mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-06 23:28:29 +08:00
Update
This commit is contained in:
youngyangyang04
@ -144,6 +144,9 @@
|
||||
* [回溯算法：求子集问题！](https://mp.weixin.qq.com/s/NNRzX-vJ_pjK4qxohd_LtA)
|
||||
* [本周小结！（回溯算法系列二）](https://mp.weixin.qq.com/s/uzDpjrrMCO8DOf-Tl5oBGw)
|
||||
* [回溯算法：求子集问题（二）](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)
|
||||
* [回溯算法：递增子序列](https://mp.weixin.qq.com/s/ePxOtX1ATRYJb2Jq7urzHQ)
|
||||
* [回溯算法：排列问题！](https://mp.weixin.qq.com/s/SCOjeMX1t41wcvJq49GhMw)
|
||||
* [回溯算法：排列问题（二）](https://mp.weixin.qq.com/s/9L8h3WqRP_h8LLWNT34YlA)
|
||||
|
||||
（持续更新中....）
|
||||
|
||||
|
||||
BIN
pics/46.全排列.png
BIN
pics/46.全排列.png
Binary file not shown.
|
Before Width: | Height: | Size: 227 KiB After Width: | Height: | Size: 230 KiB |
Binary file not shown.
|
Before Width: | Height: | Size: 263 KiB After Width: | Height: | Size: 348 KiB |
Binary file not shown.
|
Before Width: | Height: | Size: 210 KiB After Width: | Height: | Size: 232 KiB |
Binary file not shown.
|
Before Width: | Height: | Size: 258 KiB After Width: | Height: | Size: 420 KiB |
Binary file not shown.
|
Before Width: | Height: | Size: 281 KiB After Width: | Height: | Size: 291 KiB |
BIN
pics/491. 递增子序列4.png
Normal file
BIN
pics/491. 递增子序列4.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 88 KiB |
@ -1,38 +1,49 @@
|
||||
## 题目地址
|
||||
https://leetcode-cn.com/problems/permutations-ii/
|
||||
|
||||
> 排列也要去重了
|
||||
> 通知：很多录友都反馈之前看「算法汇总」的目录要一直往下拉，很麻烦，这次Carl将所有历史文章汇总到一篇文章中，有一个整体的目录，方便录友们从前面系列开始卡了，依然在公众号左下角[「算法汇总」](https://mp.weixin.qq.com/s/weyitJcVHBgFtSc19cbPdw)，这里会持续更新，大家快去瞅瞅哈
|
||||
|
||||
# 47.全排列 II
|
||||
|
||||
题目链接：https://leetcode-cn.com/problems/permutations-ii/
|
||||
|
||||
给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。
|
||||
|
||||
示例 1：
|
||||
输入：nums = [1,1,2]
|
||||
输出：
|
||||
[[1,1,2],
|
||||
[1,2,1],
|
||||
[2,1,1]]
|
||||
|
||||
示例 2：
|
||||
输入：nums = [1,2,3]
|
||||
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
|
||||
|
||||
提示：
|
||||
* 1 <= nums.length <= 8
|
||||
* -10 <= nums[i] <= 10
|
||||
|
||||
## 思路
|
||||
|
||||
这道题目和46.全排列的区别在与**给定一个可包含重复数字的序列**，要返回**所有不重复的全排列**。
|
||||
这道题目和[回溯算法：排列问题！](https://mp.weixin.qq.com/s/SCOjeMX1t41wcvJq49GhMw)的区别在与**给定一个可包含重复数字的序列**，要返回**所有不重复的全排列**。
|
||||
|
||||
这里就涉及到去重了。
|
||||
这里又涉及到去重了。
|
||||
|
||||
在[回溯算法：求组合总和（三）](https://mp.weixin.qq.com/s/_1zPYk70NvHsdY8UWVGXmQ) 、[回溯算法：求子集问题（二）](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)我们分别详细讲解了组合问题和子集问题如何去重。
|
||||
|
||||
要注意**全排列是要取树的子节点的，如果是子集问题，就取树上的所有节点。**
|
||||
那么排列问题其实也是一样的套路。
|
||||
|
||||
很多同学在去重上想不明白，其实很多题解也没有讲清楚，反正代码是能过的，感觉是那么回事，稀里糊涂的先把题目过了。
|
||||
**还要强调的是去重一定要对元素经行排序，这样我们才方便通过相邻的节点来判断是否重复使用了**。
|
||||
|
||||
这个去重为什么很难理解呢，**所谓去重，其实就是使用过的元素不能重复选取。** 这么一说好像很简单！
|
||||
|
||||
|
||||
但是什么又是“使用过”，我们把排列问题抽象为树形结构之后，**“使用过”在这个树形结构上是有两个维度的**，一个维度是同一树枝上使用过，一个维度是同一树层上使用过。
|
||||
|
||||
|
||||
**没有理解这两个层面上的“使用过” 是造成大家没有彻底理解去重的根本原因。**
|
||||
|
||||
那么排列问题，既可以在 同一树层上的“使用过”来去重，也可以在同一树枝上的“使用过”来去重！
|
||||
|
||||
理解这一本质，很多疑点就迎刃而解了。
|
||||
|
||||
**还要强调的是去重一定要对元素经行排序，这样我们才方便通过相邻的节点来判断是否重复使用了。**
|
||||
|
||||
首先把示例中的 [1,1,2] （为了方便举例，已经排序），抽象为一棵树，然后在同一树层上对nums[i-1]使用过的话，进行去重如图：
|
||||
我以示例中的 [1,1,2]为例 （为了方便举例，已经排序）抽象为一棵树，去重过程如图：
|
||||
|
||||
<img src='../pics/47.全排列II1.png' width=600> </img></div>
|
||||
|
||||
图中我们对同一树层，前一位（也就是nums[i-1]）如果使用过，那么就进行去重。
|
||||
|
||||
代码如下：
|
||||
**一般来说：组合问题和排列问题是在树形结构的叶子节点上收集结果，而子集问题就是取树上所有节点的结果**。
|
||||
|
||||
在[回溯算法：排列问题！](https://mp.weixin.qq.com/s/SCOjeMX1t41wcvJq49GhMw)中已经详解讲解了排列问题的写法，在[回溯算法：求组合总和（三）](https://mp.weixin.qq.com/s/_1zPYk70NvHsdY8UWVGXmQ) 、[回溯算法：求子集问题（二）](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)中详细讲解的去重的写法，所以这次我就不用回溯三部曲分析了，直接给出代码，如下：
|
||||
|
||||
## C++代码
|
||||
|
||||
@ -40,41 +51,40 @@ https://leetcode-cn.com/problems/permutations-ii/
|
||||
class Solution {
|
||||
private:
|
||||
vector<vector<int>> result;
|
||||
void backtracking (vector<int>& nums, vector<int>& vec, vector<bool>& used) {
|
||||
vector<int> path;
|
||||
void backtracking (vector<int>& nums, vector<bool>& used) {
|
||||
// 此时说明找到了一组
|
||||
if (vec.size() == nums.size()) {
|
||||
result.push_back(vec);
|
||||
if (path.size() == nums.size()) {
|
||||
result.push_back(path);
|
||||
return;
|
||||
}
|
||||
|
||||
for (int i = 0; i < nums.size(); i++) {
|
||||
// 这里理解used[i - 1]非常重要
|
||||
// used[i - 1] == true，说明同一树支nums[i - 1]使用过
|
||||
// used[i - 1] == true，说明同一树支nums[i - 1]使用过
|
||||
// used[i - 1] == false，说明同一树层nums[i - 1]使用过
|
||||
// 如果同一树层nums[i - 1]使用过则直接跳过
|
||||
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
|
||||
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
|
||||
continue;
|
||||
}
|
||||
if (used[i] == false) {
|
||||
used[i] = true;
|
||||
vec.push_back(nums[i]);
|
||||
backtracking(nums, vec, used);
|
||||
vec.pop_back();
|
||||
path.push_back(nums[i]);
|
||||
backtracking(nums, used);
|
||||
path.pop_back();
|
||||
used[i] = false;
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
public:
|
||||
vector<vector<int>> permuteUnique(vector<int>& nums) {
|
||||
sort(nums.begin(), nums.end());
|
||||
result.clear();
|
||||
path.clear();
|
||||
sort(nums.begin(), nums.end()); // 排序
|
||||
vector<bool> used(nums.size(), false);
|
||||
vector<int> vec;
|
||||
backtracking(nums, vec, used);
|
||||
return result;
|
||||
|
||||
}
|
||||
};
|
||||
|
||||
```
|
||||
|
||||
## 拓展
|
||||
@ -87,14 +97,14 @@ if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
|
||||
}
|
||||
```
|
||||
|
||||
可是如果把 `used[i - 1] == true` 也是正确的，去重代码如下：
|
||||
**如果改成 `used[i - 1] == true`， 也是正确的!**，去重代码如下：
|
||||
```
|
||||
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true) {
|
||||
continue;
|
||||
}
|
||||
```
|
||||
|
||||
这是为什么呢，就是上面我刚说的，如果要对树层中前一位去重，就用`used[i - 1] == false`，如果要对树枝前一位去重用用`used[i - 1] == true`。
|
||||
这是为什么呢，就是上面我刚说的，如果要对树层中前一位去重，就用`used[i - 1] == false`，如果要对树枝前一位去重用`used[i - 1] == true`。
|
||||
|
||||
**对于排列问题，树层上去重和树枝上去重，都是可以的，但是树层上去重效率更高！**
|
||||
|
||||
@ -110,5 +120,28 @@ if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true) {
|
||||
|
||||
<img src='../pics/47.全排列II3.png' width=600> </img></div>
|
||||
|
||||
大家应该很清晰的看到，树层上去重非常彻底，效率很高，树枝上去重虽然最后可能得到答案，但是多做了很多无用搜索。
|
||||
大家应该很清晰的看到，树层上对前一位去重非常彻底，效率很高，树枝上对前一位去重虽然最后可以得到答案，但是做了很多无用搜索。
|
||||
|
||||
# 总结
|
||||
|
||||
这道题其实还是用了我们之前讲过的去重思路，但有意思的是，去重的代码中，这么写：
|
||||
```
|
||||
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
|
||||
continue;
|
||||
}
|
||||
```
|
||||
和这么写：
|
||||
```
|
||||
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true) {
|
||||
continue;
|
||||
}
|
||||
```
|
||||
|
||||
都是可以的，这也是很多同学做这道题目困惑的地方，知道`used[i - 1] == false`也行而`used[i - 1] == true`也行，但是就想不明白为啥。
|
||||
|
||||
所以我通过举[1,1,1]的例子，把这两个去重的逻辑分别抽象成树形结构，大家可以一目了然：为什么两种写法都可以以及哪一种效率更高！
|
||||
|
||||
是不是豁然开朗了！！
|
||||
|
||||
就酱，很多录友表示和「代码随想录」相见恨晚，那么大家帮忙多多宣传，让更多的同学知道这里，感谢啦！
|
||||
|
||||
|
||||
@ -37,7 +37,7 @@
|
||||
|
||||
为了有鲜明的对比，我用[4, 7, 6, 7]这个数组来举例，抽象为树形结构如图：
|
||||
|
||||
<img src='../pics/491. 递增子序列1.jpg' width=600> </img></div>
|
||||
<img src='../pics/491. 递增子序列1.png' width=600> </img></div>
|
||||
|
||||
|
||||
## 回溯三部曲
|
||||
@ -69,11 +69,15 @@ if (path.size() > 1) {
|
||||
|
||||
* 单层搜索逻辑
|
||||
|
||||
<img src='../pics/491. 递增子序列1.jpg' width=600> </img></div>
|
||||
<img src='../pics/491. 递增子序列1.png' width=600> </img></div>
|
||||
在图中可以看出，**同一父节点下的同层上使用过的元素就不能在使用了**，注意这里要求的是**同一父节点下的同层**，这里和[回溯算法：求子集问题（二）](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)中去重的有本质区别。
|
||||
|
||||
在图中可以看出，同层上使用过的元素就不能在使用了，**注意这里和[回溯算法：求子集问题（二）](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)中去重的区别**。
|
||||
[回溯算法：求子集问题（二）](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)是要整棵树的同一层进行去重，所以进行排序！
|
||||
|
||||
**本题只要同层重复使用元素，递增子序列就会重复**，而[回溯算法：求子集问题（二）](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)中是排序之后看相邻元素是否重复使用。
|
||||
如图：
|
||||
|
||||
|
||||
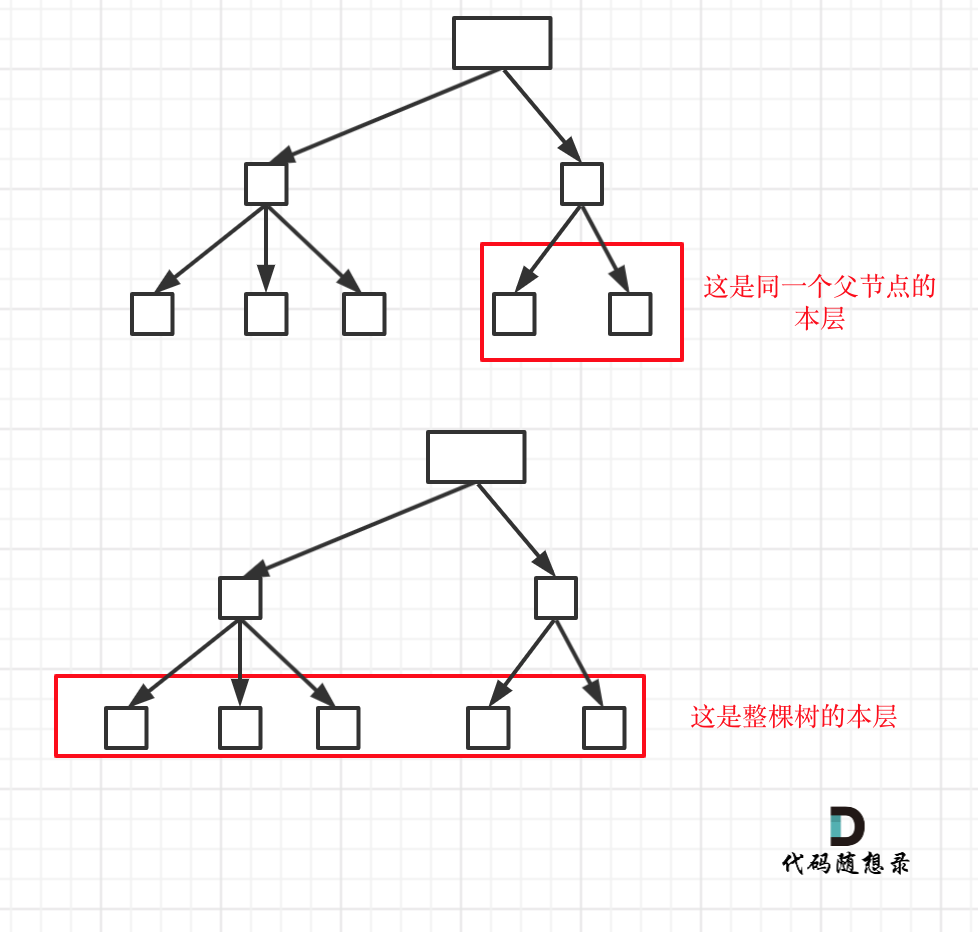
**本题只要同一父节点下的同层上重复使用元素，递增子序列就会重复**，而[回溯算法：求子集问题（二）](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)中是排序之后看相邻元素是否重复使用。
|
||||
|
||||
|
||||
还有一种情况就是如果选取的元素小于子序列最后一个元素，那么就不能是递增的，所以也要pass掉。
|
||||
|
||||
42
problems/0514.自由之路.md
Normal file
42
problems/0514.自由之路.md
Normal file
@ -0,0 +1,42 @@
|
||||
|
||||
//dp[i][j]，key的0~i位字符拼写后，ring的第j位对齐12：00方向，需要的最小步数
|
||||
//前提：key[i] = ring[j]，若不满足，dp[i][j] = INT_MAX
|
||||
|
||||
这道题目我服！ 没做出来
|
||||
|
||||
https://blog.csdn.net/qq_41855420/article/details/89058979
|
||||
|
||||
```
|
||||
class Solution {
|
||||
public:
|
||||
int findRotateSteps(string ring, string key) {
|
||||
//int dp[101][101] = {0};
|
||||
int n = ring.size();
|
||||
vector<vector<int>> dp(key.size() + 1, vector<int>(ring.size(), 0));
|
||||
for (int i = key.size() - 1; i >= 0; i--) {
|
||||
for (int j = 0; j < ring.size(); j++) {
|
||||
dp[i][j] = INT_MAX;
|
||||
for (int k = 0; k < ring.size(); k++) {
|
||||
if (ring[k] == key[i]) {
|
||||
int diff = abs(j - k);
|
||||
int step = min(diff, n - diff);
|
||||
dp[i][j] = min(dp[i][j], step + dp[i + 1][k]);
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
for (int i = 0; i < dp.size(); i++) {
|
||||
for (int j = 0; j < dp[0].size(); j++) {
|
||||
cout << dp[i][j] << " ";
|
||||
}
|
||||
cout << endl;
|
||||
}
|
||||
return dp[0][0] + key.size();
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
2 3 4 5 5 4 3
|
||||
2 1 0 0 1 2 3
|
||||
|
||||
|
||||
88
problems/0922.按奇偶排序数组II.md
Normal file
88
problems/0922.按奇偶排序数组II.md
Normal file
@ -0,0 +1,88 @@
|
||||
|
||||
## 思路
|
||||
这道题目直接的想法可能是两层for循环再加上used数组表示使用过的元素。这样的的时间复杂度是O(n^2)。
|
||||
|
||||
### 方法一
|
||||
其实这道题可以用很朴实的方法，时间复杂度就就是O(n)了，C++代码如下：
|
||||
|
||||
```
|
||||
class Solution {
|
||||
public:
|
||||
vector<int> sortArrayByParityII(vector<int>& A) {
|
||||
vector<int> even(A.size() / 2); // 初始化就确定数组大小，节省开销
|
||||
vector<int> odd(A.size() / 2);
|
||||
vector<int> result(A.size());
|
||||
int evenIndex = 0;
|
||||
int oddIndex = 0;
|
||||
int resultIndex = 0;
|
||||
// 把A数组放进偶数数组，和奇数数组
|
||||
for (int i = 0; i < A.size(); i++) {
|
||||
if (A[i] % 2 == 0) even[evenIndex++] = A[i];
|
||||
else odd[oddIndex++] = A[i];
|
||||
}
|
||||
// 把偶数数组，奇数数组分别放进result数组中
|
||||
for (int i = 0; i < evenIndex; i++) {
|
||||
result[resultIndex++] = even[i];
|
||||
result[resultIndex++] = odd[i];
|
||||
}
|
||||
return result;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
时间复杂度：O(n)
|
||||
空间复杂度：O(n)
|
||||
|
||||
### 方法二
|
||||
以上代码我是建了两个辅助数组，而且A数组还相当于遍历了两次，用辅助数组的好处就是思路清晰，优化一下就是不用这两个辅助树，代码如下：
|
||||
|
||||
```
|
||||
class Solution {
|
||||
public:
|
||||
vector<int> sortArrayByParityII(vector<int>& A) {
|
||||
vector<int> result(A.size());
|
||||
int evenIndex = 0; // 偶数下表
|
||||
int oddIndex = 1; // 奇数下表
|
||||
for (int i = 0; i < A.size(); i++) {
|
||||
if (A[i] % 2 == 0) {
|
||||
result[evenIndex] = A[i];
|
||||
evenIndex += 2;
|
||||
}
|
||||
else {
|
||||
result[oddIndex] = A[i];
|
||||
oddIndex += 2;
|
||||
}
|
||||
}
|
||||
return result;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
时间复杂度O(n)
|
||||
空间复杂度O(n)
|
||||
|
||||
### 方法三
|
||||
|
||||
当然还可以在原数组上修改，连result数组都不用了。
|
||||
|
||||
```
|
||||
class Solution {
|
||||
public:
|
||||
vector<int> sortArrayByParityII(vector<int>& A) {
|
||||
int oddIndex = 1;
|
||||
for (int i = 0; i < A.size(); i += 2) {
|
||||
if (A[i] % 2 == 1) { // 在偶数位遇到了奇数
|
||||
while(A[oddIndex] % 2 != 0) oddIndex += 2; // 在奇数位找一个偶数
|
||||
swap(A[i], A[oddIndex]); // 替换
|
||||
}
|
||||
}
|
||||
return A;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
时间复杂度：O(n)
|
||||
空间复杂度：O(1)
|
||||
|
||||
这里时间复杂度并不是O(n^2)，因为偶数位和奇数位都只操作一次，不是n/2 * n/2的关系，而是n/2 + n/2的关系！
|
||||
|
||||
@ -28,9 +28,9 @@
|
||||
回溯法，一般可以解决如下几种问题：
|
||||
|
||||
* 组合问题：N个数里面按一定规则找出k个数的集合
|
||||
* 排列问题：N个数按一定规则全排列，有几种排列方式
|
||||
* 切割问题：一个字符串按一定规则有几种切割方式
|
||||
* 子集问题：一个N个数的集合里有多少符合条件的子集
|
||||
* 排列问题：N个数按一定规则全排列，有几种排列方式
|
||||
* 棋盘问题：N皇后，解数独等等
|
||||
|
||||
**相信大家看着这些之后会发现，每个问题，都不简单！**
|
||||
|
||||
@ -1,13 +1,16 @@
|
||||
|
||||
期盼通过每个阶段的局部最优选择，从而达到全局最优
|
||||
贪心的本质是选择每一阶段的局部最优，从而达到全局最优。
|
||||
|
||||
当前子问题的最优解
|
||||
这么说有点抽象，来举一个例子：
|
||||
|
||||
一个子问题的最优解会是下一个子问题最优解的一部分，重复这个操作直到堆叠出该问题的最优解
|
||||
例如，有一堆钞票，你可以拿走十张，如果想达到最大的金额，你要怎么拿？
|
||||
|
||||
贪心算法最关键的部分在于贪心策略的选择，贪心选择的意思是对于所求问题的整体最优解可以通过一系列的局部最优选择求得。
|
||||
指定每次拿最大的，最终结果就是拿走最大数额的钱。
|
||||
|
||||
每次拿最大的就是局部最优，最后拿走最大数额的钱就是推出全局最优。
|
||||
|
||||
在举一个例子如果是 有一堆盒子，你有一个背包体积为n，如何把背包尽可能装满，如果还每次选最大的盒子，一定不行。这时候就需要动态规划。动态规划的问题在下一个系列会详细讲解。
|
||||
|
||||
而必须注意的是，贪心选择必须具备无后效性，也就是某个状态不会影响之前求得的局部最优解。
|
||||
|
||||
|
||||
很多同学做贪心的题目的时候，想不出来是贪心，想知道有没有什么套路可以一看看出来是贪心，说实话贪心算法并没有固定的套路。
|
||||
@ -16,32 +19,38 @@
|
||||
|
||||
那么如何能看出局部最优是否能退出整体最优呢？有没有什么固定策略呢？
|
||||
|
||||
不好意思，也没有，靠自己手动模拟，如果模拟可行，就可以试一试贪心策略，不过不可行，可能需要动态规划了。
|
||||
不好意思，也没有，靠自己手动模拟，如果模拟可行，就可以试一试贪心策略，不过不可行，可能需要动态规划。
|
||||
|
||||
那又有同学想手动模拟得出的结论不靠谱，想要严格的数学证明。
|
||||
那又有同学认为手动模拟得出的结论不靠谱，想要严格的数学证明。
|
||||
|
||||
做了贪心题目的时候大家就会发现，如果啥都要数学证明，就是把简单问题搞复杂了。
|
||||
看教课书上讲解贪心真的是一堆公式，估计连看都不想看。
|
||||
|
||||
举一个不太恰当的例子：我要用一下1+1 = 2，但我要先证明1+1 为什么等于2。严谨是严谨了，但有这个必要么。
|
||||
所以做了贪心题目的时候大家就会发现，如果啥都要数学证明，就是把简单问题搞复杂了。
|
||||
|
||||
虽然这个例子有点极端，但可以表达出我的意思，就是手动模拟一下感觉可以局部最优推出整体最优，那么就试一试贪心。
|
||||
举一个不太恰当的例子：我要用一下1+1 = 2，但我要先证明1+1 为什么等于2。严谨是严谨了，但没必要。
|
||||
|
||||
虽然这个例子有点极端，但可以表达这么个意思，就是手动模拟一下感觉可以局部最优推出整体最优，那么就试一试贪心。
|
||||
|
||||
刷题的时候什么时候真的需要数学推导，例如环形链表2，这道题目不用数学推导一下，就找不出环的其实位置，想试一下就不知道怎么试，这种题目确实需要数学简单推导一下。
|
||||
例如刚刚举的拿钞票的例子，就是模拟一下每次那做大的，最后就能拿到最多的钱，这还要数学证明的话，是不是感觉有点怪怪的。
|
||||
|
||||
刷题的时候什么时候真的需要数学推导呢？
|
||||
|
||||
例如环形链表2，这道题目不用数学推导一下，就找不出环的起始位置，想试一下就不知道怎么试，这种题目确实需要数学简单推导一下。
|
||||
|
||||
但贪心问题就不必了，模拟一下感觉是这么回事，就迅速试一试。
|
||||
|
||||
，但毕竟熟能生巧嘛，算法的基本思想总是固定不变的。
|
||||
贪心算法求解步骤：
|
||||
|
||||
贪心算法求解步骤
|
||||
* 将问题分解为若干个子问题
|
||||
* 找出适合的贪心策略
|
||||
* 求解每一个子问题的最优解
|
||||
* 将局部最优解堆叠成全局最优解
|
||||
|
||||
|
||||
例如，有一堆钞票，你可以拿走十张，如果想达到最大的金额，你要怎么拿？
|
||||
当前子问题的最优解
|
||||
|
||||
每次拿最大的啊，这就是局部最优，然后可以退出全局最优。
|
||||
一个子问题的最优解会是下一个子问题最优解的一部分，重复这个操作直到堆叠出该问题的最优解
|
||||
|
||||
但例如是 有一堆盒子，你有一个背包体积为n，如何把背包尽可能装满， 如果还每次选最大的盒子，一定不行。这时候就需要动态规划。
|
||||
贪心算法最关键的部分在于贪心策略的选择，贪心选择的意思是对于所求问题的整体最优解可以通过一系列的局部最优选择求得。
|
||||
|
||||
而必须注意的是，贪心选择必须具备无后效性，也就是某个状态不会影响之前求得的局部最优解。
|
||||
|
||||
Reference in New Issue
Block a user