mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-08 00:43:04 +08:00
更新回溯算法Markdown
This commit is contained in:
210
problems/0037.解数独.md
Normal file
210
problems/0037.解数独.md
Normal file
@ -0,0 +1,210 @@
|
||||
|
||||
|
||||
如果对回溯法理论还不清楚的同学,可以先看这个视频[视频来了!!带你学透回溯算法(理论篇)](https://mp.weixin.qq.com/s/wDd5azGIYWjbU0fdua_qBg)
|
||||
|
||||
## 37. 解数独
|
||||
|
||||
题目地址:https://leetcode-cn.com/problems/sudoku-solver/
|
||||
|
||||
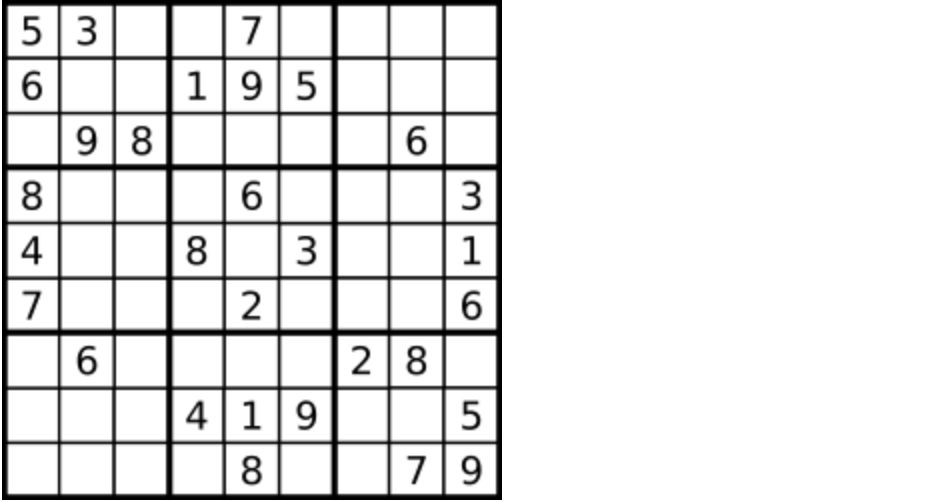
编写一个程序,通过填充空格来解决数独问题。
|
||||
|
||||
一个数独的解法需遵循如下规则:
|
||||
数字 1-9 在每一行只能出现一次。
|
||||
数字 1-9 在每一列只能出现一次。
|
||||
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。
|
||||
空白格用 '.' 表示。
|
||||
|
||||
|
||||
|
||||
一个数独。
|
||||
|
||||
|
||||
|
||||
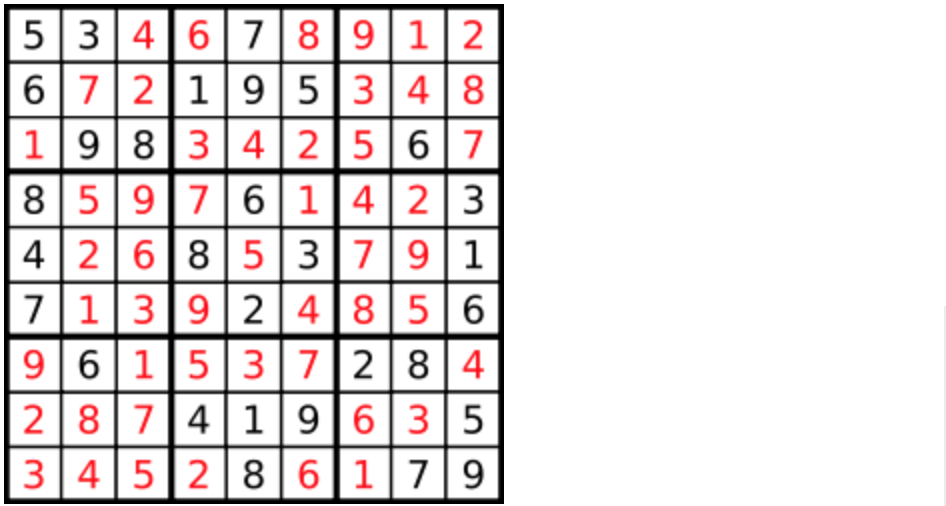
答案被标成红色。
|
||||
|
||||
提示:
|
||||
* 给定的数独序列只包含数字 1-9 和字符 '.' 。
|
||||
* 你可以假设给定的数独只有唯一解。
|
||||
* 给定数独永远是 9x9 形式的。
|
||||
|
||||
## 思路
|
||||
|
||||
棋盘搜索问题可以使用回溯法暴力搜索,只不过这次我们要做的是**二维递归**。
|
||||
|
||||
怎么做二维递归呢?
|
||||
|
||||
大家已经跟着「代码随想录」刷过了如下回溯法题目,例如:[77.组合(组合问题)](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ),[131.分割回文串(分割问题)](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q),[78.子集(子集问题)](https://mp.weixin.qq.com/s/NNRzX-vJ_pjK4qxohd_LtA),[46.全排列(排列问题)](https://mp.weixin.qq.com/s/SCOjeMX1t41wcvJq49GhMw),以及[51.N皇后(N皇后问题)](https://mp.weixin.qq.com/s/lU_QwCMj6g60nh8m98GAWg),其实这些题目都是一维递归。
|
||||
|
||||
**如果以上这几道题目没有做过的话,不建议上来就做这道题哈!**
|
||||
|
||||
[N皇后问题](https://mp.weixin.qq.com/s/lU_QwCMj6g60nh8m98GAWg)是因为每一行每一列只放一个皇后,只需要一层for循环遍历一行,递归来来遍历列,然后一行一列确定皇后的唯一位置。
|
||||
|
||||
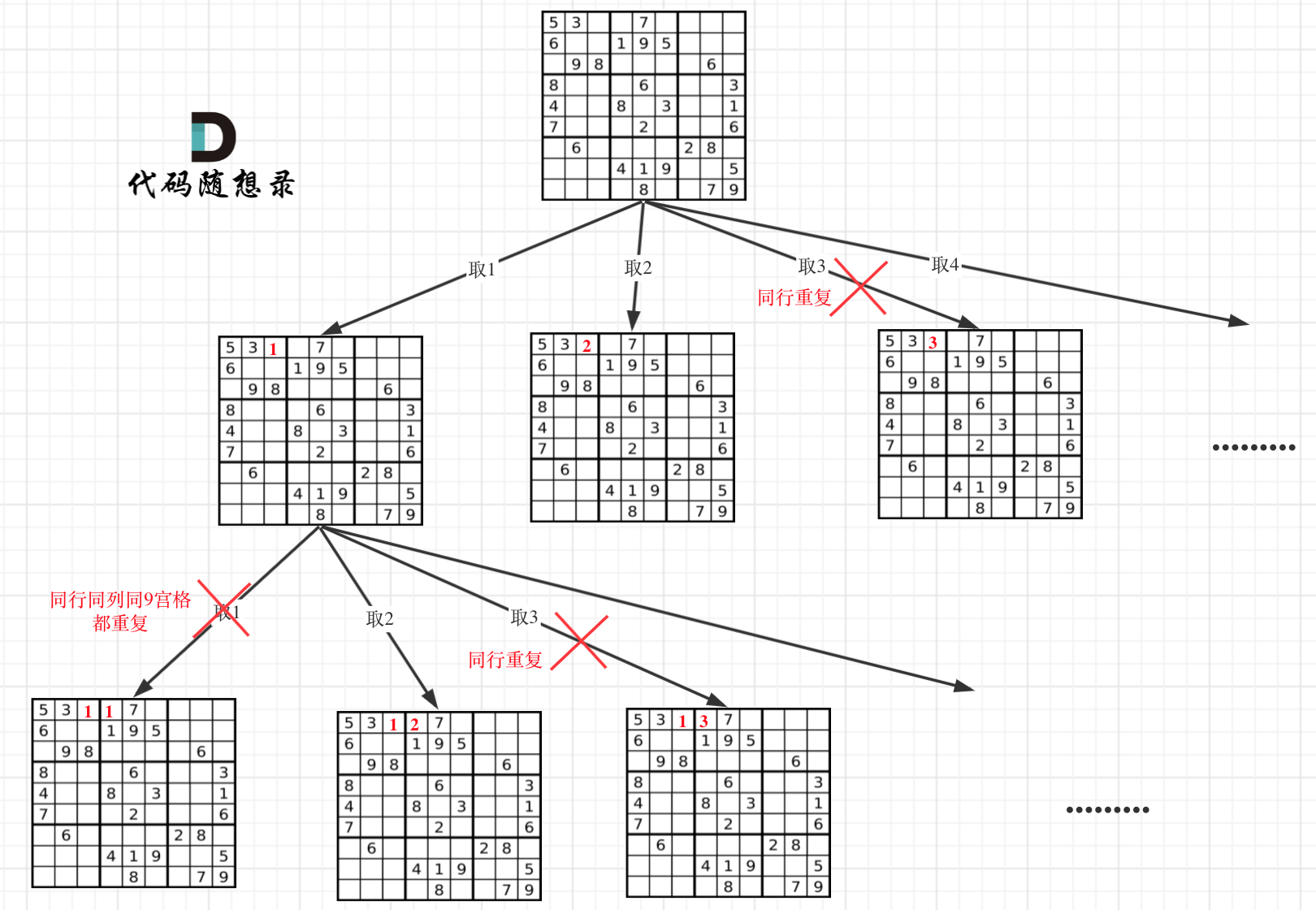
本题就不一样了,**本题中棋盘的每一个位置都要放一个数字,并检查数字是否合法,解数独的树形结构要比N皇后更宽更深**。
|
||||
|
||||
因为这个树形结构太大了,我抽取一部分,如图所示:
|
||||
|
||||
|
||||
|
||||
|
||||
## 回溯三部曲
|
||||
|
||||
* 递归函数以及参数
|
||||
|
||||
**递归函数的返回值需要是bool类型,为什么呢?**
|
||||
|
||||
因为解数独找到一个符合的条件(就在树的叶子节点上)立刻就返回,相当于找从根节点到叶子节点一条唯一路径,所以需要使用bool返回值,这一点在[回溯算法:N皇后问题](https://mp.weixin.qq.com/s/lU_QwCMj6g60nh8m98GAWg)中已经介绍过了,一样的道理。
|
||||
|
||||
代码如下:
|
||||
|
||||
```
|
||||
bool backtracking(vector<vector<char>>& board)
|
||||
```
|
||||
|
||||
* 递归终止条件
|
||||
|
||||
本题递归不用终止条件,解数独是要遍历整个树形结构寻找可能的叶子节点就立刻返回。
|
||||
|
||||
**不用终止条件会不会死循环?**
|
||||
|
||||
递归的下一层的棋盘一定比上一层的棋盘多一个数,等数填满了棋盘自然就终止(填满当然好了,说明找到结果了),所以不需要终止条件!
|
||||
|
||||
**那么有没有永远填不满的情况呢?**
|
||||
|
||||
这个问题我在递归单层搜索逻辑里在来讲!
|
||||
|
||||
* 递归单层搜索逻辑
|
||||
|
||||

|
||||
|
||||
在树形图中可以看出我们需要的是一个二维的递归(也就是两个for循环嵌套着递归)
|
||||
|
||||
**一个for循环遍历棋盘的行,一个for循环遍历棋盘的列,一行一列确定下来之后,递归遍历这个位置放9个数字的可能性!**
|
||||
|
||||
|
||||
代码如下:(**详细看注释**)
|
||||
|
||||
```C++
|
||||
bool backtracking(vector<vector<char>>& board) {
|
||||
for (int i = 0; i < board.size(); i++) { // 遍历行
|
||||
for (int j = 0; j < board[0].size(); j++) { // 遍历列
|
||||
if (board[i][j] != '.') continue;
|
||||
for (char k = '1'; k <= '9'; k++) { // (i, j) 这个位置放k是否合适
|
||||
if (isValid(i, j, k, board)) {
|
||||
board[i][j] = k; // 放置k
|
||||
if (backtracking(board)) return true; // 如果找到合适一组立刻返回
|
||||
board[i][j] = '.'; // 回溯,撤销k
|
||||
}
|
||||
}
|
||||
return false; // 9个数都试完了,都不行,那么就返回false
|
||||
}
|
||||
}
|
||||
return true; // 遍历完没有返回false,说明找到了合适棋盘位置了
|
||||
}
|
||||
```
|
||||
|
||||
**注意这里return false的地方,这里放return false 是有讲究的**。
|
||||
|
||||
因为如果一行一列确定下来了,这里尝试了9个数都不行,说明这个棋盘找不到解决数独问题的解!
|
||||
|
||||
那么会直接返回, **这也就是为什么没有终止条件也不会永远填不满棋盘而无限递归下去!**
|
||||
|
||||
## 判断棋盘是否合法
|
||||
|
||||
判断棋盘是否合法有如下三个维度:
|
||||
|
||||
* 同行是否重复
|
||||
* 同列是否重复
|
||||
* 9宫格里是否重复
|
||||
|
||||
代码如下:
|
||||
|
||||
```C++
|
||||
bool isValid(int row, int col, char val, vector<vector<char>>& board) {
|
||||
for (int i = 0; i < 9; i++) { // 判断行里是否重复
|
||||
if (board[row][i] == val) {
|
||||
return false;
|
||||
}
|
||||
}
|
||||
for (int j = 0; j < 9; j++) { // 判断列里是否重复
|
||||
if (board[j][col] == val) {
|
||||
return false;
|
||||
}
|
||||
}
|
||||
int startRow = (row / 3) * 3;
|
||||
int startCol = (col / 3) * 3;
|
||||
for (int i = startRow; i < startRow + 3; i++) { // 判断9方格里是否重复
|
||||
for (int j = startCol; j < startCol + 3; j++) {
|
||||
if (board[i][j] == val ) {
|
||||
return false;
|
||||
}
|
||||
}
|
||||
}
|
||||
return true;
|
||||
}
|
||||
```
|
||||
|
||||
最后整体代码如下:
|
||||
|
||||
## C++代码
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
private:
|
||||
bool backtracking(vector<vector<char>>& board) {
|
||||
for (int i = 0; i < board.size(); i++) { // 遍历行
|
||||
for (int j = 0; j < board[0].size(); j++) { // 遍历列
|
||||
if (board[i][j] != '.') continue;
|
||||
for (char k = '1'; k <= '9'; k++) { // (i, j) 这个位置放k是否合适
|
||||
if (isValid(i, j, k, board)) {
|
||||
board[i][j] = k; // 放置k
|
||||
if (backtracking(board)) return true; // 如果找到合适一组立刻返回
|
||||
board[i][j] = '.'; // 回溯,撤销k
|
||||
}
|
||||
}
|
||||
return false; // 9个数都试完了,都不行,那么就返回false
|
||||
}
|
||||
}
|
||||
return true; // 遍历完没有返回false,说明找到了合适棋盘位置了
|
||||
}
|
||||
bool isValid(int row, int col, char val, vector<vector<char>>& board) {
|
||||
for (int i = 0; i < 9; i++) { // 判断行里是否重复
|
||||
if (board[row][i] == val) {
|
||||
return false;
|
||||
}
|
||||
}
|
||||
for (int j = 0; j < 9; j++) { // 判断列里是否重复
|
||||
if (board[j][col] == val) {
|
||||
return false;
|
||||
}
|
||||
}
|
||||
int startRow = (row / 3) * 3;
|
||||
int startCol = (col / 3) * 3;
|
||||
for (int i = startRow; i < startRow + 3; i++) { // 判断9方格里是否重复
|
||||
for (int j = startCol; j < startCol + 3; j++) {
|
||||
if (board[i][j] == val ) {
|
||||
return false;
|
||||
}
|
||||
}
|
||||
}
|
||||
return true;
|
||||
}
|
||||
public:
|
||||
void solveSudoku(vector<vector<char>>& board) {
|
||||
backtracking(board);
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
## 总结
|
||||
|
||||
解数独可以说是非常难的题目了,如果还一直停留在单层递归的逻辑中,这道题目可以让大家瞬间崩溃。
|
||||
|
||||
所以我在开篇就提到了**二维递归**,这也是我自创词汇,希望可以帮助大家理解解数独的搜索过程。
|
||||
|
||||
一波分析之后,在看代码会发现其实也不难,唯一难点就是理解**二维递归**的思维逻辑。
|
||||
|
||||
**这样,解数独这么难的问题,也被我们攻克了**。
|
||||
|
||||
**恭喜一路上坚持打卡的录友们,回溯算法已经接近尾声了,接下来就是要一波总结了**。
|
||||
|
||||
|
||||
138
problems/0046.全排列.md
Normal file
138
problems/0046.全排列.md
Normal file
@ -0,0 +1,138 @@
|
||||
|
||||
|
||||
## 46.全排列
|
||||
|
||||
题目链接:https://leetcode-cn.com/problems/permutations/
|
||||
|
||||
给定一个 没有重复 数字的序列,返回其所有可能的全排列。
|
||||
|
||||
示例:
|
||||
输入: [1,2,3]
|
||||
输出:
|
||||
[
|
||||
[1,2,3],
|
||||
[1,3,2],
|
||||
[2,1,3],
|
||||
[2,3,1],
|
||||
[3,1,2],
|
||||
[3,2,1]
|
||||
]
|
||||
|
||||
## 思路
|
||||
|
||||
此时我们已经学习了[组合问题](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)、[切割问题](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)和[子集问题](https://mp.weixin.qq.com/s/NNRzX-vJ_pjK4qxohd_LtA),接下来看一看排列问题。
|
||||
|
||||
相信这个排列问题就算是让你用for循环暴力把结果搜索出来,这个暴力也不是很好写。
|
||||
|
||||
所以正如我们在[关于回溯算法,你该了解这些!](https://mp.weixin.qq.com/s/gjSgJbNbd1eAA5WkA-HeWw)所讲的为什么回溯法是暴力搜索,效率这么低,还要用它?
|
||||
|
||||
**因为一些问题能暴力搜出来就已经很不错了!**
|
||||
|
||||
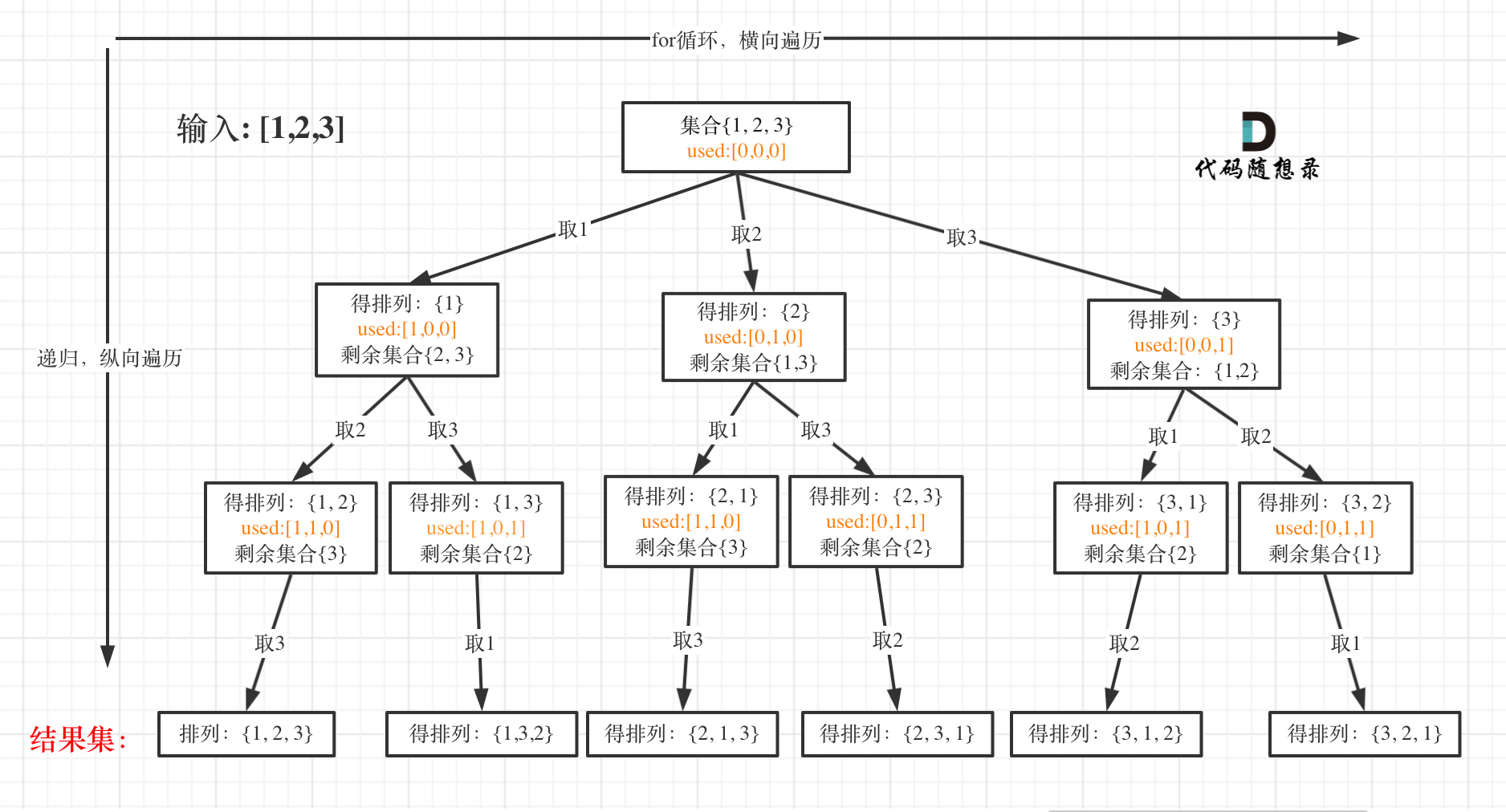
我以[1,2,3]为例,抽象成树形结构如下:
|
||||
|
||||
|
||||
|
||||
## 回溯三部曲
|
||||
|
||||
* 递归函数参数
|
||||
|
||||
**首先排列是有序的,也就是说[1,2] 和[2,1] 是两个集合,这和之前分析的子集以及组合所不同的地方**。
|
||||
|
||||
可以看出元素1在[1,2]中已经使用过了,但是在[2,1]中还要在使用一次1,所以处理排列问题就不用使用startIndex了。
|
||||
|
||||
但排列问题需要一个used数组,标记已经选择的元素,如图橘黄色部分所示:
|
||||
|
||||

|
||||
|
||||
代码如下:
|
||||
|
||||
```
|
||||
vector<vector<int>> result;
|
||||
vector<int> path;
|
||||
void backtracking (vector<int>& nums, vector<bool>& used)
|
||||
```
|
||||
|
||||
* 递归终止条件
|
||||
|
||||

|
||||
|
||||
可以看出叶子节点,就是收割结果的地方。
|
||||
|
||||
那么什么时候,算是到达叶子节点呢?
|
||||
|
||||
当收集元素的数组path的大小达到和nums数组一样大的时候,说明找到了一个全排列,也表示到达了叶子节点。
|
||||
|
||||
代码如下:
|
||||
|
||||
```
|
||||
// 此时说明找到了一组
|
||||
if (path.size() == nums.size()) {
|
||||
result.push_back(path);
|
||||
return;
|
||||
}
|
||||
```
|
||||
|
||||
* 单层搜索的逻辑
|
||||
|
||||
这里和[组合问题](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)、[切割问题](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)和[子集问题](https://mp.weixin.qq.com/s/NNRzX-vJ_pjK4qxohd_LtA)最大的不同就是for循环里不用startIndex了。
|
||||
|
||||
因为排列问题,每次都要从头开始搜索,例如元素1在[1,2]中已经使用过了,但是在[2,1]中还要再使用一次1。
|
||||
|
||||
**而used数组,其实就是记录此时path里都有哪些元素使用了,一个排列里一个元素只能使用一次**。
|
||||
|
||||
代码如下:
|
||||
|
||||
```
|
||||
for (int i = 0; i < nums.size(); i++) {
|
||||
if (used[i] == true) continue; // path里已经收录的元素,直接跳过
|
||||
used[i] = true;
|
||||
path.push_back(nums[i]);
|
||||
backtracking(nums, used);
|
||||
path.pop_back();
|
||||
used[i] = false;
|
||||
}
|
||||
```
|
||||
|
||||
整体C++代码如下:
|
||||
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
vector<vector<int>> result;
|
||||
vector<int> path;
|
||||
void backtracking (vector<int>& nums, vector<bool>& used) {
|
||||
// 此时说明找到了一组
|
||||
if (path.size() == nums.size()) {
|
||||
result.push_back(path);
|
||||
return;
|
||||
}
|
||||
for (int i = 0; i < nums.size(); i++) {
|
||||
if (used[i] == true) continue; // path里已经收录的元素,直接跳过
|
||||
used[i] = true;
|
||||
path.push_back(nums[i]);
|
||||
backtracking(nums, used);
|
||||
path.pop_back();
|
||||
used[i] = false;
|
||||
}
|
||||
}
|
||||
vector<vector<int>> permute(vector<int>& nums) {
|
||||
result.clear();
|
||||
path.clear();
|
||||
vector<bool> used(nums.size(), false);
|
||||
backtracking(nums, used);
|
||||
return result;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
## 总结
|
||||
|
||||
大家此时可以感受出排列问题的不同:
|
||||
|
||||
* 每层都是从0开始搜索而不是startIndex
|
||||
* 需要used数组记录path里都放了哪些元素了
|
||||
|
||||
排列问题是回溯算法解决的经典题目,大家可以好好体会体会。
|
||||
|
||||
|
||||
154
problems/0047.全排列II.md
Normal file
154
problems/0047.全排列II.md
Normal file
@ -0,0 +1,154 @@
|
||||
# 排列问题(二)
|
||||
|
||||
## 47.全排列 II
|
||||
|
||||
题目链接:https://leetcode-cn.com/problems/permutations-ii/
|
||||
|
||||
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
|
||||
|
||||
示例 1:
|
||||
输入:nums = [1,1,2]
|
||||
输出:
|
||||
[[1,1,2],
|
||||
[1,2,1],
|
||||
[2,1,1]]
|
||||
|
||||
示例 2:
|
||||
输入:nums = [1,2,3]
|
||||
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
|
||||
|
||||
提示:
|
||||
* 1 <= nums.length <= 8
|
||||
* -10 <= nums[i] <= 10
|
||||
|
||||
## 思路
|
||||
|
||||
这道题目和[回溯算法:排列问题!](https://mp.weixin.qq.com/s/SCOjeMX1t41wcvJq49GhMw)的区别在与**给定一个可包含重复数字的序列**,要返回**所有不重复的全排列**。
|
||||
|
||||
这里又涉及到去重了。
|
||||
|
||||
在[回溯算法:求组合总和(三)](https://mp.weixin.qq.com/s/_1zPYk70NvHsdY8UWVGXmQ) 、[回溯算法:求子集问题(二)](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)我们分别详细讲解了组合问题和子集问题如何去重。
|
||||
|
||||
那么排列问题其实也是一样的套路。
|
||||
|
||||
**还要强调的是去重一定要对元素经行排序,这样我们才方便通过相邻的节点来判断是否重复使用了**。
|
||||
|
||||
我以示例中的 [1,1,2]为例 (为了方便举例,已经排序)抽象为一棵树,去重过程如图:
|
||||
|
||||
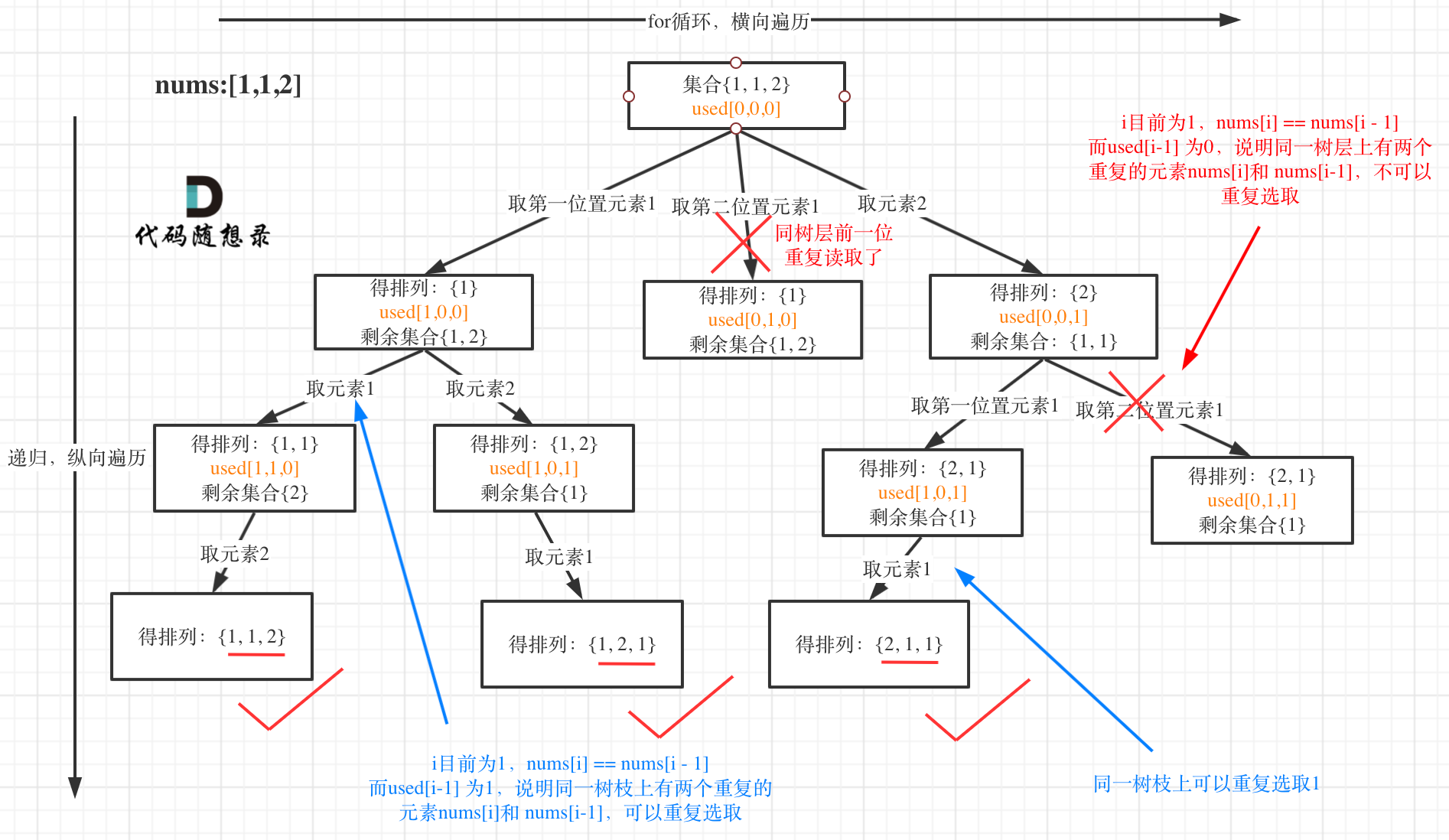
|
||||
|
||||
图中我们对同一树层,前一位(也就是nums[i-1])如果使用过,那么就进行去重。
|
||||
|
||||
**一般来说:组合问题和排列问题是在树形结构的叶子节点上收集结果,而子集问题就是取树上所有节点的结果**。
|
||||
|
||||
在[回溯算法:排列问题!](https://mp.weixin.qq.com/s/SCOjeMX1t41wcvJq49GhMw)中已经详解讲解了排列问题的写法,在[回溯算法:求组合总和(三)](https://mp.weixin.qq.com/s/_1zPYk70NvHsdY8UWVGXmQ) 、[回溯算法:求子集问题(二)](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)中详细讲解的去重的写法,所以这次我就不用回溯三部曲分析了,直接给出代码,如下:
|
||||
|
||||
## C++代码
|
||||
|
||||
```
|
||||
class Solution {
|
||||
private:
|
||||
vector<vector<int>> result;
|
||||
vector<int> path;
|
||||
void backtracking (vector<int>& nums, vector<bool>& used) {
|
||||
// 此时说明找到了一组
|
||||
if (path.size() == nums.size()) {
|
||||
result.push_back(path);
|
||||
return;
|
||||
}
|
||||
for (int i = 0; i < nums.size(); i++) {
|
||||
// used[i - 1] == true,说明同一树支nums[i - 1]使用过
|
||||
// used[i - 1] == false,说明同一树层nums[i - 1]使用过
|
||||
// 如果同一树层nums[i - 1]使用过则直接跳过
|
||||
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
|
||||
continue;
|
||||
}
|
||||
if (used[i] == false) {
|
||||
used[i] = true;
|
||||
path.push_back(nums[i]);
|
||||
backtracking(nums, used);
|
||||
path.pop_back();
|
||||
used[i] = false;
|
||||
}
|
||||
}
|
||||
}
|
||||
public:
|
||||
vector<vector<int>> permuteUnique(vector<int>& nums) {
|
||||
result.clear();
|
||||
path.clear();
|
||||
sort(nums.begin(), nums.end()); // 排序
|
||||
vector<bool> used(nums.size(), false);
|
||||
backtracking(nums, vec, used);
|
||||
return result;
|
||||
}
|
||||
};
|
||||
|
||||
```
|
||||
|
||||
## 拓展
|
||||
|
||||
大家发现,去重最为关键的代码为:
|
||||
|
||||
```
|
||||
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
|
||||
continue;
|
||||
}
|
||||
```
|
||||
|
||||
**如果改成 `used[i - 1] == true`, 也是正确的!**,去重代码如下:
|
||||
```
|
||||
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true) {
|
||||
continue;
|
||||
}
|
||||
```
|
||||
|
||||
这是为什么呢,就是上面我刚说的,如果要对树层中前一位去重,就用`used[i - 1] == false`,如果要对树枝前一位去重用`used[i - 1] == true`。
|
||||
|
||||
**对于排列问题,树层上去重和树枝上去重,都是可以的,但是树层上去重效率更高!**
|
||||
|
||||
这么说是不是有点抽象?
|
||||
|
||||
来来来,我就用输入: [1,1,1] 来举一个例子。
|
||||
|
||||
树层上去重(used[i - 1] == false),的树形结构如下:
|
||||
|
||||
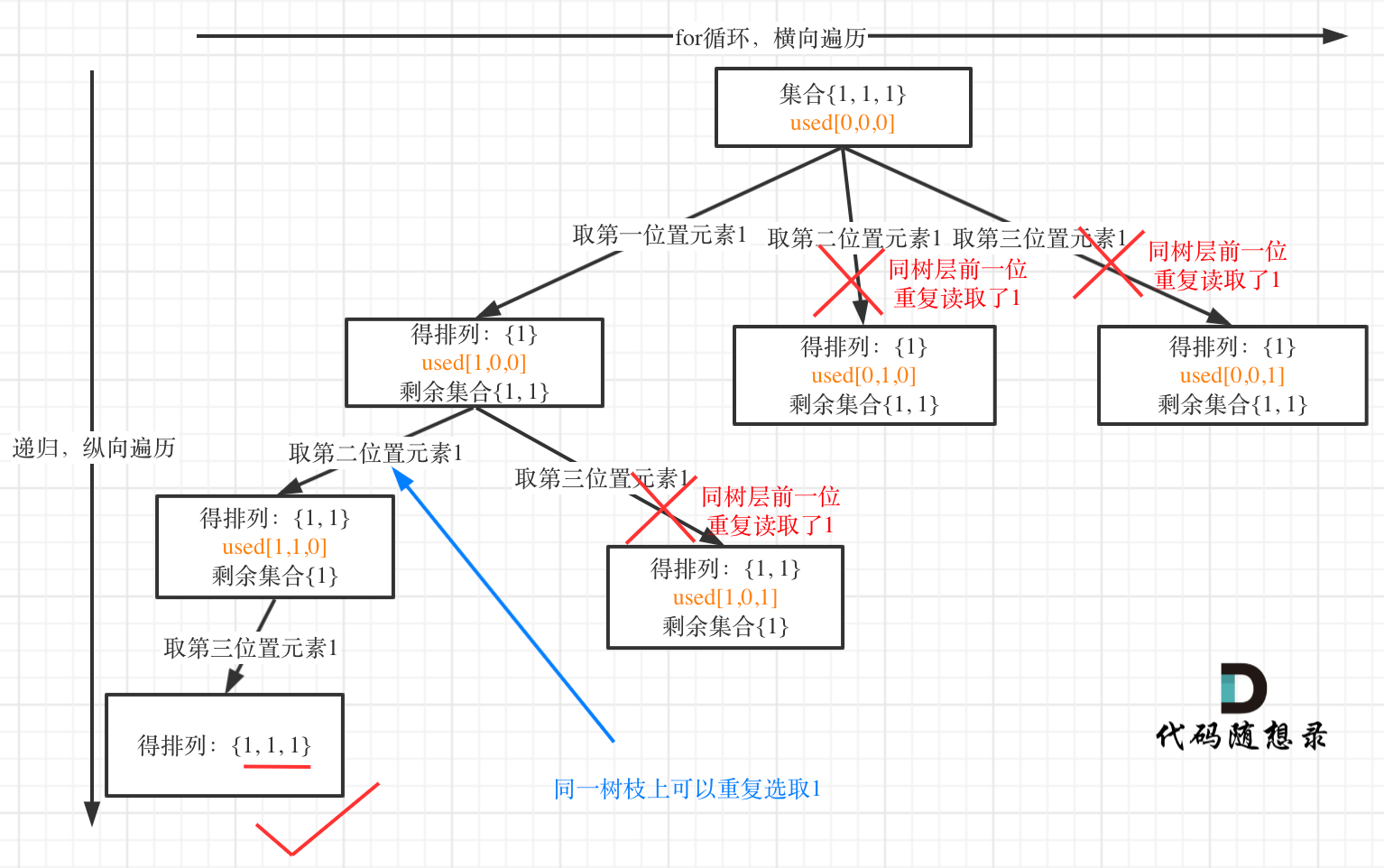
|
||||
|
||||
树枝上去重(used[i - 1] == true)的树型结构如下:
|
||||
|
||||
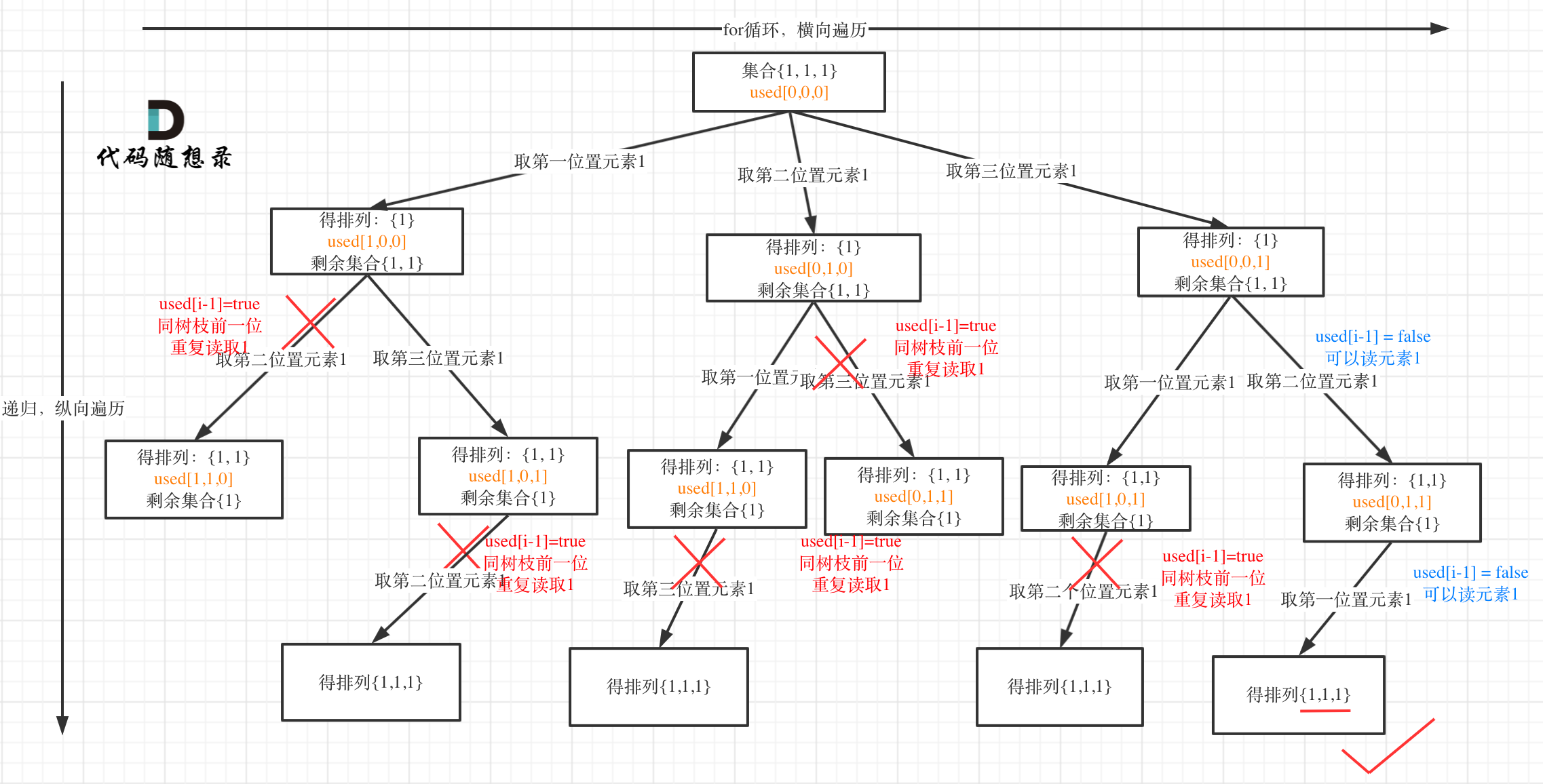
|
||||
|
||||
大家应该很清晰的看到,树层上对前一位去重非常彻底,效率很高,树枝上对前一位去重虽然最后可以得到答案,但是做了很多无用搜索。
|
||||
|
||||
## 总结
|
||||
|
||||
这道题其实还是用了我们之前讲过的去重思路,但有意思的是,去重的代码中,这么写:
|
||||
```
|
||||
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
|
||||
continue;
|
||||
}
|
||||
```
|
||||
和这么写:
|
||||
```
|
||||
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true) {
|
||||
continue;
|
||||
}
|
||||
```
|
||||
|
||||
都是可以的,这也是很多同学做这道题目困惑的地方,知道`used[i - 1] == false`也行而`used[i - 1] == true`也行,但是就想不明白为啥。
|
||||
|
||||
所以我通过举[1,1,1]的例子,把这两个去重的逻辑分别抽象成树形结构,大家可以一目了然:为什么两种写法都可以以及哪一种效率更高!
|
||||
|
||||
是不是豁然开朗了!!
|
||||
|
||||
> **相信很多小伙伴刷题的时候面对力扣上近两千道题目,感觉无从下手,我花费半年时间整理了Github项目:「力扣刷题攻略」[https://github.com/youngyangyang04/leetcode-master](https://github.com/youngyangyang04/leetcode-master)。 里面有100多道经典算法题目刷题顺序、配有40w字的详细图解,常用算法模板总结,以及难点视频讲解,按照list一道一道刷就可以了!star支持一波吧!**
|
||||
|
||||
* 公众号:[代码随想录](https://img-blog.csdnimg.cn/20201210231711160.png)
|
||||
* B站:[代码随想录](https://space.bilibili.com/525438321)
|
||||
* Github:[leetcode-master](https://github.com/youngyangyang04/leetcode-master)
|
||||
* 知乎:[代码随想录](https://www.zhihu.com/people/sun-xiu-yang-64)
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
227
problems/0051.N皇后.md
Normal file
227
problems/0051.N皇后.md
Normal file
@ -0,0 +1,227 @@
|
||||
|
||||
|
||||
## 第51题. N皇后
|
||||
|
||||
题目链接: https://leetcode-cn.com/problems/n-queens/
|
||||
|
||||
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
|
||||
|
||||
上图为 8 皇后问题的一种解法。
|
||||
|
||||
|
||||
给定一个整数 n,返回所有不同的 n 皇后问题的解决方案。
|
||||
|
||||
每一种解法包含一个明确的 n 皇后问题的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
|
||||
|
||||
示例:
|
||||
输入: 4
|
||||
输出: [
|
||||
[".Q..", // 解法 1
|
||||
"...Q",
|
||||
"Q...",
|
||||
"..Q."],
|
||||
|
||||
["..Q.", // 解法 2
|
||||
"Q...",
|
||||
"...Q",
|
||||
".Q.."]
|
||||
]
|
||||
解释: 4 皇后问题存在两个不同的解法。
|
||||
|
||||
提示:
|
||||
> 皇后,是国际象棋中的棋子,意味着国王的妻子。皇后只做一件事,那就是“吃子”。当她遇见可以吃的棋子时,就迅速冲上去吃掉棋子。当然,她横、竖、斜都可走一到七步,可进可退。(引用自 百度百科 - 皇后 )
|
||||
|
||||
|
||||
## 思路
|
||||
|
||||
都知道n皇后问题是回溯算法解决的经典问题,但是用回溯解决多了组合、切割、子集、排列问题之后,遇到这种二位矩阵还会有点不知所措。
|
||||
|
||||
首先来看一下皇后们的约束条件:
|
||||
|
||||
1. 不能同行
|
||||
2. 不能同列
|
||||
3. 不能同斜线
|
||||
|
||||
确定完约束条件,来看看究竟要怎么去搜索皇后们的位置,其实搜索皇后的位置,可以抽象为一棵树。
|
||||
|
||||
下面我用一个3 * 3 的棋牌,将搜索过程抽象为一颗树,如图:
|
||||
|
||||
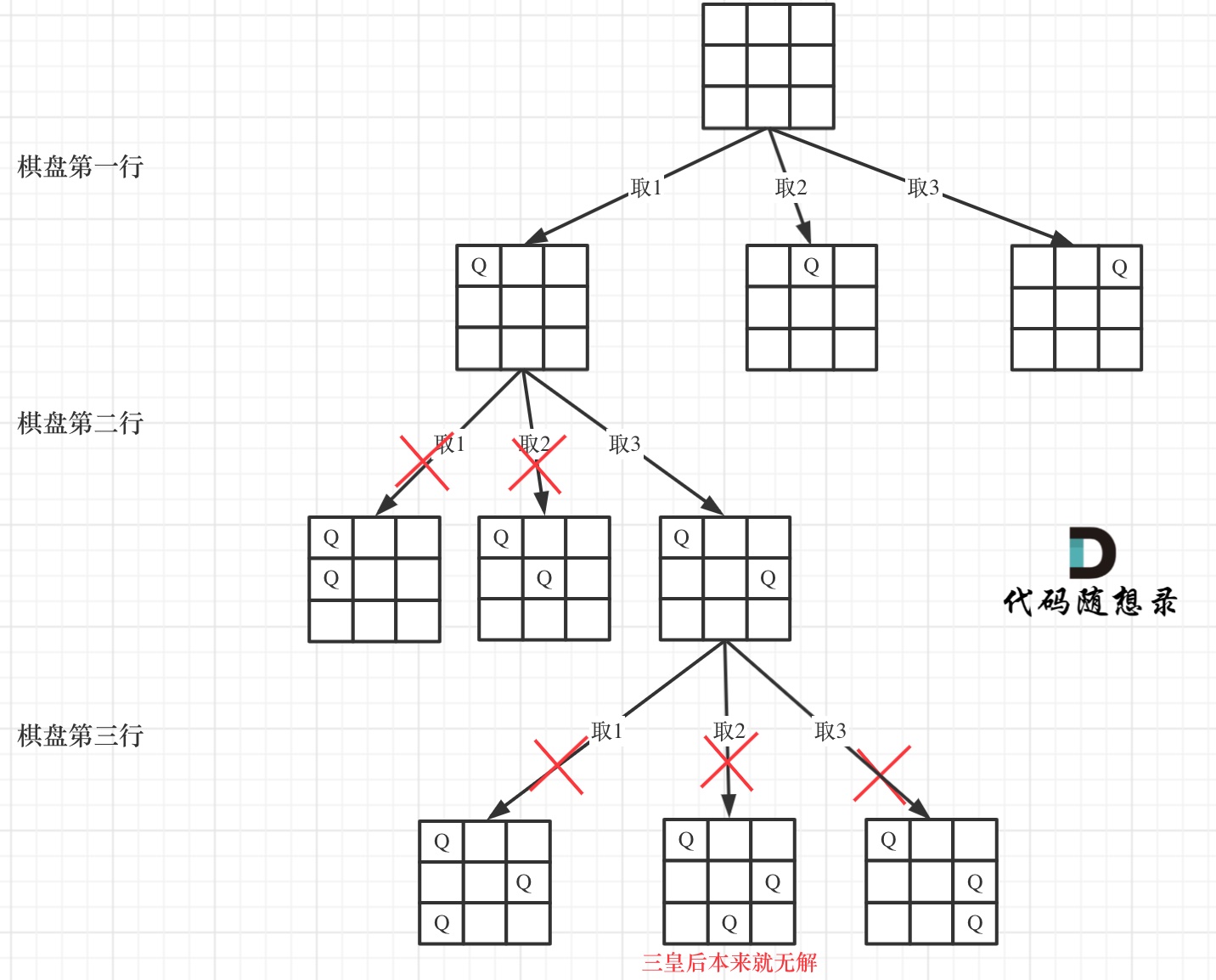
|
||||
|
||||
从图中,可以看出,二维矩阵中矩阵的高就是这颗树的高度,矩阵的宽就是树形结构中每一个节点的宽度。
|
||||
|
||||
那么我们用皇后们的约束条件,来回溯搜索这颗树,**只要搜索到了树的叶子节点,说明就找到了皇后们的合理位置了**。
|
||||
|
||||
## 回溯三部曲
|
||||
|
||||
按照我总结的如下回溯模板,我们来依次分析:
|
||||
|
||||
```
|
||||
void backtracking(参数) {
|
||||
if (终止条件) {
|
||||
存放结果;
|
||||
return;
|
||||
}
|
||||
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
|
||||
处理节点;
|
||||
backtracking(路径,选择列表); // 递归
|
||||
回溯,撤销处理结果
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* 递归函数参数
|
||||
|
||||
我依然是定义全局变量二维数组result来记录最终结果。
|
||||
|
||||
参数n是棋牌的大小,然后用row来记录当前遍历到棋盘的第几层了。
|
||||
|
||||
代码如下:
|
||||
|
||||
```
|
||||
vector<vector<string>> result;
|
||||
void backtracking(int n, int row, vector<string>& chessboard) {
|
||||
```
|
||||
|
||||
* 递归终止条件
|
||||
|
||||
在如下树形结构中:
|
||||

|
||||
|
||||
|
||||
可以看出,当递归到棋盘最底层(也就是叶子节点)的时候,就可以收集结果并返回了。
|
||||
|
||||
代码如下:
|
||||
|
||||
```
|
||||
if (row == n) {
|
||||
result.push_back(chessboard);
|
||||
return;
|
||||
}
|
||||
```
|
||||
|
||||
* 单层搜索的逻辑
|
||||
|
||||
递归深度就是row控制棋盘的行,每一层里for循环的col控制棋盘的列,一行一列,确定了放置皇后的位置。
|
||||
|
||||
每次都是要从新的一行的起始位置开始搜,所以都是从0开始。
|
||||
|
||||
代码如下:
|
||||
|
||||
```
|
||||
for (int col = 0; col < n; col++) {
|
||||
if (isValid(row, col, chessboard, n)) { // 验证合法就可以放
|
||||
chessboard[row][col] = 'Q'; // 放置皇后
|
||||
backtracking(n, row + 1, chessboard);
|
||||
chessboard[row][col] = '.'; // 回溯,撤销皇后
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* 验证棋牌是否合法
|
||||
|
||||
按照如下标准去重:
|
||||
|
||||
1. 不能同行
|
||||
2. 不能同列
|
||||
3. 不能同斜线 (45度和135度角)
|
||||
|
||||
代码如下:
|
||||
|
||||
```
|
||||
bool isValid(int row, int col, vector<string>& chessboard, int n) {
|
||||
int count = 0;
|
||||
// 检查列
|
||||
for (int i = 0; i < row; i++) { // 这是一个剪枝
|
||||
if (chessboard[i][col] == 'Q') {
|
||||
return false;
|
||||
}
|
||||
}
|
||||
// 检查 45度角是否有皇后
|
||||
for (int i = row - 1, j = col - 1; i >=0 && j >= 0; i--, j--) {
|
||||
if (chessboard[i][j] == 'Q') {
|
||||
return false;
|
||||
}
|
||||
}
|
||||
// 检查 135度角是否有皇后
|
||||
for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
|
||||
if (chessboard[i][j] == 'Q') {
|
||||
return false;
|
||||
}
|
||||
}
|
||||
return true;
|
||||
}
|
||||
```
|
||||
|
||||
在这份代码中,细心的同学可以发现为什么没有在同行进行检查呢?
|
||||
|
||||
因为在单层搜索的过程中,每一层递归,只会选for循环(也就是同一行)里的一个元素,所以不用去重了。
|
||||
|
||||
那么按照这个模板不难写出如下C++代码:
|
||||
|
||||
## C++代码
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
private:
|
||||
vector<vector<string>> result;
|
||||
// n 为输入的棋盘大小
|
||||
// row 是当前递归到棋牌的第几行了
|
||||
void backtracking(int n, int row, vector<string>& chessboard) {
|
||||
if (row == n) {
|
||||
result.push_back(chessboard);
|
||||
return;
|
||||
}
|
||||
for (int col = 0; col < n; col++) {
|
||||
if (isValid(row, col, chessboard, n)) { // 验证合法就可以放
|
||||
chessboard[row][col] = 'Q'; // 放置皇后
|
||||
backtracking(n, row + 1, chessboard);
|
||||
chessboard[row][col] = '.'; // 回溯,撤销皇后
|
||||
}
|
||||
}
|
||||
}
|
||||
bool isValid(int row, int col, vector<string>& chessboard, int n) {
|
||||
int count = 0;
|
||||
// 检查列
|
||||
for (int i = 0; i < row; i++) { // 这是一个剪枝
|
||||
if (chessboard[i][col] == 'Q') {
|
||||
return false;
|
||||
}
|
||||
}
|
||||
// 检查 45度角是否有皇后
|
||||
for (int i = row - 1, j = col - 1; i >=0 && j >= 0; i--, j--) {
|
||||
if (chessboard[i][j] == 'Q') {
|
||||
return false;
|
||||
}
|
||||
}
|
||||
// 检查 135度角是否有皇后
|
||||
for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
|
||||
if (chessboard[i][j] == 'Q') {
|
||||
return false;
|
||||
}
|
||||
}
|
||||
return true;
|
||||
}
|
||||
public:
|
||||
vector<vector<string>> solveNQueens(int n) {
|
||||
result.clear();
|
||||
std::vector<std::string> chessboard(n, std::string(n, '.'));
|
||||
backtracking(n, 0, chessboard);
|
||||
return result;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
可以看出,除了验证棋盘合法性的代码,省下来部分就是按照回溯法模板来的。
|
||||
|
||||
## 总结
|
||||
|
||||
本题是我们解决棋盘问题的第一道题目。
|
||||
|
||||
如果从来没有接触过N皇后问题的同学看着这样的题会感觉无从下手,可能知道要用回溯法,但也不知道该怎么去搜。
|
||||
|
||||
**这里我明确给出了棋盘的宽度就是for循环的长度,递归的深度就是棋盘的高度,这样就可以套进回溯法的模板里了**。
|
||||
|
||||
大家可以在仔细体会体会!
|
||||
|
||||
|
||||
168
problems/0078.子集.md
Normal file
168
problems/0078.子集.md
Normal file
@ -0,0 +1,168 @@
|
||||
|
||||
|
||||
## 第78题. 子集
|
||||
|
||||
题目地址:https://leetcode-cn.com/problems/subsets/
|
||||
|
||||
给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
|
||||
|
||||
说明:解集不能包含重复的子集。
|
||||
|
||||
示例:
|
||||
输入: nums = [1,2,3]
|
||||
输出:
|
||||
[
|
||||
[3],
|
||||
[1],
|
||||
[2],
|
||||
[1,2,3],
|
||||
[1,3],
|
||||
[2,3],
|
||||
[1,2],
|
||||
[]
|
||||
]
|
||||
|
||||
## 思路
|
||||
|
||||
求子集问题和[回溯算法:求组合问题!](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)和[回溯算法:分割问题!](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)又不一样了。
|
||||
|
||||
如果把 子集问题、组合问题、分割问题都抽象为一棵树的话,**那么组合问题和分割问题都是收集树的叶子节点,而子集问题是找树的所有节点!**
|
||||
|
||||
其实子集也是一种组合问题,因为它的集合是无序的,子集{1,2} 和 子集{2,1}是一样的。
|
||||
|
||||
**那么既然是无序,取过的元素不会重复取,写回溯算法的时候,for就要从startIndex开始,而不是从0开始!**
|
||||
|
||||
有同学问了,什么时候for可以从0开始呢?
|
||||
|
||||
求排列问题的时候,就要从0开始,因为集合是有序的,{1, 2} 和{2, 1}是两个集合,排列问题我们后续的文章就会讲到的。
|
||||
|
||||
以示例中nums = [1,2,3]为例把求子集抽象为树型结构,如下:
|
||||
|
||||

|
||||
|
||||
从图中红线部分,可以看出**遍历这个树的时候,把所有节点都记录下来,就是要求的子集集合**。
|
||||
|
||||
## 回溯三部曲
|
||||
|
||||
* 递归函数参数
|
||||
|
||||
全局变量数组path为子集收集元素,二维数组result存放子集组合。(也可以放到递归函数参数里)
|
||||
|
||||
递归函数参数在上面讲到了,需要startIndex。
|
||||
|
||||
代码如下:
|
||||
|
||||
```
|
||||
vector<vector<int>> result;
|
||||
vector<int> path;
|
||||
void backtracking(vector<int>& nums, int startIndex) {
|
||||
```
|
||||
|
||||
* 递归终止条件
|
||||
|
||||
从图中可以看出:
|
||||
|
||||

|
||||
|
||||
剩余集合为空的时候,就是叶子节点。
|
||||
|
||||
那么什么时候剩余集合为空呢?
|
||||
|
||||
就是startIndex已经大于数组的长度了,就终止了,因为没有元素可取了,代码如下:
|
||||
|
||||
```
|
||||
if (startIndex >= nums.size()) {
|
||||
return;
|
||||
}
|
||||
```
|
||||
|
||||
**其实可以不需要加终止条件,因为startIndex >= nums.size(),本层for循环本来也结束了**。
|
||||
|
||||
* 单层搜索逻辑
|
||||
|
||||
**求取子集问题,不需要任何剪枝!因为子集就是要遍历整棵树**。
|
||||
|
||||
那么单层递归逻辑代码如下:
|
||||
|
||||
```
|
||||
for (int i = startIndex; i < nums.size(); i++) {
|
||||
path.push_back(nums[i]); // 子集收集元素
|
||||
backtracking(nums, i + 1); // 注意从i+1开始,元素不重复取
|
||||
path.pop_back(); // 回溯
|
||||
}
|
||||
```
|
||||
|
||||
## C++代码
|
||||
|
||||
根据[关于回溯算法,你该了解这些!](https://mp.weixin.qq.com/s/gjSgJbNbd1eAA5WkA-HeWw)给出的回溯算法模板:
|
||||
|
||||
```
|
||||
void backtracking(参数) {
|
||||
if (终止条件) {
|
||||
存放结果;
|
||||
return;
|
||||
}
|
||||
|
||||
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
|
||||
处理节点;
|
||||
backtracking(路径,选择列表); // 递归
|
||||
回溯,撤销处理结果
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
可以写出如下回溯算法C++代码:
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
private:
|
||||
vector<vector<int>> result;
|
||||
vector<int> path;
|
||||
void backtracking(vector<int>& nums, int startIndex) {
|
||||
result.push_back(path); // 收集子集,要放在终止添加的上面,否则会漏掉自己
|
||||
if (startIndex >= nums.size()) { // 终止条件可以不加
|
||||
return;
|
||||
}
|
||||
for (int i = startIndex; i < nums.size(); i++) {
|
||||
path.push_back(nums[i]);
|
||||
backtracking(nums, i + 1);
|
||||
path.pop_back();
|
||||
}
|
||||
}
|
||||
public:
|
||||
vector<vector<int>> subsets(vector<int>& nums) {
|
||||
result.clear();
|
||||
path.clear();
|
||||
backtracking(nums, 0);
|
||||
return result;
|
||||
}
|
||||
};
|
||||
|
||||
```
|
||||
|
||||
在注释中,可以发现可以不写终止条件,因为本来我们就要遍历整颗树。
|
||||
|
||||
有的同学可能担心不写终止条件会不会无限递归?
|
||||
|
||||
并不会,因为每次递归的下一层就是从i+1开始的。
|
||||
|
||||
## 总结
|
||||
|
||||
相信大家经过了
|
||||
* 组合问题:
|
||||
* [回溯算法:求组合问题!](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)
|
||||
* [回溯算法:组合问题再剪剪枝](https://mp.weixin.qq.com/s/Ri7spcJMUmph4c6XjPWXQA)
|
||||
* [回溯算法:求组合总和!](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w)
|
||||
* [回溯算法:电话号码的字母组合](https://mp.weixin.qq.com/s/e2ua2cmkE_vpYjM3j6HY0A)
|
||||
* [回溯算法:求组合总和(二)](https://mp.weixin.qq.com/s/FLg8G6EjVcxBjwCbzpACPw)
|
||||
* [回溯算法:求组合总和(三)](https://mp.weixin.qq.com/s/_1zPYk70NvHsdY8UWVGXmQ)
|
||||
* 分割问题:
|
||||
* [回溯算法:分割回文串](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)
|
||||
* [回溯算法:复原IP地址](https://mp.weixin.qq.com/s/v--VmA8tp9vs4bXCqHhBuA)
|
||||
|
||||
洗礼之后,发现子集问题还真的有点简单了,其实这就是一道标准的模板题。
|
||||
|
||||
但是要清楚子集问题和组合问题、分割问题的的区别,**子集是收集树形结构中树的所有节点的结果**。
|
||||
|
||||
**而组合问题、分割问题是收集树形结构中叶子节点的结果**。
|
||||
|
||||
163
problems/0090.子集II.md
Normal file
163
problems/0090.子集II.md
Normal file
@ -0,0 +1,163 @@
|
||||
|
||||
|
||||
## 第90题.子集II
|
||||
|
||||
题目链接:https://leetcode-cn.com/problems/subsets-ii/
|
||||
|
||||
给定一个可能包含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
|
||||
|
||||
说明:解集不能包含重复的子集。
|
||||
|
||||
示例:
|
||||
输入: [1,2,2]
|
||||
输出:
|
||||
[
|
||||
[2],
|
||||
[1],
|
||||
[1,2,2],
|
||||
[2,2],
|
||||
[1,2],
|
||||
[]
|
||||
]
|
||||
|
||||
|
||||
## 思路
|
||||
|
||||
做本题之前一定要先做[78.子集](https://mp.weixin.qq.com/s/NNRzX-vJ_pjK4qxohd_LtA)。
|
||||
|
||||
这道题目和[回溯算法:求子集问题!](https://mp.weixin.qq.com/s/NNRzX-vJ_pjK4qxohd_LtA)区别就是集合里有重复元素了,而且求取的子集要去重。
|
||||
|
||||
那么关于回溯算法中的去重问题,**在[40.组合总和II](https://mp.weixin.qq.com/s/_1zPYk70NvHsdY8UWVGXmQ)中已经详细讲解过了,和本题是一个套路**。
|
||||
|
||||
**剧透一下,后期要讲解的排列问题里去重也是这个套路,所以理解“树层去重”和“树枝去重”非常重要**。
|
||||
|
||||
用示例中的[1, 2, 2] 来举例,如图所示: (**注意去重需要先对集合排序**)
|
||||
|
||||
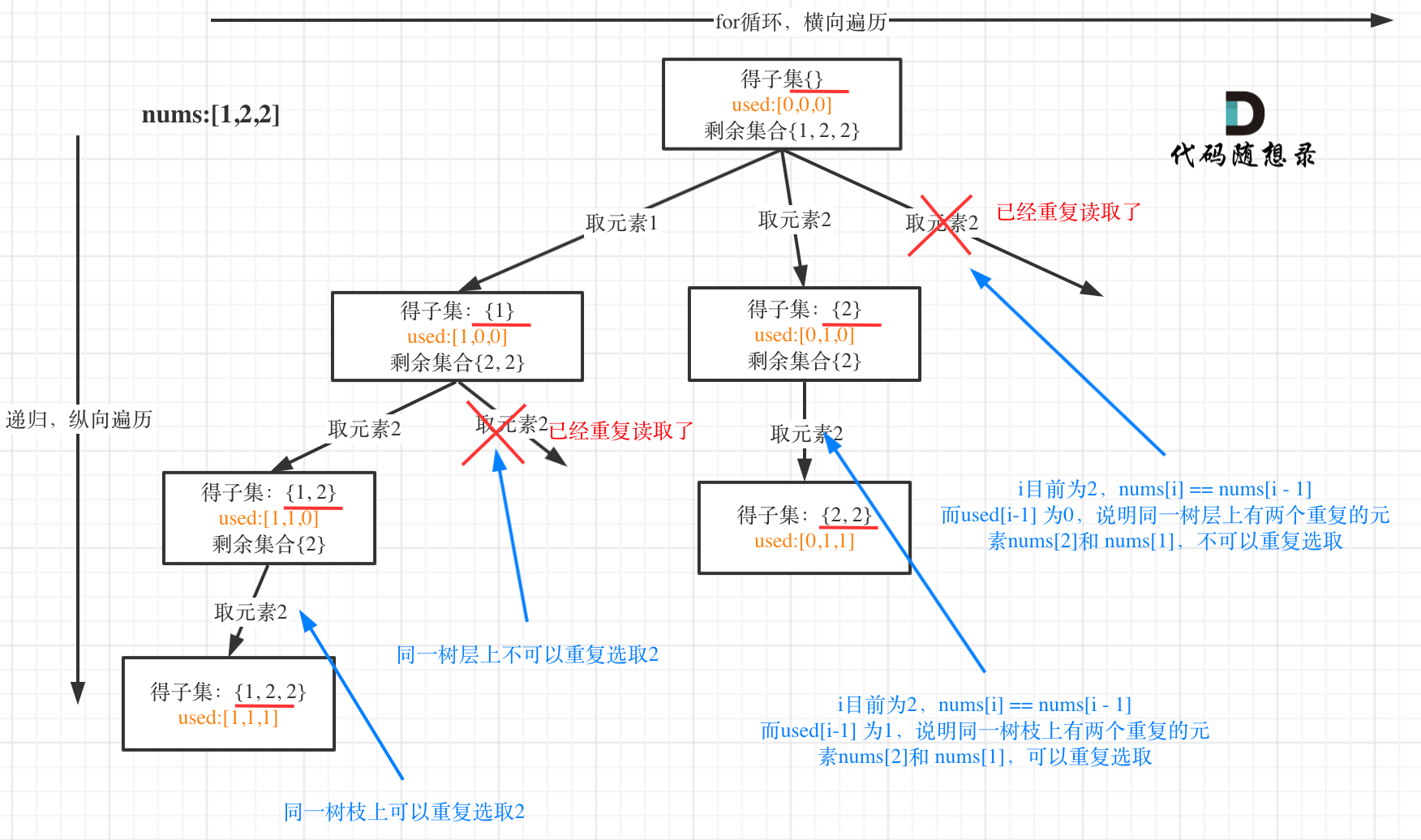
|
||||
|
||||
从图中可以看出,同一树层上重复取2 就要过滤掉,同一树枝上就可以重复取2,因为同一树枝上元素的集合才是唯一子集!
|
||||
|
||||
本题就是其实就是[回溯算法:求子集问题!](https://mp.weixin.qq.com/s/NNRzX-vJ_pjK4qxohd_LtA)的基础上加上了去重,去重我们在[回溯算法:求组合总和(三)](https://mp.weixin.qq.com/s/_1zPYk70NvHsdY8UWVGXmQ)也讲过了,所以我就直接给出代码了:
|
||||
|
||||
## C++代码
|
||||
|
||||
```
|
||||
class Solution {
|
||||
private:
|
||||
vector<vector<int>> result;
|
||||
vector<int> path;
|
||||
void backtracking(vector<int>& nums, int startIndex, vector<bool>& used) {
|
||||
result.push_back(path);
|
||||
for (int i = startIndex; i < nums.size(); i++) {
|
||||
// used[i - 1] == true,说明同一树支candidates[i - 1]使用过
|
||||
// used[i - 1] == false,说明同一树层candidates[i - 1]使用过
|
||||
// 而我们要对同一树层使用过的元素进行跳过
|
||||
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
|
||||
continue;
|
||||
}
|
||||
path.push_back(nums[i]);
|
||||
used[i] = true;
|
||||
backtracking(nums, i + 1, used);
|
||||
used[i] = false;
|
||||
path.pop_back();
|
||||
}
|
||||
}
|
||||
|
||||
public:
|
||||
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
|
||||
result.clear();
|
||||
path.clear();
|
||||
vector<bool> used(nums.size(), false);
|
||||
sort(nums.begin(), nums.end()); // 去重需要排序
|
||||
backtracking(nums, 0, used);
|
||||
return result;
|
||||
}
|
||||
};
|
||||
|
||||
```
|
||||
|
||||
使用set去重的版本。
|
||||
```
|
||||
class Solution {
|
||||
private:
|
||||
vector<vector<int>> result;
|
||||
vector<int> path;
|
||||
void backtracking(vector<int>& nums, int startIndex, vector<bool>& used) {
|
||||
result.push_back(path);
|
||||
unordered_set<int> uset;
|
||||
for (int i = startIndex; i < nums.size(); i++) {
|
||||
if (uset.find(nums[i]) != uset.end()) {
|
||||
continue;
|
||||
}
|
||||
uset.insert(nums[i]);
|
||||
path.push_back(nums[i]);
|
||||
backtracking(nums, i + 1, used);
|
||||
path.pop_back();
|
||||
}
|
||||
}
|
||||
|
||||
public:
|
||||
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
|
||||
result.clear();
|
||||
path.clear();
|
||||
vector<bool> used(nums.size(), false);
|
||||
sort(nums.begin(), nums.end()); // 去重需要排序
|
||||
backtracking(nums, 0, used);
|
||||
return result;
|
||||
}
|
||||
};
|
||||
|
||||
```
|
||||
|
||||
## 补充
|
||||
|
||||
本题也可以不适用used数组来去重,因为递归的时候下一个startIndex是i+1而不是0。
|
||||
|
||||
如果要是全排列的话,每次要从0开始遍历,为了跳过已入栈的元素,需要使用used。
|
||||
|
||||
代码如下:
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
private:
|
||||
vector<vector<int>> result;
|
||||
vector<int> path;
|
||||
void backtracking(vector<int>& nums, int startIndex) {
|
||||
result.push_back(path);
|
||||
for (int i = startIndex; i < nums.size(); i++) {
|
||||
// 而我们要对同一树层使用过的元素进行跳过
|
||||
if (i > startIndex && nums[i] == nums[i - 1] ) { // 注意这里使用i > startIndex
|
||||
continue;
|
||||
}
|
||||
path.push_back(nums[i]);
|
||||
backtracking(nums, i + 1);
|
||||
path.pop_back();
|
||||
}
|
||||
}
|
||||
|
||||
public:
|
||||
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
|
||||
result.clear();
|
||||
path.clear();
|
||||
sort(nums.begin(), nums.end()); // 去重需要排序
|
||||
backtracking(nums, 0);
|
||||
return result;
|
||||
}
|
||||
};
|
||||
|
||||
```
|
||||
|
||||
## 总结
|
||||
|
||||
其实这道题目的知识点,我们之前都讲过了,如果之前讲过的子集问题和去重问题都掌握的好,这道题目应该分分钟AC。
|
||||
|
||||
当然本题去重的逻辑,也可以这么写
|
||||
|
||||
```
|
||||
if (i > startIndex && nums[i] == nums[i - 1] ) {
|
||||
continue;
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
330
problems/0093.复原IP地址.md
Normal file
330
problems/0093.复原IP地址.md
Normal file
@ -0,0 +1,330 @@
|
||||
|
||||
|
||||
|
||||
## 93.复原IP地址
|
||||
|
||||
题目地址:https://leetcode-cn.com/problems/restore-ip-addresses/
|
||||
|
||||
给定一个只包含数字的字符串,复原它并返回所有可能的 IP 地址格式。
|
||||
|
||||
有效的 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 '.' 分隔。
|
||||
|
||||
例如:"0.1.2.201" 和 "192.168.1.1" 是 有效的 IP 地址,但是 "0.011.255.245"、"192.168.1.312" 和 "192.168@1.1" 是 无效的 IP 地址。
|
||||
|
||||
示例 1:
|
||||
输入:s = "25525511135"
|
||||
输出:["255.255.11.135","255.255.111.35"]
|
||||
|
||||
示例 2:
|
||||
输入:s = "0000"
|
||||
输出:["0.0.0.0"]
|
||||
|
||||
示例 3:
|
||||
输入:s = "1111"
|
||||
输出:["1.1.1.1"]
|
||||
|
||||
示例 4:
|
||||
输入:s = "010010"
|
||||
输出:["0.10.0.10","0.100.1.0"]
|
||||
|
||||
示例 5:
|
||||
输入:s = "101023"
|
||||
输出:["1.0.10.23","1.0.102.3","10.1.0.23","10.10.2.3","101.0.2.3"]
|
||||
|
||||
提示:
|
||||
0 <= s.length <= 3000
|
||||
s 仅由数字组成
|
||||
|
||||
|
||||
## 思路
|
||||
|
||||
做这道题目之前,最好先把[回溯算法:分割回文串](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)这个做了。
|
||||
|
||||
这道题目相信大家刚看的时候,应该会一脸茫然。
|
||||
|
||||
其实只要意识到这是切割问题,**切割问题就可以使用回溯搜索法把所有可能性搜出来**,和刚做过的[回溯算法:分割回文串](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)就十分类似了。
|
||||
|
||||
切割问题可以抽象为树型结构,如图:
|
||||
|
||||

|
||||
|
||||
|
||||
## 回溯三部曲
|
||||
|
||||
* 递归参数
|
||||
|
||||
在[回溯算法:分割回文串](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)中我们就提到切割问题类似组合问题。
|
||||
|
||||
startIndex一定是需要的,因为不能重复分割,记录下一层递归分割的起始位置。
|
||||
|
||||
本题我们还需要一个变量pointNum,记录添加逗点的数量。
|
||||
|
||||
所以代码如下:
|
||||
|
||||
```
|
||||
vector<string> result;// 记录结果
|
||||
// startIndex: 搜索的起始位置,pointNum:添加逗点的数量
|
||||
void backtracking(string& s, int startIndex, int pointNum) {
|
||||
```
|
||||
|
||||
* 递归终止条件
|
||||
|
||||
终止条件和[回溯算法:分割回文串](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)情况就不同了,本题明确要求只会分成4段,所以不能用切割线切到最后作为终止条件,而是分割的段数作为终止条件。
|
||||
|
||||
pointNum表示逗点数量,pointNum为3说明字符串分成了4段了。
|
||||
|
||||
然后验证一下第四段是否合法,如果合法就加入到结果集里
|
||||
|
||||
代码如下:
|
||||
|
||||
```
|
||||
if (pointNum == 3) { // 逗点数量为3时,分隔结束
|
||||
// 判断第四段子字符串是否合法,如果合法就放进result中
|
||||
if (isValid(s, startIndex, s.size() - 1)) {
|
||||
result.push_back(s);
|
||||
}
|
||||
return;
|
||||
}
|
||||
```
|
||||
|
||||
* 单层搜索的逻辑
|
||||
|
||||
在[回溯算法:分割回文串](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)中已经讲过在循环遍历中如何截取子串。
|
||||
|
||||
在`for (int i = startIndex; i < s.size(); i++)`循环中 [startIndex, i]这个区间就是截取的子串,需要判断这个子串是否合法。
|
||||
|
||||
如果合法就在字符串后面加上符号`.`表示已经分割。
|
||||
|
||||
如果不合法就结束本层循环,如图中剪掉的分支:
|
||||
|
||||

|
||||
|
||||
然后就是递归和回溯的过程:
|
||||
|
||||
递归调用时,下一层递归的startIndex要从i+2开始(因为需要在字符串中加入了分隔符`.`),同时记录分割符的数量pointNum 要 +1。
|
||||
|
||||
回溯的时候,就将刚刚加入的分隔符`.` 删掉就可以了,pointNum也要-1。
|
||||
|
||||
代码如下:
|
||||
|
||||
```
|
||||
for (int i = startIndex; i < s.size(); i++) {
|
||||
if (isValid(s, startIndex, i)) { // 判断 [startIndex,i] 这个区间的子串是否合法
|
||||
s.insert(s.begin() + i + 1 , '.'); // 在i的后面插入一个逗点
|
||||
pointNum++;
|
||||
backtracking(s, i + 2, pointNum); // 插入逗点之后下一个子串的起始位置为i+2
|
||||
pointNum--; // 回溯
|
||||
s.erase(s.begin() + i + 1); // 回溯删掉逗点
|
||||
} else break; // 不合法,直接结束本层循环
|
||||
}
|
||||
```
|
||||
|
||||
## 判断子串是否合法
|
||||
|
||||
最后就是在写一个判断段位是否是有效段位了。
|
||||
|
||||
主要考虑到如下三点:
|
||||
|
||||
* 段位以0为开头的数字不合法
|
||||
* 段位里有非正整数字符不合法
|
||||
* 段位如果大于255了不合法
|
||||
|
||||
代码如下:
|
||||
|
||||
```
|
||||
// 判断字符串s在左闭又闭区间[start, end]所组成的数字是否合法
|
||||
bool isValid(const string& s, int start, int end) {
|
||||
if (start > end) {
|
||||
return false;
|
||||
}
|
||||
if (s[start] == '0' && start != end) { // 0开头的数字不合法
|
||||
return false;
|
||||
}
|
||||
int num = 0;
|
||||
for (int i = start; i <= end; i++) {
|
||||
if (s[i] > '9' || s[i] < '0') { // 遇到非数字字符不合法
|
||||
return false;
|
||||
}
|
||||
num = num * 10 + (s[i] - '0');
|
||||
if (num > 255) { // 如果大于255了不合法
|
||||
return false;
|
||||
}
|
||||
}
|
||||
return true;
|
||||
}
|
||||
```
|
||||
|
||||
## C++代码
|
||||
|
||||
|
||||
根据[关于回溯算法,你该了解这些!](https://mp.weixin.qq.com/s/gjSgJbNbd1eAA5WkA-HeWw)给出的回溯算法模板:
|
||||
|
||||
```
|
||||
void backtracking(参数) {
|
||||
if (终止条件) {
|
||||
存放结果;
|
||||
return;
|
||||
}
|
||||
|
||||
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
|
||||
处理节点;
|
||||
backtracking(路径,选择列表); // 递归
|
||||
回溯,撤销处理结果
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
可以写出如下回溯算法C++代码:
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
private:
|
||||
vector<string> result;// 记录结果
|
||||
// startIndex: 搜索的起始位置,pointNum:添加逗点的数量
|
||||
void backtracking(string& s, int startIndex, int pointNum) {
|
||||
if (pointNum == 3) { // 逗点数量为3时,分隔结束
|
||||
// 判断第四段子字符串是否合法,如果合法就放进result中
|
||||
if (isValid(s, startIndex, s.size() - 1)) {
|
||||
result.push_back(s);
|
||||
}
|
||||
return;
|
||||
}
|
||||
for (int i = startIndex; i < s.size(); i++) {
|
||||
if (isValid(s, startIndex, i)) { // 判断 [startIndex,i] 这个区间的子串是否合法
|
||||
s.insert(s.begin() + i + 1 , '.'); // 在i的后面插入一个逗点
|
||||
pointNum++;
|
||||
backtracking(s, i + 2, pointNum); // 插入逗点之后下一个子串的起始位置为i+2
|
||||
pointNum--; // 回溯
|
||||
s.erase(s.begin() + i + 1); // 回溯删掉逗点
|
||||
} else break; // 不合法,直接结束本层循环
|
||||
}
|
||||
}
|
||||
// 判断字符串s在左闭又闭区间[start, end]所组成的数字是否合法
|
||||
bool isValid(const string& s, int start, int end) {
|
||||
if (start > end) {
|
||||
return false;
|
||||
}
|
||||
if (s[start] == '0' && start != end) { // 0开头的数字不合法
|
||||
return false;
|
||||
}
|
||||
int num = 0;
|
||||
for (int i = start; i <= end; i++) {
|
||||
if (s[i] > '9' || s[i] < '0') { // 遇到非数字字符不合法
|
||||
return false;
|
||||
}
|
||||
num = num * 10 + (s[i] - '0');
|
||||
if (num > 255) { // 如果大于255了不合法
|
||||
return false;
|
||||
}
|
||||
}
|
||||
return true;
|
||||
}
|
||||
public:
|
||||
vector<string> restoreIpAddresses(string s) {
|
||||
result.clear();
|
||||
if (s.size() > 12) return result; // 算是剪枝了
|
||||
backtracking(s, 0, 0);
|
||||
return result;
|
||||
}
|
||||
};
|
||||
|
||||
```
|
||||
|
||||
## 总结
|
||||
|
||||
在[回溯算法:分割回文串](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)中我列举的分割字符串的难点,本题都覆盖了。
|
||||
|
||||
而且本题还需要操作字符串添加逗号作为分隔符,并验证区间的合法性。
|
||||
|
||||
可以说是[回溯算法:分割回文串](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)的加强版。
|
||||
|
||||
在本文的树形结构图中,我已经把详细的分析思路都画了出来,相信大家看了之后一定会思路清晰不少!
|
||||
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
List<String> result = new ArrayList<>();
|
||||
|
||||
public List<String> restoreIpAddresses(String s) {
|
||||
if (s.length() > 12) return result; // 算是剪枝了
|
||||
backTrack(s, 0, 0);
|
||||
return result;
|
||||
}
|
||||
|
||||
// startIndex: 搜索的起始位置, pointNum:添加逗点的数量
|
||||
private void backTrack(String s, int startIndex, int pointNum) {
|
||||
if (pointNum == 3) {// 逗点数量为3时,分隔结束
|
||||
// 判断第四段⼦字符串是否合法,如果合法就放进result中
|
||||
if (isValid(s,startIndex,s.length()-1)) {
|
||||
result.add(s);
|
||||
}
|
||||
return;
|
||||
}
|
||||
for (int i = startIndex; i < s.length(); i++) {
|
||||
if (isValid(s, startIndex, i)) {
|
||||
s = s.substring(0, i + 1) + "." + s.substring(i + 1); //在str的后⾯插⼊⼀个逗点
|
||||
pointNum++;
|
||||
backTrack(s, i + 2, pointNum);// 插⼊逗点之后下⼀个⼦串的起始位置为i+2
|
||||
pointNum--;// 回溯
|
||||
s = s.substring(0, i + 1) + s.substring(i + 2);// 回溯删掉逗点
|
||||
} else {
|
||||
break;
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
// 判断字符串s在左闭⼜闭区间[start, end]所组成的数字是否合法
|
||||
private Boolean isValid(String s, int start, int end) {
|
||||
if (start > end) {
|
||||
return false;
|
||||
}
|
||||
if (s.charAt(start) == '0' && start != end) { // 0开头的数字不合法
|
||||
return false;
|
||||
}
|
||||
int num = 0;
|
||||
for (int i = start; i <= end; i++) {
|
||||
if (s.charAt(i) > '9' || s.charAt(i) < '0') { // 遇到⾮数字字符不合法
|
||||
return false;
|
||||
}
|
||||
num = num * 10 + (s.charAt(i) - '0');
|
||||
if (num > 255) { // 如果⼤于255了不合法
|
||||
return false;
|
||||
}
|
||||
}
|
||||
return true;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
```python
|
||||
class Solution(object):
|
||||
def restoreIpAddresses(self, s):
|
||||
"""
|
||||
:type s: str
|
||||
:rtype: List[str]
|
||||
"""
|
||||
ans = []
|
||||
path = []
|
||||
def backtrack(path, startIndex):
|
||||
if len(path) == 4:
|
||||
if startIndex == len(s):
|
||||
ans.append(".".join(path[:]))
|
||||
return
|
||||
for i in range(startIndex+1, min(startIndex+4, len(s)+1)): # 剪枝
|
||||
string = s[startIndex:i]
|
||||
if not 0 <= int(string) <= 255:
|
||||
continue
|
||||
if not string == "0" and not string.lstrip('0') == string:
|
||||
continue
|
||||
path.append(string)
|
||||
backtrack(path, i)
|
||||
path.pop()
|
||||
|
||||
backtrack([], 0)
|
||||
return ans```
|
||||
```
|
||||
|
||||
|
||||
394
problems/0332.重新安排行程.md
Normal file
394
problems/0332.重新安排行程.md
Normal file
@ -0,0 +1,394 @@
|
||||
|
||||
|
||||
> 这也可以用回溯法? 其实深搜和回溯也是相辅相成的,毕竟都用递归。
|
||||
|
||||
## 332.重新安排行程
|
||||
|
||||
题目地址:https://leetcode-cn.com/problems/reconstruct-itinerary/
|
||||
|
||||
给定一个机票的字符串二维数组 [from, to],子数组中的两个成员分别表示飞机出发和降落的机场地点,对该行程进行重新规划排序。所有这些机票都属于一个从 JFK(肯尼迪国际机场)出发的先生,所以该行程必须从 JFK 开始。
|
||||
|
||||
提示:
|
||||
* 如果存在多种有效的行程,请你按字符自然排序返回最小的行程组合。例如,行程 ["JFK", "LGA"] 与 ["JFK", "LGB"] 相比就更小,排序更靠前
|
||||
* 所有的机场都用三个大写字母表示(机场代码)。
|
||||
* 假定所有机票至少存在一种合理的行程。
|
||||
* 所有的机票必须都用一次 且 只能用一次。
|
||||
|
||||
|
||||
示例 1:
|
||||
输入:[["MUC", "LHR"], ["JFK", "MUC"], ["SFO", "SJC"], ["LHR", "SFO"]]
|
||||
输出:["JFK", "MUC", "LHR", "SFO", "SJC"]
|
||||
|
||||
示例 2:
|
||||
输入:[["JFK","SFO"],["JFK","ATL"],["SFO","ATL"],["ATL","JFK"],["ATL","SFO"]]
|
||||
输出:["JFK","ATL","JFK","SFO","ATL","SFO"]
|
||||
解释:另一种有效的行程是 ["JFK","SFO","ATL","JFK","ATL","SFO"]。但是它自然排序更大更靠后。
|
||||
|
||||
## 思路
|
||||
|
||||
这道题目还是很难的,之前我们用回溯法解决了如下问题:[组合问题](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ),[分割问题](https://mp.weixin.qq.com/s/v--VmA8tp9vs4bXCqHhBuA),[子集问题](https://mp.weixin.qq.com/s/NNRzX-vJ_pjK4qxohd_LtA),[排列问题](https://mp.weixin.qq.com/s/SCOjeMX1t41wcvJq49GhMw)。
|
||||
|
||||
直觉上来看 这道题和回溯法没有什么关系,更像是图论中的深度优先搜索。
|
||||
|
||||
实际上确实是深搜,但这是深搜中使用了回溯的例子,在查找路径的时候,如果不回溯,怎么能查到目标路径呢。
|
||||
|
||||
所以我倾向于说本题应该使用回溯法,那么我也用回溯法的思路来讲解本题,其实深搜一般都使用了回溯法的思路,在图论系列中我会再详细讲解深搜。
|
||||
|
||||
**这里就是先给大家拓展一下,原来回溯法还可以这么玩!**
|
||||
|
||||
**这道题目有几个难点:**
|
||||
|
||||
1. 一个行程中,如果航班处理不好容易变成一个圈,成为死循环
|
||||
2. 有多种解法,字母序靠前排在前面,让很多同学望而退步,如何该记录映射关系呢 ?
|
||||
3. 使用回溯法(也可以说深搜) 的话,那么终止条件是什么呢?
|
||||
4. 搜索的过程中,如何遍历一个机场所对应的所有机场。
|
||||
|
||||
针对以上问题我来逐一解答!
|
||||
|
||||
## 如何理解死循环
|
||||
|
||||
对于死循环,我来举一个有重复机场的例子:
|
||||
|
||||
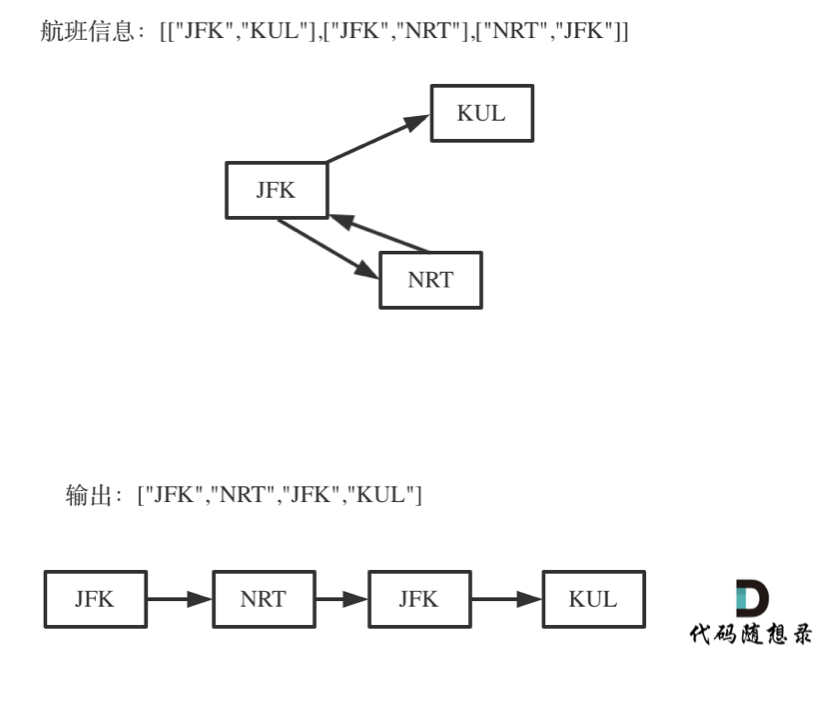
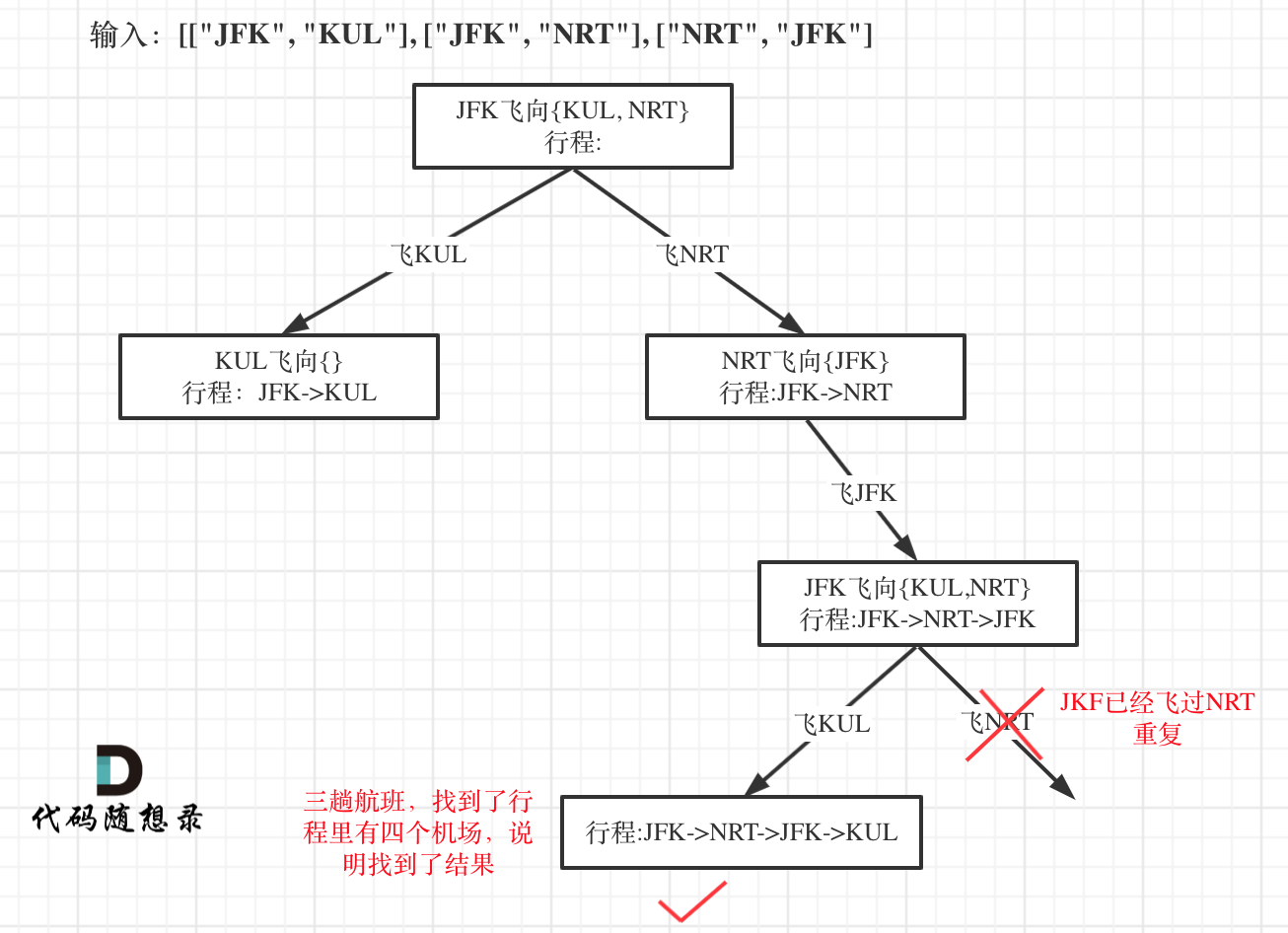
|
||||
|
||||
为什么要举这个例子呢,就是告诉大家,出发机场和到达机场也会重复的,**如果在解题的过程中没有对集合元素处理好,就会死循环。**
|
||||
|
||||
## 该记录映射关系
|
||||
|
||||
有多种解法,字母序靠前排在前面,让很多同学望而退步,如何该记录映射关系呢 ?
|
||||
|
||||
一个机场映射多个机场,机场之间要靠字母序排列,一个机场映射多个机场,可以使用std::unordered_map,如果让多个机场之间再有顺序的话,就是用std::map 或者std::multimap 或者 std::multiset。
|
||||
|
||||
如果对map 和 set 的实现机制不太了解,也不清楚为什么 map、multimap就是有序的同学,可以看这篇文章[关于哈希表,你该了解这些!](https://mp.weixin.qq.com/s/g8N6WmoQmsCUw3_BaWxHZA)。
|
||||
|
||||
这样存放映射关系可以定义为 `unordered_map<string, multiset<string>> targets` 或者 `unordered_map<string, map<string, int>> targets`。
|
||||
|
||||
含义如下:
|
||||
|
||||
`unordered_map<string, multiset<string>> targets`:`unordered_map<出发机场, 到达机场的集合> targets`
|
||||
`unordered_map<string, map<string, int>> targets`:`unordered_map<出发机场, map<到达机场, 航班次数>> targets`
|
||||
|
||||
这两个结构,我选择了后者,因为如果使用`unordered_map<string, multiset<string>> targets` 遍历multiset的时候,不能删除元素,一旦删除元素,迭代器就失效了。
|
||||
|
||||
**再说一下为什么一定要增删元素呢,正如开篇我给出的图中所示,出发机场和到达机场是会重复的,搜索的过程没及时删除目的机场就会死循环。**
|
||||
|
||||
所以搜索的过程中就是要不断的删multiset里的元素,那么推荐使用`unordered_map<string, map<string, int>> targets`。
|
||||
|
||||
在遍历 `unordered_map<出发机场, map<到达机场, 航班次数>> targets`的过程中,**可以使用"航班次数"这个字段的数字做相应的增减,来标记到达机场是否使用过了。**
|
||||
|
||||
|
||||
如果“航班次数”大于零,说明目的地还可以飞,如果如果“航班次数”等于零说明目的地不能飞了,而不用对集合做删除元素或者增加元素的操作。
|
||||
|
||||
**相当于说我不删,我就做一个标记!**
|
||||
|
||||
## 回溯法
|
||||
|
||||
这道题目我使用回溯法,那么下面按照我总结的回溯模板来:
|
||||
|
||||
```
|
||||
void backtracking(参数) {
|
||||
if (终止条件) {
|
||||
存放结果;
|
||||
return;
|
||||
}
|
||||
|
||||
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
|
||||
处理节点;
|
||||
backtracking(路径,选择列表); // 递归
|
||||
回溯,撤销处理结果
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
本题以输入:[["JFK", "KUL"], ["JFK", "NRT"], ["NRT", "JFK"]为例,抽象为树形结构如下:
|
||||
|
||||
|
||||
|
||||
开始回溯三部曲讲解:
|
||||
|
||||
* 递归函数参数
|
||||
|
||||
在讲解映射关系的时候,已经讲过了,使用`unordered_map<string, map<string, int>> targets;` 来记录航班的映射关系,我定义为全局变量。
|
||||
|
||||
当然把参数放进函数里传进去也是可以的,我是尽量控制函数里参数的长度。
|
||||
|
||||
参数里还需要ticketNum,表示有多少个航班(终止条件会用上)。
|
||||
|
||||
代码如下:
|
||||
|
||||
```
|
||||
// unordered_map<出发机场, map<到达机场, 航班次数>> targets
|
||||
unordered_map<string, map<string, int>> targets;
|
||||
bool backtracking(int ticketNum, vector<string>& result) {
|
||||
```
|
||||
|
||||
**注意函数返回值我用的是bool!**
|
||||
|
||||
我们之前讲解回溯算法的时候,一般函数返回值都是void,这次为什么是bool呢?
|
||||
|
||||
因为我们只需要找到一个行程,就是在树形结构中唯一的一条通向叶子节点的路线,如图:
|
||||
|
||||

|
||||
|
||||
所以找到了这个叶子节点了直接返回,这个递归函数的返回值问题我们在讲解二叉树的系列的时候,在这篇[二叉树:递归函数究竟什么时候需要返回值,什么时候不要返回值?](https://mp.weixin.qq.com/s/6TWAVjxQ34kVqROWgcRFOg)详细介绍过。
|
||||
|
||||
当然本题的targets和result都需要初始化,代码如下:
|
||||
```
|
||||
for (const vector<string>& vec : tickets) {
|
||||
targets[vec[0]][vec[1]]++; // 记录映射关系
|
||||
}
|
||||
result.push_back("JFK"); // 起始机场
|
||||
```
|
||||
|
||||
* 递归终止条件
|
||||
|
||||
拿题目中的示例为例,输入: [["MUC", "LHR"], ["JFK", "MUC"], ["SFO", "SJC"], ["LHR", "SFO"]] ,这是有4个航班,那么只要找出一种行程,行程里的机场个数是5就可以了。
|
||||
|
||||
所以终止条件是:我们回溯遍历的过程中,遇到的机场个数,如果达到了(航班数量+1),那么我们就找到了一个行程,把所有航班串在一起了。
|
||||
|
||||
代码如下:
|
||||
|
||||
```
|
||||
if (result.size() == ticketNum + 1) {
|
||||
return true;
|
||||
}
|
||||
```
|
||||
|
||||
已经看习惯回溯法代码的同学,到叶子节点了习惯性的想要收集结果,但发现并不需要,本题的result相当于 [回溯算法:求组合总和!](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w)中的path,也就是本题的result就是记录路径的(就一条),在如下单层搜索的逻辑中result就添加元素了。
|
||||
|
||||
* 单层搜索的逻辑
|
||||
|
||||
回溯的过程中,如何遍历一个机场所对应的所有机场呢?
|
||||
|
||||
这里刚刚说过,在选择映射函数的时候,不能选择`unordered_map<string, multiset<string>> targets`, 因为一旦有元素增删multiset的迭代器就会失效,当然可能有牛逼的容器删除元素迭代器不会失效,这里就不在讨论了。
|
||||
|
||||
**可以说本题既要找到一个对数据进行排序的容器,而且还要容易增删元素,迭代器还不能失效**。
|
||||
|
||||
所以我选择了`unordered_map<string, map<string, int>> targets` 来做机场之间的映射。
|
||||
|
||||
遍历过程如下:
|
||||
|
||||
```C++
|
||||
for (pair<const string, int>& target : targets[result[result.size() - 1]]) {
|
||||
if (target.second > 0 ) { // 记录到达机场是否飞过了
|
||||
result.push_back(target.first);
|
||||
target.second--;
|
||||
if (backtracking(ticketNum, result)) return true;
|
||||
result.pop_back();
|
||||
target.second++;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
可以看出 通过`unordered_map<string, map<string, int>> targets`里的int字段来判断 这个集合里的机场是否使用过,这样避免了直接去删元素。
|
||||
|
||||
分析完毕,此时完整C++代码如下:
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
private:
|
||||
// unordered_map<出发机场, map<到达机场, 航班次数>> targets
|
||||
unordered_map<string, map<string, int>> targets;
|
||||
bool backtracking(int ticketNum, vector<string>& result) {
|
||||
if (result.size() == ticketNum + 1) {
|
||||
return true;
|
||||
}
|
||||
for (pair<const string, int>& target : targets[result[result.size() - 1]]) {
|
||||
if (target.second > 0 ) { // 记录到达机场是否飞过了
|
||||
result.push_back(target.first);
|
||||
target.second--;
|
||||
if (backtracking(ticketNum, result)) return true;
|
||||
result.pop_back();
|
||||
target.second++;
|
||||
}
|
||||
}
|
||||
return false;
|
||||
}
|
||||
public:
|
||||
vector<string> findItinerary(vector<vector<string>>& tickets) {
|
||||
targets.clear();
|
||||
vector<string> result;
|
||||
for (const vector<string>& vec : tickets) {
|
||||
targets[vec[0]][vec[1]]++; // 记录映射关系
|
||||
}
|
||||
result.push_back("JFK"); // 起始机场
|
||||
backtracking(tickets.size(), result);
|
||||
return result;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
一波分析之后,可以看出我就是按照回溯算法的模板来的。
|
||||
|
||||
代码中
|
||||
```
|
||||
for (pair<const string, int>& target : targets[result[result.size() - 1]])
|
||||
```
|
||||
pair里要有const,因为map中的key是不可修改的,所以是`pair<const string, int>`。
|
||||
|
||||
如果不加const,也可以复制一份pair,例如这么写:
|
||||
```
|
||||
for (pair<string, int>target : targets[result[result.size() - 1]])
|
||||
```
|
||||
|
||||
|
||||
## 总结
|
||||
|
||||
本题其实可以算是一道hard的题目了,关于本题的难点我在文中已经列出了。
|
||||
|
||||
**如果单纯的回溯搜索(深搜)并不难,难还难在容器的选择和使用上**。
|
||||
|
||||
本题其实是一道深度优先搜索的题目,但是我完全使用回溯法的思路来讲解这道题题目,**算是给大家拓展一下思维方式,其实深搜和回溯也是分不开的,毕竟最终都是用递归**。
|
||||
|
||||
如果最终代码,发现照着回溯法模板画的话好像也能画出来,但难就难如何知道可以使用回溯,以及如果套进去,所以我再写了这么长的一篇来详细讲解。
|
||||
|
||||
就酱,很多录友表示和「代码随想录」相见恨晚,那么帮Carl宣传一波吧,让更多同学知道这里!
|
||||
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
python:
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
def findItinerary(self, tickets: List[List[str]]) -> List[str]:
|
||||
# defaultdic(list) 是为了方便直接append
|
||||
tickets_dict = defaultdict(list)
|
||||
for item in tickets:
|
||||
tickets_dict[item[0]].append(item[1])
|
||||
'''
|
||||
tickets_dict里面的内容是这样的
|
||||
{'JFK': ['SFO', 'ATL'], 'SFO': ['ATL'], 'ATL': ['JFK', 'SFO']})
|
||||
'''
|
||||
path = ["JFK"]
|
||||
def backtracking(start_point):
|
||||
# 终止条件
|
||||
if len(path) == len(tickets) + 1:
|
||||
return True
|
||||
tickets_dict[start_point].sort()
|
||||
for _ in tickets_dict[start_point]:
|
||||
#必须及时删除,避免出现死循环
|
||||
end_point = tickets_dict[start_point].pop(0)
|
||||
path.append(end_point)
|
||||
# 只要找到一个就可以返回了
|
||||
if backtracking(end_point):
|
||||
return True
|
||||
path.pop()
|
||||
tickets_dict[start_point].append(end_point)
|
||||
|
||||
backtracking("JFK")
|
||||
return path
|
||||
```
|
||||
|
||||
C语言版本:
|
||||
|
||||
```C
|
||||
char **result;
|
||||
bool *used;
|
||||
int g_found;
|
||||
|
||||
int cmp(const void *str1, const void *str2)
|
||||
{
|
||||
const char **tmp1 = *(char**)str1;
|
||||
const char **tmp2 = *(char**)str2;
|
||||
int ret = strcmp(tmp1[0], tmp2[0]);
|
||||
if (ret == 0) {
|
||||
return strcmp(tmp1[1], tmp2[1]);
|
||||
}
|
||||
return ret;
|
||||
}
|
||||
|
||||
void backtracting(char *** tickets, int ticketsSize, int* returnSize, char *start, char **result, bool *used)
|
||||
{
|
||||
if (*returnSize == ticketsSize + 1) {
|
||||
g_found = 1;
|
||||
return;
|
||||
}
|
||||
for (int i = 0; i < ticketsSize; i++) {
|
||||
if ((used[i] == false) && (strcmp(start, tickets[i][0]) == 0)) {
|
||||
result[*returnSize] = (char*)malloc(sizeof(char) * 4);
|
||||
memcpy(result[*returnSize], tickets[i][1], sizeof(char) * 4);
|
||||
(*returnSize)++;
|
||||
used[i] = true;
|
||||
/*if ((*returnSize) == ticketsSize + 1) {
|
||||
return;
|
||||
}*/
|
||||
backtracting(tickets, ticketsSize, returnSize, tickets[i][1], result, used);
|
||||
if (g_found) {
|
||||
return;
|
||||
}
|
||||
(*returnSize)--;
|
||||
used[i] = false;
|
||||
}
|
||||
}
|
||||
return;
|
||||
}
|
||||
|
||||
char ** findItinerary(char *** tickets, int ticketsSize, int* ticketsColSize, int* returnSize){
|
||||
if (tickets == NULL || ticketsSize <= 0) {
|
||||
return NULL;
|
||||
}
|
||||
result = malloc(sizeof(char*) * (ticketsSize + 1));
|
||||
used = malloc(sizeof(bool) * ticketsSize);
|
||||
memset(used, false, sizeof(bool) * ticketsSize);
|
||||
result[0] = malloc(sizeof(char) * 4);
|
||||
memcpy(result[0], "JFK", sizeof(char) * 4);
|
||||
g_found = 0;
|
||||
*returnSize = 1;
|
||||
qsort(tickets, ticketsSize, sizeof(tickets[0]), cmp);
|
||||
backtracting(tickets, ticketsSize, returnSize, "JFK", result, used);
|
||||
*returnSize = ticketsSize + 1;
|
||||
return result;
|
||||
}
|
||||
```
|
||||
|
||||
java 版本:
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
private Deque<String> res;
|
||||
private Map<String, Map<String, Integer>> map;
|
||||
|
||||
private boolean backTracking(int ticketNum){
|
||||
if(res.size() == ticketNum + 1){
|
||||
return true;
|
||||
}
|
||||
String last = res.getLast();
|
||||
if(map.containsKey(last)){//防止出现null
|
||||
for(Map.Entry<String, Integer> target : map.get(last).entrySet()){
|
||||
int count = target.getValue();
|
||||
if(count > 0){
|
||||
res.add(target.getKey());
|
||||
target.setValue(count - 1);
|
||||
if(backTracking(ticketNum)) return true;
|
||||
res.removeLast();
|
||||
target.setValue(count);
|
||||
}
|
||||
}
|
||||
}
|
||||
return false;
|
||||
}
|
||||
|
||||
public List<String> findItinerary(List<List<String>> tickets) {
|
||||
map = new HashMap<String, Map<String, Integer>>();
|
||||
res = new LinkedList<>();
|
||||
for(List<String> t : tickets){
|
||||
Map<String, Integer> temp;
|
||||
if(map.containsKey(t.get(0))){
|
||||
temp = map.get(t.get(0));
|
||||
temp.put(t.get(1), temp.getOrDefault(t.get(1), 0) + 1);
|
||||
}else{
|
||||
temp = new TreeMap<>();//升序Map
|
||||
temp.put(t.get(1), 1);
|
||||
}
|
||||
map.put(t.get(0), temp);
|
||||
|
||||
}
|
||||
res.add("JFK");
|
||||
backTracking(tickets.size());
|
||||
return new ArrayList<>(res);
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
191
problems/0491.递增子序列.md
Normal file
191
problems/0491.递增子序列.md
Normal file
@ -0,0 +1,191 @@
|
||||
|
||||
|
||||
> 和子集问题有点像,但又处处是陷阱
|
||||
|
||||
## 491.递增子序列
|
||||
|
||||
题目链接:https://leetcode-cn.com/problems/increasing-subsequences/
|
||||
|
||||
给定一个整型数组, 你的任务是找到所有该数组的递增子序列,递增子序列的长度至少是2。
|
||||
|
||||
示例:
|
||||
|
||||
输入: [4, 6, 7, 7]
|
||||
输出: [[4, 6], [4, 7], [4, 6, 7], [4, 6, 7, 7], [6, 7], [6, 7, 7], [7,7], [4,7,7]]
|
||||
|
||||
说明:
|
||||
* 给定数组的长度不会超过15。
|
||||
* 数组中的整数范围是 [-100,100]。
|
||||
* 给定数组中可能包含重复数字,相等的数字应该被视为递增的一种情况。
|
||||
|
||||
|
||||
## 思路
|
||||
|
||||
这个递增子序列比较像是取有序的子集。而且本题也要求不能有相同的递增子序列。
|
||||
|
||||
这又是子集,又是去重,是不是不由自主的想起了刚刚讲过的[回溯算法:求子集问题(二)](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)。
|
||||
|
||||
就是因为太像了,更要注意差别所在,要不就掉坑里了!
|
||||
|
||||
在[回溯算法:求子集问题(二)](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)中我们是通过排序,再加一个标记数组来达到去重的目的。
|
||||
|
||||
而本题求自增子序列,是不能对原数组经行排序的,排完序的数组都是自增子序列了。
|
||||
|
||||
**所以不能使用之前的去重逻辑!**
|
||||
|
||||
本题给出的示例,还是一个有序数组 [4, 6, 7, 7],这更容易误导大家按照排序的思路去做了。
|
||||
|
||||
为了有鲜明的对比,我用[4, 7, 6, 7]这个数组来举例,抽象为树形结构如图:
|
||||
|
||||
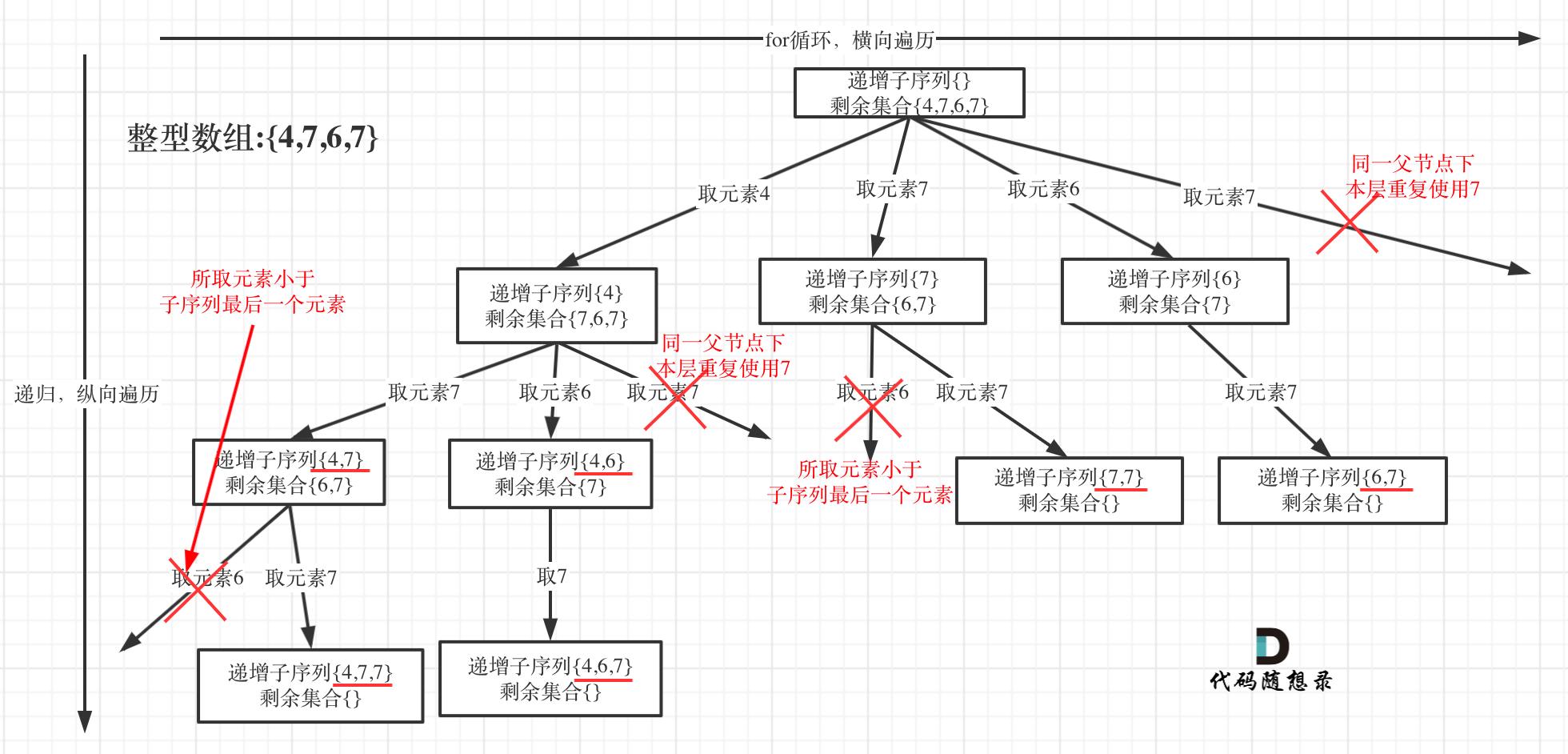
|
||||
|
||||
|
||||
## 回溯三部曲
|
||||
|
||||
* 递归函数参数
|
||||
|
||||
本题求子序列,很明显一个元素不能重复使用,所以需要startIndex,调整下一层递归的起始位置。
|
||||
|
||||
代码如下:
|
||||
|
||||
```
|
||||
vector<vector<int>> result;
|
||||
vector<int> path;
|
||||
void backtracking(vector<int>& nums, int startIndex)
|
||||
```
|
||||
|
||||
* 终止条件
|
||||
|
||||
本题其实类似求子集问题,也是要遍历树形结构找每一个节点,所以和[回溯算法:求子集问题!](https://mp.weixin.qq.com/s/NNRzX-vJ_pjK4qxohd_LtA)一样,可以不加终止条件,startIndex每次都会加1,并不会无限递归。
|
||||
|
||||
但本题收集结果有所不同,题目要求递增子序列大小至少为2,所以代码如下:
|
||||
|
||||
```
|
||||
if (path.size() > 1) {
|
||||
result.push_back(path);
|
||||
// 注意这里不要加return,因为要取树上的所有节点
|
||||
}
|
||||
```
|
||||
|
||||
* 单层搜索逻辑
|
||||
|
||||

|
||||
在图中可以看出,**同一父节点下的同层上使用过的元素就不能在使用了**
|
||||
|
||||
那么单层搜索代码如下:
|
||||
|
||||
```
|
||||
unordered_set<int> uset; // 使用set来对本层元素进行去重
|
||||
for (int i = startIndex; i < nums.size(); i++) {
|
||||
if ((!path.empty() && nums[i] < path.back())
|
||||
|| uset.find(nums[i]) != uset.end()) {
|
||||
continue;
|
||||
}
|
||||
uset.insert(nums[i]); // 记录这个元素在本层用过了,本层后面不能再用了
|
||||
path.push_back(nums[i]);
|
||||
backtracking(nums, i + 1);
|
||||
path.pop_back();
|
||||
}
|
||||
```
|
||||
|
||||
**对于已经习惯写回溯的同学,看到递归函数上面的`uset.insert(nums[i]);`,下面却没有对应的pop之类的操作,应该很不习惯吧,哈哈**
|
||||
|
||||
**这也是需要注意的点,`unordered_set<int> uset;` 是记录本层元素是否重复使用,新的一层uset都会重新定义(清空),所以要知道uset只负责本层!**
|
||||
|
||||
|
||||
最后整体C++代码如下:
|
||||
|
||||
```C++
|
||||
// 版本一
|
||||
class Solution {
|
||||
private:
|
||||
vector<vector<int>> result;
|
||||
vector<int> path;
|
||||
void backtracking(vector<int>& nums, int startIndex) {
|
||||
if (path.size() > 1) {
|
||||
result.push_back(path);
|
||||
// 注意这里不要加return,要取树上的节点
|
||||
}
|
||||
unordered_set<int> uset; // 使用set对本层元素进行去重
|
||||
for (int i = startIndex; i < nums.size(); i++) {
|
||||
if ((!path.empty() && nums[i] < path.back())
|
||||
|| uset.find(nums[i]) != uset.end()) {
|
||||
continue;
|
||||
}
|
||||
uset.insert(nums[i]); // 记录这个元素在本层用过了,本层后面不能再用了
|
||||
path.push_back(nums[i]);
|
||||
backtracking(nums, i + 1);
|
||||
path.pop_back();
|
||||
}
|
||||
}
|
||||
public:
|
||||
vector<vector<int>> findSubsequences(vector<int>& nums) {
|
||||
result.clear();
|
||||
path.clear();
|
||||
backtracking(nums, 0);
|
||||
return result;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
## 优化
|
||||
|
||||
以上代码用我用了`unordered_set<int>`来记录本层元素是否重复使用。
|
||||
|
||||
**其实用数组来做哈希,效率就高了很多**。
|
||||
|
||||
注意题目中说了,数值范围[-100,100],所以完全可以用数组来做哈希。
|
||||
|
||||
程序运行的时候对unordered_set 频繁的insert,unordered_set需要做哈希映射(也就是把key通过hash function映射为唯一的哈希值)相对费时间,而且每次重新定义set,insert的时候其底层的符号表也要做相应的扩充,也是费事的。
|
||||
|
||||
那么优化后的代码如下:
|
||||
|
||||
```C++
|
||||
// 版本二
|
||||
class Solution {
|
||||
private:
|
||||
vector<vector<int>> result;
|
||||
vector<int> path;
|
||||
void backtracking(vector<int>& nums, int startIndex) {
|
||||
if (path.size() > 1) {
|
||||
result.push_back(path);
|
||||
}
|
||||
int used[201] = {0}; // 这里使用数组来进行去重操作,题目说数值范围[-100, 100]
|
||||
for (int i = startIndex; i < nums.size(); i++) {
|
||||
if ((!path.empty() && nums[i] < path.back())
|
||||
|| used[nums[i] + 100] == 1) {
|
||||
continue;
|
||||
}
|
||||
used[nums[i] + 100] = 1; // 记录这个元素在本层用过了,本层后面不能再用了
|
||||
path.push_back(nums[i]);
|
||||
backtracking(nums, i + 1);
|
||||
path.pop_back();
|
||||
}
|
||||
}
|
||||
public:
|
||||
vector<vector<int>> findSubsequences(vector<int>& nums) {
|
||||
result.clear();
|
||||
path.clear();
|
||||
backtracking(nums, 0);
|
||||
return result;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
这份代码在leetcode上提交,要比版本一耗时要好的多。
|
||||
|
||||
**所以正如在[哈希表:总结篇!(每逢总结必经典)](https://mp.weixin.qq.com/s/1s91yXtarL-PkX07BfnwLg)中说的那样,数组,set,map都可以做哈希表,而且数组干的活,map和set都能干,但如何数值范围小的话能用数组尽量用数组**。
|
||||
|
||||
|
||||
|
||||
## 总结
|
||||
|
||||
本题题解清一色都说是深度优先搜索,但我更倾向于说它用回溯法,而且本题我也是完全使用回溯法的逻辑来分析的。
|
||||
|
||||
相信大家在本题中处处都能看到是[回溯算法:求子集问题(二)](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)的身影,但处处又都是陷阱。
|
||||
|
||||
**对于养成思维定式或者套模板套嗨了的同学,这道题起到了很好的警醒作用。更重要的是拓展了大家的思路!**
|
||||
|
||||
**就酱,如果感觉「代码随想录」很干货,就帮Carl宣传一波吧!**
|
||||
|
||||
|
||||
169
problems/周总结/20201107回溯周末总结.md
Normal file
169
problems/周总结/20201107回溯周末总结.md
Normal file
@ -0,0 +1,169 @@
|
||||
|
||||
|
||||
# 本周小结!(回溯算法系列二)
|
||||
|
||||
> 例行每周小结
|
||||
|
||||
## 周一
|
||||
|
||||
在[回溯算法:求组合总和(二)](https://mp.weixin.qq.com/s/FLg8G6EjVcxBjwCbzpACPw)中讲解的组合总和问题,和以前的组合问题还都不一样。
|
||||
|
||||
本题和[回溯算法:求组合问题!](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ),[回溯算法:求组合总和!](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w)和区别是:本题没有数量要求,可以无限重复,但是有总和的限制,所以间接的也是有个数的限制。
|
||||
|
||||
不少录友都是看到可以重复选择,就义无反顾的把startIndex去掉了。
|
||||
|
||||
**本题还需要startIndex来控制for循环的起始位置,对于组合问题,什么时候需要startIndex呢?**
|
||||
|
||||
我举过例子,如果是一个集合来求组合的话,就需要startIndex,例如:[回溯算法:求组合问题!](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ),[回溯算法:求组合总和!](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w)。
|
||||
|
||||
如果是多个集合取组合,各个集合之间相互不影响,那么就不用startIndex,例如:[回溯算法:电话号码的字母组合](https://mp.weixin.qq.com/s/e2ua2cmkE_vpYjM3j6HY0A)
|
||||
|
||||
**注意以上我只是说求组合的情况,如果是排列问题,又是另一套分析的套路,后面我再讲解排列的时候就重点介绍**。
|
||||
|
||||
最后还给出了本题的剪枝优化,如下:
|
||||
|
||||
```
|
||||
for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++)
|
||||
```
|
||||
|
||||
这个优化如果是初学者的话并不容易想到。
|
||||
|
||||
**在求和问题中,排序之后加剪枝是常见的套路!**
|
||||
|
||||
在[回溯算法:求组合总和(二)](https://mp.weixin.qq.com/s/FLg8G6EjVcxBjwCbzpACPw)第一个树形结构没有画出startIndex的作用,**这里这里纠正一下,准确的树形结构如图所示:**
|
||||
|
||||
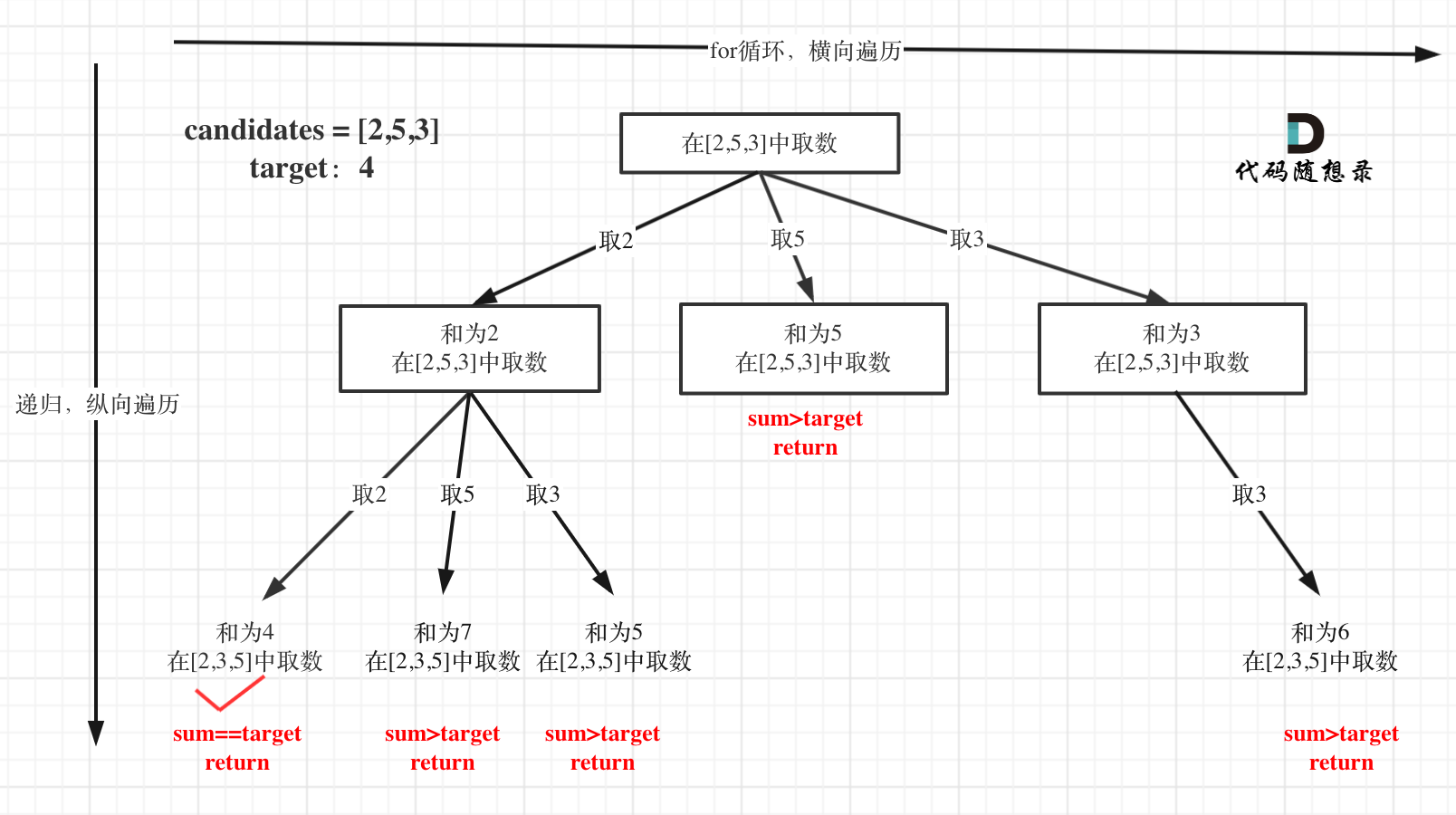
|
||||
|
||||
## 周二
|
||||
|
||||
在[回溯算法:求组合总和(三)](https://mp.weixin.qq.com/s/_1zPYk70NvHsdY8UWVGXmQ)中依旧讲解组合总和问题,本题集合元素会有重复,但要求解集不能包含重复的组合。
|
||||
|
||||
**所以难就难在去重问题上了**。
|
||||
|
||||
这个去重问题,相信做过的录友都知道有多么的晦涩难懂。网上的题解一般就说“去掉重复”,但说不清怎么个去重,代码一甩就完事了。
|
||||
|
||||
为了讲解这个去重问题,**我自创了两个词汇,“树枝去重”和“树层去重”**。
|
||||
|
||||
都知道组合问题可以抽象为树形结构,那么“使用过”在这个树形结构上是有两个维度的,一个维度是同一树枝上“使用过”,一个维度是同一树层上“使用过”。**没有理解这两个层面上的“使用过” 是造成大家没有彻底理解去重的根本原因**。
|
||||
|
||||
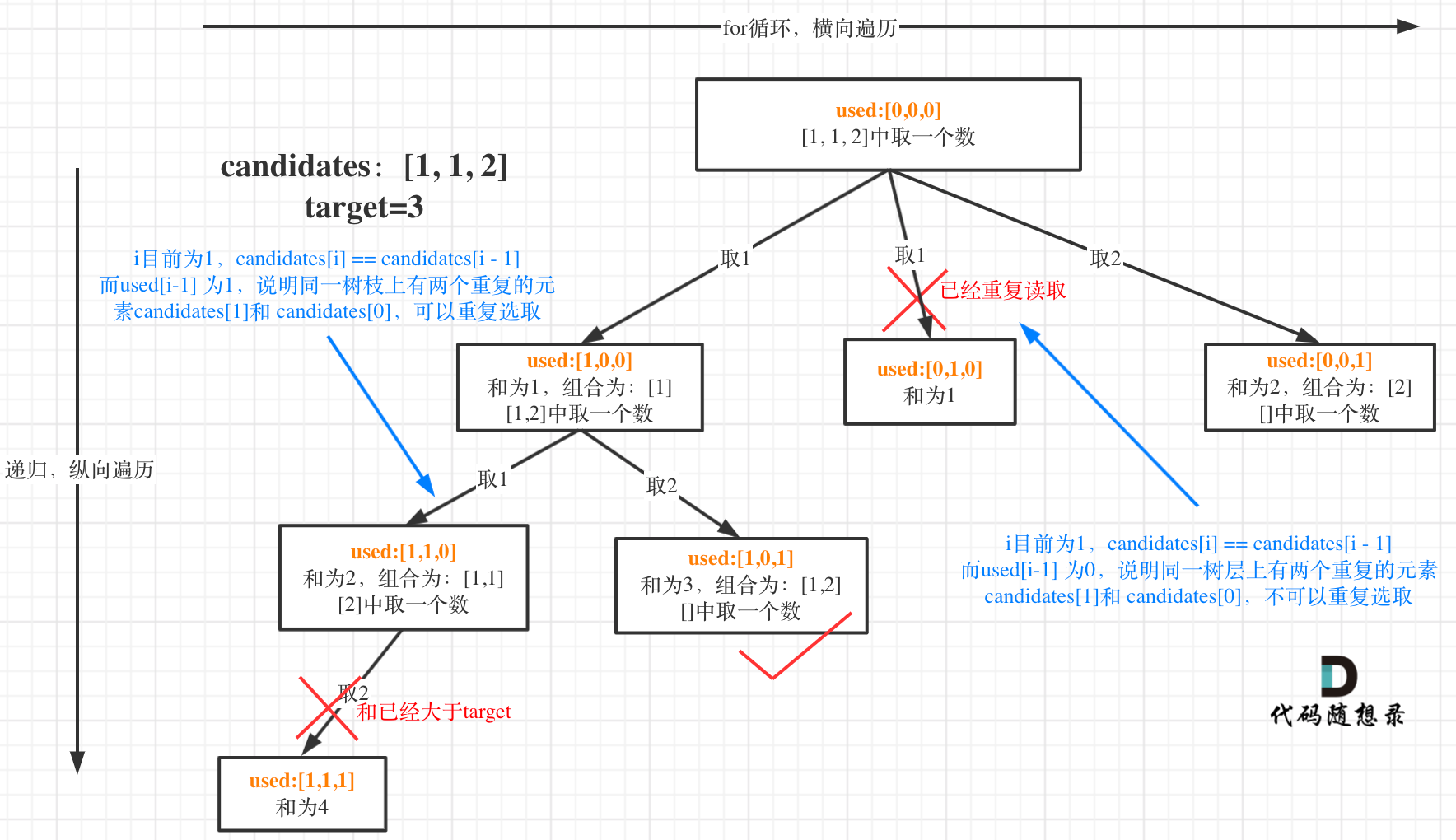
|
||||
|
||||
我在图中将used的变化用橘黄色标注上,可以看出在candidates[i] == candidates[i - 1]相同的情况下:
|
||||
|
||||
* used[i - 1] == true,说明同一树支candidates[i - 1]使用过
|
||||
* used[i - 1] == false,说明同一树层candidates[i - 1]使用过
|
||||
|
||||
**这块去重的逻辑很抽象,网上搜的题解基本没有能讲清楚的,如果大家之前思考过这个问题或者刷过这道题目,看到这里一定会感觉通透了很多!**
|
||||
|
||||
对于去重,其实排列问题也是一样的道理,后面我会讲到。
|
||||
|
||||
|
||||
## 周三
|
||||
|
||||
在[回溯算法:分割回文串](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)中,我们开始讲解切割问题,虽然最后代码看起来好像是一道模板题,但是从分析到学会套用这个模板,是比较难的。
|
||||
|
||||
我列出如下几个难点:
|
||||
|
||||
* 切割问题其实类似组合问题
|
||||
* 如何模拟那些切割线
|
||||
* 切割问题中递归如何终止
|
||||
* 在递归循环中如何截取子串
|
||||
* 如何判断回文
|
||||
|
||||
如果想到了**用求解组合问题的思路来解决 切割问题本题就成功一大半了**,接下来就可以对着模板照葫芦画瓢。
|
||||
|
||||
**但后序如何模拟切割线,如何终止,如何截取子串,其实都不好想,最后判断回文算是最简单的了**。
|
||||
|
||||
除了这些难点,**本题还有细节,例如:切割过的地方不能重复切割所以递归函数需要传入i + 1**。
|
||||
|
||||
所以本题应该是一个道hard题目了。
|
||||
|
||||
**本题的树形结构中,和代码的逻辑有一个小出入,已经判断不是回文的子串就不会进入递归了,纠正如下:**
|
||||
|
||||
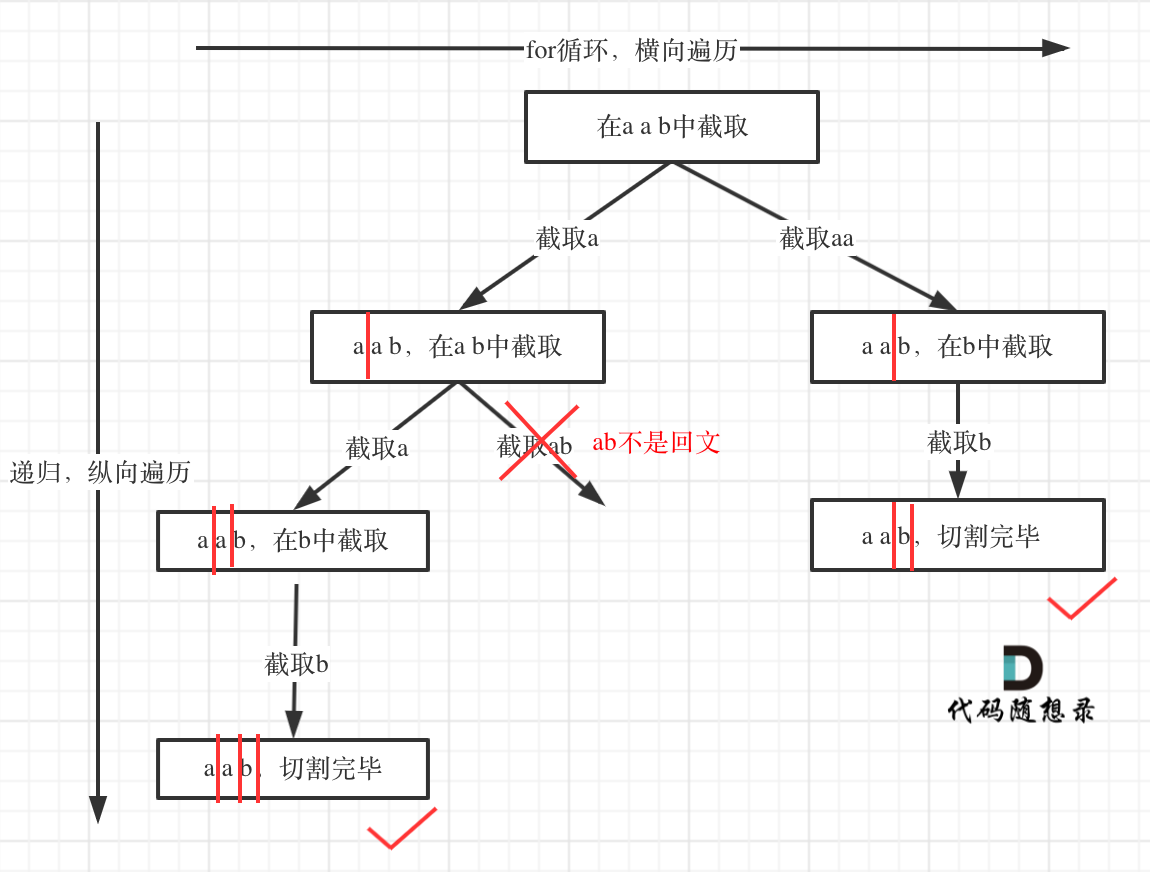
|
||||
|
||||
|
||||
## 周四
|
||||
|
||||
如果没有做过[回溯算法:分割回文串](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)的话,[回溯算法:复原IP地址](https://mp.weixin.qq.com/s/v--VmA8tp9vs4bXCqHhBuA)这道题目应该是比较难的。
|
||||
|
||||
复原IP照[回溯算法:分割回文串](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)就多了一些限制,例如只能分四段,而且还是更改字符串,插入逗点。
|
||||
|
||||
树形图如下:
|
||||
|
||||

|
||||
|
||||
在本文的树形结构图中,我已经把详细的分析思路都画了出来,相信大家看了之后一定会思路清晰不少!
|
||||
|
||||
本题还可以有一个剪枝,合法ip长度为12,如果s的长度超过了12就不是有效IP地址,直接返回!
|
||||
|
||||
代码如下:
|
||||
|
||||
```
|
||||
if (s.size() > 12) return result; // 剪枝
|
||||
|
||||
```
|
||||
|
||||
我之前给出的C++代码没有加这个限制,也没有超时,因为在第四段超过长度之后,就会截止了,所以就算给出特别长的字符串,搜索的范围也是有限的(递归只会到第三层),及时就会返回了。
|
||||
|
||||
|
||||
## 周五
|
||||
|
||||
在[回溯算法:求子集问题!](https://mp.weixin.qq.com/s/NNRzX-vJ_pjK4qxohd_LtA)中讲解了子集问题,**在树形结构中子集问题是要收集所有节点的结果,而组合问题是收集叶子节点的结果**。
|
||||
|
||||
如图:
|
||||
|
||||

|
||||
|
||||
|
||||
认清这个本质之后,今天的题目就是一道模板题了。
|
||||
|
||||
其实可以不需要加终止条件,因为startIndex >= nums.size(),本层for循环本来也结束了,本来我们就要遍历整颗树。
|
||||
|
||||
有的同学可能担心不写终止条件会不会无限递归?
|
||||
|
||||
并不会,因为每次递归的下一层就是从i+1开始的。
|
||||
|
||||
如果要写终止条件,注意:`result.push_back(path);`要放在终止条件的上面,如下:
|
||||
|
||||
```
|
||||
result.push_back(path); // 收集子集,要放在终止添加的上面,否则会漏掉自己
|
||||
if (startIndex >= nums.size()) { // 终止条件可以不加
|
||||
return;
|
||||
}
|
||||
```
|
||||
|
||||
## 周六
|
||||
|
||||
早起的哈希表系列没有总结,所以[哈希表:总结篇!(每逢总结必经典)](https://mp.weixin.qq.com/s/1s91yXtarL-PkX07BfnwLg)如约而至。
|
||||
|
||||
可能之前大家做过很多哈希表的题目,但是没有串成线,总结篇来帮你串成线,捋顺哈希表的整个脉络。
|
||||
|
||||
大家对什么时候各种set与map比较疑惑,想深入了解红黑树,哈希之类的。
|
||||
|
||||
**如果真的只是想清楚什么时候使用各种set与map,不用看那么多,把[关于哈希表,你该了解这些!](https://mp.weixin.qq.com/s/g8N6WmoQmsCUw3_BaWxHZA)看了就够了**。
|
||||
|
||||
## 总结
|
||||
|
||||
本周我们依次介绍了组合问题,分割问题以及子集问题,子集问题还没有讲完,下周还会继续。
|
||||
|
||||
**我讲解每一种问题,都会和其他问题作对比,做分析,所以只要跟着细心琢磨相信对回溯又有新的认识**。
|
||||
|
||||
最近这两天题目有点难度,刚刚开始学回溯算法的话,按照现在这个每天一题的速度来,确实有点快,学起来吃力非常正常,这些题目都是我当初学了好几个月才整明白的,哈哈。
|
||||
|
||||
**所以大家能跟上的话,已经很优秀了!**
|
||||
|
||||
还有一些录友会很关心leetcode上的耗时统计。
|
||||
|
||||
这个是很不准确的,相同的代码多提交几次,大家就知道怎么回事了。
|
||||
|
||||
leetcode上的计时应该是以4ms为单位,有的多提交几次,多个4ms就多击败50%,所以比较夸张,如果程序运行是几百ms的级别,可以看看leetcode上的耗时,因为它的误差10几ms对最终影响不大。
|
||||
|
||||
**所以我的题解基本不会写击败百分之多少多少,没啥意义,时间复杂度分析清楚了就可以了**,至于回溯算法不用分析时间复杂度了,都是一样的爆搜,就看谁剪枝厉害了。
|
||||
|
||||
一些录友表示最近回溯算法看的实在是有点懵,回溯算法确实是晦涩难懂,可能视频的话更直观一些,我最近应该会在B站(同名:「代码随想录」)出回溯算法的视频,大家也可以看视频在回顾一波。
|
||||
|
||||
**就酱,又是充实的一周,做好本周总结,迎接下一周,冲!**
|
||||
|
||||
|
||||
|
||||
97
problems/周总结/20201112回溯周末总结.md
Normal file
97
problems/周总结/20201112回溯周末总结.md
Normal file
@ -0,0 +1,97 @@
|
||||
|
||||
|
||||
# 本周小结!(回溯算法系列三)
|
||||
|
||||
## 周一
|
||||
|
||||
在[回溯算法:求子集问题(二)](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)中,开始针对子集问题进行去重。
|
||||
|
||||
本题就是[回溯算法:求子集问题!](https://mp.weixin.qq.com/s/NNRzX-vJ_pjK4qxohd_LtA)的基础上加上了去重,去重我们在[回溯算法:求组合总和(三)](https://mp.weixin.qq.com/s/_1zPYk70NvHsdY8UWVGXmQ)也讲过了。
|
||||
|
||||
所以本题对大家应该并不难。
|
||||
|
||||
树形结构如下:
|
||||
|
||||
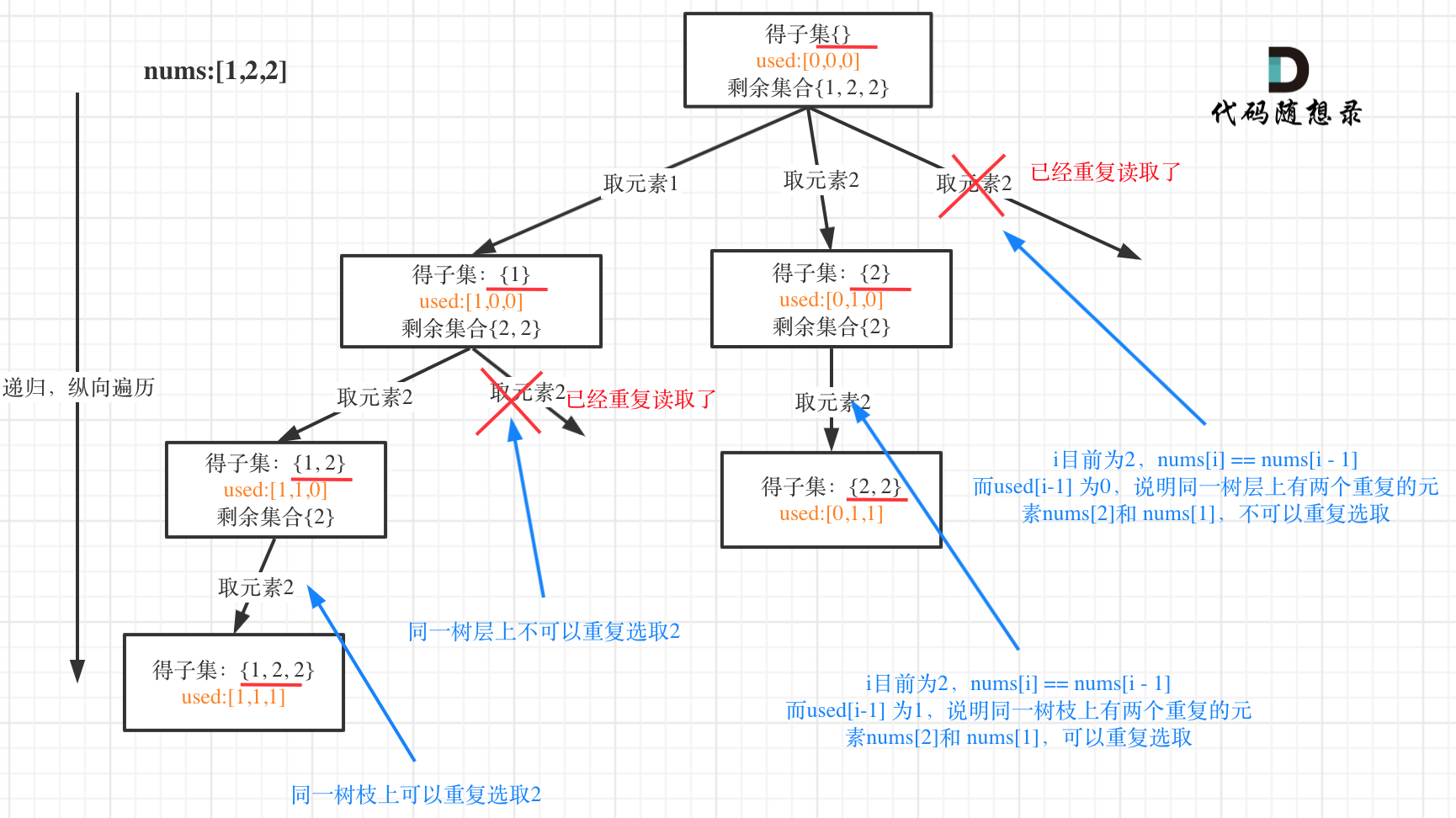
|
||||
|
||||
## 周二
|
||||
|
||||
在[回溯算法:递增子序列](https://mp.weixin.qq.com/s/ePxOtX1ATRYJb2Jq7urzHQ)中,处处都能看到子集的身影,但处处是陷阱,值得好好琢磨琢磨!
|
||||
|
||||
树形结构如下:
|
||||
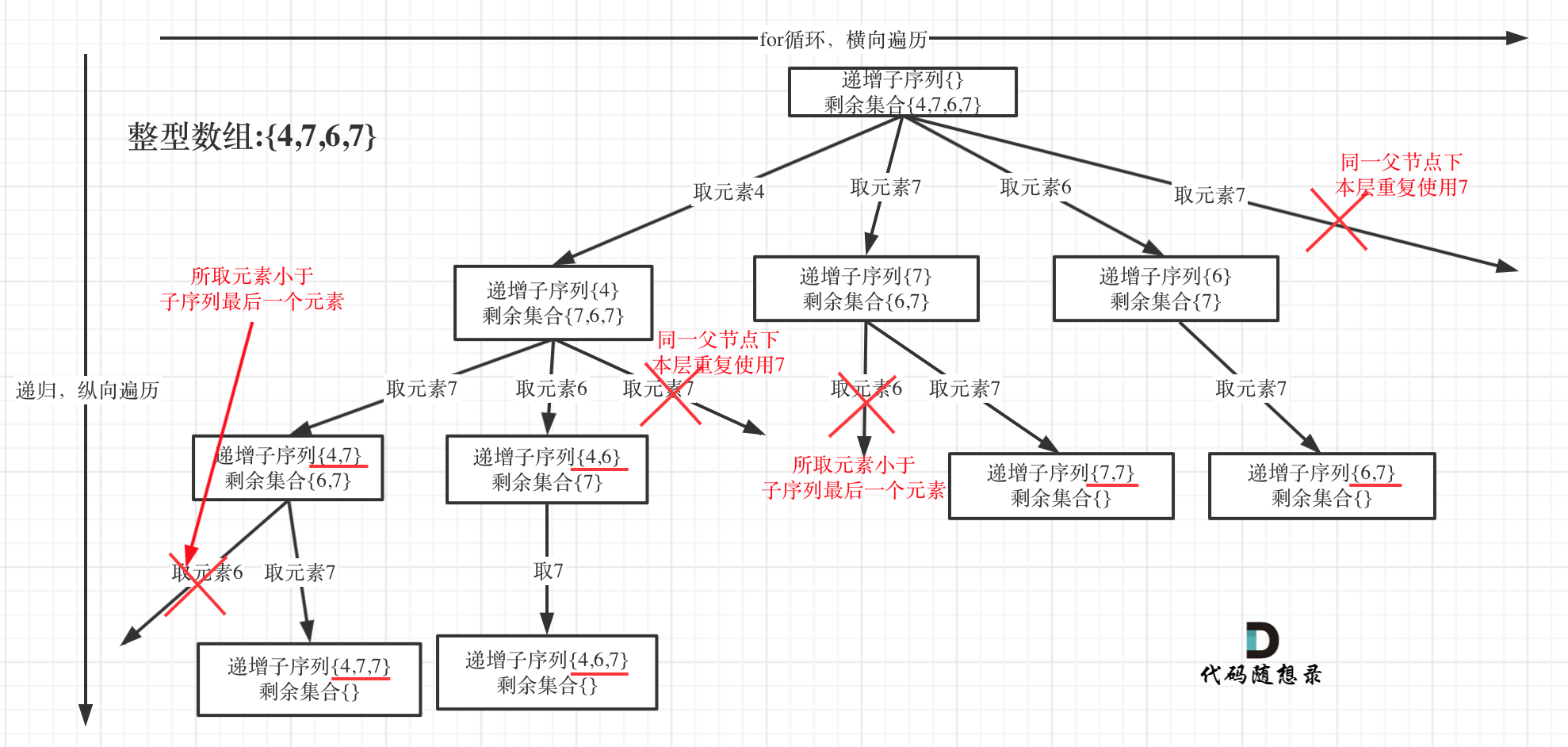
|
||||
|
||||
[回溯算法:递增子序列](https://mp.weixin.qq.com/s/ePxOtX1ATRYJb2Jq7urzHQ)留言区大家有很多疑问,主要还是和[回溯算法:求子集问题(二)](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)混合在了一起。
|
||||
|
||||
详细在[本周小结!(回溯算法系列三)续集](https://mp.weixin.qq.com/s/kSMGHc_YpsqL2j-jb_E_Ag)中给出了介绍!
|
||||
|
||||
## 周三
|
||||
|
||||
我们已经分析了组合问题,分割问题,子集问题,那么[回溯算法:排列问题!](https://mp.weixin.qq.com/s/SCOjeMX1t41wcvJq49GhMw) 又不一样了。
|
||||
|
||||
排列是有序的,也就是说[1,2] 和[2,1] 是两个集合,这和之前分析的子集以及组合所不同的地方。
|
||||
|
||||
可以看出元素1在[1,2]中已经使用过了,但是在[2,1]中还要在使用一次1,所以处理排列问题就不用使用startIndex了。
|
||||
|
||||
如图:
|
||||
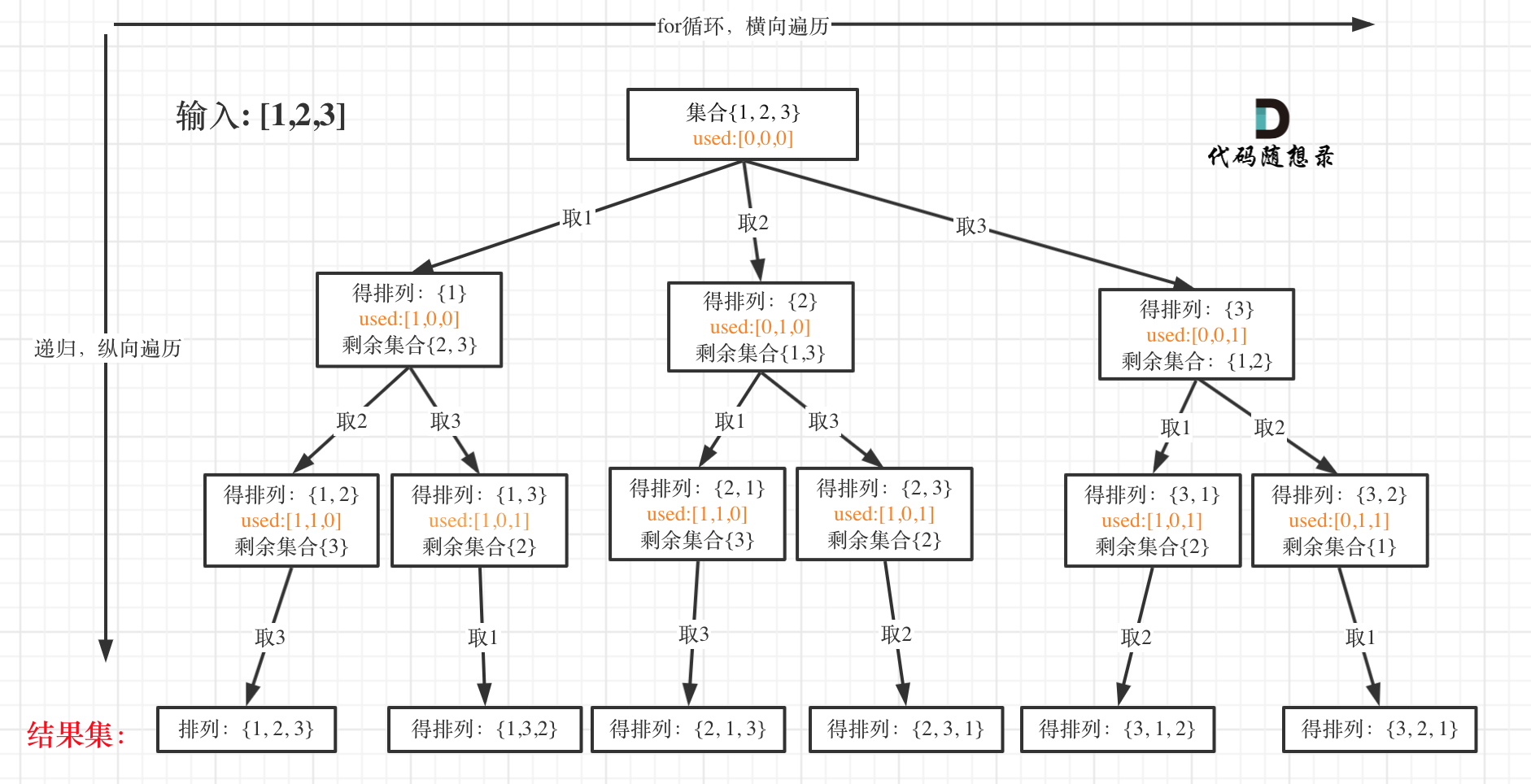
|
||||
|
||||
**大家此时可以感受出排列问题的不同:**
|
||||
|
||||
* 每层都是从0开始搜索而不是startIndex
|
||||
* 需要used数组记录path里都放了哪些元素了
|
||||
|
||||
## 周四
|
||||
|
||||
排列问题也要去重了,在[回溯算法:排列问题(二)](https://mp.weixin.qq.com/s/9L8h3WqRP_h8LLWNT34YlA)中又一次强调了“树层去重”和“树枝去重”。
|
||||
|
||||
树形结构如下:
|
||||
|
||||
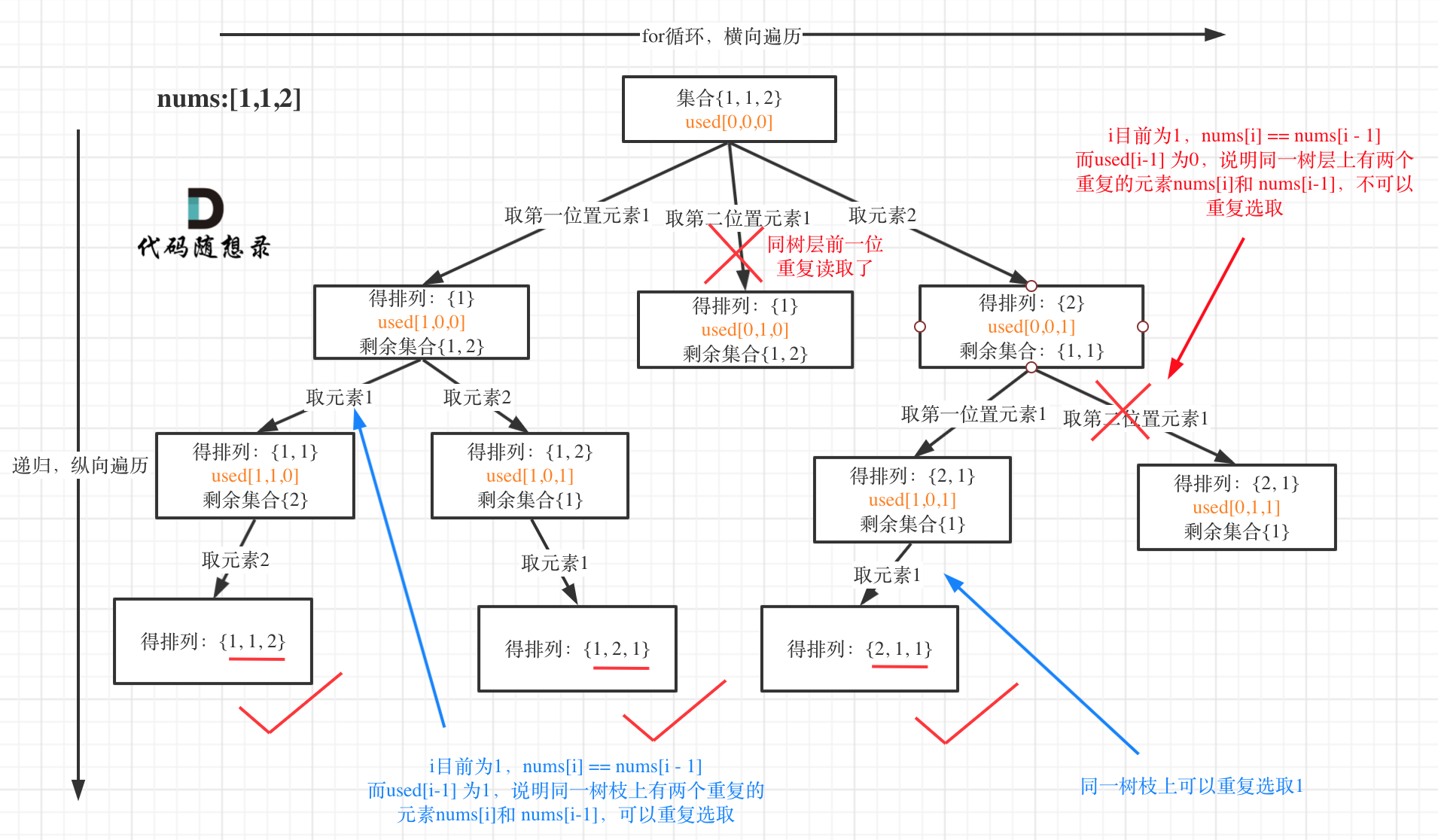
|
||||
|
||||
**这道题目神奇的地方就是used[i - 1] == false也可以,used[i - 1] == true也可以!**
|
||||
|
||||
我就用输入: [1,1,1] 来举一个例子。
|
||||
|
||||
树层上去重(used[i - 1] == false),的树形结构如下:
|
||||
|
||||
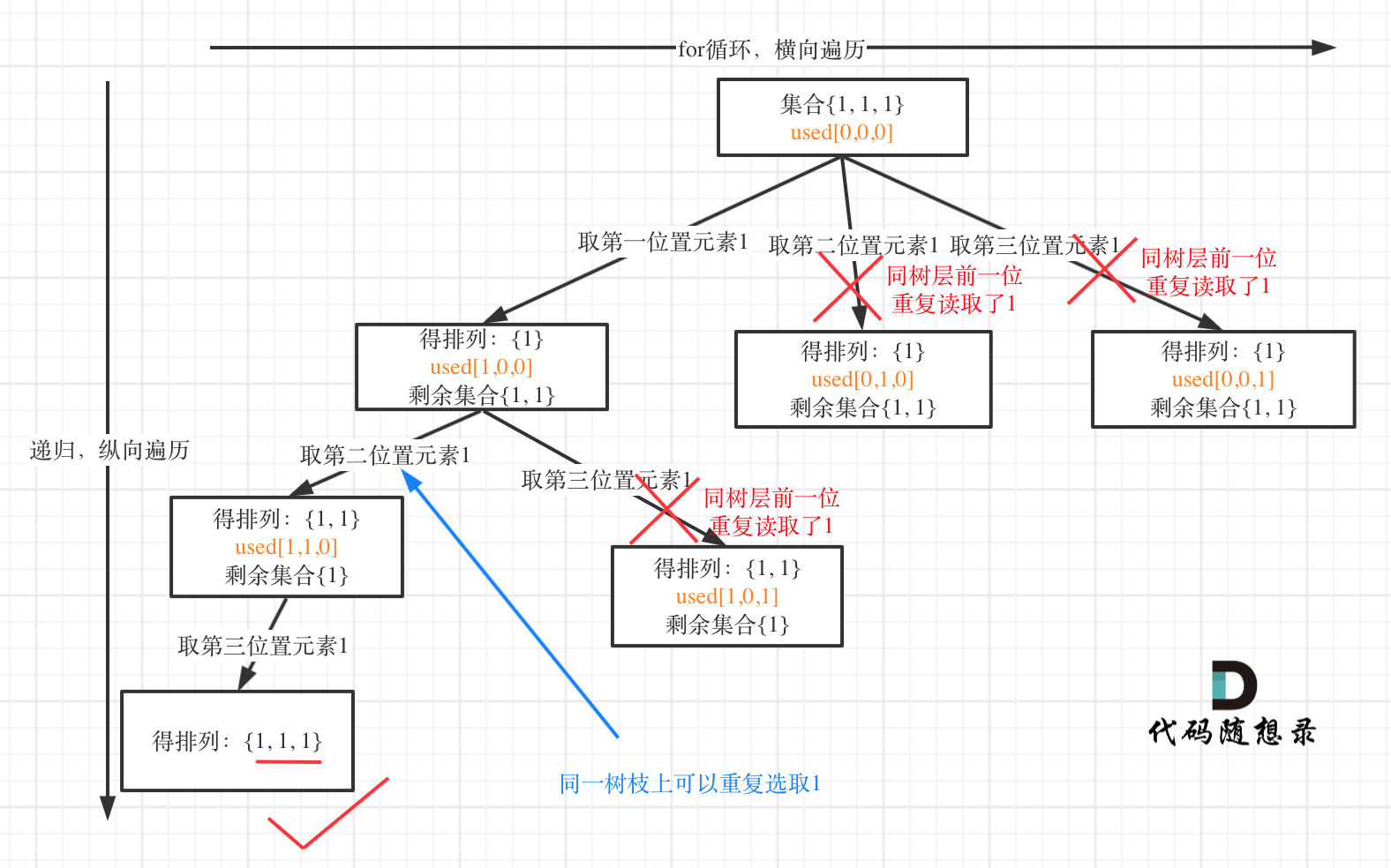
|
||||
|
||||
树枝上去重(used[i - 1] == true)的树型结构如下:
|
||||
|
||||
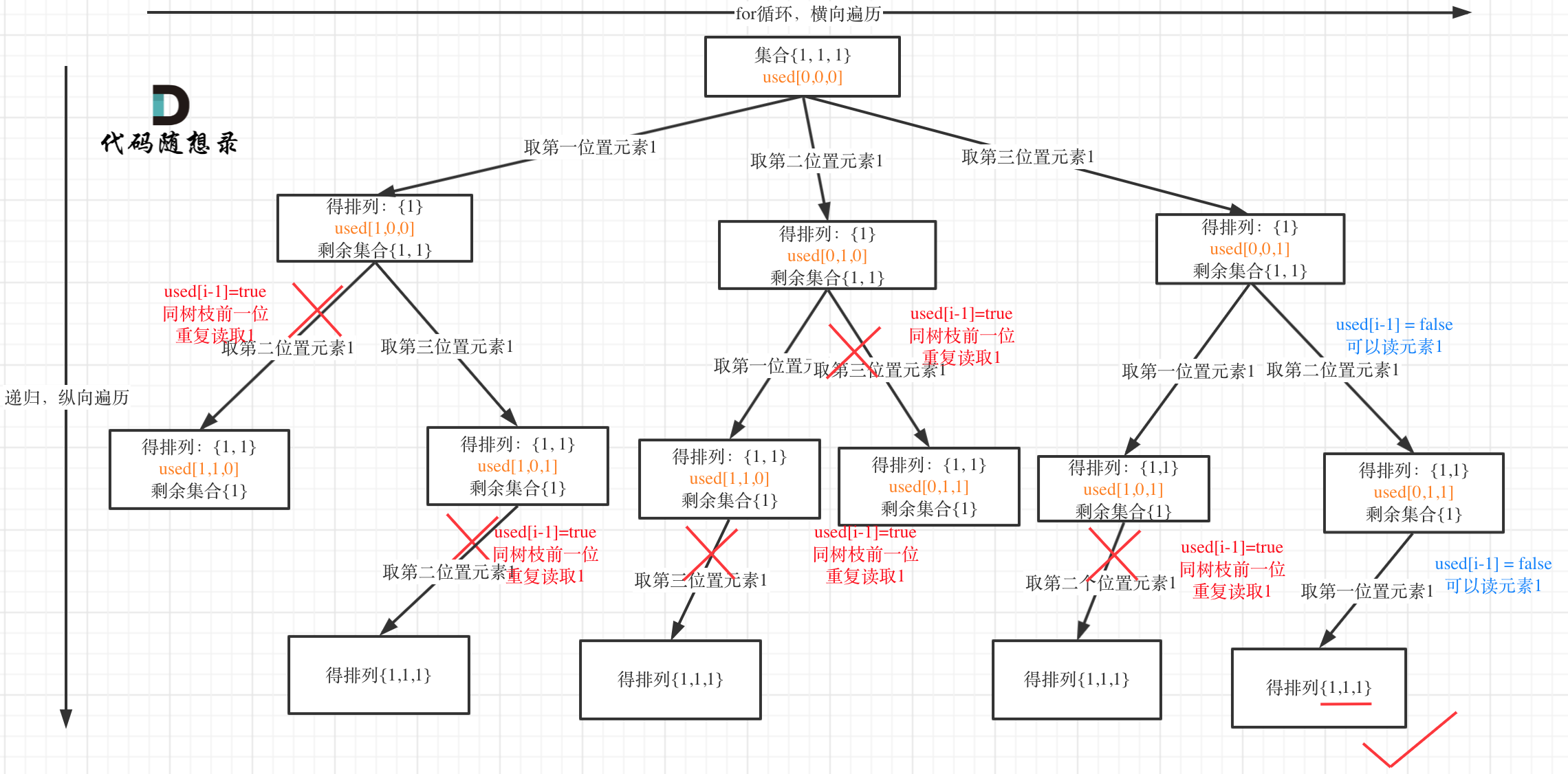
|
||||
|
||||
**可以清晰的看到使用(used[i - 1] == false),即树层去重,效率更高!**
|
||||
|
||||
## 性能分析
|
||||
|
||||
之前并没有分析各个问题的时间复杂度和空间复杂度,这次来说一说。
|
||||
|
||||
这块网上的资料鱼龙混杂,一些所谓的经典面试书籍根本不讲回溯算法,算法书籍对这块也避而不谈,感觉就像是算法里模糊的边界。
|
||||
|
||||
**所以这块就说一说我个人理解,对内容持开放态度,集思广益,欢迎大家来讨论!**
|
||||
|
||||
子集问题分析:
|
||||
* 时间复杂度:O(n * 2^n),因为每一个元素的状态无外乎取与不取,所以时间复杂度为O(2^n),构造每一组子集都需要填进数组,又有需要O(n),最终时间复杂度:O(n * 2^n)
|
||||
* 空间复杂度:O(n),递归深度为n,所以系统栈所用空间为O(n),每一层递归所用的空间都是常数级别,注意代码里的result和path都是全局变量,就算是放在参数里,传的也是引用,并不会新申请内存空间,最终空间复杂度为O(n)
|
||||
|
||||
排列问题分析:
|
||||
* 时间复杂度:O(n!),这个可以从排列的树形图中很明显发现,每一层节点为n,第二层每一个分支都延伸了n-1个分支,再往下又是n-2个分支,所以一直到叶子节点一共就是 n * n-1 * n-2 * ..... 1 = n!。
|
||||
* 空间复杂度:O(n),和子集问题同理。
|
||||
|
||||
组合问题分析:
|
||||
* 时间复杂度:O(n * 2^n),组合问题其实就是一种子集的问题,所以组合问题最坏的情况,也不会超过子集问题的时间复杂度。
|
||||
* 空间复杂度:O(n),和子集问题同理。
|
||||
|
||||
**一般说道回溯算法的复杂度,都说是指数级别的时间复杂度,这也算是一个概括吧!**
|
||||
|
||||
## 总结
|
||||
|
||||
本周我们对[子集问题进行了去重](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ),然后介绍了和子集问题非常像的[递增子序列](https://mp.weixin.qq.com/s/ePxOtX1ATRYJb2Jq7urzHQ),如果还保持惯性思维,这道题就可以掉坑里。
|
||||
|
||||
接着介绍了[排列问题!](https://mp.weixin.qq.com/s/SCOjeMX1t41wcvJq49GhMw),以及对[排列问题如何进行去重](https://mp.weixin.qq.com/s/9L8h3WqRP_h8LLWNT34YlA)。
|
||||
|
||||
最后我补充了子集问题,排列问题和组合问题的性能分析,给大家提供了回溯算法复杂度的分析思路。
|
||||
|
||||
|
||||
|
||||
@ -1,9 +1,3 @@
|
||||
<p align="center">
|
||||
<a href="https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ"><img src="https://img.shields.io/badge/知识星球-代码随想录-blue" alt=""></a>
|
||||
<a href="https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw"><img src="https://img.shields.io/badge/刷题-微信群-green" alt=""></a>
|
||||
<a href="https://img-blog.csdnimg.cn/20201210231711160.png"><img src="https://img.shields.io/badge/公众号-代码随想录-brightgreen" alt=""></a>
|
||||
<a href="https://space.bilibili.com/525438321"><img src="https://img.shields.io/badge/B站-代码随想录-orange" alt=""></a>
|
||||
</p>
|
||||
|
||||
> 20张树形结构图、14道精选回溯题目,21篇回溯法精讲文章,由浅入深,一气呵成,这是全网最强回溯算法总结!
|
||||
|
||||
|
||||
240
problems/回溯算法去重问题的另一种写法.md
Normal file
240
problems/回溯算法去重问题的另一种写法.md
Normal file
@ -0,0 +1,240 @@
|
||||
|
||||
# 回溯算法去重问题的另一种写法
|
||||
|
||||
> 在 [本周小结!(回溯算法系列三)](https://mp.weixin.qq.com/s/tLkt9PSo42X60w8i94ViiA) 中一位录友对 整颗树的本层和同一节点的本层有疑问,也让我重新思考了一下,发现这里确实有问题,所以专门写一篇来纠正,感谢录友们的积极交流哈!
|
||||
|
||||
接下来我再把这块再讲一下。
|
||||
|
||||
在[回溯算法:求子集问题(二)](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)中的去重和 [回溯算法:递增子序列](https://mp.weixin.qq.com/s/ePxOtX1ATRYJb2Jq7urzHQ)中的去重 都是 同一父节点下本层的去重。
|
||||
|
||||
[回溯算法:求子集问题(二)](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)也可以使用set针对同一父节点本层去重,但子集问题一定要排序,为什么呢?
|
||||
|
||||
我用没有排序的集合{2,1,2,2}来举例子画一个图,如图:
|
||||
|
||||
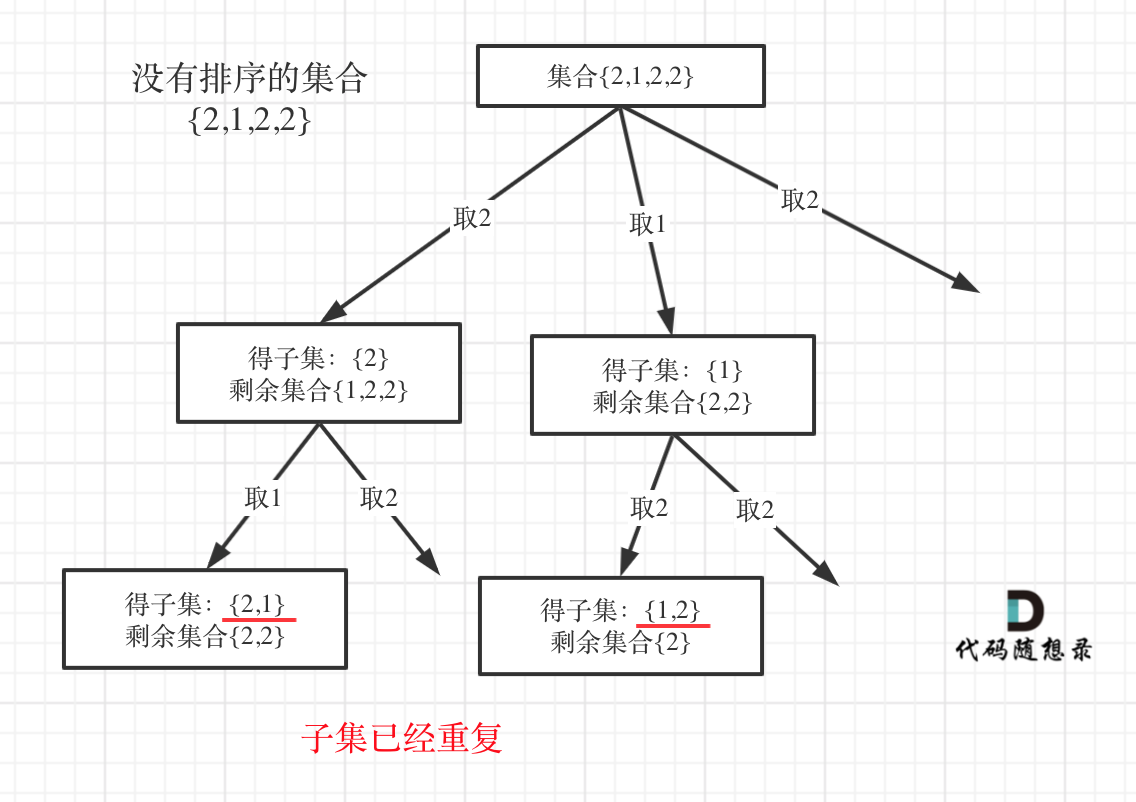
|
||||
|
||||
图中,大家就很明显的看到,子集重复了。
|
||||
|
||||
那么下面我针对[回溯算法:求子集问题(二)](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ) 给出使用set来对本层去重的代码实现。
|
||||
|
||||
## 90.子集II
|
||||
|
||||
used数组去重版本: [回溯算法:求子集问题(二)](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)
|
||||
|
||||
使用set去重的版本如下:
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
private:
|
||||
vector<vector<int>> result;
|
||||
vector<int> path;
|
||||
void backtracking(vector<int>& nums, int startIndex, vector<bool>& used) {
|
||||
result.push_back(path);
|
||||
unordered_set<int> uset; // 定义set对同一节点下的本层去重
|
||||
for (int i = startIndex; i < nums.size(); i++) {
|
||||
if (uset.find(nums[i]) != uset.end()) { // 如果发现出现过就pass
|
||||
continue;
|
||||
}
|
||||
uset.insert(nums[i]); // set跟新元素
|
||||
path.push_back(nums[i]);
|
||||
backtracking(nums, i + 1, used);
|
||||
path.pop_back();
|
||||
}
|
||||
}
|
||||
|
||||
public:
|
||||
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
|
||||
result.clear();
|
||||
path.clear();
|
||||
vector<bool> used(nums.size(), false);
|
||||
sort(nums.begin(), nums.end()); // 去重需要排序
|
||||
backtracking(nums, 0, used);
|
||||
return result;
|
||||
}
|
||||
};
|
||||
|
||||
```
|
||||
|
||||
针对留言区录友们的疑问,我再补充一些常见的错误写法,
|
||||
|
||||
|
||||
### 错误写法一
|
||||
|
||||
把uset定义放到类成员位置,然后模拟回溯的样子 insert一次,erase一次。
|
||||
|
||||
例如:
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
private:
|
||||
vector<vector<int>> result;
|
||||
vector<int> path;
|
||||
unordered_set<int> uset; // 把uset定义放到类成员位置
|
||||
void backtracking(vector<int>& nums, int startIndex, vector<bool>& used) {
|
||||
result.push_back(path);
|
||||
|
||||
for (int i = startIndex; i < nums.size(); i++) {
|
||||
if (uset.find(nums[i]) != uset.end()) {
|
||||
continue;
|
||||
}
|
||||
uset.insert(nums[i]); // 递归之前insert
|
||||
path.push_back(nums[i]);
|
||||
backtracking(nums, i + 1, used);
|
||||
path.pop_back();
|
||||
uset.erase(nums[i]); // 回溯再erase
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
在树形结构中,**如果把unordered_set<int> uset放在类成员的位置(相当于全局变量),就把树枝的情况都记录了,不是单纯的控制某一节点下的同一层了**。
|
||||
|
||||
如图:
|
||||
|
||||
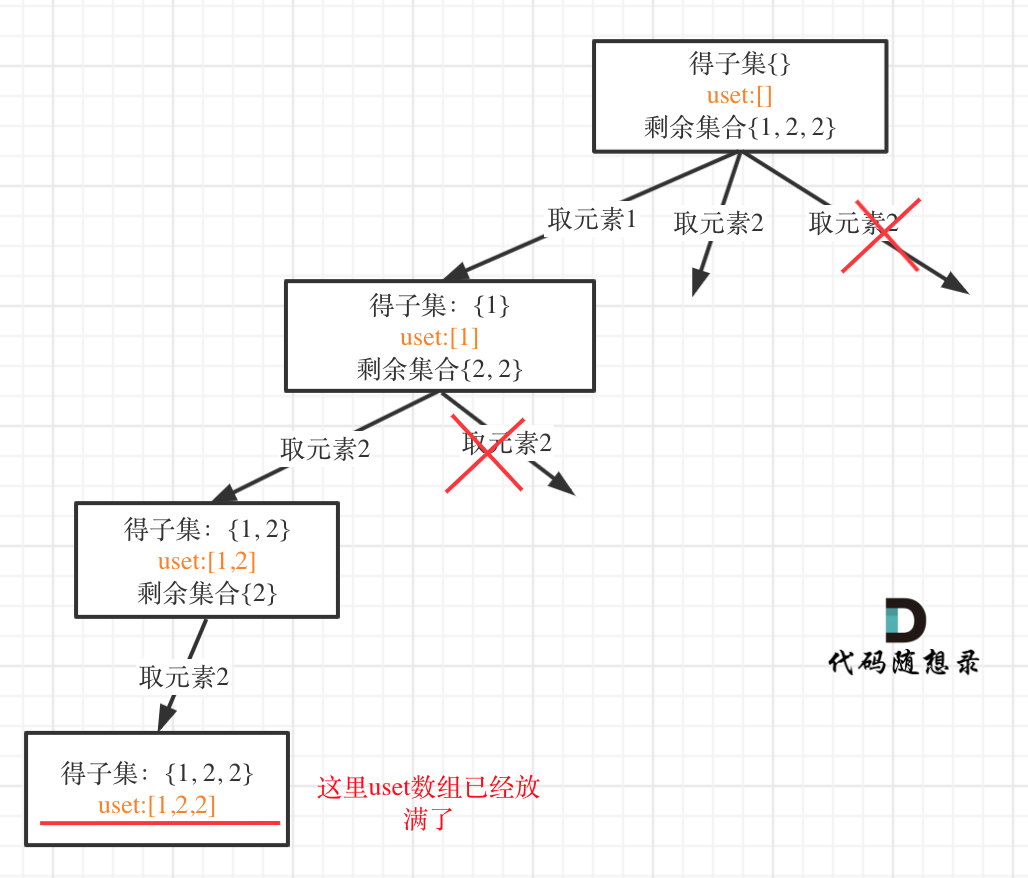
|
||||
|
||||
可以看出一旦把unordered_set<int> uset放在类成员位置,它控制的就是整棵树,包括树枝。
|
||||
|
||||
**所以这么写不行!**
|
||||
|
||||
### 错误写法二
|
||||
|
||||
有同学把 unordered_set<int> uset; 放到类成员位置,然后每次进入单层的时候用uset.clear()。
|
||||
|
||||
代码如下:
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
private:
|
||||
vector<vector<int>> result;
|
||||
vector<int> path;
|
||||
unordered_set<int> uset; // 把uset定义放到类成员位置
|
||||
void backtracking(vector<int>& nums, int startIndex, vector<bool>& used) {
|
||||
result.push_back(path);
|
||||
uset.clear(); // 到每一层的时候,清空uset
|
||||
for (int i = startIndex; i < nums.size(); i++) {
|
||||
if (uset.find(nums[i]) != uset.end()) {
|
||||
continue;
|
||||
}
|
||||
uset.insert(nums[i]); // set记录元素
|
||||
path.push_back(nums[i]);
|
||||
backtracking(nums, i + 1, used);
|
||||
path.pop_back();
|
||||
}
|
||||
}
|
||||
```
|
||||
uset已经是全局变量,本层的uset记录了一个元素,然后进入下一层之后这个uset(和上一层是同一个uset)就被清空了,也就是说,层与层之间的uset是同一个,那么就会相互影响。
|
||||
|
||||
**所以这么写依然不行!**
|
||||
|
||||
**组合问题和排列问题,其实也可以使用set来对同一节点下本层去重,下面我都分别给出实现代码**。
|
||||
|
||||
## 40. 组合总和 II
|
||||
|
||||
使用used数组去重版本:[回溯算法:求组合总和(三)](https://mp.weixin.qq.com/s/_1zPYk70NvHsdY8UWVGXmQ)
|
||||
|
||||
使用set去重的版本如下:
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
private:
|
||||
vector<vector<int>> result;
|
||||
vector<int> path;
|
||||
void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {
|
||||
if (sum == target) {
|
||||
result.push_back(path);
|
||||
return;
|
||||
}
|
||||
unordered_set<int> uset; // 控制某一节点下的同一层元素不能重复
|
||||
for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
|
||||
if (uset.find(candidates[i]) != uset.end()) {
|
||||
continue;
|
||||
}
|
||||
uset.insert(candidates[i]); // 记录元素
|
||||
sum += candidates[i];
|
||||
path.push_back(candidates[i]);
|
||||
backtracking(candidates, target, sum, i + 1);
|
||||
sum -= candidates[i];
|
||||
path.pop_back();
|
||||
}
|
||||
}
|
||||
|
||||
public:
|
||||
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
|
||||
path.clear();
|
||||
result.clear();
|
||||
sort(candidates.begin(), candidates.end());
|
||||
backtracking(candidates, target, 0, 0);
|
||||
return result;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
## 47. 全排列 II
|
||||
|
||||
使用used数组去重版本:[回溯算法:排列问题(二)](https://mp.weixin.qq.com/s/9L8h3WqRP_h8LLWNT34YlA)
|
||||
|
||||
使用set去重的版本如下:
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
private:
|
||||
vector<vector<int>> result;
|
||||
vector<int> path;
|
||||
void backtracking (vector<int>& nums, vector<bool>& used) {
|
||||
if (path.size() == nums.size()) {
|
||||
result.push_back(path);
|
||||
return;
|
||||
}
|
||||
unordered_set<int> uset; // 控制某一节点下的同一层元素不能重复
|
||||
for (int i = 0; i < nums.size(); i++) {
|
||||
if (uset.find(nums[i]) != uset.end()) {
|
||||
continue;
|
||||
}
|
||||
if (used[i] == false) {
|
||||
uset.insert(nums[i]); // 记录元素
|
||||
used[i] = true;
|
||||
path.push_back(nums[i]);
|
||||
backtracking(nums, used);
|
||||
path.pop_back();
|
||||
used[i] = false;
|
||||
}
|
||||
}
|
||||
}
|
||||
public:
|
||||
vector<vector<int>> permuteUnique(vector<int>& nums) {
|
||||
result.clear();
|
||||
path.clear();
|
||||
sort(nums.begin(), nums.end()); // 排序
|
||||
vector<bool> used(nums.size(), false);
|
||||
backtracking(nums, used);
|
||||
return result;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
## 两种写法的性能分析
|
||||
|
||||
需要注意的是:**使用set去重的版本相对于used数组的版本效率都要低很多**,大家在leetcode上提交,能明显发现。
|
||||
|
||||
原因在[回溯算法:递增子序列](https://mp.weixin.qq.com/s/ePxOtX1ATRYJb2Jq7urzHQ)中也分析过,主要是因为程序运行的时候对unordered_set 频繁的insert,unordered_set需要做哈希映射(也就是把key通过hash function映射为唯一的哈希值)相对费时间,而且insert的时候其底层的符号表也要做相应的扩充,也是费时的。
|
||||
|
||||
**而使用used数组在时间复杂度上几乎没有额外负担!**
|
||||
|
||||
**使用set去重,不仅时间复杂度高了,空间复杂度也高了**,在[本周小结!(回溯算法系列三)](https://mp.weixin.qq.com/s/tLkt9PSo42X60w8i94ViiA)中分析过,组合,子集,排列问题的空间复杂度都是O(n),但如果使用set去重,空间复杂度就变成了O(n^2),因为每一层递归都有一个set集合,系统栈空间是n,每一个空间都有set集合。
|
||||
|
||||
那有同学可能疑惑 用used数组也是占用O(n)的空间啊?
|
||||
|
||||
used数组可是全局变量,每层与每层之间公用一个used数组,所以空间复杂度是O(n + n),最终空间复杂度还是O(n)。
|
||||
|
||||
## 总结
|
||||
|
||||
本篇本打算是对[本周小结!(回溯算法系列三)](https://mp.weixin.qq.com/s/tLkt9PSo42X60w8i94ViiA)的一个点做一下纠正,没想到又写出来这么多!
|
||||
|
||||
**这个点都源于一位录友的疑问,然后我思考总结了一下,就写着这一篇,所以还是得多交流啊!**
|
||||
|
||||
如果大家对「代码随想录」文章有什么疑问,尽管打卡留言的时候提出来哈,或者在交流群里提问。
|
||||
|
||||
**其实这就是相互学习的过程,交流一波之后都对题目理解的更深刻了,我如果发现文中有问题,都会在评论区或者下一篇文章中即时修正,保证不会给大家带跑偏!**
|
||||
|
||||
|
||||
Reference in New Issue
Block a user