Merge pull request #1793 from juguagua/leetcode-modify-the-code-of-the-BinaryTree

更新完善二叉树部分：从 "左叶子之和" 到 "从中序后序序列构造二叉树"

problems/0106.从中序与后序遍历序列构造二叉树.md

@@ -34,7 +34,7 @@
 
 ## 思路
 
-首先回忆一下如何根据两个顺序构造一个唯一的二叉树，相信理论知识大家应该都清楚，就是以 后序数组的最后一个元素为切割点，先切中序数组，根据中序数组，反过来在切后序数组。一层一层切下去，每次后序数组最后一个元素就是节点元素。
+首先回忆一下如何根据两个顺序构造一个唯一的二叉树，相信理论知识大家应该都清楚，就是以 后序数组的最后一个元素为切割点，先切中序数组，根据中序数组，反过来再切后序数组。一层一层切下去，每次后序数组最后一个元素就是节点元素。
 
 如果让我们肉眼看两个序列，画一棵二叉树的话，应该分分钟都可以画出来。
 
@@ -236,7 +236,7 @@ private:
         vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
         vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());
 
-        // 一下为日志
+        // 以下为日志
         cout << "----------" << endl;
 
         cout << "leftInorder :";
@@ -275,7 +275,7 @@ public:
 };
 ```
 
-**此时应该发现了，如上的代码性能并不好，应为每层递归定定义了新的vector（就是数组），既耗时又耗空间，但上面的代码是最好理解的，为了方便读者理解，所以用如上的代码来讲解。**
+**此时应该发现了，如上的代码性能并不好，因为每层递归定义了新的vector（就是数组），既耗时又耗空间，但上面的代码是最好理解的，为了方便读者理解，所以用如上的代码来讲解。**
 
 下面给出用下标索引写出的代码版本：（思路是一样的，只不过不用重复定义vector了，每次用下标索引来分割）
 
@@ -569,7 +569,7 @@ tree2 的前序遍历是[1 2 3]， 后序遍历是[3 2 1]。
 
 之前我们讲的二叉树题目都是各种遍历二叉树，这次开始构造二叉树了，思路其实比较简单，但是真正代码实现出来并不容易。
 
-所以要避免眼高手低，踏实的把代码写出来。
+所以要避免眼高手低，踏实地把代码写出来。
 
 我同时给出了添加日志的代码版本，因为这种题目是不太容易写出来调一调就能过的，所以一定要把流程日志打出来，看看符不符合自己的思路。
 
@@ -728,25 +728,33 @@ class Solution:
  *     Right *TreeNode
  * }
  */
+var (
+    hash map[int]int
+)
 func buildTree(inorder []int, postorder []int) *TreeNode {
-    if len(inorder)<1||len(postorder)<1{return nil}
+    hash = make(map[int]int)
-    //先找到根节点（后续遍历的最后一个就是根节点）
+    for i, v := range inorder {  // 用map保存中序序列的数值对应位置
-    nodeValue:=postorder[len(postorder)-1]
+        hash[v] = i
-    //从中序遍历中找到一分为二的点，左边为左子树，右边为右子树
+    }
-    left:=findRootIndex(inorder,nodeValue)
+    // 以左闭右闭的原则进行切分
-    //构造root
+    root := rebuild(inorder, postorder, len(postorder)-1, 0, len(inorder)-1)
-    root:=&TreeNode{Val: nodeValue,
-                Left: buildTree(inorder[:left],postorder[:left]),//将后续遍历一分为二，左边为左子树，右边为右子树
-                Right: buildTree(inorder[left+1:],postorder[left:len(postorder)-1])}
     return root
 }
-func findRootIndex(inorder []int,target int) (index int){
+// rootIdx表示根节点在后序数组中的索引，l, r 表示在中序数组中的前后切分点
-    for i:=0;i<len(inorder);i++{
+func rebuild(inorder []int, postorder []int, rootIdx int, l, r int) *TreeNode {
-        if target==inorder[i]{
+    if l > r {    // 说明没有元素，返回空树
-            return i
+        return nil
     }
+    if l == r {  // 只剩唯一一个元素，直接返回
+        return &TreeNode{Val : inorder[l]}
     }
-    return -1
+    rootV := postorder[rootIdx]  // 根据后序数组找到根节点的值
+    rootIn := hash[rootV]        // 找到根节点在对应的中序数组中的位置
+    root := &TreeNode{Val : rootV}   // 构造根节点
+    // 重建左节点和右节点
+    root.Left = rebuild(inorder, postorder, rootIdx-(r-rootIn)-1, l, rootIn-1) 
+    root.Right = rebuild(inorder, postorder, rootIdx-1, rootIn+1, r)
+    return root
 }
 ```
 
@@ -761,22 +769,27 @@ func findRootIndex(inorder []int,target int) (index int){
  *     Right *TreeNode
  * }
  */
+var (
+    hash map[int]int
+)
 func buildTree(preorder []int, inorder []int) *TreeNode {
-    if len(preorder)<1||len(inorder)<1{return nil}
+    hash = make(map[int]int, len(inorder))
-    left:=findRootIndex(preorder[0],inorder)
+    for i, v := range inorder {
-    root:=&TreeNode{
+        hash[v] = i
-        Val: preorder[0],
+    }
-        Left: buildTree(preorder[1:left+1],inorder[:left]),
+    root := build(preorder, inorder, 0, 0, len(inorder)-1)  // l, r 表示构造的树在中序遍历数组中的范围
-        Right: buildTree(preorder[left+1:],inorder[left+1:])}
     return root
 }
-func findRootIndex(target int,inorder []int) int{
+func build(pre []int, in []int, root int, l, r int) *TreeNode {
-    for i:=0;i<len(inorder);i++{
+    if l > r {
-        if target==inorder[i]{
+        return nil
-            return i
     }
-    }
+    rootVal := pre[root]  // 找到本次构造的树的根节点
-    return -1
+    index := hash[rootVal]  // 根节点在中序数组中的位置
+    node := &TreeNode {Val: rootVal}
+    node.Left = build(pre, in, root + 1, l, index-1)
+    node.Right = build(pre, in, root + (index-l) + 1, index+1, r)
+    return node
 }
 ```
 

problems/0112.路径总和.md

@@ -33,7 +33,7 @@
 * 112.路径总和
 * 113.路径总和ii
 
-这道题我们要遍历从根节点到叶子节点的的路径看看总和是不是目标和。
+这道题我们要遍历从根节点到叶子节点的路径看看总和是不是目标和。
 
 ### 递归
 
@@ -167,7 +167,7 @@ public:
 };
 ```
 
-**是不是发现精简之后的代码，已经完全看不出分析的过程了，所以我们要把题目分析清楚之后，在追求代码精简。** 这一点我已经强调很多次了！
+**是不是发现精简之后的代码，已经完全看不出分析的过程了，所以我们要把题目分析清楚之后，再追求代码精简。** 这一点我已经强调很多次了！
 
 
 ### 迭代
@@ -351,28 +351,34 @@ class solution {
         if(root == null) return false;
         stack<treenode> stack1 = new stack<>();
         stack<integer> stack2 = new stack<>();
-        stack1.push(root);stack2.push(root.val);
+        stack1.push(root);
+        stack2.push(root.val);
         while(!stack1.isempty()) {
             int size = stack1.size();
+
             for(int i = 0; i < size; i++) {
-                treenode node = stack1.pop();int sum=stack2.pop();
+                treenode node = stack1.pop();
+                int sum = stack2.pop();
+
                 // 如果该节点是叶子节点了，同时该节点的路径数值等于sum，那么就返回true
-                if(node.left==null && node.right==null && sum==targetsum)return true;
+                if(node.left == null && node.right == null && sum == targetsum) {
+                    return true;
+                } 
                 // 右节点，压进去一个节点的时候，将该节点的路径数值也记录下来
                 if(node.right != null){
-                    stack1.push(node.right);stack2.push(sum+node.right.val);
+                    stack1.push(node.right);
+                    stack2.push(sum + node.right.val);
                 }
                 // 左节点，压进去一个节点的时候，将该节点的路径数值也记录下来
                 if(node.left != null) {
-                    stack1.push(node.left);stack2.push(sum+node.left.val);
+                    stack1.push(node.left);
+                    stack2.push(sum + node.left.val);
                 }
             }
         }
         return false;
     }   
-    
 }
-
 ```
 
 ### 0113.路径总和-ii

problems/0404.左叶子之和.md

@@ -35,7 +35,7 @@
 
 ![图二](https://code-thinking-1253855093.file.myqcloud.com/pics/20220902165805.png)
 
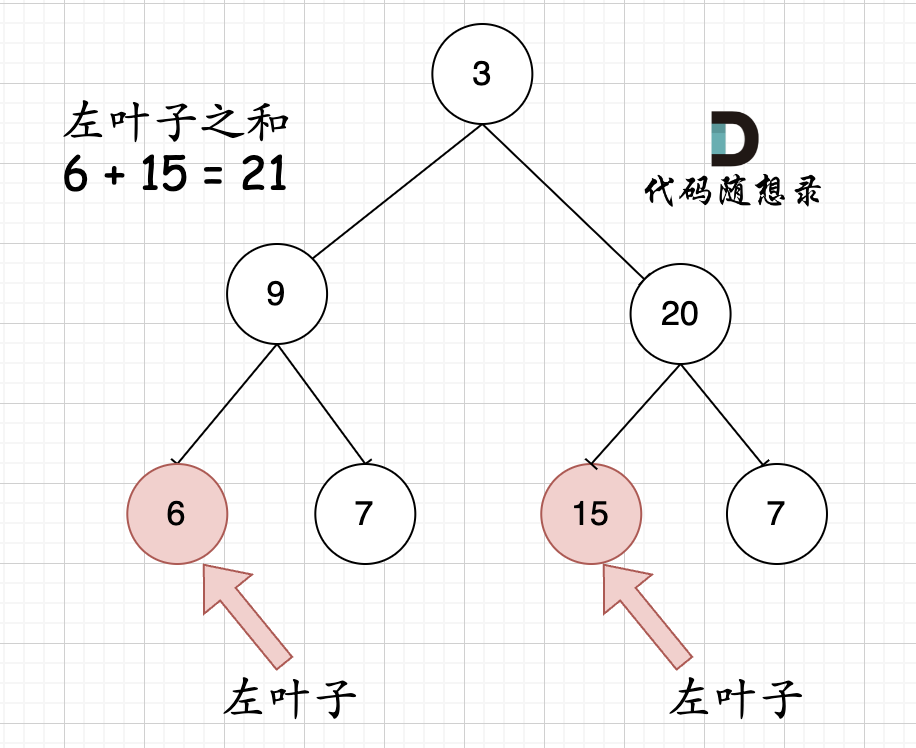
-相信通过这两个图，大家可以最左叶子的定义有明确理解了。 
+相信通过这两个图，大家对最左叶子的定义有明确理解了。 
 
 那么**判断当前节点是不是左叶子是无法判断的，必须要通过节点的父节点来判断其左孩子是不是左叶子。**
 
@@ -298,48 +298,49 @@ class Solution:
 
 ```go
 func sumOfLeftLeaves(root *TreeNode) int {
-    var  res int
+    if root == nil {
-    findLeft(root,&res)
+        return 0
-    return res
     }
-func findLeft(root *TreeNode,res *int){
+    leftValue := sumOfLeftLeaves(root.Left)   // 左
-    //左节点
+
     if root.Left != nil && root.Left.Left == nil && root.Left.Right == nil {
-        *res=*res+root.Left.Val
+        leftValue = root.Left.Val             // 中
-    }
-    if root.Left!=nil{
-        findLeft(root.Left,res)
-    }
-    if root.Right!=nil{
-        findLeft(root.Right,res)
     }
+
+    rightValue := sumOfLeftLeaves(root.Right) // 右
+
+    return leftValue + rightValue
 }
 ```
 
-**迭代法**
+**迭代法(前序遍历)**
 
 ```go
 func sumOfLeftLeaves(root *TreeNode) int {
-    var  res int
+        st := make([]*TreeNode, 0)
-    queue:=list.New()
+        if root == nil {
-    queue.PushBack(root)
+            return 0
-    for queue.Len()>0{
-        length:=queue.Len()
-        for i:=0;i<length;i++{
-            node:=queue.Remove(queue.Front()).(*TreeNode)
-            if node.Left!=nil&&node.Left.Left==nil&&node.Left.Right==nil{
-                res=res+node.Left.Val
         }
-            if node.Left!=nil{
+        st = append(st, root)
-                queue.PushBack(node.Left)
+        result := 0
+
+        for len(st) != 0 {
+            node := st[len(st)-1]
+            st = st[:len(st)-1]
+            if node.Left != nil && node.Left.Left == nil && node.Left.Right == nil {
+                result += node.Left.Val
             }
             if node.Right != nil {
-                queue.PushBack(node.Right)
+                st = append(st, node.Right)
+            }
+            if node.Left != nil {
+                st = append(st, node.Left)
             } 
         }
+
+        return result
 }
-    return res
+
-}
 ```
 
 

problems/0513.找树左下角的值.md

@@ -26,7 +26,7 @@
 
 ## 思路
 
-本地要找出树的最后一行找到最左边的值。此时大家应该想起用层序遍历是非常简单的了，反而用递归的话会比较难一点。
+本题要找出树的最后一行的最左边的值。此时大家应该想起用层序遍历是非常简单的了，反而用递归的话会比较难一点。
 
 我们依然还是先介绍递归法。
 
@@ -46,7 +46,7 @@
 
 所以要找深度最大的叶子节点。
 
-那么如果找最左边的呢？可以使用前序遍历（当然中序，后序都可以，因为本题没有 中间节点的处理逻辑，只要左优先就行），保证优先左边搜索，然后记录深度最大的叶子节点，此时就是树的最后一行最左边的值。
+那么如何找最左边的呢？可以使用前序遍历（当然中序，后序都可以，因为本题没有 中间节点的处理逻辑，只要左优先就行），保证优先左边搜索，然后记录深度最大的叶子节点，此时就是树的最后一行最左边的值。
 
 递归三部曲：
 
@@ -169,7 +169,7 @@ public:
 
 ### 迭代法
 
-本题使用层序遍历再合适不过了，比递归要好理解的多！
+本题使用层序遍历再合适不过了，比递归要好理解得多！
 
 只需要记录最后一行第一个节点的数值就可以了。
 
@@ -323,34 +323,25 @@ class Solution:
 递归法：
 
 ```go
- var maxDeep int // 全局变量 深度
+var depth int   // 全局变量 最大深度
- var  value  int //全局变量 最终值
+var res int     // 记录最终结果
 func findBottomLeftValue(root *TreeNode) int {
-     if root.Left==nil&&root.Right==nil{//需要提前判断一下（不要这个if的话提交结果会出错，但执行代码不会。防止这种情况出现，故先判断是否只有一个节点）
+    depth, res = 0, 0   // 初始化
-         return root.Val
+    dfs(root, 1)
+    return res
 }
-    findLeftValue (root,maxDeep)
+
-    return value
+func dfs(root *TreeNode, d int) {
+    if root == nil {
+        return
     }
-func findLeftValue (root *TreeNode,deep int){
+    // 因为先遍历左边，所以左边如果有值，右边的同层不会更新结果
-     //最左边的值在左边
+    if root.Left == nil && root.Right == nil && depth < d { 
-     if root.Left==nil&&root.Right==nil{
+        depth = d
-         if deep>maxDeep{
+        res = root.Val
-             value=root.Val
-             maxDeep=deep
-         }
-     }
-    //递归
-    if root.Left!=nil{
-        deep++
-        findLeftValue(root.Left,deep)
-        deep--//回溯
-    }
-    if root.Right!=nil{
-        deep++
-        findLeftValue(root.Right,deep)
-        deep--//回溯
     }
+    dfs(root.Left, d+1)   // 隐藏回溯
+    dfs(root.Right, d+1)
 }
 ```
 
@@ -358,14 +349,17 @@ func findLeftValue (root *TreeNode,deep int){
 
 ```go
 func findBottomLeftValue(root *TreeNode) int {
-    queue:=list.New()
     var gradation int
+    queue := list.New()
+    
     queue.PushBack(root)
     for queue.Len() > 0 {
         length := queue.Len()
         for i := 0; i < length; i++ {
             node := queue.Remove(queue.Front()).(*TreeNode)
-            if i==0{gradation=node.Val}
+            if i == 0 {
+                gradation = node.Val
+            }
             if node.Left != nil {
                 queue.PushBack(node.Left)
             }
@@ -394,7 +388,6 @@ var findBottomLeftValue = function(root) {
             maxPath = curPath;
             resNode = node.val;
             }
-            // return ;
         }
         node.left && dfsTree(node.left, curPath+1);
         node.right && dfsTree(node.right, curPath+1);