Merge branch 'master' into master

problems/0018.四数之和.md

@@ -35,7 +35,7 @@
 
 四数之和，和[15.三数之和](https://programmercarl.com/0015.三数之和.html)是一个思路，都是使用双指针法, 基本解法就是在[15.三数之和](https://programmercarl.com/0015.三数之和.html) 的基础上再套一层for循环。
 
-但是有一些细节需要注意，例如： 不要判断`nums[k] > target` 就返回了，三数之和 可以通过 `nums[i] > 0` 就返回了，因为 0 已经是确定的数了，四数之和这道题目 target是任意值。比如：数组是`[-4, -3, -2, -1]`，`target`是`-10`，不能因为`-4 > -10`而跳过。但是我们依旧可以去做剪枝，逻辑变成`nums[i] > target && (nums[i] >=0 || target >= 0)`就可以了。
+但是有一些细节需要注意，例如： 不要判断`nums[k] > target` 就返回了，三数之和 可以通过 `nums[i] > 0` 就返回了，因为 0 已经是确定的数了，四数之和这道题目 target是任意值。比如：数组是`[-4, -3, -2, -1]`，`target`是`-10`，不能因为`-4 > -10`而跳过。但是我们依旧可以去做剪枝，逻辑变成`nums[k] > target && (nums[k] >=0 || target >= 0)`就可以了。
 
 [15.三数之和](https://programmercarl.com/0015.三数之和.html)的双指针解法是一层for循环num[i]为确定值，然后循环内有left和right下标作为双指针，找到nums[i] + nums[left] + nums[right] == 0。
 
@@ -253,7 +253,7 @@ public class Solution {
         for (int k = 0; k < nums.length; k++) {
             // 剪枝处理
             if (nums[k] > target && nums[k] >= 0) {
-                break;
+                break;	// 此处的break可以等价于return result;
             }
             // 对nums[k]去重
             if (k > 0 && nums[k] == nums[k - 1]) {
@@ -262,7 +262,7 @@ public class Solution {
             for (int i = k + 1; i < nums.length; i++) {
                 // 第二级剪枝
                 if (nums[k] + nums[i] > target && nums[k] + nums[i] >= 0) {
-                    break;
+                    break;	// 注意是break到上一级for循环，如果直接return result;会有遗漏
                 }
                 // 对nums[i]去重
                 if (i > k + 1 && nums[i] == nums[i - 1]) {
@@ -802,3 +802,4 @@ end
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>
 </a>
+

problems/0019.删除链表的倒数第N个节点.md

@@ -129,6 +129,36 @@ class Solution {
 }
 ```
 
+
+```java
+class Solution {
+    public ListNode removeNthFromEnd(ListNode head, int n) {
+        // 创建一个新的哑节点，指向原链表头  
+        ListNode s = new ListNode(-1, head);
+        // 递归调用remove方法，从哑节点开始进行删除操作  
+        remove(s, n);
+        // 返回新链表的头（去掉可能的哑节点）  
+        return s.next;
+    }
+    
+    public int remove(ListNode p, int n) {
+        // 递归结束条件：如果当前节点为空，返回0  
+        if (p == null) {
+            return 0;
+        }
+        // 递归深入到下一个节点  
+        int net = remove(p.next, n);
+        // 如果当前节点是倒数第n个节点，进行删除操作  
+        if (net == n) {
+            p.next = p.next.next;  
+        }
+        // 返回当前节点的总深度  
+        return net + 1;
+    }
+}
+```
+
+
 ### Python:
 
 ```python

problems/0020.有效的括号.md

@@ -166,12 +166,35 @@ class Solution {
                 deque.pop();
             }
         }
-        //最后判断栈中元素是否匹配
+        //遍历结束，如果栈为空，则括号全部匹配
         return deque.isEmpty();
     }
 }
 ```
 
+```java
+// 解法二
+// 对应的另一半一定在栈顶
+class Solution {
+    public boolean isValid(String s) {
+        Stack<Character> stack = new Stack<>();
+        for(char c : s.toCharArray()){
+            // 有对应的另一半就直接消消乐
+            if(c == ')' && !stack.isEmpty() && stack.peek() == '(')
+                stack.pop();
+            else if(c == '}' && !stack.isEmpty() && stack.peek() == '{')
+                stack.pop();
+            else if(c == ']' && !stack.isEmpty() && stack.peek() == '[')
+                stack.pop();
+            else
+                stack.push(c);// 没有匹配的就放进去
+        }
+
+        return stack.isEmpty();
+    }
+}
+```
+
 ### Python：
 
 ```python
@@ -555,3 +578,4 @@ impl Solution {
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>
 </a>
+

problems/0059.螺旋矩阵II.md

@@ -715,26 +715,65 @@ object Solution {
 ### C#：
 
 ```csharp
-public class Solution {
-    public int[][] GenerateMatrix(int n) {
-        int[][] answer = new int[n][];
-        for(int i = 0; i < n; i++)
-            answer[i] = new int[n];
-        int start = 0;
-        int end = n - 1;
-        int tmp = 1;
-        while(tmp < n * n)
-        {
-            for(int i = start; i < end; i++) answer[start][i] = tmp++;
-            for(int i = start; i < end; i++) answer[i][end] = tmp++;
-            for(int i = end; i > start; i--) answer[end][i] = tmp++;
-            for(int i = end; i > start; i--) answer[i][start] = tmp++;
-            start++;
-            end--;
-        }
-        if(n % 2 == 1) answer[n / 2][n / 2] = tmp;
-        return answer;
+public int[][] GenerateMatrix(int n)
+{
+    // 参考Carl的代码随想录里面C++的思路
+    // https://www.programmercarl.com/0059.%E8%9E%BA%E6%97%8B%E7%9F%A9%E9%98%B5II.html#%E6%80%9D%E8%B7%AF
+    int startX = 0, startY = 0; // 定义每循环一个圈的起始位置
+    int loop = n / 2; // 每个圈循环几次，例如n为奇数3，那么loop = 1 只是循环一圈，矩阵中间的值需要单独处理
+    int count = 1; // 用来给矩阵每个空格赋值
+    int mid = n / 2; // 矩阵中间的位置，例如：n为3， 中间的位置就是(1，1)，n为5，中间位置为(2, 2)
+    int offset = 1;// 需要控制每一条边遍历的长度，每次循环右边界收缩一位
+
+    // 构建result二维数组
+    int[][] result = new int[n][];
+    for (int k = 0; k < n; k++)
+    {
+        result[k] = new int[n];
     }
+
+    int i = 0, j = 0; // [i,j]
+    while (loop > 0)
+    {
+        i = startX;
+        j = startY;
+        // 四个For循环模拟转一圈
+        // 第一排，从左往右遍历，不取最右侧的值(左闭右开)
+        for (; j < n - offset; j++)
+        {
+            result[i][j] = count++;
+        }
+        // 右侧的第一列，从上往下遍历，不取最下面的值(左闭右开)
+        for (; i < n - offset; i++)
+        {
+            result[i][j] = count++;
+        }
+
+        // 最下面的第一行，从右往左遍历，不取最左侧的值(左闭右开)
+        for (; j > startY; j--)
+        {
+            result[i][j] = count++;
+        }
+
+        // 左侧第一列，从下往上遍历，不取最左侧的值(左闭右开)
+        for (; i > startX; i--)
+        {
+            result[i][j] = count++;
+        }
+        // 第二圈开始的时候，起始位置要各自加1， 例如：第一圈起始位置是(0, 0)，第二圈起始位置是(1, 1)
+        startX++;
+        startY++;
+
+        // offset 控制每一圈里每一条边遍历的长度
+        offset++;
+        loop--;
+    }
+    if (n % 2 == 1)
+    {
+        // n 为奇数
+        result[mid][mid] = count;
+    }
+    return result;
 }
 ```
 

problems/0070.爬楼梯.md

@@ -130,8 +130,8 @@ public:
 };
 ```
 
-* 时间复杂度：$O(n)$
-* 空间复杂度：$O(n)$
+* 时间复杂度：O(n)
+* 空间复杂度：O(n)
 
 当然依然也可以，优化一下空间复杂度，代码如下：
 
@@ -154,8 +154,8 @@ public:
 };
 ```
 
-* 时间复杂度：$O(n)$
-* 空间复杂度：$O(1)$
+* 时间复杂度：O(n)
+* 空间复杂度：O(1)
 
 后面将讲解的很多动规的题目其实都是当前状态依赖前两个，或者前三个状态，都可以做空间上的优化，**但我个人认为面试中能写出版本一就够了哈，清晰明了，如果面试官要求进一步优化空间的话，我们再去优化**。
 
@@ -524,3 +524,4 @@ impl Solution {
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>
 </a>
+

problems/0102.二叉树的层序遍历.md

@@ -1231,6 +1231,47 @@ impl Solution {
 }
 ```
 
+#### C#:
+
+```C# 199.二叉树的右视图
+public class Solution
+{
+    public IList<int> RightSideView(TreeNode root)
+    {
+        var result = new List<int>();
+        Queue<TreeNode> queue = new();
+
+        if (root != null)
+        {
+            queue.Enqueue(root);
+        }
+        while (queue.Count > 0)
+        {
+            int count = queue.Count;
+            int lastValue = count - 1;
+            for (int i = 0; i < count; i++)
+            {
+                var currentNode = queue.Dequeue();
+                if (i == lastValue)
+                {
+                    result.Add(currentNode.val);
+                }
+
+                // lastValue == i == count -1 : left 先于 right 进入Queue
+                if (currentNode.left != null) queue.Enqueue(currentNode.left);
+                if (currentNode.right != null) queue.Enqueue(currentNode.right);
+
+                //// lastValue == i == 0: right 先于 left 进入Queue
+                // if(currentNode.right !=null ) queue.Enqueue(currentNode.right);
+                // if(currentNode.left !=null ) queue.Enqueue(currentNode.left);
+            }
+        }
+
+        return result;
+    }
+}
+```
+
 ## 637.二叉树的层平均值
 
 [力扣题目链接](https://leetcode.cn/problems/average-of-levels-in-binary-tree/)
@@ -1558,6 +1599,35 @@ impl Solution {
 }
 ```
 
+#### C#:
+
+```C# 二叉树的层平均值
+public class Solution {
+    public IList<double> AverageOfLevels(TreeNode root) {
+        var result= new List<double>();
+        Queue<TreeNode> queue = new();
+        if(root !=null) queue.Enqueue(root);
+        
+        while (queue.Count > 0)
+        {
+            int count = queue.Count;
+            double value=0;
+            for (int i = 0; i < count; i++)
+            {
+                var curentNode=queue.Dequeue();
+                value += curentNode.val;
+                if (curentNode.left!=null) queue.Enqueue(curentNode.left);
+                if (curentNode.right!=null) queue.Enqueue(curentNode.right);
+            }
+            result.Add(value/count);
+        }
+
+        return result;
+    }
+}
+
+```
+
 ## 429.N叉树的层序遍历
 
 [力扣题目链接](https://leetcode.cn/problems/n-ary-tree-level-order-traversal/)

problems/0111.二叉树的最小深度.md

@@ -40,7 +40,7 @@
 本题依然是前序遍历和后序遍历都可以，前序求的是深度，后序求的是高度。
 
 * 二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数或者节点数（取决于深度从0开始还是从1开始）
-* 二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数后者节点数（取决于高度从0开始还是从1开始）
+* 二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数或者节点数（取决于高度从0开始还是从1开始）
 
 那么使用后序遍历，其实求的是根节点到叶子节点的最小距离，就是求高度的过程，不过这个最小距离 也同样是最小深度。
 

problems/0150.逆波兰表达式求值.md

@@ -489,6 +489,67 @@ impl Solution {
 }
 ```
 
+### C:
+
+```c
+int str_to_int(char *str) {
+    // string转integer
+    int num = 0, tens = 1;
+    for (int i = strlen(str) - 1; i >= 0; i--) {
+        if (str[i] == '-') {
+            num *= -1;
+            break;
+        }
+        num += (str[i] - '0') * tens;
+        tens *= 10;
+    }
+    return num;
+}
+
+int evalRPN(char** tokens, int tokensSize) {
+
+    int *stack = (int *)malloc(tokensSize * sizeof(int));
+    assert(stack);
+    int stackTop = 0;
+
+    for (int i = 0; i < tokensSize; i++) {
+        char symbol = (tokens[i])[0];
+        if (symbol < '0' && (tokens[i])[1] == '\0') {
+
+            // pop两个数字
+            int num1 = stack[--stackTop];
+            int num2 = stack[--stackTop];
+
+            // 计算结果
+            int result;
+            if (symbol == '+') {
+                result = num1 + num2;
+            } else if (symbol == '-') {
+                result = num2 - num1;
+            } else if (symbol == '/') {
+                result = num2 / num1;
+            } else {
+                result = num1 * num2;
+            }
+
+            // push回stack
+            stack[stackTop++] = result;
+
+        } else {
+
+            // push数字进stack
+            int num = str_to_int(tokens[i]);
+            stack[stackTop++] = num;
+            
+        }
+    }
+
+    int result = stack[0];
+    free(stack);
+    return result;
+}
+```
+
 <p align="center">
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>

problems/0151.翻转字符串里的单词.md

@@ -639,7 +639,46 @@ func reverse(b []byte) {
     }
 }
 ```
-
+```go
+//双指针解法。指针逆序遍历，将遍历后得到的单词（间隔为空格，用以区分）顺序放置在额外空间
+//时间复杂度O(n)，空间复杂度O(n)
+func reverseWords(s string) string {
+    strBytes := []byte(s)
+    n := len(strBytes)
+    // 记录有效字符范围的起始和结束位置
+    start, end := 0, n-1
+    // 去除开头空格
+    for start < n && strBytes[start] == 32 {
+        start++
+    }
+    // 处理全是空格或空字符串情况
+    if start == n {
+        return ""
+    }
+    // 去除结尾空格
+    for end >= 0 && strBytes[end] == 32 {
+        end--
+    }
+    // 结果切片，预分配容量
+    res := make([]byte, 0, end-start+1)//这里挺重要的，本人之前没有预分配容量，每次循环都添加单词，导致内存超限（也可能就是我之前的思路有问题）
+    // 从后往前遍历有效字符范围
+    for i := end; i >= start; {
+        // 找单词起始位置，直接通过循环条件判断定位
+        for ; i >= start && strBytes[i] == 32; i-- {
+        }
+        j := i
+        for ; j >= start && strBytes[j]!= 32; j-- {
+        }
+        res = append(res, strBytes[j+1:i+1]...)
+        // 只在不是最后一个单词时添加空格
+        if j > start {
+            res = append(res, 32)
+        }
+        i = j
+    }
+    return string(res)
+}
+```
 
 
 ### JavaScript:

problems/0225.用队列实现栈.md

@@ -1277,6 +1277,95 @@ impl MyStack {
 }
 ```
 
+### C:
+
+> C：单队列
+
+```c
+typedef struct Node {
+    int val;
+    struct Node *next;
+} Node_t;
+
+// 用单向链表实现queue
+typedef struct {
+    Node_t *head;
+    Node_t *foot;
+    int size;
+} MyStack;
+
+MyStack* myStackCreate() {
+    MyStack *obj = (MyStack *)malloc(sizeof(MyStack));
+    assert(obj);
+    obj->head = NULL;
+    obj->foot = NULL;
+    obj->size = 0;
+    return obj;
+}
+
+void myStackPush(MyStack* obj, int x) {
+
+    Node_t *temp = (Node_t *)malloc(sizeof(Node_t));
+    assert(temp);
+    temp->val = x;
+    temp->next = NULL;
+
+    // 添加至queue末尾
+    if (obj->foot) {
+        obj->foot->next = temp;
+    } else {
+        obj->head = temp;
+    }
+    obj->foot = temp;
+    obj->size++;
+}
+
+int myStackPop(MyStack* obj) {
+
+    // 获取末尾元素
+    int target = obj->foot->val;
+
+    if (obj->head == obj->foot) {
+        free(obj->foot);
+        obj->head = NULL;
+        obj->foot = NULL;
+    } else {
+        
+        Node_t *prev = obj->head;
+        // 移动至queue尾部节点前一个节点
+        while (prev->next != obj->foot) {
+            prev = prev->next;
+        }
+
+        free(obj->foot);
+        obj->foot = prev;
+        obj->foot->next = NULL;
+    }
+
+    obj->size--;
+    return target;
+}
+
+int myStackTop(MyStack* obj) {
+    return obj->foot->val;
+}
+
+bool myStackEmpty(MyStack* obj) {
+    return obj->size == 0;
+}
+
+void myStackFree(MyStack* obj) {
+    Node_t *curr = obj->head;
+    while (curr != NULL) {
+        Node_t *temp = curr->next;
+        free(curr);
+        curr = temp;
+    }
+    free(obj);
+}
+
+```
+
 
 <p align="center">
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">

problems/0235.二叉搜索树的最近公共祖先.md

@@ -99,7 +99,7 @@ if (cur == NULL) return cur;
 
 * 确定单层递归的逻辑
 
-在遍历二叉搜索树的时候就是寻找区间[p->val, q->val]（注意这里是左闭又闭）
+在遍历二叉搜索树的时候就是寻找区间[p->val, q->val]（注意这里是左闭右闭）
 
 那么如果 cur->val 大于 p->val，同时 cur->val 大于q->val，那么就应该向左遍历（说明目标区间在左子树上）。
 

problems/0239.滑动窗口最大值.md

@@ -267,7 +267,7 @@ class Solution {
 //利用双端队列手动实现单调队列
 /**
  * 用一个单调队列来存储对应的下标，每当窗口滑动的时候，直接取队列的头部指针对应的值放入结果集即可
- * 单调队列类似 （tail -->） 3 --> 2 --> 1 --> 0 (--> head) (右边为头结点，元素存的是下标)
+ * 单调递减队列类似 （head -->） 3 --> 2 --> 1 --> 0 (--> tail) (左边为头结点，元素存的是下标)
  */
 class Solution {
     public int[] maxSlidingWindow(int[] nums, int k) {
@@ -281,7 +281,7 @@ class Solution {
             while(!deque.isEmpty() && deque.peek() < i - k + 1){
                 deque.poll();
             }
-            // 2.既然是单调，就要保证每次放进去的数字要比末尾的都大，否则也弹出
+            // 2.维护单调递减队列：新元素若大于队尾元素，则弹出队尾元素，直到满足单调性
             while(!deque.isEmpty() && nums[deque.peekLast()] < nums[i]) {
                 deque.pollLast();
             }
@@ -890,7 +890,40 @@ public:
 };
 ```
 
+### C
+
+```c
+int* maxSlidingWindow(int* nums, int numsSize, int k, int* returnSize) {
+    *returnSize = numsSize - k + 1;
+    int *res = (int*)malloc((*returnSize) * sizeof(int));
+    assert(res);
+    int *deque = (int*)malloc(numsSize * sizeof(int));
+    assert(deque);
+    int front = 0, rear = 0, idx = 0;
+
+    for (int i  = 0 ; i < numsSize ; i++) {
+        while (front < rear && deque[front] <= i - k) {
+            front++;
+        }
+
+        while (front < rear && nums[deque[rear - 1]] <= nums[i]) {
+            rear--;
+        }
+
+        deque[rear++] = i;
+
+        if (i >= k - 1) {
+            res[idx++] = nums[deque[front]];
+        }
+    }       
+
+    return res;
+}
+
+```
+
 <p align="center">
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>
 </a>
+

problems/0349.两个数组的交集.md

@@ -123,6 +123,9 @@ public:
 ### Java：
 版本一：使用HashSet
 ```Java
+// 时间复杂度O(n+m+k) 空间复杂度O(n+k)
+// 其中n是数组nums1的长度，m是数组nums2的长度，k是交集元素的个数
+
 import java.util.HashSet;
 import java.util.Set;
 
@@ -145,8 +148,15 @@ class Solution {
         }
       
         //方法1：将结果集合转为数组
-
-        return resSet.stream().mapToInt(x -> x).toArray();
+        return res.stream().mapToInt(Integer::intValue).toArray();
+        /**
+         * 将 Set<Integer> 转换为 int[] 数组：
+         * 1. stream() : Collection 接口的方法，将集合转换为 Stream<Integer>
+         * 2. mapToInt(Integer::intValue) : 
+         *    - 中间操作，将 Stream<Integer> 转换为 IntStream
+         *    - 使用方法引用 Integer::intValue，将 Integer 对象拆箱为 int 基本类型
+         * 3. toArray() : 终端操作，将 IntStream 转换为 int[] 数组。
+         */
         
         //方法2：另外申请一个数组存放setRes中的元素,最后返回数组
         int[] arr = new int[resSet.size()];
@@ -538,3 +548,4 @@ end
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>
 </a>
+

problems/0383.赎金信.md

@@ -104,7 +104,7 @@ public:
 };
 ```
 
-* 时间复杂度: O(n)
+* 时间复杂度: O(m+n)，其中m表示ransomNote的长度，n表示magazine的长度
 * 空间复杂度: O(1)
 
 
@@ -470,3 +470,4 @@ bool canConstruct(char* ransomNote, char* magazine) {
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>
 </a>
+

problems/0459.重复的子字符串.md

@@ -390,6 +390,8 @@ public:
 
 ### Java：
 
+（版本一） 前缀表 减一
+
 ```java
 class Solution {
     public boolean repeatedSubstringPattern(String s) {
@@ -420,6 +422,45 @@ class Solution {
 }
 ```
 
+（版本二） 前缀表 不减一
+
+```java
+/*
+ * 充分条件：如果字符串s是由重复子串组成的，那么它的最长相等前后缀不包含的子串一定是s的最小重复子串。
+ * 必要条件：如果字符串s的最长相等前后缀不包含的子串是s的最小重复子串，那么s必然是由重复子串组成的。
+ * 推得：当字符串s的长度可以被其最长相等前后缀不包含的子串的长度整除时，不包含的子串就是s的最小重复子串。
+ *
+ * 时间复杂度：O(n)
+ * 空间复杂度：O(n)
+ */
+class Solution {
+    public boolean repeatedSubstringPattern(String s) {
+        // if (s.equals("")) return false; 
+        // 边界判断（可以去掉，因为题目给定范围是1 <= s.length <= 10^4）
+        int n = s.length();
+
+        // Step 1.构建KMP算法的前缀表
+        int[] next = new int[n]; // 前缀表的值表示 以该位置结尾的字符串的最长相等前后缀的长度
+        int j = 0;
+        next[0] = 0;
+        for (int i = 1; i < n; i++) {
+            while (j > 0 && s.charAt(i) != s.charAt(j)) // 只要前缀后缀还不一致，就根据前缀表回退j直到起点为止
+                j = next[j - 1];
+            if (s.charAt(i) == s.charAt(j))
+                j++;
+            next[i] = j;
+        }
+
+        // Step 2.判断重复子字符串
+        if (next[n - 1] > 0 && n % (n - next[n - 1]) == 0) { // 当字符串s的长度可以被其最长相等前后缀不包含的子串的长度整除时
+            return true; // 不包含的子串就是s的最小重复子串
+        } else {
+            return false;
+        }
+    }
+}
+```
+
 ### Python：
 
 （版本一） 前缀表 减一
@@ -911,9 +952,54 @@ public bool RepeatedSubstringPattern(string s) {
     return ss.Contains(s);
 }
 ```
+### C
+
+```c
+// 前缀表不减一
+int *build_next(char* s, int len) {
+
+    int *next = (int *)malloc(len * sizeof(int));
+    assert(next);
+
+    // 初始化前缀表
+    next[0] = 0;
+
+    // 构建前缀表表
+    int i = 1, j = 0;
+    while (i < len) {
+        if (s[i] == s[j]) {
+            j++;
+            next[i] = j;
+            i++;
+        } else if (j > 0) {
+            j = next[j - 1];
+        } else {
+            next[i] = 0;
+            i++;
+        }
+    }
+    return next;
+}
+
+bool repeatedSubstringPattern(char* s) {
+
+    int len = strlen(s);
+    int *next = build_next(s, len);
+    bool result = false;
+
+    // 检查最小重复片段能否被长度整除
+    if (next[len - 1]) {
+        result = len % (len - next[len - 1]) == 0;
+    }
+
+    free(next);
+    return result;
+}
+
+```
+
 
 <p align="center">
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>
 </a>
-

problems/0494.目标和.md

@@ -151,13 +151,13 @@ if (abs(target) > sum) return 0; // 此时没有方案
 
 本题则是装满有几种方法。其实这就是一个组合问题了。
 
-1. 确定dp数组以及下标的含义
+#### 1. 确定dp数组以及下标的含义
 
 先用 二维 dp数组求解本题，dp[i][j]：使用 下标为[0, i]的nums[i]能够凑满j（包括j）这么大容量的包，有dp[i][j]种方法。
 
 01背包为什么这么定义dp数组，我在[0-1背包理论基础](https://www.programmercarl.com/%E8%83%8C%E5%8C%85%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%8001%E8%83%8C%E5%8C%85-1.html)中 确定dp数组的含义里讲解过。 
 
-2. 确定递推公式
+#### 2. 确定递推公式
 
 我们先手动推导一下，这个二维数组里面的数值。 
 
@@ -264,7 +264,7 @@ if (nums[i] > j) dp[i][j] = dp[i - 1][j];
 else dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i]];
 ```
 
-3. dp数组如何初始化
+#### 3. dp数组如何初始化
 
 先明确递推的方向，如图，求解 dp[2][2] 是由 上方和左上方推出。
 
@@ -315,7 +315,7 @@ for (int i = 0; i < nums.size(); i++) {
 }
 ```
 
-4. 确定遍历顺序
+#### 4. 确定遍历顺序
 
 在明确递推方向时，我们知道 当前值 是由上方和左上方推出。 
 
@@ -360,7 +360,7 @@ for (int j = 0; j <= bagSize; j++) { // 列，遍历背包
 这里大家可以看出，无论是以上哪种遍历，都不影响 dp[2][2]的求值，用来 推导 dp[2][2] 的数值都在。 
 
 
-5. 举例推导dp数组
+#### 5. 举例推导dp数组
 
 输入：nums: [1, 1, 1, 1, 1], target: 3
 
@@ -421,7 +421,7 @@ public:
 
 dp[i][j] 去掉 行的维度，即 dp[j]，表示：填满j（包括j）这么大容积的包，有dp[j]种方法。 
 
-2. 确定递推公式
+#### 2. 确定递推公式
 
 二维DP数组递推公式： `dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i]];` 
 
@@ -429,17 +429,17 @@ dp[i][j] 去掉 行的维度，即 dp[j]，表示：填满j（包括j）这么
 
 **这个公式在后面在讲解背包解决排列组合问题的时候还会用到！**
 
-3. dp数组如何初始化
+#### 3. dp数组如何初始化
 
 在上面 二维dp数组中，我们讲解过 dp[0][0] 初始为1，这里dp[0] 同样初始为1 ,即装满背包为0的方法有一种，放0件物品。 
 
-4. 确定遍历顺序
+#### 4. 确定遍历顺序
 
 在[动态规划：关于01背包问题，你该了解这些！（滚动数组）](https://programmercarl.com/背包理论基础01背包-2.html)中，我们系统讲过对于01背包问题一维dp的遍历。
 
 遍历物品放在外循环，遍历背包在内循环，且内循环倒序（为了保证物品只使用一次）。
 
-5. 举例推导dp数组
+#### 5. 举例推导dp数组
 
 输入：nums: [1, 1, 1, 1, 1], target: 3
 
@@ -526,7 +526,6 @@ dp[j] += dp[j - nums[i]];
 
 ## 其他语言版本
 
-
 ### Java
 ```java
 class Solution {
@@ -671,18 +670,26 @@ class Solution:
 
         # 创建二维动态规划数组，行表示选取的元素数量，列表示累加和
         dp = [[0] * (target_sum + 1) for _ in range(len(nums) + 1)]
+        dp = [[0] * (target_sum + 1) for _ in range(len(nums))]
 
         # 初始化状态
         dp[0][0] = 1
+        if nums[0] <= target_sum:
+            dp[0][nums[0]] = 1
+        numZero = 0
+        for i in range(len(nums)):
+            if nums[i] == 0:
+                numZero += 1
+            dp[i][0] = int(math.pow(2, numZero))
 
         # 动态规划过程
-        for i in range(1, len(nums) + 1):
+        for i in range(1, len(nums)):
             for j in range(target_sum + 1):
                 dp[i][j] = dp[i - 1][j]  # 不选取当前元素
                 if j >= nums[i - 1]:
-                    dp[i][j] += dp[i - 1][j - nums[i - 1]]  # 选取当前元素
+                    dp[i][j] += dp[i - 1][j - nums[i]]  # 选取当前元素
 
-        return dp[len(nums)][target_sum]  # 返回达到目标和的方案数
+        return dp[len(nums)-1][target_sum]  # 返回达到目标和的方案数
 
 
 ```

problems/0518.零钱兑换II.md

@@ -4,8 +4,6 @@
 </a>
 <p align="center"><strong><a href="./qita/join.md">参与本项目</a>，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们受益！</strong></p>
 
-
-
 # 518.零钱兑换II
 
 [力扣题目链接](https://leetcode.cn/problems/coin-change-ii/)
@@ -45,15 +43,19 @@
 
 **[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html)：[装满背包有多少种方法？组合与排列有讲究！| LeetCode：518.零钱兑换II](https://www.bilibili.com/video/BV1KM411k75j/)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
 
+## 二维dp讲解
 
+如果大家认真做完：[分割等和子集](https://www.programmercarl.com/0416.%E5%88%86%E5%89%B2%E7%AD%89%E5%92%8C%E5%AD%90%E9%9B%86.html) ， [最后一块石头的重量II](https://www.programmercarl.com/1049.%E6%9C%80%E5%90%8E%E4%B8%80%E5%9D%97%E7%9F%B3%E5%A4%B4%E7%9A%84%E9%87%8D%E9%87%8FII.html) 和 [目标和](https://www.programmercarl.com/0494.%E7%9B%AE%E6%A0%87%E5%92%8C.html)
 
+应该会知道类似这种题目：给出一个总数，一些物品，问能否凑成这个总数。  
 
-## 思路
+这是典型的背包问题！ 
 
-这是一道典型的背包问题，一看到钱币数量不限，就知道这是一个完全背包。
+本题求的是装满这个背包的物品组合数是多少。
 
+因为每一种面额的硬币有无限个，所以这是完全背包。
 
-对完全背包还不了解的同学，可以看这篇：[动态规划：关于完全背包，你该了解这些！](https://programmercarl.com/背包问题理论基础完全背包.html)
+对完全背包还不了解的同学，可以看这篇：[完全背包理论基础](https://programmercarl.com/背包问题理论基础完全背包.html)
 
 但本题和纯完全背包不一样，**纯完全背包是凑成背包最大价值是多少，而本题是要求凑成总金额的物品组合个数！**
 
@@ -69,44 +71,182 @@
 
 如果问的是排列数，那么上面就是两种排列了。
 
-**组合不强调元素之间的顺序，排列强调元素之间的顺序**。 其实这一点我们在讲解回溯算法专题的时候就讲过了哈。
+**组合不强调元素之间的顺序，排列强调元素之间的顺序**。 其实这一点我们在讲解回溯算法专题的时候就讲过。
 
 那我为什么要介绍这些呢，因为这和下文讲解遍历顺序息息相关!
 
-回归本题，动规五步曲来分析如下：
+本题其实与我们讲过 [494. 目标和](https://programmercarl.com/0494.目标和.html) 十分类似。 
 
-1. 确定dp数组以及下标的含义
+[494. 目标和](https://programmercarl.com/0494.目标和.html) 求的是装满背包有多少种方法，而本题是求装满背包有多少种组合。 
+
+这有啥区别？ 
+
+**求装满背包有几种方法其实就是求组合数**。 不过 [494. 目标和](https://programmercarl.com/0494.目标和.html) 是 01背包，即每一类物品只有一个。 
+
+以下动规五部曲：
+
+### 1、确定dp数组以及下标的含义 
+
+定义二维dp数值 dp[i][j]：使用 下标为[0, i]的coins[i]能够凑满j（包括j）这么大容量的包，有dp[i][j]种组合方法。 
+
+很多录友也会疑惑，凭什么上来就定义 dp数组，思考过程是什么样的， 这个思考过程我在 [01背包理论基础（二维数组）](https://programmercarl.com/背包理论基础01背包-1.html) 中的 “确定dp数组以及下标的含义” 有详细讲解。 
+
+（**强烈建议按照代码随想录的顺序学习，否则可能看不懂我的讲解**）
+
+
+### 2、确定递推公式
+
+> **注意**： 这里的公式推导，与之前讲解过的 [494. 目标和](https://programmercarl.com/0494.目标和.html) 、[完全背包理论基础](https://programmercarl.com/背包问题理论基础完全背包.html) 有极大重复，所以我不在重复讲解原理，而是只讲解区别。
+
+我们再回顾一下，[01背包理论基础](https://programmercarl.com/背包理论基础01背包-1.html)，中二维DP数组的递推公式为： 
+
+`dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])` 
+
+在 [完全背包理论基础](https://programmercarl.com/背包问题理论基础完全背包.html) 详细讲解了完全背包二维DP数组的递推公式为： 
+
+`dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i])`
+
+
+看去完全背包 和 01背包的差别在哪里？ 
+
+在于01背包是 `dp[i - 1][j - weight[i]] + value[i]`  ，完全背包是 `dp[i][j - weight[i]] + value[i])` 
+
+主要原因就是 完全背包单类物品有无限个。
+
+具体原因我在  [完全背包理论基础（二维）](https://programmercarl.com/背包问题理论基础完全背包.html) 的 「确定递推公式」有详细讲解，如果大家忘了，再回顾一下。 
+
+我上面有说过，本题和 [494. 目标和](https://programmercarl.com/0494.目标和.html) 是一样的，唯一区别就是  [494. 目标和](https://programmercarl.com/0494.目标和.html) 是 01背包，本题是完全背包。 
+
+
+在[494. 目标和](https://programmercarl.com/0494.目标和.html)中详解讲解了装满背包有几种方法，二维DP数组的递推公式： 
+`dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i]]`
+
+所以本题递推公式：`dp[i][j] = dp[i - 1][j] +  dp[i][j - nums[i]]`   ，区别依然是 ` dp[i - 1][j - nums[i]]` 和 `dp[i][j - nums[i]]` 
+
+这个 ‘所以’ 我省略了很多推导的内容，因为这些内容在 [494. 目标和](https://programmercarl.com/0494.目标和.html) 和 [完全背包理论基础](https://programmercarl.com/背包问题理论基础完全背包.html) 都详细讲过。
+
+这里不再重复讲解。
+
+大家主要疑惑点 
+
+1、 `dp[i][j] = dp[i - 1][j] +  dp[i][j - nums[i]]` 这个递归公式框架怎么来的，在 [494. 目标和](https://programmercarl.com/0494.目标和.html) 有详细讲解。  
+
+2、为什么是 ` dp[i][j - nums[i]]` 而不是 ` dp[i - 1][j - nums[i]]` ，在[完全背包理论基础（二维）](https://programmercarl.com/背包问题理论基础完全背包.html) 有详细讲解 
+
+
+### 3. dp数组如何初始化 
+
+那么二维数组的最上行 和 最左列一定要初始化，这是递推公式推导的基础，如图红色部分：
+
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240827103507.png)  
+
+
+这里首先要关注的就是 dp[0][0] 应该是多少？ 
+
+背包空间为0，装满「物品0」 的组合数有多少呢？  
+
+应该是 0 个， 但如果 「物品0」 的 数值就是0呢？ 岂不是可以有无限个0 组合 和为0！ 
+
+题目描述中说了`1 <= coins.length <= 300` ，所以不用考虑 物品数值为0的情况。 
+
+那么最上行dp[0][j] 如何初始化呢？ 
+
+dp[0][j]的含义：用「物品0」（即coins[0]） 装满 背包容量为j的背包，有几种组合方法。  （如果看不懂dp数组的含义，建议先学习[494. 目标和](https://programmercarl.com/0494.目标和.html)）
+
+如果 j 可以整除 物品0，那么装满背包就有1种组合方法。 
+
+初始化代码： 
+
+```CPP 
+for (int j = 0; j <= bagSize; j++) {
+    if (j % coins[0] == 0) dp[0][j] = 1;
+}
+```
+
+最左列如何初始化呢？ 
+
+dp[i][0] 的含义：用物品i（即coins[i]） 装满容量为0的背包 有几种组合方法。 
+
+都有一种方法，即不装。
+
+所以 dp[i][0] 都初始化为1 
+
+### 4. 确定遍历顺序 
+
+二维DP数组的完全背包的两个for循环先后顺序是无所谓的。 
+
+先遍历背包，还是先遍历物品都是可以的。 
+
+原理和  [01背包理论基础（二维数组）](https://programmercarl.com/背包理论基础01背包-1.html) 中的 「遍历顺序」是一样的，都是因为 两个for循环的先后顺序不影响 递推公式 所需要的数值。 
+
+具体分析过程看 [01背包理论基础（二维数组）](https://programmercarl.com/背包理论基础01背包-1.html) 中的 「遍历顺序」
+
+### 5. 打印DP数组
+
+以amount为5，coins为：[2,3,5] 为例： 
+
+dp数组应该是这样的： 
+
+```
+1 0 1 0 1 0
+1 0 1 1 1 1
+1 0 1 1 1 2
+```
+
+### 代码实现： 
+
+```CPP 
+class Solution {
+public:
+    int change(int amount, vector<int>& coins) {
+        int bagSize = amount;
+
+        vector<vector<uint64_t>> dp(coins.size(), vector<uint64_t>(bagSize + 1, 0));
+
+        // 初始化最上行
+        for (int j = 0; j <= bagSize; j++) {
+            if (j % coins[0] == 0) dp[0][j] = 1;
+        }
+        // 初始化最左列
+        for (int i = 0; i < coins.size(); i++) {
+            dp[i][0] = 1;
+        }
+        // 以下遍历顺序行列可以颠倒
+        for (int i = 1; i < coins.size(); i++) { // 行，遍历物品
+            for (int j = 0; j <= bagSize; j++) { // 列，遍历背包
+                if (coins[i] > j) dp[i][j] = dp[i - 1][j]; 
+                else dp[i][j] = dp[i - 1][j] +  dp[i][j - coins[i]];
+            }
+        }
+        return dp[coins.size() - 1][bagSize];
+    }
+};
+```
+
+## 一维dp讲解 
+
+### 1、确定dp数组以及下标的含义 
 
 dp[j]：凑成总金额j的货币组合数为dp[j]
 
-2. 确定递推公式
+### 2、确定递推公式
 
-dp[j]  就是所有的dp[j - coins[i]]（考虑coins[i]的情况）相加。
+本题 二维dp 递推公式： `dp[i][j] = dp[i - 1][j] +  dp[i][j - coins[i]]` 
 
-所以递推公式：dp[j] += dp[j - coins[i]];
+压缩成一维：`dp[j] += dp[j - coins[i]]` 
 
-**这个递推公式大家应该不陌生了，我在讲解01背包题目的时候在这篇[494. 目标和](https://programmercarl.com/0494.目标和.html)中就讲解了，求装满背包有几种方法，公式都是：dp[j] += dp[j - nums[i]];**
+这个递推公式大家应该不陌生了，我在讲解01背包题目的时候在这篇[494. 目标和](https://programmercarl.com/0494.目标和.html)中就讲解了，求装满背包有几种方法，公式都是：`dp[j] += dp[j - nums[i]]`
 
-3. dp数组如何初始化
+### 3. dp数组如何初始化 
 
-首先dp[0]一定要为1，dp[0] = 1是 递归公式的基础。如果dp[0] = 0 的话，后面所有推导出来的值都是0了。 
+装满背包容量为0 的方法是1，即不放任何物品，`dp[0] = 1`
 
-那么 dp[0] = 1 有没有含义，其实既可以说 凑成总金额0的货币组合数为1，也可以说 凑成总金额0的货币组合数为0，好像都没有毛病。
+### 4. 确定遍历顺序 
 
-但题目描述中，也没明确说 amount = 0 的情况，结果应该是多少。 
-
-这里我认为题目描述还是要说明一下，因为后台测试数据是默认，amount = 0 的情况，组合数为1的。 
-
-下标非0的dp[j]初始化为0，这样累计加dp[j - coins[i]]的时候才不会影响真正的dp[j]
-
-dp[0]=1还说明了一种情况：如果正好选了coins[i]后，也就是j-coins[i] == 0的情况表示这个硬币刚好能选，此时dp[0]为1表示只选coins[i]存在这样的一种选法。
-
-4. 确定遍历顺序
 
 本题中我们是外层for循环遍历物品（钱币），内层for遍历背包（金钱总额），还是外层for遍历背包（金钱总额），内层for循环遍历物品（钱币）呢？
 
-
-我在[动态规划：关于完全背包，你该了解这些！](https://programmercarl.com/背包问题理论基础完全背包.html)中讲解了完全背包的两个for循环的先后顺序都是可以的。
+我在[完全背包（一维DP）](./背包问题完全背包一维.md)中讲解了完全背包的两个for循环的先后顺序都是可以的。
 
 **但本题就不行了！**
 
@@ -116,7 +256,7 @@ dp[0]=1还说明了一种情况：如果正好选了coins[i]后，也就是j-coi
 
 所以纯完全背包是能凑成总和就行，不用管怎么凑的。
 
-本题是求凑出来的方案个数，且每个方案个数是为组合数。
+本题是求凑出来的方案个数，且每个方案个数是组合数。
 
 那么本题，两个for循环的先后顺序可就有说法了。
 
@@ -154,7 +294,7 @@ for (int j = 0; j <= amount; j++) { // 遍历背包容量
 
 可能这里很多同学还不是很理解，**建议动手把这两种方案的dp数组数值变化打印出来，对比看一看！（实践出真知）**
 
-5. 举例推导dp数组
+### 5. 举例推导dp数组
 
 输入: amount = 5, coins = [1, 2, 5] ，dp状态图如下：
 
@@ -208,7 +348,17 @@ public:
 
 ## 总结
 
-本题的递推公式，其实我们在[494. 目标和](https://programmercarl.com/0494.目标和.html)中就已经讲过了，**而难点在于遍历顺序！**
+本题我们从 二维 分析到 一维。 
+
+大家在刚开始学习的时候，从二维开始学习 容易理解。 
+
+之后，推荐大家直接掌握一维的写法，熟练后更容易写出来。
+
+本题中，二维dp主要是就要 想清楚和我们之前讲解的 [01背包理论基础](https://programmercarl.com/背包理论基础01背包-1.html)、[494. 目标和](https://programmercarl.com/0494.目标和.html)、 [完全背包理论基础](https://programmercarl.com/背包问题理论基础完全背包.html) 联系与区别。 
+
+这也是代码随想录安排刷题顺序的精髓所在。 
+
+本题的一维dp中，难点在于理解便利顺序。
 
 在求装满背包有几种方案的时候，认清遍历顺序是非常关键的。
 
@@ -216,8 +366,7 @@ public:
 
 **如果求排列数就是外层for遍历背包，内层for循环遍历物品**。
 
-可能说到排列数录友们已经有点懵了，后面Carl还会安排求排列数的题目，到时候在对比一下，大家就会发现神奇所在！
-
+可能说到排列数录友们已经有点懵了，后面我还会安排求排列数的题目，到时候在对比一下，大家就会发现神奇所在！
 
 
 ## 其他语言版本
@@ -397,7 +546,7 @@ object Solution {
   }
 }
 ```
-## C
+### C
 
 ```c
 int change(int amount, int* coins, int coinsSize) {

problems/0738.单调递增的数字.md

@@ -273,22 +273,20 @@ class Solution:
 ### Go 
 ```go
 func monotoneIncreasingDigits(n int) int {
-    s := strconv.Itoa(N)//将数字转为字符串，方便使用下标
-    ss := []byte(s)//将字符串转为byte数组，方便更改。
-    n := len(ss)
-    if n <= 1 {
-        return n
-    }
-    for i := n-1; i > 0; i-- {
-        if ss[i-1] > ss[i] {   //前一个大于后一位,前一位减1，后面的全部置为9
-            ss[i-1] -= 1
-            for j := i; j < n; j++ {   //后面的全部置为9
-                ss[j] = '9'
-            }
-        } 
-    }
-    res, _ := strconv.Atoi(string(ss))
-    return res 
+	s := strconv.Itoa(n)
+	// 从左到右遍历字符串，找到第一个不满足单调递增的位置
+	for i := len(s) - 2; i >= 0; i-- {
+		if s[i] > s[i+1] {
+			// 将该位置的数字减1
+			s = s[:i] + string(s[i]-1) + s[i+1:]
+			// 将该位置之后的所有数字置为9
+			for j := i + 1; j < len(s); j++ {
+				s = s[:j] + "9" + s[j+1:]
+			}
+		}
+	}
+	result, _ := strconv.Atoi(s)
+	return result
 }
 ```
 
@@ -447,3 +445,4 @@ public class Solution
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>
 </a>
+

problems/1049.最后一块石头的重量II.md

@@ -42,40 +42,41 @@
 
 ## 思路
 
-如果对背包问题不都熟悉先看这两篇：
+如果对背包问题不熟悉的话先看这两篇：
 
-* [动态规划：关于01背包问题，你该了解这些！](https://programmercarl.com/背包理论基础01背包-1.html)
-* [动态规划：关于01背包问题，你该了解这些！（滚动数组）](https://programmercarl.com/背包理论基础01背包-2.html)
+* [01背包理论基础（二维数组）](https://programmercarl.com/背包理论基础01背包-1.html)
+* [01背包理论基础（一维数组）](https://programmercarl.com/背包理论基础01背包-2.html)
 
-本题其实就是尽量让石头分成重量相同的两堆，相撞之后剩下的石头最小，**这样就化解成01背包问题了**。
+本题其实是尽量让石头分成重量相同的两堆（尽可能相同），相撞之后剩下的石头就是最小的。 
 
-是不是感觉和昨天讲解的[416. 分割等和子集](https://programmercarl.com/0416.分割等和子集.html)非常像了。
+一堆的石头重量是sum，那么我们就尽可能拼成 重量为 sum / 2 的石头堆。 这样剩下的石头堆也是 尽可能接近 sum/2 的重量。 
+那么此时问题就是有一堆石头，每个石头都有自己的重量，是否可以 装满 最大重量为 sum / 2的背包。 
 
-本题物品的重量为stones[i]，物品的价值也为stones[i]。
+看到这里，大家是否感觉和昨天讲解的 [416. 分割等和子集](https://programmercarl.com/0416.分割等和子集.html)非常像了，简直就是同一道题。
 
-对应着01背包里的物品重量weight[i]和 物品价值value[i]。
+本题**这样就化解成01背包问题了**。
+
+**[416. 分割等和子集](https://programmercarl.com/0416.分割等和子集.html) 是求背包是否正好装满，而本题是求背包最多能装多少**。
+
+物品就是石头，物品的重量为stones[i]，物品的价值也为stones[i]。 
 
 接下来进行动规五步曲：
 
-1. 确定dp数组以及下标的含义
+### 1. 确定dp数组以及下标的含义
 
 **dp[j]表示容量（这里说容量更形象，其实就是重量）为j的背包，最多可以背最大重量为dp[j]**。
 
-可以回忆一下01背包中，dp[j]的含义，容量为j的背包，最多可以装的价值为 dp[j]。
+相对于 01背包，本题中，石头的重量是 stones[i]，石头的价值也是 stones[i] 。
 
-相对于 01背包，本题中，石头的重量是 stones[i]，石头的价值也是 stones[i] ，可以 “最多可以装的价值为 dp[j]” == “最多可以背的重量为dp[j]”
+“最多可以装的价值为 dp[j]” 等同于 “最多可以背的重量为dp[j]”
 
-2. 确定递推公式
+### 2. 确定递推公式
 
 01背包的递推公式为：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
 
 本题则是：**dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);**
 
-一些同学可能看到这dp[j - stones[i]] + stones[i]中 又有- stones[i] 又有+stones[i]，看着有点晕乎。
-
-大家可以再去看 dp[j]的含义。
-
-3. dp数组如何初始化
+### 3. dp数组如何初始化
 
 既然 dp[j]中的j表示容量，那么最大容量（重量）是多少呢，就是所有石头的重量和。
 
@@ -95,7 +96,7 @@
 vector<int> dp(15001, 0);
 ```
 
-4. 确定遍历顺序
+### 4. 确定遍历顺序
 
 
 在[动态规划：关于01背包问题，你该了解这些！（滚动数组）](https://programmercarl.com/背包理论基础01背包-2.html)中就已经说明：如果使用一维dp数组，物品遍历的for循环放在外层，遍历背包的for循环放在内层，且内层for循环倒序遍历！
@@ -111,7 +112,7 @@ for (int i = 0; i < stones.size(); i++) { // 遍历物品
 
 ```
 
-5. 举例推导dp数组
+### 5. 举例推导dp数组
 
 举例，输入：[2,4,1,1]，此时target = (2 + 4 + 1 + 1)/2 = 4 ，dp数组状态图如下：
 
@@ -154,10 +155,7 @@ public:
 
 本题其实和[416. 分割等和子集](https://programmercarl.com/0416.分割等和子集.html)几乎是一样的，只是最后对dp[target]的处理方式不同。
 
-[416. 分割等和子集](https://programmercarl.com/0416.分割等和子集.html)相当于是求背包是否正好装满，而本题是求背包最多能装多少。
-
-
-
+**[416. 分割等和子集](https://programmercarl.com/0416.分割等和子集.html)相当于是求背包是否正好装满，而本题是求背包最多能装多少**。
 
 
 ## 其他语言版本

problems/1365.有多少小于当前数字的数字.md

@@ -115,7 +115,7 @@ public:
 
 ## 其他语言版本
 
-### Java： 
+### Java：
 
 ```Java 
 public int[] smallerNumbersThanCurrent(int[] nums) {
@@ -138,18 +138,51 @@ public int[] smallerNumbersThanCurrent(int[] nums) {
 
 ### Python：
 
-```python
+> 暴力法：
+
+```python3
 class Solution:
+    def smallerNumbersThanCurrent(self, nums: List[int]) -> List[int]:
+        res = [0 for _ in range(len(nums))]
+        for i in range(len(nums)):
+            cnt = 0
+            for j in range(len(nums)):
+                if j == i:
+                    continue
+                if nums[i] > nums[j]:
+                    cnt += 1
+            res[i] = cnt
+        return res
+```
+
+> 排序+hash：
+
+```python3
+class Solution:
+    # 方法一：使用字典
     def smallerNumbersThanCurrent(self, nums: List[int]) -> List[int]:
         res = nums[:]
-        hash = dict()
+        hash_dict = dict()
         res.sort() # 从小到大排序之后，元素下标就是小于当前数字的数字
         for i, num in enumerate(res):
-            if num  not in hash.keys(): # 遇到了相同的数字，那么不需要更新该 number 的情况
-                hash[num] = i       
+            if num  not in hash_dict.keys(): # 遇到了相同的数字，那么不需要更新该 number 的情况
+                hash_dict[num] = i       
         for i, num in enumerate(nums):
-            res[i] = hash[num]
+            res[i] = hash_dict[num]
         return res
+
+    # 方法二：使用数组
+    def smallerNumbersThanCurrent(self, nums: List[int]) -> List[int]:
+        # 同步进行排序和创建新数组的操作，这样可以减少一次冗余的数组复制操作，以减少一次O(n) 的复制时间开销
+        sort_nums = sorted(nums)
+        # 题意中 0 <= nums[i] <= 100，故range的参数设为101
+        hash_lst = [0 for _ in range(101)]
+        # 从后向前遍历，这样hash里存放的就是相同元素最左面的数值和下标了
+        for i in range(len(sort_nums)-1,-1,-1):
+            hash_lst[sort_nums[i]] = i
+        for i in range(len(nums)):
+            nums[i] = hash_lst[nums[i]]
+        return nums
 ```
 
 ### Go：
@@ -220,7 +253,7 @@ var smallerNumbersThanCurrent = function(nums) {
 };
 ```
 
-### TypeScript:
+### TypeScript：
 
 > 暴力法：
 
@@ -241,7 +274,7 @@ function smallerNumbersThanCurrent(nums: number[]): number[] {
 };
 ```
 
-> 排序+hash
+> 排序+hash：
 
 ```typescript
 function smallerNumbersThanCurrent(nums: number[]): number[] {
@@ -260,7 +293,7 @@ function smallerNumbersThanCurrent(nums: number[]): number[] {
 };
 ```
 
-### rust
+### Rust：
 ```rust
 use std::collections::HashMap;
 impl Solution {

problems/kamacoder/0044.开发商购买土地.md

@@ -212,13 +212,14 @@ public class Main {
         int horizontalCut = 0;
         for (int i = 0; i < n; i++) {
             horizontalCut += horizontal[i];
-            result = Math.min(result, Math.abs(sum - 2 * horizontalCut));
+            result = Math.min(result, Math.abs((sum - horizontalCut) - horizontalCut));
+            // 更新result。其中，horizontalCut表示前i行的和，sum - horizontalCut表示剩下的和，作差、取绝对值，得到题目需要的“A和B各自的子区域内的土地总价值之差”。下同。
         }
 
         int verticalCut = 0;
         for (int j = 0; j < m; j++) {
             verticalCut += vertical[j];
-            result = Math.min(result, Math.abs(sum - 2 * verticalCut));
+            result = Math.min(result, Math.abs((sum - verticalCut) - verticalCut));
         }
 
         System.out.println(result);
@@ -526,3 +527,89 @@ int main()
 }
 
 ```
+
+### Go
+
+前缀和
+
+```go
+package main
+
+import (
+    "fmt"
+    "os"
+    "bufio"
+    "strings"
+    "strconv"
+    "math"
+)
+    
+func main() {
+    var n, m int
+    
+    reader := bufio.NewReader(os.Stdin)
+    
+    line, _ := reader.ReadString('\n')
+    line = strings.TrimSpace(line)
+    params := strings.Split(line, " ")
+    
+    n, _ = strconv.Atoi(params[0])
+    m, _ = strconv.Atoi(params[1])//n和m读取完成
+    
+    land := make([][]int, n)//土地矩阵初始化
+    
+    for i := 0; i < n; i++ {
+        line, _ := reader.ReadString('\n')
+        line = strings.TrimSpace(line)
+        values := strings.Split(line, " ")
+        land[i] = make([]int, m)
+        for j := 0; j < m; j++ {
+            value, _ := strconv.Atoi(values[j])
+            land[i][j] = value
+        }
+    }//所有读取完成
+    
+    //初始化前缀和矩阵
+    preMatrix := make([][]int, n+1)
+	for i := 0; i <= n; i++ {
+		preMatrix[i] = make([]int, m+1)
+	}
+    
+    for a := 1; a < n+1; a++ {
+        for b := 1; b < m+1; b++ {
+            preMatrix[a][b] = land[a-1][b-1] + preMatrix[a-1][b] + preMatrix[a][b-1] - preMatrix[a-1][b-1]
+        }
+    }
+    
+    totalSum := preMatrix[n][m]
+    
+    minDiff := math.MaxInt32//初始化极大数，用于比较
+    
+    //按行分割
+    for i := 1; i < n; i++ {
+        topSum := preMatrix[i][m]
+        
+        bottomSum := totalSum - topSum
+        
+        diff := int(math.Abs(float64(topSum - bottomSum)))
+        if diff < minDiff {
+            minDiff = diff
+        }
+    }
+    
+    //按列分割
+    for j := 1; j < m; j++ {
+        topSum := preMatrix[n][j]
+        
+        bottomSum := totalSum - topSum
+        
+        diff := int(math.Abs(float64(topSum - bottomSum)))
+        if diff < minDiff {
+            minDiff = diff
+        }
+    }    
+    
+    fmt.Println(minDiff) 
+}
+```
+

problems/kamacoder/0054.替换数字.md

@@ -288,16 +288,6 @@ func main(){
 
 
 
-### python：
-```Python
-class Solution:
-    def change(self, s):
-        lst = list(s) # Python里面的string也是不可改的，所以也是需要额外空间的。空间复杂度：O(n)。
-        for i in range(len(lst)):
-            if lst[i].isdigit():
-                lst[i] = "number"
-        return ''.join(lst)
-```
 ### JavaScript:
 ```js
 const readline = require("readline");

problems/kamacoder/0097.小明逛公园.md

@@ -100,7 +100,8 @@ Floyd算法核心思想是动态规划。
 
 这里我们用 grid数组来存图，那就把dp数组命名为 grid。 
 
-grid[i][j][k] = m，表示 节点i 到 节点j 以[1...k] 集合为中间节点的最短距离为m。   
+grid[i][j][k] = m，表示 **节点i 到 节点j 以[1...k] 集合中的一个节点为中间节点的最短距离为m**。
+
 
 可能有录友会想，凭什么就这么定义呢？ 
 

problems/kamacoder/0108.冗余连接.md

@@ -44,7 +44,7 @@
 
 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240527110320.png)
 
-图中的 1 2，2 3，1 3 等三条边在删除后都能使原图变为一棵合法的树。但是 1 3 由于是标准输出里最后出现的那条边，所以输出结果为 1 3
+图中的 1 2，2 3，1 3 等三条边在删除后都能使原图变为一棵合法的树。但是 1 3 由于是标准输入里最后出现的那条边，所以输出结果为 1 3
 
 数据范围：
 

problems/二叉树的统一迭代法.md

@@ -238,7 +238,7 @@ class Solution {
         while (!st.empty()) {
             TreeNode node = st.peek();
             if (node != null) {
-                st.pop(); // 将该节点弹出，避免重复操作，下面再将右中左节点添加到栈中
+                st.pop(); // 将该节点弹出，避免重复操作，下面再将右左中节点添加到栈中（前序遍历-中左右，入栈顺序右左中）
                 if (node.right!=null) st.push(node.right);  // 添加右节点（空节点不入栈）
                 if (node.left!=null) st.push(node.left);    // 添加左节点（空节点不入栈）
                 st.push(node);                          // 添加中节点
@@ -266,11 +266,10 @@ public List<Integer> inorderTraversal(TreeNode root) {
     while (!st.empty()) {
         TreeNode node = st.peek();
         if (node != null) {
-            st.pop(); // 将该节点弹出，避免重复操作，下面再将右中左节点添加到栈中
+            st.pop(); // 将该节点弹出，避免重复操作，下面再将右中左节点添加到栈中（中序遍历-左中右，入栈顺序右中左）
             if (node.right!=null) st.push(node.right);  // 添加右节点（空节点不入栈）
             st.push(node);                          // 添加中节点
             st.push(null); // 中节点访问过，但是还没有处理，加入空节点做为标记。
-
             if (node.left!=null) st.push(node.left);    // 添加左节点（空节点不入栈）
         } else { // 只有遇到空节点的时候，才将下一个节点放进结果集
             st.pop();           // 将空节点弹出
@@ -294,7 +293,7 @@ class Solution {
         while (!st.empty()) {
             TreeNode node = st.peek();
             if (node != null) {
-                st.pop(); // 将该节点弹出，避免重复操作，下面再将右中左节点添加到栈中
+                st.pop(); // 将该节点弹出，避免重复操作，下面再将中右左节点添加到栈中（后序遍历-左右中，入栈顺序中右左）
                 st.push(node);                          // 添加中节点
                 st.push(null); // 中节点访问过，但是还没有处理，加入空节点做为标记。
                 if (node.right!=null) st.push(node.right);  // 添加右节点（空节点不入栈）
@@ -975,3 +974,4 @@ public IList<int> PostorderTraversal(TreeNode root)
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>
 </a>
+

problems/周总结/20210107动规周末总结.md

@@ -99,7 +99,7 @@ public:
 
 这道绝佳的面试题我没有用过，如果录友们有面试别人的需求，就把这个套路拿去吧。
 
-我在[通过一道面试题目，讲一讲递归算法的时间复杂度！](https://programmercarl.com/前序/通过一道面试题目，讲一讲递归算法的时间复杂度！.html)中，以我自己面试别人的真实经历，通过求x的n次方 这么简单的题目，就可以考察候选人对算法性能以及递归的理解深度，录友们可以看看，绝对有收获！
+我在[通过一道面试题目，讲一讲递归算法的时间复杂度！](../前序/递归算法的时间复杂度.md)中，以我自己面试别人的真实经历，通过求x的n次方 这么简单的题目，就可以考察候选人对算法性能以及递归的理解深度，录友们可以看看，绝对有收获！
 
 ## 周四
 

problems/背包理论基础01背包-1.md

@@ -41,8 +41,6 @@ leetcode上没有纯01背包的问题，都是01背包应用方面的题目，
 
 有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。**每件物品只能用一次**，求解将哪些物品装入背包里物品价值总和最大。
 
-![动态规划-背包问题](https://code-thinking-1253855093.file.myqcloud.com/pics/20210117175428387.jpg)
-
 这是标准的背包问题，以至于很多同学看了这个自然就会想到背包，甚至都不知道暴力的解法应该怎么解了。
 
 这样其实是没有从底向上去思考，而是习惯性想到了背包，那么暴力的解法应该是怎么样的呢？
@@ -73,7 +71,7 @@ leetcode上没有纯01背包的问题，都是01背包应用方面的题目，
 
 依然动规五部曲分析一波。
 
-1. 确定dp数组以及下标的含义
+#### 1. 确定dp数组以及下标的含义
 
 我们需要使用二维数组，为什么呢？ 
 
@@ -131,7 +129,7 @@ i 来表示物品、j表示背包容量。
 
 **要时刻记着这个dp数组的含义，下面的一些步骤都围绕这dp数组的含义进行的**，如果哪里看懵了，就来回顾一下i代表什么，j又代表什么。
 
-2. 确定递推公式
+#### 2. 确定递推公式
 
 这里在把基本信息给出来：
 
@@ -176,7 +174,7 @@ i 来表示物品、j表示背包容量。
 
 递归公式： `dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);`
 
-3. dp数组如何初始化
+#### 3. dp数组如何初始化
 
 **关于初始化，一定要和dp数组的定义吻合，否则到递推公式的时候就会越来越乱**。
 
@@ -197,8 +195,8 @@ dp[0][j]，即：i为0，存放编号0的物品的时候，各个容量的背包
 代码初始化如下：
 
 ```CPP
-for (int j = 0 ; j < weight[0]; j++) {  // 当然这一步，如果把dp数组预先初始化为0了，这一步就可以省略，但很多同学应该没有想清楚这一点。
-    dp[0][j] = 0;
+for (int i = 1; i < weight.size(); i++) {  // 当然这一步，如果把dp数组预先初始化为0了，这一步就可以省略，但很多同学应该没有想清楚这一点。
+    dp[i][0] = 0;
 }
 // 正序遍历
 for (int j = weight[0]; j <= bagweight; j++) {
@@ -236,7 +234,7 @@ for (int j = weight[0]; j <= bagweight; j++) {
 
 **费了这么大的功夫，才把如何初始化讲清楚，相信不少同学平时初始化dp数组是凭感觉来的，但有时候感觉是不靠谱的**。
 
-4. 确定遍历顺序
+#### 4. 确定遍历顺序
 
 在如下图中，可以看出，有两个遍历的维度：物品与背包重量
 
@@ -293,7 +291,7 @@ dp[i-1][j]和dp[i - 1][j - weight[i]] 都在dp[i][j]的左上角方向（包括
 
 **其实背包问题里，两个for循环的先后循序是非常有讲究的，理解遍历顺序其实比理解推导公式难多了**。
 
-5. 举例推导dp数组
+#### 5. 举例推导dp数组
 
 来看一下对应的dp数组的数值，如图：
 

problems/背包问题完全背包一维.md

@@ -0,0 +1,211 @@
+
+# 完全背包-一维数组
+
+本题力扣上没有原题，大家可以去[卡码网第52题](https://kamacoder.com/problempage.php?pid=1052)去练习。
+
+## 算法公开课
+
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html)：[带你学透完全背包问题！ ](https://www.bilibili.com/video/BV1uK411o7c9/)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
+
+
+## 思路  
+
+本篇我们不再做五部曲分析，核心内容 在 01背包二维 、01背包一维 和 完全背包二维 的讲解中都讲过了。 
+
+上一篇我们刚刚讲了完全背包二维DP数组的写法： 
+
+```CPP 
+for (int i = 1; i < n; i++) { // 遍历物品
+    for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
+        if (j < weight[i]) dp[i][j] = dp[i - 1][j];
+        else dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]);
+    }
+}
+```  
+
+压缩成一维DP数组，也就是将上一层拷贝到当前层。 
+
+将上一层dp[i-1] 的那一层拷贝到 当前层 dp[i] ，那么 递推公式由：`dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i])` 变成： `dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i])`
+
+这里有录友想，这样拷贝的话， dp[i - 1][j]  的数值会不会 覆盖了 dp[i][j] 的数值呢？ 
+
+并不会，因为 当前层 dp[i][j] 是空的，是没有计算过的。 
+
+变成  `dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i])` 我们压缩成一维dp数组，去掉 i 层数维度。 
+
+即：`dp[j] = max(dp[j], dp[j - weight[i]] + value[i])`
+
+
+接下来我们重点讲一下遍历顺序。 
+
+看过这两篇的话：
+
+* [01背包理论基础（二维数组）](https://programmercarl.com/背包理论基础01背包-1.html)
+* [01背包理论基础（一维数组）](https://programmercarl.com/背包理论基础01背包-2.html)
+
+就知道了，01背包中二维dp数组的两个for遍历的先后循序是可以颠倒了，一维dp数组的两个for循环先后循序一定是先遍历物品，再遍历背包容量。
+
+**在完全背包中，对于一维dp数组来说，其实两个for循环嵌套顺序是无所谓的**！
+
+因为dp[j] 是根据 下标j之前所对应的dp[j]计算出来的。 只要保证下标j之前的dp[j]都是经过计算的就可以了。
+
+遍历物品在外层循环，遍历背包容量在内层循环，状态如图：
+
+![动态规划-完全背包1](https://code-thinking-1253855093.file.myqcloud.com/pics/20210126104529605.jpg)
+
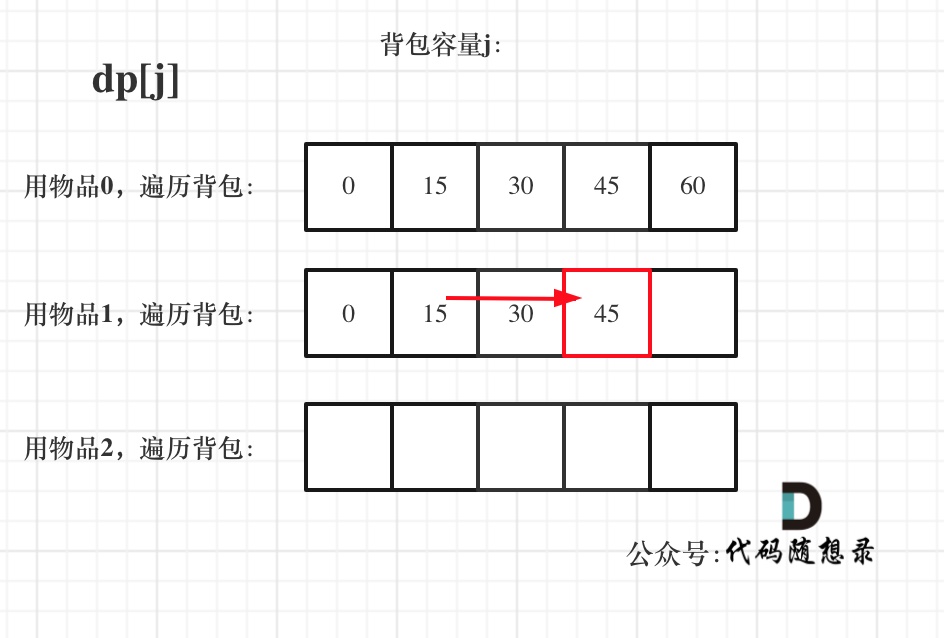
+遍历背包容量在外层循环，遍历物品在内层循环，状态如图：
+
+![动态规划-完全背包2](https://code-thinking-1253855093.file.myqcloud.com/pics/20210729234011.png)
+
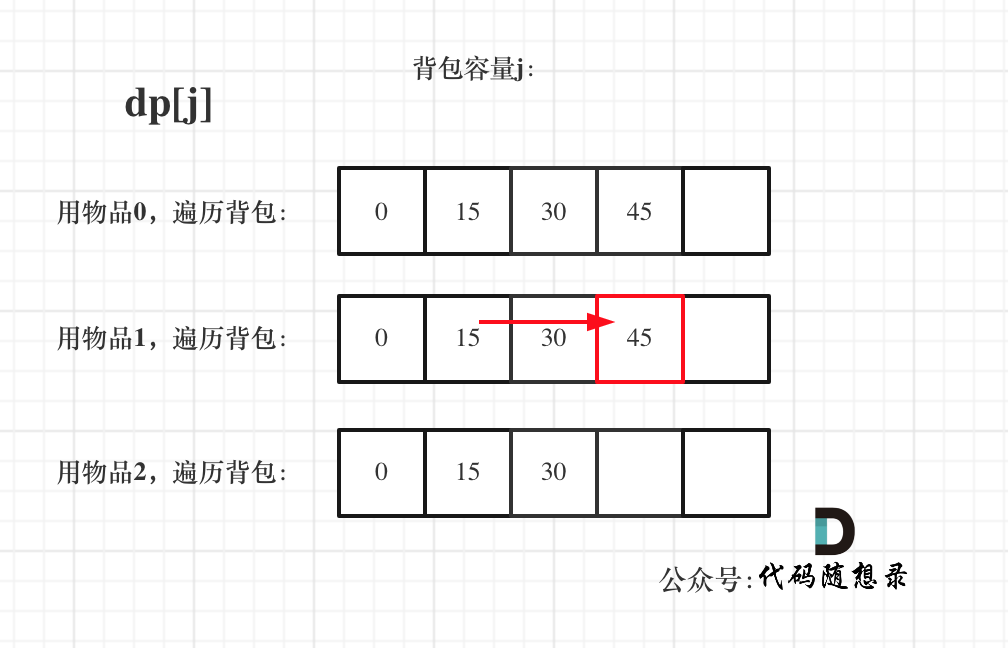
+看了这两个图，大家就会理解，完全背包中，两个for循环的先后循序，都不影响计算dp[j]所需要的值（这个值就是下标j之前所对应的dp[j]）。
+
+先遍历背包再遍历物品，代码如下：
+
+```CPP
+for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
+    for(int i = 0; i < weight.size(); i++) { // 遍历物品
+        if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
+    }
+    cout << endl;
+}
+```
+
+先遍历物品再遍历背包： 
+
+```CPP 
+for(int i = 0; i < weight.size(); i++) { // 遍历物品
+    for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
+        if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
+    }
+}
+```
+
+整体代码如下：
+
+```cpp
+#include <iostream>
+#include <vector>
+using namespace std;
+
+int main() {
+    int N, bagWeight;
+    cin >> N >> bagWeight;
+    vector<int> weight(N, 0);
+    vector<int> value(N, 0);
+    for (int i = 0; i < N; i++) {
+        int w;
+        int v;
+        cin >> w >> v;
+        weight[i] = w;
+        value[i] = v;
+    }
+
+    vector<int> dp(bagWeight + 1, 0);
+    for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
+        for(int i = 0; i < weight.size(); i++) { // 遍历物品
+            if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
+        }
+    }
+    cout << dp[bagWeight] << endl;
+
+    return 0;
+}
+```
+
+
+
+## 总结
+
+细心的同学可能发现，**全文我说的都是对于纯完全背包问题，其for循环的先后循环是可以颠倒的！**
+
+但如果题目稍稍有点变化，就会体现在遍历顺序上。
+
+如果问装满背包有几种方式的话？ 那么两个for循环的先后顺序就有很大区别了，而leetcode上的题目都是这种稍有变化的类型。
+
+这个区别，我将在后面讲解具体leetcode题目中给大家介绍，因为这块如果不结合具题目，单纯的介绍原理估计很多同学会越看越懵！
+
+别急，下一篇就是了！
+
+最后，**又可以出一道面试题了，就是纯完全背包，要求先用二维dp数组实现，然后再用一维dp数组实现，最后再问，两个for循环的先后是否可以颠倒？为什么？**
+
+这个简单的完全背包问题，估计就可以难住不少候选人了。
+
+
+## 其他语言版本
+
+### Java：
+
+```java
+import java.util.Scanner;
+
+public class Main {
+    public static void main(String[] args) {
+        Scanner scanner = new Scanner(System.in);
+        int N = scanner.nextInt();
+        int bagWeight = scanner.nextInt();
+
+        int[] weight = new int[N];
+        int[] value = new int[N];
+        for (int i = 0; i < N; i++) {
+            weight[i] = scanner.nextInt();
+            value[i] = scanner.nextInt();
+        }
+
+        int[] dp = new int[bagWeight + 1];
+
+        for (int j = 0; j <= bagWeight; j++) { // 遍历背包容量
+            for (int i = 0; i < weight.length; i++) { // 遍历物品
+                if (j >= weight[i]) {
+                    dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
+                }
+            }
+        }
+
+        System.out.println(dp[bagWeight]);
+        scanner.close();
+    }
+}
+
+```
+
+
+
+### Python：
+
+```python
+def complete_knapsack(N, bag_weight, weight, value):
+    dp = [0] * (bag_weight + 1)
+
+    for j in range(bag_weight + 1):  # 遍历背包容量
+        for i in range(len(weight)):  # 遍历物品
+            if j >= weight[i]:
+                dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
+
+    return dp[bag_weight]
+
+# 输入
+N, bag_weight = map(int, input().split())
+weight = []
+value = []
+for _ in range(N):
+    w, v = map(int, input().split())
+    weight.append(w)
+    value.append(v)
+
+# 输出结果
+print(complete_knapsack(N, bag_weight, weight, value))
+
+
+```
+
+
+### Go：
+
+```go
+
+```
+### Javascript:
+
+```Javascript
+```
+

problems/背包问题理论基础完全背包.md

@@ -5,18 +5,11 @@
 <p align="center"><strong><a href="./qita/join.md">参与本项目</a>，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们受益！</strong></p>
 
 
-# 动态规划：完全背包理论基础
+# 完全背包理论基础-二维DP数组
 
 本题力扣上没有原题，大家可以去[卡码网第52题](https://kamacoder.com/problempage.php?pid=1052)去练习，题意是一样的。
 
-## 算法公开课
-
-**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html)：[带你学透完全背包问题！ ](https://www.bilibili.com/video/BV1uK411o7c9/)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
-
-## 思路
-
-### 完全背包
-
+## 完全背包
 
 有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。**每件物品都有无限个（也就是可以放入背包多次）**，求解将哪些物品装入背包里物品价值总和最大。
 
@@ -24,14 +17,12 @@
 
 同样leetcode上没有纯完全背包问题，都是需要完全背包的各种应用，需要转化成完全背包问题，所以我这里还是以纯完全背包问题进行讲解理论和原理。
 
-在下面的讲解中，我依然举这个例子：
+在下面的讲解中，我拿下面数据举例子：
 
-背包最大重量为4。
-
-物品为：
+背包最大重量为4，物品为：
 
 |       | 重量 | 价值 |
-| ---   | ---  | ---  |
+| ----- | ---- | ---- |
 | 物品0 | 1    | 15   |
 | 物品1 | 3    | 20   |
 | 物品2 | 4    | 30   |
@@ -40,471 +31,292 @@
 
 问背包能背的物品最大价值是多少？
 
-01背包和完全背包唯一不同就是体现在遍历顺序上，所以本文就不去做动规五部曲了，我们直接针对遍历顺序经行分析！
+**如果没看到之前的01背包讲解，已经要先仔细看如下两篇，01背包是基础，本篇在讲解完全背包，之前的背包基础我将不会重复讲解**。
 
-关于01背包我如下两篇已经进行深入分析了：
+* [01背包理论基础（二维数组）](https://programmercarl.com/背包理论基础01背包-1.html)
+* [01背包理论基础（一维数组）](https://programmercarl.com/背包理论基础01背包-2.html)
 
-* [动态规划：关于01背包问题，你该了解这些！](https://programmercarl.com/背包理论基础01背包-1.html)
-* [动态规划：关于01背包问题，你该了解这些！（滚动数组）](https://programmercarl.com/背包理论基础01背包-2.html)
+动规五部曲分析完全背包，为了从原理上讲清楚，我们先从二维dp数组分析： 
 
-首先再回顾一下01背包的核心代码
-```cpp
-for(int i = 0; i < weight.size(); i++) { // 遍历物品
-    for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
-        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
-    }
+### 1. 确定dp数组以及下标的含义
+
+**dp[i][j] 表示从下标为[0-i]的物品，每个物品可以取无限次，放进容量为j的背包，价值总和最大是多少**。
+
+很多录友也会疑惑，凭什么上来就定义 dp数组，思考过程是什么样的， 这个思考过程我在 [01背包理论基础（二维数组）](https://programmercarl.com/背包理论基础01背包-1.html) 中的 “确定dp数组以及下标的含义” 有详细讲解。 
+
+
+### 2. 确定递推公式
+
+这里在把基本信息给出来：
+
+|       | 重量 | 价值 |
+| ----- | ---- | ---- |
+| 物品0 | 1    | 15   |
+| 物品1 | 3    | 20   |
+| 物品2 | 4    | 30   |
+
+对于递推公式，首先我们要明确有哪些方向可以推导出 dp[i][j]。 
+
+这里依然拿dp[1][4]的状态来举例： （[01背包理论基础（二维数组）](https://programmercarl.com/背包理论基础01背包-1.html) 中也是这个例子，要注意下面的不同之处）
+
+求取 dp[1][4] 有两种情况： 
+
+1. 放物品1  
+2. 还是不放物品1
+
+如果不放物品1， 那么背包的价值应该是 dp[0][4] 即 容量为4的背包，只放物品0的情况。 
+
+推导方向如图： 
+
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20241126112952.png)
+
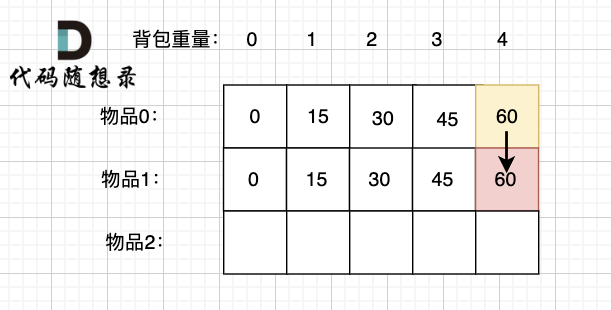
+如果放物品1， **那么背包要先留出物品1的容量**，目前容量是4，物品1 的容量（就是物品1的重量）为3，此时背包剩下容量为1。 
+
+容量为1，只考虑放物品0 和物品1 的最大价值是 dp[1][1]， **注意 这里和  [01背包理论基础（二维数组）](https://programmercarl.com/背包理论基础01背包-1.html) 有所不同了**！  
+
+在  [01背包理论基础（二维数组）](https://programmercarl.com/背包理论基础01背包-1.html) 中，背包先空留出物品1的容量，此时容量为1，只考虑放物品0的最大价值是 dp[0][1]，**因为01背包每个物品只有一个，既然空出物品1，那背包中也不会再有物品1**！ 
+
+而在完全背包中，物品是可以放无限个，所以 即使空出物品1空间重量，那背包中也可能还有物品1，所以此时我们依然考虑放 物品0 和 物品1 的最大价值即： **dp[1][1]， 而不是 dp[0][1]**
+
+所以 放物品1 的情况 = dp[1][1] + 物品1 的价值，推导方向如图：  
+
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20241126113104.png)
+
+
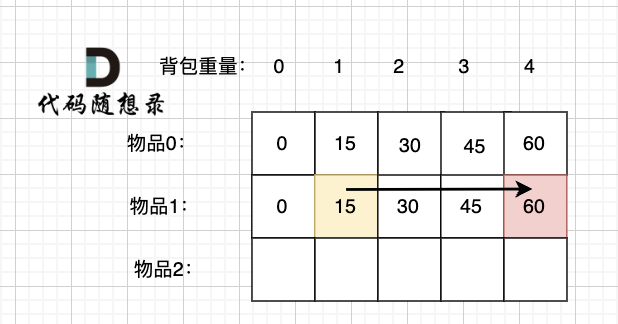
+（**注意上图和  [01背包理论基础（二维数组）](https://programmercarl.com/背包理论基础01背包-1.html) 中的区别**，对于理解完全背包很重要）
+
+两种情况，分别是放物品1 和 不放物品1，我们要取最大值（毕竟求的是最大价值） 
+
+`dp[1][4] = max(dp[0][4], dp[1][1] + 物品1 的价值) `
+
+以上过程，抽象化如下：
+
+* **不放物品i**：背包容量为j，里面不放物品i的最大价值是dp[i - 1][j]。
+
+* **放物品i**：背包空出物品i的容量后，背包容量为j - weight[i]，dp[i][j - weight[i]] 为背包容量为j - weight[i]且不放物品i的最大价值，那么dp[i][j - weight[i]] + value[i] （物品i的价值），就是背包放物品i得到的最大价值
+
+递推公式： `dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]);`
+
+（注意，完全背包二维dp数组 和 01背包二维dp数组 递推公式的区别，01背包中是 `dp[i - 1][j - weight[i]] + value[i])`）
+
+### 3. dp数组如何初始化
+
+**关于初始化，一定要和dp数组的定义吻合，否则到递推公式的时候就会越来越乱**。
+
+首先从dp[i][j]的定义出发，如果背包容量j为0的话，即dp[i][0]，无论是选取哪些物品，背包价值总和一定为0。如图：
+
+![动态规划-背包问题2](https://code-thinking-1253855093.file.myqcloud.com/pics/2021011010304192.png)
+
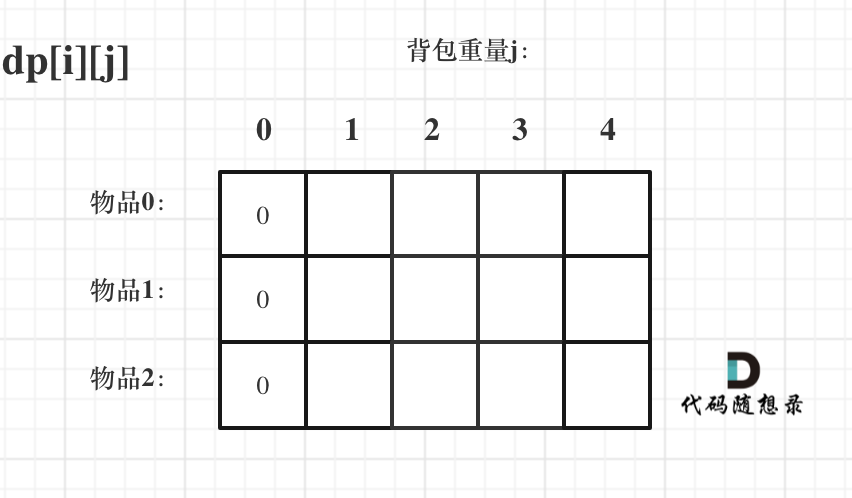
+在看其他情况。
+
+状态转移方程 `dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]);` 可以看出有一个方向 i 是由 i-1 推导出来，那么i为0的时候就一定要初始化。
+
+dp[0][j]，即：存放编号0的物品的时候，各个容量的背包所能存放的最大价值。
+
+那么很明显当 `j < weight[0]`的时候，dp[0][j] 应该是 0，因为背包容量比编号0的物品重量还小。
+
+当`j >= weight[0]`时，**dp[0][j] 如果能放下weight[0]的话，就一直装，每一种物品有无限个**。
+
+代码初始化如下：
+
+```CPP
+for (int i = 1; i < weight.size(); i++) {  // 当然这一步，如果把dp数组预先初始化为0了，这一步就可以省略，但很多同学应该没有想清楚这一点。
+    dp[i][0] = 0;
+}
+
+// 正序遍历，如果能放下就一直装物品0
+for (int j = weight[0]; j <= bagWeight; j++)
+    dp[0][j] = dp[0][j - weight[0]] + value[0];
+```
+
+（注意上面初始化和 [01背包理论基础（二维数组）](https://programmercarl.com/背包理论基础01背包-1.html)的区别在于物品有无限个）
+
+
+此时dp数组初始化情况如图所示：
+
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20241114161608.png)
+
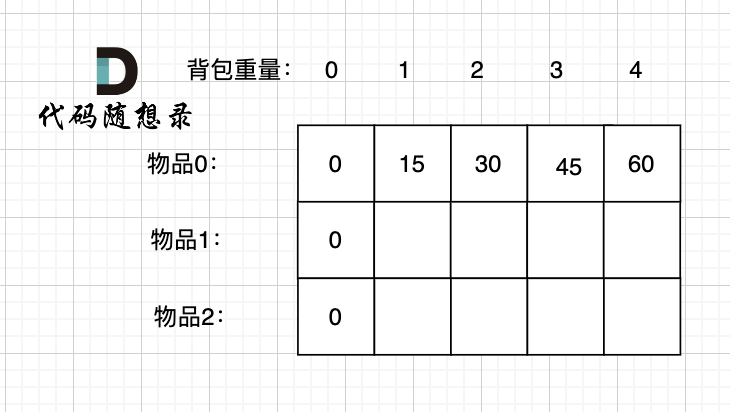
+dp[0][j] 和 dp[i][0] 都已经初始化了，那么其他下标应该初始化多少呢？
+
+其实从递归公式： dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]); 可以看出dp[i][j]  是由上方和左方数值推导出来了，那么 其他下标初始为什么数值都可以，因为都会被覆盖。
+
+但只不过一开始就统一把dp数组统一初始为0，更方便一些。
+
+最后初始化代码如下：
+
+```CPP
+// 初始化 dp
+vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
+for (int j = weight[0]; j <= bagWeight; j++) {
+    dp[0][j] = dp[0][j - weight[0]] + value[0]; 
 }
 ```
 
-我们知道01背包内嵌的循环是从大到小遍历，为了保证每个物品仅被添加一次。
 
-而完全背包的物品是可以添加多次的，所以要从小到大去遍历，即：
+### 4. 确定遍历顺序
 
-```CPP
-// 先遍历物品，再遍历背包
-for(int i = 0; i < weight.size(); i++) { // 遍历物品
-    for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量
-        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
+[01背包理论基础（二维数组）](https://programmercarl.com/背包理论基础01背包-1.html) 中我们讲过，01背包二维DP数组，先遍历物品还是先遍历背包都是可以的。 
 
-    }
-}
-```
+因为两种遍历顺序，对于二维dp数组来说，递推公式所需要的值，二维dp数组里对应的位置都有。 
 
-至于为什么，我在[动态规划：关于01背包问题，你该了解这些！（滚动数组）](https://programmercarl.com/背包理论基础01背包-2.html)中也做了讲解。
+详细可以看 [01背包理论基础（二维数组）](https://programmercarl.com/背包理论基础01背包-1.html) 中的 【遍历顺序】的讲解
 
-dp状态图如下：
-
-
-![动态规划-完全背包](https://code-thinking-1253855093.file.myqcloud.com/pics/20210126104510106.jpg)
-
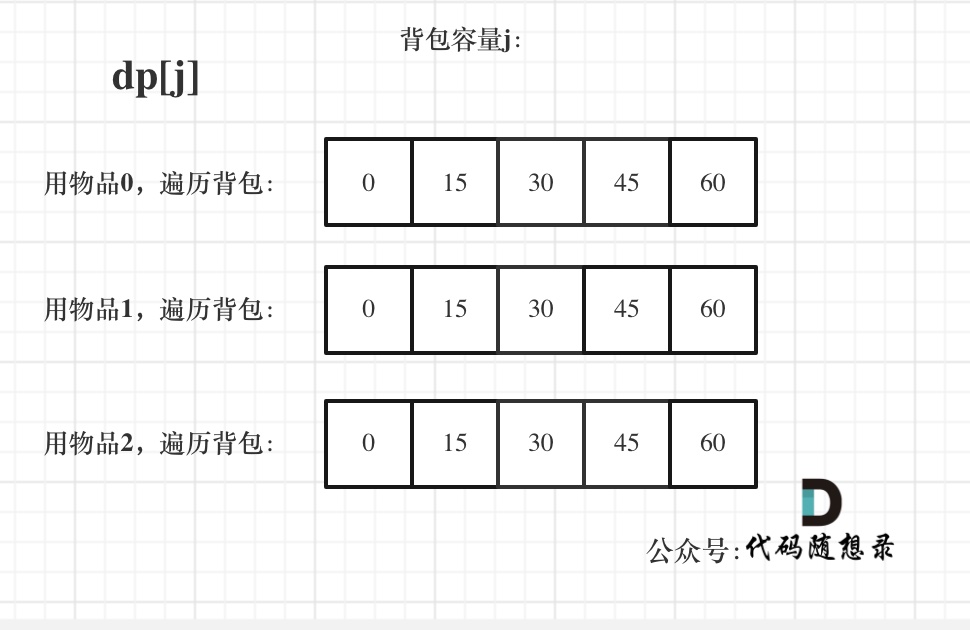
-相信很多同学看网上的文章，关于完全背包介绍基本就到为止了。
-
-**其实还有一个很重要的问题，为什么遍历物品在外层循环，遍历背包容量在内层循环？**
-
-这个问题很多题解关于这里都是轻描淡写就略过了，大家都默认 遍历物品在外层，遍历背包容量在内层，好像本应该如此一样，那么为什么呢？
-
-难道就不能遍历背包容量在外层，遍历物品在内层？
-
-
-看过这两篇的话：
-* [动态规划：关于01背包问题，你该了解这些！](https://programmercarl.com/背包理论基础01背包-1.html)
-* [动态规划：关于01背包问题，你该了解这些！（滚动数组）](https://programmercarl.com/背包理论基础01背包-2.html)
-
-就知道了，01背包中二维dp数组的两个for遍历的先后循序是可以颠倒了，一维dp数组的两个for循环先后循序一定是先遍历物品，再遍历背包容量。
-
-**在完全背包中，对于一维dp数组来说，其实两个for循环嵌套顺序是无所谓的！**
-
-因为dp[j] 是根据 下标j之前所对应的dp[j]计算出来的。 只要保证下标j之前的dp[j]都是经过计算的就可以了。
-
-遍历物品在外层循环，遍历背包容量在内层循环，状态如图：
-
-
-![动态规划-完全背包1](https://code-thinking-1253855093.file.myqcloud.com/pics/20210126104529605.jpg)
-
-遍历背包容量在外层循环，遍历物品在内层循环，状态如图：
-
-![动态规划-完全背包2](https://code-thinking-1253855093.file.myqcloud.com/pics/20210729234011.png)
-
-看了这两个图，大家就会理解，完全背包中，两个for循环的先后循序，都不影响计算dp[j]所需要的值（这个值就是下标j之前所对应的dp[j]）。
-
-先遍历背包在遍历物品，代码如下：
-
-```CPP
-// 先遍历背包，再遍历物品
-for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
-    for(int i = 0; i < weight.size(); i++) { // 遍历物品
-        if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
-    }
-    cout << endl;
-}
-```
-
-完整的C++测试代码如下：
-
-```CPP
-// 先遍历物品，在遍历背包
-void test_CompletePack() {
-    vector<int> weight = {1, 3, 4};
-    vector<int> value = {15, 20, 30};
-    int bagWeight = 4;
-    vector<int> dp(bagWeight + 1, 0);
-    for(int i = 0; i < weight.size(); i++) { // 遍历物品
-        for(int j = weight[i]; j <= bagWeight; j++) { // 遍历背包容量
-            dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
-        }
-    }
-    cout << dp[bagWeight] << endl;
-}
-int main() {
-    test_CompletePack();
-}
-
-```
-
-```CPP
-
-// 先遍历背包，再遍历物品
-void test_CompletePack() {
-    vector<int> weight = {1, 3, 4};
-    vector<int> value = {15, 20, 30};
-    int bagWeight = 4;
-
-    vector<int> dp(bagWeight + 1, 0);
+所以既可以 先遍历物品再遍历背包：
 
+```CPP 
+for (int i = 1; i < n; i++) { // 遍历物品
     for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
-        for(int i = 0; i < weight.size(); i++) { // 遍历物品
-            if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
-        }
+        if (j < weight[i]) dp[i][j] = dp[i - 1][j];
+        else dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]);
     }
-    cout << dp[bagWeight] << endl;
 }
-int main() {
-    test_CompletePack();
-}
-
 ```
 
-本题力扣上没有原题，大家可以去[卡码网第52题](https://kamacoder.com/problempage.php?pid=1052)去练习，题意是一样的，C++代码如下： 
+也可以 先遍历背包再遍历物品：
 
-```cpp
+```CPP  
+for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
+    for (int i = 1; i < n; i++) { // 遍历物品
+        if (j < weight[i]) dp[i][j] = dp[i - 1][j];
+        else dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]);
+    }
+}
+```
+
+### 5. 举例推导dp数组
+
+以本篇举例数据为例，填满了dp二维数组如图： 
+
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20241126113752.png)
+
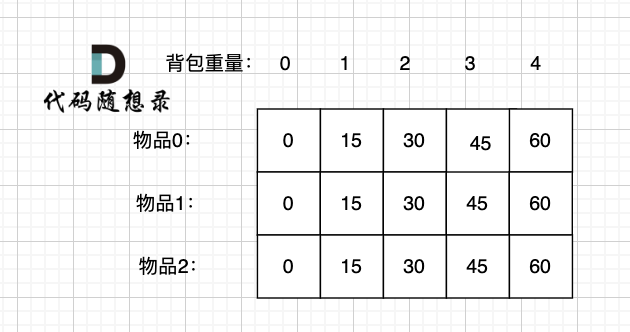
+因为 物品0 的性价比是最高的，而且 在完全背包中，每一类物品都有无限个，所以有无限个物品0，既然物品0 性价比最高，当然是优先放物品0。 
+
+
+### 本题代码：
+
+
+```CPP 
 #include <iostream>
 #include <vector>
 using namespace std;
 
-// 先遍历背包，再遍历物品
-void test_CompletePack(vector<int> weight, vector<int> value, int bagWeight) {
+int main() {
+    int n, bagWeight;
+    int w, v;
+    cin >> n >> bagWeight;
+    vector<int> weight(n);
+    vector<int> value(n);
+    for (int i = 0; i < n; i++) {
+        cin >> weight[i] >> value[i];
+    }
 
-    vector<int> dp(bagWeight + 1, 0);
+    vector<vector<int>> dp(n, vector<int>(bagWeight + 1, 0));
 
-    for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
-        for(int i = 0; i < weight.size(); i++) { // 遍历物品
-            if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
+    // 初始化
+    for (int j = weight[0]; j <= bagWeight; j++)
+        dp[0][j] = dp[0][j - weight[0]] + value[0];
+
+    for (int i = 1; i < n; i++) { // 遍历物品
+        for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
+            if (j < weight[i]) dp[i][j] = dp[i - 1][j];
+            else dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]);
         }
     }
-    cout << dp[bagWeight] << endl;
-}
-int main() {
-    int N, V;
-    cin >> N >> V;
-    vector<int> weight;
-    vector<int> value;
-    for (int i = 0; i < N; i++) {
-        int w;
-        int v;
-        cin >> w >> v;
-        weight.push_back(w);
-        value.push_back(v);
-    }
-    test_CompletePack(weight, value, V);
+
+    cout << dp[n - 1][bagWeight] << endl;
+
     return 0;
 }
+
 ```
 
-
-
-## 总结
-
-细心的同学可能发现，**全文我说的都是对于纯完全背包问题，其for循环的先后循环是可以颠倒的！**
-
-但如果题目稍稍有点变化，就会体现在遍历顺序上。
-
-如果问装满背包有几种方式的话？ 那么两个for循环的先后顺序就有很大区别了，而leetcode上的题目都是这种稍有变化的类型。
-
-这个区别，我将在后面讲解具体leetcode题目中给大家介绍，因为这块如果不结合具题目，单纯的介绍原理估计很多同学会越看越懵！
-
-别急，下一篇就是了！
-
-最后，**又可以出一道面试题了，就是纯完全背包，要求先用二维dp数组实现，然后再用一维dp数组实现，最后再问，两个for循环的先后是否可以颠倒？为什么？**
-这个简单的完全背包问题，估计就可以难住不少候选人了。
-
-
-
+关于一维dp数组，大家看这里：[完全背包一维dp数组讲解](./背包问题完全背包一维.md)
 
 ## 其他语言版本
 
-### Java：
+### Java 
 
-```java
-//先遍历物品，再遍历背包
-private static void testCompletePack(){
-    int[] weight = {1, 3, 4};
-    int[] value = {15, 20, 30};
-    int bagWeight = 4;
-    int[] dp = new int[bagWeight + 1];
-    for (int i = 0; i < weight.length; i++){ // 遍历物品
-        for (int j = weight[i]; j <= bagWeight; j++){ // 遍历背包容量
-            dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
+```Java 
+import java.util.Scanner;
+
+public class Main {
+    public static void main(String[] args) {
+        Scanner scanner = new Scanner(System.in);
+        int n = scanner.nextInt();
+        int bagWeight = scanner.nextInt();
+
+        int[] weight = new int[n];
+        int[] value = new int[n];
+
+        for (int i = 0; i < n; i++) {
+            weight[i] = scanner.nextInt();
+            value[i] = scanner.nextInt();
         }
-    }
-    for (int maxValue : dp){
-        System.out.println(maxValue + "   ");
-    }
-}
 
-//先遍历背包，再遍历物品
-private static void testCompletePackAnotherWay(){
-    int[] weight = {1, 3, 4};
-    int[] value = {15, 20, 30};
-    int bagWeight = 4;
-    int[] dp = new int[bagWeight + 1];
-    for (int i = 1; i <= bagWeight; i++){ // 遍历背包容量
-        for (int j = 0; j < weight.length; j++){ // 遍历物品
-            if (i - weight[j] >= 0){
-                dp[i] = Math.max(dp[i], dp[i - weight[j]] + value[j]);
-            }
+        int[][] dp = new int[n][bagWeight + 1];
+
+        // 初始化
+        for (int j = weight[0]; j <= bagWeight; j++) {
+            dp[0][j] = dp[0][j - weight[0]] + value[0];
         }
-    }
-    for (int maxValue : dp){
-        System.out.println(maxValue + "   ");
-    }
-}
-```
 
-
-
-### Python：
-
-先遍历物品，再遍历背包（无参版）
-```python
-def test_CompletePack():
-    weight = [1, 3, 4]
-    value = [15, 20, 30]
-    bagWeight = 4
-    dp = [0] * (bagWeight + 1)
-    for i in range(len(weight)):  # 遍历物品
-        for j in range(weight[i], bagWeight + 1):  # 遍历背包容量
-            dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
-    print(dp[bagWeight])
-
-test_CompletePack()
-
-```
-
-先遍历物品，再遍历背包（有参版）
-```python
-def test_CompletePack(weight, value, bagWeight):
-    dp = [0] * (bagWeight + 1)
-    for i in range(len(weight)):  # 遍历物品
-        for j in range(weight[i], bagWeight + 1):  # 遍历背包容量
-            dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
-    return dp[bagWeight]
-
-if __name__ == "__main__":
-    weight = [1, 3, 4]
-    value = [15, 20, 30]
-    bagWeight = 4
-    result = test_CompletePack(weight, value, bagWeight)
-    print(result)
-
-```
-先遍历背包，再遍历物品（无参版）
-```python
-def test_CompletePack():
-    weight = [1, 3, 4]
-    value = [15, 20, 30]
-    bagWeight = 4
-
-    dp = [0] * (bagWeight + 1)
-
-    for j in range(bagWeight + 1):  # 遍历背包容量
-        for i in range(len(weight)):  # 遍历物品
-            if j - weight[i] >= 0:
-                dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
-
-    print(dp[bagWeight])
-
-test_CompletePack()
-
-
-```
-
-先遍历背包，再遍历物品（有参版）
-```python
-def test_CompletePack(weight, value, bagWeight):
-    dp = [0] * (bagWeight + 1)
-    for j in range(bagWeight + 1):  # 遍历背包容量
-        for i in range(len(weight)):  # 遍历物品
-            if j - weight[i] >= 0:
-                dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
-    return dp[bagWeight]
-
-
-if __name__ == "__main__":
-    weight = [1, 3, 4]
-    value = [15, 20, 30]
-    bagWeight = 4
-    result = test_CompletePack(weight, value, bagWeight)
-    print(result)
-
-```
-
-### Go：
-
-```go
-
-// test_CompletePack1 先遍历物品, 在遍历背包
-func test_CompletePack1(weight, value []int, bagWeight int) int {
-	// 定义dp数组 和初始化
-	dp := make([]int, bagWeight+1)
-	// 遍历顺序
-	for i := 0; i < len(weight); i++ {
-		// 正序会多次添加 value[i]
-		for j := weight[i]; j <= bagWeight; j++ {
-			// 推导公式
-			dp[j] = max(dp[j], dp[j-weight[i]]+value[i])
-			// debug
-			//fmt.Println(dp)
-		}
-	}
-	return dp[bagWeight]
-}
-
-// test_CompletePack2 先遍历背包, 在遍历物品
-func test_CompletePack2(weight, value []int, bagWeight int) int {
-	// 定义dp数组 和初始化
-	dp := make([]int, bagWeight+1)
-	// 遍历顺序
-	// j从0 开始
-	for j := 0; j <= bagWeight; j++ {
-		for i := 0; i < len(weight); i++ {
-			if j >= weight[i] {
-				// 推导公式
-				dp[j] = max(dp[j], dp[j-weight[i]]+value[i])
-			}
-			// debug
-			//fmt.Println(dp)
-		}
-	}
-	return dp[bagWeight]
-}
-
-func max(a, b int) int {
-	if a > b {
-		return a
-	}
-	return b
-}
-
-func main() {
-	weight := []int{1, 3, 4}
-	price := []int{15, 20, 30}
-	fmt.Println(test_CompletePack1(weight, price, 4))
-	fmt.Println(test_CompletePack2(weight, price, 4))
-}
-```
-### JavaScript:
-
-```Javascript
-// 先遍历物品，再遍历背包容量
-function test_completePack1() {
-    let weight = [1, 3, 5]
-    let value = [15, 20, 30]
-    let bagWeight = 4 
-    let dp = new Array(bagWeight + 1).fill(0)
-    for(let i = 0; i <= weight.length; i++) {
-        for(let j = weight[i]; j <= bagWeight; j++) {
-            dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i])
-        }
-    }
-    console.log(dp)
-}
-
-// 先遍历背包容量，再遍历物品
-function test_completePack2() {
-    let weight = [1, 3, 5]
-    let value = [15, 20, 30]
-    let bagWeight = 4 
-    let dp = new Array(bagWeight + 1).fill(0)
-    for(let j = 0; j <= bagWeight; j++) {
-        for(let i = 0; i < weight.length; i++) {
-            if (j >= weight[i]) {
-                dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i])
-            }
-        }
-    }
-    console.log(2, dp);
-}
-```
-
-### TypeScript：
-
-```typescript
-// 先遍历物品，再遍历背包容量
-function test_CompletePack(): void {
-  const weight: number[] = [1, 3, 4];
-  const value: number[] = [15, 20, 30];
-  const bagSize: number = 4;
-  const dp: number[] = new Array(bagSize + 1).fill(0);
-  for (let i = 0; i < weight.length; i++) {
-    for (let j = weight[i]; j <= bagSize; j++) {
-      dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
-    }
-  }
-  console.log(dp);
-}
-test_CompletePack();
-```
-
-### Scala:
-
-```scala
-// 先遍历物品，再遍历背包容量
-object Solution {
-  def test_CompletePack() {
-    var weight = Array[Int](1, 3, 4)
-    var value = Array[Int](15, 20, 30)
-    var baseweight = 4
-
-    var dp = new Array[Int](baseweight + 1)
-
-    for (i <- 0 until weight.length) {
-      for (j <- weight(i) to baseweight) {
-        dp(j) = math.max(dp(j), dp(j - weight(i)) + value(i))
-      }
-    }
-    dp(baseweight)
-  }
-}
-```
-
-### Rust:
-
-```rust
-impl Solution {
-    // 先遍历物品
-    fn complete_pack() {
-        let (goods, bag_size) = (vec![(1, 15), (3, 20), (4, 30)], 4);
-        let mut dp = vec![0; bag_size + 1];
-        for (weight, value) in goods {
-            for j in weight..=bag_size {
-                dp[j] = dp[j].max(dp[j - weight] + value);
-            }
-        }
-        println!("先遍历物品：{}", dp[bag_size]);
-    }
-
-    // 先遍历背包
-    fn complete_pack_after() {
-        let (goods, bag_size) = (vec![(1, 15), (3, 20), (4, 30)], 4);
-        let mut dp = vec![0; bag_size + 1];
-        for i in 0..=bag_size {
-            for (weight, value) in &goods {
-                if i >= *weight {
-                    dp[i] = dp[i].max(dp[i - weight] + value);
+        // 动态规划
+        for (int i = 1; i < n; i++) {
+            for (int j = 0; j <= bagWeight; j++) {
+                if (j < weight[i]) {
+                    dp[i][j] = dp[i - 1][j];
+                } else {
+                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]);
                 }
             }
         }
-        println!("先遍历背包：{}", dp[bag_size]);
+
+        System.out.println(dp[n - 1][bagWeight]);
+        scanner.close();
     }
 }
 
-#[test]
-fn test_complete_pack() {
-    Solution::complete_pack();
-    Solution::complete_pack_after();
-}
 ```
 
+### Go 
+
+### Python 
+
+```python 
+def knapsack(n, bag_weight, weight, value):
+    dp = [[0] * (bag_weight + 1) for _ in range(n)]
+
+    # 初始化
+    for j in range(weight[0], bag_weight + 1):
+        dp[0][j] = dp[0][j - weight[0]] + value[0]
+
+    # 动态规划
+    for i in range(1, n):
+        for j in range(bag_weight + 1):
+            if j < weight[i]:
+                dp[i][j] = dp[i - 1][j]
+            else:
+                dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i])
+
+    return dp[n - 1][bag_weight]
+
+# 输入
+n, bag_weight = map(int, input().split())
+weight = []
+value = []
+for _ in range(n):
+    w, v = map(int, input().split())
+    weight.append(w)
+    value.append(v)
+
+# 输出结果
+print(knapsack(n, bag_weight, weight, value))
+
+```
+
+### JavaScript
+
+
 
 <p align="center">
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">