mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-14 15:00:42 +08:00
Merge branch 'youngyangyang04:master' into master
This commit is contained in:
@ -66,7 +66,7 @@
|
||||
|
||||
**这里每一篇题解,都是精品,值得仔细琢磨**。
|
||||
|
||||
我在题目讲解中统一使用C++,但你会发现下面几乎每篇题解都配有其他语言版本,Java、Python、Go、JavaScript等等,正是这些[热心小伙们](https://github.com/youngyangyang04/leetcode-master/graphs/contributors)的贡献的代码,当然我也会严格把控代码质量。
|
||||
我在题目讲解中统一使用C++,但你会发现下面几乎每篇题解都配有其他语言版本,Java、Python、Go、JavaScript等等,正是这些[热心小伙们](https://github.com/youngyangyang04/leetcode-master/graphs/contributors)贡献的代码,当然我也会严格把控代码质量。
|
||||
|
||||
**所以也欢迎大家参与进来,完善题解的各个语言版本,拥抱开源,让更多小伙伴们受益**。
|
||||
|
||||
|
||||
@ -444,6 +444,8 @@ public:
|
||||
};
|
||||
|
||||
```
|
||||
* 时间复杂度: O(n + m)
|
||||
* 空间复杂度: O(m), 只需要保存字符串needle的前缀表
|
||||
|
||||
# 前缀表(不减一)C++实现
|
||||
|
||||
@ -540,6 +542,9 @@ public:
|
||||
}
|
||||
};
|
||||
```
|
||||
* 时间复杂度: O(n + m)
|
||||
* 空间复杂度: O(m)
|
||||
|
||||
|
||||
# 总结
|
||||
|
||||
|
||||
@ -4,10 +4,9 @@
|
||||
</a>
|
||||
<p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||||
|
||||
|
||||
> 相对于[贪心算法:跳跃游戏](https://mp.weixin.qq.com/s/606_N9j8ACKCODoCbV1lSA)难了不少,做好心里准备!
|
||||
|
||||
# 45.跳跃游戏II
|
||||
# 45.跳跃游戏 II
|
||||
|
||||
[力扣题目链接](https://leetcode.cn/problems/jump-game-ii/)
|
||||
|
||||
@ -18,13 +17,17 @@
|
||||
你的目标是使用最少的跳跃次数到达数组的最后一个位置。
|
||||
|
||||
示例:
|
||||
* 输入: [2,3,1,1,4]
|
||||
* 输出: 2
|
||||
* 解释: 跳到最后一个位置的最小跳跃数是 2。从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
|
||||
|
||||
- 输入: [2,3,1,1,4]
|
||||
- 输出: 2
|
||||
- 解释: 跳到最后一个位置的最小跳跃数是 2。从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
|
||||
|
||||
说明:
|
||||
假设你总是可以到达数组的最后一个位置。
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[贪心算法,最少跳几步还得看覆盖范围 | LeetCode: 45.跳跃游戏 II](https://www.bilibili.com/video/BV1Y24y1r7XZ),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
## 思路
|
||||
|
||||
@ -46,7 +49,6 @@
|
||||
|
||||
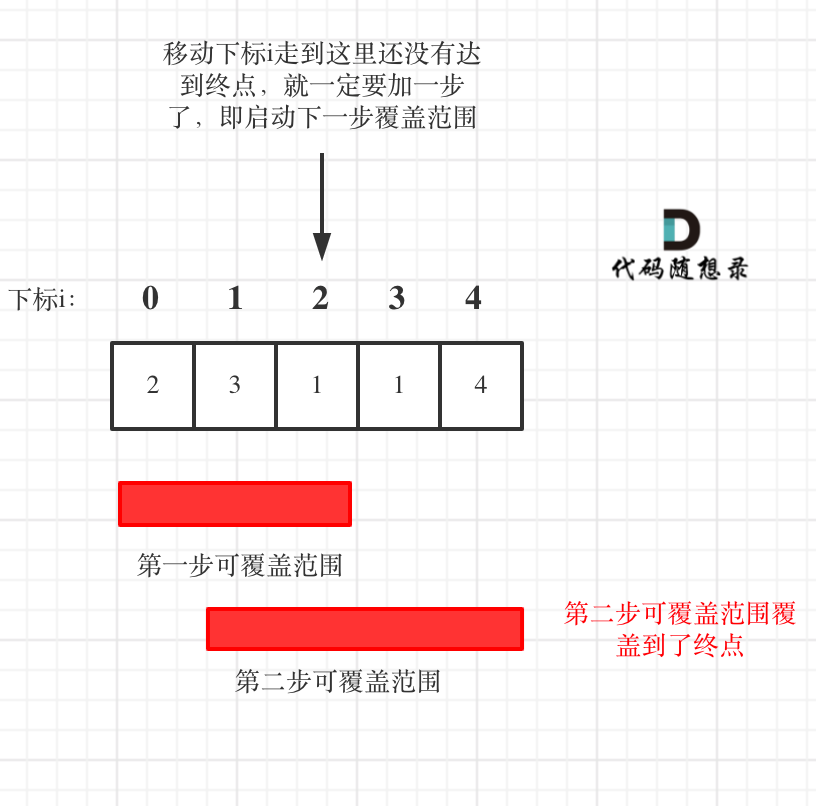
如图:
|
||||
|
||||
|
||||
|
||||
|
||||
**图中覆盖范围的意义在于,只要红色的区域,最多两步一定可以到!(不用管具体怎么跳,反正一定可以跳到)**
|
||||
@ -57,8 +59,8 @@
|
||||
|
||||
这里还是有个特殊情况需要考虑,当移动下标达到了当前覆盖的最远距离下标时
|
||||
|
||||
* 如果当前覆盖最远距离下标不是是集合终点,步数就加一,还需要继续走。
|
||||
* 如果当前覆盖最远距离下标就是是集合终点,步数不用加一,因为不能再往后走了。
|
||||
- 如果当前覆盖最远距离下标不是是集合终点,步数就加一,还需要继续走。
|
||||
- 如果当前覆盖最远距离下标就是是集合终点,步数不用加一,因为不能再往后走了。
|
||||
|
||||
C++代码如下:(详细注释)
|
||||
|
||||
@ -92,14 +94,14 @@ public:
|
||||
|
||||
**针对于方法一的特殊情况,可以统一处理**,即:移动下标只要遇到当前覆盖最远距离的下标,直接步数加一,不考虑是不是终点的情况。
|
||||
|
||||
想要达到这样的效果,只要让移动下标,最大只能移动到nums.size - 2的地方就可以了。
|
||||
想要达到这样的效果,只要让移动下标,最大只能移动到 nums.size - 2 的地方就可以了。
|
||||
|
||||
因为当移动下标指向nums.size - 2时:
|
||||
因为当移动下标指向 nums.size - 2 时:
|
||||
|
||||
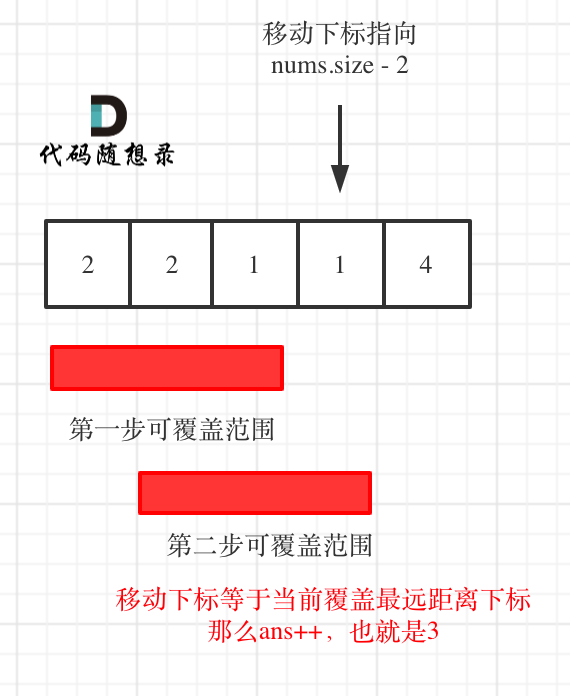
* 如果移动下标等于当前覆盖最大距离下标, 需要再走一步(即ans++),因为最后一步一定是可以到的终点。(题目假设总是可以到达数组的最后一个位置),如图:
|
||||
|
||||
- 如果移动下标等于当前覆盖最大距离下标, 需要再走一步(即 ans++),因为最后一步一定是可以到的终点。(题目假设总是可以到达数组的最后一个位置),如图:
|
||||

|
||||
|
||||
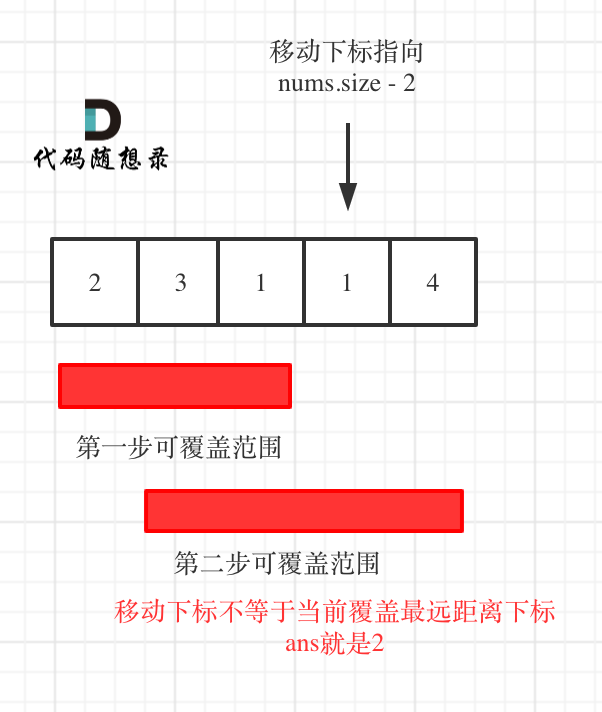
* 如果移动下标不等于当前覆盖最大距离下标,说明当前覆盖最远距离就可以直接达到终点了,不需要再走一步。如图:
|
||||
- 如果移动下标不等于当前覆盖最大距离下标,说明当前覆盖最远距离就可以直接达到终点了,不需要再走一步。如图:
|
||||
|
||||
|
||||
|
||||
@ -127,7 +129,7 @@ public:
|
||||
|
||||
可以看出版本二的代码相对于版本一简化了不少!
|
||||
|
||||
**其精髓在于控制移动下标i只移动到nums.size() - 2的位置**,所以移动下标只要遇到当前覆盖最远距离的下标,直接步数加一,不用考虑别的了。
|
||||
**其精髓在于控制移动下标 i 只移动到 nums.size() - 2 的位置**,所以移动下标只要遇到当前覆盖最远距离的下标,直接步数加一,不用考虑别的了。
|
||||
|
||||
## 总结
|
||||
|
||||
@ -137,11 +139,10 @@ public:
|
||||
|
||||
理解本题的关键在于:**以最小的步数增加最大的覆盖范围,直到覆盖范围覆盖了终点**,这个范围内最小步数一定可以跳到,不用管具体是怎么跳的,不纠结于一步究竟跳一个单位还是两个单位。
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
|
||||
### Java
|
||||
|
||||
```Java
|
||||
// 版本一
|
||||
class Solution {
|
||||
@ -230,6 +231,7 @@ class Solution:
|
||||
step += 1
|
||||
return step
|
||||
```
|
||||
|
||||
```python
|
||||
# 动态规划做法
|
||||
class Solution:
|
||||
@ -244,7 +246,6 @@ class Solution:
|
||||
|
||||
```
|
||||
|
||||
|
||||
### Go
|
||||
|
||||
```go
|
||||
@ -345,7 +346,7 @@ function jump(nums: number[]): number {
|
||||
curIndex++;
|
||||
}
|
||||
return stepNum;
|
||||
};
|
||||
}
|
||||
```
|
||||
|
||||
### Scala
|
||||
@ -379,23 +380,25 @@ object Solution {
|
||||
```Rust
|
||||
//版本一
|
||||
impl Solution {
|
||||
fn max(a: i32, b:i32) -> i32 {
|
||||
if a > b { a } else { b }
|
||||
}
|
||||
pub fn jump(nums: Vec<i32>) -> i32 {
|
||||
if nums.len() == 0 { return 0; }
|
||||
let mut cur_distance: i32 = 0;
|
||||
let mut ans: i32 = 0;
|
||||
let mut next_distance: i32 = 0;
|
||||
for i in 0..nums.len() {
|
||||
next_distance = Self::max(nums[i] + i as i32, next_distance);
|
||||
if i as i32 == cur_distance {
|
||||
if cur_distance != (nums.len() - 1) as i32 {
|
||||
if nums.len() == 1 {
|
||||
return 0;
|
||||
}
|
||||
let mut cur_distance = 0;
|
||||
let mut ans = 0;
|
||||
let mut next_distance = 0;
|
||||
for (i, &n) in nums.iter().enumerate().take(nums.len() - 1) {
|
||||
next_distance = (n as usize + i).max(next_distance);
|
||||
if i == cur_distance {
|
||||
if cur_distance < nums.len() - 1 {
|
||||
ans += 1;
|
||||
cur_distance = next_distance;
|
||||
if next_distance == (nums.len() - 1) as i32 { break; }
|
||||
if next_distance >= nums.len() - 1 {
|
||||
break;
|
||||
};
|
||||
} else {
|
||||
break;
|
||||
}
|
||||
else { break; }
|
||||
}
|
||||
}
|
||||
ans
|
||||
@ -406,16 +409,16 @@ impl Solution {
|
||||
```Rust
|
||||
//版本二
|
||||
impl Solution {
|
||||
fn max(a: i32, b:i32) -> i32 {
|
||||
if a > b { a } else { b }
|
||||
}
|
||||
pub fn jump(nums: Vec<i32>) -> i32 {
|
||||
let mut cur_distance: i32 = 0;
|
||||
let mut ans: i32 = 0;
|
||||
let mut next_distance: i32 = 0;
|
||||
for i in 0..nums.len() - 1 {
|
||||
next_distance = Self::max(nums[i] + i as i32, next_distance);
|
||||
if i as i32 == cur_distance {
|
||||
if nums.len() == 1 {
|
||||
return 0;
|
||||
}
|
||||
let mut cur_distance = 0;
|
||||
let mut ans = 0;
|
||||
let mut next_distance = 0;
|
||||
for (i, &n) in nums.iter().enumerate().take(nums.len() - 1) {
|
||||
next_distance = (n as usize + i).max(next_distance);
|
||||
if i == cur_distance {
|
||||
cur_distance = next_distance;
|
||||
ans += 1;
|
||||
}
|
||||
@ -425,7 +428,6 @@ impl Solution {
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
<p align="center">
|
||||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||||
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>
|
||||
|
||||
@ -4,7 +4,6 @@
|
||||
</a>
|
||||
<p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||||
|
||||
|
||||
# 53. 最大子序和
|
||||
|
||||
[力扣题目链接](https://leetcode.cn/problems/maximum-subarray/)
|
||||
@ -12,17 +11,21 @@
|
||||
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
|
||||
|
||||
示例:
|
||||
* 输入: [-2,1,-3,4,-1,2,1,-5,4]
|
||||
* 输出: 6
|
||||
* 解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
|
||||
|
||||
- 输入: [-2,1,-3,4,-1,2,1,-5,4]
|
||||
- 输出: 6
|
||||
- 解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[贪心算法的巧妙需要慢慢体会!LeetCode:53. 最大子序和](https://www.bilibili.com/video/BV1aY4y1Z7ya),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
## 暴力解法
|
||||
|
||||
暴力解法的思路,第一层for 就是设置起始位置,第二层for循环遍历数组寻找最大值
|
||||
暴力解法的思路,第一层 for 就是设置起始位置,第二层 for 循环遍历数组寻找最大值
|
||||
|
||||
* 时间复杂度:O(n^2)
|
||||
* 空间复杂度:O(1)
|
||||
- 时间复杂度:O(n^2)
|
||||
- 空间复杂度:O(1)
|
||||
|
||||
```CPP
|
||||
class Solution {
|
||||
@ -42,13 +45,13 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
以上暴力的解法C++勉强可以过,其他语言就不确定了。
|
||||
以上暴力的解法 C++勉强可以过,其他语言就不确定了。
|
||||
|
||||
## 贪心解法
|
||||
|
||||
**贪心贪的是哪里呢?**
|
||||
|
||||
如果 -2 1 在一起,计算起点的时候,一定是从1开始计算,因为负数只会拉低总和,这就是贪心贪的地方!
|
||||
如果 -2 1 在一起,计算起点的时候,一定是从 1 开始计算,因为负数只会拉低总和,这就是贪心贪的地方!
|
||||
|
||||
局部最优:当前“连续和”为负数的时候立刻放弃,从下一个元素重新计算“连续和”,因为负数加上下一个元素 “连续和”只会越来越小。
|
||||
|
||||
@ -56,29 +59,27 @@ public:
|
||||
|
||||
**局部最优的情况下,并记录最大的“连续和”,可以推出全局最优**。
|
||||
|
||||
|
||||
从代码角度上来讲:遍历nums,从头开始用count累积,如果count一旦加上nums[i]变为负数,那么就应该从nums[i+1]开始从0累积count了,因为已经变为负数的count,只会拖累总和。
|
||||
从代码角度上来讲:遍历 nums,从头开始用 count 累积,如果 count 一旦加上 nums[i]变为负数,那么就应该从 nums[i+1]开始从 0 累积 count 了,因为已经变为负数的 count,只会拖累总和。
|
||||
|
||||
**这相当于是暴力解法中的不断调整最大子序和区间的起始位置**。
|
||||
|
||||
|
||||
**那有同学问了,区间终止位置不用调整么? 如何才能得到最大“连续和”呢?**
|
||||
|
||||
区间的终止位置,其实就是如果count取到最大值了,及时记录下来了。例如如下代码:
|
||||
区间的终止位置,其实就是如果 count 取到最大值了,及时记录下来了。例如如下代码:
|
||||
|
||||
```
|
||||
if (count > result) result = count;
|
||||
```
|
||||
|
||||
**这样相当于是用result记录最大子序和区间和(变相的算是调整了终止位置)**。
|
||||
**这样相当于是用 result 记录最大子序和区间和(变相的算是调整了终止位置)**。
|
||||
|
||||
如动画所示:
|
||||
|
||||

|
||||
|
||||
红色的起始位置就是贪心每次取count为正数的时候,开始一个区间的统计。
|
||||
红色的起始位置就是贪心每次取 count 为正数的时候,开始一个区间的统计。
|
||||
|
||||
那么不难写出如下C++代码(关键地方已经注释)
|
||||
那么不难写出如下 C++代码(关键地方已经注释)
|
||||
|
||||
```CPP
|
||||
class Solution {
|
||||
@ -98,18 +99,16 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度:O(n)
|
||||
* 空间复杂度:O(1)
|
||||
- 时间复杂度:O(n)
|
||||
- 空间复杂度:O(1)
|
||||
|
||||
当然题目没有说如果数组为空,应该返回什么,所以数组为空的话返回啥都可以了。
|
||||
|
||||
|
||||
## 常见误区
|
||||
|
||||
误区一:
|
||||
|
||||
不少同学认为 如果输入用例都是-1,或者 都是负数,这个贪心算法跑出来的结果是0, 这是**又一次证明脑洞模拟不靠谱的经典案例**,建议大家把代码运行一下试一试,就知道了,也会理解 为什么 result 要初始化为最小负数了。
|
||||
|
||||
不少同学认为 如果输入用例都是-1,或者 都是负数,这个贪心算法跑出来的结果是 0, 这是**又一次证明脑洞模拟不靠谱的经典案例**,建议大家把代码运行一下试一试,就知道了,也会理解 为什么 result 要初始化为最小负数了。
|
||||
|
||||
误区二:
|
||||
|
||||
@ -117,19 +116,17 @@ public:
|
||||
|
||||
在动画演示用,大家可以发现, 4,遇到 -1 的时候,我们依然累加了,为什么呢?
|
||||
|
||||
因为和为3,只要连续和还是正数就会 对后面的元素 起到增大总和的作用。 所以只要连续和为正数我们就保留。
|
||||
因为和为 3,只要连续和还是正数就会 对后面的元素 起到增大总和的作用。 所以只要连续和为正数我们就保留。
|
||||
|
||||
这里也会有录友疑惑,那 4 + -1 之后 不就变小了吗? 会不会错过 4 成为最大连续和的可能性?
|
||||
|
||||
其实并不会,因为还有一个变量result 一直在更新 最大的连续和,只要有更大的连续和出现,result就更新了,那么result已经把4更新了,后面 连续和变成3,也不会对最后结果有影响。
|
||||
|
||||
|
||||
其实并不会,因为还有一个变量 result 一直在更新 最大的连续和,只要有更大的连续和出现,result 就更新了,那么 result 已经把 4 更新了,后面 连续和变成 3,也不会对最后结果有影响。
|
||||
|
||||
## 动态规划
|
||||
|
||||
当然本题还可以用动态规划来做,当前[「代码随想录」](https://img-blog.csdnimg.cn/20201124161234338.png)主要讲解贪心系列,后续到动态规划系列的时候会详细讲解本题的dp方法。
|
||||
当然本题还可以用动态规划来做,当前[「代码随想录」](https://img-blog.csdnimg.cn/20201124161234338.png)主要讲解贪心系列,后续到动态规划系列的时候会详细讲解本题的 dp 方法。
|
||||
|
||||
那么先给出我的dp代码如下,有时间的录友可以提前做一做:
|
||||
那么先给出我的 dp 代码如下,有时间的录友可以提前做一做:
|
||||
|
||||
```CPP
|
||||
class Solution {
|
||||
@ -148,8 +145,8 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度:O(n)
|
||||
* 空间复杂度:O(n)
|
||||
- 时间复杂度:O(n)
|
||||
- 空间复杂度:O(n)
|
||||
|
||||
## 总结
|
||||
|
||||
@ -159,8 +156,8 @@ public:
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
|
||||
### Java
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
public int maxSubArray(int[] nums) {
|
||||
@ -201,6 +198,7 @@ class Solution {
|
||||
```
|
||||
|
||||
### Python
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
def maxSubArray(self, nums: List[int]) -> int:
|
||||
@ -233,6 +231,7 @@ func maxSubArray(nums []int) int {
|
||||
```
|
||||
|
||||
### Rust
|
||||
|
||||
```rust
|
||||
pub fn max_sub_array(nums: Vec<i32>) -> i32 {
|
||||
let mut max_sum = i32::MIN;
|
||||
@ -247,6 +246,7 @@ pub fn max_sub_array(nums: Vec<i32>) -> i32 {
|
||||
```
|
||||
|
||||
### Javascript:
|
||||
|
||||
```Javascript
|
||||
var maxSubArray = function(nums) {
|
||||
let result = -Infinity
|
||||
@ -264,9 +264,10 @@ var maxSubArray = function(nums) {
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
### C:
|
||||
|
||||
贪心:
|
||||
|
||||
```c
|
||||
int maxSubArray(int* nums, int numsSize){
|
||||
int maxVal = INT_MIN;
|
||||
@ -286,6 +287,7 @@ int maxSubArray(int* nums, int numsSize){
|
||||
```
|
||||
|
||||
动态规划:
|
||||
|
||||
```c
|
||||
/**
|
||||
* 解题思路:动态规划:
|
||||
@ -332,7 +334,7 @@ function maxSubArray(nums: number[]): number {
|
||||
if (curSum < 0) curSum = 0;
|
||||
}
|
||||
return resMax;
|
||||
};
|
||||
}
|
||||
```
|
||||
|
||||
**动态规划**
|
||||
@ -350,7 +352,7 @@ function maxSubArray(nums: number[]): number {
|
||||
resMax = Math.max(resMax, dp[i]);
|
||||
}
|
||||
return resMax;
|
||||
};
|
||||
}
|
||||
```
|
||||
|
||||
### Scala
|
||||
|
||||
@ -4,7 +4,6 @@
|
||||
</a>
|
||||
<p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||||
|
||||
|
||||
# 55. 跳跃游戏
|
||||
|
||||
[力扣题目链接](https://leetcode.cn/problems/jump-game/)
|
||||
@ -15,20 +14,25 @@
|
||||
|
||||
判断你是否能够到达最后一个位置。
|
||||
|
||||
示例 1:
|
||||
* 输入: [2,3,1,1,4]
|
||||
* 输出: true
|
||||
* 解释: 我们可以先跳 1 步,从位置 0 到达 位置 1, 然后再从位置 1 跳 3 步到达最后一个位置。
|
||||
示例 1:
|
||||
|
||||
示例 2:
|
||||
* 输入: [3,2,1,0,4]
|
||||
* 输出: false
|
||||
* 解释: 无论怎样,你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 , 所以你永远不可能到达最后一个位置。
|
||||
- 输入: [2,3,1,1,4]
|
||||
- 输出: true
|
||||
- 解释: 我们可以先跳 1 步,从位置 0 到达 位置 1, 然后再从位置 1 跳 3 步到达最后一个位置。
|
||||
|
||||
示例 2:
|
||||
|
||||
- 输入: [3,2,1,0,4]
|
||||
- 输出: false
|
||||
- 解释: 无论怎样,你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 , 所以你永远不可能到达最后一个位置。
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[贪心算法,怎么跳跃不重要,关键在覆盖范围 | LeetCode:55.跳跃游戏](https://www.bilibili.com/video/BV1VG4y1X7kB),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
## 思路
|
||||
|
||||
刚看到本题一开始可能想:当前位置元素如果是3,我究竟是跳一步呢,还是两步呢,还是三步呢,究竟跳几步才是最优呢?
|
||||
刚看到本题一开始可能想:当前位置元素如果是 3,我究竟是跳一步呢,还是两步呢,还是三步呢,究竟跳几步才是最优呢?
|
||||
|
||||
其实跳几步无所谓,关键在于可跳的覆盖范围!
|
||||
|
||||
@ -46,14 +50,13 @@
|
||||
|
||||
如图:
|
||||
|
||||
|
||||

|
||||
|
||||
i每次移动只能在cover的范围内移动,每移动一个元素,cover得到该元素数值(新的覆盖范围)的补充,让i继续移动下去。
|
||||
i 每次移动只能在 cover 的范围内移动,每移动一个元素,cover 得到该元素数值(新的覆盖范围)的补充,让 i 继续移动下去。
|
||||
|
||||
而cover每次只取 max(该元素数值补充后的范围, cover本身范围)。
|
||||
而 cover 每次只取 max(该元素数值补充后的范围, cover 本身范围)。
|
||||
|
||||
如果cover大于等于了终点下标,直接return true就可以了。
|
||||
如果 cover 大于等于了终点下标,直接 return true 就可以了。
|
||||
|
||||
C++代码如下:
|
||||
|
||||
@ -71,6 +74,7 @@ public:
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
## 总结
|
||||
|
||||
这道题目关键点在于:不用拘泥于每次究竟跳几步,而是看覆盖范围,覆盖范围内一定是可以跳过来的,不用管是怎么跳的。
|
||||
@ -83,8 +87,8 @@ public:
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
|
||||
### Java
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
public boolean canJump(int[] nums) {
|
||||
@ -106,6 +110,7 @@ class Solution {
|
||||
```
|
||||
|
||||
### Python
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
def canJump(self, nums: List[int]) -> bool:
|
||||
@ -156,8 +161,6 @@ func max(a, b int ) int {
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
### Javascript
|
||||
|
||||
```Javascript
|
||||
@ -196,6 +199,7 @@ impl Solution {
|
||||
```
|
||||
|
||||
### C
|
||||
|
||||
```c
|
||||
#define max(a, b) (((a) > (b)) ? (a) : (b))
|
||||
|
||||
@ -217,7 +221,6 @@ bool canJump(int* nums, int numsSize){
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
### TypeScript
|
||||
|
||||
```typescript
|
||||
@ -230,10 +233,11 @@ function canJump(nums: number[]): boolean {
|
||||
cur++;
|
||||
}
|
||||
return false;
|
||||
};
|
||||
}
|
||||
```
|
||||
|
||||
### Scala
|
||||
|
||||
```scala
|
||||
object Solution {
|
||||
def canJump(nums: Array[Int]): Boolean = {
|
||||
@ -250,7 +254,6 @@ object Solution {
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
<p align="center">
|
||||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||||
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>
|
||||
|
||||
@ -22,6 +22,9 @@
|
||||
* 解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。
|
||||
* 注意:输入类型已于2019年4月15日更改。 请重置默认代码定义以获取新方法签名。
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[贪心算法,合并区间有细节!LeetCode:56.合并区间](https://www.bilibili.com/video/BV1wx4y157nD),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
## 思路
|
||||
|
||||
|
||||
@ -475,6 +475,12 @@ class solution:
|
||||
return false # 别忘记处理空treenode
|
||||
else:
|
||||
return isornot(root, targetsum - root.val)
|
||||
|
||||
class Solution: # 简洁版
|
||||
def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
|
||||
if not root: return False
|
||||
if root.left==root.right==None and root.val == targetSum: return True
|
||||
return self.hasPathSum(root.left,targetSum-root.val) or self.hasPathSum(root.right,targetSum-root.val)
|
||||
```
|
||||
|
||||
**迭代 - 层序遍历**
|
||||
@ -560,6 +566,26 @@ class Solution:
|
||||
return result
|
||||
```
|
||||
|
||||
**迭代法,前序遍历**
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:
|
||||
if not root: return []
|
||||
stack, path_stack,result = [[root,root.val]],[[root.val]],[]
|
||||
while stack:
|
||||
cur,cursum = stack.pop()
|
||||
path = path_stack.pop()
|
||||
if cur.left==cur.right==None:
|
||||
if cursum==targetSum: result.append(path)
|
||||
if cur.right:
|
||||
stack.append([cur.right,cursum+cur.right.val])
|
||||
path_stack.append(path+[cur.right.val])
|
||||
if cur.left:
|
||||
stack.append([cur.left,cursum+cur.left.val])
|
||||
path_stack.append(path+[cur.left.val])
|
||||
return result
|
||||
```
|
||||
## go
|
||||
|
||||
### 112. 路径总和
|
||||
|
||||
@ -4,43 +4,49 @@
|
||||
</a>
|
||||
<p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||||
|
||||
|
||||
# 122.买卖股票的最佳时机II
|
||||
# 122.买卖股票的最佳时机 II
|
||||
|
||||
[力扣题目链接](https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-ii/)
|
||||
|
||||
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
|
||||
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
|
||||
|
||||
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
|
||||
|
||||
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
|
||||
|
||||
|
||||
示例 1:
|
||||
* 输入: [7,1,5,3,6,4]
|
||||
* 输出: 7
|
||||
* 解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4。随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
|
||||
|
||||
- 输入: [7,1,5,3,6,4]
|
||||
- 输出: 7
|
||||
- 解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4。随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
|
||||
|
||||
示例 2:
|
||||
* 输入: [1,2,3,4,5]
|
||||
* 输出: 4
|
||||
* 解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
|
||||
|
||||
示例 3:
|
||||
* 输入: [7,6,4,3,1]
|
||||
* 输出: 0
|
||||
* 解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
|
||||
- 输入: [1,2,3,4,5]
|
||||
- 输出: 4
|
||||
- 解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
|
||||
|
||||
示例 3:
|
||||
|
||||
- 输入: [7,6,4,3,1]
|
||||
- 输出: 0
|
||||
- 解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
|
||||
|
||||
提示:
|
||||
* 1 <= prices.length <= 3 * 10 ^ 4
|
||||
* 0 <= prices[i] <= 10 ^ 4
|
||||
|
||||
- 1 <= prices.length <= 3 \* 10 ^ 4
|
||||
- 0 <= prices[i] <= 10 ^ 4
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[贪心算法也能解决股票问题!LeetCode:122.买卖股票最佳时机 II](https://www.bilibili.com/video/BV1ev4y1C7na),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
## 思路
|
||||
|
||||
本题首先要清楚两点:
|
||||
|
||||
* 只有一只股票!
|
||||
* 当前只有买股票或者卖股票的操作
|
||||
- 只有一只股票!
|
||||
- 当前只有买股票或者卖股票的操作
|
||||
|
||||
想获得利润至少要两天为一个交易单元。
|
||||
|
||||
@ -52,17 +58,16 @@
|
||||
|
||||
如何分解呢?
|
||||
|
||||
假如第0天买入,第3天卖出,那么利润为:prices[3] - prices[0]。
|
||||
假如第 0 天买入,第 3 天卖出,那么利润为:prices[3] - prices[0]。
|
||||
|
||||
相当于(prices[3] - prices[2]) + (prices[2] - prices[1]) + (prices[1] - prices[0])。
|
||||
|
||||
**此时就是把利润分解为每天为单位的维度,而不是从0天到第3天整体去考虑!**
|
||||
**此时就是把利润分解为每天为单位的维度,而不是从 0 天到第 3 天整体去考虑!**
|
||||
|
||||
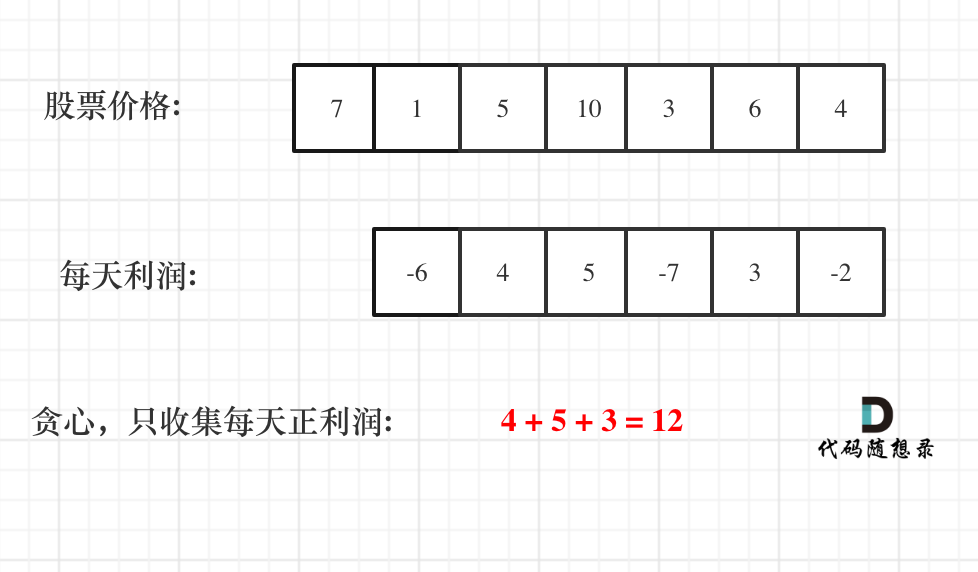
那么根据prices可以得到每天的利润序列:(prices[i] - prices[i - 1]).....(prices[1] - prices[0])。
|
||||
那么根据 prices 可以得到每天的利润序列:(prices[i] - prices[i - 1]).....(prices[1] - prices[0])。
|
||||
|
||||
如图:
|
||||
|
||||
|
||||
|
||||
|
||||
一些同学陷入:第一天怎么就没有利润呢,第一天到底算不算的困惑中。
|
||||
@ -77,7 +82,7 @@
|
||||
|
||||
局部最优可以推出全局最优,找不出反例,试一试贪心!
|
||||
|
||||
对应C++代码如下:
|
||||
对应 C++代码如下:
|
||||
|
||||
```CPP
|
||||
class Solution {
|
||||
@ -92,12 +97,12 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度:O(n)
|
||||
* 空间复杂度:O(1)
|
||||
- 时间复杂度:O(n)
|
||||
- 空间复杂度:O(1)
|
||||
|
||||
### 动态规划
|
||||
|
||||
动态规划将在下一个系列详细讲解,本题解先给出我的C++代码(带详细注释),感兴趣的同学可以自己先学习一下。
|
||||
动态规划将在下一个系列详细讲解,本题解先给出我的 C++代码(带详细注释),感兴趣的同学可以自己先学习一下。
|
||||
|
||||
```CPP
|
||||
class Solution {
|
||||
@ -119,8 +124,8 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度:$O(n)$
|
||||
* 空间复杂度:$O(n)$
|
||||
- 时间复杂度:$O(n)$
|
||||
- 空间复杂度:$O(n)$
|
||||
|
||||
## 总结
|
||||
|
||||
@ -137,6 +142,7 @@ public:
|
||||
### Java:
|
||||
|
||||
贪心:
|
||||
|
||||
```java
|
||||
// 贪心思路
|
||||
class Solution {
|
||||
@ -151,6 +157,7 @@ class Solution {
|
||||
```
|
||||
|
||||
动态规划:
|
||||
|
||||
```java
|
||||
class Solution { // 动态规划
|
||||
public int maxProfit(int[] prices) {
|
||||
@ -173,7 +180,9 @@ class Solution { // 动态规划
|
||||
```
|
||||
|
||||
### Python:
|
||||
|
||||
贪心:
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
def maxProfit(self, prices: List[int]) -> int:
|
||||
@ -184,6 +193,7 @@ class Solution:
|
||||
```
|
||||
|
||||
动态规划:
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
def maxProfit(self, prices: List[int]) -> int:
|
||||
@ -200,6 +210,7 @@ class Solution:
|
||||
### Go:
|
||||
|
||||
贪心算法
|
||||
|
||||
```go
|
||||
func maxProfit(prices []int) int {
|
||||
var sum int
|
||||
@ -212,7 +223,9 @@ func maxProfit(prices []int) int {
|
||||
return sum
|
||||
}
|
||||
```
|
||||
|
||||
动态规划
|
||||
|
||||
```go
|
||||
func maxProfit(prices []int) int {
|
||||
dp := make([][]int, len(prices))
|
||||
@ -239,6 +252,7 @@ func max(a, b int) int {
|
||||
### Javascript:
|
||||
|
||||
贪心
|
||||
|
||||
```Javascript
|
||||
var maxProfit = function(prices) {
|
||||
let result = 0
|
||||
@ -250,6 +264,7 @@ var maxProfit = function(prices) {
|
||||
```
|
||||
|
||||
动态规划
|
||||
|
||||
```javascript
|
||||
const maxProfit = (prices) => {
|
||||
let dp = Array.from(Array(prices.length), () => Array(2).fill(0));
|
||||
@ -257,24 +272,25 @@ const maxProfit = (prices) => {
|
||||
// dp[i][1] 表示第i天不持有股票所得最多现金
|
||||
dp[0][0] = 0 - prices[0];
|
||||
dp[0][1] = 0;
|
||||
for(let i = 1; i < prices.length; i++) {
|
||||
for (let i = 1; i < prices.length; i++) {
|
||||
// 如果第i天持有股票即dp[i][0], 那么可以由两个状态推出来
|
||||
// 第i-1天就持有股票,那么就保持现状,所得现金就是昨天持有股票的所得现金 即:dp[i - 1][0]
|
||||
// 第i天买入股票,所得现金就是昨天不持有股票的所得现金减去 今天的股票价格 即:dp[i - 1][1] - prices[i]
|
||||
dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] - prices[i]);
|
||||
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
|
||||
|
||||
// 在来看看如果第i天不持有股票即dp[i][1]的情况, 依然可以由两个状态推出来
|
||||
// 第i-1天就不持有股票,那么就保持现状,所得现金就是昨天不持有股票的所得现金 即:dp[i - 1][1]
|
||||
// 第i天卖出股票,所得现金就是按照今天股票佳价格卖出后所得现金即:prices[i] + dp[i - 1][0]
|
||||
dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] + prices[i]);
|
||||
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] + prices[i]);
|
||||
}
|
||||
|
||||
return dp[prices.length -1][1];
|
||||
return dp[prices.length - 1][1];
|
||||
};
|
||||
```
|
||||
|
||||
### TypeScript:
|
||||
|
||||
贪心
|
||||
```typescript
|
||||
function maxProfit(prices: number[]): number {
|
||||
let resProfit: number = 0;
|
||||
@ -282,12 +298,28 @@ function maxProfit(prices: number[]): number {
|
||||
resProfit += Math.max(prices[i] - prices[i - 1], 0);
|
||||
}
|
||||
return resProfit;
|
||||
};
|
||||
}
|
||||
```
|
||||
|
||||
动态规划
|
||||
```typescript
|
||||
function maxProfit(prices: number[]): number {
|
||||
const dp = Array(prices.length)
|
||||
.fill(0)
|
||||
.map(() => Array(2).fill(0))
|
||||
dp[0][0] = -prices[0]
|
||||
for (let i = 1; i < prices.length; i++) {
|
||||
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] - prices[i])
|
||||
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] + prices[i])
|
||||
}
|
||||
return dp[prices.length - 1][1]
|
||||
}
|
||||
```
|
||||
|
||||
### Rust
|
||||
|
||||
贪心:
|
||||
|
||||
```Rust
|
||||
impl Solution {
|
||||
fn max(a: i32, b: i32) -> i32 {
|
||||
@ -304,6 +336,7 @@ impl Solution {
|
||||
```
|
||||
|
||||
动态规划:
|
||||
|
||||
```Rust
|
||||
impl Solution {
|
||||
fn max(a: i32, b: i32) -> i32 {
|
||||
@ -323,7 +356,9 @@ impl Solution {
|
||||
```
|
||||
|
||||
### C:
|
||||
|
||||
贪心:
|
||||
|
||||
```c
|
||||
int maxProfit(int* prices, int pricesSize){
|
||||
int result = 0;
|
||||
@ -339,6 +374,7 @@ int maxProfit(int* prices, int pricesSize){
|
||||
```
|
||||
|
||||
动态规划:
|
||||
|
||||
```c
|
||||
#define max(a, b) (((a) > (b)) ? (a) : (b))
|
||||
|
||||
@ -363,6 +399,7 @@ int maxProfit(int* prices, int pricesSize){
|
||||
### Scala
|
||||
|
||||
贪心:
|
||||
|
||||
```scala
|
||||
object Solution {
|
||||
def maxProfit(prices: Array[Int]): Int = {
|
||||
|
||||
@ -45,6 +45,10 @@
|
||||
* 解释:
|
||||
你不能从 0 号或 1 号加油站出发,因为没有足够的汽油可以让你行驶到下一个加油站。我们从 2 号加油站出发,可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油。开往 0 号加油站,此时油箱有 4 - 3 + 2 = 3 升汽油。开往 1 号加油站,此时油箱有 3 - 3 + 3 = 3 升汽油。你无法返回 2 号加油站,因为返程需要消耗 4 升汽油,但是你的油箱只有 3 升汽油。因此,无论怎样,你都不可能绕环路行驶一周。
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[贪心算法,得这么加油才能跑完全程!LeetCode :134.加油站](https://www.bilibili.com/video/BV1jA411r7WX),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
|
||||
## 暴力方法
|
||||
|
||||
|
||||
@ -28,6 +28,10 @@
|
||||
* 输出: 4
|
||||
* 解释: 你可以分别给这三个孩子分发 1、2、1 颗糖果。第三个孩子只得到 1 颗糖果,这已满足上述两个条件。
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[贪心算法,两者兼顾很容易顾此失彼!LeetCode:135.分发糖果](https://www.bilibili.com/video/BV1ev4y1r7wN),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
|
||||
## 思路
|
||||
|
||||
|
||||
@ -114,6 +114,7 @@ void removeExtraSpaces(string& s) {
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
有的同学可能发现用erase来移除空格,在leetcode上性能也还行。主要是以下几点;:
|
||||
|
||||
1. leetcode上的测试集里,字符串的长度不够长,如果足够长,性能差距会非常明显。
|
||||
@ -197,6 +198,9 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度: O(n)
|
||||
* 空间复杂度: O(1) 或 O(n),取决于语言中字符串是否可变
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
@ -516,6 +520,48 @@ class Solution:
|
||||
return s[:ps] + s[ps:][::-1] # Must do the last step, because the last word is omit though the pointers are on the correct positions,
|
||||
```
|
||||
|
||||
```python
|
||||
class Solution: # 使用双指针法移除空格
|
||||
def reverseWords(self, s: str) -> str:
|
||||
|
||||
def removeextraspace(s):
|
||||
start = 0; end = len(s)-1
|
||||
while s[start]==' ':
|
||||
start+=1
|
||||
while s[end]==' ':
|
||||
end-=1
|
||||
news = list(s[start:end+1])
|
||||
slow = fast = 0
|
||||
while fast<len(news):
|
||||
while fast>0 and news[fast]==news[fast-1]==' ':
|
||||
fast+=1
|
||||
news[slow]=news[fast]
|
||||
slow+=1; fast+=1
|
||||
#return "".join(news[:slow])
|
||||
return news[:slow]
|
||||
|
||||
def reversestr(s):
|
||||
left,right = 0,len(s)-1
|
||||
news = list(s)
|
||||
while left<right:
|
||||
news[left],news[right] = news[right],news[left]
|
||||
left+=1; right-=1
|
||||
#return "".join(news)
|
||||
return news
|
||||
|
||||
news = removeextraspace(s)
|
||||
news.append(' ')
|
||||
fast=slow=0
|
||||
#print(news)
|
||||
while fast<len(news):
|
||||
while news[fast]!=' ':
|
||||
fast+=1
|
||||
news[slow:fast] = reversestr(news[slow:fast])
|
||||
# print(news[slow:fast])
|
||||
fast=slow=fast+1
|
||||
news2 = reversestr(news[:-1])
|
||||
return ''.join(news2)
|
||||
```
|
||||
Go:
|
||||
|
||||
```go
|
||||
|
||||
@ -379,6 +379,20 @@ class Solution:
|
||||
return (2 << leftDepth) - 1 #注意(2<<1) 相当于2^2,所以leftDepth初始为0
|
||||
return self.countNodes(root.left) + self.countNodes(root.right) + 1
|
||||
```
|
||||
完全二叉树写法2
|
||||
```python
|
||||
class Solution: # 利用完全二叉树特性
|
||||
def countNodes(self, root: TreeNode) -> int:
|
||||
if not root: return 0
|
||||
count = 1
|
||||
left = root.left; right = root.right
|
||||
while left and right:
|
||||
count+=1
|
||||
left = left.left; right = right.right
|
||||
if not left and not right: # 如果同时到底说明是满二叉树,反之则不是
|
||||
return 2**count-1
|
||||
return 1+self.countNodes(root.left)+self.countNodes(root.right)
|
||||
```
|
||||
|
||||
## Go
|
||||
|
||||
|
||||
@ -130,6 +130,9 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度: O(n)
|
||||
* 空间复杂度: O(1)
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
@ -4,7 +4,6 @@
|
||||
</a>
|
||||
<p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||||
|
||||
|
||||
> 本周讲解了[贪心理论基础](https://programmercarl.com/贪心算法理论基础.html),以及第一道贪心的题目:[贪心算法:分发饼干](https://programmercarl.com/0455.分发饼干.html),可能会给大家一种贪心算法比较简单的错觉,好了,接下来几天的题目难度要上来了,哈哈。
|
||||
|
||||
# 376. 摆动序列
|
||||
@ -13,25 +12,32 @@
|
||||
|
||||
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为摆动序列。第一个差(如果存在的话)可能是正数或负数。少于两个元素的序列也是摆动序列。
|
||||
|
||||
例如, [1,7,4,9,2,5] 是一个摆动序列,因为差值 (6,-3,5,-7,3) 是正负交替出现的。相反, [1,4,7,2,5] 和 [1,7,4,5,5] 不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
|
||||
例如, [1,7,4,9,2,5] 是一个摆动序列,因为差值 (6,-3,5,-7,3) 是正负交替出现的。相反, [1,4,7,2,5] 和 [1,7,4,5,5] 不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
|
||||
|
||||
给定一个整数序列,返回作为摆动序列的最长子序列的长度。 通过从原始序列中删除一些(也可以不删除)元素来获得子序列,剩下的元素保持其原始顺序。
|
||||
|
||||
示例 1:
|
||||
* 输入: [1,7,4,9,2,5]
|
||||
* 输出: 6
|
||||
* 解释: 整个序列均为摆动序列。
|
||||
|
||||
- 输入: [1,7,4,9,2,5]
|
||||
- 输出: 6
|
||||
- 解释: 整个序列均为摆动序列。
|
||||
|
||||
示例 2:
|
||||
* 输入: [1,17,5,10,13,15,10,5,16,8]
|
||||
* 输出: 7
|
||||
* 解释: 这个序列包含几个长度为 7 摆动序列,其中一个可为[1,17,10,13,10,16,8]。
|
||||
|
||||
- 输入: [1,17,5,10,13,15,10,5,16,8]
|
||||
- 输出: 7
|
||||
- 解释: 这个序列包含几个长度为 7 摆动序列,其中一个可为[1,17,10,13,10,16,8]。
|
||||
|
||||
示例 3:
|
||||
* 输入: [1,2,3,4,5,6,7,8,9]
|
||||
* 输出: 2
|
||||
|
||||
## 思路1(贪心解法)
|
||||
- 输入: [1,2,3,4,5,6,7,8,9]
|
||||
- 输出: 2
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[贪心算法,寻找摆动有细节!| LeetCode:376.摆动序列](https://www.bilibili.com/video/BV17M411b7NS),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
## 思路 1(贪心解法)
|
||||
|
||||
本题要求通过从原始序列中删除一些(也可以不删除)元素来获得子序列,剩下的元素保持其原始顺序。
|
||||
|
||||
@ -55,7 +61,7 @@
|
||||
|
||||
**这就是贪心所贪的地方,让峰值尽可能的保持峰值,然后删除单一坡度上的节点**
|
||||
|
||||
在计算是否有峰值的时候,大家知道遍历的下标i ,计算prediff(nums[i] - nums[i-1]) 和 curdiff(nums[i+1] - nums[i]),如果`prediff < 0 && curdiff > 0` 或者 `prediff > 0 && curdiff < 0` 此时就有波动就需要统计。
|
||||
在计算是否有峰值的时候,大家知道遍历的下标 i ,计算 prediff(nums[i] - nums[i-1]) 和 curdiff(nums[i+1] - nums[i]),如果`prediff < 0 && curdiff > 0` 或者 `prediff > 0 && curdiff < 0` 此时就有波动就需要统计。
|
||||
|
||||
这是我们思考本题的一个大题思路,但本题要考虑三种情况:
|
||||
|
||||
@ -69,31 +75,29 @@
|
||||
|
||||
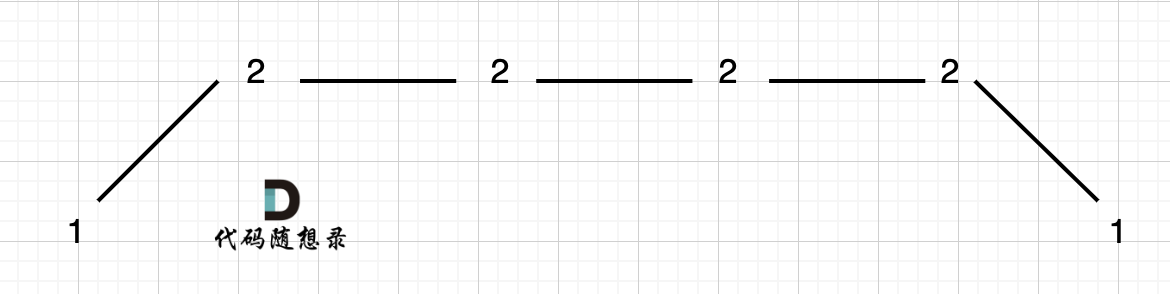
|
||||
|
||||
它的摇摆序列长度是多少呢? **其实是长度是3**,也就是我们在删除的时候 要不删除左面的三个2,要不就删除右边的三个2。
|
||||
它的摇摆序列长度是多少呢? **其实是长度是 3**,也就是我们在删除的时候 要不删除左面的三个 2,要不就删除右边的三个 2。
|
||||
|
||||
如图,可以统一规则,删除左边的三个2:
|
||||
如图,可以统一规则,删除左边的三个 2:
|
||||
|
||||
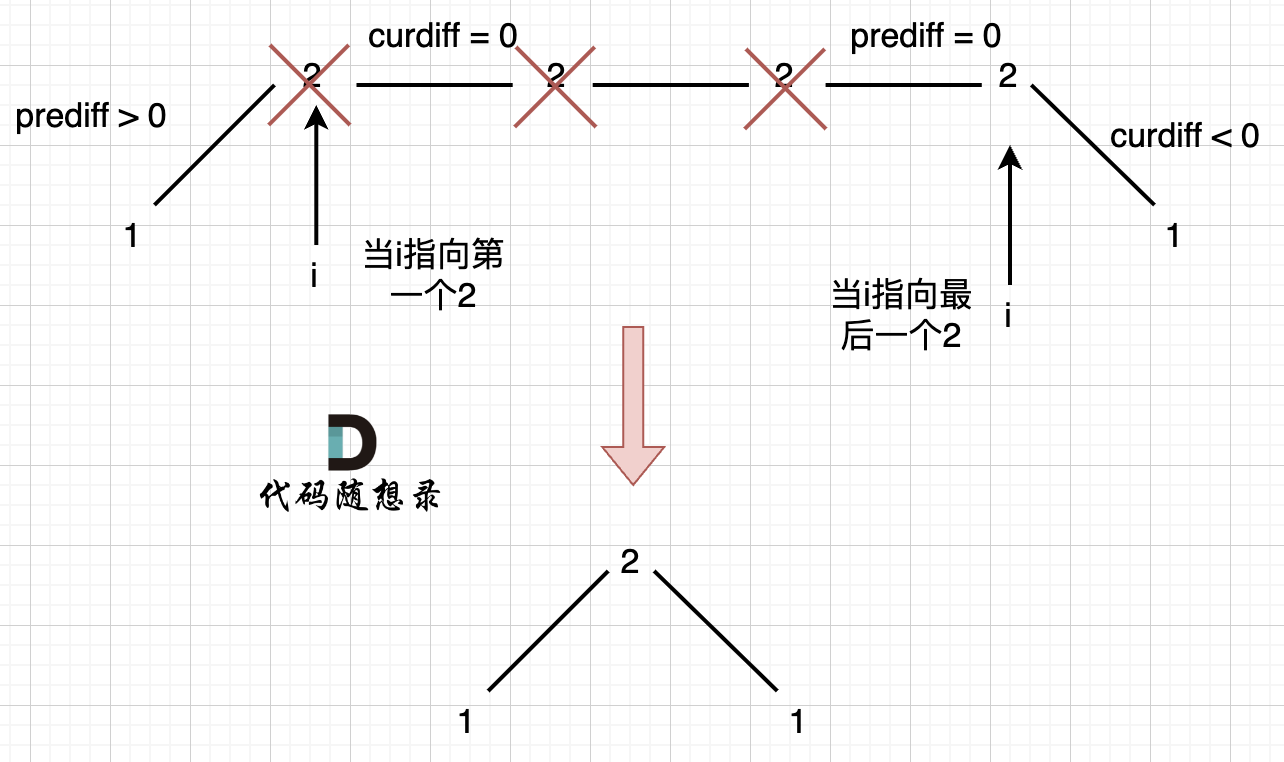
|
||||
|
||||
在图中,当i指向第一个2的时候,`prediff > 0 && curdiff = 0` ,当 i 指向最后一个2的时候 `prediff = 0 && curdiff < 0`。
|
||||
在图中,当 i 指向第一个 2 的时候,`prediff > 0 && curdiff = 0` ,当 i 指向最后一个 2 的时候 `prediff = 0 && curdiff < 0`。
|
||||
|
||||
如果我们采用,删左面三个2的规则,那么 当 `prediff = 0 && curdiff < 0` 也要记录一个峰值,因为他是把之前相同的元素都删掉留下的峰值。
|
||||
如果我们采用,删左面三个 2 的规则,那么 当 `prediff = 0 && curdiff < 0` 也要记录一个峰值,因为他是把之前相同的元素都删掉留下的峰值。
|
||||
|
||||
所以我们记录峰值的条件应该是: `(preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)`,为什么这里允许 prediff == 0 ,就是为了 上面我说的这种情况。
|
||||
|
||||
|
||||
### 情况二:数组首尾两端
|
||||
|
||||
|
||||
所以本题统计峰值的时候,数组最左面和最右面如果统计呢?
|
||||
|
||||
题目中说了,如果只有两个不同的元素,那摆动序列也是2。
|
||||
题目中说了,如果只有两个不同的元素,那摆动序列也是 2。
|
||||
|
||||
例如序列[2,5],如果靠统计差值来计算峰值个数就需要考虑数组最左面和最右面的特殊情况。
|
||||
|
||||
因为我们在计算 prediff(nums[i] - nums[i-1]) 和 curdiff(nums[i+1] - nums[i])的时候,至少需要三个数字才能计算,而数组只有两个数字。
|
||||
|
||||
这里我们可以写死,就是 如果只有两个元素,且元素不同,那么结果为2。
|
||||
这里我们可以写死,就是 如果只有两个元素,且元素不同,那么结果为 2。
|
||||
|
||||
不写死的话,如果和我们的判断规则结合在一起呢?
|
||||
|
||||
@ -101,11 +105,11 @@
|
||||
|
||||
之前我们在 讨论 情况一:相同数字连续 的时候, prediff = 0 ,curdiff < 0 或者 >0 也记为波谷。
|
||||
|
||||
那么为了规则统一,针对序列[2,5],可以假设为[2,2,5],这样它就有坡度了即preDiff = 0,如图:
|
||||
那么为了规则统一,针对序列[2,5],可以假设为[2,2,5],这样它就有坡度了即 preDiff = 0,如图:
|
||||
|
||||
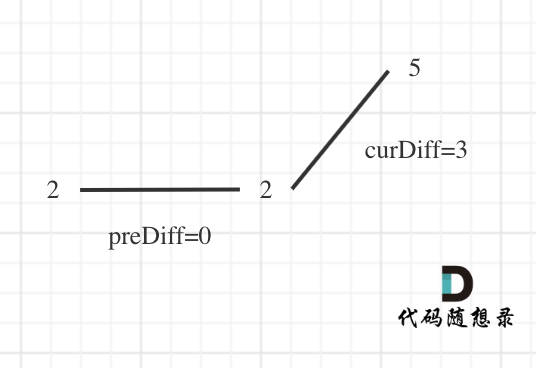
|
||||
|
||||
针对以上情形,result初始为1(默认最右面有一个峰值),此时curDiff > 0 && preDiff <= 0,那么result++(计算了左面的峰值),最后得到的result就是2(峰值个数为2即摆动序列长度为2)
|
||||
针对以上情形,result 初始为 1(默认最右面有一个峰值),此时 curDiff > 0 && preDiff <= 0,那么 result++(计算了左面的峰值),最后得到的 result 就是 2(峰值个数为 2 即摆动序列长度为 2)
|
||||
|
||||
经过以上分析后,我们可以写出如下代码:
|
||||
|
||||
@ -130,8 +134,9 @@ public:
|
||||
}
|
||||
};
|
||||
```
|
||||
* 时间复杂度:O(n)
|
||||
* 空间复杂度:O(1)
|
||||
|
||||
- 时间复杂度:O(n)
|
||||
- 空间复杂度:O(1)
|
||||
|
||||
此时大家是不是发现 以上代码提交也不能通过本题?
|
||||
|
||||
@ -143,13 +148,13 @@ public:
|
||||
|
||||
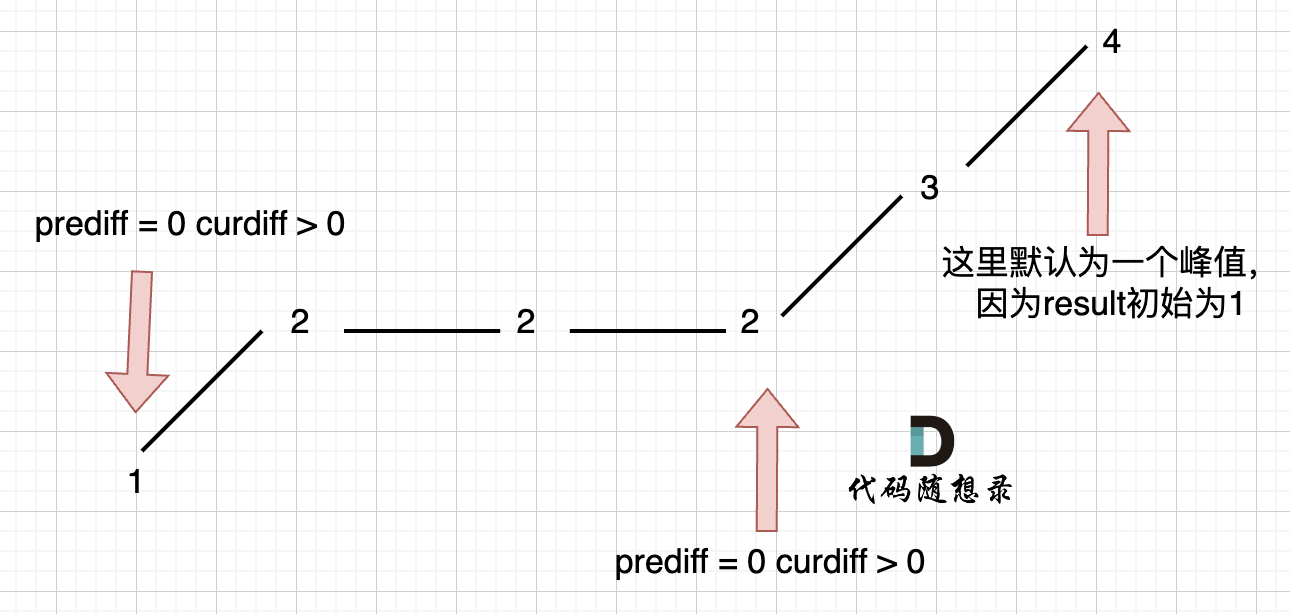
|
||||
|
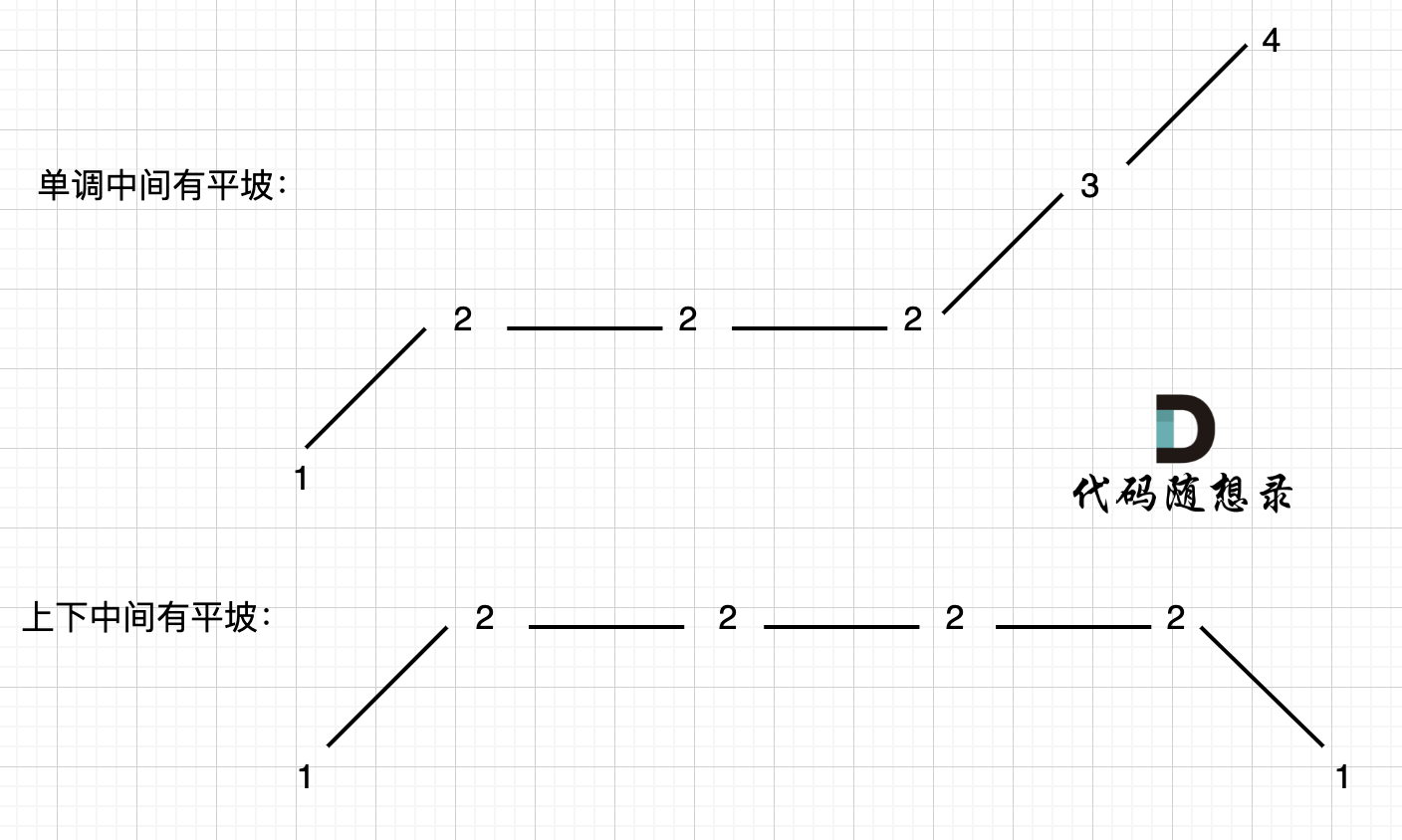
||||
图中,我们可以看出,版本一的代码在三个地方记录峰值,但其实结果因为是2,因为 单调中的平坡 不能算峰值(即摆动)。
|
||||
图中,我们可以看出,版本一的代码在三个地方记录峰值,但其实结果因为是 2,因为 单调中的平坡 不能算峰值(即摆动)。
|
||||
|
||||
之所以版本一会出问题,是因为我们实时更新了 prediff。
|
||||
|
||||
那么我们应该什么时候更新prediff呢?
|
||||
那么我们应该什么时候更新 prediff 呢?
|
||||
|
||||
我们只需要在 这个坡度 摆动变化的时候,更新prediff就行,这样prediff在 单调区间有平坡的时候 就不会发生变化,造成我们的误判。
|
||||
我们只需要在 这个坡度 摆动变化的时候,更新 prediff 就行,这样 prediff 在 单调区间有平坡的时候 就不会发生变化,造成我们的误判。
|
||||
|
||||
所以本题的最终代码为:
|
||||
|
||||
@ -182,19 +187,19 @@ public:
|
||||
|
||||
|
||||
|
||||
## 思路2(动态规划)
|
||||
## 思路 2(动态规划)
|
||||
|
||||
考虑用动态规划的思想来解决这个问题。
|
||||
|
||||
很容易可以发现,对于我们当前考虑的这个数,要么是作为山峰(即nums[i] > nums[i-1]),要么是作为山谷(即nums[i] < nums[i - 1])。
|
||||
很容易可以发现,对于我们当前考虑的这个数,要么是作为山峰(即 nums[i] > nums[i-1]),要么是作为山谷(即 nums[i] < nums[i - 1])。
|
||||
|
||||
* 设dp状态`dp[i][0]`,表示考虑前i个数,第i个数作为山峰的摆动子序列的最长长度
|
||||
* 设dp状态`dp[i][1]`,表示考虑前i个数,第i个数作为山谷的摆动子序列的最长长度
|
||||
- 设 dp 状态`dp[i][0]`,表示考虑前 i 个数,第 i 个数作为山峰的摆动子序列的最长长度
|
||||
- 设 dp 状态`dp[i][1]`,表示考虑前 i 个数,第 i 个数作为山谷的摆动子序列的最长长度
|
||||
|
||||
则转移方程为:
|
||||
|
||||
* `dp[i][0] = max(dp[i][0], dp[j][1] + 1)`,其中`0 < j < i`且`nums[j] < nums[i]`,表示将nums[i]接到前面某个山谷后面,作为山峰。
|
||||
* `dp[i][1] = max(dp[i][1], dp[j][0] + 1)`,其中`0 < j < i`且`nums[j] > nums[i]`,表示将nums[i]接到前面某个山峰后面,作为山谷。
|
||||
- `dp[i][0] = max(dp[i][0], dp[j][1] + 1)`,其中`0 < j < i`且`nums[j] < nums[i]`,表示将 nums[i]接到前面某个山谷后面,作为山峰。
|
||||
- `dp[i][1] = max(dp[i][1], dp[j][0] + 1)`,其中`0 < j < i`且`nums[j] > nums[i]`,表示将 nums[i]接到前面某个山峰后面,作为山谷。
|
||||
|
||||
初始状态:
|
||||
|
||||
@ -223,28 +228,25 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度:O(n^2)
|
||||
* 空间复杂度:O(n)
|
||||
- 时间复杂度:O(n^2)
|
||||
- 空间复杂度:O(n)
|
||||
|
||||
**进阶**
|
||||
|
||||
可以用两棵线段树来维护区间的最大值
|
||||
|
||||
* 每次更新`dp[i][0]`,则在`tree1`的`nums[i]`位置值更新为`dp[i][0]`
|
||||
* 每次更新`dp[i][1]`,则在`tree2`的`nums[i]`位置值更新为`dp[i][1]`
|
||||
* 则dp转移方程中就没有必要j从0遍历到i-1,可以直接在线段树中查询指定区间的值即可。
|
||||
- 每次更新`dp[i][0]`,则在`tree1`的`nums[i]`位置值更新为`dp[i][0]`
|
||||
- 每次更新`dp[i][1]`,则在`tree2`的`nums[i]`位置值更新为`dp[i][1]`
|
||||
- 则 dp 转移方程中就没有必要 j 从 0 遍历到 i-1,可以直接在线段树中查询指定区间的值即可。
|
||||
|
||||
时间复杂度:O(nlog n)
|
||||
|
||||
空间复杂度:O(n)
|
||||
|
||||
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
|
||||
### Java
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
public int wiggleMaxLength(int[] nums) {
|
||||
@ -270,6 +272,7 @@ class Solution {
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
```java
|
||||
// DP
|
||||
class Solution {
|
||||
@ -360,6 +363,7 @@ class Solution:
|
||||
### Go
|
||||
|
||||
**贪心**
|
||||
|
||||
```go
|
||||
func wiggleMaxLength(nums []int) int {
|
||||
n := len(nums)
|
||||
@ -383,6 +387,7 @@ func wiggleMaxLength(nums []int) int {
|
||||
```
|
||||
|
||||
**动态规划**
|
||||
|
||||
```go
|
||||
func wiggleMaxLength(nums []int) int {
|
||||
n := len(nums)
|
||||
@ -420,7 +425,9 @@ func max(a, b int) int {
|
||||
```
|
||||
|
||||
### Javascript
|
||||
|
||||
**贪心**
|
||||
|
||||
```Javascript
|
||||
var wiggleMaxLength = function(nums) {
|
||||
if(nums.length <= 1) return nums.length
|
||||
@ -437,7 +444,9 @@ var wiggleMaxLength = function(nums) {
|
||||
return result
|
||||
};
|
||||
```
|
||||
|
||||
**动态规划**
|
||||
|
||||
```Javascript
|
||||
var wiggleMaxLength = function(nums) {
|
||||
if (nums.length === 1) return 1;
|
||||
@ -458,7 +467,9 @@ var wiggleMaxLength = function(nums) {
|
||||
```
|
||||
|
||||
### Rust
|
||||
|
||||
**贪心**
|
||||
|
||||
```Rust
|
||||
impl Solution {
|
||||
pub fn wiggle_max_length(nums: Vec<i32>) -> i32 {
|
||||
@ -504,6 +515,7 @@ impl Solution {
|
||||
```
|
||||
|
||||
### C
|
||||
|
||||
**贪心**
|
||||
|
||||
```c
|
||||
@ -568,8 +580,6 @@ int wiggleMaxLength(int* nums, int numsSize){
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
### TypeScript
|
||||
|
||||
**贪心**
|
||||
@ -583,16 +593,13 @@ function wiggleMaxLength(nums: number[]): number {
|
||||
let count: number = 1;
|
||||
for (let i = 1; i < length; i++) {
|
||||
curDiff = nums[i] - nums[i - 1];
|
||||
if (
|
||||
(preDiff <= 0 && curDiff > 0) ||
|
||||
(preDiff >= 0 && curDiff < 0)
|
||||
) {
|
||||
if ((preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)) {
|
||||
preDiff = curDiff;
|
||||
count++;
|
||||
}
|
||||
}
|
||||
return count;
|
||||
};
|
||||
}
|
||||
```
|
||||
|
||||
**动态规划**
|
||||
@ -601,7 +608,7 @@ function wiggleMaxLength(nums: number[]): number {
|
||||
function wiggleMaxLength(nums: number[]): number {
|
||||
const length: number = nums.length;
|
||||
if (length <= 1) return length;
|
||||
const dp: number[][] = new Array(length).fill(0).map(_ => []);
|
||||
const dp: number[][] = new Array(length).fill(0).map((_) => []);
|
||||
dp[0][0] = 1; // 第一个数作为波峰
|
||||
dp[0][1] = 1; // 第一个数作为波谷
|
||||
for (let i = 1; i < length; i++) {
|
||||
@ -615,7 +622,7 @@ function wiggleMaxLength(nums: number[]): number {
|
||||
}
|
||||
}
|
||||
return Math.max(dp[length - 1][0], dp[length - 1][1]);
|
||||
};
|
||||
}
|
||||
```
|
||||
|
||||
### Scala
|
||||
|
||||
@ -37,6 +37,10 @@
|
||||
|
||||
题目数据确保队列可以被重建
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[贪心算法,不要两边一起贪,会顾此失彼 | LeetCode:406.根据身高重建队列](https://www.bilibili.com/video/BV1EA411675Y),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
## 思路
|
||||
|
||||
本题有两个维度,h和k,看到这种题目一定要想如何确定一个维度,然后再按照另一个维度重新排列。
|
||||
|
||||
@ -236,9 +236,222 @@ for (int j = 0; j < m; j++) {
|
||||
|
||||
空间复杂度为:O(n * m) 这个就不难理解了。开了几个 n * m 的数组。
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
|
||||
深度优先遍历:
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
// 四个位置
|
||||
private static final int[][] position = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
|
||||
|
||||
/**
|
||||
* @param heights 题目给定的二维数组
|
||||
* @param row 当前位置的行号
|
||||
* @param col 当前位置的列号
|
||||
* @param sign 记录是哪一条河,两条河中可以一个为 0,一个为 1
|
||||
* @param visited 记录这个位置可以到哪条河
|
||||
*/
|
||||
public void dfs(int[][] heights, int row, int col, int sign, boolean[][][] visited) {
|
||||
for (int[] current: position) {
|
||||
int curRow = row + current[0], curCol = col + current[1];
|
||||
// 越界
|
||||
if (curRow < 0 || curRow >= heights.length || curCol < 0 || curCol >= heights[0].length)
|
||||
continue;
|
||||
// 高度不合适或者已经被访问过了
|
||||
if (heights[curRow][curCol] < heights[row][col] || visited[curRow][curCol][sign]) continue;
|
||||
visited[curRow][curCol][sign] = true;
|
||||
dfs(heights, curRow, curCol, sign, visited);
|
||||
}
|
||||
}
|
||||
|
||||
public List<List<Integer>> pacificAtlantic(int[][] heights) {
|
||||
int rowSize = heights.length, colSize = heights[0].length;
|
||||
List<List<Integer>> ans = new ArrayList<>();
|
||||
// 记录 [row, col] 位置是否可以到某条河,可以为 true,反之为 false;
|
||||
// 假设太平洋的标记为 1,大西洋为 0
|
||||
boolean[][][] visited = new boolean[rowSize][colSize][2];
|
||||
for (int row = 0; row < rowSize; row++) {
|
||||
visited[row][colSize - 1][0] = true;
|
||||
visited[row][0][1] = true;
|
||||
dfs(heights, row, colSize - 1, 0, visited);
|
||||
dfs(heights, row, 0, 1, visited);
|
||||
}
|
||||
for (int col = 0; col < colSize; col++) {
|
||||
visited[rowSize - 1][col][0] = true;
|
||||
visited[0][col][1] = true;
|
||||
dfs(heights, rowSize - 1, col, 0, visited);
|
||||
dfs(heights, 0, col, 1, visited);
|
||||
}
|
||||
for (int row = 0; row < rowSize; row++) {
|
||||
for (int col = 0; col < colSize; col++) {
|
||||
// 如果该位置即可以到太平洋又可以到大西洋,就放入答案数组
|
||||
if (visited[row][col][0] && visited[row][col][1])
|
||||
ans.add(List.of(row, col));
|
||||
}
|
||||
}
|
||||
return ans;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
广度优先遍历:
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
// 四个位置
|
||||
private static final int[][] position = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
|
||||
|
||||
/**
|
||||
* @param heights 题目给定的二维数组
|
||||
* @param queue 记录可以到达边界的节点
|
||||
* @param visited 记录这个位置可以到哪条河
|
||||
*/
|
||||
public void bfs(int[][] heights, Queue<int[]> queue, boolean[][][] visited) {
|
||||
while (!queue.isEmpty()) {
|
||||
int[] curPos = queue.poll();
|
||||
for (int[] current: position) {
|
||||
int row = curPos[0] + current[0], col = curPos[1] + current[1], sign = curPos[2];
|
||||
// 越界
|
||||
if (row < 0 || row >= heights.length || col < 0 || col >= heights[0].length) continue;
|
||||
// 高度不合适或者已经被访问过了
|
||||
if (heights[row][col] < heights[curPos[0]][curPos[1]] || visited[row][col][sign]) continue;
|
||||
visited[row][col][sign] = true;
|
||||
queue.add(new int[]{row, col, sign});
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
public List<List<Integer>> pacificAtlantic(int[][] heights) {
|
||||
int rowSize = heights.length, colSize = heights[0].length;
|
||||
List<List<Integer>> ans = new ArrayList<>();
|
||||
boolean[][][] visited = new boolean[rowSize][colSize][2];
|
||||
// 队列,保存的数据为 [行号, 列号, 标记]
|
||||
// 假设太平洋的标记为 1,大西洋为 0
|
||||
Queue<int[]> queue = new ArrayDeque<>();
|
||||
for (int row = 0; row < rowSize; row++) {
|
||||
visited[row][colSize - 1][0] = true;
|
||||
visited[row][0][1] = true;
|
||||
queue.add(new int[]{row, colSize - 1, 0});
|
||||
queue.add(new int[]{row, 0, 1});
|
||||
}
|
||||
for (int col = 0; col < colSize; col++) {
|
||||
visited[rowSize - 1][col][0] = true;
|
||||
visited[0][col][1] = true;
|
||||
queue.add(new int[]{rowSize - 1, col, 0});
|
||||
queue.add(new int[]{0, col, 1});
|
||||
}
|
||||
bfs(heights, queue, visited);
|
||||
for (int row = 0; row < rowSize; row++) {
|
||||
for (int col = 0; col < colSize; col++) {
|
||||
// 如果该位置即可以到太平洋又可以到大西洋,就放入答案数组
|
||||
if (visited[row][col][0] && visited[row][col][1])
|
||||
ans.add(List.of(row, col));
|
||||
}
|
||||
}
|
||||
return ans;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
### Python
|
||||
|
||||
深度优先遍历
|
||||
|
||||
```Python3
|
||||
class Solution:
|
||||
def __init__(self):
|
||||
self.position = [[-1, 0], [0, 1], [1, 0], [0, -1]] # 四个方向
|
||||
|
||||
# heights:题目给定的二维数组, row:当前位置的行号, col:当前位置的列号
|
||||
# sign:记录是哪一条河,两条河中可以一个为 0,一个为 1
|
||||
# visited:记录这个位置可以到哪条河
|
||||
def dfs(self, heights: List[List[int]], row: int, col: int, sign: int, visited: List[List[List[int]]]):
|
||||
for current in self.position:
|
||||
curRow, curCol = row + current[0], col + current[1]
|
||||
# 索引下标越界
|
||||
if curRow < 0 or curRow >= len(heights) or curCol < 0 or curCol >= len(heights[0]): continue
|
||||
# 不满足条件或者已经被访问过
|
||||
if heights[curRow][curCol] < heights[row][col] or visited[curRow][curCol][sign]: continue
|
||||
visited[curRow][curCol][sign] = True
|
||||
self.dfs(heights, curRow, curCol, sign, visited)
|
||||
|
||||
def pacificAtlantic(self, heights: List[List[int]]) -> List[List[int]]:
|
||||
rowSize, colSize = len(heights), len(heights[0])
|
||||
# visited 记录 [row, col] 位置是否可以到某条河,可以为 true,反之为 false;
|
||||
# 假设太平洋的标记为 1,大西洋为 0
|
||||
# ans 用来保存满足条件的答案
|
||||
ans, visited = [], [[[False for _ in range(2)] for _ in range(colSize)] for _ in range(rowSize)]
|
||||
for row in range(rowSize):
|
||||
visited[row][0][1] = True
|
||||
visited[row][colSize - 1][0] = True
|
||||
self.dfs(heights, row, 0, 1, visited)
|
||||
self.dfs(heights, row, colSize - 1, 0, visited)
|
||||
for col in range(0, colSize):
|
||||
visited[0][col][1] = True
|
||||
visited[rowSize - 1][col][0] = True
|
||||
self.dfs(heights, 0, col, 1, visited)
|
||||
self.dfs(heights, rowSize - 1, col, 0, visited)
|
||||
for row in range(rowSize):
|
||||
for col in range(colSize):
|
||||
# 如果该位置即可以到太平洋又可以到大西洋,就放入答案数组
|
||||
if visited[row][col][0] and visited[row][col][1]:
|
||||
ans.append([row, col])
|
||||
return ans
|
||||
```
|
||||
|
||||
广度优先遍历
|
||||
|
||||
```Python3
|
||||
class Solution:
|
||||
def __init__(self):
|
||||
self.position = [[-1, 0], [0, 1], [1, 0], [0, -1]]
|
||||
|
||||
# heights:题目给定的二维数组,visited:记录这个位置可以到哪条河
|
||||
def bfs(self, heights: List[List[int]], queue: deque, visited: List[List[List[int]]]):
|
||||
while queue:
|
||||
curPos = queue.popleft()
|
||||
for current in self.position:
|
||||
row, col, sign = curPos[0] + current[0], curPos[1] + current[1], curPos[2]
|
||||
# 越界
|
||||
if row < 0 or row >= len(heights) or col < 0 or col >= len(heights[0]): continue
|
||||
# 不满足条件或已经访问过
|
||||
if heights[row][col] < heights[curPos[0]][curPos[1]] or visited[row][col][sign]: continue
|
||||
visited[row][col][sign] = True
|
||||
queue.append([row, col, sign])
|
||||
|
||||
def pacificAtlantic(self, heights: List[List[int]]) -> List[List[int]]:
|
||||
rowSize, colSize = len(heights), len(heights[0])
|
||||
# visited 记录 [row, col] 位置是否可以到某条河,可以为 true,反之为 false;
|
||||
# 假设太平洋的标记为 1,大西洋为 0
|
||||
# ans 用来保存满足条件的答案
|
||||
ans, visited = [], [[[False for _ in range(2)] for _ in range(colSize)] for _ in range(rowSize)]
|
||||
# 队列,保存的数据为 [行号, 列号, 标记]
|
||||
# 假设太平洋的标记为 1,大西洋为 0
|
||||
queue = deque()
|
||||
for row in range(rowSize):
|
||||
visited[row][0][1] = True
|
||||
visited[row][colSize - 1][0] = True
|
||||
queue.append([row, 0, 1])
|
||||
queue.append([row, colSize - 1, 0])
|
||||
for col in range(0, colSize):
|
||||
visited[0][col][1] = True
|
||||
visited[rowSize - 1][col][0] = True
|
||||
queue.append([0, col, 1])
|
||||
queue.append([rowSize - 1, col, 0])
|
||||
self.bfs(heights, queue, visited) # 广度优先遍历
|
||||
for row in range(rowSize):
|
||||
for col in range(colSize):
|
||||
# 如果该位置即可以到太平洋又可以到大西洋,就放入答案数组
|
||||
if visited[row][col][0] and visited[row][col][1]:
|
||||
ans.append([row, col])
|
||||
return ans
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
<p align="center">
|
||||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||||
|
||||
@ -30,6 +30,10 @@
|
||||
* 输出: 0
|
||||
* 解释: 你不需要移除任何区间,因为它们已经是无重叠的了。
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[贪心算法,依然是判断重叠区间 | LeetCode:435.无重叠区间](https://www.bilibili.com/video/BV1A14y1c7E1),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
## 思路
|
||||
|
||||
**相信很多同学看到这道题目都冥冥之中感觉要排序,但是究竟是按照右边界排序,还是按照左边界排序呢?**
|
||||
|
||||
@ -42,6 +42,10 @@
|
||||
* points[i].length == 2
|
||||
* -2^31 <= xstart < xend <= 2^31 - 1
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[贪心算法,判断重叠区间问题 | LeetCode:452.用最少数量的箭引爆气球](https://www.bilibili.com/video/BV1SA41167xe),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
## 思路
|
||||
|
||||
如何使用最少的弓箭呢?
|
||||
|
||||
@ -4,31 +4,35 @@
|
||||
</a>
|
||||
<p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||||
|
||||
|
||||
# 455.分发饼干
|
||||
|
||||
[力扣题目链接](https://leetcode.cn/problems/assign-cookies/)
|
||||
|
||||
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。
|
||||
|
||||
对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j] 。如果 s[j] >= g[i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
|
||||
对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j] 。如果 s[j] >= g[i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
|
||||
|
||||
示例 1:
|
||||
* 输入: g = [1,2,3], s = [1,1]
|
||||
* 输出: 1
|
||||
解释:你有三个孩子和两块小饼干,3个孩子的胃口值分别是:1,2,3。虽然你有两块小饼干,由于他们的尺寸都是1,你只能让胃口值是1的孩子满足。所以你应该输出1。
|
||||
示例 1:
|
||||
|
||||
示例 2:
|
||||
* 输入: g = [1,2], s = [1,2,3]
|
||||
* 输出: 2
|
||||
* 解释:你有两个孩子和三块小饼干,2个孩子的胃口值分别是1,2。你拥有的饼干数量和尺寸都足以让所有孩子满足。所以你应该输出2.
|
||||
- 输入: g = [1,2,3], s = [1,1]
|
||||
- 输出: 1
|
||||
解释:你有三个孩子和两块小饼干,3 个孩子的胃口值分别是:1,2,3。虽然你有两块小饼干,由于他们的尺寸都是 1,你只能让胃口值是 1 的孩子满足。所以你应该输出 1。
|
||||
|
||||
示例 2:
|
||||
|
||||
- 输入: g = [1,2], s = [1,2,3]
|
||||
- 输出: 2
|
||||
- 解释:你有两个孩子和三块小饼干,2 个孩子的胃口值分别是 1,2。你拥有的饼干数量和尺寸都足以让所有孩子满足。所以你应该输出 2.
|
||||
|
||||
提示:
|
||||
* 1 <= g.length <= 3 * 10^4
|
||||
* 0 <= s.length <= 3 * 10^4
|
||||
* 1 <= g[i], s[j] <= 2^31 - 1
|
||||
|
||||
- 1 <= g.length <= 3 \* 10^4
|
||||
- 0 <= s.length <= 3 \* 10^4
|
||||
- 1 <= g[i], s[j] <= 2^31 - 1
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[贪心算法,你想先喂哪个小孩?| LeetCode:455.分发饼干](https://www.bilibili.com/video/BV1MM411b7cq),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
## 思路
|
||||
|
||||
@ -46,9 +50,7 @@
|
||||
|
||||
|
||||
|
||||
|
||||
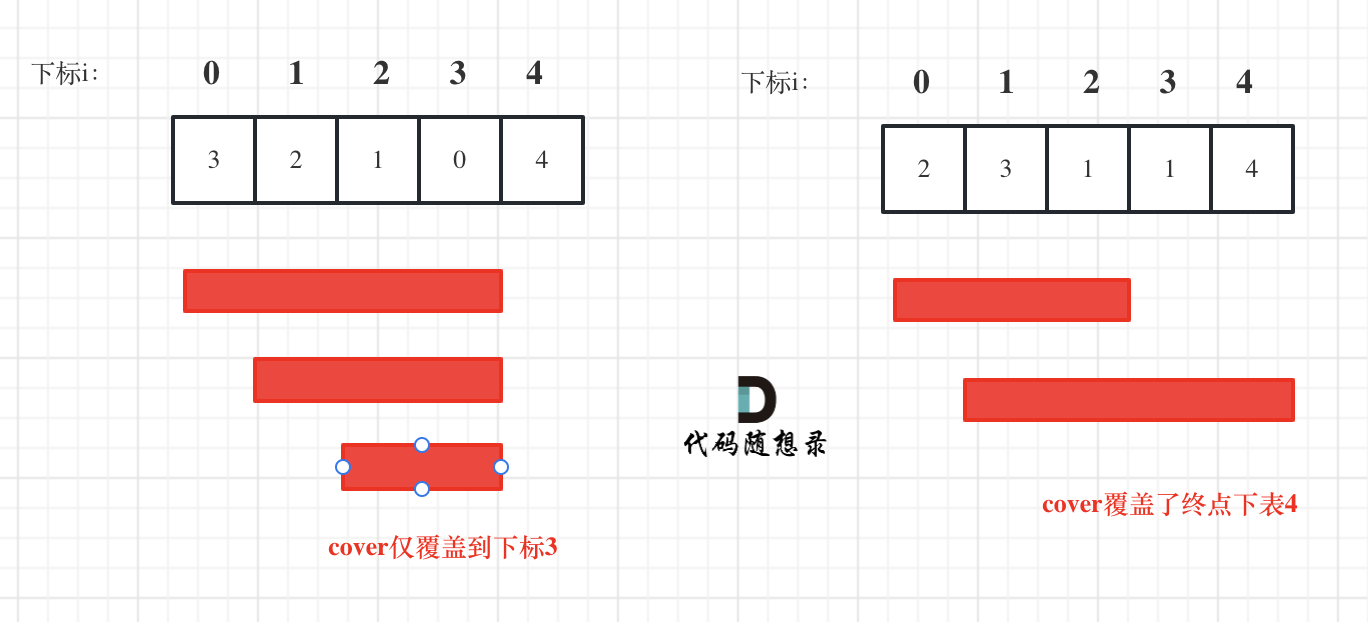
这个例子可以看出饼干9只有喂给胃口为7的小孩,这样才是整体最优解,并想不出反例,那么就可以撸代码了。
|
||||
|
||||
这个例子可以看出饼干 9 只有喂给胃口为 7 的小孩,这样才是整体最优解,并想不出反例,那么就可以撸代码了。
|
||||
|
||||
C++代码整体如下:
|
||||
|
||||
@ -74,10 +76,9 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
从代码中可以看出我用了一个index来控制饼干数组的遍历,遍历饼干并没有再起一个for循环,而是采用自减的方式,这也是常用的技巧。
|
||||
|
||||
有的同学看到要遍历两个数组,就想到用两个for循环,那样逻辑其实就复杂了。
|
||||
从代码中可以看出我用了一个 index 来控制饼干数组的遍历,遍历饼干并没有再起一个 for 循环,而是采用自减的方式,这也是常用的技巧。
|
||||
|
||||
有的同学看到要遍历两个数组,就想到用两个 for 循环,那样逻辑其实就复杂了。
|
||||
|
||||
### 注意事项
|
||||
|
||||
@ -85,16 +86,15 @@ public:
|
||||
|
||||
其实是不可以的。
|
||||
|
||||
外面的for 是里的下标i 是固定移动的,而if里面的下标 index 是符合条件才移动的。
|
||||
外面的 for 是里的下标 i 是固定移动的,而 if 里面的下标 index 是符合条件才移动的。
|
||||
|
||||
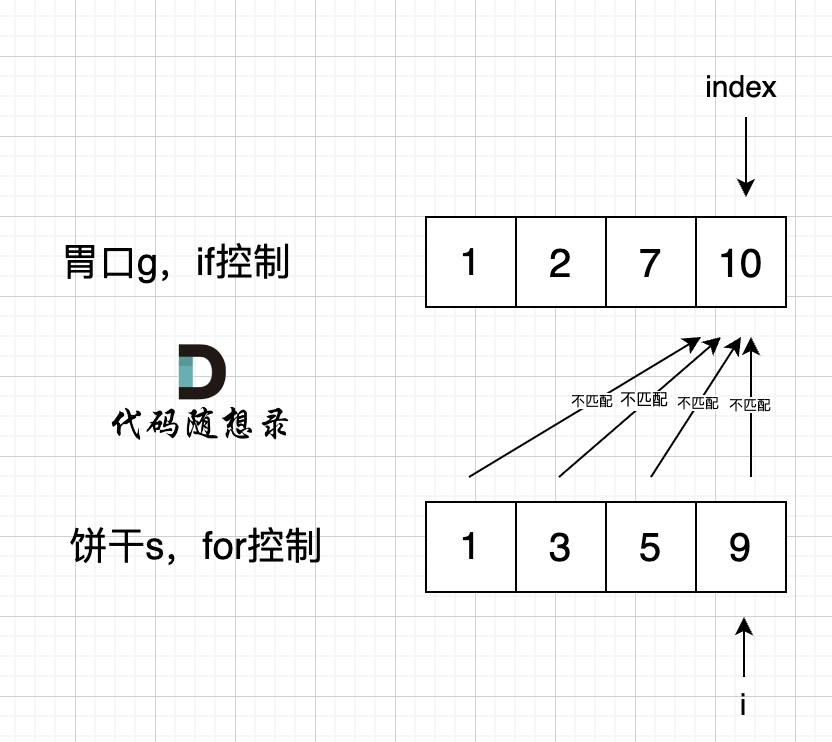
如果 for 控制的是饼干, if 控制胃口,就是出现如下情况 :
|
||||
|
||||
|
||||
|
||||
if 里的 index 指向 胃口 10, for里的i指向饼干9,因为 饼干9 满足不了 胃口10,所以 i 持续向前移动,而index 走不到` s[index] >= g[i]` 的逻辑,所以index不会移动,那么当i 持续向前移动,最后所有的饼干都匹配不上。
|
||||
|
||||
所以 一定要for 控制 胃口,里面的if控制饼干。
|
||||
if 里的 index 指向 胃口 10, for 里的 i 指向饼干 9,因为 饼干 9 满足不了 胃口 10,所以 i 持续向前移动,而 index 走不到` s[index] >= g[i]` 的逻辑,所以 index 不会移动,那么当 i 持续向前移动,最后所有的饼干都匹配不上。
|
||||
|
||||
所以 一定要 for 控制 胃口,里面的 if 控制饼干。
|
||||
|
||||
### 其他思路
|
||||
|
||||
@ -131,8 +131,8 @@ public:
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
|
||||
### Java
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
// 思路1:优先考虑饼干,小饼干先喂饱小胃口
|
||||
@ -151,6 +151,7 @@ class Solution {
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
// 思路2:优先考虑胃口,先喂饱大胃口
|
||||
@ -172,6 +173,7 @@ class Solution {
|
||||
```
|
||||
|
||||
### Python
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
# 思路1:优先考虑小胃口
|
||||
@ -184,6 +186,7 @@ class Solution:
|
||||
res += 1
|
||||
return res
|
||||
```
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
# 思路2:优先考虑大胃口
|
||||
@ -199,6 +202,7 @@ class Solution:
|
||||
```
|
||||
|
||||
### Go
|
||||
|
||||
```golang
|
||||
//排序后,局部最优
|
||||
func findContentChildren(g []int, s []int) int {
|
||||
@ -218,6 +222,7 @@ func findContentChildren(g []int, s []int) int {
|
||||
```
|
||||
|
||||
### Rust
|
||||
|
||||
```rust
|
||||
pub fn find_content_children(mut children: Vec<i32>, mut cookie: Vec<i32>) -> i32 {
|
||||
children.sort();
|
||||
@ -236,21 +241,21 @@ pub fn find_content_children(mut children: Vec<i32>, mut cookie: Vec<i32>) -> i3
|
||||
```
|
||||
|
||||
### Javascript
|
||||
```js
|
||||
var findContentChildren = function(g, s) {
|
||||
g = g.sort((a, b) => a - b)
|
||||
s = s.sort((a, b) => a - b)
|
||||
let result = 0
|
||||
let index = s.length - 1
|
||||
for(let i = g.length - 1; i >= 0; i--) {
|
||||
if(index >= 0 && s[index] >= g[i]) {
|
||||
result++
|
||||
index--
|
||||
}
|
||||
}
|
||||
return result
|
||||
};
|
||||
|
||||
```js
|
||||
var findContentChildren = function (g, s) {
|
||||
g = g.sort((a, b) => a - b);
|
||||
s = s.sort((a, b) => a - b);
|
||||
let result = 0;
|
||||
let index = s.length - 1;
|
||||
for (let i = g.length - 1; i >= 0; i--) {
|
||||
if (index >= 0 && s[index] >= g[i]) {
|
||||
result++;
|
||||
index--;
|
||||
}
|
||||
}
|
||||
return result;
|
||||
};
|
||||
```
|
||||
|
||||
### TypeScript
|
||||
@ -273,7 +278,7 @@ function findContentChildren(g: number[], s: number[]): number {
|
||||
curChild--;
|
||||
}
|
||||
return resCount;
|
||||
};
|
||||
}
|
||||
```
|
||||
|
||||
```typescript
|
||||
@ -292,7 +297,7 @@ function findContentChildren(g: number[], s: number[]): number {
|
||||
curCookie++;
|
||||
}
|
||||
return curChild;
|
||||
};
|
||||
}
|
||||
```
|
||||
|
||||
### C
|
||||
|
||||
@ -73,6 +73,8 @@ public:
|
||||
}
|
||||
};
|
||||
```
|
||||
* 时间复杂度: O(n)
|
||||
* 空间复杂度: O(1)
|
||||
|
||||
不过这种解法还有一个问题,就是 我们最终还是要判断 一个字符串(s + s)是否出现过 s 的过程,大家可能直接用contains,find 之类的库函数。 却忽略了实现这些函数的时间复杂度(暴力解法是m * n,一般库函数实现为 O(m + n))。
|
||||
|
||||
@ -185,6 +187,8 @@ public:
|
||||
}
|
||||
};
|
||||
```
|
||||
* 时间复杂度: O(n)
|
||||
* 空间复杂度: O(n)
|
||||
|
||||
|
||||
前缀表(不减一)的C++代码实现:
|
||||
@ -219,6 +223,8 @@ public:
|
||||
}
|
||||
};
|
||||
```
|
||||
* 时间复杂度: O(n)
|
||||
* 空间复杂度: O(n)
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
@ -221,8 +221,27 @@ class Solution:
|
||||
for i in range(len(res)-1): // 统计有序数组的最小差值
|
||||
r = min(abs(res[i]-res[i+1]),r)
|
||||
return r
|
||||
|
||||
|
||||
class Solution: # 双指针法,不用数组 (同Carl写法) - 更快
|
||||
def getMinimumDifference(self, root: Optional[TreeNode]) -> int:
|
||||
global pre,minval
|
||||
pre = None
|
||||
minval = 10**5
|
||||
self.traversal(root)
|
||||
return minval
|
||||
|
||||
def traversal(self,root):
|
||||
global pre,minval
|
||||
if not root: return None
|
||||
self.traversal(root.left)
|
||||
if pre and root.val-pre.val<minval:
|
||||
minval = root.val-pre.val
|
||||
pre = root
|
||||
self.traversal(root.right)
|
||||
```
|
||||
|
||||
|
||||
迭代法-中序遍历
|
||||
```python
|
||||
class Solution:
|
||||
|
||||
@ -65,6 +65,9 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度: O(n)
|
||||
* 空间复杂度: O(1)
|
||||
|
||||
|
||||
|
||||
|
||||
@ -96,6 +99,9 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度: O(n)
|
||||
* 空间复杂度: O(1)或O(n), 取决于使用的语言中字符串是否可以修改.
|
||||
|
||||
|
||||
另一种思路的解法
|
||||
|
||||
@ -116,6 +122,9 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度: O(n)
|
||||
* 空间复杂度: O(1)
|
||||
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
@ -26,6 +26,10 @@
|
||||
|
||||
说明: N 是在 [0, 10^9] 范围内的一个整数。
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[贪心算法,思路不难想,但代码不好写!LeetCode:738.单调自增的数字](https://www.bilibili.com/video/BV1Kv4y1x7tP),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
|
||||
## 暴力解法
|
||||
|
||||
|
||||
@ -284,6 +284,33 @@ func min(a, b int) int {
|
||||
return b
|
||||
}
|
||||
```
|
||||
``` GO
|
||||
第二种思路: dp[i]表示从i层起跳所需要支付的最小费用
|
||||
递推公式:
|
||||
i<n :dp[i] = min(dp[i-1],dp[i-2])+cost[i]
|
||||
i==n:dp[i] = min(dp[i-1],dp[i-2]) (登顶)
|
||||
|
||||
func minCostClimbingStairs(cost []int) int {
|
||||
n := len(cost)
|
||||
dp := make([]int, n+1)
|
||||
dp[0], dp[1] = cost[0], cost[1]
|
||||
for i := 2; i <= n; i++ {
|
||||
if i < n {
|
||||
dp[i] = min(dp[i-1], dp[i-2]) + cost[i]
|
||||
} else {
|
||||
dp[i] = min(dp[i-1], dp[i-2])
|
||||
}
|
||||
}
|
||||
return dp[n]
|
||||
}
|
||||
func min(a, b int) int {
|
||||
if a < b {
|
||||
return a
|
||||
}
|
||||
return b
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
### Javascript
|
||||
```Javascript
|
||||
|
||||
@ -24,6 +24,10 @@
|
||||
* S的长度在[1, 500]之间。
|
||||
* S只包含小写字母 'a' 到 'z' 。
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[贪心算法,寻找最远的出现位置! LeetCode:763.划分字母区间](https://www.bilibili.com/video/BV18G4y1K7d5),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
## 思路
|
||||
|
||||
一想到分割字符串就想到了回溯,但本题其实不用回溯去暴力搜索。
|
||||
|
||||
@ -50,6 +50,10 @@
|
||||
* 0 <= bills.length <= 10000
|
||||
* bills[i] 不是 5 就是 10 或是 20
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[贪心算法,看上去复杂,其实逻辑都是固定的!LeetCode:860.柠檬水找零](https://www.bilibili.com/video/BV12x4y1j7DD),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
## 思路
|
||||
|
||||
这是前几天的leetcode每日一题,感觉不错,给大家讲一下。
|
||||
|
||||
@ -38,6 +38,10 @@
|
||||
* 给定树的节点数的范围是 [1, 1000]。
|
||||
* 每个节点的值都是 0。
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[贪心算法,二叉树与贪心的结合,有点难...... LeetCode:968.监督二叉树](https://www.bilibili.com/video/BV1SA411U75i),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
|
||||
## 思路
|
||||
|
||||
|
||||
@ -34,6 +34,10 @@
|
||||
* 1 <= K <= 10000
|
||||
* -100 <= A[i] <= 100
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[贪心算法,这不就是常识?还能叫贪心?LeetCode:1005.K次取反后最大化的数组和](https://www.bilibili.com/video/BV138411G7LY),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
## 思路
|
||||
|
||||
本题思路其实比较好想了,如何可以让数组和最大呢?
|
||||
@ -231,23 +235,18 @@ var largestSumAfterKNegations = function(nums, k) {
|
||||
|
||||
```Rust
|
||||
impl Solution {
|
||||
pub fn largest_sum_after_k_negations(nums: Vec<i32>, k: i32) -> i32 {
|
||||
let mut nums = nums;
|
||||
let mut k = k;
|
||||
let len = nums.len();
|
||||
nums.sort_by(|a, b| b.abs().cmp(&a.abs()));
|
||||
for i in 0..len {
|
||||
if nums[i] < 0 && k > 0 {
|
||||
nums[i] *= -1;
|
||||
pub fn largest_sum_after_k_negations(mut nums: Vec<i32>, mut k: i32) -> i32 {
|
||||
nums.sort_by_key(|b| std::cmp::Reverse(b.abs()));
|
||||
for v in nums.iter_mut() {
|
||||
if *v < 0 && k > 0 {
|
||||
*v *= -1;
|
||||
k -= 1;
|
||||
}
|
||||
}
|
||||
if k % 2 == 1 { nums[len - 1] *= -1; }
|
||||
let mut result = 0;
|
||||
for num in nums {
|
||||
result += num;
|
||||
if k % 2 == 1 {
|
||||
*nums.last_mut().unwrap() *= -1;
|
||||
}
|
||||
result
|
||||
nums.iter().sum()
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
@ -144,6 +144,232 @@ public:
|
||||
}
|
||||
};
|
||||
```
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
|
||||
深度优先遍历版本:
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
// 四个方向
|
||||
private static final int[][] position = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
|
||||
|
||||
// 深度优先遍历,把可以通向边缘部分的 1 全部标记成 true
|
||||
public void dfs(int[][] grid, int row, int col, boolean[][] visited) {
|
||||
for (int[] current: position) {
|
||||
int newRow = row + current[0], newCol = col + current[1];
|
||||
// 下标越界直接跳过
|
||||
if (newRow < 0 || newRow >= grid.length || newCol < 0 || newCol >= grid[0].length) continue;
|
||||
// 当前位置不是 1 或者已经被访问了就直接跳过
|
||||
if (grid[newRow][newCol] != 1 || visited[newRow][newCol]) continue;
|
||||
visited[newRow][newCol] = true;
|
||||
dfs(grid, newRow, newCol, visited);
|
||||
}
|
||||
}
|
||||
|
||||
public int numEnclaves(int[][] grid) {
|
||||
int rowSize = grid.length, colSize = grid[0].length, ans = 0; // ans 记录答案
|
||||
// 标记数组记录每个值为 1 的位置是否可以到达边界,可以为 true,反之为 false
|
||||
boolean[][] visited = new boolean[rowSize][colSize];
|
||||
// 左侧边界和右侧边界查找 1 进行标记并进行深度优先遍历
|
||||
for (int row = 0; row < rowSize; row++) {
|
||||
if (grid[row][0] == 1 && !visited[row][0]) {
|
||||
visited[row][0] = true;
|
||||
dfs(grid, row, 0, visited);
|
||||
}
|
||||
if (grid[row][colSize - 1] == 1 && !visited[row][colSize - 1]) {
|
||||
visited[row][colSize - 1] = true;
|
||||
dfs(grid, row, colSize - 1, visited);
|
||||
}
|
||||
}
|
||||
// 上边界和下边界遍历,但是四个角不用遍历,因为上面已经遍历到了
|
||||
for (int col = 1; col < colSize - 1; col++) {
|
||||
if (grid[0][col] == 1 && !visited[0][col]) {
|
||||
visited[0][col] = true;
|
||||
dfs(grid, 0, col, visited);
|
||||
}
|
||||
if (grid[rowSize - 1][col] == 1 && !visited[rowSize - 1][col]) {
|
||||
visited[rowSize - 1][col] = true;
|
||||
dfs(grid, rowSize - 1, col, visited);
|
||||
}
|
||||
}
|
||||
// 查找没有标记过的 1,记录到 ans 中
|
||||
for (int row = 0; row < rowSize; row++) {
|
||||
for (int col = 0; col < colSize; col++) {
|
||||
if (grid[row][col] == 1 && !visited[row][col]) ++ans;
|
||||
}
|
||||
}
|
||||
return ans;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
广度优先遍历版本:
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
// 四个方向
|
||||
private static final int[][] position = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
|
||||
|
||||
// 广度优先遍历,把可以通向边缘部分的 1 全部标记成 true
|
||||
public void bfs(int[][] grid, Queue<int[]> queue, boolean[][] visited) {
|
||||
while (!queue.isEmpty()) {
|
||||
int[] curPos = queue.poll();
|
||||
for (int[] current: position) {
|
||||
int row = curPos[0] + current[0], col = curPos[1] + current[1];
|
||||
// 下标越界直接跳过
|
||||
if (row < 0 || row >= grid.length || col < 0 || col >= grid[0].length)
|
||||
continue;
|
||||
// 当前位置不是 1 或者已经被访问了就直接跳过
|
||||
if (visited[row][col] || grid[row][col] == 0) continue;
|
||||
visited[row][col] = true;
|
||||
queue.add(new int[]{row, col});
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
public int numEnclaves(int[][] grid) {
|
||||
int rowSize = grid.length, colSize = grid[0].length, ans = 0; // ans 记录答案
|
||||
// 标记数组记录每个值为 1 的位置是否可以到达边界,可以为 true,反之为 false
|
||||
boolean[][] visited = new boolean[rowSize][colSize];
|
||||
Queue<int[]> queue = new ArrayDeque<>();
|
||||
// 搜索左侧边界和右侧边界查找 1 存入队列
|
||||
for (int row = 0; row < rowSize; row++) {
|
||||
if (grid[row][0] == 1) {
|
||||
visited[row][0] = true;
|
||||
queue.add(new int[]{row, 0});
|
||||
}
|
||||
if (grid[row][colSize - 1] == 1) {
|
||||
visited[row][colSize - 1] = true;
|
||||
queue.add(new int[]{row, colSize - 1});
|
||||
}
|
||||
}
|
||||
// 搜索上边界和下边界遍历,但是四个角不用遍历,因为上面已经遍历到了
|
||||
for (int col = 1; col < colSize - 1; col++) {
|
||||
if (grid[0][col] == 1) {
|
||||
visited[0][col] = true;
|
||||
queue.add(new int[]{0, col});
|
||||
}
|
||||
if (grid[rowSize - 1][col] == 1 && !visited[rowSize - 1][col]) {
|
||||
visited[rowSize - 1][col] = true;
|
||||
queue.add(new int[]{rowSize - 1, col});
|
||||
}
|
||||
}
|
||||
bfs(grid, queue, visited); // 广度优先遍历
|
||||
// 查找没有标记过的 1,记录到 ans 中
|
||||
for (int row = 0; row < rowSize; row++) {
|
||||
for (int col = 0; col < colSize; col++) {
|
||||
if (grid[row][col] == 1 && !visited[row][col]) ++ans;
|
||||
}
|
||||
}
|
||||
return ans;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
### Python
|
||||
|
||||
深度优先遍历
|
||||
|
||||
```Python3
|
||||
class Solution:
|
||||
def __init__(self):
|
||||
self.position = [[-1, 0], [0, 1], [1, 0], [0, -1]] # 四个方向
|
||||
|
||||
# 深度优先遍历,把可以通向边缘部分的 1 全部标记成 true
|
||||
def dfs(self, grid: List[List[int]], row: int, col: int, visited: List[List[bool]]) -> None:
|
||||
for current in self.position:
|
||||
newRow, newCol = row + current[0], col + current[1]
|
||||
# 索引下标越界
|
||||
if newRow < 0 or newRow >= len(grid) or newCol < 0 or newCol >= len(grid[0]):
|
||||
continue
|
||||
# 当前位置值不是 1 或者已经被访问过了
|
||||
if grid[newRow][newCol] == 0 or visited[newRow][newCol]: continue
|
||||
visited[newRow][newCol] = True
|
||||
self.dfs(grid, newRow, newCol, visited)
|
||||
|
||||
def numEnclaves(self, grid: List[List[int]]) -> int:
|
||||
rowSize, colSize, ans = len(grid), len(grid[0]), 0
|
||||
# 标记数组记录每个值为 1 的位置是否可以到达边界,可以为 True,反之为 False
|
||||
visited = [[False for _ in range(colSize)] for _ in range(rowSize)]
|
||||
# 搜索左边界和右边界,对值为 1 的位置进行深度优先遍历
|
||||
for row in range(rowSize):
|
||||
if grid[row][0] == 1:
|
||||
visited[row][0] = True
|
||||
self.dfs(grid, row, 0, visited)
|
||||
if grid[row][colSize - 1] == 1:
|
||||
visited[row][colSize - 1] = True
|
||||
self.dfs(grid, row, colSize - 1, visited)
|
||||
# 搜索上边界和下边界,对值为 1 的位置进行深度优先遍历,但是四个角不需要,因为上面遍历过了
|
||||
for col in range(1, colSize - 1):
|
||||
if grid[0][col] == 1:
|
||||
visited[0][col] = True
|
||||
self.dfs(grid, 0, col, visited)
|
||||
if grid[rowSize - 1][col] == 1:
|
||||
visited[rowSize - 1][col] = True
|
||||
self.dfs(grid, rowSize - 1, col, visited)
|
||||
# 找出矩阵中值为 1 但是没有被标记过的位置,记录答案
|
||||
for row in range(rowSize):
|
||||
for col in range(colSize):
|
||||
if grid[row][col] == 1 and not visited[row][col]:
|
||||
ans += 1
|
||||
return ans
|
||||
```
|
||||
|
||||
广度优先遍历
|
||||
|
||||
```Python3
|
||||
class Solution:
|
||||
def __init__(self):
|
||||
self.position = [[-1, 0], [0, 1], [1, 0], [0, -1]] # 四个方向
|
||||
|
||||
# 广度优先遍历,把可以通向边缘部分的 1 全部标记成 true
|
||||
def bfs(self, grid: List[List[int]], queue: deque, visited: List[List[bool]]) -> None:
|
||||
while queue:
|
||||
curPos = queue.popleft()
|
||||
for current in self.position:
|
||||
row, col = curPos[0] + current[0], curPos[1] + current[1]
|
||||
# 索引下标越界
|
||||
if row < 0 or row >= len(grid) or col < 0 or col >= len(grid[0]): continue
|
||||
# 当前位置值不是 1 或者已经被访问过了
|
||||
if grid[row][col] == 0 or visited[row][col]: continue
|
||||
visited[row][col] = True
|
||||
queue.append([row, col])
|
||||
|
||||
|
||||
def numEnclaves(self, grid: List[List[int]]) -> int:
|
||||
rowSize, colSize, ans = len(grid), len(grid[0]), 0
|
||||
# 标记数组记录每个值为 1 的位置是否可以到达边界,可以为 True,反之为 False
|
||||
visited = [[False for _ in range(colSize)] for _ in range(rowSize)]
|
||||
queue = deque() # 队列
|
||||
# 搜索左侧边界和右侧边界查找 1 存入队列
|
||||
for row in range(rowSize):
|
||||
if grid[row][0] == 1:
|
||||
visited[row][0] = True
|
||||
queue.append([row, 0])
|
||||
if grid[row][colSize - 1] == 1:
|
||||
visited[row][colSize - 1] = True
|
||||
queue.append([row, colSize - 1])
|
||||
# 搜索上边界和下边界查找 1 存入队列,但是四个角不用遍历,因为上面已经遍历到了
|
||||
for col in range(1, colSize - 1):
|
||||
if grid[0][col] == 1:
|
||||
visited[0][col] = True
|
||||
queue.append([0, col])
|
||||
if grid[rowSize - 1][col] == 1:
|
||||
visited[rowSize - 1][col] = True
|
||||
queue.append([rowSize - 1, col])
|
||||
self.bfs(grid, queue, visited) # 广度优先遍历
|
||||
# 找出矩阵中值为 1 但是没有被标记过的位置,记录答案
|
||||
for row in range(rowSize):
|
||||
for col in range(colSize):
|
||||
if grid[row][col] == 1 and not visited[row][col]:
|
||||
ans += 1
|
||||
return ans
|
||||
```
|
||||
|
||||
|
||||
|
||||
## 类似题目
|
||||
|
||||
* 1254. 统计封闭岛屿的数目
|
||||
@ -153,3 +379,4 @@ public:
|
||||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||||
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>
|
||||
</a>
|
||||
|
||||
|
||||
@ -66,6 +66,9 @@ public:
|
||||
}
|
||||
};
|
||||
```
|
||||
* 时间复杂度: O(n)
|
||||
* 空间复杂度:O(1)
|
||||
|
||||
是不是发现这代码也太简单了,哈哈。
|
||||
|
||||
# 总结
|
||||
|
||||
@ -286,8 +286,70 @@ class Solution {
|
||||
}
|
||||
|
||||
```
|
||||
**90.子集II**
|
||||
```java
|
||||
class Solution {
|
||||
List<List<Integer>> reslut = new ArrayList<>();
|
||||
LinkedList<Integer> path = new LinkedList<>();
|
||||
|
||||
public List<List<Integer>> subsetsWithDup(int[] nums) {
|
||||
if(nums.length == 0){
|
||||
reslut.add(path);
|
||||
return reslut;
|
||||
}
|
||||
Arrays.sort(nums);
|
||||
backtracking(nums,0);
|
||||
return reslut;
|
||||
}
|
||||
|
||||
public void backtracking(int[] nums,int startIndex){
|
||||
reslut.add(new ArrayList<>(path));
|
||||
if(startIndex >= nums.length)return;
|
||||
HashSet<Integer> hashSet = new HashSet<>();
|
||||
for(int i = startIndex; i < nums.length; i++){
|
||||
if(hashSet.contains(nums[i])){
|
||||
continue;
|
||||
}
|
||||
hashSet.add(nums[i]);
|
||||
path.add(nums[i]);
|
||||
backtracking(nums,i+1);
|
||||
path.removeLast();
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
**40.组合总和II**
|
||||
```java
|
||||
class Solution {
|
||||
List<List<Integer>> result = new ArrayList<>();
|
||||
LinkedList<Integer> path = new LinkedList<>();
|
||||
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
|
||||
Arrays.sort( candidates );
|
||||
if( candidates[0] > target ) return result;
|
||||
backtracking(candidates,target,0,0);
|
||||
return result;
|
||||
}
|
||||
|
||||
public void backtracking(int[] candidates,int target,int sum,int startIndex){
|
||||
if( sum > target )return;
|
||||
if( sum == target ){
|
||||
result.add( new ArrayList<>(path) );
|
||||
}
|
||||
HashSet<Integer> hashSet = new HashSet<>();
|
||||
for( int i = startIndex; i < candidates.length; i++){
|
||||
if( hashSet.contains(candidates[i]) ){
|
||||
continue;
|
||||
}
|
||||
hashSet.add(candidates[i]);
|
||||
path.add(candidates[i]);
|
||||
sum += candidates[i];
|
||||
backtracking(candidates,target,sum,i+1);
|
||||
path.removeLast();
|
||||
sum -= candidates[i];
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
Python:
|
||||
|
||||
**90.子集II**
|
||||
|
||||
@ -87,7 +87,7 @@ leetcode上没有纯01背包的问题,都是01背包应用方面的题目,
|
||||
|
||||
那么可以有两个方向推出来dp[i][j],
|
||||
|
||||
* **不放物品i**:由dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时,物品i无法放进背包中,所以被背包内的价值依然和前面相同。)
|
||||
* **不放物品i**:由dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时,物品i无法放进背包中,所以背包内的价值依然和前面相同。)
|
||||
* **放物品i**:由dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值,那么dp[i - 1][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值
|
||||
|
||||
所以递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
|
||||
|
||||
Reference in New Issue
Block a user