mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-09 19:44:45 +08:00
Merge branch 'master' into master
This commit is contained in:
@ -313,54 +313,36 @@ func threeSum(nums []int)[][]int{
|
||||
javaScript:
|
||||
|
||||
```js
|
||||
/**
|
||||
* @param {number[]} nums
|
||||
* @return {number[][]}
|
||||
*/
|
||||
|
||||
// 循环内不考虑去重
|
||||
var threeSum = function(nums) {
|
||||
const len = nums.length;
|
||||
if(len < 3) return [];
|
||||
nums.sort((a, b) => a - b);
|
||||
const resSet = new Set();
|
||||
for(let i = 0; i < len - 2; i++) {
|
||||
if(nums[i] > 0) break;
|
||||
let l = i + 1, r = len - 1;
|
||||
const res = [], len = nums.length
|
||||
// 将数组排序
|
||||
nums.sort((a, b) => a - b)
|
||||
for (let i = 0; i < len; i++) {
|
||||
let l = i + 1, r = len - 1, iNum = nums[i]
|
||||
// 数组排过序,如果第一个数大于0直接返回res
|
||||
if (iNum > 0) return res
|
||||
// 去重
|
||||
if (iNum == nums[i - 1]) continue
|
||||
while(l < r) {
|
||||
const sum = nums[i] + nums[l] + nums[r];
|
||||
if(sum < 0) { l++; continue };
|
||||
if(sum > 0) { r--; continue };
|
||||
resSet.add(`${nums[i]},${nums[l]},${nums[r]}`);
|
||||
l++;
|
||||
r--;
|
||||
let lNum = nums[l], rNum = nums[r], threeSum = iNum + lNum + rNum
|
||||
// 三数之和小于0,则左指针向右移动
|
||||
if (threeSum < 0) l++
|
||||
else if (threeSum > 0) r--
|
||||
else {
|
||||
res.push([iNum, lNum, rNum])
|
||||
// 去重
|
||||
while(l < r && nums[l] == nums[l + 1]){
|
||||
l++
|
||||
}
|
||||
while(l < r && nums[r] == nums[r - 1]) {
|
||||
r--
|
||||
}
|
||||
l++
|
||||
r--
|
||||
}
|
||||
}
|
||||
}
|
||||
return Array.from(resSet).map(i => i.split(","));
|
||||
};
|
||||
|
||||
// 去重优化
|
||||
var threeSum = function(nums) {
|
||||
const len = nums.length;
|
||||
if(len < 3) return [];
|
||||
nums.sort((a, b) => a - b);
|
||||
const res = [];
|
||||
for(let i = 0; i < len - 2; i++) {
|
||||
if(nums[i] > 0) break;
|
||||
// a去重
|
||||
if(i > 0 && nums[i] === nums[i - 1]) continue;
|
||||
let l = i + 1, r = len - 1;
|
||||
while(l < r) {
|
||||
const sum = nums[i] + nums[l] + nums[r];
|
||||
if(sum < 0) { l++; continue };
|
||||
if(sum > 0) { r--; continue };
|
||||
res.push([nums[i], nums[l], nums[r]])
|
||||
// b c 去重
|
||||
while(l < r && nums[l] === nums[++l]);
|
||||
while(l < r && nums[r] === nums[--r]);
|
||||
}
|
||||
}
|
||||
return res;
|
||||
return res
|
||||
};
|
||||
```
|
||||
TypeScript:
|
||||
|
||||
@ -31,7 +31,7 @@
|
||||
|
||||
四数之和,和[15.三数之和](https://programmercarl.com/0015.三数之和.html)是一个思路,都是使用双指针法, 基本解法就是在[15.三数之和](https://programmercarl.com/0015.三数之和.html) 的基础上再套一层for循环。
|
||||
|
||||
但是有一些细节需要注意,例如: 不要判断`nums[k] > target` 就返回了,三数之和 可以通过 `nums[i] > 0` 就返回了,因为 0 已经是确定的数了,四数之和这道题目 target是任意值。(大家亲自写代码就能感受出来)
|
||||
但是有一些细节需要注意,例如: 不要判断`nums[k] > target` 就返回了,三数之和 可以通过 `nums[i] > 0` 就返回了,因为 0 已经是确定的数了,四数之和这道题目 target是任意值。比如:数组是`[-4, -3, -2, -1]`,`target`是`-10`,不能因为`-4 > -10`而跳过。但是我们依旧可以去做剪枝,逻辑变成`nums[i] > target && (nums[i] >=0 || target >= 0)`就可以了。
|
||||
|
||||
[15.三数之和](https://programmercarl.com/0015.三数之和.html)的双指针解法是一层for循环num[i]为确定值,然后循环内有left和right下标作为双指针,找到nums[i] + nums[left] + nums[right] == 0。
|
||||
|
||||
@ -72,15 +72,20 @@ public:
|
||||
vector<vector<int>> result;
|
||||
sort(nums.begin(), nums.end());
|
||||
for (int k = 0; k < nums.size(); k++) {
|
||||
// 这种剪枝是错误的,这道题目target 是任意值
|
||||
// if (nums[k] > target) {
|
||||
// return result;
|
||||
// }
|
||||
// 剪枝处理
|
||||
if (nums[k] > target && (nums[k] >= 0 || target >= 0)) {
|
||||
break; // 这里使用break,统一通过最后的return返回
|
||||
}
|
||||
// 去重
|
||||
if (k > 0 && nums[k] == nums[k - 1]) {
|
||||
continue;
|
||||
}
|
||||
for (int i = k + 1; i < nums.size(); i++) {
|
||||
// 2级剪枝处理
|
||||
if (nums[k] + nums[i] > target && (nums[k] + nums[i] >= 0 || target >= 0)) {
|
||||
break;
|
||||
}
|
||||
|
||||
// 正确去重方法
|
||||
if (i > k + 1 && nums[i] == nums[i - 1]) {
|
||||
continue;
|
||||
|
||||
@ -318,6 +318,31 @@ func searchInsert(_ nums: [Int], _ target: Int) -> Int {
|
||||
```
|
||||
|
||||
|
||||
### PHP
|
||||
|
||||
```php
|
||||
// 二分法(1):[左闭右闭]
|
||||
function searchInsert($nums, $target)
|
||||
{
|
||||
$n = count($nums);
|
||||
$l = 0;
|
||||
$r = $n - 1;
|
||||
while ($l <= $r) {
|
||||
$mid = floor(($l + $r) / 2);
|
||||
if ($nums[$mid] > $target) {
|
||||
// 下次搜索在左区间:[$l,$mid-1]
|
||||
$r = $mid - 1;
|
||||
} else if ($nums[$mid] < $target) {
|
||||
// 下次搜索在右区间:[$mid+1,$r]
|
||||
$l = $mid + 1;
|
||||
} else {
|
||||
// 命中返回
|
||||
return $mid;
|
||||
}
|
||||
}
|
||||
return $r + 1;
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
-----------------------
|
||||
|
||||
@ -370,18 +370,17 @@ func backtracking(startIndex,sum,target int,candidates,trcak []int,res *[][]int)
|
||||
```js
|
||||
var combinationSum = function(candidates, target) {
|
||||
const res = [], path = [];
|
||||
candidates.sort(); // 排序
|
||||
candidates.sort((a,b)=>a-b); // 排序
|
||||
backtracking(0, 0);
|
||||
return res;
|
||||
function backtracking(j, sum) {
|
||||
if (sum > target) return;
|
||||
if (sum === target) {
|
||||
res.push(Array.from(path));
|
||||
return;
|
||||
}
|
||||
for(let i = j; i < candidates.length; i++ ) {
|
||||
const n = candidates[i];
|
||||
if(n > target - sum) continue;
|
||||
if(n > target - sum) break;
|
||||
path.push(n);
|
||||
sum += n;
|
||||
backtracking(i, sum);
|
||||
|
||||
@ -508,22 +508,27 @@ func backtracking(startIndex,sum,target int,candidates,trcak []int,res *[][]int)
|
||||
*/
|
||||
var combinationSum2 = function(candidates, target) {
|
||||
const res = []; path = [], len = candidates.length;
|
||||
candidates.sort();
|
||||
candidates.sort((a,b)=>a-b);
|
||||
backtracking(0, 0);
|
||||
return res;
|
||||
function backtracking(sum, i) {
|
||||
if (sum > target) return;
|
||||
if (sum === target) {
|
||||
res.push(Array.from(path));
|
||||
return;
|
||||
}
|
||||
let f = -1;
|
||||
for(let j = i; j < len; j++) {
|
||||
const n = candidates[j];
|
||||
if(n > target - sum || n === f) continue;
|
||||
if(j > i && candidates[j] === candidates[j-1]){
|
||||
//若当前元素和前一个元素相等
|
||||
//则本次循环结束,防止出现重复组合
|
||||
continue;
|
||||
}
|
||||
//如果当前元素值大于目标值-总和的值
|
||||
//由于数组已排序,那么该元素之后的元素必定不满足条件
|
||||
//直接终止当前层的递归
|
||||
if(n > target - sum) break;
|
||||
path.push(n);
|
||||
sum += n;
|
||||
f = n;
|
||||
backtracking(sum, j + 1);
|
||||
path.pop();
|
||||
sum -= n;
|
||||
|
||||
@ -266,6 +266,26 @@ var merge = function(intervals) {
|
||||
};
|
||||
```
|
||||
|
||||
### TypeScript
|
||||
|
||||
```typescript
|
||||
function merge(intervals: number[][]): number[][] {
|
||||
const resArr: number[][] = [];
|
||||
intervals.sort((a, b) => a[0] - b[0]);
|
||||
resArr[0] = [...intervals[0]]; // 避免修改原intervals
|
||||
for (let i = 1, length = intervals.length; i < length; i++) {
|
||||
let interval: number[] = intervals[i];
|
||||
let last: number[] = resArr[resArr.length - 1];
|
||||
if (interval[0] <= last[1]) {
|
||||
last[1] = Math.max(interval[1], last[1]);
|
||||
} else {
|
||||
resArr.push([...intervals[i]]);
|
||||
}
|
||||
}
|
||||
return resArr;
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
|
||||
-----------------------
|
||||
|
||||
@ -30,7 +30,7 @@
|
||||
|
||||
相信很多同学刚开始做这种题目的时候,上来就是一波判断猛如虎。
|
||||
|
||||
结果运行的时候各种问题,然后开始各种修修补补,最后发现改了这里哪里有问题,改了那里这里又跑不起来了。
|
||||
结果运行的时候各种问题,然后开始各种修修补补,最后发现改了这里那里有问题,改了那里这里又跑不起来了。
|
||||
|
||||
大家还记得我们在这篇文章[数组:每次遇到二分法,都是一看就会,一写就废](https://programmercarl.com/0704.二分查找.html)中讲解了二分法,提到如果要写出正确的二分法一定要坚持**循环不变量原则**。
|
||||
|
||||
@ -47,7 +47,7 @@
|
||||
|
||||
可以发现这里的边界条件非常多,在一个循环中,如此多的边界条件,如果不按照固定规则来遍历,那就是**一进循环深似海,从此offer是路人**。
|
||||
|
||||
这里一圈下来,我们要画每四条边,这四条边怎么画,每画一条边都要坚持一致的左闭右开,或者左开又闭的原则,这样这一圈才能按照统一的规则画下来。
|
||||
这里一圈下来,我们要画每四条边,这四条边怎么画,每画一条边都要坚持一致的左闭右开,或者左开右闭的原则,这样这一圈才能按照统一的规则画下来。
|
||||
|
||||
那么我按照左闭右开的原则,来画一圈,大家看一下:
|
||||
|
||||
@ -59,7 +59,7 @@
|
||||
|
||||
一些同学做这道题目之所以一直写不好,代码越写越乱。
|
||||
|
||||
就是因为在画每一条边的时候,一会左开又闭,一会左闭右闭,一会又来左闭右开,岂能不乱。
|
||||
就是因为在画每一条边的时候,一会左开右闭,一会左闭右闭,一会又来左闭右开,岂能不乱。
|
||||
|
||||
代码如下,已经详细注释了每一步的目的,可以看出while循环里判断的情况是很多的,代码里处理的原则也是统一的左闭右开。
|
||||
|
||||
|
||||
@ -308,7 +308,58 @@ var climbStairs = function(n) {
|
||||
};
|
||||
```
|
||||
|
||||
TypeScript
|
||||
|
||||
> 爬2阶
|
||||
|
||||
```typescript
|
||||
function climbStairs(n: number): number {
|
||||
/**
|
||||
dp[i]: i阶楼梯的方法种数
|
||||
dp[1]: 1;
|
||||
dp[2]: 2;
|
||||
...
|
||||
dp[i]: dp[i - 1] + dp[i - 2];
|
||||
*/
|
||||
const dp: number[] = [];
|
||||
dp[1] = 1;
|
||||
dp[2] = 2;
|
||||
for (let i = 3; i <= n; i++) {
|
||||
dp[i] = dp[i - 1] + dp[i - 2];
|
||||
}
|
||||
return dp[n];
|
||||
};
|
||||
```
|
||||
|
||||
> 爬m阶
|
||||
|
||||
```typescript
|
||||
function climbStairs(n: number): number {
|
||||
/**
|
||||
一次可以爬m阶
|
||||
dp[i]: i阶楼梯的方法种数
|
||||
dp[1]: 1;
|
||||
dp[2]: 2;
|
||||
dp[3]: dp[2] + dp[1];
|
||||
...
|
||||
dp[i]: dp[i - 1] + dp[i - 2] + ... + dp[max(i - m, 1)]; 从i-1加到max(i-m, 1)
|
||||
*/
|
||||
const m: number = 2; // 本题m为2
|
||||
const dp: number[] = new Array(n + 1).fill(0);
|
||||
dp[1] = 1;
|
||||
dp[2] = 2;
|
||||
for (let i = 3; i <= n; i++) {
|
||||
const end: number = Math.max(i - m, 1);
|
||||
for (let j = i - 1; j >= end; j--) {
|
||||
dp[i] += dp[j];
|
||||
}
|
||||
}
|
||||
return dp[n];
|
||||
};
|
||||
```
|
||||
|
||||
### C
|
||||
|
||||
```c
|
||||
int climbStairs(int n){
|
||||
//若n<=2,返回n
|
||||
|
||||
@ -454,31 +454,36 @@ var partition = function(s) {
|
||||
|
||||
```typescript
|
||||
function partition(s: string): string[][] {
|
||||
function isPalindromeStr(s: string, left: number, right: number): boolean {
|
||||
while (left < right) {
|
||||
if (s[left++] !== s[right--]) {
|
||||
return false;
|
||||
const res: string[][] = []
|
||||
const path: string[] = []
|
||||
const isHuiwen = (
|
||||
str: string,
|
||||
startIndex: number,
|
||||
endIndex: number
|
||||
): boolean => {
|
||||
for (; startIndex < endIndex; startIndex++, endIndex--) {
|
||||
if (str[startIndex] !== str[endIndex]) {
|
||||
return false
|
||||
}
|
||||
}
|
||||
return true;
|
||||
return true
|
||||
}
|
||||
function backTracking(s: string, startIndex: number, route: string[]): void {
|
||||
let length: number = s.length;
|
||||
if (length === startIndex) {
|
||||
resArr.push(route.slice());
|
||||
return;
|
||||
const rec = (str: string, index: number): void => {
|
||||
if (index >= str.length) {
|
||||
res.push([...path])
|
||||
return
|
||||
}
|
||||
for (let i = startIndex; i < length; i++) {
|
||||
if (isPalindromeStr(s, startIndex, i)) {
|
||||
route.push(s.slice(startIndex, i + 1));
|
||||
backTracking(s, i + 1, route);
|
||||
route.pop();
|
||||
for (let i = index; i < str.length; i++) {
|
||||
if (!isHuiwen(str, index, i)) {
|
||||
continue
|
||||
}
|
||||
path.push(str.substring(index, i + 1))
|
||||
rec(str, i + 1)
|
||||
path.pop()
|
||||
}
|
||||
}
|
||||
const resArr: string[][] = [];
|
||||
backTracking(s, 0, []);
|
||||
return resArr;
|
||||
rec(s, 0)
|
||||
return res
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
@ -408,6 +408,9 @@ function canCompleteCircuit(gas: number[], cost: number[]): number {
|
||||
|
||||
### C
|
||||
|
||||
贪心算法:方法一
|
||||
|
||||
|
||||
```c
|
||||
int canCompleteCircuit(int* gas, int gasSize, int* cost, int costSize){
|
||||
int curSum = 0;
|
||||
@ -437,5 +440,36 @@ int canCompleteCircuit(int* gas, int gasSize, int* cost, int costSize){
|
||||
}
|
||||
```
|
||||
|
||||
贪心算法:方法二
|
||||
```c
|
||||
int canCompleteCircuit(int* gas, int gasSize, int* cost, int costSize){
|
||||
int curSum = 0;
|
||||
int totalSum = 0;
|
||||
int start = 0;
|
||||
|
||||
int i;
|
||||
for(i = 0; i < gasSize; ++i) {
|
||||
// 当前i站中加油量与耗油量的差
|
||||
int diff = gas[i] - cost[i];
|
||||
|
||||
curSum += diff;
|
||||
totalSum += diff;
|
||||
|
||||
// 若0到i的加油量都为负,则开始位置应为i+1
|
||||
if(curSum < 0) {
|
||||
curSum = 0;
|
||||
// 当i + 1 == gasSize时,totalSum < 0(此时i为gasSize - 1),油车不可能返回原点
|
||||
start = i + 1;
|
||||
}
|
||||
}
|
||||
|
||||
// 若总和小于0,加油车无论如何都无法返回原点。返回-1
|
||||
if(totalSum < 0)
|
||||
return -1;
|
||||
|
||||
return start;
|
||||
}
|
||||
```
|
||||
|
||||
-----------------------
|
||||
<div align="center"><img src=https://code-thinking.cdn.bcebos.com/pics/01二维码一.jpg width=500> </img></div>
|
||||
|
||||
@ -109,7 +109,7 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
# 题外话
|
||||
## 题外话
|
||||
|
||||
我们习惯看到的表达式都是中缀表达式,因为符合我们的习惯,但是中缀表达式对于计算机来说就不是很友好了。
|
||||
|
||||
@ -128,7 +128,7 @@ public:
|
||||
|
||||
|
||||
|
||||
# 其他语言版本
|
||||
## 其他语言版本
|
||||
|
||||
java:
|
||||
|
||||
|
||||
@ -145,6 +145,38 @@ public:
|
||||
|
||||
## 其他语言版本
|
||||
C:
|
||||
用原来的链表操作:
|
||||
```c
|
||||
struct ListNode* removeElements(struct ListNode* head, int val){
|
||||
struct ListNode* temp;
|
||||
// 当头结点存在并且头结点的值等于val时
|
||||
while(head && head->val == val) {
|
||||
temp = head;
|
||||
// 将新的头结点设置为head->next并删除原来的头结点
|
||||
head = head->next;
|
||||
free(temp);
|
||||
}
|
||||
|
||||
struct ListNode *cur = head;
|
||||
// 当cur存在并且cur->next存在时
|
||||
// 此解法需要判断cur存在因为cur指向head。若head本身为NULL或者原链表中元素都为val的话,cur也会为NULL
|
||||
while(cur && (temp = cur->next)) {
|
||||
// 若cur->next的值等于val
|
||||
if(temp->val == val) {
|
||||
// 将cur->next设置为cur->next->next并删除cur->next
|
||||
cur->next = temp->next;
|
||||
free(temp);
|
||||
}
|
||||
// 若cur->next不等于val,则将cur后移一位
|
||||
else
|
||||
cur = cur->next;
|
||||
}
|
||||
|
||||
// 返回头结点
|
||||
return head;
|
||||
}
|
||||
```
|
||||
设置一个虚拟头结点:
|
||||
```c
|
||||
/**
|
||||
* Definition for singly-linked list.
|
||||
|
||||
@ -112,7 +112,7 @@ public:
|
||||
|
||||
**一些录友会疑惑为什么时间复杂度是O(n)**。
|
||||
|
||||
不要以为for里放一个while就以为是O(n^2)啊, 主要是看每一个元素被操作的次数,每个元素在滑动窗后进来操作一次,出去操作一次,每个元素都是被被操作两次,所以时间复杂度是 2 × n 也就是O(n)。
|
||||
不要以为for里放一个while就以为是O(n^2)啊, 主要是看每一个元素被操作的次数,每个元素在滑动窗后进来操作一次,出去操作一次,每个元素都是被操作两次,所以时间复杂度是 2 × n 也就是O(n)。
|
||||
|
||||
## 相关题目推荐
|
||||
|
||||
|
||||
@ -168,6 +168,39 @@ func lengthOfLIS(nums []int ) int {
|
||||
}
|
||||
```
|
||||
|
||||
```go
|
||||
// 动态规划求解
|
||||
func lengthOfLIS(nums []int) int {
|
||||
// dp数组的定义 dp[i]表示取第i个元素的时候,表示子序列的长度,其中包括 nums[i] 这个元素
|
||||
dp := make([]int, len(nums))
|
||||
|
||||
// 初始化,所有的元素都应该初始化为1
|
||||
for i := range dp {
|
||||
dp[i] = 1
|
||||
}
|
||||
|
||||
ans := dp[0]
|
||||
for i := 1; i < len(nums); i++ {
|
||||
for j := 0; j < i; j++ {
|
||||
if nums[i] > nums[j] {
|
||||
dp[i] = max(dp[i], dp[j] + 1)
|
||||
}
|
||||
}
|
||||
if dp[i] > ans {
|
||||
ans = dp[i]
|
||||
}
|
||||
}
|
||||
return ans
|
||||
}
|
||||
|
||||
func max(x, y int) int {
|
||||
if x > y {
|
||||
return x
|
||||
}
|
||||
return y
|
||||
}
|
||||
```
|
||||
|
||||
Rust:
|
||||
```rust
|
||||
pub fn length_of_lis(nums: Vec<i32>) -> i32 {
|
||||
|
||||
@ -214,8 +214,8 @@ class Solution {
|
||||
|
||||
for (int i = 2; i <= prices.length; i++) {
|
||||
/*
|
||||
dp[i][0] 第i天未持有股票收益;
|
||||
dp[i][1] 第i天持有股票收益;
|
||||
dp[i][0] 第i天持有股票收益;
|
||||
dp[i][1] 第i天不持有股票收益;
|
||||
情况一:第i天是冷静期,不能以dp[i-1][1]购买股票,所以以dp[i - 2][1]买股票,没问题
|
||||
情况二:第i天不是冷静期,理论上应该以dp[i-1][1]购买股票,但是第i天不是冷静期说明,第i-1天没有卖出股票,
|
||||
则dp[i-1][1]=dp[i-2][1],所以可以用dp[i-2][1]买股票,没问题
|
||||
|
||||
@ -114,23 +114,25 @@ Java:
|
||||
```Java
|
||||
class Solution {
|
||||
public boolean canConstruct(String ransomNote, String magazine) {
|
||||
//记录杂志字符串出现的次数
|
||||
int[] arr = new int[26];
|
||||
int temp;
|
||||
for (int i = 0; i < magazine.length(); i++) {
|
||||
temp = magazine.charAt(i) - 'a';
|
||||
arr[temp]++;
|
||||
// 定义一个哈希映射数组
|
||||
int[] record = new int[26];
|
||||
|
||||
// 遍历
|
||||
for(char c : magazine.toCharArray()){
|
||||
record[c - 'a'] += 1;
|
||||
}
|
||||
for (int i = 0; i < ransomNote.length(); i++) {
|
||||
temp = ransomNote.charAt(i) - 'a';
|
||||
//对于金信中的每一个字符都在数组中查找
|
||||
//找到相应位减一,否则找不到返回false
|
||||
if (arr[temp] > 0) {
|
||||
arr[temp]--;
|
||||
} else {
|
||||
|
||||
for(char c : ransomNote.toCharArray()){
|
||||
record[c - 'a'] -= 1;
|
||||
}
|
||||
|
||||
// 如果数组中存在负数,说明ransomNote字符串总存在magazine中没有的字符
|
||||
for(int i : record){
|
||||
if(i < 0){
|
||||
return false;
|
||||
}
|
||||
}
|
||||
|
||||
return true;
|
||||
}
|
||||
}
|
||||
|
||||
@ -466,6 +466,55 @@ func sumOfLeftLeaves(_ root: TreeNode?) -> Int {
|
||||
}
|
||||
```
|
||||
|
||||
## C
|
||||
递归法:
|
||||
```c
|
||||
int sumOfLeftLeaves(struct TreeNode* root){
|
||||
// 递归结束条件:若当前结点为空,返回0
|
||||
if(!root)
|
||||
return 0;
|
||||
|
||||
// 递归取左子树的左结点和和右子树的左结点和
|
||||
int leftValue = sumOfLeftLeaves(root->left);
|
||||
int rightValue = sumOfLeftLeaves(root->right);
|
||||
|
||||
// 若当前结点的左结点存在,且其为叶子结点。取它的值
|
||||
int midValue = 0;
|
||||
if(root->left && (!root->left->left && !root->left->right))
|
||||
midValue = root->left->val;
|
||||
|
||||
return leftValue + rightValue + midValue;
|
||||
}
|
||||
```
|
||||
|
||||
迭代法:
|
||||
```c
|
||||
int sumOfLeftLeaves(struct TreeNode* root){
|
||||
struct TreeNode* stack[1000];
|
||||
int stackTop = 0;
|
||||
|
||||
// 若传入root结点不为空,将其入栈
|
||||
if(root)
|
||||
stack[stackTop++] = root;
|
||||
|
||||
int sum = 0;
|
||||
//若栈不为空,进行循环
|
||||
while(stackTop) {
|
||||
// 出栈栈顶元素
|
||||
struct TreeNode *topNode = stack[--stackTop];
|
||||
// 若栈顶元素的左孩子为左叶子结点,将其值加入sum中
|
||||
if(topNode->left && (!topNode->left->left && !topNode->left->right))
|
||||
sum += topNode->left->val;
|
||||
|
||||
// 若当前栈顶结点有左右孩子。将他们加入栈中进行遍历
|
||||
if(topNode->right)
|
||||
stack[stackTop++] = topNode->right;
|
||||
if(topNode->left)
|
||||
stack[stackTop++] = topNode->left;
|
||||
}
|
||||
return sum;
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
-----------------------
|
||||
|
||||
@ -290,6 +290,54 @@ var reconstructQueue = function(people) {
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
### C
|
||||
```c
|
||||
int cmp(const void *p1, const void *p2) {
|
||||
int *pp1 = *(int**)p1;
|
||||
int *pp2 = *(int**)p2;
|
||||
// 若身高相同,则按照k从小到大排列
|
||||
// 若身高不同,按身高从大到小排列
|
||||
return pp1[0] == pp2[0] ? pp1[1] - pp2[1] : pp2[0] - pp1[0];
|
||||
}
|
||||
|
||||
// 将start与end中间的元素都后移一位
|
||||
// start为将要新插入元素的位置
|
||||
void moveBack(int **people, int peopleSize, int start, int end) {
|
||||
int i;
|
||||
for(i = end; i > start; i--) {
|
||||
people[i] = people[i-1];
|
||||
}
|
||||
}
|
||||
|
||||
int** reconstructQueue(int** people, int peopleSize, int* peopleColSize, int* returnSize, int** returnColumnSizes){
|
||||
int i;
|
||||
// 将people按身高从大到小排列(若身高相同,按k从小到大排列)
|
||||
qsort(people, peopleSize, sizeof(int*), cmp);
|
||||
|
||||
for(i = 0; i < peopleSize; ++i) {
|
||||
// people[i]要插入的位置
|
||||
int position = people[i][1];
|
||||
int *temp = people[i];
|
||||
// 将position到i中间的元素后移一位
|
||||
// 注:因为已经排好序,position不会比i大。(举例:排序后people最后一位元素最小,其可能的k最大值为peopleSize-2,小于此时的i)
|
||||
moveBack(people, peopleSize, position, i);
|
||||
// 将temp放置到position处
|
||||
people[position] = temp;
|
||||
|
||||
}
|
||||
|
||||
|
||||
// 设置返回二维数组的大小以及里面每个一维数组的长度
|
||||
*returnSize = peopleSize;
|
||||
*returnColumnSizes = (int*)malloc(sizeof(int) * peopleSize);
|
||||
for(i = 0; i < peopleSize; ++i) {
|
||||
(*returnColumnSizes)[i] = 2;
|
||||
}
|
||||
return people;
|
||||
}
|
||||
```
|
||||
|
||||
### TypeScript
|
||||
|
||||
```typescript
|
||||
@ -309,5 +357,6 @@ function reconstructQueue(people: number[][]): number[][] {
|
||||
|
||||
|
||||
|
||||
|
||||
-----------------------
|
||||
<div align="center"><img src=https://code-thinking.cdn.bcebos.com/pics/01二维码一.jpg width=500> </img></div>
|
||||
|
||||
@ -184,13 +184,14 @@ public:
|
||||
class Solution {
|
||||
public int eraseOverlapIntervals(int[][] intervals) {
|
||||
Arrays.sort(intervals, (a, b) -> {
|
||||
if (a[0] == a[0]) return a[1] - b[1];
|
||||
return a[0] - b[0];
|
||||
// 按照区间右边界升序排序
|
||||
return a[1] - b[1];
|
||||
});
|
||||
|
||||
int count = 0;
|
||||
int edge = Integer.MIN_VALUE;
|
||||
for (int i = 0; i < intervals.length; i++) {
|
||||
// 若上一个区间的右边界小于当前区间的左边界,说明无交集
|
||||
if (edge <= intervals[i][0]) {
|
||||
edge = intervals[i][1];
|
||||
} else {
|
||||
@ -306,6 +307,55 @@ var eraseOverlapIntervals = function(intervals) {
|
||||
}
|
||||
```
|
||||
|
||||
### TypeScript
|
||||
|
||||
> 按右边界排序,从左往右遍历
|
||||
|
||||
```typescript
|
||||
function eraseOverlapIntervals(intervals: number[][]): number {
|
||||
const length = intervals.length;
|
||||
if (length === 0) return 0;
|
||||
intervals.sort((a, b) => a[1] - b[1]);
|
||||
let right: number = intervals[0][1];
|
||||
let count: number = 1;
|
||||
for (let i = 1; i < length; i++) {
|
||||
if (intervals[i][0] >= right) {
|
||||
count++;
|
||||
right = intervals[i][1];
|
||||
}
|
||||
}
|
||||
return length - count;
|
||||
};
|
||||
```
|
||||
|
||||
> 按左边界排序,从左往右遍历
|
||||
|
||||
```typescript
|
||||
function eraseOverlapIntervals(intervals: number[][]): number {
|
||||
if (intervals.length === 0) return 0;
|
||||
intervals.sort((a, b) => a[0] - b[0]);
|
||||
let right: number = intervals[0][1];
|
||||
let tempInterval: number[];
|
||||
let resCount: number = 0;
|
||||
for (let i = 1, length = intervals.length; i < length; i++) {
|
||||
tempInterval = intervals[i];
|
||||
if (tempInterval[0] >= right) {
|
||||
// 未重叠
|
||||
right = tempInterval[1];
|
||||
} else {
|
||||
// 有重叠,移除当前interval和前一个interval中右边界更大的那个
|
||||
right = Math.min(right, tempInterval[1]);
|
||||
resCount++;
|
||||
}
|
||||
}
|
||||
return resCount;
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
-----------------------
|
||||
<div align="center"><img src=https://code-thinking.cdn.bcebos.com/pics/01二维码一.jpg width=500> </img></div>
|
||||
|
||||
@ -244,6 +244,39 @@ class Solution:
|
||||
```
|
||||
|
||||
Go:
|
||||
|
||||
> 未精简版本
|
||||
```go
|
||||
func nextGreaterElement(nums1 []int, nums2 []int) []int {
|
||||
res := make([]int, len(nums1))
|
||||
for i := range res { res[i] = -1 }
|
||||
m := make(map[int]int, len(nums1))
|
||||
for k, v := range nums1 { m[v] = k }
|
||||
|
||||
stack := []int{0}
|
||||
for i := 1; i < len(nums2); i++ {
|
||||
top := stack[len(stack)-1]
|
||||
if nums2[i] < nums2[top] {
|
||||
stack = append(stack, i)
|
||||
} else if nums2[i] == nums2[top] {
|
||||
stack = append(stack, i)
|
||||
} else {
|
||||
for len(stack) != 0 && nums2[i] > nums2[top] {
|
||||
if v, ok := m[nums2[top]]; ok {
|
||||
res[v] = nums2[i]
|
||||
}
|
||||
stack = stack[:len(stack)-1]
|
||||
if len(stack) != 0 {
|
||||
top = stack[len(stack)-1]
|
||||
}
|
||||
}
|
||||
stack = append(stack, i)
|
||||
}
|
||||
}
|
||||
return res
|
||||
}
|
||||
```
|
||||
> 精简版本
|
||||
```go
|
||||
func nextGreaterElement(nums1 []int, nums2 []int) []int {
|
||||
res := make([]int, len(nums1))
|
||||
|
||||
@ -245,7 +245,29 @@ var fib = function(n) {
|
||||
};
|
||||
```
|
||||
|
||||
TypeScript
|
||||
|
||||
```typescript
|
||||
function fib(n: number): number {
|
||||
/**
|
||||
dp[i]: 第i个斐波那契数
|
||||
dp[0]: 0;
|
||||
dp[1]:1;
|
||||
...
|
||||
dp[i] = dp[i - 1] + dp[i - 2];
|
||||
*/
|
||||
const dp: number[] = [];
|
||||
dp[0] = 0;
|
||||
dp[1] = 1;
|
||||
for (let i = 2; i <= n; i++) {
|
||||
dp[i] = dp[i - 1] + dp[i - 2];
|
||||
}
|
||||
return dp[n];
|
||||
};
|
||||
```
|
||||
|
||||
### C
|
||||
|
||||
动态规划:
|
||||
```c
|
||||
int fib(int n){
|
||||
|
||||
@ -237,6 +237,45 @@ class Solution:
|
||||
```
|
||||
|
||||
Go:
|
||||
> 动态规划:
|
||||
```go
|
||||
func findLengthOfLCIS(nums []int) int {
|
||||
if len(nums) == 0 {return 0}
|
||||
res, count := 1, 1
|
||||
for i := 0; i < len(nums)-1; i++ {
|
||||
if nums[i+1] > nums[i] {
|
||||
count++
|
||||
}else {
|
||||
count = 1
|
||||
}
|
||||
if count > res {
|
||||
res = count
|
||||
}
|
||||
}
|
||||
return res
|
||||
}
|
||||
```
|
||||
|
||||
> 贪心算法:
|
||||
```go
|
||||
func findLengthOfLCIS(nums []int) int {
|
||||
if len(nums) == 0 {return 0}
|
||||
dp := make([]int, len(nums))
|
||||
for i := 0; i < len(dp); i++ {
|
||||
dp[i] = 1
|
||||
}
|
||||
res := 1
|
||||
for i := 0; i < len(nums)-1; i++ {
|
||||
if nums[i+1] > nums[i] {
|
||||
dp[i+1] = dp[i] + 1
|
||||
}
|
||||
if dp[i+1] > res {
|
||||
res = dp[i+1]
|
||||
}
|
||||
}
|
||||
return res
|
||||
}
|
||||
```
|
||||
|
||||
Rust:
|
||||
```rust
|
||||
|
||||
@ -293,6 +293,50 @@ var maxProfit = function(prices, fee) {
|
||||
};
|
||||
```
|
||||
|
||||
TypeScript:
|
||||
|
||||
> 贪心
|
||||
|
||||
```typescript
|
||||
function maxProfit(prices: number[], fee: number): number {
|
||||
if (prices.length === 0) return 0;
|
||||
let minPrice: number = prices[0];
|
||||
let profit: number = 0;
|
||||
for (let i = 1, length = prices.length; i < length; i++) {
|
||||
if (minPrice > prices[i]) {
|
||||
minPrice = prices[i];
|
||||
}
|
||||
if (minPrice + fee < prices[i]) {
|
||||
profit += prices[i] - minPrice - fee;
|
||||
minPrice = prices[i] - fee;
|
||||
}
|
||||
}
|
||||
return profit;
|
||||
};
|
||||
```
|
||||
|
||||
> 动态规划
|
||||
|
||||
```typescript
|
||||
function maxProfit(prices: number[], fee: number): number {
|
||||
/**
|
||||
dp[i][1]: 第i天不持有股票的最大所剩现金
|
||||
dp[i][0]: 第i天持有股票的最大所剩现金
|
||||
*/
|
||||
const length: number = prices.length;
|
||||
const dp: number[][] = new Array(length).fill(0).map(_ => []);
|
||||
dp[0][1] = 0;
|
||||
dp[0][0] = -prices[0];
|
||||
for (let i = 1, length = prices.length; i < length; i++) {
|
||||
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee);
|
||||
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
|
||||
}
|
||||
return Math.max(dp[length - 1][0], dp[length - 1][1]);
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
-----------------------
|
||||
<div align="center"><img src=https://code-thinking.cdn.bcebos.com/pics/01二维码一.jpg width=500> </img></div>
|
||||
|
||||
@ -225,6 +225,28 @@ var monotoneIncreasingDigits = function(n) {
|
||||
};
|
||||
```
|
||||
|
||||
### TypeScript
|
||||
|
||||
```typescript
|
||||
function monotoneIncreasingDigits(n: number): number {
|
||||
let strArr: number[] = String(n).split('').map(i => parseInt(i));
|
||||
const length = strArr.length;
|
||||
let flag: number = length;
|
||||
for (let i = length - 2; i >= 0; i--) {
|
||||
if (strArr[i] > strArr[i + 1]) {
|
||||
strArr[i] -= 1;
|
||||
flag = i + 1;
|
||||
}
|
||||
}
|
||||
for (let i = flag; i < length; i++) {
|
||||
strArr[i] = 9;
|
||||
}
|
||||
return parseInt(strArr.join(''));
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
-----------------------
|
||||
<div align="center"><img src=https://code-thinking.cdn.bcebos.com/pics/01二维码一.jpg width=500> </img></div>
|
||||
|
||||
@ -34,7 +34,7 @@
|
||||
|
||||
那么单调栈的原理是什么呢?为什么时间复杂度是O(n)就可以找到每一个元素的右边第一个比它大的元素位置呢?
|
||||
|
||||
单调栈的本质是空间换时间,因为在遍历的过程中需要用一个栈来记录右边第一个比当前元素的元素,优点是只需要遍历一次。
|
||||
单调栈的本质是空间换时间,因为在遍历的过程中需要用一个栈来记录右边第一个比当前元素大的元素,优点是只需要遍历一次。
|
||||
|
||||
|
||||
在使用单调栈的时候首先要明确如下几点:
|
||||
@ -233,7 +233,7 @@ class Solution {
|
||||
}
|
||||
```
|
||||
Python:
|
||||
``` Python3
|
||||
```python
|
||||
class Solution:
|
||||
def dailyTemperatures(self, temperatures: List[int]) -> List[int]:
|
||||
answer = [0]*len(temperatures)
|
||||
@ -277,8 +277,36 @@ func dailyTemperatures(t []int) []int {
|
||||
}
|
||||
```
|
||||
|
||||
> 单调栈法
|
||||
> 单调栈法(未精简版本)
|
||||
|
||||
```go
|
||||
func dailyTemperatures(temperatures []int) []int {
|
||||
res := make([]int, len(temperatures))
|
||||
// 初始化栈顶元素为第一个下标索引0
|
||||
stack := []int{0}
|
||||
|
||||
for i := 1; i < len(temperatures); i++ {
|
||||
top := stack[len(stack)-1]
|
||||
if temperatures[i] < temperatures[top] {
|
||||
stack = append(stack, i)
|
||||
} else if temperatures[i] == temperatures[top] {
|
||||
stack = append(stack, i)
|
||||
} else {
|
||||
for len(stack) != 0 && temperatures[i] > temperatures[top] {
|
||||
res[top] = i - top
|
||||
stack = stack[:len(stack)-1]
|
||||
if len(stack) != 0 {
|
||||
top = stack[len(stack)-1]
|
||||
}
|
||||
}
|
||||
stack = append(stack, i)
|
||||
}
|
||||
}
|
||||
return res
|
||||
}
|
||||
```
|
||||
|
||||
> 单调栈法(精简版本)
|
||||
```go
|
||||
// 单调递减栈
|
||||
func dailyTemperatures(num []int) []int {
|
||||
|
||||
@ -266,7 +266,30 @@ var minCostClimbingStairs = function(cost) {
|
||||
};
|
||||
```
|
||||
|
||||
### TypeScript
|
||||
|
||||
```typescript
|
||||
function minCostClimbingStairs(cost: number[]): number {
|
||||
/**
|
||||
dp[i]: 走到第i阶需要花费的最少金钱
|
||||
dp[0]: cost[0];
|
||||
dp[1]: cost[1];
|
||||
...
|
||||
dp[i]: min(dp[i - 1], dp[i - 2]) + cost[i];
|
||||
*/
|
||||
const dp: number[] = [];
|
||||
const length: number = cost.length;
|
||||
dp[0] = cost[0];
|
||||
dp[1] = cost[1];
|
||||
for (let i = 2; i <= length; i++) {
|
||||
dp[i] = Math.min(dp[i - 1], dp[i - 2]) + cost[i];
|
||||
}
|
||||
return Math.min(dp[length - 1], dp[length - 2]);
|
||||
};
|
||||
```
|
||||
|
||||
### C
|
||||
|
||||
```c
|
||||
int minCostClimbingStairs(int* cost, int costSize){
|
||||
//开辟dp数组,大小为costSize
|
||||
|
||||
@ -229,6 +229,31 @@ var partitionLabels = function(s) {
|
||||
};
|
||||
```
|
||||
|
||||
### TypeScript
|
||||
|
||||
```typescript
|
||||
function partitionLabels(s: string): number[] {
|
||||
const length: number = s.length;
|
||||
const resArr: number[] = [];
|
||||
const helperMap: Map<string, number> = new Map();
|
||||
for (let i = 0; i < length; i++) {
|
||||
helperMap.set(s[i], i);
|
||||
}
|
||||
let left: number = 0;
|
||||
let right: number = 0;
|
||||
for (let i = 0; i < length; i++) {
|
||||
right = Math.max(helperMap.get(s[i])!, right);
|
||||
if (i === right) {
|
||||
resArr.push(i - left + 1);
|
||||
left = i + 1;
|
||||
}
|
||||
}
|
||||
return resArr;
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
-----------------------
|
||||
<div align="center"><img src=https://code-thinking.cdn.bcebos.com/pics/01二维码一.jpg width=500> </img></div>
|
||||
|
||||
@ -250,6 +250,49 @@ var lemonadeChange = function(bills) {
|
||||
return true
|
||||
};
|
||||
|
||||
```
|
||||
### C
|
||||
```c
|
||||
bool lemonadeChange(int* bills, int billsSize){
|
||||
// 分别记录五元、十元的数量(二十元不用记录,因为不会用到20元找零)
|
||||
int fiveCount = 0; int tenCount = 0;
|
||||
|
||||
int i;
|
||||
for(i = 0; i < billsSize; ++i) {
|
||||
// 分情况讨论每位顾客的付款
|
||||
switch(bills[i]) {
|
||||
// 情况一:直接收款五元
|
||||
case 5:
|
||||
fiveCount++;
|
||||
break;
|
||||
// 情况二:收款十元
|
||||
case 10:
|
||||
// 若没有五元找零,返回false
|
||||
if(fiveCount == 0)
|
||||
return false;
|
||||
// 收款十元并找零五元
|
||||
fiveCount--;
|
||||
tenCount++;
|
||||
break;
|
||||
// 情况三:收款二十元
|
||||
case 20:
|
||||
// 若可以,优先用十元和五元找零(因为十元只能找零20,所以需要尽量用掉。而5元能找零十元和二十元)
|
||||
if(fiveCount > 0 && tenCount > 0) {
|
||||
fiveCount--;
|
||||
tenCount--;
|
||||
}
|
||||
// 若没有十元,但是有三张五元。用三张五元找零
|
||||
else if(fiveCount >= 3)
|
||||
fiveCount-=3;
|
||||
// 无法找开,返回false
|
||||
else
|
||||
return false;
|
||||
break;
|
||||
}
|
||||
}
|
||||
// 全部可以找开,返回true
|
||||
return true;
|
||||
}
|
||||
```
|
||||
|
||||
### TypeScript
|
||||
|
||||
@ -476,7 +476,35 @@ var minCameraCover = function(root) {
|
||||
};
|
||||
```
|
||||
|
||||
### TypeScript
|
||||
|
||||
```typescript
|
||||
function minCameraCover(root: TreeNode | null): number {
|
||||
/** 0-无覆盖, 1-有摄像头, 2-有覆盖 */
|
||||
type statusCode = 0 | 1 | 2;
|
||||
let resCount: number = 0;
|
||||
if (recur(root) === 0) resCount++;
|
||||
return resCount;
|
||||
function recur(node: TreeNode | null): statusCode {
|
||||
if (node === null) return 2;
|
||||
const left: statusCode = recur(node.left),
|
||||
right: statusCode = recur(node.right);
|
||||
let resStatus: statusCode = 0;
|
||||
if (left === 0 || right === 0) {
|
||||
resStatus = 1;
|
||||
resCount++;
|
||||
} else if (left === 1 || right === 1) {
|
||||
resStatus = 2;
|
||||
} else {
|
||||
resStatus = 0;
|
||||
}
|
||||
return resStatus;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
### C
|
||||
|
||||
```c
|
||||
/*
|
||||
**函数后序遍历二叉树。判断一个结点状态时,根据其左右孩子结点的状态进行判断
|
||||
|
||||
@ -11,9 +11,9 @@
|
||||
|
||||
看完本篇大家可以使用迭代法,再重新解决如下三道leetcode上的题目:
|
||||
|
||||
* 144.二叉树的前序遍历
|
||||
* 94.二叉树的中序遍历
|
||||
* 145.二叉树的后序遍历
|
||||
* [144.二叉树的前序遍历](https://leetcode-cn.com/problems/binary-tree-preorder-traversal/)
|
||||
* [94.二叉树的中序遍历](https://leetcode-cn.com/problems/binary-tree-inorder-traversal/)
|
||||
* [145.二叉树的后序遍历](https://leetcode-cn.com/problems/binary-tree-postorder-traversal/)
|
||||
|
||||
为什么可以用迭代法(非递归的方式)来实现二叉树的前后中序遍历呢?
|
||||
|
||||
|
||||
@ -99,9 +99,9 @@ void traversal(TreeNode* cur, vector<int>& vec) {
|
||||
|
||||
此时大家可以做一做leetcode上三道题目,分别是:
|
||||
|
||||
* 144.二叉树的前序遍历
|
||||
* 145.二叉树的后序遍历
|
||||
* 94.二叉树的中序遍历
|
||||
* [144.二叉树的前序遍历](https://leetcode-cn.com/problems/binary-tree-preorder-traversal/)
|
||||
* [145.二叉树的后序遍历](https://leetcode-cn.com/problems/binary-tree-postorder-traversal/)
|
||||
* [94.二叉树的中序遍历](https://leetcode-cn.com/problems/binary-tree-inorder-traversal/)
|
||||
|
||||
可能有同学感觉前后中序遍历的递归太简单了,要打迭代法(非递归),别急,我们明天打迭代法,打个通透!
|
||||
|
||||
|
||||
@ -266,7 +266,61 @@ public class Solution {
|
||||
|
||||
## Python
|
||||
|
||||
```Python
|
||||
```Python3
|
||||
class TreeNode:
|
||||
def __init__(self, val = 0, left = None, right = None):
|
||||
self.val = val
|
||||
self.left = left
|
||||
self.right = right
|
||||
|
||||
|
||||
# 根据数组构建二叉树
|
||||
|
||||
def construct_binary_tree(nums: []) -> TreeNode:
|
||||
if not nums:
|
||||
return None
|
||||
# 用于存放构建好的节点
|
||||
root = TreeNode(-1)
|
||||
Tree = []
|
||||
# 将数组元素全部转化为树节点
|
||||
for i in range(len(nums)):
|
||||
if nums[i]!= -1:
|
||||
node = TreeNode(nums[i])
|
||||
else:
|
||||
node = None
|
||||
Tree.append(node)
|
||||
if i == 0:
|
||||
root = node
|
||||
for i in range(len(Tree)):
|
||||
node = Tree[i]
|
||||
if node and (2 * i + 2) < len(Tree):
|
||||
node.left = Tree[i * 2 + 1]
|
||||
node.right = Tree[i * 2 + 2]
|
||||
return root
|
||||
|
||||
|
||||
|
||||
# 算法:中序遍历二叉树
|
||||
|
||||
class Solution:
|
||||
def __init__(self):
|
||||
self.T = []
|
||||
def inorder(self, root: TreeNode) -> []:
|
||||
if not root:
|
||||
return
|
||||
self.inorder(root.left)
|
||||
self.T.append(root.val)
|
||||
self.inorder(root.right)
|
||||
return self.T
|
||||
|
||||
|
||||
|
||||
# 验证创建二叉树的有效性,二叉排序树的中序遍历应为顺序排列
|
||||
|
||||
test_tree = [3, 1, 5, -1, 2, 4 ,6]
|
||||
root = construct_binary_tree(test_tree)
|
||||
A = Solution()
|
||||
print(A.inorder(root))
|
||||
```
|
||||
|
||||
|
||||
|
||||
@ -43,19 +43,19 @@
|
||||
|
||||
**那么二维数组在内存的空间地址是连续的么?**
|
||||
|
||||
我们来举一个例子,例如: `int[][] rating = new int[3][4];` , 这个二维数据在内存空间可不是一个 `3*4` 的连续地址空间
|
||||
我们来举一个Java的例子,例如: `int[][] rating = new int[3][4];` , 这个二维数组在内存空间可不是一个 `3*4` 的连续地址空间
|
||||
|
||||
看了下图,就应该明白了:
|
||||
|
||||
<img src='https://code-thinking.cdn.bcebos.com/pics/%E7%AE%97%E6%B3%95%E9%80%9A%E5%85%B3%E6%95%B0%E7%BB%843.png' width=600> </img></div>
|
||||
|
||||
所以**二维数据在内存中不是 `3*4` 的连续地址空间,而是四条连续的地址空间组成!**
|
||||
所以**Java的二维数组在内存中不是 `3*4` 的连续地址空间,而是四条连续的地址空间组成!**
|
||||
|
||||
# 数组的经典题目
|
||||
|
||||
在面试中,数组是必考的基础数据结构。
|
||||
|
||||
其实数据的题目在思想上一般比较简单的,但是如果想高效,并不容易。
|
||||
其实数组的题目在思想上一般比较简单的,但是如果想高效,并不容易。
|
||||
|
||||
我们之前一共讲解了四道经典数组题目,每一道题目都代表一个类型,一种思想。
|
||||
|
||||
@ -115,7 +115,7 @@
|
||||
|
||||
在这道题目中,我们再一次介绍到了**循环不变量原则**,其实这也是写程序中的重要原则。
|
||||
|
||||
相信大家又遇到过这种情况: 感觉题目的边界调节超多,一波接着一波的判断,找边界,踩了东墙补西墙,好不容易运行通过了,代码写的十分冗余,毫无章法,其实**真正解决题目的代码都是简洁的,或者有原则性的**,大家可以在这道题目中体会到这一点。
|
||||
相信大家有遇到过这种情况: 感觉题目的边界调节超多,一波接着一波的判断,找边界,拆了东墙补西墙,好不容易运行通过了,代码写的十分冗余,毫无章法,其实**真正解决题目的代码都是简洁的,或者有原则性的**,大家可以在这道题目中体会到这一点。
|
||||
|
||||
|
||||
# 总结
|
||||
|
||||
@ -380,28 +380,37 @@ func main() {
|
||||
### javascript
|
||||
|
||||
```js
|
||||
function testweightbagproblem (wight, value, size) {
|
||||
const len = wight.length,
|
||||
dp = array.from({length: len + 1}).map(
|
||||
() => array(size + 1).fill(0)
|
||||
);
|
||||
/**
|
||||
*
|
||||
* @param {Number []} weight
|
||||
* @param {Number []} value
|
||||
* @param {Number} size
|
||||
* @returns
|
||||
*/
|
||||
|
||||
for(let i = 1; i <= len; i++) {
|
||||
for(let j = 0; j <= size; j++) {
|
||||
if(wight[i - 1] <= j) {
|
||||
dp[i][j] = math.max(
|
||||
dp[i - 1][j],
|
||||
value[i - 1] + dp[i - 1][j - wight[i - 1]]
|
||||
)
|
||||
} else {
|
||||
dp[i][j] = dp[i - 1][j];
|
||||
}
|
||||
}
|
||||
}
|
||||
function testWeightBagProblem(weight, value, size) {
|
||||
const len = weight.length,
|
||||
dp = Array.from({length: len}).map(
|
||||
() => Array(size + 1)) //JavaScript 数组是引用类型
|
||||
for(let i = 0; i < len; i++) { //初始化最左一列,即背包容量为0时的情况
|
||||
dp[i][0] = 0;
|
||||
}
|
||||
for(let j = 1; j < size+1; j++) { //初始化第0行, 只有一件物品的情况
|
||||
if(weight[0] <= j) {
|
||||
dp[0][j] = value[0];
|
||||
} else {
|
||||
dp[0][j] = 0;
|
||||
}
|
||||
}
|
||||
|
||||
// console.table(dp);
|
||||
for(let i = 1; i < len; i++) { //dp[i][j]由其左上方元素推导得出
|
||||
for(let j = 1; j < size+1; j++) {
|
||||
if(j < weight[i]) dp[i][j] = dp[i - 1][j];
|
||||
else dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j - weight[i]] + value[i]);
|
||||
}
|
||||
}
|
||||
|
||||
return dp[len][size];
|
||||
return dp[len-1][size] //满足条件的最大值
|
||||
}
|
||||
|
||||
function testWeightBagProblem2 (wight, value, size) {
|
||||
|
||||
@ -24,7 +24,7 @@
|
||||
|
||||
## 双链表
|
||||
|
||||
单链表中的节点只能指向节点的下一个节点。
|
||||
单链表中的指针域只能指向节点的下一个节点。
|
||||
|
||||
双链表:每一个节点有两个指针域,一个指向下一个节点,一个指向上一个节点。
|
||||
|
||||
@ -56,7 +56,7 @@
|
||||
|
||||
|
||||
|
||||
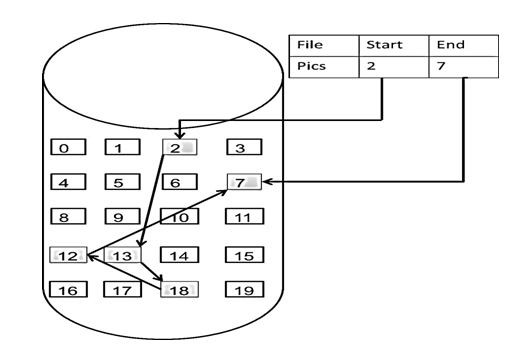
这个链表起始节点为2, 终止节点为7, 各个节点分布在内存个不同地址空间上,通过指针串联在一起。
|
||||
这个链表起始节点为2, 终止节点为7, 各个节点分布在内存的不同地址空间上,通过指针串联在一起。
|
||||
|
||||
# 链表的定义
|
||||
|
||||
|
||||
Reference in New Issue
Block a user