mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-06 23:28:29 +08:00
Update
This commit is contained in:
@ -132,6 +132,7 @@
|
||||
* [关于回溯算法,你该了解这些!](https://mp.weixin.qq.com/s/gjSgJbNbd1eAA5WkA-HeWw)
|
||||
* [回溯算法:求组合问题!](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)
|
||||
* [回溯算法:组合问题再剪剪枝](https://mp.weixin.qq.com/s/Ri7spcJMUmph4c6XjPWXQA)
|
||||
* [回溯算法:求组合总和!](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w)
|
||||
|
||||
(持续更新中....)
|
||||
|
||||
@ -305,6 +306,7 @@
|
||||
|[0051.N皇后](https://github.com/youngyangyang04/leetcode/blob/master/problems/0051.N皇后.md) |回溯|困难| **回溯**|
|
||||
|[0052.N皇后II](https://github.com/youngyangyang04/leetcode/blob/master/problems/0052.N皇后II.md) |回溯|困难| **回溯**|
|
||||
|[0053.最大子序和](https://github.com/youngyangyang04/leetcode/blob/master/problems/0053.最大子序和.md) |数组 |简单|**暴力** **贪心** 动态规划 分治|
|
||||
|[0055.跳跃游戏](https://github.com/youngyangyang04/leetcode/blob/master/problems/0053.最大子序和.md) |数组 |中等| **贪心** 经典题目|
|
||||
|[0059.螺旋矩阵II](https://github.com/youngyangyang04/leetcode/blob/master/problems/0059.螺旋矩阵II.md) |数组 |中等|**模拟**|
|
||||
|[0077.组合](https://github.com/youngyangyang04/leetcode/blob/master/problems/0077.组合.md) |回溯 |中等|**回溯**|
|
||||
|[0078.子集](https://github.com/youngyangyang04/leetcode/blob/master/problems/0078.子集.md) |回溯/数组 |中等|**回溯**|
|
||||
@ -328,6 +330,7 @@
|
||||
|[0113.路径总和II](https://github.com/youngyangyang04/leetcode/blob/master/problems/0113.路径总和II.md) |二叉树树 |简单|**深度优先搜索/递归** **回溯** **栈**|
|
||||
|[0116.填充每个节点的下一个右侧节点指针](https://github.com/youngyangyang04/leetcode/blob/master/problems/0116.填充每个节点的下一个右侧节点指针.md) |二叉树 |中等|**递归** **迭代/广度优先搜索**|
|
||||
|[0117.填充每个节点的下一个右侧节点指针II](https://github.com/youngyangyang04/leetcode/blob/master/problems/0117.填充每个节点的下一个右侧节点指针II.md) |二叉树 |中等|**递归** **迭代/广度优先搜索**|
|
||||
|[0129.求根到叶子节点数字之和](https://github.com/youngyangyang04/leetcode/blob/master/problems/0129.求根到叶子节点数字之和.md) |二叉树 |中等|**递归/回溯** 递归里隐藏着回溯,和113.路径总和II类似|
|
||||
|[0131.分割回文串](https://github.com/youngyangyang04/leetcode/blob/master/problems/0131.分割回文串.md) |回溯 |中等|**回溯**|
|
||||
|[0141.环形链表](https://github.com/youngyangyang04/leetcode/blob/master/problems/0141.环形链表.md) |链表 |简单|**快慢指针/双指针**|
|
||||
|[0142.环形链表II](https://github.com/youngyangyang04/leetcode/blob/master/problems/0142.环形链表II.md) |链表 |中等|**快慢指针/双指针**|
|
||||
|
||||
Binary file not shown.
|
Before Width: | Height: | Size: 59 KiB After Width: | Height: | Size: 125 KiB |
BIN
pics/463.岛屿的周长.png
Normal file
BIN
pics/463.岛屿的周长.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 31 KiB |
BIN
pics/463.岛屿的周长1.png
Normal file
BIN
pics/463.岛屿的周长1.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 50 KiB |
BIN
pics/55.跳跃游戏.png
Normal file
BIN
pics/55.跳跃游戏.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 62 KiB |
@ -1,64 +1,140 @@
|
||||
|
||||
|
||||
## 题目地址
|
||||
https://leetcode-cn.com/problems/letter-combinations-of-a-phone-number/
|
||||
|
||||
## 思路
|
||||
> 多个集合求组合问题。
|
||||
|
||||
本题要解决如下问题:
|
||||
# 17.电话号码的字母组合
|
||||
|
||||
题目链接:https://leetcode-cn.com/problems/letter-combinations-of-a-phone-number/
|
||||
|
||||
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。
|
||||
|
||||
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
|
||||
|
||||
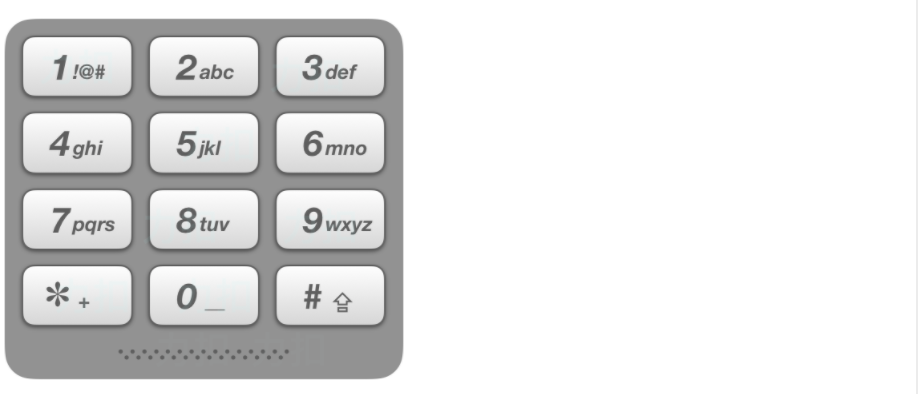
|
||||
|
||||
示例:
|
||||
输入:"23"
|
||||
输出:["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].
|
||||
|
||||
说明:尽管上面的答案是按字典序排列的,但是你可以任意选择答案输出的顺序。
|
||||
|
||||
# 思路
|
||||
|
||||
从示例上来说,输入"23",最直接的想法就是两层for循环遍历了吧,正好把组合的情况都输出了。
|
||||
|
||||
如果输入"233"呢,那么就三层for循环,如果"2333"呢,就四层for循环.......
|
||||
|
||||
大家应该感觉出和[回溯算法:求组合问题!](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)遇到的一样的问题,就是这for循环的层数如何写出来,此时又是回溯法登场的时候了。
|
||||
|
||||
理解本题后,要解决如下三个问题:
|
||||
|
||||
1. 数字和字母如何映射
|
||||
2. 两个字母我就两个for循环,三个字符我就三个for循环,以此类推,然后发现代码根本写不出来
|
||||
2. 两个字母就两个for循环,三个字符我就三个for循环,以此类推,然后发现代码根本写不出来
|
||||
3. 输入1 * #按键等等异常情况
|
||||
|
||||
接下来一一解决这几个问题。
|
||||
## 数字和字母如何映射
|
||||
|
||||
可以使用map或者定义一个二位数组,例如:string letterMap[10],来做映射,我这里定义一个二维数组,代码如下:
|
||||
|
||||
```
|
||||
const string letterMap[10] = {
|
||||
"", // 0
|
||||
"", // 1
|
||||
"abc", // 2
|
||||
"def", // 3
|
||||
"ghi", // 4
|
||||
"jkl", // 5
|
||||
"mno", // 6
|
||||
"pqrs", // 7
|
||||
"tuv", // 8
|
||||
"wxyz", // 9
|
||||
};
|
||||
```
|
||||
|
||||
## 回溯法来解决n个for循环的问题
|
||||
|
||||
对于回溯法还不了解的同学看这篇:[关于回溯算法,你该了解这些!](https://mp.weixin.qq.com/s/gjSgJbNbd1eAA5WkA-HeWw)
|
||||
|
||||
|
||||
1. 数字和字母如何映射
|
||||
|
||||
定义一个二位数组,例如:string letterMap[10],来做映射
|
||||
|
||||
2. 两个字母我就两个for循环,三个字符我就三个for循环,以此类推,然后发现代码根本写不出来。
|
||||
|
||||
**遇到这种情况,就应该想到回溯了。**
|
||||
|
||||
这是一个回溯法的经典题目,**不要以为回溯是一个性能很高的算法,回溯其实就是暴力枚举,纯暴力,搜出所有的可能性。**
|
||||
|
||||
回溯一般都伴随着递归,而这种组合问题,都可以画成一个树形结构。
|
||||
|
||||
例如:输入:"23",如图所示:
|
||||
例如:输入:"23",抽象为树形结构,如图所示:
|
||||
|
||||
<img src='../pics/17. 电话号码的字母组合.png' width=600> </img></div>
|
||||
|
||||
可以想成遍历这棵树,然后把叶子节点都保存下来,输出["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"]。
|
||||
图中可以看出遍历的深度,就是输入"23"的长度,而叶子节点就是我们要收集的结果,输出["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"]。
|
||||
|
||||
回溯三部曲:
|
||||
|
||||
3. 输入1 * #按键等等异常情况
|
||||
* 确定回溯函数参数
|
||||
|
||||
题目的测试数据中应该没有异常情况的数据,可以不考虑,但是要知道会有这些异常。
|
||||
首先需要一个字符串s来收集叶子节点的结果,然后用一个字符串数组result保存起来,这两个变量我依然定义为全局。
|
||||
|
||||
再来看参数,参数指定是有题目中给的string digits,然后还要有一个参数就是int型的index。
|
||||
|
||||
**那么在来讲一讲回溯法,回溯法的模板如下:**
|
||||
注意这个index可不是 [回溯算法:求组合问题!](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)和[回溯算法:求组合总和!](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w)中的startIndex了。
|
||||
|
||||
这个index是记录遍历第几个数字了,就是用来遍历digits的(题目中给出数字字符串),同时index也表示树的深度。
|
||||
|
||||
代码如下:
|
||||
|
||||
```
|
||||
backtracking() {
|
||||
if (终止条件) {
|
||||
存放结果;
|
||||
}
|
||||
vector<string> result;
|
||||
string s;
|
||||
void backtracking(const string& digits, int index)
|
||||
```
|
||||
|
||||
for (枚举同一个位置的所有可能性,可以想成节点孩子的数量) {
|
||||
递归,处理节点;
|
||||
backtracking();
|
||||
回溯,撤销处理结果
|
||||
}
|
||||
* 确定终止条件
|
||||
|
||||
例如输入用例"23",两个数字,那么根节点往下递归两层就可以了,叶子节点就是要收集的结果集。
|
||||
|
||||
那么终止条件就是如果index 等于 输入的数字个数(digits.size)了(本来index就是用来遍历digits的)。
|
||||
|
||||
然后收集结果,结束本层递归。
|
||||
|
||||
代码如下:
|
||||
|
||||
```
|
||||
if (index == digits.size()) {
|
||||
result.push_back(s);
|
||||
return;
|
||||
}
|
||||
```
|
||||
|
||||
按照这个模板,不难写出如下代码:
|
||||
* 确定单层遍历逻辑
|
||||
|
||||
## C++代码
|
||||
首先要取index指向的数字,并找到对应的字符集(手机键盘的字符集)。
|
||||
|
||||
然后for循环来处理这个字符集,代码如下:
|
||||
|
||||
```
|
||||
int digit = digits[index] - '0'; // 将index指向的数字转为int
|
||||
string letters = letterMap[digit]; // 取数字对应的字符集
|
||||
for (int i = 0; i < letters.size(); i++) {
|
||||
s.push_back(letters[i]); // 处理
|
||||
backtracking(digits, index + 1); // 递归,注意index+1,一下层要处理下一个数字了
|
||||
s.pop_back(); // 回溯
|
||||
}
|
||||
```
|
||||
|
||||
**注意这里for循环,可不像是在[回溯算法:求组合问题!](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)和[回溯算法:求组合总和!](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w)中从startIndex开始遍历的**。
|
||||
|
||||
**因为本题每一个数字代表的是不同集合,也就是求不同集合之间的组合,而[77. 组合](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)和[216.组合总和III](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w)都是是求同一个集合中的组合!**
|
||||
|
||||
|
||||
## 输入1 * #按键等等异常情况
|
||||
|
||||
代码中最好考虑这些异常情况,但题目的测试数据中应该没有异常情况的数据,所以我就没有加了。
|
||||
|
||||
**但是要知道会有这些异常,如果是现场面试中,一定要考虑到!**
|
||||
|
||||
|
||||
# C++代码
|
||||
关键地方都讲完了,按照[关于回溯算法,你该了解这些!](https://mp.weixin.qq.com/s/gjSgJbNbd1eAA5WkA-HeWw)中的回溯法模板,不难写出如下C++代码:
|
||||
|
||||
|
||||
```
|
||||
// 版本一
|
||||
class Solution {
|
||||
private:
|
||||
const string letterMap[10] = {
|
||||
@ -75,7 +151,53 @@ private:
|
||||
};
|
||||
public:
|
||||
vector<string> result;
|
||||
void getCombinations(const string& digits, int index, const string& s) {
|
||||
string s;
|
||||
void backtracking(const string& digits, int index) {
|
||||
if (index == digits.size()) {
|
||||
result.push_back(s);
|
||||
return;
|
||||
}
|
||||
int digit = digits[index] - '0'; // 将index指向的数字转为int
|
||||
string letters = letterMap[digit]; // 取数字对应的字符集
|
||||
for (int i = 0; i < letters.size(); i++) {
|
||||
s.push_back(letters[i]); // 处理
|
||||
backtracking(digits, index + 1); // 递归,注意index+1,一下层要处理下一个数字了
|
||||
s.pop_back(); // 回溯
|
||||
}
|
||||
}
|
||||
vector<string> letterCombinations(string digits) {
|
||||
s.clear();
|
||||
result.clear();
|
||||
if (digits.size() == 0) {
|
||||
return result;
|
||||
}
|
||||
backtracking(digits, 0);
|
||||
return result;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
一些写法,是把回溯的过程放在递归函数里了,例如如下代码,我可以写成这样:(注意注释中不一样的地方)
|
||||
|
||||
```
|
||||
// 版本二
|
||||
class Solution {
|
||||
private:
|
||||
const string letterMap[10] = {
|
||||
"", // 0
|
||||
"", // 1
|
||||
"abc", // 2
|
||||
"def", // 3
|
||||
"ghi", // 4
|
||||
"jkl", // 5
|
||||
"mno", // 6
|
||||
"pqrs", // 7
|
||||
"tuv", // 8
|
||||
"wxyz", // 9
|
||||
};
|
||||
public:
|
||||
vector<string> result;
|
||||
void getCombinations(const string& digits, int index, const string& s) { // 注意参数的不同
|
||||
if (index == digits.size()) {
|
||||
result.push_back(s);
|
||||
return;
|
||||
@ -83,10 +205,11 @@ public:
|
||||
int digit = digits[index] - '0';
|
||||
string letters = letterMap[digit];
|
||||
for (int i = 0; i < letters.size(); i++) {
|
||||
getCombinations(digits, index + 1, s + letters[i]);
|
||||
getCombinations(digits, index + 1, s + letters[i]); // 注意这里的不同
|
||||
}
|
||||
}
|
||||
vector<string> letterCombinations(string digits) {
|
||||
result.clear();
|
||||
if (digits.size() == 0) {
|
||||
return result;
|
||||
}
|
||||
@ -97,8 +220,16 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
# 拓展
|
||||
我不建议把回溯藏在递归的参数里这种写法,很不直观,我在[二叉树:以为使用了递归,其实还隐藏着回溯](https://mp.weixin.qq.com/s/ivLkHzWdhjQQD1rQWe6zWA)这篇文章中也深度分析了,回溯隐藏在了哪里。
|
||||
|
||||
请问为什么 getCombinations(const string& digits, int index, const string& s)函数里的string& s 前要加const,不加的报错
|
||||
所以大家可以按照版本一来写就可以了。
|
||||
|
||||
# 总结
|
||||
|
||||
本篇将题目的三个要点一一列出,并重点强调了和前面讲解过的[77. 组合](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)和[216.组合总和III](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w)的区别,本题是多个集合求组合,所以在回溯的搜索过程中,都有一些细节需要注意的。
|
||||
|
||||
其实本题不算难,但也处处是细节,大家还要自己亲自动手写一写。
|
||||
|
||||
**就酱,如果学到了,就帮Carl转发一波吧,让更多小伙伴知道这里!**
|
||||
|
||||
> 更多算法干货文章持续更新,可以微信搜索「代码随想录」第一时间围观,关注后,回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等,就可以获得我多年整理的学习资料。
|
||||
|
||||
41
problems/0055.跳跃游戏.md
Normal file
41
problems/0055.跳跃游戏.md
Normal file
@ -0,0 +1,41 @@
|
||||
## 链接
|
||||
https://leetcode-cn.com/problems/jump-game/
|
||||
|
||||
## 思路
|
||||
|
||||
其实贪心和动态规划很容易混在一起,在面试中,我们应该本着能用贪心就用贪心,贪心解决不了再考虑用动态规划。 毕竟贪心更容易理解,并快速写出代码。
|
||||
|
||||
刚看到本题一开始可能想:当前位置元素如果是3,我究竟是跳一步呢,还是两步呢,还是三步呢,究竟跳几步才是最优呢?
|
||||
|
||||
其实如果本题是要求只能跳元素数值大小的个数,不能多也不能少,问是否达到终点,那么一定要用动态规划了。
|
||||
|
||||
但本题其实我们就看跳到的范围能否覆盖终点,就可以了。
|
||||
|
||||
那么我们每次取最大的覆盖范围,看最后能否覆盖终点。
|
||||
|
||||
如图:
|
||||
|
||||
<img src='../pics/55.跳跃游戏.png' width=600> </img></div>
|
||||
|
||||
那么i每次移动只能在cover的范围内移动,每移动一个元素,cover得到该元素数值的补充,让i继续移动下去。
|
||||
|
||||
而cover每次只取 得到该元素数值补充后的范围 和 cover本身范围 的最大值。
|
||||
|
||||
如果cover大于等于了终点下表,直接return true就可以了。
|
||||
|
||||
C++代码如下:
|
||||
|
||||
```
|
||||
class Solution {
|
||||
public:
|
||||
bool canJump(vector<int>& nums) {
|
||||
int cover = 0;
|
||||
if (nums.size() == 1) return true; // 只有一个元素,就是能达到
|
||||
for (int i = 0; i <= cover; i++) { // 注意这里是小于等于cover
|
||||
cover = max(i + nums[i], cover);
|
||||
if (cover >= nums.size() - 1) return true; // 说明可以覆盖到终点了
|
||||
}
|
||||
return false;
|
||||
}
|
||||
};
|
||||
```
|
||||
@ -77,7 +77,7 @@ for (int i = startIndex; i <= n; i++) {
|
||||
|
||||
2. 还需要的元素个数为: k - path.size();
|
||||
|
||||
3. 在集合n中至少要从该起始位置 : n - (k - path.size()) + 1,开始遍历
|
||||
3. 在集合n中至多要从该起始位置 : n - (k - path.size()) + 1,开始遍历
|
||||
|
||||
为什么有个+1呢,因为包括起始位置,我们要是一个左闭的集合。
|
||||
|
||||
|
||||
@ -1,3 +1,5 @@
|
||||
## 链接
|
||||
https://leetcode-cn.com/problems/sum-root-to-leaf-numbers/
|
||||
|
||||
## 思路
|
||||
|
||||
@ -122,7 +124,6 @@ private:
|
||||
}
|
||||
return sum;
|
||||
}
|
||||
// 递归函数不需要返回值,因为我们要遍历整个树
|
||||
void traversal(TreeNode* cur) {
|
||||
if (!cur->left && !cur->right) { // 遇到了叶子节点
|
||||
result += vectorToInt(path);
|
||||
@ -130,14 +131,14 @@ private:
|
||||
}
|
||||
|
||||
if (cur->left) { // 左 (空节点不遍历)
|
||||
path.push_back(cur->left->val);
|
||||
path.push_back(cur->left->val); // 处理节点
|
||||
traversal(cur->left); // 递归
|
||||
path.pop_back(); // 回溯
|
||||
path.pop_back(); // 回溯,撤销
|
||||
}
|
||||
if (cur->right) { // 右 (空节点不遍历)
|
||||
path.push_back(cur->right->val);
|
||||
path.push_back(cur->right->val); // 处理节点
|
||||
traversal(cur->right); // 递归
|
||||
path.pop_back(); // 回溯
|
||||
path.pop_back(); // 回溯,撤销
|
||||
}
|
||||
return ;
|
||||
}
|
||||
@ -151,3 +152,9 @@ public:
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
# 总结
|
||||
|
||||
过于简洁的代码,很容易让初学者忽视了本题中回溯的精髓,甚至作者本身都没有想清楚自己用了回溯。
|
||||
|
||||
**我这里提供的代码把整个回溯过程充分体现出来,希望可以帮助大家看的明明白白!**
|
||||
|
||||
@ -168,6 +168,8 @@ if (sum > targetSum) { // 剪枝操作
|
||||
}
|
||||
```
|
||||
|
||||
和[回溯算法:组合问题再剪剪枝](https://mp.weixin.qq.com/s/Ri7spcJMUmph4c6XjPWXQA) 一样,for循环的范围也可以剪枝,i <= 9 - (k - path.size()) + 1就可以了。
|
||||
|
||||
最后C++代码如下:
|
||||
|
||||
```
|
||||
@ -175,10 +177,6 @@ class Solution {
|
||||
private:
|
||||
vector<vector<int>> result; // 存放结果集
|
||||
vector<int> path; // 符合条件的结果
|
||||
// targetSum:目标和,也就是题目中的n。
|
||||
// k:题目中要求k个数的集合。
|
||||
// sum:已经收集的元素的总和,也就是path里元素的总和。
|
||||
// startIndex:下一层for循环搜索的起始位置。
|
||||
void backtracking(int targetSum, int k, int sum, int startIndex) {
|
||||
if (sum > targetSum) { // 剪枝操作
|
||||
return; // 如果path.size() == k 但sum != targetSum 直接返回
|
||||
@ -187,7 +185,7 @@ private:
|
||||
if (sum == targetSum) result.push_back(path);
|
||||
return;
|
||||
}
|
||||
for (int i = startIndex; i <= 9; i++) {
|
||||
for (int i = startIndex; i <= 9 - (k - path.size()) + 1; i++) { // 剪枝
|
||||
sum += i; // 处理
|
||||
path.push_back(i); // 处理
|
||||
backtracking(targetSum, k, sum, i + 1); // 注意i+1调整startIndex
|
||||
|
||||
78
problems/0463.岛屿的周长.md
Normal file
78
problems/0463.岛屿的周长.md
Normal file
@ -0,0 +1,78 @@
|
||||
## 思路
|
||||
|
||||
岛屿问题最容易让人想到BFS或者DFS,但是这道题还真的没有必要,别把简单问题搞复杂了。
|
||||
|
||||
### 解法一:
|
||||
|
||||
遍历每一个空格,遇到岛屿,计算其上下左右的情况,遇到水域或者出界的情况,就可以计算边了。
|
||||
|
||||
如图:
|
||||
|
||||
<img src='../pics/463.岛屿的周长.png' width=600> </img></div>
|
||||
|
||||
代码如下:(详细注释)
|
||||
|
||||
```
|
||||
class Solution {
|
||||
public:
|
||||
int direction[4][2] = {0, 1, 1, 0, -1, 0, 0, -1};
|
||||
int islandPerimeter(vector<vector<int>>& grid) {
|
||||
int result = 0;
|
||||
for (int i = 0; i < grid.size(); i++) {
|
||||
for (int j = 0; j < grid[0].size(); j++) {
|
||||
if (grid[i][j] == 1) {
|
||||
for (int k = 0; k < 4; k++) { // 上下左右四个方向
|
||||
int x = i + direction[k][0];
|
||||
int y = j + direction[k][1]; // 计算周边坐标x,y
|
||||
if (x < 0 // i在边界上
|
||||
|| x >= grid.size() // i在边界上
|
||||
|| y < 0 // j在边界上
|
||||
|| y >= grid[0].size() // j在边界上
|
||||
|| grid[x][y] == 0) { // x,y位置是水域
|
||||
result++;
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
return result;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
### 解法二:
|
||||
|
||||
计算出总的岛屿数量,因为有一对相邻两个陆地,边的总数就减2,那么在计算出相邻岛屿的数量就可以了。
|
||||
|
||||
result = 岛屿数量 * 4 - cover * 2;
|
||||
|
||||
如图:
|
||||
|
||||
<img src='../pics/463.岛屿的周长1.png' width=600> </img></div>
|
||||
|
||||
代码如下:(详细注释)
|
||||
|
||||
```
|
||||
class Solution {
|
||||
public:
|
||||
int direction[4][2] = {0, 1, 1, 0, -1, 0, 0, -1};
|
||||
int islandPerimeter(vector<vector<int>>& grid) {
|
||||
int sum = 0; // 陆地数量
|
||||
int cover = 0; // 相邻数量
|
||||
for (int i = 0; i < grid.size(); i++) {
|
||||
for (int j = 0; j < grid[0].size(); j++) {
|
||||
if (grid[i][j] == 1) {
|
||||
sum++;
|
||||
// 统计上边相邻陆地
|
||||
if(i - 1 >= 0 && grid[i - 1][j] == 1) cover++;
|
||||
// 统计左边相邻陆地
|
||||
if(j - 1 >= 0 && grid[i][j - 1] == 1) cover++;
|
||||
// 为什么没统计下边和右边? 因为避免重复计算
|
||||
}
|
||||
}
|
||||
}
|
||||
return sum * 4 - cover * 2;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
Reference in New Issue
Block a user