algorithm/leetcode-master
1
0
Fork 0
mirror of https://github.com/youngyangyang04/leetcode-master.git synced 2025-07-06 23:28:29 +08:00
Code Issues Packages Projects Releases Wiki Activity

Update

Browse Source
This commit is contained in:
programmercarl
2024-05-31 10:12:41 +08:00
parent 7fc8aa199a
commit 5fabc5c1e0
9 changed files with 721 additions and 20 deletions
Download Patch File Download Diff File Expand all files Collapse all files

2
problems/0684.冗余连接.md
View File

@ -75,7 +75,7 @@ void join(int u, int v) {
2. 将两个节点接入到同一个集合，函数：join(int u, int v)，将两个节点连在同一个根节点上
3. 判断两个节点是否在同一个集合，函数：isSame(int u, int v)，就是判断两个节点是不是同一个根节点
如果还不了解并查集，可以看这里：[并查集理论基础](https://programmercarl.com/图论并查集理论基础.html)
如果还不了解并查集，可以看这里：[并查集理论基础](https://programmercarl.com/kamacoder/图论并查集理论基础.html)
我们再来看一下这道题目。

6
problems/kamacoder/0106.岛屿的周长.md
View File

@ -1,6 +1,8 @@
# 106. 岛屿的周长
[卡码网题目链接（ACM模式）](https://kamacoder.com/problempage.php?pid=1178)
题目描述
给定一个由 1（陆地）和 0（水）组成的矩阵，岛屿是被水包围，并且通过水平方向或垂直方向上相邻的陆地连接而成的。
@ -108,16 +110,14 @@ int main() {
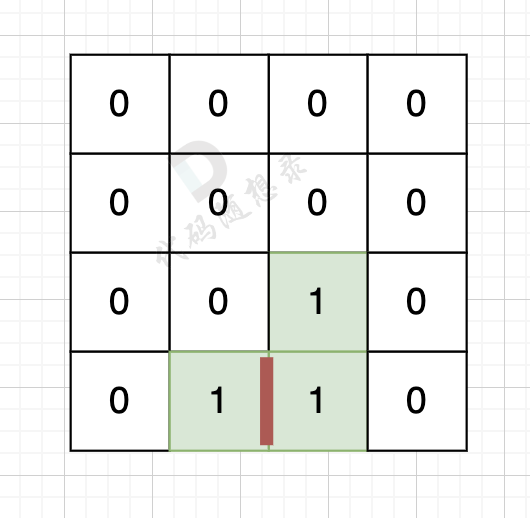
计算出总的岛屿数量，总的变数为：岛屿数量 * 4
因为有一对相邻两个陆地，边的总数就要减2，如图，有两个陆地相邻，总变数就要减2
因为有一对相邻两个陆地，边的总数就要减2，如图红线部分，有两个陆地相邻，总边数就要减2
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240524120855.png)
那么只需要在计算出相邻岛屿的数量就可以了，相邻岛屿数量为cover。
结果 result = 岛屿数量 * 4 - cover * 2;
C++代码如下：（详细注释）
```CPP

155
problems/kamacoder/0107.寻找存在的路径.md Normal file
View File

@ -0,0 +1,155 @@
# 107. 寻找存在的路径
[卡码网题目链接（ACM模式）](https://kamacoder.com/problempage.php?pid=1179)
题目描述
给定一个包含 n 个节点的无向图中，节点编号从 1 到 n （含 1 和 n ）。
你的任务是判断是否有一条从节点 source 出发到节点 destination 的路径存在。
输入描述
第一行包含两个正整数 N 和 M，N 代表节点的个数，M 代表边的个数。 
后续 M 行，每行两个正整数 s 和 t，代表从节点 s 与节点 t 之间有一条边。
最后一行包含两个正整数，代表起始节点 source 和目标节点 destination。
输出描述
输出一个整数，代表是否存在从节点 source 到节点 destination 的路径。如果存在，输出 1；否则，输出 0。
输入示例
```
5 4
1 2
1 3
2 4
3 4
1 4
```
输出示例
1
提示信息
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240527104432.png)
数据范围：
1 <= M, N <= 100。
## 思路
本题是并查集基础题目。 如果还不了解并查集，可以看这里：[并查集理论基础](https://programmercarl.com/kamacoder/图论并查集理论基础.html)
并查集可以解决什么问题呢？
主要就是集合问题，**两个节点在不在一个集合，也可以将两个节点添加到一个集合中**。
这里整理出我的并查集模板如下：
```CPP
int n = 1005; // n根据题目中节点数量而定，一般比节点数量大一点就好
vector<int> father = vector<int> (n, 0); // C++里的一种数组结构
// 并查集初始化
void init() {
for (int i = 0; i < n; ++i) {
father[i] = i;
}
}
// 并查集里寻根的过程
int find(int u) {
return u == father[u] ? u : father[u] = find(father[u]); // 路径压缩
}
// 判断 u 和 v是否找到同一个根
bool isSame(int u, int v) {
u = find(u);
v = find(v);
return u == v;
}
// 将v->u 这条边加入并查集
void join(int u, int v) {
u = find(u); // 寻找u的根
v = find(v); // 寻找v的根
if (u == v) return ; // 如果发现根相同，则说明在一个集合，不用两个节点相连直接返回
father[v] = u;
}
```
以上模板中，只要修改 n 大小就可以。
并查集主要有三个功能：
1. 寻找根节点，函数：find(int u)，也就是判断这个节点的祖先节点是哪个
2. 将两个节点接入到同一个集合，函数：join(int u, int v)，将两个节点连在同一个根节点上
3. 判断两个节点是否在同一个集合，函数：isSame(int u, int v)，就是判断两个节点是不是同一个根节点
简单介绍并查集之后，我们再来看一下这道题目。
为什么说这道题目是并查集基础题目，题目中各个点是双向图链接，那么判断 一个顶点到另一个顶点有没有有效路径其实就是看这两个顶点是否在同一个集合里。
如何算是同一个集合呢，有边连在一起，就算是一个集合。
此时我们就可以直接套用并查集模板。
使用 join(int u, int v)将每条边加入到并查集。
最后 isSame(int u, int v) 判断是否是同一个根 就可以了。
C++代码如下：
```CPP
#include <iostream>
#include <vector>
using namespace std;
int n; // 节点数量
vector<int> father = vector<int> (101, 0); // 按照节点大小定义数组大小
// 并查集初始化
void init() {
for (int i = 1; i <= n; i++) father[i] = i;
}
// 并查集里寻根的过程
int find(int u) {
return u == father[u] ? u : father[u] = find(father[u]);
}
// 判断 u 和 v是否找到同一个根
bool isSame(int u, int v) {
u = find(u);
v = find(v);
return u == v;
}
// 将v->u 这条边加入并查集
void join(int u, int v) {
u = find(u); // 寻找u的根
v = find(v); // 寻找v的根
if (u == v) return ; // 如果发现根相同，则说明在一个集合，不用两个节点相连直接返回
father[v] = u;
}
int main() {
int m, s, t, source, destination;
cin >> n >> m;
init();
while (m--) {
cin >> s >> t;
join(s, t);
}
cin >> source >> destination;
if (isSame(source, destination)) cout << 1 << endl;
else cout << 0 << endl;
}
```

128
problems/kamacoder/0108.冗余连接.md Normal file
View File

@ -0,0 +1,128 @@
# 108. 冗余连接
[卡码网题目链接（ACM模式）](https://kamacoder.com/problempage.php?pid=1181)
题目描述
树可以看成是一个图（拥有 n 个节点和 n - 1 条边的连通无环无向图）。
现给定一个拥有 n 个节点（节点编号从 1 到 n）和 n 条边的连通无向图，请找出一条可以删除的边，删除后图可以变成一棵树。
输入描述
第一行包含一个整数 N，表示图的节点个数和边的个数。
后续 N 行，每行包含两个整数 s 和 t，表示图中 s 和 t 之间有一条边。
输出描述
输出一条可以删除的边。如果有多个答案，请删除标准输入中最后出现的那条边。
输入示例
```
3
1 2
2 3
1 3
```
输出示例
1 3
提示信息
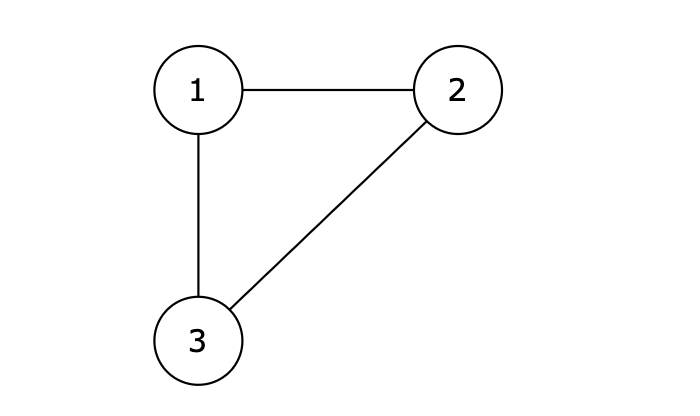
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240527110320.png)
图中的 1 2，2 3，1 3 等三条边在删除后都能使原图变为一棵合法的树。但是 1 3 由于是标准输出里最后出现的那条边，所以输出结果为 1 3
数据范围：
1 <= N <= 1000.
## 思路
这道题目也是并查集基础题目。
这里我依然降调一下，并查集可以解决什么问题：两个节点是否在一个集合，也可以将两个节点添加到一个集合中。
如果还不了解并查集，可以看这里：[并查集理论基础](https://programmercarl.com/图论并查集理论基础.html)
我们再来看一下这道题目。
题目说是无向图，返回一条可以删去的边，使得结果图是一个有着N个节点的树（即：只有一个根节点）。
如果有多个答案，则返回二维数组中最后出现的边。
那么我们就可以从前向后遍历每一条边（因为优先让前面的边连上），边的两个节点如果不在同一个集合，就加入集合（即：同一个根节点）。
如图所示：
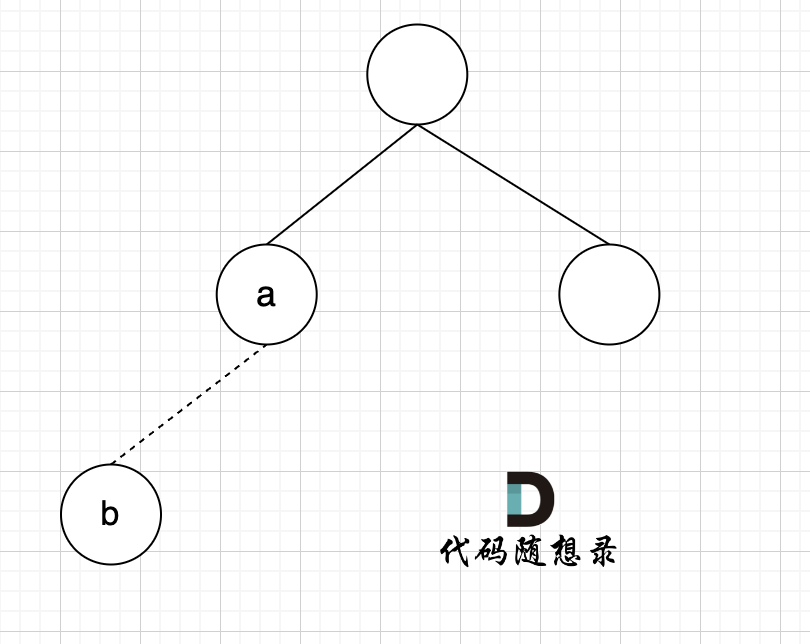
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20230604104720.png)
节点A 和节点 B 不在同一个集合，那么就可以将两个 节点连在一起。
如果边的两个节点已经出现在同一个集合里，说明着边的两个节点已经连在一起了，再加入这条边一定就出现环了。
如图所示：
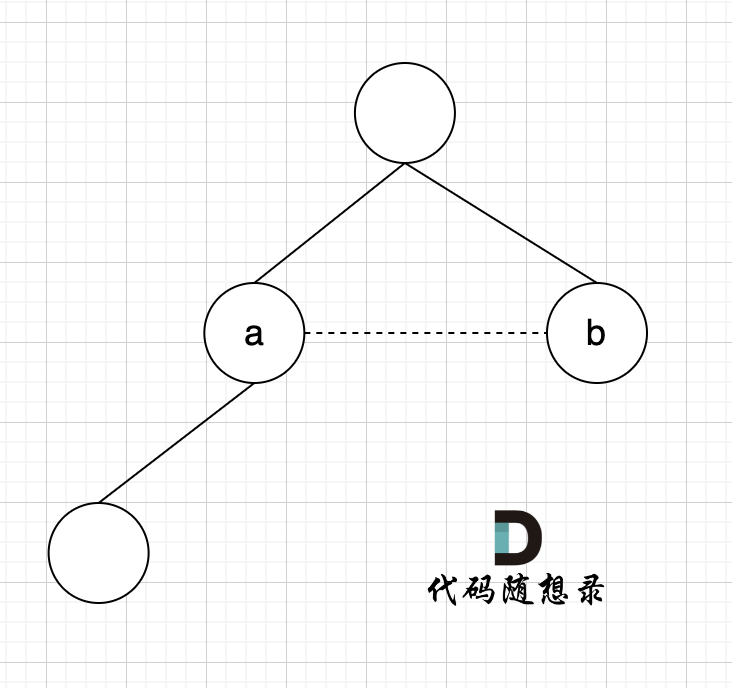
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20230604104330.png)
已经判断 节点A 和 节点B 在在同一个集合（同一个根），如果将 节点A 和 节点B 连在一起就一定会出现环。
这个思路清晰之后，代码就很好写了。
并查集C++代码如下：
```CPP
#include <iostream>
#include <vector>
using namespace std;
int n; // 节点数量
vector<int> father(1001, 0); // 按照节点大小范围定义数组
// 并查集初始化
void init() {
for (int i = 0; i <= n; ++i) {
father[i] = i;
}
}
// 并查集里寻根的过程
int find(int u) {
return u == father[u] ? u : father[u] = find(father[u]);
}
// 判断 u 和 v是否找到同一个根
bool isSame(int u, int v) {
u = find(u);
v = find(v);
return u == v;
}
// 将v->u 这条边加入并查集
void join(int u, int v) {
u = find(u); // 寻找u的根
v = find(v); // 寻找v的根
if (u == v) return ; // 如果发现根相同，则说明在一个集合，不用两个节点相连直接返回
father[v] = u;
}
int main() {
int s, t;
cin >> n;
init();
for (int i = 0; i < n; i++) {
cin >> s >> t;
if (isSame(s, t)) {
cout << s << " " << t << endl;
return 0;
} else {
join(s, t);
}
}
}
```
可以看出，主函数的代码很少，就判断一下边的两个节点在不在同一个集合就可以了。

240
problems/kamacoder/0109.冗余连接II.md Normal file
View File

@ -0,0 +1,240 @@
# 109. 冗余连接II
[卡码网题目链接（ACM模式）](https://kamacoder.com/problempage.php?pid=1182)
题目描述
有向树指满足以下条件的有向图。该树只有一个根节点，所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点，而根节点没有父节点。有向树拥有 n 个节点和 n - 1 条边。
输入一个有向图，该图由一个有着 n 个节点（节点编号 从 1 到 n），n 条边，请返回一条可以删除的边，使得删除该条边之后该有向图可以被当作一颗有向树。
输入描述
第一行输入一个整数 N，表示有向图中节点和边的个数。
后续 N 行，每行输入两个整数 s 和 t，代表 s 节点有一条连接 t 节点的单向边
输出描述
输出一条可以删除的边，若有多条边可以删除，请输出标准输入中最后出现的一条边。
输入示例
```
3
1 2
1 3
2 3
```
输出示例
2 3
提示信息
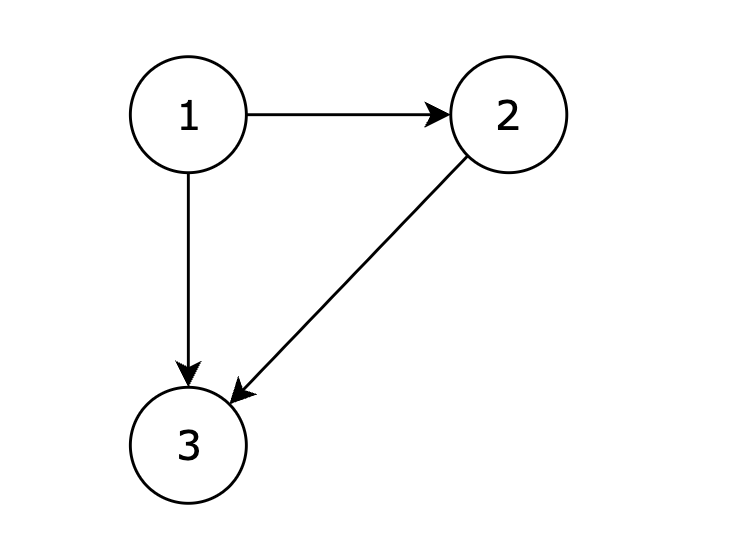
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240527112633.png)
在删除 2 3 后有向图可以变为一棵合法的有向树，所以输出 2 3
数据范围：
1 <= N <= 1000.
## 思路
本题与 [108.冗余连接](./0108.冗余连接.md) 类似，但本题是一个有向图，有向图相对要复杂一些。
本题的本质是 ：有一个有向图，是由一颗有向树 + 一条有向边组成的 （所以此时这个图就不能称之为有向树），现在让我们找到那条边 把这条边删了，让这个图恢复为有向树。
还有“**若有多条边可以删除，请输出标准输入中最后出现的一条边**”，这说明在两条边都可以删除的情况下，要删顺序靠后的边！
我们来想一下 有向树的性质，如果是有向树的话，只有根节点入度为0，其他节点入度都为1（因为该树除了根节点之外的每一个节点都有且只有一个父节点，而根节点没有父节点）。
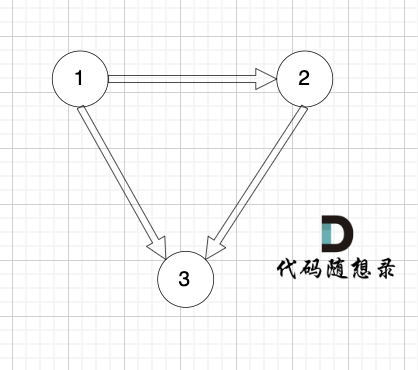
所以情况一：如果我们找到入度为2的点，那么删一条指向该节点的边就行了。
如图：
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240527115807.png)
找到了节点3 的入度为2，删 1 -> 3 或者 2 -> 3 。选择删顺序靠后便可。
但 入度为2 还有一种情况，情况二，只能删特定的一条边，如图：
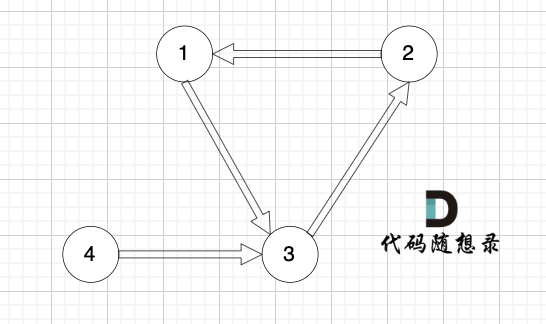
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240527151456.png)
节点3 的入度为 2，但在删除边的时候，只能删 这条边（节点1 -> 节点3），如果删这条边（节点4 -> 节点3），那么删后本图也不是有向树了（因为找不到根节点）。
综上，如果发现入度为2的节点，我们需要判断 删除哪一条边，删除后本图能成为有向树。如果是删哪个都可以，优先删顺序靠后的边。
情况三： 如果没有入度为2的点，说明 图中有环了（注意是有向环）。
如图：
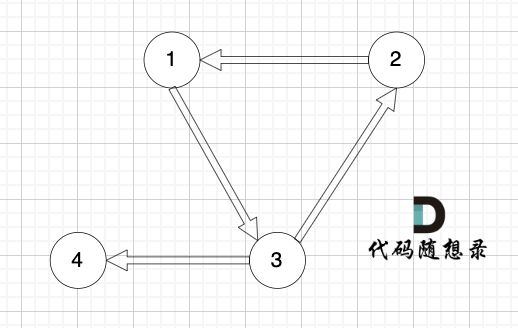
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240527120531.png)
对于情况二，删掉构成环的边就可以了。
## 写代码
把每条边记录下来，并统计节点入度：
```cpp
int s, t;
vector<vector<int>> edges;
cin >> n;
vector<int> inDegree(n + 1, 0); // 记录节点入度
for (int i = 0; i < n; i++) {
cin >> s >> t;
inDegree[t]++;
edges.push_back({s, t});
}
```
前两种入度为2的情况，一定是删除指向入度为2的节点的两条边其中的一条，如果删了一条，判断这个图是一个树，那么这条边就是答案。
同时注意要从后向前遍历，因为如果两条边删哪一条都可以成为树，就删最后那一条。
代码如下：
```cpp
vector<int> vec; // 记录入度为2的边（如果有的话就两条边）
// 找入度为2的节点所对应的边，注意要倒序，因为优先删除最后出现的一条边
for (int i = n - 1; i >= 0; i--) {
if (inDegree[edges[i][1]] == 2) {
vec.push_back(i);
}
}
if (vec.size() > 0) {
// 放在vec里的边已经按照倒叙放的，所以这里就优先删vec[0]这条边
if (isTreeAfterRemoveEdge(edges, vec[0])) {
cout << edges[vec[0]][0] << " " << edges[vec[0]][1];
} else {
cout << edges[vec[1]][0] << " " << edges[vec[1]][1];
}
return 0;
}
```
再来看情况三，明确没有入度为2的情况，那么一定有向环，找到构成环的边就是要删除的边。
可以定义一个函数，代码如下：
```cpp
// 在有向图里找到删除的那条边，使其变成树
void getRemoveEdge(const vector<vector<int>>& edges)
```
大家应该知道了，我们要解决本题要实现两个最为关键的函数：
* `isTreeAfterRemoveEdge()` 判断删一个边之后是不是有向树
* `getRemoveEdge()` 确定图中一定有了有向环，那么要找到需要删除的那条边
此时就用到**并查集**了。
如果还不了解并查集，可以看这里：[并查集理论基础](https://programmercarl.com/kamacoder/图论并查集理论基础.html)
`isTreeAfterRemoveEdge()` 判断删一个边之后是不是有向树： 将所有边的两端节点分别加入并查集，遇到要 要删除的边则跳过，如果遇到即将加入并查集的边的两端节点 本来就在并查集了，说明构成了环。
如果顺利将所有边的两端节点（除了要删除的边）加入了并查集，则说明 删除该条边 还是一个有向树
`getRemoveEdge()`确定图中一定有了有向环，那么要找到需要删除的那条边： 将所有边的两端节点分别加入并查集，如果遇到即将加入并查集的边的两端节点 本来就在并查集了，说明构成了环。
本题C++代码如下：（详细注释了）
```cpp
#include <iostream>
#include <vector>
using namespace std;
int n;
vector<int> father (1001, 0);
// 并查集初始化
void init() {
for (int i = 1; i <= n; ++i) {
father[i] = i;
}
}
// 并查集里寻根的过程
int find(int u) {
return u == father[u] ? u : father[u] = find(father[u]);
}
// 将v->u 这条边加入并查集
void join(int u, int v) {
u = find(u);
v = find(v);
if (u == v) return ;
father[v] = u;
}
// 判断 u 和 v是否找到同一个根
bool same(int u, int v) {
u = find(u);
v = find(v);
return u == v;
}
// 在有向图里找到删除的那条边，使其变成树
void getRemoveEdge(const vector<vector<int>>& edges) {
init(); // 初始化并查集
for (int i = 0; i < n; i++) { // 遍历所有的边
if (same(edges[i][0], edges[i][1])) { // 构成有向环了，就是要删除的边
cout << edges[i][0] << " " << edges[i][1];
return;
} else {
join(edges[i][0], edges[i][1]);
}
}
}
// 删一条边之后判断是不是树
bool isTreeAfterRemoveEdge(const vector<vector<int>>& edges, int deleteEdge) {
init(); // 初始化并查集
for (int i = 0; i < n; i++) {
if (i == deleteEdge) continue;
if (same(edges[i][0], edges[i][1])) { // 构成有向环了，一定不是树
return false;
}
join(edges[i][0], edges[i][1]);
}
return true;
}
int main() {
int s, t;
vector<vector<int>> edges;
cin >> n;
vector<int> inDegree(n + 1, 0); // 记录节点入度
for (int i = 0; i < n; i++) {
cin >> s >> t;
inDegree[t]++;
edges.push_back({s, t});
}
vector<int> vec; // 记录入度为2的边（如果有的话就两条边）
// 找入度为2的节点所对应的边，注意要倒序，因为优先删除最后出现的一条边
for (int i = n - 1; i >= 0; i--) {
if (inDegree[edges[i][1]] == 2) {
vec.push_back(i);
}
}
if (vec.size() > 0) {
// 放在vec里的边已经按照倒叙放的，所以这里就优先删vec[0]这条边
if (isTreeAfterRemoveEdge(edges, vec[0])) {
cout << edges[vec[0]][0] << " " << edges[vec[0]][1];
} else {
cout << edges[vec[1]][0] << " " << edges[vec[1]][1];
}
return 0;
}
// 处理情况三
// 明确没有入度为2的情况，那么一定有有向环，找到构成环的边返回就可以了
getRemoveEdge(edges);
}
```

149
problems/kamacoder/0110.字符串接龙.md Normal file
View File

@ -0,0 +1,149 @@
# 110. 字符串接龙
[卡码网题目链接（ACM模式）](https://kamacoder.com/problempage.php?pid=1182)
题目描述
字典 strList 中从字符串 beginStr 和 endStr 的转换序列是一个按下述规格形成的序列：
1. 序列中第一个字符串是 beginStr。
2. 序列中最后一个字符串是 endStr。
3. 每次转换只能改变一个字符。
4. 转换过程中的中间字符串必须是字典 strList 中的字符串。
给你两个字符串 beginStr 和 endStr 和一个字典 strList，找到从 beginStr 到 endStr 的最短转换序列中的字符串数目。如果不存在这样的转换序列，返回 0。
输入描述
第一行包含一个整数 N，表示字典 strList 中的字符串数量。 第二行包含两个字符串，用空格隔开，分别代表 beginStr 和 endStr。 后续 N 行，每行一个字符串，代表 strList 中的字符串。
输出描述
输出一个整数，代表从 beginStr 转换到 endStr 需要的最短转换序列中的字符串数量。如果不存在这样的转换序列，则输出 0。
输入示例
```
6
abc def
efc
dbc
ebc
dec
dfc
yhn
```
输出示例
4
提示信息
从 startStr 到 endStr，在 strList 中最短的路径为 abc -> dbc -> dec -> def，所以输出结果为 4
数据范围：
2 <= N <= 500
<p>
<img src="https://code-thinking-1253855093.file.myqcloud.com/pics/20240529121038.png" alt="" width="50%" />
</p>
## 思路
以示例1为例，从这个图中可以看出 abc 到 def的路线 不止一条，但最短的一条路径上是4个节点。
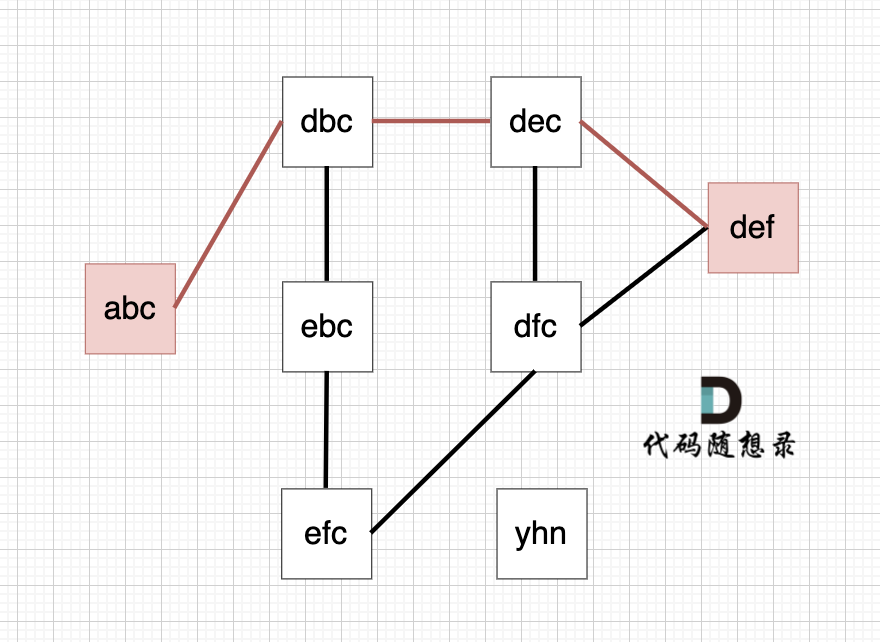
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240529121038.png)
本题只需要求出最短路径的长度就可以了，不用找出具体路径。
所以这道题要解决两个问题：
* 图中的线是如何连在一起的
* 起点和终点的最短路径长度
首先题目中并没有给出点与点之间的连线，而是要我们自己去连，条件是字符只能差一个。
所以判断点与点之间的关系，需要判断是不是差一个字符，**如果差一个字符，那就是有链接**。
然后就是求起点和终点的最短路径长度，**这里无向图求最短路，广搜最为合适，广搜只要搜到了终点，那么一定是最短的路径**。因为广搜就是以起点中心向四周扩散的搜索。
**本题如果用深搜，会比较麻烦，要在到达终点的不同路径中选则一条最短路**。 而广搜只要达到终点，一定是最短路。
另外需要有一个注意点：
* 本题是一个无向图，需要用标记位，标记着节点是否走过，否则就会死循环！
* 使用set来检查字符串是否出现在字符串集合里更快一些
C++代码如下：（详细注释）
```CPP
#include <iostream>
#include <vector>
#include <string>
#include <unordered_set>
#include <unordered_map>
#include <queue>
using namespace std;
int main() {
string beginStr, endStr, str;
int n;
cin >> n;
unordered_set<string> strSet;
cin >> beginStr >> endStr;
for (int i = 0; i < n; i++) {
cin >> str;
strSet.insert(str);
}
// 记录strSet里的字符串是否被访问过，同时记录路径长度
unordered_map<string, int> visitMap; // <记录的字符串，路径长度>
// 初始化队列
queue<string> que;
que.push(beginStr);
// 初始化visitMap
visitMap.insert(pair<string, int>(beginStr, 1));
while(!que.empty()) {
string word = que.front();
que.pop();
int path = visitMap[word]; // 这个字符串在路径中的长度
// 开始在这个str中，挨个字符去替换
for (int i = 0; i < word.size(); i++) {
string newWord = word; // 用一个新字符串替换str，因为每次要置换一个字符
// 遍历26的字母
for (int j = 0 ; j < 26; j++) {
newWord[i] = j + 'a';
if (newWord == endStr) { // 发现替换字母后，字符串与终点字符串相同
cout << path + 1 << endl; // 找到了路径
return 0;
}
// 字符串集合里出现了newWord，并且newWord没有被访问过
if (strSet.find(newWord) != strSet.end()
&& visitMap.find(newWord) == visitMap.end()) {
// 添加访问信息，并将新字符串放到队列中
visitMap.insert(pair<string, int>(newWord, path + 1));
que.push(newWord);
}
}
}
}
// 没找到输出0
cout << 0 << endl;
}
```
当然本题也可以用双向BFS，就是从头尾两端进行搜索，大家感兴趣，可以自己去实现，这里就不再做详细讲解了。

0
problems/kamacoder/00.软件构建.md → problems/kamacoder/0117.软件构建.md
View File

58
problems/kamacoder/图论总结篇.md
View File

@ -3,50 +3,78 @@
从深搜广搜 到并查集，从最小生成树到拓扑排序， 最后是最短路算法系列。
至此算上本篇，一共30篇文章，图论之旅就在此收官了。
在[0098.所有可达路径](./0098.所有可达路径.md) ，我们接触了两种图的存储方式，邻接表和邻接矩阵，数量掌握两种图的存储方式很重要。
这也是大家习惯在核心代码模式下刷题 经常忽略的 知识点。因为在力扣上刷题不需要掌握图的存储方式。
至此算上本篇，一共32篇文章，图论之旅就在此收官了。
在[0098.所有可达路径](./0098.所有可达路径.md) ，我们接触了两种图的存储方式，邻接表和邻接矩阵，掌握两种图的存储方式很重要。
图的存储方式也是大家习惯在核心代码模式下刷题 经常忽略的 知识点。因为在力扣上刷题不需要掌握图的存储方式。
## 深搜与广搜
在二叉树章节中，其实我们讲过了 深搜和广搜在二叉树上的搜索过程。
在图论章节中，深搜与广搜就是在图这个数据结构上的搜索过程。
深搜与广搜是图论里基本的搜索方法，大家需要掌握三点：
* 搜索方式：深搜是可一个方向搜，不到黄河不回头。 广搜是围绕这起点一圈一圈的去搜。
* 代码模板：需要熟练掌握深搜和广搜的基本写法。
* 应用场景：图论题目基本上可以即用深搜也可以广搜，无疑是用哪个方便而已
* 应用场景：图论题目基本上可以即用深搜也可用广搜，无疑是用哪个方便而已
### 注意事项
同样是深搜模板题，会有两种写法，
需要注意的是，同样是深搜模板题，会有两种写法。
在[0099.岛屿的数量深搜.md](./0099.岛屿的数量深搜.md) 和 [0105.有向图的完全可达性](./0105.有向图的完全可达性.md)，涉及到dfs的两种写法。
我们对dfs函数的定义是 是处理当前节点 还是处理下一个节点 很重要，决定了两种dfs的写法。
**我们对dfs函数的定义是 是处理当前节点 还是处理下一个节点 很重要**，决定了两种dfs的写法。
这也是为什么很多录友看到不同的dfs写法，结果发现提交都能过的原因。
而深搜还有细节，有的深搜题目需要回溯，有的就不用回溯，
而深搜还有细节，有的深搜题目需要用到回溯的过程，有的就不用回溯的过程，
需要计算路径的问题，一般需要回溯，如果只是染色问题 就不需要回溯。
一般是需要计算路径的问题 需要回溯，如果只是染色问题（岛屿问题系列） 就不需要回溯。
例如： [0105.有向图的完全可达性](./0105.有向图的完全可达性.md) 深搜就不需要回溯，而 [0098.所有可达路径](./0098.所有可达路径.md) 中的递归就需要回溯，文章中都有详细讲解
注意：以上说的是不需要回溯，不是没有回溯，只要有递归就会有回溯，只是我们是否需要用到回溯这个过程，这是需要考虑的。
很多录友写出来的广搜可能超时了， 例如题目：[0099.岛屿的数量广搜](./0099.岛屿的数量广搜.md)
注意：以上说的是不需要回溯，不是没有回溯，只要有递归就会有回溯，只是我们是否需要用到回溯这个过程 才是要考虑的
根本原因是**只要 加入队列就代表 走过，就需要标记，而不是从队列拿出来的时候再去标记走过**。
具体原因，我在[0099.岛屿的数量广搜](./0099.岛屿的数量广搜.md) 中详细讲了。
广搜注意事项，很多录友写广搜超时了。
在深搜与广搜的讲解中，为了防止惯性思维，我特别加入了题目 [0106.岛屿的周长](./0106.岛屿的周长.md)，提醒大家，看到类似的题目，也不要上来就想着深搜和广搜。
深搜和广搜是图论的基础，也有很多变形，我在图论里用最大岛屿问题，讲了很多
还有一些图的问题，在题目描述中，是没有图的，需要我们自己构建一个图，例如 [0110.字符串接龙](./0110.字符串接龙.md)，题目中连线都没有，需要我们自己去思考 什么样的两个字符串可以连成线。
## 并查集
并查集相对来说是比较复杂的数据结构，其实他的代码不长，但想彻底学透并查集，需要从多个维度入手，
我在理论基础篇的时候 讲解如下重点：
* 为什么要用并查集，怎么不用个二维数据，或者set、map之类的。
* 并查集能解决那些问题，哪些场景会用到并查集
* 并查集原理以及代码实现
* 并查集写法的常见误区
* 带大家去模拟一遍并查集的过程
* 路径压缩的过程
* 时间复杂度分析
上面这几个维度 大家都去思考了，并查集基本就学明白了。
其实理论基础篇就算是给大家出了一道裸的并查集题目了，所以在后面的题目安排中，会稍稍的拔高一些，重点在于并查集的应用上。
[0108.冗余连接](./0108.冗余连接.md)， [0109.冗余连接II](./0109.冗余连接II.md)
后面的两道题目，[0108.冗余连接](./0108.冗余连接.md) 和
## 最小生成树
## 拓扑排序

3
problems/kamacoder/图论理论基础.md
View File

@ -124,7 +124,8 @@
一般使用邻接表、邻接矩阵 或者用类来表示。
主流是 邻接表和邻接矩阵。
主要是 朴素存储、邻接表和邻接矩阵。
### 邻接矩阵