mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-08 00:43:04 +08:00
Merge branch 'master' of https://github.com/youngyangyang04/leetcode
This commit is contained in:
@ -107,7 +107,7 @@ public int[] twoSum(int[] nums, int target) {
|
||||
|
||||
Python:
|
||||
|
||||
```python3
|
||||
```python
|
||||
class Solution:
|
||||
def twoSum(self, nums: List[int], target: int) -> List[int]:
|
||||
hashmap={}
|
||||
|
||||
@ -148,6 +148,22 @@ class Solution {
|
||||
Python:
|
||||
|
||||
|
||||
```python3
|
||||
class Solution:
|
||||
def climbStairs(self, n: int) -> int:
|
||||
dp = [0]*(n + 1)
|
||||
dp[0] = 1
|
||||
m = 2
|
||||
# 遍历背包
|
||||
for j in range(n + 1):
|
||||
# 遍历物品
|
||||
for step in range(1, m + 1):
|
||||
if j >= step:
|
||||
dp[j] += dp[j - step]
|
||||
return dp[n]
|
||||
```
|
||||
|
||||
|
||||
Go:
|
||||
```go
|
||||
func climbStairs(n int) int {
|
||||
|
||||
@ -51,7 +51,9 @@ exection -> execution (插入 'u')
|
||||
|
||||
接下来我依然使用动规五部曲,对本题做一个详细的分析:
|
||||
|
||||
1. 确定dp数组(dp table)以及下标的含义
|
||||
-----------------------
|
||||
|
||||
### 1. 确定dp数组(dp table)以及下标的含义
|
||||
|
||||
**dp[i][j] 表示以下标i-1为结尾的字符串word1,和以下标j-1为结尾的字符串word2,最近编辑距离为dp[i][j]**。
|
||||
|
||||
@ -59,49 +61,65 @@ exection -> execution (插入 'u')
|
||||
|
||||
用i来表示也可以! 但我统一以下标i-1为结尾的字符串,在下面的递归公式中会容易理解一点。
|
||||
|
||||
2. 确定递推公式
|
||||
-----------------------
|
||||
|
||||
### 2. 确定递推公式
|
||||
|
||||
在确定递推公式的时候,首先要考虑清楚编辑的几种操作,整理如下:
|
||||
|
||||
* if (word1[i - 1] == word2[j - 1])
|
||||
* 不操作
|
||||
* if (word1[i - 1] != word2[j - 1])
|
||||
* 增
|
||||
* 删
|
||||
* 换
|
||||
```
|
||||
if (word1[i - 1] == word2[j - 1])
|
||||
不操作
|
||||
if (word1[i - 1] != word2[j - 1])
|
||||
增
|
||||
删
|
||||
换
|
||||
```
|
||||
|
||||
也就是如上四种情况。
|
||||
也就是如上4种情况。
|
||||
|
||||
if (word1[i - 1] == word2[j - 1]) 那么说明不用任何编辑,dp[i][j] 就应该是 dp[i - 1][j - 1],即dp[i][j] = dp[i - 1][j - 1];
|
||||
`if (word1[i - 1] == word2[j - 1])` 那么说明不用任何编辑,`dp[i][j]` 就应该是 `dp[i - 1][j - 1]`,即`dp[i][j] = dp[i - 1][j - 1];`
|
||||
|
||||
此时可能有同学有点不明白,为啥要即dp[i][j] = dp[i - 1][j - 1]呢?
|
||||
此时可能有同学有点不明白,为啥要即`dp[i][j] = dp[i - 1][j - 1]`呢?
|
||||
|
||||
那么就在回顾上面讲过的dp[i][j]的定义,word1[i - 1] 与 word2[j - 1]相等了,那么就不用编辑了,以下标i-2为结尾的字符串word1和以下标j-2为结尾的字符串word2的最近编辑距离dp[i - 1][j - 1] 就是 dp[i][j]了。
|
||||
那么就在回顾上面讲过的`dp[i][j]`的定义,`word1[i - 1]` 与 `word2[j - 1]`相等了,那么就不用编辑了,以下标i-2为结尾的字符串word1和以下标j-2为结尾的字符串`word2`的最近编辑距离`dp[i - 1][j - 1]`就是 `dp[i][j]`了。
|
||||
|
||||
在下面的讲解中,如果哪里看不懂,就回想一下dp[i][j]的定义,就明白了。
|
||||
在下面的讲解中,如果哪里看不懂,就回想一下`dp[i][j]`的定义,就明白了。
|
||||
|
||||
**在整个动规的过程中,最为关键就是正确理解dp[i][j]的定义!**
|
||||
**在整个动规的过程中,最为关键就是正确理解`dp[i][j]`的定义!**
|
||||
|
||||
if (word1[i - 1] != word2[j - 1]),此时就需要编辑了,如何编辑呢?
|
||||
|
||||
操作一:word1增加一个元素,使其word1[i - 1]与word2[j - 1]相同,那么就是以下标i-2为结尾的word1 与 i-1为结尾的word2的最近编辑距离 加上一个增加元素的操作。
|
||||
`if (word1[i - 1] != word2[j - 1])`,此时就需要编辑了,如何编辑呢?
|
||||
|
||||
即 dp[i][j] = dp[i - 1][j] + 1;
|
||||
操作一:word1增加一个元素,使其word1[i - 1]与word2[j - 1]相同,那么就是以下标i-2为结尾的word1 与 j-1为结尾的word2的最近编辑距离 加上一个增加元素的操作。
|
||||
|
||||
即 `dp[i][j] = dp[i - 1][j] + 1;`
|
||||
|
||||
|
||||
操作二:word2添加一个元素,使其word1[i - 1]与word2[j - 1]相同,那么就是以下标i-1为结尾的word1 与 j-2为结尾的word2的最近编辑距离 加上一个增加元素的操作。
|
||||
|
||||
即 dp[i][j] = dp[i][j - 1] + 1;
|
||||
即 `dp[i][j] = dp[i][j - 1] + 1;`
|
||||
|
||||
这里有同学发现了,怎么都是添加元素,删除元素去哪了。
|
||||
|
||||
**word2添加一个元素,相当于word1删除一个元素**,例如 word1 = "ad" ,word2 = "a",word2添加一个元素d,也就是相当于word1删除一个元素d,操作数是一样!
|
||||
**word2添加一个元素,相当于word1删除一个元素**,例如 `word1 = "ad" ,word2 = "a"`,`word1`删除元素`'d'`,`word2`添加一个元素`'d'`,变成`word1="a", word2="ad"`, 最终的操作数是一样! dp数组如下图所示意的:
|
||||
|
||||
操作三:替换元素,word1替换word1[i - 1],使其与word2[j - 1]相同,此时不用增加元素,那么以下标i-2为结尾的word1 与 j-2为结尾的word2的最近编辑距离 加上一个替换元素的操作。
|
||||
```
|
||||
a a d
|
||||
+-----+-----+ +-----+-----+-----+
|
||||
| 0 | 1 | | 0 | 1 | 2 |
|
||||
+-----+-----+ ===> +-----+-----+-----+
|
||||
a | 1 | 0 | a | 1 | 0 | 1 |
|
||||
+-----+-----+ +-----+-----+-----+
|
||||
d | 2 | 1 |
|
||||
+-----+-----+
|
||||
```
|
||||
|
||||
即 dp[i][j] = dp[i - 1][j - 1] + 1;
|
||||
操作三:替换元素,`word1`替换`word1[i - 1]`,使其与`word2[j - 1]`相同,此时不用增加元素,那么以下标`i-2`为结尾的`word1` 与 `j-2`为结尾的`word2`的最近编辑距离 加上一个替换元素的操作。
|
||||
|
||||
综上,当 if (word1[i - 1] != word2[j - 1]) 时取最小的,即:dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
|
||||
即 `dp[i][j] = dp[i - 1][j - 1] + 1;`
|
||||
|
||||
综上,当 `if (word1[i - 1] != word2[j - 1])` 时取最小的,即:`dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;`
|
||||
|
||||
递归公式代码如下:
|
||||
|
||||
@ -114,9 +132,12 @@ else {
|
||||
}
|
||||
```
|
||||
|
||||
3. dp数组如何初始化
|
||||
---
|
||||
|
||||
在回顾一下dp[i][j]的定义。
|
||||
### 3. dp数组如何初始化
|
||||
|
||||
|
||||
再回顾一下dp[i][j]的定义:
|
||||
|
||||
**dp[i][j] 表示以下标i-1为结尾的字符串word1,和以下标j-1为结尾的字符串word2,最近编辑距离为dp[i][j]**。
|
||||
|
||||
@ -135,14 +156,16 @@ for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;
|
||||
for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;
|
||||
```
|
||||
|
||||
4. 确定遍历顺序
|
||||
-----------------------
|
||||
|
||||
### 4. 确定遍历顺序
|
||||
|
||||
从如下四个递推公式:
|
||||
|
||||
* dp[i][j] = dp[i - 1][j - 1]
|
||||
* dp[i][j] = dp[i - 1][j - 1] + 1
|
||||
* dp[i][j] = dp[i][j - 1] + 1
|
||||
* dp[i][j] = dp[i - 1][j] + 1
|
||||
* `dp[i][j] = dp[i - 1][j - 1]`
|
||||
* `dp[i][j] = dp[i - 1][j - 1] + 1`
|
||||
* `dp[i][j] = dp[i][j - 1] + 1`
|
||||
* `dp[i][j] = dp[i - 1][j] + 1`
|
||||
|
||||
可以看出dp[i][j]是依赖左方,上方和左上方元素的,如图:
|
||||
|
||||
@ -164,10 +187,12 @@ for (int i = 1; i <= word1.size(); i++) {
|
||||
}
|
||||
}
|
||||
```
|
||||
-----------------------
|
||||
|
||||
5. 举例推导dp数组
|
||||
### 5. 举例推导dp数组
|
||||
|
||||
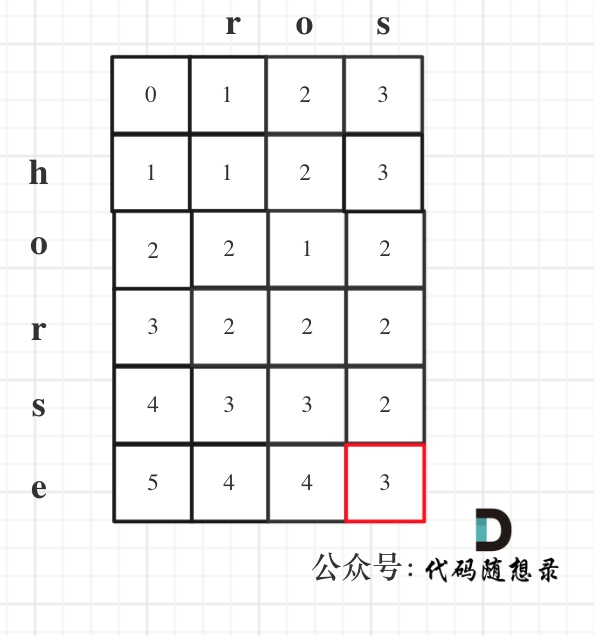
以示例1,输入:word1 = "horse", word2 = "ros"为例,dp矩阵状态图如下:
|
||||
|
||||
以示例1为例,输入:`word1 = "horse", word2 = "ros"`为例,dp矩阵状态图如下:
|
||||
|
||||
|
||||
|
||||
@ -195,7 +220,7 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
-----------------------
|
||||
## 其他语言版本
|
||||
|
||||
|
||||
@ -228,7 +253,22 @@ public int minDistance(String word1, String word2) {
|
||||
```
|
||||
|
||||
Python:
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
def minDistance(self, word1: str, word2: str) -> int:
|
||||
dp = [[0] * (len(word2)+1) for _ in range(len(word1)+1)]
|
||||
for i in range(len(word1)+1):
|
||||
dp[i][0] = i
|
||||
for j in range(len(word2)+1):
|
||||
dp[0][j] = j
|
||||
for i in range(1, len(word1)+1):
|
||||
for j in range(1, len(word2)+1):
|
||||
if word1[i-1] == word2[j-1]:
|
||||
dp[i][j] = dp[i-1][j-1]
|
||||
else:
|
||||
dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1
|
||||
return dp[-1][-1]
|
||||
```
|
||||
|
||||
Go:
|
||||
```Go
|
||||
|
||||
@ -693,6 +693,70 @@ class Solution:
|
||||
return root
|
||||
```
|
||||
Go:
|
||||
> 106 从中序与后序遍历序列构造二叉树
|
||||
|
||||
```go
|
||||
/**
|
||||
* Definition for a binary tree node.
|
||||
* type TreeNode struct {
|
||||
* Val int
|
||||
* Left *TreeNode
|
||||
* Right *TreeNode
|
||||
* }
|
||||
*/
|
||||
func buildTree(inorder []int, postorder []int) *TreeNode {
|
||||
if len(inorder)<1||len(postorder)<1{return nil}
|
||||
//先找到根节点(后续遍历的最后一个就是根节点)
|
||||
nodeValue:=postorder[len(postorder)-1]
|
||||
//从中序遍历中找到一分为二的点,左边为左子树,右边为右子树
|
||||
left:=findRootIndex(inorder,nodeValue)
|
||||
//构造root
|
||||
root:=&TreeNode{Val: nodeValue,
|
||||
Left: buildTree(inorder[:left],postorder[:left]),//将后续遍历一分为二,左边为左子树,右边为右子树
|
||||
Right: buildTree(inorder[left+1:],postorder[left:len(postorder)-1])}
|
||||
return root
|
||||
}
|
||||
func findRootIndex(inorder []int,target int) (index int){
|
||||
for i:=0;i<len(inorder);i++{
|
||||
if target==inorder[i]{
|
||||
return i
|
||||
}
|
||||
}
|
||||
return -1
|
||||
}
|
||||
```
|
||||
|
||||
> 105 从前序与中序遍历序列构造二叉树
|
||||
|
||||
```go
|
||||
/**
|
||||
* Definition for a binary tree node.
|
||||
* type TreeNode struct {
|
||||
* Val int
|
||||
* Left *TreeNode
|
||||
* Right *TreeNode
|
||||
* }
|
||||
*/
|
||||
func buildTree(preorder []int, inorder []int) *TreeNode {
|
||||
if len(preorder)<1||len(inorder)<1{return nil}
|
||||
left:=findRootIndex(preorder[0],inorder)
|
||||
root:=&TreeNode{
|
||||
Val: preorder[0],
|
||||
Left: buildTree(preorder[1:left+1],inorder[:left]),
|
||||
Right: buildTree(preorder[left+1:],inorder[left+1:])}
|
||||
return root
|
||||
}
|
||||
func findRootIndex(target int,inorder []int) int{
|
||||
for i:=0;i<len(inorder);i++{
|
||||
if target==inorder[i]{
|
||||
return i
|
||||
}
|
||||
}
|
||||
return -1
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
JavaScript
|
||||
|
||||
@ -486,6 +486,92 @@ class Solution:
|
||||
|
||||
Go:
|
||||
|
||||
> 112. 路径总和
|
||||
|
||||
```go
|
||||
//递归法
|
||||
/**
|
||||
* Definition for a binary tree node.
|
||||
* type TreeNode struct {
|
||||
* Val int
|
||||
* Left *TreeNode
|
||||
* Right *TreeNode
|
||||
* }
|
||||
*/
|
||||
func hasPathSum(root *TreeNode, targetSum int) bool {
|
||||
var flage bool //找没找到的标志
|
||||
if root==nil{
|
||||
return flage
|
||||
}
|
||||
pathSum(root,0,targetSum,&flage)
|
||||
return flage
|
||||
}
|
||||
func pathSum(root *TreeNode, sum int,targetSum int,flage *bool){
|
||||
sum+=root.Val
|
||||
if root.Left==nil&&root.Right==nil&&sum==targetSum{
|
||||
*flage=true
|
||||
return
|
||||
}
|
||||
if root.Left!=nil&&!(*flage){//左节点不为空且还没找到
|
||||
pathSum(root.Left,sum,targetSum,flage)
|
||||
}
|
||||
if root.Right!=nil&&!(*flage){//右节点不为空且没找到
|
||||
pathSum(root.Right,sum,targetSum,flage)
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
> 113 递归法
|
||||
|
||||
```go
|
||||
/**
|
||||
* Definition for a binary tree node.
|
||||
* type TreeNode struct {
|
||||
* Val int
|
||||
* Left *TreeNode
|
||||
* Right *TreeNode
|
||||
* }
|
||||
*/
|
||||
func pathSum(root *TreeNode, targetSum int) [][]int {
|
||||
var result [][]int//最终结果
|
||||
if root==nil{
|
||||
return result
|
||||
}
|
||||
var sumNodes []int//经过路径的节点集合
|
||||
hasPathSum(root,&sumNodes,targetSum,&result)
|
||||
return result
|
||||
}
|
||||
func hasPathSum(root *TreeNode,sumNodes *[]int,targetSum int,result *[][]int){
|
||||
*sumNodes=append(*sumNodes,root.Val)
|
||||
if root.Left==nil&&root.Right==nil{//叶子节点
|
||||
fmt.Println(*sumNodes)
|
||||
var sum int
|
||||
var number int
|
||||
for k,v:=range *sumNodes{//求该路径节点的和
|
||||
sum+=v
|
||||
number=k
|
||||
}
|
||||
tempNodes:=make([]int,number+1)//新的nodes接受指针里的值,防止最终指针里的值发生变动,导致最后的结果都是最后一个sumNodes的值
|
||||
for k,v:=range *sumNodes{
|
||||
tempNodes[k]=v
|
||||
}
|
||||
if sum==targetSum{
|
||||
*result=append(*result,tempNodes)
|
||||
}
|
||||
}
|
||||
if root.Left!=nil{
|
||||
hasPathSum(root.Left,sumNodes,targetSum,result)
|
||||
*sumNodes=(*sumNodes)[:len(*sumNodes)-1]//回溯
|
||||
}
|
||||
if root.Right!=nil{
|
||||
hasPathSum(root.Right,sumNodes,targetSum,result)
|
||||
*sumNodes=(*sumNodes)[:len(*sumNodes)-1]//回溯
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
JavaScript:
|
||||
|
||||
0112.路径总和
|
||||
|
||||
@ -145,7 +145,28 @@ public:
|
||||
|
||||
|
||||
Java:
|
||||
```java
|
||||
class Solution {
|
||||
public int numDistinct(String s, String t) {
|
||||
int[][] dp = new int[s.length() + 1][t.length() + 1];
|
||||
for (int i = 0; i < s.length() + 1; i++) {
|
||||
dp[i][0] = 1;
|
||||
}
|
||||
|
||||
for (int i = 1; i < s.length() + 1; i++) {
|
||||
for (int j = 1; j < t.length() + 1; j++) {
|
||||
if (s.charAt(i - 1) == t.charAt(j - 1)) {
|
||||
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
|
||||
}else{
|
||||
dp[i][j] = dp[i - 1][j];
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
return dp[s.length()][t.length()];
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
Python:
|
||||
```python
|
||||
|
||||
@ -252,6 +252,23 @@ class Solution {
|
||||
|
||||
Python:
|
||||
|
||||
```python3
|
||||
class Solution:
|
||||
def wordBreak(self, s: str, wordDict: List[str]) -> bool:
|
||||
'''排列'''
|
||||
dp = [False]*(len(s) + 1)
|
||||
dp[0] = True
|
||||
# 遍历背包
|
||||
for j in range(1, len(s) + 1):
|
||||
# 遍历单词
|
||||
for word in wordDict:
|
||||
if j >= len(word):
|
||||
dp[j] = dp[j] or (dp[j - len(word)] and word == s[j - len(word):j])
|
||||
return dp[len(s)]
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
Go:
|
||||
```Go
|
||||
|
||||
@ -183,7 +183,7 @@ public:
|
||||
int end = 0; // 反转的单词在字符串里终止位置
|
||||
bool entry = false; // 标记枚举字符串的过程中是否已经进入了单词区间
|
||||
for (int i = 0; i < s.size(); i++) { // 开始反转单词
|
||||
if ((!entry))) {
|
||||
if (!entry) {
|
||||
start = i; // 确定单词起始位置
|
||||
entry = true; // 进入单词区间
|
||||
}
|
||||
|
||||
@ -118,7 +118,7 @@ class Solution {
|
||||
if (nums == null || nums.length == 0) return 0;
|
||||
if (nums.length == 1) return nums[0];
|
||||
|
||||
int[] dp = new int[nums.length + 1];
|
||||
int[] dp = new int[nums.length];
|
||||
dp[0] = nums[0];
|
||||
dp[1] = Math.max(dp[0], nums[1]);
|
||||
for (int i = 2; i < nums.length; i++) {
|
||||
|
||||
@ -332,6 +332,66 @@ func maxSlidingWindow(nums []int, k int) []int {
|
||||
|
||||
```
|
||||
|
||||
```go
|
||||
// 封装单调队列的方式解题
|
||||
type MyQueue struct {
|
||||
queue []int
|
||||
}
|
||||
|
||||
func NewMyQueue() *MyQueue {
|
||||
return &MyQueue{
|
||||
queue: make([]int, 0),
|
||||
}
|
||||
}
|
||||
|
||||
func (m *MyQueue) Front() int {
|
||||
return m.queue[0]
|
||||
}
|
||||
|
||||
func (m *MyQueue) Back() int {
|
||||
return m.queue[len(m.queue)-1]
|
||||
}
|
||||
|
||||
func (m *MyQueue) Empty() bool {
|
||||
return len(m.queue) == 0
|
||||
}
|
||||
|
||||
func (m *MyQueue) Push(val int) {
|
||||
for !m.Empty() && val > m.Back() {
|
||||
m.queue = m.queue[:len(m.queue)-1]
|
||||
}
|
||||
m.queue = append(m.queue, val)
|
||||
}
|
||||
|
||||
func (m *MyQueue) Pop(val int) {
|
||||
if !m.Empty() && val == m.Front() {
|
||||
m.queue = m.queue[1:]
|
||||
}
|
||||
}
|
||||
|
||||
func maxSlidingWindow(nums []int, k int) []int {
|
||||
queue := NewMyQueue()
|
||||
length := len(nums)
|
||||
res := make([]int, 0)
|
||||
// 先将前k个元素放入队列
|
||||
for i := 0; i < k; i++ {
|
||||
queue.Push(nums[i])
|
||||
}
|
||||
// 记录前k个元素的最大值
|
||||
res = append(res, queue.Front())
|
||||
|
||||
for i := k; i < length; i++ {
|
||||
// 滑动窗口移除最前面的元素
|
||||
queue.Pop(nums[i-k])
|
||||
// 滑动窗口添加最后面的元素
|
||||
queue.Push(nums[i])
|
||||
// 记录最大值
|
||||
res = append(res, queue.Front())
|
||||
}
|
||||
return res
|
||||
}
|
||||
```
|
||||
|
||||
Javascript:
|
||||
```javascript
|
||||
var maxSlidingWindow = function (nums, k) {
|
||||
|
||||
@ -130,7 +130,27 @@ class Solution:
|
||||
return True
|
||||
```
|
||||
|
||||
Python写法二(没有使用数组作为哈希表,只是介绍defaultdict这样一种解题思路):
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
def isAnagram(self, s: str, t: str) -> bool:
|
||||
from collections import defaultdict
|
||||
|
||||
s_dict = defaultdict(int)
|
||||
t_dict = defaultdict(int)
|
||||
|
||||
for x in s:
|
||||
s_dict[x] += 1
|
||||
|
||||
for x in t:
|
||||
t_dict[x] += 1
|
||||
|
||||
return s_dict == t_dict
|
||||
```
|
||||
|
||||
Go:
|
||||
|
||||
```go
|
||||
func isAnagram(s string, t string) bool {
|
||||
if len(s)!=len(t){
|
||||
|
||||
@ -26,7 +26,7 @@
|
||||
输入:n = 13
|
||||
输出:2
|
||||
解释:13 = 4 + 9
|
||||
|
||||
|
||||
提示:
|
||||
* 1 <= n <= 10^4
|
||||
|
||||
@ -184,6 +184,38 @@ class Solution {
|
||||
|
||||
Python:
|
||||
|
||||
```python3
|
||||
class Solution:
|
||||
def numSquares(self, n: int) -> int:
|
||||
'''版本一'''
|
||||
# 初始化
|
||||
nums = [i**2 for i in range(1, n + 1) if i**2 <= n]
|
||||
dp = [10**4]*(n + 1)
|
||||
dp[0] = 0
|
||||
# 遍历背包
|
||||
for j in range(1, n + 1):
|
||||
# 遍历物品
|
||||
for num in nums:
|
||||
if j >= num:
|
||||
dp[j] = min(dp[j], dp[j - num] + 1)
|
||||
return dp[n]
|
||||
|
||||
def numSquares1(self, n: int) -> int:
|
||||
'''版本二'''
|
||||
# 初始化
|
||||
nums = [i**2 for i in range(1, n + 1) if i**2 <= n]
|
||||
dp = [10**4]*(n + 1)
|
||||
dp[0] = 0
|
||||
# 遍历物品
|
||||
for num in nums:
|
||||
# 遍历背包
|
||||
for j in range(num, n + 1)
|
||||
dp[j] = min(dp[j], dp[j - num] + 1)
|
||||
return dp[n]
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
Go:
|
||||
```go
|
||||
|
||||
@ -35,7 +35,7 @@
|
||||
示例 5:
|
||||
输入:coins = [1], amount = 2
|
||||
输出:2
|
||||
|
||||
|
||||
提示:
|
||||
|
||||
* 1 <= coins.length <= 12
|
||||
@ -209,6 +209,36 @@ class Solution {
|
||||
|
||||
Python:
|
||||
|
||||
```python3
|
||||
class Solution:
|
||||
def coinChange(self, coins: List[int], amount: int) -> int:
|
||||
'''版本一'''
|
||||
# 初始化
|
||||
dp = [amount + 1]*(amount + 1)
|
||||
dp[0] = 0
|
||||
# 遍历物品
|
||||
for coin in coins:
|
||||
# 遍历背包
|
||||
for j in range(coin, amount + 1):
|
||||
dp[j] = min(dp[j], dp[j - coin] + 1)
|
||||
return dp[amount] if dp[amount] < amount + 1 else -1
|
||||
|
||||
def coinChange1(self, coins: List[int], amount: int) -> int:
|
||||
'''版本二'''
|
||||
# 初始化
|
||||
dp = [amount + 1]*(amount + 1)
|
||||
dp[0] = 0
|
||||
# 遍历物品
|
||||
for j in range(1, amount + 1):
|
||||
# 遍历背包
|
||||
for coin in coins:
|
||||
if j >= coin:
|
||||
dp[j] = min(dp[j], dp[j - coin] + 1)
|
||||
return dp[amount] if dp[amount] < amount + 1 else -1
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
Go:
|
||||
```go
|
||||
@ -226,11 +256,11 @@ func coinChange1(coins []int, amount int) int {
|
||||
for i := 0; i < len(coins); i++ {
|
||||
// 遍历背包
|
||||
for j := coins[i]; j <= amount; j++ {
|
||||
//if dp[j-coins[i]] != math.MaxInt32 {
|
||||
if dp[j-coins[i]] != math.MaxInt32 {
|
||||
// 推导公式
|
||||
dp[j] = min(dp[j], dp[j-coins[i]]+1)
|
||||
fmt.Println(dp,j,i)
|
||||
//}
|
||||
//fmt.Println(dp,j,i)
|
||||
}
|
||||
}
|
||||
}
|
||||
// 没找到能装满背包的, 就返回-1
|
||||
|
||||
@ -218,7 +218,7 @@ class Solution:
|
||||
# 假设对正整数 i 拆分出的第一个正整数是 j(1 <= j < i),则有以下两种方案:
|
||||
# 1) 将 i 拆分成 j 和 i−j 的和,且 i−j 不再拆分成多个正整数,此时的乘积是 j * (i-j)
|
||||
# 2) 将 i 拆分成 j 和 i−j 的和,且 i−j 继续拆分成多个正整数,此时的乘积是 j * dp[i-j]
|
||||
for j in range(1, i):
|
||||
for j in range(1, i - 1):
|
||||
dp[i] = max(dp[i], max(j * (i - j), j * dp[i - j]))
|
||||
return dp[n]
|
||||
```
|
||||
|
||||
@ -118,7 +118,7 @@ class Solution {
|
||||
```
|
||||
|
||||
Python:
|
||||
```python3
|
||||
```python
|
||||
class Solution:
|
||||
def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
|
||||
result_set = set()
|
||||
|
||||
@ -135,8 +135,52 @@ class Solution {
|
||||
|
||||
```
|
||||
|
||||
Python:
|
||||
```py
|
||||
Python写法一(使用数组作为哈希表):
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
def canConstruct(self, ransomNote: str, magazine: str) -> bool:
|
||||
|
||||
arr = [0] * 26
|
||||
|
||||
for x in magazine:
|
||||
arr[ord(x) - ord('a')] += 1
|
||||
|
||||
for x in ransomNote:
|
||||
if arr[ord(x) - ord('a')] == 0:
|
||||
return False
|
||||
else:
|
||||
arr[ord(x) - ord('a')] -= 1
|
||||
|
||||
return True
|
||||
```
|
||||
|
||||
Python写法二(使用defaultdict):
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
def canConstruct(self, ransomNote: str, magazine: str) -> bool:
|
||||
|
||||
from collections import defaultdict
|
||||
|
||||
hashmap = defaultdict(int)
|
||||
|
||||
for x in magazine:
|
||||
hashmap[x] += 1
|
||||
|
||||
for x in ransomNote:
|
||||
value = hashmap.get(x)
|
||||
if value is None or value == 0:
|
||||
return False
|
||||
else:
|
||||
hashmap[x] -= 1
|
||||
|
||||
return True
|
||||
```
|
||||
|
||||
Python写法三:
|
||||
|
||||
```python
|
||||
class Solution(object):
|
||||
def canConstruct(self, ransomNote, magazine):
|
||||
"""
|
||||
@ -166,6 +210,7 @@ class Solution(object):
|
||||
```
|
||||
|
||||
Go:
|
||||
|
||||
```go
|
||||
func canConstruct(ransomNote string, magazine string) bool {
|
||||
record := make([]int, 26)
|
||||
|
||||
@ -144,7 +144,20 @@ Java:
|
||||
|
||||
|
||||
Python:
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
def isSubsequence(self, s: str, t: str) -> bool:
|
||||
dp = [[0] * (len(t)+1) for _ in range(len(s)+1)]
|
||||
for i in range(1, len(s)+1):
|
||||
for j in range(1, len(t)+1):
|
||||
if s[i-1] == t[j-1]:
|
||||
dp[i][j] = dp[i-1][j-1] + 1
|
||||
else:
|
||||
dp[i][j] = dp[i][j-1]
|
||||
if dp[-1][-1] == len(s):
|
||||
return True
|
||||
return False
|
||||
```
|
||||
|
||||
Go:
|
||||
|
||||
|
||||
@ -226,6 +226,71 @@ class Solution:
|
||||
```
|
||||
Go:
|
||||
|
||||
> 递归法
|
||||
|
||||
```go
|
||||
/**
|
||||
* Definition for a binary tree node.
|
||||
* type TreeNode struct {
|
||||
* Val int
|
||||
* Left *TreeNode
|
||||
* Right *TreeNode
|
||||
* }
|
||||
*/
|
||||
func sumOfLeftLeaves(root *TreeNode) int {
|
||||
var res int
|
||||
findLeft(root,&res)
|
||||
return res
|
||||
}
|
||||
func findLeft(root *TreeNode,res *int){
|
||||
//左节点
|
||||
if root.Left!=nil&&root.Left.Left==nil&&root.Left.Right==nil{
|
||||
*res=*res+root.Left.Val
|
||||
}
|
||||
if root.Left!=nil{
|
||||
findLeft(root.Left,res)
|
||||
}
|
||||
if root.Right!=nil{
|
||||
findLeft(root.Right,res)
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
> 迭代法
|
||||
|
||||
```go
|
||||
/**
|
||||
* Definition for a binary tree node.
|
||||
* type TreeNode struct {
|
||||
* Val int
|
||||
* Left *TreeNode
|
||||
* Right *TreeNode
|
||||
* }
|
||||
*/
|
||||
func sumOfLeftLeaves(root *TreeNode) int {
|
||||
var res int
|
||||
queue:=list.New()
|
||||
queue.PushBack(root)
|
||||
for queue.Len()>0{
|
||||
length:=queue.Len()
|
||||
for i:=0;i<length;i++{
|
||||
node:=queue.Remove(queue.Front()).(*TreeNode)
|
||||
if node.Left!=nil&&node.Left.Left==nil&&node.Left.Right==nil{
|
||||
res=res+node.Left.Val
|
||||
}
|
||||
if node.Left!=nil{
|
||||
queue.PushBack(node.Left)
|
||||
}
|
||||
if node.Right!=nil{
|
||||
queue.PushBack(node.Right)
|
||||
}
|
||||
}
|
||||
}
|
||||
return res
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
JavaScript:
|
||||
递归版本
|
||||
```javascript
|
||||
@ -275,6 +340,7 @@ var sumOfLeftLeaves = function(root) {
|
||||
|
||||
|
||||
|
||||
|
||||
-----------------------
|
||||
* 作者微信:[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
|
||||
* B站视频:[代码随想录](https://space.bilibili.com/525438321)
|
||||
|
||||
@ -120,7 +120,7 @@ class Solution {
|
||||
|
||||
Python:
|
||||
|
||||
```
|
||||
```python
|
||||
class Solution(object):
|
||||
def fourSumCount(self, nums1, nums2, nums3, nums4):
|
||||
"""
|
||||
@ -148,6 +148,30 @@ class Solution(object):
|
||||
count += hashmap[key]
|
||||
return count
|
||||
|
||||
# 下面这个写法更为简洁,但是表达的是同样的算法
|
||||
# class Solution:
|
||||
# def fourSumCount(self, nums1: List[int], nums2: List[int], nums3: List[int], nums4: List[int]) -> int:
|
||||
# from collections import defaultdict
|
||||
|
||||
# hashmap = defaultdict(int)
|
||||
|
||||
# for x1 in nums1:
|
||||
# for x2 in nums2:
|
||||
# hashmap[x1+x2] += 1
|
||||
|
||||
# count=0
|
||||
# for x3 in nums3:
|
||||
# for x4 in nums4:
|
||||
# key = -x3-x4
|
||||
# value = hashmap.get(key)
|
||||
|
||||
# dict的get方法会返回None(key不存在)或者key对应的value
|
||||
# 所以如果value==0,就会继续执行or,count+0,否则就会直接加value
|
||||
# 这样就不用去写if判断了
|
||||
|
||||
# count += value or 0
|
||||
|
||||
# return count
|
||||
|
||||
```
|
||||
|
||||
|
||||
@ -298,6 +298,80 @@ class Solution:
|
||||
```
|
||||
Go:
|
||||
|
||||
> 递归法
|
||||
|
||||
```go
|
||||
/**
|
||||
* Definition for a binary tree node.
|
||||
* type TreeNode struct {
|
||||
* Val int
|
||||
* Left *TreeNode
|
||||
* Right *TreeNode
|
||||
* }
|
||||
*/
|
||||
var maxDeep int // 全局变量 深度
|
||||
var value int //全局变量 最终值
|
||||
func findBottomLeftValue(root *TreeNode) int {
|
||||
if root.Left==nil&&root.Right==nil{//需要提前判断一下(不要这个if的话提交结果会出错,但执行代码不会。防止这种情况出现,故先判断是否只有一个节点)
|
||||
return root.Val
|
||||
}
|
||||
findLeftValue (root,maxDeep)
|
||||
return value
|
||||
}
|
||||
func findLeftValue (root *TreeNode,deep int){
|
||||
//最左边的值在左边
|
||||
if root.Left==nil&&root.Right==nil{
|
||||
if deep>maxDeep{
|
||||
value=root.Val
|
||||
maxDeep=deep
|
||||
}
|
||||
}
|
||||
//递归
|
||||
if root.Left!=nil{
|
||||
deep++
|
||||
findLeftValue(root.Left,deep)
|
||||
deep--//回溯
|
||||
}
|
||||
if root.Right!=nil{
|
||||
deep++
|
||||
findLeftValue(root.Right,deep)
|
||||
deep--//回溯
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
> 迭代法
|
||||
|
||||
```go
|
||||
/**
|
||||
* Definition for a binary tree node.
|
||||
* type TreeNode struct {
|
||||
* Val int
|
||||
* Left *TreeNode
|
||||
* Right *TreeNode
|
||||
* }
|
||||
*/
|
||||
func findBottomLeftValue(root *TreeNode) int {
|
||||
queue:=list.New()
|
||||
var gradation int
|
||||
queue.PushBack(root)
|
||||
for queue.Len()>0{
|
||||
length:=queue.Len()
|
||||
for i:=0;i<length;i++{
|
||||
node:=queue.Remove(queue.Front()).(*TreeNode)
|
||||
if i==0{gradation=node.Val}
|
||||
if node.Left!=nil{
|
||||
queue.PushBack(node.Left)
|
||||
}
|
||||
if node.Right!=nil{
|
||||
queue.PushBack(node.Right)
|
||||
}
|
||||
}
|
||||
}
|
||||
return gradation
|
||||
}
|
||||
```
|
||||
|
||||
JavaScript:
|
||||
1. 递归版本
|
||||
```javascript
|
||||
|
||||
@ -170,7 +170,20 @@ public class Solution {
|
||||
|
||||
|
||||
Python:
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
def longestPalindromeSubseq(self, s: str) -> int:
|
||||
dp = [[0] * len(s) for _ in range(len(s))]
|
||||
for i in range(len(s)):
|
||||
dp[i][i] = 1
|
||||
for i in range(len(s)-1, -1, -1):
|
||||
for j in range(i+1, len(s)):
|
||||
if s[i] == s[j]:
|
||||
dp[i][j] = dp[i+1][j-1] + 2
|
||||
else:
|
||||
dp[i][j] = max(dp[i+1][j], dp[i][j-1])
|
||||
return dp[0][-1]
|
||||
```
|
||||
|
||||
Go:
|
||||
```Go
|
||||
|
||||
@ -224,8 +224,37 @@ class Solution:
|
||||
return r
|
||||
```
|
||||
Go:
|
||||
> 中序遍历,然后计算最小差值
|
||||
|
||||
|
||||
```go
|
||||
/**
|
||||
* Definition for a binary tree node.
|
||||
* type TreeNode struct {
|
||||
* Val int
|
||||
* Left *TreeNode
|
||||
* Right *TreeNode
|
||||
* }
|
||||
*/
|
||||
func getMinimumDifference(root *TreeNode) int {
|
||||
var res []int
|
||||
findMIn(root,&res)
|
||||
min:=1000000//一个比较大的值
|
||||
for i:=1;i<len(res);i++{
|
||||
tempValue:=res[i]-res[i-1]
|
||||
if tempValue<min{
|
||||
min=tempValue
|
||||
}
|
||||
}
|
||||
return min
|
||||
}
|
||||
//中序遍历
|
||||
func findMIn(root *TreeNode,res *[]int){
|
||||
if root==nil{return}
|
||||
findMIn(root.Left,res)
|
||||
*res=append(*res,root.Val)
|
||||
findMIn(root.Right,res)
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
-----------------------
|
||||
|
||||
@ -104,10 +104,47 @@ public:
|
||||
|
||||
|
||||
Java:
|
||||
```java
|
||||
class Solution {
|
||||
public int minDistance(String word1, String word2) {
|
||||
int[][] dp = new int[word1.length() + 1][word2.length() + 1];
|
||||
for (int i = 0; i < word1.length() + 1; i++) dp[i][0] = i;
|
||||
for (int j = 0; j < word2.length() + 1; j++) dp[0][j] = j;
|
||||
|
||||
for (int i = 1; i < word1.length() + 1; i++) {
|
||||
for (int j = 1; j < word2.length() + 1; j++) {
|
||||
if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
|
||||
dp[i][j] = dp[i - 1][j - 1];
|
||||
}else{
|
||||
dp[i][j] = Math.min(dp[i - 1][j - 1] + 2,
|
||||
Math.min(dp[i - 1][j] + 1, dp[i][j - 1] + 1));
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
return dp[word1.length()][word2.length()];
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
Python:
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
def minDistance(self, word1: str, word2: str) -> int:
|
||||
dp = [[0] * (len(word2)+1) for _ in range(len(word1)+1)]
|
||||
for i in range(len(word1)+1):
|
||||
dp[i][0] = i
|
||||
for j in range(len(word2)+1):
|
||||
dp[0][j] = j
|
||||
for i in range(1, len(word1)+1):
|
||||
for j in range(1, len(word2)+1):
|
||||
if word1[i-1] == word2[j-1]:
|
||||
dp[i][j] = dp[i-1][j-1]
|
||||
else:
|
||||
dp[i][j] = min(dp[i-1][j-1] + 2, dp[i-1][j] + 1, dp[i][j-1] + 1)
|
||||
return dp[-1][-1]
|
||||
```
|
||||
|
||||
Go:
|
||||
|
||||
|
||||
@ -332,6 +332,43 @@ class Solution:
|
||||
|
||||
Go:
|
||||
|
||||
```go
|
||||
/**
|
||||
* Definition for a binary tree node.
|
||||
* type TreeNode struct {
|
||||
* Val int
|
||||
* Left *TreeNode
|
||||
* Right *TreeNode
|
||||
* }
|
||||
*/
|
||||
//前序遍历(递归遍历,跟105 106差不多的思路)
|
||||
func mergeTrees(t1 *TreeNode, t2 *TreeNode) *TreeNode {
|
||||
var value int
|
||||
var nullNode *TreeNode//空node,便于遍历
|
||||
nullNode=&TreeNode{
|
||||
Val:0,
|
||||
Left:nil,
|
||||
Right:nil}
|
||||
switch {
|
||||
case t1==nil&&t2==nil: return nil//终止条件
|
||||
default : //如果其中一个节点为空,则将该节点置为nullNode,方便下次遍历
|
||||
if t1==nil{
|
||||
value=t2.Val
|
||||
t1=nullNode
|
||||
}else if t2==nil{
|
||||
value=t1.Val
|
||||
t2=nullNode
|
||||
}else {
|
||||
value=t1.Val+t2.Val
|
||||
}
|
||||
}
|
||||
root:=&TreeNode{//构造新的二叉树
|
||||
Val: value,
|
||||
Left: mergeTrees(t1.Left,t2.Left),
|
||||
Right: mergeTrees(t1.Right,t2.Right)}
|
||||
return root
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
@ -284,6 +284,56 @@ class Solution {
|
||||
|
||||
Python:
|
||||
|
||||
> 动态规划:
|
||||
```python
|
||||
class Solution:
|
||||
def countSubstrings(self, s: str) -> int:
|
||||
dp = [[False] * len(s) for _ in range(len(s))]
|
||||
result = 0
|
||||
for i in range(len(s)-1, -1, -1): #注意遍历顺序
|
||||
for j in range(i, len(s)):
|
||||
if s[i] == s[j]:
|
||||
if j - i <= 1: #情况一 和 情况二
|
||||
result += 1
|
||||
dp[i][j] = True
|
||||
elif dp[i+1][j-1]: #情况三
|
||||
result += 1
|
||||
dp[i][j] = True
|
||||
return result
|
||||
```
|
||||
|
||||
> 动态规划:简洁版
|
||||
```python
|
||||
class Solution:
|
||||
def countSubstrings(self, s: str) -> int:
|
||||
dp = [[False] * len(s) for _ in range(len(s))]
|
||||
result = 0
|
||||
for i in range(len(s)-1, -1, -1): #注意遍历顺序
|
||||
for j in range(i, len(s)):
|
||||
if s[i] == s[j] and (j - i <= 1 or dp[i+1][j-1]):
|
||||
result += 1
|
||||
dp[i][j] = True
|
||||
return result
|
||||
```
|
||||
|
||||
> 双指针法:
|
||||
```python
|
||||
class Solution:
|
||||
def countSubstrings(self, s: str) -> int:
|
||||
result = 0
|
||||
for i in range(len(s)):
|
||||
result += self.extend(s, i, i, len(s)) #以i为中心
|
||||
result += self.extend(s, i, i+1, len(s)) #以i和i+1为中心
|
||||
return result
|
||||
|
||||
def extend(self, s, i, j, n):
|
||||
res = 0
|
||||
while i >= 0 and j < n and s[i] == s[j]:
|
||||
i -= 1
|
||||
j += 1
|
||||
res += 1
|
||||
return res
|
||||
```
|
||||
|
||||
Go:
|
||||
```Go
|
||||
|
||||
@ -278,6 +278,39 @@ class Solution:
|
||||
|
||||
Go:
|
||||
|
||||
> 654. 最大二叉树
|
||||
|
||||
```go
|
||||
/**
|
||||
* Definition for a binary tree node.
|
||||
* type TreeNode struct {
|
||||
* Val int
|
||||
* Left *TreeNode
|
||||
* Right *TreeNode
|
||||
* }
|
||||
*/
|
||||
func constructMaximumBinaryTree(nums []int) *TreeNode {
|
||||
if len(nums)<1{return nil}
|
||||
//首选找到最大值
|
||||
index:=findMax(nums)
|
||||
//其次构造二叉树
|
||||
root:=&TreeNode{
|
||||
Val: nums[index],
|
||||
Left:constructMaximumBinaryTree(nums[:index]),//左半边
|
||||
Right:constructMaximumBinaryTree(nums[index+1:]),//右半边
|
||||
}
|
||||
return root
|
||||
}
|
||||
func findMax(nums []int) (index int){
|
||||
for i:=0;i<len(nums);i++{
|
||||
if nums[i]>nums[index]{
|
||||
index=i
|
||||
}
|
||||
}
|
||||
return
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
@ -241,6 +241,56 @@ class Solution:
|
||||
|
||||
Go:
|
||||
|
||||
> 递归法
|
||||
|
||||
```go
|
||||
/**
|
||||
* Definition for a binary tree node.
|
||||
* type TreeNode struct {
|
||||
* Val int
|
||||
* Left *TreeNode
|
||||
* Right *TreeNode
|
||||
* }
|
||||
*/
|
||||
//递归法
|
||||
func searchBST(root *TreeNode, val int) *TreeNode {
|
||||
if root==nil||root.Val==val{
|
||||
return root
|
||||
}
|
||||
if root.Val>val{
|
||||
return searchBST(root.Left,val)
|
||||
}
|
||||
return searchBST(root.Right,val)
|
||||
}
|
||||
```
|
||||
|
||||
> 迭代法
|
||||
|
||||
```go
|
||||
/**
|
||||
* Definition for a binary tree node.
|
||||
* type TreeNode struct {
|
||||
* Val int
|
||||
* Left *TreeNode
|
||||
* Right *TreeNode
|
||||
* }
|
||||
*/
|
||||
//迭代法
|
||||
func searchBST(root *TreeNode, val int) *TreeNode {
|
||||
for root!=nil{
|
||||
if root.Val>val{
|
||||
root=root.Left
|
||||
}else if root.Val<val{
|
||||
root=root.Right
|
||||
}else{
|
||||
break
|
||||
}
|
||||
}
|
||||
return root
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
@ -158,6 +158,7 @@ private:
|
||||
|
||||
Java:
|
||||
```Java
|
||||
//单链表
|
||||
class ListNode {
|
||||
int val;
|
||||
ListNode next;
|
||||
@ -236,10 +237,110 @@ class MyLinkedList {
|
||||
pred.next = pred.next.next;
|
||||
}
|
||||
}
|
||||
|
||||
//双链表
|
||||
class MyLinkedList {
|
||||
class ListNode {
|
||||
int val;
|
||||
ListNode next,prev;
|
||||
ListNode(int x) {val = x;}
|
||||
}
|
||||
|
||||
int size;
|
||||
ListNode head,tail;//Sentinel node
|
||||
|
||||
/** Initialize your data structure here. */
|
||||
public MyLinkedList() {
|
||||
size = 0;
|
||||
head = new ListNode(0);
|
||||
tail = new ListNode(0);
|
||||
head.next = tail;
|
||||
tail.prev = head;
|
||||
}
|
||||
|
||||
/** Get the value of the index-th node in the linked list. If the index is invalid, return -1. */
|
||||
public int get(int index) {
|
||||
if(index < 0 || index >= size){return -1;}
|
||||
ListNode cur = head;
|
||||
|
||||
// 通过判断 index < (size - 1) / 2 来决定是从头结点还是尾节点遍历,提高效率
|
||||
if(index < (size - 1) / 2){
|
||||
for(int i = 0; i <= index; i++){
|
||||
cur = cur.next;
|
||||
}
|
||||
}else{
|
||||
cur = tail;
|
||||
for(int i = 0; i <= size - index - 1; i++){
|
||||
cur = cur.prev;
|
||||
}
|
||||
}
|
||||
return cur.val;
|
||||
}
|
||||
|
||||
/** Add a node of value val before the first element of the linked list. After the insertion, the new node will be the first node of the linked list. */
|
||||
public void addAtHead(int val) {
|
||||
ListNode cur = head;
|
||||
ListNode newNode = new ListNode(val);
|
||||
newNode.next = cur.next;
|
||||
cur.next.prev = newNode;
|
||||
cur.next = newNode;
|
||||
newNode.prev = cur;
|
||||
size++;
|
||||
}
|
||||
|
||||
/** Append a node of value val to the last element of the linked list. */
|
||||
public void addAtTail(int val) {
|
||||
ListNode cur = tail;
|
||||
ListNode newNode = new ListNode(val);
|
||||
newNode.next = tail;
|
||||
newNode.prev = cur.prev;
|
||||
cur.prev.next = newNode;
|
||||
cur.prev = newNode;
|
||||
size++;
|
||||
}
|
||||
|
||||
/** Add a node of value val before the index-th node in the linked list. If index equals to the length of linked list, the node will be appended to the end of linked list. If index is greater than the length, the node will not be inserted. */
|
||||
public void addAtIndex(int index, int val) {
|
||||
if(index > size){return;}
|
||||
if(index < 0){index = 0;}
|
||||
ListNode cur = head;
|
||||
for(int i = 0; i < index; i++){
|
||||
cur = cur.next;
|
||||
}
|
||||
ListNode newNode = new ListNode(val);
|
||||
newNode.next = cur.next;
|
||||
cur.next.prev = newNode;
|
||||
newNode.prev = cur;
|
||||
cur.next = newNode;
|
||||
size++;
|
||||
}
|
||||
|
||||
/** Delete the index-th node in the linked list, if the index is valid. */
|
||||
public void deleteAtIndex(int index) {
|
||||
if(index >= size || index < 0){return;}
|
||||
ListNode cur = head;
|
||||
for(int i = 0; i < index; i++){
|
||||
cur = cur.next;
|
||||
}
|
||||
cur.next.next.prev = cur;
|
||||
cur.next = cur.next.next;
|
||||
size--;
|
||||
}
|
||||
}
|
||||
|
||||
/**
|
||||
* Your MyLinkedList object will be instantiated and called as such:
|
||||
* MyLinkedList obj = new MyLinkedList();
|
||||
* int param_1 = obj.get(index);
|
||||
* obj.addAtHead(val);
|
||||
* obj.addAtTail(val);
|
||||
* obj.addAtIndex(index,val);
|
||||
* obj.deleteAtIndex(index);
|
||||
*/
|
||||
```
|
||||
|
||||
Python:
|
||||
```python3
|
||||
```python
|
||||
# 单链表
|
||||
class Node:
|
||||
|
||||
|
||||
@ -154,7 +154,25 @@ public:
|
||||
|
||||
|
||||
Java:
|
||||
```java
|
||||
class Solution {
|
||||
public int findLength(int[] nums1, int[] nums2) {
|
||||
int result = 0;
|
||||
int[][] dp = new int[nums1.length + 1][nums2.length + 1];
|
||||
|
||||
for (int i = 1; i < nums1.length + 1; i++) {
|
||||
for (int j = 1; j < nums2.length + 1; j++) {
|
||||
if (nums1[i - 1] == nums2[j - 1]) {
|
||||
dp[i][j] = dp[i - 1][j - 1] + 1;
|
||||
max = Math.max(max, dp[i][j]);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
return result;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
Python:
|
||||
|
||||
|
||||
@ -180,11 +180,86 @@ public:
|
||||
|
||||
|
||||
Java:
|
||||
|
||||
```java
|
||||
/**
|
||||
* 单调栈,栈内顺序要么从大到小 要么从小到大,本题从大到笑
|
||||
* <p>
|
||||
* 入站元素要和当前栈内栈首元素进行比较
|
||||
* 若大于栈首则 则与元素下标做差
|
||||
* 若大于等于则放入
|
||||
*
|
||||
* @param temperatures
|
||||
* @return
|
||||
*/
|
||||
public static int[] dailyTemperatures(int[] temperatures) {
|
||||
Stack<Integer> stack = new Stack<>();
|
||||
int[] res = new int[temperatures.length];
|
||||
for (int i = 0; i < temperatures.length; i++) {
|
||||
/**
|
||||
* 取出下标进行元素值的比较
|
||||
*/
|
||||
while (!stack.isEmpty() && temperatures[i] > temperatures[stack.peek()]) {
|
||||
int preIndex = stack.pop();
|
||||
res[preIndex] = i - preIndex;
|
||||
}
|
||||
/**
|
||||
* 注意 放入的是元素位置
|
||||
*/
|
||||
stack.push(i);
|
||||
}
|
||||
return res;
|
||||
}
|
||||
```
|
||||
Python:
|
||||
|
||||
Go:
|
||||
|
||||
> 暴力法
|
||||
|
||||
```go
|
||||
func dailyTemperatures(temperatures []int) []int {
|
||||
length:=len(temperatures)
|
||||
res:=make([]int,length)
|
||||
for i:=0;i<length;i++{
|
||||
j:=i+1
|
||||
if i==length-1{
|
||||
res[i]=0
|
||||
}
|
||||
for j<length&&temperatures[i]>=temperatures[j]{//大于等于
|
||||
j++
|
||||
}
|
||||
if j<length&&temperatures[i]<temperatures[j]{
|
||||
res[i]=j-i
|
||||
}
|
||||
if j==length{
|
||||
res[i]=0
|
||||
}
|
||||
}
|
||||
return res
|
||||
}
|
||||
```
|
||||
|
||||
> 单调栈法
|
||||
|
||||
```go
|
||||
func dailyTemperatures(temperatures []int) []int {
|
||||
length:=len(temperatures)
|
||||
res:=make([]int,length)
|
||||
stack:=[]int{}
|
||||
for i:=0;i<length;i++{
|
||||
//如果当前栈中存在元素,新来的元素大于栈顶的元素,则计算差值并弹出栈顶元素
|
||||
for len(stack)>0&&temperatures[i]>temperatures[stack[len(stack)-1]]{
|
||||
res[stack[len(stack)-1]]=i-stack[len(stack)-1]//存放结果集
|
||||
stack=stack[:len(stack)-1]//删除stack[len(stack)-1]的元素
|
||||
}
|
||||
//如果栈顶元素大于等于新来的元素,则加入到栈中。当栈内元素个数为0时,直接入栈
|
||||
if len(stack)==0||temperatures[i]<=temperatures[stack[len(stack)-1]]{
|
||||
stack = append(stack, i)
|
||||
}
|
||||
}
|
||||
return res
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
@ -96,8 +96,46 @@ public:
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
|
||||
Java:
|
||||
```Java
|
||||
class Solution {
|
||||
public int[] sortedSquares(int[] nums) {
|
||||
int right = nums.length - 1;
|
||||
int left = 0;
|
||||
int[] result = new int[nums.length];
|
||||
int index = result.length - 1;
|
||||
while (left <= right) {
|
||||
if (nums[left] * nums[left] > nums[right] * nums[right]) {
|
||||
result[index--] = nums[left] * nums[left];
|
||||
++left;
|
||||
} else {
|
||||
result[index--] = nums[right] * nums[right];
|
||||
--right;
|
||||
}
|
||||
}
|
||||
return result;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
public int[] sortedSquares(int[] nums) {
|
||||
int l = 0;
|
||||
int r = nums.length - 1;
|
||||
int[] res = new int[nums.length];
|
||||
int j = nums.length - 1;
|
||||
while(l <= r){
|
||||
if(nums[l] * nums[l] > nums[r] * nums[r]){
|
||||
res[j--] = nums[l] * nums[l++];
|
||||
}else{
|
||||
res[j--] = nums[r] * nums[r--];
|
||||
}
|
||||
}
|
||||
return res;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
Python:
|
||||
```Python
|
||||
@ -160,6 +198,31 @@ impl Solution {
|
||||
}
|
||||
}
|
||||
```
|
||||
Javascript:
|
||||
```Javascript
|
||||
/**
|
||||
* @desc two pointers solution
|
||||
* @link https://leetcode-cn.com/problems/squares-of-a-sorted-array/
|
||||
* @param nums Array e.g. [-4,-1,0,3,10]
|
||||
* @return {array} e.g. [0,1,9,16,100]
|
||||
*/
|
||||
const sortedSquares = function (nums) {
|
||||
let res = []
|
||||
for (let i = 0, j = nums.length - 1; i <= j;) {
|
||||
const left = Math.abs(nums[i])
|
||||
const right = Math.abs(nums[j])
|
||||
if (right > left) {
|
||||
// push element to the front of the array
|
||||
res.unshift(right * right)
|
||||
j--
|
||||
} else {
|
||||
res.unshift(left * left)
|
||||
i++
|
||||
}
|
||||
}
|
||||
return res
|
||||
}
|
||||
```
|
||||
|
||||
-----------------------
|
||||
* 作者微信:[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
|
||||
|
||||
@ -133,7 +133,7 @@ class Solution:
|
||||
A[i] *= -1
|
||||
K -= 1
|
||||
if K > 0:
|
||||
A[len(A) - 1] *= ((-1)**K)
|
||||
A[-1] *= (-1)**K #取A最后一个数只需要写-1
|
||||
return sum(A)
|
||||
```
|
||||
|
||||
|
||||
@ -337,6 +337,110 @@ class Solution:
|
||||
|
||||
Go:
|
||||
|
||||
100.相同的树
|
||||
```go
|
||||
/**
|
||||
* Definition for a binary tree node.
|
||||
* type TreeNode struct {
|
||||
* Val int
|
||||
* Left *TreeNode
|
||||
* Right *TreeNode
|
||||
* }
|
||||
*/
|
||||
func isSameTree(p *TreeNode, q *TreeNode) bool {
|
||||
switch {
|
||||
case p == nil && q == nil:
|
||||
return true
|
||||
case p == nil || q == nil:
|
||||
fallthrough
|
||||
case p.Val != q.Val:
|
||||
return false
|
||||
}
|
||||
return isSameTree(p.Left, q.Left) && isSameTree(p.Right, q.Right)
|
||||
}
|
||||
```
|
||||
|
||||
257.二叉的所有路径
|
||||
> 递归法
|
||||
|
||||
```go
|
||||
/**
|
||||
* Definition for a binary tree node.
|
||||
* type TreeNode struct {
|
||||
* Val int
|
||||
* Left *TreeNode
|
||||
* Right *TreeNode
|
||||
* }
|
||||
*/
|
||||
func binaryTreePaths(root *TreeNode) []string {
|
||||
var result []string
|
||||
traversal(root,&result,"")
|
||||
return result
|
||||
}
|
||||
func traversal(root *TreeNode,result *[]string,pathStr string){
|
||||
//判断是否为第一个元素
|
||||
if len(pathStr)!=0{
|
||||
pathStr=pathStr+"->"+strconv.Itoa(root.Val)
|
||||
}else{
|
||||
pathStr=strconv.Itoa(root.Val)
|
||||
}
|
||||
//判断是否为叶子节点
|
||||
if root.Left==nil&&root.Right==nil{
|
||||
*result=append(*result,pathStr)
|
||||
return
|
||||
}
|
||||
//左右
|
||||
if root.Left!=nil{
|
||||
traversal(root.Left,result,pathStr)
|
||||
}
|
||||
if root.Right!=nil{
|
||||
traversal(root.Right,result,pathStr)
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
> 回溯法
|
||||
|
||||
```go
|
||||
/**
|
||||
* Definition for a binary tree node.
|
||||
* type TreeNode struct {
|
||||
* Val int
|
||||
* Left *TreeNode
|
||||
* Right *TreeNode
|
||||
* }
|
||||
*/
|
||||
func binaryTreePaths(root *TreeNode) []string {
|
||||
var result []string
|
||||
var path []int
|
||||
traversal(root,&result,&path)
|
||||
return result
|
||||
}
|
||||
func traversal(root *TreeNode,result *[]string,path *[]int){
|
||||
*path=append(*path,root.Val)
|
||||
//判断是否为叶子节点
|
||||
if root.Left==nil&&root.Right==nil{
|
||||
pathStr:=strconv.Itoa((*path)[0])
|
||||
for i:=1;i<len(*path);i++{
|
||||
pathStr=pathStr+"->"+strconv.Itoa((*path)[i])
|
||||
}
|
||||
*result=append(*result,pathStr)
|
||||
return
|
||||
}
|
||||
//左右
|
||||
if root.Left!=nil{
|
||||
traversal(root.Left,result,path)
|
||||
*path=(*path)[:len(*path)-1]//回溯到上一个节点(因为traversal会加下一个节点值到path中)
|
||||
}
|
||||
if root.Right!=nil{
|
||||
traversal(root.Right,result,path)
|
||||
*path=(*path)[:len(*path)-1]//回溯
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
@ -154,7 +154,54 @@ Python:
|
||||
|
||||
|
||||
Go:
|
||||
```go
|
||||
// 遍历添加
|
||||
func replaceSpace(s string) string {
|
||||
b := []byte(s)
|
||||
result := make([]byte, 0)
|
||||
for i := 0; i < len(b); i++ {
|
||||
if b[i] == ' ' {
|
||||
result = append(result, []byte("%20")...)
|
||||
} else {
|
||||
result = append(result, b[i])
|
||||
}
|
||||
}
|
||||
return string(result)
|
||||
}
|
||||
|
||||
// 原地修改
|
||||
func replaceSpace(s string) string {
|
||||
b := []byte(s)
|
||||
length := len(b)
|
||||
spaceCount := 0
|
||||
// 计算空格数量
|
||||
for _, v := range b {
|
||||
if v == ' ' {
|
||||
spaceCount++
|
||||
}
|
||||
}
|
||||
// 扩展原有切片
|
||||
resizeCount := spaceCount * 2
|
||||
tmp := make([]byte, resizeCount)
|
||||
b = append(b, tmp...)
|
||||
i := length - 1
|
||||
j := len(b) - 1
|
||||
for i >= 0 {
|
||||
if b[i] != ' ' {
|
||||
b[j] = b[i]
|
||||
i--
|
||||
j--
|
||||
} else {
|
||||
b[j] = '0'
|
||||
b[j-1] = '2'
|
||||
b[j-2] = '%'
|
||||
i--
|
||||
j = j - 3
|
||||
}
|
||||
}
|
||||
return string(b)
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
@ -307,6 +307,41 @@ Java:
|
||||
|
||||
|
||||
Python:
|
||||
```python
|
||||
def test_2_wei_bag_problem1(bag_size, weight, value) -> int:
|
||||
rows, cols = len(weight), bag_size + 1
|
||||
dp = [[0 for _ in range(cols)] for _ in range(rows)]
|
||||
res = 0
|
||||
|
||||
# 初始化dp数组.
|
||||
for i in range(rows):
|
||||
dp[i][0] = 0
|
||||
first_item_weight, first_item_value = weight[0], value[0]
|
||||
for j in range(1, cols):
|
||||
if first_item_weight <= j:
|
||||
dp[0][j] = first_item_value
|
||||
|
||||
# 更新dp数组: 先遍历物品, 再遍历背包.
|
||||
for i in range(1, len(weight)):
|
||||
cur_weight, cur_val = weight[i], value[i]
|
||||
for j in range(1, cols):
|
||||
if cur_weight > j: # 说明背包装不下当前物品.
|
||||
dp[i][j] = dp[i - 1][j] # 所以不装当前物品.
|
||||
else:
|
||||
# 定义dp数组: dp[i][j] 前i个物品里,放进容量为j的背包,价值总和最大是多少。
|
||||
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - cur_weight]+ cur_val)
|
||||
if dp[i][j] > res:
|
||||
res = dp[i][j]
|
||||
|
||||
print(dp)
|
||||
|
||||
|
||||
if __name__ == "__main__":
|
||||
bag_size = 4
|
||||
weight = [1, 3, 4]
|
||||
value = [15, 20, 30]
|
||||
test_2_wei_bag_problem1(bag_size, weight, value)
|
||||
```
|
||||
|
||||
|
||||
Go:
|
||||
|
||||
@ -147,9 +147,56 @@ int main() {
|
||||
|
||||
Java:
|
||||
|
||||
|
||||
Python:
|
||||
|
||||
```python
|
||||
def test_multi_pack1():
|
||||
'''版本一:改变物品数量为01背包格式'''
|
||||
weight = [1, 3, 4]
|
||||
value = [15, 20, 30]
|
||||
nums = [2, 3, 2]
|
||||
bag_weight = 10
|
||||
for i in range(len(nums)):
|
||||
# 将物品展开数量为1
|
||||
while nums[i] > 1:
|
||||
weight.append(weight[i])
|
||||
value.append(value[i])
|
||||
nums[i] -= 1
|
||||
|
||||
dp = [0]*(bag_weight + 1)
|
||||
# 遍历物品
|
||||
for i in range(len(weight)):
|
||||
# 遍历背包
|
||||
for j in range(bag_weight, weight[i] - 1, -1):
|
||||
dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
|
||||
|
||||
print(" ".join(map(str, dp)))
|
||||
|
||||
def test_multi_pack2():
|
||||
'''版本:改变遍历个数'''
|
||||
weight = [1, 3, 4]
|
||||
value = [15, 20, 30]
|
||||
nums = [2, 3, 2]
|
||||
bag_weight = 10
|
||||
|
||||
dp = [0]*(bag_weight + 1)
|
||||
for i in range(len(weight)):
|
||||
for j in range(bag_weight, weight[i] - 1, -1):
|
||||
# 以上是01背包,加上遍历个数
|
||||
for k in range(1, nums[i] + 1):
|
||||
if j - k*weight[i] >= 0:
|
||||
dp[j] = max(dp[j], dp[j - k*weight[i]] + k*value[i])
|
||||
|
||||
print(" ".join(map(str, dp)))
|
||||
|
||||
|
||||
if __name__ == '__main__':
|
||||
test_multi_pack1()
|
||||
test_multi_pack2()
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
Go:
|
||||
|
||||
|
||||
Reference in New Issue
Block a user