mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-07 15:45:40 +08:00
Update
This commit is contained in:
@ -39,7 +39,7 @@
|
||||
|
||||
每改变一个0的方格,都需要重新计算一个地图的最大面积,所以 整体时间复杂度为:n^4。
|
||||
|
||||
如果对深度优先搜索不了解的录友,可以看这里:[深度优先搜索精讲](https://programmercarl.com/图论深搜理论基础.html)
|
||||
如果对深度优先搜索不了解的录友,可以看这里:[深度优先搜索精讲](https://programmercarl.com/kamacoder/图论深搜理论基础.html)
|
||||
|
||||
|
||||
## 优化思路
|
||||
|
||||
@ -8,11 +8,14 @@
|
||||
某国为促进城市间经济交流,决定对货物运输提供补贴。共有 n 个编号为 1 到 n 的城市,通过道路网络连接,网络中的道路仅允许从某个城市单向通行到另一个城市,不能反向通行。
|
||||
|
||||
|
||||
网络中的道路都有各自的运输成本和政府补贴,道路的权值计算方式为:运输成本 - 政府补贴。权值为正表示扣除了政府补贴后运输货物仍需支付的费用;权值为负则表示政府的补贴超过了支出的运输成本,实际表现为运输过程中还能赚取一定的收益。
|
||||
网络中的道路都有各自的运输成本和政府补贴,道路的权值计算方式为:运输成本 - 政府补贴。
|
||||
|
||||
权值为正表示扣除了政府补贴后运输货物仍需支付的费用;权值为负则表示政府的补贴超过了支出的运输成本,实际表现为运输过程中还能赚取一定的收益。
|
||||
|
||||
|
||||
请找出从城市 1 到城市 n 的所有可能路径中,综合政府补贴后的最低运输成本。如果最低运输成本是一个负数,它表示在遵循最优路径的情况下,运输过程中反而能够实现盈利。
|
||||
请找出从城市 1 到城市 n 的所有可能路径中,综合政府补贴后的最低运输成本。
|
||||
|
||||
如果最低运输成本是一个负数,它表示在遵循最优路径的情况下,运输过程中反而能够实现盈利。
|
||||
|
||||
城市 1 到城市 n 之间可能会出现没有路径的情况,同时保证道路网络中不存在任何负权回路。
|
||||
|
||||
@ -41,11 +44,11 @@
|
||||
1 3 5
|
||||
```
|
||||
|
||||
## 思路
|
||||
## 背景
|
||||
|
||||
本题我们来系统讲解 Bellman_ford 队列优化算法 ,也叫SPFA算法(Shortest Path Faster Algorithm)。
|
||||
|
||||
> SPFA的称呼来自 1994年西南交通大学段凡丁的论文,其实Bellman_ford 提出后不久 (20世纪50年代末期) 就有队列优化的版本,国际上不承认这个算法是是国内提出的。 所以国际上一般称呼 算法为 Bellman_ford 队列优化算法(Queue improved Bellman-Ford)
|
||||
> SPFA的称呼来自 1994年西南交通大学段凡丁的论文,其实Bellman_ford 提出后不久 (20世纪50年代末期) 就有队列优化的版本,国际上不承认这个算法是是国内提出的。 所以国际上一般称呼 该算法为 Bellman_ford 队列优化算法(Queue improved Bellman-Ford)
|
||||
|
||||
大家知道以上来历,知道 SPFA 和 Bellman_ford 队列优化算法 指的都是一个算法就好。
|
||||
|
||||
@ -72,6 +75,8 @@
|
||||
|
||||
用队列来记录。(其实用栈也行,对元素顺序没有要求)
|
||||
|
||||
## 模拟过程
|
||||
|
||||
接下来来举例这个队列是如何工作的。
|
||||
|
||||
以示例给出的所有边为例:
|
||||
@ -88,19 +93,19 @@
|
||||
|
||||
我们依然使用**minDist数组来表达 起点到各个节点的最短距离**,例如minDist[3] = 5 表示起点到达节点3 的最小距离为5
|
||||
|
||||
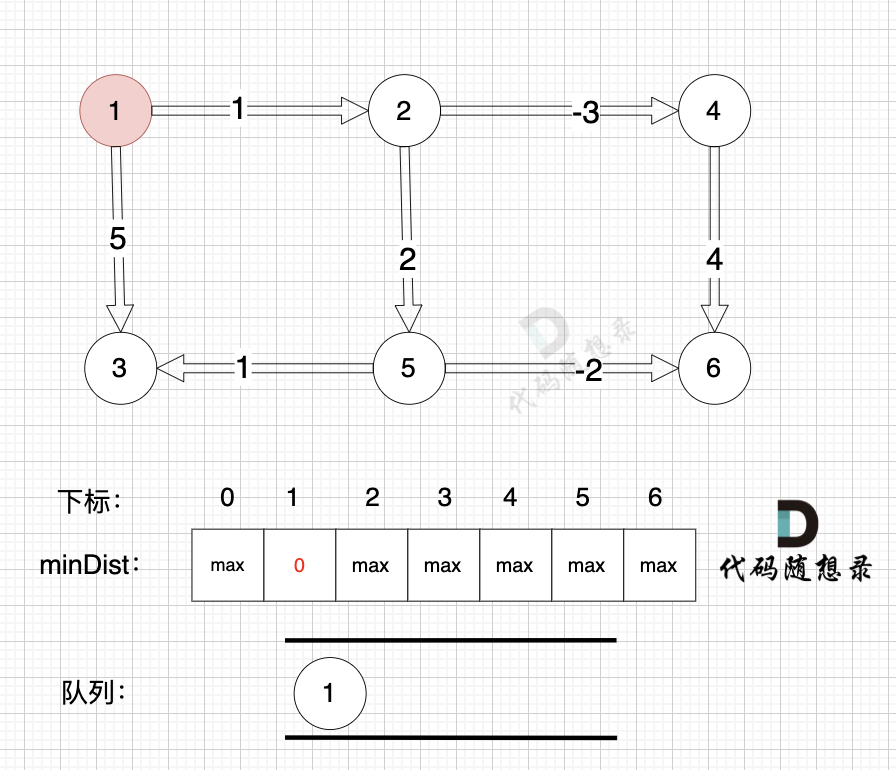
初始化,起点为节点1, 起点到起点的最短距离为0,所以minDist[1] 为 0。 将节点1 加入队列 (下次松弛送节点1开始)
|
||||
初始化,起点为节点1, 起点到起点的最短距离为0,所以minDist[1] 为 0。 将节点1 加入队列 (下次松弛从节点1开始)
|
||||
|
||||
|
||||
|
||||
------------
|
||||
|
||||
从队列里取出节点1,松弛节点1 作为出发点链接的边(节点1 -> 节点2)和边(节点1 -> 节点3)
|
||||
从队列里取出节点1,松弛节点1 作为出发点连接的边(节点1 -> 节点2)和边(节点1 -> 节点3)
|
||||
|
||||
边:节点1 -> 节点2,权值为1 ,minDist[2] > minDist[1] + 1 ,更新 minDist[2] = minDist[1] + 1 = 0 + 1 = 1 。
|
||||
|
||||
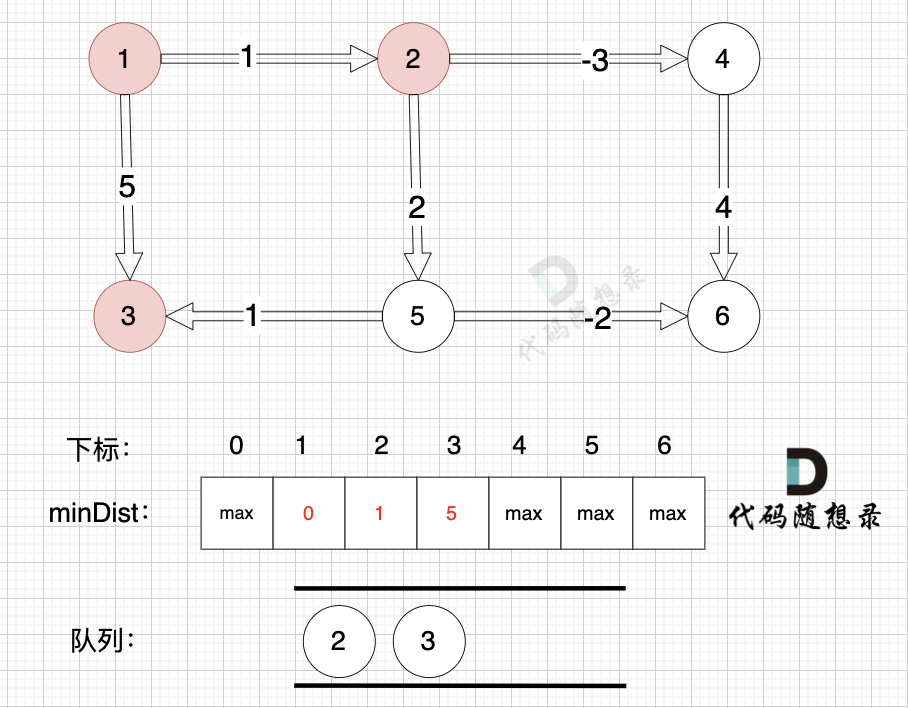
边:节点1 -> 节点3,权值为5 ,minDist[3] > minDist[1] + 5,更新 minDist[3] = minDist[1] + 5 = 0 + 5 = 5。
|
||||
|
||||
将节点2,节点3 加入队列,如图:
|
||||
将节点2、节点3 加入队列,如图:
|
||||
|
||||
|
||||
|
||||
@ -108,7 +113,7 @@
|
||||
-----------------
|
||||
|
||||
|
||||
从队列里取出节点2,松弛节点2 作为出发点链接的边(节点2 -> 节点4)和边(节点2 -> 节点5)
|
||||
从队列里取出节点2,松弛节点2 作为出发点连接的边(节点2 -> 节点4)和边(节点2 -> 节点5)
|
||||
|
||||
边:节点2 -> 节点4,权值为1 ,minDist[4] > minDist[2] + (-3) ,更新 minDist[4] = minDist[2] + (-3) = 1 + (-3) = -2 。
|
||||
|
||||
@ -123,7 +128,7 @@
|
||||
--------------------
|
||||
|
||||
|
||||
从队列里出去节点3,松弛节点3 作为出发点链接的边。
|
||||
从队列里出去节点3,松弛节点3 作为出发点连接的边。
|
||||
|
||||
因为没有从节点3作为出发点的边,所以这里就从队列里取出节点3就好,不用做其他操作,如图:
|
||||
|
||||
@ -132,11 +137,11 @@
|
||||
|
||||
------------
|
||||
|
||||
从队列中取出节点4,松弛节点4作为出发点链接的边(节点4 -> 节点6)
|
||||
从队列中取出节点4,松弛节点4作为出发点连接的边(节点4 -> 节点6)
|
||||
|
||||
边:节点4 -> 节点6,权值为4 ,minDist[6] > minDist[4] + 4,更新 minDist[6] = minDist[4] + 4 = -2 + 4 = 2 。
|
||||
|
||||
讲节点6加入队列
|
||||
将节点6加入队列
|
||||
|
||||
如图:
|
||||
|
||||
@ -145,7 +150,7 @@
|
||||
|
||||
---------------
|
||||
|
||||
从队列中取出节点5,松弛节点5作为出发点链接的边(节点5 -> 节点3),边(节点5 -> 节点6)
|
||||
从队列中取出节点5,松弛节点5作为出发点连接的边(节点5 -> 节点3),边(节点5 -> 节点6)
|
||||
|
||||
边:节点5 -> 节点3,权值为1 ,minDist[3] > minDist[5] + 1 ,更新 minDist[3] = minDist[5] + 1 = 3 + 1 = 4
|
||||
|
||||
@ -157,14 +162,14 @@
|
||||
|
||||
|
||||
|
||||
因为节点3,和 节点6 都曾经加入过队列,不用重复加入,避免重复计算。
|
||||
因为节点3 和 节点6 都曾经加入过队列,不用重复加入,避免重复计算。
|
||||
|
||||
在代码中我们可以用一个数组 visited 来记录入过队列的元素,加入过队列的元素,不再重复入队列。
|
||||
|
||||
|
||||
--------------
|
||||
|
||||
从队列中取出节点6,松弛节点6 作为出发点链接的边。
|
||||
从队列中取出节点6,松弛节点6 作为出发点连接的边。
|
||||
|
||||
节点6作为终点,没有可以出发的边。
|
||||
|
||||
@ -181,7 +186,7 @@
|
||||
|
||||
了解了大体流程,我们再看代码应该怎么写。
|
||||
|
||||
在上面模拟过程中,我们每次都要知道 一个节点作为出发点 链接了哪些节点。
|
||||
在上面模拟过程中,我们每次都要知道 一个节点作为出发点连接了哪些节点。
|
||||
|
||||
如果想方便知道这些数据,就需要使用邻接表来存储这个图,如果对于邻接表不了解的话,可以看 [kama0047.参会dijkstra堆](./kama0047.参会dijkstra堆.md) 中 图的存储 部分。
|
||||
|
||||
@ -279,7 +284,7 @@ n为其他数值的时候,也是一样的。
|
||||
|
||||
并没有计算 出队列 和 入队列的时间消耗。 因为这个在不同语言上 时间消耗也是不一定的。
|
||||
|
||||
以C++为例,以下两端代码理论上,时间复杂度都是 O(n) :
|
||||
以C++为例,以下两段代码理论上,时间复杂度都是 O(n) :
|
||||
|
||||
```CPP
|
||||
for (long long i = 0; i < n; i++) {
|
||||
@ -316,7 +321,7 @@ SPFA(队列优化版Bellman_ford) 在理论上 时间复杂度更胜一筹
|
||||
|
||||
这里可能有录友疑惑,`while (!que.empty())` 队里里 会不会造成死循环? 例如 图中有环,这样一直有元素加入到队列里?
|
||||
|
||||
其实有环的情况,要看它是 正权回路 还是 负全回路。
|
||||
其实有环的情况,要看它是 正权回路 还是 负权回路。
|
||||
|
||||
题目描述中,已经说了,本题没有 负权回路 。
|
||||
|
||||
|
||||
@ -54,14 +54,16 @@
|
||||
|
||||
这道题题目是 DFS,BFS,并查集,基础题目。
|
||||
|
||||
本题思路,是用遇到一个没有遍历过的节点陆地,计数器就加一,然后把该节点陆地所能遍历到的陆地都标记上。
|
||||
本题思路:遇到一个没有遍历过的节点陆地,计数器就加一,然后把该节点陆地所能遍历到的陆地都标记上。
|
||||
|
||||
在遇到标记过的陆地节点和海洋节点的时候直接跳过。 这样计数器就是最终岛屿的数量。
|
||||
再遇到标记过的陆地节点和海洋节点的时候直接跳过。 这样计数器就是最终岛屿的数量。
|
||||
|
||||
那么如果把节点陆地所能遍历到的陆地都标记上呢,就可以使用 DFS,BFS或者并查集。
|
||||
|
||||
### 广度优先搜索
|
||||
|
||||
如果不熟悉广搜,建议先看 [广搜理论基础](./图论广搜理论基础.md)。
|
||||
|
||||
不少同学用广搜做这道题目的时候,超时了。 这里有一个广搜中很重要的细节:
|
||||
|
||||
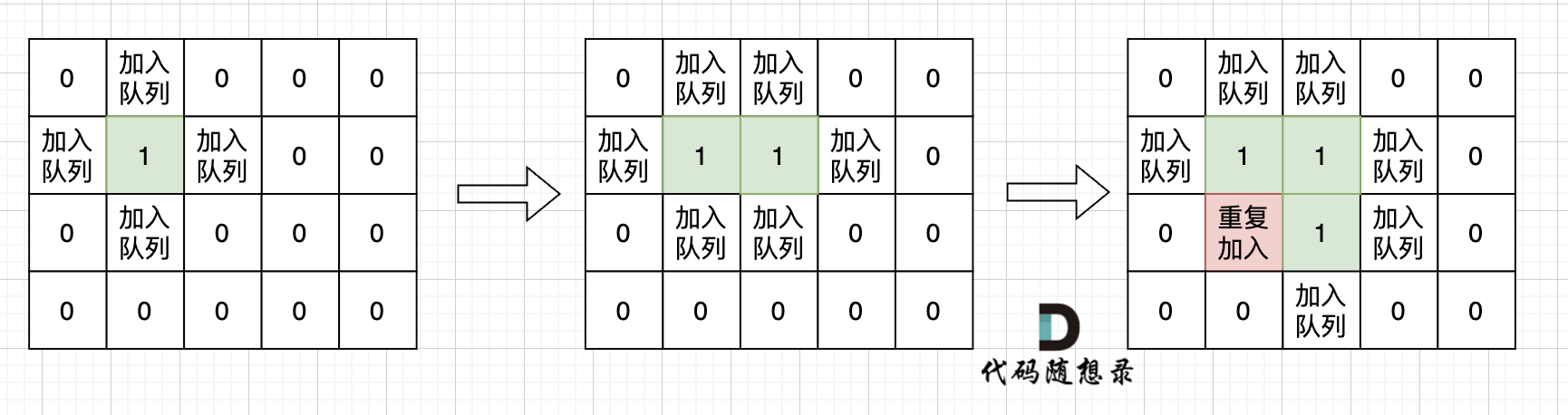
根本原因是**只要 加入队列就代表 走过,就需要标记,而不是从队列拿出来的时候再去标记走过**。
|
||||
@ -72,7 +74,7 @@
|
||||
|
||||
|
||||
|
||||
超时写法 (从队列中取出节点再标记)
|
||||
超时写法 (从队列中取出节点再标记,注意代码注释的地方)
|
||||
|
||||
```CPP
|
||||
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
|
||||
@ -98,7 +100,7 @@ void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y
|
||||
```
|
||||
|
||||
|
||||
加入队列 就代表走过,立刻标记,正确写法:
|
||||
加入队列 就代表走过,立刻标记,正确写法: (注意代码注释的地方)
|
||||
|
||||
```CPP
|
||||
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
|
||||
@ -155,7 +157,6 @@ void bfs(const vector<vector<int>>& grid, vector<vector<bool>>& visited, int x,
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
int main() {
|
||||
int n, m;
|
||||
cin >> n >> m;
|
||||
|
||||
221
problems/kamacoder/0100.岛屿的最大面积.md
Normal file
221
problems/kamacoder/0100.岛屿的最大面积.md
Normal file
@ -0,0 +1,221 @@
|
||||
|
||||
# 100. 岛屿的最大面积
|
||||
|
||||
[卡码网题目链接(ACM模式)](https://kamacoder.com/problempage.php?pid=1172)
|
||||
|
||||
[力扣题目链接](https://programmercarl.com/0695.%E5%B2%9B%E5%B1%BF%E7%9A%84%E6%9C%80%E5%A4%A7%E9%9D%A2%E7%A7%AF.html#%E6%80%9D%E8%B7%AF)
|
||||
|
||||
题目描述
|
||||
|
||||
给定一个由 1(陆地)和 0(水)组成的矩阵,计算岛屿的最大面积。岛屿面积的计算方式为组成岛屿的陆地的总数。岛屿由水平方向或垂直方向上相邻的陆地连接而成,并且四周都是水域。你可以假设矩阵外均被水包围。
|
||||
|
||||
输入描述
|
||||
|
||||
第一行包含两个整数 N, M,表示矩阵的行数和列数。后续 N 行,每行包含 M 个数字,数字为 1 或者 0,表示岛屿的单元格。
|
||||
|
||||
输出描述
|
||||
|
||||
输出一个整数,表示岛屿的最大面积。如果不存在岛屿,则输出 0。
|
||||
|
||||
输入示例
|
||||
|
||||
```
|
||||
4 5
|
||||
1 1 0 0 0
|
||||
1 1 0 0 0
|
||||
0 0 1 0 0
|
||||
0 0 0 1 1
|
||||
```
|
||||
|
||||
输出示例
|
||||
|
||||
4
|
||||
|
||||
提示信息
|
||||
|
||||

|
||||
|
||||
样例输入中,岛屿的最大面积为 4。
|
||||
|
||||
数据范围:
|
||||
|
||||
* 1 <= M, N <= 50。
|
||||
|
||||
|
||||
## 思路
|
||||
|
||||
注意题目中每座岛屿只能由**水平方向和/或竖直方向上**相邻的陆地连接形成。
|
||||
|
||||
也就是说斜角度链接是不算了, 例如示例二,是三个岛屿,如图:
|
||||
|
||||

|
||||
|
||||
这道题目也是 dfs bfs基础类题目,就是搜索每个岛屿上“1”的数量,然后取一个最大的。
|
||||
|
||||
本题思路上比较简单,难点其实都是 dfs 和 bfs的理论基础,关于理论基础我在这里都有详细讲解 :
|
||||
|
||||
* [DFS理论基础](https://programmercarl.com/kamacoder/图论深搜理论基础.html)
|
||||
* [BFS理论基础](https://programmercarl.com/kamacoder/图论广搜理论基础.html)
|
||||
|
||||
### DFS
|
||||
|
||||
很多同学写dfs其实也是凭感觉来的,有的时候dfs函数中写终止条件才能过,有的时候 dfs函数不写终止添加也能过!
|
||||
|
||||
这里其实涉及到dfs的两种写法。
|
||||
|
||||
写法一,dfs只处理下一个节点,即在主函数遇到岛屿就计数为1,dfs处理接下来的相邻陆地
|
||||
|
||||
```CPP
|
||||
// 版本一
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
using namespace std;
|
||||
int count;
|
||||
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
|
||||
void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y) {
|
||||
for (int i = 0; i < 4; i++) {
|
||||
int nextx = x + dir[i][0];
|
||||
int nexty = y + dir[i][1];
|
||||
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了,直接跳过
|
||||
if (!visited[nextx][nexty] && grid[nextx][nexty] == 1) { // 没有访问过的 同时 是陆地的
|
||||
visited[nextx][nexty] = true;
|
||||
count++;
|
||||
dfs(grid, visited, nextx, nexty);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
int main() {
|
||||
int n, m;
|
||||
cin >> n >> m;
|
||||
vector<vector<int>> grid(n, vector<int>(m, 0));
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
cin >> grid[i][j];
|
||||
}
|
||||
}
|
||||
vector<vector<bool>> visited(n, vector<bool>(m, false));
|
||||
int result = 0;
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
if (!visited[i][j] && grid[i][j] == 1) {
|
||||
count = 1; // 因为dfs处理下一个节点,所以这里遇到陆地了就先计数,dfs处理接下来的相邻陆地
|
||||
visited[i][j] = true;
|
||||
dfs(grid, visited, i, j); // 将与其链接的陆地都标记上 true
|
||||
result = max(result, count);
|
||||
}
|
||||
}
|
||||
}
|
||||
cout << result << endl;
|
||||
|
||||
}
|
||||
```
|
||||
|
||||
写法二,dfs处理当前节点,即在主函数遇到岛屿就计数为0,dfs处理接下来的全部陆地
|
||||
|
||||
dfs
|
||||
```CPP
|
||||
// 版本二
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
using namespace std;
|
||||
|
||||
int count;
|
||||
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
|
||||
void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y) {
|
||||
if (visited[x][y] || grid[x][y] == 0) return; // 终止条件:访问过的节点 或者 遇到海水
|
||||
visited[x][y] = true; // 标记访问过
|
||||
count++;
|
||||
for (int i = 0; i < 4; i++) {
|
||||
int nextx = x + dir[i][0];
|
||||
int nexty = y + dir[i][1];
|
||||
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了,直接跳过
|
||||
dfs(grid, visited, nextx, nexty);
|
||||
}
|
||||
}
|
||||
|
||||
int main() {
|
||||
int n, m;
|
||||
cin >> n >> m;
|
||||
vector<vector<int>> grid(n, vector<int>(m, 0));
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
cin >> grid[i][j];
|
||||
}
|
||||
}
|
||||
vector<vector<bool>> visited = vector<vector<bool>>(n, vector<bool>(m, false));
|
||||
int result = 0;
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
if (!visited[i][j] && grid[i][j] == 1) {
|
||||
count = 0; // 因为dfs处理当前节点,所以遇到陆地计数为0,进dfs之后在开始从1计数
|
||||
dfs(grid, visited, i, j); // 将与其链接的陆地都标记上 true
|
||||
result = max(result, count);
|
||||
}
|
||||
}
|
||||
}
|
||||
cout << result << endl;
|
||||
}
|
||||
```
|
||||
|
||||
大家通过注释可以发现,两种写法,版本一,在主函数遇到陆地就计数为1,接下来的相邻陆地都在dfs中计算。
|
||||
|
||||
版本二 在主函数遇到陆地 计数为0,也就是不计数,陆地数量都去dfs里做计算。
|
||||
|
||||
这也是为什么大家看了很多 dfs的写法 ,发现写法怎么都不一样呢? 其实这就是根本原因。
|
||||
|
||||
|
||||
### BFS
|
||||
|
||||
关于广度优先搜索,如果大家还不了解的话,看这里:[广度优先搜索精讲](https://programmercarl.com/kamacoder/图论广搜理论基础.html)
|
||||
|
||||
本题BFS代码如下:
|
||||
|
||||
```CPP
|
||||
class Solution {
|
||||
private:
|
||||
int count;
|
||||
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
|
||||
void bfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y) {
|
||||
queue<int> que;
|
||||
que.push(x);
|
||||
que.push(y);
|
||||
visited[x][y] = true; // 加入队列就意味节点是陆地可到达的点
|
||||
count++;
|
||||
while(!que.empty()) {
|
||||
int xx = que.front();que.pop();
|
||||
int yy = que.front();que.pop();
|
||||
for (int i = 0 ;i < 4; i++) {
|
||||
int nextx = xx + dir[i][0];
|
||||
int nexty = yy + dir[i][1];
|
||||
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界
|
||||
if (!visited[nextx][nexty] && grid[nextx][nexty] == 1) { // 节点没有被访问过且是陆地
|
||||
visited[nextx][nexty] = true;
|
||||
count++;
|
||||
que.push(nextx);
|
||||
que.push(nexty);
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
public:
|
||||
int maxAreaOfIsland(vector<vector<int>>& grid) {
|
||||
int n = grid.size(), m = grid[0].size();
|
||||
vector<vector<bool>> visited = vector<vector<bool>>(n, vector<bool>(m, false));
|
||||
int result = 0;
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
if (!visited[i][j] && grid[i][j] == 1) {
|
||||
count = 0;
|
||||
bfs(grid, visited, i, j); // 将与其链接的陆地都标记上 true
|
||||
result = max(result, count);
|
||||
}
|
||||
}
|
||||
}
|
||||
return result;
|
||||
}
|
||||
};
|
||||
|
||||
```
|
||||
|
||||
180
problems/kamacoder/0101.孤岛的总面积.md
Normal file
180
problems/kamacoder/0101.孤岛的总面积.md
Normal file
@ -0,0 +1,180 @@
|
||||
|
||||
# 101. 孤岛的总面积
|
||||
|
||||
[卡码网题目链接(ACM模式)](https://kamacoder.com/problempage.php?pid=1173)
|
||||
|
||||
题目描述
|
||||
|
||||
给定一个由 1(陆地)和 0(水)组成的矩阵,岛屿指的是由水平或垂直方向上相邻的陆地单元格组成的区域,且完全被水域单元格包围。孤岛是那些位于矩阵内部、所有单元格都不接触边缘的岛屿。
|
||||
|
||||
|
||||
现在你需要计算所有孤岛的总面积,岛屿面积的计算方式为组成岛屿的陆地的总数。
|
||||
|
||||
输入描述
|
||||
|
||||
第一行包含两个整数 N, M,表示矩阵的行数和列数。之后 N 行,每行包含 M 个数字,数字为 1 或者 0。
|
||||
|
||||
输出描述
|
||||
|
||||
输出一个整数,表示所有孤岛的总面积,如果不存在孤岛,则输出 0。
|
||||
|
||||
输入示例
|
||||
|
||||
```
|
||||
4 5
|
||||
1 1 0 0 0
|
||||
1 1 0 0 0
|
||||
0 0 1 0 0
|
||||
0 0 0 1 1
|
||||
```
|
||||
|
||||
|
||||
输出示例:
|
||||
|
||||
1
|
||||
|
||||
提示信息:
|
||||
|
||||
|
||||
|
||||
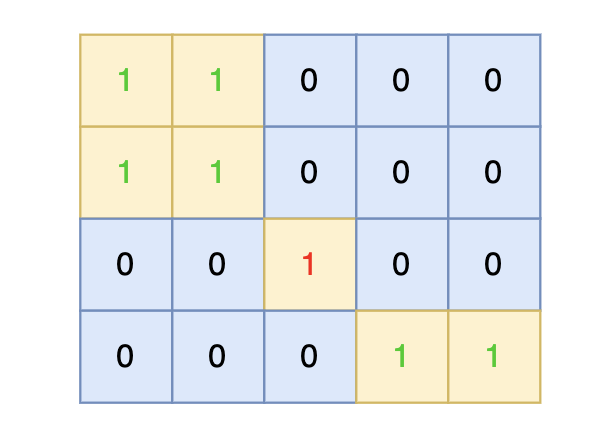
在矩阵中心部分的岛屿,因为没有任何一个单元格接触到矩阵边缘,所以该岛屿属于孤岛,总面积为 1。
|
||||
|
||||
|
||||
数据范围:
|
||||
|
||||
1 <= M, N <= 50。
|
||||
|
||||
## 思路
|
||||
|
||||
本题使用dfs,bfs,并查集都是可以的。
|
||||
|
||||
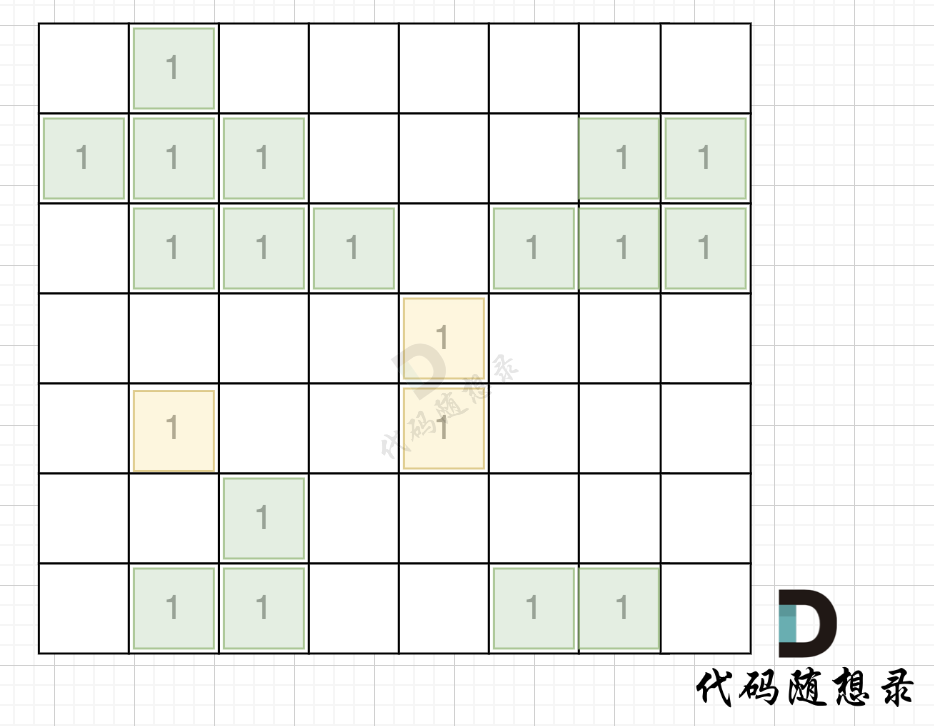
本题要求找到不靠边的陆地面积,那么我们只要从周边找到陆地然后 通过 dfs或者bfs 将周边靠陆地且相邻的陆地都变成海洋,然后再去重新遍历地图 统计此时还剩下的陆地就可以了。
|
||||
|
||||
如图,在遍历地图周围四个边,靠地图四边的陆地,都为绿色,
|
||||
|
||||
|
||||
|
||||
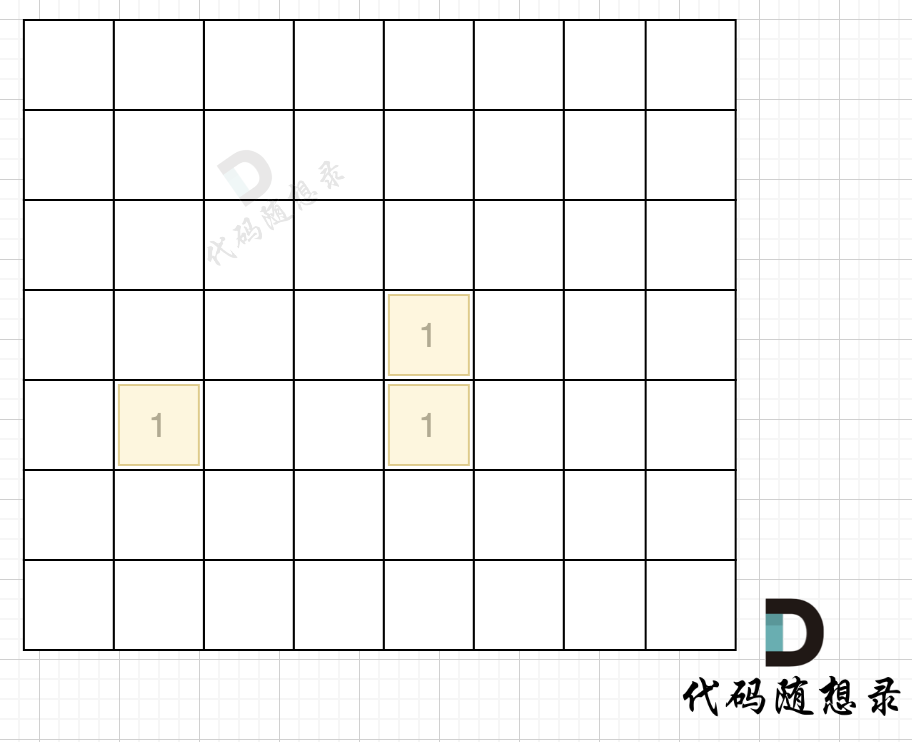
在遇到地图周边陆地的时候,将1都变为0,此时地图为这样:
|
||||
|
||||
|
||||
|
||||
然后我们再去遍历这个地图,遇到有陆地的地方,去采用深搜或者广搜,边统计所有陆地。
|
||||
|
||||
如果对深搜或者广搜不够了解,建议先看这里:[深度优先搜索精讲](https://programmercarl.com/kamacoder/图论深搜理论基础.html),[广度优先搜索精讲](https://programmercarl.com/kamacoder/图论广搜理论基础.html)。
|
||||
|
||||
|
||||
采用深度优先搜索的代码如下:
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
using namespace std;
|
||||
int dir[4][2] = {-1, 0, 0, -1, 1, 0, 0, 1}; // 保存四个方向
|
||||
int count; // 统计符合题目要求的陆地空格数量
|
||||
void dfs(vector<vector<int>>& grid, int x, int y) {
|
||||
grid[x][y] = 0;
|
||||
count++;
|
||||
for (int i = 0; i < 4; i++) { // 向四个方向遍历
|
||||
int nextx = x + dir[i][0];
|
||||
int nexty = y + dir[i][1];
|
||||
// 超过边界
|
||||
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;
|
||||
// 不符合条件,不继续遍历
|
||||
if (grid[nextx][nexty] == 0) continue;
|
||||
|
||||
dfs (grid, nextx, nexty);
|
||||
}
|
||||
return;
|
||||
}
|
||||
|
||||
int main() {
|
||||
int n, m;
|
||||
cin >> n >> m;
|
||||
vector<vector<int>> grid(n, vector<int>(m, 0));
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
cin >> grid[i][j];
|
||||
}
|
||||
}
|
||||
|
||||
// 从左侧边,和右侧边 向中间遍历
|
||||
for (int i = 0; i < n; i++) {
|
||||
if (grid[i][0] == 1) dfs(grid, i, 0);
|
||||
if (grid[i][m - 1] == 1) dfs(grid, i, m - 1);
|
||||
}
|
||||
// 从上边和下边 向中间遍历
|
||||
for (int j = 0; j < m; j++) {
|
||||
if (grid[0][j] == 1) dfs(grid, 0, j);
|
||||
if (grid[n - 1][j] == 1) dfs(grid, n - 1, j);
|
||||
}
|
||||
count = 0;
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
if (grid[i][j] == 1) dfs(grid, i, j);
|
||||
}
|
||||
}
|
||||
cout << count << endl;
|
||||
}
|
||||
```
|
||||
|
||||
采用广度优先搜索的代码如下:
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
#include <queue>
|
||||
using namespace std;
|
||||
int count = 0;
|
||||
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
|
||||
void bfs(vector<vector<int>>& grid, int x, int y) {
|
||||
queue<pair<int, int>> que;
|
||||
que.push({x, y});
|
||||
grid[x][y] = 0; // 只要加入队列,立刻标记
|
||||
count++;
|
||||
while(!que.empty()) {
|
||||
pair<int ,int> cur = que.front(); que.pop();
|
||||
int curx = cur.first;
|
||||
int cury = cur.second;
|
||||
for (int i = 0; i < 4; i++) {
|
||||
int nextx = curx + dir[i][0];
|
||||
int nexty = cury + dir[i][1];
|
||||
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了,直接跳过
|
||||
if (grid[nextx][nexty] == 1) {
|
||||
que.push({nextx, nexty});
|
||||
count++;
|
||||
grid[nextx][nexty] = 0; // 只要加入队列立刻标记
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
int main() {
|
||||
int n, m;
|
||||
cin >> n >> m;
|
||||
vector<vector<int>> grid(n, vector<int>(m, 0));
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
cin >> grid[i][j];
|
||||
}
|
||||
}
|
||||
// 从左侧边,和右侧边 向中间遍历
|
||||
for (int i = 0; i < n; i++) {
|
||||
if (grid[i][0] == 1) bfs(grid, i, 0);
|
||||
if (grid[i][m - 1] == 1) bfs(grid, i, m - 1);
|
||||
}
|
||||
// 从上边和下边 向中间遍历
|
||||
for (int j = 0; j < m; j++) {
|
||||
if (grid[0][j] == 1) bfs(grid, 0, j);
|
||||
if (grid[n - 1][j] == 1) bfs(grid, n - 1, j);
|
||||
}
|
||||
count = 0;
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
if (grid[i][j] == 1) bfs(grid, i, j);
|
||||
}
|
||||
}
|
||||
|
||||
cout << count << endl;
|
||||
}
|
||||
```
|
||||
|
||||
133
problems/kamacoder/0102.沉没孤岛.md
Normal file
133
problems/kamacoder/0102.沉没孤岛.md
Normal file
@ -0,0 +1,133 @@
|
||||
|
||||
# 102. 沉没孤岛
|
||||
|
||||
[卡码网题目链接(ACM模式)](https://kamacoder.com/problempage.php?pid=1174)
|
||||
|
||||
题目描述:
|
||||
|
||||
给定一个由 1(陆地)和 0(水)组成的矩阵,岛屿指的是由水平或垂直方向上相邻的陆地单元格组成的区域,且完全被水域单元格包围。孤岛是那些位于矩阵内部、所有单元格都不接触边缘的岛屿。
|
||||
|
||||
|
||||
现在你需要将所有孤岛“沉没”,即将孤岛中的所有陆地单元格(1)转变为水域单元格(0)。
|
||||
|
||||
输入描述:
|
||||
|
||||
第一行包含两个整数 N, M,表示矩阵的行数和列数。
|
||||
|
||||
之后 N 行,每行包含 M 个数字,数字为 1 或者 0,表示岛屿的单元格。
|
||||
|
||||
输出描述
|
||||
|
||||
输出将孤岛“沉没”之后的岛屿矩阵。
|
||||
|
||||
输入示例:
|
||||
|
||||
```
|
||||
4 5
|
||||
1 1 0 0 0
|
||||
1 1 0 0 0
|
||||
0 0 1 0 0
|
||||
0 0 0 1 1
|
||||
```
|
||||
|
||||
输出示例:
|
||||
|
||||
```
|
||||
1 1 0 0 0
|
||||
1 1 0 0 0
|
||||
0 0 0 0 0
|
||||
0 0 0 1 1
|
||||
```
|
||||
|
||||
提示信息:
|
||||
|
||||
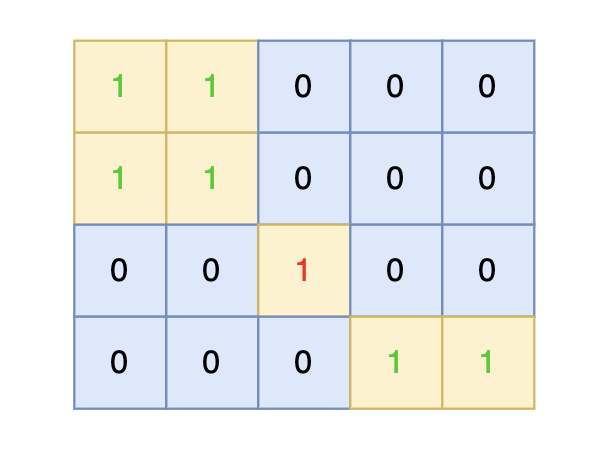
|
||||
|
||||
将孤岛沉没:
|
||||
|
||||
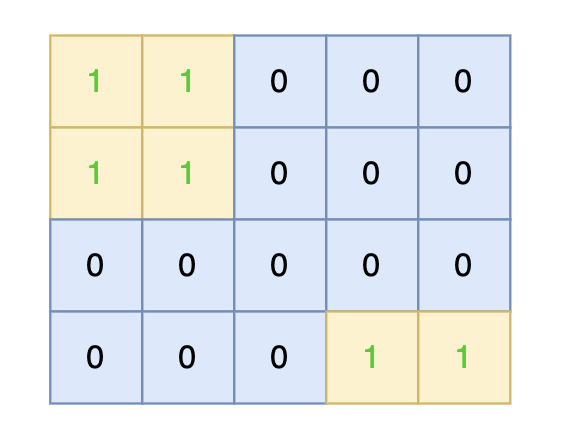
|
||||
|
||||
数据范围:
|
||||
|
||||
1 <= M, N <= 50
|
||||
|
||||
## 思路
|
||||
|
||||
这道题目和[0101.孤岛的总面积](https://kamacoder.com/problempage.php?pid=1173)正好反过来了,[0101.孤岛的总面积](https://kamacoder.com/problempage.php?pid=1173)是求 地图中间的空格数,而本题是要把地图中间的 1 都改成 0 。
|
||||
|
||||
那么两题在思路上也是差不多的。
|
||||
|
||||
思路依然是从地图周边出发,将周边空格相邻的陆地都做上标记,然后在遍历一遍地图,遇到 陆地 且没做过标记的,那么都是地图中间的 陆地 ,全部改成水域就行。
|
||||
|
||||
有的录友可能想,我在定义一个 visited 二维数组,单独标记周边的陆地,然后遍历地图的时候同时对 数组board 和 数组visited 进行判断,决定 陆地是否变成水域。
|
||||
|
||||
这样做其实就有点麻烦了,不用额外定义空间了,标记周边的陆地,可以直接改陆地为其他特殊值作为标记。
|
||||
|
||||
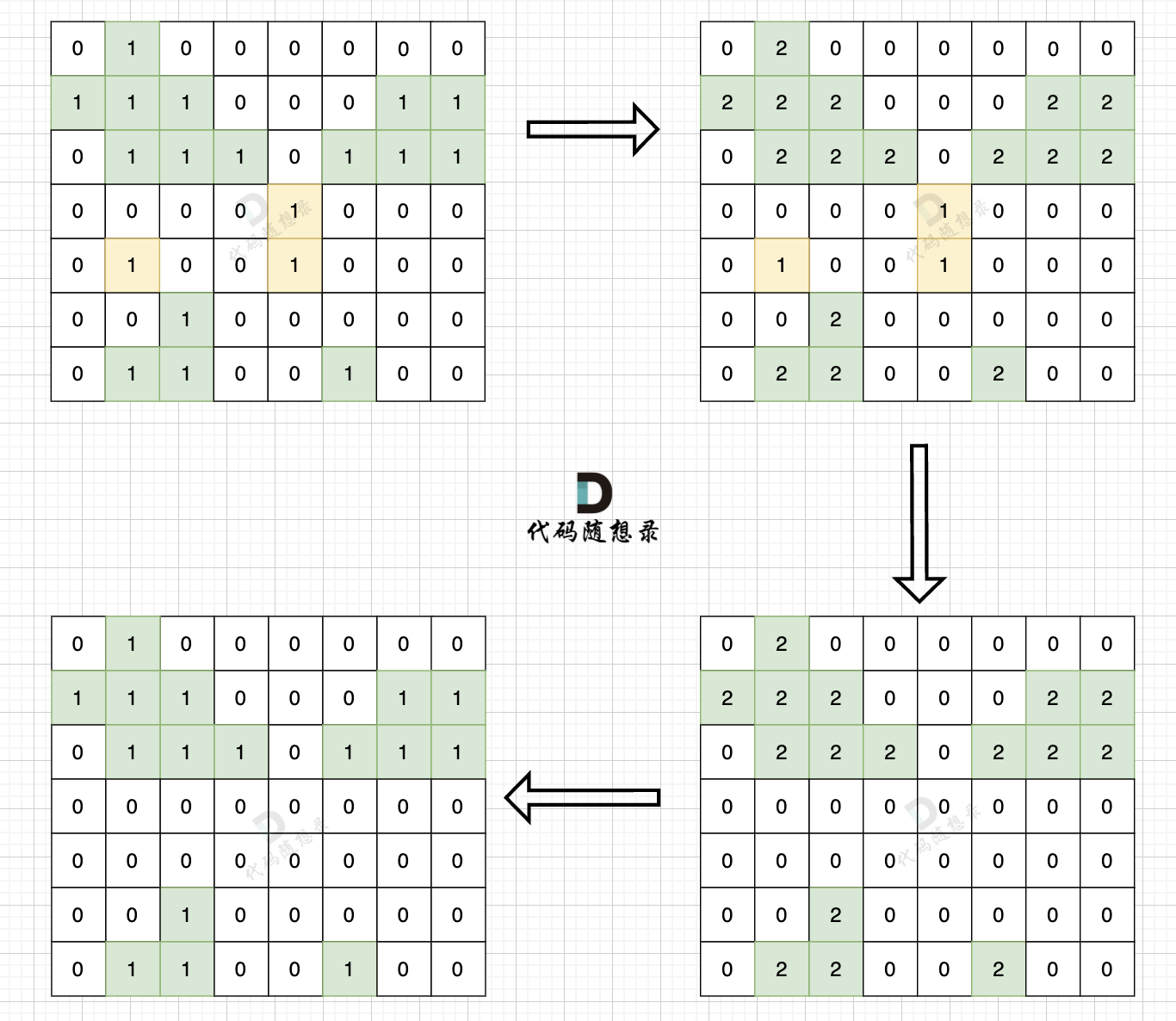
步骤一:深搜或者广搜将地图周边的 1 (陆地)全部改成 2 (特殊标记)
|
||||
|
||||
步骤二:将水域中间 1 (陆地)全部改成 水域(0)
|
||||
|
||||
步骤三:将之前标记的 2 改为 1 (陆地)
|
||||
|
||||
如图:
|
||||
|
||||
|
||||
|
||||
整体C++代码如下,以下使用dfs实现,其实遍历方式dfs,bfs都是可以的。
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
using namespace std;
|
||||
int dir[4][2] = {-1, 0, 0, -1, 1, 0, 0, 1}; // 保存四个方向
|
||||
void dfs(vector<vector<int>>& grid, int x, int y) {
|
||||
grid[x][y] = 2;
|
||||
for (int i = 0; i < 4; i++) { // 向四个方向遍历
|
||||
int nextx = x + dir[i][0];
|
||||
int nexty = y + dir[i][1];
|
||||
// 超过边界
|
||||
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;
|
||||
// 不符合条件,不继续遍历
|
||||
if (grid[nextx][nexty] == 0 || grid[nextx][nexty] == 2) continue;
|
||||
dfs (grid, nextx, nexty);
|
||||
}
|
||||
return;
|
||||
}
|
||||
|
||||
int main() {
|
||||
int n, m;
|
||||
cin >> n >> m;
|
||||
vector<vector<int>> grid(n, vector<int>(m, 0));
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
cin >> grid[i][j];
|
||||
}
|
||||
}
|
||||
|
||||
// 步骤一:
|
||||
// 从左侧边,和右侧边 向中间遍历
|
||||
for (int i = 0; i < n; i++) {
|
||||
if (grid[i][0] == 1) dfs(grid, i, 0);
|
||||
if (grid[i][m - 1] == 1) dfs(grid, i, m - 1);
|
||||
}
|
||||
|
||||
// 从上边和下边 向中间遍历
|
||||
for (int j = 0; j < m; j++) {
|
||||
if (grid[0][j] == 1) dfs(grid, 0, j);
|
||||
if (grid[n - 1][j] == 1) dfs(grid, n - 1, j);
|
||||
}
|
||||
// 步骤二、步骤三
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
if (grid[i][j] == 1) grid[i][j] = 0;
|
||||
if (grid[i][j] == 2) grid[i][j] = 1;
|
||||
}
|
||||
}
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
cout << grid[i][j] << " ";
|
||||
}
|
||||
cout << endl;
|
||||
}
|
||||
}
|
||||
```
|
||||
279
problems/kamacoder/0103.水流问题.md
Normal file
279
problems/kamacoder/0103.水流问题.md
Normal file
@ -0,0 +1,279 @@
|
||||
|
||||
# 103. 水流问题
|
||||
|
||||
[卡码网题目链接(ACM模式)](https://kamacoder.com/problempage.php?pid=1175)
|
||||
|
||||
题目描述:
|
||||
|
||||
现有一个 N × M 的矩阵,每个单元格包含一个数值,这个数值代表该位置的相对高度。矩阵的左边界和上边界被认为是第一组边界,而矩阵的右边界和下边界被视为第二组边界。
|
||||
|
||||
|
||||
矩阵模拟了一个地形,当雨水落在上面时,水会根据地形的倾斜向低处流动,但只能从较高或等高的地点流向较低或等高并且相邻(上下左右方向)的地点。我们的目标是确定那些单元格,从这些单元格出发的水可以达到第一组边界和第二组边界。
|
||||
|
||||
输入描述:
|
||||
|
||||
第一行包含两个整数 N 和 M,分别表示矩阵的行数和列数。
|
||||
|
||||
后续 N 行,每行包含 M 个整数,表示矩阵中的每个单元格的高度。
|
||||
|
||||
输出描述:
|
||||
|
||||
输出共有多行,每行输出两个整数,用一个空格隔开,表示可达第一组边界和第二组边界的单元格的坐标,输出顺序任意。
|
||||
|
||||
输入示例:
|
||||
|
||||
```
|
||||
5 5
|
||||
1 3 1 2 4
|
||||
1 2 1 3 2
|
||||
2 4 7 2 1
|
||||
4 5 6 1 1
|
||||
1 4 1 2 1
|
||||
```
|
||||
|
||||
输出示例:
|
||||
|
||||
```
|
||||
0 4
|
||||
1 3
|
||||
2 2
|
||||
3 0
|
||||
3 1
|
||||
3 2
|
||||
4 0
|
||||
4 1
|
||||
```
|
||||
|
||||
提示信息:
|
||||
|
||||
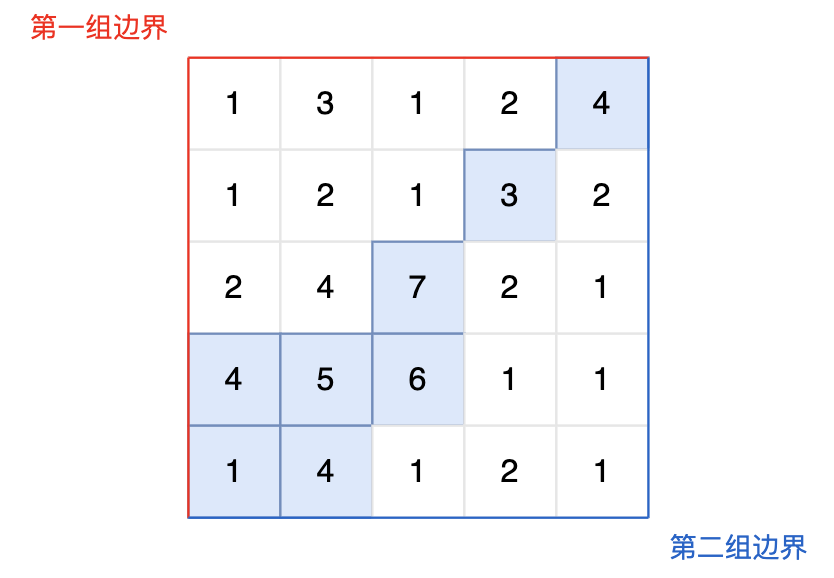
|
||||
|
||||
图中的蓝色方块上的雨水既能流向第一组边界,也能流向第二组边界。所以最终答案为所有蓝色方块的坐标。
|
||||
|
||||
|
||||
数据范围:
|
||||
|
||||
1 <= M, N <= 50
|
||||
|
||||
## 思路
|
||||
|
||||
一个比较直白的想法,其实就是 遍历每个点,然后看这个点 能不能同时到达第一组边界和第二组边界。
|
||||
|
||||
至于遍历方式,可以用dfs,也可以用bfs,以下用dfs来举例。
|
||||
|
||||
那么这种思路的实现代码如下:
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
using namespace std;
|
||||
int n, m;
|
||||
int dir[4][2] = {-1, 0, 0, -1, 1, 0, 0, 1};
|
||||
|
||||
// 从 x,y 出发 把可以走的地方都标记上
|
||||
void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y) {
|
||||
if (visited[x][y]) return;
|
||||
|
||||
visited[x][y] = true;
|
||||
|
||||
for (int i = 0; i < 4; i++) {
|
||||
int nextx = x + dir[i][0];
|
||||
int nexty = y + dir[i][1];
|
||||
if (nextx < 0 || nextx >= n || nexty < 0 || nexty >= m) continue;
|
||||
if (grid[x][y] < grid[nextx][nexty]) continue; // 高度不合适
|
||||
|
||||
dfs (grid, visited, nextx, nexty);
|
||||
}
|
||||
return;
|
||||
}
|
||||
bool isResult(vector<vector<int>>& grid, int x, int y) {
|
||||
vector<vector<bool>> visited(n, vector<bool>(m, false));
|
||||
|
||||
// 深搜,将x,y出发 能到的节点都标记上。
|
||||
dfs(grid, visited, x, y);
|
||||
bool isFirst = false;
|
||||
bool isSecond = false;
|
||||
|
||||
// 以下就是判断x,y出发,是否到达第一组边界和第二组边界
|
||||
// 第一边界的上边
|
||||
for (int j = 0; j < m; j++) {
|
||||
if (visited[0][j]) {
|
||||
isFirst = true;
|
||||
break;
|
||||
}
|
||||
}
|
||||
// 第一边界的左边
|
||||
for (int i = 0; i < n; i++) {
|
||||
if (visited[i][0]) {
|
||||
isFirst = true;
|
||||
break;
|
||||
}
|
||||
}
|
||||
// 第二边界右边
|
||||
for (int j = 0; j < m; j++) {
|
||||
if (visited[n - 1][j]) {
|
||||
isSecond = true;
|
||||
break;
|
||||
}
|
||||
}
|
||||
// 第二边界下边
|
||||
for (int i = 0; i < n; i++) {
|
||||
if (visited[i][m - 1]) {
|
||||
isSecond = true;
|
||||
break;
|
||||
}
|
||||
}
|
||||
if (isFirst && isSecond) return true;
|
||||
return false;
|
||||
}
|
||||
|
||||
|
||||
int main() {
|
||||
cin >> n >> m;
|
||||
vector<vector<int>> grid(n, vector<int>(m, 0));
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
cin >> grid[i][j];
|
||||
}
|
||||
}
|
||||
// 遍历每一个点,看是否能同时到达第一组边界和第二组边界
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
if (isResult(grid, i, j)) {
|
||||
cout << i << " " << j << endl;
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
这种思路很直白,但很明显,以上代码超时了。 来看看时间复杂度。
|
||||
|
||||
遍历每一个节点,是 m * n,遍历每一个节点的时候,都要做深搜,深搜的时间复杂度是: m * n
|
||||
|
||||
那么整体时间复杂度 就是 O(m^2 * n^2) ,这是一个四次方的时间复杂度。
|
||||
|
||||
## 优化
|
||||
|
||||
那么我们可以 反过来想,从第一组边界上的节点 逆流而上,将遍历过的节点都标记上。
|
||||
|
||||
同样从第二组边界的边上节点 逆流而上,将遍历过的节点也标记上。
|
||||
|
||||
然后**两方都标记过的节点就是既可以流太平洋也可以流大西洋的节点**。
|
||||
|
||||
从第一组边界边上节点出发,如图:
|
||||
|
||||
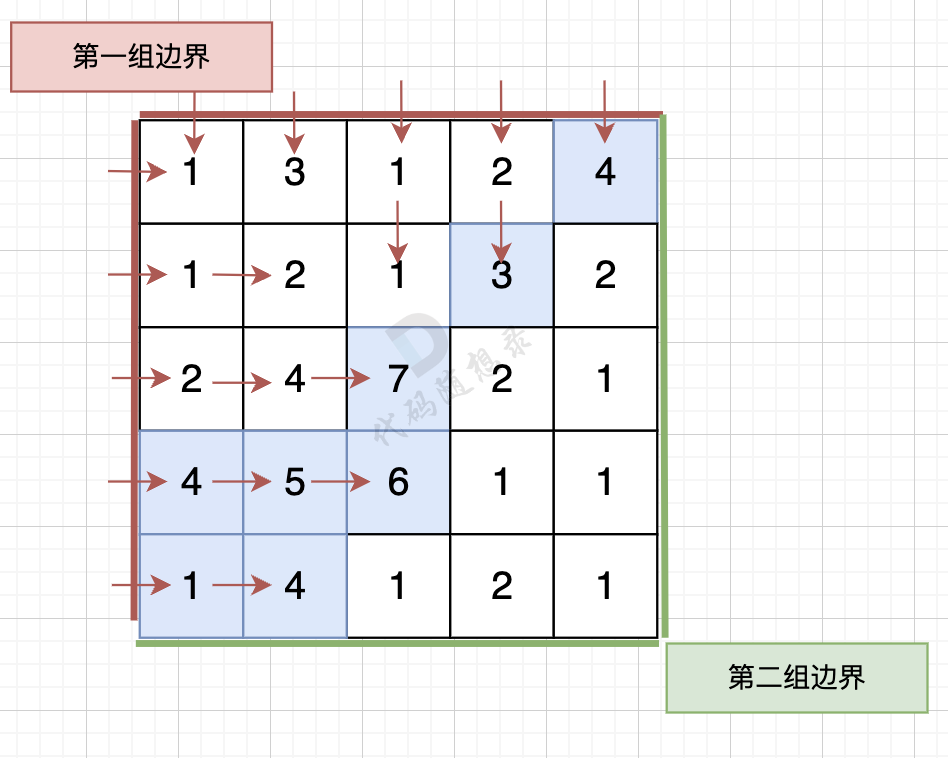
|
||||
|
||||
|
||||
从第二组边界上节点出发,如图:
|
||||
|
||||
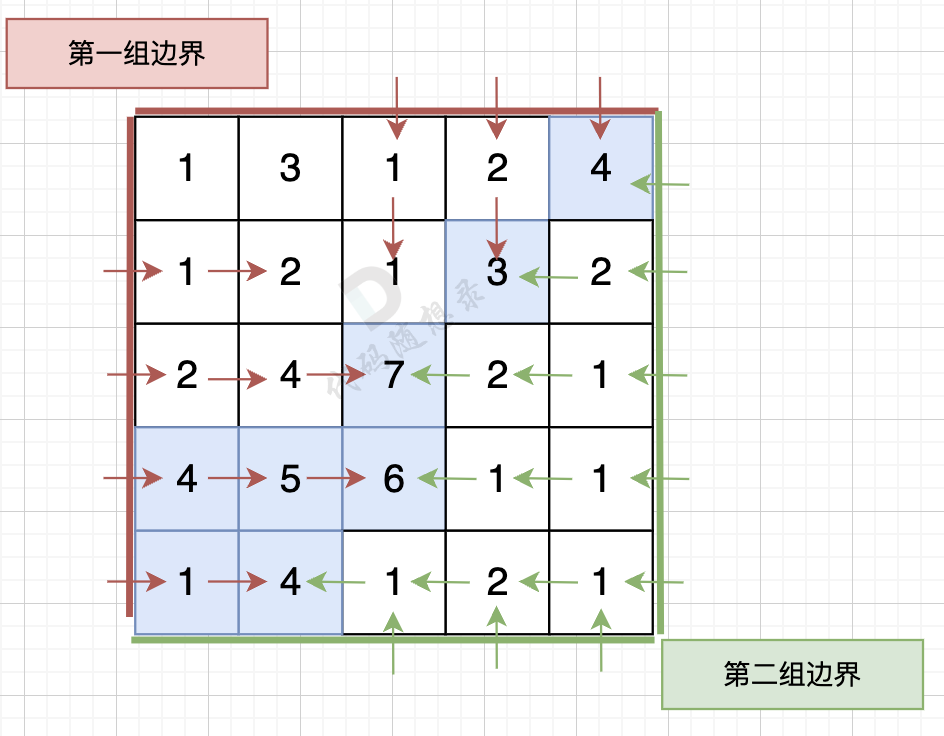
|
||||
|
||||
按照这样的逻辑,就可以写出如下遍历代码:(详细注释)
|
||||
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
using namespace std;
|
||||
int n, m;
|
||||
int dir[4][2] = {-1, 0, 0, -1, 1, 0, 0, 1};
|
||||
void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y) {
|
||||
if (visited[x][y]) return;
|
||||
|
||||
visited[x][y] = true;
|
||||
|
||||
for (int i = 0; i < 4; i++) {
|
||||
int nextx = x + dir[i][0];
|
||||
int nexty = y + dir[i][1];
|
||||
if (nextx < 0 || nextx >= n || nexty < 0 || nexty >= m) continue;
|
||||
if (grid[x][y] > grid[nextx][nexty]) continue; // 注意:这里是从低向高遍历
|
||||
|
||||
dfs (grid, visited, nextx, nexty);
|
||||
}
|
||||
return;
|
||||
}
|
||||
|
||||
|
||||
|
||||
int main() {
|
||||
|
||||
cin >> n >> m;
|
||||
vector<vector<int>> grid(n, vector<int>(m, 0));
|
||||
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
cin >> grid[i][j];
|
||||
}
|
||||
}
|
||||
// 标记从第一组边界上的节点出发,可以遍历的节点
|
||||
vector<vector<bool>> firstBorder(n, vector<bool>(m, false));
|
||||
|
||||
// 标记从第一组边界上的节点出发,可以遍历的节点
|
||||
vector<vector<bool>> secondBorder(n, vector<bool>(m, false));
|
||||
|
||||
// 从最上和最下行的节点出发,向高处遍历
|
||||
for (int i = 0; i < n; i++) {
|
||||
dfs (grid, firstBorder, i, 0); // 遍历最左列,接触第一组边界
|
||||
dfs (grid, secondBorder, i, m - 1); // 遍历最右列,接触第二组边界
|
||||
}
|
||||
|
||||
// 从最左和最右列的节点出发,向高处遍历
|
||||
for (int j = 0; j < m; j++) {
|
||||
dfs (grid, firstBorder, 0, j); // 遍历最上行,接触第一组边界
|
||||
dfs (grid, secondBorder, n - 1, j); // 遍历最下行,接触第二组边界
|
||||
}
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
// 如果这个节点,从第一组边界和第二组边界出发都遍历过,就是结果
|
||||
if (firstBorder[i][j] && secondBorder[i][j]) cout << i << " " << j << endl;;
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
|
||||
时间复杂度分析, 关于dfs函数搜索的过程 时间复杂度是 O(n * m),这个大家比较容易想。
|
||||
|
||||
关键看主函数,那么每次dfs的时候,上面还是有for循环的。
|
||||
|
||||
第一个for循环,时间复杂度是:n * (n * m) 。
|
||||
|
||||
第二个for循环,时间复杂度是:m * (n * m)。
|
||||
|
||||
所以本题看起来 时间复杂度好像是 : n * (n * m) + m * (n * m) = (m * n) * (m + n) 。
|
||||
|
||||
其实这是一个误区,大家再自己看 dfs函数的实现,其实 有visited函数记录 走过的节点,而走过的节点是不会再走第二次的。
|
||||
|
||||
所以 调用dfs函数,**只要参数传入的是 数组 firstBorder,那么地图中 每一个节点其实就遍历一次,无论你调用多少次**。
|
||||
|
||||
同理,调用dfs函数,只要 参数传入的是 数组 secondBorder,地图中每个节点也只会遍历一次。
|
||||
|
||||
所以,以下这段代码的时间复杂度是 2 * n * m。 地图用每个节点就遍历了两次,参数传入 firstBorder 的时候遍历一次,参数传入 secondBorder 的时候遍历一次。
|
||||
|
||||
```CPP
|
||||
// 从最上和最下行的节点出发,向高处遍历
|
||||
for (int i = 0; i < n; i++) {
|
||||
dfs (grid, firstBorder, i, 0); // 遍历最左列,接触第一组边界
|
||||
dfs (grid, secondBorder, i, m - 1); // 遍历最右列,接触第二组边界
|
||||
}
|
||||
|
||||
// 从最左和最右列的节点出发,向高处遍历
|
||||
for (int j = 0; j < m; j++) {
|
||||
dfs (grid, firstBorder, 0, j); // 遍历最上行,接触第一组边界
|
||||
dfs (grid, secondBorder, n - 1, j); // 遍历最下行,接触第二组边界
|
||||
}
|
||||
```
|
||||
|
||||
那么本题整体的时间复杂度其实是: 2 * n * m + n * m ,所以最终时间复杂度为 O(n * m) 。
|
||||
|
||||
空间复杂度为:O(n * m) 这个就不难理解了。开了几个 n * m 的数组。
|
||||
|
||||
|
||||
|
||||
|
||||
254
problems/kamacoder/0104.建造最大岛屿.md
Normal file
254
problems/kamacoder/0104.建造最大岛屿.md
Normal file
@ -0,0 +1,254 @@
|
||||
|
||||
# 104.建造最大岛屿
|
||||
|
||||
[卡码网题目链接(ACM模式)](https://kamacoder.com/problempage.php?pid=1176)
|
||||
|
||||
题目描述:
|
||||
|
||||
给定一个由 1(陆地)和 0(水)组成的矩阵,你最多可以将矩阵中的一格水变为一块陆地,在执行了此操作之后,矩阵中最大的岛屿面积是多少。
|
||||
|
||||
岛屿面积的计算方式为组成岛屿的陆地的总数。岛屿是被水包围,并且通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设矩阵外均被水包围。
|
||||
|
||||
输入描述:
|
||||
|
||||
第一行包含两个整数 N, M,表示矩阵的行数和列数。之后 N 行,每行包含 M 个数字,数字为 1 或者 0,表示岛屿的单元格。
|
||||
|
||||
输出描述:
|
||||
|
||||
输出一个整数,表示最大的岛屿面积。如果矩阵中不存在岛屿,则输出 0。
|
||||
|
||||
输入示例:
|
||||
|
||||
```
|
||||
4 5
|
||||
1 1 0 0 0
|
||||
1 1 0 0 0
|
||||
0 0 1 0 0
|
||||
0 0 0 1 1
|
||||
```
|
||||
|
||||
输出示例
|
||||
|
||||
6
|
||||
|
||||
提示信息
|
||||
|
||||
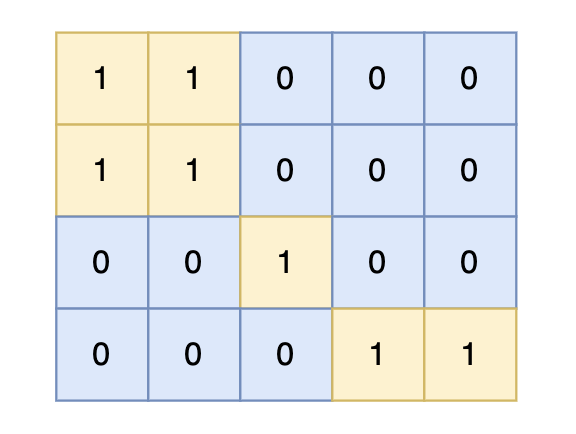
|
||||
|
||||
|
||||
对于上面的案例,有两个位置可将 0 变成 1,使得岛屿的面积最大,即 6。
|
||||
|
||||
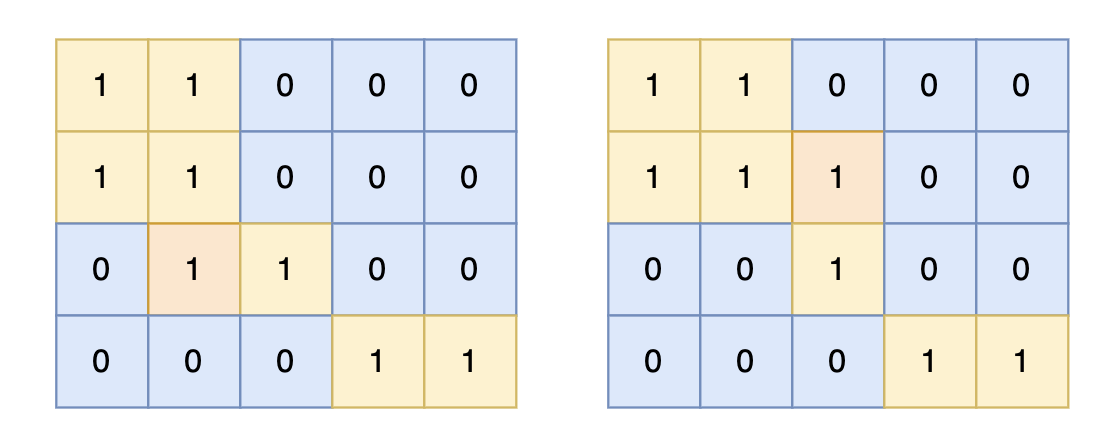
|
||||
|
||||
|
||||
数据范围:
|
||||
|
||||
1 <= M, N <= 50。
|
||||
|
||||
|
||||
## 思路
|
||||
|
||||
本题的一个暴力想法,应该是遍历地图尝试 将每一个 0 改成1,然后去搜索地图中的最大的岛屿面积。
|
||||
|
||||
计算地图的最大面积:遍历地图 + 深搜岛屿,时间复杂度为 n * n。
|
||||
|
||||
(其实使用深搜还是广搜都是可以的,其目的就是遍历岛屿做一个标记,相当于染色,那么使用哪个遍历方式都行,以下我用深搜来讲解)
|
||||
|
||||
每改变一个0的方格,都需要重新计算一个地图的最大面积,所以 整体时间复杂度为:n^4。
|
||||
|
||||
## 优化思路
|
||||
|
||||
其实每次深搜遍历计算最大岛屿面积,我们都做了很多重复的工作。
|
||||
|
||||
只要用一次深搜把每个岛屿的面积记录下来就好。
|
||||
|
||||
第一步:一次遍历地图,得出各个岛屿的面积,并做编号记录。可以使用map记录,key为岛屿编号,value为岛屿面积
|
||||
|
||||
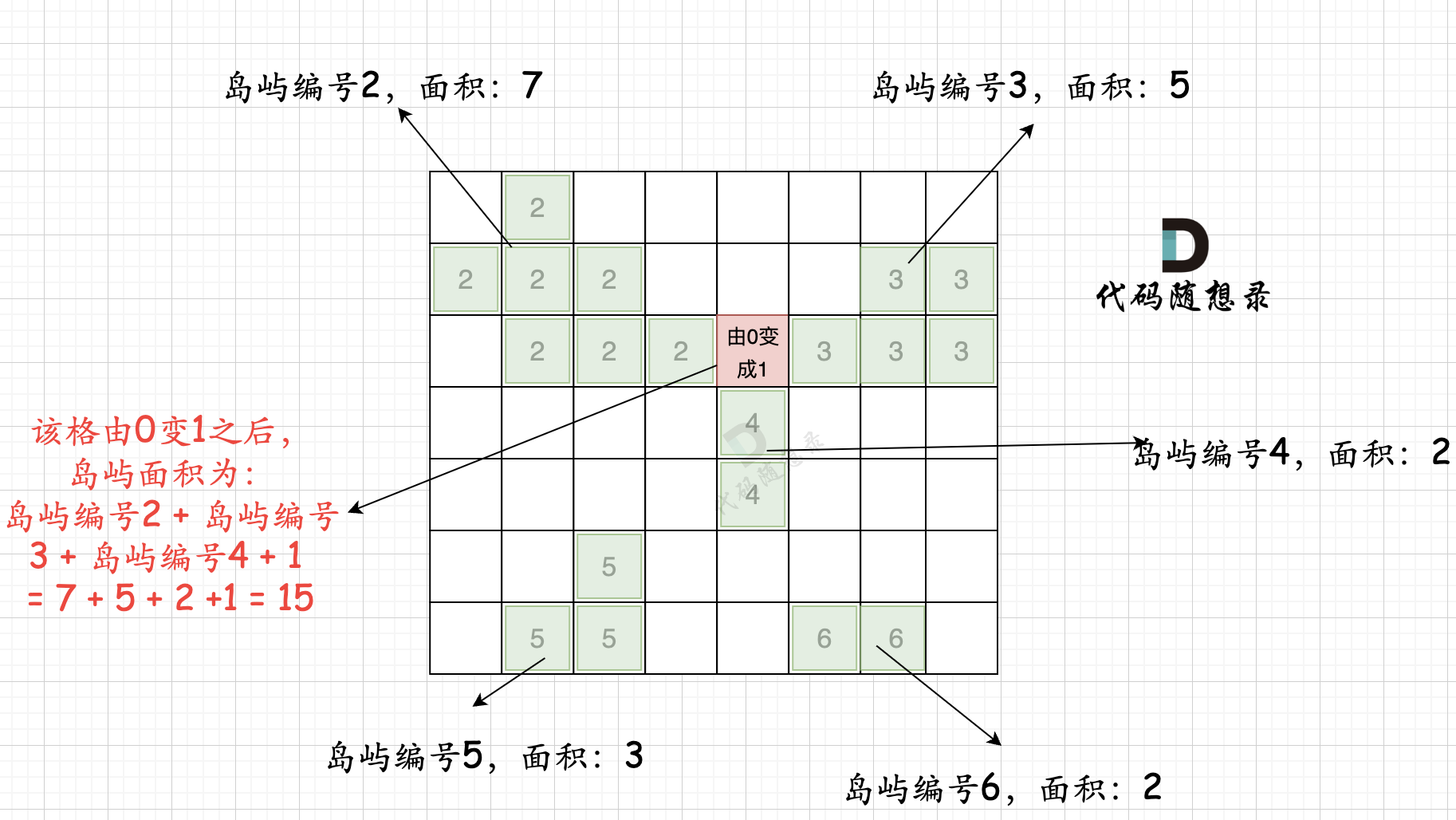
第二步:再遍历地图,遍历0的方格(因为要将0变成1),并统计该1(由0变成的1)周边岛屿面积,将其相邻面积相加在一起,遍历所有 0 之后,就可以得出 选一个0变成1 之后的最大面积。
|
||||
|
||||
拿如下地图的岛屿情况来举例: (1为陆地)
|
||||
|
||||
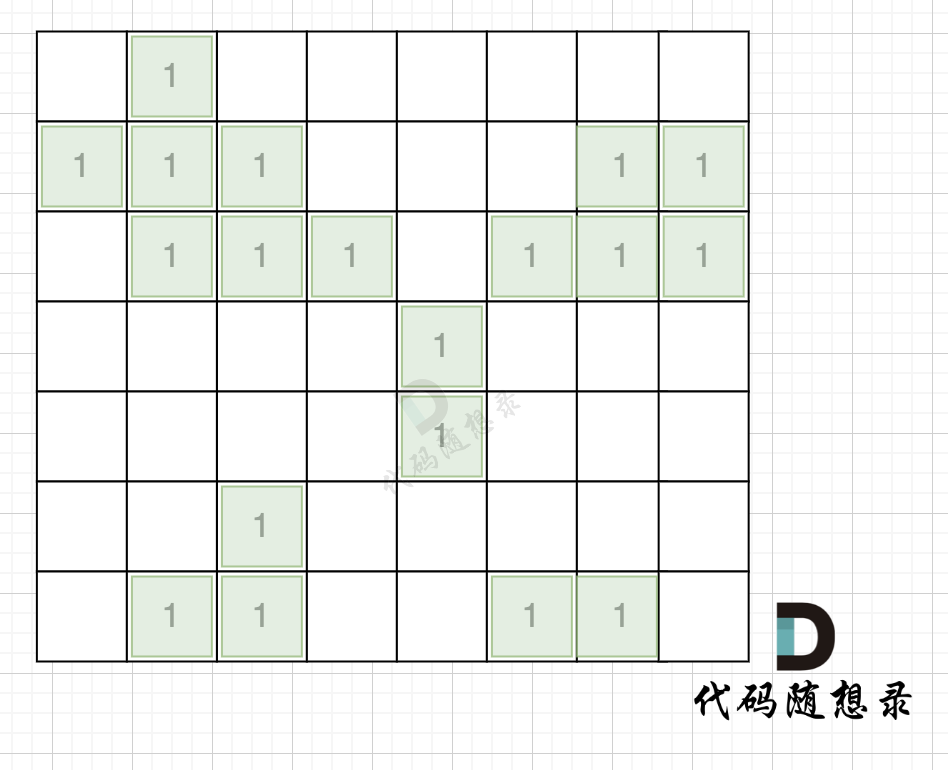
|
||||
|
||||
第一步,则遍历题目,并将岛屿到编号和面积上的统计,过程如图所示:
|
||||
|
||||
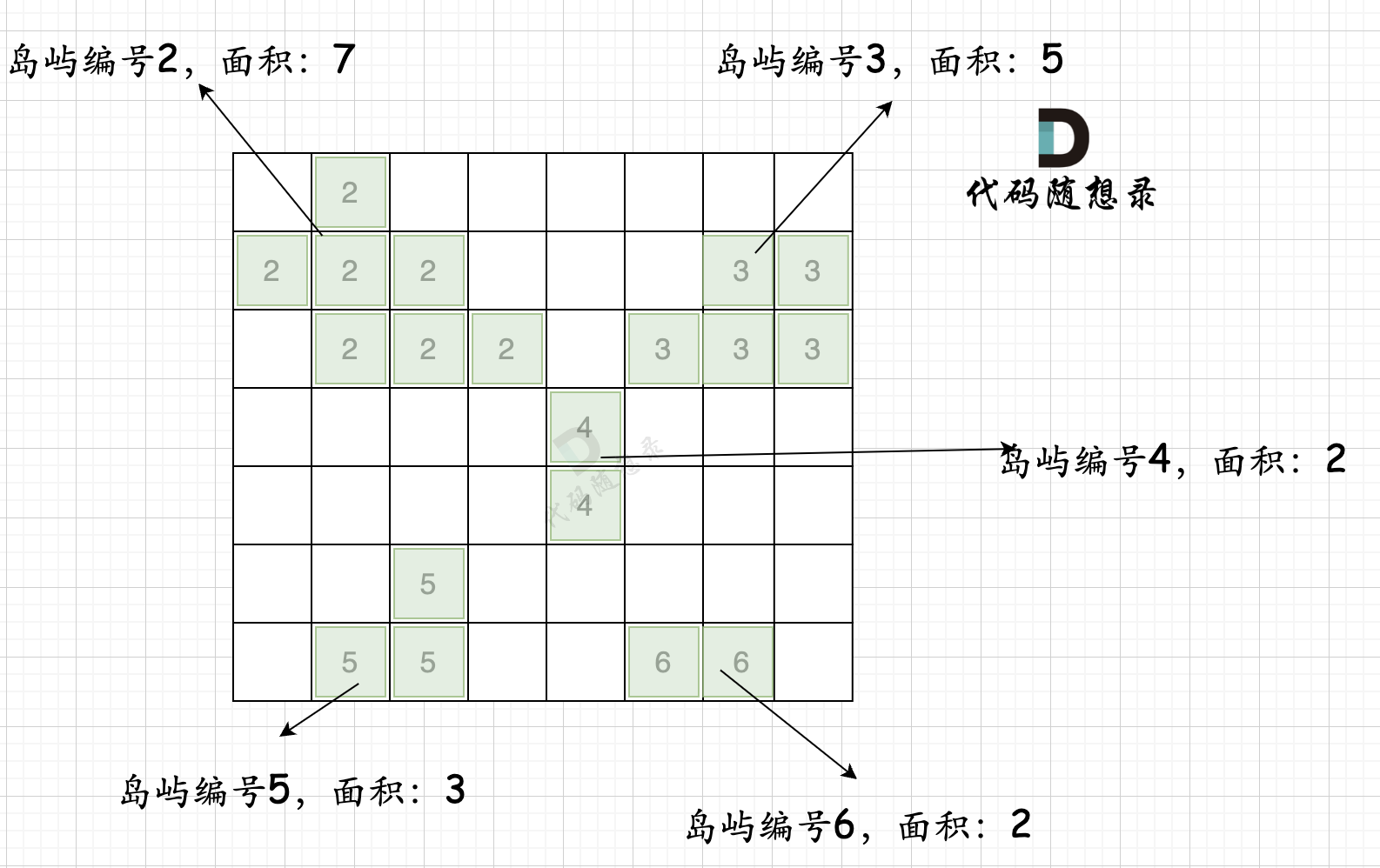
|
||||
|
||||
|
||||
本过程代码如下:
|
||||
|
||||
```CPP
|
||||
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
|
||||
void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y, int mark) {
|
||||
if (visited[x][y] || grid[x][y] == 0) return; // 终止条件:访问过的节点 或者 遇到海水
|
||||
visited[x][y] = true; // 标记访问过
|
||||
grid[x][y] = mark; // 给陆地标记新标签
|
||||
count++;
|
||||
for (int i = 0; i < 4; i++) {
|
||||
int nextx = x + dir[i][0];
|
||||
int nexty = y + dir[i][1];
|
||||
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了,直接跳过
|
||||
dfs(grid, visited, nextx, nexty, mark);
|
||||
}
|
||||
}
|
||||
|
||||
int largestIsland(vector<vector<int>>& grid) {
|
||||
int n = grid.size(), m = grid[0].size();
|
||||
vector<vector<bool>> visited = vector<vector<bool>>(n, vector<bool>(m, false)); // 标记访问过的点
|
||||
unordered_map<int ,int> gridNum;
|
||||
int mark = 2; // 记录每个岛屿的编号
|
||||
bool isAllGrid = true; // 标记是否整个地图都是陆地
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
if (grid[i][j] == 0) isAllGrid = false;
|
||||
if (!visited[i][j] && grid[i][j] == 1) {
|
||||
count = 0;
|
||||
dfs(grid, visited, i, j, mark); // 将与其链接的陆地都标记上 true
|
||||
gridNum[mark] = count; // 记录每一个岛屿的面积
|
||||
mark++; // 记录下一个岛屿编号
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
这个过程时间复杂度 n * n 。可能有录友想:分明是两个for循环下面套这一个dfs,时间复杂度怎么回事 n * n呢?
|
||||
|
||||
其实大家可以仔细看一下代码,**n * n这个方格地图中,每个节点我们就遍历一次,并不会重复遍历**。
|
||||
|
||||
第二步过程如图所示:
|
||||
|
||||
|
||||
|
||||
也就是遍历每一个0的方格,并统计其相邻岛屿面积,最后取一个最大值。
|
||||
|
||||
这个过程的时间复杂度也为 n * n。
|
||||
|
||||
所以整个解法的时间复杂度,为 n * n + n * n 也就是 n^2。
|
||||
|
||||
当然这里还有一个优化的点,就是 可以不用 visited数组,因为有mark来标记,所以遍历过的grid[i][j]是不等于1的。
|
||||
|
||||
代码如下:
|
||||
|
||||
```CPP
|
||||
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
|
||||
void dfs(vector<vector<int>>& grid, int x, int y, int mark) {
|
||||
if (grid[x][y] != 1 || grid[x][y] == 0) return; // 终止条件:访问过的节点 或者 遇到海水
|
||||
grid[x][y] = mark; // 给陆地标记新标签
|
||||
count++;
|
||||
for (int i = 0; i < 4; i++) {
|
||||
int nextx = x + dir[i][0];
|
||||
int nexty = y + dir[i][1];
|
||||
if (nextx < 0 || nextx >= n || nexty < 0 || nexty >= m) continue; // 越界了,直接跳过
|
||||
dfs(grid, nextx, nexty, mark);
|
||||
}
|
||||
}
|
||||
|
||||
int main() {
|
||||
cin >> n >> m;
|
||||
vector<vector<int>> grid(n, vector<int>(m, 0));
|
||||
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
cin >> grid[i][j];
|
||||
}
|
||||
}
|
||||
unordered_map<int ,int> gridNum;
|
||||
int mark = 2; // 记录每个岛屿的编号
|
||||
bool isAllGrid = true; // 标记是否整个地图都是陆地
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
if (grid[i][j] == 0) isAllGrid = false;
|
||||
if (grid[i][j] == 1) {
|
||||
count = 0;
|
||||
dfs(grid, i, j, mark); // 将与其链接的陆地都标记上 true
|
||||
gridNum[mark] = count; // 记录每一个岛屿的面积
|
||||
mark++; // 记录下一个岛屿编号
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
不过为了让各个变量各司其事,代码清晰一些,完整代码还是使用visited数组来标记。
|
||||
|
||||
最后,整体代码如下:
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
#include <unordered_set>
|
||||
#include <unordered_map>
|
||||
using namespace std;
|
||||
int n, m;
|
||||
int count;
|
||||
|
||||
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
|
||||
void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y, int mark) {
|
||||
if (visited[x][y] || grid[x][y] == 0) return; // 终止条件:访问过的节点 或者 遇到海水
|
||||
visited[x][y] = true; // 标记访问过
|
||||
grid[x][y] = mark; // 给陆地标记新标签
|
||||
count++;
|
||||
for (int i = 0; i < 4; i++) {
|
||||
int nextx = x + dir[i][0];
|
||||
int nexty = y + dir[i][1];
|
||||
if (nextx < 0 || nextx >= n || nexty < 0 || nexty >= m) continue; // 越界了,直接跳过
|
||||
dfs(grid, visited, nextx, nexty, mark);
|
||||
}
|
||||
}
|
||||
|
||||
int main() {
|
||||
cin >> n >> m;
|
||||
vector<vector<int>> grid(n, vector<int>(m, 0));
|
||||
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
cin >> grid[i][j];
|
||||
}
|
||||
}
|
||||
vector<vector<bool>> visited(n, vector<bool>(m, false)); // 标记访问过的点
|
||||
unordered_map<int ,int> gridNum;
|
||||
int mark = 2; // 记录每个岛屿的编号
|
||||
bool isAllGrid = true; // 标记是否整个地图都是陆地
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
if (grid[i][j] == 0) isAllGrid = false;
|
||||
if (!visited[i][j] && grid[i][j] == 1) {
|
||||
count = 0;
|
||||
dfs(grid, visited, i, j, mark); // 将与其链接的陆地都标记上 true
|
||||
gridNum[mark] = count; // 记录每一个岛屿的面积
|
||||
mark++; // 记录下一个岛屿编号
|
||||
}
|
||||
}
|
||||
}
|
||||
if (isAllGrid) {
|
||||
cout << n * m << endl; // 如果都是陆地,返回全面积
|
||||
return 0; // 结束程序
|
||||
}
|
||||
|
||||
// 以下逻辑是根据添加陆地的位置,计算周边岛屿面积之和
|
||||
int result = 0; // 记录最后结果
|
||||
unordered_set<int> visitedGrid; // 标记访问过的岛屿
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
count = 1; // 记录连接之后的岛屿数量
|
||||
visitedGrid.clear(); // 每次使用时,清空
|
||||
if (grid[i][j] == 0) {
|
||||
for (int k = 0; k < 4; k++) {
|
||||
int neari = i + dir[k][1]; // 计算相邻坐标
|
||||
int nearj = j + dir[k][0];
|
||||
if (neari < 0 || neari >= n || nearj < 0 || nearj >= m) continue;
|
||||
if (visitedGrid.count(grid[neari][nearj])) continue; // 添加过的岛屿不要重复添加
|
||||
// 把相邻四面的岛屿数量加起来
|
||||
count += gridNum[grid[neari][nearj]];
|
||||
visitedGrid.insert(grid[neari][nearj]); // 标记该岛屿已经添加过
|
||||
}
|
||||
}
|
||||
result = max(result, count);
|
||||
}
|
||||
}
|
||||
cout << result << endl;
|
||||
|
||||
}
|
||||
```
|
||||
|
||||
284
problems/kamacoder/0105.有向图的完全可达性.md
Normal file
284
problems/kamacoder/0105.有向图的完全可达性.md
Normal file
@ -0,0 +1,284 @@
|
||||
|
||||
# 105.有向图的完全可达性
|
||||
|
||||
[卡码网题目链接(ACM模式)](https://kamacoder.com/problempage.php?pid=1177)
|
||||
|
||||
【题目描述】
|
||||
|
||||
给定一个有向图,包含 N 个节点,节点编号分别为 1,2,...,N。现从 1 号节点开始,如果可以从 1 号节点的边可以到达任何节点,则输出 1,否则输出 -1。
|
||||
|
||||
【输入描述】
|
||||
|
||||
第一行包含两个正整数,表示节点数量 N 和边的数量 K。 后续 K 行,每行两个正整数 s 和 t,表示从 s 节点有一条边单向连接到 t 节点。
|
||||
|
||||
【输出描述】
|
||||
|
||||
如果可以从 1 号节点的边可以到达任何节点,则输出 1,否则输出 -1。
|
||||
|
||||
【输入示例】
|
||||
|
||||
```
|
||||
4 4
|
||||
1 2
|
||||
2 1
|
||||
1 3
|
||||
3 4
|
||||
```
|
||||
|
||||
【输出示例】
|
||||
|
||||
1
|
||||
|
||||
【提示信息】
|
||||
|
||||
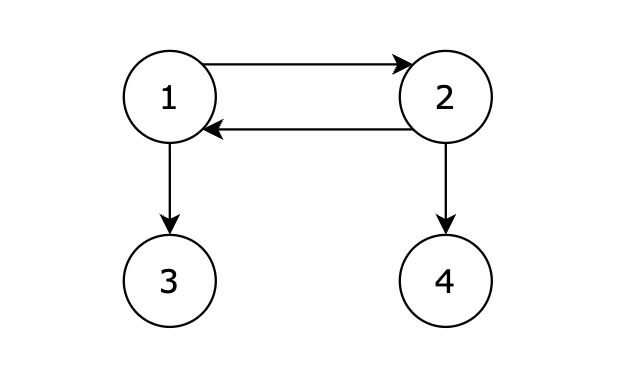
|
||||
|
||||
从 1 号节点可以到达任意节点,输出 1。
|
||||
|
||||
数据范围:
|
||||
|
||||
* 1 <= N <= 100;
|
||||
* 1 <= K <= 2000。
|
||||
|
||||
## 思路
|
||||
|
||||
本题给我们是一个有向图, 意识到这是有向图很重要!
|
||||
|
||||
接下来我们再画一个图,从图里可以直观看出来,节点6 是 不能到达节点1 的
|
||||
|
||||
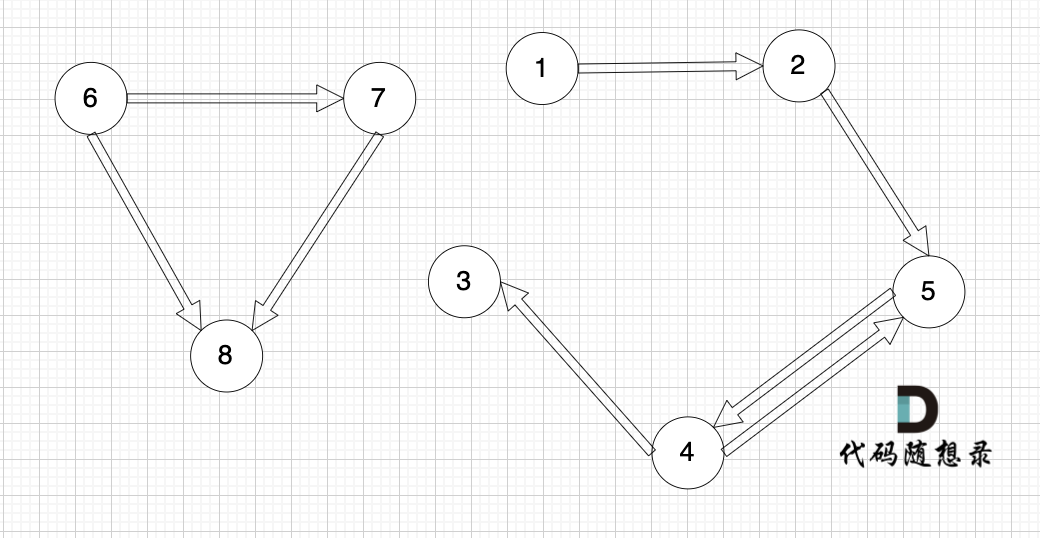
|
||||
|
||||
这就很容易让我们想起岛屿问题,只要发现独立的岛,就是不可到达的。
|
||||
|
||||
**但本题是有向图**,在有向图中,即使所有节点都是链接的,但依然不可能从0出发遍历所有边。
|
||||
|
||||
例如上图中,节点1 可以到达节点2,但节点2是不能到达节点1的。
|
||||
|
||||
所以本题是一个**有向图搜索全路径的问题**。 只能用深搜(DFS)或者广搜(BFS)来搜。
|
||||
|
||||
**以下dfs分析 大家一定要仔细看,本题有两种dfs的解法,很多题解没有讲清楚**。 看完之后 相信你对dfs会有更深的理解。
|
||||
|
||||
深搜三部曲:
|
||||
|
||||
1. 确认递归函数,参数
|
||||
|
||||
需要传入地图,需要知道当前我们拿到的key,以至于去下一个房间。
|
||||
|
||||
同时还需要一个数组,用来记录我们都走过了哪些房间,这样好知道最后有没有把所有房间都遍历的,可以定义一个一维数组。
|
||||
|
||||
所以 递归函数参数如下:
|
||||
|
||||
```C++
|
||||
// key 当前得到的可以
|
||||
// visited 记录访问过的房间
|
||||
void dfs(const vector<list<int>>& graph, int key, vector<bool>& visited) {
|
||||
```
|
||||
|
||||
2. 确认终止条件
|
||||
|
||||
遍历的时候,什么时候终止呢?
|
||||
|
||||
这里有一个很重要的逻辑,就是在递归中,**我们是处理当前访问的节点,还是处理下一个要访问的节点**。
|
||||
|
||||
这决定 终止条件怎么写。
|
||||
|
||||
首先明确,本题中什么叫做处理,就是 visited数组来记录访问过的节点,该节点默认 数组里元素都是false,把元素标记为true就是处理 本节点了。
|
||||
|
||||
如果我们是处理当前访问的节点,当前访问的节点如果是 true ,说明是访问过的节点,那就终止本层递归,如果不是true,我们就把它赋值为true,因为这是我们处理本层递归的节点。
|
||||
|
||||
代码就是这样:
|
||||
|
||||
```C++
|
||||
// 写法一:处理当前访问的节点
|
||||
void dfs(const vector<list<int>>& graph, int key, vector<bool>& visited) {
|
||||
if (visited[key]) {
|
||||
return;
|
||||
}
|
||||
visited[key] = true;
|
||||
list<int> keys = graph[key];
|
||||
for (int key : keys) {
|
||||
// 深度优先搜索遍历
|
||||
dfs(graph, key, visited);
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
如果我们是处理下一层访问的节点,而不是当前层。那么就要在 深搜三部曲中第三步:处理目前搜索节点出发的路径的时候对 节点进行处理。
|
||||
|
||||
这样的话,就不需要终止条件,而是在 搜索下一个节点的时候,直接判断 下一个节点是否是我们要搜的节点。
|
||||
|
||||
代码就是这样的:
|
||||
|
||||
```C++
|
||||
// 写法二:处理下一个要访问的节点
|
||||
void dfs(const vector<list<int>>& graph, int key, vector<bool>& visited) {
|
||||
list<int> keys = rooms[key];
|
||||
for (int key : keys) {
|
||||
if (visited[key] == false) { // 确认下一个是没访问过的节点
|
||||
visited[key] = true;
|
||||
dfs(rooms, key, visited);
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
可以看出,**如何看待 我们要访问的节点,直接决定了两种不一样的写法**,很多录友对这一块很模糊,可能做过这道题,但没有思考到这个维度上。
|
||||
|
||||
|
||||
3. 处理目前搜索节点出发的路径
|
||||
|
||||
其实在上面,深搜三部曲 第二部,就已经讲了,因为终止条件的两种写法, 直接决定了两种不一样的递归写法。
|
||||
|
||||
这里还有细节:
|
||||
|
||||
看上面两个版本的写法中, 好像没有发现回溯的逻辑。
|
||||
|
||||
我们都知道,有递归就有回溯,回溯就在递归函数的下面, 那么之前我们做的dfs题目,都需要回溯操作,例如:[0098.所有可达路径](./0098.所有可达路径), **为什么本题就没有回溯呢?**
|
||||
|
||||
代码中可以看到dfs函数下面并没有回溯的操作。
|
||||
|
||||
此时就要在思考本题的要求了,本题是需要判断 1节点 是否能到所有节点,那么我们就没有必要回溯去撤销操作了,只要遍历过的节点一律都标记上。
|
||||
|
||||
**那什么时候需要回溯操作呢?**
|
||||
|
||||
当我们需要搜索一条可行路径的时候,就需要回溯操作了,因为没有回溯,就没法“调头”, 如果不理解的话,去看我写的 [0098.所有可达路径](./0098.所有可达路径.md) 的题解。
|
||||
|
||||
|
||||
以上分析完毕,DFS整体实现C++代码如下:
|
||||
|
||||
```CPP
|
||||
// 写法一:dfs 处理当前访问的节点
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
#include <list>
|
||||
using namespace std;
|
||||
|
||||
void dfs(const vector<list<int>>& graph, int key, vector<bool>& visited) {
|
||||
if (visited[key]) {
|
||||
return;
|
||||
}
|
||||
visited[key] = true;
|
||||
list<int> keys = graph[key];
|
||||
for (int key : keys) {
|
||||
// 深度优先搜索遍历
|
||||
dfs(graph, key, visited);
|
||||
}
|
||||
}
|
||||
|
||||
int main() {
|
||||
int n, m, s, t;
|
||||
cin >> n >> m;
|
||||
|
||||
// 节点编号从1到n,所以申请 n+1 这么大的数组
|
||||
vector<list<int>> graph(n + 1); // 邻接表
|
||||
while (m--) {
|
||||
cin >> s >> t;
|
||||
// 使用邻接表 ,表示 s -> t 是相连的
|
||||
graph[s].push_back(t);
|
||||
}
|
||||
vector<bool> visited(n + 1, false);
|
||||
dfs(graph, 1, visited);
|
||||
//检查是否都访问到了
|
||||
for (int i = 1; i <= n; i++) {
|
||||
if (visited[i] == false) {
|
||||
cout << -1 << endl;
|
||||
return 0;
|
||||
}
|
||||
}
|
||||
cout << 1 << endl;
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
**第二种写法注意有注释的地方是和写法一的区别**
|
||||
|
||||
```c++
|
||||
写法二:dfs处理下一个要访问的节点
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
#include <list>
|
||||
using namespace std;
|
||||
|
||||
void dfs(const vector<list<int>>& graph, int key, vector<bool>& visited) {
|
||||
list<int> keys = rooms[key];
|
||||
for (int key : keys) {
|
||||
if (visited[key] == false) { // 确认下一个是没访问过的节点
|
||||
visited[key] = true;
|
||||
dfs(rooms, key, visited);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
int main() {
|
||||
int n, m, s, t;
|
||||
cin >> n >> m;
|
||||
|
||||
vector<list<int>> graph(n + 1);
|
||||
while (m--) {
|
||||
cin >> s >> t;
|
||||
graph[s].push_back(t);
|
||||
|
||||
}
|
||||
vector<bool> visited(n + 1, false);
|
||||
|
||||
visited[0] = true; // 节点1 预先处理
|
||||
dfs(graph, 1, visited);
|
||||
|
||||
for (int i = 1; i <= n; i++) {
|
||||
if (visited[i] == false) {
|
||||
cout << -1 << endl;
|
||||
return 0;
|
||||
}
|
||||
}
|
||||
cout << 1 << endl;
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
本题我也给出 BFS C++代码,[BFS理论基础](https://programmercarl.com/kamacoder/%E5%9B%BE%E8%AE%BA%E6%B7%B1%E6%90%9C%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html),代码如下:
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
#include <list>
|
||||
#include <queue>
|
||||
using namespace std;
|
||||
|
||||
int main() {
|
||||
int n, m, s, t;
|
||||
cin >> n >> m;
|
||||
|
||||
vector<list<int>> graph(n + 1);
|
||||
while (m--) {
|
||||
cin >> s >> t;
|
||||
graph[s].push_back(t);
|
||||
|
||||
}
|
||||
vector<bool> visited(n + 1, false);
|
||||
visited[1] = true; // 1 号房间开始
|
||||
queue<int> que;
|
||||
que.push(1); // 1 号房间开始
|
||||
|
||||
// 广度优先搜索的过程
|
||||
while (!que.empty()) {
|
||||
int key = que.front(); que.pop();
|
||||
list<int> keys = graph[key];
|
||||
for (int key : keys) {
|
||||
if (!visited[key]) {
|
||||
que.push(key);
|
||||
visited[key] = true;
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
for (int i = 1; i <= n; i++) {
|
||||
if (visited[i] == false) {
|
||||
cout << -1 << endl;
|
||||
return 0;
|
||||
}
|
||||
}
|
||||
cout << 1 << endl;
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
154
problems/kamacoder/0106.岛屿的周长.md
Normal file
154
problems/kamacoder/0106.岛屿的周长.md
Normal file
@ -0,0 +1,154 @@
|
||||
|
||||
# 106. 岛屿的周长
|
||||
|
||||
题目描述
|
||||
|
||||
给定一个由 1(陆地)和 0(水)组成的矩阵,岛屿是被水包围,并且通过水平方向或垂直方向上相邻的陆地连接而成的。
|
||||
|
||||
|
||||
你可以假设矩阵外均被水包围。在矩阵中恰好拥有一个岛屿,假设组成岛屿的陆地边长都为 1,请计算岛屿的周长。岛屿内部没有水域。
|
||||
|
||||
输入描述
|
||||
|
||||
第一行包含两个整数 N, M,表示矩阵的行数和列数。之后 N 行,每行包含 M 个数字,数字为 1 或者 0,表示岛屿的单元格。
|
||||
|
||||
输出描述
|
||||
|
||||
输出一个整数,表示岛屿的周长。
|
||||
|
||||
输入示例
|
||||
|
||||
```
|
||||
5 5
|
||||
0 0 0 0 0
|
||||
0 1 0 1 0
|
||||
0 1 1 1 0
|
||||
0 1 1 1 0
|
||||
0 0 0 0 0
|
||||
```
|
||||
|
||||
输出示例
|
||||
|
||||
14
|
||||
|
||||
提示信息
|
||||
|
||||
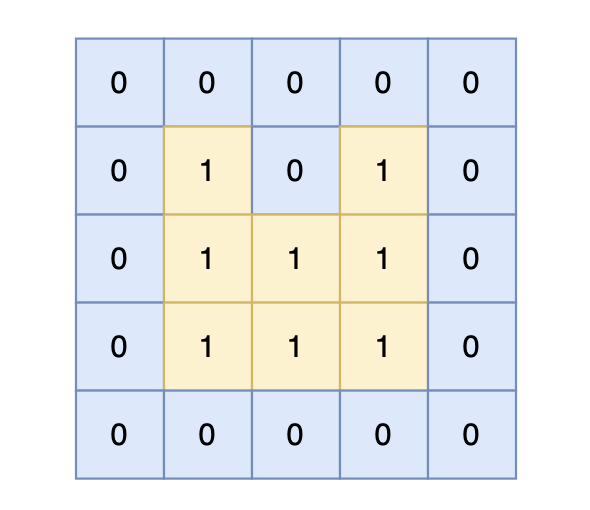
|
||||
|
||||
岛屿的周长为 14。
|
||||
|
||||
数据范围:
|
||||
|
||||
1 <= M, N <= 50。
|
||||
|
||||
## 思路
|
||||
|
||||
岛屿问题最容易让人想到BFS或者DFS,但本题确实还用不上。
|
||||
|
||||
为了避免大家惯性思维,所以给大家安排了这道题目。
|
||||
|
||||
### 解法一:
|
||||
|
||||
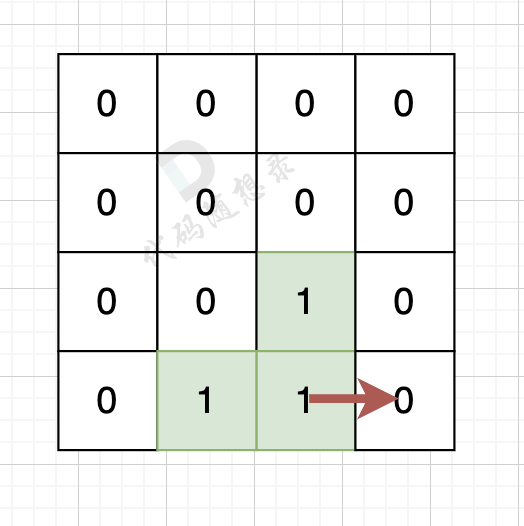
遍历每一个空格,遇到岛屿则计算其上下左右的空格情况。
|
||||
|
||||
如果该陆地上下左右的空格是有水域,则说明是一条边,如图:
|
||||
|
||||
|
||||
|
||||
陆地的右边空格是水域,则说明找到一条边。
|
||||
|
||||
|
||||
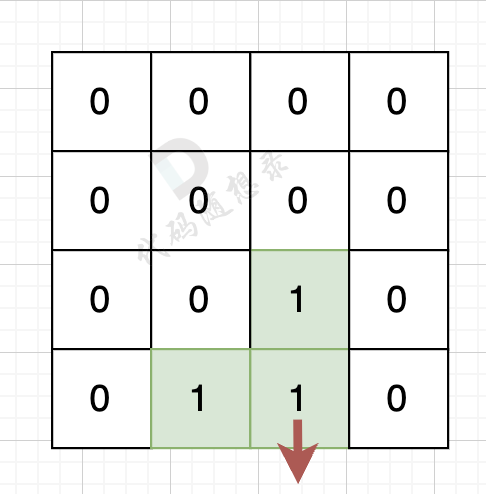
如果该陆地上下左右的空格出界了,则说明是一条边,如图:
|
||||
|
||||
|
||||
|
||||
该录友的下边空格出界了,则说明找到一条边。
|
||||
|
||||
|
||||
C++代码如下:(详细注释)
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
using namespace std;
|
||||
int main() {
|
||||
int n, m;
|
||||
cin >> n >> m;
|
||||
vector<vector<int>> grid(n, vector<int>(m, 0));
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
cin >> grid[i][j];
|
||||
}
|
||||
}
|
||||
int direction[4][2] = {0, 1, 1, 0, -1, 0, 0, -1};
|
||||
int result = 0;
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
if (grid[i][j] == 1) {
|
||||
for (int k = 0; k < 4; k++) { // 上下左右四个方向
|
||||
int x = i + direction[k][0];
|
||||
int y = j + direction[k][1]; // 计算周边坐标x,y
|
||||
if (x < 0 // x在边界上
|
||||
|| x >= grid.size() // x在边界上
|
||||
|| y < 0 // y在边界上
|
||||
|| y >= grid[0].size() // y在边界上
|
||||
|| grid[x][y] == 0) { // x,y位置是水域
|
||||
result++;
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
cout << result << endl;
|
||||
|
||||
}
|
||||
```
|
||||
|
||||
### 解法二:
|
||||
|
||||
计算出总的岛屿数量,总的变数为:岛屿数量 * 4
|
||||
|
||||
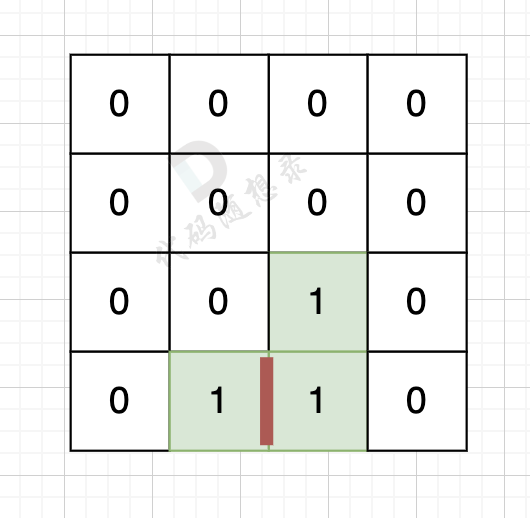
因为有一对相邻两个陆地,边的总数就要减2,如图,有两个陆地相邻,总变数就要减2
|
||||
|
||||
|
||||
|
||||
|
||||
那么只需要在计算出相邻岛屿的数量就可以了,相邻岛屿数量为cover。
|
||||
|
||||
结果 result = 岛屿数量 * 4 - cover * 2;
|
||||
|
||||
|
||||
C++代码如下:(详细注释)
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
using namespace std;
|
||||
int main() {
|
||||
int n, m;
|
||||
cin >> n >> m;
|
||||
vector<vector<int>> grid(n, vector<int>(m, 0));
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
cin >> grid[i][j];
|
||||
}
|
||||
}
|
||||
int sum = 0; // 陆地数量
|
||||
int cover = 0; // 相邻数量
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
if (grid[i][j] == 1) {
|
||||
sum++; // 统计总的陆地数量
|
||||
// 统计上边相邻陆地
|
||||
if(i - 1 >= 0 && grid[i - 1][j] == 1) cover++;
|
||||
// 统计左边相邻陆地
|
||||
if(j - 1 >= 0 && grid[i][j - 1] == 1) cover++;
|
||||
// 为什么没统计下边和右边? 因为避免重复计算
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
cout << sum * 4 - cover * 2 << endl;
|
||||
|
||||
}
|
||||
```
|
||||
@ -5,6 +5,12 @@
|
||||
|
||||
至此算上本篇,一共30篇文章,图论之旅就在此收官了。
|
||||
|
||||
在[0098.所有可达路径](./0098.所有可达路径.md) ,我们接触了两种图的存储方式,邻接表和邻接矩阵,数量掌握两种图的存储方式很重要。
|
||||
|
||||
这也是大家习惯在核心代码模式下刷题 经常忽略的 知识点。因为在力扣上刷题不需要掌握图的存储方式。
|
||||
|
||||
|
||||
|
||||
|
||||
## 深搜与广搜
|
||||
|
||||
@ -14,11 +20,30 @@
|
||||
* 代码模板:需要熟练掌握深搜和广搜的基本写法。
|
||||
* 应用场景:图论题目基本上可以即用深搜也可以广搜,无疑是用哪个方便而已
|
||||
|
||||
深搜注意事项
|
||||
|
||||
同样是深搜模板题,会有两种写法,
|
||||
|
||||
广搜注意事项
|
||||
|
||||
在[0099.岛屿的数量深搜.md](./0099.岛屿的数量深搜.md) 和 [0105.有向图的完全可达性](./0105.有向图的完全可达性.md),涉及到dfs的两种写法。
|
||||
|
||||
我们对dfs函数的定义是 是处理当前节点 还是处理下一个节点 很重要,决定了两种dfs的写法。
|
||||
|
||||
这也是为什么很多录友看到不同的dfs写法,结果发现提交都能过的原因。
|
||||
|
||||
而深搜还有细节,有的深搜题目需要回溯,有的就不用回溯,
|
||||
|
||||
需要计算路径的问题,一般需要回溯,如果只是染色问题 就不需要回溯。
|
||||
|
||||
例如: [0105.有向图的完全可达性](./0105.有向图的完全可达性.md) 深搜就不需要回溯,而 [0098.所有可达路径](./0098.所有可达路径.md) 中的递归就需要回溯,文章中都有详细讲解
|
||||
|
||||
|
||||
|
||||
注意:以上说的是不需要回溯,不是没有回溯,只要有递归就会有回溯,只是我们是否需要用到回溯这个过程 才是要考虑的
|
||||
|
||||
|
||||
广搜注意事项,很多录友写广搜超时了。
|
||||
|
||||
深搜和广搜是图论的基础,也有很多变形,我在图论里用最大岛屿问题,讲了很多
|
||||
|
||||
## 并查集
|
||||
|
||||
|
||||
Reference in New Issue
Block a user