Update

README.md

@@ -492,7 +492,7 @@
 
 大家好，我是程序员Carl，哈工大师兄，《代码随想录》作者，先后在腾讯和百度从事后端技术研发，CSDN博客专家。对算法和C++后端技术有一定的见解，利用工作之余重新刷leetcode。 
 
-加入「代码随想录」刷题小分队（微信群），可以扫下方二维码加我微信。
+加入「代码随想录」刷题小分队（微信群），可以扫下方二维码，加代码随想录客服微信。
 
 如果是已工作，备注：姓名-城市-岗位-组队刷题。如果学生，备注：姓名-学校-年级-组队刷题。**备注没有自我介绍不通过哦**
 

problems/0053.最大子序和（动态规划）.md

@@ -11,9 +11,14 @@
 给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。
 
 示例:
-输入: [-2,1,-3,4,-1,2,1,-5,4]
+* 输入: [-2,1,-3,4,-1,2,1,-5,4]
-输出: 6
+* 输出: 6
-解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。
+* 解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。
+
+## 算法公开课
+
+**《代码随想录》算法视频公开课：[看起来复杂，其实是简单动态规划 | LeetCode：53.最大子序和](https://www.bilibili.com/video/BV19V4y1F7b5)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
+
 
 ## 思路
 

problems/0115.不同的子序列.md

@@ -18,8 +18,9 @@
 
 提示：
 
-0 <= s.length, t.length <= 1000
+* 0 <= s.length, t.length <= 1000
-s 和 t 由英文字母组成
+* s 和 t 由英文字母组成
+
 
 ## 思路
 

problems/0300.最长上升子序列.md

@@ -31,6 +31,11 @@
 * 1 <= nums.length <= 2500
 * -10^4 <= nums[i] <= 104
 
+## 算法公开课
+
+**《代码随想录》算法视频公开课：[动态规划之子序列问题，元素不连续！| LeetCode：300.最长递增子序列](https://www.bilibili.com/video/BV1ng411J7xP)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
+
+
 ## 思路
 
 首先通过本题大家要明确什么是子序列，“子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序”。 

problems/0392.判断子序列.md

@@ -14,12 +14,12 @@
 字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）。
 
 示例 1：
-输入：s = "abc", t = "ahbgdc"
+* 输入：s = "abc", t = "ahbgdc"
-输出：true
+* 输出：true
 
 示例 2：
-输入：s = "axc", t = "ahbgdc"
+* 输入：s = "axc", t = "ahbgdc"
-输出：false
+* 输出：false
 
 提示：
 
@@ -28,6 +28,10 @@
 
 两个字符串都只由小写字符组成。
 
+# 算法公开课
+
+**《代码随想录》算法视频公开课：[动态规划，用相似思路解决复杂问题 | LeetCode：392.判断子序列](https://www.bilibili.com/video/BV1tv4y1B7ym/)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
+
 
 ## 思路
 

problems/0674.最长连续递增序列.md

@@ -27,6 +27,10 @@
 * 0 <= nums.length <= 10^4
 * -10^9 <= nums[i] <= 10^9
 
+## 算法公开课
+
+**《代码随想录》算法视频公开课：[动态规划之子序列问题，重点在于连续！| LeetCode：674.最长连续递增序列](https://www.bilibili.com/video/BV1bD4y1778v)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
+
 
 ## 思路
 

problems/0684.冗余连接.md

@@ -39,8 +39,8 @@
 这里整理出我的并查集模板如下：
 
 ```CPP
-int n = 1005; // 节点数量3 到 1000
+int n = 1005; // n根据题目中节点数量而定，一般比节点数量大一点就好
-int father[1005];
+vector<int> father = vector<int> (n, 0); // C++里的一种数组结构
 
 // 并查集初始化
 void init() {
@@ -50,40 +50,58 @@ void init() {
 }
 // 并查集里寻根的过程
 int find(int u) {
-    return u == father[u] ? u : father[u] = find(father[u]);
+    return u == father[u] ? u : father[u] = find(father[u]); // 路径压缩
-}
-// 将v->u 这条边加入并查集
-void join(int u, int v) {
-    u = find(u);
-    v = find(v);
-    if (u == v) return ;
-    father[v] = u;
 }
+
 // 判断 u 和 v是否找到同一个根
-bool same(int u, int v) {
+bool isSame(int u, int v) {
     u = find(u);
     v = find(v);
     return u == v;
 }
+
+// 将v->u 这条边加入并查集
+void join(int u, int v) {
+    u = find(u); // 寻找u的根
+    v = find(v); // 寻找v的根
+    if (u == v) return ; // 如果发现根相同，则说明在一个集合，不用两个节点相连直接返回
+    father[v] = u;
+}
+
 ```
 
-以上模板汇总，只要修改 n 和father数组的大小就可以了。
+以上模板 只要修改 n 就可以了，本题 节点数量不会超过1000。
 
 并查集主要有三个功能。
 
 1. 寻找根节点，函数：find(int u)，也就是判断这个节点的祖先节点是哪个
 2. 将两个节点接入到同一个集合，函数：join(int u, int v)，将两个节点连在同一个根节点上
-3. 判断两个节点是否在同一个集合，函数：same(int u, int v)，就是判断两个节点是不是同一个根节点
+3. 判断两个节点是否在同一个集合，函数：isSame(int u, int v)，就是判断两个节点是不是同一个根节点
 
 简单介绍并查集之后，我们再来看一下这道题目。
 
-题目说是无向图，返回一条可以删去的边，使得结果图是一个有着N个节点的树。
+题目说是无向图，返回一条可以删去的边，使得结果图是一个有着N个节点的树（即：只有一个根节点）。
 
 如果有多个答案，则返回二维数组中最后出现的边。
 
-那么我们就可以从前向后遍历每一条边，边的两个节点如果不在同一个集合，就加入集合（即：同一个根节点）。
+那么我们就可以从前向后遍历每一条边（因为优先让前面的边连上），边的两个节点如果不在同一个集合，就加入集合（即：同一个根节点）。
 
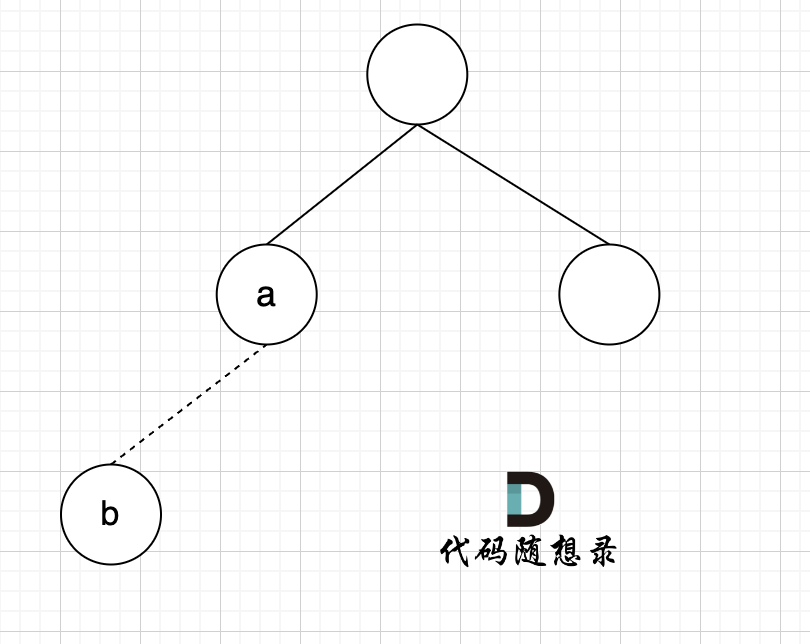
-如果边的两个节点已经出现在同一个集合里，说明着边的两个节点已经连在一起了，如果再加入这条边一定就出现环了。
+如图所示： 
+
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20230604104720.png)
+
+节点A 和节点 B 不在同一个集合，那么就可以将两个 节点连在一起。
+
+
+（如果题目中说：如果有多个答案，则返回二维数组中最前出现的边。 那我们就要 从后向前遍历每一条边了）
+
+如果边的两个节点已经出现在同一个集合里，说明着边的两个节点已经连在一起了，再加入这条边一定就出现环了。
+
+如图所示： 
+
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20230604104330.png)
+
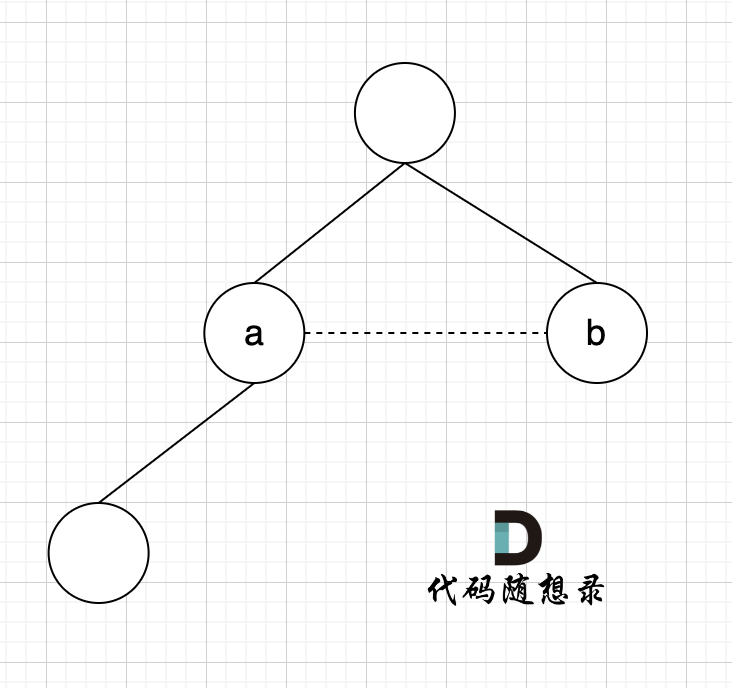
+已经判断 节点A  和 节点B 在在同一个集合（同一个根），如果将 节点A 和 节点B 连在一起就一定会出现环。 
 
 这个思路清晰之后，代码就很好写了。
 
@@ -93,7 +111,7 @@ bool same(int u, int v) {
 class Solution {
 private:
     int n = 1005; // 节点数量3 到 1000
-    int father[1005];
+    vector<int> father = vector<int> (n, 0); // C++里的一种数组结构
 
     // 并查集初始化
     void init() {
@@ -105,24 +123,22 @@ private:
     int find(int u) {
         return u == father[u] ? u : father[u] = find(father[u]);
     }
-    // 将v->u 这条边加入并查集
+    // 判断 u 和 v是否找到同一个根
-    void join(int u, int v) {
+    bool isSame(int u, int v) {
-        u = find(u);
-        v = find(v);
-        if (u == v) return ;
-        father[v] = u;
-    }
-    // 判断 u 和 v是否找到同一个根，本题用不上
-    bool same(int u, int v) {
         u = find(u);
         v = find(v);
         return u == v;
     }
+    // 将v->u 这条边加入并查集
+    void join(int u, int v) {
+        if (isSame(u, v)) return ;
+        father[v] = u;
+    }
 public:
     vector<int> findRedundantConnection(vector<vector<int>>& edges) {
         init();
         for (int i = 0; i < edges.size(); i++) {
-            if (same(edges[i][0], edges[i][1])) return edges[i];
+            if (isSame(edges[i][0], edges[i][1])) return edges[i];
             else join(edges[i][0], edges[i][1]);
         }
         return {};

problems/0685.冗余连接II.md

@@ -44,7 +44,6 @@
 
 且只有一个节点入度为2，为什么不看出度呢，出度没有意义，一棵树中随便一个父节点就有多个出度。
 
-
 第三种情况是没有入度为2的点，那么图中一定出现了有向环（**注意这里强调是有向环！**）
 
 如图：
@@ -52,7 +51,27 @@
 <img src='https://code-thinking.cdn.bcebos.com/pics/685.冗余连接II2.png' width=600> </img></div>
 
 
-首先先计算节点的入度，代码如下：
+首先先计算节点的入度，这里不少录友在计算入度的时候就搞蒙了，分不清 edges[i][j] 表示的都是什么。
+
+例如题目示例一给的是：edges = [[1,2],[1,3],[2,3]] 
+
+那大家很自然就想 对应二维数组的数值是： edges[1][2] ，edges[1][3]，edges[2][3]，但又想不出来 edges[1][2] 数值又是什么呢？ 越想约懵。
+
+其实 edges = [[1,2],[1,3],[2,3]]，表示的是 
+
+edges[0][0] = 1，edges[0][1] = 2， 
+
+edges[1][0] = 1，edges[1][1] = 3，
+
+edges[2][0] = 2，edges[2][1] = 3， 
+
+二维数组大家都学过，但是往往和图结合在一起的时候，就非常容易搞混，哪里是数组，哪里是下标了。
+
+搞清楚之后，我们如何统计入度呢？ 
+
+即 edges[i][1] 表示的节点都是 箭头指向的节点，即这个几点有一个入度！ （如果想统计出度，那么就是 edges[i][0]）。
+
+所以，统计入度的代码如下：
 
 ```cpp
 int inDegree[N] = {0}; // 记录节点入度
@@ -94,7 +113,7 @@ if (vec.size() > 0) {
 vector<int> getRemoveEdge(const vector<vector<int>>& edges)
 ```
 
-此时 大家应该知道了，我们要实现两个最为关键的函数：
+大家应该知道了，我们要实现两个最为关键的函数：
 
 * `isTreeAfterRemoveEdge()` 判断删一个边之后是不是树了
 * `getRemoveEdge` 确定图中一定有了有向环，那么要找到需要删除的那条边

problems/0718.最长重复子数组.md

@@ -23,6 +23,11 @@
 * 1 <= len(A), len(B) <= 1000
 * 0 <= A[i], B[i] < 100
 
+## 算法公开课
+
+**《代码随想录》算法视频公开课：[动态规划之子序列问题，想清楚DP数组的定义 | LeetCode：718.最长重复子数组](https://www.bilibili.com/video/BV178411H7hV)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
+
+
 
 ## 思路
 

problems/1035.不相交的线.md

@@ -17,6 +17,11 @@
 
 ![1035.不相交的线](https://code-thinking-1253855093.file.myqcloud.com/pics/2021032116363533.png)
 
+## 算法公开课
+
+**《代码随想录》算法视频公开课：[动态规划之子序列问题，换汤不换药 | LeetCode：1035.不相交的线](https://www.bilibili.com/video/BV1h84y1x7MP)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
+
+
 ## 思路
 
 相信不少录友看到这道题目都没啥思路，我们来逐步分析一下。

problems/1143.最长公共子序列.md

@@ -18,25 +18,30 @@
 
 示例 1:
 
-输入：text1 = "abcde", text2 = "ace"
+* 输入：text1 = "abcde", text2 = "ace"
-输出：3
+* 输出：3
-解释：最长公共子序列是 "ace"，它的长度为 3。
+* 解释：最长公共子序列是 "ace"，它的长度为 3。
 
 示例 2:
-输入：text1 = "abc", text2 = "abc"
+* 输入：text1 = "abc", text2 = "abc"
-输出：3
+* 输出：3
-解释：最长公共子序列是 "abc"，它的长度为 3。
+* 解释：最长公共子序列是 "abc"，它的长度为 3。
 
 示例 3:
-输入：text1 = "abc", text2 = "def"
+* 输入：text1 = "abc", text2 = "def"
-输出：0
+* 输出：0
-解释：两个字符串没有公共子序列，返回 0。
+* 解释：两个字符串没有公共子序列，返回 0。
 
 提示:
 * 1 <= text1.length <= 1000
 * 1 <= text2.length <= 1000
 输入的字符串只含有小写英文字符。
 
+## 算法公开课
+
+**《代码随想录》算法视频公开课：[动态规划子序列问题经典题目 | LeetCode：1143.最长公共子序列](https://www.bilibili.com/video/BV1ye4y1L7CQ)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
+
+
 ## 思路
 
 本题和[动态规划：718. 最长重复子数组](https://programmercarl.com/0718.最长重复子数组.html)区别在于这里不要求是连续的了，但要有相对顺序，即："ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。

problems/1971.寻找图中是否存在路径.md

@@ -3,6 +3,7 @@
   <img src="../pics/训练营.png" width="1000"/>
 </a>
 <p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！</strong></p>
+
 # 1971. 寻找图中是否存在路径 
 
 [题目链接](https://leetcode.cn/problems/find-if-path-exists-in-graph/)
@@ -30,7 +31,7 @@
 
 ## 思路
 
-这道题目也是并查集基础题目。
+本题是并查集基础题目。
 
 首先要知道并查集可以解决什么问题呢？
 
@@ -39,8 +40,8 @@
 这里整理出我的并查集模板如下：
 
 ```CPP
-int n = 1005; // 节点数量3 到 1000
+int n = 1005; // n根据题目中节点数量而定，一般比节点数量大一点就好
-int father[1005];
+vector<int> father = vector<int> (n, 0); // C++里的一种数组结构
 
 // 并查集初始化
 void init() {
@@ -50,79 +51,86 @@ void init() {
 }
 // 并查集里寻根的过程
 int find(int u) {
-    return u == father[u] ? u : father[u] = find(father[u]);
+    return u == father[u] ? u : father[u] = find(father[u]); // 路径压缩
-}
-// 将v->u 这条边加入并查集
-void join(int u, int v) {
-    u = find(u);
-    v = find(v);
-    if (u == v) return ;
-    father[v] = u;
 }
+
 // 判断 u 和 v是否找到同一个根
-bool same(int u, int v) {
+bool isSame(int u, int v) {
     u = find(u);
     v = find(v);
     return u == v;
 }
+
+// 将v->u 这条边加入并查集
+void join(int u, int v) {
+    u = find(u); // 寻找u的根
+    v = find(v); // 寻找v的根
+    if (u == v) return ; // 如果发现根相同，则说明在一个集合，不用两个节点相连直接返回
+    father[v] = u;
+}
 ```
 
-以上模板汇总，只要修改 n 和father数组的大小就可以了。
+以上模板中，只要修改 n 大小就可以，本科n不会超过2 * 10^5。
 
 并查集主要有三个功能。
 
 1. 寻找根节点，函数：find(int u)，也就是判断这个节点的祖先节点是哪个
 2. 将两个节点接入到同一个集合，函数：join(int u, int v)，将两个节点连在同一个根节点上
-3. 判断两个节点是否在同一个集合，函数：same(int u, int v)，就是判断两个节点是不是同一个根节点
+3. 判断两个节点是否在同一个集合，函数：isSame(int u, int v)，就是判断两个节点是不是同一个根节点
 
 简单介绍并查集之后，我们再来看一下这道题目。
 
-为什么说这道题目是并查集基础题目，因为 可以直接套用模板。 
+为什么说这道题目是并查集基础题目，题目中各个点是双向图链接，那么判断 一个顶点到另一个顶点有没有有效路径其实就是看这两个顶点是否在同一个集合里。 
+
+如何算是同一个集合呢，有边连在一起，就算是一个集合。 
+
+此时我们就可以直接套用并查集模板。 
 
 使用join(int u, int v)将每条边加入到并查集。 
 
-最后 same(int u, int v) 判断是否是同一个根 就可以里。 
+最后 isSame(int u, int v) 判断是否是同一个根 就可以了。 
 
-代码如下： 
+C++代码如下： 
 
-```c++ 
+```CPP
 class Solution {
-
 private:
-    int n = 200005; // 节点数量 20000 
+    int n = 200005; // 节点数量 20000
-    int father[200005];
+    vector<int> father = vector<int> (n, 0); // C++里的一种数组结构
 
     // 并查集初始化
     void init() {
-        for (int i = 0; i < n; ++i) {
+        for (int i = 0; i < n; ++i) { father[i] = i;
-            father[i] = i;
         }
     }
     // 并查集里寻根的过程
     int find(int u) {
         return u == father[u] ? u : father[u] = find(father[u]);
     }
-    // 将v->u 这条边加入并查集
+
-    void join(int u, int v) {
+    // 判断 u 和 v是否找到同一个根
-        u = find(u);
+    bool isSame(int u, int v) {
-        v = find(v);
-        if (u == v) return ;
-        father[v] = u;
-    }
-    // 判断 u 和 v是否找到同一个根，本题用不上
-    bool same(int u, int v) {
         u = find(u);
         v = find(v);
         return u == v;
     }
 
+    // 将v->u 这条边加入并查集
+    void join(int u, int v) {
+        u = find(u); // 寻找u的根
+        v = find(v); // 寻找v的根
+        if (u == v) return ; // 如果发现根相同，则说明在一个集合，不用两个节点相连直接返回
+        father[v] = u;
+    }
+
 public:
     bool validPath(int n, vector<vector<int>>& edges, int source, int destination) {
-        init(); 
+        init();
         for (int i = 0; i < edges.size(); i++) {
-            join(edges[i][0], edges[i][1]); 
+            join(edges[i][0], edges[i][1]);
         }
-        return same(source, destination);
+        return isSame(source, destination);
+
     }
 };
 ```

problems/二叉树理论基础.md

@@ -39,7 +39,7 @@
 
 什么是完全二叉树？
 
-完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2^(h-1)  个节点。
+完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层（h从1开始），则该层包含 1~ 2^(h-1)  个节点。
 
 **大家要自己看完全二叉树的定义，很多同学对完全二叉树其实不是真正的懂了。**