mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-25 01:32:21 +08:00
更新贪心算法
This commit is contained in:
114
problems/周总结/20201126贪心周末总结.md
Normal file
114
problems/周总结/20201126贪心周末总结.md
Normal file
@ -0,0 +1,114 @@
|
||||
|
||||
# 本周小结!(贪心算法系列一)
|
||||
|
||||
## 周一
|
||||
|
||||
本周正式开始了贪心算法,在[关于贪心算法,你该了解这些!](https://mp.weixin.qq.com/s/O935TaoHE9Eexwe_vSbRAg)中,我们介绍了什么是贪心以及贪心的套路。
|
||||
|
||||
**贪心的本质是选择每一阶段的局部最优,从而达到全局最优。**
|
||||
|
||||
有没有啥套路呢?
|
||||
|
||||
**不好意思,贪心没套路,就刷题而言,如果感觉好像局部最优可以推出全局最优,然后想不到反例,那就试一试贪心吧!**
|
||||
|
||||
而严格的数据证明一般有如下两种:
|
||||
|
||||
* 数学归纳法
|
||||
* 反证法
|
||||
|
||||
数学就不在讲解范围内了,感兴趣的同学可以自己去查一查资料。
|
||||
|
||||
正式因为贪心算法有时候会感觉这是常识,本就应该这么做! 所以大家经常看到网上有人说这是一道贪心题目,有人是这不是。
|
||||
|
||||
这里说一下我的依据:**如果找到局部最优,然后推出整体最优,那么就是贪心**,大家可以参考哈。
|
||||
|
||||
## 周二
|
||||
|
||||
|
||||
在[贪心算法:分发饼干](https://mp.weixin.qq.com/s/YSuLIAYyRGlyxbp9BNC1uw)中讲解了贪心算法的第一道题目。
|
||||
|
||||
这道题目很明显能看出来是用贪心,也是入门好题。
|
||||
|
||||
我在文中给出**局部最优:大饼干喂给胃口大的,充分利用饼干尺寸喂饱一个,全局最优:喂饱尽可能多的小孩**。
|
||||
|
||||
很多录友都是用小饼干优先先喂饱小胃口的。
|
||||
|
||||
后来我想一想,虽然结果是一样的,但是大家的这个思考方式更好一些。
|
||||
|
||||
**因为用小饼干优先喂饱小胃口的 这样可以尽量保证最后省下来的是大饼干(虽然题目没有这个要求)!**
|
||||
|
||||
所有还是小饼干优先先喂饱小胃口更好一些,也比较直观。
|
||||
|
||||
一些录友不清楚[贪心算法:分发饼干](https://mp.weixin.qq.com/s/YSuLIAYyRGlyxbp9BNC1uw)中时间复杂度是怎么来的?
|
||||
|
||||
就是快排O(nlogn),遍历O(n),加一起就是还是O(nlogn)。
|
||||
|
||||
## 周三
|
||||
|
||||
接下来就要上一点难度了,要不然大家会误以为贪心算法就是常识判断一下就行了。
|
||||
|
||||
在[贪心算法:摆动序列](https://mp.weixin.qq.com/s/Xytl05kX8LZZ1iWWqjMoHA)中,需要计算最长摇摆序列。
|
||||
|
||||
其实就是让序列有尽可能多的局部峰值。
|
||||
|
||||
局部最优:删除单调坡度上的节点(不包括单调坡度两端的节点),那么这个坡度就可以有两个局部峰值。
|
||||
|
||||
整体最优:整个序列有最多的局部峰值,从而达到最长摆动序列。
|
||||
|
||||
在计算峰值的时候,还是有一些代码技巧的,例如序列两端的峰值如何处理。
|
||||
|
||||
这些技巧,其实还是要多看多用才会掌握。
|
||||
|
||||
|
||||
## 周四
|
||||
|
||||
在[贪心算法:最大子序和](https://mp.weixin.qq.com/s/DrjIQy6ouKbpletQr0g1Fg)中,详细讲解了用贪心的方式来求最大子序列和,其实这道题目是一道动态规划的题目。
|
||||
|
||||
**贪心的思路为局部最优:当前“连续和”为负数的时候立刻放弃,从下一个元素重新计算“连续和”,因为负数加上下一个元素 “连续和”只会越来越小。从而推出全局最优:选取最大“连续和”**
|
||||
|
||||
代码很简单,但是思路却比较难。还需要反复琢磨。
|
||||
|
||||
针对[贪心算法:最大子序和](https://mp.weixin.qq.com/s/DrjIQy6ouKbpletQr0g1Fg)文章中给出的贪心代码如下;
|
||||
```
|
||||
class Solution {
|
||||
public:
|
||||
int maxSubArray(vector<int>& nums) {
|
||||
int result = INT32_MIN;
|
||||
int count = 0;
|
||||
for (int i = 0; i < nums.size(); i++) {
|
||||
count += nums[i];
|
||||
if (count > result) { // 取区间累计的最大值(相当于不断确定最大子序终止位置)
|
||||
result = count;
|
||||
}
|
||||
if (count <= 0) count = 0; // 相当于重置最大子序起始位置,因为遇到负数一定是拉低总和
|
||||
}
|
||||
return result;
|
||||
}
|
||||
};
|
||||
```
|
||||
不少同学都来问,如果数组全是负数这个代码就有问题了,如果数组里有int最小值这个代码就有问题了。
|
||||
|
||||
大家不要脑洞模拟哈,可以亲自构造一些测试数据试一试,就发现其实没有问题。
|
||||
|
||||
数组都为负数,result记录的就是最小的负数,如果数组里有int最小值,那么最终result就是int最小值。
|
||||
|
||||
|
||||
## 总结
|
||||
|
||||
本周我们讲解了[贪心算法的理论基础](https://mp.weixin.qq.com/s/O935TaoHE9Eexwe_vSbRAg),了解了贪心本质:局部最优推出全局最优。
|
||||
|
||||
然后讲解了第一道题目[分发饼干](https://mp.weixin.qq.com/s/YSuLIAYyRGlyxbp9BNC1uw),还是比较基础的,可能会给大家一种贪心算法比较简单的错觉,因为贪心有时候接近于常识。
|
||||
|
||||
其实我还准备一些简单的贪心题目,甚至网上很多都质疑这些题目是不是贪心算法。这些题目我没有立刻发出来,因为真的会让大家感觉贪心过于简单,而忽略了贪心的本质:局部最优和全局最优两个关键点。
|
||||
|
||||
**所以我在贪心系列难度会有所交替,难的题目在于拓展思路,简单的题目在于分析清楚其贪心的本质,后续我还会发一些简单的题目来做贪心的分析。**
|
||||
|
||||
在[摆动序列](https://mp.weixin.qq.com/s/Xytl05kX8LZZ1iWWqjMoHA)中大家就初步感受到贪心没那么简单了。
|
||||
|
||||
本周最后是[最大子序和](https://mp.weixin.qq.com/s/DrjIQy6ouKbpletQr0g1Fg),这道题目要用贪心的方式做出来,就比较有难度,都知道负数加上正数之后会变小,但是这道题目依然会让很多人搞混淆,其关键在于:**不能让“连续和”为负数的时候加上下一个元素,而不是 不让“连续和”加上一个负数**。这块真的需要仔细体会!
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
98
problems/周总结/20201203贪心周末总结.md
Normal file
98
problems/周总结/20201203贪心周末总结.md
Normal file
@ -0,0 +1,98 @@
|
||||
|
||||
|
||||
# 本周小结!(贪心算法系列二)
|
||||
|
||||
## 周一
|
||||
|
||||
一说到股票问题,一般都会想到动态规划,其实有时候贪心更有效!
|
||||
|
||||
在[贪心算法:买卖股票的最佳时机II](https://mp.weixin.qq.com/s/VsTFA6U96l18Wntjcg3fcg)中,讲到只能多次买卖一支股票,如何获取最大利润。
|
||||
|
||||
**这道题目理解利润拆分是关键点!** 不要整块的去看,而是把整体利润拆为每天的利润,就很容易想到贪心了。
|
||||
|
||||
**局部最优:只收集每天的正利润,全局最优:得到最大利润**。
|
||||
|
||||
如果正利润连续上了,相当于连续持有股票,而本题并不需要计算具体的区间。
|
||||
|
||||
如图:
|
||||
|
||||

|
||||
|
||||
## 周二
|
||||
|
||||
在[贪心算法:跳跃游戏](https://mp.weixin.qq.com/s/606_N9j8ACKCODoCbV1lSA)中是给你一个数组看能否跳到终点。
|
||||
|
||||
本题贪心的关键是:**不用拘泥于每次究竟跳几步,而是看覆盖范围,覆盖范围内一定是可以跳过来的,不用管是怎么跳的**。
|
||||
|
||||
**那么这个问题就转化为跳跃覆盖范围究竟可不可以覆盖到终点!**
|
||||
|
||||
贪心算法局部最优解:移动下标每次取最大跳跃步数(取最大覆盖范围),整体最优解:最后得到整体最大覆盖范围,看是否能到终点
|
||||
|
||||
如果覆盖范围覆盖到了终点,就表示一定可以跳过去。
|
||||
|
||||
如图:
|
||||
|
||||

|
||||
|
||||
|
||||
## 周三
|
||||
|
||||
这道题目:[贪心算法:跳跃游戏II](https://mp.weixin.qq.com/s/kJBcsJ46DKCSjT19pxrNYg)可就有点难了。
|
||||
|
||||
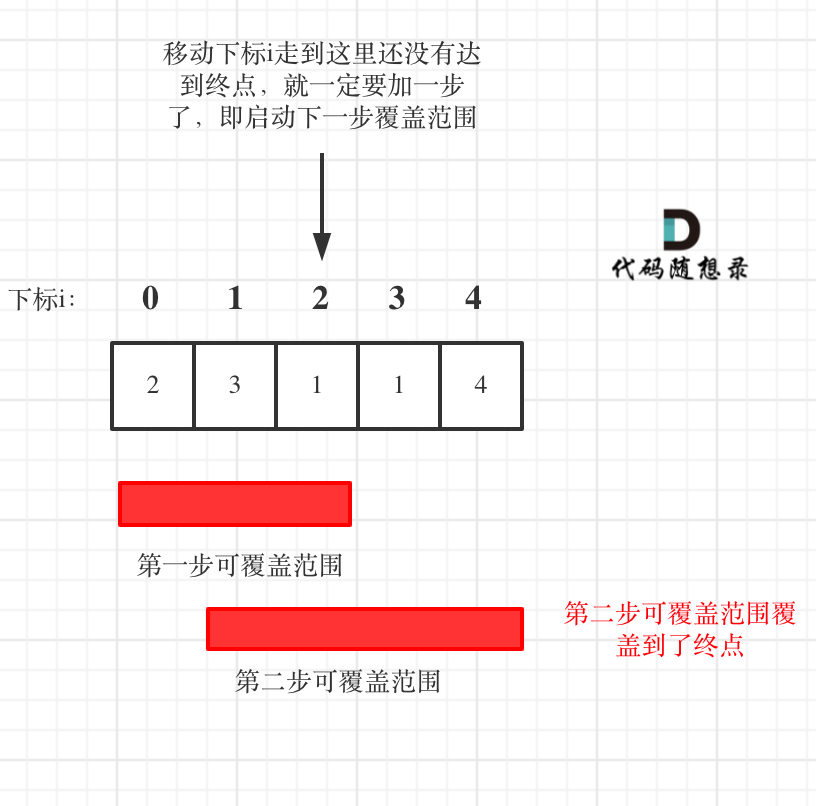
本题解题关键在于:**以最小的步数增加最大的覆盖范围,直到覆盖范围覆盖了终点**。
|
||||
|
||||
那么局部最优:求当前这步的最大覆盖,那么尽可能多走,到达覆盖范围的终点,只需要一步。整体最优:达到终点,步数最少。
|
||||
|
||||
如图:
|
||||
|
||||
|
||||
|
||||
注意:**图中的移动下标是到当前这步覆盖的最远距离(下标2的位置),此时没有到终点,只能增加第二步来扩大覆盖范围**。
|
||||
|
||||
在[贪心算法:跳跃游戏II](https://mp.weixin.qq.com/s/kJBcsJ46DKCSjT19pxrNYg)中我给出了两个版本的代码。
|
||||
|
||||
其实本质都是超过当前覆盖范围,步数就加一,但版本一需要考虑当前覆盖最远距离下标是不是数组终点的情况。
|
||||
|
||||
而版本二就比较统一的,超过范围,步数就加一,但在移动下标的范围了做了文章。
|
||||
|
||||
即如果覆盖最远距离下标是倒数第二点:直接加一就行,默认一定可以到终点。如图:
|
||||
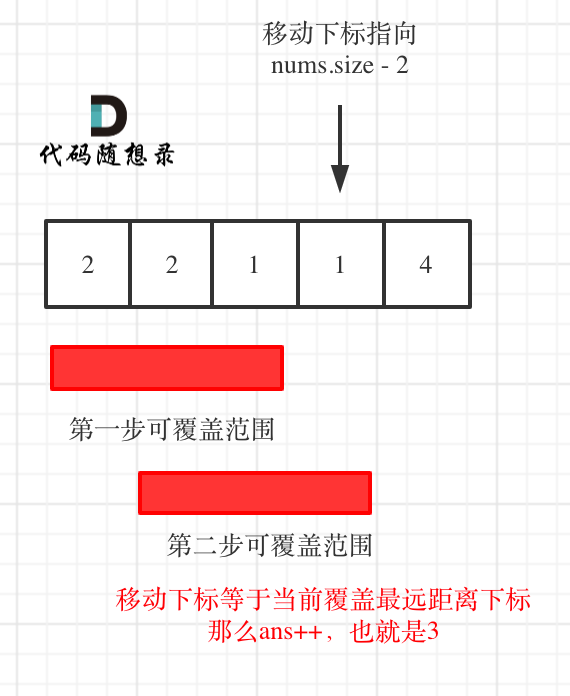
|
||||
|
||||
如果覆盖最远距离下标不是倒数第二点,说明本次覆盖已经到终点了。如图:
|
||||
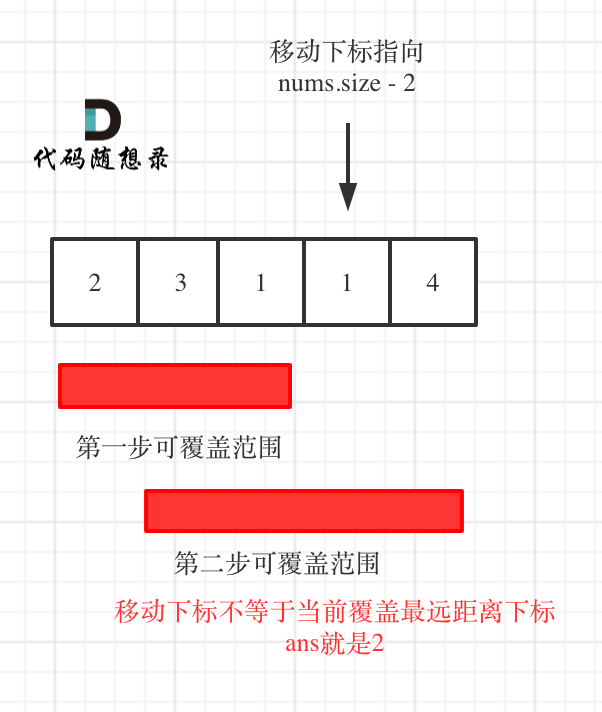
|
||||
|
||||
有的录友认为版本一好理解,有的录友认为版本二好理解,其实掌握一种就可以了,也不用非要比拼一下代码的简洁性,简洁程度都差不多了。
|
||||
|
||||
我个人倾向于版本一的写法,思路清晰一点,版本二会有点绕。
|
||||
|
||||
## 周四
|
||||
|
||||
这道题目:[贪心算法:K次取反后最大化的数组和](https://mp.weixin.qq.com/s/dMTzBBVllRm_Z0aaWvYazA)就比较简单了,哈哈,用简单题来讲一讲贪心的思想。
|
||||
|
||||
**这里其实用了两次贪心!**
|
||||
|
||||
第一次贪心:局部最优:让绝对值大的负数变为正数,当前数值达到最大,整体最优:整个数组和达到最大。
|
||||
|
||||
处理之后,如果K依然大于0,此时的问题是一个有序正整数序列,如何转变K次正负,让 数组和 达到最大。
|
||||
|
||||
第二次贪心:局部最优:只找数值最小的正整数进行反转,当前数值可以达到最大(例如正整数数组{5, 3, 1},反转1 得到-1 比 反转5得到的-5 大多了),全局最优:整个 数组和 达到最大。
|
||||
|
||||
|
||||
[贪心算法:K次取反后最大化的数组和](https://mp.weixin.qq.com/s/dMTzBBVllRm_Z0aaWvYazA)中的代码,最后while处理K的时候,其实直接判断奇偶数就可以了,文中给出的方式太粗暴了,哈哈,Carl大意了。
|
||||
|
||||
例外一位录友留言给出一个很好的建议,因为文中是使用快排,仔细看题,**题目中限定了数据范围是正负一百,所以可以使用桶排序**,这样时间复杂度就可以优化为O(n)了。但可能代码要复杂一些了。
|
||||
|
||||
|
||||
## 总结
|
||||
|
||||
大家会发现本周的代码其实都简单,但思路却很巧妙,并不容易写出来。
|
||||
|
||||
如果是第一次接触的话,其实很难想出来,就是接触过之后就会了,所以大家不用感觉自己想不出来而烦躁,哈哈。
|
||||
|
||||
相信此时大家现在对贪心算法又有一个新的认识了,加油💪
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
99
problems/周总结/20201217贪心周末总结.md
Normal file
99
problems/周总结/20201217贪心周末总结.md
Normal file
@ -0,0 +1,99 @@
|
||||
|
||||
|
||||
# 本周小结!(贪心算法系列三)
|
||||
|
||||
对于贪心,大多数同学都会感觉,不就是常识嘛,这算啥算法,那么本周的题目就可以带大家初步领略一下贪心的巧妙,贪心算法往往妙的出其不意。
|
||||
|
||||
## 周一
|
||||
|
||||
在[贪心算法:加油站](https://mp.weixin.qq.com/s/aDbiNuEZIhy6YKgQXvKELw)中给出每一个加油站的汽油和开到这个加油站的消耗,问汽车能不能开一圈。
|
||||
|
||||
这道题目咋眼一看,感觉是一道模拟题,模拟一下汽车从每一个节点出发看看能不能开一圈,时间复杂度是O(n^2)。
|
||||
|
||||
即使用模拟这种情况,也挺考察代码技巧的。
|
||||
|
||||
**for循环适合模拟从头到尾的遍历,而while循环适合模拟环形遍历,对于本题的场景要善于使用while!**
|
||||
|
||||
如果代码功力不到位,就模拟这种情况,可能写的也会很费劲。
|
||||
|
||||
本题的贪心解法,我给出两种解法。
|
||||
|
||||
对于解法一,其实我并不认为这是贪心,因为没有找出局部最优,而是直接从全局最优的角度上思考问题,但思路很巧妙,值得学习一下。
|
||||
|
||||
对于解法二,贪心的局部最优:当前累加rest[j]的和curSum一旦小于0,起始位置至少要是j+1,因为从j开始一定不行。全局最优:找到可以跑一圈的起始位置。
|
||||
|
||||
这里是可以从局部最优推出全局最优的,想不出反例,那就试试贪心。
|
||||
|
||||
**解法二就体现出贪心的精髓,同时大家也会发现,虽然贪心是常识,有些常识并不容易,甚至很难!**
|
||||
|
||||
## 周二
|
||||
|
||||
在[贪心算法:分发糖果](https://mp.weixin.qq.com/s/8MwlgFfvaNYmjGwjuMlETQ)中我们第一次接触了需要考虑两个维度的情况。
|
||||
|
||||
例如这道题,是先考虑左边呢,还是考虑右边呢?
|
||||
|
||||
**先考虑哪一边都可以! 就别两边一起考虑,那样就把自己陷进去了**。
|
||||
|
||||
先贪心一边,局部最优:只要右边评分比左边大,右边的孩子就多一个糖果,全局最优:相邻的孩子中,评分高的右孩子获得比左边孩子更多的糖果
|
||||
|
||||
如图:
|
||||
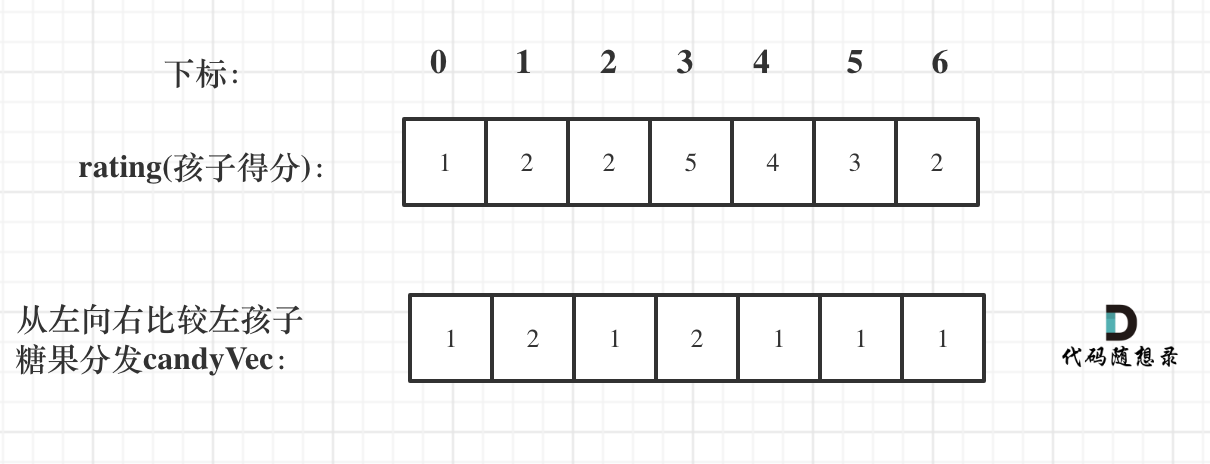
|
||||
|
||||
|
||||
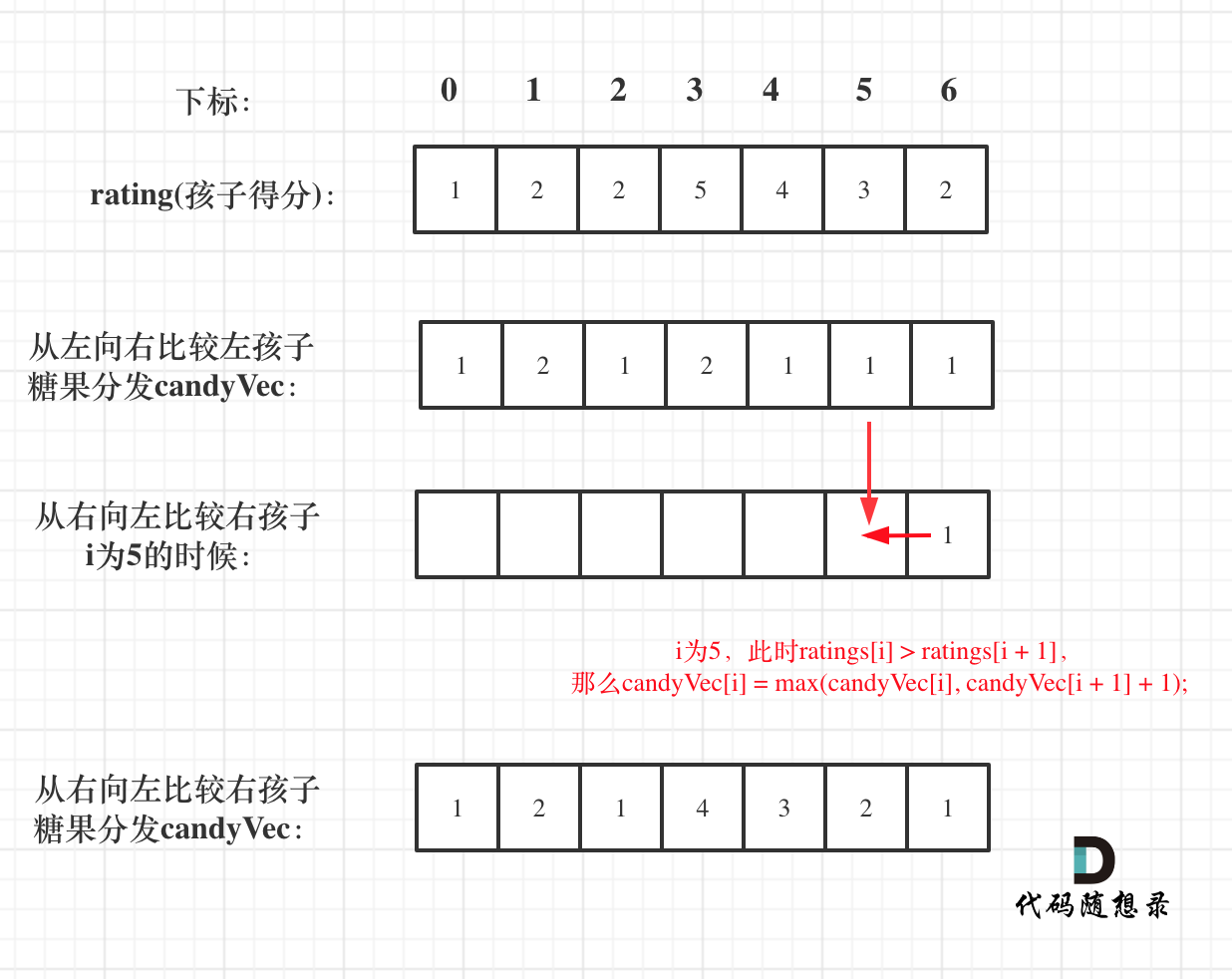
接着在贪心另一边,左孩子大于右孩子,左孩子的糖果就要比右孩子多。
|
||||
|
||||
此时candyVec[i](第i个小孩的糖果数量,左孩子)就有两个选择了,一个是candyVec[i + 1] + 1(从右孩子这个加1得到的糖果数量),一个是candyVec[i](之前比较右孩子大于左孩子得到的糖果数量)。
|
||||
|
||||
那么第二次贪心的局部最优:取candyVec[i + 1] + 1 和 candyVec[i] 最大的糖果数量,保证第i个小孩的糖果数量即大于左边的也大于右边的。全局最优:相邻的孩子中,评分高的孩子获得更多的糖果。
|
||||
|
||||
局部最优可以推出全局最优。
|
||||
|
||||
如图:
|
||||
|
||||
|
||||
|
||||
## 周三
|
||||
|
||||
在[贪心算法:柠檬水找零](https://mp.weixin.qq.com/s/0kT4P-hzY7H6Ae0kjQqnZg)中我们模拟了买柠檬水找零的过程。
|
||||
|
||||
这道题目刚一看,可能会有点懵,这要怎么找零才能保证完整全部账单的找零呢?
|
||||
|
||||
**但仔细一琢磨就会发现,可供我们做判断的空间非常少!**
|
||||
|
||||
美元10只能给账单20找零,而美元5可以给账单10和账单20找零,美元5更万能!
|
||||
|
||||
局部最优:遇到账单20,优先消耗美元10,完成本次找零。全局最优:完成全部账单的找零。
|
||||
|
||||
局部最优可以推出全局最优。
|
||||
|
||||
所以把能遇到的情况分析一下,只要分析到具体情况了,一下子就豁然开朗了。
|
||||
|
||||
这道题目其实是一道简单题,但如果一开始就想从整体上寻找找零方案,就会把自己陷进去,各种情况一交叉,只会越想越复杂了。
|
||||
|
||||
## 周四
|
||||
|
||||
在[贪心算法:根据身高重建队列](https://mp.weixin.qq.com/s/-2TgZVdOwS-DvtbjjDEbfw)中,我们再一次遇到了需要考虑两个维度的情况。
|
||||
|
||||
之前我们已经做过一道类似的了就是[贪心算法:分发糖果](https://mp.weixin.qq.com/s/8MwlgFfvaNYmjGwjuMlETQ),但本题比分发糖果难不少!
|
||||
|
||||
[贪心算法:根据身高重建队列](https://mp.weixin.qq.com/s/-2TgZVdOwS-DvtbjjDEbfw)中依然是要确定一边,然后在考虑另一边,两边一起考虑一定会蒙圈。
|
||||
|
||||
那么本题先确定k还是先确定h呢,也就是究竟先按h排序呢,还先按照k排序呢?
|
||||
|
||||
这里其实很考察大家的思考过程,如果按照k来从小到大排序,排完之后,会发现k的排列并不符合条件,身高也不符合条件,两个维度哪一个都没确定下来。
|
||||
|
||||
**所以先从大到小按照h排个序,再来贪心k**。
|
||||
|
||||
此时局部最优:优先按身高高的people的k来插入。插入操作过后的people满足队列属性。全局最优:最后都做完插入操作,整个队列满足题目队列属性。
|
||||
|
||||
局部最优可以推出全局最优,找不出反例,那么就来贪心。
|
||||
|
||||
## 总结
|
||||
|
||||
「代码随想录」里已经讲了十一道贪心题目了,大家可以发现在每一道题目的讲解中,我都是把什么是局部最优,和什么是全局最优说清楚。
|
||||
|
||||
虽然有时候感觉贪心就是常识,但如果真正是常识性的题目,其实是模拟题,就不是贪心算法了!例如[贪心算法:加油站](https://mp.weixin.qq.com/s/aDbiNuEZIhy6YKgQXvKELw)中的贪心方法一,其实我就认为不是贪心算法,而是直接从全局最优的角度上来模拟,因为方法里没有体现局部最优的过程。
|
||||
|
||||
而且大家也会发现,贪心并没有想象中的那么简单,贪心往往妙的出其不意,触不及防!哈哈
|
||||
|
||||
|
||||
104
problems/周总结/20201224贪心周末总结.md
Normal file
104
problems/周总结/20201224贪心周末总结.md
Normal file
@ -0,0 +1,104 @@
|
||||
|
||||
|
||||
# 本周小结!(贪心算法系列四)
|
||||
|
||||
## 周一
|
||||
|
||||
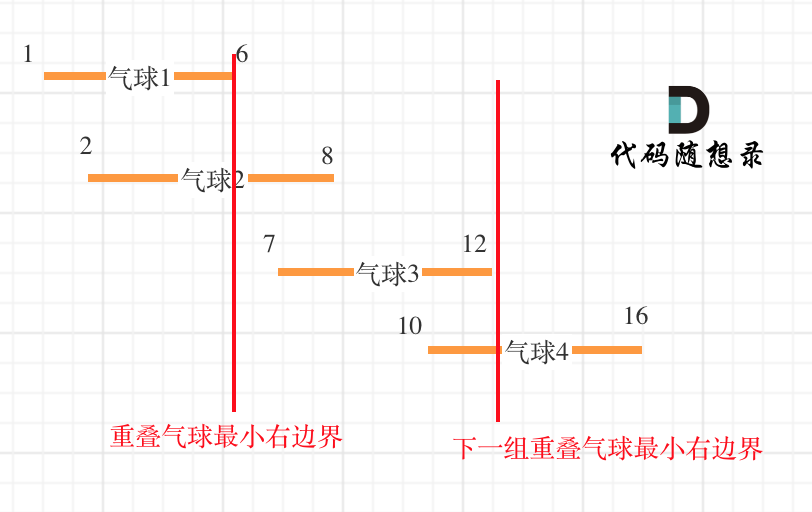
在[贪心算法:用最少数量的箭引爆气球](https://mp.weixin.qq.com/s/HxVAJ6INMfNKiGwI88-RFw)中,我们开始讲解了重叠区间问题,用最少的弓箭射爆所有气球,其本质就是找到最大的重叠区间。
|
||||
|
||||
按照左边界经行排序后,如果气球重叠了,重叠气球中右边边界的最小值 之前的区间一定需要一个弓箭
|
||||
|
||||
如图:
|
||||
|
||||
|
||||
|
||||
模拟射气球的过程,很多同学真的要去模拟了,实时把气球从数组中移走,这么写的话就复杂了,从前向后遍历重复的只要跳过就可以的。
|
||||
|
||||
## 周二
|
||||
|
||||
在[贪心算法:无重叠区间](https://mp.weixin.qq.com/s/oFOEoW-13Bm4mik-aqAOmw)中要去掉最少的区间,来让所有区间没有重叠。
|
||||
|
||||
我来按照右边界排序,从左向右记录非交叉区间的个数。最后用区间总数减去非交叉区间的个数就是需要移除的区间个数了。
|
||||
|
||||
如图:
|
||||
|
||||

|
||||
|
||||
细心的同学就发现了,此题和 [贪心算法:用最少数量的箭引爆气球](https://mp.weixin.qq.com/s/HxVAJ6INMfNKiGwI88-RFw)非常像。
|
||||
|
||||
弓箭的数量就相当于是非交叉区间的数量,只要把弓箭那道题目代码里射爆气球的判断条件加个等号(认为[0,1][1,2]不是相邻区间),然后用总区间数减去弓箭数量 就是要移除的区间数量了。
|
||||
|
||||
把[贪心算法:用最少数量的箭引爆气球](https://mp.weixin.qq.com/s/HxVAJ6INMfNKiGwI88-RFw)代码稍做修改,别可以AC本题。
|
||||
|
||||
修改后的C++代码如下:
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
// 按照区间左边界从大到小排序
|
||||
static bool cmp (const vector<int>& a, const vector<int>& b) {
|
||||
return a[0] < b[0];
|
||||
}
|
||||
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
|
||||
if (intervals.size() == 0) return 0;
|
||||
sort(intervals.begin(), intervals.end(), cmp);
|
||||
|
||||
int result = 1;
|
||||
for (int i = 1; i < intervals.size(); i++) {
|
||||
if (intervals[i][0] >= intervals[i - 1][1]) { // 需要要把> 改成 >= 就可以了
|
||||
result++; // 需要一支箭
|
||||
}
|
||||
else {
|
||||
intervals[i][1] = min(intervals[i - 1][1], intervals[i][1]); // 更新重叠气球最小右边界
|
||||
}
|
||||
}
|
||||
return intervals.size() - result;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
## 周三
|
||||
|
||||
[贪心算法:划分字母区间](https://mp.weixin.qq.com/s/pdX4JwV1AOpc_m90EcO2Hw)中我们要把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。
|
||||
|
||||
这道题目leetcode上标的是贪心,其实我不认识是贪心,因为没感受到局部最优和全局最优的关系。
|
||||
|
||||
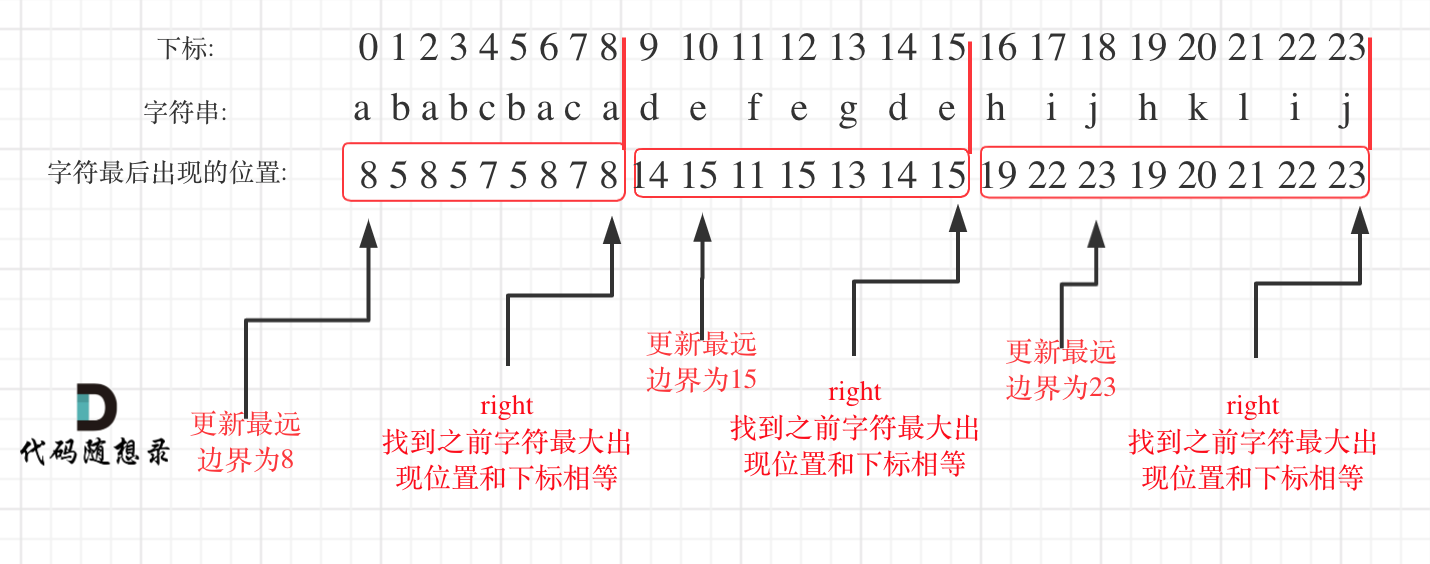
但不影响这是一道好题,思路很不错,**通过字符出现最远距离取并集的方法,把出现过的字符都圈到一个区间里**。
|
||||
|
||||
解题过程分如下两步:
|
||||
|
||||
* 统计每一个字符最后出现的位置
|
||||
* 从头遍历字符,并更新字符的最远出现下标,如果找到字符最远出现位置下标和当前下标相等了,则找到了分割点
|
||||
|
||||
如图:
|
||||
|
||||
|
||||
|
||||
|
||||
## 周四
|
||||
|
||||
[贪心算法:合并区间](https://mp.weixin.qq.com/s/royhzEM5tOkUFwUGrNStpw)中要合并所有重叠的区间。
|
||||
|
||||
相信如果录友们前几天区间问题的题目认真练习了,今天题目就应该算简单一些了。
|
||||
|
||||
按照左边界排序,排序之后局部最优:每次合并都取最大的右边界,这样就可以合并更多的区间了,整体最优:合并所有重叠的区间。
|
||||
|
||||
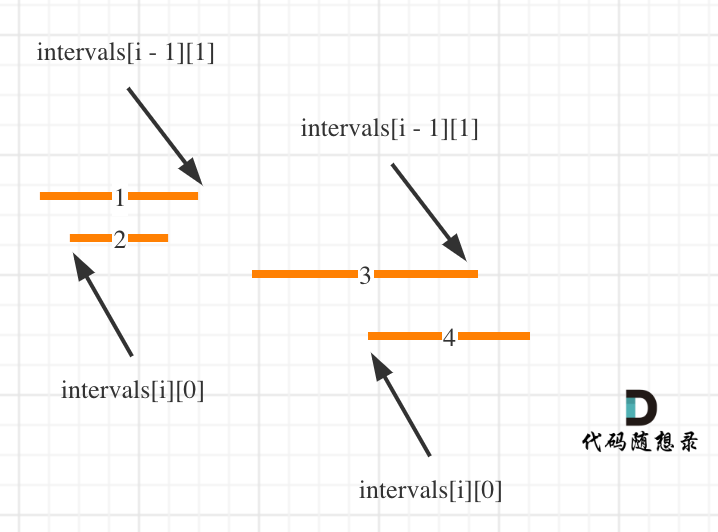
具体操作:按照左边界从小到大排序之后,如果 intervals[i][0] < intervals[i - 1][1] 即intervals[i]左边界 < intervals[i - 1]右边界,则一定有重复,因为intervals[i]的左边界一定是大于等于intervals[i - 1]的左边界。
|
||||
|
||||
如图:
|
||||
|
||||
|
||||
|
||||
|
||||
## 总结
|
||||
|
||||
本周的主题就是用贪心算法来解决区间问题,进过本周的学习,大家应该对区间的各种合并分割有一定程度的了解了。
|
||||
|
||||
其实很多区间的合并操作看起来都是常识,其实贪心算法有时候就是常识,哈哈,但也别小看了贪心算法。
|
||||
|
||||
在[贪心算法:合并区间](https://mp.weixin.qq.com/s/royhzEM5tOkUFwUGrNStpw)中就说过,对于贪心算法,很多同学都是:「如果能凭常识直接做出来,就会感觉不到自己用了贪心, 一旦第一直觉想不出来, 可能就一直想不出来了」。
|
||||
|
||||
所以还是要多看多做多练习!
|
||||
|
||||
**「代码随想录」里总结的都是经典题目,大家跟着练就节省了不少选择题目的时间了**。
|
||||
|
||||
|
||||
Reference in New Issue
Block a user