mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-07 15:45:40 +08:00
Merge branch 'youngyangyang04:master' into master
This commit is contained in:
@ -151,6 +151,96 @@ if (nums[k] + nums[i] > target && nums[i] >= 0) {
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### C:
|
||||
|
||||
```C
|
||||
/* qsort */
|
||||
static int cmp(const void* arg1, const void* arg2) {
|
||||
int a = *(int *)arg1;
|
||||
int b = *(int *)arg2;
|
||||
return (a > b);
|
||||
}
|
||||
|
||||
int** fourSum(int* nums, int numsSize, int target, int* returnSize, int** returnColumnSizes) {
|
||||
|
||||
/* 对nums数组进行排序 */
|
||||
qsort(nums, numsSize, sizeof(int), cmp);
|
||||
|
||||
int **res = (int **)malloc(sizeof(int *) * 40000);
|
||||
int index = 0;
|
||||
|
||||
/* k */
|
||||
for (int k = 0; k < numsSize - 3; k++) { /* 第一级 */
|
||||
|
||||
/* k剪枝 */
|
||||
if ((nums[k] > target) && (nums[k] >= 0)) {
|
||||
break;
|
||||
}
|
||||
/* k去重 */
|
||||
if ((k > 0) && (nums[k] == nums[k - 1])) {
|
||||
continue;
|
||||
}
|
||||
|
||||
/* i */
|
||||
for (int i = k + 1; i < numsSize - 2; i++) { /* 第二级 */
|
||||
|
||||
/* i剪枝 */
|
||||
if ((nums[k] + nums[i] > target) && (nums[i] >= 0)) {
|
||||
break;
|
||||
}
|
||||
/* i去重 */
|
||||
if ((i > (k + 1)) && (nums[i] == nums[i - 1])) {
|
||||
continue;
|
||||
}
|
||||
|
||||
/* left and right */
|
||||
int left = i + 1;
|
||||
int right = numsSize - 1;
|
||||
|
||||
while (left < right) {
|
||||
|
||||
/* 防止大数溢出 */
|
||||
long long val = (long long)nums[k] + nums[i] + nums[left] + nums[right];
|
||||
if (val > target) {
|
||||
right--;
|
||||
} else if (val < target) {
|
||||
left++;
|
||||
} else {
|
||||
int *res_tmp = (int *)malloc(sizeof(int) * 4);
|
||||
res_tmp[0] = nums[k];
|
||||
res_tmp[1] = nums[i];
|
||||
res_tmp[2] = nums[left];
|
||||
res_tmp[3] = nums[right];
|
||||
res[index++] = res_tmp;
|
||||
|
||||
/* right去重 */
|
||||
while ((right > left) && (nums[right] == nums[right - 1])) {
|
||||
right--;
|
||||
}
|
||||
/* left去重 */
|
||||
while ((left < right) && (nums[left] == nums[left + 1])) {
|
||||
left++;
|
||||
}
|
||||
|
||||
/* 更新right与left */
|
||||
left++, right--;
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
/* 返回值处理 */
|
||||
*returnSize = index;
|
||||
|
||||
int *column = (int *)malloc(sizeof(int) * index);
|
||||
for (int i = 0; i < index; i++) {
|
||||
column[i] = 4;
|
||||
}
|
||||
*returnColumnSizes = column;
|
||||
return res;
|
||||
}
|
||||
```
|
||||
|
||||
### Java:
|
||||
|
||||
```Java
|
||||
|
||||
@ -550,6 +550,27 @@ function uniquePathsWithObstacles(obstacleGrid: number[][]): number {
|
||||
};
|
||||
```
|
||||
|
||||
// 版本二: dp改為使用一維陣列,從終點開始遍歷
|
||||
```typescript
|
||||
function uniquePathsWithObstacles(obstacleGrid: number[][]): number {
|
||||
const m = obstacleGrid.length;
|
||||
const n = obstacleGrid[0].length;
|
||||
|
||||
const dp: number[] = new Array(n).fill(0);
|
||||
dp[n - 1] = 1;
|
||||
|
||||
// 由下而上,右而左進行遍歷
|
||||
for (let i = m - 1; i >= 0; i--) {
|
||||
for (let j = n - 1; j >= 0; j--) {
|
||||
if (obstacleGrid[i][j] === 1) dp[j] = 0;
|
||||
else dp[j] = dp[j] + (dp[j + 1] || 0);
|
||||
}
|
||||
}
|
||||
|
||||
return dp[0];
|
||||
};
|
||||
```
|
||||
|
||||
### Rust
|
||||
|
||||
```Rust
|
||||
|
||||
@ -605,6 +605,63 @@ func bfs(grid [][]int, i, j int) {
|
||||
}
|
||||
```
|
||||
|
||||
### JavaScript
|
||||
|
||||
```js
|
||||
/**
|
||||
* @param {number[][]} grid
|
||||
* @return {number}
|
||||
*/
|
||||
var numEnclaves = function (grid) {
|
||||
let row = grid.length;
|
||||
let col = grid[0].length;
|
||||
let count = 0;
|
||||
|
||||
// Check the first and last row, if there is a 1, then change all the connected 1s to 0 and don't count them.
|
||||
for (let j = 0; j < col; j++) {
|
||||
if (grid[0][j] === 1) {
|
||||
dfs(0, j, false);
|
||||
}
|
||||
if (grid[row - 1][j] === 1) {
|
||||
dfs(row - 1, j, false);
|
||||
}
|
||||
}
|
||||
|
||||
// Check the first and last column, if there is a 1, then change all the connected 1s to 0 and don't count them.
|
||||
for (let i = 0; i < row; i++) {
|
||||
if (grid[i][0] === 1) {
|
||||
dfs(i, 0, false);
|
||||
}
|
||||
if (grid[i][col - 1] === 1) {
|
||||
dfs(i, col - 1, false);
|
||||
}
|
||||
}
|
||||
|
||||
// Check the rest of the grid, if there is a 1, then change all the connected 1s to 0 and count them.
|
||||
for (let i = 1; i < row - 1; i++) {
|
||||
for (let j = 1; j < col - 1; j++) {
|
||||
dfs(i, j, true);
|
||||
}
|
||||
}
|
||||
|
||||
function dfs(i, j, isCounting) {
|
||||
let condition = i < 0 || i >= grid.length || j < 0 || j >= grid[0].length || grid[i][j] === 0;
|
||||
|
||||
if (condition) return;
|
||||
if (isCounting) count++;
|
||||
|
||||
grid[i][j] = 0;
|
||||
|
||||
dfs(i - 1, j, isCounting);
|
||||
dfs(i + 1, j, isCounting);
|
||||
dfs(i, j - 1, isCounting);
|
||||
dfs(i, j + 1, isCounting);
|
||||
}
|
||||
|
||||
return count;
|
||||
};
|
||||
```
|
||||
|
||||
### Rust
|
||||
|
||||
dfs:
|
||||
@ -700,3 +757,4 @@ impl Solution {
|
||||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||||
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>
|
||||
</a>
|
||||
|
||||
|
||||
@ -241,6 +241,33 @@ class Solution:
|
||||
|
||||
### Go:
|
||||
|
||||
使用栈
|
||||
```go
|
||||
func removeDuplicates(s string) string {
|
||||
stack := make([]rune, 0)
|
||||
for _, val := range s {
|
||||
if len(stack) == 0 || val != stack[len(stack)-1] {
|
||||
stack = append(stack, val)
|
||||
} else {
|
||||
stack = stack[:len(stack)-1]
|
||||
}
|
||||
}
|
||||
var res []rune
|
||||
for len(stack) != 0 { // 将栈中元素放到result字符串汇总
|
||||
res = append(res, stack[len(stack)-1])
|
||||
stack = stack[:len(stack)-1]
|
||||
}
|
||||
// 此时字符串需要反转一下
|
||||
l, r := 0, len(res)-1
|
||||
for l < r {
|
||||
res[l], res[r] = res[r], res[l]
|
||||
l++
|
||||
r--
|
||||
}
|
||||
return string(res)
|
||||
}
|
||||
```
|
||||
拿字符串直接作为栈,省去了栈还要转为字符串的操作
|
||||
```go
|
||||
func removeDuplicates(s string) string {
|
||||
var stack []byte
|
||||
|
||||
@ -655,6 +655,104 @@ int main() {
|
||||
|
||||
### Java
|
||||
|
||||
```Java
|
||||
|
||||
import java.util.*;
|
||||
|
||||
class Edge {
|
||||
int to; // 邻接顶点
|
||||
int val; // 边的权重
|
||||
|
||||
Edge(int to, int val) {
|
||||
this.to = to;
|
||||
this.val = val;
|
||||
}
|
||||
}
|
||||
|
||||
class MyComparison implements Comparator<Pair<Integer, Integer>> {
|
||||
@Override
|
||||
public int compare(Pair<Integer, Integer> lhs, Pair<Integer, Integer> rhs) {
|
||||
return Integer.compare(lhs.second, rhs.second);
|
||||
}
|
||||
}
|
||||
|
||||
class Pair<U, V> {
|
||||
public final U first;
|
||||
public final V second;
|
||||
|
||||
public Pair(U first, V second) {
|
||||
this.first = first;
|
||||
this.second = second;
|
||||
}
|
||||
}
|
||||
|
||||
public class Main {
|
||||
public static void main(String[] args) {
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
int n = scanner.nextInt();
|
||||
int m = scanner.nextInt();
|
||||
|
||||
List<List<Edge>> grid = new ArrayList<>(n + 1);
|
||||
for (int i = 0; i <= n; i++) {
|
||||
grid.add(new ArrayList<>());
|
||||
}
|
||||
|
||||
for (int i = 0; i < m; i++) {
|
||||
int p1 = scanner.nextInt();
|
||||
int p2 = scanner.nextInt();
|
||||
int val = scanner.nextInt();
|
||||
grid.get(p1).add(new Edge(p2, val));
|
||||
}
|
||||
|
||||
int start = 1; // 起点
|
||||
int end = n; // 终点
|
||||
|
||||
// 存储从源点到每个节点的最短距离
|
||||
int[] minDist = new int[n + 1];
|
||||
Arrays.fill(minDist, Integer.MAX_VALUE);
|
||||
|
||||
// 记录顶点是否被访问过
|
||||
boolean[] visited = new boolean[n + 1];
|
||||
|
||||
// 优先队列中存放 Pair<节点,源点到该节点的权值>
|
||||
PriorityQueue<Pair<Integer, Integer>> pq = new PriorityQueue<>(new MyComparison());
|
||||
|
||||
// 初始化队列,源点到源点的距离为0,所以初始为0
|
||||
pq.add(new Pair<>(start, 0));
|
||||
|
||||
minDist[start] = 0; // 起始点到自身的距离为0
|
||||
|
||||
while (!pq.isEmpty()) {
|
||||
// 1. 第一步,选源点到哪个节点近且该节点未被访问过(通过优先级队列来实现)
|
||||
// <节点, 源点到该节点的距离>
|
||||
Pair<Integer, Integer> cur = pq.poll();
|
||||
|
||||
if (visited[cur.first]) continue;
|
||||
|
||||
// 2. 第二步,该最近节点被标记访问过
|
||||
visited[cur.first] = true;
|
||||
|
||||
// 3. 第三步,更新非访问节点到源点的距离(即更新minDist数组)
|
||||
for (Edge edge : grid.get(cur.first)) { // 遍历 cur指向的节点,cur指向的节点为 edge
|
||||
// cur指向的节点edge.to,这条边的权值为 edge.val
|
||||
if (!visited[edge.to] && minDist[cur.first] + edge.val < minDist[edge.to]) { // 更新minDist
|
||||
minDist[edge.to] = minDist[cur.first] + edge.val;
|
||||
pq.add(new Pair<>(edge.to, minDist[edge.to]));
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
if (minDist[end] == Integer.MAX_VALUE) {
|
||||
System.out.println(-1); // 不能到达终点
|
||||
} else {
|
||||
System.out.println(minDist[end]); // 到达终点最短路径
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
|
||||
### Python
|
||||
|
||||
### Go
|
||||
|
||||
@ -737,6 +737,73 @@ for (int v = 1; v <= n; v++) {
|
||||
|
||||
### Java
|
||||
|
||||
```Java
|
||||
import java.util.Arrays;
|
||||
import java.util.Scanner;
|
||||
|
||||
public class Main {
|
||||
public static void main(String[] args) {
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
int n = scanner.nextInt();
|
||||
int m = scanner.nextInt();
|
||||
|
||||
int[][] grid = new int[n + 1][n + 1];
|
||||
for (int i = 0; i <= n; i++) {
|
||||
Arrays.fill(grid[i], Integer.MAX_VALUE);
|
||||
}
|
||||
|
||||
for (int i = 0; i < m; i++) {
|
||||
int p1 = scanner.nextInt();
|
||||
int p2 = scanner.nextInt();
|
||||
int val = scanner.nextInt();
|
||||
grid[p1][p2] = val;
|
||||
}
|
||||
|
||||
int start = 1;
|
||||
int end = n;
|
||||
|
||||
// 存储从源点到每个节点的最短距离
|
||||
int[] minDist = new int[n + 1];
|
||||
Arrays.fill(minDist, Integer.MAX_VALUE);
|
||||
|
||||
// 记录顶点是否被访问过
|
||||
boolean[] visited = new boolean[n + 1];
|
||||
|
||||
minDist[start] = 0; // 起始点到自身的距离为0
|
||||
|
||||
for (int i = 1; i <= n; i++) { // 遍历所有节点
|
||||
|
||||
int minVal = Integer.MAX_VALUE;
|
||||
int cur = 1;
|
||||
|
||||
// 1、选距离源点最近且未访问过的节点
|
||||
for (int v = 1; v <= n; ++v) {
|
||||
if (!visited[v] && minDist[v] < minVal) {
|
||||
minVal = minDist[v];
|
||||
cur = v;
|
||||
}
|
||||
}
|
||||
|
||||
visited[cur] = true; // 2、标记该节点已被访问
|
||||
|
||||
// 3、第三步,更新非访问节点到源点的距离(即更新minDist数组)
|
||||
for (int v = 1; v <= n; v++) {
|
||||
if (!visited[v] && grid[cur][v] != Integer.MAX_VALUE && minDist[cur] + grid[cur][v] < minDist[v]) {
|
||||
minDist[v] = minDist[cur] + grid[cur][v];
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
if (minDist[end] == Integer.MAX_VALUE) {
|
||||
System.out.println(-1); // 不能到达终点
|
||||
} else {
|
||||
System.out.println(minDist[end]); // 到达终点最短路径
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
### Python
|
||||
|
||||
### Go
|
||||
|
||||
@ -362,10 +362,43 @@ main();
|
||||
|
||||
### Scala:
|
||||
|
||||
|
||||
### PHP:
|
||||
|
||||
```php
|
||||
<?php
|
||||
// 标准输入
|
||||
$s = trim(fgets(STDIN));
|
||||
$oldLen = strlen($s);
|
||||
$count = 0;
|
||||
for ($i = 0; $i < $oldLen; $i++) {
|
||||
if (is_numeric($s[$i])) {
|
||||
$count++;
|
||||
}
|
||||
}
|
||||
|
||||
// 扩充字符串
|
||||
$s = str_pad($s, $oldLen + $count * 5);
|
||||
$newLen = strlen($s);
|
||||
while($oldLen >= 0) {
|
||||
if (is_numeric($s[$oldLen])) {
|
||||
$s[$newLen--] = 'r';
|
||||
$s[$newLen--] = 'e';
|
||||
$s[$newLen--] = 'b';
|
||||
$s[$newLen--] = 'm';
|
||||
$s[$newLen--] = 'u';
|
||||
$s[$newLen--] = 'n';
|
||||
} else {
|
||||
$s[$newLen--] = $s[$oldLen];
|
||||
}
|
||||
$oldLen--;
|
||||
}
|
||||
|
||||
echo $s;
|
||||
?>
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
### Rust:
|
||||
|
||||
|
||||
|
||||
@ -18,7 +18,7 @@
|
||||
```
|
||||
2
|
||||
abcdefg
|
||||
```
|
||||
```
|
||||
|
||||
样例输出:
|
||||
|
||||
@ -300,33 +300,50 @@ int main()
|
||||
```javascript
|
||||
// JS中字符串内不可单独修改
|
||||
|
||||
// 右旋转
|
||||
function reverseLeftWords(s, k) {
|
||||
const reverse = (sList, start, end) => {
|
||||
for (let i = start, j = end; i < j; i++, j--) {
|
||||
[sList[i], sList[j]] = [sList[j], sList[i]];
|
||||
}
|
||||
}
|
||||
const sList = Array.from(s);
|
||||
reverse(sList, 0, sList.length - k - 1);
|
||||
reverse(sList, sList.length - k, sList.length - 1);
|
||||
reverse(sList, 0, sList.length - 1);
|
||||
return sList.join('');
|
||||
const readline = require('readline')
|
||||
|
||||
const rl = readline.createInterface({
|
||||
input: process.stdin,
|
||||
output: process.stdout
|
||||
})
|
||||
|
||||
const inputs = []; // 存储输入
|
||||
|
||||
rl.on('line', function(data) {
|
||||
inputs.push(data);
|
||||
|
||||
}).on('close', function() {
|
||||
const res = deal(inputs);
|
||||
// 打印结果
|
||||
console.log(res);
|
||||
})
|
||||
|
||||
// 对传入的数据进行处理
|
||||
function deal(inputs) {
|
||||
let [k, s] = inputs;
|
||||
const len = s.length - 1;
|
||||
k = parseInt(k);
|
||||
str = s.split('');
|
||||
|
||||
str = reverseStr(str, 0, len - k)
|
||||
str = reverseStr(str, len - k + 1, len)
|
||||
str = reverseStr(str, 0, len)
|
||||
|
||||
return str.join('');
|
||||
}
|
||||
|
||||
// 左旋转
|
||||
var reverseLeftWords = function(s, n) {
|
||||
const reverse = (sList, start, end) => {
|
||||
for (let i = start, j = end; i < j; i++, j--) {
|
||||
[sList[i], sList[j]] = [sList[j], sList[i]];
|
||||
// 根据提供的范围进行翻转
|
||||
function reverseStr(s, start, end) {
|
||||
|
||||
while (start < end) {
|
||||
[s[start], s[end]] = [s[end], s[start]]
|
||||
|
||||
start++;
|
||||
end--;
|
||||
}
|
||||
}
|
||||
const sList = s.split('');
|
||||
reverse(sList, 0, n - 1);
|
||||
reverse(sList, n, sList.length - 1);
|
||||
reverse(sList, 0, sList.length - 1);
|
||||
return sList.join('');
|
||||
};
|
||||
|
||||
return s;
|
||||
}
|
||||
```
|
||||
|
||||
### TypeScript:
|
||||
@ -338,10 +355,35 @@ var reverseLeftWords = function(s, n) {
|
||||
|
||||
### PHP:
|
||||
|
||||
```php
|
||||
<?php
|
||||
// 反转函数
|
||||
function reverse(&$s, $start, $end) {
|
||||
for ($i = $start, $j = $end; $i < $j; $i++, $j--) {
|
||||
$tmp = $s[$i];
|
||||
$s[$i] = $s[$j];
|
||||
$s[$j] = $tmp;
|
||||
}
|
||||
}
|
||||
|
||||
// 标准输入:读取右旋转位数和字符串
|
||||
$n = trim(fgets(STDIN));
|
||||
$s = trim(fgets(STDIN));
|
||||
// 字符串长度
|
||||
$len = strlen($s);
|
||||
// 先部分反转
|
||||
reverse($s, $len - $n, $len - 1);
|
||||
reverse($s, 0, $len - $n - 1);
|
||||
// 再整体反转
|
||||
reverse($s, 0, $len - 1);
|
||||
|
||||
echo $s;
|
||||
?>
|
||||
```
|
||||
|
||||
|
||||
### Scala:
|
||||
|
||||
|
||||
### Rust:
|
||||
|
||||
|
||||
|
||||
191
problems/kamacoder/0058.区间和.md
Normal file
191
problems/kamacoder/0058.区间和.md
Normal file
@ -0,0 +1,191 @@
|
||||
|
||||
# 58. 区间和
|
||||
|
||||
[题目链接](https://kamacoder.com/problempage.php?pid=1070)
|
||||
|
||||
题目描述
|
||||
|
||||
给定一个整数数组 Array,请计算该数组在每个指定区间内元素的总和。
|
||||
|
||||
输入描述
|
||||
|
||||
第一行输入为整数数组 Array 的长度 n,接下来 n 行,每行一个整数,表示数组的元素。随后的输入为需要计算总和的区间,直至文件结束。
|
||||
|
||||
输出描述
|
||||
|
||||
输出每个指定区间内元素的总和。
|
||||
|
||||
输入示例
|
||||
|
||||
```
|
||||
5
|
||||
1
|
||||
2
|
||||
3
|
||||
4
|
||||
5
|
||||
0 1
|
||||
1 3
|
||||
```
|
||||
|
||||
输出示例
|
||||
|
||||
```
|
||||
3
|
||||
9
|
||||
```
|
||||
|
||||
数据范围:
|
||||
|
||||
0 < n <= 100000
|
||||
|
||||
## 思路
|
||||
|
||||
本题我们来讲解 数组 上常用的解题技巧:前缀和
|
||||
|
||||
首先来看本题,我们最直观的想法是什么?
|
||||
|
||||
那就是给一个区间,然后 把这个区间的和都累加一遍不就得了,是一道简单不能再简单的题目。
|
||||
|
||||
代码如下:
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
using namespace std;
|
||||
int main() {
|
||||
int n, a, b;
|
||||
cin >> n;
|
||||
vector<int> vec(n);
|
||||
for (int i = 0; i < n; i++) cin >> vec[i];
|
||||
while (cin >> a >> b) {
|
||||
int sum = 0;
|
||||
// 累加区间 a 到 b 的和
|
||||
for (int i = a; i <= b; i++) sum += vec[i];
|
||||
cout << sum << endl;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
代码一提交,发现超时了.....
|
||||
|
||||
我在制作本题的时候,特别制作了大数据量查询,卡的就是这种暴力解法。
|
||||
|
||||
来举一个极端的例子,如果我查询m次,每次查询的范围都是从0 到 n - 1
|
||||
|
||||
那么该算法的时间复杂度是 O(n * m) m 是查询的次数
|
||||
|
||||
如果查询次数非常大的话,这个时间复杂度也是非常大的。
|
||||
|
||||
接下来我们来引入前缀和,看看前缀和如何解决这个问题。
|
||||
|
||||
前缀和的思想是重复利用计算过的子数组之和,从而降低区间查询需要累加计算的次数。
|
||||
|
||||
**前缀和 在涉及计算区间和的问题时非常有用**!
|
||||
|
||||
前缀和的思路其实很简单,我给大家举个例子很容易就懂了。
|
||||
|
||||
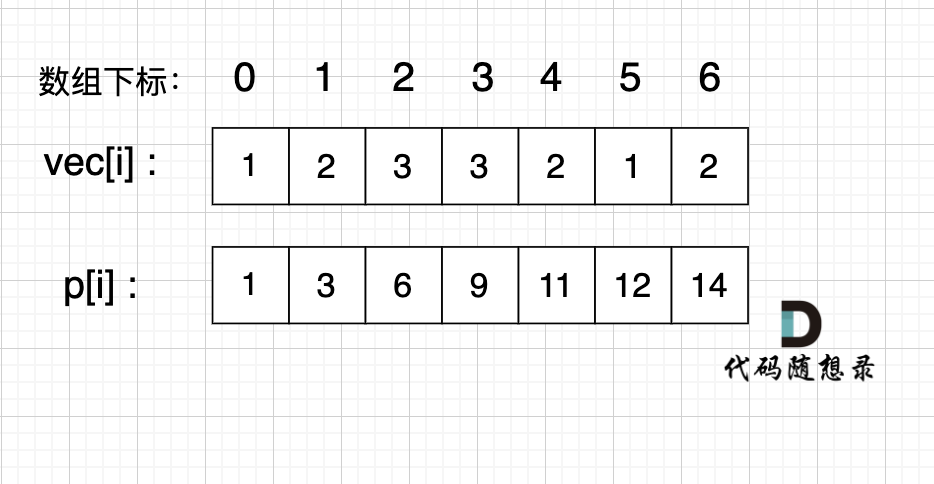
例如,我们要统计 vec[i] 这个数组上的区间和。
|
||||
|
||||
我们先做累加,即 p[i] 表示 下标 0 到 i 的 vec[i] 累加 之和。
|
||||
|
||||
如图:
|
||||
|
||||
|
||||
|
||||
|
||||
如果,我们想统计,在vec数组上 下标 2 到下标 5 之间的累加和,那是不是就用 p[5] - p[1] 就可以了。
|
||||
|
||||
为什么呢?
|
||||
|
||||
p[1] = vec[0] + vec[1];
|
||||
|
||||
p[5] = vec[0] + vec[1] + vec[2] + vec[3] + vec[4] + vec[5];
|
||||
|
||||
p[5] - p[1] = vec[2] + vec[3] + vec[4] + vec[5];
|
||||
|
||||
这不就是我们要求的 下标 2 到下标 5 之间的累加和吗。
|
||||
|
||||
如图所示:
|
||||
|
||||

|
||||
|
||||
p[5] - p[1] 就是 红色部分的区间和。
|
||||
|
||||
而 p 数组是我们之前就计算好的累加和,所以后面每次求区间和的之后 我们只需要 O(1)的操作。
|
||||
|
||||
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
using namespace std;
|
||||
int main() {
|
||||
int n, a, b;
|
||||
cin >> n;
|
||||
vector<int> vec(n);
|
||||
vector<int> p(n);
|
||||
int presum = 0;
|
||||
for (int i = 0; i < n; i++) {
|
||||
cin >> vec[i];
|
||||
presum += vec[i];
|
||||
p[i] = presum;
|
||||
}
|
||||
|
||||
while (cin >> a >> b) {
|
||||
int sum;
|
||||
if (a == 0) sum = p[b];
|
||||
else sum = p[b] - p[a - 1];
|
||||
cout << sum << endl;
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
using namespace std;
|
||||
int main() {
|
||||
int n, a, b;
|
||||
cin >> n;
|
||||
vector<int> vec(n);
|
||||
vector<int> p(n);
|
||||
int presum = 0;
|
||||
for (int i = 0; i < n; i++) {
|
||||
scanf("%d", &vec[i]);
|
||||
presum += vec[i];
|
||||
p[i] = presum;
|
||||
}
|
||||
|
||||
while (~scanf("%d%d", &a, &b)) {
|
||||
int sum;
|
||||
if (a == 0) sum = p[b];
|
||||
else sum = p[b] - p[a - 1];
|
||||
printf("%d\n", sum);
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
```CPP
|
||||
|
||||
#include<bits/stdc++.h>
|
||||
using namespace std;
|
||||
|
||||
|
||||
int main(){
|
||||
int n, a, b;
|
||||
cin >> n;
|
||||
vector<int> vec(n + 1);
|
||||
vector<int> p(n + 1, 0);
|
||||
for(int i = 1; i <= n; i++) {
|
||||
scanf("%d", &vec[i]);
|
||||
p[i] = p[i - 1] + vec[i];
|
||||
}
|
||||
while(~scanf("%d%d", &a, &b)){
|
||||
printf("%d\n", p[b + 1] - p[a]);
|
||||
}
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
@ -75,6 +75,19 @@
|
||||
|
||||
## 插曲
|
||||
|
||||
-------------
|
||||
|
||||
本题和力扣 [797.所有可能的路径](https://leetcode.cn/problems/all-paths-from-source-to-target/description/) 是一样的,录友了解深度优先搜索之后,这道题目就是模板题,是送分题。
|
||||
|
||||
力扣是核心代码模式,把图的存储方式给大家定义好了,只需要写出深搜的核心代码就可以。
|
||||
|
||||
如果笔试的时候出一道原题 (笔试都是ACM模式,部分面试也是ACM模式),不少熟练刷力扣的录友都难住了,因为不知道图应该怎么存,也不知道自己存的图如何去遍历。
|
||||
|
||||
所以这也是为什么我要让大家练习 ACM模式
|
||||
|
||||
--------
|
||||
|
||||
|
||||
这道题目是深度优先搜索,比较好的入门题。
|
||||
|
||||
如果对深度优先搜索还不够了解,可以先看这里:[深度优先搜索的理论基础](https://programmercarl.com/图论深搜理论基础.html)
|
||||
|
||||
@ -186,7 +186,56 @@ int main() {
|
||||
### Java
|
||||
|
||||
### Python
|
||||
```python
|
||||
from collections import deque
|
||||
|
||||
# 处理输入
|
||||
n, m = list(map(int, input().strip().split()))
|
||||
g = []
|
||||
for _ in range(n):
|
||||
row = list(map(int, input().strip().split()))
|
||||
g.append(row)
|
||||
|
||||
# 定义四个方向、孤岛面积(遍历完边缘后会被重置)
|
||||
directions = [[0,1], [1,0], [-1,0], [0,-1]]
|
||||
count = 0
|
||||
|
||||
# 广搜
|
||||
def bfs(r, c):
|
||||
global count
|
||||
q = deque()
|
||||
q.append((r, c))
|
||||
g[r][c] = 0
|
||||
count += 1
|
||||
|
||||
while q:
|
||||
r, c = q.popleft()
|
||||
for di in directions:
|
||||
next_r = r + di[0]
|
||||
next_c = c + di[1]
|
||||
if next_c < 0 or next_c >= m or next_r < 0 or next_r >= n:
|
||||
continue
|
||||
if g[next_r][next_c] == 1:
|
||||
q.append((next_r, next_c))
|
||||
g[next_r][next_c] = 0
|
||||
count += 1
|
||||
|
||||
|
||||
for i in range(n):
|
||||
if g[i][0] == 1: bfs(i, 0)
|
||||
if g[i][m-1] == 1: bfs(i, m-1)
|
||||
|
||||
for i in range(m):
|
||||
if g[0][i] == 1: bfs(0, i)
|
||||
if g[n-1][i] == 1: bfs(n-1, i)
|
||||
|
||||
count = 0
|
||||
for i in range(n):
|
||||
for j in range(m):
|
||||
if g[i][j] == 1: bfs(i, j)
|
||||
|
||||
print(count)
|
||||
```
|
||||
### Go
|
||||
|
||||
### Rust
|
||||
|
||||
@ -24,7 +24,7 @@
|
||||
1 2
|
||||
2 1
|
||||
1 3
|
||||
3 4
|
||||
2 4
|
||||
```
|
||||
|
||||
【输出示例】
|
||||
|
||||
@ -3,7 +3,7 @@
|
||||
|
||||
# 110. 字符串接龙
|
||||
|
||||
[卡码网题目链接(ACM模式)](https://kamacoder.com/problempage.php?pid=1182)
|
||||
[卡码网题目链接(ACM模式)](https://kamacoder.com/problempage.php?pid=1183)
|
||||
|
||||
题目描述
|
||||
|
||||
|
||||
27
problems/kamacoder/0111.构造二阶行列式.md
Normal file
27
problems/kamacoder/0111.构造二阶行列式.md
Normal file
@ -0,0 +1,27 @@
|
||||
|
||||
# 111. 构造二阶行列式
|
||||
|
||||
暴力模拟就好,每个数不超过 20, 暴力枚举其实也没多大。
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
using namespace std;
|
||||
int main() {
|
||||
int n;
|
||||
cin >> n;
|
||||
for (int x = 1; x <= 20; x++) {
|
||||
for (int y = 1; y <= 20; y++) {
|
||||
for (int i = 1; i <= 20; i++) {
|
||||
for (int j = 1; j <= 20; j++) {
|
||||
if ((x * j - y * i) == n) {
|
||||
cout << x << " " << y << endl;
|
||||
cout << i << " " << j << endl;
|
||||
return 0;
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
cout << -1 << endl;
|
||||
}
|
||||
```
|
||||
26
problems/kamacoder/0112.挑战boss.md
Normal file
26
problems/kamacoder/0112.挑战boss.md
Normal file
@ -0,0 +1,26 @@
|
||||
|
||||
# 112. 挑战boss
|
||||
|
||||
本题题意有点绕,注意看一下 题目描述中的【提示信息】,但是在笔试中,是不给这样的提示信息的。
|
||||
|
||||
简单模拟:
|
||||
|
||||
```CPP
|
||||
#include<iostream>
|
||||
using namespace std;
|
||||
int main() {
|
||||
int n, a, b, k = 0;
|
||||
cin >> n >> a >> b;
|
||||
string s;
|
||||
cin >> s;
|
||||
int result = 0;
|
||||
for (int i = 0; i < s.size(); i++) {
|
||||
int cur = a + k * b;
|
||||
result += cur;
|
||||
++k;
|
||||
if (s[i] == 'x') k = 0;
|
||||
}
|
||||
cout << result << endl;
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
29
problems/kamacoder/0114.小欧的平均数.md
Normal file
29
problems/kamacoder/0114.小欧的平均数.md
Normal file
@ -0,0 +1,29 @@
|
||||
|
||||
# 114. 小欧的平均数
|
||||
|
||||
这道题非常的脑筋急转弯, 读题都要理解半天。
|
||||
|
||||
初步读题,感觉好像是求 如何最小加减,得到三个数的平均数。
|
||||
|
||||
但题意不是这样的。
|
||||
|
||||
小欧的说的三个数平衡,只是三个数里 任何两个数 相加都能被2整除, 那么 也就是说,这三个数 要么都是 奇数,要么都是偶数,才能达到小欧所说的平衡。
|
||||
|
||||
所以题目要求的,就是,三个数,最小加减1 几次 可以让三个数都变成奇数,或者都变成偶数。
|
||||
|
||||
所以最终的结果 不是1 就是0,没有其他的。
|
||||
|
||||
录友可能想,题目出的这么绕干啥? 没办法,企业的笔试题就是这样的。
|
||||
|
||||
```CPP
|
||||
#include<iostream>
|
||||
#include<algorithm>
|
||||
using namespace std;
|
||||
int main() {
|
||||
int x, y, z;
|
||||
cin >> x >> y >> z;
|
||||
int count = (x % 2 == 0) + (y % 2 == 0) + (z % 2 == 0);
|
||||
cout << min(3 - count, count);
|
||||
}
|
||||
```
|
||||
|
||||
67
problems/kamacoder/0115.组装手机.md
Normal file
67
problems/kamacoder/0115.组装手机.md
Normal file
@ -0,0 +1,67 @@
|
||||
|
||||
# 115. 组装手机
|
||||
|
||||
这道题是比较难得哈希表题目。 把代码随想录哈希表章节理解透彻,做本题没问题。
|
||||
|
||||
思路是
|
||||
|
||||
1. 用哈希表记录 外壳售价 和 手机零件售价 出现的次数
|
||||
2. 记录总和出现的次数
|
||||
3. 遍历总和,减去 外壳售价,看 手机零件售价出现了几次
|
||||
4. 最后累加,取最大值
|
||||
|
||||
有一个需要注意的点: 数字可以重复,在计算个数的时候,如果计算重复的数字
|
||||
|
||||
例如 如果输入是
|
||||
|
||||
```
|
||||
4
|
||||
1 1 1 1
|
||||
1 1 1 1
|
||||
```
|
||||
那么输出应该是 4, 外壳售价 和 手机零件售价 是可以重复的。
|
||||
|
||||
代码如下:
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
#include <unordered_set>
|
||||
#include <unordered_map>
|
||||
using namespace std;
|
||||
int main() {
|
||||
int n;
|
||||
cin >> n;
|
||||
vector<int> aVec(n, 0);
|
||||
vector<int> bVec(n, 0);
|
||||
unordered_map<int, int > aUmap;
|
||||
unordered_map<int, int > bUmap;
|
||||
for (int i = 0; i < n; i++) {
|
||||
cin >> aVec[i];
|
||||
aUmap[aVec[i]]++;
|
||||
}
|
||||
for (int i = 0; i < n; i++) {
|
||||
cin >> bVec[i];
|
||||
bUmap[bVec[i]]++;
|
||||
}
|
||||
unordered_set<int > uset;
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < n; j++){
|
||||
uset.insert(aVec[i] + bVec[j]);
|
||||
}
|
||||
}
|
||||
int result = 0;
|
||||
for (int sum : uset) {
|
||||
//cout << p.first << endl;
|
||||
int count = 0;
|
||||
for (pair<int, int> p : aUmap) {
|
||||
//cout << p.first - aVec[i] << endl;
|
||||
if (sum - p.first > 0 && bUmap[sum - p.first] != 0) {
|
||||
count += min(bUmap[sum - p.first], p.second);
|
||||
}
|
||||
}
|
||||
result = max(result, count);
|
||||
}
|
||||
cout << result << endl;
|
||||
}
|
||||
```
|
||||
@ -167,7 +167,7 @@
|
||||
|
||||

|
||||
|
||||
--------------
|
||||
--------------
|
||||
|
||||
后面的过程一样的,节点3 和 节点4,入度都为0,选哪个都行。
|
||||
|
||||
@ -344,8 +344,107 @@ int main() {
|
||||
|
||||
### Java
|
||||
|
||||
```java
|
||||
import java.util.*;
|
||||
|
||||
|
||||
public class Main {
|
||||
public static void main(String[] args) {
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
int n = scanner.nextInt();
|
||||
int m = scanner.nextInt();
|
||||
|
||||
List<List<Integer>> umap = new ArrayList<>(); // 记录文件依赖关系
|
||||
int[] inDegree = new int[n]; // 记录每个文件的入度
|
||||
|
||||
for (int i = 0; i < n; i++)
|
||||
umap.add(new ArrayList<>());
|
||||
|
||||
for (int i = 0; i < m; i++) {
|
||||
int s = scanner.nextInt();
|
||||
int t = scanner.nextInt();
|
||||
umap.get(s).add(t); // 记录s指向哪些文件
|
||||
inDegree[t]++; // t的入度加一
|
||||
}
|
||||
|
||||
Queue<Integer> queue = new LinkedList<>();
|
||||
for (int i = 0; i < n; i++) {
|
||||
if (inDegree[i] == 0) {
|
||||
// 入度为0的文件,可以作为开头,先加入队列
|
||||
queue.add(i);
|
||||
}
|
||||
}
|
||||
|
||||
List<Integer> result = new ArrayList<>();
|
||||
|
||||
// 拓扑排序
|
||||
while (!queue.isEmpty()) {
|
||||
int cur = queue.poll(); // 当前选中的文件
|
||||
result.add(cur);
|
||||
for (int file : umap.get(cur)) {
|
||||
inDegree[file]--; // cur的指向的文件入度-1
|
||||
if (inDegree[file] == 0) {
|
||||
queue.add(file);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
if (result.size() == n) {
|
||||
for (int i = 0; i < result.size(); i++) {
|
||||
System.out.print(result.get(i));
|
||||
if (i < result.size() - 1) {
|
||||
System.out.print(" ");
|
||||
}
|
||||
}
|
||||
} else {
|
||||
System.out.println(-1);
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
### Python
|
||||
|
||||
```python
|
||||
from collections import deque, defaultdict
|
||||
|
||||
def topological_sort(n, edges):
|
||||
inDegree = [0] * n # inDegree 记录每个文件的入度
|
||||
umap = defaultdict(list) # 记录文件依赖关系
|
||||
|
||||
# 构建图和入度表
|
||||
for s, t in edges:
|
||||
inDegree[t] += 1
|
||||
umap[s].append(t)
|
||||
|
||||
# 初始化队列,加入所有入度为0的节点
|
||||
queue = deque([i for i in range(n) if inDegree[i] == 0])
|
||||
result = []
|
||||
|
||||
while queue:
|
||||
cur = queue.popleft() # 当前选中的文件
|
||||
result.append(cur)
|
||||
for file in umap[cur]: # 获取该文件指向的文件
|
||||
inDegree[file] -= 1 # cur的指向的文件入度-1
|
||||
if inDegree[file] == 0:
|
||||
queue.append(file)
|
||||
|
||||
if len(result) == n:
|
||||
print(" ".join(map(str, result)))
|
||||
else:
|
||||
print(-1)
|
||||
|
||||
|
||||
if __name__ == "__main__":
|
||||
n, m = map(int, input().split())
|
||||
edges = [tuple(map(int, input().split())) for _ in range(m)]
|
||||
topological_sort(n, edges)
|
||||
```
|
||||
|
||||
|
||||
|
||||
### Go
|
||||
|
||||
### Rust
|
||||
|
||||
@ -7,6 +7,10 @@
|
||||
|
||||
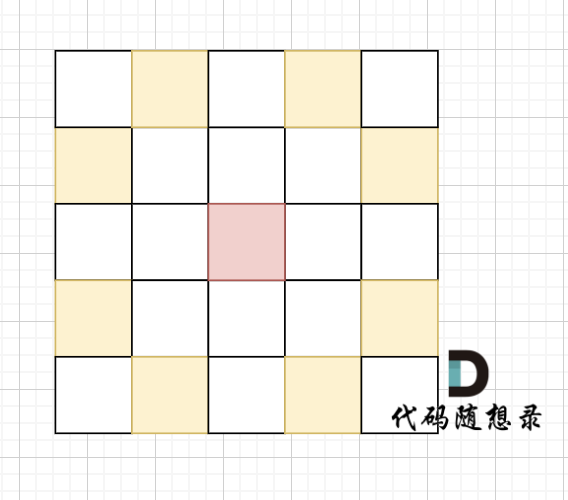
在象棋中,马和象的移动规则分别是“马走日”和“象走田”。现给定骑士的起始坐标和目标坐标,要求根据骑士的移动规则,计算从起点到达目标点所需的最短步数。
|
||||
|
||||
骑士移动规则如图,红色是起始位置,黄色是骑士可以走的地方。
|
||||
|
||||
|
||||
|
||||
棋盘大小 1000 x 1000(棋盘的 x 和 y 坐标均在 [1, 1000] 区间内,包含边界)
|
||||
|
||||
输入描述
|
||||
@ -42,6 +46,7 @@
|
||||
0
|
||||
```
|
||||
|
||||
|
||||
## 思路
|
||||
|
||||
我们看到这道题目的第一个想法就是广搜,这也是最经典的广搜类型题目。
|
||||
@ -192,7 +197,7 @@ x1, x2 为起点坐标,y1, y2 为终点坐标 ,abs 为求绝对值,sqrt
|
||||
|
||||
计算出来 F 之后,按照 F 的 大小,来选去出队列的节点。
|
||||
|
||||
可以使用 优先级队列 帮我们排好序,每次出队列,就是F最大的节点。
|
||||
可以使用 优先级队列 帮我们排好序,每次出队列,就是F最小的节点。
|
||||
|
||||
实现代码如下:(启发式函数 采用 欧拉距离计算方式)
|
||||
|
||||
|
||||
@ -1,7 +1,7 @@
|
||||
|
||||
小美的排列询问
|
||||
# 小美的排列询问
|
||||
|
||||
注意 x 和y 不分先后
|
||||
模拟题,注意 x 和y 不分先后
|
||||
|
||||
```CPP
|
||||
|
||||
@ -1,6 +1,11 @@
|
||||
|
||||
# 小美走公路
|
||||
|
||||
两个注意点
|
||||
在处理环形情况的时候,很多录友容易算懵了,不是多算一个数,就是少算一个数。
|
||||
|
||||
这里这样的题目,最好的方式是将 两个环展开,首尾相连,这样我们就可以通过 直线的思维去解题了
|
||||
|
||||
两个注意点:
|
||||
|
||||
1. x 可以比 y 大,题目没规定 x 和y 的大小顺序
|
||||
2. 累计相加的数可能超过int
|
||||
@ -1,5 +1,7 @@
|
||||
|
||||
前缀和
|
||||
# 小美的蛋糕切割
|
||||
|
||||
二维前缀和,不了解前缀和的录友 可以自行查一下,是一个很容易理解的算法思路
|
||||
|
||||
```CPP
|
||||
|
||||
|
||||
@ -36,7 +36,6 @@ void bfs(const vector<vector<char>>& grid, vector<vector<bool>>& visited, int x,
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
int main() {
|
||||
int n;
|
||||
string s;
|
||||
|
||||
@ -1,5 +1,134 @@
|
||||
# 131. 小美的树上染色
|
||||
|
||||
贪心的思路 : https://blog.csdn.net/weixin_43739821/article/details/136299012
|
||||
本题为树形dp 稍有难度,主要在于 递推公式上。
|
||||
|
||||
dp数组的定义:
|
||||
|
||||
dp[cur][1] :当前节点染色,那么当前节点为根节点及其左右子节点中,可以染色的最大数量
|
||||
|
||||
dp[cur][0] :当前节点不染色,那么当前节点为根节点及其左右子节点中,可以染色的最大数量
|
||||
|
||||
关于 dp转移方程
|
||||
|
||||
1、 情况一:
|
||||
|
||||
如果当前节点不染色,那就去 子节点 染色 或者 不染色的最大值。
|
||||
|
||||
`dp[cur][0] += max(dp[child][0], dp[child][1]);`
|
||||
|
||||
|
||||
2、情况二:
|
||||
|
||||
那么当前节点染色的话,这种情况就不好想了。
|
||||
|
||||
首先这不是二叉树,每一个节点都有可能 会有n个子节点。
|
||||
|
||||
所以我们要分别讨论,每一个子节点的情况 对父节点的影响。
|
||||
|
||||
那么父节点 针对每种情况,就要去 最大值, 也就是 `dp[cur][1] = max(dp[cur][1], 每个自孩子的情况)`
|
||||
|
||||
如图,假如节点1 是我们要计算的父节点,节点2是我们这次要计算的子节点。
|
||||
|
||||

|
||||
|
||||
选中一个节点2 作为我们这次计算的子节点,父节点染色的话,子节点必染色。
|
||||
|
||||
接下来就是计算 父节点1和该子节点2染色的话, 以子节点2 为根的 染色节点的最大数量 。
|
||||
|
||||
是:节点2不染色 且 以节点2为根节点的最大 染色数量 + 2, + 2 是因为 节点 1 和 节点2 要颜色了,染色节点增加两个。
|
||||
|
||||
代码:`dp[child][0] + 2`
|
||||
|
||||
细心的录友会发现,那我们只计算了 红色框里面的,那么框外 最大的染色数量是多少呢?
|
||||
|
||||

|
||||
|
||||
|
||||
先看 作为子节点的节点2 为根节点的最大染色数量是多少? 取一个最值,即 节点2染色 或者 不染色取最大值。
|
||||
|
||||
代码:`max(dp[child][0], dp[child][1])`
|
||||
|
||||
那么红框以外的 染色最大节点数量 就是 `dp[cur][0] - max(dp[child][0], dp[child][1])`
|
||||
|
||||
(cur是节点1,child是节点2)
|
||||
|
||||
红框以外的染色最大数量 + 父节点1和该子节点2染色的话 以子节点2 为根的 染色节点的最大数量 就是 节点1 染色的最大节点数量。
|
||||
|
||||
代码:
|
||||
|
||||
`dp[cur][1] = max(dp[cur][1], dp[cur][0] - max(dp[child][0], dp[child][1]) + dp[child][0] + 2);`
|
||||
|
||||
整体代码如下:
|
||||
|
||||
```CPP
|
||||
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
#include <cmath>
|
||||
#include <algorithm>
|
||||
#include <list>
|
||||
|
||||
using namespace std;
|
||||
|
||||
int maxN = 10005;
|
||||
vector<vector<int>> dp (maxN, vector<int>(2, 0));
|
||||
vector<list<int>> grid(maxN); // 邻接表
|
||||
vector<long> value(maxN); // 存储每个节点的权值
|
||||
|
||||
|
||||
// 在树上进行动态规划的函数
|
||||
void dpOnTheTree(int cur) {
|
||||
|
||||
for (int child : grid[cur]) {
|
||||
// 后序遍历,从下向上计算
|
||||
dpOnTheTree(child);
|
||||
// 情况一
|
||||
dp[cur][0] += max(dp[child][0], dp[child][1]);
|
||||
|
||||
}
|
||||
|
||||
// 计算dp[1] - 当前节点染色
|
||||
for (int child : grid[cur]) {
|
||||
long mul = value[cur] * value[child]; // 当前节点和相邻节点权值的乘积
|
||||
long sqrtNum = (long) sqrt(mul);
|
||||
|
||||
if (sqrtNum * sqrtNum == mul) { // 如果乘积是完全平方数
|
||||
// 情况二
|
||||
// dp[cur][0] 表示所有子节点 染色或者不染色的 最大染色数量
|
||||
// max(dp[child][0], dp[child][1]) 需要染色节点的孩子节点的最大染色数量
|
||||
// dp[cur][0] - max(dp[child][0], dp[child][1]) 除了要染色的节点及其子节点,其他孩子的最大染色数量
|
||||
// 最后 + dp[child][0] + 2 , 就是本节点染色的最大染色节点数量
|
||||
dp[cur][1] = max(dp[cur][1], dp[cur][0] - max(dp[child][0], dp[child][1]) + dp[child][0] + 2);
|
||||
}
|
||||
}
|
||||
|
||||
}
|
||||
|
||||
int main() {
|
||||
|
||||
int n;
|
||||
cin >> n; // 输入节点数量
|
||||
|
||||
// 读取节点权值
|
||||
for (int i = 1; i <= n; ++i) {
|
||||
cin >> value[i];
|
||||
}
|
||||
|
||||
// 构建树的邻接表
|
||||
for (int i = 1; i < n; ++i) {
|
||||
int x, y;
|
||||
cin >> x >> y;
|
||||
grid[x].push_back(y);
|
||||
}
|
||||
|
||||
// 从根节点(节点1)开始进行动态规划
|
||||
dpOnTheTree(1);
|
||||
|
||||
// 输出最大染色节点数量
|
||||
cout << max(dp[1][0], dp[1][1]) << endl;
|
||||
|
||||
return 0;
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
dp思路:https://www.cnblogs.com/ganyq/p/18111114
|
||||
|
||||
47
problems/kamacoder/0132.夹吃旗.md
Normal file
47
problems/kamacoder/0132.夹吃旗.md
Normal file
@ -0,0 +1,47 @@
|
||||
|
||||
# 132. 夹吃棋
|
||||
|
||||
[题目链接](https://kamacoder.com/problempage.php?pid=1209)
|
||||
|
||||
这道题是模拟题,但很多录友可能想复杂了。
|
||||
|
||||
行方向,白棋吃,只有这样的布局 `o*o`,黑棋吃,只有这样的布局 `*o*`
|
||||
|
||||
列方向也是同理的。
|
||||
|
||||
想到这一点,本题的代码就容易写了, C++代码如下:
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
using namespace std;
|
||||
int main() {
|
||||
int n;
|
||||
cin >> n;
|
||||
while (n--) {
|
||||
int black = 0, white = 0;
|
||||
vector<string> grid(3, "");
|
||||
// 判断行
|
||||
for (int i = 0; i < 3; i++) {
|
||||
cin >> grid[i];
|
||||
if (grid[i] == "o*o") white++;
|
||||
if (grid[i] == "*o*") black++;
|
||||
}
|
||||
// 判断列
|
||||
for (int i = 0; i < 3; i++) {
|
||||
string s;
|
||||
s += grid[0][i];
|
||||
s += grid[1][i];
|
||||
s += grid[2][i];
|
||||
if (s == "o*o") white++;
|
||||
if (s == "*o*") black++;
|
||||
}
|
||||
// 如果一个棋盘的局面没有一方被夹吃或者黑白双方都被对面夹吃,则认为是平局
|
||||
if ((!white && !black) || (white && black)) cout << "draw" << endl;
|
||||
// 白棋赢
|
||||
else if (white && !black) cout << "yukan" << endl;
|
||||
// 黑棋赢
|
||||
else cout << "kou" << endl;
|
||||
}
|
||||
}
|
||||
```
|
||||
48
problems/kamacoder/0133.小红买药.md
Normal file
48
problems/kamacoder/0133.小红买药.md
Normal file
@ -0,0 +1,48 @@
|
||||
|
||||
# 133. 小红买药
|
||||
|
||||
[题目链接](https://kamacoder.com/problempage.php?pid=1210)
|
||||
|
||||
本题是一道直观的模拟题,但也并不简单,很多情况容易漏了,笔试现场可能要多错几次 才能把情况都想到。
|
||||
|
||||
主要是三个情况:
|
||||
|
||||
* 小红没症状,药有副作用,统计加一,同时要给小红标记上症状
|
||||
* 小红有症状,药治不了,同时也没副症状 ,这时也要统计加一
|
||||
* 小红有症状,药可以治,给小红取消症状标记
|
||||
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
using namespace std;
|
||||
int main() {
|
||||
int n, m, q, u;
|
||||
cin >> n;
|
||||
string s;
|
||||
cin >> s;
|
||||
cin >> m;
|
||||
vector<string> a(m + 1); // 因为后面u是从1开始的
|
||||
vector<string> b(m + 1);
|
||||
for (int i = 1; i <= m; i++) {
|
||||
cin >> a[i] >> b[i];
|
||||
}
|
||||
cin >> q;
|
||||
while (q--) {
|
||||
cin >> u;
|
||||
int num = 0;
|
||||
for (int i = 0; i < n; i++) {
|
||||
// s 没症状,但b给了副作用,统计num的同时,要给s标记上症状
|
||||
if (s[i] == '0' && b[u][i] == '1') {
|
||||
num ++;
|
||||
s[i] = '1';
|
||||
}
|
||||
// s 有症状,但 a治不了,b也没副症状
|
||||
else if (s[i] == '1' && a[u][i] == '0' && a[u][i] == '0') num++;
|
||||
// s 有症状,a 可以治
|
||||
else if (s[i] == '1' && a[u][i] == '1') s[i] = '0';
|
||||
}
|
||||
cout << num << endl;
|
||||
}
|
||||
}
|
||||
```
|
||||
77
problems/kamacoder/0134.皇后移动的最小步数.md
Normal file
77
problems/kamacoder/0134.皇后移动的最小步数.md
Normal file
@ -0,0 +1,77 @@
|
||||
|
||||
# 134. 皇后移动的最小步数
|
||||
|
||||
[题目链接](https://kamacoder.com/problempage.php?pid=1211)
|
||||
|
||||
本题和 [代码随想录-不同路径](https://www.programmercarl.com/0062.%E4%B8%8D%E5%90%8C%E8%B7%AF%E5%BE%84.html) 有一些类似。
|
||||
|
||||
关键是弄清楚递推公式
|
||||
|
||||
一共分三个情况,
|
||||
|
||||
情况一,向右移动:
|
||||
|
||||
然后从 (i, j) 再向右走 到 (i, k)。 无论k 多大,步数只加1 :
|
||||
|
||||
`dp[i][k] = dp[i][j] + 1`
|
||||
|
||||
那么 `dp[i][k]` 也有可能 从其他方向得到,例如 从上到下, 或者斜上方到达 dp[i][k]
|
||||
|
||||
本题我们要求最小步数,所以取最小值:`dp[i][k] = min(dp[i][k], dp[i][j] + 1);`
|
||||
|
||||
情况二,向下移动:
|
||||
|
||||
从 (i, j) 再向下走 到 (k, j)。 无论k 多大,步数只加1 :
|
||||
|
||||
`dp[k][j] = dp[i][j] + 1;`
|
||||
|
||||
同理 `dp[i][k]` 也有可能 从其他方向得到,取最小值:`dp[k][j] = min(dp[k][j], dp[i][j] + 1);`
|
||||
|
||||
情况三,右下方移动:
|
||||
|
||||
从 (i, j) 再向右下方移动 到 (i + k, j + k)。 无论k 多大,步数只加1 :
|
||||
|
||||
`dp[i + k][j + k] = dp[i][j] + 1`
|
||||
|
||||
同理 `dp[i + k][j + k]` 也有可能 从其他方向得到,取最小值:`dp[i + k][j + k] = min(dp[i + k][j + k], dp[i][j] + 1);`
|
||||
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
using namespace std;
|
||||
const int INF = 4e6; // 最多步数也就是 2000 * 2000
|
||||
int main() {
|
||||
int n, m;
|
||||
cin >> n >> m;
|
||||
vector<vector<char>> grid(n, vector<char>(m));
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
cin >> grid[i][j];
|
||||
}
|
||||
}
|
||||
vector<vector<int>> dp(n, vector<int>(m, INF));
|
||||
dp[0][0] = 0;
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
if (grid[i][j] == '*') continue;
|
||||
// 向右移动k个格子
|
||||
for (int k = j + 1; k < m && grid[i][k] == '.'; k++) {
|
||||
dp[i][k] = min(dp[i][k], dp[i][j] + 1);
|
||||
}
|
||||
// 向下移动 k个格子
|
||||
for (int k = i + 1; k < n && grid[k][j] == '.'; k++) {
|
||||
dp[k][j] = min(dp[k][j], dp[i][j] + 1);
|
||||
}
|
||||
// 向右下移动k个格子
|
||||
for (int k = 1; i + k < n && j + k < m && grid[i + k][j + k] == '.'; k++) {
|
||||
dp[i + k][j + k] = min(dp[i + k][j + k], dp[i][j] + 1);
|
||||
}
|
||||
}
|
||||
}
|
||||
if (dp[n - 1][m - 1] == INF) cout << -1 << endl;
|
||||
else cout << dp[n - 1][m - 1] << endl;
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
50
problems/kamacoder/字符串处理器.md
Normal file
50
problems/kamacoder/字符串处理器.md
Normal file
@ -0,0 +1,50 @@
|
||||
|
||||
|
||||
```CPP
|
||||
#include<bits/stdc++.h>
|
||||
using namespace std;
|
||||
int main() {
|
||||
int index = 0;
|
||||
long long optNum;
|
||||
string s;
|
||||
string cmd;
|
||||
while(cin >> cmd){
|
||||
//cout << s << endl;
|
||||
if(cmd == "insert"){
|
||||
string buff;
|
||||
cin >> buff;
|
||||
s.insert(index, buff);
|
||||
index += buff.size();
|
||||
}
|
||||
else if(cmd == "move"){
|
||||
cin >> optNum;
|
||||
if(optNum > 0 && index + optNum <= s.size()) index += optNum;
|
||||
if(optNum < 0 && index >= -optNum) index += optNum;
|
||||
}
|
||||
else if(cmd == "delete"){
|
||||
cin >> optNum;
|
||||
if(index >= optNum && optNum != 0){
|
||||
s.erase(index - optNum, optNum);
|
||||
index -= optNum;
|
||||
}
|
||||
}
|
||||
else if(cmd == "copy"){
|
||||
if(index > 0) {
|
||||
string tmp = s.substr(0, index);
|
||||
s.insert(index, tmp);
|
||||
}
|
||||
}
|
||||
else if(cmd == "end"){
|
||||
for(int i = 0; i < index; i++) {
|
||||
cout << s[i];
|
||||
}
|
||||
cout << '|';
|
||||
for(int i = index; i < s.size(); i++){
|
||||
cout << s[i];
|
||||
}
|
||||
break;
|
||||
}
|
||||
}
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
47
problems/kamacoder/获取连通的相邻节点列表.md
Normal file
47
problems/kamacoder/获取连通的相邻节点列表.md
Normal file
@ -0,0 +1,47 @@
|
||||
|
||||
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
#include <algorithm>
|
||||
#include <unordered_set>
|
||||
using namespace std;
|
||||
int main() {
|
||||
unordered_set<int> uset;
|
||||
int n, a;
|
||||
cin >> n;
|
||||
while (n--) {
|
||||
cin >> a;
|
||||
uset.insert(a);
|
||||
}
|
||||
int m, x, vlan_id;
|
||||
long long tb;
|
||||
vector<long long> vecTB;
|
||||
cin >> m;
|
||||
while(m--) {
|
||||
cin >> tb;
|
||||
cin >> x;
|
||||
vector<long long> vecVlan_id(x);
|
||||
for (int i = 0; i < x; i++) {
|
||||
cin >> vecVlan_id[i];
|
||||
}
|
||||
for (int i = 0; i < x; i++) {
|
||||
if (uset.find(vecVlan_id[i]) != uset.end()) {
|
||||
vecTB.push_back(tb);
|
||||
break;
|
||||
}
|
||||
}
|
||||
|
||||
}
|
||||
|
||||
cout << vecTB.size() << endl;
|
||||
if (vecTB.size() != 0) {
|
||||
sort(vecTB.begin(), vecTB.end());
|
||||
for (int i = 0; i < vecTB.size() ; i++) cout << vecTB[i] << " ";
|
||||
}
|
||||
|
||||
|
||||
}
|
||||
|
||||
```
|
||||
@ -188,7 +188,7 @@ python代码
|
||||
大家提交代码的热情太高了,我有时候根本处理不过来,但我必须当天处理完,否则第二天代码冲突会越来越多。
|
||||
<div align="center"><img src='https://code-thinking-1253855093.file.myqcloud.com/pics/20210514091457392.png' width=500 alt=''></img></div>
|
||||
|
||||
一天晚分别有两位录友提交了 30多道 java代码,全部冲突,解决冲突处理的我脖子疼[哭]
|
||||
一天晚上分别有两位录友提交了 30多道 java代码,全部冲突,解决冲突处理的我脖子疼[哭]
|
||||
|
||||
那么在处理冲突的时候 保留谁的代码,删点谁的代码呢?
|
||||
|
||||
|
||||
@ -671,6 +671,62 @@ public void Traversal(TreeNode cur, IList<int> res)
|
||||
}
|
||||
```
|
||||
|
||||
### PHP
|
||||
```php
|
||||
// 144.前序遍历
|
||||
function preorderTraversal($root) {
|
||||
$output = [];
|
||||
$this->traversal($root, $output);
|
||||
return $output;
|
||||
}
|
||||
|
||||
function traversal($root, array &$output) {
|
||||
if ($root->val === null) {
|
||||
return;
|
||||
}
|
||||
|
||||
$output[] = $root->val;
|
||||
$this->traversal($root->left, $output);
|
||||
$this->traversal($root->right, $output);
|
||||
}
|
||||
```
|
||||
```php
|
||||
// 94.中序遍历
|
||||
function inorderTraversal($root) {
|
||||
$output = [];
|
||||
$this->traversal($root, $output);
|
||||
return $output;
|
||||
}
|
||||
|
||||
function traversal($root, array &$output) {
|
||||
if ($root->val === null) {
|
||||
return;
|
||||
}
|
||||
|
||||
$this->traversal($root->left, $output);
|
||||
$output[] = $root->val;
|
||||
$this->traversal($root->right, $output);
|
||||
}
|
||||
```
|
||||
```php
|
||||
// 145.后序遍历
|
||||
function postorderTraversal($root) {
|
||||
$output = [];
|
||||
$this->traversal($root, $output);
|
||||
return $output;
|
||||
}
|
||||
|
||||
function traversal($root, array &$output) {
|
||||
if ($root->val === null) {
|
||||
return;
|
||||
}
|
||||
|
||||
$this->traversal($root->left, $output);
|
||||
$this->traversal($root->right, $output);
|
||||
$output[] = $root->val;
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
<p align="center">
|
||||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||||
|
||||
@ -55,7 +55,7 @@
|
||||
|
||||
**构造二叉树有三个注意的点:**
|
||||
|
||||
* 分割时候,坚持区间不变量原则,左闭右开,或者左闭又闭。
|
||||
* 分割时候,坚持区间不变量原则,左闭右开,或者左闭右闭。
|
||||
* 分割的时候,注意后序 或者 前序已经有一个节点作为中间节点了,不能继续使用了。
|
||||
* 如何使用切割后的后序数组来切合中序数组?利用中序数组大小一定是和后序数组的大小相同这一特点来进行切割。
|
||||
|
||||
|
||||
Reference in New Issue
Block a user