mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-06 23:28:29 +08:00
Update
This commit is contained in:
@ -56,10 +56,66 @@
|
||||
|
||||
|
||||
|
||||
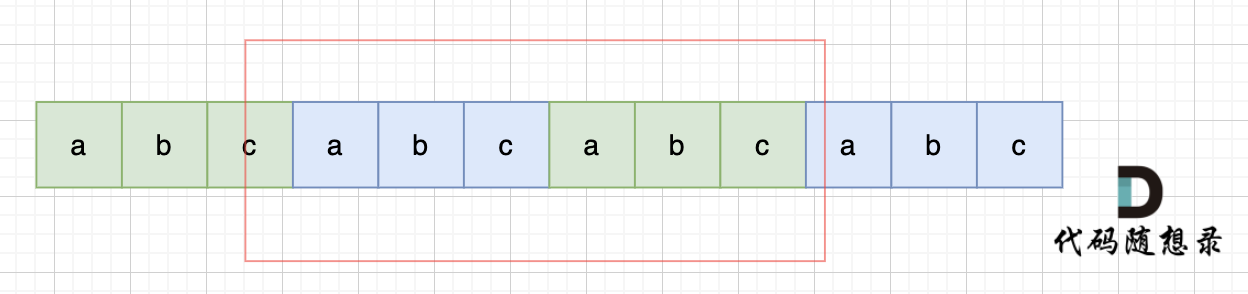
所以判断字符串s是否由重复子串组成,只要两个s拼接在一起,里面还出现一个s的话,就说明是由重复子串组成。
|
||||
|
||||
当然,我们在判断 s + s 拼接的字符串里是否出现一个s的的时候,**要刨除 s + s 的首字符和尾字符**,这样避免在s+s中搜索出原来的s,我们要搜索的是中间拼接出来的s。
|
||||
|
||||
|
||||
以上证明的充分性,接下来证明必要性:
|
||||
|
||||
如果有一个字符串s,在 s + s 拼接后, 不算首尾字符,如果能凑成s字符串,说明s 一定是重复子串组成。
|
||||
|
||||
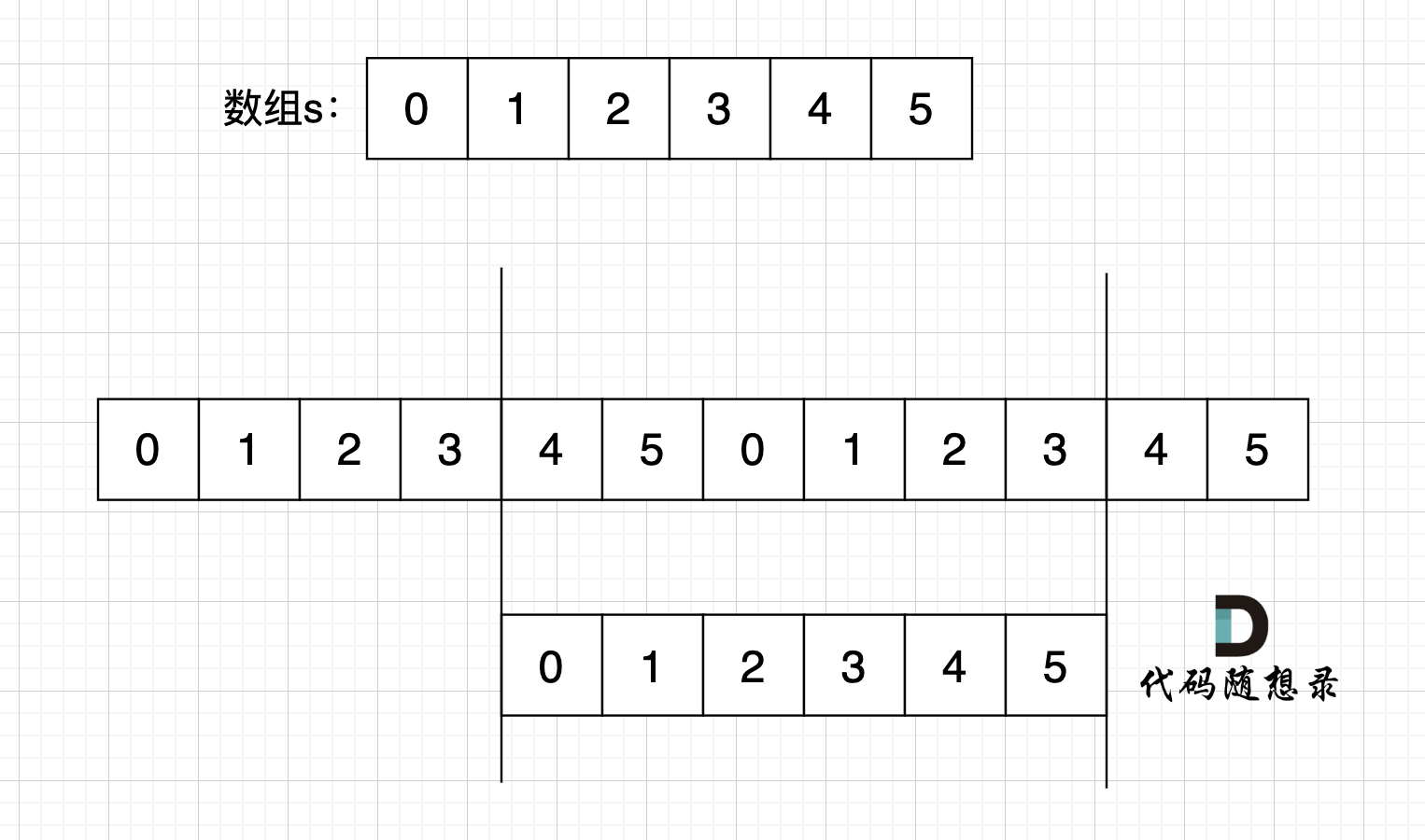
如图,字符串s,图中数字为数组下标,在 s + s 拼接后, 不算首尾字符,中间凑成s字符串。
|
||||
|
||||
|
||||
|
||||
图中,因为中间拼接成了s,根据红色框 可以知道 s[4] = s[0], s[5] = s[1], s[0] = s[2], s[1] = s[3] s[2] = s[4] ,s[3] = s[5]
|
||||
|
||||

|
||||
|
||||
以上相等关系我们串联一下:
|
||||
|
||||
s[4] = s[0] = s[2]
|
||||
|
||||
s[5] = s[1] = s[3]
|
||||
|
||||
|
||||
即:s[4],s[5] = s[0],s[1] = s[2],s[3]
|
||||
|
||||
**说明这个字符串,是由 两个字符 s[0] 和 s[1] 重复组成的**!
|
||||
|
||||
这里可以有录友想,凭什么就是这样组成的s呢,我换一个方式组成s 行不行,如图:
|
||||
|
||||

|
||||
|
||||
s[3] = s[0],s[4] = s[1] ,s[5] = s[2],s[0] = s[3],s[1] = s[4],s[2] = s[5]
|
||||
|
||||
以上相等关系串联:
|
||||
|
||||
s[3] = s[0]
|
||||
|
||||
s[1] = s[4]
|
||||
|
||||
s[2] = s[5]
|
||||
|
||||
s[0] s[1] s[2] = s[3] s[4] s[5]
|
||||
|
||||
和以上推导过程一样,最后可以推导出,这个字符串是由 s[0] ,s[1] ,s[2] 重复组成。
|
||||
|
||||
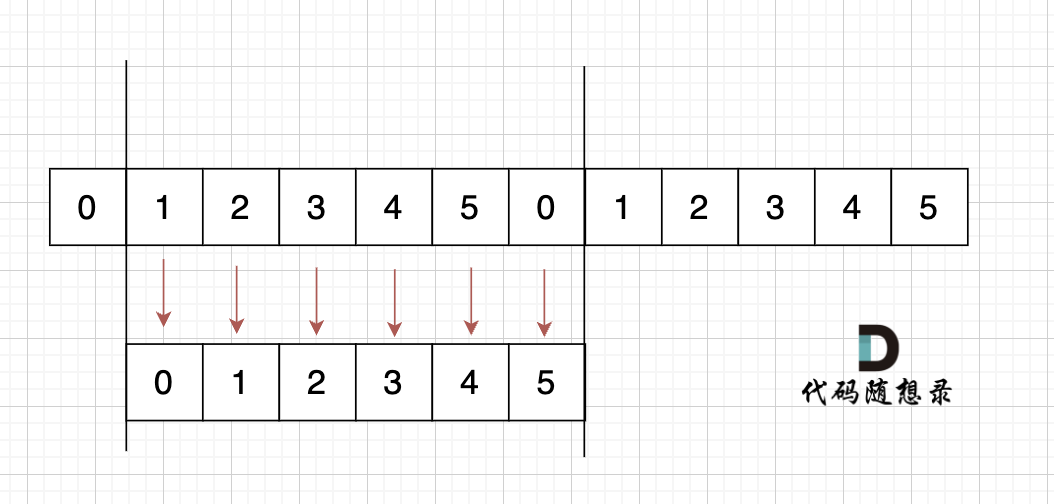
如果是这样的呢,如图:
|
||||
|
||||
|
||||
|
||||
s[1] = s[0],s[2] = s[1] ,s[3] = s[2],s[4] = s[3],s[5] = s[4],s[0] = s[5]
|
||||
|
||||
以上相等关系串联
|
||||
|
||||
s[0] = s[1] = s[2] = s[3] = s[4] = s[5]
|
||||
|
||||
最后可以推导出,这个字符串是由 s[0] 重复组成。
|
||||
|
||||
以上 充分和必要性都证明了,所以判断字符串s是否由重复子串组成,只要两个s拼接在一起,里面还出现一个s的话,就说明是由重复子串组成。
|
||||
|
||||
|
||||
代码如下:
|
||||
|
||||
```CPP
|
||||
@ -76,13 +132,14 @@ public:
|
||||
* 时间复杂度: O(n)
|
||||
* 空间复杂度: O(1)
|
||||
|
||||
不过这种解法还有一个问题,就是 我们最终还是要判断 一个字符串(s + s)是否出现过 s 的过程,大家可能直接用contains,find 之类的库函数。 却忽略了实现这些函数的时间复杂度(暴力解法是m * n,一般库函数实现为 O(m + n))。
|
||||
不过这种解法还有一个问题,就是 我们最终还是要判断 一个字符串(s + s)是否出现过 s 的过程,大家可能直接用contains,find 之类的库函数, 却忽略了实现这些函数的时间复杂度(暴力解法是m * n,一般库函数实现为 O(m + n))。
|
||||
|
||||
如果我们做过 [28.实现strStr](https://programmercarl.com/0028.实现strStr.html) 题目的话,其实就知道,**实现一个 高效的算法来判断 一个字符串中是否出现另一个字符串是很复杂的**,这里就涉及到了KMP算法。
|
||||
|
||||
### KMP
|
||||
|
||||
#### 为什么会使用KMP
|
||||
|
||||
以下使用KMP方式讲解,强烈建议大家先把以下两个视频看了,理解KMP算法,再来看下面讲解,否则会很懵。
|
||||
|
||||
* [视频讲解版:帮你把KMP算法学个通透!(理论篇)](https://www.bilibili.com/video/BV1PD4y1o7nd/)
|
||||
@ -91,7 +148,9 @@ public:
|
||||
|
||||
在一个串中查找是否出现过另一个串,这是KMP的看家本领。那么寻找重复子串怎么也涉及到KMP算法了呢?
|
||||
|
||||
KMP算法中next数组为什么遇到字符不匹配的时候可以找到上一个匹配过的位置继续匹配,靠的是有计算好的前缀表。 前缀表里,统计了各个位置为终点字符串的最长相同前后缀的长度。
|
||||
KMP算法中next数组为什么遇到字符不匹配的时候可以找到上一个匹配过的位置继续匹配,靠的是有计算好的前缀表。
|
||||
|
||||
前缀表里,统计了各个位置为终点字符串的最长相同前后缀的长度。
|
||||
|
||||
那么 最长相同前后缀和重复子串的关系又有什么关系呢。
|
||||
|
||||
@ -100,16 +159,61 @@ KMP算法中next数组为什么遇到字符不匹配的时候可以找到上一
|
||||
* 前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串;
|
||||
* 后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串
|
||||
|
||||
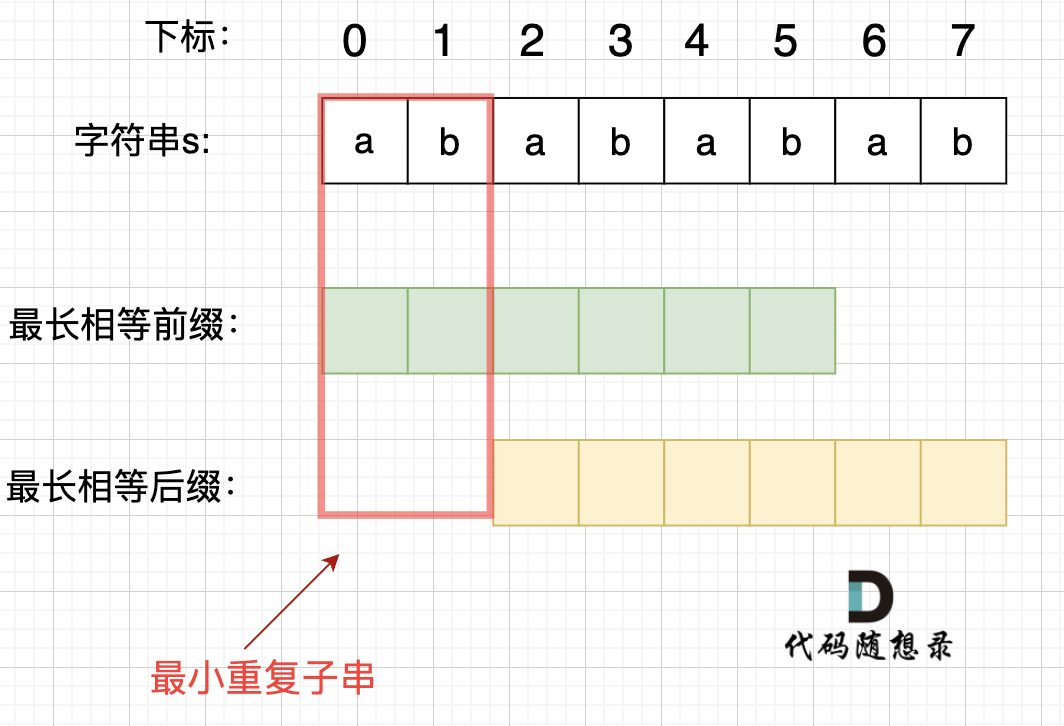
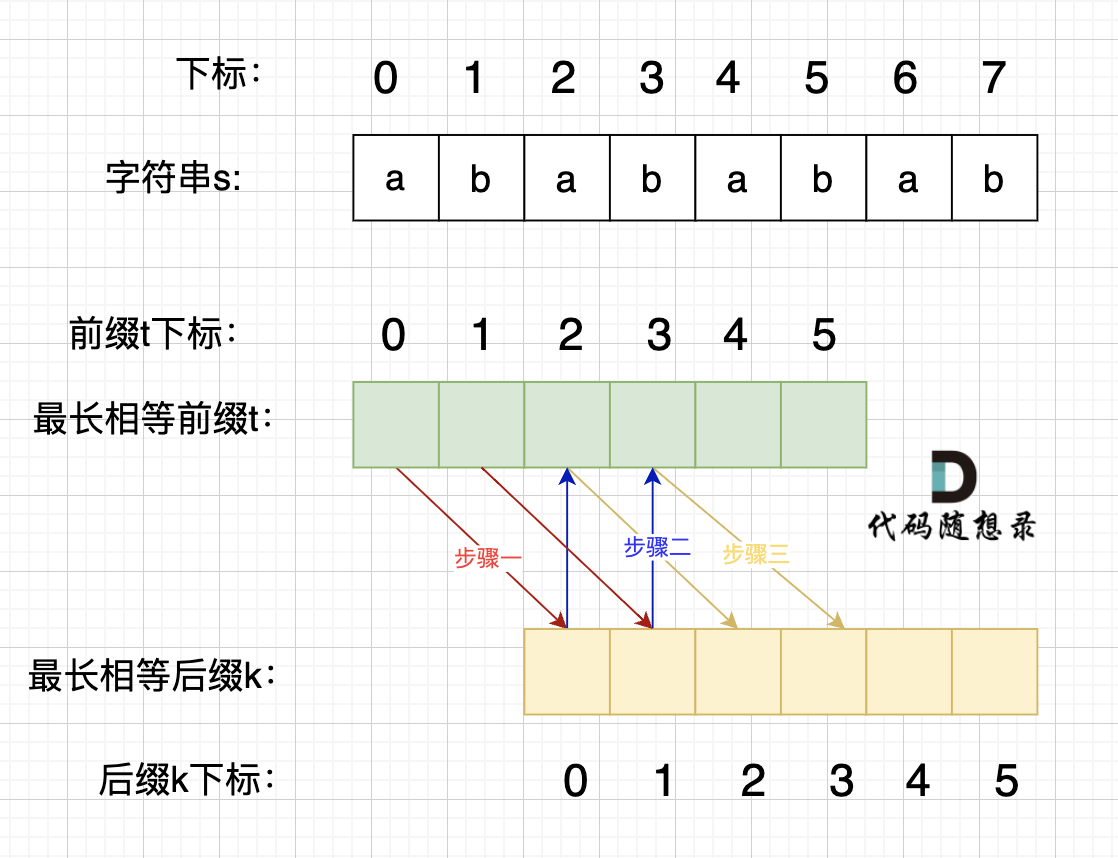
在由重复子串组成的字符串中,最长相等前后缀不包含的子串就是最小重复子串,这里拿字符串s:abababab 来举例,ab就是最小重复单位,如图所示:
|
||||
#### 充分性证明
|
||||
|
||||
|
||||
如果一个字符串s是由重复子串组成,那么 最长相等前后缀不包含的子串一定是字符串s的最小重复子串。
|
||||
|
||||
证明: 如果s 是有是有最小重复子串p组成。
|
||||
|
||||
#### 如何找到最小重复子串
|
||||
即 s = n * p
|
||||
|
||||
这里有同学就问了,为啥一定是开头的ab呢。 其实最关键还是要理解 最长相等前后缀,如图:
|
||||
那么相同前后缀可以是这样:
|
||||
|
||||
|
||||

|
||||
|
||||
也可以是这样:
|
||||
|
||||

|
||||
|
||||
最长的相等前后缀,也就是这样:
|
||||
|
||||

|
||||
|
||||
这里有录友就想:如果字符串s 是有是有最小重复子串p组成,最长相等前后缀就不能更长一些? 例如这样:
|
||||
|
||||
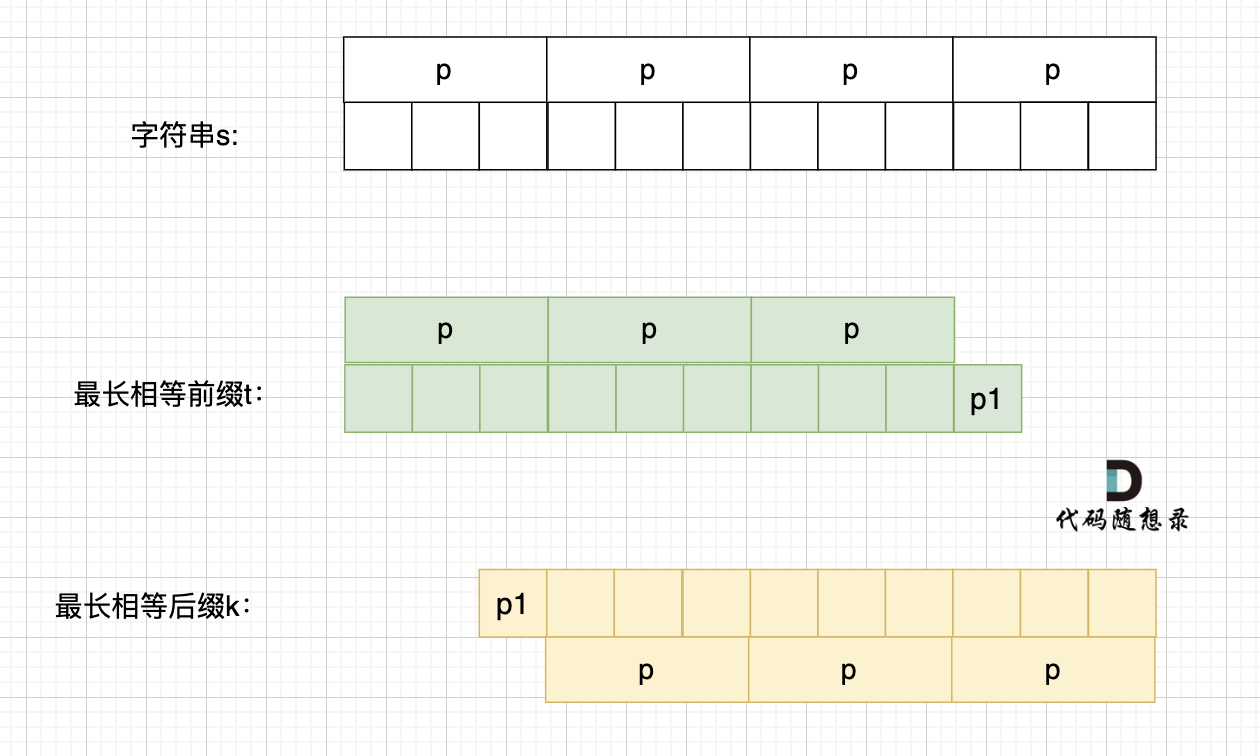
|
||||
|
||||
如果这样的话,因为前后缀要相同,所以 p2 = p1,p3 = p2,如图:
|
||||
|
||||
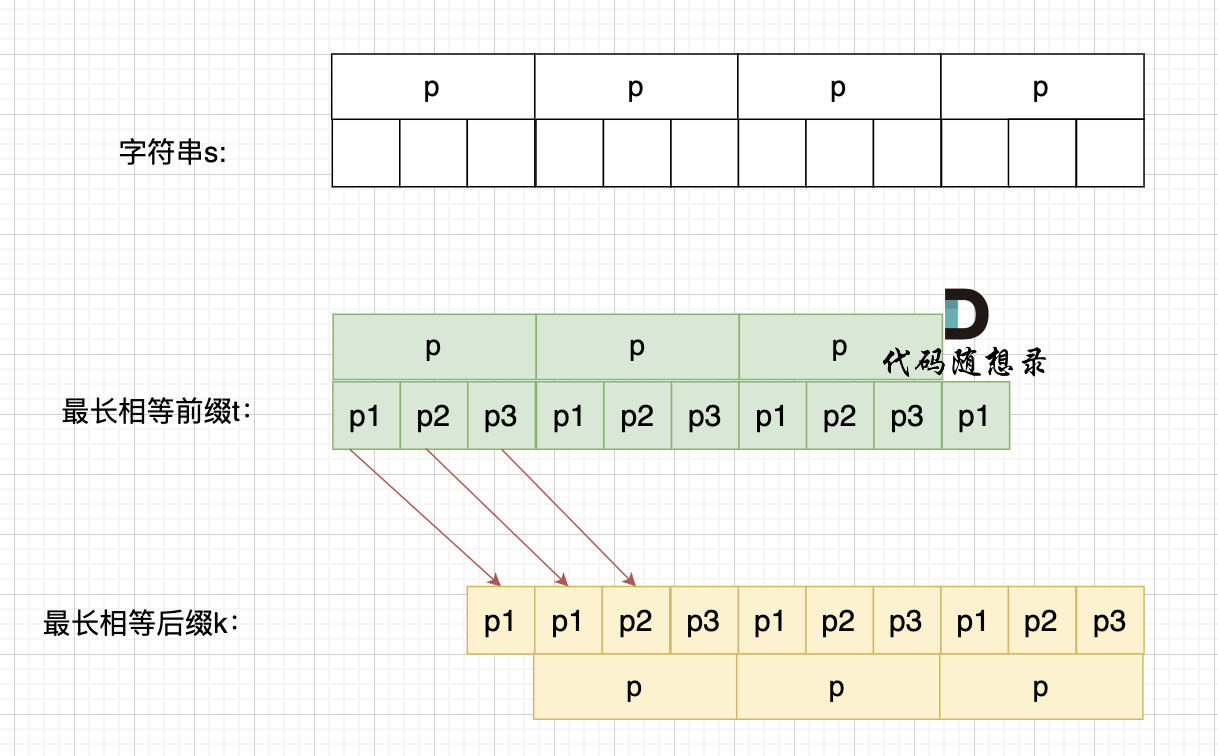
|
||||
|
||||
p2 = p1,p3 = p2 即: p1 = p2 = p3
|
||||
|
||||
说明 p = p1 * 3。
|
||||
|
||||
这样p 就不是最小重复子串了,不符合我们定义的条件。
|
||||
|
||||
所以,**如果这个字符串s是由重复子串组成,那么最长相等前后缀不包含的子串是字符串s的最小重复子串**。
|
||||
|
||||
#### 必要性证明
|
||||
|
||||
以上是充分性证明,以下是必要性证明:
|
||||
|
||||
**如果 最长相等前后缀不包含的子串是字符串s的最小重复子串, 那么字符串s一定由重复子串组成吗**?
|
||||
|
||||
最长相等前后缀不包含的子串已经是字符串s的最小重复子串,那么字符串s一定由重复子串组成,这个不需要证明了。
|
||||
|
||||
关键是要要证明:最长相等前后缀不包含的子串什么时候才是字符串s的最小重复子串呢。
|
||||
|
||||
情况一, 最长相等前后缀不包含的子串的长度 比 字符串s的一半的长度还大,那一定不是字符串s的重复子串
|
||||
|
||||
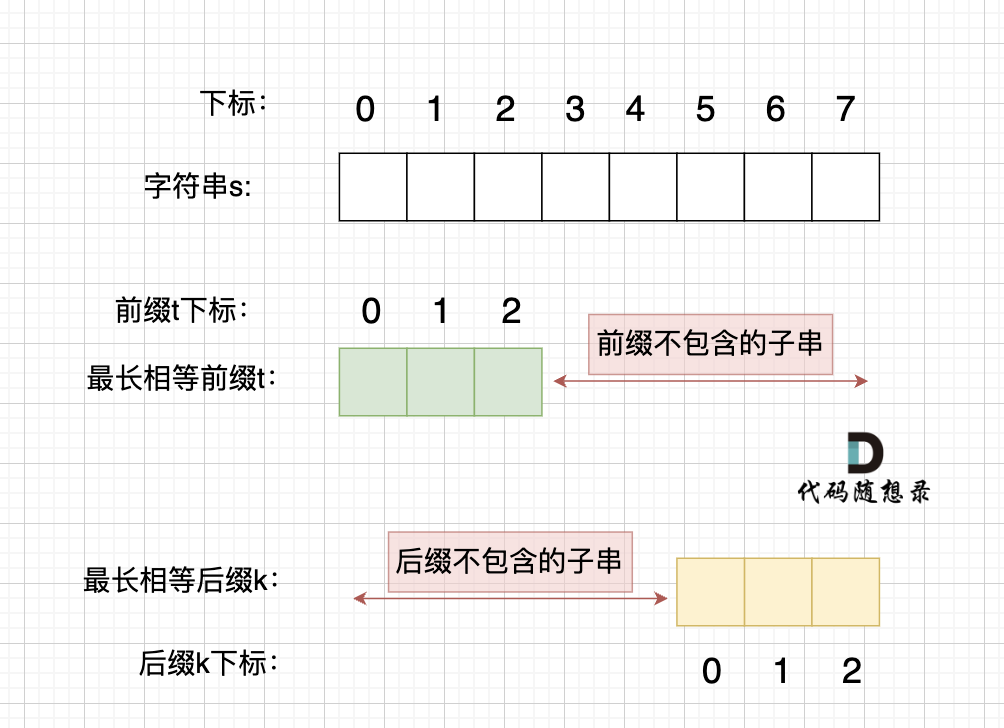
|
||||
|
||||
--------------
|
||||
|
||||
情况二,最长相等前后缀不包含的子串的长度 可以被 字符串s的长度整除,如图:
|
||||
|
||||
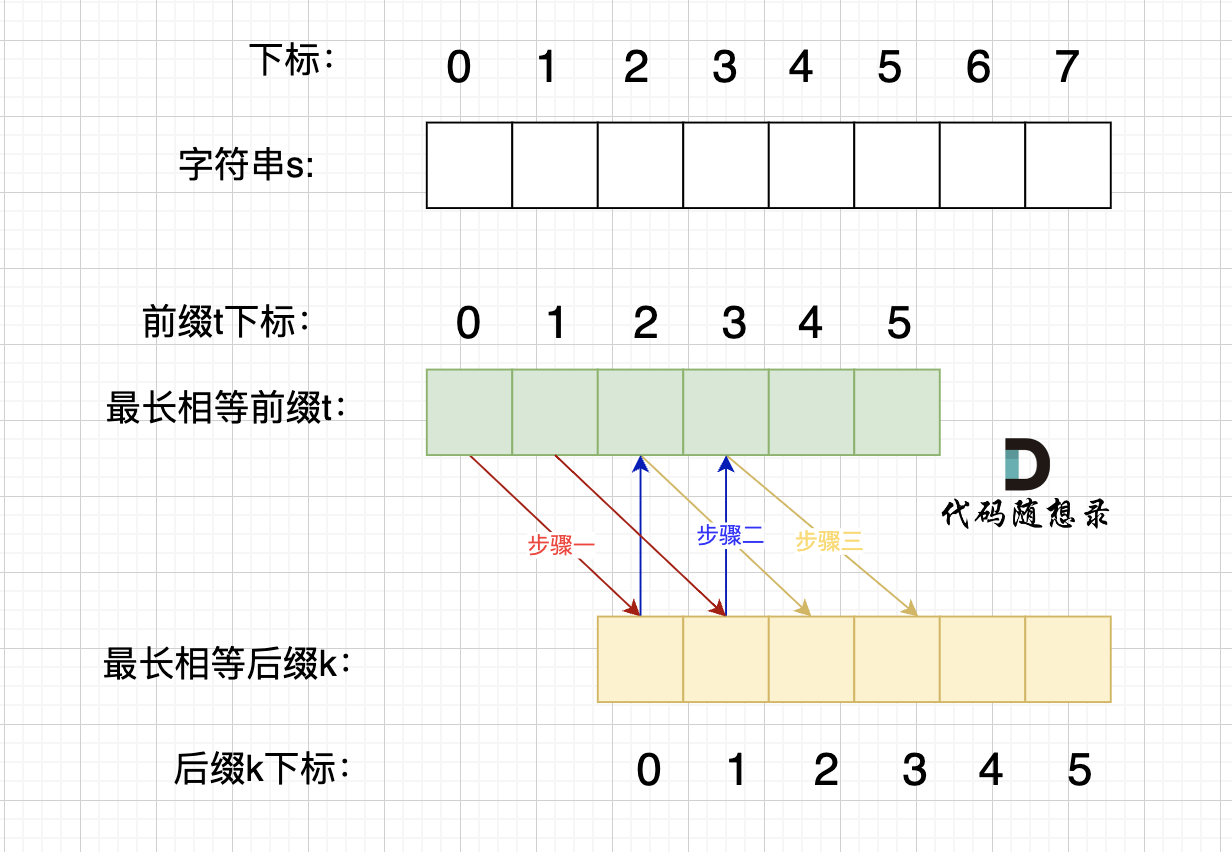
|
||||
|
||||
步骤一:因为 这是相等的前缀和后缀,t[0] 与 k[0]相同, t[1] 与 k[1]相同,所以 s[0] 一定和 s[2]相同,s[1] 一定和 s[3]相同,即:,s[0]s[1]与s[2]s[3]相同 。
|
||||
|
||||
@ -121,28 +225,79 @@ KMP算法中next数组为什么遇到字符不匹配的时候可以找到上一
|
||||
|
||||
所以字符串s,s[0]s[1]与s[2]s[3]相同, s[2]s[3] 与 s[4]s[5]相同,s[4]s[5] 与 s[6]s[7] 相同。
|
||||
|
||||
正是因为 最长相等前后缀的规则,当一个字符串由重复子串组成的,最长相等前后缀不包含的子串就是最小重复子串。
|
||||
可以推出,在由重复子串组成的字符串中,最长相等前后缀不包含的子串就是最小重复子串。
|
||||
|
||||
#### 简单推理
|
||||
即 s[0]s[1] 是最小重复子串
|
||||
|
||||
这里再给出一个数学推导,就容易理解很多。
|
||||
|
||||
假设字符串s使用多个重复子串构成(这个子串是最小重复单位),重复出现的子字符串长度是x,所以s是由n * x组成。
|
||||
以上推导中,录友可能想,你怎么知道 s[0] 和 s[1] 就不相同呢? s[0] 为什么就不能使最小重复子串。
|
||||
|
||||
因为字符串s的最长相同前后缀的长度一定是不包含s本身,所以 最长相同前后缀长度必然是m * x,而且 n - m = 1,(这里如果不懂,看上面的推理)
|
||||
如果 s[0] 和 s[1] 也相同,同时 s[0]s[1]与s[2]s[3]相同,s[2]s[3] 与 s[4]s[5]相同,s[4]s[5] 与 s[6]s[7] 相同,那么这个字符串就是有一个字符构成的字符串。
|
||||
|
||||
所以如果 nx % (n - m)x = 0,就可以判定有重复出现的子字符串。
|
||||
那么它的最长相同前后缀,就不是上图中的前后缀,而是这样的的前后缀:
|
||||
|
||||
next 数组记录的就是最长相同前后缀 [字符串:KMP算法精讲](https://programmercarl.com/0028.实现strStr.html) 这里介绍了什么是前缀,什么是后缀,什么又是最长相同前后缀), 如果 next[len - 1] != -1,则说明字符串有最长相同的前后缀(就是字符串里的前缀子串和后缀子串相同的最长长度)。
|
||||
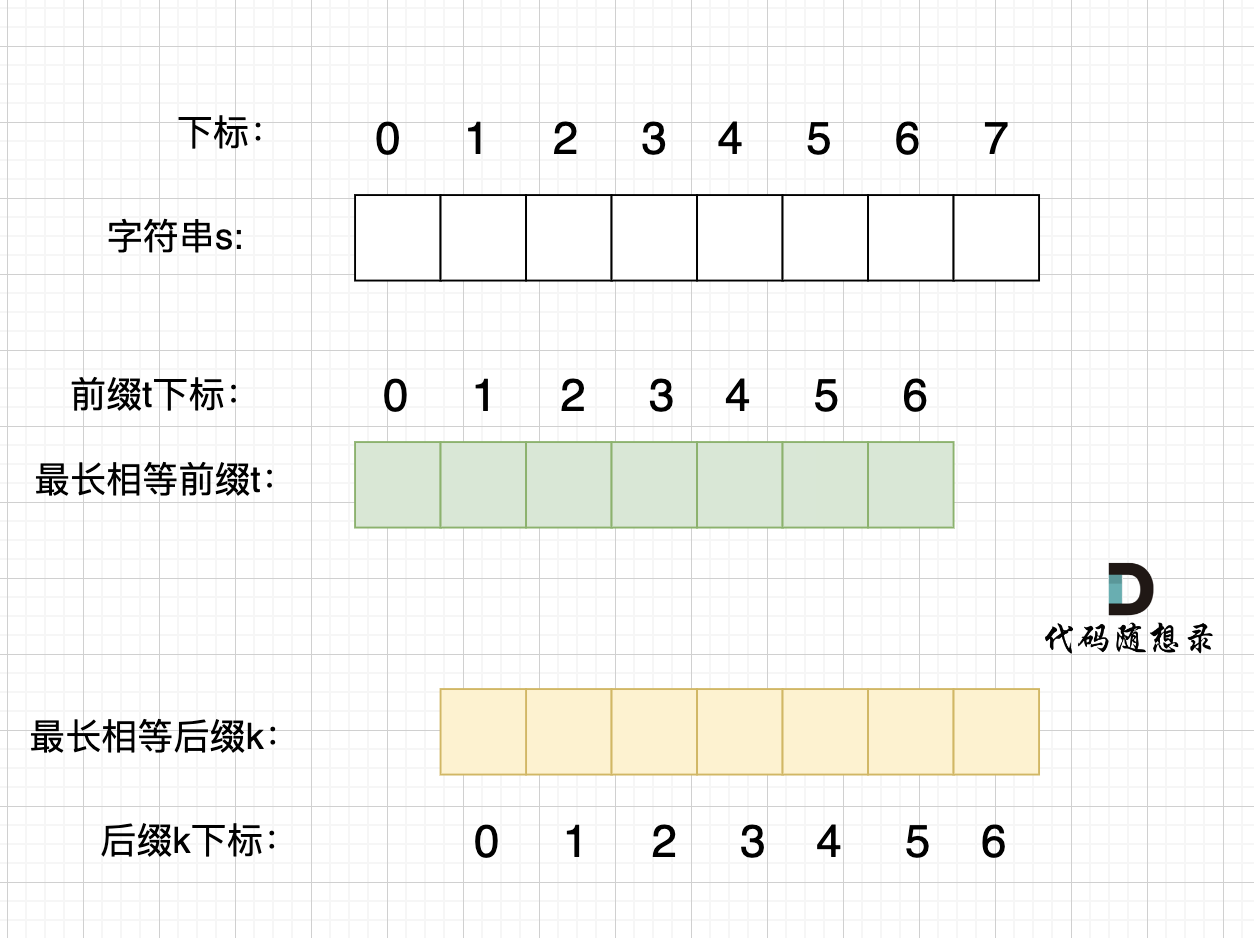
|
||||
|
||||
最长相等前后缀的长度为:next[len - 1] + 1。(这里的next数组是以统一减一的方式计算的,因此需要+1,两种计算next数组的具体区别看这里:[字符串:KMP算法精讲](https://programmercarl.com/0028.实现strStr.html))
|
||||
录友可能再问,由一个字符组成的字符串,最长相等前后缀凭什么就是这样的。
|
||||
|
||||
有这种疑惑的录友,就是还不知道 最长相等前后缀 是怎么算的。
|
||||
|
||||
可以看这里:[KMP讲解](https://programmercarl.com/0028.%E5%AE%9E%E7%8E%B0strStr.html),再去回顾一下。
|
||||
|
||||
或者说,自己举个例子,`aaaaaa`,这个字符串,他的最长相等前后缀是什么?
|
||||
|
||||
同上以上推导,最长相等前后缀不包含的子串的长度只要被 字符串s的长度整除,就是一定是最小重复子串。
|
||||
|
||||
----------------
|
||||
|
||||
**情况三,最长相等前后缀不包含的子串的长度 不被 字符串s的长度整除得情况**,如图:
|
||||
|
||||
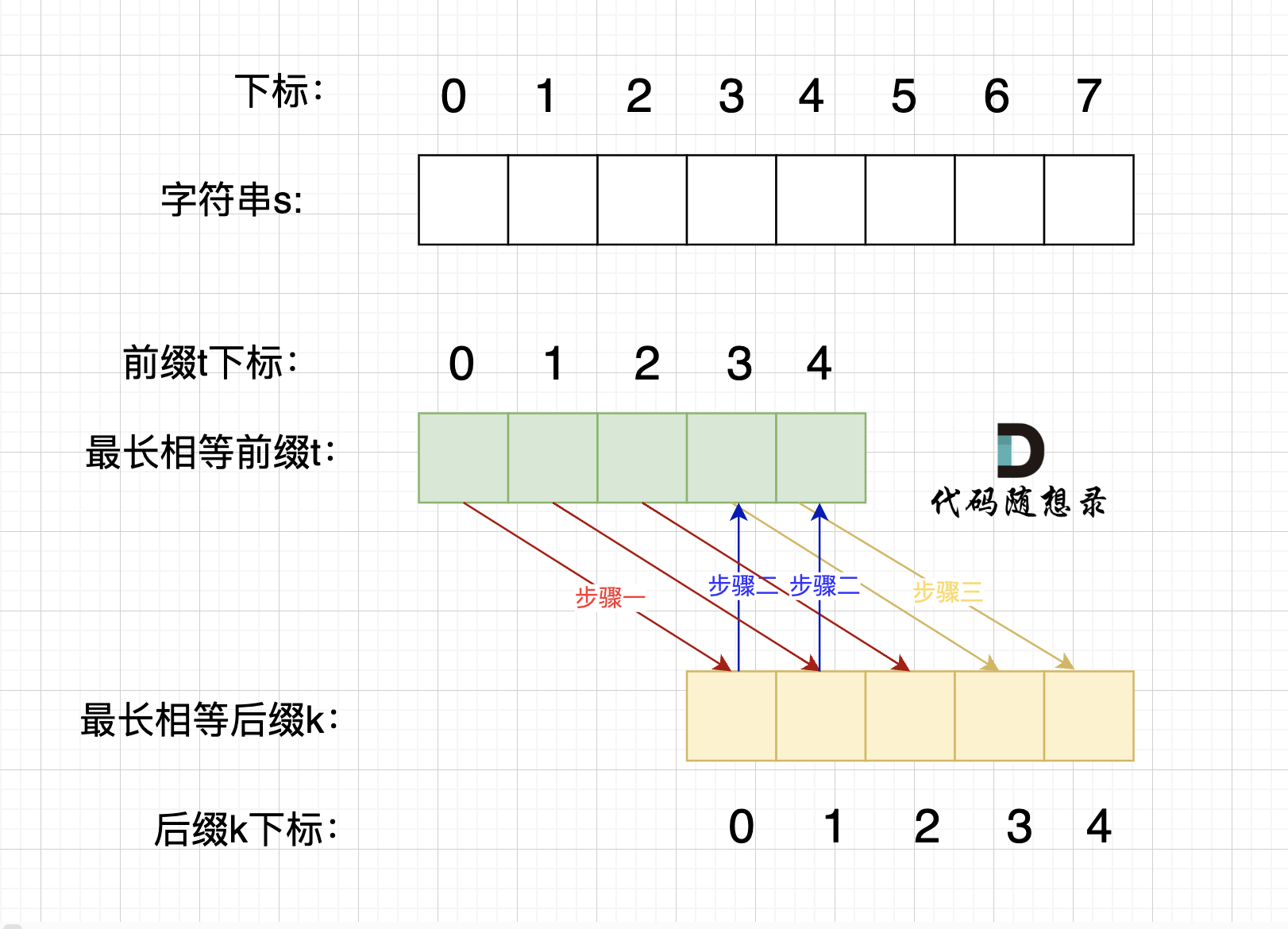
|
||||
|
||||
|
||||
步骤一:因为 这是相等的前缀和后缀,t[0] 与 k[0]相同, t[1] 与 k[1]相同,t[2] 与 k[2]相同。
|
||||
|
||||
所以 s[0] 与 s[3]相同,s[1] 与 s[4]相同,s[2] 与s[5],即:,s[0]s[1]与s[2]s[3]相同 。
|
||||
|
||||
步骤二: 因为在同一个字符串位置,所以 t[3] 与 k[0]相同,t[4] 与 k[1]相同。
|
||||
|
||||
|
||||
步骤三: 因为 这是相等的前缀和后缀,t[3] 与 k[3]相同 ,t[4]与k[5] 相同,所以,s[3]一定和s[6]相同,s[4]一定和s[7]相同,即:s[3]s[4] 与 s[6]s[7]相同。
|
||||
|
||||
|
||||
以上推导,可以得出 s[0],s[1],s[2] 与 s[3],s[4],s[5] 相同,s[3]s[4] 与 s[6]s[7]相同。
|
||||
|
||||
那么 最长相等前后缀不包含的子串的长度 不被 字符串s的长度整除 ,就不是s的重复子串
|
||||
|
||||
-----------
|
||||
|
||||
充分条件:如果字符串s是由重复子串组成,那么 最长相等前后缀不包含的子串 一定是 s的最小重复子串。
|
||||
|
||||
必要条件:如果字符串s的最长相等前后缀不包含的子串 是 s最小重复子串,那么 s是由重复子串组成。
|
||||
|
||||
在必要条件,这个是 显而易见的,都已经假设 最长相等前后缀不包含的子串 是 s的最小重复子串了,那s必然是重复子串。
|
||||
|
||||
关键是需要证明, 字符串s的最长相等前后缀不包含的子串 什么时候才是 s最小重复子串。
|
||||
|
||||
同上我们证明了,当 最长相等前后缀不包含的子串的长度 可以被 字符串s的长度整除,那么不包含的子串 就是s的最小重复子串。
|
||||
|
||||
|
||||
-------------
|
||||
|
||||
|
||||
### 代码分析
|
||||
|
||||
next 数组记录的就是最长相同前后缀( [字符串:KMP算法精讲](https://programmercarl.com/0028.实现strStr.html)), 如果 `next[len - 1] != -1`,则说明字符串有最长相同的前后缀(就是字符串里的前缀子串和后缀子串相同的最长长度)。
|
||||
|
||||
最长相等前后缀的长度为:`next[len - 1] + 1`。(这里的next数组是以统一减一的方式计算的,因此需要+1,两种计算next数组的具体区别看这里:[字符串:KMP算法精讲](https://programmercarl.com/0028.实现strStr.html))
|
||||
|
||||
数组长度为:len。
|
||||
|
||||
如果len % (len - (next[len - 1] + 1)) == 0 ,则说明数组的长度正好可以被 (数组长度-最长相等前后缀的长度) 整除 ,说明该字符串有重复的子字符串。
|
||||
`len - (next[len - 1] + 1)` 是最长相等前后缀不包含的子串的长度。
|
||||
|
||||
**数组长度减去最长相同前后缀的长度相当于是第一个周期的长度,也就是一个周期的长度,如果这个周期可以被整除,就说明整个数组就是这个周期的循环。**
|
||||
如果`len % (len - (next[len - 1] + 1)) == 0` ,则说明数组的长度正好可以被 最长相等前后缀不包含的子串的长度 整除 ,说明该字符串有重复的子字符串。
|
||||
|
||||
### 打印数组
|
||||
|
||||
**强烈建议大家把next数组打印出来,看看next数组里的规律,有助于理解KMP算法**
|
||||
|
||||
@ -150,11 +305,15 @@ next 数组记录的就是最长相同前后缀 [字符串:KMP算法精讲](ht
|
||||
|
||||

|
||||
|
||||
next[len - 1] = 7,next[len - 1] + 1 = 8,8就是此时字符串asdfasdfasdf的最长相同前后缀的长度。
|
||||
`next[len - 1] = 7`,`next[len - 1] + 1 = 8`,8就是此时字符串asdfasdfasdf的最长相同前后缀的长度。
|
||||
|
||||
(len - (next[len - 1] + 1)) 也就是: 12(字符串的长度) - 8(最长公共前后缀的长度) = 4, 4正好可以被 12(字符串的长度) 整除,所以说明有重复的子字符串(asdf)。
|
||||
`(len - (next[len - 1] + 1))` 也就是: 12(字符串的长度) - 8(最长公共前后缀的长度) = 4, 为最长相同前后缀不包含的子串长度
|
||||
|
||||
|
||||
4可以被 12(字符串的长度) 整除,所以说明有重复的子字符串(asdf)。
|
||||
|
||||
### 打码实现
|
||||
|
||||
C++代码如下:(这里使用了前缀表统一减一的实现方式)
|
||||
|
||||
```CPP
|
||||
|
||||
@ -61,7 +61,7 @@
|
||||
|
||||
left + right = sum,而sum是固定的。right = sum - left
|
||||
|
||||
公式来了, left - (sum - left) = target 推导出 left = (target + sum)/2 。
|
||||
left - (sum - left) = target 推导出 left = (target + sum)/2 。
|
||||
|
||||
target是固定的,sum是固定的,left就可以求出来。
|
||||
|
||||
@ -126,7 +126,7 @@ public:
|
||||
|
||||
x = (target + sum) / 2
|
||||
|
||||
**此时问题就转化为,装满容量为x的背包,有几种方法**。
|
||||
**此时问题就转化为,用nums装满容量为x的背包,有几种方法**。
|
||||
|
||||
这里的x,就是bagSize,也就是我们后面要求的背包容量。
|
||||
|
||||
@ -161,6 +161,8 @@ if (abs(target) > sum) return 0; // 此时没有方案
|
||||
|
||||
我们先手动推导一下,这个二维数组里面的数值。
|
||||
|
||||
------------
|
||||
|
||||
先只考虑物品0,如图:
|
||||
|
||||

|
||||
@ -173,6 +175,8 @@ if (abs(target) > sum) return 0; // 此时没有方案
|
||||
|
||||
装满背包容量为2 的方法个数是0,目前没有办法能装满容量为2的背包。
|
||||
|
||||
--------------
|
||||
|
||||
接下来 考虑 物品0 和 物品1,如图:
|
||||
|
||||
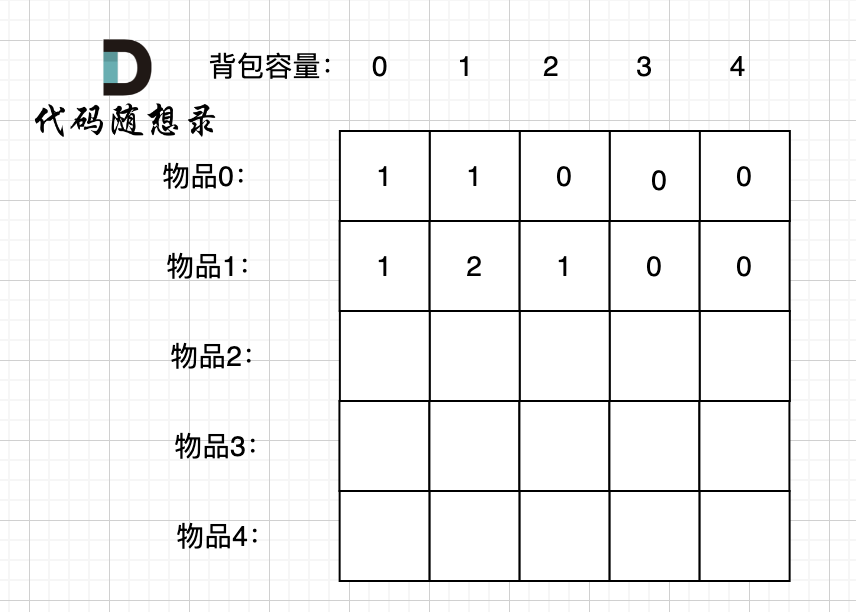
|
||||
@ -185,6 +189,8 @@ if (abs(target) > sum) return 0; // 此时没有方案
|
||||
|
||||
其他容量都不能装满,所以方法是0。
|
||||
|
||||
-----------------
|
||||
|
||||
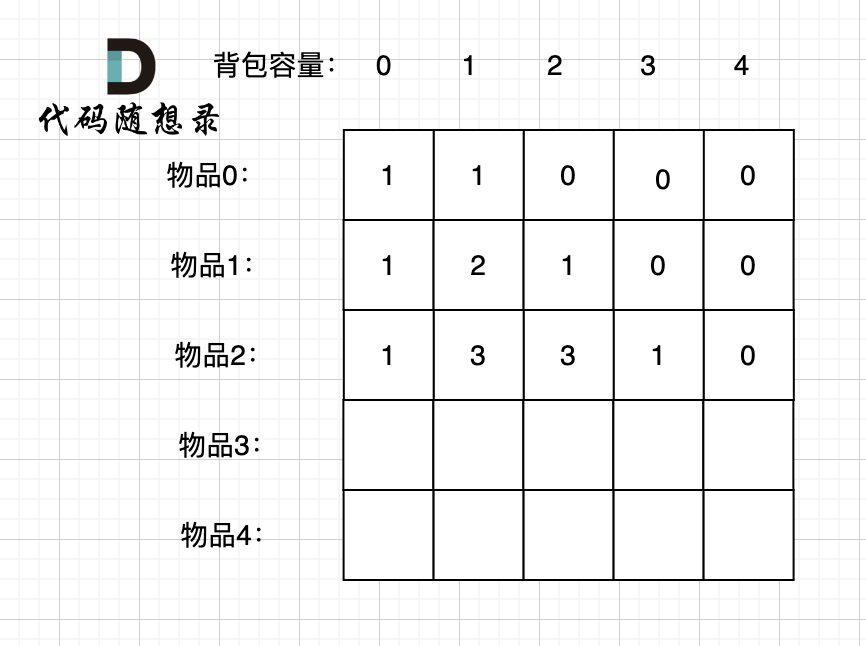
接下来 考虑 物品0 、物品1 和 物品2 ,如图:
|
||||
|
||||
|
||||
@ -193,10 +199,12 @@ if (abs(target) > sum) return 0; // 此时没有方案
|
||||
|
||||
装满背包容量为1 的方法个数是3,即 放物品0 或者 放物品1 或者 放物品2。
|
||||
|
||||
装满背包容量为2 的方法个数是3,即 放物品0 和 放物品1、放物品0 和 物品 2、 放物品1 和 物品2。
|
||||
装满背包容量为2 的方法个数是3,即 放物品0 和 放物品1、放物品0 和 物品2、放物品1 和 物品2。
|
||||
|
||||
装满背包容量为3的方法个数是1,即 放物品0 和 物品1 和 物品2。
|
||||
|
||||
---------------
|
||||
|
||||
通过以上举例,我们来看 dp[2][2] 可以有哪些方向推出来。
|
||||
|
||||
如图红色部分:
|
||||
@ -229,7 +237,7 @@ dp[2][2] = 3,即 放物品0 和 放物品1、放物品0 和 物品 2、放物
|
||||
|
||||
在上面图中,你把物品2补上就好,同样是两种方法。
|
||||
|
||||
dp[2][2] = 容量为2的背包不放物品2有几种方法 + 容量为2的背包不放物品2有几种方法
|
||||
dp[2][2] = 容量为2的背包不放物品2有几种方法 + 容量为2的背包放物品2有几种方法
|
||||
|
||||
所以 dp[2][2] = dp[1][2] + dp[1][1] ,如图:
|
||||
|
||||
@ -284,6 +292,29 @@ dp[0][j]:只放物品0, 把容量为j的背包填满有几种方法。
|
||||
|
||||
即 dp[i][0] = 1
|
||||
|
||||
但这里有例外,就是如果 物品数值就是0呢?
|
||||
|
||||
如果有两个物品,物品0为0, 物品1为0,装满背包容量为0的方法有几种。
|
||||
|
||||
* 放0件物品
|
||||
* 放物品0
|
||||
* 放物品1
|
||||
* 放物品0 和 物品1
|
||||
|
||||
此时是有4种方法。
|
||||
|
||||
其实就是算数组里有t个0,然后按照组合数量求,即 2^t 。
|
||||
|
||||
初始化如下:
|
||||
|
||||
```CPP
|
||||
int numZero = 0;
|
||||
for (int i = 0; i < nums.size(); i++) {
|
||||
if (nums[i] == 0) numZero++;
|
||||
dp[i][0] = (int) pow(2.0, numZero);
|
||||
}
|
||||
```
|
||||
|
||||
4. 确定遍历顺序
|
||||
|
||||
在明确递推方向时,我们知道 当前值 是由上方和左上方推出。
|
||||
|
||||
BIN
problems/kamacoder/.DS_Store
vendored
Normal file
BIN
problems/kamacoder/.DS_Store
vendored
Normal file
Binary file not shown.
@ -7,9 +7,15 @@
|
||||
|
||||
题目描述
|
||||
|
||||
树可以看成是一个图(拥有 n 个节点和 n - 1 条边的连通无环无向图)。
|
||||
有一个图,它是一棵树,他是拥有 n 个节点(节点编号1到n)和 n - 1 条边的连通无环无向图(其实就是一个线形图),如图:
|
||||
|
||||
现给定一个拥有 n 个节点(节点编号从 1 到 n)和 n 条边的连通无向图,请找出一条可以删除的边,删除后图可以变成一棵树。
|
||||

|
||||
|
||||
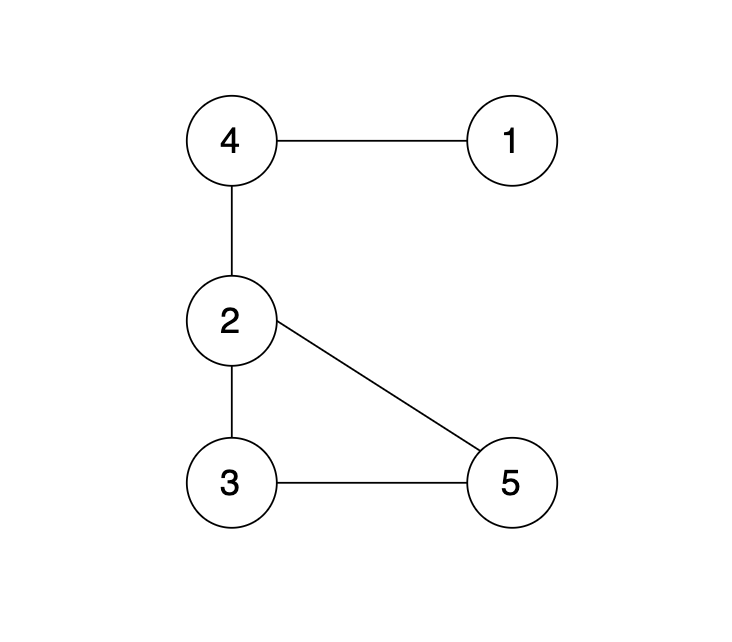
现在在这棵树上的基础上,添加一条边(依然是n个节点,但有n条边),使这个图变成了有环图,如图
|
||||
|
||||
|
||||
|
||||
先请你找出冗余边,删除后,使该图可以重新变成一棵树。
|
||||
|
||||
输入描述
|
||||
|
||||
@ -60,12 +66,11 @@
|
||||
|
||||
那么我们就可以从前向后遍历每一条边(因为优先让前面的边连上),边的两个节点如果不在同一个集合,就加入集合(即:同一个根节点)。
|
||||
|
||||
如图所示:
|
||||
|
||||
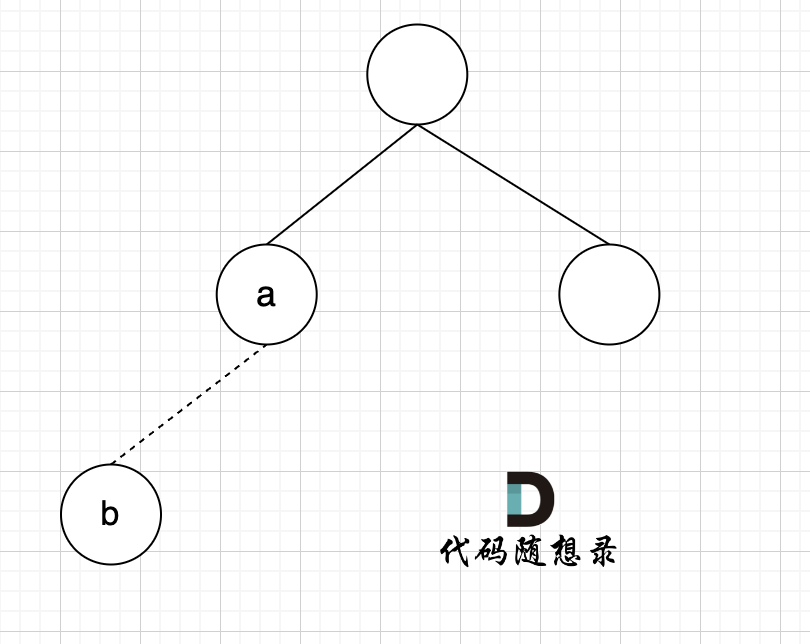
如图所示,节点A 和节点 B 不在同一个集合,那么就可以将两个 节点连在一起。
|
||||
|
||||
|
||||
|
||||
节点A 和节点 B 不在同一个集合,那么就可以将两个 节点连在一起。
|
||||
|
||||
如果边的两个节点已经出现在同一个集合里,说明着边的两个节点已经连在一起了,再加入这条边一定就出现环了。
|
||||
|
||||
如图所示:
|
||||
@ -127,6 +132,44 @@ int main() {
|
||||
|
||||
可以看出,主函数的代码很少,就判断一下边的两个节点在不在同一个集合就可以了。
|
||||
|
||||
## 拓展
|
||||
|
||||
题目要求 “请删除标准输入中最后出现的那条边” ,不少录友疑惑,这代码分明是遇到在同一个根的两个节点立刻就返回了,怎么就求出 最后出现的那条边 了呢。
|
||||
|
||||
有这种疑惑的录友是 认为发现一条冗余边后,后面还可能会有一条冗余边。
|
||||
|
||||
其实并不会。
|
||||
|
||||
题目是在 树的基础上 添加一条边,所以冗余边仅仅是一条。
|
||||
|
||||
到这一条可能靠前出现,可能靠后出现。
|
||||
|
||||
例如,题目输入示例:
|
||||
|
||||
输入示例
|
||||
|
||||
```
|
||||
3
|
||||
1 2
|
||||
2 3
|
||||
1 3
|
||||
```
|
||||
|
||||
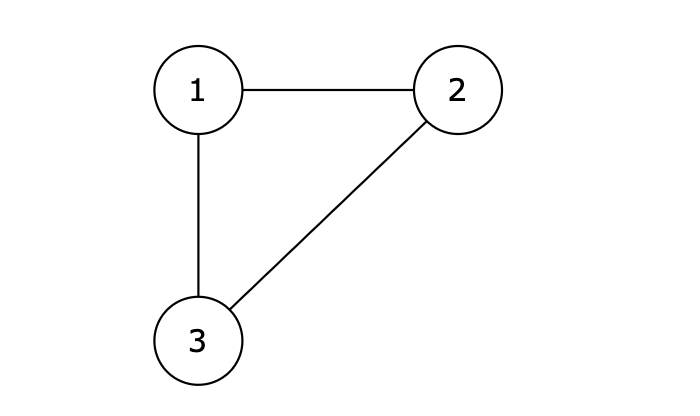
图:
|
||||
|
||||
|
||||
|
||||
输出示例
|
||||
|
||||
1 3
|
||||
|
||||
当我们从前向后遍历,优先让前面的边连上,最后判断冗余边就是 1 3。
|
||||
|
||||
如果我们从后向前便利,优先让后面的边连上,最后判断的冗余边就是 1 2。
|
||||
|
||||
题目要求“请删除标准输入中最后出现的那条边”,所以 1 3 这条边才是我们要求的。
|
||||
|
||||
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
@ -337,6 +337,38 @@ IDA * 算法 对这一空间增长问题进行了优化,关于 IDA * 算法,
|
||||
|
||||
### Python
|
||||
|
||||
```Python
|
||||
import heapq
|
||||
|
||||
n = int(input())
|
||||
|
||||
moves = [(1, 2), (2, 1), (-1, 2), (2, -1), (1, -2), (-2, 1), (-1, -2), (-2, -1)]
|
||||
|
||||
def distance(a, b):
|
||||
return ((a[0] - b[0]) ** 2 + (a[1] - b[1]) ** 2) ** 0.5
|
||||
|
||||
def bfs(start, end):
|
||||
q = [(distance(start, end), start)]
|
||||
step = {start: 0}
|
||||
|
||||
while q:
|
||||
d, cur = heapq.heappop(q)
|
||||
if cur == end:
|
||||
return step[cur]
|
||||
for move in moves:
|
||||
new = (move[0] + cur[0], move[1] + cur[1])
|
||||
if 1 <= new[0] <= 1000 and 1 <= new[1] <= 1000:
|
||||
step_new = step[cur] + 1
|
||||
if step_new < step.get(new, float('inf')):
|
||||
step[new] = step_new
|
||||
heapq.heappush(q, (distance(new, end) + step_new, new))
|
||||
return False
|
||||
|
||||
for _ in range(n):
|
||||
a1, a2, b1, b2 = map(int, input().split())
|
||||
print(bfs((a1, a2), (b1, b2)))
|
||||
```
|
||||
|
||||
### Go
|
||||
|
||||
### Rust
|
||||
|
||||
@ -252,36 +252,40 @@ import java.util.Scanner;
|
||||
public class Main {
|
||||
public static void main(String[] args) {
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
int n = scanner.nextInt();
|
||||
int bagweight = scanner.nextInt();
|
||||
|
||||
int[] weight = new int[n];
|
||||
int[] value = new int[n];
|
||||
// 读取 M 和 N
|
||||
int M = scanner.nextInt(); // 研究材料的数量
|
||||
int N = scanner.nextInt(); // 行李空间的大小
|
||||
|
||||
for (int i = 0; i < n; ++i) {
|
||||
weight[i] = scanner.nextInt();
|
||||
}
|
||||
for (int j = 0; j < n; ++j) {
|
||||
value[j] = scanner.nextInt();
|
||||
int[] costs = new int[M]; // 每种材料的空间占用
|
||||
int[] values = new int[M]; // 每种材料的价值
|
||||
|
||||
// 输入每种材料的空间占用
|
||||
for (int i = 0; i < M; i++) {
|
||||
costs[i] = scanner.nextInt();
|
||||
}
|
||||
|
||||
int[][] dp = new int[n][bagweight + 1];
|
||||
|
||||
for (int j = weight[0]; j <= bagweight; j++) {
|
||||
dp[0][j] = value[0];
|
||||
// 输入每种材料的价值
|
||||
for (int j = 0; j < M; j++) {
|
||||
values[j] = scanner.nextInt();
|
||||
}
|
||||
|
||||
for (int i = 1; i < n; i++) {
|
||||
for (int j = 0; j <= bagweight; j++) {
|
||||
if (j < weight[i]) {
|
||||
dp[i][j] = dp[i - 1][j];
|
||||
} else {
|
||||
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
|
||||
}
|
||||
// 创建一个动态规划数组 dp,初始值为 0
|
||||
int[] dp = new int[N + 1];
|
||||
|
||||
// 外层循环遍历每个类型的研究材料
|
||||
for (int i = 0; i < M; i++) {
|
||||
// 内层循环从 N 空间逐渐减少到当前研究材料所占空间
|
||||
for (int j = N; j >= costs[i]; j--) {
|
||||
// 考虑当前研究材料选择和不选择的情况,选择最大值
|
||||
dp[j] = Math.max(dp[j], dp[j - costs[i]] + values[i]);
|
||||
}
|
||||
}
|
||||
|
||||
System.out.println(dp[n - 1][bagweight]);
|
||||
// 输出 dp[N],即在给定 N 行李空间可以携带的研究材料的最大价值
|
||||
System.out.println(dp[N]);
|
||||
|
||||
scanner.close();
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
Reference in New Issue
Block a user