Update

README.md

@@ -51,6 +51,10 @@
     * [上海有这些互联网公司，你都知道么？](https://mp.weixin.qq.com/s/msqbX6eR2-JBQOYFfec4sg)
     * [成都有这些互联网公司，你都知道么？](https://mp.weixin.qq.com/s/Y9Qg22WEsBngs8B-K8acqQ)
 
+* 算法性能分析
+    * [关于时间复杂度，你不知道的都在这里！](https://mp.weixin.qq.com/s/LWBfehW1gMuEnXtQjJo-sw)
+    * [O(n)的算法居然超时了，此时的n究竟是多大？](https://mp.weixin.qq.com/s/73ryNsuPFvBQkt6BbhNzLA)
+
 * 数组
     * [必须掌握的数组理论知识](https://mp.weixin.qq.com/s/X7R55wSENyY62le0Fiawsg)
     * [数组：每次遇到二分法，都是一看就会，一写就废](https://mp.weixin.qq.com/s/fCf5QbPDtE6SSlZ1yh_q8Q)
@@ -243,6 +247,7 @@
 |[0056.合并区间](https://github.com/youngyangyang04/leetcode/blob/master/problems/0056.合并区间.md) |数组 |中等| **贪心** 以为是模拟题，其实是贪心|
 |[0057.插入区间](https://github.com/youngyangyang04/leetcode/blob/master/problems/0057.插入区间.md) |数组 |困难| **模拟**  是一道数组难题|
 |[0059.螺旋矩阵II](https://github.com/youngyangyang04/leetcode/blob/master/problems/0059.螺旋矩阵II.md) |数组 |中等|**模拟**|
+|[0062.不同路径](https://github.com/youngyangyang04/leetcode/blob/master/problems/0062.不同路径.md) |数组、动态规划 |中等|**深搜** **动态规划** **数论**|
 |[0070.爬楼梯](https://github.com/youngyangyang04/leetcode/blob/master/problems/0070.爬楼梯.md) |动态规划|简单|**动态规划** dp里求排列|
 |[0077.组合](https://github.com/youngyangyang04/leetcode/blob/master/problems/0077.组合.md) |回溯 |中等|**回溯**|
 |[0078.子集](https://github.com/youngyangyang04/leetcode/blob/master/problems/0078.子集.md) |回溯/数组 |中等|**回溯**|

problems/0062.不同路径.md

@@ -0,0 +1,176 @@
+
+# 思路
+
+## 深搜 
+
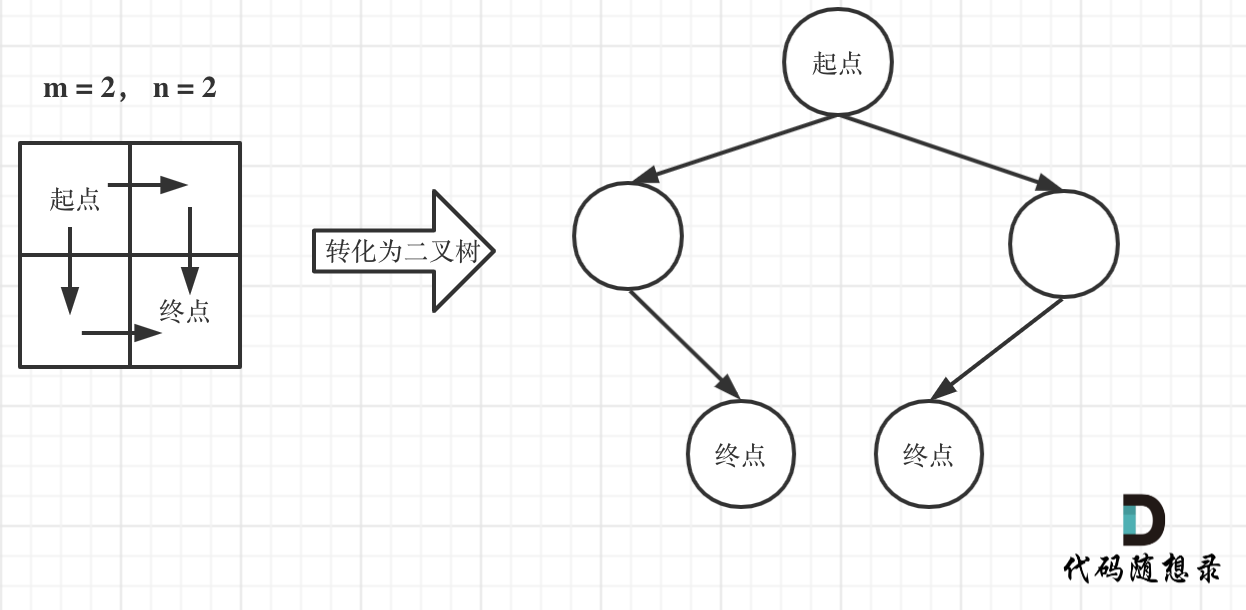
+这道题目，刚一看最直观的想法就是用图论里的深搜，来枚举出来有多少种路径。
+
+注意题目中说机器人每次只能向下或者向右移动一步，那么其实**机器人走过的路径可以抽象为一颗二叉树，而叶子节点就是终点！**
+
+如图举例：
+
+![62.不同路径](https://img-blog.csdnimg.cn/20201209113602700.png)
+
+此时问题就可以转化为求二叉树叶子节点的个数，代码如下：
+
+```C++
+class Solution {
+private:
+    int dfs(int i, int j, int m, int n) {
+        if (i > m || j > n) return 0; // 越界了
+        if (i == m && j == n) return 1; // 找到一种方法，相当于找到了叶子节点
+        return dfs(i + 1, j, m, n) + dfs(i, j + 1, m, n);
+    }
+public:
+    int uniquePaths(int m, int n) {
+        return dfs(1, 1, m, n);
+    }
+};
+```
+
+大家如果提交了代码就会发现超时了！
+
+来分析一下时间复杂度，这个深搜的算法，其实就是要遍历整个二叉树。
+
+这颗树的深度其实就是m+n-1（深度按从1开始计算）。
+
+那二叉树的节点个数就是 2^(m + n - 1) - 1。可以理解深搜的算法就是遍历了整个满二叉树（其实没有把搜索节点都遍历到，只是近似而已）
+
+所以上面深搜代码的时间复杂度为O(2^(m + n - 1) - 1)，可以看出，这是指数级别的时间复杂度，是非常大的。
+
+## 动态规划 
+
+机器人从(0 , 0) 位置触发，到(m - 1, n - 1)终点。
+
+按照动规三部曲来分析：
+
+* dp数组表述啥
+
+这里设计一个dp二维数组，dp[i][j] 表示从（0 ，0）出发，到(i, j) 有几条不同的路径。
+
+* dp数组的初始化 
+
+如何初始化呢，首先dp[i][0]一定都是1，因为从(0, 0)的位置到(i, 0)的路径只有一条，那么dp[0][j]也同理。
+
+所以初始化代码为：
+
+```
+for (int i = 0; i < m; i++) dp[i][0] = 1;
+for (int j = 0; j < n; j++) dp[0][j] = 1;
+```
+
+* 递推公式 
+
+想要求dp[i][j]，只能有两个方向来推导出来，即dp[i - 1][j] 和 dp[i][j - 1]。
+
+此时在回顾一下 dp[i-1][j] 表示啥，是从(0, 0)的位置到(i-1, j)有几条路径，dp[i][j - 1]同理。
+
+那么很自然，dp[i][j] =  dp[i-1][j] + dp[i][j - 1]，因为dp[i][j]只有这两个方向过来。
+
+如图所示：
+
+![62.不同路径1](https://img-blog.csdnimg.cn/20201209113631392.png)
+
+C++代码如下：
+
+```C++
+class Solution {
+public:
+    int uniquePaths(int m, int n) {
+        vector<vector<int>> dp(m, vector<int>(n, 0));
+        for (int i = 0; i < m; i++) dp[i][0] = 1;
+        for (int j = 0; j < n; j++) dp[0][j] = 1;
+        for (int i = 1; i < m; i++) {
+            for (int j = 1; j < n; j++) {
+                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
+            }
+        }
+        return dp[m - 1][n - 1];
+    }
+};
+```
+* 时间复杂度：O(m * n) 
+* 空间复杂度：O(m * n)
+
+其实用一个一维数组（也可以理解是滚动数组）就可以了，但是不利于理解，可以优化点空间，建议先理解了二维，在理解一维，C++代码如下：
+
+```C++
+class Solution {
+public:
+    int uniquePaths(int m, int n) {
+        vector<int> dp(n);
+        for (int i = 0; i < n; i++) dp[i] = 1;
+        for (int j = 1; j < m; j++) {
+            for (int i = 1; i < n; i++) {
+                dp[i] += dp[i - 1];
+            }
+        }
+        return dp[n - 1];
+    }
+};
+```
+* 时间复杂度：O(m * n) 
+* 空间复杂度：O(n)
+
+# 数论方法 
+
+在这个图中，可以看出一共 m，n的话，无论怎么走，走到终点都需要 m + n - 2 步。
+
+![62.不同路径](https://img-blog.csdnimg.cn/20201209113602700.png)
+
+在这m + n - 2 步中，一定有 m - 1 步是要向下走的，不用管什么时候向下走。
+
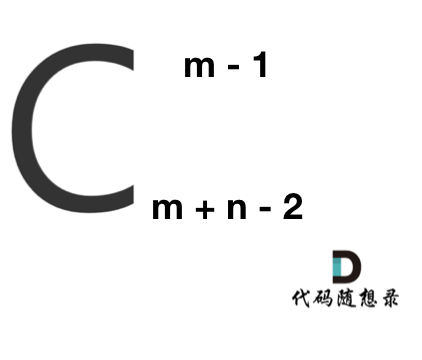
+那么有几种走法呢？ 可以转化为，给你m + n - 2个不同的数，随便取m - 1个数，有几种取法。
+
+那么这就是一个组合问题了。
+
+那么答案，如图所示：
+
+![62.不同路径2](https://img-blog.csdnimg.cn/20201209113725324.png)
+
+**求组合的时候，要防止两个int相乘溢出！** 所以不能把算式的分子都算出来，分母都算出来再做除法。
+
+```
+class Solution {
+public:
+    int uniquePaths(int m, int n) {
+        int numerator = 1, denominator = 1;
+        int count = m - 1;
+        int t = m + n - 2;
+        while (count--) numerator *= (t--); // 计算分子，此时分子就会溢出
+        for (int i = 1; i <= m - 1; i++) denominator *= i; // 计算分母
+        return numerator / denominator;
+    }
+};
+
+```
+
+需要在计算分子的时候，不算除以分母，代码如下：
+
+```
+class Solution {
+public:
+    int uniquePaths(int m, int n) {
+        long long numerator = 1; // 分子
+        int denominator = m - 1; // 分母
+        int count = m - 1;
+        int t = m + n - 2;
+        while (count--) {
+            numerator *= (t--);
+            while (denominator != 0 && numerator % denominator == 0) {
+                numerator /= denominator;
+                denominator--;
+            }
+        }
+        return numerator;
+    }
+};
+```
+
+计算组合问题的代码还是有难度的，特别是处理溢出的情况！
+
+最后这个代码还有点复杂了，还是可以优化，我就不继续优化了，有空在整理一下，哈哈，就酱！
+
+
+
+

problems/导读.md

@@ -12,7 +12,10 @@
 
 # 文章篇
 
-* 求职 
+* 代码风格
+    * [看了这么多代码，谈一谈代码风格！](https://mp.weixin.qq.com/s/UR9ztxz3AyL3qdHn_zMbqw)
+
+* 求职
     * [程序员的简历应该这么写！！（附简历模板）](https://mp.weixin.qq.com/s/nCTUzuRTBo1_R_xagVszsA)
     * [BAT级别技术面试流程和注意事项都在这里了](https://mp.weixin.qq.com/s/815qCyFGVIxwut9I_7PNFw)
     * [深圳原来有这么多互联网公司，你都知道么？](https://mp.weixin.qq.com/s/Yzrkim-5bY0Df66Ao-hoqA)
@@ -20,6 +23,10 @@
     * [上海有这些互联网公司，你都知道么？](https://mp.weixin.qq.com/s/msqbX6eR2-JBQOYFfec4sg)
     * [成都有这些互联网公司，你都知道么？](https://mp.weixin.qq.com/s/Y9Qg22WEsBngs8B-K8acqQ)
 
+* 算法性能分析
+    * [关于时间复杂度，你不知道的都在这里！](https://mp.weixin.qq.com/s/LWBfehW1gMuEnXtQjJo-sw)
+    * [O(n)的算法居然超时了，此时的n究竟是多大？](https://mp.weixin.qq.com/s/73ryNsuPFvBQkt6BbhNzLA)
+
 * 数组
     * [必须掌握的数组理论知识](https://mp.weixin.qq.com/s/X7R55wSENyY62le0Fiawsg)
     * [数组：每次遇到二分法，都是一看就会，一写就废](https://mp.weixin.qq.com/s/fCf5QbPDtE6SSlZ1yh_q8Q)