Update

README.md

@@ -106,8 +106,8 @@
 4. [数组：977.有序数组的平方](./problems/0977.有序数组的平方.md)    
 5. [数组：209.长度最小的子数组](./problems/0209.长度最小的子数组.md)
 6. [数组：区间和](./problems/kamacoder/0058.区间和.md)
-6. [数组：59.螺旋矩阵II](./problems/0059.螺旋矩阵II.md)
-8. [数组：开发商购买土地](./problems/kamacoder/0044.开发商购买土地.md)
+7. [数组：开发商购买土地](./problems/kamacoder/0044.开发商购买土地.md)
+8. [数组：59.螺旋矩阵II](./problems/0059.螺旋矩阵II.md)
 9. [数组：总结篇](./problems/数组总结篇.md)
 
 ## 链表
@@ -196,7 +196,6 @@
 12. [二叉树：110.平衡二叉树](./problems/0110.平衡二叉树.md)
 13. [二叉树：257.二叉树的所有路径](./problems/0257.二叉树的所有路径.md)
 14. [本周总结！（二叉树）](./problems/周总结/20201003二叉树周末总结.md)
-15. [二叉树：二叉树中递归带着回溯](./problems/二叉树中递归带着回溯.md)
 16. [二叉树：404.左叶子之和](./problems/0404.左叶子之和.md)
 17. [二叉树：513.找树左下角的值](./problems/0513.找树左下角的值.md)
 18. [二叉树：112.路径总和](./problems/0112.路径总和.md)

problems/0093.复原IP地址.md

@@ -376,9 +376,8 @@ class Solution {
 		// 剪枝：ip段的长度最大是3，并且ip段处于[0,255]
 		for (int i = start; i < s.length() && i - start < 3 && Integer.parseInt(s.substring(start, i + 1)) >= 0
 				&& Integer.parseInt(s.substring(start, i + 1)) <= 255; i++) {
-			// 如果ip段的长度大于1，并且第一位为0的话，continue
 			if (i + 1 - start > 1 && s.charAt(start) - '0' == 0) {
-				continue;
+				break;
 			}
 			stringBuilder.append(s.substring(start, i + 1));
 			// 当stringBuilder里的网段数量小于3时，才会加点；如果等于3，说明已经有3段了，最后一段不需要再加点

problems/0416.分割等和子集.md

@@ -47,7 +47,13 @@
 
 那么只要找到集合里能够出现 sum / 2 的子集总和，就算是可以分割成两个相同元素和子集了。
 
-本题是可以用回溯暴力搜索出所有答案的，但最后超时了，也不想再优化了，放弃回溯，直接上01背包吧。
+本题是可以用回溯暴力搜索出所有答案的，但最后超时了，也不想再优化了，放弃回溯。
+
+是否有其他解法可以解决此题。 
+
+本题的本质是，能否把容量为 sum / 2的背包装满。 
+
+**这是 背包算法可以解决的经典类型题目**。 
 
 如果对01背包不够了解，建议仔细看完如下两篇：
 
@@ -56,7 +62,7 @@
 
 ### 01背包问题
 
-背包问题，大家都知道，有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。
+01背包问题，大家都知道，有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。
 
 **背包问题有多种背包方式，常见的有：01背包、完全背包、多重背包、分组背包和混合背包等等。**
 
@@ -64,32 +70,33 @@
 
 **即一个商品如果可以重复多次放入是完全背包，而只能放入一次是01背包，写法还是不一样的。**
 
-**要明确本题中我们要使用的是01背包，因为元素我们只能用一次。**
+**元素我们只能用一次，如果使用背包，那么也是01背包**
 
 回归主题：首先，本题要求集合里能否出现总和为 sum / 2 的子集。
 
-那么来一一对应一下本题，看看背包问题如何来解决。
+既有一个 只能装重量为 sum / 2 的背包，商品为数字，这些数字能不能把 这个背包装满。 
 
-**只有确定了如下四点，才能把01背包问题套到本题上来。**
+那每一件商品是数字的话，对应的重量 和 价值是多少呢？  
 
-* 背包的体积为sum / 2
-* 背包要放入的商品（集合里的元素）重量为 元素的数值，价值也为元素的数值
-* 背包如果正好装满，说明找到了总和为 sum / 2 的子集。
-* 背包中每一个元素是不可重复放入。
+一个数字只有一个维度，即 重量等于价值。  
 
-以上分析完，我们就可以套用01背包，来解决这个问题了。
+当数字 可以装满 承载重量为 sum / 2 的背包的背包时，这个背包的价值也是 sum / 2。
+
+那么这道题就是 装满 承载重量为 sum / 2 的背包，价值最大是多少？ 
+
+如果最大价值是 sum / 2，说明正好被商品装满了。
+
+因为商品是数字，重量和对应的价值是相同的。
+
+以上分析完，我们就可以直接用01背包 来解决这个问题了。
 
 动规五部曲分析如下：
 
 1. 确定dp数组以及下标的含义
 
-01背包中，dp[j] 表示： 容量为j的背包，所背的物品价值最大可以为dp[j]。
+01背包中，dp[j] 表示： 容量（所能装的重量）为j的背包，所背的物品价值最大可以为dp[j]。
 
-本题中每一个元素的数值既是重量，也是价值。
-
-**套到本题，dp[j]表示 背包总容量（所能装的总重量）是j，放进物品后，背的最大重量为dp[j]**。
-
-那么如果背包容量为target， dp[target]就是装满 背包之后的重量，所以 当 dp[target] == target 的时候，背包就装满了。
+如果背包所载重量为target， dp[target]就是装满 背包之后的总价值，因为 本题中每一个元素的数值既是重量，也是价值，所以，当 dp[target] == target 的时候，背包就装满了。
 
 有录友可能想，那还有装不满的时候？ 
 
@@ -192,12 +199,11 @@ public:
 
 ## 总结
 
-这道题目就是一道01背包应用类的题目，需要我们拆解题目，然后套入01背包的场景。
+这道题目就是一道01背包经典应用类的题目，需要我们拆解题目，然后才能发现可以使用01背包。
 
 01背包相对于本题，主要要理解，题目中物品是nums[i]，重量是nums[i]，价值也是nums[i]，背包体积是sum/2。
 
-看代码的话，就可以发现，基本就是按照01背包的写法来的。
-
+做完本题后，需要大家清晰：背包问题，不仅可以求 背包能被的最大价值，还可以求这个背包是否可以装满。
 
 ## 其他语言版本
 

problems/kamacoder/0047.参会dijkstra朴素.md

@@ -578,7 +578,7 @@ int main() {
 更新 minDist数组，即：源点（节点1） 到 节点2 和 节点3的距离。 
 
 * 源点到节点2的最短距离为100，小于原minDist[2]的数值max，更新minDist[2] = 100 
-* 源点到节点3的最短距离为1，小于原minDist[3]的数值max，更新minDist[4] = 1 
+* 源点到节点3的最短距离为1，小于原minDist[3]的数值max，更新minDist[3] = 1 
 
 -------------------
 

problems/kamacoder/0096.城市间货物运输III.md

@@ -215,9 +215,9 @@ int main() {
 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240409111849.png)
 
 
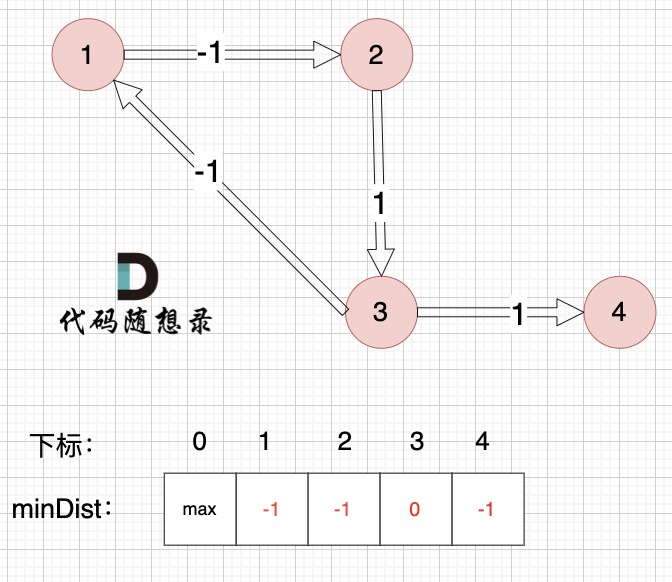
-边：节点3 -> 节点4，权值为1 ，minDist[4] > minDist[3] + 1，更新 minDist[4] = 0 + (-1) = -1 ，如图： 
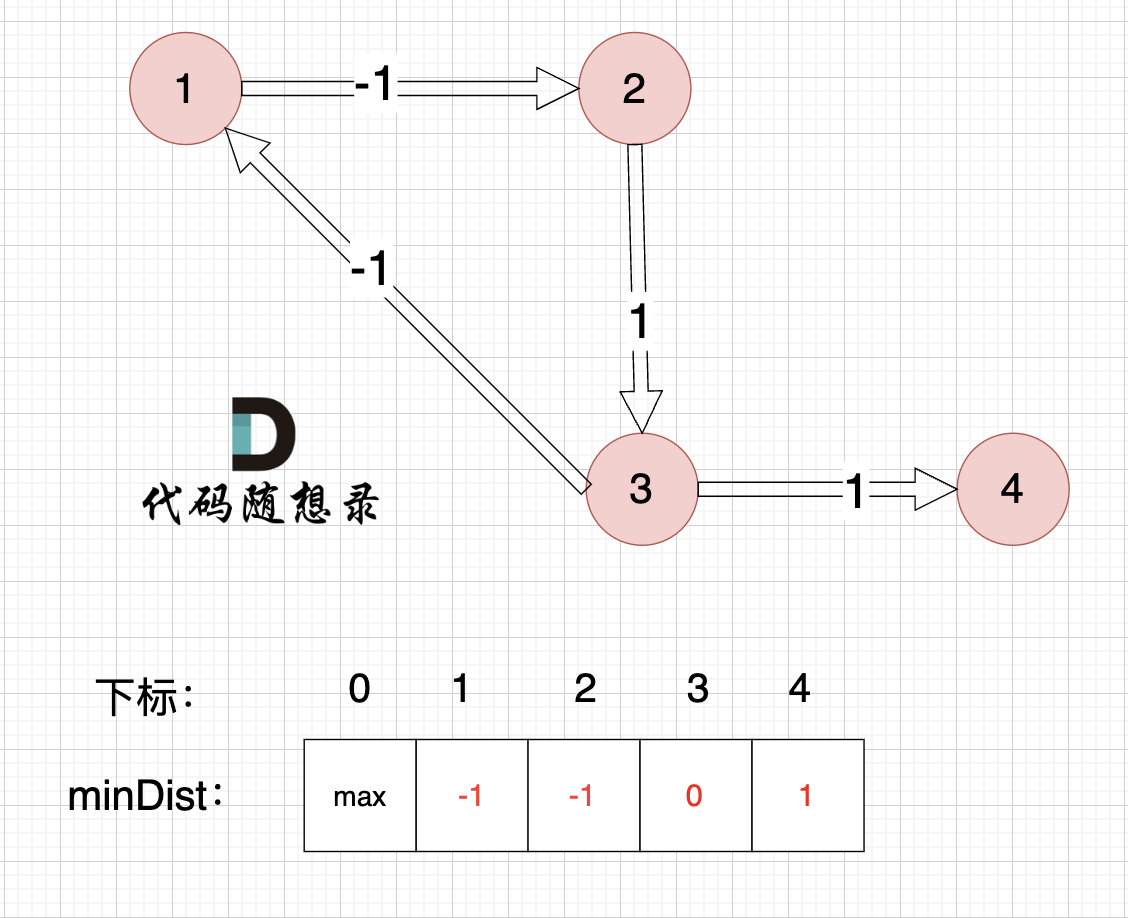
+边：节点3 -> 节点4，权值为1 ，minDist[4] > minDist[3] + 1，更新 minDist[4] = 0 + 1 = 1 ，如图： 
 
-![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240409111837.png)
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20241018192042.png)
 
 
 以上是对所有边进行的第一次松弛，最后 minDist数组为 ：-1 -1 0 1 ，（从下标1算起） 

problems/kamacoder/0126.骑士的攻击astar.md

@@ -173,7 +173,7 @@ int n=q.front();q.pop();
 
 G：起点达到目前遍历节点的距离 
 
-F：目前遍历的节点到达终点的距离
+H：目前遍历的节点到达终点的距离
 
 起点达到目前遍历节点的距离 + 目前遍历的节点到达终点的距离 就是起点到达终点的距离。