Merge pull request #971 from bqlin/master

修改错别字

problems/0040.组合总和II.md

@@ -128,7 +128,7 @@ if (sum == target) {
 
 我在图中将used的变化用橘黄色标注上，可以看出在candidates[i] == candidates[i - 1]相同的情况下：
 
-* used[i - 1] == true，说明同一树支candidates[i - 1]使用过
+* used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
 * used[i - 1] == false，说明同一树层candidates[i - 1]使用过
 
 **这块去重的逻辑很抽象，网上搜的题解基本没有能讲清楚的，如果大家之前思考过这个问题或者刷过这道题目，看到这里一定会感觉通透了很多！**
@@ -137,7 +137,7 @@ if (sum == target) {
 
 ```CPP
 for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
-    // used[i - 1] == true，说明同一树支candidates[i - 1]使用过
+    // used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
     // used[i - 1] == false，说明同一树层candidates[i - 1]使用过
     // 要对同一树层使用过的元素进行跳过
     if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) {
@@ -169,7 +169,7 @@ private:
             return;
         }
         for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
-            // used[i - 1] == true，说明同一树支candidates[i - 1]使用过
+            // used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
             // used[i - 1] == false，说明同一树层candidates[i - 1]使用过
             // 要对同一树层使用过的元素进行跳过
             if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) {
@@ -404,7 +404,7 @@ func backtracking(startIndex,sum,target int,candidates,trcak []int,res *[][]int,
     }
     if sum>target{return}
     //回溯
-    // used[i - 1] == true，说明同一树支candidates[i - 1]使用过
+    // used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
     // used[i - 1] == false，说明同一树层candidates[i - 1]使用过
     for i:=startIndex;i<len(candidates);i++{
         if i>0&&candidates[i]==candidates[i-1]&&history[i-1]==false{

problems/0047.全排列II.md

@@ -65,7 +65,7 @@ private:
             return;
         }
         for (int i = 0; i < nums.size(); i++) {
-            // used[i - 1] == true，说明同一树支nums[i - 1]使用过
+            // used[i - 1] == true，说明同一树枝nums[i - 1]使用过
             // used[i - 1] == false，说明同一树层nums[i - 1]使用过
             // 如果同一树层nums[i - 1]使用过则直接跳过
             if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
@@ -183,7 +183,7 @@ class Solution {
             }
             //如果同⼀树⽀nums[i]没使⽤过开始处理
             if (used[i] == false) {
-                used[i] = true;//标记同⼀树⽀nums[i]使⽤过，防止同一树支重复使用
+                used[i] = true;//标记同⼀树⽀nums[i]使⽤过，防止同一树枝重复使用
                 path.add(nums[i]);
                 backTrack(nums, used);
                 path.remove(path.size() - 1);//回溯，说明同⼀树层nums[i]使⽤过，防止下一树层重复

problems/0051.N皇后.md

@@ -43,13 +43,13 @@ n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，
 
 确定完约束条件，来看看究竟要怎么去搜索皇后们的位置，其实搜索皇后的位置，可以抽象为一棵树。
 
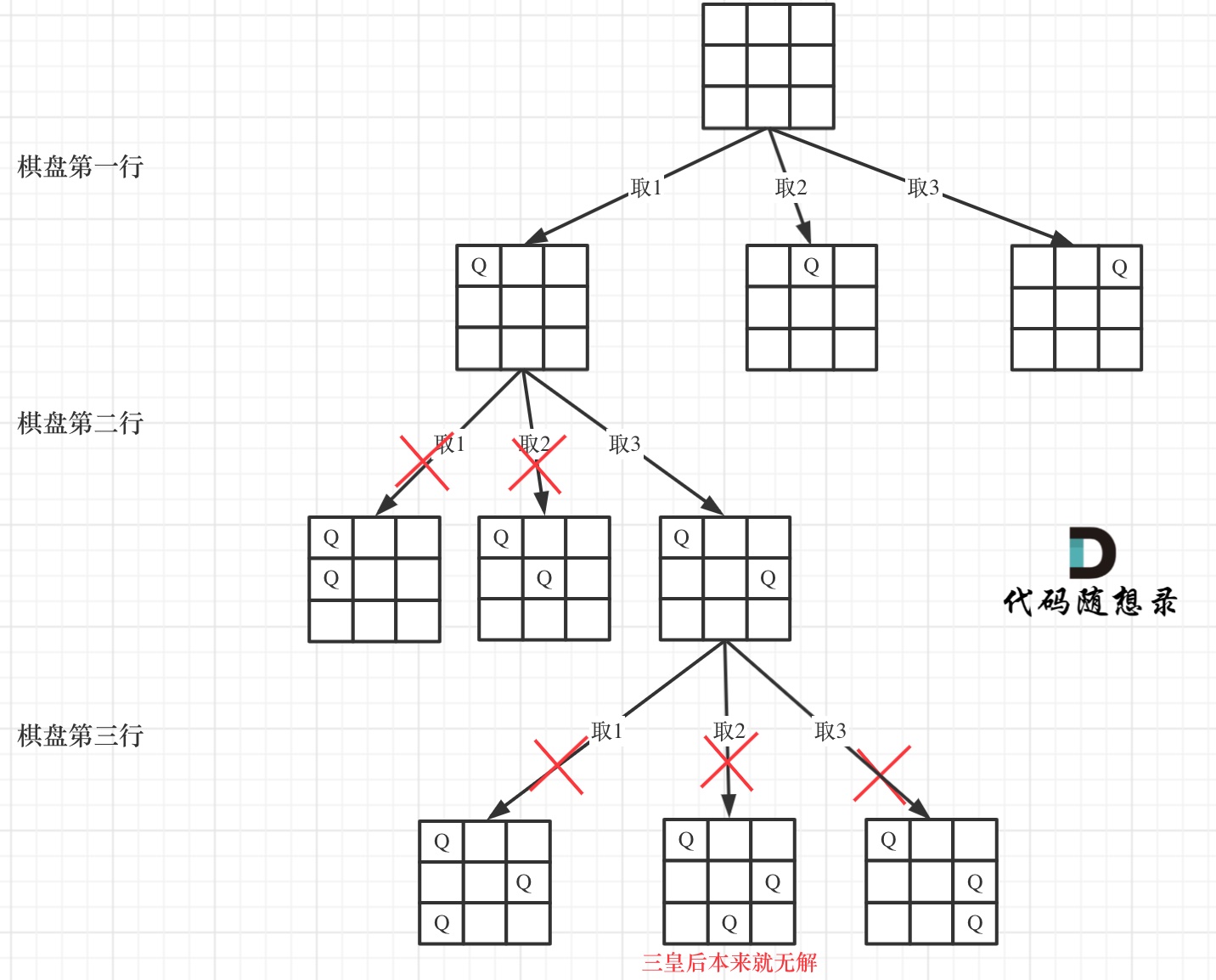
-下面我用一个 3 * 3 的棋盘，将搜索过程抽象为一颗树，如图：
+下面我用一个 3 * 3 的棋盘，将搜索过程抽象为一棵树，如图：
 
 ![51.N皇后](https://img-blog.csdnimg.cn/20210130182532303.jpg)
 
-从图中，可以看出，二维矩阵中矩阵的高就是这颗树的高度，矩阵的宽就是树形结构中每一个节点的宽度。
+从图中，可以看出，二维矩阵中矩阵的高就是这棵树的高度，矩阵的宽就是树形结构中每一个节点的宽度。
 
-那么我们用皇后们的约束条件，来回溯搜索这颗树，**只要搜索到了树的叶子节点，说明就找到了皇后们的合理位置了**。
+那么我们用皇后们的约束条件，来回溯搜索这棵树，**只要搜索到了树的叶子节点，说明就找到了皇后们的合理位置了**。
 
 ### 回溯三部曲
 

problems/0062.不同路径.md

@@ -49,7 +49,7 @@
 
 这道题目，刚一看最直观的想法就是用图论里的深搜，来枚举出来有多少种路径。
 
-注意题目中说机器人每次只能向下或者向右移动一步，那么其实**机器人走过的路径可以抽象为一颗二叉树，而叶子节点就是终点！**
+注意题目中说机器人每次只能向下或者向右移动一步，那么其实**机器人走过的路径可以抽象为一棵二叉树，而叶子节点就是终点！**
 
 如图举例：
 
@@ -76,7 +76,7 @@ public:
 
 来分析一下时间复杂度，这个深搜的算法，其实就是要遍历整个二叉树。
 
-这颗树的深度其实就是m+n-1（深度按从1开始计算）。
+这棵树的深度其实就是m+n-1（深度按从1开始计算）。
 
 那二叉树的节点个数就是 2^(m + n - 1) - 1。可以理解深搜的算法就是遍历了整个满二叉树（其实没有遍历整个满二叉树，只是近似而已）
 

problems/0077.组合.md

@@ -328,7 +328,7 @@ public:
 
 本篇我们准对求组合问题的回溯法代码做了剪枝优化，这个优化如果不画图的话，其实不好理解，也不好讲清楚。
 
-所以我依然是把整个回溯过程抽象为一颗树形结构，然后可以直观的看出，剪枝究竟是剪的哪里。
+所以我依然是把整个回溯过程抽象为一棵树形结构，然后可以直观的看出，剪枝究竟是剪的哪里。
 
 
 

problems/0077.组合优化.md

@@ -133,7 +133,7 @@ public:
 
 本篇我们准对求组合问题的回溯法代码做了剪枝优化，这个优化如果不画图的话，其实不好理解，也不好讲清楚。
 
-所以我依然是把整个回溯过程抽象为一颗树形结构，然后可以直观的看出，剪枝究竟是剪的哪里。
+所以我依然是把整个回溯过程抽象为一棵树形结构，然后可以直观的看出，剪枝究竟是剪的哪里。
 
 **就酱，学到了就帮Carl转发一下吧，让更多的同学知道这里！**
 

problems/0078.子集.md

@@ -145,7 +145,7 @@ public:
 
 ```
 
-在注释中，可以发现可以不写终止条件，因为本来我们就要遍历整颗树。
+在注释中，可以发现可以不写终止条件，因为本来我们就要遍历整棵树。
 
 有的同学可能担心不写终止条件会不会无限递归？
 

problems/0090.子集II.md

@@ -55,7 +55,7 @@ private:
     void backtracking(vector<int>& nums, int startIndex, vector<bool>& used) {
         result.push_back(path);
         for (int i = startIndex; i < nums.size(); i++) {
-            // used[i - 1] == true，说明同一树支candidates[i - 1]使用过
+            // used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
             // used[i - 1] == false，说明同一树层candidates[i - 1]使用过
             // 而我们要对同一树层使用过的元素进行跳过
             if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
@@ -115,7 +115,7 @@ public:
 
 ## 补充
 
-本题也可以不适用used数组来去重，因为递归的时候下一个startIndex是i+1而不是0。
+本题也可以不使用used数组来去重，因为递归的时候下一个startIndex是i+1而不是0。
 
 如果要是全排列的话，每次要从0开始遍历，为了跳过已入栈的元素，需要使用used。
 

problems/0096.不同的二叉搜索树.md

@@ -87,7 +87,7 @@ j相当于是头结点的元素，从1遍历到i为止。
 
 那么dp[0]应该是多少呢？
 
-从定义上来讲，空节点也是一颗二叉树，也是一颗二叉搜索树，这是可以说得通的。
+从定义上来讲，空节点也是一棵二叉树，也是一棵二叉搜索树，这是可以说得通的。
 
 从递归公式上来讲，dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量] 中以j为头结点左子树节点数量为0，也需要dp[以j为头结点左子树节点数量] = 1， 否则乘法的结果就都变成0了。
 

problems/0106.从中序与后序遍历序列构造二叉树.md

@@ -31,7 +31,7 @@
 
 首先回忆一下如何根据两个顺序构造一个唯一的二叉树，相信理论知识大家应该都清楚，就是以 后序数组的最后一个元素为切割点，先切中序数组，根据中序数组，反过来在切后序数组。一层一层切下去，每次后序数组最后一个元素就是节点元素。
 
-如果让我们肉眼看两个序列，画一颗二叉树的话，应该分分钟都可以画出来。
+如果让我们肉眼看两个序列，画一棵二叉树的话，应该分分钟都可以画出来。
 
 流程如图：
 
@@ -540,13 +540,13 @@ public:
 
 # 思考题
 
-前序和中序可以唯一确定一颗二叉树。
+前序和中序可以唯一确定一棵二叉树。
 
-后序和中序可以唯一确定一颗二叉树。
+后序和中序可以唯一确定一棵二叉树。
 
-那么前序和后序可不可以唯一确定一颗二叉树呢？
+那么前序和后序可不可以唯一确定一棵二叉树呢？
 
-**前序和后序不能唯一确定一颗二叉树！**，因为没有中序遍历无法确定左右部分，也就是无法分割。
+**前序和后序不能唯一确定一棵二叉树！**，因为没有中序遍历无法确定左右部分，也就是无法分割。
 
 举一个例子：
 
@@ -558,7 +558,7 @@ tree2 的前序遍历是[1 2 3]， 后序遍历是[3 2 1]。
 
 那么tree1 和 tree2 的前序和后序完全相同，这是一棵树么，很明显是两棵树！
 
-所以前序和后序不能唯一确定一颗二叉树！
+所以前序和后序不能唯一确定一棵二叉树！
 
 # 总结
 
@@ -570,7 +570,7 @@ tree2 的前序遍历是[1 2 3]， 后序遍历是[3 2 1]。
 
 大家遇到这种题目的时候，也要学会打日志来调试（如何打日志有时候也是个技术活），不要脑动模拟，脑动模拟很容易越想越乱。
 
-最后我还给出了为什么前序和中序可以唯一确定一颗二叉树，后序和中序可以唯一确定一颗二叉树，而前序和后序却不行。
+最后我还给出了为什么前序和中序可以唯一确定一棵二叉树，后序和中序可以唯一确定一棵二叉树，而前序和后序却不行。
 
 认真研究完本篇，相信大家对二叉树的构造会清晰很多。
 

problems/0108.将有序数组转换为二叉搜索树.md

@@ -24,7 +24,7 @@
 做这道题目之前大家可以了解一下这几道：
 
 * [106.从中序与后序遍历序列构造二叉树](https://programmercarl.com/0106.从中序与后序遍历序列构造二叉树.html)
-* [654.最大二叉树](https://programmercarl.com/0654.最大二叉树.html)中其实已经讲过了，如果根据数组构造一颗二叉树。
+* [654.最大二叉树](https://programmercarl.com/0654.最大二叉树.html)中其实已经讲过了，如果根据数组构造一棵二叉树。
 * [701.二叉搜索树中的插入操作](https://programmercarl.com/0701.二叉搜索树中的插入操作.html)
 * [450.删除二叉搜索树中的节点](https://programmercarl.com/0450.删除二叉搜索树中的节点.html)
 
@@ -36,7 +36,7 @@
 其实这里不用强调平衡二叉搜索树，数组构造二叉树，构成平衡树是自然而然的事情，因为大家默认都是从数组中间位置取值作为节点元素，一般不会随机取，**所以想构成不平衡的二叉树是自找麻烦**。
 
 
-在[二叉树：构造二叉树登场！](https://programmercarl.com/0106.从中序与后序遍历序列构造二叉树.html)和[二叉树：构造一棵最大的二叉树](https://programmercarl.com/0654.最大二叉树.html)中其实已经讲过了，如果根据数组构造一颗二叉树。
+在[二叉树：构造二叉树登场！](https://programmercarl.com/0106.从中序与后序遍历序列构造二叉树.html)和[二叉树：构造一棵最大的二叉树](https://programmercarl.com/0654.最大二叉树.html)中其实已经讲过了，如果根据数组构造一棵二叉树。
 
 **本质就是寻找分割点，分割点作为当前节点，然后递归左区间和右区间**。
 

problems/0110.平衡二叉树.md

@@ -51,7 +51,7 @@
 
 有的同学一定疑惑，为什么[104.二叉树的最大深度](https://programmercarl.com/0104.二叉树的最大深度.html)中求的是二叉树的最大深度，也用的是后序遍历。
 
-**那是因为代码的逻辑其实是求的根节点的高度，而根节点的高度就是这颗树的最大深度，所以才可以使用后序遍历。**
+**那是因为代码的逻辑其实是求的根节点的高度，而根节点的高度就是这棵树的最大深度，所以才可以使用后序遍历。**
 
 在[104.二叉树的最大深度](https://programmercarl.com/0104.二叉树的最大深度.html)中，如果真正求取二叉树的最大深度，代码应该写成如下：（前序遍历）
 

problems/0112.路径总和.md

@@ -43,8 +43,8 @@
 
 再来看返回值，递归函数什么时候需要返回值？什么时候不需要返回值？这里总结如下三点：
 
-* 如果需要搜索整颗二叉树且不用处理递归返回值，递归函数就不要返回值。（这种情况就是本文下半部分介绍的113.路径总和ii）
+* 如果需要搜索整棵二叉树且不用处理递归返回值，递归函数就不要返回值。（这种情况就是本文下半部分介绍的113.路径总和ii）
-* 如果需要搜索整颗二叉树且需要处理递归返回值，递归函数就需要返回值。 （这种情况我们在[236. 二叉树的最近公共祖先](https://programmercarl.com/0236.二叉树的最近公共祖先.html)中介绍）
+* 如果需要搜索整棵二叉树且需要处理递归返回值，递归函数就需要返回值。 （这种情况我们在[236. 二叉树的最近公共祖先](https://programmercarl.com/0236.二叉树的最近公共祖先.html)中介绍）
 * 如果要搜索其中一条符合条件的路径，那么递归一定需要返回值，因为遇到符合条件的路径了就要及时返回。（本题的情况）
 
 而本题我们要找一条符合条件的路径，所以递归函数需要返回值，及时返回，那么返回类型是什么呢？

problems/0131.分割回文串.md

@@ -48,7 +48,7 @@
 
 感受出来了不？
 
-所以切割问题，也可以抽象为一颗树形结构，如图：
+所以切割问题，也可以抽象为一棵树形结构，如图：
 
 ![131.分割回文串](https://code-thinking.cdn.bcebos.com/pics/131.%E5%88%86%E5%89%B2%E5%9B%9E%E6%96%87%E4%B8%B2.jpg)
 

problems/0236.二叉树的最近公共祖先.md

@@ -101,7 +101,7 @@ left与right的逻辑处理;
 
 **在递归函数有返回值的情况下：如果要搜索一条边，递归函数返回值不为空的时候，立刻返回，如果搜索整个树，直接用一个变量left、right接住返回值，这个left、right后序还有逻辑处理的需要，也就是后序遍历中处理中间节点的逻辑（也是回溯）**。
 
-那么为什么要遍历整颗树呢？直观上来看，找到最近公共祖先，直接一路返回就可以了。
+那么为什么要遍历整棵树呢？直观上来看，找到最近公共祖先，直接一路返回就可以了。
 
 如图：
 
@@ -161,7 +161,7 @@ else  { //  (left == NULL && right == NULL)
 
 ![236.二叉树的最近公共祖先2](https://img-blog.csdnimg.cn/202102041512582.png)
 
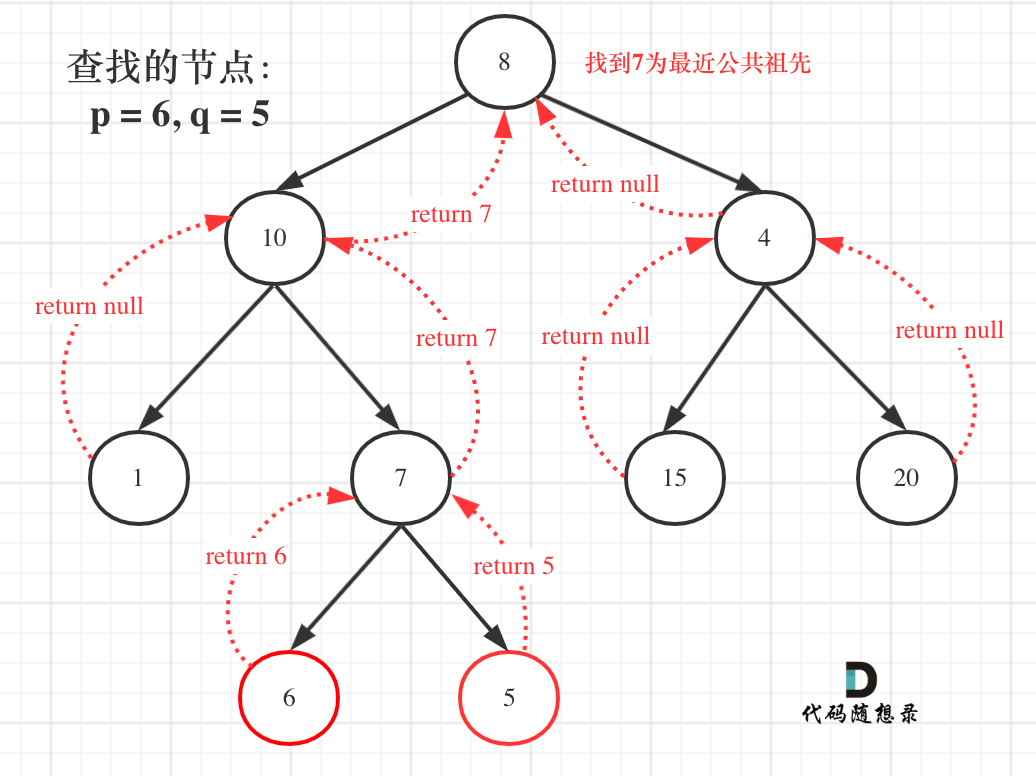
-**从图中，大家可以看到，我们是如何回溯遍历整颗二叉树，将结果返回给头结点的！**
+**从图中，大家可以看到，我们是如何回溯遍历整棵二叉树，将结果返回给头结点的！**
 
 整体代码如下：
 
@@ -208,7 +208,7 @@ public:
 
 1. 求最小公共祖先，需要从底向上遍历，那么二叉树，只能通过后序遍历（即：回溯）实现从低向上的遍历方式。
 
-2. 在回溯的过程中，必然要遍历整颗二叉树，即使已经找到结果了，依然要把其他节点遍历完，因为要使用递归函数的返回值（也就是代码中的left和right）做逻辑判断。
+2. 在回溯的过程中，必然要遍历整棵二叉树，即使已经找到结果了，依然要把其他节点遍历完，因为要使用递归函数的返回值（也就是代码中的left和right）做逻辑判断。
 
 3. 要理解如果返回值left为空，right不为空为什么要返回right，为什么可以用返回right传给上一层结果。
 

problems/0347.前K个高频元素.md

@@ -50,7 +50,7 @@
 
 什么是堆呢？
 
-**堆是一颗完全二叉树，树中每个结点的值都不小于（或不大于）其左右孩子的值。** 如果父亲结点是大于等于左右孩子就是大顶堆，小于等于左右孩子就是小顶堆。
+**堆是一棵完全二叉树，树中每个结点的值都不小于（或不大于）其左右孩子的值。** 如果父亲结点是大于等于左右孩子就是大顶堆，小于等于左右孩子就是小顶堆。
 
 所以大家经常说的大顶堆（堆头是最大元素），小顶堆（堆头是最小元素），如果懒得自己实现的话，就直接用priority_queue（优先级队列）就可以了，底层实现都是一样的，从小到大排就是小顶堆，从大到小排就是大顶堆。
 

problems/0450.删除二叉搜索树中的节点.md

@@ -66,7 +66,7 @@ if (root == nullptr) return root;
 
 ![450.删除二叉搜索树中的节点](https://tva1.sinaimg.cn/large/008eGmZEly1gnbj3k596mg30dq0aigyz.gif)
 
-动画中颗二叉搜索树中，删除元素7， 那么删除节点（元素7）的左孩子就是5，删除节点（元素7）的右子树的最左面节点是元素8。
+动画中棵二叉搜索树中，删除元素7， 那么删除节点（元素7）的左孩子就是5，删除节点（元素7）的右子树的最左面节点是元素8。
 
 将删除节点（元素7）的左孩子放到删除节点（元素7）的右子树的最左面节点（元素8）的左孩子上，就是把5为根节点的子树移到了8的左孩子的位置。
 

problems/0513.找树左下角的值.md

@@ -63,11 +63,11 @@ void traversal(TreeNode* root, int leftLen)
 
 其实很多同学都对递归函数什么时候要有返回值，什么时候不能有返回值很迷茫。
 
-**如果需要遍历整颗树，递归函数就不能有返回值。如果需要遍历某一条固定路线，递归函数就一定要有返回值！**
+**如果需要遍历整棵树，递归函数就不能有返回值。如果需要遍历某一条固定路线，递归函数就一定要有返回值！**
 
 初学者可能对这个结论不太理解，别急，后面我会安排一道题目专门讲递归函数的返回值问题。这里大家暂时先了解一下。
 
-本题我们是要遍历整个树找到最深的叶子节点，需要遍历整颗树，所以递归函数没有返回值。
+本题我们是要遍历整个树找到最深的叶子节点，需要遍历整棵树，所以递归函数没有返回值。
 
 2. 确定终止条件
 

problems/0538.把二叉搜索树转换为累加树.md

@@ -47,7 +47,7 @@
 
 一看到累加树，相信很多小伙伴都会疑惑：如何累加？遇到一个节点，然后在遍历其他节点累加？怎么一想这么麻烦呢。
 
-然后再发现这是一颗二叉搜索树，二叉搜索树啊，这是有序的啊。
+然后再发现这是一棵二叉搜索树，二叉搜索树啊，这是有序的啊。
 
 那么有序的元素如果求累加呢？
 

problems/0617.合并二叉树.md

@@ -243,7 +243,7 @@ public:
 
 合并二叉树，也是二叉树操作的经典题目，如果没有接触过的话，其实并不简单，因为我们习惯了操作一个二叉树，一起操作两个二叉树，还会有点懵懵的。
 
-这不是我们第一次操作两颗二叉树了，在[二叉树：我对称么？](https://programmercarl.com/0101.对称二叉树.html)中也一起操作了两棵二叉树。
+这不是我们第一次操作两棵二叉树了，在[二叉树：我对称么？](https://programmercarl.com/0101.对称二叉树.html)中也一起操作了两棵二叉树。
 
 迭代法中，一般一起操作两个树都是使用队列模拟类似层序遍历，同时处理两个树的节点，这种方式最好理解，如果用模拟递归的思路的话，要复杂一些。
 

problems/0685.冗余连接II.md

@@ -42,7 +42,7 @@
 
 <img src='https://code-thinking.cdn.bcebos.com/pics/685.冗余连接II1.png' width=600> </img></div>
 
-且只有一个节点入度为2，为什么不看出度呢，出度没有意义，一颗树中随便一个父节点就有多个出度。
+且只有一个节点入度为2，为什么不看出度呢，出度没有意义，一棵树中随便一个父节点就有多个出度。
 
 
 第三种情况是没有入度为2的点，那么图中一定出现了有向环（**注意这里强调是有向环！**）

problems/0701.二叉搜索树中的插入操作.md

@@ -77,7 +77,7 @@ if (root == NULL) {
 
 此时要明确，需要遍历整棵树么？
 
-别忘了这是搜索树，遍历整颗搜索树简直是对搜索树的侮辱，哈哈。
+别忘了这是搜索树，遍历整棵搜索树简直是对搜索树的侮辱，哈哈。
 
 搜索树是有方向了，可以根据插入元素的数值，决定递归方向。
 

problems/前序/ACM模式如何构建二叉树.md

@@ -24,7 +24,7 @@
 
 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20210914222335.png)
 
-一直跟着公众号学算法的录友 应该知道，我在[二叉树：构造二叉树登场！](https://mp.weixin.qq.com/s/Dza-fqjTyGrsRw4PWNKdxA)，已经讲过，**只有 中序与后序 和  中序和前序 可以确定一颗唯一的二叉树。 前序和后序是不能确定唯一的二叉树的**。
+一直跟着公众号学算法的录友 应该知道，我在[二叉树：构造二叉树登场！](https://mp.weixin.qq.com/s/Dza-fqjTyGrsRw4PWNKdxA)，已经讲过，**只有 中序与后序 和  中序和前序 可以确定一棵唯一的二叉树。 前序和后序是不能确定唯一的二叉树的**。
 
 那么[538.把二叉搜索树转换为累加树](https://mp.weixin.qq.com/s/rlJUFGCnXsIMX0Lg-fRpIw)的示例中，为什么，一个序列（数组或者是字符串）就可以确定二叉树了呢？
 

problems/前序/递归算法的时间与空间复杂度分析.md

@@ -34,13 +34,13 @@ int fibonacci(int i) {
 
 在讲解递归时间复杂度的时候，我们提到了递归算法的时间复杂度本质上是要看: **递归的次数 * 每次递归的时间复杂度**。
 
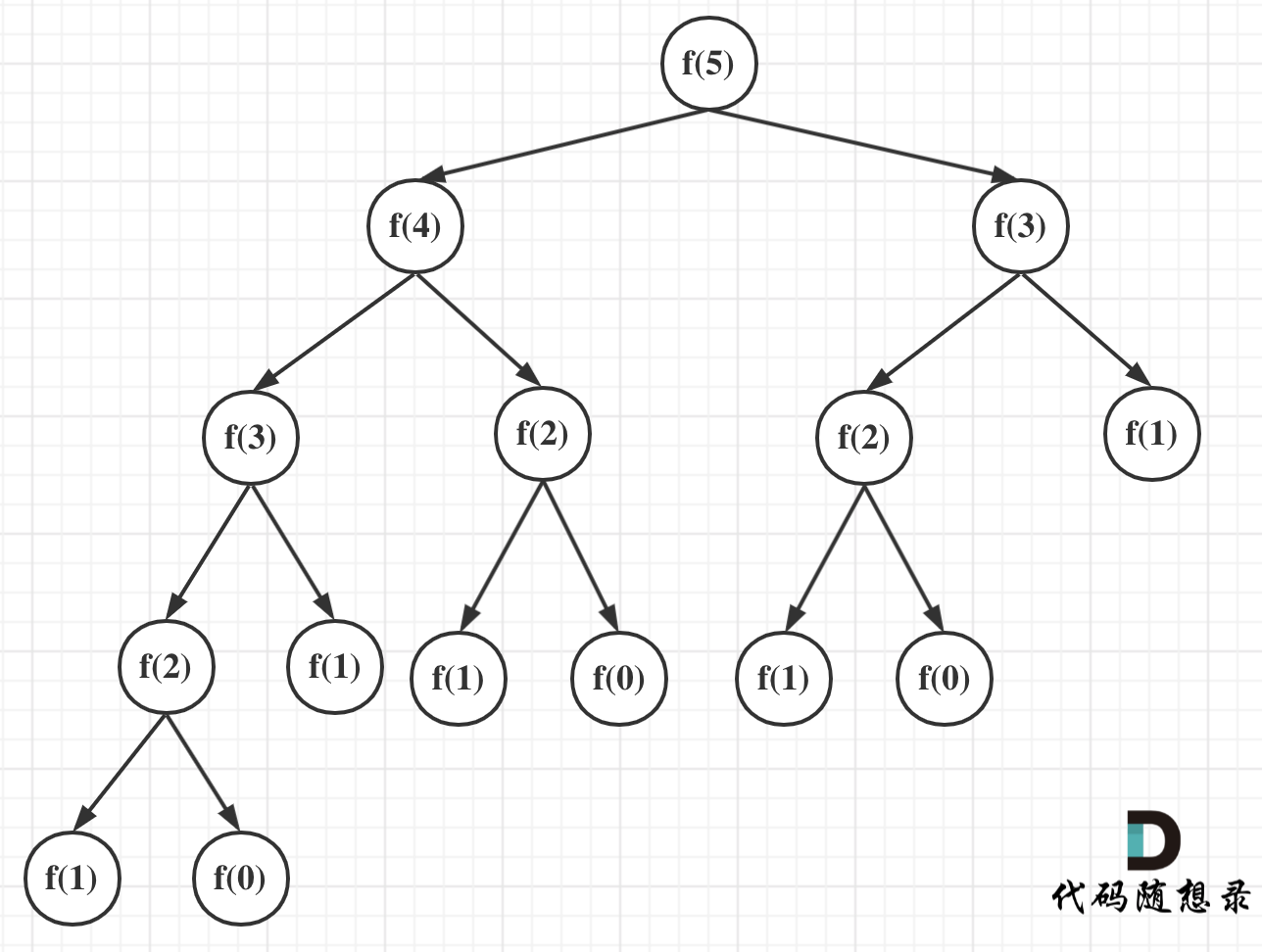
-可以看出上面的代码每次递归都是$O(1)$的操作。再来看递归了多少次，这里将i为5作为输入的递归过程 抽象成一颗递归树，如图：
+可以看出上面的代码每次递归都是$O(1)$的操作。再来看递归了多少次，这里将i为5作为输入的递归过程 抽象成一棵递归树，如图：
 
 ![递归空间复杂度分析](https://img-blog.csdnimg.cn/20210305093200104.png)
 
 从图中，可以看出f(5)是由f(4)和f(3)相加而来，那么f(4)是由f(3)和f(2)相加而来 以此类推。
 
-在这颗二叉树中每一个节点都是一次递归，那么这棵树有多少个节点呢？
+在这棵二叉树中每一个节点都是一次递归，那么这棵树有多少个节点呢？
 
 我们之前也有说到，一棵深度（按根节点深度为1）为k的二叉树最多可以有 2^k - 1 个节点。
 

problems/前序/通过一道面试题目，讲一讲递归算法的时间复杂度！.md

@@ -77,15 +77,15 @@ int function3(int x, int n) {
 
 面试官看到后微微一笑，问：“这份代码的时间复杂度又是多少呢？” 此刻有些同学可能要陷入了沉思了。
 
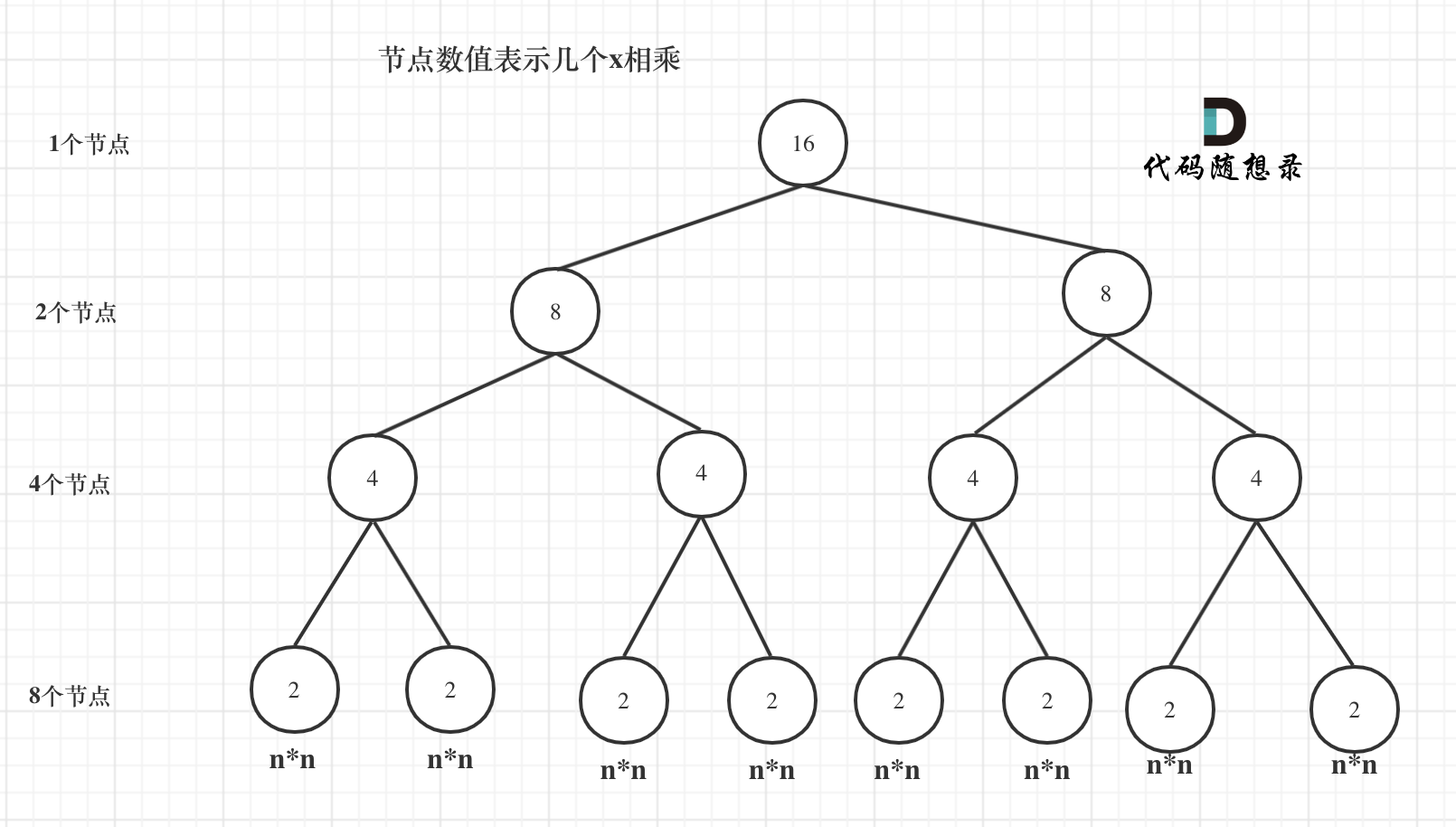
-我们来分析一下，首先看递归了多少次呢，可以把递归抽象出一颗满二叉树。刚刚同学写的这个算法，可以用一颗满二叉树来表示（为了方便表示，选择n为偶数16），如图：
+我们来分析一下，首先看递归了多少次呢，可以把递归抽象出一棵满二叉树。刚刚同学写的这个算法，可以用一棵满二叉树来表示（为了方便表示，选择n为偶数16），如图：
 
 ![递归算法的时间复杂度](https://img-blog.csdnimg.cn/20201209193909426.png)
 
-当前这颗二叉树就是求x的n次方，n为16的情况，n为16的时候，进行了多少次乘法运算呢？
+当前这棵二叉树就是求x的n次方，n为16的情况，n为16的时候，进行了多少次乘法运算呢？
 
 这棵树上每一个节点就代表着一次递归并进行了一次相乘操作，所以进行了多少次递归的话，就是看这棵树上有多少个节点。
 
-熟悉二叉树话应该知道如何求满二叉树节点数量，这颗满二叉树的节点数量就是`2^3 + 2^2 + 2^1 + 2^0 = 15`，可以发现：**这其实是等比数列的求和公式，这个结论在二叉树相关的面试题里也经常出现**。
+熟悉二叉树话应该知道如何求满二叉树节点数量，这棵满二叉树的节点数量就是`2^3 + 2^2 + 2^1 + 2^0 = 15`，可以发现：**这其实是等比数列的求和公式，这个结论在二叉树相关的面试题里也经常出现**。
 
 这么如果是求x的n次方，这个递归树有多少个节点呢，如下图所示：(m为深度，从0开始)
 

problems/周总结/20201010二叉树周末总结.md

@@ -43,7 +43,7 @@
 
 在[二叉树：递归函数究竟什么时候需要返回值，什么时候不要返回值？](https://programmercarl.com/0112.路径总和.html)中通过两道题目，彻底说清楚递归函数的返回值问题。
 
-一般情况下：**如果需要搜索整颗二叉树，那么递归函数就不要返回值，如果要搜索其中一条符合条件的路径，递归函数就需要返回值，因为遇到符合条件的路径了就要及时返回。**
+一般情况下：**如果需要搜索整棵二叉树，那么递归函数就不要返回值，如果要搜索其中一条符合条件的路径，递归函数就需要返回值，因为遇到符合条件的路径了就要及时返回。**
 
 特别是有些时候 递归函数的返回值是bool类型，一些同学会疑惑为啥要加这个，其实就是为了找到一条边立刻返回。
 
@@ -51,7 +51,7 @@
 
 ## 周五
 
-之前都是讲解遍历二叉树，这次该构造二叉树了，在[二叉树：构造二叉树登场！](https://programmercarl.com/0106.从中序与后序遍历序列构造二叉树.html)中，我们通过前序和中序，后序和中序，构造了唯一的一颗二叉树。
+之前都是讲解遍历二叉树，这次该构造二叉树了，在[二叉树：构造二叉树登场！](https://programmercarl.com/0106.从中序与后序遍历序列构造二叉树.html)中，我们通过前序和中序，后序和中序，构造了唯一的一棵二叉树。
 
 **构造二叉树有三个注意的点：**
 

problems/周总结/20201017二叉树周末总结.md

@@ -8,7 +8,7 @@
 
 在[二叉树：合并两个二叉树](https://programmercarl.com/0617.合并二叉树.html)中讲解了如何合并两个二叉树，平时我们都习惯了操作一个二叉树，一起操作两个树可能还有点陌生。
 
-其实套路是一样，只不过一起操作两个树的指针，我们之前讲过求 [二叉树：我对称么？](https://programmercarl.com/0101.对称二叉树.html)的时候，已经初步涉及到了 一起遍历两颗二叉树了。
+其实套路是一样，只不过一起操作两个树的指针，我们之前讲过求 [二叉树：我对称么？](https://programmercarl.com/0101.对称二叉树.html)的时候，已经初步涉及到了 一起遍历两棵二叉树了。
 
 **迭代法中，一般一起操作两个树都是使用队列模拟类似层序遍历，同时处理两个树的节点，这种方式最好理解，如果用模拟递归的思路的话，要复杂一些。**
 
@@ -24,7 +24,7 @@
 
 ## 周三
 
-了解了二搜索树的特性之后， 开始验证[一颗二叉树是不是二叉搜索树](https://programmercarl.com/0098.验证二叉搜索树.html)。
+了解了二搜索树的特性之后， 开始验证[一棵二叉树是不是二叉搜索树](https://programmercarl.com/0098.验证二叉搜索树.html)。
 
 首先在此强调一下二叉搜索树的特性：
 

problems/周总结/20201030回溯周末总结.md

@@ -40,7 +40,7 @@
 
 在[回溯算法：求组合问题！](https://programmercarl.com/0077.组合.html)中，我们开始用回溯法解决第一道题目，组合问题。
 
-我在文中开始的时候给大家列举k层for循环例子，进而得出都是同样是暴利解法，为什么要用回溯法。
+我在文中开始的时候给大家列举k层for循环例子，进而得出都是同样是暴力解法，为什么要用回溯法。
 
 **此时大家应该深有体会回溯法的魅力，用递归控制for循环嵌套的数量！**
 

problems/周总结/20201107回溯周末总结.md

@@ -50,7 +50,7 @@ for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target;
 
 我在图中将used的变化用橘黄色标注上，可以看出在candidates[i] == candidates[i - 1]相同的情况下：
 
-* used[i - 1] == true，说明同一树支candidates[i - 1]使用过
+* used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
 * used[i - 1] == false，说明同一树层candidates[i - 1]使用过
 
 **这块去重的逻辑很抽象，网上搜的题解基本没有能讲清楚的，如果大家之前思考过这个问题或者刷过这道题目，看到这里一定会感觉通透了很多！**
@@ -118,7 +118,7 @@ if (s.size() > 12) return result; // 剪枝
 
 认清这个本质之后，今天的题目就是一道模板题了。
 
-其实可以不需要加终止条件，因为startIndex >= nums.size()，本层for循环本来也结束了，本来我们就要遍历整颗树。
+其实可以不需要加终止条件，因为startIndex >= nums.size()，本层for循环本来也结束了，本来我们就要遍历整棵树。
 
 有的同学可能担心不写终止条件会不会无限递归？
 

problems/回溯总结.md

@@ -55,7 +55,7 @@ void backtracking(参数) {
 
 在[回溯算法：求组合问题！](https://programmercarl.com/0077.组合.html)中，我们开始用回溯法解决第一道题目：组合问题。
 
-我在文中开始的时候给大家列举k层for循环例子，进而得出都是同样是暴利解法，为什么要用回溯法！
+我在文中开始的时候给大家列举k层for循环例子，进而得出都是同样是暴力解法，为什么要用回溯法！
 
 **此时大家应该深有体会回溯法的魅力，用递归控制for循环嵌套的数量！**
 
@@ -117,7 +117,7 @@ void backtracking(参数) {
 
 最后还给出了本题的剪枝优化，如下：
 
-```
+```cpp
 for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++)
 ```
 
@@ -142,7 +142,7 @@ for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target;
 
 我在图中将used的变化用橘黄色标注上，**可以看出在candidates[i] == candidates[i - 1]相同的情况下：**
 
-* used[i - 1] == true，说明同一树支candidates[i - 1]使用过
+* used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
 * used[i - 1] == false，说明同一树层candidates[i - 1]使用过
 
 **这块去重的逻辑很抽象，网上搜的题解基本没有能讲清楚的，如果大家之前思考过这个问题或者刷过这道题目，看到这里一定会感觉通透了很多！**
@@ -202,7 +202,7 @@ for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target;
 
 认清这个本质之后，今天的题目就是一道模板题了。
 
-**本题其实可以不需要加终止条件**，因为startIndex >= nums.size()，本层for循环本来也结束了，本来我们就要遍历整颗树。
+**本题其实可以不需要加终止条件**，因为startIndex >= nums.size()，本层for循环本来也结束了，本来我们就要遍历整棵树。
 
 有的同学可能担心不写终止条件会不会无限递归？
 
@@ -331,13 +331,13 @@ used数组可是全局变量，每层与每层之间公用一个used数组，所
 
 在[回溯算法：N皇后问题](https://programmercarl.com/0051.N皇后.html)中终于迎来了传说中的N皇后。
 
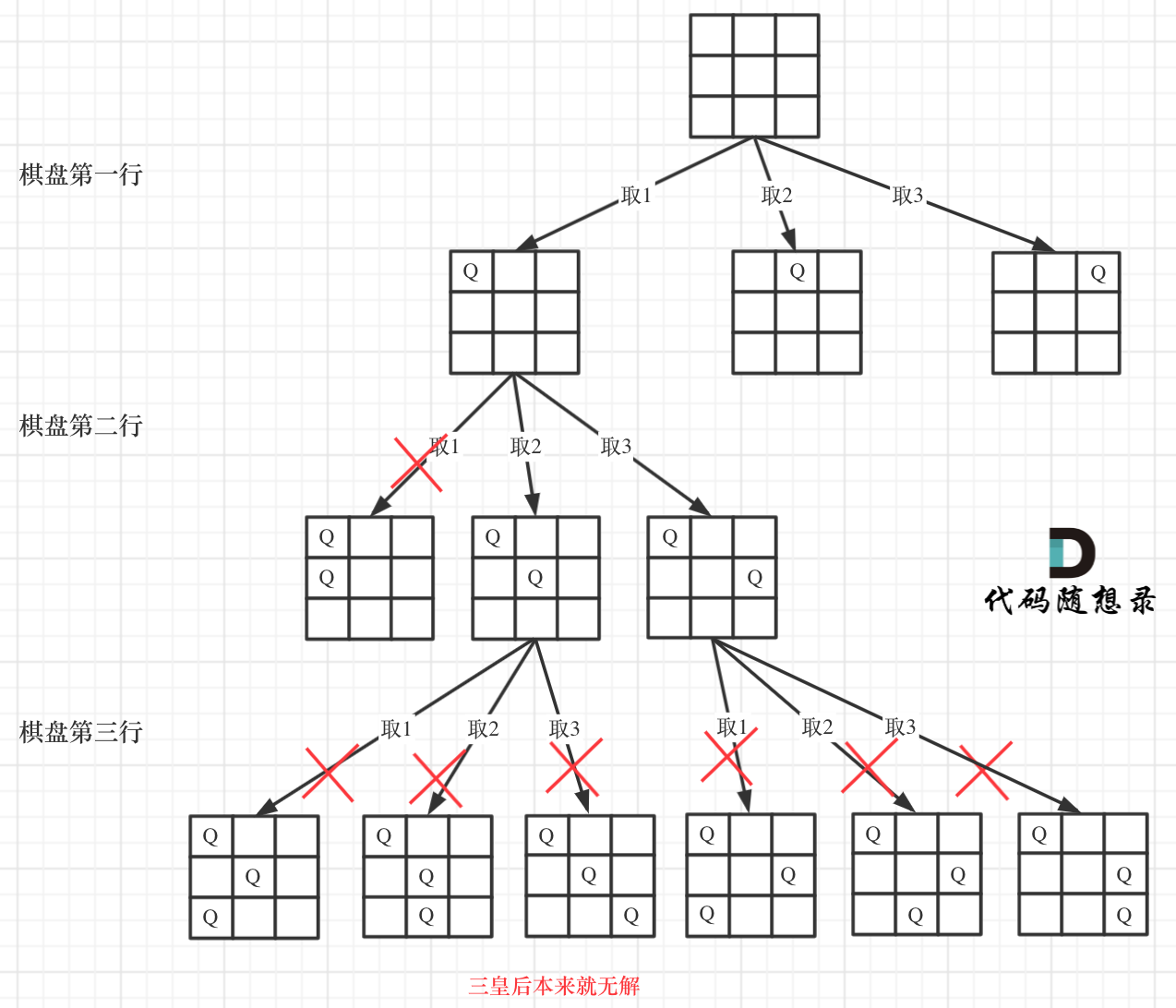
-下面我用一个3 * 3 的棋盘，将搜索过程抽象为一颗树，如图：
+下面我用一个3 * 3 的棋盘，将搜索过程抽象为一棵树，如图：
 
 ![51.N皇后](https://img-blog.csdnimg.cn/20201118225433127.png)
 
-从图中，可以看出，二维矩阵中矩阵的高就是这颗树的高度，矩阵的宽就是树形结构中每一个节点的宽度。
+从图中，可以看出，二维矩阵中矩阵的高就是这棵树的高度，矩阵的宽就是树形结构中每一个节点的宽度。
 
-那么我们用皇后们的约束条件，来回溯搜索这颗树，**只要搜索到了树的叶子节点，说明就找到了皇后们的合理位置了**。 
+那么我们用皇后们的约束条件，来回溯搜索这棵树，**只要搜索到了树的叶子节点，说明就找到了皇后们的合理位置了**。 
 
 如果从来没有接触过N皇后问题的同学看着这样的题会感觉无从下手，可能知道要用回溯法，但也不知道该怎么去搜。
 

problems/回溯算法去重问题的另一种写法.md

@@ -6,7 +6,7 @@
 
 # 回溯算法去重问题的另一种写法
 
-> 在 [本周小结！（回溯算法系列三）](https://programmercarl.com/周总结/20201112回溯周末总结.html) 中一位录友对 整颗树的本层和同一节点的本层有疑问，也让我重新思考了一下，发现这里确实有问题，所以专门写一篇来纠正，感谢录友们的积极交流哈！
+> 在 [本周小结！（回溯算法系列三）](https://programmercarl.com/周总结/20201112回溯周末总结.html) 中一位录友对 整棵树的本层和同一节点的本层有疑问，也让我重新思考了一下，发现这里确实有问题，所以专门写一篇来纠正，感谢录友们的积极交流哈！
 
 接下来我再把这块再讲一下。
 

problems/回溯算法理论基础.md

@@ -61,7 +61,7 @@
 
 因为回溯法解决的都是在集合中递归查找子集，**集合的大小就构成了树的宽度，递归的深度，都构成的树的深度**。
 
-递归就要有终止条件，所以必然是一颗高度有限的树（N叉树）。
+递归就要有终止条件，所以必然是一棵高度有限的树（N叉树）。
 
 这块可能初学者还不太理解，后面的回溯算法解决的所有题目中，我都会强调这一点并画图举相应的例子，现在有一个印象就行。
 

problems/栈与队列总结.md

@@ -135,7 +135,7 @@ cd a/b/c/../../
 
 什么是堆呢？ 
 
-**堆是一颗完全二叉树，树中每个结点的值都不小于（或不大于）其左右孩子的值。** 如果父亲结点是大于等于左右孩子就是大顶堆，小于等于左右孩子就是小顶堆。 
+**堆是一棵完全二叉树，树中每个结点的值都不小于（或不大于）其左右孩子的值。** 如果父亲结点是大于等于左右孩子就是大顶堆，小于等于左右孩子就是小顶堆。 
 
 所以大家经常说的大顶堆（堆头是最大元素），小顶堆（堆头是最小元素），如果懒得自己实现的话，就直接用priority_queue（优先级队列）就可以了，底层实现都是一样的，从小到大排就是小顶堆，从大到小排就是大顶堆。