Merge pull request #2484 from paigeman/paigeman-patch-1

Show some LaTeX formula normally

problems/0024.两两交换链表中的节点.md

@@ -81,7 +81,7 @@ public:
 
 上面的代码我第一次提交执行用时8ms，打败6.5%的用户，差点吓到我了。
 
-心想应该没有更好的方法了吧，也就$O(n)$的时间复杂度，重复提交几次，这样了：
+心想应该没有更好的方法了吧，也就 $O(n)$ 的时间复杂度，重复提交几次，这样了：
 
 ![24.两两交换链表中的节点](https://code-thinking.cdn.bcebos.com/pics/24.%E4%B8%A4%E4%B8%A4%E4%BA%A4%E6%8D%A2%E9%93%BE%E8%A1%A8%E4%B8%AD%E7%9A%84%E8%8A%82%E7%82%B9.png)
 

problems/前序/On的算法居然超时了，此时的n究竟是多大？.md

@@ -14,9 +14,9 @@
 
 也就是说程序运行的时间超过了规定的时间，一般OJ（online judge）的超时时间就是1s，也就是用例数据输入后最多要1s内得到结果，暂时还不清楚leetcode的判题规则，下文为了方便讲解，暂定超时时间就是1s。
 
-如果写出了一个$O(n)$的算法 ，其实可以估算出来n是多大的时候算法的执行时间就会超过1s了。
+如果写出了一个 $O(n)$ 的算法 ，其实可以估算出来n是多大的时候算法的执行时间就会超过1s了。
 
-如果n的规模已经足够让$O(n)$的算法运行时间超过了1s，就应该考虑log(n)的解法了。
+如果n的规模已经足够让 $O(n)$ 的算法运行时间超过了1s，就应该考虑log(n)的解法了。
 
 ## 从硬件配置看计算机的性能
 
@@ -60,7 +60,7 @@
 
 测试硬件：2015年MacPro，CPU配置：2.7 GHz Dual-Core Intel Core i5
 
-实现三个函数，时间复杂度分别是 $O(n)$ , $O(n^2)$, $O(n\log n)$，使用加法运算来统一测试。
+实现三个函数，时间复杂度分别是 $O(n)$ , $O(n^2)$ , $O(n\log n)$ ，使用加法运算来统一测试。
 
 ```CPP
 // O(n)
@@ -126,19 +126,19 @@ int main() {
 
 ![程序超时2](https://code-thinking-1253855093.file.myqcloud.com/pics/20200729200018460-20230310124315093.png)
 
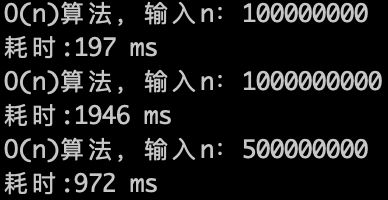
-O(n)的算法，1s内大概计算机可以运行 5 * (10^8)次计算，可以推测一下$O(n^2)$ 的算法应该1s可以处理的数量级的规模是 5 * (10^8)开根号，实验数据如下。
+O(n)的算法，1s内大概计算机可以运行 5 * (10^8)次计算，可以推测一下 $O(n^2)$ 的算法应该1s可以处理的数量级的规模是 5 * (10^8)开根号，实验数据如下。
 
 ![程序超时3](https://code-thinking-1253855093.file.myqcloud.com/pics/2020072919590970-20230310124318532.png)
 
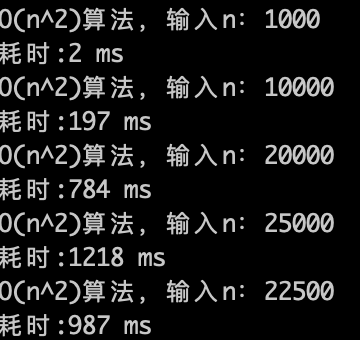
 O(n^2)的算法，1s内大概计算机可以运行 22500次计算，验证了刚刚的推测。
 
-在推测一下$O(n\log n)$的话， 1s可以处理的数据规模是什么呢？
+在推测一下 $O(n\log n)$ 的话， 1s可以处理的数据规模是什么呢？
 
-理论上应该是比 $O(n)$少一个数量级，因为$\log n$的复杂度 其实是很快，看一下实验数据。
+理论上应该是比 $O(n)$ 少一个数量级，因为 $\log n$ 的复杂度 其实是很快，看一下实验数据。
 
 ![程序超时4](https://code-thinking-1253855093.file.myqcloud.com/pics/20200729195729407-20230310124322232.png)
 
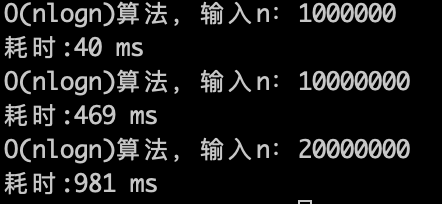
-$O(n\log n)$的算法，1s内大概计算机可以运行 2 * (10^7)次计算，符合预期。
+$O(n\log n)$ 的算法，1s内大概计算机可以运行 2 * (10^7)次计算，符合预期。
 
 这是在我个人PC上测出来的数据，不能说是十分精确，但数量级是差不多的，大家也可以在自己的计算机上测一下。
 
@@ -263,7 +263,7 @@ public class TimeComplexity {
 
 ## 总结
 
-本文详细分析了在leetcode上做题程序为什么会有超时，以及从硬件配置上大体知道CPU的执行速度，然后亲自做一个实验来看看$O(n)$的算法，跑一秒钟，这个n究竟是做大，最后给出不同时间复杂度，一秒内可以运算出来的n的大小。
+本文详细分析了在leetcode上做题程序为什么会有超时，以及从硬件配置上大体知道CPU的执行速度，然后亲自做一个实验来看看 $O(n)$ 的算法，跑一秒钟，这个n究竟是做大，最后给出不同时间复杂度，一秒内可以运算出来的n的大小。
 
 建议录友们也都自己做一做实验，测一测，看看是不是和我的测出来的结果差不多。
 

problems/前序/关于空间复杂度，可能有几个疑问？.md

@@ -32,7 +32,7 @@
 
 同样在工程实践中，计算机的内存空间也不是无限的，需要工程师对软件运行时所使用的内存有一个大体评估，这都需要用到算法空间复杂度的分析。
 
-来看一下例子，什么时候的空间复杂度是$O(1)$呢，C++代码如下：
+来看一下例子，什么时候的空间复杂度是 $O(1)$ 呢，C++代码如下：
 
 ```CPP
 int j = 0;

problems/前序/递归算法的时间与空间复杂度分析.md

@@ -191,7 +191,7 @@ int main()
 
 因为每次递归所需的空间都被压到调用栈里（这是内存管理里面的数据结构，和算法里的栈原理是一样的），一次递归结束，这个栈就是就是把本次递归的数据弹出去。所以这个栈最大的长度就是递归的深度。
 
-此时可以分析这段递归的空间复杂度，从代码中可以看出每次递归所需要的空间大小都是一样的，所以每次递归中需要的空间是一个常量，并不会随着n的变化而变化，每次递归的空间复杂度就是$O(1)$。
+此时可以分析这段递归的空间复杂度，从代码中可以看出每次递归所需要的空间大小都是一样的，所以每次递归中需要的空间是一个常量，并不会随着n的变化而变化，每次递归的空间复杂度就是 $O(1)$ 。
 
 在看递归的深度是多少呢？如图所示：
 

problems/双指针总结.md

@@ -90,7 +90,7 @@ for (int i = 0; i < array.size(); i++) {
 
 ## 总结 
 
-本文中一共介绍了leetcode上九道使用双指针解决问题的经典题目，除了链表一些题目一定要使用双指针，其他题目都是使用双指针来提高效率，一般是将O(n^2)的时间复杂度，降为$O(n)$。
+本文中一共介绍了leetcode上九道使用双指针解决问题的经典题目，除了链表一些题目一定要使用双指针，其他题目都是使用双指针来提高效率，一般是将O(n^2)的时间复杂度，降为 $O(n)$ 。
 
 建议大家可以把文中涉及到的题目在好好做一做，琢磨琢磨，基本对双指针法就不在话下了。
 

problems/周总结/20201210复杂度分析周末总结.md

@@ -54,10 +54,10 @@
 文中涉及如下问题：
 
 * 究竟什么是大O？大O表示什么意思？严格按照大O的定义来说，快排应该是$O(n^2)$的算法！
-* $O(n^2)$的算法为什么有时候比$O(n)$的算法更优？
+* $O(n^2)$ 的算法为什么有时候比 $O(n)$ 的算法更优？
 * 什么时间复杂度为什么可以忽略常数项？
 * 如何简化复杂的时间复杂度表达式，原理是什么？
-* $O(\log n)$中的log究竟是以谁为底？
+* $O(\log n)$ 中的log究竟是以谁为底？
 
 这些问题大家可能懵懵懂懂的了解一些，但一细问又答不上来。
 
@@ -96,7 +96,7 @@
 
 文中给出了四个版本的代码实现，并逐一分析了其时间复杂度。
 
-此时大家就会发现，同一道题目，同样使用递归算法，有的同学会写出了O(n)的代码，有的同学就写出了$O(\log n)$的代码。
+此时大家就会发现，同一道题目，同样使用递归算法，有的同学会写出了O(n)的代码，有的同学就写出了 $O(\log n)$ 的代码。
 
 其本质是要对递归的时间复杂度有清晰的认识，才能运用递归来有效的解决问题！
 

problems/栈与队列总结.md

@@ -142,7 +142,7 @@ cd a/b/c/../../
 
 本题就要**使用优先级队列来对部分频率进行排序。**  注意这里是对部分数据进行排序而不需要对所有数据排序！
 
-所以排序的过程的时间复杂度是$O(\log k)$，整个算法的时间复杂度是$O(n\log k)$。
+所以排序的过程的时间复杂度是 $O(\log k)$ ，整个算法的时间复杂度是 $O(n\log k)$ 。
 
 ## 总结