diff --git a/README.md b/README.md index b326046e..b1db51c9 100644 --- a/README.md +++ b/README.md @@ -299,24 +299,25 @@ 背包问题大纲 -11. [动态规划：01背包理论基础](./problems/背包理论基础01背包-1.md) -12. [动态规划：01背包理论基础（滚动数组）](./problems/背包理论基础01背包-2.md) +11. [动态规划：01背包理论基础（二维dp数组）](./problems/背包理论基础01背包-1.md) +12. [动态规划：01背包理论基础（一维dp数组）](./problems/背包理论基础01背包-2.md) 13. [动态规划：416.分割等和子集](./problems/0416.分割等和子集.md) 14. [动态规划：1049.最后一块石头的重量II](./problems/1049.最后一块石头的重量II.md) 15. [本周小结！（动态规划系列三）](./problems/周总结/20210121动规周末总结.md) 16. [动态规划：494.目标和](./problems/0494.目标和.md) 17. [动态规划：474.一和零](./problems/0474.一和零.md) -18. [动态规划：完全背包总结篇](./problems/背包问题理论基础完全背包.md) -19. [动态规划：518.零钱兑换II](./problems/0518.零钱兑换II.md) -20. [本周小结！（动态规划系列四）](./problems/周总结/20210128动规周末总结.md) -21. [动态规划：377.组合总和Ⅳ](./problems/0377.组合总和Ⅳ.md) -22. [动态规划：70.爬楼梯（完全背包版本）](./problems/0070.爬楼梯完全背包版本.md) -23. [动态规划：322.零钱兑换](./problems/0322.零钱兑换.md) -24. [动态规划：279.完全平方数](./problems/0279.完全平方数.md) -25. [本周小结！（动态规划系列五）](./problems/周总结/20210204动规周末总结.md) -26. [动态规划：139.单词拆分](./problems/0139.单词拆分.md) -27. [动态规划：多重背包理论基础](./problems/背包问题理论基础多重背包.md) -28. [背包问题总结篇](./problems/背包总结篇.md) +18. [动态规划：完全背包理论基础（二维dp数组）](./problems/背包问题理论基础完全背包.md) +19. [动态规划：完全背包理论基础（一维dp数组）](./problems/背包问题完全背包一维.md) +20. [动态规划：518.零钱兑换II](./problems/0518.零钱兑换II.md) +21. [本周小结！（动态规划系列四）](./problems/周总结/20210128动规周末总结.md) +22. [动态规划：377.组合总和Ⅳ](./problems/0377.组合总和Ⅳ.md) +23. [动态规划：70.爬楼梯（完全背包版本）](./problems/0070.爬楼梯完全背包版本.md) +24. [动态规划：322.零钱兑换](./problems/0322.零钱兑换.md) +25. [动态规划：279.完全平方数](./problems/0279.完全平方数.md) +26. [本周小结！（动态规划系列五）](./problems/周总结/20210204动规周末总结.md) +27. [动态规划：139.单词拆分](./problems/0139.单词拆分.md) +28. [动态规划：多重背包理论基础](./problems/背包问题理论基础多重背包.md) +29. [背包问题总结篇](./problems/背包总结篇.md) 打家劫舍系列： @@ -408,21 +409,6 @@ （持续更新中....） - -## 十大排序 - -## 数论 - -## 高级数据结构经典题目 - -* 并查集 -* 最小生成树 -* 线段树 -* 树状数组 -* 字典树 - -## 海量数据处理 - # 补充题目 以上题目是重中之重，大家至少要刷两遍以上才能彻底理解，如果熟练以上题目之后还在找其他题目练手，可以再刷以下题目： diff --git a/problems/0070.爬楼梯.md b/problems/0070.爬楼梯.md index a2f664a4..6a13a21c 100644 --- a/problems/0070.爬楼梯.md +++ b/problems/0070.爬楼梯.md @@ -130,8 +130,8 @@ public: }; ``` -* 时间复杂度：$O(n)$ -* 空间复杂度：$O(n)$ +* 时间复杂度：O(n) +* 空间复杂度：O(n) 当然依然也可以，优化一下空间复杂度，代码如下： @@ -154,8 +154,8 @@ public: }; ``` -* 时间复杂度：$O(n)$ -* 空间复杂度：$O(1)$ +* 时间复杂度：O(n) +* 空间复杂度：O(1) 后面将讲解的很多动规的题目其实都是当前状态依赖前两个，或者前三个状态，都可以做空间上的优化，**但我个人认为面试中能写出版本一就够了哈，清晰明了，如果面试官要求进一步优化空间的话，我们再去优化**。 @@ -524,3 +524,4 @@ impl Solution { + diff --git a/problems/0111.二叉树的最小深度.md b/problems/0111.二叉树的最小深度.md index cd7096ac..708e0532 100644 --- a/problems/0111.二叉树的最小深度.md +++ b/problems/0111.二叉树的最小深度.md @@ -40,7 +40,7 @@ 本题依然是前序遍历和后序遍历都可以，前序求的是深度，后序求的是高度。 * 二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数或者节点数（取决于深度从0开始还是从1开始） -* 二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数后者节点数（取决于高度从0开始还是从1开始） +* 二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数或者节点数（取决于高度从0开始还是从1开始） 那么使用后序遍历，其实求的是根节点到叶子节点的最小距离，就是求高度的过程，不过这个最小距离 也同样是最小深度。 diff --git a/problems/0494.目标和.md b/problems/0494.目标和.md index dda3ad75..6ddf774d 100644 --- a/problems/0494.目标和.md +++ b/problems/0494.目标和.md @@ -151,13 +151,13 @@ if (abs(target) > sum) return 0; // 此时没有方案 本题则是装满有几种方法。其实这就是一个组合问题了。 -1. 确定dp数组以及下标的含义 +#### 1. 确定dp数组以及下标的含义 先用 二维 dp数组求解本题，dp[i][j]：使用 下标为[0, i]的nums[i]能够凑满j（包括j）这么大容量的包，有dp[i][j]种方法。 01背包为什么这么定义dp数组，我在[0-1背包理论基础](https://www.programmercarl.com/%E8%83%8C%E5%8C%85%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%8001%E8%83%8C%E5%8C%85-1.html)中 确定dp数组的含义里讲解过。 -2. 确定递推公式 +#### 2. 确定递推公式 我们先手动推导一下，这个二维数组里面的数值。 @@ -264,7 +264,7 @@ if (nums[i] > j) dp[i][j] = dp[i - 1][j]; else dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i]]; ``` -3. dp数组如何初始化 +#### 3. dp数组如何初始化 先明确递推的方向，如图，求解 dp[2][2] 是由 上方和左上方推出。 @@ -315,7 +315,7 @@ for (int i = 0; i < nums.size(); i++) { } ``` -4. 确定遍历顺序 +#### 4. 确定遍历顺序 在明确递推方向时，我们知道 当前值 是由上方和左上方推出。 @@ -360,7 +360,7 @@ for (int j = 0; j <= bagSize; j++) { // 列，遍历背包 这里大家可以看出，无论是以上哪种遍历，都不影响 dp[2][2]的求值，用来 推导 dp[2][2] 的数值都在。 -5. 举例推导dp数组 +#### 5. 举例推导dp数组 输入：nums: [1, 1, 1, 1, 1], target: 3 @@ -421,7 +421,7 @@ public: dp[i][j] 去掉 行的维度，即 dp[j]，表示：填满j（包括j）这么大容积的包，有dp[j]种方法。 -2. 确定递推公式 +#### 2. 确定递推公式 二维DP数组递推公式： `dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i]];` @@ -429,17 +429,17 @@ dp[i][j] 去掉 行的维度，即 dp[j]，表示：填满j（包括j）这么 **这个公式在后面在讲解背包解决排列组合问题的时候还会用到！** -3. dp数组如何初始化 +#### 3. dp数组如何初始化 在上面 二维dp数组中，我们讲解过 dp[0][0] 初始为1，这里dp[0] 同样初始为1 ,即装满背包为0的方法有一种，放0件物品。 -4. 确定遍历顺序 +#### 4. 确定遍历顺序 在[动态规划：关于01背包问题，你该了解这些！（滚动数组）](https://programmercarl.com/背包理论基础01背包-2.html)中，我们系统讲过对于01背包问题一维dp的遍历。 遍历物品放在外循环，遍历背包在内循环，且内循环倒序（为了保证物品只使用一次）。 -5. 举例推导dp数组 +#### 5. 举例推导dp数组 输入：nums: [1, 1, 1, 1, 1], target: 3 @@ -526,7 +526,6 @@ dp[j] += dp[j - nums[i]]; ## 其他语言版本 - ### Java ```java class Solution { diff --git a/problems/0518.零钱兑换II.md b/problems/0518.零钱兑换II.md index 0d35fb7c..835df852 100644 --- a/problems/0518.零钱兑换II.md +++ b/problems/0518.零钱兑换II.md @@ -4,8 +4,6 @@

参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们受益！

- - # 518.零钱兑换II [力扣题目链接](https://leetcode.cn/problems/coin-change-ii/) @@ -45,15 +43,19 @@ **[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html)：[装满背包有多少种方法？组合与排列有讲究！| LeetCode：518.零钱兑换II](https://www.bilibili.com/video/BV1KM411k75j/)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。 +## 二维dp讲解 +如果大家认真做完：[分割等和子集](https://www.programmercarl.com/0416.%E5%88%86%E5%89%B2%E7%AD%89%E5%92%8C%E5%AD%90%E9%9B%86.html) ， [最后一块石头的重量II](https://www.programmercarl.com/1049.%E6%9C%80%E5%90%8E%E4%B8%80%E5%9D%97%E7%9F%B3%E5%A4%B4%E7%9A%84%E9%87%8D%E9%87%8FII.html) 和 [目标和](https://www.programmercarl.com/0494.%E7%9B%AE%E6%A0%87%E5%92%8C.html) +应该会知道类似这种题目：给出一个总数，一些物品，问能否凑成这个总数。 -## 思路 +这是典型的背包问题！ -这是一道典型的背包问题，一看到钱币数量不限，就知道这是一个完全背包。 +本题求的是装满这个背包的物品组合数是多少。 +因为每一种面额的硬币有无限个，所以这是完全背包。 -对完全背包还不了解的同学，可以看这篇：[动态规划：关于完全背包，你该了解这些！](https://programmercarl.com/背包问题理论基础完全背包.html) +对完全背包还不了解的同学，可以看这篇：[完全背包理论基础](https://programmercarl.com/背包问题理论基础完全背包.html) 但本题和纯完全背包不一样，**纯完全背包是凑成背包最大价值是多少，而本题是要求凑成总金额的物品组合个数！** @@ -69,44 +71,182 @@ 如果问的是排列数，那么上面就是两种排列了。 -**组合不强调元素之间的顺序，排列强调元素之间的顺序**。 其实这一点我们在讲解回溯算法专题的时候就讲过了哈。 +**组合不强调元素之间的顺序，排列强调元素之间的顺序**。 其实这一点我们在讲解回溯算法专题的时候就讲过。 那我为什么要介绍这些呢，因为这和下文讲解遍历顺序息息相关! -回归本题，动规五步曲来分析如下： +本题其实与我们讲过 [494. 目标和](https://programmercarl.com/0494.目标和.html) 十分类似。 -1. 确定dp数组以及下标的含义 +[494. 目标和](https://programmercarl.com/0494.目标和.html) 求的是装满背包有多少种方法，而本题是求装满背包有多少种组合。 + +这有啥区别？ + +**求装满背包有几种方法其实就是求组合数**。 不过 [494. 目标和](https://programmercarl.com/0494.目标和.html) 是 01背包，即每一类物品只有一个。 + +以下动规五部曲： + +### 1、确定dp数组以及下标的含义 + +定义二维dp数值 dp[i][j]：使用 下标为[0, i]的coins[i]能够凑满j（包括j）这么大容量的包，有dp[i][j]种组合方法。 + +很多录友也会疑惑，凭什么上来就定义 dp数组，思考过程是什么样的， 这个思考过程我在 [01背包理论基础（二维数组）](https://programmercarl.com/背包理论基础01背包-1.html) 中的 “确定dp数组以及下标的含义” 有详细讲解。 + +（**强烈建议按照代码随想录的顺序学习，否则可能看不懂我的讲解**） + + +### 2、确定递推公式 + +> **注意**： 这里的公式推导，与之前讲解过的 [494. 目标和](https://programmercarl.com/0494.目标和.html) 、[完全背包理论基础](https://programmercarl.com/背包问题理论基础完全背包.html) 有极大重复，所以我不在重复讲解原理，而是只讲解区别。 + +我们再回顾一下，[01背包理论基础](https://programmercarl.com/背包理论基础01背包-1.html)，中二维DP数组的递推公式为： + +`dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])` + +在 [完全背包理论基础](https://programmercarl.com/背包问题理论基础完全背包.html) 详细讲解了完全背包二维DP数组的递推公式为： + +`dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i])` + + +看去完全背包 和 01背包的差别在哪里？ + +在于01背包是 `dp[i - 1][j - weight[i]] + value[i]` ，完全背包是 `dp[i][j - weight[i]] + value[i])` + +主要原因就是 完全背包单类物品有无限个。 + +具体原因我在 [完全背包理论基础（二维）](https://programmercarl.com/背包问题理论基础完全背包.html) 的 「确定递推公式」有详细讲解，如果大家忘了，再回顾一下。 + +我上面有说过，本题和 [494. 目标和](https://programmercarl.com/0494.目标和.html) 是一样的，唯一区别就是 [494. 目标和](https://programmercarl.com/0494.目标和.html) 是 01背包，本题是完全背包。 + + +在[494. 目标和](https://programmercarl.com/0494.目标和.html)中详解讲解了装满背包有几种方法，二维DP数组的递推公式： +`dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i]]` + +所以本题递推公式：`dp[i][j] = dp[i - 1][j] + dp[i][j - nums[i]]` ，区别依然是 ` dp[i - 1][j - nums[i]]` 和 `dp[i][j - nums[i]]` + +这个 ‘所以’ 我省略了很多推导的内容，因为这些内容在 [494. 目标和](https://programmercarl.com/0494.目标和.html) 和 [完全背包理论基础](https://programmercarl.com/背包问题理论基础完全背包.html) 都详细讲过。 + +这里不再重复讲解。 + +大家主要疑惑点 + +1、 `dp[i][j] = dp[i - 1][j] + dp[i][j - nums[i]]` 这个递归公式框架怎么来的，在 [494. 目标和](https://programmercarl.com/0494.目标和.html) 有详细讲解。 + +2、为什么是 ` dp[i][j - nums[i]]` 而不是 ` dp[i - 1][j - nums[i]]` ，在[完全背包理论基础（二维）](https://programmercarl.com/背包问题理论基础完全背包.html) 有详细讲解 + + +### 3. dp数组如何初始化 + +那么二维数组的最上行 和 最左列一定要初始化，这是递推公式推导的基础，如图红色部分： + +![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240827103507.png) + + +这里首先要关注的就是 dp[0][0] 应该是多少？ + +背包空间为0，装满「物品0」 的组合数有多少呢？ + +应该是 0 个， 但如果 「物品0」 的 数值就是0呢？ 岂不是可以有无限个0 组合 和为0！ + +题目描述中说了`1 <= coins.length <= 300` ，所以不用考虑 物品数值为0的情况。 + +那么最上行dp[0][j] 如何初始化呢？ + +dp[0][j]的含义：用「物品0」（即coins[0]） 装满 背包容量为j的背包，有几种组合方法。 （如果看不懂dp数组的含义，建议先学习[494. 目标和](https://programmercarl.com/0494.目标和.html)） + +如果 j 可以整除 物品0，那么装满背包就有1种组合方法。 + +初始化代码： + +```CPP +for (int j = 0; j <= bagSize; j++) { + if (j % coins[0] == 0) dp[0][j] = 1; +} +``` + +最左列如何初始化呢？ + +dp[i][0] 的含义：用物品i（即coins[i]） 装满容量为0的背包 有几种组合方法。 + +都有一种方法，即不装。 + +所以 dp[i][0] 都初始化为1 + +### 4. 确定遍历顺序 + +二维DP数组的完全背包的两个for循环先后顺序是无所谓的。 + +先遍历背包，还是先遍历物品都是可以的。 + +原理和 [01背包理论基础（二维数组）](https://programmercarl.com/背包理论基础01背包-1.html) 中的 「遍历顺序」是一样的，都是因为 两个for循环的先后顺序不影响 递推公式 所需要的数值。 + +具体分析过程看 [01背包理论基础（二维数组）](https://programmercarl.com/背包理论基础01背包-1.html) 中的 「遍历顺序」 + +### 5. 打印DP数组 + +以amount为5，coins为：[2,3,5] 为例： + +dp数组应该是这样的： + +``` +1 0 1 0 1 0 +1 0 1 1 1 1 +1 0 1 1 1 2 +``` + +### 代码实现： + +```CPP +class Solution { +public: + int change(int amount, vector& coins) { + int bagSize = amount; + + vector> dp(coins.size(), vector(bagSize + 1, 0)); + + // 初始化最上行 + for (int j = 0; j <= bagSize; j++) { + if (j % coins[0] == 0) dp[0][j] = 1; + } + // 初始化最左列 + for (int i = 0; i < coins.size(); i++) { + dp[i][0] = 1; + } + // 以下遍历顺序行列可以颠倒 + for (int i = 1; i < coins.size(); i++) { // 行，遍历物品 + for (int j = 0; j <= bagSize; j++) { // 列，遍历背包 + if (coins[i] > j) dp[i][j] = dp[i - 1][j]; + else dp[i][j] = dp[i - 1][j] + dp[i][j - coins[i]]; + } + } + return dp[coins.size() - 1][bagSize]; + } +}; +``` + +## 一维dp讲解 + +### 1、确定dp数组以及下标的含义 dp[j]：凑成总金额j的货币组合数为dp[j] -2. 确定递推公式 +### 2、确定递推公式 -dp[j] 就是所有的dp[j - coins[i]]（考虑coins[i]的情况）相加。 +本题 二维dp 递推公式： `dp[i][j] = dp[i - 1][j] + dp[i][j - coins[i]]` -所以递推公式：dp[j] += dp[j - coins[i]]; +压缩成一维：`dp[j] += dp[j - coins[i]]` -**这个递推公式大家应该不陌生了，我在讲解01背包题目的时候在这篇[494. 目标和](https://programmercarl.com/0494.目标和.html)中就讲解了，求装满背包有几种方法，公式都是：dp[j] += dp[j - nums[i]];** +这个递推公式大家应该不陌生了，我在讲解01背包题目的时候在这篇[494. 目标和](https://programmercarl.com/0494.目标和.html)中就讲解了，求装满背包有几种方法，公式都是：`dp[j] += dp[j - nums[i]]` -3. dp数组如何初始化 +### 3. dp数组如何初始化 -首先dp[0]一定要为1，dp[0] = 1是 递归公式的基础。如果dp[0] = 0 的话，后面所有推导出来的值都是0了。 +装满背包容量为0 的方法是1，即不放任何物品，`dp[0] = 1` -那么 dp[0] = 1 有没有含义，其实既可以说 凑成总金额0的货币组合数为1，也可以说 凑成总金额0的货币组合数为0，好像都没有毛病。 +### 4. 确定遍历顺序 -但题目描述中，也没明确说 amount = 0 的情况，结果应该是多少。 - -这里我认为题目描述还是要说明一下，因为后台测试数据是默认，amount = 0 的情况，组合数为1的。 - -下标非0的dp[j]初始化为0，这样累计加dp[j - coins[i]]的时候才不会影响真正的dp[j] - -dp[0]=1还说明了一种情况：如果正好选了coins[i]后，也就是j-coins[i] == 0的情况表示这个硬币刚好能选，此时dp[0]为1表示只选coins[i]存在这样的一种选法。 - -4. 确定遍历顺序 本题中我们是外层for循环遍历物品（钱币），内层for遍历背包（金钱总额），还是外层for遍历背包（金钱总额），内层for循环遍历物品（钱币）呢？ - -我在[动态规划：关于完全背包，你该了解这些！](https://programmercarl.com/背包问题理论基础完全背包.html)中讲解了完全背包的两个for循环的先后顺序都是可以的。 +我在[完全背包（一维DP）](./背包问题完全背包一维.md)中讲解了完全背包的两个for循环的先后顺序都是可以的。 **但本题就不行了！** @@ -116,7 +256,7 @@ dp[0]=1还说明了一种情况：如果正好选了coins[i]后，也就是j-coi 所以纯完全背包是能凑成总和就行，不用管怎么凑的。 -本题是求凑出来的方案个数，且每个方案个数是为组合数。 +本题是求凑出来的方案个数，且每个方案个数是组合数。 那么本题，两个for循环的先后顺序可就有说法了。 @@ -154,7 +294,7 @@ for (int j = 0; j <= amount; j++) { // 遍历背包容量 可能这里很多同学还不是很理解，**建议动手把这两种方案的dp数组数值变化打印出来，对比看一看！（实践出真知）** -5. 举例推导dp数组 +### 5. 举例推导dp数组 输入: amount = 5, coins = [1, 2, 5] ，dp状态图如下： @@ -208,7 +348,17 @@ public: ## 总结 -本题的递推公式，其实我们在[494. 目标和](https://programmercarl.com/0494.目标和.html)中就已经讲过了，**而难点在于遍历顺序！** +本题我们从 二维 分析到 一维。 + +大家在刚开始学习的时候，从二维开始学习 容易理解。 + +之后，推荐大家直接掌握一维的写法，熟练后更容易写出来。 + +本题中，二维dp主要是就要 想清楚和我们之前讲解的 [01背包理论基础](https://programmercarl.com/背包理论基础01背包-1.html)、[494. 目标和](https://programmercarl.com/0494.目标和.html)、 [完全背包理论基础](https://programmercarl.com/背包问题理论基础完全背包.html) 联系与区别。 + +这也是代码随想录安排刷题顺序的精髓所在。 + +本题的一维dp中，难点在于理解便利顺序。 在求装满背包有几种方案的时候，认清遍历顺序是非常关键的。 @@ -216,8 +366,7 @@ public: **如果求排列数就是外层for遍历背包，内层for循环遍历物品**。 -可能说到排列数录友们已经有点懵了，后面Carl还会安排求排列数的题目，到时候在对比一下，大家就会发现神奇所在！ - +可能说到排列数录友们已经有点懵了，后面我还会安排求排列数的题目，到时候在对比一下，大家就会发现神奇所在！ ## 其他语言版本 @@ -397,7 +546,7 @@ object Solution { } } ``` -## C +### C ```c int change(int amount, int* coins, int coinsSize) { diff --git a/problems/1049.最后一块石头的重量II.md b/problems/1049.最后一块石头的重量II.md index b40ed114..0d445a71 100644 --- a/problems/1049.最后一块石头的重量II.md +++ b/problems/1049.最后一块石头的重量II.md @@ -42,40 +42,41 @@ ## 思路 -如果对背包问题不都熟悉先看这两篇： +如果对背包问题不熟悉的话先看这两篇： -* [动态规划：关于01背包问题，你该了解这些！](https://programmercarl.com/背包理论基础01背包-1.html) -* [动态规划：关于01背包问题，你该了解这些！（滚动数组）](https://programmercarl.com/背包理论基础01背包-2.html) +* [01背包理论基础（二维数组）](https://programmercarl.com/背包理论基础01背包-1.html) +* [01背包理论基础（一维数组）](https://programmercarl.com/背包理论基础01背包-2.html) -本题其实就是尽量让石头分成重量相同的两堆，相撞之后剩下的石头最小，**这样就化解成01背包问题了**。 +本题其实是尽量让石头分成重量相同的两堆（尽可能相同），相撞之后剩下的石头就是最小的。 -是不是感觉和昨天讲解的[416. 分割等和子集](https://programmercarl.com/0416.分割等和子集.html)非常像了。 +一堆的石头重量是sum，那么我们就尽可能拼成 重量为 sum / 2 的石头堆。 这样剩下的石头堆也是 尽可能接近 sum/2 的重量。 +那么此时问题就是有一堆石头，每个石头都有自己的重量，是否可以 装满 最大重量为 sum / 2的背包。 -本题物品的重量为stones[i]，物品的价值也为stones[i]。 +看到这里，大家是否感觉和昨天讲解的 [416. 分割等和子集](https://programmercarl.com/0416.分割等和子集.html)非常像了，简直就是同一道题。 -对应着01背包里的物品重量weight[i]和 物品价值value[i]。 +本题**这样就化解成01背包问题了**。 + +**[416. 分割等和子集](https://programmercarl.com/0416.分割等和子集.html) 是求背包是否正好装满，而本题是求背包最多能装多少**。 + +物品就是石头，物品的重量为stones[i]，物品的价值也为stones[i]。 接下来进行动规五步曲： -1. 确定dp数组以及下标的含义 +### 1. 确定dp数组以及下标的含义 **dp[j]表示容量（这里说容量更形象，其实就是重量）为j的背包，最多可以背最大重量为dp[j]**。 -可以回忆一下01背包中，dp[j]的含义，容量为j的背包，最多可以装的价值为 dp[j]。 +相对于 01背包，本题中，石头的重量是 stones[i]，石头的价值也是 stones[i] 。 -相对于 01背包，本题中，石头的重量是 stones[i]，石头的价值也是 stones[i] ，可以 “最多可以装的价值为 dp[j]” == “最多可以背的重量为dp[j]” +“最多可以装的价值为 dp[j]” 等同于 “最多可以背的重量为dp[j]” -2. 确定递推公式 +### 2. 确定递推公式 01背包的递推公式为：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); 本题则是：**dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);** -一些同学可能看到这dp[j - stones[i]] + stones[i]中 又有- stones[i] 又有+stones[i]，看着有点晕乎。 - -大家可以再去看 dp[j]的含义。 - -3. dp数组如何初始化 +### 3. dp数组如何初始化 既然 dp[j]中的j表示容量，那么最大容量（重量）是多少呢，就是所有石头的重量和。 @@ -95,7 +96,7 @@ vector dp(15001, 0); ``` -4. 确定遍历顺序 +### 4. 确定遍历顺序 在[动态规划：关于01背包问题，你该了解这些！（滚动数组）](https://programmercarl.com/背包理论基础01背包-2.html)中就已经说明：如果使用一维dp数组，物品遍历的for循环放在外层，遍历背包的for循环放在内层，且内层for循环倒序遍历！ @@ -111,7 +112,7 @@ for (int i = 0; i < stones.size(); i++) { // 遍历物品 ``` -5. 举例推导dp数组 +### 5. 举例推导dp数组 举例，输入：[2,4,1,1]，此时target = (2 + 4 + 1 + 1)/2 = 4 ，dp数组状态图如下： @@ -154,10 +155,7 @@ public: 本题其实和[416. 分割等和子集](https://programmercarl.com/0416.分割等和子集.html)几乎是一样的，只是最后对dp[target]的处理方式不同。 -[416. 分割等和子集](https://programmercarl.com/0416.分割等和子集.html)相当于是求背包是否正好装满，而本题是求背包最多能装多少。 - - - +**[416. 分割等和子集](https://programmercarl.com/0416.分割等和子集.html)相当于是求背包是否正好装满，而本题是求背包最多能装多少**。 ## 其他语言版本 diff --git a/problems/kamacoder/0054.替换数字.md b/problems/kamacoder/0054.替换数字.md index 443b8bfb..de0ab1a3 100644 --- a/problems/kamacoder/0054.替换数字.md +++ b/problems/kamacoder/0054.替换数字.md @@ -288,16 +288,6 @@ func main(){ -### python： -```Python -class Solution: - def change(self, s): - lst = list(s) # Python里面的string也是不可改的，所以也是需要额外空间的。空间复杂度：O(n)。 - for i in range(len(lst)): - if lst[i].isdigit(): - lst[i] = "number" - return ''.join(lst) -``` ### JavaScript: ```js const readline = require("readline"); diff --git a/problems/kamacoder/0097.小明逛公园.md b/problems/kamacoder/0097.小明逛公园.md index 27ad0eb9..dfbd6aa9 100644 --- a/problems/kamacoder/0097.小明逛公园.md +++ b/problems/kamacoder/0097.小明逛公园.md @@ -100,7 +100,8 @@ Floyd算法核心思想是动态规划。 这里我们用 grid数组来存图，那就把dp数组命名为 grid。 -grid[i][j][k] = m，表示 节点i 到 节点j 以[1...k] 集合为中间节点的最短距离为m。 +grid[i][j][k] = m，表示 **节点i 到 节点j 以[1...k] 集合中的一个节点为中间节点的最短距离为m**。 + 可能有录友会想，凭什么就这么定义呢？ diff --git a/problems/周总结/20210107动规周末总结.md b/problems/周总结/20210107动规周末总结.md index 4cab00cc..da2ebd30 100644 --- a/problems/周总结/20210107动规周末总结.md +++ b/problems/周总结/20210107动规周末总结.md @@ -99,7 +99,7 @@ public: 这道绝佳的面试题我没有用过，如果录友们有面试别人的需求，就把这个套路拿去吧。 -我在[通过一道面试题目，讲一讲递归算法的时间复杂度！](https://programmercarl.com/前序/通过一道面试题目，讲一讲递归算法的时间复杂度！.html)中，以我自己面试别人的真实经历，通过求x的n次方 这么简单的题目，就可以考察候选人对算法性能以及递归的理解深度，录友们可以看看，绝对有收获！ +我在[通过一道面试题目，讲一讲递归算法的时间复杂度！](../前序/递归算法的时间复杂度.md)中，以我自己面试别人的真实经历，通过求x的n次方 这么简单的题目，就可以考察候选人对算法性能以及递归的理解深度，录友们可以看看，绝对有收获！ ## 周四 diff --git a/problems/背包理论基础01背包-1.md b/problems/背包理论基础01背包-1.md index 259a439b..d9b953c0 100644 --- a/problems/背包理论基础01背包-1.md +++ b/problems/背包理论基础01背包-1.md @@ -41,8 +41,6 @@ leetcode上没有纯01背包的问题，都是01背包应用方面的题目， 有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。**每件物品只能用一次**，求解将哪些物品装入背包里物品价值总和最大。 -![动态规划-背包问题](https://code-thinking-1253855093.file.myqcloud.com/pics/20210117175428387.jpg) - 这是标准的背包问题，以至于很多同学看了这个自然就会想到背包，甚至都不知道暴力的解法应该怎么解了。 这样其实是没有从底向上去思考，而是习惯性想到了背包，那么暴力的解法应该是怎么样的呢？ @@ -73,7 +71,7 @@ leetcode上没有纯01背包的问题，都是01背包应用方面的题目， 依然动规五部曲分析一波。 -1. 确定dp数组以及下标的含义 +#### 1. 确定dp数组以及下标的含义 我们需要使用二维数组，为什么呢？ @@ -131,7 +129,7 @@ i 来表示物品、j表示背包容量。 **要时刻记着这个dp数组的含义，下面的一些步骤都围绕这dp数组的含义进行的**，如果哪里看懵了，就来回顾一下i代表什么，j又代表什么。 -2. 确定递推公式 +#### 2. 确定递推公式 这里在把基本信息给出来： @@ -176,7 +174,7 @@ i 来表示物品、j表示背包容量。 递归公式： `dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);` -3. dp数组如何初始化 +#### 3. dp数组如何初始化 **关于初始化，一定要和dp数组的定义吻合，否则到递推公式的时候就会越来越乱**。 @@ -197,8 +195,8 @@ dp[0][j]，即：i为0，存放编号0的物品的时候，各个容量的背包 代码初始化如下： ```CPP -for (int j = 0 ; j < weight[0]; j++) { // 当然这一步，如果把dp数组预先初始化为0了，这一步就可以省略，但很多同学应该没有想清楚这一点。 - dp[0][j] = 0; +for (int i = 1; i < weight.size(); i++) { // 当然这一步，如果把dp数组预先初始化为0了，这一步就可以省略，但很多同学应该没有想清楚这一点。 + dp[i][0] = 0; } // 正序遍历 for (int j = weight[0]; j <= bagweight; j++) { @@ -236,7 +234,7 @@ for (int j = weight[0]; j <= bagweight; j++) { **费了这么大的功夫，才把如何初始化讲清楚，相信不少同学平时初始化dp数组是凭感觉来的，但有时候感觉是不靠谱的**。 -4. 确定遍历顺序 +#### 4. 确定遍历顺序 在如下图中，可以看出，有两个遍历的维度：物品与背包重量 @@ -293,7 +291,7 @@ dp[i-1][j]和dp[i - 1][j - weight[i]] 都在dp[i][j]的左上角方向（包括 **其实背包问题里，两个for循环的先后循序是非常有讲究的，理解遍历顺序其实比理解推导公式难多了**。 -5. 举例推导dp数组 +#### 5. 举例推导dp数组 来看一下对应的dp数组的数值，如图： diff --git a/problems/背包问题完全背包一维.md b/problems/背包问题完全背包一维.md new file mode 100644 index 00000000..a8e241c3 --- /dev/null +++ b/problems/背包问题完全背包一维.md @@ -0,0 +1,211 @@ + +# 完全背包-一维数组 + +本题力扣上没有原题，大家可以去[卡码网第52题](https://kamacoder.com/problempage.php?pid=1052)去练习。 + +## 算法公开课 + +**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html)：[带你学透完全背包问题！ ](https://www.bilibili.com/video/BV1uK411o7c9/)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。 + + +## 思路 + +本篇我们不再做五部曲分析，核心内容 在 01背包二维 、01背包一维 和 完全背包二维 的讲解中都讲过了。 + +上一篇我们刚刚讲了完全背包二维DP数组的写法： + +```CPP +for (int i = 1; i < n; i++) { // 遍历物品 + for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量 + if (j < weight[i]) dp[i][j] = dp[i - 1][j]; + else dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]); + } +} +``` + +压缩成一维DP数组，也就是将上一层拷贝到当前层。 + +将上一层dp[i-1] 的那一层拷贝到 当前层 dp[i] ，那么 递推公式由：`dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i])` 变成： `dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i])` + +这里有录友想，这样拷贝的话， dp[i - 1][j] 的数值会不会 覆盖了 dp[i][j] 的数值呢？ + +并不会，因为 当前层 dp[i][j] 是空的，是没有计算过的。 + +变成 `dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i])` 我们压缩成一维dp数组，去掉 i 层数维度。 + +即：`dp[j] = max(dp[j], dp[j - weight[i]] + value[i])` + + +接下来我们重点讲一下遍历顺序。 + +看过这两篇的话： + +* [01背包理论基础（二维数组）](https://programmercarl.com/背包理论基础01背包-1.html) +* [01背包理论基础（一维数组）](https://programmercarl.com/背包理论基础01背包-2.html) + +就知道了，01背包中二维dp数组的两个for遍历的先后循序是可以颠倒了，一维dp数组的两个for循环先后循序一定是先遍历物品，再遍历背包容量。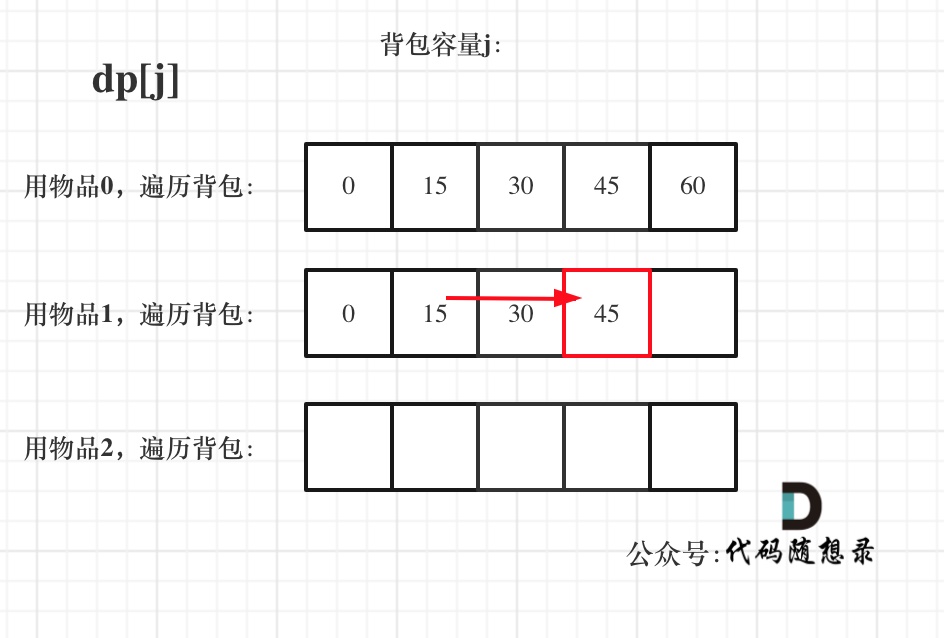 + +**在完全背包中，对于一维dp数组来说，其实两个for循环嵌套顺序是无所谓的**！ + +因为dp[j] 是根据 下标j之前所对应的dp[j]计算出来的。 只要保证下标j之前的dp[j]都是经过计算的就可以了。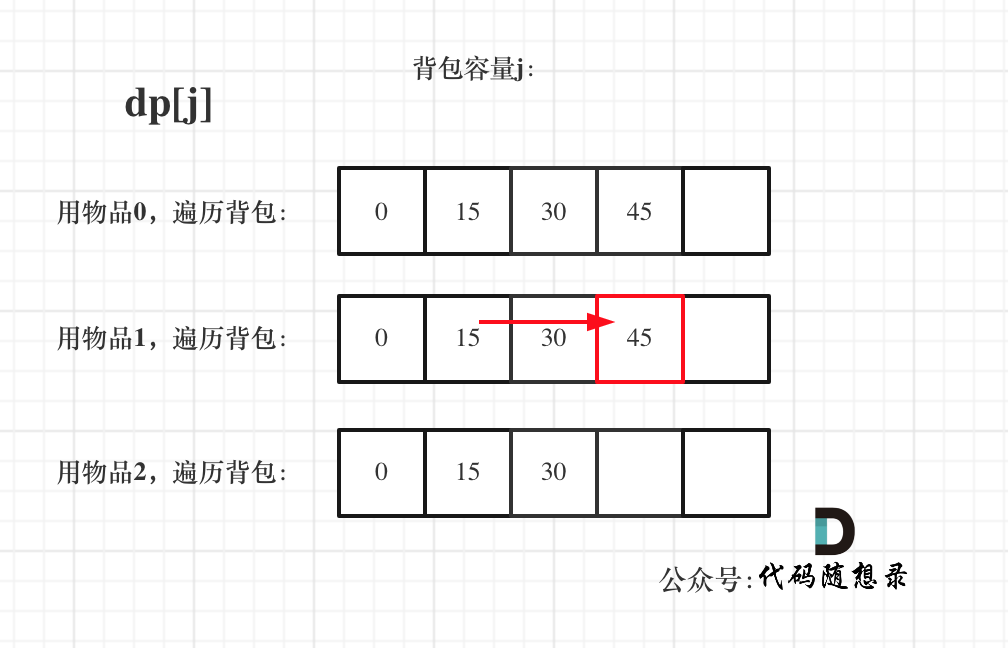 + +遍历物品在外层循环，遍历背包容量在内层循环，状态如图： + +![动态规划-完全背包1](https://code-thinking-1253855093.file.myqcloud.com/pics/20210126104529605.jpg) + +遍历背包容量在外层循环，遍历物品在内层循环，状态如图： + +![动态规划-完全背包2](https://code-thinking-1253855093.file.myqcloud.com/pics/20210729234011.png) + +看了这两个图，大家就会理解，完全背包中，两个for循环的先后循序，都不影响计算dp[j]所需要的值（这个值就是下标j之前所对应的dp[j]）。 + +先遍历背包再遍历物品，代码如下： + +```CPP +for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量 + for(int i = 0; i < weight.size(); i++) { // 遍历物品 + if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); + } + cout << endl; +} +``` + +先遍历物品再遍历背包： + +```CPP +for(int i = 0; i < weight.size(); i++) { // 遍历物品 + for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量 + if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); + } +} +``` + +整体代码如下： + +```cpp +#include +#include +using namespace std; + +int main() { + int N, bagWeight; + cin >> N >> bagWeight; + vector weight(N, 0); + vector value(N, 0); + for (int i = 0; i < N; i++) { + int w; + int v; + cin >> w >> v; + weight[i] = w; + value[i] = v; + } + + vector dp(bagWeight + 1, 0); + for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量 + for(int i = 0; i < weight.size(); i++) { // 遍历物品 + if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); + } + } + cout << dp[bagWeight] << endl; + + return 0; +} +``` + + + +## 总结 + +细心的同学可能发现，**全文我说的都是对于纯完全背包问题，其for循环的先后循环是可以颠倒的！** + +但如果题目稍稍有点变化，就会体现在遍历顺序上。 + +如果问装满背包有几种方式的话？ 那么两个for循环的先后顺序就有很大区别了，而leetcode上的题目都是这种稍有变化的类型。 + +这个区别，我将在后面讲解具体leetcode题目中给大家介绍，因为这块如果不结合具题目，单纯的介绍原理估计很多同学会越看越懵！ + +别急，下一篇就是了！ + +最后，**又可以出一道面试题了，就是纯完全背包，要求先用二维dp数组实现，然后再用一维dp数组实现，最后再问，两个for循环的先后是否可以颠倒？为什么？** + +这个简单的完全背包问题，估计就可以难住不少候选人了。 + + +## 其他语言版本 + +### Java： + +```java +import java.util.Scanner; + +public class Main { + public static void main(String[] args) { + Scanner scanner = new Scanner(System.in); + int N = scanner.nextInt(); + int bagWeight = scanner.nextInt(); + + int[] weight = new int[N]; + int[] value = new int[N]; + for (int i = 0; i < N; i++) { + weight[i] = scanner.nextInt(); + value[i] = scanner.nextInt(); + } + + int[] dp = new int[bagWeight + 1]; + + for (int j = 0; j <= bagWeight; j++) { // 遍历背包容量 + for (int i = 0; i < weight.length; i++) { // 遍历物品 + if (j >= weight[i]) { + dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]); + } + } + } + + System.out.println(dp[bagWeight]); + scanner.close(); + } +} + +``` + + + +### Python： + +```python +def complete_knapsack(N, bag_weight, weight, value): + dp = [0] * (bag_weight + 1) + + for j in range(bag_weight + 1): # 遍历背包容量 + for i in range(len(weight)): # 遍历物品 + if j >= weight[i]: + dp[j] = max(dp[j], dp[j - weight[i]] + value[i]) + + return dp[bag_weight] + +# 输入 +N, bag_weight = map(int, input().split()) +weight = [] +value = [] +for _ in range(N): + w, v = map(int, input().split()) + weight.append(w) + value.append(v) + +# 输出结果 +print(complete_knapsack(N, bag_weight, weight, value)) + + +``` + + +### Go： + +```go + +``` +### Javascript: + +```Javascript +``` + diff --git a/problems/背包问题理论基础完全背包.md b/problems/背包问题理论基础完全背包.md index ae1e9e0b..0cc6e915 100644 --- a/problems/背包问题理论基础完全背包.md +++ b/problems/背包问题理论基础完全背包.md @@ -5,18 +5,11 @@

参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们受益！

-# 动态规划：完全背包理论基础 +# 完全背包理论基础-二维DP数组 本题力扣上没有原题，大家可以去[卡码网第52题](https://kamacoder.com/problempage.php?pid=1052)去练习，题意是一样的。 -## 算法公开课 - -**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html)：[带你学透完全背包问题！ ](https://www.bilibili.com/video/BV1uK411o7c9/)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。 - -## 思路 - -### 完全背包 - +## 完全背包 有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。**每件物品都有无限个（也就是可以放入背包多次）**，求解将哪些物品装入背包里物品价值总和最大。 @@ -24,14 +17,12 @@ 同样leetcode上没有纯完全背包问题，都是需要完全背包的各种应用，需要转化成完全背包问题，所以我这里还是以纯完全背包问题进行讲解理论和原理。 -在下面的讲解中，我依然举这个例子： +在下面的讲解中，我拿下面数据举例子： -背包最大重量为4。 - -物品为： +背包最大重量为4，物品为： | | 重量 | 价值 | -| --- | --- | --- | +| ----- | ---- | ---- | | 物品0 | 1 | 15 | | 物品1 | 3 | 20 | | 物品2 | 4 | 30 | @@ -40,471 +31,292 @@ 问背包能背的物品最大价值是多少？ -01背包和完全背包唯一不同就是体现在遍历顺序上，所以本文就不去做动规五部曲了，我们直接针对遍历顺序经行分析！ +**如果没看到之前的01背包讲解，已经要先仔细看如下两篇，01背包是基础，本篇在讲解完全背包，之前的背包基础我将不会重复讲解**。 -关于01背包我如下两篇已经进行深入分析了： +* [01背包理论基础（二维数组）](https://programmercarl.com/背包理论基础01背包-1.html) +* [01背包理论基础（一维数组）](https://programmercarl.com/背包理论基础01背包-2.html) -* [动态规划：关于01背包问题，你该了解这些！](https://programmercarl.com/背包理论基础01背包-1.html) -* [动态规划：关于01背包问题，你该了解这些！（滚动数组）](https://programmercarl.com/背包理论基础01背包-2.html) +动规五部曲分析完全背包，为了从原理上讲清楚，我们先从二维dp数组分析： -首先再回顾一下01背包的核心代码 -```cpp -for(int i = 0; i < weight.size(); i++) { // 遍历物品 - for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量 - dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); - } +### 1. 确定dp数组以及下标的含义 + +**dp[i][j] 表示从下标为[0-i]的物品，每个物品可以取无限次，放进容量为j的背包，价值总和最大是多少**。 + +很多录友也会疑惑，凭什么上来就定义 dp数组，思考过程是什么样的， 这个思考过程我在 [01背包理论基础（二维数组）](https://programmercarl.com/背包理论基础01背包-1.html) 中的 “确定dp数组以及下标的含义” 有详细讲解。 + + +### 2. 确定递推公式 + +这里在把基本信息给出来： + +| | 重量 | 价值 | +| ----- | ---- | ---- | +| 物品0 | 1 | 15 | +| 物品1 | 3 | 20 | +| 物品2 | 4 | 30 | + +对于递推公式，首先我们要明确有哪些方向可以推导出 dp[i][j]。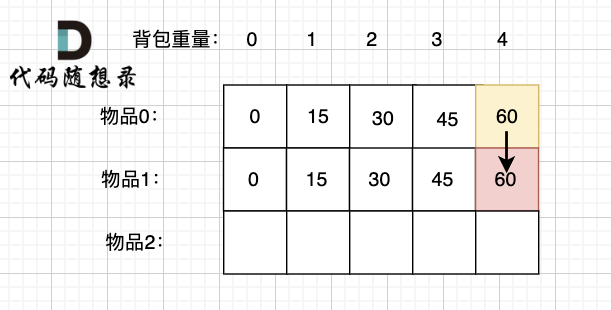 + +这里依然拿dp[1][4]的状态来举例： （[01背包理论基础（二维数组）](https://programmercarl.com/背包理论基础01背包-1.html) 中也是这个例子，要注意下面的不同之处） + +求取 dp[1][4] 有两种情况： + +1. 放物品1 +2. 还是不放物品1 + +如果不放物品1， 那么背包的价值应该是 dp[0][4] 即 容量为4的背包，只放物品0的情况。 + +推导方向如图： + +![](https://code-thinking-1253855093.file.myqcloud.com/pics/20241126112952.png) + +如果放物品1， **那么背包要先留出物品1的容量**，目前容量是4，物品1 的容量（就是物品1的重量）为3，此时背包剩下容量为1。 + +容量为1，只考虑放物品0 和物品1 的最大价值是 dp[1][1]， **注意 这里和 [01背包理论基础（二维数组）](https://programmercarl.com/背包理论基础01背包-1.html) 有所不同了**！ + +在 [01背包理论基础（二维数组）](https://programmercarl.com/背包理论基础01背包-1.html) 中，背包先空留出物品1的容量，此时容量为1，只考虑放物品0的最大价值是 dp[0][1]，**因为01背包每个物品只有一个，既然空出物品1，那背包中也不会再有物品1**！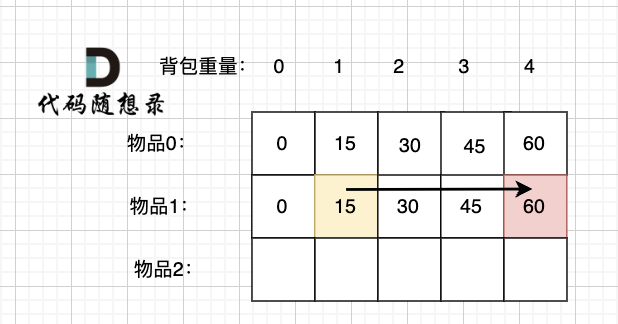 + +而在完全背包中，物品是可以放无限个，所以 即使空出物品1空间重量，那背包中也可能还有物品1，所以此时我们依然考虑放 物品0 和 物品1 的最大价值即： **dp[1][1]， 而不是 dp[0][1]** + +所以 放物品1 的情况 = dp[1][1] + 物品1 的价值，推导方向如图： + +![](https://code-thinking-1253855093.file.myqcloud.com/pics/20241126113104.png) + + +（**注意上图和 [01背包理论基础（二维数组）](https://programmercarl.com/背包理论基础01背包-1.html) 中的区别**，对于理解完全背包很重要） + +两种情况，分别是放物品1 和 不放物品1，我们要取最大值（毕竟求的是最大价值） + +`dp[1][4] = max(dp[0][4], dp[1][1] + 物品1 的价值) ` + +以上过程，抽象化如下： + +* **不放物品i**：背包容量为j，里面不放物品i的最大价值是dp[i - 1][j]。 + +* **放物品i**：背包空出物品i的容量后，背包容量为j - weight[i]，dp[i][j - weight[i]] 为背包容量为j - weight[i]且不放物品i的最大价值，那么dp[i][j - weight[i]] + value[i] （物品i的价值），就是背包放物品i得到的最大价值 + +递推公式： `dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]);` + +（注意，完全背包二维dp数组 和 01背包二维dp数组 递推公式的区别，01背包中是 `dp[i - 1][j - weight[i]] + value[i])`） + +### 3. dp数组如何初始化 + +**关于初始化，一定要和dp数组的定义吻合，否则到递推公式的时候就会越来越乱**。 + +首先从dp[i][j]的定义出发，如果背包容量j为0的话，即dp[i][0]，无论是选取哪些物品，背包价值总和一定为0。如图： + +![动态规划-背包问题2](https://code-thinking-1253855093.file.myqcloud.com/pics/2021011010304192.png) + +在看其他情况。 + +状态转移方程 `dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]);` 可以看出有一个方向 i 是由 i-1 推导出来，那么i为0的时候就一定要初始化。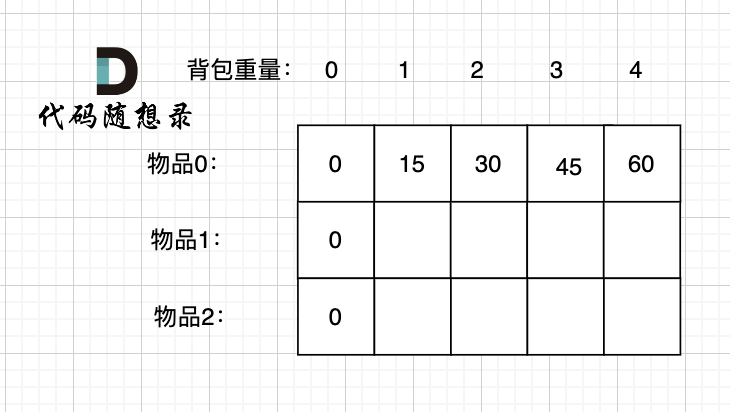 + +dp[0][j]，即：存放编号0的物品的时候，各个容量的背包所能存放的最大价值。 + +那么很明显当 `j < weight[0]`的时候，dp[0][j] 应该是 0，因为背包容量比编号0的物品重量还小。 + +当`j >= weight[0]`时，**dp[0][j] 如果能放下weight[0]的话，就一直装，每一种物品有无限个**。 + +代码初始化如下： + +```CPP +for (int i = 1; i < weight.size(); i++) { // 当然这一步，如果把dp数组预先初始化为0了，这一步就可以省略，但很多同学应该没有想清楚这一点。 + dp[i][0] = 0; +} + +// 正序遍历，如果能放下就一直装物品0 +for (int j = weight[0]; j <= bagWeight; j++) + dp[0][j] = dp[0][j - weight[0]] + value[0]; +``` + +（注意上面初始化和 [01背包理论基础（二维数组）](https://programmercarl.com/背包理论基础01背包-1.html)的区别在于物品有无限个） + + +此时dp数组初始化情况如图所示： + +![](https://code-thinking-1253855093.file.myqcloud.com/pics/20241114161608.png) + +dp[0][j] 和 dp[i][0] 都已经初始化了，那么其他下标应该初始化多少呢？ + +其实从递归公式： dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]); 可以看出dp[i][j] 是由上方和左方数值推导出来了，那么 其他下标初始为什么数值都可以，因为都会被覆盖。 + +但只不过一开始就统一把dp数组统一初始为0，更方便一些。 + +最后初始化代码如下： + +```CPP +// 初始化 dp +vector> dp(weight.size(), vector(bagweight + 1, 0)); +for (int j = weight[0]; j <= bagWeight; j++) { + dp[0][j] = dp[0][j - weight[0]] + value[0]; } ``` -我们知道01背包内嵌的循环是从大到小遍历，为了保证每个物品仅被添加一次。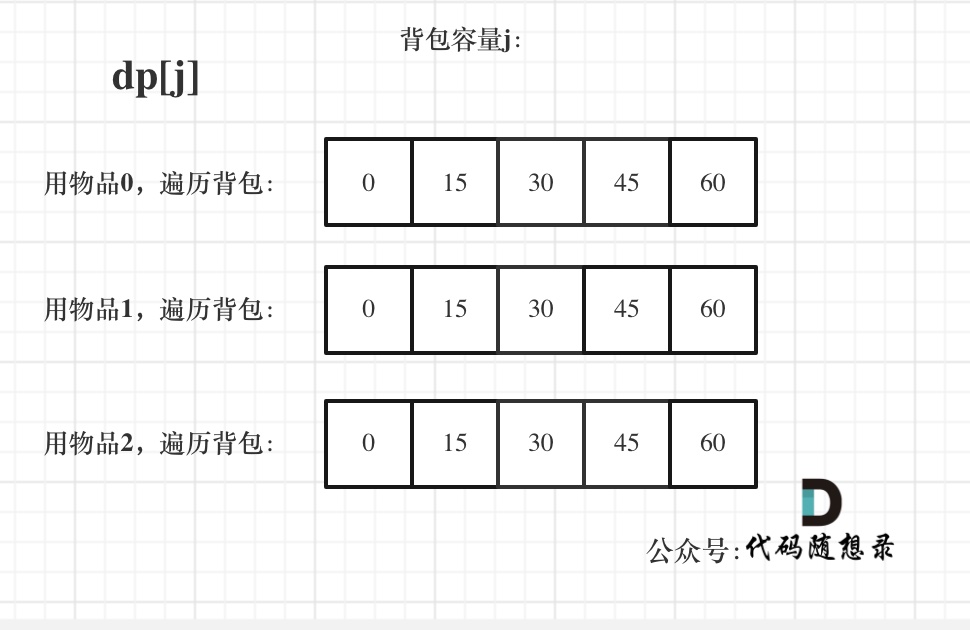 -而完全背包的物品是可以添加多次的，所以要从小到大去遍历，即： +### 4. 确定遍历顺序 -```CPP -// 先遍历物品，再遍历背包 -for(int i = 0; i < weight.size(); i++) { // 遍历物品 - for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量 - dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); +[01背包理论基础（二维数组）](https://programmercarl.com/背包理论基础01背包-1.html) 中我们讲过，01背包二维DP数组，先遍历物品还是先遍历背包都是可以的。 - } -} -``` +因为两种遍历顺序，对于二维dp数组来说，递推公式所需要的值，二维dp数组里对应的位置都有。 -至于为什么，我在[动态规划：关于01背包问题，你该了解这些！（滚动数组）](https://programmercarl.com/背包理论基础01背包-2.html)中也做了讲解。 +详细可以看 [01背包理论基础（二维数组）](https://programmercarl.com/背包理论基础01背包-1.html) 中的 【遍历顺序】的讲解 -dp状态图如下： - - -![动态规划-完全背包](https://code-thinking-1253855093.file.myqcloud.com/pics/20210126104510106.jpg) - -相信很多同学看网上的文章，关于完全背包介绍基本就到为止了。 - -**其实还有一个很重要的问题，为什么遍历物品在外层循环，遍历背包容量在内层循环？** - -这个问题很多题解关于这里都是轻描淡写就略过了，大家都默认 遍历物品在外层，遍历背包容量在内层，好像本应该如此一样，那么为什么呢？ - -难道就不能遍历背包容量在外层，遍历物品在内层？ - - -看过这两篇的话： -* [动态规划：关于01背包问题，你该了解这些！](https://programmercarl.com/背包理论基础01背包-1.html) -* [动态规划：关于01背包问题，你该了解这些！（滚动数组）](https://programmercarl.com/背包理论基础01背包-2.html) - -就知道了，01背包中二维dp数组的两个for遍历的先后循序是可以颠倒了，一维dp数组的两个for循环先后循序一定是先遍历物品，再遍历背包容量。 - -**在完全背包中，对于一维dp数组来说，其实两个for循环嵌套顺序是无所谓的！** - -因为dp[j] 是根据 下标j之前所对应的dp[j]计算出来的。 只要保证下标j之前的dp[j]都是经过计算的就可以了。 - -遍历物品在外层循环，遍历背包容量在内层循环，状态如图： - - -![动态规划-完全背包1](https://code-thinking-1253855093.file.myqcloud.com/pics/20210126104529605.jpg) - -遍历背包容量在外层循环，遍历物品在内层循环，状态如图： - -![动态规划-完全背包2](https://code-thinking-1253855093.file.myqcloud.com/pics/20210729234011.png) - -看了这两个图，大家就会理解，完全背包中，两个for循环的先后循序，都不影响计算dp[j]所需要的值（这个值就是下标j之前所对应的dp[j]）。 - -先遍历背包在遍历物品，代码如下： - -```CPP -// 先遍历背包，再遍历物品 -for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量 - for(int i = 0; i < weight.size(); i++) { // 遍历物品 - if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); - } - cout << endl; -} -``` - -完整的C++测试代码如下： - -```CPP -// 先遍历物品，在遍历背包 -void test_CompletePack() { - vector weight = {1, 3, 4}; - vector value = {15, 20, 30}; - int bagWeight = 4; - vector dp(bagWeight + 1, 0); - for(int i = 0; i < weight.size(); i++) { // 遍历物品 - for(int j = weight[i]; j <= bagWeight; j++) { // 遍历背包容量 - dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); - } - } - cout << dp[bagWeight] << endl; -} -int main() { - test_CompletePack(); -} - -``` - -```CPP - -// 先遍历背包，再遍历物品 -void test_CompletePack() { - vector weight = {1, 3, 4}; - vector value = {15, 20, 30}; - int bagWeight = 4; - - vector dp(bagWeight + 1, 0); +所以既可以 先遍历物品再遍历背包： +```CPP +for (int i = 1; i < n; i++) { // 遍历物品 for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量 - for(int i = 0; i < weight.size(); i++) { // 遍历物品 - if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); - } + if (j < weight[i]) dp[i][j] = dp[i - 1][j]; + else dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]); } - cout << dp[bagWeight] << endl; } -int main() { - test_CompletePack(); -} - ``` -本题力扣上没有原题，大家可以去[卡码网第52题](https://kamacoder.com/problempage.php?pid=1052)去练习，题意是一样的，C++代码如下： +也可以 先遍历背包再遍历物品： -```cpp +```CPP +for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量 + for (int i = 1; i < n; i++) { // 遍历物品 + if (j < weight[i]) dp[i][j] = dp[i - 1][j]; + else dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]); + } +} +``` + +### 5. 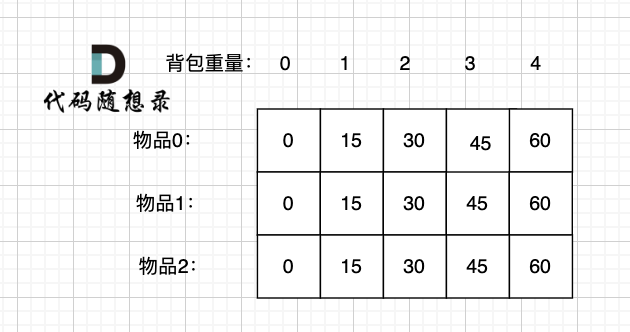举例推导dp数组 + +以本篇举例数据为例，填满了dp二维数组如图： + +![](https://code-thinking-1253855093.file.myqcloud.com/pics/20241126113752.png) + +因为 物品0 的性价比是最高的，而且 在完全背包中，每一类物品都有无限个，所以有无限个物品0，既然物品0 性价比最高，当然是优先放物品0。 + + +### 本题代码： + + +```CPP #include #include using namespace std; -// 先遍历背包，再遍历物品 -void test_CompletePack(vector weight, vector value, int bagWeight) { +int main() { + int n, bagWeight; + int w, v; + cin >> n >> bagWeight; + vector weight(n); + vector value(n); + for (int i = 0; i < n; i++) { + cin >> weight[i] >> value[i]; + } - vector dp(bagWeight + 1, 0); + vector> dp(n, vector(bagWeight + 1, 0)); - for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量 - for(int i = 0; i < weight.size(); i++) { // 遍历物品 - if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); + // 初始化 + for (int j = weight[0]; j <= bagWeight; j++) + dp[0][j] = dp[0][j - weight[0]] + value[0]; + + for (int i = 1; i < n; i++) { // 遍历物品 + for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量 + if (j < weight[i]) dp[i][j] = dp[i - 1][j]; + else dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]); } } - cout << dp[bagWeight] << endl; -} -int main() { - int N, V; - cin >> N >> V; - vector weight; - vector value; - for (int i = 0; i < N; i++) { - int w; - int v; - cin >> w >> v; - weight.push_back(w); - value.push_back(v); - } - test_CompletePack(weight, value, V); + + cout << dp[n - 1][bagWeight] << endl; + return 0; } + ``` - - -## 总结 - -细心的同学可能发现，**全文我说的都是对于纯完全背包问题，其for循环的先后循环是可以颠倒的！** - -但如果题目稍稍有点变化，就会体现在遍历顺序上。 - -如果问装满背包有几种方式的话？ 那么两个for循环的先后顺序就有很大区别了，而leetcode上的题目都是这种稍有变化的类型。 - -这个区别，我将在后面讲解具体leetcode题目中给大家介绍，因为这块如果不结合具题目，单纯的介绍原理估计很多同学会越看越懵！ - -别急，下一篇就是了！ - -最后，**又可以出一道面试题了，就是纯完全背包，要求先用二维dp数组实现，然后再用一维dp数组实现，最后再问，两个for循环的先后是否可以颠倒？为什么？** -这个简单的完全背包问题，估计就可以难住不少候选人了。 - - - +关于一维dp数组，大家看这里：[完全背包一维dp数组讲解](./背包问题完全背包一维.md) ## 其他语言版本 -### Java： +### Java -```java -//先遍历物品，再遍历背包 -private static void testCompletePack(){ - int[] weight = {1, 3, 4}; - int[] value = {15, 20, 30}; - int bagWeight = 4; - int[] dp = new int[bagWeight + 1]; - for (int i = 0; i < weight.length; i++){ // 遍历物品 - for (int j = weight[i]; j <= bagWeight; j++){ // 遍历背包容量 - dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]); +```Java +import java.util.Scanner; + +public class Main { + public static void main(String[] args) { + Scanner scanner = new Scanner(System.in); + int n = scanner.nextInt(); + int bagWeight = scanner.nextInt(); + + int[] weight = new int[n]; + int[] value = new int[n]; + + for (int i = 0; i < n; i++) { + weight[i] = scanner.nextInt(); + value[i] = scanner.nextInt(); } - } - for (int maxValue : dp){ - System.out.println(maxValue + " "); - } -} -//先遍历背包，再遍历物品 -private static void testCompletePackAnotherWay(){ - int[] weight = {1, 3, 4}; - int[] value = {15, 20, 30}; - int bagWeight = 4; - int[] dp = new int[bagWeight + 1]; - for (int i = 1; i <= bagWeight; i++){ // 遍历背包容量 - for (int j = 0; j < weight.length; j++){ // 遍历物品 - if (i - weight[j] >= 0){ - dp[i] = Math.max(dp[i], dp[i - weight[j]] + value[j]); - } + int[][] dp = new int[n][bagWeight + 1]; + + // 初始化 + for (int j = weight[0]; j <= bagWeight; j++) { + dp[0][j] = dp[0][j - weight[0]] + value[0]; } - } - for (int maxValue : dp){ - System.out.println(maxValue + " "); - } -} -``` - - -### Python： - -先遍历物品，再遍历背包（无参版） -```python -def test_CompletePack(): - weight = [1, 3, 4] - value = [15, 20, 30] - bagWeight = 4 - dp = [0] * (bagWeight + 1) - for i in range(len(weight)): # 遍历物品 - for j in range(weight[i], bagWeight + 1): # 遍历背包容量 - dp[j] = max(dp[j], dp[j - weight[i]] + value[i]) - print(dp[bagWeight]) - -test_CompletePack() - -``` - -先遍历物品，再遍历背包（有参版） -```python -def test_CompletePack(weight, value, bagWeight): - dp = [0] * (bagWeight + 1) - for i in range(len(weight)): # 遍历物品 - for j in range(weight[i], bagWeight + 1): # 遍历背包容量 - dp[j] = max(dp[j], dp[j - weight[i]] + value[i]) - return dp[bagWeight] - -if __name__ == "__main__": - weight = [1, 3, 4] - value = [15, 20, 30] - bagWeight = 4 - result = test_CompletePack(weight, value, bagWeight) - print(result) - -``` -先遍历背包，再遍历物品（无参版） -```python -def test_CompletePack(): - weight = [1, 3, 4] - value = [15, 20, 30] - bagWeight = 4 - - dp = [0] * (bagWeight + 1) - - for j in range(bagWeight + 1): # 遍历背包容量 - for i in range(len(weight)): # 遍历物品 - if j - weight[i] >= 0: - dp[j] = max(dp[j], dp[j - weight[i]] + value[i]) - - print(dp[bagWeight]) - -test_CompletePack() - - -``` - -先遍历背包，再遍历物品（有参版） -```python -def test_CompletePack(weight, value, bagWeight): - dp = [0] * (bagWeight + 1) - for j in range(bagWeight + 1): # 遍历背包容量 - for i in range(len(weight)): # 遍历物品 - if j - weight[i] >= 0: - dp[j] = max(dp[j], dp[j - weight[i]] + value[i]) - return dp[bagWeight] - - -if __name__ == "__main__": - weight = [1, 3, 4] - value = [15, 20, 30] - bagWeight = 4 - result = test_CompletePack(weight, value, bagWeight) - print(result) - -``` - -### Go： - -```go - -// test_CompletePack1 先遍历物品, 在遍历背包 -func test_CompletePack1(weight, value []int, bagWeight int) int { - // 定义dp数组 和初始化 - dp := make([]int, bagWeight+1) - // 遍历顺序 - for i := 0; i < len(weight); i++ { - // 正序会多次添加 value[i] - for j := weight[i]; j <= bagWeight; j++ { - // 推导公式 - dp[j] = max(dp[j], dp[j-weight[i]]+value[i]) - // debug - //fmt.Println(dp) - } - } - return dp[bagWeight] -} - -// test_CompletePack2 先遍历背包, 在遍历物品 -func test_CompletePack2(weight, value []int, bagWeight int) int { - // 定义dp数组 和初始化 - dp := make([]int, bagWeight+1) - // 遍历顺序 - // j从0 开始 - for j := 0; j <= bagWeight; j++ { - for i := 0; i < len(weight); i++ { - if j >= weight[i] { - // 推导公式 - dp[j] = max(dp[j], dp[j-weight[i]]+value[i]) - } - // debug - //fmt.Println(dp) - } - } - return dp[bagWeight] -} - -func max(a, b int) int { - if a > b { - return a - } - return b -} - -func main() { - weight := []int{1, 3, 4} - price := []int{15, 20, 30} - fmt.Println(test_CompletePack1(weight, price, 4)) - fmt.Println(test_CompletePack2(weight, price, 4)) -} -``` -### JavaScript: - -```Javascript -// 先遍历物品，再遍历背包容量 -function test_completePack1() { - let weight = [1, 3, 5] - let value = [15, 20, 30] - let bagWeight = 4 - let dp = new Array(bagWeight + 1).fill(0) - for(let i = 0; i <= weight.length; i++) { - for(let j = weight[i]; j <= bagWeight; j++) { - dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]) - } - } - console.log(dp) -} - -// 先遍历背包容量，再遍历物品 -function test_completePack2() { - let weight = [1, 3, 5] - let value = [15, 20, 30] - let bagWeight = 4 - let dp = new Array(bagWeight + 1).fill(0) - for(let j = 0; j <= bagWeight; j++) { - for(let i = 0; i < weight.length; i++) { - if (j >= weight[i]) { - dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]) - } - } - } - console.log(2, dp); -} -``` - -### TypeScript： - -```typescript -// 先遍历物品，再遍历背包容量 -function test_CompletePack(): void { - const weight: number[] = [1, 3, 4]; - const value: number[] = [15, 20, 30]; - const bagSize: number = 4; - const dp: number[] = new Array(bagSize + 1).fill(0); - for (let i = 0; i < weight.length; i++) { - for (let j = weight[i]; j <= bagSize; j++) { - dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]); - } - } - console.log(dp); -} -test_CompletePack(); -``` - -### Scala: - -```scala -// 先遍历物品，再遍历背包容量 -object Solution { - def test_CompletePack() { - var weight = Array[Int](1, 3, 4) - var value = Array[Int](15, 20, 30) - var baseweight = 4 - - var dp = new Array[Int](baseweight + 1) - - for (i <- 0 until weight.length) { - for (j <- weight(i) to baseweight) { - dp(j) = math.max(dp(j), dp(j - weight(i)) + value(i)) - } - } - dp(baseweight) - } -} -``` - -### Rust: - -```rust -impl Solution { - // 先遍历物品 - fn complete_pack() { - let (goods, bag_size) = (vec![(1, 15), (3, 20), (4, 30)], 4); - let mut dp = vec![0; bag_size + 1]; - for (weight, value) in goods { - for j in weight..=bag_size { - dp[j] = dp[j].max(dp[j - weight] + value); - } - } - println!("先遍历物品：{}", dp[bag_size]); - } - - // 先遍历背包 - fn complete_pack_after() { - let (goods, bag_size) = (vec![(1, 15), (3, 20), (4, 30)], 4); - let mut dp = vec![0; bag_size + 1]; - for i in 0..=bag_size { - for (weight, value) in &goods { - if i >= *weight { - dp[i] = dp[i].max(dp[i - weight] + value); + // 动态规划 + for (int i = 1; i < n; i++) { + for (int j = 0; j <= bagWeight; j++) { + if (j < weight[i]) { + dp[i][j] = dp[i - 1][j]; + } else { + dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]); } } } - println!("先遍历背包：{}", dp[bag_size]); + + System.out.println(dp[n - 1][bagWeight]); + scanner.close(); } } -#[test] -fn test_complete_pack() { - Solution::complete_pack(); - Solution::complete_pack_after(); -} ``` +### Go + +### Python + +```python +def knapsack(n, bag_weight, weight, value): + dp = [[0] * (bag_weight + 1) for _ in range(n)] + + # 初始化 + for j in range(weight[0], bag_weight + 1): + dp[0][j] = dp[0][j - weight[0]] + value[0] + + # 动态规划 + for i in range(1, n): + for j in range(bag_weight + 1): + if j < weight[i]: + dp[i][j] = dp[i - 1][j] + else: + dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]) + + return dp[n - 1][bag_weight] + +# 输入 +n, bag_weight = map(int, input().split()) +weight = [] +value = [] +for _ in range(n): + w, v = map(int, input().split()) + weight.append(w) + value.append(v) + +# 输出结果 +print(knapsack(n, bag_weight, weight, value)) + +``` + +### JavaScript + +