algorithm/leetcode-master
1
0
Fork 0
mirror of https://github.com/youngyangyang04/leetcode-master.git synced 2025-07-12 21:50:49 +08:00
Code Issues Packages Projects Releases Wiki Activity

Update

Browse Source
This commit is contained in:
programmercarl
2022-12-20 15:35:48 +08:00
parent 77f1c528b7 72d8fa4fcc
commit 38669c665b
71 changed files with 2538 additions and 1962 deletions
Download Patch File Download Diff File Expand all files Collapse all files

51
problems/0017.电话号码的字母组合.md
View File

@ -120,7 +120,7 @@ for (int i = 0; i < letters.size(); i++) {
**注意这里for循环，可不像是在[回溯算法：求组合问题！](https://programmercarl.com/0077.组合.html)和[回溯算法：求组合总和！](https://programmercarl.com/0216.组合总和III.html)中从startIndex开始遍历的**。
**因为本题每一个数字代表的是不同集合，也就是求不同集合之间的组合，而[77. 组合](https://programmercarl.com/0077.组合.html)和[216.组合总和III](https://programmercarl.com/0216.组合总和III.html)都是是求同一个集合中的组合！**
**因为本题每一个数字代表的是不同集合，也就是求不同集合之间的组合，而[77. 组合](https://programmercarl.com/0077.组合.html)和[216.组合总和III](https://programmercarl.com/0216.组合总和III.html)都是求同一个集合中的组合！**
注意：输入1 * #按键等等异常情况
@ -356,38 +356,32 @@ class Solution:
主要在于递归中传递下一个数字
```go
var (
m []string
path []byte
res []string
)
func letterCombinations(digits string) []string {
lenth:=len(digits)
if lenth==0 ||lenth>4{
return nil
m = []string{"abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"}
path, res = make([]byte, 0), make([]string, 0)
if digits == "" {
return res
}
digitsMap:= [10]string{
"", // 0
"", // 1
"abc", // 2
"def", // 3
"ghi", // 4
"jkl", // 5
"mno", // 6
"pqrs", // 7
"tuv", // 8
"wxyz", // 9
}
res:=make([]string,0)
recursion("",digits,0,digitsMap,&res)
return res
dfs(digits, 0)
return res
}
func recursion(tempString ,digits string, Index int,digitsMap [10]string, res *[]string) {//index表示第几个数字
if len(tempString)==len(digits){//终止条件，字符串长度等于digits的长度
*res=append(*res,tempString)
func dfs(digits string, start int) {
if len(path) == len(digits) { //终止条件，字符串长度等于digits的长度
tmp := string(path)
res = append(res, tmp)
return
}
tmpK:=digits[Index]-'0' // 将index指向的数字转为int（确定下一个数字）
letter:=digitsMap[tmpK]// 取数字对应的字符集
for i:=0;i<len(letter);i++{
tempString=tempString+string(letter[i])//拼接结果
recursion(tempString,digits,Index+1,digitsMap,res)
tempString=tempString[:len(tempString)-1]//回溯
digit := int(digits[start] - '0') // 将index指向的数字转为int（确定下一个数字）
str := m[digit-2] // 取数字对应的字符集（注意和map中的对应）
for j := 0; j < len(str); j++ {
path = append(path, str[j])
dfs(digits, start+1)
path = path[:len(path)-1]
}
}
```
@ -415,7 +409,6 @@ var letterCombinations = function(digits) {
backtracking(n, k, a + 1);
path.pop();
}
}
};
```

2
problems/0020.有效的括号.md
View File

@ -76,7 +76,7 @@ cd a/b/c/../../
**一些同学，在面试中看到这种题目上来就开始写代码，然后就越写越乱。**
建议要写代码之前要分析好有哪几种不匹配的情况，如果不动手之前分析好，写出的代码也会有很多问题。
建议在写代码之前要分析好有哪几种不匹配的情况，如果不在动手之前分析好，写出的代码也会有很多问题。
先来分析一下 这里有三种不匹配的情况，

17
problems/0027.移除元素.md
View File

@ -196,21 +196,26 @@ class Solution {
Python：
```python3
``` python 3
class Solution:
def removeElement(self, nums: List[int], val: int) -> int:
# 快指针遍历元素
fast = 0
# 慢指针记录位置
slow = 0
for fast in range(len(nums)):
# 快慢指针
fast = 0 # 快指针
slow = 0 # 慢指针
size = len(nums)
while fast < size: # 不加等于是因为，a = size 时，nums[a] 会越界
# slow 用来收集不等于 val 的值，如果 fast 对应值不等于 val，则把它与 slow 替换
if nums[fast] != val:
nums[slow] = nums[fast]
slow += 1
fast += 1
return slow
```
Go：
```go
func removeElement(nums []int, val int) int {

103
problems/0037.解数独.md
View File

@ -42,9 +42,9 @@
**如果以上这几道题目没有做过的话，不建议上来就做这道题哈！**
[N皇后问题](https://programmercarl.com/0051.N皇后.html)是因为每一行每一列只放一个皇后，只需要一层for循环遍历一行，递归来来遍历列，然后一行一列确定皇后的唯一位置。
[N皇后问题](https://programmercarl.com/0051.N皇后.html)是因为每一行每一列只放一个皇后，只需要一层for循环遍历一行，递归来遍历列，然后一行一列确定皇后的唯一位置。
本题就不一样了，**本题中棋盘的每一个位置都要放一个数字（而N换后是一行只放一个皇后），并检查数字是否合法，解数独的树形结构要比N皇后更宽更深**。
本题就不一样了，**本题中棋盘的每一个位置都要放一个数字（而N皇后是一行只放一个皇后），并检查数字是否合法，解数独的树形结构要比N皇后更宽更深**。
因为这个树形结构太大了，我抽取一部分，如图所示：
@ -75,7 +75,7 @@ bool backtracking(vector<vector<char>>& board)
**那么有没有永远填不满的情况呢？**
这个问题我在递归单层搜索逻辑里在来讲！
这个问题我在递归单层搜索逻辑里再来讲！
* 递归单层搜索逻辑
@ -207,7 +207,7 @@ public:
所以我在开篇就提到了**二维递归**，这也是我自创词汇，希望可以帮助大家理解解数独的搜索过程。
一波分析之后，在看代码会发现其实也不难，唯一难点就是理解**二维递归**的思维逻辑。
一波分析之后，再看代码会发现其实也不难，唯一难点就是理解**二维递归**的思维逻辑。
**这样，解数独这么难的问题，也被我们攻克了**。
@ -331,55 +331,56 @@ class Solution:
### Go
```go
func solveSudoku(board [][]byte) {
var backtracking func(board [][]byte) bool
backtracking=func(board [][]byte) bool{
for i:=0;i<9;i++{
for j:=0;j<9;j++{
//判断此位置是否适合填数字
if board[i][j]!='.'{
continue
}
//尝试填1-9
for k:='1';k<='9';k++{
if isvalid(i,j,byte(k),board)==true{//如果满足要求就填
board[i][j]=byte(k)
if backtracking(board)==true{
return true
}
board[i][j]='.'
}
}
return false
}
}
return true
}
backtracking(board)
func solveSudoku(board [][]byte) {
var backtracking func(board [][]byte) bool
backtracking = func(board [][]byte) bool {
for i := 0; i < 9; i++ {
for j := 0; j < 9; j++ {
//判断此位置是否适合填数字
if board[i][j] != '.' {
continue
}
//尝试填1-9
for k := '1'; k <= '9'; k++ {
if isvalid(i, j, byte(k), board) == true { //如果满足要求就填
board[i][j] = byte(k)
if backtracking(board) == true {
return true
}
board[i][j] = '.'
}
}
return false
}
}
return true
}
backtracking(board)
}
//判断填入数字是否满足要求
func isvalid(row,col int,k byte,board [][]byte)bool{
for i:=0;i<9;i++{//行
if board[row][i]==k{
return false
}
}
for i:=0;i<9;i++{//列
if board[i][col]==k{
return false
}
}
//方格
startrow:=(row/3)*3
startcol:=(col/3)*3
for i:=startrow;i<startrow+3;i++{
for j:=startcol;j<startcol+3;j++{
if board[i][j]==k{
return false
}
}
}
return true
func isvalid(row, col int, k byte, board [][]byte) bool {
for i := 0; i < 9; i++ { //行
if board[row][i] == k {
return false
}
}
for i := 0; i < 9; i++ { //列
if board[i][col] == k {
return false
}
}
//方格
startrow := (row / 3) * 3
startcol := (col / 3) * 3
for i := startrow; i < startrow+3; i++ {
for j := startcol; j < startcol+3; j++ {
if board[i][j] == k {
return false
}
}
}
return true
}
```

43
problems/0039.组合总和.md
View File

@ -42,7 +42,7 @@ candidates 中的数字可以无限制重复被选取。
题目中的**无限制重复被选取，吓得我赶紧想想 出现0 可咋办**，然后看到下面提示：1 <= candidates[i] <= 200，我就放心了。
本题和[77.组合](https://programmercarl.com/0077.组合.html)，[216.组合总和III](https://programmercarl.com/0216.组合总和III.html)和区别是：本题没有数量要求，可以无限重复，但是有总和的限制，所以间接的也是有个数的限制。
本题和[77.组合](https://programmercarl.com/0077.组合.html)，[216.组合总和III](https://programmercarl.com/0216.组合总和III.html)的区别是：本题没有数量要求，可以无限重复，但是有总和的限制，所以间接的也是有个数的限制。
本题搜索的过程抽象成树形结构如下：
@ -335,33 +335,32 @@ class Solution:
主要在于递归中传递下一个数字
```go
var (
res [][]int
path []int
)
func combinationSum(candidates []int, target int) [][]int {
var trcak []int
var res [][]int
backtracking(0,0,target,candidates,trcak,&res)
res, path = make([][]int, 0), make([]int, 0, len(candidates))
sort.Ints(candidates) // 排序，为剪枝做准备
dfs(candidates, 0, target)
return res
}
func backtracking(startIndex,sum,target int,candidates,trcak []int,res *[][]int){
//终止条件
if sum==target{
tmp:=make([]int,len(trcak))
copy(tmp,trcak)//拷贝
*res=append(*res,tmp)//放入结果集
func dfs(candidates []int, start int, target int) {
if target == 0 { // target 不断减小，如果为0说明达到了目标值
tmp := make([]int, len(path))
copy(tmp, path)
res = append(res, tmp)
return
}
if sum>target{return}
//回溯
for i:=startIndex;i<len(candidates);i++{
//更新路径集合和sum
trcak=append(trcak,candidates[i])
sum+=candidates[i]
//递归
backtracking(i,sum,target,candidates,trcak,res)
//回溯
trcak=trcak[:len(trcak)-1]
sum-=candidates[i]
for i := start; i < len(candidates); i++ {
if candidates[i] > target { // 剪枝，提前返回
break
}
path = append(path, candidates[i])
dfs(candidates, i, target - candidates[i])
path = path[:len(path) - 1]
}
}
```

108
problems/0040.组合总和II.md
View File

@ -110,13 +110,13 @@ if (sum == target) {
}
```
`sum > target` 这个条件其实可以省略，因为和在递归单层遍历的时候，会有剪枝的操作，下面会介绍到。
`sum > target` 这个条件其实可以省略，因为在递归单层遍历的时候，会有剪枝的操作，下面会介绍到。
* **单层搜索的逻辑**
这里与[39.组合总和](https://programmercarl.com/0039.组合总和.html)最大的不同就是要去重了。
前面我们提到：要去重的是“同一树层上的使用过”，如果判断同一树层上元素（相同的元素）是否使用过了呢。
前面我们提到：要去重的是“同一树层上的使用过”，如何判断同一树层上元素（相同的元素）是否使用过了呢。
**如果`candidates[i] == candidates[i - 1]` 并且 `used[i - 1] == false`，就说明：前一个树枝，使用了candidates[i - 1]，也就是说同一树层使用过candidates[i - 1]**。
@ -438,76 +438,74 @@ class Solution:
**使用used数组**
```go
var (
res [][]int
path []int
used []bool
)
func combinationSum2(candidates []int, target int) [][]int {
var trcak []int
var res [][]int
var history map[int]bool
history=make(map[int]bool)
sort.Ints(candidates)
backtracking(0,0,target,candidates,trcak,&res,history)
res, path = make([][]int, 0), make([]int, 0, len(candidates))
used = make([]bool, len(candidates))
sort.Ints(candidates) // 排序，为剪枝做准备
dfs(candidates, 0, target)
return res
}
func backtracking(startIndex,sum,target int,candidates,trcak []int,res *[][]int,history map[int]bool){
//终止条件
if sum==target{
tmp:=make([]int,len(trcak))
copy(tmp,trcak)//拷贝
*res=append(*res,tmp)//放入结果集
func dfs(candidates []int, start int, target int) {
if target == 0 { // target 不断减小，如果为0说明达到了目标值
tmp := make([]int, len(path))
copy(tmp, path)
res = append(res, tmp)
return
}
if sum>target{return}
//回溯
// used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
// used[i - 1] == false，说明同一树层candidates[i - 1]使用过
for i:=startIndex;i<len(candidates);i++{
if i>0&&candidates[i]==candidates[i-1]&&history[i-1]==false{
continue
for i := start; i < len(candidates); i++ {
if candidates[i] > target { // 剪枝，提前返回
break
}
//更新路径集合和sum
trcak=append(trcak,candidates[i])
sum+=candidates[i]
history[i]=true
//递归
backtracking(i+1,sum,target,candidates,trcak,res,history)
//回溯
trcak=trcak[:len(trcak)-1]
sum-=candidates[i]
history[i]=false
// used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
// used[i - 1] == false，说明同一树层candidates[i - 1]使用过
if i > 0 && candidates[i] == candidates[i-1] && used[i-1] == false {
continue
}
path = append(path, candidates[i])
used[i] = true
dfs(candidates, i+1, target - candidates[i])
used[i] = false
path = path[:len(path) - 1]
}
}
```
**不使用used数组**
```go
var (
res [][]int
path []int
)
func combinationSum2(candidates []int, target int) [][]int {
var trcak []int
var res [][]int
sort.Ints(candidates)
backtracking(0,0,target,candidates,trcak,&res)
res, path = make([][]int, 0), make([]int, 0, len(candidates))
sort.Ints(candidates) // 排序，为剪枝做准备
dfs(candidates, 0, target)
return res
}
func backtracking(startIndex,sum,target int,candidates,trcak []int,res *[][]int){
//终止条件
if sum==target{
tmp:=make([]int,len(trcak))
//拷贝
copy(tmp,trcak)
//放入结果集
*res=append(*res,tmp)
func dfs(candidates []int, start int, target int) {
if target == 0 { // target 不断减小，如果为0说明达到了目标值
tmp := make([]int, len(path))
copy(tmp, path)
res = append(res, tmp)
return
}
//回溯
for i:=startIndex;i<len(candidates) && sum+candidates[i]<=target;i++{
// 若当前树层有使用过相同的元素，则跳过
if i>startIndex&&candidates[i]==candidates[i-1]{
continue
for i := start; i < len(candidates); i++ {
if candidates[i] > target { // 剪枝，提前返回
break
}
//更新路径集合和sum
trcak=append(trcak,candidates[i])
sum+=candidates[i]
backtracking(i+1,sum,target,candidates,trcak,res)
//回溯
trcak=trcak[:len(trcak)-1]
sum-=candidates[i]
// i != start 限制了这不对深度遍历到达的此值去重
if i != start && candidates[i] == candidates[i-1] { // 去重
continue
}
path = append(path, candidates[i])
dfs(candidates, i+1, target - candidates[i])
path = path[:len(path) - 1]
}
}
```

29
problems/0045.跳跃游戏II.md
View File

@ -36,7 +36,7 @@
贪心的思路，局部最优：当前可移动距离尽可能多走，如果还没到终点，步数再加一。整体最优：一步尽可能多走，从而达到最小步数。
思路虽然是这样，但在写代码的时候还不能真的就能跳多远跳远，那样就不知道下一步最远能跳到哪里了。
思路虽然是这样，但在写代码的时候还不能真的能跳多远就跳多远，那样就不知道下一步最远能跳到哪里了。
**所以真正解题的时候，要从覆盖范围出发，不管怎么跳，覆盖范围内一定是可以跳到的，以最小的步数增加覆盖范围，覆盖范围一旦覆盖了终点，得到的就是最小步数！**
@ -234,31 +234,6 @@ class Solution:
### Go
```Go
func jump(nums []int) int {
dp := make([]int, len(nums))
dp[0] = 0//初始第一格跳跃数一定为0
for i := 1; i < len(nums); i++ {
dp[i] = i
for j := 0; j < i; j++ {
if nums[j] + j >= i {//nums[j]为起点,j为往右跳的覆盖范围,这行表示从j能跳到i
dp[i] = min(dp[j] + 1, dp[i])//更新最小能到i的跳跃次数
}
}
}
return dp[len(nums)-1]
}
func min(a, b int) int {
if a < b {
return a
} else {
return b
}
}
```
```go
// 贪心版本一
func jump(nums []int) int {
@ -320,8 +295,6 @@ func max(a, b int) int {
}
```
### Javascript
```Javascript

45
problems/0046.全排列.md
View File

@ -275,29 +275,34 @@ class Solution:
### Go
```Go
var res [][]int
var (
res [][]int
path []int
st []bool // state的缩写
)
func permute(nums []int) [][]int {
res = [][]int{}
backTrack(nums,len(nums),[]int{})
return res
}
func backTrack(nums []int,numsLen int,path []int) {
if len(nums)==0{
p:=make([]int,len(path))
copy(p,path)
res = append(res,p)
}
for i:=0;i<numsLen;i++{
cur:=nums[i]
path = append(path,cur)
nums = append(nums[:i],nums[i+1:]...)//直接使用切片
backTrack(nums,len(nums),path)
nums = append(nums[:i],append([]int{cur},nums[i:]...)...)//回溯的时候切片也要复原，元素位置不能变
path = path[:len(path)-1]
}
res, path = make([][]int, 0), make([]int, 0, len(nums))
st = make([]bool, len(nums))
dfs(nums, 0)
return res
}
func dfs(nums []int, cur int) {
if cur == len(nums) {
tmp := make([]int, len(path))
copy(tmp, path)
res = append(res, tmp)
}
for i := 0; i < len(nums); i++ {
if !st[i] {
path = append(path, nums[i])
st[i] = true
dfs(nums, cur + 1)
st[i] = false
path = path[:len(path)-1]
}
}
}
```
### Javascript

56
problems/0047.全排列II.md
View File

@ -49,7 +49,7 @@
**一般来说：组合问题和排列问题是在树形结构的叶子节点上收集结果，而子集问题就是取树上所有节点的结果**。
在[46.全排列](https://programmercarl.com/0046.全排列.html)中已经详解讲解了排列问题的写法，在[40.组合总和II](https://programmercarl.com/0040.组合总和II.html) 、[90.子集II](https://programmercarl.com/0090.子集II.html)中详细讲解的去重的写法，所以这次我就不用回溯三部曲分析了，直接给出代码，如下：
在[46.全排列](https://programmercarl.com/0046.全排列.html)中已经详细讲解了排列问题的写法，在[40.组合总和II](https://programmercarl.com/0040.组合总和II.html) 、[90.子集II](https://programmercarl.com/0090.子集II.html)中详细讲解了去重的写法，所以这次我就不用回溯三部曲分析了，直接给出代码，如下：
## C++代码
@ -225,33 +225,37 @@ class Solution:
### Go
```go
var res [][]int
func permute(nums []int) [][]int {
res = [][]int{}
backTrack(nums,len(nums),[]int{})
return res
var (
res [][]int
path []int
st []bool // state的缩写
)
func permuteUnique(nums []int) [][]int {
res, path = make([][]int, 0), make([]int, 0, len(nums))
st = make([]bool, len(nums))
sort.Ints(nums)
dfs(nums, 0)
return res
}
func backTrack(nums []int,numsLen int,path []int) {
if len(nums)==0{
p:=make([]int,len(path))
copy(p,path)
res = append(res,p)
}
used := [21]int{}//跟前一题唯一的区别，同一层不使用重复的数。关于used的思想carl在递增子序列那一题中提到过
for i:=0;i<numsLen;i++{
if used[nums[i]+10]==1{
continue
}
cur:=nums[i]
path = append(path,cur)
used[nums[i]+10]=1
nums = append(nums[:i],nums[i+1:]...)
backTrack(nums,len(nums),path)
nums = append(nums[:i],append([]int{cur},nums[i:]...)...)
path = path[:len(path)-1]
}
func dfs(nums []int, cur int) {
if cur == len(nums) {
tmp := make([]int, len(path))
copy(tmp, path)
res = append(res, tmp)
}
for i := 0; i < len(nums); i++ {
if i != 0 && nums[i] == nums[i-1] && !st[i-1] { // 去重，用st来判别是深度还是广度
continue
}
if !st[i] {
path = append(path, nums[i])
st[i] = true
dfs(nums, cur + 1)
st[i] = false
path = path[:len(path)-1]
}
}
}
```

50
problems/0051.N皇后.md
View File

@ -291,6 +291,56 @@ class Solution {
}
```
```java
// 方法2：使用boolean数组表示已经占用的直(斜)线
class Solution {
List<List<String>> res = new ArrayList<>();
boolean[] usedCol, usedDiag45, usedDiag135; // boolean数组中的每个元素代表一条直(斜)线
public List<List<String>> solveNQueens(int n) {
usedCol = new boolean[n]; // 列方向的直线条数为 n
usedDiag45 = new boolean[2 * n - 1]; // 45°方向的斜线条数为 2 * n - 1
usedDiag135 = new boolean[2 * n - 1]; // 135°方向的斜线条数为 2 * n - 1
//用于收集结果, 元素的index表示棋盘的row，元素的value代表棋盘的column
int[] board = new int[n];
backTracking(board, n, 0);
return res;
}
private void backTracking(int[] board, int n, int row) {
if (row == n) {
//收集结果
List<String> temp = new ArrayList<>();
for (int i : board) {
char[] str = new char[n];
Arrays.fill(str, '.');
str[i] = 'Q';
temp.add(new String(str));
}
res.add(temp);
return;
}
for (int col = 0; col < n; col++) {
if (usedCol[col] | usedDiag45[row + col] | usedDiag135[row - col + n - 1]) {
continue;
}
board[row] = col;
// 标记该列出现过
usedCol[col] = true;
// 同一45°斜线上元素的row + col为定值, 且各不相同
usedDiag45[row + col] = true;
// 同一135°斜线上元素row - col为定值, 且各不相同
// row - col 值有正有负, 加 n - 1 是为了对齐零点
usedDiag135[row - col + n - 1] = true;
// 递归
backTracking(board, n, row + 1);
usedCol[col] = false;
usedDiag45[row + col] = false;
usedDiag135[row - col + n - 1] = false;
}
}
}
```
### Python
```python

3
problems/0052.N皇后II.md
View File

@ -8,7 +8,7 @@
# 52. N皇后II
题目链接：https://leetcode.cn/problems/n-queens-ii/
题目链接：[https://leetcode.cn/problems/n-queens-ii/](https://leetcode.cn/problems/n-queens-ii/)
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。
@ -308,3 +308,4 @@ class Solution {
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>
</a>

22
problems/0055.跳跃游戏.md
View File

@ -72,13 +72,13 @@ public:
```
## 总结
这道题目关键点在于：不用拘泥于每次究竟跳跳几步，而是看覆盖范围，覆盖范围内一定是可以跳过来的，不用管是怎么跳的。
这道题目关键点在于：不用拘泥于每次究竟跳几步，而是看覆盖范围，覆盖范围内一定是可以跳过来的，不用管是怎么跳的。
大家可以看出思路想出来了，代码还是非常简单的。
一些同学可能感觉，我在讲贪心系列的时候，题目和题目之间貌似没有什么联系？
**是真的就是没什么联系，因为贪心无套路！**没有个整体的贪心框架解决一些列问题，只能是接触各种类型的题目锻炼自己的贪心思维！
**是真的就是没什么联系，因为贪心无套路！**没有个整体的贪心框架解决一系列问题，只能是接触各种类型的题目锻炼自己的贪心思维！
## 其他语言版本
@ -133,24 +133,6 @@ class Solution:
```
### Go
```Go
func canJUmp(nums []int) bool {
if len(nums)<=1{
return true
}
dp:=make([]bool,len(nums))
dp[0]=true
for i:=1;i<len(nums);i++{
for j:=i-1;j>=0;j--{
if dp[j]&&nums[j]+j>=i{
dp[i]=true
break
}
}
}
return dp[len(nums)-1]
}
```
```go
// 贪心

65
problems/0070.爬楼梯.md
View File

@ -53,7 +53,7 @@ dp[i]： 爬到第i层楼梯，有dp[i]种方法
2. 确定递推公式
如果可以推出dp[i]呢？
如何可以推出dp[i]呢？
从dp[i]的定义可以看出，dp[i] 可以有两个方向推出来。
@ -73,7 +73,7 @@ dp[i]： 爬到第i层楼梯，有dp[i]种方法
在回顾一下dp[i]的定义：爬到第i层楼梯，有dp[i]中方法。
那么i为0，dp[i]应该是多少呢，这个可以有很多解释，但都基本是直接奔着答案去解释的。
那么i为0，dp[i]应该是多少呢，这个可以有很多解释，但基本都是直接奔着答案去解释的。
例如强行安慰自己爬到第0层，也有一种方法，什么都不做也就是一种方法即：dp[0] = 1，相当于直接站在楼顶。
@ -91,7 +91,7 @@ dp[i]： 爬到第i层楼梯，有dp[i]种方法
我相信dp[1] = 1，dp[2] = 2，这个初始化大家应该都没有争议的。
所以我的原则是：不考虑dp[0]如果初始化，只初始化dp[1] = 1，dp[2] = 2，然后从i = 3开始递推，这样才符合dp[i]的定义。
所以我的原则是：不考虑dp[0]如何初始化，只初始化dp[1] = 1，dp[2] = 2，然后从i = 3开始递推，这样才符合dp[i]的定义。
4. 确定遍历顺序
@ -163,7 +163,7 @@ public:
这道题目还可以继续深化，就是一步一个台阶，两个台阶，三个台阶，直到 m个台阶，有多少种方法爬到n阶楼顶。
这又有难度了，这其实是一个完全背包问题，但力扣上没有这种题目，所以后续我在讲解背包问题的时候，今天这道题还会拿从背包问题的角度上来再讲一遍。
这又有难度了，这其实是一个完全背包问题，但力扣上没有这种题目，所以后续我在讲解背包问题的时候，今天这道题还会从背包问题的角度上来再讲一遍。
这里我先给出我的实现代码：
@ -194,7 +194,7 @@ public:
这一连套问下来，候选人算法能力如何，面试官心里就有数了。
**其实大厂面试最喜欢问题的就是这种简单题，然后慢慢变化，在小细节上考察候选人**。
**其实大厂面试最喜欢的问题就是这种简单题，然后慢慢变化，在小细节上考察候选人**。
@ -255,37 +255,37 @@ class Solution {
class Solution:
def climbStairs(self, n: int) -> int:
# dp[i] 为第 i 阶楼梯有多少种方法爬到楼顶
dp=[0]*(n+1)
dp[0]=1
dp[1]=1
for i in range(2,n+1):
dp[i]=dp[i-1]+dp[i-2]
dp = [0]*(n+1)
dp[0] = 1
dp[1] = 1
for i in range(2, n+1):
dp[i] = dp[i-1] + dp[i-2]
return dp[n]
# 空间复杂度为O(1)版本
class Solution:
def climbStairs(self, n: int) -> int:
dp=[0]*(n+1)
dp[0]=1
dp[1]=1
dp = [0]*(n+1)
dp[0] = 1
dp[1] = 1
for i in range(2,n+1):
tmp=dp[0]+dp[1]
dp[0]=dp[1]
dp[1]=tmp
tmp = dp[0] + dp[1]
dp[0] = dp[1]
dp[1] = tmp
return dp[1]
```
### Go
```Go
func climbStairs(n int) int {
if n==1{
if n == 1 {
return 1
}
dp:=make([]int,n+1)
dp[1]=1
dp[2]=2
for i:=3;i<=n;i++{
dp[i]=dp[i-1]+dp[i-2]
dp := make([]int, n+1)
dp[1] = 1
dp[2] = 2
for i := 3; i <= n; i++ {
dp[i] = dp[i-1] + dp[i-2]
}
return dp[n]
}
@ -303,7 +303,7 @@ var climbStairs = function(n) {
};
```
TypeScript
### TypeScript
> 爬2阶
@ -447,7 +447,26 @@ public class Solution {
}
```
### Rust
```rust
impl Solution {
pub fn climb_stairs(n: i32) -> i32 {
if n <= 2 {
return n;
}
let mut a = 1;
let mut b = 2;
let mut f = 0;
for i in 2..n {
f = a + b;
a = b;
b = f;
}
return f;
}
}
```
<p align="center">
<a href="https://programmercarl.com/other/kstar.html" target="_blank">

114
problems/0077.组合.md
View File

@ -34,7 +34,7 @@
# 思路
本题这是回溯法的经典题目。
本题是回溯法的经典题目。
直接的解法当然是使用for循环，例如示例中k为2，很容易想到 用两个for循环，这样就可以输出 和示例中一样的结果。
@ -82,13 +82,13 @@ for (int i = 1; i <= n; i++) {
如果脑洞模拟回溯搜索的过程，绝对可以让人窒息，所以需要抽象图形结构来进一步理解。
**我们在[关于回溯算法，你该了解这些！](https://programmercarl.com/回溯算法理论基础.html)中说道回溯法解决的问题都可以抽象为树形结构（N叉树），用树形结构来理解回溯就容易多了**。
**我们在[关于回溯算法，你该了解这些！](https://programmercarl.com/回溯算法理论基础.html)中说到回溯法解决的问题都可以抽象为树形结构（N叉树），用树形结构来理解回溯就容易多了**。
那么我把组合问题抽象为如下树形结构：
![77.组合](https://img-blog.csdnimg.cn/20201123195223940.png)
可以看出这个棵树，一开始集合是 1，2，3，4， 从左向右取数，取过的数，不在重复取。
可以看出这棵树，一开始集合是 1，2，3，4， 从左向右取数，取过的数，不再重复取。
第一次取1，集合变为2，3，4 ，因为k为2，我们只需要再取一个数就可以了，分别取2，3，4，得到集合[1,2] [1,3] [1,4]，以此类推。
@ -120,7 +120,7 @@ vector<int> path; // 用来存放符合条件结果
其实不定义这两个全局变量也是可以的，把这两个变量放进递归函数的参数里，但函数里参数太多影响可读性，所以我定义全局变量了。
函数里一定有两个参数，既然是集合n里面取k的数，那么n和k是两个int型的参数。
函数里一定有两个参数，既然是集合n里面取k个数，那么n和k是两个int型的参数。
然后还需要一个参数，为int型变量startIndex，这个参数用来记录本层递归的中，集合从哪里开始遍历（集合就是[1,...,n] ）。
@ -389,9 +389,8 @@ class Solution(object):
# 剪枝， 最后k - len(path)个节点直接构造结果，无需递归
last_startidx = n - (k - len(path)) + 1
result.append(path + [idx for idx in range(last_startidx, n + 1)])
for x in range(startidx, last_startidx):
for x in range(startidx, last_startidx + 1):
path.append(x)
backtracking(n, k, x + 1) # 递归
path.pop() # 回溯
@ -435,6 +434,36 @@ class Solution:
return res
```
### Go
```Go
var (
path []int
res [][]int
)
func combine(n int, k int) [][]int {
path, res = make([]int, 0, k), make([][]int, 0)
dfs(n, k, 1)
return res
}
func dfs(n int, k int, start int) {
if len(path) == k { // 说明已经满足了k个数的要求
tmp := make([]int, k)
copy(tmp, path)
res = append(res, tmp)
return
}
for i := start; i <= n; i++ { // 从start开始，不往回走，避免出现重复组合
if n - i + 1 < k - len(path) { // 剪枝
break
}
path = append(path, i)
dfs(n, k, i+1)
path = path[:len(path)-1]
}
}
```
### javascript
@ -481,82 +510,25 @@ function combine(n: number, k: number): number[][] {
};
```
### Go
```Go
var res [][]int
func combine(n int, k int) [][]int {
res=[][]int{}
if n <= 0 || k <= 0 || k > n {
return res
}
backtrack(n, k, 1, []int{})
return res
}
func backtrack(n,k,start int,track []int){
if len(track)==k{
temp:=make([]int,k)
copy(temp,track)
res=append(res,temp)
}
if len(track)+n-start+1 < k {
return
}
for i:=start;i<=n;i++{
track=append(track,i)
backtrack(n,k,i+1,track)
track=track[:len(track)-1]
}
}
```
剪枝：
```Go
var res [][]int
func combine(n int, k int) [][]int {
res=[][]int{}
if n <= 0 || k <= 0 || k > n {
return res
}
backtrack(n, k, 1, []int{})
return res
}
func backtrack(n,k,start int,track []int){
if len(track)==k{
temp:=make([]int,k)
copy(temp,track)
res=append(res,temp)
}
if len(track)+n-start+1 < k {
return
}
for i:=start;i<=n;i++{
track=append(track,i)
backtrack(n,k,i+1,track)
track=track[:len(track)-1]
}
}
```
### Rust
```Rust
impl Solution {
fn backtracking(result: &mut Vec<Vec<i32>>, path: &mut Vec<i32>, n: i32, k: i32, startIndex: i32) {
fn backtracking(result: &mut Vec<Vec<i32>>, path: &mut Vec<i32>, n: i32, k: i32, start_index: i32) {
let len= path.len() as i32;
if len == k{
result.push(path.to_vec());
return;
}
for i in startIndex..= n {
for i in start_index..= n {
path.push(i);
Self::backtracking(result, path, n, k, i+1);
path.pop();
}
}
pub fn combine(n: i32, k: i32) -> Vec<Vec<i32>> {
let mut result: Vec<Vec<i32>> = Vec::new();
let mut path: Vec<i32> = Vec::new();
let mut result = vec![];
let mut path = vec![];
Self::backtracking(&mut result, &mut path, n, k, 1);
result
}
@ -566,22 +538,22 @@ impl Solution {
剪枝
```Rust
impl Solution {
fn backtracking(result: &mut Vec<Vec<i32>>, path: &mut Vec<i32>, n: i32, k: i32, startIndex: i32) {
fn backtracking(result: &mut Vec<Vec<i32>>, path: &mut Vec<i32>, n: i32, k: i32, start_index: i32) {
let len= path.len() as i32;
if len == k{
result.push(path.to_vec());
return;
}
// 此处剪枝
for i in startIndex..= n - (k - len) + 1 {
for i in start_index..= n - (k - len) + 1 {
path.push(i);
Self::backtracking(result, path, n, k, i+1);
path.pop();
}
}
pub fn combine(n: i32, k: i32) -> Vec<Vec<i32>> {
let mut result: Vec<Vec<i32>> = Vec::new();
let mut path: Vec<i32> = Vec::new();
let mut result = vec![];
let mut path = vec![];
Self::backtracking(&mut result, &mut path, n, k, 1);
result
}

40
problems/0077.组合优化.md
View File

@ -133,7 +133,7 @@ public:
# 总结
本篇我们准对求组合问题的回溯法代码做了剪枝优化，这个优化如果不画图的话，其实不好理解，也不好讲清楚。
本篇我们针对求组合问题的回溯法代码做了剪枝优化，这个优化如果不画图的话，其实不好理解，也不好讲清楚。
所以我依然是把整个回溯过程抽象为一棵树形结构，然后可以直观的看出，剪枝究竟是剪的哪里。
@ -194,28 +194,28 @@ class Solution:
```
Go：
```Go
var res [][]int
var (
path []int
res [][]int
)
func combine(n int, k int) [][]int {
res=[][]int{}
if n <= 0 || k <= 0 || k > n {
return res
}
backtrack(n, k, 1, []int{})
return res
path, res = make([]int, 0, k), make([][]int, 0)
dfs(n, k, 1)
return res
}
func backtrack(n,k,start int,track []int){
if len(track)==k{
temp:=make([]int,k)
copy(temp,track)
res=append(res,temp)
func dfs(n int, k int, start int) {
if len(path) == k {
tmp := make([]int, k)
copy(tmp, path)
res = append(res, tmp)
return
}
if len(track)+n-start+1 < k {
return
}
for i:=start;i<=n;i++{
track=append(track,i)
backtrack(n,k,i+1,track)
track=track[:len(track)-1]
for i := start; i <= n - (k-len(path)) + 1; i++ {
path = append(path, i)
dfs(n, k, i+1)
path = path[:len(path)-1]
}
}
```

36
problems/0078.子集.md
View File

@ -227,25 +227,25 @@ class Solution:
## Go
```Go
var res [][]int
func subset(nums []int) [][]int {
res = make([][]int, 0)
sort.Ints(nums)
Dfs([]int{}, nums, 0)
return res
var (
path []int
res [][]int
)
func subsets(nums []int) [][]int {
res, path = make([][]int, 0), make([]int, 0, len(nums))
dfs(nums, 0)
return res
}
func Dfs(temp, nums []int, start int){
tmp := make([]int, len(temp))
copy(tmp, temp)
res = append(res, tmp)
for i := start; i < len(nums); i++{
//if i>start&&nums[i]==nums[i-1]{
// continue
//}
temp = append(temp, nums[i])
Dfs(temp, nums, i+1)
temp = temp[:len(temp)-1]
}
func dfs(nums []int, start int) {
tmp := make([]int, len(path))
copy(tmp, path)
res = append(res, tmp)
for i := start; i < len(nums); i++ {
path = append(path, nums[i])
dfs(nums, i+1)
path = path[:len(path)-1]
}
}
```

46
problems/0090.子集II.md
View File

@ -261,10 +261,10 @@ class Solution:
self.path.pop()
```
### Python3
#### Python3
不使用used数组
```python3
```python
class Solution:
def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
res = []
@ -291,7 +291,7 @@ class Solution:
```
使用used数组
```python3
```python
class Solution:
def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
result = []
@ -315,26 +315,30 @@ class Solution:
### Go
```Go
var res[][]int
func subsetsWithDup(nums []int)[][]int {
res=make([][]int,0)
sort.Ints(nums)
dfs([]int{},nums,0)
return res
var (
path []int
res [][]int
)
func subsetsWithDup(nums []int) [][]int {
path, res = make([]int, 0, len(nums)), make([][]int, 0)
sort.Ints(nums)
dfs(nums, 0)
return res
}
func dfs(temp, num []int, start int) {
tmp:=make([]int,len(temp))
copy(tmp,temp)
res=append(res,tmp)
for i:=start;i<len(num);i++{
if i>start&&num[i]==num[i-1]{
continue
}
temp=append(temp,num[i])
dfs(temp,num,i+1)
temp=temp[:len(temp)-1]
}
func dfs(nums []int, start int) {
tmp := make([]int, len(path))
copy(tmp, path)
res = append(res, tmp)
for i := start; i < len(nums); i++ {
if i != start && nums[i] == nums[i-1] {
continue
}
path = append(path, nums[i])
dfs(nums, i+1)
path = path[:len(path)-1]
}
}
```

78
problems/0093.复原IP地址.md
View File

@ -424,6 +424,42 @@ class Solution:
return True
```
## Go
```go
var (
path []string
res []string
)
func restoreIpAddresses(s string) []string {
path, res = make([]string, 0, len(s)), make([]string, 0)
dfs(s, 0)
return res
}
func dfs(s string, start int) {
if len(path) == 4 { // 够四段后就不再继续往下递归
if start == len(s) {
str := strings.Join(path, ".")
res = append(res, str)
}
return
}
for i := start; i < len(s); i++ {
if i != start && s[start] == '0' { // 含有前导 0，无效
break
}
str := s[start : i+1]
num, _ := strconv.Atoi(str)
if num >= 0 && num <= 255 {
path = append(path, str) // 符合条件的就进入下一层
dfs(s, i+1)
path = path[:len(path) - 1]
} else { // 如果不满足条件，再往后也不可能满足条件，直接退出
break
}
}
}
```
## JavaScript
@ -494,48 +530,6 @@ function restoreIpAddresses(s: string): string[] {
};
```
## Go
回溯（对于前导 0的IP（特别注意s[startIndex]=='0'的判断，不应该写成s[startIndex]==0，因为s截取出来不是数字））
```go
func restoreIpAddresses(s string) []string {
var res,path []string
backTracking(s,path,0,&res)
return res
}
func backTracking(s string,path []string,startIndex int,res *[]string){
//终止条件
if startIndex==len(s)&&len(path)==4{
tmpIpString:=path[0]+"."+path[1]+"."+path[2]+"."+path[3]
*res=append(*res,tmpIpString)
}
for i:=startIndex;i<len(s);i++{
//处理
path:=append(path,s[startIndex:i+1])
if i-startIndex+1<=3&&len(path)<=4&&isNormalIp(s,startIndex,i){
//递归
backTracking(s,path,i+1,res)
}else {//如果首尾超过了3个，或路径多余4个，或前导为0，或大于255，直接回退
return
}
//回溯
path=path[:len(path)-1]
}
}
func isNormalIp(s string,startIndex,end int)bool{
checkInt,_:=strconv.Atoi(s[startIndex:end+1])
if end-startIndex+1>1&&s[startIndex]=='0'{//对于前导 0的IP（特别注意s[startIndex]=='0'的判断，不应该写成s[startIndex]==0，因为s截取出来不是数字）
return false
}
if checkInt>255{
return false
}
return true
}
```
## Rust
```Rust

51
problems/0098.验证二叉搜索树.md
View File

@ -437,8 +437,6 @@ class Solution:
## Go
```Go
import "math"
func isValidBST(root *TreeNode) bool {
// 二叉搜索树也可以是空树
if root == nil {
@ -639,6 +637,55 @@ object Solution {
}
```
## rust
递归：
```rust
impl Solution {
pub fn is_valid_bst(root: Option<Rc<RefCell<TreeNode>>>) -> bool {
Self::valid_bst(i64::MIN, i64::MAX, root)
}
pub fn valid_bst(low: i64, upper: i64, root: Option<Rc<RefCell<TreeNode>>>) -> bool {
if root.is_none() {
return true;
}
let root = root.as_ref().unwrap().borrow();
if root.val as i64 <= low || root.val as i64 >= upper {
return false;
}
Self::valid_bst(low, root.val as i64, root.left.clone())
&& Self::valid_bst(root.val as i64, upper, root.right.clone())
}
}
```
辅助数组：
```rust
impl Solution {
pub fn is_valid_bst(root: Option<Rc<RefCell<TreeNode>>>) -> bool {
let mut vec = vec![];
Self::valid_bst(root, &mut vec);
for i in 1..vec.len() {
if vec[i] <= vec[i - 1] {
return false;
}
}
true
}
pub fn valid_bst(root: Option<Rc<RefCell<TreeNode>>>, mut v: &mut Vec<i64>) {
if root.is_none() {
return;
}
let node = root.as_ref().unwrap().borrow();
Self::valid_bst(node.left.clone(), v);
v.push(node.val as i64);
Self::valid_bst(node.right.clone(), v);
}
}
```
<p align="center">
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>

101
problems/0101.对称二叉树.md
View File

@ -21,7 +21,7 @@
对于二叉树是否对称，要比较的是根节点的左子树与右子树是不是相互翻转的，理解这一点就知道了**其实我们要比较的是两个树（这两个树是根节点的左右子树）**，所以在递归遍历的过程中，也是要同时遍历两棵树。
那么如果比较呢？
那么如何比较呢？
比较的是两个子树的里侧和外侧的元素是否相等。如图所示：
@ -80,7 +80,7 @@ else if (left == NULL && right == NULL) return true;
else if (left->val != right->val) return false; // 注意这里我没有使用else
```
注意上面最后一种情况，我没有使用else，而是elseif， 因为我们把以上情况都排除之后，剩下的就是 左右节点都不为空，且数值相同的情况。
注意上面最后一种情况，我没有使用else，而是else if， 因为我们把以上情况都排除之后，剩下的就是 左右节点都不为空，且数值相同的情况。
3. 确定单层递归的逻辑
@ -244,7 +244,7 @@ public:
这次我们又深度剖析了一道二叉树的“简单题”，大家会发现，真正的把题目搞清楚其实并不简单，leetcode上accept了和真正掌握了还是有距离的。
我们介绍了递归法和迭代法，递归依然通过递归三部曲来解决了这道题目，如果只看精简的代码根本看不出来递归三部曲是如果解题的。
我们介绍了递归法和迭代法，递归依然通过递归三部曲来解决了这道题目，如果只看精简的代码根本看不出来递归三部曲是如何解题的。
在迭代法中我们使用了队列，需要注意的是这不是层序遍历，而且仅仅通过一个容器来成对的存放我们要比较的元素，知道这一本质之后就发现，用队列，用栈，甚至用数组，都是可以的。
@ -259,7 +259,7 @@ public:
# 其他语言版本
## Java
Java
```Java
/**
@ -364,7 +364,7 @@ public:
```
## Python
Python
递归法:
```python
@ -464,8 +464,7 @@ class Solution:
return True
```
## Go
Go
```go
/**
* Definition for a binary tree node.
@ -488,10 +487,12 @@ func defs(left *TreeNode, right *TreeNode) bool {
}
return defs(left.Left, right.Right) && defs(right.Left, left.Right);
}
func isSymmetric(root *TreeNode) bool {
return defs(root.Left, root.Right);
}
// 迭代
func isSymmetric(root *TreeNode) bool {
var queue []*TreeNode;
@ -515,59 +516,60 @@ func isSymmetric(root *TreeNode) bool {
```
## JavaScript
JavaScript
递归判断是否为对称二叉树：
```javascript
var isSymmetric = function(root) {
//使用递归遍历左右子树 递归三部曲
// 使用递归遍历左右子树 递归三部曲
// 1. 确定递归的参数 root.left root.right和返回值true false
const compareNode=function(left,right){
//2. 确定终止条件 空的情况
if(left===null&&right!==null||left!==null&&right===null){
const compareNode = function(left, right) {
// 2. 确定终止条件 空的情况
if(left === null && right !== null || left !== null && right === null) {
return false;
}else if(left===null&&right===null){
} else if(left === null && right === null) {
return true;
}else if(left.val!==right.val){
} else if(left.val !== right.val) {
return false;
}
//3. 确定单层递归逻辑
let outSide=compareNode(left.left,right.right);
let inSide=compareNode(left.right,right.left);
return outSide&&inSide;
// 3. 确定单层递归逻辑
let outSide = compareNode(left.left, right.right);
let inSide = compareNode(left.right, right.left);
return outSide && inSide;
}
if(root===null){
if(root === null) {
return true;
}
return compareNode(root.left,root.right);
return compareNode(root.left, root.right);
};
```
队列实现迭代判断是否为对称二叉树：
```javascript
var isSymmetric = function(root) {
//迭代方法判断是否是对称二叉树
//首先判断root是否为空
if(root===null){
// 迭代方法判断是否是对称二叉树
// 首先判断root是否为空
if(root === null) {
return true;
}
let queue=[];
let queue = [];
queue.push(root.left);
queue.push(root.right);
while(queue.length){
let leftNode=queue.shift();//左节点
let rightNode=queue.shift();//右节点
if(leftNode===null&&rightNode===null){
while(queue.length) {
let leftNode = queue.shift(); //左节点
let rightNode = queue.shift(); //右节点
if(leftNode === null && rightNode === null) {
continue;
}
if(leftNode===null||rightNode===null||leftNode.val!==rightNode.val){
if(leftNode === null || rightNode === null || leftNode.val !== rightNode.val) {
return false;
}
queue.push(leftNode.left);//左节点左孩子入队
queue.push(rightNode.right);//右节点右孩子入队
queue.push(leftNode.right);//左节点右孩子入队
queue.push(rightNode.left);//右节点左孩子入队
queue.push(leftNode.left); //左节点左孩子入队
queue.push(rightNode.right); //右节点右孩子入队
queue.push(leftNode.right); //左节点右孩子入队
queue.push(rightNode.left); //右节点左孩子入队
}
return true;
};
```
@ -575,33 +577,34 @@ var isSymmetric = function(root) {
栈实现迭代判断是否为对称二叉树：
```javascript
var isSymmetric = function(root) {
//迭代方法判断是否是对称二叉树
//首先判断root是否为空
if(root===null){
// 迭代方法判断是否是对称二叉树
// 首先判断root是否为空
if(root === null) {
return true;
}
let stack=[];
let stack = [];
stack.push(root.left);
stack.push(root.right);
while(stack.length){
let rightNode=stack.pop();//左节点
let leftNode=stack.pop();//右节点
if(leftNode===null&&rightNode===null){
while(stack.length) {
let rightNode = stack.pop(); //左节点
let leftNode=stack.pop(); //右节点
if(leftNode === null && rightNode === null) {
continue;
}
if(leftNode===null||rightNode===null||leftNode.val!==rightNode.val){
if(leftNode === null || rightNode === null || leftNode.val !== rightNode.val) {
return false;
}
stack.push(leftNode.left);//左节点左孩子入队
stack.push(rightNode.right);//右节点右孩子入队
stack.push(leftNode.right);//左节点右孩子入队
stack.push(rightNode.left);//右节点左孩子入队
stack.push(leftNode.left); //左节点左孩子入队
stack.push(rightNode.right); //右节点右孩子入队
stack.push(leftNode.right); //左节点右孩子入队
stack.push(rightNode.left); //右节点左孩子入队
}
return true;
};
```
## TypeScript：
TypeScript：
> 递归法
@ -670,7 +673,7 @@ function isSymmetric(root: TreeNode | null): boolean {
};
```
## Swift:
Swift:
> 递归
```swift
@ -752,7 +755,7 @@ func isSymmetric3(_ root: TreeNode?) -> Bool {
}
```
## Scala
Scala
> 递归：
```scala

520
problems/0102.二叉树的层序遍历.md
View File

@ -47,7 +47,7 @@
层序遍历一个二叉树。就是从左到右一层一层的去遍历二叉树。这种遍历的方式和我们之前讲过的都不太一样。
需要借用一个辅助数据结构即队列来实现，**队列先进先出，符合一层一层遍历的逻辑，而是用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。**
需要借用一个辅助数据结构即队列来实现，**队列先进先出，符合一层一层遍历的逻辑，而用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。**
**而这种层序遍历方式就是图论中的广度优先遍历，只不过我们应用在二叉树上。**
@ -106,50 +106,6 @@ public:
};
```
python3代码：
```python
class Solution:
"""二叉树层序遍历迭代解法"""
def levelOrder(self, root: TreeNode) -> List[List[int]]:
results = []
if not root:
return results
from collections import deque
que = deque([root])
while que:
size = len(que)
result = []
for _ in range(size):
cur = que.popleft()
result.append(cur.val)
if cur.left:
que.append(cur.left)
if cur.right:
que.append(cur.right)
results.append(result)
return results
```
```python
# 递归法
class Solution:
def levelOrder(self, root: TreeNode) -> List[List[int]]:
res = []
def helper(root, depth):
if not root: return []
if len(res) == depth: res.append([]) # start the current depth
res[depth].append(root.val) # fulfil the current depth
if root.left: helper(root.left, depth + 1) # process child nodes for the next depth
if root.right: helper(root.right, depth + 1)
helper(root, 0)
return res
```
java:
```Java
@ -206,6 +162,51 @@ class Solution {
}
```
python3代码：
```python
class Solution:
"""二叉树层序遍历迭代解法"""
def levelOrder(self, root: TreeNode) -> List[List[int]]:
results = []
if not root:
return results
from collections import deque
que = deque([root])
while que:
size = len(que)
result = []
for _ in range(size):
cur = que.popleft()
result.append(cur.val)
if cur.left:
que.append(cur.left)
if cur.right:
que.append(cur.right)
results.append(result)
return results
```
```python
# 递归法
class Solution:
def levelOrder(self, root: TreeNode) -> List[List[int]]:
res = []
def helper(root, depth):
if not root: return []
if len(res) == depth: res.append([]) # start the current depth
res[depth].append(root.val) # fulfil the current depth
if root.left: helper(root.left, depth + 1) # process child nodes for the next depth
if root.right: helper(root.right, depth + 1)
helper(root, 0)
return res
```
go:
```go
@ -243,28 +244,31 @@ func levelOrder(root *TreeNode) [][]int {
102. 二叉树的层序遍历
*/
func levelOrder(root *TreeNode) [][]int {
res:=[][]int{}
if root==nil{//防止为空
res := [][]int{}
if root == nil{//防止为空
return res
}
queue:=list.New()
queue := list.New()
queue.PushBack(root)
var tmpArr []int
for queue.Len()>0 {
length:=queue.Len()//保存当前层的长度，然后处理当前层（十分重要，防止添加下层元素影响判断层中元素的个数）
for i:=0;i<length;i++{
node:=queue.Remove(queue.Front()).(*TreeNode)//出队列
if node.Left!=nil{
for queue.Len() > 0 {
length := queue.Len() //保存当前层的长度，然后处理当前层（十分重要，防止添加下层元素影响判断层中元素的个数）
for i := 0; i < length; i++ {
node := queue.Remove(queue.Front()).(*TreeNode) //出队列
if node.Left != nil {
queue.PushBack(node.Left)
}
if node.Right!=nil{
if node.Right != nil {
queue.PushBack(node.Right)
}
tmpArr=append(tmpArr,node.Val)//将值加入本层切片中
tmpArr = append(tmpArr, node.Val) //将值加入本层切片中
}
res=append(res,tmpArr)//放入结果集
tmpArr=[]int{}//清空层的数据
res = append(res, tmpArr) //放入结果集
tmpArr = []int{} //清空层的数据
}
return res
}
```
@ -274,22 +278,22 @@ javascript代码：
```javascript
var levelOrder = function(root) {
//二叉树的层序遍历
let res=[],queue=[];
let res = [], queue = [];
queue.push(root);
if(root===null){
if(root === null) {
return res;
}
while(queue.length!==0){
while(queue.length !== 0) {
// 记录当前层级节点数
let length=queue.length;
let length = queue.length;
//存放每一层的节点
let curLevel=[];
for(let i=0;i<length;i++){
let node=queue.shift();
let curLevel = [];
for(let i = 0;i < length; i++) {
let node = queue.shift();
curLevel.push(node.val);
// 存放当前层下一层的节点
node.left&&queue.push(node.left);
node.right&&queue.push(node.right);
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
//把每一层的结果放到结果数组
res.push(curLevel);
@ -535,31 +539,34 @@ go:
107. 二叉树的层序遍历 II
*/
func levelOrderBottom(root *TreeNode) [][]int {
queue:=list.New()
res:=[][]int{}
if root==nil{
queue := list.New()
res := [][]int{}
if root == nil{
return res
}
queue.PushBack(root)
for queue.Len()>0{
length:=queue.Len()
tmp:=[]int{}
for i:=0;i<length;i++{
node:=queue.Remove(queue.Front()).(*TreeNode)
if node.Left!=nil{
for queue.Len() > 0 {
length := queue.Len()
tmp := []int{}
for i := 0; i < length; i++ {
node := queue.Remove(queue.Front()).(*TreeNode)
if node.Left != nil {
queue.PushBack(node.Left)
}
if node.Right!=nil{
if node.Right != nil {
queue.PushBack(node.Right)
}
tmp=append(tmp,node.Val)
tmp = append(tmp, node.Val)
}
res=append(res,tmp)
res=append(res, tmp)
}
//反转结果集
for i:=0;i<len(res)/2;i++{
res[i],res[len(res)-i-1]=res[len(res)-i-1],res[i]
for i:=0; i<len(res)/2; i++ {
res[i], res[len(res)-i-1] = res[len(res)-i-1], res[i]
}
return res
}
```
@ -568,20 +575,20 @@ javascript代码
```javascript
var levelOrderBottom = function(root) {
let res=[],queue=[];
let res = [], queue = [];
queue.push(root);
while(queue.length&&root!==null){
while(queue.length && root!==null) {
// 存放当前层级节点数组
let curLevel=[];
let curLevel = [];
// 计算当前层级节点数量
let length=queue.length;
while(length--){
let node=queue.shift();
let length = queue.length;
while(length--) {
let node = queue.shift();
// 把当前层节点存入curLevel数组
curLevel.push(node.val);
// 把下一层级的左右节点存入queue队列
node.left&&queue.push(node.left);
node.right&&queue.push(node.right);
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
// 从数组前头插入值，避免最后反转数组，减少运算时间
res.unshift(curLevel);
@ -852,21 +859,23 @@ javascript代码:
```javascript
var rightSideView = function(root) {
//二叉树右视图 只需要把每一层最后一个节点存储到res数组
let res=[],queue=[];
let res = [], queue = [];
queue.push(root);
while(queue.length&&root!==null){
while(queue.length && root!==null) {
// 记录当前层级节点个数
let length=queue.length;
while(length--){
let node=queue.shift();
//length长度为0的时候表明到了层级最后一个节点
if(!length){
let length = queue.length;
while(length--) {
let node = queue.shift();
// length长度为0的时候表明到了层级最后一个节点
if(!length) {
res.push(node.val);
}
node.left&&queue.push(node.left);
node.right&&queue.push(node.right);
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
}
return res;
};
```
@ -1129,22 +1138,24 @@ javascript代码：
```javascript
var averageOfLevels = function(root) {
//层级平均值
let res=[],queue=[];
let res = [], queue = [];
queue.push(root);
while(queue.length&&root!==null){
while(queue.length && root!==null) {
//每一层节点个数
let length=queue.length;
let length = queue.length;
//sum记录每一层的和
let sum=0;
for(let i=0;i<length;i++){
let node=queue.shift();
sum+=node.val;
node.left&&queue.push(node.left);
node.right&&queue.push(node.right);
let sum = 0;
for(let i=0; i < length; i++) {
let node = queue.shift();
sum += node.val;
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
//每一层的平均值存入数组res
res.push(sum/length);
}
return res;
};
```
@ -1405,24 +1416,25 @@ go:
*/
func levelOrder(root *Node) [][]int {
queue:=list.New()
res:=[][]int{}//结果集
if root==nil{
queue := list.New()
res := [][]int{} //结果集
if root == nil{
return res
}
queue.PushBack(root)
for queue.Len()>0{
length:=queue.Len()//记录当前层的数量
for queue.Len() > 0 {
length := queue.Len() //记录当前层的数量
var tmp []int
for T:=0;T<length;T++{//该层的每个元素：一添加到该层的结果集中；二找到该元素的下层元素加入到队列中，方便下次使用
myNode:=queue.Remove(queue.Front()).(*Node)
tmp=append(tmp,myNode.Val)
for i:=0;i<len(myNode.Children);i++{
for T := 0; T < length; T++ { //该层的每个元素：一添加到该层的结果集中；二找到该元素的下层元素加入到队列中，方便下次使用
myNode := queue.Remove(queue.Front()).(*Node)
tmp = append(tmp, myNode.Val)
for i := 0; i < len(myNode.Children); i++ {
queue.PushBack(myNode.Children[i])
}
}
res=append(res,tmp)
res = append(res, tmp)
}
return res
}
```
@ -1432,23 +1444,26 @@ JavaScript代码：
```JavaScript
var levelOrder = function(root) {
//每一层可能有2个以上,所以不再使用node.left node.right
let res=[],queue=[];
let res = [], queue = [];
queue.push(root);
while(queue.length&&root!==null){
while(queue.length && root!==null) {
//记录每一层节点个数还是和二叉树一致
let length=queue.length;
let length = queue.length;
//存放每层节点 也和二叉树一致
let curLevel=[];
while(length--){
let curLevel = [];
while(length--) {
let node = queue.shift();
curLevel.push(node.val);
//这里不再是 ndoe.left node.right 而是循坏node.children
for(let item of node.children){
item&&queue.push(item);
item && queue.push(item);
}
}
res.push(curLevel);
}
return res;
};
```
@ -1708,21 +1723,23 @@ javascript代码：
```javascript
var largestValues = function(root) {
//使用层序遍历
let res=[],queue=[];
let res = [], queue = [];
queue.push(root);
while(root!==null&&queue.length){
while(root !== null && queue.length) {
//设置max初始值就是队列的第一个元素
let max=queue[0].val;
let length=queue.length;
while(length--){
let max = queue[0].val;
let length = queue.length;
while(length--) {
let node = queue.shift();
max=max>node.val?max:node.val;
node.left&&queue.push(node.left);
node.right&&queue.push(node.right);
max = max > node.val ? max : node.val;
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
//把每一层的最大值放到res数组
res.push(max);
}
return res;
};
```
@ -1964,66 +1981,6 @@ class Solution:
first = first.left # 从本层扩展到下一层
return root
```
JavaScript:
```javascript
/**
* // Definition for a Node.
* function Node(val, left, right, next) {
* this.val = val === undefined ? null : val;
* this.left = left === undefined ? null : left;
* this.right = right === undefined ? null : right;
* this.next = next === undefined ? null : next;
* };
*/
/**
* @param {Node} root
* @return {Node}
*/
var connect = function(root) {
if (root === null) return root;
let queue = [root];
while (queue.length) {
let n = queue.length;
for (let i=0; i<n; i++) {
let node = queue.shift();
if (i < n-1) {
node.next = queue[0];
}
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
}
return root;
};
```
TypeScript:
```typescript
function connect(root: Node | null): Node | null {
let helperQueue: Node[] = [];
let preNode: Node, curNode: Node;
if (root !== null) helperQueue.push(root);
while (helperQueue.length > 0) {
for (let i = 0, length = helperQueue.length; i < length; i++) {
if (i === 0) {
preNode = helperQueue.shift()!;
} else {
curNode = helperQueue.shift()!;
preNode.next = curNode;
preNode = curNode;
}
if (preNode.left) helperQueue.push(preNode.left);
if (preNode.right) helperQueue.push(preNode.right);
}
preNode.next = null;
}
return root;
};
```
go:
```GO
@ -2064,6 +2021,66 @@ func connect(root *Node) *Node {
```
JavaScript:
```javascript
/**
* // Definition for a Node.
* function Node(val, left, right, next) {
* this.val = val === undefined ? null : val;
* this.left = left === undefined ? null : left;
* this.right = right === undefined ? null : right;
* this.next = next === undefined ? null : next;
* };
*/
/**
* @param {Node} root
* @return {Node}
*/
var connect = function(root) {
if (root === null) return root;
let queue = [root];
while (queue.length) {
let n = queue.length;
for (let i = 0; i < n; i++) {
let node = queue.shift();
if (i < n-1) {
node.next = queue[0];
}
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
}
return root;
};
```
TypeScript:
```typescript
function connect(root: Node | null): Node | null {
let helperQueue: Node[] = [];
let preNode: Node, curNode: Node;
if (root !== null) helperQueue.push(root);
while (helperQueue.length > 0) {
for (let i = 0, length = helperQueue.length; i < length; i++) {
if (i === 0) {
preNode = helperQueue.shift()!;
} else {
curNode = helperQueue.shift()!;
preNode.next = curNode;
preNode = curNode;
}
if (preNode.left) helperQueue.push(preNode.left);
if (preNode.right) helperQueue.push(preNode.right);
}
preNode.next = null;
}
return root;
};
```
Swift：
```swift
@ -2226,6 +2243,45 @@ class Solution:
return root
```
go:
```GO
/**
116. 填充每个节点的下一个右侧节点指针
117. 填充每个节点的下一个右侧节点指针 II
*/
func connect(root *Node) *Node {
if root == nil { //防止为空
return root
}
queue := list.New()
queue.PushBack(root)
tmpArr := make([]*Node, 0)
for queue.Len() > 0 {
length := queue.Len() //保存当前层的长度，然后处理当前层（十分重要，防止添加下层元素影响判断层中元素的个数）
for i := 0; i < length; i++ {
node := queue.Remove(queue.Front()).(*Node) //出队列
if node.Left != nil {
queue.PushBack(node.Left)
}
if node.Right != nil {
queue.PushBack(node.Right)
}
tmpArr = append(tmpArr, node) //将值加入本层切片中
}
if len(tmpArr) > 1 {
// 遍历每层元素,指定next
for i := 0; i < len(tmpArr)-1; i++ {
tmpArr[i].Next = tmpArr[i+1]
}
}
tmpArr = []*Node{} //清空层的数据
}
return root
}
```
JavaScript:
```javascript
/**
@ -2284,44 +2340,6 @@ function connect(root: Node | null): Node | null {
};
```
go:
```GO
/**
116. 填充每个节点的下一个右侧节点指针
117. 填充每个节点的下一个右侧节点指针 II
*/
func connect(root *Node) *Node {
if root == nil { //防止为空
return root
}
queue := list.New()
queue.PushBack(root)
tmpArr := make([]*Node, 0)
for queue.Len() > 0 {
length := queue.Len() //保存当前层的长度，然后处理当前层（十分重要，防止添加下层元素影响判断层中元素的个数）
for i := 0; i < length; i++ {
node := queue.Remove(queue.Front()).(*Node) //出队列
if node.Left != nil {
queue.PushBack(node.Left)
}
if node.Right != nil {
queue.PushBack(node.Right)
}
tmpArr = append(tmpArr, node) //将值加入本层切片中
}
if len(tmpArr) > 1 {
// 遍历每层元素,指定next
for i := 0; i < len(tmpArr)-1; i++ {
tmpArr[i].Next = tmpArr[i+1]
}
}
tmpArr = []*Node{} //清空层的数据
}
return root
}
```
Swift：
```swift
@ -2461,7 +2479,6 @@ class Solution {
}
```
Python：
```python 3
class Solution:
@ -2498,20 +2515,20 @@ Go：
* }
*/
func maxDepth(root *TreeNode) int {
ans:=0
if root==nil{
ans := 0
if root == nil {
return 0
}
queue:=list.New()
queue := list.New()
queue.PushBack(root)
for queue.Len()>0{
length:=queue.Len()
for i:=0;i<length;i++{
node:=queue.Remove(queue.Front()).(*TreeNode)
if node.Left!=nil{
for queue.Len() > 0 {
length := queue.Len()
for i := 0; i < length; i++ {
node := queue.Remove(queue.Front()).(*TreeNode)
if node.Left != nil {
queue.PushBack(node.Left)
}
if node.Right!=nil{
if node.Right != nil {
queue.PushBack(node.Right)
}
}
@ -2521,8 +2538,6 @@ func maxDepth(root *TreeNode) int {
}
```
JavaScript：
```javascript
/**
@ -2763,30 +2778,29 @@ Go：
* }
*/
func minDepth(root *TreeNode) int {
ans:=0
if root==nil{
ans := 0
if root == nil {
return 0
}
queue:=list.New()
queue := list.New()
queue.PushBack(root)
for queue.Len()>0{
length:=queue.Len()
for i:=0;i<length;i++{
node:=queue.Remove(queue.Front()).(*TreeNode)
if node.Left==nil&&node.Right==nil{//当前节点没有左右节点，则代表此层是最小层
return ans+1//返回当前层 ans代表是上一层
for queue.Len() > 0 {
length := queue.Len()
for i := 0; i < length; i++ {
node := queue.Remove(queue.Front()).(*TreeNode)
if node.Left == nil && node.Right == nil { //当前节点没有左右节点，则代表此层是最小层
return ans+1 //返回当前层 ans代表是上一层
}
if node.Left!=nil{
if node.Left != nil {
queue.PushBack(node.Left)
}
if node.Right!=nil{
if node.Right != nil {
queue.PushBack(node.Right)
}
}
ans++//记录层数
}
return ans+1
}
```

12
problems/0104.二叉树的最大深度.md
View File

@ -59,7 +59,7 @@ int getdepth(treenode* node)
if (node == NULL) return 0;
```
3. 确定单层递归的逻辑：先求它的左子树的深度，再求的右子树的深度，最后取左右深度最大的数值 再+1 （加1是因为算上当前中间节点）就是目前节点为根节点的树的深度。
3. 确定单层递归的逻辑：先求它的左子树的深度，再求右子树的深度，最后取左右深度最大的数值 再+1 （加1是因为算上当前中间节点）就是目前节点为根节点的树的深度。
代码如下：
@ -591,15 +591,15 @@ var maxdepth = function(root) {
var maxdepth = function(root) {
//使用递归的方法 递归三部曲
//1. 确定递归函数的参数和返回值
const getdepth=function(node){
const getdepth = function(node) {
//2. 确定终止条件
if(node===null){
if(node === null) {
return 0;
}
//3. 确定单层逻辑
let leftdepth=getdepth(node.left);
let rightdepth=getdepth(node.right);
let depth=1+Math.max(leftdepth,rightdepth);
let leftdepth = getdepth(node.left);
let rightdepth = getdepth(node.right);
let depth = 1 + Math.max(leftdepth, rightdepth);
return depth;
}
return getdepth(root);

121
problems/0106.从中序与后序遍历序列构造二叉树.md
View File

@ -34,7 +34,7 @@
## 思路
首先回忆一下如何根据两个顺序构造一个唯一的二叉树，相信理论知识大家应该都清楚，就是以 后序数组的最后一个元素为切割点，先切中序数组，根据中序数组，反过来在切后序数组。一层一层切下去，每次后序数组最后一个元素就是节点元素。
首先回忆一下如何根据两个顺序构造一个唯一的二叉树，相信理论知识大家应该都清楚，就是以 后序数组的最后一个元素为切割点，先切中序数组，根据中序数组，反过来再切后序数组。一层一层切下去，每次后序数组最后一个元素就是节点元素。
如果让我们肉眼看两个序列，画一棵二叉树的话，应该分分钟都可以画出来。
@ -236,7 +236,7 @@ private:
vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());
// 一下为日志
// 以下为日志
cout << "----------" << endl;
cout << "leftInorder :";
@ -275,7 +275,7 @@ public:
};
```
**此时应该发现了，如上的代码性能并不好，应为每层递归定定义了新的vector（就是数组），既耗时又耗空间，但上面的代码是最好理解的，为了方便读者理解，所以用如上的代码来讲解。**
**此时应该发现了，如上的代码性能并不好，因为每层递归定义了新的vector（就是数组），既耗时又耗空间，但上面的代码是最好理解的，为了方便读者理解，所以用如上的代码来讲解。**
下面给出用下标索引写出的代码版本：（思路是一样的，只不过不用重复定义vector了，每次用下标索引来分割）
@ -569,7 +569,7 @@ tree2 的前序遍历是[1 2 3]， 后序遍历是[3 2 1]。
之前我们讲的二叉树题目都是各种遍历二叉树，这次开始构造二叉树了，思路其实比较简单，但是真正代码实现出来并不容易。
所以要避免眼高手低，踏实的把代码写出来。
所以要避免眼高手低，踏实地把代码写出来。
我同时给出了添加日志的代码版本，因为这种题目是不太容易写出来调一调就能过的，所以一定要把流程日志打出来，看看符不符合自己的思路。
@ -728,25 +728,33 @@ class Solution:
* Right *TreeNode
* }
*/
var (
hash map[int]int
)
func buildTree(inorder []int, postorder []int) *TreeNode {
if len(inorder)<1||len(postorder)<1{return nil}
//先找到根节点（后续遍历的最后一个就是根节点）
nodeValue:=postorder[len(postorder)-1]
//从中序遍历中找到一分为二的点，左边为左子树，右边为右子树
left:=findRootIndex(inorder,nodeValue)
//构造root
root:=&TreeNode{Val: nodeValue,
Left: buildTree(inorder[:left],postorder[:left]),//将后续遍历一分为二，左边为左子树，右边为右子树
Right: buildTree(inorder[left+1:],postorder[left:len(postorder)-1])}
hash = make(map[int]int)
for i, v := range inorder { // 用map保存中序序列的数值对应位置
hash[v] = i
}
// 以左闭右闭的原则进行切分
root := rebuild(inorder, postorder, len(postorder)-1, 0, len(inorder)-1)
return root
}
func findRootIndex(inorder []int,target int) (index int){
for i:=0;i<len(inorder);i++{
if target==inorder[i]{
return i
}
// rootIdx表示根节点在后序数组中的索引，l, r 表示在中序数组中的前后切分点
func rebuild(inorder []int, postorder []int, rootIdx int, l, r int) *TreeNode {
if l > r { // 说明没有元素，返回空树
return nil
}
return -1
if l == r { // 只剩唯一一个元素，直接返回
return &TreeNode{Val : inorder[l]}
}
rootV := postorder[rootIdx] // 根据后序数组找到根节点的值
rootIn := hash[rootV] // 找到根节点在对应的中序数组中的位置
root := &TreeNode{Val : rootV} // 构造根节点
// 重建左节点和右节点
root.Left = rebuild(inorder, postorder, rootIdx-(r-rootIn)-1, l, rootIn-1)
root.Right = rebuild(inorder, postorder, rootIdx-1, rootIn+1, r)
return root
}
```
@ -761,22 +769,27 @@ func findRootIndex(inorder []int,target int) (index int){
* Right *TreeNode
* }
*/
var (
hash map[int]int
)
func buildTree(preorder []int, inorder []int) *TreeNode {
if len(preorder)<1||len(inorder)<1{return nil}
left:=findRootIndex(preorder[0],inorder)
root:=&TreeNode{
Val: preorder[0],
Left: buildTree(preorder[1:left+1],inorder[:left]),
Right: buildTree(preorder[left+1:],inorder[left+1:])}
hash = make(map[int]int, len(inorder))
for i, v := range inorder {
hash[v] = i
}
root := build(preorder, inorder, 0, 0, len(inorder)-1) // l, r 表示构造的树在中序遍历数组中的范围
return root
}
func findRootIndex(target int,inorder []int) int{
for i:=0;i<len(inorder);i++{
if target==inorder[i]{
return i
}
func build(pre []int, in []int, root int, l, r int) *TreeNode {
if l > r {
return nil
}
return -1
rootVal := pre[root] // 找到本次构造的树的根节点
index := hash[rootVal] // 根节点在中序数组中的位置
node := &TreeNode {Val: rootVal}
node.Left = build(pre, in, root + 1, l, index-1)
node.Right = build(pre, in, root + (index-l) + 1, index+1, r)
return node
}
```
@ -1136,6 +1149,52 @@ object Solution {
}
```
## rust
106 从中序与后序遍历序列构造二叉树
```rust
use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
pub fn build_tree(inorder: Vec<i32>, postorder: Vec<i32>) -> Option<Rc<RefCell<TreeNode>>> {
if inorder.is_empty() {
return None;
}
let mut postorder = postorder;
let root = postorder.pop().unwrap();
let index = inorder.iter().position(|&x| x == root).unwrap();
let mut root = TreeNode::new(root);
root.left = Self::build_tree(inorder[..index].to_vec(), postorder[..index].to_vec());
root.right = Self::build_tree(inorder[index + 1..].to_vec(), postorder[index..].to_vec());
Some(Rc::new(RefCell::new(root)))
}
}
```
105 从前序与中序遍历序列构造二叉树
```rust
use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
pub fn build_tree(preorder: Vec<i32>, inorder: Vec<i32>) -> Option<Rc<RefCell<TreeNode>>> {
if preorder.is_empty() {
return None;
}
let root = preorder[0];
let index = inorder.iter().position(|&x| x == root).unwrap();
let mut root = TreeNode::new(root);
root.left = Self::build_tree(preorder[1..index + 1].to_vec(), inorder[0..index].to_vec());
root.right = Self::build_tree(
preorder[index + 1..].to_vec(),
inorder[index + 1..].to_vec(),
);
Some(Rc::new(RefCell::new(root)))
}
}
```
<p align="center">
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>

51
problems/0108.将有序数组转换为二叉搜索树.md
View File

@ -19,6 +19,10 @@
![108.将有序数组转换为二叉搜索树](https://img-blog.csdnimg.cn/20201022164420763.png)
# 算法公开课
**《代码随想录》算法视频公开课：[构造平衡二叉搜索树！| LeetCode：108.将有序数组转换为二叉搜索树](https://www.bilibili.com/video/BV1uR4y1X7qL?share_source=copy_web)，相信结合视频在看本篇题解，更有助于大家对本题的理解**。
# 思路
做这道题目之前大家可以了解一下这几道：
@ -35,7 +39,7 @@
因为只要给我们一个有序数组，如果强调平衡，都可以以线性结构来构造二叉搜索树。
例如 有序数组[-10，-3，0，5，9] 可以就可以构造成这样的二叉搜索树，如图。
例如 有序数组[-10，-3，0，5，9] 就可以构造成这样的二叉搜索树，如图。
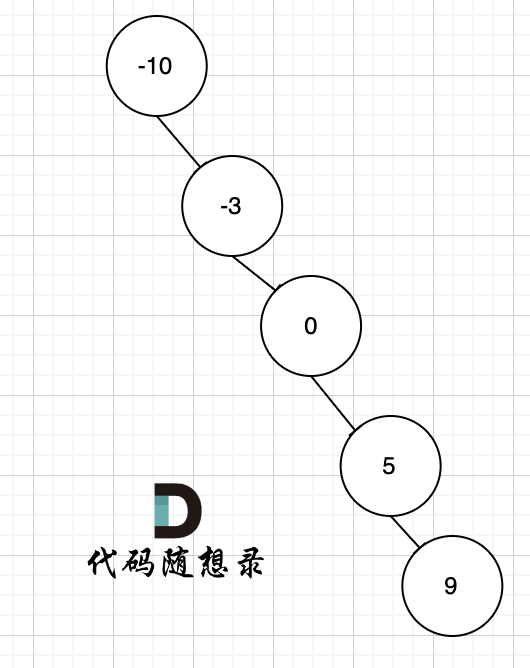
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20220930173553.png)
@ -147,7 +151,7 @@ public:
};
```
**注意：在调用traversal的时候为什么传入的left和right为什么是0和nums.size() - 1，因为定义的区间为左闭右闭**。
**注意：在调用traversal的时候传入的left和right为什么是0和nums.size() - 1，因为定义的区间为左闭右闭**。
## 迭代法
@ -354,10 +358,15 @@ class Solution:
```go
func sortedArrayToBST(nums []int) *TreeNode {
if len(nums)==0{return nil}//终止条件，最后数组为空则可以返回
root:=&TreeNode{nums[len(nums)/2],nil,nil}//按照BSL的特点，从中间构造节点
root.Left=sortedArrayToBST(nums[:len(nums)/2])//数组的左边为左子树
root.Right=sortedArrayToBST(nums[len(nums)/2+1:])//数字的右边为右子树
if len(nums) == 0 { //终止条件，最后数组为空则可以返回
return nil
}
idx := len(nums)/2
root := &TreeNode{Val: nums[idx]}
root.Left = sortedArrayToBST(nums[:idx])
root.Right = sortedArrayToBST(nums[idx+1:])
return root
}
```
@ -384,33 +393,33 @@ var sortedArrayToBST = function (nums) {
迭代
```JavaScript
var sortedArrayToBST = function(nums) {
if(nums.length===0){
if(nums.length===0) {
return null;
}
let root=new TreeNode(0); //初始根节点
let nodeQue=[root]; //放遍历的节点,并初始化
let leftQue=[0]; //放左区间的下标,初始化
let rightQue=[nums.length-1]; // 放右区间的下标
let root = new TreeNode(0); //初始根节点
let nodeQue = [root]; //放遍历的节点,并初始化
let leftQue = [0]; //放左区间的下标,初始化
let rightQue = [nums.length-1]; // 放右区间的下标
while(nodeQue.length){
let curNode=nodeQue.pop();
let left=leftQue.pop();
let right=rightQue.pop();
let mid=left+Math.floor((right-left)/2);
while(nodeQue.length) {
let curNode = nodeQue.pop();
let left = leftQue.pop();
let right = rightQue.pop();
let mid = left + Math.floor((right-left)/2);
curNode.val=nums[mid]; //将下标为mid的元素给中间节点
curNode.val = nums[mid]; //将下标为mid的元素给中间节点
// 处理左区间
if(left<=mid-1){
curNode.left=new TreeNode(0);
if(left <= mid-1) {
curNode.left = new TreeNode(0);
nodeQue.push(curNode.left);
leftQue.push(left);
rightQue.push(mid-1);
}
// 处理右区间
if(right>=mid+1){
curNode.right=new TreeNode(0);
if(right >= mid+1) {
curNode.right = new TreeNode(0);
nodeQue.push(curNode.right);
leftQue.push(mid+1);
rightQue.push(right);

71
problems/0110.平衡二叉树.md
View File

@ -158,7 +158,7 @@ if (node == NULL) {
如何判断以当前传入节点为根节点的二叉树是否是平衡二叉树呢？当然是其左子树高度和其右子树高度的差值。
分别求出其左右子树的高度，然后如果差值小于等于1，则返回当前二叉树的高度，否则则返回-1，表示已经不是二叉平衡树了。
分别求出其左右子树的高度，然后如果差值小于等于1，则返回当前二叉树的高度，否则返回-1，表示已经不是二叉平衡树了。
代码如下：
@ -342,7 +342,7 @@ public:
**例如：都知道回溯法其实就是递归，但是很少人用迭代的方式去实现回溯算法！**
因为对于回溯算法已经是非常复杂的递归了，如果在用迭代的话，就是自己给自己找麻烦，效率也并不一定高。
因为对于回溯算法已经是非常复杂的递归了，如果再用迭代的话，就是自己给自己找麻烦，效率也并不一定高。
## 总结
@ -559,37 +559,32 @@ class Solution:
### Go
```Go
func isBalanced(root *TreeNode) bool {
if root==nil{
return true
}
if !isBalanced(root.Left) || !isBalanced(root.Right){
return false
}
LeftH:=maxdepth(root.Left)+1
RightH:=maxdepth(root.Right)+1
if abs(LeftH-RightH)>1{
h := getHeight(root)
if h == -1 {
return false
}
return true
}
func maxdepth(root *TreeNode)int{
if root==nil{
// 返回以该节点为根节点的二叉树的高度，如果不是平衡二叉树了则返回-1
func getHeight(root *TreeNode) int {
if root == nil {
return 0
}
return max(maxdepth(root.Left),maxdepth(root.Right))+1
l, r := getHeight(root.Left), getHeight(root.Right)
if l == -1 || r == -1 {
return -1
}
if l - r > 1 || r - l > 1 {
return -1
}
return max(l, r) + 1
}
func max(a,b int)int{
if a>b{
func max(a, b int) int {
if a > b {
return a
}
return b
}
func abs(a int)int{
if a<0{
return -a
}
return a
}
```
### JavaScript
@ -810,6 +805,38 @@ func getHeight(_ root: TreeNode?) -> Int {
}
```
### rust
递归
```rust
use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
pub fn is_balanced(root: Option<Rc<RefCell<TreeNode>>>) -> bool {
Self::get_depth(root) != -1
}
pub fn get_depth(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
if root.is_none() {
return 0;
}
let right = Self::get_depth(root.as_ref().unwrap().borrow().left.clone());
let left = Self::get_depth(root.unwrap().borrow().right.clone());
if right == -1 {
return -1;
}
if left == -1 {
return -1;
}
if (right - left).abs() > 1 {
return -1;
}
1 + right.max(left)
}
}
```
<p align="center">
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>

80
problems/0111.二叉树的最小深度.md
View File

@ -39,7 +39,7 @@
* 二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数或者节点数（取决于深度从0开始还是从1开始）
* 二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数后者节点数（取决于高度从0开始还是从1开始）
那么使用后序遍历，其实求的是根节点到叶子节点的最小距离，就是求高度的过程，这不过这个最小距离 也同样是最小深度。
那么使用后序遍历，其实求的是根节点到叶子节点的最小距离，就是求高度的过程，不过这个最小距离 也同样是最小深度。
以下讲解中遍历顺序上依然采用后序遍历（因为要比较递归返回之后的结果，本文我也给出前序遍历的写法）。
@ -199,7 +199,7 @@ public:
如果对层序遍历还不清楚的话，可以看这篇：[二叉树：层序遍历登场！](https://programmercarl.com/0102.二叉树的层序遍历.html)
**需要注意的是，只有当左右孩子都为空的时候，才说明遍历的最低点了。如果其中一个孩子为空则不是最低点**
**需要注意的是，只有当左右孩子都为空的时候，才说明遍历到最低点了。如果其中一个孩子不为空则不是最低点**
代码如下：（详细注释）
@ -574,66 +574,48 @@ object Solution {
rust:
```rust
impl Solution {
pub fn min_depth(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
return Solution::bfs(root)
}
// 递归
pub fn dfs(node: Option<Rc<RefCell<TreeNode>>>) -> i32{
if node.is_none(){
return 0;
}
let parent = node.unwrap();
let left_child = parent.borrow_mut().left.take();
let right_child = parent.borrow_mut().right.take();
if left_child.is_none() && right_child.is_none(){
return 1;
}
let mut min_depth = i32::MAX;
if left_child.is_some(){
let left_depth = Solution::dfs(left_child);
if left_depth <= min_depth{
min_depth = left_depth
pub fn min_depth(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
if let Some(node) = root {
match (node.borrow().left.clone(), node.borrow().right.clone()) {
(Some(n1), None) => 1 + Self::min_depth(Some(n1)),
(None, Some(n2)) => 1 + Self::min_depth(Some(n2)),
(Some(n1), Some(n2)) => {
1 + std::cmp::min(Self::min_depth(Some(n1)), Self::min_depth(Some(n2)))
}
_ => 1,
}
} else {
0
}
if right_child.is_some(){
let right_depth = Solution::dfs(right_child);
if right_depth <= min_depth{
min_depth = right_depth
}
}
min_depth + 1
}
// 迭代
pub fn bfs(node: Option<Rc<RefCell<TreeNode>>>) -> i32{
let mut min_depth = 0;
if node.is_none(){
return min_depth
// 需要 use std::collections::VecDeque;
pub fn min_depth(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
let mut res = 0;
let mut queue = VecDeque::new();
if root.is_some() {
queue.push_back(root);
}
let mut stack = vec![node.unwrap()];
while !stack.is_empty(){
min_depth += 1;
let num = stack.len();
for _i in 0..num{
let top = stack.remove(0);
let left_child = top.borrow_mut().left.take();
let right_child = top.borrow_mut().right.take();
if left_child.is_none() && right_child.is_none(){
return min_depth;
while !queue.is_empty() {
res += 1;
for _ in 0..queue.len() {
let node = queue.pop_front().unwrap().unwrap();
if node.borrow().left.is_none() && node.borrow().right.is_none() {
return res;
}
if left_child.is_some(){
stack.push(left_child.unwrap());
if node.borrow().left.is_some() {
queue.push_back(node.borrow().left.clone());
}
if right_child.is_some(){
stack.push(right_child.unwrap());
if node.borrow().right.is_some() {
queue.push_back(node.borrow().right.clone());
}
}
}
min_depth
res
}
}
```
<p align="center">

159
problems/0112.路径总和.md
View File

@ -33,7 +33,7 @@
* 112.路径总和
* 113.路径总和ii
这道题我们要遍历从根节点到叶子节点的的路径看看总和是不是目标和。
这道题我们要遍历从根节点到叶子节点的路径看看总和是不是目标和。
### 递归
@ -167,7 +167,7 @@ public:
};
```
**是不是发现精简之后的代码，已经完全看不出分析的过程了，所以我们要把题目分析清楚之后，在追求代码精简。** 这一点我已经强调很多次了！
**是不是发现精简之后的代码，已经完全看不出分析的过程了，所以我们要把题目分析清楚之后，再追求代码精简。** 这一点我已经强调很多次了！
### 迭代
@ -316,13 +316,13 @@ class solution {
}
if (root.left != null) {
boolean left = haspathsum(root.left, targetsum);
if (left) {// 已经找到
if (left) { // 已经找到
return true;
}
}
if (root.right != null) {
boolean right = haspathsum(root.right, targetsum);
if (right) {// 已经找到
if (right) { // 已经找到
return true;
}
}
@ -348,31 +348,37 @@ class solution {
```java
class solution {
public boolean haspathsum(treenode root, int targetsum) {
if(root==null)return false;
if(root == null) return false;
stack<treenode> stack1 = new stack<>();
stack<integer> stack2 = new stack<>();
stack1.push(root);stack2.push(root.val);
while(!stack1.isempty()){
stack1.push(root);
stack2.push(root.val);
while(!stack1.isempty()) {
int size = stack1.size();
for(int i=0;i<size;i++){
treenode node = stack1.pop();int sum=stack2.pop();
for(int i = 0; i < size; i++) {
treenode node = stack1.pop();
int sum = stack2.pop();
// 如果该节点是叶子节点了，同时该节点的路径数值等于sum，那么就返回true
if(node.left==null && node.right==null && sum==targetsum)return true;
if(node.left == null && node.right == null && sum == targetsum) {
return true;
}
// 右节点，压进去一个节点的时候，将该节点的路径数值也记录下来
if(node.right!=null){
stack1.push(node.right);stack2.push(sum+node.right.val);
if(node.right != null){
stack1.push(node.right);
stack2.push(sum + node.right.val);
}
// 左节点，压进去一个节点的时候，将该节点的路径数值也记录下来
if(node.left!=null){
stack1.push(node.left);stack2.push(sum+node.left.val);
if(node.left != null) {
stack1.push(node.left);
stack2.push(sum + node.left.val);
}
}
}
return false;
}
}
```
### 0113.路径总和-ii
@ -715,21 +721,21 @@ var pathsum = function(root, targetsum) {
//递归方法
let respath = [],curpath = [];
// 1. 确定递归函数参数
const traveltree = function(node,count){
const traveltree = function(node,count) {
curpath.push(node.val);
count-=node.val;
if(node.left===null&&node.right===null&&count===0){
count -= node.val;
if(node.left === null && node.right === null && count === 0) {
respath.push([...curpath]);
}
node.left&&traveltree(node.left,count);
node.right&&traveltree(node.right,count);
node.left && traveltree(node.left, count);
node.right && traveltree(node.right, count);
let cur = curpath.pop();
count-=cur;
count -= cur;
}
if(root===null){
if(root === null) {
return respath;
}
travelTree(root,targetSum);
travelTree(root, targetSum);
return resPath;
};
```
@ -1213,6 +1219,111 @@ object Solution {
}
```
## rust
### 112.路径总和.md
递归：
```rust
use std::rc::Rc;
use std::cell::RefCell;
impl Solution {
pub fn has_path_sum(root: Option<Rc<RefCell<TreeNode>>>, target_sum: i32) -> bool {
if root.is_none() {
return false;
}
let node = root.unwrap();
if node.borrow().left.is_none() && node.borrow().right.is_none() {
return node.borrow().val == target_sum;
}
return Self::has_path_sum(node.borrow().left.clone(), target_sum - node.borrow().val)
|| Self::has_path_sum(node.borrow().right.clone(), target_sum - node.borrow().val);
}
}
```
迭代：
```rust
use std::rc::Rc;
use std::cell::RefCell;
impl Solution {
pub fn has_path_sum(root: Option<Rc<RefCell<TreeNode>>>, target_sum: i32) -> bool {
let mut stack = vec![];
if let Some(node) = root {
stack.push((node.borrow().val, node.to_owned()));
}
while !stack.is_empty() {
let (value, node) = stack.pop().unwrap();
if node.borrow().left.is_none() && node.borrow().right.is_none() && value == target_sum
{
return true;
}
if node.borrow().left.is_some() {
if let Some(r) = node.borrow().left.as_ref() {
stack.push((r.borrow().val + value, r.to_owned()));
}
}
if node.borrow().right.is_some() {
if let Some(r) = node.borrow().right.as_ref() {
stack.push((r.borrow().val + value, r.to_owned()));
}
}
}
false
}
```
### 113.路径总和-ii
```rust
impl Solution {
pub fn path_sum(root: Option<Rc<RefCell<TreeNode>>>, target_sum: i32) -> Vec<Vec<i32>> {
let mut res = vec![];
let mut route = vec![];
if root.is_none() {
return res;
} else {
route.push(root.as_ref().unwrap().borrow().val);
}
Self::recur(
&root,
target_sum - root.as_ref().unwrap().borrow().val,
&mut res,
&mut route,
);
res
}
pub fn recur(
root: &Option<Rc<RefCell<TreeNode>>>,
sum: i32,
res: &mut Vec<Vec<i32>>,
route: &mut Vec<i32>,
) {
let node = root.as_ref().unwrap().borrow();
if node.left.is_none() && node.right.is_none() && sum == 0 {
res.push(route.to_vec());
return;
}
if node.left.is_some() {
let left = node.left.as_ref().unwrap();
route.push(left.borrow().val);
Self::recur(&node.left, sum - left.borrow().val, res, route);
route.pop();
}
if node.right.is_some() {
let right = node.right.as_ref().unwrap();
route.push(right.borrow().val);
Self::recur(&node.right, sum - right.borrow().val, res, route);
route.pop();
}
}
}
```
<p align="center">
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>

46
problems/0122.买卖股票的最佳时机II.md
View File

@ -46,7 +46,7 @@
### 贪心算法
这道题目可能我们只会想，选一个低的买入，在选个高的卖，在选一个低的买入.....循环反复。
这道题目可能我们只会想，选一个低的买入，再选个高的卖，再选一个低的买入.....循环反复。
**如果想到其实最终利润是可以分解的，那么本题就很容易了！**
@ -198,38 +198,40 @@ class Solution:
### Go:
```golang
//贪心算法
贪心算法
```go
func maxProfit(prices []int) int {
var sum int
for i := 1; i < len(prices); i++ {
// 累加每次大于0的交易
if prices[i]-prices[i-1] > 0 {
sum += prices[i]-prices[i-1]
if prices[i] - prices[i-1] > 0 {
sum += prices[i] - prices[i-1]
}
}
return sum
}
```
```golang
//确定售卖点
动态规划
```go
func maxProfit(prices []int) int {
var result,buy int
prices=append(prices,0)//在price末尾加个0，防止price一直递增
/**
思路：检查后一个元素是否大于当前元素，如果小于，则表明这是一个售卖点，当前元素的值减去购买时候的值
如果不小于，说明后面有更好的售卖点，
**/
for i:=0;i<len(prices)-1;i++{
if prices[i]>prices[i+1]{
result+=prices[i]-prices[buy]
buy=i+1
}else if prices[buy]>prices[i]{//更改最低购买点
buy=i
}
dp := make([][]int, len(prices))
for i := 0; i < len(dp); i++ {
dp[i] = make([]int, 2)
}
return result
// dp[i][0]表示在状态i不持有股票的现金，dp[i][1]为持有股票的现金
dp[0][0], dp[0][1] = 0, -prices[0]
for i := 1; i < len(prices); i++ {
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][0] - prices[i], dp[i-1][1])
}
return dp[len(prices)-1][0]
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
```

64
problems/0131.分割回文串.md
View File

@ -43,8 +43,8 @@
例如对于字符串abcdef：
* 组合问题：选取一个a之后，在bcdef中再去选取第二个，选取b之后在cdef中在选组第三个.....。
* 切割问题：切割一个a之后，在bcdef中再去切割第二段，切割b之后在cdef中在切割第三段.....。
* 组合问题：选取一个a之后，在bcdef中再去选取第二个，选取b之后在cdef中再选取第三个.....。
* 切割问题：切割一个a之后，在bcdef中再去切割第二段，切割b之后在cdef中再切割第三段.....。
感受出来了不？
@ -78,7 +78,7 @@ void backtracking (const string& s, int startIndex) {
![131.分割回文串](https://code-thinking.cdn.bcebos.com/pics/131.%E5%88%86%E5%89%B2%E5%9B%9E%E6%96%87%E4%B8%B2.jpg)
从树形结构的图中可以看出：切割线切到了字符串最后面，说明找到了一种切割方法，此时就是本层递归的终止终止条件。
从树形结构的图中可以看出：切割线切到了字符串最后面，说明找到了一种切割方法，此时就是本层递归的终止条件。
**那么在代码里什么是切割线呢？**
@ -98,7 +98,7 @@ void backtracking (const string& s, int startIndex) {
* 单层搜索的逻辑
**来看看在递归循环，中如何截取子串呢？**
**来看看在递归循环中如何截取子串呢？**
在`for (int i = startIndex; i < s.size(); i++)`循环中，我们 定义了起始位置startIndex，那么 [startIndex, i] 就是要截取的子串。
@ -126,7 +126,7 @@ for (int i = startIndex; i < s.size(); i++) {
最后我们看一下回文子串要如何判断了，判断一个字符串是否是回文。
可以使用双指针法，一个指针从前向后，一个指针从后先前，如果前后指针所指向的元素是相等的，就是回文字符串了。
可以使用双指针法，一个指针从前向后，一个指针从后向前，如果前后指针所指向的元素是相等的，就是回文字符串了。
那么判断回文的C++代码如下：
@ -295,7 +295,7 @@ public:
除了这些难点，**本题还有细节，例如：切割过的地方不能重复切割所以递归函数需要传入i + 1**。
所以本题应该是一个道hard题目了。
所以本题应该是一道hard题目了。
**可能刷过这道题目的录友都没感受到自己原来克服了这么多难点，就把这道题目AC了**，这应该叫做无招胜有招，人码合一，哈哈哈。
@ -432,45 +432,39 @@ class Solution:
```
## Go
**注意切片（go切片是披着值类型外衣的引用类型）**
```go
var (
path []string // 放已经回文的子串
res [][]string
)
func partition(s string) [][]string {
var tmpString []string//切割字符串集合
var res [][]string//结果集合
backTracking(s,tmpString,0,&res)
path, res = make([]string, 0), make([][]string, 0)
dfs(s, 0)
return res
}
func backTracking(s string,tmpString []string,startIndex int,res *[][]string){
if startIndex==len(s){//到达字符串末尾了
//进行一次切片拷贝，怕之后的操作影响tmpString切片内的值
t := make([]string, len(tmpString))
copy(t, tmpString)
*res=append(*res,t)
func dfs(s string, start int) {
if start == len(s) { // 如果起始位置等于s的大小，说明已经找到了一组分割方案了
tmp := make([]string, len(path))
copy(tmp, path)
res = append(res, tmp)
return
}
for i:=startIndex;i<len(s);i++{
//处理（首先通过startIndex和i判断切割的区间，进而判断该区间的字符串是否为回文，若为回文，则加入到tmpString，否则继续后移，找到回文区间）（这里为一层处理）
if isPartition(s,startIndex,i){
tmpString=append(tmpString,s[startIndex:i+1])
}else{
continue
for i := start; i < len(s); i++ {
str := s[start : i+1]
if isPalindrome(str) { // 是回文子串
path = append(path, str)
dfs(s, i+1) // 寻找i+1为起始位置的子串
path = path[:len(path)-1] // 回溯过程，弹出本次已经填在的子串
}
//递归
backTracking(s,tmpString,i+1,res)
//回溯
tmpString=tmpString[:len(tmpString)-1]
}
}
//判断是否为回文
func isPartition(s string,startIndex,end int)bool{
left:=startIndex
right:=end
for ;left<right;{
if s[left]!=s[right]{
func isPalindrome(s string) bool {
for i, j := 0, len(s)-1; i < j; i, j = i+1, j-1 {
if s[i] != s[j] {
return false
}
//移动左右指针
left++
right--
}
return true
}

4
problems/0134.加油站.md
View File

@ -176,13 +176,13 @@ public:
* 时间复杂度：$O(n)$
* 空间复杂度：$O(1)$
**说这种解法为贪心算法，才是是有理有据的，因为全局最优解是根据局部最优推导出来的**。
**说这种解法为贪心算法，才是有理有据的，因为全局最优解是根据局部最优推导出来的**。
## 总结
对于本题首先给出了暴力解法，暴力解法模拟跑一圈的过程其实比较考验代码技巧的，要对while使用的很熟练。
然后给出了两种贪心算法，对于第一种贪心方法，其实我认为就是一种直接从全局选取最优的模拟操作，思路还是好巧妙的，值得学习一下。
然后给出了两种贪心算法，对于第一种贪心方法，其实我认为就是一种直接从全局选取最优的模拟操作，思路还是很巧妙的，值得学习一下。
对于第二种贪心方法，才真正体现出贪心的精髓，用局部最优可以推出全局最优，进而求得起始位置。

76
problems/0135.分发糖果.md
View File

@ -65,7 +65,7 @@ for (int i = 1; i < ratings.size(); i++) {
如果 ratings[i] > ratings[i + 1]，此时candyVec[i]（第i个小孩的糖果数量）就有两个选择了，一个是candyVec[i + 1] + 1（从右边这个加1得到的糖果数量），一个是candyVec[i]（之前比较右孩子大于左孩子得到的糖果数量）。
那么又要贪心了，局部最优：取candyVec[i + 1] + 1 和 candyVec[i] 最大的糖果数量，保证第i个小孩的糖果数量即大于左边的也大于右边的。全局最优：相邻的孩子中，评分高的孩子获得更多的糖果。
那么又要贪心了，局部最优：取candyVec[i + 1] + 1 和 candyVec[i] 最大的糖果数量，保证第i个小孩的糖果数量既大于左边的也大于右边的。全局最优：相邻的孩子中，评分高的孩子获得更多的糖果。
局部最优可以推出全局最优。
@ -172,63 +172,44 @@ class Solution:
```
### Go
```golang
```go
func candy(ratings []int) int {
/**先确定一边，再确定另外一边
1.先从左到右，当右边的大于左边的就加1
2.再从右到左，当左边的大于右边的就再加1
**/
need:=make([]int,len(ratings))
sum:=0
//初始化(每个人至少一个糖果)
for i:=0;i<len(ratings);i++{
need[i]=1
need := make([]int, len(ratings))
sum := 0
// 初始化(每个人至少一个糖果)
for i := 0; i < len(ratings); i++ {
need[i] = 1
}
//1.先从左到右，当右边的大于左边的就加1
for i:=0;i<len(ratings)-1;i++{
if ratings[i]<ratings[i+1]{
need[i+1]=need[i]+1
// 1.先从左到右，当右边的大于左边的就加1
for i := 0; i < len(ratings) - 1; i++ {
if ratings[i] < ratings[i+1] {
need[i+1] = need[i] + 1
}
}
//2.再从右到左，当左边的大于右边的就右边加1，但要花费糖果最少，所以需要做下判断
for i:=len(ratings)-1;i>0;i--{
if ratings[i-1]>ratings[i]{
need[i-1]=findMax(need[i-1],need[i]+1)
// 2.再从右到左，当左边的大于右边的就右边加1，但要花费糖果最少，所以需要做下判断
for i := len(ratings)-1; i > 0; i-- {
if ratings[i-1] > ratings[i] {
need[i-1] = findMax(need[i-1], need[i]+1)
}
}
//计算总共糖果
for i:=0;i<len(ratings);i++{
sum+=need[i]
for i := 0; i < len(ratings); i++ {
sum += need[i]
}
return sum
}
func findMax(num1 int ,num2 int) int{
if num1>num2{
func findMax(num1 int, num2 int) int {
if num1 > num2 {
return num1
}
return num2
}
```
### Rust
```rust
pub fn candy(ratings: Vec<i32>) -> i32 {
let mut candies = vec![1i32; ratings.len()];
for i in 1..ratings.len() {
if ratings[i - 1] < ratings[i] {
candies[i] = candies[i - 1] + 1;
}
}
for i in (0..ratings.len()-1).rev() {
if ratings[i] > ratings[i + 1] {
candies[i] = candies[i].max(candies[i + 1] + 1);
}
}
candies.iter().sum()
}
```
### Javascript:
```Javascript
var candy = function(ratings) {
@ -255,6 +236,25 @@ var candy = function(ratings) {
```
### Rust
```rust
pub fn candy(ratings: Vec<i32>) -> i32 {
let mut candies = vec![1i32; ratings.len()];
for i in 1..ratings.len() {
if ratings[i - 1] < ratings[i] {
candies[i] = candies[i - 1] + 1;
}
}
for i in (0..ratings.len()-1).rev() {
if ratings[i] > ratings[i + 1] {
candies[i] = candies[i].max(candies[i + 1] + 1);
}
}
candies.iter().sum()
}
```
### C
```c
#define max(a, b) (((a) > (b)) ? (a) : (b))

90
problems/0150.逆波兰表达式求值.md
View File

@ -51,7 +51,7 @@
```
逆波兰表达式：是一种后缀表达式，所谓后缀就是指算符写在后面。
逆波兰表达式：是一种后缀表达式，所谓后缀就是指运算符写在后面。
平常使用的算式则是一种中缀表达式，如 ( 1 + 2 ) * ( 3 + 4 ) 。
@ -61,11 +61,11 @@
* 去掉括号后表达式无歧义，上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
* 适合用栈操作运算：遇到数字则入栈；遇到算符则取出栈顶两个数字进行计算，并将结果压入栈中。
* 适合用栈操作运算：遇到数字则入栈；遇到运算符则取出栈顶两个数字进行计算，并将结果压入栈中。
# 思路
《代码随想录》算法视频公开课：[栈的最后表演！ | LeetCode：150. 逆波兰表达式求值](https://www.bilibili.com/video/BV1kd4y1o7on)，相信结合视频在看本篇题解，更有助于大家对本题的理解。
《代码随想录》算法视频公开课：[栈的最后表演！ | LeetCode：150. 逆波兰表达式求值](https://www.bilibili.com/video/BV1kd4y1o7on)，相信结合视频再看本篇题解，更有助于大家对本题的理解。
在上一篇文章中[1047.删除字符串中的所有相邻重复项](https://programmercarl.com/1047.删除字符串中的所有相邻重复项.html)提到了 递归就是用栈来实现的。
@ -73,7 +73,7 @@
那么来看一下本题，**其实逆波兰表达式相当于是二叉树中的后序遍历**。 大家可以把运算符作为中间节点，按照后序遍历的规则画出一个二叉树。
但我们没有必要从二叉树的角度去解决这个问题，只要知道逆波兰表达式是用后续遍历的方式把二叉树序列化了，就可以了。
但我们没有必要从二叉树的角度去解决这个问题，只要知道逆波兰表达式是用后序遍历的方式把二叉树序列化了，就可以了。
在进一步看，本题中每一个子表达式要得出一个结果，然后拿这个结果再进行运算，那么**这岂不就是一个相邻字符串消除的过程，和[1047.删除字符串中的所有相邻重复项](https://programmercarl.com/1047.删除字符串中的所有相邻重复项.html)中的对对碰游戏是不是就非常像了。**
@ -118,9 +118,9 @@ public:
我们习惯看到的表达式都是中缀表达式，因为符合我们的习惯，但是中缀表达式对于计算机来说就不是很友好了。
例如：4 + 13 / 5，这就是中缀表达式，计算机从左到右去扫描的话，扫到13，还要判断13后面是什么运算法，还要比较一下优先级，然后13还和后面的5做运算，做完运算之后，还要向前回退到 4 的位置，继续做加法，你说麻不麻烦！
例如：4 + 13 / 5，这就是中缀表达式，计算机从左到右去扫描的话，扫到13，还要判断13后面是什么运算符，还要比较一下优先级，然后13还和后面的5做运算，做完运算之后，还要向前回退到 4 的位置，继续做加法，你说麻不麻烦！
那么将中缀表达式，转化为后缀表达式之后：["4", "13", "5", "/", "+"] ，就不一样了，计算机可以利用栈里顺序处理，不需要考虑优先级了。也不用回退了， **所以后缀表达式对计算机来说是非常友好的。**
那么将中缀表达式，转化为后缀表达式之后：["4", "13", "5", "/", "+"] ，就不一样了，计算机可以利用栈来顺序处理，不需要考虑优先级了。也不用回退了， **所以后缀表达式对计算机来说是非常友好的。**
可以说本题不仅仅是一道好题，也展现出计算机的思考方式。
@ -161,6 +161,24 @@ class Solution {
}
```
python3
```python
class Solution:
def evalRPN(self, tokens: List[str]) -> int:
stack = []
for item in tokens:
if item not in {"+", "-", "*", "/"}:
stack.append(item)
else:
first_num, second_num = stack.pop(), stack.pop()
stack.append(
int(eval(f'{second_num} {item} {first_num}')) # 第一个出来的在运算符后面
)
return int(stack.pop()) # 如果一开始只有一个数，那么会是字符串形式的
```
Go:
```Go
func evalRPN(tokens []string) int {
@ -169,7 +187,7 @@ func evalRPN(tokens []string) int {
val, err := strconv.Atoi(token)
if err == nil {
stack = append(stack, val)
} else {
} else { // 如果err不为nil说明不是数字
num1, num2 := stack[len(stack)-2], stack[(len(stack))-1]
stack = stack[:len(stack)-2]
switch token {
@ -191,27 +209,31 @@ func evalRPN(tokens []string) int {
javaScript:
```js
/**
* @param {string[]} tokens
* @return {number}
*/
var evalRPN = function(tokens) {
const s = new Map([
["+", (a, b) => a * 1 + b * 1],
["-", (a, b) => b - a],
["*", (a, b) => b * a],
["/", (a, b) => (b / a) | 0]
]);
var evalRPN = function (tokens) {
const stack = [];
for (const i of tokens) {
if(!s.has(i)) {
stack.push(i);
continue;
for (const token of tokens) {
if (isNaN(Number(token))) { // 非数字
const n2 = stack.pop(); // 出栈两个数字
const n1 = stack.pop();
switch (token) { // 判断运算符类型，算出新数入栈
case "+":
stack.push(n1 + n2);
break;
case "-":
stack.push(n1 - n2);
break;
case "*":
stack.push(n1 * n2);
break;
case "/":
stack.push(n1 / n2 | 0);
break;
}
} else { // 数字
stack.push(Number(token));
}
stack.push(s.get(i)(stack.pop(),stack.pop()))
}
return stack.pop();
return stack[0]; // 因没有遇到运算符而待在栈中的结果
};
```
@ -280,24 +302,6 @@ function evalRPN(tokens: string[]): number {
};
```
python3
```python
class Solution:
def evalRPN(self, tokens: List[str]) -> int:
stack = []
for item in tokens:
if item not in {"+", "-", "*", "/"}:
stack.append(item)
else:
first_num, second_num = stack.pop(), stack.pop()
stack.append(
int(eval(f'{second_num} {item} {first_num}')) # 第一个出来的在运算符后面
)
return int(stack.pop()) # 如果一开始只有一个数，那么会是字符串形式的
```
Swift：
```Swift
func evalRPN(_ tokens: [String]) -> Int {

41
problems/0216.组合总和III.md
View File

@ -36,7 +36,7 @@
想到这一点了，做过[77. 组合](https://programmercarl.com/0077.组合.html)之后，本题是简单一些了。
本题k相当于了树的深度，9（因为整个集合就是9个数）就是树的宽度。
本题k相当于树的深度，9（因为整个集合就是9个数）就是树的宽度。
例如 k = 2，n = 4的话，就是在集合[1,2,3,4,5,6,7,8,9]中求 k（个数） = 2, n（和） = 4的组合。
@ -380,29 +380,32 @@ class Solution:
回溯+减枝
```go
var (
res [][]int
path []int
)
func combinationSum3(k int, n int) [][]int {
var track []int// 遍历路径
var result [][]int// 存放结果集
backTree(n,k,1,&track,&result)
return result
res, path = make([][]int, 0), make([]int, 0, k)
dfs(k, n, 1, 0)
return res
}
func backTree(n,k,startIndex int,track *[]int,result *[][]int){
if len(*track)==k{
var sum int
tmp:=make([]int,k)
for k,v:=range *track{
sum+=v
tmp[k]=v
}
if sum==n{
*result=append(*result,tmp)
func dfs(k, n int, start int, sum int) {
if len(path) == k {
if sum == n {
tmp := make([]int, k)
copy(tmp, path)
res = append(res, tmp)
}
return
}
for i:=startIndex;i<=9-(k-len(*track))+1;i++{//减枝（k-len(*track)表示还剩多少个可填充的元素）
*track=append(*track,i)//记录路径
backTree(n,k,i+1,track,result)//递归
*track=(*track)[:len(*track)-1]//回溯
for i := start; i <= 9; i++ {
if sum + i > n || 9-i+1 < k-len(path) {
break
}
path = append(path, i)
dfs(k, n, i+1, sum+i)
path = path[:len(path)-1]
}
}
```

136
problems/0222.完全二叉树的节点个数.md
View File

@ -63,7 +63,7 @@ int getNodesNum(TreeNode* cur) {
if (cur == NULL) return 0;
```
3. 确定单层递归的逻辑：先求它的左子树的节点数量，再求的右子树的节点数量，最后取总和再加一 （加1是因为算上当前中间节点）就是目前节点为根节点的节点数量。
3. 确定单层递归的逻辑：先求它的左子树的节点数量，再求右子树的节点数量，最后取总和再加一 （加1是因为算上当前中间节点）就是目前节点为根节点的节点数量。
代码如下：
@ -168,7 +168,7 @@ public:
可以看出如果整个树不是满二叉树，就递归其左右孩子，直到遇到满二叉树为止，用公式计算这个子树（满二叉树）的节点数量。
这里关键在于如果去判断一个左子树或者右子树是不是满二叉树呢？
这里关键在于如何去判断一个左子树或者右子树是不是满二叉树呢？
在完全二叉树中，如果递归向左遍历的深度等于递归向右遍历的深度，那说明就是满二叉树。如图：
@ -178,13 +178,13 @@ public:
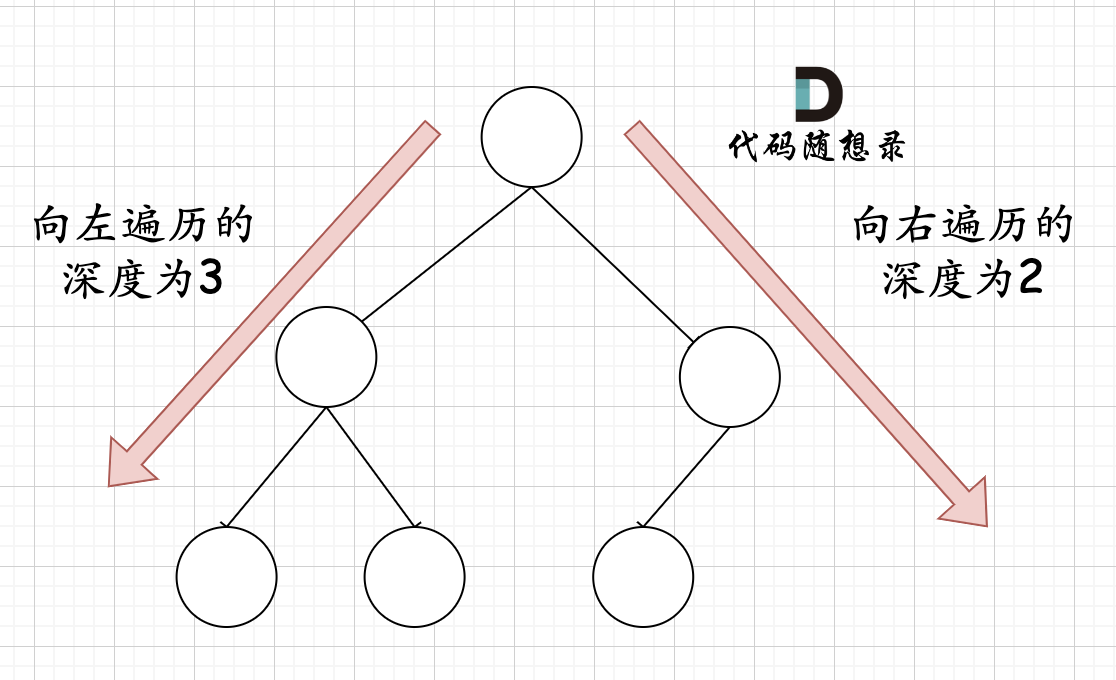
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20220829163709.png)
哪有录友说了，这种情况，递归向左遍历的深度等于递归向右遍历的深度，但也不是满二叉树，如题：
那有录友说了，这种情况，递归向左遍历的深度等于递归向右遍历的深度，但也不是满二叉树，如题：
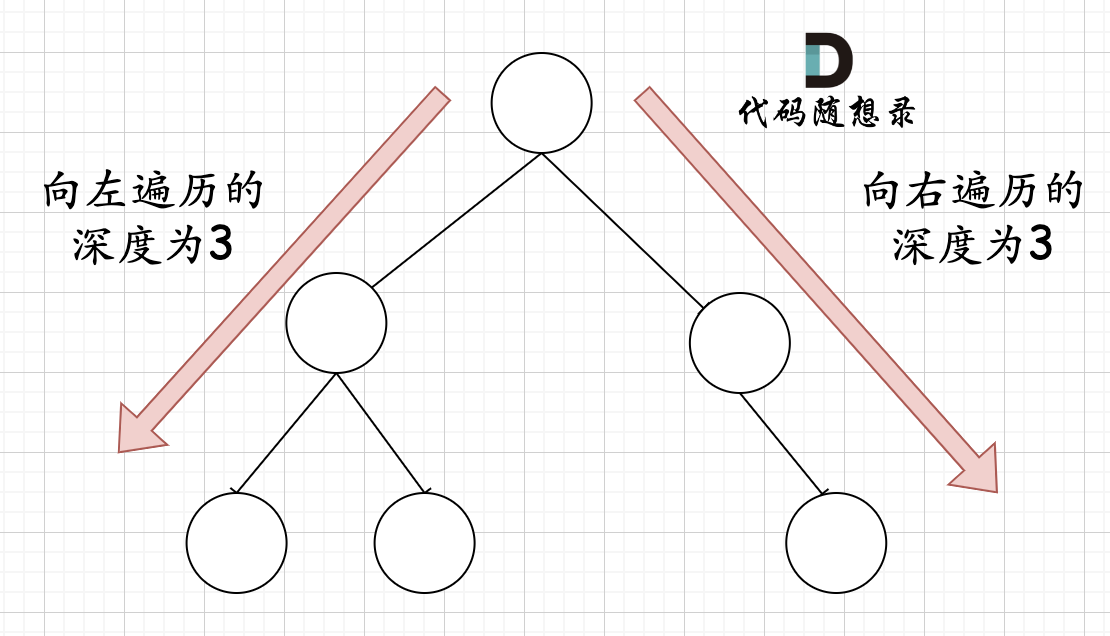
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20220829163811.png)
如果这么想，大家就是对 完全二叉树理解有误区了，**以上这棵二叉树，它根本就不是一个完全二叉树**！
判断其子树岂不是满二叉树，如果是则利用用公式计算这个子树（满二叉树）的节点数量，如果不是则继续递归，那么 在递归三部曲中，第二部：终止条件的写法应该是这样的：
判断其子树是不是满二叉树，如果是则利用公式计算这个子树（满二叉树）的节点数量，如果不是则继续递归，那么 在递归三部曲中，第二部：终止条件的写法应该是这样的：
```CPP
if (root == nullptr) return 0;
@ -292,26 +292,22 @@ class Solution {
* 满二叉树的结点数为：2^depth - 1
*/
public int countNodes(TreeNode root) {
if(root == null) {
return 0;
if (root == null) return 0;
TreeNode left = root.left;
TreeNode right = root.right;
int leftDepth = 0, rightDepth = 0; // 这里初始为0是有目的的，为了下面求指数方便
while (left != null) { // 求左子树深度
left = left.left;
leftDepth++;
}
int leftDepth = getDepth(root.left);
int rightDepth = getDepth(root.right);
if (leftDepth == rightDepth) {// 左子树是满二叉树
// 2^leftDepth其实是 （2^leftDepth - 1） + 1 ，左子树 + 根结点
return (1 << leftDepth) + countNodes(root.right);
} else {// 右子树是满二叉树
return (1 << rightDepth) + countNodes(root.left);
while (right != null) { // 求右子树深度
right = right.right;
rightDepth++;
}
}
private int getDepth(TreeNode root) {
int depth = 0;
while (root != null) {
root = root.left;
depth++;
if (leftDepth == rightDepth) {
return (2 << leftDepth) - 1; // 注意(2<<1) 相当于2^2，所以leftDepth初始为0
}
return depth;
return countNodes(root.left) + countNodes(root.right) + 1;
}
}
```
@ -397,7 +393,7 @@ class Solution:
* Right *TreeNode
* }
*/
//本题直接就是求有多少个节点，无脑存进数组算长度就行了。
//本题直接就是求有多少个节点，无脑存进结果变量就行了。
func countNodes(root *TreeNode) int {
if root == nil {
return 0
@ -473,15 +469,15 @@ func countNodes(root *TreeNode) int {
var countNodes = function(root) {
//递归法计算二叉树节点数
// 1. 确定递归函数参数
const getNodeSum=function(node){
const getNodeSum = function(node) {
//2. 确定终止条件
if(node===null){
if(node === null) {
return 0;
}
//3. 确定单层递归逻辑
let leftNum=getNodeSum(node.left);
let rightNum=getNodeSum(node.right);
return leftNum+rightNum+1;
let leftNum = getNodeSum(node.left);
let rightNum = getNodeSum(node.right);
return leftNum + rightNum + 1;
}
return getNodeSum(root);
};
@ -491,19 +487,19 @@ var countNodes = function(root) {
```javascript
var countNodes = function(root) {
//层序遍历
let queue=[];
if(root===null){
let queue = [];
if(root === null) {
return 0;
}
queue.push(root);
let nodeNums=0;
while(queue.length){
let length=queue.length;
while(length--){
let node=queue.shift();
let nodeNums = 0;
while(queue.length) {
let length = queue.length;
while(length--) {
let node = queue.shift();
nodeNums++;
node.left&&queue.push(node.left);
node.right&&queue.push(node.right);
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
}
return nodeNums;
@ -514,24 +510,24 @@ var countNodes = function(root) {
```javascript
var countNodes = function(root) {
//利用完全二叉树的特点
if(root===null){
if(root === null) {
return 0;
}
let left=root.left;
let right=root.right;
let leftDepth=0,rightDepth=0;
while(left){
left=left.left;
let left = root.left;
let right = root.right;
let leftDepth = 0, rightDepth = 0;
while(left) {
left = left.left;
leftDepth++;
}
while(right){
right=right.right;
while(right) {
right = right.right;
rightDepth++;
}
if(leftDepth==rightDepth){
return Math.pow(2,leftDepth+1)-1;
if(leftDepth == rightDepth) {
return Math.pow(2, leftDepth+1) - 1;
}
return countNodes(root.left)+countNodes(root.right)+1;
return countNodes(root.left) + countNodes(root.right) + 1;
};
```
@ -797,6 +793,52 @@ object Solution {
}
```
rust:
// 递归
```rust
use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
pub fn count_nodes(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
if root.is_none() {
return 0;
}
1 + Self::count_nodes(Rc::clone(root.as_ref().unwrap()).borrow().left.clone())
+ Self::count_nodes(root.unwrap().borrow().right.clone())
}
}
```
// 迭代
```rust
use std::rc::Rc;
use std::cell::RefCell;
use std::collections::VecDeque;
impl Solution {
pub fn count_nodes(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
let mut res = 0;
let mut queue = VecDeque::new();
if root.is_some() {
queue.push_back(root);
}
while !queue.is_empty() {
for _ in 0..queue.len() {
let node = queue.pop_front().unwrap().unwrap();
if node.borrow().left.is_some() {
queue.push_back(node.borrow().left.clone());
}
if node.borrow().right.is_some() {
queue.push_back(node.borrow().right.clone());
}
res += 1;
}
}
res
}
}
```
<p align="center">
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>

6
problems/0225.用队列实现栈.md
View File

@ -29,7 +29,7 @@
# 思路
《代码随想录》算法公开课：[队列的基本操作！ | LeetCode：225. 用队列实现栈](https://www.bilibili.com/video/BV1Fd4y1K7sm)，相信结合视频在看本篇题解，更有助于大家对链表的理解。
《代码随想录》算法公开课：[队列的基本操作！ | LeetCode：225. 用队列实现栈](https://www.bilibili.com/video/BV1Fd4y1K7sm)，相信结合视频再看本篇题解，更有助于大家对链表的理解。
（这里要强调是单向队列）
@ -44,7 +44,7 @@
所以用栈实现队列， 和用队列实现栈的思路还是不一样的，这取决于这两个数据结构的性质。
但是依然还是要用两个队列来模拟栈，只不过没有输入和输出的关系，而是另一个队列完全用又来备份的！
但是依然还是要用两个队列来模拟栈，只不过没有输入和输出的关系，而是另一个队列完全用来备份的！
如下面动画所示，**用两个队列que1和que2实现队列的功能，que2其实完全就是一个备份的作用**，把que1最后面的元素以外的元素都备份到que2，然后弹出最后面的元素，再把其他元素从que2导回que1。
@ -116,7 +116,7 @@ public:
其实这道题目就是用一个队列就够了。
**一个队列在模拟栈弹出元素的时候只要将队列头部的元素（除了最后一个元素外） 重新添加到队列尾部，此时在去弹出元素就是栈的顺序了。**
**一个队列在模拟栈弹出元素的时候只要将队列头部的元素（除了最后一个元素外） 重新添加到队列尾部，此时再去弹出元素就是栈的顺序了。**
C++优化代码

162
problems/0226.翻转二叉树.md
View File

@ -104,7 +104,7 @@ public:
### 深度优先遍历
[二叉树：听说递归能做的，栈也能做！](https://programmercarl.com/二叉树的迭代遍历.html)中给出了前中后序迭代方式的写法，所以本地可以很轻松的切出如下迭代法的代码：
[二叉树：听说递归能做的，栈也能做！](https://programmercarl.com/二叉树的迭代遍历.html)中给出了前中后序迭代方式的写法，所以本题可以很轻松的写出如下迭代法的代码：
C++代码迭代法（前序遍历）
@ -126,7 +126,7 @@ public:
}
};
```
如果这个代码看不懂的话可以在回顾一下[二叉树：听说递归能做的，栈也能做！](https://programmercarl.com/二叉树的迭代遍历.html)。
如果这个代码看不懂的话可以再回顾一下[二叉树：听说递归能做的，栈也能做！](https://programmercarl.com/二叉树的迭代遍历.html)。
我们在[二叉树：前中后序迭代方式的统一写法](https://programmercarl.com/二叉树的统一迭代法.html)中介绍了统一的写法，所以，本题也只需将文中的代码少做修改便可。
@ -258,7 +258,6 @@ public:
### Java
```Java
//DFS递归
class Solution {
@ -294,8 +293,8 @@ class Solution {
while (size-- > 0) {
TreeNode node = deque.poll();
swap(node);
if (node.left != null) {deque.offer(node.left);}
if (node.right != null) {deque.offer(node.right);}
if (node.left != null) deque.offer(node.left);
if (node.right != null) deque.offer(node.right);
}
}
return root;
@ -364,13 +363,12 @@ class Solution:
### Go
递归版本的前序遍历
```Go
func invertTree(root *TreeNode) *TreeNode {
if root ==nil{
if root == nil {
return nil
}
root.Left,root.Right=root.Right,root.Left//交换
root.Left, root.Right = root.Right, root.Left //交换
invertTree(root.Left)
invertTree(root.Right)
@ -383,12 +381,14 @@ func invertTree(root *TreeNode) *TreeNode {
```go
func invertTree(root *TreeNode) *TreeNode {
if root==nil{
if root == nil {
return root
}
invertTree(root.Left)//遍历左节点
invertTree(root.Right)//遍历右节点
root.Left,root.Right=root.Right,root.Left//交换
invertTree(root.Left) //遍历左节点
invertTree(root.Right) //遍历右节点
root.Left, root.Right = root.Right, root.Left //交换
return root
}
```
@ -397,18 +397,19 @@ func invertTree(root *TreeNode) *TreeNode {
```go
func invertTree(root *TreeNode) *TreeNode {
stack:=[]*TreeNode{}
node:=root
for node!=nil||len(stack)>0{
for node!=nil{
node.Left,node.Right=node.Right,node.Left//交换
stack=append(stack,node)
node=node.Left
stack := []*TreeNode{}
node := root
for node != nil || len(stack) > 0 {
for node != nil {
node.Left, node.Right = node.Right, node.Left //交换
stack = append(stack,node)
node = node.Left
}
node=stack[len(stack)-1]
stack=stack[:len(stack)-1]
node=node.Right
node = stack[len(stack)-1]
stack = stack[:len(stack)-1]
node = node.Right
}
return root
}
```
@ -417,25 +418,26 @@ func invertTree(root *TreeNode) *TreeNode {
```go
func invertTree(root *TreeNode) *TreeNode {
stack:=[]*TreeNode{}
node:=root
stack := []*TreeNode{}
node := root
var prev *TreeNode
for node!=nil||len(stack)>0{
for node!=nil{
stack=append(stack,node)
node=node.Left
for node != nil || len(stack) > 0 {
for node != nil {
stack = append(stack, node)
node = node.Left
}
node=stack[len(stack)-1]
stack=stack[:len(stack)-1]
if node.Right==nil||node.Right==prev{
node.Left,node.Right=node.Right,node.Left//交换
prev=node
node=nil
}else {
stack=append(stack,node)
node=node.Right
node = stack[len(stack)-1]
stack = stack[:len(stack)-1]
if node.Right == nil || node.Right == prev {
node.Left, node.Right = node.Right, node.Left //交换
prev = node
node = nil
} else {
stack = append(stack, node)
node = node.Right
}
}
return root
}
```
@ -444,21 +446,21 @@ func invertTree(root *TreeNode) *TreeNode {
```go
func invertTree(root *TreeNode) *TreeNode {
if root==nil{
if root == nil{
return root
}
queue:=list.New()
node:=root
queue := list.New()
node := root
queue.PushBack(node)
for queue.Len()>0{
length:=queue.Len()
for i:=0;i<length;i++{
e:=queue.Remove(queue.Front()).(*TreeNode)
e.Left,e.Right=e.Right,e.Left//交换
if e.Left!=nil{
for queue.Len() > 0 {
length := queue.Len()
for i := 0; i < length; i++ {
e := queue.Remove(queue.Front()).(*TreeNode)
e.Left, e.Right = e.Right, e.Left //交换
if e.Left != nil {
queue.PushBack(e.Left)
}
if e.Right!=nil{
if e.Right != nil {
queue.PushBack(e.Right)
}
}
@ -487,31 +489,31 @@ var invertTree = function(root) {
```javascript
var invertTree = function(root) {
//我们先定义节点交换函数
const invertNode=function(root,left,right){
let temp=left;
left=right;
right=temp;
root.left=left;
root.right=right;
const invertNode = function(root, left, right) {
let temp = left;
left = right;
right = temp;
root.left = left;
root.right = right;
}
//使用迭代方法的前序遍历
let stack=[];
if(root===null){
let stack = [];
if(root === null) {
return root;
}
stack.push(root);
while(stack.length){
let node=stack.pop();
if(node!==null){
while(stack.length) {
let node = stack.pop();
if(node !== null) {
//前序遍历顺序中左右 入栈顺序是前序遍历的倒序右左中
node.right&&stack.push(node.right);
node.left&&stack.push(node.left);
node.right && stack.push(node.right);
node.left && stack.push(node.left);
stack.push(node);
stack.push(null);
}else{
node=stack.pop();
} else {
node = stack.pop();
//节点处理逻辑
invertNode(node,node.left,node.right);
invertNode(node, node.left, node.right);
}
}
return root;
@ -521,27 +523,27 @@ var invertTree = function(root) {
```javascript
var invertTree = function(root) {
//我们先定义节点交换函数
const invertNode=function(root,left,right){
let temp=left;
left=right;
right=temp;
root.left=left;
root.right=right;
const invertNode = function(root, left, right) {
let temp = left;
left = right;
right = temp;
root.left = left;
root.right = right;
}
//使用层序遍历
let queue=[];
if(root===null){
let queue = [];
if(root === null) {
return root;
}
queue.push(root);
while(queue.length){
let length=queue.length;
while(length--){
let node=queue.shift();
while(queue.length) {
let length = queue.length;
while(length--) {
let node = queue.shift();
//节点处理逻辑
invertNode(node,node.left,node.right);
node.left&&queue.push(node.left);
node.right&&queue.push(node.right);
invertNode(node, node.left, node.right);
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
}
return root;
@ -760,7 +762,6 @@ func invertTree1(_ root: TreeNode?) -> TreeNode? {
}
```
### Swift
深度优先递归。
@ -808,9 +809,6 @@ func invertTree(_ root: TreeNode?) -> TreeNode? {
return root
}
```
### Scala
深度优先遍历（前序遍历）:
```scala
object Solution {

57
problems/0232.用栈实现队列.md
View File

@ -38,14 +38,14 @@ queue.empty(); // 返回 false
## 思路
《代码随想录》算法公开课：[栈的基本操作！ | LeetCode：232.用栈实现队列](https://www.bilibili.com/video/BV1nY4y1w7VC)，相信结合视频在看本篇题解，更有助于大家对链表的理解。
《代码随想录》算法公开课：[栈的基本操作！ | LeetCode：232.用栈实现队列](https://www.bilibili.com/video/BV1nY4y1w7VC)，相信结合视频再看本篇题解，更有助于大家对链表的理解。
这是一道模拟题，不涉及到具体算法，考察的就是对栈和队列的掌握程度。
使用栈来模式队列的行为，如果仅仅用一个栈，是一定不行的，所以需要两个栈**一个输入栈，一个输出栈**，这里要注意输入栈和输出栈的关系。
下面动画模拟以下队列的执行过程如下：
下面动画模拟以下队列的执行过程：
执行语句：
queue.push(1);
@ -120,7 +120,7 @@ public:
这样的项目代码会越来越乱，**一定要懂得复用，功能相近的函数要抽象出来，不要大量的复制粘贴，很容易出问题！（踩过坑的人自然懂）**
工作中如果发现某一个功能自己要经常用，同事们可能也会用到，自己就花点时间把这个功能抽象成一个好用的函数或者工具类，不仅自己方便，也方面了同事们。
工作中如果发现某一个功能自己要经常用，同事们可能也会用到，自己就花点时间把这个功能抽象成一个好用的函数或者工具类，不仅自己方便，也方便了同事们。
同事们就会逐渐认可你的工作态度和工作能力，自己的口碑都是这么一点一点积累起来的！在同事圈里口碑起来了之后，你就发现自己走上了一个正循环，以后的升职加薪才少不了你！哈哈哈
@ -231,56 +231,51 @@ class MyQueue:
Go：
```Go
type MyQueue struct {
stack []int
back []int
stackIn []int //输入栈
stackOut []int //输出栈
}
/** Initialize your data structure here. */
func Constructor() MyQueue {
return MyQueue{
stack: make([]int, 0),
back: make([]int, 0),
stackIn: make([]int, 0),
stackOut: make([]int, 0),
}
}
/** Push element x to the back of queue. */
// 往输入栈做push
func (this *MyQueue) Push(x int) {
for len(this.back) != 0 {
val := this.back[len(this.back)-1]
this.back = this.back[:len(this.back)-1]
this.stack = append(this.stack, val)
}
this.stack = append(this.stack, x)
this.stackIn = append(this.stackIn, x)
}
/** Removes the element from in front of queue and returns that element. */
// 在输出栈做pop，pop时如果输出栈数据为空，需要将输入栈全部数据导入，如果非空，则可直接使用
func (this *MyQueue) Pop() int {
for len(this.stack) != 0 {
val := this.stack[len(this.stack)-1]
this.stack = this.stack[:len(this.stack)-1]
this.back = append(this.back, val)
inLen, outLen := len(this.stackIn), len(this.stackOut)
if outLen == 0 {
if inLen == 0 {
return -1
}
for i := inLen - 1; i >= 0; i-- {
this.stackOut = append(this.stackOut, this.stackIn[i])
}
this.stackIn = []int{} //导出后清空
outLen = len(this.stackOut) //更新长度值
}
if len(this.back) == 0 {
return 0
}
val := this.back[len(this.back)-1]
this.back = this.back[:len(this.back)-1]
val := this.stackOut[outLen-1]
this.stackOut = this.stackOut[:outLen-1]
return val
}
/** Get the front element. */
func (this *MyQueue) Peek() int {
val := this.Pop()
if val == 0 {
return 0
if val == -1 {
return -1
}
this.back = append(this.back, val)
this.stackOut = append(this.stackOut, val)
return val
}
/** Returns whether the queue is empty. */
func (this *MyQueue) Empty() bool {
return len(this.stack) == 0 && len(this.back) == 0
return len(this.stackIn) == 0 && len(this.stackOut) == 0
}
```

40
problems/0235.二叉搜索树的最近公共祖先.md
View File

@ -35,14 +35,12 @@
* 所有节点的值都是唯一的。
* p、q 为不同节点且均存在于给定的二叉搜索树中。
# 视频讲解
**《代码随想录》算法视频公开课：[二叉搜索树找祖先就有点不一样了！| 235. 二叉搜索树的最近公共祖先](https://www.bilibili.com/video/BV1Zt4y1F7ww)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
# 算法公开课
**《代码随想录》算法视频公开课：[二叉搜索树找祖先就有点不一样了！| 235. 二叉搜索树的最近公共祖先](https://www.bilibili.com/video/BV1Zt4y1F7ww?share_source=copy_web)，相信结合视频在看本篇题解，更有助于大家对本题的理解**。
# 思路
做过[二叉树：公共祖先问题](https://programmercarl.com/0236.二叉树的最近公共祖先.html)题目的同学应该知道，利用回溯从底向上搜索，遇到一个节点的左子树里有p，右子树里有q，那么当前节点就是最近公共祖先。
那么本题是二叉搜索树，二叉搜索树是有序的，那得好好利用一下这个特点。
@ -65,12 +63,12 @@
而递归遍历顺序，本题就不涉及到 前中后序了（这里没有中节点的处理逻辑，遍历顺序无所谓了）。
如图所示：p为节点3，q为节点5
如图所示：p为节点6，q为节点9
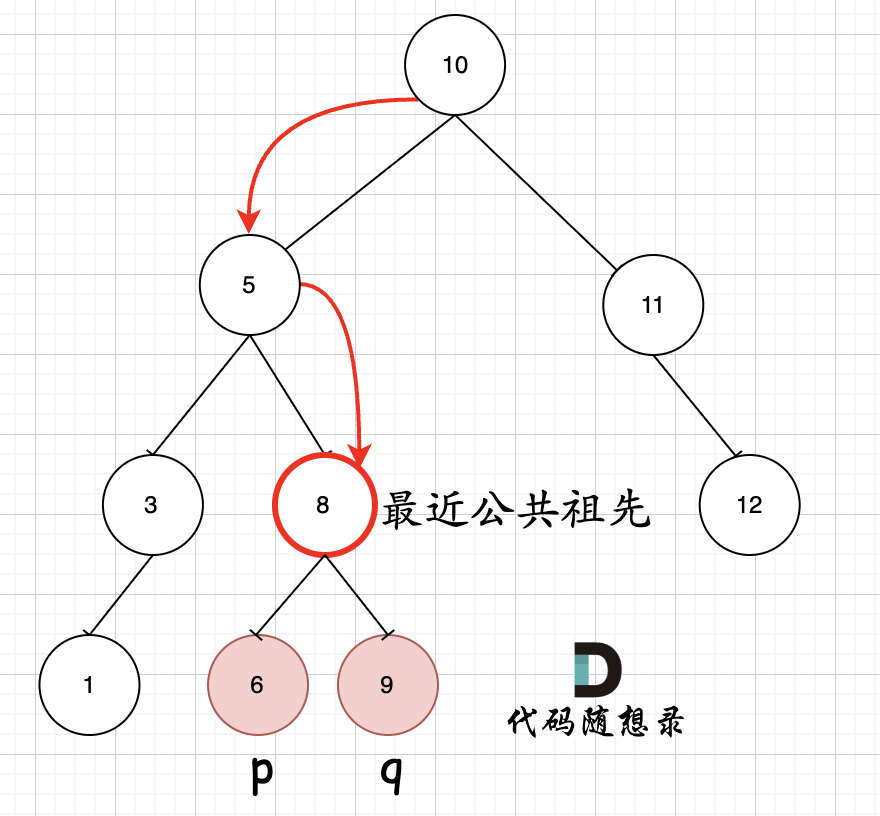
![235.二叉搜索树的最近公共祖先2](https://code-thinking-1253855093.file.myqcloud.com/pics/20220926165141.png)
可以看出直接按照指定的方向，就可以找到节点4，为最近公共祖先，而且不需要遍历整棵树，找到结果直接返回！
可以看出直接按照指定的方向，就可以找到节点8，为最近公共祖先，而且不需要遍历整棵树，找到结果直接返回！
## 递归法
@ -308,14 +306,22 @@ class Solution:
递归法：
```go
//利用BSL的性质（前序遍历有序）
func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
if root==nil{return nil}
if root.Val>p.Val&&root.Val>q.Val{//当前节点的值大于给定的值，则说明满足条件的在左边
return lowestCommonAncestor(root.Left,p,q)
}else if root.Val<p.Val&&root.Val<q.Val{//当前节点的值小于各点的值，则说明满足条件的在右边
return lowestCommonAncestor(root.Right,p,q)
}else {return root}//当前节点的值在给定值的中间（或者等于），即为最深的祖先
if root == nil {
return nil
}
for {
if root.Val > p.Val && root.Val > q.Val {
root = root.Left
}
if root.Val < p.Val && root.Val < q.Val {
root = root.Right
}
if (root.Val - p.Val) * (root.Val - q.Val) <= 0 {
return root
}
}
return root
}
```
@ -331,11 +337,11 @@ var lowestCommonAncestor = function(root, p, q) {
if(root === null) {
return root;
}
if(root.val>p.val&&root.val>q.val) {
if(root.val > p.val && root.val > q.val) {
// 向左子树查询
return root.left = lowestCommonAncestor(root.left,p,q);
}
if(root.val<p.val&&root.val<q.val) {
if(root.val < p.val && root.val < q.val) {
// 向右子树查询
return root.right = lowestCommonAncestor(root.right,p,q);
}
@ -348,9 +354,9 @@ var lowestCommonAncestor = function(root, p, q) {
var lowestCommonAncestor = function(root, p, q) {
// 使用迭代的方法
while(root) {
if(root.val>p.val&&root.val>q.val) {
if(root.val > p.val && root.val > q.val) {
root = root.left;
}else if(root.val<p.val&&root.val<q.val) {
}else if(root.val < p.val && root.val < q.val) {
root = root.right;
}else {
return root;

20
problems/0236.二叉树的最近公共祖先.md
View File

@ -48,7 +48,7 @@
后序遍历（左右中）就是天然的回溯过程，可以根据左右子树的返回值，来处理中节点的逻辑。
接下来就看如何判断一个节点是节点q和节点p的公共公共祖先呢。
接下来就看如何判断一个节点是节点q和节点p的公共祖先呢。
**首先最容易想到的一个情况：如果找到一个节点，发现左子树出现结点p，右子树出现节点q，或者 左子树出现结点q，右子树出现节点p，那么该节点就是节点p和q的最近公共祖先。** 即情况一：
@ -66,9 +66,9 @@
其实情况一 和 情况二 代码实现过程都是一样的，也可以说，实现情况一的逻辑，顺便包含了情况二。
因为遇到 q 或者 p 就返回，这样也包含了 q 或者 p 本省就是 公共祖先的情况。
因为遇到 q 或者 p 就返回，这样也包含了 q 或者 p 本身就是 公共祖先的情况。
这一点是很多录友容易忽略的，在下面的代码讲解中，可以在去体会。
这一点是很多录友容易忽略的，在下面的代码讲解中，可以再去体会。
递归三部曲：
@ -86,9 +86,9 @@ TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)
* 确定终止条件
遇到空的话，然后然后空，因为树都是空了，所以返回空。
遇到空的话，因为树都是空了，所以返回空。
那么我们来说一说，如果 root == q，或者 root == p，说明找到 q p ，则将其返回，这个返回值，后面在中节点的处理过程中会用到，那么中节点处理逻辑，后下面讲解。
那么我们来说一说，如果 root == q，或者 root == p，说明找到 q p ，则将其返回，这个返回值，后面在中节点的处理过程中会用到，那么中节点的处理逻辑，下面讲解。
代码如下：
@ -167,7 +167,7 @@ TreeNode* right = lowestCommonAncestor(root->right, p, q);
图中节点10的左子树返回null，右子树返回目标值7，那么此时节点10的处理逻辑就是把右子树的返回值（最近公共祖先7）返回上去！
这里点也很重要，可能刷过这道题目的同学，都不清楚结果究竟是如何从底层一层一层传到头结点的。
这里也很重要，可能刷过这道题目的同学，都不清楚结果究竟是如何从底层一层一层传到头结点的。
那么如果left和right都为空，则返回left或者right都是可以的，也就是返回空。
@ -231,7 +231,7 @@ public:
**那么我给大家归纳如下三点**：
1. 求最小公共祖先，需要从底向上遍历，那么二叉树，只能通过后序遍历（即：回溯）实现从低向上的遍历方式。
1. 求最小公共祖先，需要从底向上遍历，那么二叉树，只能通过后序遍历（即：回溯）实现从底向上的遍历方式。
2. 在回溯的过程中，必然要遍历整棵二叉树，即使已经找到结果了，依然要把其他节点遍历完，因为要使用递归函数的返回值（也就是代码中的left和right）做逻辑判断。
@ -332,16 +332,16 @@ var lowestCommonAncestor = function(root, p, q) {
// 1. 确定递归的函数
const travelTree = function(root,p,q) {
// 2. 确定递归终止条件
if(root === null || root === p||root === q) {
if(root === null || root === p || root === q) {
return root;
}
// 3. 确定递归单层逻辑
let left = travelTree(root.left,p,q);
let right = travelTree(root.right,p,q);
if(left !== null&&right !== null) {
if(left !== null && right !== null) {
return root;
}
if(left ===null) {
if(left === null) {
return right;
}
return left;

10
problems/0239.滑动窗口最大值.md
View File

@ -38,7 +38,7 @@
难点是如何求一个区间里的最大值呢？ （这好像是废话），暴力一下不就得了。
暴力方法，遍历一遍的过程中每次从窗口中在找到最大的数值，这样很明显是O(n × k)的算法。
暴力方法，遍历一遍的过程中每次从窗口中再找到最大的数值，这样很明显是O(n × k)的算法。
有的同学可能会想用一个大顶堆（优先级队列）来存放这个窗口里的k个数字，这样就可以知道最大的最大值是多少了， **但是问题是这个窗口是移动的，而大顶堆每次只能弹出最大值，我们无法移除其他数值，这样就造成大顶堆维护的不是滑动窗口里面的数值了。所以不能用大顶堆。**
@ -66,7 +66,7 @@ public:
**可惜了，没有！ 我们需要自己实现这么个队列。**
然后在分析一下，队列里的元素一定是要排序的，而且要最大值放在出队口，要不然怎么知道最大值呢。
然后再分析一下，队列里的元素一定是要排序的，而且要最大值放在出队口，要不然怎么知道最大值呢。
但如果把窗口里的元素都放进队列里，窗口移动的时候，队列需要弹出元素。
@ -74,9 +74,9 @@ public:
大家此时应该陷入深思.....
**其实队列没有必要维护窗口里的所有元素，只需要维护有可能成为窗口里最大值的元素就可以了，同时保证队里里的元素数值是由大到小的。**
**其实队列没有必要维护窗口里的所有元素，只需要维护有可能成为窗口里最大值的元素就可以了，同时保证队里的元素数值是由大到小的。**
那么这个维护元素单调递减的队列就叫做**单调队列，即单调递减或单调递增的队列。C++中没有直接支持单调队列，需要我们自己来一个单调队列**
那么这个维护元素单调递减的队列就叫做**单调队列，即单调递减或单调递增的队列。C++中没有直接支持单调队列，需要我们自己来实现一个单调队列**
**不要以为实现的单调队列就是 对窗口里面的数进行排序，如果排序的话，那和优先级队列又有什么区别了呢。**
@ -185,7 +185,7 @@ public:
};
```
在来看一下时间复杂度，使用单调队列的时间复杂度是 O(n)。
再来看一下时间复杂度，使用单调队列的时间复杂度是 O(n)。
有的同学可能想了，在队列中 push元素的过程中，还有pop操作呢，感觉不是纯粹的O(n)。

75
problems/0257.二叉树的所有路径.md
View File

@ -24,7 +24,7 @@
这道题目要求从根节点到叶子的路径，所以需要前序遍历，这样才方便让父节点指向孩子节点，找到对应的路径。
在这道题目中将第一次涉及到回溯，因为我们要把路径记录下来，需要回溯来回退一一个路径在进入另一个路径。
在这道题目中将第一次涉及到回溯，因为我们要把路径记录下来，需要回溯来回退一个路径再进入另一个路径。
前序遍历以及回溯的过程如图：
@ -44,7 +44,7 @@ void traversal(TreeNode* cur, vector<int>& path, vector<string>& result)
2. 确定递归终止条件
再写递归的时候都习惯了这么写：
在写递归的时候都习惯了这么写：
```
if (cur == NULL) {
@ -67,7 +67,7 @@ if (cur->left == NULL && cur->right == NULL) {
再来看一下终止处理的逻辑。
这里使用vector<int> 结构path来记录路径，所以要把vector<int> 结构的path转为string格式，在把这个string 放进 result里。
这里使用vector<int> 结构path来记录路径，所以要把vector<int> 结构的path转为string格式，再把这个string 放进 result里。
**那么为什么使用了vector<int> 结构来记录路径呢？** 因为在下面处理单层递归逻辑的时候，要做回溯，使用vector方便来做回溯。
@ -123,7 +123,7 @@ if (cur->right) {
path.pop_back();
```
这个回溯就要很大的问题，我们知道，**回溯和递归是一一对应的，有一个递归，就要有一个回溯**，这么写的话相当于把递归和回溯拆开了， 一个在花括号里，一个在花括号外。
这个回溯就有很大的问题，我们知道，**回溯和递归是一一对应的，有一个递归，就要有一个回溯**，这么写的话相当于把递归和回溯拆开了， 一个在花括号里，一个在花括号外。
**所以回溯要和递归永远在一起，世界上最遥远的距离是你在花括号里，而我在花括号外！**
@ -300,16 +300,16 @@ public:
```
**大家应该可以感受出来，如果把 `path + "->"`作为函数参数就是可以的，因为并有没有改变path的数值，执行完递归函数之后，path依然是之前的数值（相当于回溯了）**
**大家应该可以感受出来，如果把 `path + "->"`作为函数参数就是可以的，因为并没有改变path的数值，执行完递归函数之后，path依然是之前的数值（相当于回溯了）**
**综合以上，第二种递归的代码虽然精简但把很多重要的点隐藏在了代码细节里，第一种递归写法虽然代码多一些，但是把每一个逻辑处理都完整的展现了出来了。**
**综合以上，第二种递归的代码虽然精简但把很多重要的点隐藏在了代码细节里，第一种递归写法虽然代码多一些，但是把每一个逻辑处理都完整的展现出来了。**
## 拓展
这里讲解本题解的写法逻辑以及一些更具体的细节，下面的讲解中，涉及到C++语法特性，如果不是C++的录友，就可以不看了，避免越看越晕。
如果是C++的录友，建议本题独立刷过两遍，在看下面的讲解，同样避免越看越晕，造成不必要的负担。
如果是C++的录友，建议本题独立刷过两遍，再看下面的讲解，同样避免越看越晕，造成不必要的负担。
在第二版本的代码中，其实仅仅是回溯了 `->` 部分（调用两次pop_back，一个pop`>` 一次pop`-`），大家应该疑惑那么 `path += to_string(cur->val);` 这一步为什么没有回溯呢？ 一条路径能持续加节点 不做回溯吗？
@ -378,7 +378,7 @@ public:
最后我依然给出了迭代法。
对于本地充分了解递归与回溯的过程之后，有精力的同学可以在去实现迭代法。
对于本题充分了解递归与回溯的过程之后，有精力的同学可以再去实现迭代法。
@ -386,7 +386,7 @@ public:
# 其他语言版本
Java：
## Java：
```Java
//解法一
@ -466,7 +466,7 @@ class Solution {
}
```
---
Python:
## Python:
递归法+隐形回溯
```Python3
# Definition for a binary tree node.
@ -529,7 +529,7 @@ class Solution:
---
Go：
## Go：
递归法：
@ -591,28 +591,28 @@ func binaryTreePaths(root *TreeNode) []string {
```
---
JavaScript:
## JavaScript:
递归法：
```javascript
var binaryTreePaths = function(root) {
//递归遍历+递归三部曲
let res=[];
let res = [];
//1. 确定递归函数 函数参数
const getPath=function(node,curPath){
const getPath = function(node,curPath) {
//2. 确定终止条件，到叶子节点就终止
if(node.left===null&&node.right===null){
curPath+=node.val;
if(node.left === null && node.right === null) {
curPath += node.val;
res.push(curPath);
return ;
return;
}
//3. 确定单层递归逻辑
curPath+=node.val+'->';
node.left&&getPath(node.left,curPath);
node.right&&getPath(node.right,curPath);
curPath += node.val + '->';
node.left && getPath(node.left, curPath);
node.right && getPath(node.right, curPath);
}
getPath(root,'');
getPath(root, '');
return res;
};
```
@ -644,7 +644,7 @@ var binaryTreePaths = function(root) {
};
```
TypeScript：
## TypeScript：
> 递归法
@ -698,7 +698,7 @@ function binaryTreePaths(root: TreeNode | null): string[] {
};
```
Swift:
## Swift:
> 递归/回溯
```swift
@ -765,7 +765,7 @@ func binaryTreePaths(_ root: TreeNode?) -> [String] {
}
```
Scala:
## Scala:
递归:
```scala
@ -795,6 +795,33 @@ object Solution {
}
```
rust:
```rust
// 递归
impl Solution {
pub fn binary_tree_paths(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<String> {
let mut res = vec![];
Self::recur(&root, String::from(""), &mut res);
res
}
pub fn recur(node: &Option<Rc<RefCell<TreeNode>>>, mut path: String, res: &mut Vec<String>) {
let r = node.as_ref().unwrap().borrow();
path += format!("{}", r.val).as_str();
if r.left.is_none() && r.right.is_none() {
res.push(path.to_string());
return;
}
if r.left.is_some() {
Self::recur(&r.left, path.clone() + "->", res);
}
if r.right.is_some() {
Self::recur(&r.right, path + "->", res);
}
}
}
```
<p align="center">
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>

198
problems/0332.重新安排行程.md
View File

@ -86,7 +86,7 @@ unordered_map<string, map<string, int>> targets：unordered_map<出发机场, ma
在遍历 `unordered_map<出发机场, map<到达机场, 航班次数>> targets`的过程中，**可以使用"航班次数"这个字段的数字做相应的增减，来标记到达机场是否使用过了。**
如果“航班次数”大于零，说明目的地还可以飞，如果如果“航班次数”等于零说明目的地不能飞了，而不用对集合做删除元素或者增加元素的操作。
如果“航班次数”大于零，说明目的地还可以飞，如果“航班次数”等于零说明目的地不能飞了，而不用对集合做删除元素或者增加元素的操作。
**相当于说我不删，我就做一个标记！**
@ -439,68 +439,6 @@ func findItinerary(tickets [][]string) []string {
}
```
### C语言
```C
char **result;
bool *used;
int g_found;
int cmp(const void *str1, const void *str2)
{
const char **tmp1 = *(char**)str1;
const char **tmp2 = *(char**)str2;
int ret = strcmp(tmp1[0], tmp2[0]);
if (ret == 0) {
return strcmp(tmp1[1], tmp2[1]);
}
return ret;
}
void backtracting(char *** tickets, int ticketsSize, int* returnSize, char *start, char **result, bool *used)
{
if (*returnSize == ticketsSize + 1) {
g_found = 1;
return;
}
for (int i = 0; i < ticketsSize; i++) {
if ((used[i] == false) && (strcmp(start, tickets[i][0]) == 0)) {
result[*returnSize] = (char*)malloc(sizeof(char) * 4);
memcpy(result[*returnSize], tickets[i][1], sizeof(char) * 4);
(*returnSize)++;
used[i] = true;
/*if ((*returnSize) == ticketsSize + 1) {
return;
}*/
backtracting(tickets, ticketsSize, returnSize, tickets[i][1], result, used);
if (g_found) {
return;
}
(*returnSize)--;
used[i] = false;
}
}
return;
}
char ** findItinerary(char *** tickets, int ticketsSize, int* ticketsColSize, int* returnSize){
if (tickets == NULL || ticketsSize <= 0) {
return NULL;
}
result = malloc(sizeof(char*) * (ticketsSize + 1));
used = malloc(sizeof(bool) * ticketsSize);
memset(used, false, sizeof(bool) * ticketsSize);
result[0] = malloc(sizeof(char) * 4);
memcpy(result[0], "JFK", sizeof(char) * 4);
g_found = 0;
*returnSize = 1;
qsort(tickets, ticketsSize, sizeof(tickets[0]), cmp);
backtracting(tickets, ticketsSize, returnSize, "JFK", result, used);
*returnSize = ticketsSize + 1;
return result;
}
```
### Javascript
```Javascript
@ -589,6 +527,68 @@ function findItinerary(tickets: string[][]): string[] {
};
```
### C语言
```C
char **result;
bool *used;
int g_found;
int cmp(const void *str1, const void *str2)
{
const char **tmp1 = *(char**)str1;
const char **tmp2 = *(char**)str2;
int ret = strcmp(tmp1[0], tmp2[0]);
if (ret == 0) {
return strcmp(tmp1[1], tmp2[1]);
}
return ret;
}
void backtracting(char *** tickets, int ticketsSize, int* returnSize, char *start, char **result, bool *used)
{
if (*returnSize == ticketsSize + 1) {
g_found = 1;
return;
}
for (int i = 0; i < ticketsSize; i++) {
if ((used[i] == false) && (strcmp(start, tickets[i][0]) == 0)) {
result[*returnSize] = (char*)malloc(sizeof(char) * 4);
memcpy(result[*returnSize], tickets[i][1], sizeof(char) * 4);
(*returnSize)++;
used[i] = true;
/*if ((*returnSize) == ticketsSize + 1) {
return;
}*/
backtracting(tickets, ticketsSize, returnSize, tickets[i][1], result, used);
if (g_found) {
return;
}
(*returnSize)--;
used[i] = false;
}
}
return;
}
char ** findItinerary(char *** tickets, int ticketsSize, int* ticketsColSize, int* returnSize){
if (tickets == NULL || ticketsSize <= 0) {
return NULL;
}
result = malloc(sizeof(char*) * (ticketsSize + 1));
used = malloc(sizeof(bool) * ticketsSize);
memset(used, false, sizeof(bool) * ticketsSize);
result[0] = malloc(sizeof(char) * 4);
memcpy(result[0], "JFK", sizeof(char) * 4);
g_found = 0;
*returnSize = 1;
qsort(tickets, ticketsSize, sizeof(tickets[0]), cmp);
backtracting(tickets, ticketsSize, returnSize, "JFK", result, used);
*returnSize = ticketsSize + 1;
return result;
}
```
### Swift
直接迭代tickets数组：
@ -709,78 +709,6 @@ for line in tickets {
}
```
### Go
```Go
// 先排序，然后找到第一条路径即可返回
func findItinerary(tickets [][]string) []string {
var path []string // 用来保存搜索的路径
data := make(map[string]ticketSlice) // 用来保存tickets排序后的结果
var search func(airport string) bool
search = func(airport string) bool {
if len(path) == len(tickets) {
path = append(path, airport)
return true
}
to := data[airport]
for _, item := range to {
if item.Count == 0 {
// 已用完
continue
}
path = append(path, airport)
item.Count--
if search(item.To) { return true }
item.Count++
path = path[:len(path) - 1]
}
return false
}
// 排序
// 感觉这段代码有点啰嗦，不知道能不能简化一下
tmp := make(map[string]map[string]int)
for _, ticket := range tickets {
if to, ok := tmp[ticket[0]]; ok {
if _, ok2 := to[ticket[1]]; ok2 {
to[ticket[1]]++
} else {
to[ticket[1]] = 1
}
} else {
tmp[ticket[0]] = map[string]int{
ticket[1]: 1,
}
}
}
for from, to := range tmp {
var tmp ticketSlice
for to, num := range to {
tmp = append(tmp, &ticketStat{To: to, Count: num})
}
sort.Sort(tmp)
data[from] = tmp
}
search("JFK")
return path
}
type ticketStat struct {
To string
Count int
}
type ticketSlice []*ticketStat
func (p ticketSlice) Len() int { return len(p) }
func (p ticketSlice) Less(i, j int) bool { return strings.Compare(p[i].To, p[j].To) == -1 }
func (p ticketSlice) Swap(i, j int) { p[i], p[j] = p[j], p[i] }
```
### Rust
** 文中的Hashmap嵌套Hashmap的方法因为Rust的所有权问题暂时无法实现，此方法为删除哈希表中元素法 **
```Rust

68
problems/0343.整数拆分.md
View File

@ -35,7 +35,7 @@
dp[i]：分拆数字i，可以得到的最大乘积为dp[i]。
dp[i]的定义讲贯彻整个解题过程，下面哪一步想不懂了，就想想dp[i]究竟表示的是啥！
dp[i]的定义将贯彻整个解题过程，下面哪一步想不懂了，就想想dp[i]究竟表示的是啥！
2. 确定递推公式
@ -93,7 +93,7 @@ for (int i = 3; i <= n ; i++) {
}
}
```
注意 枚举j的时候，是从1开始的。从0开始的话，那么让拆分一个数拆个0的话，那么求最大乘积没有意义了。
注意 枚举j的时候，是从1开始的。从0开始的话，那么让拆分一个数拆个0，求最大乘积就没有意义了。
j的结束条件是 j < i - 1 ，其实 j < i 也是可以的，不过可以节省一步，例如让j = i - 1，的话，其实在 j = 1的时候，这一步就已经拆出来了，重复计算，所以 j < i - 1
@ -109,15 +109,15 @@ for (int i = 3; i <= n ; i++) {
}
```
因为拆分一个数n 使之乘积最大，那么一定是拆分m个成近似相同的子数相乘才是最大的。
因为拆分一个数n 使之乘积最大，那么一定是拆分成m个近似相同的子数相乘才是最大的。
例如 6 拆成 3 * 3， 10 拆成 3 * 3 * 4。 100的话 也是拆成m个近似数组的子数 相乘才是最大的。
只不过我们不知道m究竟是多少而已，但可以明确的是m一定大于等于2，既然m大于等于，也就是 最差也应该是拆成两个相同的 可能是最大值。
只不过我们不知道m究竟是多少而已，但可以明确的是m一定大于等于2，既然m大于等于2，也就是 最差也应该是拆成两个相同的 可能是最大值。
那么 j 遍历，只需要遍历到 n/2 就可以，后面就没有必要遍历了，一定不是最大值。
至于 “拆分一个数n 使之乘积最大，那么一定是拆分m个成近似相同的子数相乘才是最大的” 这个我就不去做数学证明了，感兴趣的同学，可以自己证明。
至于 “拆分一个数n 使之乘积最大，那么一定是拆分成m个近似相同的子数相乘才是最大的” 这个我就不去做数学证明了，感兴趣的同学，可以自己证明。
5. 举例推导dp数组
@ -221,14 +221,14 @@ public:
class Solution {
public int integerBreak(int n) {
//dp[i] 为正整数 i 拆分后的结果的最大乘积
int[]dp=new int[n+1];
dp[2]=1;
for(int i=3;i<=n;i++){
for(int j=1;j<=i-j;j++){
int[] dp = new int[n+1];
dp[2] = 1;
for(int i = 3; i <= n; i++) {
for(int j = 1; j <= i-j; j++) {
// 这里的 j 其实最大值为 i-j,再大只不过是重复而已，
//并且，在本题中，我们分析 dp[0], dp[1]都是无意义的，
//j 最大到 i-j,就不会用到 dp[0]与dp[1]
dp[i]=Math.max(dp[i],Math.max(j*(i-j),j*dp[i-j]));
dp[i] = Math.max(dp[i], Math.max(j*(i-j), j*dp[i-j]));
// j * (i - j) 是单纯的把整数 i 拆分为两个数 也就是 i,i-j ，再相乘
//而j * dp[i - j]是将 i 拆分成两个以及两个以上的个数,再相乘。
}
@ -254,7 +254,7 @@ class Solution:
```
### Go
```golang
```go
func integerBreak(n int) int {
/**
动态五部曲
@ -264,40 +264,25 @@ func integerBreak(n int) int {
4.确定遍历顺序
5.打印dp
**/
dp:=make([]int,n+1)
dp[1]=1
dp[2]=1
for i:=3;i<n+1;i++{
for j:=1;j<i-1;j++{
dp := make([]int, n+1)
dp[1] = 1
dp[2] = 1
for i := 3; i < n+1; i++ {
for j := 1; j < i-1; j++ {
// i可以差分为i-j和j。由于需要最大值，故需要通过j遍历所有存在的值，取其中最大的值作为当前i的最大值，在求最大值的时候，一个是j与i-j相乘，一个是j与dp[i-j].
dp[i]=max(dp[i],max(j*(i-j),j*dp[i-j]))
dp[i] = max(dp[i], max(j*(i-j), j*dp[i-j]))
}
}
return dp[n]
}
func max(a,b int) int{
if a>b{
func max(a, b int) int{
if a > b {
return a
}
return b
}
```
### Rust
```rust
pub fn integer_break(n: i32) -> i32 {
let n = n as usize;
let mut dp = vec![0; n + 1];
dp[2] = 1;
for i in 3..=n {
for j in 1..i-1 {
dp[i] = dp[i].max((i - j) * j).max(dp[i - j] * j);
}
}
dp[n] as i32
}
```
### Javascript
```Javascript
var integerBreak = function(n) {
@ -313,6 +298,21 @@ var integerBreak = function(n) {
};
```
### Rust
```rust
pub fn integer_break(n: i32) -> i32 {
let n = n as usize;
let mut dp = vec![0; n + 1];
dp[2] = 1;
for i in 3..=n {
for j in 1..i-1 {
dp[i] = dp[i].max((i - j) * j).max(dp[i - j] * j);
}
}
dp[n] as i32
}
```
### TypeScript
```typescript

4
problems/0347.前K个高频元素.md
View File

@ -204,7 +204,7 @@ class Solution:
#定义一个小顶堆，大小为k
pri_que = [] #小顶堆
#用固定大小为k的小顶堆，扫面所有频率的数值
#用固定大小为k的小顶堆，扫描所有频率的数值
for key, freq in map_.items():
heapq.heappush(pri_que, (freq, key))
if len(pri_que) > k: #如果堆的大小大于了K，则队列弹出，保证堆的大小一直为k
@ -271,7 +271,7 @@ func (h *IHeap) Pop() interface{}{
}
//方法二:利用O(logn)排序
//方法二:利用O(nlogn)排序
func topKFrequent(nums []int, k int) []int {
ans:=[]int{}
map_num:=map[int]int{}

4
problems/0376.摆动序列.md
View File

@ -286,7 +286,7 @@ class Solution:
### Go
**贪心**
```golang
```go
func wiggleMaxLength(nums []int) int {
n := len(nums)
if n < 2 {
@ -309,7 +309,7 @@ func wiggleMaxLength(nums []int) int {
```
**动态规划**
```golang
```go
func wiggleMaxLength(nums []int) int {
n := len(nums)
if n <= 1 {

129
problems/0404.左叶子之和.md
View File

@ -35,7 +35,7 @@
![图二](https://code-thinking-1253855093.file.myqcloud.com/pics/20220902165805.png)
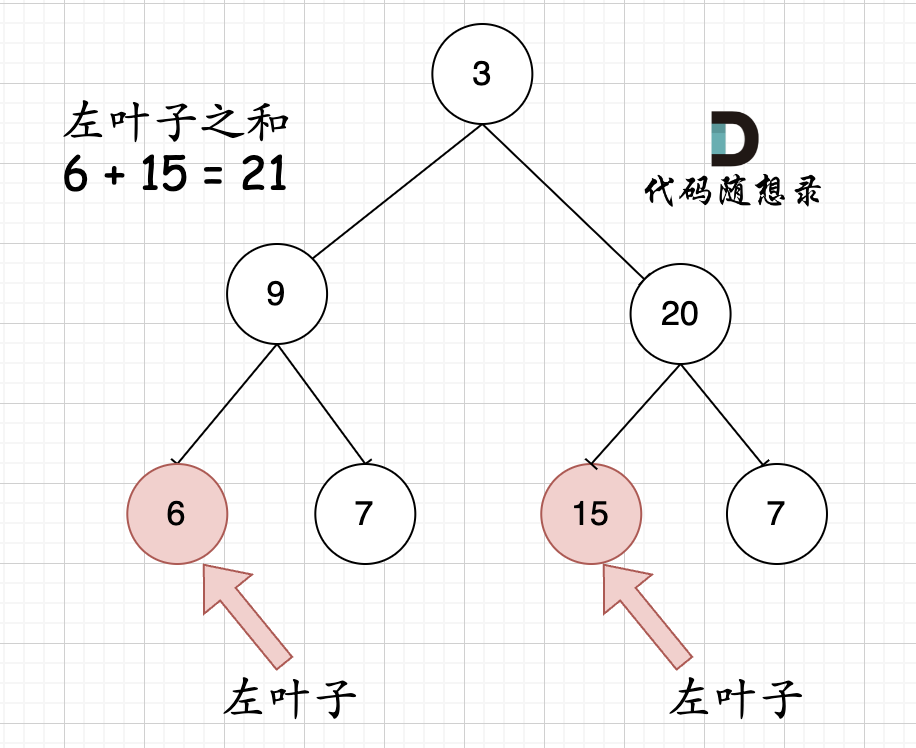
相信通过这两个图，大家可以最左叶子的定义有明确理解了。
相信通过这两个图，大家对最左叶子的定义有明确理解了。
那么**判断当前节点是不是左叶子是无法判断的，必须要通过节点的父节点来判断其左孩子是不是左叶子。**
@ -298,48 +298,49 @@ class Solution:
```go
func sumOfLeftLeaves(root *TreeNode) int {
var res int
findLeft(root,&res)
return res
}
func findLeft(root *TreeNode,res *int){
//左节点
if root.Left!=nil&&root.Left.Left==nil&&root.Left.Right==nil{
*res=*res+root.Left.Val
if root == nil {
return 0
}
if root.Left!=nil{
findLeft(root.Left,res)
}
if root.Right!=nil{
findLeft(root.Right,res)
leftValue := sumOfLeftLeaves(root.Left) // 左
if root.Left != nil && root.Left.Left == nil && root.Left.Right == nil {
leftValue = root.Left.Val // 中
}
rightValue := sumOfLeftLeaves(root.Right) // 右
return leftValue + rightValue
}
```
**迭代法**
**迭代法(前序遍历)**
```go
func sumOfLeftLeaves(root *TreeNode) int {
var res int
queue:=list.New()
queue.PushBack(root)
for queue.Len()>0{
length:=queue.Len()
for i:=0;i<length;i++{
node:=queue.Remove(queue.Front()).(*TreeNode)
if node.Left!=nil&&node.Left.Left==nil&&node.Left.Right==nil{
res=res+node.Left.Val
st := make([]*TreeNode, 0)
if root == nil {
return 0
}
st = append(st, root)
result := 0
for len(st) != 0 {
node := st[len(st)-1]
st = st[:len(st)-1]
if node.Left != nil && node.Left.Left == nil && node.Left.Right == nil {
result += node.Left.Val
}
if node.Left!=nil{
queue.PushBack(node.Left)
if node.Right != nil {
st = append(st, node.Right)
}
if node.Right!=nil{
queue.PushBack(node.Right)
if node.Left != nil {
st = append(st, node.Left)
}
}
}
return res
return result
}
```
@ -351,16 +352,16 @@ func sumOfLeftLeaves(root *TreeNode) int {
var sumOfLeftLeaves = function(root) {
//采用后序遍历 递归遍历
// 1. 确定递归函数参数
const nodesSum = function(node){
const nodesSum = function(node) {
// 2. 确定终止条件
if(node===null){
if(node === null) {
return 0;
}
let leftValue = nodesSum(node.left);
let rightValue = nodesSum(node.right);
// 3. 单层递归逻辑
let midValue = 0;
if(node.left&&node.left.left===null&&node.left.right===null){
if(node.left && node.left.left === null && node.left.right === null) {
midValue = node.left.val;
}
let sum = midValue + leftValue + rightValue;
@ -374,19 +375,19 @@ var sumOfLeftLeaves = function(root) {
```javascript
var sumOfLeftLeaves = function(root) {
//采用层序遍历
if(root===null){
if(root === null) {
return null;
}
let queue = [];
let sum = 0;
queue.push(root);
while(queue.length){
while(queue.length) {
let node = queue.shift();
if(node.left!==null&&node.left.left===null&&node.left.right===null){
if(node.left !== null && node.left.left === null && node.left.right === null) {
sum+=node.left.val;
}
node.left&&queue.push(node.left);
node.right&&queue.push(node.right);
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
return sum;
};
@ -575,6 +576,58 @@ object Solution {
}
```
### Rust
**递归**
```rust
use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
pub fn sum_of_left_leaves(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
let mut res = 0;
if let Some(node) = root {
if let Some(left) = &node.borrow().left {
if left.borrow().right.is_none() && left.borrow().right.is_none() {
res += left.borrow().val;
}
}
res + Self::sum_of_left_leaves(node.borrow().left.clone())
+ Self::sum_of_left_leaves(node.borrow().right.clone())
} else {
0
}
}
}
```
**迭代：**
```rust
use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
pub fn sum_of_left_leaves(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
let mut res = 0;
let mut stack = vec![root];
while !stack.is_empty() {
if let Some(node) = stack.pop().unwrap() {
if let Some(left) = &node.borrow().left {
if left.borrow().left.is_none() && left.borrow().right.is_none() {
res += left.borrow().val;
}
stack.push(Some(left.to_owned()));
}
if let Some(right) = &node.borrow().right {
stack.push(Some(right.to_owned()));
}
}
}
res
}
}
```
<p align="center">
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>

58
problems/0406.根据身高重建队列.md
View File

@ -39,7 +39,7 @@
## 思路
本题有两个维度，h和k，看到这种题目一定要想如何确定一个维度，然后在按照另一个维度重新排列。
本题有两个维度，h和k，看到这种题目一定要想如何确定一个维度，然后再按照另一个维度重新排列。
其实如果大家认真做了[135. 分发糖果](https://programmercarl.com/0135.分发糖果.html)，就会发现和此题有点点的像。
@ -47,7 +47,7 @@
**如果两个维度一起考虑一定会顾此失彼**。
对于本题相信大家困惑的点是先确定k还是先确定h呢，也就是究竟先按h排序呢，还先按照k排序呢？
对于本题相信大家困惑的点是先确定k还是先确定h呢，也就是究竟先按h排序呢，还是先按照k排序呢？
如果按照k来从小到大排序，排完之后，会发现k的排列并不符合条件，身高也不符合条件，两个维度哪一个都没确定下来。
@ -222,48 +222,46 @@ class Solution:
### Go
```go
func reconstructQueue(people [][]int) [][]int {
//先将身高从大到小排序，确定最大个子的相对位置
sort.Slice(people,func(i,j int)bool{
if people[i][0]==people[j][0]{
return people[i][1]<people[j][1]//这个才是当身高相同时，将K按照从小到大排序
// 先将身高从大到小排序，确定最大个子的相对位置
sort.Slice(people, func(i, j int) bool {
if people[i][0] == people[j][0] {
return people[i][1] < people[j][1] // 当身高相同时，将K按照从小到大排序
}
return people[i][0]>people[j][0]//这个只是确保身高按照由大到小的顺序来排，并不确定K是按照从小到大排序的
return people[i][0] > people[j][0] // 身高按照由大到小的顺序来排
})
//再按照K进行插入排序，优先插入K小的
result := make([][]int, 0)
for _, info := range people {
result = append(result, info)
copy(result[info[1] +1:], result[info[1]:])//将插入位置之后的元素后移动一位（意思是腾出空间）
result[info[1]] = info//将插入元素位置插入元素
// 再按照K进行插入排序，优先插入K小的
for i, p := range people {
copy(people[p[1]+1 : i+1], people[p[1] : i+1]) // 空出一个位置
people[p[1]] = p
}
return result
return people
}
```
```go
//链表法
// 链表实现
func reconstructQueue(people [][]int) [][]int {
sort.Slice(people,func (i,j int) bool {
if people[i][0]==people[j][0]{
return people[i][1]<people[j][1]//当身高相同时，将K按照从小到大排序
if people[i][0] == people[j][0] {
return people[i][1] < people[j][1] //当身高相同时，将K按照从小到大排序
}
//先将身高从大到小排序，确定最大个子的相对位置
return people[i][0]>people[j][0]
return people[i][0] > people[j][0]
})
l:=list.New()//创建链表
for i:=0;i<len(people);i++{
position:=people[i][1]
mark:=l.PushBack(people[i])//插入元素
e:=l.Front()
for position!=0{//获取相对位置
l := list.New() //创建链表
for i:=0; i < len(people); i++ {
position := people[i][1]
mark := l.PushBack(people[i]) //插入元素
e := l.Front()
for position != 0 { //获取相对位置
position--
e=e.Next()
e = e.Next()
}
l.MoveBefore(mark,e)//移动位置
l.MoveBefore(mark, e) //移动位置
}
res:=[][]int{}
for e:=l.Front();e!=nil;e=e.Next(){
res=append(res,e.Value.([]int))
res := [][]int{}
for e := l.Front(); e != nil; e = e.Next() {
res = append(res, e.Value.([]int))
}
return res
}

46
problems/0450.删除二叉搜索树中的节点.md
View File

@ -23,9 +23,13 @@
![450.删除二叉搜索树中的节点](https://img-blog.csdnimg.cn/20201020171048265.png)
# 算法公开课
**《代码随想录》算法视频公开课：[调整二叉树的结构最难！| LeetCode：450.删除二叉搜索树中的节点](https://www.bilibili.com/video/BV1tP41177us?share_source=copy_web)，相信结合视频在看本篇题解，更有助于大家对本题的理解**。
# 思路
搜索树的节点删除要比节点增加复杂的多，有很多情况需要考虑，做好心里准备。
搜索树的节点删除要比节点增加复杂的多，有很多情况需要考虑，做好心理准备。
## 递归
@ -33,7 +37,7 @@
* 确定递归函数参数以及返回值
说道递归函数的返回值，在[二叉树：搜索树中的插入操作](https://programmercarl.com/0701.二叉搜索树中的插入操作.html)中通过递归返回值来加入新节点， 这里也可以通过递归返回值删除节点。
说到递归函数的返回值，在[二叉树：搜索树中的插入操作](https://programmercarl.com/0701.二叉搜索树中的插入操作.html)中通过递归返回值来加入新节点， 这里也可以通过递归返回值删除节点。
代码如下：
@ -66,7 +70,7 @@ if (root == nullptr) return root;
![450.删除二叉搜索树中的节点](https://tva1.sinaimg.cn/large/008eGmZEly1gnbj3k596mg30dq0aigyz.gif)
动画中棵二叉搜索树中，删除元素7， 那么删除节点（元素7）的左孩子就是5，删除节点（元素7）的右子树的最左面节点是元素8。
动画中的二叉搜索树中，删除元素7， 那么删除节点（元素7）的左孩子就是5，删除节点（元素7）的右子树的最左面节点是元素8。
将删除节点（元素7）的左孩子放到删除节点（元素7）的右子树的最左面节点（元素8）的左孩子上，就是把5为根节点的子树移到了8的左孩子的位置。
@ -251,7 +255,7 @@ public:
**这里最关键的逻辑就是第五种情况（删除一个左右孩子都不为空的节点），这种情况一定要想清楚**。
而且就算想清楚了，对应的代码也未必可以写出来，所以**这道题目即考察思维逻辑，也考察代码能力**。
而且就算想清楚了，对应的代码也未必可以写出来，所以**这道题目既考察思维逻辑，也考察代码能力**。
递归中我给出了两种写法，推荐大家学会第一种（利用搜索树的特性）就可以了，第二种递归写法其实是比较绕的。
@ -390,39 +394,39 @@ class Solution:
```Go
// 递归版本
func deleteNode(root *TreeNode, key int) *TreeNode {
if root==nil{
if root == nil {
return nil
}
if key<root.Val{
root.Left=deleteNode(root.Left,key)
if key < root.Val {
root.Left = deleteNode(root.Left, key)
return root
}
if key>root.Val{
root.Right=deleteNode(root.Right,key)
if key > root.Val {
root.Right = deleteNode(root.Right, key)
return root
}
if root.Right==nil{
if root.Right == nil {
return root.Left
}
if root.Left==nil{
if root.Left == nil{
return root.Right
}
minnode:=root.Right
for minnode.Left!=nil{
minnode=minnode.Left
minnode := root.Right
for minnode.Left != nil {
minnode = minnode.Left
}
root.Val=minnode.Val
root.Right=deleteNode1(root.Right)
root.Val = minnode.Val
root.Right = deleteNode1(root.Right)
return root
}
func deleteNode1(root *TreeNode)*TreeNode{
if root.Left==nil{
pRight:=root.Right
root.Right=nil
func deleteNode1(root *TreeNode)*TreeNode {
if root.Left == nil {
pRight := root.Right
root.Right = nil
return pRight
}
root.Left=deleteNode1(root.Left)
root.Left = deleteNode1(root.Left)
return root
}
// 迭代版本

20
problems/0452.用最少数量的箭引爆气球.md
View File

@ -56,7 +56,7 @@
如果真实的模拟射气球的过程，应该射一个，气球数组就remove一个元素，这样最直观，毕竟气球被射了。
但仔细思考一下就发现：如果把气球排序之后，从前到后遍历气球，被射过的气球仅仅跳过就行了，没有必要让气球数组remote气球，只要记录一下箭的数量就可以了。
但仔细思考一下就发现：如果把气球排序之后，从前到后遍历气球，被射过的气球仅仅跳过就行了，没有必要让气球数组remove气球，只要记录一下箭的数量就可以了。
以上为思考过程，已经确定下来使用贪心了，那么开始解题。
@ -175,25 +175,25 @@ class Solution:
```
### Go
```golang
```go
func findMinArrowShots(points [][]int) int {
var res int =1//弓箭数
var res int = 1 //弓箭数
//先按照第一位排序
sort.Slice(points,func (i,j int) bool{
return points[i][0]<points[j][0]
sort.Slice(points, func (i,j int) bool {
return points[i][0] < points[j][0]
})
for i:=1;i<len(points);i++{
if points[i-1][1]<points[i][0]{//如果前一位的右边界小于后一位的左边界，则一定不重合
for i := 1; i < len(points); i++ {
if points[i-1][1] < points[i][0] { //如果前一位的右边界小于后一位的左边界，则一定不重合
res++
}else{
} else {
points[i][1] = min(points[i - 1][1], points[i][1]); // 更新重叠气球最小右边界,覆盖该位置的值，留到下一步使用
}
}
return res
}
func min(a,b int) int{
if a>b{
func min(a, b int) int {
if a > b {
return b
}
return a

43
problems/0491.递增子序列.md
View File

@ -37,7 +37,7 @@
在[90.子集II](https://programmercarl.com/0090.子集II.html)中我们是通过排序，再加一个标记数组来达到去重的目的。
而本题求自增子序列，是不能对原数组经行排序的，排完序的数组都是自增子序列了。
而本题求自增子序列，是不能对原数组进行排序的，排完序的数组都是自增子序列了。
**所以不能使用之前的去重逻辑！**
@ -78,7 +78,7 @@ if (path.size() > 1) {
* 单层搜索逻辑
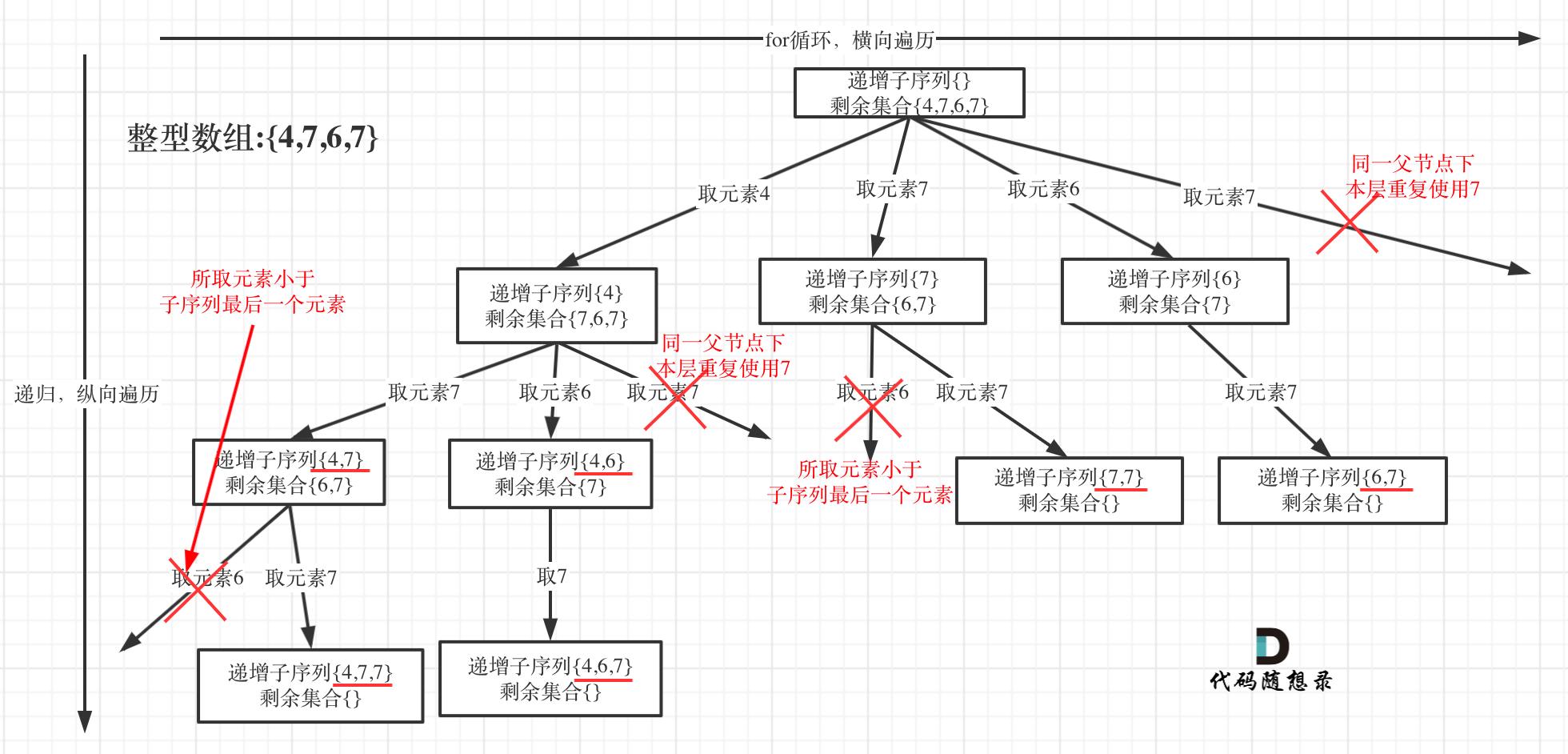
![491. 递增子序列1](https://img-blog.csdnimg.cn/20201124200229824.png)
在图中可以看出，**同一父节点下的同层上使用过的元素就不能在使用了**
在图中可以看出，**同一父节点下的同层上使用过的元素就不能再使用了**
那么单层搜索代码如下：
@ -340,30 +340,33 @@ class Solution:
```
### Go
```golang
```go
var (
res [][]int
path []int
)
func findSubsequences(nums []int) [][]int {
var subRes []int
var res [][]int
backTring(0,nums,subRes,&res)
res, path = make([][]int, 0), make([]int, 0, len(nums))
dfs(nums, 0)
return res
}
func backTring(startIndex int,nums,subRes []int,res *[][]int){
if len(subRes)>1{
tmp:=make([]int,len(subRes))
copy(tmp,subRes)
*res=append(*res,tmp)
func dfs(nums []int, start int) {
if len(path) >= 2 {
tmp := make([]int, len(path))
copy(tmp, path)
res = append(res, tmp)
}
history:=[201]int{}//记录本层元素使用记录
for i:=startIndex;i<len(nums);i++{
//分两种情况判断：一，当前取的元素小于子集的最后一个元素，则继续寻找下一个适合的元素
// 或者二，当前取的元素在本层已经出现过了，所以跳过该元素，继续寻找
if len(subRes)>0&&nums[i]<subRes[len(subRes)-1]||history[nums[i] + 100]==1{
used := make(map[int]bool, len(nums)) // 初始化used字典，用以对同层元素去重
for i := start; i < len(nums); i++ {
if used[nums[i]] { // 去重
continue
}
history[nums[i] + 100]=1//表示本层该元素使用过了
subRes=append(subRes,nums[i])
backTring(i+1,nums,subRes,res)
subRes=subRes[:len(subRes)-1]
if len(path) == 0 || nums[i] >= path[len(path)-1] {
path = append(path, nums[i])
used[nums[i]] = true
dfs(nums, i+1)
path = path[:len(path)-1]
}
}
}
```

45
problems/0501.二叉搜索树中的众数.md
View File

@ -54,7 +54,7 @@
1. 这个树都遍历了，用map统计频率
至于用前中后序那种遍历也不重要，因为就是要全遍历一遍，怎么个遍历法都行，层序遍历都没毛病！
至于用前中后序哪种遍历也不重要，因为就是要全遍历一遍，怎么个遍历法都行，层序遍历都没毛病！
这里采用前序遍历，代码如下：
@ -354,7 +354,7 @@ public:
```java
class Solution {
public int[] findMode(FindModeInBinarySearchTree.TreeNode root) {
public int[] findMode(TreeNode root) {
Map<Integer, Integer> map = new HashMap<>();
List<Integer> list = new ArrayList<>();
if (root == null) return list.stream().mapToInt(Integer::intValue).toArray();
@ -375,7 +375,7 @@ class Solution {
return list.stream().mapToInt(Integer::intValue).toArray();
}
void searchBST(FindModeInBinarySearchTree.TreeNode curr, Map<Integer, Integer> map) {
void searchBST(TreeNode curr, Map<Integer, Integer> map) {
if (curr == null) return;
map.put(curr.val, map.getOrDefault(curr.val, 0) + 1);
searchBST(curr.left, map);
@ -556,46 +556,7 @@ class Solution:
```
## Go
暴力法（非BSL）
```go
func findMode(root *TreeNode) []int {
var history map[int]int
var maxValue int
var maxIndex int
var result []int
history=make(map[int]int)
traversal(root,history)
for k,value:=range history{
if value>maxValue{
maxValue=value
maxIndex=k
}
}
for k,value:=range history{
if value==history[maxIndex]{
result=append(result,k)
}
}
return result
}
func traversal(root *TreeNode,history map[int]int){
if root.Left!=nil{
traversal(root.Left,history)
}
if value,ok:=history[root.Val];ok{
history[root.Val]=value+1
}else{
history[root.Val]=1
}
if root.Right!=nil{
traversal(root.Right,history)
}
}
```
计数法，不使用额外空间，利用二叉树性质，中序遍历
```go
func findMode(root *TreeNode) []int {
res := make([]int, 0)

162
problems/0513.找树左下角的值.md
View File

@ -26,7 +26,7 @@
## 思路
本地要找出树的最后一行找到最左边的值。此时大家应该想起用层序遍历是非常简单的了，反而用递归的话会比较难一点。
本题要找出树的最后一行的最左边的值。此时大家应该想起用层序遍历是非常简单的了，反而用递归的话会比较难一点。
我们依然还是先介绍递归法。
@ -46,7 +46,7 @@
所以要找深度最大的叶子节点。
那么如果找最左边的呢？可以使用前序遍历（当然中序，后序都可以，因为本题没有 中间节点的处理逻辑，只要左优先就行），保证优先左边搜索，然后记录深度最大的叶子节点，此时就是树的最后一行最左边的值。
那么如何找最左边的呢？可以使用前序遍历（当然中序，后序都可以，因为本题没有 中间节点的处理逻辑，只要左优先就行），保证优先左边搜索，然后记录深度最大的叶子节点，此时就是树的最后一行最左边的值。
递归三部曲：
@ -169,7 +169,7 @@ public:
### 迭代法
本题使用层序遍历再合适不过了，比递归要好理解的多！
本题使用层序遍历再合适不过了，比递归要好理解得多！
只需要记录最后一行第一个节点的数值就可以了。
@ -323,34 +323,25 @@ class Solution:
递归法：
```go
var maxDeep int // 全局变量 深度
var value int //全局变量 最终值
var depth int // 全局变量 最大深度
var res int // 记录最终结果
func findBottomLeftValue(root *TreeNode) int {
if root.Left==nil&&root.Right==nil{//需要提前判断一下（不要这个if的话提交结果会出错，但执行代码不会。防止这种情况出现，故先判断是否只有一个节点）
return root.Val
}
findLeftValue (root,maxDeep)
return value
depth, res = 0, 0 // 初始化
dfs(root, 1)
return res
}
func findLeftValue (root *TreeNode,deep int){
//最左边的值在左边
if root.Left==nil&&root.Right==nil{
if deep>maxDeep{
value=root.Val
maxDeep=deep
}
}
//递归
if root.Left!=nil{
deep++
findLeftValue(root.Left,deep)
deep--//回溯
func dfs(root *TreeNode, d int) {
if root == nil {
return
}
if root.Right!=nil{
deep++
findLeftValue(root.Right,deep)
deep--//回溯
// 因为先遍历左边，所以左边如果有值，右边的同层不会更新结果
if root.Left == nil && root.Right == nil && depth < d {
depth = d
res = root.Val
}
dfs(root.Left, d+1) // 隐藏回溯
dfs(root.Right, d+1)
}
```
@ -358,18 +349,21 @@ func findLeftValue (root *TreeNode,deep int){
```go
func findBottomLeftValue(root *TreeNode) int {
queue:=list.New()
var gradation int
queue := list.New()
queue.PushBack(root)
for queue.Len()>0{
length:=queue.Len()
for i:=0;i<length;i++{
node:=queue.Remove(queue.Front()).(*TreeNode)
if i==0{gradation=node.Val}
if node.Left!=nil{
for queue.Len() > 0 {
length := queue.Len()
for i := 0; i < length; i++ {
node := queue.Remove(queue.Front()).(*TreeNode)
if i == 0 {
gradation = node.Val
}
if node.Left != nil {
queue.PushBack(node.Left)
}
if node.Right!=nil{
if node.Right != nil {
queue.PushBack(node.Right)
}
}
@ -385,19 +379,18 @@ func findBottomLeftValue(root *TreeNode) int {
```javascript
var findBottomLeftValue = function(root) {
//首先考虑递归遍历 前序遍历 找到最大深度的叶子节点即可
let maxPath = 0,resNode = null;
let maxPath = 0, resNode = null;
// 1. 确定递归函数的函数参数
const dfsTree = function(node,curPath){
const dfsTree = function(node, curPath) {
// 2. 确定递归函数终止条件
if(node.left===null&&node.right===null){
if(curPath>maxPath){
if(node.left === null && node.right === null) {
if(curPath > maxPath) {
maxPath = curPath;
resNode = node.val;
}
// return ;
}
node.left&&dfsTree(node.left,curPath+1);
node.right&&dfsTree(node.right,curPath+1);
node.left && dfsTree(node.left, curPath+1);
node.right && dfsTree(node.right, curPath+1);
}
dfsTree(root,1);
return resNode;
@ -409,20 +402,20 @@ var findBottomLeftValue = function(root) {
var findBottomLeftValue = function(root) {
//考虑层序遍历 记录最后一行的第一个节点
let queue = [];
if(root===null){
if(root === null) {
return null;
}
queue.push(root);
let resNode;
while(queue.length){
let length = queue.length;
for(let i=0; i<length; i++){
while(queue.length) {
let length = queue.length;
for(let i = 0; i < length; i++) {
let node = queue.shift();
if(i===0){
if(i === 0) {
resNode = node.val;
}
node.left&&queue.push(node.left);
node.right&&queue.push(node.right);
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
}
return resNode;
@ -587,6 +580,77 @@ object Solution {
}
```
### rust
**层序遍历**
```rust
use std::cell::RefCell;
use std::collections::VecDeque;
use std::rc::Rc;
impl Solution {
pub fn find_bottom_left_value(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
let mut queue = VecDeque::new();
let mut res = 0;
if root.is_some() {
queue.push_back(root);
}
while !queue.is_empty() {
for i in 0..queue.len() {
let node = queue.pop_front().unwrap().unwrap();
if i == 0 {
res = node.borrow().val;
}
if node.borrow().left.is_some() {
queue.push_back(node.borrow().left.clone());
}
if node.borrow().right.is_some() {
queue.push_back(node.borrow().right.clone());
}
}
}
res
}
}
```
**递归**
```rust
use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
//*递归*/
pub fn find_bottom_left_value(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
let mut res = 0;
let mut max_depth = i32::MIN;
Self::traversal(root, 0, &mut max_depth, &mut res);
res
}
fn traversal(
root: Option<Rc<RefCell<TreeNode>>>,
depth: i32,
max_depth: &mut i32,
res: &mut i32,
) {
let node = root.unwrap();
if node.borrow().left.is_none() && node.borrow().right.is_none() {
if depth > *max_depth {
*max_depth = depth;
*res = node.borrow().val;
}
return;
}
if node.borrow().left.is_some() {
Self::traversal(node.borrow().left.clone(), depth + 1, max_depth, res);
}
if node.borrow().right.is_some() {
Self::traversal(node.borrow().right.clone(), depth + 1, max_depth, res);
}
}
}
```
<p align="center">
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>

22
problems/0530.二叉搜索树的最小绝对差.md
View File

@ -248,28 +248,6 @@ class Solution:
## Go：
中序遍历，然后计算最小差值
```go
func getMinimumDifference(root *TreeNode) int {
var res []int
findMIn(root,&res)
min:=1000000//一个比较大的值
for i:=1;i<len(res);i++{
tempValue:=res[i]-res[i-1]
if tempValue<min{
min=tempValue
}
}
return min
}
//中序遍历
func findMIn(root *TreeNode,res *[]int){
if root==nil{return}
findMIn(root.Left,res)
*res=append(*res,root.Val)
findMIn(root.Right,res)
}
```
```go
// 中序遍历的同时计算最小值
func getMinimumDifference(root *TreeNode) int {

36
problems/0538.把二叉搜索树转换为累加树.md
View File

@ -43,13 +43,17 @@
* 树中的所有值 互不相同 。
* 给定的树为二叉搜索树。
# 算法公开课
**《代码随想录》算法视频公开课：[普大喜奔！二叉树章节已全部更完啦！| LeetCode：538.把二叉搜索树转换为累加树](https://www.bilibili.com/video/BV1d44y1f7wP?share_source=copy_web)，相信结合视频在看本篇题解，更有助于大家对本题的理解**。
# 思路
一看到累加树，相信很多小伙伴都会疑惑：如何累加？遇到一个节点，然后在遍历其他节点累加？怎么一想这么麻烦呢。
一看到累加树，相信很多小伙伴都会疑惑：如何累加？遇到一个节点，然后再遍历其他节点累加？怎么一想这么麻烦呢。
然后再发现这是一棵二叉搜索树，二叉搜索树啊，这是有序的啊。
那么有序的元素如果求累加呢？
那么有序的元素如何求累加呢？
**其实这就是一棵树，大家可能看起来有点别扭，换一个角度来看，这就是一个有序数组[2, 5, 13]，求从后到前的累加数组，也就是[20, 18, 13]，是不是感觉这就简单了。**
@ -233,23 +237,23 @@ class Solution:
## Go
弄一个sum暂存其和值
```go
//右中左
func bstToGst(root *TreeNode) *TreeNode {
var sum int
RightMLeft(root,&sum)
return root
}
func RightMLeft(root *TreeNode,sum *int) *TreeNode {
if root==nil{return nil}//终止条件，遇到空节点就返回
RightMLeft(root.Right,sum)//先遍历右边
temp:=*sum//暂存总和值
*sum+=root.Val//将总和值变更
root.Val+=temp//更新节点值
RightMLeft(root.Left,sum)//遍历左节点
var pre int
func convertBST(root *TreeNode) *TreeNode {
pre = 0
traversal(root)
return root
}
func traversal(cur *TreeNode) {
if cur == nil {
return
}
traversal(cur.Right)
cur.Val += pre
pre = cur.Val
traversal(cur.Left)
}
```
## JavaScript

136
problems/0617.合并二叉树.md
View File

@ -46,7 +46,7 @@
1. **确定递归函数的参数和返回值：**
首先那么要合入两个二叉树，那么参数至少是要传入两个二叉树的根节点，返回值就是合并之后二叉树的根节点。
首先要合入两个二叉树，那么参数至少是要传入两个二叉树的根节点，返回值就是合并之后二叉树的根节点。
代码如下：
@ -56,7 +56,7 @@ TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
2. **确定终止条件：**
因为是传入了两个树，那么就有两个树遍历的节点t1 和 t2，如果t1 == NULL 了，两个树合并就应该是 t2 了啊（如果t2也为NULL也无所谓，合并之后就是NULL）。
因为是传入了两个树，那么就有两个树遍历的节点t1 和 t2，如果t1 == NULL 了，两个树合并就应该是 t2 了（如果t2也为NULL也无所谓，合并之后就是NULL）。
反过来如果t2 == NULL，那么两个数合并就是t1（如果t1也为NULL也无所谓，合并之后就是NULL）。
@ -70,7 +70,7 @@ if (t2 == NULL) return t1; // 如果t2为空，合并之后就应该是t1
3. **确定单层递归的逻辑：**
单层递归的逻辑就比较好些了，这里我们用重复利用一下t1这个树，t1就是合并之后树的根节点（就是修改了原来树的结构）。
单层递归的逻辑就比较好写了，这里我们重复利用一下t1这个树，t1就是合并之后树的根节点（就是修改了原来树的结构）。
那么单层递归中，就要把两棵树的元素加到一起。
```
@ -144,7 +144,7 @@ public:
**但是前序遍历是最好理解的，我建议大家用前序遍历来做就OK。**
如上的方法修改了t1的结构，当然也可以不修改t1和t2的结构，重新定一个树。
如上的方法修改了t1的结构，当然也可以不修改t1和t2的结构，重新定义一个树。
不修改输入树的结构，前序遍历，代码如下：
@ -214,7 +214,7 @@ public:
## 拓展
当然也可以秀一波指针的操作，这是我写的野路子，大家就随便看看就行了，以防带跑遍了。
当然也可以秀一波指针的操作，这是我写的野路子，大家就随便看看就行了，以防带跑偏了。
如下代码中，想要更改二叉树的值，应该传入指向指针的指针。
@ -252,7 +252,7 @@ public:
迭代法中，一般一起操作两个树都是使用队列模拟类似层序遍历，同时处理两个树的节点，这种方式最好理解，如果用模拟递归的思路的话，要复杂一些。
最后拓展中，我给了一个操作指针的野路子，大家随便看看就行了，如果学习C++的话，可以在去研究研究。
最后拓展中，我给了一个操作指针的野路子，大家随便看看就行了，如果学习C++的话，可以再去研究研究。
## 其他语言版本
@ -417,43 +417,7 @@ class Solution:
### Go
```go
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
//前序遍历（递归遍历，跟105 106差不多的思路）
func mergeTrees(t1 *TreeNode, t2 *TreeNode) *TreeNode {
var value int
var nullNode *TreeNode//空node，便于遍历
nullNode=&TreeNode{
Val:0,
Left:nil,
Right:nil}
switch {
case t1==nil&&t2==nil: return nil//终止条件
default : //如果其中一个节点为空，则将该节点置为nullNode，方便下次遍历
if t1==nil{
value=t2.Val
t1=nullNode
}else if t2==nil{
value=t1.Val
t2=nullNode
}else {
value=t1.Val+t2.Val
}
}
root:=&TreeNode{//构造新的二叉树
Val: value,
Left: mergeTrees(t1.Left,t2.Left),
Right: mergeTrees(t1.Right,t2.Right)}
return root
}
// 前序遍历简洁版
// 前序遍历
func mergeTrees(root1 *TreeNode, root2 *TreeNode) *TreeNode {
if root1 == nil {
return root2
@ -479,28 +443,28 @@ func mergeTrees(root1 *TreeNode, root2 *TreeNode) *TreeNode {
queue = append(queue,root1)
queue = append(queue,root2)
for size:=len(queue);size>0;size=len(queue){
for size := len(queue); size>0; size=len(queue) {
node1 := queue[0]
queue = queue[1:]
node2 := queue[0]
queue = queue[1:]
node1.Val += node2.Val
// 左子树都不为空
if node1.Left != nil && node2.Left != nil{
if node1.Left != nil && node2.Left != nil {
queue = append(queue,node1.Left)
queue = append(queue,node2.Left)
}
// 右子树都不为空
if node1.Right !=nil && node2.Right !=nil{
queue = append(queue,node1.Right)
queue = append(queue,node2.Right)
if node1.Right !=nil && node2.Right !=nil {
queue = append(queue, node1.Right)
queue = append(queue, node2.Right)
}
// 树 1 的左子树为 nil，直接接上树 2 的左子树
if node1.Left == nil{
if node1.Left == nil {
node1.Left = node2.Left
}
// 树 1 的右子树为 nil，直接接上树 2 的右子树
if node1.Right == nil{
if node1.Right == nil {
node1.Right = node2.Right
}
}
@ -691,6 +655,78 @@ object Solution {
}
```
### rust
递归：
```rust
use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
pub fn merge_trees(
root1: Option<Rc<RefCell<TreeNode>>>,
root2: Option<Rc<RefCell<TreeNode>>>,
) -> Option<Rc<RefCell<TreeNode>>> {
if root1.is_none() {
return root2;
}
if root2.is_none() {
return root1;
}
let binding = root1.clone();
let mut node1 = binding.as_ref().unwrap().borrow_mut();
let node2 = root2.as_ref().unwrap().borrow_mut();
node1.left = Self::merge_trees(node1.left.clone(), node2.left.clone());
node1.right = Self::merge_trees(node1.right.clone(), node2.right.clone());
node1.val += node2.val;
root1
}
}
```
迭代：
```rust
impl Solution {
pub fn merge_trees(
root1: Option<Rc<RefCell<TreeNode>>>,
root2: Option<Rc<RefCell<TreeNode>>>,
) -> Option<Rc<RefCell<TreeNode>>> {
if root1.is_none() {
return root2;
}
if root2.is_none() {
return root1;
}
let mut stack = vec![];
stack.push(root2);
stack.push(root1.clone());
while !stack.is_empty() {
let node1 = stack.pop().unwrap().unwrap();
let node2 = stack.pop().unwrap().unwrap();
let mut node1 = node1.borrow_mut();
let node2 = node2.borrow();
node1.val += node2.val;
if node1.left.is_some() && node2.left.is_some() {
stack.push(node2.left.clone());
stack.push(node1.left.clone());
}
if node1.right.is_some() && node2.right.is_some() {
stack.push(node2.right.clone());
stack.push(node1.right.clone());
}
if node1.left.is_none() && node2.left.is_some() {
node1.left = node2.left.clone();
}
if node1.right.is_none() && node2.right.is_some() {
node1.right = node2.right.clone();
}
}
root1
}
}
```
<p align="center">
<a href="https://programmercarl.com/other/kstar.html" target="_blank">

91
problems/0654.最大二叉树.md
View File

@ -40,7 +40,7 @@
* 确定递归函数的参数和返回值
参数就是传入的是存放元素的数组，返回该数组构造的二叉树的头结点，返回类型是指向节点的指针。
参数传入的是存放元素的数组，返回该数组构造的二叉树的头结点，返回类型是指向节点的指针。
代码如下：
@ -309,30 +309,24 @@ class Solution:
```go
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func constructMaximumBinaryTree(nums []int) *TreeNode {
if len(nums)<1{return nil}
//首选找到最大值
index:=findMax(nums)
//其次构造二叉树
root:=&TreeNode{
if len(nums) == 0 {
return nil
}
// 找到最大值
index := findMax(nums)
// 构造二叉树
root := &TreeNode {
Val: nums[index],
Left:constructMaximumBinaryTree(nums[:index]),//左半边
Right:constructMaximumBinaryTree(nums[index+1:]),//右半边
Left: constructMaximumBinaryTree(nums[:index]), //左半边
Right: constructMaximumBinaryTree(nums[index+1:]),//右半边
}
return root
}
func findMax(nums []int) (index int){
for i:=0;i<len(nums);i++{
if nums[i]>nums[index]{
index=i
func findMax(nums []int) (index int) {
for i, v := range nums {
if nums[index] < v {
index = i
}
}
return
@ -509,6 +503,63 @@ object Solution {
}
```
### Rust
新建数组：
```rust
use std::cell::RefCell;
use std::rc::Rc;
impl Solution{
pub fn construct_maximum_binary_tree(mut nums: Vec<i32>) -> Option<Rc<RefCell<TreeNode>>> {
if nums.is_empty() {
return None;
}
let mut max_value_index = 0;
for i in 0..nums.len() {
if nums[max_value_index] < nums[i] {
max_value_index = i;
}
}
let right = Self::construct_maximum_binary_tree(nums.split_off(max_value_index + 1));
let root = nums.pop().unwrap();
let left = Self::construct_maximum_binary_tree(nums);
Some(Rc::new(RefCell::new(TreeNode {
val: root,
left,
right,
})))
}
}
```
数组索引：
```rust
use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
pub fn construct_maximum_binary_tree(nums: Vec<i32>) -> Option<Rc<RefCell<TreeNode>>> {
Self::traversal(&nums, 0, nums.len())
}
pub fn traversal(nums: &Vec<i32>, left: usize, right: usize) -> Option<Rc<RefCell<TreeNode>>> {
if left >= right {
return None;
}
let mut max_value_index = left;
for i in left + 1..right {
if nums[max_value_index] < nums[i] {
max_value_index = i;
}
}
let mut root = TreeNode::new(nums[max_value_index]);
root.left = Self::traversal(nums, left, max_value_index);
root.right = Self::traversal(nums, max_value_index + 1, right);
Some(Rc::new(RefCell::new(root)))
}
}
```
<p align="center">
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>

31
problems/0657.机器人能否返回原点.md
View File

@ -150,6 +150,37 @@ var judgeCircle = function(moves) {
```
## TypeScript
```ts
var judgeCircle = function (moves) {
let x = 0
let y = 0
for (let i = 0; i < moves.length; i++) {
switch (moves[i]) {
case 'L': {
x--
break
}
case 'R': {
x++
break
}
case 'U': {
y--
break
}
case 'D': {
y++
break
}
}
}
return x === 0 && y === 0
};
```
<p align="center">
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>

60
problems/0669.修剪二叉搜索树.md
View File

@ -18,6 +18,10 @@
![669.修剪二叉搜索树1](https://img-blog.csdnimg.cn/20201014173219142.png)
# 算法公开课
**《代码随想录》算法视频公开课：[你修剪的方式不对，我来给你纠正一下！| LeetCode：669. 修剪二叉搜索树](https://www.bilibili.com/video/BV17P41177ud?share_source=copy_web)，相信结合视频在看本篇题解，更有助于大家对本题的理解**。
# 思路
相信看到这道题目大家都感觉是一道简单题（事实上leetcode上也标明是简单）。
@ -59,7 +63,7 @@ public:
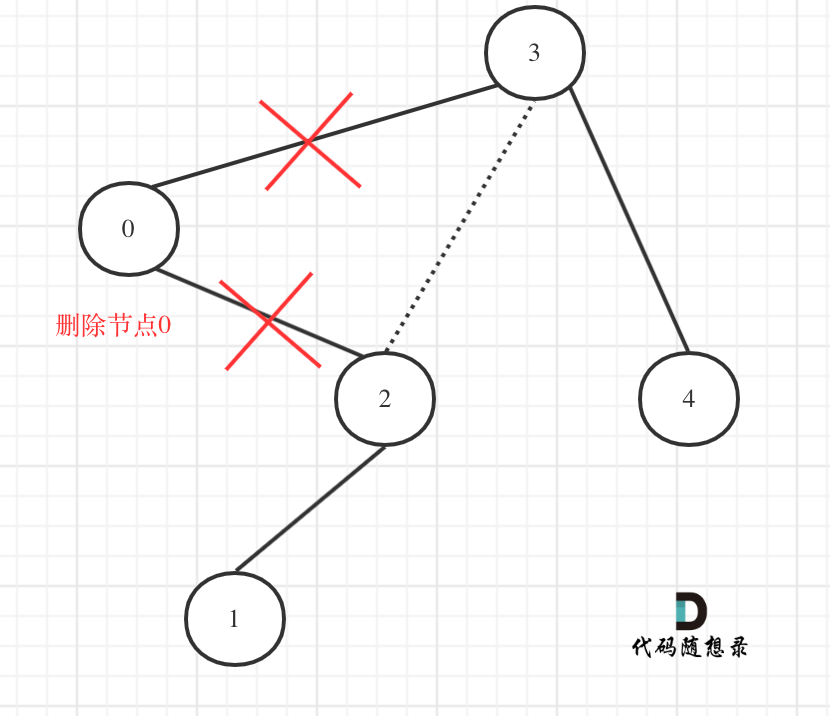
![669.修剪二叉搜索树1](https://img-blog.csdnimg.cn/20210204155327203.png)
理解了最关键部分了我们在递归三部曲：
理解了最关键部分了我们再递归三部曲：
* 确定递归函数的参数以及返回值
@ -179,7 +183,7 @@ public:
};
```
只看代码，其实不太好理解节点是符合移除的，这一块大家可以自己在模拟模拟！
只看代码，其实不太好理解节点是如何移除的，这一块大家可以自己再模拟模拟！
## 迭代法
@ -301,19 +305,19 @@ class Solution:
// 递归
func trimBST(root *TreeNode, low int, high int) *TreeNode {
if root==nil{
if root == nil {
return nil
}
if root.Val<low{//如果该节点值小于最小值，则该节点更换为该节点的右节点值，继续遍历
right:=trimBST(root.Right,low,high)
if root.Val < low { //如果该节点值小于最小值，则该节点更换为该节点的右节点值，继续遍历
right := trimBST(root.Right, low, high)
return right
}
if root.Val>high{//如果该节点的值大于最大值，则该节点更换为该节点的左节点值，继续遍历
left:=trimBST(root.Left,low,high)
if root.Val > high { //如果该节点的值大于最大值，则该节点更换为该节点的左节点值，继续遍历
left := trimBST(root.Left, low, high)
return left
}
root.Left=trimBST(root.Left,low,high)
root.Right=trimBST(root.Right,low,high)
root.Left = trimBST(root.Left, low, high)
root.Right = trimBST(root.Right, low, high)
return root
}
@ -323,25 +327,25 @@ func trimBST(root *TreeNode, low int, high int) *TreeNode {
return nil
}
// 处理 root，让 root 移动到[low, high] 范围内，注意是左闭右闭
for root != nil && (root.Val<low||root.Val>high){
if root.Val < low{
for root != nil && (root.Val < low || root.Val > high) {
if root.Val < low {
root = root.Right
}else{
} else {
root = root.Left
}
}
cur := root
// 此时 root 已经在[low, high] 范围内，处理左孩子元素小于 low 的情况（左节点是一定小于 root.Val，因此天然小于 high）
for cur != nil{
for cur.Left!=nil && cur.Left.Val < low{
for cur != nil {
for cur.Left != nil && cur.Left.Val < low {
cur.Left = cur.Left.Right
}
cur = cur.Left
}
cur = root
// 此时 root 已经在[low, high] 范围内，处理右孩子大于 high 的情况
for cur != nil{
for cur.Right!=nil && cur.Right.Val > high{
for cur != nil {
for cur.Right != nil && cur.Right.Val > high {
cur.Right = cur.Right.Left
}
cur = cur.Right
@ -359,24 +363,24 @@ var trimBST = function(root, low, high) {
if(root === null) {
return null;
}
while(root !==null &&(root.val<low||root.val>high)) {
if(root.val<low) {
while(root !== null && (root.val < low || root.val > high)) {
if(root.val < low) {
root = root.right;
}else {
root = root.left;
}
}
let cur = root;
while(cur!==null) {
while(cur.left&&cur.left.val<low) {
while(cur !== null) {
while(cur.left && cur.left.val < low) {
cur.left = cur.left.right;
}
cur = cur.left;
}
cur = root;
//判断右子树大于high的情况
while(cur!==null) {
while(cur.right&&cur.right.val>high) {
while(cur !== null) {
while(cur.right && cur.right.val > high) {
cur.right = cur.right.left;
}
cur = cur.right;
@ -391,16 +395,16 @@ var trimBST = function (root,low,high) {
if(root === null) {
return null;
}
if(root.val<low) {
let right = trimBST(root.right,low,high);
if(root.val < low) {
let right = trimBST(root.right, low, high);
return right;
}
if(root.val>high) {
let left = trimBST(root.left,low,high);
if(root.val > high) {
let left = trimBST(root.left, low, high);
return left;
}
root.left = trimBST(root.left,low,high);
root.right = trimBST(root.right,low,high);
root.left = trimBST(root.left, low, high);
root.right = trimBST(root.right, low, high);
return root;
}
```

1
problems/0695.岛屿的最大面积.md
View File

@ -197,7 +197,6 @@ class Solution:
if not visited[i][j] and grid[i][j] == 1:
# 每一个新岛屿
self.count = 0
print(f'{self.count}')
self.bfs(grid, visited, i, j)
result = max(result, self.count)

74
problems/0700.二叉搜索树中的搜索.md
View File

@ -24,7 +24,7 @@
## 思路
之前我们讲了都是普通二叉树，那么接下来看看二叉搜索树。
之前我们讲的都是普通二叉树，那么接下来看看二叉搜索树。
在[关于二叉树，你该了解这些！](https://programmercarl.com/二叉树理论基础.html)中，我们已经讲过了二叉搜索树。
@ -269,13 +269,13 @@ class Solution:
```go
//递归法
func searchBST(root *TreeNode, val int) *TreeNode {
if root==nil||root.Val==val{
if root == nil || root.Val == val {
return root
}
if root.Val>val{
return searchBST(root.Left,val)
if root.Val > val {
return searchBST(root.Left, val)
}
return searchBST(root.Right,val)
return searchBST(root.Right, val)
}
```
@ -284,13 +284,13 @@ func searchBST(root *TreeNode, val int) *TreeNode {
```go
//迭代法
func searchBST(root *TreeNode, val int) *TreeNode {
for root!=nil{
if root.Val>val{
root=root.Left
}else if root.Val<val{
root=root.Right
}else{
break
for root != nil {
if root.Val > val {
root = root.Left
} else if root.Val < val {
root = root.Right
} else {
return root
}
}
return nil
@ -414,6 +414,56 @@ object Solution {
}
```
### rust
递归：
```rust
use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
pub fn search_bst(
root: Option<Rc<RefCell<TreeNode>>>,
val: i32,
) -> Option<Rc<RefCell<TreeNode>>> {
if root.is_none() || root.as_ref().unwrap().borrow().val == val {
return root;
}
let node_val = root.as_ref().unwrap().borrow().val;
if node_val > val {
return Self::search_bst(root.as_ref().unwrap().borrow().left.clone(), val);
}
if node_val < val {
return Self::search_bst(root.unwrap().borrow().right.clone(), val);
}
None
}
}
```
迭代：
```rust
use std::cell::RefCell;
use std::rc::Rc;
use std::cmp;
impl Solution {
pub fn search_bst(
mut root: Option<Rc<RefCell<TreeNode>>>,
val: i32,
) -> Option<Rc<RefCell<TreeNode>>> {
while let Some(ref node) = root.clone() {
match val.cmp(&node.borrow().val) {
cmp::Ordering::Less => root = node.borrow().left.clone(),
cmp::Ordering::Equal => return root,
cmp::Ordering::Greater => root = node.borrow().right.clone(),
};
}
None
}
}
```
<p align="center">
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>

11
problems/0701.二叉搜索树中的插入操作.md
View File

@ -22,14 +22,13 @@
* -10^8 <= val <= 10^8
* 新值和原始二叉搜索树中的任意节点值都不同
# 视频讲解
**《代码随想录》算法视频公开课：[原来这么简单？ | LeetCode：701.二叉搜索树中的插入操作](https://www.bilibili.com/video/BV1Et4y1c78Y)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
# 算法公开课
**《代码随想录》算法视频公开课：[原来这么简单？ | LeetCode：701.二叉搜索树中的插入操作](https://www.bilibili.com/video/BV1Et4y1c78Y?share_source=copy_web)，相信结合视频在看本篇题解，更有助于大家对本题的理解**。
# 思路
其实这道题目其实是一道简单题目，**但是题目中的提示：有多种有效的插入方式，还可以重构二叉搜索树，一下子吓退了不少人**，瞬间感觉题目复杂了很多。
这道题目其实是一道简单题目，**但是题目中的提示：有多种有效的插入方式，还可以重构二叉搜索树，一下子吓退了不少人**，瞬间感觉题目复杂了很多。
其实**可以不考虑题目中提示所说的改变树的结构的插入方式。**
@ -162,7 +161,7 @@ public:
我之所以举这个例子，是想说明通过递归函数的返回值完成父子节点的赋值是可以带来便利的。
**网上千变一律的代码，可能会误导大家认为通过递归函数返回节点 这样的写法是天经地义，其实这里是有优化的！**
**网上千篇一律的代码，可能会误导大家认为通过递归函数返回节点 这样的写法是天经地义，其实这里是有优化的！**
## 迭代
@ -202,7 +201,7 @@ public:
首先在二叉搜索树中的插入操作，大家不用恐惧其重构搜索树，其实根本不用重构。
然后在递归中，我们重点讲了如果通过递归函数的返回值完成新加入节点和其父节点的赋值操作，并强调了搜索树的有序性。
然后在递归中，我们重点讲了如何通过递归函数的返回值完成新加入节点和其父节点的赋值操作，并强调了搜索树的有序性。
最后依然给出了迭代的方法，迭代的方法就需要记录当前遍历节点的父节点了，这个和没有返回值的递归函数实现的代码逻辑是一样的。

34
problems/0704.二分查找.md
View File

@ -204,18 +204,18 @@ class Solution {
```python
class Solution:
def search(self, nums: List[int], target: int) -> int:
left, right = 0, len(nums) - 1
left, right = 0, len(nums) - 1 # 定义target在左闭右闭的区间里，[left, right]
while left <= right:
middle = (left + right) // 2
middle = left + (right - left) // 2
if nums[middle] < target:
left = middle + 1
elif nums[middle] > target:
right = middle - 1
if nums[middle] > target:
right = middle - 1 # target在左区间，所以[left, middle - 1]
elif nums[middle] < target:
left = middle + 1 # target在右区间，所以[middle + 1, right]
else:
return middle
return -1
return middle # 数组中找到目标值，直接返回下标
return -1 # 未找到目标值
```
（版本二）左闭右开区间
@ -223,18 +223,18 @@ class Solution:
```python
class Solution:
def search(self, nums: List[int], target: int) -> int:
left, right = 0, len(nums)
left, right = 0, len(nums) # 定义target在左闭右开的区间里，即：[left, right)
while left < right:
middle = (left + right) // 2
while left < right: # 因为left == right的时候，在[left, right)是无效的空间，所以使用 <
middle = left + (right - left) // 2
if nums[middle] < target:
left = middle + 1
elif nums[middle] > target:
right = middle
if nums[middle] > target:
right = middle # target 在左区间，在[left, middle)中
elif nums[middle] < target:
left = middle + 1 # target 在右区间，在[middle + 1, right)中
else:
return middle
return -1
return middle # 数组中找到目标值，直接返回下标
return -1 # 未找到目标值
```
**Go：**

11
problems/0707.设计链表.md
View File

@ -106,14 +106,11 @@ public:
// 在第index个节点之前插入一个新节点，例如index为0，那么新插入的节点为链表的新头节点。
// 如果index 等于链表的长度，则说明是新插入的节点为链表的尾结点
// 如果index大于链表的长度，则返回空
// 如果index小于0，则置为0，作为链表的新头节点。
// 如果index小于0，则在头部插入节点
void addAtIndex(int index, int val) {
if (index > _size) {
return;
}
if (index < 0) {
index = 0;
}
if(index > _size) return;
if(index < 0) index = 0;
LinkedNode* newNode = new LinkedNode(val);
LinkedNode* cur = _dummyHead;
while(index--) {

79
problems/0746.使用最小花费爬楼梯.md
View File

@ -83,7 +83,7 @@ dp[i - 2] 跳到 dp[i] 需要花费 dp[i - 2] + cost[i - 2]。
那么 dp[0] 应该是多少呢？ 根据dp数组的定义，到达第0台阶所花费的最小体力为dp[0]，那么有同学可能想，那dp[0] 应该是 cost[0]，例如 cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] 的话，dp[0] 就是 cost[0] 应该是1。
这里就要说名了，本题力扣为什么改题意了，而且修改题意之后 就清晰很多的原因了。
这里就要说明本题力扣为什么改题意，而且修改题意之后 就清晰很多的原因了。
新题目描述中明确说了 “你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。” 也就是说 从 到达 第 0 个台阶是不花费的，但从 第0 个台阶 往上跳的话，需要花费 cost[0]。
@ -101,7 +101,7 @@ dp[i - 2] 跳到 dp[i] 需要花费 dp[i - 2] + cost[i - 2]。
> **但是稍稍有点难度的动态规划，其遍历顺序并不容易确定下来**。
> 例如：01背包，都知道两个for循环，一个for遍历物品嵌套一个for遍历背包容量，那么为什么不是一个for遍历背包容量嵌套一个for遍历物品呢？ 以及在使用一维dp数组的时候遍历背包容量为什么要倒序呢？
**这些都是遍历顺序息息相关。当然背包问题后续「代码随想录」都会重点讲解的！**
**这些都与遍历顺序息息相关。当然背包问题后续「代码随想录」都会重点讲解的！**
5. 举例推导dp数组
@ -182,7 +182,7 @@ public:
## 总结
大家可以发现这道题目相对于 昨天的[动态规划：爬楼梯](https://programmercarl.com/0070.爬楼梯.html)有难了一点，但整体思路是一样。
大家可以发现这道题目相对于 昨天的[动态规划：爬楼梯](https://programmercarl.com/0070.爬楼梯.html)又难了一点，但整体思路是一样的。
从[动态规划：斐波那契数](https://programmercarl.com/0509.斐波那契数.html)到 [动态规划：爬楼梯](https://programmercarl.com/0070.爬楼梯.html)再到今天这道题目，录友们感受到循序渐进的梯度了嘛。
@ -241,45 +241,56 @@ class Solution {
### Python
```python
# 第一步不支付费用
class Solution:
def minCostClimbingStairs(self, cost: List[int]) -> int:
dp = [0] * (len(cost))
dp[0] = cost[0]
dp[1] = cost[1]
for i in range(2, len(cost)):
dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i]
return min(dp[len(cost) - 1], dp[len(cost) - 2])
n = len(cost)
dp = [0]*(n+1) # 到达前两步费用为0
for i in range(2, n+1):
dp[i] = min(dp[i-1]+cost[i-1], dp[i-2]+cost[i-2])
return dp[-1]
```
```python
# 第一步支付费用
class Solution:
def minCostClimbingStairs(self, cost: List[int]) -> int:
dp = [0] * (len(cost) + 1)
dp[0] = 0
dp[1] = 0
for i in range(2, len(cost) + 1):
dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i-2])
return dp[len(cost)]
```
### Go
```Go
func minCostClimbingStairs(cost []int) int {
dp := make([]int, len(cost))
dp[0], dp[1] = cost[0], cost[1]
for i := 2; i < len(cost); i++ {
dp[i] = min(dp[i-1], dp[i-2]) + cost[i]
}
return min(dp[len(cost)-1], dp[len(cost)-2])
f := make([]int, len(cost) + 1)
f[0], f[1] = 0, 0
for i := 2; i <= len(cost); i++ {
f[i] = min(f[i-1] + cost[i-1], f[i-2] + cost[i-2])
}
return f[len(cost)]
}
func min(a, b int) int {
if a < b {
return a
}
return b
if a < b {
return a
}
return b
}
```
### Javascript
```Javascript
var minCostClimbingStairs = function(cost) {
const dp = [ cost[0], cost[1] ]
for (let i = 2; i < cost.length; ++i) {
dp[i] = Math.min(dp[i -1] + cost[i], dp[i - 2] + cost[i])
const n = cost.length;
const dp = new Array(n + 1);
dp[0] = dp[1] = 0;
for (let i = 2; i <= n; ++i) {
dp[i] = Math.min(dp[i -1] + cost[i - 1], dp[i - 2] + cost[i - 2])
}
return Math.min(dp[cost.length - 1], dp[cost.length - 2])
return dp[n]
};
```
@ -289,19 +300,19 @@ var minCostClimbingStairs = function(cost) {
function minCostClimbingStairs(cost: number[]): number {
/**
dp[i]: 走到第i阶需要花费的最少金钱
dp[0]: cost[0];
dp[1]: cost[1];
dp[0]: 0;
dp[1]: 0;
...
dp[i]: min(dp[i - 1], dp[i - 2]) + cost[i];
dp[i]: min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
*/
const dp: number[] = [];
const length: number = cost.length;
dp[0] = cost[0];
dp[1] = cost[1];
const dp = [];
const length = cost.length;
dp[0] = 0;
dp[1] = 0;
for (let i = 2; i <= length; i++) {
dp[i] = Math.min(dp[i - 1], dp[i - 2]) + cost[i];
dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
}
return Math.min(dp[length - 1], dp[length - 2]);
return dp[length];
};
```

45
problems/0860.柠檬水找零.md
View File

@ -54,7 +54,7 @@
这是前几天的leetcode每日一题，感觉不错，给大家讲一下。
这道题目刚一看，可能会有点懵，这要怎么找零才能保证完整全部账单的找零呢？
这道题目刚一看，可能会有点懵，这要怎么找零才能保证完成全部账单的找零呢？
**但仔细一琢磨就会发现，可供我们做判断的空间非常少！**
@ -179,38 +179,23 @@ class Solution:
### Go
```golang
```go
func lemonadeChange(bills []int) bool {
//left表示还剩多少 下标0位5元的个数 ，下标1为10元的个数
left:=[2]int{0,0}
//第一个元素不为5，直接退出
if bills[0]!=5{
return false
}
for i:=0;i<len(bills);i++{
//先统计5元和10元的个数
if bills[i]==5{
left[0]+=1
}
if bills[i]==10{
left[1]+=1
}
//接着处理找零的
tmp:=bills[i]-5
if tmp==5{
if left[0]>0{
left[0]-=1
}else {
ten, five := 0, 0
for i := 0; i < len(bills); i++ {
if bills[i] == 5 {
five++
} else if bills[i] == 10 {
if five == 0 {
return false
}
}
if tmp==15{
if left[1]>0&&left[0]>0{
left[0]-=1
left[1]-=1
}else if left[1]==0&&left[0]>2{
left[0]-=3
}else{
ten++; five--
} else {
if ten >= 1 && five >= 1 {
ten--; five--
} else if five >= 3 {
five -= 3
} else {
return false
}
}

9
problems/1047.删除字符串中的所有相邻重复项.md
View File

@ -50,7 +50,7 @@
![1047.删除字符串中的所有相邻重复项](https://code-thinking.cdn.bcebos.com/gifs/1047.删除字符串中的所有相邻重复项.gif)
从栈中弹出剩余元素，此时是字符串ac，因为从栈里弹出的元素是倒序的，所以在对字符串进行反转一下，就得到了最终的结果。
从栈中弹出剩余元素，此时是字符串ac，因为从栈里弹出的元素是倒序的，所以再对字符串进行反转一下，就得到了最终的结果。
C++代码 :
@ -102,9 +102,9 @@ public:
## 题外话
这道题目就像是我们玩过的游戏对对碰，如果相同的元素放在挨在一起就要消除。
这道题目就像是我们玩过的游戏对对碰，如果相同的元素挨在一起就要消除。
可能我们在玩游戏的时候感觉理所当然应该消除，但程序又怎么知道该如果消除呢，特别是消除之后又有新的元素可能挨在一起。
可能我们在玩游戏的时候感觉理所当然应该消除，但程序又怎么知道该如何消除呢，特别是消除之后又有新的元素可能挨在一起。
此时游戏的后端逻辑就可以用一个栈来实现（我没有实际考察对对碰或者爱消除游戏的代码实现，仅从原理上进行推断）。
@ -153,6 +153,8 @@ class Solution {
class Solution {
public String removeDuplicates(String s) {
// 将 res 当做栈
// 也可以用 StringBuilder 来修改字符串，速度更快
// StringBuilder res = new StringBuilder();
StringBuffer res = new StringBuffer();
// top为 res 的长度
int top = -1;
@ -470,3 +472,4 @@ impl Solution {
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>
</a>

69
problems/二叉树中递归带着回溯.md
View File

@ -617,6 +617,75 @@ func _binaryTreePaths3(_ root: TreeNode, res: inout [String], paths: inout [Int]
}
```
### Rust
> 100.相同的树
```rsut
use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
pub fn is_same_tree(
p: Option<Rc<RefCell<TreeNode>>>,
q: Option<Rc<RefCell<TreeNode>>>,
) -> bool {
match (p, q) {
(None, None) => true,
(None, Some(_)) => false,
(Some(_), None) => false,
(Some(n1), Some(n2)) => {
if n1.borrow().val == n2.borrow().val {
let right =
Self::is_same_tree(n1.borrow().left.clone(), n2.borrow().left.clone());
let left =
Self::is_same_tree(n1.borrow().right.clone(), n2.borrow().right.clone());
right && left
} else {
false
}
}
}
}
}
```
> 257.二叉树的不同路径
```rust
// 递归
use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
pub fn binary_tree_paths(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<String> {
let mut res = vec![];
let mut path = vec![];
Self::recur(&root, &mut path, &mut res);
res
}
pub fn recur(
root: &Option<Rc<RefCell<TreeNode>>>,
path: &mut Vec<String>,
res: &mut Vec<String>,
) {
let node = root.as_ref().unwrap().borrow();
path.push(node.val.to_string());
if node.left.is_none() && node.right.is_none() {
res.push(path.join("->"));
return;
}
if node.left.is_some() {
Self::recur(&node.left, path, res);
path.pop(); //回溯
}
if node.right.is_some() {
Self::recur(&node.right, path, res);
path.pop(); //回溯
}
}
}
```
<p align="center">
<a href="https://programmercarl.com/other/kstar.html" target="_blank">

6
problems/二叉树理论基础.md
View File

@ -14,7 +14,7 @@
<img src='https://img-blog.csdnimg.cn/20210219190809451.png' width=600 alt='二叉树大纲'> </img></div>
说道二叉树，大家对于二叉树其实都很熟悉了，本文呢我也不想教科书式的把二叉树的基础内容在啰嗦一遍，所以一下我讲的都是一些比较重点的内容。
说到二叉树，大家对于二叉树其实都很熟悉了，本文呢我也不想教科书式的把二叉树的基础内容再啰嗦一遍，所以以下我讲的都是一些比较重点的内容。
相信只要耐心看完，都会有所收获。
@ -83,7 +83,7 @@
那么链式存储方式就用指针， 顺序存储的方式就是用数组。
顾名思义就是顺序存储的元素在内存是连续分布的，而链式存储则是通过指针把分布在散落在各个地址的节点串联一起。
顾名思义就是顺序存储的元素在内存是连续分布的，而链式存储则是通过指针把分布在各个地址的节点串联一起。
链式存储如图：
@ -143,7 +143,7 @@
最后再说一说二叉树中深度优先和广度优先遍历实现方式，我们做二叉树相关题目，经常会使用递归的方式来实现深度优先遍历，也就是实现前中后序遍历，使用递归是比较方便的。
**之前我们讲栈与队列的时候，就说过栈其实就是递归的一种是实现结构**，也就说前中后序遍历的逻辑其实都是可以借助栈使用非递归的方式来实现的。
**之前我们讲栈与队列的时候，就说过栈其实就是递归的一种实现结构**，也就说前中后序遍历的逻辑其实都是可以借助栈使用非递归的方式来实现的。
而广度优先遍历的实现一般使用队列来实现，这也是队列先进先出的特点所决定的，因为需要先进先出的结构，才能一层一层的来遍历二叉树。

4
problems/二叉树的递归遍历.md
View File

@ -36,13 +36,13 @@
**以下以前序遍历为例：**
1. **确定递归函数的参数和返回值**：因为要打印出前序遍历节点的数值，所以参数里需要传入vector在放节点的数值，除了这一点就不需要在处理什么数据了也不需要有返回值，所以递归函数返回类型就是void，代码如下：
1. **确定递归函数的参数和返回值**：因为要打印出前序遍历节点的数值，所以参数里需要传入vector来放节点的数值，除了这一点就不需要再处理什么数据了也不需要有返回值，所以递归函数返回类型就是void，代码如下：
```cpp
void traversal(TreeNode* cur, vector<int>& vec)
```
2. **确定终止条件**：在递归的过程中，如何算是递归结束了呢，当然是当前遍历的节点是空了，那么本层递归就要要结束了，所以如果当前遍历的这个节点是空，就直接return，代码如下：
2. **确定终止条件**：在递归的过程中，如何算是递归结束了呢，当然是当前遍历的节点是空了，那么本层递归就要结束了，所以如果当前遍历的这个节点是空，就直接return，代码如下：
```cpp
if (cur == NULL) return;

6
problems/栈与队列理论基础.md
View File

@ -12,7 +12,7 @@
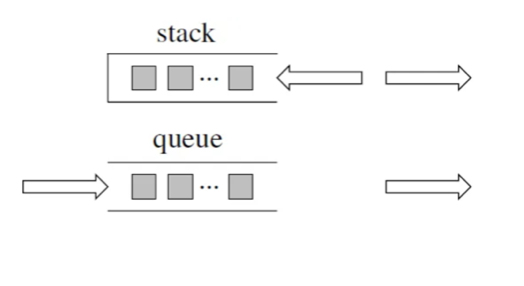
![栈与队列理论1](https://img-blog.csdnimg.cn/20210104235346563.png)
那么我这里在列出四个关于栈的问题，大家可以思考一下。以下是以C++为例，相信使用其他编程语言的同学也对应思考一下，自己使用的编程语言里栈和队列是什么样的。
那么我这里再列出四个关于栈的问题，大家可以思考一下。以下是以C++为例，使用其他编程语言的同学也对应思考一下，自己使用的编程语言里栈和队列是什么样的。
1. C++中stack 是容器么？
2. 我们使用的stack是属于哪个版本的STL？
@ -23,7 +23,7 @@
有的同学可能仅仅知道有栈和队列这么个数据结构，却不知道底层实现，也不清楚所使用栈和队列和STL是什么关系。
所以这里我在给大家扫一遍基础知识，
所以这里我再给大家扫一遍基础知识，
首先大家要知道 栈和队列是STL（C++标准库）里面的两个数据结构。
@ -83,7 +83,7 @@ std::queue<int, std::list<int>> third; // 定义以list为底层容器的队列
所以STL 队列也不被归类为容器，而被归类为container adapter（ 容器适配器）。
我这里讲的都是C++ 语言中情况， 使用其他语言的同学也要思考栈与队列的底层实现问题， 不要对数据结构的使用浅尝辄止，而要深挖起内部原理，才能夯实基础。
我这里讲的都是C++ 语言中的情况， 使用其他语言的同学也要思考栈与队列的底层实现问题， 不要对数据结构的使用浅尝辄止，而要深挖其内部原理，才能夯实基础。

71
problems/背包理论基础01背包-1.md
View File

@ -271,39 +271,64 @@ int main() {
### java
```java
public class BagProblem {
public static void main(String[] args) {
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
int bagsize = 4;
testweightbagproblem(weight, value, bagsize);
int[] weight = {1,3,4};
int[] value = {15,20,30};
int bagSize = 4;
testWeightBagProblem(weight,value,bagSize);
}
public static void testweightbagproblem(int[] weight, int[] value, int bagsize){
int wlen = weight.length, value0 = 0;
//定义dp数组：dp[i][j]表示背包容量为j时，前i个物品能获得的最大价值
int[][] dp = new int[wlen + 1][bagsize + 1];
//初始化：背包容量为0时，能获得的价值都为0
for (int i = 0; i <= wlen; i++){
dp[i][0] = value0;
/**
* 动态规划获得结果
* @param weight 物品的重量
* @param value 物品的价值
* @param bagSize 背包的容量
*/
public static void testWeightBagProblem(int[] weight, int[] value, int bagSize){
// 创建dp数组
int goods = weight.length; // 获取物品的数量
int[][] dp = new int[goods][bagSize + 1];
// 初始化dp数组
// 创建数组后，其中默认的值就是0
for (int j = weight[0]; j <= bagSize; j++) {
dp[0][j] = value[0];
}
//遍历顺序：先遍历物品，再遍历背包容量
for (int i = 1; i <= wlen; i++){
for (int j = 1; j <= bagsize; j++){
if (j < weight[i - 1]){
dp[i][j] = dp[i - 1][j];
}else{
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i - 1]] + value[i - 1]);
// 填充dp数组
for (int i = 1; i < weight.length; i++) {
for (int j = 1; j <= bagSize; j++) {
if (j < weight[i]) {
/**
* 当前背包的容量都没有当前物品i大的时候，是不放物品i的
* 那么前i-1个物品能放下的最大价值就是当前情况的最大价值
*/
dp[i][j] = dp[i-1][j];
} else {
/**
* 当前背包的容量可以放下物品i
* 那么此时分两种情况：
* 1、不放物品i
* 2、放物品i
* 比较这两种情况下，哪种背包中物品的最大价值最大
*/
dp[i][j] = Math.max(dp[i-1][j] , dp[i-1][j-weight[i]] + value[i]);
}
}
}
//打印dp数组
for (int i = 0; i <= wlen; i++){
for (int j = 0; j <= bagsize; j++){
System.out.print(dp[i][j] + " ");
// 打印dp数组
for (int i = 0; i < goods; i++) {
for (int j = 0; j <= bagSize; j++) {
System.out.print(dp[i][j] + "\t");
}
System.out.print("\n");
System.out.println("\n");
}
}
}
```
### python