Merge branch 'youngyangyang04:master' into patch-7

README.md

@@ -131,7 +131,7 @@
 1. [数组过于简单，但你该了解这些！](./problems/数组理论基础.md) 
 2. [数组：二分查找](./problems/0704.二分查找.md)
 3. [数组：移除元素](./problems/0027.移除元素.md)
-4. [数组：序数组的平方](./problems/0977.有序数组的平方.md)    
+4. [数组：有序数组的平方](./problems/0977.有序数组的平方.md)    
 5. [数组：长度最小的子数组](./problems/0209.长度最小的子数组.md)
 6. [数组：螺旋矩阵II](./problems/0059.螺旋矩阵II.md)
 7. [数组：总结篇](./problems/数组总结篇.md)

problems/0028.实现strStr.md

@@ -174,9 +174,11 @@ next数组就是一个前缀表（prefix table）。
 长度为前1个字符的子串`a`，最长相同前后缀的长度为0。（注意字符串的**前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串**；**后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串**。）
 
 <img src='https://code-thinking.cdn.bcebos.com/pics/KMP%E7%B2%BE%E8%AE%B26.png' width=600 alt='KMP精讲6'> </img></div>
+
 长度为前2个字符的子串`aa`，最长相同前后缀的长度为1。
 
 <img src='https://code-thinking.cdn.bcebos.com/pics/KMP%E7%B2%BE%E8%AE%B27.png' width=600 alt='KMP精讲7'> </img></div>
+
 长度为前3个字符的子串`aab`，最长相同前后缀的长度为0。
 
 以此类推：

problems/0042.接雨水.md

@@ -471,7 +471,7 @@ class Solution {
 ### Python:
 
 双指针法
-```python3
+```Python
 class Solution:
     def trap(self, height: List[int]) -> int:
         res = 0
@@ -510,7 +510,7 @@ class Solution:
         return result
 ```
 单调栈
-```python3
+```Python
 class Solution:
     def trap(self, height: List[int]) -> int:
         # 单调栈

problems/0045.跳跃游戏II.md

@@ -73,11 +73,11 @@ public:
         for (int i = 0; i < nums.size(); i++) {
             nextDistance = max(nums[i] + i, nextDistance);  // 更新下一步覆盖最远距离下标
             if (i == curDistance) {                         // 遇到当前覆盖最远距离下标
-                if (curDistance != nums.size() - 1) {       // 如果当前覆盖最远距离下标不是终点
+                if (curDistance < nums.size() - 1) {       // 如果当前覆盖最远距离下标不是终点
                     ans++;                                  // 需要走下一步
                     curDistance = nextDistance;             // 更新当前覆盖最远距离下标（相当于加油了）
                     if (nextDistance >= nums.size() - 1) break; // 下一步的覆盖范围已经可以达到终点，结束循环
-                } else break;                               // 当前覆盖最远距离下标是集合终点，不用做ans++操作了，直接结束
+                } else break;                               // 当前覆盖最远距到达集合终点，不用做ans++操作了，直接结束
             }
         }
         return ans;
@@ -126,7 +126,7 @@ public:
 
 可以看出版本二的代码相对于版本一简化了不少！
 
-其精髓在于控制移动下标i只移动到nums.size() - 2的位置，所以移动下标只要遇到当前覆盖最远距离的下标，直接步数加一，不用考虑别的了。
+**其精髓在于控制移动下标i只移动到nums.size() - 2的位置**，所以移动下标只要遇到当前覆盖最远距离的下标，直接步数加一，不用考虑别的了。
 
 ## 总结
 

problems/0053.最大子序和.md

@@ -12,9 +12,9 @@
 给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。
 
 示例:
-输入: [-2,1,-3,4,-1,2,1,-5,4]
-输出: 6
-解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。
+* 输入: [-2,1,-3,4,-1,2,1,-5,4]
+* 输出: 6
+* 解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。
 
 
 ## 暴力解法
@@ -103,8 +103,28 @@ public:
 
 当然题目没有说如果数组为空，应该返回什么，所以数组为空的话返回啥都可以了。
 
+
+## 常见误区 
+
+误区一： 
+
 不少同学认为 如果输入用例都是-1，或者 都是负数，这个贪心算法跑出来的结果是0， 这是**又一次证明脑洞模拟不靠谱的经典案例**，建议大家把代码运行一下试一试，就知道了，也会理解 为什么 result 要初始化为最小负数了。
 
+
+误区二：
+
+大家在使用贪心算法求解本题，经常陷入的误区，就是分不清，是遇到 负数就选择起始位置，还是连续和为负选择起始位置。 
+
+在动画演示用，大家可以发现， 4，遇到 -1 的时候，我们依然累加了，为什么呢？ 
+
+因为和为3，只要连续和还是正数就会 对后面的元素 起到增大总和的作用。 所以只要连续和为正数我们就保留。 
+
+这里也会有录友疑惑，那 4 +  -1 之后 不就变小了吗？ 会不会错过 4 成为最大连续和的可能性？ 
+
+其实并不会，因为还有一个变量result 一直在更新 最大的连续和，只要有更大的连续和出现，result就更新了，那么result已经把4更新了，后面 连续和变成3，也不会对最后结果有影响。 
+
+
+
 ## 动态规划
 
 当然本题还可以用动态规划来做，当前[「代码随想录」](https://img-blog.csdnimg.cn/20201124161234338.png)主要讲解贪心系列，后续到动态规划系列的时候会详细讲解本题的dp方法。
@@ -135,7 +155,7 @@ public:
 
 本题的贪心思路其实并不好想，这也进一步验证了，别看贪心理论很直白，有时候看似是常识，但贪心的题目一点都不简单！
 
-后续将介绍的贪心题目都挺难的，哈哈，所以贪心很有意思，别小看贪心！
+后续将介绍的贪心题目都挺难的，所以贪心很有意思，别小看贪心！
 
 ## 其他语言版本
 

problems/0055.跳跃游戏.md

@@ -78,7 +78,7 @@ public:
 
 一些同学可能感觉，我在讲贪心系列的时候，题目和题目之间貌似没有什么联系？
 
-**是真的就是没什么联系，因为贪心无套路！**没有个整体的贪心框架解决一系列问题，只能是接触各种类型的题目锻炼自己的贪心思维！
+**是真的就是没什么联系，因为贪心无套路**！没有个整体的贪心框架解决一系列问题，只能是接触各种类型的题目锻炼自己的贪心思维！
 
 ## 其他语言版本
 

problems/0072.编辑距离.md

@@ -20,24 +20,20 @@
 * 输入：word1 = "horse", word2 = "ros"
 * 输出：3
 * 解释：
-```
 horse -> rorse (将 'h' 替换为 'r')
 rorse -> rose (删除 'r')
 rose -> ros (删除 'e')
-``
 
 
 * 示例 2：
 * 输入：word1 = "intention", word2 = "execution"
 * 输出：5
 * 解释：
-```
 intention -> inention (删除 't')
 inention -> enention (将 'i' 替换为 'e')
 enention -> exention (将 'n' 替换为 'x')
 exention -> exection (将 'n' 替换为 'c')
 exection -> execution (插入 'u')
-```
 
 提示：
 

problems/0093.复原IP地址.md

@@ -40,6 +40,9 @@
 * 0 <= s.length <= 3000
 * s 仅由数字组成
 
+# 算法公开课
+
+**《代码随想录》算法视频公开课：[93.复原IP地址](https://www.bilibili.com/video/BV1XP4y1U73i/)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
 
 # 思路
 
@@ -424,6 +427,30 @@ class Solution:
         return True
 ```
 
+python3; 简单拼接版本（类似Leetcode131写法）：
+```python
+class Solution: 
+    def restoreIpAddresses(self, s: str) -> List[str]:
+        global results, path
+        results = []
+        path = []
+        self.backtracking(s,0)
+        return results
+
+    def backtracking(self,s,index):
+        global results,path
+        if index == len(s) and len(path)==4:
+            results.append('.'.join(path)) # 在连接时需要中间间隔符号的话就在''中间写上对应的间隔符
+            return
+        for i in range(index,len(s)):
+            if len(path)>3: break          # 剪枝
+            temp = s[index:i+1]
+            if (int(temp)<256 and int(temp)>0 and temp[0]!='0') or (temp=='0'):
+                path.append(temp)
+                self.backtracking(s,i+1)
+                path.pop()      
+```
+
 ## Go 
 
 ```go

problems/0102.二叉树的层序遍历.md

@@ -23,10 +23,12 @@
 * 111.二叉树的最小深度
 
 
+
 ![我要打十个](https://code-thinking.cdn.bcebos.com/gifs/%E6%88%91%E8%A6%81%E6%89%93%E5%8D%81%E4%B8%AA.gif)
 
 
 
+
 # 102.二叉树的层序遍历
 
 [力扣题目链接](https://leetcode.cn/problems/binary-tree-level-order-traversal/)
@@ -2532,20 +2534,18 @@ class Solution:
             return 0
         
         queue_ = [root]
-        result = []
+        depth = 0
         while queue_:
             length = len(queue_)
-            sub = []
             for i in range(length):
                 cur = queue_.pop(0)
                 sub.append(cur.val)
                 #子节点入队列
                 if cur.left: queue_.append(cur.left)
                 if cur.right: queue_.append(cur.right)
-            result.append(sub)
+            depth += 1
             
-
-        return len(result)
+        return depth
 ```
 
 Go：

problems/0106.从中序与后序遍历序列构造二叉树.md

@@ -397,6 +397,9 @@ public:
 };
 ```
 
+## Python 
+
+
 # 105.从前序与中序遍历序列构造二叉树
 
 [力扣题目链接](https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/)
@@ -650,6 +653,37 @@ class Solution {
 ```
 
 ## Python 
+```python
+class Solution:
+    def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:
+        # 第一步: 特殊情况讨论: 树为空. 或者说是递归终止条件
+        if not postorder:
+            return 
+
+        # 第二步: 后序遍历的最后一个就是当前的中间节点
+        root_val = postorder[-1]
+        root = TreeNode(root_val)
+        
+        # 第三步: 找切割点.
+        root_index = inorder.index(root_val)
+
+        # 第四步: 切割inorder数组. 得到inorder数组的左,右半边.
+        left_inorder = inorder[:root_index]
+        right_inorder = inorder[root_index + 1:]
+
+        # 第五步: 切割postorder数组. 得到postorder数组的左,右半边.
+        # ⭐️ 重点1: 中序数组大小一定跟后序数组大小是相同的. 
+        left_postorder = postorder[:len(left_inorder)]
+        right_postorder = postorder[len(left_inorder): len(postorder) - 1]
+
+
+        # 第六步: 递归
+        root.left = self.buildTree(left_inorder, left_postorder)
+        root.right = self.buildTree(right_inorder, right_postorder)
+
+        # 第七步: 返回答案
+        return root 
+```
 
 105.从前序与中序遍历序列构造二叉树
 

problems/0130.被围绕的区域.md

@@ -83,6 +83,7 @@ public:
 ```
 
 ## 其他语言版本 
+
 <p align="center">
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>

problems/0134.加油站.md

@@ -88,7 +88,7 @@ public:
 * 情况一：如果gas的总和小于cost总和，那么无论从哪里出发，一定是跑不了一圈的
 * 情况二：rest[i] = gas[i]-cost[i]为一天剩下的油，i从0开始计算累加到最后一站，如果累加没有出现负数，说明从0出发，油就没有断过，那么0就是起点。
 
-* 情况三：如果累加的最小值是负数，汽车就要从非0节点出发，从后向前，看哪个节点能这个负数填平，能把这个负数填平的节点就是出发节点。
+* 情况三：如果累加的最小值是负数，汽车就要从非0节点出发，从后向前，看哪个节点能把这个负数填平，能把这个负数填平的节点就是出发节点。
 
 C++代码如下：
 

problems/0150.逆波兰表达式求值.md

@@ -163,6 +163,25 @@ class Solution {
 
 python3
 
+```python
+from operator import add, sub, mul
+
+class Solution:
+    op_map = {'+': add, '-': sub, '*': mul, '/': lambda x, y: int(x / y)}
+    
+    def evalRPN(self, tokens: List[str]) -> int:
+        stack = []
+        for token in tokens:
+            if token not in {'+', '-', '*', '/'}:
+                stack.append(int(token))
+            else:
+                op2 = stack.pop()
+                op1 = stack.pop()
+                stack.append(self.op_map[token](op1, op2))  # 第一个出来的在运算符后面
+        return stack.pop()
+```
+
+另一种可行，但因为使用eval相对较慢的方法:
 ```python
 class Solution:
     def evalRPN(self, tokens: List[str]) -> int:

problems/0151.翻转字符串里的单词.md

@@ -442,7 +442,7 @@ class Solution:
             while left <= right and s[left] == ' ':    #去除开头的空格
                 left += 1
             while left <= right and s[right] == ' ':   #去除结尾的空格
-                right = right-1
+                right -= 1
             tmp = []
             while left <= right:                      #去除单词中间多余的空格
                 if s[left] != ' ':

problems/0222.完全二叉树的节点个数.md

@@ -188,7 +188,7 @@ public:
 
 ```CPP
 if (root == nullptr) return 0; 
-// 开始根据做深度和有深度是否相同来判断该子树是不是满二叉树
+// 开始根据左深度和右深度是否相同来判断该子树是不是满二叉树
 TreeNode* left = root->left;
 TreeNode* right = root->right;
 int leftDepth = 0, rightDepth = 0; // 这里初始为0是有目的的，为了下面求指数方便
@@ -843,3 +843,4 @@ impl Solution {
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>
 </a>
+

problems/0232.用栈实现队列.md

@@ -38,7 +38,7 @@ queue.empty(); // 返回 false
 
 ## 思路
 
-《代码随想录》算法公开课：[栈的基本操作！ | LeetCode：232.用栈实现队列](https://www.bilibili.com/video/BV1nY4y1w7VC)，相信结合视频再看本篇题解，更有助于大家对链表的理解。
+《代码随想录》算法公开课：[栈的基本操作！ | LeetCode：232.用栈实现队列](https://www.bilibili.com/video/BV1nY4y1w7VC)，相信结合视频再看本篇题解，更有助于大家对栈和队列的理解。
 
 
 这是一道模拟题，不涉及到具体算法，考察的就是对栈和队列的掌握程度。
@@ -662,3 +662,4 @@ impl MyQueue {
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>
 </a>
+

problems/0257.二叉树的所有路径.md

@@ -468,7 +468,7 @@ class Solution {
 ---
 ## Python:  
 递归法+隐形回溯
-```Python3
+```Python
 # Definition for a binary tree node.
 # class TreeNode:
 #     def __init__(self, val=0, left=None, right=None):
@@ -499,7 +499,7 @@ class Solution:
 
 迭代法：
 
-```python3
+```Python
 from collections import deque
 
 

problems/0349.两个数组的交集.md

@@ -137,8 +137,18 @@ class Solution {
                 resSet.add(i);
             }
         }
-        //将结果几何转为数组
+        
+        //方法1：直接将结果几何转为数组
         return resSet.stream().mapToInt(x -> x).toArray();
+        
+        //方法2：另外申请一个数组存放setRes中的元素,最后返回数组
+        int[] arr = new int[setRes.size()];
+        int j = 0;
+        for(int i : setRes){
+            arr[j++] = i;
+        }
+        
+        return arr;
     }
 }
 ```
@@ -423,3 +433,4 @@ C#:
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>
 </a>
+

problems/0376.摆动序列.md

@@ -53,21 +53,64 @@
 
 **实际操作上，其实连删除的操作都不用做，因为题目要求的是最长摆动子序列的长度，所以只需要统计数组的峰值数量就可以了（相当于是删除单一坡度上的节点，然后统计长度）**
 
-**这就是贪心所贪的地方，让峰值尽可能的保持峰值，然后删除单一坡度上的节点**。
+**这就是贪心所贪的地方，让峰值尽可能的保持峰值，然后删除单一坡度上的节点** 
 
-本题代码实现中，还有一些技巧，例如统计峰值的时候，数组最左面和最右面是最不好统计的。
+在计算是否有峰值的时候，大家知道遍历的下标i ，计算prediff（nums[i] - nums[i-1]） 和 curdiff（nums[i+1] - nums[i]），如果`prediff < 0 && curdiff > 0` 或者 `prediff > 0 && curdiff < 0` 此时就有波动就需要统计。
 
-例如序列[2,5]，它的峰值数量是2，如果靠统计差值来计算峰值个数就需要考虑数组最左面和最右面的特殊情况。
+这是我们思考本题的一个大题思路，但本题要考虑三种情况：
 
-所以可以针对序列[2,5]，可以假设为[2,2,5]，这样它就有坡度了即preDiff = 0，如图：
+1. 情况一：上下坡中有平坡  
+2. 情况二：数组首尾两端 
+3. 情况三：单调坡中有平坡
+
+### 情况一：上下坡中有平坡
+
+例如 [1,2,2,2,1]这样的数组，如图： 
+
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20230106170449.png) 
+
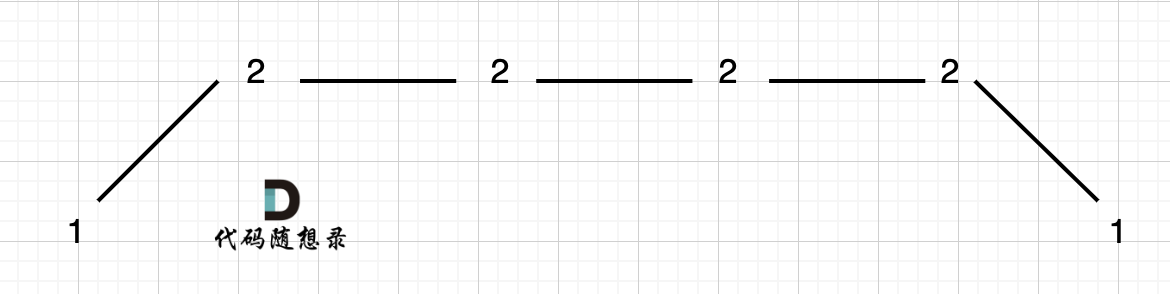
+它的摇摆序列长度是多少呢？ **其实是长度是3**，也就是我们在删除的时候 要不删除左面的三个2，要不就删除右边的三个2。  
+
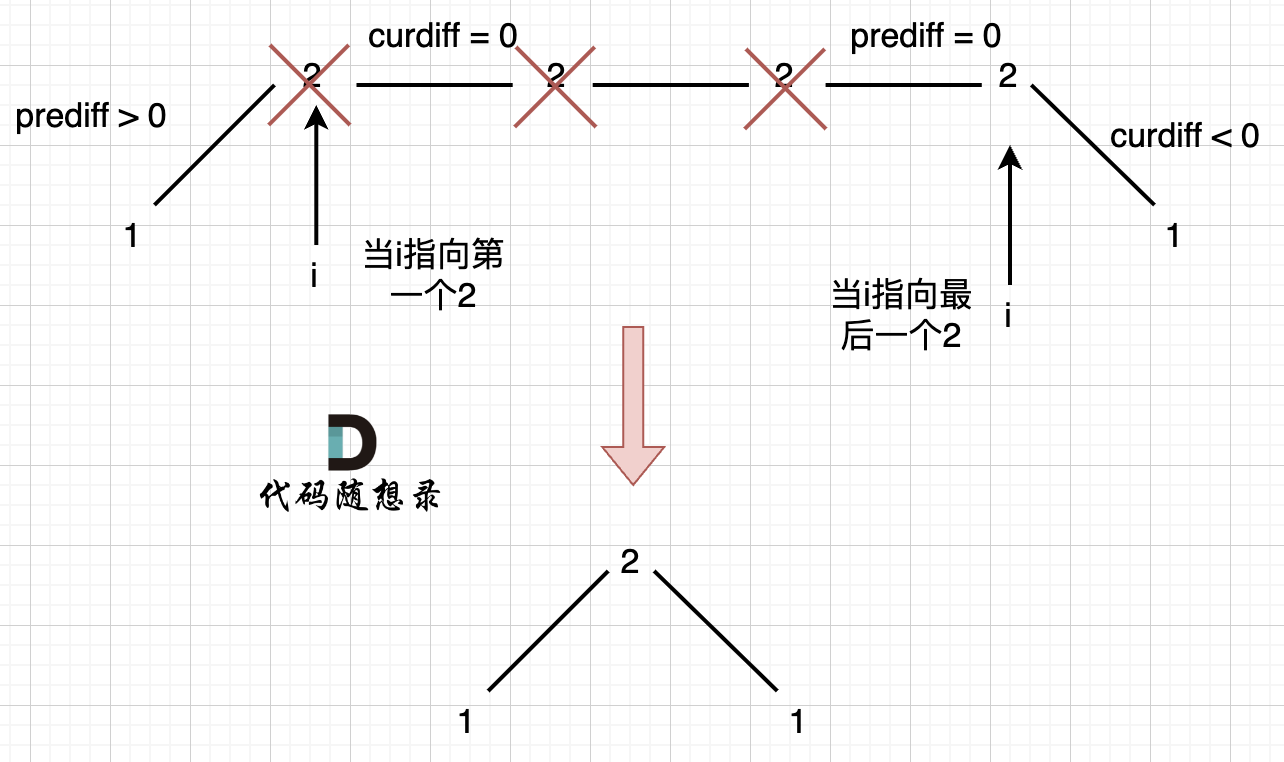
+如图，可以统一规则，删除左边的三个2：
+
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20230106172613.png)
+
+在图中，当i指向第一个2的时候，`prediff > 0 && curdiff = 0` ，当 i 指向最后一个2的时候 `prediff = 0 && curdiff < 0`。 
+
+如果我们采用，删左面三个2的规则，那么 当 `prediff = 0 && curdiff < 0` 也要记录一个峰值，因为他是把之前相同的元素都删掉留下的峰值。 
+
+所以我们记录峰值的条件应该是： `(preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)`，为什么这里允许 prediff == 0 ，就是为了 上面我说的这种情况。 
+
+
+### 情况二：数组首尾两端 
+
+
+所以本题统计峰值的时候，数组最左面和最右面如果统计呢？ 
+
+题目中说了，如果只有两个不同的元素，那摆动序列也是2。
+
+例如序列[2,5]，如果靠统计差值来计算峰值个数就需要考虑数组最左面和最右面的特殊情况。 
+
+因为我们在计算 prediff（nums[i] - nums[i-1]） 和 curdiff（nums[i+1] - nums[i]）的时候，至少需要三个数字才能计算，而数组只有两个数字。
+
+这里我们可以写死，就是 如果只有两个元素，且元素不同，那么结果为2。 
+
+不写死的话，如果和我们的判断规则结合在一起呢？ 
+
+可以假设，数组最前面还有一个数字，那这个数字应该是什么呢？ 
+
+之前我们在 讨论 情况一：相同数字连续 的时候， prediff = 0 ，curdiff < 0 或者 >0  也记为波谷。  
+
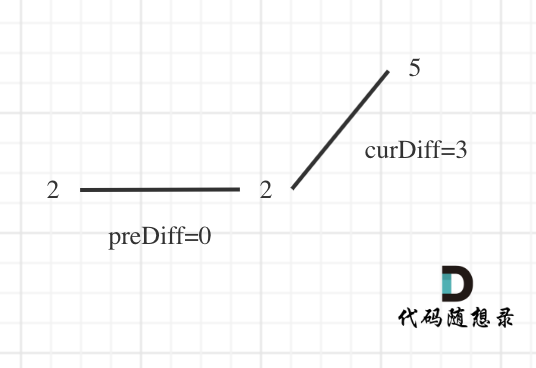
+那么为了规则统一，针对序列[2,5]，可以假设为[2,2,5]，这样它就有坡度了即preDiff = 0，如图：
 
 ![376.摆动序列1](https://img-blog.csdnimg.cn/20201124174357612.png)
 
 针对以上情形，result初始为1（默认最右面有一个峰值），此时curDiff > 0 && preDiff <= 0，那么result++（计算了左面的峰值），最后得到的result就是2（峰值个数为2即摆动序列长度为2）
 
-C++代码如下（和上图是对应的逻辑）：
+经过以上分析后，我们可以写出如下代码：
 
 ```CPP 
+// 版本一
 class Solution {
 public:
     int wiggleMaxLength(vector<int>& nums) {
@@ -78,9 +121,54 @@ public:
         for (int i = 0; i < nums.size() - 1; i++) {
             curDiff = nums[i + 1] - nums[i];
             // 出现峰值
-            if ((curDiff > 0 && preDiff <= 0) || (preDiff >= 0 && curDiff < 0)) {
+            if ((preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)) {
                 result++;
-                preDiff = curDiff;
+            }
+            preDiff = curDiff;
+        }
+        return result;
+    }
+};
+``` 
+* 时间复杂度：O(n)
+* 空间复杂度：O(1)
+
+此时大家是不是发现 以上代码提交也不能通过本题？ 
+
+所以此时我们要讨论情况三！
+
+### 情况三：单调坡度有平坡 
+
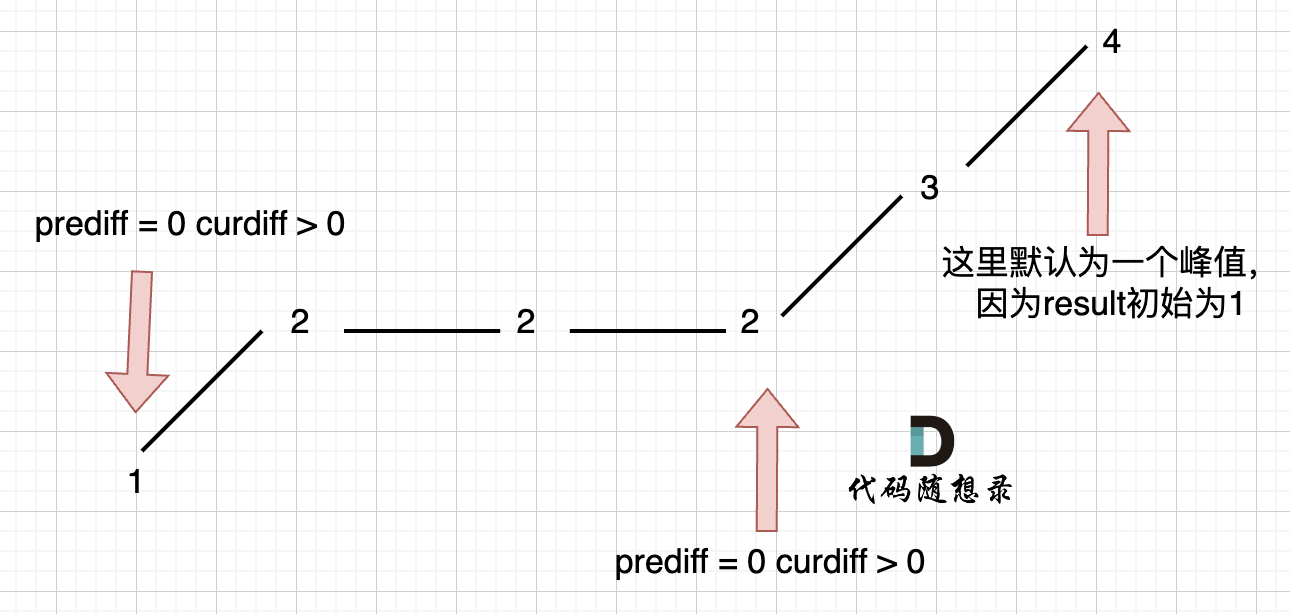
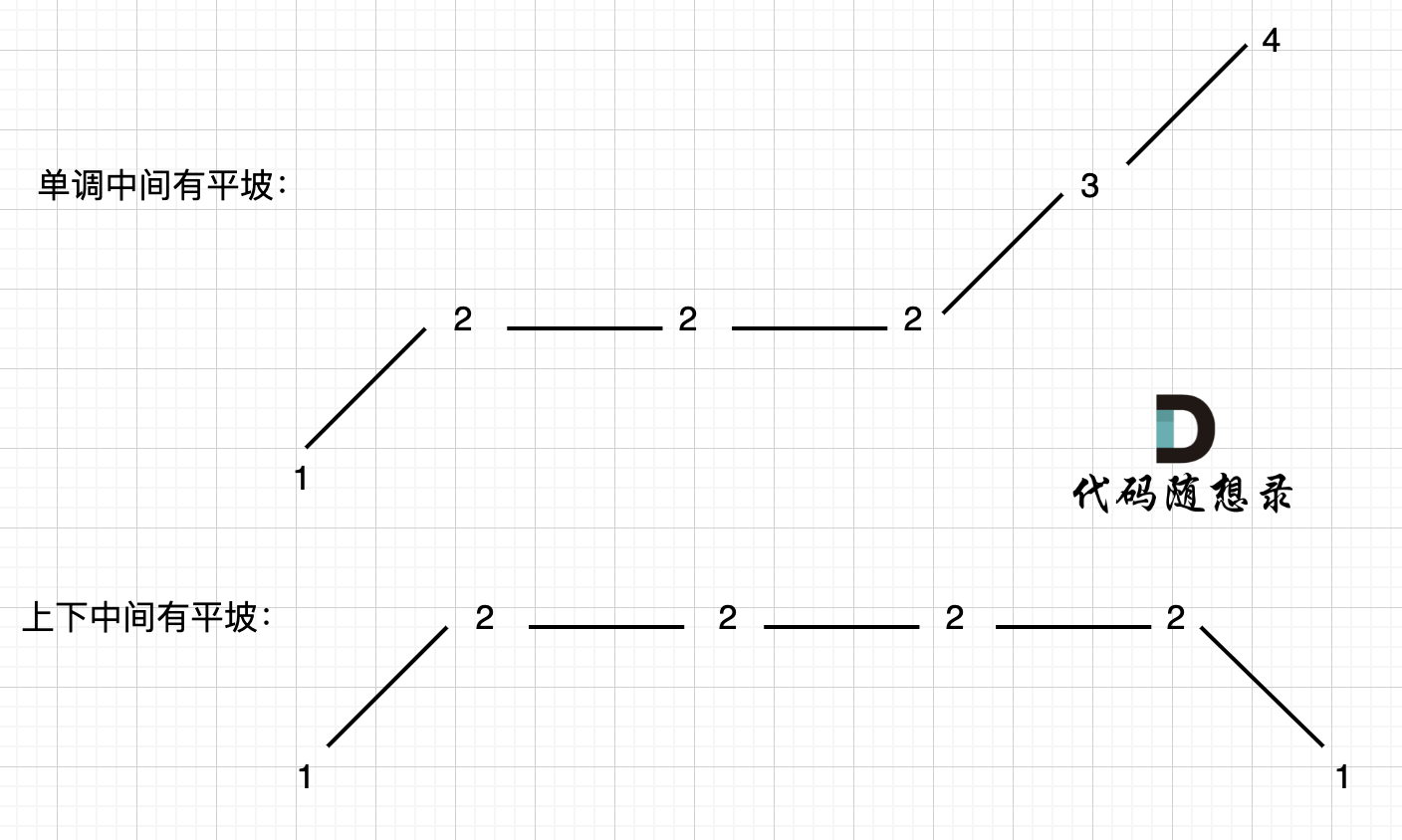
+在版本一中，我们忽略了一种情况，即 如果在一个单调坡度上有平坡，例如[1,2,2,2,3,4]，如图：  
+
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20230108171505.png)
+
+图中，我们可以看出，版本一的代码在三个地方记录峰值，但其实结果因为是2，因为 单调中的平坡 不能算峰值（即摆动）。 
+
+之所以版本一会出问题，是因为我们实时更新了 prediff。 
+
+那么我们应该什么时候更新prediff呢？ 
+
+我们只需要在 这个坡度 摆动变化的时候，更新prediff就行，这样prediff在 单调区间有平坡的时候 就不会发生变化，造成我们的误判。 
+
+所以本题的最终代码为：
+
+```CPP
+
+// 版本二 
+class Solution {
+public:
+    int wiggleMaxLength(vector<int>& nums) {
+        if (nums.size() <= 1) return nums.size();
+        int curDiff = 0; // 当前一对差值
+        int preDiff = 0; // 前一对差值
+        int result = 1;  // 记录峰值个数，序列默认序列最右边有一个峰值
+        for (int i = 0; i < nums.size() - 1; i++) {
+            curDiff = nums[i + 1] - nums[i];
+            // 出现峰值
+            if ((preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)) {
+                result++;
+                preDiff = curDiff; // 注意这里，只在摆动变化的时候更新prediff 
             }
         }
         return result;
@@ -88,8 +176,11 @@ public:
 };
 ```
 
-* 时间复杂度：O(n)
-* 空间复杂度：O(1)
+其实本题看起来好像简单，但需要考虑的情况还是很复杂的，而且很难一次性想到位。 
+
+**本题异常情况的本质，就是要考虑平坡**， 平坡分两种，一个是 上下中间有平坡，一个是单调有平坡，如图： 
+
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20230108174452.png)
 
 ## 思路2（动态规划）
 
@@ -111,25 +202,19 @@ public:
 
 C++代码如下：
 
-```c++
+```CPP
 class Solution {
 public:
     int dp[1005][2];
     int wiggleMaxLength(vector<int>& nums) {
         memset(dp, 0, sizeof dp);
         dp[0][0] = dp[0][1] = 1;
-
-        for (int i = 1; i < nums.size(); ++i)
-        {
+        for (int i = 1; i < nums.size(); ++i) {
             dp[i][0] = dp[i][1] = 1;
-
-            for (int j = 0; j < i; ++j)
-            {
+            for (int j = 0; j < i; ++j) {
                 if (nums[j] > nums[i]) dp[i][1] = max(dp[i][1], dp[j][0] + 1);
             }
-
-            for (int j = 0; j < i; ++j)
-            {
+            for (int j = 0; j < i; ++j) {
                 if (nums[j] < nums[i]) dp[i][0] = max(dp[i][0], dp[j][1] + 1);
             }
         }
@@ -153,17 +238,6 @@ public:
 
 空间复杂度：O(n)
 
-## 总结
-
-**贪心的题目说简单有的时候就是常识，说难就难在都不知道该怎么用贪心**。
-
-本题大家如果要去模拟删除元素达到最长摆动子序列的过程，那指定绕里面去了，一时半会拔不出来。
-
-而这道题目有什么技巧说一下子能想到贪心么？
-
-其实也没有，类似的题目做过了就会想到。
-
-此时大家就应该了解了：保持区间波动，只需要把单调区间上的元素移除就可以了。
 
 
 

problems/0455.分发饼干.md

@@ -52,6 +52,7 @@
 C++代码整体如下：
 
 ```CPP
+// 版本一 
 // 时间复杂度：O(nlogn)
 // 空间复杂度：O(1)
 class Solution {
@@ -61,8 +62,8 @@ public:
         sort(s.begin(), s.end());
         int index = s.size() - 1; // 饼干数组的下标
         int result = 0;
-        for (int i = g.size() - 1; i >= 0; i--) {
-            if (index >= 0 && s[index] >= g[i]) {
+        for (int i = g.size() - 1; i >= 0; i--) { // 遍历胃口 
+            if (index >= 0 && s[index] >= g[i]) { // 遍历饼干 
                 result++;
                 index--;
             }
@@ -76,6 +77,26 @@ public:
 
 有的同学看到要遍历两个数组，就想到用两个for循环，那样逻辑其实就复杂了。
 
+
+### 注意事项 
+
+注意版本一的代码中，可以看出来，是先遍历的胃口，在遍历的饼干，那么可不可以 先遍历 饼干，在遍历胃口呢？ 
+
+其实是不可以的。 
+
+外面的for 是里的下标i 是固定移动的，而if里面的下标 index 是符合条件才移动的。 
+
+如果 for 控制的是饼干， if 控制胃口，就是出现如下情况 ： 
+
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20230112102848.png)
+
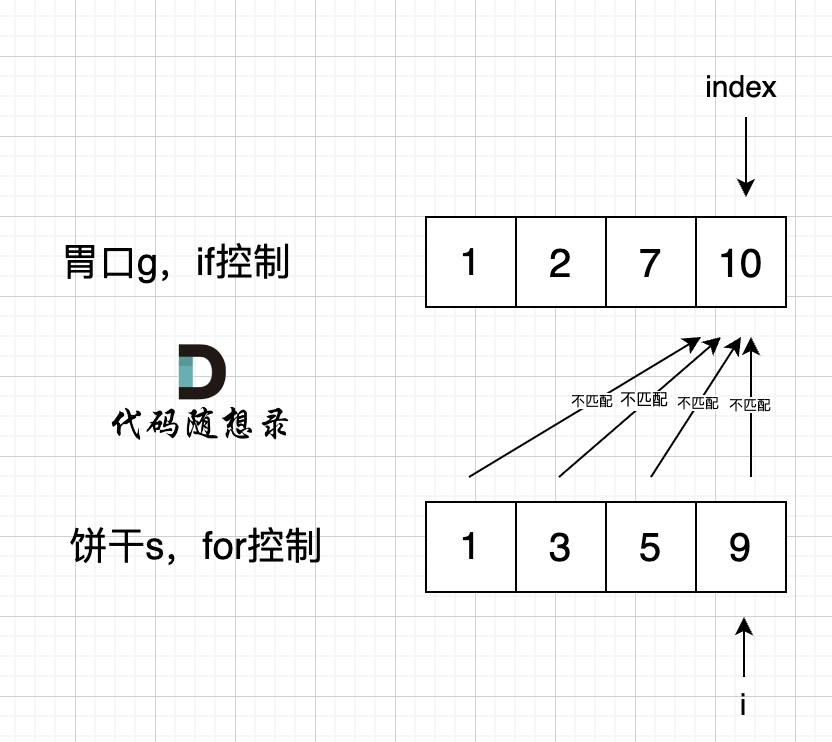
+if 里的 index 指向 胃口 10， for里的i指向饼干9，因为 饼干9 满足不了 胃口10，所以 i 持续向前移动，而index 走不到` s[index] >= g[i]` 的逻辑，所以index不会移动，那么当i 持续向前移动，最后所有的饼干都匹配不上。  
+
+所以 一定要for 控制 胃口，里面的if控制饼干。 
+
+
+### 其他思路
+
 **也可以换一个思路，小饼干先喂饱小胃口**
 
 代码如下：
@@ -87,8 +108,8 @@ public:
         sort(g.begin(),g.end());
         sort(s.begin(),s.end());
         int index = 0;
-        for(int i = 0;i < s.size();++i){
-            if(index < g.size() && g[index] <= s[i]){
+        for(int i = 0; i < s.size(); i++) { // 饼干
+            if(index < g.size() && g[index] <= s[i]){ // 胃口
                 index++;
             }
         }
@@ -97,6 +118,10 @@ public:
 };
 ``` 
 
+细心的录友可以发现，这种写法，两个循环的顺序改变了，先遍历的饼干，在遍历的胃口，这是因为遍历顺序变了，我们是从小到大遍历。 
+
+理由在上面 “注意事项”中 已经讲过。 
+
 ## 总结
 
 这道题是贪心很好的一道入门题目，思路还是比较容易想到的。
@@ -148,7 +173,7 @@ class Solution {
 ### Python
 ```python
 class Solution:
-    # 思路1：优先考虑胃饼干
+    # 思路1：优先考虑小胃口
     def findContentChildren(self, g: List[int], s: List[int]) -> int:
         g.sort()
         s.sort()
@@ -160,7 +185,7 @@ class Solution:
 ```
 ```python
 class Solution:
-    # 思路2：优先考虑胃口
+    # 思路2：优先考虑大胃口
     def findContentChildren(self, g: List[int], s: List[int]) -> int:
         g.sort()
         s.sort()

problems/0494.目标和.md

@@ -270,6 +270,8 @@ class Solution {
     public int findTargetSumWays(int[] nums, int target) {
         int sum = 0;
         for (int i = 0; i < nums.length; i++) sum += nums[i];
+	//如果target过大 sum将无法满足
+        if ( target < 0 && sum < -target) return 0;
         if ((target + sum) % 2 != 0) return 0;
         int size = (target + sum) / 2;
         if(size < 0) size = -size;

problems/0518.零钱兑换II.md

@@ -95,6 +95,8 @@ dp[j]  就是所有的dp[j - coins[i]]（考虑coins[i]的情况）相加。
 
 下标非0的dp[j]初始化为0，这样累计加dp[j - coins[i]]的时候才不会影响真正的dp[j]
 
+dp[0]=1还说明了一种情况：如果正好选了coins[i]后，也就是j-coins[i] == 0的情况表示这个硬币刚好能选，此时dp[0]为1表示只选coins[i]存在这样的一种选法。
+
 4. 确定遍历顺序
 
 本题中我们是外层for循环遍历物品（钱币），内层for遍历背包（金钱总额），还是外层for遍历背包（金钱总额），内层for循环遍历物品（钱币）呢？
@@ -316,3 +318,4 @@ object Solution {
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>
 </a>
+

problems/0538.把二叉搜索树转换为累加树.md

@@ -209,29 +209,28 @@ class Solution {
 #         self.right = right
 class Solution:
     def __init__(self):
-        self.pre = TreeNode()
+        self.count = 0
 
     def convertBST(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
+        if root == None:
+            return 
         '''
         倒序累加替换：  
-        [2, 5, 13] -> [[2]+[1]+[0], [2]+[1], [2]] -> [20, 18, 13]
         '''
-        self.traversal(root)
+        # 右
+        self.convertBST(root.right)
+
+        # 中
+        # 中节点：用当前root的值加上pre的值
+        self.count += root.val
+
+        root.val = self.count 
+
+        # 左
+        self.convertBST(root.left)
+
         return root 
         
-    def traversal(self, root: TreeNode) -> None:
-        # 因为要遍历整棵树，所以递归函数不需要返回值
-        # Base Case
-        if not root: 
-            return None
-        # 单层递归逻辑：中序遍历的反译 - 右中左
-        self.traversal(root.right)  # 右
-
-        # 中节点：用当前root的值加上pre的值
-        root.val += self.pre.val    # 中
-        self.pre = root             
-
-        self.traversal(root.left)   # 左
 ```
 
 ## Go

problems/0827.最大人工岛.md

@@ -3,8 +3,11 @@
   <img src="../pics/训练营.png" width="1000"/>
 </a>
 <p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！</strong></p>
+
 # 827. 最大人工岛 
 
+[力扣链接](https://leetcode.cn/problems/making-a-large-island/)
+
 给你一个大小为 n x n 二进制矩阵 grid 。最多 只能将一格 0 变成 1 。
 
 返回执行此操作后，grid 中最大的岛屿面积是多少？
@@ -30,7 +33,9 @@
 
 本题的一个暴力想法，应该是遍历地图尝试 将每一个 0 改成1，然后去搜索地图中的最大的岛屿面积。 
 
-计算地图的最大面积：遍历地图 + 深搜岛屿，时间复杂度为 n * n 
+计算地图的最大面积：遍历地图 + 深搜岛屿，时间复杂度为 n * n。 
+
+（其实使用深搜还是广搜都是可以的，其目的就是遍历岛屿做一个标记，相当于染色，那么使用哪个遍历方式都行，以下我用深搜来讲解） 
 
 每改变一个0的方格，都需要重新计算一个地图的最大面积，所以 整体时间复杂度为：n^4。 
 
@@ -41,7 +46,7 @@
 
 其实每次深搜遍历计算最大岛屿面积，我们都做了很多重复的工作。 
 
-只要把深搜就可以并每个岛屿的面积记录下来就好。 
+只要用一次深搜把每个岛屿的面积记录下来就好。 
 
 第一步：一次遍历地图，得出各个岛屿的面积，并做编号记录。可以使用map记录，key为岛屿编号，value为岛屿面积
 第二步：在遍历地图，遍历0的方格（因为要将0变成1），并统计该1（由0变成的1）周边岛屿面积，将其相邻面积相加在一起，遍历所有 0 之后，就可以得出 选一个0变成1 之后的最大面积。 
@@ -74,7 +79,7 @@ void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y,
 
 int largestIsland(vector<vector<int>>& grid) {
     int n = grid.size(), m = grid[0].size();
-    vector<vector<bool>> visited = vector<vector<bool>>(n, vector<bool>(m, false));
+    vector<vector<bool>> visited = vector<vector<bool>>(n, vector<bool>(m, false)); // 标记访问过的点
     unordered_map<int ,int> gridNum;
     int mark = 2; // 记录每个岛屿的编号
     bool isAllGrid = true; // 标记是否整个地图都是陆地
@@ -92,9 +97,10 @@ int largestIsland(vector<vector<int>>& grid) {
 }
 ```
 
+
 这个过程时间复杂度 n * n 。可能有录友想：分明是两个for循环下面套这一个dfs，时间复杂度怎么回事 n * n呢？ 
 
-其实大家可以自己看代码的时候，**n * n这个方格地图中，每个节点我们就遍历一次，并不会重复遍历**。
+其实大家可以仔细看一下代码，**n * n这个方格地图中，每个节点我们就遍历一次，并不会重复遍历**。
 
 第二步过程如图所示： 
 
@@ -106,6 +112,47 @@ int largestIsland(vector<vector<int>>& grid) {
 
 所以整个解法的时间复杂度，为 n * n + n * n 也就是 n^2。 
 
+当然这里还有一个优化的点，就是 可以不用 visited数组，因为有mark来标记，所以遍历过的grid[i][j]是不等于1的。 
+
+代码如下：
+
+```CPP
+    int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
+    void dfs(vector<vector<int>>& grid, int x, int y, int mark) {
+        if (grid[x][y] != 1 || grid[x][y] == 0) return; // 终止条件：访问过的节点 或者 遇到海水
+        grid[x][y] = mark; // 给陆地标记新标签
+        count++;
+        for (int i = 0; i < 4; i++) {
+            int nextx = x + dir[i][0];
+            int nexty = y + dir[i][1];
+            if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;  // 越界了，直接跳过
+            dfs(grid, nextx, nexty, mark);
+        }
+    }
+
+public:
+    int largestIsland(vector<vector<int>>& grid) {
+        int n = grid.size(), m = grid[0].size();
+        unordered_map<int ,int> gridNum;
+        int mark = 2; // 记录每个岛屿的编号
+        bool isAllGrid = true; // 标记是否整个地图都是陆地
+        for (int i = 0; i < n; i++) {
+            for (int j = 0; j < m; j++) {
+                if (grid[i][j] == 0) isAllGrid = false;
+                if (grid[i][j] == 1) {
+                    count = 0;
+                    dfs(grid, i, j, mark); // 将与其链接的陆地都标记上 true
+                    gridNum[mark] = count; // 记录每一个岛屿的面积
+                    mark++; // 记录下一个岛屿编号
+                }
+            }
+        }
+    }
+}
+```
+
+不过为了让各个变量各司其事，代码清晰一些，完整代码还是使用visited数组来标记。
+
 最后，整体代码如下： 
 
 ```CPP 
@@ -129,7 +176,7 @@ private:
 public:
     int largestIsland(vector<vector<int>>& grid) {
         int n = grid.size(), m = grid[0].size();
-        vector<vector<bool>> visited = vector<vector<bool>>(n, vector<bool>(m, false));
+        vector<vector<bool>> visited = vector<vector<bool>>(n, vector<bool>(m, false)); // 标记访问过的点
         unordered_map<int ,int> gridNum;
         int mark = 2; // 记录每个岛屿的编号
         bool isAllGrid = true; // 标记是否整个地图都是陆地
@@ -171,6 +218,7 @@ public:
     }
 };
 ```
+
 <p align="center">
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>

problems/1005.K次取反后最大化的数组和.md

@@ -44,7 +44,7 @@
 
 那么如果将负数都转变为正数了，K依然大于0，此时的问题是一个有序正整数序列，如何转变K次正负，让 数组和 达到最大。
 
-那么又是一个贪心：局部最优：只找数值最小的正整数进行反转，当前数值可以达到最大（例如正整数数组{5, 3, 1}，反转1 得到-1 比 反转5得到的-5 大多了），全局最优：整个 数组和 达到最大。
+那么又是一个贪心：局部最优：只找数值最小的正整数进行反转，当前数值和可以达到最大（例如正整数数组{5, 3, 1}，反转1 得到-1 比 反转5得到的-5 大多了），全局最优：整个 数组和 达到最大。
 
 虽然这道题目大家做的时候，可能都不会去想什么贪心算法，一鼓作气，就AC了。
 

problems/1020.飞地的数量.md

@@ -6,6 +6,8 @@
 
 # 1020. 飞地的数量 
 
+[力扣链接](https://leetcode.cn/problems/number-of-enclaves/description/)
+
 给你一个大小为 m x n 的二进制矩阵 grid ，其中 0 表示一个海洋单元格、1 表示一个陆地单元格。
 
 一次 移动 是指从一个陆地单元格走到另一个相邻（上、下、左、右）的陆地单元格或跨过 grid 的边界。
@@ -26,7 +28,7 @@
 
 ## 思路 
 
-本题使用dfs，bfs，并查集都是可以的。 本题和 417. 太平洋大西洋水流问题 很像。 
+本题使用dfs，bfs，并查集都是可以的。 
 
 本题要求找到不靠边的陆地面积，那么我们只要从周边找到陆地然后 通过 dfs或者bfs 将周边靠陆地且相邻的陆地都变成海洋，然后再去重新遍历地图的时候，统计此时还剩下的陆地就可以了。
 
@@ -142,6 +144,11 @@ public:
     }
 };
 ```
+## 类似题目 
+
+* 1254. 统计封闭岛屿的数目  
+
+
 <p align="center">
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>

problems/前序/ACM模式如何构建二叉树.md

@@ -280,7 +280,7 @@ public class Solution {
 
 ## Python 
 
-```Python3
+```Python
 class TreeNode:
     def __init__(self, val = 0, left = None, right = None):
         self.val = val

problems/前序/vim.md

@@ -66,7 +66,7 @@ IDE那么很吃内存，打开个IDE卡半天，用VIM就很轻便了，秒开
 
 ## 安装
 
-PowerVim的安防非常简单，我已经写好了安装脚本，只要执行以下就可以安装，而且不会影响你之前的vim配置，之前的配置都给做了备份，大家看一下脚本就知道备份在哪里了。
+PowerVim的安装非常简单，我已经写好了安装脚本，只要执行以下就可以安装，而且不会影响你之前的vim配置，之前的配置都给做了备份，大家看一下脚本就知道备份在哪里了。
 
 安装过程非常简单：
 ```bash