Merge branch 'master' into 583-minDistance

problems/0001.两数之和.md

@@ -341,7 +341,7 @@ impl Solution {
 }
 ```
 
-### Javascript:
+### JavaScript:
 
 ```javascript
 var twoSum = function (nums, target) {

problems/0020.有效的括号.md

@@ -275,7 +275,7 @@ def is_valid(strs)
 end
 ```
 
-### Javascript:
+### JavaScript:
 
 ```javascript
 var isValid = function (s) {

problems/0024.两两交换链表中的节点.md

@@ -286,7 +286,7 @@ func swapPairs(head *ListNode) *ListNode {
 }
 ```
 
-### Javascript:
+### JavaScript:
 
 ```javascript
 var swapPairs = function (head) {

problems/0027.移除元素.md

@@ -131,7 +131,24 @@ public:
 ## 其他语言版本
 
 ### Java：
-
+```java
+class Solution {
+    public int removeElement(int[] nums, int val) {
+	// 暴力法
+        int n = nums.length;
+        for (int i = 0; i < n; i++) {
+            if (nums[i] == val) {
+                for (int j = i + 1; j < n; j++) {
+                    nums[j - 1] = nums[j];
+                }
+                i--;
+                n--;
+            }
+        }
+        return n;
+    }
+}
+```
 ```java
 class Solution {
     public int removeElement(int[] nums, int val) {

problems/0037.解数独.md

@@ -460,7 +460,7 @@ func isvalid(row, col int, k byte, board [][]byte) bool {
 
 
 
-### Javascript
+### JavaScript
 
 ```Javascript
 var solveSudoku = function(board) {

problems/0045.跳跃游戏II.md

@@ -374,7 +374,7 @@ func max(a, b int) int {
 }
 ```
 
-### Javascript
+### JavaScript
 
 ```Javascript
 var jump = function(nums) {

problems/0046.全排列.md

@@ -201,6 +201,7 @@ class Solution {
     public void backtrack(int[] nums, LinkedList<Integer> path) {
         if (path.size() == nums.length) {
             result.add(new ArrayList<>(path));
+            return;
         }
         for (int i =0; i < nums.length; i++) {
             // 如果path中已有，则跳过
@@ -271,7 +272,7 @@ func dfs(nums []int, cur int) {
 }
 ```
 
-### Javascript 
+### JavaScript 
 
 ```js
 
@@ -524,3 +525,4 @@ public class Solution
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>
 </a>
+

problems/0047.全排列II.md

@@ -283,7 +283,7 @@ func dfs(nums []int, cur int) {
 }
 ```
 
-### Javascript
+### JavaScript
 
 ```javascript
 var permuteUnique = function (nums) {

problems/0051.N皇后.md

@@ -451,7 +451,7 @@ func isValid(n, row, col int, chessboard [][]string) bool {
 ```
 
 
-### Javascript 
+### JavaScript 
 ```Javascript
 /**
  * @param {number} n

problems/0053.最大子序和.md

@@ -240,6 +240,42 @@ class Solution:
             res = max(res, dp[i])
         return res
 ```
+
+动态规划
+
+```python
+class Solution:
+    def maxSubArray(self, nums):
+        if not nums:
+            return 0
+        dp = [0] * len(nums)    # dp[i]表示包括i之前的最大连续子序列和
+        dp[0] = nums[0]
+        result = dp[0]
+        for i in range(1, len(nums)):
+            dp[i] = max(dp[i-1]+nums[i], nums[i])   # 状态转移公式
+            if dp[i] > result:
+                result = dp[i]                      # result 保存dp[i]的最大值
+        return result
+```
+
+动态规划优化
+
+```python
+class Solution:
+    def maxSubArray(self, nums: List[int]) -> int:
+        max_sum = float("-inf") # 初始化结果为负无穷大，方便比较取最大值
+        current_sum = 0         # 初始化当前连续和
+
+        for num in nums:
+
+            # 更新当前连续和
+            # 如果原本的连续和加上当前数字之后没有当前数字大，说明原本的连续和是负数，那么就直接从当前数字开始重新计算连续和
+            current_sum = max(current_sum+num, num) 
+            max_sum = max(max_sum, current_sum) # 更新结果
+
+        return max_sum
+```
+
 ### Go
 贪心法
 ```go
@@ -290,7 +326,7 @@ pub fn max_sub_array(nums: Vec<i32>) -> i32 {
 }
 ```
 
-### Javascript:
+### JavaScript:
 
 ```Javascript
 var maxSubArray = function(nums) {

problems/0054.螺旋矩阵.md

@@ -260,7 +260,7 @@ class Solution {
 }
 ```
 
-### Javascript
+### JavaScript
 ```
 /**
  * @param {number[][]} matrix

problems/0055.跳跃游戏.md

@@ -143,6 +143,23 @@ class Solution:
         return False
 ```
 
+```python
+## 基于当前最远可到达位置判断
+class Solution:
+    def canJump(self, nums: List[int]) -> bool:
+        far = nums[0]
+        for i in range(len(nums)):
+            # 要考虑两个情况
+            # 1. i <= far - 表示 当前位置i 可以到达
+            # 2. i > far - 表示 当前位置i 无法到达
+            if i > far:
+                return False
+            far = max(far, nums[i]+i)
+        # 如果循环正常结束，表示最后一个位置也可以到达，否则会在中途直接退出
+        # 关键点在于，要想明白其实列表中的每个位置都是需要验证能否到达的
+        return True
+```
+
 ### Go
 
 ```go
@@ -166,7 +183,7 @@ func max(a, b int ) int {
 }
 ```
 
-### Javascript
+### JavaScript
 
 ```Javascript
 var canJump = function(nums) {

problems/0056.合并区间.md

@@ -215,7 +215,7 @@ func max56(a, b int) int {
 ```
 
 
-### Javascript 
+### JavaScript 
 ```javascript
 var merge = function (intervals) {
     intervals.sort((a, b) => a[0] - b[0]);

problems/0062.不同路径.md

@@ -411,7 +411,7 @@ func uniquePaths(m int, n int) int {
 }
 ```
 
-### Javascript
+### JavaScript
 
 ```Javascript
 var uniquePaths = function(m, n) {

problems/0063.不同路径II.md

@@ -465,7 +465,7 @@ func uniquePathsWithObstacles(obstacleGrid [][]int) int {
 }
 ```
 
-### Javascript
+### JavaScript
 
 ```Javascript
 var uniquePathsWithObstacles = function(obstacleGrid) {

problems/0070.爬楼梯.md

@@ -327,7 +327,7 @@ func climbStairs(n int) int {
     return dp[n]
 }
 ```
-### Javascript
+### JavaScript
 ```Javascript
 var climbStairs = function(n) {
     // dp[i] 为第 i 阶楼梯有多少种方法爬到楼顶

problems/0072.编辑距离.md

@@ -313,7 +313,7 @@ func Min(args ...int) int {
 }
 ```
 
-### Javascript：
+### JavaScript：
 
 ```javascript
 const minDistance = (word1, word2) => {

problems/0077.组合.md

@@ -468,7 +468,7 @@ func dfs(n int, k int, start int) {
 }
 ```
 
-### Javascript
+### JavaScript
 未剪枝：
 
 ```js

problems/0078.子集.md

@@ -246,7 +246,7 @@ func dfs(nums []int, start int) {
 }
 ```
 
-### Javascript
+### JavaScript
 
 ```Javascript
 var subsets = function(nums) {

problems/0090.子集II.md

@@ -376,7 +376,7 @@ func dfs(nums []int, start int) {
 ```
 
 
-### Javascript 
+### JavaScript 
 
 ```Javascript
 

problems/0093.复原IP地址.md

@@ -376,9 +376,8 @@ class Solution {
 		// 剪枝：ip段的长度最大是3，并且ip段处于[0,255]
 		for (int i = start; i < s.length() && i - start < 3 && Integer.parseInt(s.substring(start, i + 1)) >= 0
 				&& Integer.parseInt(s.substring(start, i + 1)) <= 255; i++) {
-			// 如果ip段的长度大于1，并且第一位为0的话，continue
 			if (i + 1 - start > 1 && s.charAt(start) - '0' == 0) {
-				continue;
+				break;
 			}
 			stringBuilder.append(s.substring(start, i + 1));
 			// 当stringBuilder里的网段数量小于3时，才会加点；如果等于3，说明已经有3段了，最后一段不需要再加点

problems/0096.不同的二叉搜索树.md

@@ -221,7 +221,7 @@ func numTrees(n int)int{
 }
 ```
 
-### Javascript
+### JavaScript
 
 ```Javascript
 const numTrees =(n) => {

problems/0098.验证二叉搜索树.md

@@ -22,7 +22,7 @@
 
 ## 算法公开课
 
-**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html)：[你对二叉搜索树了解的还不够！ | LeetCode：98.验证二叉搜索树](https://www.bilibili.com/video/BV18P411n7Q4)，相信结合视频在看本篇题解，更有助于大家对本题的理解**。
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html)：[你对二叉搜索树了解的还不够！ | LeetCode：98.验证二叉搜索树](https://www.bilibili.com/video/BV18P411n7Q4)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
 
 
 ## 思路

problems/0102.二叉树的层序遍历.md

@@ -356,7 +356,7 @@ func levelOrder(root *TreeNode) (res [][]int) {
 }
 ```
 
-#### Javascript：
+#### JavaScript：
 
 ```javascript
 var levelOrder = function(root) {
@@ -759,7 +759,7 @@ func levelOrderBottom(root *TreeNode) [][]int {
 }
 ```
 
-#### Javascript:
+#### JavaScript:
 
 ```javascript
 var levelOrderBottom = function (root) {
@@ -1101,7 +1101,7 @@ func rightSideView(root *TreeNode) []int {
 }
 ```
 
-#### Javascript:
+#### JavaScript:
 
 ```javascript
 var rightSideView = function(root) {
@@ -1421,7 +1421,7 @@ func averageOfLevels(root *TreeNode) []float64 {
 }
 ```
 
-#### Javascript：
+#### JavaScript：
 
 ```javascript
 var averageOfLevels = function(root) {
@@ -2109,7 +2109,7 @@ func largestValues(root *TreeNode) []int {
 }
 ```
 
-#### Javascript：
+#### JavaScript：
 
 ```javascript
 var largestValues = function (root) {

problems/0104.二叉树的最大深度.md

@@ -604,7 +604,7 @@ func maxDepth(root *Node) int {
 }
 ```
 
-### Javascript :
+### JavaScript :
 
 104.二叉树的最大深度
 

problems/0112.路径总和.md

@@ -830,7 +830,7 @@ func traverse(node *TreeNode, result *[][]int, currPath *[]int, targetSum int) {
 }
 ```
 
-### Javascript
+### JavaScript
 
 0112.路径总和
 

problems/0115.不同的子序列.md

@@ -265,7 +265,7 @@ func numDistinct(s string, t string) int {
 }
 ```
 
-### Javascript:
+### JavaScript:
 
 ```javascript
 const numDistinct = (s, t) => {

problems/0122.买卖股票的最佳时机II.md

@@ -249,7 +249,7 @@ func max(a, b int) int {
 }
 ```
 
-### Javascript:
+### JavaScript:
 
 贪心
 

problems/0122.买卖股票的最佳时机II（动态规划）.md

@@ -251,6 +251,27 @@ func max(a, b int) int {
 }
 ```
 
+```go
+// 动态规划 版本二 滚动数组
+func maxProfit(prices []int) int {
+    dp := [2][2]int{} // 注意这里只开辟了一个2 * 2大小的二维数组
+    dp[0][0] = -prices[0]
+    dp[0][1] = 0
+    for i := 1; i < len(prices); i++ {
+        dp[i%2][0] = max(dp[(i-1)%2][0], dp[(i - 1) % 2][1] - prices[i])
+        dp[i%2][1] = max(dp[(i-1)%2][1], dp[(i-1)%2][0] + prices[i])
+    }
+    return dp[(len(prices)-1)%2][1]
+}
+
+func max(x, y int) int {
+    if x > y {
+        return x
+    }
+    return y
+}
+```
+
 ### JavaScript：
 
 ```javascript

problems/0123.买卖股票的最佳时机III.md

@@ -316,6 +316,8 @@ class Solution:
 
 ### Go:
 
+> 版本一
+
 ```go
 func maxProfit(prices []int) int {
     dp := make([][]int, len(prices))
@@ -344,6 +346,80 @@ func max(a, b int) int {
 }
 ```
 
+> 版本二
+
+```go
+func maxProfit(prices []int) int {
+    if len(prices) == 0 {
+        return 0
+    }
+    dp := make([]int, 5)
+    dp[1] = -prices[0]
+    dp[3] = -prices[0]
+    for i := 1; i < len(prices); i++ {
+        dp[1] = max(dp[1], dp[0] - prices[i])
+        dp[2] = max(dp[2], dp[1] + prices[i])
+        dp[3] = max(dp[3], dp[2] - prices[i])
+        dp[4] = max(dp[4], dp[3] + prices[i])
+    }
+    return dp[4]
+}
+
+func max(x, y int) int {
+    if x > y {
+        return x
+    }
+    return y
+}
+```
+
+> 版本三
+
+```go
+func maxProfit(prices []int) int {
+    if len(prices) == 0 {
+        return 0
+    }
+    dp := make([][5]int, len(prices))
+    dp[0][1] = -prices[0]
+    dp[0][3] = -prices[0]
+    for i := 1; i < len(prices); i++ {
+        dp[i][1] = max(dp[i-1][1], 0 - prices[i])
+        dp[i][2] = max(dp[i-1][2], dp[i-1][1] + prices[i])
+        dp[i][3] = max(dp[i-1][3], dp[i-1][2] - prices[i])
+        dp[i][4] = max(dp[i-1][4], dp[i-1][3] + prices[i])
+    }
+    return dp[len(prices)-1][4]
+}
+
+func max(x, y int) int {
+    if x > y {
+        return x
+    }
+    return y
+}
+```
+
+> 版本四：一维 dp 易懂版本 
+
+```go
+func maxProfit(prices []int) int {
+    dp := make([]int, 4)
+    dp[0] = -prices[0]
+    dp[2] = -prices[0]
+
+    for _, price := range prices[1:] {
+        dc := slices.Clone(dp) // 这句话是关键，把前一天的 dp 状态保存下来，防止被覆盖掉，后面只用它，不用 dp，逻辑简单易懂
+        dp[0] = max(dc[0], -price)
+        dp[1] = max(dc[1], dc[0] + price)
+        dp[2] = max(dc[2], dc[1] - price)
+        dp[3] = max(dc[3], dc[2] + price)
+    }
+
+    return dp[3]
+}
+```
+
 ### JavaScript:
 
 > 版本一：

problems/0134.加油站.md

@@ -396,7 +396,7 @@ func canCompleteCircuit(gas []int, cost []int) int {
 }
 ```
 
-### Javascript 
+### JavaScript 
 暴力：
 ```js
 var canCompleteCircuit = function(gas, cost) {

problems/0135.分发糖果.md

@@ -177,21 +177,20 @@ class Solution {
 ```python
 class Solution:
     def candy(self, ratings: List[int]) -> int:
-        candyVec = [1] * len(ratings)
+        n = len(ratings)
+        candies = [1] * n
         
-        # 从前向后遍历，处理右侧比左侧评分高的情况
-        for i in range(1, len(ratings)):
+        # Forward pass: handle cases where right rating is higher than left
+        for i in range(1, n):
             if ratings[i] > ratings[i - 1]:
-                candyVec[i] = candyVec[i - 1] + 1
+                candies[i] = candies[i - 1] + 1
         
-        # 从后向前遍历，处理左侧比右侧评分高的情况
-        for i in range(len(ratings) - 2, -1, -1):
+        # Backward pass: handle cases where left rating is higher than right
+        for i in range(n - 2, -1, -1):
             if ratings[i] > ratings[i + 1]:
-                candyVec[i] = max(candyVec[i], candyVec[i + 1] + 1)
+                candies[i] = max(candies[i], candies[i + 1] + 1)
         
-        # 统计结果
-        result = sum(candyVec)
-        return result
+        return sum(candies)
 
 ```
 
@@ -234,7 +233,7 @@ func findMax(num1 int, num2 int) int {
 }
 ```
 
-### Javascript
+### JavaScript
 ```Javascript
 var candy = function(ratings) {
     let candys = new Array(ratings.length).fill(1)

problems/0150.逆波兰表达式求值.md

@@ -108,7 +108,7 @@ public:
             }
         }
 
-        int result = st.top();
+        long long result = st.top();
         st.pop(); // 把栈里最后一个元素弹出（其实不弹出也没事）
         return result;
     }

problems/0151.翻转字符串里的单词.md

@@ -513,6 +513,29 @@ class Solution:
 
         return "".join(result)
 ```
+
+(版本五) 遇到空格就说明前面的是一个单词，把它加入到一个数组中。
+
+```python
+class Solution:
+    def reverseWords(self, s: str) -> str:
+        words = []
+        word = ''
+        s += ' ' # 帮助处理最后一个字词
+
+        for char in s:
+            if char == ' ': # 遇到空格就说明前面的可能是一个单词
+                if word != '': # 确认是单词，把它加入到一个数组中
+                    words.append(word)
+                    word = '' # 清空当前单词
+                continue
+            
+            word += char # 收集单词的字母
+        
+        words.reverse()
+        return ' '.join(words)
+```
+
 ### Go：
 
 版本一：

problems/0188.买卖股票的最佳时机IV.md

@@ -297,8 +297,7 @@ class Solution {
 
 ### Python:
 
-版本一
-
+> 版本一
 ```python
 class Solution:
     def maxProfit(self, k: int, prices: List[int]) -> int:
@@ -313,7 +312,8 @@ class Solution:
                 dp[i][j+2] = max(dp[i-1][j+2], dp[i-1][j+1] + prices[i])
         return dp[-1][2*k]
 ```
-版本二
+
+> 版本二
 ```python
 class Solution:
     def maxProfit(self, k: int, prices: List[int]) -> int:
@@ -329,9 +329,31 @@ class Solution:
                     dp[j] = max(dp[j],dp[j-1]+prices[i])
         return dp[2*k]
 ```
+
+> 版本三: 一维 dp 数组(易理解版本)
+```python
+class Solution:
+    def maxProfit(self, k: int, prices: List[int]) -> int:
+        dp = [0] * k * 2
+        for i in range(k):
+            dp[i * 2] = -prices[0]
+
+        for price in prices[1:]:
+            dc = dp.copy() # 这句话是关键，把前一天的 dp 状态保存下来，防止被覆盖掉，后面只用它，不用 dp，逻辑简单易懂
+
+            for i in range(2 * k):
+                if i % 2 == 1:
+                    dp[i] = max(dc[i], dc[i - 1] + price)
+                else:
+                    pre = 0 if i == 0 else dc[i - 1]
+                    dp[i] = max(dc[i], pre - price)
+            
+        return dp[-1]
+```
+
 ### Go:
 
-版本一：
+> 版本一：
 
 ```go
 // 买卖股票的最佳时机IV 动态规划
@@ -368,7 +390,7 @@ func max(a, b int) int {
 }
 ```
 
-版本二: 三维 dp数组
+> 版本二: 三维 dp数组
 ```go
 func maxProfit(k int, prices []int) int {
 	length := len(prices)
@@ -443,7 +465,31 @@ func max(a, b int) int {
 }
 ```
 
+> 版本四：一维 dp 数组（易理解版本）
 
+```go
+func maxProfit(k int, prices []int) int {
+    dp := make([]int, 2 * k)
+    for i := range k {
+        dp[i * 2] = -prices[0]
+    }
+
+    for j := 1; j < len(prices); j++ {
+        dc := slices.Clone(dp) // 这句话是关键，把前一天的 dp 状态保存下来，防止被覆盖掉，后面只用它，不用 dp，逻辑简单易懂
+
+        for i := range k * 2 {
+            if i % 2 == 1 {
+                dp[i] = max(dc[i], dc[i - 1] + prices[j])
+            } else {
+                pre := 0; if i >= 1 { pre = dc[i - 1] }
+                dp[i] = max(dc[i], pre - prices[j])
+            }
+        }
+    }
+
+    return dp[2 * k - 1]
+}
+```
 
 ### JavaScript:
 

problems/0189.旋转数组.md

@@ -199,7 +199,17 @@ function reverseByRange(nums: number[], left: number, right: number): void {
 }
 ```
 
-
+### Rust
+```rust
+impl Solution {
+    pub fn rotate(nums: &mut Vec<i32>, k: i32) {
+        let k = k as usize % nums.len();
+        nums.reverse();
+        nums[..k].reverse();
+        nums[k..].reverse();
+    }
+}
+```
 
 
 <p align="center">

problems/0202.快乐数.md

@@ -534,6 +534,30 @@ public class Solution {
 }
 ```
 
+### Ruby：
+
+```ruby
+# @param {Integer} n
+# @return {Boolean}
+def is_happy(n)
+    @occurred_nums = Set.new
+
+    while true
+        n = next_value(n)
+
+        return true if n == 1
+
+        return false if @occurred_nums.include?(n)
+            
+        @occurred_nums << n
+    end
+end
+
+def next_value(n)
+    n.to_s.chars.sum { |char| char.to_i ** 2 }
+end
+```
+
 <p align="center">
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>

problems/0203.移除链表元素.md

@@ -737,7 +737,45 @@ public class Solution
     }
 }
 ```
+### Ruby#
 
+```ruby
+# 定义链表节点
+class ListNode
+  attr_accessor :val, :next
+  def initialize(val = 0, _next = nil)
+    @val = val
+    @next = _next
+  end
+end
+
+# 删除链表中值为 val 的节点
+def remove_elements(head, val)
+  # 创建一个虚拟头节点，这样可以简化删除头节点的处理
+  # 虚拟头节点的值为 0，指向当前链表的头节点
+  dummy = ListNode.new(0)
+  dummy.next = head
+  
+  # 初始化当前节点为虚拟头节点
+  current = dummy
+  
+  # 遍历链表，直到当前节点的下一个节点为空
+  while current.next
+    # 如果当前节点的下一个节点的值等于 val
+    if current.next.val == val
+      # 跳过该节点，即将当前节点的 next 指向下一个节点的 next
+      current.next = current.next.next
+    else
+      # 否则继续遍历，当前节点向前移动
+      current = current.next
+    end
+  end
+  
+  # 返回删除 val 后的新链表的头节点，虚拟头节点的 next 就是新的头节点
+  dummy.next
+end
+
+```
 
 <p align="center">
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">

problems/0209.长度最小的子数组.md

@@ -266,7 +266,7 @@ var minSubArrayLen = function(target, nums) {
 };
 ```
 
-### Typescript：
+### TypeScript：
 
 ```typescript
 function minSubArrayLen(target: number, nums: number[]): number {

problems/0232.用栈实现队列.md

@@ -113,7 +113,7 @@ public:
 
 ```
 
-* 时间复杂度: push和empty为O(1), pop和peek为O(n)
+* 时间复杂度: 都为O(1)。pop和peek看起来像O(n)，实际上一个循环n会被使用n次，最后还是O(1)。
 * 空间复杂度: O(n)
 
 

problems/0235.二叉搜索树的最近公共祖先.md

@@ -38,7 +38,7 @@
 
 ## 算法公开课 
 
-**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html)：[二叉搜索树找祖先就有点不一样了！| 235. 二叉搜索树的最近公共祖先](https://www.bilibili.com/video/BV1Zt4y1F7ww?share_source=copy_web)，相信结合视频在看本篇题解，更有助于大家对本题的理解**。
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html)：[二叉搜索树找祖先就有点不一样了！| 235. 二叉搜索树的最近公共祖先](https://www.bilibili.com/video/BV1Zt4y1F7ww?share_source=copy_web)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
 
 ## 思路
 

problems/0236.二叉树的最近公共祖先.md

@@ -36,7 +36,7 @@
 
 ## 算法公开课 
 
-**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html)：[自底向上查找，有点难度！ | LeetCode：236. 二叉树的最近公共祖先](https://www.bilibili.com/video/BV1jd4y1B7E2)，相信结合视频在看本篇题解，更有助于大家对本题的理解**。
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html)：[自底向上查找，有点难度！ | LeetCode：236. 二叉树的最近公共祖先](https://www.bilibili.com/video/BV1jd4y1B7E2)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
 
 
 ## 思路

problems/0239.滑动窗口最大值.md

@@ -299,7 +299,7 @@ class Solution {
 ```
 
 ### Python：
-
+#### 解法一：使用自定义的单调队列类
 ```python
 from collections import deque
 
@@ -339,6 +339,35 @@ class Solution:
         return result
 ```
 
+
+#### 解法二：直接用单调队列
+```python
+from collections import deque
+class Solution:
+    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
+        max_list = [] # 结果集合
+        kept_nums = deque() # 单调队列
+
+        for i in range(len(nums)):
+            update_kept_nums(kept_nums, nums[i]) # 右侧新元素加入
+
+            if i >= k and nums[i - k] == kept_nums[0]: # 左侧旧元素如果等于单调队列头元素，需要移除头元素
+                kept_nums.popleft()
+
+            if i >= k - 1:
+                max_list.append(kept_nums[0])
+
+        return max_list
+
+def update_kept_nums(kept_nums, num): # num 是新加入的元素
+    # 所有小于新元素的队列尾部元素，在新元素出现后，都是没有价值的，都需要被移除
+    while kept_nums and num > kept_nums[-1]:
+        kept_nums.pop()
+
+    kept_nums.append(num)
+
+```
+
 ### Go：
 
 ```go
@@ -401,7 +430,7 @@ func maxSlidingWindow(nums []int, k int) []int {
 }
 ```
 
-### Javascript:
+### JavaScript:
 
 ```javascript
 /**

problems/0279.完全平方数.md

@@ -346,7 +346,7 @@ func min(a, b int) int {
 }
 ```
 
-### Javascript:
+### JavaScript:
 
 ```Javascript
 // 先遍历物品，再遍历背包

problems/0283.移动零.md

@@ -169,7 +169,20 @@ void moveZeroes(int* nums, int numsSize){
 }
 ```
 
-
+### Rust
+```rust
+impl Solution {
+    pub fn move_zeroes(nums: &mut Vec<i32>) {
+        let mut slow = 0;
+        for fast in 0..nums.len() {
+            if nums[fast] != 0 {
+                nums.swap(slow, fast);
+                slow += 1;
+            }
+        }
+    }
+}
+```
 
 
 

problems/0300.最长上升子序列.md

@@ -248,7 +248,7 @@ func lengthOfLIS(nums []int ) int {
 }
 ```
 
-### Javascript:
+### JavaScript:
 
 ```javascript
 const lengthOfLIS = (nums) => {

problems/0309.最佳买卖股票时机含冷冻期.md

@@ -274,7 +274,7 @@ class Solution {
 ```
 
 ### Python：
-版本一
+> 版本一
 
 ```python
 from typing import List
@@ -294,7 +294,8 @@ class Solution:
         return max(dp[n-1][3], dp[n-1][1], dp[n-1][2])  # 返回最后一天不持有股票的最大利润
 
 ```
-版本二
+
+> 版本二
 ```python
 class Solution:
     def maxProfit(self, prices: List[int]) -> int:
@@ -320,6 +321,36 @@ class Solution:
         return max(dp[-1][1], dp[-1][2])
 
 ```
+
+> 版本三
+```python
+class Solution:
+    def maxProfit(self, prices: List[int]) -> int:
+        # 0: holding stocks 
+        #    (1) keep holding stocks: dp[i][0] = dp[i - 1][0]
+        #    (2) buy stocks: dp[i][0] = dp[i - 1][1] - price, or dp[i - 1][3] - price
+        # 1: keep no stocks: dp[i][1] = dp[i - 1][1]
+        # 2: sell stocks: dp[i][2] = dp[i - 1][0] + price
+        # 3: cooldown day: dp[i][3] = dp[i - 1][2]
+        dp = [-prices[0], 0, 0, 0]
+
+        for price in prices[1:]:
+            dc = dp.copy() # 这句话是关键，把前一天的 dp 状态保存下来，防止被覆盖掉，后面只用它，不用 dp，逻辑简单易懂
+            dp[0] = max(
+                dc[0],
+                dc[1] - price,
+                dc[3] - price
+            )
+            dp[1] = max(
+                dc[1],
+                dc[3]
+            )
+            dp[2] = dc[0] + price
+            dp[3] = dc[2]
+
+        return max(dp)
+```
+
 ### Go：
 
 ```go
@@ -393,7 +424,7 @@ func max(a, b int) int {
 
 
 
-### Javascript:
+### JavaScript:
 
 > 不同的状态定义 感觉更容易理解些
 ```javascript

problems/0322.零钱兑换.md

@@ -427,7 +427,7 @@ impl Solution {
 }
 ```
 
-### Javascript：
+### JavaScript：
 
 ```javascript
 // 遍历物品

problems/0332.重新安排行程.md

@@ -535,7 +535,7 @@ func findItinerary(tickets [][]string) []string {
 }
 ```
 
-### Javascript 
+### JavaScript 
 
 ```Javascript
 

problems/0337.打家劫舍III.md

@@ -388,19 +388,96 @@ class Solution:
 
 ### Go 
 
+暴力递归
+
+```go
+/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ *     Val int
+ *     Left *TreeNode
+ *     Right *TreeNode
+ * }
+ */
+func rob(root *TreeNode) int {
+    if root == nil {
+        return 0
+    }
+    if root.Left == nil && root.Right == nil {
+        return root.Val
+    }
+    // 偷父节点
+    val1 := root.Val
+    if root.Left != nil {
+        val1 += rob(root.Left.Left) + rob(root.Left.Right) // 跳过root->left，相当于不考虑左孩子了
+    }
+    if root.Right != nil {
+        val1 += rob(root.Right.Left) + rob(root.Right.Right) // 跳过root->right，相当于不考虑右孩子了
+    }
+    // 不偷父节点
+    val2 := rob(root.Left) + rob(root.Right) // 考虑root的左右孩子
+    return max(val1, val2)
+}
+
+func max(x, y int) int {
+    if x > y {
+        return x
+    }
+    return y
+}
+```
+
+记忆化递推
+
+```go
+/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ *     Val int
+ *     Left *TreeNode
+ *     Right *TreeNode
+ * }
+ */
+var umap = make(map[*TreeNode]int)
+
+func rob(root *TreeNode) int {
+    if root == nil {
+        return 0
+    }
+    if root.Left == nil && root.Right == nil {
+        return root.Val
+    }
+    if val, ok := umap[root]; ok {
+        return val // 如果umap里已经有记录则直接返回
+    }
+    // 偷父节点
+    val1 := root.Val
+    if root.Left != nil {
+        val1 += rob(root.Left.Left) + rob(root.Left.Right) // 跳过root->left，相当于不考虑左孩子了
+    }
+    if root.Right != nil {
+        val1 += rob(root.Right.Left) + rob(root.Right.Right) // 跳过root->right，相当于不考虑右孩子了
+    }
+    // 不偷父节点
+    val2 := rob(root.Left) + rob(root.Right) // 考虑root的左右孩子
+    umap[root] = max(val1, val2) // umap记录一下结果
+    return max(val1, val2)
+}
+
+func max(x, y int) int {
+    if x > y {
+        return x
+    }
+    return y
+}
+```
+
 动态规划
 
 ```go
 func rob(root *TreeNode) int {
 	res := robTree(root)
-	return max(res[0], res[1])
-}
-
-func max(a, b int) int {
-	if a > b {
-		return a
-	}
-	return b
+	return slices.Max(res)
 }
 
 func robTree(cur *TreeNode) []int {
@@ -414,7 +491,7 @@ func robTree(cur *TreeNode) []int {
     // 考虑去偷当前的屋子
 	robCur := cur.Val + left[0] + right[0]
     // 考虑不去偷当前的屋子
-	notRobCur := max(left[0], left[1]) + max(right[0], right[1])
+	notRobCur := slices.Max(left) + slices.Max(right)
 
     // 注意顺序：0:不偷，1:去偷
 	return []int{notRobCur, robCur}

problems/0343.整数拆分.md

@@ -385,7 +385,7 @@ func integerBreak(n int) int {
 }
 ```
 
-### Javascript
+### JavaScript
 ```Javascript
 var integerBreak = function(n) {
     let dp = new Array(n + 1).fill(0)

problems/0376.摆动序列.md

@@ -466,7 +466,7 @@ func max(a, b int) int {
 }
 ```
 
-### Javascript
+### JavaScript
 
 **贪心**
 

problems/0377.组合总和Ⅳ.md

@@ -254,7 +254,7 @@ func combinationSum4(nums []int, target int) int {
 }
 ```
 
-### Javascript：
+### JavaScript：
 
 ```javascript
 const combinationSum4 = (nums, target) => {

problems/0406.根据身高重建队列.md

@@ -270,7 +270,7 @@ func reconstructQueue(people [][]int) [][]int {
 }
 ```
 
-### Javascript 
+### JavaScript 
 
 ```Javascript
 var reconstructQueue = function(people) {

problems/0416.分割等和子集.md

@@ -47,7 +47,13 @@
 
 那么只要找到集合里能够出现 sum / 2 的子集总和，就算是可以分割成两个相同元素和子集了。
 
-本题是可以用回溯暴力搜索出所有答案的，但最后超时了，也不想再优化了，放弃回溯，直接上01背包吧。
+本题是可以用回溯暴力搜索出所有答案的，但最后超时了，也不想再优化了，放弃回溯。
+
+是否有其他解法可以解决此题。 
+
+本题的本质是，能否把容量为 sum / 2的背包装满。 
+
+**这是 背包算法可以解决的经典类型题目**。 
 
 如果对01背包不够了解，建议仔细看完如下两篇：
 
@@ -56,7 +62,7 @@
 
 ### 01背包问题
 
-背包问题，大家都知道，有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。
+01背包问题，大家都知道，有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。
 
 **背包问题有多种背包方式，常见的有：01背包、完全背包、多重背包、分组背包和混合背包等等。**
 
@@ -64,32 +70,33 @@
 
 **即一个商品如果可以重复多次放入是完全背包，而只能放入一次是01背包，写法还是不一样的。**
 
-**要明确本题中我们要使用的是01背包，因为元素我们只能用一次。**
+**元素我们只能用一次，如果使用背包，那么也是01背包**
 
 回归主题：首先，本题要求集合里能否出现总和为 sum / 2 的子集。
 
-那么来一一对应一下本题，看看背包问题如何来解决。
+既有一个 只能装重量为 sum / 2 的背包，商品为数字，这些数字能不能把 这个背包装满。 
 
-**只有确定了如下四点，才能把01背包问题套到本题上来。**
+那每一件商品是数字的话，对应的重量 和 价值是多少呢？  
 
-* 背包的体积为sum / 2
-* 背包要放入的商品（集合里的元素）重量为 元素的数值，价值也为元素的数值
-* 背包如果正好装满，说明找到了总和为 sum / 2 的子集。
-* 背包中每一个元素是不可重复放入。
+一个数字只有一个维度，即 重量等于价值。  
 
-以上分析完，我们就可以套用01背包，来解决这个问题了。
+当数字 可以装满 承载重量为 sum / 2 的背包的背包时，这个背包的价值也是 sum / 2。
+
+那么这道题就是 装满 承载重量为 sum / 2 的背包，价值最大是多少？ 
+
+如果最大价值是 sum / 2，说明正好被商品装满了。
+
+因为商品是数字，重量和对应的价值是相同的。
+
+以上分析完，我们就可以直接用01背包 来解决这个问题了。
 
 动规五部曲分析如下：
 
 1. 确定dp数组以及下标的含义
 
-01背包中，dp[j] 表示： 容量为j的背包，所背的物品价值最大可以为dp[j]。
+01背包中，dp[j] 表示： 容量（所能装的重量）为j的背包，所背的物品价值最大可以为dp[j]。
 
-本题中每一个元素的数值既是重量，也是价值。
-
-**套到本题，dp[j]表示 背包总容量（所能装的总重量）是j，放进物品后，背的最大重量为dp[j]**。
-
-那么如果背包容量为target， dp[target]就是装满 背包之后的重量，所以 当 dp[target] == target 的时候，背包就装满了。
+如果背包所载重量为target， dp[target]就是装满 背包之后的总价值，因为 本题中每一个元素的数值既是重量，也是价值，所以，当 dp[target] == target 的时候，背包就装满了。
 
 有录友可能想，那还有装不满的时候？ 
 
@@ -192,12 +199,11 @@ public:
 
 ## 总结
 
-这道题目就是一道01背包应用类的题目，需要我们拆解题目，然后套入01背包的场景。
+这道题目就是一道01背包经典应用类的题目，需要我们拆解题目，然后才能发现可以使用01背包。
 
 01背包相对于本题，主要要理解，题目中物品是nums[i]，重量是nums[i]，价值也是nums[i]，背包体积是sum/2。
 
-看代码的话，就可以发现，基本就是按照01背包的写法来的。
-
+做完本题后，需要大家清晰：背包问题，不仅可以求 背包能被的最大价值，还可以求这个背包是否可以装满。
 
 ## 其他语言版本
 

problems/0435.无重叠区间.md

@@ -311,7 +311,7 @@ func min(a, b int) int {
 }
 ```
 
-### Javascript
+### JavaScript
 - 按右边界排序
 ```Javascript
 var eraseOverlapIntervals = function(intervals) {

problems/0450.删除二叉搜索树中的节点.md

@@ -26,7 +26,7 @@
 
 ## 算法公开课 
 
-**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html)：[调整二叉树的结构最难！| LeetCode：450.删除二叉搜索树中的节点](https://www.bilibili.com/video/BV1tP41177us?share_source=copy_web)，相信结合视频在看本篇题解，更有助于大家对本题的理解**。
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html)：[调整二叉树的结构最难！| LeetCode：450.删除二叉搜索树中的节点](https://www.bilibili.com/video/BV1tP41177us?share_source=copy_web)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
 
 ## 思路
 

problems/0452.用最少数量的箭引爆气球.md

@@ -110,7 +110,7 @@ public:
 ```
 
 * 时间复杂度：O(nlog n)，因为有一个快排
-* 空间复杂度：O(1)，有一个快排，最差情况(倒序)时，需要n次递归调用。因此确实需要O(n)的栈空间
+* 空间复杂度：O(n)，有一个快排，最差情况(倒序)时，需要n次递归调用。因此确实需要O(n)的栈空间
 
 可以看出代码并不复杂。
 
@@ -180,19 +180,25 @@ class Solution:
 ```python
 class Solution: # 不改变原数组
     def findMinArrowShots(self, points: List[List[int]]) -> int:
+        if len(points) == 0:
+            return 0
+            
         points.sort(key = lambda x: x[0])
-        sl,sr = points[0][0],points[0][1]
+
+        # points已经按照第一个坐标正序排列，因此只需要设置一个变量，记录右侧坐标（阈值）
+        # 考虑一个气球范围包含两个不相交气球的情况：气球1: [1, 10], 气球2: [2, 5], 气球3: [6, 10]
+        curr_min_right = points[0][1]
         count = 1
+        
         for i in points:
-            if i[0]>sr:
-                count+=1
-                sl,sr = i[0],i[1]
+            if i[0] > curr_min_right:
+                # 当气球左侧大于这个阈值，那么一定就需要在发射一只箭，并且将阈值更新为当前气球的右侧
+                count += 1
+                curr_min_right = i[1]
             else:
-                sl = max(sl,i[0])
-                sr = min(sr,i[1])
+                # 否则的话，我们只需要求阈值和当前气球的右侧的较小值来更新阈值
+                curr_min_right = min(curr_min_right, i[1])
         return count
-
-
 ```
 ### Go
 ```go
@@ -220,7 +226,7 @@ func min(a, b int) int {
 }
 ```
 
-### Javascript 
+### JavaScript 
 ```Javascript
 var findMinArrowShots = function(points) {
     points.sort((a, b) => {

problems/0454.四数相加II.md

@@ -488,6 +488,44 @@ int fourSumCount(int* nums1, int nums1Size, int* nums2, int nums2Size, int* nums
 }
 ```
 
+### Ruby:
+
+```ruby
+# @param {Integer[]} nums1
+# @param {Integer[]} nums2
+# @param {Integer[]} nums3
+# @param {Integer[]} nums4
+# @return {Integer}
+# 新思路：和版主的思路基本相同，只是对后面两个数组的二重循环，用一个方法调用外加一重循环替代，简化了一点。
+#       简单的说，就是把四数和变成了两个两数和的统计（结果放到两个 hash 中），然后再来一次两数和为0.
+#       把四个数分成两组两个数，然后分别计算每组可能的和情况，分别存入 hash 中，key 是 和，value 是 数量；
+#       最后，得到的两个 hash 只需要遍历一次，符合和为零的 value 相乘并加总。
+def four_sum_count(nums1, nums2, nums3, nums4)
+    num_to_count_1 = two_sum_mapping(nums1, nums2)
+    num_to_count_2 = two_sum_mapping(nums3, nums4)
+
+    count_sum = 0
+
+    num_to_count_1.each do |num, count|
+        count_sum += num_to_count_2[-num] * count # 反查另一个 hash，看有没有匹配的，没有的话，hash 默认值为 0，不影响加总；有匹配的，乘积就是可能的情况
+    end
+
+    count_sum
+end
+
+def two_sum_mapping(nums1, nums2)
+    num_to_count = Hash.new(0)
+
+    nums1.each do |num1|
+        nums2.each do |nums2|
+            num_to_count[num1 + nums2] += 1 # 统计和为 num1 + nums2 的有几个
+        end
+    end
+
+    num_to_count
+end
+```
+
 <p align="center">
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>

problems/0455.分发饼干.md

@@ -278,7 +278,7 @@ pub fn find_content_children(mut children: Vec<i32>, mut cookies: Vec<i32>) -> i
 }
 ```
 
-### Javascript
+### JavaScript
 
 ```js
 var findContentChildren = function (g, s) {

problems/0474.一和零.md

@@ -362,7 +362,7 @@ func max(a,b int) int {
 }
 ```
 
-### Javascript
+### JavaScript
 ```javascript
 const findMaxForm = (strs, m, n) => {
     const dp = Array.from(Array(m+1), () => Array(n+1).fill(0));

problems/0491.递增子序列.md

@@ -375,7 +375,7 @@ func dfs(nums []int, start int) {
 }
 ```
 
-### Javascript 
+### JavaScript 
 
 ```Javascript
 

problems/0494.目标和.md

@@ -791,7 +791,7 @@ func abs(x int) int {
 }
 ```
 
-### Javascript
+### JavaScript
 ```javascript
 const findTargetSumWays = (nums, target) => {
 

problems/0501.二叉搜索树中的众数.md

@@ -35,7 +35,7 @@
 
 ## 算法公开课 
 
-**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html)：[不仅双指针，还有代码技巧可以惊艳到你！ | LeetCode：501.二叉搜索树中的众数](https://www.bilibili.com/video/BV1fD4y117gp)，相信结合视频在看本篇题解，更有助于大家对本题的理解**。
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html)：[不仅双指针，还有代码技巧可以惊艳到你！ | LeetCode：501.二叉搜索树中的众数](https://www.bilibili.com/video/BV1fD4y117gp)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
 
 
 ## 思路

problems/0503.下一个更大元素II.md

@@ -185,7 +185,7 @@ class Solution:
 
 > 版本二：针对版本一的优化
 
-```python3
+```python
 class Solution:
     def nextGreaterElements(self, nums: List[int]) -> List[int]:
         res = [-1] * len(nums)
@@ -213,6 +213,40 @@ class Solution:
 ### Go:
 
 ```go
+// 版本一
+func nextGreaterElements(nums []int) []int {
+    // 拼接一个新的nums
+    numsNew := make([]int, len(nums) * 2)
+    copy(numsNew, nums)
+    copy(numsNew[len(nums):], nums)
+    // 用新的nums大小来初始化result
+    result := make([]int, len(numsNew))
+    for i := range result {
+        result[i] = -1
+    }
+    
+    // 开始单调栈
+    st := []int{0}
+    for i := 1; i < len(numsNew); i++ {
+        if numsNew[i] < numsNew[st[len(st)-1]] {
+            st = append(st, i)
+        } else if numsNew[i] == numsNew[st[len(st)-1]] {
+            st = append(st, i)
+        } else {
+            for len(st) > 0 && numsNew[i] > numsNew[st[len(st)-1]] {
+                result[st[len(st)-1]] = numsNew[i]
+                st = st[:len(st)-1]
+            }
+            st = append(st, i)
+        }
+    }
+    result = result[:len(result)/2]
+    return result
+}
+```
+
+```go
+// 版本二
 func nextGreaterElements(nums []int) []int {
     length := len(nums)
     result := make([]int,length)

problems/0509.斐波那契数.md

@@ -292,7 +292,7 @@ func fib(n int) int {
         return c
 }
 ```
-### Javascript 
+### JavaScript 
 解法一
 ```Javascript
 var fib = function(n) {

problems/0516.最长回文子序列.md

@@ -224,7 +224,7 @@ func longestPalindromeSubseq(s string) int {
 }
 ```
 
-### Javascript：
+### JavaScript：
 
 ```javascript
 const longestPalindromeSubseq = (s) => {

problems/0518.零钱兑换II.md

@@ -349,7 +349,7 @@ impl Solution {
 }
 ```
 
-### Javascript：
+### JavaScript：
 
 ```javascript
 const change = (amount, coins) => {

problems/0530.二叉搜索树的最小绝对差.md

@@ -21,7 +21,7 @@
 
 ## 算法公开课
 
-**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html)：[二叉搜索树中，需要掌握如何双指针遍历！| LeetCode：530.二叉搜索树的最小绝对差](https://www.bilibili.com/video/BV1DD4y11779)，相信结合视频在看本篇题解，更有助于大家对本题的理解**。
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html)：[二叉搜索树中，需要掌握如何双指针遍历！| LeetCode：530.二叉搜索树的最小绝对差](https://www.bilibili.com/video/BV1DD4y11779)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
 
 
 ## 思路

problems/0541.反转字符串II.md

@@ -282,7 +282,7 @@ class Solution:
         return ''.join(res)
 ```
 
-### Python3 (v2):
+#### Python3 (v2):
 
 ```python
 class Solution:
@@ -297,6 +297,21 @@ class Solution:
         return s
 ```
 
+#### Python3 (v3):
+
+```python
+class Solution:
+    def reverseStr(self, s: str, k: int) -> str:
+        i = 0
+        chars = list(s)
+        
+        while i < len(chars):
+            chars[i:i + k] = chars[i:i + k][::-1] # 反转后，更改原值为反转后值
+            i += k * 2
+
+        return ''.join(chars)
+```
+
 ### Go：
 
 ```go

problems/0583.两个字符串的删除操作.md

@@ -290,6 +290,7 @@ func min(a, b int) int {
 }
 ```
 
+
 动态规划二
 
 ```go
@@ -318,7 +319,9 @@ func max(x, y int) int {
 }
 ```
 
-### Javascript：
+
+### JavaScript：
+
 
 ```javascript
 // 方法一

problems/0647.回文子串.md

@@ -102,7 +102,7 @@ dp[i][j]可以初始化为true么？ 当然不行，怎能刚开始就全都匹
 
 4. 确定遍历顺序
 
-遍历顺序可有有点讲究了。
+遍历顺序可就有点讲究了。
 
 首先从递推公式中可以看出，情况三是根据dp[i + 1][j - 1]是否为true，在对dp[i][j]进行赋值true的。
 
@@ -465,7 +465,7 @@ func countSubstrings(s string) int {
 }
 ```
 
-### Javascript：
+### JavaScript：
 
 > 动态规划
 ```javascript

problems/0669.修剪二叉搜索树.md

@@ -22,7 +22,7 @@
 
 ## 算法公开课
 
-**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html)：[你修剪的方式不对，我来给你纠正一下！| LeetCode：669. 修剪二叉搜索树](https://www.bilibili.com/video/BV17P41177ud?share_source=copy_web)，相信结合视频在看本篇题解，更有助于大家对本题的理解**。
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html)：[你修剪的方式不对，我来给你纠正一下！| LeetCode：669. 修剪二叉搜索树](https://www.bilibili.com/video/BV17P41177ud?share_source=copy_web)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
 
 ## 思路
 

problems/0674.最长连续递增序列.md

@@ -359,7 +359,7 @@ impl Solution {
 ```
 
 
-### Javascript：
+### JavaScript：
 
 > 动态规划：
 ```javascript

problems/0714.买卖股票的最佳时机含手续费.md

@@ -43,7 +43,7 @@
 
 在[贪心算法：122.买卖股票的最佳时机II](https://programmercarl.com/0122.买卖股票的最佳时机II.html)中使用贪心策略不用关心具体什么时候买卖，只要收集每天的正利润，最后稳稳的就是最大利润了。
 
-而本题有了手续费，就要关系什么时候买卖了，因为计算所获得利润，需要考虑买卖利润可能不足以手续费的情况。
+而本题有了手续费，就要关心什么时候买卖了，因为计算所获得利润，需要考虑买卖利润可能不足以扣减手续费的情况。
 
 如果使用贪心策略，就是最低值买，最高值（如果算上手续费还盈利）就卖。
 
@@ -122,7 +122,7 @@ public:
 * 时间复杂度：O(n)
 * 空间复杂度：O(n)
 
-当然可以对空间经行优化，因为当前状态只是依赖前一个状态。
+当然可以对空间进行优化，因为当前状态只是依赖前一个状态。
 
 C++ 代码如下：
 
@@ -243,7 +243,7 @@ func maxProfit(prices []int, fee int) int {
     return res
 }
 ```
-### Javascript
+### JavaScript
 ```Javascript
 // 贪心思路
 var maxProfit = function(prices, fee) {

problems/0714.买卖股票的最佳时机含手续费（动态规划）.md

@@ -46,7 +46,7 @@
 * 时间复杂度：O(n)
 * 空间复杂度：O(1) 
 
-本题使用贪心算法并不好理解，也很容易出错，那么我们再来看看是使用动规的方法如何解题。
+本题使用贪心算法并不好理解，也很容易出错，那么我们再来看看使用动规的方法如何解题。
 
 相对于[动态规划：122.买卖股票的最佳时机II](https://programmercarl.com/0122.买卖股票的最佳时机II（动态规划）.html)，本题只需要在计算卖出操作的时候减去手续费就可以了，代码几乎是一样的。
 
@@ -54,7 +54,7 @@
 
 这里重申一下dp数组的含义：
 
-dp[i][0] 表示第i天持有股票所省最多现金。
+dp[i][0] 表示第i天持有股票所得最多现金。
 dp[i][1] 表示第i天不持有股票所得最多现金
 
 
@@ -226,7 +226,7 @@ func max(a, b int) int {
 }
 ```
 
-### Javascript：
+### JavaScript：
 
 ```javascript
 const maxProfit = (prices,fee) => {

problems/0738.单调递增的数字.md

@@ -292,7 +292,7 @@ func monotoneIncreasingDigits(N int) int {
 }
 ```
 
-### Javascript 
+### JavaScript 
 ```Javascript
 var monotoneIncreasingDigits = function(n) {
     n = n.toString()

problems/0763.划分字母区间.md

@@ -312,7 +312,7 @@ func max(a, b int) int {
 }
 ```
 
-### Javascript 
+### JavaScript 
 ```Javascript
 var partitionLabels = function(s) {
     let hash = {}

problems/0860.柠檬水找零.md

@@ -226,7 +226,7 @@ func lemonadeChange(bills []int) bool {
 }
 ```
 
-### Javascript 
+### JavaScript 
 ```Javascript
 var lemonadeChange = function(bills) {
     let fiveCount = 0

problems/0941.有效的山脉数组.md

@@ -196,7 +196,22 @@ public class Solution {
 }
 ```
 
-
+### Rust
+```rust
+impl Solution {
+    pub fn valid_mountain_array(arr: Vec<i32>) -> bool {
+        let mut i = 0;
+        let mut j = arr.len() - 1;
+        while i < arr.len() - 1 && arr[i] < arr[i + 1] {
+            i += 1;
+        }
+        while j > 0 && arr[j] < arr[j - 1] {
+            j -= 1;
+        }
+        i > 0 && j < arr.len() - 1 && i == j
+    }
+}
+```
 
 <p align="center">
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">

problems/0968.监控二叉树.md

@@ -536,7 +536,7 @@ func min(a, b int) int {
 
 ```
 
-### Javascript
+### JavaScript
 
 ```Javascript
 var minCameraCover = function(root) {

problems/0977.有序数组的平方.md

@@ -301,7 +301,7 @@ impl Solution {
     }
 }
 ```
-### Javascript：
+### JavaScript：
 
 ```Javascript
 /**
@@ -327,7 +327,7 @@ var sortedSquares = function(nums) {
 };
 ```
 
-### Typescript：
+### TypeScript：
 
 双指针法：
 

problems/1005.K次取反后最大化的数组和.md

@@ -207,7 +207,7 @@ func largestSumAfterKNegations(nums []int, K int) int {
 ```
 
 
-### Javascript 
+### JavaScript 
 ```Javascript
 var largestSumAfterKNegations = function(nums, k) {
 

problems/1035.不相交的线.md

@@ -8,11 +8,16 @@
 
 [力扣题目链接](https://leetcode.cn/problems/uncrossed-lines/)
 
-我们在两条独立的水平线上按给定的顺序写下 A 和 B 中的整数。
+在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。
 
-现在，我们可以绘制一些连接两个数字 A[i] 和 B[j] 的直线，只要 A[i] == B[j]，且我们绘制的直线不与任何其他连线（非水平线）相交。
+现在，可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，这些直线需要同时满足：
 
-以这种方法绘制线条，并返回我们可以绘制的最大连线数。
+* nums1[i] == nums2[j]
+* 且绘制的直线不与任何其他连线（非水平线）相交。
+
+请注意，连线即使在端点也不能相交：每个数字只能属于一条连线。
+
+以这种方法绘制线条，并返回可以绘制的最大连线数。
 
 
 ![1035.不相交的线](https://code-thinking-1253855093.file.myqcloud.com/pics/2021032116363533.png)
@@ -26,16 +31,16 @@
 
 相信不少录友看到这道题目都没啥思路，我们来逐步分析一下。
 
-绘制一些连接两个数字 A[i] 和 B[j] 的直线，只要 A[i] == B[j]，且直线不能相交！
+绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，只要 nums1[i] == nums2[j]，且直线不能相交！
 
-直线不能相交，这就是说明在字符串A中 找到一个与字符串B相同的子序列，且这个子序列不能改变相对顺序，只要相对顺序不改变，链接相同数字的直线就不会相交。
+直线不能相交，这就是说明在字符串nums1中 找到一个与字符串nums2相同的子序列，且这个子序列不能改变相对顺序，只要相对顺序不改变，连接相同数字的直线就不会相交。
 
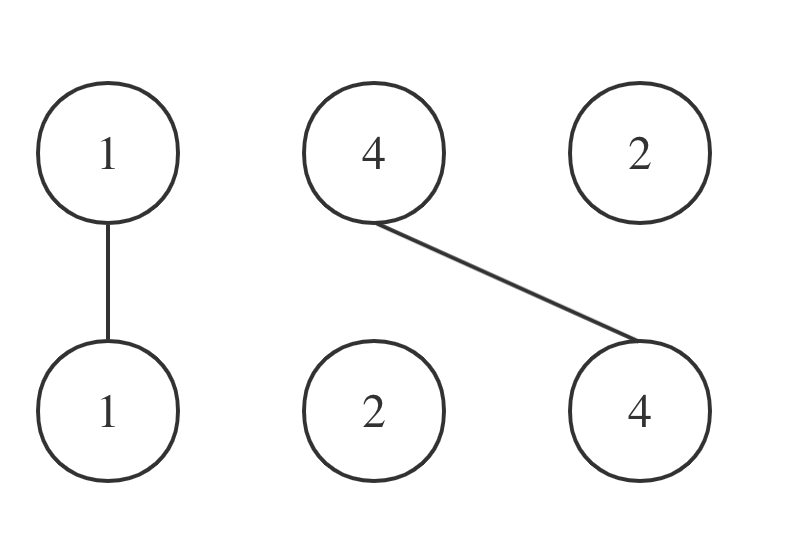
-拿示例一A = [1,4,2], B = [1,2,4]为例，相交情况如图：
+拿示例一nums1 = [1,4,2], nums2 = [1,2,4]为例，相交情况如图：
 
 
 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20210914145158.png)
 
-其实也就是说A和B的最长公共子序列是[1,4]，长度为2。 这个公共子序列指的是相对顺序不变（即数字4在字符串A中数字1的后面，那么数字4也应该在字符串B数字1的后面）
+其实也就是说nums1和nums2的最长公共子序列是[1,4]，长度为2。 这个公共子序列指的是相对顺序不变（即数字4在字符串nums1中数字1的后面，那么数字4也应该在字符串nums2数字1的后面）
 
 这么分析完之后，大家可以发现：**本题说是求绘制的最大连线数，其实就是求两个字符串的最长公共子序列的长度！**
 
@@ -52,18 +57,18 @@
 ```CPP
 class Solution {
 public:
-    int maxUncrossedLines(vector<int>& A, vector<int>& B) {
-        vector<vector<int>> dp(A.size() + 1, vector<int>(B.size() + 1, 0));
-        for (int i = 1; i <= A.size(); i++) {
-            for (int j = 1; j <= B.size(); j++) {
-                if (A[i - 1] == B[j - 1]) {
+    int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
+        vector<vector<int>> dp(nums1.size() + 1, vector<int>(nums2.size() + 1, 0));
+        for (int i = 1; i <= nums1.size(); i++) {
+            for (int j = 1; j <= nums2.size(); j++) {
+                if (nums1[i - 1] == nums2[j - 1]) {
                     dp[i][j] = dp[i - 1][j - 1] + 1;
                 } else {
                     dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
                 }
             }
         }
-        return dp[A.size()][B.size()];
+        return dp[nums1.size()][nums2.size()];
     }
 };
 ```
@@ -110,11 +115,11 @@ public:
 
 ```python
 class Solution:
-    def maxUncrossedLines(self, A: List[int], B: List[int]) -> int:
-        dp = [[0] * (len(B)+1) for _ in range(len(A)+1)]
-        for i in range(1, len(A)+1):
-            for j in range(1, len(B)+1):
-                if A[i-1] == B[j-1]:
+    def maxUncrossedLines(self, nums1: List[int], nums2: List[int]) -> int:
+        dp = [[0] * (len(nums2)+1) for _ in range(len(nums1)+1)]
+        for i in range(1, len(nums1)+1):
+            for j in range(1, len(nums2)+1):
+                if nums1[i-1] == nums2[j-1]:
                     dp[i][j] = dp[i-1][j-1] + 1
                 else:
                     dp[i][j] = max(dp[i-1][j], dp[i][j-1])
@@ -124,23 +129,22 @@ class Solution:
 ### Go:
 
 ```go
-func maxUncrossedLines(A []int, B []int) int {
-	m, n := len(A), len(B)
-	dp := make([][]int, m+1)
+func maxUncrossedLines(nums1 []int, nums2 []int) int {
+    dp := make([][]int, len(nums1) + 1)
     for i := range dp {
-        dp[i] = make([]int, n+1)
+        dp[i] = make([]int, len(nums2) + 1)
     }
 
-	for i := 1; i <= len(A); i++ {
-		for j := 1; j <= len(B); j++ {
-			if (A[i - 1] == B[j - 1]) {
+	for i := 1; i <= len(nums1); i++ {
+		for j := 1; j <= len(nums2); j++ {
+			if (nums1[i - 1] == nums2[j - 1]) {
 				dp[i][j] = dp[i - 1][j - 1] + 1
 			} else {
 				dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
 			}
 		}
 	}
-	return dp[m][n]
+	return dp[len(nums1)][len(nums2)]
 
 }
 

problems/1047.删除字符串中的所有相邻重复项.md

@@ -164,7 +164,7 @@ class Solution {
         int top = -1;
         for (int i = 0; i < s.length(); i++) {
             char c = s.charAt(i);
-            // 当 top > 0,即栈中有字符时，当前字符如果和栈中字符相等，弹出栈顶字符，同时 top--
+            // 当 top >= 0,即栈中有字符时，当前字符如果和栈中字符相等，弹出栈顶字符，同时 top--
             if (top >= 0 && res.charAt(top) == c) {
                 res.deleteCharAt(top);
                 top--;

problems/1143.最长公共子序列.md

@@ -80,7 +80,7 @@ if (text1[i - 1] == text2[j - 1]) {
 
 先看看dp[i][0]应该是多少呢？
 
-test1[0, i-1]和空串的最长公共子序列自然是0，所以dp[i][0] = 0;
+text1[0, i-1]和空串的最长公共子序列自然是0，所以dp[i][0] = 0;
 
 同理dp[0][j]也是0。
 

problems/1207.独一无二的出现次数.md

@@ -221,6 +221,28 @@ func uniqueOccurrences(arr []int) bool {
 }
 ```
 
+### Rust
+
+```rust
+use std::collections::{HashMap, HashSet};
+impl Solution {
+    pub fn unique_occurrences(arr: Vec<i32>) -> bool {
+        let mut hash = HashMap::<i32, i32>::new();
+        for x in arr {
+            *hash.entry(x).or_insert(0) += 1;
+        }
+        let mut set = HashSet::<i32>::new();
+        for (_k, v) in hash {
+            if set.contains(&v) {
+                return false
+            } else {
+                set.insert(v);
+            }
+        }
+        true
+    }
+}
+```
 
 
 

problems/1365.有多少小于当前数字的数字.md

@@ -260,6 +260,22 @@ function smallerNumbersThanCurrent(nums: number[]): number[] {
 };
 ```
 
+### rust
+```rust
+use std::collections::HashMap;
+impl Solution {
+    pub fn smaller_numbers_than_current(nums: Vec<i32>) -> Vec<i32> {
+        let mut v = nums.clone();
+        v.sort();
+        let mut hash = HashMap::new();
+        for i in 0..v.len() {
+            // rust中使用or_insert插入值, 如果存在就不插入,可以使用正序遍历
+            hash.entry(v[i]).or_insert(i as i32);
+        }
+        nums.into_iter().map(|x| *hash.get(&x).unwrap()).collect()
+    }
+}
+```
 
 
 <p align="center">

problems/1971.寻找图中是否存在路径.md

@@ -213,7 +213,7 @@ class Solution:
         return find(source) == find(destination)
 ```
 
-### Javascript：
+### JavaScript：
 
 Javascript 并查集解法如下：
 

problems/kamacoder/0047.参会dijkstra堆.md

@@ -911,7 +911,7 @@ func main() {
 
 ### Rust
 
-### Javascript
+### JavaScript
 
 ### TypeScript
 

problems/kamacoder/0047.参会dijkstra朴素.md

@@ -578,7 +578,7 @@ int main() {
 更新 minDist数组，即：源点（节点1） 到 节点2 和 节点3的距离。 
 
 * 源点到节点2的最短距离为100，小于原minDist[2]的数值max，更新minDist[2] = 100 
-* 源点到节点3的最短距离为1，小于原minDist[3]的数值max，更新minDist[4] = 1 
+* 源点到节点3的最短距离为1，小于原minDist[3]的数值max，更新minDist[3] = 1 
 
 -------------------
 
@@ -867,7 +867,7 @@ if __name__ == "__main__":
 
 ### Rust
 
-### Javascript
+### JavaScript
 
 ```js
 function dijkstra(grid, start, end) {

problems/kamacoder/0053.寻宝-Kruskal.md

@@ -547,7 +547,7 @@ if __name__ == "__main__":
 
 ### Rust
 
-### Javascript
+### JavaScript
 
 ```js
 function kruskal(v, edges) {

problems/kamacoder/0053.寻宝-prim.md

@@ -9,17 +9,17 @@
 
 在世界的某个区域，有一些分散的神秘岛屿，每个岛屿上都有一种珍稀的资源或者宝藏。国王打算在这些岛屿上建公路，方便运输。
 
-不同岛屿之间，路途距离不同，国王希望你可以规划建公路的方案，如何可以以最短的总公路距离将 所有岛屿联通起来。
+不同岛屿之间，路途距离不同，国王希望你可以规划建公路的方案，如何可以以最短的总公路距离将所有岛屿联通起来。
 
 给定一张地图，其中包括了所有的岛屿，以及它们之间的距离。以最小化公路建设长度，确保可以链接到所有岛屿。
 
 输入描述：
 
-第一行包含两个整数V 和 E，V代表顶点数，E代表边数 。顶点编号是从1到V。例如：V=2，一个有两个顶点，分别是1和2。
+第一行包含两个整数V和E，V代表顶点数，E代表边数。顶点编号是从1到V。例如：V=2，一个有两个顶点，分别是1和2。
 
-接下来共有 E 行，每行三个整数 v1，v2 和 val，v1 和 v2 为边的起点和终点，val代表边的权值。
+接下来共有E行，每行三个整数v1，v2和val，v1和v2为边的起点和终点，val代表边的权值。
 
-输出描述： 
+输出描述：
 
 输出联通所有岛屿的最小路径总距离
 
@@ -38,65 +38,65 @@
 5 6 2
 5 7 1
 6 7 1
-``` 
+```
 
-输出示例： 
+输出示例：
 
 6
 
 
-## 解题思路 
+## 解题思路
 
-本题是最小生成树的模板题，那么我们来讲一讲最小生成树。  
+本题是最小生成树的模板题，那么我们来讲一讲最小生成树。
 
-最小生成树 可以使用 prim算法 也可以使用 kruskal算法计算出来。
+最小生成树可以使用prim算法也可以使用kruskal算法计算出来。
 
-本篇我们先讲解 prim算法。
+本篇我们先讲解prim算法。
 
-最小生成树是所有节点的最小连通子图， 即：以最小的成本（边的权值）将图中所有节点链接到一起。  
+最小生成树是所有节点的最小连通子图，即：以最小的成本（边的权值）将图中所有节点链接到一起。
 
-图中有n个节点，那么一定可以用 n - 1 条边将所有节点连接到一起。  
+图中有n个节点，那么一定可以用n-1条边将所有节点连接到一起。
 
-那么如何选择 这 n-1 条边 就是 最小生成树算法的任务所在。 
+那么如何选择这n-1条边就是最小生成树算法的任务所在。
 
-例如本题示例中的无向有权图为：  
+例如本题示例中的无向有权图为：
 
 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20231206164306.png)
 
-那么在这个图中，如何选取 n-1 条边 使得 图中所有节点连接到一起，并且边的权值和最小呢？  
+那么在这个图中，如何选取n-1条边使得图中所有节点连接到一起，并且边的权值和最小呢？
 
-（图中为n为7，即7个节点，那么只需要 n-1 即 6条边就可以讲所有顶点连接到一起）
+（图中为n为7，即7个节点，那么只需要n-1即6条边就可以讲所有顶点连接到一起）
 
-prim算法 是从节点的角度 采用贪心的策略 每次寻找距离 最小生成树最近的节点 并加入到最小生成树中。
+prim算法是从节点的角度采用贪心的策略每次寻找距离最小生成树最近的节点并加入到最小生成树中。
 
-prim算法核心就是三步，我称为**prim三部曲**，大家一定要熟悉这三步，代码相对会好些很多： 
+prim算法核心就是三步，我称为**prim三部曲**，大家一定要熟悉这三步，代码相对会好些很多：
 
 1. 第一步，选距离生成树最近节点
-2. 第二步，最近节点加入生成树 
+2. 第二步，最近节点加入生成树
 3. 第三步，更新非生成树节点到生成树的距离（即更新minDist数组）
 
-现在录友们会对这三步很陌生，不知道这是干啥的，没关系，下面将会画图举例来带大家把这**prim三部曲**理解到位。 
+现在录友们会对这三步很陌生，不知道这是干啥的，没关系，下面将会画图举例来带大家把这**prim三部曲**理解到位。
 
 在prim算法中，有一个数组特别重要，这里我起名为：minDist。
 
-刚刚我有讲过 “每次寻找距离 最小生成树最近的节点 并加入到最小生成树中”，那么如何寻找距离最小生成树最近的节点呢？ 
+刚刚我有讲过“每次寻找距离最小生成树最近的节点并加入到最小生成树中”，那么如何寻找距离最小生成树最近的节点呢？
 
-这就用到了 minDist 数组， 它用来作什么呢？
+这就用到了minDist数组，它用来作什么呢？
 
-**minDist数组 用来记录 每一个节点距离最小生成树的最近距离**。 理解这一点非常重要，这也是 prim算法最核心要点所在，很多录友看不懂prim算法的代码，都是因为没有理解透 这个数组的含义。  
+**minDist数组用来记录每一个节点距离最小生成树的最近距离**。理解这一点非常重要，这也是prim算法最核心要点所在，很多录友看不懂prim算法的代码，都是因为没有理解透这个数组的含义。
 
-接下来，我们来通过一步一步画图，来带大家巩固 **prim三部曲** 以及 minDist数组 的作用。
+接下来，我们来通过一步一步画图，来带大家巩固**prim三部曲**以及minDist数组的作用。
 
-（**示例中节点编号是从1开始，所以为了让大家看的不晕，minDist数组下标我也从 1 开始计数，下标0 就不使用了，这样 下标和节点标号就可以对应上了，避免大家搞混**）
+（**示例中节点编号是从1开始，所以为了让大家看的不晕，minDist数组下标我也从1开始计数，下标0就不使用了，这样下标和节点标号就可以对应上了，避免大家搞混**）
 
 
-### 1 初始状态 
+### 1 初始状态
 
-minDist 数组 里的数值初始化为 最大数，因为本题 节点距离不会超过 10000，所以 初始化最大数为 10001就可以。 
+minDist数组里的数值初始化为最大数，因为本题节点距离不会超过10000，所以初始化最大数为10001就可以。
 
-相信这里录友就要问了，为什么这么做？ 
+相信这里录友就要问了，为什么这么做？
 
-现在 还没有最小生成树，默认每个节点距离最小生成树是最大的，这样后面我们在比较的时候，发现更近的距离，才能更新到 minDist 数组上。 
+现在还没有最小生成树，默认每个节点距离最小生成树是最大的，这样后面我们在比较的时候，发现更近的距离，才能更新到minDist数组上。
 
 如图：
 
@@ -108,125 +108,125 @@ minDist 数组 里的数值初始化为 最大数，因为本题 节点距离不
 
 1、prim三部曲，第一步：选距离生成树最近节点
 
-选择距离最小生成树最近的节点，加入到最小生成树，刚开始还没有最小生成树，所以随便选一个节点加入就好（因为每一个节点一定会在最小生成树里，所以随便选一个就好），那我们选择节点1 （符合遍历数组的习惯，第一个遍历的也是节点1） 
+选择距离最小生成树最近的节点，加入到最小生成树，刚开始还没有最小生成树，所以随便选一个节点加入就好（因为每一个节点一定会在最小生成树里，所以随便选一个就好），那我们选择节点1（符合遍历数组的习惯，第一个遍历的也是节点1）
 
-2、prim三部曲，第二步：最近节点加入生成树 
+2、prim三部曲，第二步：最近节点加入生成树
 
-此时 节点1 已经算最小生成树的节点。 
+此时节点1已经算最小生成树的节点。
 
 3、prim三部曲，第三步：更新非生成树节点到生成树的距离（即更新minDist数组）
 
-接下来，我们要更新所有节点距离最小生成树的距离，如图： 
+接下来，我们要更新所有节点距离最小生成树的距离，如图：
 
 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20231222102048.png)
 
 
-注意下标0，我们就不管它了，下标 1  与节点 1 对应，这样可以避免大家把节点搞混。 
+注意下标0，我们就不管它了，下标1与节点1对应，这样可以避免大家把节点搞混。
 
-此时所有非生成树的节点距离 最小生成树（节点1）的距离都已经跟新了 。 
+此时所有非生成树的节点距离最小生成树（节点1）的距离都已经跟新了。
 
-* 节点2 与 节点1 的距离为1，比原先的 距离值10001小，所以更新minDist[2]。 
-* 节点3 和 节点1 的距离为1，比原先的 距离值10001小，所以更新minDist[3]。
-* 节点5 和 节点1 的距离为2，比原先的 距离值10001小，所以更新minDist[5]。
+* 节点2与节点1的距离为1，比原先的距离值10001小，所以更新minDist[2]。
+* 节点3和节点1的距离为1，比原先的距离值10001小，所以更新minDist[3]。
+* 节点5和节点1的距离为2，比原先的距离值10001小，所以更新minDist[5]。
 
-**注意图中我标记了 minDist数组里更新的权值**，是哪两个节点之间的权值，例如 minDist[2] =1 ，这个 1 是 节点1 与 节点2 之间的连线，清楚这一点对最后我们记录 最小生成树的权值总和很重要。 
+**注意图中我标记了minDist数组里更新的权值**，是哪两个节点之间的权值，例如minDist[2]=1，这个1是节点1与节点2之间的连线，清楚这一点对最后我们记录最小生成树的权值总和很重要。
 
-（我在后面依然会不断重复 prim三部曲，可能基础好的录友会感觉有点啰嗦，但也是让大家感觉这三部曲求解的过程）
+（我在后面依然会不断重复prim三部曲，可能基础好的录友会感觉有点啰嗦，但也是让大家感觉这三部曲求解的过程）
 
-### 3 
+### 3
 
 1、prim三部曲，第一步：选距离生成树最近节点
 
-选取一个距离 最小生成树（节点1） 最近的非生成树里的节点，节点2，3，5 距离 最小生成树（节点1） 最近，选节点 2（其实选 节点3或者节点2都可以，距离一样的）加入最小生成树。
+选取一个距离最小生成树（节点1）最近的非生成树里的节点，节点2，3，5距离最小生成树（节点1）最近，选节点2（其实选节点3或者节点2都可以，距离一样的）加入最小生成树。
 
-2、prim三部曲，第二步：最近节点加入生成树 
+2、prim三部曲，第二步：最近节点加入生成树
 
-此时 节点1 和 节点2，已经算最小生成树的节点。
+此时节点1和节点2，已经算最小生成树的节点。
 
 
 3、prim三部曲，第三步：更新非生成树节点到生成树的距离（即更新minDist数组）
 
-接下来，我们要更新节点距离最小生成树的距离，如图： 
+接下来，我们要更新节点距离最小生成树的距离，如图：
 
-![](https://code-thinking-1253855093.file.myqcloud.com/pics/20231222102431.png) 
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20231222102431.png)
 
-此时所有非生成树的节点距离 最小生成树（节点1、节点2）的距离都已经跟新了 。  
+此时所有非生成树的节点距离最小生成树（节点1、节点2）的距离都已经跟新了。
 
-* 节点3 和 节点2 的距离为2，和原先的距离值1 小，所以不用更新。 
-* 节点4 和 节点2 的距离为2，比原先的距离值10001小，所以更新minDist[4]。
-* 节点5 和 节点2 的距离为10001（不连接），所以不用更新。 
-* 节点6 和 节点2 的距离为1，比原先的距离值10001小，所以更新minDist[6]。 
+* 节点3和节点2的距离为2，和原先的距离值1小，所以不用更新。
+* 节点4和节点2的距离为2，比原先的距离值10001小，所以更新minDist[4]。
+* 节点5和节点2的距离为10001（不连接），所以不用更新。
+* 节点6和节点2的距离为1，比原先的距离值10001小，所以更新minDist[6]。
 
-### 4 
+### 4
 
 1、prim三部曲，第一步：选距离生成树最近节点
 
-选择一个距离 最小生成树（节点1、节点2） 最近的非生成树里的节点，节点3，6 距离 最小生成树（节点1、节点2） 最近，选节点3 （选节点6也可以，距离一样）加入最小生成树。 
+选择一个距离最小生成树（节点1、节点2）最近的非生成树里的节点，节点3，6距离最小生成树（节点1、节点2）最近，选节点3（选节点6也可以，距离一样）加入最小生成树。
 
-2、prim三部曲，第二步：最近节点加入生成树 
+2、prim三部曲，第二步：最近节点加入生成树
 
-此时 节点1 、节点2 、节点3 算是最小生成树的节点。
+此时节点1、节点2、节点3算是最小生成树的节点。
 
 
 3、prim三部曲，第三步：更新非生成树节点到生成树的距离（即更新minDist数组）
 
-接下来更新节点距离最小生成树的距离，如图： 
+接下来更新节点距离最小生成树的距离，如图：
 
-![](https://code-thinking-1253855093.file.myqcloud.com/pics/20231222102457.png) 
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20231222102457.png)
 
-所有非生成树的节点距离 最小生成树（节点1、节点2、节点3 ）的距离都已经跟新了 。 
+所有非生成树的节点距离最小生成树（节点1、节点2、节点3）的距离都已经跟新了。
 
-* 节点 4 和 节点 3的距离为 1，和原先的距离值 2 小，所以更新minDist[4]为1。  
+* 节点4和节点3的距离为1，和原先的距离值2小，所以更新minDist[4]为1。
 
-上面为什么我们只比较 节点4 和 节点3 的距离呢？ 
+上面为什么我们只比较节点4和节点3的距离呢？
 
-因为节点3加入 最小生成树后，非 生成树节点  只有 节点 4 和 节点3是链接的，所以需要重新更新一下 节点4距离最小生成树的距离，其他节点距离最小生成树的距离 都不变。 
+因为节点3加入最小生成树后，非生成树节点只有节点4和节点3是链接的，所以需要重新更新一下节点4距离最小生成树的距离，其他节点距离最小生成树的距离都不变。
 
-### 5 
+### 5
 
 1、prim三部曲，第一步：选距离生成树最近节点
 
-继续选择一个距离 最小生成树（节点1、节点2、节点3） 最近的非生成树里的节点，为了巩固大家对 minDist数组的理解，这里我再啰嗦一遍：
+继续选择一个距离最小生成树（节点1、节点2、节点3）最近的非生成树里的节点，为了巩固大家对minDist数组的理解，这里我再啰嗦一遍：
 
-![](https://code-thinking-1253855093.file.myqcloud.com/pics/20231217213516.png) 
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20231217213516.png)
 
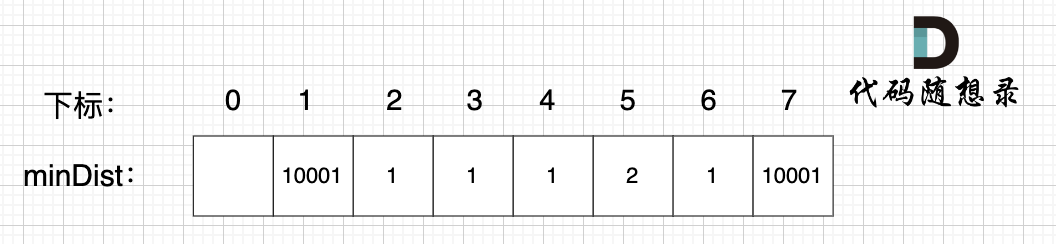
-**minDist数组 是记录了 所有非生成树节点距离生成树的最小距离**，所以 从数组里我们能看出来，非生成树节点 4 和 节点 6 距离 生成树最近。 
+**minDist数组是记录了所有非生成树节点距离生成树的最小距离**，所以从数组里我们能看出来，非生成树节点4和节点6距离生成树最近。
 
 
-任选一个加入生成树，我们选 节点4（选节点6也行） 。 
+任选一个加入生成树，我们选节点4（选节点6也行）。
 
-**注意**，我们根据 minDist数组，选取距离 生成树 最近的节点 加入生成树，那么 **minDist数组里记录的其实也是 最小生成树的边的权值**（我在图中把权值对应的是哪两个节点也标记出来了）。  
+**注意**，我们根据minDist数组，选取距离生成树最近的节点加入生成树，那么**minDist数组里记录的其实也是最小生成树的边的权值**（我在图中把权值对应的是哪两个节点也标记出来了）。
 
-如果大家不理解，可以跟着我们下面的讲解，看 minDist数组的变化， minDist数组 里记录的权值对应的哪条边。
+如果大家不理解，可以跟着我们下面的讲解，看minDist数组的变化，minDist数组里记录的权值对应的哪条边。
 
-理解这一点很重要，因为 最后我们要求 最小生成树里所有边的权值和。 
+理解这一点很重要，因为最后我们要求最小生成树里所有边的权值和。
 
-2、prim三部曲，第二步：最近节点加入生成树 
+2、prim三部曲，第二步：最近节点加入生成树
 
-此时 节点1、节点2、节点3、节点4 算是 最小生成树的节点。
+此时节点1、节点2、节点3、节点4算是最小生成树的节点。
 
 3、prim三部曲，第三步：更新非生成树节点到生成树的距离（即更新minDist数组）
 
-接下来更新节点距离最小生成树的距离，如图： 
+接下来更新节点距离最小生成树的距离，如图：
 
-![](https://code-thinking-1253855093.file.myqcloud.com/pics/20231222102618.png) 
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20231222102618.png)
 
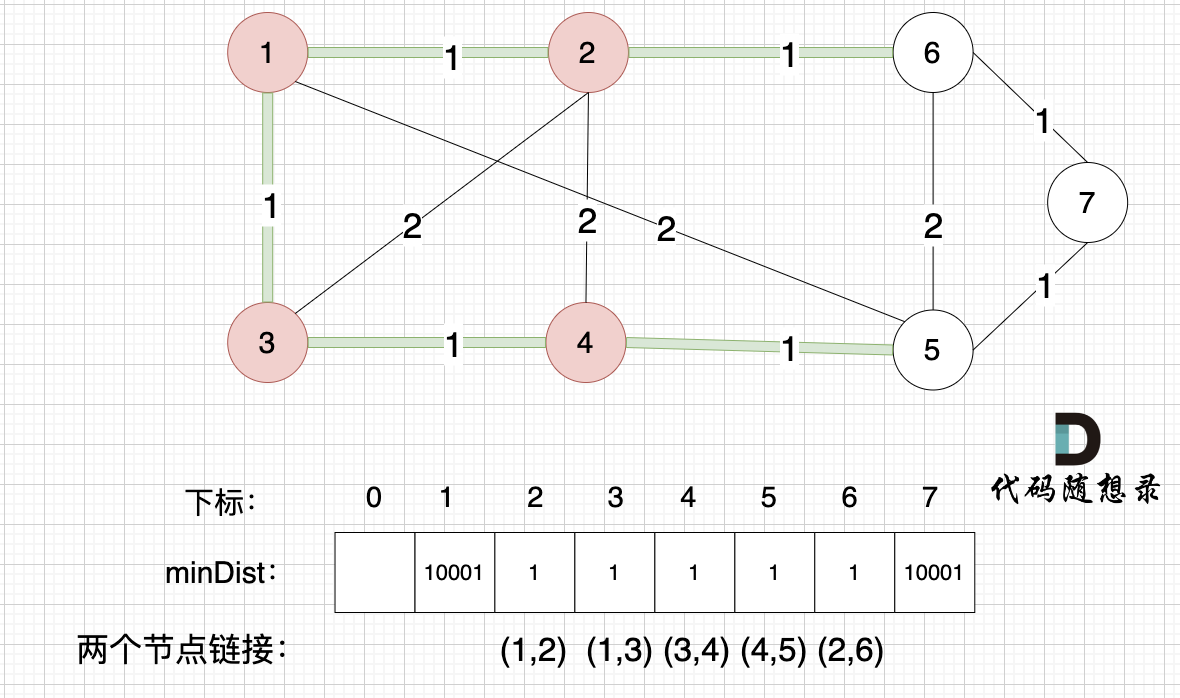
-minDist数组已经更新了 所有非生成树的节点距离 最小生成树（节点1、节点2、节点3、节点4 ）的距离 。 
+minDist数组已经更新了所有非生成树的节点距离最小生成树（节点1、节点2、节点3、节点4）的距离。
 
-* 节点 5 和 节点 4的距离为 1，和原先的距离值 2 小，所以更新minDist[5]为1。  
+* 节点5和节点4的距离为1，和原先的距离值2小，所以更新minDist[5]为1。
 
-### 6 
+### 6
 
 1、prim三部曲，第一步：选距离生成树最近节点
 
-继续选距离 最小生成树（节点1、节点2、节点3、节点4 ）最近的非生成树里的节点，只有 节点 5 和 节点6。 
+继续选距离最小生成树（节点1、节点2、节点3、节点4）最近的非生成树里的节点，只有节点5和节点6。
 
 
-选节点5 （选节点6也可以）加入 生成树。 
+选节点5（选节点6也可以）加入生成树。
 
-2、prim三部曲，第二步：最近节点加入生成树 
+2、prim三部曲，第二步：最近节点加入生成树
 
-节点1、节点2、节点3、节点4、节点5 算是 最小生成树的节点。 
+节点1、节点2、节点3、节点4、节点5算是最小生成树的节点。
 
 3、prim三部曲，第三步：更新非生成树节点到生成树的距离（即更新minDist数组）
 
@@ -234,44 +234,44 @@ minDist数组已经更新了 所有非生成树的节点距离 最小生成树
 
 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20231222102646.png)
 
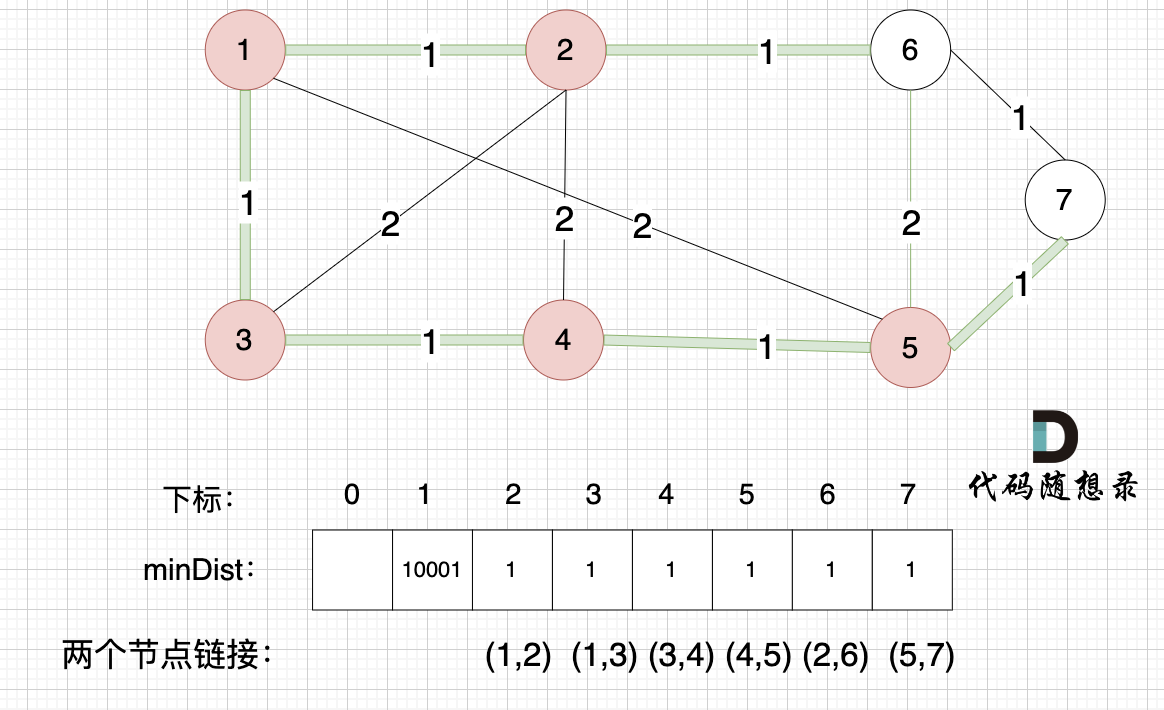
-minDist数组已经更新了 所有非生成树的节点距离 最小生成树（节点1、节点2、节点3、节点4 、节点5）的距离 。 
+minDist数组已经更新了所有非生成树的节点距离最小生成树（节点1、节点2、节点3、节点4、节点5）的距离。
 
-* 节点 6 和 节点 5 距离为 2，比原先的距离值 1 大，所以不更新 
-* 节点 7 和 节点 5 距离为 1，比原先的距离值 10001小，更新 minDist[7] 
+* 节点6和节点5距离为2，比原先的距离值1大，所以不更新
+* 节点7和节点5距离为1，比原先的距离值10001小，更新minDist[7]
 
-### 7 
+### 7
 
 1、prim三部曲，第一步：选距离生成树最近节点
 
-继续选距离 最小生成树（节点1、节点2、节点3、节点4 、节点5）最近的非生成树里的节点，只有 节点 6 和 节点7。
+继续选距离最小生成树（节点1、节点2、节点3、节点4、节点5）最近的非生成树里的节点，只有节点6和节点7。
 
-2、prim三部曲，第二步：最近节点加入生成树 
+2、prim三部曲，第二步：最近节点加入生成树
 
-选节点6 （选节点7也行，距离一样的）加入生成树。 
+选节点6（选节点7也行，距离一样的）加入生成树。
 
 3、prim三部曲，第三步：更新非生成树节点到生成树的距离（即更新minDist数组）
 
-节点1、节点2、节点3、节点4、节点5、节点6 算是 最小生成树的节点 ，接下来更新节点距离最小生成树的距离，如图： 
+节点1、节点2、节点3、节点4、节点5、节点6算是最小生成树的节点，接下来更新节点距离最小生成树的距离，如图：
 
 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20231222102732.png)
 
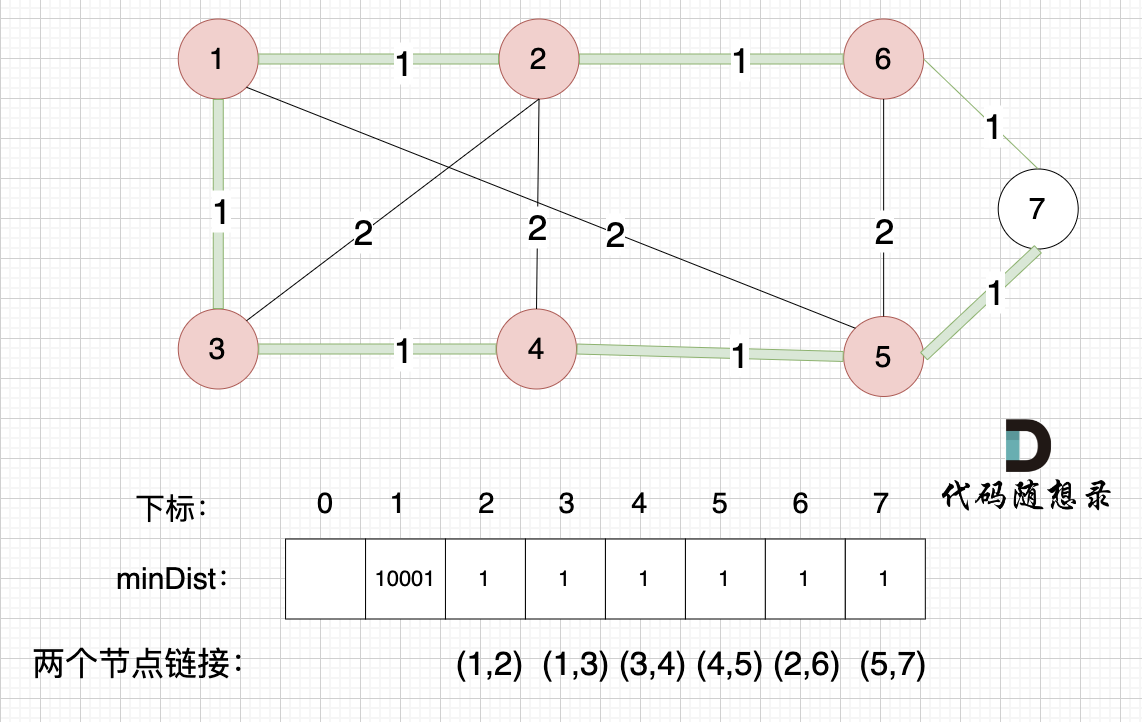
-这里就不在重复描述了，大家类推，最后，节点7加入生成树，如图： 
+这里就不在重复描述了，大家类推，最后，节点7加入生成树，如图：
 
-![](https://code-thinking-1253855093.file.myqcloud.com/pics/20231222102820.png) 
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20231222102820.png)
 
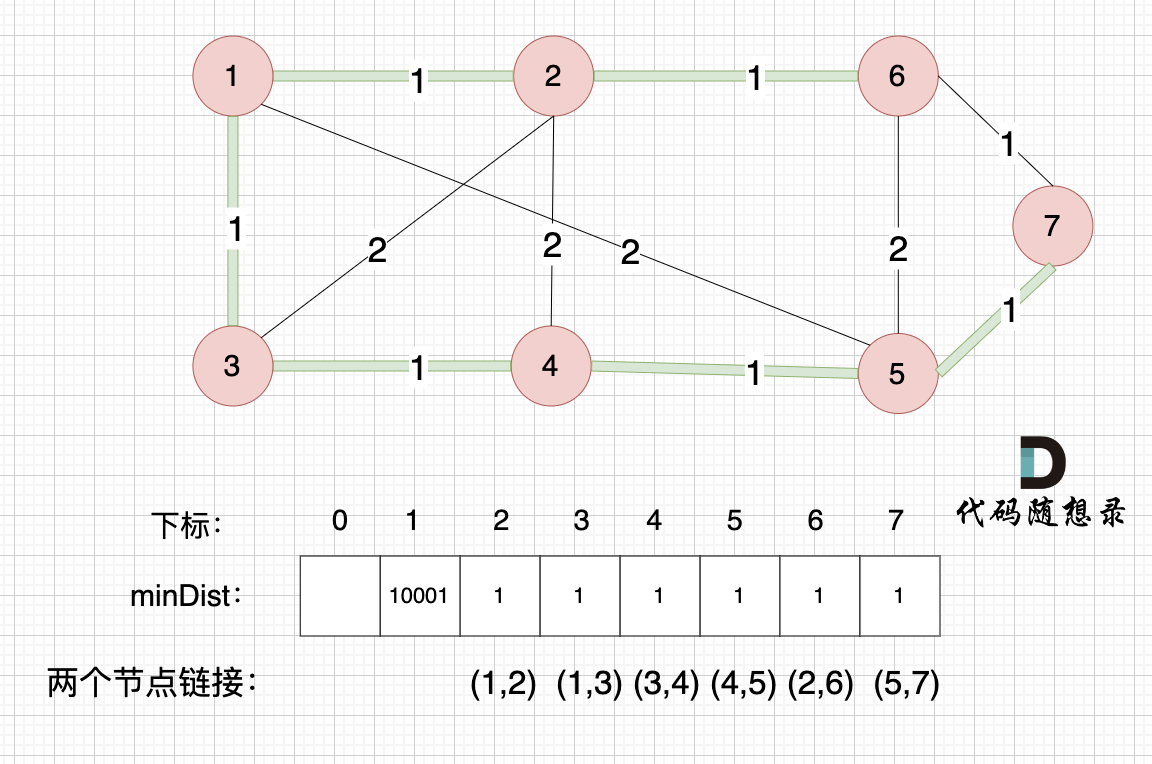
-### 最后 
+### 最后
 
-最后我们就生成了一个 最小生成树， 绿色的边将所有节点链接到一起，并且 保证权值是最小的，因为我们在更新 minDist 数组的时候，都是选距离 最小生成树最近的点 加入到树中。 
+最后我们就生成了一个最小生成树，绿色的边将所有节点链接到一起，并且保证权值是最小的，因为我们在更新minDist数组的时候，都是选距离最小生成树最近的点加入到树中。
 
-讲解上面的模拟过程的时候，我已经强调多次 minDist数组 是记录了 所有非生成树节点距离生成树的最小距离。
+讲解上面的模拟过程的时候，我已经强调多次minDist数组是记录了所有非生成树节点距离生成树的最小距离。
 
-最后，minDist数组 也就是记录的是最小生成树所有边的权值。
+最后，minDist数组也就是记录的是最小生成树所有边的权值。
 
-我在图中，特别把 每条边的权值对应的是哪两个节点 标记出来（例如minDist[7] = 1，对应的是节点5 和 节点7之间的边，而不是 节点6 和 节点7），为了就是让大家清楚， minDist里的每一个值 对应的是哪条边。 
+我在图中，特别把每条边的权值对应的是哪两个节点标记出来（例如minDist[7]=1，对应的是节点5和节点7之间的边，而不是节点6和节点7），为了就是让大家清楚，minDist里的每一个值对应的是哪条边。
 
-那么我们要求最小生成树里边的权值总和 就是 把 最后的 minDist 数组 累加一起。 
+那么我们要求最小生成树里边的权值总和就是把最后的minDist数组累加一起。
 
-以下代码，我对 prim三部曲，做了重点注释，大家根据这三步，就可以 透彻理解prim。
+以下代码，我对prim三部曲，做了重点注释，大家根据这三步，就可以透彻理解prim。
 
 ```CPP
 #include<iostream>
@@ -338,52 +338,52 @@ int main() {
 
 }
 
-``` 
+```
 
-时间复杂度为 O(n^2)，其中 n 为节点数量。 
+时间复杂度为O(n^2)，其中n为节点数量。
 
 ## 拓展
 
-上面讲解的是记录了最小生成树 所有边的权值，如果让打印出来 最小生成树的每条边呢？ 或者说 要把这个最小生成树画出来呢？  
+上面讲解的是记录了最小生成树所有边的权值，如果让打印出来最小生成树的每条边呢？或者说要把这个最小生成树画出来呢？
 
 
-此时我们就需要把 最小生成树里每一条边记录下来。
+此时我们就需要把最小生成树里每一条边记录下来。
 
-此时有两个问题： 
+此时有两个问题：
 
-* 1、用什么结构来记录 
-* 2、如何记录 
+* 1、用什么结构来记录
+* 2、如何记录
 
-如果记录边，其实就是记录两个节点就可以，两个节点连成一条边。 
+如果记录边，其实就是记录两个节点就可以，两个节点连成一条边。
 
 如何记录两个节点呢？
 
-我们使用一维数组就可以记录。 parent[节点编号] =  节点编号， 这样就把一条边记录下来了。（当然如果节点编号非常大，可以考虑使用map）
+我们使用一维数组就可以记录。parent[节点编号] =  节点编号，这样就把一条边记录下来了。（当然如果节点编号非常大，可以考虑使用map）
 
-使用一维数组记录是有向边，不过我们这里不需要记录方向，所以只关注两条边是连接的就行。 
+使用一维数组记录是有向边，不过我们这里不需要记录方向，所以只关注两条边是连接的就行。
 
-parent数组初始化代码： 
+parent数组初始化代码：
 
 ```CPP 
 vector<int> parent(v + 1, -1);
 ```
 
-接下来就是第二个问题，如何记录？ 
+接下来就是第二个问题，如何记录？
 
-我们再来回顾一下 prim三部曲， 
+我们再来回顾一下prim三部曲，
 
 1. 第一步，选距离生成树最近节点
-2. 第二步，最近节点加入生成树 
+2. 第二步，最近节点加入生成树
 3. 第三步，更新非生成树节点到生成树的距离（即更新minDist数组）
 
-大家先思考一下，我们是在第几步，可以记录 最小生成树的边呢？ 
+大家先思考一下，我们是在第几步，可以记录最小生成树的边呢？
 
-在本面上半篇 我们讲解过：“我们根据 minDist数组，选组距离 生成树 最近的节点 加入生成树，那么 **minDist数组里记录的其实也是 最小生成树的边的权值**。” 
+在本面上半篇我们讲解过：“我们根据minDist数组，选组距离生成树最近的节点加入生成树，那么**minDist数组里记录的其实也是最小生成树的边的权值**。”
 
-既然 minDist数组 记录了 最小生成树的边，是不是就是在更新  minDist数组 的时候，去更新parent数组来记录一下对应的边呢。  
+既然minDist数组记录了最小生成树的边，是不是就是在更新minDist数组的时候，去更新parent数组来记录一下对应的边呢。
 
 
-所以 在 prim三部曲中的第三步，更新 parent数组，代码如下： 
+所以在prim三部曲中的第三步，更新parent数组，代码如下：
 
 ```CPP
 for (int j = 1; j <= v; j++) {
@@ -394,23 +394,23 @@ for (int j = 1; j <= v; j++) {
 }
 ```
 
-代码中注释中，我强调了 数组指向的顺序很重要。 因为不少录友在这里会写成这样： `parent[cur] = j`  。
+代码中注释中，我强调了数组指向的顺序很重要。因为不少录友在这里会写成这样： `parent[cur] = j`  。
 
-这里估计大家会疑惑了，parent[节点编号A] = 节点编号B， 就表示A 和 B 相连，我们这里就不用在意方向，代码中 为什么 只能 `parent[j] = cur`  而不能 `parent[cur] = j` 这么写呢？ 
+这里估计大家会疑惑了，parent[节点编号A] = 节点编号B，就表示A和B相连，我们这里就不用在意方向，代码中为什么只能 `parent[j] = cur`  而不能 `parent[cur] = j` 这么写呢？ 
 
-如果写成 `parent[cur] = j`，在 for 循环中，有多个 j 满足要求， 那么 parent[cur] 就会被反复覆盖，因为 cur 是一个固定值。 
+如果写成 `parent[cur] = j`，在for循环中，有多个j满足要求，那么 parent[cur] 就会被反复覆盖，因为cur是一个固定值。
 
-举个例子，cur = 1， 在 for循环中，可能 就 j = 2， j = 3，j =4 都符合条件，那么本来应该记录 节点1 与 节点 2、节点3、节点4相连的。 
+举个例子，cur=1，在for循环中，可能就j=2，j=3，j=4都符合条件，那么本来应该记录节点1与节点2、节点3、节点4相连的。 
 
-如果  `parent[cur] = j` 这么写，最后更新的逻辑是  parent[1] = 2, parent[1] = 3， parent[1] = 4， 最后只能记录 节点1 与节点 4 相连，其他相连情况都被覆盖了。 
+如果  `parent[cur] = j` 这么写，最后更新的逻辑是  parent[1] = 2, parent[1] = 3， parent[1] = 4，最后只能记录节点1与节点4相连，其他相连情况都被覆盖了。
 
-如果这么写 `parent[j] = cur`， 那就是 parent[2] = 1, parent[3] = 1， parent[4] = 1 ，这样 才能完整表示出 节点1 与 其他节点都是链接的，才没有被覆盖。 
+如果这么写 `parent[j] = cur`，那就是 parent[2] = 1, parent[3] = 1， parent[4] = 1 ，这样才能完整表示出节点1与其他节点都是链接的，才没有被覆盖。 
 
 主要问题也是我们使用了一维数组来记录。
 
-如果是二维数组，来记录两个点链接，例如 parent[节点编号A][节点编号B] = 1 ，parent[节点编号B][节点编号A] = 1，来表示 节点A 与 节点B 相连，那就没有上面说的这个注意事项了，当然这么做的话，就是多开辟的内存空间。
+如果是二维数组，来记录两个点链接，例如 parent[节点编号A][节点编号B] = 1 ，parent[节点编号B][节点编号A] = 1，来表示节点A与节点B相连，那就没有上面说的这个注意事项了，当然这么做的话，就是多开辟的内存空间。
 
-以下是输出最小生成树边的代码，不算最后输出， 就额外添加了两行代码，我都注释标记了：
+以下是输出最小生成树边的代码，不算最后输出，就额外添加了两行代码，我都注释标记了：
 
 ```CPP
 #include<iostream>
@@ -460,7 +460,7 @@ int main() {
     }
 }
 
-``` 
+```
 
 按照本题示例，代码输入如下：  
 
@@ -476,40 +476,40 @@ int main() {
 
 注意，这里是无向图，我在输出上添加了箭头仅仅是为了方便大家看出是边的意思。 
 
-大家可以和我们本题最后生成的最小生成树的图 去对比一下 边的链接情况： 
+大家可以和我们本题最后生成的最小生成树的图去对比一下边的链接情况： 
 
 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20231229115714.png)  
 
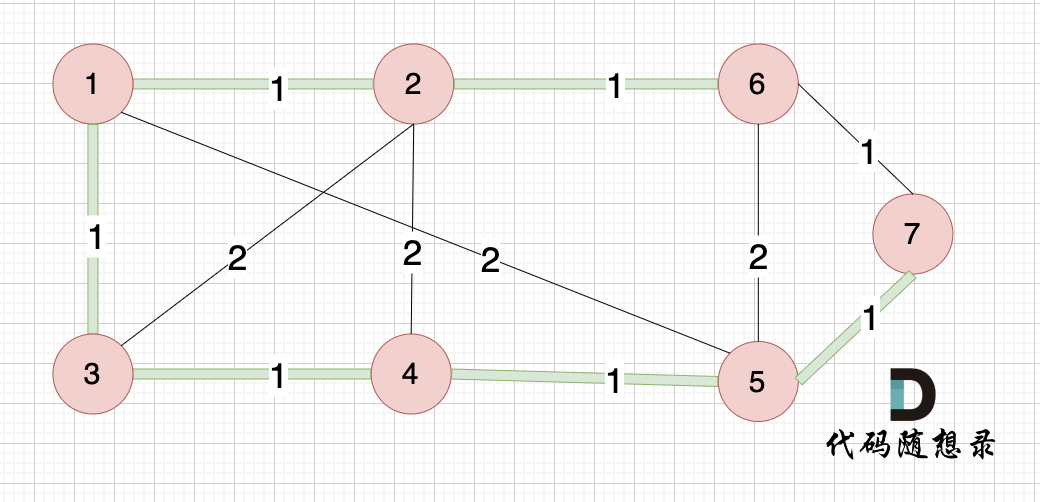
-绿色的边 是最小生成树，和我们的 输出完全一致。 
+绿色的边是最小生成树，和我们的输出完全一致。
 
-## 总结 
+## 总结
 
-此时我就把prim算法讲解完毕了，我们再来回顾一下。 
+此时我就把prim算法讲解完毕了，我们再来回顾一下。
 
-关于 prim算法，我自创了三部曲，来帮助大家理解： 
+关于prim算法，我自创了三部曲，来帮助大家理解：
 
 1. 第一步，选距离生成树最近节点
-2. 第二步，最近节点加入生成树 
+2. 第二步，最近节点加入生成树
 3. 第三步，更新非生成树节点到生成树的距离（即更新minDist数组）
 
-大家只要理解这三部曲， prim算法 至少是可以写出一个框架出来，然后在慢慢补充细节，这样不至于 自己在写prim的时候 两眼一抹黑 完全凭感觉去写。 
-这也为什么很多录友感觉 prim算法比较难，而且每次学会来，隔一段时间 又不会写了，主要是 没有一个纲领。 
+大家只要理解这三部曲，prim算法至少是可以写出一个框架出来，然后在慢慢补充细节，这样不至于自己在写prim的时候两眼一抹黑完全凭感觉去写。
+这也为什么很多录友感觉prim算法比较难，而且每次学会来，隔一段时间又不会写了，主要是没有一个纲领。
 
-理解这三部曲之后，更重要的 就是理解 minDist数组。 
+理解这三部曲之后，更重要的就是理解minDist数组。
 
-**minDist数组 是prim算法的灵魂，它帮助 prim算法完成最重要的一步，就是如何找到 距离最小生成树最近的点**。 
+**minDist数组是prim算法的灵魂，它帮助prim算法完成最重要的一步，就是如何找到距离最小生成树最近的点**。
 
-再来帮大家回顾 minDist数组 的含义：记录 每一个节点距离最小生成树的最近距离。 
+再来帮大家回顾minDist数组的含义：记录每一个节点距离最小生成树的最近距离。
 
-理解  minDist数组 ，至少大家看prim算法的代码不会懵。 
+理解minDist数组，至少大家看prim算法的代码不会懵。
 
-也正是 因为 minDist数组 的作用，我们根据 minDist数组，选取距离 生成树 最近的节点 加入生成树，那么 **minDist数组里记录的其实也是 最小生成树的边的权值**。  
+也正是因为minDist数组的作用，我们根据minDist数组，选取距离生成树最近的节点加入生成树，那么**minDist数组里记录的其实也是最小生成树的边的权值**。
 
-所以我们求 最小生成树的权值和 就是 计算后的 minDist数组 数值总和。 
+所以我们求最小生成树的权值和就是计算后的minDist数组数值总和。
 
-最后我们拓展了如何求职 最小生成树 的每一条边，其实 添加的代码很简单，主要是理解 为什么使用 parent数组 来记录边 以及 在哪里 更新parent数组。 
+最后我们拓展了如何获得最小生成树的每一条边，其实添加的代码很简单，主要是理解为什么使用parent数组来记录边以及在哪里更新parent数组。
 
-同时，因为使用一维数组，数组的下标和数组 如何赋值很重要，不要搞反，导致结果被覆盖。 
+同时，因为使用一维数组，数组的下标和数组如何赋值很重要，不要搞反，导致结果被覆盖。
 
 好了，以上为总结，录友们学习愉快。
 
@@ -692,7 +692,7 @@ if __name__ == "__main__":
 
 ### Rust
 
-### Javascript
+### JavaScript
 ```js
 function prim(v, edges) {
     const grid = Array.from({ length: v + 1 }, () => new Array(v + 1).fill(10001)); // Fixed grid initialization

problems/kamacoder/0055.右旋字符串.md

@@ -350,7 +350,29 @@ function reverseStr(s, start, end) {
 
 
 ### Swift:
+```swift
+func rotateWords(_ s: String, _ k: Int) -> String {
+    var chars = Array(s)
+    // 先反转整体
+    reverseWords(&chars, start: 0, end: s.count - 1)
+    // 反转前半段
+    reverseWords(&chars, start: 0, end: k - 1)
+    // 反转后半段
+    reverseWords(&chars, start: k, end: s.count - 1)
+    return String(chars)
+}
 
+// 反转start...end 的字符数组
+func reverseWords(_ chars: inout [Character], start: Int, end: Int) {
+    var left = start
+    var right = end
+    while left < right, right < chars.count {
+        (chars[left], chars[right]) = (chars[right], chars[left])
+        left += 1
+        right -= 1
+    }
+}
+```
 
 
 ### PHP：

problems/kamacoder/0094.城市间货物运输I-SPFA.md

@@ -462,7 +462,7 @@ if __name__ == "__main__":
 
 ### Rust
 
-### Javascript
+### JavaScript
 
 ```js
 async function main() {

problems/kamacoder/0094.城市间货物运输I.md

@@ -483,7 +483,7 @@ if __name__ == "__main__":
 
 ### Rust
 
-### Javascript
+### JavaScript
 
 ```js
 async function main() {

problems/kamacoder/0095.城市间货物运输II.md

@@ -54,7 +54,7 @@ circle
 
 ## 思路 
 
-本题是 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 延伸题目。 
+本题是 [kama94.城市间货物运输I](./0094.城市间货物运输I.md) 延伸题目。 
 
 本题是要我们判断 负权回路，也就是图中出现环且环上的边总权值为负数。
 
@@ -64,7 +64,7 @@ circle
 
 接下来我们来看 如何使用 bellman_ford 算法来判断 负权回路。 
 
-在 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 中 我们讲了 bellman_ford 算法的核心就是一句话：对 所有边 进行 n-1 次松弛。 同时文中的 【拓展】部分， 我们也讲了 松弛n次以上 会怎么样？ 
+在 [kama94.城市间货物运输I](./0094.城市间货物运输I.md) 中 我们讲了 bellman_ford 算法的核心就是一句话：对 所有边 进行 n-1 次松弛。 同时文中的 【拓展】部分， 我们也讲了 松弛n次以上 会怎么样？ 
 
 在没有负权回路的图中，松弛 n 次以上 ，结果不会有变化。 
 
@@ -72,7 +72,7 @@ circle
 
 那么每松弛一次，都会更新最短路径，所以结果会一直有变化。
 
-（如果对于 bellman_ford 不了解的录友，建议详细看这里：[kama94.城市间货物运输I](./kama94.城市间货物运输I.md)） 
+（如果对于 bellman_ford 不了解的录友，建议详细看这里：[kama94.城市间货物运输I](./0094.城市间货物运输I.md)） 
 
 以上为理论分析，接下来我们再画图举例。 
 
@@ -94,13 +94,13 @@ circle
 
 如果在负权回路多绕两圈，三圈，无穷圈，那么我们的总成本就会无限小， 如果要求最小成本的话，你会发现本题就无解了。 
 
-在 bellman_ford 算法中，松弛 n-1 次所有的边 就可以求得 起点到任何节点的最短路径，松弛 n 次以上，minDist数组（记录起到到其他节点的最短距离）中的结果也不会有改变 （如果对 bellman_ford 算法 不了解，也不知道 minDist 是什么，建议详看上篇讲解[kama94.城市间货物运输I](./kama94.城市间货物运输I.md)）  
+在 bellman_ford 算法中，松弛 n-1 次所有的边 就可以求得 起点到任何节点的最短路径，松弛 n 次以上，minDist数组（记录起到到其他节点的最短距离）中的结果也不会有改变 （如果对 bellman_ford 算法 不了解，也不知道 minDist 是什么，建议详看上篇讲解[kama94.城市间货物运输I](./0094.城市间货物运输I.md)）  
 
 而本题有负权回路的情况下，一直都会有更短的最短路，所以 松弛 第n次，minDist数组 也会发生改变。  
 
-那么解决本题的 核心思路，就是在 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 的基础上，再多松弛一次，看minDist数组 是否发生变化。
+那么解决本题的 核心思路，就是在 [kama94.城市间货物运输I](./0094.城市间货物运输I.md) 的基础上，再多松弛一次，看minDist数组 是否发生变化。
 
-代码和 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 基本是一样的，如下：（关键地方已注释） 
+代码和 [kama94.城市间货物运输I](./0094.城市间货物运输I.md) 基本是一样的，如下：（关键地方已注释） 
 
 ```CPP
 #include <iostream>
@@ -392,7 +392,7 @@ if __name__ == "__main__":
 
 ### Rust
 
-### Javascript
+### JavaScript
 
 ### TypeScript
 

problems/kamacoder/0096.城市间货物运输III.md

@@ -51,15 +51,15 @@
 
 ## 思路 
 
-本题为单源有限最短路问题，同样是 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 延伸题目。 
+本题为单源有限最短路问题，同样是 [kama94.城市间货物运输I](./0094.城市间货物运输I.md) 延伸题目。 
 
 注意题目中描述是 **最多经过 k 个城市的条件下，而不是一定经过k个城市，也可以经过的城市数量比k小，但要最短的路径**。
 
-在 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 中我们讲了：**对所有边松弛一次，相当于计算 起点到达 与起点一条边相连的节点 的最短距离**。 
+在 [kama94.城市间货物运输I](./0094.城市间货物运输I.md) 中我们讲了：**对所有边松弛一次，相当于计算 起点到达 与起点一条边相连的节点 的最短距离**。 
 
 节点数量为n，起点到终点，最多是 n-1 条边相连。 那么对所有边松弛 n-1 次 就一定能得到 起点到达 终点的最短距离。 
 
-（如果对以上讲解看不懂，建议详看 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) ） 
+（如果对以上讲解看不懂，建议详看 [kama94.城市间货物运输I](./0094.城市间货物运输I.md) ） 
 
 本题是最多经过 k 个城市， 那么是 k + 1条边相连的节点。 这里可能有录友想不懂为什么是k + 1，来看这个图： 
 
@@ -71,7 +71,7 @@
 
 对所有边松弛一次，相当于计算 起点到达 与起点一条边相连的节点 的最短距离，那么对所有边松弛 k + 1次，就是求 起点到达 与起点k + 1条边相连的节点的 最短距离。 
 
-**注意**： 本题是  [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 的拓展题，如果对 bellman_ford 没有深入了解，强烈建议先看 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 再做本题。   
+**注意**： 本题是  [kama94.城市间货物运输I](./0094.城市间货物运输I.md) 的拓展题，如果对 bellman_ford 没有深入了解，强烈建议先看 [kama94.城市间货物运输I](./0094.城市间货物运输I.md) 再做本题。   
 
 理解以上内容，其实本题代码就很容易了，bellman_ford 标准写法是松弛 n-1 次，本题就松弛 k + 1次就好。
 
@@ -215,9 +215,9 @@ int main() {
 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240409111849.png)
 
 
-边：节点3 -> 节点4，权值为1 ，minDist[4] > minDist[3] + 1，更新 minDist[4] = 0 + (-1) = -1 ，如图： 
+边：节点3 -> 节点4，权值为1 ，minDist[4] > minDist[3] + 1，更新 minDist[4] = 0 + 1 = 1 ，如图： 
 
-![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240409111837.png)
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20241018192042.png)
 
 
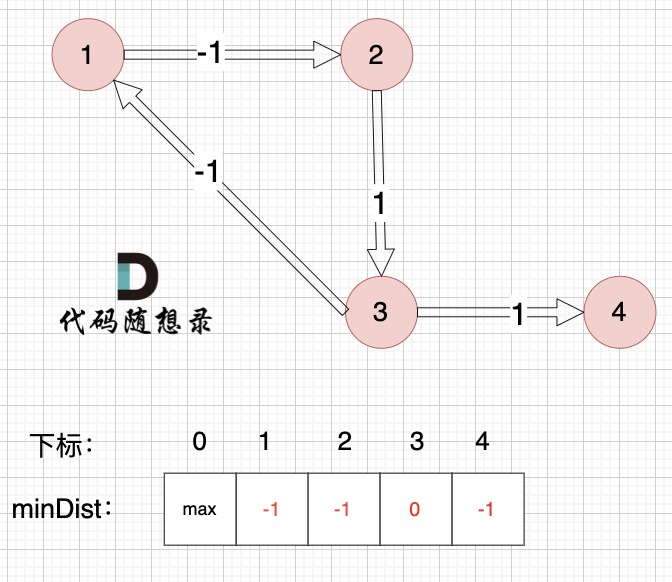
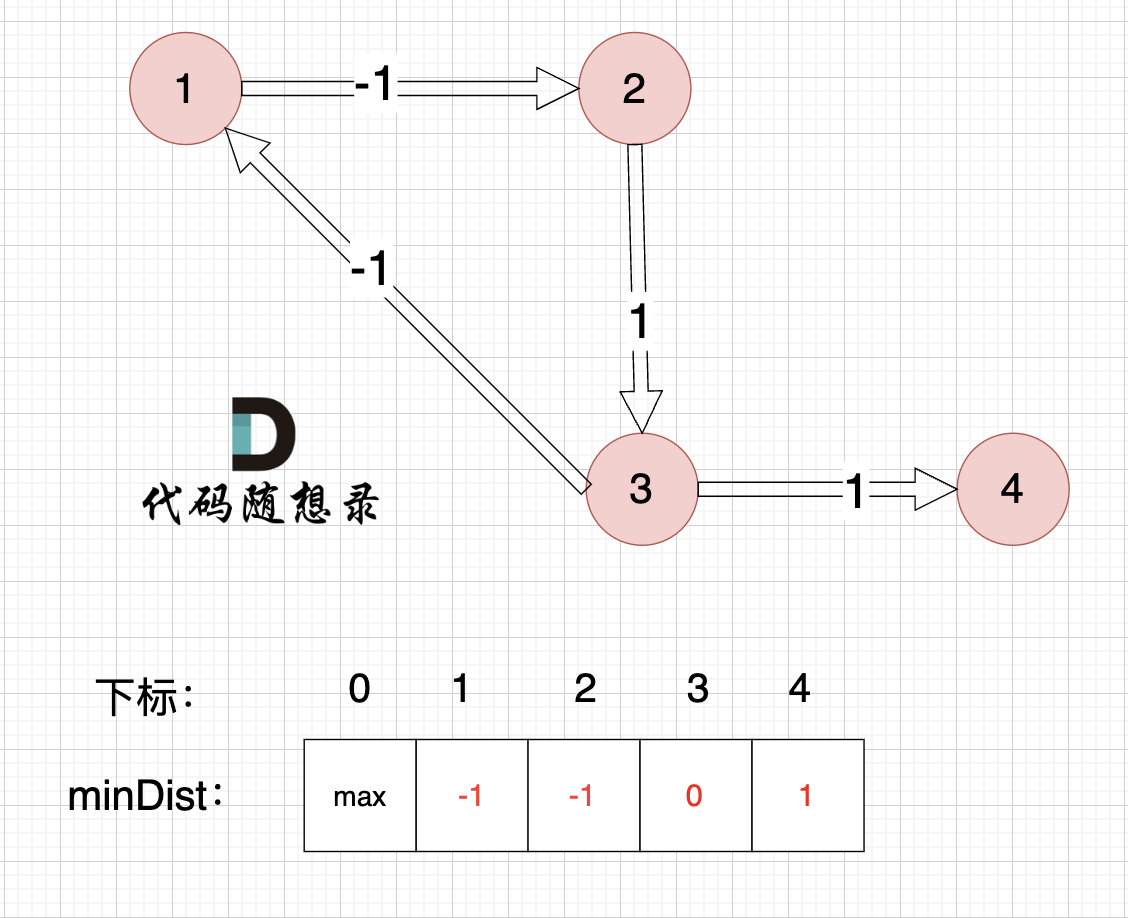
 以上是对所有边进行的第一次松弛，最后 minDist数组为 ：-1 -1 0 1 ，（从下标1算起） 
@@ -366,19 +366,19 @@ int main() {
 
 ## 拓展二（本题本质）
 
-那么前面讲解过的 [94.城市间货物运输I](./kama94.城市间货物运输I.md) 和 [95.城市间货物运输II](./kama95.城市间货物运输II.md) 也是bellman_ford经典算法，也没使用 minDist_copy，怎么就没问题呢？ 
+那么前面讲解过的 [94.城市间货物运输I](./0094.城市间货物运输I.md) 和 [95.城市间货物运输II](./0095.城市间货物运输II.md) 也是bellman_ford经典算法，也没使用 minDist_copy，怎么就没问题呢？ 
 
 > 如果没看过我上面这两篇讲解的话，建议详细学习上面两篇，再看我下面讲的区别，否则容易看不懂。
 
-[94.城市间货物运输I](./kama94.城市间货物运输I.md)， 是没有 负权回路的，那么 多松弛多少次，对结果都没有影响。  
+[94.城市间货物运输I](./0094.城市间货物运输I.md)， 是没有 负权回路的，那么 多松弛多少次，对结果都没有影响。  
 
 求 节点1 到 节点n 的最短路径，松弛n-1 次就够了，松弛 大于 n-1次，结果也不会变。 
 
 那么在对所有边进行第一次松弛的时候，如果基于 本次计算的 minDist 来计算 minDist （相当于多做松弛了），也是对最终结果没影响。 
 
-[95.城市间货物运输II](./kama95.城市间货物运输II.md) 是判断是否有 负权回路，一旦有负权回路， 对所有边松弛 n-1 次以后，在做松弛 minDist 数值一定会变，根据这一点来判断是否有负权回路。
+[95.城市间货物运输II](./0095.城市间货物运输II.md) 是判断是否有 负权回路，一旦有负权回路， 对所有边松弛 n-1 次以后，在做松弛 minDist 数值一定会变，根据这一点来判断是否有负权回路。
 
-所以，[95.城市间货物运输II](./kama95.城市间货物运输II.md) 只需要判断minDist数值变化了就行，而 minDist 的数值对不对，并不是我们关心的。 
+所以，[95.城市间货物运输II](./0095.城市间货物运输II.md) 只需要判断minDist数值变化了就行，而 minDist 的数值对不对，并不是我们关心的。 
 
 那么本题 为什么计算minDist 一定要基于上次 的 minDist 数值。 
 
@@ -744,7 +744,7 @@ if __name__ == "__main__":
 
 ### Rust
 
-### Javascript
+### JavaScript
 
 ### TypeScript
 

problems/kamacoder/0097.小明逛公园.md

@@ -492,7 +492,7 @@ if __name__ == '__main__':
 
 ### Rust
 
-### Javascript
+### JavaScript
 
 ### TypeScript
 

problems/kamacoder/0098.所有可达路径.md

@@ -277,7 +277,7 @@ ACM格式大家在输出结果的时候，要关注看看格式问题，特别
 
 有录友可能会想，ACM格式就是麻烦，有空格没有空格有什么影响，结果对了不就行了？ 
 
-ACM模式相对于核心代码模式（力扣） 更考验大家对代码的掌控能力。 例如工程代码里，输出输出都是要自己控制的。这也是为什么大公司笔试，都是ACM模式。 
+ACM模式相对于核心代码模式（力扣） 更考验大家对代码的掌控能力。 例如工程代码里，输入输出都是要自己控制的。这也是为什么大公司笔试，都是ACM模式。 
 
 以上代码中，结果都存在了 result数组里（二维数组，每一行是一个结果），最后将其打印出来。（重点看注释） 
 
@@ -726,7 +726,7 @@ func main() {
 
 ### Rust
 
-### Javascript
+### JavaScript
 
 #### 邻接矩阵写法