Merge branch 'master' into feature/nextString

problems/0005.最长回文子串.md

@@ -256,7 +256,60 @@ public:
 * 时间复杂度：O(n^2)
 * 空间复杂度：O(1)
 
+### Manacher 算法
 
+Manacher 算法的关键在于高效利用回文的对称性，通过插入分隔符和维护中心、边界等信息，在线性时间内找到最长回文子串。这种方法避免了重复计算，是处理回文问题的最优解。
+
+```c++
+//Manacher 算法
+class Solution {
+public:
+    string longestPalindrome(string s) {
+        // 预处理字符串，在每个字符之间插入 '#'
+        string t = "#";
+        for (char c : s) {
+            t += c; // 添加字符
+            t += '#';// 添加分隔符
+        }
+        int n = t.size();// 新字符串的长度
+        vector<int> p(n, 0);// p[i] 表示以 t[i] 为中心的回文半径
+        int center = 0, right = 0;// 当前回文的中心和右边界
+        
+
+        // 遍历预处理后的字符串
+        for (int i = 0; i < n; i++) {
+             // 如果当前索引在右边界内，利用对称性初始化 p[i]
+            if (i < right) {
+                p[i] = min(right - i, p[2 * center - i]);
+            }
+             // 尝试扩展回文
+            while (i - p[i] - 1 >= 0 && i + p[i] + 1 < n && t[i - p[i] - 1] == t[i + p[i] + 1]) {
+                p[i]++;// 增加回文半径
+            }
+            // 如果当前回文扩展超出右边界，更新中心和右边界
+            if (i + p[i] > right) {
+                center = i;// 更新中心
+                right = i + p[i];// 更新右边界
+            }
+        }
+       // 找到最大回文半径和对应的中心
+        int maxLen = 0, centerIndex = 0;
+        for (int i = 0; i < n; i++) {
+            if (p[i] > maxLen) {
+                maxLen = p[i];// 更新最大回文长度
+                centerIndex = i;// 更新中心索引
+            }
+        }
+        // 计算原字符串中回文子串的起始位置并返回
+        return s.substr((centerIndex - maxLen) / 2, maxLen);
+    }
+};
+```
+
+
+
+* 时间复杂度：O(n)
+* 空间复杂度：O(n)
 
 ## 其他语言版本
 
@@ -682,3 +735,4 @@ public class Solution {
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>
 </a>
+

problems/0112.路径总和.md

@@ -564,10 +564,10 @@ class Solution:
             
         return False
     
-    def hasPathSum(self, root: TreeNode, sum: int) -> bool:
+    def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
         if root is None:
             return False
-        return self.traversal(root, sum - root.val)      
+        return self.traversal(root, targetSum - root.val)      
 ```
 
 (版本二) 递归 + 精简
@@ -579,12 +579,12 @@ class Solution:
 #         self.left = left
 #         self.right = right
 class Solution:
-    def hasPathSum(self, root: TreeNode, sum: int) -> bool:
+    def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
         if not root:
             return False
-        if not root.left and not root.right and sum == root.val:
+        if not root.left and not root.right and targetSum == root.val:
             return True
-        return self.hasPathSum(root.left, sum - root.val) or self.hasPathSum(root.right, sum - root.val)
+        return self.hasPathSum(root.left, targetSum - root.val) or self.hasPathSum(root.right, targetSum - root.val)
   
 ```
 (版本三) 迭代
@@ -596,7 +596,7 @@ class Solution:
 #         self.left = left
 #         self.right = right
 class Solution:
-    def hasPathSum(self, root: TreeNode, sum: int) -> bool:
+    def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
         if not root:
             return False
         # 此时栈里要放的是pair<节点指针，路径数值>
@@ -659,13 +659,13 @@ class Solution:
 
         return
 
-    def pathSum(self, root: TreeNode, sum: int) -> List[List[int]]:
+    def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:
         self.result.clear()
         self.path.clear()
         if not root:
             return self.result
         self.path.append(root.val) # 把根节点放进路径
-        self.traversal(root, sum - root.val)
+        self.traversal(root, targetSum - root.val)
         return self.result 
 ```
 
@@ -678,7 +678,7 @@ class Solution:
 #         self.left = left
 #         self.right = right
 class Solution:
-    def pathSum(self, root: TreeNode, targetSum: int) -> List[List[int]]:
+    def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:
         
         result = []
         self.traversal(root, targetSum, [], result)
@@ -703,7 +703,7 @@ class Solution:
 #         self.left = left
 #         self.right = right
 class Solution:
-    def pathSum(self, root: TreeNode, targetSum: int) -> List[List[int]]:
+    def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:
         if not root:
             return []
         stack = [(root, [root.val])]

problems/0134.加油站.md

@@ -158,7 +158,7 @@ i从0开始累加rest[i]，和记为curSum，一旦curSum小于零，说明[0, i
 
 如果 curSum<0 说明 区间和1 + 区间和2 < 0， 那么 假设从上图中的位置开始计数curSum不会小于0的话，就是 区间和2>0。 
 
-区间和1 + 区间和2 < 0   同时 区间和2>0，只能说明区间和1 < 0， 那么就会从假设的箭头初就开始从新选择其实位置了。 
+区间和1 + 区间和2 < 0   同时 区间和2>0，只能说明区间和1 < 0， 那么就会从假设的箭头初就开始从新选择起始位置了。 
 
 
 **那么局部最优：当前累加rest[i]的和curSum一旦小于0，起始位置至少要是i+1，因为从i之前开始一定不行。全局最优：找到可以跑一圈的起始位置**。

problems/0151.翻转字符串里的单词.md

@@ -440,11 +440,10 @@ class Solution {
 ```Python
 class Solution:
     def reverseWords(self, s: str) -> str:
-        # 删除前后空白
-        s = s.strip()
         # 反转整个字符串
         s = s[::-1]
         # 将字符串拆分为单词，并反转每个单词
+        # split()函数能够自动忽略多余的空白字符
         s = ' '.join(word[::-1] for word in s.split())
         return s
 
@@ -1029,3 +1028,4 @@ public string ReverseWords(string s) {
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>
 </a>
+

problems/0459.重复的子字符串.md

@@ -64,7 +64,7 @@
 
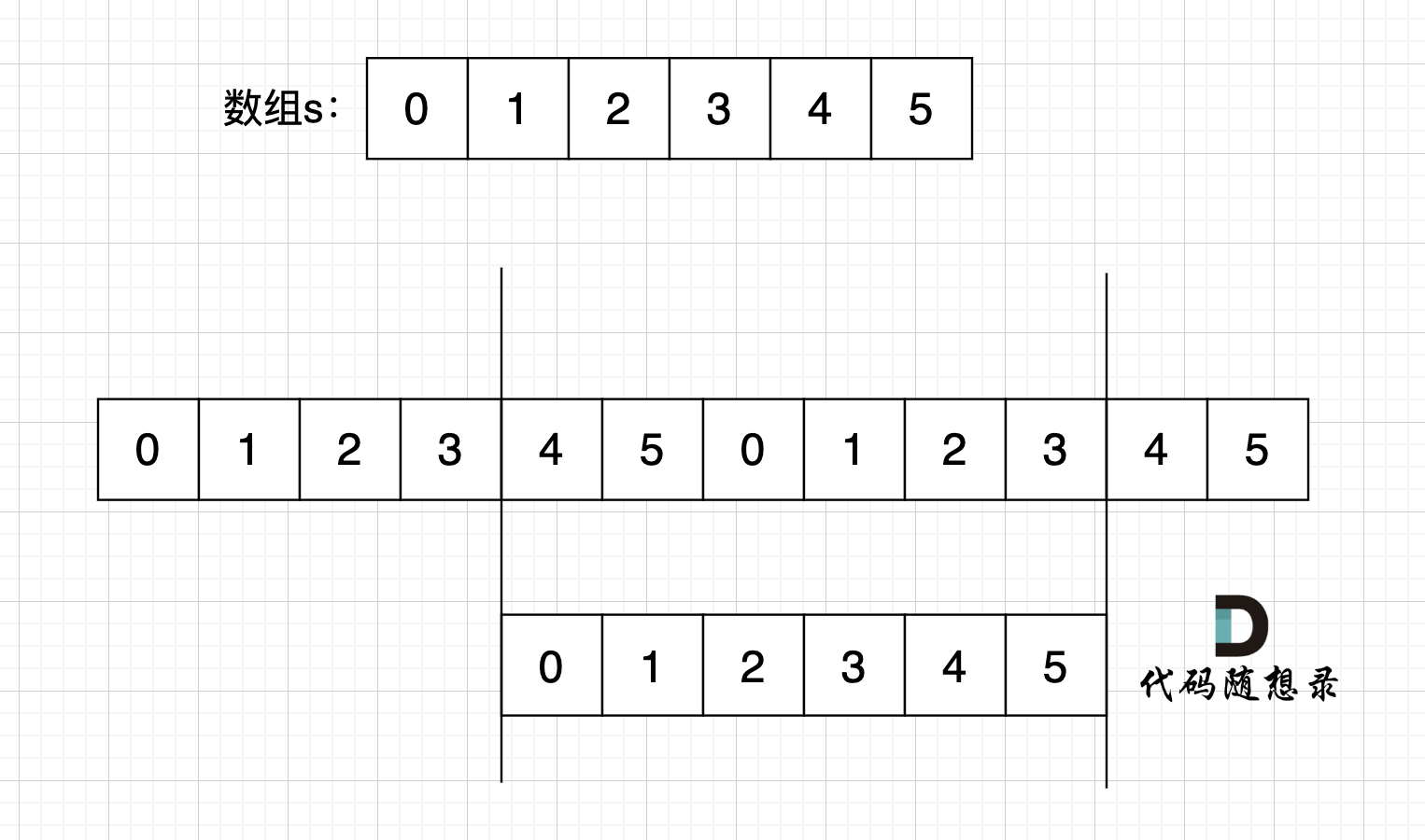
 如果有一个字符串s，在 s + s 拼接后， 不算首尾字符，如果能凑成s字符串，说明s 一定是重复子串组成。  
 
-如图，字符串s，图中数字为数组下标，在 s + s 拼接后， 不算首尾字符，中间凑成s字符串。 
+如图，字符串s，图中数字为数组下标，在 s + s 拼接后， 不算首尾字符，中间凑成s字符串。  （图中数字为数组下标）
 
 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240910115555.png) 
 
@@ -163,9 +163,7 @@ KMP算法中next数组为什么遇到字符不匹配的时候可以找到上一
 
 如果一个字符串s是由重复子串组成，那么 最长相等前后缀不包含的子串一定是字符串s的最小重复子串。  
 
-证明： 如果s 是由最小重复子串p组成。 
+如果s 是由最小重复子串p组成，即 s = n * p 
-
-即 s = n * p 
 
 那么相同前后缀可以是这样： 
 
@@ -203,12 +201,14 @@ p2 = p1，p3 = p2 即： p1 = p2 = p3
 
 最长相等前后缀不包含的子串已经是字符串s的最小重复子串，那么字符串s一定由重复子串组成，这个不需要证明了。 
 
-关键是要要证明：最长相等前后缀不包含的子串什么时候才是字符串s的最小重复子串呢。 
+关键是要证明：最长相等前后缀不包含的子串什么时候才是字符串s的最小重复子串呢。 
 
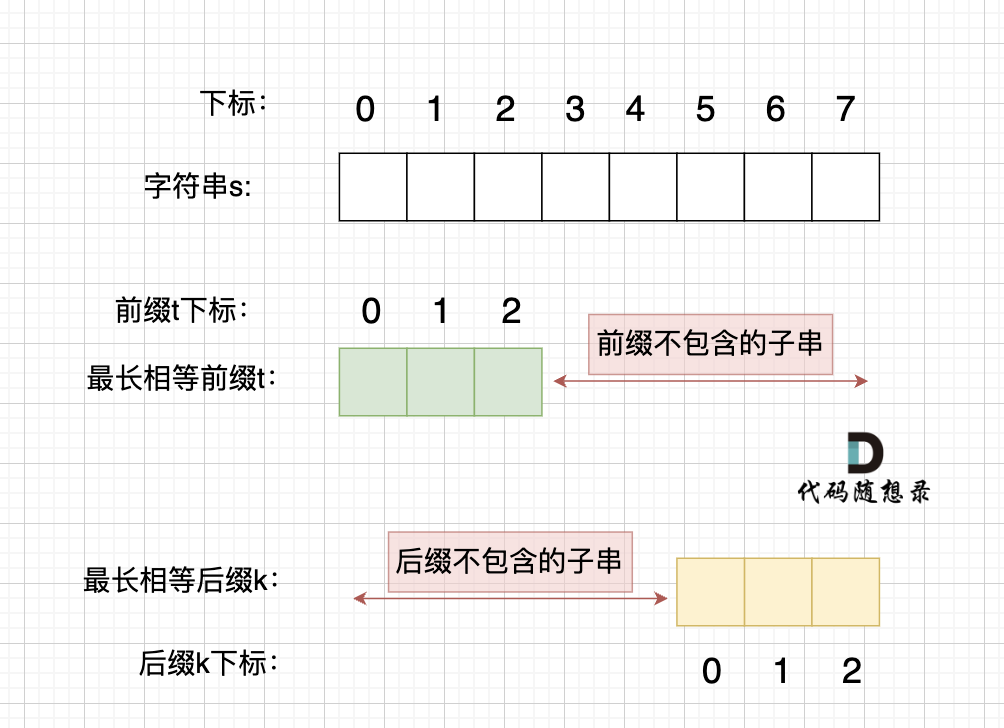
-情况一， 最长相等前后缀不包含的子串的长度 比 字符串s的一半的长度还大，那一定不是字符串s的重复子串
+情况一， 最长相等前后缀不包含的子串的长度 比 字符串s的一半的长度还大，那一定不是字符串s的重复子串，如图：
 
 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240911110236.png)
 
+图中：前后缀不包含的子串的长度 大于 字符串s的长度的 二分之一
+
 --------------
 
 情况二，最长相等前后缀不包含的子串的长度 可以被 字符串s的长度整除，如图：
@@ -230,7 +230,7 @@ p2 = p1，p3 = p2 即： p1 = p2 = p3
 即 s[0]s[1] 是最小重复子串
 
 
-以上推导中，录友可能想，你怎么知道 s[0] 和 s[1] 就不相同呢？ s[0] 为什么就不能使最小重复子串。
+以上推导中，录友可能想，你怎么知道 s[0] 和 s[1] 就不相同呢？ s[0] 为什么就不能是最小重复子串。
 
 如果 s[0] 和 s[1] 也相同，同时 s[0]s[1]与s[2]s[3]相同，s[2]s[3] 与 s[4]s[5]相同，s[4]s[5] 与 s[6]s[7] 相同，那么这个字符串就是有一个字符构成的字符串。
 
@@ -246,7 +246,7 @@ p2 = p1，p3 = p2 即： p1 = p2 = p3
 
 或者说，自己举个例子，`aaaaaa`，这个字符串，他的最长相等前后缀是什么？ 
 
-同上以上推导，最长相等前后缀不包含的子串的长度只要被 字符串s的长度整除，就是一定是最小重复子串。
+同上以上推导，最长相等前后缀不包含的子串的长度只要被 字符串s的长度整除，最长相等前后缀不包含的子串一定是最小重复子串。
 
 ----------------
 
@@ -267,7 +267,7 @@ p2 = p1，p3 = p2 即： p1 = p2 = p3
 
 以上推导，可以得出 s[0],s[1],s[2] 与 s[3],s[4],s[5] 相同，s[3]s[4] 与 s[6]s[7]相同。
 
-那么 最长相等前后缀不包含的子串的长度 不被 字符串s的长度整除 ，就不是s的重复子串
+那么 最长相等前后缀不包含的子串的长度 不被 字符串s的长度整除 ，最长相等前后缀不包含的子串就不是s的重复子串
 
 -----------
 
@@ -277,7 +277,7 @@ p2 = p1，p3 = p2 即： p1 = p2 = p3
 
 在必要条件，这个是 显而易见的，都已经假设 最长相等前后缀不包含的子串 是 s的最小重复子串了，那s必然是重复子串。 
 
-关键是需要证明， 字符串s的最长相等前后缀不包含的子串 什么时候才是 s最小重复子串。 
+**关键是需要证明， 字符串s的最长相等前后缀不包含的子串 什么时候才是 s最小重复子串**。 
 
 同上我们证明了，当 最长相等前后缀不包含的子串的长度 可以被 字符串s的长度整除，那么不包含的子串 就是s的最小重复子串。 
 
@@ -312,7 +312,7 @@ next 数组记录的就是最长相同前后缀（ [字符串：KMP算法精讲]
 
 4可以被 12(字符串的长度) 整除，所以说明有重复的子字符串（asdf）。
 
-### 打码实现
+### 代码实现
 
 C++代码如下：（这里使用了前缀表统一减一的实现方式）
 

problems/0513.找树左下角的值.md

@@ -55,7 +55,7 @@
 
 参数必须有要遍历的树的根节点，还有就是一个int型的变量用来记录最长深度。 这里就不需要返回值了，所以递归函数的返回类型为void。
 
-本题还需要类里的两个全局变量，maxLen用来记录最大深度，result记录最大深度最左节点的数值。
+本题还需要类里的两个全局变量，maxDepth用来记录最大深度，result记录最大深度最左节点的数值。
 
 代码如下：
 

problems/0518.零钱兑换II.md

@@ -168,23 +168,43 @@ for (int j = 0; j <= amount; j++) { // 遍历背包容量
 class Solution {
 public:
     int change(int amount, vector<int>& coins) {
-        vector<int> dp(amount + 1, 0);
+        vector<uint64_t> dp(amount + 1, 0); // 防止相加数据超int
-        dp[0] = 1;
+        dp[0] = 1; // 只有一种方式达到0
         for (int i = 0; i < coins.size(); i++) { // 遍历物品
             for (int j = coins[i]; j <= amount; j++) { // 遍历背包
                 dp[j] += dp[j - coins[i]];
             }
         }
-        return dp[amount];
+        return dp[amount]; // 返回组合数
     }
 };
 ```
 
+C++测试用例有两个数相加超过int的数据，所以需要在if里加上dp[i] < INT_MAX - dp[i - num]。
+
 * 时间复杂度: O(mn)，其中 m 是amount，n 是 coins 的长度
 * 空间复杂度: O(m)
 
+为了防止相加的数据 超int 也可以这么写：
+
+```CPP
+class Solution {
+public:
+    int change(int amount, vector<int>& coins) {
+        vector<int> dp(amount + 1, 0);
+        dp[0] = 1; // 只有一种方式达到0
+        for (int i = 0; i < coins.size(); i++) { // 遍历物品
+            for (int j = coins[i]; j <= amount; j++) { // 遍历背包
+                if (dp[j] < INT_MAX - dp[j - coins[i]]) { //防止相加数据超int
+                    dp[j] += dp[j - coins[i]];
+                }
+            }
+        }
+        return dp[amount]; // 返回组合数
+    }
+};
+```
 
-是不是发现代码如此精简
 
 ## 总结
 

problems/0541.反转字符串II.md

@@ -37,7 +37,7 @@
 
 因为要找的也就是每2 * k 区间的起点，这样写，程序会高效很多。
 
-**所以当需要固定规律一段一段去处理字符串的时候，要想想在在for循环的表达式上做做文章。**
+**所以当需要固定规律一段一段去处理字符串的时候，要想想在for循环的表达式上做做文章。**
 
 性能如下：
 <img src='https://code-thinking.cdn.bcebos.com/pics/541_反转字符串II.png' width=600> </img></div>
@@ -505,3 +505,4 @@ impl Solution {
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>
 </a>
+

problems/kamacoder/0047.参会dijkstra朴素.md

@@ -869,6 +869,65 @@ if __name__ == "__main__":
 
 ### Javascript
 
+```js
+function dijkstra(grid, start, end) {
+    const visited = Array.from({length: end + 1}, () => false)
+    const minDist = Array.from({length: end + 1}, () => Number.MAX_VALUE)
+    minDist[start] = 0
+    
+    for (let i = 1 ; i < end + 1 ; i++) {
+        let cur = -1
+        let tempMinDist = Number.MAX_VALUE
+        // 1. 找尋與起始點距離最近且未被訪的節點
+        for (let j = 1 ; j < end + 1 ; j++) {
+            if (!visited[j] && minDist[j] < tempMinDist) {
+                cur = j
+                tempMinDist = minDist[j]
+            }
+        }
+        if (cur === -1) break;
+        
+        // 2. 更新節點狀態為已拜訪
+        visited[cur] = true
+        
+        // 3. 更新未拜訪節點與起始點的最短距離
+        for (let j = 1 ; j < end + 1 ; j++) {
+            if(!visited[j] && grid[cur][j] != Number.MAX_VALUE 
+                && grid[cur][j] + minDist[cur] < minDist[j]
+            ) {
+                minDist[j] = grid[cur][j] + minDist[cur]
+            }
+        }
+    }
+    
+    return minDist[end] === Number.MAX_VALUE ? -1 : minDist[end]
+}
+
+
+async function main() {
+    // 輸入
+    const rl = require('readline').createInterface({ input: process.stdin })
+    const iter = rl[Symbol.asyncIterator]()
+    const readline = async () => (await iter.next()).value
+    const [n, m] = (await readline()).split(" ").map(Number)
+    const grid = Array.from({length: n + 1}, 
+        () => Array.from({length:n + 1}, () => Number.MAX_VALUE))
+    for (let i = 0 ; i < m ; i++) {
+        const [s, e, w] = (await readline()).split(" ").map(Number)
+        grid[s][e] = w
+    }
+    
+    // dijkstra
+    const result = dijkstra(grid, 1, n)
+    
+    // 輸出
+    console.log(result)
+}
+
+
+main()
+```
+
 ### TypeScript
 
 ### PhP

problems/kamacoder/0053.寻宝-Kruskal.md

@@ -549,6 +549,62 @@ if __name__ == "__main__":
 
 ### Javascript
 
+```js
+function kruskal(v, edges) {
+    const father = Array.from({ length: v + 1 }, (_, i) => i)
+    
+    function find(u){
+        if (u === father[u]) {
+            return u
+        } else {
+            father[u] = find(father[u])
+            return father[u]
+        }
+        
+    }
+    
+    function isSame(u, v) {
+        let s = find(u)
+        let t = find(v)
+        return s === t
+    }
+    
+    function join(u, v) {
+        let s = find(u)
+        let t = find(v)
+        if (s !== t) {
+            father[s] = t
+        }
+    }
+    
+    edges.sort((a, b) => a[2] - b[2])
+    let result = 0
+    for (const [v1, v2, w] of edges) {
+        if (!isSame(v1, v2)) {
+            result += w
+            join(v1 ,v2)
+        } 
+    }
+    console.log(result)
+}
+
+
+async function main() {
+    const rl = require('readline').createInterface({ input: process.stdin })
+    const iter = rl[Symbol.asyncIterator]()
+    const readline = async () => (await iter.next()).value
+    const [v, e] = (await readline()).split(" ").map(Number)
+    const edges = []
+    for (let i = 0 ; i < e ; i++) {
+        edges.push((await readline()).split(" ").map(Number))
+    }
+    kruskal(v, edges)
+}
+
+
+main()
+```
+
 ### TypeScript
 
 ### PhP

problems/kamacoder/0053.寻宝-prim.md

@@ -693,6 +693,55 @@ if __name__ == "__main__":
 ### Rust
 
 ### Javascript
+```js
+function prim(v, edges) {
+    const grid = Array.from({ length: v + 1 }, () => new Array(v + 1).fill(10001)); // Fixed grid initialization
+    const minDist = new Array(v + 1).fill(10001)
+    const isInTree = new Array(v + 1).fill(false)
+    // 建構鄰接矩陣
+    for(const [v1, v2, w] of edges) {
+        grid[v1][v2] = w
+        grid[v2][v1] = w
+    }
+    // prim 演算法
+    for (let i = 1 ; i < v ; i++) {
+        let cur = -1
+        let tempMinDist = Number.MAX_VALUE
+        // 1. 尋找距離生成樹最近的節點
+        for (let j = 1 ; j < v + 1 ; j++) {
+            if (!isInTree[j] && minDist[j] < tempMinDist) {
+                tempMinDist = minDist[j]
+                cur = j
+            }
+        }
+        // 2. 將節點放入生成樹
+        isInTree[cur] = true
+        // 3. 更新非生成樹節點與生成樹的最短距離
+        for (let j = 1 ; j < v + 1 ; j++) {
+            if (!isInTree[j] && grid[cur][j] < minDist[j]) {
+                minDist[j] = grid[cur][j]
+            }
+        }
+    }
+    console.log(minDist.slice(2).reduce((acc, cur) => acc + cur, 0))
+}
+
+
+async function main() {
+    const rl = require('readline').createInterface({ input: process.stdin })
+    const iter = rl[Symbol.asyncIterator]()
+    const readline = async () => (await iter.next()).value
+    const [v, e] = (await readline()).split(" ").map(Number)
+    const edges = []
+    for (let i = 0 ; i < e ; i++) {
+        edges.push((await readline()).split(" ").map(Number))
+    }
+    prim(v, edges)
+}
+
+
+main()
+```
 
 ### TypeScript
 

problems/kamacoder/0094.城市间货物运输I-SPFA.md

@@ -464,6 +464,60 @@ if __name__ == "__main__":
 
 ### Javascript
 
+```js
+async function main() {
+    // 輸入
+    const rl = require('readline').createInterface({ input: process.stdin })
+    const iter = rl[Symbol.asyncIterator]()
+    const readline = async () => (await iter.next()).value
+    const [n, m] = (await readline()).split(" ").map(Number)
+    const grid = {}
+    for (let i = 0 ; i < m ; i++) {
+        const [src, desc, w] = (await readline()).split(" ").map(Number)
+        if (grid.hasOwnProperty(src)) {
+            grid[src].push([desc, w])
+        } else {
+            grid[src] = [[desc, w]]
+        }
+    }
+    const minDist = Array.from({length: n + 1}, () => Number.MAX_VALUE)
+    
+    // 起始點
+    minDist[1] = 0
+    
+    const q = [1]
+    const visited = Array.from({length: n + 1}, () => false)
+    
+    while (q.length) {
+        const src = q.shift()
+        const neighbors = grid[src]
+        visited[src] = false
+        if (neighbors) {
+            for (const [desc, w] of neighbors) {
+                if (minDist[src] !== Number.MAX_VALUE 
+                && minDist[src] + w < minDist[desc]) {
+                    minDist[desc] = minDist[src] + w
+                    if (!visited[desc]) {
+                        q.push(desc)
+                        visited[desc] = true
+                    }
+                    
+                }            
+            }            
+        }
+    }
+    
+    // 輸出
+    if (minDist[n] === Number.MAX_VALUE) {
+        console.log('unconnected')
+    } else {
+        console.log(minDist[n])
+    }
+}
+
+main()
+```
+
 ### TypeScript
 
 ### PhP

problems/kamacoder/0094.城市间货物运输I.md

@@ -485,6 +485,45 @@ if __name__ == "__main__":
 
 ### Javascript
 
+```js
+async function main() {
+    // 輸入
+    const rl = require('readline').createInterface({ input: process.stdin })
+    const iter = rl[Symbol.asyncIterator]()
+    const readline = async () => (await iter.next()).value
+    const [n, m] = (await readline()).split(" ").map(Number)
+    const edges = []
+    for (let i = 0 ; i < m ; i++) {
+        edges.push((await readline()).split(" ").map(Number))
+    }
+    const minDist = Array.from({length: n + 1}, () => Number.MAX_VALUE)
+    // 起始點
+    minDist[1] = 0
+    
+    for (let i = 1 ; i < n ; i++) {
+        let update = false
+        for (const [src, desc, w] of edges) {
+            if (minDist[src] !== Number.MAX_VALUE && minDist[src] + w < minDist[desc]) {
+                minDist[desc] = minDist[src] + w
+                update = true
+            }
+        }
+        if (!update) {
+            break;
+        }
+    }
+    
+    // 輸出
+    if (minDist[n] === Number.MAX_VALUE) {
+        console.log('unconnected')
+    } else {
+        console.log(minDist[n])
+    }
+}
+
+main()
+```
+
 ### TypeScript
 
 ### PhP

problems/kamacoder/0096.城市间货物运输III.md

@@ -703,6 +703,42 @@ public class Main {
 ```
 
 ### Python
+```python
+def main():
+    # 輸入
+    n, m = map(int, input().split())
+    edges = list()
+    for _ in range(m):
+        edges.append(list(map(int, input().split() )))
+    
+    start, end, k = map(int, input().split())
+    min_dist = [float('inf') for _ in range(n + 1)]
+    min_dist[start] = 0
+    
+    # 只能經過k個城市，所以從起始點到中間有(k + 1)個邊連接
+    # 需要鬆弛(k + 1)次
+    
+    for _ in range(k + 1):
+        update = False
+        min_dist_copy = min_dist.copy()
+        for src, desc, w in edges:
+            if (min_dist_copy[src] != float('inf') and 
+            min_dist_copy[src] + w < min_dist[desc]):
+                min_dist[desc] = min_dist_copy[src] + w
+                update = True
+        if not update:
+            break
+    # 輸出
+    if min_dist[end] == float('inf'):
+        print('unreachable')
+    else:
+        print(min_dist[end])
+            
+            
+
+if __name__ == "__main__":
+    main()
+```
 
 ### Go
 

problems/kamacoder/0099.岛屿的数量广搜.md

@@ -499,6 +499,55 @@ main();
 ### Swift
 
 ### Scala
+```scala
+import scala.collection.mutable.Queue
+import util.control.Breaks._
+
+// Dev on LeetCode: https://leetcode.cn/problems/number-of-islands/description/
+object Solution {
+    def numIslands(grid: Array[Array[Char]]): Int = {
+        val row = grid.length
+        val col = grid(0).length
+        val dir = List((-1,0), (0,-1), (1,0), (0,1)) // 四个方向
+        var visited = Array.fill(row)(Array.fill(col)(false))
+        var counter = 0
+        var que = Queue.empty[Tuple2[Int, Int]]
+
+        (0 until row).map{ r =>
+            (0 until col).map{ c =>
+                breakable {
+                    if (!visited(r)(c) && grid(r)(c) == '1') {
+                        que.enqueue((r, c))
+                        visited(r)(c) // 只要加入队列，立刻标记
+                    } else break // 不是岛屿不进入queue，也不记录
+
+                    while (!que.isEmpty) {
+                        val cur = que.head
+                        que.dequeue()
+                        val x = cur(0)
+                        val y = cur(1)
+                        dir.map{ d =>
+                            val nextX = x + d(0)
+                            val nextY = y + d(1)
+                            breakable {
+                                // 越界就跳过
+                                if (nextX < 0 || nextX >= row || nextY < 0 || nextY >= col) break
+                                if (!visited(nextX)(nextY) && grid(nextX)(nextY) == '1') {
+                                    visited(nextX)(nextY) = true // 只要加入队列，立刻标记
+                                    que.enqueue((nextX, nextY))
+                                }
+                            }
+                        }
+                    }
+                    counter = counter + 1 // 找完一个岛屿后记录一下
+                }
+            }
+        }
+        
+        counter
+    }
+}
+```
 
 ### C#
 

problems/kamacoder/0100.岛屿的最大面积.md

@@ -316,6 +316,7 @@ public class Main {
                     count = 0;
                     bfs(map, visited, i, j);
                     result = Math.max(count, result);
+
                 }
             }
         }
@@ -343,8 +344,6 @@ public class Main {
 }
 
 ```
-
-
 ### Python
 
 DFS
@@ -510,6 +509,144 @@ func main() {
 
 
 ### Rust
+DFS
+
+``` rust
+use std::io;
+use std::cmp;
+
+// 定义四个方向
+const DIRECTIONS: [(i32, i32); 4] = [(0, 1), (1, 0), (-1, 0), (0, -1)];
+
+fn dfs(grid: &Vec<Vec<i32>>, visited: &mut Vec<Vec<bool>>, x: usize, y: usize, count: &mut i32) {
+    if visited[x][y] || grid[x][y] == 0 {
+        return; // 终止条件：已访问或者遇到海水
+    }
+    visited[x][y] = true; // 标记已访问
+    *count += 1;
+
+    for &(dx, dy) in DIRECTIONS.iter() {
+        let new_x = x as i32 + dx;
+        let new_y = y as i32 + dy;
+
+        // 检查边界条件
+        if new_x >= 0 && new_x < grid.len() as i32 && new_y >= 0 && new_y < grid[0].len() as i32 {
+            dfs(grid, visited, new_x as usize, new_y as usize, count);
+        }
+    }
+}
+
+fn main() {
+    let mut input = String::new();
+
+    // 读取 n 和 m
+    io::stdin().read_line(&mut input);
+    let dims: Vec<usize> = input.trim().split_whitespace().map(|s| s.parse().unwrap()).collect();
+    let (n, m) = (dims[0], dims[1]);
+
+    // 读取 grid
+    let mut grid = vec![];
+    for _ in 0..n {
+        input.clear();
+        io::stdin().read_line(&mut input);
+        let row: Vec<i32> = input.trim().split_whitespace().map(|s| s.parse().unwrap()).collect();
+        grid.push(row);
+    }
+
+    // 初始化访问记录
+    let mut visited = vec![vec![false; m]; n];
+    let mut result = 0;
+
+    // 遍历所有格子
+    for i in 0..n {
+        for j in 0..m {
+            if !visited[i][j] && grid[i][j] == 1 {
+                let mut count = 0;
+                dfs(&grid, &mut visited, i, j, &mut count);
+                result = cmp::max(result, count);
+            }
+        }
+    }
+
+    // 输出结果
+    println!("{}", result);
+}
+
+```
+BFS
+```rust
+use std::io;
+use std::collections::VecDeque;
+
+// 定义四个方向
+const DIRECTIONS: [(i32, i32); 4] = [(0, 1), (1, 0), (-1, 0), (0, -1)];
+
+fn bfs(grid: &Vec<Vec<i32>>, visited: &mut Vec<Vec<bool>>, x: usize, y: usize) -> i32 {
+    let mut count = 0;
+    let mut queue = VecDeque::new();
+    queue.push_back((x, y));
+    visited[x][y] = true; // 标记已访问
+
+    while let Some((cur_x, cur_y)) = queue.pop_front() {
+        count += 1; // 增加计数
+
+        for &(dx, dy) in DIRECTIONS.iter() {
+            let new_x = cur_x as i32 + dx;
+            let new_y = cur_y as i32 + dy;
+
+            // 检查边界条件
+            if new_x >= 0 && new_x < grid.len() as i32 && new_y >= 0 && new_y < grid[0].len() as i32 {
+                let new_x_usize = new_x as usize;
+                let new_y_usize = new_y as usize;
+
+                // 如果未访问且是陆地，加入队列
+                if !visited[new_x_usize][new_y_usize] && grid[new_x_usize][new_y_usize] == 1 {
+                    visited[new_x_usize][new_y_usize] = true; // 标记已访问
+                    queue.push_back((new_x_usize, new_y_usize));
+                }
+            }
+        }
+    }
+
+    count
+}
+
+fn main() {
+    let mut input = String::new();
+
+    // 读取 n 和 m
+    io::stdin().read_line(&mut input).expect("Failed to read line");
+    let dims: Vec<usize> = input.trim().split_whitespace().map(|s| s.parse().unwrap()).collect();
+    let (n, m) = (dims[0], dims[1]);
+
+    // 读取 grid
+    let mut grid = vec![];
+    for _ in 0..n {
+        input.clear();
+        io::stdin().read_line(&mut input).expect("Failed to read line");
+        let row: Vec<i32> = input.trim().split_whitespace().map(|s| s.parse().unwrap()).collect();
+        grid.push(row);
+    }
+
+    // 初始化访问记录
+    let mut visited = vec![vec![false; m]; n];
+    let mut result = 0;
+
+    // 遍历所有格子
+    for i in 0..n {
+        for j in 0..m {
+            if !visited[i][j] && grid[i][j] == 1 {
+                let count = bfs(&grid, &mut visited, i, j);
+                result = result.max(count);
+            }
+        }
+    }
+
+    // 输出结果
+    println!("{}", result);
+}
+
+```
 
 ### Javascript