mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-08 00:43:04 +08:00
@ -82,7 +82,7 @@ public:
|
|||||||
|
|
||||||
// ListNode *tmp = slow->next; C++释放内存的逻辑
|
// ListNode *tmp = slow->next; C++释放内存的逻辑
|
||||||
// slow->next = tmp->next;
|
// slow->next = tmp->next;
|
||||||
// delete nth;
|
// delete tmp;
|
||||||
|
|
||||||
return dummyHead->next;
|
return dummyHead->next;
|
||||||
}
|
}
|
||||||
|
|||||||
@ -42,7 +42,7 @@
|
|||||||
|
|
||||||
代码如下:
|
代码如下:
|
||||||
|
|
||||||
```
|
```cpp
|
||||||
TreeNode* deleteNode(TreeNode* root, int key)
|
TreeNode* deleteNode(TreeNode* root, int key)
|
||||||
```
|
```
|
||||||
|
|
||||||
@ -50,7 +50,7 @@ TreeNode* deleteNode(TreeNode* root, int key)
|
|||||||
|
|
||||||
遇到空返回,其实这也说明没找到删除的节点,遍历到空节点直接返回了
|
遇到空返回,其实这也说明没找到删除的节点,遍历到空节点直接返回了
|
||||||
|
|
||||||
```
|
```cpp
|
||||||
if (root == nullptr) return root;
|
if (root == nullptr) return root;
|
||||||
```
|
```
|
||||||
|
|
||||||
@ -106,7 +106,7 @@ if (root->val == key) {
|
|||||||
|
|
||||||
这里相当于把新的节点返回给上一层,上一层就要用 root->left 或者 root->right接住,代码如下:
|
这里相当于把新的节点返回给上一层,上一层就要用 root->left 或者 root->right接住,代码如下:
|
||||||
|
|
||||||
```
|
```cpp
|
||||||
if (root->val > key) root->left = deleteNode(root->left, key);
|
if (root->val > key) root->left = deleteNode(root->left, key);
|
||||||
if (root->val < key) root->right = deleteNode(root->right, key);
|
if (root->val < key) root->right = deleteNode(root->right, key);
|
||||||
return root;
|
return root;
|
||||||
|
|||||||
@ -79,7 +79,7 @@ public:
|
|||||||
|
|
||||||
代码如下:
|
代码如下:
|
||||||
|
|
||||||
```
|
```cpp
|
||||||
TreeNode* trimBST(TreeNode* root, int low, int high)
|
TreeNode* trimBST(TreeNode* root, int low, int high)
|
||||||
```
|
```
|
||||||
|
|
||||||
@ -87,7 +87,7 @@ TreeNode* trimBST(TreeNode* root, int low, int high)
|
|||||||
|
|
||||||
修剪的操作并不是在终止条件上进行的,所以就是遇到空节点返回就可以了。
|
修剪的操作并不是在终止条件上进行的,所以就是遇到空节点返回就可以了。
|
||||||
|
|
||||||
```
|
```cpp
|
||||||
if (root == nullptr ) return nullptr;
|
if (root == nullptr ) return nullptr;
|
||||||
```
|
```
|
||||||
|
|
||||||
@ -97,7 +97,7 @@ if (root == nullptr ) return nullptr;
|
|||||||
|
|
||||||
代码如下:
|
代码如下:
|
||||||
|
|
||||||
```
|
```cpp
|
||||||
if (root->val < low) {
|
if (root->val < low) {
|
||||||
TreeNode* right = trimBST(root->right, low, high); // 寻找符合区间[low, high]的节点
|
TreeNode* right = trimBST(root->right, low, high); // 寻找符合区间[low, high]的节点
|
||||||
return right;
|
return right;
|
||||||
@ -108,7 +108,7 @@ if (root->val < low) {
|
|||||||
|
|
||||||
代码如下:
|
代码如下:
|
||||||
|
|
||||||
```
|
```cpp
|
||||||
if (root->val > high) {
|
if (root->val > high) {
|
||||||
TreeNode* left = trimBST(root->left, low, high); // 寻找符合区间[low, high]的节点
|
TreeNode* left = trimBST(root->left, low, high); // 寻找符合区间[low, high]的节点
|
||||||
return left;
|
return left;
|
||||||
@ -119,7 +119,7 @@ if (root->val > high) {
|
|||||||
|
|
||||||
最后返回root节点,代码如下:
|
最后返回root节点,代码如下:
|
||||||
|
|
||||||
```
|
```cpp
|
||||||
root->left = trimBST(root->left, low, high); // root->left接入符合条件的左孩子
|
root->left = trimBST(root->left, low, high); // root->left接入符合条件的左孩子
|
||||||
root->right = trimBST(root->right, low, high); // root->right接入符合条件的右孩子
|
root->right = trimBST(root->right, low, high); // root->right接入符合条件的右孩子
|
||||||
return root;
|
return root;
|
||||||
@ -133,7 +133,7 @@ return root;
|
|||||||
|
|
||||||
如下代码相当于把节点0的右孩子(节点2)返回给上一层,
|
如下代码相当于把节点0的右孩子(节点2)返回给上一层,
|
||||||
|
|
||||||
```
|
```cpp
|
||||||
if (root->val < low) {
|
if (root->val < low) {
|
||||||
TreeNode* right = trimBST(root->right, low, high); // 寻找符合区间[low, high]的节点
|
TreeNode* right = trimBST(root->right, low, high); // 寻找符合区间[low, high]的节点
|
||||||
return right;
|
return right;
|
||||||
@ -142,7 +142,7 @@ if (root->val < low) {
|
|||||||
|
|
||||||
然后如下代码相当于用节点3的左孩子 把下一层返回的 节点0的右孩子(节点2) 接住。
|
然后如下代码相当于用节点3的左孩子 把下一层返回的 节点0的右孩子(节点2) 接住。
|
||||||
|
|
||||||
```
|
``` cpp
|
||||||
root->left = trimBST(root->left, low, high);
|
root->left = trimBST(root->left, low, high);
|
||||||
```
|
```
|
||||||
|
|
||||||
|
|||||||
@ -69,7 +69,7 @@ edges[2][0] = 2,edges[2][1] = 3,
|
|||||||
|
|
||||||
搞清楚之后,我们如何统计入度呢?
|
搞清楚之后,我们如何统计入度呢?
|
||||||
|
|
||||||
即 edges[i][1] 表示的节点都是 箭头指向的节点,即这个几点有一个入度! (如果想统计出度,那么就是 edges[i][0])。
|
即 edges[i][1] 表示的节点都是 箭头指向的节点,即这个节点有一个入度! (如果想统计出度,那么就是 edges[i][0])。
|
||||||
|
|
||||||
所以,统计入度的代码如下:
|
所以,统计入度的代码如下:
|
||||||
|
|
||||||
@ -108,7 +108,7 @@ if (vec.size() > 0) {
|
|||||||
|
|
||||||
可以定义一个函数,代码如下:
|
可以定义一个函数,代码如下:
|
||||||
|
|
||||||
```
|
```cpp
|
||||||
// 在有向图里找到删除的那条边,使其变成树,返回值就是要删除的边
|
// 在有向图里找到删除的那条边,使其变成树,返回值就是要删除的边
|
||||||
vector<int> getRemoveEdge(const vector<vector<int>>& edges)
|
vector<int> getRemoveEdge(const vector<vector<int>>& edges)
|
||||||
```
|
```
|
||||||
|
|||||||
@ -59,7 +59,7 @@
|
|||||||
|
|
||||||
代码如下:
|
代码如下:
|
||||||
|
|
||||||
```
|
```cpp
|
||||||
TreeNode* insertIntoBST(TreeNode* root, int val)
|
TreeNode* insertIntoBST(TreeNode* root, int val)
|
||||||
```
|
```
|
||||||
|
|
||||||
@ -69,7 +69,7 @@ TreeNode* insertIntoBST(TreeNode* root, int val)
|
|||||||
|
|
||||||
代码如下:
|
代码如下:
|
||||||
|
|
||||||
```
|
```cpp
|
||||||
if (root == NULL) {
|
if (root == NULL) {
|
||||||
TreeNode* node = new TreeNode(val);
|
TreeNode* node = new TreeNode(val);
|
||||||
return node;
|
return node;
|
||||||
@ -88,7 +88,7 @@ if (root == NULL) {
|
|||||||
|
|
||||||
代码如下:
|
代码如下:
|
||||||
|
|
||||||
```
|
```cpp
|
||||||
if (root->val > val) root->left = insertIntoBST(root->left, val);
|
if (root->val > val) root->left = insertIntoBST(root->left, val);
|
||||||
if (root->val < val) root->right = insertIntoBST(root->right, val);
|
if (root->val < val) root->right = insertIntoBST(root->right, val);
|
||||||
return root;
|
return root;
|
||||||
@ -120,7 +120,7 @@ public:
|
|||||||
|
|
||||||
那么递归函数定义如下:
|
那么递归函数定义如下:
|
||||||
|
|
||||||
```
|
```cpp
|
||||||
TreeNode* parent; // 记录遍历节点的父节点
|
TreeNode* parent; // 记录遍历节点的父节点
|
||||||
void traversal(TreeNode* cur, int val)
|
void traversal(TreeNode* cur, int val)
|
||||||
```
|
```
|
||||||
|
|||||||
@ -138,7 +138,7 @@ passwd gitpassword
|
|||||||
|
|
||||||
创建`.ssh` 目录,如果`.ssh` 已经存在了,可以忽略这一项
|
创建`.ssh` 目录,如果`.ssh` 已经存在了,可以忽略这一项
|
||||||
|
|
||||||
为啥用配置ssh公钥呢,同学们记不记得我急使用github上传上传代码的时候也要把自己的公钥配置上github上
|
为啥用配置ssh公钥呢,同学们记不记得我使用github上传代码的时候也要把自己的公钥配置上传到github上
|
||||||
|
|
||||||
这也是方面每次操作git仓库的时候不用再去输入密码
|
这也是方面每次操作git仓库的时候不用再去输入密码
|
||||||
|
|
||||||
@ -186,7 +186,7 @@ cd /home/git/.ssh/
|
|||||||
cat id_rsa.pub >> authorized_keys
|
cat id_rsa.pub >> authorized_keys
|
||||||
```
|
```
|
||||||
|
|
||||||
如何看我们配置的密钥是否成功呢, 在客户点直接登录git服务器,看看是否是免密登陆
|
如何看我们配置的密钥是否成功呢, 在客户端直接登录git服务器,看看是否是免密登陆
|
||||||
```
|
```
|
||||||
ssh git@git服务器ip
|
ssh git@git服务器ip
|
||||||
```
|
```
|
||||||
|
|||||||
@ -29,7 +29,7 @@
|
|||||||
|
|
||||||
所以 1GHz = 10亿Hz,表示CPU可以一秒脉冲10亿次(有10亿个时钟周期),这里不要简单理解一个时钟周期就是一次CPU运算。
|
所以 1GHz = 10亿Hz,表示CPU可以一秒脉冲10亿次(有10亿个时钟周期),这里不要简单理解一个时钟周期就是一次CPU运算。
|
||||||
|
|
||||||
例如1 + 2 = 3,cpu要执行四次才能完整这个操作,步骤一:把1放入寄存机,步骤二:把2放入寄存器,步骤三:做加法,步骤四:保存3。
|
例如1 + 2 = 3,cpu要执行四次才能完整这个操作,步骤一:把1放入寄存器,步骤二:把2放入寄存器,步骤三:做加法,步骤四:保存3。
|
||||||
|
|
||||||
|
|
||||||
而且计算机的cpu也不会只运行我们自己写的程序上,同时cpu也要执行计算机的各种进程任务等等,我们的程序仅仅是其中的一个进程而已。
|
而且计算机的cpu也不会只运行我们自己写的程序上,同时cpu也要执行计算机的各种进程任务等等,我们的程序仅仅是其中的一个进程而已。
|
||||||
@ -52,7 +52,7 @@
|
|||||||
* 火箭科学家需要大致知道一枚试射火箭的着陆点是在大海里还是在城市中;
|
* 火箭科学家需要大致知道一枚试射火箭的着陆点是在大海里还是在城市中;
|
||||||
* 医学研究者需要知道一次药物测试是会杀死还是会治愈实验对象;
|
* 医学研究者需要知道一次药物测试是会杀死还是会治愈实验对象;
|
||||||
|
|
||||||
所以**任何开发计算机程序员的软件工程师都应该能够估计这个程序的运行时间是一秒钟还是一年**。
|
所以**任何开发计算机程序的软件工程师都应该能够估计这个程序的运行时间是一秒钟还是一年**。
|
||||||
|
|
||||||
这个是最基本的,所以以上误差就不算事了。
|
这个是最基本的,所以以上误差就不算事了。
|
||||||
|
|
||||||
|
|||||||
@ -108,7 +108,7 @@ bool isSame(int u, int v) {
|
|||||||
|
|
||||||
|

|
||||||
|
|
||||||
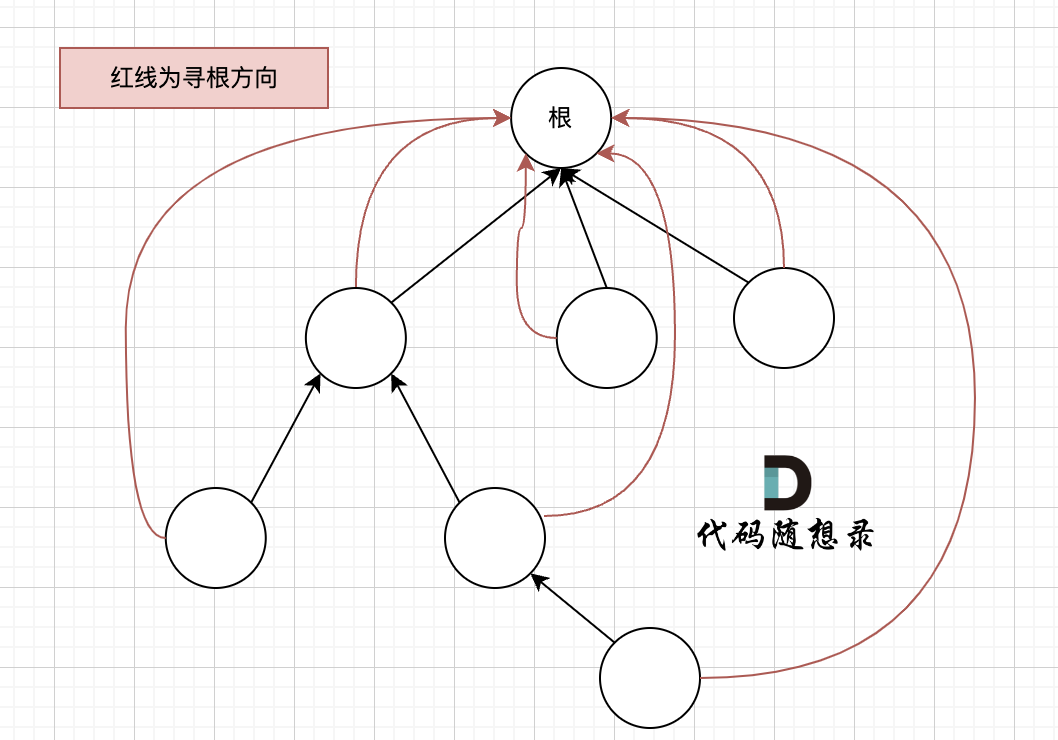
如果这棵多叉树高度很深的话,每次find函数 去寻找跟的过程就要递归很多次。
|
如果这棵多叉树高度很深的话,每次find函数 去寻找根的过程就要递归很多次。
|
||||||
|
|
||||||
我们的目的只需要知道这些节点在同一个根下就可以,所以对这棵多叉树的构造只需要这样就可以了,如图:
|
我们的目的只需要知道这些节点在同一个根下就可以,所以对这棵多叉树的构造只需要这样就可以了,如图:
|
||||||
|
|
||||||
@ -300,7 +300,7 @@ join(3, 2);
|
|||||||
|
|
||||||
**因为路经压缩了**
|
**因为路经压缩了**
|
||||||
|
|
||||||
即如下代码在寻找跟的过程中,会有路径压缩,减少 下次查询的路径长度。
|
即如下代码在寻找根的过程中,会有路径压缩,减少 下次查询的路径长度。
|
||||||
|
|
||||||
```
|
```
|
||||||
// 并查集里寻根的过程
|
// 并查集里寻根的过程
|
||||||
@ -396,7 +396,7 @@ void join(int u, int v) {
|
|||||||
if (rank[u] <= rank[v]) father[u] = v; // rank小的树合入到rank大的树
|
if (rank[u] <= rank[v]) father[u] = v; // rank小的树合入到rank大的树
|
||||||
else father[v] = u;
|
else father[v] = u;
|
||||||
|
|
||||||
if (rank[u] == rank[v] && u != v) rank[v]++; // 如果两棵树高度相同,则v的高度+1因为,方面 if (rank[u] <= rank[v]) father[u] = v; 注意是 <=
|
if (rank[u] == rank[v] && u != v) rank[v]++; // 如果两棵树高度相同,则v的高度+1,因为上面 if (rank[u] <= rank[v]) father[u] = v; 注意是 <=
|
||||||
}
|
}
|
||||||
```
|
```
|
||||||
|
|
||||||
@ -423,7 +423,7 @@ void join(int u, int v) {
|
|||||||
|
|
||||||
空间复杂度: O(n) ,申请一个father数组。
|
空间复杂度: O(n) ,申请一个father数组。
|
||||||
|
|
||||||
关于时间复杂度,如果想精确表达出来需要繁琐的数学证明,就不在本篇讲解范围内了,大家感兴趣可以自己去深入去研究。
|
关于时间复杂度,如果想精确表达出来需要繁琐的数学证明,就不在本篇讲解范围内了,大家感兴趣可以自己去深入研究。
|
||||||
|
|
||||||
这里做一个简单的分析思路。
|
这里做一个简单的分析思路。
|
||||||
|
|
||||||
|
|||||||
Reference in New Issue
Block a user