diff --git a/problems/0098.验证二叉搜索树.md b/problems/0098.验证二叉搜索树.md
index fcdd2611..a1f503e0 100644
--- a/problems/0098.验证二叉搜索树.md
+++ b/problems/0098.验证二叉搜索树.md
@@ -2,63 +2,64 @@
## 思路
-这道题目比较容易陷入两个陷阱:
-* 陷阱1 :[10,5,15,null,null,6,20] 这个case 要考虑道
-* 陷阱2:样例中根节点的val 可能是-2147483648
+中序遍历下,输出的二叉搜索树节点的数值是有序序列,有了这个特性,**验证二叉搜索树,就相当于变成了判断一个序列是不是递增的了。**
-中序遍历之后 输出的顺序就应该是一个从大到小的顺序, 可以使用一个全局变量进行比较。
+所以代码实现上,我们就使用递归法来中序遍历,遍历的过程中判断节点上的数值是不是递增的就可以了。
+
+这道题目比较容易陷入两个陷阱:
+
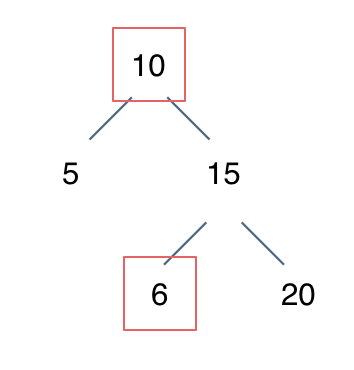
+* 陷阱1 :[10,5,15,null,null,6,20] 这个case 要考虑道
+
+
+10的右子树只能包含大于当前节点的数,而右面出现了一个6 这就不符合了!
+
+* 陷阱2:样例中根节点的val 可能是int的最小值
+
+问题可以进一步演进:如果样例中根节点的val 可能是longlong的最小值 又要怎么办呢?看下文解答!
## C++代码
-
-[10,5,15,null,null,6,20] 为什么预期结果是 false.... 这是经典陷阱
-错误代码
+定于全局变量初始化为long long最小值
```
class Solution {
public:
- bool isValidBST(TreeNode* root) {
- if (root == NULL) return true;
-
- if (root->left != NULL && root->right != NULL) {
- if (root->val > root->left->val && root->val < root->right->val) {
- return true;
- } else {
- return false;
- }
- }
-
- if (root->left != NULL && root->right == NULL) {
- if (root->val > root->left->val) {
- return true;
- }else {
- return false;
- }
- }
- if (root->left == NULL && root->right != NULL) {
- if (root->val < root->right->val) {
- return true;
- }else {
- return false;
- }
- }
- if (root->left == NULL && root->right == NULL) return true;
- return isValidBST(root->left) && isValidBST(root->right);
- }
-};
-```
-
-正确代码
-```
-class Solution {
-public:
- long long val = LONG_MIN;
+ long long maxVal = LONG_MIN;
bool isValidBST(TreeNode* root) {
if (root == NULL) return true;
bool left = isValidBST(root->left);
- if (val < root->val) val = root->val;// 中序遍历,这里相当于从大到小进行比较
+ // 中序遍历,验证遍历的元素是不是从小到大
+ if (maxVal < root->val) maxVal = root->val;
else return false;
bool right = isValidBST(root->right);
return left && right;
}
};
```
+
+其实因为后台数据有int最小值测试用例,所以都改成了longlong最小值。
+
+如果测试数据中有 longlong的最小值,怎么办?不可能在初始化一个更小的值了吧。 建议避免 初始化最小值,如下方法取到最左面的数值:
+
+```
+class Solution {
+public:
+ long long maxVal = 0; // 记录中序遍历的过程中出现过的最大值
+ bool flag = false; // 标记是否取到了最左面节点的数值
+ bool isValidBST(TreeNode* root) {
+ if (root == NULL) return true;
+ bool left = isValidBST(root->left);
+ if (!flag) {
+ maxVal = root->val;
+ flag = true;
+ } else {
+ // 中序遍历,这里相当于从大到小进行比较
+ if (maxVal < root->val) maxVal = root->val;
+ else return false;
+ }
+ bool right = isValidBST(root->right);
+ return left && right;
+ }
+};
+```
+
+> 更多算法干货文章持续更新,可以微信搜索「代码随想录」第一时间围观,关注后,回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等,就可以获得我多年整理的学习资料。
diff --git a/problems/0144.二叉树的前序遍历.md b/problems/0144.二叉树的前序遍历.md
index 8704e395..d4f6c3e8 100644
--- a/problems/0144.二叉树的前序遍历.md
+++ b/problems/0144.二叉树的前序遍历.md
@@ -177,7 +177,7 @@ public:
,然后在反转result数组,输出的结果顺序就是左右中了,如下图:

-所以后序遍历只需要前序遍历的代码稍作修改就可以了,代码如下:
+**所以后序遍历只需要前序遍历的代码稍作修改就可以了,代码如下:**
```
class Solution {
diff --git a/problems/0199.二叉树的右视图.md b/problems/0199.二叉树的右视图.md
index a99d428b..ce17ca72 100644
--- a/problems/0199.二叉树的右视图.md
+++ b/problems/0199.二叉树的右视图.md
@@ -3,7 +3,21 @@ https://leetcode-cn.com/problems/binary-tree-right-side-view/
## 思路
-广度优先搜索模板题目,层序遍历的时候,将每一层的最后元素放入result数组中
+这里再讲一遍二叉树的广度优先遍历(层序遍历)
+
+需要借用一个辅助数据结构队列来实现,**队列先进先出,符合一层一层遍历的逻辑,而是用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。**
+
+使用队列实现广度优先遍历,动画如下:
+
+
+
+这样就实现了层序从左到右遍历二叉树。
+
+建议先做一下这道题目[0102.二叉树的层序遍历](https://github.com/youngyangyang04/leetcode/blob/master/problems/0102.二叉树的层序遍历.md), 在做这道,就会发现这是一道 广度优先搜索模板题目,层序遍历的时候,将每一层的最后元素放入result数组中,
+
+层序遍历的时候,将单层的最后面的元素放进数组中,随后返回数组就可以了。
+
+代码如下:
## C++代码
diff --git a/problems/0209.长度最小的子数组.md b/problems/0209.长度最小的子数组.md
index 17fe8ec6..47049a0a 100644
--- a/problems/0209.长度最小的子数组.md
+++ b/problems/0209.长度最小的子数组.md
@@ -2,8 +2,15 @@
https://leetcode-cn.com/problems/minimum-size-subarray-sum/
## 思路
-这道题目 暴力解法当然是 两个for循环,然后不断的寻找符合条件的子序列
-这块我们还可以使用滑动窗口的细想来做这道题。所谓滑动窗口,**就是不断的调节子序列的起始位置,从而得出我们要想的结果**
+这道题目暴力解法当然是 两个for循环,然后不断的寻找符合条件的子序列,时间复杂度很明显是O(n^2) 。
+
+还可以使用滑动窗口的细想来做这道题。所谓滑动窗口,**就是不断的调节子序列的起始位置,从而得出我们要想的结果**
+
+这里还是以题目中的示例来举例,s=7, 数组是 2,3,1,2,4,3,来看一下动画效果:
+
+
+
+代码如下:
## 暴力解法
diff --git a/problems/0239.滑动窗口最大值.md b/problems/0239.滑动窗口最大值.md
index b3ee172a..513fcdc2 100644
--- a/problems/0239.滑动窗口最大值.md
+++ b/problems/0239.滑动窗口最大值.md
@@ -7,12 +7,46 @@ https://leetcode-cn.com/problems/sliding-window-maximum/
暴力方法,遍历一遍的过程中每次从窗口中在找到最大的数值,这样很明显是O(n * k)的算法。
-有的同学可能会想用一个大顶堆也就是优先级队列来存放这个窗口里的k个数字,这样就可以知道最大的最大值是多少了, 但是问题是这个窗口是移动的,而大顶堆每次只能弹出最大值,我们无法移除其他数值,这样就造成大顶堆维护的不是滑动窗口里面的数值了。所以不能用大顶堆。
+有的同学可能会想用一个大顶堆也就是优先级队列来存放这个窗口里的k个数字,这样就可以知道最大的最大值是多少了, **但是问题是这个窗口是移动的,而大顶堆每次只能弹出最大值,我们无法移除其他数值,这样就造成大顶堆维护的不是滑动窗口里面的数值了。所以不能用大顶堆。**
-使用单调队列,即单调递减或单调递增的队列。 它不是一个独立的数据结构,需要使用其他数据结构来实现单调队列,例如: deque,deque是双向队列,可以选择 从头部或者尾部pop,同样也可以从头部或者尾部push。
+**使用单调队列,即单调递减或单调递增的队列。它不是一个独立的数据结构,需要使用其他数据结构来实现单调队列**,例如: deque,deque是双向队列,可以选择 从头部或者尾部pop,同样也可以从头部或者尾部push。
不要以为实现的单调队列就是 对窗口里面的数进行排序,如果排序的话,那和优先级队列又有什么区别了呢。
+使用deque实现的单调队列如下:(代码详细注释)
+
+```
+class MyQueue { //单调队列(从大到小)
+public:
+ deque que; // 使用deque来实现单调队列
+ // 每次弹出的时候,比较当前要弹出的数值是否等于队列前端的数值,如果相等在pop数据,当然也要判断队列当前是否为空。
+ void pop(int value) {
+ if (!que.empty() && value == que.front()) {
+ que.pop_front();
+ }
+ }
+ // 如果push的数值大于后端的数值,那么就将队列后端的数值弹出,直到push的数值小于等于 队列后端的数值为止。
+ // 然后再将数值push到队列后端,这样就保持了队列里的数值是单调从大到小的了。
+ void push(int value) {
+ while (!que.empty() && value > que.back()) {
+ que.pop_back();
+ }
+ que.push_back(value);
+
+ }
+ // 查询当前队列里的最大值 直接返回队列前端也就是front就可以了。
+ int front() {
+ return que.front();
+ }
+};
+```
+
+动画解释如下:
+
+
+
+这样我们就用deque实现了一个单调队列,接下来解决滑动窗口最大值的问题就很简单了。
+
详情看代码吧,已经简洁。
## C++代码
@@ -55,5 +89,14 @@ public:
}
};
```
+来看一下时间复杂度,时间复杂度: O(n),
+有的同学可能想了,在队里中 push元素的过程中,还有pop操作呢,感觉不是纯粹了O(n)。
+
+其实,大家可以自己观察一下单调队列的实现,nums 中的每个元素最多也就被 push_back 和 pop_back 一次,没有任何多余操作,所以整体的复杂度还是 O(n)。
+
+空间复杂度因为我们定义一个辅助队列,所以是O(k)。
+
+
+
> 更过算法干货文章持续更新,可以微信搜索「代码随想录」第一时间围观,关注后,回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等,就可以获得我多年整理的学习资料。
diff --git a/problems/0700.二叉搜索树中的搜索.md b/problems/0700.二叉搜索树中的搜索.md
index dffd9707..1dab81e2 100644
--- a/problems/0700.二叉搜索树中的搜索.md
+++ b/problems/0700.二叉搜索树中的搜索.md
@@ -3,7 +3,83 @@ https://leetcode-cn.com/problems/search-in-a-binary-search-tree/
## 思路
-注意这里是二叉搜索树,是已经排序的了,两种实现,递归和迭代
+### 递归法
+
+先来看递归的实现方式。
+
+依然从递归三要素开始分析:
+
+* 确定递归函数的参数和返回值
+* 确定终止条件
+* 确定单层递归的逻辑
+
+1. 确定递归函数的参数和返回值
+
+递归函数的参数传入的就是根节点和要搜索的数值,返回的就是以这个搜索数值所在的节点。
+
+代码如下:
+
+```
+TreeNode* searchBST(TreeNode* root, int val)
+```
+
+2. 确定终止条件
+
+如果root为空,或者找到这个数值了,就返回root节点。
+
+```
+if (root == NULL || root->val == val) return root;
+```
+
+3. 确定单层递归的逻辑
+
+来看一下二叉搜索树的单层递归逻辑有何不同, 因为二叉搜索树的节点是有序的,所以可以有方向的去搜索,如果root->val > val,搜索左子树,如果root->val < val,就搜索右子树,最后如果都没有搜索到,就返回NULL。
+
+代码如下:
+
+```
+if (root->val > val) return searchBST(root->left, val);
+if (root->val < val) return searchBST(root->right, val);
+return NULL;
+```
+
+这里可能会疑惑,在递归遍历的时候,什么时候直接return 递归函数的返回值,什么时候不用加这个 return, 这取决于对递归函数的定义,这里定义的递归函数,就是返回 要查找的元素所在的节点,而这个节点就是我们所求,所以直接return递归函数的返回值。
+
+整体代码如下:
+
+```
+TreeNode* searchBST(TreeNode* root, int val) {
+ if (root == NULL || root->val == val) return root;
+ if (root->val > val) return searchBST(root->left, val);
+ if (root->val < val) return searchBST(root->right, val);
+ return NULL;
+}
+```
+
+### 迭代法
+
+一提到二叉树遍历的迭代法,可能立刻想起使用栈来模拟深度遍历,使用队列来模拟广度遍历,其实因为二叉搜索树的特殊性,也就是节点的有序性,可以不使用辅助栈或者队列就可以写出迭代法。
+
+对于一般二叉树,模拟递归的过程中还有一个回溯的过程,例如走一个左方向的分支走到头了,那么要调头,在走右分支。而对于二叉搜索树,不需要回溯的过程,因为节点的有序性就帮我们确定了搜索的方向。
+
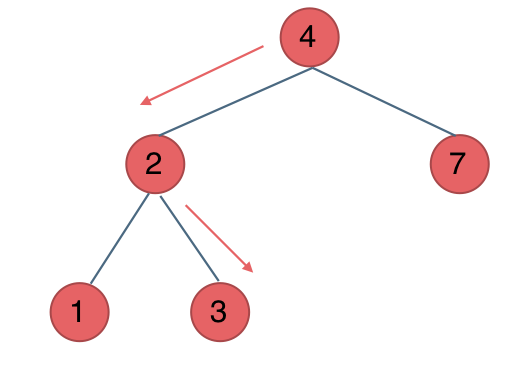
+看如下图中的这颗二叉搜索树,例如要搜索元素为3的节点,我们不需要搜索其他节点,也不需要做回溯,查找的路径已经规划好了。
+
+
+迭代法代码如下:
+
+```
+class Solution {
+public:
+ TreeNode* searchBST(TreeNode* root, int val) {
+ while (root != NULL) {
+ if (root->val > val) root = root->left;
+ else if (root->val < val) root = root->right;
+ else return root;
+ }
+ return NULL;
+ }
+};
+```
## C++代码
diff --git a/problems/1047.删除字符串中的所有相邻重复项.md b/problems/1047.删除字符串中的所有相邻重复项.md
index a9a88e41..756bbe65 100644
--- a/problems/1047.删除字符串中的所有相邻重复项.md
+++ b/problems/1047.删除字符串中的所有相邻重复项.md
@@ -3,7 +3,13 @@ https://leetcode-cn.com/problems/remove-all-adjacent-duplicates-in-string/
## 思路
-这道题目就像是我们玩过的游戏对对碰, 可以把字符串放到与一个栈中,然后如果相同的话 栈就弹出,这样最后栈里剩下的元素都是相邻不相同的元素了
+这道题目就像是我们玩过的游戏对对碰, 可以把字符串放到与一个栈中,然后如果相同的话 栈就弹出,这样最后栈里剩下的元素都是相邻不相同的元素了。
+
+如动画所示:
+
+
+
+从栈中弹出剩余元素,此时是字符串ac,因为从栈里弹出的元素是倒叙的,所以在对字符串进行反转一下,就得到了最终的结果。
## C++代码
diff --git a/video/0239.滑动窗口最大值.mp4 b/video/0239.滑动窗口最大值.mp4
new file mode 100644
index 00000000..3b984fb8
Binary files /dev/null and b/video/0239.滑动窗口最大值.mp4 differ
diff --git a/video/1047.删除字符串中的所有相邻重复项.mp4 b/video/1047.删除字符串中的所有相邻重复项.mp4
new file mode 100644
index 00000000..b8512f24
Binary files /dev/null and b/video/1047.删除字符串中的所有相邻重复项.mp4 differ
diff --git a/video/209.长度最小的子数组.mp4 b/video/209.长度最小的子数组.mp4
new file mode 100644
index 00000000..df034f52
Binary files /dev/null and b/video/209.长度最小的子数组.mp4 differ