algorithm/leetcode-master
1
0
Fork 0
mirror of https://github.com/youngyangyang04/leetcode-master.git synced 2025-07-07 15:45:40 +08:00
Code Issues Packages Projects Releases Wiki Activity

Merge branch 'youngyangyang04:master' into master

Browse Source
This commit is contained in:
Ruizheng Wu
2022-12-08 13:16:17 +08:00
committed by GitHub
parent 0131465339 29c5037a38
commit 2dab87687d
5 changed files with 101 additions and 133 deletions
Download Patch File Download Diff File Expand all files Collapse all files

49
problems/0017.电话号码的字母组合.md
View File

@ -120,7 +120,7 @@ for (int i = 0; i < letters.size(); i++) {
**注意这里for循环，可不像是在[回溯算法：求组合问题！](https://programmercarl.com/0077.组合.html)和[回溯算法：求组合总和！](https://programmercarl.com/0216.组合总和III.html)中从startIndex开始遍历的**。
**因为本题每一个数字代表的是不同集合，也就是求不同集合之间的组合，而[77. 组合](https://programmercarl.com/0077.组合.html)和[216.组合总和III](https://programmercarl.com/0216.组合总和III.html)都是是求同一个集合中的组合！**
**因为本题每一个数字代表的是不同集合，也就是求不同集合之间的组合，而[77. 组合](https://programmercarl.com/0077.组合.html)和[216.组合总和III](https://programmercarl.com/0216.组合总和III.html)都是求同一个集合中的组合！**
注意：输入1 * #按键等等异常情况
@ -356,38 +356,32 @@ class Solution:
主要在于递归中传递下一个数字
```go
var (
m []string
path []byte
res []string
)
func letterCombinations(digits string) []string {
lenth:=len(digits)
if lenth==0 ||lenth>4{
return nil
m = []string{"abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"}
path, res = make([]byte, 0), make([]string, 0)
if digits == "" {
return res
}
digitsMap:= [10]string{
"", // 0
"", // 1
"abc", // 2
"def", // 3
"ghi", // 4
"jkl", // 5
"mno", // 6
"pqrs", // 7
"tuv", // 8
"wxyz", // 9
}
res:=make([]string,0)
recursion("",digits,0,digitsMap,&res)
dfs(digits, 0)
return res
}
func recursion(tempString ,digits string, Index int,digitsMap [10]string, res *[]string) {//index表示第几个数字
if len(tempString)==len(digits){//终止条件，字符串长度等于digits的长度
*res=append(*res,tempString)
func dfs(digits string, start int) {
if len(path) == len(digits) { //终止条件，字符串长度等于digits的长度
tmp := string(path)
res = append(res, tmp)
return
}
tmpK:=digits[Index]-'0' // 将index指向的数字转为int（确定下一个数字）
letter:=digitsMap[tmpK]// 取数字对应的字符集
for i:=0;i<len(letter);i++{
tempString=tempString+string(letter[i])//拼接结果
recursion(tempString,digits,Index+1,digitsMap,res)
tempString=tempString[:len(tempString)-1]//回溯
digit := int(digits[start] - '0') // 将index指向的数字转为int（确定下一个数字）
str := m[digit-2] // 取数字对应的字符集（注意和map中的对应）
for j := 0; j < len(str); j++ {
path = append(path, str[j])
dfs(digits, start+1)
path = path[:len(path)-1]
}
}
```
@ -415,7 +409,6 @@ var letterCombinations = function(digits) {
backtracking(n, k, a + 1);
path.pop();
}
}
};
```

98
problems/0077.组合.md
View File

@ -34,7 +34,7 @@
# 思路
本题这是回溯法的经典题目。
本题是回溯法的经典题目。
直接的解法当然是使用for循环，例如示例中k为2，很容易想到 用两个for循环，这样就可以输出 和示例中一样的结果。
@ -82,13 +82,13 @@ for (int i = 1; i <= n; i++) {
如果脑洞模拟回溯搜索的过程，绝对可以让人窒息，所以需要抽象图形结构来进一步理解。
**我们在[关于回溯算法，你该了解这些！](https://programmercarl.com/回溯算法理论基础.html)中说道回溯法解决的问题都可以抽象为树形结构（N叉树），用树形结构来理解回溯就容易多了**。
**我们在[关于回溯算法，你该了解这些！](https://programmercarl.com/回溯算法理论基础.html)中说到回溯法解决的问题都可以抽象为树形结构（N叉树），用树形结构来理解回溯就容易多了**。
那么我把组合问题抽象为如下树形结构：
![77.组合](https://img-blog.csdnimg.cn/20201123195223940.png)
可以看出这个棵树，一开始集合是 1，2，3，4， 从左向右取数，取过的数，不在重复取。
可以看出这棵树，一开始集合是 1，2，3，4， 从左向右取数，取过的数，不再重复取。
第一次取1，集合变为2，3，4 ，因为k为2，我们只需要再取一个数就可以了，分别取2，3，4，得到集合[1,2] [1,3] [1,4]，以此类推。
@ -120,7 +120,7 @@ vector<int> path; // 用来存放符合条件结果
其实不定义这两个全局变量也是可以的，把这两个变量放进递归函数的参数里，但函数里参数太多影响可读性，所以我定义全局变量了。
函数里一定有两个参数，既然是集合n里面取k的数，那么n和k是两个int型的参数。
函数里一定有两个参数，既然是集合n里面取k个数，那么n和k是两个int型的参数。
然后还需要一个参数，为int型变量startIndex，这个参数用来记录本层递归的中，集合从哪里开始遍历（集合就是[1,...,n] ）。
@ -389,9 +389,8 @@ class Solution(object):
# 剪枝， 最后k - len(path)个节点直接构造结果，无需递归
last_startidx = n - (k - len(path)) + 1
result.append(path + [idx for idx in range(last_startidx, n + 1)])
for x in range(startidx, last_startidx):
for x in range(startidx, last_startidx + 1):
path.append(x)
backtracking(n, k, x + 1) # 递归
path.pop() # 回溯
@ -435,6 +434,36 @@ class Solution:
return res
```
### Go
```Go
var (
path []int
res [][]int
)
func combine(n int, k int) [][]int {
path, res = make([]int, 0, k), make([][]int, 0)
dfs(n, k, 1)
return res
}
func dfs(n int, k int, start int) {
if len(path) == k { // 说明已经满足了k个数的要求
tmp := make([]int, k)
copy(tmp, path)
res = append(res, tmp)
return
}
for i := start; i <= n; i++ { // 从start开始，不往回走，避免出现重复组合
if n - i + 1 < k - len(path) { // 剪枝
break
}
path = append(path, i)
dfs(n, k, i+1)
path = path[:len(path)-1]
}
}
```
### javascript
@ -481,63 +510,6 @@ function combine(n: number, k: number): number[][] {
};
```
### Go
```Go
var res [][]int
func combine(n int, k int) [][]int {
res=[][]int{}
if n <= 0 || k <= 0 || k > n {
return res
}
backtrack(n, k, 1, []int{})
return res
}
func backtrack(n,k,start int,track []int){
if len(track)==k{
temp:=make([]int,k)
copy(temp,track)
res=append(res,temp)
}
if len(track)+n-start+1 < k {
return
}
for i:=start;i<=n;i++{
track=append(track,i)
backtrack(n,k,i+1,track)
track=track[:len(track)-1]
}
}
```
剪枝：
```Go
var res [][]int
func combine(n int, k int) [][]int {
res=[][]int{}
if n <= 0 || k <= 0 || k > n {
return res
}
backtrack(n, k, 1, []int{})
return res
}
func backtrack(n,k,start int,track []int){
if len(track)==k{
temp:=make([]int,k)
copy(temp,track)
res=append(res,temp)
}
if len(track)+n-start+1 < k {
return
}
for i:=start;i<=n;i++{
track=append(track,i)
backtrack(n,k,i+1,track)
track=track[:len(track)-1]
}
}
```
### Rust
```Rust

36
problems/0077.组合优化.md
View File

@ -133,7 +133,7 @@ public:
# 总结
本篇我们准对求组合问题的回溯法代码做了剪枝优化，这个优化如果不画图的话，其实不好理解，也不好讲清楚。
本篇我们针对求组合问题的回溯法代码做了剪枝优化，这个优化如果不画图的话，其实不好理解，也不好讲清楚。
所以我依然是把整个回溯过程抽象为一棵树形结构，然后可以直观的看出，剪枝究竟是剪的哪里。
@ -194,28 +194,28 @@ class Solution:
```
Go：
```Go
var res [][]int
var (
path []int
res [][]int
)
func combine(n int, k int) [][]int {
res=[][]int{}
if n <= 0 || k <= 0 || k > n {
return res
}
backtrack(n, k, 1, []int{})
path, res = make([]int, 0, k), make([][]int, 0)
dfs(n, k, 1)
return res
}
func backtrack(n,k,start int,track []int){
if len(track)==k{
temp:=make([]int,k)
copy(temp,track)
res=append(res,temp)
}
if len(track)+n-start+1 < k {
func dfs(n int, k int, start int) {
if len(path) == k {
tmp := make([]int, k)
copy(tmp, path)
res = append(res, tmp)
return
}
for i:=start;i<=n;i++{
track=append(track,i)
backtrack(n,k,i+1,track)
track=track[:len(track)-1]
for i := start; i <= n - (k-len(path)) + 1; i++ {
path = append(path, i)
dfs(n, k, i+1)
path = path[:len(path)-1]
}
}
```

41
problems/0216.组合总和III.md
View File

@ -36,7 +36,7 @@
想到这一点了，做过[77. 组合](https://programmercarl.com/0077.组合.html)之后，本题是简单一些了。
本题k相当于了树的深度，9（因为整个集合就是9个数）就是树的宽度。
本题k相当于树的深度，9（因为整个集合就是9个数）就是树的宽度。
例如 k = 2，n = 4的话，就是在集合[1,2,3,4,5,6,7,8,9]中求 k（个数） = 2, n（和） = 4的组合。
@ -380,29 +380,32 @@ class Solution:
回溯+减枝
```go
var (
res [][]int
path []int
)
func combinationSum3(k int, n int) [][]int {
var track []int// 遍历路径
var result [][]int// 存放结果集
backTree(n,k,1,&track,&result)
return result
res, path = make([][]int, 0), make([]int, 0, k)
dfs(k, n, 1, 0)
return res
}
func backTree(n,k,startIndex int,track *[]int,result *[][]int){
if len(*track)==k{
var sum int
tmp:=make([]int,k)
for k,v:=range *track{
sum+=v
tmp[k]=v
}
if sum==n{
*result=append(*result,tmp)
func dfs(k, n int, start int, sum int) {
if len(path) == k {
if sum == n {
tmp := make([]int, k)
copy(tmp, path)
res = append(res, tmp)
}
return
}
for i:=startIndex;i<=9-(k-len(*track))+1;i++{//减枝（k-len(*track)表示还剩多少个可填充的元素）
*track=append(*track,i)//记录路径
backTree(n,k,i+1,track,result)//递归
*track=(*track)[:len(*track)-1]//回溯
for i := start; i <= 9; i++ {
if sum + i > n || 9-i+1 < k-len(path) {
break
}
path = append(path, i)
dfs(k, n, i+1, sum+i)
path = path[:len(path)-1]
}
}
```

4
problems/0235.二叉搜索树的最近公共祖先.md
View File

@ -60,12 +60,12 @@
而递归遍历顺序，本题就不涉及到 前中后序了（这里没有中节点的处理逻辑，遍历顺序无所谓了）。
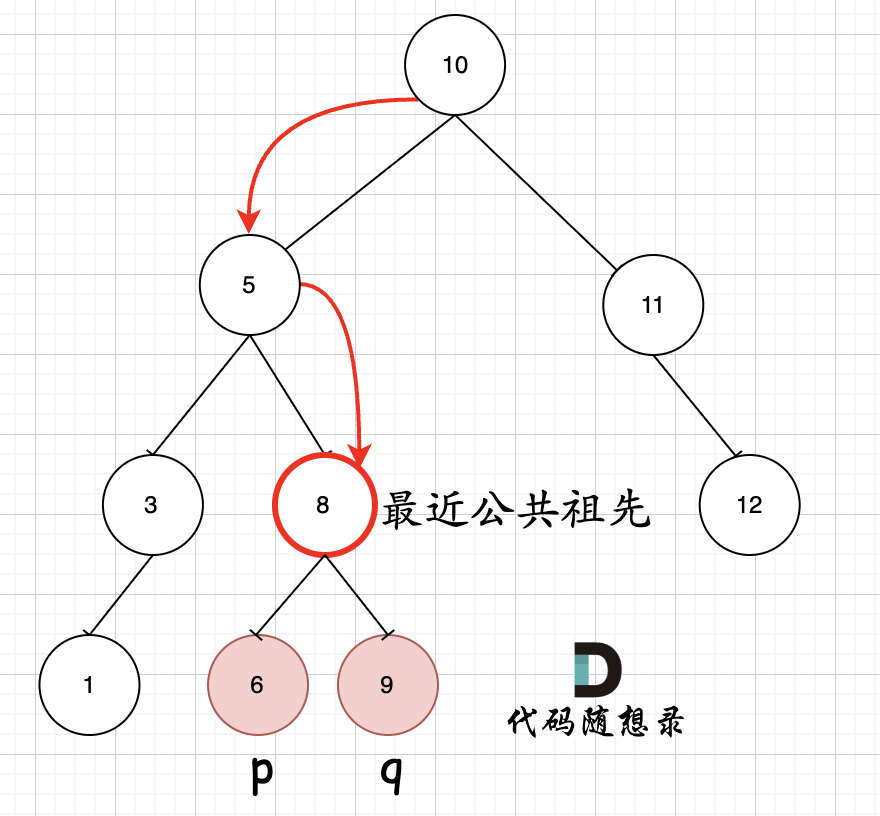
如图所示：p为节点3，q为节点5
如图所示：p为节点6，q为节点9
![235.二叉搜索树的最近公共祖先2](https://code-thinking-1253855093.file.myqcloud.com/pics/20220926165141.png)
可以看出直接按照指定的方向，就可以找到节点4，为最近公共祖先，而且不需要遍历整棵树，找到结果直接返回！
可以看出直接按照指定的方向，就可以找到节点8，为最近公共祖先，而且不需要遍历整棵树，找到结果直接返回！
## 递归法