更新回溯算法Markdown

problems/周总结/20201107回溯周末总结.md

@@ -0,0 +1,169 @@
+
+
+# 本周小结！（回溯算法系列二）
+
+> 例行每周小结
+
+## 周一
+
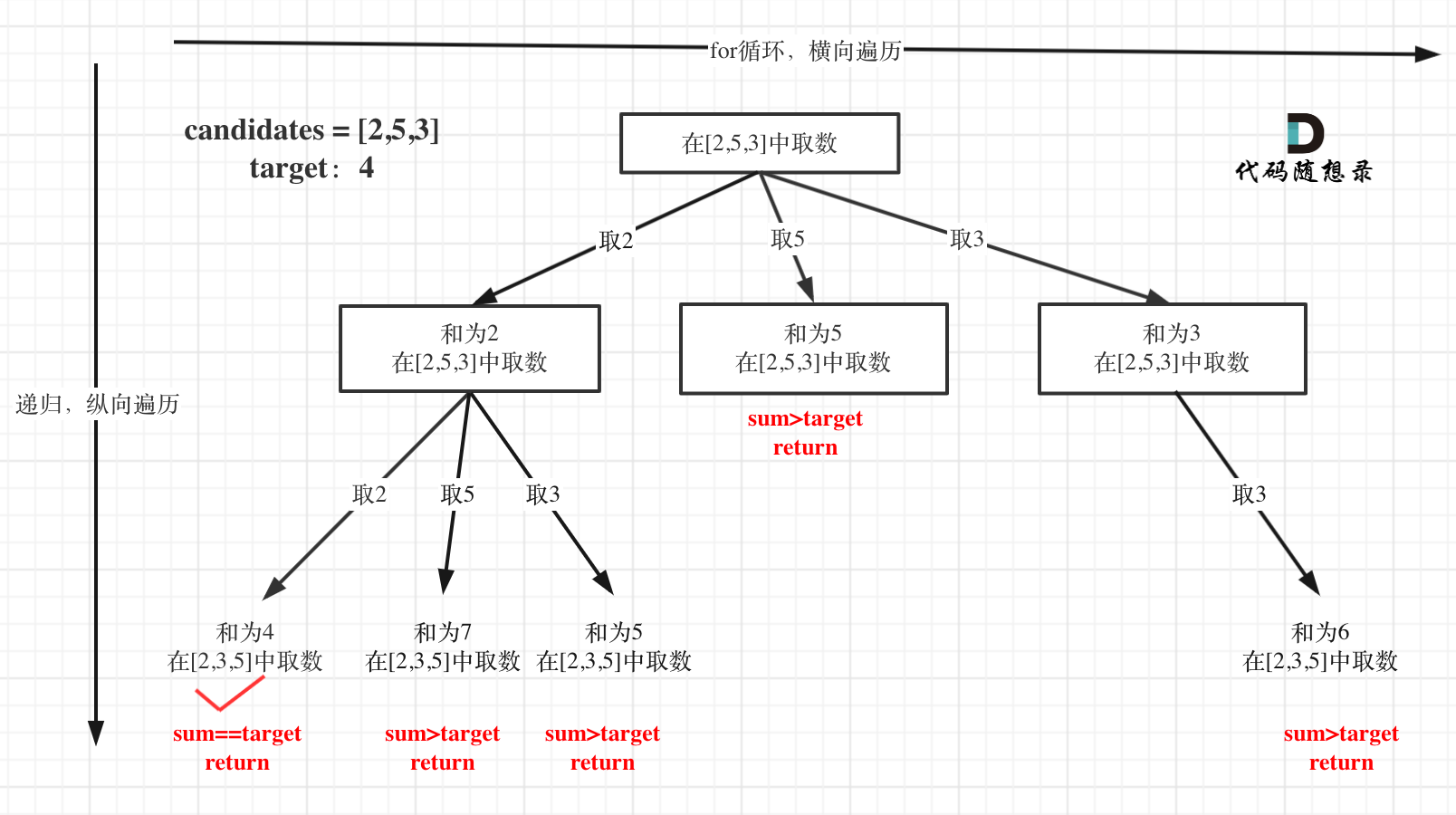
+在[回溯算法：求组合总和（二）](https://mp.weixin.qq.com/s/FLg8G6EjVcxBjwCbzpACPw)中讲解的组合总和问题，和以前的组合问题还都不一样。
+
+本题和[回溯算法：求组合问题！](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)，[回溯算法：求组合总和！](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w)和区别是：本题没有数量要求，可以无限重复，但是有总和的限制，所以间接的也是有个数的限制。
+
+不少录友都是看到可以重复选择，就义无反顾的把startIndex去掉了。
+
+**本题还需要startIndex来控制for循环的起始位置，对于组合问题，什么时候需要startIndex呢？**
+
+我举过例子，如果是一个集合来求组合的话，就需要startIndex，例如：[回溯算法：求组合问题！](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)，[回溯算法：求组合总和！](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w)。
+
+如果是多个集合取组合，各个集合之间相互不影响，那么就不用startIndex，例如：[回溯算法：电话号码的字母组合](https://mp.weixin.qq.com/s/e2ua2cmkE_vpYjM3j6HY0A)
+
+**注意以上我只是说求组合的情况，如果是排列问题，又是另一套分析的套路，后面我再讲解排列的时候就重点介绍**。
+
+最后还给出了本题的剪枝优化，如下：
+
+```
+for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++)
+```
+
+这个优化如果是初学者的话并不容易想到。
+
+**在求和问题中，排序之后加剪枝是常见的套路！**
+
+在[回溯算法：求组合总和（二）](https://mp.weixin.qq.com/s/FLg8G6EjVcxBjwCbzpACPw)第一个树形结构没有画出startIndex的作用，**这里这里纠正一下，准确的树形结构如图所示：**
+
+![39.组合总和](https://img-blog.csdnimg.cn/20201123202227835.png)
+
+## 周二
+
+在[回溯算法：求组合总和（三）](https://mp.weixin.qq.com/s/_1zPYk70NvHsdY8UWVGXmQ)中依旧讲解组合总和问题，本题集合元素会有重复，但要求解集不能包含重复的组合。
+
+**所以难就难在去重问题上了**。
+
+这个去重问题，相信做过的录友都知道有多么的晦涩难懂。网上的题解一般就说“去掉重复”，但说不清怎么个去重，代码一甩就完事了。
+
+为了讲解这个去重问题，**我自创了两个词汇，“树枝去重”和“树层去重”**。
+
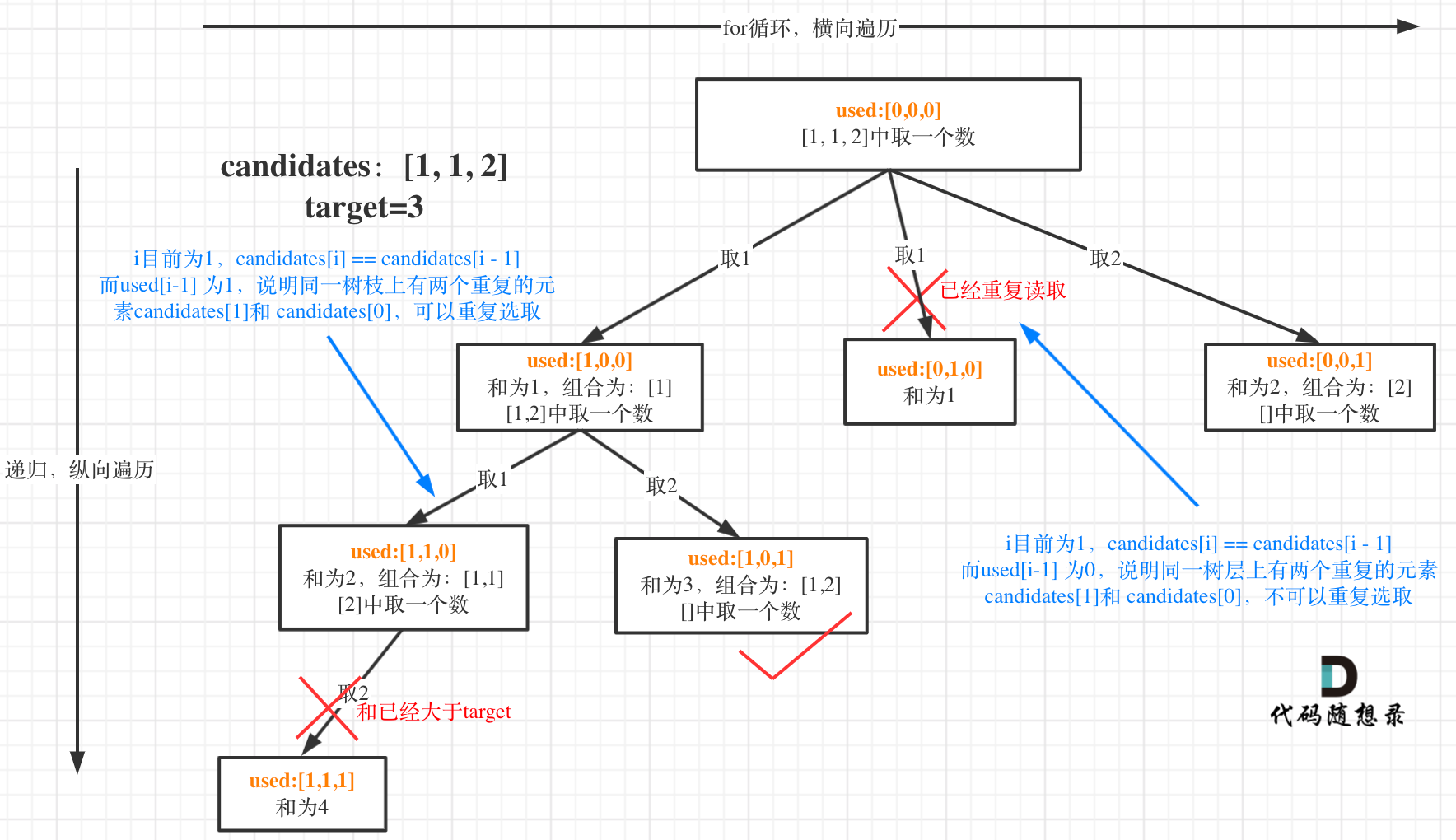
+都知道组合问题可以抽象为树形结构，那么“使用过”在这个树形结构上是有两个维度的，一个维度是同一树枝上“使用过”，一个维度是同一树层上“使用过”。**没有理解这两个层面上的“使用过” 是造成大家没有彻底理解去重的根本原因**。
+
+![40.组合总和II1](https://img-blog.csdnimg.cn/20201123202817973.png)
+
+我在图中将used的变化用橘黄色标注上，可以看出在candidates[i] == candidates[i - 1]相同的情况下：
+
+* used[i - 1] == true，说明同一树支candidates[i - 1]使用过
+* used[i - 1] == false，说明同一树层candidates[i - 1]使用过
+
+**这块去重的逻辑很抽象，网上搜的题解基本没有能讲清楚的，如果大家之前思考过这个问题或者刷过这道题目，看到这里一定会感觉通透了很多！**
+
+对于去重，其实排列问题也是一样的道理，后面我会讲到。
+
+
+## 周三
+
+在[回溯算法：分割回文串](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)中，我们开始讲解切割问题，虽然最后代码看起来好像是一道模板题，但是从分析到学会套用这个模板，是比较难的。
+
+我列出如下几个难点：
+
+* 切割问题其实类似组合问题
+* 如何模拟那些切割线
+* 切割问题中递归如何终止
+* 在递归循环中如何截取子串
+* 如何判断回文
+
+如果想到了**用求解组合问题的思路来解决 切割问题本题就成功一大半了**，接下来就可以对着模板照葫芦画瓢。
+
+**但后序如何模拟切割线，如何终止，如何截取子串，其实都不好想，最后判断回文算是最简单的了**。
+
+除了这些难点，**本题还有细节，例如：切割过的地方不能重复切割所以递归函数需要传入i + 1**。
+
+所以本题应该是一个道hard题目了。
+
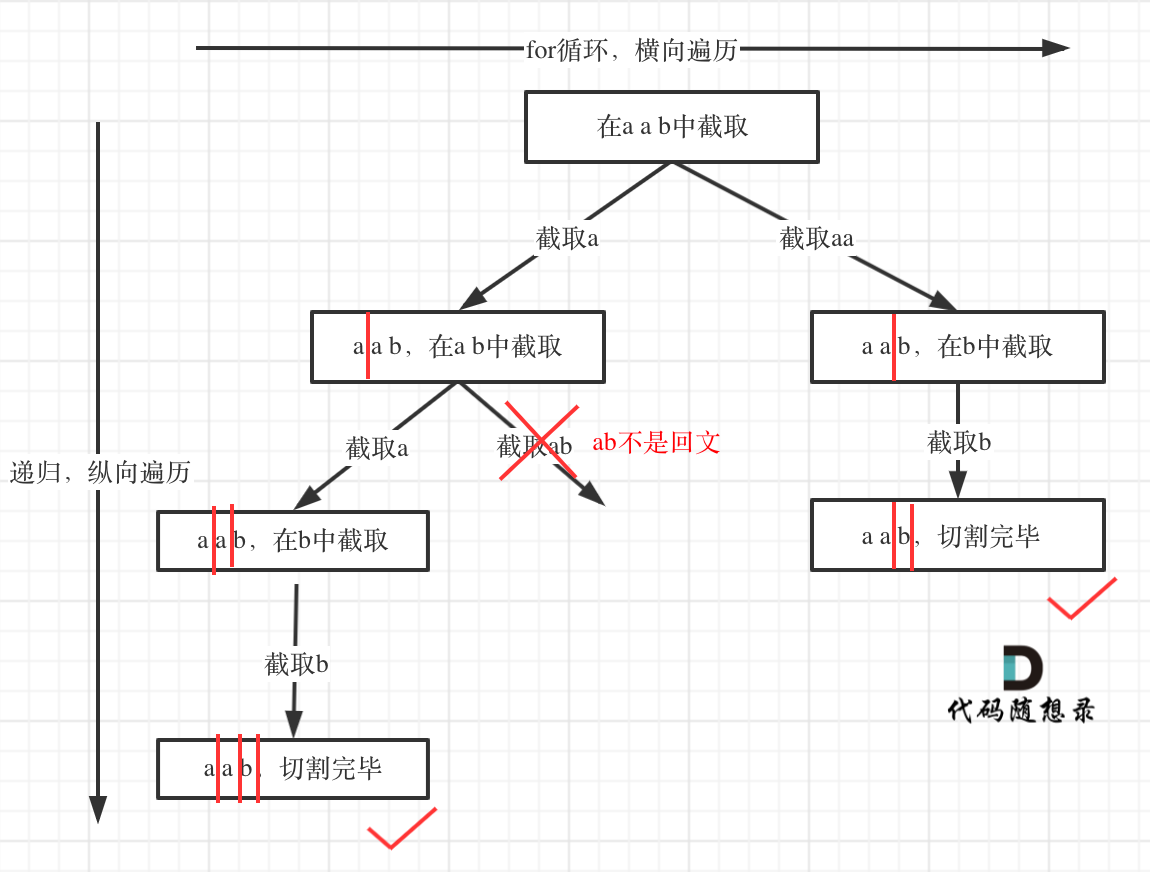
+**本题的树形结构中，和代码的逻辑有一个小出入，已经判断不是回文的子串就不会进入递归了，纠正如下：**
+
+![131.分割回文串](https://img-blog.csdnimg.cn/20201123203228309.png)
+
+
+## 周四
+
+如果没有做过[回溯算法：分割回文串](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)的话，[回溯算法：复原IP地址](https://mp.weixin.qq.com/s/v--VmA8tp9vs4bXCqHhBuA)这道题目应该是比较难的。
+
+复原IP照[回溯算法：分割回文串](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)就多了一些限制，例如只能分四段，而且还是更改字符串，插入逗点。
+
+树形图如下：
+
+![93.复原IP地址](https://img-blog.csdnimg.cn/20201123203735933.png)
+
+在本文的树形结构图中，我已经把详细的分析思路都画了出来，相信大家看了之后一定会思路清晰不少！
+
+本题还可以有一个剪枝，合法ip长度为12，如果s的长度超过了12就不是有效IP地址，直接返回！
+
+代码如下：
+
+```
+if (s.size() > 12) return result; // 剪枝
+
+```
+
+我之前给出的C++代码没有加这个限制，也没有超时，因为在第四段超过长度之后，就会截止了，所以就算给出特别长的字符串，搜索的范围也是有限的（递归只会到第三层），及时就会返回了。
+
+
+## 周五
+
+在[回溯算法：求子集问题！](https://mp.weixin.qq.com/s/NNRzX-vJ_pjK4qxohd_LtA)中讲解了子集问题，**在树形结构中子集问题是要收集所有节点的结果，而组合问题是收集叶子节点的结果**。
+
+如图：
+
+![78.子集](https://img-blog.csdnimg.cn/202011232041348.png)
+
+
+认清这个本质之后，今天的题目就是一道模板题了。
+
+其实可以不需要加终止条件，因为startIndex >= nums.size()，本层for循环本来也结束了，本来我们就要遍历整颗树。
+
+有的同学可能担心不写终止条件会不会无限递归？
+
+并不会，因为每次递归的下一层就是从i+1开始的。
+
+如果要写终止条件，注意：`result.push_back(path);`要放在终止条件的上面，如下：
+
+```
+result.push_back(path); // 收集子集，要放在终止添加的上面，否则会漏掉自己
+if (startIndex >= nums.size()) { // 终止条件可以不加
+    return;
+}
+```
+
+## 周六
+
+早起的哈希表系列没有总结，所以[哈希表：总结篇！（每逢总结必经典）](https://mp.weixin.qq.com/s/1s91yXtarL-PkX07BfnwLg)如约而至。
+
+可能之前大家做过很多哈希表的题目，但是没有串成线，总结篇来帮你串成线，捋顺哈希表的整个脉络。
+
+大家对什么时候各种set与map比较疑惑，想深入了解红黑树，哈希之类的。
+
+**如果真的只是想清楚什么时候使用各种set与map，不用看那么多，把[关于哈希表，你该了解这些！](https://mp.weixin.qq.com/s/g8N6WmoQmsCUw3_BaWxHZA)看了就够了**。
+
+## 总结
+
+本周我们依次介绍了组合问题，分割问题以及子集问题，子集问题还没有讲完，下周还会继续。
+
+**我讲解每一种问题，都会和其他问题作对比，做分析，所以只要跟着细心琢磨相信对回溯又有新的认识**。
+
+最近这两天题目有点难度，刚刚开始学回溯算法的话，按照现在这个每天一题的速度来，确实有点快，学起来吃力非常正常，这些题目都是我当初学了好几个月才整明白的，哈哈。
+
+**所以大家能跟上的话，已经很优秀了！**
+
+还有一些录友会很关心leetcode上的耗时统计。
+
+这个是很不准确的，相同的代码多提交几次，大家就知道怎么回事了。
+
+leetcode上的计时应该是以4ms为单位，有的多提交几次，多个4ms就多击败50%，所以比较夸张，如果程序运行是几百ms的级别，可以看看leetcode上的耗时，因为它的误差10几ms对最终影响不大。
+
+**所以我的题解基本不会写击败百分之多少多少，没啥意义，时间复杂度分析清楚了就可以了**，至于回溯算法不用分析时间复杂度了，都是一样的爆搜，就看谁剪枝厉害了。
+
+一些录友表示最近回溯算法看的实在是有点懵，回溯算法确实是晦涩难懂，可能视频的话更直观一些，我最近应该会在B站（同名：「代码随想录」）出回溯算法的视频，大家也可以看视频在回顾一波。
+
+**就酱，又是充实的一周，做好本周总结，迎接下一周，冲！**
+
+
+

problems/周总结/20201112回溯周末总结.md

@@ -0,0 +1,97 @@
+
+
+# 本周小结！（回溯算法系列三）
+
+## 周一
+
+在[回溯算法：求子集问题（二）](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)中，开始针对子集问题进行去重。
+
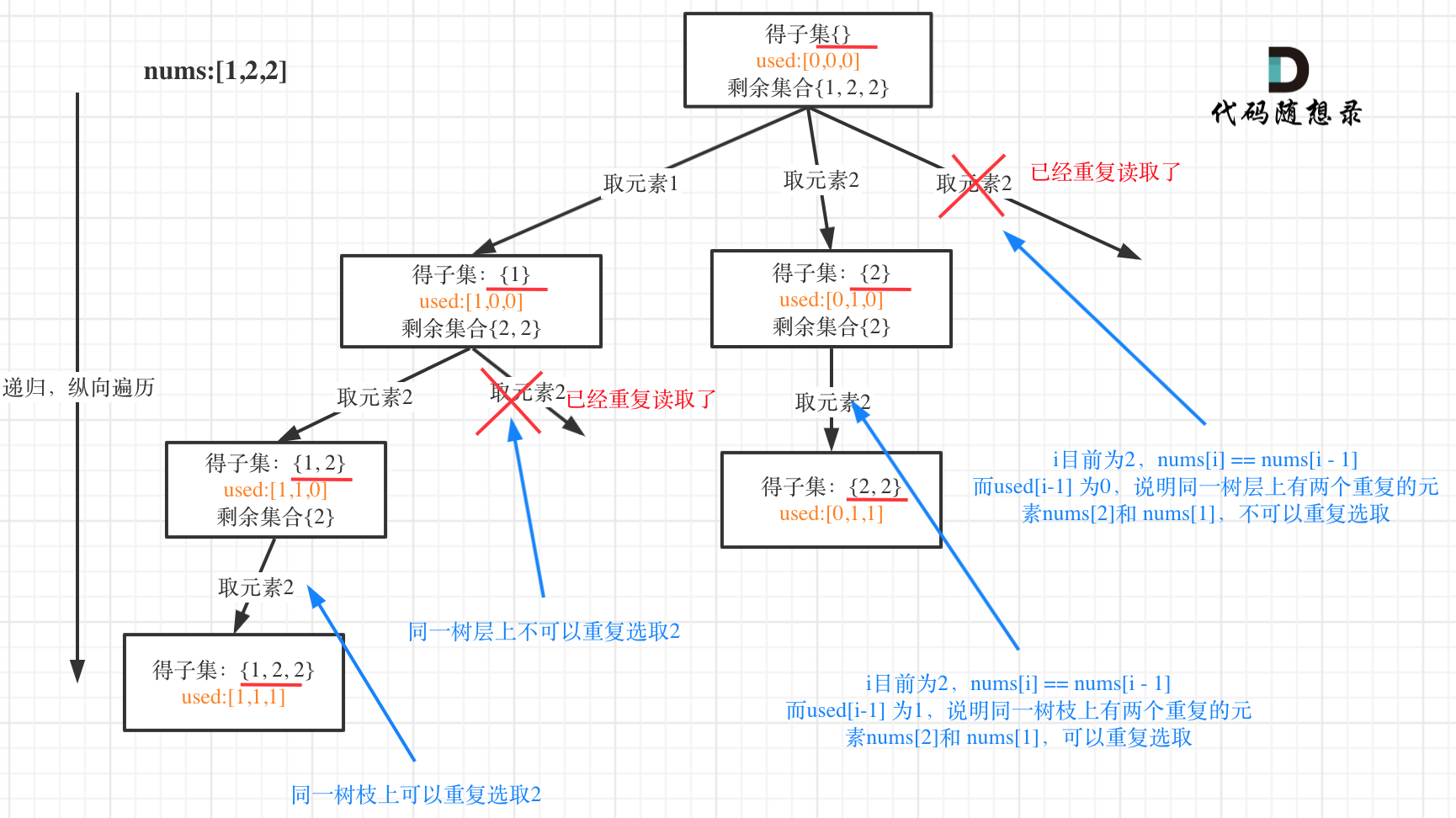
+本题就是[回溯算法：求子集问题！](https://mp.weixin.qq.com/s/NNRzX-vJ_pjK4qxohd_LtA)的基础上加上了去重，去重我们在[回溯算法：求组合总和（三）](https://mp.weixin.qq.com/s/_1zPYk70NvHsdY8UWVGXmQ)也讲过了。
+
+所以本题对大家应该并不难。
+
+树形结构如下：
+
+![90.子集II](https://img-blog.csdnimg.cn/2020111217110449.png)
+
+## 周二
+
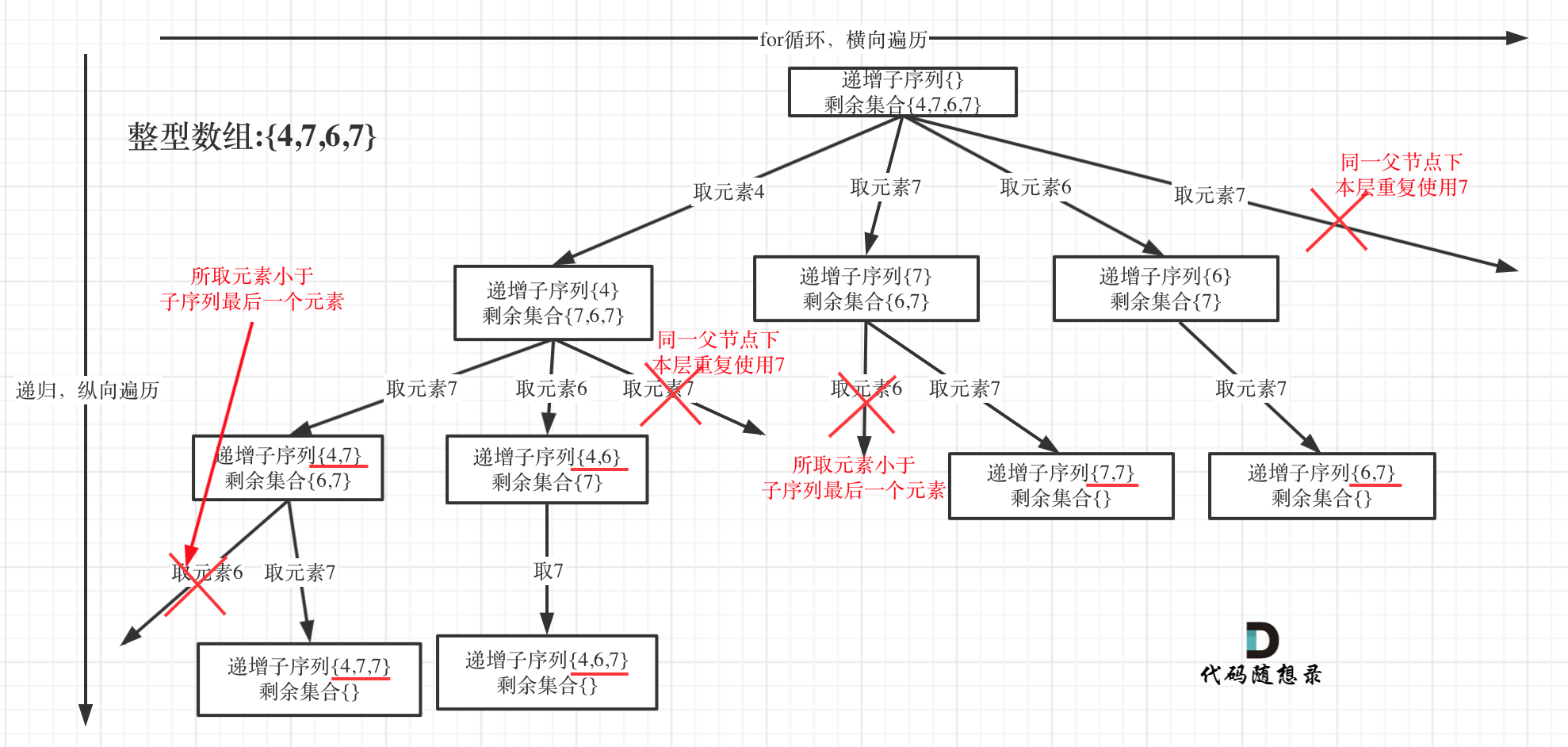
+在[回溯算法：递增子序列](https://mp.weixin.qq.com/s/ePxOtX1ATRYJb2Jq7urzHQ)中，处处都能看到子集的身影，但处处是陷阱，值得好好琢磨琢磨！
+
+树形结构如下：
+![491. 递增子序列1](https://img-blog.csdnimg.cn/20201112170832333.png)
+
+[回溯算法：递增子序列](https://mp.weixin.qq.com/s/ePxOtX1ATRYJb2Jq7urzHQ)留言区大家有很多疑问，主要还是和[回溯算法：求子集问题（二）](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)混合在了一起。
+
+详细在[本周小结！（回溯算法系列三）续集](https://mp.weixin.qq.com/s/kSMGHc_YpsqL2j-jb_E_Ag)中给出了介绍！
+
+## 周三
+
+我们已经分析了组合问题，分割问题，子集问题，那么[回溯算法：排列问题！](https://mp.weixin.qq.com/s/SCOjeMX1t41wcvJq49GhMw) 又不一样了。
+
+排列是有序的，也就是说[1,2] 和[2,1] 是两个集合，这和之前分析的子集以及组合所不同的地方。
+
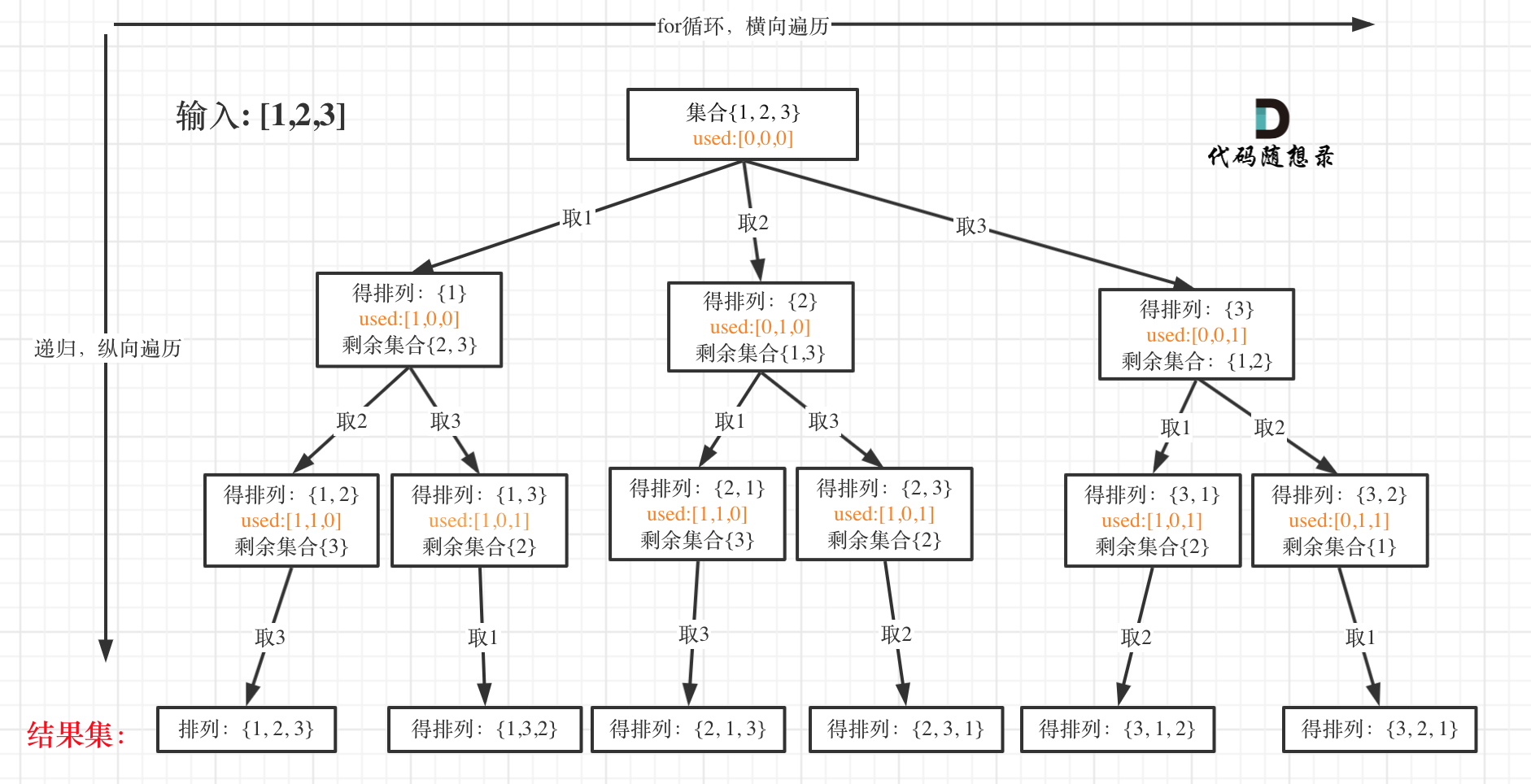
+可以看出元素1在[1,2]中已经使用过了，但是在[2,1]中还要在使用一次1，所以处理排列问题就不用使用startIndex了。
+
+如图：
+![46.全排列](https://img-blog.csdnimg.cn/20201112170304979.png)
+
+**大家此时可以感受出排列问题的不同：**
+
+* 每层都是从0开始搜索而不是startIndex
+* 需要used数组记录path里都放了哪些元素了
+
+## 周四
+
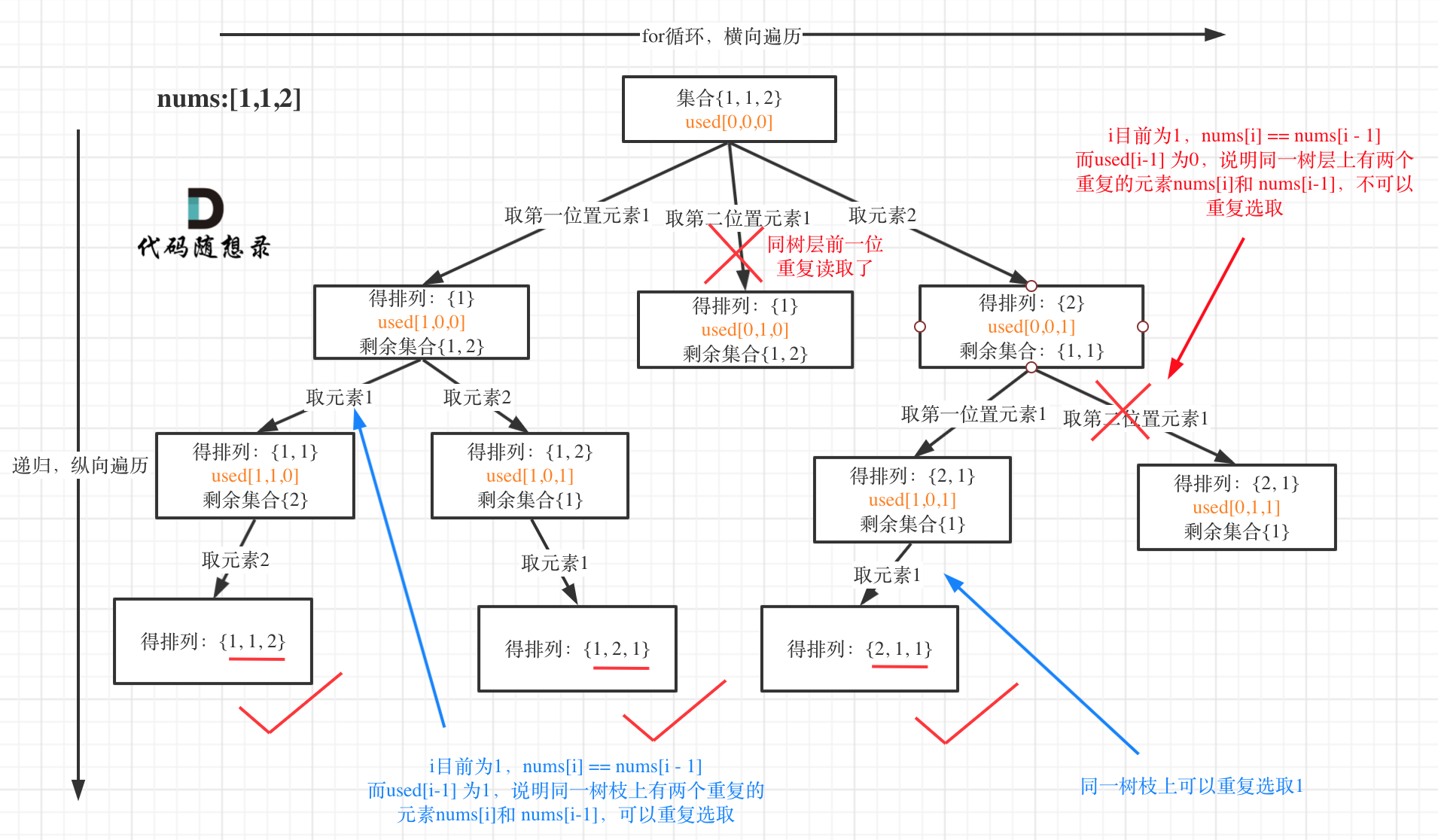
+排列问题也要去重了，在[回溯算法：排列问题（二）](https://mp.weixin.qq.com/s/9L8h3WqRP_h8LLWNT34YlA)中又一次强调了“树层去重”和“树枝去重”。
+
+树形结构如下：
+
+![47.全排列II1](https://img-blog.csdnimg.cn/20201112171930470.png)
+
+**这道题目神奇的地方就是used[i - 1] == false也可以，used[i - 1] == true也可以！**
+
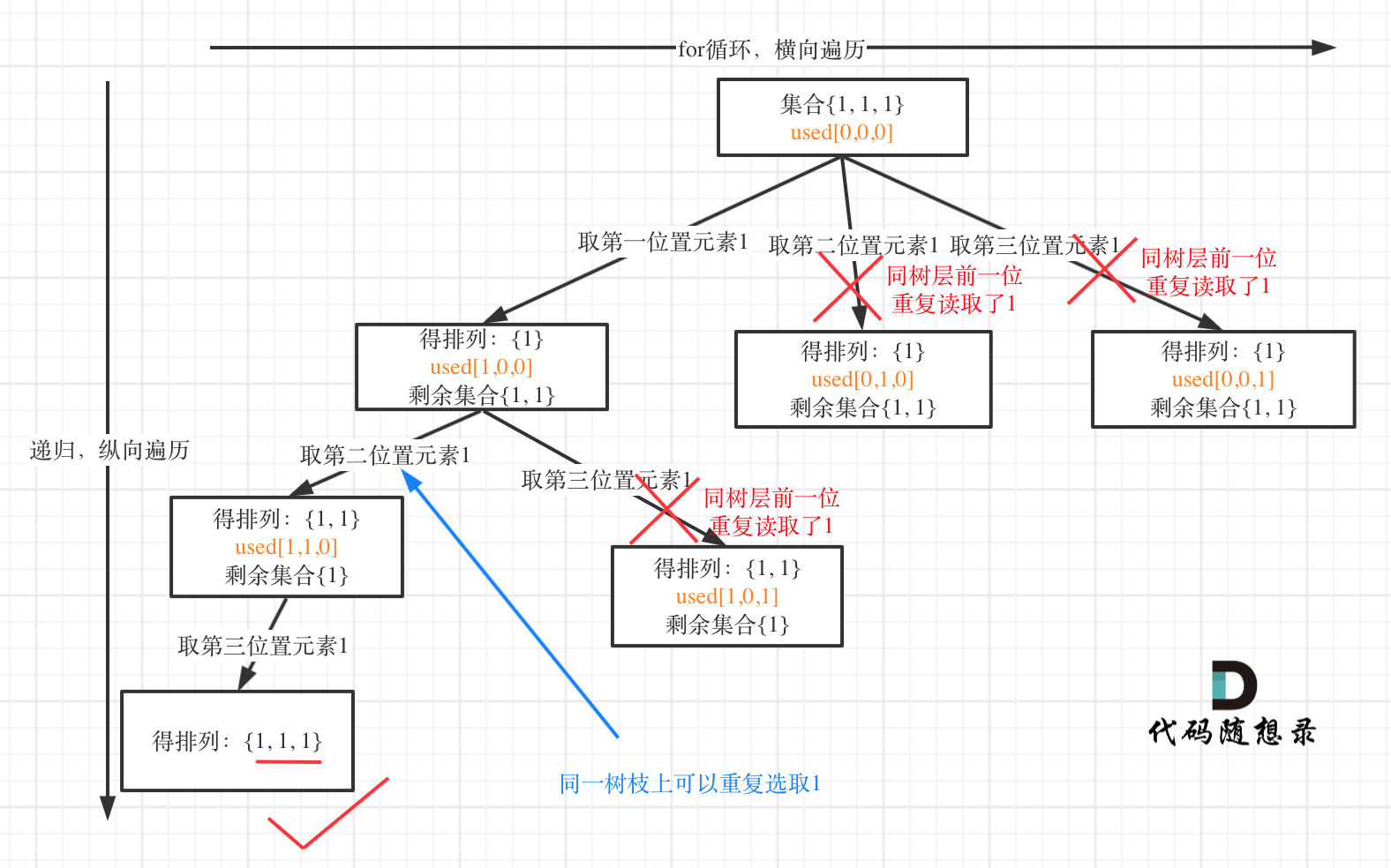
+我就用输入: [1,1,1] 来举一个例子。
+
+树层上去重(used[i - 1] == false)，的树形结构如下：
+
+![47.全排列II2.png](https://img-blog.csdnimg.cn/20201112172230434.png)
+
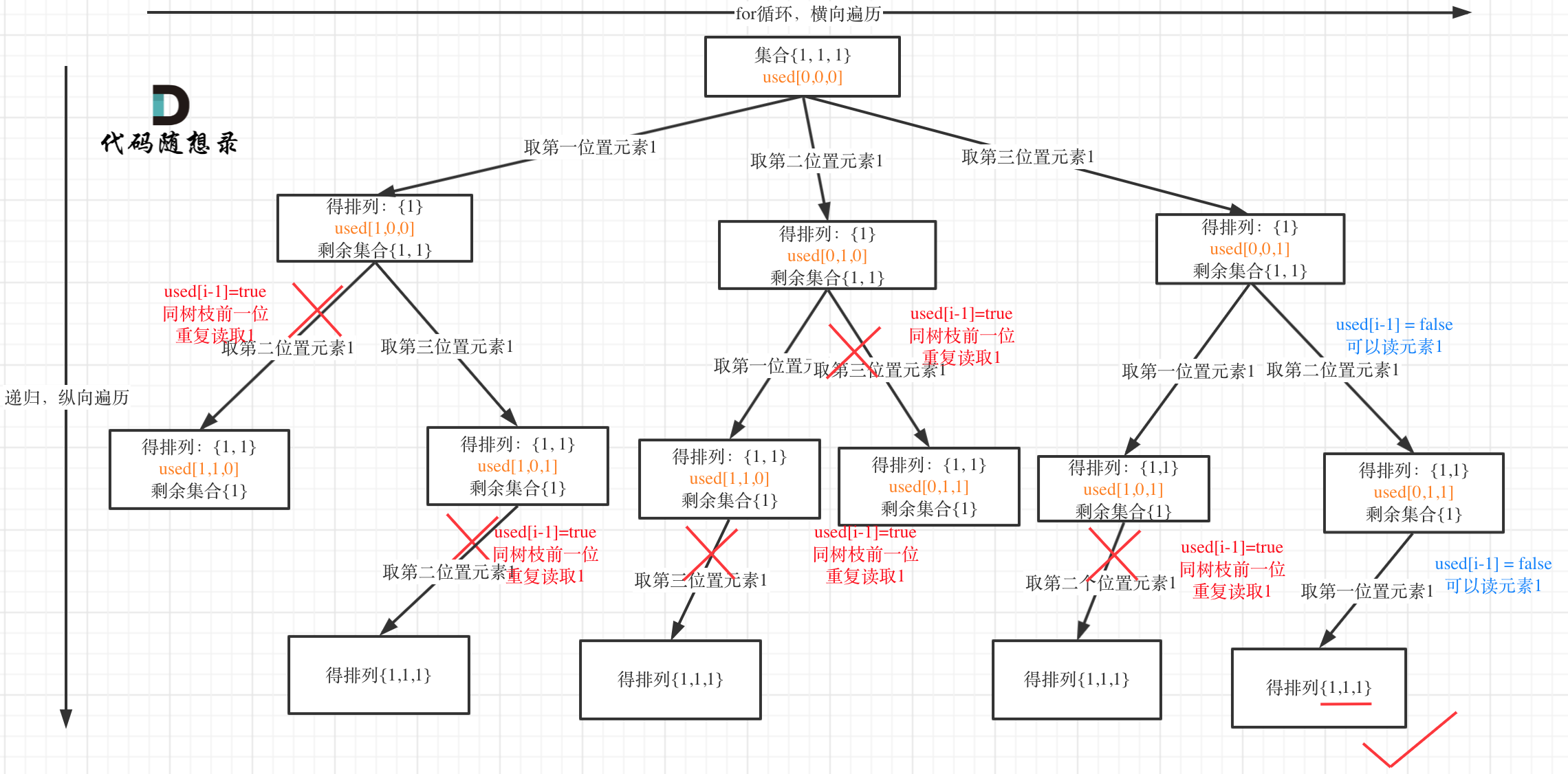
+树枝上去重（used[i - 1] == true）的树型结构如下：
+
+![47.全排列II3](https://img-blog.csdnimg.cn/20201112172327967.png)
+
+**可以清晰的看到使用(used[i - 1] == false)，即树层去重，效率更高！**
+
+## 性能分析
+
+之前并没有分析各个问题的时间复杂度和空间复杂度，这次来说一说。
+
+这块网上的资料鱼龙混杂，一些所谓的经典面试书籍根本不讲回溯算法，算法书籍对这块也避而不谈，感觉就像是算法里模糊的边界。
+
+**所以这块就说一说我个人理解，对内容持开放态度，集思广益，欢迎大家来讨论！**
+
+子集问题分析：
+* 时间复杂度：O(n * 2^n)，因为每一个元素的状态无外乎取与不取，所以时间复杂度为O(2^n)，构造每一组子集都需要填进数组，又有需要O(n)，最终时间复杂度：O(n * 2^n)
+* 空间复杂度：O(n)，递归深度为n，所以系统栈所用空间为O(n)，每一层递归所用的空间都是常数级别，注意代码里的result和path都是全局变量，就算是放在参数里，传的也是引用，并不会新申请内存空间，最终空间复杂度为O(n)
+
+排列问题分析：
+* 时间复杂度：O(n!)，这个可以从排列的树形图中很明显发现，每一层节点为n，第二层每一个分支都延伸了n-1个分支，再往下又是n-2个分支，所以一直到叶子节点一共就是 n * n-1 * n-2 * ..... 1 = n!。
+* 空间复杂度：O(n)，和子集问题同理。
+
+组合问题分析：
+* 时间复杂度：O(n * 2^n)，组合问题其实就是一种子集的问题，所以组合问题最坏的情况，也不会超过子集问题的时间复杂度。
+* 空间复杂度：O(n)，和子集问题同理。
+
+**一般说道回溯算法的复杂度，都说是指数级别的时间复杂度，这也算是一个概括吧！**
+
+## 总结
+
+本周我们对[子集问题进行了去重](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)，然后介绍了和子集问题非常像的[递增子序列](https://mp.weixin.qq.com/s/ePxOtX1ATRYJb2Jq7urzHQ)，如果还保持惯性思维，这道题就可以掉坑里。
+
+接着介绍了[排列问题！](https://mp.weixin.qq.com/s/SCOjeMX1t41wcvJq49GhMw)，以及对[排列问题如何进行去重](https://mp.weixin.qq.com/s/9L8h3WqRP_h8LLWNT34YlA)。
+
+最后我补充了子集问题，排列问题和组合问题的性能分析，给大家提供了回溯算法复杂度的分析思路。
+
+
+