algorithm/leetcode-master
1
0
Fork 0
mirror of https://github.com/youngyangyang04/leetcode-master.git synced 2025-07-07 15:45:40 +08:00
Code Issues Packages Projects Releases Wiki Activity

Merge branch 'youngyangyang04:master' into master

Browse Source
This commit is contained in:
Ryan
2023-06-09 15:55:27 +08:00
committed by GitHub
parent 5b4249d4a8 f83bbd493c
commit 26b5388f93
56 changed files with 2189 additions and 718 deletions
Download Patch File Download Diff File Expand all files Collapse all files

20
README.md
View File

@ -387,10 +387,26 @@
4. [单调栈：42.接雨水](./problems/0042.接雨水.md)
5. [单调栈：84.柱状图中最大的矩形](./problems/0084.柱状图中最大的矩形.md)
（持续更新中....）
## 图论
通知：开始更新图论内容，图论部分还没有其他语言版本，欢迎录友们提交PR，成为contributor
### 深搜广搜
* [图论：深度优先搜索理论基础](./problems/图论深搜理论基础.md)
* [图论：797.所有可能的路径](./problems/0797.所有可能的路径.md)
* [图论：广度优先搜索理论基础](./problems/图论广索理论基础.md)
* [图论：200.岛屿数量.深搜版](./problems/0200.岛屿数量.深搜版.md)
* [图论：200.岛屿数量.广搜版](./problems/0200.岛屿数量.广搜版.md)
* [图论：695.岛屿的最大面积](./problems/0695.岛屿的最大面积.md)
* [图论：1020.飞地的数量](./problems/1020.飞地的数量.md)
* [图论：130.被围绕的区域](./problems/0130.被围绕的区域.md)
* [图论：417.太平洋大西洋水流问题](./problems/0417.太平洋大西洋水流问题.md)
（持续更新中....）
## 十大排序
## 数论
@ -492,7 +508,7 @@
大家好，我是程序员Carl，哈工大师兄，《代码随想录》作者，先后在腾讯和百度从事后端技术研发，CSDN博客专家。对算法和C++后端技术有一定的见解，利用工作之余重新刷leetcode。
加入「代码随想录」刷题小分队（微信群），可以扫下方二维码加我微信。
加入「代码随想录」刷题小分队（微信群），可以扫下方二维码，加代码随想录客服微信。
如果是已工作，备注：姓名-城市-岗位-组队刷题。如果学生，备注：姓名-学校-年级-组队刷题。**备注没有自我介绍不通过哦**

22
problems/0019.删除链表的倒数第N个节点.md
View File

@ -412,6 +412,28 @@ struct ListNode* removeNthFromEnd(struct ListNode* head, int n) {
```
C#：
```csharp
public class Solution {
public ListNode RemoveNthFromEnd(ListNode head, int n) {
ListNode dummpHead = new ListNode(0);
dummpHead.next = head;
var fastNode = dummpHead;
var slowNode = dummpHead;
while(n-- != 0 && fastNode != null)
{
fastNode = fastNode.next;
}
while(fastNode.next != null)
{
fastNode = fastNode.next;
slowNode = slowNode.next;
}
slowNode.next = slowNode.next.next;
return dummpHead.next;
}
}
```
<p align="center">
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>

109
problems/0045.跳跃游戏II.md
View File

@ -205,66 +205,81 @@ class Solution {
```
### Python
贪心（版本一）
```python
class Solution:
def jump(self, nums: List[int]) -> int:
if len(nums) == 1: return 0
ans = 0
curDistance = 0
nextDistance = 0
for i in range(len(nums)):
nextDistance = max(i + nums[i], nextDistance)
if i == curDistance:
if curDistance != len(nums) - 1:
ans += 1
curDistance = nextDistance
if nextDistance >= len(nums) - 1: break
return ans
```
```python
# 贪心版本二
class Solution:
def jump(self, nums: List[int]) -> int:
def jump(self, nums):
if len(nums) == 1:
return 0
curDistance, nextDistance = 0, 0
step = 0
for i in range(len(nums)-1):
nextDistance = max(nextDistance, nums[i]+i)
if i == curDistance:
curDistance = nextDistance
step += 1
return step
cur_distance = 0 # 当前覆盖最远距离下标
ans = 0 # 记录走的最大步数
next_distance = 0 # 下一步覆盖最远距离下标
for i in range(len(nums)):
next_distance = max(nums[i] + i, next_distance) # 更新下一步覆盖最远距离下标
if i == cur_distance: # 遇到当前覆盖最远距离下标
ans += 1 # 需要走下一步
cur_distance = next_distance # 更新当前覆盖最远距离下标（相当于加油了）
if next_distance >= len(nums) - 1: # 当前覆盖最远距离达到数组末尾，不用再做ans++操作，直接结束
break
return ans
```
贪心（版本二）
```python
class Solution:
def jump(self, nums):
cur_distance = 0 # 当前覆盖的最远距离下标
ans = 0 # 记录走的最大步数
next_distance = 0 # 下一步覆盖的最远距离下标
for i in range(len(nums) - 1): # 注意这里是小于len(nums) - 1，这是关键所在
next_distance = max(nums[i] + i, next_distance) # 更新下一步覆盖的最远距离下标
if i == cur_distance: # 遇到当前覆盖的最远距离下标
cur_distance = next_distance # 更新当前覆盖的最远距离下标
ans += 1
return ans
```
贪心（版本三） 类似‘55-跳跃游戏’写法
```python
# 贪心版本三 - 类似‘55-跳跃游戏’写法
class Solution:
def jump(self, nums) -> int:
if len(nums)==1: return 0
i = 0
count = 0
cover = 0
while i<=cover:
for i in range(i,cover+1):
cover = max(nums[i]+i,cover)
if cover>=len(nums)-1: return count+1
count+=1
if len(nums)==1: # 如果数组只有一个元素，不需要跳跃，步数为0
return 0
i = 0 # 当前位置
count = 0 # 步数计数器
cover = 0 # 当前能够覆盖的最远距离
while i <= cover: # 当前位置小于等于当前能够覆盖的最远距离时循环
for i in range(i, cover+1): # 遍历从当前位置到当前能够覆盖的最远距离之间的所有位置
cover = max(nums[i]+i, cover) # 更新当前能够覆盖的最远距离
if cover >= len(nums)-1: # 如果当前能够覆盖的最远距离达到或超过数组的最后一个位置，直接返回步数+1
return count+1
count += 1 # 每一轮遍历结束后，步数+1
```
动态规划
```python
# 动态规划做法
class Solution:
def jump(self, nums: List[int]) -> int:
result = [10**4+1]*len(nums)
result[0]=0
for i in range(len(nums)):
for j in range(nums[i]+1):
if i+j<len(nums): result[i+j]=min(result[i+j],result[i]+1)
#print(result) #打印数组
return result[-1]
result = [10**4+1] * len(nums) # 初始化结果数组，初始值为一个较大的数
result[0] = 0 # 起始位置的步数为0
for i in range(len(nums)): # 遍历数组
for j in range(nums[i] + 1): # 在当前位置能够跳跃的范围内遍历
if i + j < len(nums): # 确保下一跳的位置不超过数组范围
result[i + j] = min(result[i + j], result[i] + 1) # 更新到达下一跳位置的最小步数
return result[-1] # 返回到达最后一个位置的最小步数
```

26
problems/0053.最大子序和.md
View File

@ -198,21 +198,35 @@ class Solution {
```
### Python
暴力法
```python
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
result = -float('inf')
def maxSubArray(self, nums):
result = float('-inf') # 初始化结果为负无穷大
count = 0
for i in range(len(nums)): # 设置起始位置
count = 0
for j in range(i, len(nums)): # 从起始位置i开始遍历寻找最大值
count += nums[j]
result = max(count, result) # 更新最大值
return result
```
```python
class Solution:
def maxSubArray(self, nums):
result = float('-inf') # 初始化结果为负无穷大
count = 0
for i in range(len(nums)):
count += nums[i]
if count > result:
if count > result: # 取区间累计的最大值（相当于不断确定最大子序终止位置）
result = count
if count <= 0:
if count <= 0: # 相当于重置最大子序起始位置，因为遇到负数一定是拉低总和
count = 0
return result
```
```
### Go
```go

11
problems/0053.最大子序和（动态规划）.md
View File

@ -11,9 +11,14 @@
给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。
示例:
输入: [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。
* 输入: [-2,1,-3,4,-1,2,1,-5,4]
* 输出: 6
* 解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。
## 算法公开课
**《代码随想录》算法视频公开课：[看起来复杂，其实是简单动态规划 | LeetCode：53.最大子序和](https://www.bilibili.com/video/BV19V4y1F7b5)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
## 思路

22
problems/0056.合并区间.md
View File

@ -140,18 +140,24 @@ class Solution {
### Python
```python
class Solution:
def merge(self, intervals: List[List[int]]) -> List[List[int]]:
if len(intervals) == 0: return intervals
intervals.sort(key=lambda x: x[0])
def merge(self, intervals):
result = []
result.append(intervals[0])
if len(intervals) == 0:
return result # 区间集合为空直接返回
intervals.sort(key=lambda x: x[0]) # 按照区间的左边界进行排序
result.append(intervals[0]) # 第一个区间可以直接放入结果集中
for i in range(1, len(intervals)):
last = result[-1]
if last[1] >= intervals[i][0]:
result[-1] = [last[0], max(last[1], intervals[i][1])]
if result[-1][1] >= intervals[i][0]: # 发现重叠区间
# 合并区间，只需要更新结果集最后一个区间的右边界，因为根据排序，左边界已经是最小的
result[-1][1] = max(result[-1][1], intervals[i][1])
else:
result.append(intervals[i])
result.append(intervals[i]) # 区间不重叠
return result
```
### Go

65
problems/0062.不同路径.md
View File

@ -287,17 +287,70 @@ public:
```
### Python
递归
```python
class Solution: # 动态规划
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
dp = [[1 for i in range(n)] for j in range(m)]
if m == 1 or n == 1:
return 1
return self.uniquePaths(m - 1, n) + self.uniquePaths(m, n - 1)
```
动态规划（版本一）
```python
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
# 创建一个二维列表用于存储唯一路径数
dp = [[0] * n for _ in range(m)]
# 设置第一行和第一列的基本情况
for i in range(m):
dp[i][0] = 1
for j in range(n):
dp[0][j] = 1
# 计算每个单元格的唯一路径数
for i in range(1, m):
for j in range(1, n):
dp[i][j] = dp[i][j - 1] + dp[i - 1][j]
return dp[m - 1][n - 1]
```
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
# 返回右下角单元格的唯一路径数
return dp[m - 1][n - 1]
```
动态规划（版本二）
```python
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
# 创建一个一维列表用于存储每列的唯一路径数
dp = [1] * n
# 计算每个单元格的唯一路径数
for j in range(1, m):
for i in range(1, n):
dp[i] += dp[i - 1]
# 返回右下角单元格的唯一路径数
return dp[n - 1]
```
数论
```python
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
numerator = 1 # 分子
denominator = m - 1 # 分母
count = m - 1 # 计数器，表示剩余需要计算的乘积项个数
t = m + n - 2 # 初始乘积项
while count > 0:
numerator *= t # 计算乘积项的分子部分
t -= 1 # 递减乘积项
while denominator != 0 and numerator % denominator == 0:
numerator //= denominator # 约简分子
denominator -= 1 # 递减分母
count -= 1 # 计数器减1，继续下一项的计算
return numerator # 返回最终的唯一路径数
```
### Go
```Go

151
problems/0063.不同路径II.md
View File

@ -271,69 +271,130 @@ class Solution {
### Python
动态规划（版本一）
```python
class Solution:
def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
# 构造一个DP table
row = len(obstacleGrid)
col = len(obstacleGrid[0])
dp = [[0 for _ in range(col)] for _ in range(row)]
dp[0][0] = 0 if obstacleGrid[0][0] == 1 else 1
if dp[0][0] == 0:
return 0 # 如果第一个格子就是障碍，return 0
# 第一行
for i in range(1, col):
if obstacleGrid[0][i] == 1:
# 遇到障碍物时，直接退出循环，后面默认都是0
def uniquePathsWithObstacles(self, obstacleGrid):
m = len(obstacleGrid)
n = len(obstacleGrid[0])
if obstacleGrid[m - 1][n - 1] == 1 or obstacleGrid[0][0] == 1:
return 0
dp = [[0] * n for _ in range(m)]
for i in range(m):
if obstacleGrid[i][0] == 0: # 遇到障碍物时，直接退出循环，后面默认都是0
dp[i][0] = 1
else:
break
dp[0][i] = 1
# 第一列
for i in range(1, row):
if obstacleGrid[i][0] == 1:
# 遇到障碍物时，直接退出循环，后面默认都是0
for j in range(n):
if obstacleGrid[0][j] == 0:
dp[0][j] = 1
else:
break
dp[i][0] = 1
# print(dp)
for i in range(1, m):
for j in range(1, n):
if obstacleGrid[i][j] == 1:
continue
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
return dp[m - 1][n - 1]
for i in range(1, row):
for j in range(1, col):
if obstacleGrid[i][j] == 0:
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
return dp[-1][-1]
```
动态规划（版本二）
```python
class Solution:
def uniquePathsWithObstacles(self, obstacleGrid):
m = len(obstacleGrid) # 网格的行数
n = len(obstacleGrid[0]) # 网格的列数
if obstacleGrid[m - 1][n - 1] == 1 or obstacleGrid[0][0] == 1:
# 如果起点或终点有障碍物，直接返回0
return 0
dp = [[0] * n for _ in range(m)] # 创建一个二维列表用于存储路径数
# 设置起点的路径数为1
dp[0][0] = 1 if obstacleGrid[0][0] == 0 else 0
# 计算第一列的路径数
for i in range(1, m):
if obstacleGrid[i][0] == 0:
dp[i][0] = dp[i - 1][0]
# 计算第一行的路径数
for j in range(1, n):
if obstacleGrid[0][j] == 0:
dp[0][j] = dp[0][j - 1]
# 计算其他位置的路径数
for i in range(1, m):
for j in range(1, n):
if obstacleGrid[i][j] == 1:
continue
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
return dp[m - 1][n - 1] # 返回终点的路径数
```
动态规划（版本三）
```python
class Solution:
"""
使用一维dp数组
"""
def uniquePathsWithObstacles(self, obstacleGrid):
if obstacleGrid[0][0] == 1:
return 0
dp = [0] * len(obstacleGrid[0]) # 创建一个一维列表用于存储路径数
# 初始化第一行的路径数
for j in range(len(dp)):
if obstacleGrid[0][j] == 1:
dp[j] = 0
elif j == 0:
dp[j] = 1
else:
dp[j] = dp[j - 1]
# 计算其他行的路径数
for i in range(1, len(obstacleGrid)):
for j in range(len(dp)):
if obstacleGrid[i][j] == 1:
dp[j] = 0
elif j != 0:
dp[j] = dp[j] + dp[j - 1]
return dp[-1] # 返回最后一个元素，即终点的路径数
```
动态规划（版本四）
```python
class Solution:
def uniquePathsWithObstacles(self, obstacleGrid):
if obstacleGrid[0][0] == 1:
return 0
def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
m, n = len(obstacleGrid), len(obstacleGrid[0])
# 初始化dp数组
# 该数组缓存当前行
curr = [0] * n
dp = [0] * n # 创建一个一维列表用于存储路径数
# 初始化第一行的路径数
for j in range(n):
if obstacleGrid[0][j] == 1:
break
curr[j] = 1
dp[j] = 1
for i in range(1, m): # 从第二行开始
for j in range(n): # 从第一列开始，因为第一列可能有障碍物
# 有障碍物处无法通行，状态就设成0
# 计算其他行的路径数
for i in range(1, m):
if obstacleGrid[i][0] == 1:
dp[0] = 0
for j in range(1, n):
if obstacleGrid[i][j] == 1:
curr[j] = 0
elif j > 0:
# 等价于
# dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
curr[j] = curr[j] + curr[j - 1]
# 隐含的状态更新
# dp[i][0] = dp[i - 1][0]
dp[j] = 0
else:
dp[j] += dp[j - 1]
return dp[-1] # 返回最后一个元素，即终点的路径数
return curr[n - 1]
```

64
problems/0070.爬楼梯.md
View File

@ -251,32 +251,66 @@ class Solution {
```
### Python
动态规划（版本一）
```python
# 空间复杂度为O(n)版本
class Solution:
def climbStairs(self, n: int) -> int:
# dp[i] 为第 i 阶楼梯有多少种方法爬到楼顶
dp = [0]*(n+1)
dp[0] = 1
if n <= 1:
return n
dp = [0] * (n + 1)
dp[1] = 1
for i in range(2, n+1):
dp[i] = dp[i-1] + dp[i-2]
dp[2] = 2
for i in range(3, n + 1):
dp[i] = dp[i - 1] + dp[i - 2]
return dp[n]
```
动态规划（版本二）
```python
# 空间复杂度为O(3)版本
class Solution:
def climbStairs(self, n: int) -> int:
if n <= 1:
return n
dp = [0] * 3
dp[1] = 1
dp[2] = 2
for i in range(3, n + 1):
total = dp[1] + dp[2]
dp[1] = dp[2]
dp[2] = total
return dp[2]
```
动态规划（版本三）
```python
# 空间复杂度为O(1)版本
class Solution:
def climbStairs(self, n: int) -> int:
dp = [0]*(n+1)
dp[0] = 1
dp[1] = 1
for i in range(2,n+1):
tmp = dp[0] + dp[1]
dp[0] = dp[1]
dp[1] = tmp
return dp[1]
```
if n <= 1:
return n
prev1 = 1
prev2 = 2
for i in range(3, n + 1):
total = prev1 + prev2
prev1 = prev2
prev2 = total
return prev2
```
### Go
```Go
func climbStairs(n int) int {

19
problems/0070.爬楼梯完全背包版本.md
View File

@ -225,8 +225,25 @@ function climbStairs(n: number): number {
};
```
Rust:
```rust
impl Solution {
pub fn climb_stairs(n: i32) -> i32 {
let (n, m) = (n as usize, 2);
let mut dp = vec![0; n + 1];
dp[0] = 1;
for i in 1..=n {
for j in 1..=m {
if i >= j {
dp[i] += dp[i - j];
}
}
}
dp[n]
}
}
```
<p align="center">
<a href="https://programmercarl.com/other/kstar.html" target="_blank">

13
problems/0096.不同的二叉搜索树.md
View File

@ -197,12 +197,13 @@ class Solution {
```python
class Solution:
def numTrees(self, n: int) -> int:
dp = [0] * (n + 1)
dp[0], dp[1] = 1, 1
for i in range(2, n + 1):
for j in range(1, i + 1):
dp[i] += dp[j - 1] * dp[i - j]
return dp[-1]
dp = [0] * (n + 1) # 创建一个长度为n+1的数组，初始化为0
dp[0] = 1 # 当n为0时，只有一种情况，即空树，所以dp[0] = 1
for i in range(1, n + 1): # 遍历从1到n的每个数字
for j in range(1, i + 1): # 对于每个数字i，计算以i为根节点的二叉搜索树的数量
dp[i] += dp[j - 1] * dp[i - j] # 利用动态规划的思想，累加左子树和右子树的组合数量
return dp[n] # 返回以1到n为节点的二叉搜索树的总数量
```
### Go

5
problems/0115.不同的子序列.md
View File

@ -18,8 +18,9 @@
提示：
0 <= s.length, t.length <= 1000
s 和 t 由英文字母组成
* 0 <= s.length, t.length <= 1000
* s 和 t 由英文字母组成
## 思路

6
problems/0123.买卖股票的最佳时机III.md
View File

@ -242,9 +242,9 @@ class Solution {
for (int i = 1; i < len; i++) {
dp[i][1] = Math.max(dp[i - 1][1], -prices[i]);
dp[i][2] = Math.max(dp[i - 1][2], dp[i][1] + prices[i]);
dp[i][3] = Math.max(dp[i - 1][3], dp[i][2] - prices[i]);
dp[i][4] = Math.max(dp[i - 1][4], dp[i][3] + prices[i]);
dp[i][2] = Math.max(dp[i - 1][2], dp[i - 1][1] + prices[i]);
dp[i][3] = Math.max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
dp[i][4] = Math.max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
}
return dp[len - 1][4];

76
problems/0134.加油站.md
View File

@ -249,44 +249,74 @@ class Solution {
```
### Python
暴力法
```python
# 解法1
class Solution:
def canCompleteCircuit(self, gas: List[int], cost: List[int]) -> int:
n = len(gas)
cur_sum = 0
min_sum = float('inf')
for i in range(len(cost)):
rest = gas[i] - cost[i] # 记录剩余油量
index = (i + 1) % len(cost) # 下一个加油站的索引
for i in range(n):
cur_sum += gas[i] - cost[i]
min_sum = min(min_sum, cur_sum)
while rest > 0 and index != i: # 模拟以i为起点行驶一圈（如果有rest==0，那么答案就不唯一了）
rest += gas[index] - cost[index] # 更新剩余油量
index = (index + 1) % len(cost) # 更新下一个加油站的索引
if cur_sum < 0: return -1
if min_sum >= 0: return 0
if rest >= 0 and index == i: # 如果以i为起点跑一圈，剩余油量>=0，并且回到起始位置
return i # 返回起始位置i
for j in range(n - 1, 0, -1):
min_sum += gas[j] - cost[j]
if min_sum >= 0:
return j
return -1 # 所有起始位置都无法环绕一圈，返回-1
return -1
```
贪心（版本一）
```python
# 解法2
class Solution:
def canCompleteCircuit(self, gas: List[int], cost: List[int]) -> int:
start = 0
curSum = 0
totalSum = 0
curSum = 0 # 当前累计的剩余油量
minFuel = float('inf') # 从起点出发，油箱里的油量最小值
for i in range(len(gas)):
rest = gas[i] - cost[i]
curSum += rest
if curSum < minFuel:
minFuel = curSum
if curSum < 0:
return -1 # 情况1：整个行程的总消耗大于总供给，无法完成一圈
if minFuel >= 0:
return 0 # 情况2：从起点出发到任何一个加油站时油箱的剩余油量都不会小于0，可以从起点出发完成一圈
for i in range(len(gas) - 1, -1, -1):
rest = gas[i] - cost[i]
minFuel += rest
if minFuel >= 0:
return i # 情况3：找到一个位置使得从该位置出发油箱的剩余油量不会小于0，返回该位置的索引
return -1 # 无法完成一圈
```
贪心（版本二）
```python
class Solution:
def canCompleteCircuit(self, gas: List[int], cost: List[int]) -> int:
curSum = 0 # 当前累计的剩余油量
totalSum = 0 # 总剩余油量
start = 0 # 起始位置
for i in range(len(gas)):
curSum += gas[i] - cost[i]
totalSum += gas[i] - cost[i]
if curSum < 0:
curSum = 0
start = i + 1
if totalSum < 0: return -1
if curSum < 0: # 当前累计剩余油量curSum小于0
start = i + 1 # 起始位置更新为i+1
curSum = 0 # curSum重新从0开始累计
if totalSum < 0:
return -1 # 总剩余油量totalSum小于0，说明无法环绕一圈
return start
```
### Go

16
problems/0135.分发糖果.md
View File

@ -178,13 +178,21 @@ class Solution {
class Solution:
def candy(self, ratings: List[int]) -> int:
candyVec = [1] * len(ratings)
# 从前向后遍历，处理右侧比左侧评分高的情况
for i in range(1, len(ratings)):
if ratings[i] > ratings[i - 1]:
candyVec[i] = candyVec[i - 1] + 1
for j in range(len(ratings) - 2, -1, -1):
if ratings[j] > ratings[j + 1]:
candyVec[j] = max(candyVec[j], candyVec[j + 1] + 1)
return sum(candyVec)
# 从后向前遍历，处理左侧比右侧评分高的情况
for i in range(len(ratings) - 2, -1, -1):
if ratings[i] > ratings[i + 1]:
candyVec[i] = max(candyVec[i], candyVec[i + 1] + 1)
# 统计结果
result = sum(candyVec)
return result
```
### Go

56
problems/0139.单词拆分.md
View File

@ -337,10 +337,53 @@ class Solution {
Python：
回溯
```python
class Solution:
def backtracking(self, s: str, wordSet: set[str], startIndex: int) -> bool:
# 边界情况：已经遍历到字符串末尾，返回True
if startIndex >= len(s):
return True
# 遍历所有可能的拆分位置
for i in range(startIndex, len(s)):
word = s[startIndex:i + 1] # 截取子串
if word in wordSet and self.backtracking(s, wordSet, i + 1):
# 如果截取的子串在字典中，并且后续部分也可以被拆分成单词，返回True
return True
# 无法进行有效拆分，返回False
return False
def wordBreak(self, s: str, wordDict: List[str]) -> bool:
wordSet = set(wordDict) # 转换为哈希集合，提高查找效率
return self.backtracking(s, wordSet, 0)
```
DP（版本一）
```python
class Solution:
def wordBreak(self, s: str, wordDict: List[str]) -> bool:
wordSet = set(wordDict)
n = len(s)
dp = [False] * (n + 1) # dp[i] 表示字符串的前 i 个字符是否可以被拆分成单词
dp[0] = True # 初始状态，空字符串可以被拆分成单词
for i in range(1, n + 1): # 遍历背包
for j in range(i): # 遍历单词
if dp[j] and s[j:i] in wordSet:
dp[i] = True # 如果 s[0:j] 可以被拆分成单词，并且 s[j:i] 在单词集合中存在，则 s[0:i] 可以被拆分成单词
break
return dp[n]
```
DP（版本二）
```python
class Solution:
def wordBreak(self, s: str, wordDict: List[str]) -> bool:
'''排列'''
dp = [False]*(len(s) + 1)
dp[0] = True
# 遍历背包
@ -351,17 +394,6 @@ class Solution:
dp[j] = dp[j] or (dp[j - len(word)] and word == s[j - len(word):j])
return dp[len(s)]
```
```python
class Solution: # 和视频中写法一致（和最上面C++写法一致）
def wordBreak(self, s: str, wordDict: List[str]) -> bool:
dp = [False]*(len(s)+1)
dp[0]=True
for j in range(1,len(s)+1):
for i in range(j):
word = s[i:j]
if word in wordDict and dp[i]: dp[j]=True
return dp[-1]
```

28
problems/0142.环形链表II.md
View File

@ -437,6 +437,34 @@ object Solution {
}
```
C#:
```CSharp
public class Solution
{
public ListNode DetectCycle(ListNode head)
{
ListNode fast = head;
ListNode slow = head;
while (fast != null && fast.next != null)
{
slow = slow.next;
fast = fast.next.next;
if (fast == slow)
{
fast = head;
while (fast != slow)
{
fast = fast.next;
slow = slow.next;
}
return fast;
}
}
return null;
}
}
```
<p align="center">
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>

98
problems/0198.打家劫舍.md
View File

@ -141,7 +141,36 @@ class Solution {
}
}
// 空间优化 dp数组只存与计算相关的两次数据
// 使用滚动数组思想，优化空间
// 分析本题可以发现，所求结果仅依赖于前两种状态，此时可以使用滚动数组思想将空间复杂度降低为3个空间
class Solution {
public int rob(int[] nums) {
int len = nums.length;
if (len == 0) return 0;
else if (len == 1) return nums[0];
else if (len == 2) return Math.max(nums[0],nums[1]);
int[] result = new int[3]; //存放选择的结果
result[0] = nums[0];
result[1] = Math.max(nums[0],nums[1]);
for(int i=2;i<len;i++){
result[2] = Math.max(result[0]+nums[i],result[1]);
result[0] = result[1];
result[1] = result[2];
}
return result[2];
}
}
// 进一步对滚动数组的空间优化 dp数组只存与计算相关的两次数据
class Solution {
public int rob(int[] nums) {
if (nums.length == 1) {
@ -151,11 +180,11 @@ class Solution {
// 优化空间 dp数组只用2格空间 只记录与当前计算相关的前两个结果
int[] dp = new int[2];
dp[0] = nums[0];
dp[1] = nums[0] > nums[1] ? nums[0] : nums[1];
dp[1] = Math.max(nums[0],nums[1]);
int res = 0;
// 遍历
for (int i = 2; i < nums.length; i++) {
res = (dp[0] + nums[i]) > dp[1] ? (dp[0] + nums[i]) : dp[1];
res = Math.max((dp[0] + nums[i]) , dp[1] );
dp[0] = dp[1];
dp[1] = res;
}
@ -166,30 +195,65 @@ class Solution {
```
Python：
1维DP
```python
class Solution:
def rob(self, nums: List[int]) -> int:
if len(nums) == 0:
if len(nums) == 0: # 如果没有房屋，返回0
return 0
if len(nums) == 1:
if len(nums) == 1: # 如果只有一个房屋，返回其金额
return nums[0]
# 创建一个动态规划数组，用于存储最大金额
dp = [0] * len(nums)
dp[0] = nums[0]
dp[1] = max(nums[0], nums[1])
dp[0] = nums[0] # 将dp的第一个元素设置为第一个房屋的金额
dp[1] = max(nums[0], nums[1]) # 将dp的第二个元素设置为第一二个房屋中的金额较大者
# 遍历剩余的房屋
for i in range(2, len(nums)):
dp[i] = max(dp[i-2]+nums[i], dp[i-1])
return dp[-1]
# 对于每个房屋，选择抢劫当前房屋和抢劫前一个房屋的最大金额
dp[i] = max(dp[i - 2] + nums[i], dp[i - 1])
return dp[-1] # 返回最后一个房屋中可抢劫的最大金额
```
2维DP
```python
class Solution: # 二维dp数组写法
class Solution:
def rob(self, nums: List[int]) -> int:
dp = [[0,0] for _ in range(len(nums))]
dp[0][1] = nums[0]
for i in range(1,len(nums)):
dp[i][0] = max(dp[i-1][1],dp[i-1][0])
dp[i][1] = dp[i-1][0]+nums[i]
print(dp)
return max(dp[-1])
if not nums: # 如果没有房屋，返回0
return 0
n = len(nums)
dp = [[0, 0] for _ in range(n)] # 创建二维动态规划数组，dp[i][0]表示不抢劫第i个房屋的最大金额，dp[i][1]表示抢劫第i个房屋的最大金额
dp[0][1] = nums[0] # 抢劫第一个房屋的最大金额为第一个房屋的金额
for i in range(1, n):
dp[i][0] = max(dp[i-1][0], dp[i-1][1]) # 不抢劫第i个房屋，最大金额为前一个房屋抢劫和不抢劫的最大值
dp[i][1] = dp[i-1][0] + nums[i] # 抢劫第i个房屋，最大金额为前一个房屋不抢劫的最大金额加上当前房屋的金额
return max(dp[n-1][0], dp[n-1][1]) # 返回最后一个房屋中可抢劫的最大金额
```
优化版
```python
class Solution:
def rob(self, nums: List[int]) -> int:
if not nums: # 如果没有房屋，返回0
return 0
prev_max = 0 # 上一个房屋的最大金额
curr_max = 0 # 当前房屋的最大金额
for num in nums:
temp = curr_max # 临时变量保存当前房屋的最大金额
curr_max = max(prev_max + num, curr_max) # 更新当前房屋的最大金额
prev_max = temp # 更新上一个房屋的最大金额
return curr_max # 返回最后一个房屋中可抢劫的最大金额
```
Go：
```Go

35
problems/0203.移除链表元素.md
View File

@ -596,6 +596,41 @@ class Solution {
}
```
C#
```CSharp
/**
* Definition for singly-linked list.
* public class ListNode {
* public int val;
* public ListNode next;
* public ListNode(int val=0, ListNode next=null) {
* this.val = val;
* this.next = next;
* }
* }
*/
public class Solution
{
public ListNode RemoveElements(ListNode head, int val)
{
ListNode dummyHead = new ListNode(0,head);
ListNode temp = dummyHead;
while(temp.next != null)
{
if(temp.next.val == val)
{
temp.next = temp.next.next;
}
else
{
temp = temp.next;
}
}
return dummyHead.next;
}
}
```
<p align="center">
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>

101
problems/0213.打家劫舍II.md
View File

@ -130,41 +130,94 @@ class Solution {
```
Python：
```Python
class Solution:
def rob(self, nums: List[int]) -> int:
#在198入门级的打家劫舍问题上分两种情况考虑
#一是不偷第一间房，二是不偷最后一间房
if len(nums)==1:#题目中提示nums.length>=1,所以不需要考虑len(nums)==0的情况
if len(nums) == 0:
return 0
if len(nums) == 1:
return nums[0]
val1=self.roblist(nums[1:])#不偷第一间房
val2=self.roblist(nums[:-1])#不偷最后一间房
return max(val1,val2)
def roblist(self,nums):
l=len(nums)
dp=[0]*l
dp[0]=nums[0]
for i in range(1,l):
if i==1:
dp[i]=max(dp[i-1],nums[i])
else:
dp[i]=max(dp[i-1],dp[i-2]+nums[i])
return dp[-1]
result1 = self.robRange(nums, 0, len(nums) - 2) # 情况二
result2 = self.robRange(nums, 1, len(nums) - 1) # 情况三
return max(result1, result2)
# 198.打家劫舍的逻辑
def robRange(self, nums: List[int], start: int, end: int) -> int:
if end == start:
return nums[start]
prev_max = nums[start]
curr_max = max(nums[start], nums[start + 1])
for i in range(start + 2, end + 1):
temp = curr_max
curr_max = max(prev_max + nums[i], curr_max)
prev_max = temp
return curr_max
```
2维DP
```python
class Solution: # 二维dp数组写法
class Solution:
def rob(self, nums: List[int]) -> int:
if len(nums)<3: return max(nums)
return max(self.default(nums[:-1]),self.default(nums[1:]))
def default(self,nums):
dp = [[0,0] for _ in range(len(nums))]
if len(nums) < 3:
return max(nums)
# 情况二：不抢劫第一个房屋
result1 = self.robRange(nums[:-1])
# 情况三：不抢劫最后一个房屋
result2 = self.robRange(nums[1:])
return max(result1, result2)
def robRange(self, nums):
dp = [[0, 0] for _ in range(len(nums))]
dp[0][1] = nums[0]
for i in range(1,len(nums)):
dp[i][0] = max(dp[i-1])
dp[i][1] = dp[i-1][0] + nums[i]
for i in range(1, len(nums)):
dp[i][0] = max(dp[i - 1])
dp[i][1] = dp[i - 1][0] + nums[i]
return max(dp[-1])
```
优化版
```python
class Solution:
def rob(self, nums: List[int]) -> int:
if not nums: # 如果没有房屋，返回0
return 0
if len(nums) == 1: # 如果只有一个房屋，返回该房屋的金额
return nums[0]
# 情况二：不抢劫第一个房屋
prev_max = 0 # 上一个房屋的最大金额
curr_max = 0 # 当前房屋的最大金额
for num in nums[1:]:
temp = curr_max # 临时变量保存当前房屋的最大金额
curr_max = max(prev_max + num, curr_max) # 更新当前房屋的最大金额
prev_max = temp # 更新上一个房屋的最大金额
result1 = curr_max
# 情况三：不抢劫最后一个房屋
prev_max = 0 # 上一个房屋的最大金额
curr_max = 0 # 当前房屋的最大金额
for num in nums[:-1]:
temp = curr_max # 临时变量保存当前房屋的最大金额
curr_max = max(prev_max + num, curr_max) # 更新当前房屋的最大金额
prev_max = temp # 更新上一个房屋的最大金额
result2 = curr_max
return max(result1, result2)
```
Go：

2
problems/0225.用队列实现栈.md
View File

@ -367,7 +367,7 @@ class MyStack {
```
优化，使用一个 Queue 实现，但用卡哥的逻辑实现
```
```Java
class MyStack {
Queue<Integer> queue;

69
problems/0279.完全平方数.md
View File

@ -217,36 +217,61 @@ class Solution {
Python：
先遍历物品, 再遍历背包
```python
class Solution:
def numSquares(self, n: int) -> int:
'''版本一，先遍历背包, 再遍历物品'''
# 初始化
nums = [i**2 for i in range(1, n + 1) if i**2 <= n]
dp = [10**4]*(n + 1)
dp = [float('inf')] * (n + 1)
dp[0] = 0
# 遍历背包
for j in range(1, n + 1):
# 遍历物品
for num in nums:
if j >= num:
dp[j] = min(dp[j], dp[j - num] + 1)
for i in range(1, n + 1): # 遍历背包
for j in range(1, int(i ** 0.5) + 1): # 遍历物品
# 更新凑成数字 i 所需的最少完全平方数数量
dp[i] = min(dp[i], dp[i - j * j] + 1)
return dp[n]
def numSquares1(self, n: int) -> int:
'''版本二， 先遍历物品, 再遍历背包'''
# 初始化
nums = [i**2 for i in range(1, n + 1) if i**2 <= n]
dp = [10**4]*(n + 1)
dp[0] = 0
# 遍历物品
for num in nums:
# 遍历背包
for j in range(num, n + 1):
dp[j] = min(dp[j], dp[j - num] + 1)
return dp[n]
```
先遍历背包, 再遍历物品
```python
class Solution:
def numSquares(self, n: int) -> int:
dp = [float('inf')] * (n + 1)
dp[0] = 0
for i in range(1, int(n ** 0.5) + 1): # 遍历物品
for j in range(i * i, n + 1): # 遍历背包
# 更新凑成数字 j 所需的最少完全平方数数量
dp[j] = min(dp[j - i * i] + 1, dp[j])
return dp[n]
```
其他版本
```python
class Solution:
def numSquares(self, n: int) -> int:
# 创建动态规划数组，初始值为最大值
dp = [float('inf')] * (n + 1)
# 初始化已知情况
dp[0] = 0
# 遍历背包容量
for i in range(1, n + 1):
# 遍历完全平方数作为物品
j = 1
while j * j <= i:
# 更新最少完全平方数的数量
dp[i] = min(dp[i], dp[i - j * j] + 1)
j += 1
# 返回结果
return dp[n]
```
Go：
```go
// 版本一,先遍历物品, 再遍历背包

5
problems/0300.最长上升子序列.md
View File

@ -31,6 +31,11 @@
* 1 <= nums.length <= 2500
* -10^4 <= nums[i] <= 104
## 算法公开课
**《代码随想录》算法视频公开课：[动态规划之子序列问题，元素不连续！| LeetCode：300.最长递增子序列](https://www.bilibili.com/video/BV1ng411J7xP)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
## 思路
首先通过本题大家要明确什么是子序列，“子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序”。

84
problems/0322.零钱兑换.md
View File

@ -217,36 +217,76 @@ class Solution {
Python：
先遍历物品 后遍历背包
```python
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
'''版本一'''
# 初始化
dp = [float("inf")]*(amount + 1)
dp[0] = 0
# 遍历物品
for coin in coins:
# 遍历背包
for j in range(coin, amount + 1):
dp[j] = min(dp[j], dp[j - coin] + 1)
return dp[amount] if dp[amount] != float("inf") else -1
dp = [float('inf')] * (amount + 1) # 创建动态规划数组，初始值为正无穷大
dp[0] = 0 # 初始化背包容量为0时的最小硬币数量为0
for coin in coins: # 遍历硬币列表，相当于遍历物品
for i in range(coin, amount + 1): # 遍历背包容量
if dp[i - coin] != float('inf'): # 如果dp[i - coin]不是初始值，则进行状态转移
dp[i] = min(dp[i - coin] + 1, dp[i]) # 更新最小硬币数量
if dp[amount] == float('inf'): # 如果最终背包容量的最小硬币数量仍为正无穷大，表示无解
return -1
return dp[amount] # 返回背包容量为amount时的最小硬币数量
def coinChange1(self, coins: List[int], amount: int) -> int:
'''版本二'''
# 初始化
dp = [float("inf")]*(amount + 1)
dp[0] = 0
# 遍历物品
for j in range(1, amount + 1):
# 遍历背包
for coin in coins:
if j >= coin:
dp[j] = min(dp[j], dp[j - coin] + 1)
return dp[amount] if dp[amount] != float("inf") else -1
```
先遍历背包 后遍历物品
```python
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
dp = [float('inf')] * (amount + 1) # 创建动态规划数组，初始值为正无穷大
dp[0] = 0 # 初始化背包容量为0时的最小硬币数量为0
for i in range(1, amount + 1): # 遍历背包容量
for j in range(len(coins)): # 遍历硬币列表，相当于遍历物品
if i - coins[j] >= 0 and dp[i - coins[j]] != float('inf'): # 如果dp[i - coins[j]]不是初始值，则进行状态转移
dp[i] = min(dp[i - coins[j]] + 1, dp[i]) # 更新最小硬币数量
if dp[amount] == float('inf'): # 如果最终背包容量的最小硬币数量仍为正无穷大，表示无解
return -1
return dp[amount] # 返回背包容量为amount时的最小硬币数量
```
先遍历物品 后遍历背包（优化版）
```python
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
dp = [float('inf')] * (amount + 1)
dp[0] = 0
for coin in coins:
for i in range(coin, amount + 1): # 进行优化，从能装得下的背包开始计算，则不需要进行比较
# 更新凑成金额 i 所需的最少硬币数量
dp[i] = min(dp[i], dp[i - coin] + 1)
return dp[amount] if dp[amount] != float('inf') else -1
```
先遍历背包 后遍历物品（优化版）
```python
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
dp = [float('inf')] * (amount + 1)
dp[0] = 0
for i in range(1, amount + 1): # 遍历背包容量
for coin in coins: # 遍历物品
if i - coin >= 0:
# 更新凑成金额 i 所需的最少硬币数量
dp[i] = min(dp[i], dp[i - coin] + 1)
return dp[amount] if dp[amount] != float('inf') else -1
```
Go：
```go

70
problems/0343.整数拆分.md
View File

@ -245,20 +245,68 @@ class Solution {
```
### Python
动态规划（版本一）
```python
class Solution:
def integerBreak(self, n: int) -> int:
dp = [0] * (n + 1)
dp[2] = 1
for i in range(3, n + 1):
# 假设对正整数 i 拆分出的第一个正整数是 j（1 <= j < i），则有以下两种方案：
# 1) 将 i 拆分成 j 和 i−j 的和，且 i−j 不再拆分成多个正整数，此时的乘积是 j * (i-j)
# 2) 将 i 拆分成 j 和 i−j 的和，且 i−j 继续拆分成多个正整数，此时的乘积是 j * dp[i-j]
for j in range(1, i // 2 + 1):
dp[i] = max(dp[i], max(j * (i - j), j * dp[i - j]))
return dp[n]
```
# 假设对正整数 i 拆分出的第一个正整数是 j（1 <= j < i），则有以下两种方案：
# 1) 将 i 拆分成 j 和 i−j 的和，且 i−j 不再拆分成多个正整数，此时的乘积是 j * (i-j)
# 2) 将 i 拆分成 j 和 i−j 的和，且 i−j 继续拆分成多个正整数，此时的乘积是 j * dp[i-j]
def integerBreak(self, n):
dp = [0] * (n + 1) # 创建一个大小为n+1的数组来存储计算结果
dp[2] = 1 # 初始化dp[2]为1，因为当n=2时，只有一个切割方式1+1=2，乘积为1
# 从3开始计算，直到n
for i in range(3, n + 1):
# 遍历所有可能的切割点
for j in range(1, i // 2 + 1):
# 计算切割点j和剩余部分(i-j)的乘积，并与之前的结果进行比较取较大值
dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j))
return dp[n] # 返回最终的计算结果
```
动态规划（版本二）
```python
class Solution:
def integerBreak(self, n):
if n <= 3:
return 1 * (n - 1) # 对于n小于等于3的情况，返回1 * (n - 1)
dp = [0] * (n + 1) # 创建一个大小为n+1的数组来存储最大乘积结果
dp[1] = 1 # 当n等于1时，最大乘积为1
dp[2] = 2 # 当n等于2时，最大乘积为2
dp[3] = 3 # 当n等于3时，最大乘积为3
# 从4开始计算，直到n
for i in range(4, n + 1):
# 遍历所有可能的切割点
for j in range(1, i // 2 + 1):
# 计算切割点j和剩余部分(i - j)的乘积，并与之前的结果进行比较取较大值
dp[i] = max(dp[i], dp[i - j] * dp[j])
return dp[n] # 返回整数拆分的最大乘积结果
```
贪心
```python
class Solution:
def integerBreak(self, n):
if n == 2: # 当n等于2时，只有一种拆分方式：1+1=2，乘积为1
return 1
if n == 3: # 当n等于3时，只有一种拆分方式：1+1+1=3，乘积为1
return 2
if n == 4: # 当n等于4时，有两种拆分方式：2+2=4和1+1+1+1=4，乘积都为4
return 4
result = 1
while n > 4:
result *= 3 # 每次乘以3，因为3的乘积比其他数字更大
n -= 3 # 每次减去3
result *= n # 将剩余的n乘以最后的结果
return result
```
### Go
```go
func integerBreak(n int) int {

43
problems/0377.组合总和Ⅳ.md
View File

@ -176,21 +176,37 @@ class Solution {
Python：
卡哥版
```python
class Solution:
def combinationSum4(self, nums, target):
def combinationSum4(self, nums: List[int], target: int) -> int:
dp = [0] * (target + 1)
dp[0] = 1
for i in range(1, target + 1): # 遍历背包
for j in range(len(nums)): # 遍历物品
if i - nums[j] >= 0:
dp[i] += dp[i - nums[j]]
return dp[target]
for i in range(1, target+1):
for j in nums:
if i >= j:
dp[i] += dp[i - j]
return dp[-1]
```
优化版
```python
class Solution:
def combinationSum4(self, nums: List[int], target: int) -> int:
dp = [0] * (target + 1) # 创建动态规划数组，用于存储组合总数
dp[0] = 1 # 初始化背包容量为0时的组合总数为1
for i in range(1, target + 1): # 遍历背包容量
for j in nums: # 遍历物品列表
if i >= j: # 当背包容量大于等于当前物品重量时
dp[i] += dp[i - j] # 更新组合总数
return dp[-1] # 返回背包容量为target时的组合总数
```
Go：
```go
func combinationSum4(nums []int, target int) int {
@ -253,16 +269,17 @@ Rust
```Rust
impl Solution {
pub fn combination_sum4(nums: Vec<i32>, target: i32) -> i32 {
let mut dp = vec![0; target as usize + 1];
let target = target as usize;
let mut dp = vec![0; target + 1];
dp[0] = 1;
for i in 1..=target as usize {
for &j in nums.iter() {
if i as i32 >= j {
dp[i] += dp[i- j as usize];
for i in 1..=target {
for &n in &nums {
if i >= n as usize {
dp[i] += dp[i - n as usize];
}
}
}
return dp[target as usize];
dp[target]
}
}
```

12
problems/0392.判断子序列.md
View File

@ -14,12 +14,12 @@
字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）。
示例 1：
输入：s = "abc", t = "ahbgdc"
输出：true
* 输入：s = "abc", t = "ahbgdc"
* 输出：true
示例 2：
输入：s = "axc", t = "ahbgdc"
输出：false
* 输入：s = "axc", t = "ahbgdc"
* 输出：false
提示：
@ -28,6 +28,10 @@
两个字符串都只由小写字符组成。
# 算法公开课
**《代码随想录》算法视频公开课：[动态规划，用相似思路解决复杂问题 | LeetCode：392.判断子序列](https://www.bilibili.com/video/BV1tv4y1B7ym/)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
## 思路

6
problems/0406.根据身高重建队列.md
View File

@ -191,14 +191,14 @@ class Solution {
public int[][] reconstructQueue(int[][] people) {
// 身高从大到小排（身高相同k小的站前面）
Arrays.sort(people, (a, b) -> {
if (a[0] == b[0]) return a[1] - b[1];
return b[0] - a[0];
if (a[0] == b[0]) return a[1] - b[1]; // a - b 是升序排列，故在a[0] == b[0]的狀況下，會根據k值升序排列
return b[0] - a[0]; //b - a 是降序排列，在a[0] != b[0]，的狀況會根據h值降序排列
});
LinkedList<int[]> que = new LinkedList<>();
for (int[] p : people) {
que.add(p[1],p);
que.add(p[1],p); //Linkedlist.add(index, value)，會將value插入到指定index裡。
}
return que.toArray(new int[people.length][]);

172
problems/0416.分割等和子集.md
View File

@ -218,8 +218,12 @@ class Solution {
for(int i = 0; i < n; i++) {
for(int j = target; j >= nums[i]; j--) {
//物品 i 的重量是 nums[i]，其价值也是 nums[i]
dp[j] = Math.max(dp[j], dp[j-nums[i]] + nums[i]);
dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);
}
//剪枝一下，每一次完成內層的for-loop，立即檢查是否dp[target] == target，優化時間複雜度（26ms -> 20ms）
if(dp[target] == target)
return true;
}
return dp[target] == target;
}
@ -294,64 +298,142 @@ false true false false false true true false false false false false
false true false false false true true false false false false true
false true false false false true true false false false true true
```
二維數組整數版本
```Java
class Solution {
public boolean canPartition(int[] nums) {
//using 2-D DP array.
int len = nums.length;
//check edge cases;
if(len == 0)
return false;
### Python：
```python
# 一维度数组解法
class Solution:
def canPartition(self, nums: List[int]) -> bool:
target = sum(nums)
if target % 2 == 1: return False
target //= 2
dp = [0] * (target + 1)
for i in range(len(nums)):
for j in range(target, nums[i] - 1, -1):
dp[j] = max(dp[j], dp[j - nums[i]] + nums[i])
return target == dp[target]
int sum = 0;
for (int num : nums)
sum += num;
//we only deal with even numbers. If sum is odd, return false;
if(sum % 2 == 1)
return false;
int target = sum / 2;
int[][] dp = new int[nums.length][target + 1];
// for(int j = 0; j <= target; j++){
// if(j < nums[0])
// dp[0][j] = 0;
// else
// dp[0][j] = nums[0];
// }
//initialize dp array
for(int j = nums[0]; j <= target; j++){
dp[0][j] = nums[0];
}
for(int i = 1; i < len; i++){
for(int j = 0; j <= target; j++){
if (j < nums[i])
dp[i][j] = dp[i - 1][j];
else
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - nums[i]] + nums[i]);
}
}
//print out DP array
// for(int x : dp){
// System.out.print(x + ",");
// }
// System.out.print(" "+i+" row"+"\n");
return dp[len - 1][target] == target;
}
}
//dp数组的打印结果 for test case 1.
0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
0, 1, 1, 1, 1, 5, 6, 6, 6, 6, 6, 6,
0, 1, 1, 1, 1, 5, 6, 6, 6, 6, 6, 11,
0, 1, 1, 1, 1, 5, 6, 6, 6, 6, 10, 11,
```
### Python：
卡哥版
```python
# 二维度数组解法
class Solution:
def canPartition(self, nums: List[int]) -> bool:
target = sum(nums)
nums = sorted(nums)
_sum = 0
# 做最初的判断
if target % 2 != 0:
# dp[i]中的i表示背包内总和
# 题目中说：每个数组中的元素不会超过 100，数组的大小不会超过 200
# 总和不会大于20000，背包最大只需要其中一半，所以10001大小就可以了
dp = [0] * 10001
for num in nums:
_sum += num
# 也可以使用内置函数一步求和
# _sum = sum(nums)
if _sum % 2 == 1:
return False
target = _sum // 2
# 开始 0-1背包
for num in nums:
for j in range(target, num - 1, -1): # 每一个元素一定是不可重复放入，所以从大到小遍历
dp[j] = max(dp[j], dp[j - num] + num)
# 集合中的元素正好可以凑成总和target
if dp[target] == target:
return True
return False
```
二维DP版
```python
class Solution:
def canPartition(self, nums: List[int]) -> bool:
total_sum = sum(nums)
if total_sum % 2 != 0:
return False
# 找到 target value 可以认为这个是背包的体积
target = target // 2
target_sum = total_sum // 2
dp = [[False] * (target_sum + 1) for _ in range(len(nums) + 1)]
row = len(nums)
col = target + 1
# 初始化第一行（空子集可以得到和为0）
for i in range(len(nums) + 1):
dp[i][0] = True
# 定义 dp table
dp = [[0 for _ in range(col)] for _ in range(row)]
# 初始 dp value
for i in range(row):
dp[i][0] = 0
for j in range(1, target):
if nums[0] <= j:
dp[0][j] = nums[0]
# 遍历 先遍历物品再遍历背包
for i in range(1, row):
cur_weight = nums[i]
cur_value = nums[i]
for j in range(1, col):
if cur_weight > j:
for i in range(1, len(nums) + 1):
for j in range(1, target_sum + 1):
if j < nums[i - 1]:
# 当前数字大于目标和时，无法使用该数字
dp[i][j] = dp[i - 1][j]
else:
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - cur_weight] + cur_value)
# 当前数字小于等于目标和时，可以选择使用或不使用该数字
dp[i][j] = dp[i - 1][j] or dp[i - 1][j - nums[i - 1]]
return dp[len(nums)][target_sum]
```
一维DP版
```python
class Solution:
def canPartition(self, nums: List[int]) -> bool:
total_sum = sum(nums)
if total_sum % 2 != 0:
return False
target_sum = total_sum // 2
dp = [False] * (target_sum + 1)
dp[0] = True
for num in nums:
# 从target_sum逆序迭代到num，步长为-1
for i in range(target_sum, num - 1, -1):
dp[i] = dp[i] or dp[i - num]
return dp[target_sum]
# 输出结果
return dp[-1][col - 1] == target
```
### Go：

45
problems/0435.无重叠区间.md
View File

@ -248,20 +248,45 @@ class Solution {
```
### Python
贪心 基于左边界
```python
class Solution:
def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
if len(intervals) == 0: return 0
intervals.sort(key=lambda x: x[1])
count = 1 # 记录非交叉区间的个数
end = intervals[0][1] # 记录区间分割点
for i in range(1, len(intervals)):
if end <= intervals[i][0]:
count += 1
end = intervals[i][1]
return len(intervals) - count
```
if not intervals:
return 0
intervals.sort(key=lambda x: x[0]) # 按照左边界升序排序
count = 0 # 记录重叠区间数量
for i in range(1, len(intervals)):
if intervals[i][0] < intervals[i - 1][1]: # 存在重叠区间
intervals[i][1] = min(intervals[i - 1][1], intervals[i][1]) # 更新重叠区间的右边界
count += 1
return count
```
贪心 基于左边界 把452.用最少数量的箭引爆气球代码稍做修改
```python
class Solution:
def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
if not intervals:
return 0
intervals.sort(key=lambda x: x[0]) # 按照左边界升序排序
result = 1 # 不重叠区间数量，初始化为1，因为至少有一个不重叠的区间
for i in range(1, len(intervals)):
if intervals[i][0] >= intervals[i - 1][1]: # 没有重叠
result += 1
else: # 重叠情况
intervals[i][1] = min(intervals[i - 1][1], intervals[i][1]) # 更新重叠区间的右边界
return len(intervals) - result
```
### Go
```go
func eraseOverlapIntervals(intervals [][]int) int {

55
problems/0474.一和零.md
View File

@ -210,19 +210,35 @@ class Solution {
```
### Python
DP（版本一）
```python
class Solution:
def findMaxForm(self, strs: List[str], m: int, n: int) -> int:
dp = [[0] * (n + 1) for _ in range(m + 1)] # 默认初始化0
dp = [[0] * (n + 1) for _ in range(m + 1)] # 创建二维动态规划数组，初始化为0
for s in strs: # 遍历物品
zeroNum = s.count('0') # 统计0的个数
oneNum = len(s) - zeroNum # 统计1的个数
for i in range(m, zeroNum - 1, -1): # 遍历背包容量且从后向前遍历
for j in range(n, oneNum - 1, -1):
dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1) # 状态转移方程
return dp[m][n]
```
DP（版本二）
```python
class Solution:
def findMaxForm(self, strs: List[str], m: int, n: int) -> int:
dp = [[0] * (n + 1) for _ in range(m + 1)] # 创建二维动态规划数组，初始化为0
# 遍历物品
for str in strs:
ones = str.count('1')
zeros = str.count('0')
# 遍历背包容量且从后向前遍历！
for s in strs:
ones = s.count('1') # 统计字符串中1的个数
zeros = s.count('0') # 统计字符串中0的个数
# 遍历背包容量且从后向前遍历
for i in range(m, zeros - 1, -1):
for j in range(n, ones - 1, -1):
dp[i][j] = max(dp[i][j], dp[i - zeros][j - ones] + 1)
dp[i][j] = max(dp[i][j], dp[i - zeros][j - ones] + 1) # 状态转移方程
return dp[m][n]
```
### Go
@ -491,6 +507,33 @@ object Solution {
}
```
### Rust
```rust
impl Solution {
pub fn find_max_form(strs: Vec<String>, m: i32, n: i32) -> i32 {
let (m, n) = (m as usize, n as usize);
let mut dp = vec![vec![0; n + 1]; m + 1];
for s in strs {
let (mut one_num, mut zero_num) = (0, 0);
for c in s.chars() {
match c {
'0' => zero_num += 1,
'1' => one_num += 1,
_ => (),
}
}
for i in (zero_num..=m).rev() {
for j in (one_num..=n).rev() {
dp[i][j] = dp[i][j].max(dp[i - zero_num][j - one_num] + 1);
}
}
}
dp[m][n]
}
}
```
<p align="center">
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>

24
problems/0491.递增子序列.md
View File

@ -205,6 +205,30 @@ public:
### Java
```Java
//using set, aligned with the unimproved method
class Solution {
List<List<Integer>> result = new ArrayList<>();
List<Integer> path = new ArrayList<>();
public List<List<Integer>> findSubsequences(int[] nums) {
backTracking(nums, 0);
return result;
}
private void backTracking(int[] nums, int startIndex){
if(path.size() >= 2)
result.add(new ArrayList<>(path));
HashSet<Integer> hs = new HashSet<>();
for(int i = startIndex; i < nums.length; i++){
if(!path.isEmpty() && path.get(path.size() -1 ) > nums[i] || hs.contains(nums[i]))
continue;
hs.add(nums[i]);
path.add(nums[i]);
backTracking(nums, i + 1);
path.remove(path.size() - 1);
}
}
}
```
```java
class Solution {

110
problems/0494.目标和.md
View File

@ -293,19 +293,84 @@ class Solution {
```
### Python
回溯版
```python
class Solution:
def backtracking(self, candidates, target, total, startIndex, path, result):
if total == target:
result.append(path[:]) # 将当前路径的副本添加到结果中
# 如果 sum + candidates[i] > target，则停止遍历
for i in range(startIndex, len(candidates)):
if total + candidates[i] > target:
break
total += candidates[i]
path.append(candidates[i])
self.backtracking(candidates, target, total, i + 1, path, result)
total -= candidates[i]
path.pop()
def findTargetSumWays(self, nums: List[int], target: int) -> int:
total = sum(nums)
if target > total:
return 0 # 此时没有方案
if (target + total) % 2 != 0:
return 0 # 此时没有方案，两个整数相加时要注意数值溢出的问题
bagSize = (target + total) // 2 # 转化为组合总和问题，bagSize就是目标和
# 以下是回溯法代码
result = []
nums.sort() # 需要对nums进行排序
self.backtracking(nums, bagSize, 0, 0, [], result)
return len(result)
```
二维DP
```python
class Solution:
def findTargetSumWays(self, nums: List[int], target: int) -> int:
sumValue = sum(nums)
#注意边界条件为 target>sumValue or target<-sumValue or (sumValue + target) % 2 == 1
if abs(target) > sumValue or (sumValue + target) % 2 == 1: return 0
bagSize = (sumValue + target) // 2
dp = [0] * (bagSize + 1)
dp[0] = 1
for i in range(len(nums)):
for j in range(bagSize, nums[i] - 1, -1):
dp[j] += dp[j - nums[i]]
return dp[bagSize]
total_sum = sum(nums) # 计算nums的总和
if abs(target) > total_sum:
return 0 # 此时没有方案
if (target + total_sum) % 2 == 1:
return 0 # 此时没有方案
target_sum = (target + total_sum) // 2 # 目标和
# 创建二维动态规划数组，行表示选取的元素数量，列表示累加和
dp = [[0] * (target_sum + 1) for _ in range(len(nums) + 1)]
# 初始化状态
dp[0][0] = 1
# 动态规划过程
for i in range(1, len(nums) + 1):
for j in range(target_sum + 1):
dp[i][j] = dp[i - 1][j] # 不选取当前元素
if j >= nums[i - 1]:
dp[i][j] += dp[i - 1][j - nums[i - 1]] # 选取当前元素
return dp[len(nums)][target_sum] # 返回达到目标和的方案数
```
一维DP
```python
class Solution:
def findTargetSumWays(self, nums: List[int], target: int) -> int:
total_sum = sum(nums) # 计算nums的总和
if abs(target) > total_sum:
return 0 # 此时没有方案
if (target + total_sum) % 2 == 1:
return 0 # 此时没有方案
target_sum = (target + total_sum) // 2 # 目标和
dp = [0] * (target_sum + 1) # 创建动态规划数组，初始化为0
dp[0] = 1 # 当目标和为0时，只有一种方案，即什么都不选
for num in nums:
for j in range(target_sum, num - 1, -1):
dp[j] += dp[j - num] # 状态转移方程，累加不同选择方式的数量
return dp[target_sum] # 返回达到目标和的方案数
```
### Go
@ -417,6 +482,31 @@ object Solution {
}
```
### Rust
```rust
impl Solution {
pub fn find_target_sum_ways(nums: Vec<i32>, target: i32) -> i32 {
let sum = nums.iter().sum::<i32>();
if target.abs() > sum {
return 0;
}
if (target + sum) % 2 == 1 {
return 0;
}
let size = (sum + target) as usize / 2;
let mut dp = vec![0; size + 1];
dp[0] = 1;
for n in nums {
for s in (n as usize..=size).rev() {
dp[s] += dp[s - n as usize];
}
}
dp[size]
}
}
```
<p align="center">
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>

54
problems/0509.斐波那契数.md
View File

@ -203,18 +203,9 @@ class Solution {
```
### Python
动态规划（版本一）
```python
class Solution:
def fib(self, n: int) -> int:
if n < 2:
return n
a, b, c = 0, 1, 0
for i in range(1, n):
c = a + b
a, b = b, c
return c
# 动态规划 (注释版。无修饰)
class Solution:
def fib(self, n: int) -> int:
@ -238,7 +229,48 @@ class Solution:
# 返回答案
return dp[n]
# 递归实现
```
动态规划（版本二）
```python
class Solution:
def fib(self, n: int) -> int:
if n <= 1:
return n
dp = [0, 1]
for i in range(2, n + 1):
total = dp[0] + dp[1]
dp[0] = dp[1]
dp[1] = total
return dp[1]
```
动态规划（版本三）
```python
class Solution:
def fib(self, n: int) -> int:
if n <= 1:
return n
prev1, prev2 = 0, 1
for _ in range(2, n + 1):
curr = prev1 + prev2
prev1, prev2 = prev2, curr
return prev2
```
递归（版本一）
```python
class Solution:
def fib(self, n: int) -> int:
if n < 2:

19
problems/0518.零钱兑换II.md
View File

@ -282,17 +282,18 @@ func change(amount int, coins []int) int {
Rust:
```rust
pub fn change(amount: i32, coins: Vec<i32>) -> i32 {
let amount = amount as usize;
let coins = coins.iter().map(|&c|c as usize).collect::<Vec<usize>>();
let mut dp = vec![0usize; amount + 1];
dp[0] = 1;
for i in 0..coins.len() {
for j in coins[i]..=amount {
dp[j] += dp[j - coins[i]];
impl Solution {
pub fn change(amount: i32, coins: Vec<i32>) -> i32 {
let amount = amount as usize;
let mut dp = vec![0; amount + 1];
dp[0] = 1;
for coin in coins {
for j in coin as usize..=amount {
dp[j] += dp[j - coin as usize];
}
}
dp[amount]
}
dp[amount] as i32
}
```

4
problems/0674.最长连续递增序列.md
View File

@ -27,6 +27,10 @@
* 0 <= nums.length <= 10^4
* -10^9 <= nums[i] <= 10^9
## 算法公开课
**《代码随想录》算法视频公开课：[动态规划之子序列问题，重点在于连续！| LeetCode：674.最长连续递增序列](https://www.bilibili.com/video/BV1bD4y1778v)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
## 思路

70
problems/0684.冗余连接.md
View File

@ -39,8 +39,8 @@
这里整理出我的并查集模板如下：
```CPP
int n = 1005; // 节点数量3 到 1000
int father[1005];
int n = 1005; // n根据题目中节点数量而定，一般比节点数量大一点就好
vector<int> father = vector<int> (n, 0); // C++里的一种数组结构
// 并查集初始化
void init() {
@ -50,40 +50,58 @@ void init() {
}
// 并查集里寻根的过程
int find(int u) {
return u == father[u] ? u : father[u] = find(father[u]);
}
// 将v->u 这条边加入并查集
void join(int u, int v) {
u = find(u);
v = find(v);
if (u == v) return ;
father[v] = u;
return u == father[u] ? u : father[u] = find(father[u]); // 路径压缩
}
// 判断 u 和 v是否找到同一个根
bool same(int u, int v) {
bool isSame(int u, int v) {
u = find(u);
v = find(v);
return u == v;
}
// 将v->u 这条边加入并查集
void join(int u, int v) {
u = find(u); // 寻找u的根
v = find(v); // 寻找v的根
if (u == v) return ; // 如果发现根相同，则说明在一个集合，不用两个节点相连直接返回
father[v] = u;
}
```
以上模板汇总，只要修改 n 和father数组的大小就可以了。
以上模板 只要修改 n 就可以了，本题 节点数量不会超过1000。
并查集主要有三个功能。
1. 寻找根节点，函数：find(int u)，也就是判断这个节点的祖先节点是哪个
2. 将两个节点接入到同一个集合，函数：join(int u, int v)，将两个节点连在同一个根节点上
3. 判断两个节点是否在同一个集合，函数：same(int u, int v)，就是判断两个节点是不是同一个根节点
3. 判断两个节点是否在同一个集合，函数：isSame(int u, int v)，就是判断两个节点是不是同一个根节点
简单介绍并查集之后，我们再来看一下这道题目。
题目说是无向图，返回一条可以删去的边，使得结果图是一个有着N个节点的树。
题目说是无向图，返回一条可以删去的边，使得结果图是一个有着N个节点的树（即：只有一个根节点）。
如果有多个答案，则返回二维数组中最后出现的边。
那么我们就可以从前向后遍历每一条边，边的两个节点如果不在同一个集合，就加入集合（即：同一个根节点）。
那么我们就可以从前向后遍历每一条边（因为优先让前面的边连上），边的两个节点如果不在同一个集合，就加入集合（即：同一个根节点）。
如果边的两个节点已经出现在同一个集合里，说明着边的两个节点已经连在一起了，如果再加入这条边一定就出现环了。
如图所示：
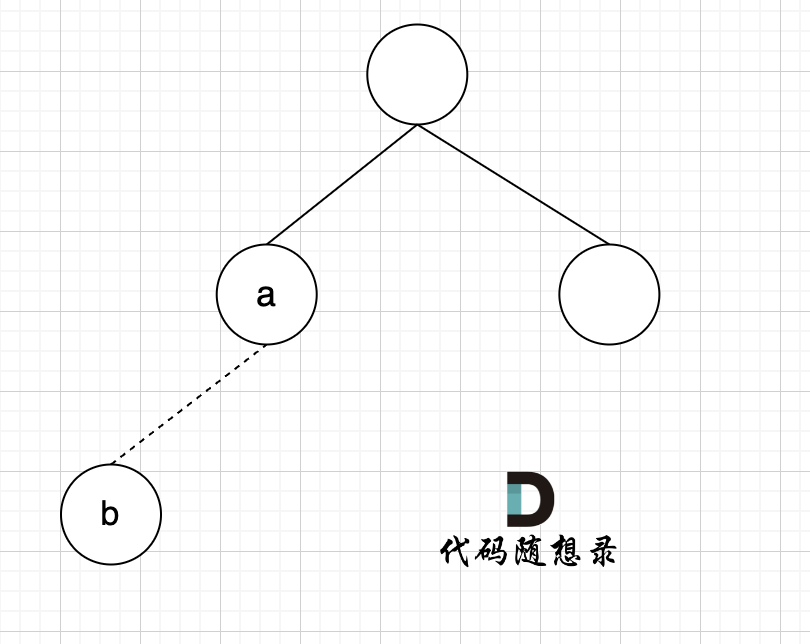
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20230604104720.png)
节点A 和节点 B 不在同一个集合，那么就可以将两个 节点连在一起。
（如果题目中说：如果有多个答案，则返回二维数组中最前出现的边。 那我们就要 从后向前遍历每一条边了）
如果边的两个节点已经出现在同一个集合里，说明着边的两个节点已经连在一起了，再加入这条边一定就出现环了。
如图所示：
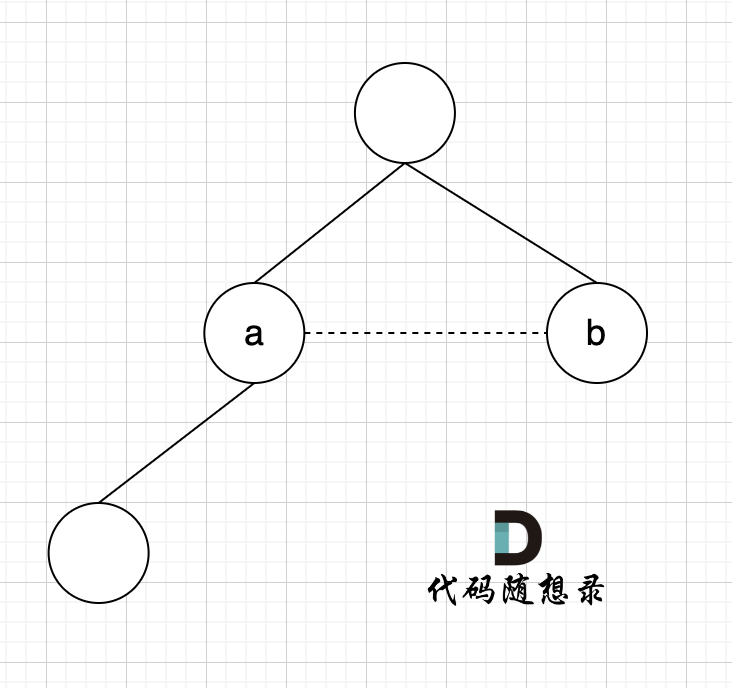
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20230604104330.png)
已经判断 节点A 和 节点B 在在同一个集合（同一个根），如果将 节点A 和 节点B 连在一起就一定会出现环。
这个思路清晰之后，代码就很好写了。
@ -93,7 +111,7 @@ bool same(int u, int v) {
class Solution {
private:
int n = 1005; // 节点数量3 到 1000
int father[1005];
vector<int> father = vector<int> (n, 0); // C++里的一种数组结构
// 并查集初始化
void init() {
@ -105,24 +123,22 @@ private:
int find(int u) {
return u == father[u] ? u : father[u] = find(father[u]);
}
// 将v->u 这条边加入并查集
void join(int u, int v) {
u = find(u);
v = find(v);
if (u == v) return ;
father[v] = u;
}
// 判断 u 和 v是否找到同一个根，本题用不上
bool same(int u, int v) {
// 判断 u 和 v是否找到同一个根
bool isSame(int u, int v) {
u = find(u);
v = find(v);
return u == v;
}
// 将v->u 这条边加入并查集
void join(int u, int v) {
if (isSame(u, v)) return ;
father[v] = u;
}
public:
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
init();
for (int i = 0; i < edges.size(); i++) {
if (same(edges[i][0], edges[i][1])) return edges[i];
if (isSame(edges[i][0], edges[i][1])) return edges[i];
else join(edges[i][0], edges[i][1]);
}
return {};

25
problems/0685.冗余连接II.md
View File

@ -44,7 +44,6 @@
且只有一个节点入度为2，为什么不看出度呢，出度没有意义，一棵树中随便一个父节点就有多个出度。
第三种情况是没有入度为2的点，那么图中一定出现了有向环（**注意这里强调是有向环！**）
如图：
@ -52,7 +51,27 @@
<img src='https://code-thinking.cdn.bcebos.com/pics/685.冗余连接II2.png' width=600> </img></div>
首先先计算节点的入度，代码如下：
首先先计算节点的入度，这里不少录友在计算入度的时候就搞蒙了，分不清 edges[i][j] 表示的都是什么。
例如题目示例一给的是：edges = [[1,2],[1,3],[2,3]]
那大家很自然就想 对应二维数组的数值是： edges[1][2] ，edges[1][3]，edges[2][3]，但又想不出来 edges[1][2] 数值又是什么呢？ 越想约懵。
其实 edges = [[1,2],[1,3],[2,3]]，表示的是
edges[0][0] = 1，edges[0][1] = 2，
edges[1][0] = 1，edges[1][1] = 3，
edges[2][0] = 2，edges[2][1] = 3，
二维数组大家都学过，但是往往和图结合在一起的时候，就非常容易搞混，哪里是数组，哪里是下标了。
搞清楚之后，我们如何统计入度呢？
即 edges[i][1] 表示的节点都是 箭头指向的节点，即这个几点有一个入度！ （如果想统计出度，那么就是 edges[i][0]）。
所以，统计入度的代码如下：
```cpp
int inDegree[N] = {0}; // 记录节点入度
@ -94,7 +113,7 @@ if (vec.size() > 0) {
vector<int> getRemoveEdge(const vector<vector<int>>& edges)
```
此时 大家应该知道了，我们要实现两个最为关键的函数：
大家应该知道了，我们要实现两个最为关键的函数：
* `isTreeAfterRemoveEdge()` 判断删一个边之后是不是树了
* `getRemoveEdge` 确定图中一定有了有向环，那么要找到需要删除的那条边

57
problems/0718.最长重复子数组.md
View File

@ -23,6 +23,11 @@
* 1 <= len(A), len(B) <= 1000
* 0 <= A[i], B[i] < 100
## 算法公开课
**《代码随想录》算法视频公开课：[动态规划之子序列问题，想清楚DP数组的定义 | LeetCode：718.最长重复子数组](https://www.bilibili.com/video/BV178411H7hV)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
## 思路
@ -198,7 +203,57 @@ public:
而且为了让 `if (dp[i][j] > result) result = dp[i][j];` 收集到全部结果，两层for训练一定从0开始遍历，这样需要加上 `&& i > 0 && j > 0`的判断。
相对于版本一来说还是多写了不少代码。而且逻辑上也复杂了一些。 优势就是dp数组的定义，更直观一点。
对于基础不牢的小白来说，在推导出转移方程后可能疑惑上述代码为什么要从`i=0,j=0`遍历而不是从`i=1,j=1`开始遍历，原因在于这里如果不是从`i=0,j=0`位置开始遍历，会漏掉如下样例结果：
```txt
nums1 = [70,39,25,40,7]
nums2 = [52,20,67,5,31]
```
当然，如果你愿意也可以使用如下代码，与上面那个c++是同一思路：
```java
class Solution {
public int findLength(int[] nums1, int[] nums2) {
int len1 = nums1.length;
int len2 = nums2.length;
int[][] result = new int[len1][len2];
int maxresult = Integer.MIN_VALUE;
for(int i=0;i<len1;i++){
if(nums1[i] == nums2[0])
result[i][0] = 1;
if(maxresult<result[i][0])
maxresult = result[i][0];
}
for(int j=0;j<len2;j++){
if(nums1[0] == nums2[j])
result[0][j] = 1;
if(maxresult<result[0][j])
maxresult = result[0][j];
}
for(int i=1;i<len1;i++){
for(int j=1;j<len2;j++){
if(nums1[i]==nums2[j])
result[i][j] = result[i-1][j-1]+1;
if(maxresult<result[i][j])
maxresult = result[i][j];
}
}
return maxresult;
}
}
```
对于小白来说一定要明确dp数组中初始化的数据是什么
整体而言相对于版本一来说还是多写了不少代码。而且逻辑上也复杂了一些。 优势就是dp数组的定义，更直观一点。
## 其他语言版本

109
problems/0738.单调递增的数字.md
View File

@ -164,17 +164,110 @@ class Solution {
### Python：
暴力
```python
class Solution:
def monotoneIncreasingDigits(self, n: int) -> int:
a = list(str(n))
for i in range(len(a)-1,0,-1):
if int(a[i]) < int(a[i-1]):
a[i-1] = str(int(a[i-1]) - 1)
a[i:] = '9' * (len(a) - i) #python不需要设置flag值，直接按长度给9就好了
return int("".join(a))
```
def checkNum(self, num):
max_digit = 10
while num:
digit = num % 10
if max_digit >= digit:
max_digit = digit
else:
return False
num //= 10
return True
def monotoneIncreasingDigits(self, N):
for i in range(N, 0, -1):
if self.checkNum(i):
return i
return 0
```
贪心（版本一）
```python
class Solution:
def monotoneIncreasingDigits(self, N: int) -> int:
# 将整数转换为字符串
strNum = str(N)
# flag用来标记赋值9从哪里开始
# 设置为字符串长度，为了防止第二个for循环在flag没有被赋值的情况下执行
flag = len(strNum)
# 从右往左遍历字符串
for i in range(len(strNum) - 1, 0, -1):
# 如果当前字符比前一个字符小，说明需要修改前一个字符
if strNum[i - 1] > strNum[i]:
flag = i # 更新flag的值，记录需要修改的位置
# 将前一个字符减1，以保证递增性质
strNum = strNum[:i - 1] + str(int(strNum[i - 1]) - 1) + strNum[i:]
# 将flag位置及之后的字符都修改为9，以保证最大的递增数字
for i in range(flag, len(strNum)):
strNum = strNum[:i] + '9' + strNum[i + 1:]
# 将最终的字符串转换回整数并返回
return int(strNum)
```
贪心（版本二）
```python
class Solution:
def monotoneIncreasingDigits(self, N: int) -> int:
# 将整数转换为字符串
strNum = list(str(N))
# 从右往左遍历字符串
for i in range(len(strNum) - 1, 0, -1):
# 如果当前字符比前一个字符小，说明需要修改前一个字符
if strNum[i - 1] > strNum[i]:
strNum[i - 1] = str(int(strNum[i - 1]) - 1) # 将前一个字符减1
# 将修改位置后面的字符都设置为9，因为修改前一个字符可能破坏了递增性质
for j in range(i, len(strNum)):
strNum[j] = '9'
# 将列表转换为字符串，并将字符串转换为整数并返回
return int(''.join(strNum))
```
贪心（版本三）
```python
class Solution:
def monotoneIncreasingDigits(self, N: int) -> int:
# 将整数转换为字符串
strNum = list(str(N))
# 从右往左遍历字符串
for i in range(len(strNum) - 1, 0, -1):
# 如果当前字符比前一个字符小，说明需要修改前一个字符
if strNum[i - 1] > strNum[i]:
strNum[i - 1] = str(int(strNum[i - 1]) - 1) # 将前一个字符减1
# 将修改位置后面的字符都设置为9，因为修改前一个字符可能破坏了递增性质
strNum[i:] = '9' * (len(strNum) - i)
# 将列表转换为字符串，并将字符串转换为整数并返回
return int(''.join(strNum))
```
贪心（版本四）精简
```python
class Solution:
def monotoneIncreasingDigits(self, N: int) -> int:
strNum = str(N)
for i in range(len(strNum) - 1, 0, -1):
# 如果当前字符比前一个字符小，说明需要修改前一个字符
if strNum[i - 1] > strNum[i]:
# 将前一个字符减1，以保证递增性质
# 使用字符串切片操作将修改后的前面部分与后面部分进行拼接
strNum = strNum[:i - 1] + str(int(strNum[i - 1]) - 1) + '9' * (len(strNum) - i)
return int(strNum)
```
### Go
```go
func monotoneIncreasingDigits(N int) int {

46
problems/0746.使用最小花费爬楼梯.md
View File

@ -245,26 +245,42 @@ class Solution {
```
### Python
动态规划（版本一）
```python
# 第一步不支付费用
class Solution:
def minCostClimbingStairs(self, cost: List[int]) -> int:
n = len(cost)
dp = [0]*(n+1) # 到达前两步费用为0
for i in range(2, n+1):
dp[i] = min(dp[i-1]+cost[i-1], dp[i-2]+cost[i-2])
return dp[-1]
```
```python
# 第一步支付费用
class Solution:
def minCostClimbingStairs(self, cost: List[int]) -> int:
dp = [0] * (len(cost) + 1)
dp[0] = 0
dp[1] = 0
dp[0] = 0 # 初始值，表示从起点开始不需要花费体力
dp[1] = 0 # 初始值，表示经过第一步不需要花费体力
for i in range(2, len(cost) + 1):
dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i-2])
return dp[len(cost)]
# 在第i步，可以选择从前一步（i-1）花费体力到达当前步，或者从前两步（i-2）花费体力到达当前步
# 选择其中花费体力较小的路径，加上当前步的花费，更新dp数组
dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])
return dp[len(cost)] # 返回到达楼顶的最小花费
```
动态规划（版本二）
```python
class Solution:
def minCostClimbingStairs(self, cost: List[int]) -> int:
dp0 = 0 # 初始值，表示从起点开始不需要花费体力
dp1 = 0 # 初始值，表示经过第一步不需要花费体力
for i in range(2, len(cost) + 1):
# 在第i步，可以选择从前一步（i-1）花费体力到达当前步，或者从前两步（i-2）花费体力到达当前步
# 选择其中花费体力较小的路径，加上当前步的花费，得到当前步的最小花费
dpi = min(dp1 + cost[i - 1], dp0 + cost[i - 2])
dp0 = dp1 # 更新dp0为前一步的值，即上一次循环中的dp1
dp1 = dpi # 更新dp1为当前步的最小花费
return dp1 # 返回到达楼顶的最小花费
```
### Go

107
problems/0763.划分字母区间.md
View File

@ -231,83 +231,56 @@ class Solution{
```
### Python
贪心（版本一）
```python
class Solution:
def partitionLabels(self, s: str) -> List[int]:
hash = [0] * 26
for i in range(len(s)):
hash[ord(s[i]) - ord('a')] = i
last_occurrence = {} # 存储每个字符最后出现的位置
for i, ch in enumerate(s):
last_occurrence[ch] = i
result = []
left = 0
right = 0
for i in range(len(s)):
right = max(right, hash[ord(s[i]) - ord('a')])
if i == right:
result.append(right - left + 1)
left = i + 1
start = 0
end = 0
for i, ch in enumerate(s):
end = max(end, last_occurrence[ch]) # 找到当前字符出现的最远位置
if i == end: # 如果当前位置是最远位置，表示可以分割出一个区间
result.append(end - start + 1)
start = i + 1
return result
# 解法二（不相交区间法）
```
贪心（版本二）与452.用最少数量的箭引爆气球 (opens new window)、435.无重叠区间 (opens new window)相同的思路。
```python
class Solution:
def partitionLabels(self, s: str) -> List[int]:
# 记录每个字母出现的区间
def getBord(s):
hash = [[-float('inf')] * 2 for _ in range(26)]
for i in range(len(s)):
if hash[ord(s[i]) - ord('a')][0] == -float('inf'):
hash[ord(s[i]) - ord('a')][0] = i
hash[ord(s[i]) - ord('a')][1] = i
# 去除字符串中未出现的字母所占用区间
hash_filter = []
for item in hash:
if item[0] != -float('inf'): hash_filter.append(item)
return hash_filter
# 得到无重叠区间题意中的输入样例格式：区间列表
hash = getBord(s)
# 按照左边界从小到大排序
hash.sort(key= lambda x: x[0])
res = []
left = 0
# 记录最大右边界
right = hash[0][1]
def countLabels(self, s):
# 初始化一个长度为26的区间列表，初始值为负无穷
hash = [[float('-inf'), float('-inf')] for _ in range(26)]
hash_filter = []
for i in range(len(s)):
if hash[ord(s[i]) - ord('a')][0] == float('-inf'):
hash[ord(s[i]) - ord('a')][0] = i
hash[ord(s[i]) - ord('a')][1] = i
for i in range(len(hash)):
# 一旦下一区间左边界大于当前右边界，即可认为出现分割点
if hash[i][0] > right:
res.append(right - left + 1)
left = hash[i][0]
# 实时更新最大右边界
right = max(right, hash[i][1])
# 最右侧区间（字符串长度为1时的特殊情况也包含于其中）
res.append(right - left + 1)
if hash[i][0] != float('-inf'):
hash_filter.append(hash[i])
return hash_filter
def partitionLabels(self, s):
res = []
hash = self.countLabels(s)
hash.sort(key=lambda x: x[0]) # 按左边界从小到大排序
rightBoard = hash[0][1] # 记录最大右边界
leftBoard = 0
for i in range(1, len(hash)):
if hash[i][0] > rightBoard: # 出现分割点
res.append(rightBoard - leftBoard + 1)
leftBoard = hash[i][0]
rightBoard = max(rightBoard, hash[i][1])
res.append(rightBoard - leftBoard + 1) # 最右端
return res
# 解法三：区间合并法 （结合下一题 56. Merge Intervals 的写法）
class Solution: #
def partitionLabels(self, s: str) -> List[int]:
aaa = list(set(s))
#aaa.sort()
bbb = list(s)
ccc = []
for i in reversed(bbb):
ccc.append(i)
intervals = []
for i in range(len(aaa)):
intervals.append([bbb.index(aaa[i]),len(bbb)-ccc.index(aaa[i])-1])
# 先求出各个字母的存在区间，之后利用区间合并方法得出所有不相邻的最大区间。
intervals.sort(key = lambda x:x[0])
newinterval = []
left, right = intervals[0][0], intervals[0][1]
for i in range(1,len(intervals)):
if intervals[i][0] in range(left, right+1):
right = max(intervals[i][1],intervals[i-1][1],right)
left = min(intervals[i-1][0],left)
else:
newinterval.append(right-left+1)
left = intervals[i][0]
right = intervals[i][1]
newinterval.append(right-left+1)
return newinterval
```
### Go

4
problems/0797.所有可能的路径.md
View File

@ -159,7 +159,7 @@ public:
## 其他语言版本
## Java
Java
```Java
// 深度优先遍历
@ -190,7 +190,7 @@ class Solution {
}
```
## Python
Python
```python
class Solution:
def __init__(self):

31
problems/0860.柠檬水找零.md
View File

@ -164,24 +164,39 @@ class Solution {
```python
class Solution:
def lemonadeChange(self, bills: List[int]) -> bool:
five, ten = 0, 0
five = 0
ten = 0
twenty = 0
for bill in bills:
# 情况一：收到5美元
if bill == 5:
five += 1
elif bill == 10:
if five < 1: return False
five -= 1
# 情况二：收到10美元
if bill == 10:
if five <= 0:
return False
ten += 1
else:
if ten > 0 and five > 0:
ten -= 1
five -= 1
# 情况三：收到20美元
if bill == 20:
# 先尝试使用10美元和5美元找零
if five > 0 and ten > 0:
five -= 1
elif five > 2:
ten -= 1
#twenty += 1
# 如果无法使用10美元找零，则尝试使用三张5美元找零
elif five >= 3:
five -= 3
#twenty += 1
else:
return False
return True
```
### Go

114
problems/0968.监控二叉树.md
View File

@ -371,56 +371,104 @@ class Solution {
### Python
贪心（版本一）
```python
class Solution:
def minCameraCover(self, root: TreeNode) -> int:
# Greedy Algo:
# Greedy Algo:
# 从下往上安装摄像头：跳过leaves这样安装数量最少，局部最优 -> 全局最优
# 先给leaves的父节点安装，然后每隔两层节点安装一个摄像头，直到Head
# 0: 该节点未覆盖
# 1: 该节点有摄像头
# 2: 该节点有覆盖
def minCameraCover(self, root: TreeNode) -> int:
# 定义递归函数
result = [0] # 用于记录摄像头的安装数量
if self.traversal(root, result) == 0:
result[0] += 1
result = 0
# 从下往上遍历：后序（左右中）
def traversal(curr: TreeNode) -> int:
nonlocal result
return result[0]
if not curr: return 2
left = traversal(curr.left)
right = traversal(curr.right)
# Case 1:
# 左右节点都有覆盖
if left == 2 and right == 2:
return 0
def traversal(self, cur: TreeNode, result: List[int]) -> int:
if not cur:
return 2
# Case 2:
# left == 0 && right == 0 左右节点无覆盖
# left == 1 && right == 0 左节点有摄像头，右节点无覆盖
# left == 0 && right == 1 左节点有无覆盖，右节点摄像头
# left == 0 && right == 2 左节点无覆盖，右节点覆盖
# left == 2 && right == 0 左节点覆盖，右节点无覆盖
elif left == 0 or right == 0:
result += 1
return 1
left = self.traversal(cur.left, result)
right = self.traversal(cur.right, result)
# Case 3:
# left == 1 && right == 2 左节点有摄像头，右节点有覆盖
# left == 2 && right == 1 左节点有覆盖，右节点有摄像头
# left == 1 && right == 1 左右节点都有摄像头
elif left == 1 or right == 1:
return 2
# 情况1: 左右节点都有覆盖
if left == 2 and right == 2:
return 0
# 其他情况前段代码均已覆盖
# 情况2:
# left == 0 && right == 0 左右节点无覆盖
# left == 1 && right == 0 左节点有摄像头，右节点无覆盖
# left == 0 && right == 1 左节点无覆盖，右节点有摄像头
# left == 0 && right == 2 左节点无覆盖，右节点覆盖
# left == 2 && right == 0 左节点覆盖，右节点无覆盖
if left == 0 or right == 0:
result[0] += 1
return 1
# 情况3:
# left == 1 && right == 2 左节点有摄像头，右节点有覆盖
# left == 2 && right == 1 左节点有覆盖，右节点有摄像头
# left == 1 && right == 1 左右节点都有摄像头
if left == 1 or right == 1:
return 2
if traversal(root) == 0:
result += 1
return result
```
贪心（版本二）利用elif精简代码
```python
class Solution:
# Greedy Algo:
# 从下往上安装摄像头：跳过leaves这样安装数量最少，局部最优 -> 全局最优
# 先给leaves的父节点安装，然后每隔两层节点安装一个摄像头，直到Head
# 0: 该节点未覆盖
# 1: 该节点有摄像头
# 2: 该节点有覆盖
def minCameraCover(self, root: TreeNode) -> int:
# 定义递归函数
result = [0] # 用于记录摄像头的安装数量
if self.traversal(root, result) == 0:
result[0] += 1
return result[0]
def traversal(self, cur: TreeNode, result: List[int]) -> int:
if not cur:
return 2
left = self.traversal(cur.left, result)
right = self.traversal(cur.right, result)
# 情况1: 左右节点都有覆盖
if left == 2 and right == 2:
return 0
# 情况2:
# left == 0 && right == 0 左右节点无覆盖
# left == 1 && right == 0 左节点有摄像头，右节点无覆盖
# left == 0 && right == 1 左节点无覆盖，右节点有摄像头
# left == 0 && right == 2 左节点无覆盖，右节点覆盖
# left == 2 && right == 0 左节点覆盖，右节点无覆盖
elif left == 0 or right == 0:
result[0] += 1
return 1
# 情况3:
# left == 1 && right == 2 左节点有摄像头，右节点有覆盖
# left == 2 && right == 1 左节点有覆盖，右节点有摄像头
# left == 1 && right == 1 左右节点都有摄像头
else:
return 2
```
### Go
```go

8
problems/0977.有序数组的平方.md
View File

@ -488,6 +488,14 @@ public class Solution {
return result;
}
}
C# LINQ：
```csharp
public class Solution {
public int[] SortedSquares(int[] nums) {
return nums.Select(x => x * x).OrderBy(x => x).ToArray();
}
}
```
<p align="center">
<a href="https://programmercarl.com/other/kstar.html" target="_blank">

18
problems/1005.K次取反后最大化的数组和.md
View File

@ -131,17 +131,23 @@ class Solution {
```
### Python
贪心
```python
class Solution:
def largestSumAfterKNegations(self, A: List[int], K: int) -> int:
A = sorted(A, key=abs, reverse=True) # 将A按绝对值从大到小排列
for i in range(len(A)):
if K > 0 and A[i] < 0:
A.sort(key=lambda x: abs(x), reverse=True) # 第一步：按照绝对值降序排序数组A
for i in range(len(A)): # 第二步：执行K次取反操作
if A[i] < 0 and K > 0:
A[i] *= -1
K -= 1
if K > 0:
A[-1] *= (-1)**K #取A最后一个数只需要写-1
return sum(A)
if K % 2 == 1: # 第三步：如果K还有剩余次数，将绝对值最小的元素取反
A[-1] *= -1
result = sum(A) # 第四步：计算数组A的元素和
return result
```
### Go

5
problems/1035.不相交的线.md
View File

@ -17,6 +17,11 @@
![1035.不相交的线](https://code-thinking-1253855093.file.myqcloud.com/pics/2021032116363533.png)
## 算法公开课
**《代码随想录》算法视频公开课：[动态规划之子序列问题，换汤不换药 | LeetCode：1035.不相交的线](https://www.bilibili.com/video/BV1h84y1x7MP)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
## 思路
相信不少录友看到这道题目都没啥思路，我们来逐步分析一下。

94
problems/1049.最后一块石头的重量II.md
View File

@ -224,18 +224,79 @@ class Solution {
```
### Python：
卡哥版
```python
class Solution:
def lastStoneWeightII(self, stones: List[int]) -> int:
sumweight = sum(stones)
target = sumweight // 2
dp = [0] * (target + 1)
for i in range(len(stones)):
for j in range(target, stones[i] - 1, -1):
dp[j] = max(dp[j], dp[j - stones[i]] + stones[i])
return sumweight - 2 * dp[target]
```
dp = [0] * 15001
total_sum = sum(stones)
target = total_sum // 2
for stone in stones: # 遍历物品
for j in range(target, stone - 1, -1): # 遍历背包
dp[j] = max(dp[j], dp[j - stone] + stone)
return total_sum - dp[target] - dp[target]
```
二维DP版
```python
class Solution:
def lastStoneWeightII(self, stones: List[int]) -> int:
total_sum = sum(stones)
target = total_sum // 2
# 创建二维dp数组，行数为石头的数量加1，列数为target加1
# dp[i][j]表示前i个石头能否组成总重量为j
dp = [[False] * (target + 1) for _ in range(len(stones) + 1)]
# 初始化第一列，表示总重量为0时，前i个石头都能组成
for i in range(len(stones) + 1):
dp[i][0] = True
for i in range(1, len(stones) + 1):
for j in range(1, target + 1):
# 如果当前石头重量大于当前目标重量j，则无法选择该石头
if stones[i - 1] > j:
dp[i][j] = dp[i - 1][j]
else:
# 可选择该石头或不选择该石头
dp[i][j] = dp[i - 1][j] or dp[i - 1][j - stones[i - 1]]
# 找到最大的重量i，使得dp[len(stones)][i]为True
# 返回总重量减去两倍的最接近总重量一半的重量
for i in range(target, -1, -1):
if dp[len(stones)][i]:
return total_sum - 2 * i
return 0
```
一维DP版
```python
class Solution:
def lastStoneWeightII(self, stones):
total_sum = sum(stones)
target = total_sum // 2
dp = [False] * (target + 1)
dp[0] = True
for stone in stones:
for j in range(target, stone - 1, -1):
# 判断当前重量是否可以通过选择之前的石头得到或选择当前石头和之前的石头得到
dp[j] = dp[j] or dp[j - stone]
for i in range(target, -1, -1):
if dp[i]:
# 返回剩余石头的重量，即总重量减去两倍的最接近总重量一半的重量
return total_sum - 2 * i
return 0
```
### Go：
```go
func lastStoneWeightII(stones []int) int {
@ -379,8 +440,23 @@ object Solution {
}
```
### Rust
```rust
impl Solution {
pub fn last_stone_weight_ii(stones: Vec<i32>) -> i32 {
let sum = stones.iter().sum::<i32>();
let target = sum as usize / 2;
let mut dp = vec![0; target + 1];
for s in stones {
for j in (s as usize..=target).rev() {
dp[j] = dp[j].max(dp[j - s as usize] + s);
}
}
sum - dp[target] * 2
}
}
```
<p align="center">
<a href="https://programmercarl.com/other/kstar.html" target="_blank">

23
problems/1143.最长公共子序列.md
View File

@ -18,25 +18,30 @@
示例 1:
输入：text1 = "abcde", text2 = "ace"
输出：3
解释：最长公共子序列是 "ace"，它的长度为 3。
* 输入：text1 = "abcde", text2 = "ace"
* 输出：3
* 解释：最长公共子序列是 "ace"，它的长度为 3。
示例 2:
输入：text1 = "abc", text2 = "abc"
输出：3
解释：最长公共子序列是 "abc"，它的长度为 3。
* 输入：text1 = "abc", text2 = "abc"
* 输出：3
* 解释：最长公共子序列是 "abc"，它的长度为 3。
示例 3:
输入：text1 = "abc", text2 = "def"
输出：0
解释：两个字符串没有公共子序列，返回 0。
* 输入：text1 = "abc", text2 = "def"
* 输出：0
* 解释：两个字符串没有公共子序列，返回 0。
提示:
* 1 <= text1.length <= 1000
* 1 <= text2.length <= 1000
输入的字符串只含有小写英文字符。
## 算法公开课
**《代码随想录》算法视频公开课：[动态规划子序列问题经典题目 | LeetCode：1143.最长公共子序列](https://www.bilibili.com/video/BV1ye4y1L7CQ)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
## 思路
本题和[动态规划：718. 最长重复子数组](https://programmercarl.com/0718.最长重复子数组.html)区别在于这里不要求是连续的了，但要有相对顺序，即："ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。

72
problems/1971.寻找图中是否存在路径.md
View File

@ -3,6 +3,7 @@
<img src="../pics/训练营.png" width="1000"/>
</a>
<p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！</strong></p>
# 1971. 寻找图中是否存在路径
[题目链接](https://leetcode.cn/problems/find-if-path-exists-in-graph/)
@ -30,7 +31,7 @@
## 思路
这道题目也是并查集基础题目。
本题是并查集基础题目。
首先要知道并查集可以解决什么问题呢？
@ -39,8 +40,8 @@
这里整理出我的并查集模板如下：
```CPP
int n = 1005; // 节点数量3 到 1000
int father[1005];
int n = 1005; // n根据题目中节点数量而定，一般比节点数量大一点就好
vector<int> father = vector<int> (n, 0); // C++里的一种数组结构
// 并查集初始化
void init() {
@ -50,79 +51,86 @@ void init() {
}
// 并查集里寻根的过程
int find(int u) {
return u == father[u] ? u : father[u] = find(father[u]);
}
// 将v->u 这条边加入并查集
void join(int u, int v) {
u = find(u);
v = find(v);
if (u == v) return ;
father[v] = u;
return u == father[u] ? u : father[u] = find(father[u]); // 路径压缩
}
// 判断 u 和 v是否找到同一个根
bool same(int u, int v) {
bool isSame(int u, int v) {
u = find(u);
v = find(v);
return u == v;
}
// 将v->u 这条边加入并查集
void join(int u, int v) {
u = find(u); // 寻找u的根
v = find(v); // 寻找v的根
if (u == v) return ; // 如果发现根相同，则说明在一个集合，不用两个节点相连直接返回
father[v] = u;
}
```
以上模板汇总，只要修改 n 和father数组的大小就可以了。
以上模板中，只要修改 n 大小就可以，本科n不会超过2 * 10^5。
并查集主要有三个功能。
1. 寻找根节点，函数：find(int u)，也就是判断这个节点的祖先节点是哪个
2. 将两个节点接入到同一个集合，函数：join(int u, int v)，将两个节点连在同一个根节点上
3. 判断两个节点是否在同一个集合，函数：same(int u, int v)，就是判断两个节点是不是同一个根节点
3. 判断两个节点是否在同一个集合，函数：isSame(int u, int v)，就是判断两个节点是不是同一个根节点
简单介绍并查集之后，我们再来看一下这道题目。
为什么说这道题目是并查集基础题目，因为 可以直接套用模板。
为什么说这道题目是并查集基础题目，题目中各个点是双向图链接，那么判断 一个顶点到另一个顶点有没有有效路径其实就是看这两个顶点是否在同一个集合里。
如何算是同一个集合呢，有边连在一起，就算是一个集合。
此时我们就可以直接套用并查集模板。
使用join(int u, int v)将每条边加入到并查集。
最后 same(int u, int v) 判断是否是同一个根 就可以里。
最后 isSame(int u, int v) 判断是否是同一个根 就可以了。
代码如下：
C++代码如下：
```c++
```CPP
class Solution {
private:
int n = 200005; // 节点数量 20000
int father[200005];
vector<int> father = vector<int> (n, 0); // C++里的一种数组结构
// 并查集初始化
void init() {
for (int i = 0; i < n; ++i) {
father[i] = i;
for (int i = 0; i < n; ++i) { father[i] = i;
}
}
// 并查集里寻根的过程
int find(int u) {
return u == father[u] ? u : father[u] = find(father[u]);
}
// 将v->u 这条边加入并查集
void join(int u, int v) {
u = find(u);
v = find(v);
if (u == v) return ;
father[v] = u;
}
// 判断 u 和 v是否找到同一个根，本题用不上
bool same(int u, int v) {
// 判断 u 和 v是否找到同一个根
bool isSame(int u, int v) {
u = find(u);
v = find(v);
return u == v;
}
// 将v->u 这条边加入并查集
void join(int u, int v) {
u = find(u); // 寻找u的根
v = find(v); // 寻找v的根
if (u == v) return ; // 如果发现根相同，则说明在一个集合，不用两个节点相连直接返回
father[v] = u;
}
public:
bool validPath(int n, vector<vector<int>>& edges, int source, int destination) {
init();
for (int i = 0; i < edges.size(); i++) {
join(edges[i][0], edges[i][1]);
}
return same(source, destination);
return isSame(source, destination);
}
};
```

2
problems/二叉树理论基础.md
View File

@ -39,7 +39,7 @@
什么是完全二叉树？
完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2^(h-1) 个节点。
完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层（h从1开始），则该层包含 1~ 2^(h-1) 个节点。
**大家要自己看完全二叉树的定义，很多同学对完全二叉树其实不是真正的懂了。**

75
problems/背包理论基础01背包-1.md
View File

@ -339,38 +339,63 @@ public class BagProblem {
```
### python
无参数版
```python
def test_2_wei_bag_problem1(bag_size, weight, value) -> int:
rows, cols = len(weight), bag_size + 1
dp = [[0 for _ in range(cols)] for _ in range(rows)]
def test_2_wei_bag_problem1():
weight = [1, 3, 4]
value = [15, 20, 30]
bagweight = 4
# 初始化dp数组.
for i in range(rows):
dp[i][0] = 0
first_item_weight, first_item_value = weight[0], value[0]
for j in range(1, cols):
if first_item_weight <= j:
dp[0][j] = first_item_value
# 二维数组
dp = [[0] * (bagweight + 1) for _ in range(len(weight))]
# 更新dp数组: 先遍历物品, 再遍历背包.
for i in range(1, len(weight)):
cur_weight, cur_val = weight[i], value[i]
for j in range(1, cols):
if cur_weight > j: # 说明背包装不下当前物品.
dp[i][j] = dp[i - 1][j] # 所以不装当前物品.
else:
# 定义dp数组: dp[i][j] 前i个物品里，放进容量为j的背包，价值总和最大是多少。
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - cur_weight]+ cur_val)
# 初始化
for j in range(weight[0], bagweight + 1):
dp[0][j] = value[0]
print(dp)
# weight数组的大小就是物品个数
for i in range(1, len(weight)): # 遍历物品
for j in range(bagweight + 1): # 遍历背包容量
if j < weight[i]:
dp[i][j] = dp[i - 1][j]
else:
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])
print(dp[len(weight) - 1][bagweight])
test_2_wei_bag_problem1()
```
有参数版
```python
def test_2_wei_bag_problem1(weight, value, bagweight):
# 二维数组
dp = [[0] * (bagweight + 1) for _ in range(len(weight))]
# 初始化
for j in range(weight[0], bagweight + 1):
dp[0][j] = value[0]
# weight数组的大小就是物品个数
for i in range(1, len(weight)): # 遍历物品
for j in range(bagweight + 1): # 遍历背包容量
if j < weight[i]:
dp[i][j] = dp[i - 1][j]
else:
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])
return dp[len(weight) - 1][bagweight]
if __name__ == "__main__":
bag_size = 4
weight = [1, 3, 4]
value = [15, 20, 30]
test_2_wei_bag_problem1(bag_size, weight, value)
weight = [1, 3, 4]
value = [15, 20, 30]
bagweight = 4
result = test_2_wei_bag_problem1(weight, value, bagweight)
print(result)
```

37
problems/背包理论基础01背包-2.md
View File

@ -246,25 +246,46 @@ int main() {
### Python
无参版
```python
def test_1_wei_bag_problem():
weight = [1, 3, 4]
value = [15, 20, 30]
bag_weight = 4
# 初始化: 全为0
dp = [0] * (bag_weight + 1)
bagWeight = 4
# 先遍历物品, 再遍历背包容量
for i in range(len(weight)):
for j in range(bag_weight, weight[i] - 1, -1):
# 递归公式
# 初始化
dp = [0] * (bagWeight + 1)
for i in range(len(weight)): # 遍历物品
for j in range(bagWeight, weight[i] - 1, -1): # 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
print(dp)
print(dp[bagWeight])
test_1_wei_bag_problem()
```
有参版
```python
def test_1_wei_bag_problem(weight, value, bagWeight):
# 初始化
dp = [0] * (bagWeight + 1)
for i in range(len(weight)): # 遍历物品
for j in range(bagWeight, weight[i] - 1, -1): # 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
return dp[bagWeight]
if __name__ == "__main__":
weight = [1, 3, 4]
value = [15, 20, 30]
bagweight = 4
result = test_1_wei_bag_problem(weight, value, bagweight)
print(result)
```
### Go
```go
func test_1_wei_bag_problem(weight, value []int, bagWeight int) int {

132
problems/背包问题理论基础多重背包.md
View File

@ -194,55 +194,127 @@ public void testMultiPack2(){
Python：
改变物品数量为01背包格式（无参版）
```python
def test_multi_pack1():
'''版本一：改变物品数量为01背包格式'''
def test_multi_pack():
weight = [1, 3, 4]
value = [15, 20, 30]
nums = [2, 3, 2]
bag_weight = 10
bagWeight = 10
# 将数量大于1的物品展开
for i in range(len(nums)):
# 将物品展开数量为1
while nums[i] > 1:
weight.append(weight[i])
value.append(value[i])
nums[i] -= 1
dp = [0]*(bag_weight + 1)
# 遍历物品
for i in range(len(weight)):
# 遍历背包
for j in range(bag_weight, weight[i] - 1, -1):
dp = [0] * (bagWeight + 1)
for i in range(len(weight)): # 遍历物品
for j in range(bagWeight, weight[i] - 1, -1): # 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
for j in range(bagWeight + 1):
print(dp[j], end=" ")
print()
print(" ".join(map(str, dp)))
def test_multi_pack2():
'''版本：改变遍历个数'''
weight = [1, 3, 4]
value = [15, 20, 30]
nums = [2, 3, 2]
bag_weight = 10
dp = [0]*(bag_weight + 1)
for i in range(len(weight)):
for j in range(bag_weight, weight[i] - 1, -1):
# 以上是01背包，加上遍历个数
for k in range(1, nums[i] + 1):
if j - k*weight[i] >= 0:
dp[j] = max(dp[j], dp[j - k*weight[i]] + k*value[i])
print(" ".join(map(str, dp)))
print(dp[bagWeight])
if __name__ == '__main__':
test_multi_pack1()
test_multi_pack2()
test_multi_pack()
```
改变遍历个数（无参版）
```python
def test_multi_pack():
weight = [1, 3, 4]
value = [15, 20, 30]
nums = [2, 3, 2]
bagWeight = 10
dp = [0] * (bagWeight + 1)
for i in range(len(weight)): # 遍历物品
for j in range(bagWeight, weight[i] - 1, -1): # 遍历背包容量
# 以上为01背包，然后加一个遍历个数
for k in range(1, nums[i] + 1): # 遍历个数
if j - k * weight[i] >= 0:
dp[j] = max(dp[j], dp[j - k * weight[i]] + k * value[i])
# 打印一下dp数组
for j in range(bagWeight + 1):
print(dp[j], end=" ")
print()
print(dp[bagWeight])
test_multi_pack()
```
改变物品数量为01背包格式（有参版）
```python
def test_multi_pack(weight, value, nums, bagWeight):
# 将数量大于1的物品展开
for i in range(len(nums)):
while nums[i] > 1:
weight.append(weight[i])
value.append(value[i])
nums[i] -= 1
dp = [0] * (bagWeight + 1)
for i in range(len(weight)): # 遍历物品
for j in range(bagWeight, weight[i] - 1, -1): # 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
for j in range(bagWeight + 1):
print(dp[j], end=" ")
print()
print(dp[bagWeight])
if __name__ == "__main__":
weight = [1, 3, 4]
value = [15, 20, 30]
nums = [2, 3, 2]
bagWeight = 10
test_multi_pack(weight, value, nums, bagWeight)
```
改变遍历个数（有参版）
```python
def test_multi_pack(weight, value, nums, bagWeight):
dp = [0] * (bagWeight + 1)
for i in range(len(weight)): # 遍历物品
for j in range(bagWeight, weight[i] - 1, -1): # 遍历背包容量
# 以上为01背包，然后加一个遍历个数
for k in range(1, nums[i] + 1): # 遍历个数
if j - k * weight[i] >= 0:
dp[j] = max(dp[j], dp[j - k * weight[i]] + k * value[i])
# 使用 join 函数打印 dp 数组
print(' '.join(str(dp[j]) for j in range(bagWeight + 1)))
print(dp[bagWeight])
if __name__ == "__main__":
weight = [1, 3, 4]
value = [15, 20, 30]
nums = [2, 3, 2]
bagWeight = 10
test_multi_pack(weight, value, nums, bagWeight)
```
Go：
```go

129
problems/背包问题理论基础完全背包.md
View File

@ -223,43 +223,81 @@ private static void testCompletePackAnotherWay(){
Python：
先遍历物品，再遍历背包（无参版）
```python
# 先遍历物品，再遍历背包
def test_complete_pack1():
def test_CompletePack():
weight = [1, 3, 4]
value = [15, 20, 30]
bag_weight = 4
dp = [0]*(bag_weight + 1)
for i in range(len(weight)):
for j in range(weight[i], bag_weight + 1):
bagWeight = 4
dp = [0] * (bagWeight + 1)
for i in range(len(weight)): # 遍历物品
for j in range(weight[i], bagWeight + 1): # 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
print(dp[bagWeight])
print(dp[bag_weight])
test_CompletePack()
# 先遍历背包，再遍历物品
def test_complete_pack2():
weight = [1, 3, 4]
value = [15, 20, 30]
bag_weight = 4
dp = [0]*(bag_weight + 1)
for j in range(bag_weight + 1):
for i in range(len(weight)):
if j >= weight[i]: dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
print(dp[bag_weight])
if __name__ == '__main__':
test_complete_pack1()
test_complete_pack2()
```
先遍历物品，再遍历背包（有参版）
```python
def test_CompletePack(weight, value, bagWeight):
dp = [0] * (bagWeight + 1)
for i in range(len(weight)): # 遍历物品
for j in range(weight[i], bagWeight + 1): # 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
return dp[bagWeight]
if __name__ == "__main__":
weight = [1, 3, 4]
value = [15, 20, 30]
bagWeight = 4
result = test_CompletePack(weight, value, bagWeight)
print(result)
```
先遍历背包，再遍历物品（无参版）
```python
def test_CompletePack():
weight = [1, 3, 4]
value = [15, 20, 30]
bagWeight = 4
dp = [0] * (bagWeight + 1)
for j in range(bagWeight + 1): # 遍历背包容量
for i in range(len(weight)): # 遍历物品
if j - weight[i] >= 0:
dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
print(dp[bagWeight])
test_CompletePack()
```
先遍历背包，再遍历物品（有参版）
```python
def test_CompletePack(weight, value, bagWeight):
dp = [0] * (bagWeight + 1)
for j in range(bagWeight + 1): # 遍历背包容量
for i in range(len(weight)): # 遍历物品
if j - weight[i] >= 0:
dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
return dp[bagWeight]
if __name__ == "__main__":
weight = [1, 3, 4]
value = [15, 20, 30]
bagWeight = 4
result = test_CompletePack(weight, value, bagWeight)
print(result)
```
Go：
```go
@ -388,6 +426,43 @@ object Solution {
}
```
Rust:
```rust
impl Solution {
// 先遍历物品
fn complete_pack() {
let (goods, bag_size) = (vec![(1, 15), (3, 20), (4, 30)], 4);
let mut dp = vec![0; bag_size + 1];
for (weight, value) in goods {
for j in weight..=bag_size {
dp[j] = dp[j].max(dp[j - weight] + value);
}
}
println!("先遍历物品：{}", dp[bag_size]);
}
// 先遍历背包
fn complete_pack_after() {
let (goods, bag_size) = (vec![(1, 15), (3, 20), (4, 30)], 4);
let mut dp = vec![0; bag_size + 1];
for i in 0..=bag_size {
for (weight, value) in &goods {
if i >= *weight {
dp[i] = dp[i].max(dp[i - weight] + value);
}
}
}
println!("先遍历背包：{}", dp[bag_size]);
}
}
#[test]
fn test_complete_pack() {
Solution::complete_pack();
Solution::complete_pack_after();
}
```
<p align="center">
<a href="https://programmercarl.com/other/kstar.html" target="_blank">