> result = new ArrayList<>();
@@ -397,7 +397,25 @@ class Solution(object):
return result
```
-Python：
+## Python
+```python
+class Solution:
+ def combine(self, n: int, k: int) -> List[List[int]]:
+ res = []
+ path = []
+ def backtrack(n, k, StartIndex):
+ if len(path) == k:
+ res.append(path[:])
+ return
+ for i in range(StartIndex, n-(k-len(path)) + 2):
+ path.append(i)
+ backtrack(n, k, i+1)
+ path.pop()
+ backtrack(n, k, 1)
+ return res
+```
+
+剪枝：
```python3
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
@@ -406,15 +424,19 @@ class Solution:
def backtrack(n,k,startIndex):
if len(path) == k:
res.append(path[:])
- return
- for i in range(startIndex,n+1):
+ return
+ for i in range(startIndex,n-(k-len(path))+2): #优化的地方
path.append(i) #处理节点
backtrack(n,k,i+1) #递归
path.pop() #回溯，撤销处理的节点
- backtrack(n,k,1)
- return res
+ backtrack(n,k,1)
+ return res
```
-javascript
+
+
+## javascript
+
+剪枝：
```javascript
let result = []
let path = []
@@ -434,8 +456,11 @@ const combineHelper = (n, k, startIndex) => {
path.pop()
}
}
-```
-Go：
+```
+
+
+
+## Go
```Go
var res [][]int
func combine(n int, k int) [][]int {
@@ -462,8 +487,35 @@ func backtrack(n,k,start int,track []int){
}
}
```
+剪枝：
+```Go
+var res [][]int
+func combine(n int, k int) [][]int {
+ res=[][]int{}
+ if n <= 0 || k <= 0 || k > n {
+ return res
+ }
+ backtrack(n, k, 1, []int{})
+ return res
+}
+func backtrack(n,k,start int,track []int){
+ if len(track)==k{
+ temp:=make([]int,k)
+ copy(temp,track)
+ res=append(res,temp)
+ }
+ if len(track)+n-start+1 < k {
+ return
+ }
+ for i:=start;i<=n;i++{
+ track=append(track,i)
+ backtrack(n,k,i+1,track)
+ track=track[:len(track)-1]
+ }
+}
+```
-C:
+## C
```c
int* path;
int pathTop;
@@ -517,6 +569,60 @@ int** combine(int n, int k, int* returnSize, int** returnColumnSizes){
}
```
+剪枝：
+```c
+int* path;
+int pathTop;
+int** ans;
+int ansTop;
+
+void backtracking(int n, int k,int startIndex) {
+ //当path中元素个数为k个时，我们需要将path数组放入ans二维数组中
+ if(pathTop == k) {
+ //path数组为我们动态申请，若直接将其地址放入二维数组，path数组中的值会随着我们回溯而逐渐变化
+ //因此创建新的数组存储path中的值
+ int* temp = (int*)malloc(sizeof(int) * k);
+ int i;
+ for(i = 0; i < k; i++) {
+ temp[i] = path[i];
+ }
+ ans[ansTop++] = temp;
+ return ;
+ }
+
+ int j;
+ for(j = startIndex; j <= n- (k - pathTop) + 1;j++) {
+ //将当前结点放入path数组
+ path[pathTop++] = j;
+ //进行递归
+ backtracking(n, k, j + 1);
+ //进行回溯，将数组最上层结点弹出
+ pathTop--;
+ }
+}
+
+int** combine(int n, int k, int* returnSize, int** returnColumnSizes){
+ //path数组存储符合条件的结果
+ path = (int*)malloc(sizeof(int) * k);
+ //ans二维数组存储符合条件的结果数组的集合。（数组足够大，避免极端情况）
+ ans = (int**)malloc(sizeof(int*) * 10000);
+ pathTop = ansTop = 0;
+
+ //回溯算法
+ backtracking(n, k, 1);
+ //最后的返回大小为ans数组大小
+ *returnSize = ansTop;
+ //returnColumnSizes数组存储ans二维数组对应下标中一维数组的长度（都为k）
+ *returnColumnSizes = (int*)malloc(sizeof(int) *(*returnSize));
+ int i;
+ for(i = 0; i < *returnSize; i++) {
+ (*returnColumnSizes)[i] = k;
+ }
+ //返回ans二维数组
+ return ans;
+}
+```
+
-----------------------
* 作者微信：[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
* B站视频：[代码随想录](https://space.bilibili.com/525438321)
diff --git a/problems/0078.子集.md b/problems/0078.子集.md
index 583fe664..fb4a8740 100644
--- a/problems/0078.子集.md
+++ b/problems/0078.子集.md
@@ -31,7 +31,7 @@
## 思路
-求子集问题和[回溯算法：求组合问题！](https://programmercarl.com/0077.组合.html)和[回溯算法：分割问题！](https://programmercarl.com/0131.分割回文串.html)又不一样了。
+求子集问题和[77.组合](https://programmercarl.com/0077.组合.html)和[131.分割回文串](https://programmercarl.com/0131.分割回文串.html)又不一样了。
如果把 子集问题、组合问题、分割问题都抽象为一棵树的话，**那么组合问题和分割问题都是收集树的叶子节点，而子集问题是找树的所有节点！**
@@ -157,7 +157,7 @@ public:
相信大家经过了
* 组合问题：
- * [回溯算法：求组合问题！](https://programmercarl.com/0077.组合.html)
+ * [回溯算法：求组合问题](https://programmercarl.com/0077.组合.html)
* [回溯算法：组合问题再剪剪枝](https://programmercarl.com/0077.组合优化.html)
* [回溯算法：求组合总和！](https://programmercarl.com/0216.组合总和III.html)
* [回溯算法：电话号码的字母组合](https://programmercarl.com/0017.电话号码的字母组合.html)
diff --git a/problems/0090.子集II.md b/problems/0090.子集II.md
index 6dc631de..c8cb42d3 100644
--- a/problems/0090.子集II.md
+++ b/problems/0090.子集II.md
@@ -32,7 +32,7 @@
做本题之前一定要先做[78.子集](https://programmercarl.com/0078.子集.html)。
-这道题目和[回溯算法：求子集问题！](https://programmercarl.com/0078.子集.html)区别就是集合里有重复元素了，而且求取的子集要去重。
+这道题目和[78.子集](https://programmercarl.com/0078.子集.html)区别就是集合里有重复元素了，而且求取的子集要去重。
那么关于回溯算法中的去重问题，**在[40.组合总和II](https://programmercarl.com/0040.组合总和II.html)中已经详细讲解过了，和本题是一个套路**。
diff --git a/problems/0093.复原IP地址.md b/problems/0093.复原IP地址.md
index 9f2ea6e7..6d01319a 100644
--- a/problems/0093.复原IP地址.md
+++ b/problems/0093.复原IP地址.md
@@ -45,11 +45,11 @@ s 仅由数字组成
## 思路
-做这道题目之前，最好先把[回溯算法：分割回文串](https://programmercarl.com/0131.分割回文串.html)这个做了。
+做这道题目之前，最好先把[131.分割回文串](https://programmercarl.com/0131.分割回文串.html)这个做了。
这道题目相信大家刚看的时候，应该会一脸茫然。
-其实只要意识到这是切割问题，**切割问题就可以使用回溯搜索法把所有可能性搜出来**，和刚做过的[回溯算法：分割回文串](https://programmercarl.com/0131.分割回文串.html)就十分类似了。
+其实只要意识到这是切割问题，**切割问题就可以使用回溯搜索法把所有可能性搜出来**，和刚做过的[131.分割回文串](https://programmercarl.com/0131.分割回文串.html)就十分类似了。
切割问题可以抽象为树型结构，如图：
@@ -60,7 +60,7 @@ s 仅由数字组成
* 递归参数
-在[回溯算法：分割回文串](https://programmercarl.com/0131.分割回文串.html)中我们就提到切割问题类似组合问题。
+在[131.分割回文串](https://programmercarl.com/0131.分割回文串.html)中我们就提到切割问题类似组合问题。
startIndex一定是需要的，因为不能重复分割，记录下一层递归分割的起始位置。
@@ -76,7 +76,7 @@ startIndex一定是需要的，因为不能重复分割，记录下一层递归
* 递归终止条件
-终止条件和[回溯算法：分割回文串](https://programmercarl.com/0131.分割回文串.html)情况就不同了，本题明确要求只会分成4段，所以不能用切割线切到最后作为终止条件，而是分割的段数作为终止条件。
+终止条件和[131.分割回文串](https://programmercarl.com/0131.分割回文串.html)情况就不同了，本题明确要求只会分成4段，所以不能用切割线切到最后作为终止条件，而是分割的段数作为终止条件。
pointNum表示逗点数量，pointNum为3说明字符串分成了4段了。
@@ -96,7 +96,7 @@ if (pointNum == 3) { // 逗点数量为3时，分隔结束
* 单层搜索的逻辑
-在[回溯算法：分割回文串](https://programmercarl.com/0131.分割回文串.html)中已经讲过在循环遍历中如何截取子串。
+在[131.分割回文串](https://programmercarl.com/0131.分割回文串.html)中已经讲过在循环遍历中如何截取子串。
在`for (int i = startIndex; i < s.size(); i++)`循环中 [startIndex, i]这个区间就是截取的子串，需要判断这个子串是否合法。
@@ -239,11 +239,11 @@ public:
## 总结
-在[回溯算法：分割回文串](https://programmercarl.com/0131.分割回文串.html)中我列举的分割字符串的难点，本题都覆盖了。
+在[131.分割回文串](https://programmercarl.com/0131.分割回文串.html)中我列举的分割字符串的难点，本题都覆盖了。
而且本题还需要操作字符串添加逗号作为分隔符，并验证区间的合法性。
-可以说是[回溯算法：分割回文串](https://programmercarl.com/0131.分割回文串.html)的加强版。
+可以说是[131.分割回文串](https://programmercarl.com/0131.分割回文串.html)的加强版。
在本文的树形结构图中，我已经把详细的分析思路都画了出来，相信大家看了之后一定会思路清晰不少！
diff --git a/problems/0102.二叉树的层序遍历.md b/problems/0102.二叉树的层序遍历.md
index 376af7a2..5128d6ec 100644
--- a/problems/0102.二叉树的层序遍历.md
+++ b/problems/0102.二叉树的层序遍历.md
@@ -6,6 +6,7 @@
欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+# 二叉树层序遍历登场！
学会二叉树的层序遍历，可以一口气打完以下十题：
@@ -20,7 +21,6 @@
* 104.二叉树的最大深度
* 111.二叉树的最小深度
-在之前写过这篇文章 [二叉树：层序遍历登场！](https://programmercarl.com/0102.二叉树的层序遍历.html)，可惜当时只打了5个，还不够，再给我一次机会，我打十个！
diff --git a/problems/0122.买卖股票的最佳时机II.md b/problems/0122.买卖股票的最佳时机II.md
index bd837eea..4bbe9e5e 100644
--- a/problems/0122.买卖股票的最佳时机II.md
+++ b/problems/0122.买卖股票的最佳时机II.md
@@ -131,9 +131,9 @@ public:
一旦想到这里了，很自然就会想到贪心了，即：只收集每天的正利润，最后稳稳的就是最大利润了。
-## 其他语言版本
+# 其他语言版本
-Java：
+## Java
```java
// 贪心思路
@@ -171,7 +171,7 @@ class Solution { // 动态规划
-Python：
+## Python
```python
class Solution:
def maxProfit(self, prices: List[int]) -> int:
@@ -181,7 +181,21 @@ class Solution:
return result
```
-Go：
+python动态规划
+```python
+class Solution:
+ def maxProfit(self, prices: List[int]) -> int:
+ length = len(prices)
+ dp = [[0] * 2 for _ in range(length)]
+ dp[0][0] = -prices[0]
+ dp[0][1] = 0
+ for i in range(1, length):
+ dp[i][0] = max(dp[i-1][0], dp[i-1][1] - prices[i]) #注意这里是和121. 买卖股票的最佳时机唯一不同的地方
+ dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i])
+ return dp[-1][1]
+```
+
+## Go
```golang
//贪心算法
func maxProfit(prices []int) int {
@@ -217,9 +231,9 @@ func maxProfit(prices []int) int {
}
```
-Javascript:
+## Javascript
+贪心
```Javascript
-// 贪心
var maxProfit = function(prices) {
let result = 0
for(let i = 1; i < prices.length; i++) {
@@ -229,7 +243,31 @@ var maxProfit = function(prices) {
};
```
-C:
+动态规划
+```javascript
+const maxProfit = (prices) => {
+ let dp = Array.from(Array(prices.length), () => Array(2).fill(0));
+ // dp[i][0] 表示第i天持有股票所得现金。
+ // dp[i][1] 表示第i天不持有股票所得最多现金
+ dp[0][0] = 0 - prices[0];
+ dp[0][1] = 0;
+ for(let i = 1; i < prices.length; i++) {
+ // 如果第i天持有股票即dp[i][0]， 那么可以由两个状态推出来
+ // 第i-1天就持有股票，那么就保持现状，所得现金就是昨天持有股票的所得现金 即：dp[i - 1][0]
+ // 第i天买入股票，所得现金就是昨天不持有股票的所得现金减去 今天的股票价格 即：dp[i - 1][1] - prices[i]
+ dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] - prices[i]);
+
+ // 在来看看如果第i天不持有股票即dp[i][1]的情况， 依然可以由两个状态推出来
+ // 第i-1天就不持有股票，那么就保持现状，所得现金就是昨天不持有股票的所得现金 即：dp[i - 1][1]
+ // 第i天卖出股票，所得现金就是按照今天股票佳价格卖出后所得现金即：prices[i] + dp[i - 1][0]
+ dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] + prices[i]);
+ }
+
+ return dp[prices.length -1][0];
+};
+```
+
+## C
```c
int maxProfit(int* prices, int pricesSize){
int result = 0;
diff --git a/problems/0122.买卖股票的最佳时机II（动态规划）.md b/problems/0122.买卖股票的最佳时机II（动态规划）.md
index 5dfe3f0e..c324d392 100644
--- a/problems/0122.买卖股票的最佳时机II（动态规划）.md
+++ b/problems/0122.买卖股票的最佳时机II（动态规划）.md
@@ -202,6 +202,7 @@ Go：
Javascript：
```javascript
+// 方法一：动态规划（dp 数组）
const maxProfit = (prices) => {
let dp = Array.from(Array(prices.length), () => Array(2).fill(0));
// dp[i][0] 表示第i天持有股票所得现金。
@@ -222,6 +223,21 @@ const maxProfit = (prices) => {
return dp[prices.length -1][0];
};
+
+// 方法二：动态规划（滚动数组）
+const maxProfit = (prices) => {
+ // 滚动数组
+ // have: 第i天持有股票最大收益; notHave: 第i天不持有股票最大收益
+ let n = prices.length,
+ have = -prices[0],
+ notHave = 0;
+ for (let i = 1; i < n; i++) {
+ have = Math.max(have, notHave - prices[i]);
+ notHave = Math.max(notHave, have + prices[i]);
+ }
+ // 最终手里不持有股票才能保证收益最大化
+ return notHave;
+}
```
diff --git a/problems/0188.买卖股票的最佳时机IV.md b/problems/0188.买卖股票的最佳时机IV.md
index bcb8a1ab..a166db72 100644
--- a/problems/0188.买卖股票的最佳时机IV.md
+++ b/problems/0188.买卖股票的最佳时机IV.md
@@ -280,6 +280,7 @@ Go：
Javascript：
```javascript
+// 方法一：动态规划
const maxProfit = (k,prices) => {
if (prices == null || prices.length < 2 || k == 0) {
return 0;
@@ -300,6 +301,30 @@ const maxProfit = (k,prices) => {
return dp[prices.length - 1][2 * k];
};
+
+// 方法二：动态规划+空间优化
+var maxProfit = function(k, prices) {
+ let n = prices.length;
+ let dp = new Array(2*k+1).fill(0);
+ // dp 买入状态初始化
+ for (let i = 1; i <= 2*k; i += 2) {
+ dp[i] = - prices[0];
+ }
+
+ for (let i = 1; i < n; i++) {
+ for (let j = 1; j < 2*k+1; j++) {
+ // j 为奇数：买入状态
+ if (j % 2) {
+ dp[j] = Math.max(dp[j], dp[j-1] - prices[i]);
+ } else {
+ // j为偶数：卖出状态
+ dp[j] = Math.max(dp[j], dp[j-1] + prices[i]);
+ }
+ }
+ }
+
+ return dp[2*k];
+};
```
-----------------------
diff --git a/problems/0216.组合总和III.md b/problems/0216.组合总和III.md
index 10491553..d7ab6cf7 100644
--- a/problems/0216.组合总和III.md
+++ b/problems/0216.组合总和III.md
@@ -30,7 +30,7 @@
输出: [[1,2,6], [1,3,5], [2,3,4]]
-## 思路
+# 思路
本题就是在[1,2,3,4,5,6,7,8,9]这个集合中找到和为n的k个数的组合。
@@ -180,7 +180,7 @@ if (sum > targetSum) { // 剪枝操作
最后C++代码如下：
-```c++
+```CPP
class Solution {
private:
vector> result; // 存放结果集
@@ -223,10 +223,10 @@ public:
-## 其他语言版本
+# 其他语言版本
-Java：
+## Java
模板方法
```java
@@ -299,7 +299,8 @@ class Solution {
}
```
-Python：
+## Python
+
```py
class Solution:
def combinationSum3(self, k: int, n: int) -> List[List[int]]:
@@ -320,10 +321,9 @@ class Solution:
return res
```
-Go：
+## Go：
-
-> 回溯+减枝
+回溯+减枝
```go
func combinationSum3(k int, n int) [][]int {
@@ -353,7 +353,7 @@ func backTree(n,k,startIndex int,track *[]int,result *[][]int){
}
```
-javaScript:
+## javaScript:
```js
// 等差数列
diff --git a/problems/0309.最佳买卖股票时机含冷冻期.md b/problems/0309.最佳买卖股票时机含冷冻期.md
index 59178c64..1bb38568 100644
--- a/problems/0309.最佳买卖股票时机含冷冻期.md
+++ b/problems/0309.最佳买卖股票时机含冷冻期.md
@@ -27,7 +27,6 @@
## 思路
-> 之前我们在[动态规划：最佳买卖股票时机含冷冻期](https://programmercarl.com/0309.最佳买卖股票时机含冷冻期.html)讲过一次这道题目，讲解的过程感觉不是很严谨，和录友们也聊过这个问题，本着对大家负责的态度，有问题的地方我都会及时纠正，所以重新发文讲解一下。
相对于[动态规划：122.买卖股票的最佳时机II](https://programmercarl.com/0122.买卖股票的最佳时机II（动态规划）.html)，本题加上了一个冷冻期
diff --git a/problems/0450.删除二叉搜索树中的节点.md b/problems/0450.删除二叉搜索树中的节点.md
index b12d40aa..f5133b84 100644
--- a/problems/0450.删除二叉搜索树中的节点.md
+++ b/problems/0450.删除二叉搜索树中的节点.md
@@ -472,7 +472,6 @@ var deleteNode = function (root, key) {
cur = cur.left;
}
cur.left = root.left;
- let temp = root;
root = root.right;
delete root;
return root;
diff --git a/problems/0491.递增子序列.md b/problems/0491.递增子序列.md
index ea113f4b..d3dc3472 100644
--- a/problems/0491.递增子序列.md
+++ b/problems/0491.递增子序列.md
@@ -33,11 +33,11 @@
这个递增子序列比较像是取有序的子集。而且本题也要求不能有相同的递增子序列。
-这又是子集，又是去重，是不是不由自主的想起了刚刚讲过的[回溯算法：求子集问题（二）](https://programmercarl.com/0090.子集II.html)。
+这又是子集，又是去重，是不是不由自主的想起了刚刚讲过的[90.子集II](https://programmercarl.com/0090.子集II.html)。
就是因为太像了，更要注意差别所在，要不就掉坑里了！
-在[回溯算法：求子集问题（二）](https://programmercarl.com/0090.子集II.html)中我们是通过排序，再加一个标记数组来达到去重的目的。
+在[90.子集II](https://programmercarl.com/0090.子集II.html)中我们是通过排序，再加一个标记数组来达到去重的目的。
而本题求自增子序列，是不能对原数组经行排序的，排完序的数组都是自增子序列了。
diff --git a/problems/0941.有效的山脉数组.md b/problems/0941.有效的山脉数组.md
index ef5739e3..607031da 100644
--- a/problems/0941.有效的山脉数组.md
+++ b/problems/0941.有效的山脉数组.md
@@ -50,7 +50,7 @@
C++代码如下：
-```c++
+```CPP
class Solution {
public:
bool validMountainArray(vector& A) {
diff --git a/problems/1035.不相交的线.md b/problems/1035.不相交的线.md
index b71a5199..a10fd381 100644
--- a/problems/1035.不相交的线.md
+++ b/problems/1035.不相交的线.md
@@ -28,8 +28,8 @@
拿示例一A = [1,4,2], B = [1,2,4]为例，相交情况如图：
-
+
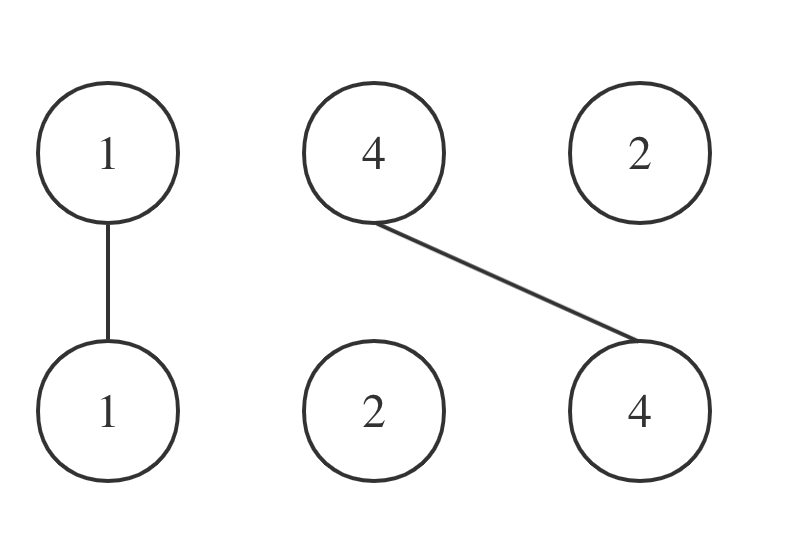
其实也就是说A和B的最长公共子序列是[1,4]，长度为2。 这个公共子序列指的是相对顺序不变（即数字4在字符串A中数字1的后面，那么数字4也应该在字符串B数字1的后面）
diff --git a/problems/前序/ACM模式如何构建二叉树.md b/problems/前序/ACM模式如何构建二叉树.md
new file mode 100644
index 00000000..682e18f5
--- /dev/null
+++ b/problems/前序/ACM模式如何构建二叉树.md
@@ -0,0 +1,243 @@
+
+
+ 
+ 
+ 
+ 
+
+欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+
+
+# 力扣上如何自己构造二叉树输入用例？
+
+经常有录友问，二叉树的题目中输入用例在ACM模式下应该怎么构造呢？
+
+力扣上的题目，输入用例就给了一个数组，怎么就能构造成二叉树呢？
+
+这次就给大家好好讲一讲！
+
+就拿最近公众号上 二叉树的打卡题目来说：
+
+[538.把二叉搜索树转换为累加树](https://mp.weixin.qq.com/s/rlJUFGCnXsIMX0Lg-fRpIw)
+
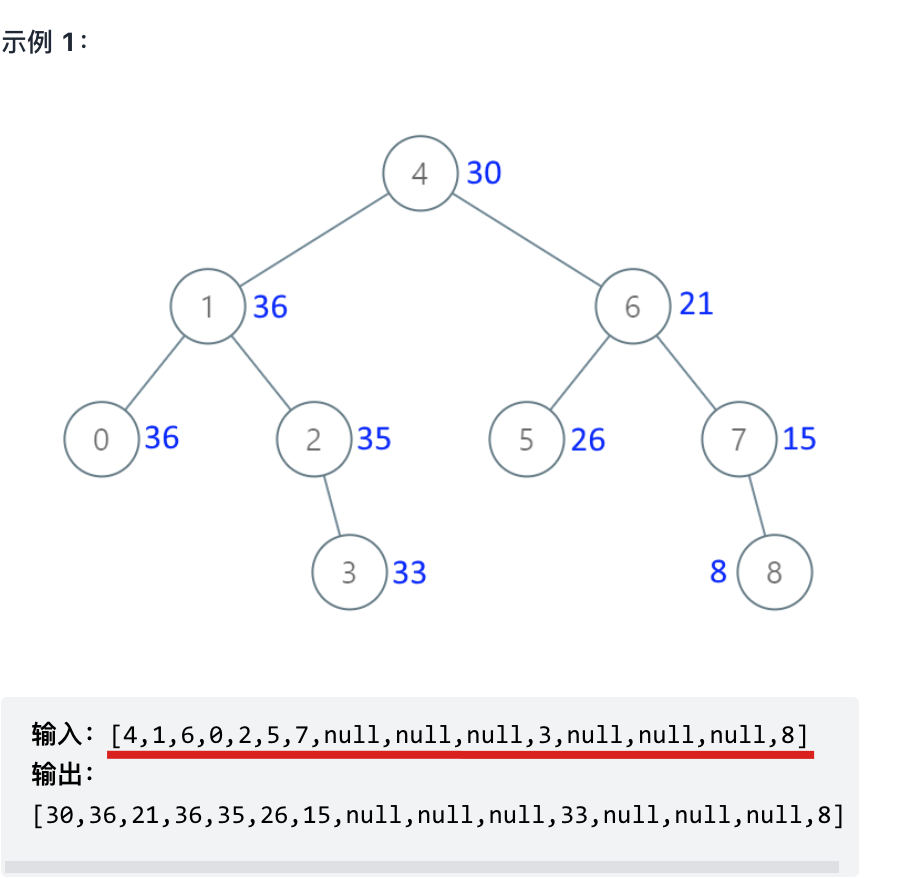
+其输入用例，就是用一个数组来表述 二叉树，如下：
+
+
+
+一直跟着公众号学算法的录友 应该知道，我在[二叉树：构造二叉树登场！](https://mp.weixin.qq.com/s/Dza-fqjTyGrsRw4PWNKdxA)，已经讲过，**只有 中序与后序 和 中序和前序 可以确定一颗唯一的二叉树。 前序和后序是不能确定唯一的二叉树的**。
+
+那么[538.把二叉搜索树转换为累加树](https://mp.weixin.qq.com/s/rlJUFGCnXsIMX0Lg-fRpIw)的示例中，为什么，一个序列（数组或者是字符串）就可以确定二叉树了呢？
+
+很明显，是后台直接明确了构造规则。
+
+再看一下 这个 输入序列 和 对应的二叉树。
+
+
+从二叉树 推导到 序列，大家可以发现这就是层序遍历。
+
+但从序列 推导到 二叉树，很多同学就看不懂了，这得怎么转换呢。
+
+我在 [关于二叉树，你该了解这些！](https://mp.weixin.qq.com/s/q_eKfL8vmSbSFcptZ3aeRA)已经详细讲过，二叉树可以有两种存储方式，一种是 链式存储，另一种是顺序存储。
+
+链式存储，就是大家熟悉的二叉树，用指针指向左右孩子。
+
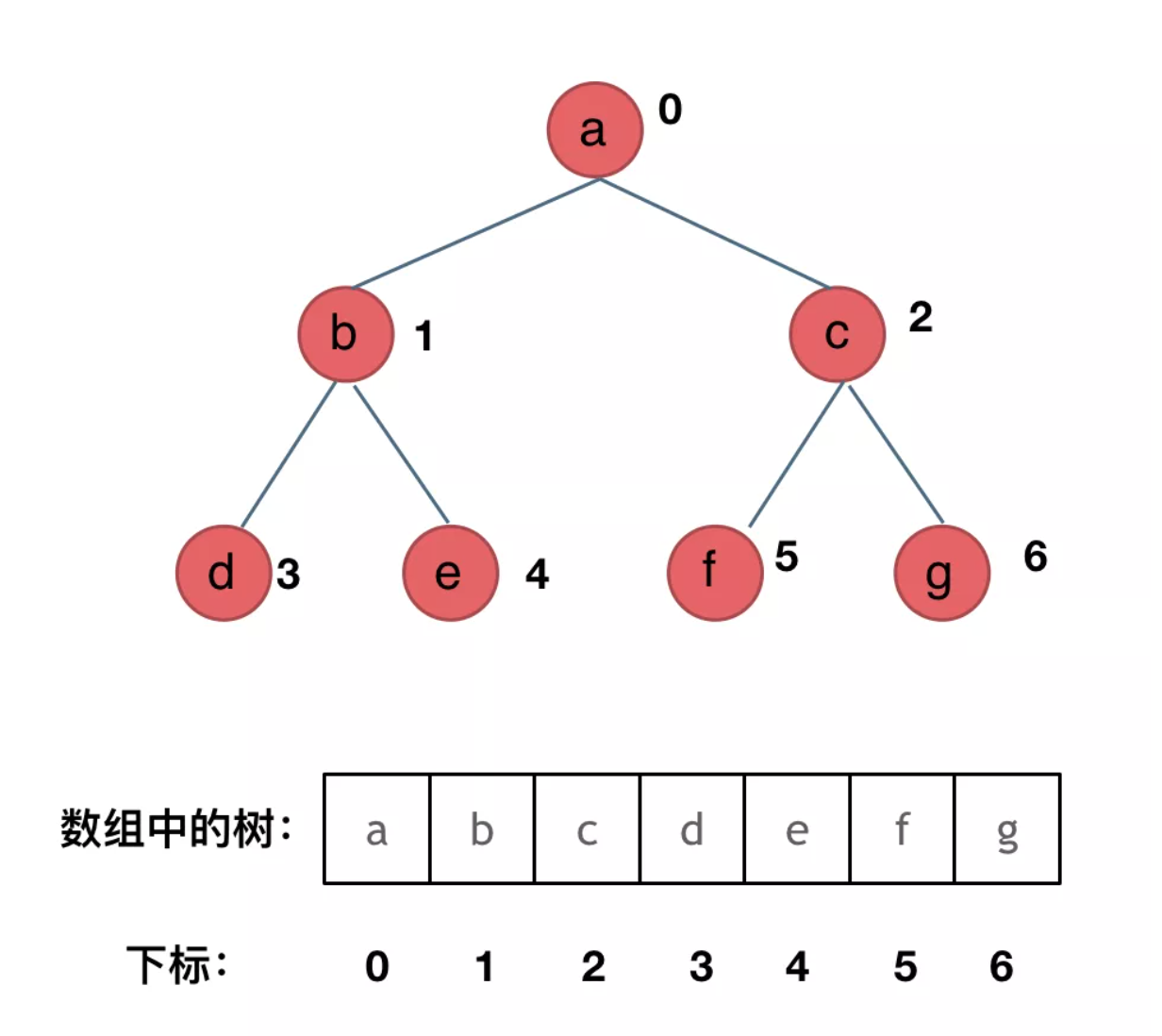
+顺序存储，就是用一个数组来存二叉树，其方式如图所示：
+
+
+
+那么此时大家是不是应该知道了，数组如何转化成 二叉树了。**如果父节点的数组下标是i，那么它的左孩子下标就是i * 2 + 1，右孩子下标就是 i * 2 + 2**。
+
+那么这里又有同学疑惑了，这些我都懂了，但我还是不知道 应该 怎么构造。
+
+来，咱上代码。 昨天晚上 速度敲了一遍实现代码。
+
+具体过程看注释：
+
+```CPP
+// 根据数组构造二叉树
+TreeNode* construct_binary_tree(const vector& vec) {
+ vector vecTree (vec.size(), NULL);
+ TreeNode* root = NULL;
+ // 把输入数值数组，先转化为二叉树节点数组
+ for (int i = 0; i < vec.size(); i++) {
+ TreeNode* node = NULL;
+ if (vec[i] != -1) node = new TreeNode(vec[i]); // 用 -1 表示null
+ vecTree[i] = node;
+ if (i == 0) root = node;
+ }
+ // 遍历一遍，根据规则左右孩子赋值就可以了
+ // 注意这里 结束规则是 i * 2 + 2 < vec.size()，避免空指针
+ for (int i = 0; i * 2 + 2 < vec.size(); i++) {
+ if (vecTree[i] != NULL) {
+ // 线性存储转连式存储关键逻辑
+ vecTree[i]->left = vecTree[i * 2 + 1];
+ vecTree[i]->right = vecTree[i * 2 + 2];
+ }
+ }
+ return root;
+}
+```
+
+这个函数最后返回的 指针就是 根节点的指针， 这就是 传入二叉树的格式了，也就是 力扣上的用例输入格式，如图：
+
+
+
+也有不少同学在做ACM模式的题目，就经常疑惑：
+
+* 让我传入数值，我会！
+* 让我传入数组，我会！
+* 让我传入链表，我也会！
+* **让我传入二叉树，我懵了，啥？ 传入二叉树？二叉树怎么传？**
+
+其实传入二叉树，就是传入二叉树的根节点的指针，和传入链表都是一个逻辑。
+
+这种现象主要就是大家对ACM模式过于陌生，说实话，ACM模式才真正的考察代码能力（注意不是算法能力），而 力扣的核心代码模式 总有一种 不够彻底的感觉。
+
+所以，如果大家对ACM模式不够了解，一定要多去练习！
+
+那么以上的代码，我们根据数组构造二叉树，接来下我们在 把 这个二叉树打印出来，看看是不是 我们输入的二叉树结构，这里就用到了层序遍历，我们在[二叉树：层序遍历登场！](https://mp.weixin.qq.com/s/4-bDKi7SdwfBGRm9FYduiA)中讲过。
+
+
+完整测试代码如下：
+
+```CPP
+#include
+#include
+#include
+using namespace std;
+
+struct TreeNode {
+ int val;
+ TreeNode *left;
+ TreeNode *right;
+ TreeNode(int x) : val(x), left(NULL), right(NULL) {}
+};
+
+// 根据数组构造二叉树
+TreeNode* construct_binary_tree(const vector& vec) {
+ vector vecTree (vec.size(), NULL);
+ TreeNode* root = NULL;
+ for (int i = 0; i < vec.size(); i++) {
+ TreeNode* node = NULL;
+ if (vec[i] != -1) node = new TreeNode(vec[i]);
+ vecTree[i] = node;
+ if (i == 0) root = node;
+ }
+ for (int i = 0; i * 2 + 2 < vec.size(); i++) {
+ if (vecTree[i] != NULL) {
+ vecTree[i]->left = vecTree[i * 2 + 1];
+ vecTree[i]->right = vecTree[i * 2 + 2];
+ }
+ }
+ return root;
+}
+
+// 层序打印打印二叉树
+void print_binary_tree(TreeNode* root) {
+ queue que;
+ if (root != NULL) que.push(root);
+ vector> result;
+ while (!que.empty()) {
+ int size = que.size();
+ vector vec;
+ for (int i = 0; i < size; i++) {
+ TreeNode* node = que.front();
+ que.pop();
+ if (node != NULL) {
+ vec.push_back(node->val);
+ que.push(node->left);
+ que.push(node->right);
+ }
+ // 这里的处理逻辑是为了把null节点打印出来，用-1 表示null
+ else vec.push_back(-1);
+ }
+ result.push_back(vec);
+ }
+ for (int i = 0; i < result.size(); i++) {
+ for (int j = 0; j < result[i].size(); j++) {
+ cout << result[i][j] << " ";
+ }
+ cout << endl;
+ }
+}
+
+int main() {
+ // 注意本代码没有考虑输入异常数据的情况
+ // 用 -1 来表示null
+ vector vec = {4,1,6,0,2,5,7,-1,-1,-1,3,-1,-1,-1,8};
+ TreeNode* root = construct_binary_tree(vec);
+ print_binary_tree(root);
+}
+
+```
+
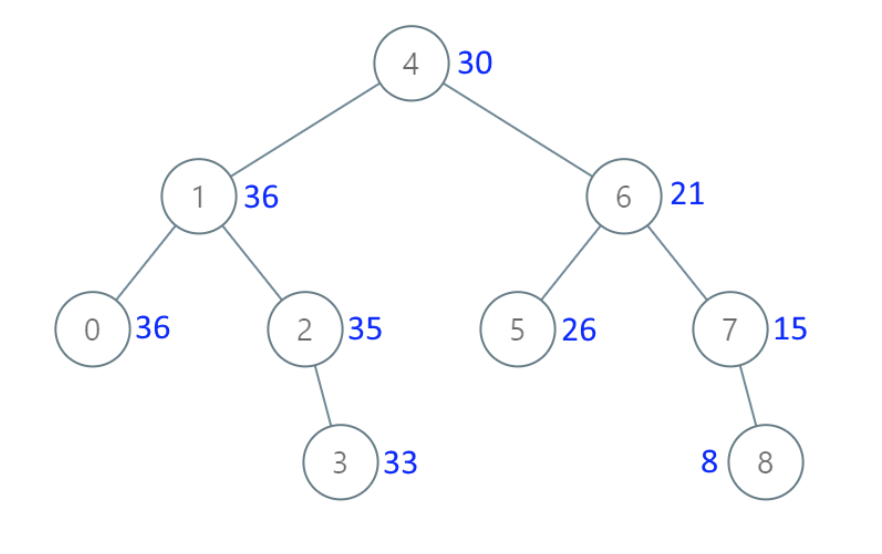
+可以看出我们传入的数组是：{4,1,6,0,2,5,7,-1,-1,-1,3,-1,-1,-1,8} ， 这里是用 -1 来表示null，
+
+和 [538.把二叉搜索树转换为累加树](https://mp.weixin.qq.com/s/rlJUFGCnXsIMX0Lg-fRpIw) 中的输入是一样的
+
+
+
+这里可能又有同学疑惑，你这不一样啊，题目是null，你为啥用-1。
+
+用-1 表示null为了方便举例，如果非要和 力扣输入一样一样的，就是简单的字符串处理，把null 替换为 -1 就行了。
+
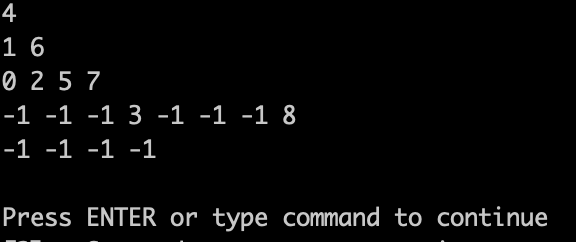
+在来看，测试代码输出的效果：
+
+
+
+可以看出和 题目中输入用例 这个图 是一样一样的。 只不过题目中图没有把 空节点 画出来而已。
+
+
+
+大家可以拿我的代码去测试一下，跑一跑。
+
+**注意：我的测试代码，并没有处理输入异常的情况（例如输入空数组之类的），处理各种输入异常，大家可以自己去练练**。
+
+
+# 总结
+
+大家可以发现，这个问题，其实涉及很多知识点，而这些知识点 其实我在文章里都讲过，而且是详细的讲过，如果大家能把这些知识点串起来，很容易解决心中的疑惑了。
+
+但为什么很多录友都没有想到这个程度呢。
+
+这也是我反复强调，**代码随想录上的 题目和理论基础，至少要详细刷两遍**。
+
+**[知识星球](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ)**里有的录友已经开始三刷：
+
+
+
+只做过一遍，真的就是懂了一点皮毛， 第二遍刷才有真的对各个题目有较为深入的理解，也会明白 我为什么要这样安排刷题的顺序了。
+
+**都是卡哥的良苦用心呀！**
+
+
+# 其他语言版本
+
+
+## Java
+
+```Java
+```
+
+
+## Python
+
+```Python
+```
+
+
+## Go
+
+```Go
+```
+
+## JavaScript
+
+```JavaScript
+```
+
+-----------------------
+* 作者微信：[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
+* B站视频：[代码随想录](https://space.bilibili.com/525438321)
+* 知识星球：[代码随想录](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ)
+
diff --git a/problems/前序/递归算法的时间与空间复杂度分析.md b/problems/前序/递归算法的时间与空间复杂度分析.md
index 7a690781..63376d11 100644
--- a/problems/前序/递归算法的时间与空间复杂度分析.md
+++ b/problems/前序/递归算法的时间与空间复杂度分析.md
@@ -247,7 +247,7 @@ int binary_search( int arr[], int l, int r, int x) {
每次递归的空间复杂度可以看出主要就是参数里传入的这个arr数组，但需要注意的是在C/C++中函数传递数组参数，不是整个数组拷贝一份传入函数而是传入的数组首元素地址。
-**也就是说每一层递归都是公用一块数组地址空间的**，所以 每次递归的时间复杂度是常数即：O(1)。
+**也就是说每一层递归都是公用一块数组地址空间的**，所以 每次递归的空间复杂度是常数即：O(1)。
再来看递归的深度，二分查找的递归深度是logn ，递归深度就是调用栈的长度，那么这段代码的空间复杂度为 1 * logn = O(logn)。
diff --git a/problems/知识星球精选/合适自己的就是最好的.md b/problems/知识星球精选/合适自己的就是最好的.md
new file mode 100644
index 00000000..2f28483e
--- /dev/null
+++ b/problems/知识星球精选/合适自己的就是最好的.md
@@ -0,0 +1,32 @@
+# 合适自己的，才是最好的！
+
+秋招已经进入下半场了，不少同学也拿到了offer，但不是说非要进大厂，每个人情况都不一样，**合适自己的，就是最好的！**。
+
+知识星球里有一位录友，就终于拿到了合适自己的offer，并不是大厂，是南京的一家公司，**但很合适自己，其实就非常值得开心**。
+
+
+
+
+
+其实我算是一路见证了这位录友披荆斩棘，**从一开始基础并不好，还是非科班，到 实验室各种不顺利，再到最后面试次次受打击，最后终于拿到自己满意的offer**。
+
+这一路下来确实不容易！
+
+这位录友是从几年五月份加入星球。
+
+
+
+然后就开始每天坚持打卡。 可以看看她每天的打卡内容。
+
+
+
+后面因为天天面试，不能坚持打卡了，也是和大部分同学一样，焦虑并努力着。
+
+
+
+星球里完整的记录了 这位录友 从五月份以来每天的学习内容和学习状态，能感觉出来 **虽然苦难重重，但依然元气满满！**
+
+我在发文的时候 看了一遍她这几个月完整的打卡过程，还是深有感触的。
+
+星球里还有很多很多这样的录友在每日奋斗着，**我相信 等大家拿到offer之后，在回头看一下当初星球里曾经每日打卡的点点滴滴，不仅会感动自己 也会感动每一位见证者**。
+
+
+
1. [关于贪心算法，你该了解这些！](./problems/贪心算法理论基础.md)
2. [贪心算法：分发饼干](./problems/0455.分发饼干.md)
diff --git a/problems/0017.电话号码的字母组合.md b/problems/0017.电话号码的字母组合.md
index 1221115c..ef485a39 100644
--- a/problems/0017.电话号码的字母组合.md
+++ b/problems/0017.电话号码的字母组合.md
@@ -29,7 +29,7 @@
如果输入"233"呢，那么就三层for循环，如果"2333"呢，就四层for循环.......
-大家应该感觉出和[回溯算法：求组合问题！](https://programmercarl.com/0077.组合.html)遇到的一样的问题，就是这for循环的层数如何写出来，此时又是回溯法登场的时候了。
+大家应该感觉出和[77.组合](https://programmercarl.com/0077.组合.html)遇到的一样的问题，就是这for循环的层数如何写出来，此时又是回溯法登场的时候了。
理解本题后，要解决如下三个问题：
@@ -75,7 +75,7 @@ const string letterMap[10] = {
再来看参数，参数指定是有题目中给的string digits，然后还要有一个参数就是int型的index。
-注意这个index可不是 [回溯算法：求组合问题！](https://programmercarl.com/0077.组合.html)和[回溯算法：求组合总和！](https://programmercarl.com/0216.组合总和III.html)中的startIndex了。
+注意这个index可不是 [77.组合](https://programmercarl.com/0077.组合.html)和[216.组合总和III](https://programmercarl.com/0216.组合总和III.html)中的startIndex了。
这个index是记录遍历第几个数字了，就是用来遍历digits的（题目中给出数字字符串），同时index也表示树的深度。
@@ -110,7 +110,7 @@ if (index == digits.size()) {
然后for循环来处理这个字符集，代码如下：
-```
+```CPP
int digit = digits[index] - '0'; // 将index指向的数字转为int
string letters = letterMap[digit]; // 取数字对应的字符集
for (int i = 0; i < letters.size(); i++) {
@@ -137,7 +137,7 @@ for (int i = 0; i < letters.size(); i++) {
关键地方都讲完了，按照[关于回溯算法，你该了解这些！](https://programmercarl.com/回溯算法理论基础.html)中的回溯法模板，不难写出如下C++代码：
-```c++
+```CPP
// 版本一
class Solution {
private:
@@ -183,7 +183,7 @@ public:
一些写法，是把回溯的过程放在递归函数里了，例如如下代码，我可以写成这样：（注意注释中不一样的地方）
-```c++
+```CPP
// 版本二
class Solution {
private:
@@ -236,10 +236,10 @@ public:
-## 其他语言版本
+# 其他语言版本
-Java：
+## Java
```Java
class Solution {
@@ -281,7 +281,7 @@ class Solution {
}
```
-Python：
+## Python
```Python
class Solution:
@@ -340,10 +340,9 @@ class Solution:
```
-Go：
+## Go
-
-> 主要在于递归中传递下一个数字
+主要在于递归中传递下一个数字
```go
func letterCombinations(digits string) []string {
@@ -382,7 +381,7 @@ func recursion(tempString ,digits string, Index int,digitsMap [10]string, res *[
}
```
-javaScript：
+## javaScript
```js
var letterCombinations = function(digits) {
diff --git a/problems/0037.解数独.md b/problems/0037.解数独.md
index b6fa0d6e..94c5c198 100644
--- a/problems/0037.解数独.md
+++ b/problems/0037.解数独.md
@@ -376,6 +376,61 @@ class Solution:
Go：
+```go
+func solveSudoku(board [][]byte) {
+ var backtracking func(board [][]byte) bool
+ backtracking=func(board [][]byte) bool{
+ for i:=0;i<9;i++{
+ for j:=0;j<9;j++{
+ //判断此位置是否适合填数字
+ if board[i][j]!='.'{
+ continue
+ }
+ //尝试填1-9
+ for k:='1';k<='9';k++{
+ if isvalid(i,j,byte(k),board)==true{//如果满足要求就填
+ board[i][j]=byte(k)
+ if backtracking(board)==true{
+ return true
+ }
+ board[i][j]='.'
+ }
+ }
+ return false
+ }
+ }
+ return true
+ }
+ backtracking(board)
+}
+//判断填入数字是否满足要求
+func isvalid(row,col int,k byte,board [][]byte)bool{
+ for i:=0;i<9;i++{//行
+ if board[row][i]==k{
+ return false
+ }
+ }
+ for i:=0;i<9;i++{//列
+ if board[i][col]==k{
+ return false
+ }
+ }
+ //方格
+ startrow:=(row/3)*3
+ startcol:=(col/3)*3
+ for i:=startrow;i