mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-06 23:28:29 +08:00
Update
This commit is contained in:
@ -25,21 +25,15 @@
|
||||
|
||||
## 思路
|
||||
|
||||
大家应该都感觉到了,此题一定要排序,那么按照左边界排序,还是右边界排序呢?
|
||||
本题的本质其实还是判断重叠区间问题。
|
||||
|
||||
都可以!
|
||||
大家如果认真做题的话,话发现和我们刚刚讲过的[452. 用最少数量的箭引爆气球](https://programmercarl.com/0452.用最少数量的箭引爆气球.html) 和 [435. 无重叠区间](https://programmercarl.com/0435.无重叠区间.html) 都是一个套路。
|
||||
|
||||
那么我按照左边界排序,排序之后局部最优:每次合并都取最大的右边界,这样就可以合并更多的区间了,整体最优:合并所有重叠的区间。
|
||||
这几道题都是判断区间重叠,区别就是判断区间重叠后的逻辑,本题是判断区间重贴后要进行区间合并。
|
||||
|
||||
局部最优可以推出全局最优,找不出反例,试试贪心。
|
||||
所以一样的套路,先排序,让所有的相邻区间尽可能的重叠在一起,按左边界,或者右边界排序都可以,处理逻辑稍有不同。
|
||||
|
||||
那有同学问了,本来不就应该合并最大右边界么,这和贪心有啥关系?
|
||||
|
||||
有时候贪心就是常识!哈哈
|
||||
|
||||
按照左边界从小到大排序之后,如果 `intervals[i][0] < intervals[i - 1][1]` 即intervals[i]左边界 < intervals[i - 1]右边界,则一定有重复,因为intervals[i]的左边界一定是大于等于intervals[i - 1]的左边界。
|
||||
|
||||
即:intervals[i]的左边界在intervals[i - 1]左边界和右边界的范围内,那么一定有重复!
|
||||
按照左边界从小到大排序之后,如果 `intervals[i][0] <= intervals[i - 1][1]` 即intervals[i]的左边界 <= intervals[i - 1]的右边界,则一定有重叠。(本题相邻区间也算重贴,所以是<=)
|
||||
|
||||
这么说有点抽象,看图:(**注意图中区间都是按照左边界排序之后了**)
|
||||
|
||||
@ -54,54 +48,21 @@ C++代码如下:
|
||||
```CPP
|
||||
class Solution {
|
||||
public:
|
||||
// 按照区间左边界从小到大排序
|
||||
static bool cmp (const vector<int>& a, const vector<int>& b) {
|
||||
return a[0] < b[0];
|
||||
}
|
||||
vector<vector<int>> merge(vector<vector<int>>& intervals) {
|
||||
vector<vector<int>> result;
|
||||
if (intervals.size() == 0) return result;
|
||||
sort(intervals.begin(), intervals.end(), cmp);
|
||||
bool flag = false; // 标记最后一个区间有没有合并
|
||||
int length = intervals.size();
|
||||
|
||||
for (int i = 1; i < length; i++) {
|
||||
int start = intervals[i - 1][0]; // 初始为i-1区间的左边界
|
||||
int end = intervals[i - 1][1]; // 初始i-1区间的右边界
|
||||
while (i < length && intervals[i][0] <= end) { // 合并区间
|
||||
end = max(end, intervals[i][1]); // 不断更新右区间
|
||||
if (i == length - 1) flag = true; // 最后一个区间也合并了
|
||||
i++; // 继续合并下一个区间
|
||||
}
|
||||
// start和end是表示intervals[i - 1]的左边界右边界,所以最优intervals[i]区间是否合并了要标记一下
|
||||
result.push_back({start, end});
|
||||
}
|
||||
// 如果最后一个区间没有合并,将其加入result
|
||||
if (flag == false) {
|
||||
result.push_back({intervals[length - 1][0], intervals[length - 1][1]});
|
||||
}
|
||||
return result;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
当然以上代码有冗余一些,可以优化一下,如下:(思路是一样的)
|
||||
|
||||
```CPP
|
||||
class Solution {
|
||||
public:
|
||||
vector<vector<int>> merge(vector<vector<int>>& intervals) {
|
||||
vector<vector<int>> result;
|
||||
if (intervals.size() == 0) return result;
|
||||
if (intervals.size() == 0) return result; // 区间集合为空直接返回
|
||||
// 排序的参数使用了lambda表达式
|
||||
sort(intervals.begin(), intervals.end(), [](const vector<int>& a, const vector<int>& b){return a[0] < b[0];});
|
||||
|
||||
// 第一个区间就可以放进结果集里,后面如果重叠,在result上直接合并
|
||||
result.push_back(intervals[0]);
|
||||
|
||||
for (int i = 1; i < intervals.size(); i++) {
|
||||
if (result.back()[1] >= intervals[i][0]) { // 合并区间
|
||||
if (result.back()[1] >= intervals[i][0]) { // 发现重叠区间
|
||||
// 合并区间,只更新右边界就好,因为result.back()的左边界一定是最小值,因为我们按照左边界排序的
|
||||
result.back()[1] = max(result.back()[1], intervals[i][1]);
|
||||
} else {
|
||||
result.push_back(intervals[i]);
|
||||
result.push_back(intervals[i]); // 区间不重叠
|
||||
}
|
||||
}
|
||||
return result;
|
||||
@ -109,25 +70,6 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度:O(nlog n) ,有一个快排
|
||||
* 空间复杂度:O(n),有一个快排,最差情况(倒序)时,需要n次递归调用。因此确实需要O(n)的栈空间
|
||||
|
||||
|
||||
## 总结
|
||||
|
||||
对于贪心算法,很多同学都是:**如果能凭常识直接做出来,就会感觉不到自己用了贪心, 一旦第一直觉想不出来, 可能就一直想不出来了**。
|
||||
|
||||
跟着「代码随想录」刷题的录友应该感受过,贪心难起来,真的难。
|
||||
|
||||
那应该怎么办呢?
|
||||
|
||||
正如我贪心系列开篇词[关于贪心算法,你该了解这些!](https://programmercarl.com/贪心算法理论基础.html)中讲解的一样,贪心本来就没有套路,也没有框架,所以各种常规解法需要多接触多练习,自然而然才会想到。
|
||||
|
||||
「代码随想录」会把贪心常见的经典题目覆盖到,大家只要认真学习打卡就可以了。
|
||||
|
||||
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
|
||||
|
||||
@ -65,7 +65,7 @@ public:
|
||||
for (int i = 0; i < cost.size(); i++) {
|
||||
int rest = gas[i] - cost[i]; // 记录剩余油量
|
||||
int index = (i + 1) % cost.size();
|
||||
while (rest > 0 && index != i) { // 模拟以i为起点行驶一圈
|
||||
while (rest > 0 && index != i) { // 模拟以i为起点行驶一圈(如果有rest==0,那么答案就不唯一了)
|
||||
rest += gas[index] - cost[index];
|
||||
index = (index + 1) % cost.size();
|
||||
}
|
||||
|
||||
@ -59,10 +59,15 @@ for (int i = 1; i < ratings.size(); i++) {
|
||||
|
||||
遍历顺序这里有同学可能会有疑问,为什么不能从前向后遍历呢?
|
||||
|
||||
因为如果从前向后遍历,根据 ratings[i + 1] 来确定 ratings[i] 对应的糖果,那么每次都不能利用上前一次的比较结果了。
|
||||
因为 rating[5]与rating[4]的比较 要利用上 rating[5]与rating[6]的比较结果,所以 要从后向前遍历。
|
||||
|
||||
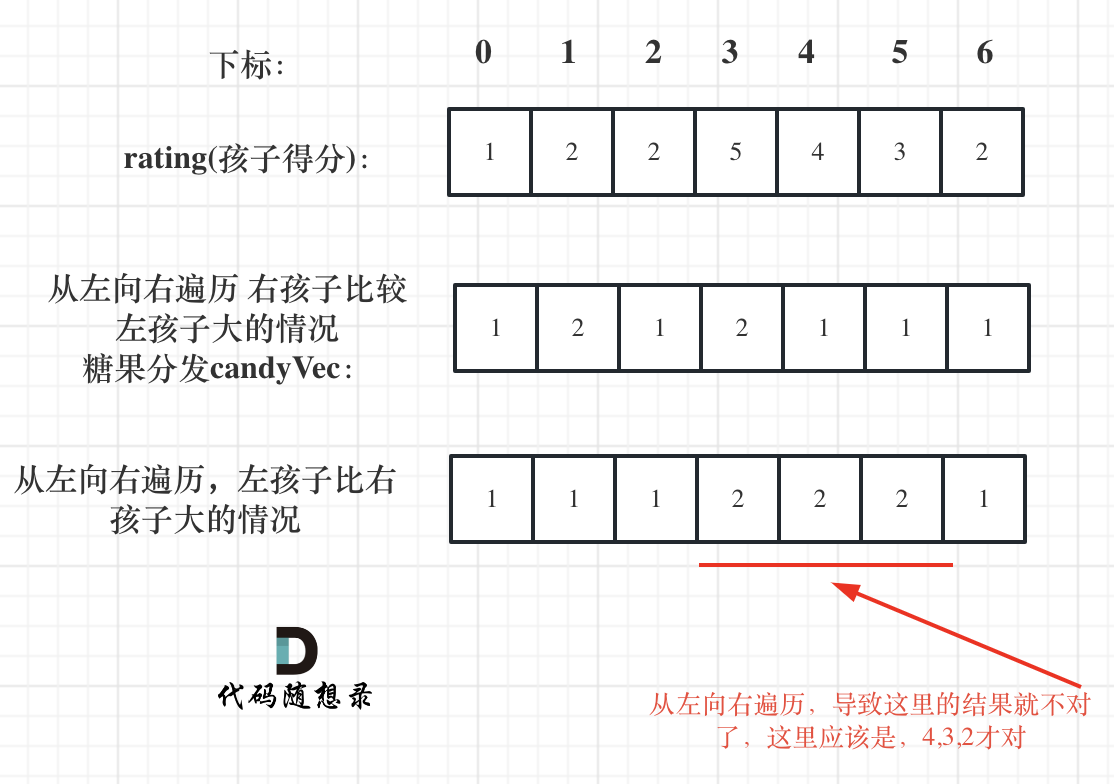
如果从前向后遍历,rating[5]与rating[4]的比较 就不能用上 rating[5]与rating[6]的比较结果了 。如图:
|
||||
|
||||
|
||||
|
||||
**所以确定左孩子大于右孩子的情况一定要从后向前遍历!**
|
||||
|
||||
|
||||
如果 ratings[i] > ratings[i + 1],此时candyVec[i](第i个小孩的糖果数量)就有两个选择了,一个是candyVec[i + 1] + 1(从右边这个加1得到的糖果数量),一个是candyVec[i](之前比较右孩子大于左孩子得到的糖果数量)。
|
||||
|
||||
那么又要贪心了,局部最优:取candyVec[i + 1] + 1 和 candyVec[i] 最大的糖果数量,保证第i个小孩的糖果数量既大于左边的也大于右边的。全局最优:相邻的孩子中,评分高的孩子获得更多的糖果。
|
||||
|
||||
@ -33,6 +33,11 @@
|
||||
* 输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
|
||||
* 输出: false
|
||||
|
||||
# 算法公开课
|
||||
|
||||
**《代码随想录》算法视频公开课:[你的背包如何装满?| LeetCode:139.单词拆分](https://www.bilibili.com/video/BV1pd4y147Rh/),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
|
||||
## 思路
|
||||
|
||||
看到这道题目的时候,大家应该回想起我们之前讲解回溯法专题的时候,讲过的一道题目[回溯算法:分割回文串](https://programmercarl.com/0131.分割回文串.html),就是枚举字符串的所有分割情况。
|
||||
|
||||
@ -16,18 +16,23 @@
|
||||
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
|
||||
|
||||
示例 1:
|
||||
输入:n = 12
|
||||
输出:3
|
||||
解释:12 = 4 + 4 + 4
|
||||
* 输入:n = 12
|
||||
* 输出:3
|
||||
* 解释:12 = 4 + 4 + 4
|
||||
|
||||
示例 2:
|
||||
输入:n = 13
|
||||
输出:2
|
||||
解释:13 = 4 + 9
|
||||
* 输入:n = 13
|
||||
* 输出:2
|
||||
* 解释:13 = 4 + 9
|
||||
|
||||
提示:
|
||||
* 1 <= n <= 10^4
|
||||
|
||||
# 算法公开课
|
||||
|
||||
**《代码随想录》算法视频公开课:[换汤不换药!| LeetCode:279.完全平方数](https://www.bilibili.com/video/BV12P411T7Br/),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
|
||||
## 思路
|
||||
|
||||
可能刚看这种题感觉没啥思路,又平方和的,又最小数的。
|
||||
|
||||
@ -13,25 +13,25 @@
|
||||
你可以认为每种硬币的数量是无限的。
|
||||
|
||||
示例 1:
|
||||
输入:coins = [1, 2, 5], amount = 11
|
||||
输出:3
|
||||
解释:11 = 5 + 5 + 1
|
||||
* 输入:coins = [1, 2, 5], amount = 11
|
||||
* 输出:3
|
||||
* 解释:11 = 5 + 5 + 1
|
||||
|
||||
示例 2:
|
||||
输入:coins = [2], amount = 3
|
||||
输出:-1
|
||||
* 输入:coins = [2], amount = 3
|
||||
* 输出:-1
|
||||
|
||||
示例 3:
|
||||
输入:coins = [1], amount = 0
|
||||
输出:0
|
||||
* 输入:coins = [1], amount = 0
|
||||
* 输出:0
|
||||
|
||||
示例 4:
|
||||
输入:coins = [1], amount = 1
|
||||
输出:1
|
||||
* 输入:coins = [1], amount = 1
|
||||
* 输出:1
|
||||
|
||||
示例 5:
|
||||
输入:coins = [1], amount = 2
|
||||
输出:2
|
||||
* 输入:coins = [1], amount = 2
|
||||
* 输出:2
|
||||
|
||||
提示:
|
||||
|
||||
@ -39,6 +39,12 @@
|
||||
* 1 <= coins[i] <= 2^31 - 1
|
||||
* 0 <= amount <= 10^4
|
||||
|
||||
# 算法公开课
|
||||
|
||||
**《代码随想录》算法视频公开课:[装满背包最少的物品件数是多少?| LeetCode:322.零钱兑换](https://www.bilibili.com/video/BV14K411R7yv/),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
|
||||
|
||||
## 思路
|
||||
|
||||
在[动态规划:518.零钱兑换II](https://programmercarl.com/0518.零钱兑换II.html)中我们已经兑换一次零钱了,这次又要兑换,套路不一样!
|
||||
|
||||
@ -172,7 +172,8 @@ return {val2, val1};
|
||||
|
||||
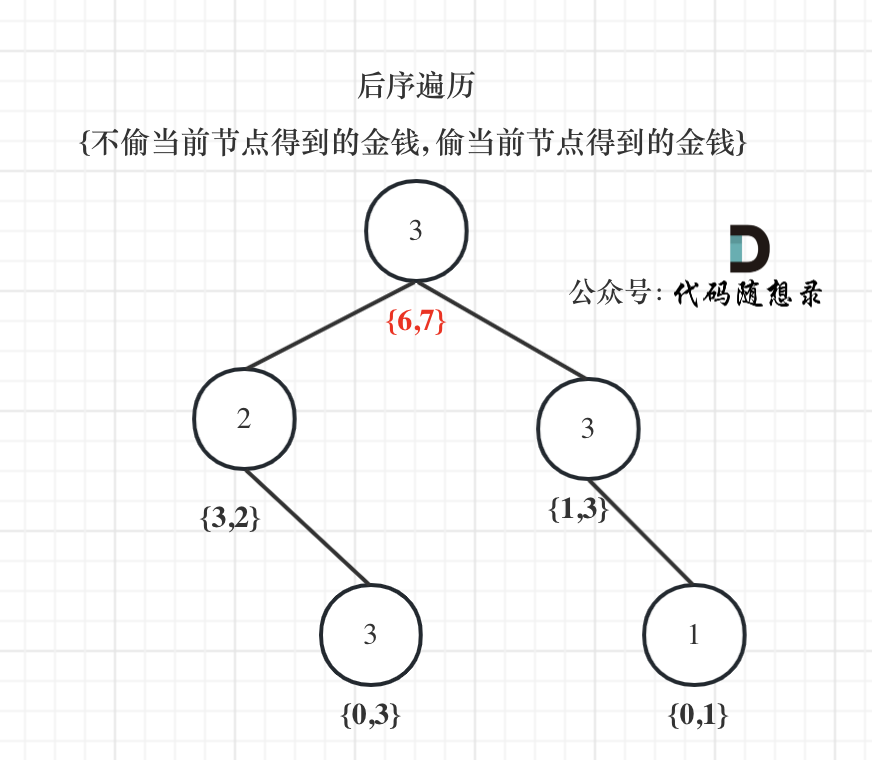
以示例1为例,dp数组状态如下:(**注意用后序遍历的方式推导**)
|
||||
|
||||

|
||||
|
||||
|
||||
|
||||
**最后头结点就是 取下标0 和 下标1的最大值就是偷得的最大金钱**。
|
||||
|
||||
|
||||
@ -15,8 +15,8 @@
|
||||
|
||||
示例:
|
||||
|
||||
nums = [1, 2, 3]
|
||||
target = 4
|
||||
* nums = [1, 2, 3]
|
||||
* target = 4
|
||||
|
||||
所有可能的组合为:
|
||||
(1, 1, 1, 1)
|
||||
@ -31,6 +31,10 @@ target = 4
|
||||
|
||||
因此输出为 7。
|
||||
|
||||
# 算法公开课
|
||||
|
||||
**《代码随想录》算法视频公开课:[装满背包有几种方法?求排列数?| LeetCode:377.组合总和IV](https://www.bilibili.com/video/BV1V14y1n7B6/),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
## 思路
|
||||
|
||||
对完全背包还不了解的同学,可以看这篇:[动态规划:关于完全背包,你该了解这些!](https://programmercarl.com/背包问题理论基础完全背包.html)
|
||||
|
||||
@ -17,19 +17,24 @@
|
||||
数组的大小不会超过 200
|
||||
|
||||
示例 1:
|
||||
输入: [1, 5, 11, 5]
|
||||
输出: true
|
||||
解释: 数组可以分割成 [1, 5, 5] 和 [11].
|
||||
* 输入: [1, 5, 11, 5]
|
||||
* 输出: true
|
||||
* 解释: 数组可以分割成 [1, 5, 5] 和 [11].
|
||||
|
||||
示例 2:
|
||||
输入: [1, 2, 3, 5]
|
||||
输出: false
|
||||
解释: 数组不能分割成两个元素和相等的子集.
|
||||
* 输入: [1, 2, 3, 5]
|
||||
* 输出: false
|
||||
* 解释: 数组不能分割成两个元素和相等的子集.
|
||||
|
||||
提示:
|
||||
* 1 <= nums.length <= 200
|
||||
* 1 <= nums[i] <= 100
|
||||
|
||||
# 算法公开课
|
||||
|
||||
**《代码随想录》算法视频公开课:[动态规划之背包问题,这个包能装满吗?| LeetCode:416.分割等和子集](https://www.bilibili.com/video/BV1rt4y1N7jE/),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
|
||||
## 思路
|
||||
|
||||
这道题目初步看,和如下两题几乎是一样的,大家可以用回溯法,解决如下两题
|
||||
|
||||
@ -44,7 +44,8 @@
|
||||
|
||||
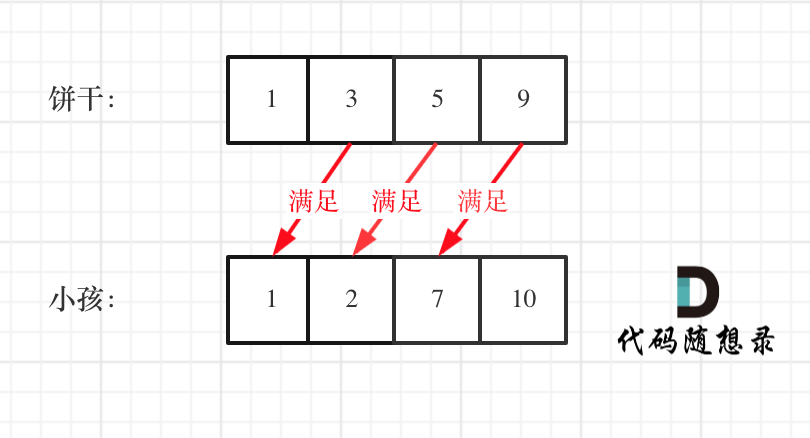
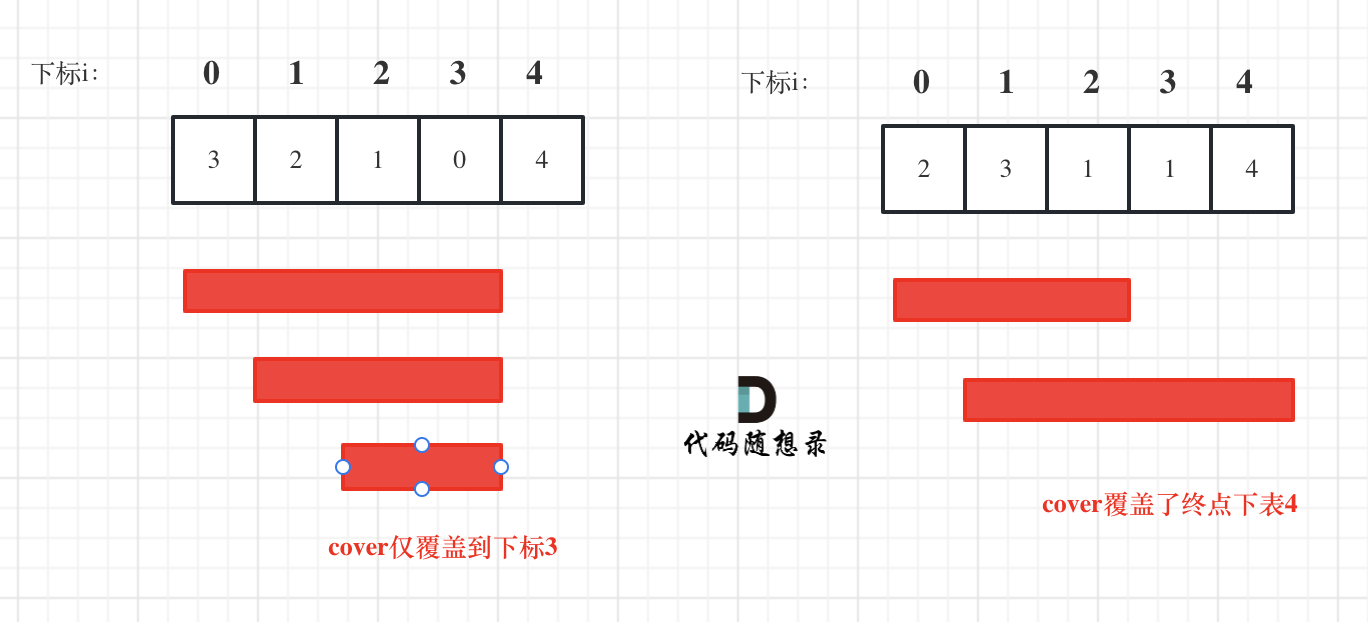
如图:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
这个例子可以看出饼干9只有喂给胃口为7的小孩,这样才是整体最优解,并想不出反例,那么就可以撸代码了。
|
||||
|
||||
|
||||
@ -16,16 +16,16 @@
|
||||
|
||||
示例 1:
|
||||
|
||||
输入:strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
|
||||
输出:4
|
||||
* 输入:strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
|
||||
* 输出:4
|
||||
|
||||
解释:最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ,因此答案是 4 。
|
||||
* 解释:最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ,因此答案是 4 。
|
||||
其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意,因为它含 4 个 1 ,大于 n 的值 3 。
|
||||
|
||||
示例 2:
|
||||
输入:strs = ["10", "0", "1"], m = 1, n = 1
|
||||
输出:2
|
||||
解释:最大的子集是 {"0", "1"} ,所以答案是 2 。
|
||||
* 输入:strs = ["10", "0", "1"], m = 1, n = 1
|
||||
* 输出:2
|
||||
* 解释:最大的子集是 {"0", "1"} ,所以答案是 2 。
|
||||
|
||||
提示:
|
||||
|
||||
@ -34,6 +34,11 @@
|
||||
* strs[i] 仅由 '0' 和 '1' 组成
|
||||
* 1 <= m, n <= 100
|
||||
|
||||
# 算法公开课
|
||||
|
||||
**《代码随想录》算法视频公开课:[装满这个背包最多用多少个物品?| LeetCode:474.一和零](https://www.bilibili.com/video/BV1rW4y1x7ZQ/),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
|
||||
## 思路
|
||||
|
||||
如果对背包问题不都熟悉先看这两篇:
|
||||
|
||||
@ -19,15 +19,15 @@
|
||||
|
||||
示例:
|
||||
|
||||
输入:nums: [1, 1, 1, 1, 1], S: 3
|
||||
输出:5
|
||||
* 输入:nums: [1, 1, 1, 1, 1], S: 3
|
||||
* 输出:5
|
||||
|
||||
解释:
|
||||
-1+1+1+1+1 = 3
|
||||
+1-1+1+1+1 = 3
|
||||
+1+1-1+1+1 = 3
|
||||
+1+1+1-1+1 = 3
|
||||
+1+1+1+1-1 = 3
|
||||
* -1+1+1+1+1 = 3
|
||||
* +1-1+1+1+1 = 3
|
||||
* +1+1-1+1+1 = 3
|
||||
* +1+1+1-1+1 = 3
|
||||
* +1+1+1+1-1 = 3
|
||||
|
||||
一共有5种方法让最终目标和为3。
|
||||
|
||||
@ -37,6 +37,11 @@
|
||||
* 初始的数组的和不会超过 1000 。
|
||||
* 保证返回的最终结果能被 32 位整数存下。
|
||||
|
||||
# 算法公开课
|
||||
|
||||
**《代码随想录》算法视频公开课:[装满背包有多少种方法?| LeetCode:494.目标和](https://www.bilibili.com/video/BV1o8411j73x/),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
|
||||
## 思路
|
||||
|
||||
如果对背包问题不都熟悉先看这两篇:
|
||||
|
||||
@ -10,8 +10,6 @@
|
||||
|
||||
[力扣题目链接](https://leetcode.cn/problems/coin-change-ii/)
|
||||
|
||||
难度:中等
|
||||
|
||||
给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。
|
||||
|
||||
示例 1:
|
||||
@ -43,6 +41,12 @@
|
||||
* 硬币种类不超过 500 种
|
||||
* 结果符合 32 位符号整数
|
||||
|
||||
# 算法公开课
|
||||
|
||||
**《代码随想录》算法视频公开课:[装满背包有多少种方法?组合与排列有讲究!| LeetCode:518.零钱兑换II](https://www.bilibili.com/video/BV1KM411k75j/),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
|
||||
|
||||
|
||||
## 思路
|
||||
|
||||
|
||||
@ -17,15 +17,15 @@
|
||||
注意:这里的一笔交易指买入持有并卖出股票的整个过程,每笔交易你只需要为支付一次手续费。
|
||||
|
||||
示例 1:
|
||||
输入: prices = [1, 3, 2, 8, 4, 9], fee = 2
|
||||
输出: 8
|
||||
* 输入: prices = [1, 3, 2, 8, 4, 9], fee = 2
|
||||
* 输出: 8
|
||||
|
||||
解释: 能够达到的最大利润:
|
||||
在此处买入 prices[0] = 1
|
||||
在此处卖出 prices[3] = 8
|
||||
在此处买入 prices[4] = 4
|
||||
在此处卖出 prices[5] = 9
|
||||
总利润: ((8 - 1) - 2) + ((9 - 4) - 2) = 8.
|
||||
* 在此处买入 prices[0] = 1
|
||||
* 在此处卖出 prices[3] = 8
|
||||
* 在此处买入 prices[4] = 4
|
||||
* 在此处卖出 prices[5] = 9
|
||||
* 总利润: ((8 - 1) - 2) + ((9 - 4) - 2) = 8.
|
||||
|
||||
注意:
|
||||
* 0 < prices.length <= 50000.
|
||||
@ -41,7 +41,7 @@
|
||||
* 时间复杂度:O(n)
|
||||
* 空间复杂度:O(1)
|
||||
|
||||
那么我们再来看看是使用动规的方法如何解题。
|
||||
本题使用贪心算法并不好理解,也很容易出错,那么我们再来看看是使用动规的方法如何解题。
|
||||
|
||||
相对于[动态规划:122.买卖股票的最佳时机II](https://programmercarl.com/0122.买卖股票的最佳时机II(动态规划).html),本题只需要在计算卖出操作的时候减去手续费就可以了,代码几乎是一样的。
|
||||
|
||||
|
||||
@ -35,6 +35,7 @@
|
||||
```CPP
|
||||
class Solution {
|
||||
private:
|
||||
// 判断一个数字的各位上是否是递增
|
||||
bool checkNum(int num) {
|
||||
int max = 10;
|
||||
while (num) {
|
||||
@ -47,15 +48,15 @@ private:
|
||||
}
|
||||
public:
|
||||
int monotoneIncreasingDigits(int N) {
|
||||
for (int i = N; i > 0; i--) {
|
||||
for (int i = N; i > 0; i--) { // 从大到小遍历
|
||||
if (checkNum(i)) return i;
|
||||
}
|
||||
return 0;
|
||||
}
|
||||
};
|
||||
```
|
||||
* 时间复杂度:$O(n × m)$ m为n的数字长度
|
||||
* 空间复杂度:$O(1)$
|
||||
* 时间复杂度:O(n × m) m为n的数字长度
|
||||
* 空间复杂度:O(1)
|
||||
|
||||
## 贪心算法
|
||||
|
||||
@ -65,20 +66,12 @@ public:
|
||||
|
||||
这一点如果想清楚了,这道题就好办了。
|
||||
|
||||
**局部最优:遇到strNum[i - 1] > strNum[i]的情况,让strNum[i - 1]--,然后strNum[i]给为9,可以保证这两位变成最大单调递增整数**。
|
||||
|
||||
**全局最优:得到小于等于N的最大单调递增的整数**。
|
||||
|
||||
**但这里局部最优推出全局最优,还需要其他条件,即遍历顺序,和标记从哪一位开始统一改成9**。
|
||||
|
||||
此时是从前向后遍历还是从后向前遍历呢?
|
||||
|
||||
从前向后遍历的话,遇到strNum[i - 1] > strNum[i]的情况,让strNum[i - 1]减一,但此时如果strNum[i - 1]减一了,可能又小于strNum[i - 2]。
|
||||
|
||||
这么说有点抽象,举个例子,数字:332,从前向后遍历的话,那么就把变成了329,此时2又小于了第一位的3了,真正的结果应该是299。
|
||||
|
||||
**所以从前后向遍历会改变已经遍历过的结果!**
|
||||
|
||||
那么从后向前遍历,就可以重复利用上次比较得出的结果了,从后向前遍历332的数值变化为:332 -> 329 -> 299
|
||||
|
||||
确定了遍历顺序之后,那么此时局部最优就可以推出全局,找不出反例,试试贪心。
|
||||
@ -108,8 +101,8 @@ public:
|
||||
|
||||
```
|
||||
|
||||
* 时间复杂度:$O(n)$,n 为数字长度
|
||||
* 空间复杂度:$O(n)$,需要一个字符串,转化为字符串操作更方便
|
||||
* 时间复杂度:O(n),n 为数字长度
|
||||
* 空间复杂度:O(n),需要一个字符串,转化为字符串操作更方便
|
||||
|
||||
## 总结
|
||||
|
||||
|
||||
@ -68,8 +68,8 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度:$O(n)$
|
||||
* 空间复杂度:$O(1)$,使用的hash数组是固定大小
|
||||
* 时间复杂度:O(n)
|
||||
* 空间复杂度:O(1),使用的hash数组是固定大小
|
||||
|
||||
## 总结
|
||||
|
||||
|
||||
@ -4,7 +4,7 @@
|
||||
</a>
|
||||
<p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||||
|
||||
## 1049. 最后一块石头的重量 II
|
||||
# 1049.最后一块石头的重量II
|
||||
|
||||
[力扣题目链接](https://leetcode.cn/problems/last-stone-weight-ii/)
|
||||
|
||||
@ -35,6 +35,11 @@
|
||||
* 1 <= stones.length <= 30
|
||||
* 1 <= stones[i] <= 1000
|
||||
|
||||
# 算法公开课
|
||||
|
||||
**《代码随想录》算法视频公开课:[这个背包最多能装多少?LeetCode:1049.最后一块石头的重量II](https://www.bilibili.com/video/BV14M411C7oV/),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
|
||||
## 思路
|
||||
|
||||
如果对背包问题不都熟悉先看这两篇:
|
||||
|
||||
@ -3,11 +3,13 @@
|
||||
<img src="../pics/训练营.png" width="1000"/>
|
||||
</a>
|
||||
<p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||||
|
||||
|
||||
# 贪心算法:根据身高重建队列(续集)
|
||||
|
||||
在讲解[贪心算法:根据身高重建队列](https://programmercarl.com/0406.根据身高重建队列.html)中,我们提到了使用vector(C++中的动态数组)来进行insert操作是费时的。
|
||||
|
||||
但是在解释的过程中有不恰当的地方,所以来专门写一篇文章来详细说一说这个问题。
|
||||
这里专门写一篇文章来详细说一说这个问题。
|
||||
|
||||
使用vector的代码如下:
|
||||
```CPP
|
||||
|
||||
@ -4,7 +4,11 @@
|
||||
</a>
|
||||
<p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||||
|
||||
# 动态规划:关于01背包问题,你该了解这些!
|
||||
# 动态规划:01背包理论基础
|
||||
|
||||
|
||||
**《代码随想录》算法视频公开课:[带你学透0-1背包问题!](https://www.bilibili.com/video/BV1cg411g7Y6/),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
|
||||
这周我们正式开始讲解背包问题!
|
||||
|
||||
|
||||
@ -4,7 +4,10 @@
|
||||
</a>
|
||||
<p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||||
|
||||
# 动态规划:关于01背包问题,你该了解这些!(滚动数组)
|
||||
# 动态规划:01背包理论基础(滚动数组)
|
||||
|
||||
**《代码随想录》算法视频公开课:[带你学透0-1背包问题!(滚动数组)](https://www.bilibili.com/video/BV1BU4y177kY/),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
|
||||
昨天[动态规划:关于01背包问题,你该了解这些!](https://programmercarl.com/背包理论基础01背包-1.html)中是用二维dp数组来讲解01背包。
|
||||
|
||||
|
||||
@ -5,10 +5,13 @@
|
||||
<p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||||
|
||||
|
||||
# 动态规划:关于完全背包,你该了解这些!
|
||||
# 动态规划:完全背包理论基础
|
||||
|
||||
**《代码随想录》算法视频公开课:[带你学透完全背包问题! ](https://www.bilibili.com/video/BV1uK411o7c9/),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
## 完全背包
|
||||
|
||||
|
||||
有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。**每件物品都有无限个(也就是可以放入背包多次)**,求解将哪些物品装入背包里物品价值总和最大。
|
||||
|
||||
**完全背包和01背包问题唯一不同的地方就是,每种物品有无限件**。
|
||||
|
||||
Reference in New Issue
Block a user