mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-25 18:08:48 +08:00
更新图床
This commit is contained in:
@ -254,5 +254,5 @@ traversal(cur->left, tmp, result);
|
||||
* Github:[leetcode-master](https://github.com/youngyangyang04/leetcode-master)
|
||||
* 知乎:[代码随想录](https://www.zhihu.com/people/sun-xiu-yang-64)
|
||||
|
||||
|
||||
|
||||
<div align="center"><img src=https://code-thinking.cdn.bcebos.com/pics/01二维码.jpg width=450> </img></div>
|
||||
|
||||
@ -1,5 +1,4 @@
|
||||
|
||||
|
||||
# 本周小结!(回溯算法系列二)
|
||||
|
||||
> 例行每周小结
|
||||
@ -32,7 +31,7 @@ for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target;
|
||||
|
||||
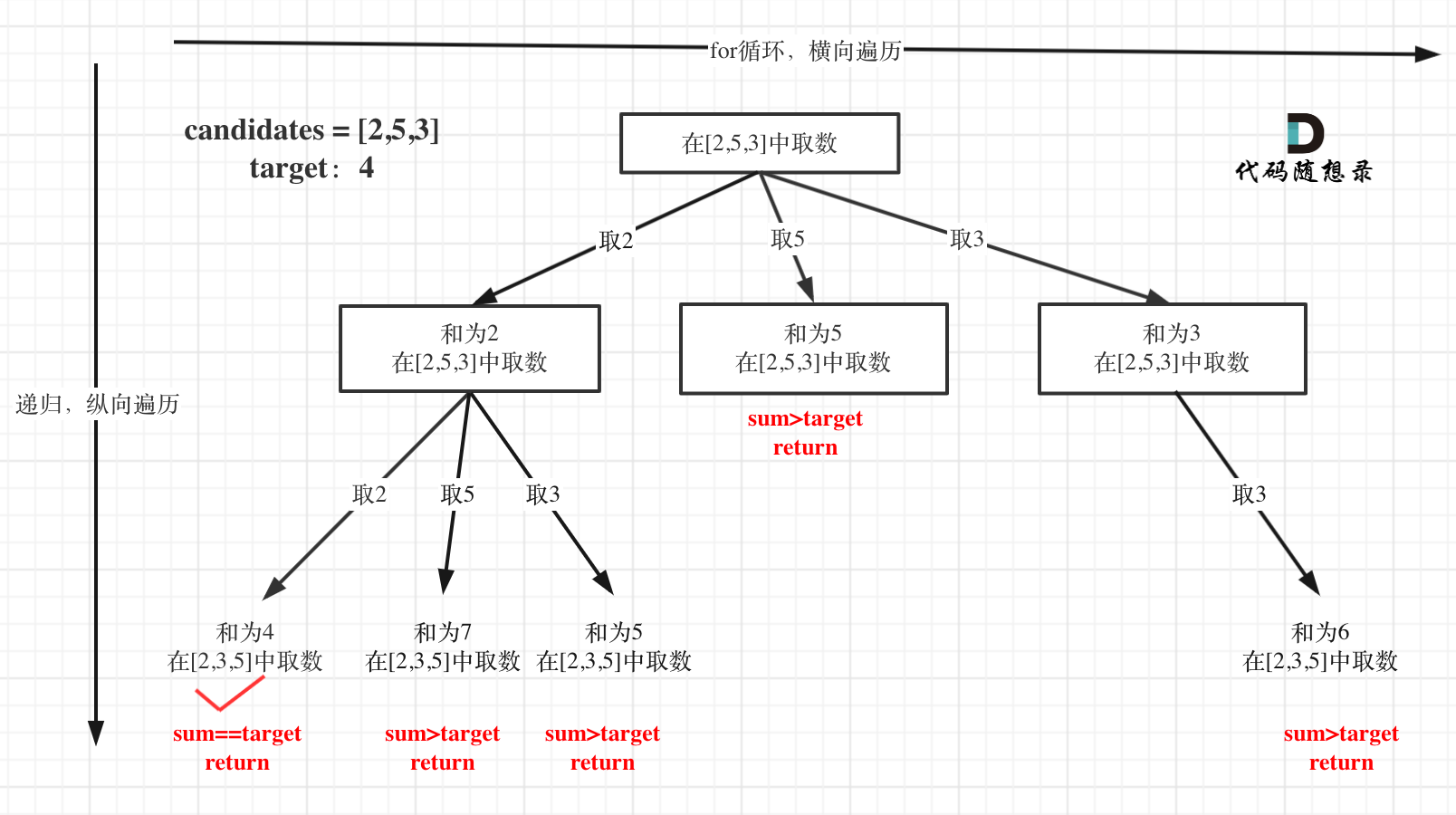
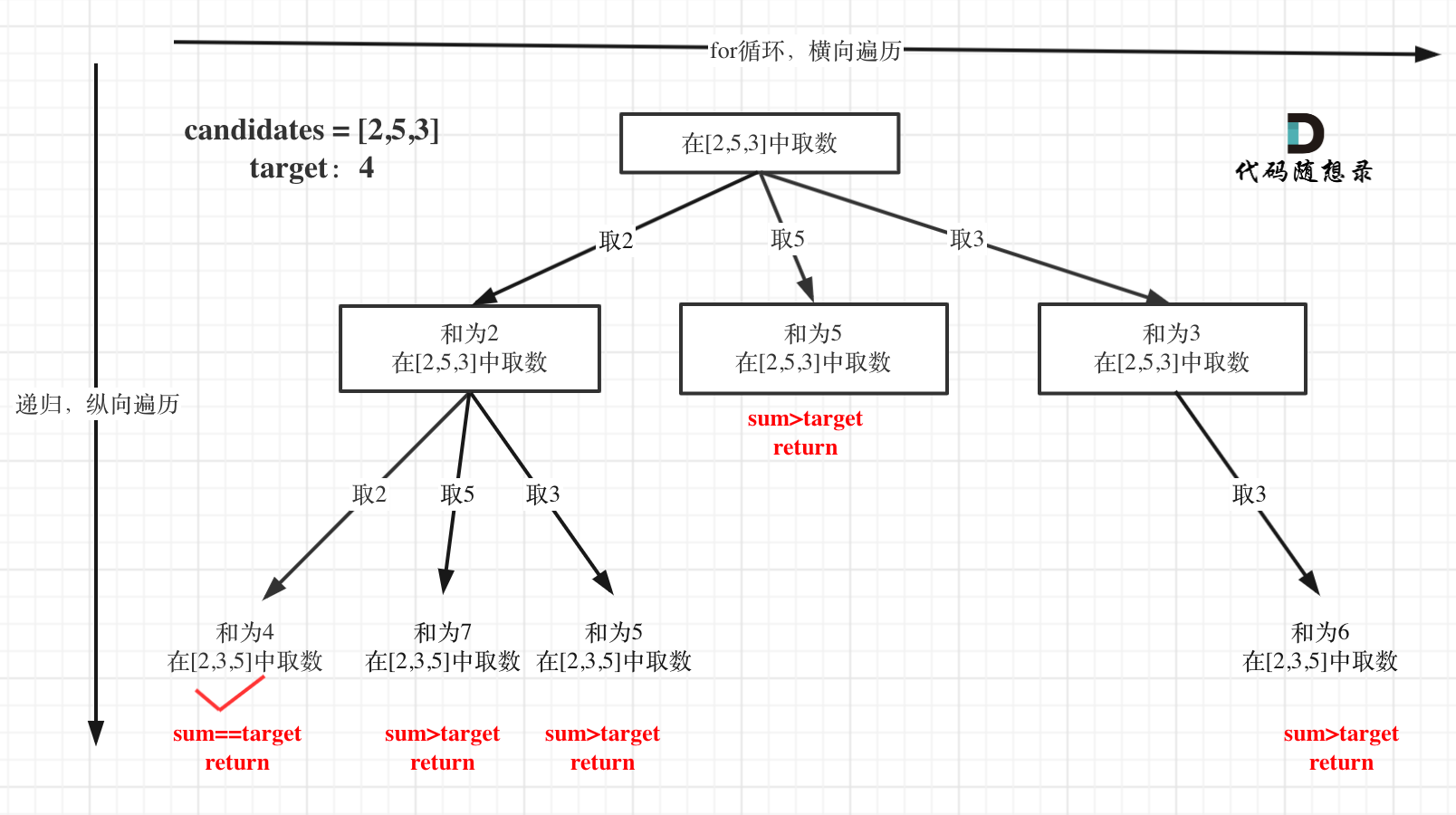
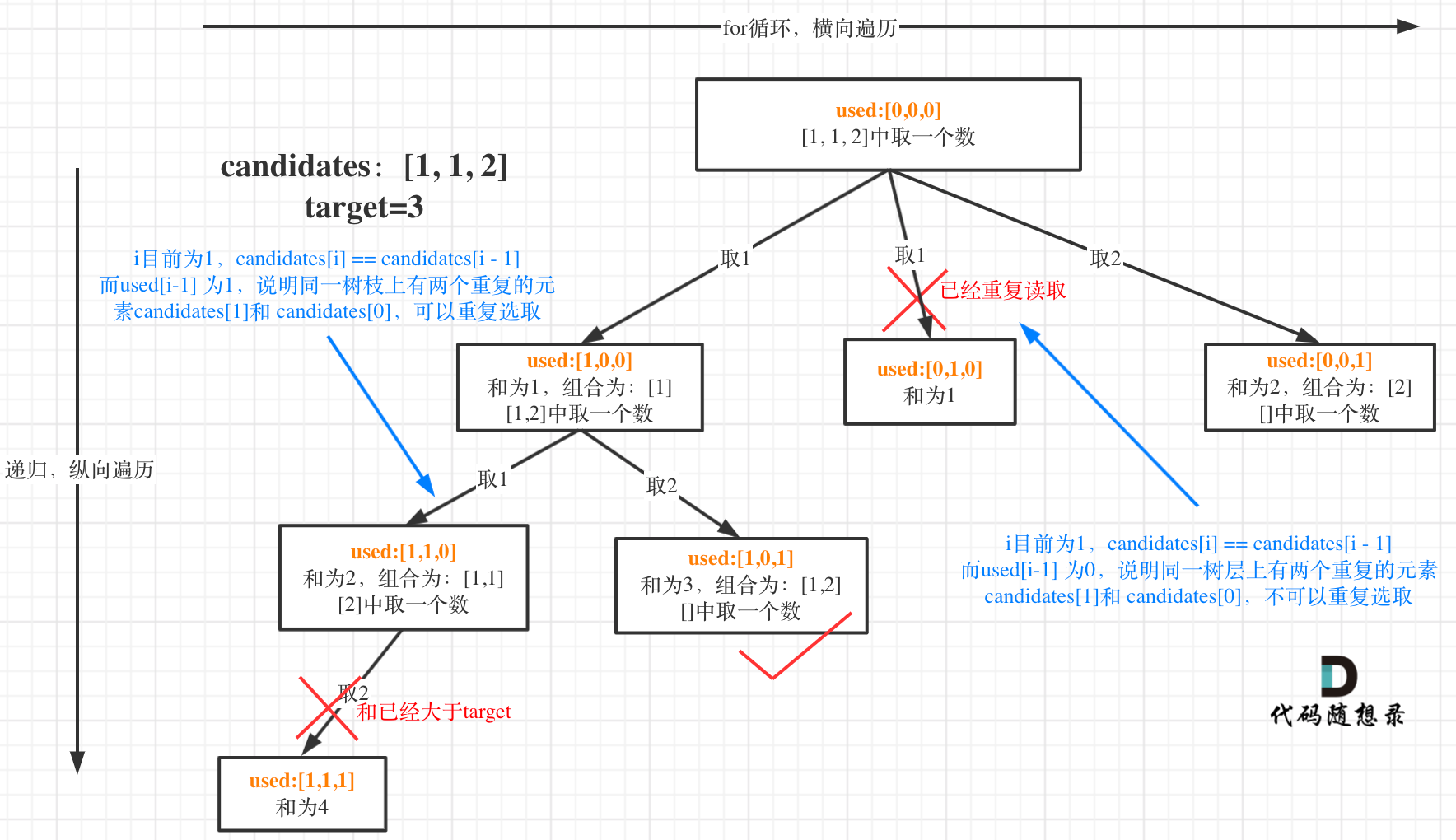
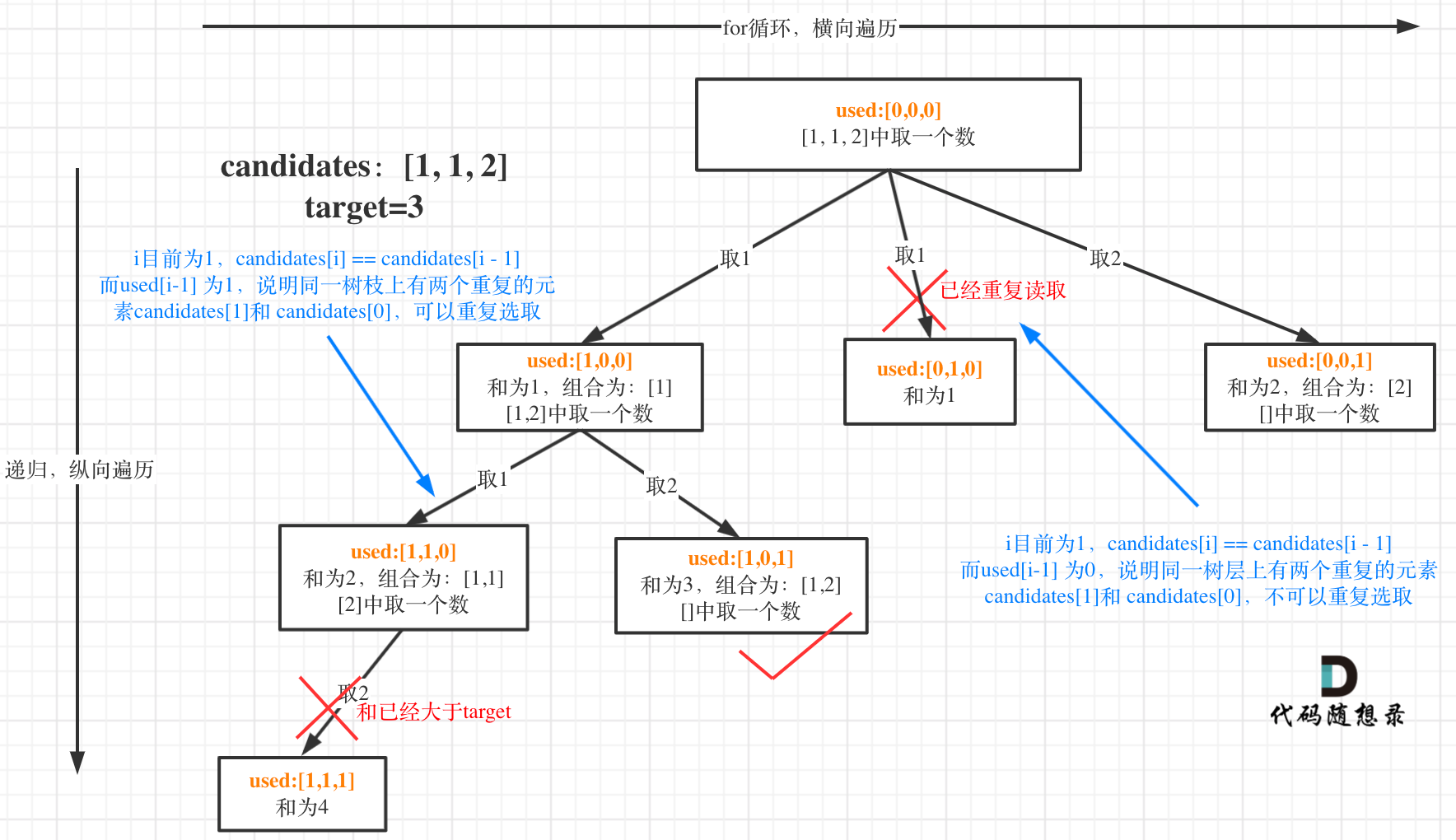
在[回溯算法:求组合总和(二)](https://programmercarl.com/0039.组合总和.html)第一个树形结构没有画出startIndex的作用,**这里这里纠正一下,准确的树形结构如图所示:**
|
||||
|
||||
|
||||
|
||||
|
||||
## 周二
|
||||
|
||||
@ -46,7 +45,7 @@ for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target;
|
||||
|
||||
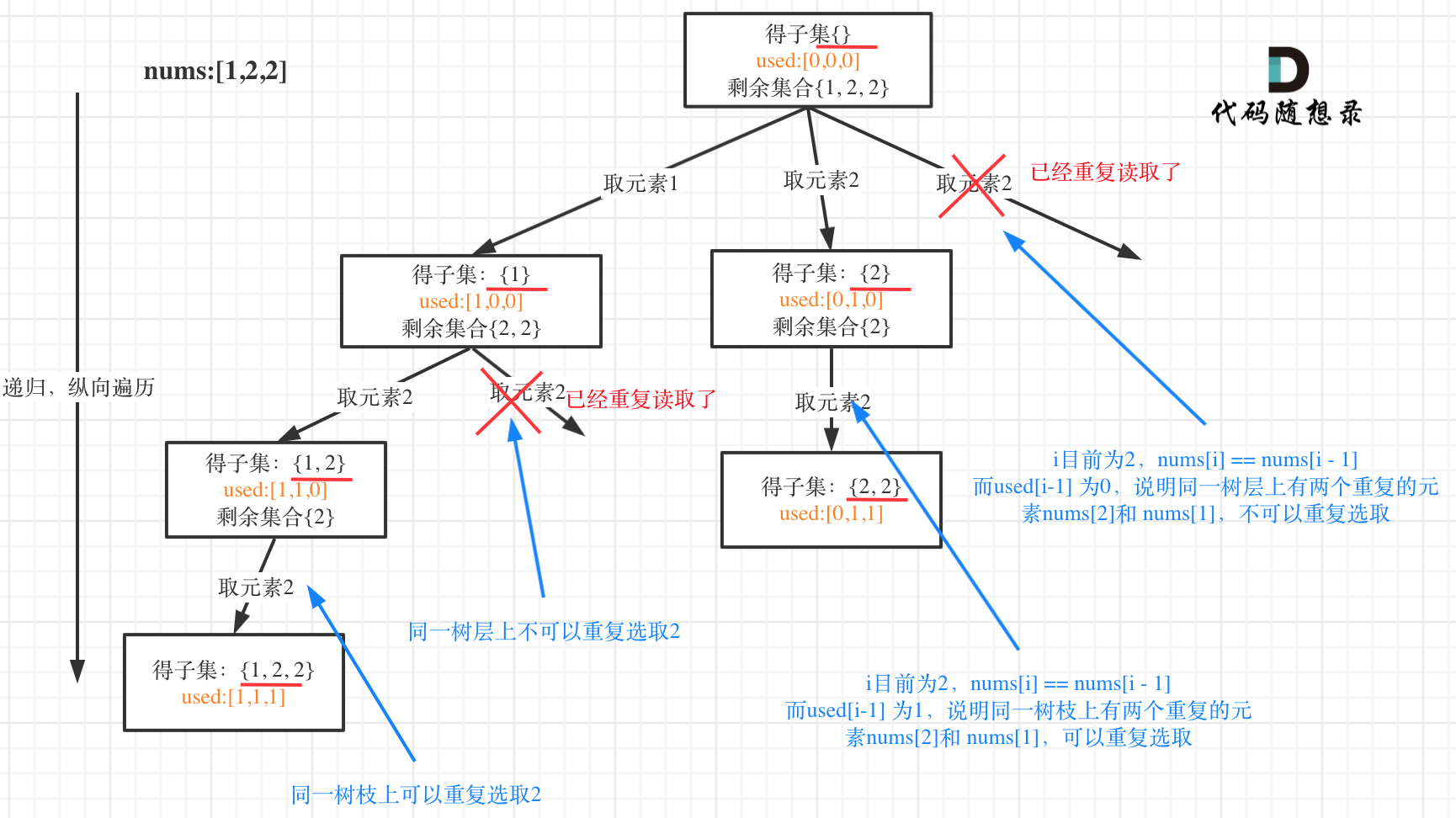
都知道组合问题可以抽象为树形结构,那么“使用过”在这个树形结构上是有两个维度的,一个维度是同一树枝上“使用过”,一个维度是同一树层上“使用过”。**没有理解这两个层面上的“使用过” 是造成大家没有彻底理解去重的根本原因**。
|
||||
|
||||
|
||||
|
||||
|
||||
我在图中将used的变化用橘黄色标注上,可以看出在candidates[i] == candidates[i - 1]相同的情况下:
|
||||
|
||||
@ -80,7 +79,7 @@ for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target;
|
||||
|
||||
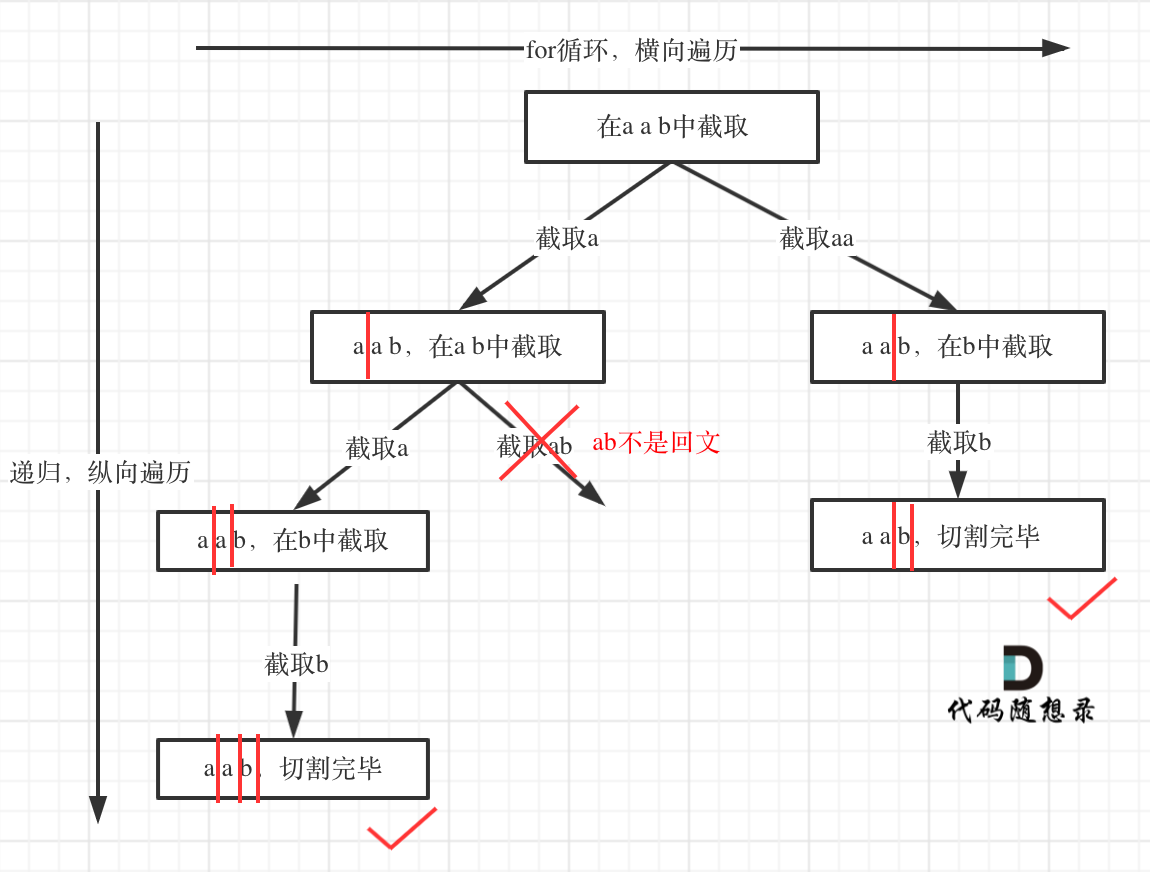
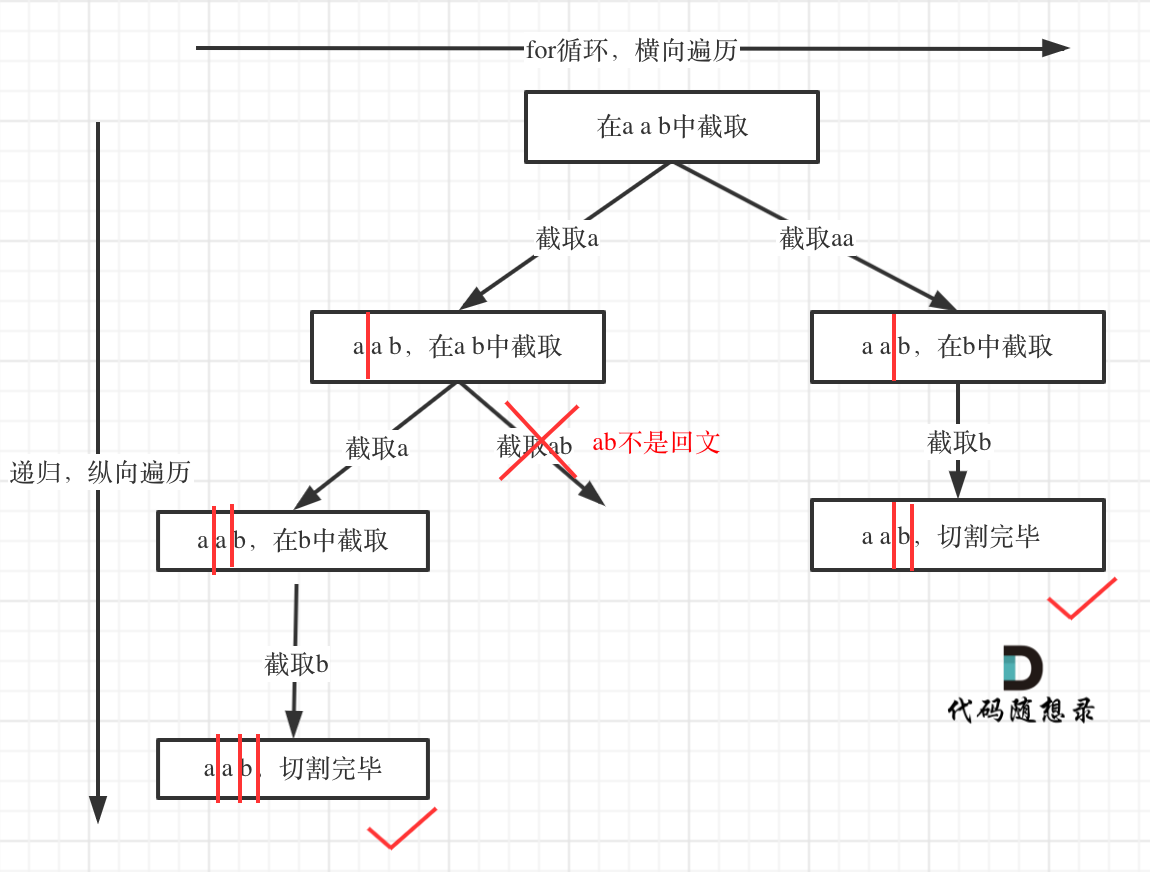
**本题的树形结构中,和代码的逻辑有一个小出入,已经判断不是回文的子串就不会进入递归了,纠正如下:**
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
## 周四
|
||||
@ -91,7 +90,7 @@ for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target;
|
||||
|
||||
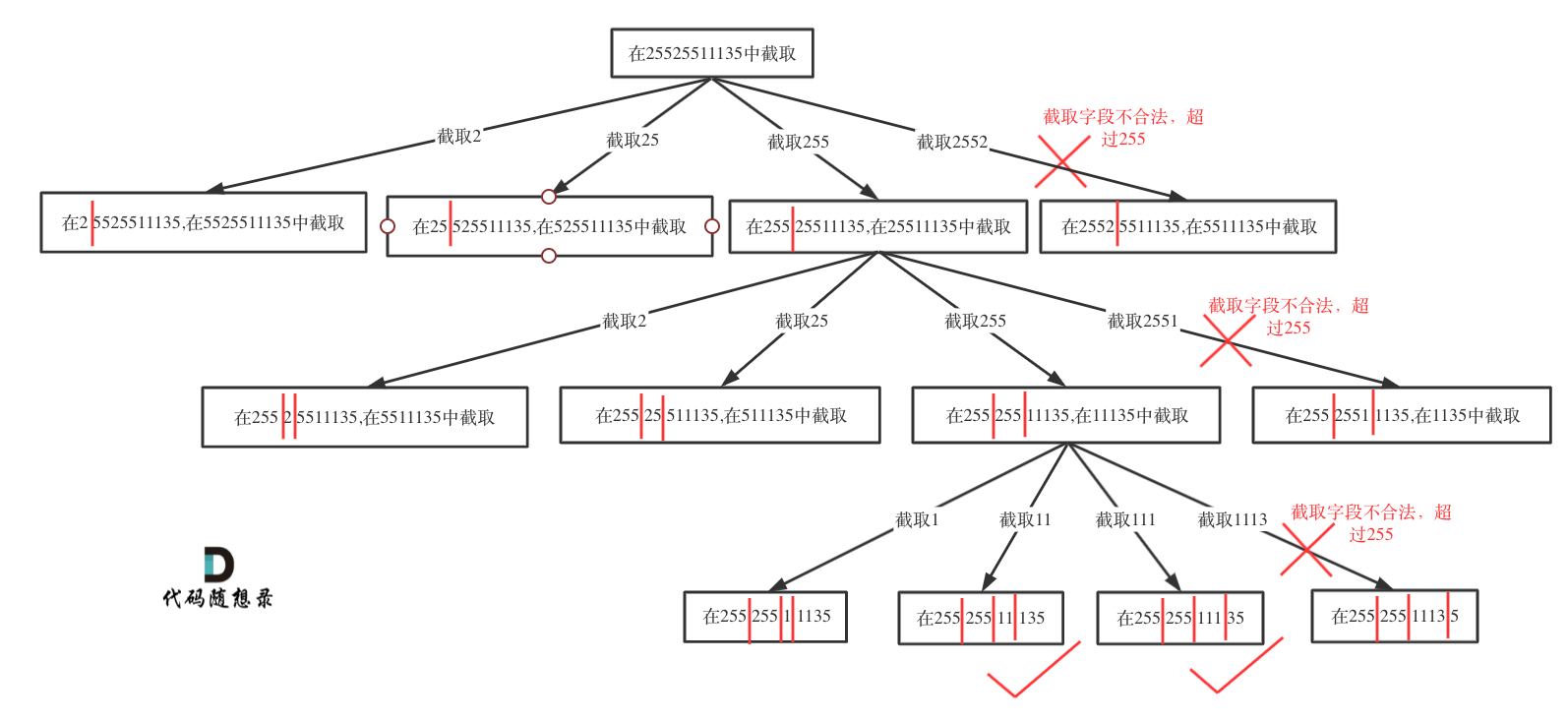
树形图如下:
|
||||
|
||||

|
||||
|
||||
|
||||
在本文的树形结构图中,我已经把详细的分析思路都画了出来,相信大家看了之后一定会思路清晰不少!
|
||||
|
||||
@ -113,7 +112,7 @@ if (s.size() > 12) return result; // 剪枝
|
||||
|
||||
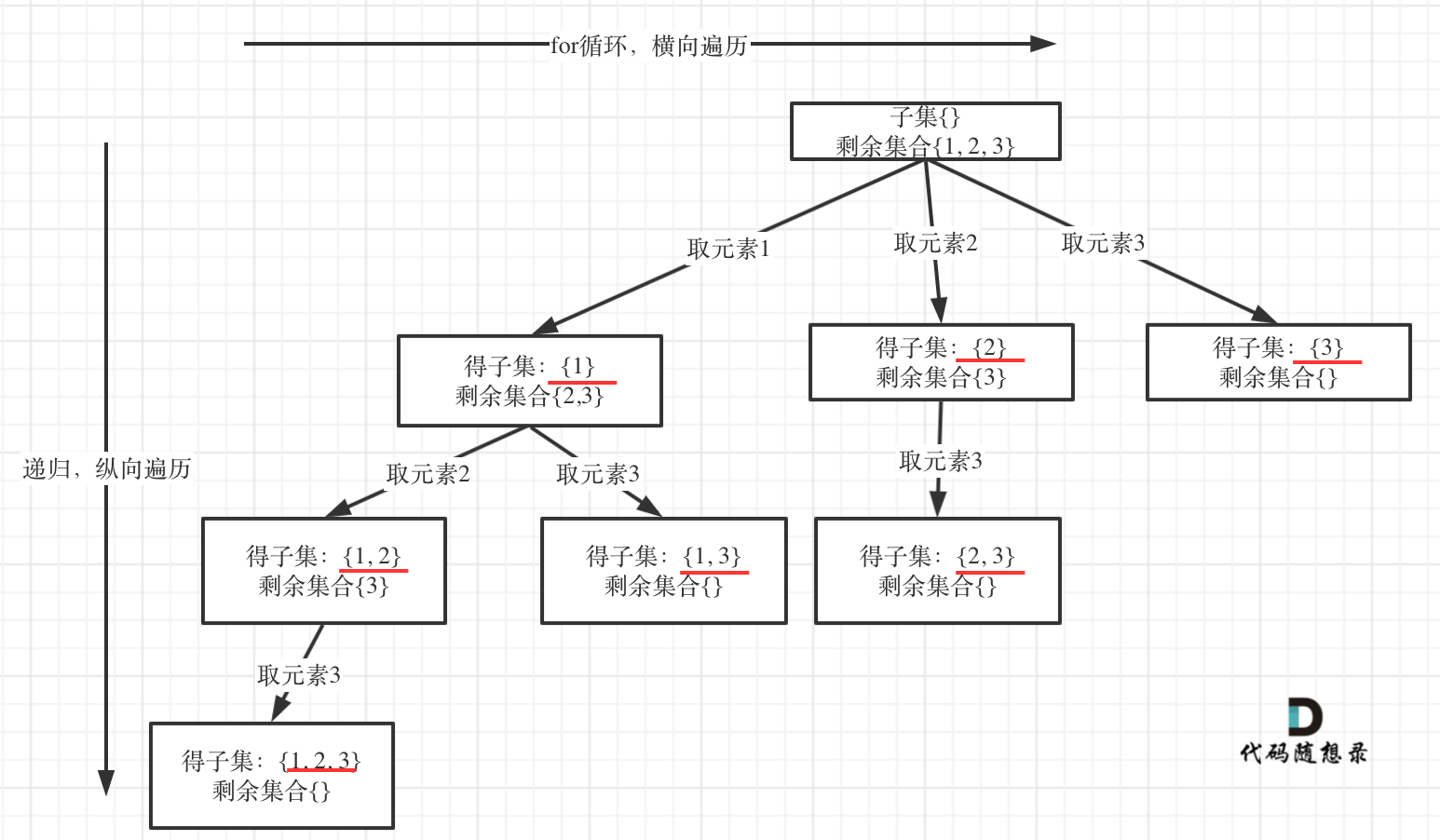
如图:
|
||||
|
||||

|
||||
|
||||
|
||||
|
||||
认清这个本质之后,今天的题目就是一道模板题了。
|
||||
|
||||
@ -1,5 +1,4 @@
|
||||
|
||||
|
||||
# 本周小结!(回溯算法系列三)
|
||||
|
||||
## 周一
|
||||
@ -12,14 +11,14 @@
|
||||
|
||||
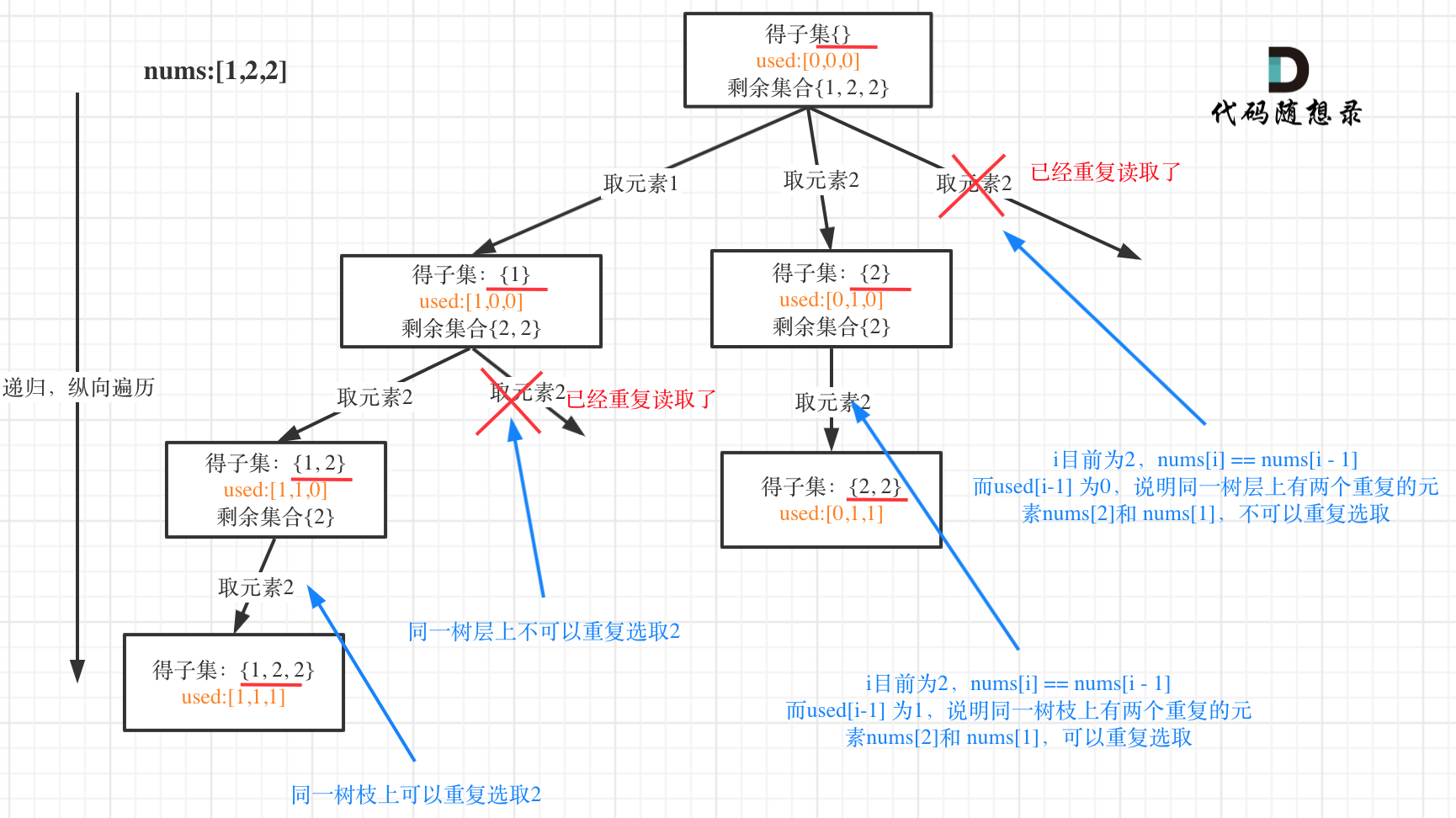
树形结构如下:
|
||||
|
||||
|
||||
|
||||
|
||||
## 周二
|
||||
|
||||
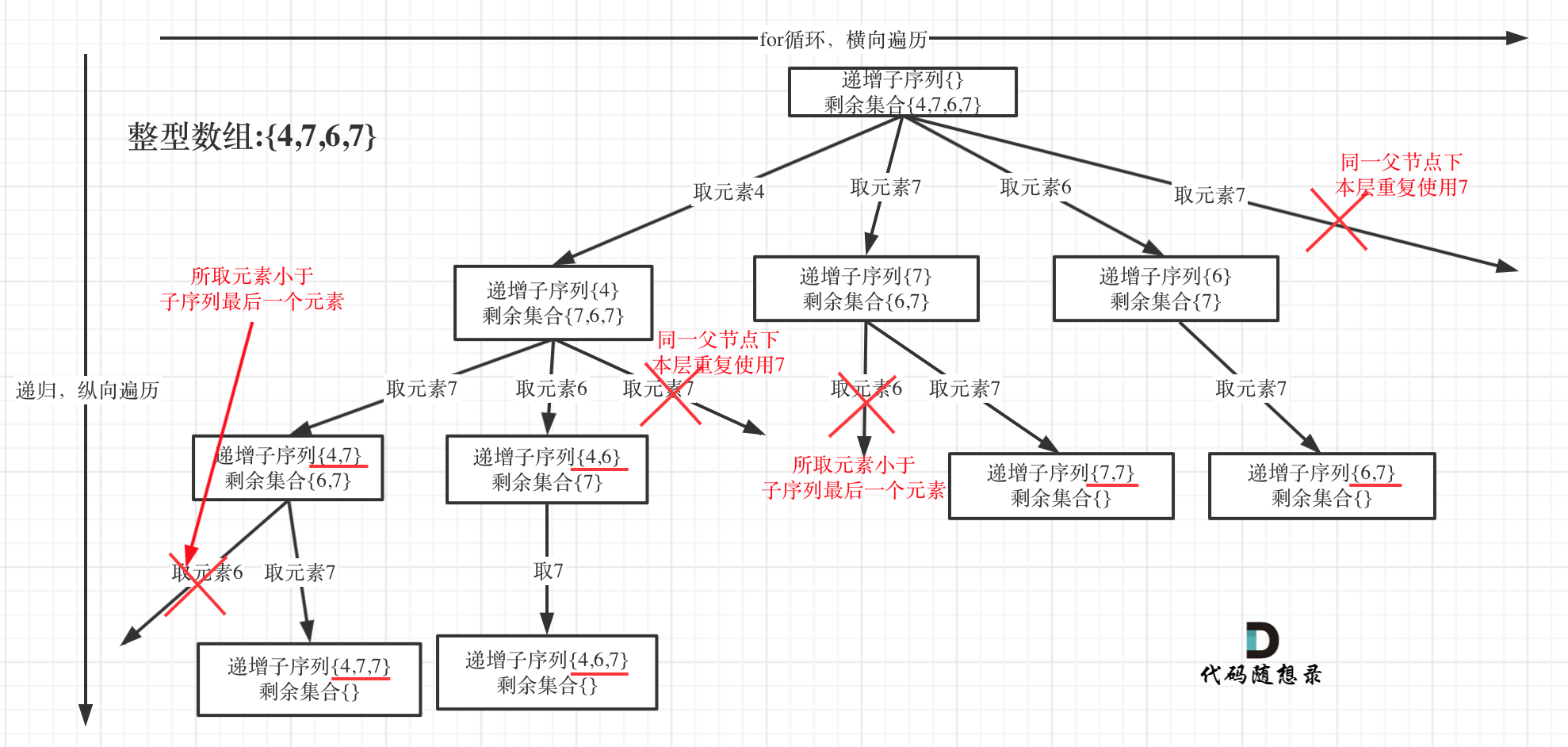
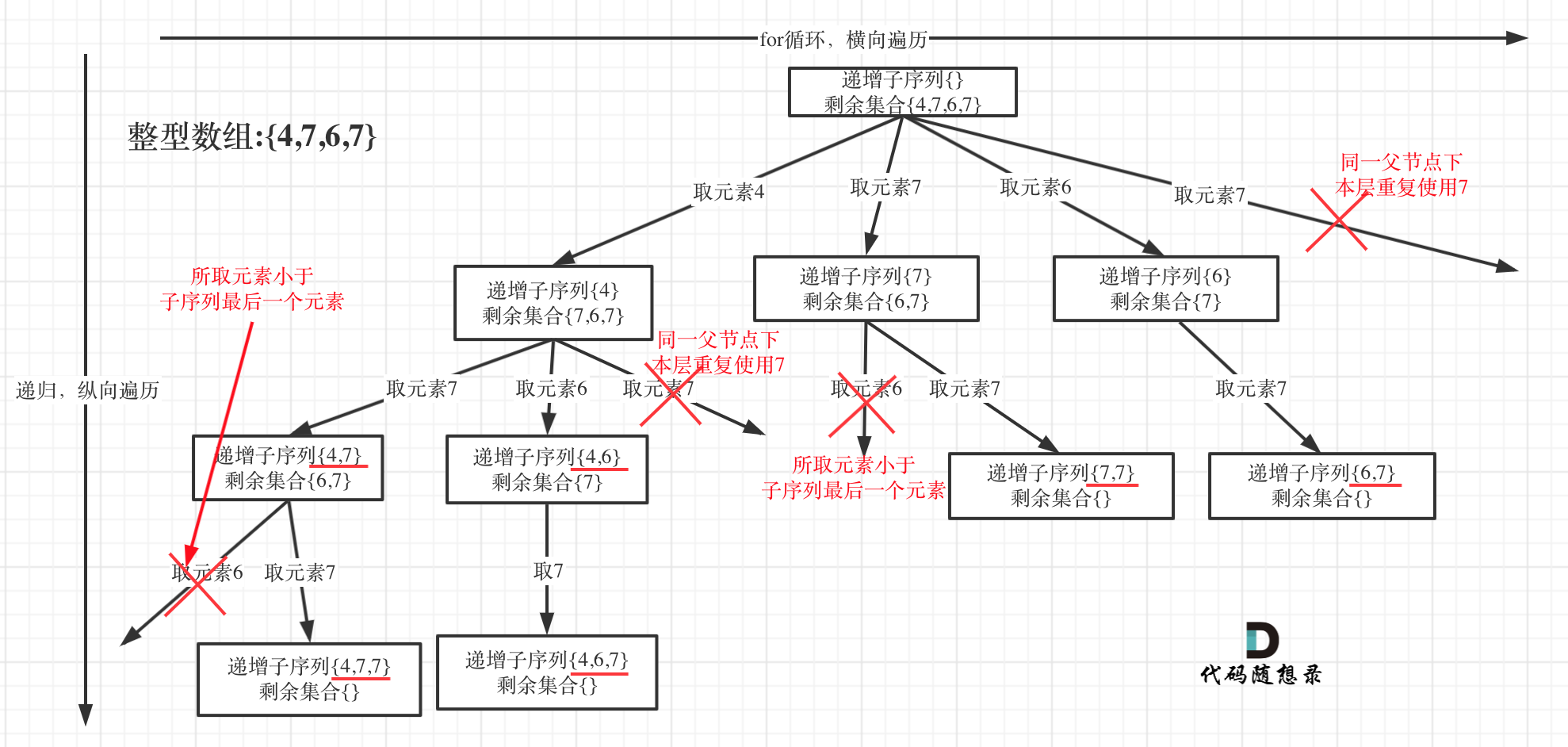
在[回溯算法:递增子序列](https://programmercarl.com/0491.递增子序列.html)中,处处都能看到子集的身影,但处处是陷阱,值得好好琢磨琢磨!
|
||||
|
||||
树形结构如下:
|
||||
|
||||
|
||||
|
||||
[回溯算法:递增子序列](https://programmercarl.com/0491.递增子序列.html)留言区大家有很多疑问,主要还是和[回溯算法:求子集问题(二)](https://programmercarl.com/0090.子集II.html)混合在了一起。
|
||||
|
||||
@ -34,7 +33,7 @@
|
||||
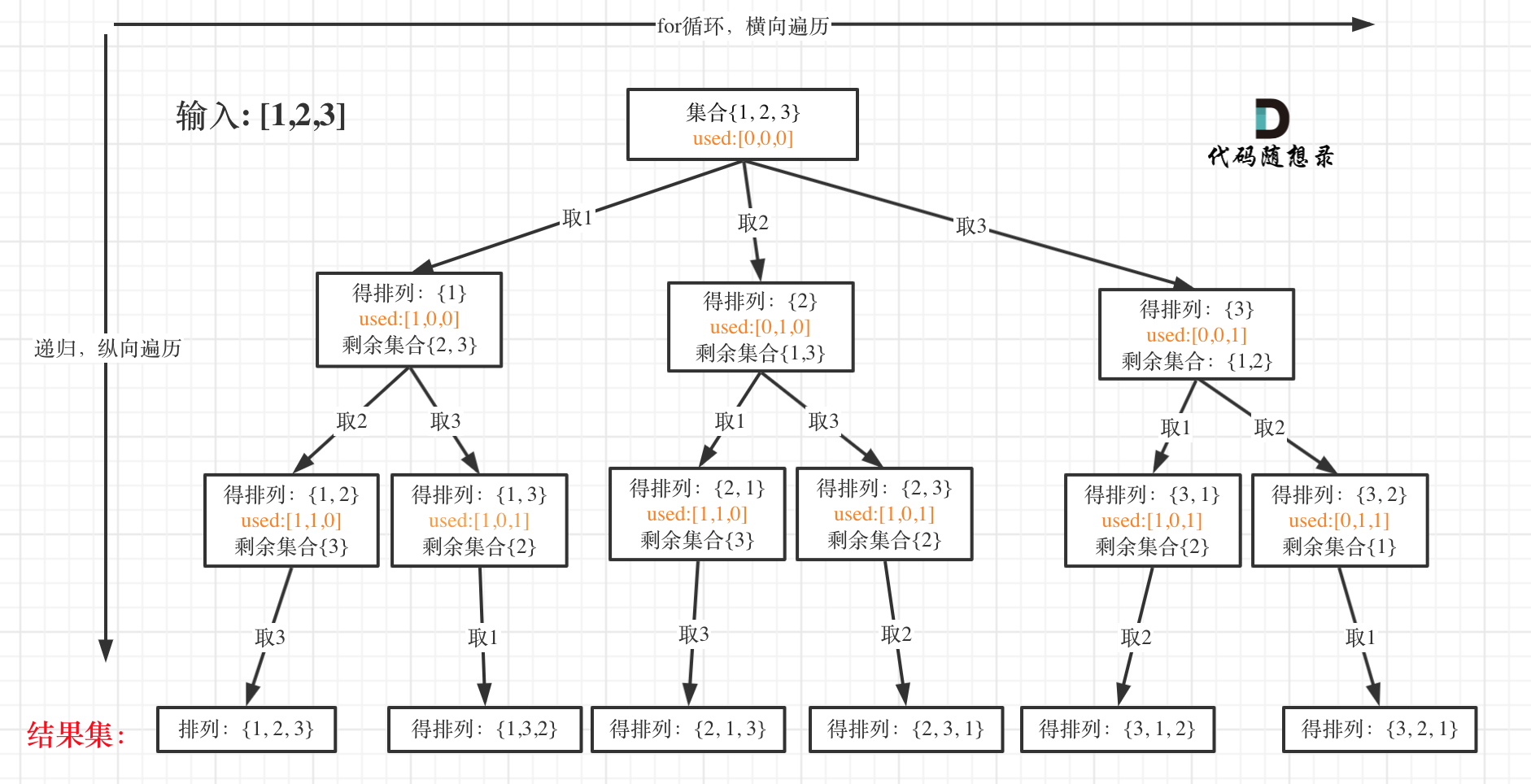
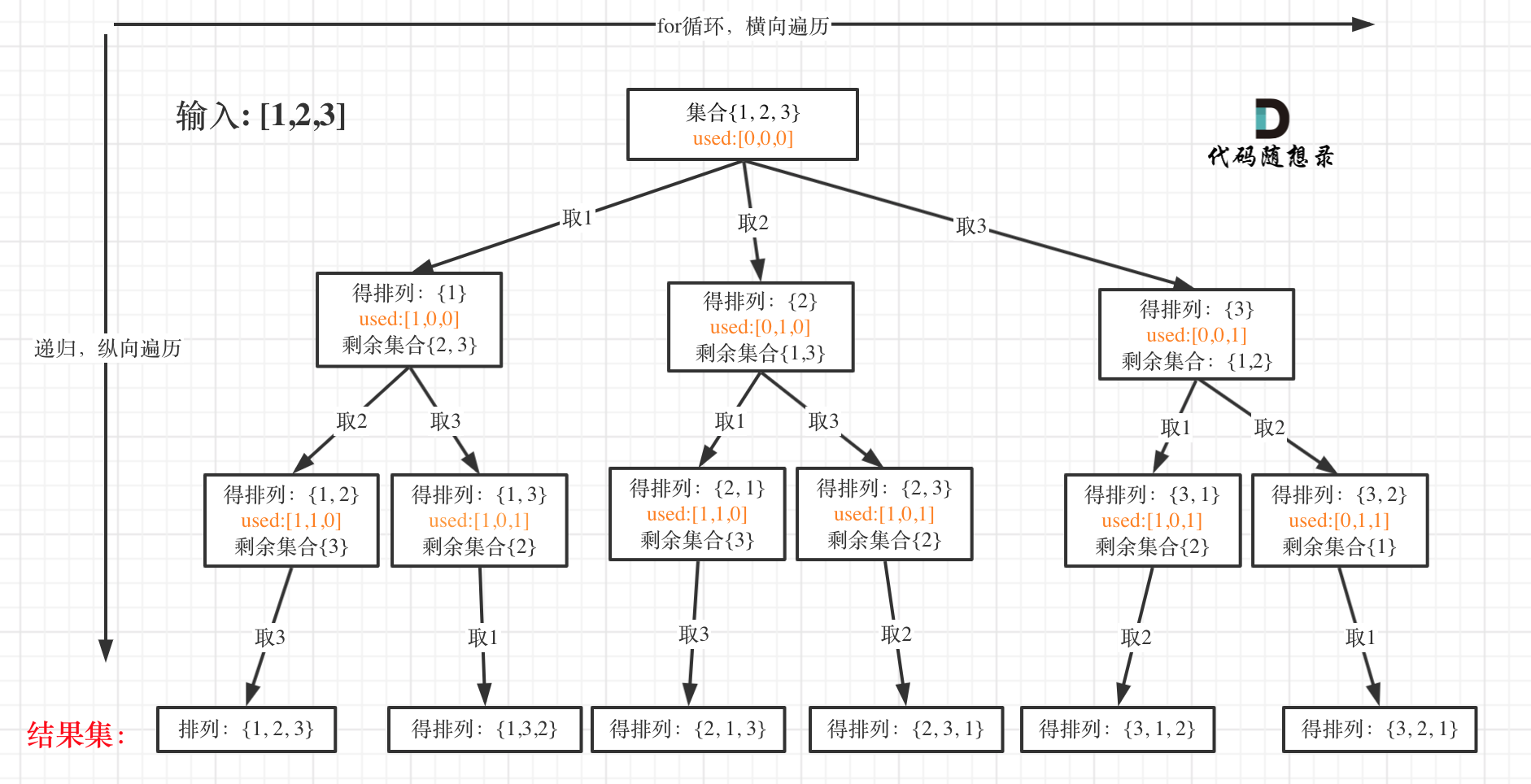
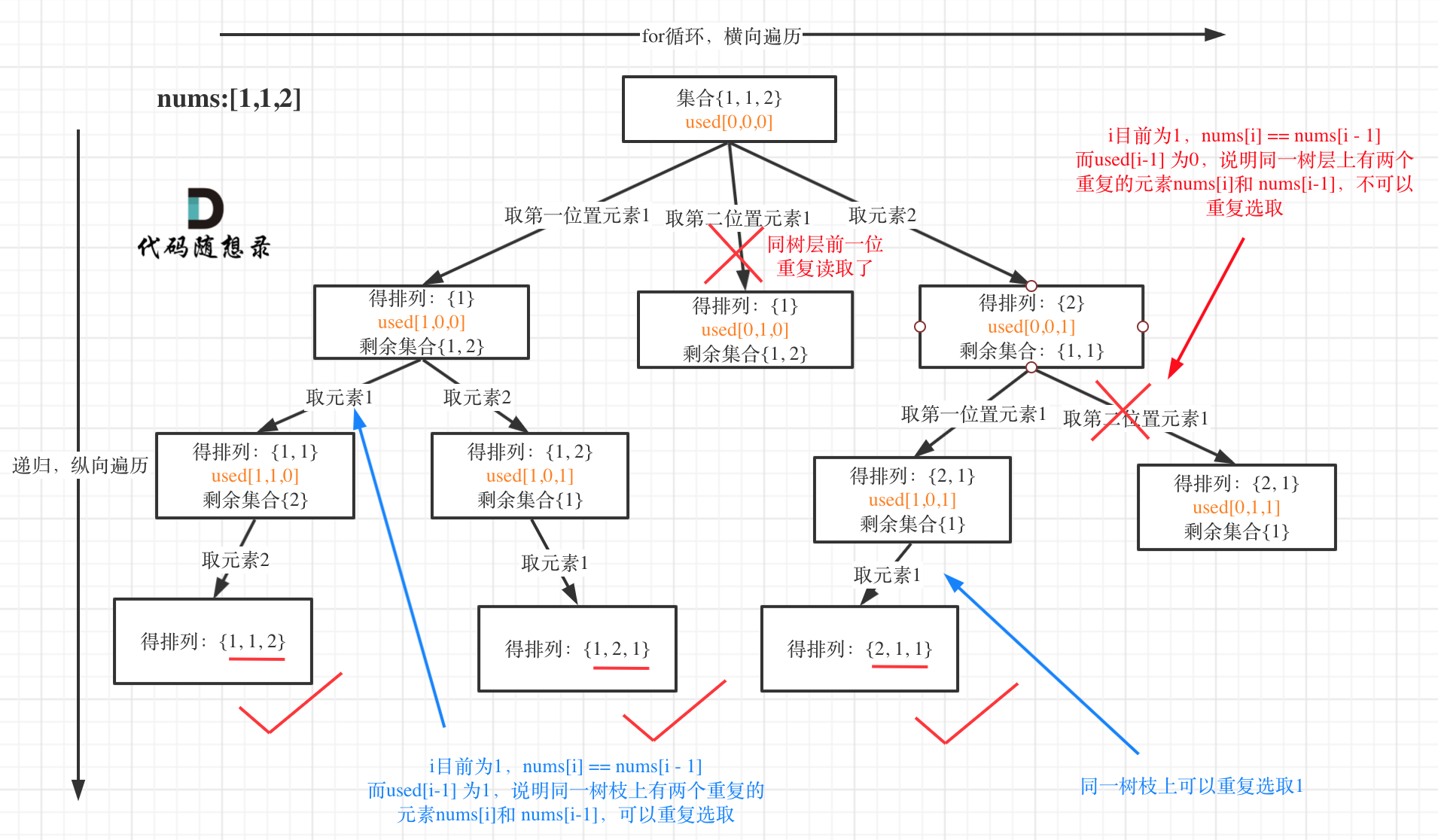
可以看出元素1在[1,2]中已经使用过了,但是在[2,1]中还要在使用一次1,所以处理排列问题就不用使用startIndex了。
|
||||
|
||||
如图:
|
||||
|
||||
|
||||
|
||||
**大家此时可以感受出排列问题的不同:**
|
||||
|
||||
@ -47,7 +46,7 @@
|
||||
|
||||
树形结构如下:
|
||||
|
||||
|
||||
|
||||
|
||||
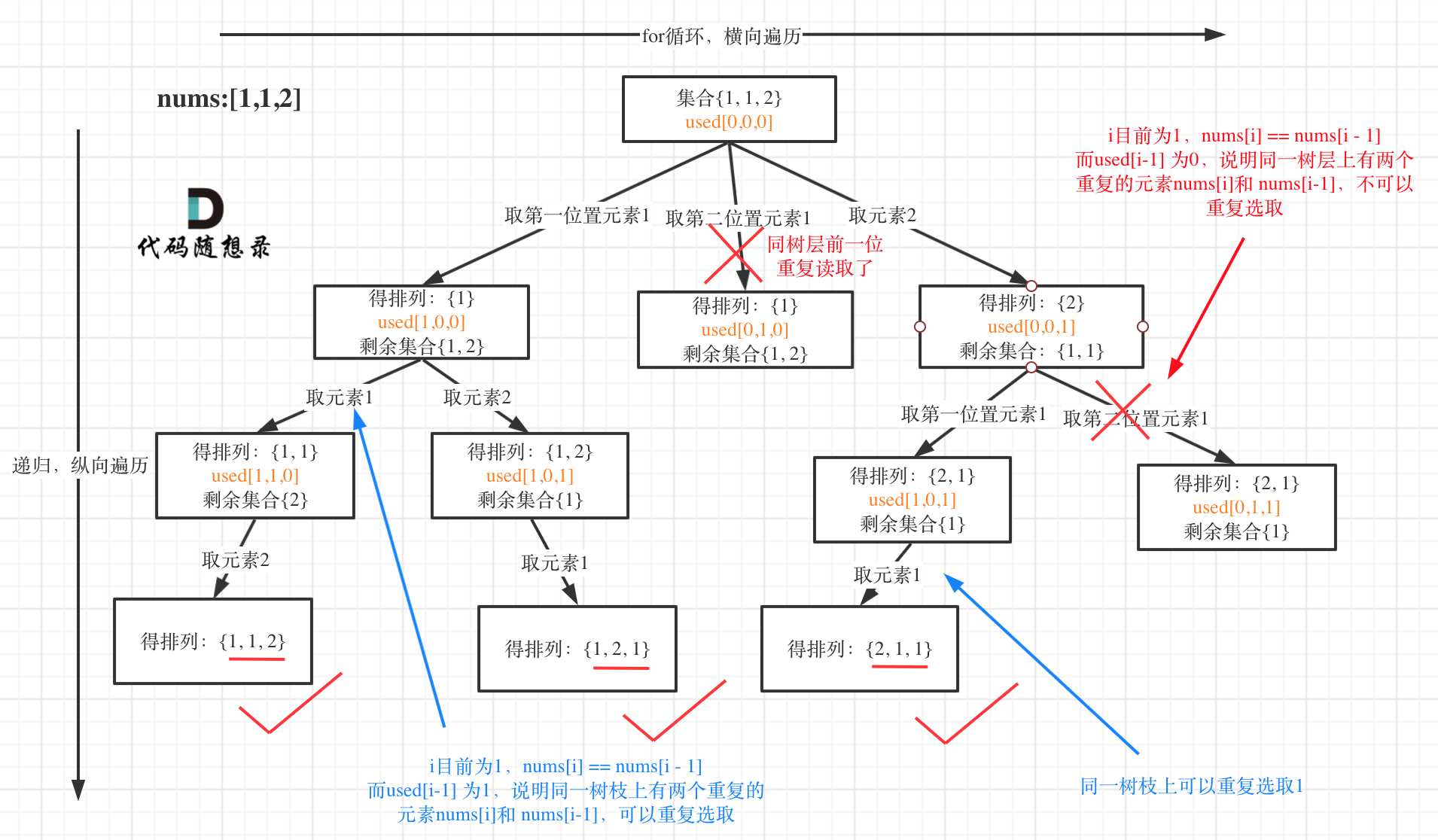
**这道题目神奇的地方就是used[i - 1] == false也可以,used[i - 1] == true也可以!**
|
||||
|
||||
@ -55,11 +54,11 @@
|
||||
|
||||
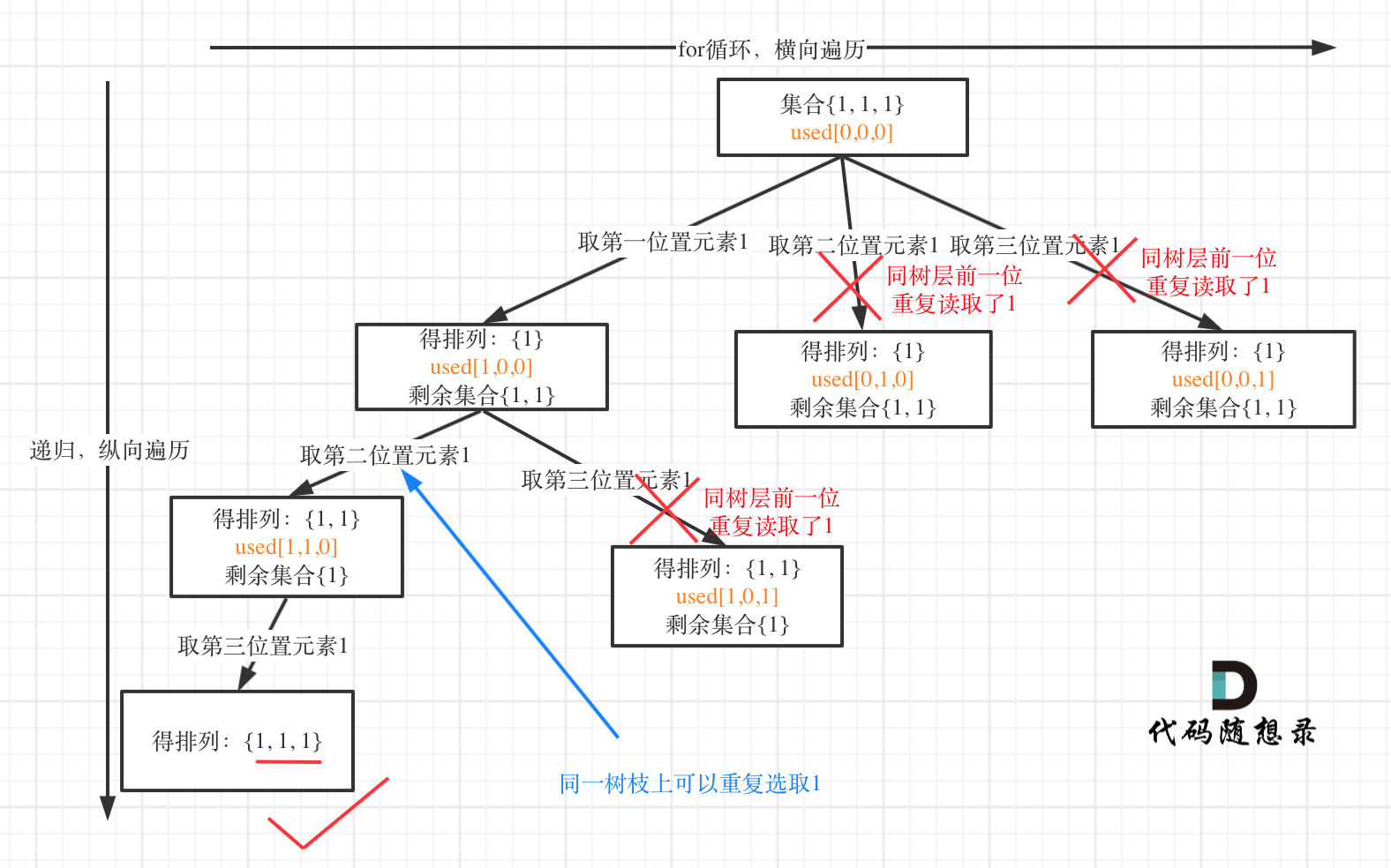
树层上去重(used[i - 1] == false),的树形结构如下:
|
||||
|
||||
|
||||
|
||||
|
||||
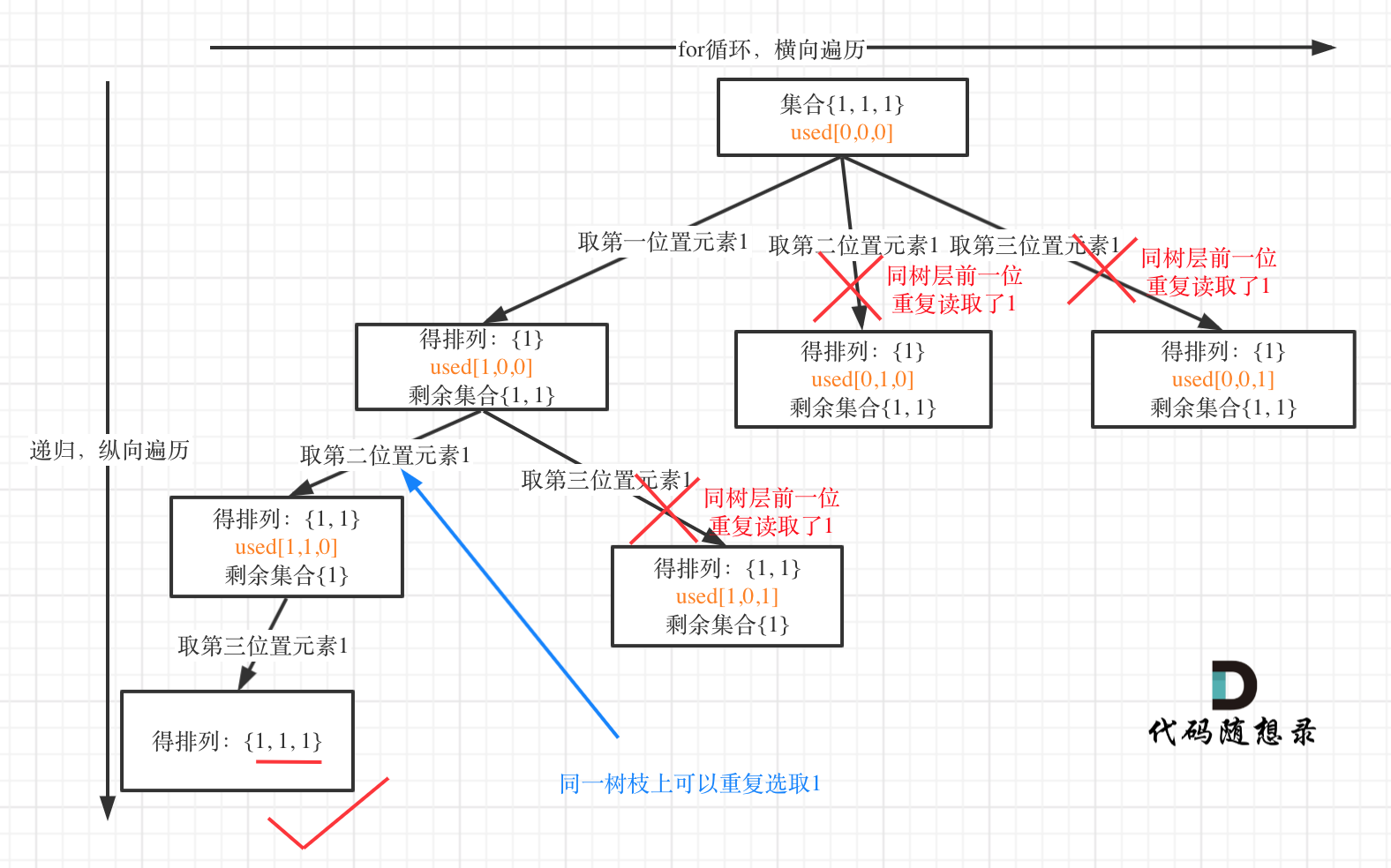
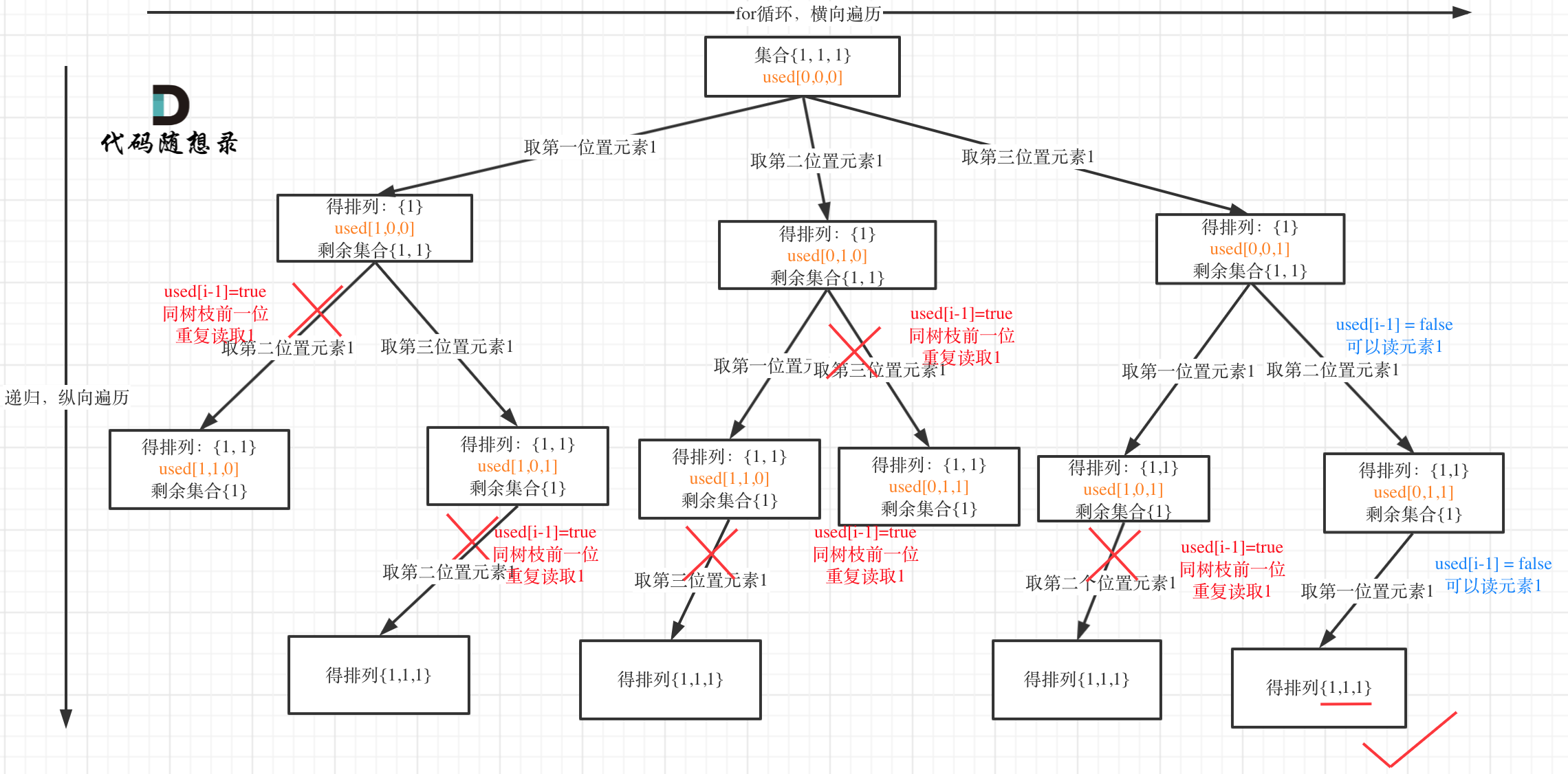
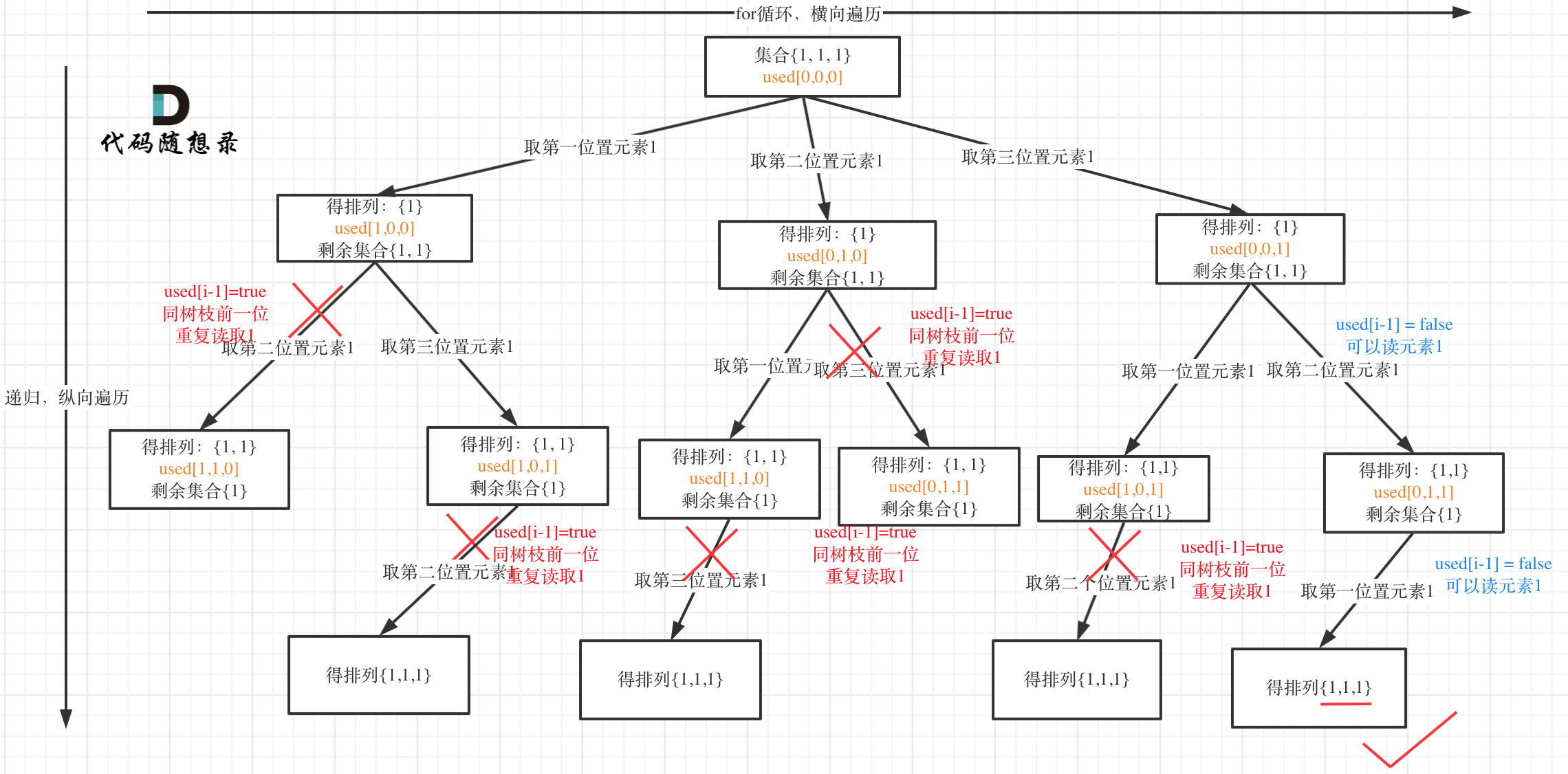
树枝上去重(used[i - 1] == true)的树型结构如下:
|
||||
|
||||
|
||||
|
||||
|
||||
**可以清晰的看到使用(used[i - 1] == false),即树层去重,效率更高!**
|
||||
|
||||
@ -72,14 +71,17 @@
|
||||
**所以这块就说一说我个人理解,对内容持开放态度,集思广益,欢迎大家来讨论!**
|
||||
|
||||
子集问题分析:
|
||||
|
||||
* 时间复杂度:$O(n × 2^n)$,因为每一个元素的状态无外乎取与不取,所以时间复杂度为$O(2^n)$,构造每一组子集都需要填进数组,又有需要$O(n)$,最终时间复杂度:$O(n × 2^n)$。
|
||||
* 空间复杂度:$O(n)$,递归深度为n,所以系统栈所用空间为$O(n)$,每一层递归所用的空间都是常数级别,注意代码里的result和path都是全局变量,就算是放在参数里,传的也是引用,并不会新申请内存空间,最终空间复杂度为$O(n)$。
|
||||
|
||||
排列问题分析:
|
||||
|
||||
* 时间复杂度:$O(n!)$,这个可以从排列的树形图中很明显发现,每一层节点为n,第二层每一个分支都延伸了n-1个分支,再往下又是n-2个分支,所以一直到叶子节点一共就是 n * n-1 * n-2 * ..... 1 = n!。每个叶子节点都会有一个构造全排列填进数组的操作(对应的代码:`result.push_back(path)`),该操作的复杂度为$O(n)$。所以,最终时间复杂度为:n * n!,简化为$O(n!)$。
|
||||
* 空间复杂度:$O(n)$,和子集问题同理。
|
||||
|
||||
组合问题分析:
|
||||
|
||||
* 时间复杂度:$O(n × 2^n)$,组合问题其实就是一种子集的问题,所以组合问题最坏的情况,也不会超过子集问题的时间复杂度。
|
||||
* 空间复杂度:$O(n)$,和子集问题同理。
|
||||
|
||||
|
||||
@ -1,5 +1,4 @@
|
||||
|
||||
|
||||
# 本周小结!(贪心算法系列二)
|
||||
|
||||
## 周一
|
||||
@ -16,7 +15,7 @@
|
||||
|
||||
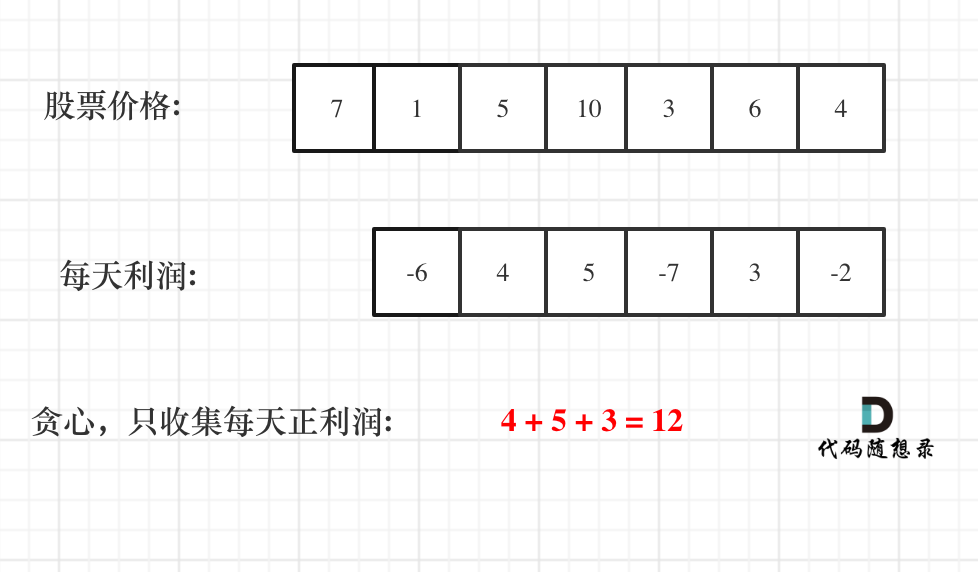
如图:
|
||||
|
||||

|
||||
|
||||
|
||||
## 周二
|
||||
|
||||
@ -32,7 +31,7 @@
|
||||
|
||||
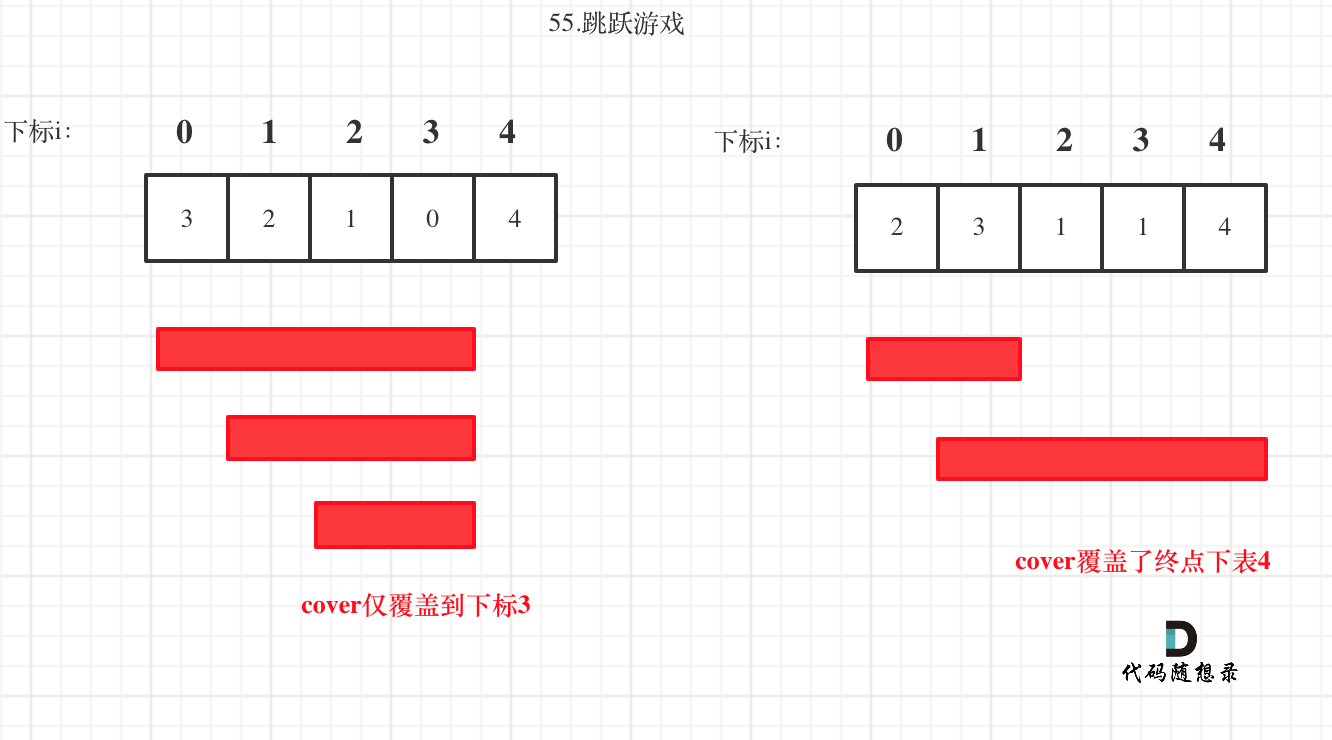
如图:
|
||||
|
||||

|
||||
|
||||
|
||||
|
||||
## 周三
|
||||
@ -45,7 +44,7 @@
|
||||
|
||||
如图:
|
||||
|
||||
|
||||
|
||||
|
||||
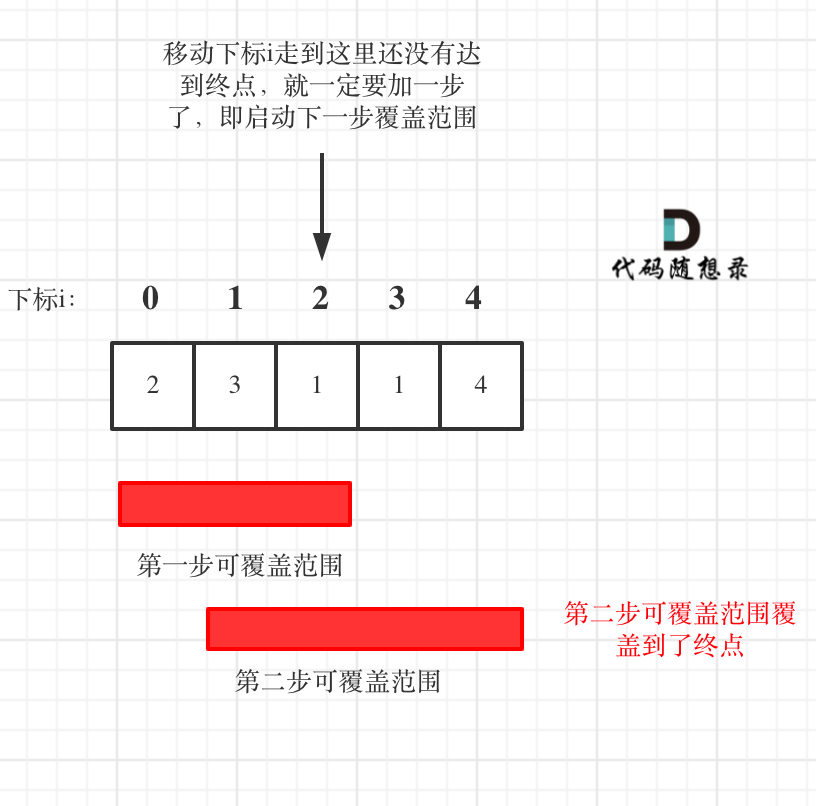
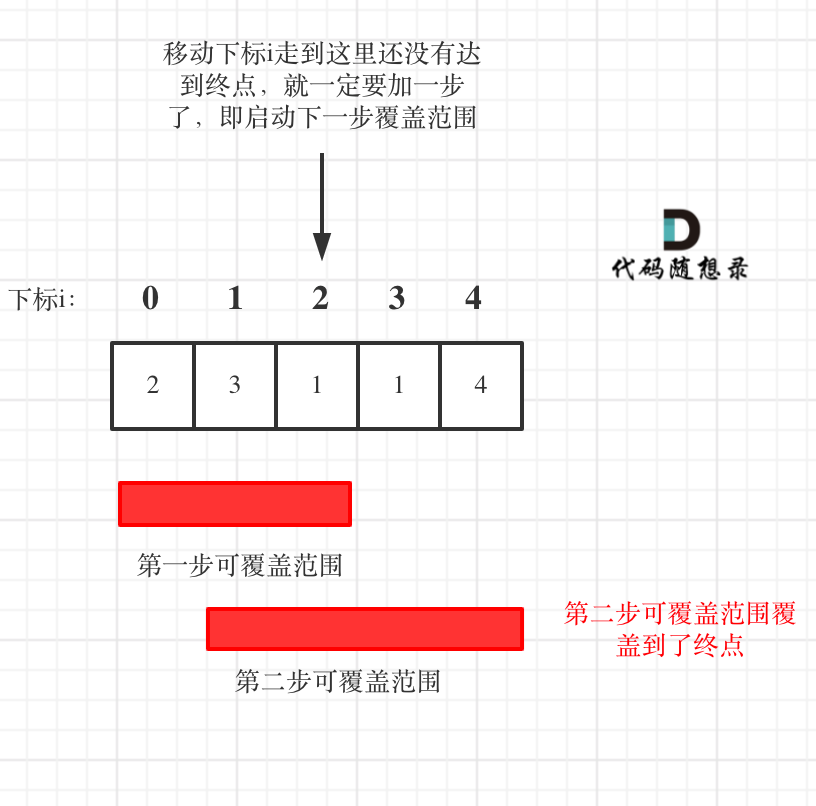
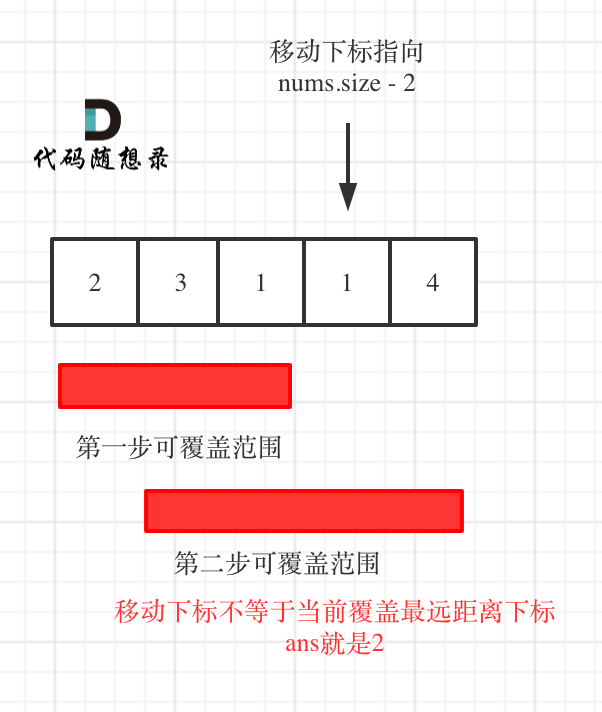
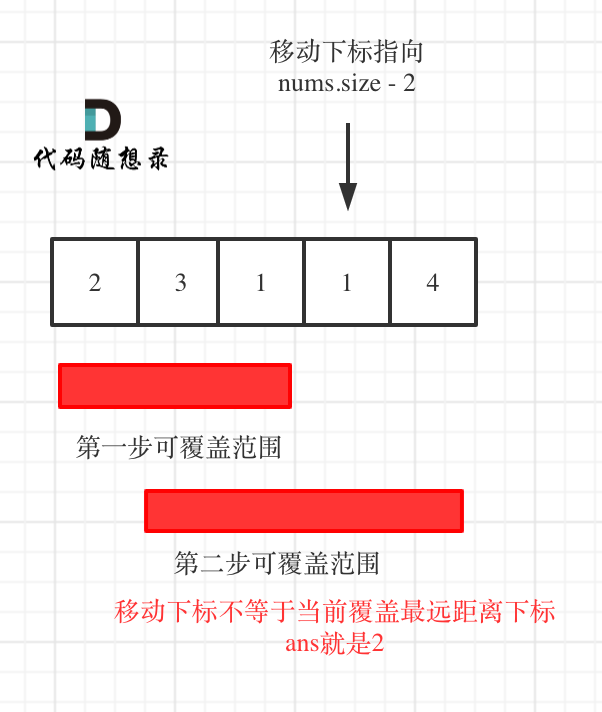
注意:**图中的移动下标是到当前这步覆盖的最远距离(下标2的位置),此时没有到终点,只能增加第二步来扩大覆盖范围**。
|
||||
|
||||
@ -56,10 +55,10 @@
|
||||
而版本二就比较统一的,超过范围,步数就加一,但在移动下标的范围了做了文章。
|
||||
|
||||
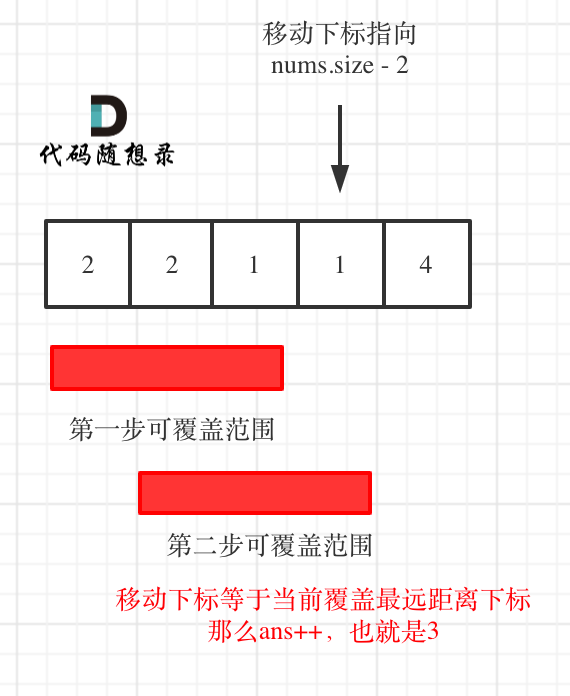
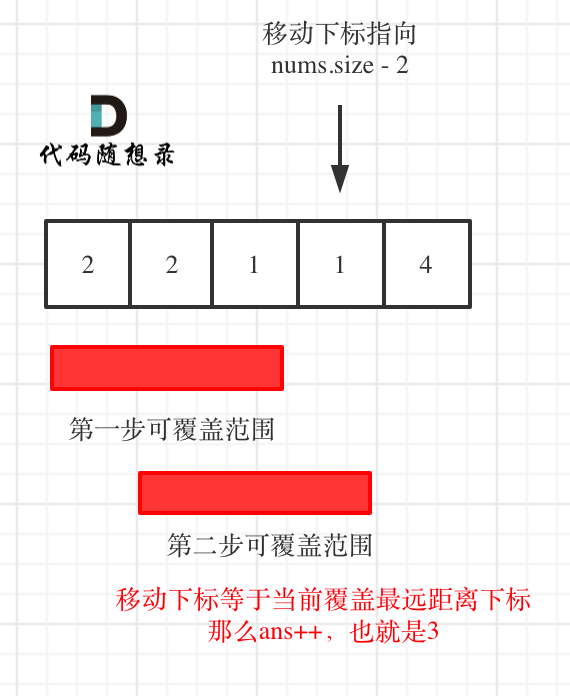
即如果覆盖最远距离下标是倒数第二点:直接加一就行,默认一定可以到终点。如图:
|
||||
|
||||
|
||||
|
||||
如果覆盖最远距离下标不是倒数第二点,说明本次覆盖已经到终点了。如图:
|
||||
|
||||
|
||||
|
||||
有的录友认为版本一好理解,有的录友认为版本二好理解,其实掌握一种就可以了,也不用非要比拼一下代码的简洁性,简洁程度都差不多了。
|
||||
|
||||
|
||||
@ -76,7 +76,8 @@
|
||||
|
||||
文中从计算机硬件出发,分析计算机的计算性能,然后亲自做实验,整理出数据如下:
|
||||
|
||||

|
||||
|
||||

|
||||
|
||||
**大家有一个数量级上的概念就可以了!**
|
||||
|
||||
|
||||
@ -37,7 +37,8 @@
|
||||
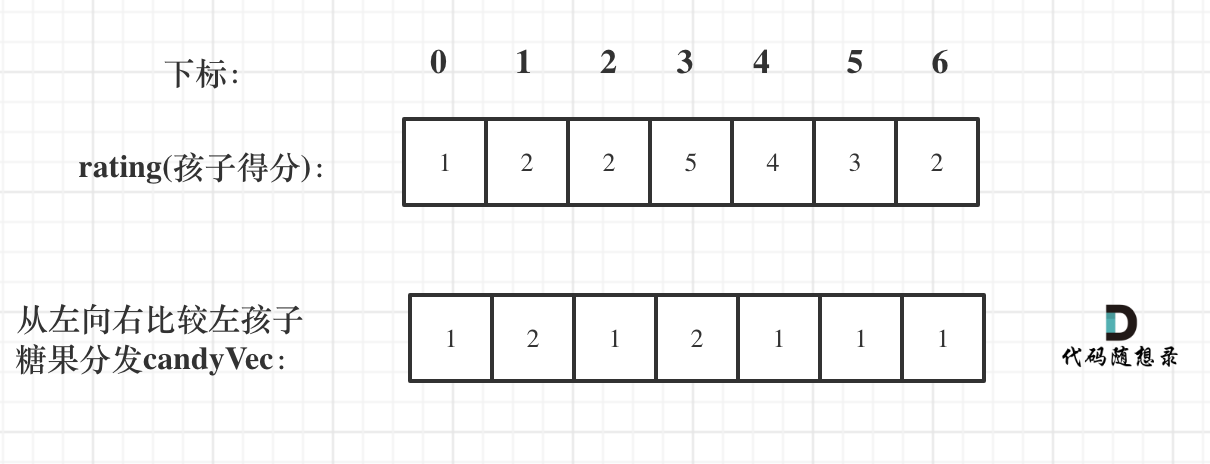
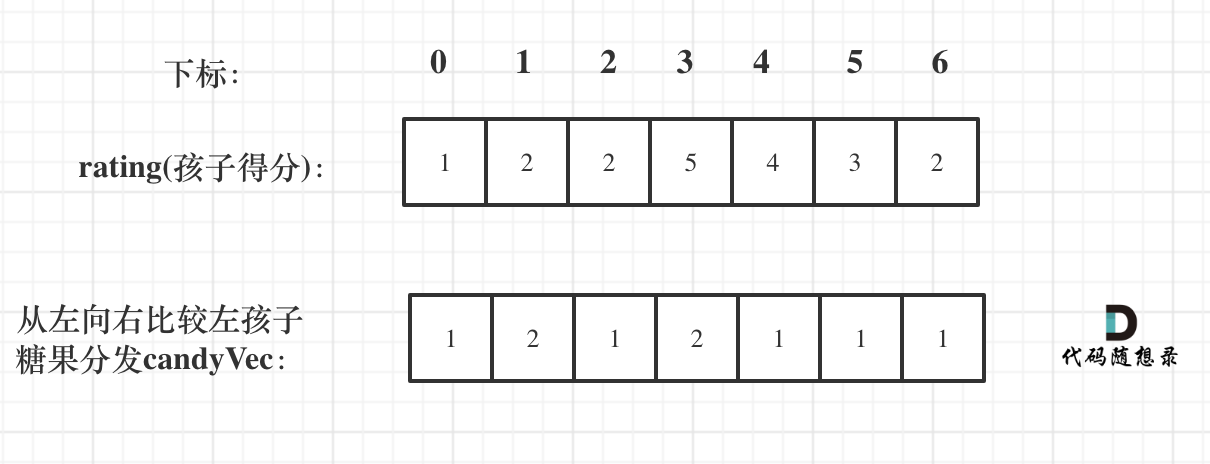
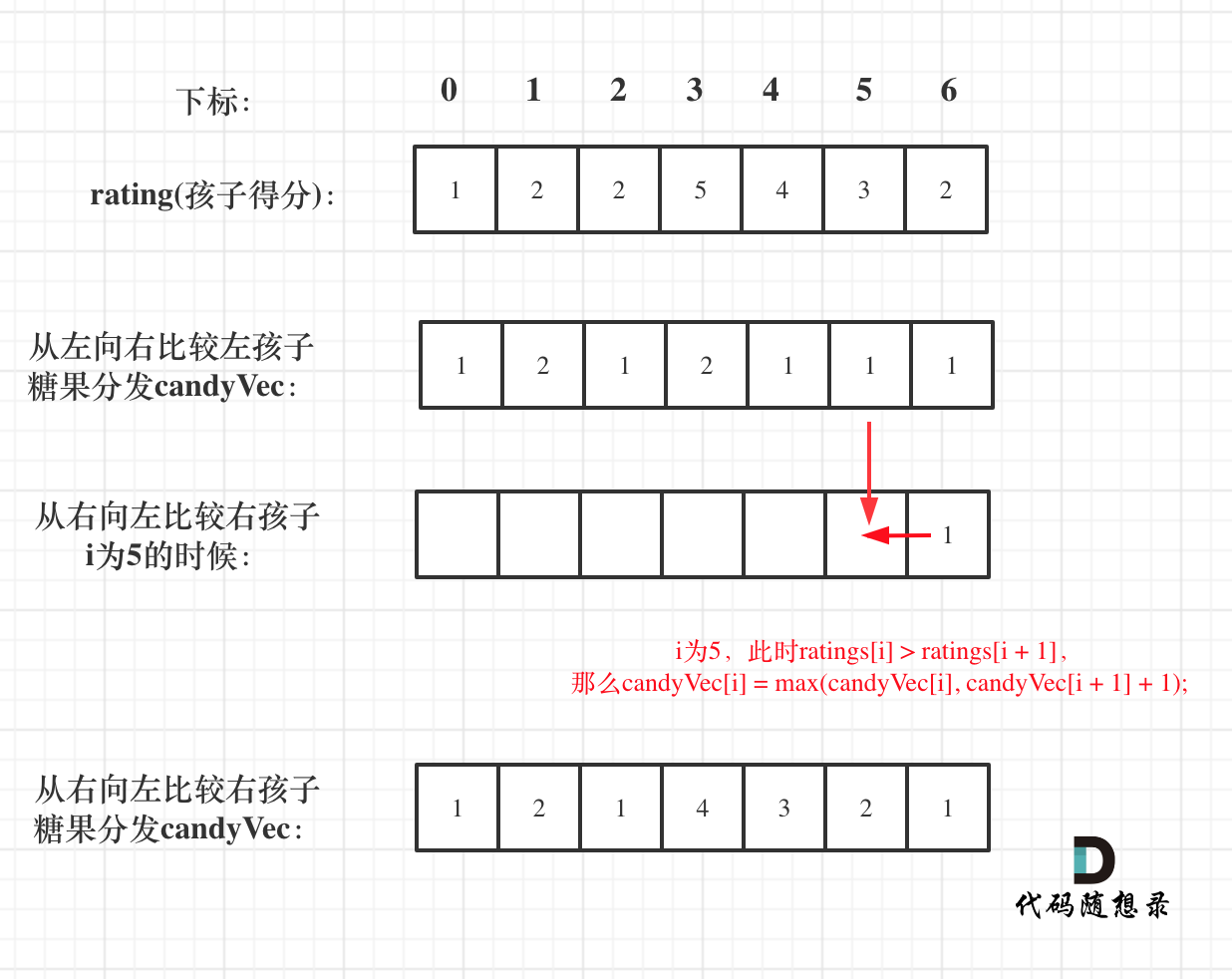
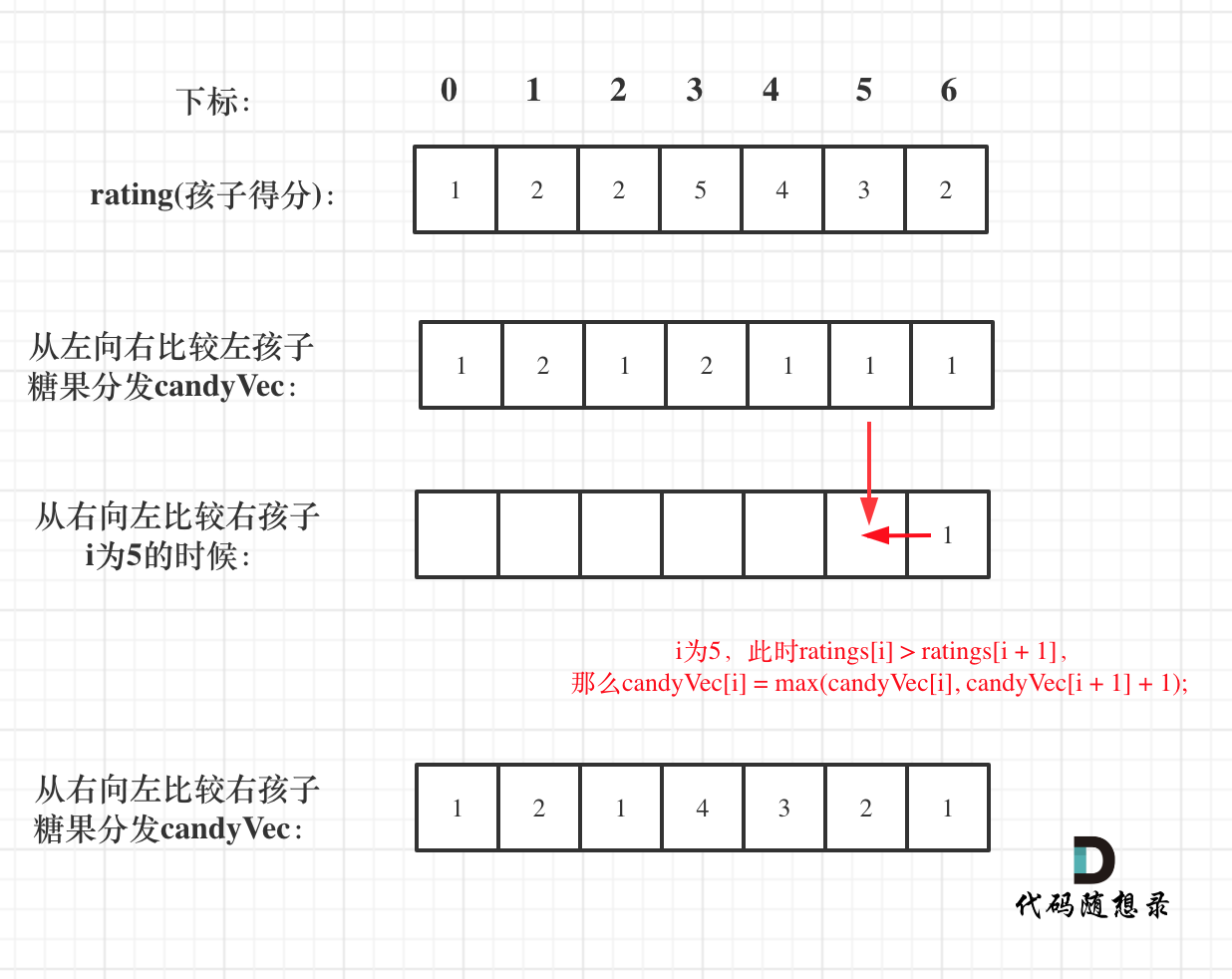
先贪心一边,局部最优:只要右边评分比左边大,右边的孩子就多一个糖果,全局最优:相邻的孩子中,评分高的右孩子获得比左边孩子更多的糖果
|
||||
|
||||
如图:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
接着在贪心另一边,左孩子大于右孩子,左孩子的糖果就要比右孩子多。
|
||||
@ -49,7 +50,7 @@
|
||||
局部最优可以推出全局最优。
|
||||
|
||||
如图:
|
||||
|
||||
|
||||
|
||||
|
||||
## 周三
|
||||
|
||||
@ -1,5 +1,4 @@
|
||||
|
||||
|
||||
# 本周小结!(贪心算法系列四)
|
||||
|
||||
## 周一
|
||||
@ -10,7 +9,7 @@
|
||||
|
||||
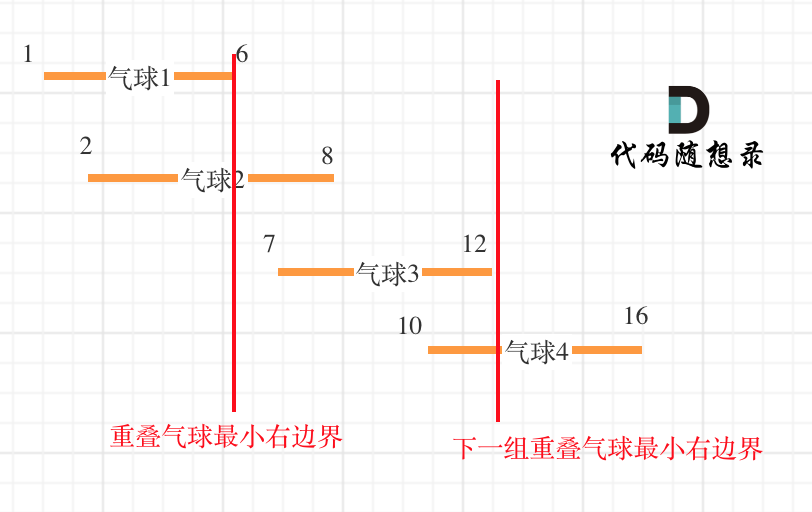
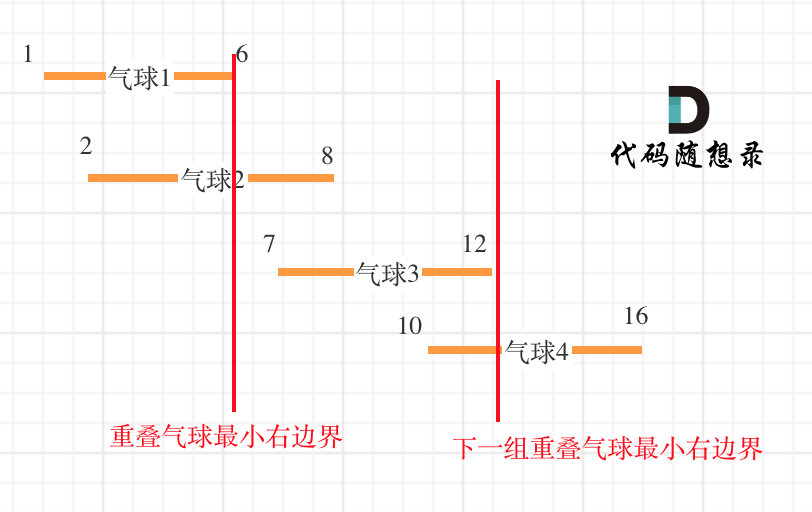
如图:
|
||||
|
||||
|
||||
|
||||
|
||||
模拟射气球的过程,很多同学真的要去模拟了,实时把气球从数组中移走,这么写的话就复杂了,从前向后遍历重复的只要跳过就可以的。
|
||||
|
||||
@ -22,7 +21,7 @@
|
||||
|
||||
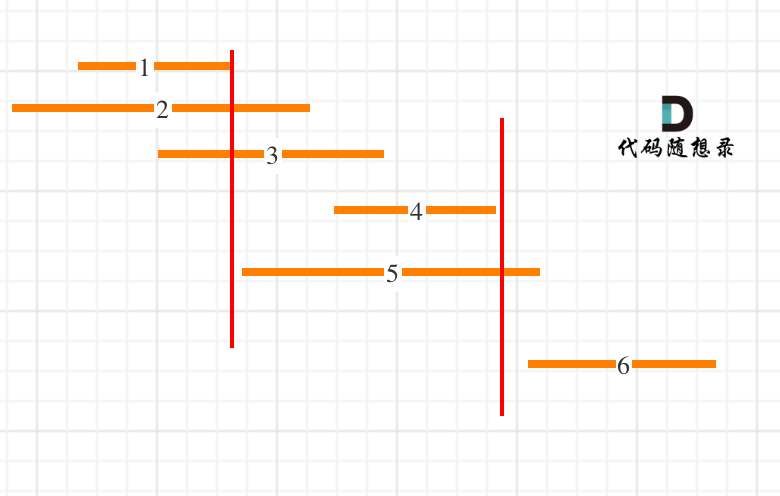
如图:
|
||||
|
||||

|
||||
|
||||
|
||||
细心的同学就发现了,此题和 [贪心算法:用最少数量的箭引爆气球](https://programmercarl.com/0452.用最少数量的箭引爆气球.html)非常像。
|
||||
|
||||
@ -31,6 +30,7 @@
|
||||
把[贪心算法:用最少数量的箭引爆气球](https://programmercarl.com/0452.用最少数量的箭引爆气球.html)代码稍做修改,就可以AC本题。
|
||||
|
||||
修改后的C++代码如下:
|
||||
|
||||
```CPP
|
||||
class Solution {
|
||||
public:
|
||||
@ -71,7 +71,7 @@ public:
|
||||
|
||||
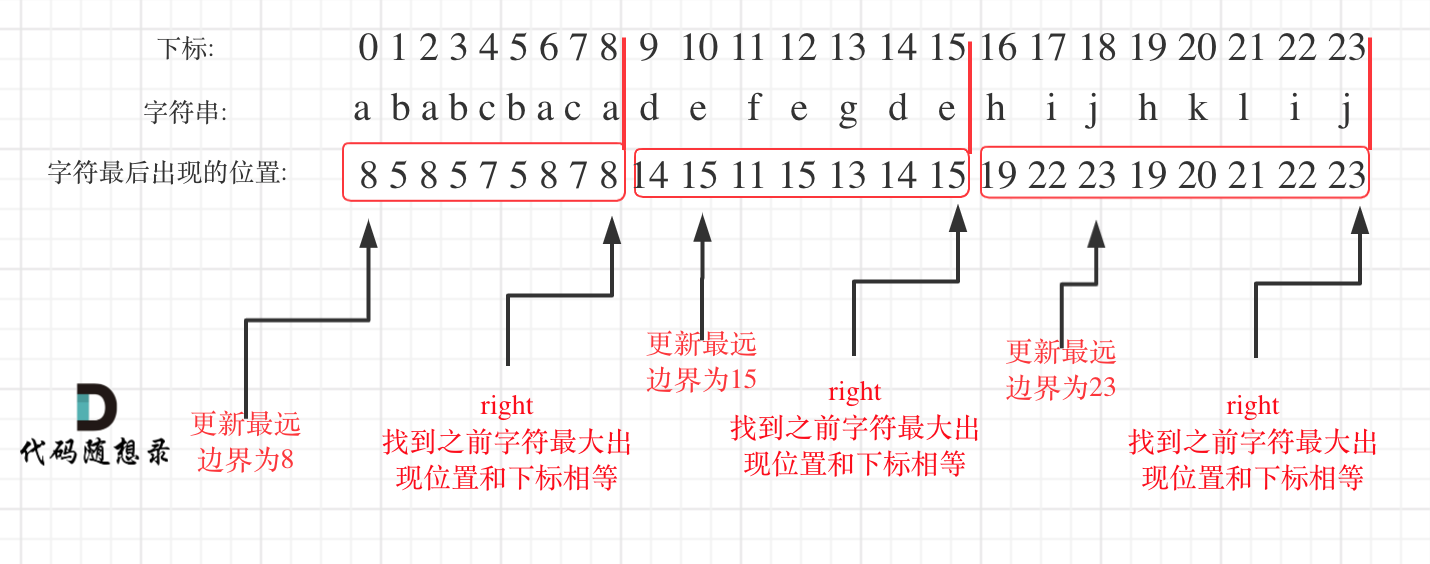
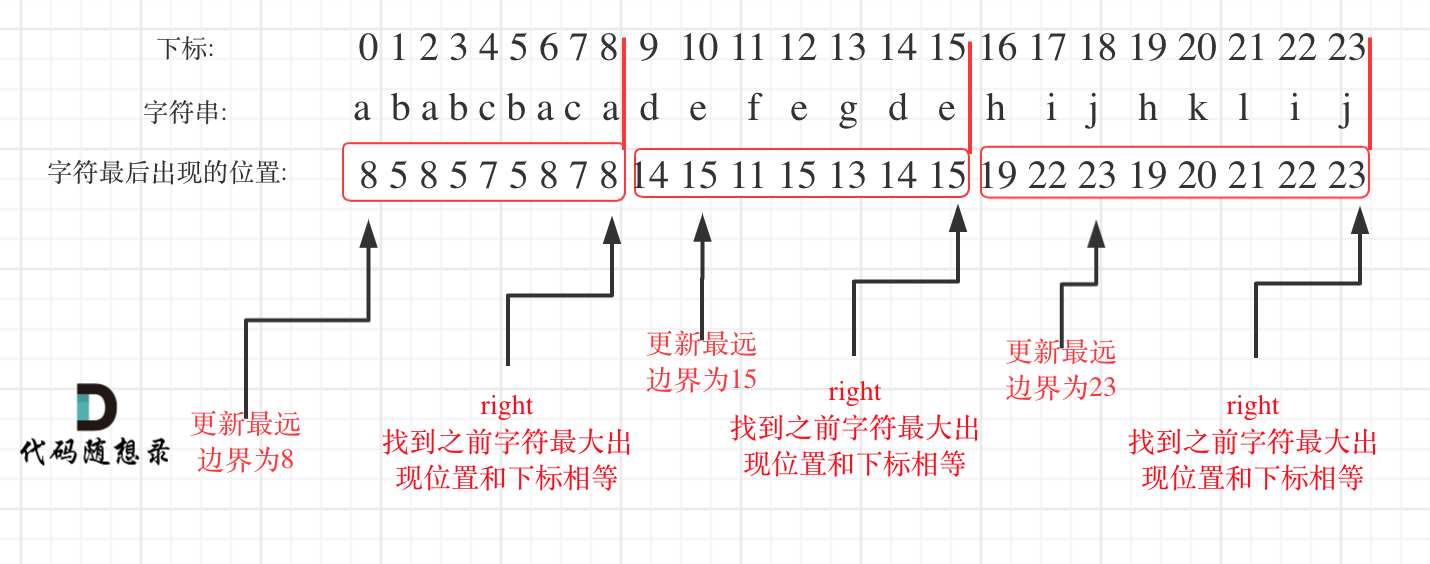
如图:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
## 周四
|
||||
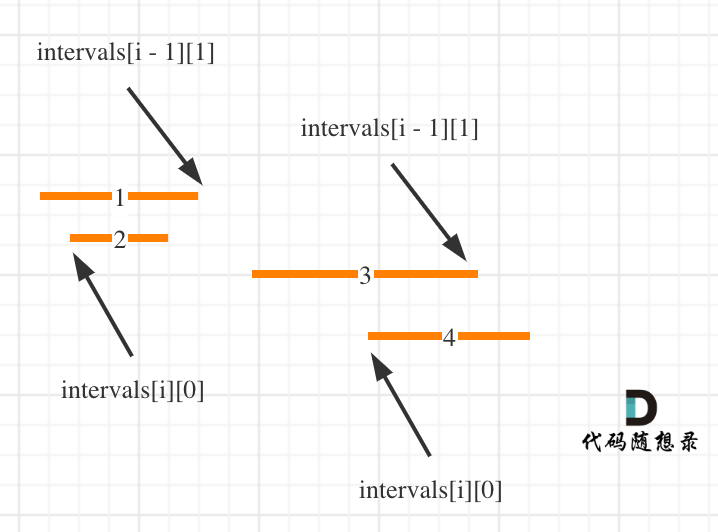
@ -86,7 +86,7 @@ public:
|
||||
|
||||
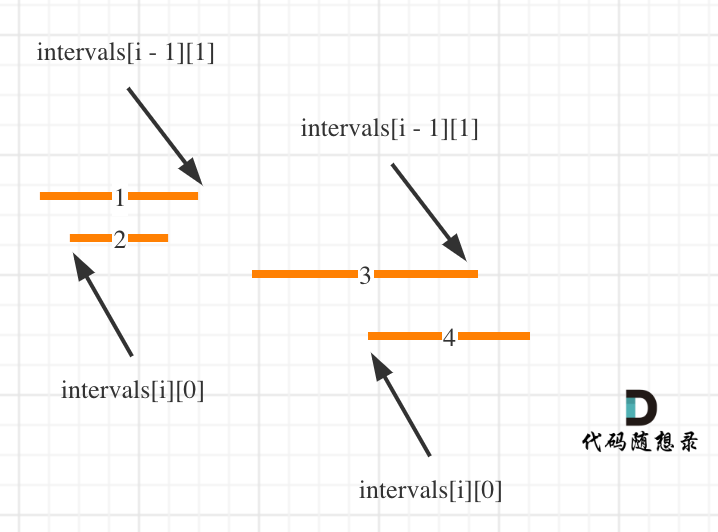
如图:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
## 总结
|
||||
|
||||
@ -30,7 +30,7 @@ for (int i = 1; i < m; i++) {
|
||||
}
|
||||
```
|
||||
|
||||

|
||||
|
||||
|
||||
|
||||
## 周二
|
||||
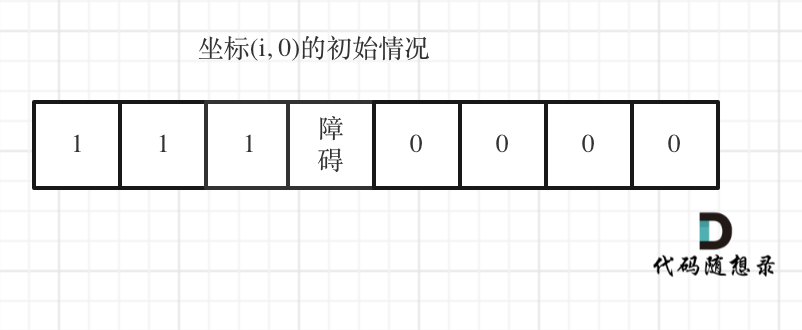
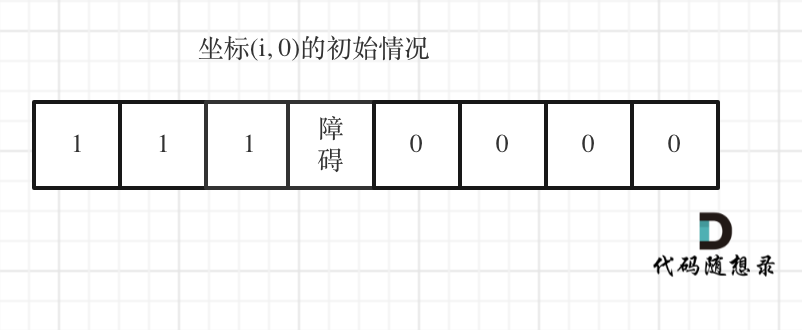
@ -44,7 +44,7 @@ dp[i][j]定义依然是:表示从(0 ,0)出发,到(i, j) 有dp[i][j]条
|
||||
|
||||
如图:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
这里难住了不少同学,代码如下:
|
||||
@ -69,11 +69,11 @@ for (int i = 1; i < m; i++) {
|
||||
|
||||
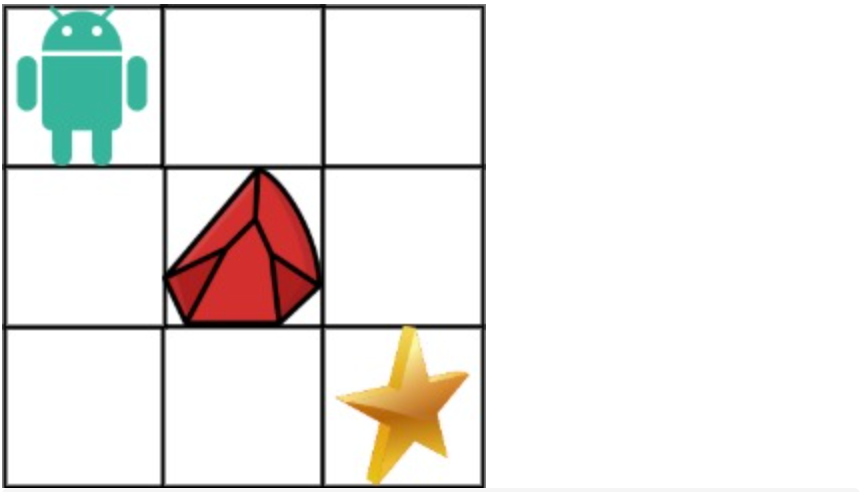
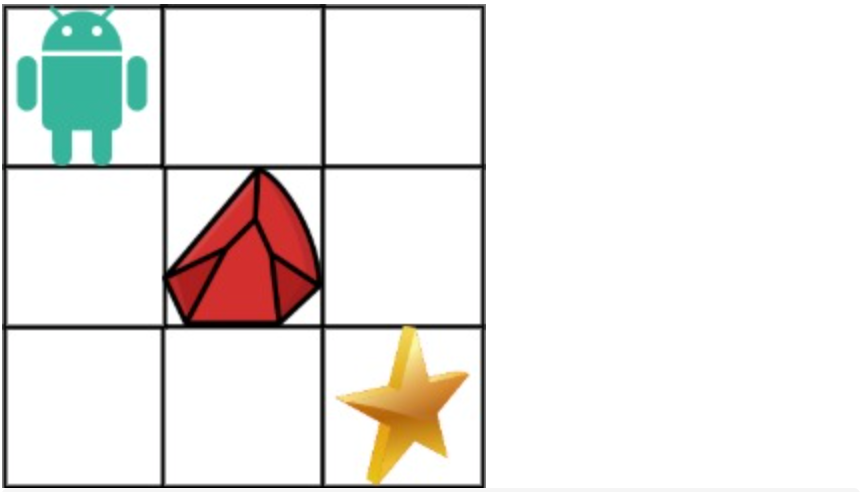
拿示例1来举例如题:
|
||||
|
||||
|
||||
|
||||
|
||||
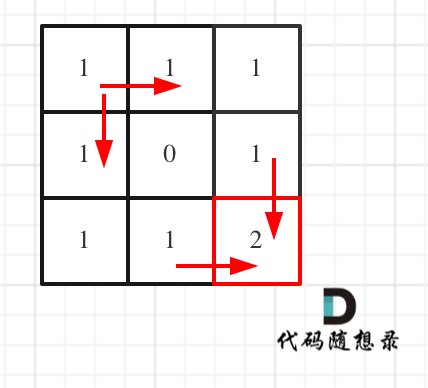
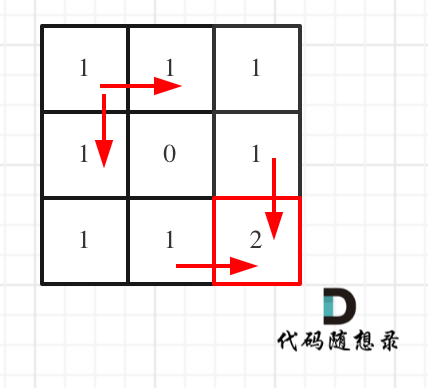
对应的dp table 如图:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
## 周三
|
||||
@ -107,9 +107,10 @@ for (int i = 3; i <= n ; i++) {
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
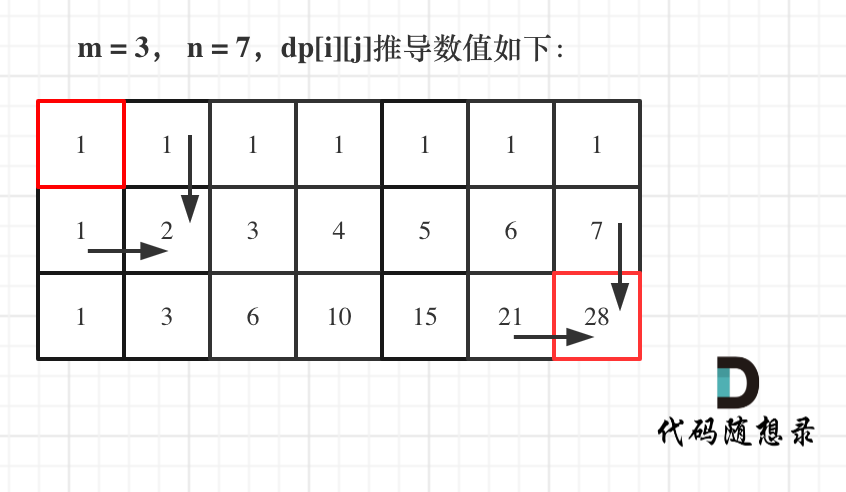
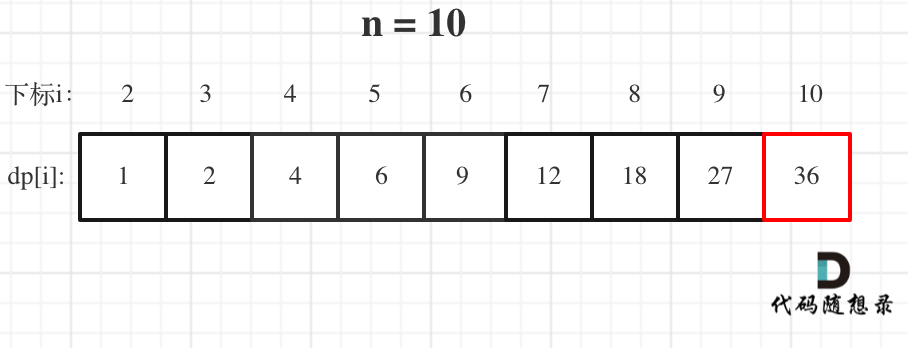
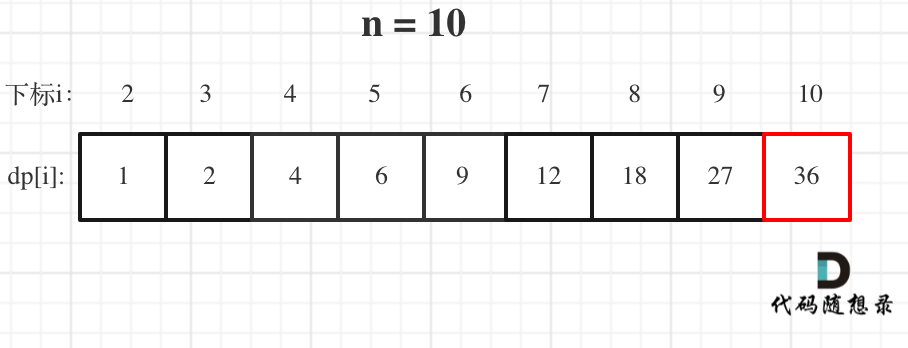
举例当n为10 的时候,dp数组里的数值,如下:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
@ -141,7 +142,7 @@ dp数组如何初始化:只需要初始化dp[0]就可以了,推导的基础
|
||||
|
||||
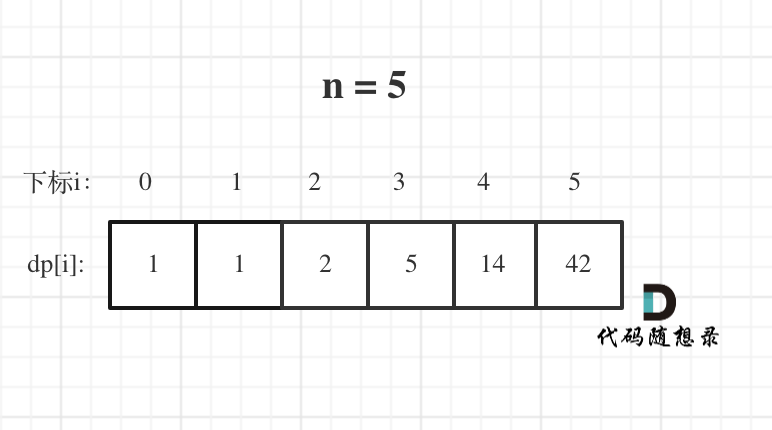
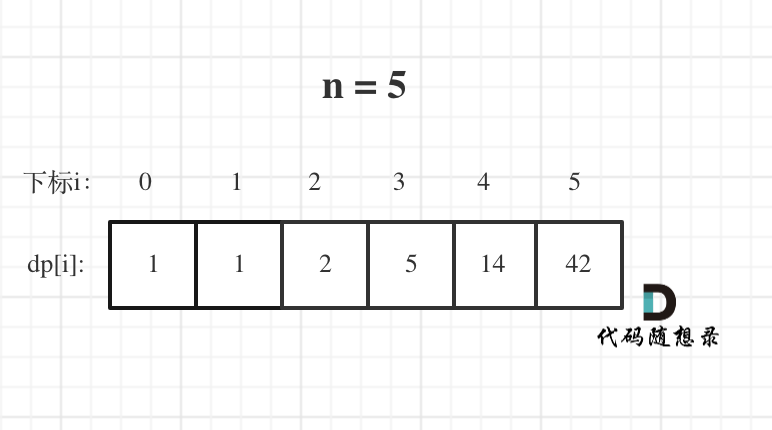
n为5时候的dp数组状态如图:
|
||||
|
||||
|
||||
|
||||
|
||||
## 总结
|
||||
|
||||
|
||||
@ -1,4 +1,6 @@
|
||||
|
||||
# 本周小结!(动态规划系列三)
|
||||
|
||||
本周我们正式开始讲解背包问题,也是动规里非常重要的一类问题。
|
||||
|
||||
背包问题其实有很多细节,如果了解个大概,然后也能一气呵成把代码写出来,但稍稍变变花样可能会陷入迷茫了。
|
||||
@ -15,7 +17,7 @@
|
||||
|
||||
关于其他几种常用的背包,大家看这张图就了然于胸了:
|
||||
|
||||
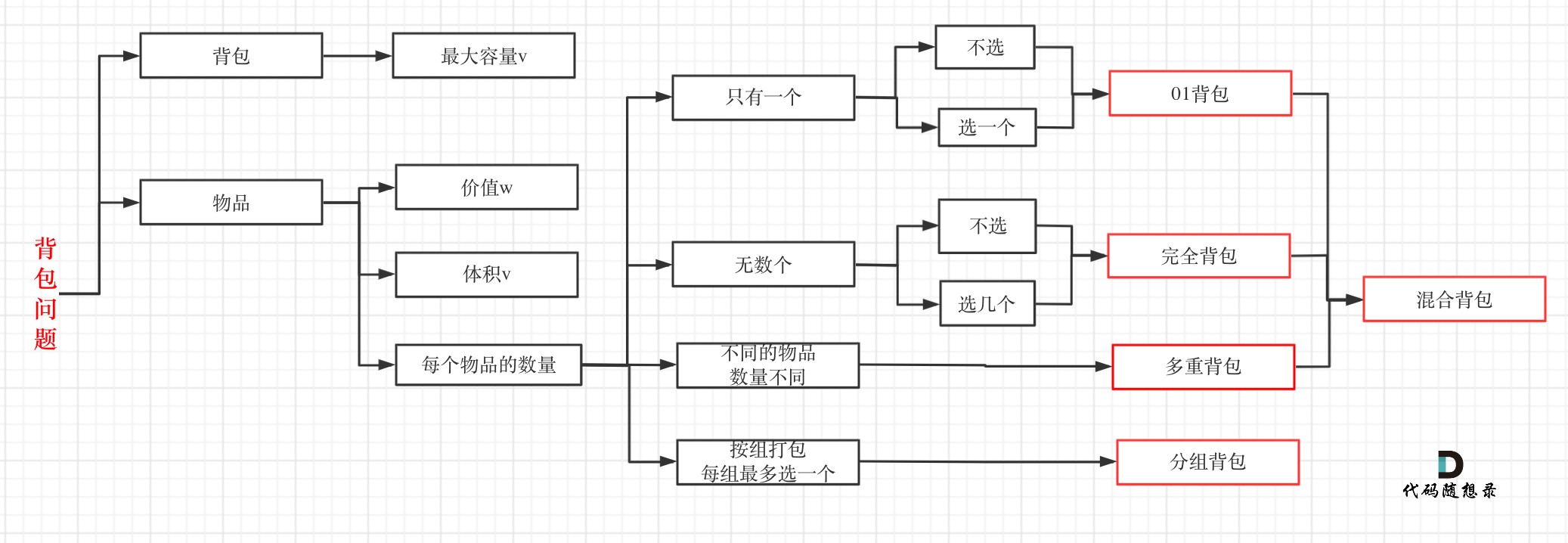
|
||||
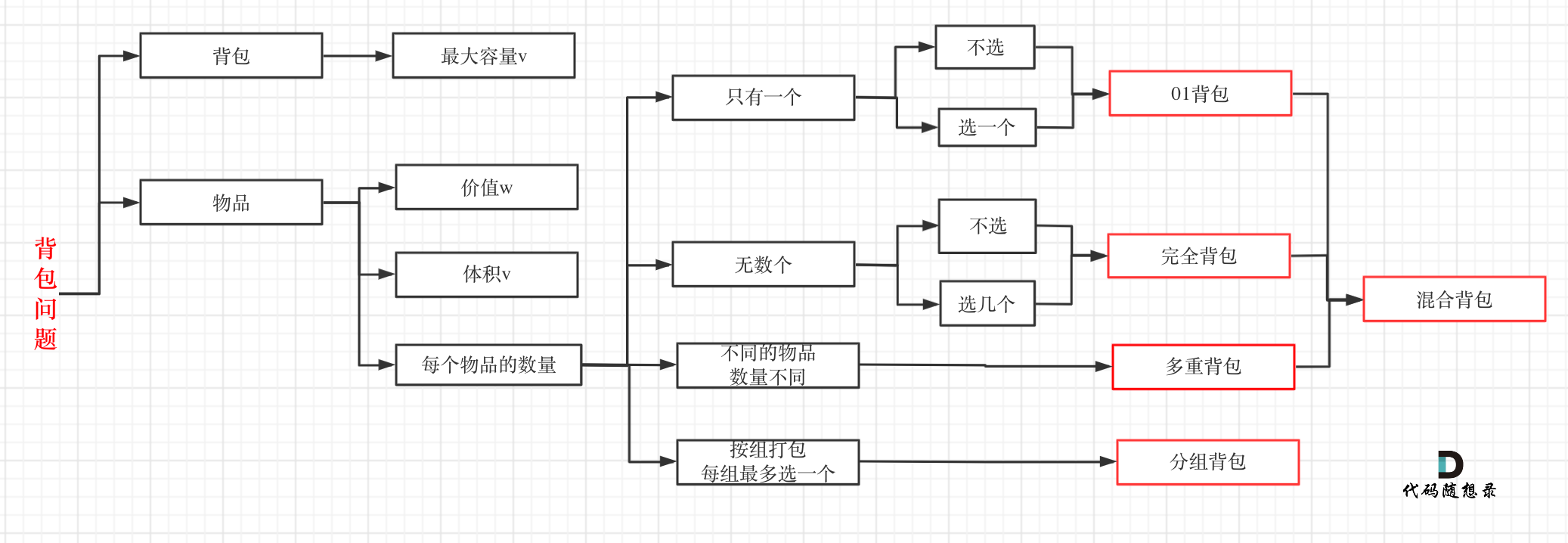
|
||||
|
||||
本文用动规五部曲详细讲解了01背包的二维dp数组的实现方法,大家其实可以发现最简单的是推导公式了,推导公式估计看一遍就记下来了,但难就难在确定初始化和遍历顺序上。
|
||||
|
||||
@ -61,14 +63,14 @@ for(int i = 1; i < weight.size(); i++) { // 遍历物品
|
||||
物品为:
|
||||
|
||||
| | 重量 | 价值 |
|
||||
| --- | --- | --- |
|
||||
| ----- | ---- | ---- |
|
||||
| 物品0 | 1 | 15 |
|
||||
| 物品1 | 3 | 20 |
|
||||
| 物品2 | 4 | 30 |
|
||||
|
||||
来看一下对应的dp数组的数值,如图:
|
||||
|
||||
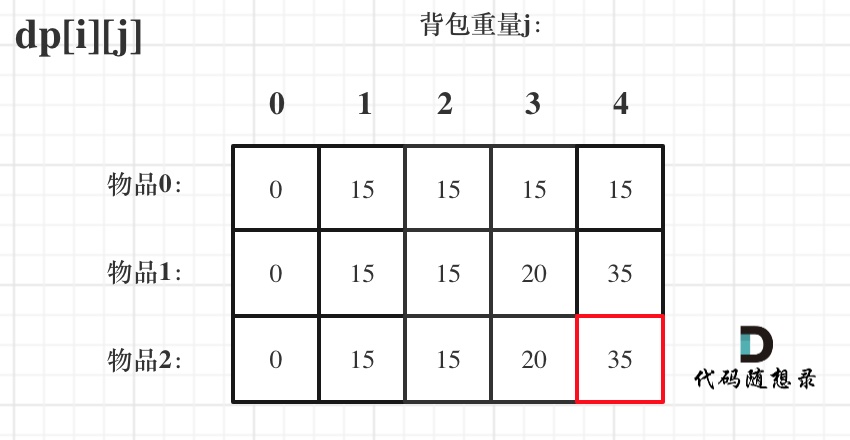
|
||||
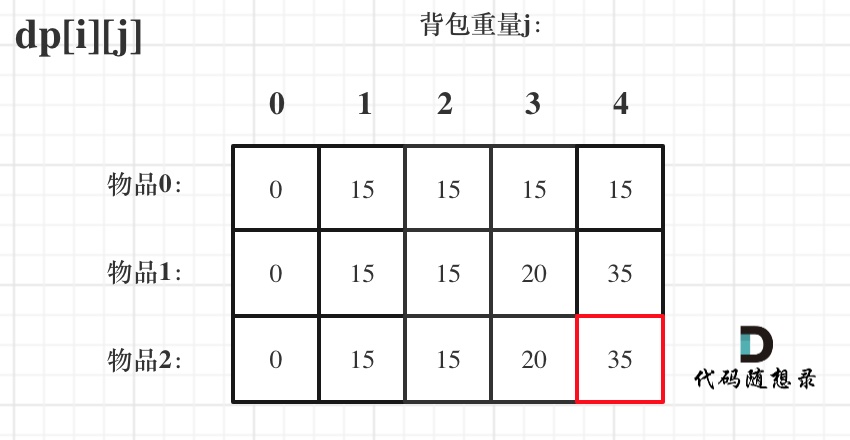
|
||||
|
||||
最终结果就是dp[2][4]。
|
||||
|
||||
@ -120,7 +122,7 @@ for(int i = 0; i < weight.size(); i++) { // 遍历物品
|
||||
|
||||
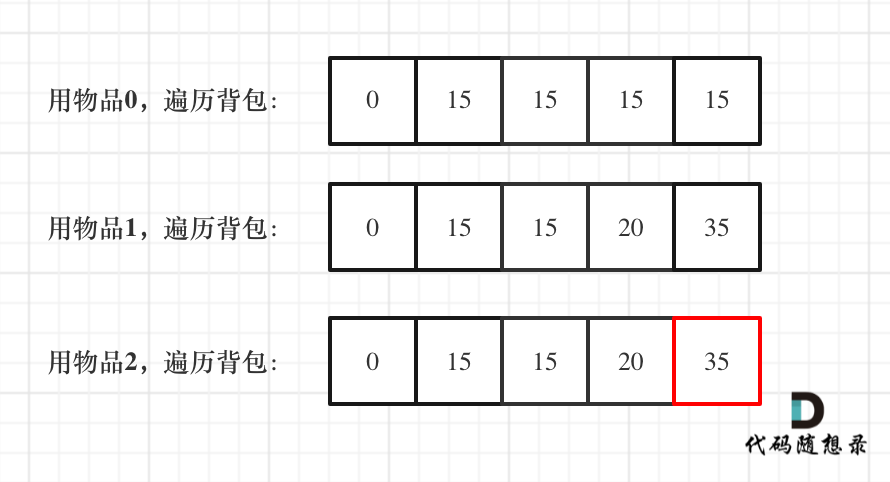
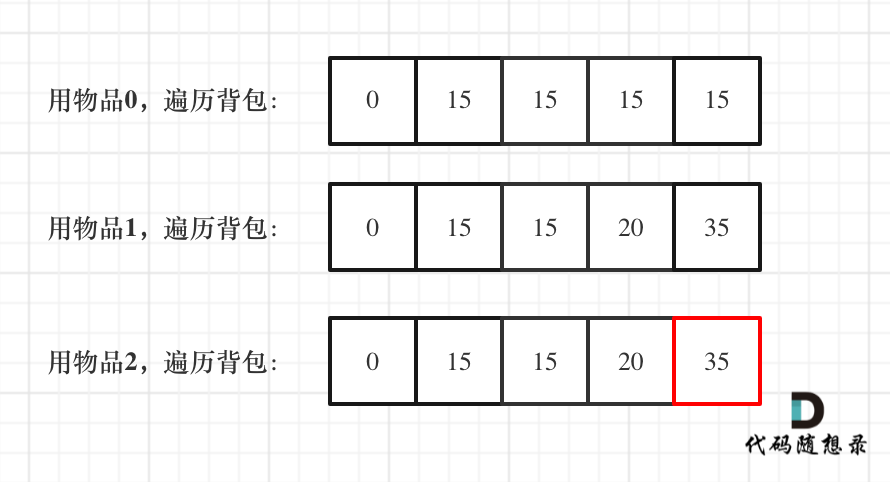
一维dp,分别用物品0,物品1,物品2 来遍历背包,最终得到结果如下:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
## 周三
|
||||
|
||||
@ -35,7 +35,7 @@ bagSize = (S + sum) / 2 = (3 + 5) / 2 = 4
|
||||
|
||||
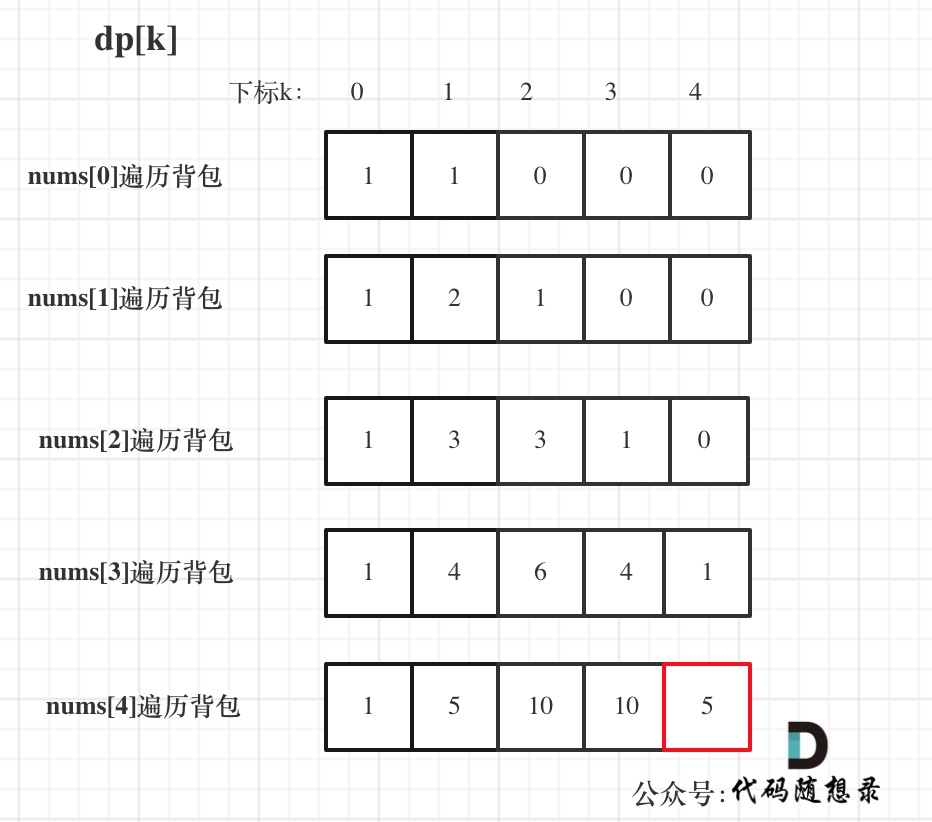
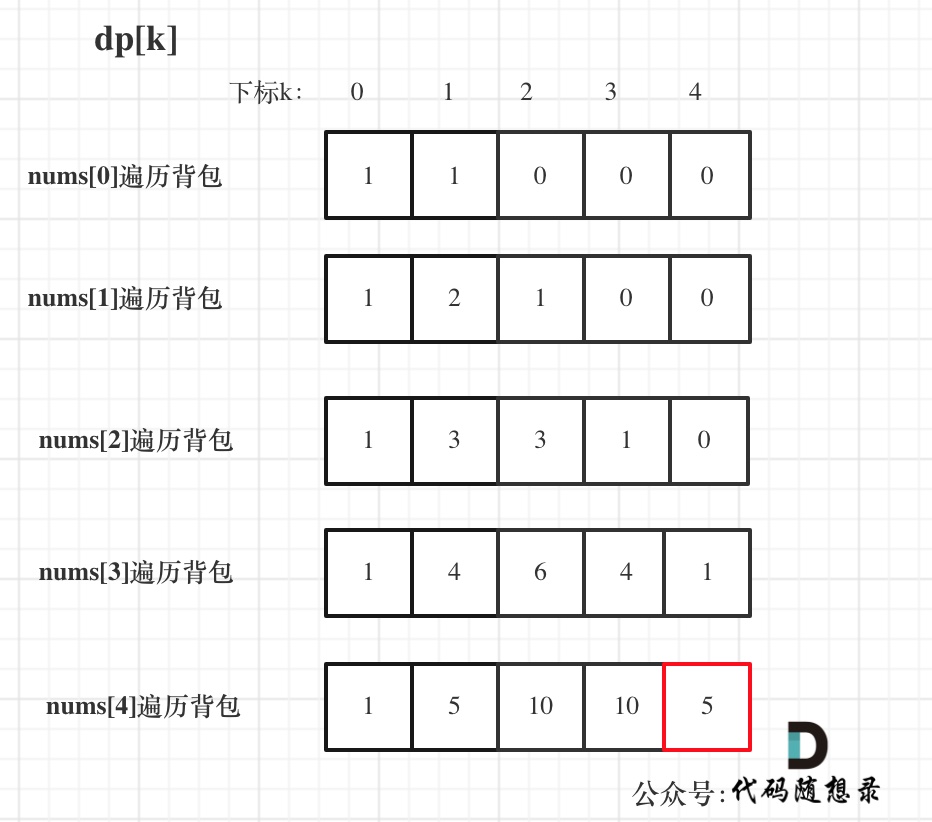
dp数组状态变化如下:
|
||||
|
||||
|
||||
|
||||
|
||||
## 周二
|
||||
|
||||
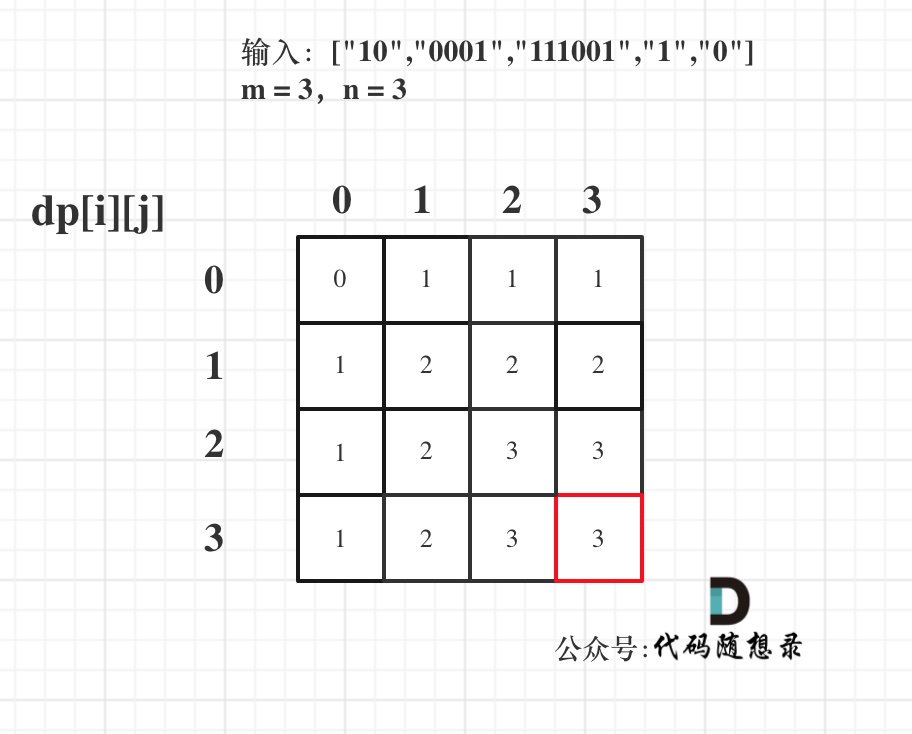
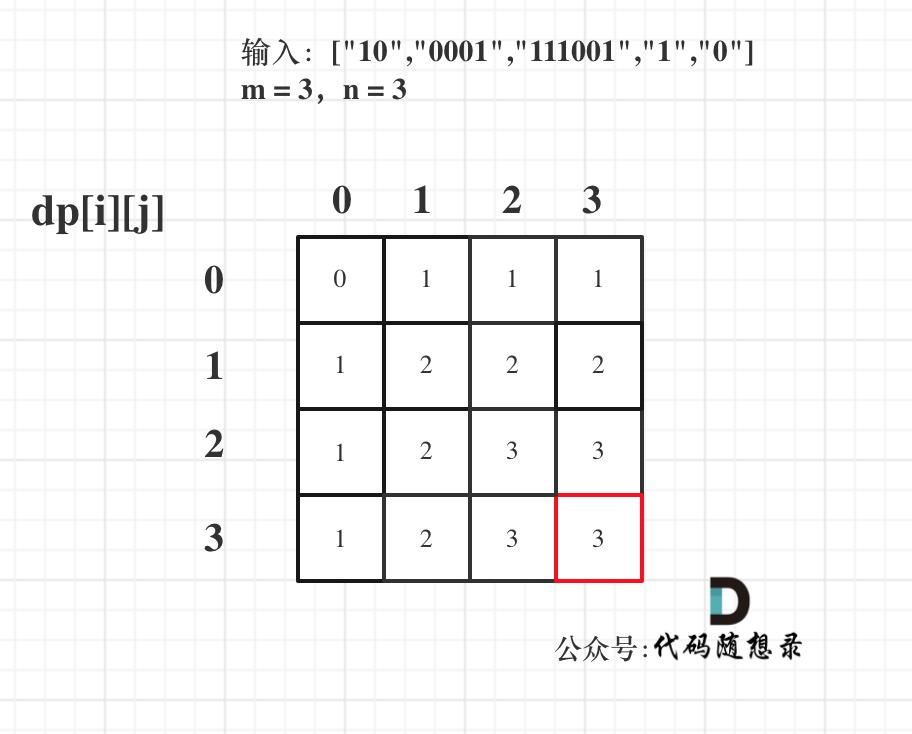
@ -72,7 +72,8 @@ dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
|
||||
|
||||
最后dp数组的状态如下所示:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
## 周三
|
||||
|
||||
|
||||
@ -29,7 +29,7 @@ dp[1] = max(nums[0], nums[1]);
|
||||
|
||||
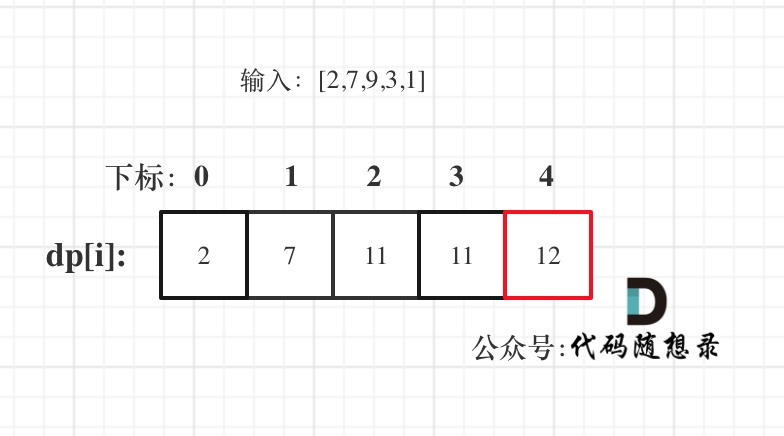
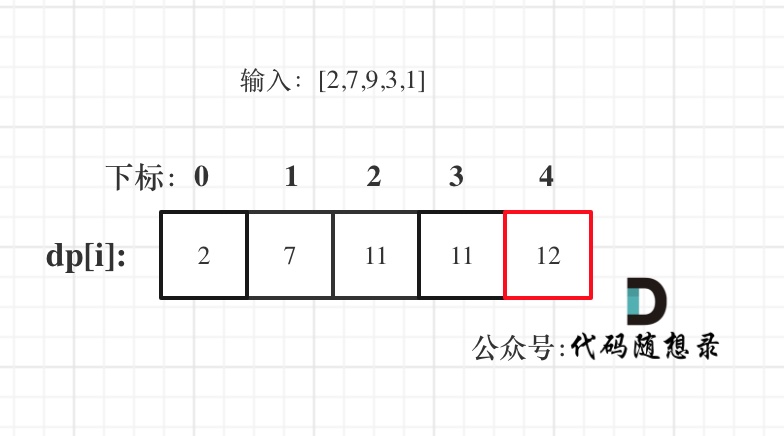
以示例二,输入[2,7,9,3,1]为例。
|
||||
|
||||
|
||||
|
||||
|
||||
红框dp[nums.size() - 1]为结果。
|
||||
|
||||
@ -41,15 +41,15 @@ dp[1] = max(nums[0], nums[1]);
|
||||
|
||||
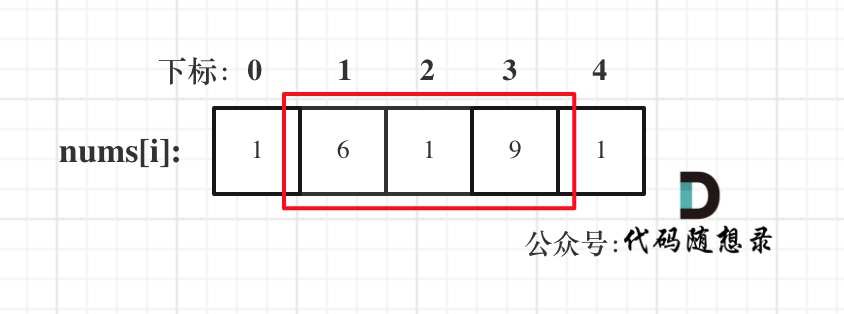
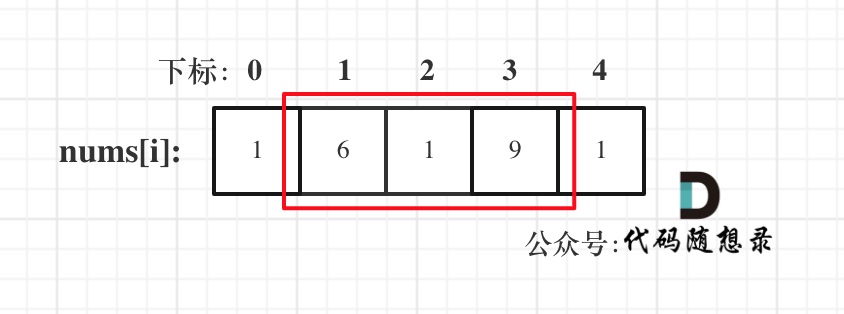
* 情况一:考虑不包含首尾元素
|
||||
|
||||
|
||||
|
||||
|
||||
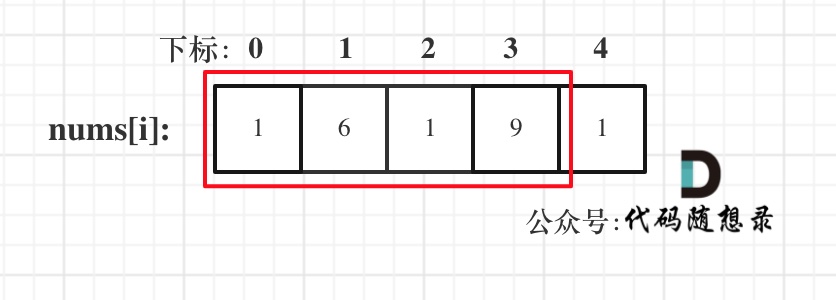
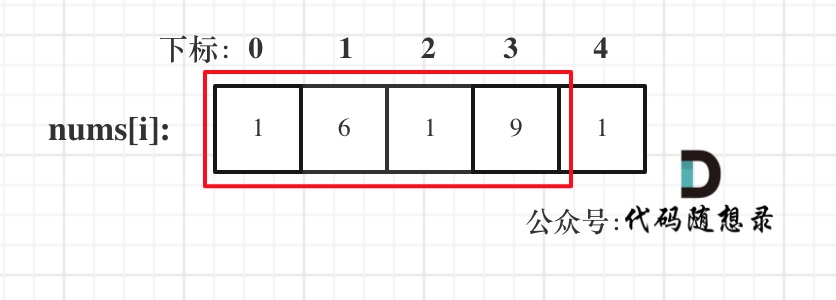
* 情况二:考虑包含首元素,不包含尾元素
|
||||
|
||||
|
||||
|
||||
|
||||
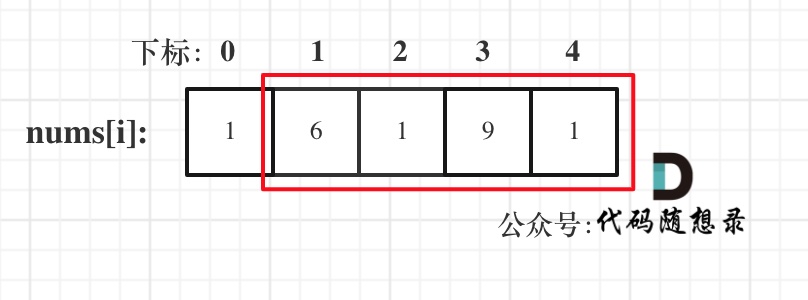
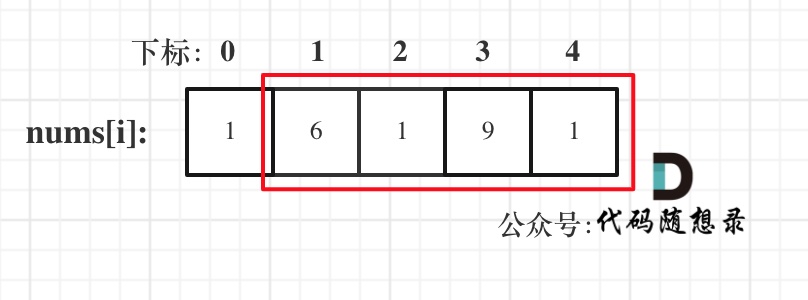
* 情况三:考虑包含尾元素,不包含首元素
|
||||
|
||||
|
||||
|
||||
|
||||
需要注意的是,**“考虑” 不等于 “偷”**,例如情况三,虽然是考虑包含尾元素,但不一定要选尾部元素!对于情况三,取nums[1] 和 nums[3]就是最大的。
|
||||
|
||||
@ -135,9 +135,11 @@ dp数组含义:下标为0记录不偷该节点所得到的的最大金钱,
|
||||
2. 确定终止条件
|
||||
|
||||
在遍历的过程中,如果遇到空间点的话,很明显,无论偷还是不偷都是0,所以就返回
|
||||
|
||||
```
|
||||
if (cur == NULL) return vector<int>{0, 0};
|
||||
```
|
||||
|
||||
3. 确定遍历顺序
|
||||
|
||||
采用后序遍历,代码如下:
|
||||
@ -175,7 +177,7 @@ return {val2, val1};
|
||||
|
||||
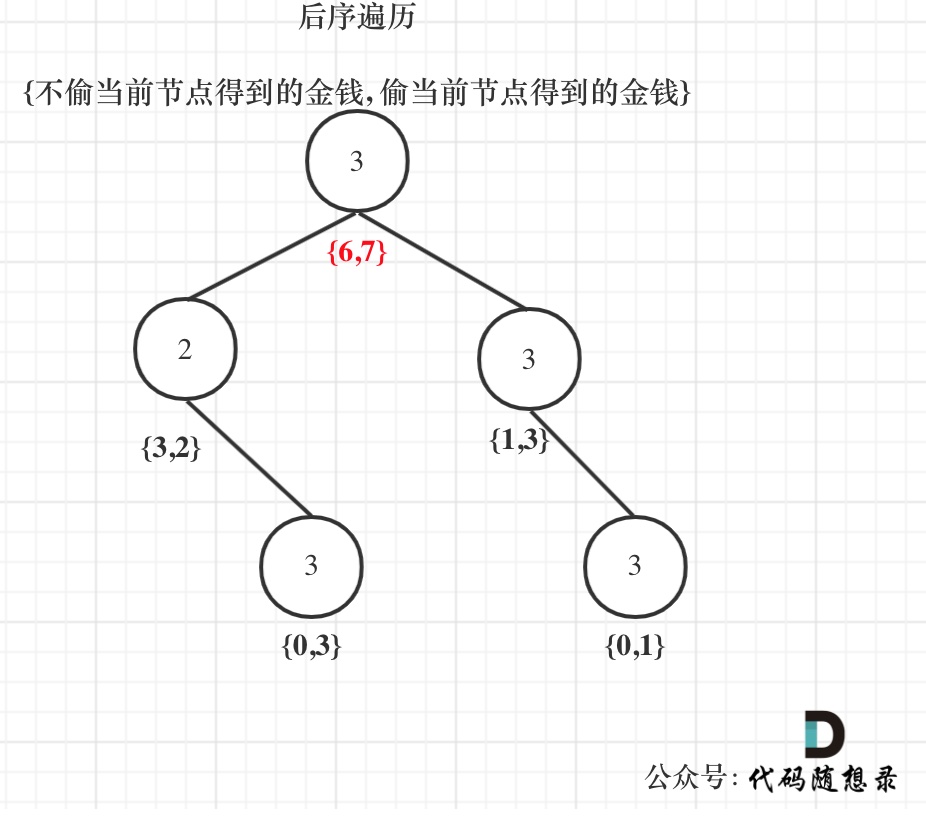
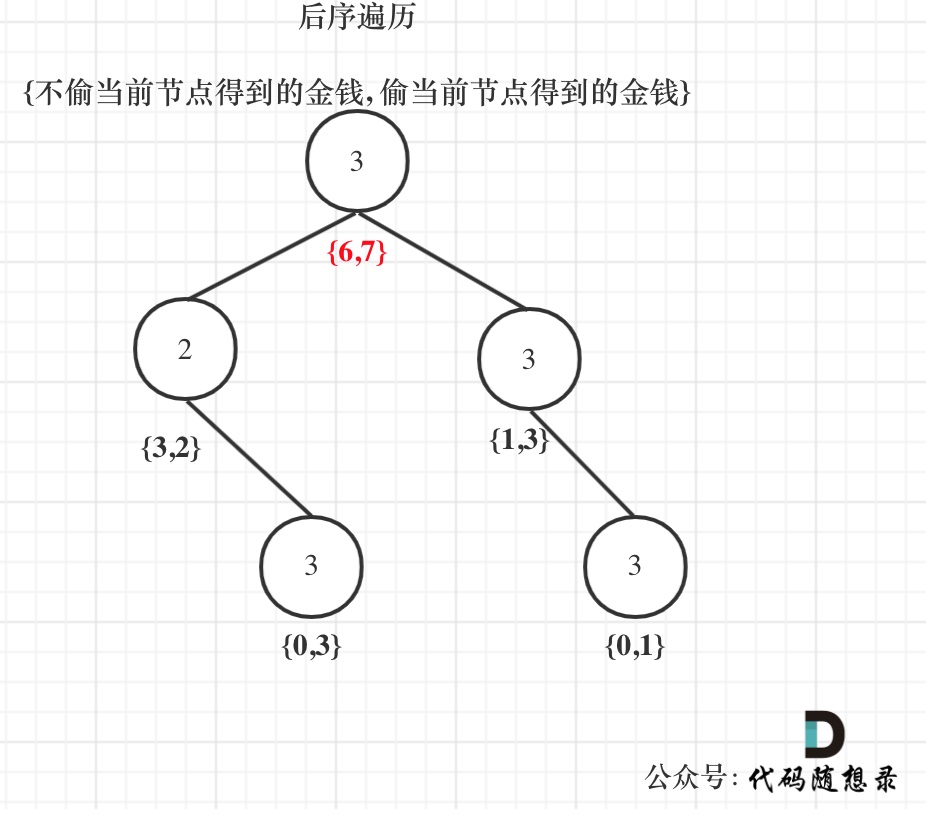
以示例1为例,dp数组状态如下:(**注意用后序遍历的方式推导**)
|
||||
|
||||
|
||||
|
||||
|
||||
**最后头结点就是 取下标0 和 下标1的最大值就是偷得的最大金钱**。
|
||||
|
||||
@ -196,6 +198,7 @@ return {val2, val1};
|
||||
这里我给出了三种解法:
|
||||
|
||||
暴力解法代码:
|
||||
|
||||
```CPP
|
||||
class Solution {
|
||||
public:
|
||||
|
||||
@ -76,7 +76,7 @@ dp[0][4] = 0;
|
||||
|
||||
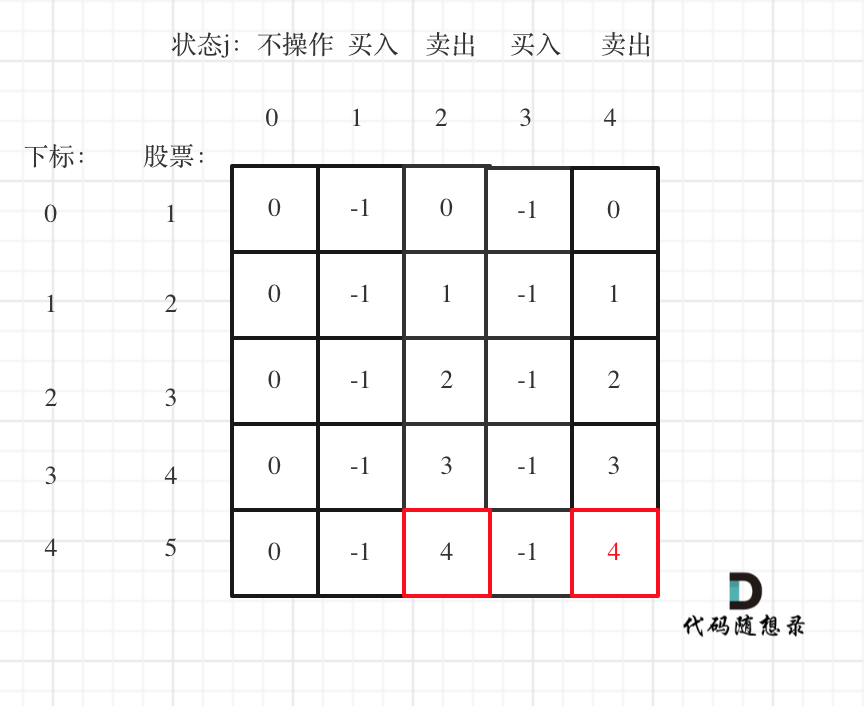
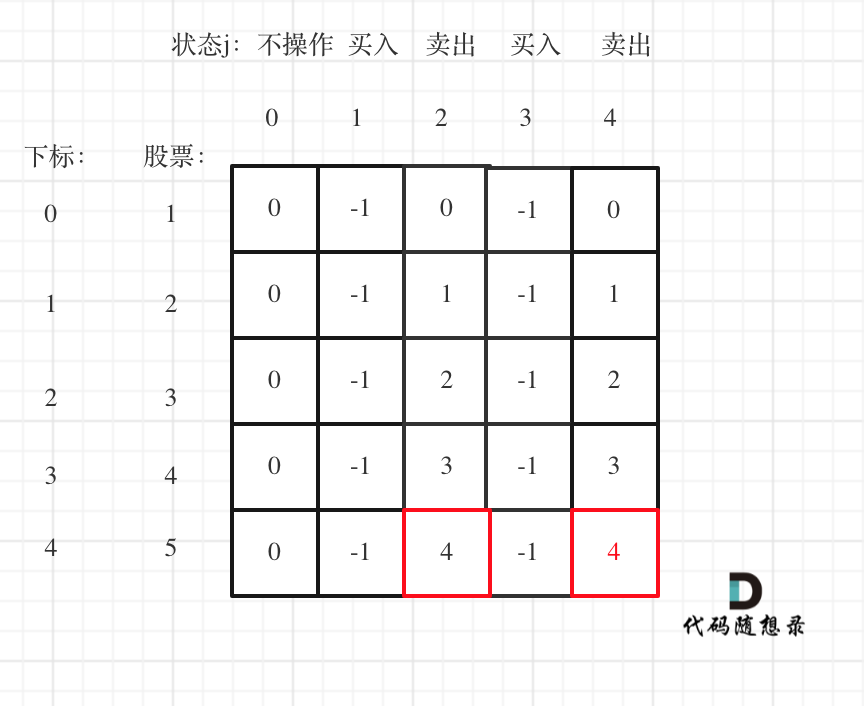
以输入[1,2,3,4,5]为例
|
||||
|
||||
|
||||
|
||||
|
||||
可以看到红色框为最后两次卖出的状态。
|
||||
|
||||
@ -142,7 +142,8 @@ for (int j = 1; j < 2 * k; j += 2) {
|
||||
|
||||
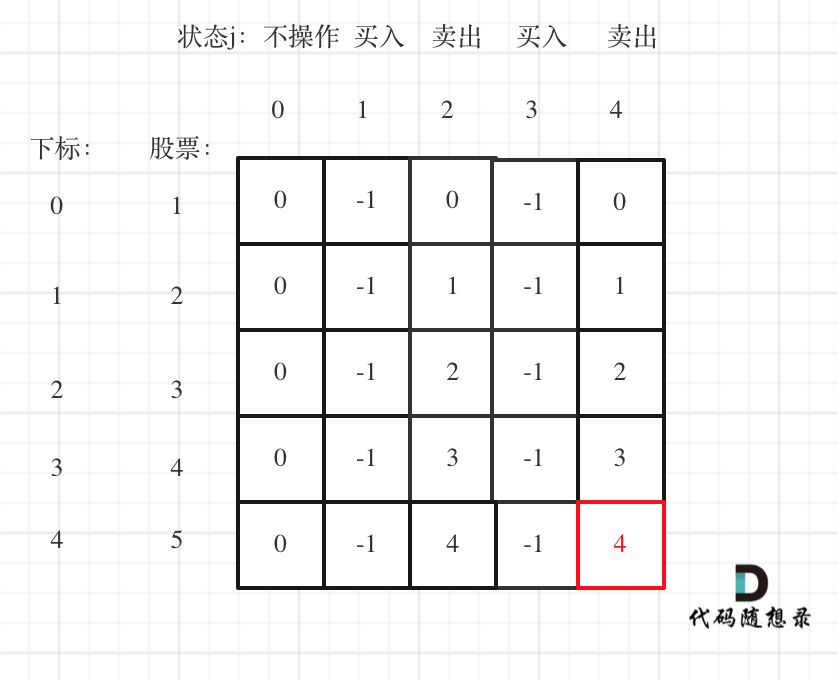
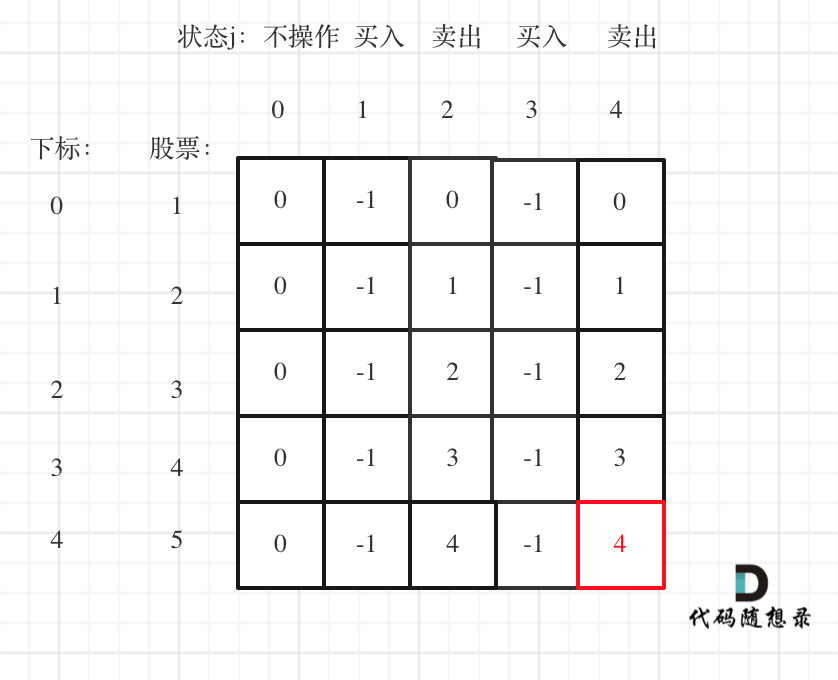
以输入[1,2,3,4,5],k=2为例。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
最后一次卖出,一定是利润最大的,dp[prices.size() - 1][2 * k]即红色部分就是最后求解。
|
||||
|
||||
@ -194,7 +195,8 @@ vector<vector<int>> dp(n, vector<int>(3, 0));
|
||||
|
||||
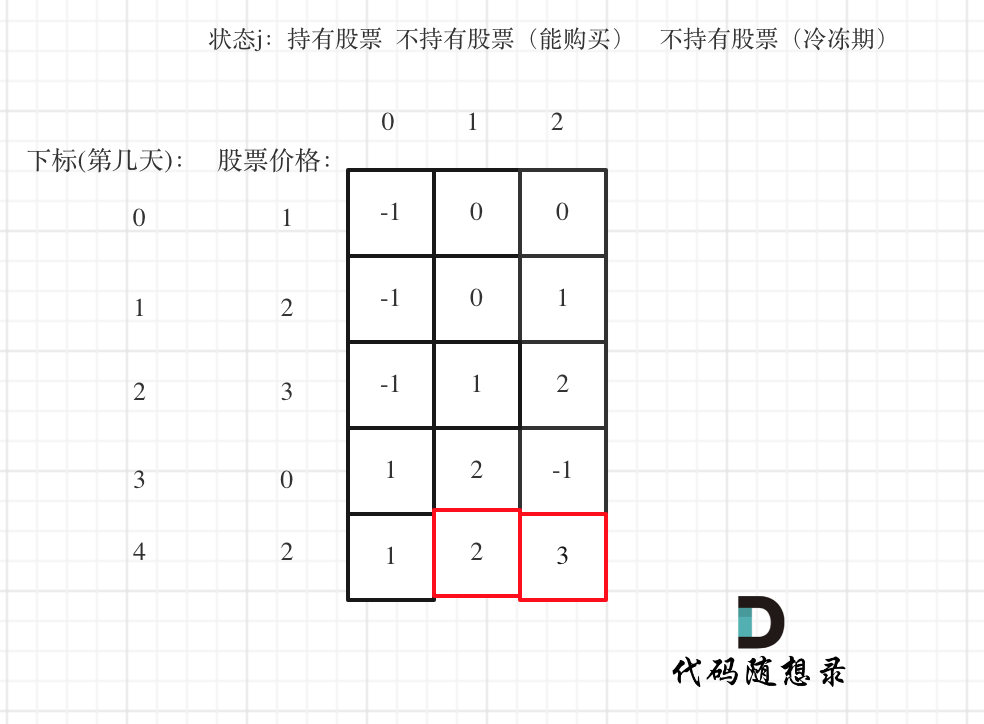
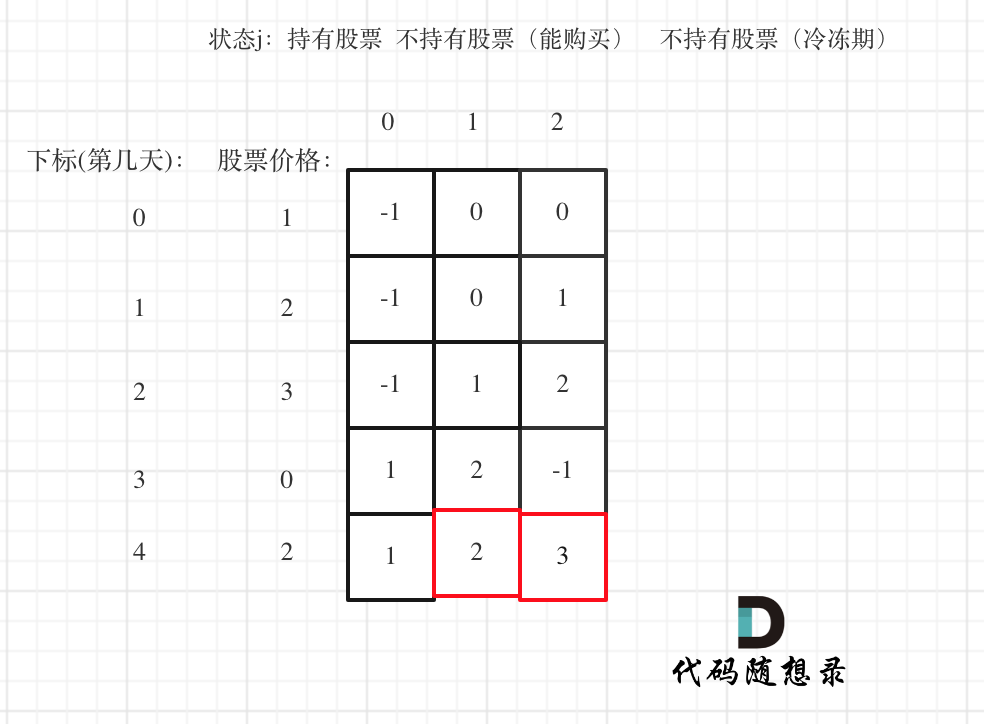
以 [1,2,3,0,2] 为例,dp数组如下:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
最后两个状态 不持有股票(能购买) 和 不持有股票(冷冻期)都有可能最后结果,取最大的。
|
||||
|
||||
|
||||
Reference in New Issue
Block a user