mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-25 18:08:48 +08:00
更新图床
This commit is contained in:
@ -8,7 +8,7 @@
|
||||
|
||||
## 超时是怎么回事
|
||||
|
||||

|
||||
|
||||
|
||||
大家在leetcode上练习算法的时候应该都遇到过一种错误是“超时”。
|
||||
|
||||
@ -48,6 +48,7 @@
|
||||
尽管有很多因素影响,但是还是可以对自己程序的运行时间有一个大体的评估的。
|
||||
|
||||
引用算法4里面的一段话:
|
||||
|
||||
* 火箭科学家需要大致知道一枚试射火箭的着陆点是在大海里还是在城市中;
|
||||
* 医学研究者需要知道一次药物测试是会杀死还是会治愈实验对象;
|
||||
|
||||
@ -99,6 +100,7 @@ void function3(long long n) {
|
||||
```
|
||||
|
||||
来看一下这三个函数随着n的规模变化,耗时会产生多大的变化,先测function1 ,就把 function2 和 function3 注释掉
|
||||
|
||||
```CPP
|
||||
int main() {
|
||||
long long n; // 数据规模
|
||||
@ -122,11 +124,11 @@ int main() {
|
||||
|
||||
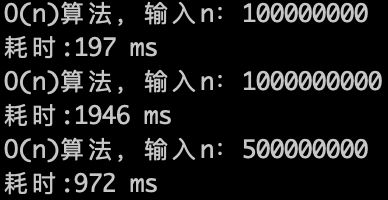
来看一下运行的效果,如下图:
|
||||
|
||||

|
||||
|
||||
|
||||
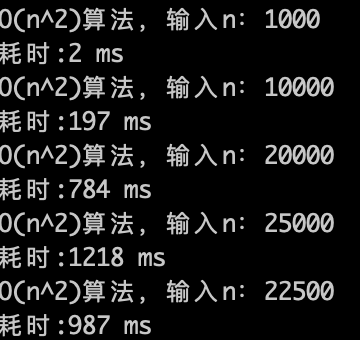
O(n)的算法,1s内大概计算机可以运行 5 * (10^8)次计算,可以推测一下$O(n^2)$ 的算法应该1s可以处理的数量级的规模是 5 * (10^8)开根号,实验数据如下。
|
||||
|
||||

|
||||
|
||||
|
||||
O(n^2)的算法,1s内大概计算机可以运行 22500次计算,验证了刚刚的推测。
|
||||
|
||||
@ -134,7 +136,7 @@ O(n^2)的算法,1s内大概计算机可以运行 22500次计算,验证了刚
|
||||
|
||||
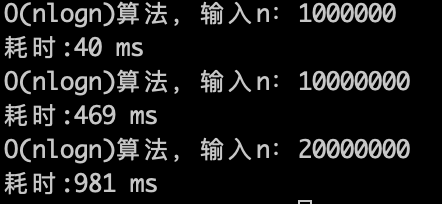
理论上应该是比 $O(n)$少一个数量级,因为$\log n$的复杂度 其实是很快,看一下实验数据。
|
||||
|
||||

|
||||
|
||||
|
||||
$O(n\log n)$的算法,1s内大概计算机可以运行 2 * (10^7)次计算,符合预期。
|
||||
|
||||
@ -142,7 +144,7 @@ $O(n\log n)$的算法,1s内大概计算机可以运行 2 * (10^7)次计算,
|
||||
|
||||
**整体测试数据整理如下:**
|
||||
|
||||

|
||||

|
||||
|
||||
至于 $O(\log n)$ 和 $O(n^3)$ 等等这些时间复杂度在1s内可以处理的多大的数据规模,大家可以自己写一写代码去测一下了。
|
||||
|
||||
@ -204,6 +206,7 @@ int main() {
|
||||
|
||||
|
||||
Java版本
|
||||
|
||||
```Java
|
||||
import java.util.Scanner;
|
||||
|
||||
@ -274,4 +277,5 @@ public class TimeComplexity {
|
||||
|
||||
|
||||
-----------------------
|
||||
|
||||
<div align="center"><img src=https://code-thinking.cdn.bcebos.com/pics/01二维码.jpg width=450> </img></div>
|
||||
|
||||
@ -57,7 +57,7 @@
|
||||
|
||||
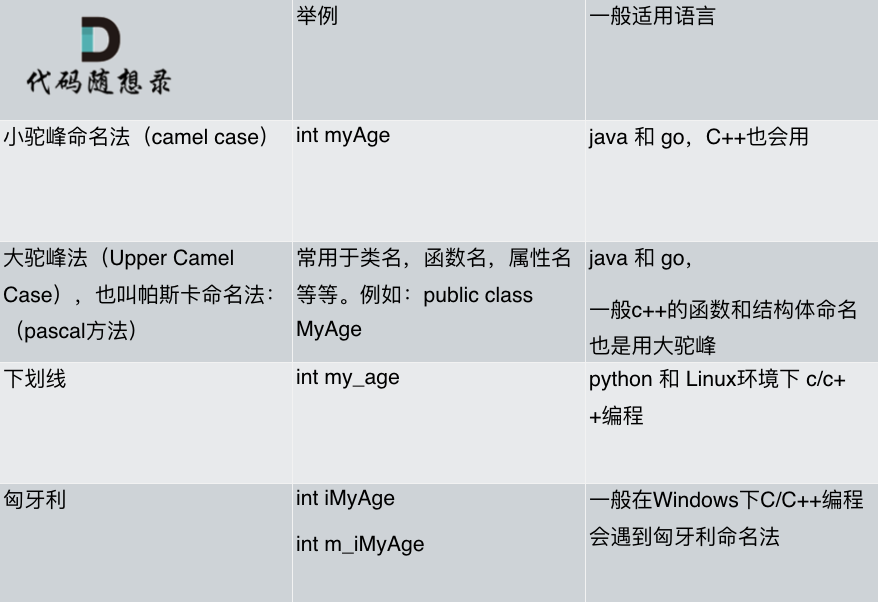
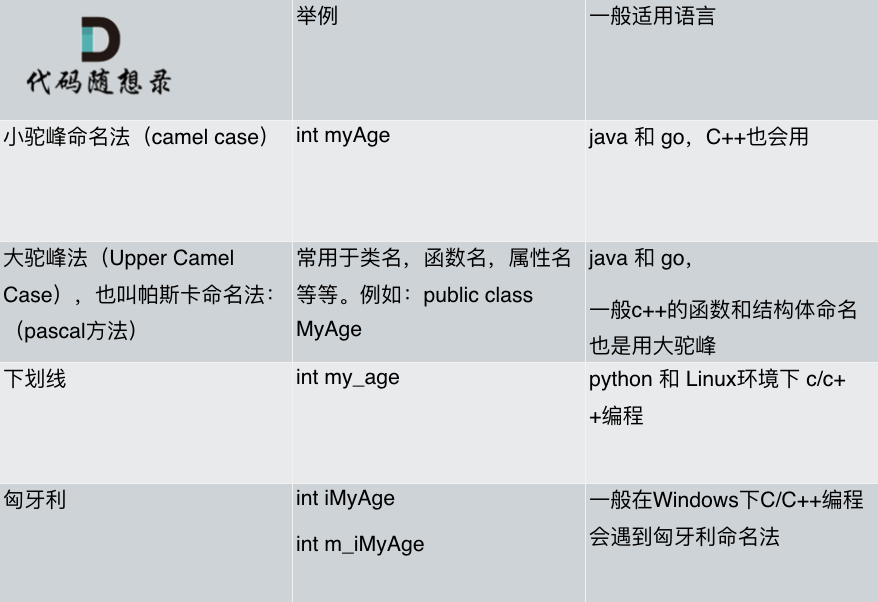
我做了一下总结如图:
|
||||
|
||||
|
||||
|
||||
|
||||
### 水平留白(代码空格)
|
||||
|
||||
|
||||
@ -38,7 +38,7 @@
|
||||
同样的同理再看一下快速排序,都知道快速排序是O(nlogn),但是当数据已经有序情况下,快速排序的时间复杂度是O(n^2) 的,**所以严格从大O的定义来讲,快速排序的时间复杂度应该是O(n^2)**。
|
||||
|
||||
**但是我们依然说快速排序是O(nlogn)的时间复杂度,这个就是业内的一个默认规定,这里说的O代表的就是一般情况,而不是严格的上界**。如图所示:
|
||||

|
||||

|
||||
|
||||
我们主要关心的还是一般情况下的数据形式。
|
||||
|
||||
@ -49,7 +49,7 @@
|
||||
|
||||
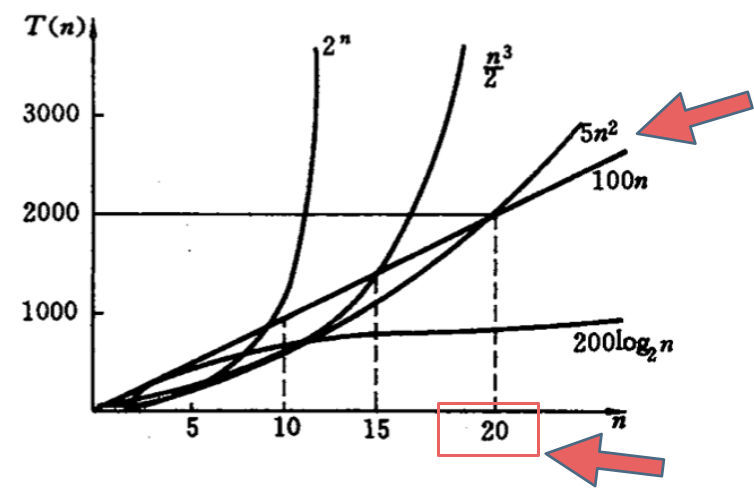
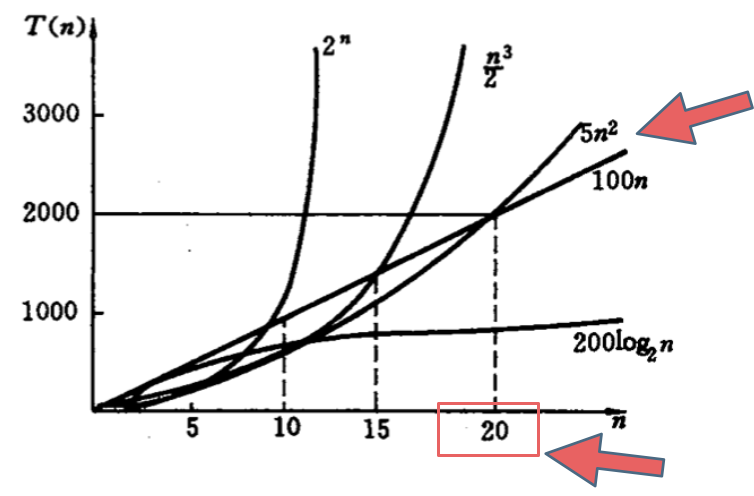
如下图中可以看出不同算法的时间复杂度在不同数据输入规模下的差异。
|
||||
|
||||
|
||||
|
||||
|
||||
在决定使用哪些算法的时候,不是时间复杂越低的越好(因为简化后的时间复杂度忽略了常数项等等),要考虑数据规模,如果数据规模很小甚至可以用O(n^2)的算法比O(n)的更合适(在有常数项的时候)。
|
||||
|
||||
@ -115,7 +115,7 @@ O(2 × n^2 + 10 × n + 1000) < O(3 × n^2),所以说最后省略掉常数项
|
||||
|
||||
为什么可以这么做呢?如下图所示:
|
||||
|
||||

|
||||

|
||||
|
||||
|
||||
假如有两个算法的时间复杂度,分别是log以2为底n的对数和log以10为底n的对数,那么这里如果还记得高中数学的话,应该不难理解`以2为底n的对数 = 以2为底10的对数 * 以10为底n的对数`。
|
||||
|
||||
@ -1,5 +1,4 @@
|
||||
|
||||
|
||||
# 刷了这么多题,你了解自己代码的内存消耗么?
|
||||
|
||||
理解代码的内存消耗,最关键是要知道自己所用编程语言的内存管理。
|
||||
@ -20,7 +19,7 @@
|
||||
|
||||
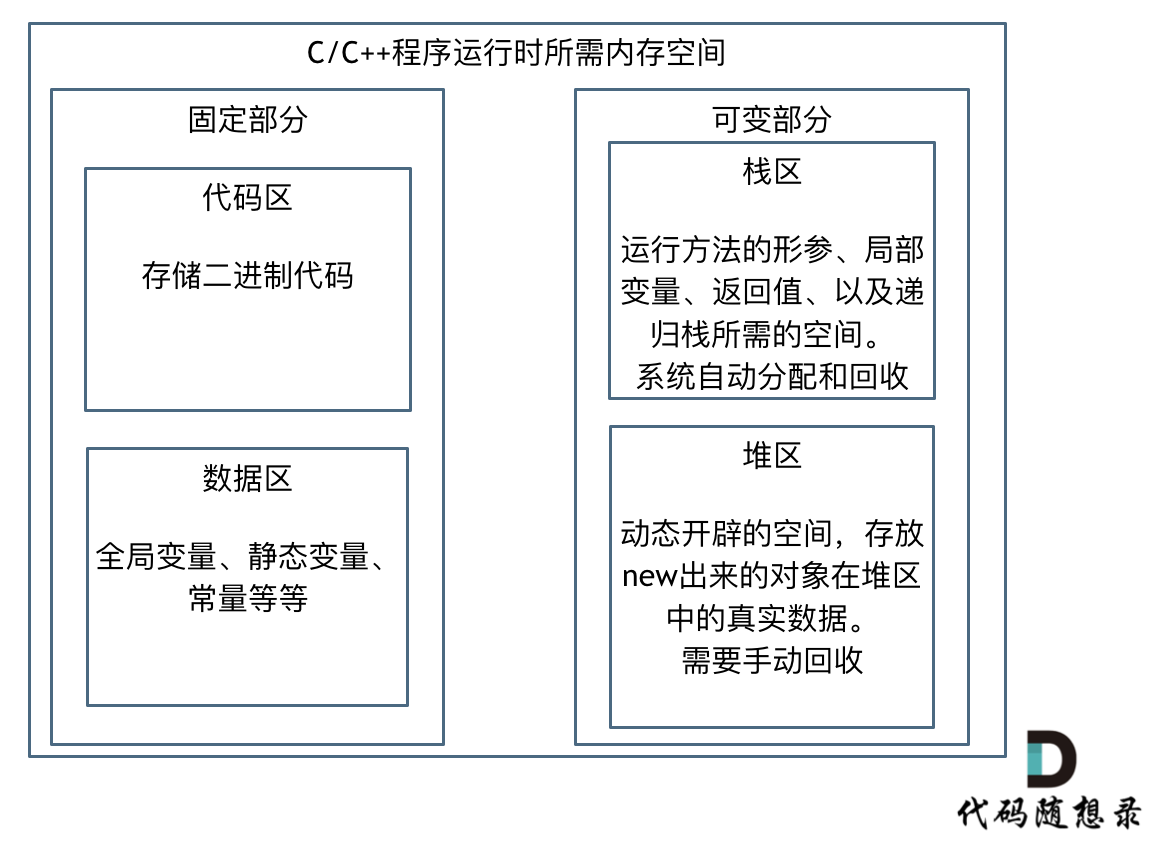
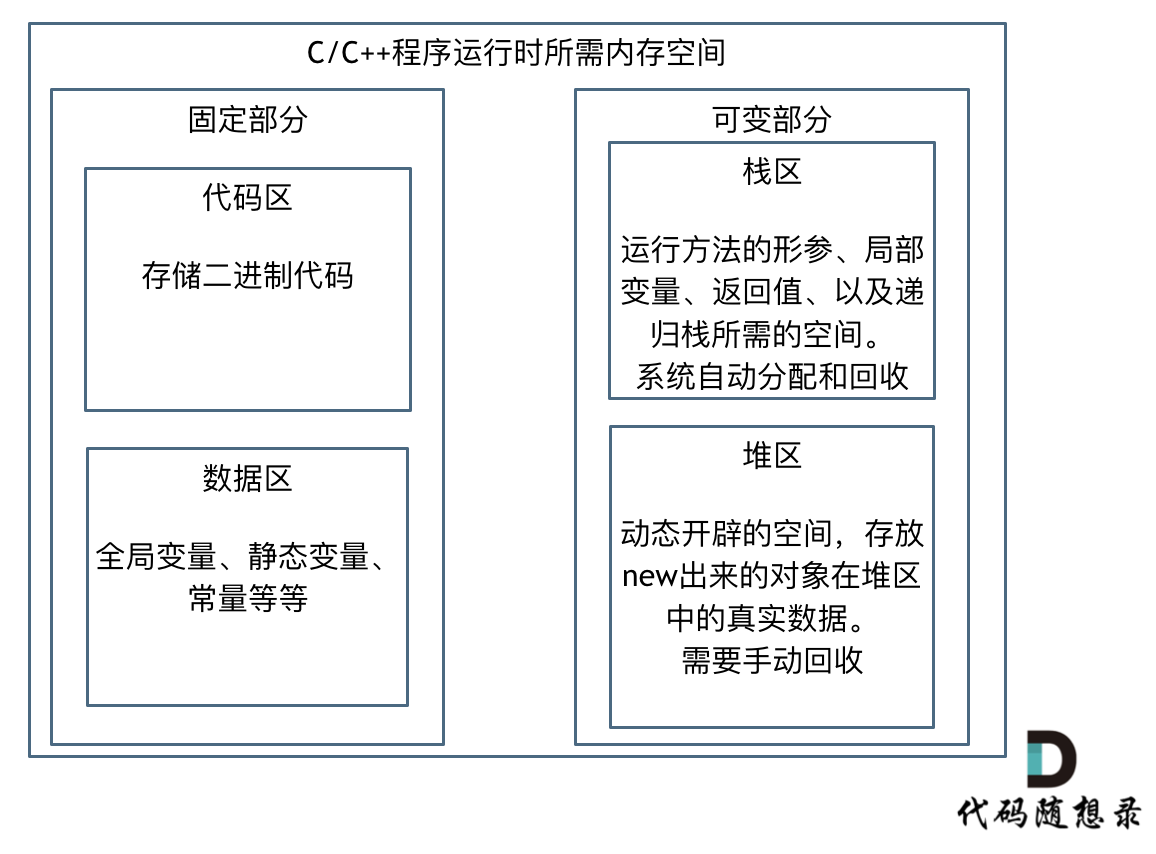
如果我们写C++的程序,就要知道栈和堆的概念,程序运行时所需的内存空间分为 固定部分,和可变部分,如下:
|
||||
|
||||
|
||||
|
||||
|
||||
固定部分的内存消耗 是不会随着代码运行产生变化的, 可变部分则是会产生变化的
|
||||
|
||||
@ -42,7 +41,7 @@
|
||||
|
||||
想要算出自己程序会占用多少内存就一定要了解自己定义的数据类型的大小,如下:
|
||||
|
||||

|
||||

|
||||
|
||||
注意图中有两个不一样的地方,为什么64位的指针就占用了8个字节,而32位的指针占用4个字节呢?
|
||||
|
||||
@ -85,9 +84,11 @@ int main() {
|
||||
cout << sizeof(st) << endl;
|
||||
}
|
||||
```
|
||||
|
||||
看一下和自己想的结果一样么, 我们来逐一分析一下。
|
||||
|
||||
其输出的结果依次为:
|
||||
|
||||
```
|
||||
4
|
||||
1
|
||||
@ -108,7 +109,7 @@ CPU读取内存不是一次读取单个字节,而是一块一块的来读取
|
||||
|
||||
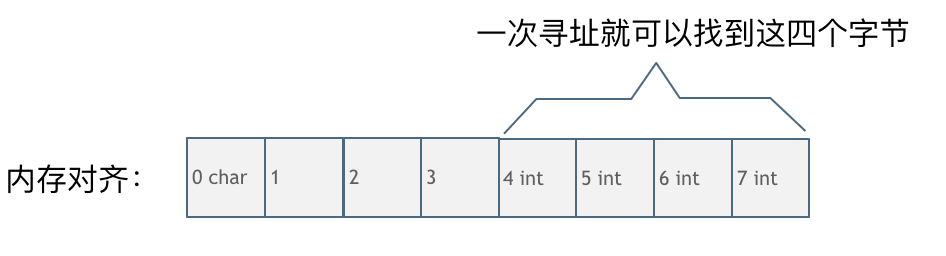
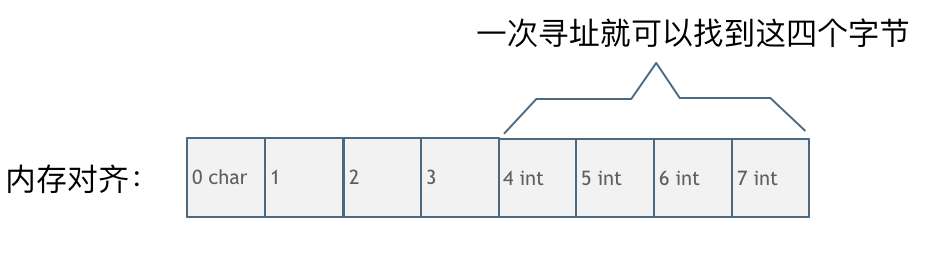
第一种就是内存对齐的情况,如图:
|
||||
|
||||
|
||||
|
||||
|
||||
一字节的char占用了四个字节,空了三个字节的内存地址,int数据从地址4开始。
|
||||
|
||||
@ -116,7 +117,7 @@ CPU读取内存不是一次读取单个字节,而是一块一块的来读取
|
||||
|
||||
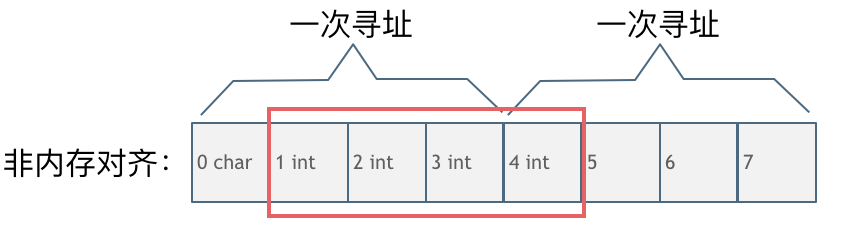
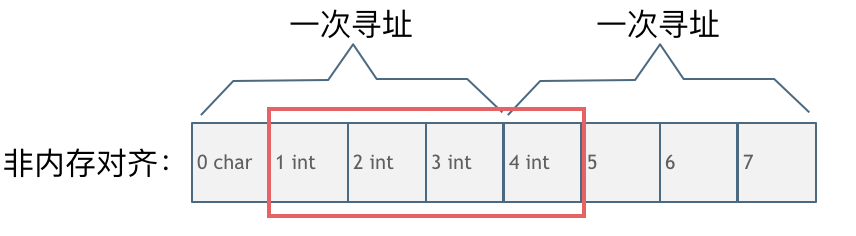
第二种是没有内存对齐的情况如图:
|
||||
|
||||
|
||||
|
||||
|
||||
char型的数据和int型的数据挨在一起,该int数据从地址1开始,那么CPU想要读这个数据的话来看看需要几步操作:
|
||||
|
||||
@ -143,4 +144,5 @@ char型的数据和int型的数据挨在一起,该int数据从地址1开始,
|
||||
|
||||
|
||||
-----------------------
|
||||
|
||||
<div align="center"><img src=https://code-thinking.cdn.bcebos.com/pics/01二维码.jpg width=450> </img></div>
|
||||
|
||||
@ -103,7 +103,7 @@ Carl校招社招都拿过大厂的offer,同时也看过很多应聘者的简
|
||||
|
||||
最后福利,把我的简历模板贡献出来!如下图所示。
|
||||
|
||||

|
||||

|
||||
|
||||
这里是简历模板中Markdown的代码:[https://github.com/youngyangyang04/Markdown-Resume-Template](https://github.com/youngyangyang04/Markdown-Resume-Template) ,可以fork到自己Github仓库上,按照这个模板来修改自己的简历。
|
||||
|
||||
|
||||
@ -28,7 +28,8 @@ int fibonacci(int i) {
|
||||
|
||||
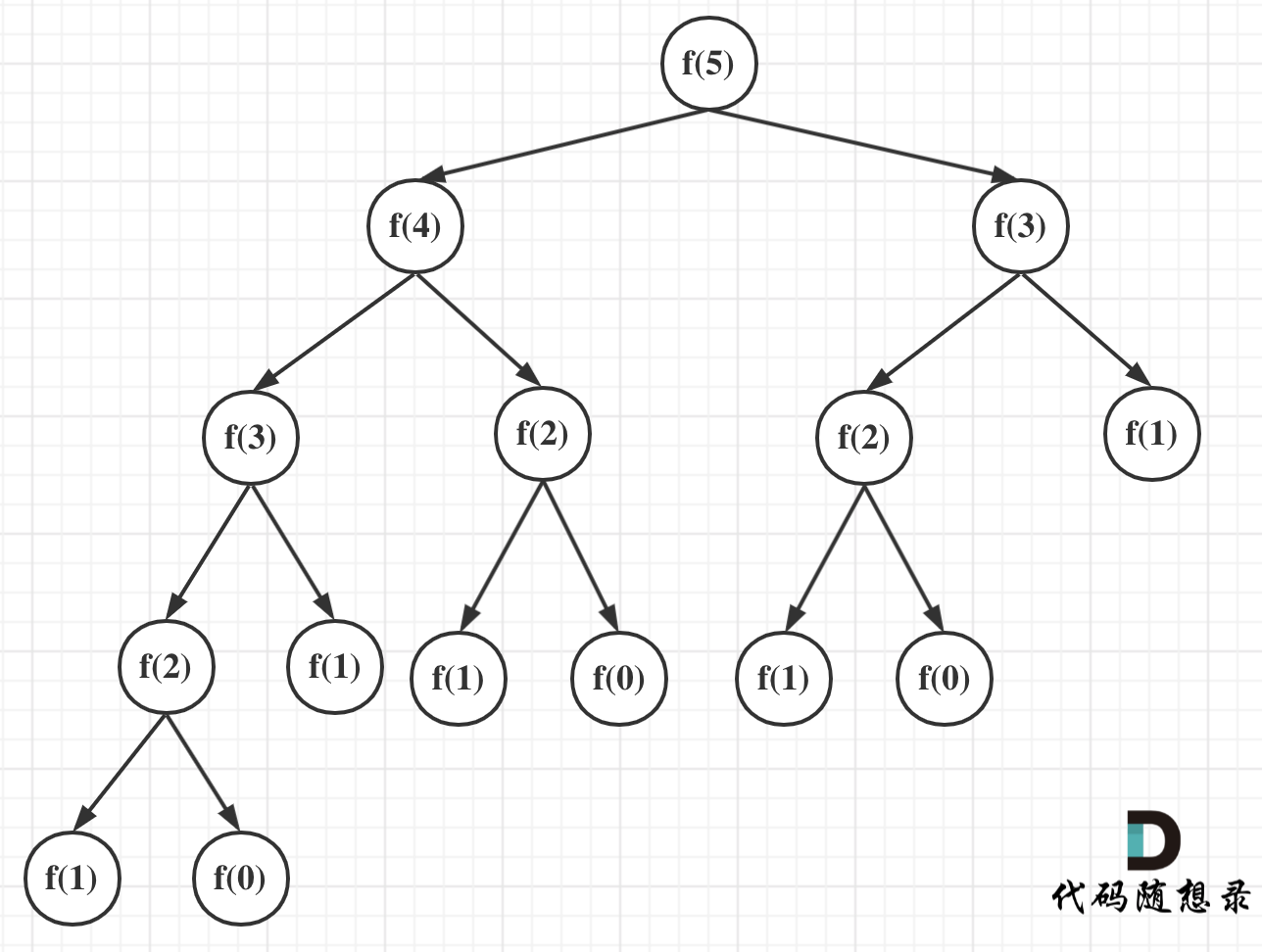
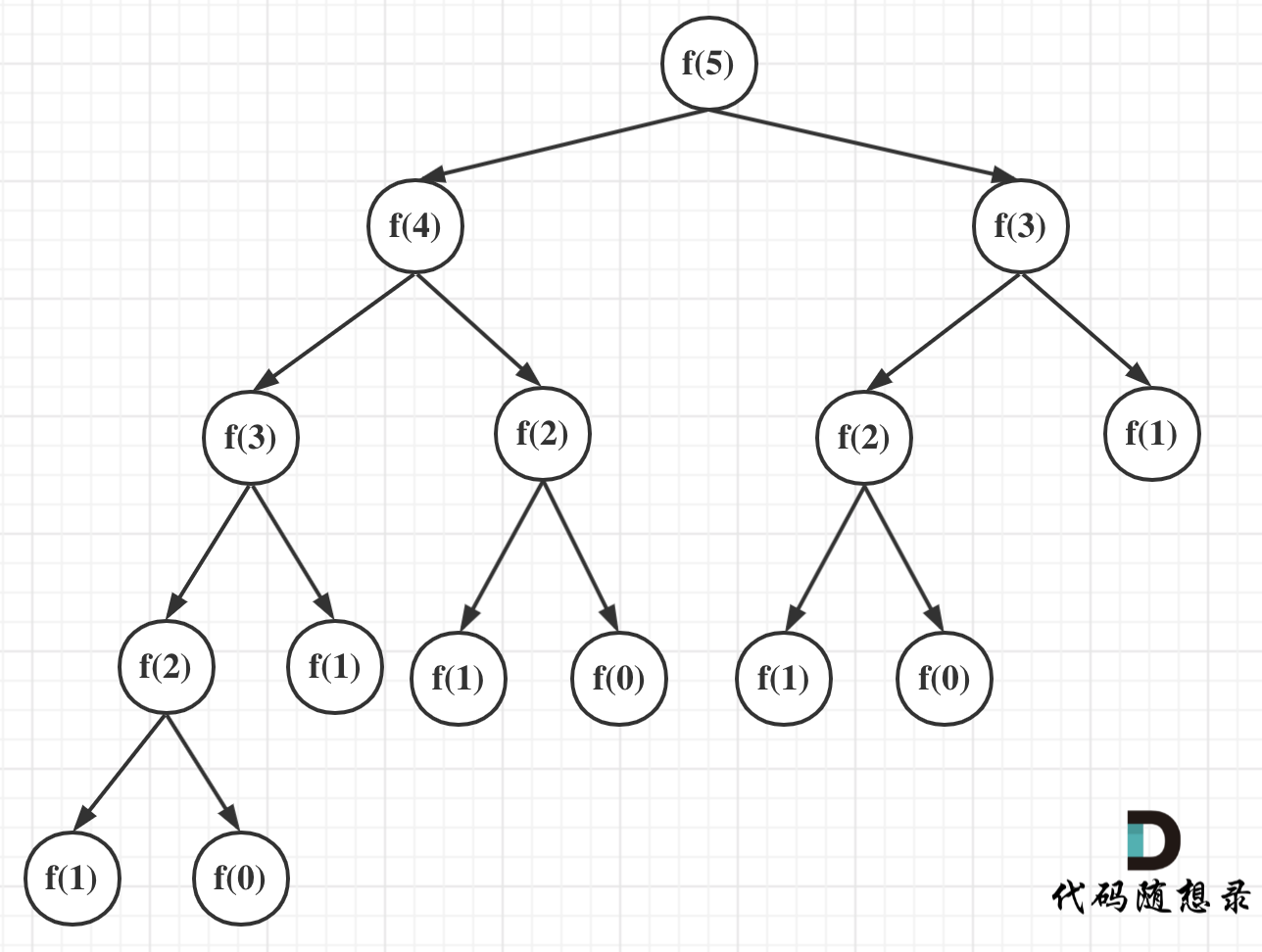
可以看出上面的代码每次递归都是O(1)的操作。再来看递归了多少次,这里将i为5作为输入的递归过程 抽象成一棵递归树,如图:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
从图中,可以看出f(5)是由f(4)和f(3)相加而来,那么f(4)是由f(3)和f(2)相加而来 以此类推。
|
||||
|
||||
@ -194,7 +195,8 @@ int main()
|
||||
|
||||
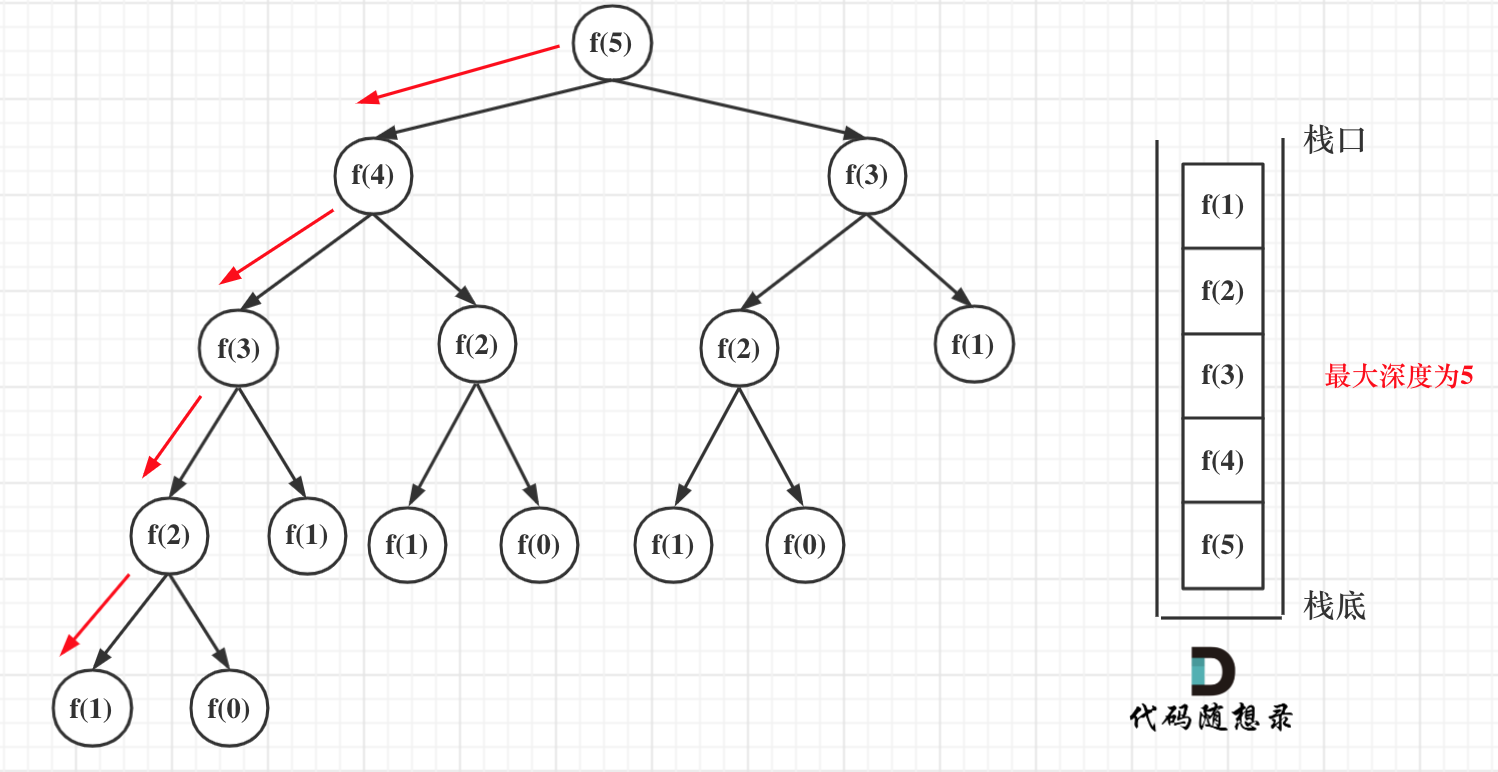
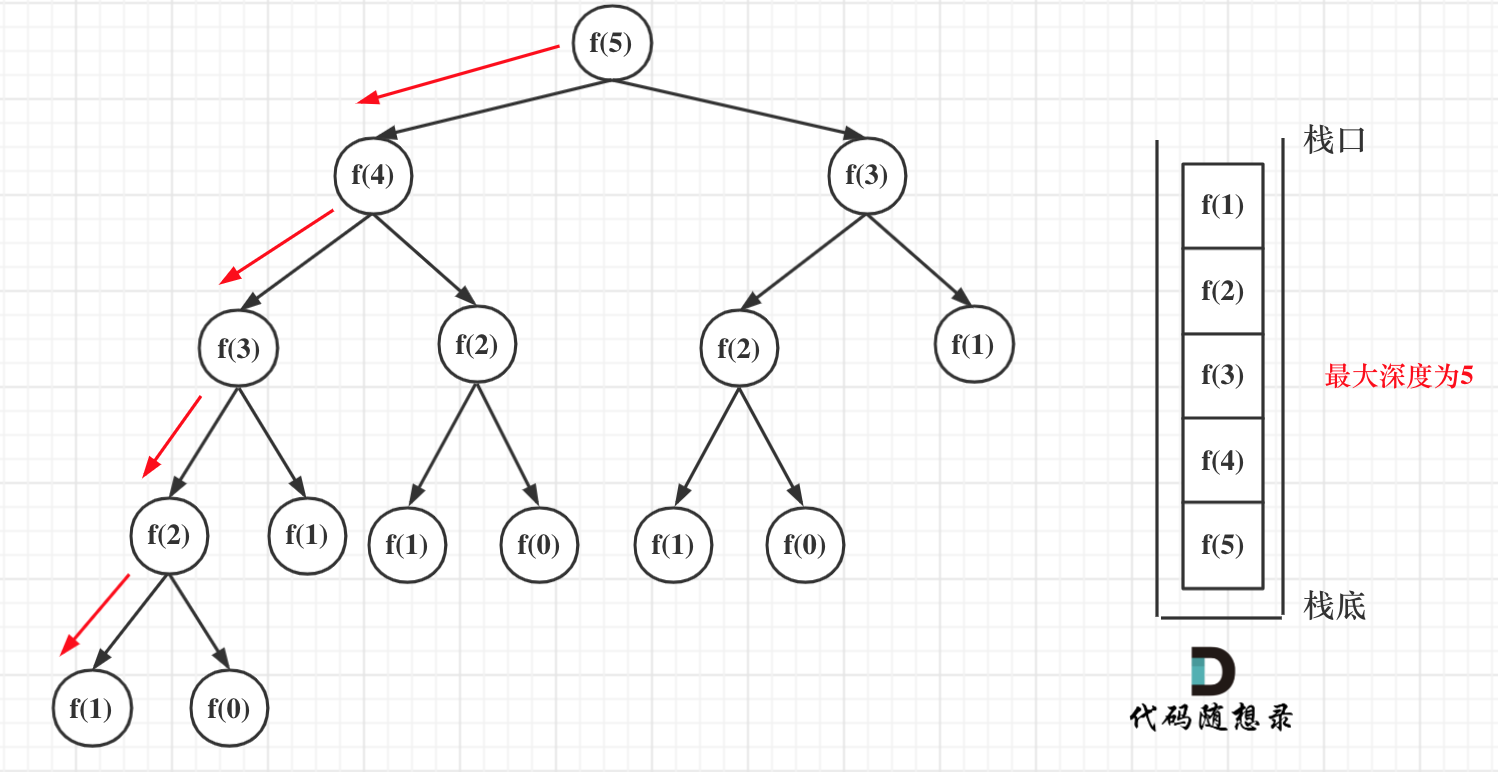
在看递归的深度是多少呢?如图所示:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
递归第n个斐波那契数的话,递归调用栈的深度就是n。
|
||||
|
||||
@ -211,7 +213,8 @@ int fibonacci(int i) {
|
||||
|
||||
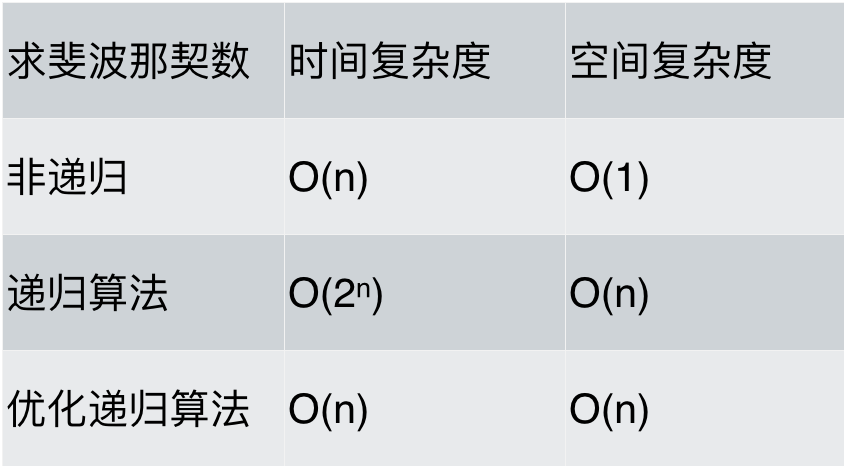
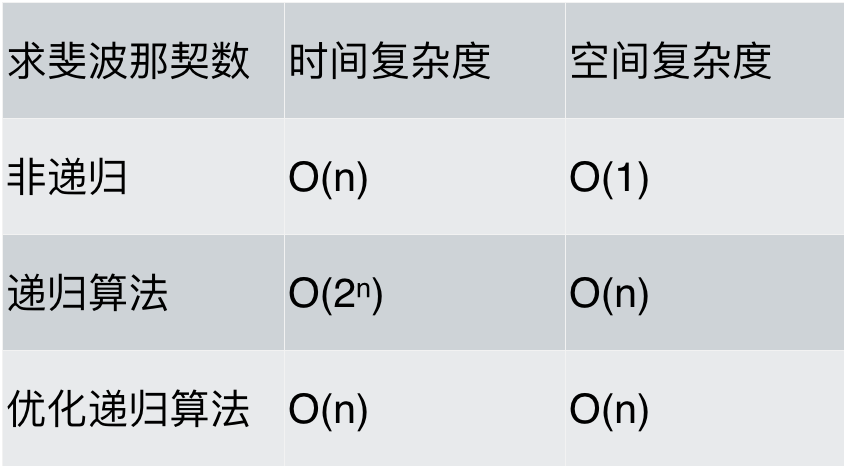
最后对各种求斐波那契数列方法的性能做一下分析,如题:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
可以看出,求斐波那契数的时候,使用递归算法并不一定是在性能上是最优的,但递归确实简化的代码层面的复杂度。
|
||||
|
||||
|
||||
@ -69,7 +69,7 @@ int function3(int x, int n) {
|
||||
|
||||
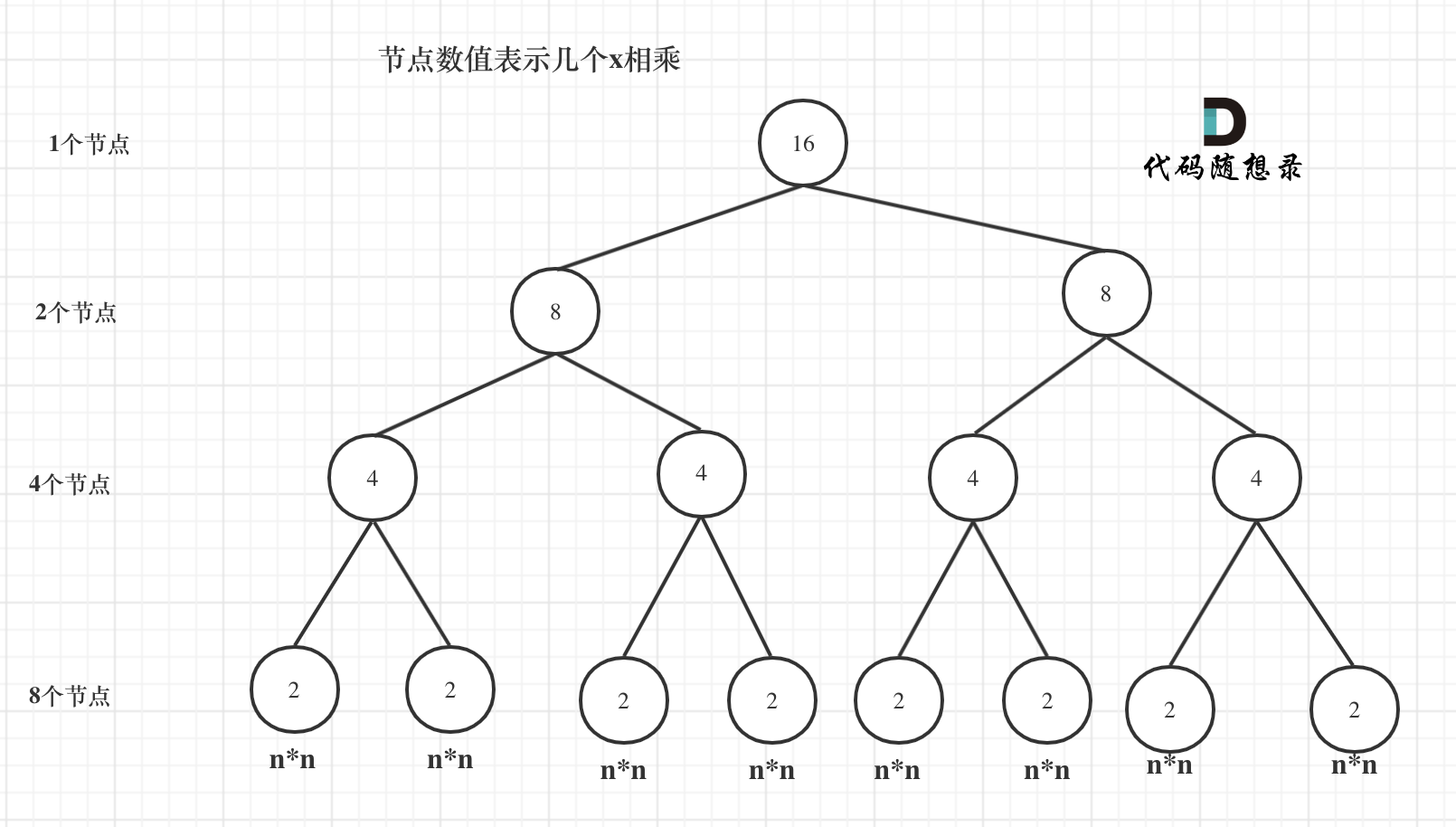
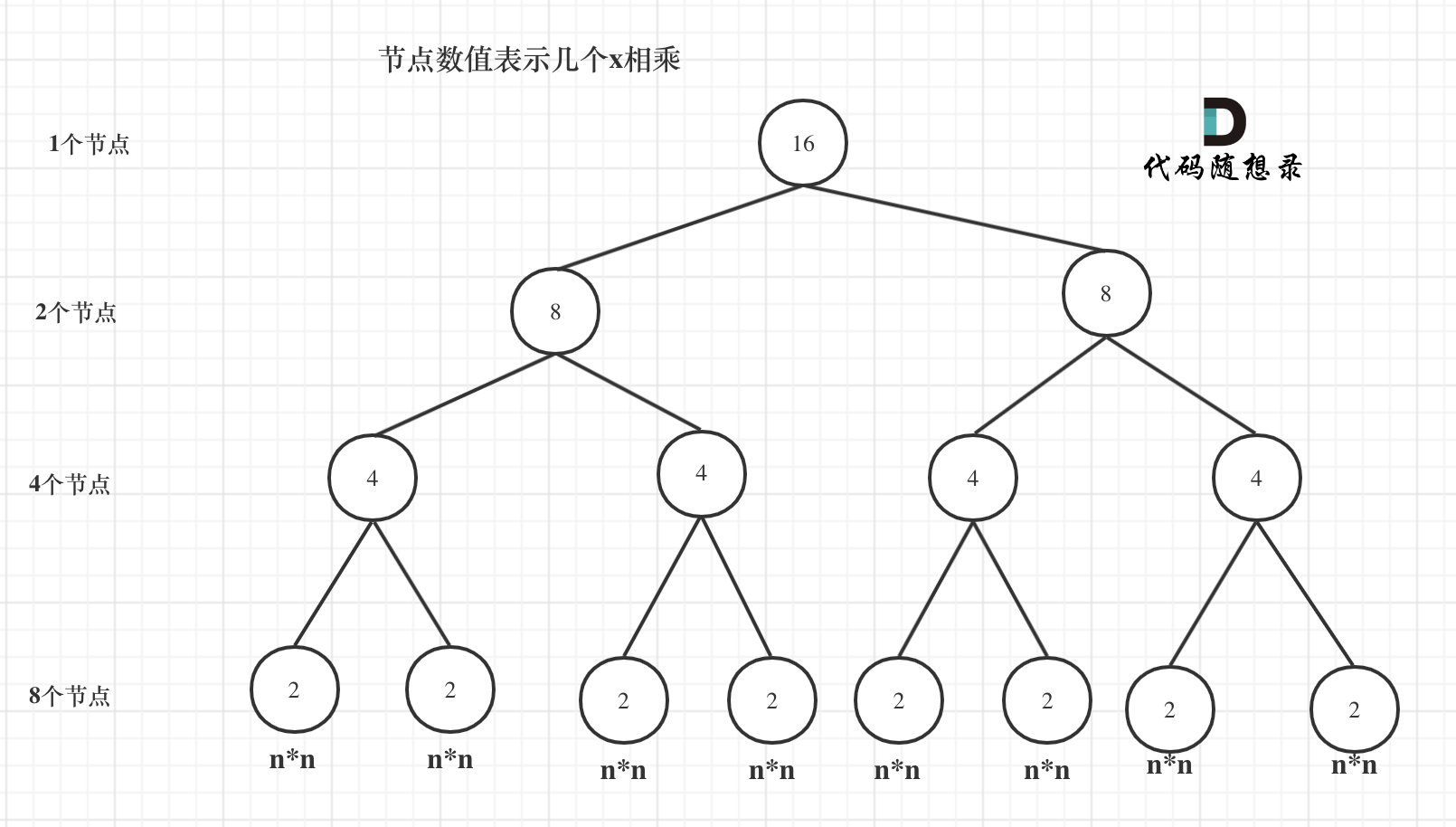
我们来分析一下,首先看递归了多少次呢,可以把递归抽象出一棵满二叉树。刚刚同学写的这个算法,可以用一棵满二叉树来表示(为了方便表示,选择n为偶数16),如图:
|
||||
|
||||
|
||||
|
||||
|
||||
当前这棵二叉树就是求x的n次方,n为16的情况,n为16的时候,进行了多少次乘法运算呢?
|
||||
|
||||
@ -79,7 +79,7 @@ int function3(int x, int n) {
|
||||
|
||||
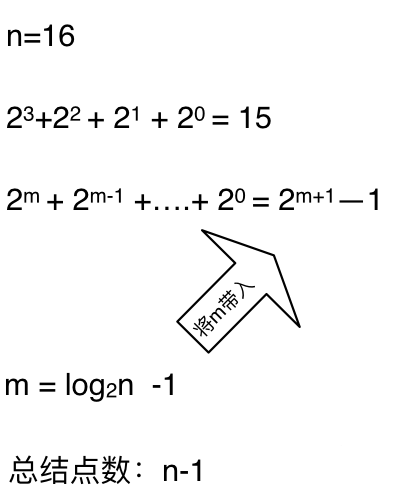
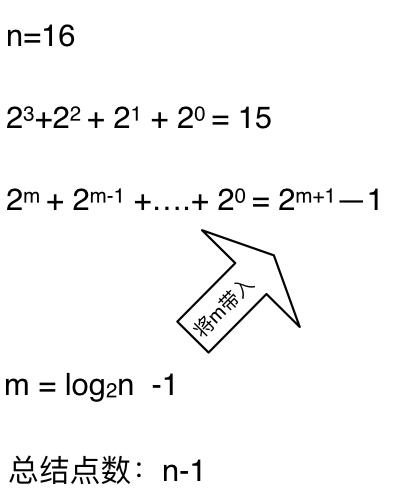
这么如果是求x的n次方,这个递归树有多少个节点呢,如下图所示:(m为深度,从0开始)
|
||||
|
||||
|
||||
|
||||
|
||||
**时间复杂度忽略掉常数项`-1`之后,这个递归算法的时间复杂度依然是O(n)**。对,你没看错,依然是O(n)的时间复杂度!
|
||||
|
||||
|
||||
Reference in New Issue
Block a user