mirror of
https://github.com/trekhleb/javascript-algorithms.git
synced 2025-12-19 08:59:05 +08:00
Chore(math-translation-FR-fr): a pack of translations for the math section (#558)
* chore(factorial): translation fr-FR * feat(math-translation-fr-FR): fast powering * feat(math-translation-fr-FR): fibonacci numbers * chore(math-translation-fr-FR): bits * chore(math-translation-fr-FR): complex number * chore(math-translation-fr-FR): euclidean algorithm * chore(math-translation-fr-FR): fibonacci number * chore(math-translation-fr-FR): fourier transform * chore(math-translation-fr-FR): fourier transform WIP * chore(math-translation-fr-FR): fourier transform done * chore(math-translation-fr-FR): fourier transform in menu
This commit is contained in:
135
src/algorithms/math/fourier-transform/README.fr-FR.md
Normal file
135
src/algorithms/math/fourier-transform/README.fr-FR.md
Normal file
@@ -0,0 +1,135 @@
|
||||
# Transformation de Fourier
|
||||
|
||||
_Read this in other languages:_
|
||||
[english](README.md).
|
||||
|
||||
## Définitions
|
||||
|
||||
La transformation de Fourier (**ℱ**) est une opération qui transforme
|
||||
une fonction intégrable sur ℝ en une autre fonction,
|
||||
décrivant le spectre fréquentiel de cette dernière
|
||||
|
||||
La **Transformée de Fourier Discrète** (**TFD**) convertit une séquence finie d'échantillons également espacés d'une fonction, dans une séquence de même longueur d'échantillons, également espacés de la Transformée de Fourier à temps discret (TFtd), qui est une fonction complexe de la fréquence.
|
||||
L'intervalle auquel le TFtd est échantillonné est l'inverse de la durée de la séquence d'entrée.
|
||||
Une TFD inverse est une série de Fourier, utilisant les échantillons TFtd comme coefficients de sinusoïdes complexes aux fréquences TFtd correspondantes. Elle a les mêmes valeurs d'échantillonnage que la
|
||||
séquence d'entrée originale. On dit donc que la TFD est une représentation du domaine fréquentiel
|
||||
de la séquence d'entrée d'origine. Si la séquence d'origine couvre toutes les
|
||||
valeurs non nulles d'une fonction, sa TFtd est continue (et périodique), et la TFD fournit
|
||||
les échantillons discrets d'une fenêtre. Si la séquence d'origine est un cycle d'une fonction périodique, la TFD fournit toutes les valeurs non nulles d'une fenêtre TFtd.
|
||||
|
||||
Transformée de Fourier Discrète converti une séquence de `N` nombres complexes:
|
||||
|
||||
{x<sub>n</sub>} = x<sub>0</sub>, x<sub>1</sub>, x<sub>2</sub> ..., x<sub>N-1</sub>
|
||||
|
||||
en une atre séquence de nombres complexes::
|
||||
|
||||
{X<sub>k</sub>} = X<sub>0</sub>, X<sub>1</sub>, X<sub>2</sub> ..., X<sub>N-1</sub>
|
||||
|
||||
décrite par:
|
||||
|
||||

|
||||
|
||||
The **Transformée de Fourier à temps discret** (**TFtd**) est une forme d'analyse de Fourier
|
||||
qui s'applique aux échantillons uniformément espacés d'une fonction continue. Le terme "temps discret" fait référence au fait que la transformée fonctionne sur des données discrètes
|
||||
(échantillons) dont l'intervalle a souvent des unités de temps.
|
||||
À partir des seuls échantillons, elle produit une fonction de fréquence qui est une somme périodique de la
|
||||
Transformée de Fourier continue de la fonction continue d'origine.
|
||||
|
||||
A **Transformation de Fourier rapide** (**FFT** pour Fast Fourier Transform) est un algorithme de calcul de la transformation de Fourier discrète (TFD). Il est couramment utilisé en traitement numérique du signal pour transformer des données discrètes du domaine temporel dans le domaine fréquentiel, en particulier dans les oscilloscopes numériques (les analyseurs de spectre utilisant plutôt des filtres analogiques, plus précis). Son efficacité permet de réaliser des filtrages en modifiant le spectre et en utilisant la transformation inverse (filtre à réponse impulsionnelle finie).
|
||||
|
||||
Cette transformation peut être illustée par la formule suivante. Sur la période de temps mesurée
|
||||
dans le diagramme, le signal contient 3 fréquences dominantes distinctes.
|
||||
|
||||
Vue d'un signal dans le domaine temporel et fréquentiel:
|
||||
|
||||
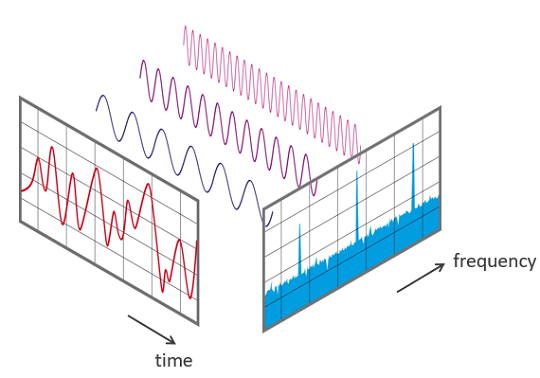
|
||||
|
||||
An FFT algorithm computes the discrete Fourier transform (DFT) of a sequence, or
|
||||
its inverse (IFFT). Fourier analysis converts a signal from its original domain
|
||||
to a representation in the frequency domain and vice versa. An FFT rapidly
|
||||
computes such transformations by factorizing the DFT matrix into a product of
|
||||
sparse (mostly zero) factors. As a result, it manages to reduce the complexity of
|
||||
computing the DFT from O(n<sup>2</sup>), which arises if one simply applies the
|
||||
definition of DFT, to O(n log n), where n is the data size.
|
||||
|
||||
Un algorithme FFT calcule la Transformée de Fourier discrète (TFD) d'une séquence, ou
|
||||
son inverse (IFFT). L'analyse de Fourier convertit un signal de son domaine d'origine
|
||||
en une représentation dans le domaine fréquentiel et vice versa. Une FFT
|
||||
calcule rapidement ces transformations en factorisant la matrice TFD en un produit de
|
||||
facteurs dispersés (généralement nuls). En conséquence, il parvient à réduire la complexité de
|
||||
calcul de la TFD de O (n <sup> 2 </sup>), qui survient si l'on applique simplement la
|
||||
définition de TFD, à O (n log n), où n est la taille des données.
|
||||
|
||||
Voici une analyse de Fourier discrète d'une somme d'ondes cosinus à 10, 20, 30, 40,
|
||||
et 50 Hz:
|
||||
|
||||
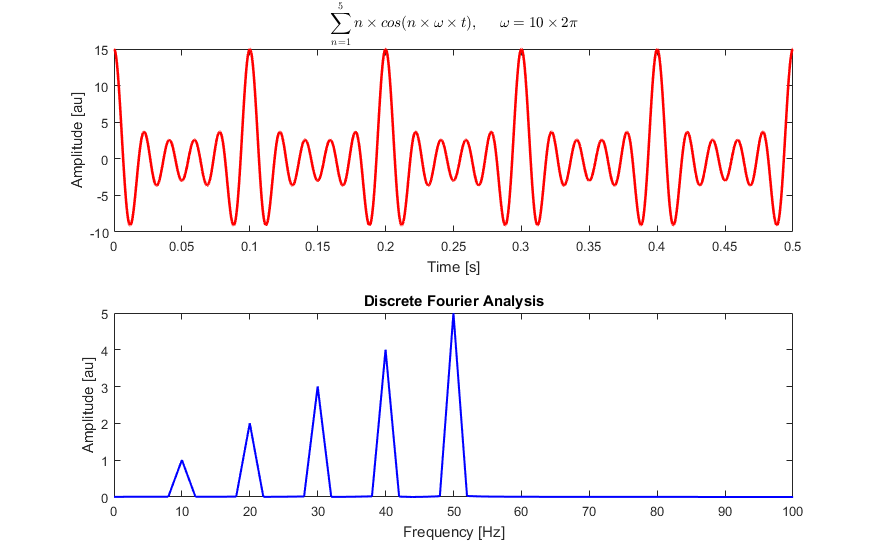
|
||||
|
||||
## Explanation
|
||||
|
||||
La Transformée de Fourier est l'une des connaissances les plus importante jamais découverte. Malheureusement, le
|
||||
son sens est enfoui dans des équations denses::
|
||||
|
||||
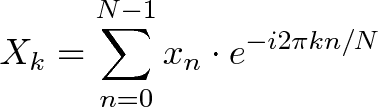
|
||||
|
||||
et
|
||||
|
||||
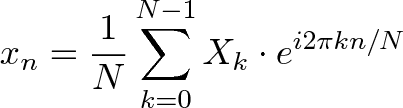
|
||||
|
||||
Plutôt que se noyer dans les symboles, faisons en premier lieu l'expérience de l'idée principale. Voici une métaphore en français simple:
|
||||
|
||||
- _Que fait la transformée de Fourier ?_ A partir d'un smoothie, elle trouve sa recette.
|
||||
- _Comment ?_ Elle passe le smoothie dans un filtre pour en extraire chaque ingrédient.
|
||||
- _Pourquoi ?_ Les recettes sont plus faciles à analyser, comparer et modifier que le smoothie lui-même.
|
||||
- _Comment récupérer le smoothie ?_ Re-mélanger les ingrédients.
|
||||
|
||||
**Pensez en cercles, pas seulement en sinusoïdes**
|
||||
|
||||
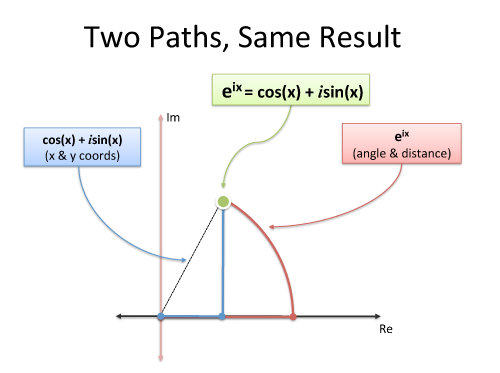
La transformée de Fourier concerne des trajectoires circulaires (pas les sinusoïdes 1-d)
|
||||
et la formuled'Euler est une manière intelligente d'en générer une:
|
||||
|
||||
|
||||
|
||||
Doit-on utiliser des exposants imaginaires pour se déplacer en cercle ? Non. Mais c'est pratique
|
||||
et compact. Et bien sûr, nous pouvons décrire notre chemin comme un mouvement coordonné en deux
|
||||
dimensions (réelle et imaginaire), mais n'oubliez pas la vue d'ensemble: nous sommes juste
|
||||
en déplacement dans un cercle.
|
||||
|
||||
**À la découverte de la transformation complète**
|
||||
|
||||
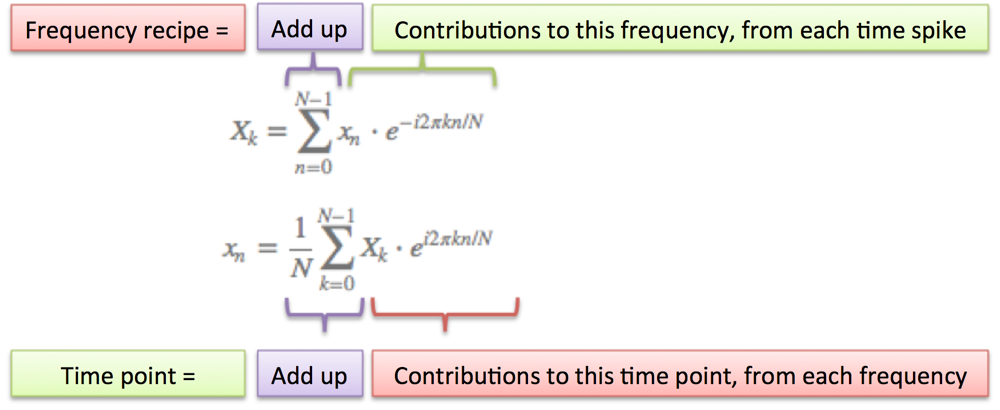
L'idée générale: notre signal n'est qu'un tas de pics de temps, d'instant T ! Si nous combinons les
|
||||
recettes pour chaque pic de temps, nous devrions obtenir la recette du signal complet.
|
||||
|
||||
La transformée de Fourier construit cette recette fréquence par fréquence:
|
||||
|
||||
|
||||
|
||||
Quelques notes
|
||||
|
||||
- N = nombre d'échantillons de temps dont nous disposons
|
||||
- n = échantillon actuellement étudié (0 ... N-1)
|
||||
- x<sub>n</sub> = valeur du signal au temps n
|
||||
- k = fréquence actuellement étudiée (0 Hertz up to N-1 Hertz)
|
||||
- X<sub>k</sub> = quantité de fréquence k dans le signal (amplitude et phase, un nombre complexe)
|
||||
- Le facteur 1 / N est généralement déplacé vers la transformée inverse (passant des fréquences au temps). Ceci est autorisé, bien que je préfère 1 / N dans la transformation directe car cela donne les tailles réelles des pics de temps. Vous pouvez être plus ambitieux et utiliser 1 / racine carrée de (N) sur les deux transformations (aller en avant et en arrière crée le facteur 1 / N).
|
||||
- n/N est le pourcentage du temps que nous avons passé. 2 _ pi _ k est notre vitesse en radians/s. e ^ -ix est notre chemin circulaire vers l'arrière. La combinaison est la distance parcourue, pour cette vitesse et ce temps.
|
||||
- Les équations brutes de la transformée de Fourier consiste simplement à "ajouter les nombres complexes". De nombreux langages de programmation ne peuvent pas gérer directement les nombres complexes, on converti donc tout en coordonnées rectangulaires, pour les ajouter.
|
||||
|
||||
Stuart Riffle a une excellente interprétation de la transformée de Fourier:
|
||||
|
||||
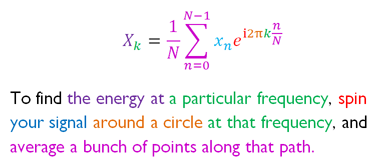
|
||||
|
||||
## Références
|
||||
|
||||
- Wikipedia
|
||||
|
||||
- [TF](https://fr.wikipedia.org/wiki/Transformation_de_Fourier)
|
||||
- [TFD](https://fr.wikipedia.org/wiki/Transformation_de_Fourier_discr%C3%A8te)
|
||||
- [FFT](https://fr.wikipedia.org/wiki/Transformation_de_Fourier_rapide)
|
||||
- [TFtd (en anglais)](https://en.wikipedia.org/wiki/Discrete-time_Fourier_transform)
|
||||
|
||||
- en Anglais
|
||||
- [An Interactive Guide To The Fourier Transform](https://betterexplained.com/articles/an-interactive-guide-to-the-fourier-transform/)
|
||||
- [DFT on YouTube by Better Explained](https://www.youtube.com/watch?v=iN0VG9N2q0U&t=0s&index=77&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
|
||||
- [FT on YouTube by 3Blue1Brown](https://www.youtube.com/watch?v=spUNpyF58BY&t=0s&index=76&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
|
||||
- [FFT on YouTube by Simon Xu](https://www.youtube.com/watch?v=htCj9exbGo0&index=78&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&t=0s)
|
||||
@@ -1,26 +1,29 @@
|
||||
# Fourier Transform
|
||||
|
||||
_Read this in other languages:_
|
||||
[français](README.fr-FR.md).
|
||||
|
||||
## Definitions
|
||||
|
||||
The **Fourier Transform** (**FT**) decomposes a function of time (a signal) into
|
||||
the frequencies that make it up, in a way similar to how a musical chord can be
|
||||
The **Fourier Transform** (**FT**) decomposes a function of time (a signal) into
|
||||
the frequencies that make it up, in a way similar to how a musical chord can be
|
||||
expressed as the frequencies (or pitches) of its constituent notes.
|
||||
|
||||
The **Discrete Fourier Transform** (**DFT**) converts a finite sequence of
|
||||
equally-spaced samples of a function into a same-length sequence of
|
||||
equally-spaced samples of the discrete-time Fourier transform (DTFT), which is a
|
||||
complex-valued function of frequency. The interval at which the DTFT is sampled
|
||||
is the reciprocal of the duration of the input sequence. An inverse DFT is a
|
||||
Fourier series, using the DTFT samples as coefficients of complex sinusoids at
|
||||
the corresponding DTFT frequencies. It has the same sample-values as the original
|
||||
input sequence. The DFT is therefore said to be a frequency domain representation
|
||||
of the original input sequence. If the original sequence spans all the non-zero
|
||||
values of a function, its DTFT is continuous (and periodic), and the DFT provides
|
||||
discrete samples of one cycle. If the original sequence is one cycle of a periodic
|
||||
The **Discrete Fourier Transform** (**DFT**) converts a finite sequence of
|
||||
equally-spaced samples of a function into a same-length sequence of
|
||||
equally-spaced samples of the discrete-time Fourier transform (DTFT), which is a
|
||||
complex-valued function of frequency. The interval at which the DTFT is sampled
|
||||
is the reciprocal of the duration of the input sequence. An inverse DFT is a
|
||||
Fourier series, using the DTFT samples as coefficients of complex sinusoids at
|
||||
the corresponding DTFT frequencies. It has the same sample-values as the original
|
||||
input sequence. The DFT is therefore said to be a frequency domain representation
|
||||
of the original input sequence. If the original sequence spans all the non-zero
|
||||
values of a function, its DTFT is continuous (and periodic), and the DFT provides
|
||||
discrete samples of one cycle. If the original sequence is one cycle of a periodic
|
||||
function, the DFT provides all the non-zero values of one DTFT cycle.
|
||||
|
||||
The Discrete Fourier transform transforms a sequence of `N` complex numbers:
|
||||
|
||||
|
||||
{x<sub>n</sub>} = x<sub>0</sub>, x<sub>1</sub>, x<sub>2</sub> ..., x<sub>N-1</sub>
|
||||
|
||||
into another sequence of complex numbers:
|
||||
@@ -31,16 +34,16 @@ which is defined by:
|
||||
|
||||

|
||||
|
||||
The **Discrete-Time Fourier Transform** (**DTFT**) is a form of Fourier analysis
|
||||
that is applicable to the uniformly-spaced samples of a continuous function. The
|
||||
The **Discrete-Time Fourier Transform** (**DTFT**) is a form of Fourier analysis
|
||||
that is applicable to the uniformly-spaced samples of a continuous function. The
|
||||
term discrete-time refers to the fact that the transform operates on discrete data
|
||||
(samples) whose interval often has units of time. From only the samples, it
|
||||
produces a function of frequency that is a periodic summation of the continuous
|
||||
(samples) whose interval often has units of time. From only the samples, it
|
||||
produces a function of frequency that is a periodic summation of the continuous
|
||||
Fourier transform of the original continuous function.
|
||||
|
||||
A **Fast Fourier Transform** (**FFT**) is an algorithm that samples a signal over
|
||||
a period of time (or space) and divides it into its frequency components. These
|
||||
components are single sinusoidal oscillations at distinct frequencies each with
|
||||
a period of time (or space) and divides it into its frequency components. These
|
||||
components are single sinusoidal oscillations at distinct frequencies each with
|
||||
their own amplitude and phase.
|
||||
|
||||
This transformation is illustrated in Diagram below. Over the time period measured
|
||||
@@ -50,22 +53,22 @@ View of a signal in the time and frequency domain:
|
||||
|
||||

|
||||
|
||||
An FFT algorithm computes the discrete Fourier transform (DFT) of a sequence, or
|
||||
its inverse (IFFT). Fourier analysis converts a signal from its original domain
|
||||
to a representation in the frequency domain and vice versa. An FFT rapidly
|
||||
computes such transformations by factorizing the DFT matrix into a product of
|
||||
sparse (mostly zero) factors. As a result, it manages to reduce the complexity of
|
||||
computing the DFT from O(n<sup>2</sup>), which arises if one simply applies the
|
||||
An FFT algorithm computes the discrete Fourier transform (DFT) of a sequence, or
|
||||
its inverse (IFFT). Fourier analysis converts a signal from its original domain
|
||||
to a representation in the frequency domain and vice versa. An FFT rapidly
|
||||
computes such transformations by factorizing the DFT matrix into a product of
|
||||
sparse (mostly zero) factors. As a result, it manages to reduce the complexity of
|
||||
computing the DFT from O(n<sup>2</sup>), which arises if one simply applies the
|
||||
definition of DFT, to O(n log n), where n is the data size.
|
||||
|
||||
Here a discrete Fourier analysis of a sum of cosine waves at 10, 20, 30, 40,
|
||||
Here a discrete Fourier analysis of a sum of cosine waves at 10, 20, 30, 40,
|
||||
and 50 Hz:
|
||||
|
||||

|
||||
|
||||
## Explanation
|
||||
|
||||
The Fourier Transform is one of deepest insights ever made. Unfortunately, the
|
||||
The Fourier Transform is one of deepest insights ever made. Unfortunately, the
|
||||
meaning is buried within dense equations:
|
||||
|
||||
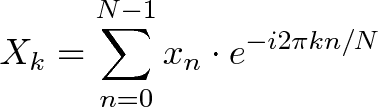
|
||||
@@ -76,26 +79,26 @@ and
|
||||
|
||||
Rather than jumping into the symbols, let's experience the key idea firsthand. Here's a plain-English metaphor:
|
||||
|
||||
- *What does the Fourier Transform do?* Given a smoothie, it finds the recipe.
|
||||
- *How?* Run the smoothie through filters to extract each ingredient.
|
||||
- *Why?* Recipes are easier to analyze, compare, and modify than the smoothie itself.
|
||||
- *How do we get the smoothie back?* Blend the ingredients.
|
||||
- _What does the Fourier Transform do?_ Given a smoothie, it finds the recipe.
|
||||
- _How?_ Run the smoothie through filters to extract each ingredient.
|
||||
- _Why?_ Recipes are easier to analyze, compare, and modify than the smoothie itself.
|
||||
- _How do we get the smoothie back?_ Blend the ingredients.
|
||||
|
||||
**Think With Circles, Not Just Sinusoids**
|
||||
|
||||
The Fourier Transform is about circular paths (not 1-d sinusoids) and Euler's
|
||||
The Fourier Transform is about circular paths (not 1-d sinusoids) and Euler's
|
||||
formula is a clever way to generate one:
|
||||
|
||||

|
||||
|
||||
Must we use imaginary exponents to move in a circle? Nope. But it's convenient
|
||||
and compact. And sure, we can describe our path as coordinated motion in two
|
||||
dimensions (real and imaginary), but don't forget the big picture: we're just
|
||||
and compact. And sure, we can describe our path as coordinated motion in two
|
||||
dimensions (real and imaginary), but don't forget the big picture: we're just
|
||||
moving in a circle.
|
||||
|
||||
**Discovering The Full Transform**
|
||||
|
||||
The big insight: our signal is just a bunch of time spikes! If we merge the
|
||||
The big insight: our signal is just a bunch of time spikes! If we merge the
|
||||
recipes for each time spike, we should get the recipe for the full signal.
|
||||
|
||||
The Fourier Transform builds the recipe frequency-by-frequency:
|
||||
@@ -110,7 +113,7 @@ A few notes:
|
||||
- k = current frequency we're considering (0 Hertz up to N-1 Hertz)
|
||||
- X<sub>k</sub> = amount of frequency k in the signal (amplitude and phase, a complex number)
|
||||
- The 1/N factor is usually moved to the reverse transform (going from frequencies back to time). This is allowed, though I prefer 1/N in the forward transform since it gives the actual sizes for the time spikes. You can get wild and even use 1/sqrt(N) on both transforms (going forward and back creates the 1/N factor).
|
||||
- n/N is the percent of the time we've gone through. 2 * pi * k is our speed in radians / sec. e^-ix is our backwards-moving circular path. The combination is how far we've moved, for this speed and time.
|
||||
- n/N is the percent of the time we've gone through. 2 _ pi _ k is our speed in radians / sec. e^-ix is our backwards-moving circular path. The combination is how far we've moved, for this speed and time.
|
||||
- The raw equations for the Fourier Transform just say "add the complex numbers". Many programming languages cannot handle complex numbers directly, so you convert everything to rectangular coordinates and add those.
|
||||
|
||||
Stuart Riffle has a great interpretation of the Fourier Transform:
|
||||
|
||||
Reference in New Issue
Block a user