mirror of
https://github.com/trekhleb/javascript-algorithms.git
synced 2025-12-19 08:59:05 +08:00
Chore(math-translation-FR-fr): a pack of translations for the math section (#558)
* chore(factorial): translation fr-FR * feat(math-translation-fr-FR): fast powering * feat(math-translation-fr-FR): fibonacci numbers * chore(math-translation-fr-FR): bits * chore(math-translation-fr-FR): complex number * chore(math-translation-fr-FR): euclidean algorithm * chore(math-translation-fr-FR): fibonacci number * chore(math-translation-fr-FR): fourier transform * chore(math-translation-fr-FR): fourier transform WIP * chore(math-translation-fr-FR): fourier transform done * chore(math-translation-fr-FR): fourier transform in menu
This commit is contained in:
49
src/algorithms/math/euclidean-algorithm/README.fr-FR.md
Normal file
49
src/algorithms/math/euclidean-algorithm/README.fr-FR.md
Normal file
@@ -0,0 +1,49 @@
|
||||
# Algorithme d'Euclide
|
||||
|
||||
_Read this in other languages:_
|
||||
[english](README.md).
|
||||
|
||||
En mathématiques, l'algorithme d'Euclide est un algorithme qui calcule le plus grand commun diviseur (PGCD) de deux entiers, c'est-à-dire le plus grand entier qui divise les deux entiers, en laissant un reste nul. L'algorithme ne connaît pas la factorisation de ces deux nombres.
|
||||
|
||||
Le PGCD de deux entiers relatifs est égal au PGCD de leurs valeurs absolues : de ce fait, on se restreint dans cette section aux entiers positifs. L'algorithme part du constat suivant : le PGCD de deux nombres n'est pas changé si on remplace le plus grand d'entre eux par leur différence. Autrement dit, `pgcd(a, b) = pgcd(b, a - b)`. Par exemple, le PGCD de `252` et `105` vaut `21` (en effet, `252 = 21 × 12` and `105 = 21 × 5`), mais c'est aussi le PGCD de `252 - 105 = 147` et `105`. Ainsi, comme le remplacement de ces nombres diminue strictement le plus grand d'entre eux, on peut continuer le processus, jusqu'à obtenir deux nombres égaux.
|
||||
|
||||
En inversant les étapes, le PGCD peut être exprimé comme une somme de
|
||||
les deux nombres originaux, chacun étant multiplié
|
||||
par un entier positif ou négatif, par exemple `21 = 5 × 105 + (-2) × 252`.
|
||||
Le fait que le PGCD puisse toujours être exprimé de cette manière est
|
||||
connue sous le nom de Théorème de Bachet-Bézout.
|
||||
|
||||
|
||||
|
||||
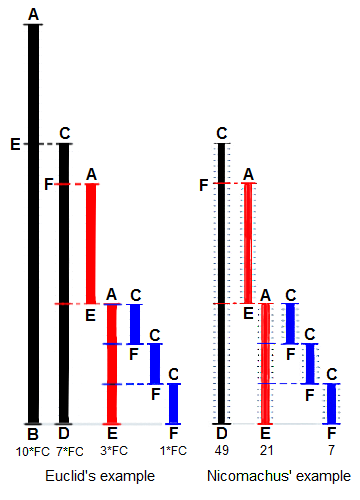
La Méthode d'Euclide pour trouver le plus grand diviseur commun (PGCD)
|
||||
de deux longueurs de départ`BA` et `DC`, toutes deux définies comme étant
|
||||
multiples d'une longueur commune. La longueur `DC` étant
|
||||
plus courte, elle est utilisée pour « mesurer » `BA`, mais une seule fois car
|
||||
le reste `EA` est inférieur à `DC`. `EA` mesure maintenant (deux fois)
|
||||
la longueur la plus courte `DC`, le reste `FC` étant plus court que `EA`.
|
||||
Alors `FC` mesure (trois fois) la longueur `EA`. Parce qu'il y a
|
||||
pas de reste, le processus se termine par `FC` étant le « PGCD ».
|
||||
À droite, l'exemple de Nicomaque de Gérase avec les nombres `49` et `21`
|
||||
ayan un PGCD de `7` (dérivé de Heath 1908: 300).
|
||||
|
||||

|
||||
|
||||
Un de rectangle de dimensions `24 par 60` peux se carreler en carrés de `12 par 12`,
|
||||
puisque `12` est le PGCD ed `24` et `60`. De façon générale,
|
||||
un rectangle de dimension `a par b` peut se carreler en carrés
|
||||
de côté `c`, seulement si `c` est un diviseur commun de `a` et `b`.
|
||||
|
||||

|
||||
|
||||
Animation basée sur la soustraction via l'algorithme euclidien.
|
||||
Le rectangle initial a les dimensions `a = 1071` et `b = 462`.
|
||||
Des carrés de taille `462 × 462` y sont placés en laissant un
|
||||
rectangle de `462 × 147`. Ce rectangle est carrelé avec des
|
||||
carrés de `147 × 147` jusqu'à ce qu'un rectangle de `21 × 147` soit laissé,
|
||||
qui à son tour estcarrelé avec des carrés `21 × 21`,
|
||||
ne laissant aucune zone non couverte.
|
||||
La plus petite taille carrée, `21`, est le PGCD de `1071` et `462`.
|
||||
|
||||
## References
|
||||
|
||||
[Wikipedia](https://fr.wikipedia.org/wiki/Algorithme_d%27Euclide)
|
||||
@@ -1,55 +1,58 @@
|
||||
# Euclidean algorithm
|
||||
|
||||
In mathematics, the Euclidean algorithm, or Euclid's algorithm,
|
||||
is an efficient method for computing the greatest common divisor
|
||||
(GCD) of two numbers, the largest number that divides both of
|
||||
_Read this in other languages:_
|
||||
[français](README.fr-FR.md).
|
||||
|
||||
In mathematics, the Euclidean algorithm, or Euclid's algorithm,
|
||||
is an efficient method for computing the greatest common divisor
|
||||
(GCD) of two numbers, the largest number that divides both of
|
||||
them without leaving a remainder.
|
||||
|
||||
The Euclidean algorithm is based on the principle that the
|
||||
greatest common divisor of two numbers does not change if
|
||||
the larger number is replaced by its difference with the
|
||||
smaller number. For example, `21` is the GCD of `252` and
|
||||
`105` (as `252 = 21 × 12` and `105 = 21 × 5`), and the same
|
||||
number `21` is also the GCD of `105` and `252 − 105 = 147`.
|
||||
Since this replacement reduces the larger of the two numbers,
|
||||
repeating this process gives successively smaller pairs of
|
||||
numbers until the two numbers become equal.
|
||||
When that occurs, they are the GCD of the original two numbers.
|
||||
The Euclidean algorithm is based on the principle that the
|
||||
greatest common divisor of two numbers does not change if
|
||||
the larger number is replaced by its difference with the
|
||||
smaller number. For example, `21` is the GCD of `252` and
|
||||
`105` (as `252 = 21 × 12` and `105 = 21 × 5`), and the same
|
||||
number `21` is also the GCD of `105` and `252 − 105 = 147`.
|
||||
Since this replacement reduces the larger of the two numbers,
|
||||
repeating this process gives successively smaller pairs of
|
||||
numbers until the two numbers become equal.
|
||||
When that occurs, they are the GCD of the original two numbers.
|
||||
|
||||
By reversing the steps, the GCD can be expressed as a sum of
|
||||
the two original numbers each multiplied by a positive or
|
||||
negative integer, e.g., `21 = 5 × 105 + (−2) × 252`.
|
||||
The fact that the GCD can always be expressed in this way is
|
||||
By reversing the steps, the GCD can be expressed as a sum of
|
||||
the two original numbers each multiplied by a positive or
|
||||
negative integer, e.g., `21 = 5 × 105 + (−2) × 252`.
|
||||
The fact that the GCD can always be expressed in this way is
|
||||
known as Bézout's identity.
|
||||
|
||||

|
||||
|
||||
Euclid's method for finding the greatest common divisor (GCD)
|
||||
of two starting lengths `BA` and `DC`, both defined to be
|
||||
multiples of a common "unit" length. The length `DC` being
|
||||
shorter, it is used to "measure" `BA`, but only once because
|
||||
remainder `EA` is less than `DC`. EA now measures (twice)
|
||||
the shorter length `DC`, with remainder `FC` shorter than `EA`.
|
||||
Then `FC` measures (three times) length `EA`. Because there is
|
||||
no remainder, the process ends with `FC` being the `GCD`.
|
||||
On the right Nicomachus' example with numbers `49` and `21`
|
||||
Euclid's method for finding the greatest common divisor (GCD)
|
||||
of two starting lengths `BA` and `DC`, both defined to be
|
||||
multiples of a common "unit" length. The length `DC` being
|
||||
shorter, it is used to "measure" `BA`, but only once because
|
||||
remainder `EA` is less than `DC`. EA now measures (twice)
|
||||
the shorter length `DC`, with remainder `FC` shorter than `EA`.
|
||||
Then `FC` measures (three times) length `EA`. Because there is
|
||||
no remainder, the process ends with `FC` being the `GCD`.
|
||||
On the right Nicomachus' example with numbers `49` and `21`
|
||||
resulting in their GCD of `7` (derived from Heath 1908:300).
|
||||
|
||||

|
||||
|
||||
A `24-by-60` rectangle is covered with ten `12-by-12` square
|
||||
tiles, where `12` is the GCD of `24` and `60`. More generally,
|
||||
an `a-by-b` rectangle can be covered with square tiles of
|
||||
A `24-by-60` rectangle is covered with ten `12-by-12` square
|
||||
tiles, where `12` is the GCD of `24` and `60`. More generally,
|
||||
an `a-by-b` rectangle can be covered with square tiles of
|
||||
side-length `c` only if `c` is a common divisor of `a` and `b`.
|
||||
|
||||

|
||||
|
||||
Subtraction-based animation of the Euclidean algorithm.
|
||||
The initial rectangle has dimensions `a = 1071` and `b = 462`.
|
||||
Squares of size `462×462` are placed within it leaving a
|
||||
`462×147` rectangle. This rectangle is tiled with `147×147`
|
||||
squares until a `21×147` rectangle is left, which in turn is
|
||||
tiled with `21×21` squares, leaving no uncovered area.
|
||||
Subtraction-based animation of the Euclidean algorithm.
|
||||
The initial rectangle has dimensions `a = 1071` and `b = 462`.
|
||||
Squares of size `462×462` are placed within it leaving a
|
||||
`462×147` rectangle. This rectangle is tiled with `147×147`
|
||||
squares until a `21×147` rectangle is left, which in turn is
|
||||
tiled with `21×21` squares, leaving no uncovered area.
|
||||
The smallest square size, `21`, is the GCD of `1071` and `462`.
|
||||
|
||||
## References
|
||||
|
||||
Reference in New Issue
Block a user