mirror of
https://github.com/trekhleb/javascript-algorithms.git
synced 2025-07-19 12:24:59 +08:00
Restructure folders.
This commit is contained in:
@ -1,14 +0,0 @@
|
||||
# Cartesian Product
|
||||
|
||||
In set theory a Cartesian product is a mathematical operation that returns a set
|
||||
(or product set or simply product) from multiple sets. That is, for sets A and B,
|
||||
the Cartesian product A × B is the set of all ordered pairs (a, b)
|
||||
where a ∈ A and b ∈ B.
|
||||
|
||||
Cartesian product `AxB` of two sets `A={x,y,z}` and `B={1,2,3}`
|
||||
|
||||

|
||||
|
||||
## References
|
||||
|
||||
[Wikipedia](https://en.wikipedia.org/wiki/Cartesian_product)
|
||||
@ -1,19 +0,0 @@
|
||||
import cartesianProduct from '../cartesianProduct';
|
||||
|
||||
describe('cartesianProduct', () => {
|
||||
it('should return null if there is not enough info for calculation', () => {
|
||||
const product1 = cartesianProduct([1], null);
|
||||
const product2 = cartesianProduct([], null);
|
||||
|
||||
expect(product1).toBeNull();
|
||||
expect(product2).toBeNull();
|
||||
});
|
||||
|
||||
it('should calculate the product of two sets', () => {
|
||||
const product1 = cartesianProduct([1], [1]);
|
||||
const product2 = cartesianProduct([1, 2], [3, 5]);
|
||||
|
||||
expect(product1).toEqual([[1, 1]]);
|
||||
expect(product2).toEqual([[1, 3], [1, 5], [2, 3], [2, 5]]);
|
||||
});
|
||||
});
|
||||
@ -1,15 +0,0 @@
|
||||
export default function cartesianProduct(setA, setB) {
|
||||
if (!setA || !setB || !setA.length || !setB.length) {
|
||||
return null;
|
||||
}
|
||||
|
||||
const product = [];
|
||||
|
||||
for (let indexA = 0; indexA < setA.length; indexA += 1) {
|
||||
for (let indexB = 0; indexB < setB.length; indexB += 1) {
|
||||
product.push([setA[indexA], setB[indexB]]);
|
||||
}
|
||||
}
|
||||
|
||||
return product;
|
||||
}
|
||||
@ -1,55 +0,0 @@
|
||||
# Combinations
|
||||
|
||||
When the order doesn't matter, it is a **Combination**.
|
||||
|
||||
When the order **does** matter it is a **Permutation**.
|
||||
|
||||
**"My fruit salad is a combination of apples, grapes and bananas"**
|
||||
We don't care what order the fruits are in, they could also be
|
||||
"bananas, grapes and apples" or "grapes, apples and bananas",
|
||||
its the same fruit salad.
|
||||
|
||||
## Combinations without repetitions
|
||||
|
||||
This is how lotteries work. The numbers are drawn one at a
|
||||
time, and if we have the lucky numbers (no matter what order)
|
||||
we win!
|
||||
|
||||
No Repetition: such as lottery numbers `(2,14,15,27,30,33)`
|
||||
|
||||
**Number of combinations**
|
||||
|
||||
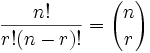
|
||||
|
||||
where `n` is the number of things to choose from, and we choose `r` of them,
|
||||
no repetition, order doesn't matter.
|
||||
|
||||
It is often called "n choose r" (such as "16 choose 3"). And is also known as the Binomial Coefficient.
|
||||
|
||||
## Combinations with repetitions
|
||||
|
||||
Repetition is Allowed: such as coins in your pocket `(5,5,5,10,10)`
|
||||
|
||||
Or let us say there are five flavours of icecream:
|
||||
`banana`, `chocolate`, `lemon`, `strawberry` and `vanilla`.
|
||||
|
||||
We can have three scoops. How many variations will there be?
|
||||
|
||||
Let's use letters for the flavours: `{b, c, l, s, v}`.
|
||||
Example selections include:
|
||||
|
||||
- `{c, c, c}` (3 scoops of chocolate)
|
||||
- `{b, l, v}` (one each of banana, lemon and vanilla)
|
||||
- `{b, v, v}` (one of banana, two of vanilla)
|
||||
|
||||
**Number of combinations**
|
||||
|
||||
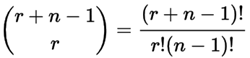
|
||||
|
||||
Where `n` is the number of things to choose from, and we
|
||||
choose `r` of them. Repetition allowed,
|
||||
order doesn't matter.
|
||||
|
||||
## References
|
||||
|
||||
[Math Is Fun](https://www.mathsisfun.com/combinatorics/combinations-permutations.html)
|
||||
@ -1,59 +0,0 @@
|
||||
import combineWithRepetitions from '../combineWithRepetitions';
|
||||
import factorial from '../../factorial/factorial';
|
||||
|
||||
describe('combineWithRepetitions', () => {
|
||||
it('should combine string with repetitions', () => {
|
||||
expect(combineWithRepetitions(['A'], 1)).toEqual([
|
||||
['A'],
|
||||
]);
|
||||
|
||||
expect(combineWithRepetitions(['A', 'B'], 1)).toEqual([
|
||||
['A'],
|
||||
['B'],
|
||||
]);
|
||||
|
||||
expect(combineWithRepetitions(['A', 'B'], 2)).toEqual([
|
||||
['A', 'A'],
|
||||
['A', 'B'],
|
||||
['B', 'B'],
|
||||
]);
|
||||
|
||||
expect(combineWithRepetitions(['A', 'B'], 3)).toEqual([
|
||||
['A', 'A', 'A'],
|
||||
['A', 'A', 'B'],
|
||||
['A', 'B', 'B'],
|
||||
['B', 'B', 'B'],
|
||||
]);
|
||||
|
||||
expect(combineWithRepetitions(['A', 'B', 'C'], 2)).toEqual([
|
||||
['A', 'A'],
|
||||
['A', 'B'],
|
||||
['A', 'C'],
|
||||
['B', 'B'],
|
||||
['B', 'C'],
|
||||
['C', 'C'],
|
||||
]);
|
||||
|
||||
expect(combineWithRepetitions(['A', 'B', 'C'], 3)).toEqual([
|
||||
['A', 'A', 'A'],
|
||||
['A', 'A', 'B'],
|
||||
['A', 'A', 'C'],
|
||||
['A', 'B', 'B'],
|
||||
['A', 'B', 'C'],
|
||||
['A', 'C', 'C'],
|
||||
['B', 'B', 'B'],
|
||||
['B', 'B', 'C'],
|
||||
['B', 'C', 'C'],
|
||||
['C', 'C', 'C'],
|
||||
]);
|
||||
|
||||
const combinationOptions = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H'];
|
||||
const combinationSlotsNumber = 4;
|
||||
const combinations = combineWithRepetitions(combinationOptions, combinationSlotsNumber);
|
||||
const n = combinationOptions.length;
|
||||
const r = combinationSlotsNumber;
|
||||
const expectedNumberOfCombinations = factorial((r + n) - 1) / (factorial(r) * factorial(n - 1));
|
||||
|
||||
expect(combinations.length).toBe(expectedNumberOfCombinations);
|
||||
});
|
||||
});
|
||||
@ -1,60 +0,0 @@
|
||||
import combineWithoutRepetitions from '../combineWithoutRepetitions';
|
||||
import factorial from '../../factorial/factorial';
|
||||
|
||||
describe('combineWithoutRepetitions', () => {
|
||||
it('should combine string without repetitions', () => {
|
||||
expect(combineWithoutRepetitions(['A', 'B'], 3)).toEqual([]);
|
||||
|
||||
expect(combineWithoutRepetitions(['A', 'B'], 1)).toEqual([
|
||||
['A'],
|
||||
['B'],
|
||||
]);
|
||||
|
||||
expect(combineWithoutRepetitions(['A'], 1)).toEqual([
|
||||
['A'],
|
||||
]);
|
||||
|
||||
expect(combineWithoutRepetitions(['A', 'B'], 2)).toEqual([
|
||||
['A', 'B'],
|
||||
]);
|
||||
|
||||
expect(combineWithoutRepetitions(['A', 'B', 'C'], 2)).toEqual([
|
||||
['A', 'B'],
|
||||
['A', 'C'],
|
||||
['B', 'C'],
|
||||
]);
|
||||
|
||||
expect(combineWithoutRepetitions(['A', 'B', 'C'], 3)).toEqual([
|
||||
['A', 'B', 'C'],
|
||||
]);
|
||||
|
||||
expect(combineWithoutRepetitions(['A', 'B', 'C', 'D'], 3)).toEqual([
|
||||
['A', 'B', 'C'],
|
||||
['A', 'B', 'D'],
|
||||
['A', 'C', 'D'],
|
||||
['B', 'C', 'D'],
|
||||
]);
|
||||
|
||||
expect(combineWithoutRepetitions(['A', 'B', 'C', 'D', 'E'], 3)).toEqual([
|
||||
['A', 'B', 'C'],
|
||||
['A', 'B', 'D'],
|
||||
['A', 'B', 'E'],
|
||||
['A', 'C', 'D'],
|
||||
['A', 'C', 'E'],
|
||||
['A', 'D', 'E'],
|
||||
['B', 'C', 'D'],
|
||||
['B', 'C', 'E'],
|
||||
['B', 'D', 'E'],
|
||||
['C', 'D', 'E'],
|
||||
]);
|
||||
|
||||
const combinationOptions = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H'];
|
||||
const combinationSlotsNumber = 4;
|
||||
const combinations = combineWithoutRepetitions(combinationOptions, combinationSlotsNumber);
|
||||
const n = combinationOptions.length;
|
||||
const r = combinationSlotsNumber;
|
||||
const expectedNumberOfCombinations = factorial(n) / (factorial(r) * factorial(n - r));
|
||||
|
||||
expect(combinations.length).toBe(expectedNumberOfCombinations);
|
||||
});
|
||||
});
|
||||
@ -1,38 +0,0 @@
|
||||
/**
|
||||
* @param {*[]} combinationOptions
|
||||
* @param {number} combinationLength
|
||||
* @return {*[]}
|
||||
*/
|
||||
|
||||
export default function combineWithRepetitions(combinationOptions, combinationLength) {
|
||||
// If combination length equal to 0 then return empty combination.
|
||||
if (combinationLength === 0) {
|
||||
return [[]];
|
||||
}
|
||||
|
||||
// If combination options are empty then return "no-combinations" array.
|
||||
if (combinationOptions.length === 0) {
|
||||
return [];
|
||||
}
|
||||
|
||||
// Init combinations array.
|
||||
const combos = [];
|
||||
|
||||
// Find all shorter combinations and attach head to each of those.
|
||||
const headCombo = [combinationOptions[0]];
|
||||
const shorterCombos = combineWithRepetitions(combinationOptions, combinationLength - 1);
|
||||
|
||||
for (let combinationIndex = 0; combinationIndex < shorterCombos.length; combinationIndex += 1) {
|
||||
const combo = headCombo.concat(shorterCombos[combinationIndex]);
|
||||
combos.push(combo);
|
||||
}
|
||||
|
||||
// Let's shift head to the right and calculate all the rest combinations.
|
||||
const combinationsWithoutHead = combineWithRepetitions(
|
||||
combinationOptions.slice(1),
|
||||
combinationLength,
|
||||
);
|
||||
|
||||
// Join all combinations and return them.
|
||||
return combos.concat(combinationsWithoutHead);
|
||||
}
|
||||
@ -1,68 +0,0 @@
|
||||
/*
|
||||
@see: https://stackoverflow.com/a/127898/7794070
|
||||
|
||||
Lets say your array of letters looks like this: "ABCDEFGH".
|
||||
You have three indices (i, j, k) indicating which letters you
|
||||
are going to use for the current word, You start with:
|
||||
|
||||
A B C D E F G H
|
||||
^ ^ ^
|
||||
i j k
|
||||
|
||||
First you vary k, so the next step looks like that:
|
||||
|
||||
A B C D E F G H
|
||||
^ ^ ^
|
||||
i j k
|
||||
|
||||
If you reached the end you go on and vary j and then k again.
|
||||
|
||||
A B C D E F G H
|
||||
^ ^ ^
|
||||
i j k
|
||||
|
||||
A B C D E F G H
|
||||
^ ^ ^
|
||||
i j k
|
||||
|
||||
Once you j reached G you start also to vary i.
|
||||
|
||||
A B C D E F G H
|
||||
^ ^ ^
|
||||
i j k
|
||||
|
||||
A B C D E F G H
|
||||
^ ^ ^
|
||||
i j k
|
||||
...
|
||||
*/
|
||||
|
||||
/**
|
||||
* @param {*[]} combinationOptions
|
||||
* @param {number} combinationLength
|
||||
* @return {*[]}
|
||||
*/
|
||||
export default function combineWithoutRepetitions(combinationOptions, combinationLength) {
|
||||
// If combination length is just 1 then return combinationOptions.
|
||||
if (combinationLength === 1) {
|
||||
return combinationOptions.map(option => [option]);
|
||||
}
|
||||
|
||||
// Init combinations array.
|
||||
const combinations = [];
|
||||
|
||||
for (let i = 0; i <= (combinationOptions.length - combinationLength); i += 1) {
|
||||
const smallerCombinations = combineWithoutRepetitions(
|
||||
combinationOptions.slice(i + 1),
|
||||
combinationLength - 1,
|
||||
);
|
||||
|
||||
for (let j = 0; j < smallerCombinations.length; j += 1) {
|
||||
const combination = [combinationOptions[i]].concat(smallerCombinations[j]);
|
||||
combinations.push(combination);
|
||||
}
|
||||
}
|
||||
|
||||
// Return all calculated combinations.
|
||||
return combinations;
|
||||
}
|
||||
@ -1,15 +0,0 @@
|
||||
# Fisher–Yates shuffle
|
||||
|
||||
The Fisher–Yates shuffle is an algorithm for generating a random
|
||||
permutation of a finite sequence—in plain terms, the algorithm
|
||||
shuffles the sequence. The algorithm effectively puts all the
|
||||
elements into a hat; it continually determines the next element
|
||||
by randomly drawing an element from the hat until no elements
|
||||
remain. The algorithm produces an unbiased permutation: every
|
||||
permutation is equally likely. The modern version of the
|
||||
algorithm is efficient: it takes time proportional to the
|
||||
number of items being shuffled and shuffles them in place.
|
||||
|
||||
## References
|
||||
|
||||
[Wikipedia](https://en.wikipedia.org/wiki/Fisher%E2%80%93Yates_shuffle)
|
||||
@ -1,19 +0,0 @@
|
||||
import fisherYates from '../fisherYates';
|
||||
import { sortedArr } from '../../../sorting/SortTester';
|
||||
import QuickSort from '../../../sorting/quick-sort/QuickSort';
|
||||
|
||||
describe('fisherYates', () => {
|
||||
it('should shuffle small arrays', () => {
|
||||
expect(fisherYates([])).toEqual([]);
|
||||
expect(fisherYates([1])).toEqual([1]);
|
||||
});
|
||||
|
||||
it('should shuffle array randomly', () => {
|
||||
const shuffledArray = fisherYates(sortedArr);
|
||||
const sorter = new QuickSort();
|
||||
|
||||
expect(shuffledArray.length).toBe(sortedArr.length);
|
||||
expect(shuffledArray).not.toEqual(sortedArr);
|
||||
expect(sorter.sort(shuffledArray)).toEqual(sortedArr);
|
||||
});
|
||||
});
|
||||
@ -1,21 +0,0 @@
|
||||
/**
|
||||
* @param {*[]} originalArray
|
||||
* @return {*[]}
|
||||
*/
|
||||
export default function fisherYates(originalArray) {
|
||||
// Clone array from preventing original array from modification (for testing purpose).
|
||||
const array = originalArray.slice(0);
|
||||
|
||||
if (array.length <= 1) {
|
||||
return array;
|
||||
}
|
||||
|
||||
for (let i = (array.length - 1); i > 0; i -= 1) {
|
||||
const randomIndex = Math.floor(Math.random() * (i + 1));
|
||||
const tmp = array[randomIndex];
|
||||
array[randomIndex] = array[i];
|
||||
array[i] = tmp;
|
||||
}
|
||||
|
||||
return array;
|
||||
}
|
||||
@ -1,42 +0,0 @@
|
||||
# Permutations
|
||||
|
||||
When the order doesn't matter, it is a **Combination**.
|
||||
|
||||
When the order **does** matter it is a **Permutation**.
|
||||
|
||||
**"The combination to the safe is 472"**. We do care about the order. `724` won't work, nor will `247`.
|
||||
It has to be exactly `4-7-2`.
|
||||
|
||||
## Permutations without repetitions
|
||||
|
||||
A permutation, also called an “arrangement number” or “order”, is a rearrangement of
|
||||
the elements of an ordered list `S` into a one-to-one correspondence with `S` itself.
|
||||
|
||||
Below are the permutations of string `ABC`.
|
||||
|
||||
`ABC ACB BAC BCA CBA CAB`
|
||||
|
||||
Or for example the first three people in a running race: you can't be first and second.
|
||||
|
||||
**Number of combinations**
|
||||
|
||||
```
|
||||
n * (n-1) * (n -2) * ... * 1 = n!
|
||||
```
|
||||
|
||||
## Permutations with repetitions
|
||||
|
||||
When repetition is allowed we have permutations with repetitions.
|
||||
For example the the lock below: it could be `333`.
|
||||
|
||||

|
||||
|
||||
**Number of combinations**
|
||||
|
||||
```
|
||||
n * n * n ... (r times) = n^r
|
||||
```
|
||||
|
||||
## References
|
||||
|
||||
[Math Is Fun](https://www.mathsisfun.com/combinatorics/combinations-permutations.html)
|
||||
@ -1,55 +0,0 @@
|
||||
import permutateWithRepetitions from '../permutateWithRepetitions';
|
||||
|
||||
describe('permutateWithRepetitions', () => {
|
||||
it('should permutate string with repetition', () => {
|
||||
const permutations0 = permutateWithRepetitions([]);
|
||||
expect(permutations0).toEqual([]);
|
||||
|
||||
const permutations1 = permutateWithRepetitions(['A']);
|
||||
expect(permutations1).toEqual([
|
||||
['A'],
|
||||
]);
|
||||
|
||||
const permutations2 = permutateWithRepetitions(['A', 'B']);
|
||||
expect(permutations2).toEqual([
|
||||
['A', 'A'],
|
||||
['A', 'B'],
|
||||
['B', 'A'],
|
||||
['B', 'B'],
|
||||
]);
|
||||
|
||||
const permutations3 = permutateWithRepetitions(['A', 'B', 'C']);
|
||||
expect(permutations3).toEqual([
|
||||
['A', 'A', 'A'],
|
||||
['A', 'A', 'B'],
|
||||
['A', 'A', 'C'],
|
||||
['A', 'B', 'A'],
|
||||
['A', 'B', 'B'],
|
||||
['A', 'B', 'C'],
|
||||
['A', 'C', 'A'],
|
||||
['A', 'C', 'B'],
|
||||
['A', 'C', 'C'],
|
||||
['B', 'A', 'A'],
|
||||
['B', 'A', 'B'],
|
||||
['B', 'A', 'C'],
|
||||
['B', 'B', 'A'],
|
||||
['B', 'B', 'B'],
|
||||
['B', 'B', 'C'],
|
||||
['B', 'C', 'A'],
|
||||
['B', 'C', 'B'],
|
||||
['B', 'C', 'C'],
|
||||
['C', 'A', 'A'],
|
||||
['C', 'A', 'B'],
|
||||
['C', 'A', 'C'],
|
||||
['C', 'B', 'A'],
|
||||
['C', 'B', 'B'],
|
||||
['C', 'B', 'C'],
|
||||
['C', 'C', 'A'],
|
||||
['C', 'C', 'B'],
|
||||
['C', 'C', 'C'],
|
||||
]);
|
||||
|
||||
const permutations4 = permutateWithRepetitions(['A', 'B', 'C', 'D']);
|
||||
expect(permutations4.length).toBe(4 * 4 * 4 * 4);
|
||||
});
|
||||
});
|
||||
@ -1,71 +0,0 @@
|
||||
import permutateWithoutRepetitions from '../permutateWithoutRepetitions';
|
||||
import factorial from '../../factorial/factorial';
|
||||
|
||||
describe('permutateWithoutRepetitions', () => {
|
||||
it('should permutate string', () => {
|
||||
const permutations0 = permutateWithoutRepetitions([]);
|
||||
expect(permutations0).toEqual([]);
|
||||
|
||||
const permutations1 = permutateWithoutRepetitions(['A']);
|
||||
expect(permutations1).toEqual([
|
||||
['A'],
|
||||
]);
|
||||
|
||||
const permutations2 = permutateWithoutRepetitions(['A', 'B']);
|
||||
expect(permutations2.length).toBe(2);
|
||||
expect(permutations2).toEqual([
|
||||
['B', 'A'],
|
||||
['A', 'B'],
|
||||
]);
|
||||
|
||||
const permutations6 = permutateWithoutRepetitions(['A', 'A']);
|
||||
expect(permutations6.length).toBe(2);
|
||||
expect(permutations6).toEqual([
|
||||
['A', 'A'],
|
||||
['A', 'A'],
|
||||
]);
|
||||
|
||||
const permutations3 = permutateWithoutRepetitions(['A', 'B', 'C']);
|
||||
expect(permutations3.length).toBe(factorial(3));
|
||||
expect(permutations3).toEqual([
|
||||
['C', 'B', 'A'],
|
||||
['B', 'C', 'A'],
|
||||
['B', 'A', 'C'],
|
||||
['C', 'A', 'B'],
|
||||
['A', 'C', 'B'],
|
||||
['A', 'B', 'C'],
|
||||
]);
|
||||
|
||||
const permutations4 = permutateWithoutRepetitions(['A', 'B', 'C', 'D']);
|
||||
expect(permutations4.length).toBe(factorial(4));
|
||||
expect(permutations4).toEqual([
|
||||
['D', 'C', 'B', 'A'],
|
||||
['C', 'D', 'B', 'A'],
|
||||
['C', 'B', 'D', 'A'],
|
||||
['C', 'B', 'A', 'D'],
|
||||
['D', 'B', 'C', 'A'],
|
||||
['B', 'D', 'C', 'A'],
|
||||
['B', 'C', 'D', 'A'],
|
||||
['B', 'C', 'A', 'D'],
|
||||
['D', 'B', 'A', 'C'],
|
||||
['B', 'D', 'A', 'C'],
|
||||
['B', 'A', 'D', 'C'],
|
||||
['B', 'A', 'C', 'D'],
|
||||
['D', 'C', 'A', 'B'],
|
||||
['C', 'D', 'A', 'B'],
|
||||
['C', 'A', 'D', 'B'],
|
||||
['C', 'A', 'B', 'D'],
|
||||
['D', 'A', 'C', 'B'],
|
||||
['A', 'D', 'C', 'B'],
|
||||
['A', 'C', 'D', 'B'],
|
||||
['A', 'C', 'B', 'D'],
|
||||
['D', 'A', 'B', 'C'],
|
||||
['A', 'D', 'B', 'C'],
|
||||
['A', 'B', 'D', 'C'],
|
||||
['A', 'B', 'C', 'D'],
|
||||
]);
|
||||
|
||||
const permutations5 = permutateWithoutRepetitions(['A', 'B', 'C', 'D', 'E', 'F']);
|
||||
expect(permutations5.length).toBe(factorial(6));
|
||||
});
|
||||
});
|
||||
@ -1,42 +0,0 @@
|
||||
/**
|
||||
* @param {*[]} permutationOptions
|
||||
* @return {*[]}
|
||||
*/
|
||||
export default function permutateWithRepetitions(permutationOptions) {
|
||||
// There is no permutations for empty array.
|
||||
if (!permutationOptions || permutationOptions.length === 0) {
|
||||
return [];
|
||||
}
|
||||
|
||||
// There is only one permutation for the 1-element array.
|
||||
if (permutationOptions.length === 1) {
|
||||
return [permutationOptions];
|
||||
}
|
||||
|
||||
// Let's create initial set of permutations.
|
||||
let previousPermutations = permutationOptions.map(option => [option]);
|
||||
let currentPermutations = [];
|
||||
let permutationSize = 1;
|
||||
|
||||
// While the size of each permutation is less then or equal to options length...
|
||||
while (permutationSize < permutationOptions.length) {
|
||||
// Reset all current permutations.
|
||||
currentPermutations = [];
|
||||
|
||||
for (let permIndex = 0; permIndex < previousPermutations.length; permIndex += 1) {
|
||||
for (let optionIndex = 0; optionIndex < permutationOptions.length; optionIndex += 1) {
|
||||
let currentPermutation = previousPermutations[permIndex];
|
||||
currentPermutation = currentPermutation.concat([permutationOptions[optionIndex]]);
|
||||
currentPermutations.push(currentPermutation);
|
||||
}
|
||||
}
|
||||
|
||||
// Make current permutations to be the previous ones.
|
||||
previousPermutations = currentPermutations.slice(0);
|
||||
|
||||
// Increase permutation size counter.
|
||||
permutationSize += 1;
|
||||
}
|
||||
|
||||
return currentPermutations;
|
||||
}
|
||||
@ -1,39 +0,0 @@
|
||||
/**
|
||||
* @param {*[]} permutationOptions
|
||||
* @return {*[]}
|
||||
*/
|
||||
export default function permutateWithoutRepetitions(permutationOptions) {
|
||||
if (permutationOptions.length === 0) {
|
||||
return [];
|
||||
}
|
||||
|
||||
if (permutationOptions.length === 1) {
|
||||
return [permutationOptions];
|
||||
}
|
||||
|
||||
const permutations = [];
|
||||
|
||||
// Get all permutations of length (n - 1).
|
||||
const previousOptions = permutationOptions.slice(0, permutationOptions.length - 1);
|
||||
const previousPermutations = permutateWithoutRepetitions(previousOptions);
|
||||
|
||||
// Insert last option into every possible position of every previous permutation.
|
||||
const lastOption = permutationOptions.slice(permutationOptions.length - 1);
|
||||
|
||||
for (
|
||||
let permutationIndex = 0;
|
||||
permutationIndex < previousPermutations.length;
|
||||
permutationIndex += 1
|
||||
) {
|
||||
const currentPermutation = previousPermutations[permutationIndex];
|
||||
|
||||
// Insert last option into every possible position of currentPermutation.
|
||||
for (let positionIndex = 0; positionIndex <= currentPermutation.length; positionIndex += 1) {
|
||||
const permutationPrefix = currentPermutation.slice(0, positionIndex);
|
||||
const permutationSuffix = currentPermutation.slice(positionIndex);
|
||||
permutations.push(permutationPrefix.concat(lastOption, permutationSuffix));
|
||||
}
|
||||
}
|
||||
|
||||
return permutations;
|
||||
}
|
||||
@ -1,12 +0,0 @@
|
||||
# Power Set
|
||||
|
||||
Power set of a set A is the set of all of the subsets of A.
|
||||
|
||||
Eg. for `{x, y, z}`, the subsets are : `{{}, {x}, {y}, {z}, {x, y}, {x, z}, {y, z}, {x, y, z}}`
|
||||
|
||||

|
||||
|
||||
## References
|
||||
|
||||
* [Wikipedia](https://en.wikipedia.org/wiki/Power_set)
|
||||
* [Math is Fun](https://www.mathsisfun.com/sets/power-set.html)
|
||||
@ -1,24 +0,0 @@
|
||||
import powerSet from '../powerSet';
|
||||
|
||||
describe('powerSet', () => {
|
||||
it('should calculate power set of given set', () => {
|
||||
const powerSets1 = powerSet([1]);
|
||||
const powerSets2 = powerSet([1, 2, 3]);
|
||||
|
||||
expect(powerSets1).toEqual([
|
||||
[],
|
||||
[1],
|
||||
]);
|
||||
|
||||
expect(powerSets2).toEqual([
|
||||
[],
|
||||
[1],
|
||||
[2],
|
||||
[1, 2],
|
||||
[3],
|
||||
[1, 3],
|
||||
[2, 3],
|
||||
[1, 2, 3],
|
||||
]);
|
||||
});
|
||||
});
|
||||
@ -1,28 +0,0 @@
|
||||
export default function powerSet(originalSet) {
|
||||
const subSets = [];
|
||||
|
||||
// We will have 2^n possible combinations (where n is a length of original set).
|
||||
// It is because for every element of original set we will decide whether to include
|
||||
// it or not (2 options for each set element).
|
||||
const numberOfCombinations = 2 ** originalSet.length;
|
||||
|
||||
// Each number in binary representation in a range from 0 to 2^n does exactly what we need:
|
||||
// it shoes by its bits (0 or 1) whether to include related element from the set or not.
|
||||
// For example, for the set {1, 2, 3} the binary number of 010 would mean that we need to
|
||||
// include only "2" to the current set.
|
||||
for (let combinationIndex = 0; combinationIndex < numberOfCombinations; combinationIndex += 1) {
|
||||
const subSet = [];
|
||||
|
||||
for (let setElementIndex = 0; setElementIndex < originalSet.length; setElementIndex += 1) {
|
||||
// Decide whether we need to include current element into the subset or not.
|
||||
if (combinationIndex & (1 << setElementIndex)) {
|
||||
subSet.push(originalSet[setElementIndex]);
|
||||
}
|
||||
}
|
||||
|
||||
// Add current subset to the list of all subsets.
|
||||
subSets.push(subSet);
|
||||
}
|
||||
|
||||
return subSets;
|
||||
}
|
||||
Reference in New Issue
Block a user