diff --git a/动态规划系列/动态规划详解进阶.md b/动态规划系列/动态规划详解进阶.md
index 92eb901..0cb4603 100644
--- a/动态规划系列/动态规划详解进阶.md
+++ b/动态规划系列/动态规划详解进阶.md
@@ -135,7 +135,7 @@ int dp(int[] memo, int n) {
 }
 ```
 
-<visual slug='mydata-fib2'/>
+<visual slug='mydata-fib2' />
 
 现在，画出递归树，你就知道「备忘录」到底做了什么。
 
@@ -179,9 +179,15 @@ int fib(int N) {
 }
 ```
 
+<visual slug='mydata-fib3' />
+
+画个图就很好理解了，而且你发现这个 DP table 特别像之前那个「剪枝」后的结果，只是反过来算而已：
+
 ![](https://labuladong.github.io/pictures/动态规划详解进阶/4.jpg)
 
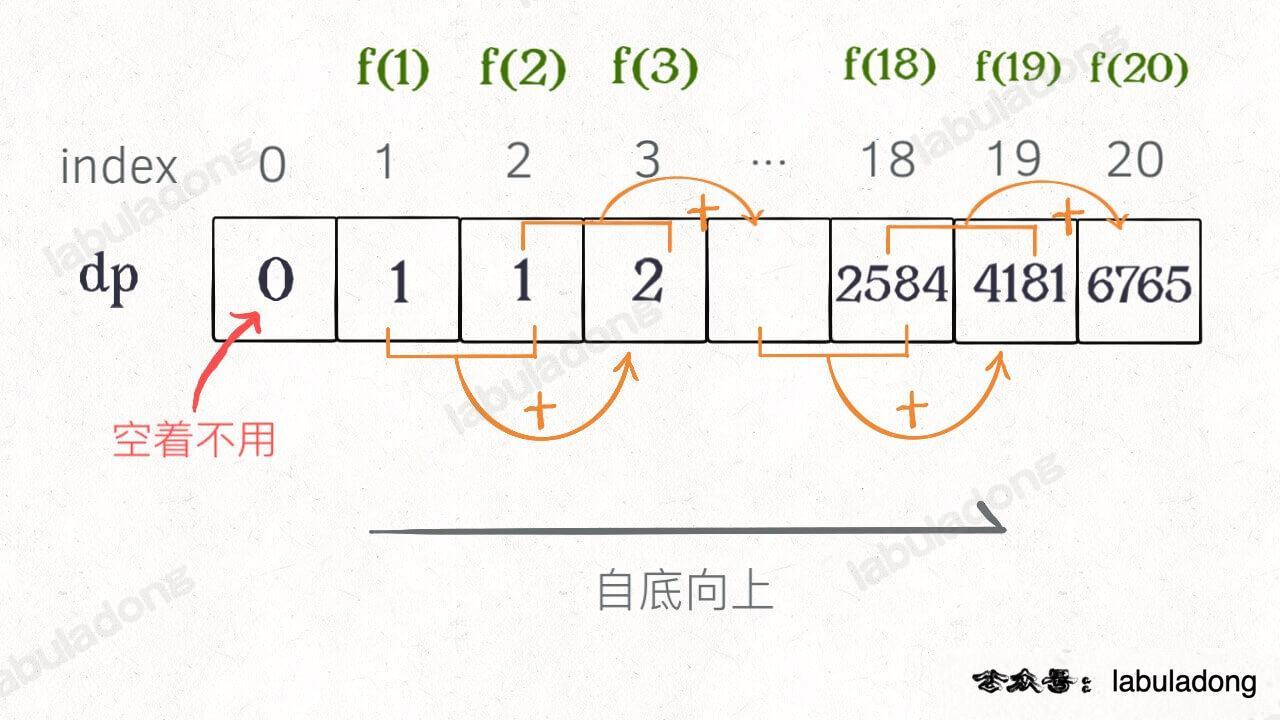
-画个图就很好理解了，而且你发现这个 DP table 特别像之前那个「剪枝」后的结果，只是反过来算而已。实际上，带备忘录的递归解法中的「备忘录」，最终完成后就是这个 DP table，所以说这两种解法其实是差不多的，大部分情况下，效率也基本相同。
+实际上，带备忘录的递归解法中的那个「备忘录」`memo` 数组，最终完成后就是这个解法中的 `dp` 数组，你对比一下可视化面板中两个算法执行的过程可以更直观地看出它俩的联系。
+
+所以说自顶向下、自底向上两种解法本质其实是差不多的，大部分情况下，效率也基本相同。
 
 这里，引出「状态转移方程」这个名词，实际上就是描述问题结构的数学形式：