update content

动态规划系列/动态规划之博弈问题.md

@@ -36,7 +36,7 @@
 
 这样推广之后就变成了一道难度比较高的动态规划问题了，力扣第 486 题「预测赢家」就是一道类似的问题：
 
-![](https://labuladong.github.io/pictures/博弈问题/title.jpg)
+<Problem slug="predict-the-winner" />
 
 函数签名如下：
 

动态规划系列/动态规划设计：最长递增子序列.md

@@ -234,7 +234,7 @@ int lengthOfLIS(int[] nums) {
 
 我们看一个经常出现在生活中的有趣问题，力扣第 354 题「俄罗斯套娃信封问题」，先看下题目：
 
-![](https://labuladong.github.io/pictures/信封嵌套/title.png)
+<Problem slug="russian-doll-envelopes" />
 
 **这道题目其实是最长递增子序列的一个变种，因为每次合法的嵌套是大的套小的，相当于在二维平面中找一个最长递增的子序列，其长度就是最多能嵌套的信封个数**。
 

动态规划系列/单词拼接.md

@@ -38,7 +38,7 @@
 
 首先看下力扣第 139 题「单词拆分」：
 
-![](https://labuladong.github.io/pictures/单词拆分/title.jpg)
+<Problem slug="word-break" />
 
 函数签名如下：
 
@@ -348,7 +348,7 @@ class Solution {
 
 有了上一道题的铺垫，力扣第 140 题「单词拆分 II」就容易多了，先看下题目：
 
-![](https://labuladong.github.io/pictures/单词拆分/title2.jpg)
+<Problem slug="word-break-ii" />
 
 相较上一题，这道题不是单单问你 `s` 是否能被拼出，还要问你是怎么拼的，其实只要把之前的解法稍微改一改就可以解决这道题。
 

动态规划系列/团灭股票问题.md

@@ -54,7 +54,7 @@ int maxProfit(vector<int>& prices) {
 
 这 6 道题目是有共性的，我们只需要抽出来力扣第 188 题「买卖股票的最佳时机 IV」进行研究，因为这道题是最泛化的形式，其他的问题都是这个形式的简化，看下题目：
 
-![](https://labuladong.github.io/pictures/股票问题/title.png)
+<Problem slug="best-time-to-buy-and-sell-stock-iv" />
 
 第一题是只进行一次交易，相当于 `k = 1`；第二题是不限交易次数，相当于 `k = +infinity`（正无穷）；第三题是只进行 2 次交易，相当于 `k = 2`；剩下两道也是不限次数，但是加了交易「冷冻期」和「手续费」的额外条件，其实就是第二题的变种，都很容易处理。
 
@@ -181,7 +181,7 @@ dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
 
 **第一题，先说力扣第 121 题「买卖股票的最佳时机」，相当于 `k = 1` 的情况**：
 
-![](https://labuladong.github.io/pictures/股票问题/title1.png)
+<Problem slug="best-time-to-buy-and-sell-stock" />
 
 直接套状态转移方程，根据 base case，可以做一些化简：
 
@@ -270,7 +270,7 @@ int maxProfit_k_1(int[] prices) {
 
 **第二题，看一下力扣第 122 题「买卖股票的最佳时机 II」，也就是 `k` 为正无穷的情况**：
 
-![](https://labuladong.github.io/pictures/股票问题/title2.png)
+<Problem slug="best-time-to-buy-and-sell-stock-ii" />
 
 题目还专门强调可以在同一天出售，但我觉得这个条件纯属多余，如果当天买当天卖，那利润当然就是 0，这不是和没有进行交易是一样的吗？这道题的特点在于没有给出交易总数 `k` 的限制，也就相当于 `k` 为正无穷。
 
@@ -322,7 +322,7 @@ int maxProfit_k_inf(int[] prices) {
 
 **第三题，看力扣第 309 题「最佳买卖股票时机含冷冻期」，也就是 `k` 为正无穷，但含有交易冷冻期的情况**：
 
-![](https://labuladong.github.io/pictures/股票问题/title3.png)
+<Problem slug="best-time-to-buy-and-sell-stock-with-cooldown" />
 
 和上一道题一样的，只不过每次 `sell` 之后要等一天才能继续交易，只要把这个特点融入上一题的状态转移方程即可：
 
@@ -381,7 +381,7 @@ int maxProfit_with_cool(int[] prices) {
 
 **第四题，看力扣第 714 题「买卖股票的最佳时机含手续费」，也就是 `k` 为正无穷且考虑交易手续费的情况**：
 
-![](https://labuladong.github.io/pictures/股票问题/title4.png)
+<Problem slug="best-time-to-buy-and-sell-stock-with-transaction-fee" />
 
 每次交易要支付手续费，只要把手续费从利润中减去即可，改写方程：
 
@@ -435,7 +435,7 @@ int maxProfit_with_fee(int[] prices, int fee) {
 
 **第五题，看力扣第 123 题「买卖股票的最佳时机 III」，也就是 `k = 2` 的情况**：
 
-![](https://labuladong.github.io/pictures/股票问题/title5.png)
+<Problem slug="best-time-to-buy-and-sell-stock-iii" />
 
 `k = 2` 和前面题目的情况稍微不同，因为上面的情况都和 `k` 的关系不太大：要么 `k` 是正无穷，状态转移和 `k` 没关系了；要么 `k = 1`，跟 `k = 0` 这个 base case 挨得近，最后也没有存在感。
 
@@ -547,7 +547,7 @@ int maxProfit_k_2(int[] prices) {
 
 **第六题，看力扣第 188 题「买卖股票的最佳时机 IV」，即 `k` 可以是题目给定的任何数的情况**：
 
-![](https://labuladong.github.io/pictures/股票问题/title.png)
+<Problem slug="best-time-to-buy-and-sell-stock-iv" />
 
 有了上一题 `k = 2` 的铺垫，这题应该和上一题的第一个解法没啥区别，你把上一题的 `k = 2` 换成题目输入的 `k` 就行了。
 

动态规划系列/编辑距离.md

@@ -31,7 +31,7 @@
 
 力扣第 72 题「编辑距离」就是这个问题，先看下题目：
 
-![](https://labuladong.github.io/pictures/editDistance/title.png)
+<Problem slug="edit-distance" />
 
 函数签名如下：
 

数据结构系列/BST1.md

@@ -64,7 +64,7 @@ void traverse(TreeNode root) {
 
 这是力扣第 230 题「二叉搜索树中第 K 小的元素」，看下题目：
 
-![](https://labuladong.github.io/pictures/BST1/title.png)
+<Problem slug="kth-smallest-element-in-a-bst" />
 
 这个需求很常见吧，一个直接的思路就是升序排序，然后找第 `k` 个元素呗。BST 的中序遍历其实就是升序排序的结果，找第 `k` 个元素肯定不是什么难事。
 
@@ -152,7 +152,7 @@ class TreeNode {
 
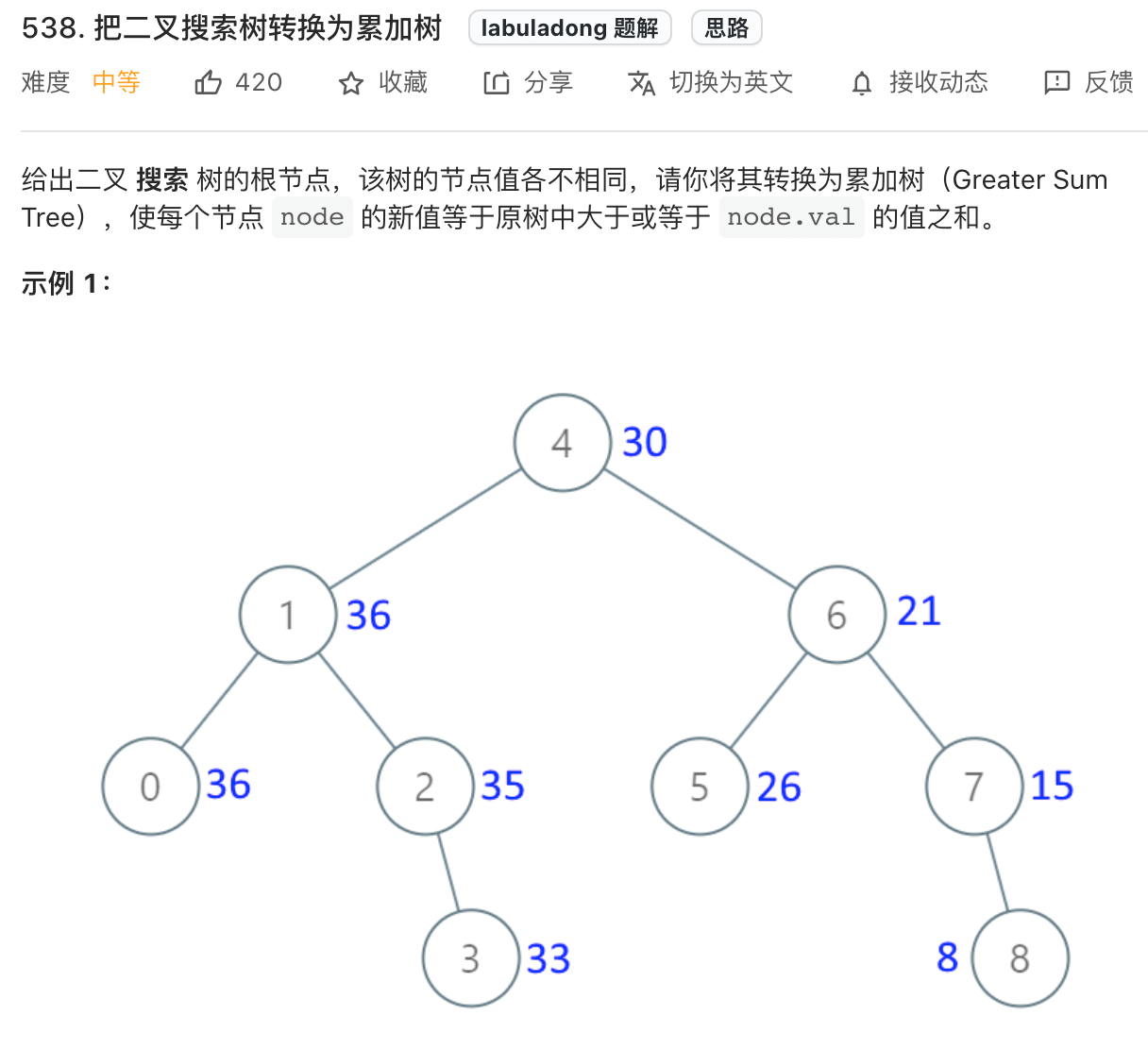
 力扣第 538 题和 1038 题都是这道题，完全一样，你可以把它们一块做掉。看下题目：
 
-![](https://labuladong.github.io/pictures/BST1/title1.png)
+<Problem slug="convert-bst-to-greater-tree" />
 
 题目应该不难理解，比如图中的节点 5，转化成累加树的话，比 5 大的节点有 6，7，8，加上 5 本身，所以累加树上这个节点的值应该是 5+6+7+8=26。
 

数据结构系列/dijkstra算法.md

@@ -503,7 +503,7 @@ Dijkstra 算法的时间复杂度是多少？你去网上查，可能会告诉
 
 第一题是力扣第 743 题「网络延迟时间」，题目如下：
 
-![](https://labuladong.github.io/pictures/dijkstra/title1.jpg)
+<Problem slug="network-delay-time" />
 
 函数签名如下：
 
@@ -615,7 +615,7 @@ int[] dijkstra(int start, List<int[]>[] graph) {
 
 感觉这道题完全没有难度，下面我们再看一道题目，力扣第 1631 题「最小体力消耗路径」：
 
-![](https://labuladong.github.io/pictures/dijkstra/title2.jpg)
+<Problem slug="path-with-minimum-effort" />
 
 函数签名如下：
 
@@ -747,7 +747,7 @@ int minimumEffortPath(int[][] heights) {
 
 最后看一道题吧，力扣第 1514 题「概率最大的路径」，看下题目：
 
-![](https://labuladong.github.io/pictures/dijkstra/title3.jpg)
+<Problem slug="path-with-maximum-probability" />
 
 函数签名如下：
 

数据结构系列/二叉树系列1.md

@@ -162,7 +162,7 @@ TreeNode invertTree(TreeNode root) {
 
 这是力扣第 116 题「填充每个二叉树节点的右侧指针」，看下题目：
 
-![](https://labuladong.github.io/pictures/二叉树系列/title1.png)
+<Problem slug="populating-next-right-pointers-in-each-node" />
 
 函数签名如下：
 
@@ -255,7 +255,7 @@ void traverse(Node node1, Node node2) {
 
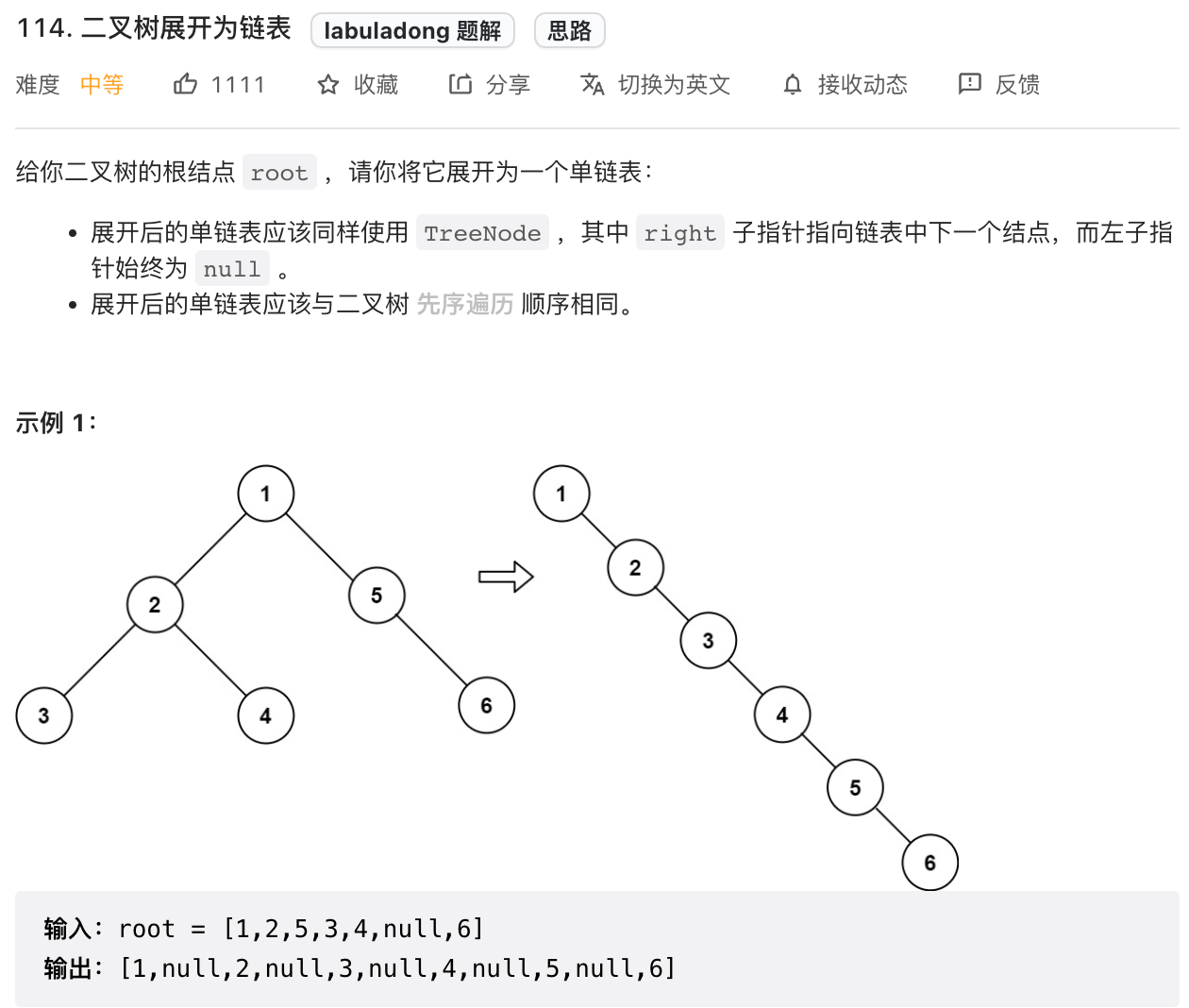
 这是力扣第 114 题「将二叉树展开为链表」，看下题目：
 
-![](https://labuladong.github.io/pictures/二叉树系列/title2.png)
+<Problem slug="flatten-binary-tree-to-linked-list" />
 
 函数签名如下：
 

数据结构系列/二叉树系列2.md

@@ -52,7 +52,7 @@
 
 先来道简单的，这是力扣第 654 题「最大二叉树」，题目如下：
 
-![](https://labuladong.github.io/pictures/二叉树系列2/title1.png)
+<Problem slug="maximum-binary-tree" />
 
 函数签名如下：
 
@@ -148,7 +148,7 @@ TreeNode build(int[] nums, int lo, int hi) {
 
 力扣第 105 题「从前序和中序遍历序列构造二叉树」就是这道经典题目，面试笔试中常考：
 
-![](https://labuladong.github.io/pictures/二叉树系列2/title3.png)
+<Problem slug="construct-binary-tree-from-preorder-and-inorder-traversal" />
 
 函数签名如下：
 
@@ -339,7 +339,7 @@ TreeNode build(int[] preorder, int preStart, int preEnd,
 
 类似上一题，这次我们利用**后序**和**中序**遍历的结果数组来还原二叉树，这是力扣第 106 题「从后序和中序遍历序列构造二叉树」：
 
-![](https://labuladong.github.io/pictures/二叉树系列2/title2.png)
+<Problem slug="construct-binary-tree-from-inorder-and-postorder-traversal" />
 
 函数签名如下：
 

数据结构系列/单调栈.md

@@ -79,7 +79,7 @@ int[] nextGreaterElement(int[] nums) {
 
 单调栈的使用技巧差不多了，首先来一个简单的变形，力扣第 496 题「下一个更大元素 I」：
 
-![](https://labuladong.github.io/pictures/单调栈/title.jpg)
+<Problem slug="next-greater-element-i" />
 
 这道题给你输入两个数组 `nums1` 和 `nums2`，让你求 `nums1` 中的元素在 `nums2` 中的下一个更大元素，函数签名如下：
 

数据结构系列/拓扑排序.md

@@ -39,7 +39,7 @@
 
 先来看看力扣第 207 题「课程表」：
 
-![](https://labuladong.github.io/pictures/拓扑排序/title1.jpg)
+<Problem slug="course-schedule" />
 
 函数签名如下：
 
@@ -264,7 +264,7 @@ class Solution {
 
 看下力扣第 210 题「课程表 II」：
 
-![](https://labuladong.github.io/pictures/拓扑排序/title2.jpg)
+<Problem slug="course-schedule-ii" />
 
 这道题就是上道题的进阶版，不是仅仅让你判断是否可以完成所有课程，而是进一步让你返回一个合理的上课顺序，保证开始修每个课程时，前置的课程都已经修完。
 

数据结构系列/递归反转链表的一部分.md

@@ -44,7 +44,7 @@ public class ListNode {
 
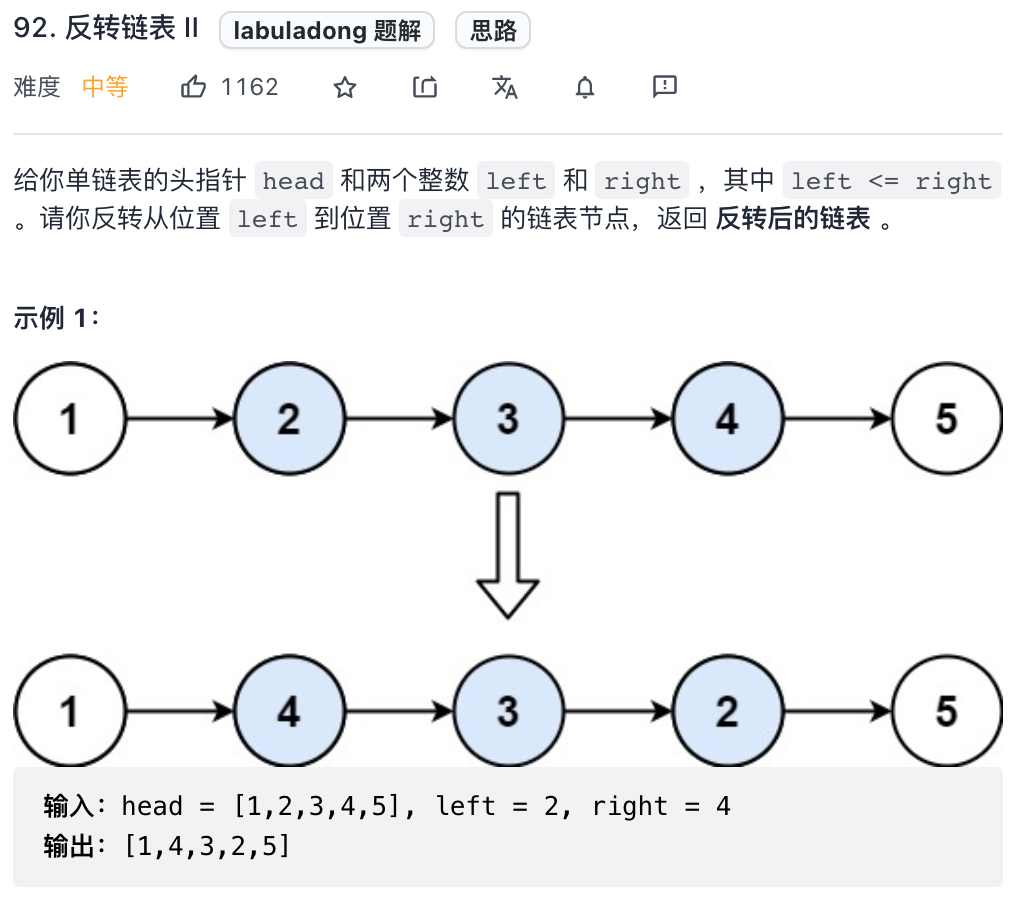
 看下力扣第 92 题「反转链表 II」：
 
-![](https://labuladong.github.io/pictures/反转链表/title.png)
+<Problem slug="reverse-linked-list-ii" />
 
 **注意这里的索引是从 1 开始的**。迭代的思路大概是：先用一个 for 循环找到第 `m` 个位置，然后再用一个 for 循环将 `m` 和 `n` 之间的元素反转。但是我们的递归解法不用一个 for 循环，纯递归实现反转。
 

算法思维系列/BFS框架.md

@@ -92,7 +92,7 @@ int BFS(Node start, Node target) {
 
 先来个简单的问题实践一下 BFS 框架吧，判断一棵二叉树的**最小**高度，这也是力扣第 111 题「二叉树的最小深度」：
 
-![](https://labuladong.github.io/pictures/BFS/title1.jpg)
+<Problem slug="minimum-depth-of-binary-tree" />
 
 怎么套到 BFS 的框架里呢？首先明确一下起点 `start` 和终点 `target` 是什么，怎么判断到达了终点？
 
@@ -169,7 +169,7 @@ BFS 可以找到最短距离，但是空间复杂度高，而 DFS 的空间复
 
 这是力扣第 752 题「打开转盘锁」，比较有意思：
 
-![](https://labuladong.github.io/pictures/BFS/title2.jpg)
+<Problem slug="open-the-lock" />
 
 函数签名如下：
 

算法思维系列/前缀和技巧.md

@@ -33,7 +33,7 @@
 
 先看一道例题，力扣第 303 题「区域和检索 - 数组不可变」，让你计算数组区间内元素的和，这是一道标准的前缀和问题：
 
-![](https://labuladong.github.io/pictures/前缀和/title1.png)
+<Problem slug="range-sum-query-immutable" />
 
 题目要求你实现这样一个类：
 
@@ -131,7 +131,7 @@ for (int i = 1; i < count.length; i++)
 
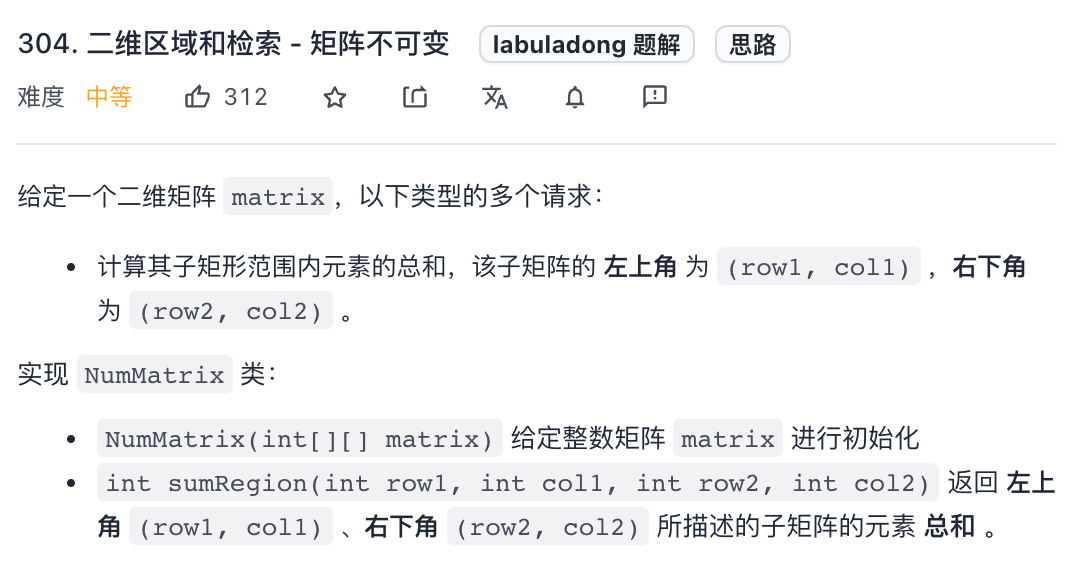
 这是力扣第 304 题「二维区域和检索 - 矩阵不可变」，其实和上一题类似，上一题是让你计算子数组的元素之和，这道题让你计算二维矩阵中子矩阵的元素之和：
 
-![](https://labuladong.github.io/pictures/前缀和/title2.png)
+<Problem slug="range-sum-query-2d-immutable" />
 
 比如说输入的 `matrix` 如下图：
 

算法思维系列/双指针技巧.md

@@ -47,7 +47,7 @@
 
 比如说看下力扣第 26 题「删除有序数组中的重复项」，让你在有序数组去重：
 
-![](https://labuladong.github.io/pictures/数组去重/title.png)
+<Problem slug="remove-duplicates-from-sorted-array" />
 
 函数签名如下：
 
@@ -137,7 +137,7 @@ ListNode deleteDuplicates(ListNode head) {
 
 比如力扣第 27 题「移除元素」，看下题目：
 
-![](https://labuladong.github.io/pictures/数组去重/title1.png)
+<Problem slug="remove-element" />
 
 函数签名如下：
 
@@ -262,7 +262,7 @@ int binarySearch(int[] nums, int target) {
 
 看下力扣第 167 题「两数之和 II」：
 
-![](https://labuladong.github.io/pictures/双指针/title.png)
+<Problem slug="two-sum-ii-input-array-is-sorted" />
 
 只要数组有序，就应该想到双指针技巧。这道题的解法有点类似二分查找，通过调节 `left` 和 `right` 就可以调整 `sum` 的大小：
 
@@ -336,7 +336,7 @@ boolean isPalindrome(String s) {
 
 这就是力扣第 5 题「最长回文子串」：
 
-![](https://labuladong.github.io/pictures/回文/title.png)
+<Problem slug="longest-palindromic-substring" />
 
 函数签名如下：
 

算法思维系列/字符串乘法.md

@@ -25,7 +25,7 @@
 
 看下力扣第 43 题「字符串相乘」：
 
-![](https://labuladong.github.io/pictures/字符串乘法/title.png)
+<Problem slug="multiply-strings" />
 
 需要注意的是，`num1` 和 `num2` 可以非常长，所以不可以把他们直接转成整型然后运算，唯一的思路就是模仿我们手算乘法。
 

算法思维系列/差分技巧.md

@@ -156,7 +156,7 @@ public void increment(int i, int j, int val) {
 
 首先，力扣第 370 题「区间加法」 就直接考察了差分数组技巧：
 
-![](https://labuladong.github.io/pictures/差分数组/title1.png)
+<Problem slug="range-addition" />
 
 那么我们直接复用刚才实现的 `Difference` 类就能把这道题解决掉：
 
@@ -181,7 +181,7 @@ int[] getModifiedArray(int length, int[][] updates) {
 
 当然，实际的算法题可能需要我们对题目进行联想和抽象，不会这么直接地让你看出来要用差分数组技巧，这里看一下力扣第 1109 题「航班预订统计」：
 
-![](https://labuladong.github.io/pictures/差分数组/title.png)
+<Problem slug="corporate-flight-bookings" />
 
 函数签名如下：
 

算法思维系列/常用的位操作.md

@@ -164,7 +164,7 @@ while (true) {
 
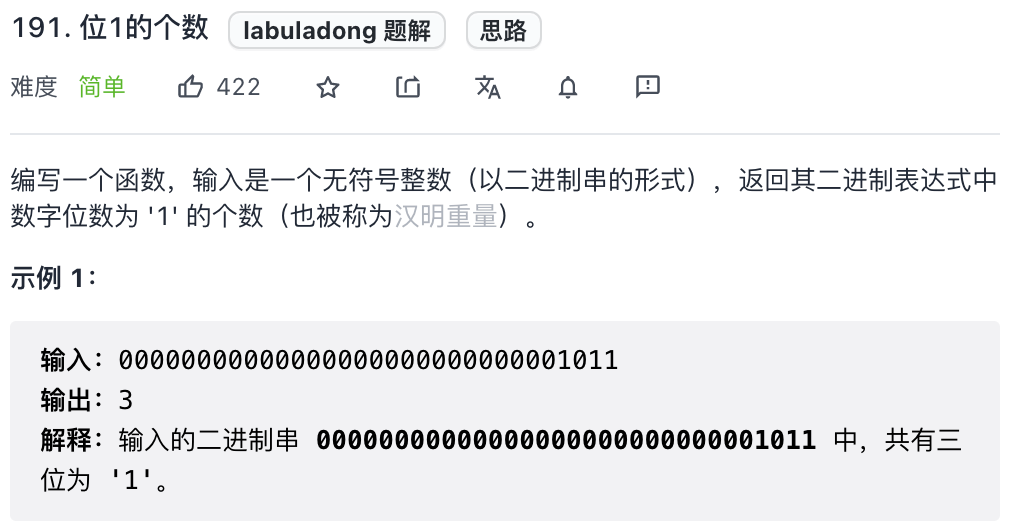
 这是力扣第 191 题「位 1 的个数」：
 
-![](https://labuladong.github.io/pictures/位操作/title.png)
+<Problem slug="number-of-1-bits" />
 
 就是让你返回 `n` 的二进制表示中有几个 1。因为 `n & (n - 1)` 可以消除最后一个 1，所以可以用一个循环不停地消除 1 同时计数，直到 `n` 变成 0 为止。
 
@@ -212,7 +212,7 @@ boolean isPowerOfTwo(int n) {
 
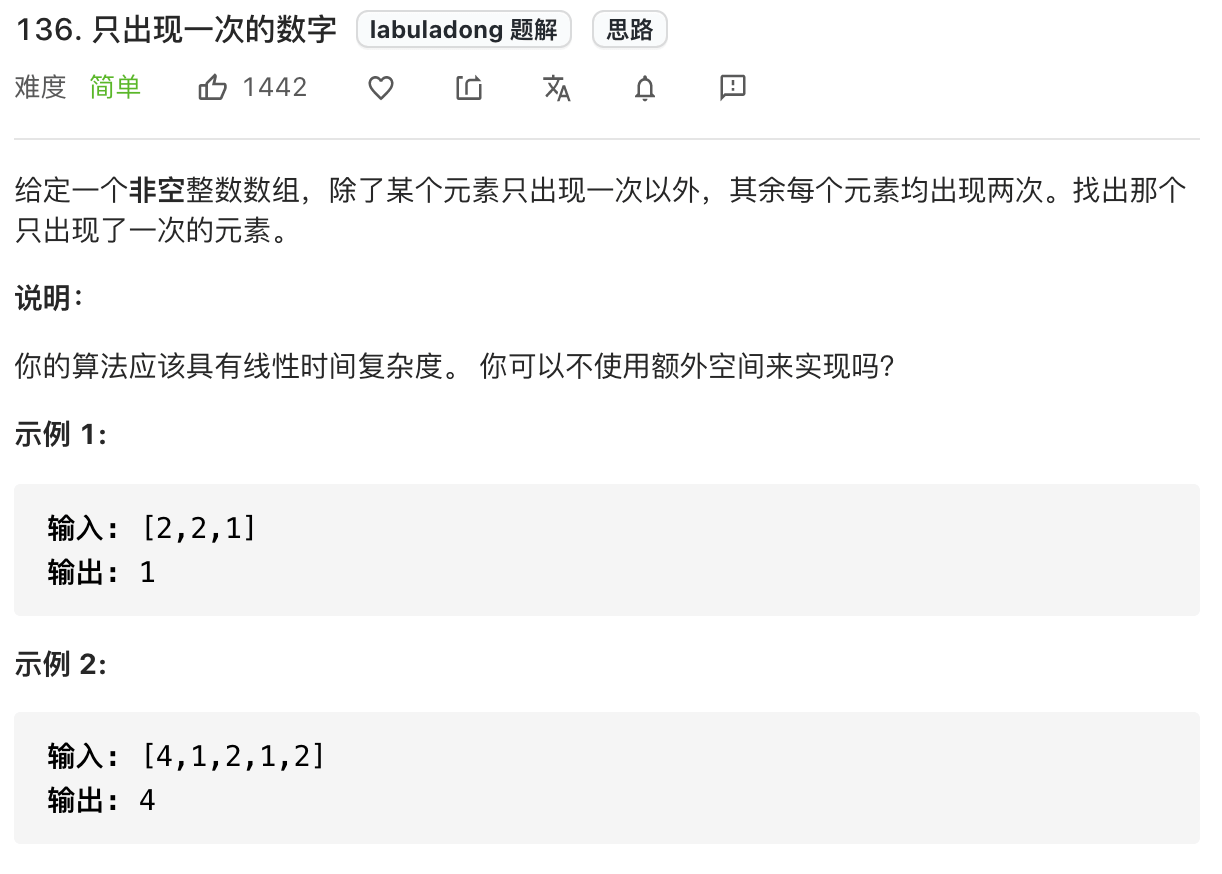
 这是力扣第 136 题「只出现一次的数字」：
 
-![](https://labuladong.github.io/pictures/位操作/title1.png)
+<Problem slug="single-number" />
 
 对于这道题目，我们只要把所有数字进行异或，成对儿的数字就会变成 0，落单的数字和 0 做异或还是它本身，所以最后异或的结果就是只出现一次的元素：
 
@@ -231,7 +231,7 @@ int singleNumber(int[] nums) {
 
 这是力扣第 268 题「丢失的数字」：
 
-![](https://labuladong.github.io/pictures/缺失元素/title.png)
+<Problem slug="missing-number" />
 
 给一个长度为 `n` 的数组，其索引应该在 `[0,n)`，但是现在你要装进去 `n + 1` 个元素 `[0,n]`，那么肯定有一个元素装不下嘛，请你找出这个缺失的元素。
 

算法思维系列/滑动窗口技巧进阶.md

@@ -130,7 +130,7 @@ void slidingWindow(string s) {
 
 先来看看力扣第 76 题「最小覆盖子串」难度 Hard：
 
-![](https://labuladong.github.io/pictures/slidingwindow/title1.png)
+<Problem slug="minimum-window-substring" />
 
 就是说要在 `S`(source) 中找到包含 `T`(target) 中全部字母的一个子串，且这个子串一定是所有可能子串中最短的。
 
@@ -277,7 +277,7 @@ string minWindow(string s, string t) {
 
 这是力扣第 567 题「字符串的排列」，难度中等：
 
-![](https://labuladong.github.io/pictures/slidingwindow/title2.png)
+<Problem slug="permutation-in-string" />
 
 注意哦，输入的 `s1` 是可以包含重复字符的，所以这个题难度不小。
 
@@ -340,7 +340,7 @@ bool checkInclusion(string t, string s) {
 
 这是力扣第 438 题「找到字符串中所有字母异位词」，难度中等：
 
-![](https://labuladong.github.io/pictures/slidingwindow/title3.png)
+<Problem slug="find-all-anagrams-in-a-string" />
 
 呵呵，这个所谓的字母异位词，不就是排列吗，搞个高端的说法就能糊弄人了吗？**相当于，输入一个串 `S`，一个串 `T`，找到 `S` 中所有 `T` 的排列，返回它们的起始索引**。
 
@@ -391,7 +391,7 @@ vector<int> findAnagrams(string s, string t) {
 
 这是力扣第 3 题「无重复字符的最长子串」，难度中等：
 
-![](https://labuladong.github.io/pictures/slidingwindow/title4.png)
+<Problem slug="longest-substring-without-repeating-characters" />
 
 这个题终于有了点新意，不是一套框架就出答案，不过反而更简单了，稍微改一改框架就行了：
 

算法思维系列/烧饼排序.md

@@ -33,7 +33,7 @@
 
 首先，需要把这个问题抽象，用数组来表示烧饼堆：
 
-![](https://labuladong.github.io/pictures/pancakeSort/title.png)
+<Problem slug="pancake-sorting" />
 
 如何解决这个问题呢？其实类似上篇文章 [递归反转链表的一部分](https://labuladong.github.io/article/fname.html?fname=递归反转链表的一部分)，这也是需要**递归思想**的。
 

算法思维系列/花式遍历.md

@@ -36,7 +36,7 @@
 
 对二维数组进行旋转是常见的笔试题，力扣第 48 题「旋转图像」就是很经典的一道：
 
-![](https://labuladong.github.io/pictures/花式遍历/title.png)
+<Problem slug="rotate-image" />
 
 题目很好理解，就是让你将一个二维矩阵顺时针旋转 90 度，**难点在于要「原地」修改**，函数签名如下：
 
@@ -180,7 +180,7 @@ void reverse(int[] arr) { /* 见上文 */}
 
 但接下来我们讲一下力扣第 54 题「螺旋矩阵」，看一看二维矩阵可以如何花式遍历：
 
-![](https://labuladong.github.io/pictures/花式遍历/title2.png)
+<Problem slug="spiral-matrix" />
 
 函数签名如下：
 
@@ -250,7 +250,7 @@ List<Integer> spiralOrder(int[][] matrix) {
 
 力扣第 59 题「螺旋矩阵 II」也是类似的题目，只不过是反过来，让你按照螺旋的顺序生成矩阵：
 
-![](https://labuladong.github.io/pictures/花式遍历/title3.png)
+<Problem slug="spiral-matrix-ii" />
 
 函数签名如下：
 

高频面试系列/k个一组反转链表.md

@@ -27,7 +27,7 @@
 
 先看下题目，不难理解：
 
-![](https://labuladong.github.io/pictures/kgroup/title.png)
+<Problem slug="reverse-nodes-in-k-group" />
 
 这个问题经常在面经中看到，而且力扣上难度是 Hard，它真的有那么难吗？
 

高频面试系列/接雨水.md

@@ -26,7 +26,7 @@
 
 先看一下题目：
 
-![](https://labuladong.github.io/pictures/接雨水/title.png)
+<Problem slug="trapping-rain-water" />
 
 就是用一个数组表示一个条形图，问你这个条形图最多能接多少水。
 
@@ -215,7 +215,7 @@ if (l_max < r_max) {
 
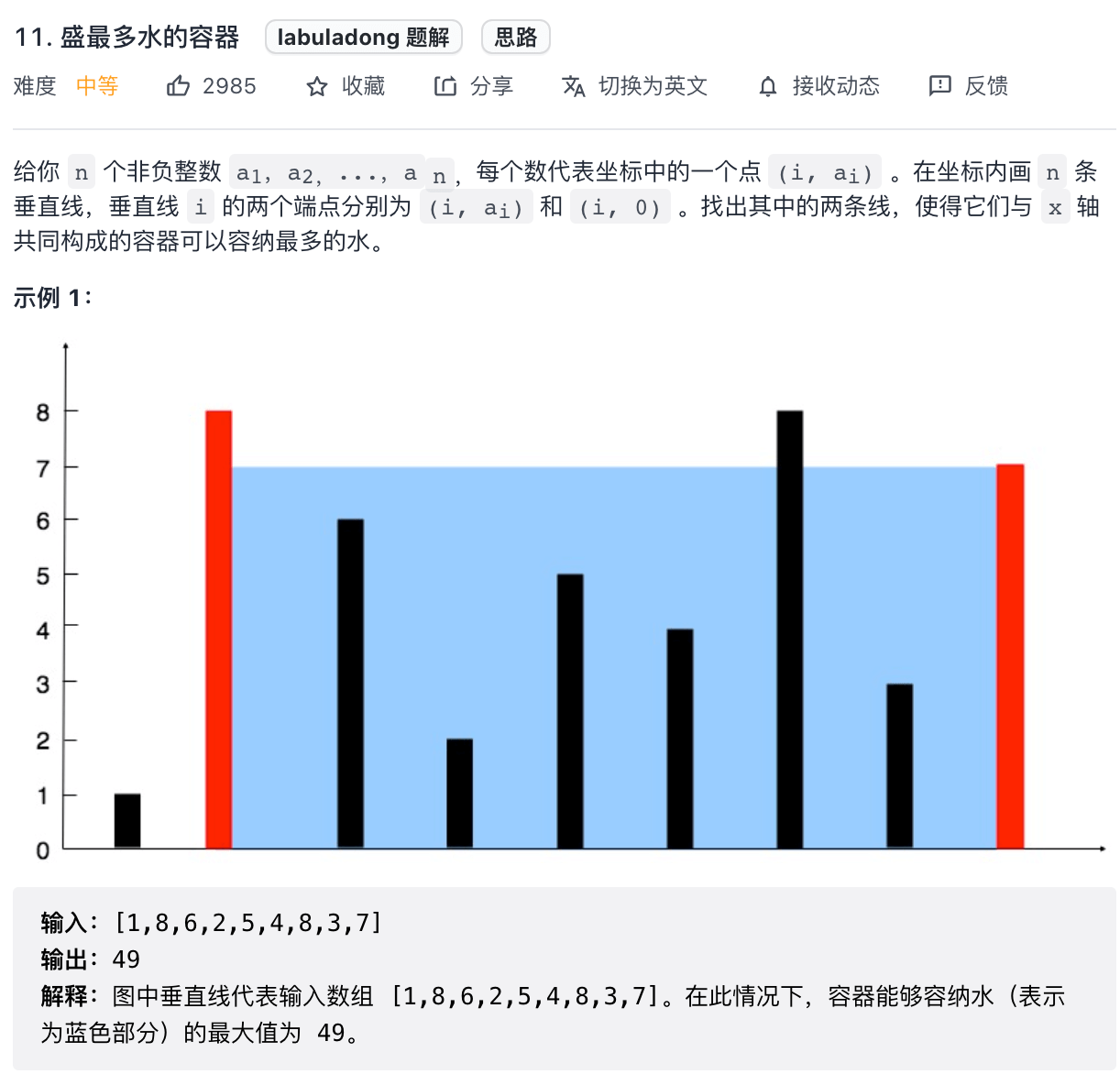
 下面我们看一道和接雨水问题非常类似的题目，力扣第 11 题「盛最多水的容器」：
 
-![](https://labuladong.github.io/pictures/接雨水/title1.png)
+<Problem slug="container-with-most-water" />
 
 函数签名如下：
 

高频面试系列/随机权重.md

@@ -48,7 +48,7 @@
 
 力扣第 528 题「按权重随机选择」就是这样一个问题：
 
-![](https://labuladong.github.io/pictures/随机权重/title.png)
+<Problem slug="random-pick-with-weight" />
 
 我们就来思考一下这个问题，解决按照权重随机选择元素的问题。