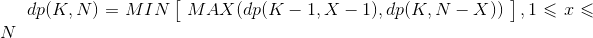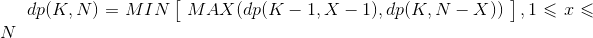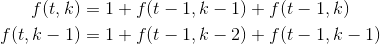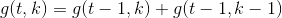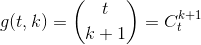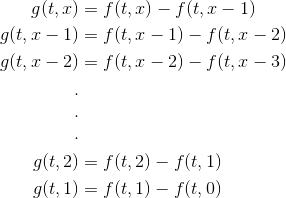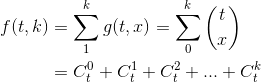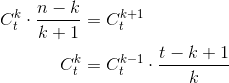# [887. Super Egg Drop](https://leetcode.com/problems/super-egg-drop/)


## 题目

You are given `K` eggs, and you have access to a building with `N` floors from `1` to `N`.

Each egg is identical in function, and if an egg breaks, you cannot drop it again.

You know that there exists a floor `F` with `0 <= F <= N` such that any egg dropped at a floor higher than `F` will break, and any egg dropped at or below floor `F` will not break.

Each *move*, you may take an egg (if you have an unbroken one) and drop it from any floor `X` (with `1 <= X <= N`).

Your goal is to know **with certainty** what the value of `F` is.

What is the minimum number of moves that you need to know with certainty what `F` is, regardless of the initial value of `F`?

**Example 1:**

    Input: K = 1, N = 2
    Output: 2
    Explanation: 
    Drop the egg from floor 1.  If it breaks, we know with certainty that F = 0.
    Otherwise, drop the egg from floor 2.  If it breaks, we know with certainty that F = 1.
    If it didn't break, then we know with certainty F = 2.
    Hence, we needed 2 moves in the worst case to know what F is with certainty.

**Example 2:**

    Input: K = 2, N = 6
    Output: 3

**Example 3:**

    Input: K = 3, N = 14
    Output: 4

**Note:**

1. `1 <= K <= 100`
2. `1 <= N <= 10000`


## 题目大意

你将获得 K 个鸡蛋，并可以使用一栋从 1 到 N  共有 N 层楼的建筑。每个蛋的功能都是一样的，如果一个蛋碎了，你就不能再把它掉下去。你知道存在楼层 F ，满足 0 <= F <= N 任何从高于 F 的楼层落下的鸡蛋都会碎，从 F 楼层或比它低的楼层落下的鸡蛋都不会破。每次移动，你可以取一个鸡蛋（如果你有完整的鸡蛋）并把它从任一楼层 X 扔下（满足 1 <= X <= N）。你的目标是确切地知道 F 的值是多少。无论 F 的初始值如何，你确定 F 的值的最小移动次数是多少？


提示：

1. 1 <= K <= 100
2. 1 <= N <= 10000


## 解题思路

- 给出 `K` 个鸡蛋，`N` 层楼，要求确定安全楼层 `F` 需要最小步数 `t`。
- 这一题是微软的经典面试题。拿到题最容易想到的是二分搜索。但是仔细分析以后会发现单纯的二分是不对的。不断的二分确实能找到最终安全的楼层，但是这里没有考虑到 `K` 个鸡蛋。鸡蛋数的限制会导致二分搜索无法找到最终楼层。题目要求要在保证能找到最终安全楼层的情况下，找到最小步数。所以单纯的二分搜索并不能解答这道题。
- 这一题如果按照题意正向考虑，动态规划的状态转移方程是 `searchTime(K, N) = max( searchTime(K-1, X-1), searchTime(K, N-X) )`。其中 `X` 是丢鸡蛋的楼层。随着 `X` 从 `[1,N]`，都能计算出一个 `searchTime` 的值，在所有这 `N` 个值之中，取最小值就是本题的答案了。这个解法可以 AC 这道题。不过这个解法不细展开了。时间复杂度 `O(k*N^2)`。    
<p align='center'>
<img src='https://img.halfrost.com/Leetcode/leetcode_887_8.png'>
</p>

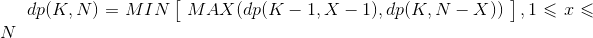
- 换个角度来看这个问题，定义 `dp[k][m]` 代表 `K` 个鸡蛋，`M` 次移动能检查的最大楼层。考虑某一步 `t` 应该在哪一层丢鸡蛋呢？一个正确的选择是在 `dp[k-1][t-1] + 1` 层丢鸡蛋，结果分两种情况：
    1. 如果鸡蛋碎了，我们首先排除了该层以上的所有楼层（不管这个楼有多高），而对于剩下的 `dp[k-1][t-1]` 层楼，我们一定能用 `k-1` 个鸡蛋在 `t-1` 步内求解。因此这种情况下，我们总共可以求解无限高的楼层。可见，这是一种非常好的情况，但并不总是发生。
    2. 如果鸡蛋没碎，我们首先排除了该层以下的 `dp[k-1][t-1]` 层楼，此时我们还有 `k` 个蛋和 `t-1` 步，那么我们去该层以上的楼层继续测得 `dp[k][t-1]` 层楼。因此这种情况下，我们总共可以求解 `dp[k-1][t-1] + 1 + dp[k][t-1]` 层楼。
- 在所有 `m` 步中只要有一次出现了第一种情况，那么我们就可以求解无限高的楼层。但题目要求我们能保证一定能找到安全楼层，所以每次丢鸡蛋的情况应该按照最差情况来，即每次都是第二种情况。于是得到转状态转移方程: `dp[k][m] = dp[k-1][m-1] + dp[k][m-1] + 1` 。这个方程可以压缩到一维，因为每个新的状态只和上一行和左一列有关。那么每一行从右往左更新，即 `dp[i] += 1 + dp[i-1]`。时间复杂度 `O(K * log N)`，空间复杂度 `O(N)`。
- 可能会有人有疑问，如果最初选择不在 `dp[k-1][t-1] + 1` 层丢鸡蛋会怎么样呢？选择在更低的层或者更高的层丢鸡蛋会怎样呢？
    1. 如果在更低的楼层丢鸡蛋也能保证找到安全楼层。那么得到的结果一定不是最小步数。因为这次丢鸡蛋没有充分的展现鸡蛋和移动次数的潜力，最终求解一定会有鸡蛋和步数剩余，即不是能探测的最大楼层了。
    2. 如果在更高的楼层丢鸡蛋，假设是第 `dp[k-1][t-1] + 2` 层丢鸡蛋，如果这次鸡蛋碎了，剩下 `k-1` 个鸡蛋和 `t-1` 步只能保证验证 `dp[k-1][t-1]` 的楼层，这里还剩**第** `dp[k-1][t-1]+ 1` 的楼层，不能保证最终一定能找到安全楼层了。
- 用反证法就能得出每一步都应该在第 `dp[k-1][t-1] + 1` 层丢鸡蛋。
- 这道题还可以用二分搜索来解答。回到上面分析的状态转移方程：`dp[k][m] = dp[k-1][m-1] + dp[k][m-1] + 1` 。用数学方法来解析这个递推关系。令 `f(t,k)` 为 `t` 和 `k` 的函数，题目所要求能测到最大楼层是 `N` 的最小步数，即要求出 `f(t,k) ≥ N` 时候的最小 `t`。由状态转移方程可以知道：`f(t,k) = f(t-1,k) + f(t-1,k-1) + 1`，当 `k = 1` 的时候，对应一个鸡蛋的情况，`f(t,1) = t`，当 `t = 1` 的时候，对应一步的情况，`f(1,k) = 1`。有状态转移方程得：    
<p align='center'>
<img src='https://img.halfrost.com/Leetcode/leetcode_887_1.png'>
</p>

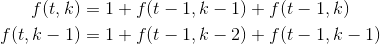
- 令 `g(t,k) = f(t,k) - f(t,k-1)`，可以得到：  

<p align='center'>
<img src='https://img.halfrost.com/Leetcode/leetcode_887_2.png'>
</p>  

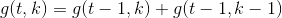
- 可以知道 `g(t,k)` 是一个杨辉三角，即二项式系数： 
 
<p align='center'>
<img src='https://img.halfrost.com/Leetcode/leetcode_887_3.png'>
</p>  

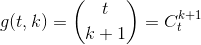
- 利用裂项相消的方法：  
<p align='center'>
<img src='https://img.halfrost.com/Leetcode/leetcode_887_4.png'>
</p>  

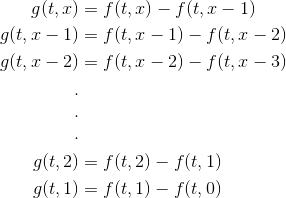
- 于是可以得到：    
<p align='center'>
<img src='https://img.halfrost.com/Leetcode/leetcode_887_5.png'>
</p>

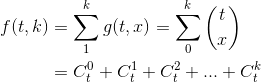
- 其中：    
<p align='center'>
<img src='https://img.halfrost.com/Leetcode/leetcode_887_6.png'>
</p>

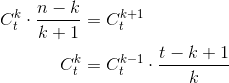
- 于是针对每一项的二项式常数，都可以由前一项乘以一个分数得到下一项。  
<p align='center'>
<img src='https://img.halfrost.com/Leetcode/leetcode_887_7.png'>
</p>

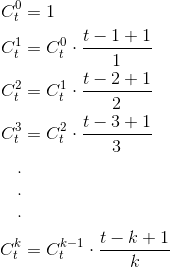
- 利用二分搜索，不断的二分 `t`，直到逼近找到 `f(t,k) ≥ N` 时候最小的 `t`。时间复杂度 `O(K * log N)`，空间复杂度 `O(1)`。