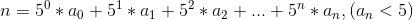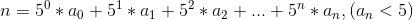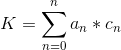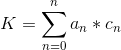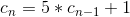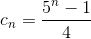# [793. Preimage Size of Factorial Zeroes Function](https://leetcode.com/problems/preimage-size-of-factorial-zeroes-function/)


## 题目

Let `f(x)` be the number of zeroes at the end of `x!`. (Recall that `x! = 1 * 2 * 3 * ... * x`, and by convention, `0! = 1`.)

For example, `f(3) = 0` because 3! = 6 has no zeroes at the end, while `f(11) = 2` because 11! = 39916800 has 2 zeroes at the end. Given `K`, find how many non-negative integers `x` have the property that `f(x) = K`.

    Example 1:
    Input: K = 0
    Output: 5
    Explanation: 0!, 1!, 2!, 3!, and 4! end with K = 0 zeroes.
    
    Example 2:
    Input: K = 5
    Output: 0
    Explanation: There is no x such that x! ends in K = 5 zeroes.

**Note:**

- `K` will be an integer in the range `[0, 10^9]`.


## 题目大意


f(x) 是 x! 末尾是0的数量。（回想一下 x! = 1 * 2 * 3 * ... * x，且0! = 1）

例如， f(3) = 0 ，因为3! = 6的末尾没有0；而 f(11) = 2 ，因为11!= 39916800末端有2个0。给定 K，找出多少个非负整数x ，有 f(x) = K 的性质。

注意：

- K 是范围在 [0, 10^9] 的整数。


## 解题思路

- 给出一个数 K，要求有多少个 n 能使得 n！末尾 0 的个数等于 K。
- 这一题是基于第 172 题的逆过程加强版。第 172 题是给出 `n`，求得末尾 0 的个数。由第 172 题可以知道，`n！`末尾 0 的个数取决于因子 5 的个数。末尾可能有 `K` 个 0，那么 `n` 最多可以等于 `5 * K`，在 `[0, 5* K]` 区间内二分搜索，判断 `mid` 末尾 0 的个数，如果能找到 `K`，那么就范围 5，如果找不到这个 `K`，返回 0 。为什么答案取值只有 0 和 5 呢？因为当 `n` 增加 5 以后，因子 5 的个数又加一了，末尾又可以多 1 个或者多个 0(如果加 5 以后，有多个 5 的因子，例如 25，125，就有可能末尾增加多个 0)。所以有效的 `K` 值对应的 `n` 的范围区间就是 5 。反过来，无效的 `K` 值对应的 `n` 是 0。`K` 在 `5^n` 的分界线处会发生跳变，所有有些值取不到。例如，`n` 在 `[0,5)` 内取值，`K = 0`；`n` 在 `[5,10)` 内取值，`K = 1`；`n` 在 `[10,15)` 内取值，`K = 2`；`n` 在 `[15,20)` 内取值，`K = 3`；`n` 在 `[20,25)` 内取值，`K = 4`；`n` 在 `[25,30)` 内取值，`K = 6`，因为 25 提供了 2 个 5，也就提供了 2 个 0，所以 `K` 永远无法取值等于 5，即当 `K = 5` 时，找不到任何的 `n` 与之对应。
- 这一题也可以用数学的方法解题。见解法二。这个解法的灵感来自于：n！末尾 0 的个数等于 [1,n] 所有数的因子 5 的个数总和。其次此题的结果一定只有 0 和 5 (分析见上一种解法)。有了这两个结论以后，就可以用数学的方法推导了。首先 n 可以表示为 5 进制的形式  
<p align='center'>
<img src='https://img.halfrost.com/Leetcode/leetcode_793_1.png'>
</p>
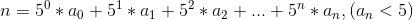
    上面式子中，所有有因子 5 的个数为：  
<p align='center'>
<img src='https://img.halfrost.com/Leetcode/leetcode_793_2.png'>
</p>

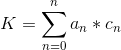
    这个总数就即是 K。针对不同的 n，an 的通项公式不同，所以表示的 K 的系数也不同。cn 的通项公式呢？  
<p align='center'>
<img src='https://img.halfrost.com/Leetcode/leetcode_793_2.png'>
</p>  
<p align='center'>
<img src='https://img.halfrost.com/Leetcode/leetcode_793_3.png'>
</p>

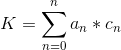
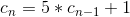
    由上面这个递推还能推出通项公式(不过这题不适用通项公式，是用递推公式更方便)：  
<p align='center'>
<img src='https://img.halfrost.com/Leetcode/leetcode_793_4.png'>
</p>
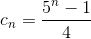
    判断 K 是否能表示成两个数列的表示形式，等价于判断 K 是否能转化为以 Cn 为基的变进制数。到此，转化成类似第 483 题了。代码实现不难，见解法二。