Add solution 0304

leetcode/0304.Range-Sum-Query-2D-Immutable/304. Range Sum Query 2D - Immutable.go

@@ -0,0 +1,31 @@
+package leetcode
+
+type NumMatrix struct {
+	cumsum [][]int
+}
+
+func Constructor(matrix [][]int) NumMatrix {
+	if len(matrix) == 0 {
+		return NumMatrix{nil}
+	}
+	cumsum := make([][]int, len(matrix)+1)
+	cumsum[0] = make([]int, len(matrix[0])+1)
+	for i := range matrix {
+		cumsum[i+1] = make([]int, len(matrix[i])+1)
+		for j := range matrix[i] {
+			cumsum[i+1][j+1] = matrix[i][j] + cumsum[i][j+1] + cumsum[i+1][j] - cumsum[i][j]
+		}
+	}
+	return NumMatrix{cumsum}
+}
+
+func (this *NumMatrix) SumRegion(row1 int, col1 int, row2 int, col2 int) int {
+	cumsum := this.cumsum
+	return cumsum[row2+1][col2+1] - cumsum[row1][col2+1] - cumsum[row2+1][col1] + cumsum[row1][col1]
+}
+
+/**
+ * Your NumMatrix object will be instantiated and called as such:
+ * obj := Constructor(matrix);
+ * param_1 := obj.SumRegion(row1,col1,row2,col2);
+ */

leetcode/0304.Range-Sum-Query-2D-Immutable/304. Range Sum Query 2D - Immutable_test.go

@@ -0,0 +1,21 @@
+package leetcode
+
+import (
+	"fmt"
+	"testing"
+)
+
+func Test_Problem304(t *testing.T) {
+	obj := Constructor(
+		[][]int{
+			{3, 0, 1, 4, 2},
+			{5, 6, 3, 2, 1},
+			{1, 2, 0, 1, 5},
+			{4, 1, 0, 1, 7},
+			{1, 0, 3, 0, 5},
+		},
+	)
+	fmt.Printf("obj = %v\n", obj.SumRegion(2, 1, 4, 3))
+	fmt.Printf("obj = %v\n", obj.SumRegion(1, 1, 2, 2))
+	fmt.Printf("obj = %v\n", obj.SumRegion(1, 2, 2, 4))
+}

leetcode/0304.Range-Sum-Query-2D-Immutable/README.md

@@ -0,0 +1,89 @@
+# [304. Range Sum Query 2D - Immutable](https://leetcode.com/problems/range-sum-query-2d-immutable/)
+
+
+## 题目
+
+Given a 2D matrix matrix, find the sum of the elements inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).
+
+![https://leetcode.com/static/images/courses/range_sum_query_2d.png](https://leetcode.com/static/images/courses/range_sum_query_2d.png)
+
+The above rectangle (with the red border) is defined by (row1, col1) = **(2, 1)** and (row2, col2) = **(4, 3)**, which contains sum = **8**.
+
+**Example:**
+
+```
+Given matrix = [
+  [3, 0, 1, 4, 2],
+  [5, 6, 3, 2, 1],
+  [1, 2, 0, 1, 5],
+  [4, 1, 0, 1, 7],
+  [1, 0, 3, 0, 5]
+]
+
+sumRegion(2, 1, 4, 3) -> 8
+sumRegion(1, 1, 2, 2) -> 11
+sumRegion(1, 2, 2, 4) -> 12
+
+```
+
+**Note:**
+
+1. You may assume that the matrix does not change.
+2. There are many calls to sumRegion function.
+3. You may assume that row1 ≤ row2 and col1 ≤ col2.
+
+## 题目大意
+
+给定一个二维矩阵，计算其子矩形范围内元素的总和，该子矩阵的左上角为 (row1, col1) ，右下角为 (row2, col2) 。
+
+## 解题思路
+
+- 这一题是一维数组前缀和的进阶版本。定义 f(x,y) 代表矩形左上角 (0,0)，右下角 (x,y) 内的元素和。{{< katex display >}} f(i,j) = \sum_{x=0}^{i}\sum_{y=0}^{j} Matrix[x][y]{{< /katex >}}
+
+	{{< katex display >}}
+    \begin{aligned}f(i,j) &= \sum_{x=0}^{i-1}\sum_{y=0}^{j-1} Matrix[x][y] + \sum_{x=0}^{i-1} Matrix[x][j] + \sum_{y=0}^{j-1} Matrix[i][y] + Matrix[i][j]\\&= (\sum_{x=0}^{i-1}\sum_{y=0}^{j-1} Matrix[x][y] + \sum_{x=0}^{i-1} Matrix[x][j]) + (\sum_{x=0}^{i-1}\sum_{y=0}^{j-1} Matrix[x][y] + \sum_{y=0}^{j-1} Matrix[i][y]) - \sum_{x=0}^{i-1}\sum_{y=0}^{j-1} Matrix[x][y] + Matrix[i][j]\\&= \sum_{x=0}^{i-1}\sum_{y=0}^{j} Matrix[x][y] + \sum_{x=0}^{i}\sum_{y=0}^{j-1} Matrix[x][y] - \sum_{x=0}^{i-1}\sum_{y=0}^{j-1} Matrix[x][y] + Matrix[i][j]\\&= f(i-1,j) + f(i,j-1) - f(i-1,j-1) + Matrix[i][j]\end{aligned}
+	{{< /katex >}}
+
+- 于是得到递推的关系式：`f(i, j) = f(i-1, j) + f(i, j-1) - f(i-1, j-1) + matrix[i][j]`，写代码为了方便，新建一个 `m+1 * n+1` 的矩阵，这样就不需要对 `row = 0` 和 `col = 0` 做单独处理了。上述推导公式如果画成图也很好理解：
+
+    ![https://img.halfrost.com/Leetcode/leetcode_304.png](https://img.halfrost.com/Leetcode/leetcode_304.png)
+
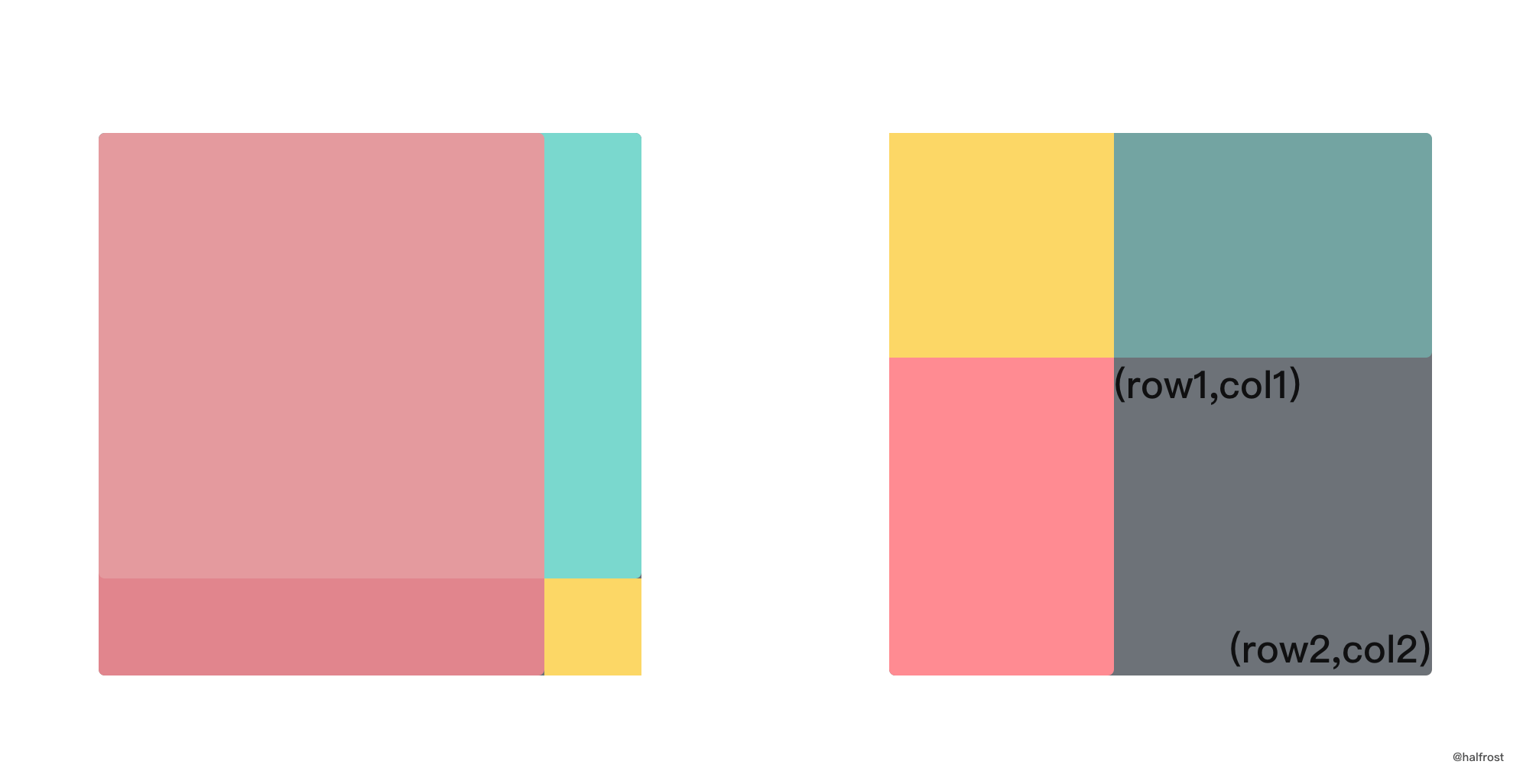
+    左图中大的矩形由粉红色的矩形 + 绿色矩形 - 粉红色和绿色重叠部分 + 黄色部分。这就对应的是上面推导出来的递推公式。左图是矩形左上角为 (0，0) 的情况，更加一般的情况是右图，左上角是任意的坐标，公式不变。
+
+- 时间复杂度：初始化 O(mn)，查询 O(1)。空间复杂度 O(mn)
+
+## 代码
+
+```go
+package leetcode
+
+type NumMatrix struct {
+	cumsum [][]int
+}
+
+func Constructor(matrix [][]int) NumMatrix {
+	if len(matrix) == 0 {
+		return NumMatrix{nil}
+	}
+	cumsum := make([][]int, len(matrix)+1)
+	cumsum[0] = make([]int, len(matrix[0])+1)
+	for i := range matrix {
+		cumsum[i+1] = make([]int, len(matrix[i])+1)
+		for j := range matrix[i] {
+			cumsum[i+1][j+1] = matrix[i][j] + cumsum[i][j+1] + cumsum[i+1][j] - cumsum[i][j]
+		}
+	}
+	return NumMatrix{cumsum}
+}
+
+func (this *NumMatrix) SumRegion(row1 int, col1 int, row2 int, col2 int) int {
+	cumsum := this.cumsum
+	return cumsum[row2+1][col2+1] - cumsum[row1][col2+1] - cumsum[row2+1][col1] + cumsum[row1][col1]
+}
+
+/**
+ * Your NumMatrix object will be instantiated and called as such:
+ * obj := Constructor(matrix);
+ * param_1 := obj.SumRegion(row1,col1,row2,col2);
+ */
+```