Add solution 1310

leetcode/0304.Range-Sum-Query-2D-Immutable/README.md

@@ -5,7 +5,7 @@
 
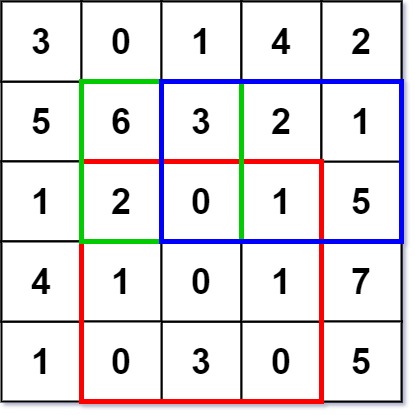
 Given a 2D matrix matrix, find the sum of the elements inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).
 
-![https://leetcode.com/static/images/courses/range_sum_query_2d.png](https://leetcode.com/static/images/courses/range_sum_query_2d.png)
+![https://leetcode.com/static/images/courses/range_sum_query_2d.png](https://assets.leetcode.com/uploads/2021/03/14/sum-grid.jpg)
 
 The above rectangle (with the red border) is defined by (row1, col1) = **(2, 1)** and (row2, col2) = **(4, 3)**, which contains sum = **8**.
 

leetcode/1310.XOR-Queries-of-a-Subarray/1310. XOR Queries of a Subarray.go

@@ -0,0 +1,17 @@
+package leetcode
+
+func xorQueries(arr []int, queries [][]int) []int {
+	xors := make([]int, len(arr))
+	xors[0] = arr[0]
+	for i := 1; i < len(arr); i++ {
+		xors[i] = arr[i] ^ xors[i-1]
+	}
+	res := make([]int, len(queries))
+	for i, q := range queries {
+		res[i] = xors[q[1]]
+		if q[0] > 0 {
+			res[i] ^= xors[q[0]-1]
+		}
+	}
+	return res
+}

leetcode/1310.XOR-Queries-of-a-Subarray/1310. XOR Queries of a Subarray_test.go

@@ -0,0 +1,48 @@
+package leetcode
+
+import (
+	"fmt"
+	"testing"
+)
+
+type question1310 struct {
+	para1310
+	ans1310
+}
+
+// para 是参数
+// one 代表第一个参数
+type para1310 struct {
+	arr     []int
+	queries [][]int
+}
+
+// ans 是答案
+// one 代表第一个答案
+type ans1310 struct {
+	one []int
+}
+
+func Test_Problem1310(t *testing.T) {
+
+	qs := []question1310{
+
+		{
+			para1310{[]int{1, 3, 4, 8}, [][]int{{0, 1}, {1, 2}, {0, 3}, {3, 3}}},
+			ans1310{[]int{2, 7, 14, 8}},
+		},
+
+		{
+			para1310{[]int{4, 8, 2, 10}, [][]int{{2, 3}, {1, 3}, {0, 0}, {0, 3}}},
+			ans1310{[]int{8, 0, 4, 4}},
+		},
+	}
+
+	fmt.Printf("------------------------Leetcode Problem 1310------------------------\n")
+
+	for _, q := range qs {
+		_, p := q.ans1310, q.para1310
+		fmt.Printf("【input】:%v       【output】:%v\n", p, xorQueries(p.arr, p.queries))
+	}
+	fmt.Printf("\n\n\n")
+}

leetcode/1310.XOR-Queries-of-a-Subarray/README.md

@@ -0,0 +1,75 @@
+# [1310. XOR Queries of a Subarray](https://leetcode.com/problems/xor-queries-of-a-subarray/)
+
+
+## 题目
+
+Given the array `arr` of positive integers and the array `queries` where `queries[i] = [Li,Ri]`, for each query `i` compute the **XOR** of elements from `Li` to `Ri` (that is, `arr[Li]xor arr[Li+1]xor ...xor arr[Ri]`). Return an array containing the result for the given `queries`.
+
+**Example 1:**
+
+```
+Input: arr = [1,3,4,8], queries = [[0,1],[1,2],[0,3],[3,3]]
+Output: [2,7,14,8]
+Explanation:
+The binary representation of the elements in the array are:
+1 = 0001
+3 = 0011
+4 = 0100
+8 = 1000
+The XOR values for queries are:
+[0,1] = 1 xor 3 = 2
+[1,2] = 3 xor 4 = 7
+[0,3] = 1 xor 3 xor 4 xor 8 = 14
+[3,3] = 8
+
+```
+
+**Example 2:**
+
+```
+Input: arr = [4,8,2,10], queries = [[2,3],[1,3],[0,0],[0,3]]
+Output: [8,0,4,4]
+
+```
+
+**Constraints:**
+
+- `1 <= arr.length <= 3 * 10^4`
+- `1 <= arr[i] <= 10^9`
+- `1 <= queries.length <= 3 * 10^4`
+- `queries[i].length == 2`
+- `0 <= queries[i][0] <= queries[i][1] < arr.length`
+
+## 题目大意
+
+有一个正整数数组 arr，现给你一个对应的查询数组 queries，其中 queries[i] = [Li, Ri]。对于每个查询 i，请你计算从 Li 到 Ri 的 XOR 值（即 arr[Li] xor arr[Li+1] xor ... xor arr[Ri]）作为本次查询的结果。并返回一个包含给定查询 queries 所有结果的数组。
+
+## 解题思路
+
+- 此题求区间异或，很容易让人联想到区间求和。区间求和利用前缀和，可以使得 query 从 O(n) 降为 O(1)。区间异或能否也用类似前缀和的思想呢？答案是肯定的。利用异或的两个性质，x ^ x = 0，x ^ 0 = x。那么有：（由于 LaTeX 中异或符号 ^ 是特殊字符，笔者用 $\oplus$ 代替异或）
+
+    $$\begin{aligned}Query(left,right) &=arr[left] \oplus \cdots  \oplus arr[right]\\&=(arr[0] \oplus \cdots  \oplus arr[left-1]) \oplus (arr[0] \oplus \cdots  \oplus arr[left-1]) \oplus (arr[left] \oplus \cdots  \oplus arr[right])\\ &=(arr[0] \oplus \cdots  \oplus arr[left-1]) \oplus (arr[0] \oplus \cdots  \oplus arr[right])\\ &=xors[left] \oplus xors[right+1]\\ \end{aligned}$$
+
+    按照这个思路解题，便可以将 query 从 O(n) 降为 O(1)，总的时间复杂度为 O(n)。
+
+## 代码
+
+```go
+package leetcode
+
+func xorQueries(arr []int, queries [][]int) []int {
+	xors := make([]int, len(arr))
+	xors[0] = arr[0]
+	for i := 1; i < len(arr); i++ {
+		xors[i] = arr[i] ^ xors[i-1]
+	}
+	res := make([]int, len(queries))
+	for i, q := range queries {
+		res[i] = xors[q[1]]
+		if q[0] > 0 {
+			res[i] ^= xors[q[0]-1]
+		}
+	}
+	return res
+}
+```