mirror of
https://github.com/halfrost/LeetCode-Go.git
synced 2025-07-06 09:23:19 +08:00
Add solution 0665、0669、1423、1463、1579
This commit is contained in:
@ -0,0 +1,17 @@
|
||||
package leetcode
|
||||
|
||||
func checkPossibility(nums []int) bool {
|
||||
count := 0
|
||||
for i := 0; i < len(nums)-1; i++ {
|
||||
if nums[i] > nums[i+1] {
|
||||
count++
|
||||
if count > 1 {
|
||||
return false
|
||||
}
|
||||
if i > 0 && nums[i+1] < nums[i-1] {
|
||||
nums[i+1] = nums[i]
|
||||
}
|
||||
}
|
||||
}
|
||||
return true
|
||||
}
|
||||
@ -0,0 +1,47 @@
|
||||
package leetcode
|
||||
|
||||
import (
|
||||
"fmt"
|
||||
"testing"
|
||||
)
|
||||
|
||||
type question665 struct {
|
||||
para665
|
||||
ans665
|
||||
}
|
||||
|
||||
// para 是参数
|
||||
// one 代表第一个参数
|
||||
type para665 struct {
|
||||
nums []int
|
||||
}
|
||||
|
||||
// ans 是答案
|
||||
// one 代表第一个答案
|
||||
type ans665 struct {
|
||||
one bool
|
||||
}
|
||||
|
||||
func Test_Problem665(t *testing.T) {
|
||||
|
||||
qs := []question665{
|
||||
|
||||
{
|
||||
para665{[]int{4, 2, 3}},
|
||||
ans665{true},
|
||||
},
|
||||
|
||||
{
|
||||
para665{[]int{4, 2, 1}},
|
||||
ans665{false},
|
||||
},
|
||||
}
|
||||
|
||||
fmt.Printf("------------------------Leetcode Problem 665------------------------\n")
|
||||
|
||||
for _, q := range qs {
|
||||
_, p := q.ans665, q.para665
|
||||
fmt.Printf("【input】:%v 【output】:%v\n", p, checkPossibility(p.nums))
|
||||
}
|
||||
fmt.Printf("\n\n\n")
|
||||
}
|
||||
59
leetcode/0665.Non-decreasing-Array/README.md
Normal file
59
leetcode/0665.Non-decreasing-Array/README.md
Normal file
@ -0,0 +1,59 @@
|
||||
# [665. Non-decreasing Array](https://leetcode.com/problems/non-decreasing-array/)
|
||||
|
||||
## 题目
|
||||
|
||||
Given an array `nums` with `n` integers, your task is to check if it could become non-decreasing by modifying **at most one element**.
|
||||
|
||||
We define an array is non-decreasing if `nums[i] <= nums[i + 1]` holds for every `i` (**0-based**) such that (`0 <= i <= n - 2`).
|
||||
|
||||
**Example 1:**
|
||||
|
||||
```
|
||||
Input: nums = [4,2,3]
|
||||
Output: true
|
||||
Explanation: You could modify the first 4 to 1 to get a non-decreasing array.
|
||||
```
|
||||
|
||||
**Example 2:**
|
||||
|
||||
```
|
||||
Input: nums = [4,2,1]
|
||||
Output: false
|
||||
Explanation: You can't get a non-decreasing array by modify at most one element.
|
||||
```
|
||||
|
||||
**Constraints:**
|
||||
|
||||
- `n == nums.length`
|
||||
- `1 <= n <= 104`
|
||||
- `-10^5 <= nums[i] <= 10^5`
|
||||
|
||||
## 题目大意
|
||||
|
||||
给你一个长度为 n 的整数数组,请你判断在 最多 改变 1 个元素的情况下,该数组能否变成一个非递减数列。我们是这样定义一个非递减数列的: 对于数组中任意的 i (0 <= i <= n-2),总满足 nums[i] <= nums[i + 1]。
|
||||
|
||||
## 解题思路
|
||||
|
||||
- 简单题。循环扫描数组,找到 `nums[i] > nums[i+1]` 这种递减组合。一旦这种组合超过 2 组,直接返回 false。找到第一组递减组合,需要手动调节一次。如果 `nums[i + 1] < nums[i - 1]`,就算交换 `nums[i+1]` 和 `nums[i]`,交换结束,`nums[i - 1]` 仍然可能大于 `nums[i + 1]`,不满足题意。正确的做法应该是让较小的那个数变大,即 `nums[i + 1] = nums[i]`。两个元素相等满足非递减的要求。
|
||||
|
||||
## 代码
|
||||
|
||||
```go
|
||||
package leetcode
|
||||
|
||||
func checkPossibility(nums []int) bool {
|
||||
count := 0
|
||||
for i := 0; i < len(nums)-1; i++ {
|
||||
if nums[i] > nums[i+1] {
|
||||
count++
|
||||
if count > 1 {
|
||||
return false
|
||||
}
|
||||
if i > 0 && nums[i+1] < nums[i-1] {
|
||||
nums[i+1] = nums[i]
|
||||
}
|
||||
}
|
||||
}
|
||||
return true
|
||||
}
|
||||
```
|
||||
@ -0,0 +1,32 @@
|
||||
package leetcode
|
||||
|
||||
import (
|
||||
"github.com/halfrost/LeetCode-Go/structures"
|
||||
)
|
||||
|
||||
// TreeNode define
|
||||
type TreeNode = structures.TreeNode
|
||||
|
||||
/**
|
||||
* Definition for a binary tree node.
|
||||
* type TreeNode struct {
|
||||
* Val int
|
||||
* Left *TreeNode
|
||||
* Right *TreeNode
|
||||
* }
|
||||
*/
|
||||
|
||||
func trimBST(root *TreeNode, low int, high int) *TreeNode {
|
||||
if root == nil {
|
||||
return root
|
||||
}
|
||||
if root.Val > high {
|
||||
return trimBST(root.Left, low, high)
|
||||
}
|
||||
if root.Val < low {
|
||||
return trimBST(root.Right, low, high)
|
||||
}
|
||||
root.Left = trimBST(root.Left, low, high)
|
||||
root.Right = trimBST(root.Right, low, high)
|
||||
return root
|
||||
}
|
||||
@ -0,0 +1,68 @@
|
||||
package leetcode
|
||||
|
||||
import (
|
||||
"fmt"
|
||||
"testing"
|
||||
|
||||
"github.com/halfrost/LeetCode-Go/structures"
|
||||
)
|
||||
|
||||
type question669 struct {
|
||||
para669
|
||||
ans669
|
||||
}
|
||||
|
||||
// para 是参数
|
||||
// one 代表第一个参数
|
||||
type para669 struct {
|
||||
one []int
|
||||
low int
|
||||
high int
|
||||
}
|
||||
|
||||
// ans 是答案
|
||||
// one 代表第一个答案
|
||||
type ans669 struct {
|
||||
one []int
|
||||
}
|
||||
|
||||
func Test_Problem669(t *testing.T) {
|
||||
|
||||
qs := []question669{
|
||||
|
||||
{
|
||||
para669{[]int{1, 0, 2}, 1, 2},
|
||||
ans669{[]int{1, structures.NULL, 2}},
|
||||
},
|
||||
|
||||
{
|
||||
para669{[]int{3, 0, 4, structures.NULL, 2, structures.NULL, structures.NULL, 1}, 1, 3},
|
||||
ans669{[]int{3, 2, structures.NULL, 1}},
|
||||
},
|
||||
|
||||
{
|
||||
para669{[]int{1}, 1, 2},
|
||||
ans669{[]int{1}},
|
||||
},
|
||||
|
||||
{
|
||||
para669{[]int{1, structures.NULL, 2}, 1, 3},
|
||||
ans669{[]int{1, structures.NULL, 2}},
|
||||
},
|
||||
|
||||
{
|
||||
para669{[]int{1, structures.NULL, 2}, 2, 4},
|
||||
ans669{[]int{2}},
|
||||
},
|
||||
}
|
||||
|
||||
fmt.Printf("------------------------Leetcode Problem 669------------------------\n")
|
||||
|
||||
for _, q := range qs {
|
||||
_, p := q.ans669, q.para669
|
||||
fmt.Printf("【input】:%v ", p)
|
||||
root := structures.Ints2TreeNode(p.one)
|
||||
fmt.Printf("【output】:%v \n", structures.Tree2ints(trimBST(root, p.low, p.high)))
|
||||
}
|
||||
fmt.Printf("\n\n\n")
|
||||
}
|
||||
100
leetcode/0669.Trim-a-Binary-Search-Tree/README.md
Normal file
100
leetcode/0669.Trim-a-Binary-Search-Tree/README.md
Normal file
@ -0,0 +1,100 @@
|
||||
# [669. Trim a Binary Search Tree](https://leetcode.com/problems/trim-a-binary-search-tree/)
|
||||
|
||||
|
||||
## 题目
|
||||
|
||||
Given the `root` of a binary search tree and the lowest and highest boundaries as `low` and `high`, trim the tree so that all its elements lies in `[low, high]`. Trimming the tree should **not** change the relative structure of the elements that will remain in the tree (i.e., any node's descendant should remain a descendant). It can be proven that there is a **unique answer**.
|
||||
|
||||
Return *the root of the trimmed binary search tree*. Note that the root may change depending on the given bounds.
|
||||
|
||||
**Example 1:**
|
||||
|
||||

|
||||
|
||||
```
|
||||
Input: root = [1,0,2], low = 1, high = 2
|
||||
Output: [1,null,2]
|
||||
```
|
||||
|
||||
**Example 2:**
|
||||
|
||||

|
||||
|
||||
```
|
||||
Input: root = [3,0,4,null,2,null,null,1], low = 1, high = 3
|
||||
Output: [3,2,null,1]
|
||||
```
|
||||
|
||||
**Example 3:**
|
||||
|
||||
```
|
||||
Input: root = [1], low = 1, high = 2
|
||||
Output: [1]
|
||||
```
|
||||
|
||||
**Example 4:**
|
||||
|
||||
```
|
||||
Input: root = [1,null,2], low = 1, high = 3
|
||||
Output: [1,null,2]
|
||||
```
|
||||
|
||||
**Example 5:**
|
||||
|
||||
```
|
||||
Input: root = [1,null,2], low = 2, high = 4
|
||||
Output: [2]
|
||||
```
|
||||
|
||||
**Constraints:**
|
||||
|
||||
- The number of nodes in the tree in the range `[1, 10^4]`.
|
||||
- `0 <= Node.val <= 10^4`
|
||||
- The value of each node in the tree is **unique**.
|
||||
- `root` is guaranteed to be a valid binary search tree.
|
||||
- `0 <= low <= high <= 10^4`
|
||||
|
||||
## 题目大意
|
||||
|
||||
给你二叉搜索树的根节点 root ,同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树,使得所有节点的值在[low, high]中。修剪树不应该改变保留在树中的元素的相对结构(即,如果没有被移除,原有的父代子代关系都应当保留)。 可以证明,存在唯一的答案。所以结果应当返回修剪好的二叉搜索树的新的根节点。注意,根节点可能会根据给定的边界发生改变。
|
||||
|
||||
## 解题思路
|
||||
|
||||
- 这一题考察二叉搜索树中的递归遍历。递归遍历二叉搜索树每个结点,根据有序性,当前结点如果比 high 大,那么当前结点的右子树全部修剪掉,再递归修剪左子树;当前结点如果比 low 小,那么当前结点的左子树全部修剪掉,再递归修剪右子树。处理完越界的情况,剩下的情况都在区间内,分别递归修剪左子树和右子树即可。
|
||||
|
||||
## 代码
|
||||
|
||||
```go
|
||||
package leetcode
|
||||
|
||||
import (
|
||||
"github.com/halfrost/LeetCode-Go/structures"
|
||||
)
|
||||
|
||||
// TreeNode define
|
||||
type TreeNode = structures.TreeNode
|
||||
|
||||
/**
|
||||
* Definition for a binary tree node.
|
||||
* type TreeNode struct {
|
||||
* Val int
|
||||
* Left *TreeNode
|
||||
* Right *TreeNode
|
||||
* }
|
||||
*/
|
||||
|
||||
func trimBST(root *TreeNode, low int, high int) *TreeNode {
|
||||
if root == nil {
|
||||
return root
|
||||
}
|
||||
if root.Val > high {
|
||||
return trimBST(root.Left, low, high)
|
||||
}
|
||||
if root.Val < low {
|
||||
return trimBST(root.Right, low, high)
|
||||
}
|
||||
root.Left = trimBST(root.Left, low, high)
|
||||
root.Right = trimBST(root.Right, low, high)
|
||||
return root
|
||||
}
|
||||
```
|
||||
@ -0,0 +1,20 @@
|
||||
package leetcode
|
||||
|
||||
func maxScore(cardPoints []int, k int) int {
|
||||
windowSize, sum := len(cardPoints)-k, 0
|
||||
for _, val := range cardPoints[:windowSize] {
|
||||
sum += val
|
||||
}
|
||||
minSum := sum
|
||||
for i := windowSize; i < len(cardPoints); i++ {
|
||||
sum += cardPoints[i] - cardPoints[i-windowSize]
|
||||
if sum < minSum {
|
||||
minSum = sum
|
||||
}
|
||||
}
|
||||
total := 0
|
||||
for _, pt := range cardPoints {
|
||||
total += pt
|
||||
}
|
||||
return total - minSum
|
||||
}
|
||||
@ -0,0 +1,63 @@
|
||||
package leetcode
|
||||
|
||||
import (
|
||||
"fmt"
|
||||
"testing"
|
||||
)
|
||||
|
||||
type question1423 struct {
|
||||
para1423
|
||||
ans1423
|
||||
}
|
||||
|
||||
// para 是参数
|
||||
// one 代表第一个参数
|
||||
type para1423 struct {
|
||||
cardPoints []int
|
||||
k int
|
||||
}
|
||||
|
||||
// ans 是答案
|
||||
// one 代表第一个答案
|
||||
type ans1423 struct {
|
||||
one int
|
||||
}
|
||||
|
||||
func Test_Problem1423(t *testing.T) {
|
||||
|
||||
qs := []question1423{
|
||||
|
||||
{
|
||||
para1423{[]int{1, 2, 3, 4, 5, 6, 1}, 3},
|
||||
ans1423{12},
|
||||
},
|
||||
|
||||
{
|
||||
para1423{[]int{2, 2, 2}, 2},
|
||||
ans1423{4},
|
||||
},
|
||||
|
||||
{
|
||||
para1423{[]int{9, 7, 7, 9, 7, 7, 9}, 7},
|
||||
ans1423{55},
|
||||
},
|
||||
|
||||
{
|
||||
para1423{[]int{1, 1000, 1}, 1},
|
||||
ans1423{1},
|
||||
},
|
||||
|
||||
{
|
||||
para1423{[]int{1, 79, 80, 1, 1, 1, 200, 1}, 3},
|
||||
ans1423{202},
|
||||
},
|
||||
}
|
||||
|
||||
fmt.Printf("------------------------Leetcode Problem 1423------------------------\n")
|
||||
|
||||
for _, q := range qs {
|
||||
_, p := q.ans1423, q.para1423
|
||||
fmt.Printf("【input】:%v 【output】:%v\n", p, maxScore(p.cardPoints, p.k))
|
||||
}
|
||||
fmt.Printf("\n\n\n")
|
||||
}
|
||||
@ -0,0 +1,90 @@
|
||||
# [1423. Maximum Points You Can Obtain from Cards](https://leetcode.com/problems/maximum-points-you-can-obtain-from-cards/)
|
||||
|
||||
|
||||
## 题目
|
||||
|
||||
There are several cards **arranged in a row**, and each card has an associated number of points The points are given in the integer array `cardPoints`.
|
||||
|
||||
In one step, you can take one card from the beginning or from the end of the row. You have to take exactly `k` cards.
|
||||
|
||||
Your score is the sum of the points of the cards you have taken.
|
||||
|
||||
Given the integer array `cardPoints` and the integer `k`, return the *maximum score* you can obtain.
|
||||
|
||||
**Example 1:**
|
||||
|
||||
```
|
||||
Input: cardPoints = [1,2,3,4,5,6,1], k = 3
|
||||
Output: 12
|
||||
Explanation: After the first step, your score will always be 1. However, choosing the rightmost card first will maximize your total score. The optimal strategy is to take the three cards on the right, giving a final score of 1 + 6 + 5 = 12.
|
||||
```
|
||||
|
||||
**Example 2:**
|
||||
|
||||
```
|
||||
Input: cardPoints = [2,2,2], k = 2
|
||||
Output: 4
|
||||
Explanation: Regardless of which two cards you take, your score will always be 4.
|
||||
```
|
||||
|
||||
**Example 3:**
|
||||
|
||||
```
|
||||
Input: cardPoints = [9,7,7,9,7,7,9], k = 7
|
||||
Output: 55
|
||||
Explanation: You have to take all the cards. Your score is the sum of points of all cards.
|
||||
```
|
||||
|
||||
**Example 4:**
|
||||
|
||||
```
|
||||
Input: cardPoints = [1,1000,1], k = 1
|
||||
Output: 1
|
||||
Explanation: You cannot take the card in the middle. Your best score is 1.
|
||||
```
|
||||
|
||||
**Example 5:**
|
||||
|
||||
```
|
||||
Input: cardPoints = [1,79,80,1,1,1,200,1], k = 3
|
||||
Output: 202
|
||||
```
|
||||
|
||||
**Constraints:**
|
||||
|
||||
- `1 <= cardPoints.length <= 10^5`
|
||||
- `1 <= cardPoints[i] <= 10^4`
|
||||
- `1 <= k <= cardPoints.length`
|
||||
|
||||
## 题目大意
|
||||
|
||||
几张卡牌 排成一行,每张卡牌都有一个对应的点数。点数由整数数组 cardPoints 给出。每次行动,你可以从行的开头或者末尾拿一张卡牌,最终你必须正好拿 k 张卡牌。你的点数就是你拿到手中的所有卡牌的点数之和。给你一个整数数组 cardPoints 和整数 k,请你返回可以获得的最大点数。
|
||||
|
||||
## 解题思路
|
||||
|
||||
- 这一题是滑动窗口题的简化题。从卡牌两边取 K 张牌,可以转换成在中间连续取 n-K 张牌。从两边取牌的点数最大,意味着剩下来中间牌的点数最小。扫描一遍数组,在每一个窗口大小为 n-K 的窗口内计算累加和,记录下最小的累加和。题目最终求的最大点数等于牌的总和减去中间最小的累加和。
|
||||
|
||||
## 代码
|
||||
|
||||
```go
|
||||
package leetcode
|
||||
|
||||
func maxScore(cardPoints []int, k int) int {
|
||||
windowSize, sum := len(cardPoints)-k, 0
|
||||
for _, val := range cardPoints[:windowSize] {
|
||||
sum += val
|
||||
}
|
||||
minSum := sum
|
||||
for i := windowSize; i < len(cardPoints); i++ {
|
||||
sum += cardPoints[i] - cardPoints[i-windowSize]
|
||||
if sum < minSum {
|
||||
minSum = sum
|
||||
}
|
||||
}
|
||||
total := 0
|
||||
for _, pt := range cardPoints {
|
||||
total += pt
|
||||
}
|
||||
return total - minSum
|
||||
}
|
||||
```
|
||||
@ -1,45 +1,52 @@
|
||||
package leetcode
|
||||
|
||||
func cherryPickup(grid [][]int) int {
|
||||
m, n := len(grid), len(grid[0])
|
||||
old, new := make([]int, n*n), make([]int, n*n)
|
||||
for i := range old {
|
||||
old[i] = -0xffffff
|
||||
rows, cols := len(grid), len(grid[0])
|
||||
dp := make([][][]int, rows)
|
||||
for i := 0; i < rows; i++ {
|
||||
dp[i] = make([][]int, cols)
|
||||
for j := 0; j < cols; j++ {
|
||||
dp[i][j] = make([]int, cols)
|
||||
}
|
||||
}
|
||||
old[n-1] = grid[0][0]+grid[0][n-1]
|
||||
|
||||
// dp
|
||||
for k:=1; k<m; k++ {
|
||||
for s:=0; s<n*n; s++ {
|
||||
new[s] = -0xffffff
|
||||
c1, c2 := s/n, s%n
|
||||
toadd := grid[k][c1]
|
||||
if c1 != c2 {
|
||||
toadd += grid[k][c2]
|
||||
}
|
||||
for _, d1 := range []int{1,0,-1} {
|
||||
for _, d2 := range []int{1,0,-1} {
|
||||
nc1, nc2 := c1+d1, c2+d2
|
||||
if nc1>=0 && nc1<n && nc2>=0 && nc2<n && old[nc1*n+nc2]>=0 {
|
||||
new[s] = max(new[s], old[nc1*n+nc2]+toadd)
|
||||
for i := 0; i < rows; i++ {
|
||||
for j := 0; j <= i && j < cols; j++ {
|
||||
for k := cols - 1; k >= cols-1-i && k >= 0; k-- {
|
||||
max := 0
|
||||
for a := j - 1; a <= j+1; a++ {
|
||||
for b := k - 1; b <= k+1; b++ {
|
||||
sum := isInBoard(dp, i-1, a, b)
|
||||
if a == b && i > 0 && a >= 0 && a < cols {
|
||||
sum -= grid[i-1][a]
|
||||
}
|
||||
if sum > max {
|
||||
max = sum
|
||||
}
|
||||
}
|
||||
}
|
||||
if j == k {
|
||||
max += grid[i][j]
|
||||
} else {
|
||||
max += grid[i][j] + grid[i][k]
|
||||
}
|
||||
dp[i][j][k] = max
|
||||
}
|
||||
}
|
||||
old, new = new, old
|
||||
}
|
||||
allmax := 0
|
||||
for _, v := range old {
|
||||
if v>allmax {
|
||||
allmax = v
|
||||
count := 0
|
||||
for j := 0; j < cols && j < rows; j++ {
|
||||
for k := cols - 1; k >= 0 && k >= cols-rows; k-- {
|
||||
if dp[rows-1][j][k] > count {
|
||||
count = dp[rows-1][j][k]
|
||||
}
|
||||
}
|
||||
}
|
||||
return allmax
|
||||
return count
|
||||
}
|
||||
|
||||
func max(a, b int) int {
|
||||
if a>b {
|
||||
return a
|
||||
func isInBoard(dp [][][]int, i, j, k int) int {
|
||||
if i < 0 || j < 0 || j >= len(dp[0]) || k < 0 || k >= len(dp[0]) {
|
||||
return 0
|
||||
}
|
||||
return b
|
||||
return dp[i][j][k]
|
||||
}
|
||||
|
||||
@ -5,65 +5,65 @@ import (
|
||||
"testing"
|
||||
)
|
||||
|
||||
type question1436 struct {
|
||||
para1436
|
||||
ans1436
|
||||
type question1463 struct {
|
||||
para1463
|
||||
ans1463
|
||||
}
|
||||
|
||||
type para1436 struct {
|
||||
type para1463 struct {
|
||||
grid [][]int
|
||||
}
|
||||
|
||||
type ans1436 struct {
|
||||
type ans1463 struct {
|
||||
ans int
|
||||
}
|
||||
|
||||
func Test_Problem1436(t *testing.T) {
|
||||
func Test_Problem1463(t *testing.T) {
|
||||
|
||||
qs := []question1436{
|
||||
qs := []question1463{
|
||||
|
||||
{
|
||||
para1436{[][]int{
|
||||
para1463{[][]int{
|
||||
{3, 1, 1},
|
||||
{2, 5, 1},
|
||||
{1, 5, 5},
|
||||
{2, 1, 1},
|
||||
}},
|
||||
ans1436{24},
|
||||
ans1463{24},
|
||||
},
|
||||
|
||||
{
|
||||
para1436{[][]int{
|
||||
para1463{[][]int{
|
||||
{1, 0, 0, 0, 0, 0, 1},
|
||||
{2, 0, 0, 0, 0, 3, 0},
|
||||
{2, 0, 9, 0, 0, 0, 0},
|
||||
{0, 3, 0, 5, 4, 0, 0},
|
||||
{1, 0, 2, 3, 0, 0, 6},
|
||||
}},
|
||||
ans1436{28},
|
||||
ans1463{28},
|
||||
},
|
||||
{
|
||||
para1436{[][]int{
|
||||
para1463{[][]int{
|
||||
{1, 0, 0, 3},
|
||||
{0, 0, 0, 3},
|
||||
{0, 0, 3, 3},
|
||||
{9, 0, 3, 3},
|
||||
}},
|
||||
ans1436{22},
|
||||
ans1463{22},
|
||||
},
|
||||
{
|
||||
para1436{[][]int{
|
||||
para1463{[][]int{
|
||||
{1, 1},
|
||||
{1, 1},
|
||||
}},
|
||||
ans1436{4},
|
||||
ans1463{4},
|
||||
},
|
||||
}
|
||||
|
||||
fmt.Printf("------------------------Leetcode Problem 1436------------------------\n")
|
||||
fmt.Printf("------------------------Leetcode Problem 1463------------------------\n")
|
||||
|
||||
for _, q := range qs {
|
||||
_, p := q.ans1436, q.para1436
|
||||
_, p := q.ans1463, q.para1463
|
||||
fmt.Printf("【input】:%v ", p)
|
||||
fmt.Printf("【output】:%v \n", cherryPickup(p.grid))
|
||||
}
|
||||
|
||||
@ -1,44 +1,148 @@
|
||||
# [1463. Cherry Pickup II](https://leetcode.com/problems/cherry-pickup-ii/)
|
||||
Given a rows x cols matrix grid representing a field of cherries. Each cell in grid represents the number of cherries that you can collect.
|
||||
|
||||
You have two robots that can collect cherries for you, Robot #1 is located at the top-left corner (0,0) , and Robot #2 is located at the top-right corner (0, cols-1) of the grid.
|
||||
## 题目
|
||||
|
||||
Return the maximum number of cherries collection using both robots by following the rules below:
|
||||
Given a `rows x cols` matrix `grid` representing a field of cherries. Each cell in `grid` represents the number of cherries that you can collect.
|
||||
|
||||
From a cell (i,j), robots can move to cell (i+1, j-1) , (i+1, j) or (i+1, j+1).
|
||||
When any robot is passing through a cell, It picks it up all cherries, and the cell becomes an empty cell (0).
|
||||
When both robots stay on the same cell, only one of them takes the cherries.
|
||||
Both robots cannot move outside of the grid at any moment.
|
||||
Both robots should reach the bottom row in the grid.
|
||||
You have two robots that can collect cherries for you, Robot #1 is located at the top-left corner (0,0) , and Robot #2 is located at the top-right corner (0, cols-1) of the grid.
|
||||
|
||||
Return the maximum number of cherries collection using both robots by following the rules below:
|
||||
|
||||
- From a cell (i,j), robots can move to cell (i+1, j-1) , (i+1, j) or (i+1, j+1).
|
||||
- When any robot is passing through a cell, It picks it up all cherries, and the cell becomes an empty cell (0).
|
||||
- When both robots stay on the same cell, only one of them takes the cherries.
|
||||
- Both robots cannot move outside of the grid at any moment.
|
||||
- Both robots should reach the bottom row in the `grid`.
|
||||
|
||||
**Example 1:**
|
||||
|
||||
|
||||
|
||||
## Example 1:
|
||||
```
|
||||
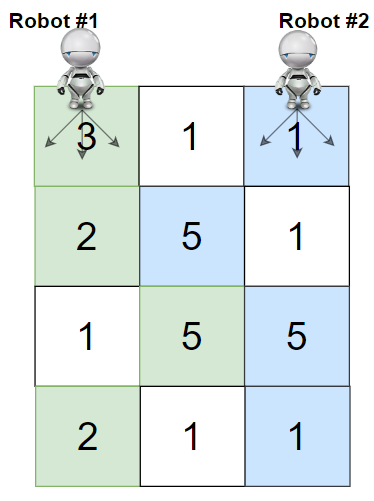
Input: grid = [[3,1,1],[2,5,1],[1,5,5],[2,1,1]]
|
||||
Output: 24
|
||||
Explanation: Path of robot #1 and #2 are described in color green and blue respectively.
|
||||
Explanation: Path of robot #1 and #2 are described in color green and blue respectively.
|
||||
Cherries taken by Robot #1, (3 + 2 + 5 + 2) = 12.
|
||||
Cherries taken by Robot #2, (1 + 5 + 5 + 1) = 12.
|
||||
Total of cherries: 12 + 12 = 24.
|
||||
```
|
||||
|
||||
## Example 2:
|
||||
**Example 2:**
|
||||
|
||||
|
||||
|
||||
```
|
||||
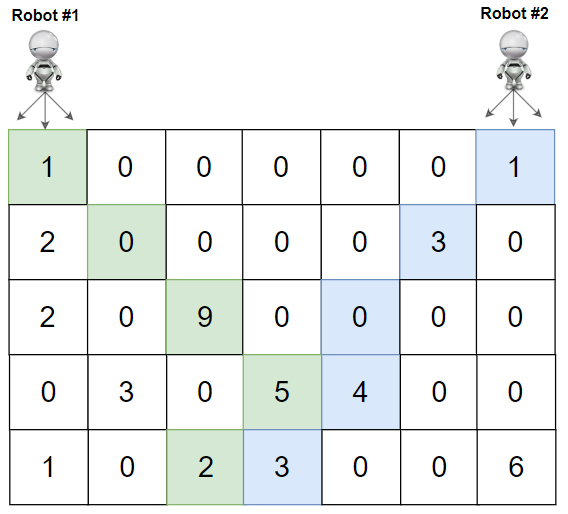
Input: grid = [[1,0,0,0,0,0,1],[2,0,0,0,0,3,0],[2,0,9,0,0,0,0],[0,3,0,5,4,0,0],[1,0,2,3,0,0,6]]
|
||||
Output: 28
|
||||
Explanation: Path of robot #1 and #2 are described in color green and blue respectively.
|
||||
Explanation: Path of robot #1 and #2 are described in color green and blue respectively.
|
||||
Cherries taken by Robot #1, (1 + 9 + 5 + 2) = 17.
|
||||
Cherries taken by Robot #2, (1 + 3 + 4 + 3) = 11.
|
||||
Total of cherries: 17 + 11 = 28.
|
||||
```
|
||||
|
||||
## Example 3:
|
||||
**Example 3:**
|
||||
|
||||
```
|
||||
Input: grid = [[1,0,0,3],[0,0,0,3],[0,0,3,3],[9,0,3,3]]
|
||||
Output: 22
|
||||
```
|
||||
|
||||
## Example 4:
|
||||
**Example 4:**
|
||||
|
||||
```
|
||||
Input: grid = [[1,1],[1,1]]
|
||||
Output: 4
|
||||
```
|
||||
|
||||
**Constraints:**
|
||||
|
||||
- `rows == grid.length`
|
||||
- `cols == grid[i].length`
|
||||
- `2 <= rows, cols <= 70`
|
||||
- `0 <= grid[i][j] <= 100`
|
||||
|
||||
## 题目大意
|
||||
|
||||
给你一个 rows x cols 的矩阵 grid 来表示一块樱桃地。 grid 中每个格子的数字表示你能获得的樱桃数目。你有两个机器人帮你收集樱桃,机器人 1 从左上角格子 (0,0) 出发,机器人 2 从右上角格子 (0, cols-1) 出发。请你按照如下规则,返回两个机器人能收集的最多樱桃数目:
|
||||
|
||||
- 从格子 (i,j) 出发,机器人可以移动到格子 (i+1, j-1),(i+1, j) 或者 (i+1, j+1) 。
|
||||
- 当一个机器人经过某个格子时,它会把该格子内所有的樱桃都摘走,然后这个位置会变成空格子,即没有樱桃的格子。
|
||||
- 当两个机器人同时到达同一个格子时,它们中只有一个可以摘到樱桃。
|
||||
- 两个机器人在任意时刻都不能移动到 grid 外面。
|
||||
- 两个机器人最后都要到达 grid 最底下一行。
|
||||
|
||||
## 解题思路
|
||||
|
||||
- 如果没有思路可以先用暴力解法 DFS 尝试。读完题可以分析出求最多樱桃数目,里面包含了很多重叠子问题,于是乎自然而然思路是用动态规划。数据规模上看,100 的数据规模最多能保证 O(n^3) 时间复杂度的算法不超时。
|
||||
- 这一题的变量有 2 个,一个是行号,另外一个是机器人所在的列。具体来说,机器人每走一步的移动范围只能往下走,不能往上走,所以 2 个机器人所在行号一定相同。两个机器人的列号不同。综上,变量有 3 个,1 个行号和2 个列号。定义 `dp[i][j][k]` 代表第一个机器人从 (0,0) 走到 (i,k) 坐标,第二个机器人从 (0,n-1) 走到 (i,k) 坐标,两者最多能收集樱桃的数目。状态转移方程为 :
|
||||
|
||||
{{< katex display >}}
|
||||
dp[i][j][k] = max \begin{pmatrix}\begin{array}{lr} dp[i-1][f(j_1))][f(j_2)] + grid[i][j_1] + grid[i][j_2], j_1\neq j_2 \\ dp[i-1][f(j_1))][f(j_2)] + grid[i][j_1], j_1 = j_2 \end{array} \end{pmatrix}
|
||||
{{< /katex>}}
|
||||
|
||||
其中:
|
||||
|
||||
{{< katex display >}}
|
||||
\left\{\begin{matrix}f(j_1) \in [0,n), f(j_1) - j_1 \in [-1,0,1]\\ f(j_2) \in [0,n), f(j_2) - j_2 \in [-1,0,1]\end{matrix}\right.
|
||||
{{< /katex>}}
|
||||
|
||||
即状态转移过程中需要在 `[j1 - 1, j1, j1 + 1]` 中枚举 `j1`,同理,在 在 `[j2 - 1, j2, j2 + 1]` 中枚举 `j2`,每个状态转移需要枚举这 3*3 = 9 种状态。
|
||||
|
||||
- 边界条件 `dp[i][0][n-1] = grid[0][0] + grid[0][n-1]`,最终答案存储在 `dp[m-1]` 行中,循环找出 `dp[m-1][j1][j2]` 中的最大值,到此该题得解。
|
||||
|
||||
## 代码
|
||||
|
||||
```go
|
||||
package leetcode
|
||||
|
||||
func cherryPickup(grid [][]int) int {
|
||||
rows, cols := len(grid), len(grid[0])
|
||||
dp := make([][][]int, rows)
|
||||
for i := 0; i < rows; i++ {
|
||||
dp[i] = make([][]int, cols)
|
||||
for j := 0; j < cols; j++ {
|
||||
dp[i][j] = make([]int, cols)
|
||||
}
|
||||
}
|
||||
for i := 0; i < rows; i++ {
|
||||
for j := 0; j <= i && j < cols; j++ {
|
||||
for k := cols - 1; k >= cols-1-i && k >= 0; k-- {
|
||||
max := 0
|
||||
for a := j - 1; a <= j+1; a++ {
|
||||
for b := k - 1; b <= k+1; b++ {
|
||||
sum := isInBoard(dp, i-1, a, b)
|
||||
if a == b && i > 0 && a >= 0 && a < cols {
|
||||
sum -= grid[i-1][a]
|
||||
}
|
||||
if sum > max {
|
||||
max = sum
|
||||
}
|
||||
}
|
||||
}
|
||||
if j == k {
|
||||
max += grid[i][j]
|
||||
} else {
|
||||
max += grid[i][j] + grid[i][k]
|
||||
}
|
||||
dp[i][j][k] = max
|
||||
}
|
||||
}
|
||||
}
|
||||
count := 0
|
||||
for j := 0; j < cols && j < rows; j++ {
|
||||
for k := cols - 1; k >= 0 && k >= cols-rows; k-- {
|
||||
if dp[rows-1][j][k] > count {
|
||||
count = dp[rows-1][j][k]
|
||||
}
|
||||
}
|
||||
}
|
||||
return count
|
||||
}
|
||||
|
||||
func isInBoard(dp [][][]int, i, j, k int) int {
|
||||
if i < 0 || j < 0 || j >= len(dp[0]) || k < 0 || k >= len(dp[0]) {
|
||||
return 0
|
||||
}
|
||||
return dp[i][j][k]
|
||||
}
|
||||
```
|
||||
@ -0,0 +1,30 @@
|
||||
package leetcode
|
||||
|
||||
import (
|
||||
"github.com/halfrost/LeetCode-Go/template"
|
||||
)
|
||||
|
||||
func maxNumEdgesToRemove(n int, edges [][]int) int {
|
||||
alice, bob, res := template.UnionFind{}, template.UnionFind{}, len(edges)
|
||||
alice.Init(n)
|
||||
bob.Init(n)
|
||||
for _, e := range edges {
|
||||
x, y := e[1]-1, e[2]-1
|
||||
if e[0] == 3 && (!(alice.Find(x) == alice.Find(y)) || !(bob.Find(x) == bob.Find(y))) {
|
||||
alice.Union(x, y)
|
||||
bob.Union(x, y)
|
||||
res--
|
||||
}
|
||||
}
|
||||
ufs := [2]*template.UnionFind{&alice, &bob}
|
||||
for _, e := range edges {
|
||||
if tp := e[0]; tp < 3 && !(ufs[tp-1].Find(e[1]-1) == ufs[tp-1].Find(e[2]-1)) {
|
||||
ufs[tp-1].Union(e[1]-1, e[2]-1)
|
||||
res--
|
||||
}
|
||||
}
|
||||
if alice.TotalCount() > 1 || bob.TotalCount() > 1 {
|
||||
return -1
|
||||
}
|
||||
return res
|
||||
}
|
||||
@ -0,0 +1,53 @@
|
||||
package leetcode
|
||||
|
||||
import (
|
||||
"fmt"
|
||||
"testing"
|
||||
)
|
||||
|
||||
type question1579 struct {
|
||||
para1579
|
||||
ans1579
|
||||
}
|
||||
|
||||
// para 是参数
|
||||
// one 代表第一个参数
|
||||
type para1579 struct {
|
||||
n int
|
||||
edges [][]int
|
||||
}
|
||||
|
||||
// ans 是答案
|
||||
// one 代表第一个答案
|
||||
type ans1579 struct {
|
||||
one int
|
||||
}
|
||||
|
||||
func Test_Problem1579(t *testing.T) {
|
||||
|
||||
qs := []question1579{
|
||||
|
||||
{
|
||||
para1579{4, [][]int{{3, 1, 2}, {3, 2, 3}, {1, 1, 3}, {1, 2, 4}, {1, 1, 2}, {2, 3, 4}}},
|
||||
ans1579{2},
|
||||
},
|
||||
|
||||
{
|
||||
para1579{4, [][]int{{3, 1, 2}, {3, 2, 3}, {1, 1, 4}, {2, 1, 4}}},
|
||||
ans1579{0},
|
||||
},
|
||||
|
||||
{
|
||||
para1579{4, [][]int{{3, 2, 3}, {1, 1, 2}, {2, 3, 4}}},
|
||||
ans1579{-1},
|
||||
},
|
||||
}
|
||||
|
||||
fmt.Printf("------------------------Leetcode Problem 1579------------------------\n")
|
||||
|
||||
for _, q := range qs {
|
||||
_, p := q.ans1579, q.para1579
|
||||
fmt.Printf("【input】:%v 【output】:%v \n", p, maxNumEdgesToRemove(p.n, p.edges))
|
||||
}
|
||||
fmt.Printf("\n\n\n")
|
||||
}
|
||||
@ -0,0 +1,103 @@
|
||||
# [1579. Remove Max Number of Edges to Keep Graph Fully Traversable](https://leetcode.com/problems/remove-max-number-of-edges-to-keep-graph-fully-traversable/)
|
||||
|
||||
|
||||
## 题目
|
||||
|
||||
Alice and Bob have an undirected graph of `n` nodes and 3 types of edges:
|
||||
|
||||
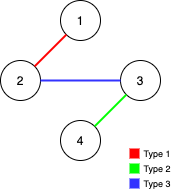
- Type 1: Can be traversed by Alice only.
|
||||
- Type 2: Can be traversed by Bob only.
|
||||
- Type 3: Can by traversed by both Alice and Bob.
|
||||
|
||||
Given an array `edges` where `edges[i] = [typei, ui, vi]` represents a bidirectional edge of type `typei` between nodes `ui` and `vi`, find the maximum number of edges you can remove so that after removing the edges, the graph can still be fully traversed by both Alice and Bob. The graph is fully traversed by Alice and Bob if starting from any node, they can reach all other nodes.
|
||||
|
||||
Return *the maximum number of edges you can remove, or return* `-1` *if it's impossible for the graph to be fully traversed by Alice and Bob.*
|
||||
|
||||
**Example 1:**
|
||||
|
||||
|
||||
|
||||
```
|
||||
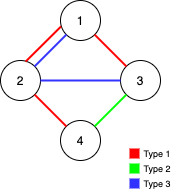
Input: n = 4, edges = [[3,1,2],[3,2,3],[1,1,3],[1,2,4],[1,1,2],[2,3,4]]
|
||||
Output: 2
|
||||
Explanation: If we remove the 2 edges [1,1,2] and [1,1,3]. The graph will still be fully traversable by Alice and Bob. Removing any additional edge will not make it so. So the maximum number of edges we can remove is 2.
|
||||
```
|
||||
|
||||
**Example 2:**
|
||||
|
||||
|
||||
|
||||
```
|
||||
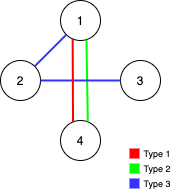
Input: n = 4, edges = [[3,1,2],[3,2,3],[1,1,4],[2,1,4]]
|
||||
Output: 0
|
||||
Explanation: Notice that removing any edge will not make the graph fully traversable by Alice and Bob.
|
||||
```
|
||||
|
||||
**Example 3:**
|
||||
|
||||
|
||||
|
||||
```
|
||||
Input: n = 4, edges = [[3,2,3],[1,1,2],[2,3,4]]
|
||||
Output: -1
|
||||
Explanation: In the current graph, Alice cannot reach node 4 from the other nodes. Likewise, Bob cannot reach 1. Therefore it's impossible to make the graph fully traversable.
|
||||
```
|
||||
|
||||
**Constraints:**
|
||||
|
||||
- `1 <= n <= 10^5`
|
||||
- `1 <= edges.length <= min(10^5, 3 * n * (n-1) / 2)`
|
||||
- `edges[i].length == 3`
|
||||
- `1 <= edges[i][0] <= 3`
|
||||
- `1 <= edges[i][1] < edges[i][2] <= n`
|
||||
- All tuples `(typei, ui, vi)` are distinct.
|
||||
|
||||
## 题目大意
|
||||
|
||||
Alice 和 Bob 共有一个无向图,其中包含 n 个节点和 3 种类型的边:
|
||||
|
||||
- 类型 1:只能由 Alice 遍历。
|
||||
- 类型 2:只能由 Bob 遍历。
|
||||
- 类型 3:Alice 和 Bob 都可以遍历。
|
||||
|
||||
给你一个数组 edges ,其中 edges[i] = [typei, ui, vi] 表示节点 ui 和 vi 之间存在类型为 typei 的双向边。请你在保证图仍能够被 Alice和 Bob 完全遍历的前提下,找出可以删除的最大边数。如果从任何节点开始,Alice 和 Bob 都可以到达所有其他节点,则认为图是可以完全遍历的。返回可以删除的最大边数,如果 Alice 和 Bob 无法完全遍历图,则返回 -1 。
|
||||
|
||||
## 解题思路
|
||||
|
||||
- 本题是第 1319 题的加强版。在第 1319 题中只有一个人,同样也是判断在保证图可连通的基础上,删掉最多边的条数。这一题只不过变成了 2 个人。解题思路依旧是并查集。
|
||||
- 初始化 2 个并查集,分别表示 Alice 和 Bob。先合并公共边,每合并一条边,可删除的最大总边数便减少 1 。再合并 2 人各自的单独的边,同样是每合并一条边,每合并一条边,可删除的最大总边数便减少 1 。合并完所有的边,2 人的并查集内部集合数仍大于 1,那么则代表 2 人无法完全遍历图,则输出 -1。如果 2 人的并查集内部集合都是 1,代表整个图都连通了。输出可以删除的最大边数。
|
||||
|
||||
## 代码
|
||||
|
||||
```go
|
||||
package leetcode
|
||||
|
||||
import (
|
||||
"github.com/halfrost/LeetCode-Go/template"
|
||||
)
|
||||
|
||||
func maxNumEdgesToRemove(n int, edges [][]int) int {
|
||||
alice, bob, res := template.UnionFind{}, template.UnionFind{}, len(edges)
|
||||
alice.Init(n)
|
||||
bob.Init(n)
|
||||
for _, e := range edges {
|
||||
x, y := e[1]-1, e[2]-1
|
||||
if e[0] == 3 && (!(alice.Find(x) == alice.Find(y)) || !(bob.Find(x) == bob.Find(y))) {
|
||||
alice.Union(x, y)
|
||||
bob.Union(x, y)
|
||||
res--
|
||||
}
|
||||
}
|
||||
ufs := [2]*template.UnionFind{&alice, &bob}
|
||||
for _, e := range edges {
|
||||
if tp := e[0]; tp < 3 && !(ufs[tp-1].Find(e[1]-1) == ufs[tp-1].Find(e[2]-1)) {
|
||||
ufs[tp-1].Union(e[1]-1, e[2]-1)
|
||||
res--
|
||||
}
|
||||
}
|
||||
if alice.TotalCount() > 1 || bob.TotalCount() > 1 {
|
||||
return -1
|
||||
}
|
||||
return res
|
||||
}
|
||||
```
|
||||
Reference in New Issue
Block a user