mirror of
https://github.com/halfrost/LeetCode-Go.git
synced 2025-07-13 07:14:17 +08:00
Add solution 1631、1691
This commit is contained in:
@ -25,7 +25,7 @@ Given an unsorted array of integers, find the length of longest increasing subse
|
||||
|
||||
## 解题思路
|
||||
|
||||
- 给定一个整数序列,求其中的最长上升子序列的长度。这一题就是经典的最长上升子序列的问题。
|
||||
- 给定一个整数序列,求其中的最长上升子序列的长度。这一题就是经典的 LIS 最长上升子序列的问题。
|
||||
- `dp[i]` 代表为第 i 个数字为结尾的最长上升子序列的长度。换种表述,dp[i] 代表 [0,i] 范围内,选择数字 nums[i] 可以获得的最长上升子序列的长度。状态转移方程为 `dp[i] = max( 1 + dp[j]) ,其中 j < i && nums[j] > nums[i]`,取所有满足条件的最大值。时间复杂度 O(n^2)
|
||||
- 这道题还有一种更快的解法。考虑这样一个问题,我们是否能用一个数组,记录上升子序列的最末尾的一个数字呢?如果这个数字越小,那么这个子序列往后面添加数字的几率就越大,那么就越可能成为最长的上升子序列。举个例子:nums = [4,5,6,3],它的所有的上升子序列为
|
||||
|
||||
@ -34,7 +34,8 @@ Given an unsorted array of integers, find the length of longest increasing subse
|
||||
len = 2 : [4, 5], [5, 6] => tails[1] = 5
|
||||
len = 3 : [4, 5, 6] => tails[2] = 6
|
||||
```
|
||||
- 其中 `tails[i]` 中存储的是所有长度为 i + 1 的上升子序列中末尾最小的值。也很容易证明 `tails` 数组里面的值一定是递增的(因为我们用末尾的数字描述最长递增子序列)。既然 tails 是有序的,我们就可以用二分查找的方法去更新这个 tail 数组里面的值。更新策略如下:(1). 如果 x 比所有的 tails 元素都要大,那么就直接放在末尾,并且 tails 数组长度加一;(2). 如果 `tails[i-1] < x <= tails[i]`,则更新 tails[i],因为 x 更小,更能获得最长上升子序列。最终 tails 数组的长度即为最长的上升子序列。这种做法的时间复杂度 O(n log n)。
|
||||
- 其中 `tails[i]` 中存储的是所有长度为 i + 1 的上升子序列中末尾最小的值。也很容易证明 `tails` 数组里面的值一定是递增的(因为我们用末尾的数字描述最长递增子序列)。既然 tails 是有序的,我们就可以用二分查找的方法去更新这个 tail 数组里面的值。更新策略如下:(1). 如果 x 比所有的 tails 元素都要大,那么就直接放在末尾,并且 tails 数组长度加一,这里对应解法二中,二分搜索找不到对应的元素值,直接把 num 放在 dp[] 的最后;(2). 如果 `tails[i-1] < x <= tails[i]`,则更新 tails[i],因为 x 更小,更能获得最长上升子序列,这一步对应解法二中将 dp[i] 更新为 num。最终 tails 数组的长度即为最长的上升子序列。这种做法的时间复杂度 O(n log n)。
|
||||
- 此题是一维的 LIS 问题。二维的 LIS 问题是第 354 题。三维的 LIS 问题是第 1691 题。
|
||||
|
||||
|
||||
|
||||
|
||||
@ -29,6 +29,7 @@ What is the maximum number of envelopes can you Russian doll? (put one inside ot
|
||||
|
||||
- 给出一组信封的宽度和高度,如果组成俄罗斯套娃,问最多能套几层。只有当一个信封的宽度和高度都比另外一个信封大的时候,才能套在小信封上面。
|
||||
- 这一题的实质是第 300 题 Longest Increasing Subsequence 的加强版。能组成俄罗斯套娃的条件就是能找到一个最长上升子序列。但是这题的条件是二维的,要求能找到在二维上都能满足条件的最长上升子序列。先降维,把宽度排序。然后在高度上寻找最长上升子序列。这里用到的方法和第 300 题的方法一致。解题思路详解见第 300 题。
|
||||
- 此题是二维的 LIS 问题。一维的 LIS 问题是第 300 题。三维的 LIS 问题是第 1691 题。
|
||||
|
||||
|
||||
## 代码
|
||||
|
||||
@ -106,5 +106,5 @@ func maxNumEdgesToRemove(n int, edges [][]int) int {
|
||||
----------------------------------------------
|
||||
<div style="display: flex;justify-content: space-between;align-items: center;">
|
||||
<p><a href="https://books.halfrost.com/leetcode/ChapterFour/1500~1599/1573.Number-of-Ways-to-Split-a-String/">⬅️上一页</a></p>
|
||||
<p><a href="https://books.halfrost.com/leetcode/ChapterFour/1600~1699/1640.Check-Array-Formation-Through-Concatenation/">下一页➡️</a></p>
|
||||
<p><a href="https://books.halfrost.com/leetcode/ChapterFour/1600~1699/1631.Path-With-Minimum-Effort/">下一页➡️</a></p>
|
||||
</div>
|
||||
|
||||
@ -0,0 +1,177 @@
|
||||
# [1631. Path With Minimum Effort](https://leetcode.com/problems/path-with-minimum-effort/)
|
||||
|
||||
## 题目
|
||||
|
||||
You are a hiker preparing for an upcoming hike. You are given `heights`, a 2D array of size `rows x columns`, where `heights[row][col]` represents the height of cell `(row, col)`. You are situated in the top-left cell, `(0, 0)`, and you hope to travel to the bottom-right cell, `(rows-1, columns-1)` (i.e., **0-indexed**). You can move **up**, **down**, **left**, or **right**, and you wish to find a route that requires the minimum **effort**.
|
||||
|
||||
A route's **effort** is the **maximum absolute difference** in heights between two consecutive cells of the route.
|
||||
|
||||
Return *the minimum **effort** required to travel from the top-left cell to the bottom-right cell.*
|
||||
|
||||
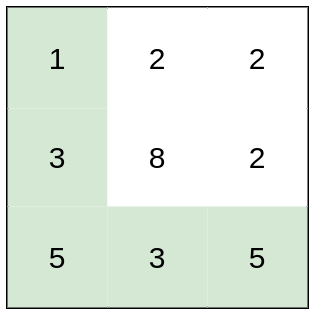
**Example 1:**
|
||||
|
||||
|
||||
|
||||
```
|
||||
Input: heights = [[1,2,2],[3,8,2],[5,3,5]]
|
||||
Output: 2
|
||||
Explanation: The route of [1,3,5,3,5] has a maximum absolute difference of 2 in consecutive cells.
|
||||
This is better than the route of [1,2,2,2,5], where the maximum absolute difference is 3.
|
||||
```
|
||||
|
||||
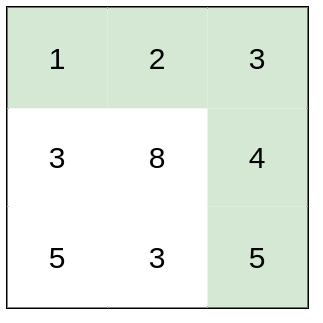
**Example 2:**
|
||||
|
||||
|
||||
|
||||
```
|
||||
Input: heights = [[1,2,3],[3,8,4],[5,3,5]]
|
||||
Output: 1
|
||||
Explanation: The route of [1,2,3,4,5] has a maximum absolute difference of 1 in consecutive cells, which is better than route [1,3,5,3,5].
|
||||
```
|
||||
|
||||
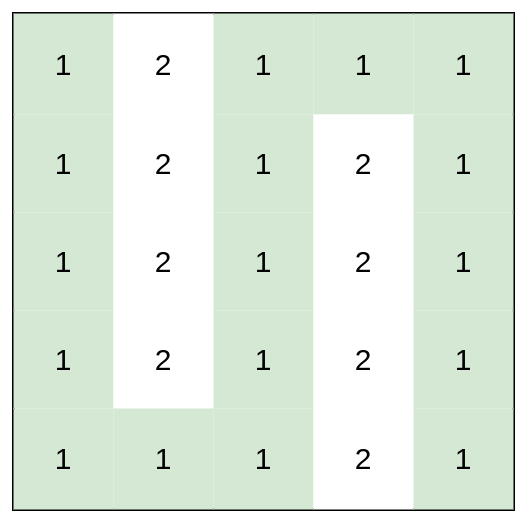
**Example 3:**
|
||||
|
||||
|
||||
|
||||
```
|
||||
Input: heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
|
||||
Output: 0
|
||||
Explanation: This route does not require any effort.
|
||||
```
|
||||
|
||||
**Constraints:**
|
||||
|
||||
- `rows == heights.length`
|
||||
- `columns == heights[i].length`
|
||||
- `1 <= rows, columns <= 100`
|
||||
- `1 <= heights[i][j] <= 10^6`
|
||||
|
||||
## 题目大意
|
||||
|
||||
你准备参加一场远足活动。给你一个二维 `rows x columns` 的地图 `heights` ,其中 `heights[row][col]` 表示格子 `(row, col)` 的高度。一开始你在最左上角的格子 `(0, 0)` ,且你希望去最右下角的格子 `(rows-1, columns-1)` (注意下标从 0 开始编号)。你每次可以往 上,下,左,右 四个方向之一移动,你想要找到耗费 体力 最小的一条路径。一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。请你返回从左上角走到右下角的最小 体力消耗值 。
|
||||
|
||||
## 解题思路
|
||||
|
||||
- 此题和第 778 题解题思路完全一致。在第 778 题中求的是最短连通时间。此题求的是连通路径下的最小体力值。都是求的最小值,只是 2 个值的意义不同罢了。
|
||||
- 按照第 778 题的思路,本题也有多种解法。第一种解法是 DFS + 二分。先将题目变换一个等价问法。题目要求找到最小体力消耗值,也相当于问是否存在一个体力消耗值 x,只要大于等于 x,一定能连通。利用二分搜索来找到这个临界值。体力消耗值是有序的,此处满足二分搜索的条件。题目给定柱子高度是 [1,10^6],所以体力值一定在 [0,10^6-1] 这个区间内。判断是否取中值的条件是用 DFS 或者 BFS 搜索 (0,0) 点和 (N-1, N-1) 点之间是否连通。时间复杂度:O(mnlogC),其中 m 和 n 分别是地图的行数和列数,C 是格子的最大高度。C 最大为 10^6,所以 logC 常数也很小。空间复杂度 O(mn)。
|
||||
- 第二种解法是并查集。将图中所有边按照权值从小到大进行排序,并依次加入并查集中。直到加入一条权值为 x 的边以后,左上角到右下角连通了。最小体力消耗值也就找到了。注意加入边的时候,只加入 `i-1` 和 `i` ,`j-1` 和 `j` 这 2 类相邻的边。因为最小体力消耗意味着不走回头路。上下左右四个方向到达一个节点,只可能从上边和左边走过来。从下边和右边走过来肯定是浪费体力了。时间复杂度:O(mnlog(mn)),其中 m 和 n 分别是地图的行数和列数,图中的边数为 O(mn)。空间复杂度 O(mn),即为存储所有边以及并查集需要的空间。
|
||||
|
||||
## 代码
|
||||
|
||||
```go
|
||||
package leetcode
|
||||
|
||||
import (
|
||||
"sort"
|
||||
|
||||
"github.com/halfrost/LeetCode-Go/template"
|
||||
)
|
||||
|
||||
var dir = [4][2]int{
|
||||
{0, 1},
|
||||
{1, 0},
|
||||
{0, -1},
|
||||
{-1, 0},
|
||||
}
|
||||
|
||||
// 解法一 DFS + 二分
|
||||
func minimumEffortPath(heights [][]int) int {
|
||||
n, m := len(heights), len(heights[0])
|
||||
visited := make([][]bool, n)
|
||||
for i := range visited {
|
||||
visited[i] = make([]bool, m)
|
||||
}
|
||||
low, high := 0, 1000000
|
||||
for low < high {
|
||||
threshold := low + (high-low)>>1
|
||||
if !hasPath(heights, visited, 0, 0, threshold) {
|
||||
low = threshold + 1
|
||||
} else {
|
||||
high = threshold
|
||||
}
|
||||
for i := range visited {
|
||||
for j := range visited[i] {
|
||||
visited[i][j] = false
|
||||
}
|
||||
}
|
||||
}
|
||||
return low
|
||||
}
|
||||
|
||||
func hasPath(heights [][]int, visited [][]bool, i, j, threshold int) bool {
|
||||
n, m := len(heights), len(heights[0])
|
||||
if i == n-1 && j == m-1 {
|
||||
return true
|
||||
}
|
||||
visited[i][j] = true
|
||||
res := false
|
||||
for _, d := range dir {
|
||||
ni, nj := i+d[0], j+d[1]
|
||||
if ni < 0 || ni >= n || nj < 0 || nj >= m || visited[ni][nj] || res {
|
||||
continue
|
||||
}
|
||||
diff := abs(heights[i][j] - heights[ni][nj])
|
||||
if diff <= threshold && hasPath(heights, visited, ni, nj, threshold) {
|
||||
res = true
|
||||
}
|
||||
}
|
||||
return res
|
||||
}
|
||||
|
||||
func abs(a int) int {
|
||||
if a < 0 {
|
||||
a = -a
|
||||
}
|
||||
return a
|
||||
}
|
||||
|
||||
func min(a, b int) int {
|
||||
if a < b {
|
||||
return a
|
||||
}
|
||||
return b
|
||||
}
|
||||
|
||||
func max(a, b int) int {
|
||||
if a < b {
|
||||
return b
|
||||
}
|
||||
return a
|
||||
}
|
||||
|
||||
// 解法二 并查集
|
||||
func minimumEffortPath1(heights [][]int) int {
|
||||
n, m, edges, uf := len(heights), len(heights[0]), []edge{}, template.UnionFind{}
|
||||
uf.Init(n * m)
|
||||
for i, row := range heights {
|
||||
for j, h := range row {
|
||||
id := i*m + j
|
||||
if i > 0 {
|
||||
edges = append(edges, edge{id - m, id, abs(h - heights[i-1][j])})
|
||||
}
|
||||
if j > 0 {
|
||||
edges = append(edges, edge{id - 1, id, abs(h - heights[i][j-1])})
|
||||
}
|
||||
}
|
||||
}
|
||||
sort.Slice(edges, func(i, j int) bool { return edges[i].diff < edges[j].diff })
|
||||
for _, e := range edges {
|
||||
uf.Union(e.v, e.w)
|
||||
if uf.Find(0) == uf.Find(n*m-1) {
|
||||
return e.diff
|
||||
}
|
||||
}
|
||||
return 0
|
||||
}
|
||||
|
||||
type edge struct {
|
||||
v, w, diff int
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
----------------------------------------------
|
||||
<div style="display: flex;justify-content: space-between;align-items: center;">
|
||||
<p><a href="https://books.halfrost.com/leetcode/ChapterFour/1500~1599/1579.Remove-Max-Number-of-Edges-to-Keep-Graph-Fully-Traversable/">⬅️上一页</a></p>
|
||||
<p><a href="https://books.halfrost.com/leetcode/ChapterFour/1600~1699/1640.Check-Array-Formation-Through-Concatenation/">下一页➡️</a></p>
|
||||
</div>
|
||||
@ -97,6 +97,6 @@ func canFormArray(arr []int, pieces [][]int) bool {
|
||||
|
||||
----------------------------------------------
|
||||
<div style="display: flex;justify-content: space-between;align-items: center;">
|
||||
<p><a href="https://books.halfrost.com/leetcode/ChapterFour/1500~1599/1579.Remove-Max-Number-of-Edges-to-Keep-Graph-Fully-Traversable/">⬅️上一页</a></p>
|
||||
<p><a href="https://books.halfrost.com/leetcode/ChapterFour/1600~1699/1631.Path-With-Minimum-Effort/">⬅️上一页</a></p>
|
||||
<p><a href="https://books.halfrost.com/leetcode/ChapterFour/1600~1699/1641.Count-Sorted-Vowel-Strings/">下一页➡️</a></p>
|
||||
</div>
|
||||
|
||||
@ -133,5 +133,5 @@ func max(a, b int) int {
|
||||
----------------------------------------------
|
||||
<div style="display: flex;justify-content: space-between;align-items: center;">
|
||||
<p><a href="https://books.halfrost.com/leetcode/ChapterFour/1600~1699/1689.Partitioning-Into-Minimum-Number-Of-Deci-Binary-Numbers/">⬅️上一页</a></p>
|
||||
<p><a href="https://books.halfrost.com/leetcode/ChapterFour/1600~1699/1694.Reformat-Phone-Number/">下一页➡️</a></p>
|
||||
<p><a href="https://books.halfrost.com/leetcode/ChapterFour/1600~1699/1691.Maximum-Height-by-Stacking-Cuboids/">下一页➡️</a></p>
|
||||
</div>
|
||||
|
||||
@ -0,0 +1,113 @@
|
||||
# [1691. Maximum Height by Stacking Cuboids](https://leetcode.com/problems/maximum-height-by-stacking-cuboids/)
|
||||
|
||||
## 题目
|
||||
|
||||
Given `n` `cuboids` where the dimensions of the `ith` cuboid is `cuboids[i] = [widthi, lengthi, heighti]` (**0-indexed**). Choose a **subset** of `cuboids` and place them on each other.
|
||||
|
||||
You can place cuboid `i` on cuboid `j` if `widthi <= widthj` and `lengthi <= lengthj` and `heighti <= heightj`. You can rearrange any cuboid's dimensions by rotating it to put it on another cuboid.
|
||||
|
||||
Return *the **maximum height** of the stacked* `cuboids`.
|
||||
|
||||
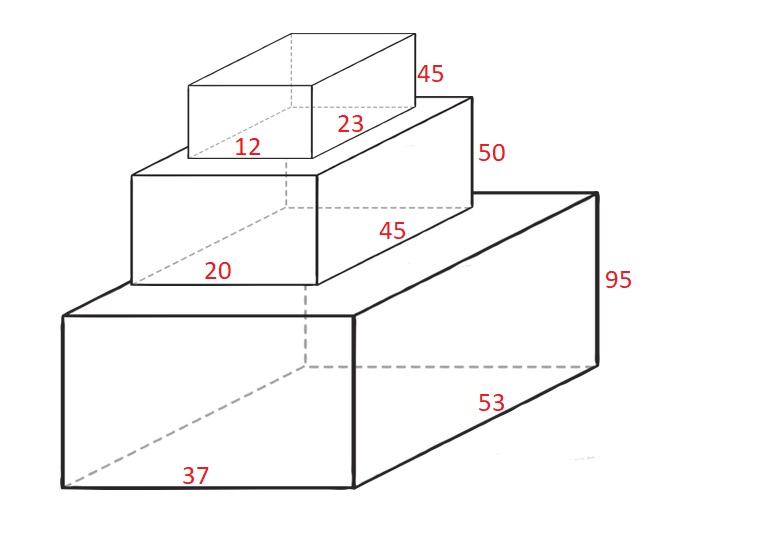
**Example 1:**
|
||||
|
||||
|
||||
|
||||
```
|
||||
Input: cuboids = [[50,45,20],[95,37,53],[45,23,12]]
|
||||
Output: 190
|
||||
Explanation:
|
||||
Cuboid 1 is placed on the bottom with the 53x37 side facing down with height 95.
|
||||
Cuboid 0 is placed next with the 45x20 side facing down with height 50.
|
||||
Cuboid 2 is placed next with the 23x12 side facing down with height 45.
|
||||
The total height is 95 + 50 + 45 = 190.
|
||||
```
|
||||
|
||||
**Example 2:**
|
||||
|
||||
```
|
||||
Input: cuboids = [[38,25,45],[76,35,3]]
|
||||
Output: 76
|
||||
Explanation:
|
||||
You can't place any of the cuboids on the other.
|
||||
We choose cuboid 1 and rotate it so that the 35x3 side is facing down and its height is 76.
|
||||
```
|
||||
|
||||
**Example 3:**
|
||||
|
||||
```
|
||||
Input: cuboids = [[7,11,17],[7,17,11],[11,7,17],[11,17,7],[17,7,11],[17,11,7]]
|
||||
Output: 102
|
||||
Explanation:
|
||||
After rearranging the cuboids, you can see that all cuboids have the same dimension.
|
||||
You can place the 11x7 side down on all cuboids so their heights are 17.
|
||||
The maximum height of stacked cuboids is 6 * 17 = 102.
|
||||
```
|
||||
|
||||
**Constraints:**
|
||||
|
||||
- `n == cuboids.length`
|
||||
- `1 <= n <= 100`
|
||||
- `1 <= widthi, lengthi, heighti <= 100`
|
||||
|
||||
## 题目大意
|
||||
|
||||
给你 n 个长方体 cuboids ,其中第 i 个长方体的长宽高表示为 cuboids[i] = [widthi, lengthi, heighti](下标从 0 开始)。请你从 cuboids 选出一个 子集 ,并将它们堆叠起来。如果 widthi <= widthj 且 lengthi <= lengthj 且 heighti <= heightj ,你就可以将长方体 i 堆叠在长方体 j 上。你可以通过旋转把长方体的长宽高重新排列,以将它放在另一个长方体上。返回 堆叠长方体 cuboids 可以得到的 最大高度 。
|
||||
|
||||
## 解题思路
|
||||
|
||||
- 这一题是 LIS 最长递增子序列系列问题的延续。一维 LIS 问题是第 300 题。二维 LIS 问题是 354 题。这一题是三维的 LIS 问题。
|
||||
- 题目要求最终摞起来的长方体尽可能的高,那么把长宽高中最大的值旋转为高。这是针对单个方块的排序。多个方块间还要排序,因为他们摞起来有要求,大的方块必须放在下面。所以针对多个方块,按照长,宽,高的顺序进行排序。两次排序完成以后,可以用动态规划找出最大值了。定义 `dp[i]` 为以 `i` 为最后一块砖块所能堆叠的最高高度。由于长和宽已经排好序了。所以只需要在 [0, i - 1] 这个区间内动态更新 dp 最大值。
|
||||
|
||||
## 代码
|
||||
|
||||
```go
|
||||
package leetcode
|
||||
|
||||
import "sort"
|
||||
|
||||
func maxHeight(cuboids [][]int) int {
|
||||
n := len(cuboids)
|
||||
for i := 0; i < n; i++ {
|
||||
sort.Ints(cuboids[i]) // 立方体三边内部排序
|
||||
}
|
||||
// 立方体排序,先按最短边,再到最长边
|
||||
sort.Slice(cuboids, func(i, j int) bool {
|
||||
if cuboids[i][0] != cuboids[j][0] {
|
||||
return cuboids[i][0] < cuboids[j][0]
|
||||
}
|
||||
if cuboids[i][1] != cuboids[j][1] {
|
||||
return cuboids[i][1] < cuboids[j][1]
|
||||
}
|
||||
return cuboids[i][2] < cuboids[j][2]
|
||||
})
|
||||
res := 0
|
||||
dp := make([]int, n)
|
||||
for i := 0; i < n; i++ {
|
||||
dp[i] = cuboids[i][2]
|
||||
res = max(res, dp[i])
|
||||
}
|
||||
for i := 1; i < n; i++ {
|
||||
for j := 0; j < i; j++ {
|
||||
if cuboids[j][0] <= cuboids[i][0] && cuboids[j][1] <= cuboids[i][1] && cuboids[j][2] <= cuboids[i][2] {
|
||||
dp[i] = max(dp[i], dp[j]+cuboids[i][2])
|
||||
}
|
||||
}
|
||||
res = max(res, dp[i])
|
||||
}
|
||||
return res
|
||||
}
|
||||
|
||||
func max(x, y int) int {
|
||||
if x > y {
|
||||
return x
|
||||
}
|
||||
return y
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
----------------------------------------------
|
||||
<div style="display: flex;justify-content: space-between;align-items: center;">
|
||||
<p><a href="https://books.halfrost.com/leetcode/ChapterFour/1600~1699/1690.Stone-Game-VII/">⬅️上一页</a></p>
|
||||
<p><a href="https://books.halfrost.com/leetcode/ChapterFour/1600~1699/1694.Reformat-Phone-Number/">下一页➡️</a></p>
|
||||
</div>
|
||||
@ -137,6 +137,6 @@ func reformatNumber(number string) string {
|
||||
|
||||
----------------------------------------------
|
||||
<div style="display: flex;justify-content: space-between;align-items: center;">
|
||||
<p><a href="https://books.halfrost.com/leetcode/ChapterFour/1600~1699/1690.Stone-Game-VII/">⬅️上一页</a></p>
|
||||
<p><a href="https://books.halfrost.com/leetcode/ChapterFour/1600~1699/1691.Maximum-Height-by-Stacking-Cuboids/">⬅️上一页</a></p>
|
||||
<p><a href="https://books.halfrost.com/leetcode/ChapterFour/1600~1699/1695.Maximum-Erasure-Value/">下一页➡️</a></p>
|
||||
</div>
|
||||
|
||||
@ -36,7 +36,7 @@ weight: 1
|
||||
|0064|Minimum Path Sum|[Go]({{< relref "/ChapterFour/0001~0099/0064.Minimum-Path-Sum.md" >}})|Medium| O(n^2)| O(n^2)||56.1%|
|
||||
|0066|Plus One|[Go]({{< relref "/ChapterFour/0001~0099/0066.Plus-One.md" >}})|Easy||||42.3%|
|
||||
|0074|Search a 2D Matrix|[Go]({{< relref "/ChapterFour/0001~0099/0074.Search-a-2D-Matrix.md" >}})|Medium||||37.6%|
|
||||
|0075|Sort Colors|[Go]({{< relref "/ChapterFour/0001~0099/0075.Sort-Colors.md" >}})|Medium| O(n)| O(1)|❤️|49.2%|
|
||||
|0075|Sort Colors|[Go]({{< relref "/ChapterFour/0001~0099/0075.Sort-Colors.md" >}})|Medium| O(n)| O(1)|❤️|49.3%|
|
||||
|0078|Subsets|[Go]({{< relref "/ChapterFour/0001~0099/0078.Subsets.md" >}})|Medium| O(n^2)| O(n)|❤️|64.9%|
|
||||
|0079|Word Search|[Go]({{< relref "/ChapterFour/0001~0099/0079.Word-Search.md" >}})|Medium| O(n^2)| O(n^2)|❤️|36.7%|
|
||||
|0080|Remove Duplicates from Sorted Array II|[Go]({{< relref "/ChapterFour/0001~0099/0080.Remove-Duplicates-from-Sorted-Array-II.md" >}})|Medium| O(n)| O(1||46.0%|
|
||||
|
||||
@ -192,9 +192,10 @@ func peakIndexInMountainArray(A []int) int {
|
||||
|1157|Online Majority Element In Subarray|[Go]({{< relref "/ChapterFour/1100~1199/1157.Online-Majority-Element-In-Subarray.md" >}})|Hard||||39.6%|
|
||||
|1170|Compare Strings by Frequency of the Smallest Character|[Go]({{< relref "/ChapterFour/1100~1199/1170.Compare-Strings-by-Frequency-of-the-Smallest-Character.md" >}})|Medium||||59.6%|
|
||||
|1201|Ugly Number III|[Go]({{< relref "/ChapterFour/1200~1299/1201.Ugly-Number-III.md" >}})|Medium||||26.4%|
|
||||
|1235|Maximum Profit in Job Scheduling|[Go]({{< relref "/ChapterFour/1200~1299/1235.Maximum-Profit-in-Job-Scheduling.md" >}})|Hard||||47.4%|
|
||||
|1235|Maximum Profit in Job Scheduling|[Go]({{< relref "/ChapterFour/1200~1299/1235.Maximum-Profit-in-Job-Scheduling.md" >}})|Hard||||47.3%|
|
||||
|1283|Find the Smallest Divisor Given a Threshold|[Go]({{< relref "/ChapterFour/1200~1299/1283.Find-the-Smallest-Divisor-Given-a-Threshold.md" >}})|Medium||||49.4%|
|
||||
|1300|Sum of Mutated Array Closest to Target|[Go]({{< relref "/ChapterFour/1300~1399/1300.Sum-of-Mutated-Array-Closest-to-Target.md" >}})|Medium||||43.2%|
|
||||
|1631|Path With Minimum Effort|[Go]({{< relref "/ChapterFour/1600~1699/1631.Path-With-Minimum-Effort.md" >}})|Medium||||50.1%|
|
||||
|1649|Create Sorted Array through Instructions|[Go]({{< relref "/ChapterFour/1600~1699/1649.Create-Sorted-Array-through-Instructions.md" >}})|Hard||||36.3%|
|
||||
|1658|Minimum Operations to Reduce X to Zero|[Go]({{< relref "/ChapterFour/1600~1699/1658.Minimum-Operations-to-Reduce-X-to-Zero.md" >}})|Medium||||33.4%|
|
||||
|------------|-------------------------------------------------------|-------| ----------------| ---------------|-------------|-------------|-------------|
|
||||
|
||||
@ -14,7 +14,7 @@ weight: 9
|
||||
|0099|Recover Binary Search Tree|[Go]({{< relref "/ChapterFour/0001~0099/0099.Recover-Binary-Search-Tree.md" >}})|Hard| O(n)| O(1)||42.4%|
|
||||
|0100|Same Tree|[Go]({{< relref "/ChapterFour/0100~0199/0100.Same-Tree.md" >}})|Easy| O(n)| O(1)||54.1%|
|
||||
|0101|Symmetric Tree|[Go]({{< relref "/ChapterFour/0100~0199/0101.Symmetric-Tree.md" >}})|Easy| O(n)| O(1)||48.0%|
|
||||
|0104|Maximum Depth of Binary Tree|[Go]({{< relref "/ChapterFour/0100~0199/0104.Maximum-Depth-of-Binary-Tree.md" >}})|Easy| O(n)| O(1)||67.9%|
|
||||
|0104|Maximum Depth of Binary Tree|[Go]({{< relref "/ChapterFour/0100~0199/0104.Maximum-Depth-of-Binary-Tree.md" >}})|Easy| O(n)| O(1)||68.0%|
|
||||
|0105|Construct Binary Tree from Preorder and Inorder Traversal|[Go]({{< relref "/ChapterFour/0100~0199/0105.Construct-Binary-Tree-from-Preorder-and-Inorder-Traversal.md" >}})|Medium||||51.6%|
|
||||
|0106|Construct Binary Tree from Inorder and Postorder Traversal|[Go]({{< relref "/ChapterFour/0100~0199/0106.Construct-Binary-Tree-from-Inorder-and-Postorder-Traversal.md" >}})|Medium||||49.5%|
|
||||
|0108|Convert Sorted Array to Binary Search Tree|[Go]({{< relref "/ChapterFour/0100~0199/0108.Convert-Sorted-Array-to-Binary-Search-Tree.md" >}})|Easy| O(n)| O(1)||60.3%|
|
||||
@ -69,7 +69,7 @@ weight: 9
|
||||
|0947|Most Stones Removed with Same Row or Column|[Go]({{< relref "/ChapterFour/0900~0999/0947.Most-Stones-Removed-with-Same-Row-or-Column.md" >}})|Medium||||55.4%|
|
||||
|0959|Regions Cut By Slashes|[Go]({{< relref "/ChapterFour/0900~0999/0959.Regions-Cut-By-Slashes.md" >}})|Medium||||67.1%|
|
||||
|0968|Binary Tree Cameras|[Go]({{< relref "/ChapterFour/0900~0999/0968.Binary-Tree-Cameras.md" >}})|Hard||||38.7%|
|
||||
|0979|Distribute Coins in Binary Tree|[Go]({{< relref "/ChapterFour/0900~0999/0979.Distribute-Coins-in-Binary-Tree.md" >}})|Medium||||69.6%|
|
||||
|0979|Distribute Coins in Binary Tree|[Go]({{< relref "/ChapterFour/0900~0999/0979.Distribute-Coins-in-Binary-Tree.md" >}})|Medium||||69.7%|
|
||||
|0980|Unique Paths III|[Go]({{< relref "/ChapterFour/0900~0999/0980.Unique-Paths-III.md" >}})|Hard| O(n log n)| O(n)||77.2%|
|
||||
|0987|Vertical Order Traversal of a Binary Tree|[Go]({{< relref "/ChapterFour/0900~0999/0987.Vertical-Order-Traversal-of-a-Binary-Tree.md" >}})|Hard||||38.7%|
|
||||
|1020|Number of Enclaves|[Go]({{< relref "/ChapterFour/1000~1099/1020.Number-of-Enclaves.md" >}})|Medium||||58.9%|
|
||||
@ -84,6 +84,7 @@ weight: 9
|
||||
|1302|Deepest Leaves Sum|[Go]({{< relref "/ChapterFour/1300~1399/1302.Deepest-Leaves-Sum.md" >}})|Medium||||84.2%|
|
||||
|1306|Jump Game III|[Go]({{< relref "/ChapterFour/1300~1399/1306.Jump-Game-III.md" >}})|Medium||||62.6%|
|
||||
|1319|Number of Operations to Make Network Connected|[Go]({{< relref "/ChapterFour/1300~1399/1319.Number-of-Operations-to-Make-Network-Connected.md" >}})|Medium||||55.4%|
|
||||
|1631|Path With Minimum Effort|[Go]({{< relref "/ChapterFour/1600~1699/1631.Path-With-Minimum-Effort.md" >}})|Medium||||50.1%|
|
||||
|------------|-------------------------------------------------------|-------| ----------------| ---------------|-------------|-------------|-------------|
|
||||
|
||||
|
||||
|
||||
@ -53,7 +53,7 @@ weight: 7
|
||||
|1049|Last Stone Weight II|[Go]({{< relref "/ChapterFour/1000~1099/1049.Last-Stone-Weight-II.md" >}})|Medium||||45.2%|
|
||||
|1074|Number of Submatrices That Sum to Target|[Go]({{< relref "/ChapterFour/1000~1099/1074.Number-of-Submatrices-That-Sum-to-Target.md" >}})|Hard||||61.7%|
|
||||
|1105|Filling Bookcase Shelves|[Go]({{< relref "/ChapterFour/1100~1199/1105.Filling-Bookcase-Shelves.md" >}})|Medium||||57.5%|
|
||||
|1235|Maximum Profit in Job Scheduling|[Go]({{< relref "/ChapterFour/1200~1299/1235.Maximum-Profit-in-Job-Scheduling.md" >}})|Hard||||47.4%|
|
||||
|1235|Maximum Profit in Job Scheduling|[Go]({{< relref "/ChapterFour/1200~1299/1235.Maximum-Profit-in-Job-Scheduling.md" >}})|Hard||||47.3%|
|
||||
|1423|Maximum Points You Can Obtain from Cards|[Go]({{< relref "/ChapterFour/1400~1499/1423.Maximum-Points-You-Can-Obtain-from-Cards.md" >}})|Medium||||46.6%|
|
||||
|1463|Cherry Pickup II|[Go]({{< relref "/ChapterFour/1400~1499/1463.Cherry-Pickup-II.md" >}})|Hard||||69.3%|
|
||||
|1641|Count Sorted Vowel Strings|[Go]({{< relref "/ChapterFour/1600~1699/1641.Count-Sorted-Vowel-Strings.md" >}})|Medium||||76.9%|
|
||||
@ -62,6 +62,7 @@ weight: 7
|
||||
|1659|Maximize Grid Happiness|[Go]({{< relref "/ChapterFour/1600~1699/1659.Maximize-Grid-Happiness.md" >}})|Hard||||35.3%|
|
||||
|1664|Ways to Make a Fair Array|[Go]({{< relref "/ChapterFour/1600~1699/1664.Ways-to-Make-a-Fair-Array.md" >}})|Medium||||60.6%|
|
||||
|1690|Stone Game VII|[Go]({{< relref "/ChapterFour/1600~1699/1690.Stone-Game-VII.md" >}})|Medium||||47.6%|
|
||||
|1691|Maximum Height by Stacking Cuboids|[Go]({{< relref "/ChapterFour/1600~1699/1691.Maximum-Height-by-Stacking-Cuboids.md" >}})|Hard||||49.9%|
|
||||
|------------|-------------------------------------------------------|-------| ----------------| ---------------|-------------|-------------|-------------|
|
||||
|
||||
|
||||
|
||||
@ -61,7 +61,7 @@ weight: 12
|
||||
|0949|Largest Time for Given Digits|[Go]({{< relref "/ChapterFour/0900~0999/0949.Largest-Time-for-Given-Digits.md" >}})|Medium||||36.2%|
|
||||
|0952|Largest Component Size by Common Factor|[Go]({{< relref "/ChapterFour/0900~0999/0952.Largest-Component-Size-by-Common-Factor.md" >}})|Hard||||36.1%|
|
||||
|0970|Powerful Integers|[Go]({{< relref "/ChapterFour/0900~0999/0970.Powerful-Integers.md" >}})|Medium||||40.0%|
|
||||
|0976|Largest Perimeter Triangle|[Go]({{< relref "/ChapterFour/0900~0999/0976.Largest-Perimeter-Triangle.md" >}})|Easy| O(n log n)| O(log n) ||58.5%|
|
||||
|0976|Largest Perimeter Triangle|[Go]({{< relref "/ChapterFour/0900~0999/0976.Largest-Perimeter-Triangle.md" >}})|Easy| O(n log n)| O(log n) ||58.6%|
|
||||
|0996|Number of Squareful Arrays|[Go]({{< relref "/ChapterFour/0900~0999/0996.Number-of-Squareful-Arrays.md" >}})|Hard| O(n log n)| O(n) ||48.3%|
|
||||
|1017|Convert to Base -2|[Go]({{< relref "/ChapterFour/1000~1099/1017.Convert-to-Base--2.md" >}})|Medium||||59.6%|
|
||||
|1025|Divisor Game|[Go]({{< relref "/ChapterFour/1000~1099/1025.Divisor-Game.md" >}})|Easy| O(1)| O(1)||66.2%|
|
||||
|
||||
@ -20,7 +20,7 @@ weight: 14
|
||||
|:--------:|:------- | :--------: | :----------: | :----: | :-----: | :-----: |:-----: |
|
||||
|0056|Merge Intervals|[Go]({{< relref "/ChapterFour/0001~0099/0056.Merge-Intervals.md" >}})|Medium| O(n log n)| O(log n)||40.9%|
|
||||
|0057|Insert Interval|[Go]({{< relref "/ChapterFour/0001~0099/0057.Insert-Interval.md" >}})|Medium| O(n)| O(1)||35.0%|
|
||||
|0075|Sort Colors|[Go]({{< relref "/ChapterFour/0001~0099/0075.Sort-Colors.md" >}})|Medium| O(n)| O(1)|❤️|49.2%|
|
||||
|0075|Sort Colors|[Go]({{< relref "/ChapterFour/0001~0099/0075.Sort-Colors.md" >}})|Medium| O(n)| O(1)|❤️|49.3%|
|
||||
|0147|Insertion Sort List|[Go]({{< relref "/ChapterFour/0100~0199/0147.Insertion-Sort-List.md" >}})|Medium| O(n)| O(1) |❤️|44.3%|
|
||||
|0148|Sort List|[Go]({{< relref "/ChapterFour/0100~0199/0148.Sort-List.md" >}})|Medium|O(n log n)| O(log n)|❤️|46.1%|
|
||||
|0164|Maximum Gap|[Go]({{< relref "/ChapterFour/0100~0199/0164.Maximum-Gap.md" >}})|Hard| O(n log n)| O(log n) |❤️|36.7%|
|
||||
@ -29,7 +29,7 @@ weight: 14
|
||||
|0242|Valid Anagram|[Go]({{< relref "/ChapterFour/0200~0299/0242.Valid-Anagram.md" >}})|Easy| O(n)| O(n) ||58.5%|
|
||||
|0274|H-Index|[Go]({{< relref "/ChapterFour/0200~0299/0274.H-Index.md" >}})|Medium| O(n)| O(n) ||36.3%|
|
||||
|0315|Count of Smaller Numbers After Self|[Go]({{< relref "/ChapterFour/0300~0399/0315.Count-of-Smaller-Numbers-After-Self.md" >}})|Hard||||42.5%|
|
||||
|0324|Wiggle Sort II|[Go]({{< relref "/ChapterFour/0300~0399/0324.Wiggle-Sort-II.md" >}})|Medium| O(n)| O(n)|❤️|30.7%|
|
||||
|0324|Wiggle Sort II|[Go]({{< relref "/ChapterFour/0300~0399/0324.Wiggle-Sort-II.md" >}})|Medium| O(n)| O(n)|❤️|30.6%|
|
||||
|0327|Count of Range Sum|[Go]({{< relref "/ChapterFour/0300~0399/0327.Count-of-Range-Sum.md" >}})|Hard||||36.0%|
|
||||
|0349|Intersection of Two Arrays|[Go]({{< relref "/ChapterFour/0300~0399/0349.Intersection-of-Two-Arrays.md" >}})|Easy| O(n)| O(n) ||64.7%|
|
||||
|0350|Intersection of Two Arrays II|[Go]({{< relref "/ChapterFour/0300~0399/0350.Intersection-of-Two-Arrays-II.md" >}})|Easy| O(n)| O(n) ||52.0%|
|
||||
@ -41,16 +41,17 @@ weight: 14
|
||||
|0922|Sort Array By Parity II|[Go]({{< relref "/ChapterFour/0900~0999/0922.Sort-Array-By-Parity-II.md" >}})|Easy| O(n)| O(1) ||70.5%|
|
||||
|0969|Pancake Sorting|[Go]({{< relref "/ChapterFour/0900~0999/0969.Pancake-Sorting.md" >}})|Medium| O(n log n)| O(log n) |❤️|68.6%|
|
||||
|0973|K Closest Points to Origin|[Go]({{< relref "/ChapterFour/0900~0999/0973.K-Closest-Points-to-Origin.md" >}})|Medium| O(n log n)| O(log n) ||64.6%|
|
||||
|0976|Largest Perimeter Triangle|[Go]({{< relref "/ChapterFour/0900~0999/0976.Largest-Perimeter-Triangle.md" >}})|Easy| O(n log n)| O(log n) ||58.5%|
|
||||
|0976|Largest Perimeter Triangle|[Go]({{< relref "/ChapterFour/0900~0999/0976.Largest-Perimeter-Triangle.md" >}})|Easy| O(n log n)| O(log n) ||58.6%|
|
||||
|1030|Matrix Cells in Distance Order|[Go]({{< relref "/ChapterFour/1000~1099/1030.Matrix-Cells-in-Distance-Order.md" >}})|Easy| O(n^2)| O(1) ||66.9%|
|
||||
|1054|Distant Barcodes|[Go]({{< relref "/ChapterFour/1000~1099/1054.Distant-Barcodes.md" >}})|Medium| O(n log n)| O(log n) |❤️|44.2%|
|
||||
|1122|Relative Sort Array|[Go]({{< relref "/ChapterFour/1100~1199/1122.Relative-Sort-Array.md" >}})|Easy||||68.1%|
|
||||
|1235|Maximum Profit in Job Scheduling|[Go]({{< relref "/ChapterFour/1200~1299/1235.Maximum-Profit-in-Job-Scheduling.md" >}})|Hard||||47.4%|
|
||||
|1235|Maximum Profit in Job Scheduling|[Go]({{< relref "/ChapterFour/1200~1299/1235.Maximum-Profit-in-Job-Scheduling.md" >}})|Hard||||47.3%|
|
||||
|1305|All Elements in Two Binary Search Trees|[Go]({{< relref "/ChapterFour/1300~1399/1305.All-Elements-in-Two-Binary-Search-Trees.md" >}})|Medium||||77.8%|
|
||||
|1329|Sort the Matrix Diagonally|[Go]({{< relref "/ChapterFour/1300~1399/1329.Sort-the-Matrix-Diagonally.md" >}})|Medium||||81.8%|
|
||||
|1640|Check Array Formation Through Concatenation|[Go]({{< relref "/ChapterFour/1600~1699/1640.Check-Array-Formation-Through-Concatenation.md" >}})|Easy||||60.2%|
|
||||
|1647|Minimum Deletions to Make Character Frequencies Unique|[Go]({{< relref "/ChapterFour/1600~1699/1647.Minimum-Deletions-to-Make-Character-Frequencies-Unique.md" >}})|Medium||||54.5%|
|
||||
|1648|Sell Diminishing-Valued Colored Balls|[Go]({{< relref "/ChapterFour/1600~1699/1648.Sell-Diminishing-Valued-Colored-Balls.md" >}})|Medium||||30.8%|
|
||||
|1691|Maximum Height by Stacking Cuboids|[Go]({{< relref "/ChapterFour/1600~1699/1691.Maximum-Height-by-Stacking-Cuboids.md" >}})|Hard||||49.9%|
|
||||
|------------|-------------------------------------------------------|-------| ----------------| ---------------|-------------|-------------|-------------|
|
||||
|
||||
|
||||
|
||||
@ -18,7 +18,7 @@ weight: 6
|
||||
|0101|Symmetric Tree|[Go]({{< relref "/ChapterFour/0100~0199/0101.Symmetric-Tree.md" >}})|Easy| O(n)| O(1)||48.0%|
|
||||
|0102|Binary Tree Level Order Traversal|[Go]({{< relref "/ChapterFour/0100~0199/0102.Binary-Tree-Level-Order-Traversal.md" >}})|Medium| O(n)| O(1)||56.5%|
|
||||
|0103|Binary Tree Zigzag Level Order Traversal|[Go]({{< relref "/ChapterFour/0100~0199/0103.Binary-Tree-Zigzag-Level-Order-Traversal.md" >}})|Medium| O(n)| O(n)||50.0%|
|
||||
|0104|Maximum Depth of Binary Tree|[Go]({{< relref "/ChapterFour/0100~0199/0104.Maximum-Depth-of-Binary-Tree.md" >}})|Easy| O(n)| O(1)||67.9%|
|
||||
|0104|Maximum Depth of Binary Tree|[Go]({{< relref "/ChapterFour/0100~0199/0104.Maximum-Depth-of-Binary-Tree.md" >}})|Easy| O(n)| O(1)||68.0%|
|
||||
|0105|Construct Binary Tree from Preorder and Inorder Traversal|[Go]({{< relref "/ChapterFour/0100~0199/0105.Construct-Binary-Tree-from-Preorder-and-Inorder-Traversal.md" >}})|Medium||||51.6%|
|
||||
|0106|Construct Binary Tree from Inorder and Postorder Traversal|[Go]({{< relref "/ChapterFour/0100~0199/0106.Construct-Binary-Tree-from-Inorder-and-Postorder-Traversal.md" >}})|Medium||||49.5%|
|
||||
|0107|Binary Tree Level Order Traversal II|[Go]({{< relref "/ChapterFour/0100~0199/0107.Binary-Tree-Level-Order-Traversal-II.md" >}})|Easy| O(n)| O(1)||55.1%|
|
||||
@ -60,7 +60,7 @@ weight: 6
|
||||
|0872|Leaf-Similar Trees|[Go]({{< relref "/ChapterFour/0800~0899/0872.Leaf-Similar-Trees.md" >}})|Easy||||64.6%|
|
||||
|0897|Increasing Order Search Tree|[Go]({{< relref "/ChapterFour/0800~0899/0897.Increasing-Order-Search-Tree.md" >}})|Easy||||74.5%|
|
||||
|0968|Binary Tree Cameras|[Go]({{< relref "/ChapterFour/0900~0999/0968.Binary-Tree-Cameras.md" >}})|Hard||||38.7%|
|
||||
|0979|Distribute Coins in Binary Tree|[Go]({{< relref "/ChapterFour/0900~0999/0979.Distribute-Coins-in-Binary-Tree.md" >}})|Medium||||69.6%|
|
||||
|0979|Distribute Coins in Binary Tree|[Go]({{< relref "/ChapterFour/0900~0999/0979.Distribute-Coins-in-Binary-Tree.md" >}})|Medium||||69.7%|
|
||||
|0987|Vertical Order Traversal of a Binary Tree|[Go]({{< relref "/ChapterFour/0900~0999/0987.Vertical-Order-Traversal-of-a-Binary-Tree.md" >}})|Hard||||38.7%|
|
||||
|0993|Cousins in Binary Tree|[Go]({{< relref "/ChapterFour/0900~0999/0993.Cousins-in-Binary-Tree.md" >}})|Easy| O(n)| O(1)||52.3%|
|
||||
|1026|Maximum Difference Between Node and Ancestor|[Go]({{< relref "/ChapterFour/1000~1099/1026.Maximum-Difference-Between-Node-and-Ancestor.md" >}})|Medium||||69.4%|
|
||||
|
||||
@ -44,7 +44,7 @@ weight: 3
|
||||
|0030|Substring with Concatenation of All Words|[Go]({{< relref "/ChapterFour/0001~0099/0030.Substring-with-Concatenation-of-All-Words.md" >}})|Hard| O(n)| O(n)|❤️|26.1%|
|
||||
|0042|Trapping Rain Water|[Go]({{< relref "/ChapterFour/0001~0099/0042.Trapping-Rain-Water.md" >}})|Hard| O(n)| O(1)|❤️|51.0%|
|
||||
|0061|Rotate List|[Go]({{< relref "/ChapterFour/0001~0099/0061.Rotate-List.md" >}})|Medium| O(n)| O(1)||31.7%|
|
||||
|0075|Sort Colors|[Go]({{< relref "/ChapterFour/0001~0099/0075.Sort-Colors.md" >}})|Medium| O(n)| O(1)|❤️|49.2%|
|
||||
|0075|Sort Colors|[Go]({{< relref "/ChapterFour/0001~0099/0075.Sort-Colors.md" >}})|Medium| O(n)| O(1)|❤️|49.3%|
|
||||
|0076|Minimum Window Substring|[Go]({{< relref "/ChapterFour/0001~0099/0076.Minimum-Window-Substring.md" >}})|Hard| O(n)| O(n)|❤️|35.9%|
|
||||
|0080|Remove Duplicates from Sorted Array II|[Go]({{< relref "/ChapterFour/0001~0099/0080.Remove-Duplicates-from-Sorted-Array-II.md" >}})|Medium| O(n)| O(1||46.0%|
|
||||
|0086|Partition List|[Go]({{< relref "/ChapterFour/0001~0099/0086.Partition-List.md" >}})|Medium| O(n)| O(1)|❤️|43.3%|
|
||||
|
||||
@ -39,7 +39,8 @@ weight: 16
|
||||
|0990|Satisfiability of Equality Equations|[Go]({{< relref "/ChapterFour/0900~0999/0990.Satisfiability-of-Equality-Equations.md" >}})|Medium| O(n)| O(n)||46.7%|
|
||||
|1202|Smallest String With Swaps|[Go]({{< relref "/ChapterFour/1200~1299/1202.Smallest-String-With-Swaps.md" >}})|Medium||||48.7%|
|
||||
|1319|Number of Operations to Make Network Connected|[Go]({{< relref "/ChapterFour/1300~1399/1319.Number-of-Operations-to-Make-Network-Connected.md" >}})|Medium||||55.4%|
|
||||
|1579|Remove Max Number of Edges to Keep Graph Fully Traversable|[Go]({{< relref "/ChapterFour/1500~1599/1579.Remove-Max-Number-of-Edges-to-Keep-Graph-Fully-Traversable.md" >}})|Hard||||46.2%|
|
||||
|1579|Remove Max Number of Edges to Keep Graph Fully Traversable|[Go]({{< relref "/ChapterFour/1500~1599/1579.Remove-Max-Number-of-Edges-to-Keep-Graph-Fully-Traversable.md" >}})|Hard||||46.3%|
|
||||
|1631|Path With Minimum Effort|[Go]({{< relref "/ChapterFour/1600~1699/1631.Path-With-Minimum-Effort.md" >}})|Medium||||50.1%|
|
||||
|------------|-------------------------------------------------------|-------| ----------------| ---------------|-------------|-------------|-------------|
|
||||
|
||||
|
||||
|
||||
Reference in New Issue
Block a user