mirror of
https://github.com/halfrost/LeetCode-Go.git
synced 2025-07-06 09:23:19 +08:00
Merge branch 'master' of https://github.com/halfrost/LeetCode-Go
This commit is contained in:
@ -10,8 +10,9 @@ Rotate the image by 90 degrees (clockwise).
|
||||
|
||||
You have to rotate the image **[in-place](https://en.wikipedia.org/wiki/In-place_algorithm)**, which means you have to modify the input 2D matrix directly. **DO NOT** allocate another 2D matrix and do the rotation.
|
||||
|
||||
**Example 1:**
|
||||
**Example 1**:
|
||||
|
||||

|
||||
|
||||
Given input matrix =
|
||||
[
|
||||
@ -28,8 +29,9 @@ You have to rotate the image **[in-place](https://en.wikipedia.org/wiki/In-plac
|
||||
]
|
||||
|
||||
|
||||
**Example 2:**
|
||||
**Example 2**:
|
||||
|
||||

|
||||
|
||||
Given input matrix =
|
||||
[
|
||||
|
||||
@ -16,19 +16,51 @@ type TreeNode = structures.TreeNode
|
||||
* }
|
||||
*/
|
||||
|
||||
// 解法一 dfs
|
||||
func isSymmetric(root *TreeNode) bool {
|
||||
var dfs func(rootLeft, rootRight *TreeNode) bool
|
||||
dfs = func(rootLeft, rootRight *TreeNode) bool {
|
||||
if rootLeft == nil && rootRight == nil {
|
||||
return true
|
||||
}
|
||||
if rootLeft == nil || rootRight == nil {
|
||||
return false
|
||||
}
|
||||
if rootLeft.Val != rootRight.Val {
|
||||
return false
|
||||
}
|
||||
return dfs(rootLeft.Left, rootRight.Right) && dfs(rootLeft.Right, rootRight.Left)
|
||||
}
|
||||
return root == nil || dfs(root.Left, root.Right)
|
||||
}
|
||||
|
||||
func dfs(rootLeft, rootRight *TreeNode) bool {
|
||||
if rootLeft == nil && rootRight == nil {
|
||||
return true
|
||||
}
|
||||
if rootLeft == nil || rootRight == nil {
|
||||
return false
|
||||
}
|
||||
if rootLeft.Val != rootRight.Val {
|
||||
return false
|
||||
}
|
||||
return dfs(rootLeft.Left, rootRight.Right) && dfs(rootLeft.Right, rootRight.Left)
|
||||
}
|
||||
|
||||
// 解法二
|
||||
func isSymmetric1(root *TreeNode) bool {
|
||||
if root == nil {
|
||||
return true
|
||||
}
|
||||
return isSameTree(invertTree(root.Left), root.Right)
|
||||
}
|
||||
|
||||
func isSameTree(p *TreeNode, q *TreeNode) bool {
|
||||
if p == nil && q == nil {
|
||||
return true
|
||||
} else if p != nil && q != nil {
|
||||
if p.Val != q.Val {
|
||||
return false
|
||||
}
|
||||
return isSameTree(p.Left, q.Left) && isSameTree(p.Right, q.Right)
|
||||
} else {
|
||||
return false
|
||||
}
|
||||
}
|
||||
|
||||
func invertTree(root *TreeNode) *TreeNode {
|
||||
if root == nil {
|
||||
return nil
|
||||
}
|
||||
invertTree(root.Left)
|
||||
invertTree(root.Right)
|
||||
root.Left, root.Right = root.Right, root.Left
|
||||
return root
|
||||
}
|
||||
|
||||
@ -6,8 +6,83 @@ import (
|
||||
"github.com/halfrost/LeetCode-Go/template"
|
||||
)
|
||||
|
||||
// 解法一 线段树 Segment Tree,时间复杂度 O(n log n)
|
||||
// 解法一 树状数组,时间复杂度 O(n log n)
|
||||
const LEFTSIDE = 1
|
||||
const RIGHTSIDE = 2
|
||||
|
||||
type Point struct {
|
||||
xAxis int
|
||||
side int
|
||||
index int
|
||||
}
|
||||
|
||||
func getSkyline(buildings [][]int) [][]int {
|
||||
res := [][]int{}
|
||||
if len(buildings) == 0 {
|
||||
return res
|
||||
}
|
||||
allPoints, bit := make([]Point, 0), BinaryIndexedTree{}
|
||||
// [x-axis (value), [1 (left) | 2 (right)], index (building number)]
|
||||
for i, b := range buildings {
|
||||
allPoints = append(allPoints, Point{xAxis: b[0], side: LEFTSIDE, index: i})
|
||||
allPoints = append(allPoints, Point{xAxis: b[1], side: RIGHTSIDE, index: i})
|
||||
}
|
||||
sort.Slice(allPoints, func(i, j int) bool {
|
||||
if allPoints[i].xAxis == allPoints[j].xAxis {
|
||||
return allPoints[i].side < allPoints[j].side
|
||||
}
|
||||
return allPoints[i].xAxis < allPoints[j].xAxis
|
||||
})
|
||||
bit.Init(len(allPoints))
|
||||
kth := make(map[Point]int)
|
||||
for i := 0; i < len(allPoints); i++ {
|
||||
kth[allPoints[i]] = i
|
||||
}
|
||||
for i := 0; i < len(allPoints); i++ {
|
||||
pt := allPoints[i]
|
||||
if pt.side == LEFTSIDE {
|
||||
bit.Add(kth[Point{xAxis: buildings[pt.index][1], side: RIGHTSIDE, index: pt.index}], buildings[pt.index][2])
|
||||
}
|
||||
currHeight := bit.Query(kth[pt] + 1)
|
||||
if len(res) == 0 || res[len(res)-1][1] != currHeight {
|
||||
if len(res) > 0 && res[len(res)-1][0] == pt.xAxis {
|
||||
res[len(res)-1][1] = currHeight
|
||||
} else {
|
||||
res = append(res, []int{pt.xAxis, currHeight})
|
||||
}
|
||||
}
|
||||
}
|
||||
return res
|
||||
}
|
||||
|
||||
type BinaryIndexedTree struct {
|
||||
tree []int
|
||||
capacity int
|
||||
}
|
||||
|
||||
// Init define
|
||||
func (bit *BinaryIndexedTree) Init(capacity int) {
|
||||
bit.tree, bit.capacity = make([]int, capacity+1), capacity
|
||||
}
|
||||
|
||||
// Add define
|
||||
func (bit *BinaryIndexedTree) Add(index int, val int) {
|
||||
for ; index > 0; index -= index & -index {
|
||||
bit.tree[index] = max(bit.tree[index], val)
|
||||
}
|
||||
}
|
||||
|
||||
// Query define
|
||||
func (bit *BinaryIndexedTree) Query(index int) int {
|
||||
sum := 0
|
||||
for ; index <= bit.capacity; index += index & -index {
|
||||
sum = max(sum, bit.tree[index])
|
||||
}
|
||||
return sum
|
||||
}
|
||||
|
||||
// 解法三 线段树 Segment Tree,时间复杂度 O(n log n)
|
||||
func getSkyline1(buildings [][]int) [][]int {
|
||||
st, ans, lastHeight, check := template.SegmentTree{}, [][]int{}, 0, false
|
||||
posMap, pos := discretization218(buildings)
|
||||
tmp := make([]int, len(posMap))
|
||||
@ -54,8 +129,8 @@ func max(a int, b int) int {
|
||||
return b
|
||||
}
|
||||
|
||||
// 解法二 扫描线 Sweep Line,时间复杂度 O(n log n)
|
||||
func getSkyline1(buildings [][]int) [][]int {
|
||||
// 解法三 扫描线 Sweep Line,时间复杂度 O(n log n)
|
||||
func getSkyline2(buildings [][]int) [][]int {
|
||||
size := len(buildings)
|
||||
es := make([]E, 0)
|
||||
for i, b := range buildings {
|
||||
|
||||
@ -30,6 +30,16 @@ func Test_Problem218(t *testing.T) {
|
||||
para218{[][]int{{2, 9, 10}, {3, 7, 15}, {5, 12, 12}, {15, 20, 10}, {19, 24, 8}}},
|
||||
ans218{[][]int{{2, 10}, {3, 15}, {7, 12}, {12, 0}, {15, 10}, {20, 8}, {24, 0}}},
|
||||
},
|
||||
|
||||
{
|
||||
para218{[][]int{{1, 2, 1}, {1, 2, 2}, {1, 2, 3}, {2, 3, 1}, {2, 3, 2}, {2, 3, 3}}},
|
||||
ans218{[][]int{{1, 3}, {3, 0}}},
|
||||
},
|
||||
|
||||
{
|
||||
para218{[][]int{{4, 9, 10}, {4, 9, 15}, {4, 9, 12}, {10, 12, 10}, {10, 12, 8}}},
|
||||
ans218{[][]int{{4, 15}, {9, 0}, {10, 10}, {12, 0}}},
|
||||
},
|
||||
}
|
||||
|
||||
fmt.Printf("------------------------Leetcode Problem 218------------------------\n")
|
||||
|
||||
@ -1,8 +1,6 @@
|
||||
package leetcode
|
||||
|
||||
import (
|
||||
"github.com/halfrost/LeetCode-Go/template"
|
||||
)
|
||||
import "github.com/halfrost/LeetCode-Go/template"
|
||||
|
||||
// NumArray define
|
||||
type NumArray struct {
|
||||
@ -23,6 +21,11 @@ func (this *NumArray) Update(i int, val int) {
|
||||
this.st.Update(i, val)
|
||||
}
|
||||
|
||||
// SumRange define
|
||||
func (this *NumArray) SumRange(i int, j int) int {
|
||||
return this.st.Query(i, j)
|
||||
}
|
||||
|
||||
//解法二 prefixSum,sumRange 时间复杂度 O(1)
|
||||
|
||||
// // NumArray define
|
||||
@ -60,6 +63,30 @@ func (this *NumArray) Update(i int, val int) {
|
||||
// return this.prefixSum[j]
|
||||
// }
|
||||
|
||||
// 解法三 树状数组
|
||||
// type NumArray struct {
|
||||
// bit template.BinaryIndexedTree
|
||||
// data []int
|
||||
// }
|
||||
|
||||
// // Constructor define
|
||||
// func Constructor307(nums []int) NumArray {
|
||||
// bit := template.BinaryIndexedTree{}
|
||||
// bit.InitWithNums(nums)
|
||||
// return NumArray{bit: bit, data: nums}
|
||||
// }
|
||||
|
||||
// // Update define
|
||||
// func (this *NumArray) Update(i int, val int) {
|
||||
// this.bit.Add(i+1, val-this.data[i])
|
||||
// this.data[i] = val
|
||||
// }
|
||||
|
||||
// // SumRange define
|
||||
// func (this *NumArray) SumRange(i int, j int) int {
|
||||
// return this.bit.Query(j+1) - this.bit.Query(i)
|
||||
// }
|
||||
|
||||
/**
|
||||
* Your NumArray object will be instantiated and called as such:
|
||||
* obj := Constructor(nums);
|
||||
|
||||
@ -12,9 +12,25 @@ func Test_Problem307(t *testing.T) {
|
||||
obj.Update(1, 2)
|
||||
fmt.Printf("obj = %v\n", obj)
|
||||
fmt.Printf("SumRange(0,2) = %v\n", obj.SumRange(0, 2))
|
||||
}
|
||||
|
||||
// SumRange define
|
||||
func (ma *NumArray) SumRange(i int, j int) int {
|
||||
return ma.st.Query(i, j)
|
||||
obj = Constructor307([]int{-1})
|
||||
fmt.Printf("obj = %v\n", obj)
|
||||
fmt.Printf("SumRange(0,2) = %v\n", obj.SumRange(0, 0))
|
||||
obj.Update(0, 1)
|
||||
fmt.Printf("obj = %v\n", obj)
|
||||
fmt.Printf("SumRange(0,2) = %v\n", obj.SumRange(0, 0))
|
||||
|
||||
obj = Constructor307([]int{7, 2, 7, 2, 0})
|
||||
fmt.Printf("obj = %v\n", obj)
|
||||
obj.Update(4, 6)
|
||||
obj.Update(0, 2)
|
||||
obj.Update(0, 9)
|
||||
fmt.Printf("SumRange(0,2) = %v\n", obj.SumRange(4, 4))
|
||||
obj.Update(3, 8)
|
||||
fmt.Printf("obj = %v\n", obj)
|
||||
fmt.Printf("SumRange(0,2) = %v\n", obj.SumRange(0, 4))
|
||||
obj.Update(4, 1)
|
||||
fmt.Printf("SumRange(0,2) = %v\n", obj.SumRange(0, 3))
|
||||
fmt.Printf("SumRange(0,2) = %v\n", obj.SumRange(0, 4))
|
||||
obj.Update(0, 4)
|
||||
}
|
||||
|
||||
@ -48,3 +48,4 @@ sumRange(0, 2) -> 8
|
||||
- 给出一个数组,数组里面的数都是`**可变**`的,设计一个数据结构能够满足查询数组任意区间内元素的和。
|
||||
- 对比第 303 题,这一题由于数组里面的元素都是**`可变`**的,所以第一个想到的解法就是线段树,构建一颗线段树,父结点内存的是两个子结点的和,初始化建树的时间复杂度是 O(log n),查询区间元素和的时间复杂度是 O(log n),更新元素值的时间复杂度是 O(log n)。
|
||||
- 如果此题还用 prefixSum 的思路解答呢?那每次 update 操作的时间复杂度都是 O(n),因为每次更改一个值,最坏情况就是所有的 prefixSum 都要更新一次。prefixSum 的方法在这道题上面也可以 AC,只不过时间排名在 5%,非常差。
|
||||
- 此题也可以用树状数组解决。代码很直白,区间查询即是两个区间前缀和相减。最简单的树状数组应用。
|
||||
|
||||
@ -6,6 +6,7 @@ import (
|
||||
"github.com/halfrost/LeetCode-Go/template"
|
||||
)
|
||||
|
||||
// 解法一 线段树
|
||||
func countSmaller(nums []int) []int {
|
||||
if len(nums) == 0 {
|
||||
return []int{}
|
||||
@ -35,3 +36,31 @@ func countSmaller(nums []int) []int {
|
||||
}
|
||||
return res
|
||||
}
|
||||
|
||||
// 解法二 树状数组
|
||||
func countSmaller1(nums []int) []int {
|
||||
// copy 一份原数组至所有数字 allNums 数组中
|
||||
allNums, res := make([]int, len(nums)), []int{}
|
||||
copy(allNums, nums)
|
||||
// 将 allNums 离散化
|
||||
sort.Ints(allNums)
|
||||
k := 1
|
||||
kth := map[int]int{allNums[0]: k}
|
||||
for i := 1; i < len(allNums); i++ {
|
||||
if allNums[i] != allNums[i-1] {
|
||||
k++
|
||||
kth[allNums[i]] = k
|
||||
}
|
||||
}
|
||||
// 树状数组 Query
|
||||
bit := template.BinaryIndexedTree{}
|
||||
bit.Init(k)
|
||||
for i := len(nums) - 1; i >= 0; i-- {
|
||||
res = append(res, bit.Query(kth[nums[i]]-1))
|
||||
bit.Add(kth[nums[i]], 1)
|
||||
}
|
||||
for i := 0; i < len(res)/2; i++ {
|
||||
res[i], res[len(res)-1-i] = res[len(res)-1-i], res[i]
|
||||
}
|
||||
return res
|
||||
}
|
||||
|
||||
@ -39,3 +39,4 @@ You are given an integer array nums and you have to return a new counts arra
|
||||
|
||||
- 给出一个数组,要求输出数组中每个元素相对于数组中的位置右边比它小的元素。
|
||||
- 这一题是第 327 题的缩水版。由于需要找数组位置右边比当前位置元素小的元素,所以从数组右边开始往左边扫。构造一颗线段树,线段树里面父节点存的是子节点出现的次数和。有可能给的数据会很大,所以构造线段树的时候先离散化。还需要注意的是数组里面可能有重复元素,所以构造线段树要先去重并排序。从右往左扫的过程中,依次添加数组中的元素,添加了一次就立即 query 一次。query 的区间是 [minNum, nums[i]-1]。如果是 minNum 则输出 0,并且也要记得插入这个最小值。这一题的思路和第 327 题大体类似,详解可见第 327 题。
|
||||
- 这一题同样可以用树状数组来解答。相比 327 题简单很多。第一步还是把所有用到的元素放入 allNums 数组中,第二步排序 + 离散化。由于题目要求输出右侧更小的元素,所以第三步倒序插入构造树状数组,Query 查询 `[1,i-1]` 区间内元素总数即为右侧更小元素个数。注意最终输出是顺序输出,计算是逆序计算的,最终数组里面的答案还需要逆序一遍。相同的套路题有,第 327 题,第 493 题。
|
||||
@ -40,8 +40,39 @@ func countRangeSum(nums []int, lower int, upper int) int {
|
||||
return res
|
||||
}
|
||||
|
||||
// 解法二 暴力,时间复杂度 O(n^2)
|
||||
// 解法二 树状数组,时间复杂度 O(n log n)
|
||||
func countRangeSum1(nums []int, lower int, upper int) int {
|
||||
n := len(nums)
|
||||
// 计算前缀和 preSum,以及后面统计时会用到的所有数字 allNums
|
||||
allNums, preSum, res := make([]int, 1, 3*n+1), make([]int, n+1), 0
|
||||
for i, v := range nums {
|
||||
preSum[i+1] = preSum[i] + v
|
||||
allNums = append(allNums, preSum[i+1], preSum[i+1]-lower, preSum[i+1]-upper)
|
||||
}
|
||||
// 将 allNums 离散化
|
||||
sort.Ints(allNums)
|
||||
k := 1
|
||||
kth := map[int]int{allNums[0]: k}
|
||||
for i := 1; i <= 3*n; i++ {
|
||||
if allNums[i] != allNums[i-1] {
|
||||
k++
|
||||
kth[allNums[i]] = k
|
||||
}
|
||||
}
|
||||
// 遍历 preSum,利用树状数组计算每个前缀和对应的合法区间数
|
||||
bit := template.BinaryIndexedTree{}
|
||||
bit.Init(k)
|
||||
bit.Add(kth[0], 1)
|
||||
for _, sum := range preSum[1:] {
|
||||
left, right := kth[sum-upper], kth[sum-lower]
|
||||
res += bit.Query(right) - bit.Query(left-1)
|
||||
bit.Add(kth[sum], 1)
|
||||
}
|
||||
return res
|
||||
}
|
||||
|
||||
// 解法三 暴力,时间复杂度 O(n^2)
|
||||
func countRangeSum2(nums []int, lower int, upper int) int {
|
||||
res, n := 0, len(nums)
|
||||
for i := 0; i < n; i++ {
|
||||
tmp := 0
|
||||
|
||||
@ -17,11 +17,10 @@ Given an integer array `nums`, return the number of range sums that lie in `[l
|
||||
## 题目大意
|
||||
|
||||
|
||||
给定一个整数数组 nums,返回区间和在 [lower, upper] 之间的个数,包含 lower 和 upper。区间和 S(i, j) 表示在 nums 中,位置从 i 到 j 的元素之和,包含 i 和 j (i ≤ j)。
|
||||
|
||||
说明:
|
||||
最直观的算法复杂度是 O(n^2) ,请在此基础上优化你的算法。
|
||||
给定一个整数数组 nums 。区间和 S(i, j) 表示在 nums 中,位置从 i 到 j 的元素之和,包含 i 和 j (i ≤ j)。请你以下标 i (0 <= i <= nums.length )为起点,元素个数逐次递增,计算子数组内的元素和。当元素和落在范围 [lower, upper] (包含 lower 和 upper)之内时,记录子数组当前最末元素下标 j ,记作 有效 区间和 S(i, j) 。求数组中,值位于范围 [lower, upper] (包含 lower 和 upper)之内的 有效 区间和的个数。
|
||||
|
||||
注意:
|
||||
最直观的算法复杂度是 O(n2) ,请在此基础上优化你的算法。
|
||||
|
||||
## 解题思路
|
||||
|
||||
@ -75,3 +74,5 @@ Given an integer array `nums`, return the number of range sums that lie in `[l
|
||||
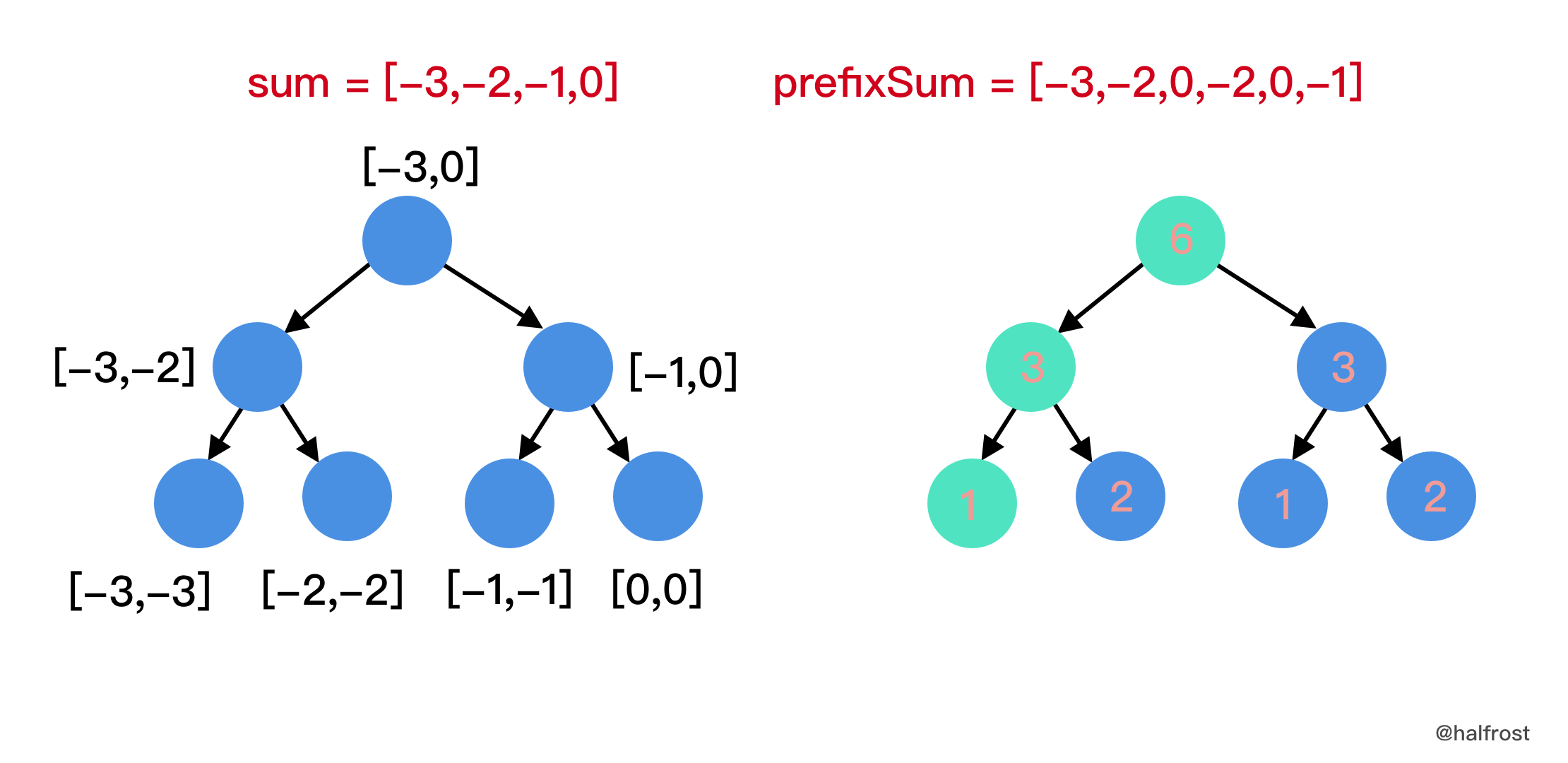
|
||||
|
||||
这时候查找区间变为了 `[-3 + prefixSum[0-1], -1 + prefixSum[0-1]] = [-3,-1]`,注意 `prefixSum[-1] = 0`,即判断 `-3 ≤ sum(0, 0,1,2,3,4,5) ≤ -1`,满足等式的有几种情况,这里有六种情况,即 `j = 0`、`j = 1`、`j = 2`、 `j = 3` 、`j = 4` 或者 `j = 5`,满足等式的有 `j = 0`、`j = 1`、 `j = 3` 和 `j = 5`,即 `-3 ≤ sum(0, 0) ≤ -1` 、 `-3 ≤ sum(0, 1) ≤ -1`、`-3 ≤ sum(0, 3) ≤ -1` 和 `-3 ≤ sum(0, 5) ≤ -1`。所以这一步 `res = 4`。最后的答案就是把每一步的结果都累加,`res = 1 + 0 + 2 + 0 + 0 + 4 = 7`。
|
||||
|
||||
- 此题同样可以用树状数组来解答。同样把问题先转化成区间 Query 的模型,`lower ≤ prefixSum(j) - prefixSum(i-1) ≤ upper` 等价于 `prefixSum(j) - upper ≤ prefixSum(i-1) ≤ prefixSum(j) - lower`,`i` 的取值在 `[0,j-1]` 区间内。所以题目可以转化为 `i` 在 `[0,j-1]` 区间内取值,问数组 `prefixSum[0...j-1]` 中的所有取值,位于区间 `[prefixSum(j) - upper, prefixSum(j) - lower]` 内的次数。在树状数组中,区间内的前缀和可以转化为 2 个区间的前缀和相减,即 `Query([i,j]) = Query(j) - Query(i-1)`。所以这道题枚举数组 `prefixSum[0...j-1]` 中每个值是否出现在指定区间内出现次数即可。第一步先将所有的前缀和 `prefixSum(j)` 以及 `[prefixSum(j) - upper, prefixSum(j) - lower]` 计算出来。第二步排序和离散化,离散化以后的点区间为 `[1,n]`。最后根据数组 `prefixSum(j)` 的值在指定区间内查询出现次数即可。相同的套路题有,第 315 题,第 493 题。
|
||||
@ -0,0 +1,33 @@
|
||||
package leetcode
|
||||
|
||||
import "sort"
|
||||
|
||||
func largestDivisibleSubset(nums []int) []int {
|
||||
sort.Ints(nums)
|
||||
dp, res := make([]int, len(nums)), []int{}
|
||||
for i := range dp {
|
||||
dp[i] = 1
|
||||
}
|
||||
maxSize, maxVal := 1, 1
|
||||
for i := 1; i < len(nums); i++ {
|
||||
for j, v := range nums[:i] {
|
||||
if nums[i]%v == 0 && dp[j]+1 > dp[i] {
|
||||
dp[i] = dp[j] + 1
|
||||
}
|
||||
}
|
||||
if dp[i] > maxSize {
|
||||
maxSize, maxVal = dp[i], nums[i]
|
||||
}
|
||||
}
|
||||
if maxSize == 1 {
|
||||
return []int{nums[0]}
|
||||
}
|
||||
for i := len(nums) - 1; i >= 0 && maxSize > 0; i-- {
|
||||
if dp[i] == maxSize && maxVal%nums[i] == 0 {
|
||||
res = append(res, nums[i])
|
||||
maxVal = nums[i]
|
||||
maxSize--
|
||||
}
|
||||
}
|
||||
return res
|
||||
}
|
||||
@ -0,0 +1,47 @@
|
||||
package leetcode
|
||||
|
||||
import (
|
||||
"fmt"
|
||||
"testing"
|
||||
)
|
||||
|
||||
type question368 struct {
|
||||
para368
|
||||
ans368
|
||||
}
|
||||
|
||||
// para 是参数
|
||||
// one 代表第一个参数
|
||||
type para368 struct {
|
||||
one []int
|
||||
}
|
||||
|
||||
// ans 是答案
|
||||
// one 代表第一个答案
|
||||
type ans368 struct {
|
||||
one []int
|
||||
}
|
||||
|
||||
func Test_Problem368(t *testing.T) {
|
||||
|
||||
qs := []question368{
|
||||
|
||||
{
|
||||
para368{[]int{1, 2, 3}},
|
||||
ans368{[]int{1, 2}},
|
||||
},
|
||||
|
||||
{
|
||||
para368{[]int{1, 2, 4, 8}},
|
||||
ans368{[]int{1, 2, 4, 8}},
|
||||
},
|
||||
}
|
||||
|
||||
fmt.Printf("------------------------Leetcode Problem 368------------------------\n")
|
||||
|
||||
for _, q := range qs {
|
||||
_, p := q.ans368, q.para368
|
||||
fmt.Printf("【input】:%v 【output】:%v\n", p, largestDivisibleSubset(p.one))
|
||||
}
|
||||
fmt.Printf("\n\n\n")
|
||||
}
|
||||
86
leetcode/0368.Largest-Divisible-Subset/README.md
Normal file
86
leetcode/0368.Largest-Divisible-Subset/README.md
Normal file
@ -0,0 +1,86 @@
|
||||
# [368. Largest Divisible Subset](https://leetcode.com/problems/largest-divisible-subset/)
|
||||
|
||||
|
||||
## 题目
|
||||
|
||||
Given a set of **distinct** positive integers `nums`, return the largest subset `answer` such that every pair `(answer[i], answer[j])` of elements in this subset satisfies:
|
||||
|
||||
- `answer[i] % answer[j] == 0`, or
|
||||
- `answer[j] % answer[i] == 0`
|
||||
|
||||
If there are multiple solutions, return any of them.
|
||||
|
||||
**Example 1:**
|
||||
|
||||
```
|
||||
Input: nums = [1,2,3]
|
||||
Output: [1,2]
|
||||
Explanation: [1,3] is also accepted.
|
||||
|
||||
```
|
||||
|
||||
**Example 2:**
|
||||
|
||||
```
|
||||
Input: nums = [1,2,4,8]
|
||||
Output: [1,2,4,8]
|
||||
|
||||
```
|
||||
|
||||
**Constraints:**
|
||||
|
||||
- `1 <= nums.length <= 1000`
|
||||
- `1 <= nums[i] <= 2 * 109`
|
||||
- All the integers in `nums` are **unique**.
|
||||
|
||||
## 题目大意
|
||||
|
||||
给你一个由 无重复 正整数组成的集合 nums ,请你找出并返回其中最大的整除子集 answer ,子集中每一元素对 (answer[i], answer[j]) 都应当满足:
|
||||
|
||||
- answer[i] % answer[j] == 0 ,或
|
||||
- answer[j] % answer[i] == 0
|
||||
|
||||
如果存在多个有效解子集,返回其中任何一个均可。
|
||||
|
||||
## 解题思路
|
||||
|
||||
- 根据题目数据规模 1000,可以估计此题大概率是动态规划,并且时间复杂度是 O(n^2)。先将集合排序,以某一个小的数作为基准,不断的选择能整除的数加入集合。按照这个思路考虑,此题和第 300 题经典的 LIS 解题思路一致。只不过 LIS 每次选择更大的数,此题除了选择更大的数,只不过多了一个判断,这个更大的数能否整除当前集合里面的所有元素。按照此法一定可以找出最大的集合。
|
||||
- 剩下的问题是如何输出最大集合。这道题的集合具有重叠子集的性质,例如 [2,4,8,16] 这个集合,长度是 4,它一定包含长度为 3 的子集,因为从它里面随便取 3 个数形成的子集也满足元素相互能整除的条件。同理,它也一定包含长度为 2,长度为 1 的子集。由于有这个性质,可以利用 dp 数组里面的数据,输出最大集合。例如,[2,4,6,8,9,13,16,40],由动态规划可以找到最大集合是 [2,4,8,16]。长度为 4 的找到了,再找长度为 3 的,[2,4,8],[2,4,40]。在最大集合中,最大元素是 16,所以 [2,4,40] 这个集合排除,它的最大元素大于 16。选定 [2,4,8] 这个集合,此时最大元素是 8 。以此类推,筛选到最后,便可以输出 [16,8,4,2] 这个组最大集合的答案了。
|
||||
|
||||
## 代码
|
||||
|
||||
```go
|
||||
package leetcode
|
||||
|
||||
import "sort"
|
||||
|
||||
func largestDivisibleSubset(nums []int) []int {
|
||||
sort.Ints(nums)
|
||||
dp, res := make([]int, len(nums)), []int{}
|
||||
for i := range dp {
|
||||
dp[i] = 1
|
||||
}
|
||||
maxSize, maxVal := 1, 1
|
||||
for i := 1; i < len(nums); i++ {
|
||||
for j, v := range nums[:i] {
|
||||
if nums[i]%v == 0 && dp[j]+1 > dp[i] {
|
||||
dp[i] = dp[j] + 1
|
||||
}
|
||||
}
|
||||
if dp[i] > maxSize {
|
||||
maxSize, maxVal = dp[i], nums[i]
|
||||
}
|
||||
}
|
||||
if maxSize == 1 {
|
||||
return []int{nums[0]}
|
||||
}
|
||||
for i := len(nums) - 1; i >= 0 && maxSize > 0; i-- {
|
||||
if dp[i] == maxSize && maxVal%nums[i] == 0 {
|
||||
res = append(res, nums[i])
|
||||
maxVal = nums[i]
|
||||
maxSize--
|
||||
}
|
||||
}
|
||||
return res
|
||||
}
|
||||
```
|
||||
@ -1,6 +1,20 @@
|
||||
package leetcode
|
||||
|
||||
func combinationSum4(nums []int, target int) int {
|
||||
dp := make([]int, target+1)
|
||||
dp[0] = 1
|
||||
for i := 1; i <= target; i++ {
|
||||
for _, num := range nums {
|
||||
if i-num >= 0 {
|
||||
dp[i] += dp[i-num]
|
||||
}
|
||||
}
|
||||
}
|
||||
return dp[target]
|
||||
}
|
||||
|
||||
// 暴力解法超时
|
||||
func combinationSum41(nums []int, target int) int {
|
||||
if len(nums) == 0 {
|
||||
return 0
|
||||
}
|
||||
@ -34,7 +34,7 @@ func Test_Problem377(t *testing.T) {
|
||||
|
||||
{
|
||||
para377{[]int{1, 2, 3}, 32},
|
||||
ans377{7},
|
||||
ans377{181997601},
|
||||
},
|
||||
}
|
||||
|
||||
98
leetcode/0377.Combination-Sum-IV/README.md
Normal file
98
leetcode/0377.Combination-Sum-IV/README.md
Normal file
@ -0,0 +1,98 @@
|
||||
# [377. Combination Sum IV](https://leetcode.com/problems/combination-sum-iv/)
|
||||
|
||||
|
||||
## 题目
|
||||
|
||||
Given an array of **distinct** integers `nums` and a target integer `target`, return *the number of possible combinations that add up to* `target`.
|
||||
|
||||
The answer is **guaranteed** to fit in a **32-bit** integer.
|
||||
|
||||
**Example 1:**
|
||||
|
||||
```
|
||||
Input: nums = [1,2,3], target = 4
|
||||
Output: 7
|
||||
Explanation:
|
||||
The possible combination ways are:
|
||||
(1, 1, 1, 1)
|
||||
(1, 1, 2)
|
||||
(1, 2, 1)
|
||||
(1, 3)
|
||||
(2, 1, 1)
|
||||
(2, 2)
|
||||
(3, 1)
|
||||
Note that different sequences are counted as different combinations.
|
||||
|
||||
```
|
||||
|
||||
**Example 2:**
|
||||
|
||||
```
|
||||
Input: nums = [9], target = 3
|
||||
Output: 0
|
||||
```
|
||||
|
||||
**Constraints:**
|
||||
|
||||
- `1 <= nums.length <= 200`
|
||||
- `1 <= nums[i] <= 1000`
|
||||
- All the elements of `nums` are **unique**.
|
||||
- `1 <= target <= 1000`
|
||||
|
||||
**Follow up:** What if negative numbers are allowed in the given array? How does it change the problem? What limitation we need to add to the question to allow negative numbers?
|
||||
|
||||
## 题目大意
|
||||
|
||||
给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。题目数据保证答案符合 32 位整数范围。
|
||||
|
||||
## 解题思路
|
||||
|
||||
- Combination Sum 这是系列问题。拿到题目,笔者先用暴力解法 dfs 尝试了一版,包含的重叠子问题特别多,剪枝条件也没有写好,果然超时。元素只有 [1,2,3] 这三种,target = 32,这组数据居然有 181997601 这么多种情况。仔细看了题目数据规模 1000,基本可以断定此题是动态规划,并且时间复杂度是 O(n^2)。
|
||||
- 本题和完全背包有点像,但是还是有区别。完全背包的取法内部不区分顺序。例如 5 = 1 + 2 + 2。但是本题是 3 种答案 (1,2,2),(2,1,2),(2,2,1)。定义 dp[i] 为总和为 target = i 的组合总数。最终答案存在 dp[target] 中。状态转移方程为:
|
||||
|
||||
$$dp[i] =\left\{\begin{matrix}1,i=0\\ \sum dp[i-j],i\neq 0\end{matrix}\right.$$
|
||||
|
||||
- 这道题最后有一个进阶问题。如果给定的数组中含有负数,则会导致出现无限长度的排列。例如,假设数组 nums 中含有正整数 a 和负整数 −b(其中 a>0,b>0,-b<0),则有 a×b+(−b)×a=0,对于任意一个元素之和等于 target 的排列,在该排列的后面添加 b 个 a 和 a 个 −b 之后,得到的新排列的元素之和仍然等于 target,而且还可以在新排列的后面继续 b 个 a 和 a 个 −b。因此只要存在元素之和等于 target 的排列,就能构造出无限长度的排列。如果允许负数出现,则必须限制排列的最大长度,不然会出现无限长度的排列。
|
||||
|
||||
## 代码
|
||||
|
||||
```go
|
||||
package leetcode
|
||||
|
||||
func combinationSum4(nums []int, target int) int {
|
||||
dp := make([]int, target+1)
|
||||
dp[0] = 1
|
||||
for i := 1; i <= target; i++ {
|
||||
for _, num := range nums {
|
||||
if i-num >= 0 {
|
||||
dp[i] += dp[i-num]
|
||||
}
|
||||
}
|
||||
}
|
||||
return dp[target]
|
||||
}
|
||||
|
||||
// 暴力解法超时
|
||||
func combinationSum41(nums []int, target int) int {
|
||||
if len(nums) == 0 {
|
||||
return 0
|
||||
}
|
||||
c, res := []int{}, 0
|
||||
findcombinationSum4(nums, target, 0, c, &res)
|
||||
return res
|
||||
}
|
||||
|
||||
func findcombinationSum4(nums []int, target, index int, c []int, res *int) {
|
||||
if target <= 0 {
|
||||
if target == 0 {
|
||||
*res++
|
||||
}
|
||||
return
|
||||
}
|
||||
for i := 0; i < len(nums); i++ {
|
||||
c = append(c, nums[i])
|
||||
findcombinationSum4(nums, target-nums[i], i, c, res)
|
||||
c = c[:len(c)-1]
|
||||
}
|
||||
}
|
||||
```
|
||||
@ -6,8 +6,69 @@ import (
|
||||
"github.com/halfrost/LeetCode-Go/template"
|
||||
)
|
||||
|
||||
// 解法一 线段树,时间复杂度 O(n log n)
|
||||
// 解法一 归并排序 mergesort,时间复杂度 O(n log n)
|
||||
func reversePairs(nums []int) int {
|
||||
buf := make([]int, len(nums))
|
||||
return mergesortCount(nums, buf)
|
||||
}
|
||||
|
||||
func mergesortCount(nums, buf []int) int {
|
||||
if len(nums) <= 1 {
|
||||
return 0
|
||||
}
|
||||
mid := (len(nums) - 1) / 2
|
||||
cnt := mergesortCount(nums[:mid+1], buf)
|
||||
cnt += mergesortCount(nums[mid+1:], buf)
|
||||
for i, j := 0, mid+1; i < mid+1; i++ { // Note!!! j is increasing.
|
||||
for ; j < len(nums) && nums[i] <= 2*nums[j]; j++ {
|
||||
}
|
||||
cnt += len(nums) - j
|
||||
}
|
||||
copy(buf, nums)
|
||||
for i, j, k := 0, mid+1, 0; k < len(nums); {
|
||||
if j >= len(nums) || i < mid+1 && buf[i] > buf[j] {
|
||||
nums[k] = buf[i]
|
||||
i++
|
||||
} else {
|
||||
nums[k] = buf[j]
|
||||
j++
|
||||
}
|
||||
k++
|
||||
}
|
||||
return cnt
|
||||
}
|
||||
|
||||
// 解法二 树状数组,时间复杂度 O(n log n)
|
||||
func reversePairs1(nums []int) (cnt int) {
|
||||
n := len(nums)
|
||||
if n <= 1 {
|
||||
return
|
||||
}
|
||||
// 离散化所有下面统计时会出现的元素
|
||||
allNums := make([]int, 0, 2*n)
|
||||
for _, v := range nums {
|
||||
allNums = append(allNums, v, 2*v)
|
||||
}
|
||||
sort.Ints(allNums)
|
||||
k := 1
|
||||
kth := map[int]int{allNums[0]: k}
|
||||
for i := 1; i < 2*n; i++ {
|
||||
if allNums[i] != allNums[i-1] {
|
||||
k++
|
||||
kth[allNums[i]] = k
|
||||
}
|
||||
}
|
||||
bit := template.BinaryIndexedTree{}
|
||||
bit.Init(k)
|
||||
for i, v := range nums {
|
||||
cnt += i - bit.Query(kth[2*v])
|
||||
bit.Add(kth[v], 1)
|
||||
}
|
||||
return
|
||||
}
|
||||
|
||||
// 解法三 线段树,时间复杂度 O(n log n)
|
||||
func reversePairs2(nums []int) int {
|
||||
if len(nums) < 2 {
|
||||
return 0
|
||||
}
|
||||
@ -42,35 +103,3 @@ func reversePairs(nums []int) int {
|
||||
}
|
||||
return res
|
||||
}
|
||||
|
||||
// 解法二 mergesort
|
||||
func reversePairs1(nums []int) int {
|
||||
buf := make([]int, len(nums))
|
||||
return mergesortCount(nums, buf)
|
||||
}
|
||||
|
||||
func mergesortCount(nums, buf []int) int {
|
||||
if len(nums) <= 1 {
|
||||
return 0
|
||||
}
|
||||
mid := (len(nums) - 1) / 2
|
||||
cnt := mergesortCount(nums[:mid+1], buf)
|
||||
cnt += mergesortCount(nums[mid+1:], buf)
|
||||
for i, j := 0, mid+1; i < mid+1; i++ { // Note!!! j is increasing.
|
||||
for ; j < len(nums) && nums[i] <= 2*nums[j]; j++ {
|
||||
}
|
||||
cnt += len(nums) - j
|
||||
}
|
||||
copy(buf, nums)
|
||||
for i, j, k := 0, mid+1, 0; k < len(nums); {
|
||||
if j >= len(nums) || i < mid+1 && buf[i] > buf[j] {
|
||||
nums[k] = buf[i]
|
||||
i++
|
||||
} else {
|
||||
nums[k] = buf[j]
|
||||
j++
|
||||
}
|
||||
k++
|
||||
}
|
||||
return cnt
|
||||
}
|
||||
|
||||
@ -31,6 +31,11 @@ func Test_Problem493(t *testing.T) {
|
||||
ans493{2},
|
||||
},
|
||||
|
||||
{
|
||||
para493{[]int{9, 8, 7, 4, 7, 2, 3, 8, 7, 0}},
|
||||
ans493{18},
|
||||
},
|
||||
|
||||
{
|
||||
para493{[]int{2, 4, 3, 5, 1}},
|
||||
ans493{3},
|
||||
|
||||
@ -38,5 +38,6 @@ You need to return the number of important reverse pairs in the given array.
|
||||
|
||||
- 给出一个数组,要求找出满足条件的所有的“重要的反转对” (i,j)。重要的反转对的定义是:`i<j`,并且 `nums[i] > 2*nums[j]`。
|
||||
- 这一题是 327 题的变种题。首先将数组中所有的元素以及各自的 `2*nums[i] + 1` 都放在字典中去重。去重以后再做离散化处理。这一题的测试用例会卡离散化,如果不离散化,Math.MaxInt32 会导致数字溢出,见测试用例中 2147483647, -2147483647 这组测试用例。离散后,映射关系 保存在字典中。从左往右遍历数组,先 query ,再 update ,这个顺序和第 327 题是反的。先 query 查找 `[2*nums[i] + 1, len(indexMap)-1]` 这个区间内满足条件的值,这个区间内的值都是 `> 2*nums[j]` 的。这一题移动的是 `j`,`j` 不断的变化,往线段树中不断插入的是 `i`。每轮循环先 query 一次前一轮循环中累积插入线段树中的 `i`,这些累积在线段树中的代表的是所有在 `j` 前面的 `i`。query 查询的是本轮 `[2*nums[j] + 1, len(indexMap)-1]`,如果能找到,即找到了这样一个 `j`,能满足 `nums[i] > 2*nums[j`, 把整个数组都扫完,累加的 query 出来的 count 计数就是最终答案。
|
||||
- 另外一种解法是树状数组。树状数组最擅长解答逆序对的问题。先将原数组中所有的元素值的 2 倍算出来,和原数组合并到一个大数组中。这个大数组中装了所有可能产生 2 倍逆序对的元素值。然后再将他们所有值排序,离散化。离散化以后便将问题集转化成 `[1,N]` 这个区间。于是回到了树状数组经典的求逆序对的问题。逆序插入原数组构造树状数组,或者正序插入原数组构造树状数组都可以解答此题。
|
||||
- 类似的题目:第 327 题,第 315 题。
|
||||
- 这一题用线段树并不是最优解,用线段树解这一题是为了训练线段树这个数据结构。最优解是解法二中的 mergesort。
|
||||
- 这一题用线段树和树状数组并不是最优解,用线段树和树状数组解这一题是为了训练线段树和树状数组这两个数据结构。最优解是解法一中的 mergesort。
|
||||
|
||||
@ -0,0 +1,43 @@
|
||||
package leetcode
|
||||
|
||||
// Definition for a Node.
|
||||
type Node struct {
|
||||
Val int
|
||||
Children []*Node
|
||||
}
|
||||
|
||||
// 解法一 非递归
|
||||
func preorder(root *Node) []int {
|
||||
res := []int{}
|
||||
if root == nil {
|
||||
return res
|
||||
}
|
||||
stack := []*Node{root}
|
||||
for len(stack) > 0 {
|
||||
r := stack[len(stack)-1]
|
||||
stack = stack[:len(stack)-1]
|
||||
res = append(res, r.Val)
|
||||
tmp := []*Node{}
|
||||
for _, v := range r.Children {
|
||||
tmp = append([]*Node{v}, tmp...) // 逆序存点
|
||||
}
|
||||
stack = append(stack, tmp...)
|
||||
}
|
||||
return res
|
||||
}
|
||||
|
||||
// 解法二 递归
|
||||
func preorder1(root *Node) []int {
|
||||
res := []int{}
|
||||
preorderdfs(root, &res)
|
||||
return res
|
||||
}
|
||||
|
||||
func preorderdfs(root *Node, res *[]int) {
|
||||
if root != nil {
|
||||
*res = append(*res, root.Val)
|
||||
for i := 0; i < len(root.Children); i++ {
|
||||
preorderdfs(root.Children[i], res)
|
||||
}
|
||||
}
|
||||
}
|
||||
@ -0,0 +1,82 @@
|
||||
package leetcode
|
||||
|
||||
import (
|
||||
"fmt"
|
||||
"testing"
|
||||
|
||||
"github.com/halfrost/LeetCode-Go/structures"
|
||||
)
|
||||
|
||||
type question589 struct {
|
||||
para589
|
||||
ans589
|
||||
}
|
||||
|
||||
// para 是参数
|
||||
// one 代表第一个参数
|
||||
type para589 struct {
|
||||
one []int
|
||||
}
|
||||
|
||||
// ans 是答案
|
||||
// one 代表第一个答案
|
||||
type ans589 struct {
|
||||
one []int
|
||||
}
|
||||
|
||||
func Test_Problem589(t *testing.T) {
|
||||
|
||||
qs := []question589{
|
||||
|
||||
{
|
||||
para589{[]int{1, structures.NULL, 3, 2, 4, structures.NULL, 5, 6}},
|
||||
ans589{[]int{1, 3, 5, 6, 2, 4}},
|
||||
},
|
||||
|
||||
{
|
||||
para589{[]int{1, structures.NULL, 2, 3, 4, 5, structures.NULL, structures.NULL, 6, 7, structures.NULL, 8, structures.NULL, 9, 10, structures.NULL, structures.NULL, 11, structures.NULL, 12, structures.NULL, 13, structures.NULL, structures.NULL, 14}},
|
||||
ans589{[]int{1, 2, 3, 6, 7, 11, 14, 4, 8, 12, 5, 9, 13, 10}},
|
||||
},
|
||||
}
|
||||
|
||||
fmt.Printf("------------------------Leetcode Problem 589------------------------\n")
|
||||
|
||||
for _, q := range qs {
|
||||
_, p := q.ans589, q.para589
|
||||
fmt.Printf("【input】:%v ", p)
|
||||
rootOne := int2NaryNode(p.one)
|
||||
fmt.Printf("【output】:%v \n", preorder(rootOne))
|
||||
}
|
||||
fmt.Printf("\n\n\n")
|
||||
}
|
||||
|
||||
func int2NaryNode(nodes []int) *Node {
|
||||
root := &Node{}
|
||||
if len(nodes) > 1 {
|
||||
root.Val = nodes[0]
|
||||
}
|
||||
queue := []*Node{}
|
||||
queue = append(queue, root)
|
||||
i := 1
|
||||
count := 0
|
||||
for i < len(nodes) {
|
||||
node := queue[0]
|
||||
|
||||
childrens := []*Node{}
|
||||
for ; i < len(nodes) && nodes[i] != structures.NULL; i++ {
|
||||
tmp := &Node{Val: nodes[i]}
|
||||
childrens = append(childrens, tmp)
|
||||
queue = append(queue, tmp)
|
||||
}
|
||||
count++
|
||||
if count%2 == 0 {
|
||||
queue = queue[1:]
|
||||
count = 1
|
||||
}
|
||||
if node != nil {
|
||||
node.Children = childrens
|
||||
}
|
||||
i++
|
||||
}
|
||||
return root
|
||||
}
|
||||
90
leetcode/0589.N-ary-Tree-Preorder-Traversal/README.md
Normal file
90
leetcode/0589.N-ary-Tree-Preorder-Traversal/README.md
Normal file
@ -0,0 +1,90 @@
|
||||
# [589. N-ary Tree Preorder Traversal](https://leetcode.com/problems/n-ary-tree-preorder-traversal/)
|
||||
|
||||
## 题目
|
||||
|
||||
Given the `root` of an n-ary tree, return *the preorder traversal of its nodes' values*.
|
||||
|
||||
Nary-Tree input serialization is represented in their level order traversal. Each group of children is separated by the null value (See examples)
|
||||
|
||||
**Example 1:**
|
||||
|
||||

|
||||
|
||||
```
|
||||
Input: root = [1,null,3,2,4,null,5,6]
|
||||
Output: [1,3,5,6,2,4]
|
||||
```
|
||||
|
||||
**Example 2:**
|
||||
|
||||

|
||||
|
||||
```
|
||||
Input: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
|
||||
Output: [1,2,3,6,7,11,14,4,8,12,5,9,13,10]
|
||||
```
|
||||
|
||||
**Constraints:**
|
||||
|
||||
- The number of nodes in the tree is in the range `[0, 104]`.
|
||||
- `0 <= Node.val <= 10^4`
|
||||
- The height of the n-ary tree is less than or equal to `1000`.
|
||||
|
||||
**Follow up:** Recursive solution is trivial, could you do it iteratively?
|
||||
|
||||
## 题目大意
|
||||
|
||||
给定一个 N 叉树,返回其节点值的 **前序遍历** 。N 叉树 在输入中按层序遍历进行序列化表示,每组子节点由空值 `null` 分隔(请参见示例)。
|
||||
|
||||
## 解题思路
|
||||
|
||||
- N 叉树和二叉树的前序遍历原理完全一样。二叉树非递归解法需要用到栈辅助,N 叉树同样如此。将父节点的所有孩子节点**逆序**入栈,逆序的目的是为了让前序节点永远在栈顶。依次循环直到栈里所有元素都出栈。输出的结果即为 N 叉树的前序遍历。时间复杂度 O(n),空间复杂度 O(n)。
|
||||
- 递归解法非常简单,见解法二。
|
||||
|
||||
## 代码
|
||||
|
||||
```go
|
||||
package leetcode
|
||||
|
||||
// Definition for a Node.
|
||||
type Node struct {
|
||||
Val int
|
||||
Children []*Node
|
||||
}
|
||||
|
||||
// 解法一 非递归
|
||||
func preorder(root *Node) []int {
|
||||
res := []int{}
|
||||
if root == nil {
|
||||
return res
|
||||
}
|
||||
stack := []*Node{root}
|
||||
for len(stack) > 0 {
|
||||
r := stack[len(stack)-1]
|
||||
stack = stack[:len(stack)-1]
|
||||
res = append(res, r.Val)
|
||||
tmp := []*Node{}
|
||||
for _, v := range r.Children {
|
||||
tmp = append([]*Node{v}, tmp...) // 逆序存点
|
||||
}
|
||||
stack = append(stack, tmp...)
|
||||
}
|
||||
return res
|
||||
}
|
||||
|
||||
// 解法二 递归
|
||||
func preorder1(root *Node) []int {
|
||||
res := []int{}
|
||||
preorderdfs(root, &res)
|
||||
return res
|
||||
}
|
||||
|
||||
func preorderdfs(root *Node, res *[]int) {
|
||||
if root != nil {
|
||||
*res = append(*res, root.Val)
|
||||
for i := 0; i < len(root.Children); i++ {
|
||||
preorderdfs(root.Children[i], res)
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
@ -0,0 +1,21 @@
|
||||
package leetcode
|
||||
|
||||
func countBinarySubstrings(s string) int {
|
||||
last, res := 0, 0
|
||||
for i := 0; i < len(s); {
|
||||
c, count := s[i], 1
|
||||
for i++; i < len(s) && s[i] == c; i++ {
|
||||
count++
|
||||
}
|
||||
res += min(count, last)
|
||||
last = count
|
||||
}
|
||||
return res
|
||||
}
|
||||
|
||||
func min(a, b int) int {
|
||||
if a < b {
|
||||
return a
|
||||
}
|
||||
return b
|
||||
}
|
||||
@ -0,0 +1,57 @@
|
||||
package leetcode
|
||||
|
||||
import (
|
||||
"fmt"
|
||||
"testing"
|
||||
)
|
||||
|
||||
type question696 struct {
|
||||
para696
|
||||
ans696
|
||||
}
|
||||
|
||||
// para 是参数
|
||||
// one 代表第一个参数
|
||||
type para696 struct {
|
||||
one string
|
||||
}
|
||||
|
||||
// ans 是答案
|
||||
// one 代表第一个答案
|
||||
type ans696 struct {
|
||||
one int
|
||||
}
|
||||
|
||||
func Test_Problem696(t *testing.T) {
|
||||
|
||||
qs := []question696{
|
||||
|
||||
{
|
||||
para696{"00110011"},
|
||||
ans696{6},
|
||||
},
|
||||
|
||||
{
|
||||
para696{"10101"},
|
||||
ans696{4},
|
||||
},
|
||||
|
||||
{
|
||||
para696{"0110001111"},
|
||||
ans696{6},
|
||||
},
|
||||
|
||||
{
|
||||
para696{"0001111"},
|
||||
ans696{3},
|
||||
},
|
||||
}
|
||||
|
||||
fmt.Printf("------------------------Leetcode Problem 696------------------------\n")
|
||||
|
||||
for _, q := range qs {
|
||||
_, p := q.ans696, q.para696
|
||||
fmt.Printf("【input】:%v 【output】:%v\n", p, countBinarySubstrings(p.one))
|
||||
}
|
||||
fmt.Printf("\n\n\n")
|
||||
}
|
||||
69
leetcode/0696.Count-Binary-Substrings/README.md
Normal file
69
leetcode/0696.Count-Binary-Substrings/README.md
Normal file
@ -0,0 +1,69 @@
|
||||
# [696. Count Binary Substrings](https://leetcode.com/problems/count-binary-substrings/)
|
||||
|
||||
|
||||
## 题目
|
||||
|
||||
Give a string `s`, count the number of non-empty (contiguous) substrings that have the same number of 0's and 1's, and all the 0's and all the 1's in these substrings are grouped consecutively.
|
||||
|
||||
Substrings that occur multiple times are counted the number of times they occur.
|
||||
|
||||
**Example 1:**
|
||||
|
||||
```
|
||||
Input: "00110011"
|
||||
Output: 6
|
||||
Explanation: There are 6 substrings that have equal number of consecutive 1's and 0's: "0011", "01", "1100", "10", "0011", and "01".
|
||||
|
||||
Notice that some of these substrings repeat and are counted the number of times they occur.
|
||||
|
||||
Also, "00110011" is not a valid substring becauseall the 0's (and 1's) are not grouped together.
|
||||
|
||||
```
|
||||
|
||||
**Example 2:**
|
||||
|
||||
```
|
||||
Input: "10101"
|
||||
Output: 4
|
||||
Explanation: There are 4 substrings: "10", "01", "10", "01" that have equal number of consecutive 1's and 0's.
|
||||
|
||||
```
|
||||
|
||||
**Note:**
|
||||
|
||||
- `s.length` will be between 1 and 50,000.
|
||||
- `s` will only consist of "0" or "1" characters.
|
||||
|
||||
## 题目大意
|
||||
|
||||
给定一个字符串 s,计算具有相同数量 0 和 1 的非空(连续)子字符串的数量,并且这些子字符串中的所有 0 和所有 1 都是连续的。重复出现的子串要计算它们出现的次数。
|
||||
|
||||
## 解题思路
|
||||
|
||||
- 简单题。先分组统计 0 和 1 的个数,例如,`0110001111` 按照 0 和 1 分组统计出来的结果是 [1, 2, 3, 4]。再拼凑结果。相邻 2 组取两者最短的,例如 `0110001111`,凑成的结果应该是 min(1,2),min(2,3),min(3,4),即 `01`,`01`,`10`,`1100`,`0011`,`000111`。时间复杂度 O(n),空间复杂度 O(1)。
|
||||
|
||||
## 代码
|
||||
|
||||
```go
|
||||
package leetcode
|
||||
|
||||
func countBinarySubstrings(s string) int {
|
||||
last, res := 0, 0
|
||||
for i := 0; i < len(s); {
|
||||
c, count := s[i], 1
|
||||
for i++; i < len(s) && s[i] == c; i++ {
|
||||
count++
|
||||
}
|
||||
res += min(count, last)
|
||||
last = count
|
||||
}
|
||||
return res
|
||||
}
|
||||
|
||||
func min(a, b int) int {
|
||||
if a < b {
|
||||
return a
|
||||
}
|
||||
return b
|
||||
}
|
||||
```
|
||||
@ -11,6 +11,8 @@ Two submatrices `(x1, y1, x2, y2)` and `(x1', y1', x2', y2')` are different
|
||||
|
||||
**Example 1:**
|
||||
|
||||
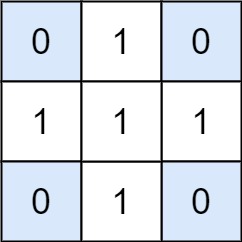
|
||||
|
||||
Input: matrix = [[0,1,0],[1,1,1],[0,1,0]], target = 0
|
||||
Output: 4
|
||||
Explanation: The four 1x1 submatrices that only contain 0.
|
||||
|
||||
@ -0,0 +1,48 @@
|
||||
package leetcode
|
||||
|
||||
// 解法一 stack
|
||||
func removeDuplicates(s string, k int) string {
|
||||
stack, arr := [][2]int{}, []byte{}
|
||||
for _, c := range s {
|
||||
i := int(c - 'a')
|
||||
if len(stack) > 0 && stack[len(stack)-1][0] == i {
|
||||
stack[len(stack)-1][1]++
|
||||
if stack[len(stack)-1][1] == k {
|
||||
stack = stack[:len(stack)-1]
|
||||
}
|
||||
} else {
|
||||
stack = append(stack, [2]int{i, 1})
|
||||
}
|
||||
}
|
||||
for _, pair := range stack {
|
||||
c := byte(pair[0] + 'a')
|
||||
for i := 0; i < pair[1]; i++ {
|
||||
arr = append(arr, c)
|
||||
}
|
||||
}
|
||||
return string(arr)
|
||||
}
|
||||
|
||||
// 解法二 暴力
|
||||
func removeDuplicates1(s string, k int) string {
|
||||
arr, count, tmp := []rune{}, 0, '#'
|
||||
for _, v := range s {
|
||||
arr = append(arr, v)
|
||||
for len(arr) > 0 {
|
||||
count = 0
|
||||
tmp = arr[len(arr)-1]
|
||||
for i := len(arr) - 1; i >= 0; i-- {
|
||||
if arr[i] != tmp {
|
||||
break
|
||||
}
|
||||
count++
|
||||
}
|
||||
if count == k {
|
||||
arr = arr[:len(arr)-k]
|
||||
} else {
|
||||
break
|
||||
}
|
||||
}
|
||||
}
|
||||
return string(arr)
|
||||
}
|
||||
@ -0,0 +1,53 @@
|
||||
package leetcode
|
||||
|
||||
import (
|
||||
"fmt"
|
||||
"testing"
|
||||
)
|
||||
|
||||
type question1209 struct {
|
||||
para1209
|
||||
ans1209
|
||||
}
|
||||
|
||||
// para 是参数
|
||||
// one 代表第一个参数
|
||||
type para1209 struct {
|
||||
s string
|
||||
k int
|
||||
}
|
||||
|
||||
// ans 是答案
|
||||
// one 代表第一个答案
|
||||
type ans1209 struct {
|
||||
one string
|
||||
}
|
||||
|
||||
func Test_Problem1209(t *testing.T) {
|
||||
|
||||
qs := []question1209{
|
||||
|
||||
// {
|
||||
// para1209{"abcd", 2},
|
||||
// ans1209{"abcd"},
|
||||
// },
|
||||
|
||||
{
|
||||
para1209{"deeedbbcccbdaa", 3},
|
||||
ans1209{"aa"},
|
||||
},
|
||||
|
||||
{
|
||||
para1209{"pbbcggttciiippooaais", 2},
|
||||
ans1209{"ps"},
|
||||
},
|
||||
}
|
||||
|
||||
fmt.Printf("------------------------Leetcode Problem 1209------------------------\n")
|
||||
|
||||
for _, q := range qs {
|
||||
_, p := q.ans1209, q.para1209
|
||||
fmt.Printf("【input】:%v 【output】:%v\n", p, removeDuplicates(p.s, p.k))
|
||||
}
|
||||
fmt.Printf("\n\n\n")
|
||||
}
|
||||
@ -0,0 +1,106 @@
|
||||
# [1209. Remove All Adjacent Duplicates in String II](https://leetcode.com/problems/remove-all-adjacent-duplicates-in-string-ii/)
|
||||
|
||||
|
||||
## 题目
|
||||
|
||||
Given a string `s`, a *k* *duplicate removal* consists of choosing `k` adjacent and equal letters from `s` and removing them causing the left and the right side of the deleted substring to concatenate together.
|
||||
|
||||
We repeatedly make `k` duplicate removals on `s` until we no longer can.
|
||||
|
||||
Return the final string after all such duplicate removals have been made.
|
||||
|
||||
It is guaranteed that the answer is unique.
|
||||
|
||||
**Example 1:**
|
||||
|
||||
```
|
||||
Input: s = "abcd", k = 2
|
||||
Output: "abcd"
|
||||
Explanation:There's nothing to delete.
|
||||
```
|
||||
|
||||
**Example 2:**
|
||||
|
||||
```
|
||||
Input: s = "deeedbbcccbdaa", k = 3
|
||||
Output: "aa"
|
||||
Explanation:
|
||||
First delete "eee" and "ccc", get "ddbbbdaa"
|
||||
Then delete "bbb", get "dddaa"
|
||||
Finally delete "ddd", get "aa"
|
||||
```
|
||||
|
||||
**Example 3:**
|
||||
|
||||
```
|
||||
Input: s = "pbbcggttciiippooaais", k = 2
|
||||
Output: "ps"
|
||||
```
|
||||
|
||||
**Constraints:**
|
||||
|
||||
- `1 <= s.length <= 10^5`
|
||||
- `2 <= k <= 10^4`
|
||||
- `s` only contains lower case English letters.
|
||||
|
||||
## 题目大意
|
||||
|
||||
给你一个字符串 s,「k 倍重复项删除操作」将会从 s 中选择 k 个相邻且相等的字母,并删除它们,使被删去的字符串的左侧和右侧连在一起。你需要对 s 重复进行无限次这样的删除操作,直到无法继续为止。在执行完所有删除操作后,返回最终得到的字符串。本题答案保证唯一。
|
||||
|
||||
## 解题思路
|
||||
|
||||
- 暴力解法。每增加一个字符,就往前扫描 `k` 位,判断是否存在 `k` 个连续相同的字符。消除了 `k` 个相同字符后,重新组成的字符串还可能再次产出 `k` 位相同的字符,(类似消消乐,`k` 个相同的字符碰到一起就“消除”),还需要继续消除。最差情况要再次扫描一次字符串。时间复杂度 O(n^2),空间复杂度 O(n)。
|
||||
- 暴力解法的低效在于重复统计字符频次,如果每个字符的频次统计一次就好了。按照这个思路,利用 stack ,每个栈元素存 2 个值,一个是字符,一个是该字符对应的频次。有了栈顶字符频次信息,就不需要重复往前扫描了。只要栈顶字符频次到达了 `k`,就弹出该字符。如此反复,最终剩下的字符串为所求。时间复杂度 O(n),空间复杂度 O(n)。
|
||||
|
||||
## 代码
|
||||
|
||||
```go
|
||||
package leetcode
|
||||
|
||||
// 解法一 stack
|
||||
func removeDuplicates(s string, k int) string {
|
||||
stack, arr := [][2]int{}, []byte{}
|
||||
for _, c := range s {
|
||||
i := int(c - 'a')
|
||||
if len(stack) > 0 && stack[len(stack)-1][0] == i {
|
||||
stack[len(stack)-1][1]++
|
||||
if stack[len(stack)-1][1] == k {
|
||||
stack = stack[:len(stack)-1]
|
||||
}
|
||||
} else {
|
||||
stack = append(stack, [2]int{i, 1})
|
||||
}
|
||||
}
|
||||
for _, pair := range stack {
|
||||
c := byte(pair[0] + 'a')
|
||||
for i := 0; i < pair[1]; i++ {
|
||||
arr = append(arr, c)
|
||||
}
|
||||
}
|
||||
return string(arr)
|
||||
}
|
||||
|
||||
// 解法二 暴力
|
||||
func removeDuplicates1(s string, k int) string {
|
||||
arr, count, tmp := []rune{}, 0, '#'
|
||||
for _, v := range s {
|
||||
arr = append(arr, v)
|
||||
for len(arr) > 0 {
|
||||
count = 0
|
||||
tmp = arr[len(arr)-1]
|
||||
for i := len(arr) - 1; i >= 0; i-- {
|
||||
if arr[i] != tmp {
|
||||
break
|
||||
}
|
||||
count++
|
||||
}
|
||||
if count == k {
|
||||
arr = arr[:len(arr)-k]
|
||||
} else {
|
||||
break
|
||||
}
|
||||
}
|
||||
}
|
||||
return string(arr)
|
||||
}
|
||||
```
|
||||
@ -0,0 +1,35 @@
|
||||
package leetcode
|
||||
|
||||
import (
|
||||
"sort"
|
||||
)
|
||||
|
||||
func maxEvents(events [][]int) int {
|
||||
sort.Slice(events, func(i, j int) bool {
|
||||
if events[i][0] == events[j][0] {
|
||||
return events[i][1] < events[j][1]
|
||||
}
|
||||
return events[i][0] < events[j][0]
|
||||
})
|
||||
attended, current := 1, events[0]
|
||||
for i := 1; i < len(events); i++ {
|
||||
prev, event := events[i-1], events[i]
|
||||
if event[0] == prev[0] && event[1] == prev[1] && event[1] == event[0] {
|
||||
continue
|
||||
}
|
||||
start, end := max(current[0], event[0]-1), max(current[1], event[1])
|
||||
if end-start > 0 {
|
||||
current[0] = start + 1
|
||||
current[1] = end
|
||||
attended++
|
||||
}
|
||||
}
|
||||
return attended
|
||||
}
|
||||
|
||||
func max(a, b int) int {
|
||||
if a > b {
|
||||
return a
|
||||
}
|
||||
return b
|
||||
}
|
||||
@ -0,0 +1,67 @@
|
||||
package leetcode
|
||||
|
||||
import (
|
||||
"fmt"
|
||||
"testing"
|
||||
)
|
||||
|
||||
type question1353 struct {
|
||||
para1353
|
||||
ans1353
|
||||
}
|
||||
|
||||
// para 是参数
|
||||
// one 代表第一个参数
|
||||
type para1353 struct {
|
||||
events [][]int
|
||||
}
|
||||
|
||||
// ans 是答案
|
||||
// one 代表第一个答案
|
||||
type ans1353 struct {
|
||||
one int
|
||||
}
|
||||
|
||||
func Test_Problem1353(t *testing.T) {
|
||||
|
||||
qs := []question1353{
|
||||
|
||||
{
|
||||
para1353{[][]int{{1, 2}, {2, 3}, {3, 4}}},
|
||||
ans1353{3},
|
||||
},
|
||||
|
||||
{
|
||||
para1353{[][]int{{1, 4}, {4, 4}, {2, 2}, {3, 4}, {1, 1}}},
|
||||
ans1353{4},
|
||||
},
|
||||
|
||||
{
|
||||
para1353{[][]int{{1, 100000}}},
|
||||
ans1353{1},
|
||||
},
|
||||
|
||||
{
|
||||
para1353{[][]int{{1, 1}, {2, 2}, {1, 3}, {1, 4}, {1, 5}, {1, 6}, {1, 7}}},
|
||||
ans1353{7},
|
||||
},
|
||||
|
||||
{
|
||||
para1353{[][]int{{1, 2}, {2, 2}, {3, 3}, {3, 4}, {3, 4}}},
|
||||
ans1353{4},
|
||||
},
|
||||
|
||||
{
|
||||
para1353{[][]int{{1, 10}, {2, 2}, {2, 2}, {2, 2}, {2, 2}}},
|
||||
ans1353{2},
|
||||
},
|
||||
}
|
||||
|
||||
fmt.Printf("------------------------Leetcode Problem 1353------------------------\n")
|
||||
|
||||
for _, q := range qs {
|
||||
_, p := q.ans1353, q.para1353
|
||||
fmt.Printf("【input】:%v 【output】:%v\n", p, maxEvents(p.events))
|
||||
}
|
||||
fmt.Printf("\n\n\n")
|
||||
}
|
||||
@ -0,0 +1,113 @@
|
||||
# [1353. Maximum Number of Events That Can Be Attended](https://leetcode.com/problems/maximum-number-of-events-that-can-be-attended/)
|
||||
|
||||
|
||||
## 题目
|
||||
|
||||
Given an array of `events` where `events[i] = [startDayi, endDayi]`. Every event `i` starts at `startDayi` and ends at `endDayi`.
|
||||
|
||||
You can attend an event `i` at any day `d` where `startTimei <= d <= endTimei`. Notice that you can only attend one event at any time `d`.
|
||||
|
||||
Return *the maximum number of events* you can attend.
|
||||
|
||||
**Example 1:**
|
||||
|
||||
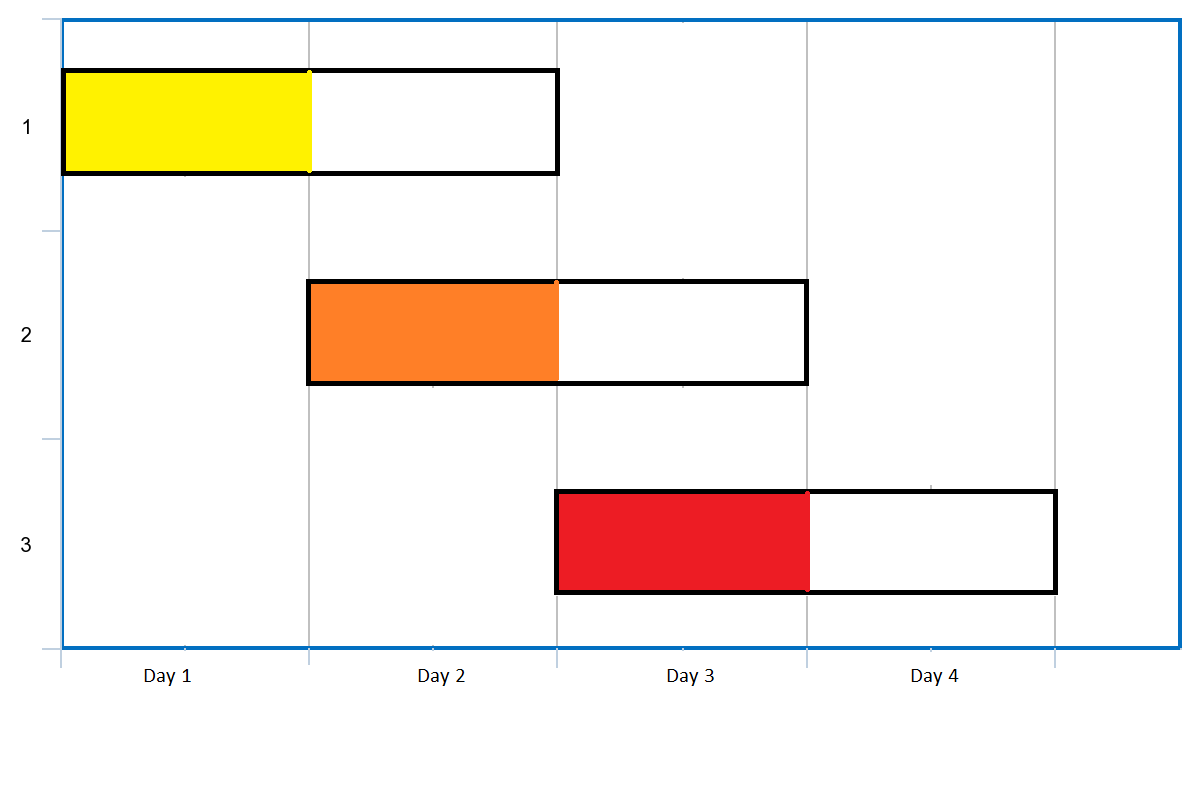
|
||||
|
||||
```
|
||||
Input: events = [[1,2],[2,3],[3,4]]
|
||||
Output: 3
|
||||
Explanation: You can attend all the three events.
|
||||
One way to attend them all is as shown.
|
||||
Attend the first event on day 1.
|
||||
Attend the second event on day 2.
|
||||
Attend the third event on day 3.
|
||||
|
||||
```
|
||||
|
||||
**Example 2:**
|
||||
|
||||
```
|
||||
Input: events= [[1,2],[2,3],[3,4],[1,2]]
|
||||
Output: 4
|
||||
|
||||
```
|
||||
|
||||
**Example 3:**
|
||||
|
||||
```
|
||||
Input: events = [[1,4],[4,4],[2,2],[3,4],[1,1]]
|
||||
Output: 4
|
||||
|
||||
```
|
||||
|
||||
**Example 4:**
|
||||
|
||||
```
|
||||
Input: events = [[1,100000]]
|
||||
Output: 1
|
||||
|
||||
```
|
||||
|
||||
**Example 5:**
|
||||
|
||||
```
|
||||
Input: events = [[1,1],[1,2],[1,3],[1,4],[1,5],[1,6],[1,7]]
|
||||
Output: 7
|
||||
|
||||
```
|
||||
|
||||
**Constraints:**
|
||||
|
||||
- `1 <= events.length <= 10^5`
|
||||
- `events[i].length == 2`
|
||||
- `1 <= startDayi <= endDayi <= 10^5`
|
||||
|
||||
## 题目大意
|
||||
|
||||
给你一个数组 events,其中 events[i] = [startDayi, endDayi] ,表示会议 i 开始于 startDayi ,结束于 endDayi 。你可以在满足 startDayi <= d <= endDayi 中的任意一天 d 参加会议 i 。注意,一天只能参加一个会议。请你返回你可以参加的 最大 会议数目。
|
||||
|
||||
## 解题思路
|
||||
|
||||
- 关于会议安排,活动安排这类题,第一直觉是贪心问题。先按照会议开始时间从小到大排序,如果开始时间相同,再按照结束时间从小到大排序。贪心策略是,优先选择参加早结束的会议。因为一个结束时间晚的会议,代表这个会议持续时间长,先参加马上要结束的会议,这样可以参加更多的会议。
|
||||
- 注意题目给的数据代表的是天数。比较大小的时候最好转换成坐标轴上的坐标点。例如 [1,2] 代表这个会议持续 2 天,如果在坐标轴上表示,是 [0,2],0-1 表示第一天,1-2 表示第二天。所以比较会议时需要把开始时间减一。选定了这个会议以后记得要把这一天排除,例如选择了第二天,那么下次对比起始时间需要从坐标 2 开始,因为第二天的时间范围是 1-2,所以下一轮比较会议前需要把开始时间加一。从左往右依次扫描各个会议时间段,选择结束时间大于起始时间的会议,不断累加次数,扫描完所有会议,最终结果即为可参加的最大会议数。
|
||||
- 测试数据中有一组很恶心的数据,见 test 文件中最后一组数据。这组数据在同一天叠加了多个会议,并且起始时间完全一致。这种特殊情况需要加判断条件排除,见下面代码 continue 条件。
|
||||
|
||||
## 代码
|
||||
|
||||
```go
|
||||
package leetcode
|
||||
|
||||
import (
|
||||
"sort"
|
||||
)
|
||||
|
||||
func maxEvents(events [][]int) int {
|
||||
sort.Slice(events, func(i, j int) bool {
|
||||
if events[i][0] == events[j][0] {
|
||||
return events[i][1] < events[j][1]
|
||||
}
|
||||
return events[i][0] < events[j][0]
|
||||
})
|
||||
attended, current := 1, events[0]
|
||||
for i := 1; i < len(events); i++ {
|
||||
prev, event := events[i-1], events[i]
|
||||
if event[0] == prev[0] && event[1] == prev[1] && event[1] == event[0] {
|
||||
continue
|
||||
}
|
||||
start, end := max(current[0], event[0]-1), max(current[1], event[1])
|
||||
if end-start > 0 {
|
||||
current[0] = start + 1
|
||||
current[1] = end
|
||||
attended++
|
||||
}
|
||||
}
|
||||
return attended
|
||||
}
|
||||
|
||||
func max(a, b int) int {
|
||||
if a > b {
|
||||
return a
|
||||
}
|
||||
return b
|
||||
}
|
||||
```
|
||||
@ -1,12 +1,26 @@
|
||||
package leetcode
|
||||
|
||||
import (
|
||||
"github.com/halfrost/LeetCode-Go/template"
|
||||
"sort"
|
||||
|
||||
"github.com/halfrost/LeetCode-Go/template"
|
||||
)
|
||||
|
||||
// 解法一 线段树 SegmentTree
|
||||
// 解法一 树状数组 Binary Indexed Tree
|
||||
func createSortedArray(instructions []int) int {
|
||||
bit, res := template.BinaryIndexedTree{}, 0
|
||||
bit.Init(100001)
|
||||
for i, v := range instructions {
|
||||
less := bit.Query(v - 1)
|
||||
greater := i - bit.Query(v)
|
||||
res = (res + min(less, greater)) % (1e9 + 7)
|
||||
bit.Add(v, 1)
|
||||
}
|
||||
return res
|
||||
}
|
||||
|
||||
// 解法二 线段树 SegmentTree
|
||||
func createSortedArray1(instructions []int) int {
|
||||
if len(instructions) == 0 {
|
||||
return 0
|
||||
}
|
||||
@ -49,58 +63,3 @@ func min(a int, b int) int {
|
||||
}
|
||||
return a
|
||||
}
|
||||
|
||||
// 解法二 树状数组 Binary Indexed Tree
|
||||
func createSortedArray1(instructions []int) int {
|
||||
b := newBIT(make([]int, 100001))
|
||||
var res int
|
||||
cnt := map[int]int{}
|
||||
for i, n := range instructions {
|
||||
less := b.get(n - 1)
|
||||
greater := i - less - cnt[n]
|
||||
res = (res + min(less, greater)) % (1e9 + 7)
|
||||
b.update(n, 1)
|
||||
cnt[n]++
|
||||
}
|
||||
|
||||
return res % (1e9 + 7)
|
||||
}
|
||||
|
||||
func max(x, y int) int {
|
||||
if x > y {
|
||||
return x
|
||||
}
|
||||
return y
|
||||
}
|
||||
|
||||
type BIT struct {
|
||||
data []int
|
||||
}
|
||||
|
||||
func newBIT(nums []int) *BIT {
|
||||
data := make([]int, len(nums)+1)
|
||||
b := &BIT{data}
|
||||
for i, n := range nums {
|
||||
b.update(i, n)
|
||||
}
|
||||
|
||||
return b
|
||||
}
|
||||
|
||||
func (b *BIT) update(i, num int) {
|
||||
i++
|
||||
for i < len(b.data) {
|
||||
b.data[i] += num
|
||||
i += (i & -i)
|
||||
}
|
||||
}
|
||||
|
||||
func (b *BIT) get(i int) int {
|
||||
i++
|
||||
var sum int
|
||||
for i > 0 {
|
||||
sum += b.data[i]
|
||||
i -= (i & -i)
|
||||
}
|
||||
return sum
|
||||
}
|
||||
|
||||
@ -83,12 +83,26 @@ The total cost is 0 + 0 + 0 + 0 + 1 + 0 + 1 + 0 + 2 = 4.
|
||||
package leetcode
|
||||
|
||||
import (
|
||||
"github.com/halfrost/LeetCode-Go/template"
|
||||
"sort"
|
||||
|
||||
"github.com/halfrost/LeetCode-Go/template"
|
||||
)
|
||||
|
||||
// 解法一 线段树 SegmentTree
|
||||
// 解法一 树状数组 Binary Indexed Tree
|
||||
func createSortedArray(instructions []int) int {
|
||||
bit, res := template.BinaryIndexedTree{}, 0
|
||||
bit.Init(100001)
|
||||
for i, v := range instructions {
|
||||
less := bit.Query(v - 1)
|
||||
greater := i - bit.Query(v)
|
||||
res = (res + min(less, greater)) % (1e9 + 7)
|
||||
bit.Add(v, 1)
|
||||
}
|
||||
return res
|
||||
}
|
||||
|
||||
// 解法二 线段树 SegmentTree
|
||||
func createSortedArray1(instructions []int) int {
|
||||
if len(instructions) == 0 {
|
||||
return 0
|
||||
}
|
||||
@ -132,58 +146,4 @@ func min(a int, b int) int {
|
||||
return a
|
||||
}
|
||||
|
||||
// 解法二 树状数组 Binary Indexed Tree
|
||||
func createSortedArray1(instructions []int) int {
|
||||
b := newBIT(make([]int, 100001))
|
||||
var res int
|
||||
cnt := map[int]int{}
|
||||
for i, n := range instructions {
|
||||
less := b.get(n - 1)
|
||||
greater := i - less - cnt[n]
|
||||
res = (res + min(less, greater)) % (1e9 + 7)
|
||||
b.update(n, 1)
|
||||
cnt[n]++
|
||||
}
|
||||
|
||||
return res % (1e9 + 7)
|
||||
}
|
||||
|
||||
func max(x, y int) int {
|
||||
if x > y {
|
||||
return x
|
||||
}
|
||||
return y
|
||||
}
|
||||
|
||||
type BIT struct {
|
||||
data []int
|
||||
}
|
||||
|
||||
func newBIT(nums []int) *BIT {
|
||||
data := make([]int, len(nums)+1)
|
||||
b := &BIT{data}
|
||||
for i, n := range nums {
|
||||
b.update(i, n)
|
||||
}
|
||||
|
||||
return b
|
||||
}
|
||||
|
||||
func (b *BIT) update(i, num int) {
|
||||
i++
|
||||
for i < len(b.data) {
|
||||
b.data[i] += num
|
||||
i += (i & -i)
|
||||
}
|
||||
}
|
||||
|
||||
func (b *BIT) get(i int) int {
|
||||
i++
|
||||
var sum int
|
||||
for i > 0 {
|
||||
sum += b.data[i]
|
||||
i -= (i & -i)
|
||||
}
|
||||
return sum
|
||||
}
|
||||
```
|
||||
Reference in New Issue
Block a user