Update 0315、0327

leetcode/0315.Count-of-Smaller-Numbers-After-Self/315. Count of Smaller Numbers After Self.go

@@ -6,6 +6,7 @@ import (
 	"github.com/halfrost/LeetCode-Go/template"
 )
 
+// 解法一 线段树
 func countSmaller(nums []int) []int {
 	if len(nums) == 0 {
 		return []int{}
@@ -35,3 +36,31 @@ func countSmaller(nums []int) []int {
 	}
 	return res
 }
+
+// 解法二 树状数组
+func countSmaller1(nums []int) []int {
+	// copy 一份原数组至所有数字 allNums 数组中
+	allNums, res := make([]int, len(nums)), []int{}
+	copy(allNums, nums)
+	// 将 allNums 离散化
+	sort.Ints(allNums)
+	k := 1
+	kth := map[int]int{allNums[0]: k}
+	for i := 1; i < len(allNums); i++ {
+		if allNums[i] != allNums[i-1] {
+			k++
+			kth[allNums[i]] = k
+		}
+	}
+	// 树状数组 Query
+	bit := template.BinaryIndexedTree{}
+	bit.Init(k)
+	for i := len(nums) - 1; i >= 0; i-- {
+		res = append(res, bit.Query(kth[nums[i]]-1))
+		bit.Add(kth[nums[i]], 1)
+	}
+	for i := 0; i < len(res)/2; i++ {
+		res[i], res[len(res)-1-i] = res[len(res)-1-i], res[i]
+	}
+	return res
+}

leetcode/0315.Count-of-Smaller-Numbers-After-Self/README.md

@@ -39,3 +39,4 @@ You are given an integer array nums and you have to return a new counts arra
 
 - 给出一个数组，要求输出数组中每个元素相对于数组中的位置右边比它小的元素。
 - 这一题是第 327 题的缩水版。由于需要找数组位置右边比当前位置元素小的元素，所以从数组右边开始往左边扫。构造一颗线段树，线段树里面父节点存的是子节点出现的次数和。有可能给的数据会很大，所以构造线段树的时候先离散化。还需要注意的是数组里面可能有重复元素，所以构造线段树要先去重并排序。从右往左扫的过程中，依次添加数组中的元素，添加了一次就立即 query 一次。query 的区间是 [minNum, nums[i]-1]。如果是 minNum 则输出 0，并且也要记得插入这个最小值。这一题的思路和第 327 题大体类似，详解可见第 327 题。
+- 这一题同样可以用树状数组来解答。相比 327 题简单很多。第一步还是把所有用到的元素放入 allNums 数组中，第二步排序 + 离散化。由于题目要求输出右侧更小的元素，所以第三步倒序插入构造树状数组，Query 查询 `[1,i-1]` 区间内元素总数即为右侧更小元素个数。注意最终输出是顺序输出，计算是逆序计算的，最终数组里面的答案还需要逆序一遍。相同的套路题有，第 327 题，第 493 题。

leetcode/0327.Count-of-Range-Sum/327. Count of Range Sum.go

@@ -40,8 +40,39 @@ func countRangeSum(nums []int, lower int, upper int) int {
 	return res
 }
 
-// 解法二 暴力，时间复杂度 O(n^2)
+// 解法二 树状数组，时间复杂度 O(n log n)
 func countRangeSum1(nums []int, lower int, upper int) int {
+	n := len(nums)
+	// 计算前缀和 preSum，以及后面统计时会用到的所有数字 allNums
+	allNums, preSum, res := make([]int, 1, 3*n+1), make([]int, n+1), 0
+	for i, v := range nums {
+		preSum[i+1] = preSum[i] + v
+		allNums = append(allNums, preSum[i+1], preSum[i+1]-lower, preSum[i+1]-upper)
+	}
+	// 将 allNums 离散化
+	sort.Ints(allNums)
+	k := 1
+	kth := map[int]int{allNums[0]: k}
+	for i := 1; i <= 3*n; i++ {
+		if allNums[i] != allNums[i-1] {
+			k++
+			kth[allNums[i]] = k
+		}
+	}
+	// 遍历 preSum，利用树状数组计算每个前缀和对应的合法区间数
+	bit := template.BinaryIndexedTree{}
+	bit.Init(k)
+	bit.Add(kth[0], 1)
+	for _, sum := range preSum[1:] {
+		left, right := kth[sum-upper], kth[sum-lower]
+		res += bit.Query(right) - bit.Query(left-1)
+		bit.Add(kth[sum], 1)
+	}
+	return res
+}
+
+// 解法三 暴力，时间复杂度 O(n^2)
+func countRangeSum2(nums []int, lower int, upper int) int {
 	res, n := 0, len(nums)
 	for i := 0; i < n; i++ {
 		tmp := 0

leetcode/0327.Count-of-Range-Sum/README.md

@@ -17,11 +17,10 @@ Given an integer array `nums`, return the number of range sums that lie in `[l
 ## 题目大意
 
 
-给定一个整数数组 nums，返回区间和在 [lower, upper] 之间的个数，包含 lower 和 upper。区间和 S(i, j) 表示在 nums 中，位置从 i 到 j 的元素之和，包含 i 和 j (i ≤ j)。
-
-说明:   
-最直观的算法复杂度是 O(n^2) ，请在此基础上优化你的算法。
+给定一个整数数组 nums 。区间和 S(i, j) 表示在 nums 中，位置从 i 到 j 的元素之和，包含 i 和 j (i ≤ j)。请你以下标 i （0 <= i <= nums.length ）为起点，元素个数逐次递增，计算子数组内的元素和。当元素和落在范围 [lower, upper] （包含 lower 和 upper）之内时，记录子数组当前最末元素下标 j ，记作 有效 区间和 S(i, j) 。求数组中，值位于范围 [lower, upper] （包含 lower 和 upper）之内的 有效 区间和的个数。
 
+注意：
+最直观的算法复杂度是 O(n2) ，请在此基础上优化你的算法。
 
 ## 解题思路
 
@@ -75,3 +74,5 @@ Given an integer array `nums`, return the number of range sums that lie in `[l
     ![](https://img.halfrost.com/Leetcode/leetcode_327_8_.png)
 
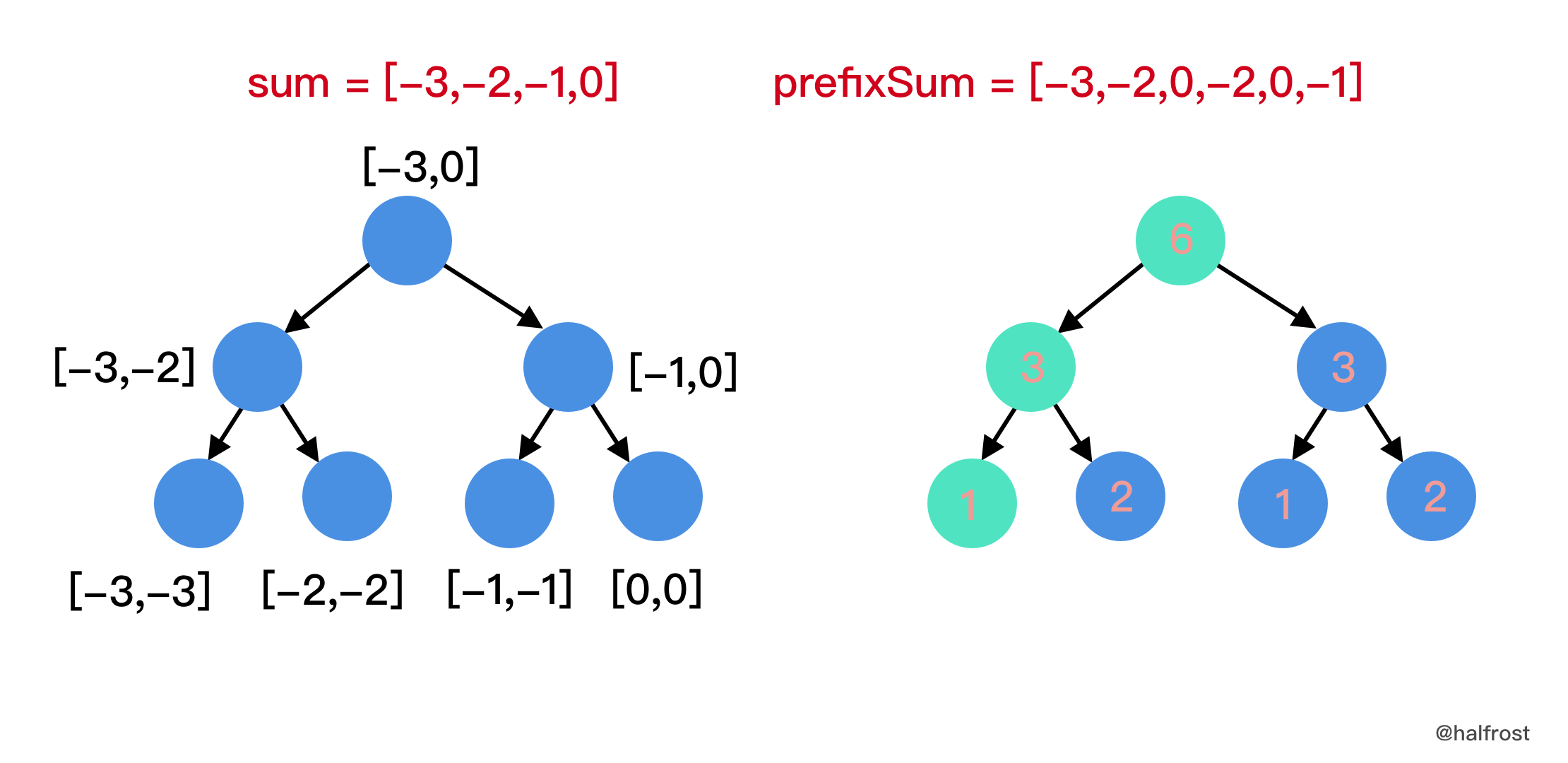
     这时候查找区间变为了 `[-3 + prefixSum[0-1], -1 + prefixSum[0-1]] = [-3,-1]`，注意 `prefixSum[-1] = 0`，即判断 `-3 ≤ sum(0,  0,1,2,3,4,5) ≤ -1`，满足等式的有几种情况，这里有六种情况，即 `j = 0`、`j = 1`、`j = 2`、 `j = 3` 、`j = 4` 或者 `j = 5`，满足等式的有 `j = 0`、`j = 1`、 `j = 3` 和 `j = 5`，即 `-3 ≤ sum(0, 0) ≤ -1` 、 `-3 ≤ sum(0, 1) ≤ -1`、`-3 ≤ sum(0, 3) ≤ -1` 和 `-3 ≤ sum(0, 5) ≤ -1`。所以这一步 `res = 4`。最后的答案就是把每一步的结果都累加，`res = 1 + 0 + 2 + 0 + 0 + 4 = 7`。
+
+- 此题同样可以用树状数组来解答。同样把问题先转化成区间 Query 的模型，`lower ≤ prefixSum(j) - prefixSum(i-1) ≤ upper` 等价于 `prefixSum(j) - upper ≤ prefixSum(i-1) ≤ prefixSum(j) - lower`，`i` 的取值在 `[0,j-1]` 区间内。所以题目可以转化为 `i` 在 `[0,j-1]` 区间内取值，问数组 `prefixSum[0...j-1]` 中的所有取值，位于区间 `[prefixSum(j) - upper, prefixSum(j) - lower]` 内的次数。在树状数组中，区间内的前缀和可以转化为 2 个区间的前缀和相减，即 `Query([i,j]) = Query(j) - Query(i-1)`。所以这道题枚举数组 `prefixSum[0...j-1]` 中每个值是否出现在指定区间内出现次数即可。第一步先将所有的前缀和 `prefixSum(j)` 以及 `[prefixSum(j) - upper, prefixSum(j) - lower]` 计算出来。第二步排序和离散化，离散化以后的点区间为 `[1,n]`。最后根据数组 `prefixSum(j)` 的值在指定区间内查询出现次数即可。相同的套路题有，第 315 题，第 493 题。