Micro fix

leetcode/0547.Number-of-Provinces/README.md

@@ -1,4 +1,4 @@
-# [547. Friend Circles](https://leetcode.com/problems/friend-circles/)
+# [547. Number of Provinces](https://leetcode.com/problems/number-of-provinces/)
 
 ## 题目
 

leetcode/0828.Count-Unique-Characters-of-All-Substrings-of-a-Given-String/README.md

@@ -1,16 +1,44 @@
-# [828. Unique Letter String](https://leetcode.com/problems/unique-letter-string/)
+# [828. Count Unique Characters of All Substrings of a Given String](https://leetcode.com/problems/count-unique-characters-of-all-substrings-of-a-given-string/)
+
 
 ## 题目
 
-THIS PROBLEM COPYRIGHT BELONGS TO CODILITY.COM
+Let's define a function `countUniqueChars(s)` that returns the number of unique characters on `s`, for example if `s = "LEETCODE"` then `"L"`, `"T"`,`"C"`,`"O"`,`"D"` are the unique characters since they appear only once in `s`, therefore `countUniqueChars(s) = 5`.On this problem given a string `s` we need to return the sum of `countUniqueChars(t)` where `t` is a substring of `s`. Notice that some substrings can be repeated so on this case you have to count the repeated ones too.
+
+Since the answer can be very large, return the answer modulo `10 ^ 9 + 7`.
 
 **Example 1:**
 
+```
+Input: s = "ABC"
+Output: 10
+Explanation: All possible substrings are: "A","B","C","AB","BC" and "ABC".
+Evey substring is composed with only unique letters.
+Sum of lengths of all substring is 1 + 1 + 1 + 2 + 2 + 3 = 10
 
+```
 
 **Example 2:**
 
+```
+Input: s = "ABA"
+Output: 8
+Explanation: The same as example 1, except countUniqueChars("ABA") = 1.
 
+```
+
+**Example 3:**
+
+```
+Input: s = "LEETCODE"
+Output: 92
+
+```
+
+**Constraints:**
+
+- `0 <= s.length <= 10^4`
+- `s` contain upper-case English letters only.
 
 ## 题目大意
 
@@ -18,11 +46,56 @@ THIS PROBLEM COPYRIGHT BELONGS TO CODILITY.COM
 
 对于给定字符串 S，计算其所有非空子串的独特字符的个数（即 UNIQ(substring)）之和。如果在 S 的不同位置上出现两个甚至多个相同的子串，那么我们认为这些子串是不同的。考虑到答案可能会非常大，规定返回格式为：结果 mod 10 ^ 9 + 7。
 
-
 ## 解题思路
 
 - 这一题可以先用暴力解法尝试解题，不过提交以后会发现判题结果是超时。出错的一组数据是一个有 10000 个字符的字符串。暴力解法中间由于遍历了太多的子区间，导致了超时。
 - 这道题换一个角度思考问题。当子字符串中字符 X 出现了 2 次以上，那么它就对最终结果没有任何影响，所以只有当某个字符只出现一次的时候才会影响最终结果。再者，一个子字符串中不重复的字符的总个数，也就是这个子字符串 UNIQ 值。例如，“ABC”，这个子字符串的 UNIQ 值是 3，可以这样计算，它属于 A 的独特的字符串，也属于 B 的独特的字符串，也属于 C 的独特的字符串，那么计算这个子字符串的问题可以分解成计算 A 有多少个独特的子字符串，B 有多少个独特的子字符串，C 有多少个独特的子字符串的问题。在计算 A 有多少个子字符串的问题的时候，里面肯定会包含 "ABC" 这个子字符串的。所以原问题就转换成了分别计算给出的字符串中每个字符出现在独特字符串中的总数之和。
-- 假设原字符串是 BAABBABBBAAABA，这个字符串中出现了很多 A 和很多 B，假设我们当前计算到了第 3 个 A 的位置了(index = 5)，即标红色的那个 A。如何计算这个 A 在哪些子字符串中是独特的呢？由于子字符串题目中要求必须是连续的区间，所以这个问题很简单。找到这个 A 前一个 A 的下标位置(index = 2)，再找到这个 A 后一个 A 的下标位置(index = 9)，即 BAABBABBBAAABA，第一个 A 和当前计算的 A 中间区间有 2 个字符，第三个 A 和当前计算的 A 中间有 3 个字符。那么当前计算的 A 出现在 `(2 + 1) * (3 + 1) = 12` 个子字符串中是独特的，这 12 个字符串是：`A`，`BA`，`BBA`，`AB`，`ABB`，`ABBB`，`BAB`，`BABB`，`BABBB`，`BBAB`，`BBABB`，`BBABBB`。计算方法，假设当前待计算的字符的下标是 i ，找到当前字符前一次出现的下标位置 left，再找到当前字符后一次出现的下标位置 right，那么左边区间 (left,i) 的**开区间**内包含的字符数是 i - left - 1，右边区间 (i,right) 的**开区间**内包含的字符数是 right - i - 1。左右两边都还需要考虑空字符串的情况，即左右两边都可以不取任何字符，那么对应的就是只有中间这个待计算的字符 `A`。所以左右两边都还需要再加上空串的情况，左边 i - left - 1 + 1 = i - left，右边 right - i - 1 + 1 = right - i。左右两边的情况进行排列组合，即 (i - left) * (right - i)。针对字符串的每个字符都计算这样的值，最后累积的总和就是题目中要求的总 UNIQ 值。
+- 假设原字符串是 BAABBABBBAAABA，这个字符串中出现了很多 A 和很多 B，假设我们当前计算到了第 3 个 A 的位置了(index = 5)，即标红色的那个 A。如何计算这个 A 在哪些子字符串中是独特的呢？由于子字符串题目中要求必须是连续的区间，所以这个问题很简单。找到这个 A 前一个 A 的下标位置(index = 2)，再找到这个 A 后一个 A 的下标位置(index = 9)，即 BAABBABBBAAABA，第一个 A 和当前计算的 A 中间区间有 2 个字符，第三个 A 和当前计算的 A 中间有 3 个字符。那么当前计算的 A 出现在 `(2 + 1) * (3 + 1) = 12` 个子字符串中是独特的，这 12 个字符串是：`A`，`BA`，`BBA`，`AB`，`ABB`，`ABBB`，`BAB`，`BABB`，`BABBB`，`BBAB`，`BBABB`，`BBABBB`。计算方法，假设当前待计算的字符的下标是 i ，找到当前字符前一次出现的下标位置 left，再找到当前字符后一次出现的下标位置 right，那么左边区间 (left,i) 的***开区间****内包含的字符数是 i - left - 1，右边区间 (i,right) 的***开区间****内包含的字符数是 right - i - 1。左右两边都还需要考虑空字符串的情况，即左右两边都可以不取任何字符，那么对应的就是只有中间这个待计算的字符 `A`。所以左右两边都还需要再加上空串的情况，左边 i - left - 1 + 1 = i - left，右边 right - i - 1 + 1 = right - i。左右两边的情况进行排列组合，即 (i - left) * (right - i)。针对字符串的每个字符都计算这样的值，最后累积的总和就是题目中要求的总 UNIQ 值。
 
+## 代码
 
+```go
+package leetcode
+
+func uniqueLetterString(S string) int {
+	res, left, right := 0, 0, 0
+	for i := 0; i < len(S); i++ {
+		left = i - 1
+		for left >= 0 && S[left] != S[i] {
+			left--
+		}
+		right = i + 1
+		for right < len(S) && S[right] != S[i] {
+			right++
+		}
+		res += (i - left) * (right - i)
+	}
+	return res % 1000000007
+}
+
+// 暴力解法，超时！时间复杂度 O(n^2)
+func uniqueLetterString1(S string) int {
+	if len(S) == 0 {
+		return 0
+	}
+	res, mod := 0, 1000000007
+	for i := 0; i < len(S); i++ {
+		letterMap := map[byte]int{}
+		for j := i; j < len(S); j++ {
+			letterMap[S[j]]++
+			tmp := 0
+			for _, v := range letterMap {
+				if v > 1 {
+					tmp++
+				}
+			}
+			if tmp == len(letterMap) {
+				continue
+			} else {
+				res += len(letterMap) - tmp
+			}
+		}
+	}
+	return res % mod
+}
+```

website/content/ChapterFour/0098.Validate-Binary-Search-Tree.md

@@ -11,7 +11,7 @@ Assume a BST is defined as follows:
 - The right subtree of a node contains only nodes with keys **greater than** the node's key.
 - Both the left and right subtrees must also be binary search trees.
 
-**xample 1:**
+**Example 1**:
 
         2
        / \

website/content/ChapterFour/0130.Surrounded-Regions.md

@@ -22,7 +22,7 @@ After running your function, the board should be:
     X X X X
     X O X X
 
-**Explanation:**
+**Explanation**:
 
 Surrounded regions shouldn’t be on the border, which means that any `'O'` on the border of the board are not flipped to `'X'`. Any `'O'` that is not on the border and it is not connected to an `'O'` on the border will be flipped to `'X'`. Two cells are connected if they are adjacent cells connected horizontally or vertically.
 

website/content/ChapterFour/0146.LRU-Cache.md

@@ -10,9 +10,9 @@ Implement the `LRUCache` class:
 - `int get(int key)` Return the value of the `key` if the key exists, otherwise return `1`.
 - `void put(int key, int value)` Update the value of the `key` if the `key` exists. Otherwise, add the `key-value` pair to the cache. If the number of keys exceeds the `capacity` from this operation, **evict** the least recently used key.
 
-**Follow up:**Could you do `get` and `put` in `O(1)` time complexity?
+**Follow up**:Could you do `get` and `put` in `O(1)` time complexity?
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input
@@ -35,7 +35,7 @@ lRUCache.get(4);    // return 4
 
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= capacity <= 3000`
 - `0 <= key <= 3000`

website/content/ChapterFour/0189.Rotate-Array.md

@@ -4,12 +4,12 @@
 
 Given an array, rotate the array to the right by *k* steps, where *k* is non-negative.
 
-**Follow up:**
+**Follow up**:
 
 - Try to come up as many solutions as you can, there are at least 3 different ways to solve this problem.
 - Could you do it in-place with O(1) extra space?
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: nums = [1,2,3,4,5,6,7], k = 3
@@ -20,7 +20,7 @@ rotate 2 steps to the right: [6,7,1,2,3,4,5]
 rotate 3 steps to the right: [5,6,7,1,2,3,4]
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: nums = [-1,-100,3,99], k = 2
@@ -30,7 +30,7 @@ rotate 1 steps to the right: [99,-1,-100,3]
 rotate 2 steps to the right: [3,99,-1,-100]
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= nums.length <= 2 * 10^4`
 - `-2^31 <= nums[i] <= 2^31 - 1`

website/content/ChapterFour/0228.Summary-Ranges.md

@@ -12,7 +12,7 @@ Each range `[a,b]` in the list should be output as:
 - `"a->b"` if `a != b`
 - `"a"` if `a == b`
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: nums = [0,1,2,4,5,7]
@@ -24,7 +24,7 @@ Explanation: The ranges are:
 
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: nums = [0,2,3,4,6,8,9]
@@ -37,7 +37,7 @@ Explanation: The ranges are:
 
 ```
 
-**Example 3:**
+**Example 3**:
 
 ```
 Input: nums = []
@@ -45,7 +45,7 @@ Output: []
 
 ```
 
-**Example 4:**
+**Example 4**:
 
 ```
 Input: nums = [-1]
@@ -53,7 +53,7 @@ Output: ["-1"]
 
 ```
 
-**Example 5:**
+**Example 5**:
 
 ```
 Input: nums = [0]
@@ -61,7 +61,7 @@ Output: ["0"]
 
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `0 <= nums.length <= 20`
 - `231 <= nums[i] <= 231 - 1`

website/content/ChapterFour/0460.LFU-Cache.md

@@ -13,7 +13,7 @@ Implement the `LFUCache` class:
 
 **Notice that** the number of times an item is used is the number of calls to the `get` and `put` functions for that item since it was inserted. This number is set to zero when the item is removed.
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input
@@ -37,12 +37,12 @@ lfu.get(4);      // return 4
 
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `0 <= capacity, key, value <= 104`
 - At most `10^5` calls will be made to `get` and `put`.
 
-**Follow up:** Could you do both operations in `O(1)` time complexity?
+**Follow up**: Could you do both operations in `O(1)` time complexity?
 
 ## 题目大意
 

website/content/ChapterFour/0493.Reverse-Pairs.md

@@ -7,12 +7,12 @@ Given an array `nums`, we call `(i, j)` an **important reverse pair** if `
 
 You need to return the number of important reverse pairs in the given array.
 
-**Example1:**
+**Example1**:
 
     Input: [1,3,2,3,1]
     Output: 2
 
-**Example2:**
+**Example2**:
 
     Input: [2,4,3,5,1]
     Output: 3

website/content/ChapterFour/0497.Random-Point-in-Non-overlapping-Rectangles.md

@@ -31,7 +31,7 @@ Given a list of **non-overlapping** axis-aligned rectangles `rects`, write a
     Output: 
     [null,[-1,-2],[2,0],[-2,-1],[3,0],[-2,-2]]
 
-**Explanation of Input Syntax:**
+**Explanation of Input Syntax**:
 
 The input is two lists: the subroutines called and their arguments. `Solution`'s constructor has one argument, the array of rectangles `rects`. `pick` has no arguments. Arguments are always wrapped with a list, even if there aren't any.
 

website/content/ChapterFour/0528.Random-Pick-with-Weight.md

@@ -25,7 +25,7 @@ Given an array `w` of positive integers, where `w[i]` describes the weight o
     [[[1,3]],[],[],[],[],[]]
     Output: [null,0,1,1,1,0]
 
-**Explanation of Input Syntax:**
+**Explanation of Input Syntax**:
 
 The input is two lists: the subroutines called and their arguments. `Solution`'s constructor has one argument, the array `w`. `pickIndex` has no arguments. Arguments are always wrapped with a list, even if there aren't any.
 

website/content/ChapterFour/0541.Reverse-String-II.md

@@ -10,7 +10,7 @@ Given a string and an integer k, you need to reverse the first k characters for
     Input: s = "abcdefg", k = 2
     Output: "bacdfeg"
 
-**Restrictions:**
+**Restrictions**:
 
 1. The string consists of lower English letters only.
 2. Length of the given string and k will in the range [1, 10000]

website/content/ChapterFour/0547.Number-of-Provinces.md

@@ -1,4 +1,4 @@
-# [547. Friend Circles](https://leetcode.com/problems/friend-circles/)
+# [547. Number of Provinces](https://leetcode.com/problems/number-of-provinces/)
 
 ## 题目
 

website/content/ChapterFour/0605.Can-Place-Flowers.md

@@ -6,21 +6,21 @@ You have a long flowerbed in which some of the plots are planted, and some are n
 
 Given an integer array `flowerbed` containing `0`'s and `1`'s, where `0` means empty and `1` means not empty, and an integer `n`, return *if* `n` new flowers can be planted in the `flowerbed` without violating the no-adjacent-flowers rule.
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: flowerbed = [1,0,0,0,1], n = 1
 Output: true
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: flowerbed = [1,0,0,0,1], n = 2
 Output: false
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= flowerbed.length <= 2 * 104`
 - `flowerbed[i]` is `0` or `1`.

website/content/ChapterFour/0785.Is-Graph-Bipartite.md

@@ -32,7 +32,7 @@ The graph is given in the following form: `graph[i]` is a list of indexes `j`
 	We cannot find a way to divide the set of nodes into two independent subsets.
 
 
-**Note:**
+**Note**:
 
 - `graph` will have length in range `[1, 100]`.
 - `graph[i]` will contain integers in range `[0, graph.length - 1]`.

website/content/ChapterFour/0828.Count-Unique-Characters-of-All-Substrings-of-a-Given-String.md

@@ -1,16 +1,44 @@
-# [828. Unique Letter String](https://leetcode.com/problems/unique-letter-string/)
+# [828. Count Unique Characters of All Substrings of a Given String](https://leetcode.com/problems/count-unique-characters-of-all-substrings-of-a-given-string/)
+
 
 ## 题目
 
-THIS PROBLEM COPYRIGHT BELONGS TO CODILITY.COM
+Let's define a function `countUniqueChars(s)` that returns the number of unique characters on `s`, for example if `s = "LEETCODE"` then `"L"`, `"T"`,`"C"`,`"O"`,`"D"` are the unique characters since they appear only once in `s`, therefore `countUniqueChars(s) = 5`.On this problem given a string `s` we need to return the sum of `countUniqueChars(t)` where `t` is a substring of `s`. Notice that some substrings can be repeated so on this case you have to count the repeated ones too.
+
+Since the answer can be very large, return the answer modulo `10 ^ 9 + 7`.
 
 **Example 1**:
 
+```
+Input: s = "ABC"
+Output: 10
+Explanation: All possible substrings are: "A","B","C","AB","BC" and "ABC".
+Evey substring is composed with only unique letters.
+Sum of lengths of all substring is 1 + 1 + 1 + 2 + 2 + 3 = 10
 
+```
 
 **Example 2**:
 
+```
+Input: s = "ABA"
+Output: 8
+Explanation: The same as example 1, except countUniqueChars("ABA") = 1.
 
+```
+
+**Example 3**:
+
+```
+Input: s = "LEETCODE"
+Output: 92
+
+```
+
+**Constraints**:
+
+- `0 <= s.length <= 10^4`
+- `s` contain upper-case English letters only.
 
 ## 题目大意
 
@@ -18,20 +46,15 @@ THIS PROBLEM COPYRIGHT BELONGS TO CODILITY.COM
 
 对于给定字符串 S，计算其所有非空子串的独特字符的个数（即 UNIQ(substring)）之和。如果在 S 的不同位置上出现两个甚至多个相同的子串，那么我们认为这些子串是不同的。考虑到答案可能会非常大，规定返回格式为：结果 mod 10 ^ 9 + 7。
 
-
 ## 解题思路
 
 - 这一题可以先用暴力解法尝试解题，不过提交以后会发现判题结果是超时。出错的一组数据是一个有 10000 个字符的字符串。暴力解法中间由于遍历了太多的子区间，导致了超时。
 - 这道题换一个角度思考问题。当子字符串中字符 X 出现了 2 次以上，那么它就对最终结果没有任何影响，所以只有当某个字符只出现一次的时候才会影响最终结果。再者，一个子字符串中不重复的字符的总个数，也就是这个子字符串 UNIQ 值。例如，“ABC”，这个子字符串的 UNIQ 值是 3，可以这样计算，它属于 A 的独特的字符串，也属于 B 的独特的字符串，也属于 C 的独特的字符串，那么计算这个子字符串的问题可以分解成计算 A 有多少个独特的子字符串，B 有多少个独特的子字符串，C 有多少个独特的子字符串的问题。在计算 A 有多少个子字符串的问题的时候，里面肯定会包含 "ABC" 这个子字符串的。所以原问题就转换成了分别计算给出的字符串中每个字符出现在独特字符串中的总数之和。
-- 假设原字符串是 BAABBABBBAAABA，这个字符串中出现了很多 A 和很多 B，假设我们当前计算到了第 3 个 A 的位置了(index = 5)，即标红色的那个 A。如何计算这个 A 在哪些子字符串中是独特的呢？由于子字符串题目中要求必须是连续的区间，所以这个问题很简单。找到这个 A 前一个 A 的下标位置(index = 2)，再找到这个 A 后一个 A 的下标位置(index = 9)，即 BAABBABBBAAABA，第一个 A 和当前计算的 A 中间区间有 2 个字符，第三个 A 和当前计算的 A 中间有 3 个字符。那么当前计算的 A 出现在 `(2 + 1) * (3 + 1) = 12` 个子字符串中是独特的，这 12 个字符串是：`A`，`BA`，`BBA`，`AB`，`ABB`，`ABBB`，`BAB`，`BABB`，`BABBB`，`BBAB`，`BBABB`，`BBABBB`。计算方法，假设当前待计算的字符的下标是 i ，找到当前字符前一次出现的下标位置 left，再找到当前字符后一次出现的下标位置 right，那么左边区间 (left,i) 的**开区间**内包含的字符数是 i - left - 1，右边区间 (i,right) 的**开区间**内包含的字符数是 right - i - 1。左右两边都还需要考虑空字符串的情况，即左右两边都可以不取任何字符，那么对应的就是只有中间这个待计算的字符 `A`。所以左右两边都还需要再加上空串的情况，左边 i - left - 1 + 1 = i - left，右边 right - i - 1 + 1 = right - i。左右两边的情况进行排列组合，即 (i - left) * (right - i)。针对字符串的每个字符都计算这样的值，最后累积的总和就是题目中要求的总 UNIQ 值。
+- 假设原字符串是 BAABBABBBAAABA，这个字符串中出现了很多 A 和很多 B，假设我们当前计算到了第 3 个 A 的位置了(index = 5)，即标红色的那个 A。如何计算这个 A 在哪些子字符串中是独特的呢？由于子字符串题目中要求必须是连续的区间，所以这个问题很简单。找到这个 A 前一个 A 的下标位置(index = 2)，再找到这个 A 后一个 A 的下标位置(index = 9)，即 BAABBABBBAAABA，第一个 A 和当前计算的 A 中间区间有 2 个字符，第三个 A 和当前计算的 A 中间有 3 个字符。那么当前计算的 A 出现在 `(2 + 1) * (3 + 1) = 12` 个子字符串中是独特的，这 12 个字符串是：`A`，`BA`，`BBA`，`AB`，`ABB`，`ABBB`，`BAB`，`BABB`，`BABBB`，`BBAB`，`BBABB`，`BBABBB`。计算方法，假设当前待计算的字符的下标是 i ，找到当前字符前一次出现的下标位置 left，再找到当前字符后一次出现的下标位置 right，那么左边区间 (left,i) 的***开区间****内包含的字符数是 i - left - 1，右边区间 (i,right) 的***开区间****内包含的字符数是 right - i - 1。左右两边都还需要考虑空字符串的情况，即左右两边都可以不取任何字符，那么对应的就是只有中间这个待计算的字符 `A`。所以左右两边都还需要再加上空串的情况，左边 i - left - 1 + 1 = i - left，右边 right - i - 1 + 1 = right - i。左右两边的情况进行排列组合，即 (i - left) * (right - i)。针对字符串的每个字符都计算这样的值，最后累积的总和就是题目中要求的总 UNIQ 值。
-
-
-
 
 ## 代码
 
 ```go
-
 package leetcode
 
 func uniqueLetterString(S string) int {
@@ -75,6 +98,4 @@ func uniqueLetterString1(S string) int {
 	}
 	return res % mod
 }
-
-
 ```

website/content/ChapterFour/0830.Positions-of-Large-Groups.md

@@ -13,7 +13,7 @@ A group is considered **large** if it has 3 or more characters.
 
 Return *the intervals of every **large** group sorted in **increasing order by start index***.
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: s = "abbxxxxzzy"
@@ -21,7 +21,7 @@ Output: [[3,6]]
 Explanation: "xxxx" is the only large group with start index 3 and end index 6.
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: s = "abc"
@@ -29,7 +29,7 @@ Output: []
 Explanation: We have groups "a", "b", and "c", none of which are large groups.
 ```
 
-**Example 3:**
+**Example 3**:
 
 ```
 Input: s = "abcdddeeeeaabbbcd"
@@ -37,14 +37,14 @@ Output: [[3,5],[6,9],[12,14]]
 Explanation: The large groups are "ddd", "eeee", and "bbb".
 ```
 
-**Example 4:**
+**Example 4**:
 
 ```
 Input: s = "aba"
 Output: []
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= s.length <= 1000`
 - `s` contains lower-case English letters only.

website/content/ChapterFour/0910.Smallest-Range-II.md

@@ -8,7 +8,7 @@ After this process, we have some array `B`.
 
 Return the smallest possible difference between the maximum value of `B` and the minimum value of `B`.
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: A = [1], K = 0
@@ -16,7 +16,7 @@ Output: 0
 Explanation: B = [1]
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: A = [0,10], K = 2
@@ -24,7 +24,7 @@ Output: 6
 Explanation: B = [2,8]
 ```
 
-**Example 3:**
+**Example 3**:
 
 ```
 Input: A = [1,3,6], K = 3
@@ -32,7 +32,7 @@ Output: 3
 Explanation: B = [4,6,3]
 ```
 
-**Note:**
+**Note**:
 
 1. `1 <= A.length <= 10000`
 2. `0 <= A[i] <= 10000`

website/content/ChapterFour/1018.Binary-Prefix-Divisible-By-5.md

@@ -7,7 +7,7 @@ Given an array `A` of `0`s and `1`s, consider `N_i`: the i-th subarray from
 
 Return a list of booleans `answer`, where `answer[i]` is `true` if and only if `N_i` is divisible by 5.
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: [0,1,1]
@@ -17,7 +17,7 @@ The input numbers in binary are 0, 01, 011; which are 0, 1, and 3 in base-10.  O
 
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: [1,1,1]
@@ -25,7 +25,7 @@ Output: [false,false,false]
 
 ```
 
-**Example 3:**
+**Example 3**:
 
 ```
 Input: [0,1,1,1,1,1]
@@ -33,7 +33,7 @@ Output: [true,false,false,false,true,false]
 
 ```
 
-**Example 4:**
+**Example 4**:
 
 ```
 Input: [1,1,1,0,1]
@@ -41,7 +41,7 @@ Output: [false,false,false,false,false]
 
 ```
 
-**Note:**
+**Note**:
 
 1. `1 <= A.length <= 30000`
 2. `A[i]` is `0` or `1`

website/content/ChapterFour/1093.Statistics-from-a-Large-Sample.md

@@ -22,7 +22,7 @@ Return the minimum, maximum, mean, median, and mode of the sample respectively,
     Input: count = [0,4,3,2,2,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]
     Output: [1.00000,4.00000,2.18182,2.00000,1.00000]
 
-**Constraints:**
+**Constraints**:
 
 1. `count.length == 256`
 2. `1 <= sum(count) <= 10^9`

website/content/ChapterFour/1105.Filling-Bookcase-Shelves.md

@@ -23,7 +23,7 @@ Return the minimum possible height that the total bookshelf can be after placing
     The sum of the heights of the 3 shelves are 1 + 3 + 2 = 6.
     Notice that book number 2 does not have to be on the first shelf.
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= books.length <= 1000`
 - `1 <= books[i][0] <= shelf_width <= 1000`

website/content/ChapterFour/1108.Defanging-an-IP-Address.md

@@ -17,7 +17,7 @@ A *defanged IP address* replaces every period `"."` with `"[.]"`.
     Input: address = "255.100.50.0"
     Output: "255[.]100[.]50[.]0"
 
-**Constraints:**
+**Constraints**:
 
 - The given `address` is a valid IPv4 address.
 

website/content/ChapterFour/1111.Maximum-Nesting-Depth-of-Two-Valid-Parentheses-Strings.md

@@ -33,7 +33,7 @@ Return an `answer` array (of length `seq.length`) that encodes such a choice
     Input: seq = "()(())()"
     Output: [0,0,0,1,1,0,1,1]
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= seq.size <= 10000`
 

website/content/ChapterFour/1122.Relative-Sort-Array.md

@@ -12,7 +12,7 @@ Sort the elements of `arr1` such that the relative ordering of items in `arr1
     Input: arr1 = [2,3,1,3,2,4,6,7,9,2,19], arr2 = [2,1,4,3,9,6]
     Output: [2,2,2,1,4,3,3,9,6,7,19]
 
-**Constraints:**
+**Constraints**:
 
 - `arr1.length, arr2.length <= 1000`
 - `0 <= arr1[i], arr2[i] <= 1000`

website/content/ChapterFour/1123.Lowest-Common-Ancestor-of-Deepest-Leaves.md

@@ -30,7 +30,7 @@ Recall that:
     Input: root = [1,2,3,4,5]
     Output: [2,4,5]
 
-**Constraints:**
+**Constraints**:
 
 - The given tree will have between 1 and 1000 nodes.
 - Each node of the tree will have a distinct value between 1 and 1000.

website/content/ChapterFour/1128.Number-of-Equivalent-Domino-Pairs.md

@@ -12,7 +12,7 @@ Return the number of pairs `(i, j)` for which `0 <= i < j < dominoes.length`,
     Input: dominoes = [[1,2],[2,1],[3,4],[5,6]]
     Output: 1
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= dominoes.length <= 40000`
 - `1 <= dominoes[i][j] <= 9`

website/content/ChapterFour/1137.N-th-Tribonacci-Number.md

@@ -22,7 +22,7 @@ Given `n`, return the value of Tn.
     Input: n = 25
     Output: 1389537
 
-**Constraints:**
+**Constraints**:
 
 - `0 <= n <= 37`
 - The answer is guaranteed to fit within a 32-bit integer, ie. `answer <= 2^31 - 1`.

website/content/ChapterFour/1154.Day-of-the-Year.md

@@ -26,7 +26,7 @@ Given a string `date` representing a [Gregorian calendar](https://en.wikiped
     Input: date = "2004-03-01"
     Output: 61
 
-**Constraints:**
+**Constraints**:
 
 - `date.length == 10`
 - `date[4] == date[7] == '-'`, and all other `date[i]`'s are digits

website/content/ChapterFour/1157.Online-Majority-Element-In-Subarray.md

@@ -19,7 +19,7 @@ Each `query(...)` returns the element in `arr[left], arr[left+1], ..., arr[ri
     majorityChecker.query(0,3,3); // returns -1
     majorityChecker.query(2,3,2); // returns 2
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= arr.length <= 20000`
 - `1 <= arr[i] <= 20000`

website/content/ChapterFour/1170.Compare-Strings-by-Frequency-of-the-Smallest-Character.md

@@ -18,7 +18,7 @@ Now, given string arrays `queries` and `words`, return an integer array `ans
     Output: [1,2]
     Explanation: On the first query only f("bbb") < f("aaaa"). On the second query both f("aaa") and f("aaaa") are both > f("cc").
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= queries.length <= 2000`
 - `1 <= words.length <= 2000`

website/content/ChapterFour/1171.Remove-Zero-Sum-Consecutive-Nodes-from-Linked-List.md

@@ -25,7 +25,7 @@ After doing so, return the head of the final linked list. You may return any suc
     Input: head = [1,2,3,-3,-2]
     Output: [1]
 
-**Constraints:**
+**Constraints**:
 
 - The given linked list will contain between `1` and `1000` nodes.
 - Each node in the linked list has `-1000 <= node.val <= 1000`.

website/content/ChapterFour/1175.Prime-Arrangements.md

@@ -20,7 +20,7 @@ Since the answer may be large, return the answer **modulo `10^9 + 7`**.
     Input: n = 100
     Output: 682289015
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= n <= 100`
 

website/content/ChapterFour/1184.Distance-Between-Bus-Stops.md

@@ -32,7 +32,7 @@ Return the shortest distance between the given `start` and `destination` sto
     Output: 4
     Explanation: Distance between 0 and 3 is 6 or 4, minimum is 4.
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= n <= 10^4`
 - `distance.length == n`

website/content/ChapterFour/1185.Day-of-the-Week.md

@@ -24,7 +24,7 @@ Return the answer as one of the following values `{"Sunday", "Monday", "Tuesday
     Input: day = 15, month = 8, year = 1993
     Output: "Sunday"
 
-**Constraints:**
+**Constraints**:
 
 - The given dates are valid dates between the years `1971` and `2100`.
 

website/content/ChapterFour/1189.Maximum-Number-of-Balloons.md

@@ -26,7 +26,7 @@ You can use each character in `text` **at most once**. Return the maximum numb
     Input: text = "leetcode"
     Output: 0
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= text.length <= 10^4`
 - `text` consists of lower case English letters only.

website/content/ChapterFour/1200.Minimum-Absolute-Difference.md

@@ -27,7 +27,7 @@ Return a list of pairs in ascending order(with respect to pairs), each pair `[a
     Input: arr = [3,8,-10,23,19,-4,-14,27]
     Output: [[-14,-10],[19,23],[23,27]]
 
-**Constraints:**
+**Constraints**:
 
 - `2 <= arr.length <= 10^5`
 - `-10^6 <= arr[i] <= 10^6`

website/content/ChapterFour/1201.Ugly-Number-III.md

@@ -30,7 +30,7 @@ Ugly numbers are **positive integers** which are divisible by `a` **or** `b
     Input: n = 1000000000, a = 2, b = 217983653, c = 336916467
     Output: 1999999984
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= n, a, b, c <= 10^9`
 - `1 <= a * b * c <= 10^18`

website/content/ChapterFour/1202.Smallest-String-With-Swaps.md

@@ -35,7 +35,7 @@ Return the lexicographically smallest string that `s` can be changed to after
     Swap s[1] and s[2], s = "bac"
     Swap s[0] and s[1], s = "abc"
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= s.length <= 10^5`
 - `0 <= pairs.length <= 10^5`

website/content/ChapterFour/1207.Unique-Number-of-Occurrences.md

@@ -21,7 +21,7 @@ Given an array of integers `arr`, write a function that returns `true` if an
     Input: arr = [-3,0,1,-3,1,1,1,-3,10,0]
     Output: true
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= arr.length <= 1000`
 - `-1000 <= arr[i] <= 1000`

website/content/ChapterFour/1208.Get-Equal-Substrings-Within-Budget.md

@@ -29,7 +29,7 @@ If there is no substring from `s` that can be changed to its corresponding sub
     Output: 1
     Explanation: You can't make any change, so the maximum length is 1.
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= s.length, t.length <= 10^5`
 - `0 <= maxCost <= 10^6`

website/content/ChapterFour/1217.Minimum-Cost-to-Move-Chips-to-The-Same-Position.md

@@ -26,7 +26,7 @@ Return the minimum cost needed to move all the chips to the same position (any
     Output: 2
     Explanation: Both fourth and fifth chip will be moved to position two with cost 1. Total minimum cost will be 2.
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= chips.length <= 100`
 - `1 <= chips[i] <= 10^9`

website/content/ChapterFour/1221.Split-a-String-in-Balanced-Strings.md

@@ -27,7 +27,7 @@ Return the maximum amount of splitted balanced strings.
     Output: 1
     Explanation: s can be split into "LLLLRRRR".
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= s.length <= 1000`
 - `s[i] = 'L' or 'R'`

website/content/ChapterFour/1232.Check-If-It-Is-a-Straight-Line.md

@@ -20,7 +20,7 @@ You are given an array `coordinates`, `coordinates[i] = [x, y]`, where `[x, y
     Input: coordinates = [[1,1],[2,2],[3,4],[4,5],[5,6],[7,7]]
     Output: false
 
-**Constraints:**
+**Constraints**:
 
 - `2 <= coordinates.length <= 1000`
 - `coordinates[i].length == 2`

website/content/ChapterFour/1234.Replace-the-Substring-for-Balanced-String.md

@@ -35,7 +35,7 @@ Return 0 if the string is already **balanced**.
     Output: 3
     Explanation: We can replace the last 3 'Q' to make s = "QWER".
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= s.length <= 10^5`
 - `s.length` is a multiple of `4`

website/content/ChapterFour/1235.Maximum-Profit-in-Job-Scheduling.md

@@ -34,7 +34,7 @@ If you choose a job that ends at time `X` you will be able to start another j
     Input: startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4]
     Output: 6
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= startTime.length == endTime.length == profit.length <= 5 * 10^4`
 - `1 <= startTime[i] < endTime[i] <= 10^9`

website/content/ChapterFour/1252.Cells-with-Odd-Values-in-a-Matrix.md

@@ -25,7 +25,7 @@ Return *the number of cells with odd values* in the matrix after applying the
     Output: 0
     Explanation: Final matrix = [[2,2],[2,2]]. There is no odd number in the final matrix.
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= n <= 50`
 - `1 <= m <= 50`

website/content/ChapterFour/1266.Minimum-Time-Visiting-All-Points.md

@@ -26,7 +26,7 @@ You can move according to the next rules:
     Input: points = [[3,2],[-2,2]]
     Output: 5
 
-**Constraints:**
+**Constraints**:
 
 - `points.length == n`
 - `1 <= n <= 100`

website/content/ChapterFour/1275.Find-Winner-on-a-Tic-Tac-Toe-Game.md

@@ -68,7 +68,7 @@ Explanation: The game has not finished yet.
 
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= moves.length <= 9`
 - `moves[i].length == 2`

website/content/ChapterFour/1539.Kth-Missing-Positive-Number.md

@@ -6,7 +6,7 @@ Given an array `arr` of positive integers sorted in a **strictly increasing
 
 *Find the* `kth` *positive integer that is missing from this array.*
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: arr = [2,3,4,7,11], k = 5
@@ -14,7 +14,7 @@ Output: 9
 Explanation: The missing positive integers are [1,5,6,8,9,10,12,13,...]. The 5th missing positive integer is 9.
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: arr = [1,2,3,4], k = 2
@@ -22,7 +22,7 @@ Output: 6
 Explanation: The missing positive integers are [5,6,7,...]. The 2nd missing positive integer is 6.
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= arr.length <= 1000`
 - `1 <= arr[i] <= 1000`

website/content/ChapterFour/1573.Number-of-Ways-to-Split-a-String.md

@@ -9,7 +9,7 @@ Return the number of ways `s` can be split such that the number of characters
 
 Since the answer may be too large, return it modulo 10^9 + 7.
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: s = "10101"
@@ -22,7 +22,7 @@ Explanation: There are four ways to split s in 3 parts where each part contain t
 
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: s = "1001"
@@ -30,7 +30,7 @@ Output: 0
 
 ```
 
-**Example 3:**
+**Example 3**:
 
 ```
 Input: s = "0000"
@@ -42,7 +42,7 @@ Explanation: There are three ways to split s in 3 parts.
 
 ```
 
-**Example 4:**
+**Example 4**:
 
 ```
 Input: s = "100100010100110"
@@ -50,7 +50,7 @@ Output: 12
 
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `3 <= s.length <= 10^5`
 - `s[i]` is `'0'` or `'1'`.

website/content/ChapterFour/1640.Check-Array-Formation-Through-Concatenation.md

@@ -7,14 +7,14 @@ You are given an array of **distinct** integers `arr` and an array of intege
 
 Return `true` *if it is possible to form the array* `arr` *from* `pieces`. Otherwise, return `false`.
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: arr = [85], pieces = [[85]]
 Output: true
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: arr = [15,88], pieces = [[88],[15]]
@@ -22,7 +22,7 @@ Output: true
 Explanation: Concatenate [15] then [88]
 ```
 
-**Example 3:**
+**Example 3**:
 
 ```
 Input: arr = [49,18,16], pieces = [[16,18,49]]
@@ -30,7 +30,7 @@ Output: false
 Explanation: Even though the numbers match, we cannot reorder pieces[0].
 ```
 
-**Example 4:**
+**Example 4**:
 
 ```
 Input: arr = [91,4,64,78], pieces = [[78],[4,64],[91]]
@@ -38,7 +38,7 @@ Output: true
 Explanation: Concatenate [91] then [4,64] then [78]
 ```
 
-**Example 5:**
+**Example 5**:
 
 ```
 Input: arr = [1,3,5,7], pieces = [[2,4,6,8]]
@@ -46,7 +46,7 @@ Output: false
 
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= pieces.length <= arr.length <= 100`
 - `sum(pieces[i].length) == arr.length`

website/content/ChapterFour/1646.Get-Maximum-in-Generated-Array.md

@@ -12,7 +12,7 @@ You are given an integer `n`. An array `nums` of length `n + 1` is generate
 
 Return *****the **maximum** integer in the array* `nums`.
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: n = 7
@@ -30,7 +30,7 @@ Hence, nums = [0,1,1,2,1,3,2,3], and the maximum is 3.
 
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: n = 2
@@ -39,7 +39,7 @@ Explanation: According to the given rules, the maximum between nums[0], nums[1],
 
 ```
 
-**Example 3:**
+**Example 3**:
 
 ```
 Input: n = 3
@@ -48,7 +48,7 @@ Explanation: According to the given rules, the maximum between nums[0], nums[1],
 
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `0 <= n <= 100`
 

website/content/ChapterFour/1647.Minimum-Deletions-to-Make-Character-Frequencies-Unique.md

@@ -9,7 +9,7 @@ Given a string `s`, return *the **minimum** number of characters you need to
 
 The **frequency** of a character in a string is the number of times it appears in the string. For example, in the string `"aab"`, the **frequency** of `'a'` is `2`, while the **frequency** of `'b'` is `1`.
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: s = "aab"
@@ -18,7 +18,7 @@ Explanation: s is already good.
 
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: s = "aaabbbcc"
@@ -27,7 +27,7 @@ Explanation: You can delete two 'b's resulting in the good string "aaabcc".
 Another way it to delete one 'b' and one 'c' resulting in the good string "aaabbc".
 ```
 
-**Example 3:**
+**Example 3**:
 
 ```
 Input: s = "ceabaacb"
@@ -37,7 +37,7 @@ Note that we only care about characters that are still in the string at the end
 
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= s.length <= 105`
 - `s` contains only lowercase English letters.

website/content/ChapterFour/1648.Sell-Diminishing-Valued-Colored-Balls.md

@@ -11,7 +11,7 @@ You are given an integer array, `inventory`, where `inventory[i]` represents
 
 Return *the **maximum** total value that you can attain after selling* `orders` *colored balls*. As the answer may be too large, return it **modulo** `109 + 7`.
 
-**Example 1:**
+**Example 1**:
 
 ![https://assets.leetcode.com/uploads/2020/11/05/jj.gif](https://assets.leetcode.com/uploads/2020/11/05/jj.gif)
 
@@ -23,7 +23,7 @@ The maximum total value is 2 + 5 + 4 + 3 = 14.
 
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: inventory = [3,5], orders = 6
@@ -32,14 +32,14 @@ Explanation: Sell the 1st color 2 times (3 + 2) and the 2nd color 4 times (5 + 4
 The maximum total value is 3 + 2 + 5 + 4 + 3 + 2 = 19.
 ```
 
-**Example 3:**
+**Example 3**:
 
 ```
 Input: inventory = [2,8,4,10,6], orders = 20
 Output: 110
 ```
 
-**Example 4:**
+**Example 4**:
 
 ```
 Input: inventory = [1000000000], orders = 1000000000
@@ -47,7 +47,7 @@ Output: 21
 Explanation: Sell the 1st color 1000000000 times for a total value of 500000000500000000. 500000000500000000 modulo 109 + 7 = 21.
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= inventory.length <= 10^5`
 - `1 <= inventory[i] <= 10^9`

website/content/ChapterFour/1649.Create-Sorted-Array-through-Instructions.md

@@ -11,7 +11,7 @@ For example, if inserting element `3` into `nums = [1,2,3,5]`, the **cost**
 
 Return *the **total cost** to insert all elements from* `instructions` *into* `nums`. Since the answer may be large, return it **modulo** `10^9 + 7`
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: instructions = [1,5,6,2]
@@ -24,7 +24,7 @@ Insert 2 with cost min(1, 2) = 1, now nums = [1,2,5,6].
 The total cost is 0 + 0 + 0 + 1 = 1.
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: instructions = [1,2,3,6,5,4]
@@ -39,7 +39,7 @@ Insert 4 with cost min(3, 2) = 2, now nums = [1,2,3,4,5,6].
 The total cost is 0 + 0 + 0 + 0 + 1 + 2 = 3.
 ```
 
-**Example 3:**
+**Example 3**:
 
 ```
 Input: instructions = [1,3,3,3,2,4,2,1,2]
@@ -57,7 +57,7 @@ Insert 2 with cost min(2, 4) = 2, now nums = [1,1,2,2,2,3,3,3,4].
 The total cost is 0 + 0 + 0 + 0 + 1 + 0 + 1 + 0 + 2 = 4.
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= instructions.length <= 105`
 - `1 <= instructions[i] <= 105`

website/content/ChapterFour/1652.Defuse-the-Bomb.md

@@ -15,7 +15,7 @@ As `code` is circular, the next element of `code[n-1]` is `code[0]`, and th
 
 Given the **circular** array `code` and an integer key `k`, return *the decrypted code to defuse the bomb*!
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: code = [5,7,1,4], k = 3
@@ -23,7 +23,7 @@ Output: [12,10,16,13]
 Explanation: Each number is replaced by the sum of the next 3 numbers. The decrypted code is [7+1+4, 1+4+5, 4+5+7, 5+7+1]. Notice that the numbers wrap around.
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: code = [1,2,3,4], k = 0
@@ -31,7 +31,7 @@ Output: [0,0,0,0]
 Explanation: When k is zero, the numbers are replaced by 0. 
 ```
 
-**Example 3:**
+**Example 3**:
 
 ```
 Input: code = [2,4,9,3], k = -2
@@ -39,7 +39,7 @@ Output: [12,5,6,13]
 Explanation: The decrypted code is [3+9, 2+3, 4+2, 9+4]. Notice that the numbers wrap around again. If k is negative, the sum is of the previous numbers.
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `n == code.length`
 - `1 <= n <= 100`

website/content/ChapterFour/1653.Minimum-Deletions-to-Make-String-Balanced.md

@@ -9,7 +9,7 @@ You can delete any number of characters in `s` to make `s` **balanced**. `s
 
 Return *the **minimum** number of deletions needed to make* `s` ***balanced***.
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: s = "aababbab"
@@ -19,7 +19,7 @@ Delete the characters at 0-indexed positions 2 and 6 ("aababbab" -> "aaabbb"), o
 Delete the characters at 0-indexed positions 3 and 6 ("aababbab" -> "aabbbb").
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: s = "bbaaaaabb"
@@ -27,7 +27,7 @@ Output: 2
 Explanation: The only solution is to delete the first two characters.
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= s.length <= 105`
 - `s[i]` is `'a'` or `'b'`.

website/content/ChapterFour/1654.Minimum-Jumps-to-Reach-Home.md

@@ -16,7 +16,7 @@ The bug may jump forward **beyond** its home, but it **cannot jump** to posi
 
 Given an array of integers `forbidden`, where `forbidden[i]` means that the bug cannot jump to the position `forbidden[i]`, and integers `a`, `b`, and `x`, return *the minimum number of jumps needed for the bug to reach its home*. If there is no possible sequence of jumps that lands the bug on position `x`, return `1.`
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: forbidden = [14,4,18,1,15], a = 3, b = 15, x = 9
@@ -24,14 +24,14 @@ Output: 3
 Explanation: 3 jumps forward (0 -> 3 -> 6 -> 9) will get the bug home.
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: forbidden = [8,3,16,6,12,20], a = 15, b = 13, x = 11
 Output: -1
 ```
 
-**Example 3:**
+**Example 3**:
 
 ```
 Input: forbidden = [1,6,2,14,5,17,4], a = 16, b = 9, x = 7
@@ -40,7 +40,7 @@ Explanation: One jump forward (0 -> 16) then one jump backward (16 -> 7) will ge
 
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= forbidden.length <= 1000`
 - `1 <= a, b, forbidden[i] <= 2000`

website/content/ChapterFour/1655.Distribute-Repeating-Integers.md

@@ -11,7 +11,7 @@ You are given an array of `n` integers, `nums`, where there are at most `50`
 
 Return `true` *if it is possible to distribute* `nums` *according to the above conditions*.
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: nums = [1,2,3,4], quantity = [2]
@@ -19,7 +19,7 @@ Output: false
 Explanation: The 0th customer cannot be given two different integers.
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: nums = [1,2,3,3], quantity = [2]
@@ -27,7 +27,7 @@ Output: true
 Explanation: The 0th customer is given [3,3]. The integers [1,2] are not used.
 ```
 
-**Example 3:**
+**Example 3**:
 
 ```
 Input: nums = [1,1,2,2], quantity = [2,2]
@@ -35,7 +35,7 @@ Output: true
 Explanation: The 0th customer is given [1,1], and the 1st customer is given [2,2].
 ```
 
-**Example 4:**
+**Example 4**:
 
 ```
 Input: nums = [1,1,2,3], quantity = [2,2]
@@ -43,7 +43,7 @@ Output: false
 Explanation: Although the 0th customer could be given [1,1], the 1st customer cannot be satisfied.
 ```
 
-**Example 5:**
+**Example 5**:
 
 ```
 Input: nums = [1,1,1,1,1], quantity = [2,3]
@@ -51,7 +51,7 @@ Output: true
 Explanation: The 0th customer is given [1,1], and the 1st customer is given [1,1,1].
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `n == nums.length`
 - `1 <= n <= 105`

website/content/ChapterFour/1656.Design-an-Ordered-Stream.md

@@ -11,7 +11,7 @@ Implement the `OrderedStream` class:
 - `OrderedStream(int n)` Constructs the stream to take `n` values.
 - `String[] insert(int id, String value)` Inserts the pair `(id, value)` into the stream, then returns the **largest possible chunk** of currently inserted values that appear next in the order.
 
-**Example:**
+**Example**:
 
 ![https://assets.leetcode.com/uploads/2020/11/10/q1.gif](https://assets.leetcode.com/uploads/2020/11/10/q1.gif)
 
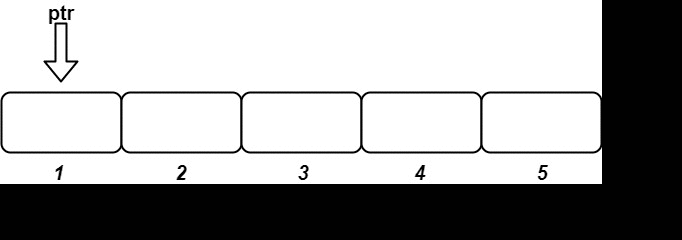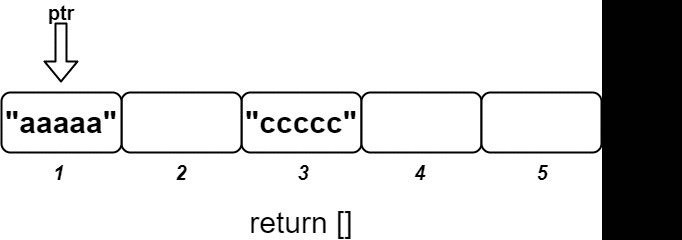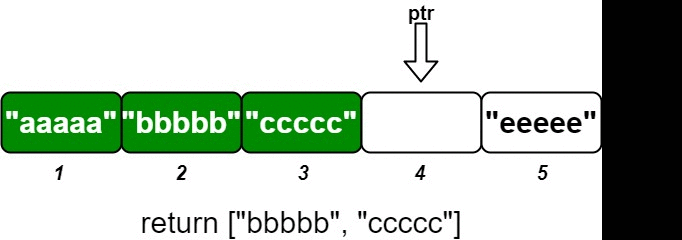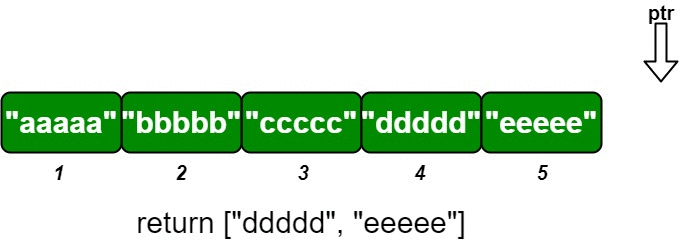
@@ -36,7 +36,7 @@ os.insert(4, "ddddd"); // Inserts (4, "ddddd"), returns ["ddddd", "eeeee"].
 
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= n <= 1000`
 - `1 <= id <= n`

website/content/ChapterFour/1657.Determine-if-Two-Strings-Are-Close.md

@@ -14,7 +14,7 @@ You can use the operations on either string as many times as necessary.
 
 Given two strings, `word1` and `word2`, return `true` *if* `word1` *and* `word2` *are **close**, and* `false` *otherwise.*
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: word1 = "abc", word2 = "bca"
@@ -25,7 +25,7 @@ Apply Operation 1: "acb" -> "bca"
 
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: word1 = "a", word2 = "aa"
@@ -34,7 +34,7 @@ Explanation: It is impossible to attain word2 from word1, or vice versa, in any
 
 ```
 
-**Example 3:**
+**Example 3**:
 
 ```
 Input: word1 = "cabbba", word2 = "abbccc"
@@ -46,7 +46,7 @@ Apply Operation 2: "baaccc" -> "abbccc"
 
 ```
 
-**Example 4:**
+**Example 4**:
 
 ```
 Input: word1 = "cabbba", word2 = "aabbss"
@@ -55,7 +55,7 @@ Explanation: It is impossible to attain word2 from word1, or vice versa, in any
 
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= word1.length, word2.length <= 105`
 - `word1` and `word2` contain only lowercase English letters.

website/content/ChapterFour/1658.Minimum-Operations-to-Reduce-X-to-Zero.md

@@ -7,7 +7,7 @@ You are given an integer array `nums` and an integer `x`. In one operation, y
 
 Return *the **minimum number** of operations to reduce* `x` *to **exactly*** `0` *if it's possible, otherwise, return* `1`.
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: nums = [1,1,4,2,3], x = 5
@@ -16,7 +16,7 @@ Explanation: The optimal solution is to remove the last two elements to reduce x
 
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: nums = [5,6,7,8,9], x = 4
@@ -24,7 +24,7 @@ Output: -1
 
 ```
 
-**Example 3:**
+**Example 3**:
 
 ```
 Input: nums = [3,2,20,1,1,3], x = 10
@@ -33,7 +33,7 @@ Explanation: The optimal solution is to remove the last three elements and the f
 
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= nums.length <= 105`
 - `1 <= nums[i] <= 104`

website/content/ChapterFour/1659.Maximize-Grid-Happiness.md

@@ -15,7 +15,7 @@ Neighbors live in the directly adjacent cells north, east, south, and west of a
 
 The **grid happiness** is the **sum** of each person's happiness. Return *the **maximum possible grid happiness**.*
 
-**Example 1:**
+**Example 1**:
 
 ![https://assets.leetcode.com/uploads/2020/11/05/grid_happiness.png](https://assets.leetcode.com/uploads/2020/11/05/grid_happiness.png)
 
@@ -31,7 +31,7 @@ The grid happiness is 120 + 60 + 60 = 240.
 The above figure shows the grid in this example with each person's happiness. The introvert stays in the light green cell while the extroverts live on the light purple cells.
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: m = 3, n = 1, introvertsCount = 2, extrovertsCount = 1
@@ -43,14 +43,14 @@ Explanation: Place the two introverts in (1,1) and (3,1) and the extrovert at (2
 The grid happiness is 90 + 80 + 90 = 260.
 ```
 
-**Example 3:**
+**Example 3**:
 
 ```
 Input: m = 2, n = 2, introvertsCount = 4, extrovertsCount = 0
 Output: 240
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= m, n <= 5`
 - `0 <= introvertsCount, extrovertsCount <= min(m * n, 6)`

website/content/ChapterFour/1662.Check-If-Two-String-Arrays-are-Equivalent.md

@@ -7,7 +7,7 @@ Given two string arrays `word1` and `word2`, return **`true` *if the two ar
 
 A string is **represented** by an array if the array elements concatenated **in order** forms the string.
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: word1 = ["ab", "c"], word2 = ["a", "bc"]
@@ -18,21 +18,21 @@ word2 represents string "a" + "bc" -> "abc"
 The strings are the same, so return true.
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: word1 = ["a", "cb"], word2 = ["ab", "c"]
 Output: false
 ```
 
-**Example 3:**
+**Example 3**:
 
 ```
 Input: word1  = ["abc", "d", "defg"], word2 = ["abcddefg"]
 Output: true
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= word1.length, word2.length <= 103`
 - `1 <= word1[i].length, word2[i].length <= 103`

website/content/ChapterFour/1663.Smallest-String-With-A-Given-Numeric-Value.md

@@ -10,7 +10,7 @@ You are given two integers `n` and `k`. Return *the **lexicographically sma
 
 Note that a string `x` is lexicographically smaller than string `y` if `x` comes before `y` in dictionary order, that is, either `x` is a prefix of `y`, or if `i` is the first position such that `x[i] != y[i]`, then `x[i]` comes before `y[i]` in alphabetic order.
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: n = 3, k = 27
@@ -18,14 +18,14 @@ Output: "aay"
 Explanation: The numeric value of the string is 1 + 1 + 25 = 27, and it is the smallest string with such a value and length equal to 3.
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: n = 5, k = 73
 Output: "aaszz"
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= n <= 105`
 - `n <= k <= 26 * n`

website/content/ChapterFour/1664.Ways-to-Make-a-Fair-Array.md

@@ -15,7 +15,7 @@ An array is **fair** if the sum of the odd-indexed values equals the sum of th
 
 Return the ***number** of indices that you could choose such that after the removal,* `nums` *is **fair**.*
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: nums = [2,1,6,4]
@@ -28,7 +28,7 @@ Remove index 3: [2,1,6] -> Even sum: 2 + 6 = 8. Odd sum: 1. Not fair.
 There is 1 index that you can remove to make nums fair.
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: nums = [1,1,1]
@@ -36,7 +36,7 @@ Output: 3
 Explanation: You can remove any index and the remaining array is fair.
 ```
 
-**Example 3:**
+**Example 3**:
 
 ```
 Input: nums = [1,2,3]
@@ -44,7 +44,7 @@ Output: 0
 Explanation: You cannot make a fair array after removing any index.
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= nums.length <= 105`
 - `1 <= nums[i] <= 104`

website/content/ChapterFour/1665.Minimum-Initial-Energy-to-Finish-Tasks.md

@@ -13,7 +13,7 @@ You can finish the tasks in **any order** you like.
 
 Return *the **minimum** initial amount of energy you will need* *to finish all the tasks*.
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: tasks = [[1,2],[2,4],[4,8]]
@@ -26,7 +26,7 @@ Starting with 8 energy, we finish the tasks in the following order:
 Notice that even though we have leftover energy, starting with 7 energy does not work because we cannot do the 3rd task.
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: tasks = [[1,3],[2,4],[10,11],[10,12],[8,9]]
@@ -40,7 +40,7 @@ Starting with 32 energy, we finish the tasks in the following order:
     - 5th task. Now energy = 9 - 8 = 1.
 ```
 
-**Example 3:**
+**Example 3**:
 
 ```
 Input: tasks = [[1,7],[2,8],[3,9],[4,10],[5,11],[6,12]]
@@ -56,7 +56,7 @@ Starting with 27 energy, we finish the tasks in the following order:
 
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= tasks.length <= 105`
 - `1 <= actuali <= minimumi <= 104`

website/content/ChapterFour/1668.Maximum-Repeating-Substring.md

@@ -7,7 +7,7 @@ For a string `sequence`, a string `word` is **`k`-repeating** if `word` c
 
 Given strings `sequence` and `word`, return *the **maximum `k`-repeating value** of `word` in `sequence`*.
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: sequence = "ababc", word = "ab"
@@ -15,7 +15,7 @@ Output: 2
 Explanation: "abab" is a substring in "ababc".
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: sequence = "ababc", word = "ba"
@@ -23,7 +23,7 @@ Output: 1
 Explanation: "ba" is a substring in "ababc". "baba" is not a substring in "ababc".
 ```
 
-**Example 3:**
+**Example 3**:
 
 ```
 Input: sequence = "ababc", word = "ac"
@@ -31,7 +31,7 @@ Output: 0
 Explanation: "ac" is not a substring in "ababc". 
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= sequence.length <= 100`
 - `1 <= word.length <= 100`

website/content/ChapterFour/1669.Merge-In-Between-Linked-Lists.md

@@ -13,7 +13,7 @@ The blue edges and nodes in the following figure incidate the result:
 
 *Build the result list and return its head.*
 
-**Example 1:**
+**Example 1**:
 
 ![https://assets.leetcode.com/uploads/2020/11/05/merge_linked_list_ex1.png](https://assets.leetcode.com/uploads/2020/11/05/merge_linked_list_ex1.png)
 
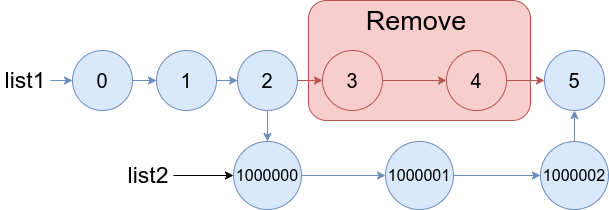
@@ -24,7 +24,7 @@ Explanation: We remove the nodes 3 and 4 and put the entire list2 in their place
 
 ```
 
-**Example 2:**
+**Example 2**:
 
 ![https://assets.leetcode.com/uploads/2020/11/05/merge_linked_list_ex2.png](https://assets.leetcode.com/uploads/2020/11/05/merge_linked_list_ex2.png)
 
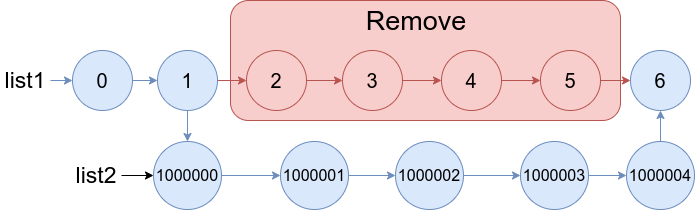
@@ -35,7 +35,7 @@ Explanation: The blue edges and nodes in the above figure indicate the result.
 
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `3 <= list1.length <= 104`
 - `1 <= a <= b < list1.length - 1`

website/content/ChapterFour/1670.Design-Front-Middle-Back-Queue.md

@@ -20,7 +20,7 @@ Implement the `FrontMiddleBack` class:
 - Pushing `6` into the middle of `[1, 2, 3, 4, 5]` results in `[1, 2, 6, 3, 4, 5]`.
 - Popping the middle from `[1, 2, 3, 4, 5, 6]` returns `3` and results in `[1, 2, 4, 5, 6]`.
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input:
@@ -43,7 +43,7 @@ q.popFront();     // return -1 -> [] (The queue is empty)
 
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= val <= 109`
 - At most `1000` calls will be made to `pushFront`, `pushMiddle`, `pushBack`, `popFront`, `popMiddle`, and `popBack`.

website/content/ChapterFour/1672.Richest-Customer-Wealth.md

@@ -7,7 +7,7 @@ You are given an `m x n` integer grid `accounts` where `accounts[i][j]` is
 
 A customer's **wealth** is the amount of money they have in all their bank accounts. The richest customer is the customer that has the maximum **wealth**.
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: accounts = [[1,2,3],[3,2,1]]
@@ -17,7 +17,7 @@ Explanation:1st customer has wealth = 1 + 2 + 3 = 6
 Both customers are considered the richest with a wealth of 6 each, so return 6.
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: accounts = [[1,5],[7,3],[3,5]]
@@ -29,14 +29,14 @@ Explanation:
 The 2nd customer is the richest with a wealth of 10.
 ```
 
-**Example 3:**
+**Example 3**:
 
 ```
 Input: accounts = [[2,8,7],[7,1,3],[1,9,5]]
 Output: 17
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `m == accounts.length`
 - `n == accounts[i].length`

website/content/ChapterFour/1673.Find-the-Most-Competitive-Subsequence.md

@@ -9,7 +9,7 @@ An array's subsequence is a resulting sequence obtained by erasing some (possibl
 
 We define that a subsequence `a` is more **competitive** than a subsequence `b` (of the same length) if in the first position where `a` and `b` differ, subsequence `a` has a number **less** than the corresponding number in `b`. For example, `[1,3,4]` is more competitive than `[1,3,5]` because the first position they differ is at the final number, and `4` is less than `5`.
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: nums = [3,5,2,6], k = 2
@@ -18,7 +18,7 @@ Explanation: Among the set of every possible subsequence: {[3,5], [3,2], [3,6],
 
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: nums = [2,4,3,3,5,4,9,6], k = 4
@@ -26,7 +26,7 @@ Output: [2,3,3,4]
 
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= nums.length <= 105`
 - `0 <= nums[i] <= 109`

website/content/ChapterFour/1674.Minimum-Moves-to-Make-Array-Complementary.md

@@ -8,7 +8,7 @@ The array `nums` is **complementary** if for all indices `i` (**0-indexed*
 
 Return the ***minimum** number of moves required to make* `nums` ***complementary***.
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: nums = [1,2,4,3], limit = 4
@@ -21,7 +21,7 @@ nums[3] + nums[0] = 3 + 1 = 4.
 Therefore, nums[i] + nums[n-1-i] = 4 for every i, so nums is complementary.
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: nums = [1,2,2,1], limit = 2
@@ -29,7 +29,7 @@ Output: 2
 Explanation: In 2 moves, you can change nums to [2,2,2,2]. You cannot change any number to 3 since 3 > limit.
 ```
 
-**Example 3:**
+**Example 3**:
 
 ```
 Input: nums = [1,2,1,2], limit = 2
@@ -37,7 +37,7 @@ Output: 0
 Explanation: nums is already complementary.
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `n == nums.length`
 - `2 <= n <= 105`

website/content/ChapterFour/1678.Goal-Parser-Interpretation.md

@@ -6,7 +6,7 @@ You own a **Goal Parser** that can interpret a string `command`. The `comman
 
 Given the string `command`, return *the **Goal Parser**'s interpretation of* `command`.
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: command = "G()(al)"
@@ -18,21 +18,21 @@ G -> G
 The final concatenated result is "Goal".
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: command = "G()()()()(al)"
 Output: "Gooooal"
 ```
 
-**Example 3:**
+**Example 3**:
 
 ```
 Input: command = "(al)G(al)()()G"
 Output: "alGalooG"
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= command.length <= 100`
 - `command` consists of `"G"`, `"()"`, and/or `"(al)"` in some order.

website/content/ChapterFour/1679.Max-Number-of-K-Sum-Pairs.md

@@ -9,7 +9,7 @@ In one operation, you can pick two numbers from the array whose sum equals `k`
 
 Return *the maximum number of operations you can perform on the array*.
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: nums = [1,2,3,4], k = 5
@@ -20,7 +20,7 @@ Explanation: Starting with nums = [1,2,3,4]:
 There are no more pairs that sum up to 5, hence a total of 2 operations.
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: nums = [3,1,3,4,3], k = 6
@@ -30,7 +30,7 @@ Explanation: Starting with nums = [3,1,3,4,3]:
 There are no more pairs that sum up to 6, hence a total of 1 operation.
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= nums.length <= 105`
 - `1 <= nums[i] <= 109`

website/content/ChapterFour/1680.Concatenation-of-Consecutive-Binary-Numbers.md

@@ -5,7 +5,7 @@
 
 Given an integer `n`, return *the **decimal value** of the binary string formed by concatenating the binary representations of* `1` *to* `n` *in order, **modulo*** `109 + 7`.
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: n = 1
@@ -13,7 +13,7 @@ Output: 1
 Explanation: "1" in binary corresponds to the decimal value 1. 
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: n = 3
@@ -22,7 +22,7 @@ Explanation: In binary, 1, 2, and 3 corresponds to "1", "10", and "11".
 After concatenating them, we have "11011", which corresponds to the decimal value 27.
 ```
 
-**Example 3:**
+**Example 3**:
 
 ```
 Input: n = 12
@@ -32,7 +32,7 @@ The decimal value of that is 118505380540.
 After modulo 109 + 7, the result is 505379714.
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= n <= 10^5`
 

website/content/ChapterFour/1681.Minimum-Incompatibility.md

@@ -11,7 +11,7 @@ Return *the **minimum possible sum of incompatibilities** of the* `k` *subs
 
 A subset is a group integers that appear in the array with no particular order.
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: nums = [1,2,1,4], k = 2
@@ -21,7 +21,7 @@ The incompatibility is (2-1) + (4-1) = 4.
 Note that [1,1] and [2,4] would result in a smaller sum, but the first subset contains 2 equal elements.
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: nums = [6,3,8,1,3,1,2,2], k = 4
@@ -31,7 +31,7 @@ The incompatibility is (2-1) + (3-2) + (8-6) + (3-1) = 6.
 
 ```
 
-**Example 3:**
+**Example 3**:
 
 ```
 Input: nums = [5,3,3,6,3,3], k = 3
@@ -40,7 +40,7 @@ Explanation: It is impossible to distribute nums into 3 subsets where no two ele
 
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= k <= nums.length <= 16`
 - `nums.length` is divisible by `k`

website/content/ChapterFour/1684.Count-the-Number-of-Consistent-Strings.md

@@ -7,7 +7,7 @@ You are given a string `allowed` consisting of **distinct** characters and a
 
 Return *the number of **consistent** strings in the array* `words`.
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: allowed = "ab", words = ["ad","bd","aaab","baa","badab"]
@@ -16,7 +16,7 @@ Explanation: Strings "aaab" and "baa" are consistent since they only contain cha
 
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: allowed = "abc", words = ["a","b","c","ab","ac","bc","abc"]
@@ -25,7 +25,7 @@ Explanation: All strings are consistent.
 
 ```
 
-**Example 3:**
+**Example 3**:
 
 ```
 Input: allowed = "cad", words = ["cc","acd","b","ba","bac","bad","ac","d"]
@@ -34,7 +34,7 @@ Explanation: Strings "cc", "acd", "ac", and "d" are consistent.
 
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= words.length <= 104`
 - `1 <= allowed.length <= 26`

website/content/ChapterFour/1685.Sum-of-Absolute-Differences-in-a-Sorted-Array.md

@@ -9,7 +9,7 @@ Build and return *an integer array* `result` *with the same length as* `nums
 
 In other words, `result[i]` is equal to `sum(|nums[i]-nums[j]|)` where `0 <= j < nums.length` and `j != i` (**0-indexed**).
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: nums = [2,3,5]
@@ -20,14 +20,14 @@ result[1] = |3-2| + |3-3| + |3-5| = 1 + 0 + 2 = 3,
 result[2] = |5-2| + |5-3| + |5-5| = 3 + 2 + 0 = 5.
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: nums = [1,4,6,8,10]
 Output: [24,15,13,15,21]
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `2 <= nums.length <= 105`
 - `1 <= nums[i] <= nums[i + 1] <= 104`

website/content/ChapterFour/1688.Count-of-Matches-in-Tournament.md

@@ -10,7 +10,7 @@ You are given an integer `n`, the number of teams in a tournament that has stra
 
 Return *the number of matches played in the tournament until a winner is decided.*
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: n = 7
@@ -22,7 +22,7 @@ Explanation: Details of the tournament:
 Total number of matches = 3 + 2 + 1 = 6.
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: n = 14
@@ -35,7 +35,7 @@ Explanation: Details of the tournament:
 Total number of matches = 7 + 3 + 2 + 1 = 13.
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= n <= 200`
 

website/content/ChapterFour/1689.Partitioning-Into-Minimum-Number-Of-Deci-Binary-Numbers.md

@@ -6,7 +6,7 @@ A decimal number is called **deci-binary** if each of its digits is either `0
 
 Given a string `n` that represents a positive decimal integer, return *the **minimum** number of positive **deci-binary** numbers needed so that they sum up to* `n`*.*
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: n = "32"
@@ -14,21 +14,21 @@ Output: 3
 Explanation: 10 + 11 + 11 = 32
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: n = "82734"
 Output: 8
 ```
 
-**Example 3:**
+**Example 3**:
 
 ```
 Input: n = "27346209830709182346"
 Output: 9
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= n.length <= 105`
 - `n` consists of only digits.

website/content/ChapterFour/1690.Stone-Game-VII.md

@@ -10,7 +10,7 @@ Bob found that he will always lose this game (poor Bob, he always loses), so he
 
 Given an array of integers `stones` where `stones[i]` represents the value of the `ith` stone **from the left**, return *the **difference** in Alice and Bob's score if they both play **optimally**.*
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: stones = [5,3,1,4,2]
@@ -24,14 +24,14 @@ Explanation:
 The score difference is 18 - 12 = 6.
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: stones = [7,90,5,1,100,10,10,2]
 Output: 122
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `n == stones.length`
 - `2 <= n <= 1000`

website/content/ChapterFour/1694.Reformat-Phone-Number.md

@@ -15,7 +15,7 @@ The blocks are then joined by dashes. Notice that the reformatting process shoul
 
 Return *the phone number after formatting.*
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: number = "1-23-45 6"
@@ -27,7 +27,7 @@ Joining the blocks gives "123-456".
 
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: number = "123 4-567"
@@ -39,7 +39,7 @@ Joining the blocks gives "123-45-67".
 
 ```
 
-**Example 3:**
+**Example 3**:
 
 ```
 Input: number = "123 4-5678"
@@ -52,7 +52,7 @@ Joining the blocks gives "123-456-78".
 
 ```
 
-**Example 4:**
+**Example 4**:
 
 ```
 Input: number = "12"
@@ -60,7 +60,7 @@ Output: "12"
 
 ```
 
-**Example 5:**
+**Example 5**:
 
 ```
 Input: number = "--17-5 229 35-39475 "
@@ -68,7 +68,7 @@ Output: "175-229-353-94-75"
 
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `2 <= number.length <= 100`
 - `number` consists of digits and the characters `'-'` and `' '`.

website/content/ChapterFour/1695.Maximum-Erasure-Value.md

@@ -9,7 +9,7 @@ Return *the **maximum score** you can get by erasing **exactly one** subarr
 
 An array `b` is called to be a subarray of `a` if it forms a contiguous subsequence of `a`, that is, if it is equal to `a[l],a[l+1],...,a[r]` for some `(l,r)`.
 
-**Example 1:**
+**Example 1**:
 
 ```
 Input: nums = [4,2,4,5,6]
@@ -17,7 +17,7 @@ Output: 17
 Explanation: The optimal subarray here is [2,4,5,6].
 ```
 
-**Example 2:**
+**Example 2**:
 
 ```
 Input: nums = [5,2,1,2,5,2,1,2,5]
@@ -25,7 +25,7 @@ Output: 8
 Explanation: The optimal subarray here is [5,2,1] or [1,2,5].
 ```
 
-**Constraints:**
+**Constraints**:
 
 - `1 <= nums.length <= 105`
 - `1 <= nums[i] <= 104`

website/content/menu/index.md

@@ -317,7 +317,7 @@ headless: true
     - [0537.Complex-Number-Multiplication]({{< relref "/ChapterFour/0537.Complex-Number-Multiplication.md" >}})
     - [0541.Reverse-String-II]({{< relref "/ChapterFour/0541.Reverse-String-II.md" >}})
     - [0542.01-Matrix]({{< relref "/ChapterFour/0542.01-Matrix.md" >}})
-    - [0547.Friend-Circles]({{< relref "/ChapterFour/0547.Friend-Circles.md" >}})
+    - [0547.Number-of-Provinces]({{< relref "/ChapterFour/0547.Number-of-Provinces.md" >}})
     - [0557.Reverse-Words-in-a-String-III]({{< relref "/ChapterFour/0557.Reverse-Words-in-a-String-III.md" >}})
     - [0561.Array-Partition-I]({{< relref "/ChapterFour/0561.Array-Partition-I.md" >}})
     - [0563.Binary-Tree-Tilt]({{< relref "/ChapterFour/0563.Binary-Tree-Tilt.md" >}})
@@ -397,7 +397,7 @@ headless: true
     - [0817.Linked-List-Components]({{< relref "/ChapterFour/0817.Linked-List-Components.md" >}})
     - [0819.Most-Common-Word]({{< relref "/ChapterFour/0819.Most-Common-Word.md" >}})
     - [0826.Most-Profit-Assigning-Work]({{< relref "/ChapterFour/0826.Most-Profit-Assigning-Work.md" >}})
-    - [0828.COPYRIGHT-PROBLEM-XXX]({{< relref "/ChapterFour/0828.COPYRIGHT-PROBLEM-XXX.md" >}})
+    - [0828.Count-Unique-Characters-of-All-Substrings-of-a-Given-String]({{< relref "/ChapterFour/0828.Count-Unique-Characters-of-All-Substrings-of-a-Given-String.md" >}})
     - [0830.Positions-of-Large-Groups]({{< relref "/ChapterFour/0830.Positions-of-Large-Groups.md" >}})
     - [0832.Flipping-an-Image]({{< relref "/ChapterFour/0832.Flipping-an-Image.md" >}})
     - [0834.Sum-of-Distances-in-Tree]({{< relref "/ChapterFour/0834.Sum-of-Distances-in-Tree.md" >}})