add leetcode logo

leetcode/0850.Rectangle-Area-II/README.md

@@ -56,7 +56,7 @@ Find the total area covered by all `rectangles` in the plane. Since the answer
 
     需要注意的一点是，**每次 query 的结果并不一定是连续线段**。如上图最右边的图，中间有一段是可能出现镂空的。这种情况看似复杂，其实很简单，因为每段线段树的线段代表的权值高度是不同的，每次 query 最大高度得到的结果已经考虑了中间可能有镂空的情况了。
 
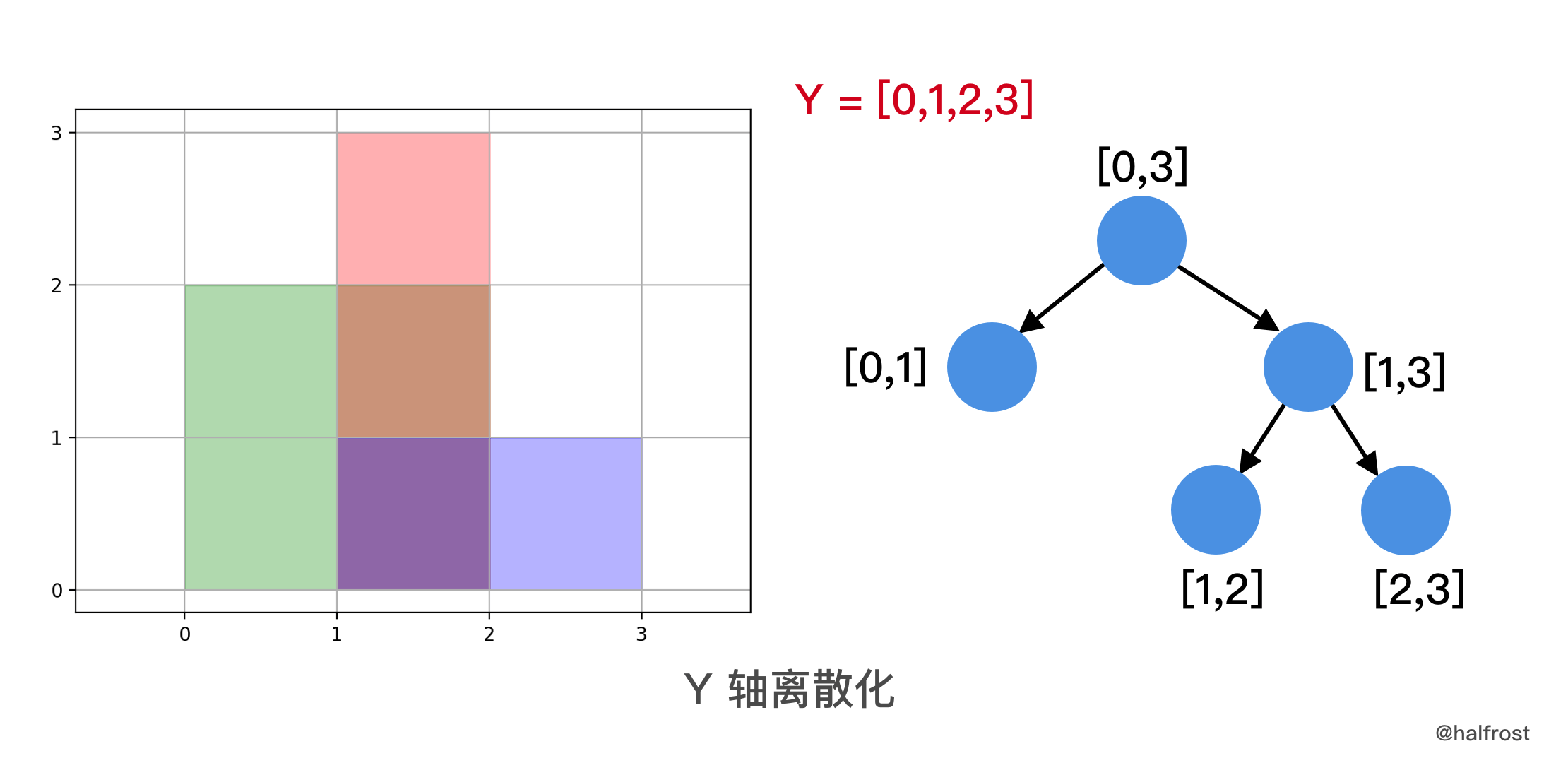
-- 具体做法，先把各个矩形在 Y 轴方向上离散化，这里的**线段树叶子节点不再是一个点了，而是一个区间长度为 1 的区间段。**
+- 具体做法，先把各个矩形在 Y 轴方向上离散化，这里的**线段树叶子节点不再是一个点了，而是一个区间长度为 1 的区间段**。
 
     ![](https://img.halfrost.com/Leetcode/leetcode_850_0.png)
 

leetcode/1157.Online-Majority-Element-In-Subarray/README.md

@@ -73,6 +73,6 @@ Each `query(...)` returns the element in `arr[left], arr[left+1], ..., arr[ri
         		return segmentItem{candidate: j.candidate, count: j.count - i.count}
         	}
 
-    直到根节点的 candidate 和 count 都填满。**注意，这里的 count 并不是元素出现的总次数，而是摩尔投票中坚持没有被投出去的轮数。**当线段树构建完成以后，就可以开始查询任意区间内的众数了，candidate 即为众数。接下来还要确定众数是否满足 `threshold` 的条件。
+    直到根节点的 candidate 和 count 都填满。**注意，这里的 count 并不是元素出现的总次数，而是摩尔投票中坚持没有被投出去的轮数**。当线段树构建完成以后，就可以开始查询任意区间内的众数了，candidate 即为众数。接下来还要确定众数是否满足 `threshold` 的条件。
 
 - 用一个字典记录每个元素在数组中出现位置的下标，例如上述这个例子，用 map 记录下标：count = map[1:[0 1 4 5] 2:[2 3]]。由于下标在记录过程中是递增的，所以满足二分查找的条件。利用这个字典就可以查出在任意区间内，指定元素出现的次数。例如这里要查找 1 在 [0,5] 区间内出现的个数，那么利用 2 次二分查找，分别找到 `lowerBound` 和 `upperBound`，在 [lowerBound，upperBound) 区间内，都是元素 1 ，那么区间长度即是该元素重复出现的次数，和 `threshold` 比较，如果 ≥ `threshold` 说明找到了答案，否则没有找到就输出 -1 。