mirror of
https://github.com/halfrost/LeetCode-Go.git
synced 2025-07-06 17:44:10 +08:00
Add solution 1656、1657、1658、1659
This commit is contained in:
@ -0,0 +1,40 @@
|
||||
package leetcode
|
||||
|
||||
func minOperations(nums []int, x int) int {
|
||||
total := 0
|
||||
for _, n := range nums {
|
||||
total += n
|
||||
}
|
||||
target := total - x
|
||||
if target < 0 {
|
||||
return -1
|
||||
}
|
||||
if target == 0 {
|
||||
return len(nums)
|
||||
}
|
||||
left, right, sum, res := 0, 0, 0, -1
|
||||
for right < len(nums) {
|
||||
if sum < target {
|
||||
sum += nums[right]
|
||||
right++
|
||||
}
|
||||
for sum >= target {
|
||||
if sum == target {
|
||||
res = max(res, right-left)
|
||||
}
|
||||
sum -= nums[left]
|
||||
left++
|
||||
}
|
||||
}
|
||||
if res == -1 {
|
||||
return -1
|
||||
}
|
||||
return len(nums) - res
|
||||
}
|
||||
|
||||
func max(a, b int) int {
|
||||
if a > b {
|
||||
return a
|
||||
}
|
||||
return b
|
||||
}
|
||||
@ -0,0 +1,53 @@
|
||||
package leetcode
|
||||
|
||||
import (
|
||||
"fmt"
|
||||
"testing"
|
||||
)
|
||||
|
||||
type question1658 struct {
|
||||
para1658
|
||||
ans1658
|
||||
}
|
||||
|
||||
// para 是参数
|
||||
// one 代表第一个参数
|
||||
type para1658 struct {
|
||||
nums []int
|
||||
x int
|
||||
}
|
||||
|
||||
// ans 是答案
|
||||
// one 代表第一个答案
|
||||
type ans1658 struct {
|
||||
one int
|
||||
}
|
||||
|
||||
func Test_Problem1658(t *testing.T) {
|
||||
|
||||
qs := []question1658{
|
||||
|
||||
{
|
||||
para1658{[]int{1, 1, 4, 2, 3}, 5},
|
||||
ans1658{2},
|
||||
},
|
||||
|
||||
{
|
||||
para1658{[]int{5, 6, 7, 8, 9}, 4},
|
||||
ans1658{-1},
|
||||
},
|
||||
|
||||
{
|
||||
para1658{[]int{3, 2, 20, 1, 1, 3}, 10},
|
||||
ans1658{5},
|
||||
},
|
||||
}
|
||||
|
||||
fmt.Printf("------------------------Leetcode Problem 1658------------------------\n")
|
||||
|
||||
for _, q := range qs {
|
||||
_, p := q.ans1658, q.para1658
|
||||
fmt.Printf("【input】:%v 【output】:%v \n", p, minOperations(p.nums, p.x))
|
||||
}
|
||||
fmt.Printf("\n\n\n")
|
||||
}
|
||||
@ -0,0 +1,96 @@
|
||||
# [1658. Minimum Operations to Reduce X to Zero](https://leetcode.com/problems/minimum-operations-to-reduce-x-to-zero/)
|
||||
|
||||
|
||||
## 题目
|
||||
|
||||
You are given an integer array `nums` and an integer `x`. In one operation, you can either remove the leftmost or the rightmost element from the array `nums` and subtract its value from `x`. Note that this **modifies** the array for future operations.
|
||||
|
||||
Return *the **minimum number** of operations to reduce* `x` *to **exactly*** `0` *if it's possible, otherwise, return* `1`.
|
||||
|
||||
**Example 1:**
|
||||
|
||||
```
|
||||
Input: nums = [1,1,4,2,3], x = 5
|
||||
Output: 2
|
||||
Explanation: The optimal solution is to remove the last two elements to reduce x to zero.
|
||||
|
||||
```
|
||||
|
||||
**Example 2:**
|
||||
|
||||
```
|
||||
Input: nums = [5,6,7,8,9], x = 4
|
||||
Output: -1
|
||||
|
||||
```
|
||||
|
||||
**Example 3:**
|
||||
|
||||
```
|
||||
Input: nums = [3,2,20,1,1,3], x = 10
|
||||
Output: 5
|
||||
Explanation: The optimal solution is to remove the last three elements and the first two elements (5 operations in total) to reduce x to zero.
|
||||
|
||||
```
|
||||
|
||||
**Constraints:**
|
||||
|
||||
- `1 <= nums.length <= 105`
|
||||
- `1 <= nums[i] <= 104`
|
||||
- `1 <= x <= 109`
|
||||
|
||||
## 题目大意
|
||||
|
||||
给你一个整数数组 nums 和一个整数 x 。每一次操作时,你应当移除数组 nums 最左边或最右边的元素,然后从 x 中减去该元素的值。请注意,需要 修改 数组以供接下来的操作使用。如果可以将 x 恰好 减到 0 ,返回 最小操作数 ;否则,返回 -1 。
|
||||
|
||||
## 解题思路
|
||||
|
||||
- 给定一个数组 nums 和一个整数 x,要求从数组两端分别移除一些数,使得这些数加起来正好等于整数 x,要求输出最小操作数。
|
||||
- 要求输出最小操作数,即数组两头的数字个数最少,并且加起来和正好等于整数 x。由于在数组的两头,用 2 个指针分别操作不太方便。我当时解题的时候的思路是把它变成循环数组,这样两边的指针就在一个区间内了。利用滑动窗口找到一个最小的窗口,使得窗口内的累加和等于整数 k。这个方法可行,但是代码挺多的。
|
||||
- 有没有更优美的方法呢?有的。要想两头的长度最少,也就是中间这段的长度最大。这样就转换成直接在数组上使用滑动窗口求解,累加和等于一个固定值的连续最长的子数组。
|
||||
- 和这道题类似思路的题目,209,1040(循环数组),325。强烈推荐这 3 题。
|
||||
|
||||
## 代码
|
||||
|
||||
```go
|
||||
package leetcode
|
||||
|
||||
func minOperations(nums []int, x int) int {
|
||||
total := 0
|
||||
for _, n := range nums {
|
||||
total += n
|
||||
}
|
||||
target := total - x
|
||||
if target < 0 {
|
||||
return -1
|
||||
}
|
||||
if target == 0 {
|
||||
return len(nums)
|
||||
}
|
||||
left, right, sum, res := 0, 0, 0, -1
|
||||
for right < len(nums) {
|
||||
if sum < target {
|
||||
sum += nums[right]
|
||||
right++
|
||||
}
|
||||
for sum >= target {
|
||||
if sum == target {
|
||||
res = max(res, right-left)
|
||||
}
|
||||
sum -= nums[left]
|
||||
left++
|
||||
}
|
||||
}
|
||||
if res == -1 {
|
||||
return -1
|
||||
}
|
||||
return len(nums) - res
|
||||
}
|
||||
|
||||
func max(a, b int) int {
|
||||
if a > b {
|
||||
return a
|
||||
}
|
||||
return b
|
||||
}
|
||||
```
|
||||
@ -0,0 +1,107 @@
|
||||
package leetcode
|
||||
|
||||
import (
|
||||
"math"
|
||||
)
|
||||
|
||||
func getMaxGridHappiness(m int, n int, introvertsCount int, extrovertsCount int) int {
|
||||
// lineStatus 将每一行中 3 种状态进行编码,空白 - 0,内向人 - 1,外向人 - 2,每行状态用三进制表示
|
||||
// lineStatusList[729][6] 每一行的三进制表示
|
||||
// introvertsCountInner[729] 每一个 lineStatus 包含的内向人数
|
||||
// extrovertsCountInner[729] 每一个 lineStatus 包含的外向人数
|
||||
// scoreInner[729] 每一个 lineStatus 包含的行内得分(只统计 lineStatus 本身的得分,不包括它与上一行的)
|
||||
// scoreOuter[729][729] 每一个 lineStatus 包含的行外得分
|
||||
// dp[上一行的 lineStatus][当前处理到的行][剩余的内向人数][剩余的外向人数]
|
||||
n3, lineStatus, introvertsCountInner, extrovertsCountInner, scoreInner, scoreOuter, lineStatusList, dp := math.Pow(3.0, float64(n)), 0, [729]int{}, [729]int{}, [729]int{}, [729][729]int{}, [729][6]int{}, [729][6][7][7]int{}
|
||||
for i := 0; i < 729; i++ {
|
||||
lineStatusList[i] = [6]int{}
|
||||
}
|
||||
for i := 0; i < 729; i++ {
|
||||
dp[i] = [6][7][7]int{}
|
||||
for j := 0; j < 6; j++ {
|
||||
dp[i][j] = [7][7]int{}
|
||||
for k := 0; k < 7; k++ {
|
||||
dp[i][j][k] = [7]int{-1, -1, -1, -1, -1, -1, -1}
|
||||
}
|
||||
}
|
||||
}
|
||||
// 预处理
|
||||
for lineStatus = 0; lineStatus < int(n3); lineStatus++ {
|
||||
tmp := lineStatus
|
||||
for i := 0; i < n; i++ {
|
||||
lineStatusList[lineStatus][i] = tmp % 3
|
||||
tmp /= 3
|
||||
}
|
||||
introvertsCountInner[lineStatus], extrovertsCountInner[lineStatus], scoreInner[lineStatus] = 0, 0, 0
|
||||
for i := 0; i < n; i++ {
|
||||
if lineStatusList[lineStatus][i] != 0 {
|
||||
// 个人分数
|
||||
if lineStatusList[lineStatus][i] == 1 {
|
||||
introvertsCountInner[lineStatus]++
|
||||
scoreInner[lineStatus] += 120
|
||||
} else if lineStatusList[lineStatus][i] == 2 {
|
||||
extrovertsCountInner[lineStatus]++
|
||||
scoreInner[lineStatus] += 40
|
||||
}
|
||||
// 行内分数
|
||||
if i-1 >= 0 {
|
||||
scoreInner[lineStatus] += closeScore(lineStatusList[lineStatus][i], lineStatusList[lineStatus][i-1])
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
// 行外分数
|
||||
for lineStatus0 := 0; lineStatus0 < int(n3); lineStatus0++ {
|
||||
for lineStatus1 := 0; lineStatus1 < int(n3); lineStatus1++ {
|
||||
scoreOuter[lineStatus0][lineStatus1] = 0
|
||||
for i := 0; i < n; i++ {
|
||||
scoreOuter[lineStatus0][lineStatus1] += closeScore(lineStatusList[lineStatus0][i], lineStatusList[lineStatus1][i])
|
||||
}
|
||||
}
|
||||
}
|
||||
return dfs(0, 0, introvertsCount, extrovertsCount, m, int(n3), &dp, &introvertsCountInner, &extrovertsCountInner, &scoreInner, &scoreOuter)
|
||||
}
|
||||
|
||||
// 如果 x 和 y 相邻,需要加上的分数
|
||||
func closeScore(x, y int) int {
|
||||
if x == 0 || y == 0 {
|
||||
return 0
|
||||
}
|
||||
// 两个内向的人,每个人要 -30,一共 -60
|
||||
if x == 1 && y == 1 {
|
||||
return -60
|
||||
}
|
||||
if x == 2 && y == 2 {
|
||||
return 40
|
||||
}
|
||||
return -10
|
||||
}
|
||||
|
||||
// dfs(上一行的 lineStatus,当前处理到的行,剩余的内向人数,剩余的外向人数)
|
||||
func dfs(lineStatusLast, row, introvertsCount, extrovertsCount, m, n3 int, dp *[729][6][7][7]int, introvertsCountInner, extrovertsCountInner, scoreInner *[729]int, scoreOuter *[729][729]int) int {
|
||||
// 边界条件:如果已经处理完,或者没有人了
|
||||
if row == m || introvertsCount+extrovertsCount == 0 {
|
||||
return 0
|
||||
}
|
||||
// 记忆化
|
||||
if dp[lineStatusLast][row][introvertsCount][extrovertsCount] != -1 {
|
||||
return dp[lineStatusLast][row][introvertsCount][extrovertsCount]
|
||||
}
|
||||
best := 0
|
||||
for lineStatus := 0; lineStatus < n3; lineStatus++ {
|
||||
if introvertsCountInner[lineStatus] > introvertsCount || extrovertsCountInner[lineStatus] > extrovertsCount {
|
||||
continue
|
||||
}
|
||||
score := scoreInner[lineStatus] + scoreOuter[lineStatus][lineStatusLast]
|
||||
best = max(best, score+dfs(lineStatus, row+1, introvertsCount-introvertsCountInner[lineStatus], extrovertsCount-extrovertsCountInner[lineStatus], m, n3, dp, introvertsCountInner, extrovertsCountInner, scoreInner, scoreOuter))
|
||||
}
|
||||
dp[lineStatusLast][row][introvertsCount][extrovertsCount] = best
|
||||
return best
|
||||
}
|
||||
|
||||
func max(a int, b int) int {
|
||||
if a > b {
|
||||
return a
|
||||
}
|
||||
return b
|
||||
}
|
||||
@ -0,0 +1,55 @@
|
||||
package leetcode
|
||||
|
||||
import (
|
||||
"fmt"
|
||||
"testing"
|
||||
)
|
||||
|
||||
type question1659 struct {
|
||||
para1659
|
||||
ans1659
|
||||
}
|
||||
|
||||
// para 是参数
|
||||
// one 代表第一个参数
|
||||
type para1659 struct {
|
||||
m int
|
||||
n int
|
||||
introvertsCount int
|
||||
extrovertsCount int
|
||||
}
|
||||
|
||||
// ans 是答案
|
||||
// one 代表第一个答案
|
||||
type ans1659 struct {
|
||||
one int
|
||||
}
|
||||
|
||||
func Test_Problem1659(t *testing.T) {
|
||||
|
||||
qs := []question1659{
|
||||
|
||||
{
|
||||
para1659{2, 3, 1, 2},
|
||||
ans1659{240},
|
||||
},
|
||||
|
||||
{
|
||||
para1659{3, 1, 2, 1},
|
||||
ans1659{260},
|
||||
},
|
||||
|
||||
{
|
||||
para1659{2, 2, 4, 0},
|
||||
ans1659{240},
|
||||
},
|
||||
}
|
||||
|
||||
fmt.Printf("------------------------Leetcode Problem 1659------------------------\n")
|
||||
|
||||
for _, q := range qs {
|
||||
_, p := q.ans1659, q.para1659
|
||||
fmt.Printf("【input】:%v 【output】:%v \n", p, getMaxGridHappiness(p.m, p.n, p.introvertsCount, p.extrovertsCount))
|
||||
}
|
||||
fmt.Printf("\n\n\n")
|
||||
}
|
||||
185
leetcode/1659.Maximize-Grid-Happiness/README.md
Normal file
185
leetcode/1659.Maximize-Grid-Happiness/README.md
Normal file
@ -0,0 +1,185 @@
|
||||
# [1659. Maximize Grid Happiness](https://leetcode.com/problems/maximize-grid-happiness/)
|
||||
|
||||
## 题目
|
||||
|
||||
You are given four integers, `m`, `n`, `introvertsCount`, and `extrovertsCount`. You have an `m x n` grid, and there are two types of people: introverts and extroverts. There are `introvertsCount` introverts and `extrovertsCount` extroverts.
|
||||
|
||||
You should decide how many people you want to live in the grid and assign each of them one grid cell. Note that you **do not** have to have all the people living in the grid.
|
||||
|
||||
The **happiness** of each person is calculated as follows:
|
||||
|
||||
- Introverts **start** with `120` happiness and **lose** `30` happiness for each neighbor (introvert or extrovert).
|
||||
- Extroverts **start** with `40` happiness and **gain** `20` happiness for each neighbor (introvert or extrovert).
|
||||
|
||||
Neighbors live in the directly adjacent cells north, east, south, and west of a person's cell.
|
||||
|
||||
The **grid happiness** is the **sum** of each person's happiness. Return *the **maximum possible grid happiness**.*
|
||||
|
||||
**Example 1:**
|
||||
|
||||
|
||||
|
||||
```
|
||||
Input: m = 2, n = 3, introvertsCount = 1, extrovertsCount = 2
|
||||
Output: 240
|
||||
Explanation: Assume the grid is 1-indexed with coordinates (row, column).
|
||||
We can put the introvert in cell (1,1) and put the extroverts in cells (1,3) and (2,3).
|
||||
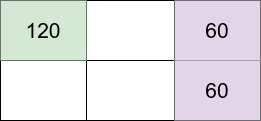
- Introvert at (1,1) happiness: 120 (starting happiness) - (0 * 30) (0 neighbors) = 120
|
||||
- Extrovert at (1,3) happiness: 40 (starting happiness) + (1 * 20) (1 neighbor) = 60
|
||||
- Extrovert at (2,3) happiness: 40 (starting happiness) + (1 * 20) (1 neighbor) = 60
|
||||
The grid happiness is 120 + 60 + 60 = 240.
|
||||
The above figure shows the grid in this example with each person's happiness. The introvert stays in the light green cell while the extroverts live on the light purple cells.
|
||||
```
|
||||
|
||||
**Example 2:**
|
||||
|
||||
```
|
||||
Input: m = 3, n = 1, introvertsCount = 2, extrovertsCount = 1
|
||||
Output: 260
|
||||
Explanation: Place the two introverts in (1,1) and (3,1) and the extrovert at (2,1).
|
||||
- Introvert at (1,1) happiness: 120 (starting happiness) - (1 * 30) (1 neighbor) = 90
|
||||
- Extrovert at (2,1) happiness: 40 (starting happiness) + (2 * 20) (2 neighbors) = 80
|
||||
- Introvert at (3,1) happiness: 120 (starting happiness) - (1 * 30) (1 neighbor) = 90
|
||||
The grid happiness is 90 + 80 + 90 = 260.
|
||||
```
|
||||
|
||||
**Example 3:**
|
||||
|
||||
```
|
||||
Input: m = 2, n = 2, introvertsCount = 4, extrovertsCount = 0
|
||||
Output: 240
|
||||
```
|
||||
|
||||
**Constraints:**
|
||||
|
||||
- `1 <= m, n <= 5`
|
||||
- `0 <= introvertsCount, extrovertsCount <= min(m * n, 6)`
|
||||
|
||||
## 题目大意
|
||||
|
||||
给你四个整数 m、n、introvertsCount 和 extrovertsCount 。有一个 m x n 网格,和两种类型的人:内向的人和外向的人。总共有 introvertsCount 个内向的人和 extrovertsCount 个外向的人。请你决定网格中应当居住多少人,并为每个人分配一个网格单元。 注意,不必 让所有人都生活在网格中。每个人的 幸福感 计算如下:
|
||||
|
||||
- 内向的人 开始 时有 120 个幸福感,但每存在一个邻居(内向的或外向的)他都会 失去 30 个幸福感。
|
||||
- 外向的人 开始 时有 40 个幸福感,每存在一个邻居(内向的或外向的)他都会 得到 20 个幸福感。
|
||||
|
||||
邻居是指居住在一个人所在单元的上、下、左、右四个直接相邻的单元中的其他人。网格幸福感 是每个人幸福感的 总和 。 返回 最大可能的网格幸福感 。
|
||||
|
||||
## 解题思路
|
||||
|
||||
- 给出 `m` x `n` 网格和两种人,要求如何安排这两种人能使得网格的得分最大。两种人有各自的初始分,相邻可能会加分也有可能减分。
|
||||
- 这一题状态很多。首先每个格子有 3 种状态,那么每一行有 3^6 = 729 种不同的状态。每行行内分数变化值可能是 -60(两个内向),+40(两个外向),-10(一个内向一个外向)。两行行间分数变化值可能是 -60(两个内向),+40(两个外向),-10(一个内向一个外向)。那么我们可以把每行的状态压缩成一个三进制,那么网格就变成了一维,每两个三进制之间的关系是行间关系,每个三进制内部还需要根据内向和外向的人数决定行内最终分数。定义 `dp[lineStatusLast][row][introvertsCount][extrovertsCount]` 代表在上一行 `row - 1` 的状态是 `lineStatusLast` 的情况下,当前枚举到了第 `row` 行,内向还有 `introvertsCount` 个人,外向还有 `extrovertsCount` 个人能获得的最大分数。状态转移方程是 `dp[lineStatusLast(row-1)][row][introvertsCount][extrovertsCount] = max{dp[lineStatusLast(row)][row+1][introvertsCount - countIC(lineStatusLast(row)) ][extrovertsCount - countEC(lineStatusLast(row)) ] + scoreInner(lineStatusLast(row)) + scoreOuter(lineStatusLast(row-1),lineStatusLast(row))}` ,这里有 2 个统计函数,`countIC` 是统计当前行状态三进制里面有多少个内向人。`countEC` 是统计当前行状态三进制里面有多少个外向人。`scoreInner` 是计算当前行状态三进制的行内分数。`scoreOuter` 是计算 `row -1` 行和 `row` 行之间的行间分数。
|
||||
- 由于这个状态转移方程的计算量是巨大的。所以需要预先初始化一些计算结果。比如把 729 中行状态分别对应的行内、行间的分数都计算好,在动态规划状态转移的时候,直接查表获取分数即可。这样我们在深搜的时候,利用 dp 的记忆化,可以大幅减少时间复杂度。
|
||||
- 题目中还提到,人数可以不用完。如果 `introvertsCount = 0`, `extrovertsCount = 0` ,即人数都用完了的情况,这时候 `dp = 0`。如果 `row = m`,即已经枚举完了所有行,那么不管剩下多少人,这一行的 `dp = 0` 。
|
||||
- 初始化的时候,注意,特殊处理 0 的情况,0 行 0 列都初始化为 -1 。
|
||||
|
||||
## 代码
|
||||
|
||||
```go
|
||||
package leetcode
|
||||
|
||||
import (
|
||||
"math"
|
||||
)
|
||||
|
||||
func getMaxGridHappiness(m int, n int, introvertsCount int, extrovertsCount int) int {
|
||||
// lineStatus 将每一行中 3 种状态进行编码,空白 - 0,内向人 - 1,外向人 - 2,每行状态用三进制表示
|
||||
// lineStatusList[729][6] 每一行的三进制表示
|
||||
// introvertsCountInner[729] 每一个 lineStatus 包含的内向人数
|
||||
// extrovertsCountInner[729] 每一个 lineStatus 包含的外向人数
|
||||
// scoreInner[729] 每一个 lineStatus 包含的行内得分(只统计 lineStatus 本身的得分,不包括它与上一行的)
|
||||
// scoreOuter[729][729] 每一个 lineStatus 包含的行外得分
|
||||
// dp[上一行的 lineStatus][当前处理到的行][剩余的内向人数][剩余的外向人数]
|
||||
n3, lineStatus, introvertsCountInner, extrovertsCountInner, scoreInner, scoreOuter, lineStatusList, dp := math.Pow(3.0, float64(n)), 0, [729]int{}, [729]int{}, [729]int{}, [729][729]int{}, [729][6]int{}, [729][6][7][7]int{}
|
||||
for i := 0; i < 729; i++ {
|
||||
lineStatusList[i] = [6]int{}
|
||||
}
|
||||
for i := 0; i < 729; i++ {
|
||||
dp[i] = [6][7][7]int{}
|
||||
for j := 0; j < 6; j++ {
|
||||
dp[i][j] = [7][7]int{}
|
||||
for k := 0; k < 7; k++ {
|
||||
dp[i][j][k] = [7]int{-1, -1, -1, -1, -1, -1, -1}
|
||||
}
|
||||
}
|
||||
}
|
||||
// 预处理
|
||||
for lineStatus = 0; lineStatus < int(n3); lineStatus++ {
|
||||
tmp := lineStatus
|
||||
for i := 0; i < n; i++ {
|
||||
lineStatusList[lineStatus][i] = tmp % 3
|
||||
tmp /= 3
|
||||
}
|
||||
introvertsCountInner[lineStatus], extrovertsCountInner[lineStatus], scoreInner[lineStatus] = 0, 0, 0
|
||||
for i := 0; i < n; i++ {
|
||||
if lineStatusList[lineStatus][i] != 0 {
|
||||
// 个人分数
|
||||
if lineStatusList[lineStatus][i] == 1 {
|
||||
introvertsCountInner[lineStatus]++
|
||||
scoreInner[lineStatus] += 120
|
||||
} else if lineStatusList[lineStatus][i] == 2 {
|
||||
extrovertsCountInner[lineStatus]++
|
||||
scoreInner[lineStatus] += 40
|
||||
}
|
||||
// 行内分数
|
||||
if i-1 >= 0 {
|
||||
scoreInner[lineStatus] += closeScore(lineStatusList[lineStatus][i], lineStatusList[lineStatus][i-1])
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
// 行外分数
|
||||
for lineStatus0 := 0; lineStatus0 < int(n3); lineStatus0++ {
|
||||
for lineStatus1 := 0; lineStatus1 < int(n3); lineStatus1++ {
|
||||
scoreOuter[lineStatus0][lineStatus1] = 0
|
||||
for i := 0; i < n; i++ {
|
||||
scoreOuter[lineStatus0][lineStatus1] += closeScore(lineStatusList[lineStatus0][i], lineStatusList[lineStatus1][i])
|
||||
}
|
||||
}
|
||||
}
|
||||
return dfs(0, 0, introvertsCount, extrovertsCount, m, int(n3), &dp, &introvertsCountInner, &extrovertsCountInner, &scoreInner, &scoreOuter)
|
||||
}
|
||||
|
||||
// 如果 x 和 y 相邻,需要加上的分数
|
||||
func closeScore(x, y int) int {
|
||||
if x == 0 || y == 0 {
|
||||
return 0
|
||||
}
|
||||
// 两个内向的人,每个人要 -30,一共 -60
|
||||
if x == 1 && y == 1 {
|
||||
return -60
|
||||
}
|
||||
if x == 2 && y == 2 {
|
||||
return 40
|
||||
}
|
||||
return -10
|
||||
}
|
||||
|
||||
// dfs(上一行的 lineStatus,当前处理到的行,剩余的内向人数,剩余的外向人数)
|
||||
func dfs(lineStatusLast, row, introvertsCount, extrovertsCount, m, n3 int, dp *[729][6][7][7]int, introvertsCountInner, extrovertsCountInner, scoreInner *[729]int, scoreOuter *[729][729]int) int {
|
||||
// 边界条件:如果已经处理完,或者没有人了
|
||||
if row == m || introvertsCount+extrovertsCount == 0 {
|
||||
return 0
|
||||
}
|
||||
// 记忆化
|
||||
if dp[lineStatusLast][row][introvertsCount][extrovertsCount] != -1 {
|
||||
return dp[lineStatusLast][row][introvertsCount][extrovertsCount]
|
||||
}
|
||||
best := 0
|
||||
for lineStatus := 0; lineStatus < n3; lineStatus++ {
|
||||
if introvertsCountInner[lineStatus] > introvertsCount || extrovertsCountInner[lineStatus] > extrovertsCount {
|
||||
continue
|
||||
}
|
||||
score := scoreInner[lineStatus] + scoreOuter[lineStatus][lineStatusLast]
|
||||
best = max(best, score+dfs(lineStatus, row+1, introvertsCount-introvertsCountInner[lineStatus], extrovertsCount-extrovertsCountInner[lineStatus], m, n3, dp, introvertsCountInner, extrovertsCountInner, scoreInner, scoreOuter))
|
||||
}
|
||||
dp[lineStatusLast][row][introvertsCount][extrovertsCount] = best
|
||||
return best
|
||||
}
|
||||
|
||||
func max(a int, b int) int {
|
||||
if a > b {
|
||||
return a
|
||||
}
|
||||
return b
|
||||
}
|
||||
```
|
||||
Reference in New Issue
Block a user