mirror of
https://github.com/halfrost/LeetCode-Go.git
synced 2025-07-06 17:44:10 +08:00
Add solution 0119、1439
This commit is contained in:
@ -0,0 +1,10 @@
|
||||
package leetcode
|
||||
|
||||
func getRow(rowIndex int) []int {
|
||||
row := make([]int, rowIndex+1)
|
||||
row[0] = 1
|
||||
for i := 1; i <= rowIndex; i++ {
|
||||
row[i] = row[i-1] * (rowIndex - i + 1) / i
|
||||
}
|
||||
return row
|
||||
}
|
||||
@ -0,0 +1,47 @@
|
||||
package leetcode
|
||||
|
||||
import (
|
||||
"fmt"
|
||||
"testing"
|
||||
)
|
||||
|
||||
type question119 struct {
|
||||
para119
|
||||
ans119
|
||||
}
|
||||
|
||||
// para 是参数
|
||||
// one 代表第一个参数
|
||||
type para119 struct {
|
||||
rowIndex int
|
||||
}
|
||||
|
||||
// ans 是答案
|
||||
// one 代表第一个答案
|
||||
type ans119 struct {
|
||||
one []int
|
||||
}
|
||||
|
||||
func Test_Problem119(t *testing.T) {
|
||||
|
||||
qs := []question119{
|
||||
|
||||
{
|
||||
para119{3},
|
||||
ans119{[]int{1, 3, 3, 1}},
|
||||
},
|
||||
|
||||
{
|
||||
para119{0},
|
||||
ans119{[]int{1}},
|
||||
},
|
||||
}
|
||||
|
||||
fmt.Printf("------------------------Leetcode Problem 119------------------------\n")
|
||||
|
||||
for _, q := range qs {
|
||||
_, p := q.ans119, q.para119
|
||||
fmt.Printf("【input】:%v 【output】:%v\n", p, getRow(p.rowIndex))
|
||||
}
|
||||
fmt.Printf("\n\n\n")
|
||||
}
|
||||
72
leetcode/0119.Pascals-Triangle-II/README.md
Normal file
72
leetcode/0119.Pascals-Triangle-II/README.md
Normal file
@ -0,0 +1,72 @@
|
||||
# [119. Pascal's Triangle II](https://leetcode.com/problems/pascals-triangle-ii/)
|
||||
|
||||
|
||||
## 题目
|
||||
|
||||
Given an integer `rowIndex`, return the `rowIndexth` row of the Pascal's triangle.
|
||||
|
||||
Notice that the row index starts from **0**.
|
||||
|
||||

|
||||
|
||||
In Pascal's triangle, each number is the sum of the two numbers directly above it.
|
||||
|
||||
**Follow up:**
|
||||
|
||||
Could you optimize your algorithm to use only *O*(*k*) extra space?
|
||||
|
||||
**Example 1:**
|
||||
|
||||
```
|
||||
Input: rowIndex = 3
|
||||
Output: [1,3,3,1]
|
||||
```
|
||||
|
||||
**Example 2:**
|
||||
|
||||
```
|
||||
Input: rowIndex = 0
|
||||
Output: [1]
|
||||
```
|
||||
|
||||
**Example 3:**
|
||||
|
||||
```
|
||||
Input: rowIndex = 1
|
||||
Output: [1,1]
|
||||
```
|
||||
|
||||
**Constraints:**
|
||||
|
||||
- `0 <= rowIndex <= 33`
|
||||
|
||||
## 题目大意
|
||||
|
||||
给定一个非负索引 k,其中 k ≤ 33,返回杨辉三角的第 k 行。
|
||||
|
||||
## 解题思路
|
||||
|
||||
- 题目中的三角是杨辉三角,每个数字是 `(a+b)^n` 二项式展开的系数。题目要求我们只能使用 O(k) 的空间。那么需要找到两两项直接的递推关系。由组合知识得知:
|
||||
|
||||
$$\begin{aligned}C_{n}^{m} &= \frac{n!}{m!(n-m)!} \\C_{n}^{m-1} &= \frac{n!}{(m-1)!(n-m+1)!}\end{aligned}$$
|
||||
|
||||
于是得到递推公式:
|
||||
|
||||
$$C_{n}^{m} = C_{n}^{m-1} \times \frac{n-m+1}{m}$$
|
||||
|
||||
利用这个递推公式即可以把空间复杂度优化到 O(k)
|
||||
|
||||
## 代码
|
||||
|
||||
```go
|
||||
package leetcode
|
||||
|
||||
func getRow(rowIndex int) []int {
|
||||
row := make([]int, rowIndex+1)
|
||||
row[0] = 1
|
||||
for i := 1; i <= rowIndex; i++ {
|
||||
row[i] = row[i-1] * (rowIndex - i + 1) / i
|
||||
}
|
||||
return row
|
||||
}
|
||||
```
|
||||
@ -0,0 +1,82 @@
|
||||
package leetcode
|
||||
|
||||
import "container/heap"
|
||||
|
||||
func kthSmallest(mat [][]int, k int) int {
|
||||
if len(mat) == 0 || len(mat[0]) == 0 || k == 0 {
|
||||
return 0
|
||||
}
|
||||
prev := mat[0]
|
||||
for i := 1; i < len(mat); i++ {
|
||||
prev = kSmallestPairs(prev, mat[i], k)
|
||||
}
|
||||
if k < len(prev) {
|
||||
return -1
|
||||
}
|
||||
return prev[k-1]
|
||||
}
|
||||
|
||||
func kSmallestPairs(nums1 []int, nums2 []int, k int) []int {
|
||||
res := []int{}
|
||||
if len(nums2) == 0 {
|
||||
return res
|
||||
}
|
||||
pq := newPriorityQueue()
|
||||
for i := 0; i < len(nums1) && i < k; i++ {
|
||||
heap.Push(pq, &pddata{
|
||||
n1: nums1[i],
|
||||
n2: nums2[0],
|
||||
n2Idx: 0,
|
||||
})
|
||||
}
|
||||
for pq.Len() > 0 {
|
||||
i := heap.Pop(pq)
|
||||
data := i.(*pddata)
|
||||
res = append(res, data.n1+data.n2)
|
||||
k--
|
||||
if k <= 0 {
|
||||
break
|
||||
}
|
||||
idx := data.n2Idx
|
||||
idx++
|
||||
if idx >= len(nums2) {
|
||||
continue
|
||||
}
|
||||
heap.Push(pq, &pddata{
|
||||
n1: data.n1,
|
||||
n2: nums2[idx],
|
||||
n2Idx: idx,
|
||||
})
|
||||
}
|
||||
return res
|
||||
}
|
||||
|
||||
type pddata struct {
|
||||
n1 int
|
||||
n2 int
|
||||
n2Idx int
|
||||
}
|
||||
|
||||
type priorityQueue []*pddata
|
||||
|
||||
func newPriorityQueue() *priorityQueue {
|
||||
pq := priorityQueue([]*pddata{})
|
||||
heap.Init(&pq)
|
||||
return &pq
|
||||
}
|
||||
|
||||
func (pq priorityQueue) Len() int { return len(pq) }
|
||||
func (pq priorityQueue) Swap(i, j int) { pq[i], pq[j] = pq[j], pq[i] }
|
||||
func (pq priorityQueue) Less(i, j int) bool { return pq[i].n1+pq[i].n2 < pq[j].n1+pq[j].n2 }
|
||||
func (pq *priorityQueue) Pop() interface{} {
|
||||
old := *pq
|
||||
val := old[len(old)-1]
|
||||
old[len(old)-1] = nil
|
||||
*pq = old[0 : len(old)-1]
|
||||
return val
|
||||
}
|
||||
|
||||
func (pq *priorityQueue) Push(i interface{}) {
|
||||
val := i.(*pddata)
|
||||
*pq = append(*pq, val)
|
||||
}
|
||||
@ -0,0 +1,56 @@
|
||||
package leetcode
|
||||
|
||||
import (
|
||||
"fmt"
|
||||
"testing"
|
||||
)
|
||||
|
||||
type question1439 struct {
|
||||
para1439
|
||||
ans1439
|
||||
}
|
||||
|
||||
// para 是参数
|
||||
// one 代表第一个参数
|
||||
type para1439 struct {
|
||||
mat [][]int
|
||||
k int
|
||||
}
|
||||
|
||||
// ans 是答案
|
||||
// one 代表第一个答案
|
||||
type ans1439 struct {
|
||||
one int
|
||||
}
|
||||
|
||||
func Test_Problem1439(t *testing.T) {
|
||||
|
||||
qs := []question1439{
|
||||
|
||||
{
|
||||
para1439{[][]int{{1, 3, 11}, {2, 4, 6}}, 5},
|
||||
ans1439{7},
|
||||
},
|
||||
|
||||
{
|
||||
para1439{[][]int{{1, 3, 11}, {2, 4, 6}}, 9},
|
||||
ans1439{17},
|
||||
},
|
||||
{
|
||||
para1439{[][]int{{1, 10, 10}, {1, 4, 5}, {2, 3, 6}}, 7},
|
||||
ans1439{9},
|
||||
},
|
||||
{
|
||||
para1439{[][]int{{1, 1, 10}, {2, 2, 9}}, 7},
|
||||
ans1439{12},
|
||||
},
|
||||
}
|
||||
|
||||
fmt.Printf("------------------------Leetcode Problem 1439------------------------\n")
|
||||
|
||||
for _, q := range qs {
|
||||
_, p := q.ans1439, q.para1439
|
||||
fmt.Printf("【input】:%v 【output】:%v\n", p, kthSmallest(p.mat, p.k))
|
||||
}
|
||||
fmt.Printf("\n\n\n")
|
||||
}
|
||||
@ -0,0 +1,144 @@
|
||||
# [1439. Find the Kth Smallest Sum of a Matrix With Sorted Rows](https://leetcode.com/problems/find-the-kth-smallest-sum-of-a-matrix-with-sorted-rows/)
|
||||
|
||||
|
||||
## 题目
|
||||
|
||||
You are given an `m * n` matrix, `mat`, and an integer `k`, which has its rows sorted in non-decreasing order.
|
||||
|
||||
You are allowed to choose exactly 1 element from each row to form an array. Return the Kth **smallest** array sum among all possible arrays.
|
||||
|
||||
**Example 1:**
|
||||
|
||||
```
|
||||
Input: mat = [[1,3,11],[2,4,6]], k = 5
|
||||
Output: 7
|
||||
Explanation: Choosing one element from each row, the first k smallest sum are:
|
||||
[1,2], [1,4], [3,2], [3,4], [1,6]. Where the 5th sum is 7.
|
||||
```
|
||||
|
||||
**Example 2:**
|
||||
|
||||
```
|
||||
Input: mat = [[1,3,11],[2,4,6]], k = 9
|
||||
Output: 17
|
||||
```
|
||||
|
||||
**Example 3:**
|
||||
|
||||
```
|
||||
Input: mat = [[1,10,10],[1,4,5],[2,3,6]], k = 7
|
||||
Output: 9
|
||||
Explanation: Choosing one element from each row, the first k smallest sum are:
|
||||
[1,1,2], [1,1,3], [1,4,2], [1,4,3], [1,1,6], [1,5,2], [1,5,3]. Where the 7th sum is 9.
|
||||
```
|
||||
|
||||
**Example 4:**
|
||||
|
||||
```
|
||||
Input: mat = [[1,1,10],[2,2,9]], k = 7
|
||||
Output: 12
|
||||
```
|
||||
|
||||
**Constraints:**
|
||||
|
||||
- `m == mat.length`
|
||||
- `n == mat.length[i]`
|
||||
- `1 <= m, n <= 40`
|
||||
- `1 <= k <= min(200, n ^ m)`
|
||||
- `1 <= mat[i][j] <= 5000`
|
||||
- `mat[i]` is a non decreasing array.
|
||||
|
||||
## 题目大意
|
||||
|
||||
给你一个 m * n 的矩阵 mat,以及一个整数 k ,矩阵中的每一行都以非递减的顺序排列。你可以从每一行中选出 1 个元素形成一个数组。返回所有可能数组中的第 k 个 最小数组和。
|
||||
|
||||
## 解题思路
|
||||
|
||||
- 这一题是第 373 题的升级版。在第 373 题中,给定 2 个有序数组,要求分别从这 2 个数组中选出一个数组成一个数对,最终输出和最小的 K 组。这一题中给出的是 m*n 的矩阵。其实是将第 373 题的 2 个数组升级为了 m 个数组。无非外层多了一层循环。这层循环依次从每一行中选出一个数,先从第 0 行和第 1 行取数,找到前 K 小的组合以后,再从第 2 行取数,以此类推。其他做法和第 373 题一致。维护一个长度为 k 的最小堆。每次从堆中 pop 出最小的数组和 sum 和对应的下标 index,然后依次将下标向后移动一位,生成新的 sum,加入堆中。
|
||||
|
||||
## 代码
|
||||
|
||||
```go
|
||||
package leetcode
|
||||
|
||||
import "container/heap"
|
||||
|
||||
func kthSmallest(mat [][]int, k int) int {
|
||||
if len(mat) == 0 || len(mat[0]) == 0 || k == 0 {
|
||||
return 0
|
||||
}
|
||||
prev := mat[0]
|
||||
for i := 1; i < len(mat); i++ {
|
||||
prev = kSmallestPairs(prev, mat[i], k)
|
||||
}
|
||||
if k < len(prev) {
|
||||
return -1
|
||||
}
|
||||
return prev[k-1]
|
||||
}
|
||||
|
||||
func kSmallestPairs(nums1 []int, nums2 []int, k int) []int {
|
||||
res := []int{}
|
||||
if len(nums2) == 0 {
|
||||
return res
|
||||
}
|
||||
pq := newPriorityQueue()
|
||||
for i := 0; i < len(nums1) && i < k; i++ {
|
||||
heap.Push(pq, &pddata{
|
||||
n1: nums1[i],
|
||||
n2: nums2[0],
|
||||
n2Idx: 0,
|
||||
})
|
||||
}
|
||||
for pq.Len() > 0 {
|
||||
i := heap.Pop(pq)
|
||||
data := i.(*pddata)
|
||||
res = append(res, data.n1+data.n2)
|
||||
k--
|
||||
if k <= 0 {
|
||||
break
|
||||
}
|
||||
idx := data.n2Idx
|
||||
idx++
|
||||
if idx >= len(nums2) {
|
||||
continue
|
||||
}
|
||||
heap.Push(pq, &pddata{
|
||||
n1: data.n1,
|
||||
n2: nums2[idx],
|
||||
n2Idx: idx,
|
||||
})
|
||||
}
|
||||
return res
|
||||
}
|
||||
|
||||
type pddata struct {
|
||||
n1 int
|
||||
n2 int
|
||||
n2Idx int
|
||||
}
|
||||
|
||||
type priorityQueue []*pddata
|
||||
|
||||
func newPriorityQueue() *priorityQueue {
|
||||
pq := priorityQueue([]*pddata{})
|
||||
heap.Init(&pq)
|
||||
return &pq
|
||||
}
|
||||
|
||||
func (pq priorityQueue) Len() int { return len(pq) }
|
||||
func (pq priorityQueue) Swap(i, j int) { pq[i], pq[j] = pq[j], pq[i] }
|
||||
func (pq priorityQueue) Less(i, j int) bool { return pq[i].n1+pq[i].n2 < pq[j].n1+pq[j].n2 }
|
||||
func (pq *priorityQueue) Pop() interface{} {
|
||||
old := *pq
|
||||
val := old[len(old)-1]
|
||||
old[len(old)-1] = nil
|
||||
*pq = old[0 : len(old)-1]
|
||||
return val
|
||||
}
|
||||
|
||||
func (pq *priorityQueue) Push(i interface{}) {
|
||||
val := i.(*pddata)
|
||||
*pq = append(*pq, val)
|
||||
}
|
||||
```
|
||||
@ -1,6 +1,6 @@
|
||||
package structures
|
||||
|
||||
// intHeap 实现了 heap 的接口
|
||||
// intHeap 实现了最小堆 heap 的接口
|
||||
type intHeap []int
|
||||
|
||||
func (h intHeap) Len() int {
|
||||
|
||||
@ -63,5 +63,5 @@ func generate(numRows int) [][]int {
|
||||
----------------------------------------------
|
||||
<div style="display: flex;justify-content: space-between;align-items: center;">
|
||||
<p><a href="https://books.halfrost.com/leetcode/ChapterFour/0100~0199/0114.Flatten-Binary-Tree-to-Linked-List/">⬅️上一页</a></p>
|
||||
<p><a href="https://books.halfrost.com/leetcode/ChapterFour/0100~0199/0120.Triangle/">下一页➡️</a></p>
|
||||
<p><a href="https://books.halfrost.com/leetcode/ChapterFour/0100~0199/0119.Pascals-Triangle-II/">下一页➡️</a></p>
|
||||
</div>
|
||||
|
||||
@ -0,0 +1,83 @@
|
||||
# [119. Pascal's Triangle II](https://leetcode.com/problems/pascals-triangle-ii/)
|
||||
|
||||
|
||||
## 题目
|
||||
|
||||
Given an integer `rowIndex`, return the `rowIndexth` row of the Pascal's triangle.
|
||||
|
||||
Notice that the row index starts from **0**.
|
||||
|
||||

|
||||
|
||||
In Pascal's triangle, each number is the sum of the two numbers directly above it.
|
||||
|
||||
**Follow up:**
|
||||
|
||||
Could you optimize your algorithm to use only *O*(*k*) extra space?
|
||||
|
||||
**Example 1:**
|
||||
|
||||
```
|
||||
Input: rowIndex = 3
|
||||
Output: [1,3,3,1]
|
||||
```
|
||||
|
||||
**Example 2:**
|
||||
|
||||
```
|
||||
Input: rowIndex = 0
|
||||
Output: [1]
|
||||
```
|
||||
|
||||
**Example 3:**
|
||||
|
||||
```
|
||||
Input: rowIndex = 1
|
||||
Output: [1,1]
|
||||
```
|
||||
|
||||
**Constraints:**
|
||||
|
||||
- `0 <= rowIndex <= 33`
|
||||
|
||||
## 题目大意
|
||||
|
||||
给定一个非负索引 k,其中 k ≤ 33,返回杨辉三角的第 k 行。
|
||||
|
||||
## 解题思路
|
||||
|
||||
- 题目中的三角是杨辉三角,每个数字是 `(a+b)^n` 二项式展开的系数。题目要求我们只能使用 O(k) 的空间。那么需要找到两两项直接的递推关系。由组合知识得知:
|
||||
|
||||
{{< katex display >}}
|
||||
\begin{aligned}C_{n}^{m} &= \frac{n!}{m!(n-m)!} \\C_{n}^{m-1} &= \frac{n!}{(m-1)!(n-m+1)!}\end{aligned}
|
||||
{{< /katex>}}
|
||||
|
||||
于是得到递推公式:
|
||||
|
||||
{{< katex display >}}
|
||||
C_{n}^{m} = C_{n}^{m-1} \times \frac{n-m+1}{m}
|
||||
{{< /katex>}}
|
||||
|
||||
利用这个递推公式即可以把空间复杂度优化到 O(k)
|
||||
|
||||
## 代码
|
||||
|
||||
```go
|
||||
package leetcode
|
||||
|
||||
func getRow(rowIndex int) []int {
|
||||
row := make([]int, rowIndex+1)
|
||||
row[0] = 1
|
||||
for i := 1; i <= rowIndex; i++ {
|
||||
row[i] = row[i-1] * (rowIndex - i + 1) / i
|
||||
}
|
||||
return row
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
----------------------------------------------
|
||||
<div style="display: flex;justify-content: space-between;align-items: center;">
|
||||
<p><a href="https://books.halfrost.com/leetcode/ChapterFour/0100~0199/0118.Pascals-Triangle/">⬅️上一页</a></p>
|
||||
<p><a href="https://books.halfrost.com/leetcode/ChapterFour/0100~0199/0120.Triangle/">下一页➡️</a></p>
|
||||
</div>
|
||||
@ -91,6 +91,6 @@ func minimumTotal1(triangle [][]int) int {
|
||||
|
||||
----------------------------------------------
|
||||
<div style="display: flex;justify-content: space-between;align-items: center;">
|
||||
<p><a href="https://books.halfrost.com/leetcode/ChapterFour/0100~0199/0118.Pascals-Triangle/">⬅️上一页</a></p>
|
||||
<p><a href="https://books.halfrost.com/leetcode/ChapterFour/0100~0199/0119.Pascals-Triangle-II/">⬅️上一页</a></p>
|
||||
<p><a href="https://books.halfrost.com/leetcode/ChapterFour/0100~0199/0121.Best-Time-to-Buy-and-Sell-Stock/">下一页➡️</a></p>
|
||||
</div>
|
||||
|
||||
@ -78,7 +78,7 @@ func (pq PriorityQueue) Len() int {
|
||||
}
|
||||
|
||||
func (pq PriorityQueue) Less(i, j int) bool {
|
||||
// 注意:因为golang中的heap是按最小堆组织的,所以count越大,Less()越小,越靠近堆顶.
|
||||
// 注意:因为 golang 中的 heap 默认是按最小堆组织的,所以 count 越大,Less() 越小,越靠近堆顶。这里采用 >,变为最大堆
|
||||
return pq[i].count > pq[j].count
|
||||
}
|
||||
|
||||
|
||||
@ -76,5 +76,5 @@ func kLengthApart(nums []int, k int) bool {
|
||||
----------------------------------------------
|
||||
<div style="display: flex;justify-content: space-between;align-items: center;">
|
||||
<p><a href="https://books.halfrost.com/leetcode/ChapterFour/1300~1399/1389.Create-Target-Array-in-the-Given-Order/">⬅️上一页</a></p>
|
||||
<p><a href="https://books.halfrost.com/leetcode/ChapterFour/1400~1499/1455.Check-If-a-Word-Occurs-As-a-Prefix-of-Any-Word-in-a-Sentence/">下一页➡️</a></p>
|
||||
<p><a href="https://books.halfrost.com/leetcode/ChapterFour/1400~1499/1439.Find-the-Kth-Smallest-Sum-of-a-Matrix-With-Sorted-Rows/">下一页➡️</a></p>
|
||||
</div>
|
||||
|
||||
@ -0,0 +1,151 @@
|
||||
# [1439. Find the Kth Smallest Sum of a Matrix With Sorted Rows](https://leetcode.com/problems/find-the-kth-smallest-sum-of-a-matrix-with-sorted-rows/)
|
||||
|
||||
|
||||
## 题目
|
||||
|
||||
You are given an `m * n` matrix, `mat`, and an integer `k`, which has its rows sorted in non-decreasing order.
|
||||
|
||||
You are allowed to choose exactly 1 element from each row to form an array. Return the Kth **smallest** array sum among all possible arrays.
|
||||
|
||||
**Example 1:**
|
||||
|
||||
```
|
||||
Input: mat = [[1,3,11],[2,4,6]], k = 5
|
||||
Output: 7
|
||||
Explanation: Choosing one element from each row, the first k smallest sum are:
|
||||
[1,2], [1,4], [3,2], [3,4], [1,6]. Where the 5th sum is 7.
|
||||
```
|
||||
|
||||
**Example 2:**
|
||||
|
||||
```
|
||||
Input: mat = [[1,3,11],[2,4,6]], k = 9
|
||||
Output: 17
|
||||
```
|
||||
|
||||
**Example 3:**
|
||||
|
||||
```
|
||||
Input: mat = [[1,10,10],[1,4,5],[2,3,6]], k = 7
|
||||
Output: 9
|
||||
Explanation: Choosing one element from each row, the first k smallest sum are:
|
||||
[1,1,2], [1,1,3], [1,4,2], [1,4,3], [1,1,6], [1,5,2], [1,5,3]. Where the 7th sum is 9.
|
||||
```
|
||||
|
||||
**Example 4:**
|
||||
|
||||
```
|
||||
Input: mat = [[1,1,10],[2,2,9]], k = 7
|
||||
Output: 12
|
||||
```
|
||||
|
||||
**Constraints:**
|
||||
|
||||
- `m == mat.length`
|
||||
- `n == mat.length[i]`
|
||||
- `1 <= m, n <= 40`
|
||||
- `1 <= k <= min(200, n ^ m)`
|
||||
- `1 <= mat[i][j] <= 5000`
|
||||
- `mat[i]` is a non decreasing array.
|
||||
|
||||
## 题目大意
|
||||
|
||||
给你一个 m * n 的矩阵 mat,以及一个整数 k ,矩阵中的每一行都以非递减的顺序排列。你可以从每一行中选出 1 个元素形成一个数组。返回所有可能数组中的第 k 个 最小数组和。
|
||||
|
||||
## 解题思路
|
||||
|
||||
- 这一题是第 373 题的升级版。在第 373 题中,给定 2 个有序数组,要求分别从这 2 个数组中选出一个数组成一个数对,最终输出和最小的 K 组。这一题中给出的是 m*n 的矩阵。其实是将第 373 题的 2 个数组升级为了 m 个数组。无非外层多了一层循环。这层循环依次从每一行中选出一个数,先从第 0 行和第 1 行取数,找到前 K 小的组合以后,再从第 2 行取数,以此类推。其他做法和第 373 题一致。维护一个长度为 k 的最小堆。每次从堆中 pop 出最小的数组和 sum 和对应的下标 index,然后依次将下标向后移动一位,生成新的 sum,加入堆中。
|
||||
|
||||
## 代码
|
||||
|
||||
```go
|
||||
package leetcode
|
||||
|
||||
import "container/heap"
|
||||
|
||||
func kthSmallest(mat [][]int, k int) int {
|
||||
if len(mat) == 0 || len(mat[0]) == 0 || k == 0 {
|
||||
return 0
|
||||
}
|
||||
prev := mat[0]
|
||||
for i := 1; i < len(mat); i++ {
|
||||
prev = kSmallestPairs(prev, mat[i], k)
|
||||
}
|
||||
if k < len(prev) {
|
||||
return -1
|
||||
}
|
||||
return prev[k-1]
|
||||
}
|
||||
|
||||
func kSmallestPairs(nums1 []int, nums2 []int, k int) []int {
|
||||
res := []int{}
|
||||
if len(nums2) == 0 {
|
||||
return res
|
||||
}
|
||||
pq := newPriorityQueue()
|
||||
for i := 0; i < len(nums1) && i < k; i++ {
|
||||
heap.Push(pq, &pddata{
|
||||
n1: nums1[i],
|
||||
n2: nums2[0],
|
||||
n2Idx: 0,
|
||||
})
|
||||
}
|
||||
for pq.Len() > 0 {
|
||||
i := heap.Pop(pq)
|
||||
data := i.(*pddata)
|
||||
res = append(res, data.n1+data.n2)
|
||||
k--
|
||||
if k <= 0 {
|
||||
break
|
||||
}
|
||||
idx := data.n2Idx
|
||||
idx++
|
||||
if idx >= len(nums2) {
|
||||
continue
|
||||
}
|
||||
heap.Push(pq, &pddata{
|
||||
n1: data.n1,
|
||||
n2: nums2[idx],
|
||||
n2Idx: idx,
|
||||
})
|
||||
}
|
||||
return res
|
||||
}
|
||||
|
||||
type pddata struct {
|
||||
n1 int
|
||||
n2 int
|
||||
n2Idx int
|
||||
}
|
||||
|
||||
type priorityQueue []*pddata
|
||||
|
||||
func newPriorityQueue() *priorityQueue {
|
||||
pq := priorityQueue([]*pddata{})
|
||||
heap.Init(&pq)
|
||||
return &pq
|
||||
}
|
||||
|
||||
func (pq priorityQueue) Len() int { return len(pq) }
|
||||
func (pq priorityQueue) Swap(i, j int) { pq[i], pq[j] = pq[j], pq[i] }
|
||||
func (pq priorityQueue) Less(i, j int) bool { return pq[i].n1+pq[i].n2 < pq[j].n1+pq[j].n2 }
|
||||
func (pq *priorityQueue) Pop() interface{} {
|
||||
old := *pq
|
||||
val := old[len(old)-1]
|
||||
old[len(old)-1] = nil
|
||||
*pq = old[0 : len(old)-1]
|
||||
return val
|
||||
}
|
||||
|
||||
func (pq *priorityQueue) Push(i interface{}) {
|
||||
val := i.(*pddata)
|
||||
*pq = append(*pq, val)
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
----------------------------------------------
|
||||
<div style="display: flex;justify-content: space-between;align-items: center;">
|
||||
<p><a href="https://books.halfrost.com/leetcode/ChapterFour/1400~1499/1437.Check-If-All-1s-Are-at-Least-Length-K-Places-Away/">⬅️上一页</a></p>
|
||||
<p><a href="https://books.halfrost.com/leetcode/ChapterFour/1400~1499/1455.Check-If-a-Word-Occurs-As-a-Prefix-of-Any-Word-in-a-Sentence/">下一页➡️</a></p>
|
||||
</div>
|
||||
@ -100,6 +100,6 @@ func isPrefixOfWord(sentence string, searchWord string) int {
|
||||
|
||||
----------------------------------------------
|
||||
<div style="display: flex;justify-content: space-between;align-items: center;">
|
||||
<p><a href="https://books.halfrost.com/leetcode/ChapterFour/1400~1499/1437.Check-If-All-1s-Are-at-Least-Length-K-Places-Away/">⬅️上一页</a></p>
|
||||
<p><a href="https://books.halfrost.com/leetcode/ChapterFour/1400~1499/1439.Find-the-Kth-Smallest-Sum-of-a-Matrix-With-Sorted-Rows/">⬅️上一页</a></p>
|
||||
<p><a href="https://books.halfrost.com/leetcode/ChapterFour/1400~1499/1463.Cherry-Pickup-II/">下一页➡️</a></p>
|
||||
</div>
|
||||
|
||||
@ -71,9 +71,9 @@ Explanation: Sell the 1st color 1000000000 times for a total value of 5000000005
|
||||
- 拿到这个题目以后很容易想到优先队列,建立大根堆以后,`pop` 出当前最大值 `maxItem`,累加,以后把 `maxItem` 减一再 `push` 回去。循环执行 `orders` 次以后即是最终结果。题目是这个意思,但是我们不能这么写代码,因为题目条件里面给出了 `orders` 的数据大小。orders 最大为 10^9。按照优先队列的这个方法一定会超时,时间复杂度为 O(orders⋅logn)。那就换一个思路。优先队列这个思路中,重复操作了 `orders` 次,其实在这些操作中,有一些是没有必要的废操作。这些大量的“废”操作导致了超时。试想,在 `orders` 次操作中,能否合并 `n` 个 `pop` 操作,一口气先 `pop` 掉 `n` 个前 `n` 大的数呢?这个是可行的,因为每次 `pop` 出去,元素都只会减一,这个是非常有规律的。
|
||||
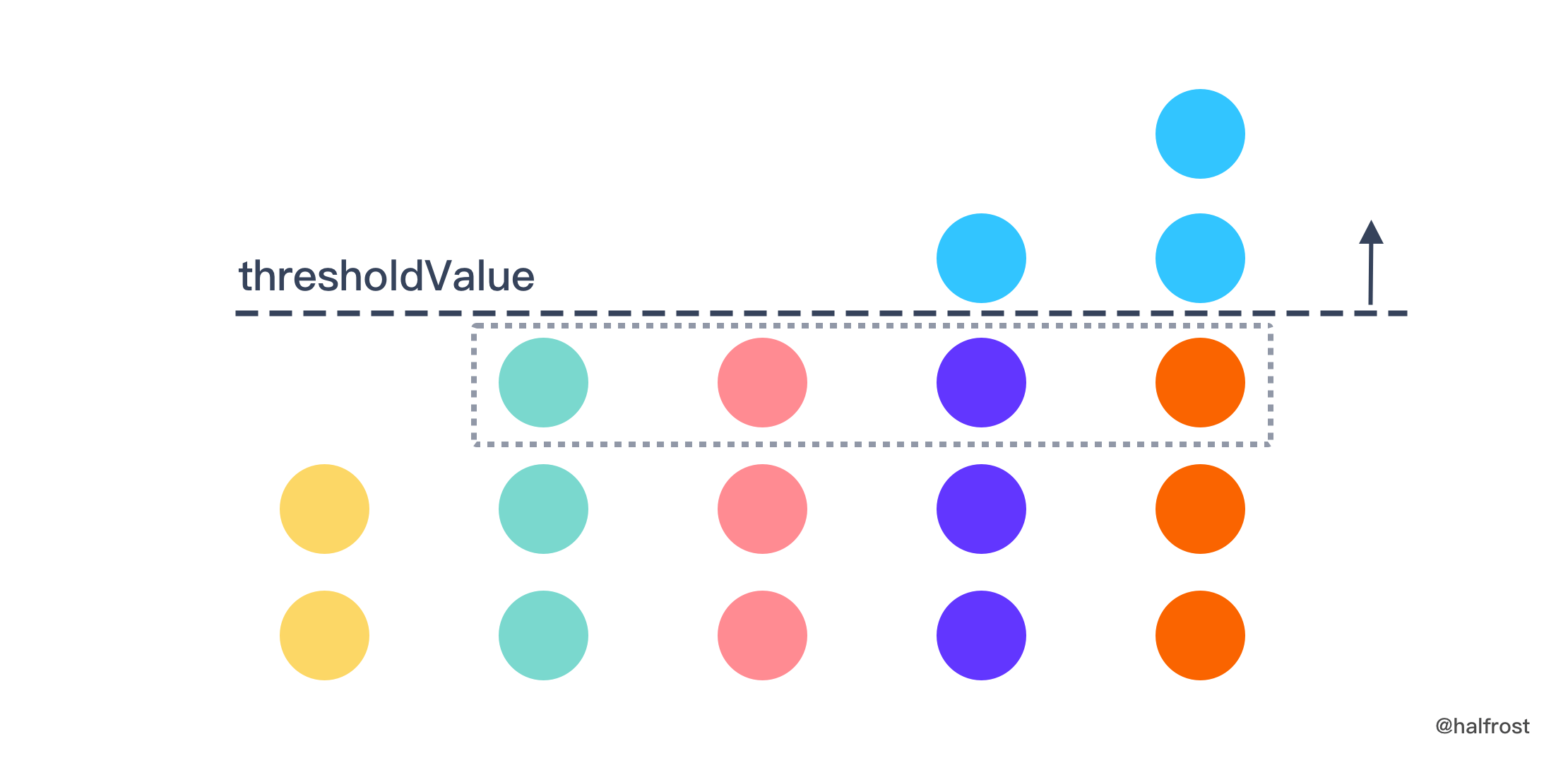
- 为了接下来的描述更加清晰易懂,还需要再定义 1 个值, `thresholdValue` 为操作 `n` 次以后,当前 `inventory` 数组的最大值。关于 `thresholdValue` 的理解,这里要说明一下。 `thresholdValue` 的来源有 2 种,一种是本来数组里面就有这个值,还有一种来源是 `inventory[i]` 元素减少到了 `thresholdValue` 这个值。举个例子:原始数组是 [2,3,3,4,5],`orders` = 4,取 4 次以后,剩下的数组是 [2,2,3,3,3]。3 个 3 里面其中一个 3 就来自于 `4-1=3`,或者 `5-2=3`。
|
||||
- 用二分搜索在 [0,max(`inventory`)] 区间内找到这个 `thresholdValue` 值,能满足下列不等式的最小 `thresholdValue` 值:
|
||||
|
||||
$$\sum_{inventory[i]\geqslant thresholdValue}^{} \left ( inventory[i] - thresholdValue \right )\leqslant orders$$
|
||||
|
||||
{{< katex display >}}
|
||||
\sum_{inventory[i]\geqslant thresholdValue}^{} \left ( inventory[i] - thresholdValue \right )\leqslant orders
|
||||
{{< /katex >}}
|
||||
`thresholdValue` 越小,不等式左边的值越大,随着 `thresholdValue` 的增大,不等式左边的值越来越小,直到刚刚能小于等于 `orders`。求出了 `thresholdValue` 值以后,还需要再判断有多少值等于 `thresholdValue - 1` 值了。
|
||||
|
||||
|
||||
|
||||
@ -46,6 +46,7 @@ weight: 1
|
||||
|0105|Construct Binary Tree from Preorder and Inorder Traversal|[Go]({{< relref "/ChapterFour/0100~0199/0105.Construct-Binary-Tree-from-Preorder-and-Inorder-Traversal.md" >}})|Medium||||51.6%|
|
||||
|0106|Construct Binary Tree from Inorder and Postorder Traversal|[Go]({{< relref "/ChapterFour/0100~0199/0106.Construct-Binary-Tree-from-Inorder-and-Postorder-Traversal.md" >}})|Medium||||49.5%|
|
||||
|0118|Pascal's Triangle|[Go]({{< relref "/ChapterFour/0100~0199/0118.Pascals-Triangle.md" >}})|Easy||||54.7%|
|
||||
|0119|Pascal's Triangle II|[Go]({{< relref "/ChapterFour/0100~0199/0119.Pascals-Triangle-II.md" >}})|Easy||||52.1%|
|
||||
|0120|Triangle|[Go]({{< relref "/ChapterFour/0100~0199/0120.Triangle.md" >}})|Medium| O(n^2)| O(n)||45.7%|
|
||||
|0121|Best Time to Buy and Sell Stock|[Go]({{< relref "/ChapterFour/0100~0199/0121.Best-Time-to-Buy-and-Sell-Stock.md" >}})|Easy| O(n)| O(1)||51.5%|
|
||||
|0122|Best Time to Buy and Sell Stock II|[Go]({{< relref "/ChapterFour/0100~0199/0122.Best-Time-to-Buy-and-Sell-Stock-II.md" >}})|Easy| O(n)| O(1)||58.4%|
|
||||
@ -84,7 +85,7 @@ weight: 1
|
||||
|0697|Degree of an Array|[Go]({{< relref "/ChapterFour/0600~0699/0697.Degree-of-an-Array.md" >}})|Easy||||54.4%|
|
||||
|0713|Subarray Product Less Than K|[Go]({{< relref "/ChapterFour/0700~0799/0713.Subarray-Product-Less-Than-K.md" >}})|Medium| O(n)| O(1)||40.5%|
|
||||
|0714|Best Time to Buy and Sell Stock with Transaction Fee|[Go]({{< relref "/ChapterFour/0700~0799/0714.Best-Time-to-Buy-and-Sell-Stock-with-Transaction-Fee.md" >}})|Medium| O(n)| O(1)||56.0%|
|
||||
|0717|1-bit and 2-bit Characters|[Go]({{< relref "/ChapterFour/0700~0799/0717.1-bit-and-2-bit-Characters.md" >}})|Easy||||47.3%|
|
||||
|0717|1-bit and 2-bit Characters|[Go]({{< relref "/ChapterFour/0700~0799/0717.1-bit-and-2-bit-Characters.md" >}})|Easy||||47.4%|
|
||||
|0718|Maximum Length of Repeated Subarray|[Go]({{< relref "/ChapterFour/0700~0799/0718.Maximum-Length-of-Repeated-Subarray.md" >}})|Medium||||50.3%|
|
||||
|0719|Find K-th Smallest Pair Distance|[Go]({{< relref "/ChapterFour/0700~0799/0719.Find-K-th-Smallest-Pair-Distance.md" >}})|Hard||||32.5%|
|
||||
|0724|Find Pivot Index|[Go]({{< relref "/ChapterFour/0700~0799/0724.Find-Pivot-Index.md" >}})|Easy||||45.3%|
|
||||
@ -107,7 +108,7 @@ weight: 1
|
||||
|0985|Sum of Even Numbers After Queries|[Go]({{< relref "/ChapterFour/0900~0999/0985.Sum-of-Even-Numbers-After-Queries.md" >}})|Easy||||60.7%|
|
||||
|0989|Add to Array-Form of Integer|[Go]({{< relref "/ChapterFour/0900~0999/0989.Add-to-Array-Form-of-Integer.md" >}})|Easy||||44.8%|
|
||||
|0999|Available Captures for Rook|[Go]({{< relref "/ChapterFour/0900~0999/0999.Available-Captures-for-Rook.md" >}})|Easy||||67.7%|
|
||||
|1002|Find Common Characters|[Go]({{< relref "/ChapterFour/1000~1099/1002.Find-Common-Characters.md" >}})|Easy||||68.5%|
|
||||
|1002|Find Common Characters|[Go]({{< relref "/ChapterFour/1000~1099/1002.Find-Common-Characters.md" >}})|Easy||||68.6%|
|
||||
|1011|Capacity To Ship Packages Within D Days|[Go]({{< relref "/ChapterFour/1000~1099/1011.Capacity-To-Ship-Packages-Within-D-Days.md" >}})|Medium||||59.7%|
|
||||
|1018|Binary Prefix Divisible By 5|[Go]({{< relref "/ChapterFour/1000~1099/1018.Binary-Prefix-Divisible-By-5.md" >}})|Easy||||47.8%|
|
||||
|1040|Moving Stones Until Consecutive II|[Go]({{< relref "/ChapterFour/1000~1099/1040.Moving-Stones-Until-Consecutive-II.md" >}})|Medium||||54.1%|
|
||||
@ -128,7 +129,7 @@ weight: 1
|
||||
|1217|Minimum Cost to Move Chips to The Same Position|[Go]({{< relref "/ChapterFour/1200~1299/1217.Minimum-Cost-to-Move-Chips-to-The-Same-Position.md" >}})|Easy||||71.2%|
|
||||
|1232|Check If It Is a Straight Line|[Go]({{< relref "/ChapterFour/1200~1299/1232.Check-If-It-Is-a-Straight-Line.md" >}})|Easy||||43.7%|
|
||||
|1252|Cells with Odd Values in a Matrix|[Go]({{< relref "/ChapterFour/1200~1299/1252.Cells-with-Odd-Values-in-a-Matrix.md" >}})|Easy||||78.8%|
|
||||
|1260|Shift 2D Grid|[Go]({{< relref "/ChapterFour/1200~1299/1260.Shift-2D-Grid.md" >}})|Easy||||61.9%|
|
||||
|1260|Shift 2D Grid|[Go]({{< relref "/ChapterFour/1200~1299/1260.Shift-2D-Grid.md" >}})|Easy||||61.8%|
|
||||
|1266|Minimum Time Visiting All Points|[Go]({{< relref "/ChapterFour/1200~1299/1266.Minimum-Time-Visiting-All-Points.md" >}})|Easy||||79.5%|
|
||||
|1275|Find Winner on a Tic Tac Toe Game|[Go]({{< relref "/ChapterFour/1200~1299/1275.Find-Winner-on-a-Tic-Tac-Toe-Game.md" >}})|Easy||||52.9%|
|
||||
|1287|Element Appearing More Than 25% In Sorted Array|[Go]({{< relref "/ChapterFour/1200~1299/1287.Element-Appearing-More-Than-25-In-Sorted-Array.md" >}})|Easy||||60.2%|
|
||||
@ -139,7 +140,7 @@ weight: 1
|
||||
|1313|Decompress Run-Length Encoded List|[Go]({{< relref "/ChapterFour/1300~1399/1313.Decompress-Run-Length-Encoded-List.md" >}})|Easy||||85.4%|
|
||||
|1329|Sort the Matrix Diagonally|[Go]({{< relref "/ChapterFour/1300~1399/1329.Sort-the-Matrix-Diagonally.md" >}})|Medium||||81.8%|
|
||||
|1380|Lucky Numbers in a Matrix|[Go]({{< relref "/ChapterFour/1300~1399/1380.Lucky-Numbers-in-a-Matrix.md" >}})|Easy||||70.8%|
|
||||
|1385|Find the Distance Value Between Two Arrays|[Go]({{< relref "/ChapterFour/1300~1399/1385.Find-the-Distance-Value-Between-Two-Arrays.md" >}})|Easy||||66.5%|
|
||||
|1385|Find the Distance Value Between Two Arrays|[Go]({{< relref "/ChapterFour/1300~1399/1385.Find-the-Distance-Value-Between-Two-Arrays.md" >}})|Easy||||66.4%|
|
||||
|1389|Create Target Array in the Given Order|[Go]({{< relref "/ChapterFour/1300~1399/1389.Create-Target-Array-in-the-Given-Order.md" >}})|Easy||||84.8%|
|
||||
|1437|Check If All 1's Are at Least Length K Places Away|[Go]({{< relref "/ChapterFour/1400~1499/1437.Check-If-All-1s-Are-at-Least-Length-K-Places-Away.md" >}})|Easy||||62.8%|
|
||||
|1464|Maximum Product of Two Elements in an Array|[Go]({{< relref "/ChapterFour/1400~1499/1464.Maximum-Product-of-Two-Elements-in-an-Array.md" >}})|Easy||||77.2%|
|
||||
@ -149,7 +150,7 @@ weight: 1
|
||||
|1539|Kth Missing Positive Number|[Go]({{< relref "/ChapterFour/1500~1599/1539.Kth-Missing-Positive-Number.md" >}})|Easy||||55.1%|
|
||||
|1640|Check Array Formation Through Concatenation|[Go]({{< relref "/ChapterFour/1600~1699/1640.Check-Array-Formation-Through-Concatenation.md" >}})|Easy||||60.2%|
|
||||
|1646|Get Maximum in Generated Array|[Go]({{< relref "/ChapterFour/1600~1699/1646.Get-Maximum-in-Generated-Array.md" >}})|Easy||||53.5%|
|
||||
|1652|Defuse the Bomb|[Go]({{< relref "/ChapterFour/1600~1699/1652.Defuse-the-Bomb.md" >}})|Easy||||63.0%|
|
||||
|1652|Defuse the Bomb|[Go]({{< relref "/ChapterFour/1600~1699/1652.Defuse-the-Bomb.md" >}})|Easy||||62.9%|
|
||||
|1656|Design an Ordered Stream|[Go]({{< relref "/ChapterFour/1600~1699/1656.Design-an-Ordered-Stream.md" >}})|Easy||||82.2%|
|
||||
|1672|Richest Customer Wealth|[Go]({{< relref "/ChapterFour/1600~1699/1672.Richest-Customer-Wealth.md" >}})|Easy||||88.4%|
|
||||
|------------|-------------------------------------------------------|-------| ----------------| ---------------|-------------|-------------|-------------|
|
||||
|
||||
@ -118,7 +118,7 @@ func updateMatrix_BFS(matrix [][]int) [][]int {
|
||||
|0093|Restore IP Addresses|[Go]({{< relref "/ChapterFour/0001~0099/0093.Restore-IP-Addresses.md" >}})|Medium| O(n)| O(n)|❤️|37.4%|
|
||||
|0126|Word Ladder II|[Go]({{< relref "/ChapterFour/0100~0199/0126.Word-Ladder-II.md" >}})|Hard| O(n)| O(n^2)|❤️|23.6%|
|
||||
|0131|Palindrome Partitioning|[Go]({{< relref "/ChapterFour/0100~0199/0131.Palindrome-Partitioning.md" >}})|Medium| O(n)| O(n^2)|❤️|51.8%|
|
||||
|0211|Design Add and Search Words Data Structure|[Go]({{< relref "/ChapterFour/0200~0299/0211.Design-Add-and-Search-Words-Data-Structure.md" >}})|Medium| O(n)| O(n)|❤️|40.0%|
|
||||
|0211|Design Add and Search Words Data Structure|[Go]({{< relref "/ChapterFour/0200~0299/0211.Design-Add-and-Search-Words-Data-Structure.md" >}})|Medium| O(n)| O(n)|❤️|40.1%|
|
||||
|0212|Word Search II|[Go]({{< relref "/ChapterFour/0200~0299/0212.Word-Search-II.md" >}})|Hard| O(n^2)| O(n^2)|❤️|36.9%|
|
||||
|0216|Combination Sum III|[Go]({{< relref "/ChapterFour/0200~0299/0216.Combination-Sum-III.md" >}})|Medium| O(n)| O(1)|❤️|60.2%|
|
||||
|0306|Additive Number|[Go]({{< relref "/ChapterFour/0300~0399/0306.Additive-Number.md" >}})|Medium| O(n^2)| O(1)|❤️|29.6%|
|
||||
@ -130,7 +130,7 @@ func updateMatrix_BFS(matrix [][]int) [][]int {
|
||||
|0980|Unique Paths III|[Go]({{< relref "/ChapterFour/0900~0999/0980.Unique-Paths-III.md" >}})|Hard| O(n log n)| O(n)||77.2%|
|
||||
|0996|Number of Squareful Arrays|[Go]({{< relref "/ChapterFour/0900~0999/0996.Number-of-Squareful-Arrays.md" >}})|Hard| O(n log n)| O(n) ||48.3%|
|
||||
|1079|Letter Tile Possibilities|[Go]({{< relref "/ChapterFour/1000~1099/1079.Letter-Tile-Possibilities.md" >}})|Medium| O(n^2)| O(1)|❤️|75.9%|
|
||||
|1641|Count Sorted Vowel Strings|[Go]({{< relref "/ChapterFour/1600~1699/1641.Count-Sorted-Vowel-Strings.md" >}})|Medium||||77.0%|
|
||||
|1641|Count Sorted Vowel Strings|[Go]({{< relref "/ChapterFour/1600~1699/1641.Count-Sorted-Vowel-Strings.md" >}})|Medium||||76.9%|
|
||||
|1655|Distribute Repeating Integers|[Go]({{< relref "/ChapterFour/1600~1699/1655.Distribute-Repeating-Integers.md" >}})|Hard||||40.4%|
|
||||
|1659|Maximize Grid Happiness|[Go]({{< relref "/ChapterFour/1600~1699/1659.Maximize-Grid-Happiness.md" >}})|Hard||||35.4%|
|
||||
|1681|Minimum Incompatibility|[Go]({{< relref "/ChapterFour/1600~1699/1681.Minimum-Incompatibility.md" >}})|Hard||||35.4%|
|
||||
|
||||
@ -160,7 +160,7 @@ func peakIndexInMountainArray(A []int) int {
|
||||
|0367|Valid Perfect Square|[Go]({{< relref "/ChapterFour/0300~0399/0367.Valid-Perfect-Square.md" >}})|Easy||||42.0%|
|
||||
|0378|Kth Smallest Element in a Sorted Matrix|[Go]({{< relref "/ChapterFour/0300~0399/0378.Kth-Smallest-Element-in-a-Sorted-Matrix.md" >}})|Medium||||56.1%|
|
||||
|0392|Is Subsequence|[Go]({{< relref "/ChapterFour/0300~0399/0392.Is-Subsequence.md" >}})|Easy| O(n)| O(1)||49.5%|
|
||||
|0410|Split Array Largest Sum|[Go]({{< relref "/ChapterFour/0400~0499/0410.Split-Array-Largest-Sum.md" >}})|Hard||||46.2%|
|
||||
|0410|Split Array Largest Sum|[Go]({{< relref "/ChapterFour/0400~0499/0410.Split-Array-Largest-Sum.md" >}})|Hard||||46.3%|
|
||||
|0436|Find Right Interval|[Go]({{< relref "/ChapterFour/0400~0499/0436.Find-Right-Interval.md" >}})|Medium||||48.5%|
|
||||
|0441|Arranging Coins|[Go]({{< relref "/ChapterFour/0400~0499/0441.Arranging-Coins.md" >}})|Easy||||42.3%|
|
||||
|0454|4Sum II|[Go]({{< relref "/ChapterFour/0400~0499/0454.4Sum-II.md" >}})|Medium| O(n^2)| O(n) ||54.6%|
|
||||
@ -181,10 +181,10 @@ func peakIndexInMountainArray(A []int) int {
|
||||
|0793|Preimage Size of Factorial Zeroes Function|[Go]({{< relref "/ChapterFour/0700~0799/0793.Preimage-Size-of-Factorial-Zeroes-Function.md" >}})|Hard||||40.7%|
|
||||
|0852|Peak Index in a Mountain Array|[Go]({{< relref "/ChapterFour/0800~0899/0852.Peak-Index-in-a-Mountain-Array.md" >}})|Easy||||71.7%|
|
||||
|0862|Shortest Subarray with Sum at Least K|[Go]({{< relref "/ChapterFour/0800~0899/0862.Shortest-Subarray-with-Sum-at-Least-K.md" >}})|Hard||||25.2%|
|
||||
|0875|Koko Eating Bananas|[Go]({{< relref "/ChapterFour/0800~0899/0875.Koko-Eating-Bananas.md" >}})|Medium||||53.5%|
|
||||
|0875|Koko Eating Bananas|[Go]({{< relref "/ChapterFour/0800~0899/0875.Koko-Eating-Bananas.md" >}})|Medium||||53.4%|
|
||||
|0878|Nth Magical Number|[Go]({{< relref "/ChapterFour/0800~0899/0878.Nth-Magical-Number.md" >}})|Hard||||28.8%|
|
||||
|0887|Super Egg Drop|[Go]({{< relref "/ChapterFour/0800~0899/0887.Super-Egg-Drop.md" >}})|Hard||||27.1%|
|
||||
|0911|Online Election|[Go]({{< relref "/ChapterFour/0900~0999/0911.Online-Election.md" >}})|Medium||||51.3%|
|
||||
|0911|Online Election|[Go]({{< relref "/ChapterFour/0900~0999/0911.Online-Election.md" >}})|Medium||||51.2%|
|
||||
|0927|Three Equal Parts|[Go]({{< relref "/ChapterFour/0900~0999/0927.Three-Equal-Parts.md" >}})|Hard||||34.6%|
|
||||
|0981|Time Based Key-Value Store|[Go]({{< relref "/ChapterFour/0900~0999/0981.Time-Based-Key-Value-Store.md" >}})|Medium||||54.1%|
|
||||
|1011|Capacity To Ship Packages Within D Days|[Go]({{< relref "/ChapterFour/1000~1099/1011.Capacity-To-Ship-Packages-Within-D-Days.md" >}})|Medium||||59.7%|
|
||||
|
||||
@ -49,7 +49,7 @@ X & ~X = 0
|
||||
|0137|Single Number II|[Go]({{< relref "/ChapterFour/0100~0199/0137.Single-Number-II.md" >}})|Medium| O(n)| O(1)|❤️|53.7%|
|
||||
|0169|Majority Element|[Go]({{< relref "/ChapterFour/0100~0199/0169.Majority-Element.md" >}})|Easy| O(n)| O(1)|❤️|60.0%|
|
||||
|0187|Repeated DNA Sequences|[Go]({{< relref "/ChapterFour/0100~0199/0187.Repeated-DNA-Sequences.md" >}})|Medium| O(n)| O(1)||41.4%|
|
||||
|0190|Reverse Bits|[Go]({{< relref "/ChapterFour/0100~0199/0190.Reverse-Bits.md" >}})|Easy| O(n)| O(1)|❤️|41.9%|
|
||||
|0190|Reverse Bits|[Go]({{< relref "/ChapterFour/0100~0199/0190.Reverse-Bits.md" >}})|Easy| O(n)| O(1)|❤️|42.0%|
|
||||
|0191|Number of 1 Bits|[Go]({{< relref "/ChapterFour/0100~0199/0191.Number-of-1-Bits.md" >}})|Easy| O(n)| O(1)||53.6%|
|
||||
|0201|Bitwise AND of Numbers Range|[Go]({{< relref "/ChapterFour/0200~0299/0201.Bitwise-AND-of-Numbers-Range.md" >}})|Medium| O(n)| O(1)|❤️|39.6%|
|
||||
|0231|Power of Two|[Go]({{< relref "/ChapterFour/0200~0299/0231.Power-of-Two.md" >}})|Easy| O(1)| O(1)||43.8%|
|
||||
@ -65,7 +65,7 @@ X & ~X = 0
|
||||
|0401|Binary Watch|[Go]({{< relref "/ChapterFour/0400~0499/0401.Binary-Watch.md" >}})|Easy| O(1)| O(1)||48.4%|
|
||||
|0405|Convert a Number to Hexadecimal|[Go]({{< relref "/ChapterFour/0400~0499/0405.Convert-a-Number-to-Hexadecimal.md" >}})|Easy| O(n)| O(1)||44.4%|
|
||||
|0421|Maximum XOR of Two Numbers in an Array|[Go]({{< relref "/ChapterFour/0400~0499/0421.Maximum-XOR-of-Two-Numbers-in-an-Array.md" >}})|Medium| O(n)| O(1)|❤️|54.0%|
|
||||
|0461|Hamming Distance|[Go]({{< relref "/ChapterFour/0400~0499/0461.Hamming-Distance.md" >}})|Easy| O(n)| O(1)||73.2%|
|
||||
|0461|Hamming Distance|[Go]({{< relref "/ChapterFour/0400~0499/0461.Hamming-Distance.md" >}})|Easy| O(n)| O(1)||73.1%|
|
||||
|0476|Number Complement|[Go]({{< relref "/ChapterFour/0400~0499/0476.Number-Complement.md" >}})|Easy| O(n)| O(1)||65.1%|
|
||||
|0477|Total Hamming Distance|[Go]({{< relref "/ChapterFour/0400~0499/0477.Total-Hamming-Distance.md" >}})|Medium| O(n)| O(1)||50.6%|
|
||||
|0693|Binary Number with Alternating Bits|[Go]({{< relref "/ChapterFour/0600~0699/0693.Binary-Number-with-Alternating-Bits.md" >}})|Easy| O(n)| O(1)|❤️|59.8%|
|
||||
|
||||
@ -22,13 +22,13 @@ weight: 10
|
||||
|0207|Course Schedule|[Go]({{< relref "/ChapterFour/0200~0299/0207.Course-Schedule.md" >}})|Medium| O(n^2)| O(n^2)||44.3%|
|
||||
|0210|Course Schedule II|[Go]({{< relref "/ChapterFour/0200~0299/0210.Course-Schedule-II.md" >}})|Medium| O(n^2)| O(n^2)||42.5%|
|
||||
|0513|Find Bottom Left Tree Value|[Go]({{< relref "/ChapterFour/0500~0599/0513.Find-Bottom-Left-Tree-Value.md" >}})|Medium||||62.5%|
|
||||
|0515|Find Largest Value in Each Tree Row|[Go]({{< relref "/ChapterFour/0500~0599/0515.Find-Largest-Value-in-Each-Tree-Row.md" >}})|Medium| O(n)| O(n)||62.1%|
|
||||
|0515|Find Largest Value in Each Tree Row|[Go]({{< relref "/ChapterFour/0500~0599/0515.Find-Largest-Value-in-Each-Tree-Row.md" >}})|Medium| O(n)| O(n)||62.2%|
|
||||
|0529|Minesweeper|[Go]({{< relref "/ChapterFour/0500~0599/0529.Minesweeper.md" >}})|Medium||||61.0%|
|
||||
|0542|01 Matrix|[Go]({{< relref "/ChapterFour/0500~0599/0542.01-Matrix.md" >}})|Medium| O(n)| O(1)||40.8%|
|
||||
|0785|Is Graph Bipartite?|[Go]({{< relref "/ChapterFour/0700~0799/0785.Is-Graph-Bipartite.md" >}})|Medium||||48.3%|
|
||||
|0815|Bus Routes|[Go]({{< relref "/ChapterFour/0800~0899/0815.Bus-Routes.md" >}})|Hard||||43.3%|
|
||||
|0863|All Nodes Distance K in Binary Tree|[Go]({{< relref "/ChapterFour/0800~0899/0863.All-Nodes-Distance-K-in-Binary-Tree.md" >}})|Medium||||57.8%|
|
||||
|0864|Shortest Path to Get All Keys|[Go]({{< relref "/ChapterFour/0800~0899/0864.Shortest-Path-to-Get-All-Keys.md" >}})|Hard||||41.8%|
|
||||
|0864|Shortest Path to Get All Keys|[Go]({{< relref "/ChapterFour/0800~0899/0864.Shortest-Path-to-Get-All-Keys.md" >}})|Hard||||41.9%|
|
||||
|0993|Cousins in Binary Tree|[Go]({{< relref "/ChapterFour/0900~0999/0993.Cousins-in-Binary-Tree.md" >}})|Easy| O(n)| O(1)||52.3%|
|
||||
|1306|Jump Game III|[Go]({{< relref "/ChapterFour/1300~1399/1306.Jump-Game-III.md" >}})|Medium||||62.6%|
|
||||
|1319|Number of Operations to Make Network Connected|[Go]({{< relref "/ChapterFour/1300~1399/1319.Number-of-Operations-to-Make-Network-Connected.md" >}})|Medium||||55.3%|
|
||||
|
||||
@ -22,8 +22,8 @@ weight: 9
|
||||
|0110|Balanced Binary Tree|[Go]({{< relref "/ChapterFour/0100~0199/0110.Balanced-Binary-Tree.md" >}})|Easy| O(n)| O(1)||44.7%|
|
||||
|0111|Minimum Depth of Binary Tree|[Go]({{< relref "/ChapterFour/0100~0199/0111.Minimum-Depth-of-Binary-Tree.md" >}})|Easy| O(n)| O(1)||39.4%|
|
||||
|0112|Path Sum|[Go]({{< relref "/ChapterFour/0100~0199/0112.Path-Sum.md" >}})|Easy| O(n)| O(1)||42.3%|
|
||||
|0113|Path Sum II|[Go]({{< relref "/ChapterFour/0100~0199/0113.Path-Sum-II.md" >}})|Medium| O(n)| O(1)||48.9%|
|
||||
|0114|Flatten Binary Tree to Linked List|[Go]({{< relref "/ChapterFour/0100~0199/0114.Flatten-Binary-Tree-to-Linked-List.md" >}})|Medium| O(n)| O(1)||51.7%|
|
||||
|0113|Path Sum II|[Go]({{< relref "/ChapterFour/0100~0199/0113.Path-Sum-II.md" >}})|Medium| O(n)| O(1)||49.0%|
|
||||
|0114|Flatten Binary Tree to Linked List|[Go]({{< relref "/ChapterFour/0100~0199/0114.Flatten-Binary-Tree-to-Linked-List.md" >}})|Medium| O(n)| O(1)||51.8%|
|
||||
|0124|Binary Tree Maximum Path Sum|[Go]({{< relref "/ChapterFour/0100~0199/0124.Binary-Tree-Maximum-Path-Sum.md" >}})|Hard| O(n)| O(1)||35.4%|
|
||||
|0129|Sum Root to Leaf Numbers|[Go]({{< relref "/ChapterFour/0100~0199/0129.Sum-Root-to-Leaf-Numbers.md" >}})|Medium| O(n)| O(1)||50.8%|
|
||||
|0130|Surrounded Regions|[Go]({{< relref "/ChapterFour/0100~0199/0130.Surrounded-Regions.md" >}})|Medium||||29.3%|
|
||||
@ -32,20 +32,20 @@ weight: 9
|
||||
|0200|Number of Islands|[Go]({{< relref "/ChapterFour/0200~0299/0200.Number-of-Islands.md" >}})|Medium| O(n^2)| O(n^2)||48.9%|
|
||||
|0207|Course Schedule|[Go]({{< relref "/ChapterFour/0200~0299/0207.Course-Schedule.md" >}})|Medium| O(n^2)| O(n^2)||44.3%|
|
||||
|0210|Course Schedule II|[Go]({{< relref "/ChapterFour/0200~0299/0210.Course-Schedule-II.md" >}})|Medium| O(n^2)| O(n^2)||42.5%|
|
||||
|0211|Design Add and Search Words Data Structure|[Go]({{< relref "/ChapterFour/0200~0299/0211.Design-Add-and-Search-Words-Data-Structure.md" >}})|Medium||||40.0%|
|
||||
|0257|Binary Tree Paths|[Go]({{< relref "/ChapterFour/0200~0299/0257.Binary-Tree-Paths.md" >}})|Easy| O(n)| O(1)||53.4%|
|
||||
|0211|Design Add and Search Words Data Structure|[Go]({{< relref "/ChapterFour/0200~0299/0211.Design-Add-and-Search-Words-Data-Structure.md" >}})|Medium||||40.1%|
|
||||
|0257|Binary Tree Paths|[Go]({{< relref "/ChapterFour/0200~0299/0257.Binary-Tree-Paths.md" >}})|Easy| O(n)| O(1)||53.5%|
|
||||
|0329|Longest Increasing Path in a Matrix|[Go]({{< relref "/ChapterFour/0300~0399/0329.Longest-Increasing-Path-in-a-Matrix.md" >}})|Hard||||44.7%|
|
||||
|0337|House Robber III|[Go]({{< relref "/ChapterFour/0300~0399/0337.House-Robber-III.md" >}})|Medium||||51.8%|
|
||||
|0394|Decode String|[Go]({{< relref "/ChapterFour/0300~0399/0394.Decode-String.md" >}})|Medium| O(n)| O(n)||52.6%|
|
||||
|0491|Increasing Subsequences|[Go]({{< relref "/ChapterFour/0400~0499/0491.Increasing-Subsequences.md" >}})|Medium||||47.5%|
|
||||
|0494|Target Sum|[Go]({{< relref "/ChapterFour/0400~0499/0494.Target-Sum.md" >}})|Medium||||45.8%|
|
||||
|0513|Find Bottom Left Tree Value|[Go]({{< relref "/ChapterFour/0500~0599/0513.Find-Bottom-Left-Tree-Value.md" >}})|Medium||||62.5%|
|
||||
|0515|Find Largest Value in Each Tree Row|[Go]({{< relref "/ChapterFour/0500~0599/0515.Find-Largest-Value-in-Each-Tree-Row.md" >}})|Medium| O(n)| O(n)||62.1%|
|
||||
|0515|Find Largest Value in Each Tree Row|[Go]({{< relref "/ChapterFour/0500~0599/0515.Find-Largest-Value-in-Each-Tree-Row.md" >}})|Medium| O(n)| O(n)||62.2%|
|
||||
|0526|Beautiful Arrangement|[Go]({{< relref "/ChapterFour/0500~0599/0526.Beautiful-Arrangement.md" >}})|Medium||||61.8%|
|
||||
|0529|Minesweeper|[Go]({{< relref "/ChapterFour/0500~0599/0529.Minesweeper.md" >}})|Medium||||61.0%|
|
||||
|0538|Convert BST to Greater Tree|[Go]({{< relref "/ChapterFour/0500~0599/0538.Convert-BST-to-Greater-Tree.md" >}})|Medium||||59.1%|
|
||||
|0542|01 Matrix|[Go]({{< relref "/ChapterFour/0500~0599/0542.01-Matrix.md" >}})|Medium| O(n)| O(1)||40.8%|
|
||||
|0547|Number of Provinces|[Go]({{< relref "/ChapterFour/0500~0599/0547.Number-of-Provinces.md" >}})|Medium||||60.3%|
|
||||
|0547|Number of Provinces|[Go]({{< relref "/ChapterFour/0500~0599/0547.Number-of-Provinces.md" >}})|Medium||||60.4%|
|
||||
|0563|Binary Tree Tilt|[Go]({{< relref "/ChapterFour/0500~0599/0563.Binary-Tree-Tilt.md" >}})|Easy||||52.9%|
|
||||
|0638|Shopping Offers|[Go]({{< relref "/ChapterFour/0600~0699/0638.Shopping-Offers.md" >}})|Medium||||52.8%|
|
||||
|0685|Redundant Connection II|[Go]({{< relref "/ChapterFour/0600~0699/0685.Redundant-Connection-II.md" >}})|Hard||||32.9%|
|
||||
@ -62,12 +62,12 @@ weight: 9
|
||||
|0841|Keys and Rooms|[Go]({{< relref "/ChapterFour/0800~0899/0841.Keys-and-Rooms.md" >}})|Medium||||65.4%|
|
||||
|0851|Loud and Rich|[Go]({{< relref "/ChapterFour/0800~0899/0851.Loud-and-Rich.md" >}})|Medium||||52.6%|
|
||||
|0863|All Nodes Distance K in Binary Tree|[Go]({{< relref "/ChapterFour/0800~0899/0863.All-Nodes-Distance-K-in-Binary-Tree.md" >}})|Medium||||57.8%|
|
||||
|0872|Leaf-Similar Trees|[Go]({{< relref "/ChapterFour/0800~0899/0872.Leaf-Similar-Trees.md" >}})|Easy||||64.5%|
|
||||
|0872|Leaf-Similar Trees|[Go]({{< relref "/ChapterFour/0800~0899/0872.Leaf-Similar-Trees.md" >}})|Easy||||64.6%|
|
||||
|0897|Increasing Order Search Tree|[Go]({{< relref "/ChapterFour/0800~0899/0897.Increasing-Order-Search-Tree.md" >}})|Easy||||74.5%|
|
||||
|0924|Minimize Malware Spread|[Go]({{< relref "/ChapterFour/0900~0999/0924.Minimize-Malware-Spread.md" >}})|Hard||||41.8%|
|
||||
|0928|Minimize Malware Spread II|[Go]({{< relref "/ChapterFour/0900~0999/0928.Minimize-Malware-Spread-II.md" >}})|Hard||||41.2%|
|
||||
|0947|Most Stones Removed with Same Row or Column|[Go]({{< relref "/ChapterFour/0900~0999/0947.Most-Stones-Removed-with-Same-Row-or-Column.md" >}})|Medium||||55.5%|
|
||||
|0959|Regions Cut By Slashes|[Go]({{< relref "/ChapterFour/0900~0999/0959.Regions-Cut-By-Slashes.md" >}})|Medium||||67.0%|
|
||||
|0959|Regions Cut By Slashes|[Go]({{< relref "/ChapterFour/0900~0999/0959.Regions-Cut-By-Slashes.md" >}})|Medium||||67.1%|
|
||||
|0968|Binary Tree Cameras|[Go]({{< relref "/ChapterFour/0900~0999/0968.Binary-Tree-Cameras.md" >}})|Hard||||38.7%|
|
||||
|0979|Distribute Coins in Binary Tree|[Go]({{< relref "/ChapterFour/0900~0999/0979.Distribute-Coins-in-Binary-Tree.md" >}})|Medium||||69.6%|
|
||||
|0980|Unique Paths III|[Go]({{< relref "/ChapterFour/0900~0999/0980.Unique-Paths-III.md" >}})|Hard| O(n log n)| O(n)||77.2%|
|
||||
|
||||
@ -26,7 +26,7 @@ weight: 7
|
||||
|0198|House Robber|[Go]({{< relref "/ChapterFour/0100~0199/0198.House-Robber.md" >}})|Medium| O(n)| O(n)||42.8%|
|
||||
|0213|House Robber II|[Go]({{< relref "/ChapterFour/0200~0299/0213.House-Robber-II.md" >}})|Medium| O(n)| O(n)||37.5%|
|
||||
|0300|Longest Increasing Subsequence|[Go]({{< relref "/ChapterFour/0300~0399/0300.Longest-Increasing-Subsequence.md" >}})|Medium| O(n log n)| O(n)||43.9%|
|
||||
|0303|Range Sum Query - Immutable|[Go]({{< relref "/ChapterFour/0300~0399/0303.Range-Sum-Query---Immutable.md" >}})|Easy||||47.4%|
|
||||
|0303|Range Sum Query - Immutable|[Go]({{< relref "/ChapterFour/0300~0399/0303.Range-Sum-Query---Immutable.md" >}})|Easy||||47.5%|
|
||||
|0309|Best Time to Buy and Sell Stock with Cooldown|[Go]({{< relref "/ChapterFour/0300~0399/0309.Best-Time-to-Buy-and-Sell-Stock-with-Cooldown.md" >}})|Medium| O(n)| O(n)||48.1%|
|
||||
|0322|Coin Change|[Go]({{< relref "/ChapterFour/0300~0399/0322.Coin-Change.md" >}})|Medium| O(n)| O(n)||37.1%|
|
||||
|0337|House Robber III|[Go]({{< relref "/ChapterFour/0300~0399/0337.House-Robber-III.md" >}})|Medium||||51.8%|
|
||||
@ -35,7 +35,7 @@ weight: 7
|
||||
|0354|Russian Doll Envelopes|[Go]({{< relref "/ChapterFour/0300~0399/0354.Russian-Doll-Envelopes.md" >}})|Hard||||36.2%|
|
||||
|0357|Count Numbers with Unique Digits|[Go]({{< relref "/ChapterFour/0300~0399/0357.Count-Numbers-with-Unique-Digits.md" >}})|Medium| O(1)| O(1)||48.8%|
|
||||
|0392|Is Subsequence|[Go]({{< relref "/ChapterFour/0300~0399/0392.Is-Subsequence.md" >}})|Easy| O(n)| O(1)||49.5%|
|
||||
|0410|Split Array Largest Sum|[Go]({{< relref "/ChapterFour/0400~0499/0410.Split-Array-Largest-Sum.md" >}})|Hard||||46.2%|
|
||||
|0410|Split Array Largest Sum|[Go]({{< relref "/ChapterFour/0400~0499/0410.Split-Array-Largest-Sum.md" >}})|Hard||||46.3%|
|
||||
|0416|Partition Equal Subset Sum|[Go]({{< relref "/ChapterFour/0400~0499/0416.Partition-Equal-Subset-Sum.md" >}})|Medium| O(n^2)| O(n)||44.8%|
|
||||
|0474|Ones and Zeroes|[Go]({{< relref "/ChapterFour/0400~0499/0474.Ones-and-Zeroes.md" >}})|Medium||||43.6%|
|
||||
|0494|Target Sum|[Go]({{< relref "/ChapterFour/0400~0499/0494.Target-Sum.md" >}})|Medium||||45.8%|
|
||||
@ -54,7 +54,7 @@ weight: 7
|
||||
|1074|Number of Submatrices That Sum to Target|[Go]({{< relref "/ChapterFour/1000~1099/1074.Number-of-Submatrices-That-Sum-to-Target.md" >}})|Hard||||61.7%|
|
||||
|1105|Filling Bookcase Shelves|[Go]({{< relref "/ChapterFour/1100~1199/1105.Filling-Bookcase-Shelves.md" >}})|Medium||||57.5%|
|
||||
|1235|Maximum Profit in Job Scheduling|[Go]({{< relref "/ChapterFour/1200~1299/1235.Maximum-Profit-in-Job-Scheduling.md" >}})|Hard||||47.3%|
|
||||
|1641|Count Sorted Vowel Strings|[Go]({{< relref "/ChapterFour/1600~1699/1641.Count-Sorted-Vowel-Strings.md" >}})|Medium||||77.0%|
|
||||
|1641|Count Sorted Vowel Strings|[Go]({{< relref "/ChapterFour/1600~1699/1641.Count-Sorted-Vowel-Strings.md" >}})|Medium||||76.9%|
|
||||
|1654|Minimum Jumps to Reach Home|[Go]({{< relref "/ChapterFour/1600~1699/1654.Minimum-Jumps-to-Reach-Home.md" >}})|Medium||||26.2%|
|
||||
|1655|Distribute Repeating Integers|[Go]({{< relref "/ChapterFour/1600~1699/1655.Distribute-Repeating-Integers.md" >}})|Hard||||40.4%|
|
||||
|1659|Maximize Grid Happiness|[Go]({{< relref "/ChapterFour/1600~1699/1659.Maximize-Grid-Happiness.md" >}})|Hard||||35.4%|
|
||||
|
||||
@ -19,14 +19,14 @@ weight: 13
|
||||
|0076|Minimum Window Substring|[Go]({{< relref "/ChapterFour/0001~0099/0076.Minimum-Window-Substring.md" >}})|Hard| O(n)| O(n)|❤️|35.9%|
|
||||
|0094|Binary Tree Inorder Traversal|[Go]({{< relref "/ChapterFour/0001~0099/0094.Binary-Tree-Inorder-Traversal.md" >}})|Medium| O(n)| O(1)||65.7%|
|
||||
|0136|Single Number|[Go]({{< relref "/ChapterFour/0100~0199/0136.Single-Number.md" >}})|Easy||||66.5%|
|
||||
|0138|Copy List with Random Pointer|[Go]({{< relref "/ChapterFour/0100~0199/0138.Copy-List-with-Random-Pointer.md" >}})|Medium| O(n)| O(1)||40.5%|
|
||||
|0138|Copy List with Random Pointer|[Go]({{< relref "/ChapterFour/0100~0199/0138.Copy-List-with-Random-Pointer.md" >}})|Medium| O(n)| O(1)||40.6%|
|
||||
|0187|Repeated DNA Sequences|[Go]({{< relref "/ChapterFour/0100~0199/0187.Repeated-DNA-Sequences.md" >}})|Medium||||41.4%|
|
||||
|0202|Happy Number|[Go]({{< relref "/ChapterFour/0200~0299/0202.Happy-Number.md" >}})|Easy| O(log n)| O(1)||51.2%|
|
||||
|0204|Count Primes|[Go]({{< relref "/ChapterFour/0200~0299/0204.Count-Primes.md" >}})|Easy||||32.2%|
|
||||
|0205|Isomorphic Strings|[Go]({{< relref "/ChapterFour/0200~0299/0205.Isomorphic-Strings.md" >}})|Easy| O(log n)| O(n)||40.4%|
|
||||
|0217|Contains Duplicate|[Go]({{< relref "/ChapterFour/0200~0299/0217.Contains-Duplicate.md" >}})|Easy| O(n)| O(n)||56.6%|
|
||||
|0219|Contains Duplicate II|[Go]({{< relref "/ChapterFour/0200~0299/0219.Contains-Duplicate-II.md" >}})|Easy| O(n)| O(n)||38.6%|
|
||||
|0242|Valid Anagram|[Go]({{< relref "/ChapterFour/0200~0299/0242.Valid-Anagram.md" >}})|Easy| O(n)| O(n) ||58.1%|
|
||||
|0242|Valid Anagram|[Go]({{< relref "/ChapterFour/0200~0299/0242.Valid-Anagram.md" >}})|Easy| O(n)| O(n) ||58.5%|
|
||||
|0274|H-Index|[Go]({{< relref "/ChapterFour/0200~0299/0274.H-Index.md" >}})|Medium| O(n)| O(n) ||36.3%|
|
||||
|0290|Word Pattern|[Go]({{< relref "/ChapterFour/0200~0299/0290.Word-Pattern.md" >}})|Easy| O(n)| O(n) ||38.3%|
|
||||
|0347|Top K Frequent Elements|[Go]({{< relref "/ChapterFour/0300~0399/0347.Top-K-Frequent-Elements.md" >}})|Medium| O(n)| O(n) ||62.3%|
|
||||
@ -58,7 +58,7 @@ weight: 13
|
||||
|0739|Daily Temperatures|[Go]({{< relref "/ChapterFour/0700~0799/0739.Daily-Temperatures.md" >}})|Medium| O(n)| O(n) ||64.5%|
|
||||
|0748|Shortest Completing Word|[Go]({{< relref "/ChapterFour/0700~0799/0748.Shortest-Completing-Word.md" >}})|Easy||||57.5%|
|
||||
|0771|Jewels and Stones|[Go]({{< relref "/ChapterFour/0700~0799/0771.Jewels-and-Stones.md" >}})|Easy||||86.9%|
|
||||
|0781|Rabbits in Forest|[Go]({{< relref "/ChapterFour/0700~0799/0781.Rabbits-in-Forest.md" >}})|Medium||||55.4%|
|
||||
|0781|Rabbits in Forest|[Go]({{< relref "/ChapterFour/0700~0799/0781.Rabbits-in-Forest.md" >}})|Medium||||55.5%|
|
||||
|0811|Subdomain Visit Count|[Go]({{< relref "/ChapterFour/0800~0899/0811.Subdomain-Visit-Count.md" >}})|Easy||||71.4%|
|
||||
|0884|Uncommon Words from Two Sentences|[Go]({{< relref "/ChapterFour/0800~0899/0884.Uncommon-Words-from-Two-Sentences.md" >}})|Easy||||64.0%|
|
||||
|0895|Maximum Frequency Stack|[Go]({{< relref "/ChapterFour/0800~0899/0895.Maximum-Frequency-Stack.md" >}})|Hard| O(n)| O(n) ||62.3%|
|
||||
@ -68,7 +68,7 @@ weight: 13
|
||||
|0970|Powerful Integers|[Go]({{< relref "/ChapterFour/0900~0999/0970.Powerful-Integers.md" >}})|Medium||||40.0%|
|
||||
|0981|Time Based Key-Value Store|[Go]({{< relref "/ChapterFour/0900~0999/0981.Time-Based-Key-Value-Store.md" >}})|Medium||||54.1%|
|
||||
|0992|Subarrays with K Different Integers|[Go]({{< relref "/ChapterFour/0900~0999/0992.Subarrays-with-K-Different-Integers.md" >}})|Hard| O(n)| O(n) |❤️|50.6%|
|
||||
|1002|Find Common Characters|[Go]({{< relref "/ChapterFour/1000~1099/1002.Find-Common-Characters.md" >}})|Easy||||68.5%|
|
||||
|1002|Find Common Characters|[Go]({{< relref "/ChapterFour/1000~1099/1002.Find-Common-Characters.md" >}})|Easy||||68.6%|
|
||||
|1078|Occurrences After Bigram|[Go]({{< relref "/ChapterFour/1000~1099/1078.Occurrences-After-Bigram.md" >}})|Easy||||64.9%|
|
||||
|1160|Find Words That Can Be Formed by Characters|[Go]({{< relref "/ChapterFour/1100~1199/1160.Find-Words-That-Can-Be-Formed-by-Characters.md" >}})|Easy||||67.9%|
|
||||
|1189|Maximum Number of Balloons|[Go]({{< relref "/ChapterFour/1100~1199/1189.Maximum-Number-of-Balloons.md" >}})|Easy||||61.7%|
|
||||
|
||||
@ -31,11 +31,11 @@ weight: 4
|
||||
|0025|Reverse Nodes in k-Group|[Go]({{< relref "/ChapterFour/0001~0099/0025.Reverse-Nodes-in-k-Group.md" >}})|Hard| O(log n)| O(1)|❤️|44.7%|
|
||||
|0061|Rotate List|[Go]({{< relref "/ChapterFour/0001~0099/0061.Rotate-List.md" >}})|Medium| O(n)| O(1)||31.7%|
|
||||
|0082|Remove Duplicates from Sorted List II|[Go]({{< relref "/ChapterFour/0001~0099/0082.Remove-Duplicates-from-Sorted-List-II.md" >}})|Medium| O(n)| O(1)||39.2%|
|
||||
|0083|Remove Duplicates from Sorted List|[Go]({{< relref "/ChapterFour/0001~0099/0083.Remove-Duplicates-from-Sorted-List.md" >}})|Easy| O(n)| O(1)||46.4%|
|
||||
|0083|Remove Duplicates from Sorted List|[Go]({{< relref "/ChapterFour/0001~0099/0083.Remove-Duplicates-from-Sorted-List.md" >}})|Easy| O(n)| O(1)||46.5%|
|
||||
|0086|Partition List|[Go]({{< relref "/ChapterFour/0001~0099/0086.Partition-List.md" >}})|Medium| O(n)| O(1)|❤️|43.3%|
|
||||
|0092|Reverse Linked List II|[Go]({{< relref "/ChapterFour/0001~0099/0092.Reverse-Linked-List-II.md" >}})|Medium| O(n)| O(1)|❤️|40.5%|
|
||||
|0109|Convert Sorted List to Binary Search Tree|[Go]({{< relref "/ChapterFour/0100~0199/0109.Convert-Sorted-List-to-Binary-Search-Tree.md" >}})|Medium| O(log n)| O(n)||50.1%|
|
||||
|0138|Copy List with Random Pointer|[Go]({{< relref "/ChapterFour/0100~0199/0138.Copy-List-with-Random-Pointer.md" >}})|Medium||||40.5%|
|
||||
|0138|Copy List with Random Pointer|[Go]({{< relref "/ChapterFour/0100~0199/0138.Copy-List-with-Random-Pointer.md" >}})|Medium||||40.6%|
|
||||
|0141|Linked List Cycle|[Go]({{< relref "/ChapterFour/0100~0199/0141.Linked-List-Cycle.md" >}})|Easy| O(n)| O(1)|❤️|42.8%|
|
||||
|0142|Linked List Cycle II|[Go]({{< relref "/ChapterFour/0100~0199/0142.Linked-List-Cycle-II.md" >}})|Medium| O(n)| O(1)|❤️|39.6%|
|
||||
|0143|Reorder List|[Go]({{< relref "/ChapterFour/0100~0199/0143.Reorder-List.md" >}})|Medium| O(n)| O(1)|❤️|40.5%|
|
||||
@ -55,7 +55,7 @@ weight: 4
|
||||
|1019|Next Greater Node In Linked List|[Go]({{< relref "/ChapterFour/1000~1099/1019.Next-Greater-Node-In-Linked-List.md" >}})|Medium| O(n)| O(1)||58.2%|
|
||||
|1171|Remove Zero Sum Consecutive Nodes from Linked List|[Go]({{< relref "/ChapterFour/1100~1199/1171.Remove-Zero-Sum-Consecutive-Nodes-from-Linked-List.md" >}})|Medium||||41.4%|
|
||||
|1290|Convert Binary Number in a Linked List to Integer|[Go]({{< relref "/ChapterFour/1200~1299/1290.Convert-Binary-Number-in-a-Linked-List-to-Integer.md" >}})|Easy||||81.8%|
|
||||
|1669|Merge In Between Linked Lists|[Go]({{< relref "/ChapterFour/1600~1699/1669.Merge-In-Between-Linked-Lists.md" >}})|Medium||||77.2%|
|
||||
|1669|Merge In Between Linked Lists|[Go]({{< relref "/ChapterFour/1600~1699/1669.Merge-In-Between-Linked-Lists.md" >}})|Medium||||77.1%|
|
||||
|1670|Design Front Middle Back Queue|[Go]({{< relref "/ChapterFour/1600~1699/1670.Design-Front-Middle-Back-Queue.md" >}})|Medium||||54.5%|
|
||||
|------------|-------------------------------------------------------|-------| ----------------| ---------------|-------------|-------------|-------------|
|
||||
|
||||
|
||||
@ -46,7 +46,7 @@ weight: 12
|
||||
|0633|Sum of Square Numbers|[Go]({{< relref "/ChapterFour/0600~0699/0633.Sum-of-Square-Numbers.md" >}})|Medium||||32.5%|
|
||||
|0645|Set Mismatch|[Go]({{< relref "/ChapterFour/0600~0699/0645.Set-Mismatch.md" >}})|Easy||||42.5%|
|
||||
|0753|Cracking the Safe|[Go]({{< relref "/ChapterFour/0700~0799/0753.Cracking-the-Safe.md" >}})|Hard||||52.3%|
|
||||
|0781|Rabbits in Forest|[Go]({{< relref "/ChapterFour/0700~0799/0781.Rabbits-in-Forest.md" >}})|Medium||||55.4%|
|
||||
|0781|Rabbits in Forest|[Go]({{< relref "/ChapterFour/0700~0799/0781.Rabbits-in-Forest.md" >}})|Medium||||55.5%|
|
||||
|0812|Largest Triangle Area|[Go]({{< relref "/ChapterFour/0800~0899/0812.Largest-Triangle-Area.md" >}})|Easy||||58.9%|
|
||||
|0836|Rectangle Overlap|[Go]({{< relref "/ChapterFour/0800~0899/0836.Rectangle-Overlap.md" >}})|Easy||||44.7%|
|
||||
|0878|Nth Magical Number|[Go]({{< relref "/ChapterFour/0800~0899/0878.Nth-Magical-Number.md" >}})|Hard||||28.8%|
|
||||
@ -76,7 +76,7 @@ weight: 12
|
||||
|1281|Subtract the Product and Sum of Digits of an Integer|[Go]({{< relref "/ChapterFour/1200~1299/1281.Subtract-the-Product-and-Sum-of-Digits-of-an-Integer.md" >}})|Easy||||85.6%|
|
||||
|1317|Convert Integer to the Sum of Two No-Zero Integers|[Go]({{< relref "/ChapterFour/1300~1399/1317.Convert-Integer-to-the-Sum-of-Two-No-Zero-Integers.md" >}})|Easy||||56.8%|
|
||||
|1512|Number of Good Pairs|[Go]({{< relref "/ChapterFour/1500~1599/1512.Number-of-Good-Pairs.md" >}})|Easy||||87.7%|
|
||||
|1641|Count Sorted Vowel Strings|[Go]({{< relref "/ChapterFour/1600~1699/1641.Count-Sorted-Vowel-Strings.md" >}})|Medium||||77.0%|
|
||||
|1641|Count Sorted Vowel Strings|[Go]({{< relref "/ChapterFour/1600~1699/1641.Count-Sorted-Vowel-Strings.md" >}})|Medium||||76.9%|
|
||||
|1648|Sell Diminishing-Valued Colored Balls|[Go]({{< relref "/ChapterFour/1600~1699/1648.Sell-Diminishing-Valued-Colored-Balls.md" >}})|Medium||||30.8%|
|
||||
|1680|Concatenation of Consecutive Binary Numbers|[Go]({{< relref "/ChapterFour/1600~1699/1680.Concatenation-of-Consecutive-Binary-Numbers.md" >}})|Medium||||52.4%|
|
||||
|1685|Sum of Absolute Differences in a Sorted Array|[Go]({{< relref "/ChapterFour/1600~1699/1685.Sum-of-Absolute-Differences-in-a-Sorted-Array.md" >}})|Medium||||61.9%|
|
||||
|
||||
@ -43,7 +43,7 @@ weight: 18
|
||||
|0327|Count of Range Sum|[Go]({{< relref "/ChapterFour/0300~0399/0327.Count-of-Range-Sum.md" >}})|Hard| O(n log n)| O(n)|❤️|36.0%|
|
||||
|0493|Reverse Pairs|[Go]({{< relref "/ChapterFour/0400~0499/0493.Reverse-Pairs.md" >}})|Hard| O(n log n)| O(n)||26.8%|
|
||||
|0699|Falling Squares|[Go]({{< relref "/ChapterFour/0600~0699/0699.Falling-Squares.md" >}})|Hard| O(n log n)| O(n)|❤️|42.5%|
|
||||
|0715|Range Module|[Go]({{< relref "/ChapterFour/0700~0799/0715.Range-Module.md" >}})|Hard| O(log n)| O(n)|❤️|40.1%|
|
||||
|0715|Range Module|[Go]({{< relref "/ChapterFour/0700~0799/0715.Range-Module.md" >}})|Hard| O(log n)| O(n)|❤️|40.2%|
|
||||
|0732|My Calendar III|[Go]({{< relref "/ChapterFour/0700~0799/0732.My-Calendar-III.md" >}})|Hard| O(log n)| O(n)|❤️|61.7%|
|
||||
|0850|Rectangle Area II|[Go]({{< relref "/ChapterFour/0800~0899/0850.Rectangle-Area-II.md" >}})|Hard| O(n log n)| O(n)|❤️|48.3%|
|
||||
|1157|Online Majority Element In Subarray|[Go]({{< relref "/ChapterFour/1100~1199/1157.Online-Majority-Element-In-Subarray.md" >}})|Hard| O(log n)| O(n)|❤️|39.6%|
|
||||
|
||||
@ -26,7 +26,7 @@ weight: 14
|
||||
|0164|Maximum Gap|[Go]({{< relref "/ChapterFour/0100~0199/0164.Maximum-Gap.md" >}})|Hard| O(n log n)| O(log n) |❤️|36.7%|
|
||||
|0179|Largest Number|[Go]({{< relref "/ChapterFour/0100~0199/0179.Largest-Number.md" >}})|Medium| O(n log n)| O(log n) |❤️|30.6%|
|
||||
|0220|Contains Duplicate III|[Go]({{< relref "/ChapterFour/0200~0299/0220.Contains-Duplicate-III.md" >}})|Medium| O(n log n)| O(1) |❤️|21.3%|
|
||||
|0242|Valid Anagram|[Go]({{< relref "/ChapterFour/0200~0299/0242.Valid-Anagram.md" >}})|Easy| O(n)| O(n) ||58.1%|
|
||||
|0242|Valid Anagram|[Go]({{< relref "/ChapterFour/0200~0299/0242.Valid-Anagram.md" >}})|Easy| O(n)| O(n) ||58.5%|
|
||||
|0274|H-Index|[Go]({{< relref "/ChapterFour/0200~0299/0274.H-Index.md" >}})|Medium| O(n)| O(n) ||36.3%|
|
||||
|0315|Count of Smaller Numbers After Self|[Go]({{< relref "/ChapterFour/0300~0399/0315.Count-of-Smaller-Numbers-After-Self.md" >}})|Hard||||42.5%|
|
||||
|0324|Wiggle Sort II|[Go]({{< relref "/ChapterFour/0300~0399/0324.Wiggle-Sort-II.md" >}})|Medium| O(n)| O(n)|❤️|30.6%|
|
||||
@ -37,7 +37,7 @@ weight: 14
|
||||
|0524|Longest Word in Dictionary through Deleting|[Go]({{< relref "/ChapterFour/0500~0599/0524.Longest-Word-in-Dictionary-through-Deleting.md" >}})|Medium| O(n)| O(1) ||49.0%|
|
||||
|0710|Random Pick with Blacklist|[Go]({{< relref "/ChapterFour/0700~0799/0710.Random-Pick-with-Blacklist.md" >}})|Hard| O(n)| O(n) ||32.7%|
|
||||
|0767|Reorganize String|[Go]({{< relref "/ChapterFour/0700~0799/0767.Reorganize-String.md" >}})|Medium| O(n log n)| O(log n) |❤️|50.0%|
|
||||
|0853|Car Fleet|[Go]({{< relref "/ChapterFour/0800~0899/0853.Car-Fleet.md" >}})|Medium| O(n log n)| O(log n) ||43.8%|
|
||||
|0853|Car Fleet|[Go]({{< relref "/ChapterFour/0800~0899/0853.Car-Fleet.md" >}})|Medium| O(n log n)| O(log n) ||43.7%|
|
||||
|0922|Sort Array By Parity II|[Go]({{< relref "/ChapterFour/0900~0999/0922.Sort-Array-By-Parity-II.md" >}})|Easy| O(n)| O(1) ||70.5%|
|
||||
|0969|Pancake Sorting|[Go]({{< relref "/ChapterFour/0900~0999/0969.Pancake-Sorting.md" >}})|Medium| O(n log n)| O(log n) |❤️|68.6%|
|
||||
|0973|K Closest Points to Origin|[Go]({{< relref "/ChapterFour/0900~0999/0973.K-Closest-Points-to-Origin.md" >}})|Medium| O(n log n)| O(log n) ||64.6%|
|
||||
|
||||
@ -27,7 +27,7 @@ weight: 5
|
||||
|0145|Binary Tree Postorder Traversal|[Go]({{< relref "/ChapterFour/0100~0199/0145.Binary-Tree-Postorder-Traversal.md" >}})|Medium| O(n)| O(1)||57.4%|
|
||||
|0150|Evaluate Reverse Polish Notation|[Go]({{< relref "/ChapterFour/0100~0199/0150.Evaluate-Reverse-Polish-Notation.md" >}})|Medium| O(n)| O(1)||37.8%|
|
||||
|0155|Min Stack|[Go]({{< relref "/ChapterFour/0100~0199/0155.Min-Stack.md" >}})|Easy| O(n)| O(n)||46.3%|
|
||||
|0173|Binary Search Tree Iterator|[Go]({{< relref "/ChapterFour/0100~0199/0173.Binary-Search-Tree-Iterator.md" >}})|Medium| O(n)| O(1)||59.9%|
|
||||
|0173|Binary Search Tree Iterator|[Go]({{< relref "/ChapterFour/0100~0199/0173.Binary-Search-Tree-Iterator.md" >}})|Medium| O(n)| O(1)||60.0%|
|
||||
|0224|Basic Calculator|[Go]({{< relref "/ChapterFour/0200~0299/0224.Basic-Calculator.md" >}})|Hard| O(n)| O(n)||38.1%|
|
||||
|0225|Implement Stack using Queues|[Go]({{< relref "/ChapterFour/0200~0299/0225.Implement-Stack-using-Queues.md" >}})|Easy| O(n)| O(n)||47.2%|
|
||||
|0232|Implement Queue using Stacks|[Go]({{< relref "/ChapterFour/0200~0299/0232.Implement-Queue-using-Stacks.md" >}})|Easy| O(n)| O(n)||52.0%|
|
||||
@ -41,7 +41,7 @@ weight: 5
|
||||
|0636|Exclusive Time of Functions|[Go]({{< relref "/ChapterFour/0600~0699/0636.Exclusive-Time-of-Functions.md" >}})|Medium| O(n)| O(n)||54.3%|
|
||||
|0682|Baseball Game|[Go]({{< relref "/ChapterFour/0600~0699/0682.Baseball-Game.md" >}})|Easy| O(n)| O(n)||66.7%|
|
||||
|0726|Number of Atoms|[Go]({{< relref "/ChapterFour/0700~0799/0726.Number-of-Atoms.md" >}})|Hard| O(n)| O(n) |❤️|51.1%|
|
||||
|0735|Asteroid Collision|[Go]({{< relref "/ChapterFour/0700~0799/0735.Asteroid-Collision.md" >}})|Medium| O(n)| O(n) ||43.3%|
|
||||
|0735|Asteroid Collision|[Go]({{< relref "/ChapterFour/0700~0799/0735.Asteroid-Collision.md" >}})|Medium| O(n)| O(n) ||43.2%|
|
||||
|0739|Daily Temperatures|[Go]({{< relref "/ChapterFour/0700~0799/0739.Daily-Temperatures.md" >}})|Medium| O(n)| O(n) ||64.5%|
|
||||
|0844|Backspace String Compare|[Go]({{< relref "/ChapterFour/0800~0899/0844.Backspace-String-Compare.md" >}})|Easy| O(n)| O(n) ||46.9%|
|
||||
|0856|Score of Parentheses|[Go]({{< relref "/ChapterFour/0800~0899/0856.Score-of-Parentheses.md" >}})|Medium| O(n)| O(n)||62.4%|
|
||||
|
||||
@ -50,7 +50,7 @@ weight: 2
|
||||
|1662|Check If Two String Arrays are Equivalent|[Go]({{< relref "/ChapterFour/1600~1699/1662.Check-If-Two-String-Arrays-are-Equivalent.md" >}})|Easy||||83.3%|
|
||||
|1668|Maximum Repeating Substring|[Go]({{< relref "/ChapterFour/1600~1699/1668.Maximum-Repeating-Substring.md" >}})|Easy||||38.5%|
|
||||
|1678|Goal Parser Interpretation|[Go]({{< relref "/ChapterFour/1600~1699/1678.Goal-Parser-Interpretation.md" >}})|Easy||||85.7%|
|
||||
|1684|Count the Number of Consistent Strings|[Go]({{< relref "/ChapterFour/1600~1699/1684.Count-the-Number-of-Consistent-Strings.md" >}})|Easy||||83.4%|
|
||||
|1684|Count the Number of Consistent Strings|[Go]({{< relref "/ChapterFour/1600~1699/1684.Count-the-Number-of-Consistent-Strings.md" >}})|Easy||||83.3%|
|
||||
|1694|Reformat Phone Number|[Go]({{< relref "/ChapterFour/1600~1699/1694.Reformat-Phone-Number.md" >}})|Easy||||66.2%|
|
||||
|------------|-------------------------------------------------------|-------| ----------------| ---------------|-------------|-------------|-------------|
|
||||
|
||||
|
||||
@ -26,26 +26,26 @@ weight: 6
|
||||
|0110|Balanced Binary Tree|[Go]({{< relref "/ChapterFour/0100~0199/0110.Balanced-Binary-Tree.md" >}})|Easy| O(n)| O(1)||44.7%|
|
||||
|0111|Minimum Depth of Binary Tree|[Go]({{< relref "/ChapterFour/0100~0199/0111.Minimum-Depth-of-Binary-Tree.md" >}})|Easy| O(n)| O(1)||39.4%|
|
||||
|0112|Path Sum|[Go]({{< relref "/ChapterFour/0100~0199/0112.Path-Sum.md" >}})|Easy| O(n)| O(1)||42.3%|
|
||||
|0113|Path Sum II|[Go]({{< relref "/ChapterFour/0100~0199/0113.Path-Sum-II.md" >}})|Medium| O(n)| O(1)||48.9%|
|
||||
|0114|Flatten Binary Tree to Linked List|[Go]({{< relref "/ChapterFour/0100~0199/0114.Flatten-Binary-Tree-to-Linked-List.md" >}})|Medium| O(n)| O(1)||51.7%|
|
||||
|0113|Path Sum II|[Go]({{< relref "/ChapterFour/0100~0199/0113.Path-Sum-II.md" >}})|Medium| O(n)| O(1)||49.0%|
|
||||
|0114|Flatten Binary Tree to Linked List|[Go]({{< relref "/ChapterFour/0100~0199/0114.Flatten-Binary-Tree-to-Linked-List.md" >}})|Medium| O(n)| O(1)||51.8%|
|
||||
|0124|Binary Tree Maximum Path Sum|[Go]({{< relref "/ChapterFour/0100~0199/0124.Binary-Tree-Maximum-Path-Sum.md" >}})|Hard| O(n)| O(1)||35.4%|
|
||||
|0129|Sum Root to Leaf Numbers|[Go]({{< relref "/ChapterFour/0100~0199/0129.Sum-Root-to-Leaf-Numbers.md" >}})|Medium| O(n)| O(1)||50.8%|
|
||||
|0144|Binary Tree Preorder Traversal|[Go]({{< relref "/ChapterFour/0100~0199/0144.Binary-Tree-Preorder-Traversal.md" >}})|Medium| O(n)| O(1)||57.4%|
|
||||
|0145|Binary Tree Postorder Traversal|[Go]({{< relref "/ChapterFour/0100~0199/0145.Binary-Tree-Postorder-Traversal.md" >}})|Medium| O(n)| O(1)||57.4%|
|
||||
|0173|Binary Search Tree Iterator|[Go]({{< relref "/ChapterFour/0100~0199/0173.Binary-Search-Tree-Iterator.md" >}})|Medium| O(n)| O(1)||59.9%|
|
||||
|0173|Binary Search Tree Iterator|[Go]({{< relref "/ChapterFour/0100~0199/0173.Binary-Search-Tree-Iterator.md" >}})|Medium| O(n)| O(1)||60.0%|
|
||||
|0199|Binary Tree Right Side View|[Go]({{< relref "/ChapterFour/0100~0199/0199.Binary-Tree-Right-Side-View.md" >}})|Medium| O(n)| O(1)||56.3%|
|
||||
|0222|Count Complete Tree Nodes|[Go]({{< relref "/ChapterFour/0200~0299/0222.Count-Complete-Tree-Nodes.md" >}})|Medium| O(n)| O(1)||49.1%|
|
||||
|0226|Invert Binary Tree|[Go]({{< relref "/ChapterFour/0200~0299/0226.Invert-Binary-Tree.md" >}})|Easy| O(n)| O(1)||66.8%|
|
||||
|0230|Kth Smallest Element in a BST|[Go]({{< relref "/ChapterFour/0200~0299/0230.Kth-Smallest-Element-in-a-BST.md" >}})|Medium| O(n)| O(1)||62.4%|
|
||||
|0235|Lowest Common Ancestor of a Binary Search Tree|[Go]({{< relref "/ChapterFour/0200~0299/0235.Lowest-Common-Ancestor-of-a-Binary-Search-Tree.md" >}})|Easy| O(n)| O(1)||51.6%|
|
||||
|0236|Lowest Common Ancestor of a Binary Tree|[Go]({{< relref "/ChapterFour/0200~0299/0236.Lowest-Common-Ancestor-of-a-Binary-Tree.md" >}})|Medium| O(n)| O(1)||48.5%|
|
||||
|0257|Binary Tree Paths|[Go]({{< relref "/ChapterFour/0200~0299/0257.Binary-Tree-Paths.md" >}})|Easy| O(n)| O(1)||53.4%|
|
||||
|0257|Binary Tree Paths|[Go]({{< relref "/ChapterFour/0200~0299/0257.Binary-Tree-Paths.md" >}})|Easy| O(n)| O(1)||53.5%|
|
||||
|0337|House Robber III|[Go]({{< relref "/ChapterFour/0300~0399/0337.House-Robber-III.md" >}})|Medium||||51.8%|
|
||||
|0404|Sum of Left Leaves|[Go]({{< relref "/ChapterFour/0400~0499/0404.Sum-of-Left-Leaves.md" >}})|Easy| O(n)| O(1)||52.2%|
|
||||
|0437|Path Sum III|[Go]({{< relref "/ChapterFour/0400~0499/0437.Path-Sum-III.md" >}})|Medium| O(n)| O(1)||48.1%|
|
||||
|0508|Most Frequent Subtree Sum|[Go]({{< relref "/ChapterFour/0500~0599/0508.Most-Frequent-Subtree-Sum.md" >}})|Medium||||59.0%|
|
||||
|0513|Find Bottom Left Tree Value|[Go]({{< relref "/ChapterFour/0500~0599/0513.Find-Bottom-Left-Tree-Value.md" >}})|Medium||||62.5%|
|
||||
|0515|Find Largest Value in Each Tree Row|[Go]({{< relref "/ChapterFour/0500~0599/0515.Find-Largest-Value-in-Each-Tree-Row.md" >}})|Medium| O(n)| O(n)||62.1%|
|
||||
|0515|Find Largest Value in Each Tree Row|[Go]({{< relref "/ChapterFour/0500~0599/0515.Find-Largest-Value-in-Each-Tree-Row.md" >}})|Medium| O(n)| O(n)||62.2%|
|
||||
|0538|Convert BST to Greater Tree|[Go]({{< relref "/ChapterFour/0500~0599/0538.Convert-BST-to-Greater-Tree.md" >}})|Medium||||59.1%|
|
||||
|0563|Binary Tree Tilt|[Go]({{< relref "/ChapterFour/0500~0599/0563.Binary-Tree-Tilt.md" >}})|Easy||||52.9%|
|
||||
|0572|Subtree of Another Tree|[Go]({{< relref "/ChapterFour/0500~0599/0572.Subtree-of-Another-Tree.md" >}})|Easy||||44.5%|
|
||||
@ -56,7 +56,7 @@ weight: 6
|
||||
|0685|Redundant Connection II|[Go]({{< relref "/ChapterFour/0600~0699/0685.Redundant-Connection-II.md" >}})|Hard||||32.9%|
|
||||
|0834|Sum of Distances in Tree|[Go]({{< relref "/ChapterFour/0800~0899/0834.Sum-of-Distances-in-Tree.md" >}})|Hard||||45.8%|
|
||||
|0863|All Nodes Distance K in Binary Tree|[Go]({{< relref "/ChapterFour/0800~0899/0863.All-Nodes-Distance-K-in-Binary-Tree.md" >}})|Medium||||57.8%|
|
||||
|0872|Leaf-Similar Trees|[Go]({{< relref "/ChapterFour/0800~0899/0872.Leaf-Similar-Trees.md" >}})|Easy||||64.5%|
|
||||
|0872|Leaf-Similar Trees|[Go]({{< relref "/ChapterFour/0800~0899/0872.Leaf-Similar-Trees.md" >}})|Easy||||64.6%|
|
||||
|0897|Increasing Order Search Tree|[Go]({{< relref "/ChapterFour/0800~0899/0897.Increasing-Order-Search-Tree.md" >}})|Easy||||74.5%|
|
||||
|0968|Binary Tree Cameras|[Go]({{< relref "/ChapterFour/0900~0999/0968.Binary-Tree-Cameras.md" >}})|Hard||||38.7%|
|
||||
|0979|Distribute Coins in Binary Tree|[Go]({{< relref "/ChapterFour/0900~0999/0979.Distribute-Coins-in-Binary-Tree.md" >}})|Medium||||69.6%|
|
||||
|
||||
@ -23,7 +23,7 @@ weight: 16
|
||||
|0130|Surrounded Regions|[Go]({{< relref "/ChapterFour/0100~0199/0130.Surrounded-Regions.md" >}})|Medium| O(m\*n)| O(m\*n)||29.3%|
|
||||
|0200|Number of Islands|[Go]({{< relref "/ChapterFour/0200~0299/0200.Number-of-Islands.md" >}})|Medium| O(m\*n)| O(m\*n)||48.9%|
|
||||
|0399|Evaluate Division|[Go]({{< relref "/ChapterFour/0300~0399/0399.Evaluate-Division.md" >}})|Medium| O(n)| O(n)||54.2%|
|
||||
|0547|Number of Provinces|[Go]({{< relref "/ChapterFour/0500~0599/0547.Number-of-Provinces.md" >}})|Medium| O(n^2)| O(n)||60.3%|
|
||||
|0547|Number of Provinces|[Go]({{< relref "/ChapterFour/0500~0599/0547.Number-of-Provinces.md" >}})|Medium| O(n^2)| O(n)||60.4%|
|
||||
|0684|Redundant Connection|[Go]({{< relref "/ChapterFour/0600~0699/0684.Redundant-Connection.md" >}})|Medium| O(n)| O(n)||58.9%|
|
||||
|0685|Redundant Connection II|[Go]({{< relref "/ChapterFour/0600~0699/0685.Redundant-Connection-II.md" >}})|Hard| O(n)| O(n)||32.9%|
|
||||
|0721|Accounts Merge|[Go]({{< relref "/ChapterFour/0700~0799/0721.Accounts-Merge.md" >}})|Medium| O(n)| O(n)|❤️|51.6%|
|
||||
@ -35,7 +35,7 @@ weight: 16
|
||||
|0928|Minimize Malware Spread II|[Go]({{< relref "/ChapterFour/0900~0999/0928.Minimize-Malware-Spread-II.md" >}})|Hard| O(m\*n)| O(n)|❤️|41.2%|
|
||||
|0947|Most Stones Removed with Same Row or Column|[Go]({{< relref "/ChapterFour/0900~0999/0947.Most-Stones-Removed-with-Same-Row-or-Column.md" >}})|Medium| O(n)| O(n)||55.5%|
|
||||
|0952|Largest Component Size by Common Factor|[Go]({{< relref "/ChapterFour/0900~0999/0952.Largest-Component-Size-by-Common-Factor.md" >}})|Hard| O(n)| O(n)|❤️|36.1%|
|
||||
|0959|Regions Cut By Slashes|[Go]({{< relref "/ChapterFour/0900~0999/0959.Regions-Cut-By-Slashes.md" >}})|Medium| O(n^2)| O(n^2)|❤️|67.0%|
|
||||
|0959|Regions Cut By Slashes|[Go]({{< relref "/ChapterFour/0900~0999/0959.Regions-Cut-By-Slashes.md" >}})|Medium| O(n^2)| O(n^2)|❤️|67.1%|
|
||||
|0990|Satisfiability of Equality Equations|[Go]({{< relref "/ChapterFour/0900~0999/0990.Satisfiability-of-Equality-Equations.md" >}})|Medium| O(n)| O(n)||46.7%|
|
||||
|1202|Smallest String With Swaps|[Go]({{< relref "/ChapterFour/1200~1299/1202.Smallest-String-With-Swaps.md" >}})|Medium||||48.7%|
|
||||
|1319|Number of Operations to Make Network Connected|[Go]({{< relref "/ChapterFour/1300~1399/1319.Number-of-Operations-to-Make-Network-Connected.md" >}})|Medium||||55.3%|
|
||||
|
||||
Reference in New Issue
Block a user